Radioactive multi-omics collaborative learning for adaptive radiation therapy eligibility prediction in nasopharyngeal carcinoma
-
摘要: 针对传统的放射多组学(影像组学、剂量组学和轮廓组学)模型往往采用特征拼接的方式,容易忽略不同组学特定统计属性、产生过拟合的问题,提出了以一致性约束和自适应权重为核心构建的多组学协同学习算法(multi-omics collaborative learning, MOCL)。该算法采用一致性约束挖掘不同组学特征之间的互补模式,再通过香农熵自适应学习不同组学特征的权重,最后引入紧致度图来避免过拟合现象。通过将MOCL在311名鼻咽癌患者组成的临床影像数据上得到的实验结果与3种传统的机器学习算法以及2种多视角算法进行比较,结果表明MOCL在多组学协同学习上,具有一定的优势,能为鼻咽癌自适应放疗资格预测提供有价值的决策依据。Abstract: Traditional radiation omics models, including radiomics, dosiomics, and contouromics, typically adopt feature splicing, which tends to ignore the specific statistical attributes of different omics and therefore leads to overfitting. A multi-omics collaborative learning (MOCL) algorithm focused on consistency constraints and adaptive weights was proposed in the study to address this problem. The MOCL algorithm employs consistency constraints to explore complementary patterns among heterogeneous omics features and adaptively learns their weights using Shannon entropy while avoiding overfitting through compactness mapping. An experiment was conducted on the clinical imaging data of 311 patients with nasopharyngeal carcinoma using MOCL. The experimental result is compared with three traditional machine learning algorithms and two multiperspective algorithms. The results demonstrate that MOCL has certain advantages in collaborative learning of multi-omics and can provide a valuable prediction basis for adaptive radiotherapy qualification in the case of nasopharyngeal carcinoma.
-
鼻咽癌(nasopharyngeal carcinoma, NPC)是指发生于鼻咽腔顶部和侧壁的恶性肿瘤。根据国际癌症研究机构的数据[1],2020年,在世界范围内估计有1930万新的癌症病例,其中大概有13.3万例鼻咽癌新发病例,死亡人数约为8万人,表现出较高的死亡率。在中国,鼻咽癌的发病人数明显高于世界平均水平(1.9万/10万)[2-3],主要发生在香港和南方五省(广东、广西、湖南、福建和江西),是当地头颈部恶性肿瘤的首位。
随着人工智能技术的发展,影像组学被广泛应用于癌症的临床分期、治疗方法选择、疗效评估以及预后分析等领域,并且取得了一定的研究成果。在鼻咽癌领域,Liu等[4]从鼻咽癌患者的CT图像提取影像组学数据并与患者的唾液量相结合,通过预测患者的预期唾液量来构建预测患者未来急性口干燥症的可能性和程度的模型,该模型能在早期准确地预测患者的唾液量,并提前预防口干症状;金哲等[5]从1393例鼻咽癌患者的MRI图像中提取影像组学特征并结合患者的临床指标构建鼻咽癌远端转移预测模型,在预测鼻咽癌远端转移风险方面具有较高效能。
但影像组学数据也有自己的局限性[6–9],由于各个医院之间所采用的机器不同、协议不同、参数不同,以及负责感兴趣区域(volume of interest, VOI)标注的临床医师的不同,使得影像组学特征的再现性受到影响,进而影响模型的准确性和可重复性。因此,影像组学数据融合其他组学或临床指标的方法逐渐开始受到重视。将影像组学与其他组学相结合的研究方式,可以充分利用来自不同组学特征进行互补,也可以避免单组学特征冗余度过高的问题,以提高模型的预测精度和泛用性。例如, Zhou等[10]结合影像组学和基于EQD2的剂量组学,建立了基于CT的放射性肺炎(padiation poisoning, RP)预测模型,发现剂量组学结合影像组学的训练效果要优于传统的剂量−体积直方图(dose-volume histogram, DVH)、影像组学+DVH,且具有统计学意义;Cai等[11]将水平计算机断层扫描(CT)融合剂量学,所建立的融合剂量学模型均优于单一的CT/剂量模型;Cui等[12]在深度学习中整合了PET(positron emission tomography)影像组学、细胞因子和miRNA的多组学信息,构建了预测正常组织并发症概率/肿瘤控制概率的模型,要优于传统的预测模型。
在多组学研究中,处理多组学数据传统方法之一是将来自不同组学的特征向量连接成特征新向量,然后在连接后的向量上应用单视角算法进行处理。而这样简单的特征拼接处理容易带来以下问题:1)忽略了不同组学之间的信息互补关系;2)特征数量会随着组学数量的增加而增加,造成维度灾难。最终导致过拟合,模型精度较差等问题[13]。多组学问题应当基于多视角学习的原则设计[14]:1)假设视角之间的分歧是分类误差的上限,力求最大限度地保证每个视角的预测一致性;2)假设每个视角都包含其他视角没有的信息,从每个视角中提取差异,同时保留共享信息。因此,采用合适的多组学融合方案是多组学研究的关键。对此,本研究针对影像组学、剂量组学和轮廓组学,设计了一种多组学协同学习算法(multi-omics collaborative learning, MOCL)。MOCL通过一致性约束挖掘不同组学特征之间的互补模式,另外还通过香农熵自适应学习不同组学特征的权重。通过在真实临床影像数据上的实验结果表明,MOCL对鼻咽癌远端转移有较好的预测作用。另外,和引入的对比算法的比较结果表明,MOCL在多组学协同学习上具有一定的优势。
1. 放射多组学协同学习
1.1 问题提出
鼻咽癌患者在治疗过程中,从其CT、MRI等常规放射影像学资料中,可以获取的组学特征包括影像组学、剂量组学以及轮廓组学。已有研究表明,影像组学、剂量组学以及轮廓组学特征均和患者的治疗预后密切相关[15-16],只使用单一组学构建模型往往会出现模式信息有限的问题,如何有效地挖掘不同组学特征所包含的互补信息对于准确预测患者预后来说显得非常重要。传统的学习策略将各组学进行拼接,人为地割裂了各个组学之间潜在的联系,只是简单地将单独学习的结果进行集成,很难达到较为满意的学习效果。因此,基于多组学协同学习的问题描述如下。
假设{X,Y}为一个多组学训练集,其中,每个组学特征空间可以表示为
${\boldsymbol{X}}_{k}\in {\mathbf{R}}^{N\times d}$ ,则多组学协同学习的问题可以形式化描述为$$ \begin{gathered} \mathop {\min }\limits_f \sum\limits_k {{\rm{L}}(f({{\boldsymbol{X}}_k}),Y)} + \sum\limits_{k,t,k \ne t} {C(f({{\boldsymbol{X}}_k}),f({{\boldsymbol{X}}_t}))} + \parallel f\parallel _F^2 \end{gathered} $$ (1) 式中:第1项为各个组学特征空间上的损失之和;第2项为各组学之间的一致性约束,用于保障同一对象在不同组学特征空间预测的一致性;第3项为泛化项,用于保障模型的泛化能力。
1.2 多组学特征空间损失
在使用机器学习进行线性分类的过程中,对于每个样本,可以使用一个转置矩阵将其映射到一个低维空间中,即模型对该样本的预测值
$ f\left(X\right) $ 。但需要对模型的预测值$ f\left(X\right) $ 与真实值$ Y $ 的差异程度的进行估算。两者相差值越小,说明模型的预测精度就越好。在描述多组学的特征空间损失时,具体定义如下:$$ \sum\limits_{k = 1}^K {{\omega _k}\parallel {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - Y\parallel _F^2} $$ (2) 式中:K是数据集中所包含的组学的数量,
$ {\omega }_{k} $ 是第k个组学所占的权重,${\boldsymbol{X}}_{k}$ 为第k个组学的特征向量,${\boldsymbol{A}}_{k}$ 代表第k个组学特征的转置矩阵。通过最小化式(2),能保证训练过程中得到的标签和真实结果误差尽可能最小。1.3 一致性约束
为了确保各组学特征空间之间预测结果的一致性,即认为同一个鼻咽癌患者,在不同视图下,其放疗预后的结果应该尽量保持一致,设置一个先验知识,具体定义如下:
$$ \mathop \sum \limits_{k = 1}^K \left\| {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - \frac{1}{{K - 1}}\mathop \sum \limits_{l = 1,l \ne k}^K {{\boldsymbol{X}}_l}{\tilde {\boldsymbol{A}}_l}\right\| _F^2 $$ (3) 其中
${\tilde {\boldsymbol{A}}_l}$ 是针对每个组学特征空间单独预先训练得到的一个转换矩阵。通过最小化式(3),能保证从任意组学特征空间进行预测时,都能与其余组学特征空间得到的预测结果的差异最小,保证同一样本在不同组学特征空间预测的结果尽量一致。同时为了从不同的角度来探索一致或互补的信息,本文提出了一种基于信息论的多视图加权机制,即自适应权重。具体来说,引入了一个基于“香农熵”的视图加权惩罚项来自适应学习每个组学的权重系数,对于包含模式信息较少的特征空间,为其分配较小的权重,反之,则为其分配较大的权重其定义如下:
$$ \mathop \sum \limits_{k = 1}^K {\omega _k}\ln {\omega _k} $$ (4) 通过最小化式(4),能使得包含更多有效特征的组学在训练中被给予更大的权重。
1.4 泛化性能提升
为了减少在迭代过程中可能出现的过拟合现象,基于流形学习的方法,采用紧致度图来尽可能避免过拟合问题。在紧致度图中,同一标签的两个不同的样本对应的两个节点由一条无向边连接,其权重定义如下:
$$ {{\boldsymbol{W}}_{ij}} = \left\{ \begin{array}{l} {{{\rm{e}}^{ - \frac{{{\parallel x_i} - {x_j}\parallel {^2}}}{\sigma }}}},\quad\;{{x_i},\;{x_j}}\text{标签相同}\\ 0,\quad\;{{x_i},\;{x_j}}\text{标签不同} \end{array}\right. $$ (5) 其中
$\sigma $ 是热核参数。如果$ {{\boldsymbol{W}}}_{ij} $ 能够保证具有相同标签的样本彼此应该相互靠近,那么两个具有相同标签的样本$ {f}_{i} $ 和$ {f}_{j} $ 就应该被赋予更大的权重$ {{\boldsymbol{W}}}_{ij} $ [17]。选择映射的合理标准是最小化以下目标函数:$$ \underset{f}{{\rm{min}}}{\displaystyle \sum\limits_{ij}}\Vert {f}_{i}-{f}_{j}{\Vert }^{2}{{\boldsymbol{W}}}_{i,j} $$ (6) 其中:
$ {f}_{i} $ 和$ {f}_{j} $ 表示$ {x}_{i} $ 和$ {x}_{j} $ 进行变换后的结果,通过最小化该式,能进一步确保$ {f}_{i} $ 和$ {f}_{j} $ 在空间中的相对接近。因此,可以通过式(6),保持样本在变换空间中的紧致性。再引入拉普拉斯矩阵之后,式(6)可以进一步变化为$$ \lambda \mathop \sum \limits_{k = 1}^K \left( {{\boldsymbol{A}}_k^{\rm{T}}{\boldsymbol{X}}_k^{\rm{T}}{{\boldsymbol{L}}_k}{{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k}} \right) $$ (7) 式中:
${{\boldsymbol{L}}_k}$ 是拉普拉斯矩阵,定义为${\boldsymbol{ L}} = {\boldsymbol{Z}} - {\boldsymbol{W}}$ ;Z是对角矩阵,它的对角项可以由${{\boldsymbol{Z}}_{ij}} = \displaystyle\sum\limits_J {{\boldsymbol{W}}_{ij}}$ 计算。1.5 目标函数和优化
基于式(2)~(4)、(7)所设计的组件,多组学协同学习算法的目标函数可以表示为
$$ \begin{gathered} {{J}}({\omega _k},{{\boldsymbol{A}}_k}) = \mathop {\min }\limits_{\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_k},{\omega _k}} \\ \end{array}} \mathop \sum \limits_{k = 1}^K {\omega _k}\parallel {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - Y\parallel _F^2 + \\ \eta \mathop \sum \limits_{k = 1}^K \left\| {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - \frac{1}{{k - 1}}\mathop \sum \limits_{l = 1,l \ne k}^K {{\boldsymbol{X}}_l}{{\tilde {\boldsymbol{A}}}_l}\right\| _F^2 + \\ \lambda \mathop \sum \limits_{k = 1}^K \left( {{\boldsymbol{A}}_k^{\rm{T}}{\boldsymbol{X}}_k^{\rm{T}}{{\boldsymbol{L}}_k}{{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k}} \right) + \beta \mathop \sum \limits_{k = 1}^K {\omega _k}\ln {\omega _k} \\ {\text{s}}.{\text{t}}.\mathop \sum \limits_{k = 1}^K {\omega _k} = 1 \end{gathered} $$ (8) 其中,
$ \eta 、\lambda 、\beta $ 作为平衡参数且>0,以调配目标函数中不同部分的影响。定理1 针对
${J}({\omega }_{k},{\boldsymbol{A}}_{k}$ ),当$ {\omega }_{k} $ 固定时,求得最佳的${\boldsymbol{A}}_{K}$ 计算如下:$$ {{\boldsymbol{A}}_K} = {\left[ {\left( {{\omega _k} + \eta } \right){\boldsymbol{X}}_k^{\rm{T}}{\boldsymbol{X}} + \lambda {\boldsymbol{X}}_k^{\rm{T}}{{\boldsymbol{L}}_k}{{\boldsymbol{X}}_k}} \right]^{ - 1}} \left({\omega }_{k}{{\boldsymbol{X}}}_{k}^{{\rm{T}}}+\eta {{\boldsymbol{X}}}_{k}^{{\rm{T}}}\tilde{D}\right) $$ (9) 其中
$\tilde D = \dfrac{1}{{k - 1}} \displaystyle\sum\limits_{l = 1,l \ne k}^K {{\boldsymbol{X}}_l}{\tilde {\boldsymbol{A}}_l}$ 。证明 给定任意
$ {\omega }_{k} $ ,式(8)中的目标函数可以重新表达为$$ \begin{gathered} {{J}}\left( {{{\boldsymbol{A}}_k}} \right) = \mathop {\min }\limits_{\begin{array}{*{20}{c}} {{A_k},{\omega _k}} \\ \end{array}} \mathop \sum \limits_{k = 1}^K {\omega _k}\parallel {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - Y\parallel _F^2 + \\ \eta \mathop \sum \limits_{k = 1}^K \parallel {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - \tilde D\parallel _F^2 + \lambda \mathop \sum \limits_{k = 1}^K \left( {{\boldsymbol{A}}_k^{\rm{T}}{\boldsymbol{X}}_k^{\rm{T}}{{\boldsymbol{L}}_k}{{\boldsymbol{A}}_k}{{\boldsymbol{X}}_k}} \right) \\ \end{gathered} $$ (10) 其中
$\tilde D = \dfrac{1}{{k - 1}}\displaystyle\sum\limits_{l = 1,l \ne k}^K {{\boldsymbol{X}}_l}{\tilde {\boldsymbol{A}}_l}$ ,通过将${J}\left({\boldsymbol{A}}_{k}\right)$ 对${\boldsymbol{A}}_{k}$ 的偏导数设为0,可以得到$$\begin{gathered} \dfrac{{\partial {{J}}({{\boldsymbol{A}}_k})}}{{\partial {{\boldsymbol{A}}_k}}} = 0\\ \Rightarrow 2{\omega _k}{{\boldsymbol{X}}_k}^{\rm{T}}{{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - 2{\omega _k}{{\boldsymbol{X}}_k}^{\rm{T}}Y + \\ 2\lambda {{\boldsymbol{X}}_k}^{\rm{T}}{{\boldsymbol{L}}_k}{{\boldsymbol{A}}_k}{{\boldsymbol{X}}_k} + 2\eta ({{\boldsymbol{X}}_k}^{\rm{T}}{{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - {{\boldsymbol{X}}_k}^{\rm{T}}\tilde {D)} = 0 \\ \Rightarrow \left({\omega }_{k}{{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{X}}}_{k}+\lambda {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{L}}}_{k}{{\boldsymbol{X}}}_{k}+\eta {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{X}}}_{k}\right){{\boldsymbol{A}}}_{k}= \\ {\omega }_{k}{{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}Y+\eta {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}\tilde{D}\end{gathered} $$ 则
$$ \begin{gathered}{{\boldsymbol{A}}}_{k}={\omega }_{k}{{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{X}}}_{k}+\lambda {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{L}}}_{k}{{\boldsymbol{X}}}_{k}+ \eta {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}{{\boldsymbol{X}}}_{k)}{}^{-1}\left({\omega }_{k}{{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}Y+\eta {{\boldsymbol{X}}}_{k}{}^{{\rm{T}}}\tilde{D}\right)\end{gathered}$$ 证毕。
定理2 针对
${J}({\omega }_{k},{\boldsymbol{A}}_{k}$ ),当${\boldsymbol{A}}_{k}$ 固定时,可以求得最佳$ {\omega }_{k} $ :$$ {\omega }_{k}=\frac{{{\rm{e}}}^{\frac{-\parallel {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\parallel }_{F}^{2}}{\beta }}}{{{\displaystyle \sum\limits_{k=1}^{K} }}{{\rm{e}}}^{\frac{-\parallel {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\parallel }_{F}^{2}}{\beta }}} $$ (12) 证明 给定任意的
${\boldsymbol{A}}_{k}$ ,式(8)中的目标函数可以被重新表达为$$ \begin{gathered} {{J}}\left( {{\omega _k}} \right) = \mathop {\min }\limits_{{{\boldsymbol{A}}_k},{\omega _k}} \mathop \sum\limits_{k = 1}^K {\omega _k}\parallel {{\boldsymbol{X}}_k}{{\boldsymbol{A}}_k} - Y\parallel _F^2 + \beta \mathop \sum \limits_{k = 1}^K {\omega _k}\ln {\omega _k} \\ {\text{s}}.{\text{t}}.\mathop \sum \limits_{k = 1}^K {\omega _k} = 1 \end{gathered}$$ (13) 通过将
$ {{J}(\omega }_{k}) $ 对$ {\omega }_{k} $ 的偏导数设置为0,可以得到$$\begin{gathered}\dfrac{{\partial {\rm{J}}({\omega _k})}}{{\partial {\omega _k}}} = 0\\ \stackrel{}{\Rightarrow }-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}+ \beta \left(\mathrm{ln}{\omega }_{k}+1\right)+\varphi =0\\ \underset{}{\Rightarrow }\mathrm{ln}{\omega }_{k}=\frac{-\varphi -\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }-1\\ \stackrel{}{\Rightarrow }{\omega }_{k}={{\rm{e}}}^{\frac{-\varphi -\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }-1}={{\rm{e}}}^{-\frac{-\varphi }{\beta }}{{\rm{e}}}^{\frac{-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }}{{\rm{e}}}^{-1}\end{gathered}$$ 由
$\displaystyle \sum\limits_{k = 1}^K {\omega _k} = 1$ 可得:$$\begin{array}{l} {\displaystyle\sum_{k=1}^{K} }{{\rm{e}}}^{-\frac{-\varphi }{\beta }}{{\rm{e}}}^{\frac{-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }}{{\rm{e}}}^{-1}=1 \stackrel{}{\Rightarrow }{{\rm{e}}}^{-\frac{-\varphi }{\beta }}{{\rm{e}}}^{-1}=\dfrac{1}{{{\displaystyle \sum _{k=1}^{K}{{\rm{e}}}^{\frac{-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }}}}}\end{array} $$ 将
${{\rm{e}}^{ - \frac{{ - \varphi }}{\beta }}}{{\rm{e}}^{ - 1}}$ 代入${\omega _k}$ ,可得:$$ {\omega }_{k}=\frac{{{\rm{e}}}^{\frac{-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }}}{{{\displaystyle \sum _{k=1}^{K}{{\rm{e}}}^{\frac{-\Vert {{\boldsymbol{X}}}_{k}{{\boldsymbol{A}}}_{k}-Y{\Vert }_{F}^{2}}{\beta }}}}} $$ (14) 证毕。
1.6 MOCL算法描述
根据
${\boldsymbol{A}}_{k}$ 和$ {\omega }_{k} $ 的计算原则,具体算法计算流程如下。算法1 MOCL训练
输入 多组学训练样本
$\{{\boldsymbol{X}}_{k},Y\}$ ,正则化参数$ \eta 、\lambda $ 、$\beta $ ,迭代次数t输出
${\boldsymbol{A}}_{k}$ 和$ {\omega }_{k} $ 1) 计算影像组学、轮廓组学和剂量组学的转置矩阵
${\tilde{\boldsymbol{A}}}_{l}$ ;2) 为每一个组学特征空间计算
${\boldsymbol{L}}_{m}$ ;3) 以1/K为每个组学特征空间赋予初始权重
${\omega _k}$ 重复;4) 为每个组学特征空间计算
${\boldsymbol{A}}_{k}$ ;5) 为每个组学特征空间计算
$ {\omega }_{k} $ 直到($\Vert {\boldsymbol{A}}_{k}^{\left(t\right)}- {\boldsymbol{A}}_{k}^{(t-1)}\leqslant {10}^{-4}\Vert$ );6) 返回
${\boldsymbol{A}}_{k}$ 和$ {\omega }_{k} $ 。算法2 MOCL测试
输入 测试集
$\left\{{\hat{\boldsymbol{X}}}_{k}\right\},{\boldsymbol{A}}_{k}$ 和$ {\omega }_{k} $ 输出
$\hat Y = \displaystyle\sum \limits_{k = 1}^K {\omega _k}{\hat {\boldsymbol{X}}_k}{{\boldsymbol{A}}_k}$ 2. 实验分析
2.1 数据来源和预处理
2.1.1 患者数据
本研究对2012—2015年期间在香港伊利沙伯医院接受放疗的311名NPC患者进行了回顾性分析。研究对象包括符合以下条件的患者:1)初次诊断为经组织活检证实的原发性鼻咽癌,无远处转移和合并其他类型肿瘤;2)接受了治愈性的同步放化疗(concurrent chemoradiation,CCRT)或CCRT加辅助化疗(AC);3)接受了螺旋调强放疗治疗。被排除的患者包括:1)在接受CCRT治疗之前接受过新辅助化疗的患者;2)接受放疗但未同时接受化疗的患者;3)未注射造影剂进行计划对比增强CT(contrast enhancement CT, CECT)或计划对比增强T1-w(CET1-w)磁共振成像的患者;4)没有完整的临床/影像数据的患者。个体患者以在放疗后是否需要进行自适应复查(adaptive review)来进行分类,其中需要进行自适应复查的标记为1,不需要的标记为0。
2.1.2 感兴趣区域
本研究涉及8个不同的器官结构的VOI,包括原发性NPC肿瘤(GTVnp)和转移淋巴结(GTVn)的总肿瘤体积、同侧腮腺(IpsiPG)、对侧腮腺(ContraPG)、脑干(BS)、脊髓(SC)、淋巴结计划靶体积的高剂量和低剂量区(分别为处方剂量为70-Gy的PTVn_high_dose和处方剂量为60-Gy的PTVn_low_dose)。图1结出了本研究中涉及的每个VOI的位置。
其中GTVnp是与计划MRI图像对准后,在轴向CT层面上手动勾画出来的,GTVn是由一名丰富经验且获得认证的头颈放射肿瘤学家按照国际颈部水平CT描绘指南在CECT图像上绘制的。为了区分患者的同侧腮腺和对策腮腺,本文按照以下策略进行:1)确定腮腺(PG)体积上特定体素点与GTVnp表面上所有体素点之间的最小几何距离;2)选择另一体素点,重复(1)过程,直到确定整个PG上所有体素点相对于GTVnp的最小距离;3)计算所有最小距离的中值,并以此确定各个患者的PG与GTVnp的总体接近度。中值较小的认为是同侧腮腺,较大的认为是对侧腮腺。所有分割均使用Varian ARIA和Eclipse治疗计划系统v13(加利福尼亚州帕洛阿尔托的Varian医疗系统公司)进行。
2.1.3 影像组学特征
在实验中,由GTVnp、GTVn、IpsiParotid和ContraParotid 4种来自不同器官结构的VOI参与影像组学的特征提取的计算。使用Python中的SimpleITK(v1.2.4)和Pyradiomics(v2.2.0)对原始医学图像进行提取。一般来说,影像组学特征可以分为3类:一阶统计特征、形态特征、二阶及高阶纹理特征。一阶统计特征反应所测体素的对称性、均匀性以及局部强度分布变化。包括中值、平均值、最小值、最大值、标准差、偏度、峰度等。形态特征定量描述感兴趣区的几何特性,如肿瘤的表面积、体积、表面积和体积比、球形度、紧凑性和三维直径等,这些特征可以描述肿瘤三维的大小和形态信息。二阶及高阶纹理特征能够反映图像体素灰度之间的空间排列关系,可以分为灰度共生矩阵(gray-level covarionce matrix, GLCM)、灰度游程长度矩阵(gray-level run-length matrix, GLRLM)和灰度尺寸区域矩阵(gray-level size zone matrix, GLSZM)。在对CECT、CET1-w和T2-w磁振图像进行影像组学特征计算的过程中,以高斯−拉普拉斯滤波器(核大小:1、3、6 mm)和小波滤波器(HHH、HLL、LHL、LLH、LHH、HLH、HHL、LLL)进行滤波。在本研究中,将4个VOI的形态学特征全部分离出来,为每个研究的VOI提供了总共6348个影像组学特征。同时将4个VOI (GTVnp、GTVn、IpsiPG和ContraPG)的伸长、平整度、最小轴长、长轴长、小轴长、最大2D直径列、最大2D直径行、最大2D直径切片、最大3D直径网格体积、球度、表面积、表面体积比、体素体积14个形态学特征组合起来的56个特征作为一组。影像组学和形态学特征的详细定义可在Pyradiomics文档中找到。
2.1.4 剂量组学特征
因为传统的剂量−体积直方图(DVH)不包含辐照器官内空间剂量分布的信息,所以本文采用RT剂量数据对8种不同器官结构的VOI进行剂量学特征计算。相比之下,剂量组学能够表征所研究的8个VOI内局部辐射剂量分布的空间格局,在癌症预后和治疗反应的各种预测模型中得到了广泛的研究[18-19]。本研究采用Gabryovic等[20]的方法计算了8种VOI的DVH曲线点的剂量学特征,示例包括但不限于最大剂量、最小剂量、平均剂量、至少接受一定剂量水平的VOI的体积以及一定体积的VOI接受的最小剂量。此外,本文提取了每个研究VOI内的空间剂量分布,以全面描述沉积剂量的异质性,如沿3个成像轴(x、y和z方向)的剂量梯度。这些特征的定义在Buettner等[21]之前的出版物中描述过。同时,本文将每个研究VOI内的三维剂量分布都转换为3D图像,以便后续使用Pyradiomics包计算与影像组学特征相似的剂量组学特征;所提取的特征包括一阶剂量统计量、灰度依赖矩阵(gray-level dependence matrix, GLDM)、GLCM、GLRLM、GLSZM和相邻灰度差分矩阵(neighboring gray tone difference matrix, NGTDM)等。本研究共从8个VOI中提取了1608个剂量组学特征。
2.1.5 轮廓组学特征
在本研究中,是否需要实施自适应放疗(adaptive radiotherapy, ART)是由头颈部不同内部器官几何关系的变化决定的。故我们提取了能描述4对器官结构的VOI (GTVnp与IpsiPG、GTVnp与ContraPG、GTVnp与SC、PTVn_low_dose与SC)之间复杂几何关系的特征。这些特征是从RT等高线数据中提取的,作为“轮廓组学”特征。对于每个VOI对,从距离描述符重叠体积直方图(overlapping volume nistogram, OVH)中计算一系列轮廓特征;例如,在治疗计划阶段,SC与PTVn_low_dose之间的最大和最小距离分别作为零和满体积时OVH上的距离。在本研究中,OVH的计算使用了Wu等[22]设计的算法。此外还使用投影重叠体积(projected overlap volume, POV),即一个VOI与另一个VOI在特定投影角度的平行投影重叠,来进一步揭示VOI对潜在的轮廓特征。本研究共从4对VOI中提取了132个轮廓特征。表1总结了计算所研究的4种组学特征所涉及的VOIs的来源(“—”表示无相应组学特征)。
表 1 3种组学特征涉及到的VOIs来源Table 1 Source of VOIs involved in the three histological profiles影像组学 剂量组学 轮廓组学 CECT-GTVnp GTVnp PTVn_low_dose-SC CECT-GTVn GTVn GTVnp-IpsiPG CECT-IpsiPG IpsiPG GTVnp-ContraPG CECT-ContraPG ContraPG GTVnp-SC CET1w-GTVnp BS — CET1w-IpsiPG SC — CET1w-ContraPG PTVn_high_dose — T2w-GTVnp PTVn_low_dose — T2w-IpsiPG — — T2w-ContraPG — — 2.2 特征选择
在最小化模型过度拟合的风险时,特征选择(feature selection, FS)能减少建模阶段的冗余和不相关性较高的特征,是机器学习中必不可少的步骤。在这项研究中,仿照了Li等[23]的方法选取了6种常用的无监督FS算法和4种有监督FS算法产生24组FS组合。进行多次随机分割作为训练集和验证集,以每种FS组合的可分辨性和再现性的乘积作为评价指标,且各组学独立进行特征选择过程,互相无影响。最佳的特征选择方法依次是费舍尔得分Fisher Score和Pearson Score、T_score和Pearson Score、T_score和Lap_score,组成311×35、311×4和311×8的数据集。
2.3 实验设置
为了综合评估MOCL算法对于多组学数据的预测性能,选取了3种传统的单视角机器学习算法SVM、C4_5决策树、Adaboost元算法和Zhang等[24]提出的DICS、Yang等[25]提出的WeightReg两种多视角算法进行比较。针对单视角算法,采用传统的特征拼接方法,即影像组学、剂量组学、轮廓组学的3组特征向量拼接成一组新特征向量,进行归一化后直接使用单视角算法对拼接后的向量进行处理。本实验的评价指标设置为接收者操作特征曲线下的面积(area under curve, AUC)和F1_score。
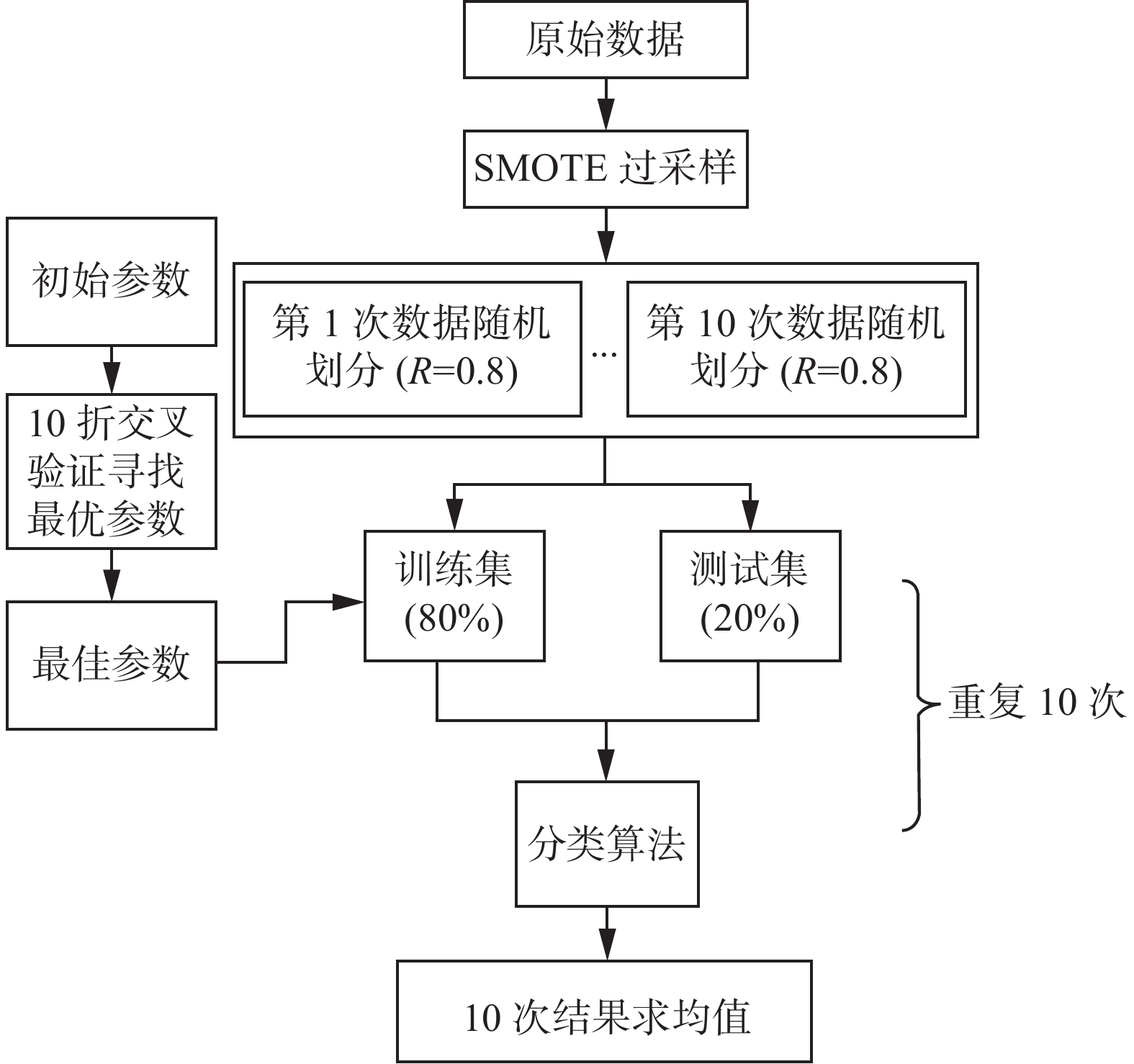
为了进行公正的比较,每一种算法都进行了相对公平的参数设定和评价指标。所有的算法都是在搭载了win10操作系统的机器上运行的。具体流程如图2所示,其中支持向量机(support vector machines, SVM)算法和MOCL算法都额外使用10折交叉验证寻找最佳参数;由于Adaboost元算法是通过迭代的方式不断优化分类器的性能,故取20个分类器中最优分类器的实验精度作为10次随机划分的结果并求均值。表2给出了实验过程中,各算法参数的设定值。
表 2 各算法参数设定值Table 2 Parameter settings for each algorithm算法 参数表 SVM RBF核函数γ$ \in ${−10∶1∶10},
正则化项系数C$\in ${−10∶1∶10},
s =10−4,v =10C4_5决策树 防过拟合参数N $ \in ${5,6,7,8,9,10} Adaboost N = 20 DICS K1 =5,K3 =10,K2 =5,K4 =10,
α=0.1,β=10,γ=100,i=200,f=10WeightReg γ =1.0,i =200,e =5×10−3 MOCL β$ \in ${0.01,0.1,1,10},η$ \in ${0.01,0.1,1,10},
λ$ \in ${ 0.01,0.1,1,10}MOCL消融 λ$ \in ${0.01,0.1,1,10,100} 2.4 实验结果和分析
首先,给出MOCL及其对比算法的分类准确率,如表3所示。可以看到和传统的单视角机器学习算法相比,采用自适应权重和一致性约束的MOCL算法能取得较为优秀的实验结果。其中SVM和Adaboost元算法也都有较好的结果,可能是因为所使用的数据中,影像组学的特征占比较大,对于拼接后的特征向量,剂量组学和轮廓组学特征带来的影响比较小。同时相对于两种针对多视角的算法,MOCL算法明显取得了更加优秀的实验结果。DISC采用联合非负矩阵分解将多视图数据分解为公共部分和视图特定部分,而这种方法的结果对于子空间维数相当敏感,在面对不同的设定时结果差异很大;WeightReg算法设计了一种基于判别回归的框架将多视图数据映射到统一的低维判别子空间,并引入了一组可学习的权重参数保留原始视图的相关和互补信息在投影子空间中,这种设计在处理不同视角特征数目不等的真实数据集合时可能存在一定的不足。
表 3 MOCL及其对比算法结果平均值(标准差)Table 3 Mean of results for MOCL and its comparison algorithims (standard deviation)分类算法 AUC F1_score 单视角
算法SVM 0.7657(0.0573) 0.7738(0.0462) C4_5决策树 0.6236(0.0560) 0.6104(0.0521) Adaboost元算法 0.7310(0.0602) 0.7298(0.0480) 多视角
算法DICS 0.7188(0.0806) 0.6012(0.0892) WeightReg 0.7161(0.0709) 0.7163(0.0483) MOCL 0.7950(0.0522) 0.7067(0.0639) 2.5 消融分析
为了确定采用多组学协作学习算法构建模型和使用单一组学特征构建模型确实存在差异,将MOCL算法进行消融,即去除其中有关自适应权重和一致性约束的计算,将其改造为针对单一组学特征空间的算法。对3个组学特征进行单独10次随机划分后、训练和验证,并以10次验证结果的均值作为最终结果,结果如表4所示。可以看出,综合考虑AUC和F1_score两项评价指标,采取多组学协作学习的方式构建模型相比单独考虑单一组学特征空间,能取得更好的预测精度。
表 4 MOCL与其消融算法结果对比平均值(标准差)Table 4 Mean of results for MOCL and its ablation algorithms (standard deviation)MOCL消融 AUC F1_score 特征空间1(轮廓组学) 0.6444(0.0366) 0.6027(0.0364) 特征空间2(剂量组学) 0.7274(0.0358) 0.6687(0.0278) 特征空间3(影像组学) 0.7711(0.0339) 0.6907(0.0356) 3个特征空间合计 0.7143(0.0262) 0.6541(0.0224) MOCL 0.7950(0.0522) 0.7067(0.0639) 2.6 统计分析
为了进一步确定每一种对比算法和MOCL算法是否存在统计学上的差别,依次将对比算法与MOCL进行了T检验,设定α为0.05,具体结果如表5所示。可以看出,MOCL算法与SVM算法在AUC不存在显著的差异,能达到类似的性能,但从F1的角度评估与SVM还有一定差距。而与其余算法相比,MOCL改良算法至少在一项评价指标上显现出显著差异,证明无论是与单视角算法对比还是已有的多视角算法对比,MOCL都有较为优秀的分类性能和稳定性。MOCL消融算法和MOCL的显著差异也更一步体现,使用多组学协作学习的方式相较于应用单一组学的方式能取得更好的模型性能。
表 5 MOCL与其对比算法统计学比较Table 5 Statistical comparison of MOCL with its comparison algorithm对比算法 AUC
(p-value)是否接受
差异(H)F1
(p-value)是否接受
差异(H)MOCL-SVM 0.52 0 0.03 1 MOCL-C4_5 1.33×10−6 1 0.0003 1 MOCL_Adaboost 0.048 1 0.68 0 MOCL-DICS 0.0501 0 0.0027 1 MOCL-WeightReg 0.0258 1 0.8717 0 MOCL-MOCL消融 0.000295 1 0.0021 1 3. 结束语
由于影像组学特征的再现性容易受到多种因素影响,使用多组学融合进行研究的方法越来越收到重视。而如何挖掘不同组学之间的互补信息是多组学研究的关键。针对此,本文设计了一种基于放射多组学的协同学习算法用于预测鼻咽癌患者是否需要进行ART,并在来自香港伊利沙伯医院311名患者的真实数据上完成验证。相比已有的一些针对多视角的算法,能够更好地适应多组学数据,有较好的实验精度。但相比SVM、Adaboost两种经典的机器学习算法,没有显示出统计学上的明显差异。可能是因为所使用的数据集中,剂量组学和轮廓组学特征数量较小,在计算过程中权重影响较低,在接下来的研究中会着重于剂量组学和轮廓组学的特征提取和选择,尽可能扩大其特征数量。总的来说,本算法在预测鼻咽癌患者是否需要进行ART时,可以为临床决策提供较为可靠的参考意见,更早发现有可能发生转移的病人,提高病人的存活率。
-
表 1 3种组学特征涉及到的VOIs来源
Table 1 Source of VOIs involved in the three histological profiles
影像组学 剂量组学 轮廓组学 CECT-GTVnp GTVnp PTVn_low_dose-SC CECT-GTVn GTVn GTVnp-IpsiPG CECT-IpsiPG IpsiPG GTVnp-ContraPG CECT-ContraPG ContraPG GTVnp-SC CET1w-GTVnp BS — CET1w-IpsiPG SC — CET1w-ContraPG PTVn_high_dose — T2w-GTVnp PTVn_low_dose — T2w-IpsiPG — — T2w-ContraPG — — 表 2 各算法参数设定值
Table 2 Parameter settings for each algorithm
算法 参数表 SVM RBF核函数γ$ \in ${−10∶1∶10},
正则化项系数C$\in ${−10∶1∶10},
s =10−4,v =10C4_5决策树 防过拟合参数N $ \in ${5,6,7,8,9,10} Adaboost N = 20 DICS K1 =5,K3 =10,K2 =5,K4 =10,
α=0.1,β=10,γ=100,i=200,f=10WeightReg γ =1.0,i =200,e =5×10−3 MOCL β$ \in ${0.01,0.1,1,10},η$ \in ${0.01,0.1,1,10},
λ$ \in ${ 0.01,0.1,1,10}MOCL消融 λ$ \in ${0.01,0.1,1,10,100} 表 3 MOCL及其对比算法结果平均值(标准差)
Table 3 Mean of results for MOCL and its comparison algorithims (standard deviation)
分类算法 AUC F1_score 单视角
算法SVM 0.7657(0.0573) 0.7738(0.0462) C4_5决策树 0.6236(0.0560) 0.6104(0.0521) Adaboost元算法 0.7310(0.0602) 0.7298(0.0480) 多视角
算法DICS 0.7188(0.0806) 0.6012(0.0892) WeightReg 0.7161(0.0709) 0.7163(0.0483) MOCL 0.7950(0.0522) 0.7067(0.0639) 表 4 MOCL与其消融算法结果对比平均值(标准差)
Table 4 Mean of results for MOCL and its ablation algorithms (standard deviation)
MOCL消融 AUC F1_score 特征空间1(轮廓组学) 0.6444(0.0366) 0.6027(0.0364) 特征空间2(剂量组学) 0.7274(0.0358) 0.6687(0.0278) 特征空间3(影像组学) 0.7711(0.0339) 0.6907(0.0356) 3个特征空间合计 0.7143(0.0262) 0.6541(0.0224) MOCL 0.7950(0.0522) 0.7067(0.0639) 表 5 MOCL与其对比算法统计学比较
Table 5 Statistical comparison of MOCL with its comparison algorithm
对比算法 AUC
(p-value)是否接受
差异(H)F1
(p-value)是否接受
差异(H)MOCL-SVM 0.52 0 0.03 1 MOCL-C4_5 1.33×10−6 1 0.0003 1 MOCL_Adaboost 0.048 1 0.68 0 MOCL-DICS 0.0501 0 0.0027 1 MOCL-WeightReg 0.0258 1 0.8717 0 MOCL-MOCL消融 0.000295 1 0.0021 1 -
[1] SUNG H, FERLAY J, SIEGEL R L, et al. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries[J]. CA:a cancer journal for clinicians, 2021, 71(3): 209–249. doi: 10.3322/caac.21660 [2] 梁锌, 杨剑, 高婷, 等. 中国鼻咽癌流行概况[J]. 中国肿瘤, 2016, 25(11): 835–840. doi: 10.11735/j.issn.1004-0242.2016.11.A001 LIANG Xin, YANG Jian, GAO Ting, et al. Nasopharynx cancer epidemiology in China[J]. China cancer, 2016, 25(11): 835–840. doi: 10.11735/j.issn.1004-0242.2016.11.A001 [3] CHEN Yupei, CHAN A T C, LE Q T, et al. Nasopharyngeal carcinoma[J]. Lancet, 2019, 394(10192): 64–80. doi: 10.1016/S0140-6736(19)30956-0 [4] LIU Yanxia, SHI Hongyu, HUANG Sijuan, et al. Early prediction of acute xerostomia during radiation therapy for nasopharyngeal cancer based on delta radiomics from CT images[J]. Quantitative imaging in medicine and surgery, 2019, 9(7): 1288–1302. doi: 10.21037/qims.2019.07.08 [5] 金哲, 张斌, 张璐, 等. 基于多参数MRI影像组学及临床特征的鼻咽癌远处转移可解释性机器学习预测模型[J]. 磁共振成像, 2022, 13(11): 22–29. doi: 10.12015/issn.1674-8034.2022.11.005 JIN Zhe, ZHANG Bin, ZHANG Lu, et al. Prediction of distant metastasis in nasopharyngeal carcinoma by interpretable machine learning model based on multiparametric MRI radiomics and clinical factors[J]. Chinese journal of magnetic resonance imaging, 2022, 13(11): 22–29. doi: 10.12015/issn.1674-8034.2022.11.005 [6] ZHANG Xingping, ZHANG Yanchun, ZHANG Guijuan, et al. Deep learning with radiomics for disease diagnosis and treatment: challenges and potential[J]. Frontiers in oncology, 2022, 12: 773840. doi: 10.3389/fonc.2022.773840 [7] MAYERHOEFER M E, MATERKA A, LANGS G, et al. Introduction to radiomics[J]. Journal of nuclear medicine: official publication, Society of Nuclear Medicine, 2020, 61(4): 488–495. [8] HARDING-THEOBALD E, LOUISSAINT J, MARAJ B, et al. Systematic review: radiomics for the diagnosis and prognosis of hepatocellular carcinoma[J]. Alimentary pharmacology & therapeutics, 2021, 54(7): 890–901. [9] AVANZO M, STANCANELLO J, EL NAQA I. Beyond imaging: the promise of radiomics[J]. Physica medica, 2017, 38: 122–139. doi: 10.1016/j.ejmp.2017.05.071 [10] ZHOU Lu, WEN Yuefeng, ZHANG Guoqian, et al. Machine learning-based multiomics prediction model for radiation pneumonitis[J]. Journal of oncology, 2023, 2023: 1–9. [11] CAI C, LYU Wenbing, CHI F, et al. Prognostic generalization of multi-level CT-dose fusion dosiomics from primary tumor and lymph node in nasopharyngeal carcinoma[J]. Medical physics, 2023, 50(2): 922–934. doi: 10.1002/mp.16044 [12] CUI Sunan, TEN HAKEN R K, EL NAQA I. Integrating multiomics information in deep learning architectures for joint actuarial outcome prediction in non-small cell lung cancer patients after radiation therapy[J]. International journal of radiation oncology biology physics, 2021, 110(3): 893–904. doi: 10.1016/j.ijrobp.2021.01.042 [13] TONG Li, WU Hang, WANG M D. Integrating multi-omics data by learning modality invariant representations for improved prediction of overall survival of cancer[J]. Methods, 2021, 189: 74–85. doi: 10.1016/j.ymeth.2020.07.008 [14] XU Chang, TAO Dacheng, XU Chao. A survey on multi-view learning[EB/OL]. (2013−04−20)[2023−03−24]. https://arxiv.org/abs/1304.5634.pdf. [15] 包丹, 罗德红. 基于MR的影像组学在鼻咽癌中的研究进展[J]. 国际医学放射学杂志, 2020, 43(5): 560–564. doi: 10.19300/j.2020.Z18099 BAO Dan, LUO Dehong. Research progress in MR-based radiomics of nasopharyngeal carcinoma[J]. International journal of medical radiology, 2020, 43(5): 560–564. doi: 10.19300/j.2020.Z18099 [16] FANETTI G, AVANZO M, PIRRONE G, et al. PO-122 CT/PET based dosiomics and radiomics model predicts local control of nasopharyngeal carcinoma[J]. Radiotherapy and oncology, 2019, 132: 62–63. doi: 10.1016/S0167-8140(19)30288-9 [17] FANG Xiaozhao, XU Yong, LI Xuelong, et al. Regularized label relaxation linear regression[J]. IEEE transactions on neural networks and learning systems, 2018, 29(4): 1006–1018. doi: 10.1109/TNNLS.2017.2648880 [18] WU Aiqian, LI Yongbao, QI Mengke, et al. Dosiomics improves prediction of locoregional recurrence for intensity modulated radiotherapy treated head and neck cancer cases[J]. Oral oncology, 2020, 104: 104625. doi: 10.1016/j.oraloncology.2020.104625 [19] LEE S H, HAN Peijin, HALES R K, et al. Multi-view radiomics and dosiomics analysis with machine learning for predicting acute-phase weight loss in lung cancer patients treated with radiotherapy[J]. Physics in medicine & biology, 2020, 65(19): 195015. [20] GABRYŚ H S, BUETTNER F, STERZING F, et al. Design and selection of machine learning methods using radiomics and dosiomics for normal tissue complication probability modeling of xerostomia[J]. Frontiers in oncology, 2018, 8: 35. doi: 10.3389/fonc.2018.00035 [21] BUETTNER F, MIAH A B, GULLIFORD S L, et al. Novel approaches to improve the therapeutic index of head and neck radiotherapy: an analysis of data from the PARSPORT randomised phase III trial[J]. Radiotherapy and oncology, 2012, 103(1): 82–87. doi: 10.1016/j.radonc.2012.02.006 [22] WU Binbin, RICCHETTI F, SANGUINETI G, et al. Patient geometry-driven information retrieval for IMRT treatment plan quality control[J]. Medical physics, 2009, 36(12): 5497–5505. doi: 10.1118/1.3253464 [23] LI Bing, ZHENG Xiaoli, GUO Wei, et al. Radiation pneumonitis prediction using multi- omics fusion based on a novel machine learning pipeline[J]. Human-centric computing and information sciences, 2022, 12: 49. [24] ZHANG Zhong, QIN Zhili, LI Peiyan, et al. Multi-view discriminative learning via joint non-negative matrix factorization[C]//International Conference on Database Systems for Advanced Applications. Cham: Springer, 2018: 542−557. [25] YANG Muli, DENG Cheng, NIE Feiping. Adaptive-weighting discriminative regression for multi-view classification[J]. Pattern recognition, 2019, 88: 236–245. doi: 10.1016/j.patcog.2018.11.015













































































 下载:
下载: