Image super-resolution reconstruction by fusing layered features with residual distillation connections
-
摘要: 针对目前诸多图像超分辨率重建算法通过采用单一通道网络结构无法充分利用特征信息的问题，提出了一种可以高效利用特征信息的融合分层特征与残差蒸馏连接的超分辨率重建算法。该方法首先设计了一种将分层特征融合与残差连接相结合的连接方式，对图像深层特征与浅层特征进行充分融合，提升了网络对于特征信息的利用率；其次设计出一种残差蒸馏注意力模块，使网络更高效地关注图像关键特征，从而可以更好地恢复出重建图像的细节特征。实验结果表明，所提出的算法模型不仅在4种测试集上呈现出更优秀的客观评价指标，而且在主观视觉效果上也呈现出更好的重建效果。具体在Set14测试集上，该模型4倍重建结果的峰值信噪比相对于对比模型平均提升了0.85 dB，结构相似度平均提升了0.034，充分证明了该算法模型的有效性。Abstract: Aiming at the issue that several current image super-resolution reconstruction algorithms cannot fully utilize the feature information by adopting a single-channel network structure, a super-resolution reconstruction algorithm that fuses hierarchical features and residual distillation connections is proposed. In this method, a connection method that combines layered features with residual connections is adopted to fully fuse the deep and shallow features of an image, improving the utilization of feature information by the network. Further, a residual distillation attention module is used, which enables the network to focus on the key features of the image efficiently, allowing efficient recovery of the detailed features of the reconstructed image. The experimental results showed that the proposed algorithmic model exhibits better objective evaluation indexes on four test sets and has a superior reconstruction effect on the subjective visual effect. Specifically, on the Set14 test set, the peak signal-to-noise ratio of the four-fold reconstruction results of the model is improved by 0.85 dB on average relative to the comparison model and the structural similarity is improved by 0.034 on average, demonstrating the effectiveness of the algorithmic model.
-
在计算机视觉与图像处理领域中，图像的质量直接影响到很多应用的精度与效果，图像超分辨率重建技术可以在不借助外部设备条件的情况下将低分辨率图像转换为高分辨率图像，从而达到提高图像质量的目的，近年来逐渐成为国内外学者的研究热点。当下图像超分辨率重建技术已成功地应用到各种领域当中，例如最近比较热门的人脸识别技术[1]经常被用于学校、公司、小区的安防监控中。除此之外，此技术同样被成功应用于医疗领域[2]、遥感影像领域[3-4]以及智慧矿山领域[5]中，具有非常广阔的应用前景。
目前图像超分辨率重建技术由3类方法组成：基于插值的方法[6]、基于重建的方法[7-8]和基于学习[9]的方法。基于插值的方法优点是可以快速得到结果，但重建图像会存在边缘模糊的问题；基于重建的方法优点在于计算量少，但在重建过程中会忽略掉图像的高频细节信息，从而导致重建图片不真实。
相比较而言，基于学习的方法可以提取到更丰富、更具体的图像细节信息，图像重建效果明显优于传统插值和重建方法，其主要通过早期的浅层机器学习与当下常用的深度学习来完成图像超分辨率重建任务。例如Yang等[10]提出基于稀疏编码理论的重建方法, 该方法主要通过图像的稀疏表示学习获得高分辨率字典与低分辨率字典，并根据高低分辨率图像之间的映射关系成功对图像进行了重建。
Dong等[11]首次将深度学习带入到图像超分辨率重建领域当中，提出了SRCNN（super resolution convolutional neural network）网络模型，但是SRCNN网络具有明显的局限性，其只适用于3层网络结构，当图像超分辨率重建的尺度因子为4倍以上时，SRCNN模型重建速度较慢且重建出的图像视觉效果较差；之后Dong等[12]针对SRCNN网络训练速度慢、重建效率低的缺点，在SRCNN的基础上进而提出了FSRCNN（fast super-resolution convolutional neural network）网络模型，通过在网络结构中引入可以改变特征图维度的反卷积层，实现了加速模型训练效率的目的；同年Shi等[13]提出ESPCN（efficient sub-pixel convolutional neural network）模型，实现了在网络中对图像进行缩放的目的，但当网络深度较大时，训练难度会增大且重建效果不佳；接着，He等[14]提出了残差网络ResNet（residual network），用来解决网络深度较大时训练困难的问题，Kim等[15]首次将残差网络的思想应用于图像超分辨率领域，提出了VDSR（very deep convolution networks for super-resolution）模型，该模型将网络结构层数从3层增加到20层，并且证明了残差结构的确可以有效提升模型的重建性能；Lim等[16]提出了EDSR（enhanced deep super-resolution network）网络简化了残差连接结构，并意识到了残差结构的局限性，加入了新的批归一化层[17]作为非线性映射层的堆叠模块，从而使EDSR成功构建出更深的网络结构，提高了网络的整体性能。
随后Zhang等[18]在EDSR网络的基础上提出了基于RIR（residual in residual）结构的RCAN（residual channel attention networks）网络模型，其通过引入注意力机制对图像中各部分的特征信息进行分类，关注更加有用的特征信息，提高了网络对于关键特征获取的效率；随后Zhang等[19]继续在深层残差网络的基础上进行思考，利用密集连接将各层级之间的特征信息进行充分融合，提出了残差密集网络RDN（residual dense network）结构，得到了更好的图像重建效果。之后Chen等[20]在残差密集网络结构的基础上，加深网络结构的深度的同时对网络进行内容导向化，实现图像超分辨率重建。程德强等[21]利用残差网络提出多通道递归残差网络的图像超分辨率重建，将不同层次间的特征信息进行跨尺度融合，改变传统跳跃连接得到了更好的图像重建效果。
近期Haris等[22]利用迭代反投影法，有效挖掘图像特征的先验信息，在8倍尺度因子下的超分辨率重建中取得了优异的效果。Purohit等[23]提出了一种从混合网络派生而来的混合密度连接网路，以最大程度地提高超分辨率网络的效率，并从残余和密集连接中受益。Faramarzi等[24]将图像像素信息抽象成空间域的数值信号，利用傅里叶变换将信号转换成频域，对频率杂乱的噪声进行滤波处理，然后再逆变换生成重建图像，这样即可达到去除图像噪声的效果。Ahn等[25]利用层组的跳转连接在处理残差数据时将神经网络层划分为多个层组，使得隐藏层单元中的处理数据分布范围更广，有利于输入数据的特征信息能更稳健地传输到输出。
研究人员不断地在卷积神经网络的基础上对模型进行改进与创新，使重建出的图像呈现出更好的效果。虽然以上算法对于图像超分辨率重建具有较好的重建性能，但大部分算法仍然存在以下问题：
1）诸多超分辨率重建算法都只采用单一通道的网络结构，图像特征信息在传输过程中极易丢失，使模型无法充分利用网络所提取到的特征信息，导致模型的重建性能下降。
2）诸多超分辨率重建算法通过不断堆叠卷积块的方式来提升模型对特征信息的获取能力，但是该方式会使模型无差别地对待图像特征信息，无法对图像关键特征信息进行有效提取，并且随着网络深度的加深容易出现高频细节信息丢失的问题，导致模型重建性能下降。
针对上述问题，本文提出一种融合分层特征与残差蒸馏连接的超分辨率重建模型，本模型首先设计了一种将分层特征融合与残差连接相结合的连接方式，将图像的深层特征与浅层特征进行充分融合，大幅度提高了模型对于图像特征信息的利用率，并且残差连接的存在可以大大降低网络模型的训练难度，有效防止了梯度爆炸、梯度消失、模型退化等问题的出现；其次提出了一种基于增强空间注意力机制的残差蒸馏模块，通过在残差块中融入增强空间注意力机制，分别对不同空间的特征信息赋予不同的权重，使模型在训练过程中可以更高效地关注权重较高的图像特征信息，加强了模型对于图像关键特征信息的获取能力，同时减少了图像细节特征信息在残差块中的损失，解决了图像重建后边缘模糊的问题，使重建后的图像细节信息更加完善，效果更加清晰。
1. 本文方法
1.1 本文整体网络结构
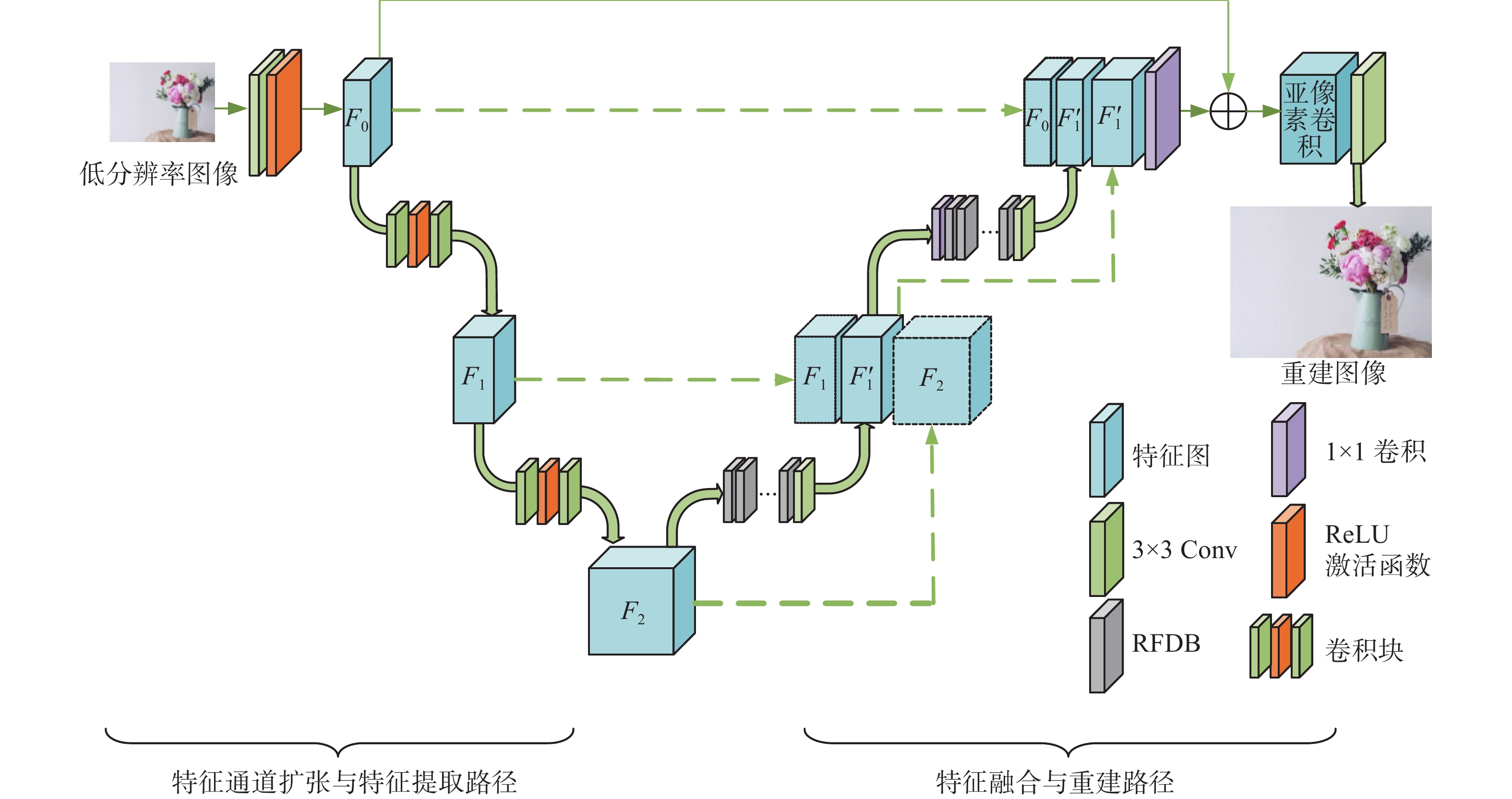
为了提高图像的特征信息在网络中的传递与提取，同时为了满足图像超分辨率重建任务的需求，本文对U-Net结构进行改进与创新。首先改进U-Net网络的下采样结构，本文模型去除最大池化层，不再改变特征图尺寸的大小，最大程度减少图像分辨率的丢失，只扩大提取图像特征图的通道数；其次为了降低模型的训练难度，本文不再使用原U-Net网络的5层结构，只使用3层结构，即对特征图通道数只进行两次扩张，每一次扩张都会使本层特征图的通道数扩大为上一层的2倍；然后在U-Net上采样操作中引入残差蒸馏注意力模块对提取到的特征图进行关键特征提取并对其进行优化处理；最后通过残差学习与特征融合结合的方式，利用特征融合操作使深层特征与浅层特征充分融合，利用残差连接防止梯度爆炸、梯度消失、模型退化等问题的出现，以此来确保获取到的图像特征信息被充分利用，最终获得一个整体3层的网络结构，如图1所示。
图 1 融合分层特征U型网络结构Fig. 1 Fused hierarchical feature U-shaped network structure
下载:
全尺寸图片
首先向网络输入通道数为3的低分辨率RGB图像，初始卷积由64个3×3大小的卷积核与ReLU函数组成，目的是为了将RGB三通道的低分辨率图像转换成通道数为64的特征图
$ F_{0} $ ，接着进入向下卷积模块中，此模块由128个3×3大小的卷积核与ReLU函数组成，目的是为了在向下卷积的过程中将通道数扩大为原来的2倍得到新的特征图$ F_{1} $ (128层)。同样地，第2层向下卷积操作通过由256个3×3大小的卷积核与ReLU函数组成的卷积块将特征图$ F_{1} $ 扩大为2倍，生成新的特征图$ F_{2} $ (256层)。具体运算如下：$$ F_{{i = }}{f_{\text{c}}} ({F_{{{i}}-1}}),({{i}}=1,2)$$ (1) 其中
$f_{\text{c}}$ (convolution block)表示向下卷积块操作，卷积块由不同数量的卷积核与ReLU函数组成，其作用是在扩大图像特征通道数的同时增强模型的非线性能力。之后将卷积块特征提取操作得到的特征图$ F_{2} $ 送入特征图融合重建路径中的残差特征蒸馏注意力模块(residual feature fusion attention distillation block, RFAB)中进行特征提取。本文模型中，每层RFAB模块数量设置为4，RFAB模块的输出将继续经过一个拥有128个卷积核大小3×3的卷积层将特征图$ F_{2} $ (256层)融合为128层的特征图${F'_{1}}$ ，具体运算如下：$$ {F'_{1}}=f_{{\text{3}} \times {\text{3}}}(f_{\text{RFAB}}(F_{\text{2}})) $$ (2) 式中：
$f_{{\text{3}} \times {\text{3}} }$ 为3×3卷积层处理特征通道数的操作，$f_{\text{RFAB}}$ 为特征图通过RFAB模块的操作。此时${F'_{1}}$ 的通道数与$ F_{1} $ 相同，方便进行特征拼接。为了提高特征图的利用率，本文模型将通过U型网络对称的特点将${F'_{1}}$ 与$ F_{1} $ 进行特征融合得到$ F $ ，此时特征通道数为两者之和128层，同时利用残差学习的特点，将深层特征$ F_{2} $ 输入到融合层之中，与浅层特征${F'_{11}}$ 进行拼接得到${F'_{12}}$ ，这样可以使网络充分地对深层特征与浅层特征进行融合，获得细节特征更具体的特征图。具体运算如下：$$ \left\{\begin{array}{l}{F'_{11}}=H_{\text{concat}}(F_1{,}\;F'_1)\\ {F'_{12}}=H_{\text{concat}}({F'_{11}}{,}\;F_2)\end{array}\right. $$ (3) 紧接着将
${F'_{12}}$ 通过1×1的卷积层进行降维处理，再次送入新的一层RFAB模块中，最后通过3×3的卷积层将特征图${F'_{12}}$ 的通道数融合为通道数为64的特征图$ F'_{0}{ } $ ，与U型网络左侧输送来的浅层特征$ F_{0} $ 进行融合得到${F'_{00}}$ ；同时利用残差学习的特点，将上一层的${F'_{1}}$ 输送到本层特征融合层与${F'_{00}}$ 进行再次拼接得到${F'_{01}}$ ，具体运算如下：$$ \left\{ \begin{gathered} {F'_{0}} = f_{3 \times 3}(f_{\text{RFAB}}(f_{{\text{1}} \times {\text{1}}}({{{F'_{12}}))}}) \\ {F'_{00}} = H_{\text{concat}}(F_{\text{0,}}{F'_{0}}{{)}} \\ {F'_{01}} = H_{\text{concat}}({F'_{00}}{{,}}{F'_{1}}{{)}} \\ \end{gathered} \right. $$ (4) 将经过两层特征提取模块的
${F'_{01}}$ 送入到1×1的卷积层当中进行降维处理，同时利用本文整体网络的残差结构，进行残差学习之后送入到亚像素卷积模块生成高分辨率图像。具体运算图下：$$ F_{\text{SR = }}f_{3 \times 3}(f_{\text{PS}}(f_{1 \times 1}({F'_{01}}) + F_0{\text{)}}) $$ (5) 式中：
$ F_{0} $ 为低分辨率图像最开始经过卷积处理后的粗特征图，$f_{\text{PS}}$ 为亚像素卷积方法中的像素重排操作。重排之后的图像经过3×3的卷积层将图像通道数还原为通道数为3的RGB图像，得到重建后的图像为$F_{\text{SR}}$ 。其中
$ F_{1} $ 与$ F_{2} $ 的特征图通道数量是$ F_{0} $ 的2倍和4倍，分别为128层与256层，${F'_{1}}$ 与${F'_{0}}$ 的特征图通道数量与$ F_{1} $ 和$ F_{0} $ 相同，分别为128层与64层；图中第一层特征融合层中的${F'_{11}}$ 为$ F_{1} $ 与${F'_{1}}$ 融合得到，特征通道数为256层，${F'_{12}}$ 为${F'_{11}}$ 与$ F_{2} $ 融合得到，特征通道数为512层；第二层特征融合层中的${F'_{00}}$ 为$ F_{0} $ 与${F'_{0}}$ 融合得到，特征通道数为128层，${F'_{01}}$ 为${F'_{00}}$ 与${F'_{1}}$ 融合得到，特征通道数为256层，具体模型中每一功能模块的输入输出特征通道数如表1所示。表 1 各功能模块输入与输出通道数Table 1 Input and output channels of each function module模块名称 输入通道数 输出通道数 图像特征图提取模块 3( $F_{\text{LR} }$) 64( $ F_{0} $) 向下卷积模块CB1 64( $ F_{0} $) 128( $ F_{1} $) 向下卷积模块CB2 128( $ F_{1} $) 256( $ F_{2} $) 残差特征注意力
蒸馏模块(RFAB×4)256( $ F_{2} $) 128( ${F'_{1}}$) 第一层特征融合层 128+128+256
( $ F_{1} $+ ${F'_{1}}$+ $ F_{2} $)512
( ${F'_{11}}$+ $ F_{2} $= ${F'_{12}}$)1×1降维卷积层 512 ( ${F'_{12}}$) 128( ${F'_{12}}$) 残差特征注意力
蒸馏模块(RFAB×4)128( ${F'_{12}}$) 64( ${F'_{0}}$) 第二层特征融合层 64+64+128
( $ F_{0} $+ ${F'_{0}}$+ ${F'_{1}}$)256
( ${F'_{01} }$= ${F'_{1}}$+ ${F'_{00}}$)1×1降维卷积层 256( ${F'_{01} }$) 64( ${F'_{01}}$) 图像重建模块 64( ${F'_{01}}$) 3( $F_{\text{SR} }$) 1.2 残差蒸馏注意力模块
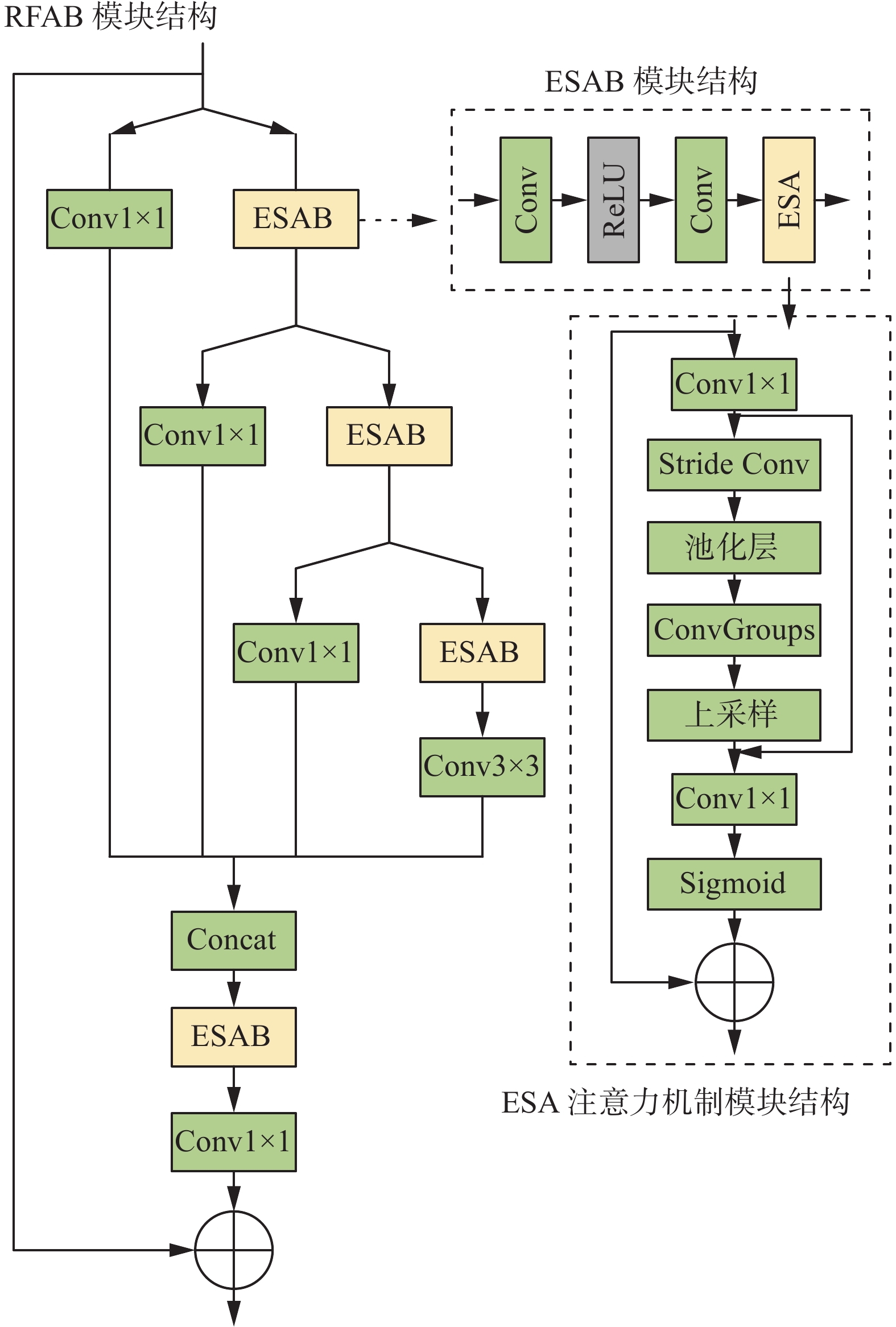
在CNN网络中，输入进网络的是图片最基本的特征，网络通过卷积层来对图像的特征信息进行提取，但是过多的卷积层会导致图细节特征信息的丢失，最终导致重建效果不佳，本文所引用的残差特征蒸馏连接，是在残差连接的基础上进行改进，可以在防止梯度消失的同时，提高网络的运算效率，并且对残差块所引起的图像细节特征丢失进行补偿。2020年，Liu等[26]提出了一种更灵活更快速的残差蒸馏连接方式，信息蒸馏操作是通过卷积以一定比例压缩特征通道来实现的，来达到降低网络训练难度的目的。本文所改进后的残差蒸馏注意力模块，在残差蒸馏连接的基础上，增加了创新的增强空间注意力模块(enhanced spatial attention block, ESAB)，在引入空间注意力机制之后，可以使模型在训练过程中获得更大的感受野，更好地根据空间上下文内容自适应地重新分配特征信息，从而着重关注到关键特征信息，使重建出的图像细节信息更加丰富，边缘信息更加清晰。此模块的引入可以保证网络能够有效地学习更高级复杂地图像特征，得到区域相关性更强的注意力特征图，有利于提升图像超分辨率重建质量。
图2给出了残差蒸馏注意力模块（residual feature fusion attention distillation block, RFAB）的整体结构，它包含一个3×3的卷积核、一个恒等连接分支以及一个激活单元，ESAB在不引入额外参数的情况下，还可以从残差学习中获益。RFAB模块首先采用通道分离操作将输入特征图分为两部分，一部分特征图通过1×1的卷积进行降维处理并进行保留，另一部分则作为新的输入融入到下个阶段的蒸馏步骤中。ESAB是构成RFAB的基础残差模块，ESA(enhanced feature attention)是结构中引进的增强空间注意力模块，具体结构均在图2中标出。
图 2 残差蒸馏注意力模块Fig. 2 Residual feature fusion attention distillation block下载:
全尺寸图片
然后将各层蒸馏特征操作后保留的特征图进行特征融合，融合后的特征图送入增强注意力模块得到最后的输出特征图。其具体运算可以表示为
$$ \left\{ \begin{gathered} F_{\text{dis = }}H_{\text{concat}}(F_{\text{dis}\_1,}F_{\text{dis}\_2,}F_{\text{dis}\_3,}F_{\text{dis}\_4}{\text{}} ) \\ F_{\text{out = }}f_{\text{c}}(f_{\text{ESA}}(F_{\text{dis }})+F_{\text{in}} ) \\ \end{gathered} \right. $$ (6) 其中：
${F_{{{\rm{dis}}{\_}i}}{(i = 1,2,3,4)}}$ 为每一层蒸馏操作，$f_{\text{ESA}}$ 为增强空间注意力机制，$f_{\text{c}}$ 为卷积层操作，$H_{\text{concat}}$ 为特征融合操作。首先，对输入使用1×1的卷积组进行通道数的降维操作，为了使注意力区域更好地完成图像重建目标，需要扩大感受野的范围，所以在降维后再通过stride为2的卷积、2×2的最大池化层以及卷积组来达到目的，其中卷积组是由7×7的最大池化层和stride为3的卷积组成。此时输出的特征经过上采样得到和输入尺寸大小相等的特征，经过跳跃链接后的特征进行1×1卷积和Sigmoid函数，与输入点乘，得到ESA的输出特征。此结构保证了图像中较为平滑的低频信息在网络中可以有效地传递，还可以利用注意力机制对高频信息进行高效的学习，也保证了网络的训练效率，有利于提高输出图像的重建效果。
2. 实验结果与分析
2.1 实验相关准备
本实验训练测试的硬件环境为：Intel(R) Core(TM) i9-10980XE CPU@3. 00 GHz，18核36线程；系统内存为64 GB；显卡为NVIDIA RTX 3090，24 GB显存容量。软件环境为：Ubuntu20.04系统；Pytorch1.8深度学习框架；cuda11.4加速学习；编程语言为Python3.7。网络迭代训练500次，初始学习率设置为0.0001，当网络训练次数达到300次时，学习率减半，优化方法采用自适应矩估计(adaptive momentum estimation，Adam)优化器，其参数β1=0.9，β2=0.99。损失函数采用L1损失函数。
2.2 实验数据集与性能评价指标
本文采用的训练数据集为公开数据集DIV2K，该数据集提供了1000张不同场景下不同分辨率的图片。通过双三次插值下采样得到输入的低分辨率(low resolution, LR)图像，尺度因子分别为×4与×8。测试集上，本文选用Set5[27]、Set14[28]、B100[29]以及Urban100[30]这4种经典数据集作为测试集。
本文在测试集上的对比实验，首先选用峰值信噪比(peak signal to noise ratio, PSNR)来作为客观评价指标，PSNR指标值的大小与图像的质量成正比，实验所得到的值越大，其代表的图像质量就越高，单位为dB；其次本文将选用结构相似度(structural similarity, SSIM)对图像质量进行二次评价，SSIM指标与PSNR值经常搭配在一起使用，其值越大，代表所对应图像质量也就越高，并且值越接近1，说明重建后的图像与原高清图像越相似。
2.3 实验对比模型选取
为了验证本文算法在图像超分辨率重建任务中的有效性，在实验中，对比模型采用双三次插值法Bicubic、SRCNN、EDSR、RCAN、DBPN（deep back-projection networks）、CSNLN（cross-scale non-local attention networks）[31]、NLSN（non-local sparse attention networks）[32]以及EFDN（edge-enhanced feature distillation network）网络模型[33]进行对比，本文所选用的对比模型在图像超分辨率重建领域中具有一定的代表性，所运用到的技术对本文算法有一定的启示作用。
其中，Bicubic是传统插值中最具代表性的经典算法；SRCNN网络是在图像超分辨率重建领域中首次将深度学习与卷积神经网络作为研究基础的算法模型，在图像超分辨率重建领域中具有开创性的意义；EDSR网络是在VDSR的基础上优化的深度残差网络；RCAN网络是首次在残差块的基础上引入RIR结构并利用注意力机制对图像特征信息进行选择获取的网络；DBPN网络则是在上采样的过程中进行创新迭代，在8倍模型上取得了比以往模型更好的重建效果；CSNLN网络则是在RCAN的基础上，探索了不同尺度间的特征信息，将不同尺度间的特征信息进行部分融合，获得了更好的重建效果；NLSN网络将非局部的自注意力机制与稀疏表示相结合，对特征信息进行分组，使自相关更加精确；EFDN网络中构建了一种更加精细和有效的重参数化模块，通过堆叠更多的边缘增强模块，来获取更多高级结构信息。通过上述对比模型与本文模型进行对比实验，可以更好地对本文模型的重建性能进行评估。
2.4 模型性能对比
为了具体地说明本文模型在重建任务中所带来的性能提升，下面将通过两种角度来对本文模型进行分析。首先从客观评价指标的角度上，通过重建后的图像与原始图像计算得出的PSNR值与SSIM值来评价本文模型的重建性能；其次从人体主观视觉效果角度出发，将本文模型重建出的图像与对比模型重建出的图像进行观察对比，比较重建图像的完整度与清晰度。
2.4.1 不同模型客观评价指标对比
在实验测试集上，本文选用4种完全不同的测试集分别在×4、×8两种尺度因子进行测试，对比模型选用上文所介绍的8种代表模型，实验所得出的PSNR与SSIM两种客观评价指标数据如表2、3所示，其中下划数值为次优结果，加粗数值为最优结果。
表 2 不同算法模型在4种测试集上的PSNR指标对比Table 2 Comparison of PSNR metrics of different algorithmic models on four test setsdB 测试集 尺度因子 Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Set5 ×4 28.42 29.33 32.25 32.45 32.39 32.64 32.68 32.69 32.69 ×8 24.32 25.02 26.89 27.21 27.25 27.29 27.36 27.34 27.38 Set14 ×4 25.89 26.11 28.67 28.78 28.66 28.88 28.91 28.93 28.95 ×8 23.19 23.45 25.02 25.16 25.18 25.22 25.24 25.26 25.31 Urban100 ×4 23.12 24.16 26.15 26.51 26.38 26.76 27.24 27.24 27.28 ×8 20.64 21.20 22.52 22.82 22.72 22.84 22.87 22.89 22.91 B100 ×4 25.26 25.77 26.85 26.92 25.97 26.97 27.06 27.05 27.08 ×8 22.07 23.82 24.76 25.49 25.52 25.78 25.88 25.91 25.96 表 3 不同算法模型在4种测试集上的SSIM指标对比Table 3 Comparison of SSIM metrics of different algorithmic models on four test sets测试集 尺度因子 Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Set5 ×4 0.8102 0.8442 0.9066 0.9112 0.9091 0.9116 0.9120 0.9121 0.9121 ×8 0.6568 0.6971 0.7742 0.7872 0.7875 0.7891 0.7897 0.7902 0.7905 Set14 ×4 0.7026 0.7899 0.8669 0.8713 0.8653 0.8715 0.8720 0.8722 0.8724 ×8 0.5682 0.5981 0.6415 0.6491 0.6510 0.6517 0.6523 0.6525 0.6528 Urban100 ×4 0.6981 0.7520 0.7911 0.8087 0.7946 0.8159 0.8172 0.8170 0.8174 ×8 0.5150 0.5541 0.6180 0.6431 0.6359 0.6433 0.6437 0.6439 0.6441 B100 ×4 0.6453 0.6662 0.7095 0.7149 0.6725 0.7154 0.7158 0.7159 0.7163 ×8 0.5047 0.5514 0.6112 0.6521 0.6522 0.6712 0.6779 0.6787 0.6789 从表2~3的数据可以看出，本文模型在4种不同测试集上呈现出比其他对比模型更优异的客观评价指标，PSNR值与SSIM值均有所提高。以Set14测试集为例，将本文网络分别8种对比模型进行客观评价指标对比，可以得出在尺度×4时，本文模型PSNR值提高了3.06、2.84、0.28、0.17、0.29、0.07、0.04、0.02 dB，SSIM结构相似度则分别提高了0.1698、0.0825、0.0055、0.0011、0.0071、0.0009、0.0004、0.0002；在尺度×8时, PSNR值分别提高了2.12、1.86、0.29、0.15、0.13、0.09、0.07、0.05 dB, SSIM结构相似度则分别提高了0.0846、0.0547、0.0113、0.0037、0.0018、0.0005、0.0003。说明本文模型基于在模型结构上的改进与创新分别在×4、×8两种尺度因子上均表现出比其他对比模型更优秀的重建性能。
为更加具体地验证本文模型对于单幅低分辨率图像的重建性能，本文将对Set5数据集中的5幅图像单独进行尺度因子为×4的超分辨率重建，每幅图像两种客观评价指标值如表4、5所示，其中下划数值为次优结果，加粗数值为最优结果。
表 4 不同算法模型在Set5上的PSNR指标对比Table 4 Comparison of PSNR metrics of different algorithmic models on Set5dB 图像(×4) Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EDFN[33] 本文算法 Baby 31.77 32.20 33.76 33.94 33.78 33.95 33.99 34.02 34.02 Bird 30.17 31.12 35.14 35.81 35.59 35.84 35.87 35.88 35.90 Butterfly 22.09 24.04 28.78 29.29 29.00 29.31 29.36 29.38 29.41 Head 31.57 31.58 32.97 32.88 32.98 32.92 33.02 33.03 33.03 Woman 26.46 27.72 30.58 30.91 30.61 31.22 31.38 31.37 31.41 均值 28.41 29.33 32.25 32.56 32.39 32.65 32.72 32.74 32.75 表 5 不同算法模型在Set5上的SSIM指标对比Table 5 Comparison of SSIM metrics of different algorithmic models on Set5图像(×4) Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Baby 0.9275 0.9322 0.9555 0.9562 0.9551 0.9562 0.9565 0.9567 0.9569 Bird 0.8726 0.8846 0.9452 0.9501 0.9492 0.9513 0.9517 0.9516 0.9520 Butterfly 0.7362 0.8007 0.9261 0.9335 0.9286 0.9344 0.9346 0.9348 0.9350 Head 0.7536 0.7515 0.7968 0.7974 0.7972 0.7977 0.7986 0.7988 0.7991 Woman 0.8315 0.8513 0.9139 0.9182 0.9147 0.9198 0.9205 0.9203 0.9206 均值 0.8243 0.8441 0.9075 0.9111 0.9089 0.9119 0.9124 0.9124 0.9127 从表4~5中可以看出，在Set5中的5幅图像上本文模型相对于其他对比模型客观评价指标上都得到了有效提升，其中PSNR均值分别提升了4.34、3.42、0.50、0.19、0.36、0.10、0.03、0.01 dB；SSIM均值相对于其他模型分别提升了0.1018、0. 0676、0.0060、0.0055、0.0009、0.0030、0.0002、0.0001。可以看出，本文模型在对Set5的5幅图像进行单独重建时，均表现出相对于对比模型更加优秀的客观评价指标。充分说明了本文模型对于测试集中的每一幅图像的超分辨率重建均展现出较好的重建性能。
综上所述，本文模型在4种测试集上均表现出比8种对比模型更优异的客观评价指标，其主要归功于本文模型对U型网络结构上的改进与创新，通过特征融合层图像浅层特征信息与深层特征信息进行充分融合，提升模型对于特征信息的利用率；并在模型整体外侧加入残差连接对模型进行优化调整，防止模型性能退化与梯度爆炸问题的出现，使模型可以更好地进行训练；以及本文模型在重建路径中创新并引入的的RFAB模块可以在重建过程中利用增强空间注意力机制提取到更多的图像关键特征信息。基于以上3点，本文模型在客观评价指标上呈现出相对与对比模型更加优秀的结果。
2.4.2 不同模型主观视觉效果对比
在对模型进行客观评价指标定性对比之外，本文还将通过人体主观视觉效果的角度分别在4种测试集中选取一张图像进行主观视觉效果对比。在重建效果图中，为了更好地展示出本文模型对细节特征的恢复能力，本文对重建图像的局部放大图进行对比。左侧部分为HR(high resolution)高清图像，图像中红框部分为图像局部区域放大图，右侧部分分别展示不同对比模型以及本文模型对于该图像的重建效果图。
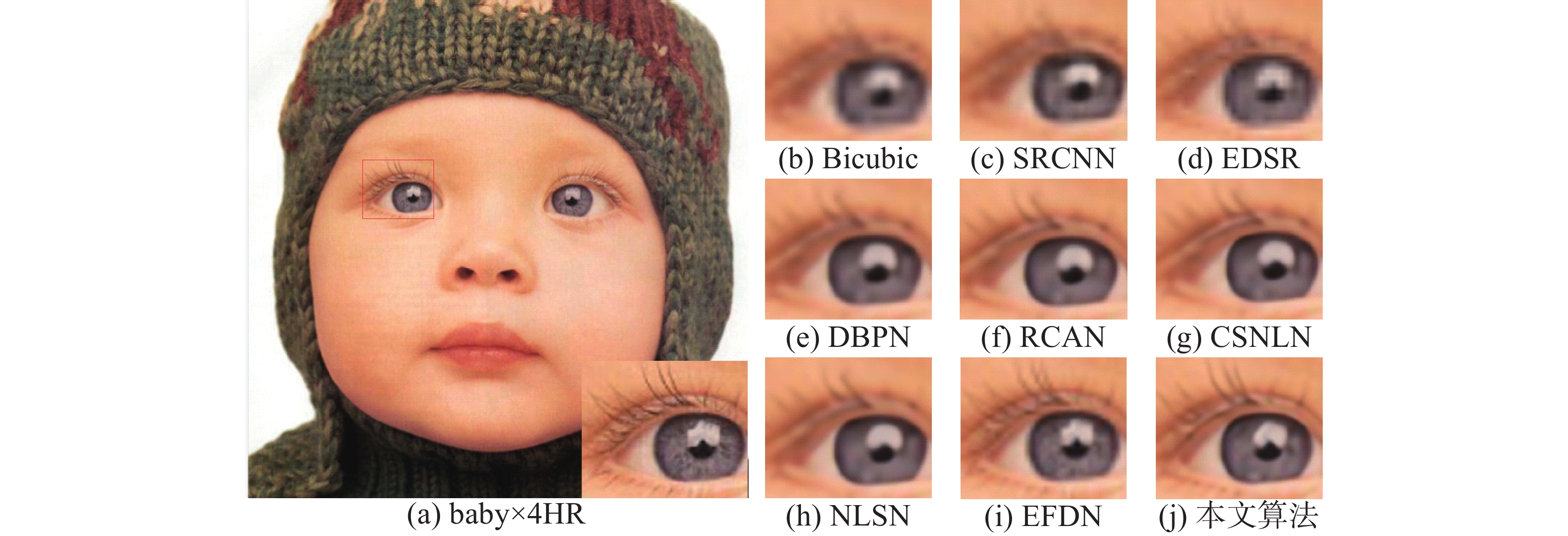
图3给出了不同模型对测试集Set5中图像baby.png在尺度为×4时的重建效果对比，方框部分为局部放大图，可以看出本文算法重建出的图像更加清晰。具体地，Bicubic、SRCNN只能重建出眼部大概的轮廓；EDSR、RCAN、CSNLN、NLSN模型通过引入不同的注意力机制，使得模型的重建图像的细节部分得到了部分恢复，但依然不够清晰；EFDN模型重建出的图像对细节特征处理得较好，但仍存在边缘模糊的现象；本文模型重建出的图像对图像细节特征掌握的更加充分，睫毛部分更加清晰，更加接近于左侧HR图像呈现出的效果。
图 3 不同算法对Set5中baby.png在尺度为×4时的重建效果对比Fig. 3 Contrast of reconstruction effects of various algorithms on baby.png in Set5(×4)下载:
全尺寸图片
图4给出了不同模型对测试集B100中的图像86000.png在尺度为×4时的重建效果对比，红框部分为局部放大图，可以看出本文算法的重建图像更加清晰。具体地，Bicubic、SRCNN以及EDSR 3种模型重建出的图像出现了伪影现象；而DBPN、RCAN、CSNLN、NLSN模型重建出的图像视觉效果比较模糊；EFDN模型重建出的图像在边缘部分仍存在少量残影，而本文模型重建出的图像在边缘信息上基本还原了外立面的像素排列方式，重建效果比较理想，更接近于左侧HR图像呈现出的效果。
图 4 不同算法对B100中86000.png在尺度为×4时重建效果对比Fig. 4 Contrast of reconstruction effects of various algorithms on 86000.png in B100(×4)下载:
全尺寸图片
图5给出了不同模型对测试集Set14中的图像ppt3.png在尺度为×8时的重建效果对比，红框部分为局部放大图，可以看出本文算法重建出的图像更加清晰。对比模型中，前6种模型在重建后的放大图左侧区域均出现了黄色边缘伪影现象；NLSN模型重建图像的数字部分“2002”比较模糊；而EFDN与本文模型重建出的图像消除了伪影部分，重建图像更加清晰，更贴近于左侧HR图像呈现出的效果。
图 5 不同算法对Set14中ppt3.png在尺度为×8时重建效果对比Fig. 5 Contrast of reconstruction effects of various algorithms on ppt3.png in Set14(×8)下载:
全尺寸图片
图6给出了不同模型对测试集Urban100中的图像img062.png在尺度为×8时的重建效果对比，红框部分为局部放大图，可以看出本文模型重建出的图像对更加清晰，8种对比模型重建图像的窗框部分细节特征恢复不够理想；而本文模型相对于对比模型，不仅恢复了图像的整体结构，而且图像的边缘信息与细节信息得到了更好的恢复，重建效果相对比较理想，更贴近于左侧HR图像呈现出的效果。
图 6 不同算法对Urban100中img062.png在尺度为×8时重建效果对比Fig. 6 Contrast of effects of various algorithms on img062.png in Urban100(×8)下载:
全尺寸图片
以上4张图片分别展示了不同模型在×4与×8两种尺度因子的重建效果，通过对比可知本文模型基于结构上的改进与创新使重建图像的细节信息更加丰富，呈现出更好的主观视觉效果。
2.5 本文模型消融实验
2.5.1 不同组合的RFAB模块对模型重建性能的影响
本文模型的重建路径由两组残差蒸馏注意力模块构成，每一组包含4个RFAB模块，为了说明本文选取的两组残差蒸馏注意力组对于模型重建性能的提升，接下来以4倍尺度下的Set14测试集为例，分别对含有不同组合方式的RFAB模块的模型进行测试，表6中G代表组数，B代表每组中的RFAB模块数量，例如G2B1代表本文模型由两组RFAB模块组成，每组中含有一个RFAB模块，实验结果如表6所示，其中下划数值为次优结果，加粗数值为最优结果。
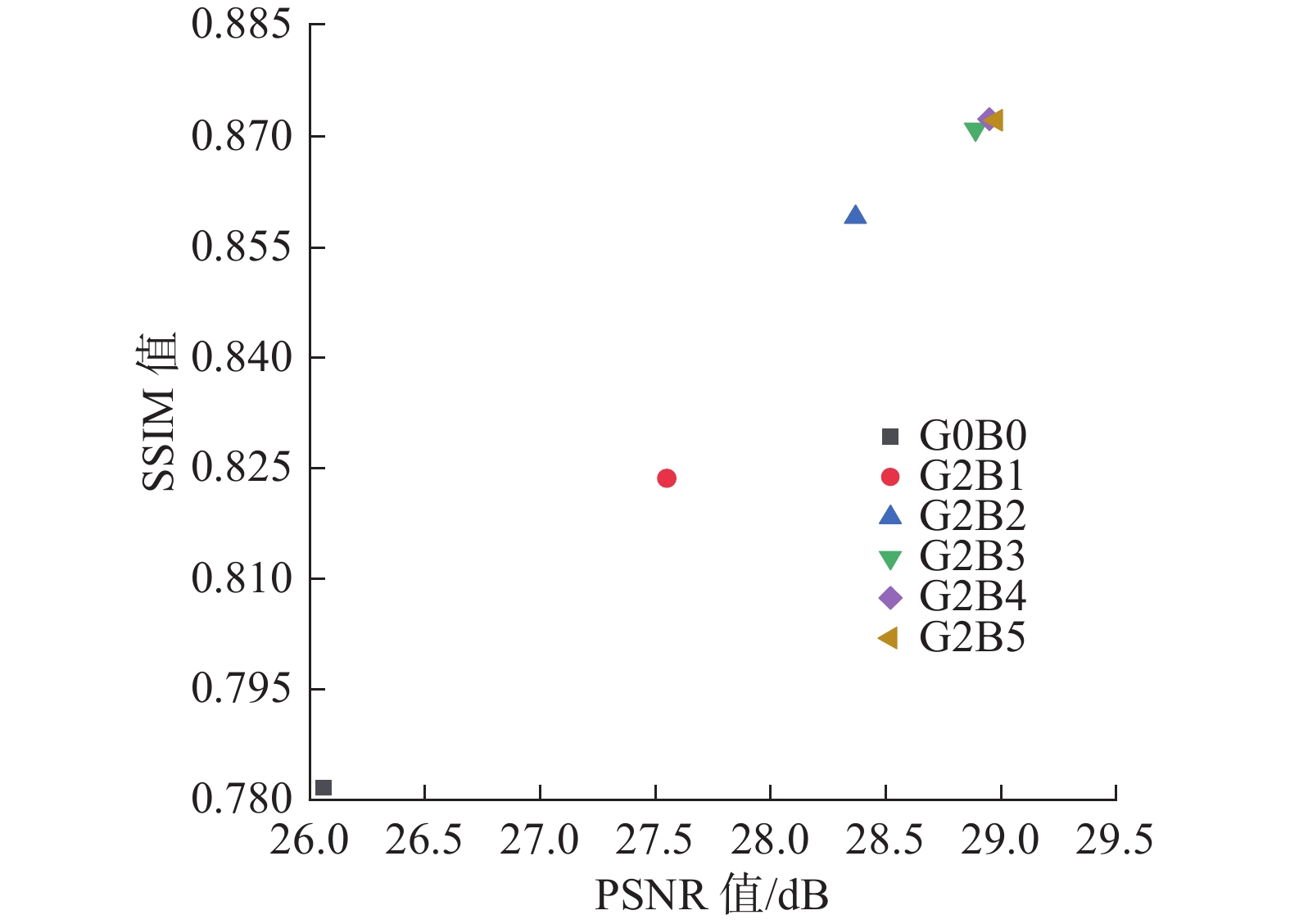
表 6 含有不同数量RFAB模块的模型的客观评价指标Table 6 Objective evaluation index of models with different number of RFAB modules参数 G0B0 G2B1 G2B2 G2B3 G2B4 G2B5 PSNR/dB 26.06 27.55 28.37 28.89 28.95 28.98 SSIM 0.7816 0.8236 0.8591 0.8710 0.8724 0.8722 从表6可以看出本文模型（G2B4组合）呈现出的PSNR值分别比G0B0、G2B1、G2B2、G2B3提升了2.89、1.40、0.58、0.06 dB；SSIM值分别提高了0.0908、0.0488、0.0133、0.0014。当RFAB模块组合方式为G2B5时，其经过测试后呈现出的PSNR值虽然比本文模型提升了0.03 dB，但结构相似度SSIM指标却降低了0.0002，为了更方便地说明由不同数量的RFAB模块组成的模型PSNR值与SSIM值之间的关系，可以通过坐标图7来进行进一步分析。
图 7 不同数量的RFAB模型客观评价指标关系Fig. 7 Relationship diagram of objective evaluation indexes of different numbers of RFAB下载:
全尺寸图片
当重建模块没有嵌入RFAB模块时，本文模型在Set14数据集上所表现出的两种客观评价指标均为最低值，当RFAB模块组合方式为G2B1、G2B2、G2B3、G2B4（本文模型）时，其测试出的 PSNR值与SSIM值均稳步递增。当RFAB模块组合方式为G2B5组时，其呈现出的PSNR值虽然比本文模型的组合方式G2B4略高一些，但其结构相似度SSIM指标反而出现了逆增长现象，说明当RFAB模块达到8个以上时，模型性能已趋于饱和，此时，如果继续堆叠RFAB模块，会大大增加网络整体的训练难度，而且模型的重建性能也不会得到有效提升，所以本文选用R2B4的组合方式嵌入到重建路径中基本可以达到本文模型的最佳性能。
2.5.2 不同组合的连接方式对模型性能的影响
本文模型由两层深层特征融合层与一层浅层残差连接组成，以Urban100测试集为例，在尺度因子为×4的基础上，本文将分别对不同组合方式进行对比实验，下表中本文模型第1层特征融合层简称为融合层A，第2层特征融合层简称融合层B，实验结果如表7所示，其中下划数值为次优结果，加粗数值为最优结果。
表 7 含有不同组合方式的模型在Urban100(×4)表现出的客观评价指标Table 7 Objective evaluation indexes of models with different combinations in Urban100(×4)组合方式 PSNR值/dB SSIM值 融合层A 26.17 0.7916 融合层B 26.25 0.7953 融合层A+残差连接 26.53 0.8092 融合层B+残差连接 26.72 0.8138 融合层A+融合层B 26.75 0.8136 融合层A+融合层B+残差连接 27.28 0.8174 从客观评级指标的角度出发，当模型只拥有特征融合层A或者特征融合层B时，其表现出的客观评价指标不够理想，因为模型获取的特征图较少；当分别在融合层A、融合层B添加残差连接之后，模型表现出的客观评价指标均有明显提升，残差连接使模型更好地进行训练，防止了一些边缘信息的丢失；当融合层A与融合层B组合时，其表现出的客观评价指标并无明显增长，这是由于在对模型进行卷积堆叠时，过多的卷积层虽然会使模型对于特征信息提取能力增强，但同时也容易出现高频细节信息丢失的问题；在此基础上加入残差连接，即本文模型的连接方式时，其模型所陈先出的PSNR值与SSIM值均得到明显提升；从主观视觉效果角度上出发，分别对4种不同组合方式的模型在Urban100测试集中进行测试，选取img088图像进行×4尺度因子的重建效果对比，如图8所示。
图 8 含有不同组合方式的模型在img088.png上在尺度为×4时的重建效果对比Fig. 8 Comparison of SR images of models with different combinations in img088.png(×4)下载:
全尺寸图片
可以看出，当模型结构的组合方式为图8(a)时，其模型对图像特征信息的获取不够充分，导致重建图像过于模糊；当模型结构的组合方式为图8(b)时，模型重建出的图像出现了伪影现象；当模型结构的组合方式为图8(c)时，重建效果相对于图8(b)方式基本没有发生变化，这是由于过多的卷积块的叠加会造成高频细节信息丢失，从而导致重建效果不佳；当模型结构的组合方式为本文模型结构图8(d)时，相比前3种方式，重建出的图像效果得到明显提升，基本消除了图像重建过程中出现的伪影现象。残差连接的存在可以更好地对模型进行训练，防止模型性能出现退化现象，所以本文模型的组合方式可以充分提高对于图像特征信息的利用率，表现出更加优秀的重建效果。
3. 结束语
本文提出一种融合分层特征与残差蒸馏连接的超分辨率重建模型，本模型首先设计了一种将分层特征融合与残差连接相结合的连接方式，将图像的深层特征与浅层特征进行充分融合，大幅度提高了模型对于图像特征信息的利用率；其次提出了一种基于增强空间注意力机制的残差蒸馏模块，通过在残差块中融入增强空间注意力机制，分别对不同空间的特征信息赋予不同的权重，加强了模型对于图像关键特征信息的获取能力，同时减少了图像细节特征信息在残差块中的损失，使重建后的图像细节信息更加完善，效果更加清晰。为了验证本文模型的有效性，本文实验部分选取了8种具有代表性的超分辨率重建算法在4种不同的测试集上进行对比实验，实验结果表明本文模型重建图像的客观评价指标与主观视觉效果均优于8种对比模型，充分说明了本算法模型的有效性。虽然本文模型表现出了非常优秀的重建性能，但是模型所带来的参数量导致模型复杂度较高的问题有待进一步分析与优化。在未来工作中，我们将分析多重递归连接与多重交叉连接对模型性能的影响，对模型探索更科学有效的连接方式，并分析不同方式对模型复杂度的影响，从而根据分析结果构建出性能更高效且模型复杂度更低的算法模型。
-
图 1 融合分层特征U型网络结构
Fig. 1 Fused hierarchical feature U-shaped network structure
下载:
全尺寸图片
图 2 残差蒸馏注意力模块
Fig. 2 Residual feature fusion attention distillation block
下载:
全尺寸图片
图 3 不同算法对Set5中baby.png在尺度为×4时的重建效果对比
Fig. 3 Contrast of reconstruction effects of various algorithms on baby.png in Set5(×4)
下载:
全尺寸图片
图 4 不同算法对B100中86000.png在尺度为×4时重建效果对比
Fig. 4 Contrast of reconstruction effects of various algorithms on 86000.png in B100(×4)
下载:
全尺寸图片
图 5 不同算法对Set14中ppt3.png在尺度为×8时重建效果对比
Fig. 5 Contrast of reconstruction effects of various algorithms on ppt3.png in Set14(×8)
下载:
全尺寸图片
图 6 不同算法对Urban100中img062.png在尺度为×8时重建效果对比
Fig. 6 Contrast of effects of various algorithms on img062.png in Urban100(×8)
下载:
全尺寸图片
图 7 不同数量的RFAB模型客观评价指标关系
Fig. 7 Relationship diagram of objective evaluation indexes of different numbers of RFAB
下载:
全尺寸图片
图 8 含有不同组合方式的模型在img088.png上在尺度为×4时的重建效果对比
Fig. 8 Comparison of SR images of models with different combinations in img088.png(×4)
下载:
全尺寸图片
表 1 各功能模块输入与输出通道数
Table 1 Input and output channels of each function module
模块名称 输入通道数 输出通道数 图像特征图提取模块 3( $F_{\text{LR} }$) 64( $ F_{0} $) 向下卷积模块CB1 64( $ F_{0} $) 128( $ F_{1} $) 向下卷积模块CB2 128( $ F_{1} $) 256( $ F_{2} $) 残差特征注意力
蒸馏模块(RFAB×4)256( $ F_{2} $) 128( ${F'_{1}}$) 第一层特征融合层 128+128+256
( $ F_{1} $+ ${F'_{1}}$+ $ F_{2} $)512
( ${F'_{11}}$+ $ F_{2} $= ${F'_{12}}$)1×1降维卷积层 512 ( ${F'_{12}}$) 128( ${F'_{12}}$) 残差特征注意力
蒸馏模块(RFAB×4)128( ${F'_{12}}$) 64( ${F'_{0}}$) 第二层特征融合层 64+64+128
( $ F_{0} $+ ${F'_{0}}$+ ${F'_{1}}$)256
( ${F'_{01} }$= ${F'_{1}}$+ ${F'_{00}}$)1×1降维卷积层 256( ${F'_{01} }$) 64( ${F'_{01}}$) 图像重建模块 64( ${F'_{01}}$) 3( $F_{\text{SR} }$) 表 2 不同算法模型在4种测试集上的PSNR指标对比
Table 2 Comparison of PSNR metrics of different algorithmic models on four test sets
dB 测试集 尺度因子 Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Set5 ×4 28.42 29.33 32.25 32.45 32.39 32.64 32.68 32.69 32.69 ×8 24.32 25.02 26.89 27.21 27.25 27.29 27.36 27.34 27.38 Set14 ×4 25.89 26.11 28.67 28.78 28.66 28.88 28.91 28.93 28.95 ×8 23.19 23.45 25.02 25.16 25.18 25.22 25.24 25.26 25.31 Urban100 ×4 23.12 24.16 26.15 26.51 26.38 26.76 27.24 27.24 27.28 ×8 20.64 21.20 22.52 22.82 22.72 22.84 22.87 22.89 22.91 B100 ×4 25.26 25.77 26.85 26.92 25.97 26.97 27.06 27.05 27.08 ×8 22.07 23.82 24.76 25.49 25.52 25.78 25.88 25.91 25.96 表 3 不同算法模型在4种测试集上的SSIM指标对比
Table 3 Comparison of SSIM metrics of different algorithmic models on four test sets
测试集 尺度因子 Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Set5 ×4 0.8102 0.8442 0.9066 0.9112 0.9091 0.9116 0.9120 0.9121 0.9121 ×8 0.6568 0.6971 0.7742 0.7872 0.7875 0.7891 0.7897 0.7902 0.7905 Set14 ×4 0.7026 0.7899 0.8669 0.8713 0.8653 0.8715 0.8720 0.8722 0.8724 ×8 0.5682 0.5981 0.6415 0.6491 0.6510 0.6517 0.6523 0.6525 0.6528 Urban100 ×4 0.6981 0.7520 0.7911 0.8087 0.7946 0.8159 0.8172 0.8170 0.8174 ×8 0.5150 0.5541 0.6180 0.6431 0.6359 0.6433 0.6437 0.6439 0.6441 B100 ×4 0.6453 0.6662 0.7095 0.7149 0.6725 0.7154 0.7158 0.7159 0.7163 ×8 0.5047 0.5514 0.6112 0.6521 0.6522 0.6712 0.6779 0.6787 0.6789 表 4 不同算法模型在Set5上的PSNR指标对比
Table 4 Comparison of PSNR metrics of different algorithmic models on Set5
dB 图像(×4) Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EDFN[33] 本文算法 Baby 31.77 32.20 33.76 33.94 33.78 33.95 33.99 34.02 34.02 Bird 30.17 31.12 35.14 35.81 35.59 35.84 35.87 35.88 35.90 Butterfly 22.09 24.04 28.78 29.29 29.00 29.31 29.36 29.38 29.41 Head 31.57 31.58 32.97 32.88 32.98 32.92 33.02 33.03 33.03 Woman 26.46 27.72 30.58 30.91 30.61 31.22 31.38 31.37 31.41 均值 28.41 29.33 32.25 32.56 32.39 32.65 32.72 32.74 32.75 表 5 不同算法模型在Set5上的SSIM指标对比
Table 5 Comparison of SSIM metrics of different algorithmic models on Set5
图像(×4) Bicubic[6] SRCNN[11] EDSR[16] RCAN[18] DBPN[22] CSNLN[31] NLSN[32] EFDN[33] 本文算法 Baby 0.9275 0.9322 0.9555 0.9562 0.9551 0.9562 0.9565 0.9567 0.9569 Bird 0.8726 0.8846 0.9452 0.9501 0.9492 0.9513 0.9517 0.9516 0.9520 Butterfly 0.7362 0.8007 0.9261 0.9335 0.9286 0.9344 0.9346 0.9348 0.9350 Head 0.7536 0.7515 0.7968 0.7974 0.7972 0.7977 0.7986 0.7988 0.7991 Woman 0.8315 0.8513 0.9139 0.9182 0.9147 0.9198 0.9205 0.9203 0.9206 均值 0.8243 0.8441 0.9075 0.9111 0.9089 0.9119 0.9124 0.9124 0.9127 表 6 含有不同数量RFAB模块的模型的客观评价指标
Table 6 Objective evaluation index of models with different number of RFAB modules
参数 G0B0 G2B1 G2B2 G2B3 G2B4 G2B5 PSNR/dB 26.06 27.55 28.37 28.89 28.95 28.98 SSIM 0.7816 0.8236 0.8591 0.8710 0.8724 0.8722 表 7 含有不同组合方式的模型在Urban100(×4)表现出的客观评价指标
Table 7 Objective evaluation indexes of models with different combinations in Urban100(×4)
组合方式 PSNR值/dB SSIM值 融合层A 26.17 0.7916 融合层B 26.25 0.7953 融合层A+残差连接 26.53 0.8092 融合层B+残差连接 26.72 0.8138 融合层A+融合层B 26.75 0.8136 融合层A+融合层B+残差连接 27.28 0.8174 -
[1] CHENG Deqiang, LI Jiahan, KOU Qiqi, et al. H-net: unsupervised domain adaptation person re-identification network based on hierarchy[J]. Image and vision computing, 2022, 124: 104493. doi: 10.1016/j.imavis.2022.104493 [2] 韩璐, 毕晓君. 多尺度特征融合网络的视网膜OCT图像分类[J]. 智能系统学报, 2022, 17(2): 360–367. HAN Lu, BI Xiaojun. Retinal optical coherence tomography image classification based on multiscale feature fusion[J]. CAAI transactions on intelligent systems, 2022, 17(2): 360–367. [3] 毕晓君, 潘梦迪. 基于生成对抗网络的机载遥感图像超分辨率重建[J]. 智能系统学报, 2020, 15(1): 74–83. doi: 10.11992/tis.202002002 BI Xiaojun, PAN Mengdi. Super-resolution reconstruction of airborne remote sensing images based on the generative adversarial networks[J]. CAAI transactions on intelligent systems, 2020, 15(1): 74–83. doi: 10.11992/tis.202002002 [4] 王宇昊, 王铸. 卫星遥感影像特定目标的超分辨率重建算法[J]. 遥感信息, 2022, 37(5): 108–115. WANG Yuhao, WANG Zhu. Super-resolution reconstruction algorithm for specific target in satellite remote sensing imagery[J]. Remote sensing information, 2022, 37(5): 108–115. [5] 程德强, 陈杰, 寇旗旗, 等. 融合层次特征和注意力机制的轻量化矿井图像超分辨率重建方法[J]. 仪器仪表学报, 2022, 43(8): 73–84. CHENG Deqiang, CHEN Jie, KOU Qiqi, et al. Lightweight super-resolution reconstruction method based on hierarchical features fusion and attention mechanism for mine image[J]. Chinese journal of scientific instrument, 2022, 43(8): 73–84. [6] TAO Hongjiu, TANG Xinjian, LIU Jian, et al. Superresolution remote sensing image processing algorithm based on wavelet transform and interpolation[J]. Image processing and pattern recognition in remote sensing, 2003, 4898: 259–263. [7] CHENG Deqiang, CHEN Liangliang, LYU Chen, et al. Light-guided and cross-fusion U-net for anti-illumination image super-resolution[J]. IEEE transactions on circuits and systems for video technology, 2022, 32(12): 8436–8449. doi: 10.1109/TCSVT.2022.3194169 [8] WANG Yetong, XING Kongduo, WANG Baji, et al. Image super-resolution reconstruction method based on residual mechanism[J]. Journal of electronic imaging, 2022, 31(3): 033010. [9] 王凡超, 丁世飞. 基于广泛激活深度残差网络的图像超分辨率重建[J]. 智能系统学报, 2022, 17(2): 440–446. WANG Fanchao, DING Shifei. Image super-resolution reconstruction based on widely activated deep residual networks[J]. CAAI transactions on intelligent systems, 2022, 17(2): 440–446. [10] YANG Shuyuan, LIU Zhizhou, WANG Min, et al. Multitask dictionary learning and sparse representation based single-image super-resolution reconstruction[J]. Neurocomputing, 2011, 74(17): 3193–3203. doi: 10.1016/j.neucom.2011.04.014 [11] DONG Chao, LOY C C, HE Kaiming, et al. Learning a deep convolutional network for image super-resolution[C]//European Conference on Computer Vision. Cham: Springer, 2014: 184−199. [12] DONG Chao, LOY C C, TANG Xiaoou. Accelerating the super-resolution convolutional neural network[EB/OL]. (2016−08−01)[2023−04−06]. https://arxiv.org/abs/1608.00367. [13] SHI Wenzhe, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1874−1883. [14] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [15] KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1646−1654. [16] LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu: IEEE, 2017: 1132−1140. [17] SEGU M, TONIONI A, TOMBARI F. Batch normalization embeddings for deep domain generalization[J]. Pattern recognition, 2023, 135: 109115. doi: 10.1016/j.patcog.2022.109115 [18] ZHANG Yulun, LI Kunpeng, LI Kai, et al. Image super-resolution using very deep residual channel attention networks[C]//European Conference on Computer Vision. Cham: Springer, 2018: 294−310. [19] ZHANG Yulun, TIAN Yapeng, KONG Yu, et al. Residual dense network for image super-resolution[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 2472−2481. [20] CHEN Liangliang, KOU Qiqi, CHENG Deqiang, et al. Content-guided deep residual network for single image super-resolution[J]. Optik, 2020, 202: 163678. doi: 10.1016/j.ijleo.2019.163678 [21] 程德强, 郭昕, 陈亮亮, 等. 多通道递归残差网络的图像超分辨率重建[J]. 中国图象图形学报, 2021, 26(3): 605–618. doi: 10.11834/jig.200108 CHENG Deqiang, GUO Xin, CHEN Liangliang, et al. Image super-resolution reconstruction from multi-channel recursive residual network[J]. Journal of image and graphics, 2021, 26(3): 605–618. doi: 10.11834/jig.200108 [22] HARIS M, SHAKHNAROVICH G, UKITA N. Deep back-projection networks for super-resolution[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 1664−1673. [23] PUROHIT K, MANDAL S, RAJAGOPALAN A N. Mixed-dense connection networks for image and video super-resolution[J]. Neurocomputing, 2020, 398: 360–376. doi: 10.1016/j.neucom.2019.02.069 [24] FARAMARZI A, AHMADYFARD A, KHOSRAVI H. Adaptive image super-resolution algorithm based on fractional Fourier transform[J]. Image analysis & stereology, 2022, 41(2): 133–144. [25] AHN H, YIM C. Convolutional neural networks using skip connections with layer groups for super-resolution image reconstruction based on deep learning[J]. Applied sciences, 2020, 10(6): 1959. doi: 10.3390/app10061959 [26] LIU Jie, TANG Jie, WU Gangshan. Residual feature distillation network for lightweight image super-resolution[M]//Computer Vision-ECCV 2020 Workshops. Cham: Springer International Publishing, 2020: 41−55. [27] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[C]//Proceedings of the British Machine Vision Conference 2012. Surrey: British Machine Vision Association, 2012. [28] ROMANO Y, PROTTER M, ELAD M. Single image interpolation via adaptive nonlocal sparsity-based modeling[J]. IEEE transactions on image processing, 2014, 23(7): 3085–3098. doi: 10.1109/TIP.2014.2325774 [29] LIU Yun, CHENG Mingming, HU Xiaowei, et al. Richer convolutional features for edge detection[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(8): 1939–1946. doi: 10.1109/TPAMI.2018.2878849 [30] HUANG Jiabin, SINGH A, AHUJA N. Single image super-resolution from transformed self-exemplars[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 5197−5206. [31] MEI Yiqun, FAN Yuchen, ZHOU Yuqian, et al. Image super-resolution with cross-scale non-local attention and exhaustive self-exemplars mining[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 5689−5698. [32] MEI Yiqun, FAN Yuchen, ZHOU Yuqian. Image super-resolution with non-local sparse attention[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 3516−3525. [33] WANG Yan. Edge-enhanced feature distillation network for efficient super-resolution[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. New Orleans: IEEE, 2022: 776−784.
