Multi-scale deep learning method for 3D point cloud registration
-
摘要: 针对近几年三维视觉领域基于深度学习点云配准算法鲁棒性差和精度较差等问题，设计了一种基于深度学习的三维点云配准方法。首先抽取具有明显几何特征的点作为兴趣点，通过区域生长算法对兴趣点进行聚合，并基于多尺度分析方法进行特征提取以及特征融合。为进一步提取特征数据中包含的深层局部信息，使用多层感知机（multilayer perceptron，MLP）网络进行二次特征提取，并加入修改过的Transformer网络补充特征。设计了匹配矩阵生成及优化算法，并通过奇异值分解（singular value decomposition，SVD）计算得到变换矩阵。通过在ModelNet40数据集上进行比较实验，证明本文的配准算法远优于传统配准算法，并在配准精度和鲁棒性方面优于近几年流行的深度配准网络DCPNet和RPMNet。本文分析结果可为提高点云配准鲁棒性以及精度提供参考。Abstract: In order to solve the problems of poor robustness and poor accuracy of the point cloud registration algorithm based on deep learning in the field of 3D vision in recent years, a 3D point cloud registration method based on deep learning is designed. Firstly, the points with obvious geometric features are extracted as points of interest, and the points of interest are aggregated by the regional growth algorithm, and feature extraction and feature fusion are carried out based on the multi-scale analysis method. In order to further extract the deep local information contained in the feature data, the multilayer perceptron(MLP) network is used for secondary feature extraction, and the modified Transformer network is added to supplement the features. The matching matrix generation and optimization algorithm is designed, and the transformation matrix is obtained by singular value decomposition(SVD) calculation. Through comparative experiments on the ModelNet40 dataset, it is proved that the registration algorithm in this paper is far superior to the traditional registration algorithm, and is better than the popular deep registration networks DCPNet and RPMNet in recent years in terms of registration accuracy and robustness. The analysis results in this paper provide a reference for improving the robustness and accuracy of point cloud registration.
-
点云配准是寻找一个点集到另一个点集空间映射变换的过程[1]，其广泛地应用于三维重建[2]、医学图像分析[3]、同时定位与地图重建[4]和景圆分割等领域。因此如何提高三维点云配准性能成为当下研究热点。目前点云配准主要有2类算法，分别是基于全局分布状态直接求解的变换估计算法和基于局部特征提取的特征匹配算法[5]。随着深度学习技术的不断发展，学界出现了很多基于深度学习技术的点云特征提取方法。来自斯坦福的开拓者提出PointNet[6]用于处理无序点云后，许多学者基于PointNet 提出了许多新的关键点提取与特征提取算法。3DMatch[7]是局部特征提取的典型算法，通过对关键点及其周围点一起进行体素化处理后，设计正负样本，然后送入Siamese 网络训练，使得相似关键点的特征相似度高，而差异较大的关键点的特征相似度低，进而完成对关键点的匹配。Elbaz等[8]提出的LORAX则是选择用球体对点云进行划分得到多个局部点云子集，再使用自动编码器提取局部点集的特征描述，使用这些特征描述完成点集匹配并根据匹配结果估计大致的变换参数，最后使用迭代最近点算法进行微调。Usip[9]是新加坡国立大学提出的一种无监督学习关键点提取与特征提取算法，该算法首先将输入点云进行随机旋转和平移变换，并使用最远点采样提取到较为分散的节点，基于这些节点使用点到节点的划分策略对点云进行划分，得到局部点集并输入到基于 PointNet 的深度网络得到关键点和关键特征，取得了很好的效果。RSKDD-Net[10]则是基于Usip 进行改进，使用膨胀节点的感受野并随机采样的策略增大关键节点的感受域，并引入注意力机制，使用带真实变换的点云对进行训练得到了更好的配准效果与更优的计算速度。3DFeat-Net [11] 通过设计算法提取关键点，并使用弱监督学习来学习局部点云匹配的特征描述符，该算法不需要手动标注匹配点集，其选用包含 GPS/INS 标记的点云并使用注意力机制 Transformer来完成关键点以及特征的提取；该方法使用 Triplet-Loss[12]作为目标函数完成网络训练，没有用到点与点之间的空间关系。
基于全局进行特征匹配最广泛应用的是 Paul 与 Neil 提出的 ICP(iterative closest point) 算法以及它的各种变体[13]。Myronenko等[14]提出的CPD（coherent point drift）与Gao等[15]提出的 FilterReg则是基于高斯混合模型使用最大化期望算法[16]优化求解最优变换，这类变换计算量非常大，难以在包含大量空间点的点云上应用。基于PointNet也有许多直接估计变换的算法，Li等[17]于 2019 年提出的 DeepMapping 基于视线遮挡原理设计了一种巧妙的双段式网络，在第一个网络 L-Net 中直接估计多幅点云中采集装置的相对位置与姿态, 点云正确配准后的点云当中通常不会出现采集装置与点之间的视线遮挡，在第2个网络 M-Net 中根据这一原理将回归问题转化为二分类问题，从而完成了无监督配准。PointNetLK则认为 PointNet本身可以看作是可理解的特征表达功能[18]，因此可以将经典视觉算法LK（Lucas &Kanade）[19]用于该问题，作者修改 LK 算法以适应 PointNet 特征提取的功能，并将 PointNet 和 LK 算法展开为单个可训练的递归深度神经网络。PCRNet[20]与 PointNetLK类似，也是通过迭代特征与配准迭代完成最终的变换估计，区别在于 PCRNet 配准阶段也使用的是纯神经网络的方法。Wang等[21]提出算法 DCP（deep closet point）将自然语言处理中的 Transformer[22]应用到了点云配准问题中，通过 Transformer 模块中的注意力机制 Attention[23]，去估计一个虚拟的目标点云, 使用损失函数进行约束，将虚拟点云向真实点云逼近，进而完成点云之间的配准。上述基于全局分布状态的深度学习配准算法在图形学生成的点云模型上取得了不错的效果，然而在点云之间存在较大差异的采集数据集上难以完成有效配准。
本文基于近年来流行的深度神经网络，设计了一种基于深度学习的三维点云配准方法，主要工作有：点云全局和局部特征提取，包括兴趣点查找、基于区域生长算法的兴趣点聚合、多尺度特征提取与融合、二次特征提取和补充；相似度匹配矩阵及优化、对应点奇异值分解、损失函数、神经网络训练以及实验结果及分析。
1. 基于区域生长算法的兴趣点聚合
为构建深度神经网络输入层的局部信息，基于分割思想，对点云数据进行聚集分类。本文设计基于区域生长算法[24]的兴趣点聚合对点云数据进行分割，作为后续多尺度特征提取与融合的准备工作。区域生长是根据事先定义的准则将像素或者子区域聚合成更大区域的过程。其基本思想是从一组生长点开始，将与该生长点性质相似的相邻像素或者区域与生长点合并，形成新的生长点，重复此过程直到不能生长为止。使用区域增长算法对三维点云进行分割，可有效划分具有鲜明区域信息的局部区域。在此基础上，以各生长点为中心，构建多尺度的特征提取，进而对全局信息进一步补充。
1.1 确定生长兴趣点
内部形态描述子(intrinsic shape signatures，ISS)[25]可表征立体几何形状，因此可用来进行兴趣点选择。设兴趣点
$ {p_i} $ 、搜索半径为$ r $ ，主要步骤如下：1） 建立兴趣点的局部坐标系。
2） 求兴趣点与邻域点的协方差矩阵。
每个点的权重为
$$ {w_j} = \frac{1}{{\left| {\{ {p_k}\text{:}{{\left\| {{p_k} - {p_j}} \right\|}_2} < r\} } \right|}} $$ 计算加权协方差公式为
$$ {{\rm{conv}}}({p_i}) = \frac{{\displaystyle\sum\limits_{{{\left\| {{p_i} - {p_j}} \right\|}_2} < r} {{w_j}({p_j} - {p_i}){{({p_j} - {p_i})}^{{\rm{T}}}}} }}{{\displaystyle\sum\limits_{{{\left\| {{p_i} - {p_j}} \right\|}_2} < r} {{w_j}} }} $$ 由标量转矩阵运算时可表示为
$$ {\displaystyle\sum\limits_{{{\left\| {{p_i} - {p_j}} \right\|}_2} < r} {{w_j}({p_j} - {p_i})({p_j} - {p_i})} ^{{\rm{T}}}} = \displaystyle\sum\limits_j {{w_j}{x_j}{x_j}^{{\rm{T}}} = {{\boldsymbol{XWX}}^{{\rm{T}}}}} $$ 3）计算每个点的特征值，由大到小
$ \{ \lambda _i^1,\lambda _i^2,\lambda _i^3\} $ ，利用协方差矩阵的特征值之间关系来形容该点的特征程度。若存在特征值相等的情况，则对应线或者平面，需要进行排除。4）对步骤3）的结果进行非极大值抑制。满足下式即为兴趣点。
$$ \frac{{\lambda _i^2}}{{\lambda _i^1}} < {\gamma _{21}},\;\;\;\;\frac{{\lambda _i^3}}{{\lambda _i^2}} < {\gamma _{32}} $$ 通过以上步骤处理全部点云数据，比较后即可得到期望的生长兴趣点。
1.2 生成聚类点集
得到兴趣点后，就可以根据区域生长算法，对三维点云数据进行聚合分类，生长准则选取经典的法线曲率判断，便于使用协方差矩阵得出结果。此方案是针对小曲率变化面设计的，尤其适合对于变化平面进行分割，适用于多种复杂零件的提取。具体算法的实现步骤如下：
1) 从兴趣点集中选择生长种子点；
2) 以该种子点为中心，近邻策略搜索附近点集；
3) 从附近点集中顺序选择一个未判断点，判断法线方向是否相近或曲率是否足够小，满足2件则该点并入聚类点集，若只满足条件 1，则将其并入该种子点集；
4) 重复步骤 3）至附近点集为空，跳回步骤1）新选择种子生长点；
5) 从某个种子点出发，循环重复步骤 1）~4）至数据集无空点，即“子种子”不再出现，则类聚集完成。
2. 多尺度特征提取与融合
局部点云的特征提取是基于特征匹配算法中的重要步骤，基于兴趣点的特征描述符将有助于找到源点云与目标点云之间的匹配关系，从而估计变换矩阵。其中特征提取的目的是为了从点云空间结构中找到所需要的结构特征。
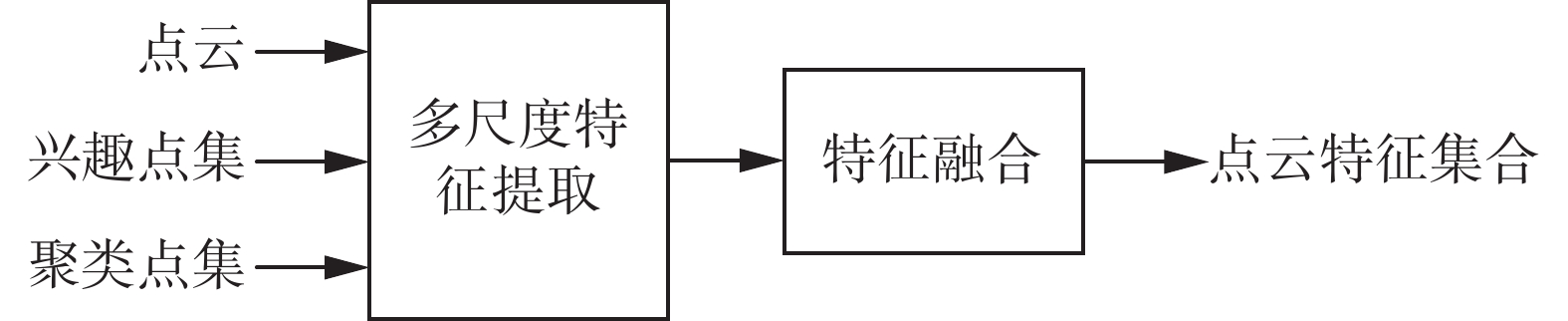
本文采用的提取思路为在确定的聚类点集内，以各生长兴趣点为中心，进行多尺度提取，然后和点云本身的空间信息融合，得到可输入后续网络的混合特征。主要流程如图1所示。
图 1 特征提取流程Fig. 1 Feature extraction process
下载:
全尺寸图片
2.1 特征提取
考虑到兴趣点的生成方法是基于曲率法线数据的筛选得到，而聚类的点集也几何性较弱，形状不稳定，且规模适中，而对于非大型点云，欧氏空间信息仍具有重要意义，为了进行信息补充，同时也方便计算，本文采用最近邻分类算法（K-nearest neighbours，KNN）对聚类点集进行多尺度查询并提取特征。KNN邻近分类算法是数据挖掘技术中经典的方法之一。所谓
$K$ 最近邻，就是$K$ 个最近的邻居的意思，表达的是每个样本都可以用它最接近的$K$ 个邻近值或其特征来代表。在确定数据集上，以数量为界，根据点数分层查询，即在不同的
$K$ 参数下多次提取局部特征信息，为了对应需求框架信息的整体策略，仍然使用协方差矩阵计算，保留每一层的最小特征值作为显著性度量指标。ModelNet40 数据集为小规模点云，根据生长聚类可视化效果的分析，层数应选取适中，定为 3 层，即在同一聚类点集中，多尺度特征为三层点云分别计算得到的最小特征值$\lambda $ ，整合得到多尺度特征${\lambda _c} = ({\lambda ^1},{\lambda ^2},{\lambda ^3})$ ，维数3。2.2 特征融合
使用特征融合法对点云原本的空间信息进行补充，得到每一个点均为空间坐标，聚类中心点和多尺度特征的基础混合特征。
$$ F = ({x_c},{x_o},{\lambda _c}) $$ 式中：
${x_c}$ 为$x$ 点的三维空间坐标$(x,y,z)$ ，${x_0}$ 为该点所在聚类空间的中心生长点，${\lambda _c}$ 为多尺度结构特征。为体现聚类点集中框架特征对于全局、局部信息的融合及补充，本文使用的结构为该点空间坐标+该点多尺度特征+与邻域点的聚类中心点的空间距离+与邻域点的空间距离，以此作为后续估计点云变换神经网络的输入数据：
$$ {H_{{{\rm{Features}}}}} = ({x_c},{\lambda _c},\Delta ({x_c},{x_{io}}),\Delta ({x_c},{x_i})) $$ 式中：
$ {x_i} $ 为邻域$ N(x) $ 中一点，$ {x_{io}} $ 为聚类中心点，$ \Delta (x,y) = {\left\| {x - y} \right\|_2} $ 为三维空间点欧氏距离。3. 二次特征提取和补充
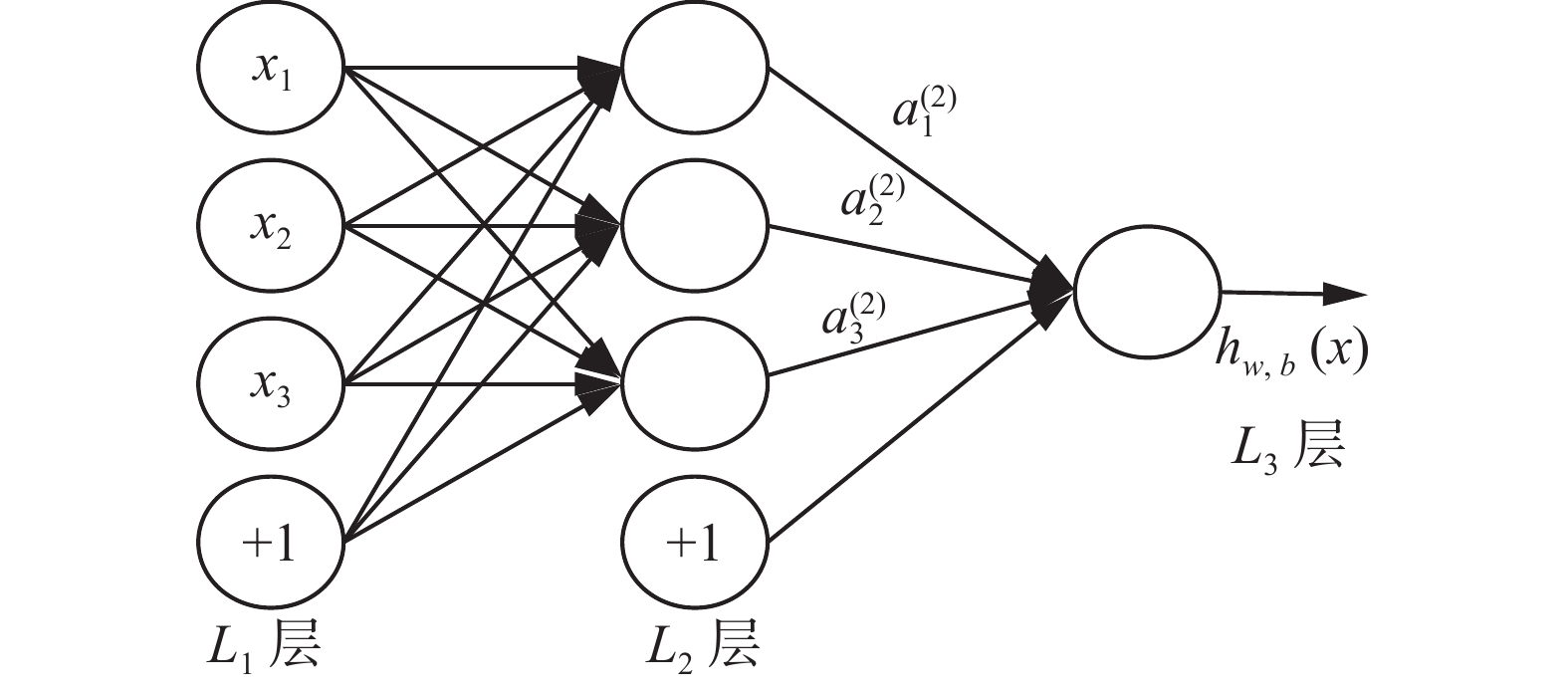
为进一步提取特征数据中包含的深层局部信息，使用 MLP 网络再次进行二次特征提取。最简单的MLP是三层结构，如图2所示。
图 2 三层感知机模型Fig. 2 Three layer perceptron model下载:
全尺寸图片
根据第2部分定义设定，对每一个点
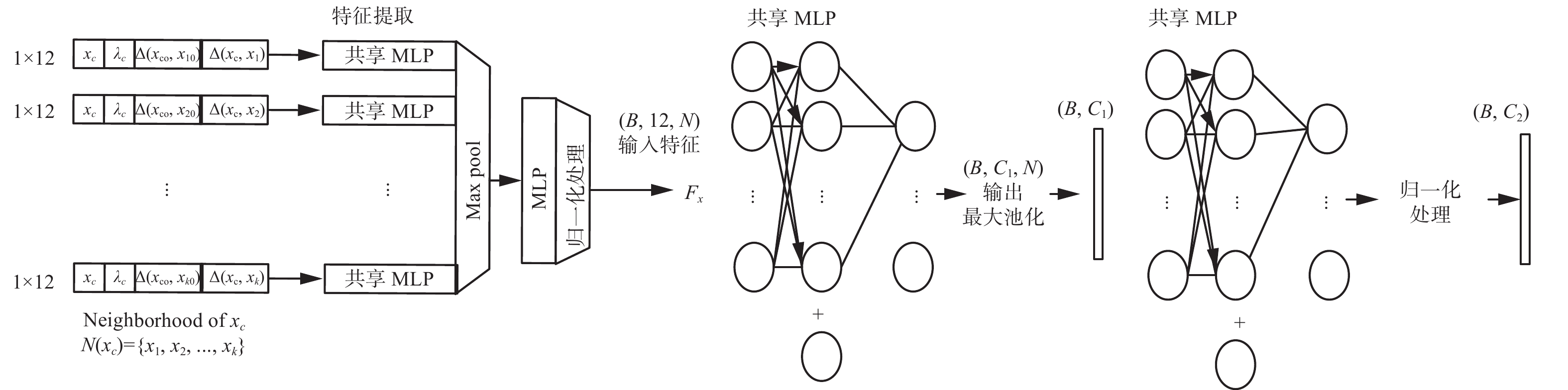
$x$ 都进一步定义邻域$N(x)$ ，其结构为该点空间坐标+该点多尺度特征+与领域点的聚类中心点的空间距离+与领域点的空间距离，以此作为特征提取模块的输入数据，其构成一个 12 维向量，batch 的数据格式为(B, 12, N)，送入到一个给定共享参数的 MLP，得到维度为(B, C1, N)的特征；而后经过Max Pooling，得到维度为(B, C1)的特征；接着再次 MLP，得到维度为(B, C2)的特征进行归一化；最终产生维度为(B, C2)的结果特征。本文MLP网络采用两层架构，输出维度为 128，使用Adam优化器以 lr =
0.0001 的学习率进行训练，并且在除最后一层之外的所有层上，都使用ReLU 激活函数和组归一化处理。邻域基础特征输入后得到二次提取的混合特征值，提取过程如图3所示。
图 3 MLP 特征提取模块结构Fig. 3 MLP feature extraction module structure下载:
全尺寸图片
在以往的学习匹配算法中，得到最终的点云特征后，一般都会进入匹配网络，生成软对应矩阵确定点对关系，但效果往往不理想，原因是源点云和目标点云的信息都是单独嵌入然后进行比较的，并不包含对方的变换信息，这一点被称为匹配信息的忽略，应加以补充，为此在网络中加入DCPNet中的Transformer 模块。其通过捕获自我注意和条件注意来学习共同信息，对点云特征进行补充。在处理点云配准问题时，可以将2个待匹配的点云，分别看作2个无序的序列，而配准目标是找到2个序列之间的位置转换关系。通过捕获自我注意和条件注意来学习共同信息，得到相互的“条件”残差变化量，以此对点云特征进行补充。
对于二次提取后得到的特征
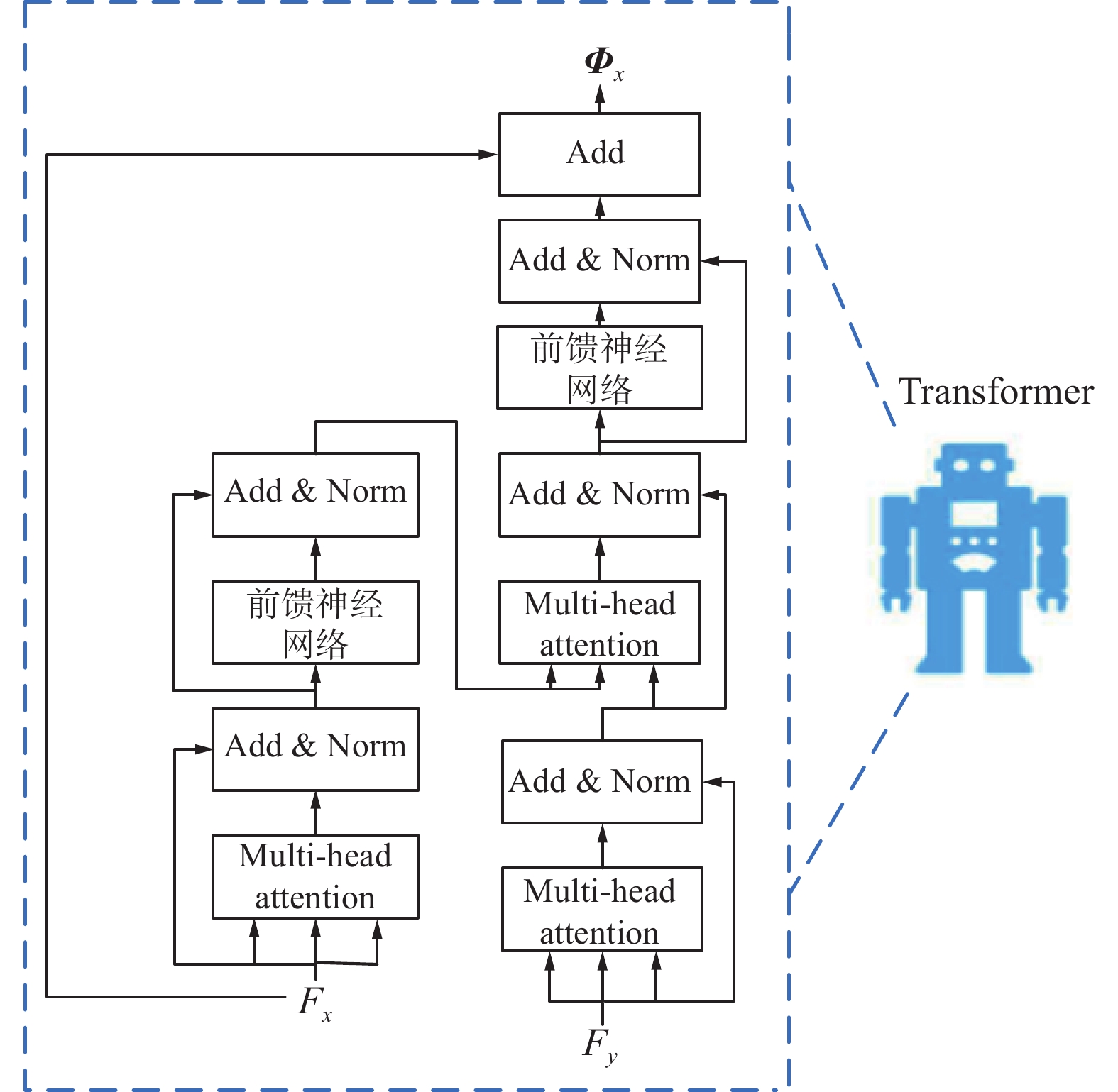
${{\boldsymbol{F}}_x}$ 、${{\boldsymbol{F}}_y}$ ，在计算过程中彼此独立，为了让二者能产生关系，彼此知道对方的存在，从而更好地计算出“如何才能调整到对方的位置”，本文使用修改过的Transformer网络，其输出为$$ \begin{gathered} {\boldsymbol{\varPhi}} _x = {\boldsymbol{F}}_x + \phi ({\boldsymbol{F}}_x,{\boldsymbol{F}}_y) \\ {\boldsymbol{\varPhi}} _y = {\boldsymbol{F}}_y + \phi ({\boldsymbol{F}}_y,{\boldsymbol{F}}_x) \\ \end{gathered} $$ (1) 式中
$ \phi $ 为Transformer 对特征学习到一个“条件”残差变化量。例如，对于$ {\boldsymbol{F}}_x $ ，$ \phi ({\boldsymbol{F}}_x,{\boldsymbol{F}}_y) $ 表示要将$x$ 调整到$y$ ，应该怎么调整$x$ 的特征。相当于以$ {\boldsymbol{F}}_y $ 作为条件，计算出$x$ 的残差变化量$ {\boldsymbol{\varPhi}} _x $ ，如图4所示。
图 4 改进后的Transformer网络Fig. 4 Revamped Transformer network下载:
全尺寸图片
Transformer 模块中的多头注意力与全连接前馈网络的结合，就是类似与传统 seq2seq 问题中编码器与解码器的存在，并在2个子层之间加入残差连接。在每一层中，multi-head attention 的数量为 4，嵌入维度为 512，每层后同样接组归一化 LayerNorm，训练中使用 Adam 优化网络参数，初始学习率为 0.001，并参考 DCPNet 的实验设置，在第 75、150 和 200 次训练后将学习率除以 10，整个网络的训练次数为500。
4. 相似度匹配矩阵和优化
经过了二次提取和信息互补后，点云数据包含了更加丰富的可匹配信息，就可以进入后续的环节，生成匹配矩阵。
为了避免得到不可微的硬分配，本文使用概率方法生成两点云“软映射”，即利用补充信息后的点云特征点乘计算相似度，得到了基于概率的点对点对应关系，生成软对应矩阵，对应概率越大的对应关系越紧密。
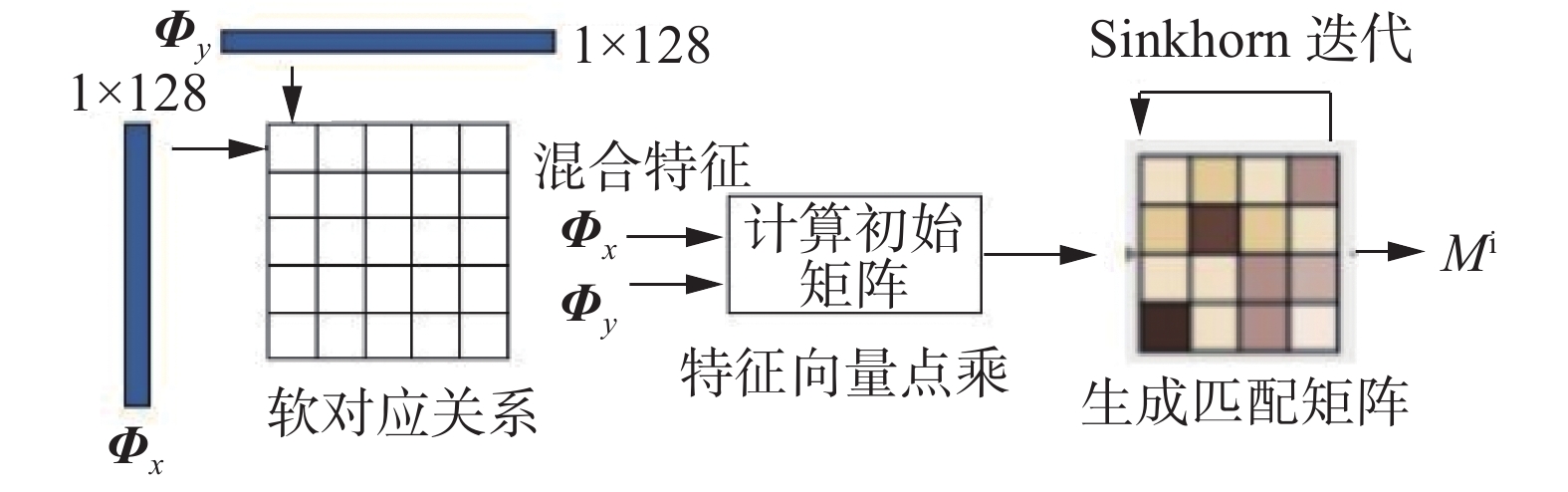
如图5所示为匹配矩阵计算模块。通过
$ {\boldsymbol{\varPhi}} _x $ 、$ {\boldsymbol{\varPhi}} _y $ 计算出soft pointer，本质上是将源点云和目标点云进行点积运算，得到相似度，softmax将相似度转化为概率，即$ {x_i} $ 与点云$y$ 中每个点的带权重关系的map。
图 5 匹配矩阵计算模块Fig. 5 Matching matrix calculation module下载:
全尺寸图片
$$ m({x_i},y) = {\rm{soft}}\; \max ({\boldsymbol{\varPhi}} _y {\boldsymbol{\varPhi}} _{{x_i}}^{\text{T}}) $$ (2) 式中：
$ {\boldsymbol{\varPhi}} _y \in {{\bf{R}}^{N \times P}} $ 表示点云经过 Attention 模块处理后$N$ 个点的特征；$ {\boldsymbol{\varPhi}} _{x_i} \in {{\bf{R}}^{1 \times P}} $ 表示点云$x$ 经过Attention 模块处理后点$ {x_i} $ 的特征；${\boldsymbol{\varPhi}} _y{\boldsymbol{\varPhi}} _{{x_i}}^{\rm{T}} \in {{\bf{R}}^{N \times 1}}$ 表示用点$ {x_i} $ 的特征，分别与$ {\boldsymbol{\varPhi}} _y $ 中每个点的特征做点积运算，得到$ {x_i} $ 与点云$ y $ 中每个点的相似度。得到点与点的对应关系后，下一步就是计算出到底该如何调整
$x$ ，使其尽量对齐$y$ 。在匹配矩阵中，寻找2个点之间的对应关系，其本质上是一种最优传输问题，而使用Sinkhorn迭代则可以使整个对应关系的损失最小，即达到熵正则化的条件。正则化鼓励利用多数小流量路径的传输，而惩罚稀疏的，利用少数大流量路径的传输，由此达到减少计算复杂度的目的。换句话说，就是在迭代中寻找最优的分配关系，以达到最优传输，对于点云匹配来说，就是两点云间最佳的对应关系。假设有源点云
$x$ 与目标点云$y$ ，定义一个匹配矩阵${\boldsymbol{M}}$ 来表示点对应的赋值，其中每个元素为$$ {{\boldsymbol{m}}}_{jk}=\left\{\begin{array}{l}1,\quad \text{ 点}{{x}}_{{j}}\text{对应}{{y}}_{{k}}\\ 0,\quad \text{ }其他\end{array} \right.$$ (3) 此假设为理想情况，一般都是由软分配得到。对于方阵
${\boldsymbol{M}}$ ，配准问题可以描述为找到刚性变换{R，t}和对应矩阵${\boldsymbol{M}}$ ，它能够将$x$ 中的点最好地映射到$y$ 上。$$ \begin{gathered} \mathop {\arg \min }\limits_{{\boldsymbol{M,R,t}}} = \displaystyle\sum\limits_{j = 1}^J {\displaystyle\sum\limits_{k = 1}^K {{m_{jk}}\left({{\left\| {{\boldsymbol{R}}{{\boldsymbol{x}}_j} + {\boldsymbol{t}} - {{\boldsymbol{y}}_k}} \right\|}_2}^2 - \alpha \right)} } \\ {\rm{s}} . {\rm{t}} . \displaystyle\sum\limits_{k = 1}^K {{m_{jk}}} = 1,\forall j;\displaystyle\sum\limits_{k = 1}^J {{m_{jk}}} = 1,\forall k \\ {m_{jk}} \in \left\{ {0,1} \right\},\forall jk \end{gathered} $$ 这3个约束条件要求
$M$ 是一个置换矩阵。$ \alpha $ 是一个参数，用于控制匹配的参考量，和前文实验中内点率测试的原理相同，转换后误差符合的便视为内点。由于提取混合特征具有很强的匹配信息，所以以相似度矩阵作为分配初始值，通过 Sinkhorn 迭代来获取一个双随机限制的矩阵，在运算上就是交替进行行归一化和列归一化，3~5 次后便得到最终的匹配矩阵，为保证效果，本实验固定为 5 次。该算法在以往工作中已经模块化，加入网络中就可以应用，使用一系列矩阵乘法即可求解。
5. 对应点SVD及损失函数
在通过不断优化初始矩阵得到最终的对应关系矩阵后，依据概率得到平均对应点。最后输入经典的 SVD 模块中，计算得到旋转平移矩阵参数 R、t。
5.1 SVD主要步骤
假设源点云和目标点云为
$ \{ {p_i}\} $ 、$ \{ {p_i}'\} $ ，则2点云对应关系为$$ {p_i} = {\boldsymbol{R}}{p_i}' + {\boldsymbol{T}} + {{\boldsymbol{N}}_i} $$ 式中：R 为旋转矩阵，T 为位移向量，
$ {{\boldsymbol{N}}_i} $ 为噪声向量。求解步骤可简述为分别求2个点云的质心，然后求各点相对于质心的位移向量，利用质心位移向量得到的矩阵进行SVD分解，并基于分解结果求得旋转与位移矩阵。5.2 损失函数
经过一系列的模块运算，得到了点云的估计变换结果{R，t}，为评价配准结果，使用以下损失函数来衡量模型与真实刚性运动的一致性：
$$ L = {\left\| {{\boldsymbol{R}}_{xy}^{\text{T}}{\boldsymbol{R}}_{xy}^g - {\boldsymbol{I}}} \right\|^2} + {\left\| {{{\boldsymbol{t}}_{xy}} - {\boldsymbol{t}}_{xy}^g} \right\|^2} + \lambda {\left\| \theta \right\|^2} $$ 式中：角标 g为真实情况，
${{\boldsymbol{R}}_{xy}}$ 和${{\boldsymbol{t}}_{xy}}$ 为网络输出的旋转和平移参数，${\boldsymbol{R}}_{xy}^g$ 和${\boldsymbol{t}}_{xy}^g$ 为实际旋转和平移参数。前2项定义了刚性变换上的简单距离，第3项系数$\theta $ 表示正则化补偿，限制缩小解的范围，用于降低网络复杂性。6. 神经网络训练
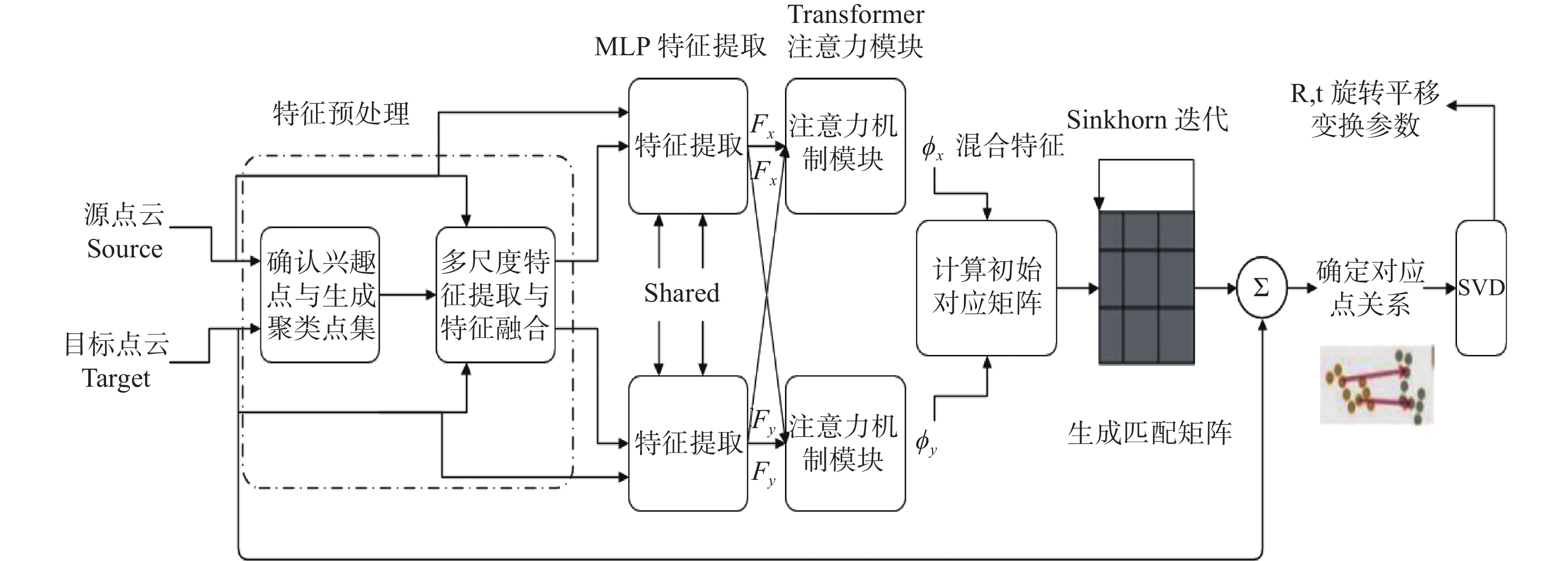
整个网络被视为一个可循环的整体，可以实现端对端的直接输出，如图6所示为本文点云配准总体结构，其中需要训练的主要部分为两分支共享参数的 MLP 模块以及跟在后面的 Transformer 注意力机制模块。
图 6 点云配准总体结构Fig. 6 Overall structure of point cloud registration下载:
全尺寸图片
在此网络基础上，结合梯度下降和反向传播算法对该网络进行训练，其中梯度下降算法指引网络向最优解的方向移动，其方向指出了所求目标函数，在给定点变化最快的方向，通常的数学定义公式为
$$ \varTheta ' = {\varTheta ^0} - \alpha \nabla J(\varTheta ) $$ 式中：
$ J $ 为关于$ \varTheta $ 的函数，$ \alpha $ 为步长，$ \varTheta $ 为网络中需要训练的神经元权重以及偏置大小。因为梯度向量表示的是损失函数增长最快的方向，所以减法运算代表目标指向下降最快的方向，即当损失函数大时，表示网络效果差，需要向相反方向快速移动。在本实验中，在训练集中的源点云与目标点云进行特征预处理得到邻域基础特征后，将其作为训练集输入，根据网络结构向前传播，其中初始网络权重采用随机生成，然后得到网络中其余所有参数的值，如混合特征和匹配矩阵等，并通过点对应关系输出预测的变换参数值。然后根据目标函数计算预测变换值与实际目标值之间的误差，用匹配矩阵计算的线型函数反推到网络中Transformer训练模块的输出层，再由梯度下降法，更新该层与上一层之间的权重与偏置值以减少误差，并再推导出上一层的真实值，不断前推至 MLP 模块，更新网络权重参数后，进行下一次训练，不断重复前向计算，反向回传的过程，以达到减小目标函数误差、训练神经网络的目的。
需要注意的是，在网络训练中，尽管梯度的运算可以从一次迭代流向另一次迭代，但在实践中，这并不会提高性能，而且可能导致训练不稳定。所以采用在每次迭代开始时，停止{R, t}梯度的简单解决方案，这意味着每次迭代都是独立的，在训练期间可以多次执行，稳定的同时也允许更频繁查看网络中较小错位的数据，从而学习如何在后续迭代中改进配准，所以本文在训练中的循环次数设定为 2，测试中则为 5 或者更多，以此来实现更精确的配准。
7. 实验结果及分析
7.1 实验环境
本文实验在Ubuntu18.04系统上进行操作，基于Python3.7版本和PyTorch神经网络框架。使用ModelNet40数据集评估算法效果，ModelNet40数据集是普林斯顿大学公开的用于计算机视觉、计算机图形学、机器人学和认知科学领域研究的三维CAD模型集合。
7.2 点云兴趣点提取与聚合实验结果
本实验在经过预处理的ModelNet40数据集上进行实验，评估关键点（兴趣点）提取的方法以及聚类点集的划分。同时对当前流行的经典算法进行对比试验，对比算法效果是否有效。实验中的固定设置如表1所示。
表 1 实验参数Table 1 Experimental parameters参数 数值 临近点数量 60 输入点云大小 1024 旋转角度/(°) [0,60] 位移大小/cm [0,20] 本文采用常用的评价指标计算效率来进行性能测试，计算效率指标是评价算法可行性的关键指标，它可以很好地评价一个关键点提取算法的实用性，算法计算关键点时间越短，算法落地的可能性就更大。
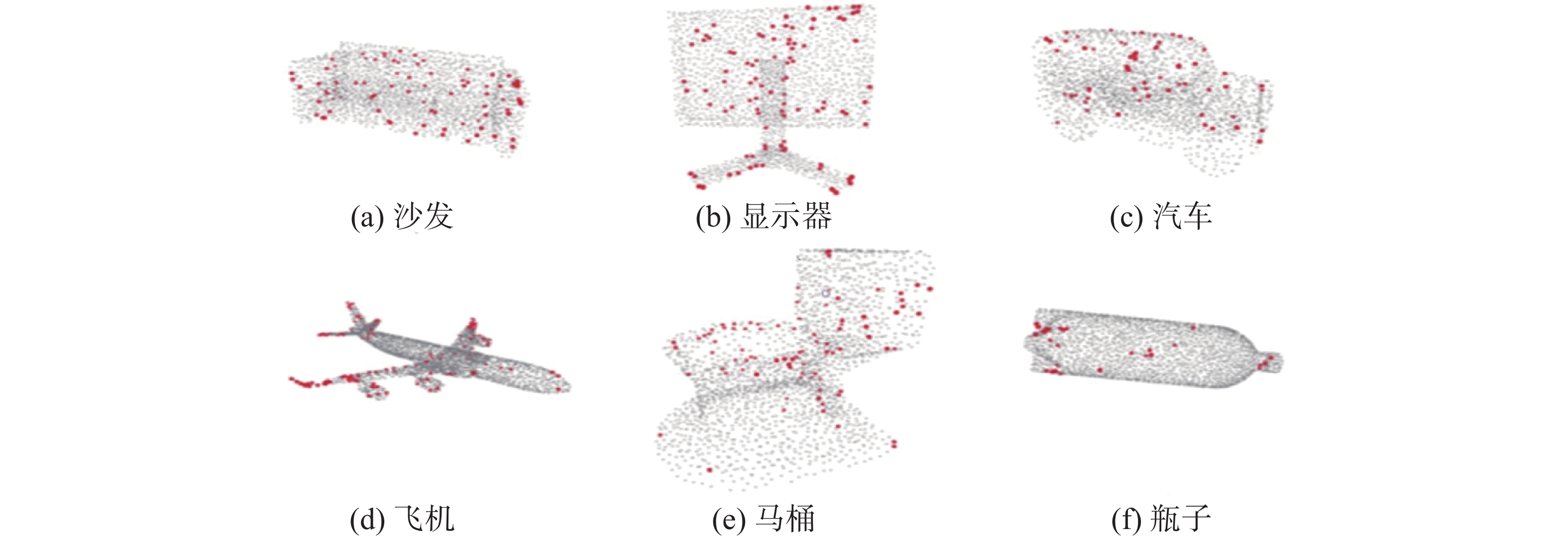
图7是本文关键点提取算法在数据集部分点云帧中提取的关键点分布，可以看到主要分布在点云中空间信息丰富的位置，符合参考分割算法中期望的整体框架特征，能有效代表主要局部空间。
图 7 ModelNet40 数据集中的关键点提取Fig. 7 Key point extraction in ModelNet40 data set下载:
全尺寸图片
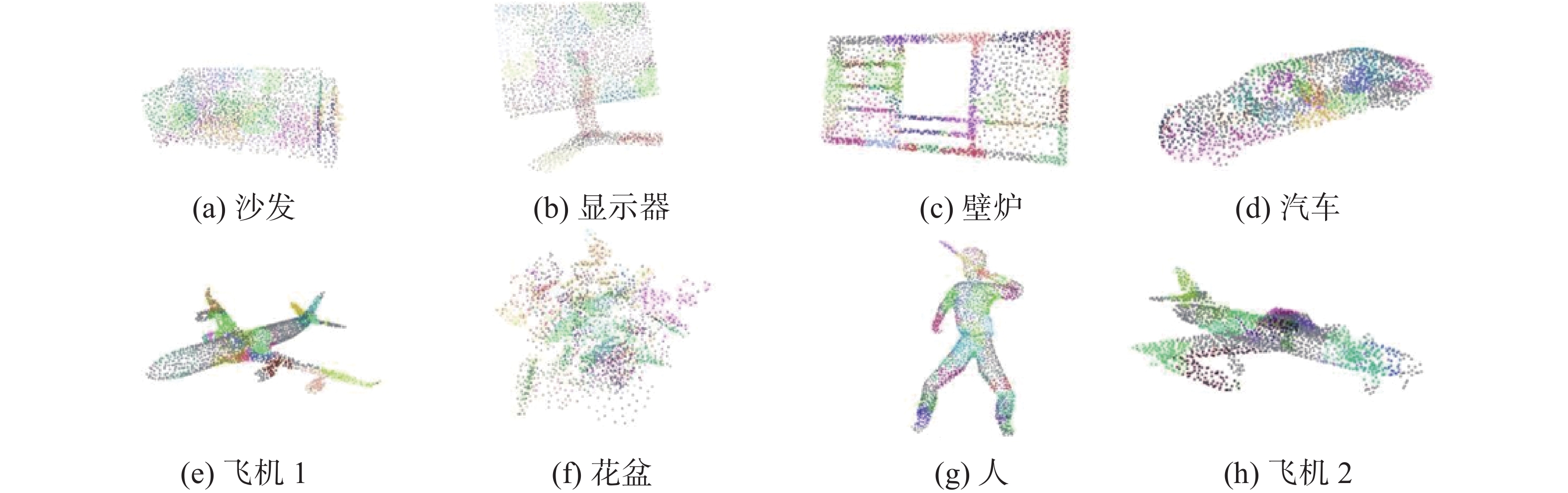
为了更好地评价算法性能，对经典算法 SIFT-3D、USIP、RSKDD-Net 进行实验，其中 SIFT-3D 是传统算法，USIP 是无监督算法，RSKDD-Net 是有监督算法。本文分别统计提取 64、128 个关键点时算法的时间消耗，并与 SIFT-3D、USIP 和 RSKDD-Net 进行比较。结果如表2所示，可以看到基于深度学习的关键点提取算法效率要大大领先传统算法，本文关键点提取时间受限于ISS思想略慢于传统深度学习方法，但整体表现良好。最后使用本文方案，根据生长聚类算法得到聚类点集的划分结果，如图8所示可看出该方案有效，可以在其基础上进行后续工作。
表 2 不同关键点提取模型的耗时Table 2 Time spent on model extraction for different key pointsms 关键点检测算法 64个关键点 128个关键点 本文算法 8.3 10.6 USIP 7.8 11.2 SIFT-3D 17.7 25.3 RSKDD-Net 4.2 5.6 
图 8 区域生长的聚类点集Fig. 8 Cluster point set of regional growth下载:
全尺寸图片
7.3 点云配准实验结果
本文在 ModelNet40 数据集上进行实验，遵循之前的实验设置，从每个模型的外表面均匀采样
1024 个点，重新缩放居中以适应单位球体，并且原数据中没有出现除$(x,y,{\textit{z}})$ 坐标以外的特征，其中部分配准结果如图9所示。
图 9 ModelNet40数据集的配准结果Fig. 9 Registration results for the ModelNet40 dataset下载:
全尺寸图片
为了更好地评估实验效果，将本文模型与 ICP、快速全局匹配 (fast global registration，FGR)、PointNetLK、DCPNet 和 RPMNet 深度学习方法进行比较。对于 ICP 和 FGR，使用Open3D 中的代码实现，其余则使用原作者的代码。在所有实验中，并没有假设给出好的初始姿态，测试点云的生成方式与训练点云相同， ICP使用恒等变换矩阵进行初始化。
使用均方误差 (mean square error，MSE)、均方根误差 (root mean squared error，RMSE) 和平均绝对误差 (mean absolute error，MAE)来测量真实值和预测值之间的误差，如MSE(R)为旋转矩阵的均方误差，而MSE(t)为平移矩阵均分误差。理想情况下，如果刚性对齐是完美的，所有这些误差指标都应该为零。
$$ {L_{{\text{MSE}}}} = \frac{1}{m}\displaystyle\sum\limits_{i = 1}^m {{{({y_i} - {{\hat y}_i})}^2}} $$ $$ {L_{{{\rm{RMSE}}}}} = \sqrt {\frac{1}{m}\displaystyle\sum\limits_{i = 1}^m {{{({y_i} - {{\hat y}_i})}^2}} } $$ $$ {L_{{{\rm{MAE}}}}} = \frac{1}{m}\displaystyle\sum\limits_{i = 1}^m {\left| {{y_i} - {{\hat y}_i}} \right|} $$ 式中：
$ {y_i} $ 为真实值，$ {\hat y_i} $ 为拟合值。表3中评估了本文算法与其他算法的使用效果，可以看出所有指标都优于传统方法，与近几年流行的DCPNet和RPMNet深度网络相比具有一定的提升。为验证算法鲁棒性，本文还尝试向输入点云添加噪声。对独立的高斯噪声进行采样，限制为 [−0.05, 0.05]，并在测试期间将其添加到数据中。本实验中，使用的模型在无噪声数据集上进行训练，表4给出了该实验的结果。ICP 通常会收敛到远处的固定点，而 FGR 对噪声很敏感。其余学习方法对噪声均保持鲁棒性。
表 3 不同算法的配准性能Table 3 Registration performance of different algorithms配准算法 MSE(R) RMSE(R) MAE(R) MSE(t) RMSE(t) MAE(t) ICP 498.560 29.920 28.170 0.084 0.290 0.275 FGR 87.660 9.367 1.989 0.003 0.015 0.007 PointNetLK 227.870 15.090 4.255 0.004 0.022 0.005 DCPNet 6.481 2.545 1.506 0.001 0.001 0.001 RPMNet 4.753 2.505 1.963 0.001 0.002 0.001 本文算法 4.501 1.493 1.144 0.000 0.001 0.001 表 4 高斯噪声下不同算法的配准性能Table 4 Registration performance of different algorithms under Gaussian noise配准算法 MSE(R) RMSE(R) MAE(R) MSE(t) RMSE(t) MAE(t) ICP 558.590 29.700 23.170 0.084 0.279 0.240 FGR 481.760 29.360 10.890 0.001 0.107 0.027 PointNetLK 256.170 16.890 4.590 0.005 0.021 0.006 DCPNet 6.982 2.631 1.515 0.000 0.002 0.002 RPMNet 5.701 2.004 1.667 0.001 0.002 0.002 本文算法 4.902 1.999 2.089 0.000 0.001 0.001 在效率上，相同实验环境下进行推理时间分析；计算时间以秒为单位，通过平均 100个结果计算得出。如表5所示，传统方法都普遍较慢，本文在学习方法中的表现不错。
表 5 不同算法下的配准效率Table 5 Registration efficiency under different algorithmss 点数 ICP FGR PointNetLK DCPNet RPMNet 本文算法 64 0.0041 0.0426 0.04889 0.0021 0.0038 0.0027 128 0.0059 0.0824 0.05001 0.0023 0.0042 0.0031 总体来说，本文提出的基于神经网络的三维物体点云配准在 ModelNet40 数据集上应用有效，能够稳定高效地完成点云配准任务。
8. 结束语
1)本文基于近年来流行的神经网络方法，开展了一种基于深度学习的三维点配准研究。以基于局部特征提取的特征匹配算法为基础，设计了基于区域生长算法兴趣点提取和聚合，使用多尺度分析方法来强化特征描述提取，引入深度神经网络捕获更加丰富的结构信息并寻找点对关系，完成了点云配准工作。
2)设计兴趣点提取与聚合实验、点云配准实验，兴趣点提取实验与传统的SIFT-3D和流行的深度学习提取网络USIP以及RSKDD-Net作对比，验证了本文特征提取的有效性，并以此得到聚类点集。
3)点云配准实验中本文方法在配准性能和速度方面远优于传统方法ICP和FGR，并略优于近几年流行的深度网络DCPNet和RPMNet，验证了在加入噪声时本文配准方案的鲁棒性。
-
图 1 特征提取流程
Fig. 1 Feature extraction process
下载:
全尺寸图片
图 2 三层感知机模型
Fig. 2 Three layer perceptron model
下载:
全尺寸图片
图 3 MLP 特征提取模块结构
Fig. 3 MLP feature extraction module structure
下载:
全尺寸图片
图 4 改进后的Transformer网络
Fig. 4 Revamped Transformer network
下载:
全尺寸图片
图 5 匹配矩阵计算模块
Fig. 5 Matching matrix calculation module
下载:
全尺寸图片
图 6 点云配准总体结构
Fig. 6 Overall structure of point cloud registration
下载:
全尺寸图片
图 7 ModelNet40 数据集中的关键点提取
Fig. 7 Key point extraction in ModelNet40 data set
下载:
全尺寸图片
图 8 区域生长的聚类点集
Fig. 8 Cluster point set of regional growth
下载:
全尺寸图片
图 9 ModelNet40数据集的配准结果
Fig. 9 Registration results for the ModelNet40 dataset
下载:
全尺寸图片
表 1 实验参数
Table 1 Experimental parameters
参数 数值 临近点数量 60 输入点云大小 1024 旋转角度/(°) [0,60] 位移大小/cm [0,20] 表 2 不同关键点提取模型的耗时
Table 2 Time spent on model extraction for different key points
ms 关键点检测算法 64个关键点 128个关键点 本文算法 8.3 10.6 USIP 7.8 11.2 SIFT-3D 17.7 25.3 RSKDD-Net 4.2 5.6 表 3 不同算法的配准性能
Table 3 Registration performance of different algorithms
配准算法 MSE(R) RMSE(R) MAE(R) MSE(t) RMSE(t) MAE(t) ICP 498.560 29.920 28.170 0.084 0.290 0.275 FGR 87.660 9.367 1.989 0.003 0.015 0.007 PointNetLK 227.870 15.090 4.255 0.004 0.022 0.005 DCPNet 6.481 2.545 1.506 0.001 0.001 0.001 RPMNet 4.753 2.505 1.963 0.001 0.002 0.001 本文算法 4.501 1.493 1.144 0.000 0.001 0.001 表 4 高斯噪声下不同算法的配准性能
Table 4 Registration performance of different algorithms under Gaussian noise
配准算法 MSE(R) RMSE(R) MAE(R) MSE(t) RMSE(t) MAE(t) ICP 558.590 29.700 23.170 0.084 0.279 0.240 FGR 481.760 29.360 10.890 0.001 0.107 0.027 PointNetLK 256.170 16.890 4.590 0.005 0.021 0.006 DCPNet 6.982 2.631 1.515 0.000 0.002 0.002 RPMNet 5.701 2.004 1.667 0.001 0.002 0.002 本文算法 4.902 1.999 2.089 0.000 0.001 0.001 表 5 不同算法下的配准效率
Table 5 Registration efficiency under different algorithms
s 点数 ICP FGR PointNetLK DCPNet RPMNet 本文算法 64 0.0041 0.0426 0.04889 0.0021 0.0038 0.0027 128 0.0059 0.0824 0.05001 0.0023 0.0042 0.0031 -
[1] REN Tianyu, WU Ruicheng. An acceleration algorithmof 3D point cloud registration based on iterative closet point[C]//2020 Asia-Pacific Conference on Image Processing, Electronics and Computers. Dalian: IEEE, 2020: 271−276. [2] FENG Shanshan, LIN Yun, WANG Yanping, et al. 3D point cloud reconstruction using inversely mapping and voting from single pass CSAR images[J]. Remote sensing, 2021, 13(17): 3534. doi: 10.3390/rs13173534 [3] 李姗姗, 张娜娜, 张媛媛, 等. 基于MSD-Vnet的三维医学图像配准[J]. 电视技术, 2021, 45(1): 51–56. LI Shanshan, ZHANG Nana, ZHANG Yuanyuan, et al. Three-dimensional medical image registration based on MSD-Vnet[J]. Television technology, 2021, 45(1): 51–56. [4] 鹿道玺. 基于多源信息融合的SLAM算法研究[J]. 无线互联科技, 2022, 19(24): 141–144. doi: 10.3969/j.issn.1672-6944.2022.24.043 LU Daoxi. Research on SLAM algorithm based on multi-source information fusion[J]. Wireless internet technology, 2022, 19(24): 141–144. doi: 10.3969/j.issn.1672-6944.2022.24.043 [5] SAYED H, AHMED E, AHMED S, et al. A computer-aided diagnostic system for diabetic retinopathy based on local and global extracted features[J]. Applied sciences, 2022, 12(16): 8326–8326. doi: 10.3390/app12168326 [6] QI C R, SU Hao, MO Kaichun, et al. Pointnet: deep learning on point sets for 3d classification and segmentation[C]//Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 52−660. [7] ZENG Andy, SONG Shuran, NIEBNER M, et al. 3DMatch: learning local geometric descriptors from RGB-dreconstructions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 1802−1811. [8] ELBAZ G, AVRAHAM T, FISCHER A. 3D point cloud registration for localization using a deep neuralnetwork auto-encoder[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. Honolulu: IEEE, 2017: 4631−4640. [9] LI J, LEE G H. Usip: unsupervised stable interest point detection from 3d point clouds[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 361−370. [10] LU Fan, CHEN Guang, LIU Yinlong, et al. Rskdd-net: random sample-based keypoint detector and descriptor[EB/OL]. (2020−10−23)[2023−04−01]. https://doi.org/10.48550/arXiv.2010.12394. [11] YEW Z J, LEE G H. 3D featnet: weakly supervised local 3d features for point cloud registration[C]//Proceedings of the European Conference on Computer Vision. Berlin: Springer, 2018: 607−623. [12] SCHROFF F, KALENICHENKO D, PHILBIN J. Facenet: a unified embedding for face recognition and clustering[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 815−823. [13] ELIZEU M O J, DANIEL R S, GIOVANA A R M. A new variant of the ICP algorithm for pairwise 3D point cloud registration[J]. American academic scientific research journal for engineering, technology, and sciences, 2022, 85(1): 71–88. [14] MYRONENKO A, SONG X. Point set registration: coherent point drift[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(12): 2262–2275. doi: 10.1109/TPAMI.2010.46 [15] GAO W, TEDRAKE R. Filterreg: robust and efficient probabilistic point-set registration using gaussian filter and twist parameterization[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 11095−11104. [16] JIANG Huijun, LI Quefeng, LIN J T, et al. Classification of disease recurrence using transition likelihoods with expectation-maximization algorithm[J]. Statistics in medicine, 2022, 41(23): 4697–4715. doi: 10.1002/sim.9534 [17] LI Ding, CHEN Feng. Deep mapping: unsupervised map estimation from multiple point clouds[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 8650−8659. [18] AOKI Y, GOFORTH H, SRIVATSAN R A, et al. Pointnetlk: robust & efficient point cloud registrationusing pointnet[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 7163−7172. [19] 林桂潮, 张青, 邹湘军. 基于改进Lucas-Kanade的亚像素级零件图像配准[J]. 计算机应用研究, 2017, 34(5): 1577–1580, 1593. doi: 10.3969/j.issn.1001-3695.2017.05.067 LIN Guichao, ZHANG Qing, ZOU Xiangjun. Subpixel level parts image registration based on improved lucas-kanade[J]. Application research of computers, 2017, 34(5): 1577–1580, 1593. doi: 10.3969/j.issn.1001-3695.2017.05.067 [20] SARODE V, LI X, GOFORTH H, et al. PCRNet: point cloud registration network using pointNet encoding[EB/OL]. (2019−08−21)[2023−04−01]. https://doi.org/10.48550/arXiv.1908.07906. [21] WANG Y, SOLOMON J M. Deep closest point: learning representations for point cloud registration[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 3523−3532. [22] GU Fengwei, LU Jun, CAI Chengtao. RPformer: a robust parallel transformer for visual tracking in complex scenes[J]. IEEE transactions on instrumentation and measurement, 2022, 71: 1–14. [23] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[EB/OL]. (2017−06−12)[2023−04−01]. https://doi.org/10.48550/arXiv.1706.03762. [24] 何翠萍. 应用区域生长的无人船红外图像精确分割方法[J]. 信息与电脑(理论版), 2022, 34(24): 81–83. HE Cuiping. Accurate segmentation method of infrared image of unmanned ship growing in application area[J]. Information and computer(theoretical edition), 2022, 34(24): 81–83. [25] YU Zhong, Intrinsic shape signatures: a shape descriptor for 3D object recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Kyoto: IEEE, 2009: 689−696.
