Gait recognition with united local multiscale and global context features
-
摘要: 现有步态识别方法在空间上能提取丰富的步态信息，但是在时间上通常忽略局部区域内的细粒度时间特征和不同子区域间的时间上下文信息。考虑到步态识别为细粒度识别问题同时每个人行走的时间上下文信息具有独特性，提出一种联合局部多尺度和全局上下文时间特征的步态识别方法。将整个步态序列按多个时间分辨率划分并提取局部子序列内的多分辨率细粒度时间特征。在子序列之间基于Transformer提取时间上下文信息，并基于上下文信息融合所有子序列形成全局特征。在2个公开数据集上进行大量的实验，在CASIA-B数据集的3种行走状态下取得98.0%、95.4%和87.0%的rank-1准确率，在OU-MVLP数据集上取得90.7%的rank-1准确率。本文提出的方法得到的结果可为其他步态识别方法提供参考。Abstract: Existing gait recognition methods can extract rich gait information in the spatial dimension. However, they often overlook fine-grained temporal features within local regions and temporal contextual information across different sub-regions. Considering that gait recognition is a fine-grained recognition problem, and each individual’s gait carries unique temporal context information, we propose a gait recognition method that combines local multiscale and global contextual temporal features. The entire gait sequence is divided into multiple time resolutions and fine-grained temporal features within local sub-sequences are extracted. Transformer is used to extract temporal context information among different subsequences, and the global features are formed by integrating all subsequences based on the contextual information. We have conducted extensive experiments on two public datasets. The proposed model achieves rank-1 accuracies of 98.0%, 95.4%, and 87.0% on three walking conditions of the CASIA-B dataset. On the OU-MVLP dataset, the model achieves a rank-1 accuracy of 90.7%. The method proposed in this paper has achieved state-of-the-art results and can provide reference for other gait recognition methods.
-
步态识别具有对图像分辨率要求低、可远距离识别、无需受试者合作、难以隐藏或伪装等优势，在安防监控和调查取证等领域有着广阔的应用前景[1]。虽然步态识别已经吸引了许多研究者的兴趣[2-4]，但是步态识别的性能受到许多条件的影响，例如，更换衣服、携带条件、跨视角、速度变化和分辨率[5]。因此，提高复杂外部环境中步态识别的性能仍然是非常必要的。在当前的研究中步态识别方法可以分为基于3维步态信息的识别方法、基于视角转换模型的识别方法、基于视角不变特征的识别方法和基于深度学习的识别方法[1]4类。目前主流的步态识别方法通常采用基于深度学习的方法，利用深度神经网络对步态特征进行提取通常分为空间特征提取和时间特征提取2个部分，其中如何同时提取有效的时空特征是决定识别效果的关键因素。
近年来许多方法致力于在空间维度上提取更具表征能力的步态特征[6-9]。这些研究将不同的身体部位设置为不同的运动模式，并将步态序列在空间上划分为不同的子区域。每个子区域分别送到不同的网络中，以按不同的运动模式提取各自的空间特征。特别是在文献[10]中同时提取全局空间特征和局部空间特征进行联合利用，从而获得更鲁棒的特征表示。除了提取空间特征外，一些学者致力于在时间维度上提取更具表征能力的步态特征。在时间维度上早期工作侧重于提取全局特征。先前的方法通常使用3D卷积[11]或长短期记忆网络 (long short-term memory, LSTM)[9]提取时间特征。3Dlocal[12]将步态数据在空间上按部位划分，并对每个部位分别使用3D卷积提取全局时间步态特征。GaitNet[13]提出了一种自动编码器框架，用于从原始RGB图像中提取步态相关的特征，然后使用LSTM对全部步态序列的时间变化进行建模。Zhang等[14]使用在自然图像分类任务中预先训练的模型，直接应用3D卷积于整个步态序列来提取序列信息。然而，同时提取全局时间特征会导致网络忽略局部区域细粒度特征，从而在面对视角变化时缺乏区分力。Lin等[15]将完整步态序列在时间维度上划分子序列，在子序列内应用3D卷积提取的局部时空特征。更进一步，上下文敏感时间特征学习网络(context-sensitive temporal feature learning, CSTL)[16]采取多个时间尺度提取不同尺度的局部时间特征，并对多尺度的步态特征进行融合，以获得更具判别性的特征表示。这些方法要么只关注全局时间特征忽略更能代表身份的局部时间信息，要么只关注局部时间特征忽略全局不同区域的上下文信息。
人们在观察整个步态运动时通常会聚焦于几个局部区域上，在每个子区域内更关注局部区域的细粒度步态特征，再通过连续的几帧获得人的身份信息，综合利用不同的局部区域步态特征的上下文信息最终判断步态身份。经过7名志愿者的投票显示，在整个序列中人们通常更关注脚在离地最大高度的局部段、脚刚触地的局部段、手臂在最大高度的局部段等，然后再综合利用上述局部段的上下文信息做出判断。受此启发，本文提出了联合局部多尺度和全局上下文时间特征提取网络。本算法的主要贡献可以概括如下：
1)考虑到步态识别是一个细粒度分类问题，本文将整个步态序列分成多个子序列，提出了一个局部多分辨率细粒度时间特征提取器来提取不同分辨率下每个子序列的局部细粒度时间特征。
2)本文提出一个多分支特征融合模块，让不同分辨率分支特征在侧重自身分辨率信息的基础上，基于其自身子序列位置融合其他分辨率特征，以提高每个分支的特征多样性和表达能力。
3)在充分考虑局部细粒度时间特征基础上，由于每个人行走习惯不同，不同人的子序列时间上下文特征应当是独一无二的。本文提出了一个全局自注意力上下文时间特征提取器来提取子序列的上下文时间信息，提取更具判别性的步态特征。
4)在CASIA-B和OU-MVLP共2个公共数据集上的大量实验表明，此方法达到了当前最先进的性能。此外，消融实验证明了每个模块的有效性。
1. 相关理论
1.1 3D卷积网络
3D卷积已广泛应用于计算机视觉领域，并在各种应用中取得了巨大成功[17-18]，但是仅用3D卷积堆叠构建的网络可能不会获得良好的性能。一方面，堆叠3D卷积块会在训练期间造成巨大的资源消耗；另一方面，过多的卷积块也使得参数冗余。因此，许多现有方法通过将3D参数矩阵分解成低秩矩阵来提高性能。R(2+1)D[19]引入了一种新的时空卷积块，通过将3D参数矩阵分解为1D和2D参数矩阵来提高性能。P3D[20]提出了伪3D 的网络结构，以减少模型的参数，提取更鲁棒的3D特征。虽然可以提取稳健的时空特征，但这些结构可能会导致信息丢失。B3D[15]通过结合3D卷积和低秩矩阵来构建3D网络的基本结构，将低秩结构作为一个分支来增强3D卷积的能力。本文的3D卷积采用这种结构。
1.2 Transformer网络
Transformer网络[21]是一项相对较新的进步，在许多自然语言处理和计算机视觉任务中取得了令人印象深刻的成果，如手语识别[22] 、定位[23]、翻译[24]和生成[25]、对象检测[26]、场景分割[27]、视频理解[28]。Transformer利用自注意力机制对输入数据进行编码解码使其在翻译领域得到很好的发展。本文利用Transformer的这种特性对全局步态特征进行编解码使其获得丰富的上下文信息，并基于这种上下文信息自适应地进行特征融合，从而得到优于基于静态融合方法的效果。
2. 联合局部多尺度和全局上下文时间特征提取网络
2.1 整体结构
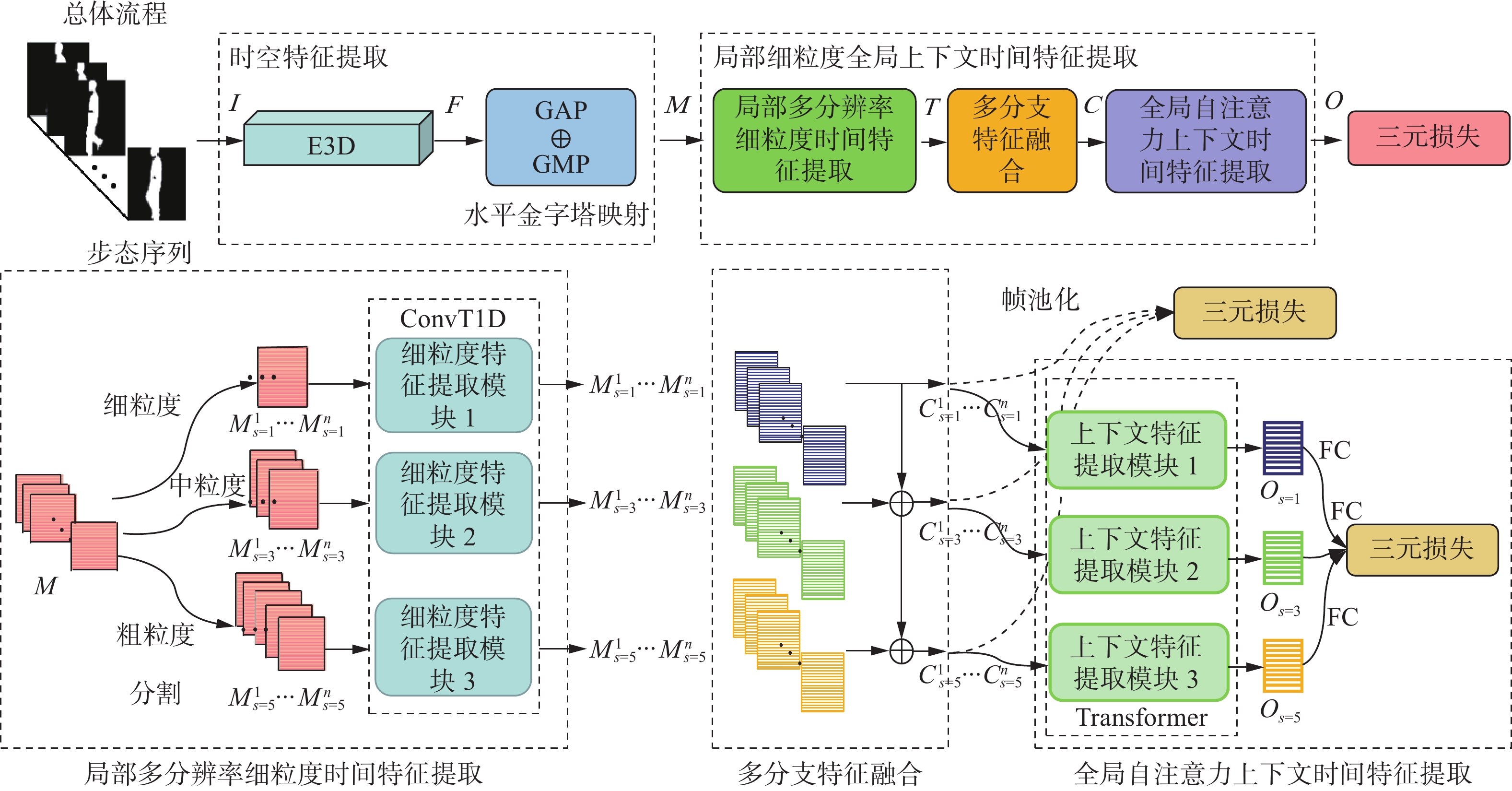
本文方法的整体流程如图1所示，其目的是提取更具代表性的步态特征。它主要由时空特征提取器、局部多分辨率细粒度时间特征提取器、多分支特征融合和全局自注意力上下文时间特征提取器4个部分组成。
图 1 联合局部多尺度和全局上下文时间特征提取网络的整体流程Fig. 1 Overall process of the joint local multiscale and global context temporal feature extraction network
下载:
全尺寸图片
输入的步态数据
$\{ {\boldsymbol{I}_j} \in {\bf{R}}^{h \times w},j{\text{ = }}1,2,\cdots ,n\}$ 为n帧步态轮廓图，每帧高为h，宽为w。首先，将I送入一个4层的3D卷积骨干网络${{\rm{E3D}}(} \cdot {)}$ ，以提取得到时空特征：$$ {\boldsymbol{F}} = {{\rm{E}}} 3{\rm{D}}({\boldsymbol{I}}) $$ 式中：
${\boldsymbol{F}} \in {\bf{R}}^{n \times c \times {h_2} \times {w_2}}$ ，${h_2}$ 、${w_2}$ 为特征F的空间水平和垂直维度，c为通道数。E3D网络由4层3D卷积堆叠而成，利用3D卷积的时空特征提取能力，对原始步态数据进行初步处理，提取出简单的时空特征，便于后续网络模块进一步提取出更丰富的时间特征。之后对特征F进行水平金字塔映射，将F在水平方向上划分为m个子区域，并将划分后的子特征图分别送入全局平均池化${{\rm{GAP}}(} \cdot {)}$ 和全局最大池化${{\rm{GMP}}(} \cdot {)}$ [24]得到特征${\boldsymbol{M}} \in {\bf{R}}^{n \times c \times m}$ ，公式为$$ {\boldsymbol{M }}= {{\rm{GAP}}(}{\boldsymbol{F}}{)} + {{\rm{GMP}}(}{\boldsymbol{F}}{)} $$ 本文将特征图在空间维度上划分为m个空间局部区域，特征F维度由
${h_2}$ ×${w_2}$ 降到m维。得到特征M后，为了便于后续可以提取局部细粒度的时间特征，本文将特征M在时间维度上重叠地分割成多个子序列。将每一个子序列分别送入局部多分辨率细粒度时间特征提取器来提取每个子序列的局部细粒度时间特征。此外为了获得更丰富的局部时间特征，本文采用不同的时间尺度来分割子序列。每一个分割尺度对应一个局部时间特征提取分支。对每一个分支的所有子序列区域分别提取，得到局部细粒度时间特征后，将所有特征作为多分支特征融合模块的输入，通过该模块对不同分支的对应子序列特征进行信息交互，以提高每个分支特征的表达能力。之后将增强后的各分支特征分别送入全局自注意力上下文时间特征提取器，获得不同子序列区域的时间上下文信息，并基于上下文信息进行自适应的时间特征融合，加强关键区域、抑制非关键区域以得到全局时间特征。最后将得到的全局特征送入全连接层进行映射送入三元损失用于训练。在2.2~2.4节将分别对局部多分辨率细粒度时间特征提取器、多分支特征融合和全局自注意力上下文时间特征提取器进行详细介绍。
2.2 局部多分辨率细粒度时间特征提取器
如第2.1节所述，本文应用E3D(·)网络提取步态特征，然后采用全局最大池化和全局平均池化来降低特征的空间维度并保持时间维度。此外，人类在观察时通常将注意力集中到连续的几帧上，在每个局部区域内观察细粒度的步态特征。因此，本文认为局部区域内包含了更多的身份信息。
为了提取细粒度的局部时间特征，本文将整个步态特征序列重叠的按尺度s分成n个子序列：
$$ {\boldsymbol{M}}_s^i \in {\bf{R}}^{s \times c \times m} $$ 式中：
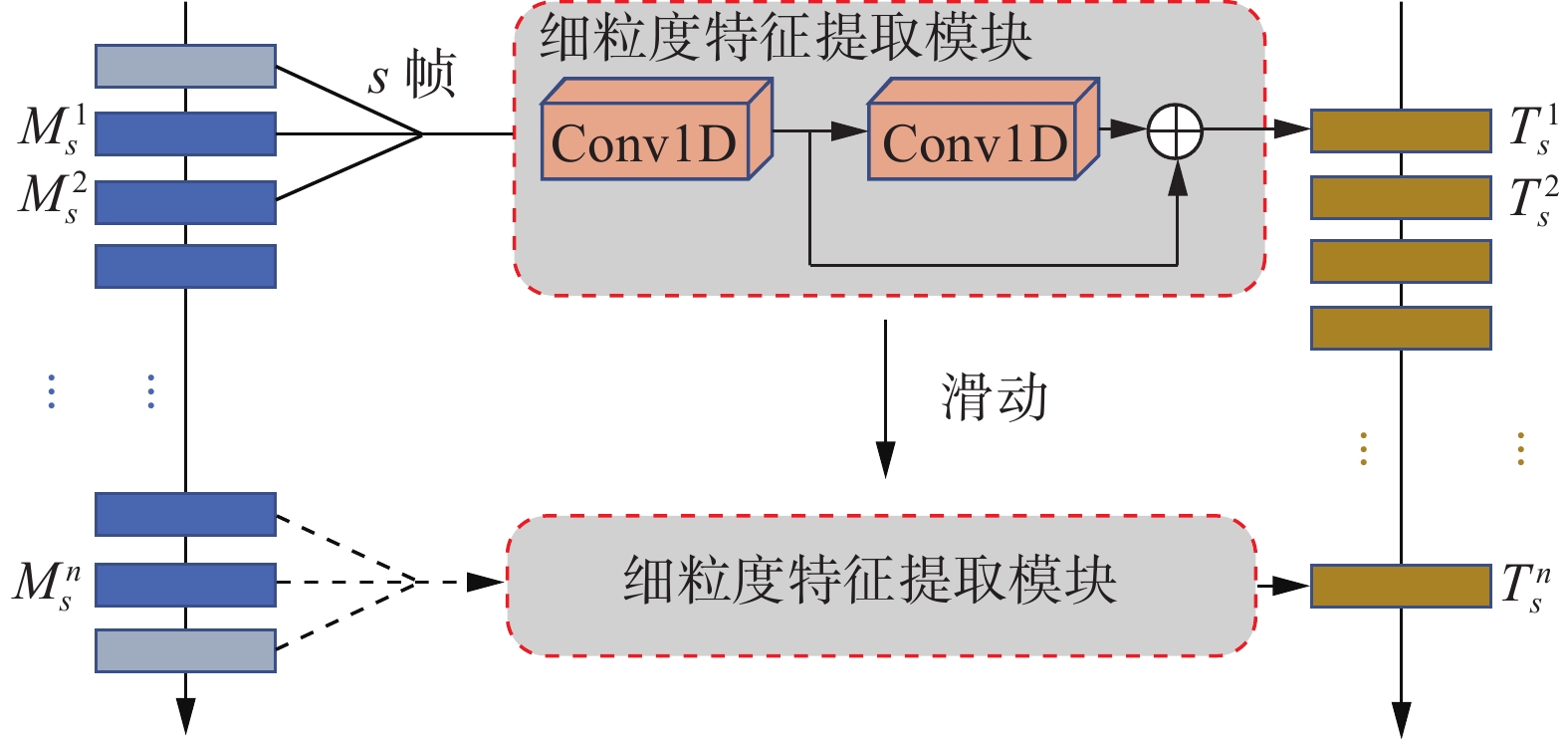
$i \in {\{ 1,2,} \cdots {,n\} }$ ，s为每s帧划分为一个子序列，i为第i个子序列。之后通过细粒度特征提取函数提取每个子序列内的局部细粒度时间特征。模块结构在图2中给出。
图 2 细粒度特征提取模块的详细结构Fig. 2 Detailed structure of fine grained feature extractor下载:
全尺寸图片
为了捕获局部时间特征，模块由2个串联的内核大小为s的1D卷积组成，并且应用ResNet模块，捕获局部时间特征的公式为
$$ \begin{gathered} {\boldsymbol{T}}_s^i ={{\rm{ConvT}}} 1{{\rm{D}}} ({\boldsymbol{M}}_s^i) = \\ {\text{ }}{{\rm{Re}}} \left( {{\boldsymbol{M}}_s^i \circ k_{}^1 + b_{}^1} \right) + {{\rm{Re}}} \left( {{{\rm{Re}}} \left( {{\boldsymbol{M}}_s^i \circ k_{}^1 + b_{}^1} \right) \circ k_{}^2 + b_{}^2} \right) \end{gathered} $$ 式中：
${\boldsymbol{M}}_s^i$ 为输入特征，$ \circ $ 为卷积运算，k1、k2分别为第1层、第2层卷积核参数，b1、b2分别为第1层、第2层卷积偏置值，${{\rm{Re}}(} \cdot {)}$ 为ReLU激活函数。提取后的特征${\boldsymbol{T}}_s^i \in {\bf{R}}^{1 \times c \times m}$ 。这使得网络能够更关注局部运动模式，以便提取更细粒度的时间特征。为了提取更丰富的局部时间特征，本文采用3个分支，每个分支以不同尺度s切割子序列，通过实验发现s分别为1、3、5时实验效果最好。
2.3 多分支特征融合
在2.2节中以不同的尺度提取局部时间特征之后，将提取到的多分支特征送入多分支特征融合模块。该模块让每一分支在侧重自身分辨率下的细粒度信息的基础上融合其他分辨率下的细粒度特征，来丰富每个分支的特征表达能力。该模型分别对3个分支每一个对应子区域的特征进行融合，模型具体公式为
$$ {\boldsymbol{C}}_{s'}^i = {{\rm{H}}} \left( {{\boldsymbol{T}}_{s = 1}^i,{\boldsymbol{T}}_{s = 3}^i,{\boldsymbol{T}}_{s = 5}^i} \right);i \in \{ 1,2, \cdots ,{{n}}\} ,s' = \{ 1,3,5\} $$ 式中：
${{\rm{H}}} \left( \cdot \right)$ 为多分支特征融合函数，${\boldsymbol{T}}_s^i \in {\bf{R}}^{1 \times c \times m}$ ，${\boldsymbol{C}}_{s'}^i \in {\bf{R}}^{1 \times c \times m}$ ，i为第i个子区域。本文介绍2种方法来实现${{\rm{H}}} \left( \cdot \right)$ 。通过实验发现尽管这几种方法会影响性能，但它们并没有很大的不同。1）静态方法。在静态方法中，一个简单的选择是以不同分支的特征求和结果作为新分支的特征。文中采用自细粒度特征向粗粒度特征进行累加。每个分支的新特征等于所有不大于自身粒度分支的原特征之和。公式为
$$ \begin{gathered} {{\boldsymbol{C}}_{s = 1}^i }= {\boldsymbol{T}}_{s = 1}^i\\ {{\boldsymbol{C}}_{s = 3}^i }= {\boldsymbol{T}}_{s = 1}^i \oplus {\boldsymbol{T}}_{s = 3}^i\\ {{\boldsymbol{C}}_{s = 5}^i } = {\boldsymbol{T}}_{s = 1}^i \oplus {\boldsymbol{T}}_{s = 3}^i \oplus {\boldsymbol{T}}_{s = 5}^i \end{gathered}$$ 具体而言，融合后的细粒度分支特征等于原细粒度分支特征本身，但融合后的中粒度分支特征等于原细粒度分支特征加原中粒度分支特征，同样的融合后的粗粒度分子特征等于原细粒度分支特征加原中粒度分支特征加原粗粒度分支特征。这种方法，不增加网络的参数量，可以降低计算的开销。
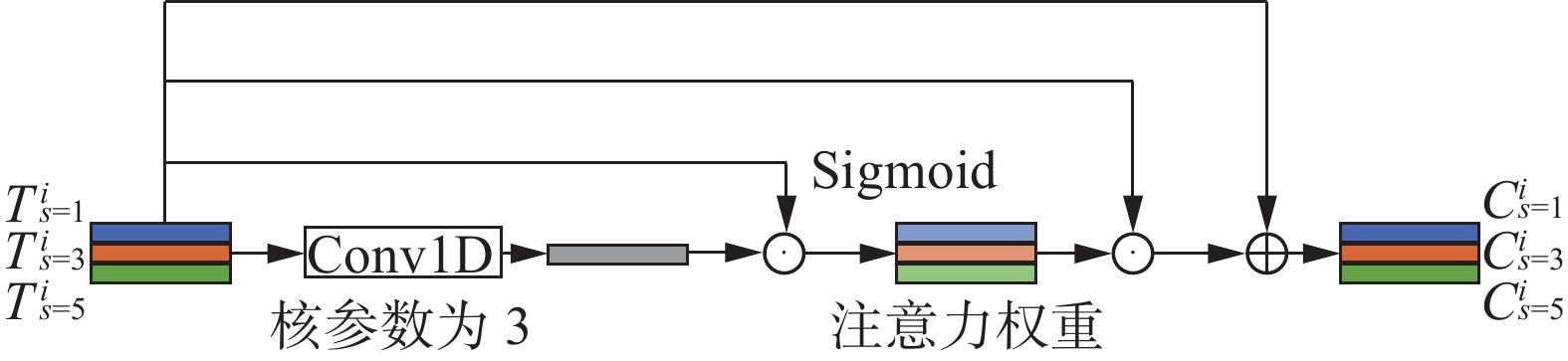
2）注意力机制。基于注意力机制的方法已经成功应用于很多领域。本文用注意力机制来融合不同分支的特征，该结构如图3所示。
图 3 基于注意力机制的多分支特征融合Fig. 3 Multibranch feature fusion based on attention mechanism下载:
全尺寸图片
输入特征
${\boldsymbol{T}}_{}^i = ({\boldsymbol{T}}_{s = 1}^i,{\boldsymbol{T}}_{s = 3}^i,{\boldsymbol{T}}_{s = 5}^i) \in {\bf{R}}^{3 \times c \times m}$ 被送入该网络。首先，将所有分支特征送入1D卷积进行融合得到融合特征；之后使每个分支特征与融合特征按位相乘再送入${{\rm{Sigmoid}}(} \cdot {)}$ 函数来获得每个分支的注意力权重；最后将每个分支的特征乘以注意力权重并与输入特征残差连接以得到每个分支特征基于相互关系更新后的特征${\boldsymbol{C}}_{}^i = ({\boldsymbol{C}}_{s = 1}^i, {\boldsymbol{C}}_{s = 3}^i,{\boldsymbol{C}}_{s = 5}^i) \in {\bf{R}}^{3 \times c \times m}$ 。公式为$$ {\boldsymbol{C}}_{}^i = {{\rm{S}}} \left( {{\boldsymbol{T}}_{}^i \circ k + b,{\boldsymbol{T}}_{}^i} \right) \odot {\boldsymbol{T}}_{}^i + {\boldsymbol{T}}_{}^i $$ 式中：k为1D卷积卷积核参数，b为偏置值，
${{\rm{S}}(} \cdot {)}$ 为Sigmoid函数，将相关性归一化到(−1，1)作为注意力权重。2.4 全局自注意力上下文时间特征提取器
先前研究中对于全局时间特征融合方法主要有
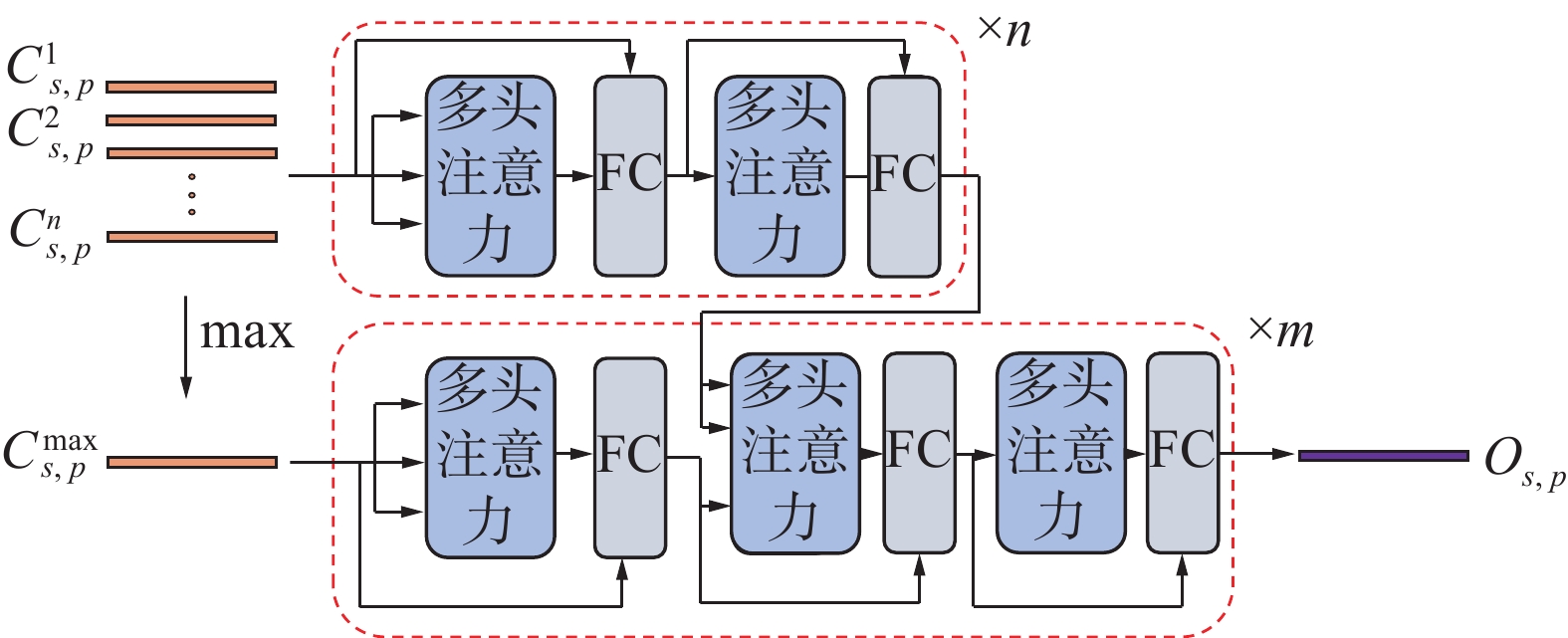
${{\rm{Max}}(} \cdot {)}$ 、${{\rm{Mean}}(} \cdot {)}$ 和${{\rm{Median}}(} \cdot {)}$ 或它们的组合等静态融合方法。这些方法认为整个序列的所有局部时间区域是同等重要的，并不能获得不同子区域的上下文关系来自适应地进行特征融合。因此本文基于Transformer的编解码结构，通过编码器来获得不同子序列间的上下文关系，同时利用解码器基于这种上下文关系来自适应地融合不同子序列的特征，来获得全局步态时间特征。2.3节中得到的特征$ {\boldsymbol{C}}_s^1,{\boldsymbol{C}}_s^2, \cdots ,{\boldsymbol{C}}_s^n $ 每个水平子区域分别送入Transformer网络得到基于时间上下文关系的全局时间融合特征。全局自注意力上下文时间特征提取器结构如图4所示。
图 4 全局自注意力上下文时间特征提取器的结构Fig. 4 Detailed structure of global self attention context temporal feature extractor下载:
全尺寸图片
时间特征提取器公式为
$$ \begin{gathered} {{\boldsymbol{O}}_{s,p}} = {\rm{{Transformer}}} ({\boldsymbol{C}}_{s,p}^1,{\boldsymbol{C}}_{s,p}^2, \cdots ,{\boldsymbol{C}}_{s,p}^n) = \\ {{\rm{Dec}}} ({{\rm{Enc}}} ({\boldsymbol{C}}_{s,p}^1,{\boldsymbol{C}}_{s,p}^2, \cdots ,{\boldsymbol{C}}_{s,p}^n),{\boldsymbol{C}}_{s,p}^{{\text{max}}})) \end{gathered} $$ 式中：编码器
${{\rm{Enc}}(} \cdot {)}$ 输入${\{ }{\boldsymbol{C}}_{s,p}^i \in {\bf{R}}^{1\times c},i = 1,2, \cdots ,n{\} }$ ，$ p \in {\{ 1,2,} \cdots {,}m{\} } $ 代表水平空间第p个子区域；解码器${{\rm{Dec}}(} \cdot {)}$ 输入${\boldsymbol{C}}_{s,p}^{{\text{max}}} \in {\bf{R}}^{1\times c}$ ，由输入$ {\boldsymbol{C}}_{s,p}^1,{\boldsymbol{C}}_{s,p}^2, \cdots ,{\boldsymbol{C}}_{s,p}^n $ 在时间维度上做最大池化得到，输出${{\boldsymbol{O}}_{s,p}} \in {\bf{R}}^{1\times c}$ 。输入
$ {\boldsymbol{C}}_{s,p}^1,{\boldsymbol{C}}_{s,p}^2, \cdots ,{\boldsymbol{C}}_{s,p}^n $ 被送到编码器，以基于上下文信息获得编码特征。具体来说，将${\boldsymbol{C}}_{s,p}^1,{\boldsymbol{C}}_{s,p}^2, \cdots , {\boldsymbol{C}}_{s,p}^n$ 经过线性变换分别得到Transformer的Q、K、V。$$ {\boldsymbol{Q}}_{s,p}^i = {\boldsymbol{C}}_{s,p}^i \times {{\boldsymbol{W}}^Q};{\boldsymbol{K}}_{s,p}^i = {\boldsymbol{C}}_{s,p}^i \times {{\boldsymbol{W}}^K};{\boldsymbol{V}}_{s,p}^i = {\boldsymbol{C}}_{s,p}^i \times {{\boldsymbol{W}}^V} $$ 式中：变换矩阵
${{\boldsymbol{W}}^Q},{{\boldsymbol{W}}^K},{{\boldsymbol{W}}^V} \in {\bf{R}}^{c\times c'}$ ，$c'$ 为线性变换后的特征维度。自注意力特征$u_{s,p}^{}$ 通过${\boldsymbol{Q}}_{s,p}^{}$ 、${\boldsymbol{K}}_{s,p}^{}$ 、${\boldsymbol{V}}_{s,p}^{}$ 送入自注意力函数A(·)得到，公式为$$ {u_{s,p}} = {{\rm{A}}} ({\boldsymbol{Q}}_{s,p},{\boldsymbol{K}}_{s,p},{\boldsymbol{V}}_{s,p}) = {{\rm{softmax}}} \left(\frac{{\boldsymbol{Q}}_{s,p}{\boldsymbol{K}}_{s,p}^{\text{T}}}{{\sqrt {{d_k}} }}\right)V_{s,p} $$ 为了使编码效果更好，本文使用了多头注意力机制获得更丰富的编码特征。具体操作类似于文献[21]。之后，将自注意力特征
$u_{s,p}^{}$ 送入到前馈网络${{\rm{FFN}}(} \cdot {)}$ 获得编码特征${{\boldsymbol{U}}_{s,p}}$ ，前馈网络公式为$$ {{\boldsymbol{U}}_{s,p}} = {{\rm{FFN}}} ({{\boldsymbol{u}}_{s,p}}) = \max (0,{u_{s,p}} \times {{{W}}_1} + {{{b}}_1}) \times {{{W}}_2} + {{{b}}_2} $$ 式中W1、W2、b1、b2分别为前馈网络第1层、第2层的权重和偏置。经过n个编码层堆叠，得到最终的编码器编码特征
${\boldsymbol{U}}_{s,p}^{^{{\text{enc}}}} \in {\bf{R}}^{n\times c}$ ，编码特征${\boldsymbol{U}}_{s,p}^{^{{\text{enc}}}}$ 被视为解码器的${\boldsymbol{K}}_{s,p}^{}$ 、${\boldsymbol{V}}_{s,p}^{}$ 输入。${\boldsymbol{C}}_{s,p}^{{\text{max}}}$ 作为解码器${\boldsymbol{Q}}_{s,p}^{}$ 的输入。${\boldsymbol{U}}_{s,p}^{^{{\text{enc}}}}$ 和${\boldsymbol{C}}_{s,p}^{{\text{max}}}$ 在解码器中通过与编码器同样的自注意力函数和前馈网络来获得最终的解码特征：$$ {{\boldsymbol{O}}_{s,p}} = {{\rm{Dec}}} ({\boldsymbol{U}}_{s,p}^{{\text{enc}}},{\boldsymbol{C}}_{_{s,p}}^{{\text{max}}}),{{\boldsymbol{O}}_{s,p}} \in {\bf{R}}^{1 \times c} $$ m个水平空间区域的解码特征
${{\boldsymbol{O}}_{s,p}}$ 共同构成第s分支的全局自注意力时间上下文特征${{\boldsymbol{O}}_s} \in {\bf{R}} ^{m \times c}$ 。2.5 损失函数
为了有效地训练所提出的步态识别模型，本文使用三元损失提高类间距离，降低类内距离。在训练阶段，将
$ {\boldsymbol{C}}_s^1,{\boldsymbol{C}}_s^2, \cdots ,{\boldsymbol{C}}_s^n $ 在时间维度上做最大池化得到${\boldsymbol{C}}_s^{{\text{max}}} = {\max _{\rm{T}}}({\boldsymbol{C}}_s^1,{\boldsymbol{C}}_s^2, \cdots ,{\boldsymbol{C}}_s^n)$ 作为第1个三元损失的输入得到${L_{{\rm{{tri1}}}}}$ 。${{\boldsymbol{O}}_s}$ 作为第2个三元损失输入得到${L_{{{\rm{tri2}}}}}$ 。其中${L_{{{\rm{tri1}}}}}$ 和${L_{{{\rm{tri2}}}}}$ 分别表示为$$\begin{gathered} {L_{{\rm{{tri1}}}}} = \\ \left[ {{{\rm{D}}} \big( {{\rm{G}}\big( {{\boldsymbol{C}}_s^{{{\rm{max}}},{a_1}}} \big),{\rm{G}}\big( {{\boldsymbol{C}}_s^{{{\rm{max}}},b}} \big)} \big) {{\rm{D}}} \big( {{\rm{G}}\big( {{\boldsymbol{C}}_s^{{{\rm{max}}},{a_1}}} \big),{\rm{G}}\big( {{\boldsymbol{C}}_s^{{{\rm{max}},}{a_2}}} \big)} \big) + m} \right]_ + \\ {L_{{{\rm{tri2}}}}} = \\ {\left[ {{{\rm{D}}} \big( {{\rm{G}}\big( {{\boldsymbol{O}}_s^{{a_1}}} \big),{\rm{G}}\big( {{\boldsymbol{O}}_s^b} \big)} \big) - {{\rm{D}}} \big( {{\rm{G}}\big( {{\boldsymbol{O}}_s^{{a_1}}} \big),{\rm{G}}\big( {{\boldsymbol{O}}_s^{{a_2}}} \big)} \big) + m} \right]_ + } \end{gathered}$$ 式中：a1和a2为来自相同类别的不同样本，而b表示来自另外一种类别的样本；
${{\rm{G}}(} \cdot {)}$ 为全连接层，对${{\boldsymbol{Q}}_s}$ 做特征映射改变特征维度；${{\rm{D}}(}{{{{d}}}_{1}}{, }{{{{d}}}_{2}}{)}$ 为d1和d2之间的欧几里德距离；m为三元损失的阈值。运算${{[}\gamma {]}_ + }$ 等同于${{\rm{max}}(\gamma , 0)}$ 。整个网络的训练损失由局部细粒度特征提取损失${L_{{{\rm{tri1}}}}}$ 和全局损失${L_{{{\rm{tri2}}}}}$ 共2部分构成，总损失函数${L_{{{\rm{com}}}}}$ 可定义为$$ {L_{{{\rm{com}}}}} = {L_{{{\rm{tri1}}}}} + {L_{{{\rm{tri2}}}}} $$ 其中，局部细粒度特征提取损失
${L_{{{\rm{tri1}}}}}$ 可以确保网络的局部细粒度特征提取模块能够准确地提取局部细粒度特征。防止后续增加全局自注意力上下文时间特征提取模块后网络层数加深导致前面的网络梯度消失，训练变得困难。全局损失${L_{{{\rm{tri2}}}}}$ 能够不断调整模型参数以最小化损失值，确保网络的全局自注意力上下文时间特征提取模块的准确性。3. 实验过程及结果
3.1 数据集
CASIA-B数据集[6]是最常用的步态数据集，包含124名受试者。每名受试者在3种情况下包含6组正常行走(normal walking status, NM)、2组拎包行走(walking status with a bag, BG)和2组穿着衣服行走(walking status in a coat, CL)共10个不同的组。每组包含11个不同的角度(0°~180°，增量为18°)。数据集包含大样本训练(large-sample training, LT: 74名训练对象和50名测试对象)、中样本训练(medium-sample training, MT: 62名训练对象和62名测试对象)和小样本训练(small-sample training, ST: 24名训练对象和100名测试对象)3种设置。在每个设置中，测试数据被分成一个注册集和一个预测集。注册集合包括NM条件下的4个组，预测集合包括其余组。
OU-MVLP[29]是世界上最大的公共步态数据集，包含
10307 名受试者。每个受试者包含14个视图(0°、15°、…、90°；180°、195°、……、270°)，每个视图包含2个序列(00和01)。实验中使用的协议与文献[3]相同。所有序列按受试者分为训练和测试(5153 名训练对象，5154 名测试对象)。在测试集中，seq01是注册集，seq00是预测集。3.2 实现细节
3.2.1 训练细节
在所有实验中，使用与文献[26]相同的处理方法来对齐每个帧，并调整大小为64×44。使用Adam作为优化器[30]，学习率为1×10−4，动量为0.9。当使用一个batch中所有样本计算三元损失时，三元损失阈值设置为0.2。此外，在每个卷积层之后应用Leaky ReLU[31]激活函数。模型在4个NVIDIA 2080ti GPU上训练。在一个Batch中，采样的受试者的数量记为p，每个受试者采样序列的数量记作k。具体来讲，在CASIA-B上，(p，k)设置为(8，8)，在OU-MVLP上设置为(32，8)。对于每个输入序列，在训练时固定使用30帧，并在测试时使用全部帧。在CASIA-B中，本文先对局部多分辨率细粒度时间特征提取器进行80×103次迭代，并在70×103次迭代时将学习率降低到1×10−5。之后加入全局自注意力上下文时间特征提取器联合训练30×103次迭代。
3.2.2 超参数设置
1)在CASIA-B和OU-MVLP数据集上，4个卷积层的通道数分别设置为32/64、64/128、128/256和128/256。所有卷积的内核大小为3。2)对于局部多分辨率细粒度时间特征提取器，分支设置为3，每个分支的s值分别设置为1、3、5。3)对于全局自注意力上下文时间特征提取器，将(n，m)的值设置为(4，4)。
3.3 与现有方法的比较
3.3.1 基于CASIA-B数据集
在表1中，文中将所提出的方法与几种最先进的步态识别方法进行了比较，包括GaitSet[32]、GaitSet+[33]、GaitPart[8]、CSTL[16]、MT3D[11]和GLFE[10]。可以观察到，本文提出的模型在所有外观条件和角度下都显示出优越性。
表 1 CASIA-B数据集上不同视角的实验结果Table 1 Expriment results of the different identical-view cases on OU-MVLP% 数据设置 表观 模型 角度/(°) 平均 0 18 36 54 72 90 108 126 144 162 180 LT NM GaitSet[32] 90.8 97.9 99.4 96.9 93.6 91.7 95.0 97.8 98.9 96.8 85.8 95.0 GaitSet+[33] 95.8 99.3 99.8 98.3 96.1 94.6 96.2 98.6 99.2 98.7 93.8 97.3 GaitPart[8] 94.1 98.6 99.3 98.5 94.0 92.3 95.9 98.4 99.2 97.8 90.4 96.2 MT3D[11] 95.7 98.2 99.0 97.5 95.1 93.9 96.1 98.6 99.2 98.2 92.0 96.7 GLFE[10] 96.0 98.3 99.0 97.9 96.9 95.4 97.0 98.9 99.3 98.8 94.0 97.4 CSTL[16] 97.2 99.0 99.2 98.1 96.2 95.5 97.7 98.7 99.2 98.9 96.5 97.8 本文算法 97.0 99.5 99.3 98.8 97.4 96.2 97.4 98.9 99.5 99.5 94.3 98.0 BG GaitSet[32] 83.8 91.2 91.8 88.8 83.3 81.0 84.1 90.0 92.2 94.4 79.0 87.2 GaitSet+[33] 92.2 97.0 96.0 94.7 92.0 90.4 92.0 96.1 97.6 97.8 88.5 94.0 GaitPart[8] 89.1 94.8 96.7 95.1 88.3 84.9 89.0 93.5 96.1 93.8 85.8 91.5 MT3D[11] 91.0 95.4 97.5 94.2 92.3 86.9 91.2 95.6 97.3 96.4 86.6 93.0 GLFE[10] 92.6 96.6 96.8 95.5 93.5 89.3 92.2 96.5 98.2 96.9 91.5 94.5 CSTL[16] 91.7 96.5 97.0 95.4 90.9 88.0 91.5 95.8 97.0 95.5 90.3 93.6 本文算法 93.4 97.8 99.9 96.6 94.7 89.3 93.6 98.0 99.7 98.8 89.0 95.4 CL GaitSet[32] 61.4 75.4 80.7 77.3 72.1 70.1 71.5 73.5 73.5 68.4 50.0 70.4 GaitSet+[33] 76.8 88.3 88.0 85.0 81.9 78.0 78.9 81.7 83.9 83.3 73.3 81.7 GaitPart[8] 70.7 85.5 86.9 83.3 77.1 72.5 76.9 82.2 83.8 80.2 66.5 78.7 MT3D[11] 76.0 87.6 89.8 85.0 81.2 75.7 81.0 84.5 85.4 82.2 68.1 81.5 GLFE[10] 76.6 90.0 90.3 87.1 84.5 79.0 84.1 87.0 87.3 84.4 69.5 83.6 CSTL[16] 78.1 89.4 91.6 86.6 82.1 79.9 81.8 86.3 88.7 86.6 75.3 84.2 本文算法 81.5 93.1 95.3 90.5 86.7 81.2 86.5 90.0 90.9 87.7 73.6 87.0 注：加黑代表效果最好，下同。 在GaitSet中，LT设置下，在NM、BG和CL共3种外观条件下的识别准确率分别为95.0%、87.2%和70.4%。本文方法中，在3种条件下的识别准确度分别为98.3%、95.6%和85.1%，分别提高了3.3%、8.4%和14.6%。这表明本文方法在外观变化的情况下具有更强的鲁棒性。
另外，在交叉视角识别方面，从表1可以观察到，本文方法在几乎所有角度都达到了最高的识别精度。与其他模型相比，本文模型在不同相机视角下的性能差异很小。例如，在LT设置的NM条件下，在36°和180°视角下，GaitSet的准确率分别为99.4%和85.8%，准确度相差近10%。但是本文方法在每个视角中都达到了94%以上的准确率，因此本文模型对不同视角具有更强的鲁棒性。
3.3.2 基于OU-MVLP数据集
为了评估本文网络的泛化能力，还在全球最大的公共步态数据集OU-MVLP[21]上完成了实验。为了公平比较，使用了3.1节中提到的测试协议，与文献[3]相同。结果如表2所示，与当前先进的方法相比，联合局部多尺度和全局上下文时间特征的步态识别网络在所有视角下都取得了更好的性能。
表 2 OU-MVLP数据集上不同视角的实验结果Table 2 Expriment results of the different identical-view cases on OU-MVLP% NM视角/(°) 算法 GaitSet[32] GaitPart[8] GLFE[10] 本文算法 0 79.5 82.6 83.8 88.4 15 87.9 88.9 90.0 91.6 30 89.9 90.8 91.0 91.5 45 90.2 91.0 91.2 91.8 60 88.1 89.7 90.3 91.4 75 88.7 89.9 90.0 91.1 90 87.8 89.5 89.4 90.7 180 81.7 85.2 85.3 90.7 195 86.7 88.1 89.1 90.8 210 89.0 90.0 90.5 91.6 225 89.3 90.1 90.6 91.5 240 87.2 89.0 89.6 91.0 255 87.8 89.1 89.3 90.5 270 86.2 88.2 88.5 90.0 平均 87.1 88.7 89.2 90.9 3.4 消融实验
联合局部多尺度和全局上下文时间特征提取网络主要由以下关键组件组成：首先，局部多分辨率细粒度时间特征提取器用于提取细粒度的局部时间特征；其次，引入全局自注意力上下文时间特征提取器来提取全局时间特征。本文通过不同的消融实验来进一步分析每个关键部件的作用。
3.4.1 局部多分辨率细粒度时间特征提取模块
不同于以往只提取一个尺度的时间特征的方法，本文在特征层使用多分辨率来提取细粒度局部时间特征。本文研究了不同分支的重要性，表3给出了CASIA-B数据集上LT设置下的实验结果。从结果中可以观察到，当仅使用一个分支时，无论哪个分支，平均准确率都低于90%。当合并2个分支时，无论是哪一种(帧级别和小尺度、帧级别和大尺度、小尺度和大尺度)，效果都比单独使用一个分支要好。当结合3个分支时，效果最好，与合并2个分支的情况相比，平均精度提高了1.2%。
表 3 CASIA-B数据集上LT设置的不同分支实验结果Table 3 Expriment results of the different branches with the LT settings on CASIA-B尺度选择 rank-1精度/% 帧级别 小尺度 大尺度 NM BG CL 平均 ✓ 96.0 92.6 81.2 89.9 ✓ 95.4 92.2 80.9 89.5 ✓ 95.2 92.0 80.6 89.4 ✓ ✓ 97.9 95.2 84.7 92.6 ✓ ✓ 97.3 94.0 82.8 91.4 ✓ ✓ 97.6 95.0 84.4 92.3 ✓ ✓ ✓ 98.0 95.4 87.0 93.5 3.4.2 多分支特征融合模块不同实现方法
在2.3节中分别介绍了不同多分支特征融合模块的实现方式。本节对这些方法进行对比，观察不同方法的区别，结果如表4所示。从表4中可以看到，当使用静态方法时，网络的训练时间和参数量都少于使用注意力的方法。并且在训练准确率上使用注意力的方法与使用静态方法的差别并不大，注意力网络并没有显著地增加步态识别模型的识别准确率。因此，综合计算成本和识别效果，在本文模型中最终选择了静态方法来实现多分支特征融合模块。其次在静态方法中，可以使用2个方向对多个分支的特征进行融合。
表 4 多分支特征融合模块不同实现方法的贡献Table 4 Contributions of different implementation methods for multi branch feature fusion modules融合方式 推理时间/s 网络参数量/MB NM/% BG/% CL/% 静态方法
（Ts=1→Ts=5）545 95.6 98.0 95.4 87.0 静态方法
（Ts=5→Ts=1）547 95.6 97.8 95.1 86.5 注意力方法 720 102 98.5 95.7 85.4 $$ （{{T_{s=1}}}\to {{T_{s=5}}}、{{T_{s=5}}}\to {{T_{s=1}}}） $$ 式中：Ts=1→Ts=5代表从细粒度特征逐渐向粗粒度特征累加，Ts=5→Ts=1代表从粗粒度特征向细粒度特征累加。具体累加方式详见2.3节。从实验结果可以看出，Ts=1→Ts=5可以取得更高的识别准确率。说明从细粒度特征逐渐向粗粒度特征累加的效果更好。此外，在细粒度、中粒度、粗粒度之间进行比较的话，细粒度分支包含了更多的身份信息。所以从细粒度逐渐向其他分支累加时，细粒度分支的步态特征对其他分支特征进行了丰富和扩充，提高了其他分支的步态特征表达能力。以此提高了整个步态识别网络的识别准确率。
3.4.3 全局自注意力上下文时间特征提取器
传统的集合池化使用
${\rm{Max}}( \cdot )$ 、${\rm{Mean}}( \cdot )$ 或${\rm{Median}}( \cdot )$ 来聚合全局步态信息，这样并不能获得不同区域的上下文信息。因此，本文介绍了全局自注意力上下文时间特征提取器。实验结果如表5所示。表 5 全局自注意力上下文时间特征提取器贡献的实验数据结果Table 5 The experimental data results on the contribution of the global self attention context time feature extractor% 模型 NM BG CL Baseline 96.0 92.6 81.2 Baseline+Transformer(4×4) 97.7 94.7 83.4 Baseline+ConvT+Transformer(1×1) 97.8 95.0 85.4 Baseline+ConvT+Transformer(4×4) 98.0 95.4 87.0 GaitSet 95.0 87.2 70.4 GaitSet+Transformer(4×4) 97.0 89.2 74.5 MT3D 96.5 93.4 81.6 MT3D+Transformer(4×4) 97.3 94.5 83.6 基线模型是具有4层3Dconv的网络骨架。从结果中可以观察到，基线模型和全局自注意力上下文时间特征提取器相结合能够实现比基线更高的精度。这表明将全局自注意力上下文时间特征提取器用于自适应帧池化是有效的。并且，将Gaitset、MT3D与全局自注意力上下文时间特征提取器相结合时，平均精度也会提高。这表明全局自注意力上下文时间特征提取器是通用的，它可以与其他基本网络相结合以提高准确性。此外，结果表明当全局自注意力上下文时间特征提取器的m和n都设置为4时，模型的性能最好。
4. 结束语
本文提出了一种新的步态识别框架，可以充分提取局部细粒度时间特征和全局上下文时间特征。同时全局上下文时间特征提取器可以与其他多种网络结合改进先前的静态帧池化方法。在公共数据集上的实验分析揭示了网络各个模块的有效性。在未来的工作中，将在其他视频理解任务中应用联合利用局部多尺度和全局上下文时间特征提取的方法。
-
图 1 联合局部多尺度和全局上下文时间特征提取网络的整体流程
Fig. 1 Overall process of the joint local multiscale and global context temporal feature extraction network
下载:
全尺寸图片
图 2 细粒度特征提取模块的详细结构
Fig. 2 Detailed structure of fine grained feature extractor
下载:
全尺寸图片
图 3 基于注意力机制的多分支特征融合
Fig. 3 Multibranch feature fusion based on attention mechanism
下载:
全尺寸图片
图 4 全局自注意力上下文时间特征提取器的结构
Fig. 4 Detailed structure of global self attention context temporal feature extractor
下载:
全尺寸图片
表 1 CASIA-B数据集上不同视角的实验结果
Table 1 Expriment results of the different identical-view cases on OU-MVLP
% 数据设置 表观 模型 角度/(°) 平均 0 18 36 54 72 90 108 126 144 162 180 LT NM GaitSet[32] 90.8 97.9 99.4 96.9 93.6 91.7 95.0 97.8 98.9 96.8 85.8 95.0 GaitSet+[33] 95.8 99.3 99.8 98.3 96.1 94.6 96.2 98.6 99.2 98.7 93.8 97.3 GaitPart[8] 94.1 98.6 99.3 98.5 94.0 92.3 95.9 98.4 99.2 97.8 90.4 96.2 MT3D[11] 95.7 98.2 99.0 97.5 95.1 93.9 96.1 98.6 99.2 98.2 92.0 96.7 GLFE[10] 96.0 98.3 99.0 97.9 96.9 95.4 97.0 98.9 99.3 98.8 94.0 97.4 CSTL[16] 97.2 99.0 99.2 98.1 96.2 95.5 97.7 98.7 99.2 98.9 96.5 97.8 本文算法 97.0 99.5 99.3 98.8 97.4 96.2 97.4 98.9 99.5 99.5 94.3 98.0 BG GaitSet[32] 83.8 91.2 91.8 88.8 83.3 81.0 84.1 90.0 92.2 94.4 79.0 87.2 GaitSet+[33] 92.2 97.0 96.0 94.7 92.0 90.4 92.0 96.1 97.6 97.8 88.5 94.0 GaitPart[8] 89.1 94.8 96.7 95.1 88.3 84.9 89.0 93.5 96.1 93.8 85.8 91.5 MT3D[11] 91.0 95.4 97.5 94.2 92.3 86.9 91.2 95.6 97.3 96.4 86.6 93.0 GLFE[10] 92.6 96.6 96.8 95.5 93.5 89.3 92.2 96.5 98.2 96.9 91.5 94.5 CSTL[16] 91.7 96.5 97.0 95.4 90.9 88.0 91.5 95.8 97.0 95.5 90.3 93.6 本文算法 93.4 97.8 99.9 96.6 94.7 89.3 93.6 98.0 99.7 98.8 89.0 95.4 CL GaitSet[32] 61.4 75.4 80.7 77.3 72.1 70.1 71.5 73.5 73.5 68.4 50.0 70.4 GaitSet+[33] 76.8 88.3 88.0 85.0 81.9 78.0 78.9 81.7 83.9 83.3 73.3 81.7 GaitPart[8] 70.7 85.5 86.9 83.3 77.1 72.5 76.9 82.2 83.8 80.2 66.5 78.7 MT3D[11] 76.0 87.6 89.8 85.0 81.2 75.7 81.0 84.5 85.4 82.2 68.1 81.5 GLFE[10] 76.6 90.0 90.3 87.1 84.5 79.0 84.1 87.0 87.3 84.4 69.5 83.6 CSTL[16] 78.1 89.4 91.6 86.6 82.1 79.9 81.8 86.3 88.7 86.6 75.3 84.2 本文算法 81.5 93.1 95.3 90.5 86.7 81.2 86.5 90.0 90.9 87.7 73.6 87.0 注：加黑代表效果最好，下同。 表 2 OU-MVLP数据集上不同视角的实验结果
Table 2 Expriment results of the different identical-view cases on OU-MVLP
% NM视角/(°) 算法 GaitSet[32] GaitPart[8] GLFE[10] 本文算法 0 79.5 82.6 83.8 88.4 15 87.9 88.9 90.0 91.6 30 89.9 90.8 91.0 91.5 45 90.2 91.0 91.2 91.8 60 88.1 89.7 90.3 91.4 75 88.7 89.9 90.0 91.1 90 87.8 89.5 89.4 90.7 180 81.7 85.2 85.3 90.7 195 86.7 88.1 89.1 90.8 210 89.0 90.0 90.5 91.6 225 89.3 90.1 90.6 91.5 240 87.2 89.0 89.6 91.0 255 87.8 89.1 89.3 90.5 270 86.2 88.2 88.5 90.0 平均 87.1 88.7 89.2 90.9 表 3 CASIA-B数据集上LT设置的不同分支实验结果
Table 3 Expriment results of the different branches with the LT settings on CASIA-B
尺度选择 rank-1精度/% 帧级别 小尺度 大尺度 NM BG CL 平均 ✓ 96.0 92.6 81.2 89.9 ✓ 95.4 92.2 80.9 89.5 ✓ 95.2 92.0 80.6 89.4 ✓ ✓ 97.9 95.2 84.7 92.6 ✓ ✓ 97.3 94.0 82.8 91.4 ✓ ✓ 97.6 95.0 84.4 92.3 ✓ ✓ ✓ 98.0 95.4 87.0 93.5 表 4 多分支特征融合模块不同实现方法的贡献
Table 4 Contributions of different implementation methods for multi branch feature fusion modules
融合方式 推理时间/s 网络参数量/MB NM/% BG/% CL/% 静态方法
（Ts=1→Ts=5）545 95.6 98.0 95.4 87.0 静态方法
（Ts=5→Ts=1）547 95.6 97.8 95.1 86.5 注意力方法 720 102 98.5 95.7 85.4 表 5 全局自注意力上下文时间特征提取器贡献的实验数据结果
Table 5 The experimental data results on the contribution of the global self attention context time feature extractor
% 模型 NM BG CL Baseline 96.0 92.6 81.2 Baseline+Transformer(4×4) 97.7 94.7 83.4 Baseline+ConvT+Transformer(1×1) 97.8 95.0 85.4 Baseline+ConvT+Transformer(4×4) 98.0 95.4 87.0 GaitSet 95.0 87.2 70.4 GaitSet+Transformer(4×4) 97.0 89.2 74.5 MT3D 96.5 93.4 81.6 MT3D+Transformer(4×4) 97.3 94.5 83.6 -
[1] 许文正, 黄天欢, 贲晛烨, 等. 跨视角步态识别综述[J]. 中国图象图形学报, 2023, 28(5): 1265–1286. XU Wenzheng, HUANG Tianhuan, BEN Xianye, et al. Cross-view gait recognition: a review[J]. Journal of image and graphics, 2023, 28(5): 1265–1286. [2] 吕卓纹, 王一斌, 邢向磊, 等. 加权CCA多信息融合的步态表征方法[J]. 智能系统学报, 2019, 14(3): 449–454. LYU Zhuowen, WANG Yibin, XING Xianglei, et al. A gait representation method based on weighted CCA for multi-information fusion[J]. CAAI transactions on intelligent systems, 2019, 14(3): 449–454. [3] 李一波, 李昆. 双视角下多特征信息融合的步态识别[J]. 智能系统学报, 2013, 8(1): 74–79. LI Yibo, LI Kun. Gait recognition based on dual view and multiple feature information fusion[J]. CAAI transactions on intelligent systems, 2013, 8(1): 74–79. [4] CONNOR P, ROSS A. Biometric recognition by gait: a survey of modalities and features[J]. Computer vision & image understanding, 2018, 167(1): 1–27. [5] LIAO R, CAO C, GARCIA E B, et al. Pose-based temporal-spatial network (PTSN) for gait recognition with carrying and clothing variations[C]//12th Chinese Conference on Biometric Recognition. Shenzhen: Springer international publishing, 2017: 474−483. [6] YU Shiqi, TAN Daoliang, TAN Tieniu. A framework for evaluating the effect of view angle, clothing and carrying condition on gait recognition[C]//18th International Conference on Pattern Recognition. Hong Kong: IEEE, 2006, 4: 441−444. [7] ZHANG Yuqi, HUANG Yongzhen, YU Shiqi, et al. Cross-view gait recognition by discriminative feature learning[J]. IEEE transactions on image processing, 2019, 29: 1001–1015. [8] FAN Chao, PENG Yunjie, CAO Chunshui, et al. Gaitpart: Temporal part-based model for gait recognition[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 14225−14233. [9] SEPAS-MOGHADDAM A, ETEMAD A. View-invariant gait recognition with attentive recurrent learning of partial representations[J]. IEEE transactions on biometrics, behavior, and identity science, 2020, 3(1): 124–137. [10] LIN Beibei, ZHANG Shunli, YU Xin. Gait recognition via effective global-local feature representation and local temporal aggregation[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 14648−14656. [11] WOLF T, BABAEE M, RIGOLL G. Multi-view gait recognition using 3D convolutional neural networks[C]//2016 IEEE International Conference on Image Processing. Phoenix: IEEE, 2016: 4165−4169. [12] HUANG Zhen, XUE Dixiu, SHEN Xu, et al. 3D local convolutional neural networks for gait recognition[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 14920−14929. [13] ZHANG Ziyuan, TRAN Luan, LIU Feng, et al. On learning disentangled representations for gait recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2020, 44(1): 345–360. [14] ZHANG Ziyuan, TRAN Luan, YIN Xi, et al. Gait recognition via disentangled representation learning[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 4710−4719. [15] LIN Beibei, ZHANG Shunli, BAO Feng. Gait recognition with multiple-temporal-scale 3d convolutional neural network[C]//Proceedings of the 28th ACM International Conference on Multimedia. New York: ACM, 2020: 3054−3062. [16] HUANG Xiaohu, ZHU Duowang, WANG Hao, et al. Context-sensitive temporal feature learning for gait recognition[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 12909−12918. [17] JI Shuiwang, XU Wei, YANG Ming, et al. 3D convolutional neural networks for human action recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 35(1): 221–231. [18] TRAN D, BOURDEV L, FERGUS R, et al. Learning spatiotemporal features with 3d convolutional networks[C]//Proceedings of the IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 4489−4497. [19] TRAN D, WANG H, TORRESANI L, et al. A closer look at spatiotemporal convolutions for action recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6450−6459. [20] QIU Zhaofan, YAO Ting, MEI Tao. Learning spatio-temporal representation with pseudo-3D residual networks[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Venice: IEEE, 2017: 5534−5542. [21] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30: 6000–6010. [22] CAMGOZ N C, KOLLER O, HADFIELD S, et al. Sign language transformers: Joint end-to-end sign language recognition and translation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 10023−10033. [23] VAROL G, MOMENI L, ALBANIE S, et al. Read and attend: temporal localisation in sign language videos[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 16857−16866. [24] CAMGOZ N C, KOLLER O, HADFIELDS, et al. Multi-channel transformers for multi-articulatory sign language translation[C]//16th European Conference on Computer Vision. Glasgow: Springer International Publishing, 2020: 301−319. [25] SAUNDERS B, CAMGOZ N C, BOWDEN R. Progressive transformers for end-to-end sign language production[C]//16th European Conference on Computer Vision. Glasgow: Springer International Publishing, 2020: 687−705. [26] CARION N, MASSA F, SYNNAEVE G, et al. End-to-end object detection with transformers[C]//16th European Conference on Computer Vision. Glasgow: Springer International Publishing, 2020: 213−229. [27] FU Jun, LIU Jing, TIAN Haijie, et al. Dual attention network for scene segmentation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019: 3146−3154. [28] SUN Chen, MYERS A, VONDRICK C, et al. Videobert: a joint model for video and language representation learning[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 7464−7473. [29] TAKEMURA N, MAKIHARA Y, MURAMATSU D, et al. Multi-view large population gait dataset and its performance evaluation for cross-view gait recognition[J]. IPSJ transactions on computer vision and applications, 2018, 10: 1–14. doi: 10.1186/s41074-017-0037-0 [30] KINGMA D P, BA J. Adam: a method for stochastic optimization[J]. International conference on learning representations, 2014, 1: 1–13. [31] MAAS A L, HANNUN A Y, NG A Y. Rectifier nonlinearities improve neural network acoustic models[J]. Computer science, 2013, 30(1): 3–8. [32] CHAO Hanqing, WANG Kun, HE Yiwei, et al. GaitSet: cross-view gait recognition through utilizing gait as a deep set[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 44(7): 3467–3478. [33] 刘正道, 努尔毕亚·亚地卡尔, 木特力甫·马木提, 等. 基于优化GaitSet模型的步态识别研究[J]. 东北师范大学学报, 2022, 54(4): 77–86. LIU Zhengdao, NURBIYA·Yadikar, MUTELEP·Mamut, et al. Research on gait recognition based on optimized GaitSet model[J]. Journal of Northeastern University, 2022, 54(4): 77–86.
