Action segmentation based on multigraph fusion constraint semi-nonnegative matrix factorization
-
摘要: 基于聚类的无监督动作分割方法主要利用序列中相邻帧之间的结构相似性来提高动作分割的准确性。这在实现动作片段内部一致划分的同时给不同动作边界的准确分割带来隐患。为此提出了一种基于多图融合约束矩阵分解的动作分割方法。通过融合序列中的结构相似性和度量相似性信息构造多图融合约束项，融入到半非负矩阵分解中获得序列的低维表示，进而获得序列的k近邻图并利用图割的方法实现准确分割。在两类动作序列上的实验表明，所提方法在保持动作内部一致划分的同时能够准确划分动作边界，明显提升了分割准确性，时间效率也明显提升。Abstract: Most clustering-based action segmentation methods mainly exploit the structure similarity information between adjacent frames (points) in the sequence to improve the accuracy of action segmentation. These methods improve the consistency of segmentation inside each action but introduce potential issues for accurately segmenting action boundaries. Hence, this paper presents a novel action segmentation method based on multigraph fusion constraint semi-nonnegative matrix factorization (MGSeNMF). In this method, the structural and measurement similarity information is fused to build a multigraph fusion constraint term, which is fused to semi-NMF to obtain a low-dimensional representation. A k-nearest neighbor graph is also generated for the action sequences, realizing accurate segmentation using the graph cut method. Experimental results on two kinds of real-action datasets show that MGSeNMF can accurately divide the boundary of actions while maintaining consistent segmentation inside each action. Thus, the proposed method improves the accuracy of segmentation and efficiency of running time significantly.
-
动作分割是将采集到的动作序列数据分割成若干个不同的动作片段，其在人体行为理解[1]、人机交互[2]、机器人控制[3]、数据挖掘[4]等多个领域具有广泛的应用。与其他数据相比，动作序列数据通常包含多个动作片段。一般认为，序列中相邻帧（点）的变化是连续的、缓慢的，具有较高的相似性[5]。动作分割时，属于同一个动作片段内的相邻帧应划分到一起；而在不同动作片段边界上的相邻帧应分别划分到对应的动作片段中。因此动作分割的关键包括同一动作片段内所有帧的一致分割和动作片段边界帧的准确分割 (即动作边界的准确判断)。目前已有大量工作对该问题进行了深入研究，取得了一系列成果，提出了许多基于监督[6]或无监督学习[7]动作分割方法。如基于深度学习模型的方法[8]通过训练数据集上学到的不同粒度、类型的时序特征，可以实现较好的动作分割效果。然而此类基于监督的方法需要大量标注数据，对计算资源要求也相对较高。相比之下，基于聚类的无监督学习方法将不同动作片段看作一类，动作分割就是将动作序列中所有帧聚类到相应动作片段中。这种方法简单、直观，建模灵活，受到越来越多的重视。
考虑到动作序列中的结构相似性特点，即相邻帧之间是平滑的、缓慢变化的，它们之间具有较高的相似性，因此在基于聚类的分割方法中，特征表示学习过程中融入结构相似性是提升分割准确性的关键。如基于子空间聚类 (subspace clustering, SC) [9]，TSC（temporal subspace clustering）[5]构造了相邻帧之间的约束正则项嵌入到子空间投影过程中；TLRSC (temporal plus low-rank subspace clustering) [10]在子空间投影中引入结构相似性约束和低秩约束，这些结构相似性的引入可以帮助获得更好的动作序列图表示用于聚类。而基于半非负矩阵分解(semi-nonnegative matrix factorization, Semi-NMF)方法[11]，文献[12]在降维的过程中融入了多近邻帧结构相似性约束，可以获得更准确的动作序列低维特征表示用于后续的聚类。TW-FINCH (temporally- weighted hierarchical clustering)[13] 是一种层次聚类方法，在相似性度量中利用结构最近邻的高相似性来约束相邻帧尽可能的划分到同一动作中。ABD (action boundary detection)[1]通过寻找动过片段的边界来分割不同动作，同样也利用结构相似性来实现快速分割。显然这些方法的核心思路是利用结构相似性约束相邻帧尽可能一致归属到相同类，通过实现动作片段内部聚类的准确性有效提升动作分割的准确性。
然而，结构相似性虽然可以确保动作片段内部的一致归属，但是如果相邻帧处在不同动作片段的边界上，带来的问题就是会造成边界分割的不准确。这是因为边界处的相邻帧在实际中如果差异确实较大，那么该差异信息是准确判断不同动作片段的依据，而结构相似性约束减小了这种边界处的差异信息，使得边界处不同动作的帧之间相似性关系增强，边界变得更加难以判断，给分割造成困难；并且在结构相似性约束中引入的相邻帧数越多，差异信息减少越多，动作边界越难以判断，导致动作分割的准确性很难进一步提升，这是动作分割的难点[14]。针对该问题，可以考虑采用其他相似性信息来提升分割效果。如文献[15]利用k近邻相似性约束来提升聚类的准确性，该约束是一种度量相似性，通过使用距离函数计算帧间相似性来寻找前k个高相似性关系，并在特征表示学习中保持该相似性关系。对于动作序列而言，如果边界上的相邻帧差异较大，那么该约束不会影响边界处的差异性，可以减少边界处的错误分割；但是如果不同动作片段中存在一些相似帧 (如跑步与跳跃动作中都存在双脚离地的帧) ，那么该约束可能会将那些本属于不同动作片段的帧归属到相同类，造成动作片段内部分割的不一致。可见，对于动作分割而言，不同的相似性约束各有利弊，为了实现准确分割，尽可能保持动作片段内所有帧的相同归属和边界处的准确分割十分有必要。
基于以上分析，不同于当前大多数方法仅利用结构相似性约束来提升动作分割的准确性，为了发挥不同相似性约束的优势，本文提出了融合结构相似性和度量相似性信息的多图融合约束Semi-NMF (multi-raph constraint Semi-NMF, MGSeNMF)动作分割方法。该方法首先在特征表示学习过程中，通过融合两种相似性关系图构造正则约束项约束Semi-NMF获得序列的低维表示；进而生成动作序列的k近邻图[16], 再使用图割[17]进行分割。
本文工作可概括如下：
1) 提出一种融合结构相似性和度量相似性信息的多图融合约束Semi-NMF动作序列特征表示学习算法，在动作序列的表示中保持更合理、更准确的近邻关系。
2) 提出一种求解多图融合约束Semi-NMF优化问题的方法，获得动作序列的低维表示并生成动作序列的k近邻图。
3) 在视频和捕获这两类真实动作序列数据集上进行分割实验。实验结果表明与其他经典方法相比，所提方法适用于不同类型数据，能在保持动作片段内部一致归属的同时准确分割动作边界，提升分割准确性，整体运行效率更高。
1. 相关工作
当前基于聚类的动作分割方法主要思路是：首先在基于SC、Semi-NMF等特征表示学习的过程中融入相似性信息，确保近邻帧之间具有较高相似性；再利用k-means、图割等对获得的特征表示进行类划分，实现分割的目的。其中融入结构相似性约束是此类方法的主要工作。本节主要从基于Semi-NMF的特征表示学习和结构相似性约束正则项构造两方面展开论述。
1.1 基于Semi-NMF的特征表示学习
设输入动作序列
${\boldsymbol{X}} \in {{\mathbf{R}}^{d \times n}}$ ，包含$ n $ 个连续的数据帧（点）记作：$\left\{ {{x_1},{x_2}, \cdots ,} \right.\left. {{x_n}} \right\}$ ，每个数据帧的特征维度为$ d $ 。基于SC的各种方法可以获得序列${\boldsymbol{X}}$ 的关系图表示${\boldsymbol{G }}\in {{\bf{R}}^{n \times n}}$ ，而基于Semi-NMF的方法是在特征空间${\boldsymbol{Z}} \in {{\bf{R}}^{d \times p}}$ 上获得一个低维特征表示${\boldsymbol{ H}} \in {{\bf{R}}^{p \times n}}$ ，再利用其他方法获得关系图表示${\boldsymbol{G}}$ ，其中$ p $ 表示降维后的特征维数。因此，基于Semi-NMF的特征表示学习可描述为一个优化问题：$$ \mathop {\min }\limits_{{{\boldsymbol{Z}}}\;{\boldsymbol{H}}} J = \left\| {{\boldsymbol{X }}- {\boldsymbol{ZH}}} \right\|_F^2\quad{\rm{s.t.}}\;\;{\boldsymbol{H}} \geqslant 0 $$ (1) 其中
${\boldsymbol{H}}$ 中的元素为非负值。Semi-NMF能够处理负值数据，具有建模简单灵活，可解释性强等特点。研究表明在Semi-NMF过程中施加相似性约束可以提高特征学习的质量[15,18]，从而实现聚类性能的提升。为了融入这种关系，通常设近邻关系图
${\boldsymbol{W}} \in {{{\bf{R}}}^{n \times n}}$ 描述了原始数据之间的近邻相似性关系，则约束Semi-NMF可描述为$$ \mathop {\min }\limits_{{{\boldsymbol{Z}}}\;{\boldsymbol{H}}} J = \left\| {{\boldsymbol{X}} - {\boldsymbol{ZH}}} \right\|_F^2 + \alpha {\text{tr}}{\left( {{\boldsymbol{HLH{}}^{\rm{T}}}} \right)_{}}_{}\quad{\rm{s.t.}}\;\;{_{}}_{}{\boldsymbol{H}} \geqslant 0 $$ (2) 式中
${\boldsymbol{L }}$ 是${\boldsymbol{W}}$ 的拉普拉斯矩阵。${\boldsymbol{D}}$ 是对角矩阵，定义为${\boldsymbol{D }}= \displaystyle\sum\limits_i{\boldsymbol{ W}}$ ，有${\boldsymbol{L }}= {\boldsymbol{D}} -{\boldsymbol{ W}}$ 。通过在优化模型中施加此类相似性关系约束，Semi-NMF在迭代中保持原数据点之间的关系，从而提高特征学习的性能。特别地，针对动作序列而言，设计结构相似性约束正则项融入到特征学习中是序列数据聚类的研究重点。1.2 结构相似性约束正则项构造
为了在特征表示学习的过程中融入结构相似性，文献[5]认为在动作关系图
${\boldsymbol{G }}$ 的学习过程中，当前数据帧$ {x_i} $ 与它之后的数据帧$ {x_{i + 1}} $ 之间的差异应该尽可能的小。为此可以引入正则约束项${\left\| {{\boldsymbol{GR}}} \right\|_1}$ ，其中${\boldsymbol{ R}} \in {{\bf{R}}^{n \times n}}$ 是近邻指示矩阵，定义如下：$${\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&0& \cdots &0\\ 1&{ - 1}&0& \cdots &0\\ 0&1&{ - 1}& \cdots &0\\ 0&0&1& \cdots &0\\ \vdots &{\vdots }&{\vdots }&{\cdots }&{ }\vdots\\ 0&0&0& \cdots &{ - 1}\\ 0&0&0& \cdots &1 \end{array}} \right]$$ (3) 该约束项通过L1范数使得
$ {x_i} $ 与$ {x_{i + 1}} $ 之间的差异尽可能小。基于此约束项，人们设计了许多基于结构约束聚类的动作分割方法[19]。文献[12]认为$ {x_i} $ 与其前后不止一个近邻帧具有相似性，可以在构造约束项时同时考虑多个近邻帧，因此可在低维特征表示${\boldsymbol{H}}$ 学习过程中，利用L2,1范数构造正则约束项${\left\| {{\boldsymbol{HR}}} \right\|_{2,1}}$ ，其中，包含$ q $ 个结构近邻的近邻指示矩阵${\boldsymbol{R}}$ 表示如下：$${\boldsymbol{R}} = \begin{array}{*{20}{c}} {}\\ {\overline \uparrow }\\ q\\ {\underline \downarrow }\\ {_{}}\\ {}\\ {}\\ {} \end{array}\left[ {\begin{array}{*{20}{c}} { - {q_{11}}}&0&0& \cdots &0\\ {{1_{21}}}&{ - {q_{22}}}&0& \cdots &0\\ {{1_{31}}}&{{1_{32}}}&{ - {q_{33}}}& \cdots &0\\ {{1_{\left( {q + 1} \right)1}}}&{{1_{\left( {q + 1} \right)2}}}&1& \cdots &0\\ \vdots &{\vdots }&{\vdots }&{\cdots }&{}\vdots\\ 0&0&0& \cdots &{ - {q_{\left( {n - q} \right)\left( {n - q} \right)}}}\\ \vdots &{\vdots }&{\vdots }&{\cdots }&{}\vdots\\ 0&0&0& \cdots &{{1_{n\left( {n - q} \right)}}} \end{array}} \right]$$ (4) 文献[20]认为此类多近邻相似性约束项中，离序列点越远的点，其相似性越低，所占权重应当不同。因此，在关系图
${\boldsymbol{G}}$ 学习中引入遗忘因子来构造约束项${\left\| {{\boldsymbol{G}} - {\boldsymbol{GR}}{^{\rm{T}}}} \right\|_2}$ ，包含3个结构近邻的近邻指示矩阵${\boldsymbol{ R}}$ 可描述为：$${\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} \beta &0&0& \cdots &0\\ {\alpha \beta }&\beta &0& \cdots &0\\ {{\alpha ^2}\beta }&{\alpha \beta }&\beta & \cdots &0\\ 0&{{\alpha ^2}\beta }&{\alpha \beta }& \cdots &0\\ \vdots &{\vdots }&{\vdots }&{\cdots }&{}\vdots\\ 0&0&{{\alpha ^2}\beta }& \cdots &\beta \end{array}} \right] $$ (5) 式中：参数
$ \beta = 1 - \alpha $ ，$ \alpha $ 是遗忘因子。相关实验表明，增加相邻帧的个数，可以强化动作片段内部的划分一致性，提升动作分割的准确性。综上可见，目前多数研究主要考虑如何设计更合理的结构近邻约束，忽视了近邻约束给动作边界处的准确分割可能带来的问题。如果要进一步提升动作分割的准确性，边界处的准确分割也同样重要。因此为了兼顾动作片段内部的一致归属和边界处的分割问题，本文通过融合不同近邻约束来有效降低目前方法存在的潜在弊端，实现更准确的动作分割。
2. 基于多图融合约束矩阵分解的特征表示
2.1 多图融合约束项构建
2.1.1 两种相似性关系图的构建
设
$ {x_i} $ 是动作序列中的一帧，考虑利用$ {x_i} $ 前后的各$ q $ 个近邻来构造该点结构近邻约束，则$ {x_i} $ 的结构近邻集合可描述为$$ {{C}}\left({x}_{i}\right)=\left\{{x}_{j}|\left|j-i\right|\leqslant {q}{且}j\ne i\right\} $$ (6) 式中：
${{C}}\left( {{x_i}} \right)$ 表示$ {x_i} $ 的$ q $ 结构近邻集合，$ i $ 和$ j $ 分别表示$ {x_i} $ 和$ {x_j} $ 在序列中所处的位置，若它们之间所处位置相差不超过$ q $ ，则$ {x_j} $ 是$ {x_i} $ 的一个结构近邻。 此时序列中所有帧的$ q $ 结构近邻集合构成了序列的结构近邻相似性关系，描述为一个无向无权图${{\boldsymbol{W}}_1} = \left[ {{{V}}\;{{{E}}_1}} \right]$ 。其顶点${{V}} = \left\{ {{x_1},{x_2}, \cdots ,} \right.\left. {{x_n}} \right\}$ 是序列中所有帧的集合，${{{E}}_1}$ 是顶点之间边的集合，定义如下：$$ E_1\left({x}_{i},{x}_{j}\right)=\left\{ \begin{array}{l}{{}_{}}_{}1{,}\quad{x}_{j}\in {{C}}{\left({x}_{i}\right)}_{}{或}_{}{x}_{i}\in {{C}}\left({x}_{j}\right)\\ {{}_{}}_{}{\text{0,}}\quad 其他\end{array}\right. $$ (7) 同时，对于度量相似性关系，选择经典的k近邻进行描述[15]。采用“binary”距离计算所有帧与
$ {x_i} $ 的距离，距离越小，说明与$ {x_i} $ 相似性越高，其中距离最小的前k个帧就构成了$ {x_i} $ 的k近邻集合，描述为$$ N\left( {{x_i}} \right) = \left\{ {{x_j}\left| {{d_{{x_i},{x_j}}} \leqslant {d_{ik}}} \right.} \right\} $$ (8) 式中：
$ {d_{{x_i},{x_j}}} $ 表示$ {x_i} $ 和$ {x_j} $ 之间的距离，$ {d_{ik}} $ 表示从最短距离开始的第k个最短距离。若$ {d_{{x_i},{x_j}}} \leqslant {d_{ik}} $ ，表明$ {x_j} $ 是$ {x_i} $ 的一个k近邻帧。同理，序列中所有帧的k近邻集合就构成了序列度量相似性关系，描述为无向无权图${{{{\boldsymbol{W}}}}_2} = \left[ {{{V}}\;{{{E}}_2}} \right]$ 。顶点${{V}}$ 也是序列中所有帧的集合，而$ {E_2} $ 是顶点之间边的集合，其定义如下:$$ E_2\left({x}_{i},{x}_{j}\right)=\left\{ \begin{array}{l}{{}_{}}_{}1{,}\quad {x}_{j}\in {\rm{N}}{\left({x}_{i}\right)}_{}{或}_{}{x}_{i}\in {\rm{N}}\left({x}_{j}\right)\\ {{}_{}}_{}{\text{0,}}\quad 其他\end{array}\right. $$ (9) 2.1.2 两多关系图的融合
如前所述，
${{\boldsymbol{W}}_1}$ 和${{\boldsymbol{W}}_2}$ 从不同相似性角度描述了帧间关系，各有利弊，为了充分吸收它们的优点，可以融合这两种相似性信息来实现融合约束，提升特征表示学习的质量。基本思路是采用线性组合的策略[21]，对${{\boldsymbol{W}}_1}$ 和${{\boldsymbol{W}}_2}$ 进行融合。为此构建多图融合约束项如下：$$ \sum\limits_{i = 1}^2 {{\tau _i}{\text{tr}}\left( {{\boldsymbol{HL}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} $$ (10) 其中
${{\boldsymbol{L}}_i}$ 表示第i个关系图的拉普拉斯矩阵，定义为${{\boldsymbol{L}}_i} = {{\boldsymbol{D}}_i} - {{\boldsymbol{W}}_i}$ ，${{\boldsymbol{D}}_i} = \displaystyle\sum\limits_i {{{\boldsymbol{W}}_i}}$ ，$ {\tau _i} $ 表示第i 个关系图在组合中的权重，定义为$$ {\tau _i} = \frac{{{{\tilde \tau }_i}}}{{\displaystyle\sum\limits_i {{{\tilde \tau }_i}} }},{\tilde \tau _i} = \frac{1}{{2\sqrt {{\text{tr}}\left( {{\boldsymbol{HL}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} }} $$ (11) 显然，在融合约束项中，不同图约束项的权重取决于各自图差异值计算的结果。计算结果越小，说明相似性越高，该约束项权重越大。考虑到同一动作片段内，相邻帧之间相似性较高，此时
$ {x_{i + 1}} $ 既是$ {x_i} $ 的结构近邻又是度量近邻，那么融合约束项可以有效保持它们之间的近邻关系；而在边界处，若$ {x_{i + 1}} $ 不是$ {x_i} $ 的度量近邻，那么图$ {{\boldsymbol{W}}_1} $ 计算所得相似性结果要小于$ {{\boldsymbol{W}}_2} $ 计算结果，$ {{\boldsymbol{W}}_1} $ 在融合约束项中权重小于$ {{\boldsymbol{W}}_2} $ 权重，因此结构相似性约束力度将会减小，从而有利于边界处差异性特征的保留。2.2 多图融合约束Semi-NMF低维特征学习
对于输入序列，将上述多图融合约束项融入到Semi-NMF中，构建低维特征学习优化模型如下所示：
$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{Z}}\;{\boldsymbol{H}}} J = \left\| {{\boldsymbol{X }}- {\boldsymbol{ZH}}} \right\|_F^2 + \alpha \sum\limits_{i = 1}^2 {{\tau _i}{\text{tr}}\left( {{\boldsymbol{HL}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} \\ {\rm{s.t.}}\;{\boldsymbol{H}} \geqslant 0,{\tau _i} = \frac{{{{\tilde \tau }_i}}}{{\displaystyle\sum\limits_i {{{\tilde \tau }_i}} }},{{\tilde \tau }_i} = \frac{1}{{2\sqrt {{\text{tr}}\left( {{\boldsymbol{HL}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} }} \\ \end{gathered} $$ (12) 式中：
$ \alpha $ 是多图融合约束项的权重参数，$\left\| {\;} \right\|_F^2$ 表示L2范数，$ \tau $ 为不同关系图在多图融合约束项中所占权重。求解该优化模型是一个非凸优化问题，根据文献[11]，可采用交替迭代的思路获得局部最优解。具体方法如下：1）更新
$ {\boldsymbol{Z}} $ 固定其他变量，由于
${\boldsymbol{Z}}$ 可以取负值，此时根据矩阵运算规则，可得${\boldsymbol{Z}}$ 的闭式解为$$ {\boldsymbol{Z}} = {\boldsymbol{XH}}{^{\rm{T}}}{\left( {{\boldsymbol{HH}}{^{\rm{T}}}} \right)^{ - 1}} $$ (13) 2）更新
${\boldsymbol{H}}$ 固定其他变量，
${\boldsymbol{H}}$ 的求解转化为关于${\boldsymbol{H}}$ 的如下问题：$$ \begin{array}{c} {\rm{mi}}{\rm{n}}\;L\left( {\boldsymbol{H}} \right) = {\rm{tr}}\left( {{\boldsymbol{XX}}{^{\rm{T}}} - 2{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{ZH}} + {{\boldsymbol{H}}^{\rm{T}}}{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{ZH}}} \right)+\\ \alpha \displaystyle\sum\limits_{i = 1}^2 {{\tau _i}{\rm{tr}}\left( {{\boldsymbol{HD}}{_i}{{\boldsymbol{H}}^{\rm{T}}} - {\boldsymbol{HW}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} \end{array} $$ (14) 考虑到
${\boldsymbol{X}}$ 和${\boldsymbol{Z}}$ 均可取负值，不失一般地，令${{\boldsymbol{M}}^{\text{ + }}}$ 、${{\boldsymbol{M}}^ - }$ 分别表示矩阵${\boldsymbol{M}}$ 非负部分和负值部分，即：${{\boldsymbol{M}}^{\text{ + }}}{\text{ = }}{{\left( {\left| {\boldsymbol{M}} \right|{\text{ + }}{\boldsymbol{M}}} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {\boldsymbol{M}} \right|{\text{ + }}{\boldsymbol{M}}} \right)} {\text{2}}}} \right. } {\text{2}}}$ ，$ {M^ - }{\text{ = }}{{\left( {\left| M \right| - M} \right)} \mathord{\left/ {\vphantom {{\left( {\left| M \right| - M} \right)} {\text{2}}}} \right. } {\text{2}}} $ ，于是问题可改写为$$ \begin{array}{c} {\rm{mi}}{\rm{n}}\;{{L}}\left( {\boldsymbol{H}} \right) = {\rm{tr}}\left( {{\boldsymbol{X}}{{\boldsymbol{X}}^{\rm{T}}} - 2{{\left( {{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ + }{\boldsymbol{H}} + 2{{\left( {{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ - }{\boldsymbol{H}}} \right) +\\ {\rm{tr}}\left( {{{\boldsymbol{H}}^{\rm{T}}}{{\left( {{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ + }{\boldsymbol{H}} - {{\boldsymbol{H}}^{\rm{T}}}{{\left( {{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ - }{\boldsymbol{H}}} \right)+ \\ \alpha \displaystyle\sum\limits_{i = 1}^2 {{\tau _i}{\rm{tr}}\left( {{\boldsymbol{HD}}{_i}{{\boldsymbol{H}}^{\rm{T}}} - {\boldsymbol{HW}}{_i}{{\boldsymbol{H}}^{\rm{T}}}} \right)} \end{array} $$ (15) 根据Semi-NMF的迭代规则求解理论[11]，
$ {\boldsymbol{H}} $ 的更新规则推导可以通过构造辅助函数并求解该函数来完成。$ L\left( {\boldsymbol{H}} \right) $ 的辅助函数$ G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) $ 需满足$ G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) \geqslant L\left( {\boldsymbol{H}} \right) $ 且$ G\left( {{\boldsymbol{H}},{\boldsymbol{H}}} \right) = L\left( {\boldsymbol{H}} \right) $ 。可以定义$ L\left( {\boldsymbol{H}} \right) $ 的辅助函数为：$$ \begin{array}{c} G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) = \displaystyle\sum\limits_{ij} {{X_{ij}}{X_{ij}}} - 2\displaystyle\sum\limits_{ij} {\left( {{{\boldsymbol{Z}}^{\rm{T}}}X} \right)_{ij}^ + {\boldsymbol{H}}_{ij}^t\left( {1 + \log \frac{{{{\boldsymbol{H}}_{ij}}}}{{{\boldsymbol{H}}_{ij}^t}}} \right)} +\\ \displaystyle\sum\limits_{ij} {\left( {{{\boldsymbol{Z}}^{\rm{T}}}X} \right)_{ij}^ - \left( {\frac{{{\boldsymbol{H}}_{ij}^2 + {\boldsymbol{H}}_{ij}^{t2}}}{{{\boldsymbol{H}}_{ij}^t}}} \right)} + \displaystyle\sum\limits_{ij} {{{\left( {{{\left( {{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ + }{{\boldsymbol{H}}^t}} \right)}_{ij}}\frac{{{\boldsymbol{H}}_{ij}^2}}{{{\boldsymbol{H}}_{ij}^t}}} -\\ \displaystyle\sum\limits_{ijl} {\left( {\left( {{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{Z}}} \right)_{jl}^ - {\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{jl}^t} \right)\left( {1 + \log \frac{{{{\boldsymbol{H}}_{ij}}{{\boldsymbol{H}}_{il}}}}{{{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{il}^t}}} \right)} + \\ \alpha \displaystyle\sum\limits_{k = 1}^2 {{\tau _k}\left( {\displaystyle\sum\limits_{ij} {{{\left( {{{\boldsymbol{H}}^t}{{\boldsymbol{D}}_k}} \right)}_{ij}}\frac{{{\boldsymbol{H}}_{ij}^2}}{{{\boldsymbol{H}}_{ij}^t}}} } \right.} -\\ \left. { \displaystyle\sum\limits_{ijl} {{{\left( {{{\boldsymbol{W}}_k}} \right)}_{jl}}{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{jl}^t\left( {1 + \log \frac{{{{\boldsymbol{H}}_{ij}}{{\boldsymbol{H}}_{il}}}}{{{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{il}^t}}} \right)} } \right) \\ \end{array} $$ 首先需要证明
$ G\left( {{\boldsymbol{H}} ,{{\boldsymbol{H}} ^t}} \right) $ 是$ L\left( {\boldsymbol{H}} \right) $ 的一个辅助函数。证明 显然
$G\left( {{\boldsymbol{H}} ,{\boldsymbol{H}} } \right) = L\left( {\boldsymbol{H}} \right)$ 满足，重点证明$G\left( {{\boldsymbol{H}} , {{\boldsymbol{H}} ^t}} \right) \geqslant L\left( {\boldsymbol{H}} \right)$ 。当非负矩阵
${\boldsymbol{S}} \in {{\bf{R}}^{n \times n}}$ 、${\boldsymbol{B}} \in {{\bf{R}}^{p \times p}}$ 是对角矩阵时，如下不等式成立：$$ {\text{tr}}\left( {{{\boldsymbol{H}} ^{\rm{T}}}{\boldsymbol{SHB}} } \right) \leqslant \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^p {\left( {{{\boldsymbol{SH}} ^t}{\boldsymbol{B}}} \right)} } \frac{{{\boldsymbol{H}} _{ij}^2}}{{{\boldsymbol{H}} _{ij}^t}} $$ (16) 利用该不等式，可得：
$$ {\text{tr}}\left( {{{\boldsymbol{H}} ^{\rm{T}}}{{\left( {{{\boldsymbol{Z}} ^{\rm{T}}}{\boldsymbol{Z}} } \right)}^ + }{\boldsymbol{H}} } \right) \leqslant \sum\limits_{ij} {{{\left( {{{\left( {{{\boldsymbol{Z}} ^{\rm{T}}}{\boldsymbol{Z}} } \right)}^ + }{{\boldsymbol{H}} ^t}} \right)}_{ij}}\frac{{{\boldsymbol{H}} _{ij}^2}}{{{\boldsymbol{H}} _{ij}^t}}} $$ (17) $$ \sum\limits_{k = 1}^2 {{\tau _k}} {\text{tr}}\left( {{\boldsymbol{H}} {{\boldsymbol{D}} _k}{{\boldsymbol{H}} ^{\rm{T}}}} \right) \leqslant \sum\limits_{k = 1}^2 {{\tau _k}\sum\nolimits_{ij} {{{\left( {{{\boldsymbol{H}} ^t}{{\boldsymbol{D}} _k}} \right)}_{ij}}\frac{{{\boldsymbol{H}} _{ij}^2}}{{{\boldsymbol{H}} _{ij}^t}}} } $$ (18) 利用不等式
${\textit{z}} > 1 + \log\; {\textit{z}}$ （${\textit{z}} > 0$ ），可得：$$ {\text{tr}}\left( {{{\left( {{{\boldsymbol{X}} ^ {\rm{T}}}{\boldsymbol{Z}} } \right)}^ + }{\boldsymbol{H}} } \right) \geqslant \sum\limits_{ij} {\left( {{{\boldsymbol{Z}} ^ {\rm{T}}}{\boldsymbol{X}} } \right)_{ij}^ + {\boldsymbol{H}} _{ij}^t\left( {1 + \log \frac{{{{\boldsymbol{H}} _{ij}}}}{{{\boldsymbol{H}} _{ij}^t}}} \right)} $$ (19) $$ \begin{gathered} {\text{tr}}\left( {{{\boldsymbol{H}}^ {\rm{T}}}{{\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{Z}}} \right)}^ - }{\boldsymbol{H}}} \right) \geqslant \\ \sum\limits_{ijl} {\left( {\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{Z}}} \right)_{jl}^ - {\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{jl}^t} \right)\left( {1 + \log \frac{{{{\boldsymbol{H}}_{ij}}{{\boldsymbol{H}}_{il}}}}{{{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{il}^t}}} \right)} \end{gathered} $$ (20) $$ \begin{gathered} \sum\limits_{k = 1}^2 {{\tau _k}} {\text{tr}}\left( {{\boldsymbol{H}}{{\boldsymbol{W}}_k}{{\boldsymbol{H}}^{\rm{T}}}} \right) \geqslant \\ \sum\limits_{k = 1}^2 {{\tau _k}} \sum\limits_{ijl} {\left( {{{\boldsymbol{W}}_k}} \right)_{jl}^{}{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{jl}^t\left( {1 + \log \frac{{{{\boldsymbol{H}}_{ij}}{{\boldsymbol{H}}_{il}}}}{{{\boldsymbol{H}}_{ij}^t{\boldsymbol{H}}_{il}^t}}} \right)} \end{gathered} $$ (21) 利用该不等式
$ {a^2} + {b^2} \geqslant 2ab $ （$ a,b > 0 $ ），可得：$$ {\text{2tr}}\left( {{{\left( {{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Z}}} \right)}^ - }{\boldsymbol{H}}} \right) \leqslant \sum\limits_{ij} {\left( {{{\boldsymbol{Z}}^{\rm{T}}}{\boldsymbol{X}}} \right)_{ij}^ - \left( {\frac{{{\boldsymbol{H}}_{ij}^2 + {\boldsymbol{H}}_{ij}^{t2}}}{{{\boldsymbol{H}}_{ij}^t}}} \right)} $$ (22) 综上可得：
$ G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) \geqslant L\left( {\boldsymbol{H}} \right) $ ，因此它是$ L\left( {\boldsymbol{H}} \right) $ 的辅助函数。证毕。
其次通过求解
$ G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) $ 来求解优化问题(14)，考虑到$ G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right) $ 是一个凸优化，令：$$ \frac{{\partial G\left( {{\boldsymbol{H}},{{\boldsymbol{H}}^t}} \right)}}{{\partial {{\boldsymbol{H}}_{ij}}}} = 0 $$ (23) 可得
${\boldsymbol{H}}$ 迭代规则：$$ {\boldsymbol{H}} \leftarrow {\boldsymbol{H}}\sqrt {\frac{{{{\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{X}}} \right)}^ + } + {{\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{Z}}} \right)}^ - }{\boldsymbol{H}} + \alpha \displaystyle\sum\limits_{i = 1}^2 {{\tau _i}{\boldsymbol{HW}}{_i}} }}{{{{\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{X}}} \right)}^ - } + {{\left( {{{\boldsymbol{Z}}^ {\rm{T}}}{\boldsymbol{Z}}} \right)}^ + }{\boldsymbol{H}} + \alpha \displaystyle\sum\limits_{i = 1}^2 {{\tau _i}{\boldsymbol{HD}}{_i}} }}} $$ (24) 3）更新
$ \tau $ 为了确定不同关系图的权重，需要根据每次迭代过程中
$ {\boldsymbol{H}}$ 的重新确定$ {{\boldsymbol{W}}_1} $ 和$ {{\boldsymbol{W}}_2} $ 的权重系数。因此迭代中$ \tau $ 需要按照式（11）重新计算权重。通过以上的迭代更新，最终可以获得动作序列的低维特征表示
${\boldsymbol{H}}$ ，利用该特征表示可以获取序列的k近邻图表示。3. 基于k近邻图的动作分割
考虑到获得的矩阵
${\boldsymbol{H}}$ 中蕴含丰富的各种帧间相似性关系，可以清晰地通过这种相似性关系描述整个动作序列的关系图，因此矩阵${\boldsymbol{H}}$ 生成k近邻图${\boldsymbol{G}} \in {{\bf{R}}^{n \times n}}$ 是一个无向无权图${\boldsymbol{G}} = \left[ {{{V}}\;{{E}}} \right]$ ，顶点${{V}}$ 是序列中所有帧的集合，${{E}}$ 是顶点之间边的集合，定义如下：$$ E\left({h}_{i},{h}_{j}\right)=\left\{ \begin{array}{l}{}_{}1{,}\;\;\;{h}_{j}\in N{\left({h}_{i}\right)}_{}{或}_{}{h}_{i}\in N\left({h}_{j}\right)\\ {}_{}{\text{0,}}\;\;\;其他\end{array}\right. $$ (25) 其中
${{N}}\left( {{h_i}} \right)$ 表示利用特征表示矩阵${\boldsymbol{H}}$ 计算获取的第i帧的k近邻集合，k近邻计算同样按照文献[14]方法进行。最后利用图割方法对
${\boldsymbol{G}}$ 进行分割，获得动作分割结果。Ncut是常用的图分割方法，其利用${\boldsymbol{D}}$ 的拉普拉斯特征值第2小所对应的特征向量来分割，详细介绍可参考文献[17]。综上，本文提出的MGSeNMF动作分割方法可描述如下：
算法 基于MGSeNMF动作分割
输入
${\boldsymbol{X}}$ ,$ q $ ，k，$ \alpha $ 1)初始化:
$\left( {{\boldsymbol{Z}},{\boldsymbol{H}}} \right) \leftarrow {\rm{Semi}} - {\rm{NMF}}\left( X \right)$ ，${{\boldsymbol{W}}_1} \leftarrow $ 式(6~7)，${{\boldsymbol{W}}_2} \leftarrow $ 式(8~9) ，$ {\tau _1} = {\tau _2} = 0.5 $ 2)while 没有收敛 do
${\boldsymbol{Z}} \leftarrow $ 式(13)，${\boldsymbol{H}}\leftarrow $ 式(24)，$\tau \leftarrow$ 式(11)3)end while
4)生成k近邻图：
${\boldsymbol{G}}$ $ \leftarrow $ ${\boldsymbol{H}}$ 5)聚类: Ncut
$\left( {\boldsymbol{G}} \right)$ 输出 分割结果
其中初始矩阵
${\boldsymbol{Z}}$ 、${\boldsymbol{H}}$ 采用经典Semi-NMF进行赋值，$ \tau $ 初始值都是0.5表示两种图关系的权重相同。4. 实验与讨论
4.1 数据集及比较方法
实验在两类不同的真实动作序列共6个数据集上进行。一类是视频序列，包括Weizmann (Weiz)、Keck和UT-Interaction (UT-I)[22]。其中Weiz和UT-I是人体动作序列，Keck是手势动作序列。与文献[22]一样，提取HoG 特征作为这些序列的输入数据。另一类来自 CMU Mocap database 86号运动捕获序列数据[23]。这些运动序列主要由各个关节附着传感器的人在一定时间内做出不同的动作而生成，共14组。选取其中的第1、2、3组，记作：mo-1、mo-2、mo-3。这些数据集信息如表1所示。
表 1 实验数据集信息Table 1 Characteristics of datasets数据集 序列帧数 特征维度 动作数 重复动作 Weiz 701 324 10 无 Keck 1245 324 10 无 UT-I 650 1024 6 无 mo-1 954 42 4 有 mo-2 2192 42 8 有 mo-3 1760 42 7 有 为了比较不同方法动作分割的效果，与TSC、TLRSC、SC-NMF、TW-FINCH等基于聚类的动作分割方法进行比较。其中：TSC和TLRSC是基于SC的动作分割方法；SC-NMF是基于Semi-NMF的方法，它在低维表示过程中引入了
$ q $ 个结构近邻构造的约束项，再生成一个k近邻图用于动作分割；TW-FINCH是一个基于层次聚类的动作分割方法。实验的参数分别根据文献的推荐进行设置。其中MGSeNMF与SC-NMF一样，设置Weiz、Keck、UT-I的特征维数为60，mo-1、mo-2、mo-3的特征维数为15；
$ \alpha $ 取值范围[0.001, 0.01, 0.1, 1, 10, 100, 1000]。 MGSeNMF设置$ q $ 取值范围[1, 2, 3, 4, 5, 6, 8, 10]，k与$ q $ 相同。SC-NMF中$ q $ 的取值与文献保持一致，为MGSeNMF中$ q $ 的2倍。所有方法获取最优结果作为输出。评价指标采用标准的ACC和NMI进行衡量[24-25]。4.2 动作分割结果比较
表2和表3所示是不同方法动作分割的ACC和NMI性能比较。可以看到，MGSeNMF在大多数数据集上都获得了更好的动作分割效果，特别是在3个视频序列数据集上性能提升效果明显；在mo-1和mo-3 上，MGSeNMF也可以获得最好的ACC和NMI值，在mo-2上稍差于SC-NMF。
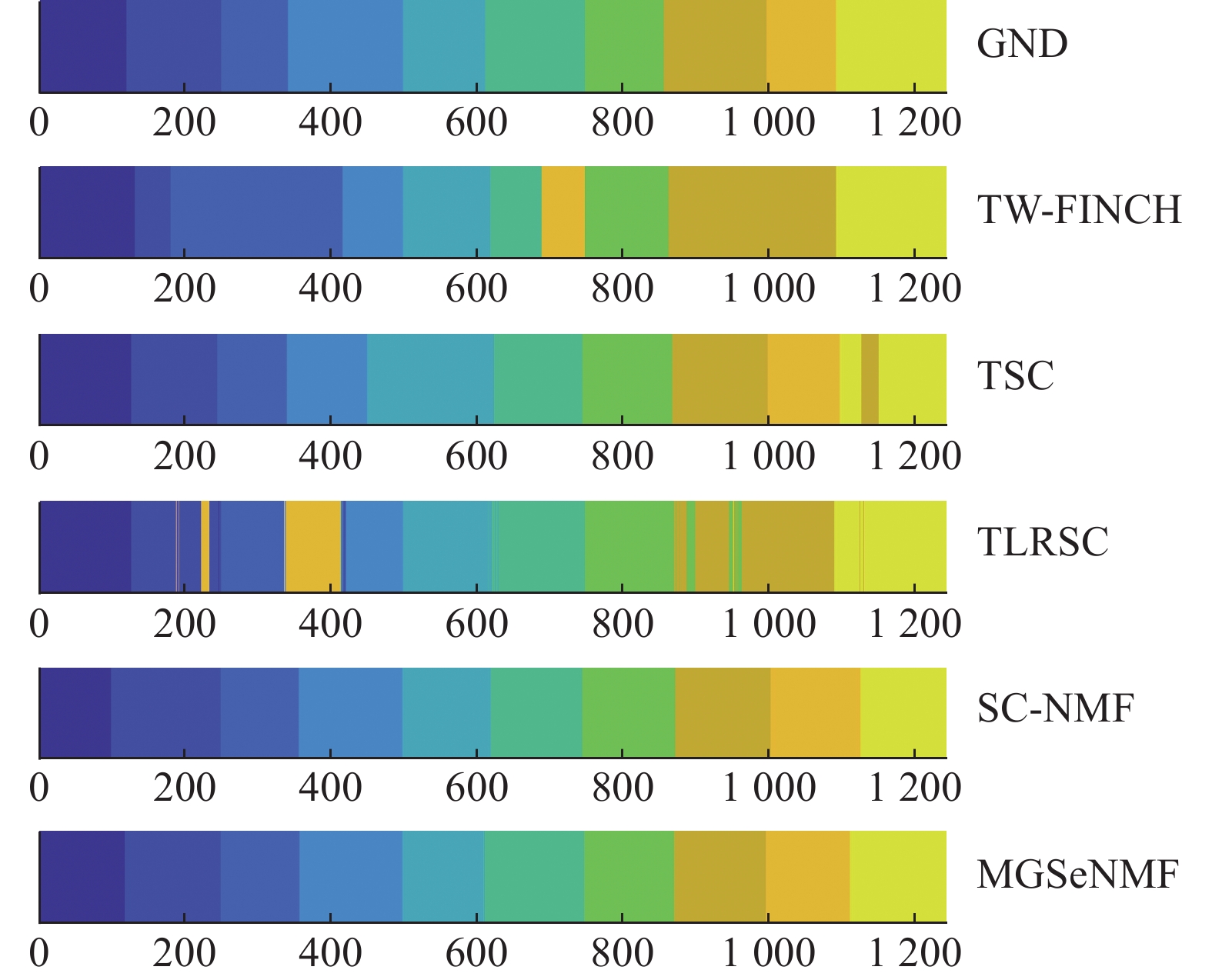
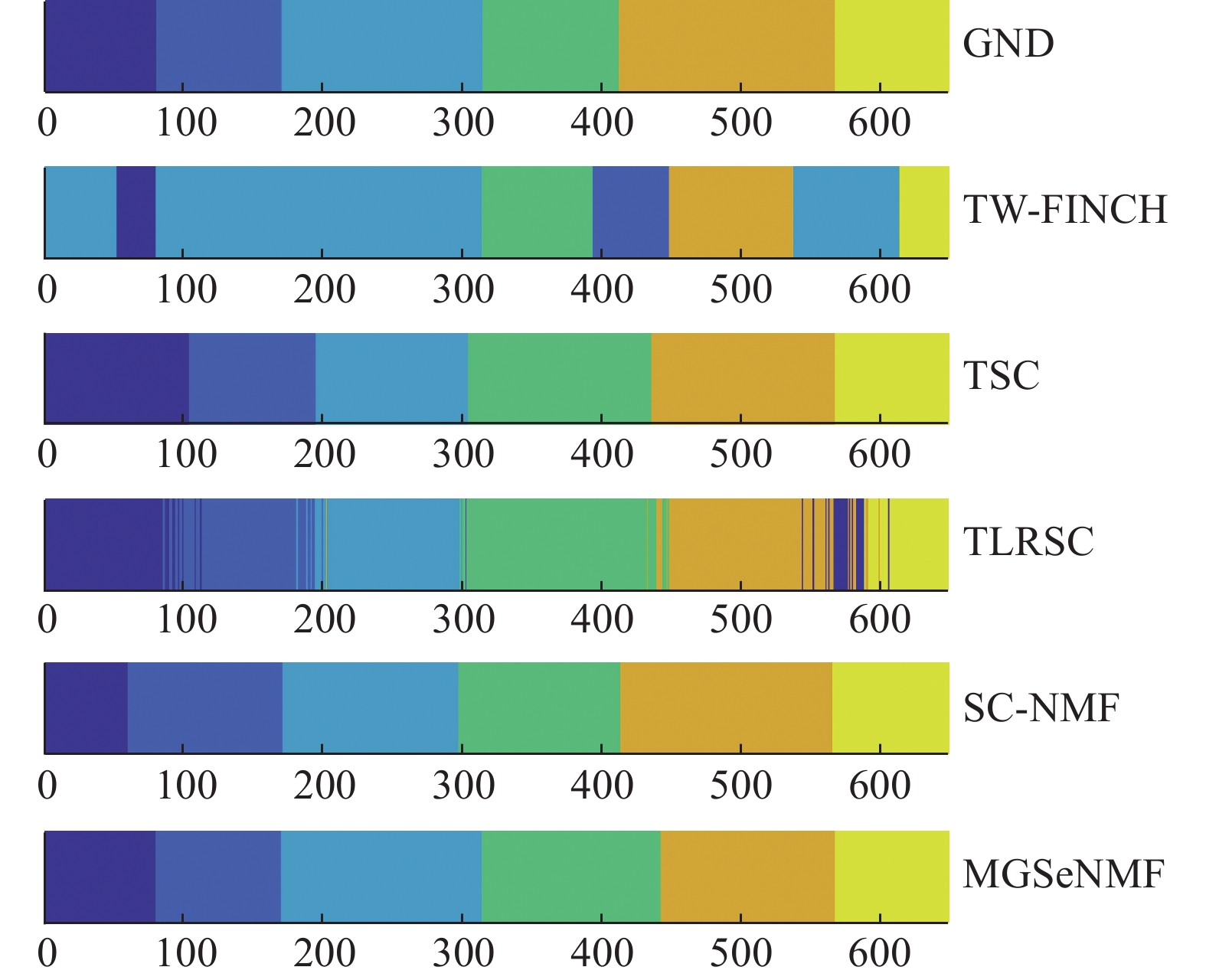
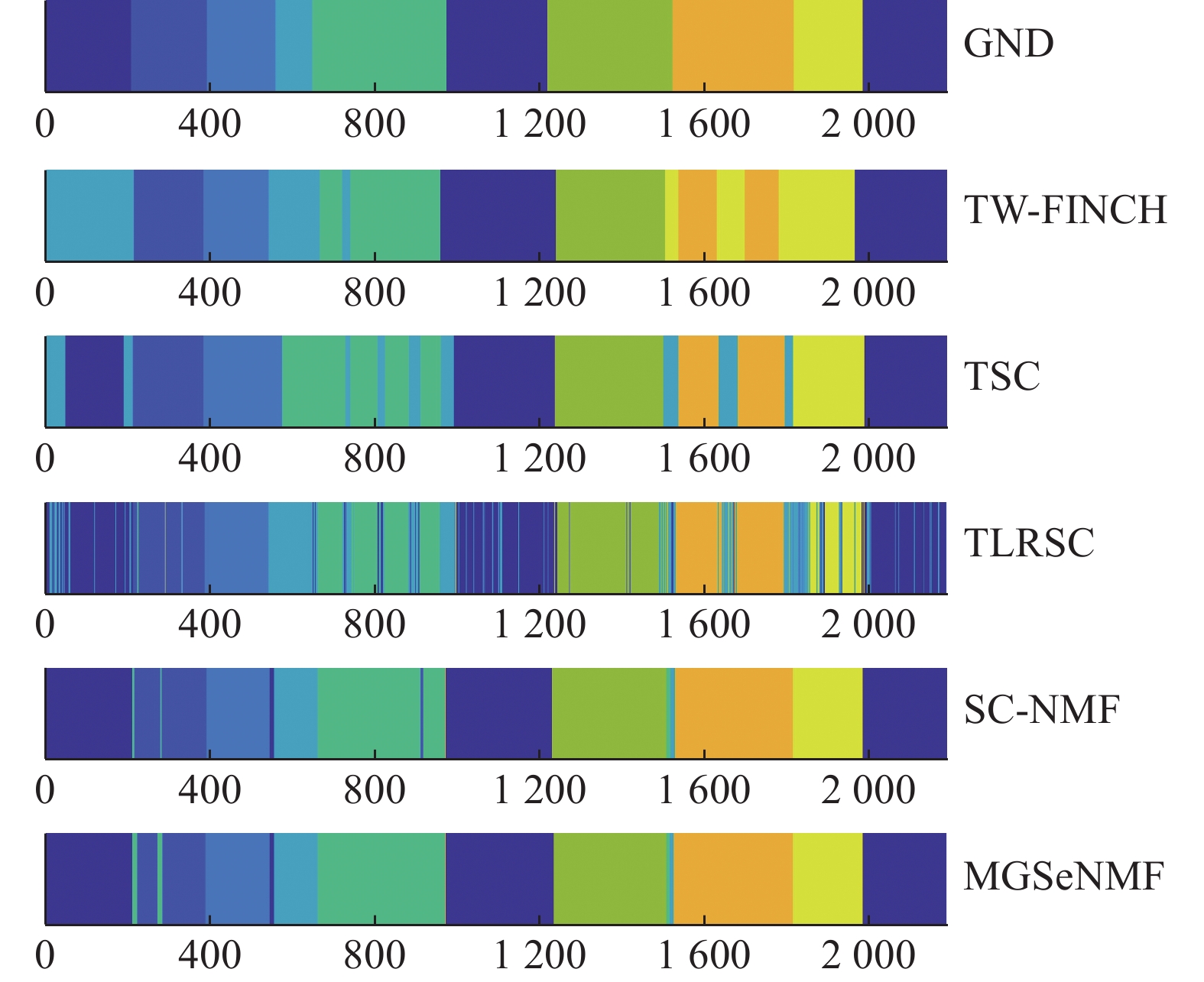
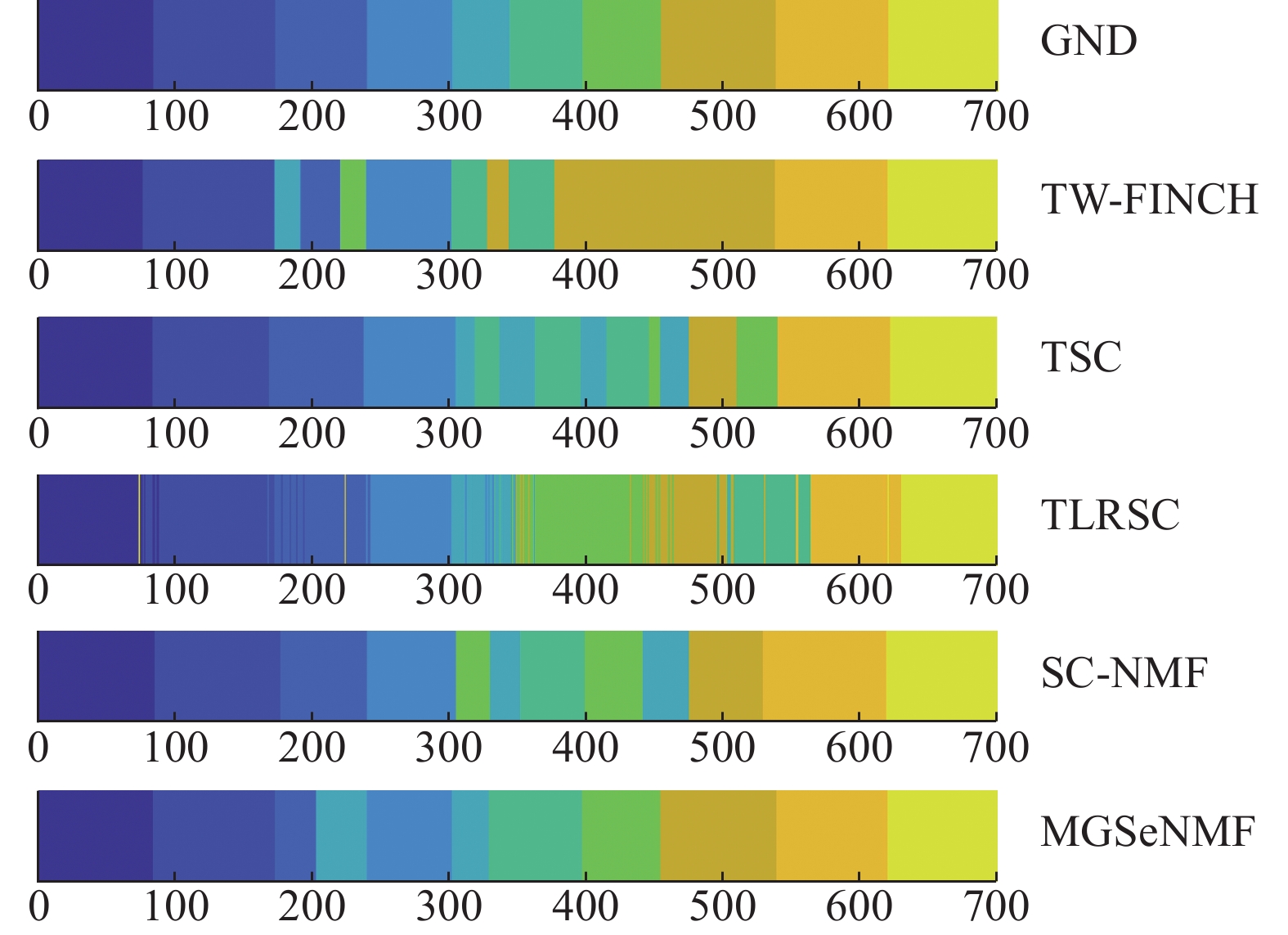
表 2 不同方法的ACC性能比较Table 2 ACC comparison with different methods数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.7874 0.7789 0.8759 0.7660 0.9244 Keck 0.9044 0.8000 0.9173 0.7406 0.9566 UT-I 0.8738 0.8277 0.9369 0.5800 0.9534 mo-1 0.6709 0.8899 0.9644 0.6583 0.9644 mo-2 0.8244 0.8166 0.9630 0.7865 0.9576 mo-3 0.7364 0.7432 0.9489 0.8051 0.9517 表 3 不同方法的NMI性能比较Table 3 NMI comparison with different methods数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.8303 0.8116 0.8769 0.8279 0.9468 Keck 0.8799 0.8689 0.8939 0.8231 0.9389 UT-I 0.8112 0.7255 0.8937 0.5057 0.9336 mo-1 0.6515 0.6822 0.8693 0.6021 0.8733 mo-2 0.8007 0.7107 0.9119 0.7498 0.9021 mo-3 0.7561 0.6757 0.8698 0.7465 0.8786 为进一步分析动作分割效果，图1~6所示为不同方法的最终动作分割结果（不同颜色表示不同的动作片段）比较，其中GND表示数据集的标准结果。
图 1 Weiz数据集上的动作分割结果Fig. 1 The action segmentation yielded on Weiz
下载:
全尺寸图片
图 2 Keck数据集上的动作分割结果Fig. 2 The action segmentation yielded on Keck下载:
全尺寸图片
图 3 UT-I数据集上的动作分割结果Fig. 3 The action segmentation yielded on UT-I下载:
全尺寸图片
图 4 mo-1数据集上的动作分割结果Fig. 4 The action segmentation yielded on mo-1下载:
全尺寸图片
图 5 mo-2数据集上的动作分割结果Fig. 5 The action segmentation yielded on mo-2下载:
全尺寸图片
图 6 mo-3数据集上的动作分割结果Fig. 6 The action segmentation yielded on mo-3下载:
全尺寸图片
可以看到，与其他方法相比，MGSeNMF与SC-NMF基本都可以保持动作序列内部的一致归属。它们的主要区别在于动作边界处的分割结果。由于MGSeNMF引入k近邻图信息，在保持有效近邻关系的同时，弱化了结构近邻图的强制性约束，从而可以在动作边界处实现更客观准确的分割。如在Weiz数据集上，虽然MGSeNMF将动作3的结束部分划分到动作5，但是主要动作之间的边界都是清晰的， 与标准分割一致，没有出现如SC-NMF那样将动作7的结束和动作8的开始分割为一个独立新动作之类的错误。Keck数据集上，动作1和动作2、动作9和动作10之间的分割更接近标准。可见利用多图融合信息，MGSeNMF在确保动作片段内一致归属的同时，边界处的准确分割得到了进一步增强，从而使得动作分割的准确性得到了进一步提升。
4.3 参数分析
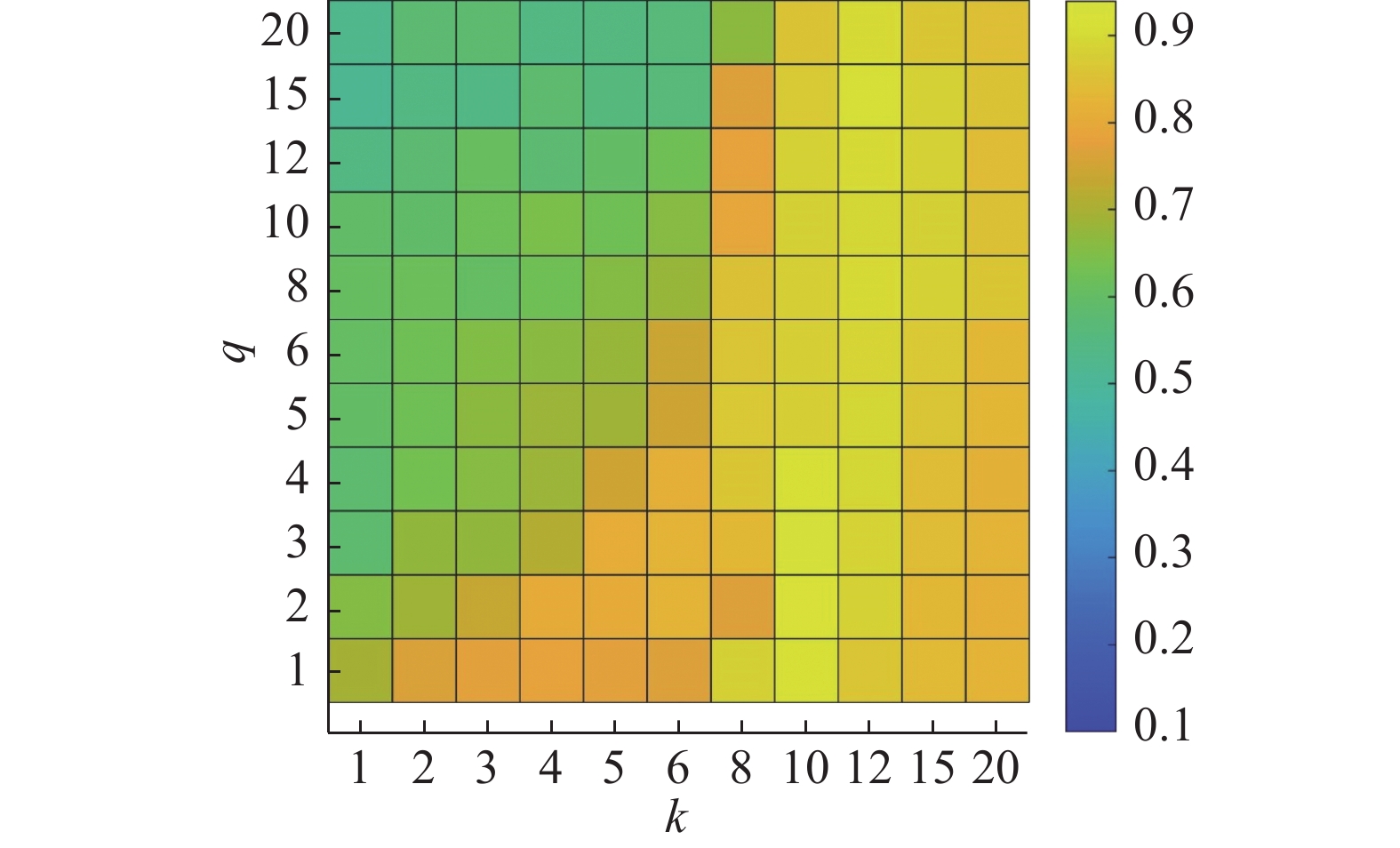
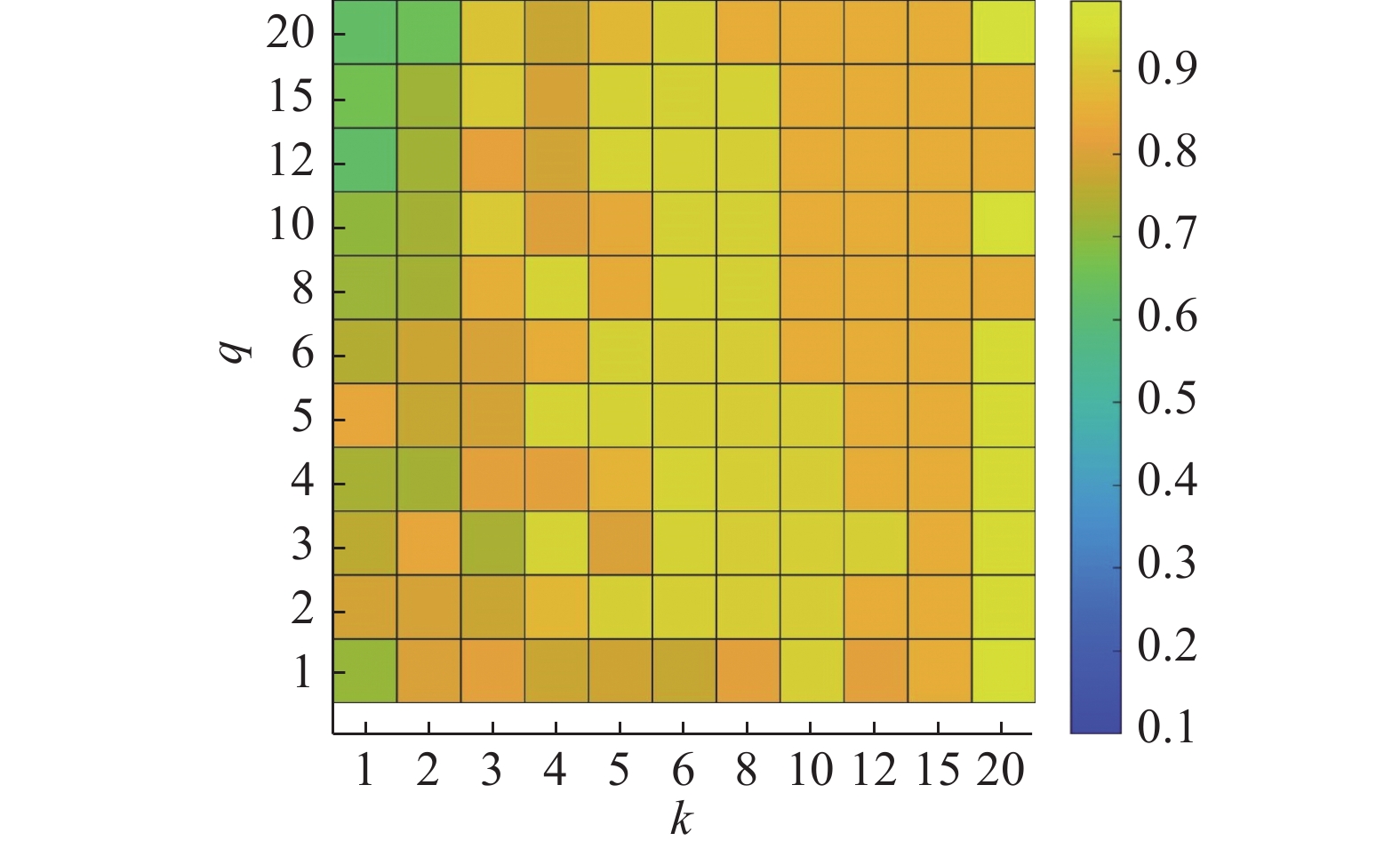
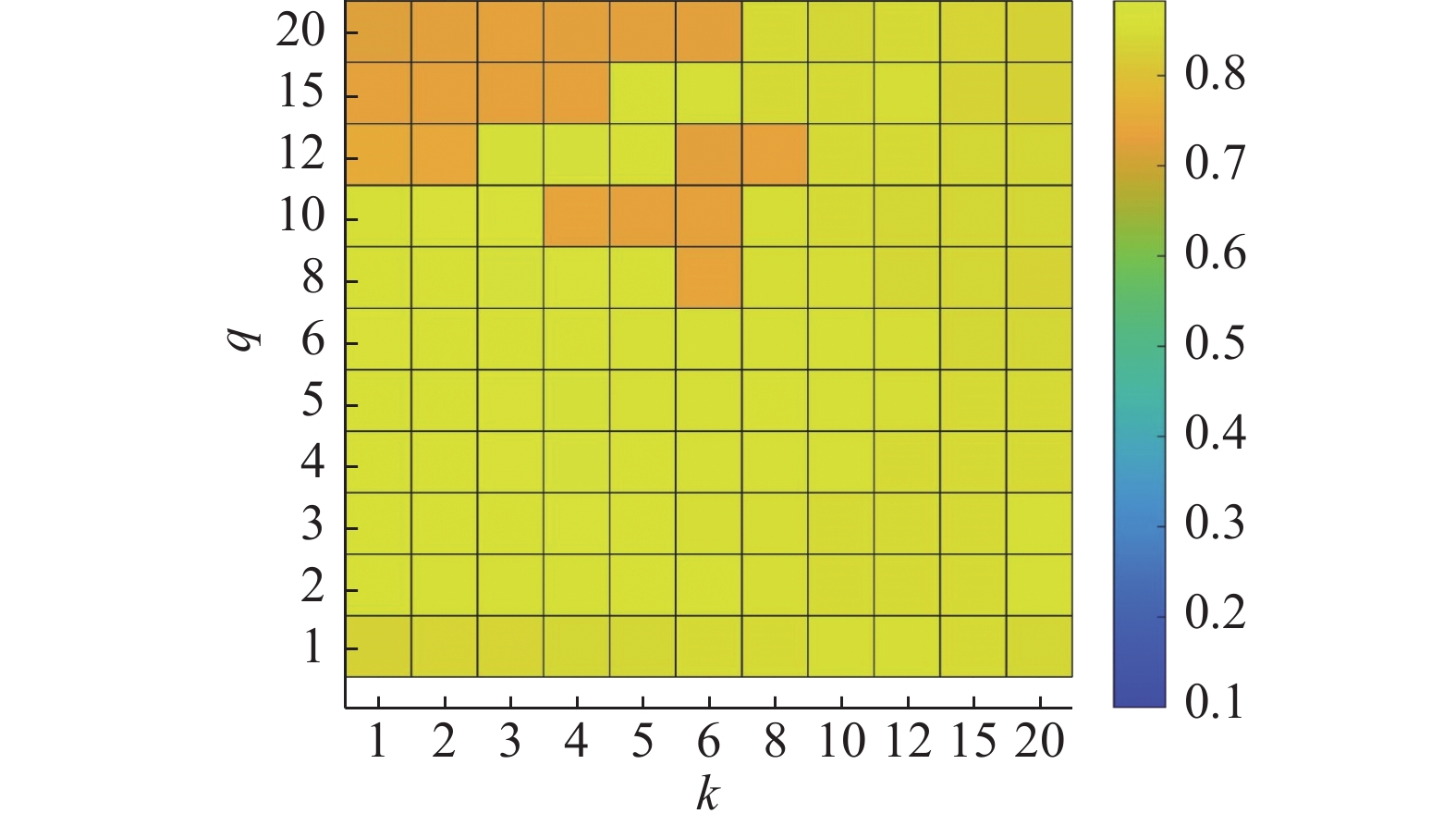
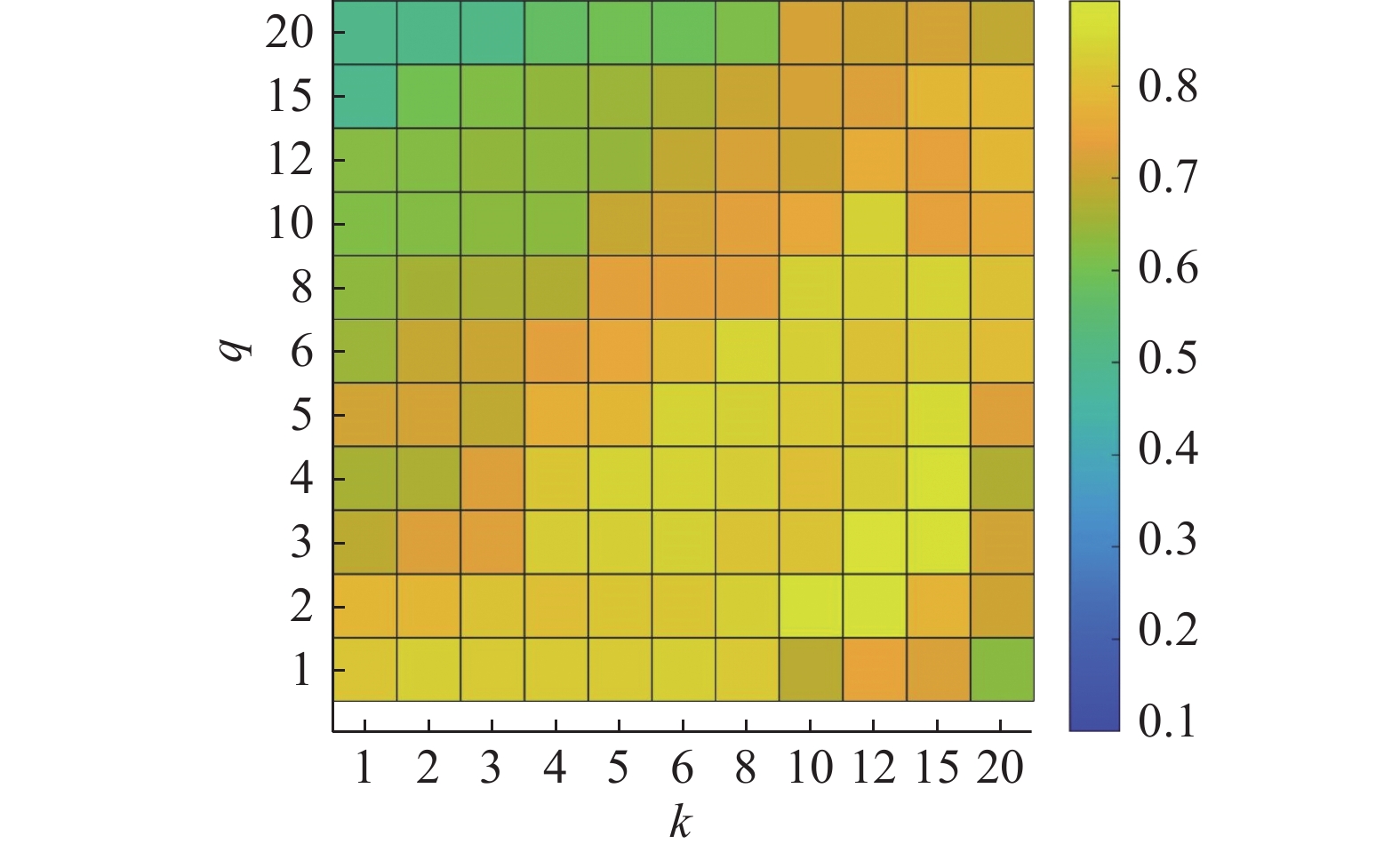
MGSeNMF中参数k和
$ q $ 分别描述两种相似图中近邻的个数，实验取值在[1，2，3，4，5，6，8，10，12，15，20]范围内，如图7~12所示为不同取值下的NMI性能。可以看到，同时增大k和$ q $ ，NMI性能在Weiz、Keck、UT-I、mo-3上提升明显，说明引入较多的结构近邻节点，可以更有效约束动作序列结构近邻之间表示尽可能的一致，从而确保动作片段内部归属到相同类。同时需要注意到，过大的$ q $ 仍意味着会将不同动作边界处的数据帧建立高相似性关系，从而导致错误分割。如当$ q $ =20时，NMI性能在Weiz、Keck、UT-I、mo-1、mo-3上下降明显，在其他数据集上也有下降，因此$ q $ 的选择不能过大。同理对于k的取值，和文献[14]所得结论一样，过大的k也将导致性能的下降，因此对k的讨论本文不再赘述。
图 7 Weiz数据集上不同q和k下的NMI值Fig. 7 The NMI with different q and k on Weiz下载:
全尺寸图片
图 8 Keck数据集上不同q和k下的NMI值Fig. 8 The NMI with different q and k on Keck下载:
全尺寸图片
图 9 UT-I数据集上不同q和k下的NMI值Fig. 9 The NMI with different q and k on UT-I下载:
全尺寸图片
图 10 mo-1数据集上不同q和k下的NMI值Fig. 10 The NMI with different q and k on mo-1下载:
全尺寸图片
图 11 mo-2数据集上不同q和k下的NMI值Fig. 11 The NMI with different q and k on mo-2下载:
全尺寸图片
图 12 mo-3数据集上不同q和k下的NMI值Fig. 12 The NMI with different q and k on mo-3下载:
全尺寸图片
MGSeNMF中参数
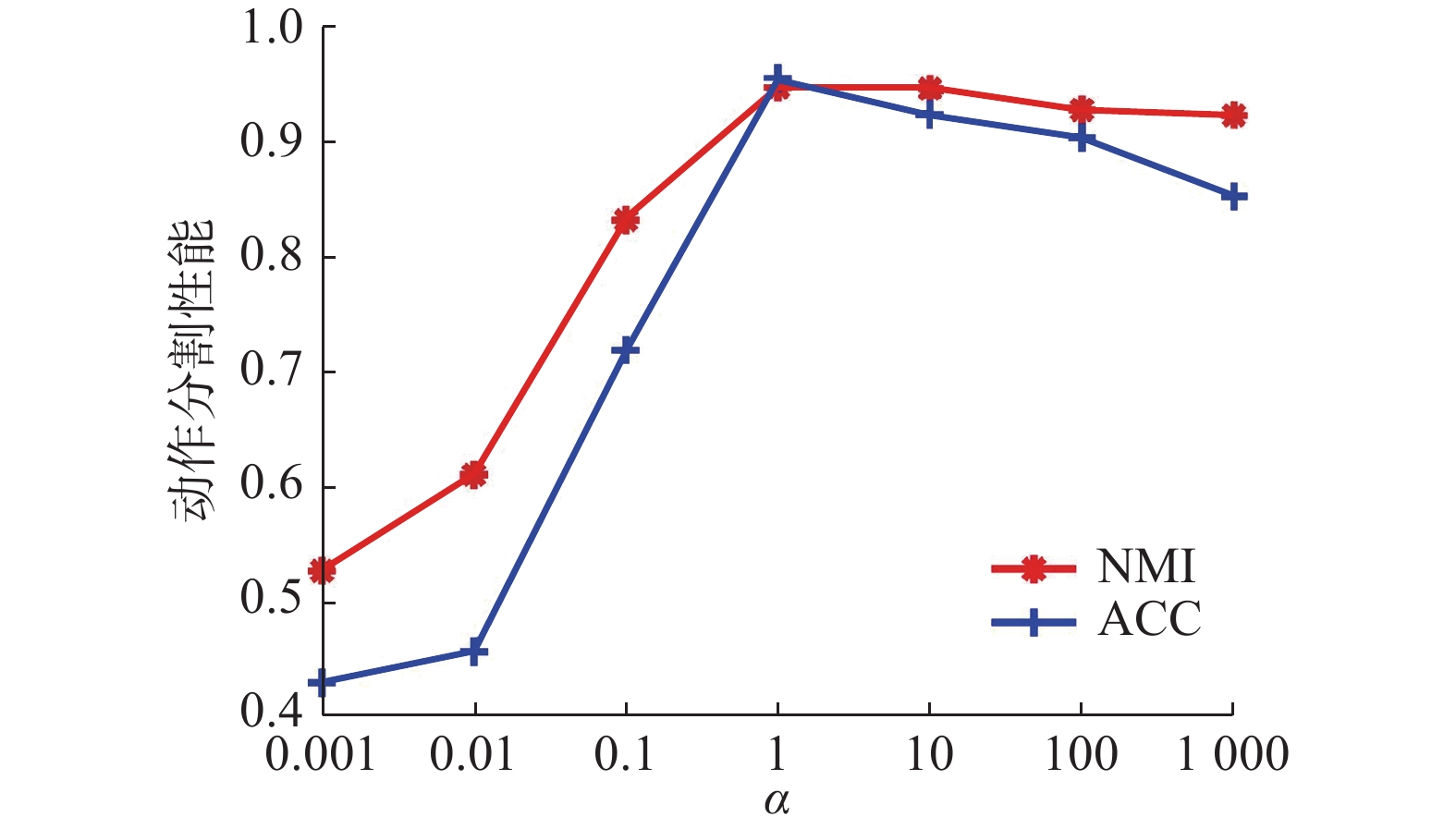
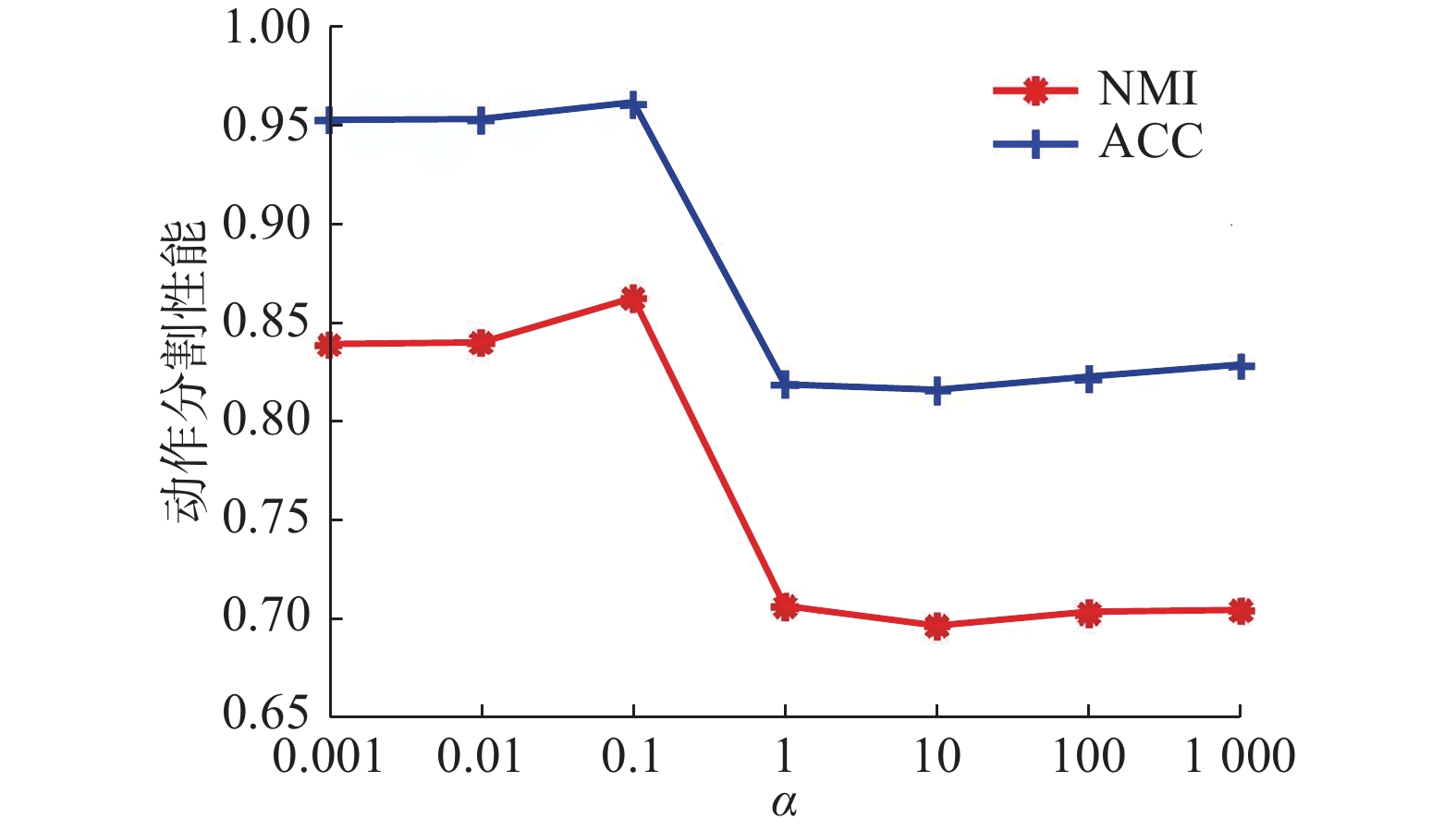
$ \alpha $ 描述了多图融合约束项在优化目标中的权重。固定其他参数，设置$ \alpha $ 取值[0.001, 0.01, 0.1, 1, 10,100, 1000]，以Weiz和mo-1为例，图13~14所示为不同$ \alpha $ 取值下的ACC和NMI值。可以看到，在Weiz数据集上，当$ \alpha \leqslant 1 $ 时，ACC和NMI提升明显，之后略有下降；与之相反，在mo-1数据集上，当$ \alpha \geqslant 0.1 $ 时，ACC和NMI下降明显。这是因为对于Weiz之类的高维数据而言，需要较大的$ \alpha $ 值来提升多图融合约束项在整个优化模型中的权重；反之对于mo-1等数据而言，由于原始数据特征维数相对较小，因此需要较小的$ \alpha $ 值来调节多图融合约束项在优化模型中的权重。
图 13 Weiz数据集上ACC和NMI值随$ \alpha $ 变化情况Fig. 13 The ACC and NMI with different set of$ \alpha $ on Weiz下载:
全尺寸图片
图 14 mo-1数据集上ACC和NMI值随$ \alpha $ 变化情况Fig. 14 The ACC and NMI with different set of$ \alpha $ on mo-1下载:
全尺寸图片
4.4 运行时间分析
表4为不同方法所需时间的统计。可以看到，TW-FINCH所需时间最少，SC-NMF方法最耗时，TLRSC次之。结合前述分割性能分析可以看到，在整体上取得更好分割准确性的情况下，MGSeNMF运行所需时间大大缩小，运行效率明显提升。这说明虽然增加了一个图约束，但是MGSeNMF的多图融合约束项设计采用L2范数，计算比SC-NMF中的L2,1 更高效，因此MGSeNMF整体计算效率更高。特别是随着数据量的增大，MGSeNMF运行效率更具优势。
表 4 不同方法的运行时间比较Table 4 The comparison of the running time with different methodss 数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.8683 1.3697 5.6972 0.4058 2.4358 Keck 1.6168 4.8103 24.3205 0.4389 5.1995 UT-I 0.8986 1.0194 5.2796 0.7519 2.7492 mo-1 1.1796 1.7360 10.5217 0.3990 2.9585 mo-2 2.9823 20.9330 113.3782 0.4305 6.9445 mo-3 2.2592 12.1045 60.1259 0.4135 4.9526 合计 9.8048 41.9729 219.3231 2.8396 25.2401 5. 结束语
针对当前基于聚类的动作分割方法常采用结构相似性约束易导致边界上的错误而造成动作分割不准确的问题，提出了一种融合结构相似性和度量相似性的基于多图融合约束Semi-NMF的动作分割方法MGSeNMF。该方法主要在特征表示学习中，利用不同权重的相似性关系图融合约束实现序列的降维，从而确保了后续获得更好的序列关系图表示和更准确的动作分割。实验表明该方法可以有效提升动作分割的准确性，特别是在视频序列中，平均精度较第二名方法SC-NMF提升了近4%；并且在准确性得到提高的同时，运行效率明显提升，与SC-NMF相比，总的运行时间缩短了近一个数量级。下一步，针对自动设置最优近邻个数，更准确确定动作边界以及运用多模态数据实现更优动作分割等问题持续开展研究。
-
图 1 Weiz数据集上的动作分割结果
Fig. 1 The action segmentation yielded on Weiz
下载:
全尺寸图片
图 2 Keck数据集上的动作分割结果
Fig. 2 The action segmentation yielded on Keck
下载:
全尺寸图片
图 3 UT-I数据集上的动作分割结果
Fig. 3 The action segmentation yielded on UT-I
下载:
全尺寸图片
图 4 mo-1数据集上的动作分割结果
Fig. 4 The action segmentation yielded on mo-1
下载:
全尺寸图片
图 5 mo-2数据集上的动作分割结果
Fig. 5 The action segmentation yielded on mo-2
下载:
全尺寸图片
图 6 mo-3数据集上的动作分割结果
Fig. 6 The action segmentation yielded on mo-3
下载:
全尺寸图片
图 7 Weiz数据集上不同q和k下的NMI值
Fig. 7 The NMI with different q and k on Weiz
下载:
全尺寸图片
图 8 Keck数据集上不同q和k下的NMI值
Fig. 8 The NMI with different q and k on Keck
下载:
全尺寸图片
图 9 UT-I数据集上不同q和k下的NMI值
Fig. 9 The NMI with different q and k on UT-I
下载:
全尺寸图片
图 10 mo-1数据集上不同q和k下的NMI值
Fig. 10 The NMI with different q and k on mo-1
下载:
全尺寸图片
图 11 mo-2数据集上不同q和k下的NMI值
Fig. 11 The NMI with different q and k on mo-2
下载:
全尺寸图片
图 12 mo-3数据集上不同q和k下的NMI值
Fig. 12 The NMI with different q and k on mo-3
下载:
全尺寸图片
图 13 Weiz数据集上ACC和NMI值随
$ \alpha $ 变化情况Fig. 13 The ACC and NMI with different set of
$ \alpha $ on Weiz下载:
全尺寸图片
图 14 mo-1数据集上ACC和NMI值随
$ \alpha $ 变化情况Fig. 14 The ACC and NMI with different set of
$ \alpha $ on mo-1下载:
全尺寸图片
表 1 实验数据集信息
Table 1 Characteristics of datasets
数据集 序列帧数 特征维度 动作数 重复动作 Weiz 701 324 10 无 Keck 1245 324 10 无 UT-I 650 1024 6 无 mo-1 954 42 4 有 mo-2 2192 42 8 有 mo-3 1760 42 7 有 表 2 不同方法的ACC性能比较
Table 2 ACC comparison with different methods
数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.7874 0.7789 0.8759 0.7660 0.9244 Keck 0.9044 0.8000 0.9173 0.7406 0.9566 UT-I 0.8738 0.8277 0.9369 0.5800 0.9534 mo-1 0.6709 0.8899 0.9644 0.6583 0.9644 mo-2 0.8244 0.8166 0.9630 0.7865 0.9576 mo-3 0.7364 0.7432 0.9489 0.8051 0.9517 表 3 不同方法的NMI性能比较
Table 3 NMI comparison with different methods
数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.8303 0.8116 0.8769 0.8279 0.9468 Keck 0.8799 0.8689 0.8939 0.8231 0.9389 UT-I 0.8112 0.7255 0.8937 0.5057 0.9336 mo-1 0.6515 0.6822 0.8693 0.6021 0.8733 mo-2 0.8007 0.7107 0.9119 0.7498 0.9021 mo-3 0.7561 0.6757 0.8698 0.7465 0.8786 表 4 不同方法的运行时间比较
Table 4 The comparison of the running time with different methods
s 数据集 TSC TLRSC SC-NMF TW-FINCH MGSeNMF Weiz 0.8683 1.3697 5.6972 0.4058 2.4358 Keck 1.6168 4.8103 24.3205 0.4389 5.1995 UT-I 0.8986 1.0194 5.2796 0.7519 2.7492 mo-1 1.1796 1.7360 10.5217 0.3990 2.9585 mo-2 2.9823 20.9330 113.3782 0.4305 6.9445 mo-3 2.2592 12.1045 60.1259 0.4135 4.9526 合计 9.8048 41.9729 219.3231 2.8396 25.2401 -
[1] DU Zexing, WANG Xue, ZHOU Guoqing, et al. Fast and unsupervised action boundary detection for action segmentation[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 3313−3322. [2] CHAKRABORTY B K, SARMA D, BHUYAN M K, et al. Review of constraints on vision-based gesture recognition for human-computer interaction[J]. IET computer vision, 2018, 12(1): 3–15. doi: 10.1049/iet-cvi.2017.0052 [3] 邵振洲, 赵红发, 渠瀛, 等. 一种面向多模态手术轨迹的快速无监督分割方法[J]. 小型微型计算机系统, 2018, 39(10): 2296–2302. SHAO Zhenzhou, ZHAO Hongfa, QU Ying, et al. Fast unsupervised approach for multi-modality surgical trajectory segmentation[J]. Journal of Chinese computer systems, 2018, 39(10): 2296–2302. [4] CHEN Wanjun, ZHANG Erhu, ZHANG Zhuomin. A Laplacian structured representation model in subspace clustering for enhanced motion segmentation[J]. Neurocomputing, 2016, 208: 174–182. doi: 10.1016/j.neucom.2015.12.123 [5] LI Sheng, LI Kang, FU Yun. Temporal subspace clustering for human motion segmentation[C]//2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2016: 4453−4461. [6] GAO Shanghua, HAN Qi, LI Zhongyu, et al. Global2Local: efficient structure search for video action segmentation[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 16800−16809. [7] ZHOU Tao, FU Huazhu, GONG Chen, et al. Consistency and diversity induced human motion segmentation[J]. IEEE transactions on pattern analysis and machine intelligence, 2023, 45(1): 197–210. doi: 10.1109/TPAMI.2022.3147841 [8] LEI Peng, TODOROVIC S. Temporal deformable residual networks for action segmentation in videos[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6742−6751. [9] ELHAMIFAR E, VIDAL R. Sparse subspace clustering: algorithm, theory, and applications[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(11): 2765–2781. doi: 10.1109/TPAMI.2013.57 [10] ZHENG Jianwei, YANG Ping, SHEN Guojiang, et al. Enhanced low-rank constraint for temporal subspace clustering and its acceleration scheme[J]. Pattern recognition, 2021, 111: 107678. doi: 10.1016/j.patcog.2020.107678 [11] DING C H Q, LI Tao, JORDAN M I. Convex and semi-nonnegative matrix factorizations[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(1): 45–55. doi: 10.1109/TPAMI.2008.277 [12] GAO Hongbo, LYU Chen, ZHANG Tong, et al. A structure constraint matrix factorization framework for human behavior segmentation[J]. IEEE transactions on cybernetics, 2022, 52(12): 12978–12988. doi: 10.1109/TCYB.2021.3095357 [13] SARFRAZ M S, MURRAY N, SHARMA V, et al. Temporally-weighted hierarchical clustering for unsupervised action segmentation[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 11220−11229. [14] WANG Xiumei, GUO Dingning, CHENG Peitao. Support structure representation learning for sequential data clustering[J]. Pattern recognition, 2022, 122: 108326. doi: 10.1016/j.patcog.2021.108326 [15] CAI Deng, HE Xiaofei, HAN Jiawei, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(8): 1548–1560. doi: 10.1109/TPAMI.2010.231 [16] CAI Yongda, HUANG J Z, YIN Jianfei. A new method to build the adaptive k-nearest neighbors similarity graph matrix for spectral clustering[J]. Neurocomputing, 2022, 493: 191–203. doi: 10.1016/j.neucom.2022.04.030 [17] SHI Jianbo, MALIK J. Normalized cuts and image segmentation[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(8): 888–905. doi: 10.1109/34.868688 [18] HE Yangcheng, LU Hongtao, HUANG Lei, et al. Pairwise constrained concept factorization for data representation[J]. Neural networks, 2014, 52: 1–17. doi: 10.1016/j.neunet.2013.12.007 [19] XIA Guiyu, CHEN Beijia, SUN Huaijiang, et al. Nonconvex low-rank kernel sparse subspace learning for keyframe extraction and motion segmentation[J]. IEEE transactions on neural networks and learning systems, 2021, 32(4): 1612–1626. doi: 10.1109/TNNLS.2020.2985817 [20] LIU Haijun, CHENG Jian, WANG Feng. Sequential subspace clustering via temporal smoothness for sequential data segmentation[J]. IEEE transactions on image processing, 2018, 27(2): 866–878. doi: 10.1109/TIP.2017.2767785 [21] ZHANG Kexin, ZHAO Xuezhuan, PENG Siyuan. Multiple graph regularized semi-supervised nonnegative matrix factorization with adaptive weights for clustering[J]. Engineering applications of artificial intelligence, 2021, 106: 104499. doi: 10.1016/j.engappai.2021.104499 [22] WANG Lichen, DING Zhengming, FU Yun. Low-rank transfer human motion segmentation[J]. IEEE transactions on image processing, 2019, 28(2): 1023–1034. doi: 10.1109/TIP.2018.2870945 [23] JIANG Zhuolin, LIN Zhe, DAVIS L. Recognizing human actions by learning and matching shape-motion prototype trees[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(3): 533–547. doi: 10.1109/TPAMI.2011.147 [24] ZHU Xiaofeng, ZHANG Shichao, HE Wei, et al. One-step multi-view spectral clustering[J]. IEEE transactions on knowledge and data engineering, 2019, 31(10): 2022–2034. doi: 10.1109/TKDE.2018.2873378 [25] BAI Yue, WANG Lichen, LIU Yunyu, et al. Human motion segmentation via velocity-sensitive dual-side auto-encoder[J]. IEEE transactions on image processing, 2023, 32: 524–536. doi: 10.1109/TIP.2022.3217720
