一种多策略改进鲸鱼优化算法的混沌系统参数辨识

潘悦悦,  吴立飞,  杨晓忠

downloadPDF
潘悦悦, 吴立飞, 杨晓忠. 一种多策略改进鲸鱼优化算法的混沌系统参数辨识 [J]. 智能系统学报, 2024, 19(1): 176-189. doi: 10.11992/tis.202303043
引用本文: 潘悦悦, 吴立飞, 杨晓忠. 一种多策略改进鲸鱼优化算法的混沌系统参数辨识 [J]. 智能系统学报, 2024, 19(1): 176-189. doi: 10.11992/tis.202303043
shu
PAN Yueyue, WU Lifei, YANG Xiaozhong. Parameter identification of chaotic system based on a multi-strategy improved whale optimization algorithm [J]. CAAI Transactions on Intelligent Systems, 2024, 19(1): 176-189. doi: 10.11992/tis.202303043
Citation: PAN Yueyue, WU Lifei, YANG Xiaozhong. Parameter identification of chaotic system based on a multi-strategy improved whale optimization algorithm [J]. CAAI Transactions on Intelligent Systems, 2024, 19(1): 176-189. doi: 10.11992/tis.202303043
shu

一种多策略改进鲸鱼优化算法的混沌系统参数辨识

doi: 10.11992/tis.202303043
  • 1.

    华北电力大学 控制与计算机工程学院, 北京 102206;

  • 2.

    华北电力大学 数理学院信息与计算研究所, 北京 102206

基金项目: 中央高校基本科研业务费专项基金项目(2021MS045)；华北电力大学国内外联合培养博士生资助项目(2020).
详细信息
    作者简介:

    潘悦悦，博士研究生，主要研究方向为智能优化算法。E-mail：panyueyue@ncepu.edu.cn;

    吴立飞，高级工程师，博士，主要研究方向为系统辨识、过程控制。主持教育部中央高校基本科研业务费专项基金2项。发表学术论文30 余篇。E-mail：wulf@ncepu.edu.cn;

    杨晓忠，教授，博士生导师，主要研究方向为智能优化算法、人工智能。主持国家科技重大专项子课题3项、国家自然科学基金面上项目2项。发表学术论文100 余篇。E-mail：yxiaozh@ncepu.edu.cn.

    通讯作者:

    杨晓忠. E-mail：yxiaozh@ncepu.edu.cn.

  • 中图分类号: TP18

Parameter identification of chaotic system based on a multi-strategy improved whale optimization algorithm

  • 1.

    School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China;

  • 2.

    Institute of Information and Computing, School of Mathematics and Physics, North China Electric Power University, Beijing 102206, China

    摘要
  • 摘要: 针对混沌系统参数辨识精度不高的问题，以鲸鱼优化算法(whale optimization algorithm，WOA)为基础，提出一种多策略改进鲸鱼优化算法(multi-strategy improved whale optimization algorithm，MIWOA)。采用Chebyshev混沌映射选取高质量初始种群，采用非线性收敛因子和自适应权重，提高算法收敛速度，为了避免算法陷入局部最优，动态选择自适应t分布或蚁狮优化算法更新后期位置，提高处理局部极值的能力。通过对10个基准函数和高维测试函数进行仿真试验，表明MIWOA具有良好的稳定性和收敛精度。将MIWOA应用于辨识$ {\rm{R}}\ddot {\rm{o}}{\rm{ssler}} $和$ {\rm{L}}\ddot {\rm{u}} $混沌系统参数，仿真结果优于现有成果，表明本文MIWOA辨识混沌系统参数的高效性和实用性。

     

    Abstract: Aimed at the problem of low parameter identification accuracy of chaotic systems, a multi-strategy improved whale optimization algorithm (MIWOA) is proposed based on the whale optimization algorithm (WOA). MIWOA uses Chebyshev chaotic mapping to select high-quality initial populations, and nonlinear convergence factor and adaptive weight to improve the convergence speed of the algorithm. In order to avoid falling into local optimal solution, MIWOA dynamically selects adaptive t distribution or ant lion optimization algorithm to update the later position and improve the ability to handle local extremum. Through simulation experiments on 10 benchmark functions and high-dimensional test functions, it is shown that MIWOA has good stability and convergence accuracy. Applying MIWOA to identify the parameters of $ {\rm{R}}\ddot {\rm{o}}{\rm{ssler}} $ and $ {\rm{L}}\ddot {\rm{u}} $ chaotic systems, the simulation results are superior to existing achievements, indicating the efficiency and practicality of MIWOA in identifying chaotic system parameters in this paper.

     

    • HTML全文

  • 在非线性科学领域，混沌系统的控制与同步是研究热点，其在信息科学、保密通信等方面应用广泛[1-2]，准确的混沌系统模型是实现同步控制的基础。然而，实际应用中，混沌系统结构复杂，部分参数不可知，因此精确辨识混沌系统参数具有重要的现实意义[3-4]。

    近年来，许多学者开始关注和研究混沌系统参数辨识问题，并应用智能优化算法辨识系统参数。Chen等(2019年)[5]使用改进花授粉算法估计混沌和超混沌系统参数。数值模拟证明了新算法的有效性和鲁棒性。Ahandani等(2020年)[6]提出一种混洗复杂进化算法解决混沌系统参数估计问题，数值结果表明改进算法提高了参数估计的收敛速度和精度。Turgut等(2021年)[7]使用单元拓扑改进鲸鱼算法和正余弦算法，辨识混沌系统参数，测试结果证明，新算法成功地解决了参数识别问题。Ebrahimi等(2021年)[8]提出了一种改进洛兹映射混沌优化算法，数值结果表明，改进算法能够高效、准确地估计混沌系统参数。

    鲸鱼优化算法(whale optimization algorithm，WOA)是一种新型群智能算法[9]，具有搜索能力强、计算稳定等特点，在最优控制、光伏系统等方面应用广泛[10-11]。然而WOA存在全局和局部搜索不平衡，易陷入局部最优等问题，因此国内外学者对WOA进行了有效的改进。Chen等(2020年)[12]提出一种准对立混沌WOA(whale optimization algorithm with chaos mechanism based on quasi-opposition, OBCWOA)，数值仿真结果证明了改进算法的全局搜索能力。Chen等(2020年)[13] 为提高WOA的收敛精度和速度，提出一种双自适应随机备用增强WOA(reinforced whale optimization algorithm, RDWOA)。仿真结果验证了RDWOA的有效性。Chakraborty等(2021年)[14]为解决高维问题，结合多种策略，提出一种增强WOA(enhanced whale optimization algorithm, eWOA)，测试结果表明所提算法能有效解决高维问题。Shen等(2023年)[15]提出一种多策略进化WOA(whale optimization algorithm based on multi-population evolution, MEWOA)，试验结果证明了MEWOA求解优化问题的有效性。Deng等(2023年)[16]提出了一种具有多策略混合算法的改进WOA(improved whale optimization algorithm, IWOA)，仿真结果表明，IWOA有较好的收敛速度和稳定性。

    以上改进算法虽然有一定提升，但在收敛精度和速度方面仍有待提高，本文在已有工作的基础上，以WOA为基础，使用Chebyshev混沌映射产生均匀分布种群，增加初始种群多样性。将收敛因子非线性化，增加自适应权重，兼顾全局搜索和局部挖掘。动态选择自适应t分布或蚁狮优化算法[17-18]，跳出局部最优。通过对10个基准函数和高维测试函数进行仿真试验，验证了MIWOA的优越性。将MIWOA应用于$ {\rm{R}}\ddot {\rm{o}}{\rm{ssler}} $和$ {\rm{L}}\ddot {\rm{u}} $混沌系统参数辨识，仿真结果证明了MIWOA辨识混沌系统参数的有效性。

    1.   多策略改进鲸鱼优化算法的建立

    1.1   基本WOA

    WOA模拟了鲸鱼捕食行为，其仿生学原理描述如下：

    1) 包围捕食阶段。

    鲸鱼寻找食物时，当前鲸鱼根据最佳鲸鱼位置更新自身位置，公式为

    $$ D = \left| {C \cdot {X^ * }(t) - X(t)} \right| $$ (1)
    $$ X(t + 1) = {X^ * }(t) - A \cdot D $$ (2)
    $$ A = 2a \cdot {r_1} - a $$ (3)
    $$ C = 2 \cdot {r_2} $$ (4)

    式中：$ a = 2 - {{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. } T} $，$ t $和$ T $分别为当前迭代次数和最大迭代次数，$ {X^ * }(t) $和$ X(t) $分别为最佳鲸鱼位置和当前位置，$ {r}_{1}、{r}_{2} $为[0,1]的随机数。

    2) 螺旋更新阶段。

    在螺旋更新位置时，鲸鱼通过螺旋向上的方式，靠近群体中最优位置，更新公式为

    $$ X(t + 1) = {X^*}(t) + D' \cdot {{\rm{e}}^{bl}}\cos (2 \text{π} l) $$ (5)
    $$ D' = |{X^*}(t) - X(t)| $$ (6)

    式中：$ D' $为第$ i $只鲸鱼和猎物之间的距离，$ b $为改变螺旋形状的常数，$ l $为$ [ - 1,1] $中的随机数。

    在鲸鱼搜索猎物时，收缩包围和螺旋更新同步进行，位置更新公式为

    $$ X(t + 1) = \left\{ {\begin{array}{l} {{X^ * }(t) - A \cdot D,{\text{ }}p < 0.5} \\ {{X^ * }(t) + D' \cdot {{\rm{e}}^{bl}}\cos (2 \text{π} l),{\text{ }}p \geqslant 0.5} \end{array}} \right. $$ (7)

    式中$ p $为$ [0,1] $之间的随机数。

    3) 随机搜寻阶段。

    鲸鱼通过$ \left| A \right| $大小，选择随机搜寻或者包围捕食。当$ \left| A \right| > 1 $时，鲸鱼在包围圈外，通过随机搜寻获得猎物信息，位置更新公式为

    $$ D = |C \cdot {X_{{\text{rand}}}}(t) - X(t)| $$ (8)
    $$ X(t + 1) = {X_{{\text{rand}}}}(t) - A \cdot D $$ (9)

    式中$ {X_{{\text{rand}}}} $为当前的一个随机鲸鱼位置。

    1.2   WOA的改进

    WOA初始化种群时采用随机搜索策略，全局搜索能力弱。包围捕食和螺旋更新阶段，收敛因子线性递减不能平衡全局和局部搜索。算法后期容易陷入局部最优。针对以上缺点，本文通过Chebyshev混沌映射初始化种群。包围捕食和螺旋更新阶段，非线性化收敛因子，加入自适应权重。算法后期，动态使用自适应t分布或蚁狮优化算法更新鲸鱼位置，对WOA进行改进。

    1) Chebyshev混沌映射。

    Chebyshev混沌映射对初值敏感[19]，可产生大量无周期实值序列。本文采用Chebyshev混沌映射对WOA进行种群初始化，迭代方式为

    $$ {x_{n + 1}} = \cos (k(\arccos ({x_n}))),{\text{ }}{x_n} \in [ - 1,1] $$ (10)

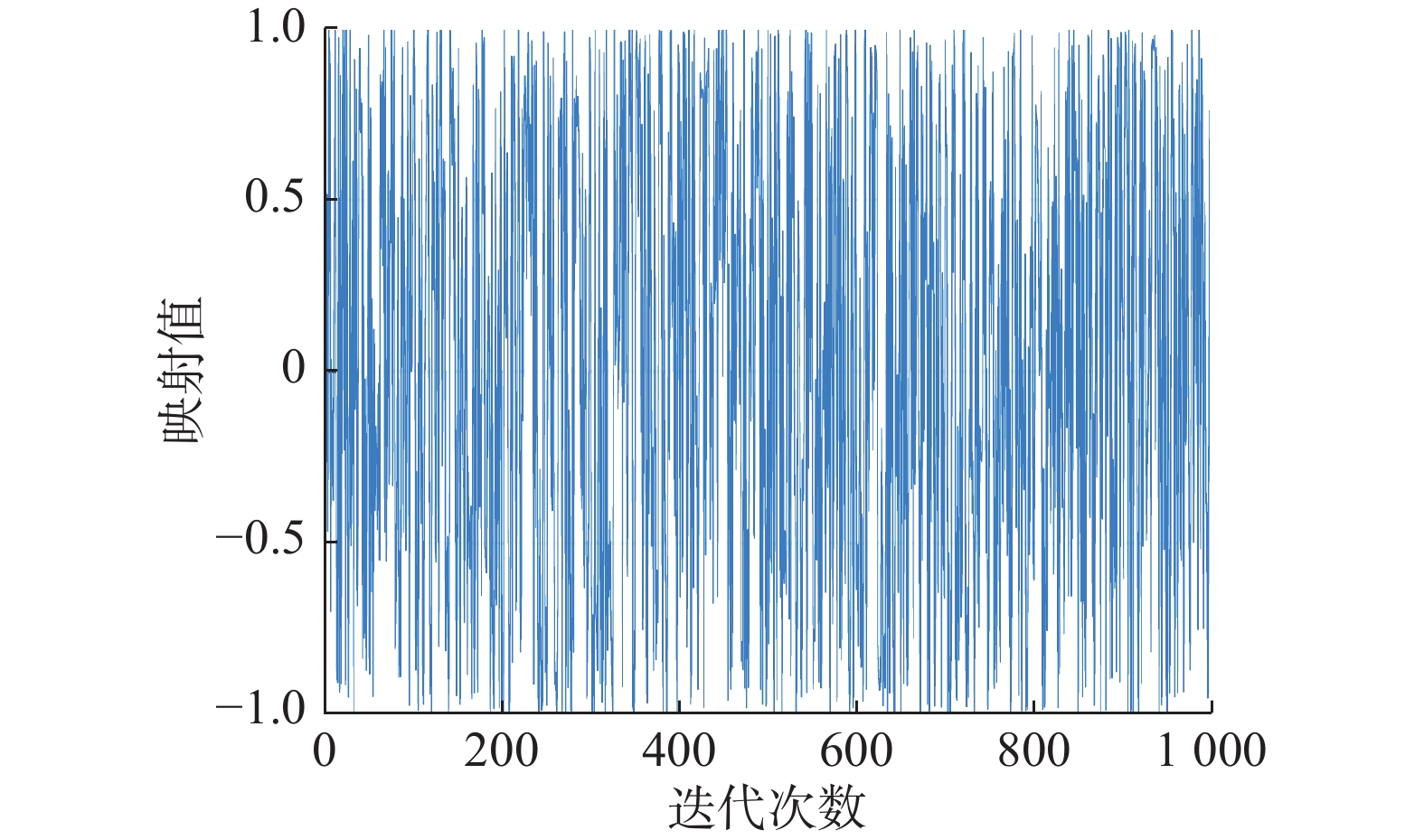
    式中$ k $为阶次。Chebyshev映射迭代1 000次的分布如图1所示。

    图  1  Chebyshev映射分布
    Fig.  1  Chebyshev map distribution
    下载: 全尺寸图片

    由图1可知，映射值分布于$ [ - 1,1] $，Chebyshev混沌映射能更均衡地选取初始种群。将Chebyshev混沌序列映射到WOA解空间中，规定鲸鱼种群数为$ N $，随机产生第1只鲸鱼个体向量，$ {\boldsymbol{Y}} = ({y_1}, $$ {y_2}, \cdots ,{y_d}) $。使用式(10)对$ {\boldsymbol{Y}} $的各维进行$ n - 1 $次迭代，产生其余的$ n - 1 $只鲸鱼。映射生成$ n $只鲸鱼个体为

    $$ {x_{id}} = {l_d} + (1 + {y_{id}}) \times ({u_d} - {l_d})/2 $$ (11)

    式中：$ {u_d} $和$ {l_d} $分别为搜索空间第$ d $维的上下界，$ {y_{id}} $和$ {x_{id}} $分别为第$ d $维的第$ i $只鲸鱼和第$ i $只鲸鱼的坐标值。

    2) 非线性收敛因子和自适应权重。

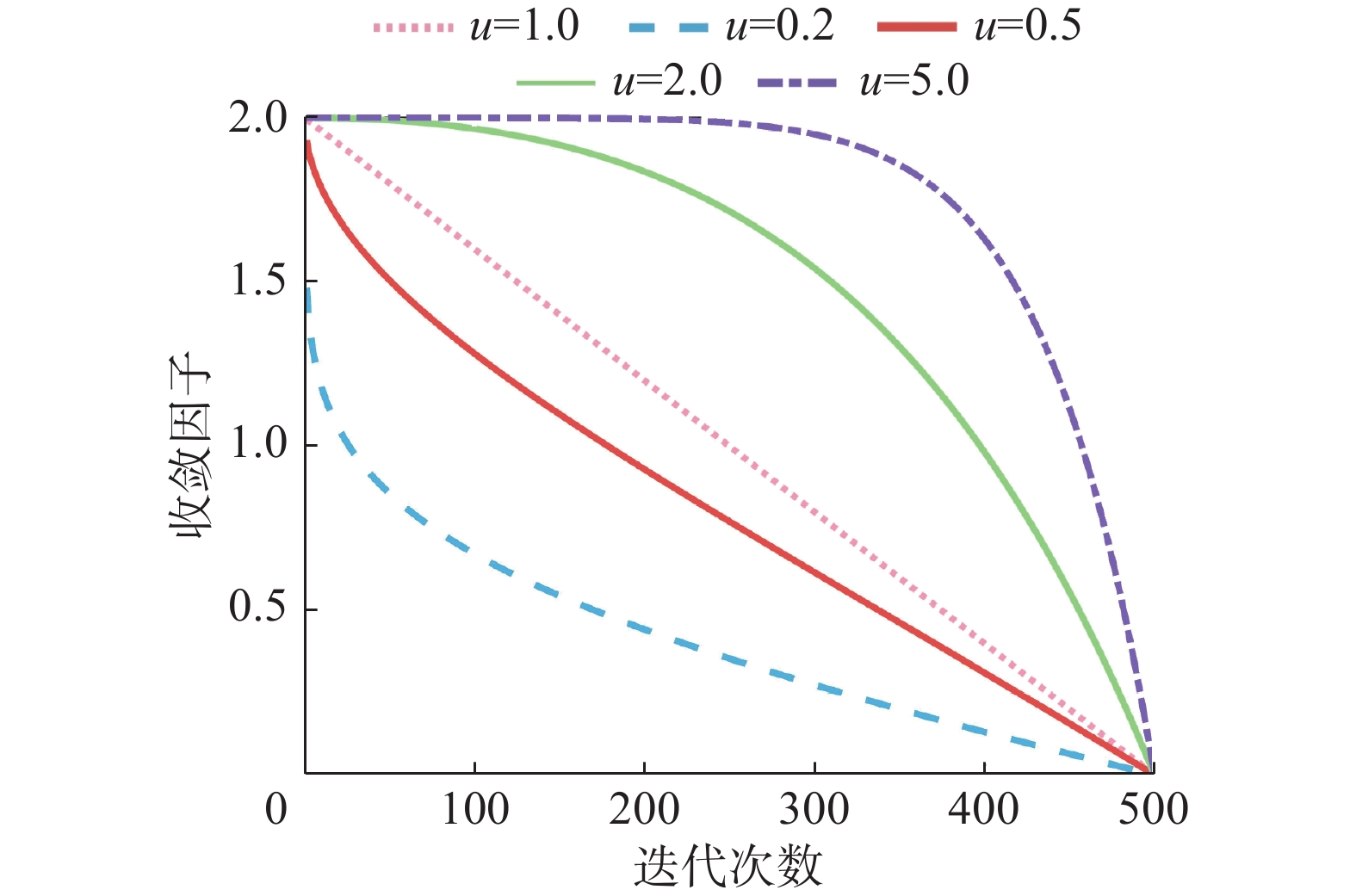
    WOA中，参数$ A \in [ - a,a] $调节全局搜索和局部挖掘。当$ |A| \geqslant 1 $时，算法进行全局搜索，当$ |A| < 1 $时，算法进行局部挖掘。随着迭代的进行，$a = 2 - {{2t} \mathord{\left/ {\vphantom {{2t} T}} \right. } T}$线性递减不能体现实际优化过程，因此改进收敛因子，公式为[20]

    $$ a = 2 - 2{\left(\frac{{{{\rm{e}}^{{t \mathord{\left/ {\vphantom {t T}} \right. } T}}} - 1}}{{{\rm{e}} - 1}}\right)^u} $$ (12)

    式中：$ u $为大于零的常数，调节$ a $的衰减程度。$ T = 500 $时，图2为$ a $随$ u $的变化曲线。

    图  2  a的衰减曲线
    Fig.  2  Attenuation curves of a
    下载: 全尺寸图片

    如图2，与WOA相比，$ u $越大，$ a > 1 $所占的迭代次数比例越大，算法全局搜索能力越强，局部挖掘能力越弱。反之，$ u $越小，$ a < 1 $所占的比例越大，算法局部挖掘能力越强，全局搜索能力越弱。所以$ a $的变化趋势很大程度地影响优化求解。由于本文提出的Chebyshev混沌映射初始化种群策略，可以有效提高算法全局搜索能力，故选取$ u = 0.6 $，增强局部挖掘能力，加快收敛速度，提高精度。

    针对WOA后期局部挖掘时，权重固定，不利于算法寻优，本文提出一种自适应权重策略，公式为

    $$ \omega = \frac{a}{2} $$ (13)
    $$ X(t + 1) = \omega {X^*}(t) - AD $$ (14)
    $$ X(t + 1) = \omega {X^*}(t) - D'{{\rm{e}}^{bl}}\cos (2 \text{π} l) $$ (15)

    3) 自适应t分布。

    t分布又称学生分布，概率密度函数为[17]

    $$ {p_t}(x) = \frac{{\varGamma \left(\dfrac{{n + 1}}{2}\right)}}{{\sqrt {n \text{π} } \varGamma \left(\dfrac{n}{2}\right)}} \cdot {\left(1 + \dfrac{{{x^2}}}{n}\right)^{ - \tfrac{{n + 1}}{2}}} $$ (16)

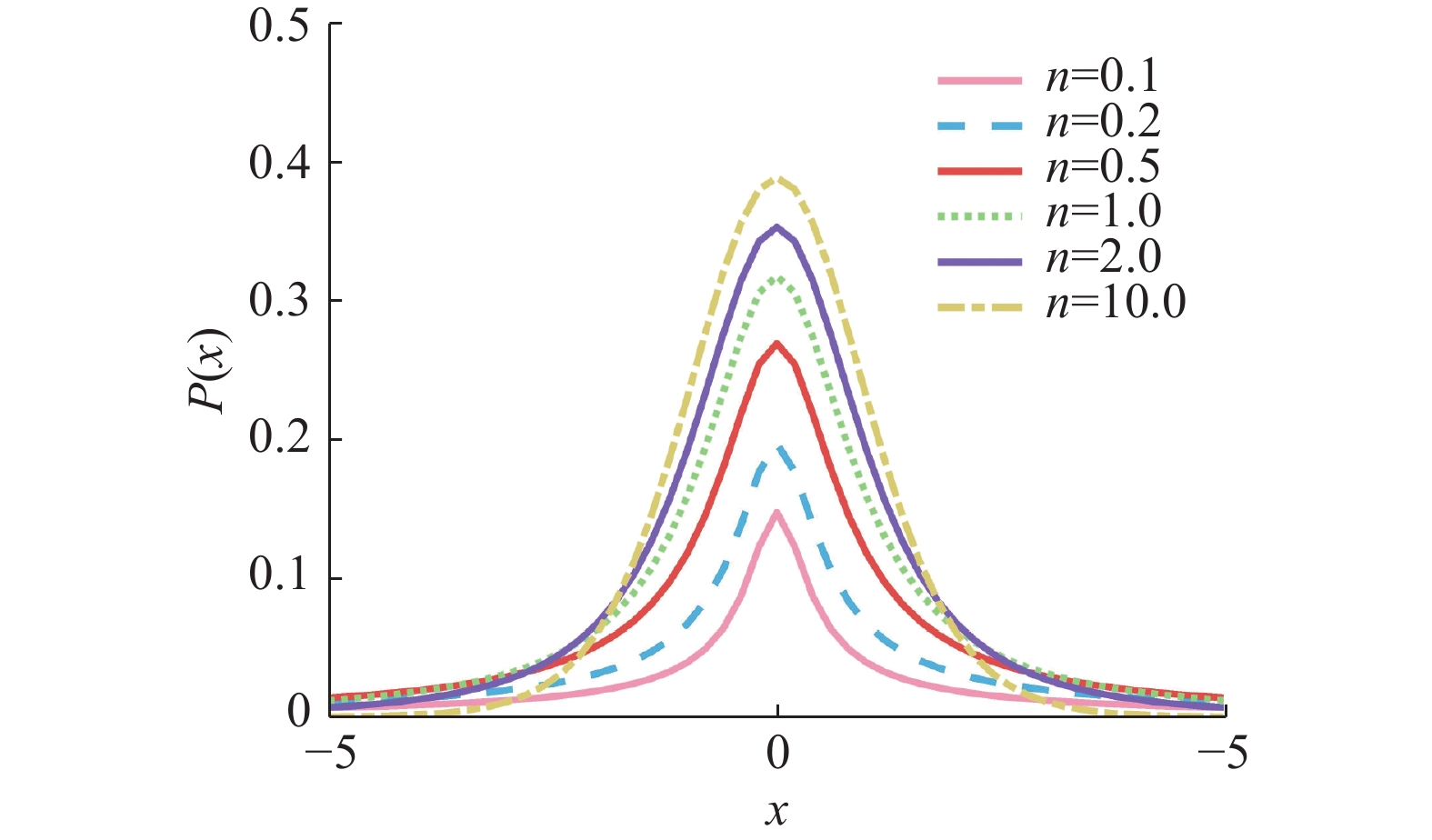
    式中$\varGamma \left(\dfrac{{n + 1}}{2}\right) = \displaystyle\int_0^{ + \infty } {{x^{\tfrac{{n + 1}}{2} - 1}}{{\rm{e}}^{ - x}}{\rm{d}}x}$。图3为$ n $取不同值时t分布图像对比。

    图  3  函数分布对比
    Fig.  3  Function distribution comparison
    下载: 全尺寸图片

    由图3可知，t分布的自由度$ n $越小，曲线的双尾翘越高，中间峰值越小，整体越平滑。反之，自由度$ n $越大，中间峰值越大，整体越陡峭。自适应t分布对鲸鱼位置的更新为

    $$ x_i^t = {x_i} + {x_i} \times t(n) $$ (17)

    式中：$ x_i^t $为更新后的鲸鱼位置，$n$和$t(n)$分别为迭代次数和以迭代次数为自由度的t分布函数。

    4) 蚁狮优化算法。

    在蚁狮优化算法中，蚂蚁通过随机游走更新位置，公式为[18]

    $$ \begin{array}{c} X(t) = [0,{\text{ }}{\rm{cumsum}}(2r({t_1}) - 1), \\ {\rm{cumsum}}(2r({t_2}) - 1), \cdots ,{\rm{cumsum}}(2r({t_T}) - 1)] \\ \end{array} $$ (18)

    式中：cumsum为蚂蚁游走位置累加和，$ T $为最大迭代次数，$ t $为当前迭代次数，$ r(t) $为0或1的随机数。蚂蚁随机游走公式的标准化形式为

    $$ X_i^t = \frac{{(X_i^t - {a_i}) \times (d_i^t - c_i^t)}}{{({b_i} - {a_i})}} + c_i^t $$ (19)

    式中：$ {a_i} $和$ {b_i} $分别为第$ i $个变量的最小值和最大值，$ c_i^t $和$ d_i^t $分别为第$ t $代第$ i $个变量的最小值和最大值。

    2.   混沌系统参数辨识的MIWOA

    2.1   混沌系统的参数辨识原理

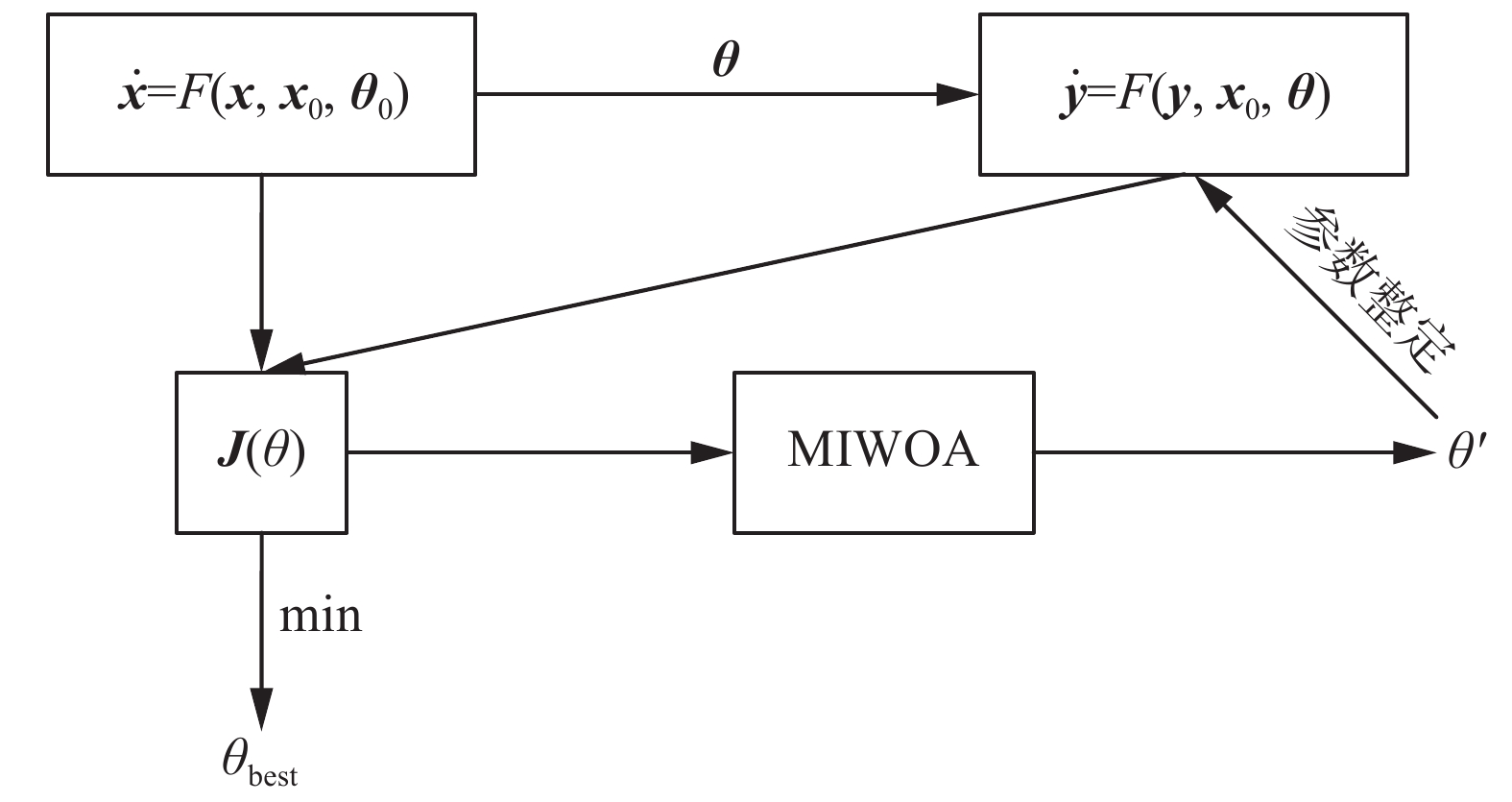
    混沌系统参数辨识原理如图4所示。

    图  4  混沌系统参数辨识原理
    Fig.  4  Principle of parameter identification for chaotic system
    下载: 全尺寸图片

    考虑如下n维混沌动力学系统：

    $$ {{\dot {\boldsymbol{x}}}} = F({\boldsymbol{x}},{{\boldsymbol{x}}_0},{{\boldsymbol{\theta}}_0}) $$

    式中：${\boldsymbol{x}} = {[{x_1}\;\;{x_2}\;\; \cdots \;\;{x_n}]^{\rm{T}}} \in {{\bf{R}}^n}$为系统的n维状态变量，${{\boldsymbol{x}}_0}$为初始状态量，${{\boldsymbol{\theta}}_0} = {[{\theta _{10}}\;\;{\theta _{20}}\;\; \cdots \;\;{\theta _{m0}}]^{\rm{T}}}$为参数真实值。当辨识系统参数时，假设结构为

    $$ {{\dot {\boldsymbol{y}}}} = F({\boldsymbol{y}},{{\boldsymbol{x}}_0},{\boldsymbol{\theta}}) $$

    式中：${\boldsymbol{y}} = {[{y_1}\;\;{y_2}\;\; \cdots \;\;{y_n}]^{\rm{T}}} \in {{\bf{R}}^n}$为辨识系统的状态变量，${\boldsymbol{\theta}} = {[{\theta _1}\;\;{\theta _2} \;\; \cdots \;\;{\theta _m}]^{\rm{T}}}$为参数估计值。系统参数辨识是寻找一组最优未知参数，使系统真值${\boldsymbol{x}}$和估计值${\boldsymbol{y}}$的误差值最小：

    $$ \min J(\theta ) = \frac{1}{m}\sum\limits_{k = 1}^m {{{\left\| {{{\boldsymbol{x}}_k} - {{\boldsymbol{y}}_k}} \right\|}^2}} $$

    式中：${{\boldsymbol{x}}_k}$和${{\boldsymbol{y}}_k}$分别为$ k $时刻的系统真值和估计值，$ m $为参数辨识状态变量序列的长度。目标泛函$ J(\theta ) $的值越小，参数辨识的精度越高。MIWOA流程如图5所示。

    图  5  MIWOA流程
    Fig.  5  Flow chart of MIWOA
    下载: 全尺寸图片

    2.2   MIWOA的时间复杂度分析

    设种群规模为$ N $，搜索空间维度为$ D $，最大迭代次数为$ T $，WOA的时间复杂度为$ {O}(NDT) $。本文MIWOA以WOA为基础进行改进，Chebyshev 混沌映射初始化种群的时间复杂度为$ {O}(ND) $，非线性收敛因子和自适应权重未在基本WOA基础上增加循环嵌套，时间复杂度为$ {O}(NDT) $，动态选择自适应t分布或蚁狮优化算法的时间为$ {t_1} $，则其时间复杂度为$ {O}(NDT + {t_1}) $，虽然MIWOA的时间复杂度相对WOA有所增加，但在可接受范围内，下面通过数值试验说明MIWOA的卓越性。

    3.   MIWOA性能测试与分析

    3.1   测试函数的选取

    仿真试验基于AMD Ryzen R7 5700U CPU@1.80 GHz，在Matlab R2019a 环境下运行。为了验证MIWOA有更好的寻优性能，选取表1的10个基准函数进行测试，$ \varepsilon $表示绝对误差精度。$ {f_1} \sim {f_7} $为单峰函数， $ {f_8} \sim {f_{10}} $为多峰函数，10个测试函数的最优值均为0。

    表  1  基准函数
    Table  1  Benchmark functions
    函数搜索范围$ \varepsilon $
    Sphere Function($ {f_1} $)[−100,100]0.001
    Schwefel’s Problem 2.22($ {f_2} $)[−10,10]0.001
    Schwefel’s Problem 1.2($ {f_3} $)[−100,100]0.001
    Schwefel’s Problem 2.21($ {f_4} $)[−100,100]0.001
    Rosenbrock’s Function($ {f_5} $)[−30,30]0.010
    续表 1
    函数搜索范围$ \varepsilon $
    Step Function($ {f_6} $)[−100,100]0.010
    Quartic Function($ {f_7} $)[−1.28,1.28]0.010
    Schwefel’s Problem 2.26($ {f_8} $)[−500,500]100.000
    Rastrigin’s Function($ {f_9} $)[−5.12,5.12]0.010
    Ackley’s Function($ {f_{10}} $)[−32,32]0.010

    3.2   MIWOA与其他智能算法对比

    采用10个基准函数检验MIWOA的性能，与WOA、粒子群算法(particle swarm optimization，PSO)[21]、人工蜂群算法(artificial bee colony algorithm, ABC)[22]、灰狼算法(grey wolf optimizer，GWO)[23]和哈里斯鹰算法(harris hawks optimization，HHO)[24]进行测试结果比较。令$ N = 30 $，$ D = 30 $，$ T = 1\;000 $，运行30次，表2为6种算法的最优值、最差值、平均值和标准差(黑色粗体为最优结果)。

    表  2  测试函数优化结果
    Table  2  Test function optimization results
    函数指标WOAPSOABCGWOHHOMIWOA
    $ f_{1} $最优值2.57×10−1654.01×1012.74×10−19.58×10−619.90×10−2140
    最差值3.15×10−1491.38×1021.46×1008.42×10−591.29×10−1850
    平均值3.21×10−1508.22×1016.20×10−12.04×10−591.29×10−1860
    标准差9.44×10−1503.09×1013.26×10−12.37×10−5900
    $ f_{2} $最优值1.81×10−1112.59×1005.32×10−25.40×10−368.33×10−1070
    最差值3.52×10−1021.03×1025.81×1014.23×10−344.72×10−950
    平均值3.58×10−1033.89×1011.41×1011.30×10−344.89×10−960
    标准差1.05×10−1022.63×1012.27×1011.18×10−341.41×10−950
    $ f_{3} $最优值3.69×1033.59×1033.28×1043.14×10−193.62×10−1760
    最差值4.64×1042.10×1048.86×1041.60×10−132.18×10−1490
    平均值2.01×1041.10×1046.78×1041.65×10−142.41×10−1500
    标准差1.32×1045.27×1031.68×1044.80×10−146.51×10−1500
    $ f_{4} $最优值3.58×10−21.94×1005.27×1019.39×10−161.53×10−1020
    最差值8.89×1016.66×1006.61×1011.72×10−132.05×10−900
    平均值2.47×1013.62×1005.92×1012.65×10−142.15×10−910
    标准差2.75×1011.29×1004.60×1005.01×10−146.14×10−910
    $ f_{5} $最优值2.79×1013.95×1031.37×1062.79×1011.61×10−32.80×101
    最差值2.87×1016.29×1032.29×1062.87×1015.45×10−32.88×101
    平均值2.84×1015.36×1031.93×1062.84×1013.92×10−32.82×101
    标准差4.23×10−11.15×1034.53×1053.96×10−11.88×10−32.76×10−1
    $ f_{6} $最优值8.77×10−21.44×1024.45×10−19.96×10−11.77×10−59.23×10−3
    最差值2.72×10−13.09×1026.81×10−11.26×1006.11×10−52.72×10−1
    平均值1.98×10−12.43×1025.86×10−11.15×1004.37×10−54.41×10−2
    标准差9.03×10−28.11×1011.15×10−11.30×10−12.12×10−56.35×10−2
    $ f_{7} $最优值1.78×10−43.84×10−22.16×10−14.57×10−42.27×10−61.59×10−6
    最差值5.24×10−31.58×10−18.24×10−12.07×10−31.25×10−49.40×10−5
    平均值2.04×10−37.45×10−25.37×10−19.18×10−46.13×10−52.69×10−5
    标准差1.57×10−33.40×10−21.75×10−14.24×10−44.43×10−53.15×10−5
    续表 2
    函数指标WOAPSOABCGWOHHOMIWOA
    $ f_{8} $最优值−1.26×104−1.04×104−8.22×10112−6.60×103−1.26×104−1.26×104
    最差值−7.69×103−5.75×103−2.27×10119−4.95×103−5.78×103−6.37×103
    平均值−1.12×104−8.14×103−2.41×10118−6.06×103−1.19×104−1.15×104
    标准差1.84×1031.39×1036.77×101185.09×1022.04×1031.74×103
    $ f_{9} $最优值01.23×1021.91×102000
    最差值02.58×1022.50×1029.98×10−100
    平均值01.90×1022.31×1021.99×10−100
    标准差03.51×1011.67×1013.99×10−100
    $ f_{10} $最优值8.88×10−161.71×1003.03×1007.99×10−158.88×10−168.88×10−16
    最差值7.99×10−152.20×1015.29×1002.58×10−148.88×10−168.88×10−16
    平均值4.80×10−157.40×1004.01×1001.58×10−148.88×10−168.88×10−16
    标准差2.49×10−156.32×1007.33×10−14.71×10−1500

    由表2数据可知，对于单峰函数$ {f_1} $、$ {f_2} $，MIWOA的寻优结果均为0， WOA的计算结果优于PSO、ABC和GWO算法。在$ {f_3} $、$ {f_4} $测试函数上，MIWOA的计算结果优于HHO，可取得理论最小值。对于$ {f_5}\sim{f_7} $函数，虽然MIWOA没有达到最小值，但优于WOA。对于多峰函数$ {f_8}\sim{f_{10}} $，MIWOA可收敛到最优值附近，其中$ {f_9} $函数可收敛到最优值，说明MIWOA相对于其他算法有更好的收敛精度和稳定性。

    基准测试函数的收敛曲线可以清晰地展现算法的收敛速度，图6(a)~(d)和(e)~(f)分别为单峰和多峰函数的平均收敛曲线。由图6可以看出，对于6个测试函数，在收敛精度相同的情况下，MIWOA收敛速度更快，说明Chebyshev混沌映射初始化种群策略提高了种群中高质量个体的比例，非线性收敛因子和自适应权重平衡了全局和局部搜索，加速收敛。MIWOA收敛曲线波动下降，说明自适应t分布或蚁狮优化算法的动态选择策略有助于算法跳出局部最优，提高收敛精度。

    图  6  30维测试函数的平均收敛曲线
    Fig.  6  Average convergence curves of 30 dimensional test functions
    下载: 全尺寸图片

    3.3   Wilcoxon秩和检验

    Wilcoxon秩和检验能够检测更为复杂的数据分布，并与算法多次运行的数据对比，公平地体现MIWOA的优越性[24]。实验设定显著性差异为 5% ，当$ p < 5\% $判定两算法有明显差异，反之无明显差异。符号“＋”“－”和“＝”分别表示MIWOA的性能优于、劣于和相当于对比算法，N/A表示无法进行显著性判断。选取MIWOA在10个测试函数的运行结果与WOA、PSO、ABC、GWO以及HHO运行结果进行Wilcoxon秩和检验，计算p值。表3结果显示大部分$ p < 5\% $，说明MIWOA的寻优能力优于5种对比算法。

    表  3  Wilcoxon秩和检验结果
    Table  3  Results of Wilcoxon rank sum test
    函数WOAPSOABCGWOHHO
    $ f_{1} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $ f_{2} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{3}$2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $ f_{4} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{5}$1.25×10−12.00×10−62.00×10−68.51×10−22.00×10−6
    $ f_{6} $6.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{7}$2.00×10−62.00×10−62.00×10−62.00×10−61.47×10−2
    $ f_{8} $3.13×10−12.30×10−5N/A2.00×10−61.40×10−2
    $f_{9}$N/A2.00×10−62.00×10−62.00×10−3N/A
    $ f_{10} $9.00×10−62.00×10−62.00×10−69.03×10−7N/A
    +/=/−7/1/210/0/09/1/09/0/18/2/0

    3.4   MIWOA不同改进策略的有效性分析

    为比较3种改进策略对MIWOA性能的影响，令$ N = 30 $，$ D = 30 $，$ T = 500 $，对$ {f_1}\sim{f_{10}} $进行寻优计算，将MIWOA与WOA、WOA1(采用Chebyshev混沌映射)、WOA2(采用非线性收敛因子和自适应权重)和WOA3(采用自适应t分布或蚁狮优化算法)比较，计算结果如表4。

    表  4  不同改进策略算法性能对比
    Table  4  Performance comparison of algorithms for different improved strategies
    函数指标WOAWOA1WOA2WOA3MIWOA
    $ f_{1} $最优值1.25×10−853.72×10−84000
    最差值1.27×10−712.16×10−72000
    平均值6.84×10−731.08×10−73000
    标准差2.62×10−724.04×10−73000
    $ f_{2} $最优值1.45×10−581.14×10−573.45×10−26400
    最差值2.85×10−491.73×10−495.63×10−24500
    平均值1.01×10−508.04×10−511.88×10−24600
    标准差5.11×10−503.12×10−50000
    $ f_{3} $最优值1.46×1042.48×104000
    最差值7.97×1041.41×105000
    平均值4.70×1048.05×104000
    标准差1.56×1042.81×104000
    $ f_{4} $最优值1.54×1004.04×10−15.95×10−25500
    最差值8.70×1019.66×1016.93×10−24200
    平均值3.93×1015.40×1014.02×10−24300
    标准差3.07×1013.29×101000
    $ f_{5} $最优值2.72×1012.71×1012.75×1011.12×10−61.38×10−5
    最差值2.88×1012.88×1012.88×1011.51×10−18.58×10−4
    平均值2.79×1012.79×1012.81×1012.10×10−23.27×10−4
    标准差4.78×10−15.12×10−13.63×10−13.84×10−22.84×10−4
    续表 4
    函数指标WOAWOA1WOA2WOA3MIWOA
    $f_{6}$最优值1.20×10−11.01×10−12.52×10−11.44×10−71.27×10−7
    最差值1.29×1008.20×10−18.25×10−11.40×10−24.15×10−6
    平均值4.82×10−13.58×10−14.80×10−11.39×10−31.65×10−6
    标准差2.86×10−11.98×10−11.76×10−13.06×10−31.46×10−6
    $f_{7}$最优值1.33×10−51.66×10−47.12×10−72.25×10−62.03×10−6
    最差值9.45×10−31.77×10−23.71×10−42.71×10−42.86×10−5
    平均值3.17×10−34.21×10−31.01×10−45.79×10−51.06×10−5
    标准差2.78×10−34.76×10−38.87×10−55.22×10−58.36×10−6
    $ f_{8} $最优值−1.26×104−1.26×104−1.26×104−1.26×104−1.25×104
    最差值−7.44×103−7.61×103−1.11×104−1.13×104−1.17×104
    平均值−1.02×104−1.01×104−1.24×104−1.24×104−1.22×104
    标准差1.60×1031.75×1033.85×1022.49×1023.40×102
    $f_{9}$最优值00000
    最差值00000
    平均值00000
    标准差00000
    $ f_{10} $最优值8.88×10−168.88×10−168.88×10−168.88×10−168.88×10−16
    最差值7.99×10−157.99×10−158.88×10−168.88×10−168.88×10−16
    平均值4.56×10−153.97×10−158.88×10−168.88×10−168.88×10−16
    标准差2.51×10−152.71×10−15000

    由表4可知，3种改进策略对WOA均有不同程度的提升，WOA3的改进效果最好，WOA2次之，WOA1的计算结果低于其他2种算法的计算结果，但对WOA仍有明显的改进效果。将3种改进策略相结合时，算法搜索最精确，明显优于WOA1、WOA2和WOA3，表明3种改进策略是有效的。

    3.5   MIWOA与不同策略改进WOA对比

    为了对比MIWOA与其他改进WOA的改进效果，令$ N = 30 $，$ D = 500 $，$ T = 500 $，引用3种算法(OBCWOA [12]、eWOA [14]和MEWOA [15])的数据，在相同测试条件下，对$ {f_1}\sim{f_{10}} $测试，结果如表5。

    表  5  MIWOA与其他改进WOA性能对比
    Table  5  Performance comparison between MIWOA and other improved WOAs
    函数指标OBCWOA[12]eWOA[14]MEWOA[15]MIWOA
    $ f_{1} $平均值1.44×10−2721.30×10−20900
    标准差0000
    $ f_{2} $平均值2.09×10−1421.25×10−10500
    标准差1.08×10−1414.43×10−10500
    $ f_{3} $平均值3.47×10−2392.76×10−11000
    标准差01.30×10−10900
    $ f_{4} $平均值3.02×10−1342.83×10−9900
    标准差1.24×10−1331.47×10−9800
    $f_{5}$平均值4.95×1039.51×1028.32×1024.98×102
    标准差2.26×10−17.91×1003.01×1009.44×10−2
    续表 5
    函数指标OBCWOA[12]eWOA[14]MEWOA[15]MIWOA
    $f_{6}$平均值2.84×1022.86×1012.06×1011.11×102
    标准差6.57×1013.28×1014.09×1002.31×100
    $f_{7}$平均值1.80×10−42.07×10−43.30×10−44.15×10−6
    标准差1.47×10−41.88×10−43.53×10−42.80×10−6
    $ f_{8} $平均值−2.05×105−2.03×105−2.09×105−6.21×104
    标准差9.53×1031.50×1043.10×1024.04×103
    $f_{9}$平均值0000
    标准差0000
    $ f_{10} $平均值1.01×10−158.88×10−168.88×10−168.88×10−16
    标准差6.49×10−16000

    表5结果显示，对于函数$ {f_1}\sim{f_4} $，MIWOA与MEWOA可以在有限次迭代收敛到最优值，而OBCWOA和eWOA相对收敛精度较低。对于函数$ {f_5}\sim{f_{10}} $，MIWOA可以使用更少的迭代次数收敛到最优值，说明MIWOA比其他改进WOA寻优效果更好。

    平均绝对误差(mean absolute error, MAE)是评价算法有效可行的重要指标，计算公式为[23]

    $$ E_{{\rm{MAE}}} = \frac{{\displaystyle\sum\limits_{i = 1}^{{N_f}} {|{m_i} - {o_i}|} }}{{{N_f}}} $$ (20)

    式中：$ {m_i} $为算法求解结果平均值，$ {o_i} $为各测试函数理论值，$ {N_f} $为测试函数个数。表6为除理论值非零的$ {f_8} $函数外，4种算法的MAE排序，由计算结果可知，MIWOA的MAE值最小，排名第1，证明了本文改进策略的有效性。

    表  6  4种改进WOA的MAE排名
    Table  6  MAE ranking of four improved WOAs
    算法MAE排名
    MIWOA6.77×1011
    MEWOA9.47×1012
    eWOA1.09×1023
    OBCWOA5.82×1024

    3.6   MIWOA求解高维函数的实验分析

    由上述计算结果可知，对于低维测试函数，本文MIWOA寻优效果良好，但实际应用中高维大规模问题普遍存在，为了检验MIWOA求解高维问题的可行性，将其在10个基准函数，$ N = 30 $， $ T = 500 $，$ D = 200、500、1\;000 $情况下，运行30次取平均值，根据文献[25]求解算法寻优成功率。绝对误差精度如表1所示，计算结果如表7。

    表  7  高维测试函数优化对比
    Table  7  High dimensional test functions optimization comparison
    维数函数WOAMIWOA
    平均值标准差成功率/%平均值标准差成功率/%
    200$ {f_1} $6.20×10−1041.22×10−10310000100
    $ {f_2} $6.90×10−611.05×10−6010000100
    $ {f_3} $2.94×1063.68×105000100
    $ {f_4} $6.41×1013.00×101000100
    $ {f_5} $1.96×1026.86×10−201.99×1021.03×10−10
    $ {f_6} $8.71×10−17.01×10−204.20×1011.87×1000
    $ {f_7} $4.88×10−45.71×10−41001.10×10−59.27×10−6100
    $ {f_8} $−8.16×1042.68×1030−2.69×1042.72×1030
    $ {f_9} $0010000100
    $ {f_{10}} $4.44×10−1501008.88×10−160100
    续表 7
    维数函数WOAMIWOA
    平均值标准差成功率/%平均值标准差成功率/%
    500$ {f_1} $2.12×10−1094.20×10−10910000100
    $ {f_2} $5.06×10−608.84×10−6010000100
    $ {f_3} $1.65×1072.51×106000100
    $ {f_4} $9.23×1014.44×100000100
    $ {f_5} $4.93×1022.68×10−104.98×1029.44×10−20
    $ {f_6} $1.41×1002.68×10−101.11×1022.31×1000
    $ {f_7} $1.01×10−46.41×10−51004.15×10−62.80×10−6100
    $ {f_8} $−2.02×1051.02×1040−6.21×1044.04×1030
    $ {f_9} $0010000100
    $ {f_{10}} $8.88×10−1601008.88×10−160100
    1000$ {f_1} $5.77×10−1151.15×10−11410000100
    $ {f_2} $4.31×10−648.17×10−6410000100
    $ {f_3} $6.16×1078.23×106000100
    $ {f_4} $1.82×1013.13×1012000100
    $ {f_5} $9.89×1022.71×10−109.98×1021.64×10−10
    $ {f_6} $2.21×1004.32×10−102.26×1023.83×1000
    $ {f_7} $2.22×10−41.68×10−41001.54×10−61.03×10−6100
    $ {f_8} $−4.17×1052.64×1030−1.27×1051.32×1040
    $ {f_9} $0010000100
    $ {f_{10}} $4.44×10−152.25×10−151008.88×10−160100

    从表7可以看出，两算法在求解高维测试函数时，寻优精度比求低维函数略有下降，但整体仍可达到较高精度，获得理想结果。MIWOA在7个基准函数上寻优成功率达到了100%，相同维度下，MIWOA的寻优效果比WOA更好，说明MIWOA对于求解高维优化问题具有较高的计算精度和稳定性。

    3.7   MIWOA平均运行时间分析

    为了验证MIWOA的计算速度，将其与PSO、ABC、GWO、HHO、WOA、WOA1、WOA2、WOA3运行30次的平均时间对比，$ N = 30 $，$ D = 1\;000 $，$ T = 500 $，计算结果如表8。

    表  8  基准函数寻优平均时间对比
    Table  8  Comparison of average time for optimization of benchmark function s
    函数PSOABCGWOHHOWOAWOA1WOA2WOA3MIWOA
    $ {f_1} $0.1859650.8965581.8413940.4746760.9904460.9933900.7913722.6402942.831416
    $ {f_2} $0.2100071.0423121.9061510.4995801.0012651.0157370.8068342.6932932.949955
    $ {f_3} $11.73320024.23192013.34820028.45170012.42321012.66927012.75003014.62622014.395090
    $ {f_4} $0.1908020.8883691.8764430.6474020.9972291.0127850.8054262.6448092.827659
    $ {f_5} $0.2299611.1602962.0823100.9721871.0662101.1922950.9740363.0345232.931688
    $ {f_6} $0.1897150.9042811.8474580.7939470.9938770.9938180.7787922.6234572.742954
    $ {f_7} $0.6356812.2107402.6177101.5024351.7240801.7839971.5130493.5063163.821165
    $ {f_8} $0.6474232.3777152.4029961.6587021.5597841.6122481.3993423.1828733.422051
    $ {f_9} $0.4779261.9270732.2454311.2499361.3793081.4149271.2288203.0351983.260680
    $ {f_{10}} $0.4947071.9965122.2190101.2526471.4286661.4102181.1903163.0992083.261962

    由表8可知，对于元启发式算法，WOA与ABC、HHO运行时间相近，可以快速收敛到最优值。对于改进算法，WOA、WOA1和WOA2的平均时长相当，说明WOA1和WOA2的改进策略未增加WOA运行时间。由于算法后期动态选择自适应t分布或蚁狮优化算法，增加了循环嵌套，WOA3耗时多于WOA。融合多种改进策略的MIWOA搜索范围变广，寻优时间增加，但均在合理范围内，与理论分析相符。

    4.   MIWOA辨识混沌系统参数

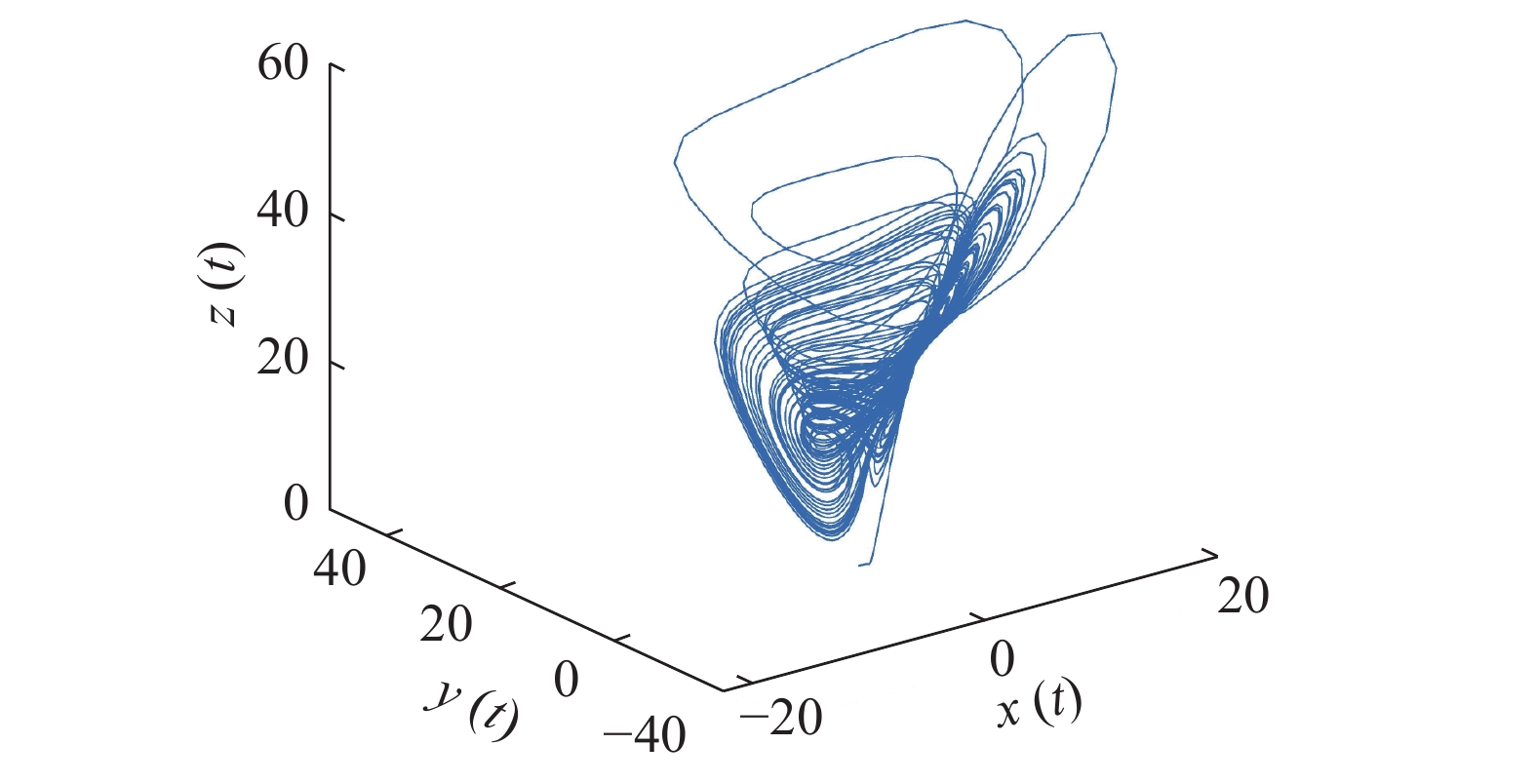
    4.1   MIWOA对$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统的参数辨识

    $ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $系统具有简单、非对称吸引子结构，在保密通信中承担非常重要的作用。以典型$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统为例，验证MIWOA可以精确辨识混沌系统参数。$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $系统表达式为[7]

    $$ \left\{ {\begin{array}{l} {\dot x = - y - {\textit{z}}} \\ {\dot y = x + ay} \\ {\dot {\textit{z}} = b + x{\textit{z}} - c{\textit{z}}} \end{array}} \right. $$ (21)

    当参数$ a = 0.2 $，$ b = 0.2 $，$ c = 5.7 $时，系统为混沌状态，其演化过程如图7所示。令初值向量为$ {[ - 1\;\; 0\;\; 1 ]^{\rm{T}}} $，步长$ h = 0.01 $，使用四阶Runge-Kutta法解式(21)，利用前100个解及PSO、WOA、MIWOA辨识待定参数$ {[a\;\; b\;\; c]^{\rm{T}}} $，各算法独立运行20次。

    图  7  $ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统动力学轨迹
    Fig.  7  Dynamic track of $ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $ chaotic system
    下载: 全尺寸图片

    首先测试3种算法在具有一个未知参数的$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $系统参数辨识中的搜索性能，即每次只辨识$ a、b、c $ 3个参数中的一个，测试结果如表9。由表中数据可知，对于参数$ a $，MIWOA可收敛到理论最优值，其最差值优于其他2种算法的最优值。对于参数$ b $，WOA和MIWOA均可达到理论最优值，但MIWOA寻优效果更好。对于参数$ c $，MIWOA的适应度值小于PSO和WOA的适应度值，估计值很接近真实值，说明MIWOA具有良好的全局搜索能力和计算鲁棒性。

    表  9  不同算法的一维参数估计结果比较
    Table  9  Comparison of one-dimensional parameter estimation results for different algorithms
    评价指标算法实验1 ($ a $未知)实验2 ($ b $未知)实验3 ($ c $未知)
    $ a $$ J $$ b $$ J $$ c $$ J $
    最优值PSO0.2000006.45×10−130.1999999.08×10−135.6999934.87×10−12
    WOA0.2000001.27×10−140.2000002.29×10−145.6999995.86×10−14
    MIWOA0.20000000.20000005.7000000
    平均值PSO0.2000004.38×10−120.2000014.03×10−125.7000051.13×10−11
    WOA0.2000001.63×10−120.2000002.06×10−135.7000038.71×10−12
    MIWOA0.2000001.73×10−150.2000004.22×10−165.7000001.09×10−14
    最差值PSO0.2000011.45×10−110.2000028.55×10−125.7000141.79×10−11
    WOA0.1999995.75×10−120.2000003.72×10−135.7000152.15×10−11
    MIWOA0.2000008.88×10−150.2000002.00×10−155.6999993.13×10−14

    然后测试各算法在具有2个未知参数的混沌系统参数辨识中的搜索性能，计算结果如表10。从表10估计$ a $和$ b $可以看出，各算法搜索精度相似，相对于一个未知参数的情况，搜索精度略有下降，但MIWOA的计算结果仍优于PSO和WOA。另外2种情况也得出同样的结论，验证了MIWOA辨识2个未知参数$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $系统的可行性。

    表  10  不同算法的二维参数估计结果比较
    Table  10  Comparison of two-dimensional parameter estimation results for different algorithms
    评价指标算法实验1 ($ a $和$ b $未知)实验2 ($ a $和$ c $未知)实验3 ($ b $和$ c $未知)
    $ a $$ b $$ J $$ a $$ c $$ J $$ b $$ c $$ J $
    最优值PSO0.1999750.1999745.63×10−80.2007965.6946136.15×10−50.2012535.7019712.36×10−5
    WOA0.2000590.2002191.07×10−70.1991525.7020575.07×10−60.1991075.6976267.13×10−7
    MIWOA0.1999860.2000161.19×10−80.2002315.6997501.08×10−60.1999665.6992996.91×10−8
    平均值PSO0.2000000.2000521.41×10−70.2001255.6981978.91×10−50.1992245.6991313.36×10−5
    WOA0.2000000.1999994.16×10−70.2001235.6996751.48×10−50.1997805.6994241.29×10−6
    MIWOA0.1999990.1999705.22×10−80.2001945.7000612.84×10−60.2002635.6999598.13×10−7
    最差值PSO0.2001630.2004313.59×10−70.1964355.7339731.24×10−40.1916695.6660206.88×10−5
    WOA0.1997670.2008661.66×10−60.2024155.6941144.12×10−50.1986385.6963741.66×10−6
    MIWOA0.1999090.1997451.15×10−70.2008105.7049614.65×10−60.2011585.6949331.34×10−6

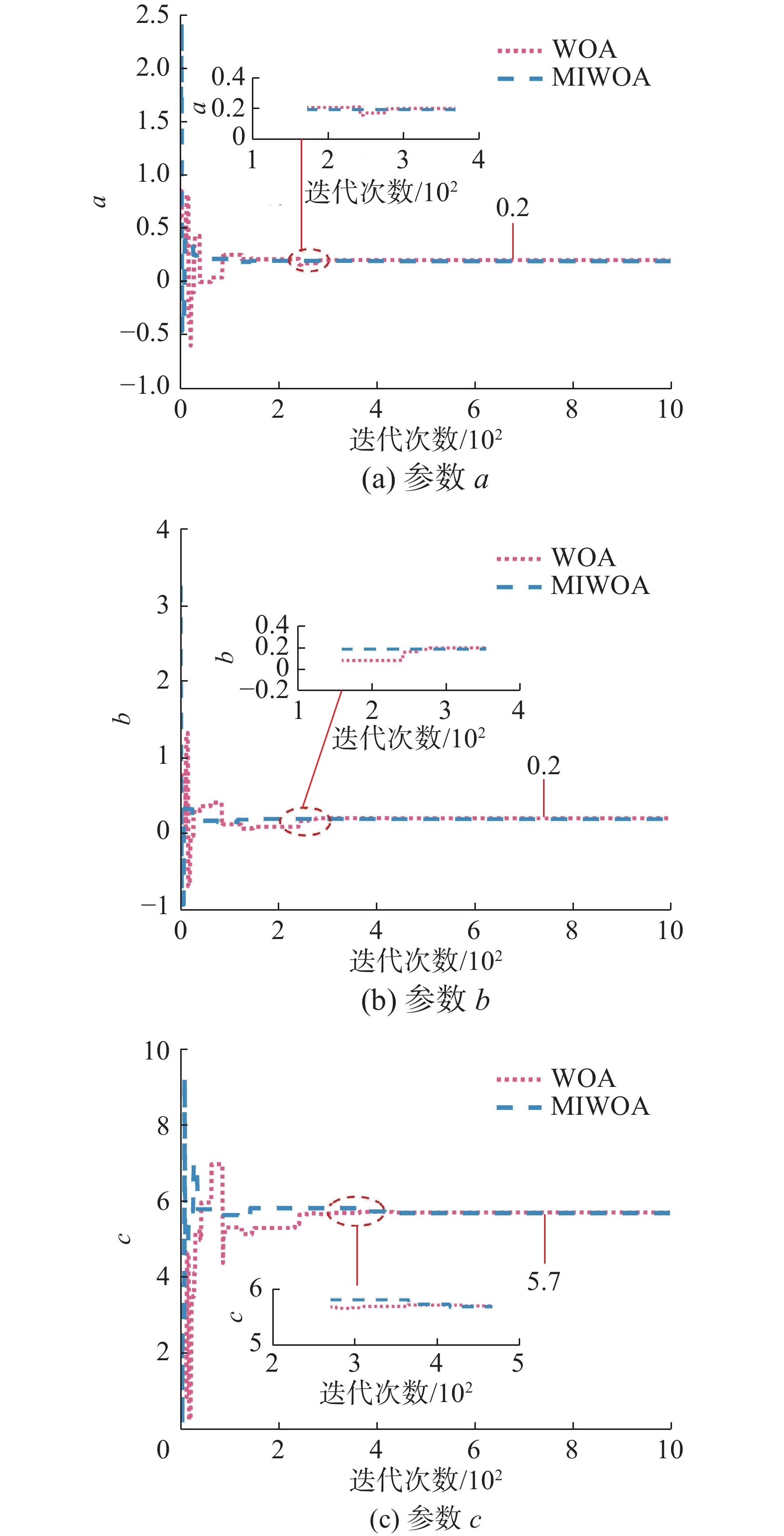
    最后，使用3种算法辨识具有3个未知参数的混沌系统，表11为各算法运行20次的统计结果。由表11中数据可知，各算法的搜索精度下降，但MIWOA的最差值优于PSO和WOA的最优值，在3种算法中搜索精度最高，表明MIWOA对$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统参数辨识更具有效性。

    表  11  不同算法的三维参数估计结果比较
    Table  11  Comparison of three-dimensional parameter estimation results for different algorithms
    评价指标算法abcJ
    最优值PSO0.2013490.1999045.6996981.06×10−3
    WOA0.2006030.1982185.6934751.02×10−4
    MIWOA0.2000130.1994825.6979902.10×10−5
    平均值PSO0.2025460.2118775.7299511.57×10−3
    WOA0.2008520.2009925.7011047.11×10−4
    MIWOA0.1994940.1992685.7041615.08×10−5
    最差值PSO0.2141860.2377015.8773062.00×10−3
    WOA0.1877810.2316055.7855841.47×10−3
    MIWOA0.1971970.2093525.7359409.02×10−5

    图8和图9分别是WOA和MIWOA对$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统的参数辨识曲线和适应度值曲线，从图中可以看到MIWOA的参数估计值可以快速收敛到真实值，适应度值迅速逼近0，表明MIWOA高效的全局搜索能力和快速收敛速度。

    图  8  WOA和MIWOA参数辨识曲线
    Fig.  8  Parameter identification curves of WOA and MIWOA
    下载: 全尺寸图片
    图  9  WOA和MIWOA适应度值曲线
    Fig.  9  Fitness value curves of WOA and MIWOA
    下载: 全尺寸图片

    4.2   MIWOA对$ {\rm{L}}\ddot {\rm{u}} $混沌系统的参数辨识

    为了验证MIWOA对混沌系统参数辨识的普适性，以$ {\rm{L}}\ddot {\rm{u}} $系统为例进行仿真，表达式为[26]

    $$ \left\{ {\begin{array}{l} {\dot x = a(y - x)} \\[-3pt] {\dot y = - x{\textit{z}} + by} \\[-3pt] {\dot {\textit{z}} = xy - c{\textit{z}}} \end{array}} \right. $$ (22)

    其中，系统参数真实值为$ a = 30 $，$ b = 22.2 $，$ c = {{8.8} \mathord{\left/ {\vphantom {{8.8} 3}} \right. } 3} $时，系统为混沌状态，其演化过程如图10所示。

    图  10  $ {\rm{L}}\ddot {\rm{u}} $混沌系统动力学轨迹
    Fig.  10  Dynamic track of $ {\rm{L}}\ddot {\rm{u}} $ chaotic system
    下载: 全尺寸图片

    令初值向量为${[ - 1\;\; 0\;\; 1]^{\rm{T}}}$，使用PSO、WOA和MIWOA辨识$ {\rm{L}}\ddot {\rm{u}} $混沌系统3个参数未知时的情况，3种算法独立运行20次，辨识结果如表12所示。

    表  12  各算法的三维参数估计结果比较
    Table  12  Comparison of three-dimensional parameter estimation results for each algorithm
    评价指标算法$ a $$ b $$ c $$ J $
    最优值PSO30.21260422.2488502.9248351.0056×10−3
    WOA30.02425222.2650872.9321202.3900×10−5
    MIWOA29.99942722.1390152.9358867.8900×10−5
    平均值PSO29.97153922.3327462.9250841.4468×10−3
    WOA29.64116021.9485052.9297577.6355×10−3
    MIWOA29.95337722.1795342.9330541.6305×10−4
    最差值PSO28.71845722.7847622.9005862.1256×10−3
    WOA25.86708824.9742652.9031073.9871×10−2
    MIWOA29.64389922.4437692.9263062.3000×10−4

    由表12中数据可知，除了MIWOA的最优适应度值大于WOA的最优适应度值，MIWOA的计算结果均优于其他2种算法，说明MIWOA辨识混沌系统具有普适性。

    5.   结束语

    本文以WOA为基础，提出一种MIWOA。通过分析初始种群分布，使用Chebyshev混沌映射提高了初始种群质量。采用非线性收敛因子和自适应权重，提高了算法全局和局部搜索能力。动态选择自适应t分布或蚁狮优化算法更新鲸鱼位置，避免过早收敛。通过对10个基准函数和高维测试函数进行测试，以及Wilcoxon秩和检验，证明了MIWOA的优越性。

    将MIWOA应用于$ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $和$ {\rm{L}}\ddot {\rm{u}} $混沌系统的参数辨识，仿真结果优于PSO和WOA，验证了MIWOA辨识混沌系统参数的高效性。今后将继续研究WOA的优化策略，将其应用到混沌系统控制与同步等其他领域。

    致谢　本文作者衷心感谢德国阿尔弗雷德韦格纳研究所 Sergey Danilov 教授和王强博士在写作过程中提出的宝贵建议和意见！

  • 图  1   Chebyshev映射分布

    Fig.  1   Chebyshev map distribution

    下载: 全尺寸图片

    图  2   a的衰减曲线

    Fig.  2   Attenuation curves of a

    下载: 全尺寸图片

    图  3   函数分布对比

    Fig.  3   Function distribution comparison

    下载: 全尺寸图片

    图  4   混沌系统参数辨识原理

    Fig.  4   Principle of parameter identification for chaotic system

    下载: 全尺寸图片

    图  5   MIWOA流程

    Fig.  5   Flow chart of MIWOA

    下载: 全尺寸图片

    图  6   30维测试函数的平均收敛曲线

    Fig.  6   Average convergence curves of 30 dimensional test functions

    下载: 全尺寸图片

    图  7   $ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $混沌系统动力学轨迹

    Fig.  7   Dynamic track of $ {\rm{R}}\ddot {\rm{o}} {\rm{ssler}} $ chaotic system

    下载: 全尺寸图片

    图  8   WOA和MIWOA参数辨识曲线

    Fig.  8   Parameter identification curves of WOA and MIWOA

    下载: 全尺寸图片

    图  9   WOA和MIWOA适应度值曲线

    Fig.  9   Fitness value curves of WOA and MIWOA

    下载: 全尺寸图片

    图  10   $ {\rm{L}}\ddot {\rm{u}} $混沌系统动力学轨迹

    Fig.  10   Dynamic track of $ {\rm{L}}\ddot {\rm{u}} $ chaotic system

    下载: 全尺寸图片

    表  1   基准函数

    Table  1   Benchmark functions

    函数搜索范围$ \varepsilon $
    Sphere Function($ {f_1} $)[−100,100]0.001
    Schwefel’s Problem 2.22($ {f_2} $)[−10,10]0.001
    Schwefel’s Problem 1.2($ {f_3} $)[−100,100]0.001
    Schwefel’s Problem 2.21($ {f_4} $)[−100,100]0.001
    Rosenbrock’s Function($ {f_5} $)[−30,30]0.010
    续表 1
    函数搜索范围$ \varepsilon $
    Step Function($ {f_6} $)[−100,100]0.010
    Quartic Function($ {f_7} $)[−1.28,1.28]0.010
    Schwefel’s Problem 2.26($ {f_8} $)[−500,500]100.000
    Rastrigin’s Function($ {f_9} $)[−5.12,5.12]0.010
    Ackley’s Function($ {f_{10}} $)[−32,32]0.010

    表  2   测试函数优化结果

    Table  2   Test function optimization results

    函数指标WOAPSOABCGWOHHOMIWOA
    $ f_{1} $最优值2.57×10−1654.01×1012.74×10−19.58×10−619.90×10−2140
    最差值3.15×10−1491.38×1021.46×1008.42×10−591.29×10−1850
    平均值3.21×10−1508.22×1016.20×10−12.04×10−591.29×10−1860
    标准差9.44×10−1503.09×1013.26×10−12.37×10−5900
    $ f_{2} $最优值1.81×10−1112.59×1005.32×10−25.40×10−368.33×10−1070
    最差值3.52×10−1021.03×1025.81×1014.23×10−344.72×10−950
    平均值3.58×10−1033.89×1011.41×1011.30×10−344.89×10−960
    标准差1.05×10−1022.63×1012.27×1011.18×10−341.41×10−950
    $ f_{3} $最优值3.69×1033.59×1033.28×1043.14×10−193.62×10−1760
    最差值4.64×1042.10×1048.86×1041.60×10−132.18×10−1490
    平均值2.01×1041.10×1046.78×1041.65×10−142.41×10−1500
    标准差1.32×1045.27×1031.68×1044.80×10−146.51×10−1500
    $ f_{4} $最优值3.58×10−21.94×1005.27×1019.39×10−161.53×10−1020
    最差值8.89×1016.66×1006.61×1011.72×10−132.05×10−900
    平均值2.47×1013.62×1005.92×1012.65×10−142.15×10−910
    标准差2.75×1011.29×1004.60×1005.01×10−146.14×10−910
    $ f_{5} $最优值2.79×1013.95×1031.37×1062.79×1011.61×10−32.80×101
    最差值2.87×1016.29×1032.29×1062.87×1015.45×10−32.88×101
    平均值2.84×1015.36×1031.93×1062.84×1013.92×10−32.82×101
    标准差4.23×10−11.15×1034.53×1053.96×10−11.88×10−32.76×10−1
    $ f_{6} $最优值8.77×10−21.44×1024.45×10−19.96×10−11.77×10−59.23×10−3
    最差值2.72×10−13.09×1026.81×10−11.26×1006.11×10−52.72×10−1
    平均值1.98×10−12.43×1025.86×10−11.15×1004.37×10−54.41×10−2
    标准差9.03×10−28.11×1011.15×10−11.30×10−12.12×10−56.35×10−2
    $ f_{7} $最优值1.78×10−43.84×10−22.16×10−14.57×10−42.27×10−61.59×10−6
    最差值5.24×10−31.58×10−18.24×10−12.07×10−31.25×10−49.40×10−5
    平均值2.04×10−37.45×10−25.37×10−19.18×10−46.13×10−52.69×10−5
    标准差1.57×10−33.40×10−21.75×10−14.24×10−44.43×10−53.15×10−5
    续表 2
    函数指标WOAPSOABCGWOHHOMIWOA
    $ f_{8} $最优值−1.26×104−1.04×104−8.22×10112−6.60×103−1.26×104−1.26×104
    最差值−7.69×103−5.75×103−2.27×10119−4.95×103−5.78×103−6.37×103
    平均值−1.12×104−8.14×103−2.41×10118−6.06×103−1.19×104−1.15×104
    标准差1.84×1031.39×1036.77×101185.09×1022.04×1031.74×103
    $ f_{9} $最优值01.23×1021.91×102000
    最差值02.58×1022.50×1029.98×10−100
    平均值01.90×1022.31×1021.99×10−100
    标准差03.51×1011.67×1013.99×10−100
    $ f_{10} $最优值8.88×10−161.71×1003.03×1007.99×10−158.88×10−168.88×10−16
    最差值7.99×10−152.20×1015.29×1002.58×10−148.88×10−168.88×10−16
    平均值4.80×10−157.40×1004.01×1001.58×10−148.88×10−168.88×10−16
    标准差2.49×10−156.32×1007.33×10−14.71×10−1500

    表  3   Wilcoxon秩和检验结果

    Table  3   Results of Wilcoxon rank sum test

    函数WOAPSOABCGWOHHO
    $ f_{1} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $ f_{2} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{3}$2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $ f_{4} $2.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{5}$1.25×10−12.00×10−62.00×10−68.51×10−22.00×10−6
    $ f_{6} $6.00×10−62.00×10−62.00×10−62.00×10−62.00×10−6
    $f_{7}$2.00×10−62.00×10−62.00×10−62.00×10−61.47×10−2
    $ f_{8} $3.13×10−12.30×10−5N/A2.00×10−61.40×10−2
    $f_{9}$N/A2.00×10−62.00×10−62.00×10−3N/A
    $ f_{10} $9.00×10−62.00×10−62.00×10−69.03×10−7N/A
    +/=/−7/1/210/0/09/1/09/0/18/2/0

    表  4   不同改进策略算法性能对比

    Table  4   Performance comparison of algorithms for different improved strategies

    函数指标WOAWOA1WOA2WOA3MIWOA
    $ f_{1} $最优值1.25×10−853.72×10−84000
    最差值1.27×10−712.16×10−72000
    平均值6.84×10−731.08×10−73000
    标准差2.62×10−724.04×10−73000
    $ f_{2} $最优值1.45×10−581.14×10−573.45×10−26400
    最差值2.85×10−491.73×10−495.63×10−24500
    平均值1.01×10−508.04×10−511.88×10−24600
    标准差5.11×10−503.12×10−50000
    $ f_{3} $最优值1.46×1042.48×104000
    最差值7.97×1041.41×105000
    平均值4.70×1048.05×104000
    标准差1.56×1042.81×104000
    $ f_{4} $最优值1.54×1004.04×10−15.95×10−25500
    最差值8.70×1019.66×1016.93×10−24200
    平均值3.93×1015.40×1014.02×10−24300
    标准差3.07×1013.29×101000
    $ f_{5} $最优值2.72×1012.71×1012.75×1011.12×10−61.38×10−5
    最差值2.88×1012.88×1012.88×1011.51×10−18.58×10−4
    平均值2.79×1012.79×1012.81×1012.10×10−23.27×10−4
    标准差4.78×10−15.12×10−13.63×10−13.84×10−22.84×10−4
    续表 4
    函数指标WOAWOA1WOA2WOA3MIWOA
    $f_{6}$最优值1.20×10−11.01×10−12.52×10−11.44×10−71.27×10−7
    最差值1.29×1008.20×10−18.25×10−11.40×10−24.15×10−6
    平均值4.82×10−13.58×10−14.80×10−11.39×10−31.65×10−6
    标准差2.86×10−11.98×10−11.76×10−13.06×10−31.46×10−6
    $f_{7}$最优值1.33×10−51.66×10−47.12×10−72.25×10−62.03×10−6
    最差值9.45×10−31.77×10−23.71×10−42.71×10−42.86×10−5
    平均值3.17×10−34.21×10−31.01×10−45.79×10−51.06×10−5
    标准差2.78×10−34.76×10−38.87×10−55.22×10−58.36×10−6
    $ f_{8} $最优值−1.26×104−1.26×104−1.26×104−1.26×104−1.25×104
    最差值−7.44×103−7.61×103−1.11×104−1.13×104−1.17×104
    平均值−1.02×104−1.01×104−1.24×104−1.24×104−1.22×104
    标准差1.60×1031.75×1033.85×1022.49×1023.40×102
    $f_{9}$最优值00000
    最差值00000
    平均值00000
    标准差00000
    $ f_{10} $最优值8.88×10−168.88×10−168.88×10−168.88×10−168.88×10−16
    最差值7.99×10−157.99×10−158.88×10−168.88×10−168.88×10−16
    平均值4.56×10−153.97×10−158.88×10−168.88×10−168.88×10−16
    标准差2.51×10−152.71×10−15000

    表  5   MIWOA与其他改进WOA性能对比

    Table  5   Performance comparison between MIWOA and other improved WOAs

    函数指标OBCWOA[12]eWOA[14]MEWOA[15]MIWOA
    $ f_{1} $平均值1.44×10−2721.30×10−20900
    标准差0000
    $ f_{2} $平均值2.09×10−1421.25×10−10500
    标准差1.08×10−1414.43×10−10500
    $ f_{3} $平均值3.47×10−2392.76×10−11000
    标准差01.30×10−10900
    $ f_{4} $平均值3.02×10−1342.83×10−9900
    标准差1.24×10−1331.47×10−9800
    $f_{5}$平均值4.95×1039.51×1028.32×1024.98×102
    标准差2.26×10−17.91×1003.01×1009.44×10−2
    续表 5
    函数指标OBCWOA[12]eWOA[14]MEWOA[15]MIWOA
    $f_{6}$平均值2.84×1022.86×1012.06×1011.11×102
    标准差6.57×1013.28×1014.09×1002.31×100
    $f_{7}$平均值1.80×10−42.07×10−43.30×10−44.15×10−6
    标准差1.47×10−41.88×10−43.53×10−42.80×10−6
    $ f_{8} $平均值−2.05×105−2.03×105−2.09×105−6.21×104
    标准差9.53×1031.50×1043.10×1024.04×103
    $f_{9}$平均值0000
    标准差0000
    $ f_{10} $平均值1.01×10−158.88×10−168.88×10−168.88×10−16
    标准差6.49×10−16000

    表  6   4种改进WOA的MAE排名

    Table  6   MAE ranking of four improved WOAs

    算法MAE排名
    MIWOA6.77×1011
    MEWOA9.47×1012
    eWOA1.09×1023
    OBCWOA5.82×1024

    表  7   高维测试函数优化对比

    Table  7   High dimensional test functions optimization comparison

    维数函数WOAMIWOA
    平均值标准差成功率/%平均值标准差成功率/%
    200$ {f_1} $6.20×10−1041.22×10−10310000100
    $ {f_2} $6.90×10−611.05×10−6010000100
    $ {f_3} $2.94×1063.68×105000100
    $ {f_4} $6.41×1013.00×101000100
    $ {f_5} $1.96×1026.86×10−201.99×1021.03×10−10
    $ {f_6} $8.71×10−17.01×10−204.20×1011.87×1000
    $ {f_7} $4.88×10−45.71×10−41001.10×10−59.27×10−6100
    $ {f_8} $−8.16×1042.68×1030−2.69×1042.72×1030
    $ {f_9} $0010000100
    $ {f_{10}} $4.44×10−1501008.88×10−160100
    续表 7
    维数函数WOAMIWOA
    平均值标准差成功率/%平均值标准差成功率/%
    500$ {f_1} $2.12×10−1094.20×10−10910000100
    $ {f_2} $5.06×10−608.84×10−6010000100
    $ {f_3} $1.65×1072.51×106000100
    $ {f_4} $9.23×1014.44×100000100
    $ {f_5} $4.93×1022.68×10−104.98×1029.44×10−20
    $ {f_6} $1.41×1002.68×10−101.11×1022.31×1000
    $ {f_7} $1.01×10−46.41×10−51004.15×10−62.80×10−6100
    $ {f_8} $−2.02×1051.02×1040−6.21×1044.04×1030
    $ {f_9} $0010000100
    $ {f_{10}} $8.88×10−1601008.88×10−160100
    1000$ {f_1} $5.77×10−1151.15×10−11410000100
    $ {f_2} $4.31×10−648.17×10−6410000100
    $ {f_3} $6.16×1078.23×106000100
    $ {f_4} $1.82×1013.13×1012000100
    $ {f_5} $9.89×1022.71×10−109.98×1021.64×10−10
    $ {f_6} $2.21×1004.32×10−102.26×1023.83×1000
    $ {f_7} $2.22×10−41.68×10−41001.54×10−61.03×10−6100
    $ {f_8} $−4.17×1052.64×1030−1.27×1051.32×1040
    $ {f_9} $0010000100
    $ {f_{10}} $4.44×10−152.25×10−151008.88×10−160100

    表  8   基准函数寻优平均时间对比

    Table  8   Comparison of average time for optimization of benchmark function s

    函数PSOABCGWOHHOWOAWOA1WOA2WOA3MIWOA
    $ {f_1} $0.1859650.8965581.8413940.4746760.9904460.9933900.7913722.6402942.831416
    $ {f_2} $0.2100071.0423121.9061510.4995801.0012651.0157370.8068342.6932932.949955
    $ {f_3} $11.73320024.23192013.34820028.45170012.42321012.66927012.75003014.62622014.395090
    $ {f_4} $0.1908020.8883691.8764430.6474020.9972291.0127850.8054262.6448092.827659
    $ {f_5} $0.2299611.1602962.0823100.9721871.0662101.1922950.9740363.0345232.931688
    $ {f_6} $0.1897150.9042811.8474580.7939470.9938770.9938180.7787922.6234572.742954
    $ {f_7} $0.6356812.2107402.6177101.5024351.7240801.7839971.5130493.5063163.821165
    $ {f_8} $0.6474232.3777152.4029961.6587021.5597841.6122481.3993423.1828733.422051
    $ {f_9} $0.4779261.9270732.2454311.2499361.3793081.4149271.2288203.0351983.260680
    $ {f_{10}} $0.4947071.9965122.2190101.2526471.4286661.4102181.1903163.0992083.261962

    表  9   不同算法的一维参数估计结果比较

    Table  9   Comparison of one-dimensional parameter estimation results for different algorithms

    评价指标算法实验1 ($ a $未知)实验2 ($ b $未知)实验3 ($ c $未知)
    $ a $$ J $$ b $$ J $$ c $$ J $
    最优值PSO0.2000006.45×10−130.1999999.08×10−135.6999934.87×10−12
    WOA0.2000001.27×10−140.2000002.29×10−145.6999995.86×10−14
    MIWOA0.20000000.20000005.7000000
    平均值PSO0.2000004.38×10−120.2000014.03×10−125.7000051.13×10−11
    WOA0.2000001.63×10−120.2000002.06×10−135.7000038.71×10−12
    MIWOA0.2000001.73×10−150.2000004.22×10−165.7000001.09×10−14
    最差值PSO0.2000011.45×10−110.2000028.55×10−125.7000141.79×10−11
    WOA0.1999995.75×10−120.2000003.72×10−135.7000152.15×10−11
    MIWOA0.2000008.88×10−150.2000002.00×10−155.6999993.13×10−14

    表  10   不同算法的二维参数估计结果比较

    Table  10   Comparison of two-dimensional parameter estimation results for different algorithms

    评价指标算法实验1 ($ a $和$ b $未知)实验2 ($ a $和$ c $未知)实验3 ($ b $和$ c $未知)
    $ a $$ b $$ J $$ a $$ c $$ J $$ b $$ c $$ J $
    最优值PSO0.1999750.1999745.63×10−80.2007965.6946136.15×10−50.2012535.7019712.36×10−5
    WOA0.2000590.2002191.07×10−70.1991525.7020575.07×10−60.1991075.6976267.13×10−7
    MIWOA0.1999860.2000161.19×10−80.2002315.6997501.08×10−60.1999665.6992996.91×10−8
    平均值PSO0.2000000.2000521.41×10−70.2001255.6981978.91×10−50.1992245.6991313.36×10−5
    WOA0.2000000.1999994.16×10−70.2001235.6996751.48×10−50.1997805.6994241.29×10−6
    MIWOA0.1999990.1999705.22×10−80.2001945.7000612.84×10−60.2002635.6999598.13×10−7
    最差值PSO0.2001630.2004313.59×10−70.1964355.7339731.24×10−40.1916695.6660206.88×10−5
    WOA0.1997670.2008661.66×10−60.2024155.6941144.12×10−50.1986385.6963741.66×10−6
    MIWOA0.1999090.1997451.15×10−70.2008105.7049614.65×10−60.2011585.6949331.34×10−6

    表  11   不同算法的三维参数估计结果比较

    Table  11   Comparison of three-dimensional parameter estimation results for different algorithms

    评价指标算法abcJ
    最优值PSO0.2013490.1999045.6996981.06×10−3
    WOA0.2006030.1982185.6934751.02×10−4
    MIWOA0.2000130.1994825.6979902.10×10−5
    平均值PSO0.2025460.2118775.7299511.57×10−3
    WOA0.2008520.2009925.7011047.11×10−4
    MIWOA0.1994940.1992685.7041615.08×10−5
    最差值PSO0.2141860.2377015.8773062.00×10−3
    WOA0.1877810.2316055.7855841.47×10−3
    MIWOA0.1971970.2093525.7359409.02×10−5

    表  12   各算法的三维参数估计结果比较

    Table  12   Comparison of three-dimensional parameter estimation results for each algorithm

    评价指标算法$ a $$ b $$ c $$ J $
    最优值PSO30.21260422.2488502.9248351.0056×10−3
    WOA30.02425222.2650872.9321202.3900×10−5
    MIWOA29.99942722.1390152.9358867.8900×10−5
    平均值PSO29.97153922.3327462.9250841.4468×10−3
    WOA29.64116021.9485052.9297577.6355×10−3
    MIWOA29.95337722.1795342.9330541.6305×10−4
    最差值PSO28.71845722.7847622.9005862.1256×10−3
    WOA25.86708824.9742652.9031073.9871×10−2
    MIWOA29.64389922.4437692.9263062.3000×10−4
    • 参考文献(26)
  • [1] 张昊, 王兴元. 复杂混沌系统同步及其应用[M]. 北京: 科学出版社, 2021.
    [2] 郭荣伟. 混沌系统的控制问题研究及其应用[M]. 北京: 科学出版社, 2020.
    [3] DING Zhenghao, LU Zhongrong, LIU Jike. Parameters identification of chaotic systems based on artificial bee colony algorithm combined with cuckoo search strategy[J]. Science China technological sciences, 2018, 61(3): 417–426. doi: 10.1007/s11431-016-9026-4
    [4] 尚荣华, 焦李成, 刘芳, 等. 智能算法导论[M]. 北京: 清华大学出版社, 2021.
    [5] CHEN Yang, PI Dechang, WANG Bi. Enhanced global flower pollination algorithm for parameter identification of chaotic and hyper-chaotic system[J]. Nonlinear dynamics, 2019, 97(2): 1343–1358. doi: 10.1007/s11071-019-05052-z
    [6] AHANDANI M A, KHARRATI H. A corporate shuffled complex evolution for parameter identification[J]. Artificial intelligence review, 2020, 53(4): 2933–2956. doi: 10.1007/s10462-019-09751-2
    [7] TURGUT M S, SAĞBAN H M, TURGUT O E, et al. Whale optimization and sine-cosine optimization algorithms with cellular topology for parameter identification of chaotic systems and Schottky barrier diode models[J]. Soft computing, 2021, 25(2): 1365–1409. doi: 10.1007/s00500-020-05227-6
    [8] EBRAHIMI S M, MALEKZADEH M, ALIZADEH M, et al. Parameter identification of nonlinear system using an improved Lozi map based chaotic optimization algorithm (ILCOA)[J]. Evolving systems, 2021, 12(2): 255–272. doi: 10.1007/s12530-019-09266-9
    [9] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008
    [10] 包子阳, 余继周, 杨杉. 智能优化算法及其MATLAB实例[M]. 3版. 北京: 电子工业出版社, 2021.
    [11] 李士勇, 李研, 林永茂. 智能优化算法与涌现计算[M]. 2版. 北京: 清华大学出版社, 2022.
    [12] CHEN Hui, LI Weide, YANG Xuan. A whale optimization algorithm with chaos mechanism based on quasi-opposition for global optimization problems[J]. Expert systems with applications, 2020, 158: 113612. doi: 10.1016/j.eswa.2020.113612
    [13] CHEN Huiling, YANG Chenjun, HEIDARI A A, et al. An efficient double adaptive random spare reinforced whale optimization algorithm[J]. Expert systems with applications, 2020, 154: 113018. doi: 10.1016/j.eswa.2019.113018
    [14] CHAKRABORTY S, SAHA A K, CHAKRABORTY R, et al. An enhanced whale optimization algorithm for large scale optimization problems[J]. Knowledge-based systems, 2021, 233: 107543. doi: 10.1016/j.knosys.2021.107543
    [15] SHEN Ya, ZHANG Chen, GHAREHCHOPOGH F S, et al. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems[J]. Expert systems with applications, 2023, 215: 119269. doi: 10.1016/j.eswa.2022.119269
    [16] DENG Huaijun, LIU Linna, FANG Jianyin, et al. A novel improved whale optimization algorithm for optimization problems with multi-strategy and hybrid algorithm[J]. Mathematics and computers in simulation, 2023, 205: 794–817. doi: 10.1016/j.matcom.2022.10.023
    [17] YAN Aijun, GUO Jingcheng, WANG Dianhui. Robust stochastic configuration networks for industrial data modelling with Student’s-t mixture distribution[J]. Information sciences, 2022, 607: 493–505. doi: 10.1016/j.ins.2022.05.105
    [18] AN Yining, WANG Jianzhou, LU Haiyan, et al. Research of a combined wind speed model based on multi-objective ant lion optimization algorithm[J]. International transactions on electrical energy systems, 2021, 31(12): e13189.
    [19] ZHANG Liping, ZHU Yue, REN Wei, et al. An energy-efficient authentication scheme based on Chebyshev chaotic map for smart grid environments[J]. IEEE Internet of things journal, 2021, 8(23): 17120–17130. doi: 10.1109/JIOT.2021.3078175
    [20] 黄元春, 张凌波. 改进的鲸鱼优化算法及其应用[J]. 计算机工程与应用, 2019, 55(21): 220–226,270. doi: 10.3778/j.issn.1002-8331.1901-0296

    HUANG Yuanchun, ZHANG Lingbo. Improved whale optimization algorithm and its application[J]. Computer engineering and applications, 2019, 55(21): 220–226,270. doi: 10.3778/j.issn.1002-8331.1901-0296
    [21] 陈强, 王宇嘉, 梁海娜, 等. 目标空间映射策略的高维多目标粒子群优化算法[J]. 智能系统学报, 2021, 16(2): 362–370. doi: 10.11992/tis.202006042

    CHEN Qiang, WANG Yujia, LIANG Haina, et al. Multi-objective particle swarm optimization algorithm based on an objective space papping strategy[J]. CAAI transactions on intelligent systems, 2021, 16(2): 362–370. doi: 10.11992/tis.202006042
    [22] ZHOU Xinyu, WU Yanlin, ZHONG Maosheng, et al. Artificial bee colony algorithm based on adaptive neighborhood topologies[J]. Information sciences, 2022, 610: 1078–1101. doi: 10.1016/j.ins.2022.08.001
    [23] WANG Erlei, XIA Jiangying, LI Jia, et al. Parameters exploration of SOFC for dynamic simulation using adaptive chaotic grey wolf optimization algorithm[J]. Energy, 2022, 261: 125146. doi: 10.1016/j.energy.2022.125146
    [24] 贾鹤鸣, 刘庆鑫, 刘宇翔, 等. 融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法[J]. 智能系统学报, 2023, 18(1): 104–116. doi: 10.11992/tis.202108031

    JIA Heming, LIU Qingxin, LIU Yuxiang, et al. Hybrid Aquila and Harris Hawks optimization algorithm with dynamic opposition-based learning[J]. CAAI transactions on intelligent systems, 2023, 18(1): 104–116. doi: 10.11992/tis.202108031
    [25] 刘成汉, 何庆. 融合多策略的黄金正弦黑猩猩优化算法[J]. 自动化学报, 2023, 49(11): 2360–2373. doi: 10.16383/j.aas.c210313

    LIU Chenghan, HE Qing. Golden sine chimp optimization algorithm integrating multiple strategies[J]. Acta automatica sinica, 2023, 49(11): 2360–2373. doi: 10.16383/j.aas.c210313
    [26] LIU Hongwei, HE Ping, LI Guodong, et al. Multi-directional annular multi-wing chaotic system based on Julia fractals[J]. Chaos, solitons & fractals, 2022, 165: 112799.
WeChat 点击查看大图
图(10)  /  表(17)
出版历程
  • 收稿日期:  2023-03-30
  • 网络出版日期:  2023-09-20

目录

    /

    返回文章
    返回