规则耦合下的多异构子网络MADDPG博弈对抗算法

张钰欣,  赵恩娇,  赵玉新

downloadPDF
张钰欣, 赵恩娇, 赵玉新. 规则耦合下的多异构子网络MADDPG博弈对抗算法 [J]. 智能系统学报, 2024, 19(1): 190-208. doi: 10.11992/tis.202303037
引用本文: 张钰欣, 赵恩娇, 赵玉新. 规则耦合下的多异构子网络MADDPG博弈对抗算法 [J]. 智能系统学报, 2024, 19(1): 190-208. doi: 10.11992/tis.202303037
shu
ZHANG Yuxin, ZHAO Enjiao, ZHAO Yuxin. MADDPG game confrontation algorithm of polyisomer network based on rule coupling based on rule coupling [J]. CAAI Transactions on Intelligent Systems, 2024, 19(1): 190-208. doi: 10.11992/tis.202303037
Citation: ZHANG Yuxin, ZHAO Enjiao, ZHAO Yuxin. MADDPG game confrontation algorithm of polyisomer network based on rule coupling based on rule coupling [J]. CAAI Transactions on Intelligent Systems, 2024, 19(1): 190-208. doi: 10.11992/tis.202303037
shu

规则耦合下的多异构子网络MADDPG博弈对抗算法

doi: 10.11992/tis.202303037

  • 哈尔滨工程大学 智能科学与工程学院, 黑龙江 哈尔滨 150001

基金项目: 国家自然科学基金项目（61903099）；黑龙江省自然科学基金项目 （LH2020F025）；重庆市教育委员会科学技术研究计划（KJZD-K20200470）；中国博士后科学基金面上项目（2021M690812）； 黑龙江省博士后基金面上项目（LBH-Z21048）.
详细信息
    作者简介:

    张钰欣，硕士研究生，主要研究方向为多智能体深度强化学习和多智能体博弈对抗。E-mail：15140294516@163.com;

    赵恩娇，副教授，主要研究方向为集群无人系统协同控制、智能化航海，主持国家自然科学基金项目、黑龙江省自然科学基金项目、中国博士后科学基金项目、黑龙江省博士后科学基金项目等 10 余项。发表学术论文 20余篇。E-mail：zhaoenjiao935@ hrbeu.edu.cn;

    赵玉新，教授，博士生导师，中国青年科技奖、霍英东教育教学奖获得者，入选国家科技创新领军人才支持计划，首批龙江科技英才，担任“导航仪器”教育部工程研究中心主任、工信部研究型教学团队负责人、国家级虚拟教研室负责人、国家级一流本科课程负责人，主要研究方向为船舶导航与海洋仪器技术。承担国防973课题、国家重大科技专项课题、国家自然科学基金项目等多项任务。发表学术论文50余篇，出版专著4部。E-mail：zhaoyuxin@hrbeu.edu.cn.

    通讯作者:

    赵恩娇. E-mail：zhaoenjiao935@hrbeu.edu.cn.

  • 中图分类号: V279

MADDPG game confrontation algorithm of polyisomer network based on rule coupling based on rule coupling

  • College of Intelligent Systems Science and Engineering, Harbin Engineering University, Harbin 150001, China

    摘要
  • 摘要: 针对多无人机博弈对抗过程中无人机数量动态衰减问题和传统深度强化学习算法中的稀疏奖励问题及无效经验抽取频率过高问题，本文以攻防能力及通信范围受限条件下的多无人机博弈对抗任务为研究背景，构建了红、蓝两方无人机群的博弈对抗模型，在多智能体深度确定性策略梯度(multi-agent deep deterministic policy gradient, MADDPG)算法的Actor-Critic框架下，根据博弈环境的特点对原始的MADDPG算法进行改进。为了进一步提升算法对有效经验的探索和利用，本文构建了规则耦合模块以在无人机的决策过程中对Actor网络进行辅助。仿真实验表明，本文设计的算法在收敛速度、学习效率和稳定性方面都取了一定的提升，异构子网络的引入使算法更适用于无人机数量动态衰减的博弈场景；奖励势函数和重要性权重耦合的优先经验回放方法提升了经验差异的细化程度及优势经验利用率；规则耦合模块的引入实现了无人机决策网络对先验知识的有效利用。

     

    Abstract: In order to overcome of dynamic attenuation of the number of UAVs in the process of multi-UAV game confrontation, and solve the sparse reward problem in the traditional deep reinforcement learning algorithm and the high frequency of invalid experience extraction, a game model of red and blue UAV clusters is built in this paper based on the background of multi-unmanned aerial vehicles (Multi-UAVs) game with limited attack and defense capabilities and communication range. Under the Actor-Critic framework of multi-agent deep deterministic policy gradient (MADDPG) algorithm, the original MADDPG algorithm is improved according to the characteristics of the game scenario to solve the problem of the number attenuation, sparse rewards and high extraction frequency of invalid experience of UAVs in the original algorithm. On this basis, in order to improve the exploration and utilization of algorithm for effective experiences, a rule coupling module is built to assist UAV. The simulation experiment shows that the algorithm designed in this paper has improved the convergence speed, learning efficiency and stability. The use of polyisomer network makes the algorithm more suitable for the game scenario that the number of UAVs declines dynamically; the reward potential function and the priority experience playback method based on the importance weight coupling improve the degree of refinement of experience difference and the utilization rate of superior experience; the introduction of rule coupling module realizes the effective utilization of UAV decision network for priori knowledge.

     

    • HTML全文

  • 随着现代战争的复杂性日益提升，智能化空战对无人机自主决策的需求日渐迫切。在多无人机博弈对抗过程中，无人机的自主决策方法已成为空战对抗问题中的重要研究课题。多无人机博弈对抗是指在博弈区域内的两方无人机以一对多或多对多的形式针对敌方无人机进行打击、协同围捕或逃逸敌方无人机的围捕。参与博弈对抗的无人机通常需要根据观测信息进行决策，使无人机群在尽可能保证组内个体存活的同时完成对敌方无人机的协同围捕或击毁[1]。基于多智能体深度强化学习(multi-agent deep reinforcement learning, MADRL)的智能算法在上述多无人机博弈对抗过程中的应用能够对决策机制起到有效的辅助作用，使无人机在动态环境中的机动能力大幅提升，并为智能空战中的策略应用提供参考。因此，开展基于MADRL的多无人机博弈对抗算法的研究具有重要的工程意义。本文选取多个具有相同打击能力、防御能力、探测能力及机动性能的无人机组成参与博弈的双方并在有限区域内进行对抗。通过对上述博弈问题的研究，设计基于MADRL的多无人机博弈对抗算法以提升无人机的对抗性能。

    目前，学者们针对基于MADRL的多无人机博弈对抗问题提出了多种研究方法并取得了大量的研究成果，依据其核心内容的不同，主要分为观测信息预处理、网络结构设计、目标函数设置、奖励机制细化、经验采样和先验知识开发利用6个方向。

    在观测信息预处理方面，由于博弈环境的高度复杂性，环境信息通常是不可完全观测的，若直接将所有无人机的观测信息作为共享信息全部输入网络则会为网络输入端引入大量冗余信息。针对观测信息冗余问题，研究者通常会基于观测信息序列为网络设计注意力机制以提取特征信息；针对观测信息缺失问题，研究者通常会为网络设计信息共享机制以生成局部观测信息从而弥补缺失信息[2-5]。

    在网络结构设计方面，经典的Actor-Critic网络框架虽然能够解决多种复杂问题，但在某些特殊情况下仍然无法做出合理的决策。在传统的网络结构基础上引入额外的辅助网络或丰富传统网络的层次结构可以对网络输出进行有效的约束，在提高网络鲁棒性的同时强化网络性能[6-7]。

    在目标函数设置方面，目标函数是网络参数更新的基础，由于网络参数以目标函数梯度进行更新迭代从而逼近最优解，合理的目标函数设置方法不仅能够提升网络学习的收敛速度，还能在一定程度上避免过拟合问题[8-9]，如将交叉熵项引入目标函数可以在提高网络泛化能力的同时强化网络在干扰环境中的自我调整能力。

    在奖励机制细化方面，稀疏奖励问题是网络学习过程中需要解决的重点问题之一，存储经验的奖励值分布稀疏通常会导致网络学习效率低下，由于参数更新迭代缺乏合理的引导，网络参数始终无法逼近最优解。为博弈问题设计细化的奖励机制能够有效避免稀疏奖励问题，对网络参数的更新以及决策也起到了一定的指导作用[10-11]。

    在经验采样方面，传统的经验抽取通常以均匀采样的方式抽取一个批次的样本，由于优势经验数量较少，对经验进行等概率随机采样通常会导致网络学习效率低下，网络难以学习优秀的成功经验。针对上述问题，研究者通常会对经验生成、存储和采样机制进行优化设计以提升对优势经验的利用效率[12-13]。

    在先验知识开发利用方面，完全依靠自主探索积累经验的学习方式虽然能够达到预期的学习目标，但完全摒弃了对先验知识的利用。专家经验对网络学习能够起到良好的指导作用从而提升网络学习效率[14-15]。部分学者在网络学习过程中引入专家经验对其进行指导，如建立专家经验库以辅助决策或生成成功的伪经验以辅助训练。实验表明，上述方法在网络训练和决策阶段均能够起到良好的辅助作用。

    随着MADRL算法的发展，学者们开始将其应用于多无人机博弈对抗问题的研究中。传统的多无人机博弈对抗方法以基于统计决策和知识推理进行决策或基于最优决策方法在解空间内进行迭代寻优为核心思想，上述传统方法虽然使无人机具有一定的决策能力，但其灵活性、适应性和鲁棒性等性能仍有待提升，在具有连续状态、动作空间的复杂环境中难以取得优秀的表现。基于MADRL的决策方法赋予无人机自我学习和扩展的能力，为智能无人机博弈对抗决策研究的发展带来新契机。混合Q值(QMIX)算法是一种基于价值学习的早期MADRL算法，可以以集中的端到端方式训练分散策略，算法基于局部观测将联合动作值估计为每个无人机Q值的复杂非线性组合。多智能体深度Q学习网络(multi-agent deep Q-learning network, MADQN)将深度Q网络(deep Q-learning network, DQN)算法扩展至多智能体领域，为每个无人机分配了一套独立的DQN，无人机个体以获取最优Q函数为学习目标。虽然QMIX算法和MADQN算法在对多无人机博弈对抗的研究中已经取得了一定的成果，但是从任一单无人机的角度来看，由于其他个体策略的未知性导致环境不稳定，状态转换受到影响，从而违反了马尔科夫决策标准，同时该问题还会导致经验回放在逼近状态对概率进行转换时变的不准确。MADDPG算法以“集中评价−分布执行”为框架以适应多无人机博弈对抗过程的复杂环境，算法在“捕食者−猎物”(predator-prey)问题的研究中取得了初步的成果，但上述问题中无人机群主要以协同围捕作为主要目标而非对抗[16]。针对无人机群博弈对抗过程的特点，通信多智能体深度确定性策略梯度(communication multi-agent deep deterministic policy gradient, COM-MADDPG)算法对经典的MADDPG算法进行改进，使无人机群能够完成协同围捕和打击任务，但无人机仍以粒子的形式参与博弈对抗任务，并未对无人机进行具体的建模[17]。在博弈对抗过程中无人机所处环境通常具有高度复杂性而其自身也受到一定的约束，同步目标分配路径规划(simultaneous target assignment and path planning, STAPP)算法对参与博弈的无人机进行简单建模并构建了具有威胁区的复杂博弈环境以解决多无人机目标分配和路径规划问题(multi-UAV target assignment and path planning, MUTAPP)，但任务的高度复杂性使无效经验的比例大幅度提升，降低了网络模型的学习效率[18]；奖励生成多智能体深度确定性策略梯度(reward shaping multi-agent deep deterministic policy gradient, RS-MADDPG)算法对无人机进行完整建模并提出了相应的约束条件以增加任务复杂性和真实性，同时算法对奖励机制进行优化设计以指导网络参数的更新方向，但所设计的奖励机制更加适用于近距离打击任务而非完整的博弈任务[19]。虽然大部分基于MADRL的智能算法在多无人机博弈对抗过程中已经取得了良好的表现，但无人机完全依赖自身对环境的探索以积累经验的学习方式通常不具有较高的学习效率，与在环境中进行试错学习的纯基于算法的学习方式相比，以合理的规则辅助决策可以减少无效的探索操作，并提升决策能力。基于规则的MADDPG算法将先验知识与MADDPG算法结合，在保留博弈环境复杂性和无人机自身约束的同时，为算法制定规则集以指导无人机在特殊情况下进行决策，虽然规则集在决策阶段起到了有效的指导作用，但决策网络的性能并未得到显著提升且并未考虑到无人机数量衰减这一实际问题[20]。

    综上所述，现有研究成果均利用MADRL算法对各自提出的问题进行研究并改进了原始的MADDPG算法。然而环境的非平稳性、状态空间和动作空间的连续性会导致训练效率低下且学习阶段过于漫长；对有效经验的利用率不高会导致学习的策略与最优策略相差甚远。部分算法虽然对上述问题进行了研究和改进，但涉及到真实博弈场景中多无人机博弈对抗问题的研究实则较少，无人机的有限打击能力和有限防御能力等特性极大地提高了博弈问题的复杂性且参与博弈的无人机数量的动态衰减问题为网络决策增添了冗余信息。因此，将基于MADRL的博弈对抗算法应用于多无人机空战问题时，算法的网络结构、有效经验利用以及奖励函数设计等方面仍存在许多值得探索和研究的内容，如何在经典MADDPG算法的基础上进行研究并针对特定博弈场景进行改进以提升算法的学习效率、收敛速度和稳定性是本文研究的核心目标。

    本文主要针对有限区域内的多无人机博弈对抗问题，在考虑无人机有限打击能力和有限防御能力等约束条件的同时，利用MADRL算法对无人机攻击、逃逸的机动决策方案进行研究。根据MADDPG算法“状态评估−自主决策−环境反馈−网络训练”的自举博弈及训练方法在多无人机博弈对抗问题的应用中存在的无人机数量衰减问题、先验知识利用问题、稀疏奖励问题和有效经验抽取问题，对原始算法的网络结构、奖励机制、决策机制及经验采样方法进行改进并提出了基于规则耦合的多异构子网络MADDPG算法；为了提升算法的收敛速度和稳定性，提出了各子网络在迁移场景中独立训练、在目标场景中联合训练的场景迁移训练方法。

    1.   无人机群博弈对抗问题描述与建模

    1.1   多无人机博弈对抗问题

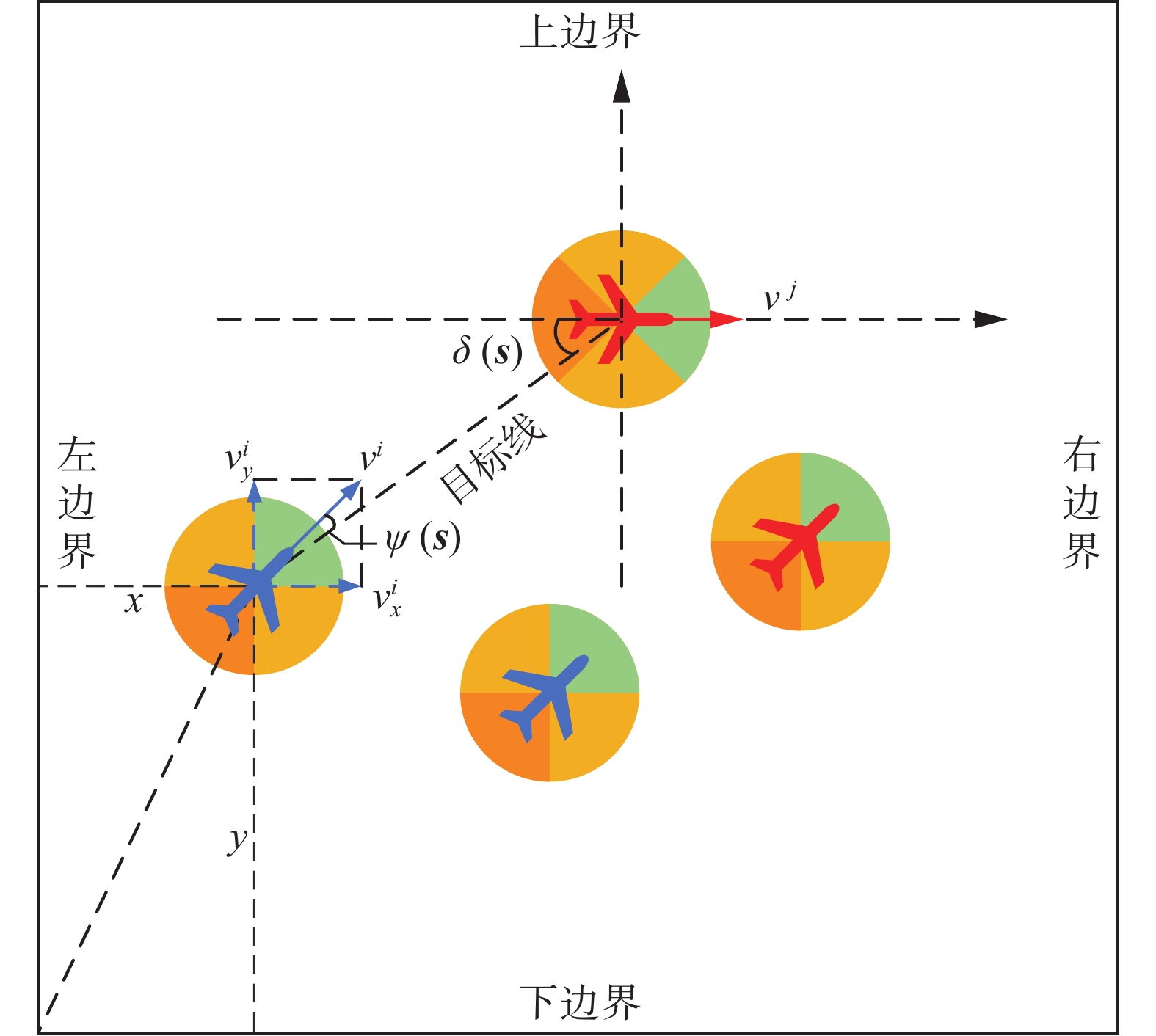
    本文基于2-vs-2多无人机博弈对抗问题对实验环境进行构建，如图1所示。

    图  1  无人机群对抗场景
    Fig.  1  UAVs game confrontation scenario
    下载: 全尺寸图片

    在300 m × 300 m的有限博弈区域内，红、蓝两方各有2架作战无人机参与博弈。与某一无人机距离最近的敌方无人机称为目标无人机，无人机可以通过机载雷达、电子陀螺仪等装置对环境进行观测以获取自身的绝对位置信息以及与目标无人机间的相对位置信息。无人机通过机载通信装置实现主体与友方的观测信息共享，使无人机群具有一定的协同能力，但受限于通信能力，无人机群只能在博弈区域内进行信息共享。若无人机被击毁或离开博弈区域则无法参与后续的对抗任务且由于通信范围受限，被击毁或离开博弈区域的无人机将停止与己方无人机的信息共享。参与博弈的无人机需要在博弈区域内根据融合后的共享观测信息对目标无人机进行攻击或逃离目标无人机的攻击区域。综上所述，本文的研究内容与真实的空战场景更加接近。

    每个无人机的单体状态${{\boldsymbol{s}}^{\boldsymbol{o}}}$为

    $$ {{\boldsymbol{s}}^{\boldsymbol{o}}} = \left[ {x\quad y\quad {v_x}\quad {v_y}\quad d\quad \psi \quad \delta } \right] $$ (1)

    式中：$\left( {x,y} \right)$为无人机在区域内的位置坐标，m；$\left( {{v_x},{v_y}} \right)$为无人机沿$x$轴正方向和$y$轴正方向的分速度，m/s；$d$为目标无人机与当前无人机的相对距离，m；$\psi $为当前无人机的天线列角(antenna train angle, ATA)，rad；$\delta $为目标无人机相对当前无人机的方位角(aspect angle, AA)，rad。

    无人机$i$的状态序列中，目标无人机$j$相对于无人机$i$的距离$d\left( {i,j} \right)$、无人机$i$针对目标无人机$j$的天线列角$\psi \left( {i,j} \right)$和目标无人机$j$的方位角$\delta \left( {i,j} \right)$为

    $$ \left\{ \begin{gathered} d(i,j) = \sqrt {{{(w_x^{ij})}^2} + {{(w_y^{ij})}^2}} \\ \psi (i,j) = {\cos ^{ - 1}}\left[ {{{\left( {v_x^i \cdot w_x^{ij} + v_y^i \cdot w_y^{ij}} \right)} \mathord{\left/ {\vphantom {{\left( {v_x^i \cdot w_x^{ij} + v_y^i \cdot w_y^{ij}} \right)} {\left( {d(i,j) \cdot {v^i}} \right)}}} \right. } {\left( {d(i,j) \cdot {v^i}} \right)}}} \right] \\ \delta (i,j) = {\cos ^{ - 1}}\left[ {{{\left( {v_x^j \cdot w_x^{ij} + v_y^j \cdot w_y^{ij}} \right)} \mathord{\left/ {\vphantom {{\left( {v_x^j \cdot w_x^{ij} + v_y^j \cdot w_y^{ij}} \right)} {\left( {d(i,j) \cdot {v^j}} \right)}}} \right. } {\left( {d(i,j) \cdot {v^j}} \right)}}} \right] \\ \end{gathered} \right. $$ (2)

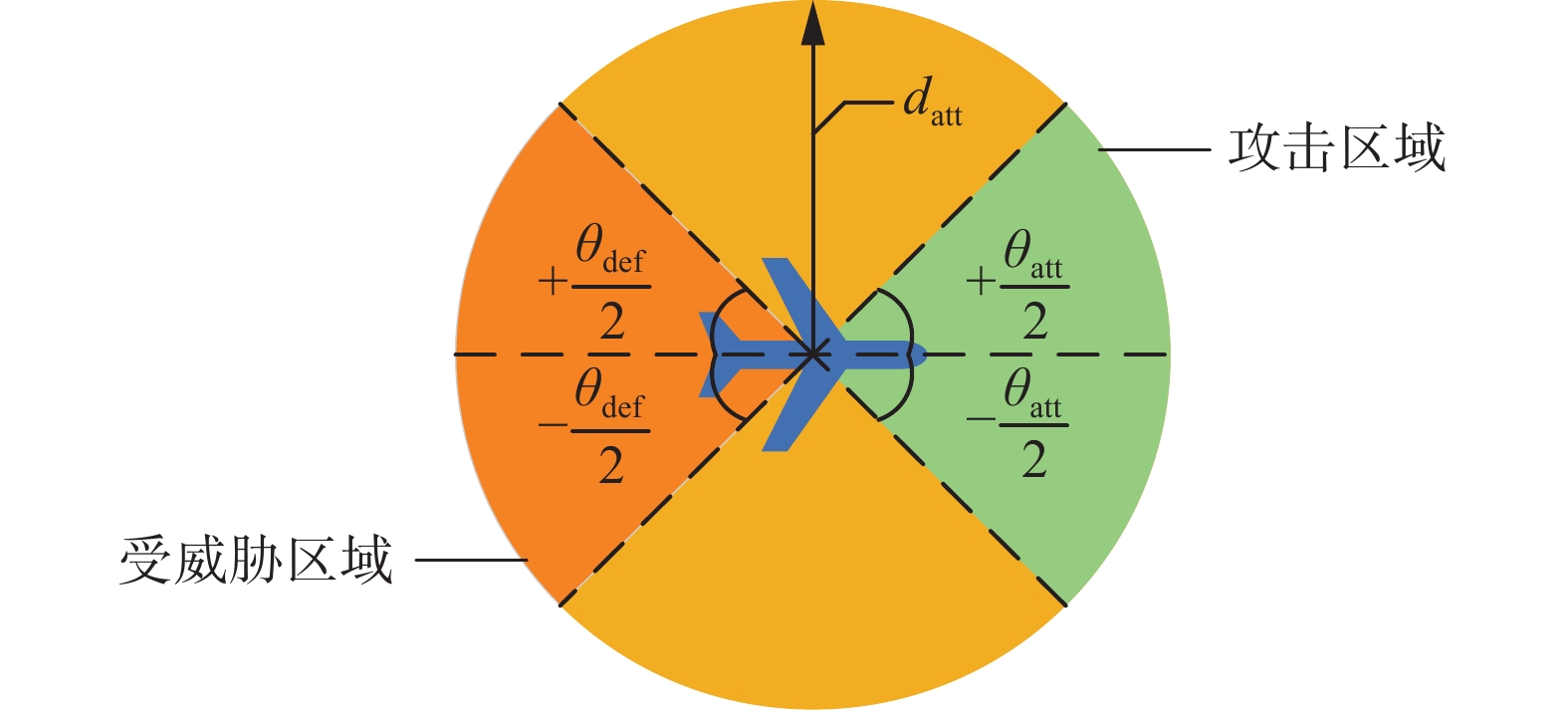
    式中：$w_x^{ij}$、$w_y^{ij}$分别为无人机$i$与目标无人机$j$在$x$方向和$y$方向上的相对距离，$ v_x^i $、$ v_y^i $分别为无人机$i$在$x$方向和$y$方向上的分速度，$ v_x^j $、$ v_y^j $分别为目标无人机$j$在$x$方向和$y$方向上的分速度，$ {v^i} $、$ {v^j} $分别为无人机$ i $和目标无人机$j$的绝对速度，其关系为

    $$ \left\{ \begin{gathered} w_x^{ij} = {x^j} - {x^i} \\ w_y^{ij} = {y^j} - {y^i} \\ {v^i} = \sqrt {{{\left( {v_x^i} \right)}^2} + {{\left( {v_y^i} \right)}^2}} \\ {v^j} = \sqrt {{{\left( {v_x^j} \right)}^2} + {{\left( {v_y^j} \right)}^2}} \\ \end{gathered} \right. $$ (3)

    对于作战无人机来说，其搭载的自行火炮打击能力通常会受到武器射程的限制，机载武器的搭载方式和机械结构对火炮转角也起到约束作用，而无人机的防御能力通常会受到自身机动能性能的约束[21]。无人机的攻防约束条件如图2所示。

    图  2  无人机攻防约束条件
    Fig.  2  UAV attack and defense constrains
    下载: 全尺寸图片

    在本文中，每个无人机的最大攻击距离为${d_{{\rm{att}}}}$，m；在以${d_{{\rm{att}}}}$为半径的圆形区域内，无人机的攻击范围被限制在一个扇形区域内，该区域位于无人机前端，其左右边界与无人机主轴的夹角为$\pm {{{\theta _{{\rm{att}}}}} \mathord{\left/ {\vphantom {{{\theta _{att}}} 2}} \right. } 2}$，rad；而无人机的受威胁范围同样也被限制在一个扇形区域内，该区域位于无人机的尾端，其左右边界与无人机主轴的夹角为$\pm {{{\theta _{{\rm{def}}}}} \mathord{\left/ {\vphantom {{{\theta _{def}}} 2}} \right. } 2}$，rad；当敌方无人机的方位角$\delta $大于$\left| {{{{\theta _{{\rm{def}}}}} \mathord{\left/ {\vphantom {{{\theta _{{\rm{def}}}}} 2}} \right. } 2}} \right|$时，无人机可以有效躲避敌方无人机的攻击以避免被击毁。

    当某一无人机探测到目标无人机时，只有其状态序列满足以下3个条件时才能判定为成功将目标无人机击毁：

    1) 攻击者$i$与目标$j$之间的距离小于攻击距离${d_{{\rm{att}}}}$；

    2) 目标$j$位于攻击者$i$的攻击区域内；

    3) 攻击者$i$位于目标$j$的受威胁区内。

    上述击毁条件可描述为

    $$ \left\{ \begin{array}{l} d\left( {i,j} \right) < {d_{{\rm{att}}}} \\ \varphi \left( {i,j} \right) < {{{\theta _{{\rm{att}}}}} \mathord{\left/ {\vphantom {{{\theta _{att}}} 2}} \right. } 2} \\ \delta \left( {i,j} \right) < {{{\theta _{{\rm{def}}}}} \mathord{\left/ {\vphantom {{{\theta _{def}}} 2}} \right. } 2} \\ \end{array} \right. $$ (4)

    1.2   无人机数学模型

    每个无人机个体的动作序列${{\boldsymbol{a}}^{\boldsymbol{o}}}$为

    $$ {{\boldsymbol{a}}^{\boldsymbol{o}}} = \left[ {{a_x}\quad {a_y}} \right] $$ (5)

    式中：${a_x}$为无人机沿$x$轴正方向加速度，m/s2；${a_y}$为无人机沿$y$轴正方向加速度，m/s2。无人机的动作序列直接决定了其状态空间中的$\left( {x,y,{v_x},{v_y}} \right)$元组，其关系为

    $$ \left\{ \begin{array}{l} v_x^{t + 1} = v_x^t + a_x^t \cdot \Delta t \\ v_y^{t + 1} = v_y^t + a_y^t \cdot \Delta t \\ {x^{t + 1}} = {x^t} + v_x^t \cdot \Delta t + {{a_x^t \cdot {{(\Delta t)}^2}} \mathord{\left/ {\vphantom {{a_x^t \cdot {{(\Delta t)}^2}} 2}} \right. } 2} \\ {y^{t + 1}} = {y^t} + v_y^t \cdot \Delta t + {{a_y^t \cdot {{(\Delta t)}^2}} \mathord{\left/ {\vphantom {{a_y^t \cdot {{(\Delta t)}^2}} 2}} \right. } 2} \\ \end{array} \right. $$ (6)

    在执行过程中，各无人机仅能以己方共享的状态信息和动作信息作为决策依据并生成动作序列${{\boldsymbol{a}}^{\boldsymbol{o}}}$。每一组编队中的无人机均通过控制机体沿各方向的加速度以实现对博弈区域这一未知环境的边界探索；在未跨越博弈区域边界的情况下，对各自锁定的目标无人机进行追捕、打击；在编队中的无人机锁定了相同的目标无人机时，对目标无人机进行协同围捕。

    2.   基于MADRL的多无人机博弈模型

    2.1   马尔可夫博弈

    在MADRL领域中，各个智能体通过与环境的交互来改进自身的策略模型，而智能体本身仅能获取自身的信息或团队的信息，敌方的策略对其来说则是未知的，这也导致了每个智能体所处的环境对其本身来说是极度复杂多变的。

    多智能体博弈对抗的过程被称为马尔可夫博弈(Markov game)或随机博弈(stochastic game)。$N$个智能体的博弈通常以元组$\left( {N,S,A,O,R,P,\gamma } \right)$表示。其中$S$为全局环境状态序列空间，${\boldsymbol{ s}} \in S$；动作序列空间集合$A$为

    $$ A = \left\{ {{A_{1}},A_2, \cdots ,{A_N}} \right\} $$ (7)

    式中：${A_i}$为智能体$i$的动作序列空间，${{\boldsymbol{a}}_{\boldsymbol{i}}} \in {A_i}$；智能体观测状态序列空间集合$O$为

    $$ O = \left\{ {{O_{1}}, O_2, \cdots ,{O_N}} \right\} $$ (8)

    式中：${O_i}$为智能体$i$的观测序列空间，${{\boldsymbol{o}}_{\boldsymbol{i}}} \in {O_i}$；智能体的奖励集合$R$为

    $$ \left\{ \begin{gathered} R = \left\{ {{R_{1}},R_2, \cdots ,{R_N}} \right\} \\ {\rm{s}}.{\rm{t}}. \\ {\boldsymbol{a}} = \left\{ {{{\boldsymbol{a}}_{1}},{\boldsymbol{a}}_2, \cdots ,{{\boldsymbol{a}}_{\boldsymbol{N}}}} \right\} \\ \end{gathered} \right. $$ (9)

    式中：${R_i}:S \times A \to \bf{R}$为智能体$i$的奖励函数，所有智能体在全局环境状态${\boldsymbol{s}}$下执行联合动作${\boldsymbol{a}}$后智能体$i$获得的奖励值${r_i}$为

    $$ {r_i} = {R_i}({\boldsymbol{s}},{\boldsymbol{a}}) $$ (10)

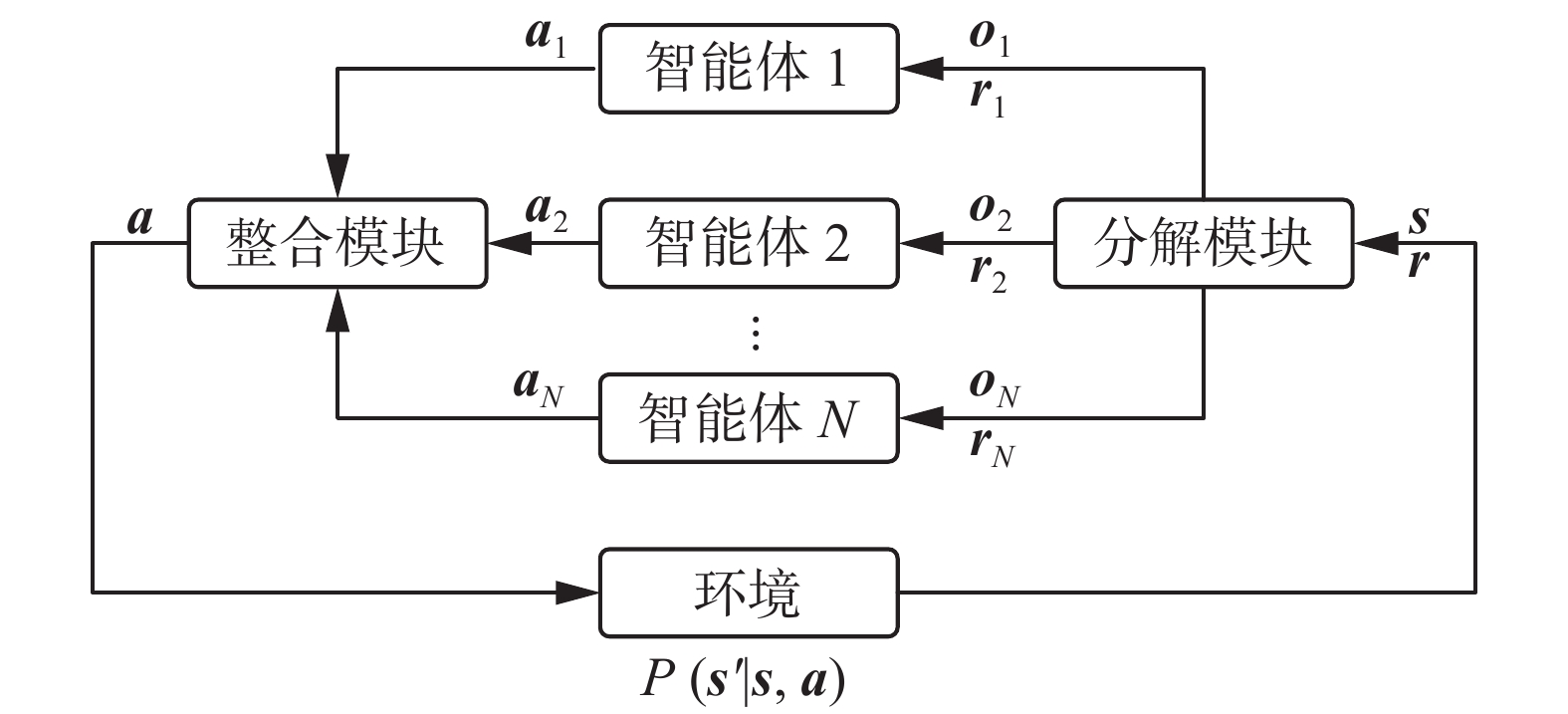
    奖励值的大小不仅取决于自身的动作序列，还受到其他智能体的动作序列影响；$P$为智能体在环境中的状态转移概率函数，即$P:S \times A \times S \to \left[ {0,1} \right]$表示所有智能体在全局环境状态${\boldsymbol{s}}$下执行联合动作${\boldsymbol{a}}$后全局环境状态转移到${\boldsymbol{s}}'$的概率分布；$\gamma \in \left[ {0,1} \right]$为累积奖励值的衰减因子。多智能体与环境交互的过程如图3所示。

    图  3  智能体与环境交互过程
    Fig.  3  Interaction between agent and environment
    下载: 全尺寸图片

    在马尔可夫博弈中，智能体$i$的确定性策略对应的概率密度函数为

    $$ {\pi _{\boldsymbol{i}}}({{\boldsymbol{a}}_{\boldsymbol{i}}}\left| {{{\boldsymbol{o}}_{\boldsymbol{i}}}} \right.) = \left\{ {\begin{array}{*{20}{c}} {1,}&{{{\boldsymbol{a}}_{\boldsymbol{i}}} = \mu ({{\boldsymbol{o}}_{\boldsymbol{i}}};{{\boldsymbol{\theta}} _{\boldsymbol{i}}})} \\ {0,}&{{{\boldsymbol{a}}_{\boldsymbol{i}}} \ne \mu ({{\boldsymbol{o}}_{\boldsymbol{i}}};{{\boldsymbol{\theta}} _{\boldsymbol{i}}})} \end{array}} \right. $$ (11)

    式中：$\mu $为智能体$i$的策略网络，${{\boldsymbol{\theta}} _{\boldsymbol{i}}}$为策略网络参数。由于网络输出确定性策略，故执行策略网络输出的动作序列的概率为1。智能体$i$的累积折扣奖励为

    $$ G_i^t = r_i^{t + 1} + \gamma \cdot r_i^{t + 2} + \cdots = \sum\limits_{k = 0}^\infty {\left\{ {{\gamma ^k} \cdot r_i^{t + 1 + k}} \right\}} $$ (12)

    式中：$r_i^t$为智能体在时刻$t$获得的即时奖励。智能体$i$的累积期望奖励为

    $$ {V_{{\pi _i};\pi _i^ - }}(s) = {\boldsymbol{E}_{{\pi _i};\pi _i^ - }}\left\{ {G_i^t\left| {{{\boldsymbol{S}}_t}} \right. = {\boldsymbol{s}}} \right\} $$ (13)

    式中：$\pi _i^ - $为除智能体$i$以外的所有智能体的联合策略。在本文中，每一个智能体不仅需要与敌方智能体进行对抗还需要与己方智能体进行合作，本质上属于混合博弈问题。所有智能体的学习目标均为最大化累计奖励期望值：

    $$ \begin{array}{*{20}{c}} {{\boldsymbol{\theta}} _i^* = \mathop {\arg \max }\limits_{{{\boldsymbol{\theta}} _i}} \left\{ {{V_{{\pi _i};\pi _i^ - }}({\boldsymbol{s}})} \right\}}&{(i = 1,2, \cdots ,N)} \end{array} $$ (14)

    2.2   MADDPG算法

    MADDPG算法是一种适用于多智能体博弈对抗问题的经典算法[22]，算法框架如图4所示。

    图  4  MADDPG算法框架
    Fig.  4  MADDPG algorithm framework
    下载: 全尺寸图片

    算法采用的“集中式训练−分布式执行”方式使智能体能够在训练时通过Critic网络对全局状态进行评价以适应不稳定的环境，而在决策时通过Actor网络依据本地信息生成动作序列。

    对于参与博弈的$N$个智能体，每一个智能体的决策核心由2个网络组成，即Critic评价网络和Actor策略网络。智能体$ i $的Online Critic网络参数为${{\boldsymbol{\theta}} _{\boldsymbol{i}}}$，Online Actor网络参数为${{\boldsymbol{w}}_{\boldsymbol{i}}}$，为了使训练具有良好的稳定性，算法额外引入了Target Critic网络和Target Actor网络，其网络参数为和${{\boldsymbol{w}}_{\boldsymbol{i}}}'$。智能体的Critic网络将全局信息${{{\boldsymbol{s}}^{{\boldsymbol{gl}}}}}$和${{{\boldsymbol{a}}^{{\boldsymbol{gl}}}}}$作为输入，表示为

    $$ \left\{ \begin{gathered} {{\boldsymbol{s}}^{{\boldsymbol{gl}}}} = \left[ {{{\boldsymbol{s}}^{{\boldsymbol{o}}}}\quad {{\boldsymbol{s}}^{tm}}\quad {{\boldsymbol{s}}^{{\boldsymbol{en}}}}} \right] \\ {{\boldsymbol{a}}^{{\boldsymbol{gl}}}} = \left[ {{{\boldsymbol{a}}^{{\boldsymbol{o}}}}\quad {{\boldsymbol{a}}^{tm}}\quad {{\boldsymbol{a}}^{{\boldsymbol{en}}}}} \right] \\ \end{gathered} \right. $$ (15)

    式中：${{\boldsymbol{s}}^{\boldsymbol{o}}}$、${{\boldsymbol{a}}^{\boldsymbol{o}}}$为当前进行网络参数更新的智能体(待更新智能体)的状态序列和动作序列，${{\boldsymbol{s}}^{{\boldsymbol{tm}}}}$、${{\boldsymbol{a}}^{{\boldsymbol{tm}}}}$为待更新智能体的全部友方智能体的联合状态序列和联合动作序列，${{{\boldsymbol{s}}}^{{\boldsymbol{en}}}}$、${{\boldsymbol{a}}^{{\boldsymbol{en}}}}$为待更新智能体的全部敌方智能体的联合状态序列和联合动作序列。智能体的Actor网络则将局部信息${{\boldsymbol{s}}^{{\boldsymbol{lo}}}}$作为输入，表示为

    $$ {{\boldsymbol{s}}^{{\boldsymbol{lo}}}} = \left[ {{{\boldsymbol{s}}^{\boldsymbol{o}}}\quad {{\boldsymbol{s}}^{{\boldsymbol{tm}}}}} \right] $$ (16)

    网络的输入和输出关系为

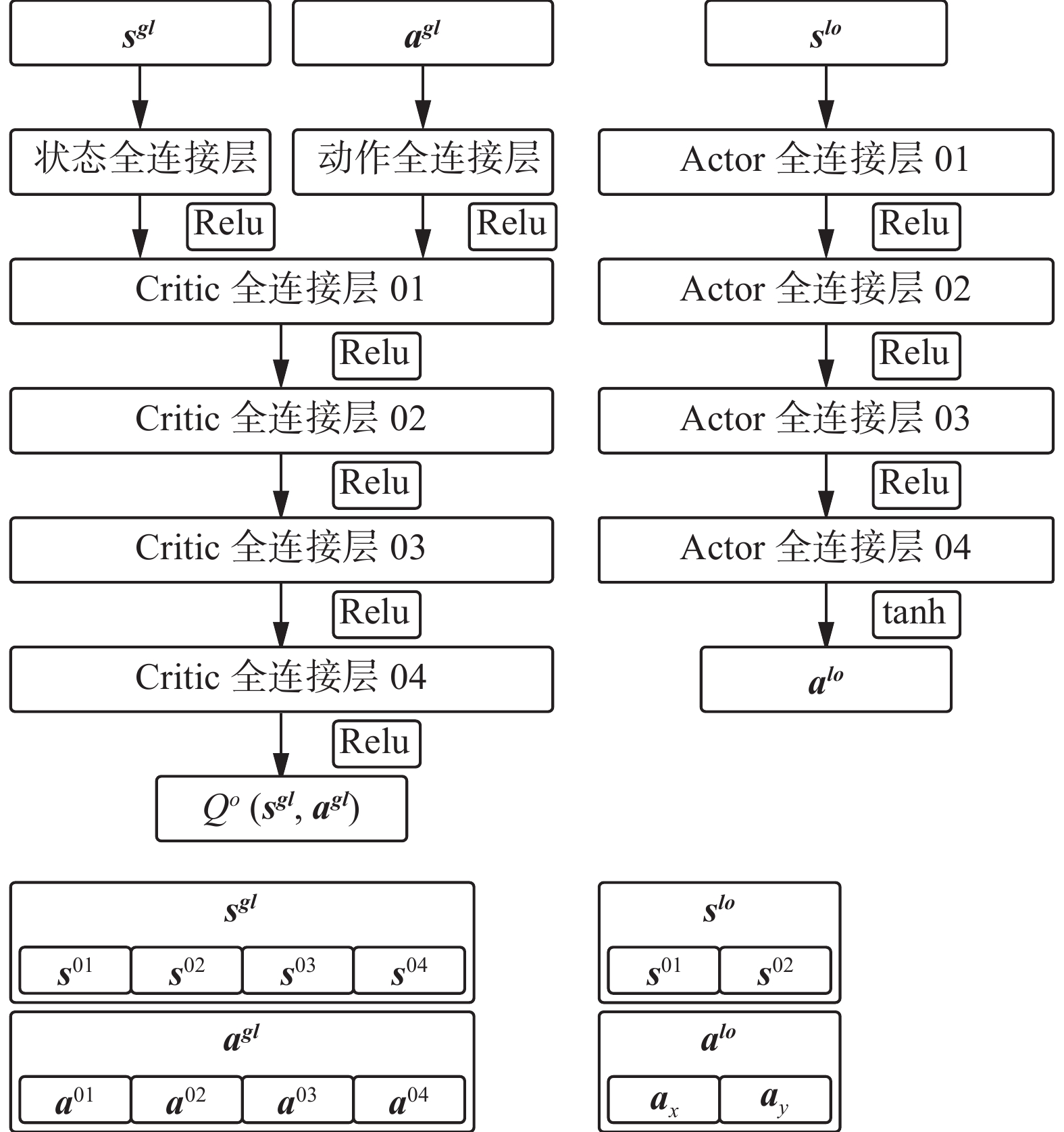
    $$ \left\{ \begin{gathered} {{\boldsymbol{a}}_i} = \mu ({{\boldsymbol{s}}^{{\boldsymbol{lo}}}};{{\boldsymbol{w}}_{\boldsymbol{i}}}) \\ {q_i} = Q({{\boldsymbol{s}}^{{\boldsymbol{gl}}}},{{\boldsymbol{a}}^{{\boldsymbol{gl}}}};{{\boldsymbol{\theta}} _{\boldsymbol{i}}}) \\ \end{gathered} \right. $$ (17)

    原始MADDPG算法的Actor-Critic网络结构如图5所示。

    图  5  Critic网络和Actor网络
    Fig.  5  Critic network and actor network
    下载: 全尺寸图片

    分析网络输入、输出可知，Critic网络利用全局观测信息对当前智能体的状态−动作价值评价，即“集中评价”，Actor网络仅利用本地观测信息进行决策，即“分布执行”，该框架适用于多无人机博弈对抗问题。

    网络参数的训练采用经验回放机制，即为网络设置经验池${ \mathcal{D}} $以存储经验$\left( {{{\boldsymbol{o}}^{\boldsymbol{j}}},{{\boldsymbol{a}}^{\boldsymbol{j}}},{{\boldsymbol{r}}^{\boldsymbol{j}}},{\boldsymbol{o}}{'^{\boldsymbol{j}}}} \right)$，每一步博弈结束后，智能体会从经验池$\mathcal{D}$中抽取一定数量的经验分别训练Critic网络和Actor网络。

    对于智能体$i$的Online Critic网络，其梯度更新为

    $$ \left\{ \begin{array}{l} {\nabla _{{{\boldsymbol{\theta}} _i}}}J({{\boldsymbol{\theta}} _i}) = \dfrac{1}{m} \cdot \displaystyle\sum\limits_{j = 1}^m {\left\{ {{\nabla _Q}T{D^2} \cdot {\nabla _{{{\boldsymbol{\theta }}_i}}}Q({{\boldsymbol{o}}^j},{{\boldsymbol{a}}^j};{{\boldsymbol{\theta}} _i})} \right\}} \\ y_i^j = r_i^j + \gamma \cdot Q({\boldsymbol{o}}'{^j},{\boldsymbol{a}}'{^j};{{\boldsymbol{\theta}} _i}')\\ TD = y_i^j - Q({{\boldsymbol{o}}^j},{{\boldsymbol{a}}^j};{{\boldsymbol{\theta}} _i})\\ {\boldsymbol{a}}'{^j} = \left[ {\mu \left({\boldsymbol{o}}^{\prime j}_{1};{{\boldsymbol{w}}_{1}}'\right)\;\;\; \mu \left({\boldsymbol{o}}^{\prime j}_2;{{\boldsymbol{w}}_2}'\right)\;\; \cdots \;\; \mu \left({\boldsymbol{o}}^{\prime j}_N;{{\boldsymbol{w}}_N}'\right)} \right] \end{array} \right. $$ (18)

    对于智能体$i$的Online Actor网络，其梯度更新为

    $$ \left\{ \begin{gathered} {\nabla _{{{\boldsymbol{w}}_i}}}J({{\boldsymbol{w}}_i}) = \frac{1}{m} \cdot \sum\limits_{j = 1}^m {\left\{ {\left[ {{\nabla _{{\boldsymbol{a}}'}}Q({{\boldsymbol{o}}^j},{\boldsymbol{a}}';{{\boldsymbol{\theta}} _i})} \right] \cdot {\nabla _{{{\boldsymbol{w}}_i}}}{\boldsymbol{a}}'} \right\}} \\ {\nabla _{{{\boldsymbol{w}}_i}}}{\boldsymbol{a}}' = {\nabla _{{{\boldsymbol{w}}_i}}}\mu ({\boldsymbol{o}}_i^j;{{\boldsymbol{w}}_i}) \\ {\boldsymbol{a}}' = \left[ {{{\boldsymbol{a}}_{1}},{\boldsymbol{a}}_2,\cdots ,{{\boldsymbol{a}}_i}', \cdots ,{{\boldsymbol{a}}_N}} \right] \\ {{\boldsymbol{a}}_i}' = \mu ({\boldsymbol{o}}_i^j;{{\boldsymbol{w}}_i}) \\ \end{gathered} \right. $$ (19)

    所有智能体的Target网络则不依据梯度进行更新，而是采用软更新的方式进行参数迭代。因此Online Critic网络和Target Critic网络参数的更新为

    $$ \left\{ \begin{gathered} {{\boldsymbol{\theta}} _{\boldsymbol{i}}} = {{\boldsymbol{\theta}} _{\boldsymbol{i}}} - {\beta _{{\rm{Critic}}}} \cdot {\nabla _{{{\boldsymbol{\theta}} _{\boldsymbol{i}}}}}J({{\boldsymbol{\theta}} _{\boldsymbol{i}}}) \\ {{\boldsymbol{\theta}} _{\boldsymbol{i}}}' = \tau \cdot {{\boldsymbol{\theta}} _{\boldsymbol{i}}} + (1 - \tau ) \cdot {{\boldsymbol{\theta}} _{\boldsymbol{i}}}' \\ \end{gathered} \right. $$ (20)

    Online Actor网络和Target Actor网络参数的更新公式为

    $$ \left\{ \begin{gathered} {{\boldsymbol{w}} _{\boldsymbol{i}}} = {{\boldsymbol{w}} _{\boldsymbol{i}}} - {\alpha _{{\rm{Actor}}}} \cdot {\nabla _{{{\boldsymbol{w}} _{\boldsymbol{i}}}}}J({{\boldsymbol{w}} _{\boldsymbol{i}}}) \\ {{\boldsymbol{w}} _{\boldsymbol{i}}}' = \tau \cdot {{\boldsymbol{w}} _{\boldsymbol{i}}} + (1 - \tau ) \cdot {{\boldsymbol{w}} _{\boldsymbol{i}}}' \\ \end{gathered} \right. $$ (21)

    式中：${\beta _{{\rm{Critic}}}}$为Online Critic网络学习率，${\alpha _{{\rm{Actor}}}}$为Online Actor网络学习率，$\tau \in \left[ {0,1} \right]$为软更新系数。

    3.   基于规则耦合方法的多异构子网络改进MADDPG算法

    3.1   状态评估——基于博弈无人机数量衰减问题构造异构子网络

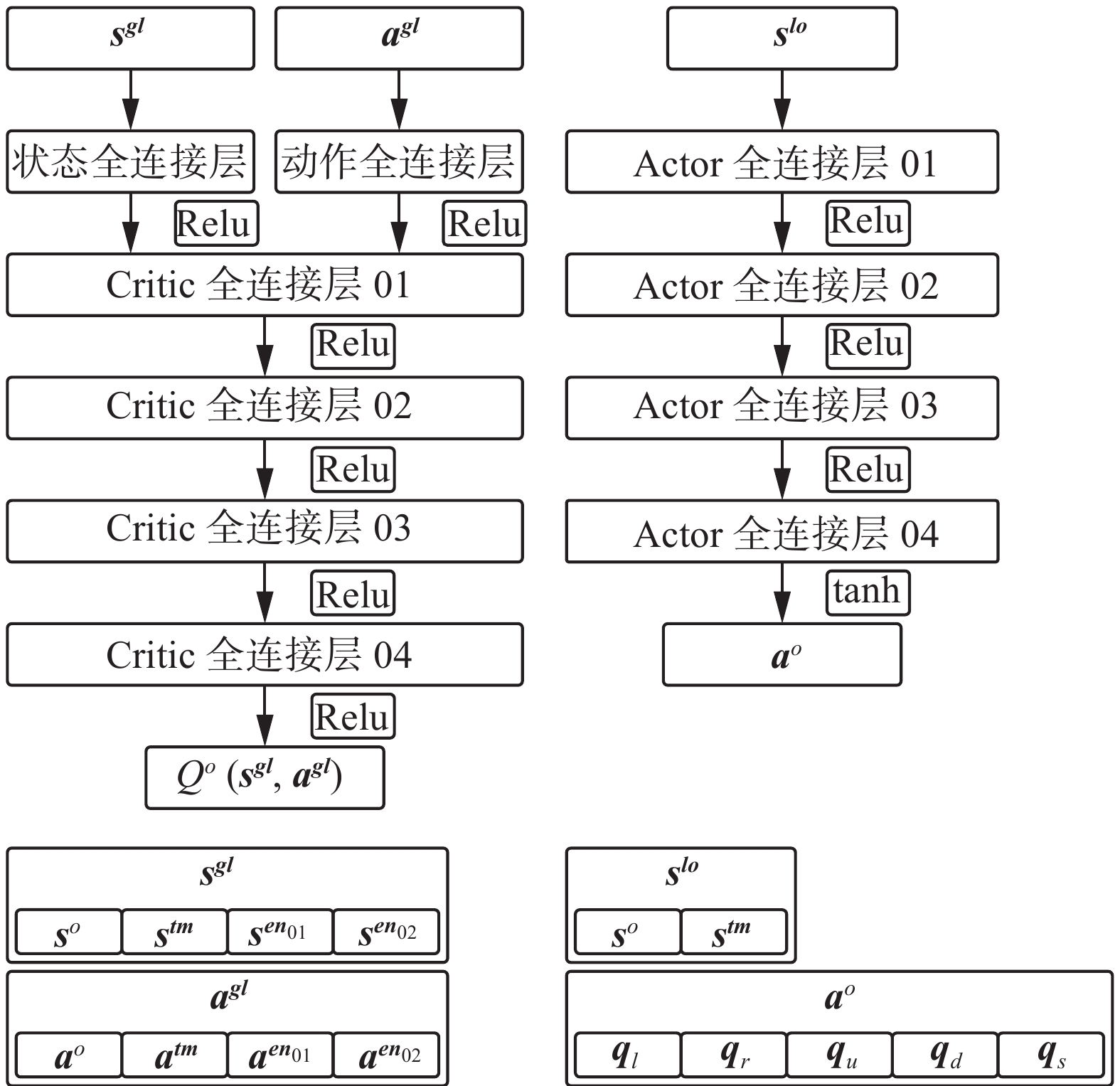
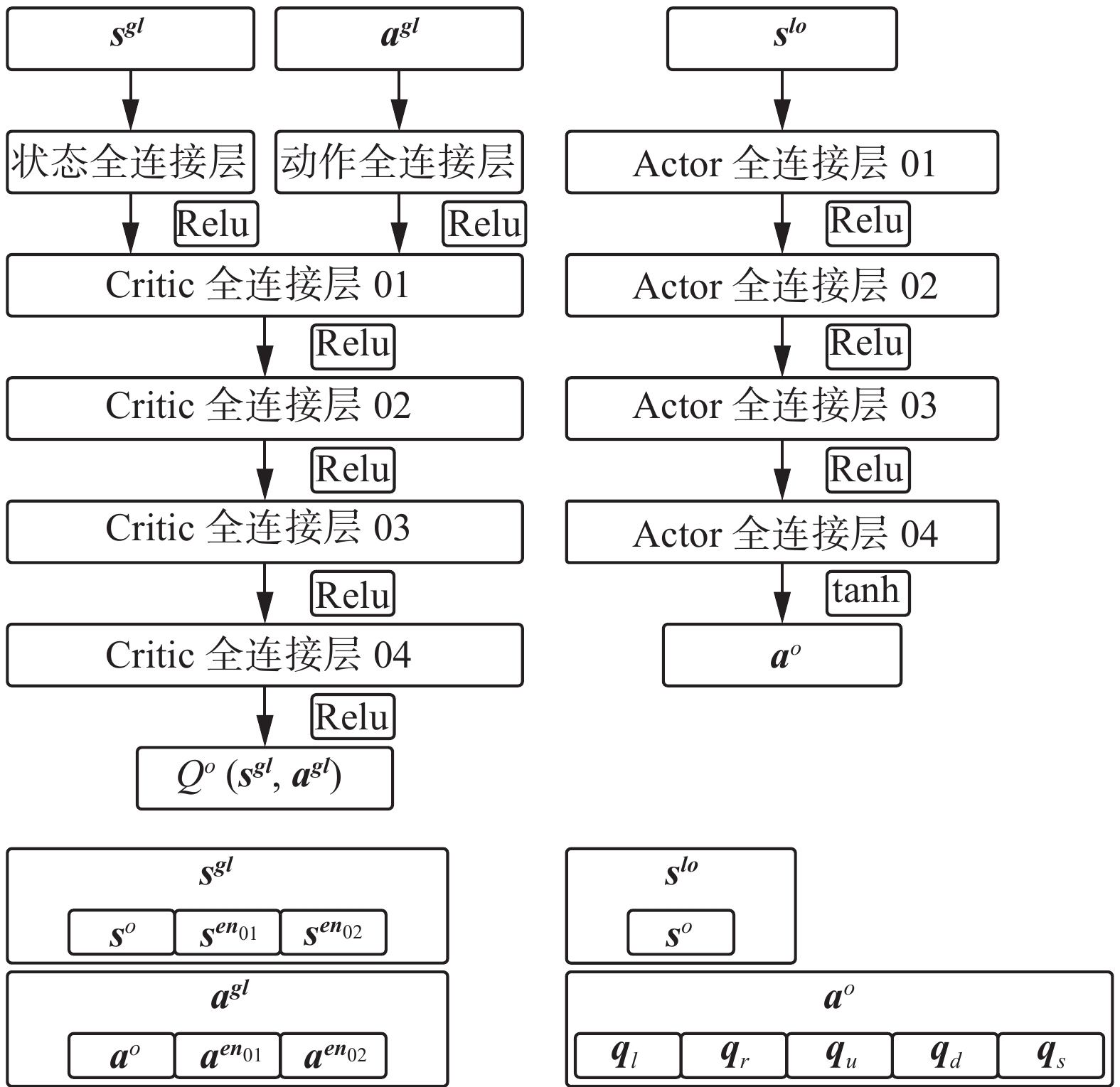
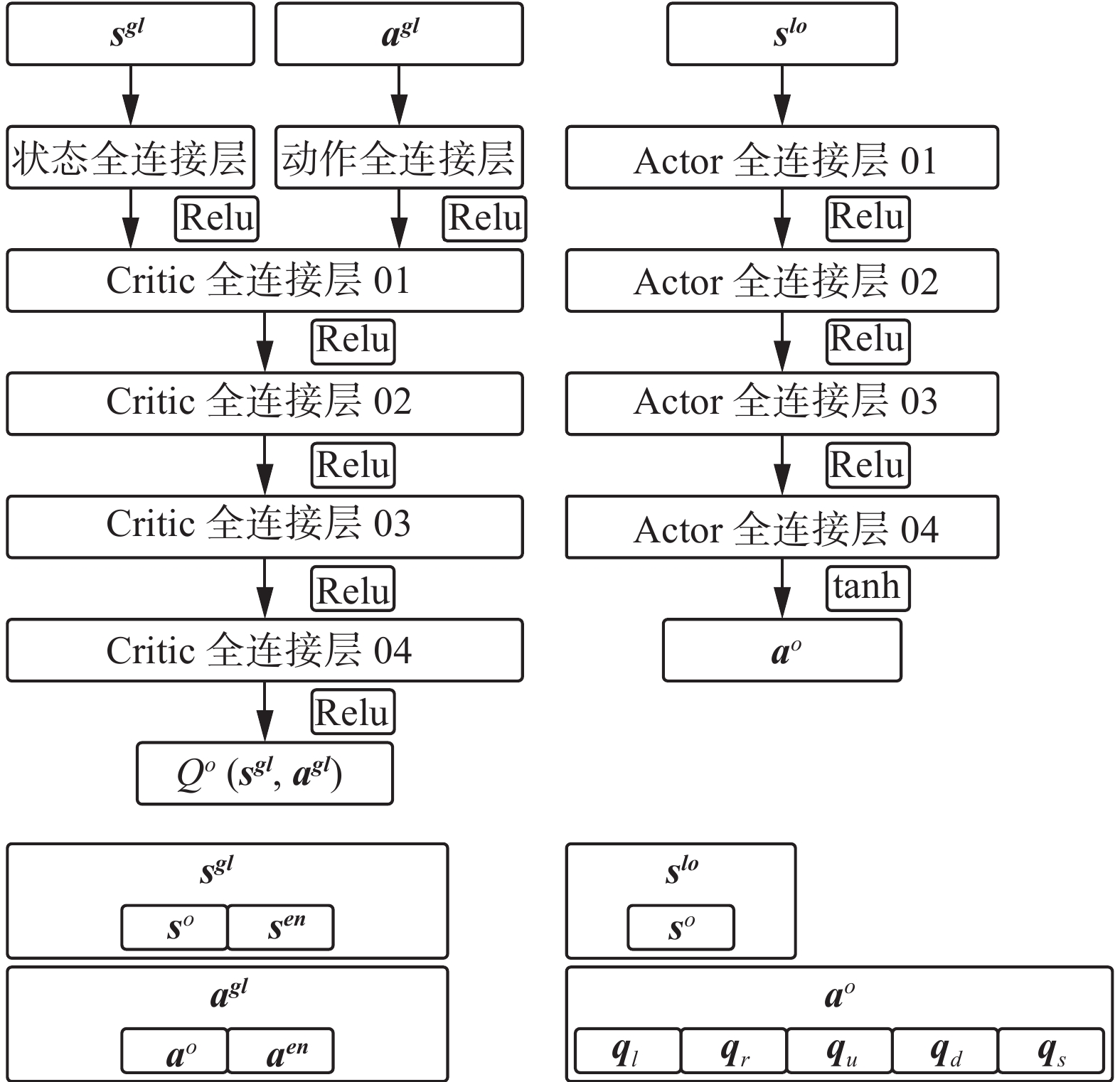
    传统的MADDPG算法中，无人机的Actor网络输入己方所有无人机的联合状态，即局部状态${{\boldsymbol{s}}^ {\boldsymbol{lo}}}$，Critic网络输入双方无人机的联合状态，即全局状态${{\boldsymbol{s}}^ {{\boldsymbol{gl}}}}$。在多无人机博弈对抗问题中，若某一个无人机被击毁，而其友方无人机仍然存活，则该无人机在后续博弈中的状态难以定义且由于团队奖励函数的设计，被击毁的无人机会因为友方的良好表现而获得额外的奖励。上述情况会导致“Lazy无人机”出现，造成学习效率低下，因为无人机在击毁状态下是没有必要进行状态−动作价值评估的，而且在该状态下无人机的任何决策都是无效的。在基于MADRL的多无人机博弈对抗问题中，若无人机数量衰减，保留学习效果较好的无人机使其继续参与博弈同时舍弃学习效果较差的无人机并重新定义其信息序列一直是一项挑战[23]。

    本文基于2-vs-2的小规模多无人机博弈对抗问题，为3种可能出现的博弈场景设置了4个不同结构的子网络，即2-vs-2子网络、2-vs-1子网络、1-vs-2子网络和1-vs-1子网络，在每个博弈场景下只需要为对应的子网络输入存活无人机的状态序列和动作序列并将任意一架无人机被击毁时对应的状态作为博弈的终止状态即可。若某一个博弈场景结束训练则直接切换至下一个博弈场景以继续训练对应的子网络，上述方法不仅可以提升网络的学习效率，还能够使所有无人机的状态在下一个场景中得到继承以积累更多的有价值经验。在博弈对抗中，所有无人机的任务目标相同，因此两方无人机群的网络参数可以实现共享。公共网络参数的共享使参与博弈的无人机具备相同的观测信息转化能力，可将其视为一种公共知识[24]。公共知识能够使系统更快地从环境状态的突发性改变中恢复过来，网络参数更新所需的计算量也会更小。各场景对应的子网络结构如图6~9所示。

    图  6  2-vs-2 Critic网络和Actor网络
    Fig.  6  2-vs-2 Critic network and actor network
    下载: 全尺寸图片
    图  7  2-vs-1 Critic网络和Actor网络
    Fig.  7  2-vs-1 Critic network and actor network
    下载: 全尺寸图片
    图  8  1-vs-2 Critic网络和Actor网络
    Fig.  8  1-vs-2 Critic network and actor network
    下载: 全尺寸图片
    图  9  1-vs-1 Critic网络和Actor网络
    Fig.  9  1-vs-1 Critic network and actor network
    下载: 全尺寸图片

    每个无人机单体在训练时只需要对全局观测序列进行初等变换以组成专属的全局观测序列和局部观测序列并将信息序列输入网络即可。无人机的Critic网络需要根据全局观测序列对其状态−动作价值进行评估，故输入网络的全局状态序列和联合动作序列$\left[ {{{\boldsymbol{s}}^{{\boldsymbol{gl}}}}\quad {{\boldsymbol{a}}^{{\boldsymbol{gl}}}}} \right]$为

    $$ \left\{ \begin{gathered} {{\boldsymbol{s}}^{\boldsymbol{gl}}} = \left[ {{{\boldsymbol{s}}^{\boldsymbol{o}}}\quad {{\boldsymbol{s}}^{\boldsymbol{tm}}}\quad {{\boldsymbol{s}}^{{\boldsymbol{en}}{_{{{\textit{01}}}}}}}\quad {{\boldsymbol{s}}^{{\boldsymbol{en}}{_{{{\textit{02}}}}}}}} \right] \\ {{\boldsymbol{a}}^{\boldsymbol{gl}}} = \left[ {{{\boldsymbol{a}}^{\boldsymbol{o}}}\quad {{\boldsymbol{a}}^{\boldsymbol{tm}}}\quad {{\boldsymbol{a}}^{{\boldsymbol{en}}{_{{{\textit{01}}}}}}}\quad {{\boldsymbol{a}}^{{\boldsymbol{en}}{_{{{\textit{02}}}}}}}} \right] \\ \end{gathered} \right. $$ (22)

    无人机的Actor网络需要根据局部观测序列计算动作序列，故输入网络的局部状态序列${s{\boldsymbol{}}^{{\boldsymbol{lo}}}}$为

    $$ {{\boldsymbol{s}}^{{\boldsymbol{lo}}}} = \left[ {{{\boldsymbol{s}}^{\boldsymbol{o}}}\quad {{\boldsymbol{s}}^{{\boldsymbol{tm}}}}} \right] $$ (23)

    如果Actor网络直接输出执行动作序列$\left[ {{a_x}\quad {a_y}} \right]$，通常会产生严重的过拟合问题，导致策略模型的稳定性较差[25]。本文中，Actor网络输出的动作序列由5个基本动作对应的动作价值组成：

    $$ {{\boldsymbol{a}}^{\boldsymbol{o}}} = \left[ {{q_l}\quad {q_r}\quad {q_u}\quad {q_d}\quad {q_s}} \right] $$ (24)

    式中：${q_l}$为无人机沿$x$轴负方向的加速度价值，${q_r}$为无人机沿$x$轴正方向的加速度价值，${q_u}$为无人机沿$y$轴正方向的加速度价值，${q_d}$为无人机沿$y$轴负方向的加速度价值，$ {q_s} $将无人机的加速度限制在一定范围内。对Actor网络输出的价值序列${{\boldsymbol{a}}^{\boldsymbol{o}}}$进行Softmax处理后得到基本动作序列${{\boldsymbol{a}}_{\boldsymbol{b}}}$为

    $$ \left\{ \begin{gathered} {a_i} = {{{e^{{q_i}}}} \mathord{\left/ {\vphantom {{{e^{{q_i}}}} {\sum\limits_{j \in Se{t_b}} {\displaystyle\{ {{e^{{q_j}}}} \displaystyle\}} }}} \right. } {\sum\limits_{j \in Se{t_b}} {\left\{ {{e^{{q_j}}}} \right\}} }} \\ {{\boldsymbol{a}}_{\boldsymbol{b}}} = \left[ {{a_l}\quad {a_r}\quad {a_u}\quad {a_d}\quad {a_s}} \right] \\ \end{gathered} \right. $$ (25)

    式中：$Se{t_b}$为基本动作(无人机加速度方向)集合$\left\{ {{\rm{left}},{\rm{right}},{\rm{up}},{\rm{down}},{\rm{stay}}} \right\}$，该集合可缩写为$\left\{ {l,r,u,d,s} \right\}$；${q_i}$、$ {q_j} $分别为Actor网络输出的动作价值序列中与基本动作$i$、$j$相对应的输出值；${a_i}$为无人机沿方向$i$的加速度。无人机的5个基本动作和执行动作的关系为

    $$ \left\{ \begin{gathered} {a_x} = \alpha \cdot ({a_r} - {a_l}) \\ {a_y} = \alpha \cdot ({a_u} - {a_d}) \\ \qquad\quad {\rm{s}}.{\rm{t}}. \\ {a_l} + {a_r} + {a_u} + {a_d} + {a_s} = 1 \\ \end{gathered} \right. $$ (26)

    3.2   环境反馈——基于势函数的奖励机制优化设计方法

    强化学习问题中，奖励函数是一种环境反馈信息，实现了环境与算法之间的沟通以及对学习目标的数学化描述，因此奖励机制设计的合理性对于策略的学习至关重要[26]。本文中，参与博弈的无人机具有相同的任务目标，故所有无人机奖励机制相同。无人机的团队奖励机制以离散奖励函数对成功打击目标、离开博弈区域等基本任务节点对无人机的奖励函数进行设置，其目的是引导无人机团队学习简单的竞争、合作策略。无人机基本任务节点的团队离散奖励函数${r_b}$设置为

    $$ {r_b} = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {200},&{所有敌方无人机被消灭} \end{array}\\ \begin{array}{*{20}{c}} { - 100},&{没有敌方无人机被消灭} \end{array}\\ \begin{array}{*{20}{c}} {40},&{击毁一架敌方无人机} \end{array}\\ \begin{array}{*{20}{c}} {20},&{友方无人机击毁一架敌方无人机} \end{array}\\ \begin{array}{*{20}{c}} { - 40},&{被敌方无人机击毁} \end{array}\\ \begin{array}{*{20}{c}} { - 20},&{友方无人机被敌方击毁} \end{array}\\ \begin{array}{*{20}{c}} { - 40},&{离开博弈区域} \end{array}\\ \begin{array}{*{20}{c}} { - 20},&{友方无人机离开博弈区域} \end{array} \end{array} \right.$$ (27)

    如果在博弈对抗过程中，无人机只有在完成基本任务时才能获得奖励，则会导致训练过程缺乏环境反馈引导[27]。由于在一次博弈中，无人机需要在开始阶段对区域进行探索，而探索环境的无人机很难完成基本任务，故几乎不会获得奖励，即稀疏奖励问题。奖励函数设计不合理导致的稀疏奖励问题可能会延长算法的收敛时间或增大学习策略与最优策略的偏差，甚至会导致学习策略永远无法达到预期目标[28- 29]。

    本文中，为避免稀疏奖励问题且使无人机能够学习如何接近目标无人机的受威胁区域，对基于势函数的个体连续奖励机制进行设计。该机制为无人机的每一步动作计算奖励值，在原有的基本任务节点奖励函数的基础上，额外增加了基于势函数构造的奖励函数${R_{{\rm{po}}}}$。综合奖励势函数$ \phi \left( {\boldsymbol{s}} \right) $由常规奖励势函数${\phi _{{\rm{no}}}}\left( {\boldsymbol{s}} \right)$和特殊奖励势函数${\phi _{{\rm{sp}}}}\left( {\boldsymbol{s}} \right)$组成。常规奖励势函数${\phi _{{\rm{no}}}}\left( {\boldsymbol{s}} \right)$由3项基于状态的子奖励势函数组成，即角度奖励势函数${\phi _0}\left( {\boldsymbol{s}} \right)$、距离奖励势函数${\phi _{{\rm{dis}}}}\left( {\boldsymbol{s}} \right)$和速度奖励势函数${\phi _{{\rm{vel}}}}\left( {\boldsymbol{s}} \right)$，其作用为引导当前无人机对目标无人机进行打击；特殊奖励势函数${\phi _{{\rm{sp}}}}\left( {\boldsymbol{s}} \right)$由2项基于状态的子奖励势函数组成，即边界安全奖励势函数$ {\phi _{{\rm{bou}}}}\left( {\boldsymbol{s}} \right) $和逃避追击奖励势函数${\phi _{{\rm{esp}}}}\left( {\boldsymbol{s}} \right)$，二者仅在无人机状态满足特定条件时有效且由于该状态下的无人机以保证个体存活为优先任务，常规奖励势函数在该状态下无效。

    角度奖励势函数${\phi _0}\left( {\boldsymbol{s}} \right)$根据当前无人机的速度矢量与目标线的夹角${\psi ^o}\left( {\boldsymbol{s}} \right)$(rad)和目标无人机的速度矢量与目标线的夹角${\delta ^t}({\boldsymbol{s}})$(rad)进行设置为

    $$ {\phi _0}({\boldsymbol{s}}) = \frac{1}{\text{π}} \cdot \left[ {\text{π} - (\left| {{\psi ^o}({\boldsymbol{s}})} \right| + \left| {{\delta ^t}({\boldsymbol{s}})} \right|)} \right] $$ (28)

    距离奖励势函数${\phi _{{\rm{dis}}}}\left( {\boldsymbol{s}} \right)$在${\phi _0}\left( {\boldsymbol{s}} \right)$基础上额外考虑到了无人机间的距离为

    $$ \left\{ \begin{gathered} {\phi _{{\rm{dis}}}}({\boldsymbol{s}}) = {\phi _0}({\boldsymbol{s}}) \cdot {{\rm{e}}^{ - {k_{{\rm{dis}}}} \cdot \left| {{D_e} - D\left( {\boldsymbol{s}} \right)} \right|}} \\ D({\boldsymbol{s}}) = \sqrt {{{({x^o} - {x^t})}^2} + {{({y^o} - {y^t})}^2}} \\ \end{gathered} \right. $$ (29)

    式中：${D_e}$为最适合无人机攻击的距离且满足$0 < {D_e} < {d_{{\rm{att}}}}$，m；$D\left( {\boldsymbol{s}} \right)$为当前无人机与目标无人机间的距离，m；$ {k_{{\rm{dis}}}} \in \left[ {0,1} \right] $为相对距离系数。

    速度奖励势函数${\phi _{{\rm{vel}}}}\left( {\boldsymbol{s}} \right)$则在${\phi _0}\left({\boldsymbol{ s}} \right)$基础上额外考虑到了无人机间的速度差值：

    $$ {\phi _{{\rm{vel}}}}({\boldsymbol{s}}) = {\phi _0}({\boldsymbol{s}}) \cdot {{\rm{e}}^{ - {k_{{\rm{vel}}}} \cdot \left| {{v^o} - {v^t}} \right|}} $$ (30)

    式中：${v^o}$为当前无人机速度，m/s；${v^t}$为目标无人机速度，m/s；${k_{{\rm{vel}}}} \in \left[ {0,1} \right]$为相对速度系数。

    边界安全奖励势函数${\phi _{{\rm{bou}}}}\left( {\boldsymbol{s}} \right)$在当前无人机距战场边界距离小于安全距离${d_{{\rm{bou}}}}$(m)时有效：

    $$ {\phi _{{\rm{bou}}}}\left( {\boldsymbol{s}} \right) = {{\rm{e}}^{ - {k_{{\rm{bou}}}} \cdot \left| {{D_{{\rm{bou}}}}\left( {\boldsymbol{s}} \right) - {d_{{\rm{bou}}}}} \right|}} $$ (31)

    式中：${D_{{\rm{bou}}}}\left( {\boldsymbol{s}} \right)$为无人机距边界的最小距离，m；${k_{{\rm{bou}}}} \in \left[ {0,1} \right]$为边界距离系数。

    逃避追击奖励势函数${\phi _{{\rm{esp}}}}\left( {\boldsymbol{s}} \right)$在当前无人机与敌方无人机距离小于危险距离${d_{{\rm{dan}}}}$(m)且敌方无人机的速度矢量与目标线夹角${\psi ^{en}}\left( {\boldsymbol{s}} \right)$(rad)和当前无人机的速度矢量与敌方无人机目标线夹角${\delta ^o}\left( {\boldsymbol{s}} \right)$(rad)满足攻击条件时有效：

    $$ \left\{ \begin{gathered} {\phi _{{\rm{esp}}}}\left( {\boldsymbol{s}} \right) = \phi _0^{en}\left( {\boldsymbol{s}} \right) \cdot {{\rm{e}}^{ - {k_{{\rm{esp}}}} \cdot \left| {{D_{{\rm{esp}}}}\left( {\boldsymbol{s}} \right) - {d_{{\rm{dan}}}}} \right|}} \\ \phi _0^{en}\left( {\boldsymbol{s}} \right) = \frac{1}{\text{π} } \cdot \left[ {\left( {\left| {{\psi ^{en}}\left( {\boldsymbol{s}} \right)} \right| + \left| {{\delta ^o}\left( {\boldsymbol{s}} \right)} \right|} \right) - \text{π} } \right] \\ \end{gathered} \right. $$ (32)

    称满足式(32)条件的敌方无人机为威胁无人机，则式(32)中${D_{{\rm{esp}}}}\left({\boldsymbol{ s}} \right)$为当前无人机与威胁无人机的距离，m；${k_{{\rm{esp}}}} \in \left[ {0,1} \right]$为威胁距离系数。

    综合奖励势函数$\phi \left({\boldsymbol{ s}} \right)$由上述各项子奖励势函数组成，无人机的奖励机制根据每个无人机的当前状态序列$s$选择对应的子奖励势函数并生成奖励值。最终得到的综合奖励势函数(个体连续奖励函数)$\phi \left( {\boldsymbol{s }}\right)$为

    $$\phi \left( {\boldsymbol{s}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\phi _{{\rm{sp}}}}\left( {\boldsymbol{s}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\phi _{{\rm{bou}}}}\left( {\boldsymbol{s}} \right),{D_{{\rm{bou}}}}\left( {\boldsymbol{s}} \right) < {d_{{\rm{bou}}}}}\\ {{\phi _{{\rm{esp}}}}\left( s \right),\left\{ {\begin{array}{*{20}{l}} {{D_{{\rm{esp}}}}\left( {\boldsymbol{s}} \right) < {d_{{\rm{dan}}}}}\\ {{\psi ^{en}}\left( {\boldsymbol{s}} \right) < {{{\theta _{{\rm{att}}}}} / 2}}\\ {{{\delta} ^o}\left( {\boldsymbol{s}} \right) < {{{\theta _{{\rm{def}}}}} / 2}} \end{array}} \right.} \end{array}} \right.}\\ {{\phi _{{\rm{no}}}}\left( {\boldsymbol{s}} \right) = {\phi _0}\left( {\boldsymbol{s}} \right) + {\phi _{{\rm{dis}}}}\left( {\boldsymbol{s}} \right) + {\phi _{{\rm{vel}}}}\left( s \right),\quad 其他} \end{array}} \right.$$ (33)

    由式(27)~(32)可知，组成综合奖励势函数的子奖励势函数的取值均被限制在一定范围内且具有一定差异。各项子奖励势函数取值范围如表1所示。

    表  1  子奖励势函数取值范围
    Table  1  Value range of sub incentive potential function
    奖励势函数取值范围
    $\phi_0({\boldsymbol{s}})$[−1, 1]
    $\phi_{{\rm{dis}}}({\boldsymbol{s} })$[−1, 1]
    $\phi_{{\rm{vel}}}({\boldsymbol{s} })$[−1, 1]
    $\phi_{{\rm{bou}}}({\boldsymbol{s} })$[0, 1]
    $\phi_{{\rm{esp}}}({\boldsymbol{s} })$[−1, 1]

    由表1中数据可知，组合后的常规奖励势函数${\phi _{{\rm{no}}}}\left( {\boldsymbol{s}} \right) \in \left[ { - 3,3} \right]$，而组合后的特殊奖励势函数${\phi _{{\rm{sp}}}}\left( {\boldsymbol{s}} \right) \in \left[ { - 1,1} \right]$。综上所述，若要将综合奖励势函数与基本任务节点的奖励函数${r_b}$相结合且尽可能避免网络学习过程中出现振荡等不稳定现象，需要根据离散奖励值的大小对$\phi \left( s \right)$进行标准化处理，最终奖励值${R_{{\rm{fin}}}}$为

    $$ \left\{ \begin{gathered} \overline \phi \left( {\boldsymbol{s}} \right) = {w_\phi } \cdot \phi \left( {\boldsymbol{s}} \right) \\ {R_{{\rm{fin}}}} = {r_b} + {R_{{\rm{po}}}} = {r_b} + \gamma \cdot \overline \phi \left( {s'} \right) - \overline \phi \left( {\boldsymbol{s}} \right) \\ \end{gathered} \right. $$ (34)

    式中：${w_\phi }$为奖励函数归一化参数，其作用为平衡个体竞争经验和团队合作经验对策略模型学习的影响，避免奖励值差异导致网络学习收敛至次优解。

    3.3   自主决策——规则耦合模块构造

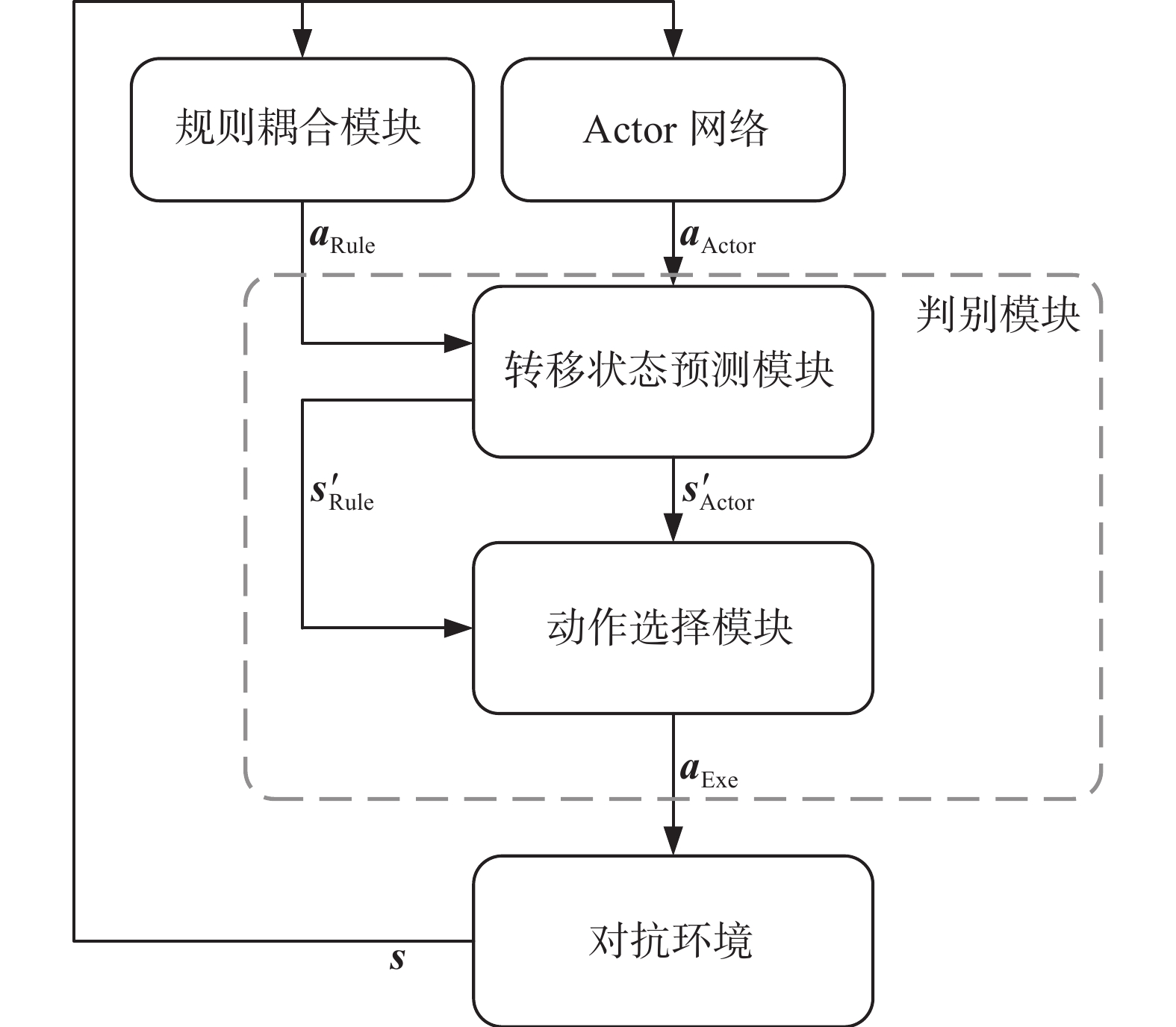
    仅基于客观事实对奖励函数进行优化设计以学习最优策略的方法对于多无人机博弈对抗问题来说是不现实的，与完全基于算法在环境中不断进行试错学习的策略相比，使用某些已经由人类总结出来的规则作为辅助的策略可以减少无人机的无效探索并在某些情况下做出更加合理的决策。本文建立了一个基于专家经验的规则耦合模块并与Actor网络相互耦合，规则耦合模块参与博弈的过程如图10所示。

    图  10  规则耦合模块参与博弈过程
    Fig.  10  Game process with rule coupling
    下载: 全尺寸图片

    在决策阶段，根据无人机在环境中的状态对算法输出的动作序列和规则耦合模块输出的动作序列进行评估以选择实际动作序列的方法在网络的学习过程中通常能够起到较好的指导作用[30]。

    转移状态预测模块基于无人机当前的局部状态对执行规则耦合模块输出的基本动作序列${{\boldsymbol{a}}_{{\rm{Rule}}}}$和Actor网络输出的基本动作序列${{\boldsymbol{a}}_{{\rm{Actor}}}}$后的转移状态进行预测；动作选择模块则基于预测转移状态的奖励势函数$\phi \left( {{{\boldsymbol{s}}_{{\rm{Rule}}}'}} \right)$和$\phi \left( {{{\boldsymbol{s}}_{{\rm{Actor}}}'}} \right)$对进行采样以生成执行动作序列${{\boldsymbol{a}}_{{\rm{Exe}}}}$，对基本动作序列的采样概率为

    $$ \left\{ \begin{gathered} P\left( {{{\boldsymbol{a}}_{{\rm{Rule}}}}} \right) = {{{\lambda _e}} \mathord{\left/ {\vphantom {{{\lambda _e}} {\left[ {1 + {{{e^{\phi \left( {{{\boldsymbol{s}}_{{\rm{Actor}}}'}} \right)}}} \mathord{\left/ {\vphantom {{{e^{\phi \left( {{{\boldsymbol{s}}_{{\boldsymbol{Actor}}}}'} \right)}}} {{e^{\phi \left( {{{\boldsymbol{s}}_{{\rm{Rule}}}'}} \right)}}}}} \right. } {{e^{\phi \left( {{s_{{\rm{Rule}}}'}} \right)}}}}} \right]}}} \right. } {\left[ {1 + {{{e^{\phi \left( {{s_{{\rm{Actor}}}'}} \right)}}} \mathord{\left/ {\vphantom {{{e^{\phi \left( {{s_{{\boldsymbol{Actor}}}}'} \right)}}} {{e^{\phi \left( {{s_{{\boldsymbol{Rule}}}}'} \right)}}}}} \right. } {{e^{\phi \left( {{s_{{\rm{Rule}}}'}} \right)}}}}} \right]}} \\ P\left( {{{\boldsymbol{a}}_{{\rm{Actor}}}}} \right) = 1 - P\left( {{a_{{\rm{Rule}}}}} \right) \\ {\lambda _e} = 1 - {{p} \mathord{\left/ {\vphantom {{p} {M}}} \right. } {M}} \\ p \in \left[ {0,M} \right] \\ \end{gathered} \right. $$ (35)

    式中：$P\left( {{{\boldsymbol{a}}_{{\rm{Rule}}}}} \right)$、$P\left( {{{\boldsymbol{a}}_{{\rm{Actor}}}}} \right)$为规则耦合模块和Actor网络输出基本动作序列的采样概率，由动作选择模块计算；${\lambda _e}$为模块依赖参数，其值随着网络训练幕数$p$的增加而逐渐衰减。动作采样概率表明，在网络模型的训练过程中，无人机对规则耦合模块的依赖程度降低，决策机制逐渐放弃对保守策略的依赖并开始对复杂度更高的战术性策略进行探索，即网络学习对“搜索”策略和“开发”策略的平衡。

    规则耦合模块中集成的约束规则触发条件如图11所示。

    图  11  约束规则触发条件示意
    Fig.  11  Diagram of constraint trigger conditions
    下载: 全尺寸图片

    规则耦合模块针对出界、追踪、逃逸和锁定4种情况制定了约束规则。当无人机与边界的距离小于边界安全距离${d_{{\rm{bou}}}}$(m)时，规则耦合模块的出界约束参与规则耦合，模块输出的动作序列使无人机沿远离边界方向以最大加速度运动；当无人机与目标无人机的距离大于探索距离${d_{{\rm{exp}}}}$(m)时，无人机执行未完成训练的Actor网络输出的动作序列通常会导致无价值经验增加，此时规则耦合模块的追踪约束参与规则耦合，模块输出的动作序列使无人机直接向目标无人机靠近；当无人机与任一敌方无人机距离小于危险距离${d_{{\rm{dan}}}}$(m)且敌方无人机位于当前无人机的受威胁区时，规则耦合模块的逃逸约束参与规则耦合，模块输出的动作序列使无人机向远离构成威胁的敌方无人机的方向以最大加速度运动；当无人机与目标无人机的距离小于攻击距离${d_{{\rm{att}}}}$时，规则耦合模块的锁定约束参与规则耦合，模块输出的动作序列使无人机的速度矢量、目标线和目标无人机的速度矢量尽可能位于同一直线。

    3.4   网络训练——重要性权重耦合的经验优先回放采样

    原始的经验回放机制可以解释为将每一步博弈产生的经验元组存入经验池，而在网络参数更新时则以均匀采样的方式随机抽取多个训练元组进行策略改进。经验回放机制的引入，在提高经验利用率的同时降低了经验池中各经验元组间的关联度，进而提升了网络训练效率[31]。

    为了让无人机的网络模型能够对成功击毁敌方无人机的优质经验进行优先学习，优先经验回放机制(prioritized experience replay, PER)根据每个经验元组的TD-Error绝对值$\left| {{\delta _k}} \right|$的大小为其分配优先级，TD-Error为

    $$ {\delta _k} = {r_k} + \gamma \cdot Q({\boldsymbol{s}}',{\boldsymbol{a}}';{{\boldsymbol{\theta}} _i}') - Q({\boldsymbol{s}},{\boldsymbol{a}};{{\boldsymbol{\theta }}_i})$$ (36)

    TD-Error可以隐含地反映智能体从经验中学习的程度，从而使网络评估结果更符合未来数据的趋势。较大的TD-Error表明Target网络的评估值与该状态的实际价值之间存在显著差异，因此算法需要增加对该经验元组的采样频率，以尽快更新Target网络和Online网络的参数从而达到最佳训练效果。根据PER机制定义的经验抽取概率为

    $$ \left\{ \begin{array}{l} P({e_k}) = {{{{({D_k})}^\alpha }} \bigg/{\displaystyle\sum\limits_{j = 1}^K {{{({D_j})}^\alpha }} }}\\ {D_k} = {1 /{{\rm{rank}}({e_k})}} \end{array} \right. $$ (37)

    式中：${\rm{rank}}({e_k})$为所有经验根据其TD-Error绝对值进行由大到小排序后经验${e_k }$对应的序号，参数$\alpha \in \left[ {0,1} \right]$决定采样依赖优先级的程度，当$\alpha=0$时，经验回放将完全采用均匀采样的方式抽取经验。从采样概率的定义可以看出，即使是TD-Error绝对值较小的经验也可能会被抽取，这种非零的概率分布确保了采样经验的多样性，防止网络训练产生过拟合问题。

    虽然根据PER机制抽取经验能够为所有经验分配合适的抽取概率，但TD-Error绝对值较高的经验通常会被更频繁地抽取，即各个经验被采样的频率会产生严重的不均衡问题，这不仅会导致训练过程出现振荡或发散的不稳定问题，甚至仍无法避免网络的训练产生过拟合问题或陷入局部最优问题[32-33]。

    本文中，在PER的基础上，为每条经验分配一个重要性权重${w_k}$，使网络在训练阶段的经验抽取更加偏向于有较大的学习价值的经验而又不完全舍弃无效的探索经验，重要性权重为

    $$ {w_k} = {1 \mathord{\left/ {\vphantom {1 {\left\{ {\left( {1 + \eta \cdot epi \cdot ps{e_k}} \right) \cdot {S^\beta } \cdot {{\left[ {P(ex{p_k})} \right]}^\beta }} \right\}}}} \right. } {\left\{ {\left( {1 + \eta \cdot p \cdot {p_k}} \right) \cdot {S^\beta } \cdot {{\left[ {P({e_k})} \right]}^\beta }} \right\}}} $$ (38)

    式中：$S$为经验池的大小；参数$\beta \in \left[ {0,1} \right]$用于控制经验${e_k}$的重要性权重${w_k}$对网络学习的影响，随着$\beta $的增加，经验池中高优先级经验的重要性权重几乎不变，而低优先级经验的重要性权重则会大幅增长；$p$为仿真博弈的幕数；参数$\eta \in \left[ {0,1} \right]$用于控制规则耦合模块生成的伪经验的重要性权重对网络学习的影响；${p_k}$为${e_k}$的伪经验标志位，若${e_k}$来自规则耦合模块则${p_k}$为1，否则${p_k}$为0，随着$p$的增加，伪经验的重要性权重将逐渐减小，即网络学习对伪经验的依赖程度将逐渐降低。在完成一个样本批次(one batch)的抽取后，算法会计算批次中所有经验的重要性权重并对其进行归一化处理，最终根据采样经验及其重要性权重对用于Critic网络更新的损失函数进行计算，重要性权重耦合的损失函数为

    $$ \left\{ \begin{gathered} {\mathcal{L}_{{\rm{Criti}}{{\rm{c}}_i}}}({{\boldsymbol{\theta }}_i}) = \frac{1}{K} \cdot \sum\limits_{k = 1}^K {\left\{ {{{\overline w_k}} \cdot {\delta _k}^2} \right\}} \\ {{\overline w_k}} = {{{w_k}} \mathord{\left/ {\vphantom {{{w_k}} {\mathop {\max }\limits_j \left\{ {{w_j}} \right\}}}} \right. } {\mathop {\max }\limits_j \left\{ {{w_j}} \right\}}} \\ \end{gathered} \right. $$ (39)

    式中：$K$为一个样本批次所抽取的经验数(batch size)，${{\overline w_k}} $为归一化重要性权重。

    如果在每次采样时均对经验池中所有经验的抽取概率进行计算，则需要消耗巨大的计算量，导致训练速度大幅降低。本文中，改进算法使用小批量抽取并逐渐累积经验的方法进行经验抽取以减少每次训练网络所需的计算量。每一轮从经验池中仅抽取$M$条经验并计算其抽取概率，依据概率进行经验抽取后，若累积抽取经验数已经达到一个样本批次的经验数，则停止采样，否则继续下一轮采样。每存储一条经验的同时，算法还会计算其重要性权重${w_k}$并将其与经验元组一同存入本次采样的样本批次中。经验采样过程如图12所示。

    图  12  重要性权重耦合的经验采样流程
    Fig.  12  Experience sampling process based on importance weights
    下载: 全尺寸图片

    3.5   算法流程设计

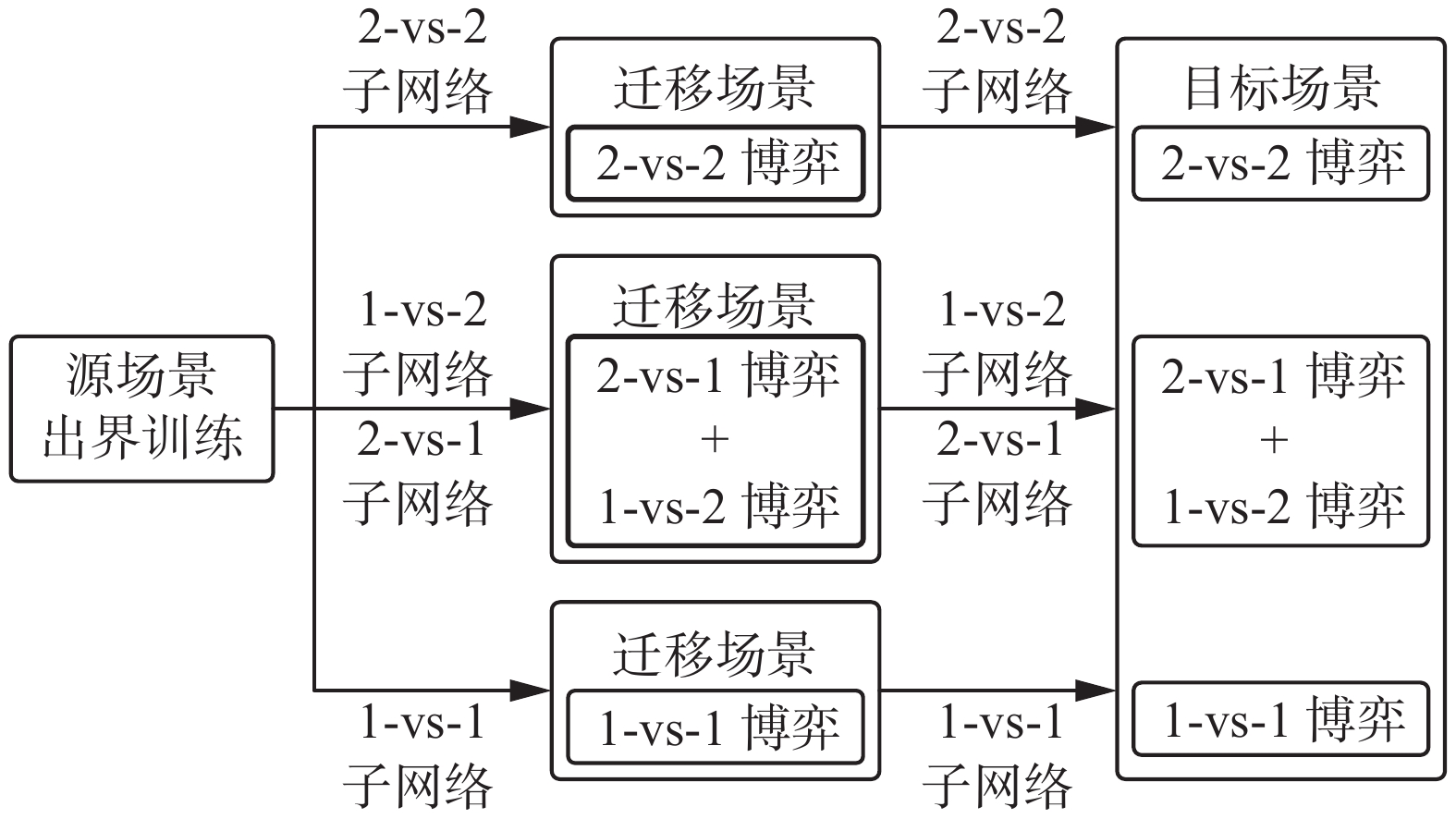
    在本实验初始阶段，算法运行子博弈场景以进行子网络的预训练，子网络完成在3个子博弈场景中的预训练后即可被迁移至完整的目标博弈场景中以进行进一步的网络训练。本文中，当无人机数量衰减时，用于决策的子网络也需要同时切换。无模型的MADRL算法通常需要大量的训练已学习最优策略，而无人机通常需要耗费大量的时间对具有高维状态−动作空间的复杂环境进行探索，导致训练效果难以得到有效提升。直接在目标场景中对所有子网络进行串行训练的方法通常会导致子博弈场景过早结束，难以积累有效的学习经验。基于上述问题，子网络的训练将采用“子场景迁移训练−目标场景联合训练”的训练优化方法。迁移学习的核心思想是将智能体针对简单任务的学习所获得的知识应用到对相关性较高的复杂任务的学习中[34]。本文中，各个子网络分别在其对应的博弈场景中进行训练属于简单任务，所有子网络在相互衔接的博弈场景中进行训练则属于复杂任务，2个学习任务虽然有所差异却具有较高的相似性，因此相比于直接训练由2-vs-2博弈场景开始直到某一方无人机被全部击毁的复杂任务，将各个博弈场景作为迁移场景分别进行训练并逐渐过渡到目标场景训练，即简单任务向复杂任务迁移训练的方式能够实现知识的继承，从而取得更好的训练效果。训练子网络由迁移场景向目标场景过渡的流程如图13所示。

    图  13  迁移场景训练流程
    Fig.  13  Migration scenario training process
    下载: 全尺寸图片

    4.   实验设置

    本文实验中的环境参数如表2所示，算法的超参数设置如表3所示。当无人机的位置超出博弈区域时，无人机被判定为出界。当无人机的动作序列使其绝对速度超出上限时，无人机的绝对速度大小将会被限制在最大值而仅按照$ {v_x} $和${v_y}$的比例改变方向。

    表  2  环境参数设置
    Table  2  Environment parameter settings
    参数名称参数数值
    博弈区域大小$300 \times 300 $
    边界安全距离${d_{{\rm{bou}}} }$/m20
    危险距离${d_{{\rm{dan}}}} $/m70
    攻击距离${d_{{\rm{att}}} }$/m50
    探索距离${d_{{\rm{exp}}}} $/m100
    攻击区张角${\theta _{{\rm{att}}}} $/rad1.7
    受威胁区张角${\theta _{{\rm{def}}}} $/rad1.57
    速度上限${v_{{\rm{max}}}} $/(m/s)20
    速度下限${v_{{\rm{min}}}} $/(m/s)1
    加速度上限${a_{{\rm{max}}}} $/(m/s2)5
    表  3  超参数设置
    Table  3  Hyperparameter settings
    参数名称参数数值
    Actor网络学习率${\alpha _{{\rm{Actor} } } }$0.8
    Critic网络学习率${\beta _{{\rm{Critic} } } }$0.8
    软更新系数$\tau $0.5
    折扣系数$\gamma $0.8
    噪声方差$\sigma $0.1
    经验池容量 10000
    采样批次数 1024
    最大幕数 15000
    最大步数500
    相对距离系数${k_{{\rm{dis}}}} $0.5
    相对速度系数${k_{{\rm{vel}}}} $0.5
    边界距离系数${k_{{\rm{bou}}}} $0.5
    威胁距离系数${k_{{\rm{esp}}}} $0.5
    PER系数$\alpha $0.8
    重要性权重系数$\beta $0.8
    奖励归一化系数${w_\phi } $10
    伪经验依赖系数$\eta $0.8
    仿真步长$\Delta t $1

    各个子网络模型的Critic网络结构参数如表4所示，Actor网络结构参数如表5所示。

    表  4  Critic子网络结构
    Table  4  Critic subnetwork structure
    网络 数据输入隐层01~05输出
    0102~05
    2-vs-2
    子网络    		State281281281
    Action201281281
    2-vs-1
    子网络    		State211281281
    Action151281281
    1-vs-2
    子网络    		State211281281
    Action151281281
    1-vs-1
    子网络    		State141281281
    Action101281281
    表  5  Actor子网络结构
    Table  5  Actor subnetwork structure
    网络输入隐层01~04输出
    2-vs-2
    子网络    		141285
    2-vs-1
    子网络    		141285
    1-vs-2
    子网络    		71285
    1-vs-1
    子网络    		71285

    5.   仿真实验

    5.1   训练过程

    基于MADRL的多无人机博弈对抗算法以最大化参与博弈的无人机获得的累积奖励值为学习目标。平均奖励是一幕博弈的每一步所获得奖励的平均值，平均奖励收敛速度越快、收敛平稳性越好说明网络的训练效果越好。在本实验中，每完成100幕网络训练即运行一幕测试博弈，并计算测试环境中无人机的平均奖励。

    在3.1节中提出的3个迁移场景中，分别使用本文提出的改进MADDPG算法、基于奖励势函数的MADDPG算法(MADDPG-I)、基于规则耦合方法的MADDPG算法(MADDPG-II)、重要性权重耦合的PER-MADDPG算法(MADDPG-III)和原始的MADDPG算法对场景中的子网络进行训练并通过对比无人机的平均奖励曲线以验证各改进方法的有效性。与上述5种算法对应的平均奖励曲线如图14所示。

    图  14  改进方案平均奖励曲线
    Fig.  14  Average reward curve of plans
    下载: 全尺寸图片

    分析图14中数据可知，上述3种改进方案均能够提升原始MADDPG算法的网络训练效率，但是算法的性能无法得到显著的提升。联合3种方案的改进算法则能够通过改进方案的相互辅助以大幅提升算法的性能。

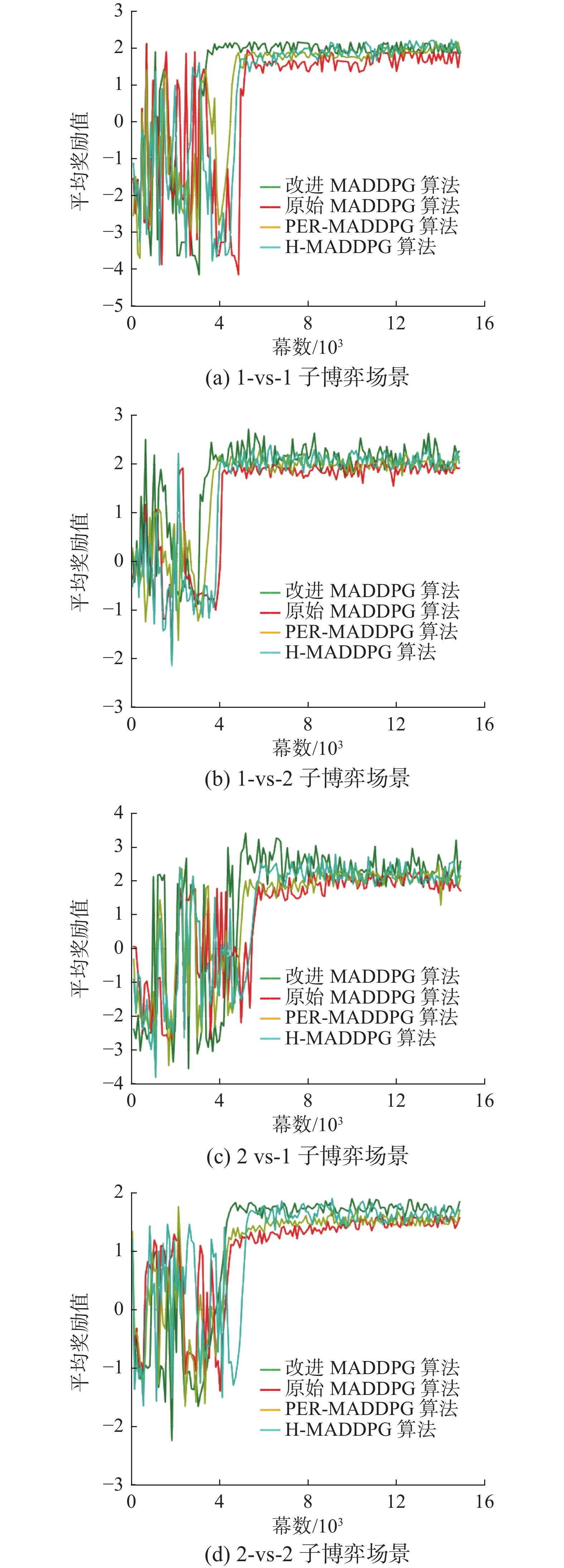
    在3个迁移场景中，分别使用传统的MADDPG算法、PER-MADDPG算法、H-MADDPG算法和改进MADDPG算法对场景中的子网络进行预训练并绘制4种算法的平均奖励曲线以验证改进算法的性能。上述4种算法中，PER-MADDPG算法将PER机制与传统的MADDPG算法结合以提升网络学习效率[35]；H-MADDPG算法将线性奖励函数和“后知后觉单元”引入MADDPG算法，线性奖励函数为训练经验引入了连续奖励值，一定程度上解决了稀疏奖励问题，提升了网络训练效率，“后知后觉单元”则在一幕仿真结束后对经验序列进行分析并生成相对成功的伪经验，伪经验与真实经验同时被存入经验池并参与经验回放，提升了算法对先验知识的利用率；改进MADDPG算法在原始算法的基础上引入规则耦合模块并基于势函数对算法的奖励机制进行设计，同时采用重要性权重耦合的PER方法对原始算法进行改进。子网络在各个子博弈场景中的训练效果如图15所示。

    图  15  改进算法平均奖励曲线
    Fig.  15  Average reward curve of algorithms
    下载: 全尺寸图片

    对平均奖励曲线的信息进行分析，计算各算法的评价指标，各算法的收敛均值和收敛时间如表6所示。

    表  6  算法收敛情况
    Table  6  Algorithm convergence
    算法博弈场景收敛时间/幕收敛均值
    MADDPG1-vs-153001.6348
    1-vs-243001.8785
    2-vs-160001.8919
    2-vs-248001.3937
    H-MADDPG1-vs-150001.8865
    1-vs-241002.0728
    2-vs-158002.1974
    2-vs-254001.7362
    PER-MADDPG1-vs-147001.8277
    1-vs-240002.0126
    2-vs-154002.0308
    2-vs-247001.4887
    改进MADDPG1-vs-135001.9834
    1-vs-236002.1508
    2-vs-150002.4312
    2-vs-246001.7271

    联合分析图15和表6中的数据可知，相比于3个对比算法，改进算法具有更高的优越性。在1-vs-1子博弈场景和2-vs-2子博弈场景中，与改进算法对应的平均奖励曲线收敛更快且曲线收敛后具有更加良好的平稳性，其平均奖励值基准线始终保持在与对比算法对应的平均奖励值基准线之上。

    5.2   测试结果

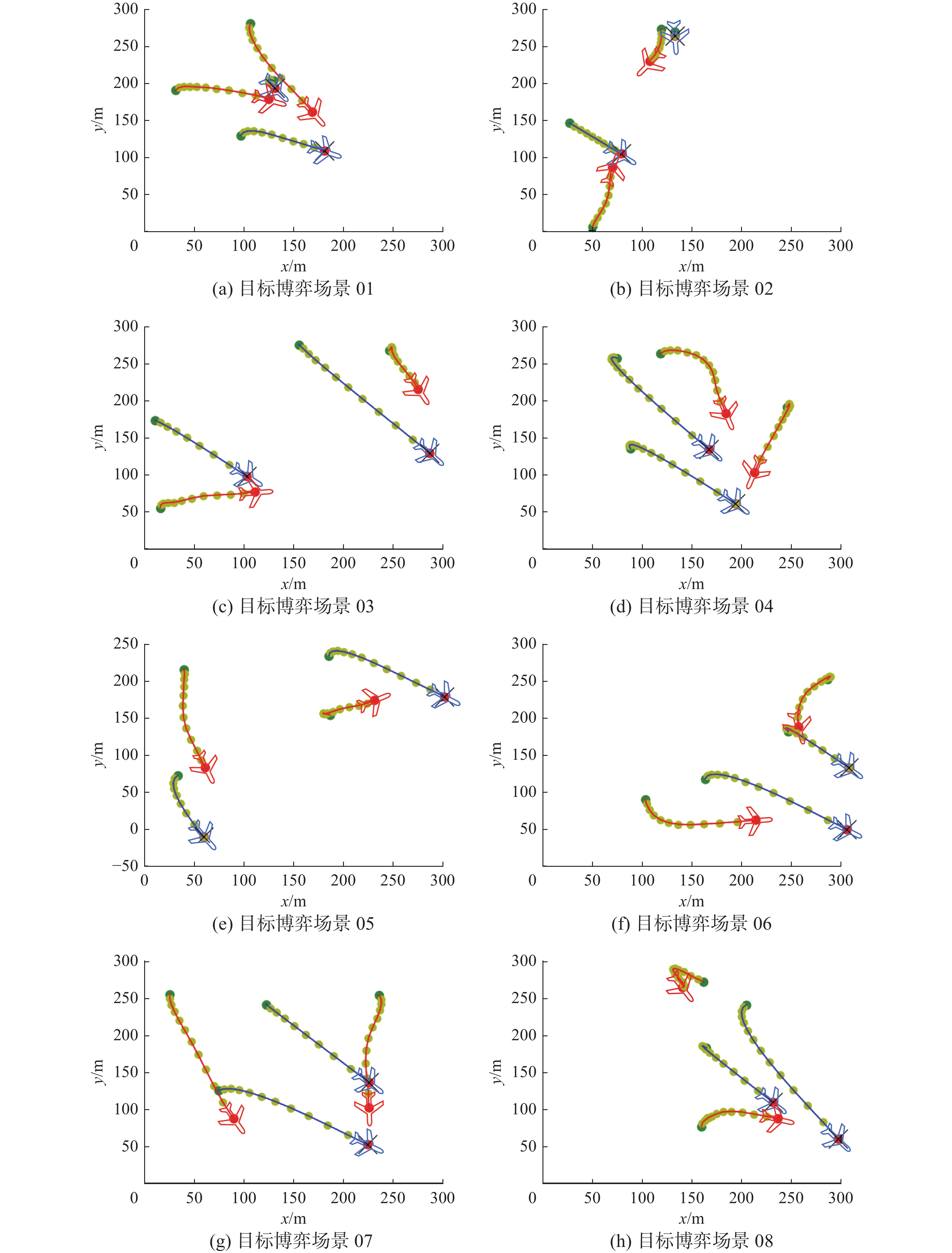
    在无人机的策略模型收敛后，为研究与改进对应的策略模型在博弈对抗中的表现，以进一步验证基于规则耦合的多异构子网络MADDPG算法在多无人机博弈对抗问题中的优势，实验将在测试环境中运行150幕完整的博弈对抗场景以相对直观地表明根据改进算法进行训练的Actor网络的优越性。本文从大量无人机博弈轨迹图中选择了一组具有代表性的轨迹数据进行分析，如图16所示。

    图  16  目标博弈场景博弈轨迹
    Fig.  16  Game curves in target game scenarios
    下载: 全尺寸图片

    测试博弈场景中，红方无人机使用以改进算法进行训练的Actor网络作为决策网络且引入规则耦合模块辅助网络决策而蓝方无人机分别使用以传统的MADDPG算法、H-MADDPG算法、PER-MADDPG算法和RS-MADDPG算法进行训练的Actor网络作为决策网络且不引入任何辅助模块。如引言所述，RS-MADDPG算法对无人机博弈对抗环境进行了完整的建模并引入了优化奖励机制以提升网络的训练效率和无人机Actor网络的决策能力。

    初步分析无人机轨迹可知，以改进算法进行训练的网络模型能够使无人机有效避免出界问题，模型具有一定的智能性且无人机在分工、合作等方面均表现出了良好的决策能力。在目标博弈场景01和目标博弈场景04中，红方无人机具有相同的目标无人机，故团队以合作的方式对蓝方无人机实施打击；在目标博弈场景02和目标博弈场景03中，红方无人机的目标无人机不同，故团队以分工的方式分别对各自的目标无人机实施打击；在目标博弈场景05和目标博弈场景06中，红方无人机则利用环境因素，将蓝方无人机驱赶至边界以完成对抗任务，即将目标无人机逼入绝境。在目标博弈场景07和目标博弈场景08中，红方无人机则展现出了更加智能灵活的博弈策略，无人机通过学习已经能够将分工、合作以及围捕等基础策略进行结合并应用于部分目标场景中。

    为了研究策略模型在收敛后的表现，进一步验证以改进算法训练的网络模型在多无人机博弈对抗问题中的决策优势，实验对150幕完整博弈过程中红、蓝两方无人机的仿真对抗数据进行统计。

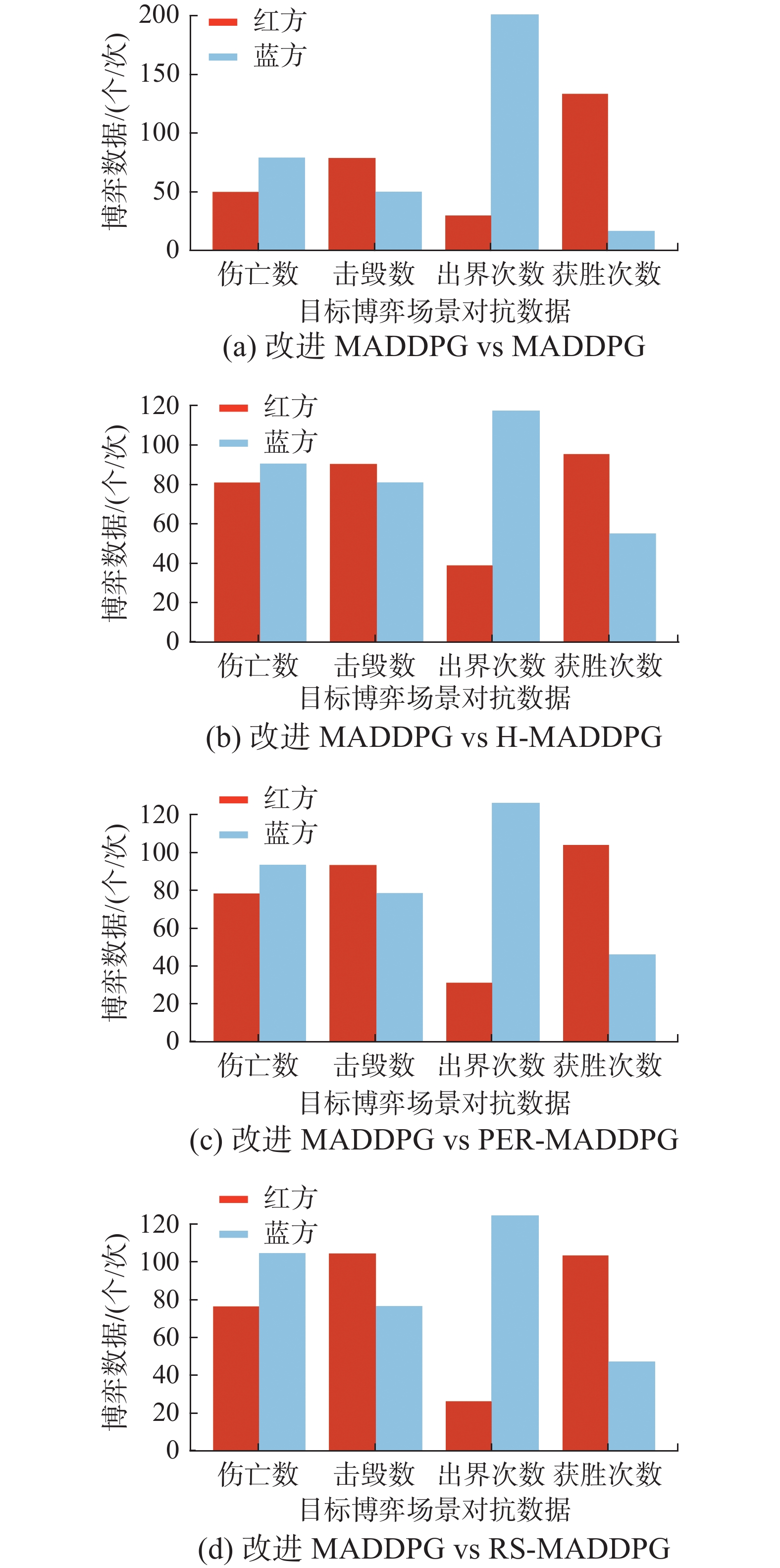
    测试实验中，博弈场景中红方无人机使用以改进算法进行训练的Actor网络作为决策网络，且引入规则耦合模块辅助网络决策，而蓝方无人机分别使用以传统的MADDPG算法、PER-MADDPG算法、H-MADDPG算法和RS-MADDPG算法进行训练的Actor网络作为决策网络且不引入任何辅助模块。双方在2-vs-1子博弈场景、1-vs-2子博弈场景和目标博弈场景中的对抗结果见图17~19。

    图  17  2-vs-1子博弈场景对抗数据统计
    Fig.  17  Statistical data in 2-vs-1 scenarios
    下载: 全尺寸图片
    图  18  1-vs-2子博弈场景对抗数据统计
    Fig.  18  Statistical data in 1-vs-2 scenarios
    下载: 全尺寸图片

    综合分析图17~19中的数据和仿真轨迹图可知，使用以改进算法进行训练的策略模型进行决策的红方无人机在博弈过程中的出界次数较少且具有更强的追踪打击能力和安全逃逸能力，即使红方无人机处于1-vs-2的劣势下，其策略模型仍然能够将胜率控制在50%左右，而使用以原始算法进行训练的策略模型进行决策的蓝方无人机的博弈对抗能力相对较弱且出界次数较多，以其他对比算法进行训练的策略模型的博弈对抗能力虽然优于以原始的MADDPG算法进行训练的策略模型但仍然无法完全超越以改进MADDPG算法进行训练的策略模型。

    图  19  目标博弈场景对抗数据统计
    Fig.  19  Statistical data in target scenarios
    下载: 全尺寸图片

    6.   结束语

    本文针对基于MADRL的多无人机博弈对抗问题进行研究，建立了与真实空战场景相似度较高的2-vs-2无人机博弈对抗场景。首先，对经典的MADDPG算法进行介绍并提出了算法在多无人机博弈对抗环境应用中存在的问题。其次，针对文中提出的问题对MADDPG算法进行改进，为算法设计异构子网络和规则耦合模块并引入奖励势函数以生成优质经验，同时设计了重要性权重耦合的PER方法以提高优势经验的利用率。最后，仿真实验结果表明：

    1) 规则耦合模块能够为算法引入更优质的经验，提升了网络模型的收敛速度和决策能力。在无人机的决策过程中，模块也能够起到良好的辅助作用。

    2) 对博弈任务进行分解并引入子网络的方法能够在不增加网络学习所需计算量的同时解决无人机团队在博弈过程中的团队成员数量动态衰减问题，可以满足小规模无人机团队博弈对抗任务的需求且不会引入冗余信息或丢失特征信息。

    3) 以势函数构建的奖励机制解决了网络模型学习过程中的稀疏奖励问题，对网络参数迭代能够起到良好的指导作用。

    4) 重要性权重耦合的PER机制使算法能够优先抽取TD-Error较大的经验以对网络模型进行训练且未完全放弃对探索经验的参考，随着学习时间的增加，重要性权重使网络学习对规则耦合模块的依赖程度逐渐降低，提升了网络学习效率。

    虽然算法在多无人机博弈对抗问题中取得了良好的学习效果，但当无人机数量增加时异构子网络的数量也会大幅增加。如果将大型无人机编队划分为多个小型编队并为若干小型编队分配相同的专属任务，则可以使一个或多个小型编队专注于完成全局任务的一部分即专注于完成子任务。在训练阶段，算法需要为具有相同子任务的小型编队设置局部Critic网络并为全体无人机构成的大型无人机编队设计全局Critic网络，而不需要对小型编队内无人机的Actor网络和Critic网络进行额外的修改。在今后的研究中将基于上述方案对算法进行进一步优化以使其适用于更大规模的多无人机博弈对抗任务。

  • 图  1   无人机群对抗场景

    Fig.  1   UAVs game confrontation scenario

    下载: 全尺寸图片

    图  2   无人机攻防约束条件

    Fig.  2   UAV attack and defense constrains

    下载: 全尺寸图片

    图  3   智能体与环境交互过程

    Fig.  3   Interaction between agent and environment

    下载: 全尺寸图片

    图  4   MADDPG算法框架

    Fig.  4   MADDPG algorithm framework

    下载: 全尺寸图片

    图  5   Critic网络和Actor网络

    Fig.  5   Critic network and actor network

    下载: 全尺寸图片

    图  6   2-vs-2 Critic网络和Actor网络

    Fig.  6   2-vs-2 Critic network and actor network

    下载: 全尺寸图片

    图  7   2-vs-1 Critic网络和Actor网络

    Fig.  7   2-vs-1 Critic network and actor network

    下载: 全尺寸图片

    图  8   1-vs-2 Critic网络和Actor网络

    Fig.  8   1-vs-2 Critic network and actor network

    下载: 全尺寸图片

    图  9   1-vs-1 Critic网络和Actor网络

    Fig.  9   1-vs-1 Critic network and actor network

    下载: 全尺寸图片

    图  10   规则耦合模块参与博弈过程

    Fig.  10   Game process with rule coupling

    下载: 全尺寸图片

    图  11   约束规则触发条件示意

    Fig.  11   Diagram of constraint trigger conditions

    下载: 全尺寸图片

    图  12   重要性权重耦合的经验采样流程

    Fig.  12   Experience sampling process based on importance weights

    下载: 全尺寸图片

    图  13   迁移场景训练流程

    Fig.  13   Migration scenario training process

    下载: 全尺寸图片

    图  14   改进方案平均奖励曲线

    Fig.  14   Average reward curve of plans

    下载: 全尺寸图片

    图  15   改进算法平均奖励曲线

    Fig.  15   Average reward curve of algorithms

    下载: 全尺寸图片

    图  16   目标博弈场景博弈轨迹

    Fig.  16   Game curves in target game scenarios

    下载: 全尺寸图片

    图  17   2-vs-1子博弈场景对抗数据统计

    Fig.  17   Statistical data in 2-vs-1 scenarios

    下载: 全尺寸图片

    图  18   1-vs-2子博弈场景对抗数据统计

    Fig.  18   Statistical data in 1-vs-2 scenarios

    下载: 全尺寸图片

    图  19   目标博弈场景对抗数据统计

    Fig.  19   Statistical data in target scenarios

    下载: 全尺寸图片

    表  1   子奖励势函数取值范围

    Table  1   Value range of sub incentive potential function

    奖励势函数取值范围
    $\phi_0({\boldsymbol{s}})$[−1, 1]
    $\phi_{{\rm{dis}}}({\boldsymbol{s} })$[−1, 1]
    $\phi_{{\rm{vel}}}({\boldsymbol{s} })$[−1, 1]
    $\phi_{{\rm{bou}}}({\boldsymbol{s} })$[0, 1]
    $\phi_{{\rm{esp}}}({\boldsymbol{s} })$[−1, 1]

    表  2   环境参数设置

    Table  2   Environment parameter settings

    参数名称参数数值
    博弈区域大小$300 \times 300 $
    边界安全距离${d_{{\rm{bou}}} }$/m20
    危险距离${d_{{\rm{dan}}}} $/m70
    攻击距离${d_{{\rm{att}}} }$/m50
    探索距离${d_{{\rm{exp}}}} $/m100
    攻击区张角${\theta _{{\rm{att}}}} $/rad1.7
    受威胁区张角${\theta _{{\rm{def}}}} $/rad1.57
    速度上限${v_{{\rm{max}}}} $/(m/s)20
    速度下限${v_{{\rm{min}}}} $/(m/s)1
    加速度上限${a_{{\rm{max}}}} $/(m/s2)5

    表  3   超参数设置

    Table  3   Hyperparameter settings

    参数名称参数数值
    Actor网络学习率${\alpha _{{\rm{Actor} } } }$0.8
    Critic网络学习率${\beta _{{\rm{Critic} } } }$0.8
    软更新系数$\tau $0.5
    折扣系数$\gamma $0.8
    噪声方差$\sigma $0.1
    经验池容量 10000
    采样批次数 1024
    最大幕数 15000
    最大步数500
    相对距离系数${k_{{\rm{dis}}}} $0.5
    相对速度系数${k_{{\rm{vel}}}} $0.5
    边界距离系数${k_{{\rm{bou}}}} $0.5
    威胁距离系数${k_{{\rm{esp}}}} $0.5
    PER系数$\alpha $0.8
    重要性权重系数$\beta $0.8
    奖励归一化系数${w_\phi } $10
    伪经验依赖系数$\eta $0.8
    仿真步长$\Delta t $1

    表  4   Critic子网络结构

    Table  4   Critic subnetwork structure

    网络 数据输入隐层01~05输出
    0102~05
    2-vs-2
    子网络    		State281281281
    Action201281281
    2-vs-1
    子网络    		State211281281
    Action151281281
    1-vs-2
    子网络    		State211281281
    Action151281281
    1-vs-1
    子网络    		State141281281
    Action101281281

    表  5   Actor子网络结构

    Table  5   Actor subnetwork structure

    网络输入隐层01~04输出
    2-vs-2
    子网络    		141285
    2-vs-1
    子网络    		141285
    1-vs-2
    子网络    		71285
    1-vs-1
    子网络    		71285

    表  6   算法收敛情况

    Table  6   Algorithm convergence

    算法博弈场景收敛时间/幕收敛均值
    MADDPG1-vs-153001.6348
    1-vs-243001.8785
    2-vs-160001.8919
    2-vs-248001.3937
    H-MADDPG1-vs-150001.8865
    1-vs-241002.0728
    2-vs-158002.1974
    2-vs-254001.7362
    PER-MADDPG1-vs-147001.8277
    1-vs-240002.0126
    2-vs-154002.0308
    2-vs-247001.4887
    改进MADDPG1-vs-135001.9834
    1-vs-236002.1508
    2-vs-150002.4312
    2-vs-246001.7271
    • 参考文献(35)
  • [1] 贾永楠, 田似营, 李擎. 无人机集群研究进展综述[J]. 航空学报, 2020, 41(S1): 4–14.

    JIA Yongnan, TIAN Siying, LI Qing. Recent development of unmanned aerial vehicle swarms[J]. Acta aeronautica et astronautica sinica, 2020, 41(S1): 4–14.
    [2] 李静晨, 史豪斌, 黄国胜. 基于自注意力机制和策略映射重组的多智能体强化学习算法[J]. 计算机学报, 2022, 45(9): 1842–1858.

    LI Jingchen, SHI Haobin, HUANG Guosheng. A multi-agent reinforcement learning method based on self-attention mechanism and policy mapping recombination[J]. Chinese journal of computers, 2022, 45(9): 1842–1858.
    [3] ZHANG Yu, MOU Zhiyu, GAO Feifei, et al. UAV-enabled secure communications by multi-agent deep reinforcement learning[J]. IEEE transactions on vehicular technology, 2020, 69(10): 11599–11611. doi: 10.1109/TVT.2020.3014788
    [4] ZHANG Lixiang, LI Jingchen, ZHU Yi’an, et al. Multi-agent reinforcement learning by the actor-critic model with an attention interface[J]. Neurocomputing, 2022, 471: 275–284. doi: 10.1016/j.neucom.2021.06.049
    [5] SIMÕES D, LAU N, REIS L P. Exploring communication protocols and centralized critics in multi-agent deep learning[J]. Integrated computer-aided engineering, 2020, 27(4): 333–351. doi: 10.3233/ICA-200631
    [6] SINGH A, JHA S S. Learning safe cooperative policies in autonomous multi-UAV navigation[C]//2021 IEEE 18th India Council International Conference . Piscataway: IEEE, 2022: 1−6.
    [7] WANG Bennian, GAO Yang, CHEN Zhaoqian, et al. A two-layered multi-agent reinforcement learning model and algorithm[J]. Journal of network and computer applications, 2007, 30(4): 1366–1376. doi: 10.1016/j.jnca.2006.09.004
    [8] WANG Zihao, ZHANG Yanxin, YIN Chenkun, et al. Multi-agent deep reinforcement learning based on maximum entropy[C]//2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference. Piscataway: IEEE, 2021: 1402−1406.
    [9] DING Feng, MA Guanfeng, CHEN Zhikui, et al. Averaged soft actor-critic for deep reinforcement learning[J]. Complexity, 2021, 2021: 1–16.
    [10] 符小卫, 王辉, 徐哲. 基于DE-MADDPG的多无人机协同追捕策略[J]. 航空学报, 2022, 43(5): 325311.

    FU Xiaowei, WANG Hui, XU Zhe. Cooperative pursuit strategy for multi-UAVs based on DE-MADDPG algorithm[J]. Acta aeronautica et astronautica sinica, 2022, 43(5): 325311.
    [11] ZHOU Xiao, SONG Zhou, MOU Xingang, et al. Multirobot collaborative pursuit target robot by improved MADDPG[J]. Computational intelligence and neuroscience, 2022, 2022: 1–10.
    [12] LI Chengjing, WANG Li, HUANG Zirong. Hindsight-aware deep reinforcement learning algorithm for multi-agent systems[J]. International journal of machine learning and cybernetics, 2022, 13(7): 2045–2057. doi: 10.1007/s13042-022-01505-x
    [13] WAN Kaifang, WU Dingwei, LI Bo, et al. ME-MADDPG: an efficient learning-based motion planning method for multiple agents in complex environments[J]. International journal of intelligent systems, 2022, 37(3): 2393–2427. doi: 10.1002/int.22778
    [14] WAN Kaifang, WU Dingwei, ZHAI Yiwei, et al. An improved approach towards multi-agent pursuit-evasion game decision-making using deep reinforcement learning[J]. Entropy, 2021, 23(11): 1433. doi: 10.3390/e23111433
    [15] LUO Wentao, ZHANG Jianfu, FENG Pingfa, et al. A deep transfer-learning-based dynamic reinforcement learning for intelligent tightening system[J]. International journal of intelligent systems, 2021, 36(3): 1345–1365. doi: 10.1002/int.22345
    [16] SUN Yu, LAI Jun, CAO Lei, et al. A novel multi-agent parallel-critic network architecture for cooperative-competitive reinforcement learning[J]. IEEE access, 2020, 8: 135605–135616. doi: 10.1109/ACCESS.2020.3011670
    [17] JIANG Longting, WEI Ruixuan, WANG Dong. UAVs rounding up inspired by communication multi-agent depth deterministic policy gradient[J]. Applied intelligence, 2023, 53(10): 11474–11489. doi: 10.1007/s10489-022-03986-3
    [18] QIE Han, SHI Dianxi, SHEN Tianlong, et al. Joint optimization of multi-UAV target assignment and path planning based on multi-agent reinforcement learning[J]. IEEE access, 2019, 7: 146264–146272. doi: 10.1109/ACCESS.2019.2943253
    [19] KONG Weiren, ZHOU Deyun, YANG Zhen. Air combat strategies generation of CGF based on MADDPG and reward shaping[C]//2020 International Conference on Computer Vision, Image and Deep Learning. Piscataway: IEEE, 2020: 651−655.
    [20] XIANG Lei, XIE Tao. Research on UAV swarm confrontation task based on MADDPG algorithm[C]//2020 5th International Conference on Mechanical, Control and Computer Engineering. Piscataway: IEEE, 2021: 1513−1518.
    [21] LIU Jianxing, AN Hao, GAO Yabin, et al. Adaptive control of hypersonic flight vehicles with limited angle-of-attack[J]. IEEE/ASME transactions on mechatronics, 2018, 23(2): 883–894. doi: 10.1109/TMECH.2018.2800089
    [22] LOWE R, WU Yi, TAMAR A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[EB/OL]. (2017−06−07)[2023−03−30]. https://arxiv.org/abs/1706.02275.
    [23] 邹长杰, 郑皎凌, 张中雷. 基于GAED-MADDPG多智能体强化学习的协作策略研究[J]. 计算机应用研究, 2020, 37(12): 3656–3661. doi: 10.19734/j.issn.1001-3695.2019.09.0546

    ZOU Changjie, ZHENG Jiaoling, ZHANG Zhonglei. Research on collaborative strategy based on GAED-MADDPG multi-agent reinforcement learning[J]. Application research of computers, 2020, 37(12): 3656–3661. doi: 10.19734/j.issn.1001-3695.2019.09.0546
    [24] WANG Zhaolei, ZHANG Jun, LI Yue, et al. Automated reinforcement learning based on parameter sharing network architecture search[C]//2021 6th International Conference on Robotics and Automation Engineering (ICRAE). Piscataway: IEEE, 2022: 358−363.
    [25] HUANG Liwei, FU Mingsheng, QU Hong, et al. A deep reinforcement learning-based method applied for solving multi-agent defense and attack problems[J]. Expert systems with applications, 2021, 176: 114896. doi: 10.1016/j.eswa.2021.114896
    [26] REN Jinsheng, GUO Shangqi, CHEN Feng. Orientation-preserving rewards’ balancing in reinforcement learning[J]. IEEE transactions on neural networks and learning systems, 2022, 33(11): 6458–6472. doi: 10.1109/TNNLS.2021.3080521
    [27] 陈灿, 莫雳, 郑多, 等. 非对称机动能力多无人机智能协同攻防对抗[J]. 航空学报, 2020, 41(12): 324152. doi: 10.7527/S1000-6893.2020.24152

    CHEN Can, MO Li, ZHENG Duo, et al. Cooperative attack-defense game of multiple UAVs with asymmetric maneuverability[J]. Acta aeronautica et astronautica sinica, 2020, 41(12): 324152. doi: 10.7527/S1000-6893.2020.24152
    [28] KONG Weiren, ZHOU Deyun, ZHANG Kai, et al. Air combat autonomous maneuver decision for one-on-one within visual range engagement base on robust multi-agent reinforcement learning[C]//2020 IEEE 16th International Conference on Control & Automation. Piscataway: IEEE, 2020: 506−512.
    [29] ZUO Guoyu, ZHAO Qishen, LU Jiahao, et al. Efficient hindsight reinforcement learning using demonstrations for robotic tasks with sparse rewards[J]. International journal of advanced robotic systems, 2020, 17(1): 172988141989834.
    [30] FU Yuchuan, LI Changle, YU F R, et al. Hybrid autonomous driving guidance strategy combining deep reinforcement learning and expert system[J]. IEEE transactions on intelligent transportation systems, 2022, 23(8): 11273–11286. doi: 10.1109/TITS.2021.3102432
    [31] YANG Ruyue, WANG Ding, QIAO Junfei. Policy gradient adaptive critic design with dynamic prioritized experience replay for wastewater treatment process control[J]. IEEE transactions on industrial informatics, 2022, 18(5): 3150–3158. doi: 10.1109/TII.2021.3106402
    [32] NI Zhen, MALLA N, ZHONG Xiangnan. Prioritizing useful experience replay for heuristic dynamic programming-based learning systems[J]. IEEE transactions on cybernetics, 2019, 49(11): 3911–3922. doi: 10.1109/TCYB.2018.2853582
    [33] YUAN Wei, LI Yueyuan, ZHUANG Hanyang, et al. Prioritized experience replay-based deep Q learning: multiple-reward architecture for highway driving decision making[J]. IEEE robotics & automation magazine, 2021, 28(4): 21–31.
    [34] LIU Wenzhang, DONG Lu, LIU Jian, et al. Knowledge transfer in multi-agent reinforcement learning with incremental number of agents[J]. Journal of systems engineering and electronics, 2022, 33(2): 447–460. doi: 10.23919/JSEE.2022.000045
    [35] 高昂, 董志明, 李亮, 等. MADDPG算法并行优先经验回放机制[J]. 系统工程与电子技术, 2021, 43(2): 420–433. doi: 10.12305/j.issn.1001-506X.2021.02.17

    GAO Ang, DONG Zhiming, LI Liang, et al. Parallel priority experience replay mechanism of MADDPG algorithm[J]. Systems engineering and electronics, 2021, 43(2): 420–433. doi: 10.12305/j.issn.1001-506X.2021.02.17
WeChat 点击查看大图
图(19)  /  表(6)
出版历程
  • 收稿日期:  2023-03-30
  • 网络出版日期:  2023-07-31

目录

    /

    返回文章
    返回