Hybrid genetic long-nosed raccoon optimization algorithm for maintenance resource allocation and scheduling
-
摘要: 鉴于传统的资源受限的项目调度问题（resource-constrained project scheduling problem，RCPSP）已经难以满足当下实际需求，对资源受限的项目调度问题进行扩展已是大势所趋，所以本文结合设备动态发布维修任务的特性，对原RCPSP问题进行抽象，加入了与设备相关的多模式的资源配置问题，从而建立了面向多维修中心的多模式的动态资源分配调度模型。为了更好地求解所提出的模型，本文提出了一种遗传−长鼻浣熊混合优化算法，该算法是在原长鼻浣熊优化算法的基础之上加入了遗传算法的选择、交叉以及变异算子，主要用于扩大搜索范围，从而跳出局部最优；为了进一步提高候选解的质量，还加入了贪婪算子的操作。通过对仿真实验结果的对比分析，发现不论是从收敛速度还是求解质量等方面，新提出的遗传−长鼻浣熊混合优化算法均以绝对的优势优于其他算法。Abstract: Traditional resource-constrained project scheduling problems (RCPSPs) can hardly meet current practical needs. Hence, expanding the RCPSP is an inevitable trend. Therefore, this paper abstracts the original RCPSP problem based on the characteristics of dynamically releasing maintenance tasks for equipment, adding multimodal resource allocation issues related to equipment. Thus, a multimode dynamic resource allocation and scheduling model for multiple maintenance centers is established. This paper proposes a hybrid optimization algorithm combining genetic and long-nosed raccoon algorithms to solve the proposed model effectively. The algorithm is added with the selection, crossover, and mutation operators of the genetic algorithm based on the original coati optimization algorithm, which are mainly used to expand the search range, thereby jumping out of local optimization. Furthermore, greedy operator functions are added to further improve the quality of candidate solutions. Comparative analysis of the results of simulative experiments revealed that the newly proposed genetic long-nosed raccoon hybrid optimization algorithm is superior to other algorithms in terms of convergence speed and solution quality.
-
多维修中心系统[1]以多个维修中心的优势脱颖而出，它涉及维修检查、维修资源供应调度和维修资源分配调度等部分，在很大程度上降低了由于系统故障[2]或者串行维修[3]所导致的长时间的维修停滞问题[4]。多维修中心系统具有两大鲜明的优势，其一是多维修中心系统进行维修任务时，可以并行没有优先级限制[5]的维修任务，极大地提高维修效率，节约维修成本；另外，由于所要维修的设备所处的位置并不固定，所以单一维修系统可能会拉长维修时间，但多维修中心系统采用“就近原则”进行维修，尽可能地降低了损失，提高了维修成功的机会。另一大优势在于多维修中心系统结合了区块链的核心思想[6]，是一种“去中心化”[7]的系统。多维修系统不但弥补了单维修系统维修效率低的问题，而且还分散了敌方的攻击目标，解决了以往单一维修后勤保障系统受到攻击而失去后勤保障能力[8]的弊病。
在实际维修任务中，不难发现关于设备的维修任务的资源调度问题隶属于经典资源受限项目调度问题[9-10]的范畴。
在国外的研究中，Oztemel等[11]为求解单资源的RCPSP问题，提出了人工蜂群算法；为了更好地处理基于无线通信与雷达系统的多核心的任务调度平台，Krishnakumar等[12]提出了一种关于模仿学习的方法；基于多模式的资源受限的项目调度问题，Kosztyan等[13]提出了一种基于矩阵的新思路；针对具有优先级先后顺序约束的多任务的资源受限的项目调度问题，Chakrabortty等[14]提出一种变邻域的启发式搜索算法；Zaman等[15]提出一种将浮动资源进行合理安排的方案。
在国内的研究中，田启华等[16]在多目标理想方法的基础上进行拓展，构建了任务的评价指标函数；鉴于资源存在空窗期的特性，陆志强等[17]针对作业的开始时间，提出了一种改进的遗传算法。事实上，实际任务的工期只是一个预期值，并不是确定的，针对这种实际情况，谢芳等[18]建立了基于资源受限项目调度问题的马尔可夫决策过程模型；最近，张宇哲等[19]针对所研究的问题，将传统的整数规划模型细化为约束主问题以及子问题，并且提出一种列生成的方法用于求解模型。最后通过实验发现，所提出的新算法拥有较好的求解性能。
通过对国内外任务调度技术的相关研究不难发现，现阶段还存在以下问题：
1）与维修设备的任务调度相关的研究较少；
2）经典静态模型已难以满足当下实际需求，对其进行拓展，使其更符合实际场景要求已迫在眉睫；
3）模型进行拓展之后，提出适用于新模型的改进算法至关重要。
结合多维修中心系统的优势，以维修资源为研究对象，采用适应当下实际需求的优化目标，以合理高效的资源调度策略，建立相应的资源调度模型并提出更好的求解算法，进而更加出色地完成所部署的维修任务。
1. 维修任务中的资源调度
1.1 问题描述与概念解释
维修任务是安全保障体系的重要组分之一，是受损设备经维修操作后恢复其作战状态的过程。资源调度则是指在任务的流水作业执行过程中，运用计算机、人工智能以及智能优化算法等相关技术，对所涉及的维修资源进行合理地监管与分配，以尽可能地提高维修效率，降低维修成本。
在维修任务的资源调度中，会涉及如下概念：
1）工件
工件是指所要维修的目标，可能是设备、备品备件，也可能是设备的零部件。
2）工序
工序是完成一项维修任务的最小单元。就维修一个小型设备而言，包括运输工序、修复工序、检验工序等。值得一提的是，工序之间存在严格的优先级关系，一旦工序顺序发生改变，很可能导致维修任务的失败；另外，工序一旦开始便不可中断，否则会直接影响后续工序的执行。
3）资源
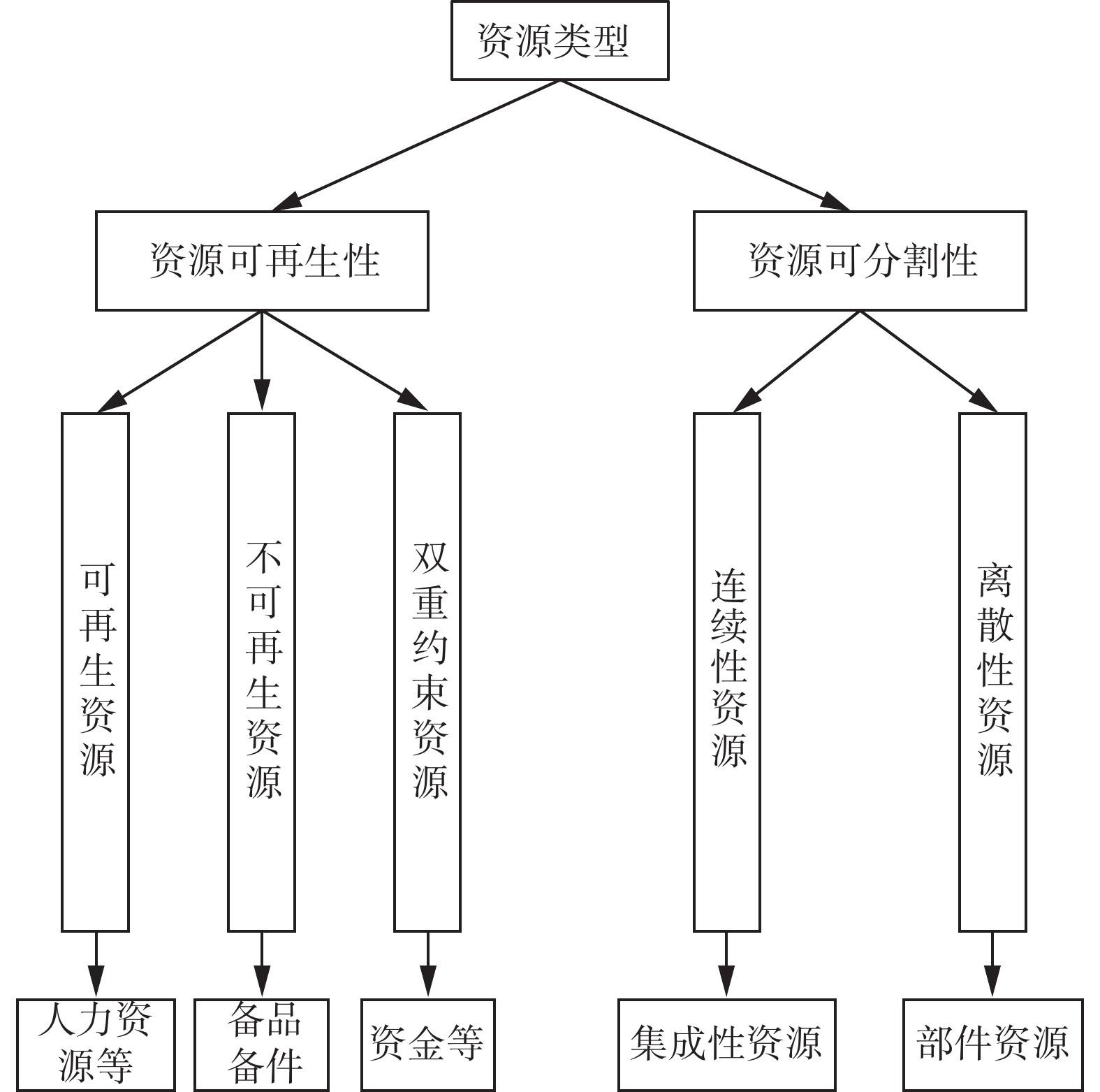
依据不同的分类标准，资源可以划分为不同的类型。资源大致可分为两大类，具体如图1所示。
图 1 资源的分类Fig. 1 Classification of resources
下载:
全尺寸图片
1.2 约束条件的分析
在实际维修保障体系中，维修任务是纷繁复杂的，其发布时间具有一定的随机性，进入维修队列的任务也会受到新任务的影响。除此之外，多维修中心系统主要是按照维修任务管理中心的维修检修计划来工作的。因此，一般是在当前设备使用的空闲期进行维修，并且还得确保一定的时效性。
显然，面向多维修中心的维修任务隶属于动态任务发布模式范畴，在执行当前任务时，有极大可能受到新加入任务的干涉，这使得其资源约束条件相较于静态调度问题更加严苛与抽象。
通过对维修任务的深入研究与分析，资源分配调度中的约束条件主要可以概括为以下4种：
1）时间约束
多维修中心的任务是不定时发布的，任务一经发布，系统通过维修任务分析预测模块对其需求的资源以及排队时间等指标进行预测，并依据设备具体使用时间等指标，综合考虑该待修设备进行维修任务的开始和截止时间。此外，维修任务必须在该时间范围内执行，否则会造成不可估量的损失。
2）资源约束
多维修中心系统以设备的维修为主，而设备的维修过程复杂多变，通常需要多种不同类型的资源的同时参与。因维修难度以及设备需求时间等差异，维修所需资源也不尽相同。一般而言，同一时间某维修资源仅为某工序所有，在该工序执行结束后，不可再生资源被消耗，有限的资源数量减少；而可再生资源在一定范围内可重复利用，总数量恒定。基于可再生资源可重复使用的特性，可以初步将可再生资源粗分为“空闲”与“忙碌”两种状态，以便后续建模等工作的顺利开展。
3）模式约束
在维修活动中包含着不同种类的维修工人和维修设备，由于维修人员所掌握的技能和熟练程度的差异，所以维修人员的级别可简单分为高级工、中级工和普通工；由于工作强度与维修难度的不同，维修设备的维修效率也存在差异。对于同一道工序，使用不同类型的资源配置方式，其实际执行时间不尽相同。假设就执行某道维修工序而言，高级工配置高效率设备只需要0.5 h就能完成，但普工配置低效率设备则可能需要2 h才能完成。同一工序的不同类型的资源配置方式称为工序模式，而不同的工序模式意味着不同的维修工期。
4）优先级约束
对于维修设备而言，维修次序不是随意的，而是具有严格要求的。设备的生产以及维修是厂商依据一定的规范条约严格执行的，维修工人必须严格按照要求进行损坏设备的维修，比如先拆解再分块维修，最后整装调试。显然，维修工序在时序上具有优化级约束。
2. 资源分配调度模型的建立
2.1 模型概述与资源调度策略
鉴于经典的RCPSP模型已经难以满足当下多维修中心系统保障体系的实际需求。所以，本文结合维修设备动态发布维修任务的特征，将维修任务涉及的维修资源简单划分为可再生资源（renewable resource，RR)和不可再生资源NRR（non-renewable resource，NRR），将维修任务抽象为RCPSP模型中的项目，维修工序抽象为RCPSP模型中的活动。另外，本文还考虑了不同模式的选择问题，进而构建了多模式的动态资源分配调度模型，但有如下限制：
1）考虑到维修任务具有发布时间随机等动态任务相关的特性，故可将其视为可以实时进入维修任务管理中心并随时等待安排维修处理的任务。另外，维修任务的执行时间必须在发布时间之后。
2）由于本文涉及的是资源受限类相关问题，所以资源并不是理想状态下的无限资源，而是有限数量的资源。具体为使用前后数量保持不变的RR和不可以重复使用，使用频次与剩余数量成反比的NRR。
3）维修工序不可轻易中断，维修任务一旦开始，涉及的资源将被占用，直至所有的维修工序均已完成，其所占用的RR才能被释放。
4）在资源配置阶段，倘若当前可用的RR不能满足当前需求，那么当前工序便被挂起，直至可用的RR数量满足当下需求才可被重新唤醒。
5）由于实际的维修任务纷繁复杂，影响维修任务的因素颇多，所以很难准确保证维修任务所需时间，一般在维修任务规定的到期时间前后小范围波动，则表明当前维修任务能够顺利完成。若在任务规定时间之前完成，则有一定的奖励，否则，会有相应的惩罚。
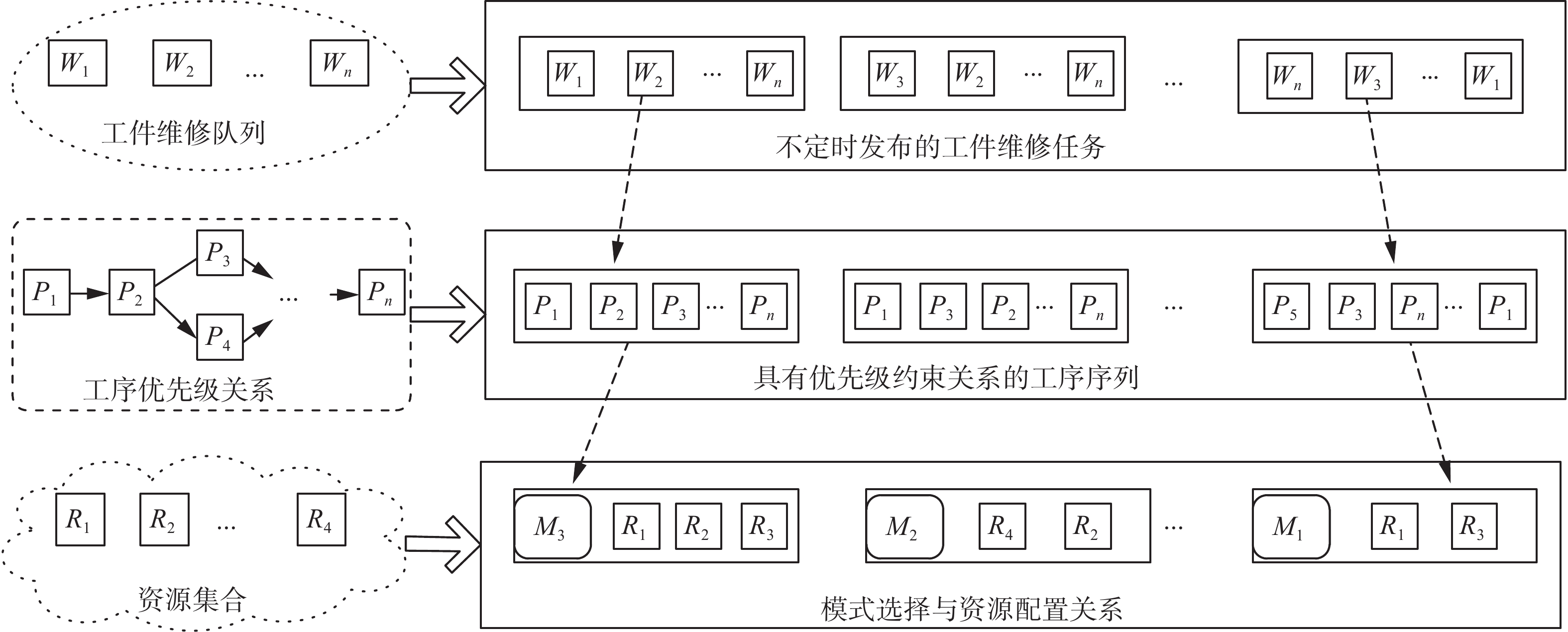
如图2所示，本文所建立的多模式动态受限资源分配调度模型主要涉及这几部分：不定时工件维修任务的发布、依据工序优先级关系所确定的作业执行次序以及不同模式的选择与需求资源的配置。
图 2 多模式动态受限资源分配调度模型结构Fig. 2 Structure chart of multimode dynamic constrained resource allocation and scheduling model下载:
全尺寸图片
2.2 数学模型的建立
鉴于同一符号参数被多次使用，为了方便管理与查阅，现对所建立的数学模型所涉及的符号参数进行详细地介绍，以便理解后续相关公式的具体含义，具体如表1、2所示。
表 1 变量释义与索引范围Table 1 Variable definition and index range变量 含义 索引范围 $i$ 任务序号 $1\leqslant i\leqslant I $ $j $ 工序序号 $1\leqslant j\leqslant J $ $m $ 模式序号 $ 1\leqslant m\leqslant M $ $t $ 时间序号 $0\leqslant t\leqslant T $ $r $ 可再生资源序号 $1\leqslant r\leqslant R $ $k $ 不可再生资源序号 $1\leqslant k\leqslant K $ 表 2 决策变量及其含义Table 2 Decision variables and their meanings决策变量 含义 $ Y_{ijt}$ 表征维修工作开始的决策变量，若第i任务中工序j在t时刻开始工作，那么此时该决策变量取1，否则取0 $X_{i}^{{\rm{ed}}}$ 表征第i维修任务提早日期完成的决策变量，若第i维修任务提早完成，那么此时该决策变量取1，否则取0 $X_{i}^{ {\rm{td} } } $ 表征第i维修任务超时日期完成的决策变量，若第i维修任务超时完成，那么此时该决策变量取1，否则取0 $X_{ijmt}^{ {\rm{rs} } } $ 表征资源充裕状态的决策变量，当第i任务中工序j在t时刻以m模式准备开展维修工作时，若剩余资源数量可以满足需求，则该决策变量取1，否则取0 $X_{ijm} $ 表征工序模式执行的决策变量，若第i任务中工序j按照m模式进行工作，那么此时该决策变量取1，否则取0 本文参考了不少学者采用的多目标加权优化的方法，采用专家评分系统进行权重的估量，具体得到如下结果：时间成本40%、经济成本30%、资源利用率30%，所以依次可以得到1.2、0.9、0.9这样的系数，取三者之和记为总成本
$ C $ 。$$ \min C = \sum\limits_{i = 1}^I {(1.2{C_i}^{{\text{time}}} + 0.9R_{C_i} } ) + 0.9\sum\limits_{r = 1}^R {C_r}^{{\text{idle}}} $$ (1) $$ {\rm{s.t.}} \;A_{i{j^{}}}^s \geqslant A_{i{j^\prime }}^f,\quad \left( {{j^\prime },j} \right) \in P_{d_i} $$ (2) $$ \sum\limits_{m = 1}^M {X_{ijm}^{}} = 1 $$ (3) $$ S_{T_i} = \min \left( {A_{ij}^s} \right)\quad \forall \{ j = 1,2, \cdots ,J\} $$ (4) $$ F_{T_i} = \max \left( {A_{ij}^f} \right)\quad \forall \{ j = 1,2, \cdots ,J\} $$ (5) $$ S_{T_i} \geqslant R_{T_i} $$ (6) $$ F_{T_i} \leqslant D_{D_i} $$ (7) $$ A_{ij}^f = A_{ij}^s + \sum\limits_{m = 1}^M {A_{ijm}^d} \cdot X_{ijm}^{} $$ (8) $$ A_{i{j^\prime }}^s \geqslant \max \left( {A_{ij}^f} \right) + {l_{i{j^\prime }}},\quad \forall \left( {j,{j^\prime }} \right) \in {{P}}_{{{d}}_i} $$ (9) $$ A_{(i + 1)1}^s \geqslant \max \left\{ {R_{i + 1}^{{\text{Task}}},A_{i1}^s} \right\} + {l_{(i + 1)1}} $$ (10) $$ {l}_{ij}=t\text{，}\text{ }当\left({\displaystyle \sum _{t=0}^{T}{Y}_{ijt}}\cdot {X}_{ijmt}^{\text{rs}}\right)\text=1 $$ (11) $$ \sum\limits_{t = 0}^T {{Y_{ijt}}} = 1\;, \forall \{ j = 1,2, \cdots ,J\} $$ (12) $$ \sum\limits_{i = 1}^I {R_{ik}^{{\text{nr}}}} \leqslant T_k^{{\text{nr}}} $$ (13) $$ \sum\limits_{j = 1}^J { \sum\limits_{m = 1}^M {R_{ijmr}^r} } \cdot X_{ijm}^{} \cdot {Y_{ijt}} \leqslant T_R^r \;\;\;\forall \{ t = 0,1,2, \cdots ,T\} $$ (14) 其中，式（1）表示最小化总成本这一目标函数，第1项表示时间成本、第2项表示经济成本、最后一项表示资源利用率；式（2~14）为约束条件，式（2）要求只有当
$ j $ 工序的前驱工序$ {j^\prime } $ 完成后才能开始；式（3）要求某一任务的某道工序一旦采用某种模式开始执行，则中途不允许进行模式的切换；式（4）和（5）指出某一任务的实际开始时间由最早工序的开始时间所决定，而某一任务的实际完成时间则由最晚工序的完成时间所决定；式（6）和（7）要求某一维修任务的实际开始时间不能早于该任务的发布时间；而某一维修任务的实际完成时间不能晚于该任务的到期时间；式（8）指出第$ i $ 维修任务的工序$ j $ 的实际完成时间一般由工序$ j $ 开始工作时对应的时间与完成工序$ j $ 所耗费的执行时间共同决定；另外，若当前闲置的可再生资源的数量不能满足第$ i $ 任务的$ {j^\prime } $ 工序的需求，那么需要耗费额外的等待时间$ {l_{i{j^\prime }}} $ 去等待可再生资源的释放。与此同时，式（9）要求工序$ {j^\prime } $ 的实际开始运行时间$ A_{i{j^\prime }}^s $ 应当不早于其前驱工序$ j $ 中最晚结束的时间与等待可再生资源所额外耗费的时间之和；就维修队列中连续的两个维修任务而言，式（10）指出第$ i+1 $ 维修任务的首个工序的实际开始工作时间$ A_{(i+1) 1}^{s} $ 由第$ i+1 $ 任务的发布时间$ R_{i + 1}^{{\text{Task}}} $ 、第$i$ 任务的首个工序的实际开始执行时间$ A_{i 1}^{s} $ 以及第$ i+1 $ 任务的首道工序所要耗费的额外可再生资源的等待时间$l_{(i+1)1}$ 来综合决定；式（11）指出当第$ i $ 任务的$ j $ 工序在0时刻开始执行，此时对应的空闲可再生资源的数量从不满足需求到满足需求所耗费的时间$ t $ 即为空闲资源等待时间$ {l_{ij}} $ ；式（12）要求每道工序有且仅有一次调度机会；式（13）要求不可再生资源在维修任务中的使用总量不应超过其总的库存量；式（14）要求某一时刻下该类资源的使用量不应超过当下库存总量$ T_R^r $ 。3. 遗传−长鼻浣熊混合优化算法
众所周知，受限资源的优化调度问题是经典的NP难问题，那么开展关于设备维修任务的动态多模式的资源分配调度问题的研究无疑是个极具挑战力的事情，看似是简单地将经典静态资源调度问题变成动态多模式的受限资源调度问题，但实际上其研究难度倍增，约束条件也会变得异常复杂，同济大学丁雪枫等[20]在文献中也曾指出，若采用精确求解算法求解该类问题其算法复杂程度空前绝后，随着任务数量的增加，求解时间指数级倍增。本文就2022年提出的长鼻浣熊优化算法[21]（coati optimization algorithm，COA）所存在的问题，结合遗传算法[22]及贪心算法[23]的相关思想进行改进，提出了一种新颖的算法——遗传−长鼻浣熊混合优化算法（hybrid genetic and coati optimization algorithm，GCOA）。
3.1 食物位置的编码与解码
1）编码策略
在GCOA中，每一个食物位置都代表着一个候选解，而每个候选解对应一个具体的调度策略，本文所建立的多模式动态受限资源分配调度模型中的调度方案主要包含具体的设备维修任务、维修工序以及维修的执行模式等部分。采用变量
$ i $ 表示维修任务，变量$ j $ 表示维修工序，变量$ m $ 则表示具体的某项维修任务的某道工序所选择的执行模式。将$ （i,j,m） $ 三元组构成的向量抽象为本章所建数学模型的一个具体的调度策略。鬣蜥位置的具体生成方式可以概括如下：首先根据维修任务管理中心的维修等待队列中任务的数量随机生成
$ {\boldsymbol{I }}$ 向量；随后将同一任务的不同工序经全排列后插入对应位置从而得到工序向量${\boldsymbol{J}}$ ；最后，将3种不同资源配置的模式随机分配给各道工序，每道工序有且仅有一种模式，这样就得到了与工序向量对应的模式向量${\boldsymbol{M}}$ ，具体如图3所示。
图 3 食物位置编码图Fig. 3 Food location coding chart下载:
全尺寸图片
在图3中，第一维行向量
${\boldsymbol{I}}$ 代表维修任务，其中各数字代表维修任务的编号；第二维行向量${\boldsymbol{J}}$ 代表维修工序，其数字代表工序编号；第三维行向量${\boldsymbol{M}}$ 代表执行模式，其数字表示工序所选择的具体执行模式。另外，不同的颜色对应不同的维修任务。2）解码策略
从上述编码阶段不难发现，该阶段仅涉及维修任务向量
${\boldsymbol{I}}$ 、维修工序向量${\boldsymbol{J}}$ 、执行模式向量${\boldsymbol{M}}$ ，并没有关于维修任务的资源剩余情况以及任务调度要求等相关信息，但是在解码中需要结合实际设备维修任务的发布时间$ D_{{\text{Release}}}^{} $ 、维修任务的到期时间$ D_{{\text{Due}}}^{} $ 、具体任务的具体工序在不同执行模式下的工作时间$ D_{{\text{Execution}}}^{} $ 以及资源的需求情况$ R_{{\text{Requirement}}}^{} $ 等，对开始调度时间$ T $ 、要求的最晚调度结束时间$ T_{{\text{max}}}^{} $ 以及资源的剩余数量$ R_{{\text{surplus}}}^{} $ 等参数进行初始化操作是解码策略的前提，具体可以参见鬣蜥位置解码的伪代码。解码是基于编码而来，故解码策略需要根据编码策略的特点来进行，也即按照编码策略中从左至右的顺序为具体任务的每道工序依照不同执行模式的不同要求进行资源的合理配置。
算法 鬣蜥位置解码伪代码
输入
$ T_{{\text{Task}}}^{} $ =$ I $ ,$ P_{{\text{Procedure}}}^{} $ =$ J $ ,$ M_{{\text{mode}}}^{} $ =$ M $ ,$ D_{{\text{Release}}}^{} $ = RD,$ D_{{\text{Execution}}}^{} $ = ED，$ R_{{\text{Requirement}}}^{} $ = RR，$ D_{{\text{Due}}}^{} $ = DD输出
$ S_{{\text{Time}}}^{} $ ,$ F_{{\text{Time}}}^{} $ ,$ P_{{\text{Start}}}^{} $ ,$ P_{{\text{End}}}^{} $ ,$ R_{{\text{surplus}}}^{} $ 初始化
$ T $ = 0,$ T_{{\text{max}}}^{} $ = 2000,$ R_{{\text{surplus}}}^{} $ = RS // 对应可进行资源调度的开始和结束时间,更新当前可用资源的剩余量。1) for
$ i $ ←0 to$ P_{{\text{Procedure}}}^{} $ .length do // 遵循编码策略的特点遍历每道工序2) while T < Tmax do // 资源分配调度循环计时条件
3) if
$ T $ >=$ D_{{\text{Release}}}^{} $ .get($ i $ ) then // 判断当前时间是否不早于任务的发布时间4) if
$ R_{{\text{surplus}}}^{} $ >=$ R_{{\text{Requirement}}}^{} $ .get($ M_{{\text{mode}}}^{} $ .get($ i $ )) then5) 根据工序具体资源需求情况进行资源的分配，并更新[
$ T $ ,$ T $ +$ D_{{\text{Execution}}}^{} $ .get($ i $ )]这个时间段对应需求资源的剩余量$ R_{{\text{surplus}}}^{} $ 6)
$ P_{{\text{Start}}}^{} $ .set($ T $ ) // 确定当前工序的开始时间7)
$ P_{{\text{End}}}^{} $ .set($ T $ +$ D_{{\text{Execution}}}^{} $ .get($ i $ )) // 确定当前工序的完成时间8) if
$ P_{{\text{Procedure}}}^{} $ .get($ i $ ) = 1 then // 判断是否为第$ i $ 任务的首道工序9)
$ S_{{\text{Time}}}^{} $ .set($ T $ ) // 确定任务的开始时间10) else if
$ P_{{\text{Procedure}}}^{} $ .get($ i $ ) =$ P_{{\text{Procedure}}}^{} $ .max then // 判断是否为第$ i $ 任务的最后一道工序11)
$ F_{{\text{Time}}}^{} $ .set($ T $ +$ D_{{\text{Execution}}}^{} $ .get($ i $ )) // 确定第$ i $ 任务的完成时间 // 值得注意的是，这里的$ T $ 对应第$ i $ 任务的最后一道工序的开始时间12) if (
$ T $ +$ D_{{\text{Execution}}}^{} $ .get($ i $ )) >=$ D_{{\text{Due}}}^{} $ then13) 该调度方案不合理，需要重新进行资源分配调度的安排
14) end if
15) else
16)
$T$ ++ // 当前没有足够的空闲资源可分配，当前工序进入等待队列，进入挂起等待状态，并且调度开始时间仍然持续推进17) end if
18) else
19)
$T$ ++ // 时间持续推进，直至不早于任务的发布时间20) end if
21) end while // 结束调度时间的预分配
22) end for // 结束遍历维修任务的工序集
23) end
3.2 算法核心要素
1）活动范围
在COA中，候选解是在长鼻浣熊的猎取鬣蜥区以及逃避天敌区的范围内随机生成的，所以不难发现，长鼻浣熊活动范围内候选解的数量也即鬣蜥的总数量
$ {N_{{\text{sum}}}} $ 对解的质量影响较大。由于猎取鬣蜥区域是长鼻浣熊的主要捕食区，而逃避天敌区域的核心目标是躲避天敌。基于此，在本文所提出的GCOA中，设置猎取鬣蜥区域中食物鬣蜥数量为$ {N_{{\text{hunt}}}} $ ，而逃避天敌区域中鬣蜥数量为$ {N_{{\text{escape}}}} $ ，它们之间的具体关系为$$ {N_{{\text{sum}}}} = {N_{{\text{hunt}}}} + {N_{{\text{escape}}}} $$ (15) $$ {N_{{\text{hunt}}}} = 4 \cdot {N_{{\text{escape}}}} $$ (16) 2）适应度函数
由于本文所建立的多模式动态受限资源分配调度模型的优化目标是最小化总成本，所以更高适应度的解也就意味着总的调度成本更低，相应的解的质量也就越高，适应度也就越高，具体表现为
$$ f(i) = \frac{1}{{C(i)}} $$ (17) 其中：
$ C(i) $ 表示在所有候选解中第$ i $ 候选解所对应的目标函数值的大小，也即对应本文所建立的数学模型的第$ i $ 候选解所对应的调度策略的总成本；$ f(i) $ 则表示该候选解的适应度大小。3）迁移因子和保留频次
若长鼻浣熊在连续多次迭代过程中其位置始终保持不变，那么该算法很有可能陷入局部最优。对此，引入了迁移因子（migration factor，MF）的概念，当长鼻浣熊在连续的迁移因子
$ M $ 次迭代中其位置始终保持不变，那么便将长鼻浣熊强制迁移至临近的一个随机位置处，增大其搜索范围，以使其尽可能跳出局部最优状态。为了便于记录长鼻浣熊随着迭代次数的增加其当前位置保持不变的迭代次数，本文引入了保留频次（retention frequency，RF）这一概念，若当前迭代后发现长鼻浣熊的位置仍然保持在迭代前的位置，那么保留频次
$ F $ 加1，否则须将$ F $ 置为0；若长鼻浣熊在连续的$ M $ 次迭代中其位置始终保持不变，那么需要将长鼻浣熊迁移至当前活动范围外的临近随机位置处，具体强制迁移条件如下所示：$$ F = \left\{ \begin{gathered} F + 1,\quad l_i^{{\text{current}}} = l_{i - 1}^{{\text{current}}} \\ 0,\quad l_i^{{\text{current}}} \ne l_{i - 1}^{{\text{current}}} \\ \end{gathered} \right. $$ (18) $$ l_i^{{\text{current}}} = \left\{ {\begin{array}{*{20}{l}} {l_i^{{\text{random}}}}\;,&{{\text{ }}M \leqslant F} \\ {l_{i - 1}^{{\text{current}}}}\;,&{{\text{ }}M{\text{ > }}F} \end{array}} \right. $$ (19) 式中：
$ l_i^{{\text{current}}} $ 表示长鼻浣熊当前位置，而$ l_i^{{\text{random}}} $ 则表示长鼻浣熊所处的随机位置。4）优化的选择操作
本文采用精英保留与轮盘赌相结合的策略来进行算法的选择操作，这样不但保留了优秀个体而且还极大地丰富了种群基因的多样性，从而使算法尽快朝着预期方向进行收敛。
首先，采取精英选择策略来保留候选解中质量较高的
$ N_{}^{{\text{single}}} $ 个个体，具体流程为：对当前活动范围的各个候选解进行适应度大小的排列，选择适应度较高的前$ N_{}^{{\text{single}}} $ 个个体不经过遗传而直接通过复制的方式进入子代，而$ N_{}^{{\text{single}}} $ 的具体计算方式为$$ N_{}^{{\text{single}}} = (1 - G) \cdot {N_{{\text{sum}}}} $$ (20) 式中：
$ G $ 表示区间$ (0,1) $ 范围内的代沟值，$ {N_{{\text{sum}}}} $ 反映了种群的大小规模。不难发现，精英选择策略可以有效保留种群中较优秀的个体，避免最优个体被交叉操作而破坏。
$ N_{}^{{\text{single}}} $ 个质量较高的个体通过精英选择策略进行保留，而剩余的$ G \cdot {N_{{\text{sum}}}} $ 个个体则采用轮盘赌的方式进行抉择：首先，利用式（17）计算每个个体的适应度；其次，通过式（21）计算第$ i $ 个体$ N_i^{{\text{single}}} $ 的保留概率$ p{\text{(}}N_i^{{\text{single}}}{\text{)}} $ ；然后，使用式（22）计算出各个个体的累积概率$ q{\text{(}}N_i^{{\text{single}}}{\text{)}} $ ；最后，随机生成$ G \cdot {N_{{\text{sum}}}} $ 个(0,1]区间的随机数，依据所落区间个数的多少，择优选择对应的个体。不难发现，保留概率较小的个体也有被选中的概率，这样便极大地丰富了候选解的多样性，同时也增大了算法搜索到更优质解的能力。$$ p{\text{(}}N_i^{{\text{single}}}{\text{) = }}\frac{{f(N_i^{{\text{single}}}){\text{ }}}}{{\displaystyle\sum\limits_{j = {\text{1}}}^{{N_{{\text{sum}}}}} {f(N_j^{{\text{single}}})} }} $$ (21) $$ q{\text{(}}N_i^{{\text{single}}}{\text{) = }}\sum\limits_{j = {\text{1}}}^i {p{\text{(}}N_j^{{\text{single}}}{\text{)}}} $$ (22) 式中：
$ f(N_i^{{\text{single}}}) $ 为个体$ N_i^{{\text{single}}} $ 对应的适应度值，$ p{\text{(}}N_i^{{\text{single}}}{\text{)}} $ 反映了个体$ N_i^{{\text{single}}} $ 被选择保留下来的概率，$ q{\text{(}}N_i^{{\text{single}}}{\text{)}} $ 表示第$ i $ 个体的累积概率。5）交叉操作
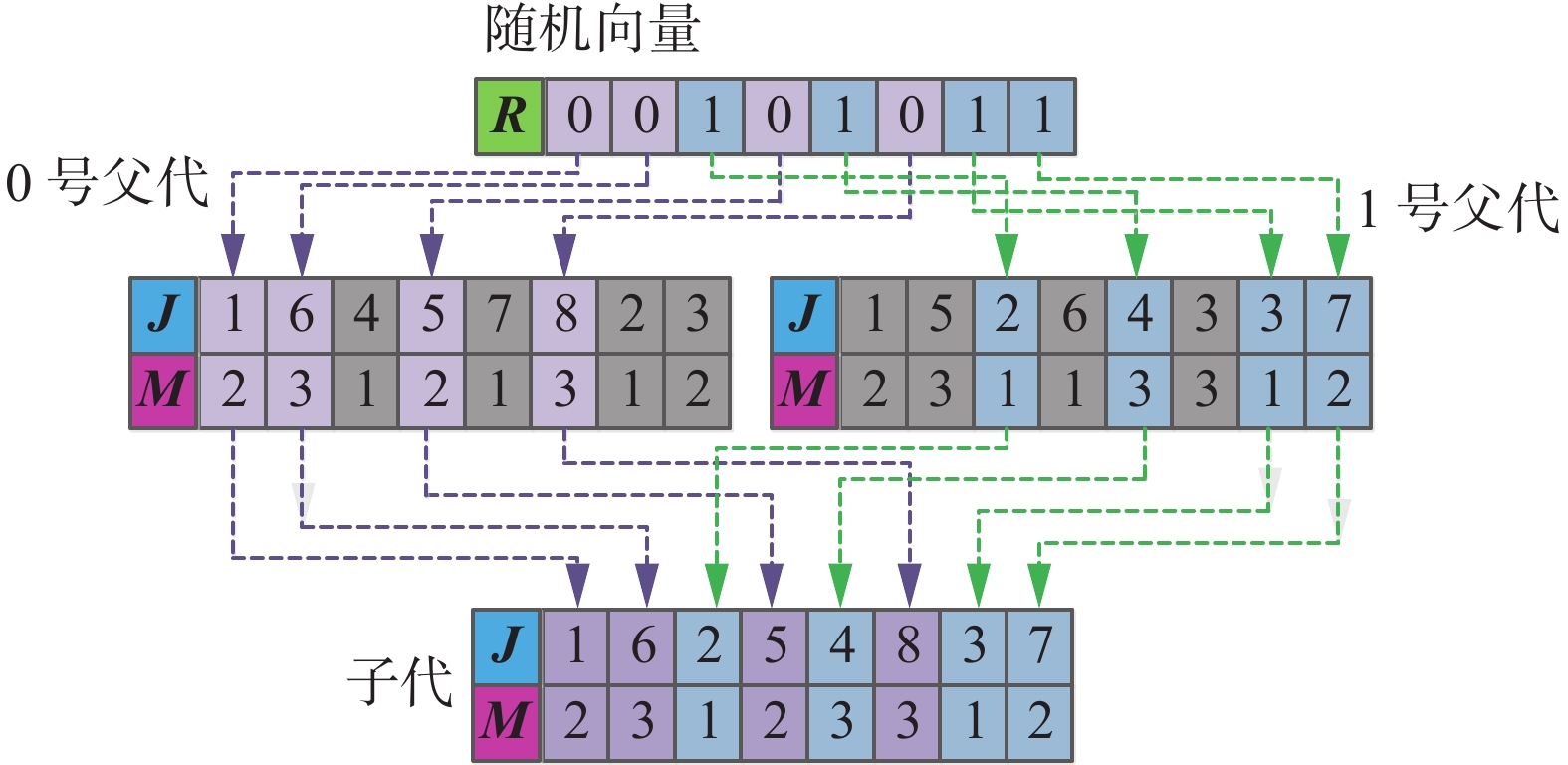
选取当前活动范围的两个鬣蜥位置作为父本，引入随机向量
${\boldsymbol{R}}$ ，按照随机向量的约束，交叉重组得到子代所对应的候选解。本文所设计的算法的交叉操作主要针对维修工序${\boldsymbol{J}}$ 和执行模式${\boldsymbol{M}}$ 而言，具体如图4所示。
图 4 交叉操作示意Fig. 4 Schematic diagram of cross operation下载:
全尺寸图片
6）变异操作
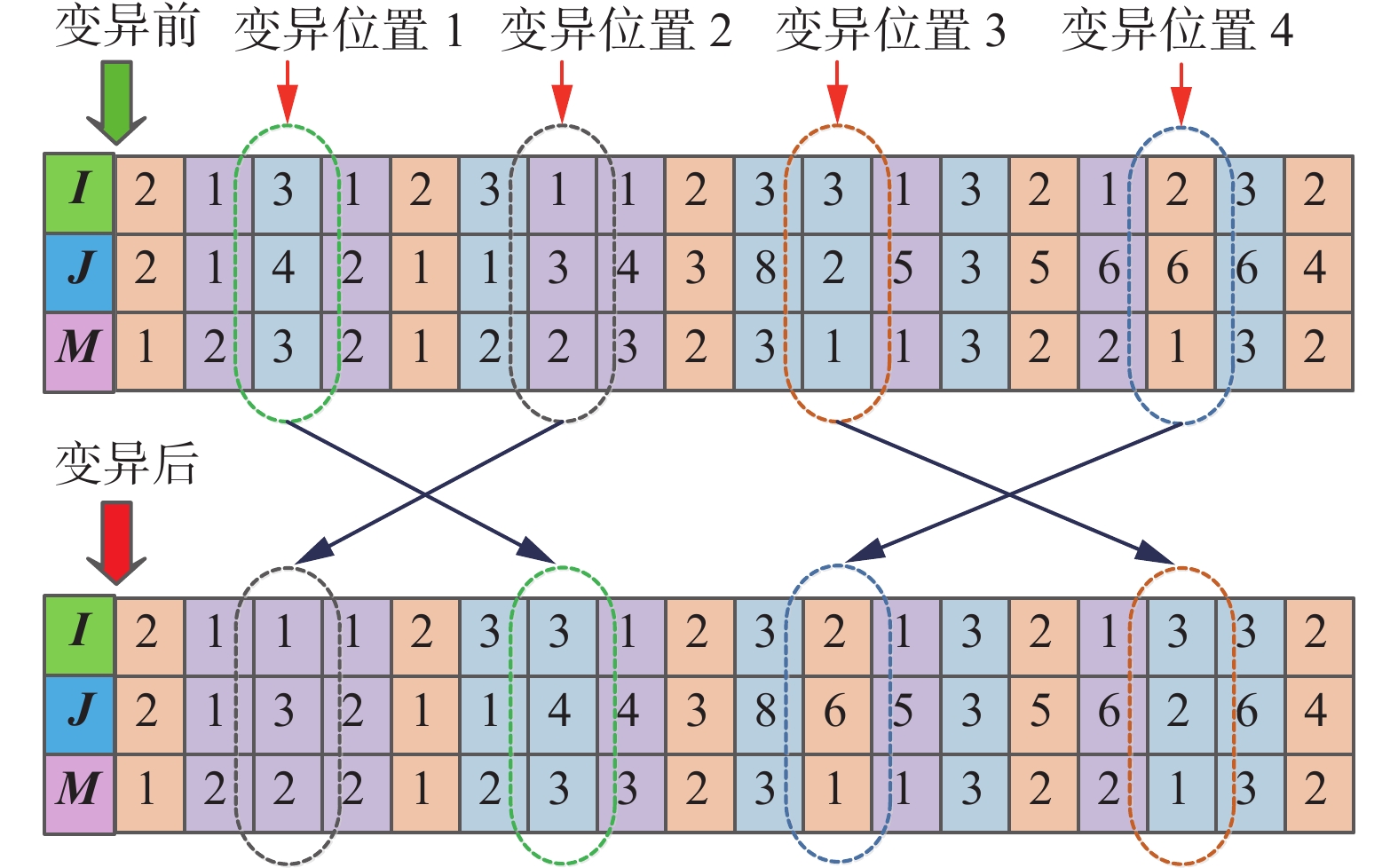
本文主要采用了一种随机多点交换的策略来实现算法的变异操作，其实质上一种基于进化逆转操作来实现的变异方式。由于任务之间是相互独立的，不同任务的维修工序之间不存在优先级约束，所以将维修任务
${\boldsymbol{I}}$ 、维修工序${\boldsymbol{J}}$ 以及执行模式${\boldsymbol{M}}$ 构成的鬣蜥位置编码三元组$ （i,j,m） $ 按照维修任务的不同，随机选择4个不同的位置进行两两交换，从而来实现GCOA算法的变异操作，具体如图5变异操作示意图所示。
图 5 变异操作示意Fig. 5 Schematic diagram of variation operation下载:
全尺寸图片
不难发现，采用这种变异操作的方式可以较大程度的保留任务内部维修工序的约束关系，在一定程度上增强了候选解的可行性，同时也增加了候选解的多样性。另外，针对实际设备维修任务所设计的食物位置的编码方式受诸多约束条件的限制，所以并非对候选解进行多重叠加操作就会有更好的结果，反而可能造成候选解逆向退化。据此，以变异执行概率
$ {P_m} $ 随机选择$ {P_m} \cdot {N_{{\text{sum}}}} $ 个鬣蜥位置实现变异操作；再在剩余的候选解中以交叉执行概率$ {P_c} $ 随机选择$ {P_c} \cdot {N_{{\text{sum}}}} $ 个候选解进行交叉操作。7）引入贪婪算子
为了提高候选解的质量，也即进一步优化求解目标，降低总维修成本，本文基于贪婪思想提出了一种贪心算子的操作。贪婪操作的对象是鬣蜥位置编码三元组中的维修工序
${\boldsymbol{J}}$ 和执行模式${\boldsymbol{M}}$ ，具体过程如下：①在新生成的长鼻浣熊活动范围中随机选取一定数量的鬣蜥位置作为贪婪算子的候选解；
②按照从左至右的顺序依次检查各个候选解的不同维修工序所对应的执行模式，筛选出包含2种或2种以上工作模式的维修工序；
③分别计算这些维修工序的各个模式所对应的不同资源配置下的总维修成本；
④若该工序其他模式的资源使用成本中，存在小于当前编码执行模式资源使用成本的模式，修改当前维修工序的执行模式为最小总维修成本所对应的执行模式；
⑤判断当前工序是否为最后一道工序，若不是鬣蜥位置编码中的最后一道工序，则转到3），继续后一道维修工序的执行模式的贪婪搜索；若是，则输出当前最优的解决方案。
3.3 可行性分析与维护
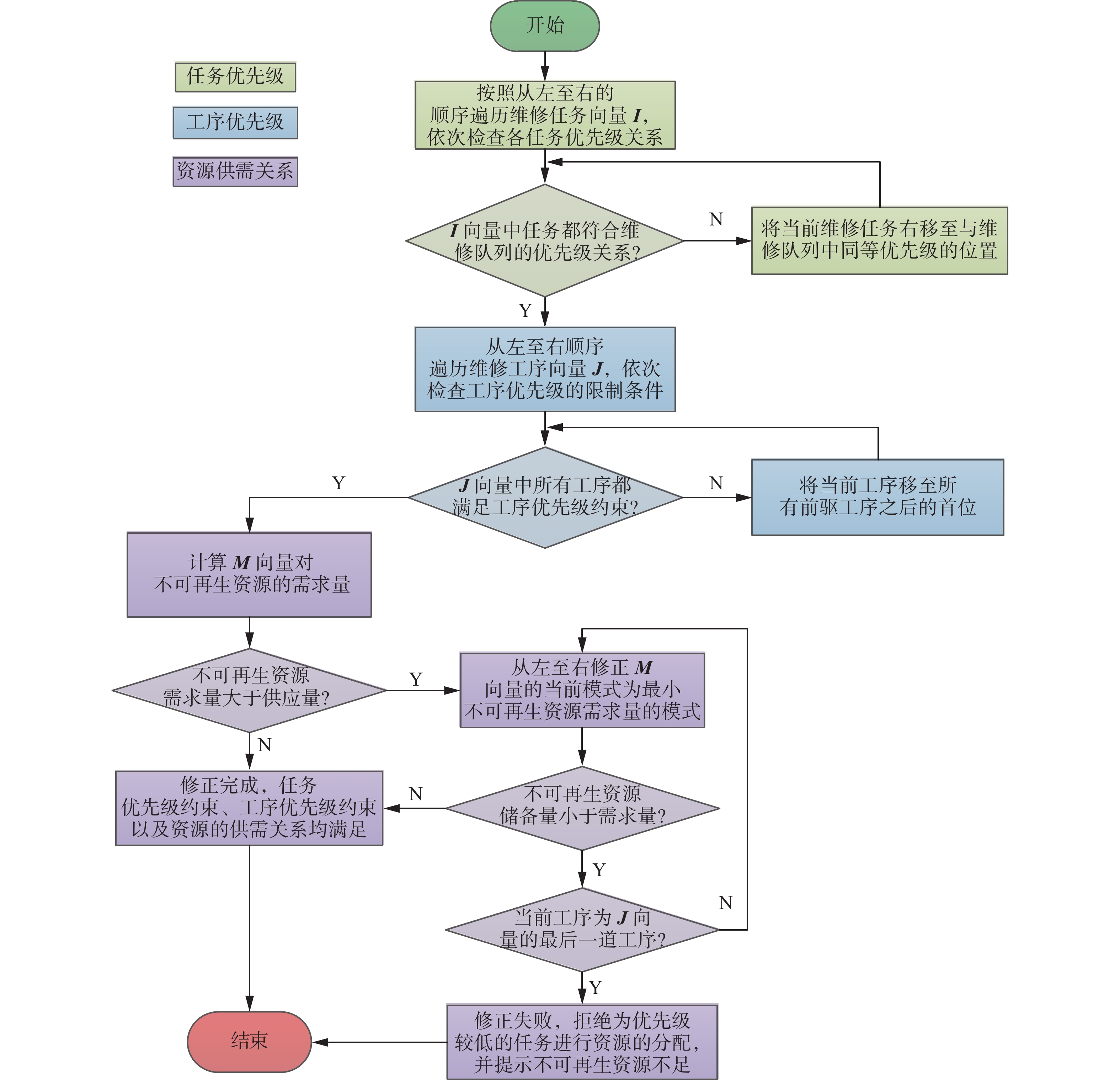
新提出的GCOA是采用随机生成的方式生成维修任务的，并且调度中存在大量的约束条件，所以初始解中存在大量不可行解，需要将其剔除或者修正。此外，原来的维修工序也是通过全排列的随机生成的方式插入到对应任务中去的，而且3种不同资源配置的执行模式也是随机分配给各道工序的，所以势必存在大量不可行解，对于这些不可行解的分析检查与修正是必要的，具体如图6所示。
图 6 可行性分析与维护流程Fig. 6 Feasibility analysis and maintenance flow下载:
全尺寸图片
不难发现，可行性分析与维护主要包含以下3部分：1）任务优先顺序的检查与维护；2）工序优先级的检查与维护；3）资源供需关系的检查与修正。
3.4 GCOA算法流程图
GCOA算法可以简单概括为初始化、全局捕食和局部避敌3部分，GCOA算法具体流程图如图7所示。
图 7 GCOA算法流程Fig. 7 Flow of genetic and coati hybrid optimization algorithm下载:
全尺寸图片
4. 实验设计与结果分析
4.1 实验数据与算法参数
鉴于目前还没有公开的可供研究使用的设备维修数据，此次研究将PSPLIB标准问题库中的部分数据进行按需改造，进而展开相应的仿真实验。PSPLIB标准问题库是Project Scheduling Problem Library的缩写，由Kolisch等[24]通过设计ProGen软件首次产出拥有不同目标的项目调度问题集；随后，Schwindt等[25]结合资源性质、模式类别以及倒换时间等因素，设计出更符合实际需求的新软件ProGen/Max，进而得到PSPLIB标准问题库。
本文参考了文献[26]的数据处理方式，具体则是选取PSPLIB标准问题库的j10.mm、j14.mm以及j30.mm的基准实例进行整合从而得到此次研究所需要的数据，依据数据来源与规模的差异，从而得到如表3所示的4种不同大小规模的仿真实验算例。
表 3 仿真实验算例详细信息Table 3 Detailed information of simulation experiment examples算例
编号数据来源 工序数量/道 任务总数/个 工序总数/道 模式总数/个 R1数量/个 R2数量/个 K1数量/个 K2数量/个 任务发布
时间/h1 j10，j14 12 15 180 540 160 132 450 440 随机 2 j14，j30 22 7 154 462 98 120 446 360 随机 3 j10，j14 12 30 360 1080 330 175 900 880 随机 4 j14，j30 22 14 308 924 200 250 892 720 随机 为了模拟多维修中心系统中维修任务管理中心不定时发布新维修任务的过程，此次仿真实验所采用的实验算例中所涉及的所有维修任务也均是按照随机时间发布的。由于此次实验涉及两大类不同的资源：可再生资源RR和不可再生资源NRR，而每类资源又可细分为两种资源，所以为每种资源分别设定相应的调度成本是很有必要的。为便于求解以及后续不同算法间性能的比较，此次调度成本具体设定详情如表4所示。
表 4 调度成本参数值详情Table 4 Details of dispatch cost parameter values参数名称 设定值 R1资源使用成本/（元·个−1·h−1） 2 R2资源使用成本/（元·位−1·h−1） 3 K1资源损耗成本/（元/个） 15 K2资源损耗成本/（元/个） 12 R1资源闲置成本/（元·个−1·h−1） 0.50 R2资源闲置成本/（元·位−1·h−1） 0.75 提前完成任务奖励成本/（元/h） 80 超时完成任务惩罚成本/（元/h） 160 鉴于本文所提出的GCOA算法的求解性能受迁移因子、交叉算子、变异算子以及贪心算子等参数的影响，所以在表5给出了GCOA各参数具体取值详情。
表 5 GCOA各参数取值参考Table 5 Reference for GCOA parameter values参数名称 参数值 鬣蜥总数量 $ {N_{{\text{sum}}}} $/只 100（小规模）
200（大规模）猎取鬣蜥区鬣蜥数量 $ {N_{{\text{hunt}}}} $/只 80（小规模）
160（大规模）逃离天敌区鬣蜥数量 $ {N_{{\text{escape}}}} $/只 20（小规模）
40（大规模）迁移因子 $ M $ 50 交叉算子概率 $ {P_c} $ 0.7 变异算子概率 $ {P_m} $ 0.2 贪心算子概率 $ {P_g} $ 0.4 迭代次数 $ N $ 2000 4.2 算法性能的对比分析
由于涉及的算法都属于元启发式算法，故皆受随机因素的影响，所以选择在各个算例上运行10次取均值的方式来提高算法的可靠性。此外，秉持对比实验的公平性，同一算例下的算法保持相同的初始解、迭代次数以及食物数量等信息。
1）算法收敛性能对比
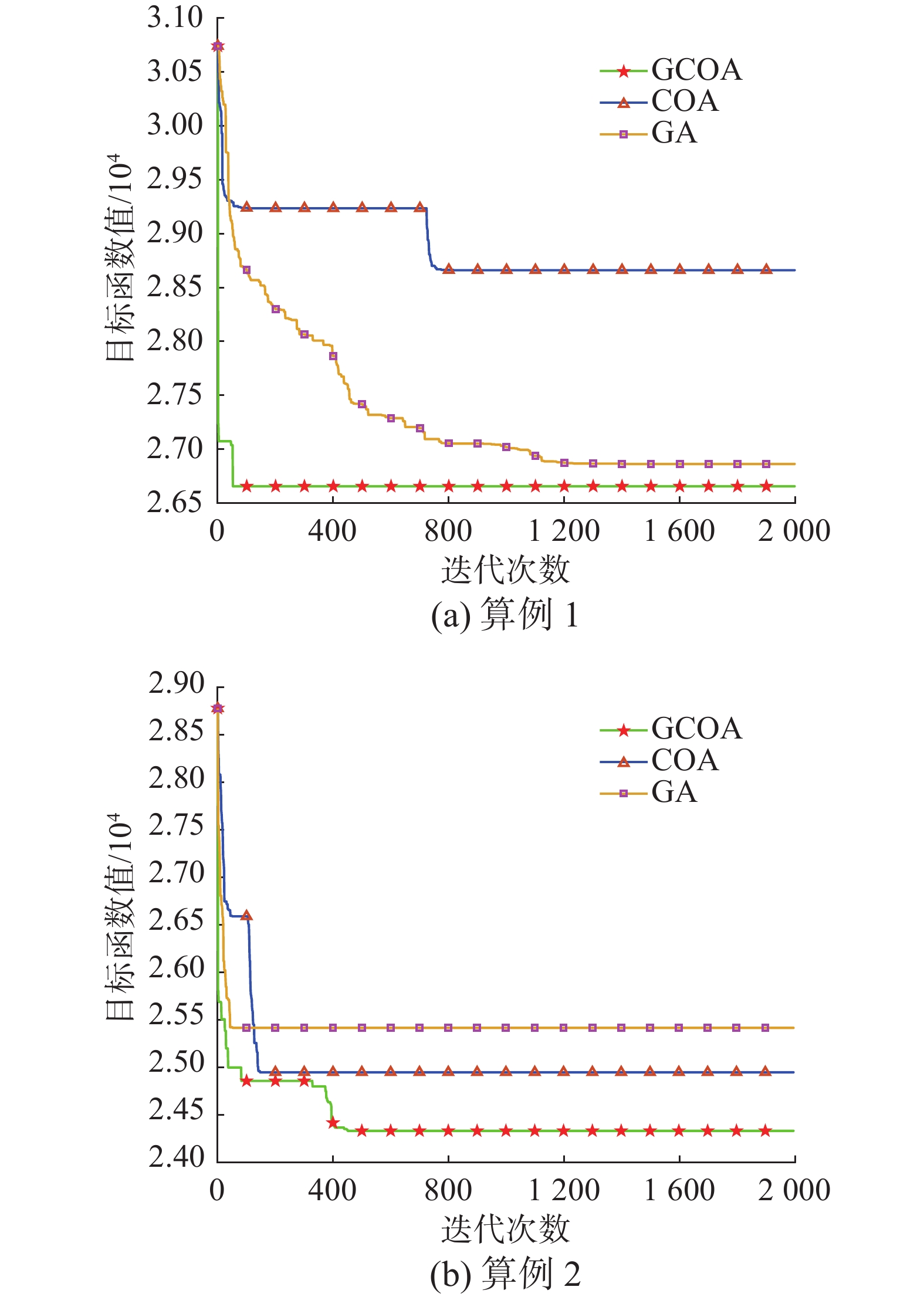
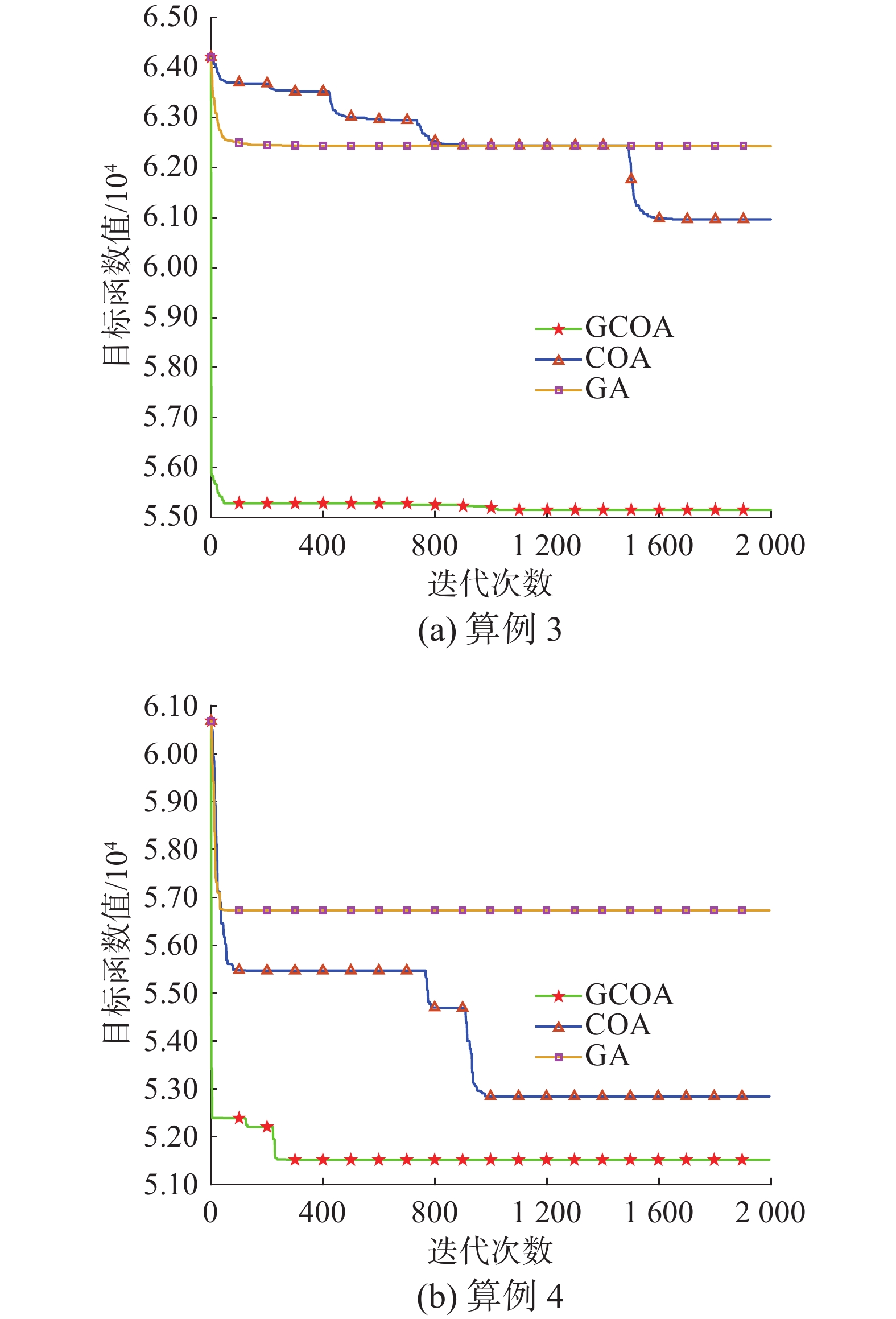
为更加直观地比对不同算法在不同规模的算例上的收敛情况，此次实验选择对不同大小规模的算例进行实验，得到如图8所示的较小规模算例收敛曲线以及图9所示的较大规模算例收敛曲线。
图 8 较小规模算例收敛曲线Fig. 8 Convergence curves for smaller scale examples下载:
全尺寸图片
图 9 较大规模算例收敛曲线Fig. 9 Convergence curves for larger scale examples下载:
全尺寸图片
从不同规模算例的收敛曲线不难发现：本文所提出的GCOA算法不论是在较小规模的算例1和算例2上还是在较大规模的算例3和算例4上，在迭代初期下降速率较遗传算法GA和改进前COA算法都是最快的；另外，就首次找到满意解方面，GCOA算法表现也是比较突出的，可以在较小迭代次数下找到满意解，但不可否认的是，不论是在较小规模算例2上，还是在较大规模算例3和算例4上，GA算法相较于GCOA算法和COA算法而言，它均可以在更小的迭代次数内初次找到满意解，并且在较大规模算例3中COA算法较GCOA 算法可以在更小的迭代次数内初次找到满意解；然而，就最终所得到的目标函数值方面，不论是在较小规模算例1和算例2上，还是在较大规模算例3和算例4上，GCOA算法均以绝对的优势胜于其他算法。
值得一提的是，本文所提出的GCOA算法在收敛性能方面较其他几种适用性较强的算法而言是最优的。之所以在部分算例中会出现GCOA算法初次找到满意解方面晚于GA算法和COA算法，是因为GA算法和COA算法过早收敛，陷入了局部最优，这也正是最终所得的目标函数值不如GCOA算法的根本。另外，虽然在较简单的维修任务层面，GA算法与COA算法的表现与GCOA算法相差不大，但是在较复杂的维修任务方面，本文所提出的 GCOA算法以绝对的优势胜于其他几种算法，这也正是本文所提新算法的价值所在。此外，本文所提出的新GCOA算法可以在较小的迭代次数内获得调度成本最小的解决方案，这是其他几种算法不可比拟的，但却是多维修中心系统最为重视的，这也进一步说明了本文所提出的新算法更符合多维修中心系统保障体系的需求。
2）算法求解质量的对比
尽管从前面所介绍的收敛速度曲线图中可以直观地对比不同算法的优劣，但是却不能进行数字化的定量分析，所以为了更加全面地分析不同算法的求解性能，本文还从初次找到满意解的平均所需时间、目标函数值的平均值、目标函数值的最优值、对资源的利用率（resource utilization，RU）以及目标函数值的相对百分比偏差（relative percentage deviation，RPD）等角度进行了不同算法的对比。
相对百分比偏差
$ {V_{{\text{RPD}}}} $ 的具体计算方式为$$ {V}_{\text{RPD}}=\frac{{C}_{\text{avg}}(n)-{C}_{\text{best}}}{{C}_{\text{best}}}\cdot 100\%\;\;\;(n=1,2,3) $$ (23) 式中：分子首项表示第
$ n $ 个算法的目标函数的平均值；$ {C_{{\text{best}}}} $ 表示所有算法中目标函数值的平均值中最小的值，也即对应于最优算法的目标函数值的平均值。本文所指的资源利用率
$ {R_{{\text{RU}}}} $ 具体是指单位时间内对资源的利用程度，具体计算方式为$$ {R_{{\text{RU}}}} = \frac{{\displaystyle\sum\limits_{r = 1}^R {\displaystyle\sum\limits_{i = 1}^I {\displaystyle\sum\limits_{j = 1}^J {\displaystyle\sum\limits_{m = 1}^m {R_{ijmr}^r \cdot A_{ijm}^d \cdot X_{ijm}^{}} } } } }}{{\displaystyle\sum\limits_{r = 1}^R {T_R^r \cdot (\max \{ F_{T_{i}}\} - \min \{ S_{T_{i}}\} )} }} \cdot 100\% (n=1,2,3) $$ (24) 式中：分子
$ R_{ijmr}^r、A_{ijm}^d、X_{ijm}^{} $ 依次表示第$ i $ 个任务中工序$ j $ 在模式$ m $ 下对于可再生资源$ r $ 的需求数量、第$ i $ 个任务中工序$ j $ 在模式$ m $ 下的具体执行时间、第$ i $ 个任务中工序$ j $ 是否在模式$ m $ 下执行的决策变量，若第$ i $ 个任务中工序$ j $ 是在模式$ m $ 下执行的，那么结果取1，否则取0；而分母中$T_R^r、S_{T_{i}}、F_{T_{i}}$ 依次表示可再生资源$ r $ 总的储备量、第$ i $ 个任务的实际维修任务的开始时间以及第$ i $ 个任务的实际维修任务的完成时间。表 6 算例1算法求解质量对比Table 6 Comparison of algorithm solution quality for example 1算法
名称初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 570.23 27310.75 26862.25 2.41 35.45 COA 344.02 28880.07 28660.00 8.29 36.23 GCOA 293.81 26667.99 26655.25 0.00 37.37 表 7 算例2算法求解质量对比Table 7 Comparison of algorithm solution quality for example 2算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 582.53 25427.20 25405.50 4.05 29.88 COA 374.45 25050.35 24936.25 2.51 31.26 GCOA 357.34 24436.73 24318.50 0.00 34.84 表 8 算例3算法求解质量对比Table 8 Comparison of algorithm solution quality for example 3算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比偏差RPD/% 资源利用率
RU/%GA 1105.73 61565.55 61519.75 11.49 34.59 COA 920.32 62427.52 60962.75 13.04 33.21 GCOA 1136.38 55222.80 55151.50 0.00 34.79 表 9 算例4算法求解质量对比Table 9 Comparison of algorithm solution quality for example 4算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 1161.25 56756.29 56731.00 9.97 32.26 COA 1366.42 54070.09 52843.25 4.76 31.39 GCOA 1419.05 51611.10 51515.75 0.00 33.20 从表6~9不难得到以下结论：从整体来看，不论是目标函数值的平均值还是目标函数值的最优值方面，本文新提出的GCOA算法均以绝对的优势胜于同类型的GA算法与COA算法，并且相对百分比偏差在不同规模的4个算例上均为0；在资源利用率方面，新提出的GCOA算法也是相较GA算法与COA算法更优。从局部来看，本文新提出的GCOA算法在初次找到满意解平均所需时间方面也是比较好的，尤其在较小规模算例1和算例2上所耗费时间较同类型其他算法更短，但是在较大规模算例3和算例4上所耗费的时间要略大于同类型的其他算法，这是一种在时间成本可控的前提下尽可能提高求解质量的思想，结果也是不失所望，舍弃了一些时间成本但是换来了较同类型的GA算法与COA算法更高的求解质量，这在某种意义上也进一步反映出本文所提出的GCOA算法的有效性。
本文采用了遗传算法思想中的遗传算子、变异算子以及贪婪算法思想中的贪婪算子，这在一定程度上极大地提高了候选解的质量，使得全局搜索能力得到提升，从而尽可能得到更高质量的全局最优解，这也与此次维修任务尽可能降低维修任务最大完工时间、最小化维修任务成本的目标相契合。
5. 结束语
本文主要研究了面向多维修中心的维修任务的动态资源分配调度[27]问题。首先，介绍了设备维修任务的相关概念以及限制条件，明确了此次研究的主要目标是选择合适的执行模式在尽可能降低维修任务时间成本的同时，最小化维修任务的经济成本，并且最大程度地利用已分配到的资源来完成当下所要完成的维修任务；然后，在经典静态RCPSP的基础上结合多维修中心系统不定时发布任务的特点以及不同资源配置所对应的不同执行模式问题，建立了一种多模式动态受限资源分配调度的数学模型。
为了更好地求解此次所建立的数学模型，本章提出了一种遗传−长鼻浣熊混合优化算法。该算法是在2022年新提出的长鼻浣熊优化算法的基础之上加入了遗传算法以及贪婪算法的相关思想优化而来。基于遗传思想的相关操作扩大了候选解的搜索范围，丰富了候选解的多样性；而基于贪婪思想的相关操作提高了候选解的质量，也契合了最小化总维修成本的目标。最后，本文对PSPLIB基准问题库中的部分数据进行改造，得到不同规模的算例，在这些不同规模的算例上进行同类型算法的仿真实验，通过从不同角度对实验结果的对比分析，发现不论是从收敛速度还是求解质量等方面，新提出的GCOA混合优化算法均以绝对的优势优于其他算法，这也进一步说明了新提出的算法在求解该模型方面的优势所在。
-
图 1 资源的分类
Fig. 1 Classification of resources
下载:
全尺寸图片
图 2 多模式动态受限资源分配调度模型结构
Fig. 2 Structure chart of multimode dynamic constrained resource allocation and scheduling model
下载:
全尺寸图片
图 3 食物位置编码图
Fig. 3 Food location coding chart
下载:
全尺寸图片
图 4 交叉操作示意
Fig. 4 Schematic diagram of cross operation
下载:
全尺寸图片
图 5 变异操作示意
Fig. 5 Schematic diagram of variation operation
下载:
全尺寸图片
图 6 可行性分析与维护流程
Fig. 6 Feasibility analysis and maintenance flow
下载:
全尺寸图片
图 7 GCOA算法流程
Fig. 7 Flow of genetic and coati hybrid optimization algorithm
下载:
全尺寸图片
图 8 较小规模算例收敛曲线
Fig. 8 Convergence curves for smaller scale examples
下载:
全尺寸图片
图 9 较大规模算例收敛曲线
Fig. 9 Convergence curves for larger scale examples
下载:
全尺寸图片
表 1 变量释义与索引范围
Table 1 Variable definition and index range
变量 含义 索引范围 $i$ 任务序号 $1\leqslant i\leqslant I $ $j $ 工序序号 $1\leqslant j\leqslant J $ $m $ 模式序号 $ 1\leqslant m\leqslant M $ $t $ 时间序号 $0\leqslant t\leqslant T $ $r $ 可再生资源序号 $1\leqslant r\leqslant R $ $k $ 不可再生资源序号 $1\leqslant k\leqslant K $ 表 2 决策变量及其含义
Table 2 Decision variables and their meanings
决策变量 含义 $ Y_{ijt}$ 表征维修工作开始的决策变量，若第i任务中工序j在t时刻开始工作，那么此时该决策变量取1，否则取0 $X_{i}^{{\rm{ed}}}$ 表征第i维修任务提早日期完成的决策变量，若第i维修任务提早完成，那么此时该决策变量取1，否则取0 $X_{i}^{ {\rm{td} } } $ 表征第i维修任务超时日期完成的决策变量，若第i维修任务超时完成，那么此时该决策变量取1，否则取0 $X_{ijmt}^{ {\rm{rs} } } $ 表征资源充裕状态的决策变量，当第i任务中工序j在t时刻以m模式准备开展维修工作时，若剩余资源数量可以满足需求，则该决策变量取1，否则取0 $X_{ijm} $ 表征工序模式执行的决策变量，若第i任务中工序j按照m模式进行工作，那么此时该决策变量取1，否则取0 表 3 仿真实验算例详细信息
Table 3 Detailed information of simulation experiment examples
算例
编号数据来源 工序数量/道 任务总数/个 工序总数/道 模式总数/个 R1数量/个 R2数量/个 K1数量/个 K2数量/个 任务发布
时间/h1 j10，j14 12 15 180 540 160 132 450 440 随机 2 j14，j30 22 7 154 462 98 120 446 360 随机 3 j10，j14 12 30 360 1080 330 175 900 880 随机 4 j14，j30 22 14 308 924 200 250 892 720 随机 表 4 调度成本参数值详情
Table 4 Details of dispatch cost parameter values
参数名称 设定值 R1资源使用成本/（元·个−1·h−1） 2 R2资源使用成本/（元·位−1·h−1） 3 K1资源损耗成本/（元/个） 15 K2资源损耗成本/（元/个） 12 R1资源闲置成本/（元·个−1·h−1） 0.50 R2资源闲置成本/（元·位−1·h−1） 0.75 提前完成任务奖励成本/（元/h） 80 超时完成任务惩罚成本/（元/h） 160 表 5 GCOA各参数取值参考
Table 5 Reference for GCOA parameter values
参数名称 参数值 鬣蜥总数量 $ {N_{{\text{sum}}}} $/只 100（小规模）
200（大规模）猎取鬣蜥区鬣蜥数量 $ {N_{{\text{hunt}}}} $/只 80（小规模）
160（大规模）逃离天敌区鬣蜥数量 $ {N_{{\text{escape}}}} $/只 20（小规模）
40（大规模）迁移因子 $ M $ 50 交叉算子概率 $ {P_c} $ 0.7 变异算子概率 $ {P_m} $ 0.2 贪心算子概率 $ {P_g} $ 0.4 迭代次数 $ N $ 2000 表 6 算例1算法求解质量对比
Table 6 Comparison of algorithm solution quality for example 1
算法
名称初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 570.23 27310.75 26862.25 2.41 35.45 COA 344.02 28880.07 28660.00 8.29 36.23 GCOA 293.81 26667.99 26655.25 0.00 37.37 表 7 算例2算法求解质量对比
Table 7 Comparison of algorithm solution quality for example 2
算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 582.53 25427.20 25405.50 4.05 29.88 COA 374.45 25050.35 24936.25 2.51 31.26 GCOA 357.34 24436.73 24318.50 0.00 34.84 表 8 算例3算法求解质量对比
Table 8 Comparison of algorithm solution quality for example 3
算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比偏差RPD/% 资源利用率
RU/%GA 1105.73 61565.55 61519.75 11.49 34.59 COA 920.32 62427.52 60962.75 13.04 33.21 GCOA 1136.38 55222.80 55151.50 0.00 34.79 表 9 算例4算法求解质量对比
Table 9 Comparison of algorithm solution quality for example 4
算法名称 初次找到满意解
平均所需时间/s目标函数
平均值目标函数
最优值相对百分比
偏差RPD/%资源利用率
RU/%GA 1161.25 56756.29 56731.00 9.97 32.26 COA 1366.42 54070.09 52843.25 4.76 31.39 GCOA 1419.05 51611.10 51515.75 0.00 33.20 -
[1] 齐小刚, 张仲华, 宋卫星, 等. 多中心维修任务分配研究现状[J]. 智能系统学报, 2022, 17(3): 448–458. QI Xiaogang, ZHANG Zhonghua, SONG Weixing, et al. Research status of multicenter maintenance task assignment[J]. CAAI transactions on intelligent systems, 2022, 17(3): 448–458. [2] ERYILMAZ S, YALCIN F. The number of failed components upon system failure when the lifetimes are discretely distributed[J]. Reliability engineering & system safety, 2022, 225: 108632. [3] 鄢超波, 张雷. 串行生产线中机器维修工人的任务分配问题研究[J]. 自动化学报, 2021, 47(11): 2578–2584. YAN Chaobo, ZHANG Lei. Formulation and solution methodology for repairman allocation problem in serial production lines[J]. Acta automatica sinica, 2021, 47(11): 2578–2584. [4] DZULKIFLI N, SARBINI N N, IBRAHIM I S, et al. Review on maintenance issues toward building maintenance management best practices[J]. Journal of building engineering, 2021, 44: 102985. doi: 10.1016/j.jobe.2021.102985 [5] GBALLOU Y T, KIDJEGBO A T, TIECOURA Y, et al. Assessment of the performance of a buffer management system to improve high priority message delivery time limit[J]. International journal of advanced research, 2021, 9(1): 1092–1104. doi: 10.21474/IJAR01/12396 [6] SHI Long, WANG Taotao, LI Jun, et al. Pooling is not favorable: decentralize mining power of PoW blockchain using age-of-work[J]. IEEE transactions on cloud computing, 2023, 11(3): 2756–2769. [7] TAN Xin, ZHOU Minghui. Scaling open source software communities: challenges and practices of decentralization[J]. IEEE software, 2022, 39(1): 70–75. doi: 10.1109/MS.2020.3025959 [8] 苏喜生, 刘楠, 贺德富, 等. 一种后勤保障能力评估系统: CN115392651A[P]. 2022−11−25. [9] GARCÍA-NIEVES J D, PONZ-TIENDA J L, SALCEDO-BERNAL A, et al. The multimode resource-constrained project scheduling problem for repetitive activities in construction projects[J]. Computer-aided civil and infrastructure engineering, 2018, 33(8): 655–671. doi: 10.1111/mice.12356 [10] 李猛. 面向自主维修保障的资源调度与优化技术研究[D]. 西安电子科技大学, 2021. LI Meng. Research on resource scheduling and optimization technology for autonomous maintenance support [D]. Xi’an: Xidian University, 2021. [11] OZTEMEL E, SELAM A A. Bees Algorithm for multi-mode, resource-constrained project scheduling in molding industry[J]. Computers & industrial engineering, 2017, 112: 187–196. [12] KRISHNAKUMAR A, ARDA S E, GOKSOY A A, et al. Runtime task scheduling using imitation learning for heterogeneous many-core systems[J]. IEEE transactions on computer-aided design of integrated circuits and systems, 2020, 39(11): 4064–4077. doi: 10.1109/TCAD.2020.3012861 [13] KOSZTYÁN Z T, SZALKAI I. Multimode resource-constrained project scheduling in flexible projects[J]. Journal of global optimization, 2020, 76(1): 211–241. doi: 10.1007/s10898-019-00832-8 [14] CHAKRABORTTY R K, ABBASI A, RYAN M J. Multi-mode resource-constrained project scheduling using modified variable neighborhood search heuristic[J]. International transactions in operational research, 2020, 27(1): 138–167. doi: 10.1111/itor.12644 [15] ZAMAN F, ELSAYED S M, SAKER R, et al. Resource constrained project scheduling with dynamic disruption recovery[J]. IEEE access, 2020, 8: 144866–144879. doi: 10.1109/ACCESS.2020.3014940 [16] 田启华, 黄佳康, 明文豪, 等. 资源约束下产品开发任务调度的多目标优化[J]. 计算机集成制造系统, 2022, 28(2): 564–573. TIAN Qihua, HUANG Jiakang, MING Wenhao, et al. Multi-objective optimization of product development task scheduling under resource constraints[J]. Computer integrated manufacturing systems, 2022, 28(2): 564–573. [17] 陆志强, 石婷. 考虑资源空窗期的资源投入问题的建模与优化[J]. 上海交通大学学报, 2019, 53(5): 600–609. LU Zhiqiang, SHI Ting. Modeling and optimization of resource investment problem with resource vacations[J]. Journal of Shanghai Jiao Tong University, 2019, 53(5): 600–609. [18] 谢芳, 李洪波, 柏庆国. 随机多模式资源受限项目调度[J]. 中国管理科学, 2022, 30(10): 155–164. XIE Fang, LI Hongbo, BAI Qingguo. Stochastic multi-mode resource-constrained project scheduling[J]. Chinese journal of management science, 2022, 30(10): 155–164. [19] 张宇哲, 董兴业, 周正. 求解资源受限项目调度问题的分支定价算法[J]. 计算机科学, 2022, 49(12): 274–282. ZHANG Yuzhe, DONG Xingye, ZHOU Zheng. Branch & price algorithm for resource-constrained project scheduling problem[J]. Computer science, 2022, 49(12): 274–282. [20] 尤建新. 多模式资源受限项目调度问题的混合优化算法研究[C]//第十四届中国管理科学学术年会. 济南: [s. n. ], 2012: 159−164. You Jianxin. Research on hybrid optimization algorithms for multimodal resource constrained project scheduling problems[C]//The 14th China Annual Conference of Management Science. Jinan: [s. n. ], 2012: 159−164. [21] DEHGHANI M, MONTAZERI Z, TROJOVSKÁ E, et al. Coati Optimization Algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems[J]. Knowledge-based systems, 2023, 259: 110011. doi: 10.1016/j.knosys.2022.110011 [22] HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. Cambridge, Mass. : MIT Press, 1992. [23] QIN Haoxiang, HAN Yuyan, LIU Yiping, et al. A collaborative iterative greedy algorithm for the scheduling of distributed heterogeneous hybrid flow shop with blocking constraints[J]. Expert systems with applications, 2022, 201: 117256. doi: 10.1016/j.eswa.2022.117256 [24] KOLISCH R, SPRECHER A. PSPLIB - A project scheduling problem library[J]. European journal of operational research, 1997, 96(1): 205–216. doi: 10.1016/S0377-2217(96)00170-1 [25] SCHWINDT C. Generation of resource-constrained project scheduling problems subject to temporal constraints[EB/OL]. (2018-04-05) [2023-03-25].https://publikationen.bibliothek.kit.edu/78698. [26] WAUTERS T, KINABLE J, SMET P, et al. The multi-mode resource-constrained multi-project scheduling problem[J]. Journal of scheduling, 2016, 19(3): 271–283. doi: 10.1007/s10951-014-0402-0 [27] DANG Qianlong, XU Wei, YUAN Yangfei. A dynamic resource allocation strategy with reinforcement learning for multimodal multi-objective optimization[J]. Machine intelligence research, 2022, 19(2): 138–152. doi: 10.1007/s11633-022-1314-7
