基于K-means聚类和特征空间增强的噪声标签深度学习算法

吕佳,  邱小龙

downloadPDF
吕佳, 邱小龙. 基于K-means聚类和特征空间增强的噪声标签深度学习算法 [J]. 智能系统学报, 2024, 19(2): 267-277. doi: 10.11992/tis.202303014
引用本文: 吕佳, 邱小龙. 基于K-means聚类和特征空间增强的噪声标签深度学习算法 [J]. 智能系统学报, 2024, 19(2): 267-277. doi: 10.11992/tis.202303014
shu
LYU Jia, QIU Xiaolong. A noisy label deep learning algorithm based on K-means clustering and feature space augmentation [J]. CAAI Transactions on Intelligent Systems, 2024, 19(2): 267-277. doi: 10.11992/tis.202303014
Citation: LYU Jia, QIU Xiaolong. A noisy label deep learning algorithm based on K-means clustering and feature space augmentation [J]. CAAI Transactions on Intelligent Systems, 2024, 19(2): 267-277. doi: 10.11992/tis.202303014
shu

基于K-means聚类和特征空间增强的噪声标签深度学习算法

doi: 10.11992/tis.202303014
  • 1.

    重庆师范大学 计算机与信息科学学院，重庆 401331;

  • 2.

    重庆市数字农业服务工程技术研究中心，重庆 401331

基金项目: 国家自然科学基金重大项目(11991024)；重庆市教委“成渝地区双城经济圈建设”科技创新项目(KJCX2020024)；重庆市高校创新研究群体资助项目(CXQT20015)；重庆市教委科研项目重点项目(KJZD-K202200511).
详细信息
    作者简介:

    吕佳，教授，博士，主要研究方向为机器学习、数据挖掘，中国计算机学会会员。主持或参与的国家级、省部级科研项目20项，发表学术论文70余篇。E-mail：lvjia@cqnu.edu.cn;

    邱小龙，硕士研究生，主要研究方向为机器学习、数据挖掘、噪声标签学习算法。E-mail：2021210516067@stu.cqnu.edu.cn.

    通讯作者:

    吕佳. E-mail: lvjia@cqnu.edu.cn.

  • 中图分类号: TP181

A noisy label deep learning algorithm based on K-means clustering and feature space augmentation

  • 1.

    College of Computer and Information Sciences, Chongqing Normal University, Chongqing 401331, China;

  • 2.

    Chongqing Digital Agriculture Service Engineering Technology Research Center, Chongqing 401331, China

    摘要
  • 摘要: 深度学习中神经网络的性能依赖于高质量的样本，然而噪声标签会降低网络的分类准确率。为降低噪声标签对网络性能的影响，噪声标签学习算法被提出。该算法首先将训练样本集划分成干净样本集和噪声样本集，然后使用半监督学习算法对噪声样本集赋予伪标签。然而，错误的伪标签以及训练样本数量不足的问题仍然限制着噪声标签学习算法性能的提升。为解决上述问题，提出基于K-means聚类和特征空间增强的噪声标签深度学习算法。首先，该算法利用K-means聚类算法对干净样本集进行标签聚类，并根据噪声样本集与聚类中心的距离大小筛选出难以分类的噪声样本，以提高训练样本的质量；其次，使用mixup算法扩充干净样本集和噪声样本集，以增加训练样本的数量；最后，采用特征空间增强算法抑制mixup算法新生成的噪声样本，从而提高网络的分类准确率。并在CIFAR10、CIFAR100、MNIST和ANIMAL-10共4个数据集上试验验证了该算法的有效性。

     

    Abstract: The performance of neural networks in deep learning relies on high-quality samples. However, the presence of noisy labels reduces the classification accuracy of the network. To reduce the impact of noisy labels, we propose a learning algorithm that categorizes training samples into clean and noisy subsets, assigning pseudo-labels to the noisy samples using a semisupervised learning algorithm. Despite these measures, the performance of the noisy label learning algorithm can be hindered by inaccurate pseudo-labels and a lack of sufficient training samples. To address the aforementioned problems, we propose a noisy label deep learning algorithm that leverages K-means clustering and feature space augmentation. First, the algorithm applies the K-means clustering algorithm to cluster the clean samples based on their labels. It then selects noisy samples that are difficult to classify according to the distance between the noisy samples and the cluster center. This process enhances the quality of the training samples. Second, the mix-up algorithm is used to expand both the clean and noisy samples, thereby increasing the number of training samples. Finally, a feature space augmentation algorithm is used to suppress the noise samples generated by the mix-up algorithm, leading to improved network classification accuracy. The effectiveness of the proposed algorithm has been validated on four data sets: CIFAR10, CIFAR100, MNIST, and ANIMAL-10.

     

    • HTML全文

  • 神经网络的性能依赖于高质量的样本，但获取高质量的样本标签需要投入大量的时间与人力成本。为了降低样本标注的时间和成本，通常会借助众包技术[1]，通过雇佣众包工人来标注样本。然而该方式会产生噪声标签，其在训练过程中会降低网络的分类准确率[2]。为了解决该问题，研究者们在噪声标签学习算法中采用样本划分策略[3-5]和半监督学习算法[6-9]来提高网络的抗噪性。

    噪声标签学习算法采用样本划分策略来移除噪声样本，从而降低噪声标签对网络训练的影响。Han等[3]提出协同教学(co-teaching，CT)算法，该算法通过双网络模型来划分训练样本，利用网络之间的差异性来过滤噪声样本。随着网络的不断更新，双网络过滤出的噪声样本的质量会逐渐降低。为了更好地利用双网络的差异性，Yu等[4]提出co-teaching+算法，该算法选择双网络预测分歧的样本作为训练样本，然而分歧样本的数量会不断减少，使得网络的分类准确率降低。为了解决该问题，Wei等[5]提出联合正则化训练算法(joint training method with co-regularization，JOCOR)，该算法使用联合正则化损失来保持2个网络的一致性，通过正则化损失选择干净样本集来训练网络。然而上述算法仅使用干净样本集进行训练，忽略了噪声样本中潜在的语义信息。

    噪声标签学习算法利用半监督学习的思想，将干净样本集视为有标签样本集，将噪声样本集视为无标签样本集，通过少量的有标签样本集和大量的无标签样本集来训练网络。Li等[6]提出的dividemix算法首次在噪声标签算法中应用半监督学习算法。该算法首先利用高斯混合模型将训练样本集划分为干净样本集和噪声样本集，随后使用半监督学习算法纠正噪声样本集的标签，最后通过mixup算法扩充有效的训练样本数量。为了提高干净样本集的质量，Cordeiro等[7]对样本进行多次预测，选取多次被预测为高置信度的样本作为干净样本，再利用mixup算法扩充有效的样本数量来进行半监督训练。除了静态数据存在噪声标签外，流式数据中也有类似的问题。为了解决流式数据中的噪声标签，Karim等[8]首先建立样本缓冲区，将干净数据流和噪声数据流分别存放在干净样本缓冲区和噪声样本缓冲区中，然后同时使用弱增强算法[9]和mixup算法来增加2个缓冲区中有效训练样本数量，最后使用半监督学习算法训练样本。上述算法均使用mixup算法扩充训练样本数量，然而新生成的样本会带有噪声信息，使得网络在学习过程中易受到错误样本的干扰。

    综上所述，噪声标签学习算法通过样本划分策略和半监督学习算法来提升网络的抗噪性，但上述工作仍存在以下问题：

    1)由于初始时网络的分类性能较弱，在使用样本划分策略时，易将边界样本错误地划分到干净样本集中，从而降低了网络的泛化性。

    2)由于mixup算法生成的新样本会包含新的噪声信息，使网络易受到错误样本的干扰，从而降低网络的分类准确率。

    为了解决上述问题，本研究提出一种基于K-means聚类和特征空间增强的噪声标签深度学习算法(noisy label deep learning algorithm based on K-means clustering and feature space augmentation，NLDLBKCFSA)。针对问题1)，对噪声样本进行二次划分，采用K-means聚类算法对干净样本集进行聚类，根据噪声样本集与聚类中心的距离大小，筛选出难以分类的噪声样本；针对问题2)，本研究提出了样本组合与矩交换增强(mixup and moment exchange augmentation，MMEA)算法，该算法首先使用mixup算法进行样本组合增强，增加训练样本数量，再采用特征空间增强算法生成样本的组合特征，帮助网络学习新生成样本的特征信息，从而提高网络的分类准确率。

    1.   理论基础

    1.1   变量说明

    本研究涉及到的变量以及相关说明如表1所示。其中，$D=\{(x_i,\; y_i)\} _i^N=1$，xi表示第i个样本，yi表示第i个样本的噪声标签，N为样本数量，yi∈{1,2,···,C}，C为样本类别数。

    表  1  变量描述
    Table  1  Description of variables
    变量变量说明
    D训练样本集
    X从训练样本集D中划分出的带有正确标签的干净样本集
    U从训练样本集D中划分出的带有错误标签的噪声样本集
    Us从噪声样本集中U中划分出的易分类的噪声样本集
    Uuns从噪声样本集U中划分出来的难以分类的边界噪声样本集
    $u_{{\rm{uns}}}^s $对边界噪声样本集Uuns中的样本进行强增强后的样本
    $u_{{\rm{uns}}}^w $对边界噪声样本集Uuns中的样本进行弱增强后的样本

    1.2   样本划分策略

    通过样本划分策略比较样本损失值与噪声阈值的大小，从而筛选出噪声样本。

    基于固定阈值的样本划分策略首先设置一个阈值用于筛选噪声样本，再使用下式计算xi的损失值。

    $$ {L_{{\rm{CE}}}} = - \sum\limits_i {{y_i}\log f\left( {{x_i};\theta } \right)} + \left( {1 - {y_i}} \right)\log \left( {1 - f\left( {{x_i};\theta } \right)} \right) $$ (1)

    其中，$f({x_i};\theta )$表示网络对样本xi的预测值。

    并根据损失值的大小筛选出噪声样本。然而，过大或过小的固定阈值会使得网络产生错误的样本划分，从而降低网络的分类准确率。

    为了解决固定阈值导致的错误分类问题，Cheng等[10]提出动态阈值划分策略。

    $$ {L_{{\rm{CR}}}}\left( {{x_i}} \right) = - \beta \cdot {\rm{E}}[{L_{{\rm{CE}}}}] $$ (2)
    $$ {\alpha }_{i,t}=\frac{1}{N}{\displaystyle \sum {L}_{{\rm{CE}}}^{\left(t\right)}+{L}_{{\rm{CR}}}\left({x}_{i}\right)} $$ (3)
    $$ L = L_{{\rm{CE}}}^{\left( t \right)} + {L_{{\rm{CR}}}}\left( {{x_i}} \right) $$ (4)
    $$ v_i^{(t)}={\mathbb{1}}\;\; (L < \alpha _{i,t}) $$ (5)

    式中：β为样本损失的权重因子；${\mathbb{1}} $(·)为指示函数；当$v_i^{(t)}=0 $时表示样本i为噪声样本，$v_i^{(t)}=1 $时表示样本i为干净样本。

    该策略使用式(2)中的正则化损失LCR来提高网络对干净样本的置信度，再通过式(3)调整当前第t轮的噪声阈值$ {\alpha _{i,t}} $，并按照式(4)计算当前样本的整体损失值L，最后根据式(5)比较损失值与当前噪声阈值的大小，从中筛选出大于阈值的样本作为噪声样本。

    1.3   数据增强

    数据增强通过对样本添加微弱的标签扰动或生成新样本来丰富样本的多样性。传统的数据增强包括图像平移、转换、颜色变换等方式。Zhang等[11]提出了mixup算法。

    $$ {\boldsymbol{x}}' = \lambda {{\boldsymbol{x}}_i} + \left( {1 - \lambda } \right){{\boldsymbol{x}}_j} $$ (6)
    $$ {\boldsymbol{y}}' = \lambda {{\boldsymbol{y}}_i} + \left( {1 - \lambda } \right){{\boldsymbol{y}}_j} $$ (7)

    其中，$ \lambda $用于控制数据增强的比例。

    mixup算法依据式(6)和式(7)对任意2个样本(xi, yi)和(xj, yj)进行线性增强，从而生成新样本(x', y')。

    然而，mixup算法在增加训练样本的过程中易产生新的噪声样本，从而误导网络学习错误的样本信息。为了降低新样本中噪声的干扰，Li等[12]提出空间增强算法，该算法通过组合样本的特征矩来进行特征增强。

    $$ {\boldsymbol{u}}=\frac{1}{N}\sum _{N}{\boldsymbol{x}} $$ (8)
    $$ {\boldsymbol{\sigma}} =\sqrt{\frac{1}{N}\sum _{N}{\left({\boldsymbol{x}}-{\boldsymbol{u}}\right)}^{2}+\varepsilon } $$ (9)
    $$ {\boldsymbol{x}}_i^{(j)} = {{\boldsymbol{\sigma }}_j}\frac{{{{\boldsymbol{x}}_i} - {{\boldsymbol{\mu}} _i}}}{{{\boldsymbol{{\sigma}} _i}}} + {{\boldsymbol{\mu}} _j} $$ (10)

    式中：ε为常数；${\boldsymbol{x}}_i^{(j)} $是生成的样本组合特征。首先根据式(8)和式(9)分别提取xi和xj的一阶特征矩ui、uj和二阶特征矩σi、σj，再根据式(10)将xi的特征矩与xj的特征矩进行融合以实现特征矩之间的组合，从而协助网络学习新样本的组合特征。

    2.   本研究算法

    2.1   NLDLBKCFSA算法

    本研究提出了一种基于K-means聚类和特征空间增强的噪声标签深度学习算法。由于同一类别的样本应归属于同一簇，故利用K-means聚类算法对X进行聚类，并根据U与聚类中心的距离大小筛选出难以分类的噪声样本，从而提高训练样本的质量。为了降低mixup算法生成的噪声样本对网络的干扰，使用特征空间增强算法对样本特征表示进行增强，以提高网络对新生成样本的预测准确率。

    本算法采用双网络模型来交叉更新网络参数。在每一轮迭代中，动态调整噪声阈值进行样本划分。首先，利用K-means聚类算法对X进行聚类，从U中筛选出难以分类的边界噪声样本，将其加入到Uuns中，并将剩余的噪声样本加入到Us中。随后使用半监督学习算法纠正Us中的噪声标签，并利用MMEA算法增强X和Us中的样本。为了进一步利用样本中的潜在信息，本研究对Uuns中的样本分别使用弱增强算法和强增强算法，再计算增强后样本的KL散度值，最后通过一致性正则化策略引导网络对同一样本的不同形态产生相近的预测值。算法NLDLBKCFSA的整体框架如图1所示。

    图  1  NLDLBKCFSA算法框架
    Fig.  1  Framework of NLDLBKCFSA algorithm
    下载: 全尺寸图片

    2.2   边界样本筛选策略

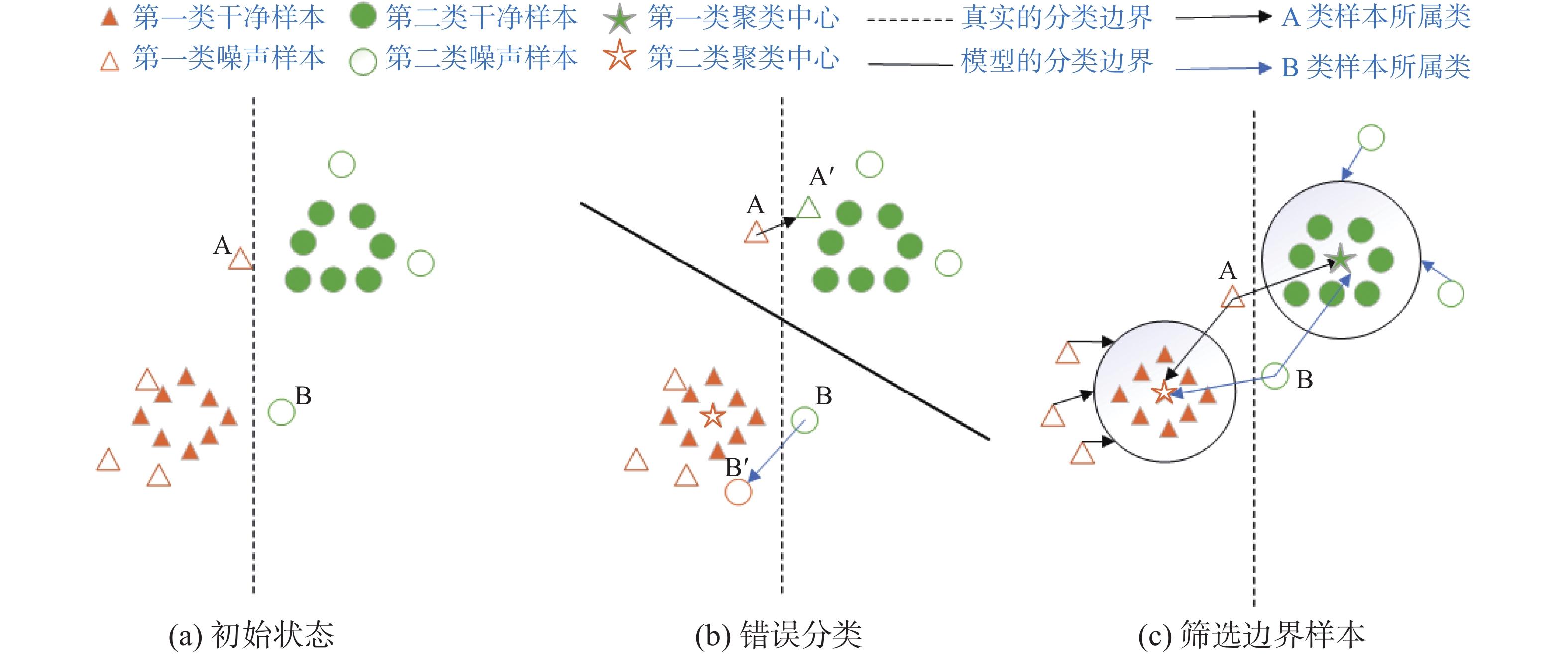
    网络初始分类性能较弱的问题易导致边界噪声样本被错分，使得网络学习到错误的样本信息。图2为筛选误分类样本示意图，其中三角形和圆形分别表示D中的2个类别，实心图形表示X中的样本，空心图形表示U中的样本。图2(a)为样本的初始分类状态，虚线表示样本空间中的真实分类边界，样本A和样本B分别为处于分类边界周围的2个噪声样本。由于网络的初始分类准确率较差，在对A和B进行分类时，网络会将A和B划分到不正确的类别中，如图2(b)所示。为了解决该问题，本研究提出了边界样本筛选策略。该策略使用K-means聚类算法对X进行聚类，生成对应的聚类簇(实心五角星为聚类中心)，再计算A、B与聚类中心的距离大小来筛选出U中难以分类的噪声样本，从而提高训练样本的质量，图2(c)为筛选边界样本的过程。

    图  2  筛选误分类样本示意
    Fig.  2  Schematic diagram of filtering misclassified sample
    下载: 全尺寸图片
    $$ \widehat D = \frac{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1,j \ne i}^M {({x_i} \times {{{c}}_j})} } }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^N {{{({x_i})}^2}} } \times \sqrt {\displaystyle\sum\limits_{j = 1,j \ne i}^M {{{({c_j})}^2}} } }} $$ (11)

    式(11)用于计算噪声样本(xi,yi)与聚类中心(cj,yj)的距离$ \widehat D $。

    $$ d = |{\widehat D_1} - {\widehat D_2}| $$ (12)

    在计算出噪声样本与聚类中心的距离后，边界样本筛选策略会根据式(12)计算最近距离$ {\widehat D_1} $和次近距离$ {\widehat D_2} $的差的绝对值d，然后将其与预设的边界阈值进行比较，若d小于边界阈值，则说明该样本会导致分类结果不可靠，从而筛选出该噪声样本以提高训练样本质量。

    2.3   特征空间增强

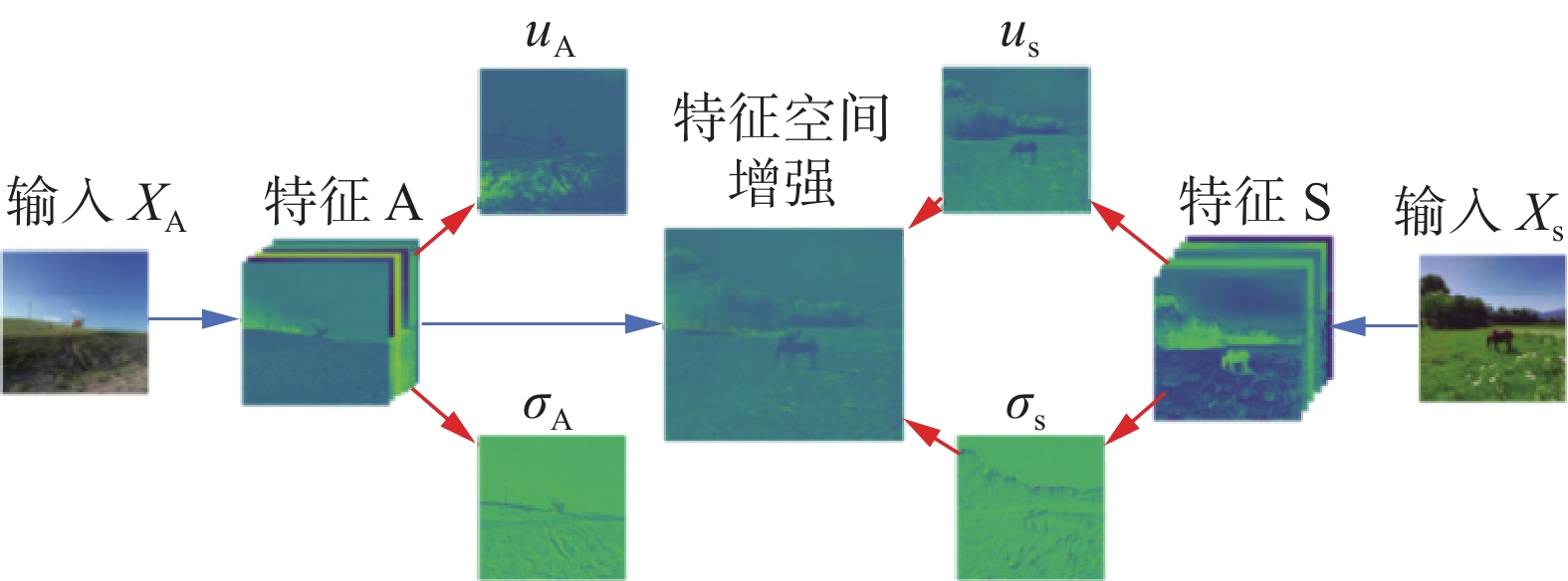
    为了增加有效的训练样本数量，本研究使用mixup算法对D进行增强。该算法根据式(6)和式(7)对D中任意2个样本进行线性组合，生成新样本用于网络训练。图3为mixup算法过程图，其中图3(a)和图3(b)分别为D中的2个训练样本，利用mixup算法生成图3(c)的新样本。然而，Berthelot等[13]研究发现，mixup算法生成的新样本是原样本间像素的简单组合，该方式会不可避免地产生部分噪声信息，使得网络对新样本产生错误的类别预测。例如图3(c)是由类别马和类别骆驼组合生成的新样本，其真实标签为马和骆驼的组合类别，然而网络在学习过程中易将其识别为其他类别，从而降低了网络的分类准确率。为了解决该问题，本研究提出了MMEA算法。首先使用mixup算法扩充训练样本数量，接着利用特征空间增强算法进行特征组合增强，根据式(8)和式(9)分别提取图3(a)和图3(b)的特征一阶矩和特征二阶矩，并按照式(10)对特征矩进行组合增强，生成新的样本特征。网络通过学习2个样本及其组合生成的特征信息，能够提高对新生成样本的预测，图4为特征空间增强算法的过程。MMEA算法通过mixup算法生成新的训练样本，并采用特征空间增强算法生成样本的组合特征。网络通过学习该组合特征来提高对新样本的预测准确率，从而减少新样本中的噪声信息对网络的干扰，进而提高网络的分类准确率。

    图  3  mixup算法图像生成示意
    Fig.  3  Schematic diagram of mixup algorithm image generation
    下载: 全尺寸图片
    图  4  特征空间增强算法示意
    Fig.  4  Schematic diagram of feature space enhancement algorithm
    下载: 全尺寸图片
    $$ p' = \frac{1}{2}\sum\limits_{{x_i} \in X} {\left( {f\left( {{x_i};{\theta ^{\left( 1 \right)}}} \right) + f\left( {{x_i};{\theta ^{\left( 2 \right)}}} \right)} \right)} $$ (13)
    $$ y' = (1 - r)y + rp' $$ (14)

    式中：$ {\theta ^{\left( 1 \right)}} $和$ {\theta ^{\left( 2 \right)}} $分别为网络1和网络2的训练参数；r为样本标签的错误比例。

    为了降低潜在噪声标签对网络的影响，根据式(13)对X中的样本进行预测，得到预测值p'，并利用式(14)将p'与y进行组合，得到软标签值y'，从而提高X中样本标签的可信度。

    2.4   损失函数

    NLDLBKCFSA算法属于有监督学习算法，其整体损失Lall分别由X的损失Lx，U的损失Lu以及一致性正则化损失LKL组成。

    $$ {L_{{\rm{all}}}} = {L_x} + {\lambda _u}{L_u} + {\lambda _k}{L_{{\rm{KL}}}} $$ (15)

    式中：λu和λk为调整Lx和Lu的权重因子，Lx和Lu的表达式分别为

    $$ {L_x} = - \frac{1}{{\left| X \right|}}\sum\limits_{i = 1}^{|X|} {{y_i}\log \left( {f({v_i};\theta )} \right)} $$ (16)
    $$ {L}_{u}=\frac{1}{\left|{U}_{{\rm{s}}}\right|}{\displaystyle \sum _{j=1}^{\left|{U}_{s}\right|}\left|\right|{y}_{j}-f({u}_{j};\theta )|{|}_{2}^{2}} $$ (17)

    其中，(vi,yi)∈X，(uj,yj)∈Us。

    对于Uuns样本集，本研究采用一致性正则化策略[14]。

    $$ {L_{KL}} = {\text{KL}}(u_{{\rm{uns}}}^s\parallel u_{{\rm{uns}}}^w) = \sum u_{{\rm{uns}}}^s\log \dfrac{{u_{{\rm{uns}}}^s}}{{u_{{\rm{uns}}}^w}} $$ (18)

    该策略首先利用弱增强算法和强增强算法[15]对Uuns中的样本进行增强，分别生成$u_{{\rm{uns}}}^s $和$u_{{\rm{uns}}}^w $，再根据式(18)计算KL散度值来衡量网络对不同增强形态下样本的预测概率分布差异，并引导网络产生一致性预测。

    3.   试验结果与分析

    3.1   试验设置与数据集描述

    本研究选择2种噪声类型进行研究：对称噪声和非对称噪声。对称噪声以r的概率将样本的真实标签随机替换成其他类型的标签，非对称噪声以r的概率将样本的真实标签替换成指定类型的标签。本研究参照文献[6,16]所使用的网络训练参数和相应的r进行试验，分别使用20%、40%、60%和80%的对称噪声率以及10%、20%、30%和40%的非对称噪声率。CIFAR10和CIFAR100均使用网络PreAct ResNet18进行训练，并采用随机梯度下降法，动量为0.9，权重衰减为0.0005，batch-size大小为64，训练轮次为300 epochs，初始学习率为0.01，在第150 epoch时降低为0.001。CIFAR10和CIFAR100分别采用10 epochs和30 epochs进行预热（warm-up）操作。ANIMAL-10N采用PreAct ResNet34进行训练，网络参数与CIFAR10、CIFAR100共享，batch-size大小设置为32，训练轮数共200 epochs，初始学习率为0.001，并在第100 epochs后降低为0.0001，warm-up训练轮数设为5。超参数λu从{0, 25, 50}中进行选择，λk值设置为0.4。算法采用K-means聚类算法进行噪声样本的二次划分，其中聚类个数K为X的类别总数。

    为验证本研究所提NLDLBKCFSA算法的有效性，共选取4个数据集进行试验，详细的数据集信息如表2所示，其中前3个数据集均采用人工合成的方式将正确的样本标签转换成对称噪声标签和非对称噪声标签，ANIMAL-10N为真实收集的噪声样本集，该样本集的噪声率为8%。

    表  2  数据集描述
    Table  2  Description of data sets
    数据集样本数大小类别数
    CIFAR10[17]6000032$ \times $3210
    CIFAR100[17]6000032$ \times $32100
    MNIST[18]7000032$ \times $3210
    ANIMAL-10N[19]6000064$ \times $6410

    本研究在Pytorch环境详细的配置环境见表3。

    表  3  试验配置环境
    Table  3  The environment of experimental configuration
    配置环境版本
    编程语言Python 3.8
    CPUIntel(R)Core(TM)i5-12400
    RAM16 GB
    操作系统
    显卡    		Windows 10 专业版
    NVIDIA 3060

    3.2   对比试验

    为了证明NLDLBKCFSA算法在对称噪声和非对称噪声下的分类准确率，本研究选取了13个噪声标签学习算法进行对比试验。

    1) Cross-Entropy：使用传统的交叉熵损失进行噪声标签学习。

    2) Co-teaching[3]：训练2个网络进行噪声标签学习，并且交叉更新2个网络的参数。

    3) F-correction[20]：使用标准的网络估计噪声转移矩阵，并利用该矩阵纠正网络预测。

    4) GCE[21]：改进交叉熵损失来提升网络的抗噪性，并使用改进后的损失函数进行噪声标签学习。

    5) M-correction[22]：通过拟合BMM模型划分X和U，并使用划分后的样本进行噪声标签训练。

    6) DivideMix[6]：使用GMM模型对每个batch的训练样本进行划分，并使用半监督学习算法对划分后的样本进行训练。

    7) DivideMix+[23]：使用GMM模型对每个mini-batch的训练样本进行划分，并使用半监督学习算法对划分后的样本进行训练。

    8) F-Class2Sim[16]：将噪声样本类别转换为噪声标签之间的相似度关系，并使用相似度关系进行噪声标签学习。

    9) GCE+SR[24]：使用空间正则化损失函数训练网络，提高网络对噪声样本的抗噪性。

    10) Taylor-CE[25]：对交叉熵损失进行Taylor分解，并使用Taylor损失函数进行噪声标签学习，提高网络的抗噪性。

    11) CTRR[26]：使用对比正则化函数学习噪声样本的特征表示。

    12) OVA[15]：采用多个二进制分类器联合进行噪声标签学习任务。

    13) PHuber-CE[27]：从梯度裁剪的角度对交叉熵损失进行线性优化，从而提高损失函数的抗噪性。

    以上13个算法和本研究所提出的算法在CIFAR10、CIFAR100和MNIST共3个数据集上进行训练。试验结果如表4-9所示。

    表  4  在对称噪声率下，各算法在CIFAR10上的平均准确率
    Table  4  Average accuracy of each algorithm on CIFAR10 under symmetric noise rate %
    算法噪声率
    20%40%60%80%
    Cross-Entropy83.48±0.1768.49±0.4048.65±0.0627.56±0.43
    Co-teaching[3]67.73±0.7162.83±0.7248.81±0.7827.56±2.71
    F-correction[20]83.27±0.0473.67±0.3077.64±0.1163.95±0.32
    GCE[21]89.72±0.1087.75±0.0584.11±0.2663.95±0.32
    M-correction[22]89.72±0.1090.09±0.6885.90±0.2270.57±0.85
    DivideMix[6]94.82±0.0993.95±0.1492.28±0.0889.30±0.17
    DivideMix+[23]94.84±0.1294.03±0.2093.08±0.1991.91±0.07
    F-Class2Simi[16]91.38±0.1988.22±0.1979.45±0.5332.95±0.01
    GCE+SR[24]87.93±0.2784.82±0.0677.65±0.0551.97±1.13
    Taylor-CE[25]85.96±0.0980.51±0.1178.18±0.3633.48±0.44
    CTRR[20]93.05±0.3292.16±0.3178.18±0.3633.48±0.44
    OVA[15]65.38±0.4260.84±0.6854.55±0.8234.42±0.61
    PHuber-CE[27]90.73±0.0786.05±0.3774.06±0.9232.97±0.32
    NLDLBKCFSA(本研究)95.86±0.4095.27±0.1394.64±0.2091.83±0.48
    注：加粗的为最优分类准确率，下划线为次优分类准确率，下同。
    表  5  在对称噪声率下，各算法在CIFAR100上的平均准确率
    Table  5  Average accuracy of each algorithm on CIFAR100 under symmetric noise rate %
    算法噪声率
    20%40%60%80%
    Cross-Entropy60.93±0.4046.24±0.7429.00±0.3811.42±0.19
    Co-teaching[3]60.93±0.4060.00±0.6048.30±0.1016.10±1.10
    F-correction[20]60.49±0.2948.93±0.2148.74±0.4122.93±0.78
    GCE[21]69.20±0.1065.90±0.2557.33±0.1818.19±1.15
    M-correction[22]67.96±0.1764.48±0.7655.37±0.7224.21±1.06
    DivideMix[6]73.17±0.2871.01±0.1666.61±0.1843.25±0.82
    DivideMix+[23]73.17±0.2871.03±0.3267.52±0.1958.07±0.71
    F-Class2Simi[16]60.26±0.1854.85±0.6040.38±0.5821.86±0.01
    GCE+SR[24]67.03±0.4660.68±0.9044.66±0.8417.35±0.42
    Taylor-CE[25]59.11±0.1150.99±0.0938.31±0.1215.96±0.31
    CTRR[20]70.09±0.4565.32±0.2054.20±0.3443.69±0.28
    OVA[15]59.29±0.0151.61±0.0433.85±0.0718.26±0.09
    PHuber-CE[27]57.90±0.3152.36±0.7737.93±0.8613.83±0.25
    NLDLBKCFSA(本研究)78.15±0.1677.28±0.2371.56±0.1252.53±0.09
    表  6  在对称噪声率下，各算法在MNIST上的平均准确率
    Table  6  Average accuracy of each algorithm on MNIST under symmetric noise rate %
    算法噪声率
    20%40%60%80%
    Cross-Entropy86.16±0.3470.39±0.5950.35±0.5123.41±0.96
    Co-teaching[3]91.20±0.0390.02±0.0283.21±0.7125.33±0.84
    F-correction[20]93.93±0.1084.30±0.4365.06±0.6429.81±0.63
    GCE[21]94.36±0.1193.61±0.1792.46±0.2085.04±0.66
    M-correction[22]97.25±0.0396.63±0.0495.07±0.0886.19±0.42
    DivideMix[6]96.80±0.0896.53±0.0696.47±0.0495.15±0.25
    DivideMix+[23]96.83±0.0696.79±0.0696.69±0.0395.91±0.10
    F-Class2Simi[16]99.26±0.0799.18±0.0698.91±0.0980.80±0.16
    GCE+SR[24]99.13±0.0799.06±0.0298.84±0.0998.37±0.26
    Taylor-CE[25]98.99±0.1498.46±0.1297.53±0.2391.14±0.18
    CTRR[20]96.98±0.4998.73±0.4198.05±0.4196.17±0.41
    OVA[15]98.10±0.0297.48±0.0195.88±0.1374.21±0.59
    PHuber-CE[27]98.46±0.0897.60±0.1195.37±0.0790.08±0.15
    NLDLBKCFSA(本研究)99.48±0.0399.25±0.0499.24±0.0298.21±0.15
    表  7  在非对称噪声率下，各算法在CIFAR10上的平均准确率
    Table  7  Average accuracy of each algorithm on CIFAR10 under asymmetric noise rate %
    算法噪声率
    10%20%30%40%
    Cross-Entropy90.85±0.0687.23±0.4081.92±0.3276.23±0.45
    Co-teaching[3]62.85±2.2061.04±1.3154.50±0.3951.68±1.66
    F-correction[20]89.79±0.3386.79±0.6783.34±0.3076.81±1.08
    GCE[21]90.40±0.0989.30±0.1386.89±0.2282.60±0.17
    M-correction[22]92.28±0.1292.13±0.1791.38±0.1190.43±0.23
    DivideMix[6]93.61±0.1592.99±0.2192.82±0.2890.57±0.31
    DivideMix+[23]94.27±0.2393.92±0.2091.79±0.3691.91±0.24
    F-Class2Simi[16]90.50±0.0291.24±0.2788.28±0.0287.79±0.36
    GCE+SR[24]89.14±0.0287.55±0.0884.69±0.4679.01±0.18
    Taylor-CE[25]87.34±0.1285.02±0.1185.63±0.0772.65±0.11
    CTRR[20]86.82±0.3886.42±0.3980.97±0.3976.89±0.41
    OVA[15]66.36±0.0664.62±0.5059.10±0.1644.28±0.66
    PHuber-CE[27]87.91±0.1384.87±0.2679.01±0.3872.65±0.11
    NLDLBKCFSA(本研究)94.45±0.4094.02±0.1392.93±0.2391.43±0.50
    表  8  在非对称噪声率下，各算法在CIFAR100上的平均准确率
    Table  8  Average accuracy of each algorithm on CIFAR100 under asymmetric noise rate %
    算法噪声率
    10%20%30%40%
    Cross-Entropy68.58±0.3468.82±0.2253.99±0.5044.31±0.23
    Co-teaching[3]−63.40±0.9057.60±0.3049.20±0.30
    F-correction[20]68.87±0.0664.11±0.3756.45±0.5946.44±0.50
    GCE[21]70.77±0.1469.22±0.1564.60±0.2551.72±1.17
    M-correction[22]69.44±0.5267.25±0.8163.16±1.5552.90±1.79
    DivideMix[6]74.00±0.2973.28±0.4272.84±0.3654.33±0.69
    DivideMix+[23]73.49±0.3173.30±0.2272.36±0.4355.63±0.60
    F-Class2Simi[16]63.53±0.0159.10±0.1358.63±0.0352.99±0.78
    GCE+SR[24]68.99±0.0364.35±0.7857.22±0.8049.51±1.31
    Taylor-CE[25]60.96±0.2155.45±0.1245.81±0.1935.45±0.25
    CTRR[20]56.24±0.4049.58±0.4243.02±0.3836.23±0.37
    OVA[15]61.50±0.0157.93±0.0254.76±0.0244.29±0.05
    PHuber-CE[27]60.07±0.0953.30±0.1044.39±0.1435.36±0.13
    NLDLBKCFSA(本研究)77.71±1.4076.18±0.2172.93±1.0355.56±0.38
    表  9  在非对称噪声率下，各算法在MNIST上的平均准确率
    Table  9  Average accuracy of each algorithm on MNIST under asymmetric noise rate %
    算法噪声率
    10%20%30%40%
    Cross-Entropy95.78±0.1991.15±0.2686.01±0.2579.92±0.32
    Co-teaching[3]90.32±0.0289.03±0.0279.80±0.2764.94±0.02
    F-correction[20]96.39±0.0494.27±0.2189.33±0.9481.61±0.42
    GCE[21]94.61±0.1394.43±0.0794.00±0.1293.42±0.12
    M-correction[22]96.74±0.0396.70±0.1096.67±0.0794.85±0.40
    DivideMix[6]96.17±0.0696.11±0.0995.88±0.0595.83±0.05
    DivideMix+[23]96.67±0.0496.66±0.0796.50±0.0496.46±0.04
    F-Class2Simi[16]99.33±0.0199.25±0.0599.18±0.0299.08±0.07
    GCE+SR[24]99.28±0.0499.22±0.0299.13±0.0599.09±0.02
    Taylor-CE[25]99.01±0.0698.84±0.0997.53±0.2391.14±0.18
    CTRR[20]99.19±0.3899.10±0.4598.71±0.3997.12±0.43
    OVA[15]98.23±0.0297.80±0.1094.31±0.5480.25±1.25
    PHuber-CE[27]98.65±0.0796.97±0.1193.98±0.0987.37±0.19
    NLDLBKCFSA(本研究)99.36±0.0799.25±0.1399.20±0.0598.16±0.23

    表4-6分别给出了NLDLBKCFSA算法与上述对比算法在对称噪声下的分类准确率。通过分析可以发现，当噪声率分别为20%、40%和60%时，NLDLBKCFSA算法的分类准确率均优于其他噪声标签学习算法。其原因在于网络在进行样本选择的过程中，使用K-means聚类筛选出难以分类的边界噪声样本，以提高训练样本的质量。然而，在噪声率为80%的情况下，本研究提出的算法的准确率低于次优算法。这是因为在高噪声率条件下，X中的样本类别数量会减少，因此当使用K-means算法对X进行聚类时，K的数量亦减少，这会导致部分边界噪声样本所属的聚类簇会不存在，从而无法筛选出干扰网络分类的边界噪声样本。

    表7-9分别给出了NLDLBKCFSA与上述对比算法在非对称噪声下的分类准确率。分析表7-9发现，当噪声率分别为10%、20%和30%时，本算法的分类准确率优于其他噪声标签学习算法。在CIFAR10数据集上，相较于其余算法中的最优算法，本算法的分类准确率分别提高了0.19%，0.11%和0.12%，在CIFAR100数据集上，与其余算法中的最优算法相比，本算法的分类准确率分别提高了5.01%，3.93%和0.12%，在MNIST数据集上，本算法的分类准确率相比于其余算法中的最优算法，分别提高了0.03%，0.08%和0.09%。然而当非对称噪声率达到40%时，网络的分类准确率较低于其他噪声标签学习算法。一方面，在高噪声率条件下，X的数量会变少，使得网络无法学习到充足的样本信息。另一方面，随着U的数量不断增加，mixup算法会选择2个噪声样本进行组合增强，生成带有噪声标签的新样本，如图5所示，样本的错误标签会误导网络学习无关特征信息，从而降低网络的分类准确率。

    图  5  MNIST中生成的组合样本
    Fig.  5  Mixed generated samples in MNIST
    下载: 全尺寸图片

    3.3   真实数据集对比试验

    通过上述试验可知，NLDLBKCFSA算法在人工合成的噪声样本集上表现较好。为了进一步验证本算法对真实数据集是否有效，本研究在ANIMAL-10数据集上进行试验，并将试验结果与以下4种噪声标签学习算法进行对比。

    1) Cross-Entropy：使用传统的交叉熵损失进行噪声标签学习。

    2) SELFIE[28]：选择高置信度的噪声样本进行标签纠正，并将纠正后的样本与X共同进行噪声标签学习。

    3) PLC[29]：利用网络迭代的纠正噪声标签进行训练。

    4) Nested-CE[30]：对Nested-Dropout[31]算法施加正则化方法来对抗噪声标签。

    表10给出了不同算法在ANIMAL-10上的分类准确率，由表10可知，NLDLBKCFSA算法的分类准确率优于其他噪声标签学习算法。这是因为本研究不仅使用K-means聚类算法获取高质量样本，还利用MMEA算法提高了网络对mixup算法新生成样本的预测准确率，从而引导网络具有良好的抗噪性。因此，NLDLBKCFSA算法在真实世界的噪声标签训练集上具有较好的分类准确率。

    表  10  在真实数据集ANIMAL-10上的分类准确率
    Table  10  Accuracy on the real data ANIMAL-10 %
    算法准确率
    Cross-Entropy79.4
    SELFIE[28]81.8
    PLC[29]83.4
    Nested-CE[30]84.1
    NLDLBKCFSA(本研究)87.7

    3.4   消融试验

    为了验证NLDLBKCFSA算法中MMEA算法模块的有效性，本研究在CIFAR10数据集上，分别采用20%、40%、60%和80%的对称噪声率进行消融试验，试验结果见表11，其中Baseline为不采用mixup算法和空间增强算法的噪声标签学习算法。通过表11可知，MMEA算法相较于Baseline、Baseline+mixup算法及Baseline+feature spaceaugmention均有明显的提升。原因在于本研究不仅使用mixup算法对训练样本集进行有效地扩充，还使用特征空间增强算法来帮助网络学习2个样本的组合特征，缓解了新样本中的噪声对网络学习的干扰，从而进一步提高网络的分类准确率。

    表  11  不同数据增强部分对网络准确率的影响
    Table  11  The impact of different data augmentation parts on network accuracy %
    算法噪声率
    20%40%60%80%
    Baseline88.2185.1878.6164.69
    Baseline + mixup95.1394.8393.8793.16
    Baseline + feature
    space augmention    		92.8187.4885.9685.08
    NLDLBKCFSA
    (Baseline + MMEA)    		96.0695.3294.7694.38

    4.   结束语

    本研究针对噪声样本在训练过程中会降低网络分类准确率的问题，提出了一种基于K-means聚类和特征空间增强的噪声标签深度学习算法。该算法首先对X进行K-means聚类，接着计算U中的样本与聚类中心的距离大小来筛选出难以分类的边界噪声样本，从而提高训练样本的质量，然后使用mixup算法增加有效的训练样本数量，最后使用特征空间增强算法来协助网络学习样本的组合特征，以减少新生成样本中噪声信息对网络训练的干扰，从而提高网络的分类准确率。

    然而随着样本噪声率的提高，X和U的数量会产生显著差异，导致网络无法从X中学习到有效的样本信息来纠正U中的噪声标签，从而降低网络的分类准确率。因此在后续工作中，将继续研究如何在高噪声条件下，利用少量的干净样本来筛选出难分类样本的噪声样本，从而提升网络的泛化性。

  • 图  1   NLDLBKCFSA算法框架

    Fig.  1   Framework of NLDLBKCFSA algorithm

    下载: 全尺寸图片

    图  2   筛选误分类样本示意

    Fig.  2   Schematic diagram of filtering misclassified sample

    下载: 全尺寸图片

    图  3   mixup算法图像生成示意

    Fig.  3   Schematic diagram of mixup algorithm image generation

    下载: 全尺寸图片

    图  4   特征空间增强算法示意

    Fig.  4   Schematic diagram of feature space enhancement algorithm

    下载: 全尺寸图片

    图  5   MNIST中生成的组合样本

    Fig.  5   Mixed generated samples in MNIST

    下载: 全尺寸图片

    表  1   变量描述

    Table  1   Description of variables

    变量变量说明
    D训练样本集
    X从训练样本集D中划分出的带有正确标签的干净样本集
    U从训练样本集D中划分出的带有错误标签的噪声样本集
    Us从噪声样本集中U中划分出的易分类的噪声样本集
    Uuns从噪声样本集U中划分出来的难以分类的边界噪声样本集
    $u_{{\rm{uns}}}^s $对边界噪声样本集Uuns中的样本进行强增强后的样本
    $u_{{\rm{uns}}}^w $对边界噪声样本集Uuns中的样本进行弱增强后的样本

    表  2   数据集描述

    Table  2   Description of data sets

    数据集样本数大小类别数
    CIFAR10[17]6000032$ \times $3210
    CIFAR100[17]6000032$ \times $32100
    MNIST[18]7000032$ \times $3210
    ANIMAL-10N[19]6000064$ \times $6410

    表  3   试验配置环境

    Table  3   The environment of experimental configuration

    配置环境版本
    编程语言Python 3.8
    CPUIntel(R)Core(TM)i5-12400
    RAM16 GB
    操作系统
    显卡    		Windows 10 专业版
    NVIDIA 3060

    表  4   在对称噪声率下，各算法在CIFAR10上的平均准确率

    Table  4   Average accuracy of each algorithm on CIFAR10 under symmetric noise rate %

    算法噪声率
    20%40%60%80%
    Cross-Entropy83.48±0.1768.49±0.4048.65±0.0627.56±0.43
    Co-teaching[3]67.73±0.7162.83±0.7248.81±0.7827.56±2.71
    F-correction[20]83.27±0.0473.67±0.3077.64±0.1163.95±0.32
    GCE[21]89.72±0.1087.75±0.0584.11±0.2663.95±0.32
    M-correction[22]89.72±0.1090.09±0.6885.90±0.2270.57±0.85
    DivideMix[6]94.82±0.0993.95±0.1492.28±0.0889.30±0.17
    DivideMix+[23]94.84±0.1294.03±0.2093.08±0.1991.91±0.07
    F-Class2Simi[16]91.38±0.1988.22±0.1979.45±0.5332.95±0.01
    GCE+SR[24]87.93±0.2784.82±0.0677.65±0.0551.97±1.13
    Taylor-CE[25]85.96±0.0980.51±0.1178.18±0.3633.48±0.44
    CTRR[20]93.05±0.3292.16±0.3178.18±0.3633.48±0.44
    OVA[15]65.38±0.4260.84±0.6854.55±0.8234.42±0.61
    PHuber-CE[27]90.73±0.0786.05±0.3774.06±0.9232.97±0.32
    NLDLBKCFSA(本研究)95.86±0.4095.27±0.1394.64±0.2091.83±0.48
    注：加粗的为最优分类准确率，下划线为次优分类准确率，下同。

    表  5   在对称噪声率下，各算法在CIFAR100上的平均准确率

    Table  5   Average accuracy of each algorithm on CIFAR100 under symmetric noise rate %

    算法噪声率
    20%40%60%80%
    Cross-Entropy60.93±0.4046.24±0.7429.00±0.3811.42±0.19
    Co-teaching[3]60.93±0.4060.00±0.6048.30±0.1016.10±1.10
    F-correction[20]60.49±0.2948.93±0.2148.74±0.4122.93±0.78
    GCE[21]69.20±0.1065.90±0.2557.33±0.1818.19±1.15
    M-correction[22]67.96±0.1764.48±0.7655.37±0.7224.21±1.06
    DivideMix[6]73.17±0.2871.01±0.1666.61±0.1843.25±0.82
    DivideMix+[23]73.17±0.2871.03±0.3267.52±0.1958.07±0.71
    F-Class2Simi[16]60.26±0.1854.85±0.6040.38±0.5821.86±0.01
    GCE+SR[24]67.03±0.4660.68±0.9044.66±0.8417.35±0.42
    Taylor-CE[25]59.11±0.1150.99±0.0938.31±0.1215.96±0.31
    CTRR[20]70.09±0.4565.32±0.2054.20±0.3443.69±0.28
    OVA[15]59.29±0.0151.61±0.0433.85±0.0718.26±0.09
    PHuber-CE[27]57.90±0.3152.36±0.7737.93±0.8613.83±0.25
    NLDLBKCFSA(本研究)78.15±0.1677.28±0.2371.56±0.1252.53±0.09

    表  6   在对称噪声率下，各算法在MNIST上的平均准确率

    Table  6   Average accuracy of each algorithm on MNIST under symmetric noise rate %

    算法噪声率
    20%40%60%80%
    Cross-Entropy86.16±0.3470.39±0.5950.35±0.5123.41±0.96
    Co-teaching[3]91.20±0.0390.02±0.0283.21±0.7125.33±0.84
    F-correction[20]93.93±0.1084.30±0.4365.06±0.6429.81±0.63
    GCE[21]94.36±0.1193.61±0.1792.46±0.2085.04±0.66
    M-correction[22]97.25±0.0396.63±0.0495.07±0.0886.19±0.42
    DivideMix[6]96.80±0.0896.53±0.0696.47±0.0495.15±0.25
    DivideMix+[23]96.83±0.0696.79±0.0696.69±0.0395.91±0.10
    F-Class2Simi[16]99.26±0.0799.18±0.0698.91±0.0980.80±0.16
    GCE+SR[24]99.13±0.0799.06±0.0298.84±0.0998.37±0.26
    Taylor-CE[25]98.99±0.1498.46±0.1297.53±0.2391.14±0.18
    CTRR[20]96.98±0.4998.73±0.4198.05±0.4196.17±0.41
    OVA[15]98.10±0.0297.48±0.0195.88±0.1374.21±0.59
    PHuber-CE[27]98.46±0.0897.60±0.1195.37±0.0790.08±0.15
    NLDLBKCFSA(本研究)99.48±0.0399.25±0.0499.24±0.0298.21±0.15

    表  7   在非对称噪声率下，各算法在CIFAR10上的平均准确率

    Table  7   Average accuracy of each algorithm on CIFAR10 under asymmetric noise rate %

    算法噪声率
    10%20%30%40%
    Cross-Entropy90.85±0.0687.23±0.4081.92±0.3276.23±0.45
    Co-teaching[3]62.85±2.2061.04±1.3154.50±0.3951.68±1.66
    F-correction[20]89.79±0.3386.79±0.6783.34±0.3076.81±1.08
    GCE[21]90.40±0.0989.30±0.1386.89±0.2282.60±0.17
    M-correction[22]92.28±0.1292.13±0.1791.38±0.1190.43±0.23
    DivideMix[6]93.61±0.1592.99±0.2192.82±0.2890.57±0.31
    DivideMix+[23]94.27±0.2393.92±0.2091.79±0.3691.91±0.24
    F-Class2Simi[16]90.50±0.0291.24±0.2788.28±0.0287.79±0.36
    GCE+SR[24]89.14±0.0287.55±0.0884.69±0.4679.01±0.18
    Taylor-CE[25]87.34±0.1285.02±0.1185.63±0.0772.65±0.11
    CTRR[20]86.82±0.3886.42±0.3980.97±0.3976.89±0.41
    OVA[15]66.36±0.0664.62±0.5059.10±0.1644.28±0.66
    PHuber-CE[27]87.91±0.1384.87±0.2679.01±0.3872.65±0.11
    NLDLBKCFSA(本研究)94.45±0.4094.02±0.1392.93±0.2391.43±0.50

    表  8   在非对称噪声率下，各算法在CIFAR100上的平均准确率

    Table  8   Average accuracy of each algorithm on CIFAR100 under asymmetric noise rate %

    算法噪声率
    10%20%30%40%
    Cross-Entropy68.58±0.3468.82±0.2253.99±0.5044.31±0.23
    Co-teaching[3]−63.40±0.9057.60±0.3049.20±0.30
    F-correction[20]68.87±0.0664.11±0.3756.45±0.5946.44±0.50
    GCE[21]70.77±0.1469.22±0.1564.60±0.2551.72±1.17
    M-correction[22]69.44±0.5267.25±0.8163.16±1.5552.90±1.79
    DivideMix[6]74.00±0.2973.28±0.4272.84±0.3654.33±0.69
    DivideMix+[23]73.49±0.3173.30±0.2272.36±0.4355.63±0.60
    F-Class2Simi[16]63.53±0.0159.10±0.1358.63±0.0352.99±0.78
    GCE+SR[24]68.99±0.0364.35±0.7857.22±0.8049.51±1.31
    Taylor-CE[25]60.96±0.2155.45±0.1245.81±0.1935.45±0.25
    CTRR[20]56.24±0.4049.58±0.4243.02±0.3836.23±0.37
    OVA[15]61.50±0.0157.93±0.0254.76±0.0244.29±0.05
    PHuber-CE[27]60.07±0.0953.30±0.1044.39±0.1435.36±0.13
    NLDLBKCFSA(本研究)77.71±1.4076.18±0.2172.93±1.0355.56±0.38

    表  9   在非对称噪声率下，各算法在MNIST上的平均准确率

    Table  9   Average accuracy of each algorithm on MNIST under asymmetric noise rate %

    算法噪声率
    10%20%30%40%
    Cross-Entropy95.78±0.1991.15±0.2686.01±0.2579.92±0.32
    Co-teaching[3]90.32±0.0289.03±0.0279.80±0.2764.94±0.02
    F-correction[20]96.39±0.0494.27±0.2189.33±0.9481.61±0.42
    GCE[21]94.61±0.1394.43±0.0794.00±0.1293.42±0.12
    M-correction[22]96.74±0.0396.70±0.1096.67±0.0794.85±0.40
    DivideMix[6]96.17±0.0696.11±0.0995.88±0.0595.83±0.05
    DivideMix+[23]96.67±0.0496.66±0.0796.50±0.0496.46±0.04
    F-Class2Simi[16]99.33±0.0199.25±0.0599.18±0.0299.08±0.07
    GCE+SR[24]99.28±0.0499.22±0.0299.13±0.0599.09±0.02
    Taylor-CE[25]99.01±0.0698.84±0.0997.53±0.2391.14±0.18
    CTRR[20]99.19±0.3899.10±0.4598.71±0.3997.12±0.43
    OVA[15]98.23±0.0297.80±0.1094.31±0.5480.25±1.25
    PHuber-CE[27]98.65±0.0796.97±0.1193.98±0.0987.37±0.19
    NLDLBKCFSA(本研究)99.36±0.0799.25±0.1399.20±0.0598.16±0.23

    表  10   在真实数据集ANIMAL-10上的分类准确率

    Table  10   Accuracy on the real data ANIMAL-10 %

    算法准确率
    Cross-Entropy79.4
    SELFIE[28]81.8
    PLC[29]83.4
    Nested-CE[30]84.1
    NLDLBKCFSA(本研究)87.7

    表  11   不同数据增强部分对网络准确率的影响

    Table  11   The impact of different data augmentation parts on network accuracy %

    算法噪声率
    20%40%60%80%
    Baseline88.2185.1878.6164.69
    Baseline + mixup95.1394.8393.8793.16
    Baseline + feature
    space augmention    		92.8187.4885.9685.08
    NLDLBKCFSA
    (Baseline + MMEA)    		96.0695.3294.7694.38
    • 参考文献(31)
  • [1] ZHANG Jing, WU Xindong, SHENG V S. Learning from crowdsourced labeled data: a survey[J]. Artificial intelligence review, 2016, 46(4): 543–576. doi: 10.1007/s10462-016-9491-9
    [2] 伏博毅, 彭云聪, 蓝鑫, 等. 基于深度学习的标签噪声学习算法综述[J]. 计算机应用, 2023, 43(3): 674–684.

    FU Boyi, PENG Yuncong, LAN Xin, et al. Survey of label noise learning algorithms based on deep learning[J]. Journal of computer applications, 2023, 43(3): 674–684.
    [3] HAN Bo, YAO Quanming, YU Xingrui, et al. Co-teaching: robust training of deep neural networks with extremely noisy labels[C]//Advances in Neural Information Processing Systems. Montreal: NIPS, 2018: 1602−1613.
    [4] YU Xingrui, HAN Bo, YAO Jiangchao, et al. How does disagreement help generalization against label corruption [EB/OL]. (2019−01−14)[2022−12−25]. https://arxiv.org/abs/1901.04215.pdf.
    [5] WEI Hongxin, FENG Lei, CHEN Xiangyu, et al. Combating noisy labels by agreement: a joint training method with co-regularization[C]//2020 IEEE Conference on Computer Vision and Pattern Recognition. Washington: IEEE, 2020: 13723−13732.
    [6] LI Junnan, SOCHER R, HOI S C H. DivideMix: learning with noisy labels as semi-supervised learning[EB/OL]. (2020−02−18)[2022−12−25]. https://arxiv.org/abs/2002.07394.pdf.
    [7] CORDEIRO F R, SACHDEVA R, BELAGIANNIS V, et al. LongReMix: robust learning with high confidence samples in a noisy label environment[J]. Pattern recognition, 2023, 133(1): 565–581.
    [8] KARIM N, KHALID U, ESMAEILI A, et al. CNLL: a semi-supervised approach for continual noisy label learning[C]//2022 IEEE Conference on Computer Vision and Pattern Recognition Workshops. New Orleans: IEEE, 2022: 3877−3887.
    [9] ZAHEER M Z, LEE Jinha, ASTRID M, et al. Cleaning label noise with clusters for minimally supervised anomaly detection[EB/OL]. (2021−04−30)[2022−12−25]. https://arxiv.org/abs/2104.14770.pdf.
    [10] CHENG Hao, ZHU Zhaowei, LI Xingyu, et al. Learning with instance-dependent label noise: a sample sieve appro-ach[EB/OL]. (2020−10−05)[2022−12−25]. https://arxiv.org/abs/2010.02347.pdf.
    [11] ZHANG Hongyi, CISSE M, DAUPHIN Y N, et al. Mixup: beyond empirical risk minimization[EB/OL]. (2018−04−27)[2022−12−25]. https://arxiv.org/abs/1710.09412.pdf.
    [12] LI Boyi, WU F, LIM S N, et al. On feature normalization and data augmentation[C]//2021 IEEE Conference on Computer Vision and Pattern Recognition. Kuala Lumpur: IEEE, 2021: 12378−12387.
    [13] BERTHELOT D, RAFFEL C, ROY A, et al. Understanding and improving interpolation in autoencoders via an adversarial regularizer[EB/OL]. (2018−07−23)[2022−12−.25]. https://arxiv.org/abs/1807.07543.pdf.
    [14] SOHN K, BERTHELOT D, CARLINI N, et al. Fixmatch: simplifying semi-supervised learning with consistency and confidence[C]//Advances in Neural Information Processing Systems. Addis Ababa: NIPS, 2020: 596−608.
    [15] LIU Defu, ZHAO Jiayi, WU Jinzhao, et al. Multi-category classification with label noise by robust binary loss[J]. Neurocomputing, 2022, 482(16): 14–26.
    [16] WU Songhua, XIA Xiaobo, LIU Tongliang, et al. Class2Simi: a noise reduction perspective on learning with noisy labels[C]//International Conference on Machine Learning. London: ACM, 2021: 11285−11295.
    [17] SHARMA N, JAIN V, MISHRA A. An analysis of convolutional neural networks for image classification[J]. Procedia computer science, 2018, 132(9): 377–384.
    [18] DENG L. The mnist database of handwritten digit images for machine learning research[J]. IEEE signal processing magazine, 2012, 29(6): 141–142. doi: 10.1109/MSP.2012.2211477
    [19] TAN C, XIA J, WU L, et al. Co-learning: Learning from noisy labels with self-supervision[C]//Proceedings of the 29th ACM International Conference on Multimedia. Chengdu: ACM, 2021: 1405−1413.
    [20] PATRINI G, ROZZA A, MENON A K, et al. Making deep neural networks robust to label noise: a loss correction approach[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 2233−2241.
    [21] ZHANG Z, SABUNCU M. Generalized cross entropy loss fortraining deep neural networks with noisy labels[C]//Avances in Neural Information Processing Systems. Montreal: NIPS, 2018: 11400−11411.
    [22] ARAZO E, ORTEGO D, ALBERT P, et al. Unsupervised label noise modeling and loss correction[C]//International Conference on Machine Learning. Los Angeles: ACM, 2019: 312−321.
    [23] WANG Zhuowei, JIANG Jing, HAN Bo, et al. SemiNLL: a framework of noisy-label learning by semi-supervised learning[EB/OL]. (2020−11−02)[2022−12−27]. https://arxiv.org/abs/2012.00925.pdf.
    [24] ZHOU Xiong, LIU Xianming, WANG Chenyang, et al. Learning with noisy labels via sparse regularization[C]//2021 IEEE International Conference on Computer Vision. Montreal: IEEE, 2022: 72−81.
    [25] FENG Lei, SHU Senlin, LIN Zhuoyi, et al. Can cross entropy loss be robust to label noise[C]//Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence. Yokohama: ACM, 2020: 2206−2212.
    [26] YI Li, LIU Sheng, SHE Qi, et al. On learning contrastive representations for learning with noisy labels[C]//2022 IEEE Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 16661−16670.
    [27] MENON A K, RAWAT A S, REDDI S J, et al. Can gradient clipping mitigate label noise[C]//International Conference on Learning Representations. Addis Ababa: ACM, 2020: 6204−6231.
    [28] SONG H, KIM M, LEE J G. Selfie: Refurbishing unclean samples for robust deep learning[C]//International Conference on Machine Learning, Los Angeles: ACM, 2019: 5907−5915.
    [29] ZHANG Yikai, ZHENG Songzhu, WU Pengxiang, et al. Learning with feature dependent label noise: a progressiv-e approach[EB/OL]. (2021−05−27)[2022−12−25]. https://ar-xiv.org/abs/2103.07756.pdf.
    [30] CHEN Yingyi, SHEN Xi, HU S X, et al. Boosting co-teaching with compression regularization for label noise[C]//2021 IEEE Conference on Computer Vision and Pattern Recognition Kuala Lumpur, IEEE, 2021: 2682−2686.
    [31] RIPPEL O, GELBART M, ADAMS R. Learning ordered representations with nested dropout[C]//International Conference on Machine Learning. Beijing: ACM, 2014: 1746−1754.
WeChat 点击查看大图
图(5)  /  表(11)
出版历程
  • 收稿日期:  2023-03-07
  • 网络出版日期:  2023-12-25

目录

    /

    返回文章
    返回