Path planning of mobile robots based on improved RRT* algorithm
-
摘要: 针对传统快速随机搜索树*(rapidly-exploring random tree*, RRT*)算法收敛速率较慢，且不适用于动态场景等问题，提出一种基于目标点偏置和冗余节点删除的改进RRT*算法，用于解决移动机器人快速找到无碰撞最优路径的问题。此算法在RRT*算法基础上，首先对采样点进行优化处理，保证路径最优的同时减少搜寻时间；其次引入路径节点最大值概念，删除扩展树冗余节点以提高算法效率；最后结合动态窗口(dynamic window approaches, DWA)算法提高路径的安全性和平滑性，实现对动态障碍物的避障。通过3种不同地图下的仿真验证，改进算法能有效提升路径质量，且大幅降低运行时间。Abstract: To address the problems associated with the traditional rapidly-exploring random tree* (RRT*) algorithm, including its slow convergence rate and unsuitability for dynamic environments, we propose an improved RRT* algorithm. This new approach biases toward the target point and eliminates redundant nodes to efficiently find collision-free optimal paths for mobile robots. The improved algorithm begins by optimizing the sampling points, which ensures the discovery of the optimal path while reducing search time. Then, it introduces the concept of path maximization to identify and remove redundant nodes from the extended tree, thereby enhancing algorithm efficiency. Additionally, the improved algorithm is integrated with the dynamic window approaches algorithm, which enhances the safety and smoothness of the path and enables effective obstacle avoidance in dynamic environments. Simulations conducted on three different maps demonstrate that the improved algorithm significantly improves path quality and greatly reduces running time.
-
Keywords:
- mobile robot /
- dynamic environment /
- optimal path /
- RRT* algorithm /
- dynamic window approaches algorithm /
- redundant node /
- safety /
- smoothness
-
在机器人领域，路径规划一直是研究的核心问题。路径规划指从起点开始到终点规划出一条安全且无碰撞的高效路径，并且越来越多应用在复杂及人为干涉困难的环境，这就要求规划出的路径满足路径短、用时少、有效避障等特点[1-3]。现阶段根据路径规划算法的发展趋势可分为基于搜索的路径规划算法和基于采样的路径规划算法[4-5]。基于搜索的路径规划算法包括Dijkstra算法、A*算法等[6-9]。成怡等[10]提出一种改进的A*算法与Morphin搜索树算法相结合的混合算法，改进关键点的选取方式并删除冗余节点，利用平均滤波的方法进行路径平滑处理，再结合Morphin搜索树算法进行动态的局部优化。基于采样的路径规划算法主要有概率路线图算法(probabilistic road maps, PRM)、快速随机搜索树算法(rapidly-exploring random tree, RRT)等[11-14]，此类算法具有灵活强大的搜索能力，且无需对空间进行建模，能够较快地获取路径解，但由于其采样方式随机，得到的路径并非最优路径。为获得最优路径，Karaman等[15]提出引入了父节点重选和节点重连的RRT*算法，得到的路径能够收敛到全局最优解；Gammell等[16]提出Informed-RRT*(下文简称为In-RRT*)算法，规划出一个椭圆作为采样范围，缩短路径长度的同时加快算法收敛速率，但随着节点数量的增加，计算复杂度和运行时间也随之增长。针对此问题，李娟等[17]在未知的三维环境中，建立搜索实时地图和决策函数以提高搜索效率；Spanogianopoulos等[18]提出一种RRT*FN (RRT fixed nodes)算法可以减少路径上的多余叶子节点，提高规划速度；张腾龙等[19]提出固定节点数的动态双向渐进最优快速随机扩展树算法(bidrectional RRT* fix-node dynamic, B-RRT* FND)，采用双向贪婪搜索方法来加快路径搜索速度，利用固定节点算法减少计算量，并引入动态更新以及路径修复思想，实现了移动障碍物下的避障功能。
受RRT*衍生算法的启发，本文提出一种改进的RRT*算法，首先利用目标点信息对采样点进行择优选择，加快算法收敛速度；其次引入路径节点最大值概念对搜索树的冗余节点进行删除，降低在后续过程中过多冗余节点造成的额外搜索成本，拉伸路径的同时提高算法效率；最后利用获取的全局路径结合动态窗口(dynamic window approaches, DWA)算法进行局部规划，提升路径平滑度和安全性，实现动态避障。
1. 相关工作
1.1 问题描述
定义
$ X = {R_n} $ 为路径规划问题的状态空间，定义${{X}_{\rm obs}} \subset {X}$ 为障碍物所在空间，可得机器人活动的空间为$ {X_{\rm free}} = {C_X}(X \cap {X_{\rm obs}}) $ ，给定机器人初始节点Xstart，目标节点Xgoal，有$ {X_{\rm start}},{X_{\rm goal}} \in {X_{\rm free}} $ 。定义$ \sigma :[0,1] \to {R_n} $ 为机器人的可行路径，且$ \sigma (0) = {X_{\rm start}},\sigma (1) = {X_{\rm goal}} $ 。因此路径规划问题转化为在机器人自由活动空间Xfree中求解点集$ \sigma :[0,1] $ ，定义$ \varSigma $ 表示所有可行路径集合，$ c:\varSigma \to R \geqslant 0 $ 为所有路径代价集合。对于路径最优解问题，路径代价和路径优势成反比，代价越小表示路径越优[20]，则最优路径求解问题可被描述为：在自由空间Xfree中求解使路径代价最小的可行路径
${\sigma ^*}$ ：$$ \begin{gathered} {\sigma ^*} = {\mathrm{argmin}}\left\{ {c(\sigma )} \right.|\sigma (0) = {X_{\rm start}},\sigma (1) = {X_{\rm goal}}, \\ \forall x \in [0,1],\sigma (x) \in \left. {{X_{\rm free}}} \right\} \end{gathered} $$ (1) 1.2 RRT算法
RRT算法是基于采样的路径规划算法中最具代表性的路径规划算法，该算法的本质是在整个空间中随机采样并生成路径点，规划出一条起点到终点的无碰撞且唯一的路径[21-22]。RRT算法的具体实现步骤如下[23]：
1)创建地图空间S，起始点Xstart，目标点Xgoal和障碍物。
2)在Xfree中随机取得采样点Xrand。
3)从与Xrand最近的节点Xnear以步长L向采样点Xrand方向生长，并得到新的路径节点Xnew，若碰撞障碍物则不选用。
4)不断重复步骤2)和3)扩展树枝，当树生长到Xgoal或Xnew与Xgoal的连线与障碍物不相交时，找到可行路径
$\sigma $ 。1.3 RRT*算法
RRT算法具有概率完备性，其规划速度相对于其他路径规划算法较快，但由于其随机性，因此所得路径不是最优路径[24]。RRT*算法在RRT算法的基础上引进了对路径的寻优思想，主要有两点改进，具体实现步骤如下[25]：
1)重选父节点
①计算搜索树总节点数len(n_node)，以新节点Xnew为圆心计算范围半径：
$$ {r_{\rm range}} = \sqrt {\rm lg(len(n\_node))/len(n\_node)} $$ (2) ②遍历式(2)所求圆内节点，分别计算与Xnew的距离，记录为新的父节点库，再检验库中节点与Xnew连线是否碰撞障碍物，返回无碰撞且连线最短的节点作为新的父节点。
2)节点重连
以Xnew为父节点，遍历半径为rrange的范围内节点，分别计算与Xnew间的距离并与Xnew当前路径长度相加记为s_cost，若小于原路径长度且与障碍物无碰撞，则此节点为Xnew的子节点。
2. 改进RRT*算法
2.1 采样点择优
由于传统RRT*算法的采样随机性较强，搜索目标点的过程需花费大量时间，因此改进算法在保留RRT*算法特有的随机采样特点下利用目标点信息对采样点进行择优选择以提升搜索速率[26]。具体实现步骤如下：
1)引入启发式思想[27]，以一定概率将目标点Xgoal选取为采样点：
$$ {X_{\rm sample}} = \left\{ {\begin{array}{*{20}{c}} {{X_{\rm goal}}, \qquad p \leqslant a} \\ {{X_{\rm rand}}, \qquad p > a} \end{array}} \right. $$ (3) 式中：Xsample为最终采样点，Xrand为随机采样点，p为0~1的随机数，为防止失去RRT类算法特有的随机采样特性，a设置为0.1。
2)从离采样点最近的节点Xnear出发，以机器人步长L向采样点扩展，生成新节点Xnew。
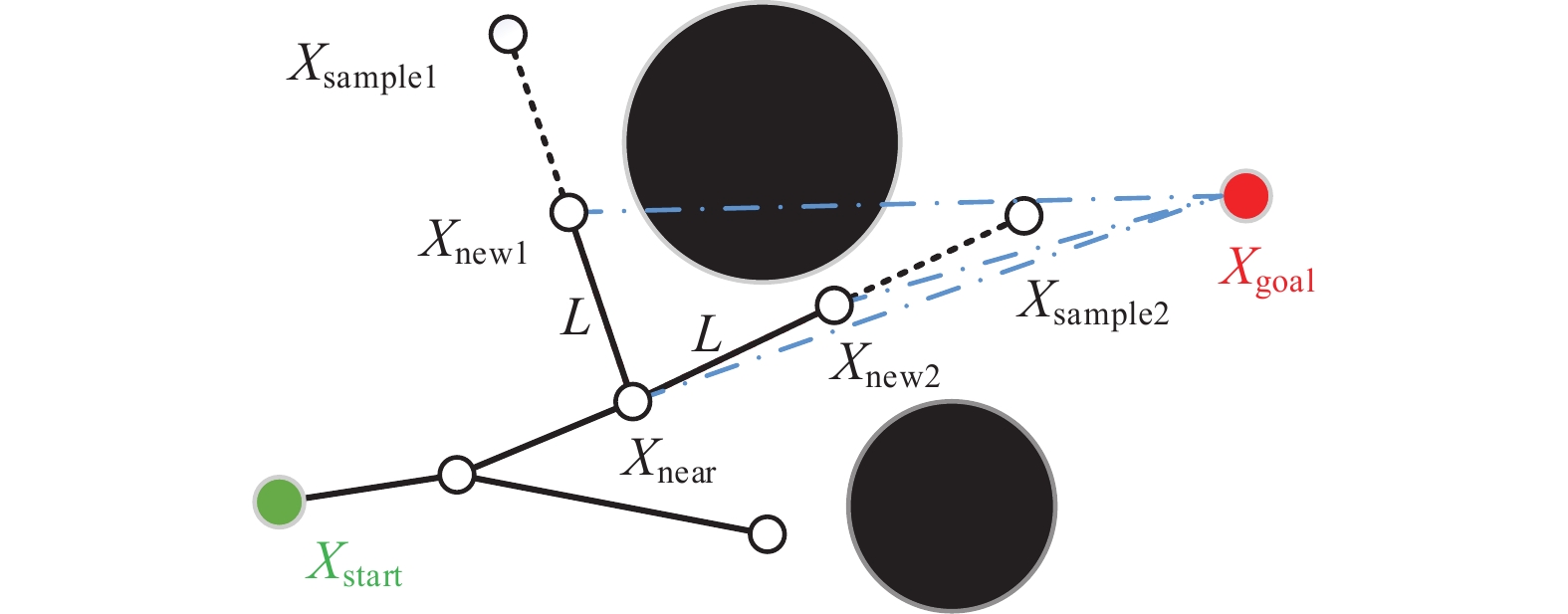
3)分别计算Xnear和Xnew到Xgoal的欧氏距离，并进行对比，若Xnew到Xgoal的距离小于Xnear到Xgoal的距离则认为采样成功，否则返回步骤1）重新采样，如图1所示。
图 1 改进RRT*算法采样过程Fig. 1 Improved RRT * algorithm sampling process
下载:
全尺寸图片
2.2 冗余节点删除
除此之外，RRT*算法在寻优过程中会产生大量冗余节点，使得算法的复杂度和运行时间呈指数级增长、寻优效率低下[28-29]。对此，引入路径节点最大值概念对冗余节点枝干进行修剪，减少算法的搜索成本。具体实现步骤如下：
1)遍历最优路径节点，分别计算与起终点连线的距离，取最大值并记录为节点最大值：
$$ d_{\mathrm{MAX} }=\max \left\{i \mid\left\|X_i\left(X_{\text {start }}+t \cdot\left(X_{\text {goal }}-X_{\text {start }}\right)\right)\right\|\right\} $$ (4) 式中：i为可行路径上节点的下标，t为可行路径上Xi节点在起、终点连线上的映射点到Xstart的距离与起、终点连线的距离之比。
2)遍历树上所有节点，随机取出节点计算其与起终点连线的距离为
$$ {d}_{{\mathrm{T}} j}=\Vert {X}_{i}({X}_{\text{start}}+t\cdot ({X}_{\text{goal}}-{X}_{\text{start}}))\Vert $$ (5) 式中j为树上其余节点下标。
3)将式(5)中计算出的dTj与式(4)的dMAX进行对比，若dTj>dMAX，删除此节点及其附属枝干，反之保留此节点。
4)不断重复步骤2)和3)，直至所有节点均计算完毕，如图2所示，其中，XMAX为最优路径节点垂直于起终点连线的最大值节点。
图 2 删除冗余节点过程示意Fig. 2 Schematic of the process of removing redundant nodes下载:
全尺寸图片
剔除冗余节点，选择关键节点，从而提升算法运行速率。与此同时，对采样过程进行二次约束。改进RRT*算法的采样过程中，通过判断新生成的节点与目标点之间的距离来确定是否有效，生成的新节点离目标点会更近的同时可能会造成路径总长度的增加。而删除冗余节点过程中计算出的dMAX同样对采样生成的点有约束作用，相当于变相拉伸可行路径，使得路径长度减小，提高了算法的容错率，如图3所示。
图 3 二次约束示意Fig. 3 Schematic of secondary constraint下载:
全尺寸图片
2.3 DWA算法
本文引入DWA算法沿全局路径进行局部路径规划。DWA算法将机器人速度选择问题转化到其线速度v和角速度
$\omega $ 组成的速度矢量空间$ ({v},\omega ) $ 中，对于速度矢量空间$ ({v},\omega ) $ 的约束条件主要有3点，具体如下[30]：1)由机器人自身限制的线速度和角速度约束。机器人的采样速度需控制在自身的最大速度和最小速度之间，约束公式为
$$ \begin{split} {V_s} = \{ ({v},\omega )|{{v}_{\rm min}} \leqslant {v} \leqslant {{v}_{\rm max}}, {\omega _{\rm min}} \leqslant \omega \leqslant {\omega _{\rm max}}\} \end{split} $$ 式中：v为机器人的线速度，
$\omega $ 为其角速度。2)由电机性能限制的加速度与减速度约束。机器人的加速度会受到电机输出扭矩的限制，因此线速度v和角速度
$\omega $ 都存在最大加速度及最大减速度，约束公式为$$ \begin{gathered} {V_d} = \left\{ {({v},\omega )|} \right.{v} \in [{{v}_t} - {\alpha _{v}}\Delta t,{v_t} + {\alpha _{v}}\Delta t], \\ {\text{ }}\left. {\omega \in [{\omega _t} - {\alpha _\omega }\Delta t,{\omega _t} + {\alpha _\omega }\Delta t]} \right\} \end{gathered} $$ 式中：
$ ({{v}_t},{\omega _t}) $ 分别为当前时刻机器人的线速度和角速度，${\alpha _v}$ 为最大线加速度，${\alpha _w}$ 为最大角加速度，$ \Delta t $ 为变化时间间隔。3)由环境因素限制的制动距离约束。为防止机器人因为速度原因碰撞到障碍物，提出满足机器人安全性的速度约束空间，约束公式为
$$ \begin{array}{c}{V}_{a}=\{( {v},\omega )| {v}\leqslant \sqrt{2{d}_{s}({ {v}}_{t},{\omega }_{t}){\alpha }_{ {v}}}，\\ \omega \leqslant \sqrt{2{d}_{{s}}({ {v}}_{t},{\omega }_{t}){\alpha }_{\omega }}\} \end{array} $$ $$ \begin{array}{c}{V}_{m}=\{( {v},\omega )| {v}\leqslant \sqrt{2{d}_{s}({ {v}}_{t},{w}_{t}){a}_{ {v}}}，\\ \text{ }\omega \leqslant \sqrt{2{d}_{s}({ {v}}_{t},{w}_{t}){a}_{\omega }}\} \end{array} $$ 式中：
${d_s}({v_t},{\omega _t})$ 为机器人在t时刻的速度$(v,\omega )$ 下到静态障碍物的最近距离,${d_m}({v_t},{\omega _t})$ 为机器人在t时刻的速度$(v,\omega )$ 下到动态障碍物的最近距离。因此机器人的速度空间由上述3条约束条件共同约束，最终机器人的速度空间满足：
$$ {V_r} = {V_s} \cap {V_d} \cap {V_a} \cap {V_m} $$ 此外，DWA算法在上述机器人速度空间Vr的约束下进行速度的采样以及离散化，得到可行的速度集合，并根据速度集合和轨迹预测时间段生成预测轨迹，之后通过评价函数对预测的轨迹集进行评价，选取最优路径，具体评价函数如下：
$$ \begin{gathered} G(v,\omega ) = \{ \alpha \cdot {\mathrm{head}} (v,\omega ) + \beta \cdot {\mathrm{vel}}(v,\omega )+ \\ \gamma \cdot {d_s}(v,\omega ) + \eta \cdot {d_m}(v,\omega )\} \end{gathered} $$ 式中：
$G(v,\omega )$ 为机器人在保证不碰到障碍物的情况下的最大速度；${\mathrm{head}}(v,\omega )$ 为方位角评价函数，用来评估机器人在当前速度下模拟轨迹的末端方向与目标点方向之间的角度差；$\alpha $ 为其权重系数；${\mathrm{vel}}(v,\omega )$ 为速度评价函数，表示机器人当前的运行速度；$ \,\beta $ 为其权重系数；$ {d}_{s}(v,\omega )、{d}_{m}(v,\omega ) $ 为距离评价函数，前者表示机器人位置与最近静态障碍物的关系，后者表示机器人与最近动态障碍物的关系，若当前轨迹无障碍物，记$ {d}_{s}(v,\omega )、{d}_{m}(v,\omega ) $ 为常数；$ \gamma 、 \;\eta $ 为其各自对应权重系数。2.4 融合算法实现
融合算法首先利用改进RRT*算法提升采样性能，能够在短时间内规划出一条起点到终点的可行路径，并且在之后的迭代中删除冗余节点，减少计算复杂度，其次结合DWA局部路径规划算法实现动态避障，融合算法具体实现流程如图4所示。
图 4 融合算法流程Fig. 4 Fusion algorithm flow下载:
全尺寸图片
3. 仿真实验与分析
为验证改进算法的有效性，将改进RRT*算法与其他算法在简单、复杂和存在移动障碍物3种地图下进行对比，并评价其性能指标。本文将不规则障碍物膨胀化为规则图形，并将机器人看作质点，为减小RRT类算法随机采样带来的不稳定性，分别对每种地图设置50次独立仿真实验，最终取平均值进行对比分析。本次实验采用处理器为Intel(R)Core(TM)i5-4460 CPU @ 3.20 GHz、内存为8 GB的64位WIN7操作系统，实验平台为Python3.6.8。
3.1 简单地图仿真
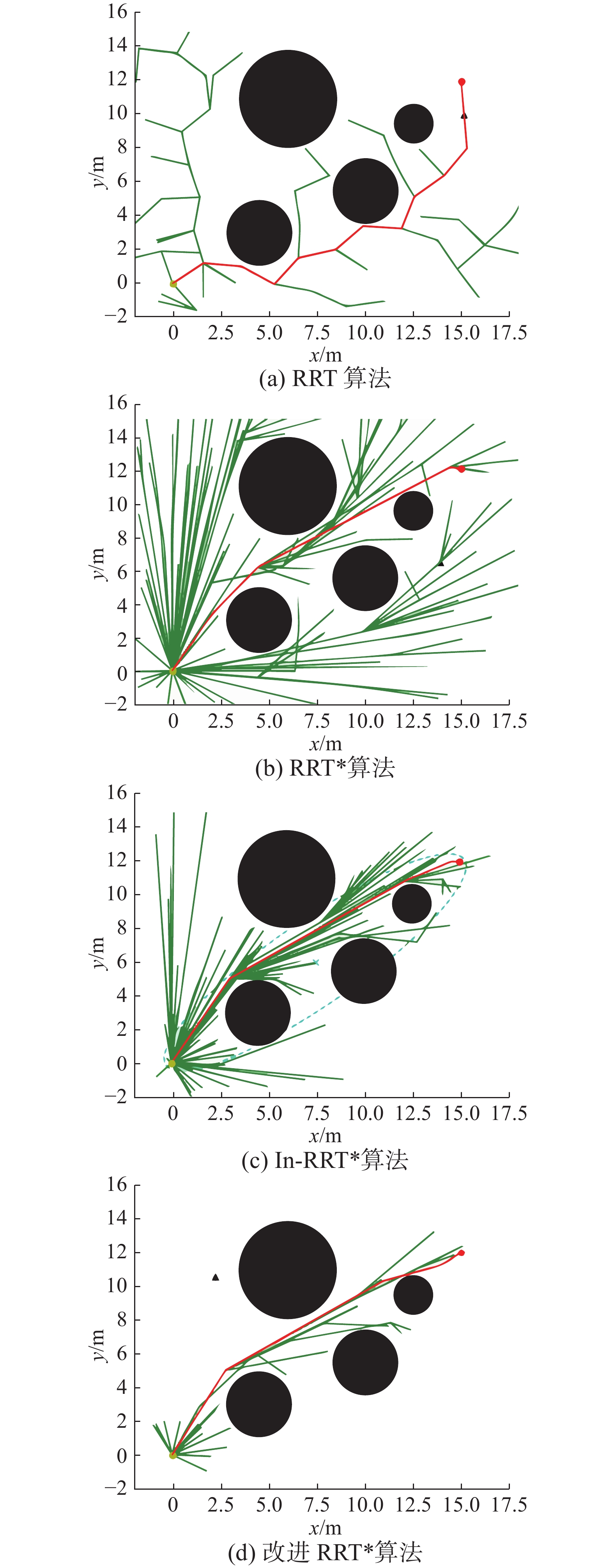
简单地图下各算法路径规划结果示意如图5所示，地图大小设置为20 m×17 m，横向和纵向坐标向负扩展2 m，移动机器人的起点终点位置为[0,0] m、[15,12] m，分别用黄、红圆点表示，黑色实心圆表示障碍物，绿色线表示搜索树枝干，红色线表示搜索到的最优路径。
图 5 简单地图下各算法路径规划结果示意Fig. 5 Schematic of path planning results of algorithms under simple map下载:
全尺寸图片
分别用 RRT、RRT*、In-RRT*、改进RRT*算法分别在简单地图中进行路径规划，迭代次数均为200，将50次独立仿真实验记录并求得平均值列于表1。
表 1 简单地图各算法数据Table 1 Algorithm data of simple map对比算法 平均路径长度/m 平均运行时间/s 平均迭代次数 RRT 24.398 3.700 85 RRT* 20.192 9.171 82 In-RRT* 19.923 17.861 118 改进RRT* 19.860 5.417 79 从表1中可看出，虽然RRT算法运行时间最小，但其搜索的路径最差，改进RRT*算法所求得路径最优，且平均运行时间和迭代次数小于RRT*、In-RRT*寻优算法。相比RRT*算法，改进RRT*所的路径长度减小了1.644%，时间缩短了40.933%，而相比In-RRT*算法，改进RRT*所得路径长度缩短较小，但其运行时间缩短了69.671%。由此可得改进RRT*算法通过对采样点的择优和冗余节点的删除，有效降低路径长度和计算复杂度的同时提升算法效率。
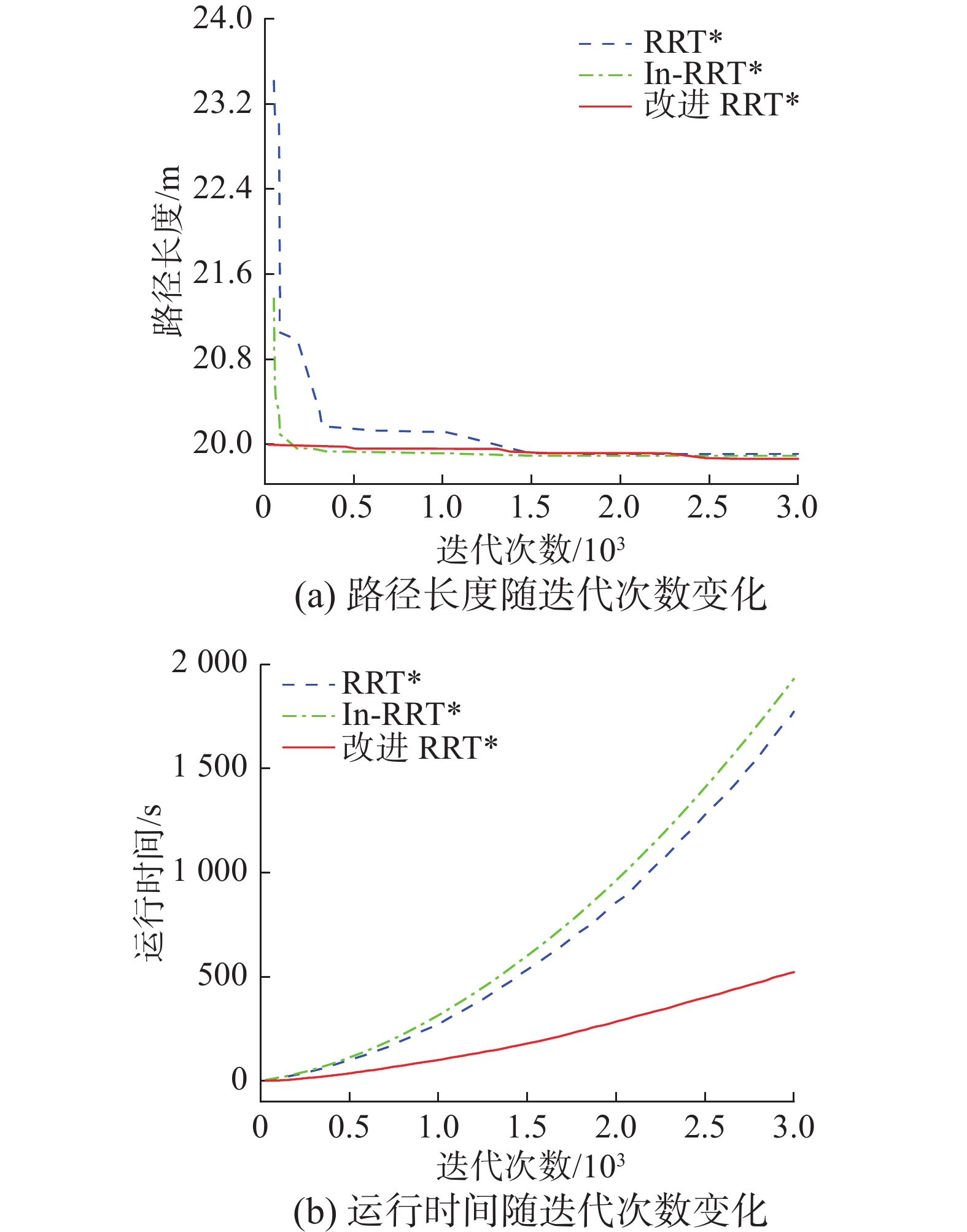
此外，将迭代次数提升至2 000，简单地图各算法性能对比如图6所示，改进RRT*算法搜索到的路径优于RRT*并且与In-RRT*在迭代1 600次以后基本持平(如图6(a))，但由于In-RRT*算法存在大量冗余节点，运行时间随迭代次数的增加快速增大，2 000次迭代后共花费980.774 s，而改进RRT*上升曲线相对平缓，用时347.413 s(如图6(b))。
图 6 简单地图各算法性能对比Fig. 6 Performance comparison of simple map algorithms下载:
全尺寸图片
3.2 复杂地图仿真
复杂地图下各算法路径规划结果示意如图7所示，除障碍物设置外，其余设置如同3.1节。从图7中可看出，在存在大量障碍物的复杂地图下，RRT算法获取的路径转折点多，路径长度大，不利于移动机器人的运动，RRT*和In-RRT*算法获得的路径转折点少，路径也更优，但存在许多不必要的搜索路径，改进RRT*获得的路径接近上述两类算法，但减少了不必要的搜索路径，即删除了过多冗余节点。分别将各类算法的50次独立仿真记录并求得平均值列于表2。
图 7 复杂地图下各算法路径规划结果示意Fig. 7 Schematic of path planning results of algorithms under complex map下载:
全尺寸图片
表 2 复杂地图各算法数据Table 2 Algorithm data of complex map对比算法 平均路径
长度/m平均运行
时间/s平均迭
代次数节点利
用率/%RRT 26.156 4.722 76 37.651 RRT* 20.782 9.087 122 4.467 In-RRT* 20.552 12.861 136 5.686 改进RRT* 20.165 2.954 72 7.051 从表2中可看出，RRT的路径长度远大于其他3种算法，因此不作考虑；而RRT*、In-RRT*的路径虽短，但由于其冗余节点的存在加大了算法运行时间；改进RRT*算法相较RRT*算法，获取的路径长度减少2.969%，运行时间降低67.492%，相较于In-RRT*算法，获取的路径长度减少1.883%，运行时间降低77.031%，同时将节点占用率提升到7.051%，节点利用率是指路径上的节点数目与搜索树上的节点数目之比，节点利用率越大，算法搜寻最优路径的效率越高。
将迭代次数提升至3 000，复杂地图各算法性能对比如图8所示，由于采样点在多障碍物的情况下难以选取，导致RRT*和In-RRT*算法的路径搜索效率降低，花费大量的运行时间，而改进RRT*算法最优路径收敛较快，且迭代次数到达3 000时的运行时间为522.019 s，远小于其他两种算法。
图 8 复杂地图各算法性能对比Fig. 8 Performance comparison of algorithms for complex maps下载:
全尺寸图片
3.3 动态地图仿真
为进一步探究改进RRT*算法在动态环境下的性能，本文设置了含有动态障碍物、大小为20 m×17 m的动态地图，引入DWA局部路径规划算法，将移动机器人的最大线速度、最大角速度、最大线加速度、最大角加速度、线速度分辨率、角速度分辨率、时间间隔、模拟轨迹持续时间分别为3 m/s、50 (°)/s、0.5 m/s2、30 (°)/s2、0.01 m/s、0.1 (°)/s、0.1 s、4 s。动态障碍物地图下各算法路径规划结果示意如图9所示。
图 9 动态地图下各算法路径规划结果示意Fig. 9 Schematic of path planning results of each algorithm under dynamic map下载:
全尺寸图片
从图9中可看出，RRT-DWA算法因路径节点过多而产生较大转折，其他3类算法规划出的路径较为平滑，将50次独立仿真记录并求得平均值列于表3。
表 3 动态地图各算法数据Table 3 Algorithm data of dynamic map对比算法 平均路径长度/m 平均运行时间/s RRT-DWA 29.344 717.503 RRT*-DWA 21.406 367.994 In-RRT*-DWA 20.809 402.117 改进RRT*-DWA 20.414 294.721 从表3中可看出，RRT-DWA算法引入局部规划算法后得到的路径长度最大，运行时间也最久；其他3类算法规划出的路径都接近最优路径，其中利用改进RRT*-DWA算法得到的路径平均长度比RRT*-DWA算法、In-RRT*-DWA算法分别减少4.634 %、1.898 %，平均运行时间与之对比分别降低19.911 %、26.708 %，由此可得，本文算法在动态环境下具有较好的动态规划能力。
4. 结束语
针对传统RRT*算法收敛速度慢、无法应用于动态环境等问题，提出了一种改进RRT*算法结合DWA算法的路径规划方法。该算法首先对随机树的采样点进行择优选取，避免无效搜寻；其次对树上冗余节点进行删除，提高算法运算速率，同时对采样点进行二次择优；最后引入DWA算法，实现动态环境下的避障功能。通过仿真实验与各搜索算法对比，验证所提融合算法在二维平面路径规划中能够有效提升路径质量，大幅减少算法运行时间，并提升在动态障碍物环境下的路径规划性能。
-
图 1 改进RRT*算法采样过程
Fig. 1 Improved RRT * algorithm sampling process
下载:
全尺寸图片
图 2 删除冗余节点过程示意
Fig. 2 Schematic of the process of removing redundant nodes
下载:
全尺寸图片
图 3 二次约束示意
Fig. 3 Schematic of secondary constraint
下载:
全尺寸图片
图 4 融合算法流程
Fig. 4 Fusion algorithm flow
下载:
全尺寸图片
图 5 简单地图下各算法路径规划结果示意
Fig. 5 Schematic of path planning results of algorithms under simple map
下载:
全尺寸图片
图 6 简单地图各算法性能对比
Fig. 6 Performance comparison of simple map algorithms
下载:
全尺寸图片
图 7 复杂地图下各算法路径规划结果示意
Fig. 7 Schematic of path planning results of algorithms under complex map
下载:
全尺寸图片
图 8 复杂地图各算法性能对比
Fig. 8 Performance comparison of algorithms for complex maps
下载:
全尺寸图片
图 9 动态地图下各算法路径规划结果示意
Fig. 9 Schematic of path planning results of each algorithm under dynamic map
下载:
全尺寸图片
表 1 简单地图各算法数据
Table 1 Algorithm data of simple map
对比算法 平均路径长度/m 平均运行时间/s 平均迭代次数 RRT 24.398 3.700 85 RRT* 20.192 9.171 82 In-RRT* 19.923 17.861 118 改进RRT* 19.860 5.417 79 表 2 复杂地图各算法数据
Table 2 Algorithm data of complex map
对比算法 平均路径
长度/m平均运行
时间/s平均迭
代次数节点利
用率/%RRT 26.156 4.722 76 37.651 RRT* 20.782 9.087 122 4.467 In-RRT* 20.552 12.861 136 5.686 改进RRT* 20.165 2.954 72 7.051 表 3 动态地图各算法数据
Table 3 Algorithm data of dynamic map
对比算法 平均路径长度/m 平均运行时间/s RRT-DWA 29.344 717.503 RRT*-DWA 21.406 367.994 In-RRT*-DWA 20.809 402.117 改进RRT*-DWA 20.414 294.721 -
[1] GUL F, MIR I, ABUALIGAH L, et al. A consolidated review of path planning and optimization techniques: technical perspectives and future directions[J]. Electronics, 2021, 10(18): 2250. doi: 10.3390/electronics10182250 [2] WU Xiaojing, XU Lei, ZHEN Ran, et al. Biased sampling potentially guided intelligent bidirectional RRT algorithm for UAV path planning in 3D environment[J]. Mathematical problems in engineering, 2019, 2019: 5157403. [3] LYU Desheng, CHEN Ziwei, CAI Zesu, et al. Robot path planning by leveraging the graph-encoded Floyd algorithm[J]. Future generation computer systems, 2021, 122: 204−208. doi: 10.1016/j.future.2021.03.007 [4] 张子迎, 宫思远, 徐东, 等. 多机器人任务分配与路径规划算法[J]. 哈尔滨工程大学学报, 2019, 40(10): 1753−1759. ZHANG Ziying, GONG Siyuan, XU Dong, et al. Research on multi-robot task assignment and path planning algorithm[J]. Journal of Harbin Engineering University, 2019, 40(10): 1753−1759. [5] 崔永杰, 王寅初, 何智, 等. 基于改进RRT算法的猕猴桃采摘机器人全局路径规划[J]. 农业机械学报, 2022, 53(6): 151−158. CUI Yongjie, WANG Yinchu, HE Zhi, et al. Global path planning of kiwifruit harvesting robot based on improved RRT algorithm[J]. Transactions of the Chinese society for agricultural machinery, 2022, 53(6): 151−158. [6] 张飞, 白伟, 乔耀华, 等. 基于改进D*算法的无人机室内路径规划[J]. 智能系统学报, 2019, 14(4): 662−669. ZHANG Fei, BAI Wei, QIAO Yaohua, et al. UAV indoor path planning based on improved D* algorithm[J]. CAAI transactions on intelligent systems, 2019, 14(4): 662−669. [7] 李颀, 汪伟. 多全向轮协同分拣平台的路径规划[J]. 系统仿真学报, 2021, 33(3): 698−709. LI Qi, WANG Wei. Path designing of multi-omnidirectional wheel collaborative sorting platform[J]. Journal of system simulation, 2021, 33(3): 698−709. [8] 黄鑫, 董红斌. 面向无人机路径规划的双层多目标粒子群算法[J]. 应用科技, 2023, 50(3): 1−10. HUANG Xin, DONG Hongbin. Double-layer multi-objective particle swarm algorithm for UAV path planning[J]. Applied science and technology, 2023, 50(3): 1−10. [9] 申铉京, 施英杰, 黄永平, 等. 基于双向蚁群算法的路径规划研究[J]. 哈尔滨工程大学学报, 2023, 44(5): 865−875. SHEN Xuanjing, SHI Yingjie, HUANG Yongping, et al. Path planning optimization using the bidirectional ant colony algorithm[J]. Journal of Harbin Engineering University, 2023, 44(5): 865−875. [10] 成怡, 肖宏图. 融合改进A*算法和Morphin算法的移动机器人动态路径规划[J]. 智能系统学报, 2020, 15(3): 546−552. CHENG Yi, XIAO Hongtu. Mobile-robot dynamic path planning based on improved A* and Morphin algorithms[J]. CAAI transactions on intelligent systems, 2020, 15(3): 546−552. [11] 邹宇星, 李立君, 高自成. 基于改进PRM的采摘机器人机械臂避障路径规划[J]. 传感器与微系统, 2019, 38(1): 52−56. ZOU Yuxing, LI Lijun, GAO Zicheng. Obstacle avoidance path planning for harvesting robot arm based on improved PRM[J]. Transducer and microsystem technologies, 2019, 38(1): 52−56. [12] WANG Hao, LI Guoqing, HOU Jie, et al. A path planning method for underground intelligent vehicles based on an improved RRT* algorithm[J]. Electronics, 2022, 11(3): 294. doi: 10.3390/electronics11030294 [13] 许万, 杨晔, 余磊涛, 等. 一种基于改进RRT*的全局路径规划算法[J]. 控制与决策, 2022, 37(4): 829−838. XU Wan, YANG Ye, YU Leitao, et al. A global path planning algorithm based on improved RRT*[J]. Control and decision, 2022, 37(4): 829−838. [14] 夏炎, 隋岩. PRM路径规划算法优化研究[J]. 应用科技, 2010, 37(10): 1−5. XIA Yan, SUI Yan. Research on optimization of PRM path planning algorithm[J]. Applied science and technology, 2010, 37(10): 1−5. [15] KARAMAN S, FRAZZOLI E. Sampling-based algorithms for optimal motion planning[J]. International journal of robotics research, 2011, 30(7): 846−894. doi: 10.1177/0278364911406761 [16] GAMMELL J D, SRINIVASA S S, BARFOOT T D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic[C]//2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago: IEEE, 2014: 2997−3004. [17] 李娟, 张韵, 陈涛. 改进RRT算法在未知三维环境下AUV目标搜索中的应用[J]. 智能系统学报, 2022, 17(2): 368−375. LI Juan, ZHANG Yun, CHEN Tao. Application of the improved RRT algorithm to AUV target search in an unknown 3D environment[J]. CAAI transactions on intelligent systems, 2022, 17(2): 368−375. [18] SPANOGIANOPOULOS S, SIRLANTZIS K. Non-holonomic path planning of car-like robot using RRT*FN[C]//2015 12th International Conference on Ubiquitous Robots and Ambient Intelligence. Goyangi: IEEE, 2015: 53−57. [19] 张腾龙, 李擎. 基于B-RRT*FND算法的移动机器人路径规划[J]. 控制与决策, 2023, 38(11): 3121−3127. ZHANG Tenglong, LI Qing. Path planning of AGV based on B-RRT*FND algorithm[J]. Control and decision, 2023, 38(11): 3121−3127. [20] QIN Hongwei, SHAO Shiliang, WANG Ting, et al. Review of autonomous path planning algorithms for mobile robots[J]. Drones, 2023, 7(3): 211. doi: 10.3390/drones7030211 [21] PEREIRA N, RIBEIRO A F, LOPES G, et al. Path planning towards non-compulsory multiple targets using TWIN-RRT[J]. Industrial robot, 2016, 43(4): 370−379. doi: 10.1108/IR-02-2016-0069 [22] 刘成菊, 韩俊强, 安康. 基于改进RRT算法的RoboCup机器人动态路径规划[J]. 机器人, 2017, 39(1): 8−15. LIU Chengju, HAN Junqiang, AN Kang. Dynamic path planning based on an improved RRT algorithm for RoboCup robot[J]. Robot, 2017, 39(1): 8−15. [23] CHAI Qisen, WANG Yujun. RJ-RRT: improved RRT for path planning in narrow passages[J]. Applied sciences, 2022, 12(23): 12033. doi: 10.3390/app122312033 [24] WANG Jiankun, CHI Wenzheng, LI Chenming, et al. Neural RRT*: learning-based optimal path planning[J]. IEEE transactions on automation science and engineering, 2020, 17(4): 1748−1758. doi: 10.1109/TASE.2020.2976560 [25] ZHOU Lintao, WU Nanpeng, CHEN Hu, et al. RRT*-fuzzy dynamic window approach (RRT*-FDWA) for collision-free path planning[J]. Applied sciences, 2023, 13(9): 5234. doi: 10.3390/app13095234 [26] DAM T, CHALVATZAKI G, PETERS J, et al. Monte-Carlo robot path planning[J]. IEEE robotics and automation letters, 2022, 7(4): 11213−11220. doi: 10.1109/LRA.2022.3199674 [27] FRANSEN K, EEKELEN J V. Efficient path planning for automated guided vehicles using A* (Astar) algorithm incorporating turning costs in search heuristic[J]. International journal of production research, 2021, 61: 707−725. [28] MENG B H, GODAGE I S, KANJ I. RRT*-based path planning for continuum arms[J]. IEEE robotics and automation letters, 2022, 7(3): 6830−6837. doi: 10.1109/LRA.2022.3174257 [29] DING Jun, ZHOU Yinxuan, HUANG Xia, et al. An improved RRT* algorithm for robot path planning based on path expansion heuristic sampling[J]. Journal of computational science, 2023, 67: 101937. doi: 10.1016/j.jocs.2022.101937 [30] 蒲兴成, 谭令. 基于自适应动态窗口改进细菌算法与移动机器人路径规划[J]. 智能系统学报, 2023, 18(2): 314−324. PU Xingcheng, TAN Ling. A mobile robot path planning method based on adaptive DWA and an improved bacteria algorithm[J]. CAAI transactions on intelligent systems, 2023, 18(2): 314−324.
