Knowledge tracing model via exercise transfer representation
-
摘要: 针对多数知识追踪研究在表征题目时仅利用了题目包含的概念等显性特征,未能考虑到题目中概念的考察侧重程度这一隐性特征,也未表征迁移过程中题目的迁移程度的问题,本文提出题目迁移表征的知识追踪模型。在题目侧重表征方面,采用加性注意力机制提取题目中各个概念的考察侧重程度;在题目迁移方面,利用相似性和通道注意力机制融合建模历史题目多角度的迁移程度;在迁移遗忘方面,使用门限机制建模学习迁移的遗忘过程。最终得到题目迁移表征,以此来预测学习者未来的答题表现。在实验阶段,与6种相关模型在3个真实数据集上进行对比实验,结果表明提出模型的曲线下面积(area under the curve, AUC)和准确率(accuracy, ACC)均有更好表现,尤其在ASSISTments2012数据集上表现最佳,相较于其他对比模型分别提升了3.5%~20.1%和2.3%~18.5%;在可解释性方面,使用图表可视化描述了题目迁移表征生成路径。本研究建模的学习迁移内在机制可为知识追踪模型的设计提供参考。Abstract: In most knowledge tracing research, the representation of questions typically relies solely on explicit features such as the concepts contained within the questions, neglecting the implicit feature of the emphasis level on concepts and failing to characterize the degree of question transfer during the transfer process. This paper presents a knowledge tracing model via exercise transfer representation. In terms of the representation of the focus of the exercise, the additive attention mechanism is used to extract the focus of each concept in the exercise. In terms of exercise transfer, the multi-angle transfer degree of historical exercises is modeled by fusion of similarity and channel attention mechanism. In terms of transfer forgetting, a threshold mechanism is used to model the forgetting process of learning transfer. Finally, the exercise transfer representation is obtained to predict the learner’s future answering performance. Experimental results show that the proposed model outperforms six benchmark models across three real datasets, particularly excelling on the ASSISTments 2012 dataset with improvements ranging from 3.5% to 20.1% for area under the curve (AUC) and 2.3% to 18.5% for accuracy (ACC). The interpretability aspect is enhanced through graphical visualization of the question transfer representation generation pathway. The internal mechanisms of learning transfer modeled in this paper provide valuable insights for the design of knowledge tracing models.
-
近年来,国家智慧教育公共服务平台、学堂在线、超星学习通等智慧教学环境快速发展,既打破了传统课堂教学场所的限制,同时也给学习者带来了更丰富的学习资源。最初智慧教学环境并未对学习者提供个性化的教学辅导。然而在实际学习中,每位学习者的知识状态不可能完全相同,如果学习者无法得到针对性的教学支持,其学习效果就可能受到影响。基于因材施教的目的,建模不同学习者各自的知识状态,成为了智慧教学环境首先要解决的关键问题。知识追踪[1-2]在这种需求驱动之下应运而生,利用智慧教学环境的学习数据,如题目、概念、作答情况和答题间隔时间等作为输入,建模学习者的知识状态,预测学习者的未来答题表现,是智慧教学环境提供个性化教与学的基础设施。
早期的知识追踪模型主要是基于隐马尔可夫模型[3](hidden Markov model, HMM)的贝叶斯知识追踪模型[4](Bayesian knowledge tracing, BKT)及其延伸BF-BKT[5](behavior-forgetting Bayesian knowledge tracing)等。后续的方法主要基于深度模型,如深度知识追踪[6](deep knowledge tracing, DKT)、动态键值记忆网络[7](dynamic key-value memory networks, DKVMN)及其延伸DKVMN-BORUTA[8]、MSKT[9]、DKVMN-GBRT[10]和DKVMN-DT[11]等。上述知识追踪模型对整个领域的发展起到了重要的推动作用。然而它们在表征题目时往往仅利用了题目包含的概念等显性特征,这种方法无法区分包含相同概念的不同题目。另一方面,学习迁移[12]是运用已有的知识经验去学习新的知识,形成新的知识状态。然而以往的研究仅利用深度模型本身的缺省功能将学习迁移结果隐式地建模于知识状态中,并未深入刻画历史题目到当前题目的学习迁移过程,仅是对学习迁移机制的结果表达。
为了更加准确地表征学习迁移,本文提出题目迁移表征的知识追踪模型(knowledge tracing model via exercise transfer representation, ETKT),从学习迁移的角度建模题目迁移表征。第一,通过加性注意力机制获取题目中每个概念对题目本身的重要性,将其转化为每个概念的权重,从而得到题目中每个概念的考察侧重程度。第二,使用相似性注意力机制建模历史题目与当前题目的相似度,将上述相似度转化为历史题目到当前题目的迁移程度;使用通道注意力机制捕获迁移的全局信息,获取间隔时间对迁移全局的影响权重。第三,使用门限机制建模遗忘过程,最终增强题目在迁移中的表征,更好地预测学习者未来的学习表现。
1. 知识追踪相关工作
1.1 题目侧重
DKT将深度模型引入知识追踪领域,利用循环神经网络[13](recurrent neural network, RNN)在一定程度上建模了历史题目到当前题目的迁移过程。但DKT仅将题目包含的单个概念作为题目表示,既忽视了考察相同概念的不同题目间的差异,也未考虑到一道题目考察多个概念的情况。后续的知识追踪模型对考察了相同概念的不同题目进行了区分,考虑了题目包含的多个概念对题目迁移的影响。IDKT[14](interpretable DKT)利用题目与概念的关联以及题目共现信息来表征当前题目,客观上描述了历史题目包含的多个概念对当前题目产生的迁移作用。GIKT[15](graph-based knowledge tracing)考虑到题目中包含的多个概念对迁移的影响,利用图卷积神经网络[16](graph convolutional network, GCN)聚合题目及其包含的多个概念,然后从高阶信息中挖掘题目和概念的特征,对题目进行了更丰富的表征。Liu等[17]通过构建题目与概念关系、题目相似关系、概念相似关系的二分图,利用神经网络预训练得到题目表征。上述模型的工作重点在于从不同的角度利用概念表征题目。但它们的隐含假设是同一道题目中包含的所有概念考察侧重程度相等,事实上,一道题目考察的概念数量通常为一个或以上,且这些概念在题目中的考察侧重程度并不一定完全相同。上述模型都未能区分题目中概念的考察侧重程度的差异。
1.2 题目迁移
DKT-CF[18](DKT collaborative filtering)利用深度模型的缺省功能将题目的迁移隐式建模于学习过程。ATCKT[19](temporal convolutional knowledge tracing with attention mechanism)使用时间卷积网络[20]建模题目迁移。AKT[21](contex-aware knowledge tracing)在时间卷积网络的基础上加入了注意力机制[22]隐式地建模了题目的迁移过程。上述研究利用了深度模型固有的缺省功能客观上表示了题目迁移过程。但它们将所有历史题目到当前题目的迁移程度同等对待,忽视了实际情况中历史题目由于本身信息的差异迁移程度并不一定完全相同的事实。这些研究都未能明确区分不同历史题目的迁移程度。
1.3 迁移遗忘
许多知识追踪模型对学习迁移过程中的遗忘现象进行了建模,DKT+forgetting[23]在DKT的基础上加入了相同题目时间间隔、相邻题目时间间隔和题目历史练习次数等特征,使用深度模型的缺省功能建模了遗忘现象。DKVMN通过记忆擦除机制消除值矩阵中遗忘的知识状态。LFKT[24](learning and forgetting behavior modeling for knowledge tracing)使用学习者重复学习概念的间隔时间、重复学习概念的次数、顺序答题间隔时间以及学习者针对概念的掌握程度等建模遗忘现象。王璨等[25]提出了时间卷积知识追踪模型TCN-KT(temporal convolutional network knowledge tracing),该模型采用多种类型的信息来表示复杂的遗忘行为,例如学习者回答相同题目的时间间隔、相邻题目的时间间隔以及历史作答题目的次数。Pandey等[26]提出了一种基于关系感知和自注意力的知识追踪模型RKT(relation knowledge tracing),通过建立指数衰减的核函数集成了遗忘行为信息。Gan等[27]提出了一种遗忘的建模方法KTM-DLF(knowledge tracing machine by modeling cognitive item difficulty and learning and forgetting),将相同概念间隔时间、相同题目间隔时间和相邻交互间隔时间作为衡量遗忘的因素,即学习某个概念的间隔越长,遗忘的可能性越大。上述模型直接操作学习者的知识状态,仅能描述遗忘机制的结果,忽视了对遗忘机制过程的建模。
2. 题目迁移表征的知识追踪模型
2.1 问题定义
对于知识追踪而言,其任务是通过题目及其包含的概念等特征建模题目的迁移过程来描述学习者的知识状态,从而预测学习者作答题目的概率
$ {{P(}}{r_t}{|}{q_1},{q_2}, \cdots ,{q_t}{\text{,}}{r_1}{\text{,}}{r_2}{\text{,}} \cdots {\text{,}}{r_{t - 1}}{\text{)}} $ 。其中$t$ 为当前时刻,$ {q_i}(1 \leqslant i \leqslant t) $ 为学习者作答的题目,$ {r_i}(1 \leqslant i \leqslant t) $ 为对应的答题结果。通常情况下,$ {r_i} = 0 $ 表示答错,$ {r_i} = 1 $ 表示答对。2.2 模型输入
本文使用题目、概念、答题间隔时间和答题情况等数据作为模型的输入,来建模题目迁移表征。
记题目
${\boldsymbol{q}_t}$ 的one-hot编码为$O({\boldsymbol{q}_t}) \in {{\bf{R}}^{N \times 1}}$ ,与嵌入矩阵$ {{\boldsymbol{W}}_q} \in {{\bf{R}}^{N \times d}} $ 相乘得到题目的嵌入向量$ {{\boldsymbol{q}}_t} \in {{\bf{R}}^{d \times 1}} $ ,表示为$$ {{\boldsymbol{q}}_t} = {\boldsymbol{W}}_q^{\rm{T}} \times O({\boldsymbol{q}_t}) $$ 式中:
$ N $ 为题目总数,$d$ 为题目嵌入维度。记概念
${\boldsymbol{c}_i}$ 的one-hot编码为$O({\boldsymbol{c}_i}) \in {{\bf{R}}^{M \times 1}}$ ,与嵌入矩阵${{\boldsymbol{W}}_c} \in {{\bf{R}}^{M \times d}}$ 相乘得到概念的嵌入向量${{\boldsymbol{c}}_i} \in {{\bf{R}}^{d \times 1}}$ ,表示为$$ {{\boldsymbol{c}}_i} = {\boldsymbol{W}}_c^{\rm{T}} \times O({\boldsymbol{c}_i}) $$ 式中:
$ M $ 是概念总数,$d$ 为概念嵌入维度。将历史题目到当前题目的答题间隔时间离散化,记答题间隔时间
${i_{t,h}}$ 离散化后的one-hot编码为$O({\boldsymbol{i}_{t,h}}) \in {{\bf{R}}^{F \times 1}}$ ,与嵌入矩阵${{\boldsymbol{W}}_i} \in {{\bf{R}}^{F \times d}}$ 相乘得到嵌入向量$ {{\boldsymbol{i}}_{t,h}} \in {{\bf{R}}^{d \times 1}} $ ,如下式所示:$$ {{\boldsymbol{i}}_{t,h}} = {\boldsymbol{W}}_i^{\rm{T}} \times O({\boldsymbol{i}_{t,h}}) $$ 式中:
$ F $ 为离散化后的答题间隔时间总数,$d$ 为答题间隔时间嵌入维度。2.3 模型框架
题目迁移表征的知识追踪模型ETKT的整体架构如图1所示。主要有5个部分,分别是题目侧重表征、迁移权重表征、迁移遗忘表征、题目迁移表征和预测模块。题目侧重表征以题目中概念的考察侧重程度来建模题目表征;迁移权重表征建模历史题目到当前题目的迁移程度;迁移遗忘表征建模遗忘机制的过程;题目迁移表征融合迁移权重和迁移遗忘表征对;预测模块通过长短期记忆网络[28](long short-term memory, LSTM)来预测学习者在
$ t $ 时刻的答题情况。2.3.1 题目侧重表征
传统模型假设题目中的概念考察侧重程度是相同的。然而实际情况中,每道题目包含的概念考察侧重程度并非完全相同。例如,学习者作答了某道包含加法、减法、乘法3个概念的题目:
$263.689 \times 109.261 \times 116.452 + 1 - 0$ ,显然该题目更侧重于考察乘法这一概念。这种概念考察侧重程度不同的情况在传统模型中未能表示,这里本文使用概念考察权重来表示题目中不同概念的考察侧重程度,某概念的权重越大说明这个概念在题目中的考察侧重程度越大。本小节将建模题目包含的概念考察权重。以题目
$ \boldsymbol{q} $ 及其包含的概念集合$ {\boldsymbol{ C}_q} $ ,作为题目侧重表征的输入。本节通过加性注意力机制[29]描述概念对题目的重要性以获取概念的考察权重。具体地,将$ {\boldsymbol{q}} \in {{\bf{R}}^{d \times 1}} $ 通过单位矩阵$ {{\boldsymbol{W}}_1} \in {{\bf{R}}^{1 \times M}} $ 扩展为$ {\boldsymbol{Q}} \in {{\bf{R}}^{d \times M}} $ 。将$ {\boldsymbol{Q }}$ 及其包含的概念集合的嵌入表示$ {{\boldsymbol{C}}_q} \in {{\bf{R}}^{d \times M}} $ 映射到更高维度,即对题目和概念的嵌入向量进行共享线性变换,分别得到$ {\boldsymbol{WQ}} $ 和$ {\boldsymbol{WC}}_q $ ,其中$ {\boldsymbol{W}} \in {{\bf{R}}^{d' \times d}} $ 为共享线性变换矩阵。拼接
$ {\boldsymbol{WQ}} $ 和$ {\boldsymbol{WC}}_q $ 得到$ [{\boldsymbol{WQ}}||{\boldsymbol{WC}}_q] \in {{\bf{R}}^{2d' \times M}} $ ,再和共享参数向量$ {\boldsymbol{a}} \in {{\bf{R}}^{2d' \times 1}} $ 作点积后通过激活函数LeakyReLu得到${\boldsymbol{ e}} \in {{\bf{R}}^{1 \times M}} $ ,表示为$$ {\boldsymbol{e}} = {{\rm{LeakyReLu}}} ({{\boldsymbol{a}}^{\rm{T}}}([{\boldsymbol{Wq}}||{\boldsymbol{WC}}_q])) $$ 式中:
${\boldsymbol{ e}} \in {{\bf{R}}^{1 \times M}} $ 为注意力系数向量,表示概念集合$ {\boldsymbol{ C}_q} $ 中每一个概念对题目$ \boldsymbol{q} $ 的重要性,重要性越高表明题目中该概念考察程度越高。输出$ {\boldsymbol{e}} $ 经过$ \text{softmax} $ 激活函数映射得到题目$ \boldsymbol{q} $ 对概念集合$ {\boldsymbol{ C}_q} $ 中每一个概念的考察权重${\boldsymbol{ s}} = \sigma ({\boldsymbol{e}}) $ ,$ {\boldsymbol{s}} \in {{\bf{R}}^{1 \times M}} $ 。将
$ {\boldsymbol{s}} $ 与全体概念集合$ {\boldsymbol{C}} \in {{\bf{R}}^{M \times d}} $ 相乘得到加权后的概念表示,再与嵌入矩阵$ {{\boldsymbol{W}}_{{q_1}}} \in {{\bf{R}}^{d \times d}} $ 相乘得到${{\boldsymbol{W}}_{{q_1}}}{{\boldsymbol{C}}^{\rm{T}}}{\boldsymbol{s}}_i^{\rm{T}}$ ,即题目$\boldsymbol{q}$ 包含的全部概念的嵌入表示。将嵌入矩阵$ {{\boldsymbol{W}}_{{q_2}}} \in {{\bf{R}}^{d \times d}} $ 与${\boldsymbol{ q}} $ 相乘后得到$ {{\boldsymbol{W}}_{{q_2}}}{\boldsymbol{q}} $ ,即题目$ \boldsymbol{q} $ 的嵌入表示。将上述概念表示与题目表示相加,通过${\text{sigmoid}}$ 激活函数得到融合不同概念考察权重的题目表征$ {\boldsymbol{q}}' \in {{\bf{R}}^{d \times 1}} $ 。$$ {\boldsymbol{q}}' = \sigma ({{\boldsymbol{W}}_{{q_1}}}{{\boldsymbol{C}}^{\rm{T}}}{{\boldsymbol{s}}^{\rm{T}}} + {{\boldsymbol{W}}_{{q_2}}}{\boldsymbol{q}}) $$ 2.3.2 迁移权重表征
多数传统模型将所有历史题目到当前题目的迁移程度同等对待。这种做法忽视了学习迁移过程中2次学习相似度越高,迁移程度越高的情况。例如,历史题目1是
$263.6 \times 109.2 \times 116.2 + 26.2 - 12.9$ 和历史题目2是求一个圆形面积。当学习者作答当前题目$12.56 \times 251 \times 121 + 18 - 12$ 的时候,则更容易从历史题目1进行迁移,即历史题目1的迁移程度比历史题目2的迁移程度要高。上述迁移程度的差异在传统模型中未有表示。采用注意力机制,让模型将更多的权重放在与当前题目相似度较高的历史题目上。具体地,单个历史题目
$ {{\boldsymbol{q}}_h} \in {{\bf{R}}^{d \times 1}} $ ,$F$ 道历史题目拼接表征为$ {{\boldsymbol{Q}}_h} \in {{\bf{R}}^{d \times F}} $ ,利用余弦相似度计算$F$ 道历史题目集合$ {{\boldsymbol{Q}}_h} $ 基于其本身信息到当前题目$ {{\boldsymbol{q}}_t} $ 的迁移权重:$$ {{\boldsymbol{\alpha}} _{t,h}} = \cos ({{\boldsymbol{q}}_t},{{\boldsymbol{Q}}_h}) = \frac{{{\boldsymbol{q}}_t^{\rm{T}}}}{{|{{\boldsymbol{q}}_t}|}} \cdot \frac{{{{\boldsymbol{Q}}_h}}}{{|{{\boldsymbol{Q}}_h}|}} $$ 式中:
${{\boldsymbol{\alpha}} _{t,h}} \in {{\bf{R}}^{1 \times F}}$ ,$ |{{\boldsymbol{q}}_t}| $ 为向量的$ {{\boldsymbol{q}}_t} $ 的长度,$ |{{\boldsymbol{Q}}_h}| $ 为矩阵$ {{\boldsymbol{Q}}_h} $ 的行列式。然而,仅利用题目信息,没有考虑到题目迁移的间隔时间,可能会忽视时间对迁移过程的影响。通常情况下,迁移会被答题间隔时间影响,历史题目与当前题目间隔时间越短,学习者对题目印象更深刻,则越容易进行迁移。此处利用通道注意力机制,捕获迁移的全局信息,将历史题目集合
$ {{\boldsymbol{Q}}_h}_{} $ 距当前题目$ {{\boldsymbol{q}}_t} $ 的间隔时间$ {{\boldsymbol{I}}_{t,h}} \in {{\bf{R}}^{F \times d}}_{} $ 转化为对迁移影响的相对权重$ {{\boldsymbol{g}}_{t,h}} \in {{\bf{R}}^{1 \times F}}_{} $ 。$$ {{\boldsymbol{g}}_{t,h}} = \sigma (\text{ReLu}({{\boldsymbol{W}}_{{g_1}}}{\boldsymbol{I}}_{t,h}^{\rm{T}} + {{\boldsymbol{b}}_{{g_1}}}){{\boldsymbol{W}}_{{g_2}}} + {{\boldsymbol{b}}_{{g_2}}}) $$ 式中:
$ {{\boldsymbol{g}}_{t,h}} $ 为注意力系数向量,其中$ {{\boldsymbol{W}}_{{g_1}}} \in {{\bf{R}}^{1 \times d}} $ 、$ {{\boldsymbol{W}}_{{g_2}}} \in {{\bf{R}}^{F \times F}} $ 为参数矩阵,$ {{\boldsymbol{b}}_{{g_1}}},{{\boldsymbol{b}}_{{g_2}}} \in {{\bf{R}}^{1 \times F}} $ 为偏置项,再将$ {{\boldsymbol{g}}_{t,h}} $ 经过$ {{\rm{softmax}}} $ 归一化,得到历史题目集合$ {{\boldsymbol{Q}}_h} $ 基于间隔时间到当前题目$ {{\boldsymbol{q}}_t} $ 的迁移权重$ {{\boldsymbol{\beta}} _{t,h}} = \sigma ({{\boldsymbol{g}}_{t,h}}) $ ,$ {{\boldsymbol{\beta}} _{t,h}} \in {{\bf{R}}^{1 \times F}} $ 。2.3.3 迁移遗忘表征
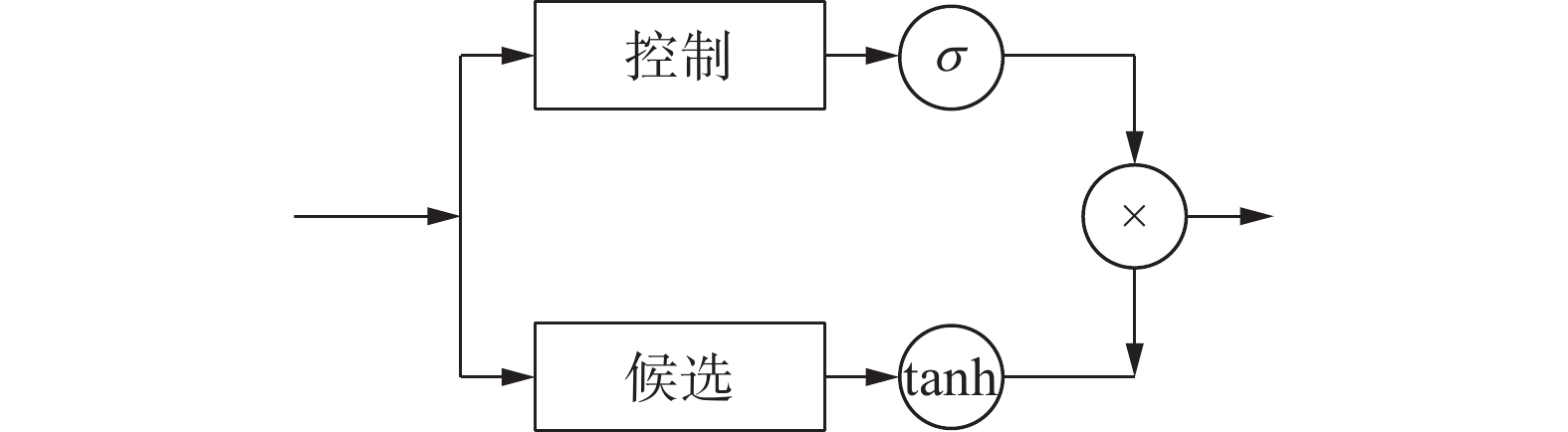
迁移遗忘表征来源于学习科学对学习迁移内在机制的描述,是迁移过程中的重要环节,其缺失不符合学习迁移的客观规律。以往研究多数直接操作学习者的知识状态仅能描述遗忘机制的结果,未能建模遗忘机制的过程[23-27]。针对上述问题,本小节利用门限功能实现对遗忘机制过程的建模,从而获取迁移遗忘权重。具体包括控制部分和候选部分,如图2所示。
单个历史题目
$ {{\boldsymbol{q}}'_h} \in {{\bf{R}}^{d \times 1}} $ ,$F$ 道历史题目拼接表征为$ {{\boldsymbol{Q}}'_h} \in {{\bf{R}}^{d \times F}} $ 。候选部分使用$ {\tanh _{}} $ 激活函数,将$ {{\boldsymbol{Q}}'_h} $ 作为输入,利用$ {\tanh _{}} $ 函数将待遗忘的内容控制在一定范围内。控制部分使用$ {{{\rm{Sigmoid}}} _{}} $ 激活函数,将$ {{\boldsymbol{Q}}'_h} $ 作为输入,利用$ {{{\rm{Sigmoid}}} _{}} $ 函数控制迁移遗忘。上述2部分的输出相乘,即控制部分的输出决定候选部分的重要程度,如下:$$ {{\boldsymbol{Q}}''_h} = \sigma ({{\boldsymbol{W}}_{{f_1}}}{{\boldsymbol{Q}}'_h} + {{\boldsymbol{b}}_{{f_1}}}) \cdot \tanh ({{\boldsymbol{W}}_{{f_2}}}{{\boldsymbol{Q}}'_h} + {{\boldsymbol{b}}_{{f_2}}}) $$ 式中:
${{\boldsymbol{Q}}''_h} \in {{\bf{R}}^{d \times F}}$ 为历史题目集合对当前题目$ {{\boldsymbol{q}}_t}_{} $ 经过遗忘的学习迁移表征,$ {{\boldsymbol{W}}_{{f_1}}},{{\boldsymbol{W}}_{{f_2}}} \in {{\bf{R}}^{d \times d}} $ 为需要训练的权重矩阵,$ {{\boldsymbol{b}}_{{f_1}}},{{\boldsymbol{b}}_{{f_2}}} \in {{\bf{R}}^{d \times F}} $ 为偏置项。2.3.4 题目迁移表征
通过
$ {{\boldsymbol{\alpha }}_{t,h}} $ 和$ {{\boldsymbol{\beta}} _{t,h}} $ 对$ {{\boldsymbol{Q}}''_h} $ 分别作加权和操作,然后进行拼接。$$ {\boldsymbol{h}}_t^\alpha = {\boldsymbol{W}}_{{{\boldsymbol{\alpha }}_1}}^{}{{\boldsymbol{Q}}''_h}{\boldsymbol{\alpha }}_{t,h}^{\rm{T}} + {{\boldsymbol{W}}_{{{\boldsymbol{\alpha }}_2}}}{{\boldsymbol{q}}'_t} $$ $$ {\boldsymbol{h}}_t^\beta = {\boldsymbol{W}}_{{\beta _1}}^{}{{\boldsymbol{Q}}''_h}\beta _{t,h}^{\rm{T}} + {{\boldsymbol{W}}_{{\beta _2}}}{{\boldsymbol{q}}'_t} $$ 式中
$ {{\boldsymbol{W}}_{{{\boldsymbol{\alpha }}_1}}},{{\boldsymbol{W}}_{{{\boldsymbol{\alpha }}_2}}} \in {{\bf{R}}^{d \times d}} $ 、${{\boldsymbol{W}}_{{\beta _1}}},{{\boldsymbol{W}}_{{\beta _2}}} \in {{\bf{R}}^{d \times d}}$ 为需要训练的权重矩阵。拼接$ {\boldsymbol{h}}_t^\alpha ,{\boldsymbol{h}}_t^\beta $ ,通过激活函数得到题目迁移表征$ {\boldsymbol{x}}_t^{} \in {{\bf{R}}^{1 \times M}} $ ,$M$ 为题目迁移表征嵌入维度。$$ {{\boldsymbol{x}}_t} = {\rm{ReLu}}({[{\boldsymbol{h}}_t^\alpha \parallel {\boldsymbol{h}}_t^\beta ]^{\rm{T}}}{{\boldsymbol{W}}_h} + {{\boldsymbol{b}}_h}) $$ 式中:
${{\boldsymbol{W}}_h} \in {{\bf{R}}^{2d \times M}}$ 为需要训练的权重矩阵,$ {{\boldsymbol{b}}_h} \in {{\bf{R}}^{1 \times M}} $ 为偏置项。2.3.5 预测模块
由于答题结果对学生的学习状态影响不同。根据文献[30],先将答题结果
$ {r_{t - 1}} $ 转化为与${\boldsymbol{ x}}_t^{} \in {{\bf{R}}^{1 \times M}} $ 维度相同的零向量,再将题目迁移表征${\boldsymbol{ x}}_t^{} \in {{\bf{R}}^{1 \times M}} $ 与答题结果$ {r_{t - 1}} $ 扩展为LSTM的输入向量$ {{\boldsymbol{a}}_t} \in {{\bf{R}}^{1 \times {\text{2M}}}} $ ,表示为$$ {{\boldsymbol{a}}_t} = \left\{ \begin{aligned} &[{\boldsymbol{0}}\|{{\boldsymbol{x}}_t}], \quad {r_{t-1}} = 1 \\ & [{{\boldsymbol{x}}_t}\|{\boldsymbol{0}}], \quad {r_{t-1}} = 0 \end{aligned} \right. $$ 式中:
$ || $ 为连接2个向量的操作,$ {r_{t - 1}} = 1 $ 为学生在$ t - 1 $ 时刻答题正确,$ {r_{t - 1}} = 0 $ 为学生在$ t - 1 $ 时刻答题错误。将$ {{\boldsymbol{a}}_t} $ 作为LSTM的输入得到预测结果$ {y_t} $ ,即$$ {y_t} = {{\rm{LSTM}}} ({{\boldsymbol{a}}_t}) $$ 2.4 损失函数
本文选择交叉熵损失函数来最小化预测值
$ {y_t} $ 和真实标签$ {r_t} $ 之间的差异性。交叉熵用来衡量当前训练得到的概率分布与真实分布的差异情况。它描述的是预测值与真实标签的距离,当交叉熵值越小时,2个概率分布就越接近。交叉熵损失函数的具体表达式为$$ L = - \sum\limits_t {({r_t}\ln {y_t} + (1 - {r_t})\ln (1 - {y_t}))} $$ 交叉熵损失函数是凸函数,因此在训练过程中,使用梯度下降法得到极小值,从而使得模型能够更准确地预测学习者的知识掌握情况。
3. 实验结果与分析
3.1 实验设置
3.1.1 知识追踪数据集
为了验证本文模型的有效性,实验分别在ASSISTments2009[31](ASSIST09)、ASSISTments2012(ASSIST12)[32]、EdNet[33]等3个公开的知识追踪数据集上进行性能验证。
ASSIST09和ASSIST12是ASSISTments在线辅导平台收集的答题记录数据,EdNet来自英语教学系统Santa。上述3个数据集来自于学习者与在线智能导学系统的交互日志,其中包含了关于学习者和题目以及交互记录,交互记录为学生与系统互动的详细记录,这包括学生对特定问题的回答情况以及问题所考察的概念,此外,它还涵盖了系统根据学生的回答提供的反馈以及学生对这些反馈的响应。因此它们非常适合于追踪学习者长期知识状态的变化。表1给出了这3个真实数据集的基本信息。
表 1 数据集信息Table 1 Datasets information数据集 学习者数 交互记录数 题目数 概念数 ASSIST09 3841 190320 15911 123 ASSIST12 27405 1867167 47104 265 EdNet 5000 222141 13169 188 3.1.2 实验设置
本实验所用实验设备为2.30 GHz的Intel(R) Core(TM) i5-8300H CPU,配备NVIDIA GeForce GTX
1060 显卡,配置了16 GB的内存。在Windos10操作系统中完成,采用Python 3.7编程语言,PyTorch 1.9.0深度学习框架。为充分利用GPU加速深度学习训练过程,使用了CUDA 11.0版本。训练前,在每个数据集中将70%的数据划分为训练集,30%的数据划分为测试集。在训练过程中,优化器选用Adam优化器,初始学习率设置为0.01, 参数的初始化选择服从
$\mathcal{N}(0,1)$ 分布。3.1.3 对比模型
为了验证该模型的有效性,本研究在3个公开的知识追踪数据集ASSIST09、ASSIST12、EdNet上与BKT、DKT、DKVMN、AKT、GIKT、IDKT模型性能表现进行对比实验。
选择上述模型的原因在于:BKT将迁移隐式表现在了学习者的知识状态中;DKT使用RNN的缺省机制客观上建模迁移过程;DKVMN使用动态键值记忆神经网络建模迁移遗忘;AKT使用注意力机制获取每个历史题目到当前题目的迁移过程;GIKT通过图神经网络对题目的迁移进行更丰富的表征;IDKT描述了历史题目包含的多个概念对当前题目产生的迁移作用。
3.2 性能比较
为了验证本文模型的有效性,将本文模型与传统的BKT、DKT、DKVMN、AKT、GIKT和IDKT等模型进行模型的曲线下面积(area under the curve, AUC)和准确率(accuracy, ACC)值对比。
AUC为受试者特征曲线(receiver operator characteristic curve, ROC)下与坐标轴围成的面积,这个面积的取值范围在0.5~1,如果AUC的值为0.5,说明模型是随机预测模型,AUC值越高则说明模型预测性能越好,AUC值越低则说明预测性能越差。ACC为准确率,即正确预测结果占所有预测结果的百分比,ACC的值越大,说明模型预测的越准确;ACC值越小,则说明模型预测的越不准确。实验对比结果如表2所示。
表 2 模型AUC/ACC对比Table 2 Model AUC/ACC comparison模型 ASSIST09 ASSIST12 EdNet AUC ACC AUC ACC AUC ACC BKT 0.657 0.611 0.620 0.596 0.602 0.593 DKT 0.756 0.653 0.728 0.708 0.682 0.673 DKVMN 0.755 0.726 0.728 0.703 0.696 0.684 AKT 0.789 0.714 0.772 0.752 0.731 0.713 GIKT 0.789 0.742 0.775 0.747 0.752 0.716 IDKT 0.779 0.751 0.786 0.758 0.744 0.717 ETKT 0.816 0.807 0.821 0.781 0.753 0.728 表2的对比模型可分为概率模型和深度模型。在深度模型中,IDKT在ASSIST09、ASSIST12和EdNet数据集上的AUC值达到了0.779、0.786和0.744,属对比模型中最高,整体表现良好,这是由于相较于其他对比模型IDKT描述了历史题目包含的多个概念对当前题目产生的迁移作用。AKT和GIKT在多个数据集上的性能表现较为平稳,虽未描述历史题目包含的多个概念对当前题目产生的迁移作用,但对题目的迁移进行了较为丰富的表征,与传统深度模型相比均有更好的表现。从实验结果可以看出,本文提出ETKT模型的AUC值和ACC值在3个公共数据集上远超概率模型,也超过对比的深度模型,具体地,在ASSIST09、ASSIST12和EdNet上的AUC值分别达到了0.816、0.821和0.753,ACC值分别达到了0.807、0.781和0.728,并且性能表现也很平稳。加入题目迁移表征能够改善知识追踪模型的性能,这是因为文中根据学习科学对学习迁移内在机制的描述建模了迁移权重和迁移遗忘,融合生成题目迁移表征,能够真实地反映题目迁移过程的本质信息。由实验结果可以看出,本文提出的ETKT模型相较于其他对比模型能够达到更准确的预测效果。
3.3 消融实验
本小节使用消融实验对比分析题目侧重表征、迁移权重表征和迁移遗忘表征在模型中的有效性。其中,ETKT-E表示熔断题目侧重表征部分,ETKT-W表示熔断迁移权重表征部分,ETKT-F表示熔断迁移遗忘表征部分。实验结果的AUC值对比如表3所示。
表 3 不同部分对模型性能的影响(AUC)Table 3 Impact of different data on model performance(AUC)消融模型 ASSIST09 ASSIST12 EdNet ETKT-E 0.759 0.736 0.716 ETKT-W 0.767 0.743 0.721 ETKT-F 0.784 0.747 0.737 ETKT 0.816 0.821 0.753 从实验结果来看,加入了题目侧重表征、迁移权重表征和迁移遗忘表征的模型其AUC值优于不加上述3个表征部分的模型。这表明本文建模题目迁移表征是有效的,归因于文中基于学习科学理论对学习迁移机制的建模构建了题目迁移表征,有效捕捉了题目迁移过程中的核心特征。ETKT-E模型在3个数据集上的AUC值低于ETKT-W和ETKT-F模型,说明熔断题目侧重表征部分会导致模型无法将更多的权重放在重点考察的概念上,无法有效提升模型的性能。ETKT-W和ETKT-F模型在3个真实数据集上的AUC值低于ETKT模型,说明仅建模概念考察侧重程度而忽略建模题目权重表征和迁移遗忘表征会导致学习迁移建模不完整,同样也无法显著提升模型的性能。
3.4 迁移可解释性验证
本文提出的ETKT模型通过题目侧重表征描述历史题目包含的概念考察侧重程度,迁移权重表征描述每道历史题目的迁移程度,迁移遗忘表征描述历史题目在迁移过程中的遗忘程度。
图3给出了ASSIST2009中随机选取的一位学习者作答15道题目的学习迁移过程。当前题目编号为15,包含概念2和61;历史题目编号为1~14,包含概念的序列如图3所示。本小节从题目侧重表征、迁移权重表征和迁移遗忘表征等层次来分析学习者作答的14道历史题目的学习迁移轨迹。
1)题目侧重表征层次。本文重点观察迁移权重较大的题目5、6和迁移权重较小的题目8。根据图3,题目5对概念2的考察权重为0.12,题目6对概念61的考察权重为0.84。题目8与当前题目15不包含相同概念2和61,其概念74的考察权重为0.74。可见本文提出的模型ETKT能够建模题目对不同概念的考察侧重程度。
2)迁移权重表征层次。所有历史题目中5和6迁移权重最大,分别为0.24和0.32。这是因为它们与当前题目15包含有共同概念2或61,可见ETKT能够建模学习迁移过程中与当前题目有共同概念的历史题目迁移程度更大的客观事实。而与当前题目不包含共同概念的历史题目8中概念74的考察权重较大,但最后迁移权重较小,为0.04。可见ETKT同时能够建模与当前题目无共同概念的历史题目迁移程度更小的客观事实。
3)迁移遗忘表征层次。历史题目5和6迁移遗忘权重较小,分别为0.29和0.11。这是因为它们与当前题目有共同概念2或61。可见ETKT能够建模迁移遗忘中与当前题目有共同概念的历史题目迁移遗忘程度更小的客观事实。历史题目8迁移遗忘权重较大,为0.84。这是因为它与当前题目无共同概念。可见ETKT能够建模迁移遗忘中与当前题目无共同概念的历史题目迁移遗忘程度更大的客观事实。
4. 结束语
本文针对现有知识追踪模型对学习迁移机制挖掘不深、无法显式表征题目迁移的问题,提出了一种题目迁移表征的知识追踪模型ETKT。首先在题目侧重表征方面,建模了迁移过程中题目包含的概念考察侧重程度;其次在迁移权重表征方面,衡量了历史题目到当前题目的迁移程度;然后迁移遗忘表征部分模拟了学习迁移中的遗忘过程;最终通过题目迁移表征融合迁移权重和迁移遗忘表征。通过在真实数据集上进行的多个实验,验证了本文提出的ETKT模型的有效性。同时进行了可解释性验证,相较于现有方法,为预测结果提供迁移路径层面的可视化解释。今后将探究更深层次的学习迁移机理,更合理地建模学习迁移过程,为学习者提供更好的自主学习支撑。
-
表 1 数据集信息
Table 1 Datasets information
数据集 学习者数 交互记录数 题目数 概念数 ASSIST09 3841 190320 15911 123 ASSIST12 27405 1867167 47104 265 EdNet 5000 222141 13169 188 表 2 模型AUC/ACC对比
Table 2 Model AUC/ACC comparison
模型 ASSIST09 ASSIST12 EdNet AUC ACC AUC ACC AUC ACC BKT 0.657 0.611 0.620 0.596 0.602 0.593 DKT 0.756 0.653 0.728 0.708 0.682 0.673 DKVMN 0.755 0.726 0.728 0.703 0.696 0.684 AKT 0.789 0.714 0.772 0.752 0.731 0.713 GIKT 0.789 0.742 0.775 0.747 0.752 0.716 IDKT 0.779 0.751 0.786 0.758 0.744 0.717 ETKT 0.816 0.807 0.821 0.781 0.753 0.728 表 3 不同部分对模型性能的影响(AUC)
Table 3 Impact of different data on model performance(AUC)
消融模型 ASSIST09 ASSIST12 EdNet ETKT-E 0.759 0.736 0.716 ETKT-W 0.767 0.743 0.721 ETKT-F 0.784 0.747 0.737 ETKT 0.816 0.821 0.753 -
[1] LIU Qi, SHEN Shuanghong, HUANG Zhenya, et al. A survey of knowledge tracing[EB/OL]. (2021−05−06)[2023−01−05]. https://ar5iv.org/abs/2105.15106.pdf. [2] 刘铁园, 陈威, 常亮, 等. 基于深度学习的知识追踪研究进展[J]. 计算机研究与发展, 2022, 59(1): 81–104. LIU Tieyuan, CHEN Wei, CHANG Liang, et al. Research progress in knowledge tracking based on deep learning[J]. Computer research and development, 2022, 59(1): 81–104. [3] RABINER L, JUANG B. An introduction to hidden Markov models[J]. IEEE ASSP magazine, 1986, 3(1): 4–16. doi: 10.1109/MASSP.1986.1165342 [4] CORBETT A T, ANDERSON J R. Knowledge tracing: modeling the acquisition of procedural knowledge[J]. User modeling and user-adapted interaction, 1994, 4(4): 253–278. [5] 黄诗雯, 刘朝晖, 罗凌云, 等. 融合行为和遗忘因素的贝叶斯知识追踪模型研究[J]. 计算机应用研究, 2021, 38(7): 1993–1997. HUANG Shiwen, LIU Zhaohui, LUO Lingyun, et al. Research on Bayesian knowledge tracing model integrating behavior and forgetting factors[J]. Computer application research, 2021, 38(7): 1993–1997. [6] PIECH C, BASSEN J, HUANG J. Deep knowledge tracing[J]. Advances in neural information processing systems, 2015, 28: 19–23. [7] ZHANG Jiani, SHI Xingjian, KING I, et al. Dynamic key-value memory networks for knowledge tracing[C]//Proceedings of the 26th International Conference on World Wide Web. New York: ACM, 2017: 765−774. [8] 李浩君, 卢佳琪, 吴嘉铭. 融合学习过程特征的深度知识追踪方法[J]. 浙江工业大学学报, 2022, 50(3): 245–252. LI Haojun, LU Jiaqi, WU Jiaming, et al. In-depth knowledge tracing method integrating learning process characteristics[J]. Journal of Zhejiang University of Technology, 2022, 50(3): 245–252. [9] 宗晓萍, 陶泽泽. 基于掌握速度的知识追踪模型[J]. 计算机工程与应用, 2021, 57(6): 117–123. ZONG Xiaoping, TAO Zeze. Knowledge tracing model based on mastery speed[J]. Computer engineering and application, 2021, 57(6): 117–123. [10] 李浩君, 高鹏. 融合梯度提升回归树的深度知识追踪优化模型[J]. 系统科学与数学, 2021, 41(8): 2101–2112. LI Haojun, GAO Peng. Deep knowledge tracing optimization model integrated with gradient boosting regression tree[J]. Systems science and mathematics, 2021, 41(8): 2101–2112. [11] SUN Xia, ZHAO Xu, MA Yuna, et al. Muti-behavior features based knowledge tracking using decision tree improved DKVMN[C]//Proceedings of the ACM Turing Celebration Conference. Chengdu: ACM, 2019: 1−6. [12] 姚梅林. 学习迁移研究的新进展[J]. 北京师范大学学报(社会科学版), 1994(5): 99–104. YAO Meilin. New progress in learning transfer research[J]. Journal of Beijing Normal University (social science edition), 1994(5): 99–104. [13] ZAREMBA W, SUTSKEVER I, VINYALS O. Recurrent neural network regularization[EB/OL]. (2014−09−08)[2023−01−06]. https://ar5iv.org/abs/1409.2329.pdf. [14] 刘坤佳, 李欣奕, 唐九阳, 等. 可解释深度知识追踪模型[J]. 计算机研究与发展, 2021, 58(12): 2618–2629. LIU KunJia, LI Xinyi, TANG Jiuyang, et al. Interpretable deep knowledge tracing model[J]. Computer research and development, 2021, 58(12): 2618–2629. [15] YANG Yang, SHEN Jian, QU Yanru, et al. GIKT: a graph-based interaction model for knowledge tracing[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Cham: Springer, 2020: 299−315. [16] DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[J]. Advances in neural information processing systems, 2016, 29: 3844–3852. [17] LIU Yunfei, YANG Yang, CHEN Xianyu, et al. Improving knowledge tracing via pre-training question embeddings[EB/OL]. (2020−12−09)[2023−01−05]. https://ar5iv.org/abs/2012.05031.pdf. [18] 马骁睿, 徐圆, 朱群雄. 一种结合深度知识追踪的个性化习题推荐方法[J]. 小型微型计算机系统, 2020, 41(5): 990–995. MA Xiaorui, XU Yuan, ZHU Qunxiong. A personalized exercise recommendation method combined with deep knowledge tracing[J]. Small microcomputer system, 2020, 41(5): 990–995. [19] 邵小萌, 张猛. 融合注意力机制的时间卷积知识追踪模型[J]. 计算机应用, 2023, 43(2): 343–348. SHAO Xiaomeng, ZHANG Meng. Temporal convolutional knowledge tracing model with attention mechanism[J]. Journal of computer applications, 2023, 43(2): 343–348. [20] BAI S, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. (2018−03−04)[2023−01−06]. https://ar5iv.org/abs/1803.01271.pdf. [21] GHOSH A, HEFFERNAN N, LAN A S. Context-aware attentive knowledge tracing[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020: 2330−2339. [22] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30: 5998–6008. [23] NAGATANI K, ZHANG Q, SATO M, et al. Augmenting knowledge tracing by considering forgetting behavior[C]//The World Wide Web Conference. New York: IW3C2, 2019: 3101−3107. [24] 李晓光, 魏思齐, 张昕, 等. LFKT: 学习与遗忘融合的深度知识追踪模型[J]. 软件学报, 2021, 32(3): 818–830. LI Xiaoguang, WEI Siqi, ZHANG Xin, et al. LFKT: deep knowledge tracing model with learning and forgetting behavior merging[J]. Journal of software, 2021, 32(3): 818–830. [25] 王璨, 刘朝晖, 王蓓, 等. TCN-KT: 个人基础与遗忘融合的时间卷积知识追踪模型[J]. 计算机应用研究, 2022, 39(5): 1496–1500. WANG Can, LIU Zhaohui, WANG Bei, et al. TCN-KT: time convolutional knowledge tracing model for fusion of personal basis and forgetting[J]. Computer application research, 2022, 39(5): 1496–1500. [26] PANDEY S, SRIVASTAVA J. RKT: relation-aware self-attention for knowledge tracing[C]//Proceedings of the 29th ACM International Conference on Information & Knowledge Management. New York: ACM, 2020: 1205−1214. [27] GAN W, SUN Y, PENG X, et al. Modeling learner’s dynamic knowledge construction procedure and cognitive item difficulty for knowledge tracing[J]. Applied intelligence, 2020, 50: 3894–3912. doi: 10.1007/s10489-020-01756-7 [28] SCHMIDHUBER J, HOCHREITER S. Long short-term memory[J]. Neural comput, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735 [29] BAHDANAU D, CHO K, BENGIO Y. Neural machine translation by jointly learning to align and translate[EB/OL]. (2014−09−01)[2023−01−05]. https://ar5iv.org/abs/1409.0473.pdf. [30] SU Yu, LIU Qingwen, LIU Qi, et al. Exercise-enhanced sequential modeling for student performance prediction[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2018: 2435−2443. [31] FENG M, HEFFERNAN N, KOEDINGER K. Addressing the assessment challenge with an online system that tutors as it assesses[J]. User modeling and user-adapted interaction, 2009, 19: 243–266. doi: 10.1007/s11257-009-9063-7 [32] KOEDINGER K R, BAKER R S J, CUNNINGHAM K, et al. A data repository for the EDM community: the PSLC datashop[J]. Handbook of educational data mining, 2010, 43: 43–56. [33] CHOI Y, LEE Y, SHIN D, et al. Ednet: a large-scale hierarchical dataset in education[C]//21st International Conference on Artificial Intelligence in Education. Cham: Springer, 2020: 69-73.






























 下载:
下载: