Local path planning for AUV with fusion of DWA and RRT algorithms in a complex environment
-
摘要: 针对复杂水下环境下的自主水下航行器（autonomous underwater vehicle，AUV）局部路径规划问题，传统动态窗口法(dynamic window approach，DWA）存在复杂障碍物中陷入局部停滞，动态避障性能不佳等问题，本文提出了一种基于DWA与快速随机搜索树（rapid-exploration random tree，RRT)算法融合的路径规划算法。改进的DWA算法速度空间根据整个动态窗口的周期生成，重设了评价函数并结合AUV任务环境引入洋流能耗评价函数；改进的RRT算法在局部已知空间内规划导引点，帮助DWA脱离局部停滞状态并实现更安全的动态避障。将2种算法融合，实现了AUV在复杂水下环境中的局部路径规划。仿真表明，该融合算法能够降低AUV在洋流中的能耗代价，解决了DWA在复杂障碍物中陷入局部停滞的问题，能够安全有效地躲避动态避障物。Abstract: For the local path planning problem of autonomous underwater vehicle (AUV) in a complex underwater environment, traditional dynamic window approach(DWA) has the problems of getting into local stagnation in complex obstacles and poor dynamic obstacle avoidance performance, etc. In this paper, we propose a path planning algorithm based on the fusion of DWA and Rapid-exploration random tree(RRT) algorithms. The improved DWA algorithm generates the velocity space based on the whole dynamic window period, resets the evaluation function and introduces the evaluation function of ocean current energy consumption in an AUV mission environment; the improved RRT algorithm plans the guide points in a local known space, which helps DWA to get out of the local stagnation and achieve a safer dynamic obstacle avoidance. The two algorithms are fused to achieve local path planning for AUV in a complex underwater environment. Simulations show that the fusion algorithm can reduce the energy cost of AUV in ocean currents, solve the problem of DWA getting into local stagnation in complex obstacles, and can avoid dynamic obstacles safely and effectively.
-
路径规划是自主水下航行器（autonomous underwater vehicle，AUV）进行水下任务的基础。水下环境复杂多变[1-2]，存在无法预先获知的静态、动态障碍物。为了保证水下任务的可执行性，AUV需具备局部规划能力，即使在复杂障碍物环境中也要具备对目标点的可到达性[3-4]，对动态障碍物也要能安全有效地避碰[5]。
目前常用的移动机器人局部路径规划算法有人工势场法（artificial potential field，APF）、速度障碍法（velocity obstacle，VO）、动态窗口法（dynamic window approach，DWA）、时间弹性带法（time elastic band，TEB）等[6-8]，其中DWA算法能够生成包含速度、航向角和时间等运动状态信息的运动轨迹，可构建多指标的评价函数，计算复杂度低，能够动态规划实时避障,但避障效果一般[9]。Molinos等[10]提出用以处理动态障碍物的动态障碍动态窗口算法（dynamic window approach for dynamic obstacles，DW4DO）和动态窗口障碍树算法（dynamic window approach for dynamic obstacles tree，DW4DOT），在栅格中加入障碍物占用时间等信息，扩展了栅格的数据维度，并在动态窗口内实现多级速度预测，实现了比传统DWA更安全、平滑的路径规划。Shen等[11]引入Q-learning强化学习算法，用于学习DWA目标函数的权值，可以在不同的环境中选择合适的权值，提高DWA在复杂环境中的适用性。张伟龙等[12]引入障碍物预测轨迹和权重因子改进了传统DWA的距离评价函数,提高了水面无人船（unmanned surface vessel，USV）躲避多个动态障碍物的能力。庞永旭等[13]对传统A星搜素算法（a star，A*）进行改进，并融合DWA实现动态实时避障。张振等[14]在传统 A*算法的评价函数中加入环境中障碍物信息和父节点到目标点的代价信息，提高路径搜索效率并基于安全阈值提取路径关键点，优化搜索路径；将优化后的关键点作为 DWA 算法的临时目标点，将2种算法融合规划出一条基于全局最优的圆滑曲线路径。综合已有的研究成果，发现以上研究都存在不足，文献[10]实现动态窗口内的多级速度预测，但仍不是动态窗口可达到的全部速度空间；文献[11-12]对于DWA算法的改进虽提升了避障性能，但未解决DWA由于局部评价值最优而导致停滞在局部的问题；文献[13-14]提出的A*与DWA融合算法适用于全局路径规划，不能很好地应用在未知复杂障碍物环境中。
快速扩展随机树（rapidly exploring random tree，RRT）算法结构简单，具有高效、随机、环境建模简单等优势[15]。文献[16-17]将双向快速随机搜索树算法与粒子群算法相结合，不仅具备了对未知空间的搜索能力且得到了较为平滑的路径。文献[18]将滚动规划与改进RRT算法相结合，实现了AUV在未知三维环境中的路径规划。基于此类算法研究，虽能将RRT引入至未知环境的路径规划，且保证全局目标的可到达性，但规划的路径只考虑障碍物的约束并不考虑对象的运动状态，因此规划的路径并非实际可达，无法对于动态障碍物进行避障。 针对以上问题，本文提出了一种DWA与RRT算法融合的局部路径规划算法，该算法能够降低AUV在洋流环境中的能耗代价，解决DWA在复杂障碍物中陷入局部停滞的问题，并实现更安全的动态避障，其主要创新点有：1）改进RRT，将RRT用于局部目标点的搜索，并加入关键点提取策略剔除冗余节点；2）改进DWA算法的速度空间和评价函数，新增洋流能耗评价函数；3）加入障碍物采样窗口，当在窗口内无法绕开障碍物时，引入改进RRT为DWA规划导引点，避免陷入局部停滞；4）根据障碍物运动状态，计算避障风险、危险区域，当存在碰撞危险时引入改进RRT规划导引点及时躲避；5）将RRT规划的导引点加入DWA 算法的评价体系中，实现算法融合。
1. 问题描述及模型建立
1.1 问题描述
本文研究了AUV的局部路径规划问题，考虑水下环境中的洋流、未知的复杂障碍物和动态障碍物等干扰。环境空间栅格化处理映射至连续空间，AUV在连续空间中运动，考虑其旋转和前向运动以及速度限制，AUV的任务为安全到达目标点。本文的分析中提出以下假设：
假设1 洋流、障碍物与AUV处于同一水平面。
假设2 AUV能够借助海流计、声呐等传感器设备获取环境信息，包括洋流速度、障碍物的位置、动态障碍物的大小和速度。
假设3 AUV按规划路径航行，且运动参数与规划参数一致。
1.2 AUV运动学模型
本文选取文献[19]中介绍的Minesniper MkII 鱼雷型AUV为研究对象，引入了AUV运动学模型。将
$ {{\boldsymbol{S}}_k} = \left\{ {{x_k},{y_k},{\varphi _k}} \right\} $ 定义为AUV状态向量，其中$\left\{ {{x_k},{y_k}} \right\}$ 代表AUV在k时刻的位置，${\varphi _k}$ 代表AUV艏向角，即AUV水平转角。AUV运动学方程可以简化为$$ {{\boldsymbol{S}}_{k + 1}} = {{\boldsymbol{S}}_{k + 1}} + f\left( {{{\boldsymbol{S}}_k},{v_k},{{\dot \varphi }_k}} \right) $$ 其中
$$ f\left( {{{\boldsymbol{S}}_k},{v_k},{{\dot \varphi }_k}} \right) = \left[ {\begin{array}{*{20}{c}} {\left( {{v_k} + {{\dot v}_k}} \right)\cos \left( {{\varphi _k} + {{\dot \varphi }_k} \cdot \Delta t} \right) \cdot \Delta t} \\ {\left( {{v_k} + {{\dot v}_k}} \right)\sin \left( {{\varphi _k} + {{\dot \varphi }_k} \cdot \Delta t} \right) \cdot \Delta t} \\ {{\varphi _k} + {{\dot \varphi }_k} \cdot \Delta t} \end{array}} \right] $$ 式中
${v_k}$ 为AUV运动速度。根据AUV性能参数和任务要求，AUV在进行动态路径规划时应满足以下约束条件：$$ \left\{\begin{array}{l}0 \leqslant {v}_{k} \leqslant 2\\ -\dfrac{\text{π}}{3} \leqslant {\dot \varphi }_{k} \leqslant \dfrac{\text{π}}{3}\end{array} \right.$$ 1.3 声呐模型
本文引入文献[20]中的声呐模型，采用英国Tritech公司的Micron DST紧凑型数字成像声呐用于地图构建和信息探测。它能通过不断旋转换能器，发送一个狭窄的扇形声束来扫描周围的环境。该声呐的工作频率为700 kHz，水平波束角和垂直波束角分别为30°和3°，能够实现一个完整的360°扇区扫描，最大范围可达100 m。
AUV大范围路径规划多处于同一水平面，且二维与三维规划算法无本质区别，文中对声呐进行简化。满足以下条件的物体可被 AUV 声呐探测到：
$$ {\left(x-{x}_{0}\right)}^{2}+{\left(y-{y}_{0}\right)}^{2} \leqslant {r}^{2} $$ 式中：
$ \left( {{x_0},{y_0}} \right) $ 为 AUV 的坐标，$ \left( {x,y} \right) $ 为物体坐标，$r$ 为探测距离阈值。1.4 水下环境模型
1.4.1 静态障碍物模型
由静态栅格组成存在半封闭空间的不规则障碍物模型，用于模拟海底山脉、峡谷等复杂地形。黑色栅格区域表示障碍物区域，空白区域表示可通行区域[21]。
1.4.2 动态障碍物模型
为增加动态避障的安全性，根据动态障碍物的体长将其膨胀为等直径的圆形，假设在局部区域内运动呈线性，运动学方程可以表示为
$$ \left[ {\begin{array}{*{20}{l}} {{x_{k + 1}}} \\ {{{\dot x}_{k + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 1&T \\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{x_k}} \\ {{{\dot x}_k}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} 1&0 \\ 1&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\omega _k}} \\ {{{\ddot x}_k}} \end{array}} \right] $$ 式中：
${x_k}$ 、${\dot x_k}$ 、${\ddot x_k}$ 分别为目标在$k$ 时刻的位置、速度和加速度，${\omega _k}$ 为高斯白噪声，$T$ 为采样时间。1.4.3 洋流模型
将一系列具有潮汐成分频率的正、余弦函数作为时间基函数。并用
$y$ 来表示洋流在东西和南北方向上的速度，洋流速度模型为$$ \begin{gathered} y(p,t) = {y_0}(p) + \\ \sum\limits_{i = 1}^N {\left[ {{g_i}(p)\cos \left( {{a_i}t} \right) + \sum\limits_{i = 1}^N {\left[ {{h_i}(p)\sin \left( {{a_i}t} \right)} \right]} } \right]} \\ \end{gathered} $$ 式中：
$N$ 为海域中频率成分个数，$p$ 为节点的位置，${y_0}(p)$ 表示在观察时间段内洋流速度的平均值，${g_i}(p)$ 、${h_i}(p)$ 是与节点位置相关的函数[22]。洋流在地图中栅格化表示，每个栅格中洋流速度大小和方向与栅格中心点保持一致。2. 基于改进DWA算法的AUV局部路径规划
本文局部路径规划方法基于DWA，该方法是基于速度采样的局部规划算法。它在空间中对多组速度和艏向角速度
$ \left( {v,\omega } \right) $ 进行采样，并模拟AUV在预测周期内的轨迹[23]，选出最优轨迹进入下一运动周期，重复此过程在线实时规划路径。本文对DWA进行改进以避障性能和环境适应性。2.1 轨迹模拟
基于运动方程和采样速度预估AUV在预测周期内的运动轨迹，预测周期分为多个时刻，2个相邻时刻之间的间隔为一个运动周期，由于间隔较短，因此可以将AUV在每个运动周期内的运动简化为线性运动，并根据下式更新轨迹信息：
$$ \left[ {\begin{array}{*{20}{l}} {{x_{k + 1}}} \\ {{y_{k + 1}}} \\ {{\varphi _{k + 1}}} \\ {{v_{k + 1}}} \\ {{\omega _{k + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_k}} \\ {{y_k}} \\ {{\varphi _k}} \\ 0 \\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\varphi _k}} \right) \cdot \tau }&0 \\ {\sin \left( {{\varphi _k}} \right) \cdot \tau }&0 \\ 0&\tau \\ 1&0 \\ 0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{v_u}} \\ {{\omega _u}} \end{array}} \right] $$ 式中
$ {v_u} $ 、$ {\omega _u} $ 为下一时刻期望的速度和艏向角速度。2.2 改进速度空间
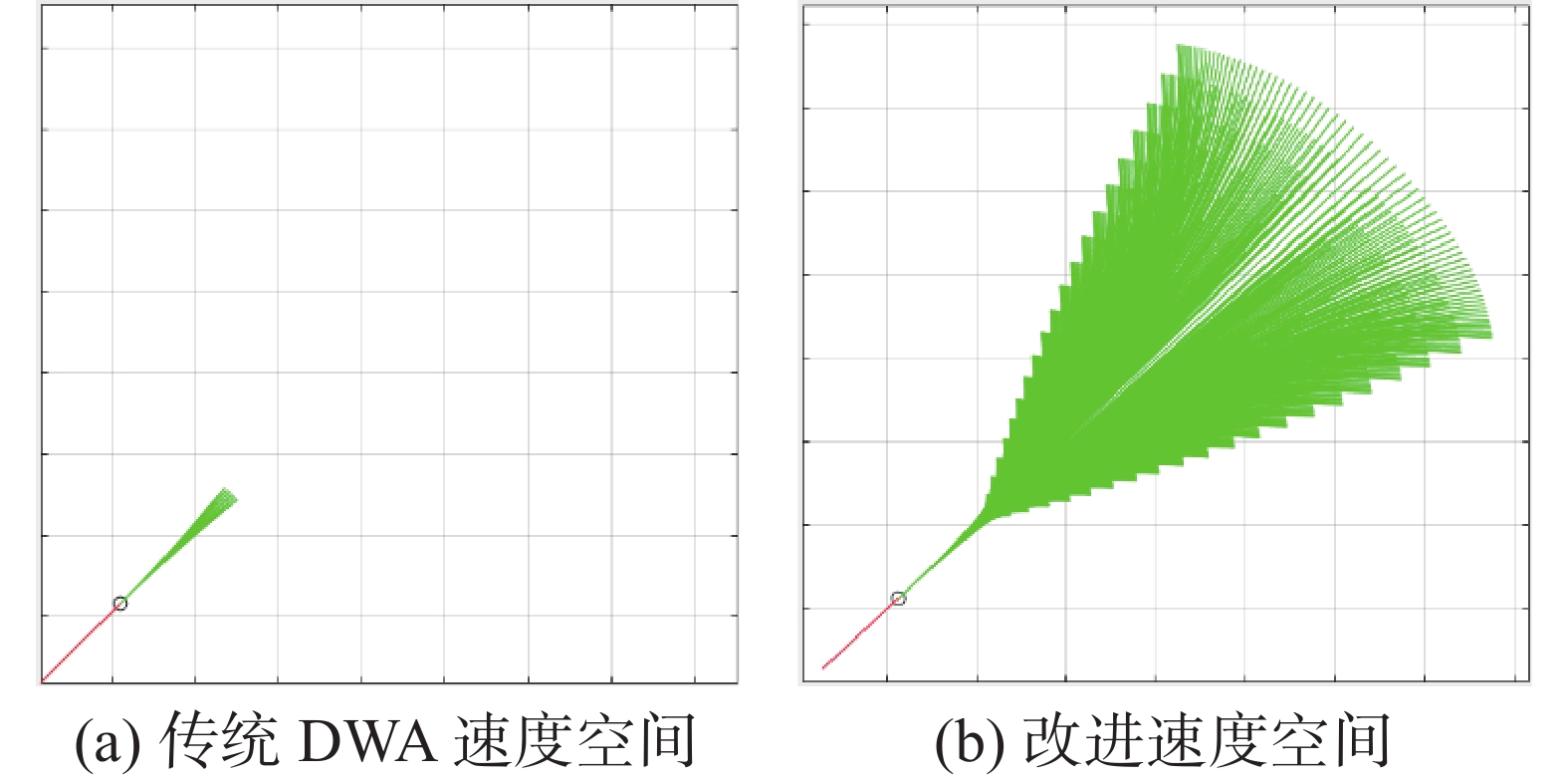
传统DWA只根据第一个运动周期后能达到的速度范围建立速度空间，这种方式预测出的轨迹不能完整体现AUV的运动性能，可能会损失实际可行且更优的运动轨迹。改进后的DWA算法会计算AUV在动态窗口内的所有运动周期后能达到的速度空间，用于采样生成预测轨迹。改进后的速度空间为
$$ {{\boldsymbol{V}}_w} = \left\{ {{{\left[ {{v_w},{\omega _w}} \right]}^{\rm{T}}}} \right\} $$ 其中
$$ \left\{ \begin{gathered} {v_w} \in \left[ {\max \left( {0,{v_{a0}} - aT} \right),\min \left( {{v_{\max }},{v_{a0}} + aT} \right)} \right] \\ {\omega _w} \in \left[ {\max \left( { - {\omega _{\max }},{\omega _{a0}} - \alpha T} \right),\min \left( {{\omega _{\max }},{\omega _{a0}} + \alpha } \right)} \right] \\ \end{gathered} \right. $$ 式中：
$ {v_w} $ 、$ {\omega _w} $ 分别为动态窗口内AUV速度、艏向角速度，$ {v_{a0}} $ 、$ {\omega _{a0}} $ 分别为窗口初始AUV速度、艏向角速度，$ a $ 、$ \alpha $ 分别为AUV最大加速度、最大艏向角加速度，$ {v_{\max }} $ 为AUV最大速度，$ T $ 为预测周期，max(∙)为最大值函数，min(∙)为最小值函数。生成速度空间后，以采样率
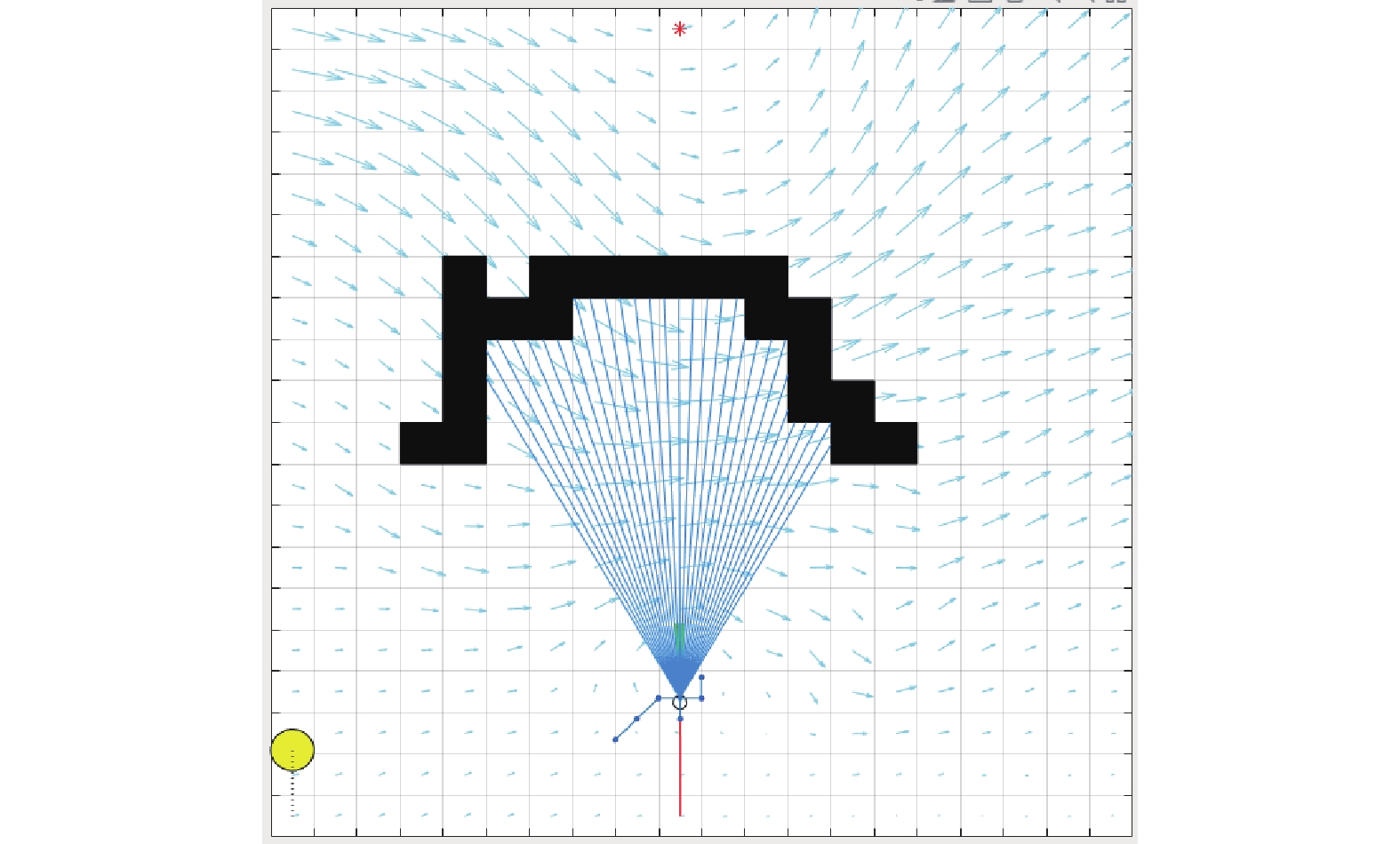
$l_s$ 进行采样，每种采样速度状态${{\boldsymbol{V}}_s} = \left\{ {{v_s},{\omega _s}} \right\}$ 作为一条轨迹的预期速度状态，结合AUV运动模型生成预测周期内的轨迹，如图1所示，绿色实线为预测轨迹，改进速度空间后每个预测周期内可评价轨迹的数量和广度都将显著增加。
图 1 AUV预测轨迹Fig. 1 AUV predicted trajectory
下载:
全尺寸图片
由于AUV性能限制，有些采样速度需要若干个运动周期才能达到，所以每条轨迹的每个运动周期都计算并刷新一次速度状态
$ {{\boldsymbol{V}}_{{s_i}}} = \left[ {{v_{{s_i}}},{\omega _{{s_i}}}} \right] $ ，其中：$$ {v_{{s_i}}} = \left\{ \begin{array}{*{20}{l}} {\max \left( {{v_{{s_{i - 1}}}} - a\tau ,{v_{{s_i}}}} \right),}\;\;\;\;{{v_{{s_{i - 1}}}} > {v_s}}\\ {\min \left( {{v_{{s_{i - 1}}}} + a\tau ,{v_{{s_i}}}} \right),}\;\;\;\;{{v_{{s_{i - 1}}}} < {v_s}}\\ {{v_s},}\;\;\;\;其他 \end{array} \right. $$ $$ {\omega _{{s_i}}} = \left\{ \begin{array}{*{20}{l}} {\max \left( {{\omega _{{s_{i - 1}}}} - a\tau ,{\omega _{{s_i}}}} \right),}\;\;\;\;{{\omega _{{s_{i - 1}}}} > {\omega _s}}\\ {\min \left( {{\omega _{{s_{i - 1}}}} + a\tau ,{\omega _{{s_i}}}} \right),}\;\;\;\;{{\omega _{{s_{i - 1}}}} < {\omega _s}}\\ {{\omega _s},}\;\;\;\;其他 \end{array} \right. $$ 式中：
$ {v_{{s_i}}} $ 、$ {\omega _{{s_i}}} $ 分别表示当前运动周期的速度与艏向角速度，$ {v_{{s_{i - 1}}}} $ 、$ {\omega _{{s_{i - 1}}}} $ 分别为上个运动周期的速度与艏向角速度，$ \tau $ 为运动周期。2.3 改进评价函数
DWA根据评价函数为每条预测轨迹打分，选出评价值最高的一条轨迹[24]，作为AUV的期望运动轨迹。传统DWA包括航向、速度以及障碍物距离3种评价函数。本文优化并重设了评价函数，新增洋流能耗评价函数，帮助AUV在动态洋流环境中节省能耗，新的评价函数为
$$ \begin{gathered} {f_{{\text{eval }}}}(v,\omega ) = \frac{{{C_{{\text{goal }}}} \cdot {{\rm{goal}}} (v,\omega )}}{{\displaystyle\sum\limits_{i = 1}^{{n_t}} {{{\rm{goal}}} } {{(v,\omega )}_i}}} + \frac{{{C_{{\text{velocity }}}} \cdot {\text{velocity }}(v)}}{{\displaystyle\sum\limits_{i = 1}^{{n_t}} {{{\rm{velocity}}} } {{(v)}_i}}} + \\ \frac{{{C_{{\text{obstacle }}}} \cdot {\text{obstacle }}(v,\omega )}}{{\displaystyle\sum\limits_{i = 1}^{{n_t}} {{{\rm{velocity}}} } {{(v)}_i}}} + \frac{{{C_{{\text{currentE }}}} \cdot {\text{currentE }}(v,\omega )}}{{\displaystyle\sum\limits_{i = 1}^{{n_t}} {{\text{ currentE }}} {{(v,\omega )}_i}}} \\ \end{gathered} $$ 式中：
$ {{\rm{goal}}} (v,\omega ) $ 为目标评价函数，$ {\text{velocity }}(v) $ 为速度评价函数，$ {\text{obstacle }}(v,\omega ) $ 为障碍物评价函数，$ {\text{currentE }}(v,\omega ) $ 为洋流能耗评价函数，$ {C_{{\text{goal }}}} $ 、$ {C_{{\text{velocity }}}} $ 、$ {C_{{\text{obstacle }}}} $ 和$ {C_{{\text{currentE }}}} $ 分别为各评价函数对应的权重系数。2.3.1 目标评价函数
目标评价函数根据AUV与目标点的航向差异和距离进行评价，期望AUV能够朝向目标点行驶，且与目标点的欧氏距离越来越小。目标评价函数为
$$ \begin{array}{l}\mathrm{goal}(v,\omega )=\left\{\begin{array}{l}\dfrac{\text{π}-\left|\mathrm{atan}2\left({X}_{\text{goal }}-{X}_{a}\right)-{\varphi }_{a}\right|}{{C}_{{d}}\Vert {X}_{\text{goal }}-{X}_{a}\Vert },\;\;\;\Delta \varphi \leqslant \text{π}\\ \dfrac{\left|\mathrm{atan}2\left({X}_{\text{goal }}-{X}_{a}\right)-{\varphi }_{a}\right|-\text{π}}{{C}_{{d}}\Vert {X}_{\text{goal }}-{X}_{a}\Vert }\text{, }\;\;\;其他\end{array}\right. \end{array} $$ 式中：
$ {X_a} $ 、$ {X_{{\text{goal}}}} $ 分别为预测轨迹末端AUV的笛卡尔空间坐标和目标点的笛卡尔空间坐标，$ {\varphi _a} $ 、$ \Delta \varphi $ 分别为预测轨迹末端AUV的艏向角、艏向角与目标方向的差角，$ {C_d} $ 为权重调节系数，$ \mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}2 ({{x}}_{2}-{{x}}_{1}) $ 函数返回点$X_1$ 至点$X_2$ 的方位角。2.3.2 速度评价函数
速度评价函数期望找到通行速度更快的轨迹，从而减少达到目标的时间。由于局部规划算法没有全局视野，可能无法找全局时间最短的路径。但该评价函数被证明有效，如果没有该评价函数可能会因其他评价函数互相抗衡而导致机器人速度过慢，甚至停滞于局部[10]。
传统DWA由于每条轨迹中速度保持一致，速度评价函数根据各轨迹的采样速度进行评价，改进DWA允许轨迹中存在速度变化，所以速度评价函数改为根据每条轨迹的平均速度进行评价，表达式为
$$ {{\rm{velocity}}} (v) = \frac{{\displaystyle\sum\limits_{i = 2}^{{T}/{\tau }} {\left\| {{X_i} - {X_{i - 1}}} \right\|} }}{\tau } $$ 式中
$ {X_{i - 1}} $ 、$ {X_i} $ 为前一时刻和后一时刻AUV位置坐标。2.3.3 障碍物评价函数
传统DWA的障碍物评价函数根据轨迹末端与障碍物的距离进行评价，并不能全面客观地评价整条轨迹与障碍物的距离关系，改进后的障碍物评价函数根据轨迹与障碍物的最短距离进行评价，距离越远评价值越高，表达式为
$$ {{\rm{obstacle}}} (v,\omega ) = \min \left( {\left\| {{X_{oi}} - {X_{ai}}} \right\|} \right) $$ 式中
$ {X_{ai}} $ 、$ {X_{oi}} $ 分别${\mathrm{y}}_{{a}{i}}$ 为轨迹中某节点的坐标和据该点最近的障碍物点坐标。为保证安全性，根据AUV速度计算AUV与障碍物间需保持的安全距离，当预测轨迹中存在小于安全距离的节点时不会将该轨迹加入待评价轨迹簇中。安全距离计算表达式为
$$ {S_d} = \frac{{{v_a}^2}}{{2a}} $$ 2.3.4 洋流能耗评价函数
新增洋流能耗评价函数，根据轨迹中所有节点所受洋流能耗代价之和进行评价，能耗代价越小评价值越高。表达式为
$$ {{\rm{currentE}}} (v,\omega ) = \sum\limits_{i = 1}^{{T}/{\tau }} {{E_{{\text{nod}}{{\text{e}}_i}}}} $$ 式中：
$ {E_{{\text{nod}}{{\text{e}}_i}}} $ 为轨迹中某节点的洋流能耗代价，基于动能公式，根据AUV与洋流的速度、方向角关系计算，计算方法为当
${v}_{ai} \geqslant {v}_{ci}$ 且$\Delta {\varphi _i} = 2k{\text{π }}(k = 0,1, \cdots )$ 时$$ {E_{{\text{nod}}{{\text{e}}_i}}} = \frac{{2{\text{π }}}}{{ - v_{ci}^2}} $$ 当
$ {v_{ai}} < {v_{ci}} $ 且$\Delta {\varphi _i} = 2k{\text{π }}(k = 0,1, \cdots )$ 时$$ {E_{{\text{nod}}{{\text{e}}_i}}} = \frac{{2{\text{π }}}}{{{{\left( {{v_{ci}} - {v_{ai}}} \right)}^2}}} $$ 当
$0 < \Delta {\varphi _i} < \dfrac{{\text{π }}}{2}$ 时$$ {E_{{\text{nod}}{{\text{e}}_i}}} = \frac{{2{\text{π }} - \left| {{\varphi _{ci}} - {\varphi _{ai}}} \right|}}{{v_{ci}^2\left( {{{\sin }^2}\left| {{\varphi _{ai}} - {\varphi _{ci}}} \right| - {{\cos }^2}\left| {{\varphi _{ai}} - {\varphi _{ci}}} \right|} \right)}} $$ 当
$ {\text{π }} < \Delta {\varphi _i} < 2{\text{π }} $ 且$2{\text{π }} - \left( {\left| {{\varphi _{ai}}} \right| + \left| {{\varphi _{ai}}} \right|} \right) < \dfrac{{\text{π }}}{2}$ 时$$ {E_{{\text{nod}}{{\text{e}}_i}}} = \frac{{\left( {\left| {{\varphi _{ai}}} \right| + \left| {{\varphi _{ci}}} \right|} \right)}}{{v_{ci}^2\left( {{{\sin }^2}\left( {2{\text{π }} - \left| {{\varphi _{ai}}} \right| - \left| {{\varphi _{ci}}} \right|} \right)} \right. - \left. {{{\cos }^2}\left( {2{\text{π }} - \left| {{\varphi _{ai}}} \right| - \left| {{\varphi _{ci}}} \right|} \right)} \right)}}{\text{ }} $$ 其余情况时
$$ {E_{{\text{nod}}{{\text{e}}_i}}} = \frac{{\text{π }}}{{v_{ci}^2}} $$ 式中：
$ {v_{ai}} $ 、$ {\varphi _{ai}} $ 为某节点处AUV的速度和艏向角，$ {v_{ci}} $ 、$ {\varphi _{ci}} $ 为该节点处洋流的速度与方向角，$ \Delta {\varphi _i} $ 为该节点处AUV艏向角与洋流方向的夹角。2.4 加入障碍物采样窗口
传统DWA在进入复杂障碍物半封闭空间或与前方障碍物距离过近时会因评价值的局部最优陷入停滞状态[25]，无法规划绕开障碍物的路径。为解决该问题，在声呐范围内加入采样窗口，如图2所示，用于判断前方是否存在连续的障碍物空间，对是否会陷入停滞进行预测。
图 2 障碍物采样窗口Fig. 2 Obstacle sampling window下载:
全尺寸图片
以AUV坐标点位为原点，AUV艏向为极轴建立极坐标系，采样窗口的空间为
$$ {{\boldsymbol{S}}_w} = \left\{ {{{\left( {{\theta _w},{d_w}} \right)}^{\rm{T}}}\mid {\theta _w} \in \left[ {0,{\theta _r}} \right] \cup \left( {0,2{\text{π }} - {\theta _r}} \right],{d_w} \in [0,\rho ]} \right\} $$ 式中：
$ {\theta _w} $ 为采样角度，$ {d_w} $ 为采样距离，$ {\theta _r} $ 为开角参数，$ \rho $ 为距离参数。在此空间内以采样角度
$ {\theta _r} $ 和距离$ \rho $ 设置采样线。若采样线被障碍物遮挡，则该采样线被障碍物占用，占用值$ {l_{oi}} $ 为1，根据每条采样线的占用值计算窗口的占用值。$$ {F}_{a}=\left\{\begin{array}{l}1,\;\;\;\;{F}_{o}=0 \\ 0,\;\;\;\; 其他\text{ } \end{array} \right.$$ 其中
$$ {F_o} = \sum\limits_{i = 1}^{\tfrac{{2{\theta _r}}}{{{\theta _w}}} + 1} {\left| {{l_{oi}} - 1} \right|} $$ 式中：
$ {l_{oi}} $ 为采样线占用值；$ {F_o} $ 为所有采样线占用值的相反数之和；$ {F_a} $ 为窗口的占用值，当$ {F_a} $ =1时，认为窗口被障碍物占用，AUV运动前向没有可以逃离障碍物的通路，存在陷入停滞的风险。为避免算法陷入局部停滞，本文提出将DWA与RRT算法融合，利用RRT的快速性和大范围搜索能力规划避障导引点，引导DWA规划路径及时逃离局部障碍物区域。
3. 融合改进DWA算法与改进RRT算法后的局部路径规划
3.1 融合算法流程
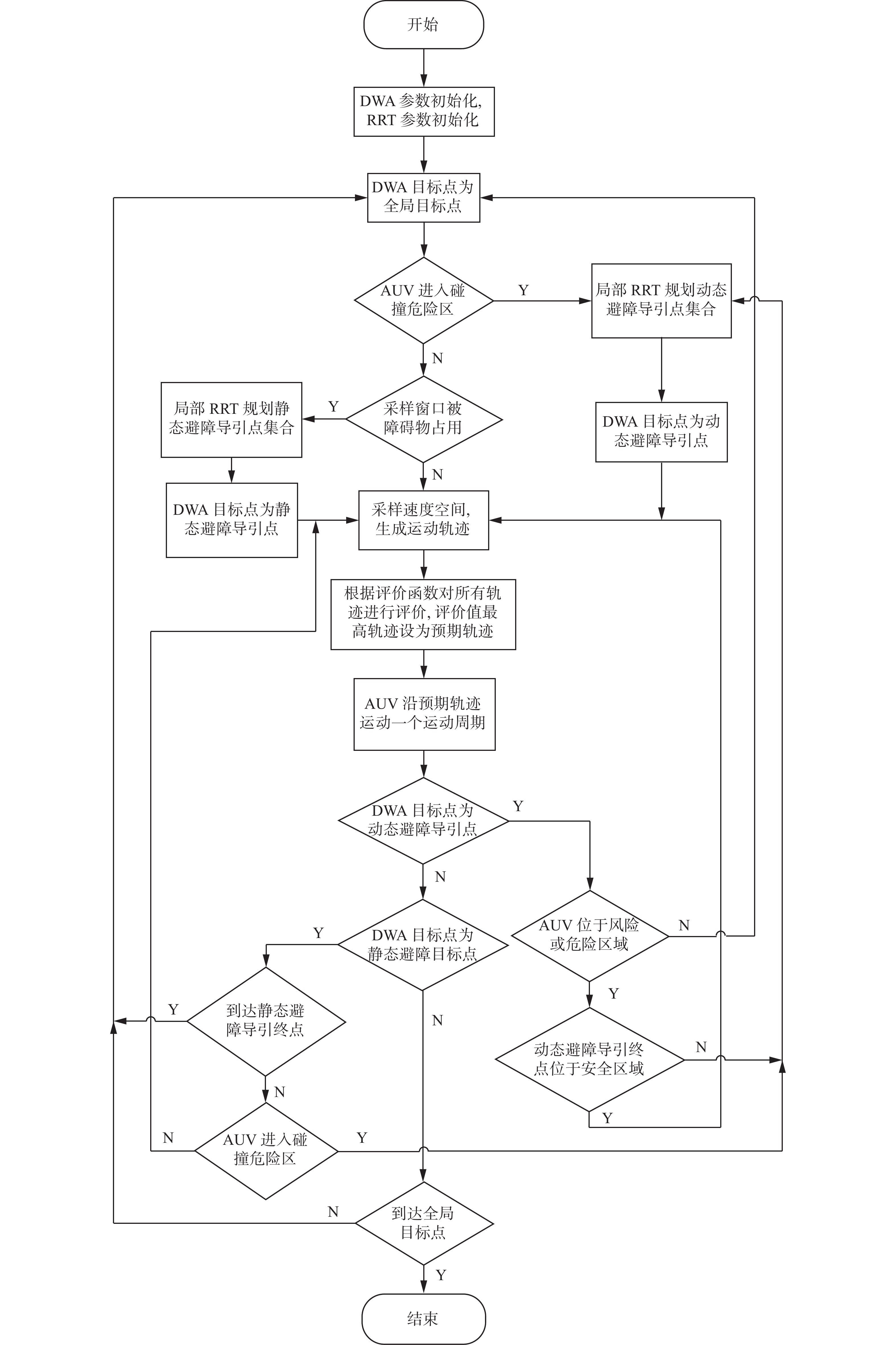
DWA算法与RRT算法融合的基本思想是：在DWA算法存在局部避障困难时，引入改进RRT算法规划局部导引点，将导引点依次作为DWA的目标点，从而避免发生局部停滞，并实现更安全的动态避障，图3为融合算法的流程。
图 3 融合算法流程Fig. 3 Fusion algorithm flow下载:
全尺寸图片
3.2 基于改进RRT的局部导引点规划
3.2.1 基本的RRT算法
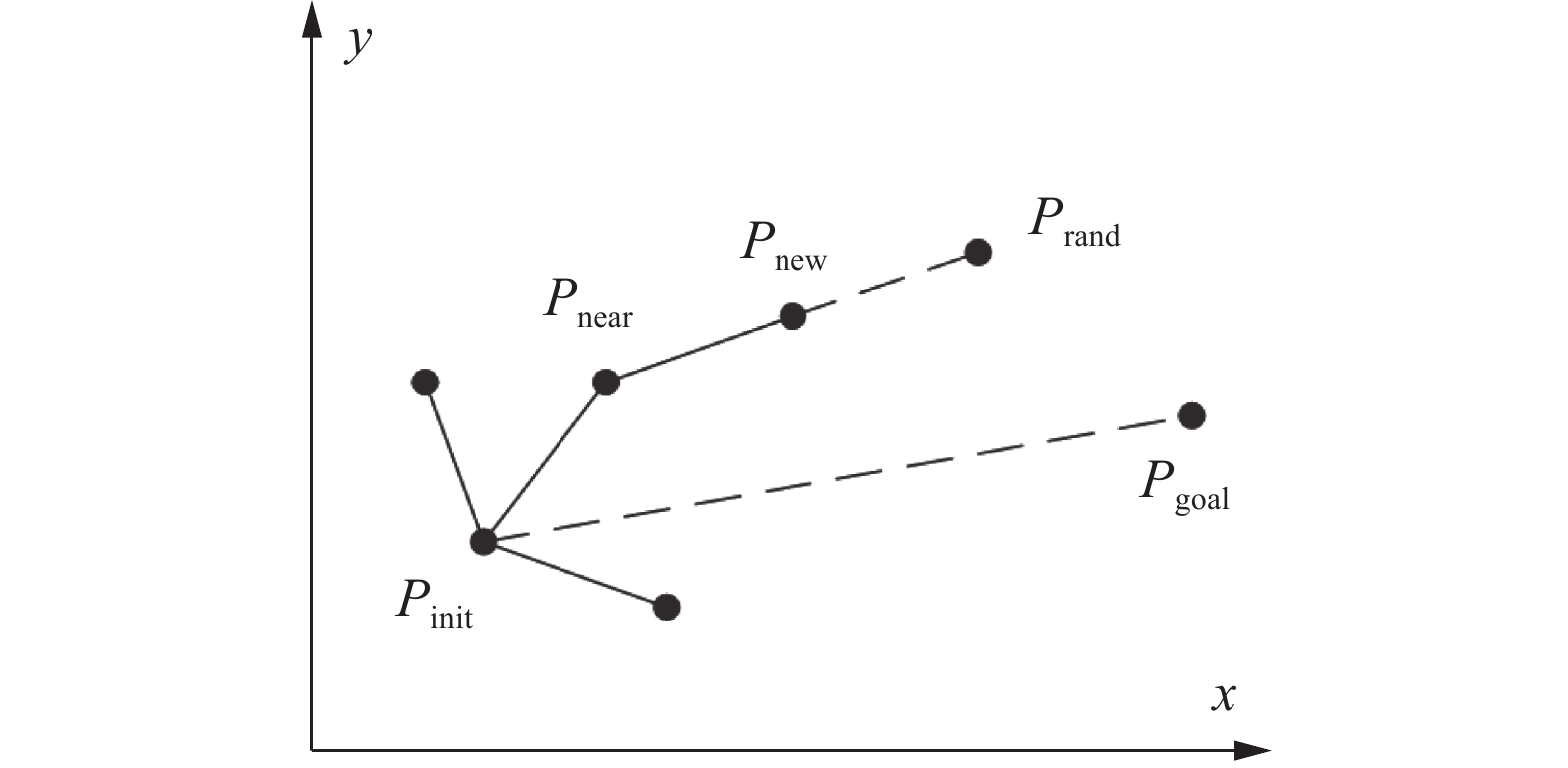
随机树的扩展过程如图4所示。设该笛卡尔空间为AUV所处的水下状态空间， AUV的初始坐标作为随机树的根节点Pinit，根节点作为父节点在空间中随机采样得到Prand，找到距Prand欧氏距离最近的节点Pnear，然后以设定步长从Pnear向Prand扩展得到新节点Pnew，若Pnear与Pnew的连线通过了碰撞检测，则将新节点Pnew以及连线加入到随机树上。对上述过程重复进行，直到到达目标点。将随机树上的从根节点到目标点之间的树节点连接即为所规划的路径。
图 4 RRT扩展过程Fig. 4 RRT Extension Process下载:
全尺寸图片
由随机树的基本原理可知，一方面节点选取的随机性较强[26]，会规划出不必要的节点，造成航行时间加长；另一方面，RRT通常用于全局规划，需已知起始点、目标点和环境中的障碍物信息，不能用于未知环境和局部规划[27]，因此需要对RRT算法进行改进，在必要时为DWA算法规划局部导引点，提高DWA算法局部规划性能，实现更安全的动态避障。为考虑实际情况的约束，提高AUV航行效率，算法需满足要求：1）在已知区域内搜索节点，找到可以引导AUV逃离复杂障碍物的导引点集合；2）动态避障时，导引点终点需位于不会与动态障碍物发生碰撞的安全位置；3）删除冗余节点，提取关键导引点集合。
综合以上方面，对RRT的改进方法如下。
3.2.2 静态避障导引点规划
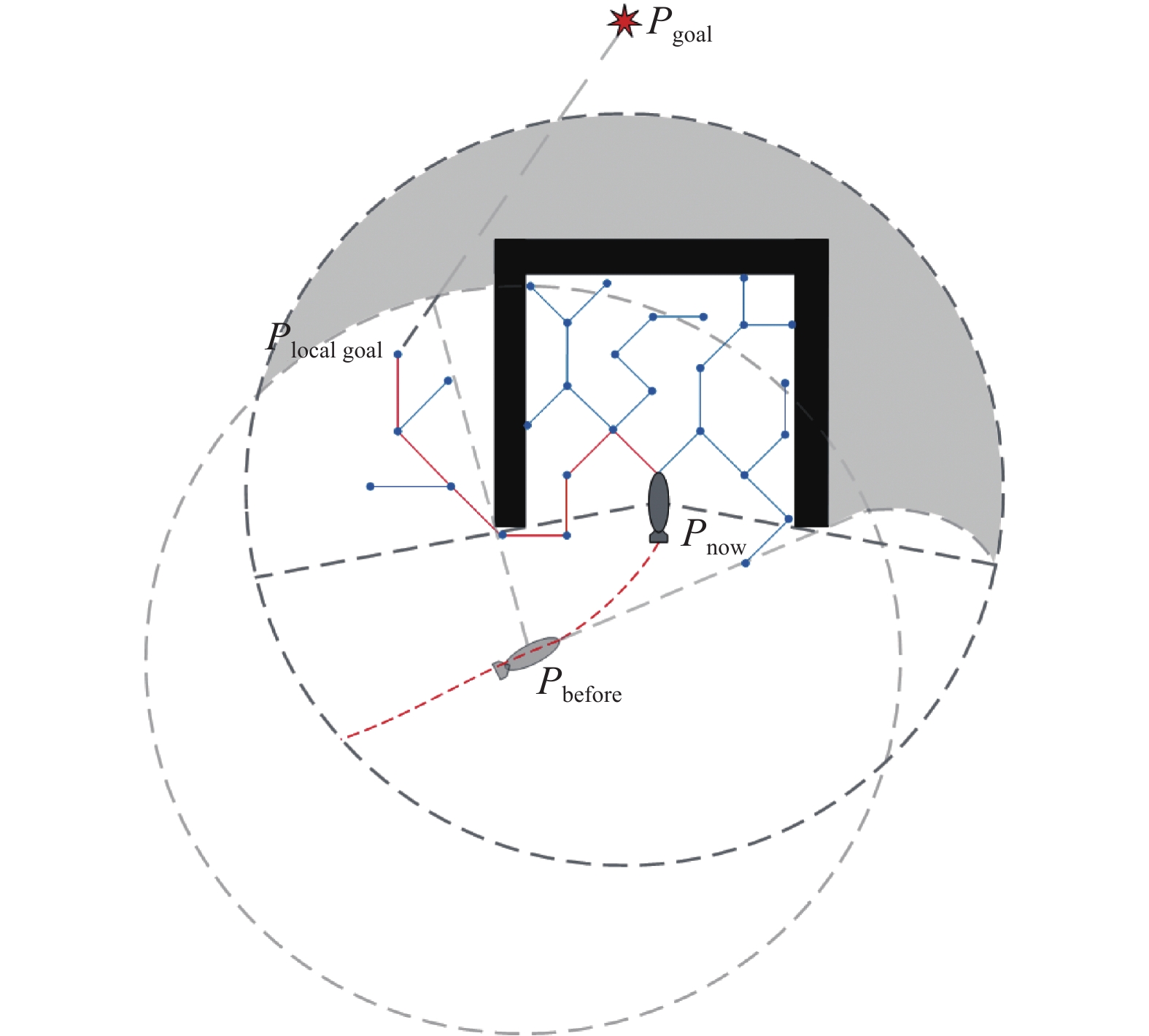
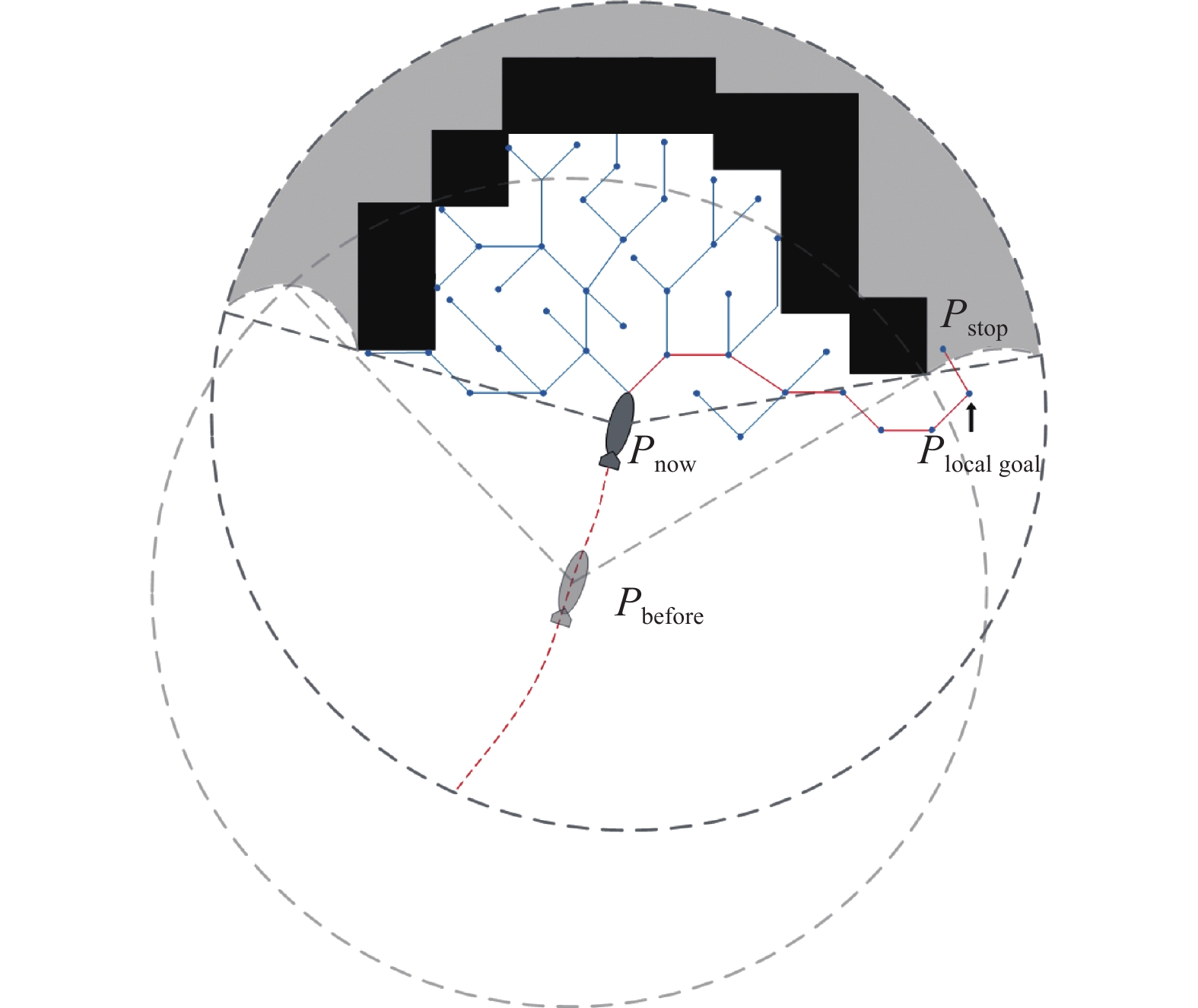
传统局部规划算法常在复杂障碍物区域因局部最优而陷入停滞[28]，本文将RRT引入局部，规划静态避障导引点，避免发生局部停滞，原理如图5、6所示。
图 5 全局目标点线性连通节点作为RRT局部目标点Fig. 5 Linear connection node with global target point as RRT local target point下载:
全尺寸图片
图 6 临界节点作为RRT局部目标点Fig. 6 Critical node as RRT local target point下载:
全尺寸图片
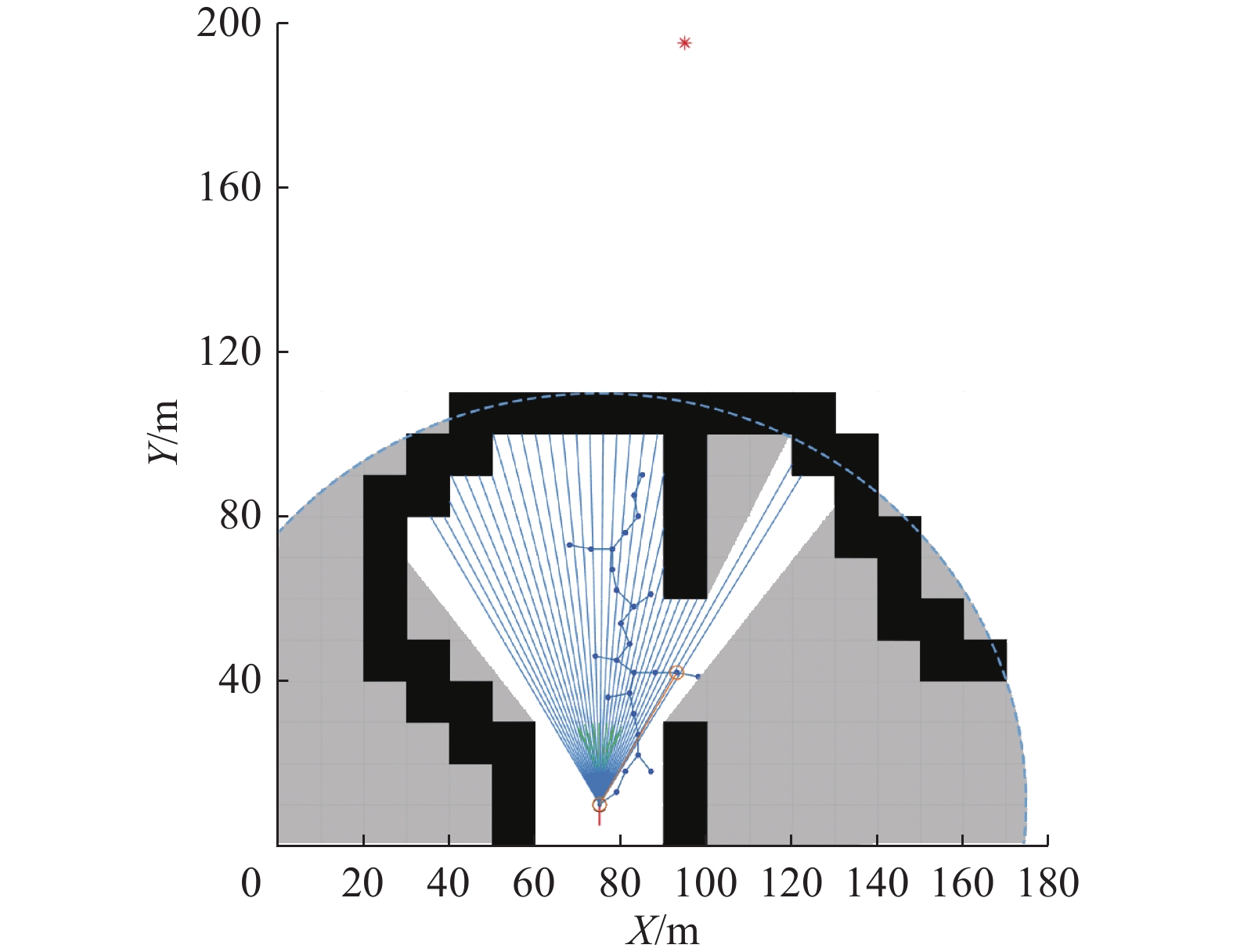
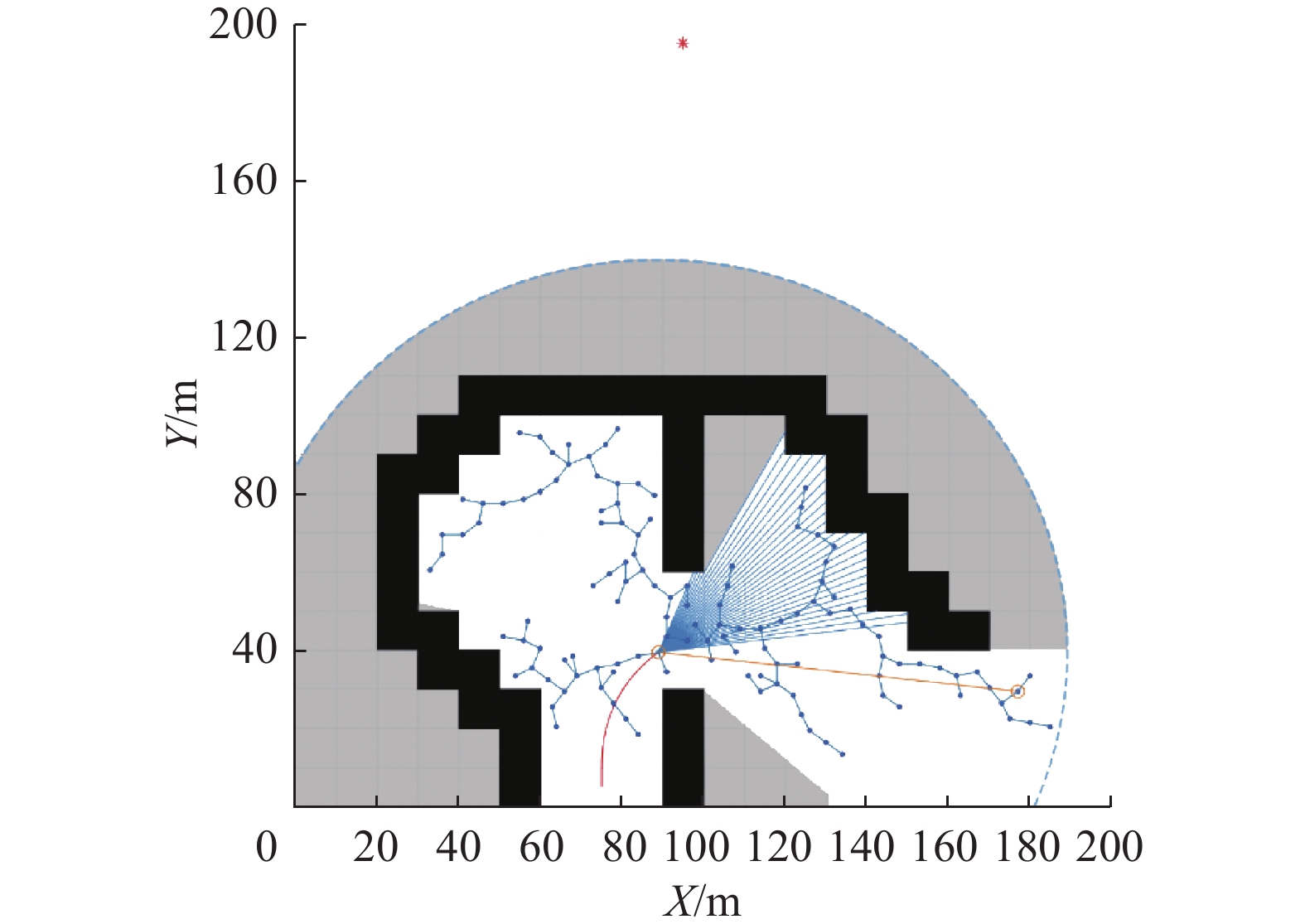
图5、6中，黑色区域为障碍物区域，灰色虚线为AUV的声呐窗口，灰色区域为声呐窗口内因障碍物遮挡而存在的未知区域，白色区域为已知区域，蓝色节点为RRT的搜索节点，蓝色实线为连接节点的路径，红色实线为连接规划出的导引点的路径。
当存在停滞风险时，改进RRT在已知区域内搜索非障碍物区域节点，判断标准为在已知区域内与全局目标点间无已知障碍物遮挡，搜索到该节点后将该节点设为局部目标点Plocal goal，如图5所示，回溯Plocal goal至AUV当前位置Pnow的路径，将路径中所有连接节点加入导引点集合。若已知区域内未搜索到非障碍物区域节点，则RRT将引导AUV到未知区域继续探索，RRT将在未知区域节点Pstop处停止搜索，如图6所示，为保证当未知区域存在障碍物时不发生碰撞，且无障碍物时对于未知区域可到达，将未知区域节点的前一已知区域父节点设为局部目标点Plocal goal，回溯路径节点建立导引点集合。
若AUV到达局部目标点后仍陷于障碍物区域，则将新探知的区域纳入已知区域，重复以上局部RRT搜索过程，直至逃离障碍物区域。
3.2.3 动态避障导引点规划
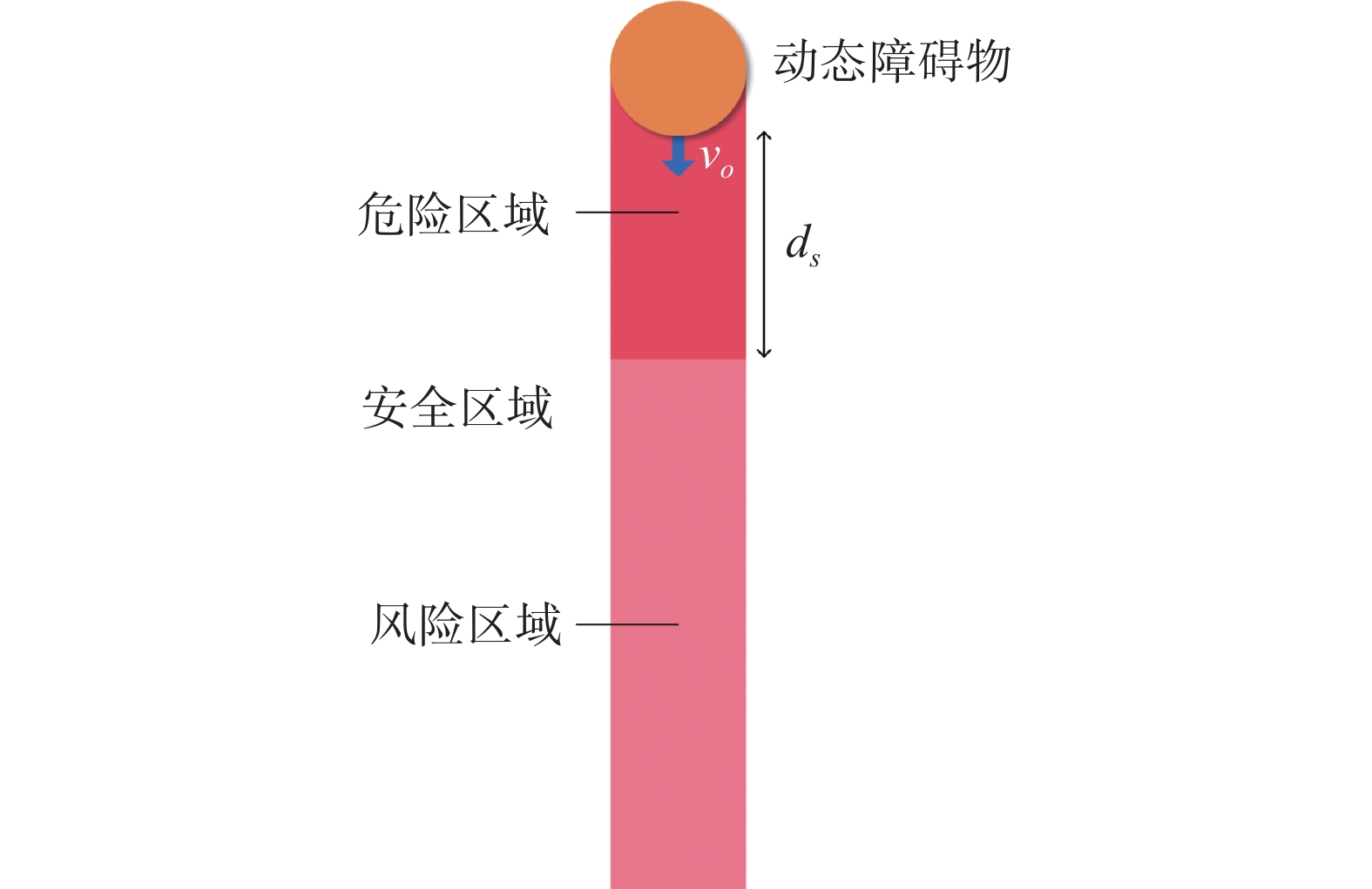
传统局部规划算法在遭遇体积较大，运动速度较快的动态障碍物时避障效果不佳[29]，本文将RRT引入局部，规划动态避障导引点，实现更安全的动态避障。为了提高安全性，将障碍物膨胀为以长度为直径的圆形区域，根据AUV的性能指标和动态障碍物的速度、运动方向等状态信息，设立碰撞风险区域、危险区域和安全区域，如图7所示。图7中黄色圆形为动态障碍物区域，浅红色区域为AUV对于动态障碍物的碰撞风险区域，深红色区域为碰撞危险区域。
图 7 碰撞安全区域、风险区域和危险区域设置Fig. 7 Setting of collision avoidance safety area, risk area and dangerous area下载:
全尺寸图片
以端点在动态障碍物区域边界上，与边界相切且与障碍物速度
$ {v_o} $ 方向同向的两条射线作为边界，若AUV处于2条射线以内的区域，则存在与动态障碍物相撞的风险，该区域即为碰撞风险区域。对于碰撞危险区域的设置，最大化考虑AUV在风险区域内机动所需的时间，包括减速、掉头、加速、转向并逃离风险区域一系列运动过程所需要的时间，根据AUV当前速度、最大加速度和障碍物速度计算风险区内AUV与障碍物之间的距离阈值$ {d_s} $ 。$$ {d_s} = {v_o}\left[ {\frac{{{v_{\max }} + {v_o}}}{a} + {t_\omega } + \sqrt {\frac{{2{d_o}}}{a}} } \right] + \frac{{{v_{\max }^2} + v_o^2}}{{2a}} + {d_p} $$ 式中：
$ {d_o} $ 为动态障碍物膨胀圆直径，$ {d_p} $ 为距离阈值调节参数，$ {t_\omega } $ 为AUV完成所有转向机动需要的时间，表达式为$$ {t}_{\omega }=\left\{\begin{array}{l}\dfrac{3\text{π}}{2\omega }+\dfrac{2\omega }{\alpha },\;\;\;\alpha > \dfrac{{\text{π}}^{2}}{\omega } \\ \sqrt{\dfrac{2\text{π}}{\alpha }}+\sqrt{\dfrac{4\text{π}}{\alpha },}\;\;\;其他\text{ } \end{array} \right.$$ 碰撞风险区域内距离障碍物的距离小于等于
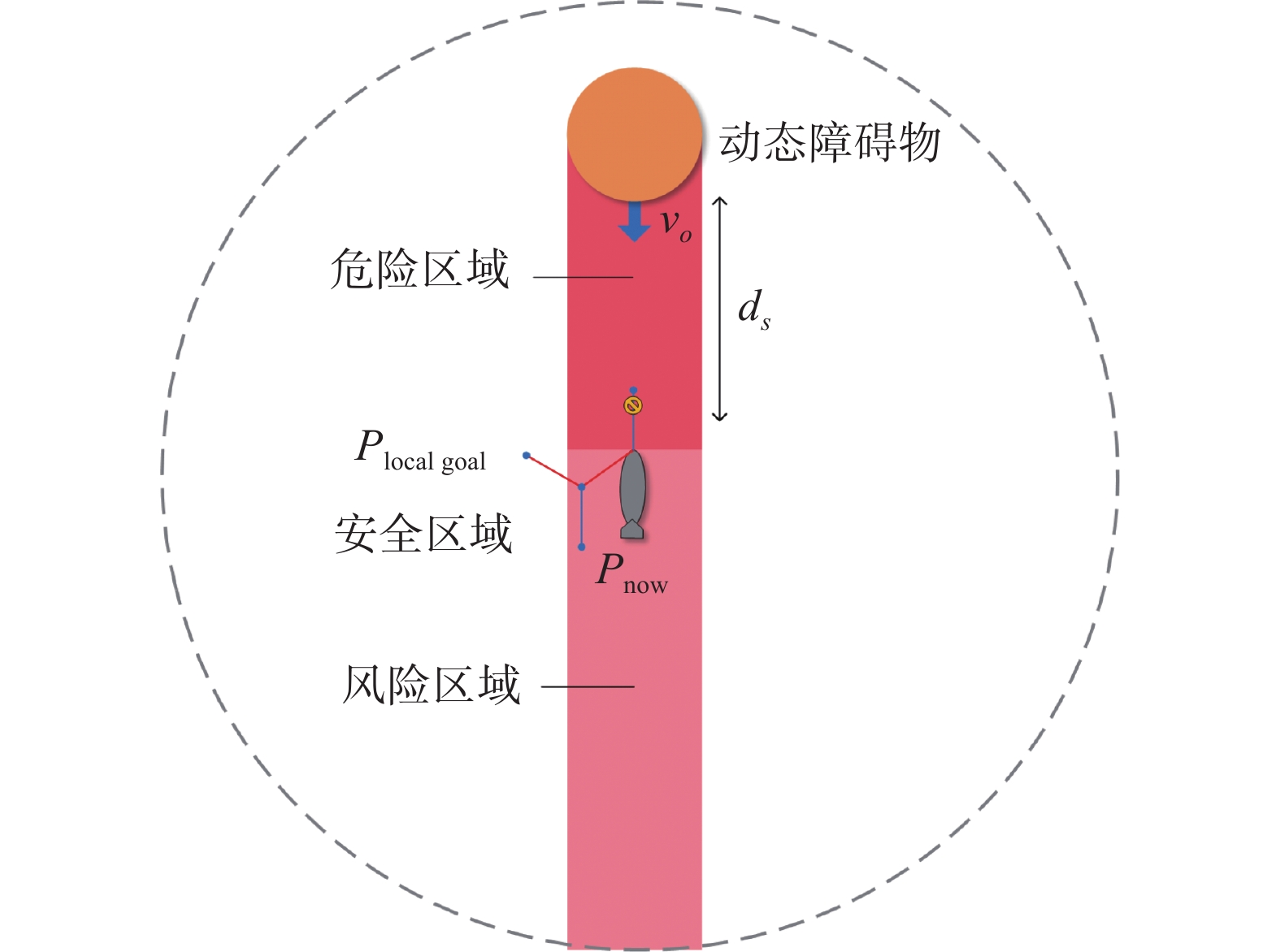
$ {d_s} $ 的区域设为碰撞危险区域。动态避障导引点规划原理如图8所示。当AUV位于非危险区域的风险区域时，存在碰撞风险但暂无危险，此时不干预AUV的局部规划，当AUV进入危险区域边界时则认为仅凭局部规划算法不能安全有效避障，引入改进RRT规划动态避障导引点。局部RRT规划时会裁剪位于危险区域内的搜索节点，当搜索节点处于风险区域之外时停止搜索，将该节点设为动态避障局部目标点Plocal goal，回溯路径节点建立导引点集合。
图 8 引入局部RRT动态避障Fig. 8 Introducing local RRT dynamic obstacle avoidance下载:
全尺寸图片
3.2.4 提取关键导引点集合
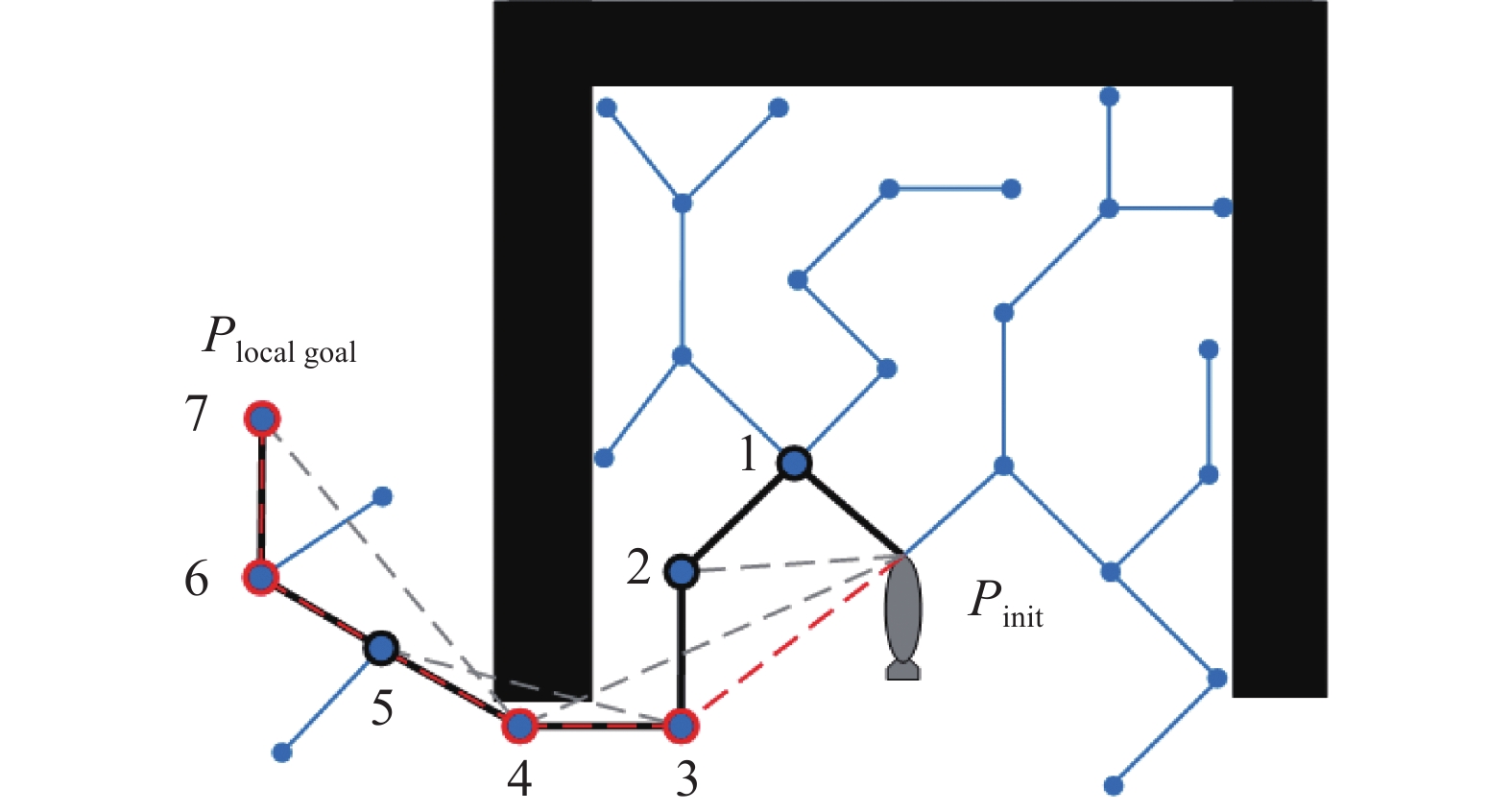
局部RRT得到初始导引点集合后，其中可能会存在冗余导引点，即该导引点非AUV避障必须到达的关键位置，会造成航行路径的冗余。为提高AUV航行效率，引入关键导引点选取规则。原理如图9所示，先将从起始点Pinit到局部目标节点7之间的所有连接节点加入导引点集合，从起始点Pinit开始，跳过导引点1，连接起始点和导引点2，如连接的路径与障碍物不发生碰撞，则认为导引点1为冗余导引点从集合中删除，继续连接起始点与导引点3进行判断；若某次连接的路径发生碰撞，如起始点和导引点4之间的路径与障碍物发生碰撞，则认为上一导引点3为关键导引点在集合中保留，之后继续从导引点3开始，跳过导引点4与导引点5连接进行判断。重复上述判断过程，直到遍历所有初始导引点，生成关键导引点集合。图9中的关键引导点集合为{3，4，6，7}。
图 9 提取关键导引点Fig. 9 Extract key guidance points下载:
全尺寸图片
4. 仿真结果及分析
为证明本文所设计算法的有效性，使用传统DWA算法和文献[30]所使用的动态路径规划算法作为对比算法与本文算法进行对比仿真实验。设置了简单障碍物环境、洋流–障碍物环境、复杂障碍物环境和动态复杂障碍物环境4种工况，每种工况设置了3组不同的起点、终点以进一步验证算法的有效性和鲁棒性。
4.1 简单障碍物环境路径规划仿真
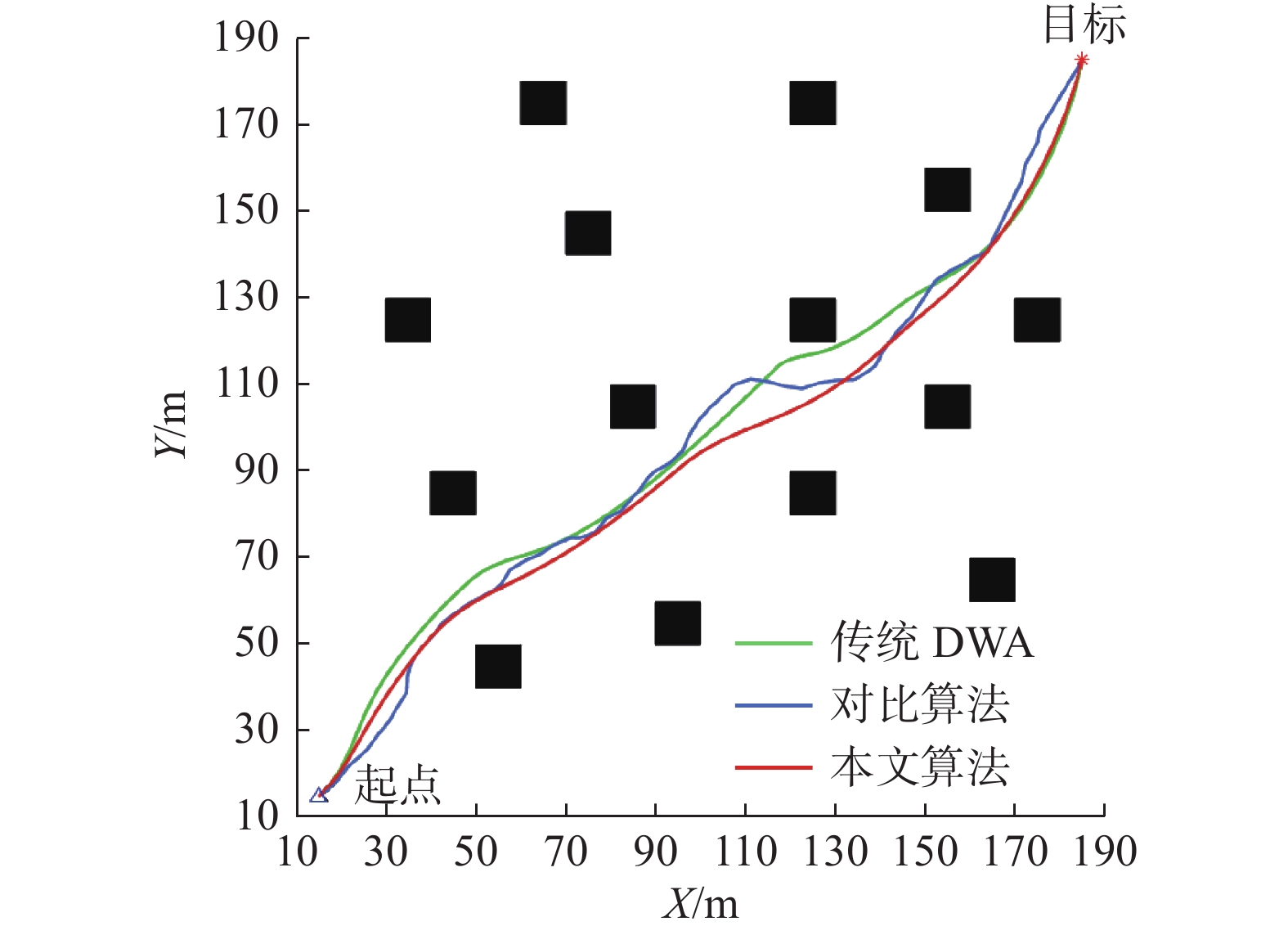
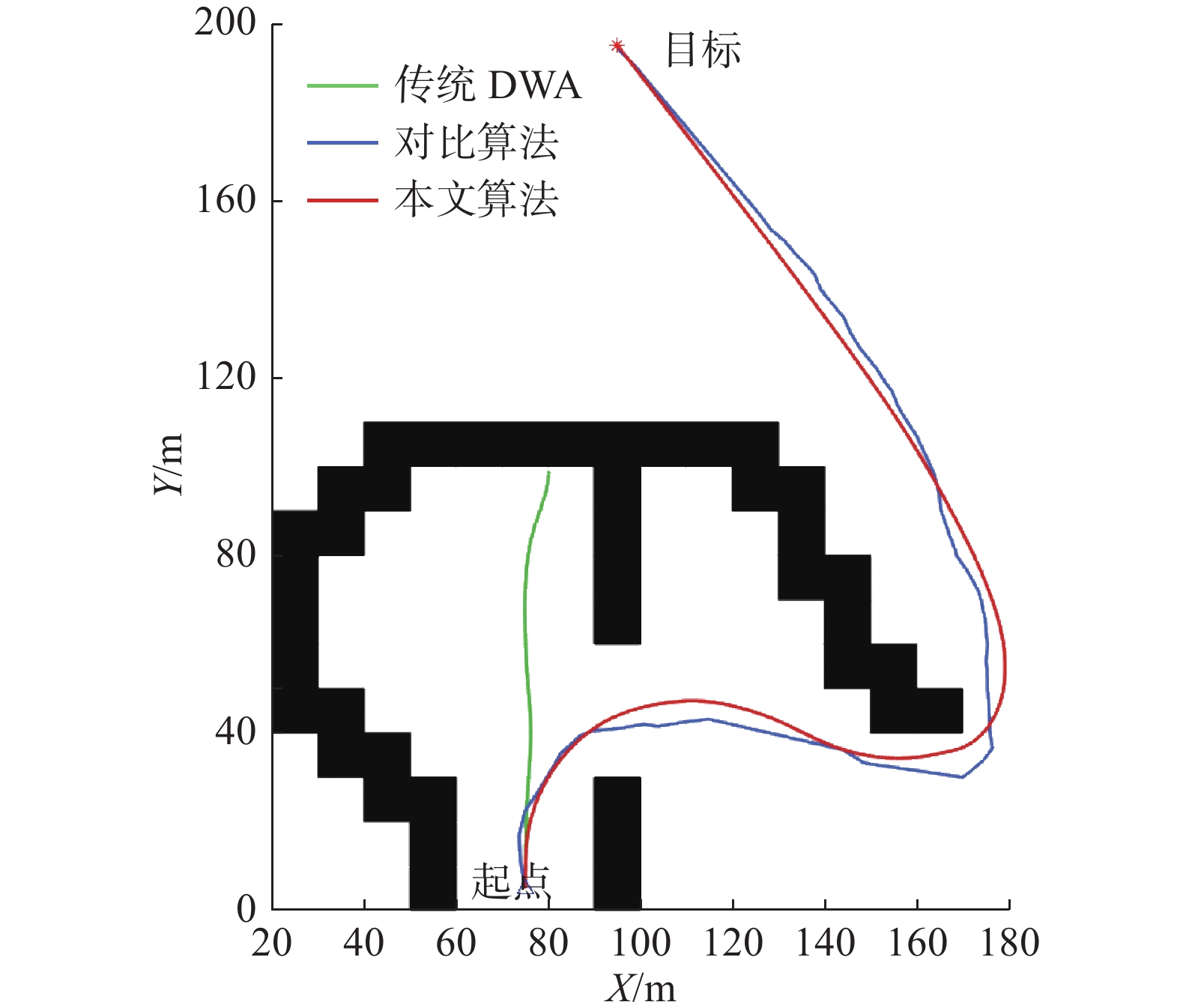
本节仿真环境200 m×200 m，黑色区域为障碍物区域，白色区域为可自由通行区域。DWA的预测周期为10 s，运动周期为0.1 s。图10给出了起点为（15，15）、终点为（185，185）时，传统DWA算法、对比算法和本文算法在简单障碍物环境中的路径规划仿真结果，3种算法规划的路径分别对应图10中的绿色、蓝色和红色曲线。表1为3种算法在3种不同起点、终点设置下的路径规划数据对比。
图 10 简单障碍物环境路径规划仿真Fig. 10 Simple obstacle environment path planning simulation下载:
全尺寸图片
表 1 简单障碍物环境下3种算法路径规划结果对比Table 1 Comparison of path planning results of three algorithms in simple obstacle environment起点
终点算法 路径长度/m 航行时间/s 转角代价/rad (15,15)
(185,185)传统DWA 247.8 172.9 5.5 对比算法 257.1 189.4 11.3 本文算法 245.7 156.6 4.1 (5,185)
(185,25)传统DWA 244.4 154.3 4.6 对比算法 252.5 171.0 8.0 本文算法 242.4 149.2 3.5 (55,25)
(175,175)传统DWA 193.5 145.6 4.0 对比算法 204.8 165.2 7.7 本文算法 192.5 129.2 3.0 对比3种算法的路径规划结果，可以得出本文算法在路径长度、航行时间和转角代价指标相较于其他算法均有一定的提升。因改进速度空间采样提高了算法的前瞻性，减少了机动次数，提高了路径的平滑性，所以对于转角代价的优化较为明显。
4.2 洋流–障碍物环境路径规划仿真
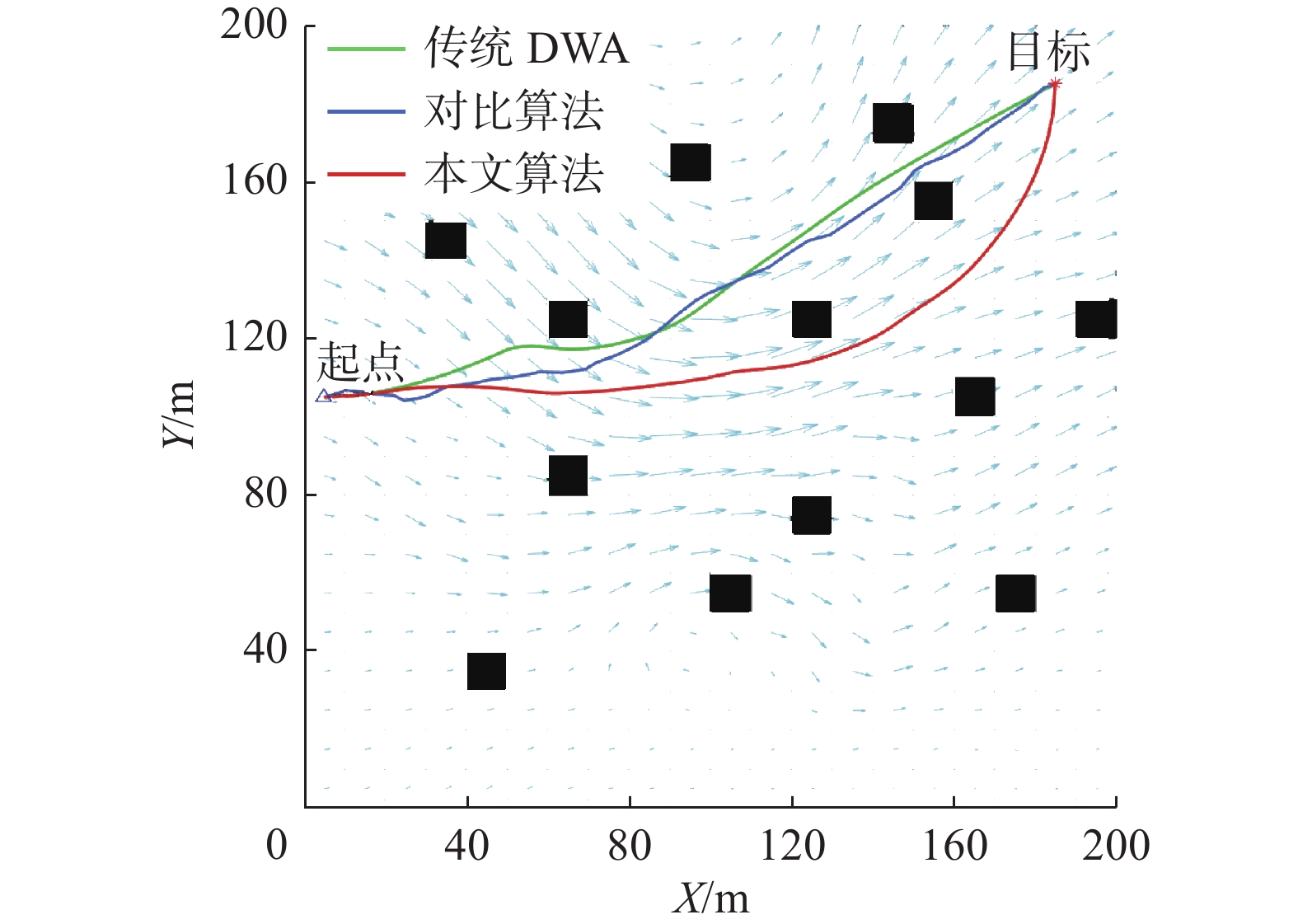
本节在仿真环境中加入了洋流。洋流的速度为0~0.5 m/s，大小和方向每秒发生变化。图11给出了起点为（5，105）、终点为（185，185）时3种算法的路径规划仿真结果，图中蓝色箭头长短表示洋流速度的大小，箭头方向表示洋流速度方向。表2为3种算法在3种不同起点终点设置下的路径规划数据对比。对比3种算法的路径规划结果，可以得出相较于其他算法本文算法加入洋流能耗评价函数后，在洋流速度较大时，规划路径更倾向于顺应洋流速度方向，可以更好地借助洋流，节约更多能耗。
图 11 洋流-障碍物环境路径规划仿真Fig. 11 Current-obstacle environment path planning simulation下载:
全尺寸图片
表 2 洋流–障碍物环境下3种算法路径规划结果对比Table 2 Comparison of path planning results of three algorithms in the ocean current-obstacle environment起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad洋流能耗
代价/J(5,105)
(185,185)传统DWA 200.2 142.9 3.7 − 2479.8 对比算法 204.0 135.0 5.2 − 2783.5 本文算法 216.0 128.4 4.0 − 3662.2 (15,15)
(185,175)传统DWA 243.8 137.5 4.3 − 1510.9 对比算法 252.1 165.5 6.6 − 1530.3 本文算法 239.8 134.7 4.5 − 3550.3 (95,195)
(175,25)传统DWA 188.3 121.6 3.9 1370.3 对比算法 246.6 155.7 9.1 1460.3 本文算法 190.1 114.3 4.1 975.8 4.3 复杂障碍物环境仿真
本节仿真环境设置了存在陷阱区域的复杂障碍物。声呐传感器探测半径为100 m，随机树的扩展步长为5 m。
图12和图13给出了本文算法在规划中2次启动改进RRT算法为DWA算法规划导引点的过程。图中蓝色虚线为声呐传感器边界，灰色区域为声呐探测范围内的未知区域；蓝色射线为障碍物采样窗口，蓝色实心节点为RRT算法搜索节点，黄色空心节点为提取的关键导引点，黄色线段为AUV位置与导引点的连线，红色实线为AUV已走过的路径。表3为传统RRT和本文改进RRT规划导引点数量的对比，可以看出改进RRT算法通过引入关键导引点提取，裁剪了冗余导引点，大大减少了导引点数量。
图 12 第1次引入改进RRT规划导引点Fig. 12 Introduction of improved RRT planning guidance point for the first time下载:
全尺寸图片
图 13 第2次引入改进RRT规划导引点Fig. 13 Introducing improved RRT planning guidance points for the second time下载:
全尺寸图片
表 3 传统RRT同改进RRT规划导引点数量对比Table 3 Comparison of the number of planning guidance points between traditional RRT and improved RRT算法 第1次 第2次 传统RRT 9 22 改进RRT 1 1 图14给出起点为（75，5）、终点为（95，195）时3种算法的路径规划仿真结果。表4为3种算法在3种不同起点、终点设置下的路径规划数据对比。对比3种算法的路径规划结果可知，本文算法可以解决传统DWA因局部最优而停滞于局部的问题，同时相较于同样可以到达目标的对比算法，本文算法在路径长度、航行时间和转角代价指标下表现更优。
图 14 复杂障碍物环境路径规划仿真Fig. 14 Dynamic obstacle avoidance based on fusion algorithm in this paper下载:
全尺寸图片
表 4 复杂障碍物环境下3种算法路径规划结果对比Table 4 Comparison of path planning results of three algorithms in complex obstacle environment起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad是否到达
目标(75,5)
(95,195)传统DWA 94.68 97.6 2.6 否 对比算法 317.1 227.9 9.3 是 本文算法 310.3 203.6 6.5 是 (115,155)
(65,85)传统DWA 87.1 84.5 4.6 否 对比算法 286.2 201.2 11.0 是 本文算法 260.5 186.1 9.5 是 (55,85)
(175,135)传统DWA 38.5 80.7 18.5 否 对比算法 255.0 182.0 8.4 是 本文算法 239.2 151.3 7.3 是 4.4 动态复杂障碍物环境路径规划仿真
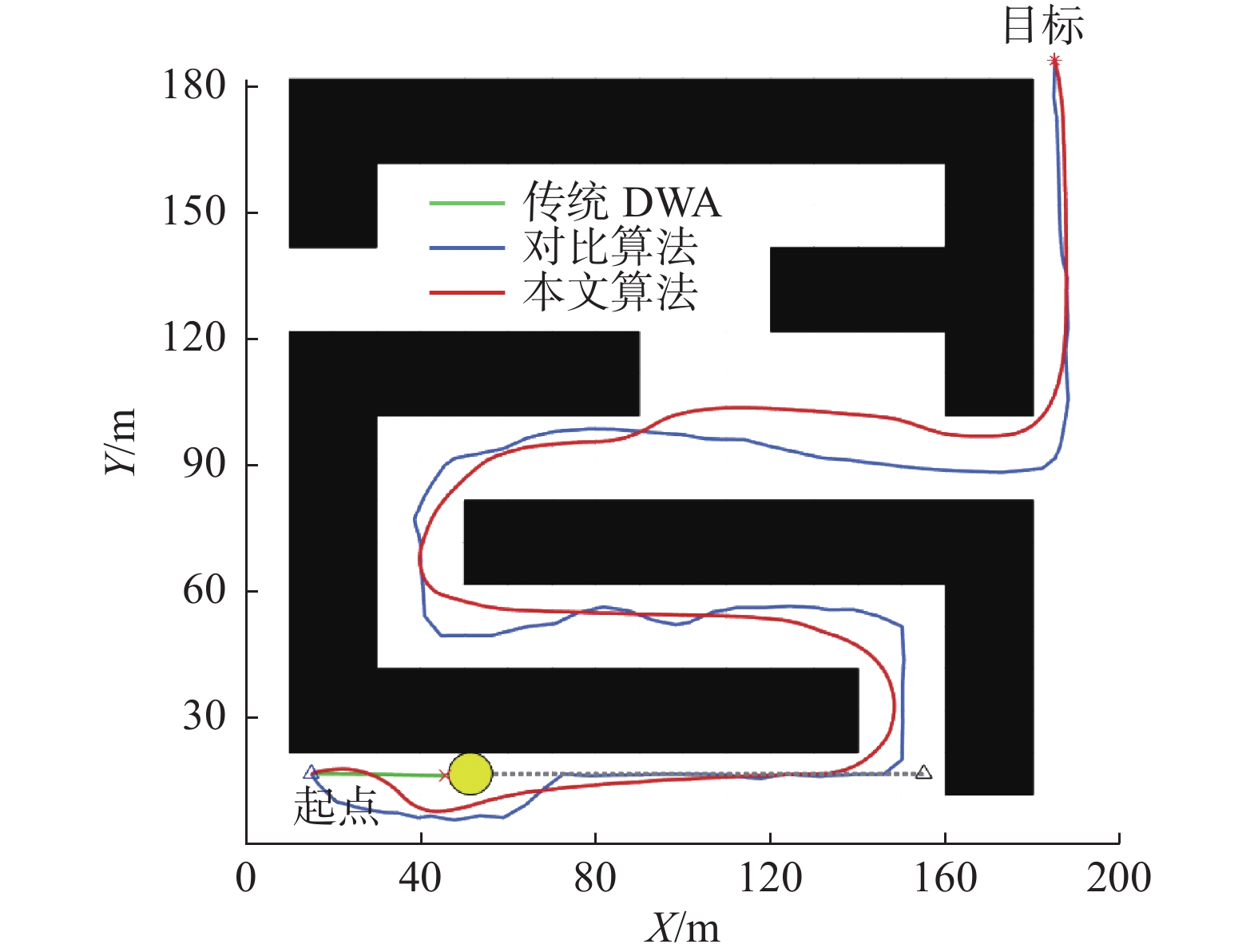
本节设置了第2种复杂障碍物环境，包含曲折的通路和陷阱区域，同时在AUV运动路线中设置了动态障碍物。图15给出了起点为（15，15）、终点为（185，185）时3种算法的路径规划仿真结果，图中黄色圆形为动态障碍物，其半径为5 m，速度为5.6 m/s，灰色虚线为动态障碍物运动路径。表5为3种算法在3种不同起点终点设置下的路径规划数据对比。对比3种算法的路径规划结果可知，采用传统DWA算法的AUV与动态障碍物发生碰撞，无法实现安全有效的避障。本文提出的融合算法能够及时规划动态避障导引点，将AUV引导至无碰撞风险的安全区域，避免与动态障碍物相撞，动态避障安全性相较于传统DWA算法明显提高。同时相较于对比算法本文算法依然在路径长度、航行时间和转角代价指标下表现更优。
图 15 复杂障碍物环境路径规划仿真Fig. 15 Simulation of path planning in complex obstacle environment下载:
全尺寸图片
表 5 动态复杂障碍物环境下3种算法路径规划结果对比Table 5 Comparison of path planning results of three algorithms in dynamic complex obstacle environment起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad是否到达
目标是否
碰撞(15,15)
(185,185)传统DWA 30.7 18.8 1.8 否 是 对比算法 565.8 353.2 17.1 是 否 本文算法 511.7 273.9 14.8 是 否 (145,25)
(155,155)传统DWA 33.7 64.3 2.3 否 是 对比算法 309.3 201.6 11.8 是 否 本文算法 296.5 178.4 10.4 是 否 (25,135)
(105,45)传统DWA 16.5 10.9 2.0 否 是 对比算法 269.6 170.7 12.3 是 否 本文算法 241.8 144.8 8.9 是 否 5. 结束语
本文提出复杂环境下基于RRT与DWA融合的路径规划算法。通过改进速度空间和评价函数增强DWA的多目标优化性能，提高算法前瞻性，并且降低了AUV在洋流环境中的能耗代价。提出适用于局部未知环境和动态避障导引点规划的局部RRT算法，利用RRT算法的快速性和大范围搜索能力为DWA算法规划导引点，并得到最简导引点集合，解决了传统DWA算法在复杂未知障碍物环境下容易陷入局部停滞的问题，且提高了动态避障的安全性，最后通过仿真验证了算法的有效性。另外在洋流环境中，当洋流速度过大时，算法容易出现在尾段不优先朝向目标行驶的情况，参数设置较为复杂；对于局部路径规划，还可以在路径长度和全局性上进一步优化，DWA还存在距离目标点较近时速度变慢的问题，影响航行效率和动态避障的安全性，针对以上问题仍有必要继续深入研究。
-
图 1 AUV预测轨迹
Fig. 1 AUV predicted trajectory
下载:
全尺寸图片
图 2 障碍物采样窗口
Fig. 2 Obstacle sampling window
下载:
全尺寸图片
图 3 融合算法流程
Fig. 3 Fusion algorithm flow
下载:
全尺寸图片
图 4 RRT扩展过程
Fig. 4 RRT Extension Process
下载:
全尺寸图片
图 5 全局目标点线性连通节点作为RRT局部目标点
Fig. 5 Linear connection node with global target point as RRT local target point
下载:
全尺寸图片
图 6 临界节点作为RRT局部目标点
Fig. 6 Critical node as RRT local target point
下载:
全尺寸图片
图 7 碰撞安全区域、风险区域和危险区域设置
Fig. 7 Setting of collision avoidance safety area, risk area and dangerous area
下载:
全尺寸图片
图 8 引入局部RRT动态避障
Fig. 8 Introducing local RRT dynamic obstacle avoidance
下载:
全尺寸图片
图 9 提取关键导引点
Fig. 9 Extract key guidance points
下载:
全尺寸图片
图 10 简单障碍物环境路径规划仿真
Fig. 10 Simple obstacle environment path planning simulation
下载:
全尺寸图片
图 11 洋流-障碍物环境路径规划仿真
Fig. 11 Current-obstacle environment path planning simulation
下载:
全尺寸图片
图 12 第1次引入改进RRT规划导引点
Fig. 12 Introduction of improved RRT planning guidance point for the first time
下载:
全尺寸图片
图 13 第2次引入改进RRT规划导引点
Fig. 13 Introducing improved RRT planning guidance points for the second time
下载:
全尺寸图片
图 14 复杂障碍物环境路径规划仿真
Fig. 14 Dynamic obstacle avoidance based on fusion algorithm in this paper
下载:
全尺寸图片
图 15 复杂障碍物环境路径规划仿真
Fig. 15 Simulation of path planning in complex obstacle environment
下载:
全尺寸图片
表 1 简单障碍物环境下3种算法路径规划结果对比
Table 1 Comparison of path planning results of three algorithms in simple obstacle environment
起点
终点算法 路径长度/m 航行时间/s 转角代价/rad (15,15)
(185,185)传统DWA 247.8 172.9 5.5 对比算法 257.1 189.4 11.3 本文算法 245.7 156.6 4.1 (5,185)
(185,25)传统DWA 244.4 154.3 4.6 对比算法 252.5 171.0 8.0 本文算法 242.4 149.2 3.5 (55,25)
(175,175)传统DWA 193.5 145.6 4.0 对比算法 204.8 165.2 7.7 本文算法 192.5 129.2 3.0 表 2 洋流–障碍物环境下3种算法路径规划结果对比
Table 2 Comparison of path planning results of three algorithms in the ocean current-obstacle environment
起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad洋流能耗
代价/J(5,105)
(185,185)传统DWA 200.2 142.9 3.7 − 2479.8 对比算法 204.0 135.0 5.2 − 2783.5 本文算法 216.0 128.4 4.0 − 3662.2 (15,15)
(185,175)传统DWA 243.8 137.5 4.3 − 1510.9 对比算法 252.1 165.5 6.6 − 1530.3 本文算法 239.8 134.7 4.5 − 3550.3 (95,195)
(175,25)传统DWA 188.3 121.6 3.9 1370.3 对比算法 246.6 155.7 9.1 1460.3 本文算法 190.1 114.3 4.1 975.8 表 3 传统RRT同改进RRT规划导引点数量对比
Table 3 Comparison of the number of planning guidance points between traditional RRT and improved RRT
算法 第1次 第2次 传统RRT 9 22 改进RRT 1 1 表 4 复杂障碍物环境下3种算法路径规划结果对比
Table 4 Comparison of path planning results of three algorithms in complex obstacle environment
起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad是否到达
目标(75,5)
(95,195)传统DWA 94.68 97.6 2.6 否 对比算法 317.1 227.9 9.3 是 本文算法 310.3 203.6 6.5 是 (115,155)
(65,85)传统DWA 87.1 84.5 4.6 否 对比算法 286.2 201.2 11.0 是 本文算法 260.5 186.1 9.5 是 (55,85)
(175,135)传统DWA 38.5 80.7 18.5 否 对比算法 255.0 182.0 8.4 是 本文算法 239.2 151.3 7.3 是 表 5 动态复杂障碍物环境下3种算法路径规划结果对比
Table 5 Comparison of path planning results of three algorithms in dynamic complex obstacle environment
起点
终点算法 路径
长度/m航行
时间/s转角
代价/rad是否到达
目标是否
碰撞(15,15)
(185,185)传统DWA 30.7 18.8 1.8 否 是 对比算法 565.8 353.2 17.1 是 否 本文算法 511.7 273.9 14.8 是 否 (145,25)
(155,155)传统DWA 33.7 64.3 2.3 否 是 对比算法 309.3 201.6 11.8 是 否 本文算法 296.5 178.4 10.4 是 否 (25,135)
(105,45)传统DWA 16.5 10.9 2.0 否 是 对比算法 269.6 170.7 12.3 是 否 本文算法 241.8 144.8 8.9 是 否 -
[1] SUI Fuli, TANG Xiaoke, DONG Zihao, et al. ACO+ PSO+ A*: a bi-layer hybrid algorithm for multi-task path planning of an AUV[J]. Computers & industrial engineering, 2022, 175: 108905. [2] 李杰, 马徐琨. 远程投送水下航行器自主航行安全性策略设计方法[J]. 水下无人系统学报, 2019, 27(4): 463–468. LI Jie, MA Xukun. Design method of autonomous navigation safety strategy for remotely delivered underwater vehicles[J]. Journal of underwater unmanned systems, 2019, 27(4): 463–468. [3] HAO Kun, ZHAO Jiale, LI Zhisheng, et al. Dynamic path planning of a three-dimensional underwater AUV based on an adaptive genetic algorithm[J]. Ocean engineering, 2022, 263(11): 112421. [4] 赵苗, 高永琪, 吴笛霄, 等. 复杂海战场环境下AUV全局路径规划方法[J]. 国防科技大学学报, 2021, 43(1): 41–48. ZHAO Miao, GAO Yongqi, WU Dixiao, et al. A global path planning method for AUV in complex naval battlefield environment[J]. Journal of the National University of Defense Technology, 2021, 43(1): 41–48. [5] 章飞, 胡春磊. 基于滚动速度障碍法的AUV动态避障路径规划[J]. 水下无人系统学报, 2021, 29(1): 30–38. ZHANG Fei, HU Chunlei. Dynamic obstacle avoidance path planning for AUV based on rolling speed obstacle method[J]. Journal of underwater unmanned systems, 2021, 29(1): 30–38. [6] 马思远, 黄大志, 徐慧丽, 等. 水面无人艇路径规划算法综述[J]. 自动化博览, 2021, 38(11): 68–71. MA Siyuan, HUANG Dazhi, XU Huili, et al. Overview of path planning algorithms for surface unmanned craft[J]. Automation expo, 2021, 38(11): 68–71. [7] 代婉玉, 张丽娟, 吴佳峰, 等. 改进TEB算法的局部路径规划算法研究[J]. 计算机工程与应用, 2022, 58(8): 283–288. DAI WanYu, ZHANG LiJuan, WU Jiafeng et al. Research on local path planning algorithm with improved TEB algorithm[J]. Computer engineering and applications, 2022, 58(8): 283–288. [8] 王豪杰, 马向华, 代婉玉, 等. 改进DWA算法的移动机器人避障研究[J]. 计算机工程与应用, 2023, 59(6): 326–332. WANG Haojie, MA Xianghua, DAI Wangyu, et al. Improved DWA algorithm for mobile robot obstacle avoidance[J]. Computer engineering and applications, 2023, 59(6): 326–332. [9] 常路, 单梁, 戴跃伟, 等. 未知环境下基于改进DWA的多机器人编队控制[J]. 控制与决策, 2022, 37(10): 2524–2534. CHANG Lu, SHAN Liang, DAI Yuewei, et al. Improved DWA-based multi-robot formation control in unknown environments[J]. Control and decision, 2022, 37(10): 2524–2534. [10] MOLINOS E J, LLAMAZARES A, OCAÑA M. Dynamic window based approaches for avoiding obstacles in moving[J]. Robotics and autonomous systems, 2019, 118: 112–130. doi: 10.1016/j.robot.2019.05.003 [11] SHEN Yue, XU Han, WANG Dianrui, et al. Real-time obstacle avoidance for AUV based on reinforcement learning and dynamic window approach[C]//Global Oceans. Singapore-Biloxi: IEEE, 2020: 1−4. [12] 张伟龙, 单梁, 常路, 等. 基于改进DWA的多无人水面艇分布式避碰算法[J]. 控制与决策, 2023, 38(4): 951–962. ZHANG Weilong, SHAN Liang, CHANG Lu, et al. Distributed collision avoidance algorithm for multiple unmanned surface craft based on improved DWA[J]. Control and decision, 2023, 38(4): 951–962. [13] 庞永旭, 袁德成. 融合改进A*与DWA算法的移动机器人路径规划[J]. 计算机与现代化, 2022(1): 103–107. PANG Yongxu, YUAN Decheng. Mobile robot path planning based on improved A* and DWA algorithm[J]. Computer and modernization, 2022(1): 103–107. [14] 张振, 张华良, 邓永胜, 等. 融合改进A*算法与DWA算法的机器人实时路径规划[J]. 无线电工程, 2022, 52(11): 1984–1993. ZHANG Zhen, ZHANG Hualiang, DENG Yongsheng, et al. Real time path planning for robots integrating improved A* algorithm and DWA algorithm[J]. Radio engineering, 2022, 52(11): 1984–1993. [15] 张伟, 孙毅. 基于改进RRT算法的水下无人航行器路径规划方法[J]. 信息与电脑(理论版), 2020, 32(12): 74–77. ZHANG Wei, SUN Yi. Path planning method for underwater unmanned vehicle based on improved RRT algorithm[J]. Information and computer (theoretical edition), 2020, 32(12): 74–77. [16] 武晓晶, 许磊, 甄然, 等. 动态步长BI—RRT的无人机航迹规划算法[J]. 河北科技大学学报, 2019, 40(5): 414–422. WU Xiaojing, XU Lei, ZHEN Ran, et al. UAV path planning algorithm based on dynamic step BI-RRT[J]. Journal of Hebei University of Science and Technology, 2019, 40(5): 414–422. [17] 陈志梅, 李敏, 邵雪卷, 等. 基于改进RRT算法的桥式起重机避障路径规划[J]. 系统仿真学报, 2021, 33(8): 1832–1838. CHEN Zhimei, LI Min, SHAO Xuejuan, et al. Obstacle avoidance path planning of bridge crane based on improved RRT algorithm[J]. Journal of system simulation, 2021, 33(8): 1832–1838. [18] 李娟, 张韵, 陈涛. 改进RRT算法在未知三维环境下 AUV 目标搜索中的应用[J]. 智能系统学报, 2021, 17(2): 368–375. LI Juan, ZHANG Yun, CHEN Tao. Application of improved RRT algorithm in AUV target search under unknown 3D environment[J]. CAAI transactions on intelligent systems, 2021, 17(2): 368–375. [19] REFSNES J E, SORENSEN A J, PETTERSEN K Y. Model-based output feedback control of slender-body underactuated AUVs: Theory and experiments[J]. IEEE transactions on control systems technology, 2008, 16(5): 930–946. doi: 10.1109/TCST.2007.916347 [20] CAO Xiang, SUN Hongbing, JAN G E. Multi-AUV cooperative target search and tracking in unknown underwater environment[J]. Ocean engineering, 2018, 150: 1–11. doi: 10.1016/j.oceaneng.2017.12.037 [21] 杨恒, 李越, 孙寒挺, 等. 路径最优的移动机器人路径规划研究[J]. 机械设计, 2022, 39(8): 58−67. YANG Heng, LI Yue, SUN Hanting, et al. Research on path planning of mobile robot with optimal path[J] Mechanical design, 2022, 39 (8): 58−67. [22] 刘丽萍, 陈梦, 晋泽炎. UWSNs节点运动模型及预测定位[J]. 哈尔滨工业大学学报, 2018, 50(9): 156–163. LIU Liping, CHEN Meng, JIN Zeyan. Motion model and predictive positioning of UWSNs nodes[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 156–163. [23] 王子静, 陈熙源. 基于改进A*和DWA的无人艇路径规划算法[J]. 传感技术学报, 2021, 34(2): 249–254. WANG Zijing, CHEN Xiyuan. Path planning algorithm for unmanned craft based on improved A* and DWA[J]. Journal of sensing technology, 2021, 34(2): 249–254. [24] 陈凯旋, 孟祥娟, 沈安文, 等. 考虑扰动的AGV动态窗口法路径跟踪研究[J]. 工业控制计算机, 2021, 34(1): 28–30. doi: 10.3969/j.issn.1001-182X.2021.01.011 CHEN Kaixuan, MENG Xiangjuan, SHEN Anwen, et al. Research on AGV dynamic window method path tracking considering disturbance[J]. Industrial control computer, 2021, 34(1): 28–30. doi: 10.3969/j.issn.1001-182X.2021.01.011 [25] 魏立新, 张钰锟, 孙浩, 等. 基于改进蚁群和DWA算法的机器人动态路径规划[J]. 控制与决策, 2022, 37(9): 2211–2216. WEI Lixin, ZHANG Yukun, SUN Hao, et al. Robot dynamic path planning based on improved ant colony algorithm and DWA algorithm[J]. Control and decision, 2022, 37(9): 2211–2216. [26] 王稷尧, 袁锋伟. 一种改进的RRT路径规划算法[J]. 机电工程技术, 2022, 51(3): 161–164. WANG Jiyao, YUAN Fengwei. An improved RRT path planning algorithm[J]. Electromechanical engineering technology, 2022, 51(3): 161–164. [27] 刘紫燕, 张杰, 袁浩, 等. 融合改进RRT和DWA算法的移动机器人路径规划[J]. 机械设计与制造, 2023(11): 224–229. LIU Ziyan, ZHANG Jie, YUAN Hao, et al. Mobile robot path planning using improved RRT and DWA algorithms[J]. Mechanical design and manufacturing, 2023(11): 224–229. [28] 苗红霞, 陈家林, 齐本胜, 等. 基于改进RRT和人工势场法的路径规划算法[J]. 自动化与仪器仪表, 2023(12): 9–14. MIAO Hongxia, CHEN Jialin, QI Bensheng, et al. A path planning algorithm based on improved RRT and APF method[J]. Automation and instrumentation, 2023(12): 9–14. [29] 杨敏豪, 张国良, 罗国攀, 等. 融合间隙与DWA的移动机器人动态避障规[J]. 国外电子测量技术, 2023, 42(11): 190–196. YANG Minhao, ZHANG Guoliang, LUO Guopan, et al. Dynamic obstacle avoidance regulations for mobile robots integrating gap and DWA[J]. Foreign electronic measurement technology, 2023, 42(11): 190–196. [30] 司徒华杰, 雷海波, 庄春刚. 动态环境下基于人工势场引导的RRT路径规划算法[J]. 计算机应用研究, 2021, 38(3): 714–717. SITU Huajie, LEI Haibo, ZHUANG Chungang. RRT path planning algorithm based on artificial potential field guidance in dynamic environments[J]. Computer application research, 2021, 38(3): 714–717.
