Unsupervised learning method for surface defect detection of slate materials
-
摘要: 石板材表面缺陷检测是一项具有挑战性的任务，尤其对于边缘磕碰、裂缝等细微缺陷，检测难度大。此外，冗余特征的存在会影响训练效果，多尺度特征学习需要进行多维计算，计算复杂度高。针对上述问题，本文提出一种基于无监督学习的石板材表面缺陷检测方法，它能够有效解决该任务存在的问题。首先，对预训练网络提取到的图像多尺度特征，采用正半交嵌入特征降维方式减少冗余特征的影响。然后，通过多过程特征学习降低计算中的时间复杂度，提高训练效率。最后，根据训练模型得出待测图像的局部马氏距离，提高检测性能。相关实验表明，本方法在石板材数据集上的结果优于当前几种先进方法，同时在石板材表面缺陷检测和定位方面证明本方法的有效性。Abstract: The surface defect detection of slate is a challenging task, particularly for small defects like edge bumps and cracks. In addition, the existence of redundant features will influence the training effect, multiscale feature learning will require multidimensional calculation, and the calculation complexity will increase. Considering the above problems, this paper proposes a method for detecting surface defects in slate materials based on unsupervised learning to solve the problem in this task effectively. First, the semiorthogonal embedding feature dimension reduction is used on the multiscale features of the image extracted using a pretraining network to reduce the effect of redundant features. Further, the time complexity of calculation is reduced through multiprocess feature learning, increasing training efficiency. Finally, the local Markov distance of the image to be measured is obtained in accordance with the training model to improve the detection performance. Relevant experiments show that the results of this method on the slate data set are superior to several advanced methods at present, and the effectiveness of this method is verified by detecting and locating surface defects in slate materials.
-
作为一种被广泛应用于家居建材、生产设备、公共设施等领域的重要材料，石板材与人们的日常生活息息相关[1]。为了提供优质的产品，石板材的质量检测环节就显得极为重要。由于人工检测效率低，极大地制约了石板材制造行业的整体生产水平，成为行业的瓶颈。因此，开发一种针对石板材表面缺陷的工业视觉缺陷检测方法以减少人工操作的需求变得越来越急迫。
基于无监督工业视觉缺陷检测的现有工作依赖于通过自动编码方法[2-4]、GANs[5-7]或其他无监督学习方法[8-9]学习标称分布模型。最近，文献[10]和文献[11]建议利用ImageNet[12]分类的常见深度表示，而不适应目标分布。使用深度神经网络提取描述整个图像的有意义向量，用于异常检测[13-14]或用于异常定位的图像块[15-16]，是当下热门的研究方向。通常情况下，向量可以参考包括普通图像嵌入球状体的中心[9]、高斯分布参数[17]或整个嵌入向量集[14]。SPADE[11]使用最后一种方式，该方法在异常检测和定位方面的报告结果较好。然而，它的推理复杂度与数据集大小成线性关系，阻碍该方法的工业应用。PaDiM[18]类似于上述方法，并使用随机嵌入来进行特征降维，消除冗余特征的影响。由于这种方式随机性强，很可能会剔除对检测有益的特征。在此基础上，PatchCore[19]提出减少特征的提取层数，提高检测效率。在包含较明显缺陷的图像检测中，这种方法很有效，但对于拥有大量细微缺陷的石板材图像来说，特征层数的减少会影响检测效果。在嵌入特征方面，Johnson-Lindenstrauss引理[20]检验了从高维到低维欧氏空间的嵌入，样本之间的距离实际上保持不变，例如正交投影。一些工作使用随机正交矩阵来近似Gram矩阵[21]，或提出正交低秩嵌入损失，以减少类内方差[22]。对于无监督异常检测，使用局部马氏距离优于比较方法[18]。最后，多尺度特征能够检测不同阶段之间相互作用的异常[18,23]以及神经网络中不同大小的感受野。然而，这种方式需要为特征图中的每个位置计算马氏距离[24]的精度矩阵，从而形成了多维张量的批量逆，这增加了最终的计算开销。综上所述，本工作需要在保留多尺度特征的情况下，减少冗余特征的影响，减少计算复杂度，获得更好的检测性能。
针对上述问题，本文提出了一种基于无监督学习的石板材表面缺陷检测方法。本方法主要分为特征学习和检测两部分。在特征学习阶段，使用未标注的正常石板材图片作为训练对象，采用在ImageNet[12]上进行预处理的网络，基于半正交特征嵌入特征降维进行多过程特征学习。在检测阶段，本文通过计算马氏距离矩阵，进而得到测试图像的异常分数并进行缺陷检测和分割。
1. 基于无监督学习的石板材表面缺陷检测问题描述
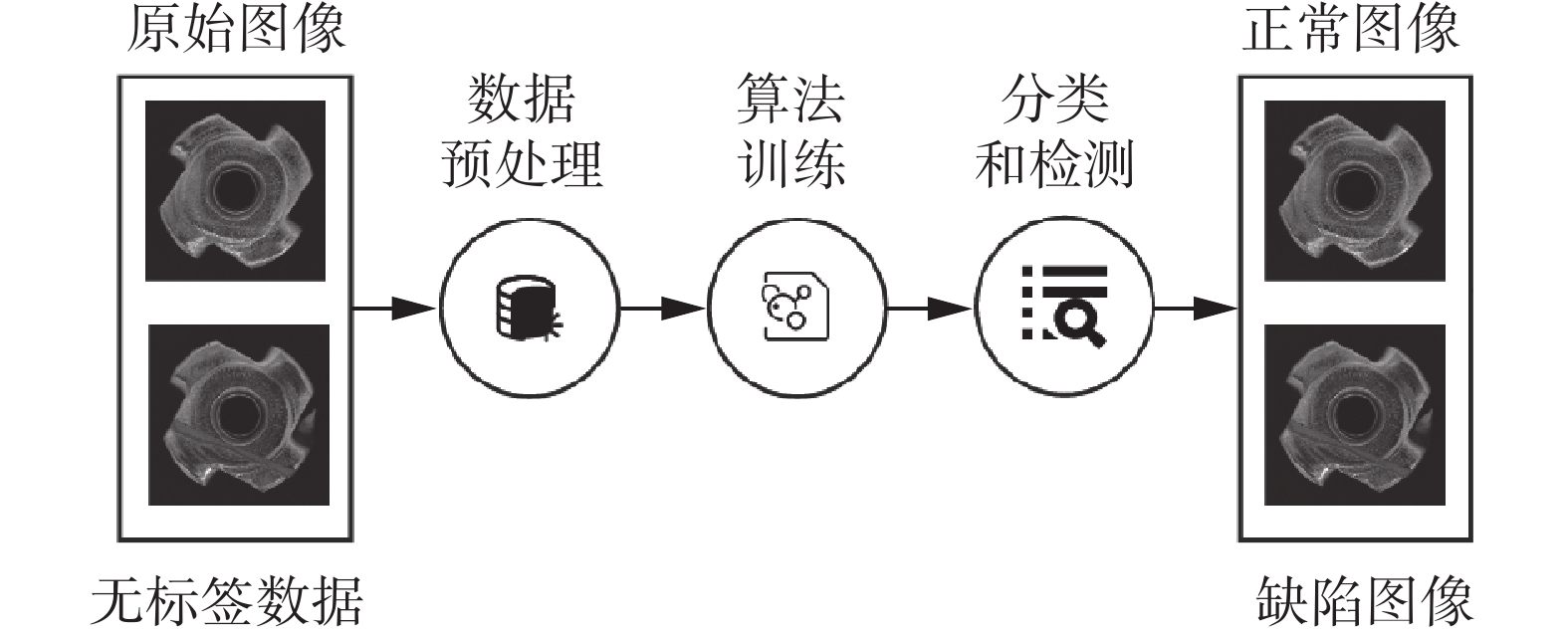
与有监督学习可以基于数据的标签信息进行训练不同，无监督学习是一种在没有标签信息的情况下对该数据进行操作的机器学习方式。基于无监督学习的缺陷检测工作原理如图1所示。由于输入数据没有标签信息，训练难度较有监督学习更大，因此，从繁杂的数据中获取到尽可能有用的信息并加以训练成为无监督学习研究的重要课题。对于石板材表面缺陷来说，其多样的缺陷种类和形式，以及自身表面纹理的存在亦增加了任务的艰巨程度。同时，大量的细微缺陷使得数据图片的分辨率不能过低，而这增加了计算复杂度，降低了训练和检测效率。在训练结束以后，如何利用训练模型对石板材测试图像数据进行检测也是亟待解决的问题。
图 1 基于无监督学习的缺陷检测工作原理Fig. 1 Operating principle of defect detection based on unsupervised learning
下载:
全尺寸图片
本文所提出的无监督缺陷检测方法，结合石板材实际缺陷检测场景，使用半正交嵌入特征降维获取有效信息，采用多过程计算减少时间复杂度，计算局部马氏距离作为缺陷检测依据。本方法训练时间短，检测效率高，可以胜任石板材缺陷检测任务。
2. 融合多尺度特征的无监督缺陷检测模型
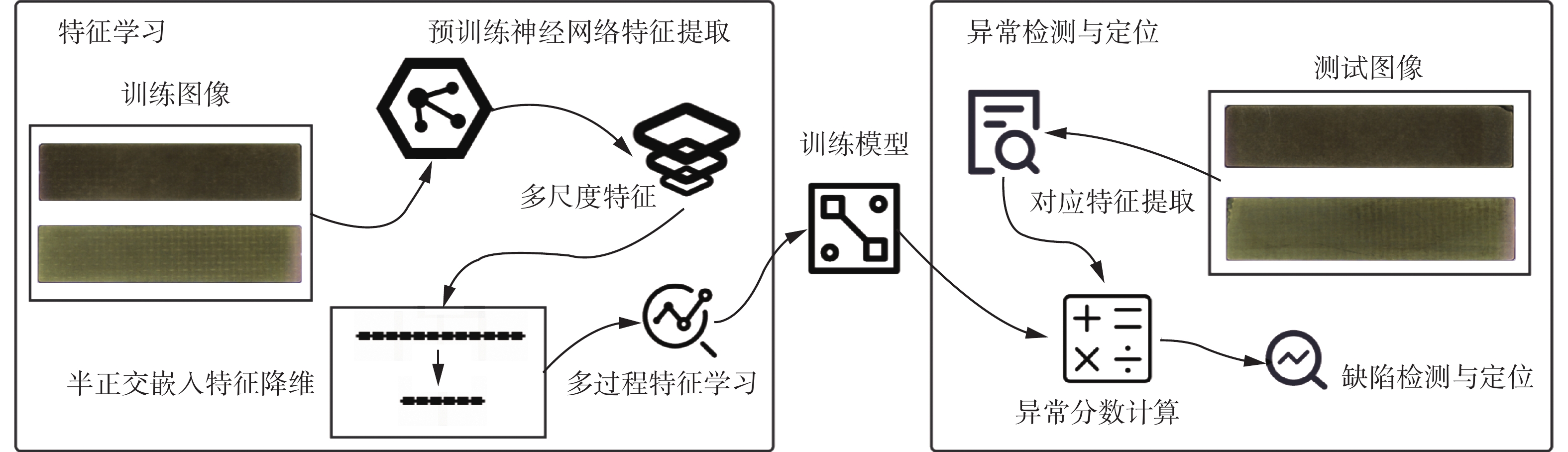
图2给出了本文提出的融合多尺度特征的无监督缺陷检测模型框架。该方法框架主要由两个阶段组成：特征学习和异常检测与定位。在特征学习阶段，首先，将训练图像输入预训练好的神经网络中，提取其多尺度特征。然后，采用半正交嵌入特征降维减少冗余特征的影响。最后，分步计算特征学习中的参数，以降低开销，提高学习效率，并获取训练模型。在异常检测与定位阶段，为了获取较为精确的异常图计算结果，使用局部马氏距离作为异常分数计算方式，对待测图像进行检测。
图 2 融合多尺度特征的无监督缺陷检测模型框架Fig. 2 Unsupervised defect detection model framework based on mutil-scale features下载:
全尺寸图片
2.1 特征学习
将图片输入经过ImageNet[12]预处理的神经网络中，提取到前3层特征层相对应的特征图。通过插值将不同尺寸大小的感受野与提取到的最大尺寸(即第一层特征层的尺寸)相匹配后，所得到的多尺度视觉特征有助于检测不同大小的异常缺陷。将特征进行筛选和提取，并通过多过程学习，得到缺陷训练模型。特征学习的过程如图2左侧部分所示。
2.1.1 半正交嵌入特征降维
由于实验设备的限制和数据集尺寸的影响，利用图像全部的特征进行训练，效率低下且耗费巨大。Defard等[18]通过实验证明图像的部分特征含有冗余信息，对训练效果没有益处，并使用随机降维的方式解决这一问题。但是在这种降维方式随机性过高，不易利用好对检测有益的特征。基于上述问题，根据概率论中的中心极限定理，当样本容量无穷大时，分布的极限就是高斯分布。故本文采用半正交嵌入特征降维方式取代随机降维，更好地利用对训练有益的特征，减少冗余特征的影响。
基于对正交不变性的观察，Kim等[25]建议使用标准正交向量来嵌入特征向量，这些向量由酉变换组成。正交向量
${\boldsymbol{S}}$ 由高斯分布随机变量生成：$$ {\boldsymbol{S}} \in {r^{H \times k}} \sim N\left( {0,1} \right) $$ (1) 式中：
$H$ 为神经网络提取到的特征维度数量；$k$ 为秩约束，即需要保留的特征维数。$k$ 越小，则保留的特征维数越少，相应地计算复杂度也会降低，但是$k$ 过大或过小也会影响训练效果，需要找到它的相对平衡点。且由${\rm{QR}}$ 分解得出：${\boldsymbol{S}} = {\boldsymbol{QR}}$ 。对于特征图的每一个位置，本方法均使用相同的嵌入。根据Mezzadri[26]提出的方法，计算大小为$H \times k$ 的近似矩阵${\boldsymbol{W}}$ ：$$ {\boldsymbol{W}} = {\boldsymbol{Q}} * {\rm{sign}}\left( {{\rm{diag}}\left( {\boldsymbol{R}} \right)} \right) $$ (2) 式中：
$ {\rm{diag}}(·) $ 得到给定矩阵的对角线矩阵，$ {\rm{sign}}(·) $ 返回矩阵形状相同的元素符号，进而使其呈标准正态分布。在线性代数中，矩阵${\boldsymbol{W}}$ 又被称为半正交矩阵，即它具有如下性质：${{\boldsymbol{W}}{\rm{^T}}}{\boldsymbol{W}} = {{\boldsymbol{I}}_k} \in {{\bf{R}}^{k \times k}}$ ，且${\boldsymbol{W}}{{\boldsymbol{W}}^{\rm{T}}} \ne {{\boldsymbol{I}}_F} \in {{\bf{R}}^{H \times H}}$ 。再根据先前所获得的大小为$H \times N$ ，特征尺寸为$w \times h$ 的多尺度特征${\boldsymbol{F}}$ ，$w \times h$ 为第一特征层中单个特征的尺寸，$N$ 为输入的图片总体数量，本文可以得到大小为$k \times N$ ，特征尺寸为$w \times h$ 的半正交嵌入特征${{\boldsymbol{F}}_r}$ ：$$ {{\boldsymbol{F}}_r} = {{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{F}} $$ (3) 在进行特征提取的同时，需要将所用特征向量的对应维数序号按顺序记录到列表中：
$$ {\boldsymbol{L}} = [x] $$ (4) 式中：
${\boldsymbol{L}}$ 为记录序号的单列列表，$x \in [0,X)$ 为多尺度特征${\boldsymbol{F}}$ 中所用特征向量的对应序号，$X$ 为多尺度特征的最大序号(即特征的最大维数)。最后一并储存在训练模型中，以备后续的异常检测与定位时使用。经过上述步骤后，获取到的半正交嵌入特征${{\boldsymbol{F}}_r}$ 可以用于特征学习，形成训练模型。2.1.2 多过程特征学习
通常情况下，学习位置
$\left( {i,j} \right)$ 处的正常图像特征时，需要首先计算位于$\left( {i,j} \right)$ 处的嵌入特征向量集${{\boldsymbol{F}}_{i,j}}$ 。为了总结图像特征所携带的信息，样本协方差估计如下：$$ {{\boldsymbol{C}}_{i,j}} = {\rm{Cov}}\left( {{{\boldsymbol{F}}_{i,j}},{\boldsymbol{F}}_{i,j}^{\rm{T}}} \right) $$ (5) 式中：
${{\boldsymbol{C}}_{i,j}}$ 为该位置的协方差矩阵，$ {\rm{Cov}}(·) $ 返回特征向量协方差的计算结果。由于多尺度特征下直接按式(5)进行样本协方差计算会导致计算的复杂性问题，影响训练效率。因此，本文将它的计算拆分为初始向量计算、平均向量计算、初始协方差计算和协方差矩阵计算4个子过程，每个子过程按顺序依次进行，以降低计算复杂度，提高特征学习效率。
首先，生成初始向量
${{\boldsymbol{M}}_0}$ ：$$ {{\boldsymbol{M}}_{\text{0}}}{\text{ = }}\sum\limits_{i = 1}^N {{f_i}} $$ (6) 式中：
${f_i}$ 为第$i$ 个输入图片的半正交嵌入特征向量，$N$ 为输入的图片总体数量。该步骤的时间复杂度为$O\left( {Nwh} \right)$ 。然后，计算平均向量${\boldsymbol{M}}$ ：$$ {\boldsymbol{M}} = \frac{{{{\boldsymbol{M}}_0}}}{N} $$ (7) 由于平均向量
${{\boldsymbol{M}}_0}$ 的大小为$wh \times k$ ，故时间复杂度为$O\left( {whk} \right)$ 。接着，根据半正交嵌入特征${{\boldsymbol{F}}_r}$ 生成大小为$k \times k$ ，特征尺寸为$w \times h$ 的初始协方差矩阵${\boldsymbol{C}}'$ ：$$ {\boldsymbol{C}}' = {{\boldsymbol{F}}_r}{\boldsymbol{F}}_r^{\rm{T}} $$ (8) 该步骤时间复杂度为
$O\left( {N{k^2}} \right)$ 。最后，再计算第$i$ 个特征($i \in \left[ {0,wh} \right)$ )的协方差矩阵${{\boldsymbol{C}}_i}$ ：$$ {{\boldsymbol{C}}_i} = \frac{{{{{\boldsymbol{C}}'}_i} - N \times {{\boldsymbol{M}}_i}^{\rm{T}}{{\boldsymbol{M}}_i}}}{{N - 1}} + \varepsilon {\boldsymbol{I}} $$ (9) 式中：
${{\boldsymbol{C}}'_i}$ 表示位于第$i$ 个特征下的初始协方差矩阵，${{\boldsymbol{M}}_i}$ 表示${\boldsymbol{M}}$ 第$i$ 行元素，$\varepsilon $ 为可设定的单位系数，${\boldsymbol{I}}$ 是秩为$k$ 的单位对角阵，正则化项$\varepsilon {\boldsymbol{I}}$ 可以保证协方差矩阵${\boldsymbol{C}}$ 满秩且可逆。由于平均向量${\boldsymbol{M}}$ 的大小为$wh \times k$ ，且本方法中$wh \ll {k^2}$ ,故公式(9)的时间复杂度为$O\left( {{\text{5}}wh{k^2}} \right)$ 。综上所述，本方法计算的时间复杂度为$O\left( {\left( {{\text{5}}wh + N} \right){k^2}} \right)$ ，小于直接计算下的时间复杂度$O\left( {wh{k^3}} \right)$ 。经过上述步骤，本文就可以在降低时间复杂度的前提下，有效率地学习不同尺度的特征信息。同时，对预处理卷积神经网络不同语义级别之间的这些关系进行建模有助于提高异常定位性能[19]。
2.2 异常检测与定位
异常检测与定位流程如图2右侧部分所示。在通过特征学习得到训练模型后，本方法将测试集图片数据输入神经网络中，根据特征学习时的特征序号列表
$L$ ，定向提取多尺度特征中的特征向量，并插值匹配到第一特征层尺寸大小。若训练模型参数与检测用特征向量无法一一对应，则会导致最终检测结果出现严重偏差，对整个工业生产造成极其严重的影响。随后，进行异常分数计算，获得每个像素点对应分数组成的分数图。由此，可以根据实际需求选定合适的阈值，进行缺陷检测与定位。为了获得较为精确的异常图计算结果，本文使用改进后的马氏距离[23]作为测试图像在该位置
$\left( {i,j} \right)$ 处的异常分数。与特征学习阶段相似，本方法同样在第一特征层的尺度上进行马氏距离计算。局部马氏距离${d_{i,j}}$ 在本方法中可以解释为$\left( {i,j} \right)$ 处的测试图像嵌入特征${{\boldsymbol{F}}_{i,j}}$ 和平均向量${{\boldsymbol{M}}_{i,j}}$ 之间的距离，具体计算过程如下：$$ {d_{i,j}} = \sqrt {{{\left( {{{\boldsymbol{F}}_{i,j}} - {{\boldsymbol{M}}_{i,j}}} \right)}^{\rm{T}}}{\Sigma _{i,j}}^{{{ - 1}}}\left( {{{\boldsymbol{F}}_{i,j}} - {{\boldsymbol{M}}_{i,j}}} \right)} $$ (10) 式中
${\Sigma _{i,j}}$ 为特征学习得出的协方差矩阵${\boldsymbol{C}}$ 在位置$\left( {i,j} \right)$ 处的协方差矩阵形式。由此，可以计算形成异常分数图的马氏距离矩阵
${\boldsymbol{D}} = \left[ {{d_{i,j}}} \right]$ ，通过双线性插值上采样还原成输入图像的尺寸，以和图像具体位置一一对应。在分类情况下，整张图像的最终异常得分是异常分数图的最大值。在进行缺陷分割时，这张异常分数图上高于检测阈值的高分部分，即表示为检测出缺陷的异常区域。在测试时，由于不包含KNN的思想，不需要计算和排序大量距离值以获得补丁的异常得分，因此基于KNN的方法[16]而产生的可伸缩性问题，在本方法中并不存在。3. 实验与结果分析
在本章节中，本文将所提方法与其他先进方法在同一石板材缺陷数据集上的性能进行了对比，以验证本方法在石板材缺陷检测领域的有效性。此外，本文还比较了特征维数在不同取值的情况下对检测结果的影响，验证了冗余特征及特征维数过低都会干扰缺陷检测结果。最终实验结果表明，所提方法选用具有更大深度与宽度的网络作为基干网络，实际检测效果更好。
3.1 实验用数据集
本文所使用的石板材数据集由石板材正面和石板材反面两大类组成，图像分辨率为1275×279，包括1200张正常图像和242张缺陷图像，如图3所示。图4给出了石板材数据集中的4种缺陷模式：正常、磕边、裂纹和沙眼。除正常情况外，在其余3种缺陷模式下均进行了标记。本次实验选取大部分未作标记的正常图像作为训练集，剩余图像作为测试集，训练集和测试集数量按7∶3划分。
图 3 石板材数据集图片示例Fig. 3 Sample pictures of slate dataset下载:
全尺寸图片
图 4 石板材数据集缺陷模式示例Fig. 4 Examples of defect mode for slate dataset下载:
全尺寸图片
MVTec数据集作为一个开源的缺陷检测数据集，由15种类别组成，包括3629张训练图片，1725张测试图片，图像分辨率在700×700~1024×1024之间。它的训练集由无标注的正常图像组成，测试集则由正常图像和缺陷图像混合组成，其中缺陷图像均做了标注。本实验选用该数据集以验证本方法通用性和可靠性。
3.2 实验设置
本文使用英特尔14核CPU处理器，16 GB显存、32 GB内存的电脑设备，采用Python3.8进行实验。将石板材数据集中的输入图像分辨率大小统一调整为512×112，以WideResnet-50[27]为主干网，复现了PaDiM[18]和PatchCore[19]的模型，同时采用CFLOW-AD[28]的官方代码。包括本文方法，所有参与比较的方法所使用的神经网络均在ImageNet上进行了预处理。本文从前3层提取特征嵌入向量，并将其余特征层与第一特征层的尺寸相匹配，这3层特征图的尺寸大小分别为[1，256，128，28]、[1，512，64，14]和[1，512，64，14]，其中第1列为输入图像数量，第2列为特征维数，第3、4列为特征尺寸。经过插值匹配后的特征图尺寸为[1，1792，128，28]。以便组合来自不同语义级别的信息，同时保持足够高的分辨率以完成定位任务。为了更好地评估性能，本文使用接收器工作特性曲线下的面积(area under the receiver operating characteristic curve，ROC)，其中真阳性率是正确分类为异常的像素的百分比。由于ROC偏向于较大的异常，本文后续也采用了每个区域的重叠分数(PRO分数)进行计算比较。
3.3 实验结果及分析
在本小节中，本文给出了基于石板材数据集的实验结果，包括与现有的先进无监督缺陷检测方法的比较、采用不同特征维数和多种主干网络的比较结果。图5给出了部分通过本文方法得到的缺陷检测效果图。其中，从左到右分别为原图、异常分数热力图和缺陷分割结果图。
图 5 本文方法得到的部分石板材缺陷检测效果Fig. 5 Defect detection renderings of some slates obtained by our method下载:
全尺寸图片
3.3.1 与当前先进方法的比较
在石板材数据集上的图像级异常检测的结果如表1和表2所示。在所有情况下，本文方法在所有子数据集上都取得了更好的图像缺陷检测性能。表1为ROC度量中的检测结果，本文采用WideResNet-50为主干网络在图像级缺陷检测方面达到89.70%，比当前最先进的方法高出1.26%，在像素级缺陷定位方面达到95.39%，比最好的方法高出1.76%。表2包括PRO分数下的像素级缺陷定位检测结果比较。与其他先进方法相比，本文的方法在两类图像中的表现均更加出色，平均达到91.88%，比表现最好的PaDim高出1.75%。
表 1 石板材数据集缺陷检测结果(图片级分类ROC，像素级定位ROC)Table 1 Defect detection results of slate dataset (picture-level classification ROC, pixel-level localization ROC)% 石板材正/背面 CFLOW-AD PatchCore PaDiM 本文方法 石板材正面 (81.12,90.15) (85.05,90.92) (89.73,94.74) (91.36,96.73) 石板材背面 (79.88,88.72) (86.01,89.10) (87.15,92.51) (88.04,94.05) 总计 (80.05,89.44) (85.53,90.01) (88.44,93.63) (89.70,95.39) 表 2 石板材数据集缺陷检测结果(PRO分数)Table 2 Flaw detection results of slate dataset (PRO-score)% 石板材正/背面 CFLOW-AD PatchCore PaDiM 本文方法 石板材正面 84.86 86.06 93.32 95.63 石板材背面 81.07 86.25 86.94 88.12 总计 82.97 86.16 90.13 91.88 本文选用MVTec数据集验证本方法的通用性和可靠性，实验结果如表3所示。其中，为了适应数据集图像的尺寸和对比方法的实验设置，本实验统一将输入图像的尺寸调整为224像素×224像素，其余设置与石板材数据集实验保持一致，其中对比方法的结果由相应文献中得到。由于部分文献缺少图片级分类ROC的结果，本实验选择在像素级定位ROC和PRO分数度量中进行对比。本方法在像素级定位ROC度量中与几种先进方法互有优劣，而在PRO分数度量中总体优于对比方法，很好地验证了本方法的通用性和有效性。
表 3 MVTec数据集检测结果(像素级定位ROC，PRO分数)Table 3 Defect detection results of MVTec dataset (pixel-level localization ROC，PRO-score)% 纹理及类别 CFLOW-AD PatchCore PaDiM 本文方法 Bottle (98.98,96.80) (98.60,96.10) (98.30,94.80) (98.40,98.64) Cable (97.64,93.53) (98.50,92.60) (96.70,88.80) (96.73,96.98) Capsule (98.98,93.40) (98.90,95.50) (98.50,93.50) (98.56,98.34) Carpet (99.25,97.70) (99.10,96.60) (99.10,96.20) (99.01,98.93) Grid (98.99,96.08) (98.70,95.90) (97.30,94.60) (95.27,96.37) Hazelnut (99.66,96.68) (98.70,93.90) (98.20,92.60) (98.46,98.50) Leather (98.56,99.35) (99.30,98.90) (99.20,97.80) (99.27,99.52) Metal Nut (98.56,91.65) (98.60,91.30) (97.20,85.60) (97.74,97.96) Pill (95.39,95.39) (97.60,94.10) (95.70,92.70) (95.50,98.29) Screw (98.86,95.30) (99.40,97.90) (98.50,94.40) (98.21,98.06) Tile (98.01,94.34) (95.90,87.40) (94.10,86.00) (94.83,95.82) Toothbrush (98.93,95.06) (98.70,91.40) (98.80,93.10) (98.85,97.95) Transistor (97.99,81.40) (96.40,83.50) (98.50,84.50) (97.52,97.91) Wood (96.65,95.79) (95.10,89.60) (94.90,91.10) (94.92,97.63) Zipper (99.08,96.60) (98.90,97.10) (98.50,95.90) (98.15,98.17) 总计 (98.62,94.60) (98.10,93.50) (97.50,92.10) (97.43,97.94) 3.3.2 时间开销比较
在检测时间方面，本方法在几种方法中同样做到了最好，结果统计如表4所示。经过多次实验验证，本方法平均每张图片的检测时间仅需14.94 ms，检测效率远高于其他方法。同样地，得益于本方法的针对性优化措施，石板材数据集每个类别的整个训练及检测流程可以在3 min左右完成。相应地，PatchCore需要7 min，PaDim需要10 min左右，而基于流模型的CFLOW-AD则要耗费40 min。
表 4 石板材数据集平均缺陷检测时间Table 4 Average defect detection time on slate dataset方法 CFLOW-AD PatchCore PaDiM 本文方法 检测时间/ms 24.07 20.13 21.54 14.94 3.3.3 特征维数研究
尽管将全部的特征用于训练，可以实现最好的缺陷检测性能。但是，由于数据集大小及自身检测设备的限制，使得减小特征维度的数量变得很有必要。同时，减小嵌入特征维数的大小可以降低模型的计算复杂度。另一方面，若降维幅度过大，很有可能将含有必要信息的特征滤除，导致检测效果下降。因此，本文把嵌入特征分别下降到不同的维数
$k$ ，以研究半正交嵌入特征维数在石板材数据集中的表现，并寻找最佳性能下的特征维数。此外，本文也采用随机降维的方法，将特征向量下降相同的幅度。在这种情况下，本文训练多个模型并取平均的ROC度量分数及PRO分数。不同维度$k$ 下的缺陷检测结果如表5所示。表 5 改变降维幅度后的石板材数据集缺陷检测结果Table 5 Defect detection results of slate dataset under changing dimension reduction amplitude% 降维幅度 图片级分类ROC 像素级定位ROC 像素级定位PRO分数 半正交嵌入降维( $k = 100$) 88.90 95.16 91.25 半正交嵌入降维( $k = {\text{2}}00$) 89.70 95.39 91.88 半正交嵌入降维( $k = {\text{3}}00$) 89.67 95.11 91.70 半正交嵌入降维( $k = {\text{4}}00$) 89.39 95.07 91.71 随机降维( $k = {\text{2}}00$) 88.06 93.47 90.59 实验表现为这样一种现象：当特征维度保留过多时，检测性能会有一定程度的下降；而降维幅度过大，又会使得缺陷检测结果变差。之所以会呈现出这种情况，是由于特征维度保留过多时，包含不必要信息的特征向量也会一并保存下来。这些冗余特征在训练阶段使网络进行近乎无效训练的同时，还会干扰正常训练，让网络把训练权重转向自己，而不是具有必要信息的特征向量。上述问题导致神经网络训练效果不佳。而当降维幅度过大时，丢失的必要特征信息过多，使得检测性能降低。由实验结果可以看出，当特征向量采用半正交嵌入下降到200维时，本文方法的检测表现最好，在图片级检测ROC、像素级定位ROC和像素级定位PRO分数中，分别至少比选择其他维度高出0.17%、0.23%、0.17%。
Defard等[18]建议使用随机采样特征来减小协方差大小。然而，从表5中还可以注意到，对于相同数量的维度，半正交嵌入降维在石板材缺陷数据集上比随机降维检测性能更好，在ROC度量中分别高1.64%和1.92%，在PRO分数中高1.29%。相比较于随机降维，半正交嵌入降维更有助于区分正常类和异常类的维度。
3.3.4 主干网络选取研究
为了实验不同的主干网络对所提出的方法的影响，本文分别选用不同规格的残差网络，设定特征参数
$k{\text{ = 200}}$ ，本文方法在石板材数据集上得到检测结果如表6所示。根据表6可以得出，在其他参数变量保持一致的条件下，本文方法所使用的神经网络深度越深、宽度越宽，相应地，其缺陷检测性能就越优秀。表 6 不同主干网络下的石板材数据集缺陷检测结果Table 6 Defect detection eesults of slate datasets under different backbone networks% 主干网络名称 图片级检测ROC 像素级定位ROC 像素级定位PRO分数 ResNet-18 87.26 93.88 90.60 ResNet-50 89.33 94.72 91.61 WideResNet-50 89.70 95.39 91.88 4. 结束语
本文提出了一种新的基于无监督学习的石板材缺陷检测方法，减少了特征学习中冗余特征的影响，降低了计算复杂度，提高了缺陷检测的性能。在该方法的特征学习阶段中，使用容易获得的未标志图像数据，使用正半交嵌入特征降维方式，减少冗余特征的影响；通过多过程特征学习，减少计算中的时间复杂度，提高训练效率。然后，在检测阶段中，通过计算马氏距离作为异常分数，以得到更好的检测性能。在实验中，本文方法在石板材缺陷数据集取得了比现有先进方法更好的结果，同时在获得了石板材缺陷检测和定位中证明了本文方法的有效性。并通过在MVTec数据集上的实验，验证了本文方法的通用性和可靠性。
本文分析了本文方法中特征维数和网络结构分别对检测性能的影响。保留适当的特征维数可以有效将正常样本与缺陷样本区分开，而过大或过小都会降低最终检测效果。同时，更深更宽的神经网络也是提高缺陷检测性能的重要条件。本文通过定量实验验证了本文的上述分析。
尽管本文提出的方法在石板材缺陷检测方面展现出很高的效率，但其通用性受到各种原因的限制。这一问题可以通过与所使用功能的适应性结合来解决，将会在未来工作中进行深入研究与探索。
-
图 1 基于无监督学习的缺陷检测工作原理
Fig. 1 Operating principle of defect detection based on unsupervised learning
下载:
全尺寸图片
图 2 融合多尺度特征的无监督缺陷检测模型框架
Fig. 2 Unsupervised defect detection model framework based on mutil-scale features
下载:
全尺寸图片
图 3 石板材数据集图片示例
Fig. 3 Sample pictures of slate dataset
下载:
全尺寸图片
图 4 石板材数据集缺陷模式示例
Fig. 4 Examples of defect mode for slate dataset
下载:
全尺寸图片
图 5 本文方法得到的部分石板材缺陷检测效果
Fig. 5 Defect detection renderings of some slates obtained by our method
下载:
全尺寸图片
表 1 石板材数据集缺陷检测结果(图片级分类ROC，像素级定位ROC)
Table 1 Defect detection results of slate dataset (picture-level classification ROC, pixel-level localization ROC)
% 石板材正/背面 CFLOW-AD PatchCore PaDiM 本文方法 石板材正面 (81.12,90.15) (85.05,90.92) (89.73,94.74) (91.36,96.73) 石板材背面 (79.88,88.72) (86.01,89.10) (87.15,92.51) (88.04,94.05) 总计 (80.05,89.44) (85.53,90.01) (88.44,93.63) (89.70,95.39) 表 2 石板材数据集缺陷检测结果(PRO分数)
Table 2 Flaw detection results of slate dataset (PRO-score)
% 石板材正/背面 CFLOW-AD PatchCore PaDiM 本文方法 石板材正面 84.86 86.06 93.32 95.63 石板材背面 81.07 86.25 86.94 88.12 总计 82.97 86.16 90.13 91.88 表 3 MVTec数据集检测结果(像素级定位ROC，PRO分数)
Table 3 Defect detection results of MVTec dataset (pixel-level localization ROC，PRO-score)
% 纹理及类别 CFLOW-AD PatchCore PaDiM 本文方法 Bottle (98.98,96.80) (98.60,96.10) (98.30,94.80) (98.40,98.64) Cable (97.64,93.53) (98.50,92.60) (96.70,88.80) (96.73,96.98) Capsule (98.98,93.40) (98.90,95.50) (98.50,93.50) (98.56,98.34) Carpet (99.25,97.70) (99.10,96.60) (99.10,96.20) (99.01,98.93) Grid (98.99,96.08) (98.70,95.90) (97.30,94.60) (95.27,96.37) Hazelnut (99.66,96.68) (98.70,93.90) (98.20,92.60) (98.46,98.50) Leather (98.56,99.35) (99.30,98.90) (99.20,97.80) (99.27,99.52) Metal Nut (98.56,91.65) (98.60,91.30) (97.20,85.60) (97.74,97.96) Pill (95.39,95.39) (97.60,94.10) (95.70,92.70) (95.50,98.29) Screw (98.86,95.30) (99.40,97.90) (98.50,94.40) (98.21,98.06) Tile (98.01,94.34) (95.90,87.40) (94.10,86.00) (94.83,95.82) Toothbrush (98.93,95.06) (98.70,91.40) (98.80,93.10) (98.85,97.95) Transistor (97.99,81.40) (96.40,83.50) (98.50,84.50) (97.52,97.91) Wood (96.65,95.79) (95.10,89.60) (94.90,91.10) (94.92,97.63) Zipper (99.08,96.60) (98.90,97.10) (98.50,95.90) (98.15,98.17) 总计 (98.62,94.60) (98.10,93.50) (97.50,92.10) (97.43,97.94) 表 4 石板材数据集平均缺陷检测时间
Table 4 Average defect detection time on slate dataset
方法 CFLOW-AD PatchCore PaDiM 本文方法 检测时间/ms 24.07 20.13 21.54 14.94 表 5 改变降维幅度后的石板材数据集缺陷检测结果
Table 5 Defect detection results of slate dataset under changing dimension reduction amplitude
% 降维幅度 图片级分类ROC 像素级定位ROC 像素级定位PRO分数 半正交嵌入降维( $k = 100$) 88.90 95.16 91.25 半正交嵌入降维( $k = {\text{2}}00$) 89.70 95.39 91.88 半正交嵌入降维( $k = {\text{3}}00$) 89.67 95.11 91.70 半正交嵌入降维( $k = {\text{4}}00$) 89.39 95.07 91.71 随机降维( $k = {\text{2}}00$) 88.06 93.47 90.59 表 6 不同主干网络下的石板材数据集缺陷检测结果
Table 6 Defect detection eesults of slate datasets under different backbone networks
% 主干网络名称 图片级检测ROC 像素级定位ROC 像素级定位PRO分数 ResNet-18 87.26 93.88 90.60 ResNet-50 89.33 94.72 91.61 WideResNet-50 89.70 95.39 91.88 -
[1] 马立修. 激光切割及其在切割石板材中的应用研究[J]. 应用激光, 2008, 28(4): 292–294. MA Lixiu. The laser cutting and its application in cutting the stone plate[J]. Applied laser, 2008, 28(4): 292–294. [2] SAKURADA M, YAIRI T. Anomaly detection using autoencoders with nonlinear dimensionality reduction[C]//Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis. Gold Coast: ACM, 2014: 4−11. [3] 杨文元. 多标记学习自编码网络无监督维数约简[J]. 智能系统学报, 2018, 13(5): 808–817. YANG Wenyuan. Unsupervised dimensionality reduction of multi-label learning via autoencoder networks[J]. CAAI transactions on intelligent systems, 2018, 13(5): 808–817. [4] NGUYEN D T, LOU Z, KLAR M, et al. Anomaly detection with multiple-hypotheses predictions[EB/OL]. (2018−10−31)[2022−12−06]. https://arxiv.org/abs/1810.13292. [5] AKCAY S, ATAPOUR-ABARGHOUEI A, BRECKON T P. GANomaly: semi-supervised anomaly detection via adversarial training[C]//Asian Conference on Computer Vision. Cham: Springer, 2019: 622−637. [6] PIDHORSKYI S, ALMOHSEN R, ADJEROH D A, et al. Generative probabilistic novelty detection with adversarial autoencoders[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: ACM, 2018: 6823−6834. [7] SABOKROU M, KHALOOEI M, FATHY M, et al. Adversarially learned one-class classifier for novelty detection[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 3379−3388. [8] YI Jihun, YOON S. Patch SVDD: patch-level SVDD for anomaly detection and segmentation[C]//Asian Conference on Computer Vision. Cham: Springer, 2021: 375−390. [9] RUDOLPH M, WANDT B, ROSENHAHN B. Same same but DifferNet: semi-supervised defect detection with normalizing flows[C]//2021 IEEE Winter Conference on Applications of Computer Vision. Waikoloa: IEEE, 2021: 1906−1915. [10] BERGMAN L, COHEN N, HOSHEN Y. Deep nearest neighbor anomaly detection[EB/OL]. (2020−02−10) [2022−12−06]. https://arxiv.org/abs/2002.10445. [11] COHEN N, HOSHEN Y. Sub-image anomaly detection with deep pyramid correspondences[EB/OL]. (2020− 05−02) [2022−12−06]. https://arxiv.org/abs/2005.02357. [12] DENG Jia, DONG Wei, SOCHER R, et al. ImageNet: a large-scale hierarchical image database[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 248−255. [13] RUFF L, VANDERMEULEN R, GOERNITZ N, et al. Deep one-class classification[C]//35th International Conference on Machine Learning. Stockholm: PMLR, 2018, 80: 4393−4402. [14] BERGMAN L, HOSHEN Y. Classification-based anomaly detection for general data[EB/OL]. (2020−05−10) [2022−12−06]. https://www.researchgate.net/publication/341175574_Classification-Based_Anomaly_Detection_for_General_Data. [15] NAPOLETANO P, PICCOLI F, SCHETTINI R. Anomaly detection in nanofibrous materials by CNN-based self-similarity[J]. Sensors, 2018, 18(2): 209. doi: 10.3390/s18010209 [16] BERGMANN P, FAUSER M, SATTLEGGER D, et al. Uninformed students: student-teacher anomaly detection with discriminative latent embeddings[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 4182−4191. [17] LEE K, LEE K, LEE H, et al. A simple unified framework for detecting out-of-distribution samples and adversarial attacks[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: ACM, 2018: 7167−7177. [18] DEFARD T, SETKOV A, LOESCH A, et al. PaDiM: A patch distribution modeling framework for anomaly detection and localization[C]//International Conference on Pattern Recognition. Cham: Springer, 2021: 475−489. [19] ROTH K, PEMULA L, ZEPEDA J, et al. Towards total recall in industrial anomaly detection[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022: 14298−14308. [20] JOHNSON W B, LINDENSTRAUSS J. Extensions of lipschitz mappings into a Hilbert space[J]. Contemporary mathematics, 1984, 26(1): 189–206. [21] CHOROMANSKI K, ROWLAND M, WELLER A. The unreasonable effectiveness of structured random orthogonal embeddings[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017: 218−227. [22] LEZAMA J, QIU Qiang, MUSÉ P, et al. OLE: orthogonal low-rank embedding, A plug and play geometric loss for deep learning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 8109−8118. [23] SALEHI M, SADJADI N, BASELIZADEH S, et al. Multiresolution knowledge distillation for anomaly detection[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 14897−14907. [24] MAHALANOBIS P C. On the generalised distance in statistics[EB/OL]. (2016−08−15) [2022−12−06]. http://bayes.acs.unt.edu:8083/BayesContent/class/Jon/MiscDocs/1936_Mahalanobis.pdf. [25] KIM J H, KIM D H, YI S, et al. Semi-orthogonal embedding for efficient unsupervised anomaly segmentation[EB/OL]. (2021−05−31)[2022−12−06]. https://arxiv.org/abs/2105.14737.pdf [26] MEZZADRI F. How to generate random matrices from the classical compact groups[J]. Notices of the AMS, 2006, 54(5): 592–604. [27] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 770−778. [28] GUDOVSKIY D, ISHIZAKA S, KOZUKA K. CFLOW-AD: real-time unsupervised anomaly detection with localization via conditional normalizing flows[C]//2022 IEEE/CVF Winter Conference on Applications of Computer Vision. Waikoloa: IEEE, 2022: 1819−1828.
