Three-dimensional path planning of AUV based on improved ant colony optimization algorithm
-
摘要: 针对蚁群算法在三维路径规划时收敛速度慢且难以收敛至最优的缺点，提出一种新的改进蚁群算法，并将其应用于自主式水下机器人(autonomous underwater vehicle，AUV)三维路径规划。与现有算法相比，改进算法优点主要体现在3个方面：首先，引进伪随机状态转移概率提升算法全局搜索能力；其次，将距离和轨迹限定因子引入启发式函数，距离因子保证搜索不断趋近目标点，在轨迹限定因子约束下，轨迹累计转角更小，以此提升收敛速度和精度；最后，通过扩大信息素增量差距并逐步提高信息素衰减系数，进一步提高路径规划效率。实验结果表明，改进蚁群算法能够获得累计转角更小路径，且路径长度更小，收敛速度更快。Abstract: A new and improved ant colony algorithm is proposed and applied to AUV in 3D path planning. This method addresses the disadvantages of slow convergence and difficulty in achieving the optimum of conventional ant colony algorithms in 3D path planning. Compared with existing algorithms, the improved algorithm mainly has three advantages. First, the pseudorandom state transition probability is introduced to improve the global search ability of the algorithm. Second, the distance and trajectory limitations are considered in the heuristic function, using the distance factor to ensure the search continues to approach the target point. Under the constraint of trajectory limitation, the cumulative rotation angle of the trajectory is small, thereby increasing the convergence speed and accuracy. Finally, the path planning efficiency can be further improved by expanding the incremental gap of pheromones and gradually increasing the attenuation coefficient of pheromones. Test results show that, by using the improved ant colony algorithm, a reduced path of the accumulative turning angle can be obtained, the path length decreases, and the convergence speed accelerates.
-
自主式水下机器人(autonomous underwater vehicle，AUV)是新型水下无人平台，该平台具有比较好的自主、隐蔽、环境适应和可部署性以及低费效比等优点。因此，AUV在海底勘探、水下救援、反潜、情报搜集和目标攻击等军民领域有广泛的应用前景，受到国内外学者高度关注并得到深入研究[1-5]。近年来，随着AUV技术快速发展，它的应用场景也越来越复杂。在此情形下，AUV路径规划问题已经成为相关领域一个研究热点。不同于二维地形，面对水下复杂多变的三维地形，如何规划最优路径是AUV面临的首要问题。一般来说，路径规划分为局部和全局路径规划两类。局部路径规划需要实时收集空间和障碍物信息，然后规划出一条当前点到子目标节点的最优路径，因此该规划也叫做动态规划。全局路径规划是指在空间信息已知情况下，根据障碍分布情况，对起点到目标点进行路径规划，因此该规划属于静态规划。目前，用于全局路径规划的传统方法主要有RRT算法[6-7]、A*算法[8-9]、D*算法[10-11]和Dijkstra算法[12-13]等。这些基于数学模型的算法很难在复杂的三维环境中规划有效路径。在此情况下，有学者提出模拟动物行为的群智能算法，如蚁群算法(ant colony optimization, ACO) [14-15]、粒子群算法[16-17]、遗传算法[18-19]和人工蜂群算法等[20-21]。相比于其他群智能算法，蚁群算法具有更强解决高复杂度问题能力。
蚁群算法是一种模拟蚂蚁觅食行为的进化算法，具备较强的寻优能力和鲁棒性，早期被用于解决旅行商问题并取得了较好成效，其缺点是当问题维度变大时，算法收敛速度变慢且难以收敛至最优。标准蚁群算法在进行三维路径规划时，可选择的点数量很多，导致收敛精度不足，搜索时间长。文献[22]提出了一种基于安全、距离和路径偏移因子的启发式函数，该函数能大幅提升算法收敛精度，但完全收敛速度依然很慢。文献[23]提出一种具有局部可见性启发函数，该函数虽能有效提高蚂蚁前期搜索到较优路径概率和收敛速度，但会使搜索空间减小，容易产生局部最优问题。针对标准蚁群算法收敛速度慢和难以收敛至最优的缺点，改进状态转移概率，逐渐降低启发函数权重，再将新的距离和轨迹限制因子引入启发函数，以减少AUV转弯次数，从而改善收敛精度。在信息素更新时，放大信息素差距并使信息素衰减率逐渐提高，以提升算法整体收敛精度和收敛速度。
1. 环境建模和搜索空间
1.1 环境建模
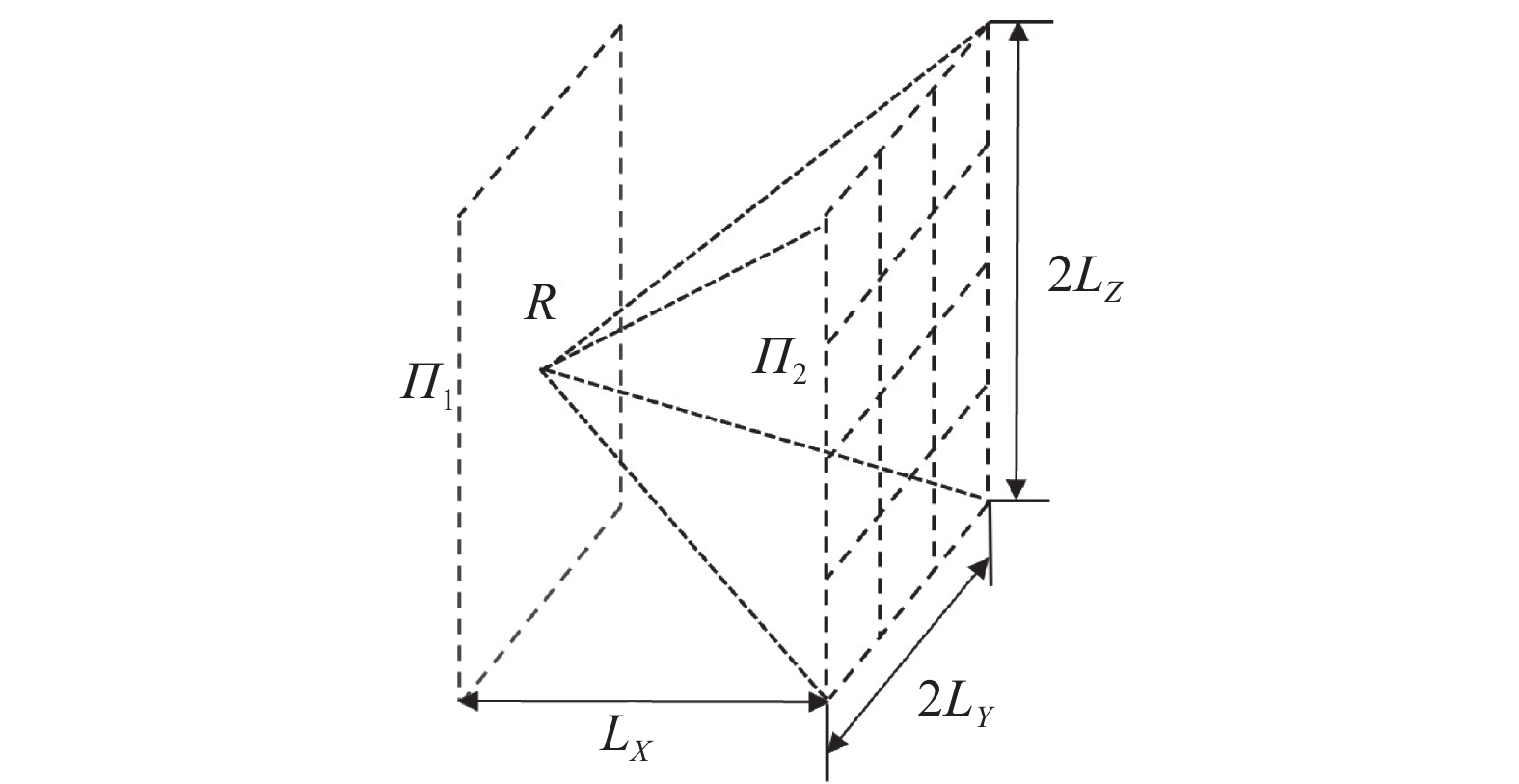
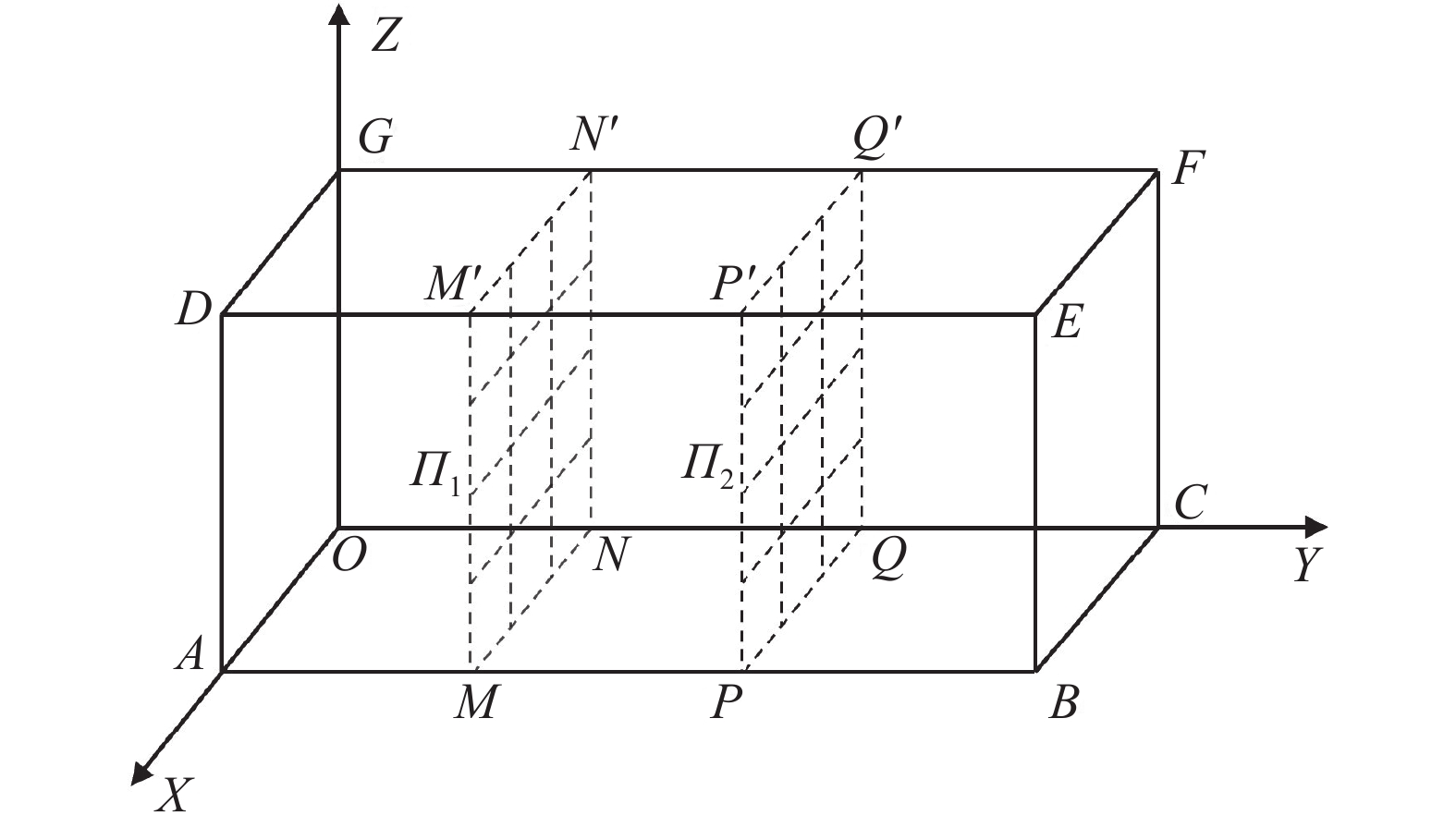
针对AUV三维路径规划问题，采用栅格法进行水下环境建模，具体构建方法如图1。
图 1 栅格法建模示意Fig. 1 Schematic diagram of grid method modeling
下载:
全尺寸图片
水下三维地图建模主要分为以下3步。
1) 建立一个空间坐标系O-XYZ，在该坐标系内以原点O为顶点构建立方体OABC-DEFG。OA、OC和OG分别代表了地图中X、Y和Z 3个方向上最大尺度。
2) 沿着OC（即Y轴）将立方体均分为
$n$ 个部分，生成$n + 1$ 个平面$\varPi_i {(i = 1,2, \cdots ,n + 1)}$ 。3）将每一个生成的平面
${\varPi _i}$ 沿着OA（即X轴）均分为$m$ 部分，沿着OG（即Z轴）均分为$l$ 部分，每个平面被分为$m \times l$ 部分，整个空间被分为了$n \times m \times l$ 个小立方体。经过这样划分后，可求出该空间坐标系每个点的离散坐标。这些离散点有两套坐标，即$({x_i},{y_j},{{\textit{z}}_k})$ 表示离散点在空间坐标系中的具体坐标，下标$(i,j,k)$ 表示该点的序列号。1.2 搜索空间
为降低三维环境搜索空间复杂度，采用逐层递进和平面搜索模式，如图2所示。
图 2 搜索空间示意图Fig. 2 Schematic diagram of the search space下载:
全尺寸图片
该搜索模式通过限制X、Y和Z轴的搜索范围，从而减小搜索空间。将X轴设为搜索主方向，
${L_{X}}$ 表示前进（X轴）最大距离，代表两个相邻平面${\varPi _1}$ 和${\varPi_2}$ 在X轴上距离。${L_Y}$ 表示横向最大移动距离（Y轴）。${L_Z}$ 表示纵向最大移动距离（Z轴）。2. 蚁群算法
2.1 蚁群算法基本原理
蚂蚁在觅食过程中，会不断地散发信息素，信息素浓度随时间不断衰减，路径越长，蚂蚁行走时间越长，信息素浓度就越低。而其他蚂蚁能感知信息素浓度并倾向选择信息素浓度高的路径。经过一段时间后，蚂蚁逐渐汇集到同一条路径中，最终找到一条最优路径。
2.2 状态转移概率
蚂蚁选择下一个点取决于信息素浓度和启发函数。在第
$t$ 次迭代中，蚂蚁$k$ 由节点$i$ 选择下一节点$j$ 的转移概率为$$ {P}_{ij}^{k}(t)=\left\{\begin{array}{l}\dfrac{{\tau }_{ij}^{\alpha }\left(t\right){\eta }_{ij}^{\beta }\left(t\right)}{{\displaystyle \sum _{s\in {\omega }_{k}}{\tau }_{is}^{\alpha }\left(t\right){\eta }_{is}^{\beta }\left(t\right)}},\qquad j\in {\omega }_{k}\\ 0,\qquad 其他\end{array}\right. $$ (1) $$ {\eta _{ij}} = \frac{1}{{{d_{ij}}}} $$ (2) 式中：
${\tau _{ij}}$ 表示路径$(i,j)$ 的信息素浓度；$ {\eta _{ij}} $ 为路径$(i,j)$ 的启发函数；${d_{ij}}$ 为当前节点$i$ 和待选节点$j$ 的欧氏距离；$\alpha $ 为信息素因子，反应信息素在路径选择中的比重；$\beta $ 为启发函数因子，反应启发函数在路径中选择的比重；$ {\omega _k} $ 表示所有下一可达节点的集合。2.3 信息素更新
一次迭代中所有蚂蚁找到通往目标点的路径后，对其残留信息素进行挥发处理，则
$t + 1$ 时刻在路径$(i,j)$ 上的信息素更新方式为$$ {\tau _{ij}}\left( {t + 1} \right) = (1 - \rho ){\tau _{ij}}\left( t \right) + \Delta {\tau _{ij}}(t,t + 1) $$ (3) 其中：
$ \,\rho $ 表示信息素衰减系数；$ \Delta {\tau _{ij}}(t,t + 1) $ 表示$t$ 到$t + 1$ 时刻信息素增量，计算公式为$$ \Delta {\tau _{ij}}(t,t + 1) = \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} $$ (4) $$ \Delta {\tau }_{ij}^{k}=\left\{\begin{array}{l}Q/{L}_{k},\qquad \left(i,j\right)\in {\psi }_{k}\\ 0,\qquad 其他\end{array} \right.$$ (5) 式中：
$ \Delta \tau _{ij}^k $ 表示蚂蚁$k$ 在路径$(i,j)$ 上分泌的信息素增量，$Q$ 为常量，${L_k}$ 表示蚂蚁$k$ 走过的总路径长度，$ {\psi _k} $ 是蚂蚁$ k $ 经过的路径集合。3. 蚁群算法的改进
3.1 转移概率的改进
针对标准蚁群算法收敛速度慢的问题，在原始状态转移概率基础上，引入伪随机规则来保证算法前期收敛速度，具体计算为
$$ j=\left\{\begin{array}{l}\underset{s\in {\omega }_{k}}{\overset{\mathrm{max}}{\mathrm{arg}}}\left({\tau }_{ij}^{\alpha }\times {\eta }_{ij}^{\beta }\right),\qquad q \leqslant {q}_{0}\\ {p}_{ij}^{k}(t),\qquad 其他\end{array}\right. $$ (6) 式中：
$q$ 是一个取值范围在$(0,1)$ 的随机数，${q_0}$ 是与迭代次数成反比的参数，其具体计算为$$ {q_0} = 1 - \xi \times {{\text{e}}^{ - \frac{1}{N}}} $$ (7) 信息素因子
$\alpha $ 为一固定值；而由式（6）可知，启发函数因子$\,\beta $ 取值影响路径初始规划，该值越大越接近贪心算法，越容易陷入局部最优，越小越无法找到目标点。因此，可以在算法前期取较大值来寻找一条初始路径，之后逐渐减小$\,\beta $ 的值，实现扩大算法搜索范围目的，相关计算为$$ \beta = {{\text{c}}_1} \times {{\text{e}}^{ - \frac{N}{{{N_{\max }}}}}} + 1 $$ (8) 其中：
$\xi $ 代表下限系数，$\xi \in (0,1)$ ；$N$ 是当前迭代次数；${N_{\max }}$ 是最大迭代次数；${c_1}$ 是常数。3.2 启发函数的改进
标准蚁群算法的启发函数只考虑当前节点
$i$ 和待选节点$j$ 的关系，没有考虑到与终点关系，容易使蚂蚁陷入局部最优。同时，在三维环境中，不仅需要考虑路径长度和避障，还需考虑蚁群算法在三维空间因过多转弯产生不必要消耗，因此提出一种新的启发函数。该启发函数由安全因子、距离因子和轨迹限制因子组成。下面对这些因子做简单介绍。1）安全因子
为了保障AUV航行安全，自主避开所有障碍及威胁，在启发函数中引入安全因子
$O$ 。安全因子判断机器人下一点$j$ 是否会撞上障碍，计算公式为$$ O = \left\{ \begin{gathered} 1,\qquad j \in {\omega _k} \\ 0,\qquad j \notin {\omega _k} \\ \end{gathered} \right. $$ (9) 2）距离因子
为使规划路径长度最短，引入距离因子
$D$ ，尽可能选取路径最短并且靠近终点的节点，$D$ 计算公式为$$ D = \frac{1}{{{d_{ij}} + {d_{jE}} - {d_{iE}} + {c_2}}} $$ (10) 其中：
${d_{jE}}$ 表示目标点和终点的距离，${d_{iE}}$ 表示当前点和终点的距离，${c_2}$ 是常数。3）轨迹限制因子
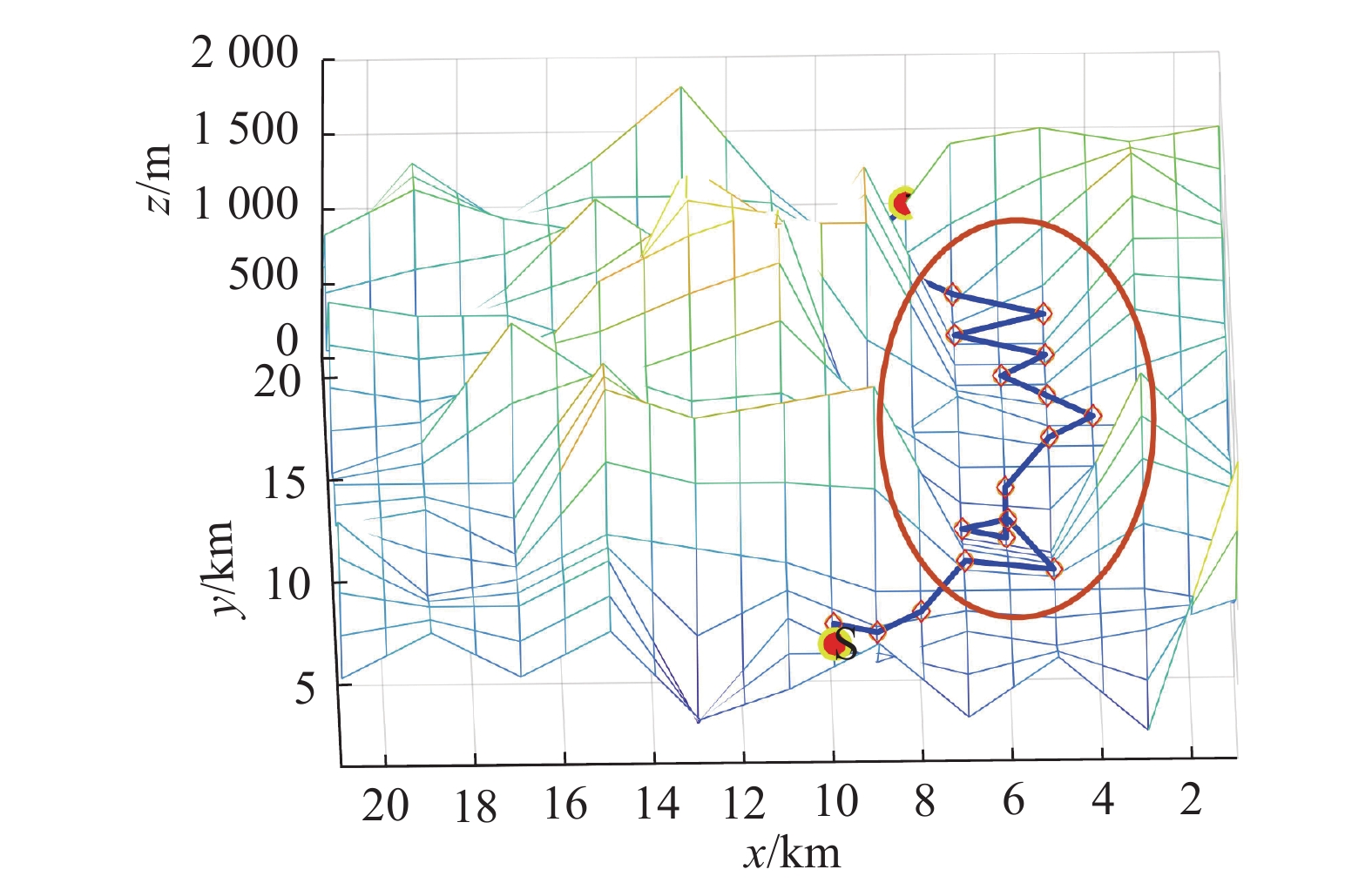
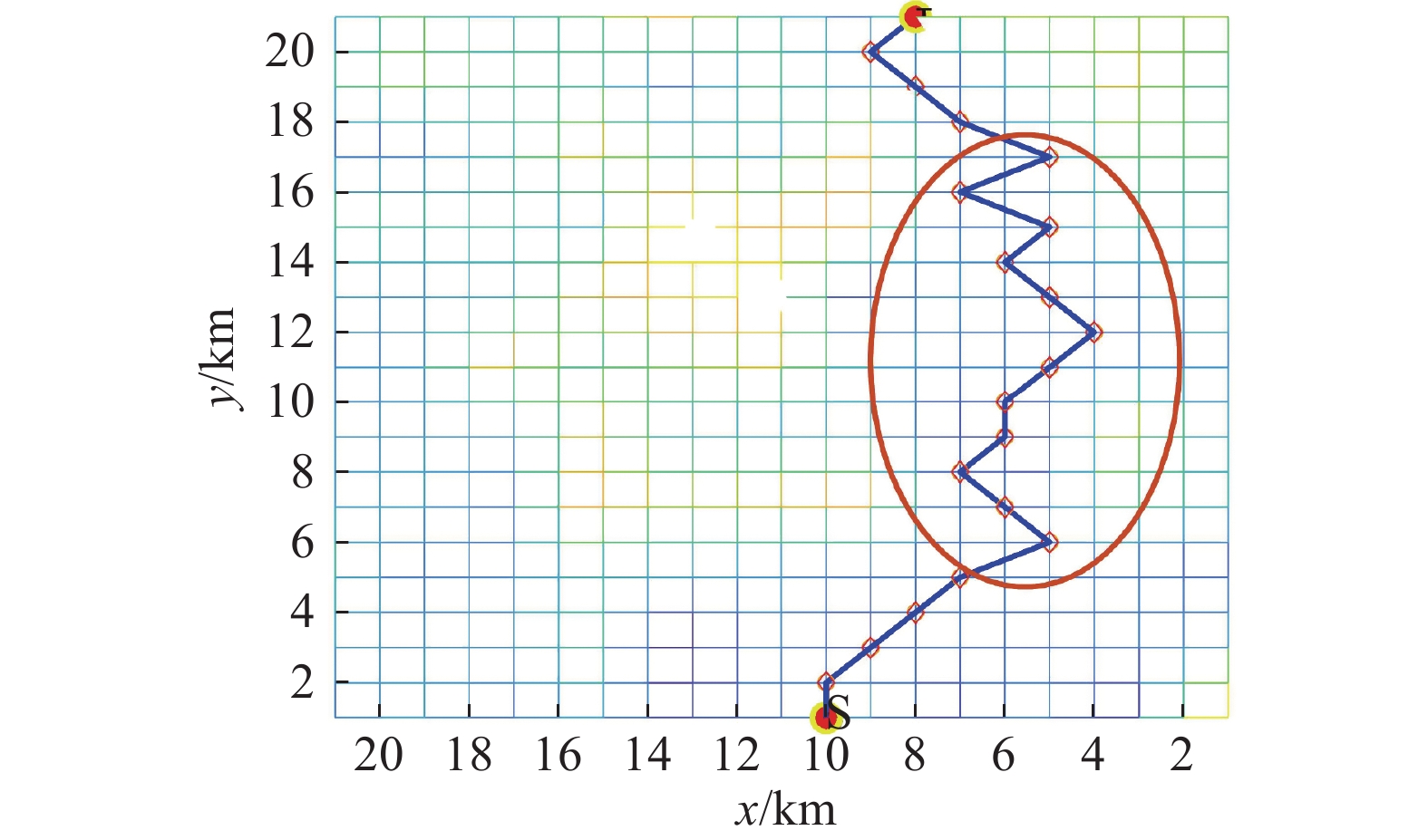
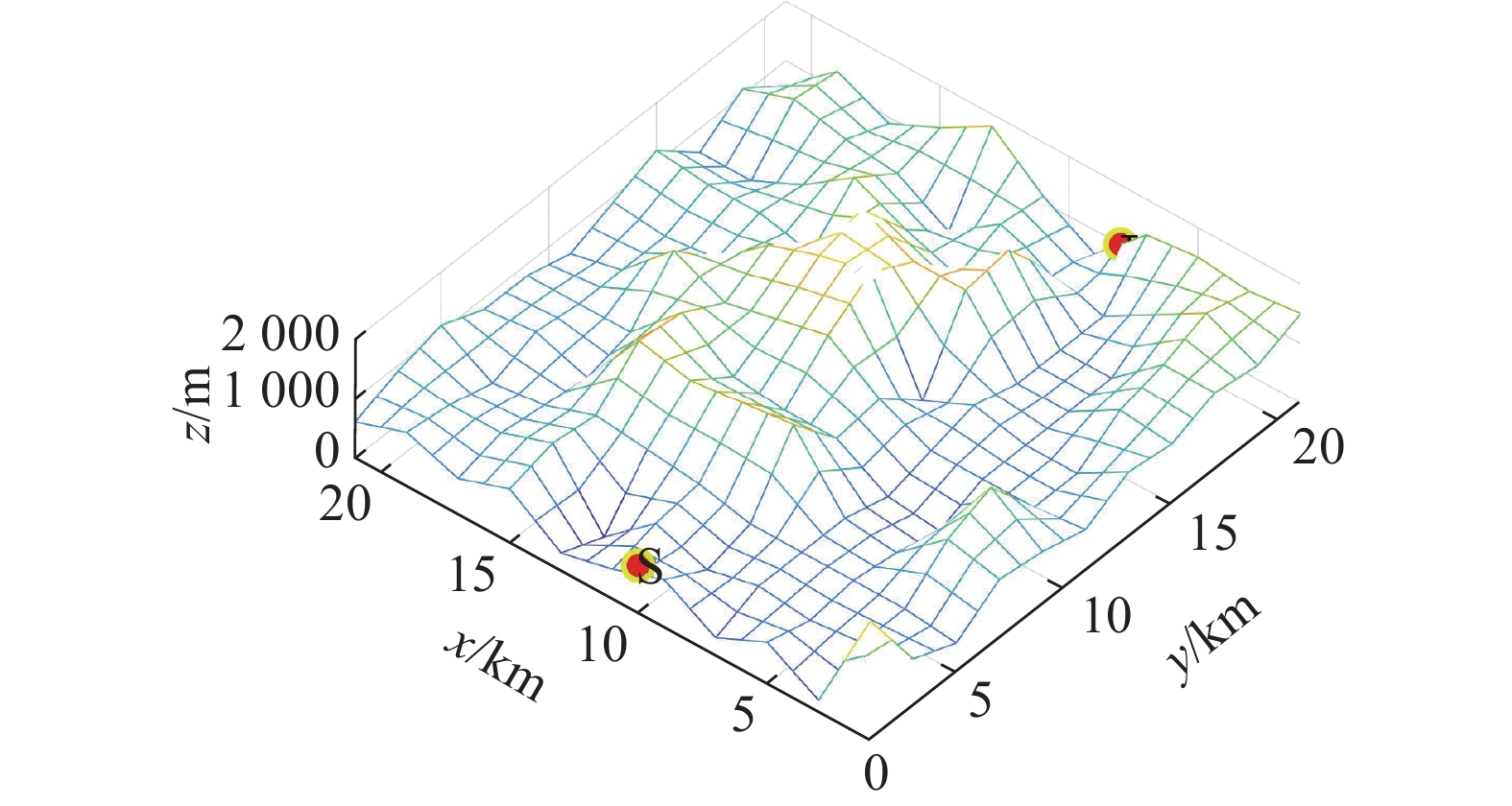
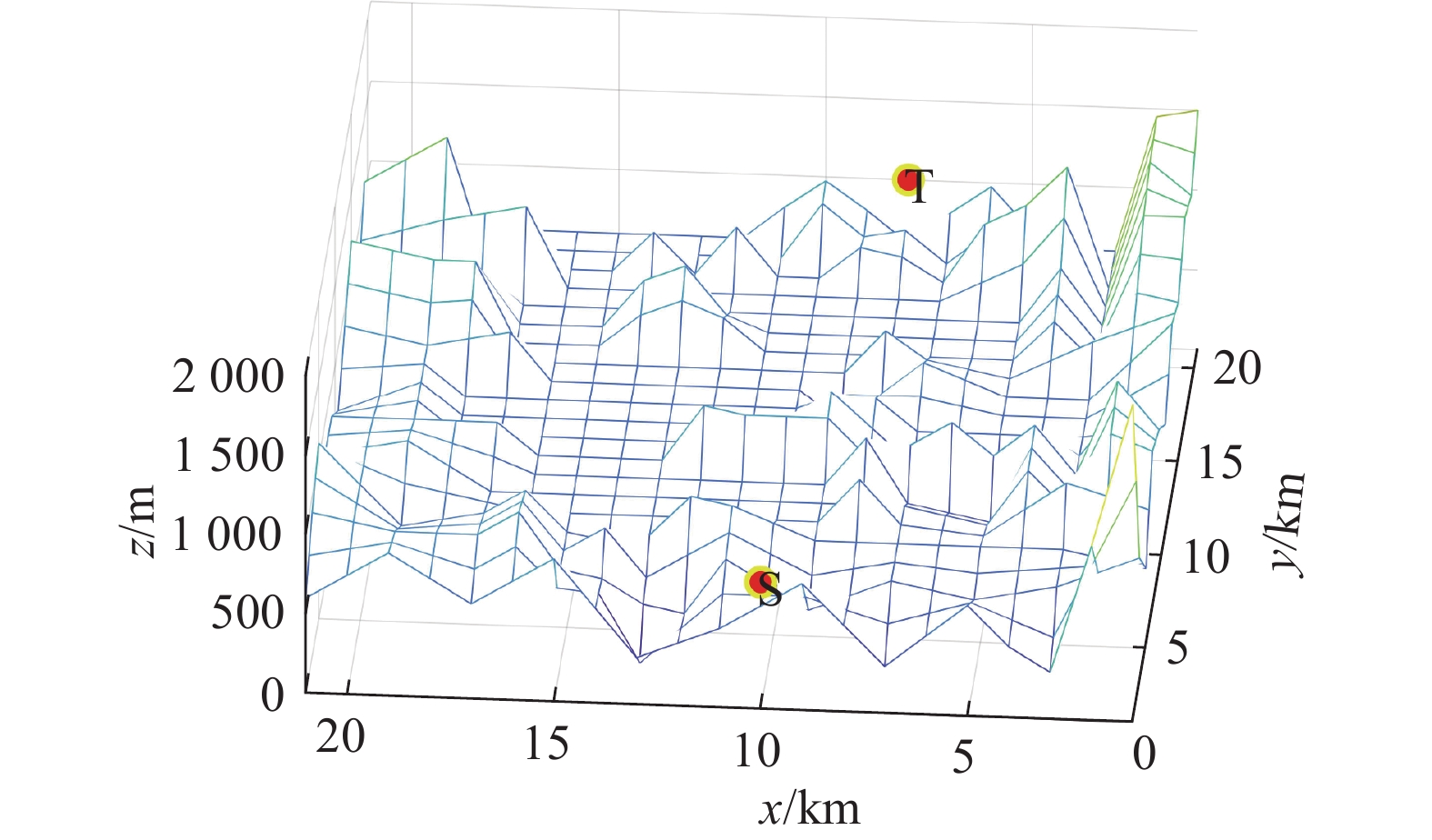
将标准蚁群算法应用于AUV三维环境路径规划时，搜索结果具有多样性，因此路径中有很多转折点，如图3和图4所示。在此情形下，路径中每一次转折都会增加路径长度和危险性。
图 3 标准蚁群算法路径Fig. 3 Original ant colony algorithm path下载:
全尺寸图片
图 4 标准蚁群算法路径俯视图Fig. 4 Vertical view of original ant colony algorithm path下载:
全尺寸图片
为此，引入轨迹限制因子，具体计算为
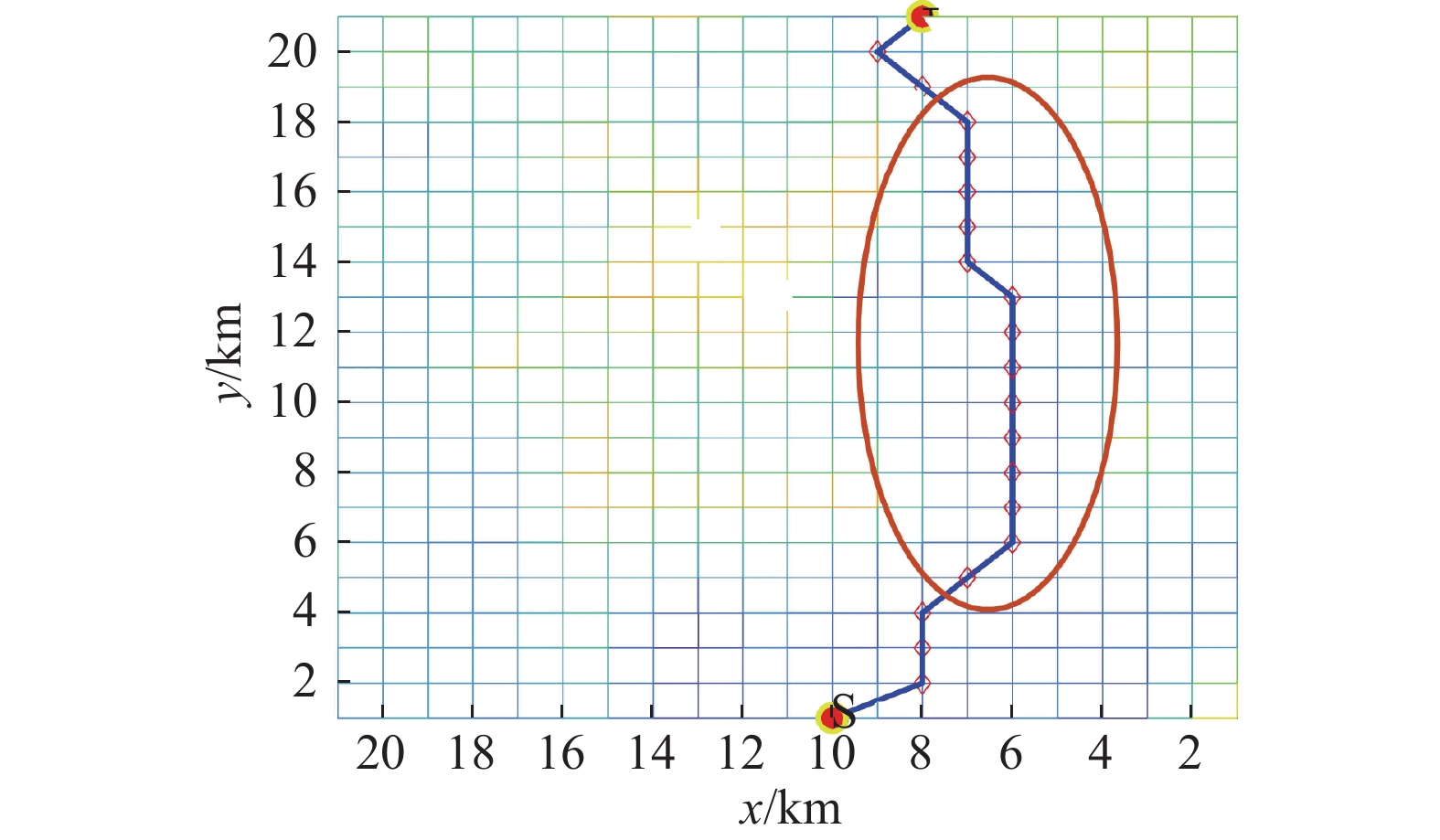
$$ T = \frac{1}{{{{\text{e}}^{| {{i_y} - {j_y}} | + \left| {{i_{\textit{z}}} - {j_{\textit{z}}}} \right| + \left| {{j_{\textit{z}}} + 1} \right|}}}} $$ (11) 式中：
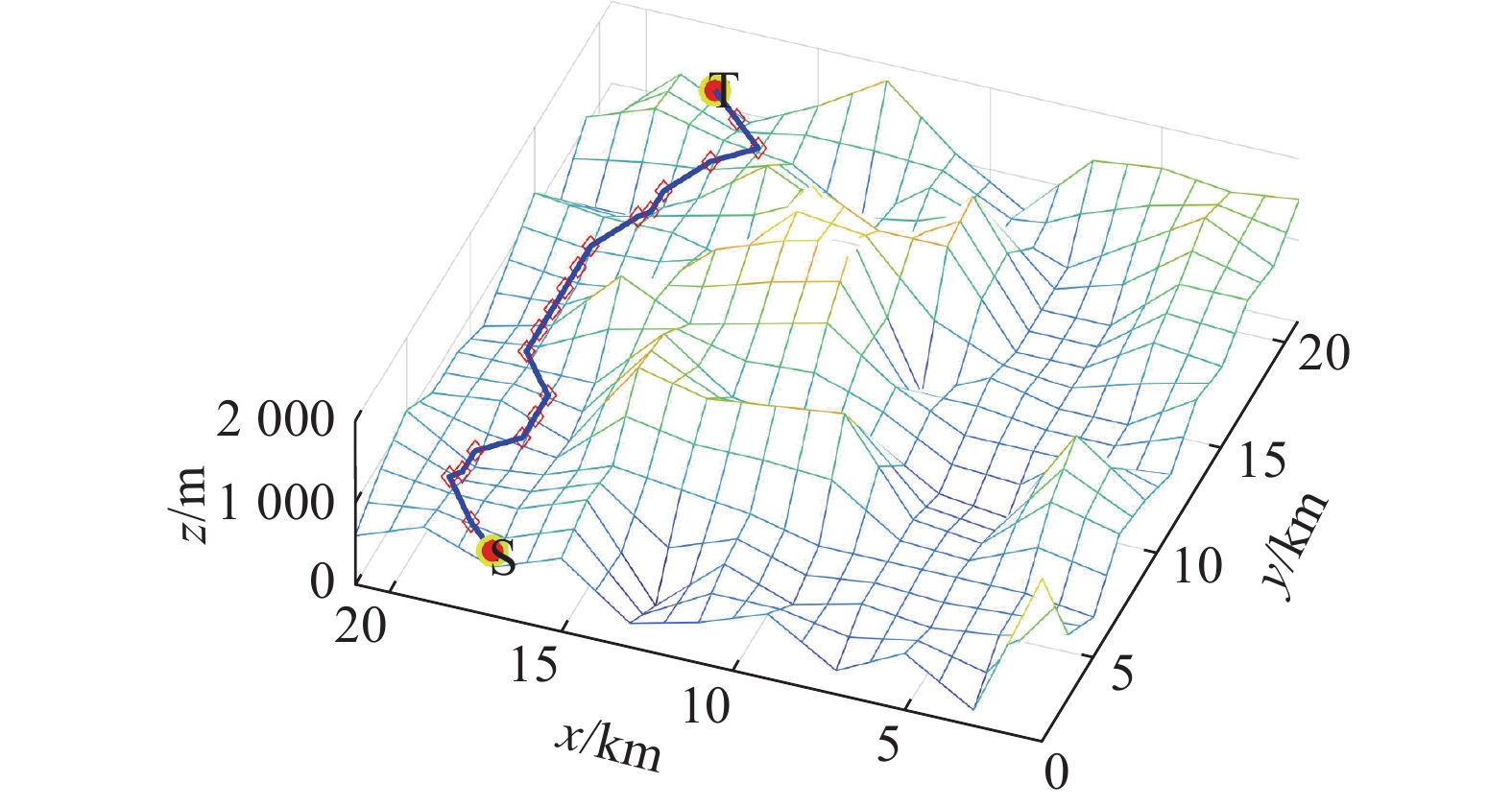
${i_y}$ 和${j_y}$ 分别表示当前点和下一点$y$ 轴高度。$ {i_{\textit{z}}} $ 和$ {j_{\textit{z}}} $ 分别表示当前点和下一点${\textit{z}}$ 轴高度。经过限制后的AUV轨迹如图5和图6所示。
图 5 改进蚁群算法路径Fig. 5 Improved ant colony algorithm path下载:
全尺寸图片
图 6 改进蚁群算法路径俯视图Fig. 6 Vertical view of improved ant colony algorithm path下载:
全尺寸图片
在安全和距离因子共同作用下，AUV在三维空间中能选择更加安全和全局最优路径。此外，轨迹限制因子能够减少拐点，从而规划出转角更小路径，并进一步提高搜索效率。
综合以上考虑，改进算法采用如下启发函数计算公式：
$$ \eta = O \times D \times T $$ (12) 3.3 信息素更新方式改进
标准蚁群算法只使用全局信息素更新方式，这样在一定程度上会导致信息素更新延迟。反之，若信息素更新采用局部更新策略，从某种程度上可解决信息素更新延迟问题，并且能在迭代时尽量确保其他蚂蚁有更大概率去选择未探索节点，从而达到扩大搜索范围和增强搜索能力目的。因此，同时使用局部和全局信息素更新方式更利于寻找全局最优解。下面具体介绍一下局部信息素更新、全局信息素更新和信息素最小值计算方式。
1) 局部信息素更新计算：
$$ {\tau _{ijk}}(t + 1) = (1 - \mu ){\tau _{ijk}}(t) $$ (13) 式中：
$\,\mu $ 为局部信息素衰减系数，是一个介于$(0,1)$ 的参数；$ {\tau _{ijk}}(t) $ 表示$t$ 时间在节点$(i,j,k)$ 上的信息素。2) 全局信息素更新计算：
$$ {\tau _{ijk}}(t + 1) = (1 - \sigma ){\tau _{ijk}}(t) + \sigma \cdot \Delta {\tau _{ijk}}(t) $$ (14) 式中：
$\sigma $ 表示全局信息素衰减系数，$\Delta {\tau _{ijk}}$ 表示第$t$ 次迭代信息素增量。在标准蚁群算法中，
$\sigma $ 是一个常量。在算法中后期，因信息素衰减量较小，路径信息素浓度大，该算法对不同路径的分辨能力较差。为解决这一问题，引入一种自适应全局信息素衰减系数方法。该方法中，算法前期$\sigma $ 值较小，在中后期逐渐增大，这样，蚂蚁就更能选择出最短路径。$\sigma $ 具体计算公式为$$ \sigma = 0.2 \times {2^{\frac{{2N}}{{{N_{\max }}}}}} $$ (15) 此外，标准蚁群算法在信息素更新时，不同路径信息素增量
$ {\tau _{ijk}}(t) $ 差距非常小，很难让蚂蚁规划出一条较优路径。基于这一原因，引入一种放大信息素增量差距方法，具体计算为$$ \Delta {\tau }_{ijk}(t)=\left\{\begin{array}{l}\dfrac{{c}_{3}\cdot {N}_{\mathrm{max}}}{2{L}_{m}}-{c}_{3},\text{ }(i,j,k)\in {\psi }_{k}\\ 0,\text{ }其他\end{array}\right. $$ (16) 式中：
$ {c_3} $ 为常数，表示信息素差距放大倍数；${L_m}$ 为一次迭代结束后的最优路径长度。3) 信息素最小值
算法中后期，经过多次信息素更新，未走过路径的信息素趋近于0。而根据式(1)，节点信息素小于1会使蚂蚁倾向避开此节点，为了让蚂蚁能探索更多节点，增强搜索能力，因此设置信息素最小值为1。
$$ {\tau _{ijk}} = \left\{ \begin{gathered} {\tau _{ijk}},{\text{ }}{\tau _{ijk}} \geqslant 1 \\ 1,{\text{ }}{\tau _{ijk}} < 1 \\ \end{gathered} \right. $$ (17) 3.4 算法步骤和流程
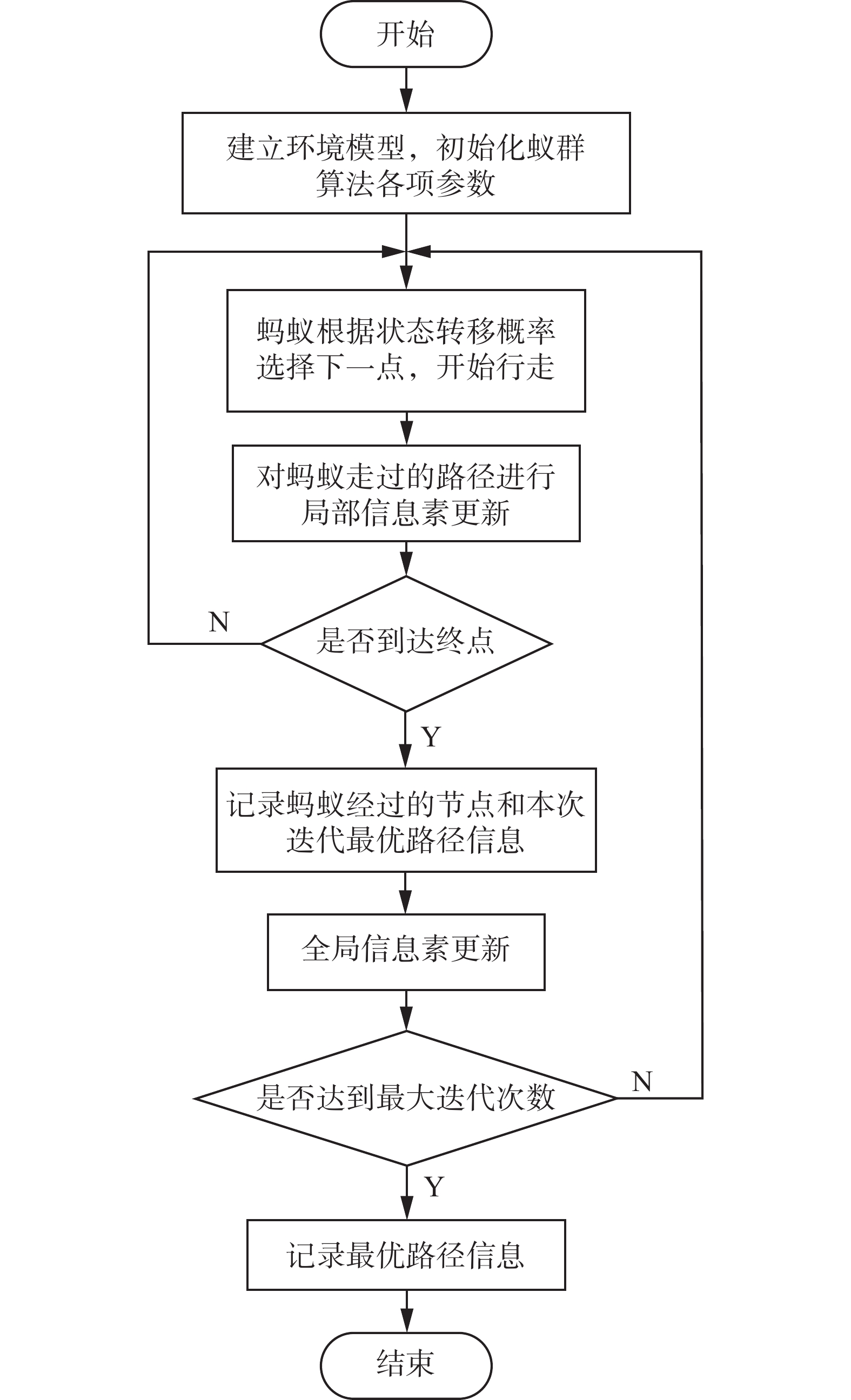
本小节主要介绍改进算法步骤和流程。主要有6个步骤，具体如图7所示。
图 7 算法流程Fig. 7 Algorithm flow chart下载:
全尺寸图片
4. 仿真实验
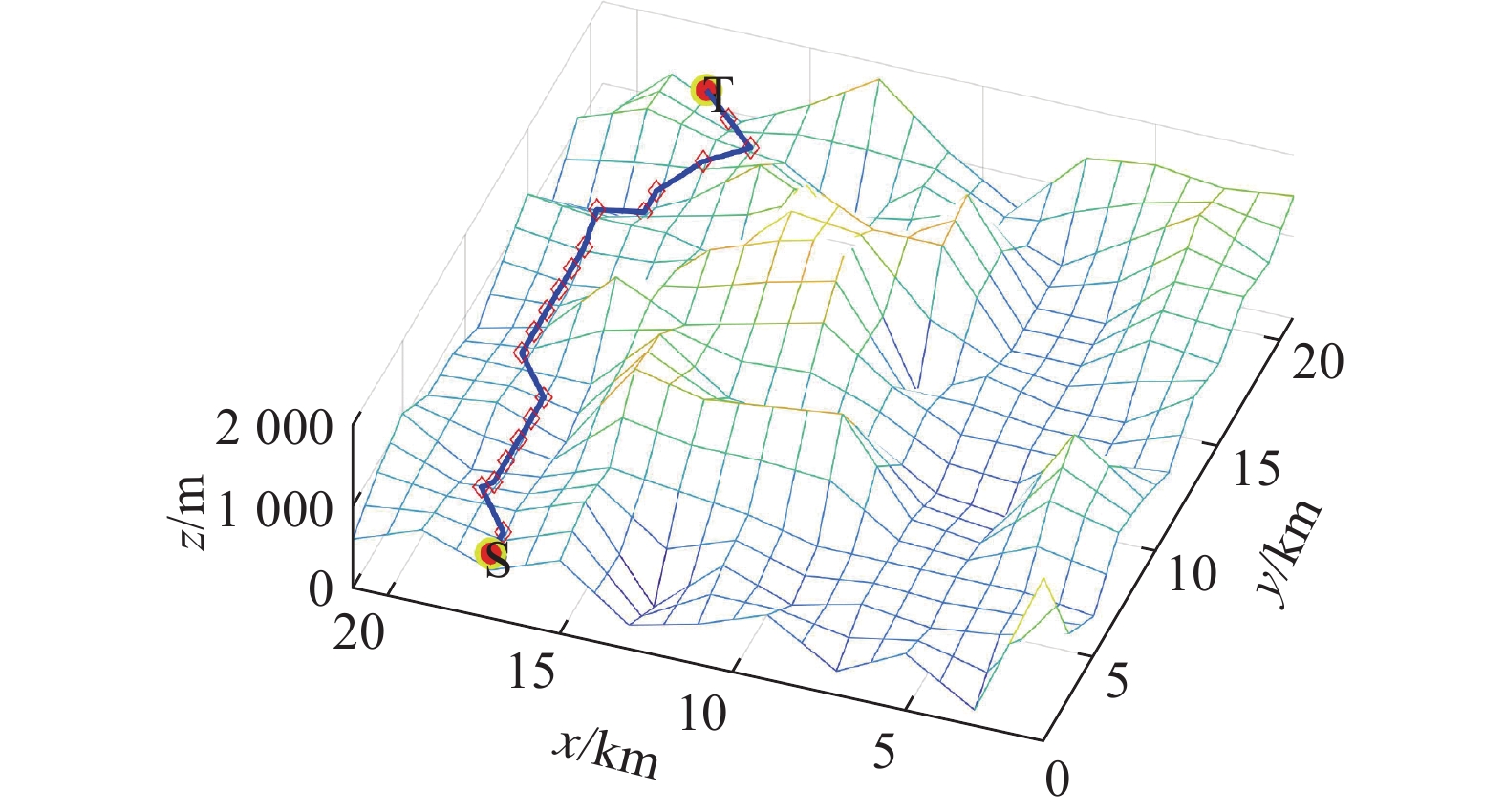
为验证改进蚁群算法有效性，进行对比实验，改进蚁群算法(MyIACO)采用与文献[24](IACO)和文献[25](NIACO)完全相同的两张随机三维地图，如图8、9所示，实验参数设置如表1所示。
图 8 第1张三维地图Fig. 8 First three-dimensional map下载:
全尺寸图片
图 9 第2张三维地图Fig. 9 Second three-dimensional map下载:
全尺寸图片
表 1 实验参数设置Table 1 Experiment parameter settings参数名 符号 设定值 最大移动距离（y、z轴） $ {L_y} $、${L_{\textit{z}}}$ 2 迭代次数 ${N_{\max }}$ 200 蚁群规模 $ m $ 100 信息素启发因子 $ \alpha $ 1 下限系数 $\xi $ 0.9 局部信息素衰减系数 $\mu $ 0.2 常数 ${c_1}$、${c_2}$、$ {c_3} $ 7、1、10 图10~16分别给出了不同算法下路径规划情况。第一组路径实验结果如图10~13所示。
图 10 IACO的第一条路径Fig. 10 First path of IACO下载:
全尺寸图片
图 11 NIACO的第一条路径Fig. 11 First path of NIACO下载:
全尺寸图片
图 12 MyIACO的第一条路径Fig. 12 First path of MyIACO下载:
全尺寸图片
图 13 第1组路径的路径长度变化趋势Fig. 13 Change trend graph of the first group of paths下载:
全尺寸图片
图 14 第1组路径多次实验路径长度Fig. 14 Path length of the first group of multiple experiments下载:
全尺寸图片
图 15 第2组路径多次实验路径长度Fig. 15 Path length of the second group of multiple experiments下载:
全尺寸图片
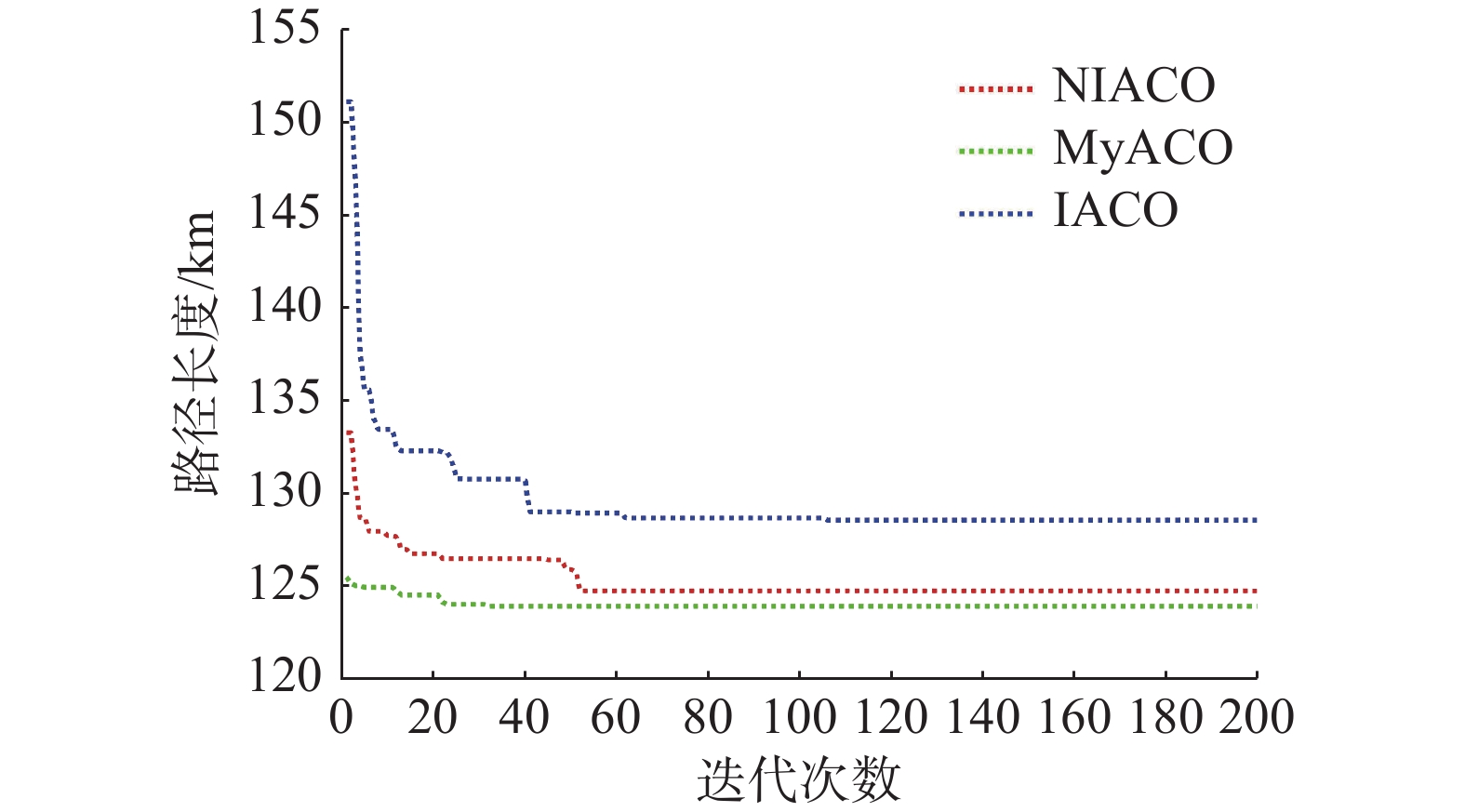
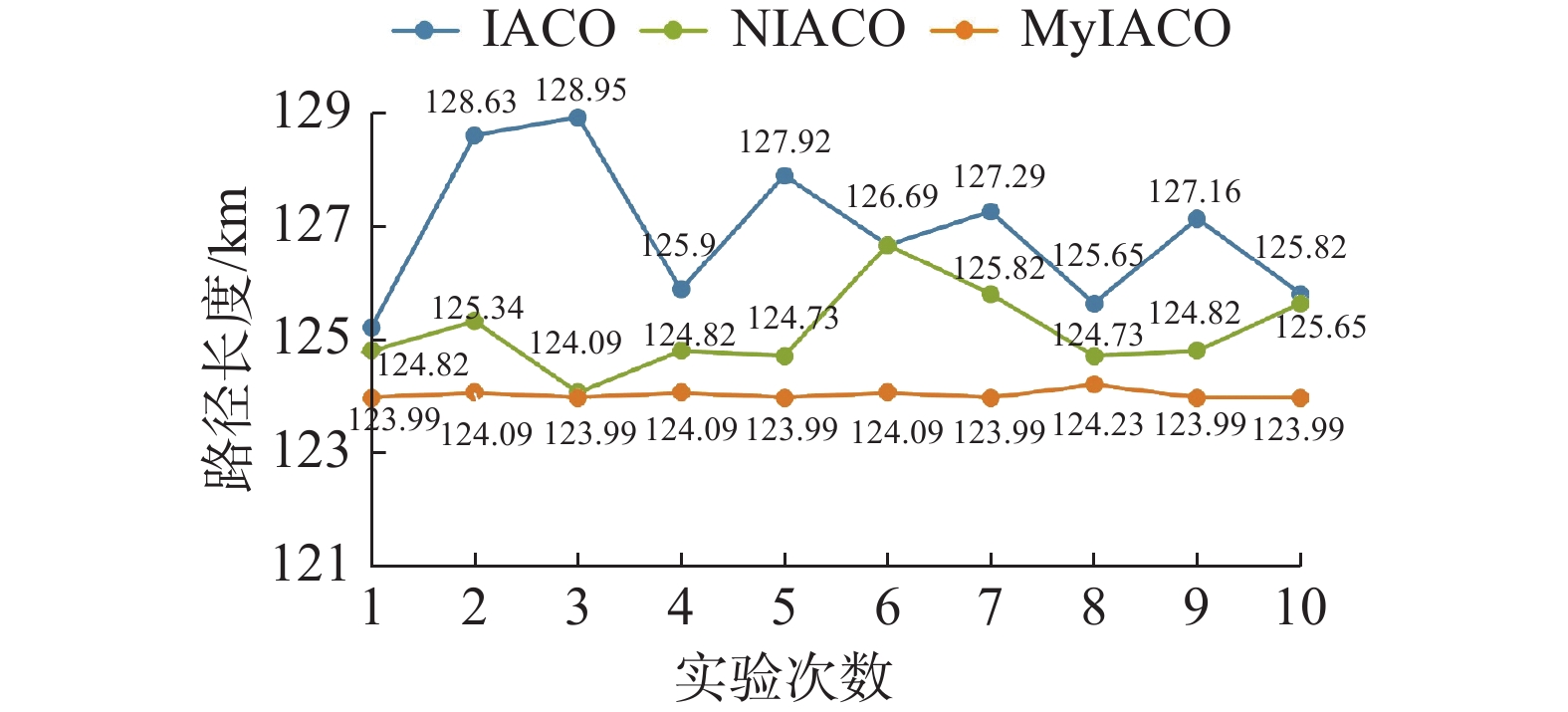
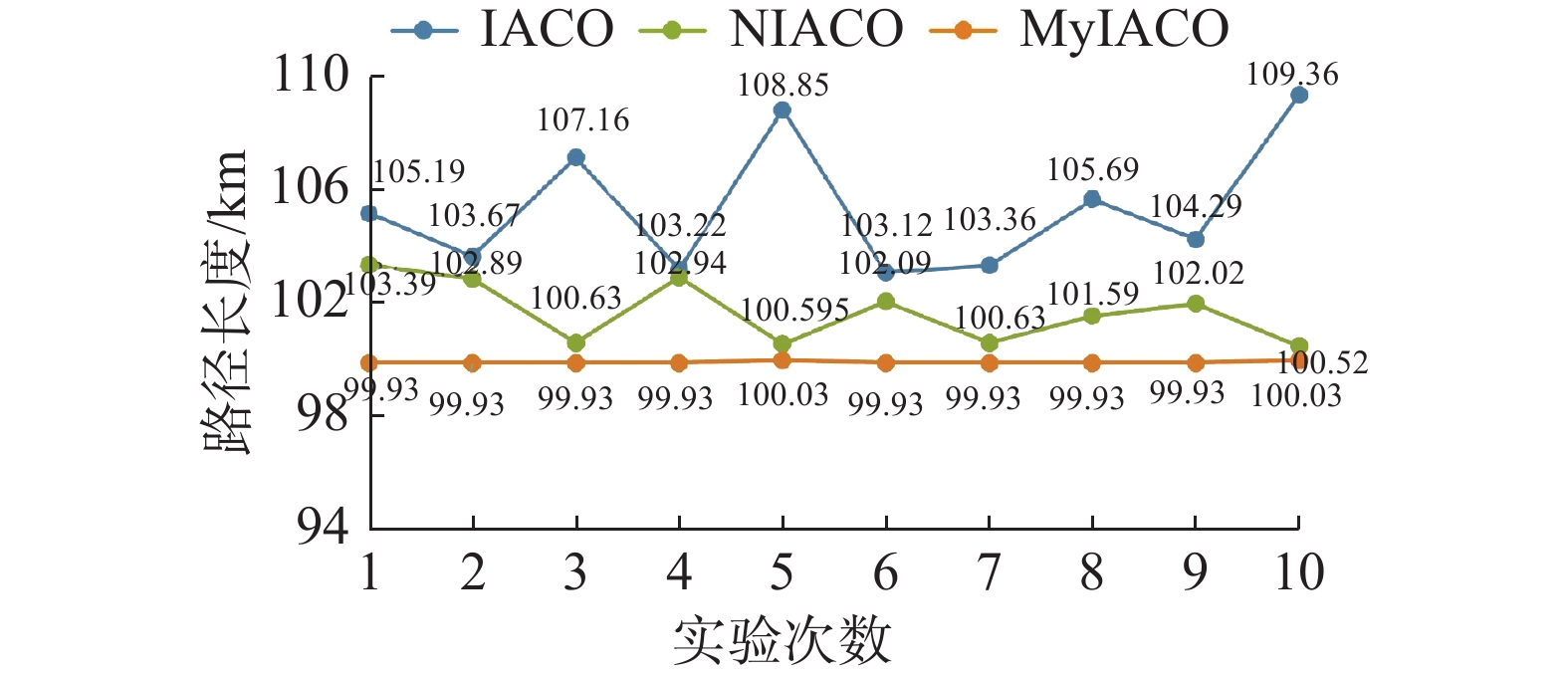
3种算法下第1组路径的多次实验路径长度如图14所示，具体平均数据如表2所示。3种算法第2组路径的多次实验路径长度如图15所示，具体平均数据如表3所示。
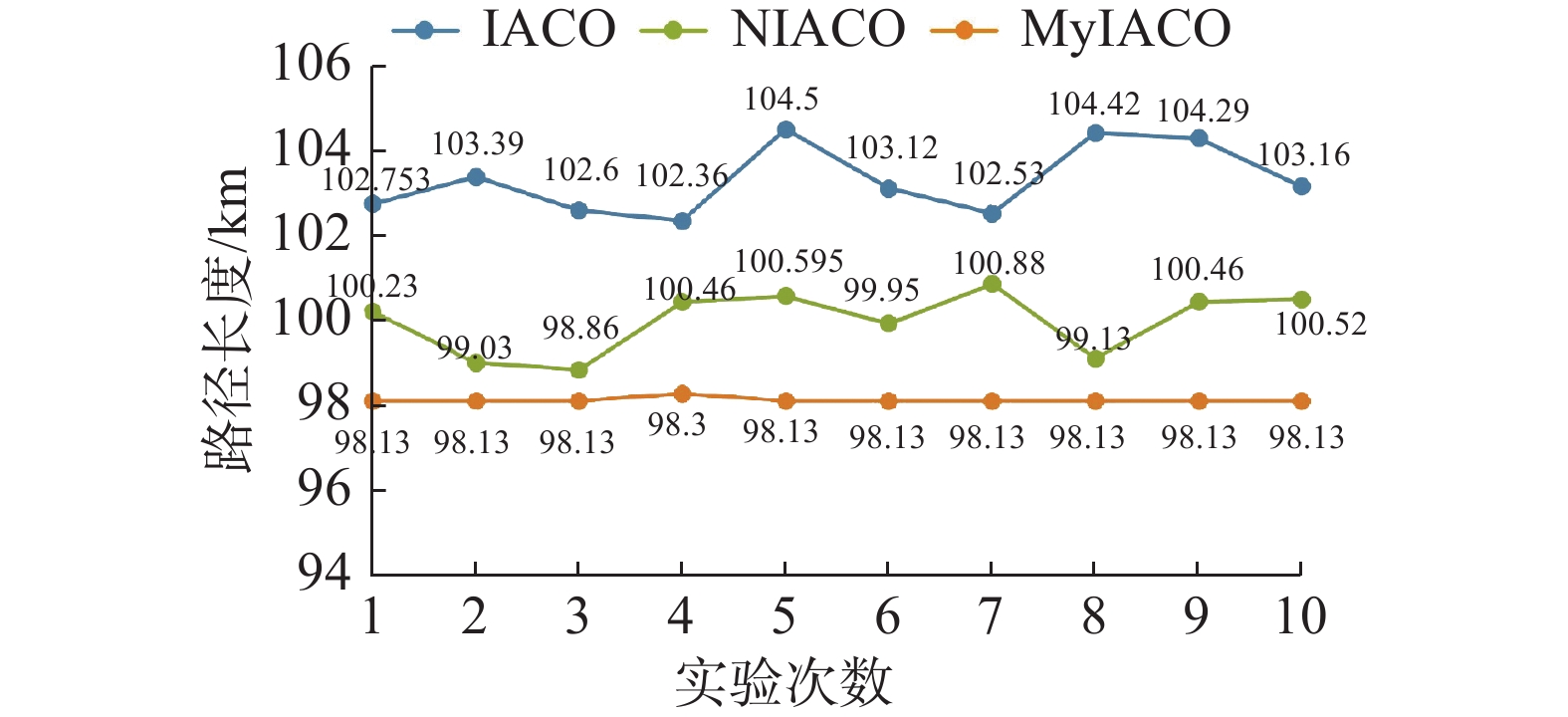
3种算法第3组路径的多次实验路径长度如图16所示，具体平均数据如表4所示。
图 16 第3组路径多次实验路径长度Fig. 16 Path length of the second map of multiple experiments下载:
全尺寸图片
由图10可知，由IACO算法产生的路径中出现了很多多余拐点。同样，由图11可以看出，NICAO算法运行时也会出现少量多余拐点。不管是哪种情况，都会增加AUV路径长度和危险性。但从图12可以看出利用改进算法MyIACO产生的路径没有出现多余拐点。从图14、15、16可以看出，改进算法MyIACO在大部分情况下已经能收敛至一个固定值，且没有向下波动，考虑到其轨迹中没有多余拐点的情况，可以认定收敛至最优。而从表2、3、4可以看出，MyIACO相比于其他两个算法的累计转角、收敛次数，运行时间都有一定的提升。
综上所述，改进算法MyIACO能有效克服蚁群算法收敛速度慢和难以收敛至最优的缺点。由此可见，利用改进蚁群算法规划路径能有效减少转弯次数，且能获得更短路径长度、更少收敛次数和运行时间等。
5. 结束语
针对蚁群算法在三维路径规划时收敛速度慢且难以收敛至最优的缺点，提出一种新的改进算法，并将该改进算法应用于AUV三维路径规划。改进算法结合伪随机状态转移概率的优点，以提升算法前期收敛速度，同时改进启发函数，以减少转角，降低路径长度。最后，提出新的信息素更新方式，扩大搜索范围，使蚂蚁趋向更短路径，且在一定程度上加快了算法收敛速度。仿真对比实验表明本文改进算法路径长度、累计转角、收敛速度和运行时间比文献[24]和文献[25]都得到了提升，考虑到AUV在海底环境中需要节能以运行更长时间，本文算法在实际应用中能发挥更好效果。此外，海底环境复杂多变，基于随机干扰的路径规划是研究难点，有待进一步深入研究。
-
图 1 栅格法建模示意
Fig. 1 Schematic diagram of grid method modeling
下载:
全尺寸图片
图 2 搜索空间示意图
Fig. 2 Schematic diagram of the search space
下载:
全尺寸图片
图 3 标准蚁群算法路径
Fig. 3 Original ant colony algorithm path
下载:
全尺寸图片
图 4 标准蚁群算法路径俯视图
Fig. 4 Vertical view of original ant colony algorithm path
下载:
全尺寸图片
图 5 改进蚁群算法路径
Fig. 5 Improved ant colony algorithm path
下载:
全尺寸图片
图 6 改进蚁群算法路径俯视图
Fig. 6 Vertical view of improved ant colony algorithm path
下载:
全尺寸图片
图 7 算法流程
Fig. 7 Algorithm flow chart
下载:
全尺寸图片
图 8 第1张三维地图
Fig. 8 First three-dimensional map
下载:
全尺寸图片
图 9 第2张三维地图
Fig. 9 Second three-dimensional map
下载:
全尺寸图片
图 10 IACO的第一条路径
Fig. 10 First path of IACO
下载:
全尺寸图片
图 11 NIACO的第一条路径
Fig. 11 First path of NIACO
下载:
全尺寸图片
图 12 MyIACO的第一条路径
Fig. 12 First path of MyIACO
下载:
全尺寸图片
图 13 第1组路径的路径长度变化趋势
Fig. 13 Change trend graph of the first group of paths
下载:
全尺寸图片
图 14 第1组路径多次实验路径长度
Fig. 14 Path length of the first group of multiple experiments
下载:
全尺寸图片
图 15 第2组路径多次实验路径长度
Fig. 15 Path length of the second group of multiple experiments
下载:
全尺寸图片
图 16 第3组路径多次实验路径长度
Fig. 16 Path length of the second map of multiple experiments
下载:
全尺寸图片
表 1 实验参数设置
Table 1 Experiment parameter settings
参数名 符号 设定值 最大移动距离（y、z轴） $ {L_y} $、${L_{\textit{z}}}$ 2 迭代次数 ${N_{\max }}$ 200 蚁群规模 $ m $ 100 信息素启发因子 $ \alpha $ 1 下限系数 $\xi $ 0.9 局部信息素衰减系数 $\mu $ 0.2 常数 ${c_1}$、${c_2}$、$ {c_3} $ 7、1、10 表 2 第1组路径平均实验数据
Table 2 Experimental data of the first group of paths
表 3 第2组路径平均实验数据
Table 3 Experimental data of the second group of paths
-
[1] 吴有生, 赵羿羽, 郎舒妍, 等. 智能无人潜水器技术发展研究[J]. 中国工程科学, 2020, 22(6): 26–31. doi: 10.15302/J-SSCAE-2020.06.004 WU Yousheng, ZHAO Yiyu, LANG Shuyan, et al. Development of autonomous underwater vehicles technology[J]. Strategic study of CAE, 2020, 22(6): 26–31. doi: 10.15302/J-SSCAE-2020.06.004 [2] CONSTABLE S, KOWALCZYK P, BLOOMER S. Measuring marine self-potential using an autonomous underwater vehicle[J]. Geophysical journal international, 2018, 215(1): 49–60. doi: 10.1093/gji/ggy263 [3] 封锡盛, 李一平, 徐会希, 等. 深海自主水下机器人发展及其在资源调查中的应用[J]. 中国有色金属学报, 2021, 31(10): 2746–2756. doi: 10.11817/j.ysxb.1004.0609.2021-37984 FENG Xisheng, LI Yiping, XU Huixi, et al. Development of deep-sea autonomous underwater vehicle and its applications in resource survey[J]. The Chinese journal of nonferrous metals, 2021, 31(10): 2746–2756. doi: 10.11817/j.ysxb.1004.0609.2021-37984 [4] WU Jiehong, SONG Chengxin, MA Jian, et al. Reinforcement learning and particle swarm optimization supporting real-time rescue assignments for multiple autonomous underwater vehicles[J]. IEEE transactions on intelligent transportation systems, 2022, 23(7): 6807–6820. doi: 10.1109/TITS.2021.3062500 [5] 钱东, 赵江, 杨芸. 军用UUV发展方向与趋势(上): 美军用无人系统发展规划分析解读[J]. 水下无人系统学报, 2017, 25(2): 1–30. QIAN Dong, ZHAO Jiang, YANG Yun. Development trend of military UUV(Ⅰ): a review of U. S. military unmanned system development plan[J]. Journal of unmanned undersea systems, 2017, 25(2): 1–30. [6] 刘成菊, 韩俊强, 安康. 基于改进RRT算法的RoboCup机器人动态路径规划[J]. 机器人, 2017, 39(1): 8–15. LIU Chengju, HAN Junqiang, AN Kang. Dynamic path planning based on an improved RRT algorithm for RoboCup robot[J]. Robot, 2017, 39(1): 8–15. [7] 张伟民, 付仕雄. 基于改进RRT*算法的移动机器人路径规划[J]. 华中科技大学学报(自然科学版), 2021, 49(1): 31–36. ZHANG Weimin, FU Shixiong. Mobile robot path planning based on improved RRT* algorithm[J]. Journal of Huazhong university of science and technology (natural science edition), 2021, 49(1): 31–36. [8] LIU Chenguang, MAO Qingzhou, CHU Xiumin, et al. An improved A-star algorithm considering water current, traffic separation and berthing for vessel path planning[J]. Applied sciences, 2019, 9(6): 1057. doi: 10.3390/app9061057 [9] 赵晓, 王铮, 黄程侃, 等. 基于改进A*算法的移动机器人路径规划[J]. 机器人, 2018, 40(6): 903–910. ZHAO Xiao, WANG Zheng, HUANG Chengkan, et al. Mobile robot path planning based on an improved A* algorithm[J]. Robot, 2018, 40(6): 903–910. [10] 史久根, 刘春霞, 席海强. CA模型下的改进D*路径规划算法[J]. 电子测量与仪器学报, 2016, 30(1): 30–37. SHI Jiugen, LIU Chunxia, XI Haiqiang. Improved D* path planning algorithm based on CA model[J]. Journal of electronic measurement and instrumentation, 2016, 30(1): 30–37. [11] 朱蟋蟋, 孙兵, 朱大奇. 基于改进D*算法的AUV三维动态路径规划[J]. 控制工程, 2021, 28(4): 736–743. ZHU Xixi, SUN Bing, ZHU Daqi. Three-dimensional dynamic path planning of AUV based on improved D* algorithm[J]. Control engineering of China, 2021, 28(4): 736–743. [12] 姜辰凯, 李智, 盘书宝, 等. 基于改进Dijkstra算法的AGVs无碰撞路径规划[J]. 计算机科学, 2020, 47(8): 272–277. JIANG Chenkai, LI Zhi, PAN Shubao, et al. Collision-free path planning of AGVs based on improved Dijkstra algorithm[J]. Computer science, 2020, 47(8): 272–277. [13] 陈亚琳, 庄丽阳, 朱龙彪, 等. 基于改进Dijkstra算法的泊车系统路径规划研究[J]. 现代制造工程, 2017(8): 63–67. CHEN Yalin, ZHUANG Liyang, ZHU Longbiao, et al. Research on path planing of parking system based on the improved Dijkstra algorithm[J]. Modern manufacturing engineering, 2017(8): 63–67. [14] DORIGO M, MANIEZZO V, COLORNI A. Ant system: An autocatalytic optimizing process technical report 91-016[J]. Clustering, 1991, 3(12): 340. [15] HAN Zhenhua, LIU Shugui, YU Fei, et al. A 3D measuring path planning strategy for intelligent CMMs based on an improved ant colony algorithm[J]. The international journal of advanced manufacturing technology, 2017, 93(1): 1487–1497. [16] 方群, 徐青. 基于改进粒子群算法的无人机三维航迹规划[J]. 西北工业大学学报, 2017, 35(1): 66–73. doi: 10.3969/j.issn.1000-2758.2017.01.011 FANG Qun, XU Qing. 3D route planning for UAV based on improved PSO algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1): 66–73. doi: 10.3969/j.issn.1000-2758.2017.01.011 [17] XIA Shuang, ZHANG Xiangyin. Constrained path planning for unmanned aerial vehicle in 3D terrain using modified multi-objective particle swarm optimization[J]. Actuators, 2021, 10(10): 255. doi: 10.3390/act10100255 [18] LEE J, KIM D W. An effective initialization method for genetic algorithm-based robot path planning using a directed acyclic graph[J]. Information sciences, 2016, 332: 1–18. doi: 10.1016/j.ins.2015.11.004 [19] 贺娇, 谭代伦. 基于视野范围和遗传算法的三维地形路径规划[J]. 计算机工程与应用, 2021, 57(15): 279–285. doi: 10.3778/j.issn.1002-8331.2103-0071 HE Jiao, TAN Dailun. Three-dimensional terrain path planning based on sight range and genetic algorithm[J]. Computer engineering and applications, 2021, 57(15): 279–285. doi: 10.3778/j.issn.1002-8331.2103-0071 [20] HAN Zengliang, CHEN Mou, SHAO Shuyi, et al. Improved artificial bee colony algorithm-based path planning of unmanned autonomous helicopter using multi-strategy evolutionary learning[J]. Aerospace science and technology, 2022, 122: 107374. doi: 10.1016/j.ast.2022.107374 [21] XU Feiyi, LI Haolun, PUN C M, et al. A new global best guided artificial bee colony algorithm with application in robot path planning[J]. Applied soft computing, 2020, 88: 106037. doi: 10.1016/j.asoc.2019.106037 [22] 魏江, 王建军, 王健, 等. 基于改进蚁群算法的三维航迹规划[J]. 计算机工程与应用, 2020, 56(17): 217–223. WEI Jiang, WANG Jianjun, WANG Jian, et al. 3D path planning based on improved ant colony algorithm[J]. Computer engineering and applications, 2020, 56(17): 217–223. [23] GAO Wenxiang, TANG Qing, YE Beifa, et al. An enhanced heuristic ant colony optimization for mobile robot path planning[J]. Soft computing, 2020, 24(8): 6139–6150. doi: 10.1007/s00500-020-04749-3 [24] WANG Lanfei, KAN Jiangming, GUO Jun, et al. 3D path planning for the ground robot with improved ant colony optimization[J]. Sensors, 2019, 19(4): 815. doi: 10.3390/s19040815 [25] PU Xingcheng, XIONG Chaowen, JI Lianghao, et al. 3D path planning for a robot based on improved ant colony algorithm[J]. Evolutionary intelligence, 2024, 17(1): 55–65. doi: 10.1007/s12065-020-00397-6
