Continuous classification of garbage based on the elastic weightconsolidation and knowledge distillation
-
摘要: 针对目前的垃圾分类方法仅仅是对固定类别的常见生活垃圾分类，无法满足垃圾类别数量增长带来的动态持续分类要求的问题，本文提出了一种弹性权重巩固与知识蒸馏（elastic weight consolidation and knowledge distillation，EWC-KD）垃圾持续分类方法。该方法通过EWC正则化损失函数和蒸馏损失函数增强模型的记忆能力，EWC正则化损失函数限制重要参数的更新范围，带有温度系数的蒸馏损失函数通过保护类别标签中携带的类别信息增强模型的泛化能力。在5个垃圾分类任务上进行实验，结果表明该方法的性能优于对比方法，可以在所有任务上保持较高的分类准确率和较低的后向转移值，能够增强垃圾分类系统的持续分类能力。Abstract: The current garbage classification methods focus on the classification of common domestic garbage of fixed classes, which cannot meet the dynamic and continuous classification requirements brought by the growth of the number of garbage classes. To solve this problem, the paper proposes an elastic weight consolidation and knowledge distillation (EWC-KD) continuous garbage classification method. The method enhances the memory ability of the model through EWC regularization loss function and distillation loss function. EWC regularization loss function limits the update range of important parameters, and the distillation loss function with temperature coefficient enhances the generalization ability of the model by protecting the class information carried in the class label. Experiments on five garbage classification tasks show that the performance of this method is better than that of the comparison method. Our method can maintain high classification accuracy and low backward transfer value on all tasks, and can enhance the continuous classification ability of the garbage classification system.
-
随着我国经济的飞速发展和人民生活水平的提升，生活垃圾的数量和种类迅猛增长。有效的垃圾分类不仅能减少环境污染，改善人居环境，而且有助于再生资源循环利用，节约原生资源。住建部、发改委等九部门在2019年6月联合印发的《关于在全国地级及以上城市全面开展生活垃圾分类工作的通知》提出，到2025年，全国地级及以上城市基本建成生活垃圾分类处理系统。垃圾分类已经成为我国加强生态环境保护和污染防治的重要举措[1]。
传统的垃圾分类主要由人工进行分拣和分类，存在劳动强度大、分选效率低、工作环境差等缺点，急需智能化、自动化的分类方法来替代[2]。Kang等[3]从输入图像的多特征融合、残差单元的特征重用、激活函数的设计3个方面对ResNet-34网络结构进行进一步优化。张涛[4]以ResNet-18为主干网络构建了一个全局感知特征聚合模块与全新的核心自注意力机制的垃圾识别分类网络。许玉蕊等[5]将Inception模块和残差模块进行结合来提高特征提取能力，提出了一种基于特征融合的轻量级网络模型。杨旺功等[6]为了增强特征表示，采用双线性汇合方法计算不同空间位置的外积，并对不同空间位置计算平均汇合以得到双线性特征。Zeng等[7]提出一种多任务分类算法，其中一个任务识别生活垃圾的4个主要类别，另一个任务识别10个子类垃圾。Meng等[8]基于Xception网络，结合DenseNet网络中密集连接和多尺度特征融合的思想构造了X-DenseNet网络对视觉传感器获取的垃圾图像进行分类。Shi等[9]针对垃圾图像训练数据不足的问题，通过扩展分支来扩展网络，然后使用添加层来实现特征信息的融合。Bircanoğlu等[10]通过修改DenseNet密集块内跳跃连接的连接方式将网络中的参数数量从700万减少到约300万，缩短了网络的预测时间。Mao等[11]利用遗传算法优化DenseNet-121的全连接层以提高垃圾分类精度。
目前的相关研究大多是基于深度学习训练一个针对固定类别的常见生活垃圾分类模型，但忽略了生活垃圾的类别数量是逐渐增加的。如从早期的菜叶、纸张、炉渣等垃圾，到如今的塑料、针织、电子元件等。甚至已经分类好的垃圾到了垃圾处理厂还需要再分选，如塑料里会混杂 PP、PE、PVC 等各种塑料，电池还包含蓄电池、纽扣电池、干电池等。Yang等[12]提出的GarbageNet通过卷积神经网络（convolutional neural networks，CNN）特征提取器将现有样本和新样本投影到特征空间，然后通过寻找测试样本的最近邻对新样本进行分类，但是需要保存现有样本的样本池。
针对垃圾种类日益增加的问题，如果用未能识别的垃圾图像重新训练分类模型，模型对已学习垃圾图像的分类准确率会下降，发生灾难性遗忘。面对以上问题，可以采用多任务学习（multi-task learning，MTL）方法或单任务学习（single-task learning，STL）方法。如果采用多任务学习（MTL）方法, 即用全部的垃圾图像重新训练分类模型会消耗大量的时间成本；如果采用单任务学习（STL）方法, 即针对每个垃圾图像数据集单独训练一个分类模型，会造成分类模型参数的线性增长。持续学习（也称增量学习、终生学习）算法可以帮助分类模型实现持续有效的分类，在兼顾模型的稳定性和可塑性的同时，缩短模型的训练时间，缓解分类模型参数的线性增长问题。Delange等[13]认为持续学习方法按照不同任务中特定信息的存储和使用方式可以分为3个方向：基于回放、基于参数隔离和基于正则化。基于回放的持续学习方法[14-17]需要保留部分具有代表性的旧数据或利用生成模型生成旧数据，然后和新数据一起参与训练。基于参数隔离的持续学习方法[18-20]为每个任务分配不同的模型参数。基于正则化的持续学习方法[21-25]使用新数据、辅助数据或之前模型的参数先验知识限制网络参数的更新。在现实场景中，之前类别的垃圾图像可能由于内存或隐私限制无法获取，网络模型的空间大小也不应随着垃圾类别的增多无限扩大，所以基于正则化的持续学习方法更加适用垃圾分类场景。
本文提出了一种弹性权重巩固与知识蒸馏（elastic weight consolidation and knowledge distillation，EWC-KD）持续学习方法实现多个生活垃圾分类任务的持续有效分类。首先，由于垃圾种类繁多，为了充分利用卷积层提取到的特征信息的同时防止发生梯度弥散，本文选择ResNet-18作为垃圾持续分类模型的主干网络。其次，本文通过EWC持续学习算法中的Fisher信息矩阵限制参数更新的方式，另外引入了知识蒸馏方法以保持模型在旧任务上的输出不变。最后，在本文构造的5个垃圾分类任务上的实验结果显示， EWC-KD持续学习方法在保证新的生活垃圾分类任务有较高分类准确率的同时，更大限度保持了旧的生活垃圾分类任务的分类准确率。
1. 损失函数
在实际环境中，未来的垃圾分类任务和垃圾图像是无法预测的。假设目前有
$K$ 个垃圾分类任务$\{ {{{T}}_k}|k \in \{ 1,2,\cdots, K\} \}$ ,${T_k}$ 包括第$k$ 个任务中所有类别的垃圾图像，不同的任务之间没有数据交集和类别交集。则不加任何约束时${T_k}$ 训练过程中的损失函数可以表示为$$ {L_{k - {\rm{classify}}}}{\text{(}}\theta {\text{)}} = {l} {\text{(}}{f_{k - 1}}{\text{(}}\theta ,k,{x_k}{\text{)}},{y_k}{\text{)}} $$ (1) 式中：
${x_k}$ 为${T_k}$ 中的垃圾图像；${y_k}$ 为图像${x_k}$ 对应的类别标签；$K$ 个垃圾分类任务按照次序依次参与训练，${T_{k - 1}}$ 完全训练后的垃圾分类网络表示为${f_{k - 1}}$ ；$ \theta $ 是垃圾分类网络的参数。式（1）是对单个垃圾分类任务监督训练时的损失函数。在多个垃圾分类任务依次训练的场景下，如果不保存之前任务的旧数据和不扩展网络参数，只将式（1）的梯度进行反向传播势必会导致灾难性遗忘。本文的目的是通过添加额外的损失限制网络参数的更新，在
${T_k}$ 经过充分训练且有较高的分类准确率时，任务$ {T_j}(j < k) $ 能够最大限度地保持初始分类准确率：$$ {f_k}({x_j}) = {y_j} \text{，} {f_k}({x_k}) = {y_k} $$ (2) 最终
$ {T_k} $ 训练过程中的损失函数表示为$$ {L_k}{\text{(}}\theta {\text{)}} = {L_{k - {\rm{classify}}}}{\text{(}}\theta {\text{)}} + {L_{k - {\rm{extra}}}}{\text{(}}\theta {\text{)}} $$ (3) 式中
${L_{k - {\rm{extra}}}}$ 是额外的损失限制项。2. 持续学习方法
2.1 EWC持续学习方法
EWC持续学习方法[21]的思想来源于哺乳动物在学习新技能时，大脑皮层中一定比例的神经元树突棘体积增大，尽管后续学习了其他新技能，这些扩大的树突棘仍然存在，从而记忆之前学习的技能。神经网络中的参数可看作树突棘，体积增大的树突棘即对任务重要性大的参数。参数的不同组合也会有相同的性能，所以在新任务的学习过程中需要减缓重要参数的学习速度，约束参数保持在以旧任务参数为中心的旧任务的低误差区域来保护旧任务的性能。
EWC持续学习方法用参数的二阶导来评估参数的重要性：
$$ F_i^{(k - 1)} = \frac{1}{{|{D_{k - 1}}|}}\sum\limits_{B \in {D_{k - 1}}} {\frac{{{\partial ^2}L{{(B,}}{\theta ^{(k - 1)}})}}{{\partial {{(\theta _i^{(k - 1)})}^2}}}} $$ (4) 式中：
$ {D_{k - 1}} $ 是第$ k - 1 $ 个任务数据集，$ B $ 是训练过程中的一个数据集批次；$ \theta _i^{{\text{(}}k - 1{\text{)}}} $ 是第$ k - 1 $ 个任务中的第$ i $ 个参数；$ L $ 是任务损失函数；$ F_i^{{\text{(}}k - 1{\text{)}}} $ 是$ \theta _i^{{\text{(}}k - 1{\text{)}}} $ 的重要性估计。为了降低计算复杂度，按照点估计理论用梯度平方的平均值对式（4）做近似：$$ F_i^{{\text{(}}k - 1{\text{)}}} = \frac{1}{{|{D_{k - 1}}|}}\sum\limits_{B \in {\rm{ }}{D_{k - 1}}} {\frac{{\partial L{{{{(B,}}{\theta ^{{\text{(}}k - 1{\text{)}}}}{\text{)}}}^2}}}{{\partial {{{\text{(}}\theta _i^{{\text{(}}k - 1{\text{)}}}{\text{)}}}^2}}}} $$ (5) $ F_i^{{\text{(}}k - 1{\text{)}}} $ 有3个重要性质：1）等价于损失函数在最小值处的二阶导数；2）可以从一阶导数计算，因此即使对于大型模型也很容易计算；3）保证是正半定的。因此，可以通过增加一个正则化损失函数限制旧任务参数的更新：$$ {L_{k - {\rm{ewc}}}} = \sum\limits_i {\frac{\lambda }{2}} F_i^{{\text{(}}k - 1{\text{)}}}{{\text{(}}\theta _i^{{\text{(}}k{\text{)}}} - \theta _i^{{\text{(}}k - 1{\text{)}}}{\text{)}}^2} $$ (6) 式中
$ \lambda $ 用来衡量旧任务相对于新任务的重要性。如果有多个旧任务，需要多个任务的Fisher信息矩阵衡量参数对每个旧任务的重要性。EWC++[26]使用滑动平均对$ {F_i} $ 进行高效更新：$$ F_i^{{\text{(}}k - 1{\text{)}}} = \alpha F_i^{{\text{(}}k - 1{\text{)}}} + {\text{(}}1 - \alpha {\text{)}}F_i^{{\text{(}}k - 2{\text{)}}} $$ (7) 式中
$ \alpha $ 用来衡量不同旧任务的重要性。2.2 知识蒸馏
知识蒸馏（knowledge distillation, KD）[27]最早由Hinton在2015年首次提出应用于模型压缩，其由教师模型和学生模型组成。教师模型的参数以及教师模型输出的监督信息都可称为知识，学生模型学习教师模型的参数和监督信息的过程称为蒸馏。知识蒸馏可以帮助学生模型向教师模型学习以提高学生模型的精度，也可以压缩教师网络的参数量以降低教师模型的时延。知识蒸馏也可用于迁移学习中，可以将一个模型的中间层特征知识、任务相关知识或表征相关知识迁移到另一个模型中。
对于图像分类任务，传统的深度学习训练过程是对类别标签求极大似然估计，所有负标签的类别概率都是0；但是加入知识蒸馏的训练过程是将教师模型Softmax层输出的类别概率作为学生模型训练时的软标签，对类别概率求极大似然估计。Softmax层的输出除了正标签外，负标签也携带大量类别信息，比传统的训练过程更有效，所以学生模型的泛化能力甚至优于教师模型。在多个连续分类任务中，当前任务的分类模型即学生模型，上一个任务的分类模型即教师模型，学生模型需要通过知识蒸馏学习教师模型在上一个任务中学习到的参数信息。在第
$ k $ 个任务中，假设分类模型在第$ i $ 类上的输出为$ \hat y_k^{(i)} $ ，第$ i $ 类的类别标签为$ y_k^{(i)} $ ，经过带有温度系数$ T $ 的Softmax层输出在第$ i $ 类上的类别概率为$ p_k^{T{(i)}} $ ，其计算公式为$$ p_k^{T(i)} = \frac{{{\text{exp(}}y_k^{{\text{(}}i{\text{)}}}{{/T)}}}}{{\displaystyle\sum\limits_{j = 0}^N {{\text{exp(}}y_k^{{\text{(}}j{\text{)}}}{{/T)}}} }} $$ (8) 式中
$ N $ 为类别总数。$ T $ 取1时式（8）就是Softmax层，根据逻辑回归值输出各个类别的概率。Softmax层做归一化可以凸显每个类别之间的差别。直接使用Softmax层的输出值作为软标签会带来一个问题：当Softmax层输出的概率分布熵相对较小时，负标签的值都很接近0，对损失函数的贡献小到可以忽略不计。如果$ T $ 接近0，则最大的值会接近1，其他值会接近0，近似于单值标签。$ T $ 越高，Softmax层的输出概率分布越趋于平滑，其分布的熵越大，负标签携带的信息会被相对地放大，模型训练将更加关注负标签，起到保留相似信息的作用。蒸馏损失定义为$$ {L_{k - {\rm{dl}}}} = - \sum\limits_{j = 0}^N {p_k^{T(j)} \cdot {\text{log}}} (p_{k - 1}^{T(j)}) $$ (9) 3. EWC-KD持续学习方法
EWC持续学习方法可以限制重要参数的更新，但是重要性小的参数还是会随着新任务的训练向新任务最优解的梯度方向更新，导致新模型的输出偏离旧任务模型的输出。虽然偏离程度比较微小，但是随着任务数量的增多偏离程度会叠加放大，对更早的训练任务的遗忘程度也会越来越严重。尤其在任务差异较大时，在将旧任务的后验概率最大化公式化为式（6）时泰勒展开的高阶项不能近似为0，式（6）就无法保留旧任务的重要信息，导致EWC持续学习算法性能下降。
神经网络模型是一个黑箱模型，神经网络的训练是通过不断地对训练样本回放，有监督地加强训练样本与类别标签之间的联系，是一种综合出的效果，无法准确分析中间层的权重系数和偏差系数。不同组合的系数完全有可能呈现出相同的效果。因此，知识蒸馏虽然可以限制新模型的输出无限接近旧模型的输出，但是中间某些对旧任务重要性大的权重可能已经远离了原始参数空间。这种不关注具体参数更新的方式也会随着任务数量的增加展现出弊端，无法保证之前所有旧任务上的性能。
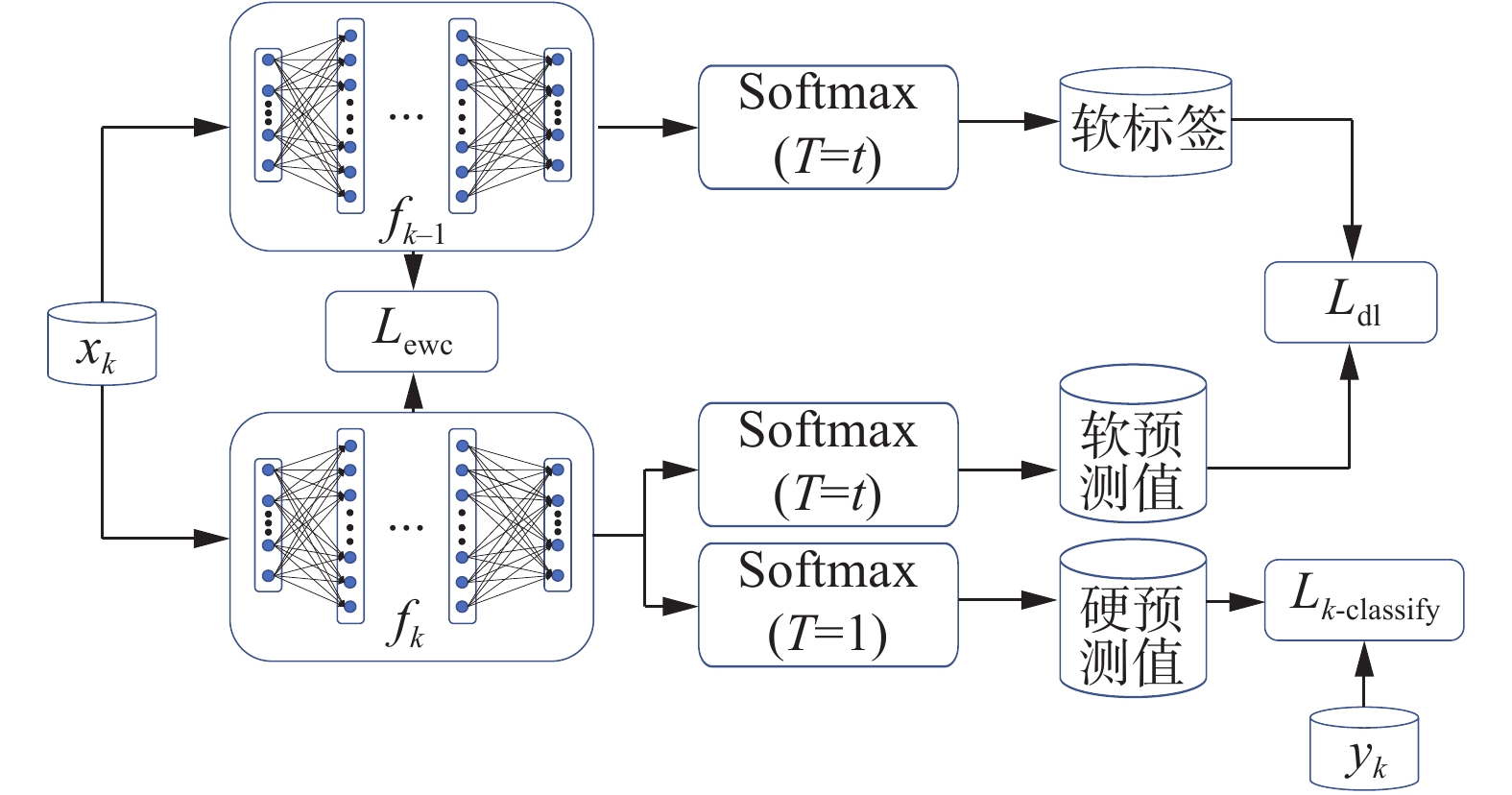
EWC持续学习方法关注神经网络中具体参数的更新空间范围，知识蒸馏关注神经网络的输出不变性，知识蒸馏可以有效弥补EWC持续学习方法的短板。本文提出的EWC-KD持续学习方法框图如图1。式（3）中总的损失函数包括3项：新任务的分类损失函数
${L_{k - {\rm{classify}}}}$ 、EWC损失函数${L_{k - {\rm{ewc}}}}$ 和蒸馏损失函数${L_{k - {\rm{dl}}}}$ 。
图 1 EWC-KD持续学习方法Fig. 1 Block diagram of EWC-KD continuous learning method
下载:
全尺寸图片
$$ {L_k}{\text{(}}\theta {\text{)}} = {L_{k - {\rm{classify}}}}{\text{(}}\theta {\text{)}} + {L_{k - {\rm{ewc}}}}{\text{(}}\theta {\text{) + }}{L_{k - {\rm{dl}}}}{\text{(}}\theta {\text{)}} $$ (10) 本文中采用标准交叉熵损失函数对新任务进行分类训练：
$$ {L_{k - {\rm{classify}}}}{\text{(}}\theta {\text{) = }} - {y_k} \cdot {\text{log(}}{{f} _{k - 1}}{\text{(}}\theta ,k,{x_k}{\text{))}} $$ (11) 由于所有的垃圾分类任务都需要正确分类，本文将所有任务视为同等重要，即式（7）中
$ \alpha $ 设为1。在每个任务训练完毕后Fisher信息矩阵的值都更新一次。$$ F_i^{{\text{(}}k - 1{\text{)}}} = F_i^{{\text{(}}k - 1{\text{)}}} + F_i^{{\text{(}}k - 2{\text{)}}} + \cdots + F_i^{{\text{(2)}}} + F_i^{{\text{(1)}}} $$ (12) 4. 垃圾分类模型
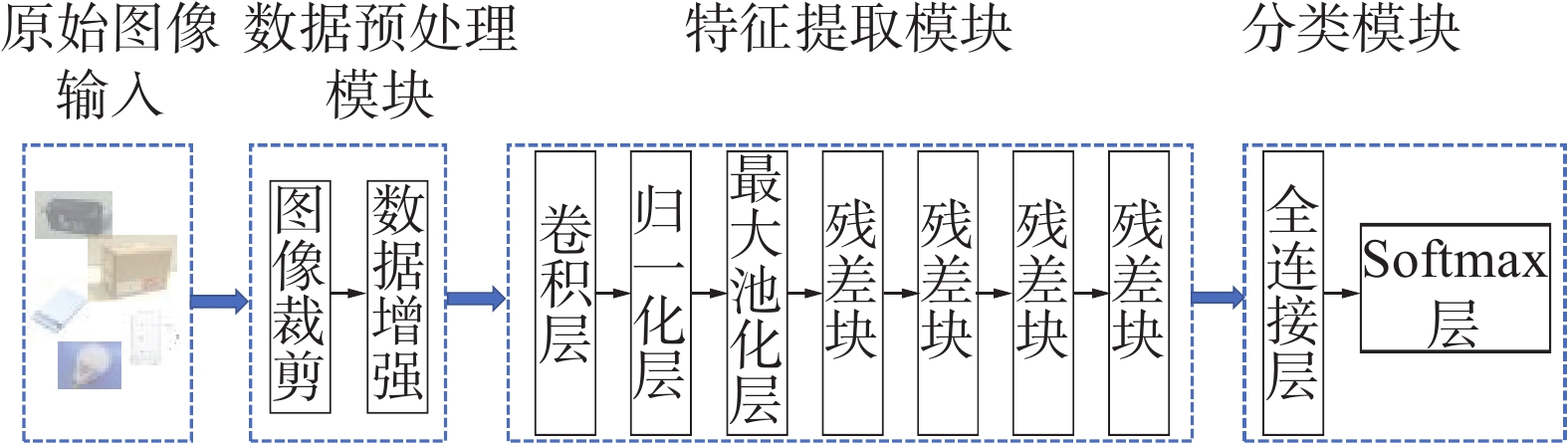
垃圾分类模型输入的图片尺寸是固定的，但是不同垃圾图像的尺寸大小不一，所以必须将垃圾图像进行统一尺寸的裁剪。图像裁剪中常见的插值方法有最近邻插值法、双线性插值法和双三次插值法。最近邻插值法是一种最基本、最简单的图像缩放算法，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真。双线型插值法和双三次插值缩放效果比简单的最近邻插值好，但双三次插值计算代价过大，所以本文平衡缩放效果和计算速度选择双线性插值法。
为了增加训练的数据量,提高模型的泛化能力，本文采用图像亮度调整、图像水平翻转、图像垂直翻转3种数据增强技术对裁剪后的图像进行预处理。
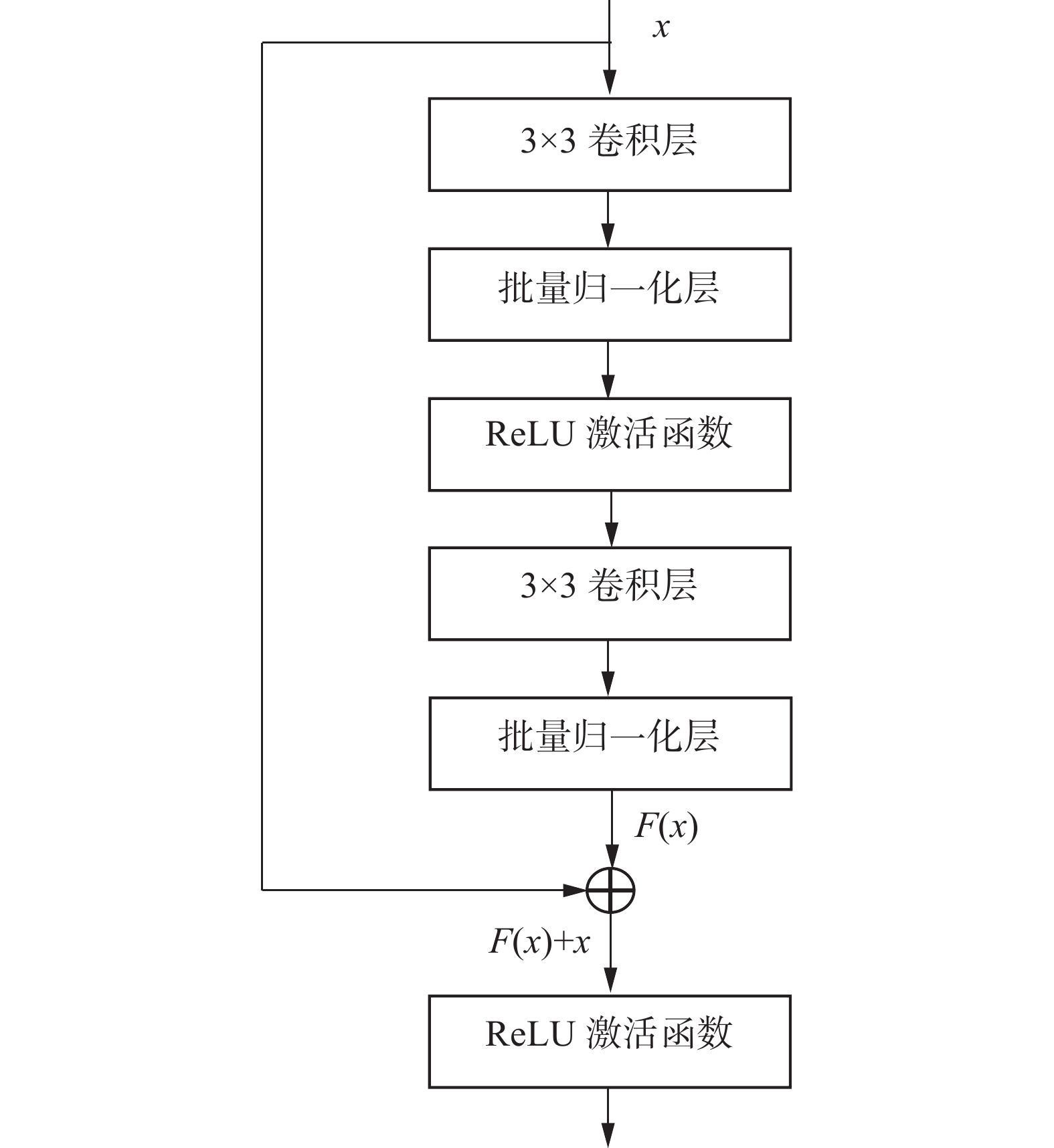
由于不同垃圾种类的特征差异较大，在缺陷分类网络的前端构建多个卷积层可以扩大感受野，充分提取输入图像的局部特征和全局特征。并且通过叠加层，将 ReLU 等激活函数夹在卷积层的中间可以进一步提高网络的表现力。但实践证明，网络结构的加深会使梯度爆炸、梯度消失的风险增加。AlexNet[28]包含5个卷积层和3个全连接层，使用ReLU作为CNN的激活函数成功解决了Sigmoid在网络较深时的梯度弥散问题，使用Dropout避免模型过拟合，并且使用最大池化避免平均池化的模糊效果，但是卷积核只与某一部分的特征图进行卷积，模型的泛化能力有所下降。DenseNet-121[29]包含4个密集块，相邻密集块之间通过卷积层和池化层相连，每一层都以前面所有的特征图作为输入。连接不同层学习到的特征图会增加后续层输入的变化，从而提高效率，但是由于通道叠加原因，频繁读取内存拖慢了训练速度。Resnet-18[30]包含4个残差块，残差块结构如图2所示，每个残差块中输入可以直接加在最后的ReLU激活函数前，这样带短连接的网络拟合高维函数的能力比普通连接的网络更强，可以避免简单地增加深度导致的网络退化。考虑到分类模型的效率和时效性，本文采用ResNet-18作为模型的骨干网。
图 2 ResNet网络残差块结构Fig. 2 Residual block structure of ResNet network下载:
全尺寸图片
本文垃圾分类模型的分类模块由一个全连接层和一个Softmax层组成。全连接层可以将特征提取模块学到的“分布式特征表示”映射到样本标记空间，减少特征位置对分类的影响。Softmax层根据全连接层的输出值做归一化输出各个类别的概率，可以凸显每个类别之间的差别。
因此，如图3所示，本文的垃圾分类模型由3个模块构成：数据预处理模块、特征提取模块和分类模块。
图 3 垃圾分类模型Fig. 3 Garbage classification model下载:
全尺寸图片
5. 实验设置
5.1 任务划分及实验细节
本文从公开的垃圾分类数据集[31]中挑选15类垃圾构造了5个垃圾分类任务，每个任务包含3种类别的垃圾，类别内部按照2∶1划分为训练集和测试集，任务内部的垃圾类别和垃圾图像数量如表1所示，垃圾图像如图4所示。任务1~5分别需要对电池垃圾、纸质垃圾、充电垃圾、玻璃垃圾和灯类垃圾分类。本文将5个垃圾分类任务数据集依次加入模型中进行训练，之前的任务数据集不参与当前任务数据集的训练。
表 1 垃圾分类任务Table 1 Garbage classification task任务序号 垃圾类别 训练集样本
数量/张测试集样本
数量/张任务1 蓄电池 229 76 纽扣电池 126 41 干电池 174 57 任务2 纸箱 239 79 报纸 191 63 纸袋 259 86 任务3 充电宝 83 27 充电头 78 26 充电线 109 36 任务4 玻璃壶 399 132 量杯 195 64 玻璃球 143 47 任务5 台灯 183 61 LED灯泡 164 54 玻璃灯管 68 22 
图 4 垃圾图像Fig. 4 Garbage dataset images下载:
全尺寸图片
本文运行实验程序的显卡配置为RTX 3050Ti，实验模型使用Pytorch深度学习框架编写，利用Adam作为目标函数的优化器，垃圾图像裁剪为128×128，训练集图像采用数据增强技术，训练步数为50，样本批次大小为10，学习率为0.0003。
本文将微调（fine-tuning）方法、知识蒸馏（KD）[27]方法、EWC[23]方法、无遗忘学习（learning without forgetting，LWF）[24]方法、STL方法和MTL方法与本文的EWC-KD方法做了对比实验。fine-tuning方法只使用交叉熵损失作为模型的损失函数，势必会发生灾难性遗忘，作为持续学习方法的参考下限。KD方法在损失函数中添加了蒸馏损失项来保留网络在旧任务上学习到的知识。EWC方法在损失函数中添加了正则化项来限制重要参数的更新。LWF方法的训练分为2步：第1步冻结旧任务的参数而训练新任务参数；第2步采用知识蒸馏训练整个分类模型。STL方法针对每个任务训练一个分类模型，忽略了任务之间所富含的丰富的关联信息，泛化能力较弱，也会造成模型参数的线性增长，作为模型参数量的参考上限。MTL方法是将目前任务的数据集和之前所有任务的数据集加在一起重新训练，其使用交叉熵损失作为模型的损失函数。随着任务数量的增加，MTL方法既耗时又占用大量内存，作为持续学习方法的参考上限。
5.2 评价指标
本文计算平均准确率（average accuracy, ACC）和后向转移（backward transfer, BWT）作为持续学习方法的评价指标。ACC评价分类模型在所有任务上的分类准确率，BWT评价后续任务的训练对之前任务分类准确率的遗忘程度。定义任务
$ T $ 结束时任务$ k $ 的准确率为$ {R_{T,k}} $ ，ACC和BWT分别表示为$$ {{R}}_{\text{ACC}} = \frac{1}{T}\sum_{k = 1}^T {{R_{T,k}}} $$ $$ {{R}}_{\text{BWT}} = \frac{1}{{T - 1}}\sum_{k = 1}^{T - 1} {{R_{T,k}} - } {R_{k,k}} $$ 式中：
${{R}}_{\text{ACC}}$ 为平均准确率，${{R}}_{\text{BWT}}$ 为后向转移。6. 实验结果
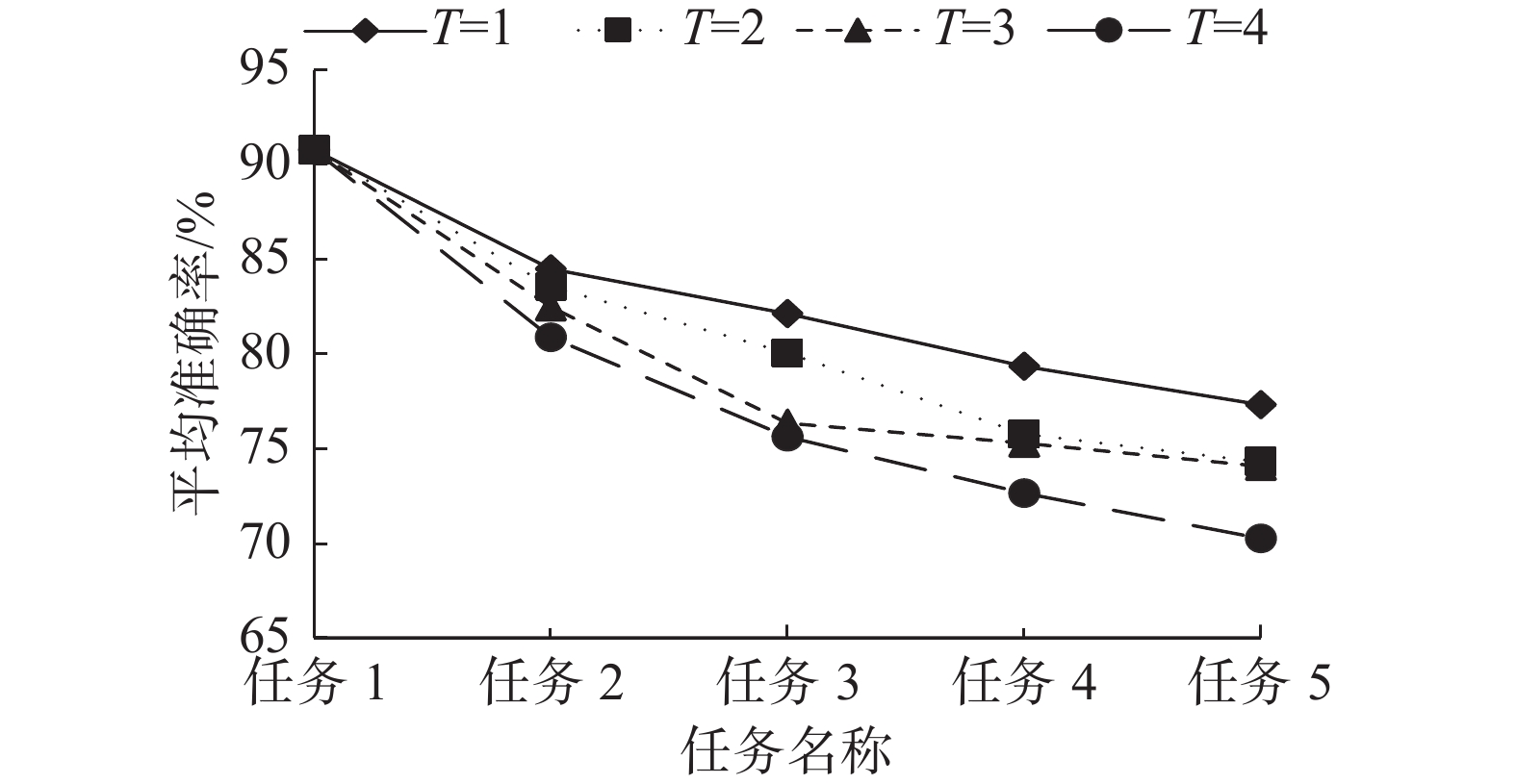
知识蒸馏中温度系数的选择是知识迁移效果的关键因素。图5是不同温度系数下知识蒸馏方法在5个垃圾分类任务上的遗忘曲线图，横轴代表5个垃圾分类任务数据集的训练次序，纵轴是垃圾分类模型在已训练任务测试集上的平均准确率。比较图5中的各条曲线可以观察到，随着温度系数
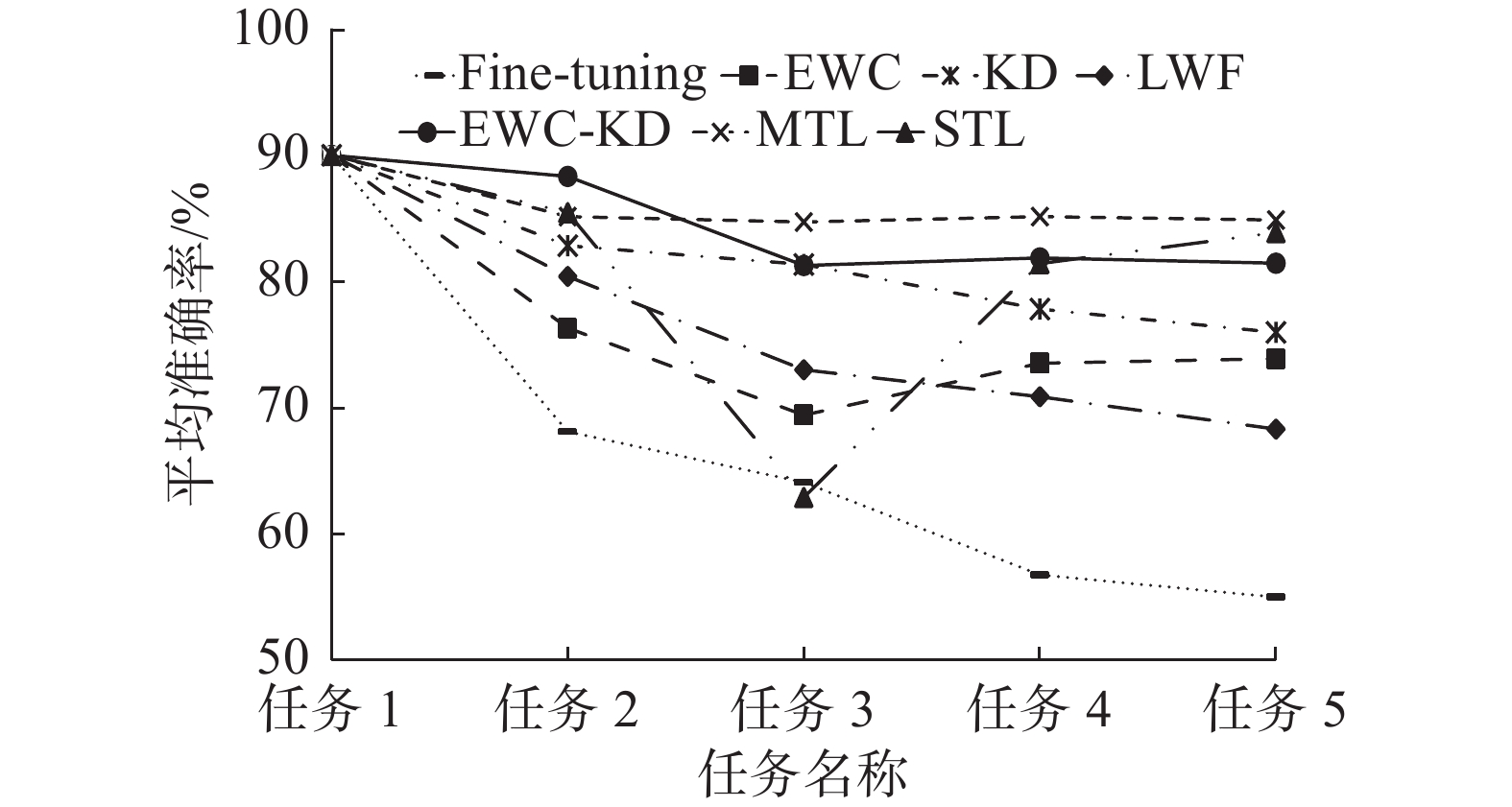
$ T $ 的增加，即每个类别所获得的相似度越来越平均，知识蒸馏方法在已训练数据集上的平均准确率逐渐下降。$ T = 1 $ 时知识蒸馏方法可以更好地保留之前任务上学到的知识，但是还是会发生较大程度的遗忘。
图 5 不同温度系数下知识蒸馏方法在5个垃圾分类任务上的遗忘曲线Fig. 5 Forgetting curves of knowledge distillation method on five garbage classification tasks under different temperature coefficients下载:
全尺寸图片
表2是不同方法在5个垃圾分类任务依次训练后的平均准确率和第5个垃圾分类任务训练后的后向转移值，图6是对应表2中数据的遗忘曲线图。从图6可以观察到，EWC、KD、LWF和EWC-KD在5个任务上的平均准确率都高于fine-tuning，可以不同程度缓解遗忘现象。本文的EWC-KD方法结合了EWC和KD的优点，平均准确率远高于EWC，相比KD在任务2、任务3和任务5训练后的平均准确率都有提升，甚至在任务2训练后的平均准确率高于MTL。表2中第5列数据显示，在5个垃圾分类任务的平均准确率方面，本文提出的EWC-KD方法比fine-tuning方法提高了26.51%，比EWC方法提高了7.58%，比KD方法提高了5.49%，比LWF方法提高了13.17%，证明了本文提出的方法能够有效提高垃圾持续分类的效果。表2中后向转移结果显示，EWC-KD（−0.84%）比fine-tuning（−37.82%）、EWC（−8.87%）、KD（−10.21%）和LWF（−17.04%）展现出了更强的稳定性，接近MTL（−0.65%），可以有效防止遗忘。STL方法最后训练得到5个分类模型，不考察后向转移值。
表 2 不同方法在5个垃圾分类任务依次训练后的平均准确率和第5个垃圾分类任务训练后的后向转移Table 2 ACC of different methods after the training of five garbage classification tasks in turn and the BWT after the training of the fifth garbage classification task% 方法 不同任务训练后的ACC BWT 任务1 任务2 任务3 任务4 任务5 fine-tuning 90.08 68.14 64.11 56.77 55 −37.82 EWC 90.08 76.37 69.45 73.57 73.93 −8.87 KD 90.08 82.9 81.41 77.87 76.02 −10.21 LWF 90.08 80.46 73.05 70.91 68.34 −17.04 EWC-KD 90.08 88.4 81.33 81.93 81.51 −0.84 MTL 90.08 86.23 86.78 83.88 86.12 −0.65 STL 90.08 85.53 62.92 81.48 83.94 — 
图 6 不同方法在5个垃圾分类任务上的遗忘曲线Fig. 6 Forgetting curves of different methods on five garbage classification tasks下载:
全尺寸图片
另外，本文考虑了模型在不同方法下的训练时间和模型参数量。由表3对比可知，STL方法的模型参数量是其他方法的5倍，MTL方法的模型训练时间远高于其他方法。虽然EWC、KD和LWF能节省模型训练时间，不需要扩展模型大小，但表2中的平均准确率远低于本文提出的EWC-KD方法。总之，本文提出的EWC-KD持续学习方法可以为垃圾持续分类提供良好的解决方案。
表 3 不同方法的模型训练时间和模型参数量Table 3 Model training time and model parameters in different methods方法 模型训练时间/s 模型参数量/M fine-tuning 1770.39 11.18 EWC 1821.26 11.18 KD 1823.16 11.18 LWF 3247.21 11.18 EWC-KD 1939.35 11.18 MTL 5325.80 11.18 STL 1816.18 55.9 7. 结束语
本文提出了EWC-KD持续学习方法对多个垃圾分类任务进行分类。该方法计算Fisher信息矩阵评估每个参数在旧任务上的重要性，并加入EWC正则化损失函数限制重要参数的更新，同时结合知识蒸馏方法保持旧任务的数据在新模型和旧模型上的输出一致。在构造的5个垃圾分类任务上，通过消融实验选择知识蒸馏中最佳的温度系数，并通过与相关方法的对比实验表明，本文提出的方法可以最大程度保留模型在之前任务上学到的分类知识，兼顾模型的稳定性和可塑性，能够在多个垃圾分类任务上保持较高的分类准确率。尽管本文的方法在各个分类任务上表现良好，但旧任务知识的保留过程限制了新任务的学习，无法充分利用学习到的知识，与MTL方法有较大的差距，这将是我们以后的改进方向。
-
图 1 EWC-KD持续学习方法
Fig. 1 Block diagram of EWC-KD continuous learning method
下载:
全尺寸图片
图 2 ResNet网络残差块结构
Fig. 2 Residual block structure of ResNet network
下载:
全尺寸图片
图 3 垃圾分类模型
Fig. 3 Garbage classification model
下载:
全尺寸图片
图 4 垃圾图像
Fig. 4 Garbage dataset images
下载:
全尺寸图片
图 5 不同温度系数下知识蒸馏方法在5个垃圾分类任务上的遗忘曲线
Fig. 5 Forgetting curves of knowledge distillation method on five garbage classification tasks under different temperature coefficients
下载:
全尺寸图片
图 6 不同方法在5个垃圾分类任务上的遗忘曲线
Fig. 6 Forgetting curves of different methods on five garbage classification tasks
下载:
全尺寸图片
表 1 垃圾分类任务
Table 1 Garbage classification task
任务序号 垃圾类别 训练集样本
数量/张测试集样本
数量/张任务1 蓄电池 229 76 纽扣电池 126 41 干电池 174 57 任务2 纸箱 239 79 报纸 191 63 纸袋 259 86 任务3 充电宝 83 27 充电头 78 26 充电线 109 36 任务4 玻璃壶 399 132 量杯 195 64 玻璃球 143 47 任务5 台灯 183 61 LED灯泡 164 54 玻璃灯管 68 22 表 2 不同方法在5个垃圾分类任务依次训练后的平均准确率和第5个垃圾分类任务训练后的后向转移
Table 2 ACC of different methods after the training of five garbage classification tasks in turn and the BWT after the training of the fifth garbage classification task
% 方法 不同任务训练后的ACC BWT 任务1 任务2 任务3 任务4 任务5 fine-tuning 90.08 68.14 64.11 56.77 55 −37.82 EWC 90.08 76.37 69.45 73.57 73.93 −8.87 KD 90.08 82.9 81.41 77.87 76.02 −10.21 LWF 90.08 80.46 73.05 70.91 68.34 −17.04 EWC-KD 90.08 88.4 81.33 81.93 81.51 −0.84 MTL 90.08 86.23 86.78 83.88 86.12 −0.65 STL 90.08 85.53 62.92 81.48 83.94 — 表 3 不同方法的模型训练时间和模型参数量
Table 3 Model training time and model parameters in different methods
方法 模型训练时间/s 模型参数量/M fine-tuning 1770.39 11.18 EWC 1821.26 11.18 KD 1823.16 11.18 LWF 3247.21 11.18 EWC-KD 1939.35 11.18 MTL 5325.80 11.18 STL 1816.18 55.9 -
[1] TONG Yeqing, LIU Jiafa, LIU Sizhe. China is implementing “Garbage Classification” action[J]. Environmental pollution, 2020, 259: 113707. doi: 10.1016/j.envpol.2019.113707 [2] 李金玉, 陈晓雷, 张爱华, 等. 基于深度学习的垃圾分类方法综述[J]. 计算机工程, 2022, 48(2): 1–9. LI Jinyu, CHEN Xiaolei, ZHANG Aihua, et al. Survey of garbage classification methods based on deep learning[J]. Computer engineering, 2022, 48(2): 1–9. [3] KANG Zhuang, YANG Jie, LI Guilan, et al. An automatic garbage classification system based on deep learning[J]. IEEE access, 2020, 8: 140019–140029. doi: 10.1109/ACCESS.2020.3010496 [4] 张涛. 基于GAICNet的垃圾识别分类检测网络[J]. 智能计算机与应用, 2022, 12(4): 47–53. doi: 10.3969/j.issn.2095-2163.2022.04.009 ZHANG Tao. Garbage identification classification and detection method based on GAICNet[J]. Intelligent computer and applications, 2022, 12(4): 47–53. doi: 10.3969/j.issn.2095-2163.2022.04.009 [5] 许玉蕊, 刘银华, 高鑫. 基于特征融合卷积神经网络的垃圾分类[J]. 自动化与仪表, 2021, 36(9): 11–16. doi: 10.19557/j.cnki.1001-9944.2021.09.003 XU Yurui, LIU Yinhua, GAO Xin. Garbage classification based on feature fusion convolutional neural network[J]. Automation & instrumentation, 2021, 36(9): 11–16. doi: 10.19557/j.cnki.1001-9944.2021.09.003 [6] 杨旺功, 赵一飞. 注意力机制与双线性网络的垃圾图像分类研究[J]. 计算机仿真, 2021, 38(12): 222–226. doi: 10.3969/j.issn.1006-9348.2021.12.045 YANG Wanggong, ZHAO Yifei. Research on garbage image classification based on attention mechanism and bilinear network[J]. Computer simulation, 2021, 38(12): 222–226. doi: 10.3969/j.issn.1006-9348.2021.12.045 [7] ZENG Ming, LU Xiangzhe, XU Wenkang, et al. PublicGarbageNet: a deep learning framework for public garbage classification[C]// 39th Chinese Control Conference. Piscataway: IEEE, 2020: 7200−7205. [8] MENG Sha, ZHANG Ning, REN Yunwen. X-DenseNet: deep learning for garbage classification based on visual images[J]. Journal of physics:conference series, 2020, 1575(1): 012139. doi: 10.1088/1742-6596/1575/1/012139 [9] SHI Cuiping, XIA Ruiyang, WANG Liguo. A novel multi-branch channel expansion network for garbage image classification[J]. IEEE access, 2020, 8: 154436–154452. doi: 10.1109/ACCESS.2020.3016116 [10] BIRCANOĞLU C, ATAY M, BEŞER F, et al. RecycleNet: intelligent waste sorting using deep neural networks[C]//2018 Innovations in Intelligent Systems and Applications. Piscataway: IEEE, 2018: 1−7. [11] MAO Weilung, CHEN Weichun, WANG Chien, et al. Recycling waste classification using optimized convolutional neural network[J]. Resources, conservation and recycling, 2021, 164: 105132. doi: 10.1016/j.resconrec.2020.105132 [12] YANG Jianfei, ZENG Zhaoyang, WANG Kai, et al. GarbageNet: a unified learning framework for robust garbage classification[J]. IEEE transactions on artificial intelligence, 2021, 2(4): 372–380. doi: 10.1109/TAI.2021.3081055 [13] DE LANGE M, ALJUNDI R, MASANA M, et al. A continual learning survey: defying forgetting in classification tasks[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(7): 3366–3385. [14] REBUFFI S A, KOLESNIKOV A, SPERL G, et al. iCaRL: incremental classifier and representation learning[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2017: 5533−5542. [15] SHIN H, LEE J K, KIM J, et al. Continual learning with deep generative replay[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 2994−3003. [16] LOPEZ-PAZ D, RANZATO M. Gradient episodic memory for continual learning[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 6470−6479. [17] CHAUDHRY A, RANZATO M, ROHRBACH M, et al. Efficient lifelong learning with A-GEM[EB/OL]. (2018−12−02)[2022−11−16]. https://arxiv.org/abs/1812.00420 [18] MALLYA A, LAZEBNIK S. PackNet: adding multiple tasks to a single network by iterative pruning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 7765−7773. [19] FERNANDO C, BANARSE D, BLUNDELL C, et al. PathNet: evolution channels gradient descent in super neural networks[EB/OL]. (2017−01−30)[2022−11−16].https://arxiv.org/abs/1701.08734 [20] ALJUNDI R, CHAKRAVARTY P, TUYTELAARS T. Expert gate: lifelong learning with a network of experts[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2017: 7120−7129. [21] KIRKPATRICK J, PASCANU R, RABINOWITZ N, et al. Overcoming catastrophic forgetting in neural networks[J]. Proceedings of the national academy of sciences of the United States of America, 2017, 114(13): 3521–3526. doi: 10.1073/pnas.1611835114 [22] LIU Xialei, MASANA M, HERRANZ L, et al. Rotate your networks: better weight consolidation and less catastrophic forgetting[C]//2018 24th International Conference on Pattern Recognition. Piscataway: IEEE, 2018: 2262−2268. [23] LEE S W, KIM J H, JUN J, et al. Overcoming catastrophic forgetting by incremental moment matching[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: ACM, 2017: 4655−4665. [24] LI Zhizhong, HOIEM D. Learning without forgetting[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(12): 2935–2947. doi: 10.1109/TPAMI.2017.2773081 [25] RANNEN A, ALJUNDI R, BLASCHKO M B, et al. Encoder based lifelong learning[C]//2017 IEEE International Conference on Computer Vision. Piscataway: IEEE, 2017: 1329−1337. [26] CHAUDHRY A, DOKANIA P K, AJANTHAN T, et al. Riemannian walk for incremental learning: understanding forgetting and intransigence[M]//Computer Vision - ECCV 2018. Cham: Springer International Publishing, 2018: 556−572. [27] HINTON G, VINYALS O, DEAN J. Distilling the knowledge in a neural network[EB/OL]. (2015−03−09)[2022−11−16]. https://arxiv.org/abs/1503.02531. [28] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84–90. doi: 10.1145/3065386 [29] HUANG Gao, LIU Zhuang, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2017: 2261−2269. [30] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2016: 770−778. [31] YAN Xin. Garbagenet: a large-scale garbage dataset for image classification[EB/OL]. (2023−01−20)[2023−03−10]. https://git.openi.org.cn/Garbage sorting/GarbageNet.
