Cohesive group query approach for collective spatial keywords
-
摘要: 给定一个道路网络和社交网络，集合空间关键字查询的目的是找到一组兴趣点，该组兴趣点的文本信息包含所有查询关键字，与查询的位置较近且彼此之间的距离较小。内聚组查询的目的是找到在地理位置和社交关系上紧密联系的一组用户；而集合空间关键字内聚组查询的目的是找到满足查询要求的一对最佳匹配的兴趣点集合和用户集合。针对这一问题，提出一种新的集合空间关键字内聚组查询处理模式。首先通过快速贪心查询过程获得候选兴趣点集合，然后使用core-tree结构存储(k,c)-core核心分解的结果，从而提高内聚组查询效率，并且保证查询结果能够同时满足用户之间的社会关系约束和兴趣点之间的空间位置约束。通过在真实数据集上开展实验，结果表明提出的方法比枚举方法的查询效率快1~2个数量级，并且具有较高查询准确性。Abstract: Given a road network and a social network, the collective spatial keyword query aims to find a set of points of interest (POIs) in which the text information contains all query keywords close to the query location and with a small mutual distance. The query goal of the cohesive group is to identify a group of users that are closely connected geographically and socially, whereas the query purpose of the collective spatial keyword cohesive group is to determine a pair of optimally matched POI sets and user sets that satisfy the query requirements. To address this problem, a novel type of cohesive group query mode is proposed for collective spatial keywords. Initially, the candidate POI set is obtained through a fast greedy query process. Then, the core tree structure is used to store the results of (k,c)-core decomposition to improve the efficiency of cohesive group query and ensure that the query results can satisfy the social constraints among users and the spatial constraints among POIs simultaneously. The experiments conducted on real datasets show that the proposed method is one to two orders of magnitude faster than the query efficiency of the enumeration method, and the results exhibit high query accuracy.
-
位置社交网络（location based social network，LBSN）上的集合空间关键字查询(collective spatial keyword query, CSKQ)[1-2]和内聚组查询(cohesive group query, Co-GQ)[3-4]在空间文本数据查询领域备受关注。CSKQ的目的是找到一组兴趣点(point of interest, POI)，该组兴趣点满足3个条件：1)所关联的文本信息包含所有的查询关键字，2)靠近查询位置，3)组内兴趣点之间的距离较小。Co-GQ的目的是找到一组社会关系紧密的用户，且彼此之间的位置距离不超过给定阈值。然而，现有方法不能满足集合空间关键字内聚组查询(collective spatial keywords cohesive group query, CSKCGQ)，CSKCGQ查询的目的是找到一对满足查询要求的最佳匹配的兴趣点集合和用户集合。例如，用户A想和朋友一起去逛公园、购物和享受美食，但是并没有明确的朋友选择和地点访问计划。此时，A通过发起CSKCGQ查询，获得的结果将包含一组兴趣点和一组朋友，并且满足如下条件：1)兴趣点集合的文本信息必须包含“公园”“商场”和“餐厅”关键字，2)用户集合必须满足一定的社会关系亲密度要求，3)兴趣点集合与用户集合在位置上相互靠近，4)集合中的兴趣点之间的位置距离较近。实现CSKCGQ查询需要考虑以下空间位置和社会关系因素：1)选定的用户需要与兴趣点在位置上尽量接近，从而减少活动的等待时间；2)用户之间要具有紧密的社交关系，以便增加活动的凝聚力。
尽笔者所知，本文研究的CSKCGQ是一种新的空间文本数据查询处理模式，其主要面临以下挑战：1）按顺序使用现有集合空间关键字查询CSKQ和内聚组查询Co-GQ查询虽然能够实现CSKCGQ，但会产生不正确的查询结果。原因是，如果先执行CSKQ查询得到一组兴趣点，然后再根据得到的兴趣点集合获取对应的用户集合，但这种方式返回的用户集合很可能不满足社会关系紧密度的约束条件；反之，会导致得到的兴趣点集合中地点之间的距离较远。2）兴趣点集合的选取需要考虑道路网络，用户集合的选取需要考虑社交网络，如何综合考虑路网和社交网络来获取查询结果并且具有较高查询效率，也是CSKCGQ面临的一个挑战。
本文提出的集合空间关键字内聚组查询方法，综合考虑社交网络和道路网络上的社会关系约束和位置距离约束，提出了core-tree结构，用于快速检索满足约束条件的用户集合和兴趣点集合。
1. 相关工作
1.1 空间关键字查询和索引结构
空间关键字查询是指在包含位置和文本信息的空间对象集合中，根据查询的位置和文本信息，返回最符合用户查询条件的空间对象。目前研究最多的空间关键字查询工作主要分为两类，排序空间关键字查询与范围空间关键字查询[5]。排序空间关键字查询的代表性模型是top-k检索[6-8]，其思想是从一个数据集合中找出最符合某种排序标准的前k个元素。范围空间关键字查询要求返回的对象既要包含给定的关键字，又要落在给定的空间范围内[9]。
为加快空间关键字的查询匹配效率，研究者提出多种空间文本索引结构，经典的索引结构包括IR-tree[10]、IL-Quadtree[11]等及其各种变体（比如IR2-tree[12]、AIR-tree[13]等），上述索引结构是基于欧几里得空间的索引结构。在现实中，空间对象主要分布在路网上。文献[14]提出的ROAD索引结构，通过预先计算不同子网(Rnets)中边界顶点的最短路径距离来加快查询速度。Zhong等[15]提出的G-tree用于大型路网的最短距离计算和最近邻查询，它将道路网络拆分为多个子网络，然后构建平衡树，但缺点是需要预处理数据和维护索引结构。随着机器学习的发展，相应技术也被用于处理路网查询。如文献[16]提出了基于学习的RNE方法计算路网中的最短路径，虽然查询结果不是精确值，但误差的范围非常小。本文提出的查询方法也是基于路网结构，使用G-tree作为基本索引加快查询效率。
1.2 社交网络上的群组查询
本文的用户集合查找以社交网络为基础，社交网络上的群组查询旨在检索包含查询用户的密集子图。常用的密集子图模型包括clique[17]、k-core[18]、k-truss[19]等。文献[19-20]研究了k-truss社区模型，寻找包含查询节点的密集连接社区，但是没有考虑社区的影响力、用户的亲密关系等因素。文献[21-22]研究了具有属性的社区搜索问题，且根据这些属性来定义社区的质量或影响力。Liu等[23]在此基础上进一步提出了一种顶点中心属性社区模型，既考虑了网络结构的密度，也考虑了节点属性的相似性。文献[24]研究了基于用户收藏的top-t个最喜爱的k-truss社区查询问题，并提出反向查询算法以加速过滤社交网络中的用户。上述研究工作结合用户之间的关系和属性进行社区查找，文献[3,25-26]还考虑了用户在道路网络上的位置信息以及用户之间的社交关系，其中文献[3,25]使用k-core模型衡量用户关系，文献[26]使用了基于k-truss的模型。上述研究工作为本文在社交网络上的用户群组查询提供了基本思路。
1.3 集合空间关键字查询
Zhang等[27]首次提出mCK查询，给定m个查询关键字，mCK查询旨在获取一组m个对象，这些对象可以共同覆盖所有查询关键字并且具有最小直径。Cao等[28]首次提出了集合空间关键字查询，并利用IR-tree索引加快CSKQ查询效率，但该研究中的距离是基于欧氏空间的。Gao等[1]又进一步研究了基于路网的集合空间关键字查询问题，提出滑动窗口(sliding window, SW)算法解决该问题。Su等[29]研究路网上基于组的集合关键字(group-based collective keyword, GBCK)查询问题，发起查询的用户为一组用户，而不是单个用户。Chen等[30]提出时间感知型集合空间关键字查询问题，除了考虑对象和查询之间的位置相关性与文本相关性，还考虑了对象的时间相关性。李艳红等[31]研究了移动对象的查询问题，能根据查询对象的移动不断返回查询结果。文献[32]研究了时间依赖路网上的集合空间关键字查询，揭示了路网中边的权重随时间变化的规律。
综上可见，社会群组查询和空间关键字查询已经在各个方面展开，但是上述查询方法都是针对某一类型的查询(如仅查询用户和兴趣点)，没有同时考虑用户集合与兴趣点集合之间的匹配查询。针对这一需求，本文综合考虑空间关键字查询和社会群组查询方法，提出一种新的集合空间关键字内聚组查询方法，目的是为查询者找到一对满足查询要求的最佳匹配兴趣点集合和用户集合。
2. 问题定义
2.1 问题描述
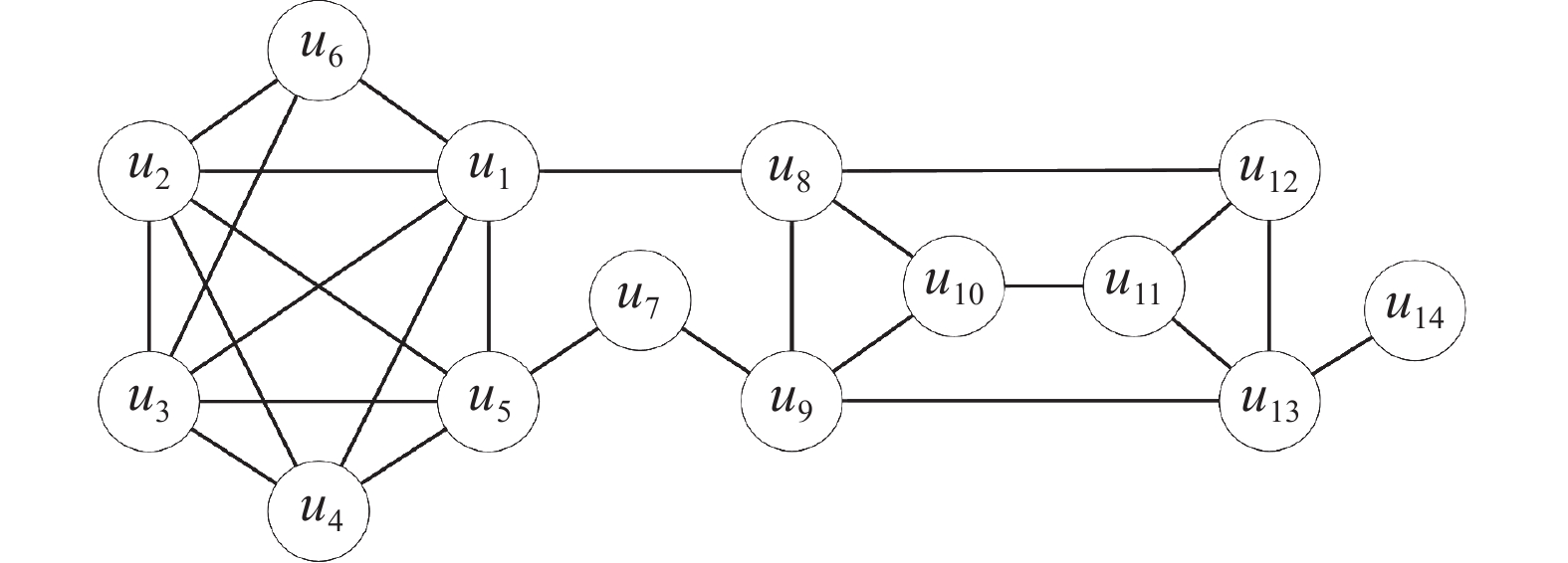
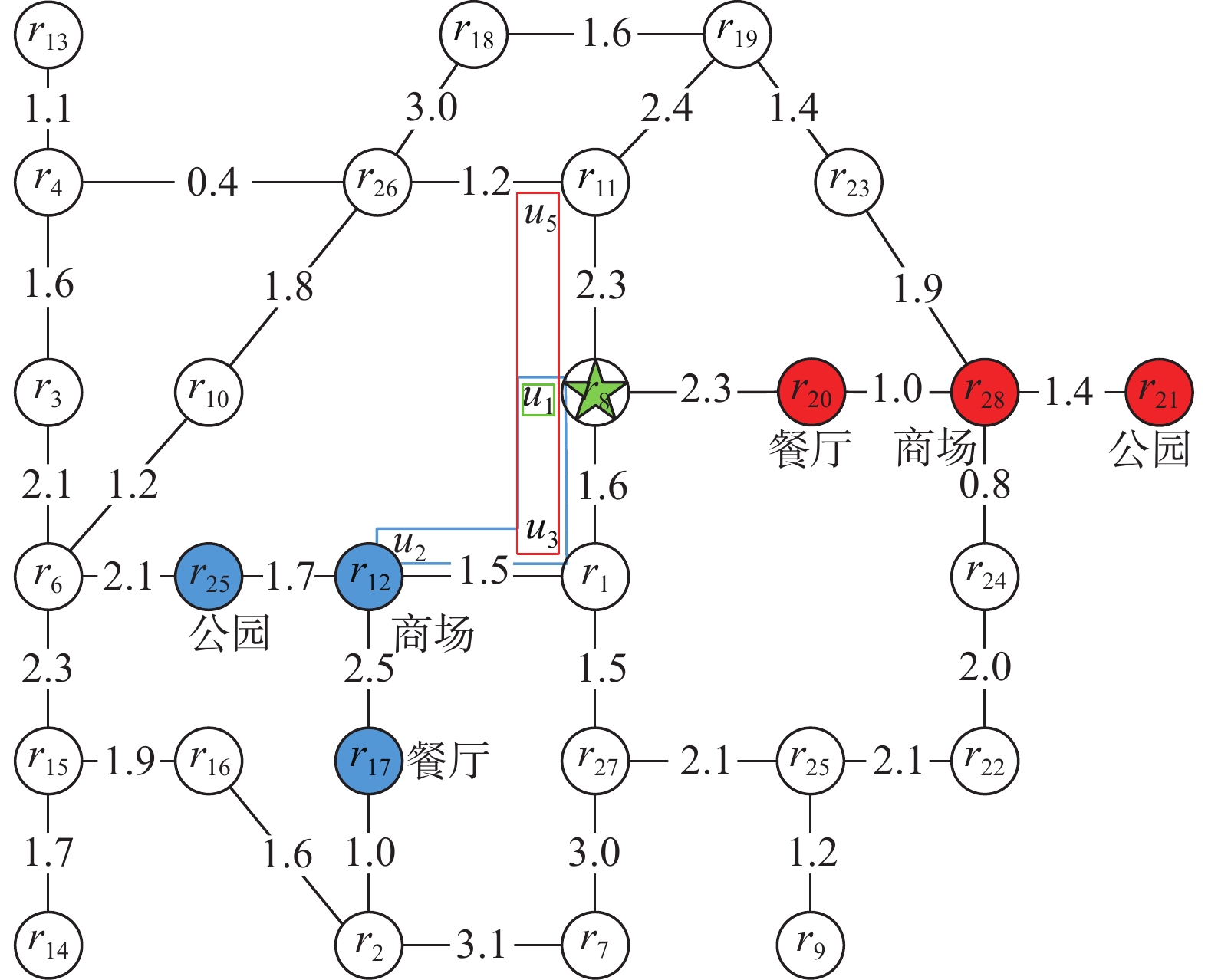
图1和图2分别给出道路网络（路网）和社会关系示例，图2中的边代表用户之间的朋友关系。在图1中，用户u1位于r8处，提出查询关键字为{公园, 餐厅, 商场}，并希望和其余2个朋友同去。路网中的红色和蓝色分别标注一组满足查询关键字条件的兴趣点集合，查询返回的结果可以是{{u1, u2, u3},{r12, r17, r25}}或{{u1, u3, u5},{r20, r28, r21}}。两个结果中用户集合都满足一定的社会亲密度关系，兴趣点集合的文本信息共同包含查询关键字且兴趣点之间的位置临近。
图 1 道路网络Fig. 1 Road network
下载:
全尺寸图片
图 2 用户社会关系Fig. 2 Users social network下载:
全尺寸图片
2.2 相关定义
2.2.1 道路网络
道路网络表示为带权无向图
$ {G_r} = (V,E,W) $ ，其中V是路网顶点的集合，E是边的集合，$ \forall e\left( {u,v} \right) \in E $ 上有权重$ w(u,v) \in W $ ，权重表示通行道路成本(如时间、距离等)。给定顶点u和v之间一条可达路径，构成该路径所有边的权重之和称为路径的距离，记为d(u,v)。在u和v之间所有路径中，具有最小路径距离的路径称为最短路径，令s(u,v)表示u和v之间的最短路径距离。下文中提到两点间距离都是指最短路径距离。路网的作用是将兴趣点和用户位置映射到路网上，通过其所在的顶点计算兴趣点之间、用户之间、用户与兴趣点之间的路网距离。2.2.2 社交网络
社交网络表示为带权无向图
$ {G_s} = (V,E,W) $ ，其中V为用户的集合，$ \forall v \in V $ 代表一个用户，如果$ \exists e(i,j) \in E $ ，表示用户i和j之间存在直接的亲密关系，边e(i, j)的权重$ w(i,j) \in W $ 表示用户i和j的亲密度，如果$w(i,j) > w(i,k)$ ，表示对于用户j和k，用户i和j更亲密。需要说明的是，本文暂不考虑用户之间的亲密度权重。社交网络主要用于表示用户关系，通过分析不同用户群体组成的子图结构度量用户间亲密度，以选取关系紧密的朋友集合。2.2.3 目标对象在路网上的位置
用户和兴趣点统称为目标对象，目标对象落在路网Gr的顶点V上，记为(o,v)，其中o代表目标对象，v为Gr中的顶点。计算两个目标对象间距离则是计算两个目标对象所在顶点间的距离。
2.3 路网索引结构
本文使用G-tree[15]作为路网索引。路网被建模为带权无向图，G-tree递归的将路网划分为子图
$ {G_i} \subseteq G $ ，并预先计算子图中边界顶点之间的距离。在G-tree基础上，再增加倒排文件来索引空间对象的文本信息。通过使用G-tree，对路网上不需参与计算的顶点进行剪枝，从而提高查询效率。2.4 度量方法
定义 1 诱导子图。给定图G，一个诱导子图
$ {G'} = ({V'},{E'}) $ 满足以下条件：1)$ {V'} \subseteq V $ ；2)如果顶点$ u,v \in {V'} $ 且$ \exists e(u,v) \in E $ ，那么$ e(u,v) \in E' $ ；3)对于G中顶点和边的每个属性，也对应存在于G′中。k-core概念广泛用于描述内聚子图，定义如下：
定义 2 k-core。给定一个图G和正整数k，如果一个诱导子图G′满足
$ \forall u \in {V'},\delta (u) \geqslant k $ ，其中$ \delta (u) $ 表示顶点u的度数，则子图G′为k-core。但子图G′可能不连通。如图2中由顶点[u1, u2, u3, u4, u5, u6, u8, u9, u10, u11, u12, u13]组成子图G′，$ \forall u \in {V'},\delta (u) \geqslant 3 $ ，所以G′是3-core，且这个子图不是连通图。图G的核心值为图中所有顶点度数的最小值，定义为
${{{\rm{gk}} - {\rm{core}}}}(G) = {\min _{v \in V}}\delta (v)$ 。顶点u的核心值定义为包含顶点u所有子图中最大的核心值，记为${{{\rm{vk}} - {\rm{core}}}}(u) = \max {{{\rm{gk}} - {\rm{core}}}}({G'}),{G'} \subseteq G \wedge v \in {V'}$ 。如果一个k-core子图G′包含所有可以组成k-core子图的顶点，则称G′为最大k-core子图，记为kmax-core。定义 3 (k,c)-core。给定k-core子图G′，如果G′含有c个顶点，即|V′|=c，称G′为(k,c)-core。
社会关系度量。本文使用用户集合形成(k,c)-core子图的核心值来评估社交关系。如果将社交图中的边视为朋友关系，那么k-core对社交关系亲密度的解释是：两个用户之间共同朋友越多，形成的团体就越有凝聚力。对于图2中的社交关系，用户u1可以形成两个(k,5)-core，分别是{u1, u2, u3, u4, u5}和{u1, u5, u7, u8, u9}。第1组用户形成诱导子图
$ G_1' $ 的核心值为4，而$ G_2' $ 的核心值为2，因此认为由子图$ G_1' $ 组成的用户集合具有更高社会凝聚力。空间距离度量。对于两个目标对象之间的距离，用对象之间的最短距离s(u,v)来衡量，其中u、v分别表示两个对象在路网中所处位置。对于CSKQ查询，常用的距离成本函数是
$ {C_{{{\max }^2}}}(q,S) $ [28]，计算q与S中对象之间的最大距离和S中任意两个对象之间的最大距离的加权和，计算方法为$$ {C_{{{\max }^2}}}(q,S) = \alpha \cdot \mathop {\max }\limits_{o \in S} d(q,o) + (1 - \alpha ) \cdot \mathop {\max }\limits_{{o^1},{o^2} \in S} d({o^1},{o^2}) $$ (1) 对于兴趣点集合与用户集合之间距离度量使用改进的成本函数评估，计算方法为
$$ \begin{gathered} C(P,U) = \alpha \cdot \sum\limits_{u \in U} {\frac{{\mathop {\max }\limits_{p \in P} s(u,p) + \mathop {\min }\limits_{p \in P} s(u,p)}}{2}} + \\ { (1 - \alpha )} \cdot \mathop {\max }\limits_{{p_1},{p_2} \in P} s({p_1},{p_2}) \end{gathered} $$ (2) 式中：U和P分别代表用户集合和兴趣点集合，成本函数第1部分是每个用户到兴趣点距离的最大值和最小值的平均值之和，第2部分是兴趣点集合中任意两个兴趣点之间的最大距离。本文同等考虑两个距离的影响，设置
$ \alpha $ 值为0.5。2.5 查询定义
给定一个道路网络Gr和一个社交网络Gs，CSKCGQ目的是找到满足查询要求的最佳匹配兴趣点集合和用户集合。问题定义如下：
给定一个查询
$ Q = \{ {u_q},{\text{keywords}},r,c\} $ ，其中uq是发起查询的用户，keywords是查询关键字，r是可接受最远距离阈值，c是用户集合中用户数量。返回结果集为$ R = \{ {U_s},{P_s}\} $ ，其中Us是一组满足内聚组查询需求的用户集合，Ps是兴趣点集合，兴趣点集合关联的文本信息共同覆盖所有查询关键字。例1 以图1和图2为例，表1给出了每个路网节点拥有的用户和兴趣点。用户u1位于r8，希望和朋友一起去购物、吃美食、逛公园，发起的查询条件可表示为：Q={u1,{商场, 餐厅, 公园}, 6, 5}，得到结果为R={{u1, u2, u3, u4, u5}, {r12, r17, r25}}，用户集合核心值为4，总距离成本为23.45。
表 1 路网顶点信息Table 1 Road network vertex information节点 用户 兴趣点 节点 用户 兴趣点 r1 u3 r2 u12 r3 餐厅 r4 u9 商场 r5 r6 餐厅 r7 r8 u1 r9 公园 r10 u8 r11 u5 餐厅 r12 u2 商场 r13 公园 r14 餐厅 r15 u13 r16 酒吧 r17 餐厅 r18 酒吧 r19 u7 商场 r20 餐厅 r21 u11 公园 r22 u6 餐厅 r23 餐厅 r24 u14 餐厅、商场 r25 公园 r26 u10 餐厅 r27 u4 r28 商场 2.6 问题复杂性分析
首先分析找到包含uq的(k,c)-core的复杂度，可以在O(m)时间复杂度内找到kmax-core，其中m表示图Gs中边数，要找到一个恰好包含c个顶点的k-core是一个挑战。(k,c)-core问题定义如下：给定一个图G，一个顶点u，正整数k和c，判断一个连通k-core子图是否存在，包括u共有c个顶点。
定理 1 (k,c)-core问题是NP-complete。
证明 通过将最大团(maximum clique)问题简化为(k,c)-core问题来证明这一点，最大团问题已被证明是NP-complete[33]。给定图G和整数n，最大团问题是检查G中是否包含大小为n的clique。给定一个图G和参数n，从G找到一个clique子图G′，满足|V′|=n，由clique性质可知子图G′也是(k,c)-core，其中c=n，k=n−1。同样的，给定一个图H，在图H中找到一个(k,c)-core子图H′，满足k=c−1，通过(k,c)-core和clique性质可推断出H′是一个大小为c的clique。所以，(k,c)-core问题也是NP-complete。
3. CSKCGQ查询解决方法
3.1 基于枚举策略的CSKCGQ查询方法
对于集合空间关键字查询部分，通常的解决方案是：对于每个包含查询关键字文本的兴趣点，将不同的关键字组合起来，得到共同覆盖查询关键字的兴趣点集合。对于内聚用户组查询问题，从(k,c)-core定义可知，寻找(k,c)-core的直接方法是检查kmax-core中每包含c个顶点的组合是否最终可以形成一个k-core。基于这种思想，可以推导出以下枚举策略：首先获取满足CSKQ的兴趣点集合，然后获取包含查询用户的(k,c)-core用户集合，最后对两种集合进行枚举组合，根据设计的评分函数对组合进行评分，返回成本代价最小的组合作为结果。
3.1.1 改进SW算法的兴趣点集合查找方法
上述枚举方法对于CSKQ选择非常耗时，随机组合又会产生许多无效的结果，因此文献[1]提出滑动窗口(sliding window, SW)算法来加快查询过程。SW算法的基本思想是距查询位置相近的兴趣点可能彼此非常接近，该算法通过剪枝策略提前结束兴趣点的查找，然后对所有满足条件的兴趣点按照不同关键字进行组合得到满足查询条件的结果。
原始SW算法的问题是没有对枚举组合的结果进行筛选。本文在SW算法基础上进行改进，得到兴趣点组合后再进行一次判断，提前过滤掉不满足条件的组合，具体执行过程如算法1所示。
算法 1 改进SW算法
输入 Q={uq,keywords,r}、 Gr
输出 满足CSKQ查询的兴趣点集合Rset
1）Rset ← 原始SW算法返回兴趣点集合
2）Rset ← Ø
3）for each set in Rset do :
4）max_d1 ←
${\text{max}}(s({u_q},v),v \in {\rm{set}})$ 5）max_d2←
${\text{max}}(s(m,n),m,n \in {\rm{set}})$ 先通过原始SW算法获取所有兴趣点组合，优化部分对每个组合进行一次判断。优化操作计算两个距离，max_d1代表用户到set中兴趣点的最远距离，max_d2代表set中任意两个兴趣点之间的最远距离，如果max_d2>max_d1则说明当前set中兴趣点分布过于分散，可以直接丢弃。
6）if max_d1>max_d2:
改进的SW算法对查询时间的优化分析：假设通过原始SW算法得到Rset共有n个兴趣点集合，且每个兴趣点只包含一个查询关键字，则每个兴趣点集合有k个兴趣点(k为查询关键字个数)。后续查询过程需要计算每个兴趣点集合和用户集合之间的距离，计算距离的算法时间复杂度为一个固定值t，则使用原始SW算法生成的Rset计算C(P,U)的消耗时间为
$ n \cdot [k \cdot |U| + k \cdot (k - 1)] \cdot t $ 。假设Rset中有x个兴趣点集合过于分散，则使用改进的SW算法可以为后续查询过程节约$ x \cdot \left(k \cdot \dfrac{{|U| - 1}}{{|U|}}\right) \cdot t $ 时间。7）add set to Rset
8）return Rset
3.1.2 (k,c)-core用户集合查找算法
寻找(k,c)-core的方法是先对图Gs进行核心分解[31]，从最大可能核心值k=min(vk-core(uq), Q.c-1)开始，在Gs中提取包含uq的kmax-core，依次判断kmax-core中包含uq在内含有c个顶点的连通子图是否可形成k-core，如果当前k值不存在，则将k值减1(k最小值为1)，直到找到(k,c)-core。
上述方法需要考虑大量组合，并且对于较大的图是不切实际的，因为形成的kmax-core子图通常含有大量顶点，进行枚举得到结果的代价很大。对于这个问题，文献[3]通过使用n-plex属性修剪不符合结果的顶点来加速查询。
定义 4 n-plex。给定一个图G和一个正整数n，G′是G的一个连通子图，如果满足条件：
$ \forall v \in {V'},\delta (v) \geqslant \left| {{V'}} \right| - n $ ，则G′具有n-plex性质。如果没有其他n-plex连通子图${G{''}} $ 存在使得$ {G'} \subseteq {G{''}} $ ，则子图G′是最大的n-plex，记为nmax-plex。n-plex具有良好的闭包性：一个n-plex图的任何连通子图也是n-plex。例如，一个1-plex图H有5个顶点，那么它包含4个顶点的子图H′也是1-plex。根据(k,c)-core和n-plex的定义，推断出(k,c)-core和(c-k)-plex是等价的，并且(c-k)-plex存在于(c-k)max-plex中，因此(c-k)max-plex中任何c个顶点都可以组成(k,c)-core。
定义 5 图直径。给定一个图G，图直径定义为任意两点间最短距离的最大值，记为ddiam(G)。计算方法如下：
$$ {d_{{\text{diam}}}}(G) = \max \{ s(u,v)|u,v \in V\} $$ (3) 根据(c-k)-plex和ddiam(G)的定义，以及文献[33]中的命题，得出加快(k,c)-core搜索速度的结论。
对于包含c个顶点的(c-k)-plex图G：
1) 如果c < 2k+ 2，则ddiam(G) ≤ 2。
2) 如果c ≥ 2k + 2，则ddiam(G)≤ c−2k +2。
根据以上对(k,c)-core分析，设计一个(k,c)-core查找算法(如算法2所示)。
算法 2 (k,c)-core查找算法
输入 uq、U、c、r、Gs
输出 满足条件的用户集合Rset
1）U←U中到uq距离于r的用户
2）
$ G_s' $ ←Gs中由U组成的子图3）对
$ G_s' $ 进行核心分解4）k ← min{core(uq),c-1}
5）while k > 0 do:
6）
$ G{_s'^{[k]}} $ ← 从$ G_s' $ 中提取包含uq的kmax-core7）
$ G{_s{''}^{[k]}} $ ← 对$ G{_s'^{[k]}} $ 进行直径修剪操作8）C ← 从
$ G{_s{''}^{[k]}} $ 中获取满足条件的(k,c)-core9）if C is not empty: return C
10）k ← k-1
11）return Ø
3.1.3 基于枚举的CSKCGQ查询方法
基于枚举的CSKCGQ查询处理过程如算法3所示。首先使用算法1获得满足条件的CSKQ兴趣点集合，然后使用算法2获取满足(k,c)-core性质的用户集合。对用户集合和兴趣点集合进行组合枚举，判断每一个可能组合，并根据组合的成本对结果R进行更新，返回最好的结果。
算法 3 精确CSKCGQ方法
输入 Q={uq, keywords, r, c}、Gr、Gs
输出 结果R
1）poi_set ←算法1，满足条件的CSKQ集合
2）user_set←算法2，满足条件的(k,c)-core集合
3）对poi_set 和user_set中每个元素进行组合
4）for each combination do:
5）res = {p_set,u_set}
6）cost_res = COST(res)
7）使用res和cost_res更新R
8）return R
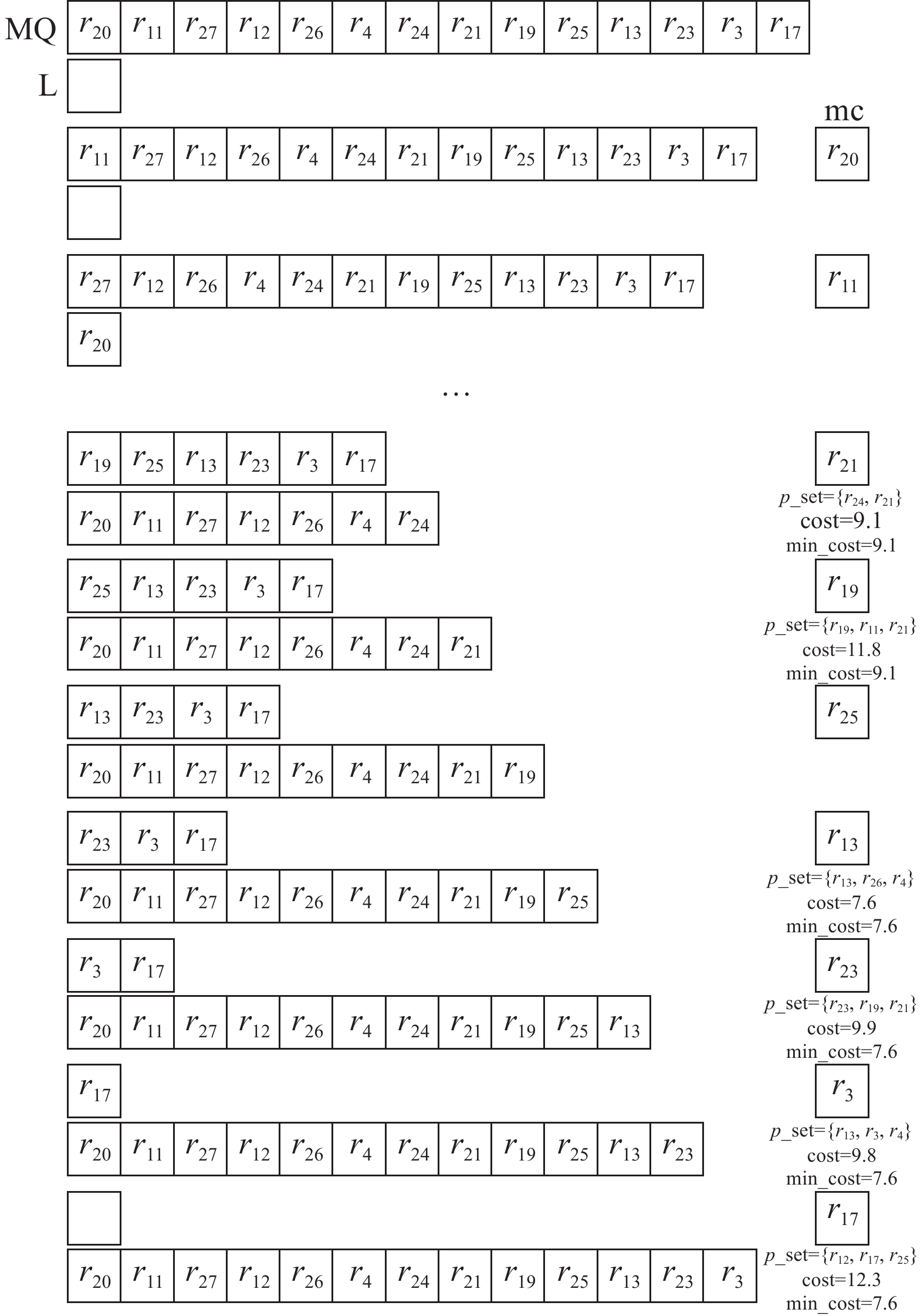
例2 沿用例1中的例子来说明CSKCGQ查询过程。首先，使用SW算法可以进一步过滤兴趣点到[r20, r11, r27, r12, r26, r4, r24, r21, r19, r25, r13, r23]；将列表中兴趣点按照其包含的查询关键字进行分类{餐厅: r20, r11, r26, r24, r23}, {公园: r21, r25, r13,}, {商场: r27, r12, r4, r24, r19,}, 根据不同关键字枚举所有CSKQ组合，对于每个组合使用改进的部分判断是否满足条件。例如，组合{r4, r25, r20}，计算出4.8 < 7.1，所以丢弃这个组合。然后，用范围搜索得到用户列表[u1, u2, u3, u4, u5, u7, u8, u9, u10, u11, u14]，得到子图
$ G_s' $ ，对$ G_s' $ 做核心分解得到k=4和${G_s'^{[4]}}$ ={u1, u2, u3, u4, u5}，得到$ G{_s'^{[4]}} $ 中的(k,c)-core，结果是{u1, u2, u3, u4, u5}。计算poi_set和user_set之间的成本，选择成本最小的组合作为结果返回，结果是{{u1, u2, u3, u4, u5}, {r25, r17, r12}, 4, 23.45}。3.2 基于core-tree的CSKCGQ查询方法
3.2.1 兴趣点集合的快速查询算法
在基于枚举的CSKCGQ查询方法中，不仅需要枚举包含关键字的兴趣点组合，还需要考虑组合结果是否满足条件。对于兴趣点集合查询结果，希望集合中兴趣点之间的距离越近越好，因此本节提出一种快速贪心查询算法，选择距离相互靠近的兴趣点形成集合，并且跳过枚举过程。
算法 4 Fast Greedy 查询过程
输入 O、keywords
输出 满足CSKQ条件的兴趣点集合poi_set
1）poi_list←Ø
2）Q←Ø, L←Ø //Q是最小优先队列
3）将O中的POI加入Q中
4）min_cost ←
$\infty $ 5）while Q not empty：
6）mc = Q.get()
7）L.add(mc)
8）d = s(uq,mc)
9）if d> min_cost : break
10）p←range_search(mc, L, d)
11）p_set←get_combination(p,keywords)
12）if p_set is not empty:
13）poi_list.add(p_set)
14）min_cost = min(min_cost,cost(p_set))
15）return poi_list
首先，根据到查询用户的距离对所有包含查询关键字的兴趣点排序，将其存储到一个最小优先级队列中(第3行)，然后迭代查询队列中的兴趣点得到兴趣点集合。例如，优先级队列Q=[p1, p2, p3, p4, p5, p6, p7, p8]，辅助列表L。将p1从队列Q中移除，添加到L中(第6~7行)，然后从p1发起范围查询，目标是L中兴趣点，查询阈值是p1到查询用户uq的距离(第10行)，选择最接近p1包含其余查询关键字的兴趣点形成集合(第11行)，记录查询过程中组合的最小成本(第14行)。然后继续对Q中的下一个元素搜索，如果优先队列中兴趣点的距离大于查询过程中的最小成本，则查询过程中断(第9行)，最后返回所有满足条件的兴趣点集合。
3.2.2 core-tree结构
为构建core-tree，首先对社交网络图进行核心分解过程，得到不同k值的kmax-core子图，并以树节点结构存储；然后，将(k+1)max-core子图形成的树节点记录为kmax-core子图所在树节点的子节点，并从kmax-core所在的树节点中删除(k+1)max-core中包含的顶点。树节点中的顶点集是其子节点顶点集的超集，因此可删除节点中与子节点共享的冗余顶点，每个顶点在树中只存储一次。
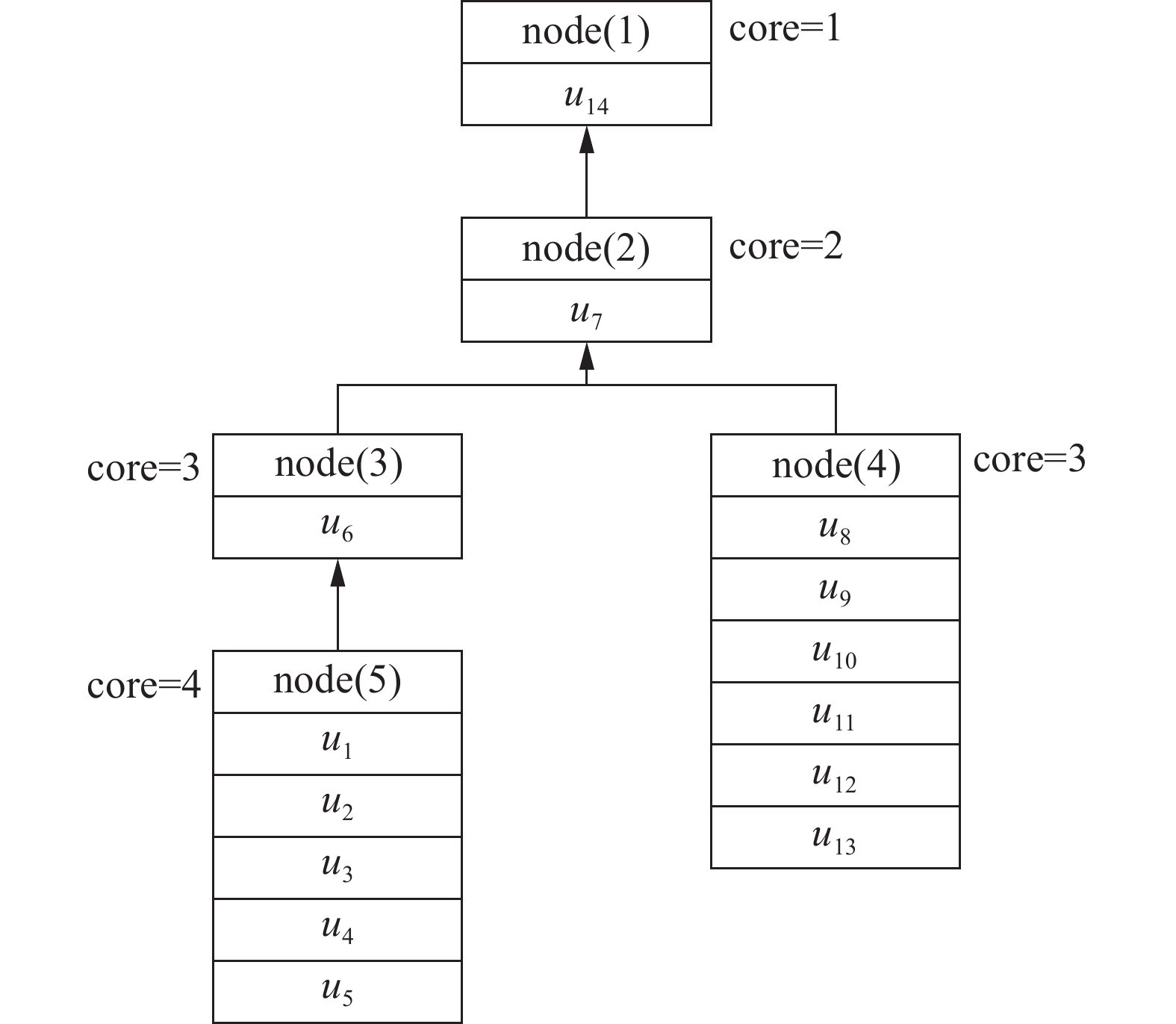
例3 使用图2中的社交网络来说明core-tree结构，如图3所示。node(5)有5个用户，可以组成一个4-core；node(3)有一个用户u6和一个子节点node(5)，包含用户{u1, u2, u3, u4, u5, u6}，所以node(3)是一个3-core；node(4)也是3-core，但是node(3)和node(4)不连通，记录为两个不同的树节点；对于node(1)，表示1-core，包括所有用户。
图 3 core-tree结构示例Fig. 3 The example of core-tree structure下载:
全尺寸图片
3.2.3 基于core-tree的查询算法
首先，使用快速贪心算法来获得兴趣点(poi)集合，然后将每个组合传入到core-tree，并更新core-tree中每个用户和传入组合之间的距离，进而使用贪心策略将最近的用户添加到用户集合中。对于当前k值，如果找到一组(k,c)-core用户集，则结束对当前k值的(k,c)-core查询。执行过程如算法5所示。
算法 5 基于core-tree的快速查询方法
输入 Q={uq, keywords, r, c}、Gr、Gs
输出 结果R
1）O←获取包含keywords中关键字的poi
2）O←范围查询range_search(Q.uq、O、Q.r)
3）poi_set_list←fast_greed(O、keywords)
4）U←range_search(Q.uq、Gs.users、Q.r)
5）ct←使用U中的用户构建core-tree
6）for each poi_set in poi_set_list do:
7）ct.calculate_d(poi_set)
8）r ←ct.ge_user_set()
9）update(R) with r
10）return R
11）method core-tree.get_user_set:
12）k←uq的最大核心值
13）while k>0 :
14）user_set ← greedy choose (k,c)-core
15）if user_set is not empty：
16）return user_set
17）k←k-1
18）return Ø
例4 沿用例1中的查询条件。首先通过范围查询得到O，快速贪心的过程如图4所示，通过快速贪心过程，得到6个兴趣点组合。然后使用范围查询得到U并构建一个core-tree，并传入兴趣点组合返回结果。首先得到core-tree最大核心数为4，所以只计算4max-core，如果当前k值不存在(k,c)-core，减小k的值并继续搜索。在该例中，得到{u1, u2, u3, u4, u5}作为(4,5)-core，作为用户集合结果，对于每个兴趣点集合，计算用户集合和兴趣点集合之间的评分，选择评分最小的组合作为结果的{{u1, u2, u3, u4, u5}, {r12, r17, r25}, 4, 23.45}。
图 4 快速贪心算法过程Fig. 4 Process of fast greedy algorithm下载:
全尺寸图片
4. 实验
4.1 实验设置
实验使用两个道路网络(DC、DE)和两个社交网络(Facebook、Twitch)数据集，兴趣点数据集使用Yelp-dataset。数据集的详细信息如表2所示。
表 2 数据集信息表Table 2 Datasets information table路网 节点数 边数 边平均权重 DC 9522 14832 122.48 DE 115055 130893 225.12 社交网络 节点数 变数 节点平均度数 Facebook 4039 88234 43.69 Twitch 34118 429113 25.15 社交网络 节点数 变数 节点平均度数 POIs dataset keywords max average top 10 10 8 1.4 通过将兴趣点和用户映射到路网上，使用路网距离衡量两个对象间的距离，模拟真实的距离查找场景。使用社交网络表达用户间的亲密度关系，根据密集子图的查找结果表示用户的凝聚力组查找结果。通过结合路网、社交网络和兴趣点数据集得到实验数据集，使用DC+Fb表示由DC和Facebook组成的道路−社交网络，NH+Tw表示由NH和Twitch组成的道路−社交网络。随机选择
$\left| {V({G_r})} \right| \times 0.6$ 个顶点作为POI所在的位置。实验过程考虑3个参数：关键字个数k，用户数量c和距离阈值r，这些参数的范围及其默认值如表3所示。k表示查询条件中包含的关键字个数，k值主要根据兴趣点数据集中每个兴趣点涵盖的关键字个数来设置，平均每个兴趣点包含1.4个关键字一组兴趣点集合通常包含3~5个兴趣点，因此设置k的范围为2~5，默认值为3；c表示希望返回的用户集合中包含的用户数，该参数的设置依据社交网络的平均出度和(k,c)-core查找性质，如果设置的值过大会无法产生结果；r表示查询的距离阈值，r的默认值设置为DC和DE的平均边权重的15倍，并通过上下浮动来定义不同的范围。
表 3 参数设置表Table 3 Parameters settings table参数 范围 默认值 k 2,3,4,5 3 c(DC+Fb) 3,4,5,6,8 5 r(DC+Fb) 1×103,2×103,3×103,4×103 2000 c(DE+Tw) 3,4,5,6 4 r(DE+Tw) 3×103,4×103,5×103,6×103, 4000 4.2 实验结果
4.2.1 CSKQ查询效果的比较
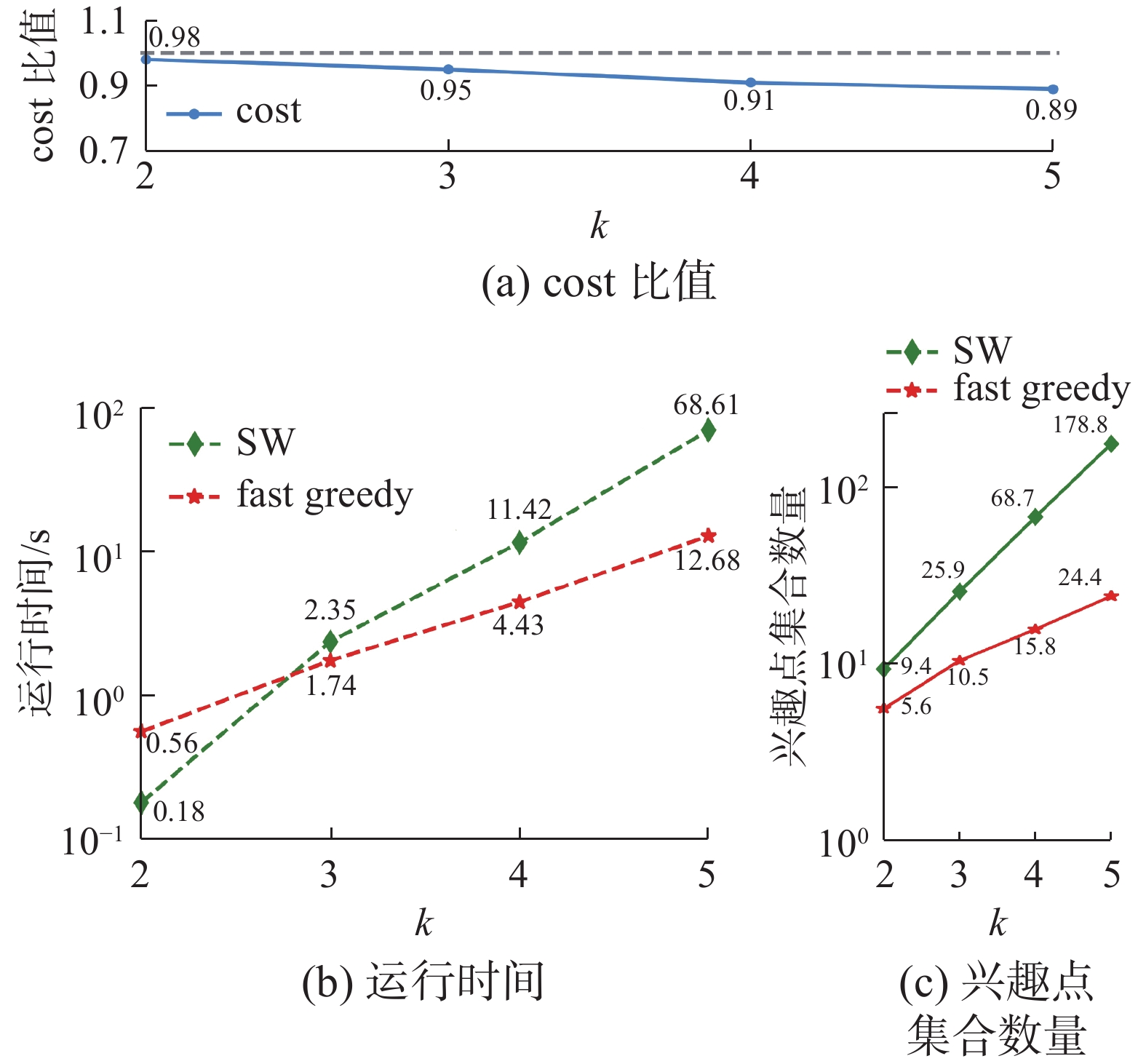
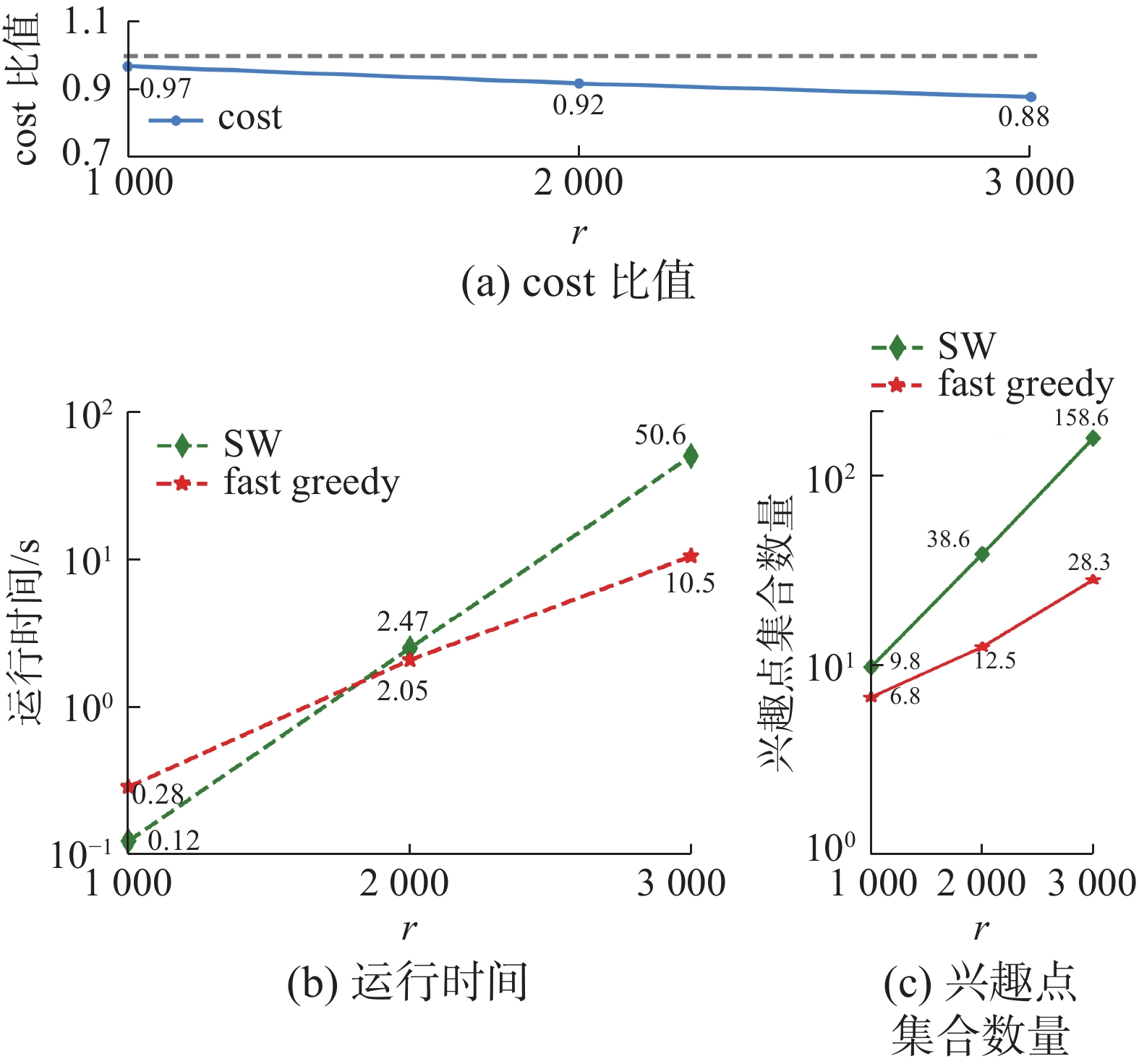
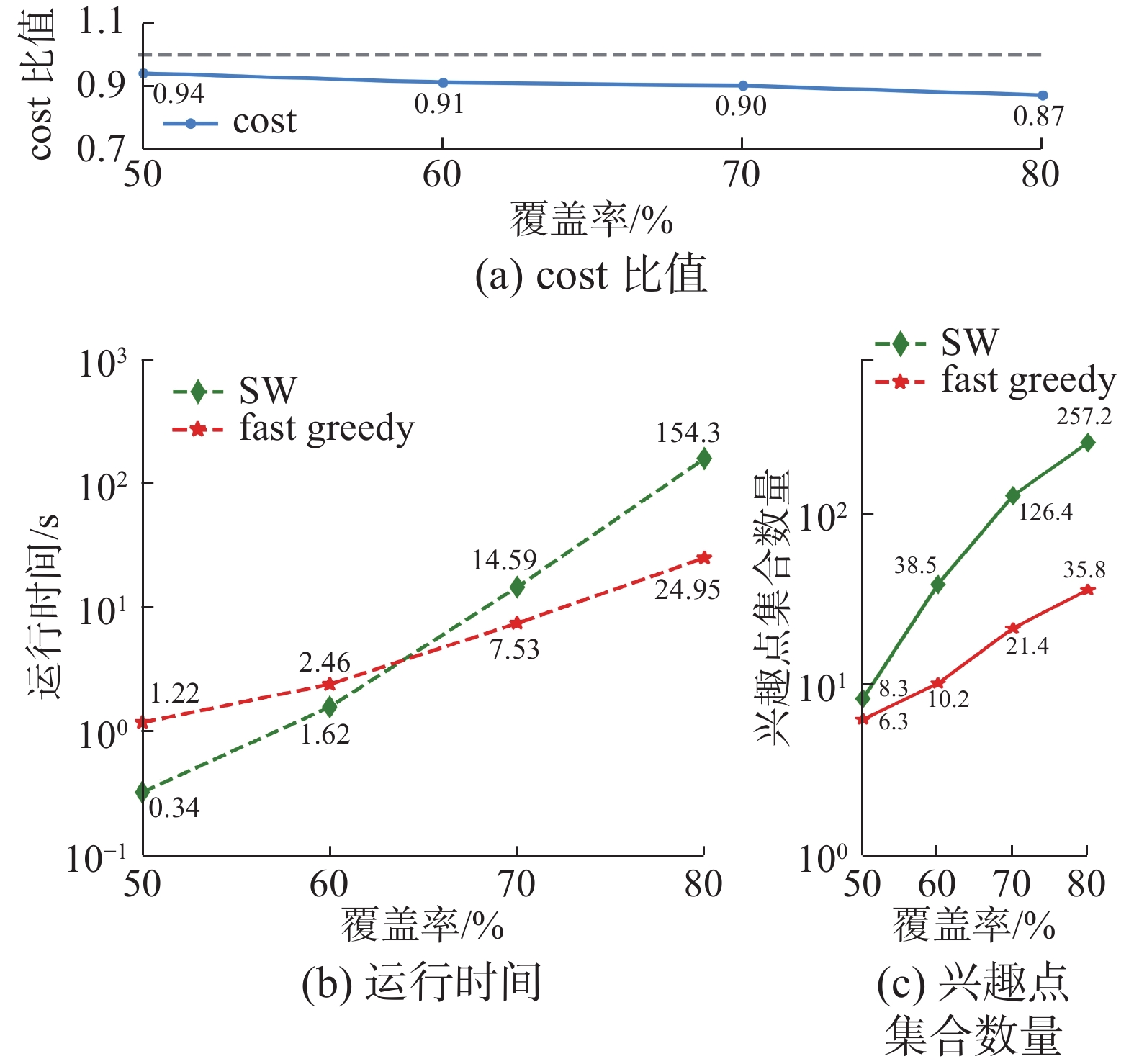
该实验目的是对比提出的fast greedy方法和SW算法的效果。实验使用DC+Fb数据集，分别对不同关键字个数k，查询距离阈值r以及兴趣点的覆盖率进行实验，实验结果如图5~7所示。
图 5 不同k值Fig. 5 Varying k values下载:
全尺寸图片
图 6 不同r值Fig. 6 Varying r values下载:
全尺寸图片
图 7 不同覆盖率Fig. 7 Varying cover ratio下载:
全尺寸图片
实验结果考虑3个指标：1)fast greedy与SW返回的兴趣点集合的cost比值，2)算法运行时间，3)算法得到的兴趣点集合数量。cost计算使用式（1），其比值ratio的计算公式为
$ {r_{{\text{atio}}}} = \dfrac{{{c_{{\text{SW}}}}}}{{{c_{{\text{fast}}}}}} $ ，ratio的值越接近1则说明fast greedy方法查询结果与SW算法的结果越接近，准确率越高。对每个参数使用随机生成的查询条件，每个参数进行20次查询，取结果的平均值作为实验结果。从图5~7的(a)可看出，fast greedy具有良好的准确性。随着参数的增加，准确性不会产生太大波动。当3个参数较小时，CSKQ的查询结果较少，fast greedy与SW结果接近。随着参数增大，fast greedy的修剪过程可能会将最佳CSKQ结果过滤掉，从而导致准确率下降，下降的准确率低于0.1。
图5~7中(b)则给出了不同参数下两种方法的运行时间对比。当参数较小时，SW枚举组合的结果较少，运行速度快；相反，fast greedy通过查询修剪来获得结果，当兴趣点较少时查询的开销大于枚举。但随着参数增长，满足条件的兴趣点也不断增多，枚举方法消耗的时间呈指数增加。fast greedy没有枚举过程，所以当参数增大时，只会增加查询次数，运行时间的变化幅度较小。如参数覆盖率会影响阈值范围内的兴趣点数量，参数覆盖率从60%增加到70%过程中，SW的时间消耗变成了10倍，而fast greedy时间消耗只增加了2倍。
图5~7中的 (c)对比了两个方法在运行过程中产生的兴趣点集合数量。随着3个参数的增长，候选兴趣点数量不断增加，导致SW枚举兴趣点组合数量也急剧变化。相比之下，本文的fast greedy方法通过范围查询过滤，减少了运行过程中需要考虑的兴趣点集合数量。
综上可见，SW对于CSKQ的参数变化特别敏感，运行时间和产生的组合数会随着参数变化而呈指数变化趋势，而fast greedy则不会有明显变化。
4.2.2 CSKCGQ查询的比较
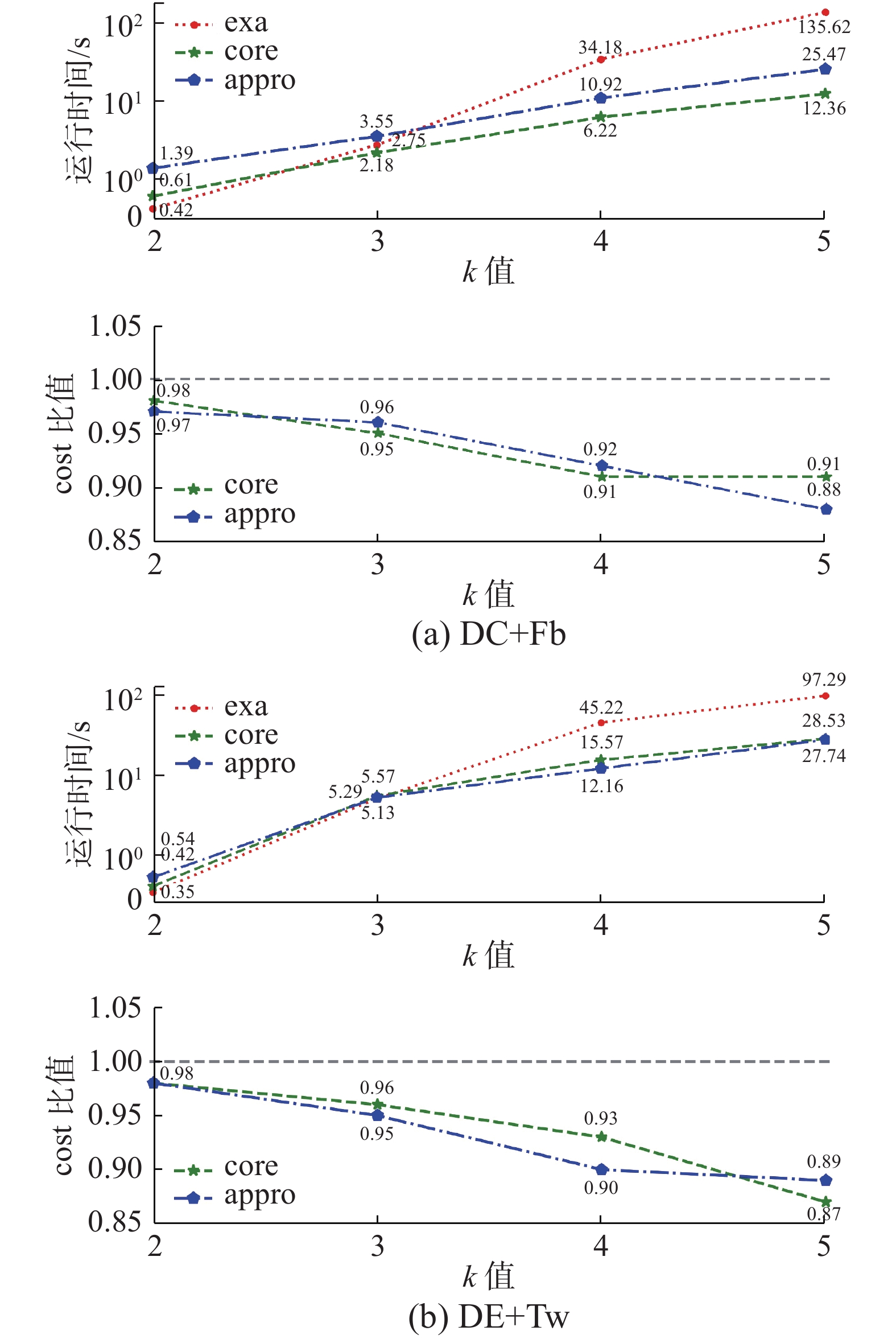
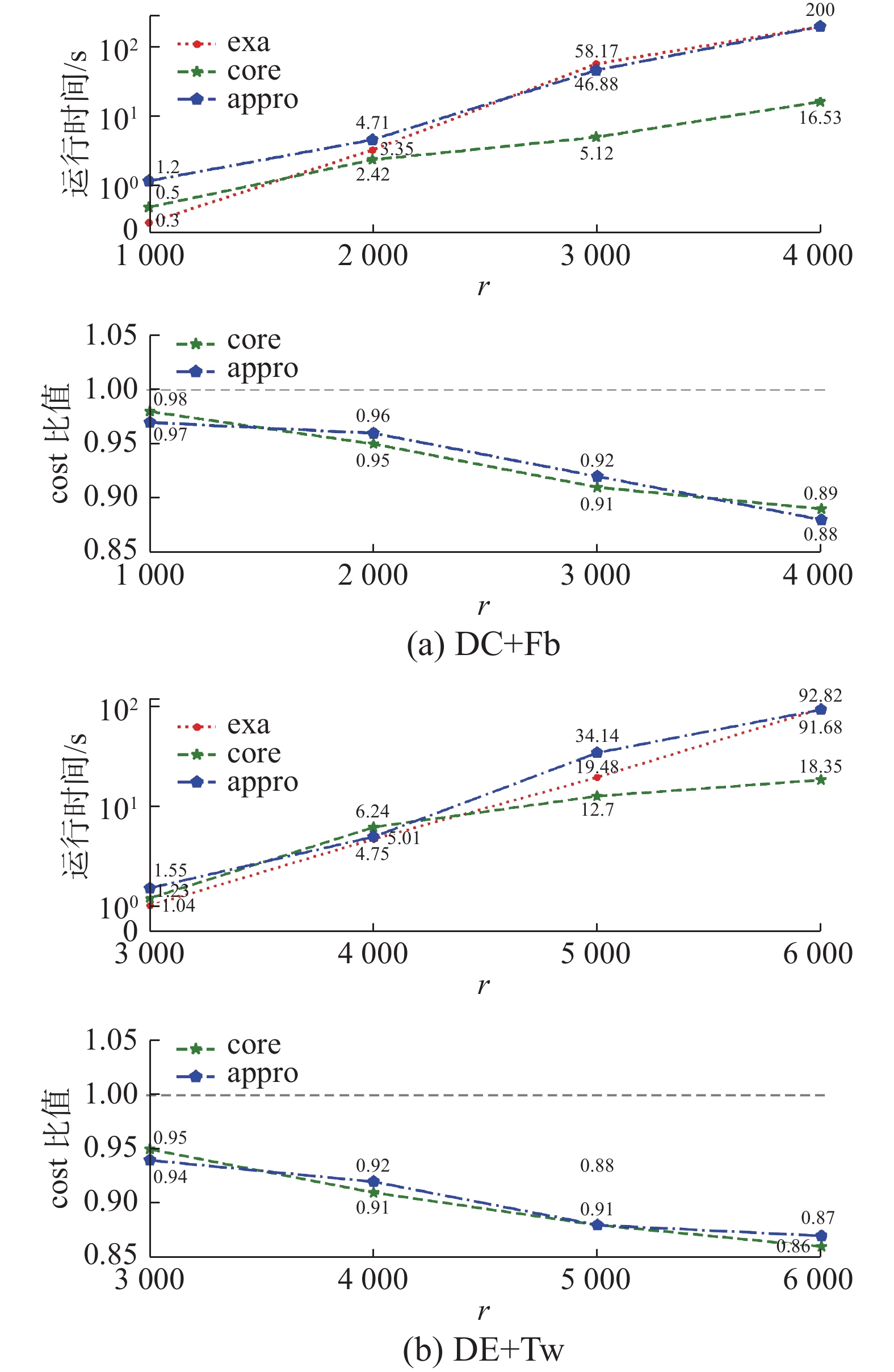
该实验目的是验证本文提出的基于core-tree查询方法的效率和准确性。文献[29]提出的GBCK查询与本文工作最为接近，并提出了APPRO方法解决查询问题。本文使用(k,c)-core方法与APPRO方法作为对比实验。实验过程中，如果程序运行时间超过200 s，记录运行时间为200 s。图8~10给出了不同算法的运行时间和cost比值。
图 8 不同k值Fig. 8 Varying k value下载:
全尺寸图片
图 9 不同c值Fig. 9 Varying c value下载:
全尺寸图片
图 10 不同r值Fig. 10 Varying r value下载:
全尺寸图片
图8给出了在两个数据集上3个算法对于不同k值的运行结果。k值主要影响兴趣点集合结果部分，在两个数据集上有相同的变化规律。当参数k值较小时，兴趣点组合数量较少，3种方法的运行时间十分接近。但是随着k值增大，基于枚举的查询方法(exa)的运行时间成倍增加，因为k值增大会增加枚举过程中兴趣点组合的数量，从而大幅度增加运算时间。而结合(k,c)-core与APPRO方法(appro)和基于core-tree查询方法(core)时间波动较为平缓，因为k值变化只会影响查询过程中兴趣点集合的规模，不会影响某类关键字兴趣点的数量，而这两种方法都没有对兴趣点组合的枚举查找过程，所以运行时间波动较小。
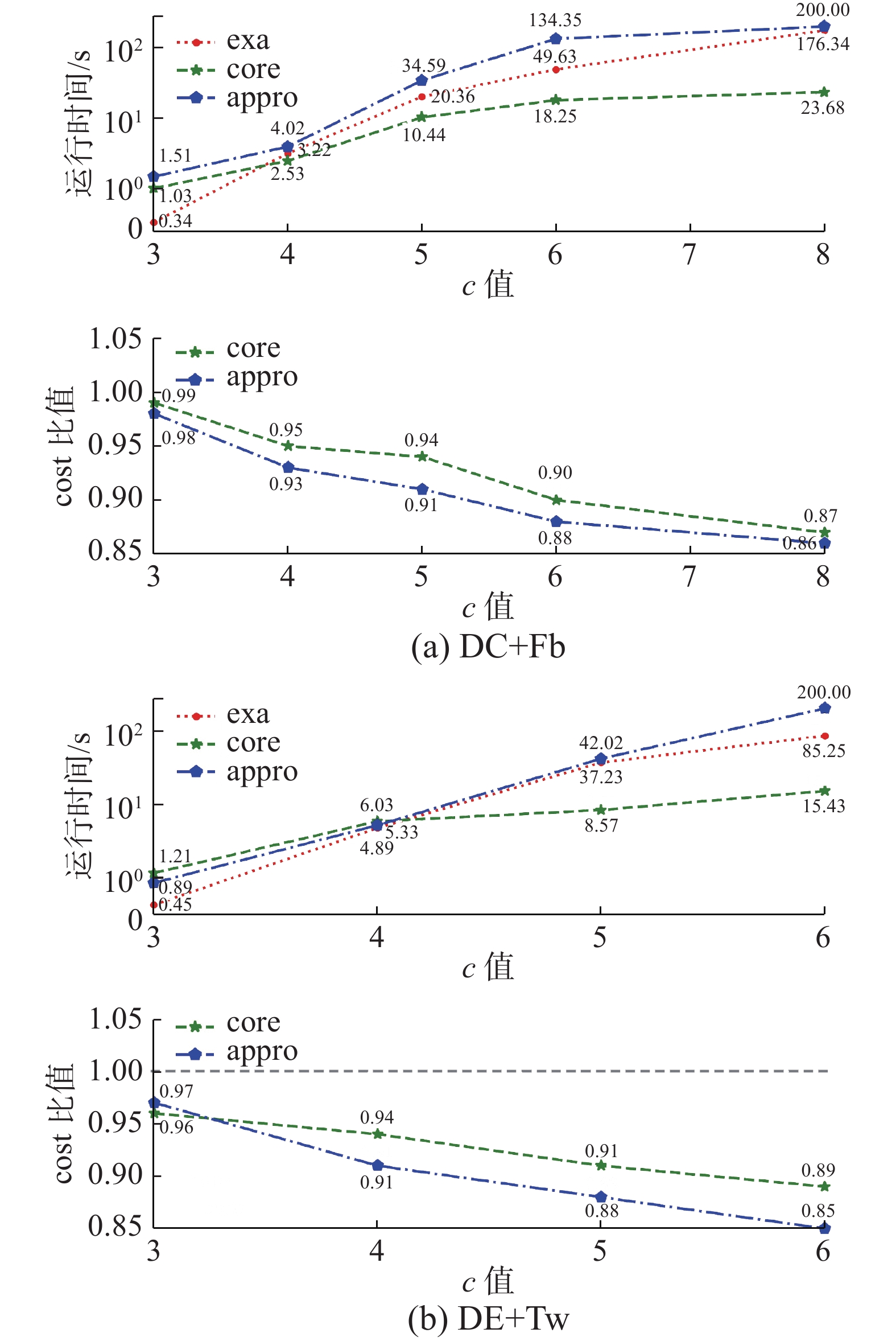
图9给出了随着查询参数c变化下每种方法的运行结果。参数c的变化会影响用户集合的查询结果，参数c的增大会导致满足(k,c)-core条件的用户集合数量增加，appro方法会对每个可能的用户集合发起一次GBCK查询，所以appro方法运行消耗的时间会极大增加。同样，exa方法则增加兴趣点集合与用户集合匹配组合的数量，运行时间也会大幅度增加，但变化趋势没有appro方法剧烈。本文提出的core方法使用core-tree结构存储了用户的核心分解结果，结果的返回过程中以贪心方式选择距离兴趣点集合最近的用户，并没有对所有可能的用户集合进行判断，参数c对core-tree方法的主要影响是增加了图核心分解过程的时间消耗。
图10给出了对于不同距离阈值参数r的运行结果。随着参数r的增加，需要考虑的用户和兴趣点会增多，同时满足条件的兴趣点集合和用户集合数量也会增加，所以exa方法和appro方法的运行时间会大幅度提高。比较两个数据集上的结果，DC+Fb数据集对r值的变化波动较大，因为Fb构成的社交网络具有更高的聚合度，随着查询范围的扩大，所形成的用户组合也会更多。但本文提出的基于core-tree查询方法使用fast greedy搜索过程加速了兴趣点集合查找，且使用core-tree结构存储用户内聚组合，使用贪心思想返回凝聚力最高的用户集合，并不会对所有的用户集合进行判断，所以运行结果的波动较小。
相应的，从图8~10的结果cost比值可以看出，本文提出的基于core-tree查询方法的结果准确性无法与exa方法相比，因为fast greedy查询过程与core-tree结构都基于贪心思想，修剪掉了某些兴趣点集合或者用户集合，但其组合结果可能是最佳结果，因此查询的准确率比exa方法有所下降。
综上考虑，本文提出的CSKCGQ方法具有较高查询准确性，且对不同参数变化有较好适应性。
5. 结束语
本文通过分析现有的查询工作定义了道路社交网络上的集合空间关键字内聚组查询处理模式。提出了一种基于core-tree的快速查询方法来解决集合空间关键字凝聚组查询问题，返回一组用户集合与兴趣点集合的最佳匹配作为结果。在查询执行的过程中，通过使用快速贪心查询方法，提前修剪了不满足条件的兴趣点，同时也大幅度减少了CSKQ集合的数量；根据k-core和n-plex的性质，设计了core-tree结构保存核心分解的结果，加快了满足(k,c)-core条件的用户组查询。实验部分通过改变不同的参数进行实验，实验结果证明了所提出的方法的效率和准确性。下一步的研究工作将会考虑兴趣点的时间感知属性，以及用户之间的亲密度权重，使查询的结果更贴合用户需求。
-
图 1 道路网络
Fig. 1 Road network
下载:
全尺寸图片
图 2 用户社会关系
Fig. 2 Users social network
下载:
全尺寸图片
图 3 core-tree结构示例
Fig. 3 The example of core-tree structure
下载:
全尺寸图片
图 4 快速贪心算法过程
Fig. 4 Process of fast greedy algorithm
下载:
全尺寸图片
图 5 不同k值
Fig. 5 Varying k values
下载:
全尺寸图片
图 6 不同r值
Fig. 6 Varying r values
下载:
全尺寸图片
图 7 不同覆盖率
Fig. 7 Varying cover ratio
下载:
全尺寸图片
图 8 不同k值
Fig. 8 Varying k value
下载:
全尺寸图片
图 9 不同c值
Fig. 9 Varying c value
下载:
全尺寸图片
图 10 不同r值
Fig. 10 Varying r value
下载:
全尺寸图片
表 1 路网顶点信息
Table 1 Road network vertex information
节点 用户 兴趣点 节点 用户 兴趣点 r1 u3 r2 u12 r3 餐厅 r4 u9 商场 r5 r6 餐厅 r7 r8 u1 r9 公园 r10 u8 r11 u5 餐厅 r12 u2 商场 r13 公园 r14 餐厅 r15 u13 r16 酒吧 r17 餐厅 r18 酒吧 r19 u7 商场 r20 餐厅 r21 u11 公园 r22 u6 餐厅 r23 餐厅 r24 u14 餐厅、商场 r25 公园 r26 u10 餐厅 r27 u4 r28 商场 表 2 数据集信息表
Table 2 Datasets information table
路网 节点数 边数 边平均权重 DC 9522 14832 122.48 DE 115055 130893 225.12 社交网络 节点数 变数 节点平均度数 Facebook 4039 88234 43.69 Twitch 34118 429113 25.15 社交网络 节点数 变数 节点平均度数 POIs dataset keywords max average top 10 10 8 1.4 表 3 参数设置表
Table 3 Parameters settings table
参数 范围 默认值 k 2,3,4,5 3 c(DC+Fb) 3,4,5,6,8 5 r(DC+Fb) 1×103,2×103,3×103,4×103 2000 c(DE+Tw) 3,4,5,6 4 r(DE+Tw) 3×103,4×103,5×103,6×103, 4000 -
[1] GAO Yunjun, ZHAO Jingwen, ZHENG Baihua, et al. Efficient collective spatial keyword query processing on road networks[J]. IEEE transactions on intelligent transportation systems, 2016, 17(2): 469–480. doi: 10.1109/TITS.2015.2477837 [2] LI Yun, WANG Ziheng, CHEN Jing, et al. Multiple query point based collective spatial keyword querying[C]// International Conference on Advanced Data Mining and Applications. Cham: Springer, 2019: 63–78. [3] LI Qiyan, ZHU Yuanyuan, YU J X. Skyline cohesive group queries in large road-social networks[C]//2020 IEEE 36th International Conference on Data Engineering. Dallas: IEEE, 2020: 397–408. [4] GUO Fangda, YUAN Ye, WANG Guoren, et al. Cohesive group nearest neighbor queries over road-social networks[C]//2019 IEEE 35th International Conference on Data Engineering. Macao: IEEE, 2019: 434–445. [5] CHEN Lisi, CONG Gao, JENSEN C S, et al. Spatial keyword query processing[J]. Proceedings of the VLDB endowment, 2013, 6(3): 217–228. doi: 10.14778/2535569.2448955 [6] ZHANG Xiaoyan, MENG Xiangfu, SUN Jinguang, et al. An efficient top: spatial keyword typicality and semantic query[J]. IEEE access, 2019, 7: 138122–138135. doi: 10.1109/ACCESS.2019.2941760 [7] 孟祥福, 张霄雁, 赵路路, 等. 基于位置−文本关系的空间对象top-k查询与排序方法[J]. 智能系统学报, 2020, 15(2): 235–242. doi: 10.11992/tis.201808011 MENG Xiangfu, ZHANG Xiaoyan, ZHAO Lulu, et al. A location-text correlation-based top-k query and ranking approach for spatial objects[J]. CAAI transactions on intelligent systems, 2020, 15(2): 235–242. doi: 10.11992/tis.201808011 [8] ZHU Huaijie, LI Wenbin, LIU Wei, et al. Top k optimal sequenced route query with POI preferences[J]. Data science and engineering, 2022, 7(1): 3–15. doi: 10.1007/s41019-022-00177-5 [9] 刘喜平, 万常选, 刘德喜, 等. 空间关键词搜索研究综述[J]. 软件学报, 2016, 27(2): 329–347. LIU Xiping, WAN Changxuan, LIU Dexi, et al. Survey on spatial keyword search[J]. Journal of software, 2016, 27(2): 329–347. [10] LI Zhisheng, LEE K C K, ZHENG Baihua, et al. IR-tree: an efficient index for geographic document search[J]. IEEE transactions on knowledge and data engineering, 2011, 23(4): 585–599. doi: 10.1109/TKDE.2010.149 [11] ZHANG Chengyuan, ZHANG Ying, ZHANG Wenjie, et al. Inverted linear quadtree: efficient top K spatial keyword search[J]. IEEE transactions on knowledge and data engineering, 2016, 28(7): 1706–1721. doi: 10.1109/TKDE.2016.2530060 [12] DE FELIPE I, HRISTIDIS V, RISHE N. Keyword search on spatial databases[C]//2008 IEEE 24th International Conference on Data Engineering. Cancun: IEEE, 2008: 656–665. [13] MENG Xiangfu, LI Pan, ZHANG Xiaoyan. A personalized and approximated spatial keyword query approach[J]. IEEE access, 2863, 8: 44889–44902. [14] LEE K C K, LEE W C, ZHENG Baihua, et al. ROAD: a new spatial object search framework for road networks[J]. IEEE transactions on knowledge and data engineering, 2012, 24(3): 547–560. doi: 10.1109/TKDE.2010.243 [15] ZHONG Ruicheng, LI Guoliang, TAN K L, et al. G-tree: an efficient and scalable index for spatial search on road networks[J]. IEEE transactions on knowledge and data engineering, 2015, 27(8): 2175–2189. doi: 10.1109/TKDE.2015.2399306 [16] ZHAO Tianyu, HUANG Shuai, WANG Yong, et al. RNE: computing shortest paths using road network embedding[J]. The VLDB journal, 2022, 31(3): 507–528. doi: 10.1007/s00778-021-00705-1 [17] 张绍雪, 王丽珍, 陈文和. CPM-MCHM: 一种基于极大团和哈希表的空间并置模式挖掘算法[J]. 计算机学报, 2022, 45(3): 526–541. doi: 10.11897/SP.J.1016.2022.00526 ZHANG Shaoxue, WANG Lizhen, TRAN Vanha. CPM-MCHM: a spatial co-location pattern mining algorithm based on maximal clique and hash map[J]. Chinese journal of computers, 2022, 45(3): 526–541. doi: 10.11897/SP.J.1016.2022.00526 [18] BARBIERI N, BONCHI F, GALIMBERTI E, et al. Efficient and effective community search[J]. Data mining and knowledge discovery, 2015, 29(5): 1406–1433. doi: 10.1007/s10618-015-0422-1 [19] AKBAS E, ZHAO Peixiang. Truss-based community search[J]. Proceedings of the VLDB endowment, 2017, 10(11): 1298–1309. doi: 10.14778/3137628.3137640 [20] 徐兰天, 李荣华, 王国仁, 等. 面向时序图的K-truss社区搜索算法研究[J]. 计算机科学与探索, 2020, 14(9): 1482–1489. doi: 10.3778/j.issn.1673-9418.1909050 XU Lantian, LI Ronghua, WANG Guoren, et al. Research on K-truss community search algorithm for temporal networks[J]. Journal of frontiers of computer science and technology, 2020, 14(9): 1482–1489. doi: 10.3778/j.issn.1673-9418.1909050 [21] LI Ronghua, QIN Lu, YE Fanghua, et al. Skyline community search in multi-valued networks[C]//Proceedings of the 2018 International Conference on Management of Data. Houston: ACM, 2018: 457–472. [22] FANG Yixiang, CHENG R, CHEN Yankai, et al. Effective and efficient attributed community search[J]. The VLDB journal, 2017, 26(6): 803–828. doi: 10.1007/s00778-017-0482-5 [23] LIU Qing, ZHU Yifan, ZHAO Minjun, et al. VAC: vertex-centric attributed community search[C]//2020 IEEE 36th International Conference on Data Engineering. Dallas: IEEE, 2020: 937–948. [24] YANG Zhibang, LI Xiaoxue, ZHANG Xu, et al. K-truss community most favorites query based on top-T[J]. World wide web, 2022, 25(2): 949–969. doi: 10.1007/s11280-021-00947-7 [25] KIM J, GUO Tao, FENG Kaiyu, et al. Densely connected user community and location cluster search in location-based social networks[C]//Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. Portland: ACM, 2020: 2199–2209. [26] AL-BAGHDADI A, LIAN Xiang. Topic-based community search over spatial-social networks[J]. Proceedings of the VLDB endowment, 2020, 13(12): 2104–2117. doi: 10.14778/3407790.3407812 [27] ZHANG Dongxiang, CHEE Y M, MONDAL A, et al. Keyword search in spatial databases: towards searching by document[C]//2009 IEEE 25th International Conference on Data Engineering. Shanghai: IEEE, 2009: 688–699. [28] CAO Xin, CONG Gao, JENSEN C S, et al. Collective spatial keyword querying[C]//Proceedings of the 2011 ACM SIGMOD International Conference on Management of data. Athens: ACM, 2011: 373–384. [29] SU Sen, ZHAO Sen, CHENG Xiang, et al. Group-based collective keyword querying in road networks[J]. Information processing letters, 2017, 118: 83–90. doi: 10.1016/j.ipl.2016.10.008 [30] CHEN Zijun, ZHAO Tingting, LIU Wenyuan. Time-aware collective spatial keyword query[J]. Computer science and information systems, 2021, 18(3): 1077–1100. doi: 10.2298/CSIS200131034C [31] 李艳红, 李国徽, 周斌. 路网移动对象空间关键字连续Top-k查询[J]. 华中科技大学学报(自然科学版), 2014, 42(6): 127–132. LI Yanhong, LI Guohui, ZHOU Bin. Continuous top-kspatial keyword queries over moving objects in road networks[J]. Journal of Huazhong university of science and technology (natural science edition), 2014, 42(6): 127–132. [32] XUE Jingtao, WU Chunyu, ZHAO Bin, et al. Collective spatial keyword query on time dependent road networks[C]//2022 Tenth International Conference on Advanced Cloud and Big Data. Guilin: IEEE, 2022: 7–12. [33] BRANDES U. Network analysis: methodological foundations[M]. Berlin: Springer Science & Business Media, 2005.
