目前，电力线巡线机器人主要有飞行式巡线机器人、攀爬式巡线机器人和混合式巡线机器人。飞行式巡线机器人是以无人机为载体，通过在机体上搭载巡检设备，采用飞行方式对电力线进行巡检。攀爬式巡线机器人的典型特征是有两个或者多个与电力线垂直的机械臂，机械臂上安装有行走轮，行走轮与电力线相接触且在电机的驱动下沿电力线行走^[1]。混合式巡线机器人是一种将攀爬式巡线机器人的行走功能和飞行式巡线机器人的飞行功能相结合的巡线机器人^[2]，能够利用飞行功能将机器人悬挂到电力线上，利用行走功能控制机器人沿电力线移动^[1]。遇到障碍物时可以通过飞行模式或爬行模式穿越障碍物。而由于输电线路走廊常常被架设在雪山、河谷、沙漠、戈壁等特殊地形，且伴随风雪、沙尘、雨露等天气的侵扰^[3]，增加了混合式巡线机器人的巡检难度。近年来，如何提高巡线机器人的稳定性和可靠性，是其面向实际应用的难点。

对于飞行式巡线机器人和攀爬式巡线机器人，它们的稳定性和可靠性控制方式均有所不同。其中飞行式巡线机器人主要是对飞行稳定性和可靠性进行控制。例如，诸多学者利用了滑模控制技术来应对飞行器控制过程中所受外部干扰问题^[4-6]。文献[7]采用积分反步法，应对风场效应对飞行器的干扰。文献[8]针对飞行器轨迹跟踪控制问题，提出了一种模糊自适应动态面轨迹跟踪控制方法。攀爬式巡线机器人的稳定性和可靠性控制主要集中在行走控制。文献[9]提出了一种模糊控制方法，控制机器人的转向行为。文献[10]采用了预编程和传感器定位相结合的方法，实现机器人自主越障控制。文献[11]提出了一种基于重力模型的PD控制律和模糊打滑控制方法，实现巡线机器人打滑和越障控制。飞行式巡线机器人的飞行控制目前有较为广泛的研究，但其存在续航时间短、无法有效克服强气流干扰等缺点，稳定性和续航时间不及攀爬式巡线机器人。而攀爬式巡线机器人虽然依托电力线，具有续航时间长、稳定性高等优点，但结构设计复杂、无法自主上下电力线，成为其在电力线巡检上的应用瓶颈。

混合式巡线机器人在多变的野外环境下，频繁的飞走切换，使其需不断地在呈柔索特性的电力线上完成起落，对机器人的稳定控制提出了较大挑战。为了使混合式巡线机器人能有效应对复杂的电力线环境，采用单一控制模式已无法满足需求，因此需采用多模式控制方法，旨在机器人能在不同环境下工作时都有一套合适的控制模式与之匹配。目前，多模式控制方法已经广泛应用于车辆、机器人等领域，并取得了一定的成果。文献[12]针对复杂的交通环境，设计了定速巡航、稳态跟随、接近前车、强加速、强减速和避撞6种模式，并利用经验型碰撞时间倒数来实现模式切换。文献[13]设计了一个可用于野外地质探测的陆空两栖平台，划分了飞行和陆地行走两种控制模式，并采用差值判定法实现陆空两种模式切换。文献[14]针对四旋翼飞行器室外环境因素对飞行的影响，将控制模式划分为起降、平稳、增稳和失控保护4种模式，并以俯仰角、翻滚角和高度为模式切换变量进行模式切换。

为了提升巡线机器人在复杂电力线环境中的稳定性和可靠性，本文以FPLIR为研究对象，提出了一种多模式切换混杂控制方法。针对飞走巡线机器人(flying-walking power line inspection robot，FPLIR)的工作原理建立了4种模式的混杂自动机模型和模式切换监测器模型，并利用Lyapunov函数法和力角稳定性判据(force-angle stability margin，FASM)分别分析FPLIR在行走状态下多模式切换的稳定性和基于力学特性的稳定性。基于各种控制模式侧重的控制目标，提出了滑模控制、模型预测控制、变论域模糊控制、EGO-Planer等控制策略，并进行仿真和实验。仿真和实验结果表明，所提出的控制方法取得了较好的控制效果。

1.   FPLIR机构描述

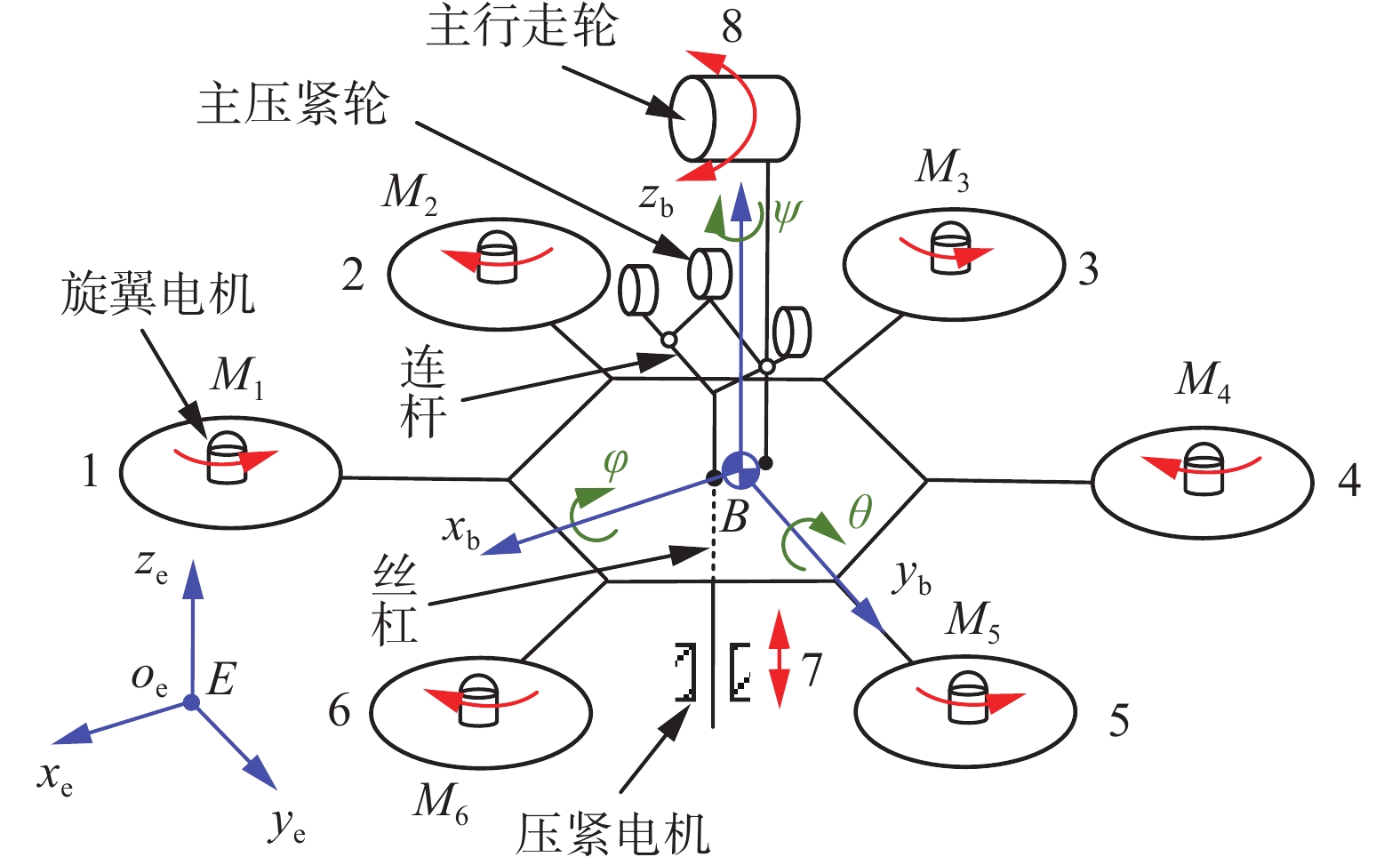
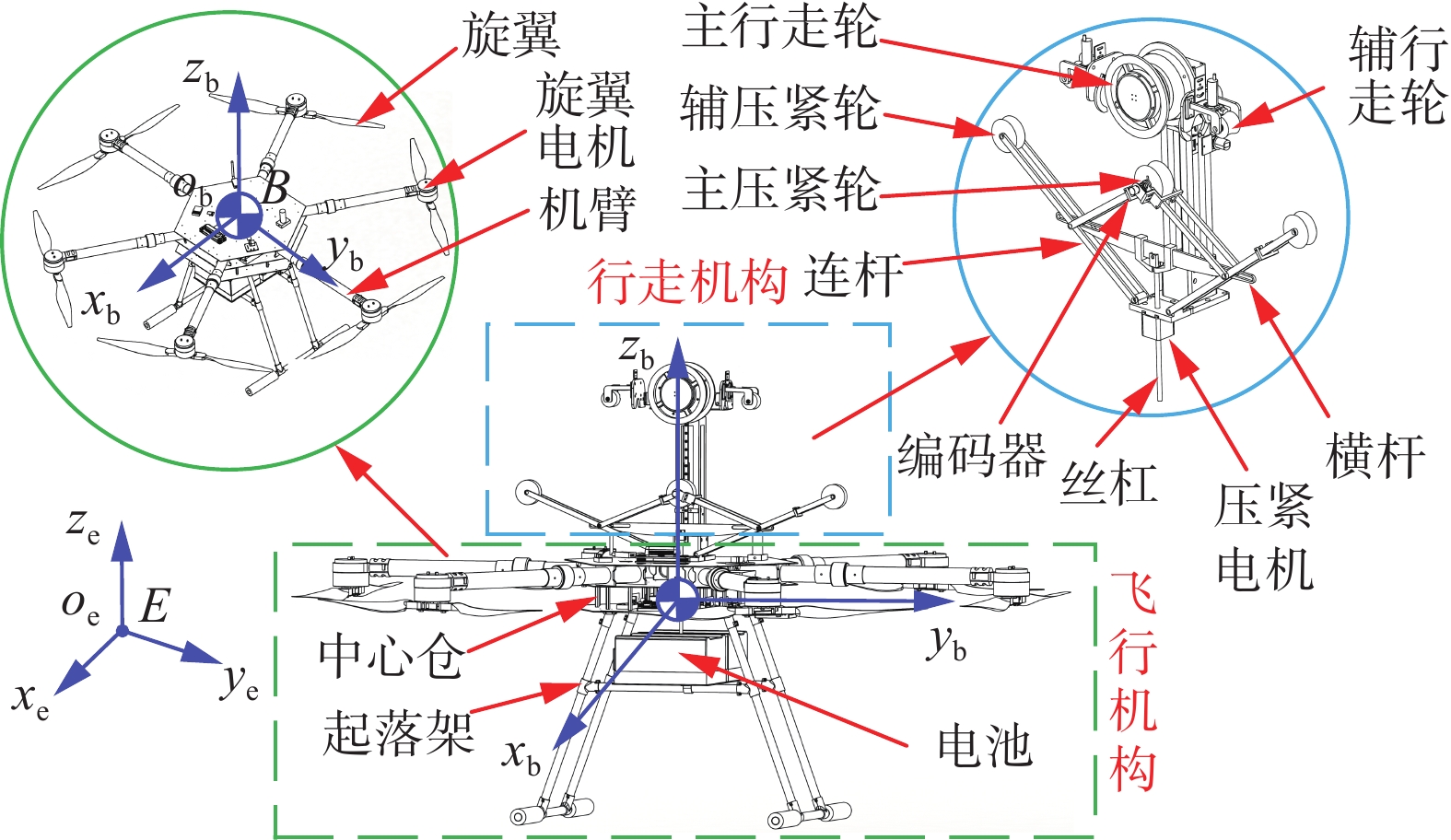
自主研发的FPLIR主要由飞行机构和行走机构两部分构成，其模型如图1所示。

图  1  FPLIR机械结构图

Fig.  1  Mechanical structure of FPLIR

下载: 全尺寸图片

其中飞行机构采用X型结构设计，6个旋翼电机均匀分布在中心仓的四周序号为M₁~M₆。行走机构包括主行走轮、辅行走轮、主压紧轮、编码器等。在机器人运动空间中基于右手螺旋定则建立惯性坐标系 $ \left\{ E \right\} $ 和重心坐标系 $ \left\{ B \right\} $ 。其中重心坐标系的 $ {x}_{{\rm{b}}} $ 轴指向机器人正前方， $ {y}_{\text{b}} $ 轴指向机器人正左方， ${z_{\rm{b}}}$ 轴垂直于平面 $ {x_{\text{b}}}{o_{\text{b}}}{y_{\text{b}}} $ 竖直向上。惯性坐标系 $ \left\{ E \right\} $ 的 $ x_{{\rm{e}}} $ 轴指向正北方， $ y_{\mathrm{e}} $ 轴指向正西方， ${z_{\text{e}}}$ 轴方向铅锤向上。

图2为FPLIR的机构构型，图中标号1~8表示机器人的驱动器件，为8个控制输入。在飞行状态下，飞行机构被激活，行走机构被关闭，该状态下机器人具有6个自由度。行走状态下，飞行机构被关闭，行走机构被激活，此时机器人具有2个自由度，分别为行走轮挂线行走时的沿线运动和压紧组件（主压紧轮、辅压紧轮、丝杠、连杆等）在压紧电机驱动下的上下运动。图中， $ \varphi $ 为沿 ${x_{\rm{b}}}$ 轴旋转的横滚角， $ \psi $ 为沿 ${z_{\rm{b}}}$ 轴旋转的偏航角， $ \theta $ 为沿 ${y_{\text{b}}}$ 轴旋转的俯仰角。为方便对机器人进行飞行状态下的动力学分析，定义重心坐标系 $ \left\{ B \right\} $ 为机体坐标系，重心与中心重合。

图  2  FPLIR的机构构型

Fig.  2  Mechanism diagram of FPLIR

下载: 全尺寸图片

设机体坐标系按照 $xyz$ 旋转顺序得到惯性坐标系，则旋转矩阵为

设机体角速度为 ${{\boldsymbol{\omega }}_{\rm{b}}} = {\left[ {\begin{array}{*{20}{c}} {{\omega _{{\text{b}}x}}}\quad{{\omega _{{\text{b}}y}}}\quad{{\omega _{{\text{b}}z}}} \end{array}} \right]^{\text{T}}}$ ，则 ${{\boldsymbol{\omega }}_{\rm{b}}}$ 与姿态角速度之间的关系为

2.   FPLIR动力学模型

2.1   飞行机构动力学模型

2.1.1   位置动力学模型

根据牛顿第二定律，机器人运动学方程为

式中： $m$ 为机器人的质量， $ {{\boldsymbol{E}}}_{{\rm{e}}} $ 为惯性坐标系下的位移量， ${\boldsymbol{G}}$ 为重力， ${{\boldsymbol{T}}_{{\rm{e}}}}$ 为惯性坐标系下机器人的升力， ${{\boldsymbol{F}}_{{\rm{e}}}}$ 为空气阻力。

设机体坐标系下机器人升力为

式中： $ {k_{\rm{F}}} $ 为升力系数， $ {\varOmega _i} $ ( $i = 1,2, \cdot \cdot \cdot ,6$ )为旋翼转速。

通过旋转矩阵 ${\boldsymbol{R}}_{\rm{b}}^{\rm{e}}$ 转换得到机器人的升力在惯性坐标系下的表达式：

空气阻力表达式为

其中， ${k_{{\text{a}}x}}$ 、 ${k_{{\text{a}}y}}$ 、 $ {k}_{\text{a}z} $ 分别为 $ {x}_{\text{b}} $ 、 ${y_{\text{b}}}$ 、 ${z_{\text{b}}}$ 3个轴向的空气阻尼系数。

联立式(1)~(6)得到机器人位置动力学模型：

式中 $ g $ 为重力加速度。

2.1.2   姿态动力学模型

根据牛顿—欧拉方程建立机体坐标系下FPLIR的姿态动力学方程：

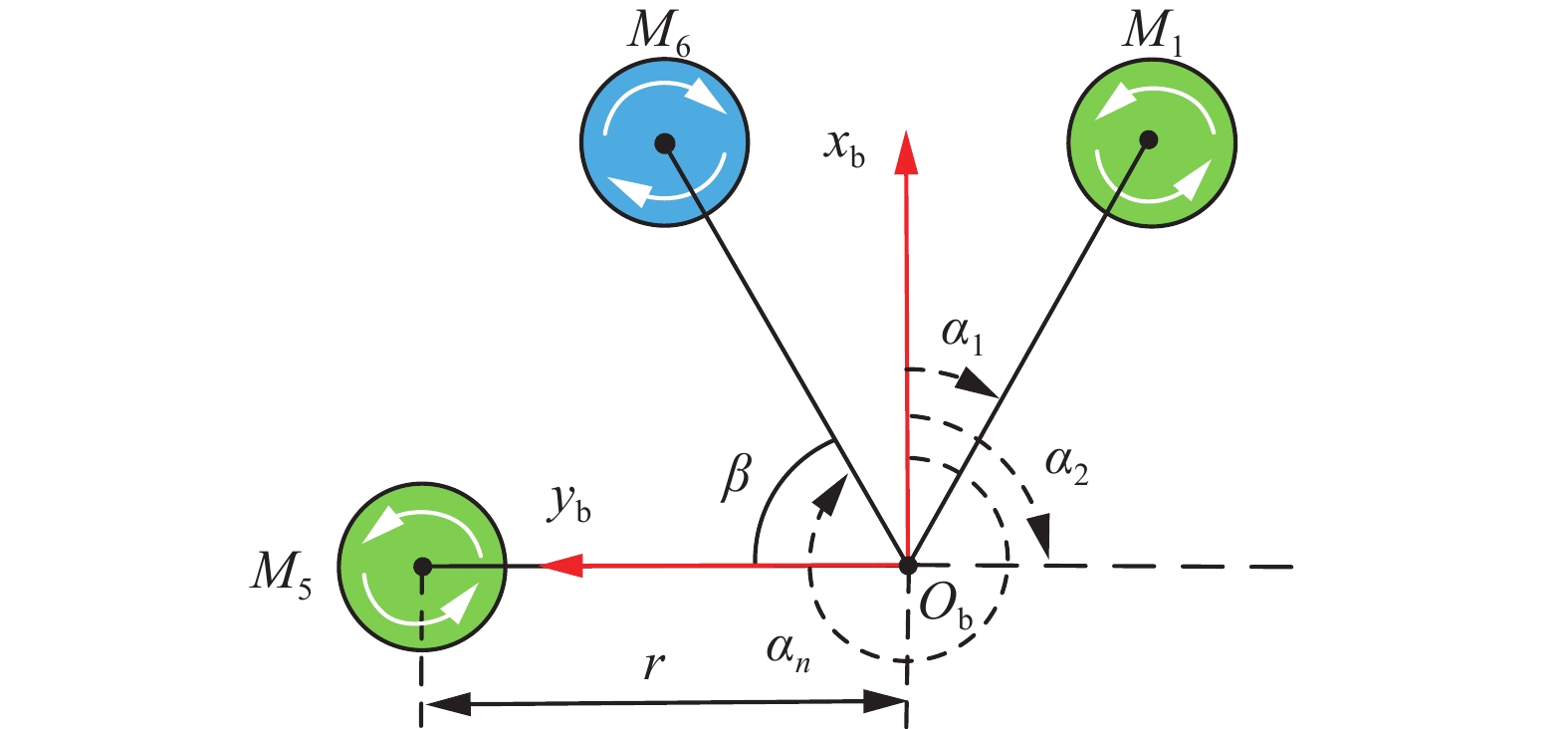
式中： $ {{\boldsymbol{G}}_{\rm{b}}} $ 为旋翼产生的陀螺力矩， ${{\boldsymbol{\varGamma}} _{\rm{b}}} = $ ${[ {{\varGamma _{{\rm{b}}x}}}\quad{{\varGamma _{{\rm{b}}y}}}\quad{{\varGamma _{{\rm{b}}z}}} ]^{\text{T}}}$ 为旋翼在机体轴上产生的力矩， ${\boldsymbol{ I}} = {\text{diag}}\left( {\begin{array}{*{20}{c}} {{I_x}}&{{I_y}}&{{I_z}} \end{array}} \right)$ 为FPLIR的转动惯量。

如图3所示， $ r $ 为机器人中心到机臂末端的距离， $\beta = 60^\circ $ 表示两机臂之间的夹角， ${\alpha _n}\left( {n = 1,2, \cdot \cdot \cdot ,6} \right)$ 为机臂与 $ x_{{\rm{b}}} $ 轴正方向的夹角， $ k_{m} $ 为反扭矩系数，则旋翼在机体轴上产生的力矩为

图  3  FPLIR机臂布局示意图

Fig.  3  Schematic diagram of FPLIR arm layout

下载: 全尺寸图片

对式(2)求逆矩阵，并采用小角度假设得：

联立式(2)、(8)、(9)、(10)得到FPLIR的姿态动力学方程为

2.1.3   模型线性化

为方便控制器设计，将式(8)简化为 ${{\boldsymbol{\varGamma}} _{{\rm{b}}}} = {\boldsymbol{I}}{\dot{\boldsymbol{ \omega}} _{{\rm{b}}}}$ ，在速度较小的情况下忽略空气阻力的影响，则：

2.2   行走机构动力学模型

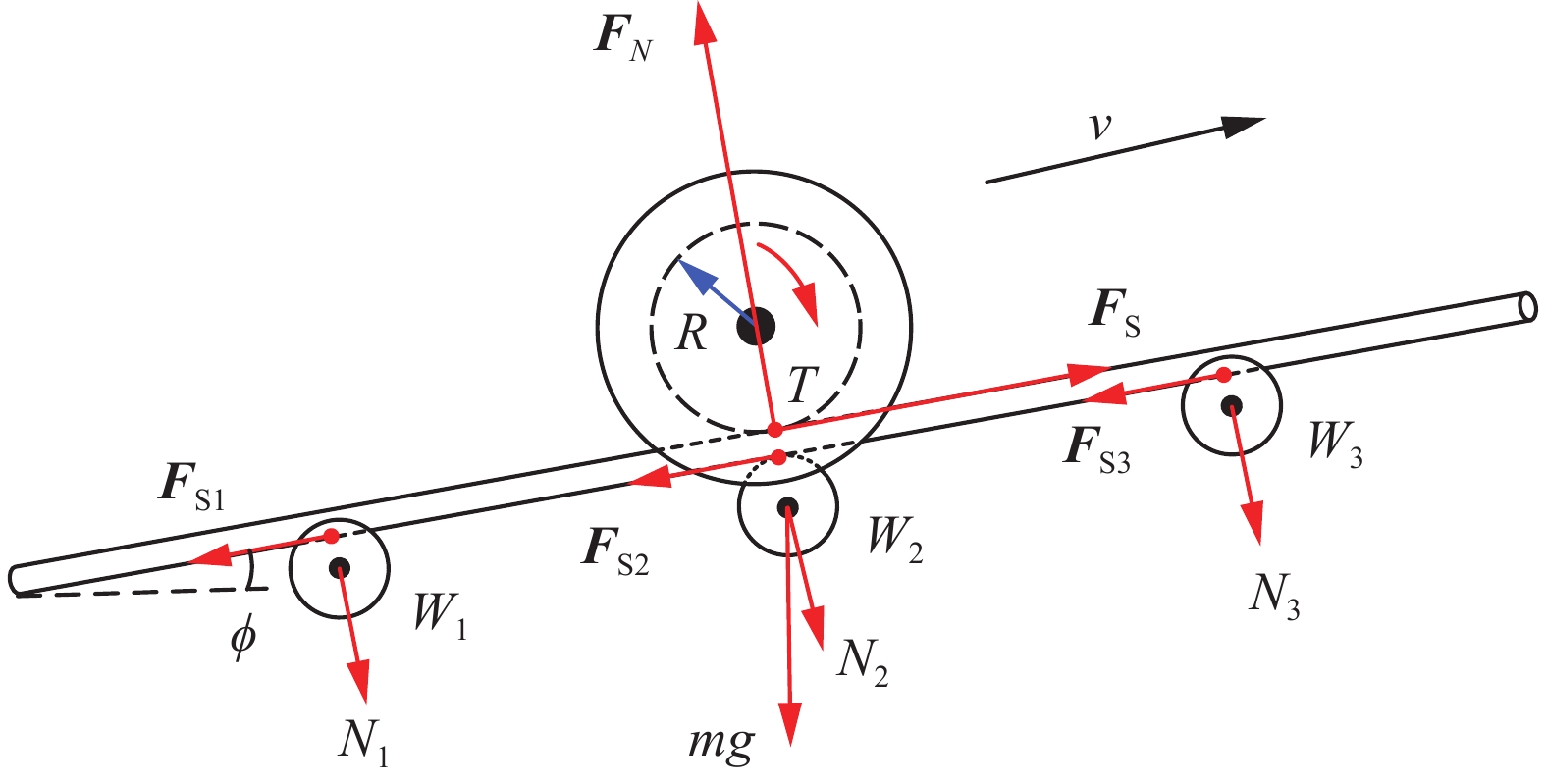
机器人在挂线行走工况下旋翼电机停止工作对行走机构的影响可忽略，辅行走轮质量较轻且主要起导向作用忽略其对电力线的影响，因此在沿线行走工况下对机器人进行如图4所示的受力分析。

图  4  FPLIR滚轮与电力线之间的受力分析

Fig.  4  Force analysis between FPLIR roller and power line

下载: 全尺寸图片

在惯性坐标系下设电力线倾角为 $ \phi $ ，则机器人沿电力线匀速行走时受力平衡方程为

式中： $ {F_N} $ 为电力线对主行走轮的作用力， $ {N_j} $ 为主压紧轮 $ {{\text{W}}_2} $ 和辅压紧轮 $ {{\text{W}}_1} $ 、 $ {\text{W}}_{3} $ 与电力线之间的相互作用力 $ (j = 1,2,3) $ ， $ {F}_{{\rm{S}}} $ 为主行走轮与电力线之间的静摩擦力， $ {F_{{\text{S}}i}} $ 为主压紧轮、辅压紧轮和电力线之间的静摩擦力 $ (i=1,2,3) $ ， $ \varepsilon $ 为主行走轮、主压紧轮和辅压紧轮与电力线的摩擦系数， $ R $ 为主行走轮的半径， $ T $ 为主行走轮的驱动力矩。

则机器人沿线行走时的动力学方程为

式中v为机器人沿线行走时的速度。

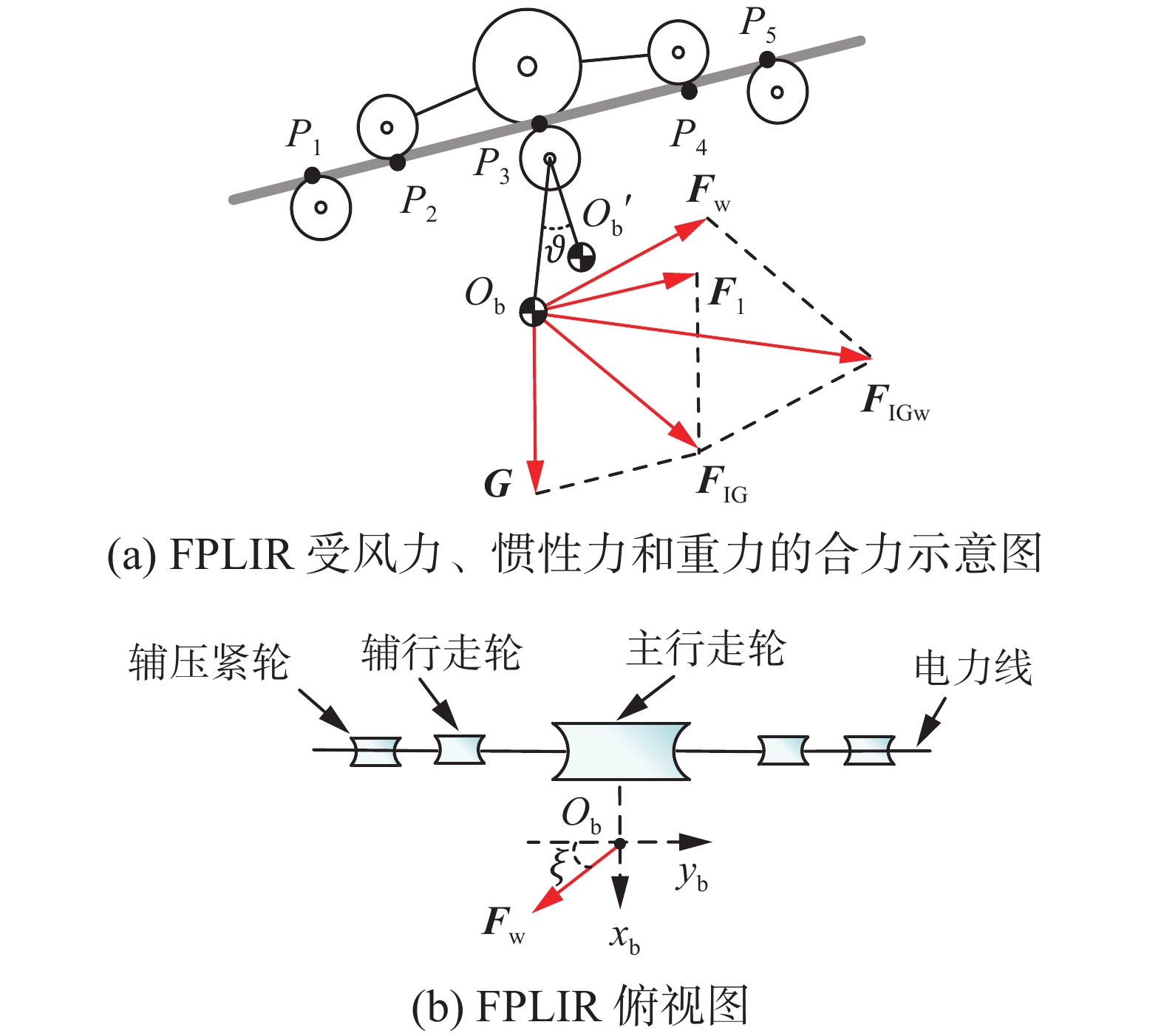
机器人沿线行走时除了受到滚轮（主压紧轮、辅压紧轮、主行走轮、辅行走轮）与电力线之间力的影响，亦会受到风力 $ {{\boldsymbol{F}}}_{\text{w}} $ 和惯性力 $ {{\boldsymbol{F}}_{{\rm{I}}}} $ 的影响，其受力如图5(a)所示。

图  5  挂线行走时FPLIR受力分析

Fig.  5  Force analysis of FPLIR along the power line

下载: 全尺寸图片

图中P₁、P₂、P₃、P₄、P₅为滚轮与电力线的接触点， $ \vartheta $ 为机器人摆角。机器人受风力影响的俯视图如图5(b)所示，风力 $ {{\boldsymbol{F}}}_{\text{w}} $ 与 $ {y_{\rm{b}}} $ 轴的夹角为 $ \xi $ ，则机器人所受合力为

式中： $ {{\boldsymbol{F}}_{{\rm{IG}}}} $ 为 $ {\boldsymbol{G}} $ 和 $ {{\boldsymbol{F}}_{{\rm{I}}}} $ 的合力， ${{\boldsymbol{F}}_{{{\rm{IGw}}}}}$ 为 $ {{\boldsymbol{F}}_{{{\rm{IG}}}}} $ 和 $ {{\boldsymbol{F}}_{{\rm{w}}}} $ 的合力。

3.   FPLIR混杂自动机模型及多模式切换监督器设计

3.1   FPLIR控制模式划分及切换

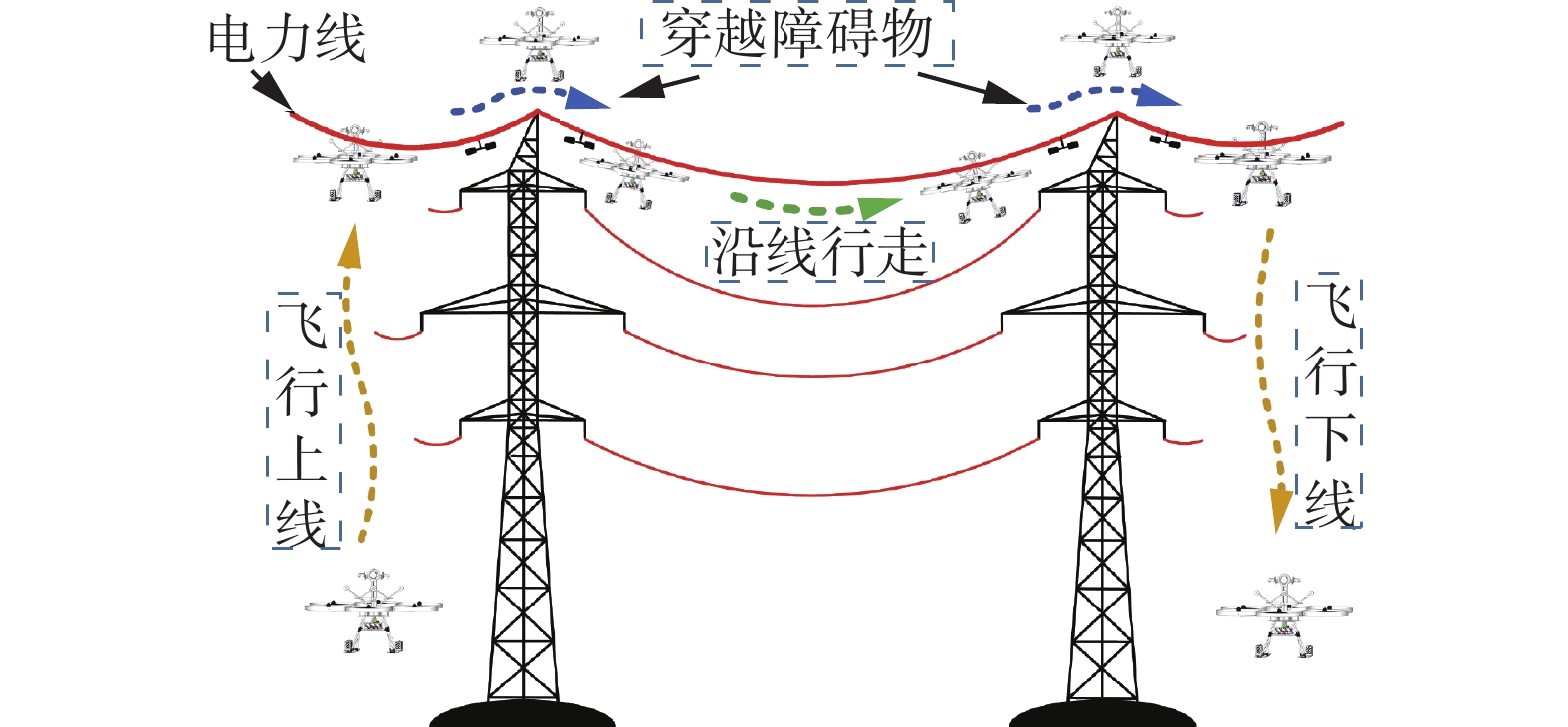
FPLIR的工作原理如图6所示：机器人从地面起飞，通过飞行的方式完成落线。安全落线后，机器人开始线上行走巡检。在行走过程中遇到障碍物时，机器人通过飞行或行走穿越的方式越过障碍物。当完成单档段的巡检任务后，通过飞行的方式飞越杆塔到下一个档段。当机器人完成巡检任务后，通过飞行完成下线。

图  6  FPLIR工作原理

Fig.  6  Working principle of FPLIR

下载: 全尺寸图片

输电线路因其循环往复的结构化分布特征，以及FPLIR灵活切换的运行机制，将FPLIR的工作划分为如表1所示的5种控制模式。

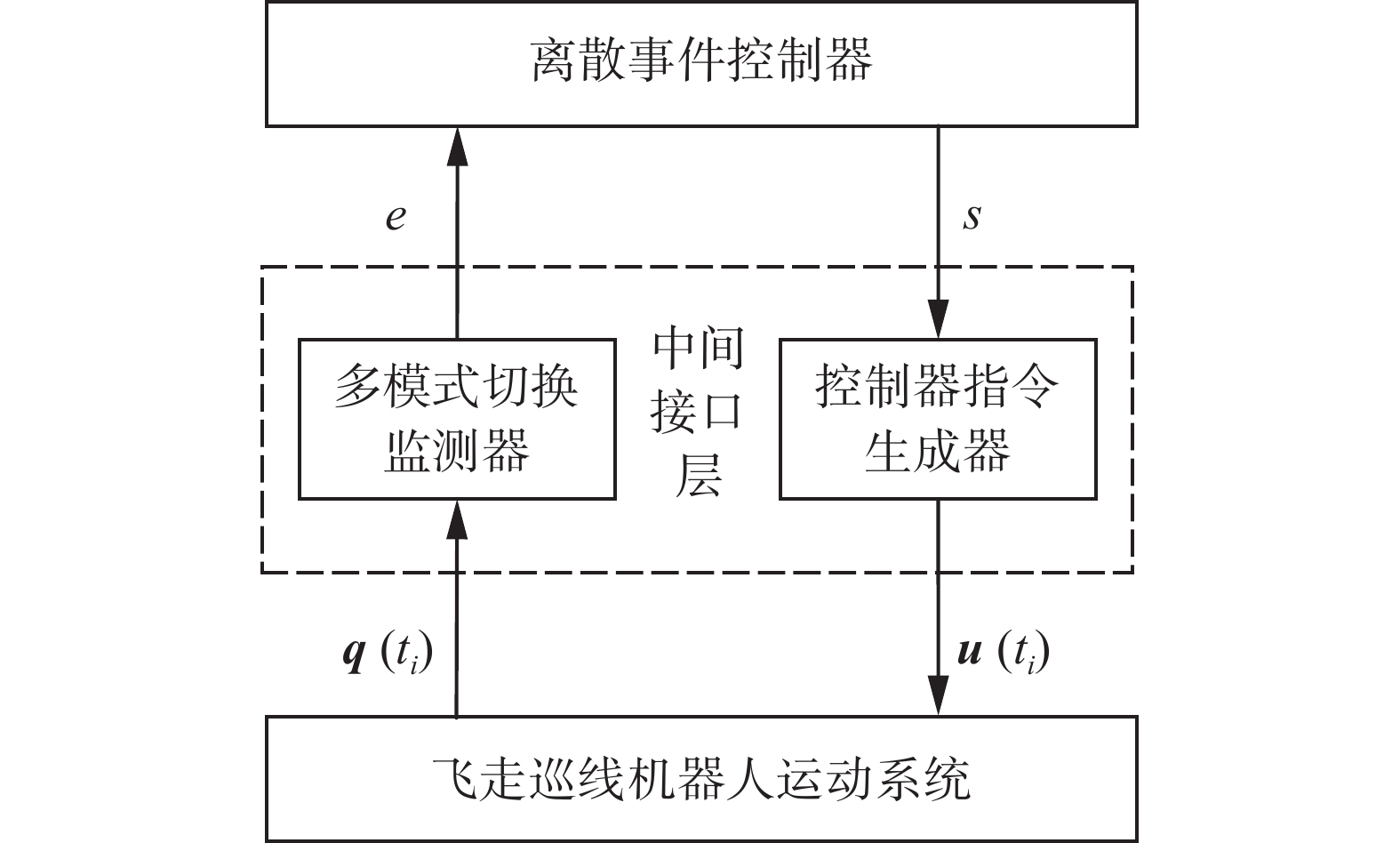
表中每种控制模式分别对应着FPLIR的一种状态，这些状态通过离散事件的触发实现相互切换^[15]，对此本文引入一种如图7所示的多模式切换监控框架。FPLIR巡检过程中，设机器人任意时刻 $ {t}_{i} $ 的运动状态为 ${\boldsymbol{q}}\left( {{t_i}} \right) \in {\boldsymbol{Q}}$ ，当多模式切换监测器检测到离散事件满足触发条件时，多模式切换监测器将机器人状态信息，映射为系统的离散事件 $e \in {{E}}$ 。离散事件控制器计算出离散控制策略 $s \in {{S}}$ ，控制指令生成器将离散控制策略转化为对机器人的连续操纵命令^[16] ${\boldsymbol{u}}\left( {{t_i}} \right) \in {\boldsymbol{U}}$ ，通过命令的执行，改变机器人的运动状态。

图  7  FPLIR多模式切换监控框架

Fig.  7  FPLIR multi-mode switching monitoring framework

下载: 全尺寸图片

3.2   FPLIR多模式切换混杂系统模型

由于FPLIR控制系统是一个典型的混杂动态系统，无法单一地用离散或连续的数学模型来准确地描述，因此建立如下所示的混杂自动机模型。

式中： $ {{S}} = \left\{ {{s_1},{s_2},{s_3},{s_4}} \right\} $ ， $ {s}_{1} $ 为落线模式、 $ {s_2} $ 为打滑模式、 $ {s_3} $ 为行走越障模式、 $ {s_4} $ 为飞越杆塔模式； ${{E}}$ 为4种控制模式切换的逻辑判决条件集， $ {{E}} = \left\{ {{e_{12}},{e_{23}}, \cdot \cdot \cdot ,{e_{ij}}} \right\} $ $(i = 1,2, 3 ,4;j = 1,2, 3 ,4)$ ； $ {\boldsymbol{Q}} $ 为 $ n $ 维连续变量状态空间， $ {{\boldsymbol{Q}}}_{ }\subseteq {{\bf{R}}}^{n} $ ； $ {{\boldsymbol{U}}}_{ } $ 为 $ m $ 维连续动态控制输入空间， $ {{\boldsymbol{U}}}_{ }\subseteq {{\bf{R}}}^{m} $ ； ${\boldsymbol{f}}$ 为连续状态向量 ${\boldsymbol{ x}}\left( {\boldsymbol{t}} \right) $ 的向量场， $ {\boldsymbol{f}}:{{\boldsymbol{Q}}}_{ }\times {{\boldsymbol{U}}}_{ }\to {{\boldsymbol{Q}}}_{ } $ 。

图8描述了控制模式的切换过程，在 ${t_i}$ 时刻控制模式为 ${s_i}$ ，离散事件 ${e_{ij}}$ 发生之前，遵循连续动态行为 $\dot {\boldsymbol{q}}\left( {{t_i}} \right) = {\boldsymbol{f}}\left( {{\boldsymbol{q}}\left( {{t_i}} \right),{\boldsymbol{u}}\left( {{t_i}} \right)} \right)$ ，在 ${t_j}$ 时刻，离散事件 ${e_{ij}}$ 发生，控制模式变迁为 ${s_j}$ ，此后系统将遵循新控制模式下的连续动态行为^[17] $\dot {\boldsymbol{q}}\left( {{t_j}} \right) = {\boldsymbol{f}}\left( {{\boldsymbol{q}}\left( {{t_j}} \right),{\boldsymbol{u}}\left( {{t_j}} \right)} \right)$ 。从图中可知，在具有结构化工况特点的电力线环境中机器人的运行具有一定的规律性，其模式的切换亦存在规律性。

图  8  混杂自动机切换模型

Fig.  8  Switching model of hybrid automata

下载: 全尺寸图片

3.3   FPLIR多模式切换监测器设计

FPLIR多模式切换监测器用于监测机器人状态的连续变化过程中产生的离散事件，依据控制模式的划分规则，设计每种离散事件监测器模型，包括：

1) 落线模式监测器模型

落线模式需要机器人飞行到一定的高度后才能被触发，则监测器模型为

式中： $ h $ 为机器人的飞行高度； $ H $ 为地线的高度； $ \Delta h $ 为允许的高度偏差。

2) 打滑模式监测器模型

FPLIR在挂线巡检过程中，通过监测机器人摆角 $ \vartheta $ 是否小于安全阈值，以及主压紧轮的线速度与主行走轮的线速度之比是否小于设定的打滑度 ${\eta _{{\rm{des}}}}$ ，从而判定是否打滑，则监测器模型为

其中： ${v_t}$ 为主压紧轮的速度， $ {v}_{\text{ref}} $ 为主行走轮的速度， $ {\vartheta }_{\mathrm{max}} $ 为摆角安全阈值。

3) 行走越障模式监测器模型

机器人挂线行走时，检测到前方小型穿越型障碍物与机器人的距离为 $ {x_d} $ ，触发行走越障模式的设定距离为 $D$ ，允许的检测距离偏差为 ${{\Delta }}{d_{{\text{max}}}}$ ，则：

4) 飞越杆塔模式监测器模型

机器人在挂线巡检过程中，为保证机器人不与杆塔发生碰撞，需要与杆塔之间保持一个最小安全距离 ${l_{{\text{min}}}}$ 。当机器人检测到与杆塔的距离为 ${l_{{\text{min}}}}$ 时，系统切换至飞越杆塔模式，则监测器模型为

其中： ${x_l}$ 为机器人与杆塔之间的距离， ${{\Delta }}l$ 为允许的距离偏差。

4.   FPLIR多模式切换控制方法

4.1   FPLIR稳定性分析

4.1.1   行走状态下多模式切换稳定性分析

机器人沿线行走时的控制系统是一个非线性系统，其稳定性比通常的由连续或离散子系统组成的切换系统稳定性要复杂^[18]。

定理1　对于非线性切换系统^[19]，如果存在正定Lyapunov函数 ${V_i}\left( {x\left( t \right),t} \right)$ ，K类函数 $ {\alpha _i} $ ， $ i = 1,2, \cdot \cdot \cdot , p $ 满足：

1) ${\alpha _1}\left( {\parallel x\left( t \right)\parallel } \right) \leqslant {V_i}\left( {x\left( t \right),t} \right)$ ， $i = 1, 2, \cdot \cdot \cdot ,p$ ；

2) $ {\dot V_i}\left( {x\left( t \right),t} \right) \leqslant 0 $ ， $ i = 1,2, \cdot \cdot \cdot ,p $ ， $ x \in {{\text{B}}_r} = \{ x:\| x \| \leqslant r, r > 0 \} $ ；

3) $ {V_{i + 1}}\left( {x\left( t \right),t} \right) \leqslant {V_i}\left( {x\left( t \right),t} \right) $ ， $ i = 1,2, \cdot \cdot \cdot ,p $ ；那么平衡点是在Lyapunov意义下稳定的。

定理2　对于非线性切换系统，若存在正定Lyapunov函数 ${V_i}\left( {x\left( t \right),t} \right)$ ，K类函数 ${\alpha _i}$ 和 ${\beta _i}$ ，满足下面条件：

1) ${\alpha _1}\left(\, {\parallel x\left(\, t \,\right)\parallel } \,\right) \leqslant {V_i}\left( \,{x\left( t \,\right),t} \right) \leqslant {\beta _i}\left(\, {\parallel x\left( t\, \right)\parallel } \right)$ , $i = 1, 2, \cdot \cdot \cdot , p$ ；

2) $ {\dot V_i}\left( {x\left( t \right),t} \right) \leqslant 0 $ ， $ i = 1,2, \cdot \cdot \cdot ,p $ ， $x \in {{\text{B}}_r} = \{x:\left\| x \right\| \leqslant r, r > 0 \}$ ；

3) ${V_{i + 1}}\left( {x\left( t \right),t} \right) \leqslant {V_i}\left( {x\left( t \right),t} \right)$ ， $i = 1,2, \cdot \cdot \cdot ,p$ ；则平衡点在Lyapunov意义下是一致稳定的。

由定理1和2可知，Lyapunov函数值既要求在每个连续子系统的时间区间上是非增，也要求在切换过程中是非增的。对于FPLIR而言，机器人沿线行走时各个模式具有相同的数学模型，因此选用共同Lyapunov函数法对多模式切换进行稳定性分析。FPLIR协调控制器的控制律和Lyapunov函数为

式中： $\varUpsilon = {\eta _{{\rm{des}}}}(t) - \eta (t)$ ， $k$ 为量化因子， ${\text{sat}}$ 为饱和函数。机器人在低速穿越障碍物过程中压紧组件降下不输出压紧力，无法进行打滑控制，忽略此时的打滑情况，并设此时的打滑度 $ \eta (t) = 1 $ 。对 $ V $ 求导得：

当 $ {\eta _{{\rm{des}}}}(t) - \eta (t) $ 变号时 $\dot V$ 变号，从而得出 $\dot V < 0$ 恒成立。

式中， $ 2{\eta _{{\rm{des}}}}(t) - {\eta _{i + 1}}(t) - {\eta _i}(t) > 0 $ ， $ {\eta _i}(t) - {\eta _{i + 1}}(t) < 0 $ ，因此 $ {V_{i + 1}}\left( {x(t),t} \right) - {V_i}\left( {x(t),t} \right) > 0 $ 。

综上分析，机器人在行走状态下多模式切换是稳定的，这样保证了机器人沿线行走时速度与主行走轮转速的跟随性。

4.1.2   行走状态下基于力学特性的稳定性分析

对已有机器人稳定性判别法进行综合分析^[20]，并结合FPLIR的机械结构特点，采用力—角稳定性判据法对FPLIR线上行走进行稳定性分析。

如图9所示，机器人滚轮与电力线的5个接触点共线，所以5个点组成倾翻轴线，向量记为

图  9  FASM稳定裕度分析示意图

Fig.  9  Diagram of FASM stability margin analysis

下载: 全尺寸图片

式中， $ {{\boldsymbol{P}}_5} $ 、 $ {{\boldsymbol{P}}_1} $ 为重心 ${O_{\rm{b}}}$ 到接触点 ${{{P}}_5}$ 和 ${{{P}}_1}$ 的向量。

过重心 ${O_{\rm{b}}}$ 作与倾翻轴线 $ {\boldsymbol{b}} $ 的法向量为

其中 $ \hat {\boldsymbol{b}} = \dfrac{{\boldsymbol{b}}}{{\left\| {\boldsymbol{b}} \right\|}} $ 。

${{\boldsymbol{F}}_{{{\rm{IGw}}}}}$ 在以 $ \hat {\boldsymbol{b}} $ 为法向量的平面A上的投影为

机器人边线倾翻角为 ${{\boldsymbol{F}}_{{{\rm{IGw}}}}}$ 的投影 $ {{{\boldsymbol{L}}}_{2}} $ 与 $ {{\boldsymbol{L}}_1} $ 的夹角：

根据文献[1]和文献[21]可知： $ {L_1} $ 的长度为40.9 cm，当风力与 $ {y_{\text{b}}} $ 轴的夹角为 $ \xi = 90^\circ $ ，风速为15.5 m/s（7级风），压紧轮（主、辅压紧轮）没有对电力线输出压紧力时，机器人沿 $ x_{{\rm{b}}} $ 轴方向的摆动位移最大为5.9 cm。由于辅行走轮在起到导向作用的同时，也能够减小机器人沿 ${y_{\rm{b}}}$ 轴方向的摆动，因此忽略机器人沿 $ y_{{\rm{b}}} $ 轴方向的惯性力，经计算得 $ \lambda $ =8.29， $ {T_{{\text{fasm}}}} > 0 $ ，故机器人沿线行走时在风速为15.5 m/s的情况下依旧具有稳定性。

4.1.3   飞行和行走状态切换稳定性分析

对机器人飞行状态和行走状态的切换选用Lyapunov直接法进行稳定性分析。

Lyapunov直接法^[22]：设系统状态方程为 $\dot x = f\left( x \right)$ ， $t \geqslant 0$ ，平衡状态为 ${x_{\rm{e}}} = 0$ ，若存在一个标量函数 $ V(x) $ 对所有 $ x $ 都有连续一阶偏导，满足：

1)稳定性判据1：① $V\left( x \right)$ 正定， $\dot V\left( x \right)$ 负定，则系统在平衡状态 ${x_{\rm{e}}}$ 是渐近稳定的；② $\left\| x \right\| \to \infty $ ， $V(x)\to \infty $ ，则系统在平衡状态 ${x_{\rm{e}}}$ 大范围渐近稳定。

2)稳定性判据2：① $V\left( x \right)$ 正定， $\dot V\left( x \right)$ 半负定，在非零状态 $\dot V\left( x \right)\not \equiv 0$ ，则系统在平衡状态 ${x_{\rm{e}}}$ 是渐近稳定的；② $\left\| x \right\| \to \infty $ ， $V(x) \to \infty $ 则系统在平衡状态 ${x_{\rm{e}}}$ 是大范围渐近稳定的。

3)稳定性判据3： $V\left( x \right)$ 正定， $\dot V\left( x \right)$ 半负定，在非零状态 $\dot V\left( x \right) \equiv 0$ ，则系统在平衡状 ${x_{\rm{e}}}$ 是Lyapunov意义下稳定的。

由图1所示的机器人的行走机构可知，为保证机器人能够安全、平稳落线，需要机器人的主行走轮能够准确落到电力线上。

当主行走轮位于电力线正上方时，机器人沿z轴匀速缓慢降落，此时忽略其x轴和y轴的微小位移，则z轴的加速度矢量为

机器人接触到电力线上但未完全停稳时，其 $x$ 轴和 $y$ 轴速度为0， $z$ 轴加速度矢量为

由于当机器人落到线上时，旋翼提供的升力逐渐减小至0，而电力线对机器人提供的支持力逐渐增大，因此机器人将做加速度逐渐变小的减速运动。

设 $ V\left( x \right) = a_2^2 - a_1^2 $ ，则 $ \dot V\left( x \right) = 2{a_2} \cdot {\dot a_2} - 2{a_1} \cdot {\dot a_1} $ 。由于 $V\left( x \right)$ 正定， $\dot V\left( x \right)$ 负定，故飞行状态切换至行走状态的过程稳定，同理可得行走状态切换至飞行状态过程稳定。

4.2   控制模式设计

4.2.1   增稳模式

由于滑模变结构控制能有效处理系统信号通道中突然出现的干扰或者信号大幅变化的情况^[6]，所以增稳模式采用滑模变结构控制方法。以俯仰通道为例进行控制器设计：

选取滑模面为线性滑模面：

选取指数趋近律：

令 $ \theta_{r} $ 为参考输入， $ \theta $ 为实际俯仰角，则：

将式(32)、(33)代入式(30)、(31)中得：

将式(34)代入式(12)得：

同理可得其他通道的控制器。

4.2.2   落线模式

为了能够让机器人安全、平稳落线，需要让机器人以零速度到达期望的落线位置。由于模型预测控制(model predictive control，MPC)方法能够预测被控对象的未来行为，通过对输入和状态变量的约束，可以保证机器人降落的安全性^[23]，因此采用MPC作为落线模式的控制方法。

设连续时间的动力学系统常微分方程为

其中：机器人状态向量和输入向量分别为 ${\boldsymbol{x}}\left( t \right) = \left[ {{\boldsymbol{p}}^{\rm{T}}}\;\;\;{{{\dot {\boldsymbol{p}}}^{\rm{T}}}}\;\;\;\, \varphi \;\;\;\, \theta \;\;\;\, \psi \;\;\;\, {\dot \varphi }\;\;\;\, {\dot \theta }\;\;\;\, {\dot \psi } \right]^{\text{T}}$ 和 ${\boldsymbol{u}}\left( t \right) = \left[ {T_{\text{b}}}\;\;\;{{\varGamma _x}}\;\;\;{{\varGamma _y}}\;\;\; {{\varGamma _z}} \right]^{\text{T}}，$ 则最优控制问题为

其中： $ \Delta {\boldsymbol{u}}(t) $ 表示控制增量， ${{\boldsymbol{x}}_{{r}}}(t)$ 表示参考状态向量，Q和F表示正常数。在实际控制过程中，往往需要对系统状态机控制量进行约束，一般如下：

因此，模型预测控制在的每一步的都带约束优化求解问题都等价于求解二次规划问题。当每个控制周期完成求解后，可以得到控制时域内的一系列控制输入增量。

根据模型预测控制基本原理，将该控制序列中的第一个元素作为实际的控制输入增量作用于系统，即：

当控制系统执行这一控制量直到下一时刻。在新的时刻，系统根据状态信息重新预测下一段时域的输出，通过优化过程得到一个新的控制增量序列。

4.2.3   打滑模式

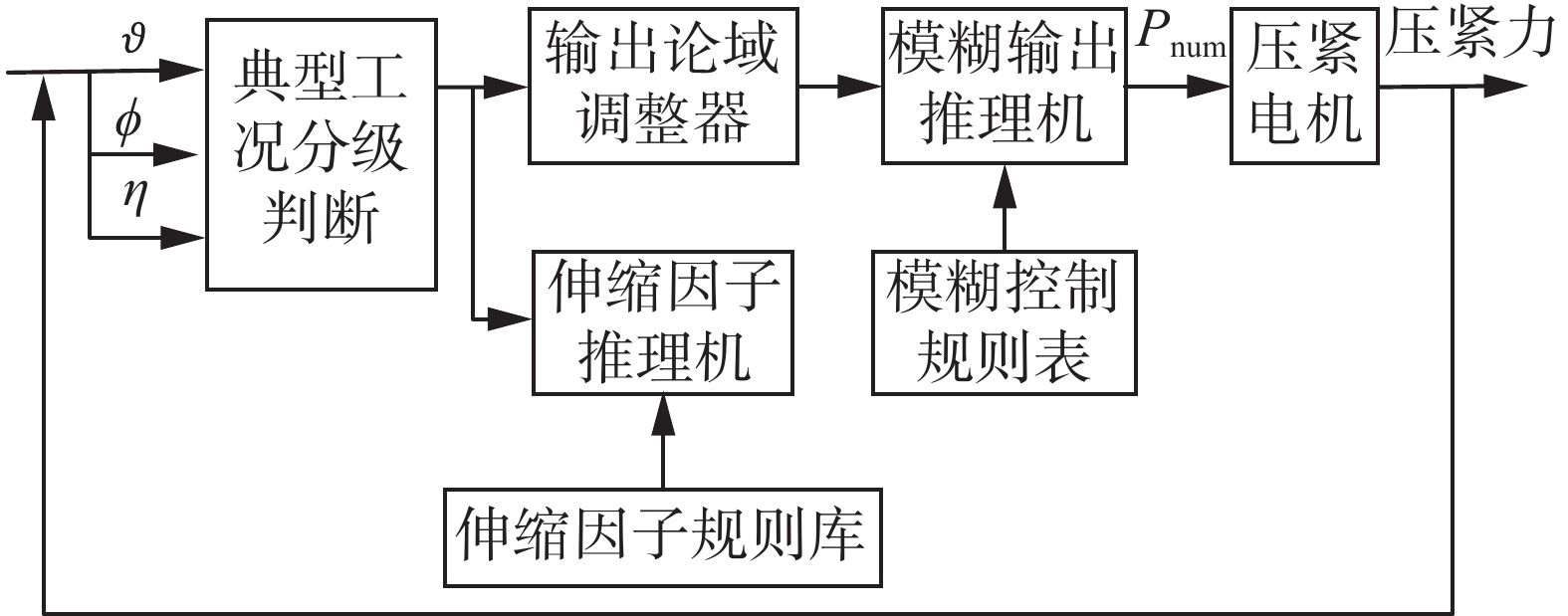
机器人沿线巡检过程中，主行走轮可能发生打滑主要有以下3种情况：1)电力线坡度较大，且压紧力不足；2)在雨雪天气等影响下，使电力线表面的摩擦系数变小；3)有较大风扰时会使机器人发生摆动。这些工况会对机器人的行走稳定性造成严重影响。因此，针对电力线坡度、风扰、磨损等诸多因素，本文采用一种基于多工况变论域模糊控制(variable universe fuzzy control，VUFC)方法^[24]。该控制系统能够根据机器人在不同工况下，改变输出变量的论域从而获得更好的控制效果。

由2.2节分析可知，若机器人沿线行走时主行走轮不打滑应满足以下条件：

线上行走打滑控制系统流程图如图10所示。以电力线坡度、打滑度和机器人摆角作为控制器的输入变量，以三者的值作为工况分级的判断依据，压紧电机接收的脉冲数 $ {P_{{\rm{num}}}} $ 作为输出变量。输入变量的论域如表2所示，输出变量的论域受伸缩因子 ${y_{\rm{p}}}$ 的影响。

图  10  变论域模糊控制系统流程

Fig.  10  Flow of variable domain fuzzycontrol system

下载: 全尺寸图片

电力线坡度采用高斯型隶属度函数进行模糊化；打滑度主要采用三角形隶属度函数进行模糊化，对于 $ \eta \geqslant 0.95 $ （不打滑）和 $ \eta < 0.6 $ （严重打滑）两个临界点，则选择梯形隶属度函数；摆动角程度分为小(0°< $\vartheta \leqslant $ 2°)，中(2°< $\vartheta \leqslant $ 12°)，大( $\vartheta $ >12°)，并分别采用高斯型隶属度函数、三角形隶属度函数和梯形隶属函数进行模糊化，其中摆动角度为小时认定机器人稳定。输入和输出变量的隶属度函数如图11所示。

图  11  输入和输出隶属度函数

Fig.  11  Input and output membership functions

下载: 全尺寸图片

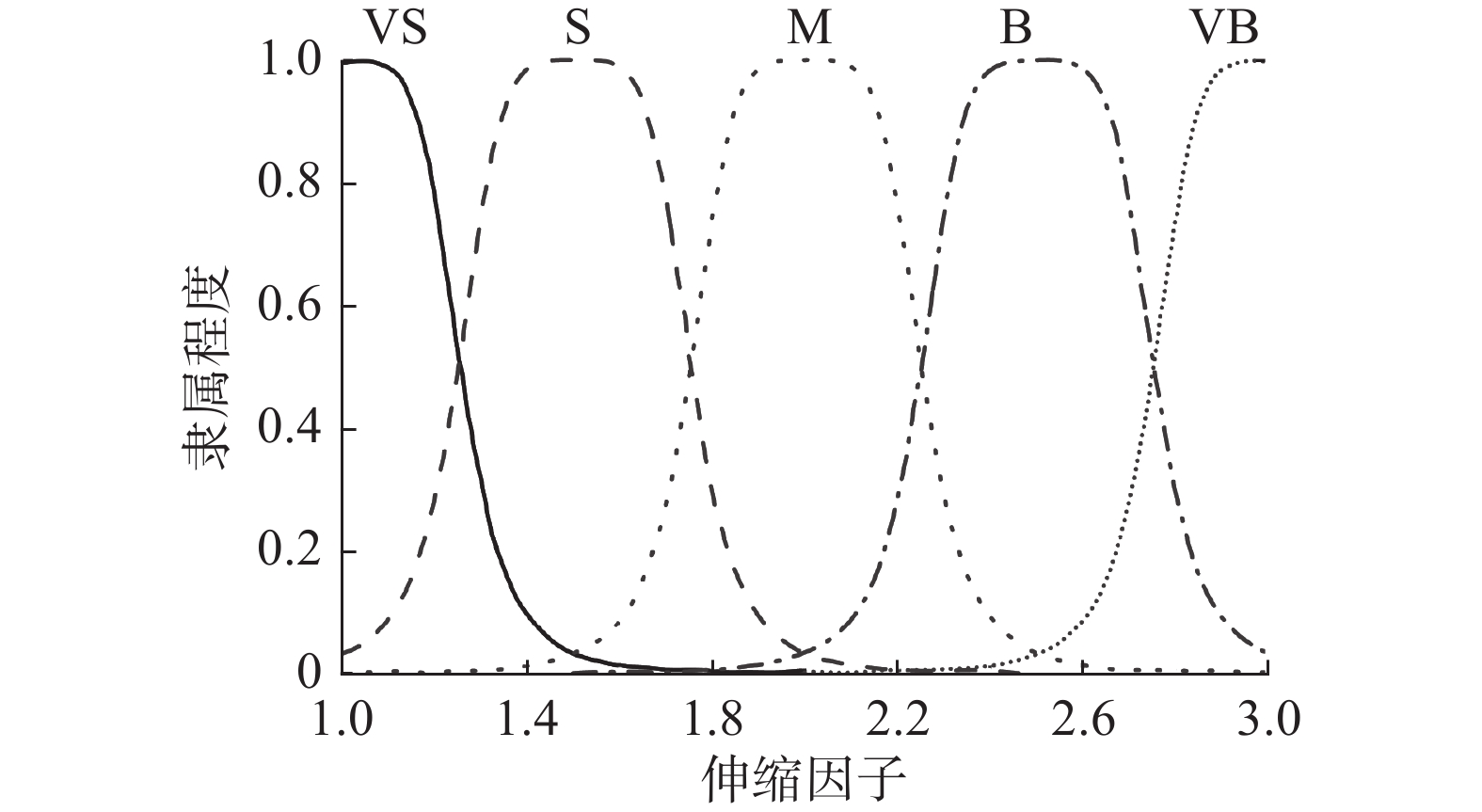
伸缩因子 ${y_p}$ 的隶属度函数如图12所示。解模糊方法采用最大隶属度函数法。

图  12  伸缩因子隶属度函数

Fig.  12  Membership function diagram of expansion factor

下载: 全尺寸图片

4.2.4   行走越障模式

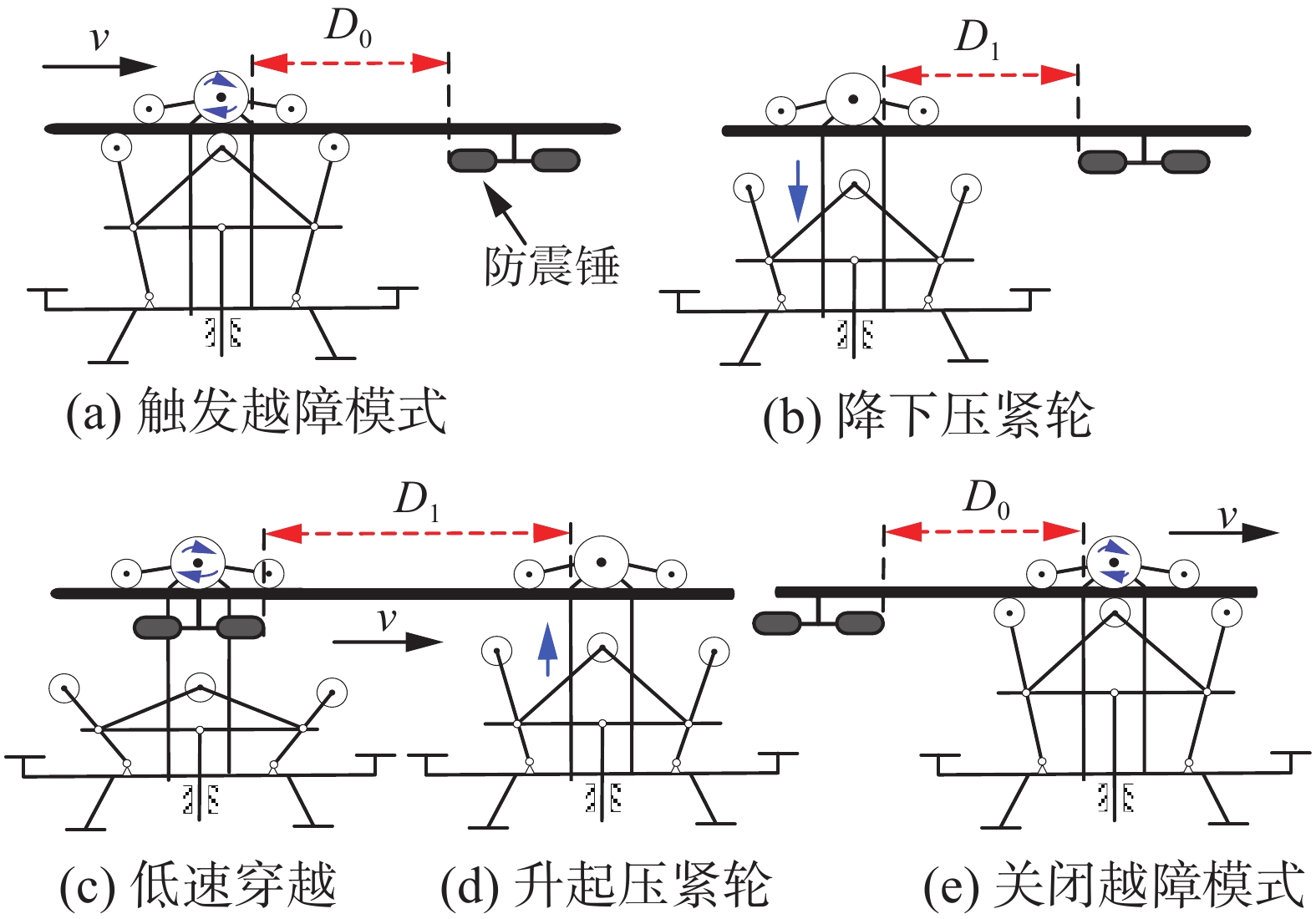
机器人沿线巡检过程中遇到可以通过行走越过的小型障碍物如防震锤等，控制系统切换至行走越障模式，其越障过程如图13所示。当机器人与防震锤的距离为 $ {x_d} > {D_0} $ 时，机器人速度为 ${v_0}$ ；当机器人与防震锤的距离为 $ {D_1} < {x_d} \leqslant {D_0} $ 时，触发行走越障模式，机器人速度为 ${v_1}$ ；当机器人与防震锤的距离为 $ {x_d} \leqslant {D_1} $ 时，机器人降下主、辅压紧轮，速度为 ${v_2}$ ；当机器人越过防震锤之后，若 $ {x_d} \leqslant {D_1} $ ，则机器人以速度 ${v_2}$ 前进，若 $ {D_1} < {x_d} \leqslant {D_0} $ ，则机器人主、辅压紧轮重新压紧电力线，速度为 ${v_1}$ ，若 ${x_d} > {D_0}$ ，则机器人退出行走越障模式，以速度 ${v_0}$ 前进。

图  13  FPLIR穿越小型障碍物(防震锤)示意

Fig.  13  Schematic of FPLIR crossing a small obstacle (shockproof hammer)

下载: 全尺寸图片

机器人沿线行走时速度突变会对机器人的稳定性造成影响，为保证在越障过程中速度变化时的平滑性，采用一种基于插值规则的控制方法，如下式所示。该控制方法是以机器人与障碍物的距离 $ {x_d} $ 为自变量，速度 $ v $ 为因变量。由于机器人在不断接近或远离障碍物的过程中距离 $ {x_d} $ 是连续平滑变化的，因此可以保证机器人速度 $ v $ 变化的平滑性。

式中： ${D_0}$ 是机器人越过防震锤之前触发行走越障模式的最大距离，以及越过防震锤之后退出行走越障模式的最大距离； ${D_1}$ 是机器人越过防震锤之前降下主、辅压紧轮的最小距离，以及越过防震锤之后升起主、辅压紧轮的最小距离。

4.2.5   飞越杆塔模式

为保证机器人能够安全飞越杆塔，本文采用基于无ESDF梯度的局部规划器(ESDF-free gradient-based local planner，EGO Planner)^[25]作为飞越杆塔模式的控制方法。通过对机器人飞行路径的规划，以及设置膨胀半径，能够让机器人沿着安全飞行路径飞越杆塔，也可让机器人与杆塔保持一定的安全距离，确保机器人飞越杆塔的安全性。

首先，生成一个满足约束但忽略障碍物的B样条曲线 $ \varPhi $ ，然后对曲线 $ \varPhi $ 进行碰撞检测，并用A^*算法生成一条无碰撞路径，对于每一条碰撞段中的控制点 $ {{\boldsymbol{Q}}_i} $ 都会分配一个 $ \left\{ {{\boldsymbol{p}},{\boldsymbol{v}}} \right\} $ 对。

为防止轨迹在被拉出当前障碍物前重复生成 $ \left\{ {{\boldsymbol{p}},{\boldsymbol{v}}} \right\} $ 对，则给出以下约束条件：

式中 ${d_{ij}}$ 表示 $ {{\boldsymbol{Q}}_i} $ 到第j个障碍物的距离。若满足 ${d_{ij}} > 0$ ，则认为控制点 $ {{\boldsymbol{Q}}_i} $ 在新的障碍物中，反之则认为是已发现的障碍物。

使用均匀B样条曲线 $\varPhi$ 表示轨迹，每个节点向量与父节点向量有相同的时间间隔 $\Delta t = {t_{m + 1}} - {t_m}$ 。

根据B样条曲线 $\varPhi$ 的一阶、二阶、三阶控制点分别为

式中： $ {{\boldsymbol{V}}_i} $ 表示控制点的速度， $ {{\boldsymbol{A}}_i} $ 表示加速度， $ {{\boldsymbol{J}}_i} $ 表示加加速度。

根据无人机的微分平坦特性，降低要规划的变量，则目标函数为

其中： $ {J_s} $ 是平滑项惩罚， $ {J_c} $ 是碰撞项惩罚， $ {J_d} $ 是可行性惩罚， $ {\lambda _s} $ 、 $ {\lambda _c} $ 、 $ {\lambda _d} $ 为惩罚项的权值。

根据上述得到的安全轨迹 $ {\varPhi _s} $ ，需要通过合理的时间重新分配，重新生成均匀的B样条轨迹 $ {\varPhi _f} $ 。通过利用各向异性曲线拟合法，保持与 $ {\varPhi _s} $ 几乎相同的形状，同时使 $ {\varPhi _f} $ 可以自由优化控制点满足高阶导数的约束。

超限比例的计算方法为

式中， $i \in \left\{ {1, 2,\cdots ,{N} - 1} \right\}$ ， $j \in \left\{ {1, 2,\cdots ,{N_c} - 2} \right\}$ ， $k \in\left\{ 1,\right. \left.2, \cdots , {N_c} - 3 \right\}$ 和 $ r \in \{ x,y,z\} $ 轴。 $ {r_e} $ 表示相对于 $ {\varPhi _s} $ ， $ {\varPhi _f} $ 需要分配的时长。 $ {{\boldsymbol{V}}_i} $ ， $ {{\boldsymbol{A}}_i} $ 和 $ {{\boldsymbol{J}}_k} $ 与 $ \Delta t $ 的一次、二次和三次成反比。则 $ {\varPhi _f} $ 新的时间间隔为

通过求解闭式的最小二乘问题，在约束条件下初始生成时间间隔为 $ {{\Delta }}t' $ 的轨迹 $ {\varPhi _f} $ ，同时保持与 $ {\varPhi _s} $ 相同的控制点数和形状，然后重新计算光滑项惩罚和动力学可行项惩罚得到新的目标函数：

其中： $ {\lambda _f} $ 为拟合项权重， $ {J_f} $ 为 $ {\varPhi _f}(\alpha T') $ 到 $ {\varPhi _s}(\alpha T) $ 的各向异性位移的积分， $ \alpha \in \left[ {0,1} \right] $ ， $ T' $ 、 $ T $ 为 $ {\varPhi _s} $ 和 $ {\varPhi _f} $ 的持续时间。

对于两条曲线，用带有低权重的轴向位移来放宽光滑调整限制，用高权重的径向位移来防止碰撞。

5.   仿真和实验

为验证多模式切换控制方法的有效性，本文以仿真和实验相结合的方式进行验证。仿真以Gazebo等软件为平台，搭建FPLIR飞行动力学模型，对FPLIR飞行状态下的多模式切换控制策略进行了仿真测试。实验研究以FPLIR为载体，在电力线实验台架上通过人为设置障碍物工况、打滑工况、改变地线表面摩擦系数等，验证线上行走状态下多模式切换控制策略的有效性。FPLIR和实验台架的具体设计参数如表3所示。

5.1   仿真及结果分析

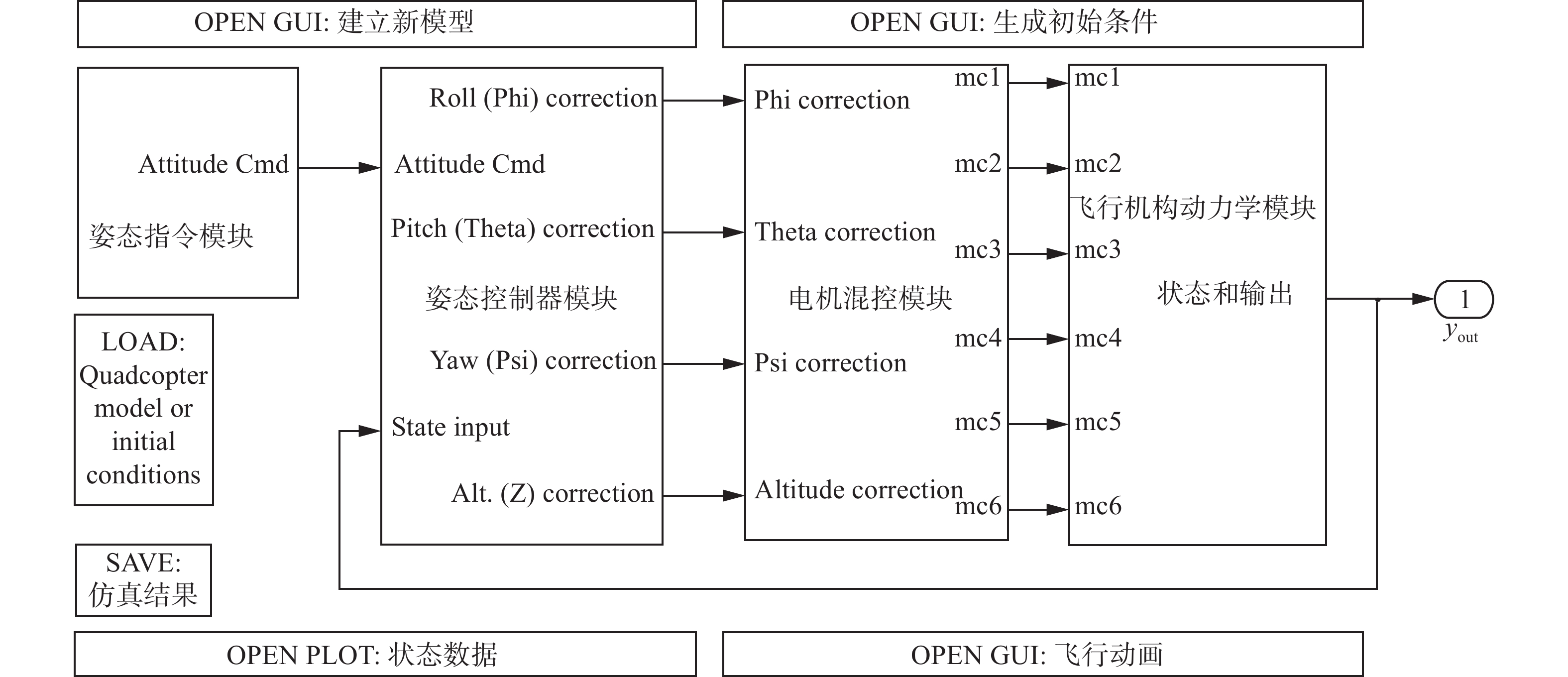
本文采用与PID控制算法对比的方式验证滑模变结构控制算法的鲁棒性。结合前文对FPLIR动力学模型的分析，利用仿真平台对增稳模式进行仿真验证，控制器模型如图14所示。该模型主要包括姿态指令模块、姿态控制器模块、电机混控模块和飞行机构动力学模块。姿态指令模块用于对机器人施加姿态干扰；姿态控制器模块包含PID和滑模控制算法，用于对姿态进行调控；电机混控模块用于将控制器的输出解算为单个电机的控制指令；飞行机构动力学模块包含机器人飞行状态下的动力学模型，用于完成电机控制指令到转速的转换以及机器人飞行状态的更新。

图  14  增稳模式仿真平台

Fig.  14  Simulation platform of stability mode

下载: 全尺寸图片

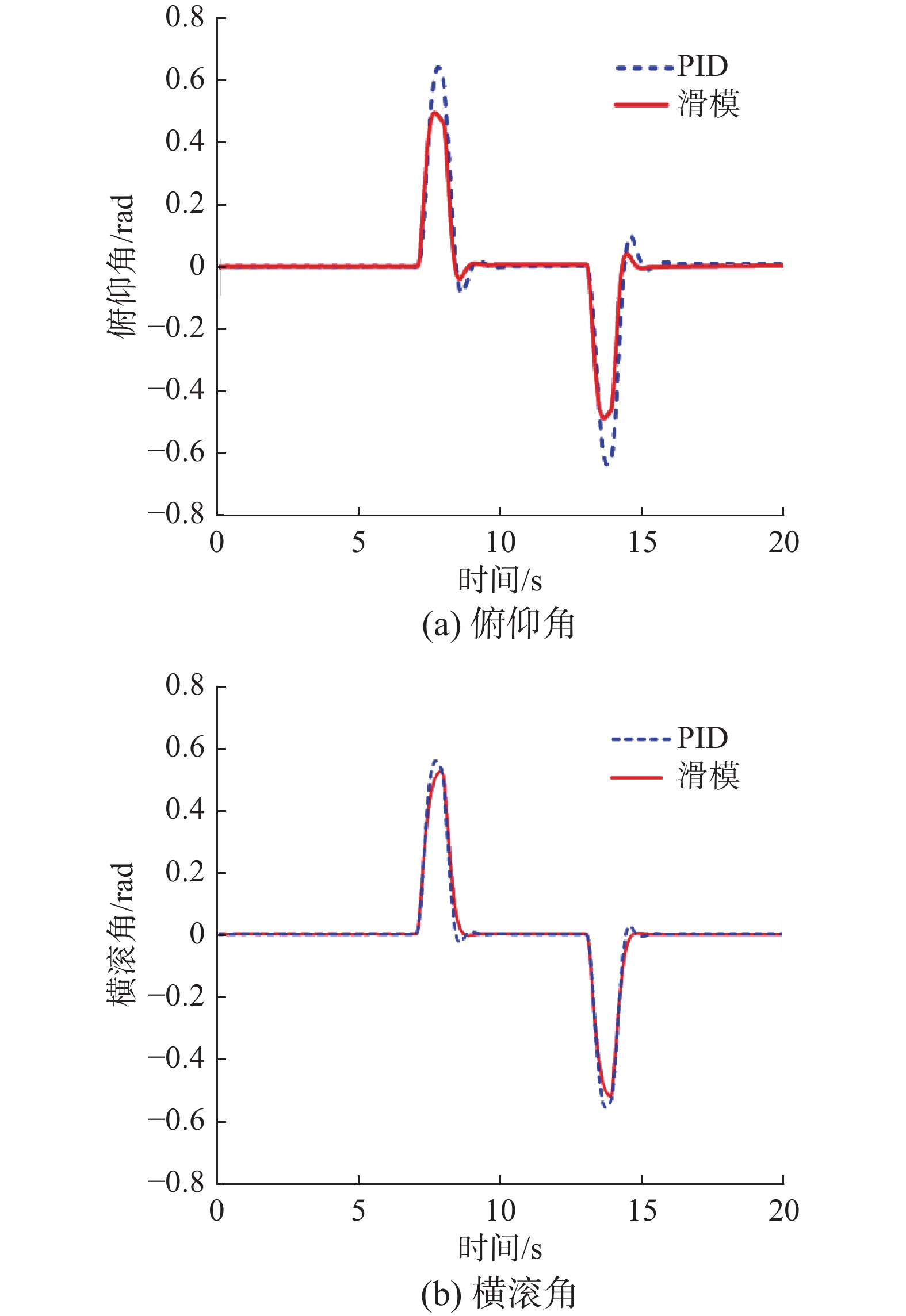
根据表3中FPLIR的模型参数在仿真平台中进行参数设置，设 $ g = 9.8\;{\text{m/}}{{\text{s}}^{\text{2}}} $ 。如图15所示，为模拟机器人在飞行过程中遇到阵风的情况，在7 s和13 s时对机器人的俯仰角和横滚角加入一个30°和−30°信号突变。为验证控制方法的有效性，设置横滚通道的滑模控制器参数为： ${k_x} = 0.28$ ， ${c_x} = 0.01$ ， ${\varepsilon _x} = 0.001$ ，PID控制器的参数为： ${P_x} = 0.14$ ， ${I_x} = 0.19$ ， ${D_x} = 0.032$ ；俯仰角通道的滑模控制器参数为： ${k_y} = 0.53$ ， ${c_y} = 0.31$ ， ${\varepsilon _y} = 0.003$ ，PID控制器的参数为： ${P_y} = 0.35$ ， ${I_y} = 0.21$ ， ${D_y} = 0.035$ 。

图  15  控制效果对比

Fig.  15  Control effect comparison diagram

下载: 全尺寸图片

通过对比滑模变结构控制算法和PID控制算法的控制效果可知，机器人在滑模变结构控制算法的控制下姿态角超调量小于在PID控制算法控制下的超调量，避免了机器人在强干扰下因超调量过大导致机器人失稳的危险情况发生。

为有效验证机器人落线模式和飞越杆塔模式，本文采用Gazebo软件对这两种模式进行仿真模拟，仿真平台如图16所示。仿真场景中使用的机器人模型与实际机器人相同，电力线杆塔模型略小于实际电力线杆塔，使用的飞行控制器与实际一致为Pixhawk4。

图  16  落线模式仿真平台

Fig.  16  Simulation platform of flying off line mode

下载: 全尺寸图片

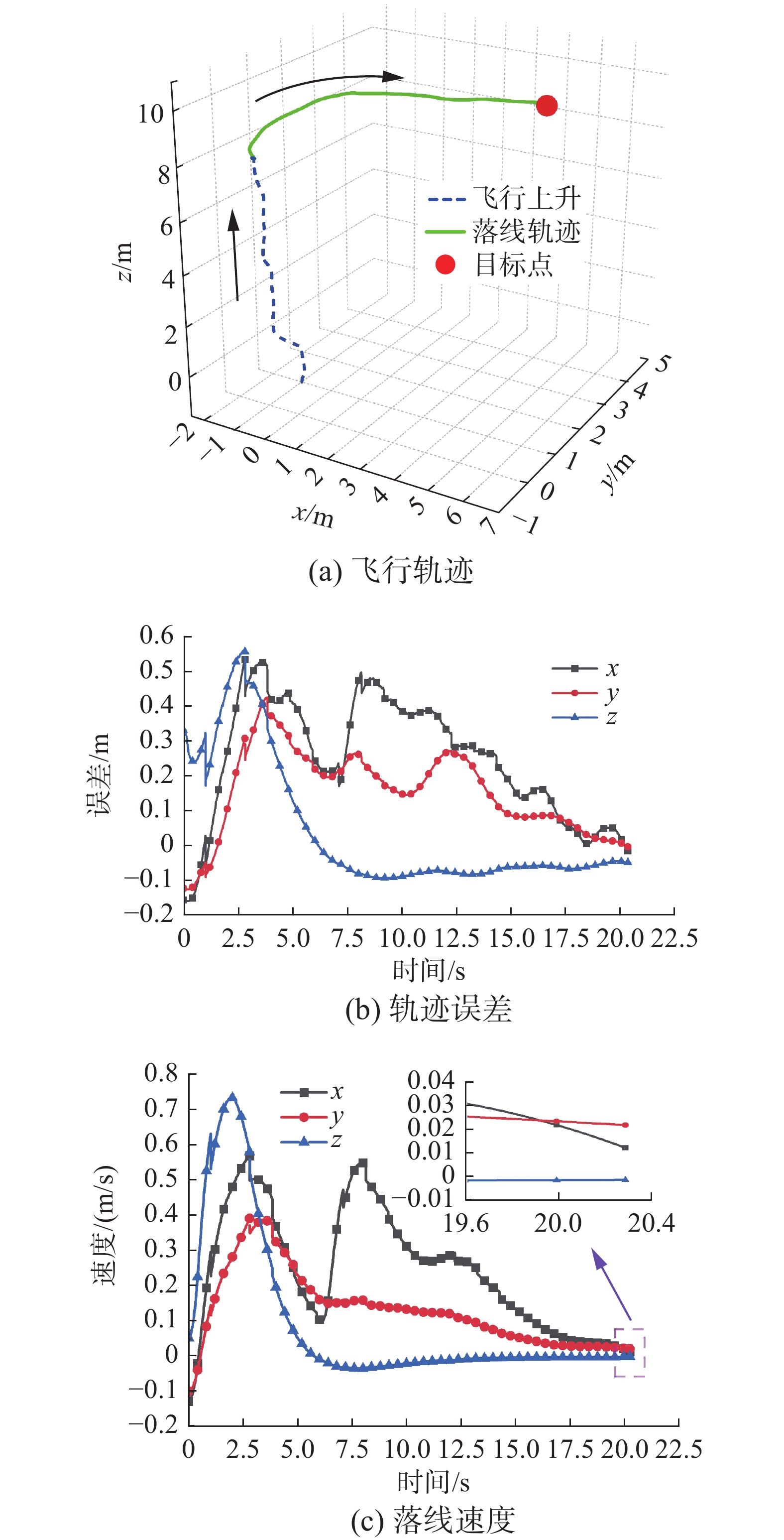
落线模式仿真搭建：使用ACADO工具箱建立了非线性控制问题，并使用qpOASES作为求解器。通过使用代码生成工具导出高效的C代码，该代码集成到ROS节点中。离散化步长被设置为 $ d_t = 0.2\;{\rm{s}} $ ，时间范围为 $ {t_h} = 2\;{\text{s}} $ 。在精度和速度的权衡下，将预测时域设置为 $ {{P}} = 20 $ ，控制时域设置为 $ {{M}} = 10 $ 。对于权重矩阵，将位置的权重设置为5，速度的权重设置为2，其余的都设置为1。对于输入权重矩阵 $ {{\boldsymbol{R}}} $ 和输入量 $ {u_1} $ 、 $ {u_2} $ 、 $ {u_3} $ 、 $ {u_4} $ 的权重设置为0.2，输入量的变化率权重设置为0.1。为了保证对机器人的足够敏捷性，控制回路频率为设置为100 Hz。

落线模式仿真中，地线高度为10.2 m，设定的飞行高度为8.2 m。地线与机器人飞行高度差为2 m，旨在留下一定的调节范围，减小精准落线过程中姿态的调整。图17(a)显示了机器人落线的飞行轨迹，当机器人飞行到空中高度为8.19 m时，控制系统切换至落线模式。图17(b)显示了FPLIR实际运行轨迹与航点轨迹误差的对比效果，从图中可以看出在20.3 s时 $x$ 、 $y$ 、 $z$ 3个轴的误差分别为0.0147 m、0.002 m和0.046 m，两点的距离差为0.048 m。图17(c)显示了机器人在靠近目标点时速度收敛于原点，在20.3 s时， $x$ 、 $y$ 、 $z$ 3个轴的速度分别为0.011 m/s，0.021 m/s和0.0015 m/s，线速度为0.023 m/s。

图  17  FPLIR飞行轨迹和速度

Fig.  17  Flight path and speed of FPLIR

下载: 全尺寸图片

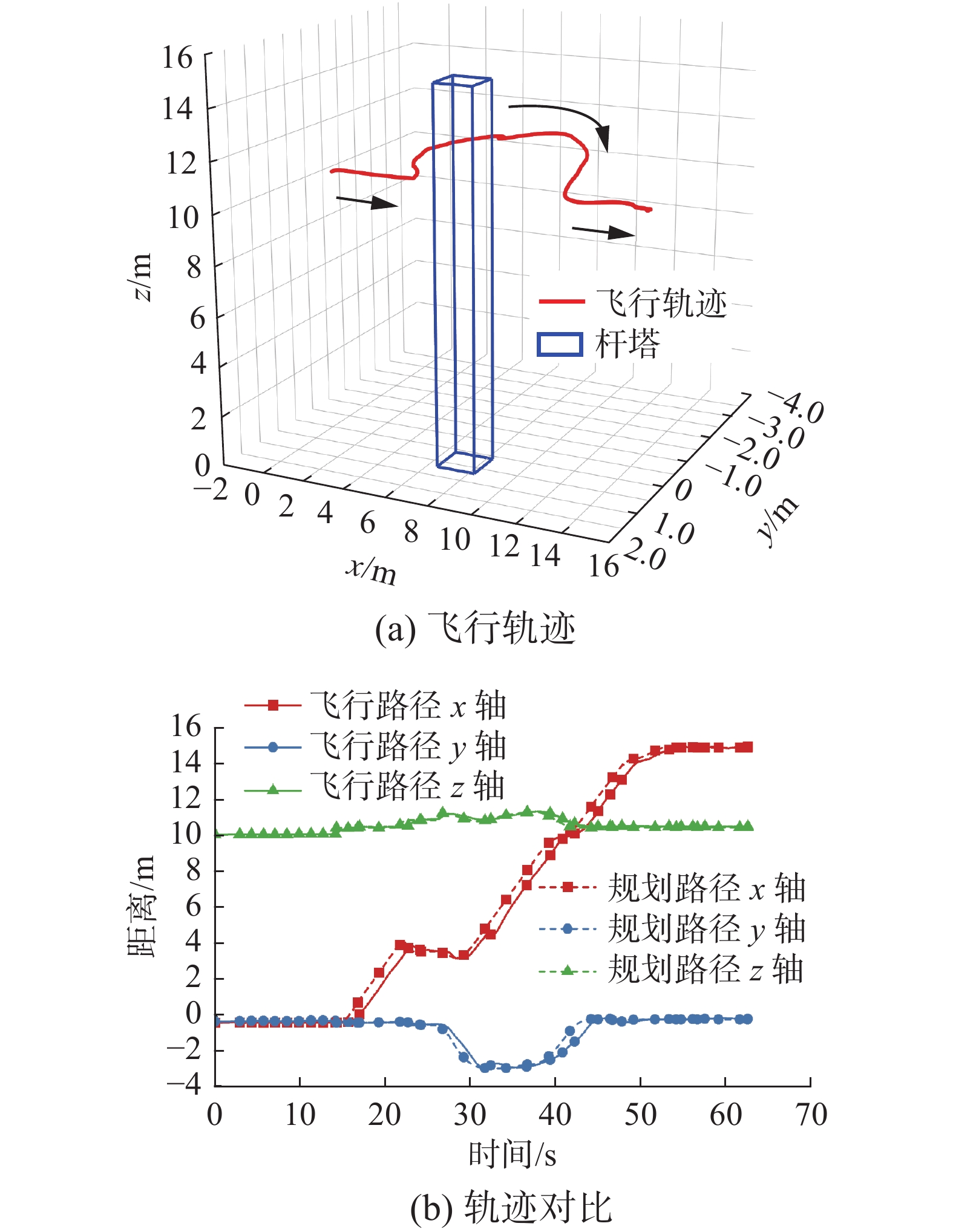
此外，本文落线系统与文献[26]中的降落系统进行了比较，对比结果如表4所示。由表4可知，本文的落线系统让机器人在完成降落后坐标误差的绝对值以及 $x$ 、 $y$ 、 $z$ 三轴方向上的速度均小于文献[26]。而相较于本文的FPLIR和降落目标而言，文献[26]的中的机器人质量更轻(6.5 kg)，更容易控制，目标物更大，更容易识别，且在软抓手降落装置的辅助下，更容易实现稳定降落。因此，使用本文的落线系统可以实现更加准确和安全的降落。

对飞越杆塔模式下的仿真参数进行如下设置：将EGO-Planner规划器的建图沿 $ x $ 、 $ y $ 、 $ z $ 3个轴的大小分别设为50 m、50 m和30 m，地图分辨率设置为0.52。由于膨胀半径不大于分辨率4倍，因此将EGO-Planner规划器的膨胀半径为设置为2 m。无人机的最大速度和最大加速度分别设置为1 m/s和3 m/s²。

如图18(a)所示，杆塔被化成长方体，其底面中心坐标为(7.3,0.4) m，长宽为1 m，高为15 m，规定机器人挂线行走时与杆塔保持的最小安全距离l_min=3 m。从图18(b)中可知，在23 s时机器人的坐标为(3.9,−0.3,10.7) m，与杆塔的距离为2.9 m，此时飞越杆塔监测器被触发，控制系统切换至飞越杆塔模式，EGO-Planner规划器生成越障轨迹。飞越杆塔的过程中，在38 s时机器人的坐标为(4.3,−2.7,11.3) m。此时机器人与杆塔的距离最近为3.2 m。通过仿真可以发现，飞越杆塔模式能够保证机器人在与杆塔保持安全距离的情况下越过杆塔。

图  18  飞越杆塔轨迹

Fig.  18  Trajectory over the tower

下载: 全尺寸图片

5.2   实验及结果分析

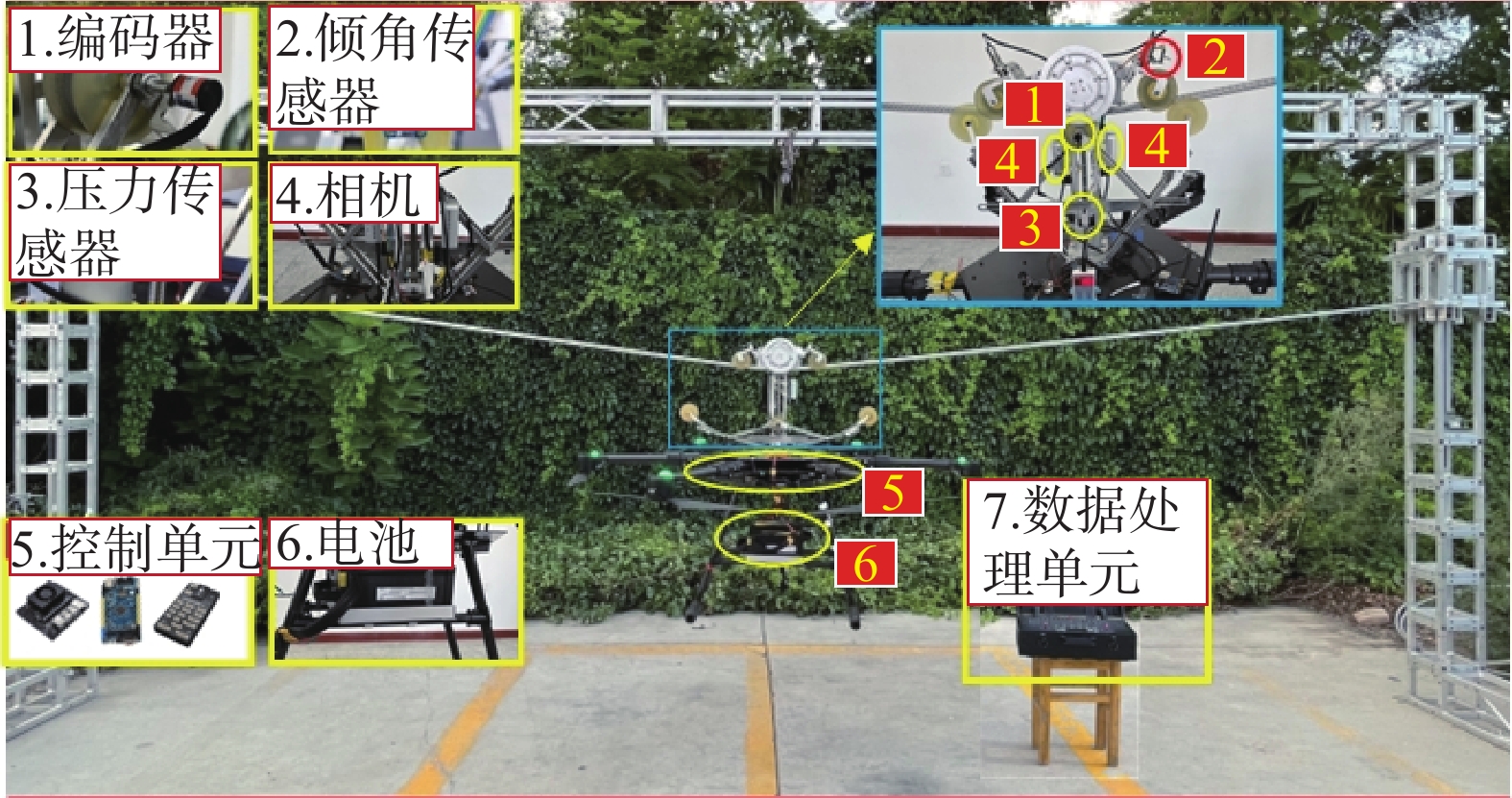
实验平台如图19所示，包括电力线实验台架和FPLIR。其中FPLIR包括传感器（编码器、压力传感器、相机、倾角传感器），控制单元（NIVIDA、STM32F4、Pixhawk4），驱动单元（驱动电机、压紧电机）。其中安装在主压紧轮上的编码器用来检测主压紧轮的转速，压力传感器用于检测压紧轮的附线压力值。相机用于检测机器人与目标物的距离，倾角传感器安装在辅行走轮上，用于检测机器人所处电力线坡度。机器人的控制系统框图如图20所示，其中3个控制器彼此之间通过串行通信的方式实现数据交互。

图  19  实验平台

Fig.  19  Test platform

下载: 全尺寸图片

图  20  机器人控制系统框图

Fig.  20  Control system block diagram of robot

下载: 全尺寸图片

实验平台参数如表3所示。打滑实验过程为机器人先下坡后爬坡，初始时机器人所处坡度为−18°，行走速度为35 cm/s，在电力线5 m处减小其与主行走轮的静摩擦系数至0.21。实验结果如图21所示，其中图(a)为变论域模糊控制的实验结果图，图(b)为模糊控制和变论域模糊控制对机器人的控制效果对比图。表5为两种控制方法重要实验参数的对比数据表。

图  21  打滑模式下的试验曲线

Fig.  21  Test curves in sliding mode

下载: 全尺寸图片

在坡度为−17.6°时，由于压紧力偏小导致机器人在行走时出现了打滑现象，打滑度低于0.95，此时系统进入打滑控制模式。当压紧力达到156 N时，打滑度大于0.95。坡度在15.8°~22.4°这一段中，由于机器人摆角大于2°打滑度低于0.95，此时压紧力增量较大，旨在让机器人在较短时间内不打滑，减小摆动。当机器人处于5.6°、−6.1°等坡度时，打滑度大于0.95且摆角小于2°，此时压紧力减小，当打滑度低于0.95或摆角大于2°时，则压紧力又开始增大。此过程是一个动态过程，旨在让压紧力输出一个合适的值，避免压紧力过大造成摩擦力变大，影响机器人的巡线速度，增加能耗，以及压紧力不足，导致出现滑坡的现象。

通过表5可知，采用变论域模糊控制时，平均打滑度为0.93满足实验要求。变论域模糊控制相较于模糊控制而言机器人爬坡能力提升了6.92%，抑制打滑能力提升了9.44%，平均摆动角度降低了48.8%。由此可见，采用变论域模糊控制能明显降低复杂工况对机器人的干扰，提高行走稳定性。

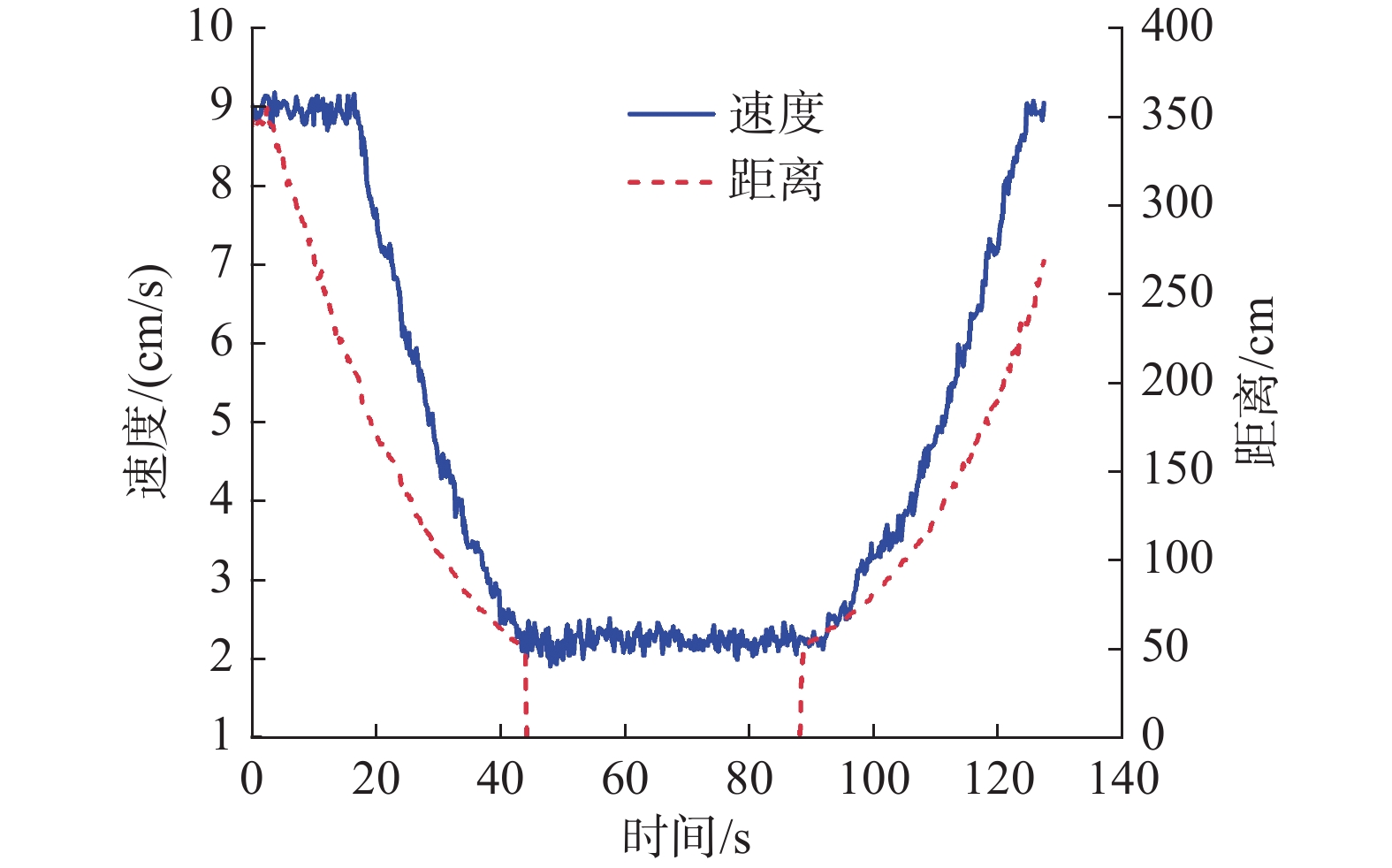
行走越障实验是以防震锤为机器人的越障对象，实验结果如图22所示。当机器人与防震锤的距离 ${x_d} > 2\;{\text{m}}$ ，此时设定初始速度 $v = 8.91\;{\text{cm}}/{\text{s}}$ 进行定速巡航。由于机器人惯性较大，在线上行走过程中速度存在±0.4 cm/s的波动误差。当机器人与防震锤的距离 ${x_d} \leqslant 2\;{\text{m}}$ 时，行走越障模式被触发，机器人进入行走越障模式。其中，当 $2\;{\text{m}} \geqslant {x_d} > 0.5\;{\text{m}}$ 时，机器人的速度采用式(44)的控制方法平滑递减。当距离时 ${x_d} \leqslant 0.5\;{\text{m}}$ ，此时机器人保持 $v = 2.22\;{\text{cm}}/{\text{s}}$ 的恒定速度越过防震锤，NIVIDA传送回来的距离数据为0 cm。同理，当机器人越过防震锤后的距离 $2\;{\text{m}} \geqslant {x_d} > 0.5\;{\text{m}}$ 时，机器人的速度以同样的控制方法平滑递增；当机器人与防震锤的距离 ${x_d} > 2\;{\text{m}}$ 时，机器人速度为 $v = 8.91\;{\text{cm}}/{\text{s}}$ 。从图中可以看出，机器人进入越障模式时模式切换过程平稳，行走速度变化平缓没有出现陡增陡降的现象，保证了机器人在越障过程中的稳定性。

图  22  越障模式下速度与距离

Fig.  22  Speed and distance in obstacle crossing mode

下载: 全尺寸图片

6.   结束语

针对一种飞走巡线机器人，分析了机器人在结构化柔索环境下的多模式切换过程，设计了多模式切换监测器模型和各模式的控制策略。在Gazebo等软件平台上建立了FPLIR的仿真模型，并对FPLIR线上行走进行了实验，验证了FPLIR在飞行和行走状态下监测器和控制策略的性能。

1) 仿真结果表明，针对所设计的增稳控制模式，有效地增强了FPLIR飞行时的稳定性。落线模式保证了FPLIR能以接近零速度和坐标误差最大为0.048 m的情况下完成落线，避免了FPLIR在速度较大的情况下由于惯性导致落线失败的情况发生。飞越杆塔模式则保证了FPLIR能以最小3.2 m的安全距离避开电力线杆塔，完成档段的切换。

2) 实验研究发现，行走越障模式下通过对驱动电机的有效控制，保证了FPLIR在线上行走越障过程中速度的平滑变换，保障了机器人在越障过程中的安全性和稳定性。打滑模式下，控制器根据变论域模糊控制规则，通过对压紧力的合理输出，将打滑度均值维持在0.93，摆角均值维持在1.27°，有效抑制了打滑和风扰的影响。