Obstacle avoidance method for intelligent vehicles in complex environments
-
摘要: 为了提高智能车辆避障的安全性与舒适性，提出了一种基于改进势场模型与隐马尔可夫模型的避障方法。首先建立了考虑车辆特性、道路环境与行驶状态等因素的改进势场模型，预测碰撞风险的动态变化；其次利用隐马尔可夫模型进行避障方式决策，并在改进的势场模型中融入隐马尔可夫决策层，完成自车避障路径规划；然后利用模型预测控制方法对规划的避障路径进行实时跟踪，并在控制器中加入松弛因子与约束条件防止出现无最优解；最后应用联合仿真对提出的避障方法进行验证，结果表明，所提出的方法可在复杂交通环境下获得无碰撞的避障路径，实现动态避障的同时，提高了车辆的安全性与舒适性。Abstract: An obstacle avoidance method based on an improved potential field model and hidden Markov model (HMM) is proposed to enhance the safety and comfort of intelligent vehicles during obstacle avoidance. First, the method constructed an improved field model by considering typical elements of vehicle attributes, road environment, and driving states to predict the dynamic changes in collision risk. Further, HMM was used for obstacle avoidance decision making, and path planning was performed by incorporating HMM into the improved potential field model. Next, the model predictive control was used to track the planning paths in real time, and a relaxation factor and constraints were added to the controller to prevent the problem of unavailable optimal solutions. Finally, the cosimulations by CarSim and MATLAB/Simulink were conducted to verify the effectiveness of the proposed method. Results show that the proposed method can enhance driving safety and ride comfort while obtaining collision-free driving paths in various situations and realizing dynamic obstacle avoidance.
-
Keywords:
- intelligent vehicle /
- potential model /
- HMM /
- dynamic obstacle avoidance /
- path planning /
- tracking control /
- MPC /
- complex environments
-
随着人工智能、V2X技术以及大数据等技术的兴起，智能驾驶受到广泛关注[1]。复杂道路工况下的避障方法一直是智能驾驶研究的热点问题[2]。目前，适用于避障路径规划的主要方法包括随机搜索法[3]、Dijkstra算法[4]、MPC方法[5-6]、蚁群算法[7-8]、深度强化学习[9]、人工势场法(artificial potential field, APF)[10]等。Zhou等[11]提出了基于改进的APF，通过对汽车施加引力和排斥力来实现智能车辆避障路径规划。Cao等[12]根据谐波函数设计了障碍物、道路边界以及目标点势场模型，通过势场下降法得到最优轨迹。Ji等[13]通过构建环境势场，利用三角函数和指数函数构建道路边界势能和障碍物势能得到最优轨迹，随后通过模型预测控制实现轨迹跟踪。徐杨等[14]利用APF与MPC规划无人车辆轨迹的同时，实现了车辆的纵向耦合控制。赵治国等[15]基于驾驶预瞄模型与粒子群算法设计了避障路径跟踪控制器，李军等[16]基于预瞄距离发生器, 解决预瞄误差模型中固定预瞄距离的问题。Wang等[17]提出了一种驾驶安全场模型，该模型考虑了交通各因素影响。
综上，在智能车辆避障研究中存在以下问题：1) 车辆在行驶过程中会受到道路环境的影响，如能见度、坡度、道路曲率等，但目前大多数的避障方法未考虑上述影响；2) 碰撞风险会随着车辆状态的改变而变化，现有研究工作大多只致力于势能场与车辆物理尺寸之间的关系，很少涉及车辆状态对势能场的影响；3) 目前基于势场法的避障策略较少考虑在复杂路况下车辆是否具备换道避障的条件。针对上述问题，提出一种基于改进势场模型和HMM的智能车辆避障方法。主要创新点和贡献如下：1) 建立了包含道路条件参数的改进势场模型，分析了车辆特性对碰撞风险的影响；2)建立了基于HMM的智能车辆避障决策方法，并融入改进的势场模型，完成自车避障路径规划；3) 建立了基于自适应MPC避障路径跟踪控制器，并在控制器中加入松弛因子与约束条件防止出现无最优解。
1. 改进势场模型的构建
为了预测行车安全的动态变化，对传统势场模型进行改进，对智能车辆在行驶过程中的交通环境进行建模，考虑到车辆和道路环境对行车安全的影响，将驾驶风险场模型分为道路场和障碍场两部分，用ET表示驾驶风险场，ER表示道路势场，EK表示障碍势场，驾驶风险场模型表示为
$$ {E_T} = {E_K} + {E_R} $$ (1) 1.1 道路势场模型
道路场模型由边界势能(Eroad)和车道势能(Elane)两部分组成[17]，即
$$ {E_R} = {E_{{\text{road}}}} + {E_{{\text{lane}}}} $$ (2) 边界势能通过在道路边缘施加无限大的势场力来防止车辆离开道路。指数函数可通过调节曲率因子ζ 改变下降速率，使车辆在边界车道行驶时容错率更高，利用指数函数模拟边界势能，即：
$$ {E_{{\text{road}}}} = {A_r}\exp ( - \zeta y + {y_{r,t}}) $$ (3) 式中：Ar为比例因子，决定边界势能大小；ζ为曲率因子，决定边界势能的上升/下降速度；t∈{1,2}；yr,t为第t条道路边界线的位置。
车道势能会为车辆换道带来阻力，并将车辆逼迫到车道中心，同时势场力不宜过大，以便在换道时足以克服阻力。利用高斯函数模拟车道势能[18]：
$$ {E_{{\text{lane}}}} = {A_l}\exp [ - {(y - {y_{l,l}})^2}/\sigma _l^2] $$ (4) 式中：Al为车道标记类型，由交通法规定义的优先级确定，优先级越高，Al越大；yl,l是第l条车道划分的横向位置；σl确定车道势能上升/下降的速度。
1.2 障碍势场模型
障碍势能场表示障碍物对行驶安全影响的物理场，其场强大小和方向由自身属性、状态和道路条件共同决定。障碍势场可保证自车与其周围车辆的相对安全，引导自车进行避障。文献[17]建立了考虑道路条件和车辆状态的势场模型，该模型采用指数函数建模，导致车尾的势场不能达到指定值，且没有考虑弯道曲率对势场模型方向的影响。本文对障碍车辆势场模型(EK)进行了改进，具体为
$$ {E_K} = \dfrac{{{A_q}{W_q}({k_2} + v\cos \theta / \pm {T_q})}}{{|{{\boldsymbol{d}}_q}{|^{{k_1}}}}} $$ (5) 式中：Aq为不确定性常数，用于标定模型；k1为梯度系数，k2为大于0的修正系数，根据各路段历史交通事故数据确定，用于标定速度对驾驶风险的影响；dq表示物体周围各位置到物体所在位置的距离矢量，且与场强方向相同；v为运动物体的速度；θ是物体速度方向与dq形成的夹角，逆时针方向为正；Tq为道路曲率因子，±表示转弯方向(+为左，−为右)；Wq为道路状况因子。
注1 不同于文献[17]将梯度系数k1视为常数，本文设计的障碍势场不仅考虑了道路曲率对势场模型方向的影响，而且详细设计了k1。
注2 不同于文献[14]将道路状况因子Wq视为常数，本文所设计的Wq包括道路的附着系数、能见度、坡度等因素，统一用Wq来表达。
1.2.1 梯度系数
对于车道上的障碍物，如果类型相同，物体的质量越大，在发生碰撞时就会造成更大的损失。当质量和速度相同时，物体类型不同，碰撞造成的损失也不同。将障碍车辆特征参数如质量、类型纳入势场模型，得到梯度系数为
$$ {k_1} = \eta f(\Delta v)Hm $$ (6) 式中：m为障碍物体的质量，H为物体的类型，Δv为车速标准差(km/h)，f(Δv)为事故率函数，η为梯度系数的修正参数。
碰撞风险随着车辆的固有属性和运动状态改变而改变。如车辆的质量和速度越大，避障时所需的制动距离越长，碰撞损失就越大。车辆的固有属性和运动状态等效为虚拟质量。研究发现，事故率与车辆速度的标准差呈正相关，具体模型为[18]
$$ f(\Delta v) = - 35.472 + 16.435 \cdot \ln (\Delta v) $$ (7) 使用单位化拟合曲线公式确定梯度系数k1为
$$ {k_1} = \eta \left[ {16.435 \cdot \ln (\Delta v) - 35.472} \right]mH $$ (8) 需要说明的是本文将障碍车的特征参数视为已知数，但目前障碍车的质量难以通过自车的车载传感器直接获取，可以采用交通工程应用中的常用方法，如基于车型分类基础上的质量统计模型[19]，解决车辆质量的估计问题。随着车联网的不断发展，未来可通过车联网获取车辆的特征参数。
1.2.2 道路曲率因子
车辆转向时，会受到牵引力和离心力的共同作用，在水平方向的受力大小和方向会发生变化，导致势能场模型的大小和梯度方向发生改变。转弯过程中的合力为
$$ {F_w} = \dfrac{{{T_s}}}{{v{R_T}}} $$ (9) $$ {F_{{\text{cf}}}} = m{v^2}K $$ (10) $$ {F_{{\text{rf}}}} = \sqrt {F_w^2 + F_{{\text{cf}}}^{\text{2}}} $$ (11) 式中：Fw是驱动力；Fcf是离心力；Frf是驱动力和离心力的合力；Ts为变速器输出轴转矩，可通过在轮胎处加装转矩传感器获取；α为牵引力与合力间的夹角；RT为车轮滚动半径；K为道路曲率。
合力方向与速度方向之间的余弦值为
$$ {T_q} = \cos \alpha = \dfrac{{{T_s}}}{{\sqrt {{m^2}{v^6}{K^2}{R^2} + T_s^2} }} $$ (12) 由于惯性效应，势场模型的最大梯度方向由车速方向变为合力方向。
1.2.3 道路状况因子
道路状况主要受天气和道路设施的影响[20]，势能场与道路条件息息相关。恶劣的道路条件会导致更高的驾驶风险。道路状况因子Wq可定义为[14]
$$ {W_q} = {W_q}(\mu ,\eta ,\beta ) = \left\{ \begin{array}{l} {\beta _1}\dfrac{\tau }{{{\tau ^*}}},\quad v = 0 \\ {\beta _2}\dfrac{\tau }{{{\tau ^*}}}\dfrac{{{\mu ^*}}}{\mu }\exp (\lambda ),\quad v \ne 0 \\ \end{array} \right. $$ (13) 式中：β1和β2为修正系数，根据该路段发生过的事故数据进行修正；μ为道路附着系数；τ为能见度系数；β为道路坡度系数；τ*和μ*分别为能见度系数和道路附着系数的标定值，道路附着系数μ≤1，取μ*=1。
1）能见度系数
能见度系数与道路可视距离有关，可视距离越长，能见度系数越小。利用雾天时不同可视距离对应发生的交通事故率拟合得到能见度系数分布函数，其表达式为[21]
$$ \tau = \dfrac{{0.287\;7}}{{[1 + {{({D_{{\text{is}}}}/0.110\;2)}^{1.54}}]}} + 0.007\;4 $$ (14) 式中Dis为可视距离。
2）道路坡度系数
整车纵向动力学可表示为
$$ ma = \dfrac{{{T_s}}}{R} - mg(\sin \psi + \mu \cos \psi ) - \dfrac{{\rho {C_d}A{v^2}}}{2} $$ (15) 式中：Ts为变速器输出轴转矩，R为车轮滚动半径，g为重力加速度，ψ为坡度角，μ为道路附着系数，ρ为空气密度，Cd为空气阻力系数，A为迎风面积，a为纵向加速度。
由于实际坡度难以实时测量，本文利用等效坡度[22]及式(15)得道路坡度系数为
$$ \beta = \sin \psi + \mu \cos \psi = \dfrac{{{T_s}}}{{2Rmg}} - \dfrac{{\rho {C_d}A{v^2}}}{{2mg}} - \dfrac{a}{g} $$ (16) 由式(16)可知，当道路坡度为0°时，等效坡度值等于道路附着系数。
3）道路附着系数
道路附着系数难以利用传感器进行直接测量，主要采用基于汽车纵向动力学或横向动力学模型等方法进行估计[23]，路面附着系数与车轮滑移率s、车速v的关系为
$$ \mu = ({C_1}(1 - {{\rm{e}}^{-{C_2} {s}}}) - {C_3}s){{\rm{e}}^{-{ C_4}{s \cdot v}}} $$ (17) 式中：C1、C2、C3为轮胎附着特征参数；C4为车速对附着特性的影响参数，范围为[0.02, 0.04]。相关参数在不同道路情况下的取值如表1所示。
表 1 不同道路的附着相关参数Table 1 Friction parameters at different road conditions道路情况 C1 C2 C3 干沥青道路 1.280 1 23.990 0.520 0 干混凝土道路 1.197 3 25.186 0.537 3 雪地道路 0.050 0 306.390 0.000 0 结冰道路 0.194 6 94.129 0.064 6 2. 避障路径规划
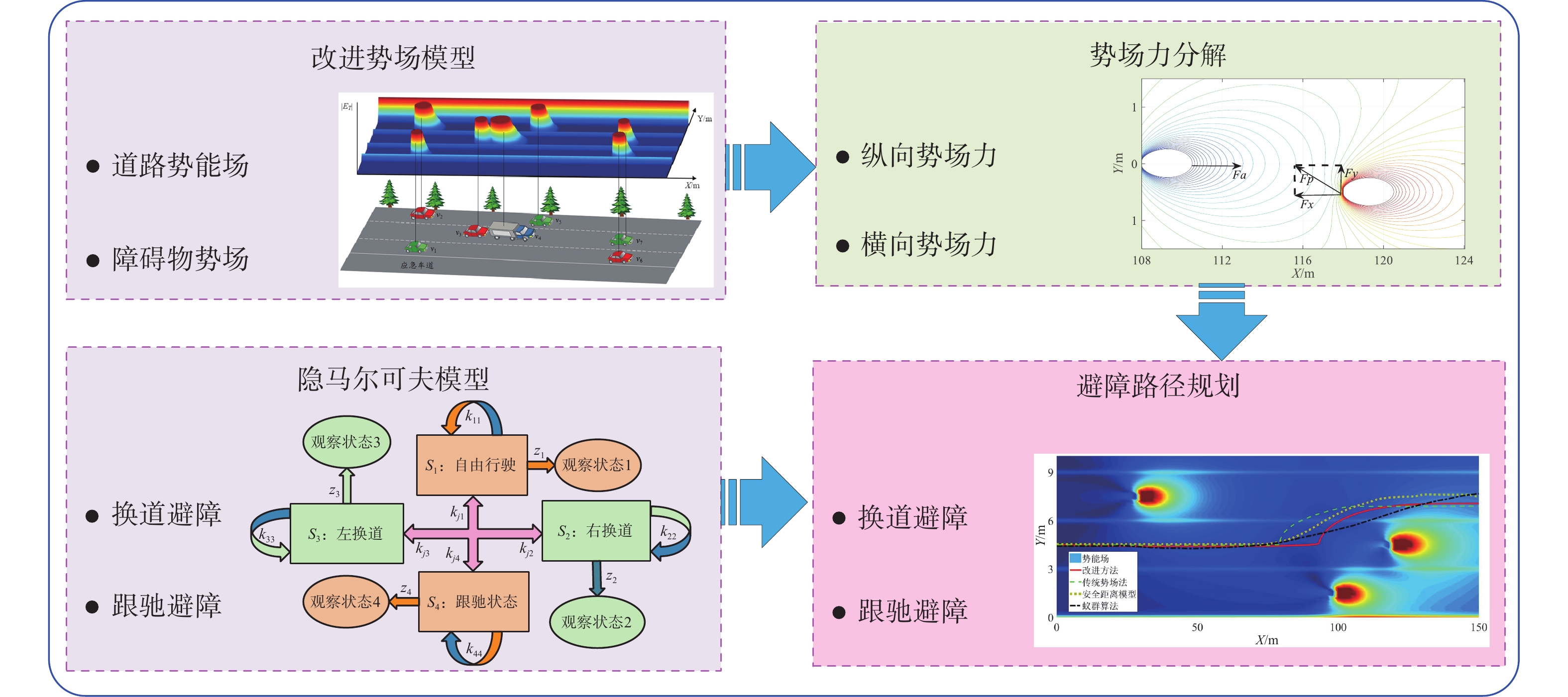
通过融合改进的势场模型和HMM模型，建立智能车辆避障路径规划方法。具体思路为：基于建立的势场模型，对势场的横向、纵向梯度力进行分解，得到最小势场力点；利用HMM进行状态预测，判断自车的避障方式，完成避障路径规划。流程如图1所示。
图 1 避障流程Fig. 1 Flow of obstacle avoidance
下载:
全尺寸图片
2.1 势场力分解
势场中的可行路径与虚拟力相关，且势场力与势场的关系可表示为[24]
$$ F = - {\text{grad}}(E) $$ (18) 式中：“−”表示场力方向，由高势能处向低势能延伸；grad为梯度函数。
为使车辆朝前方行驶，传统的人工势场法是设置一个引力点驱动车辆向目标点行驶。然而车辆只需沿着道路方向行驶，对车辆的纵向引力模型进行改进，将车辆前进方向作为引力方向，其表达式为
$$ {F_a} = {k_3}|{x_{{\text{end}}}} - {x_{{\text{start}}}}| $$ (19) 式中：k3是引力系数，xend是自车的前端，xstrat是道路的起点。
2.1.1 纵向势场力
车辆在势场环境下会受到引力和排斥力的作用，在离障碍物不同位置产生的纵向排斥力为
$$ F_b=\left\{\begin{array}{lr} F_{\max }, \quad d_q \leq d_{\min } \\ \dfrac{A_q W_q\left(k_2+v \cos \theta \cos \phi\right)}{\left|d_q\right|^{k_1}}, \quad d_{\min }<d_q<d_{\max } \\ 0, \quad d_q \geq d_{\max } \end{array}\right.$$ (20) 其中
$ \phi $ 为v与X轴的夹角。从式(20)可以看出，定义的车辆纵向位置排斥力具有约束性和可控性。2.1.2 横向势场力
在势场环境下的避障过程中，车辆在Y轴方向同样会受到障碍物的排斥作用，基于建立的道路势场模型和障碍势场模型，使车辆换道避障。其中，道路势场模型驱使目标车辆一直沿道路行驶，更符合实际情况。为了保证车辆不驶出车道边界，边界势能需足够大，排斥力足够强；车道排斥力可使车辆保持在车道上行驶，但也要足以克服，确保车辆正常变道。边界排斥力与车道排斥力分别表示为
$$ {F_{c1}} = \zeta {A_r}\exp ( - \zeta y + {y_{r,j}}) $$ (21) $$ {F_{c2}} = 2(y - {y_{l,i}}){A_l}\exp [ - {(y - {y_{l,i}})^2}/\sigma _l^2]/\sigma _l^2 $$ (22) 其中δl为车道势能因子。
障碍车需产生足够的侧向排斥力，保证车辆之间有一定的安全距离，并可以在安全距离内换道避障。障碍车的侧向排斥力表示如下：
$$ {F}_{c3}=\left\{\begin{array}{l}{F}_{\mathrm{max}},\quad {d}_{q}\leqslant {r}_{\mathrm{min}}\\ {q}_{i}\dfrac{{A}_{q}{W}_{q}({k}_{2}+{v}_{q}\mathrm{cos}\;\theta \mathrm{sin}\;\phi )}{|{d}_{q}{|}^{{k}_{1}}}\text{，}{r}_{\mathrm{min}} < {d_q} < {r_{max}}\\ 0,\quad {d}_{q}\geqslant{r}_{\mathrm{max}}\end{array} \right.$$ (23) 其中qi为横向避障决策系数。
2.2 避障方式决策
HMM被用于决策车辆在复杂交通环境中的避障方式，HMM能够分析时间序列的动态信号，并根据相邻状态间的关系完成避障模式识别[25]，即跟驰避障和换道避障。HMM可根据观察到的参数确定该过程的隐含参数，并利用这些参数来做进一步分析。将车辆位置、速度和相邻车道的车辆间距等特征参数作为观测变量，障碍车与道路的侧向排斥力作为隐藏状态，通过观测变量来预测隐藏状态。
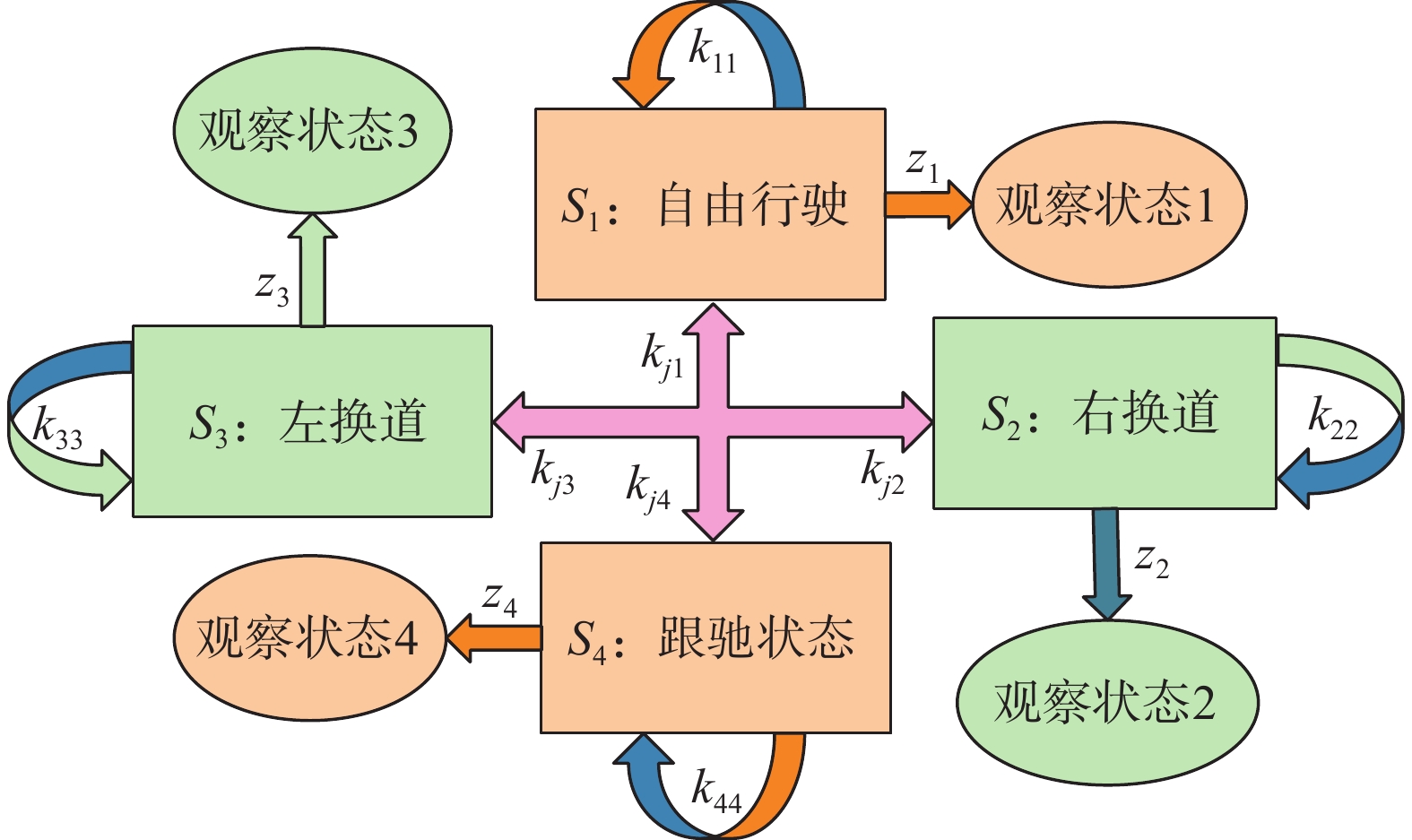
车辆行驶过程可分为跟驰、左换道、右换道和自由行驶4种状态[26]，建立HMM如图2所示。图2中，K为状态转移概率矩阵，Z为观测概率分布矩阵，Z=[z1 z2 z3 z4]。当自车观测到周围无任何车辆，即观察状态1；当自车观测到左侧和前方有车辆行驶，则为观察状态2；当自车观测到右侧和前方有车辆行驶，则为观察状态3；当自车观测到左右两侧和前方有车辆行驶，根据观测变量判断是否能换道，若能，则根据观测变量计算车辆驾驶状态；若不能，则为观察状态4。4种行驶状态可根据观察状态而相互转化。其中，分布矩阵K是通过12个概率k11~k44组成：
图 2 隐马尔可夫模型Fig. 2 Hidden Markov model下载:
全尺寸图片
$$ {\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {{k_{11}}}&{{k_{12}}}&{{k_{13}}}&{{k_{14}}} \\ {{k_{21}}}&{{k_{22}}}&{{k_{23}}}&{{k_{24}}} \\ {{k_{31}}}&{{k_{32}}}&{{k_{33}}}&{{k_{34}}} \\ {{k_{41}}}&{{k_{42}}}&{{k_{43}}}&{{k_{44}}} \end{array}} \right] $$ (24) 式中kij表示隐藏状态从Si变化到Sj的概率值，即
$$ {k_{ij}} = P{\kern 1pt} {\kern 1pt} [S(t) = {S_j}|S(t - 1) = {S_i})] $$ (25) 观测序列由多个观测向量O组成[27]，每个向量O包含4个元素，分别为车辆速度v、车辆加速度a、数字化转向行为指数ρ和车辆横向偏移指数vl, 即：
$$ {{{{\boldsymbol{O}}}}_i}(t) = \left[ {\begin{array}{*{20}{c}} {{o_{i1}}(t)} \\ {{o_{i2}}(t)} \\ {{o_{i3}}(t)} \\ {{o_{i4}}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_i}(t)} \\ {{a_i}(t)} \\ {{\rho _i}(t)} \\ {{v_{li}}(t)} \end{array}} \right] $$ (26) 式中：ρ由转向角和转向角速率计算得到，vl为车辆横向偏移对车道线的时间导数。由观测变量和驾驶状态可得到下一时刻车辆的驾驶状态：
$$ {p_{n + 1}}(i) = \dfrac{{\displaystyle\sum\limits_j {{p_n}(j)} \cdot {k_{ji}} \cdot {z_i}[{\boldsymbol{O}}({t_n})]}}{{\displaystyle\sum\limits_i {\displaystyle\sum\limits_j {{p_n}(j){k_{ji}} \cdot {z_i}[{\boldsymbol{O}}({t_n})]} } }} $$ (27) 式中：pn(i)为当前时刻n车运动状态的概率，pn+1(i)为下一时刻n+1车运动状态的概率，pn(1)表示自由行驶状态概率，pn(2)表示右换道状态概率，pn(3)表示左换道状态概率，pn(4)表示跟驰状态概率，O(tn)为观测变量矩阵，zi[O(tn)]表示观测概率分布。
$$ {\boldsymbol{P}}_{n+1}=[p_{n+1}(1)\,p_{n+1}(2)\,p_{n+1}(3)\,p_{n+1}(4)] $$ 由式(27)可预测自车的横向运动状态，根据该预测模型可计算出自车运动的避障决策系数，即：
$$ {q_i} = \left\{ {\begin{array}{*{20}{c}} {1,\begin{array}{*{20}{c}} {}&{\arg \max [\mathop {\boldsymbol{P}}\limits_{i \in {s_i}} (i|n + 1)] = I} \end{array}} \\ {0,\begin{array}{*{20}{c}} {}&{\arg \max [\mathop {\boldsymbol{P}}\limits_{i \in {s_i}} (i|n + 1)] \ne I} \end{array}} \end{array}} \right. $$ (28) 其中I=2,3表示横向运动，分别为左换道和右换道。
2.3 避障路径规划
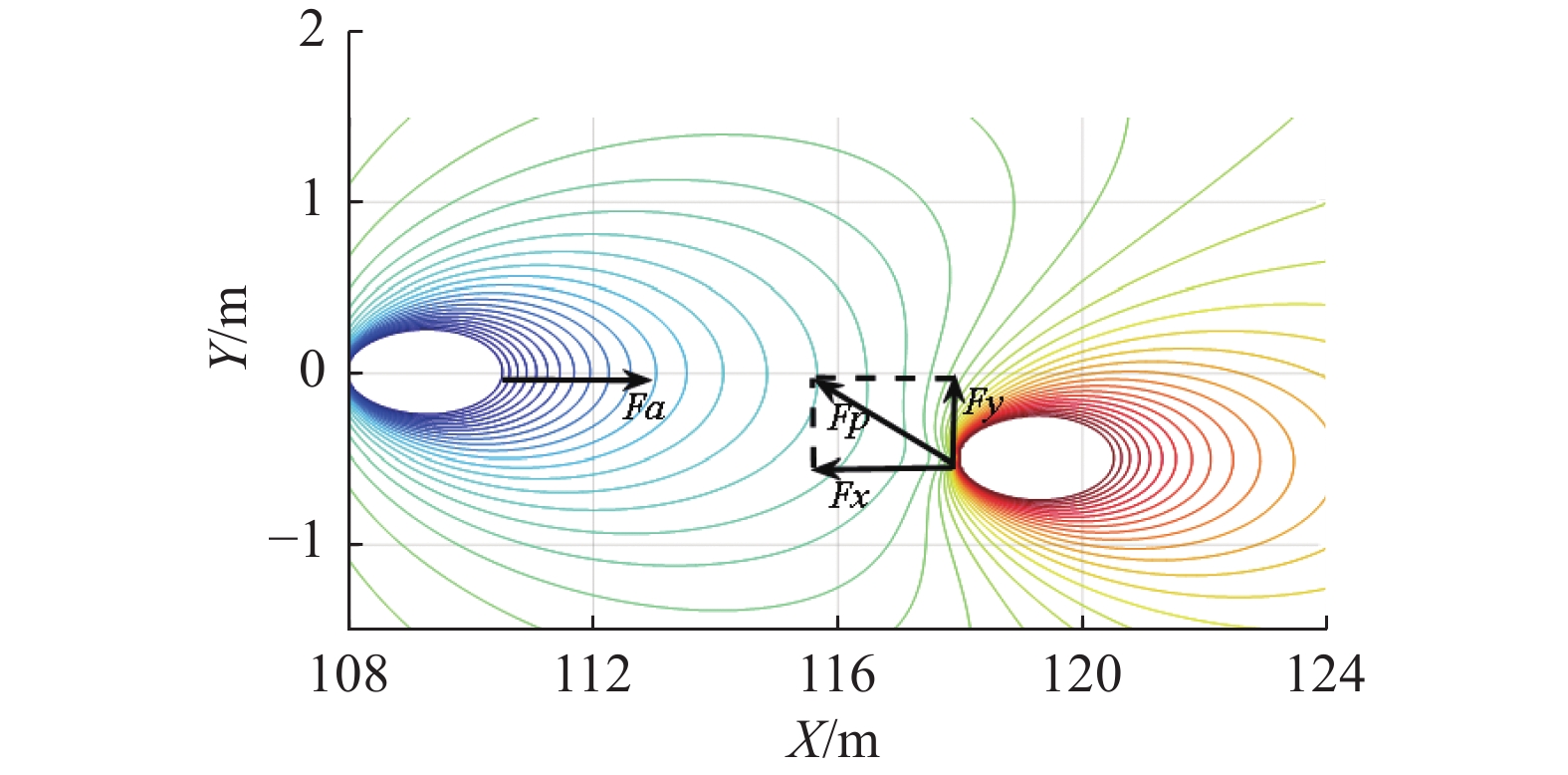
由建立的HMM，自车可根据周围车辆状态进行决策。当正前方有障碍车时，在速度不变的情况下，采取换道避障，由分解势场力得到该工况下的势场力最小点，随后以势场力最小点作为下一刻避障路径点。具体思路为：自车始终受到前方吸引力Fa，当前方有障碍车时，自车将形成排斥场，且离障碍车越近，排斥力越大。一旦受到排斥力的影响，HHM就会计算出决策因子qi，确定自车是否可以改变车道避障。如果是，障碍车辆的排斥力Fp将被分解成X轴方向的排斥力Fx和Y轴方向的排斥力Fy。势场力分解如图3所示，自车为低势能，为了直观表现，给予一定的形状大小，障碍车辆为高势能，随后通过受力分析可使自车沿低势能点进行避障。
图 3 势场力分解示意Fig. 3 Diagram of potential field force decomposition下载:
全尺寸图片
若前方道路上有n个障碍车辆，由式(19)~(23)可得道路上综合外力的平衡方程为
$$ \sum\limits_{i{\text{ = }}1}^n {{F_{xi}}} \cdot {{\boldsymbol{e}}_x} + \sum\limits_{i{\text{ = }}1}^n {{F_{yi}}} \cdot {{\boldsymbol{e}}_y} + {F_{c1}} + {F_{c2}} = 0 $$ (29) 其中ex、ey分表示纵横向矢量。
通过牛顿迭代法求解式(29)，得到道路的最小势场力点，拟合每个势场力最小点，得到所需的安全避障路径。当qi = 0，即车辆不能变道，此时横向排斥力始终为0，目标车只受障碍车纵向斥力的影响，并且最小斥力点总是在障碍车的后方。由道路边界和车道线形成的势场力总是向两侧延伸，只产生横向斥力，而不产生纵向斥力，且车道产生的势场力只会使被控车辆始终保持在车道中心线附近。
3. 测试分析
为测试势能场模型和避障方法的有效性，将自车设置为一个受势场力作用的全向点，设计了几种模拟场景，所设计的工况为障碍物在不同车道及位置处以不同速度移动。测试参数如表2所示。
表 2 仿真参数Table 2 Simulation parameters参数 值 参数 值 mq/kg 1500 ζ 1 Hq 1.3 δl 1 Gq 1 k1 0.1 Aq 0.01 k2 50 Tc 1 Wq 0.8 β/(°) 0 Tq 1 Ar 10 η1 1 Al 30 η2 1 Dis/m 100~1000 μ 0.8 Np 15 ε 2 Nc 2 Cf 61224 a,b/m 1.23,1.47 Cr 42500 3.1 模型测试
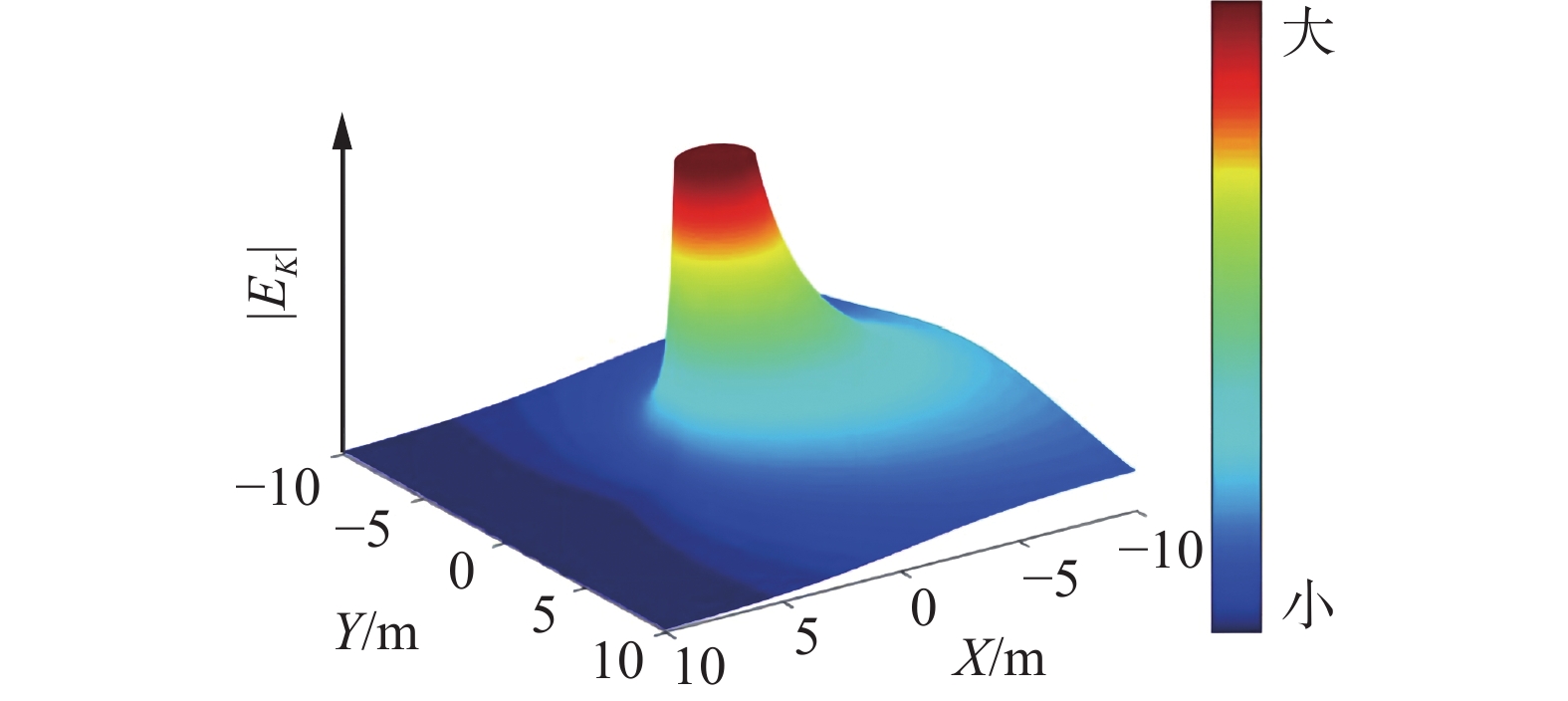
模拟的硬件条件是AMD 3700X处理器、GTX 1660S显卡和16 GB运行内存，图4为运动物体产生的势场图。
图 4 障碍物势场Fig. 4 Obstacle potential field下载:
全尺寸图片
由图4可知，障碍势能场的中心是物体的质心，在等距离处，越接近车辆正前方，障碍势能场的势能越大，符合实际车辆驾驶的风险特点。
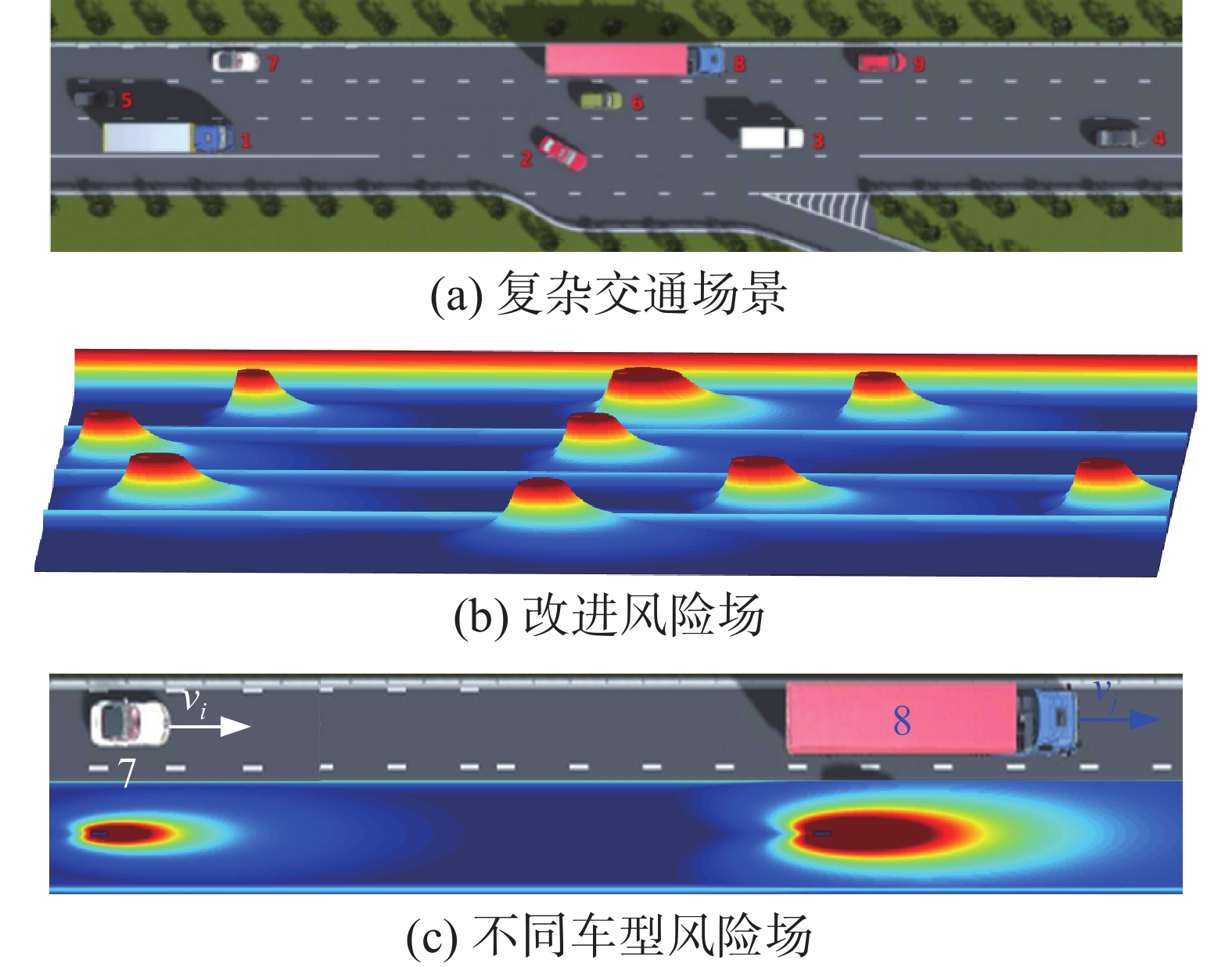
为分析不同车辆特性如质量、类型、速度对驾驶风险场的影响，设计复杂交通场景，如图5(a)所示，在该场景中，3条主干道上分布着9辆不同类型的汽车，每辆车都以不同的车速行驶。具体仿真参数如表3所示。根据行车风险场的分布图可判断出各个位置行车危险程度的大小。复杂交通场景下驾驶风险场场强如图5(b)、(c)所示。
图 5 复杂交通场景的驾驶风险场Fig. 5 Driving risk field in complex traffic scenario下载:
全尺寸图片
表 3 仿真参数Table 3 Vehicle characteristic parameters类型 型号 质量/kg 车速/(km/h) 1 (卡车) MercedesBenz_Actros_6x2 2750 85 2 (轿车) Roewe_550_S_Sedan 1590 65 3 (卡车) Nissan_Cabstar_Boxtruck 2150 90 4 (轿车) Audi_A8_Sedan 1770 95 5 (轿车) Toyota_Yaris_Hatchback 1420 96 6 (轿车) Ford_Fiesta_Hatchback 1480 97 7 (轿车) BMW_Z3_Convertible 1690 100 8 (卡车) MercedesBenzActros+Trailer 4970 98 9 (轿车) Ford_Focus_Stationwagon 1450 108 从图5可以看出，质量越大，发生碰撞风险也更大；越接近车辆正前方，障碍势能越大。
3.2 路径规划仿真
对所提出的路径规划系统在3种情况下进行了模拟。
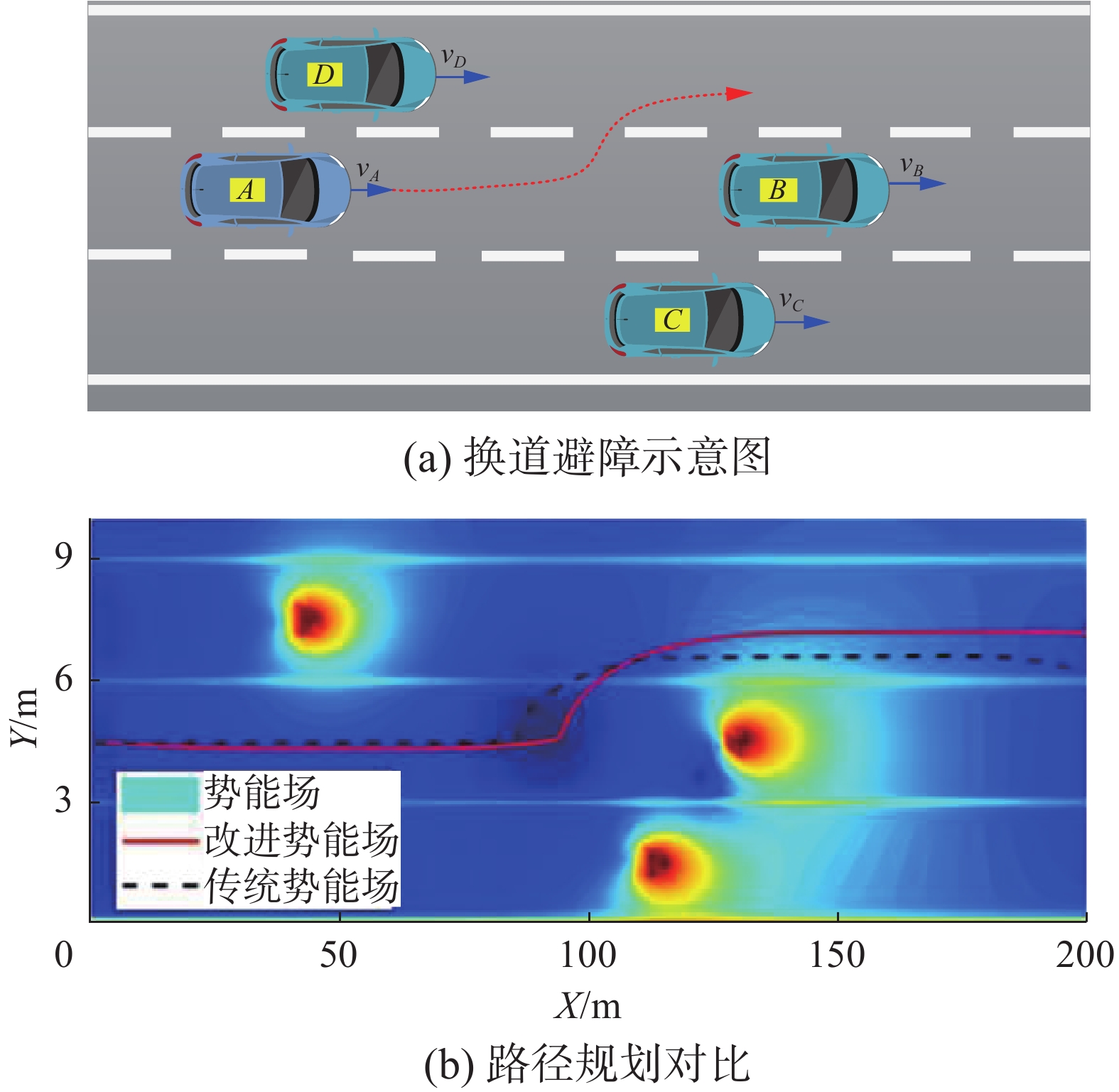
场景1 设计智能车辆 (A) ，即自车所处车道和两侧车道均有障碍车辆，分别标记为B、C、D，且自车A的车速大于障碍车辆的行驶速度，如图6(a)所示。根据HMM，自车将进行左换道避障，为了评估路径规划方法的性能，对改进前后路径规划方法进行了模拟计算。改进后的势场法与传统势场法的路径规划结果对比如图6(b)所示。
图 6 换道避障路径规划Fig. 6 Path planning by lane change下载:
全尺寸图片
由图6(b)可知，与传统的势场方法相比，所提出的方法的转弯曲率明显改善，避障完成后，目标车不必换回原始车道，在保证安全的情况下，尽量减少了自车的动作，提高车辆的舒适性和经济性。
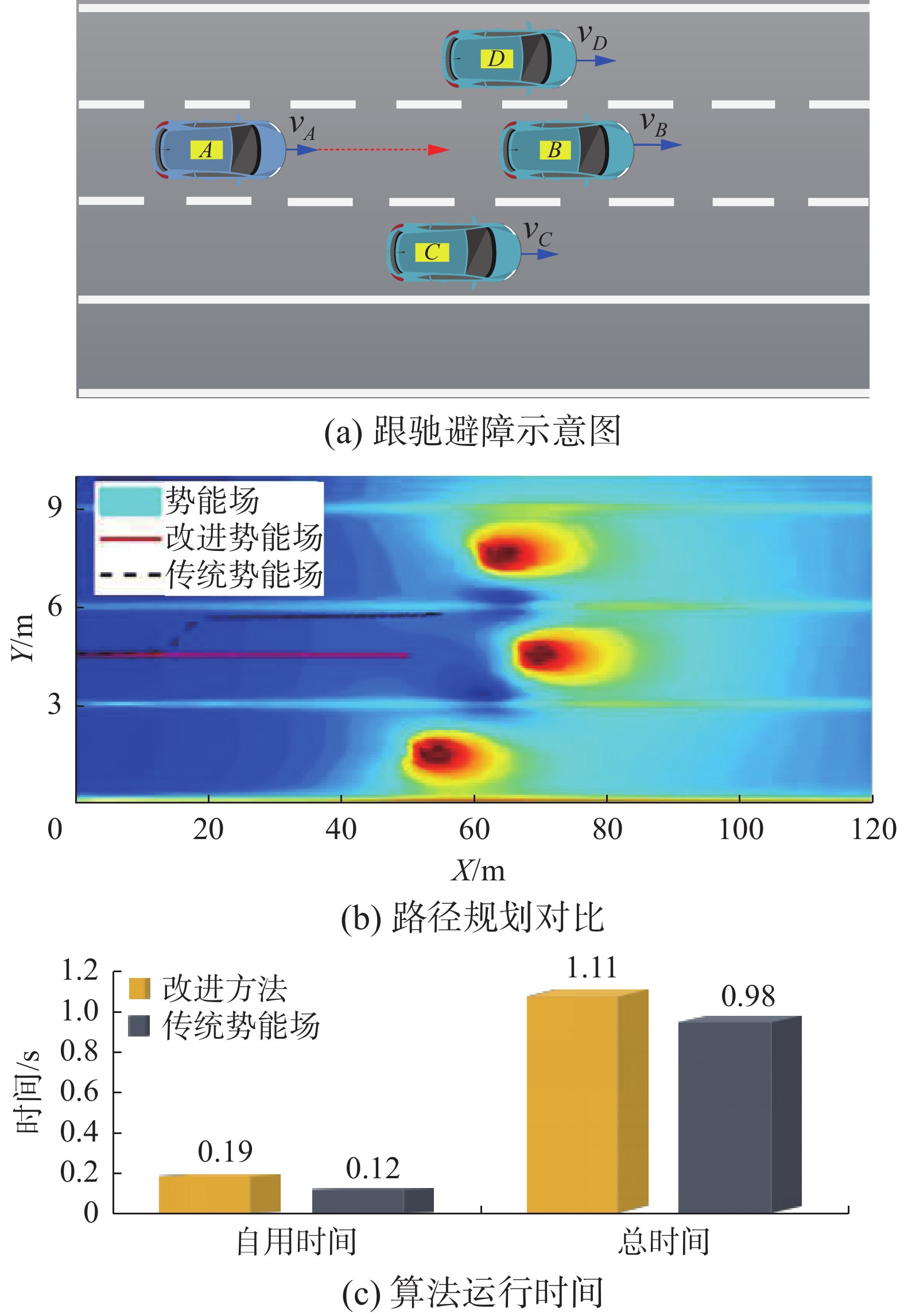
场景2 设计A车所处车道和两侧车道均有障碍车B、C、D，且A车车速大于障碍车，如图7(a)所示。根据HMM，决策系数等于0，不满足换道条件，此时分解的横向势场力也等于0，即不存在横向力而只有纵向力，以纵向力最小点为下一刻避障路径起点，进行跟驰避障。改进势场法与传统势场法的路径规划对比如图7(b)所示。图7(c)为改进前后完成避障路径规划所需的运行时间。
图 7 跟驰避障路径规划Fig. 7 Path planning by car following下载:
全尺寸图片
由图7可见，当自车相邻的两车道上都有障碍车，且领先障碍车辆的速度，进行跟驰避障。传统势场法虽然能确保规划的路径是安全的，但是规划的路径会偏离车道中心，陷入局部最小值，这与交通法规不一致。改进的方法避免了此问题，保证车辆在车道内行驶。改进的势场法运行时间比传统势场法略有增加，但仍处于可接受范围内。
在改进的势场法的基础上加入了HMM决策层，可避免陷入局部最小值，保证了避障路径的有效性。
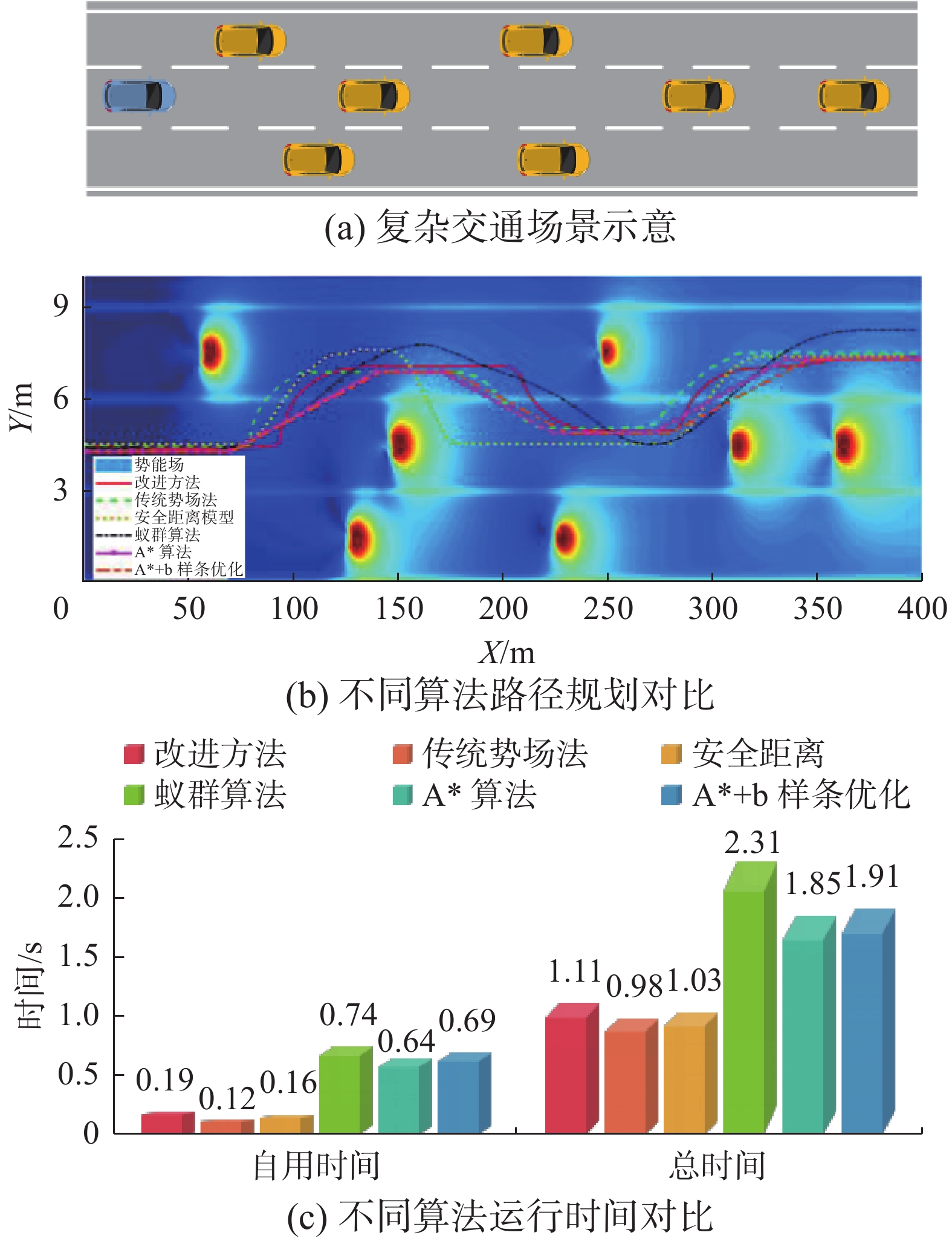
场景3 自车（蓝色）在复杂交通场景下行驶，障碍车均为黄色，如图8(a)表示。本次模拟将与传统的势场法[28]、安全距离模型[29]、蚁群算法[30]和A*算法[31]进行对比，复杂交通环境下不同算法的路径规划、运行时间对比如图8(b)、(c)所示。
图 8 复杂交通场景路径规划Fig. 8 Path planning in complex environments下载:
全尺寸图片
从图8中可以看出，改进方法的避障距离比其他5种方法略小，在避开障碍物后始终保持在车道的中心位置；传统的势场法运行时间最短，在避障过程中会干扰其他车辆的势场，且总选择最小值点；安全距离模型在避障后需要变回原来的车道，这增加了驾驶的复杂性；蚁群算法得到的避障路径更加平滑，但运行时间最长；A*算法和A*+b样条曲线算法规划的路径更加笔直，但运行时间较长。
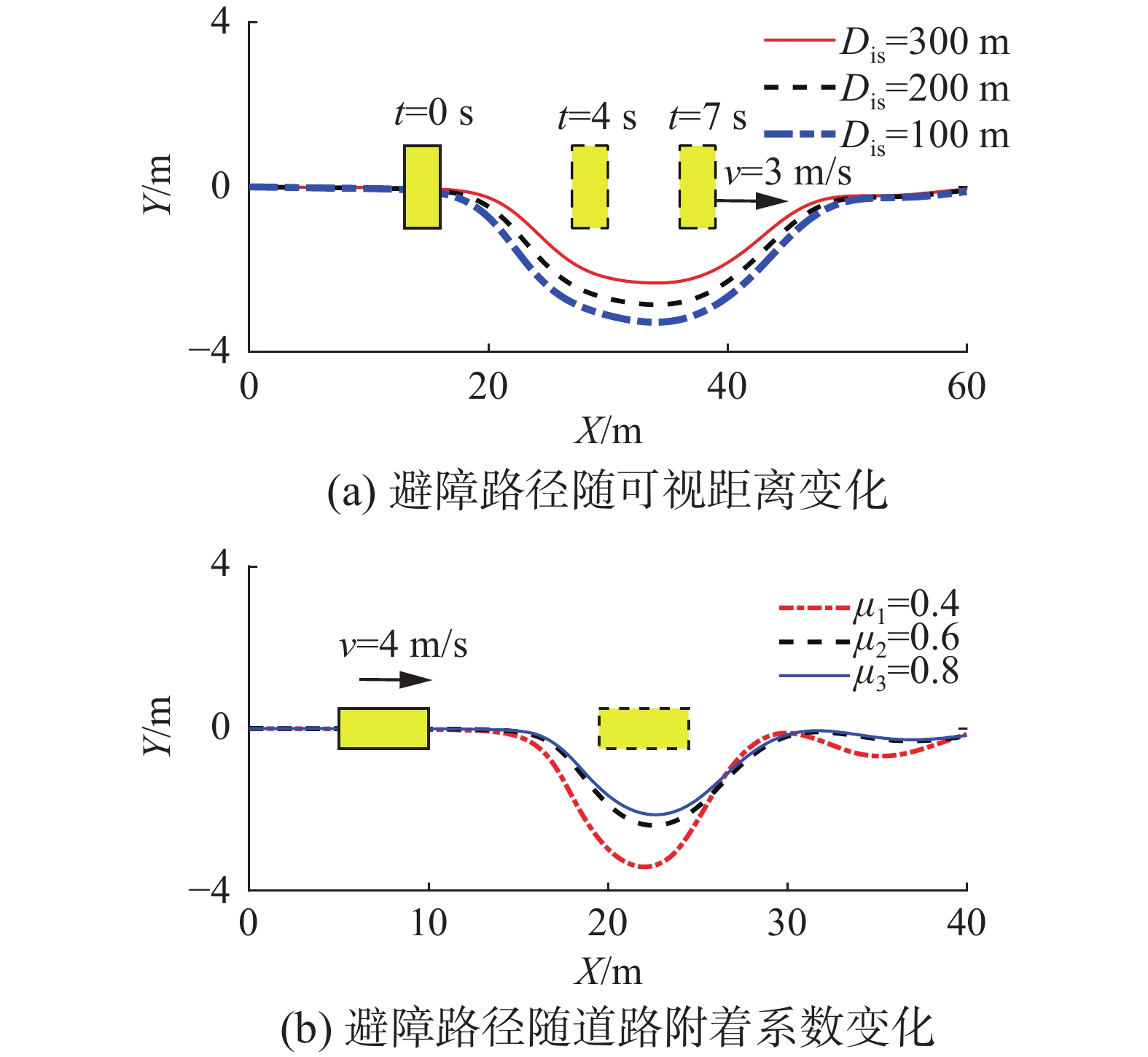
为了说明改进势场模型参数的取值对路径规划的影响规律，其他参数保持不变，动态障碍物运动速度为3 m/s，可视距离Dis分别取100、200、300 m时，得到的避障路径如图9(a)所示；分别取道路附着系数μ1=0.4、μ2=0.6、μ3=0.8，得到的避障路径如图9(b)所示。从图9可知，当可视距离变大时，所规划的避障路径会更加靠近障碍车辆，且自车的回正距离变小；当道路附着系数不断减小时，障碍车的势能场不断变大，碰撞风险不断上升，因此所规划的路径会随着附着系数的减小而远离障碍车辆。
图 9 不同参数取值的路径规划Fig. 9 Path planning with different parameters下载:
全尺寸图片
3.3 路径跟踪分析
为了验证提出的避障方法的有效性和合理性，利用MPC控制器实现车辆实时避障路径跟踪。
3.3.1 避障跟踪控制器
MPC采用二自由度车辆模型，同时对车辆动力学模型进行离散化，得到离散化后的预测模型为[14]
$$ \xi (t + 1) = f(\xi (t),{u_T}(t)) $$ (30) $$ {u_T}(t) = u(t - 1) + \Delta u(t) $$ (31) 式中控制量为车辆的前轮转角。
将改进势场模型规划出的路径作为模型预测控制的目标输入，该目标函数表示为
$$ \begin{array}{c}J(\xi (t)\text{，}u(t-1)\text{，}\Delta U(t))=\\ {\displaystyle \sum _{i=1}^{{N}_{p}}\left|\right|\lambda (t+i|t)-{\lambda }_{\text{ref}}(t+i|t)}|{|}_{Q}^{2}+{\displaystyle \sum _{i=1}^{{N}_{c}-1}\left|\right|\Delta u(t+i\text{|}t)}|{|}_{R}^{2}+\rho {\varepsilon }^{2}\end{array} $$ (32) 式中：
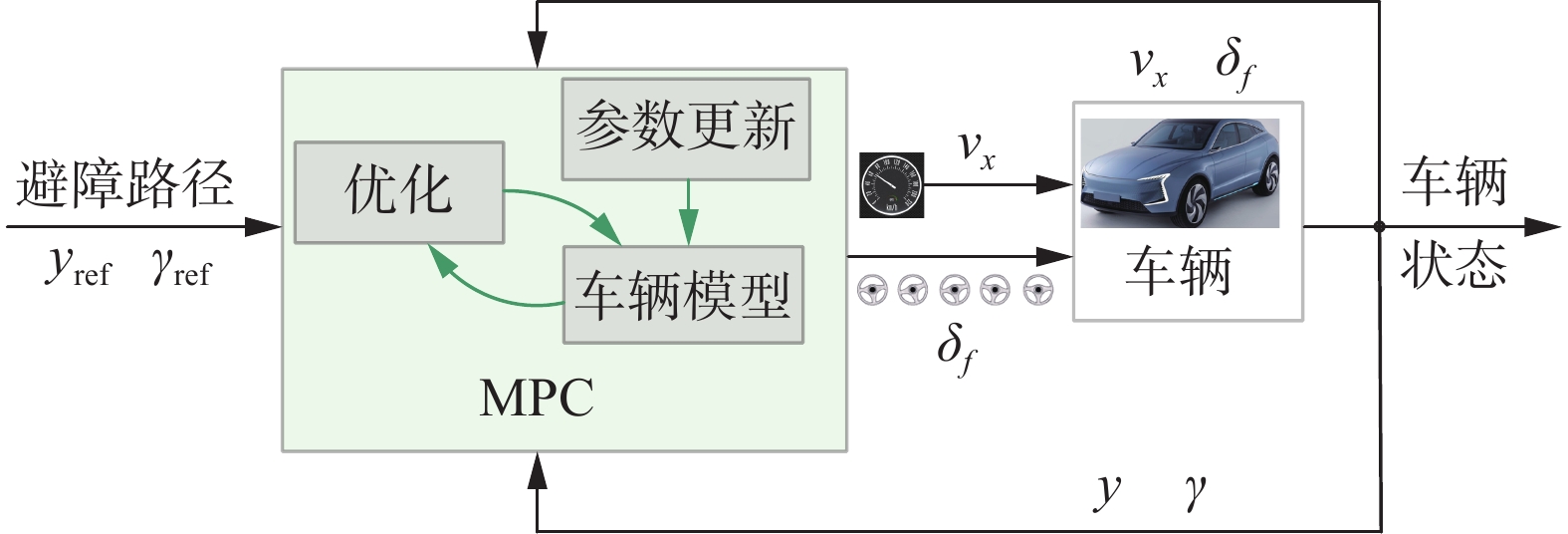
$ \xi (t) $ 为当前t时刻的状态量，ΔU(t)为t时刻的控制输入，u(t−1)为上一时刻的控制量，λref =yref为预测控制器输出的参考路径，Np为预测时域，Nc为控制时域，Q、R和ρ为权重系数，ε为松弛因子。考虑车速的变化，建立MPC，如图10所示。
图 10 MPC路径跟踪Fig. 10 MPC for path tracking下载:
全尺寸图片
以自车当前的位置、速度、横摆角速度为状态变量，以规划的实施避障路径(yref)、横摆角速度(γref)为控制输入量加入到MPC中。在对MPC的车辆与道路权重系数进行设计时，需从3个方面进行考虑：1)根据权重因素的重要性进行排序；2)影响因素的物理含义及可测性；3) 影响因素的数值大小。文章通过对实际道路进行检测，获得道路影响因素的数值，车辆等因素按照安全性、驾驶性、经济性、舒适性的轻重顺序准则确定权重系数。
为了保证车辆行驶的稳定性，在求解目标函数时添加的约束条件满足：
$$ {u_{\min }} \leqslant u(t + i) \leqslant {u_{\max }}\quad i = 0,1, \cdots ,{N_c} - 1 $$ (33) $$ \Delta {u_{\min }} \leqslant \Delta u(t + i) \leqslant \Delta {u_{\max }}\quad i = 0,1, \cdots ,{N_c} - 1 $$ (34) 式中：
$ \Delta u $ 为控制量的前轮转角变化率，$ \Delta {u_{\max }} $ =0.2 rad/s，$ \Delta {u_{\min }} = - 0.2{\text{rad}}/{\text{s}} $ ，umin=−0.3 rad，umax=0.3 rad。除控制量和控制增量约束外，还需增加车辆动力学约束，文献[32]对不同路况下车辆稳定行驶的质心侧偏角进行了研究。车辆在某些极限工况下失稳是由于车辆轮胎力达到饱和，并且轮胎力饱和与轮胎侧偏角存在一定关系，因此，需对轮胎侧偏角进行约束，轮胎侧偏力的约束如下：
$$ {\alpha _{\min }} \leqslant {\alpha _{f,\;r}} \leqslant {\alpha _{\max }} $$ (35) 其中αmin和αmax分别为轮胎侧偏角的上下限。
根据轮胎的侧偏特性可知,在轮胎侧偏角不超过5°时，侧偏角与侧偏力呈线性关系。因此，本文设置轮胎侧偏力的取值范围为−2.5°~2.5°。此外，车辆动力学不仅要考虑驱动力的约束，还需考虑路面对车辆附着条件的限制，车辆的纵向加速度和横向加速度存在如下关系：
$$ \sqrt {a_x^2 + a_y^2} \leqslant \mu g $$ (36) 当车辆纵向匀速行驶时，式(36)可化简为
$$ |{a_y}| \leqslant \mu g $$ (37) 此约束在路面附着条件较好时比较宽松，但侧向加速度过大时会使车辆稳定降低，过小又会导致无最优解[24]，因此将该约束设为软约束条件，具体如下：
$$ {a_{y,\min }} - \varepsilon \leqslant {a_y} \leqslant {a_{y,\min }} + \varepsilon $$ (38) 3.3.2 避障跟踪仿真
为了验证所提避障方法的有效性，分别对3.2节部分3种场景下的避障路径进行跟踪控制仿真。
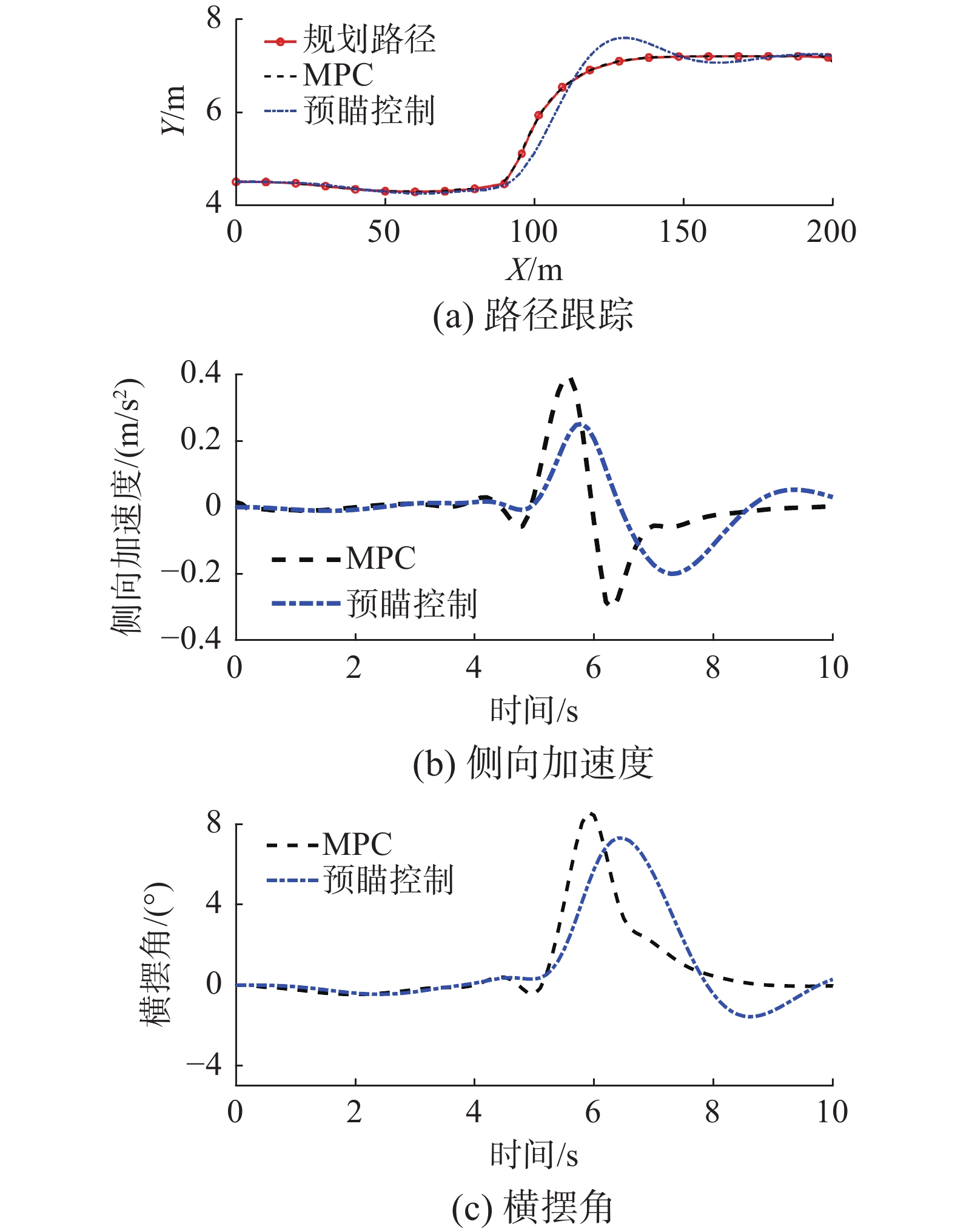
1）场景1(图6)
设定自车初始速度为20 m/s (72 km/h)，自车车速度大于障碍车的行驶速度，根据提出的避障方法，避障路径跟踪仿真结果如图11所示。从图11(a)可以看出，预瞄控制和MPC都能较好跟踪避障路径，但MPC跟踪误差更小，且在车辆转向时，预瞄控制会出现较大偏差，而MPC中加入软约束和权重系数，能够更好地跟踪路径。从图11(b)、(c)可以看出，MPC控制的汽车的侧向加速度、横摆角相对于预瞄控制有不同程度增大，这是为了获得更高的跟踪精度，但输出状态仍在约束条件范围内。
图 11 换道避障路径跟踪对比Fig. 11 Path tracking of obstacle avoidance by lane-change下载:
全尺寸图片
2）场景2(图7)
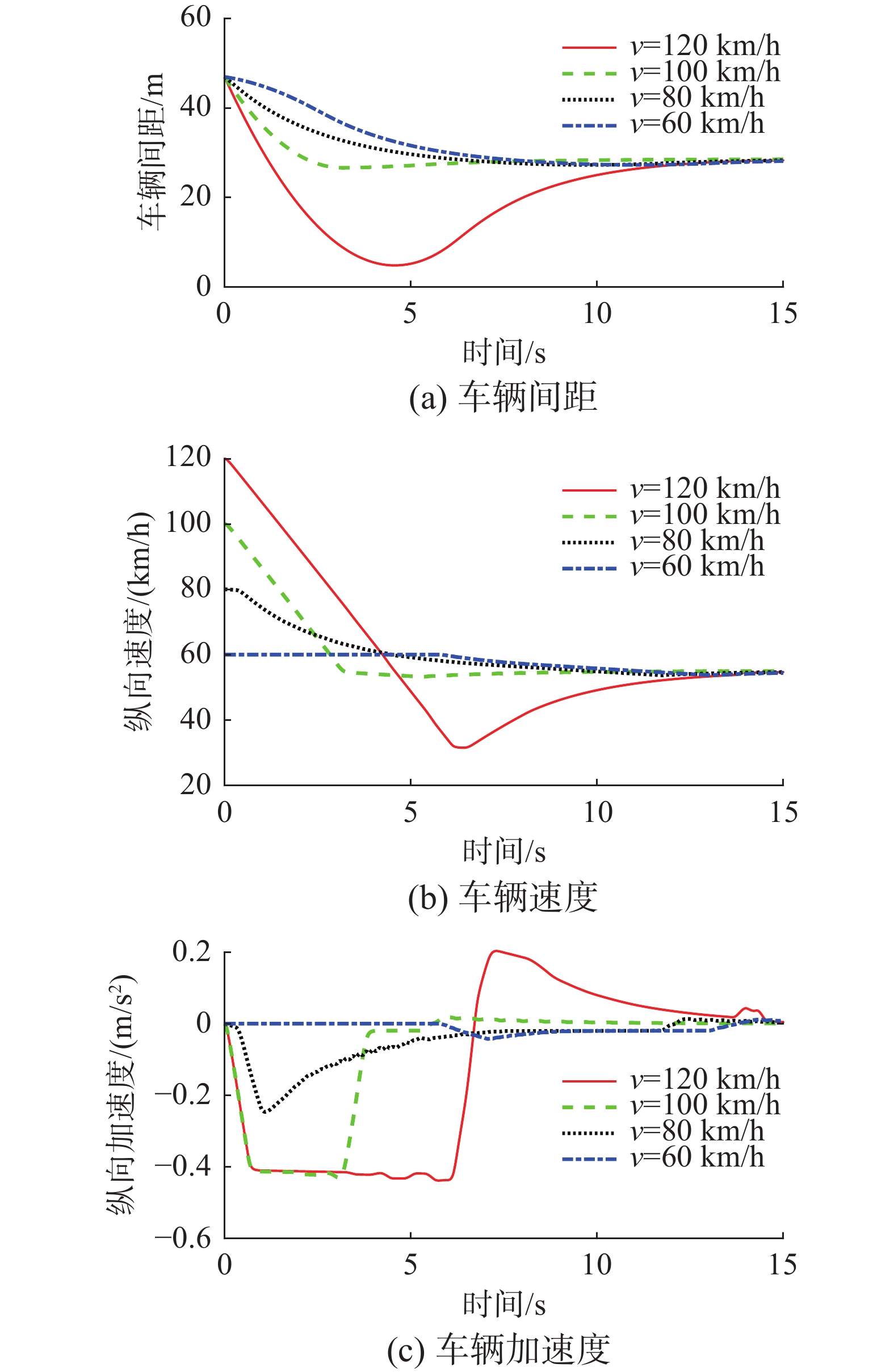
自车在无法进行换道避障时，会采取减速制动，避免与前方车辆发生碰撞。在确保不会与前车发生碰撞后，停止减速；当自车速度小于前方障碍车辆的速度，MPC控制器会使汽车加速，直到再次受到前方车辆势场力的作用，自车会与前方障碍车辆保持相同速度。
对自车设定不同的初始速度，通过避障仿真实验，获取车辆间距、自车速度和加速度的变化规律。不同自车速度的避障结果如图12所示。由图12可知，当v=120 km/h时，自车在0~5 s期间速度从初始避障车速开始减速，在确保与前车不会发生碰撞后，自车会停止制动，最终减速到35 km/h；自车在> 5~10 s期间，制动后的车速小于前方障碍车时，自车会进行一定的缓慢加速，直到受到前方车辆势场力的作用，自车会与前方障碍车辆保持相同的速度，以避免碰撞。通过对自车设定不同的初始速度可以看出，自车的速度越小，制动时间和车辆间距恢复到势场力影响阈值时间也越短。
图 12 不同速度的跟驰避障对比Fig. 12 Obstacle avoidance with different velocities下载:
全尺寸图片
3）场景3(图8)
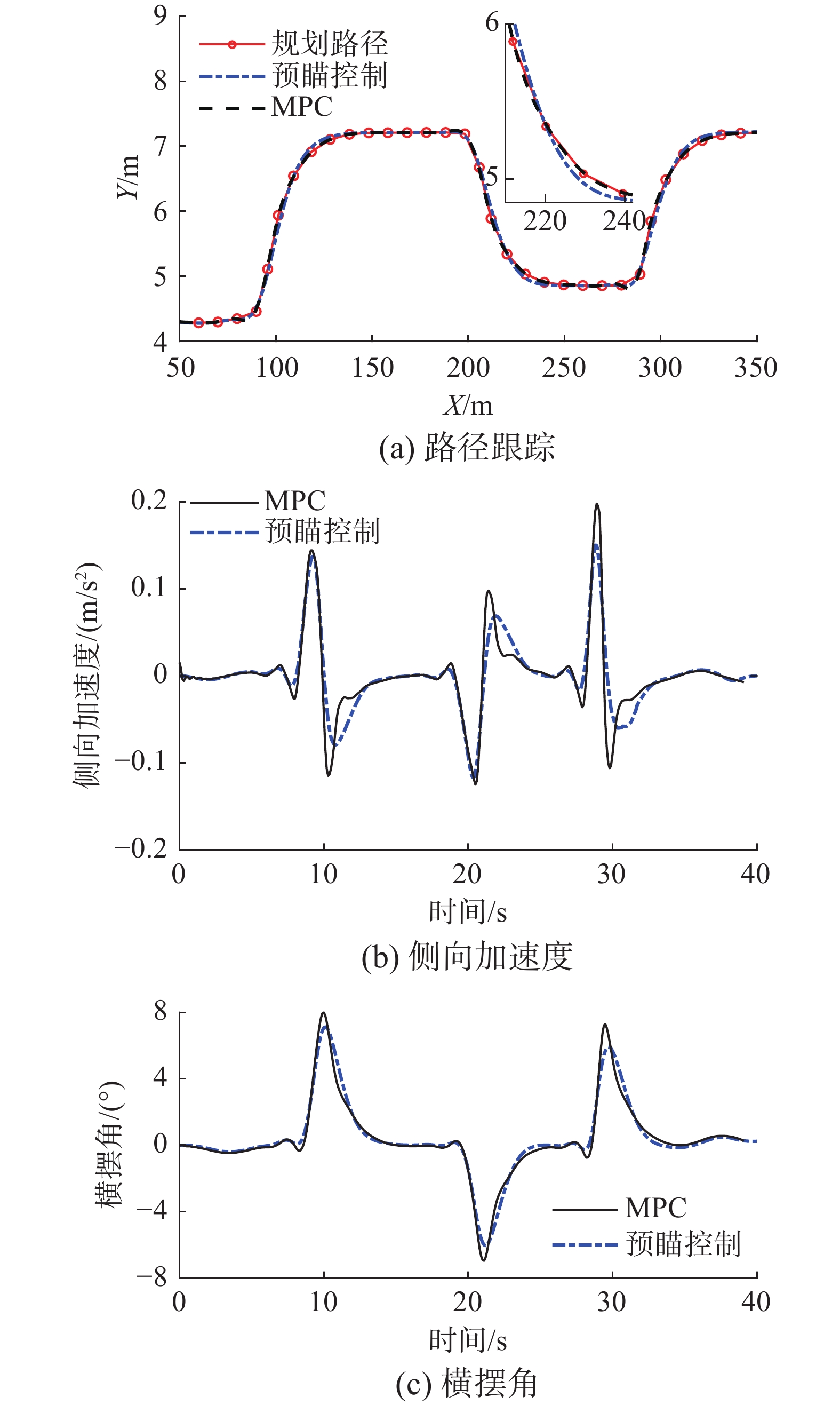
设定车速度大于障碍车辆的行驶速度，障碍车分别以不同的速度在3个车道内行驶。避障路径跟踪仿真结果如图13所示。
图 13 复杂交通场景避障路径跟踪对比Fig. 13 Path tracking in complex environments下载:
全尺寸图片
从图13可得，复杂交通场景下与预瞄控制相比，MPC跟踪精度更高，同时MPC作用的侧向加速度、横摆角响应亦有所增加，但仍在允许范围内。
4. 结束语
提出了一种基于改进势场模型和HMM的避障路径规划方法，并利用MPC对规划的避障路径进行跟踪。1）建立了包含道路条件、车辆状态参数的改进势场模型，分析了车辆特性对碰撞风险的影响，并将该参数纳入到势场的梯度系数中，提高风险预测精度；2）对势场的纵向与横向梯度力进行了分解，利用HMM预测避障方式，完成避障路径规划，与传统势场法相比，所提改进方法在复杂交通环境中可以避免规划路径陷入局部最小值中，改善转弯曲率，减少自车的动作；3）建立了基于MPC的避障路径跟踪控制器，实现动态避障的同时，提高了车辆的安全性与舒适性。
-
图 1 避障流程
Fig. 1 Flow of obstacle avoidance
下载:
全尺寸图片
图 2 隐马尔可夫模型
Fig. 2 Hidden Markov model
下载:
全尺寸图片
图 3 势场力分解示意
Fig. 3 Diagram of potential field force decomposition
下载:
全尺寸图片
图 4 障碍物势场
Fig. 4 Obstacle potential field
下载:
全尺寸图片
图 5 复杂交通场景的驾驶风险场
Fig. 5 Driving risk field in complex traffic scenario
下载:
全尺寸图片
图 6 换道避障路径规划
Fig. 6 Path planning by lane change
下载:
全尺寸图片
图 7 跟驰避障路径规划
Fig. 7 Path planning by car following
下载:
全尺寸图片
图 8 复杂交通场景路径规划
Fig. 8 Path planning in complex environments
下载:
全尺寸图片
图 9 不同参数取值的路径规划
Fig. 9 Path planning with different parameters
下载:
全尺寸图片
图 10 MPC路径跟踪
Fig. 10 MPC for path tracking
下载:
全尺寸图片
图 11 换道避障路径跟踪对比
Fig. 11 Path tracking of obstacle avoidance by lane-change
下载:
全尺寸图片
图 12 不同速度的跟驰避障对比
Fig. 12 Obstacle avoidance with different velocities
下载:
全尺寸图片
图 13 复杂交通场景避障路径跟踪对比
Fig. 13 Path tracking in complex environments
下载:
全尺寸图片
表 1 不同道路的附着相关参数
Table 1 Friction parameters at different road conditions
道路情况 C1 C2 C3 干沥青道路 1.280 1 23.990 0.520 0 干混凝土道路 1.197 3 25.186 0.537 3 雪地道路 0.050 0 306.390 0.000 0 结冰道路 0.194 6 94.129 0.064 6 表 2 仿真参数
Table 2 Simulation parameters
参数 值 参数 值 mq/kg 1500 ζ 1 Hq 1.3 δl 1 Gq 1 k1 0.1 Aq 0.01 k2 50 Tc 1 Wq 0.8 β/(°) 0 Tq 1 Ar 10 η1 1 Al 30 η2 1 Dis/m 100~1000 μ 0.8 Np 15 ε 2 Nc 2 Cf 61224 a,b/m 1.23,1.47 Cr 42500 表 3 仿真参数
Table 3 Vehicle characteristic parameters
类型 型号 质量/kg 车速/(km/h) 1 (卡车) MercedesBenz_Actros_6x2 2750 85 2 (轿车) Roewe_550_S_Sedan 1590 65 3 (卡车) Nissan_Cabstar_Boxtruck 2150 90 4 (轿车) Audi_A8_Sedan 1770 95 5 (轿车) Toyota_Yaris_Hatchback 1420 96 6 (轿车) Ford_Fiesta_Hatchback 1480 97 7 (轿车) BMW_Z3_Convertible 1690 100 8 (卡车) MercedesBenzActros+Trailer 4970 98 9 (轿车) Ford_Focus_Stationwagon 1450 108 -
[1] 李克强, 戴一凡, 李升波, 等. 智能网联汽车(ICV)技术的发展现状及趋势[J]. 汽车安全与节能学报, 2017, 8(1): 1–14. LI Keqian, DAI Yifan, LI Shengbo, et al. Development status and trend of intelligent networked vehicle (ICV) technology[J]. Journal of automotive safety and energy, 2017, 8(1): 1–14. [2] MAN J H, JIAN W, HONG M Q, et al. Coordinated collision avoidance for connected vehicles using relative kinetic energy density[J]. International journal of automotive technology, 2017, 18(5): 923–932. doi: 10.1007/s12239-017-0090-9 [3] 阮晓钢, 周静, 张晶晶, 等. 基于子目标搜索的机器人目标导向RRT路径规划算法[J]. 控制与决策, 2020, 35(10): 2543–2548. RUAN Xiaogang, ZHOU Jing, ZHANG Jingjing, et al. Robot goal guide RRT path planning based on sub-target search[J]. Control and Decision, 2020, 35(10): 2543–2548. [4] RADMANESH M, KUMAR M, GUENTERT P H, et al. Overview of path planning and obstacle avoidance algorithms for UAVs: a comparative study[J]. Unmanned systems, 2018, 6(2): 95–118. doi: 10.1142/S2301385018400022 [5] 张伟, 郁晨曦, 滕延斌, 等. 基于模型预测控制的UUV路径跟踪控制研究[J]. 仪器仪表学报, 2017, 38(11): 2659–2666. doi: 10.3969/j.issn.0254-3087.2017.11.006 ZHANG Wei, YU Chenxi, TENG Yanbin, et al. Research on UUV path tracking control based on model predictive control[J]. Chinese journal of scientific instrument, 2017, 38(11): 2659–2666. doi: 10.3969/j.issn.0254-3087.2017.11.006 [6] CHENG S, LI L, CHEN X, et al. Model-predictive- control-based path tracking controller of autonomous vehicle considering parametric uncertainties and velocity varying[J]. IEEE transactions on industrial electronics, 2021, 68(9): 8698–8707. doi: 10.1109/TIE.2020.3009585 [7] 江明, 王飞, 葛愿, 等. 基于改进蚁群算法的移动机器人路径规划研究[J]. 仪器仪表学报, 2019, 40(2): 113–121. doi: 10.19650/j.cnki.cjsi.J1804429 JIANG Ming, WANG Fei, GE Yuan, et al. Research on path planning of mobile robot based on improved ant colony algorithm[J]. Chinese journal of scientific instrument, 2019, 40(2): 113–121. doi: 10.19650/j.cnki.cjsi.J1804429 [8] 孙功武, 苏义鑫, 顾轶超, 等. 基于改进蚁群算法的水面无人艇路径规划[J]. 控制与决策, 2021, 36(4): 847–856. SUN Gongwu, SU Yixin, GU Yichao, et al. Path planning for unmanned surface vehicle based on improved ant colony algorithm[J]. Control and decision, 2021, 36(4): 847–856. [9] 欧阳勇平, 魏长, 蔡帛良. 动态环境下分布式异构多机器人避障方法研究[J]. 智能系统学报, 2022, 17(4): 752–763. OUYANG Yongping, WEI Changyun, CAI Boliang. Collision avoidance approach for distributed heterogeneous multirobot systems in dynamic environments[J]. CAAI transactions on intelligent systems, 2022, 17(4): 752–763. [10] HUANG Y, DING H, ZHANG Y, et al. A motion planning and tracking framework for autonomous vehicles based on artificial potential field elaborated resistance network approach[J]. IEEE transactions on industrial electronics, 2019, 67(2): 1376–1386. [11] ZHOU L, LI W. A potential field method approach to intelligent vehicle path planning[J]. Journal of computational information systems, 2015, 11(9): 3285–3295. [12] CAO Haotian, SONG Xiaolin, HUANG Zhengyu, et al. Simulation research on emergency path planning of an active collision avoidance system combined with longitudinal control for an autonomous vehicle[J]. Proceedings of the institution of mechanical engineers, part d:journal of automobile engineering, 2016, 230(12): 1624–1653. doi: 10.1177/0954407015618533 [13] JI J, KHAJEPOUR A, MELEK W W, et al. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints[J]. IEEE transactions on vehicular technology, 2017, 66(2): 952–964. doi: 10.1109/TVT.2016.2555853 [14] 徐杨, 陆丽萍, 褚端峰, 等. 无人车辆轨迹规划与 跟踪控制的统一建模方法[J]. 自动化学报, 2019, 45(4): 799–807. XU Yang, LU Liping, CHU Duanfeng, et al. Unified modeling of trajectory planning and tracking for unmanned vehicle[J]. Acta automatica sinica, 2019, 45(4): 799–807. [15] 赵治国, 周良杰, 朱强. 无人驾驶车辆路径跟踪控制预瞄距离自适应优化[J]. 机械工程学报, 2018, 54(24): 166–173. doi: 10.3901/JME.2018.24.166 ZHAO Zhiguo, ZHOU Liangjie, ZHU Qiang. Preview distance adaptive optimization for the path tracking control of unmanned vehicle[J]. Journal of mechanical engineering, 2018, 54(24): 166–173. doi: 10.3901/JME.2018.24.166 [16] 李军, 唐爽, 黄志祥, 等. 融合稳定性的高速无人驾驶车辆纵横向协调控制方法[J]. 交通运输工程学报, 2020, 20(2): 205–218. LI Jun, TANG Shuang, HUANG Zhixiang, et al. Longitudinal and lateral coordination control method of high-speed unmanned vehicles with integrated stability[J]. Journal of traffic and transportation engineering, 2020, 20(2): 205–218. [17] WANG J, WU J, LI Y. The driving safety field based on driver-vehicle-road interactions[J]. IEEE transactions on intelligent transportation systems, 2015, 16(4): 2203–2214. doi: 10.1109/TITS.2015.2401837 [18] HOU D J, SUN X D, HE Y L. Study on the relationship between speed difference and crash rate on freeway[C]//Tenth International Conference of Chinese Transportation Professionals. Beijing: [s.n.], 2010: 354−359. [19] 李巧茹, 刁文文, 陈亮, 等. 多车型自适应性动态称重阈值模型及评价[J]. 河北工业大学学报, 2014, 43(2): 92–96. doi: 10.14081/j.cnki.hgdxb.2014.02.016 LI Qiaoru, DIAO Wenwen, CHEN Liang, et al. Formulation and evaluation of multi-truck-type dynamic weight threshold model for WIM operations[J]. Journal of Hebei University of Technology, 2014, 43(2): 92–96. doi: 10.14081/j.cnki.hgdxb.2014.02.016 [20] ASHLEY W S, STRADER S, DZIUBLA D C, et al. Driving blind: weather-related vision hazards and fatal motor vehicle crashes[J]. Bulletin of the american meteorological society, 2015, 96(5): 755–778. doi: 10.1175/BAMS-D-14-00026.1 [21] 冯蕾, 邓毅萍, 李蔼恂, 等. 雾天高速公路交通事故的特征及与能见度的关系[J]. 科技导报, 2020, 38(11): 160–168. doi: 10.3981/j.issn.1000-7857.2020.11.018 FENG Lei, DENG Yipin, LI Aixun, et al. The characteristics of traffic accidents in expressway in fog days and their relationship with visibility[J]. Science & technology review, 2020, 38(11): 160–168. doi: 10.3981/j.issn.1000-7857.2020.11.018 [22] 李磊, 章国胜, 宋健, 等. 基于等效坡度的自动手动变速器换档规律研究[J]. 公路交通科技, 2011, 28(2): 144–148. doi: 10.3969/j.issn.1002-0268.2011.02.025 LI Lei, ZHANG Guosheng, SONG Jian, et al. Research on automated manual transmission shift schedule based on equivalent slope[J]. Journal of highway and transportation research and development, 2011, 28(2): 144–148. doi: 10.3969/j.issn.1002-0268.2011.02.025 [23] ZHAO Youqun, LI Haiqing, LIN Fen, et al. Estimation of road friction coefficient in different road conditions based on vehicle braking dynamics[J]. Chinese journal of mechanical engineering, 2017, 30: 982–990. doi: 10.1007/s10033-017-0143-z [24] MOREAU J, MELCHIOR P, VICTOR S, et al. Path planning with fractional potential fields for autonomous vehicles[J]. IFAC-PapersOnLine, 2017, 50(1): 14533–14538. doi: 10.1016/j.ifacol.2017.08.2076 [25] 刘志强, 吴雪刚, 倪捷, 等. 基于HMM和SVM级联算法的驾驶意图识别[J]. 汽车工程, 2018, 40(7): 858–864. doi: 10.19562/j.chinasae.qcgc.2018.07.017 LIU Zhiqiang, WU Xuegang, NI Jie, et al. Driving intention recognition based on HMM and SVM cascade algorithm[J]. Automotive engineering, 2018, 40(7): 858–864. doi: 10.19562/j.chinasae.qcgc.2018.07.017 [26] 田洪清, 丁峰, 郑讯佳, 等. 基于势能场虚拟力的智能网联车辆运动规划[J]. 汽车工程, 2021, 43(4): 518–526. doi: 10.19562/j.chinasae.qcgc.2021.04.009 TIAN Hongqing, DING Feng, ZHENG Xunjia, et al. Motion planning based on virtual force of potential field for intelligent connected vehicles[J]. Automotive engineering, 2021, 43(4): 518–526. doi: 10.19562/j.chinasae.qcgc.2021.04.009 [27] 丁洁云, 党睿娜, 王建强, 等. 驾驶人换道决策分析及意图识别算法设计[J]. 清华大学学报(自然科学版), 2015, 55(7): 769–774. doi: 10.16511/j.cnki.qhdxxb.2015.07.011 DING Jieyun, DANG Ruina, WANG Jianqiang, et al. Driver lane change decision analysis and intention recognition algorithm[J]. Journal of Tsinghua University (science and technology edition), 2015, 55(7): 769–774. doi: 10.16511/j.cnki.qhdxxb.2015.07.011 [28] 汪波, 张建勋, 侯之旭. 应用人工势场算法的智能车路径规划[J]. 重庆理工大学学报(自然科学版), 2015, 29(6): 107–111. WANG Bo, ZHANG Jianxun, HOU Zhixu. Path planning for intelligent vehicle based on artificial potential field method[J]. Journal of Chongqing University of Technology (natural science edition), 2015, 29(6): 107–111. [29] GUO C, WANG X, Su L, et al. Safety distance model for longitudinal collision avoidance of logistics vehicles considering slope and road adhesion coefficient[J]. Proceedings of the institution of mechanical engineers, Part D: journal of automobile engineering, 2020, 235(1): 1–15. [30] WANG Yang, MA Jianming, WANG Ying. Application of ant colony algorithm in path planning of the data center room robot[J]. AIP conference proceedings, 2017, 1839(1): 1–5. [31] 劳彩莲, 李鹏, 冯宇. 基于改进A*与DWA算法融合的温室机器人路径规划[J]. 农业机械学报, 2021, 52(1): 14–22. LAO Cailian, LI Peng and FENG Yu. Path planning of greenhouse robot based on fusion of improved A* algorithm and dynamic window approach[J]. Transactions of the Chinese society for agricultural machinery, 2021, 52(1): 14–22. [32] 李升波, 王建强, 李克强. 软约束线性模型预测控制系统的稳定性方法[J]. 清华大学学报(自然科学版), 2010, 50(11): 1848–185. doi: 10.16511/j.cnki.qhdxxb.2010.11.029 LI Shengbo, WANG Jianqiang, LI Keqiang. Stability method of soft constrained linear model predictive control system[J]. Journal of Qinghua University (natural science edition), 2010, 50(11): 1848–185. doi: 10.16511/j.cnki.qhdxxb.2010.11.029
