Submarine cable vibration signal recognition based on BS-1DCNN
-
摘要: 光纤振动信号是非线性的，传统的非线性振动信号识别方法通常需要信号分析和特征选择，既耗时又复杂。本文提出一种光纤振动信号识别新方法，可以直接提取特征，对原始信号进行分类，简化识别过程。本方法用支持向量机代替Softmax分类器，优化一维卷积神经网络（one-dimensional convolution neural network，1DCNN），以提高1DCNN结果在小样本条件下的稳定性。采用鸟群算法（bird swarm algorithm，BSA）对支持向量机(support vector machine，SVM)参数进行了优化，有效地提高识别精度。将本文提出的BS-1DCNN方法与1DCNN、VMD-GA-SVM、VMD-PSO-SVM、VMD-BSA-SVM共4种方法进行比较，结果表明，BS-1DCNN在识别准确率和测试时间方面性能表现良好。该算法能有效提高海缆振动信号识别率，且在不同样本比例下均能达到较好的识别效果。Abstract: Optical fiber vibration signals are nonlinear. Conventional nonlinear vibration signals recognition methods usually require signal analysis and features selection, both time-consuming and complex. In this paper, we propose a new method for optical fiber vibration signals recognition that can directly extract features, classify original signals and simplify the recognition process. In our method, the one-dimensional convolutional neural network (1DCNN) is improved by replacing the Softmax classifier with a support vector machine, so as to improve the stability of 1DCNN results under small sample conditions. Moreover, the bird swarm algorithm (BSA) is applied to optimize the support vector machine(SVM) parameters, improving the recognition accuracy effectively. The performance of the proposed method is compared with that of other four methods, namely 1DCNN, variational mode decomposition (VMD) and SVM optimized by genetic algorithm (VMD-GA-SVM), VMD and SVM optimized by particle swarm optimization (VMD-PSO-SVM), VMD and SVM optimized by bird wwarm algorithm (VMD-BSA-SVM). The results show that our BS-1DCNN method performs better in accuracy and timeliness and the recognition accuracy is satisfactory. The algorithm can effectively improve the recognition rate of marine cable vibration signals, and can achieve better recognition effect under different sample proportions.
-
随着国内近海岛礁经济的快速发展和近海风电建设的推进，光纤复合海底电缆（以下简称“海缆”）在跨海输电和通信传输中的重要性不断增加[1]。然而，由于海缆所处的海洋环境复杂多变，它经常会受到冲刷、摩擦和锚砸等多种因素的影响，这些因素对海缆的安全和可靠运行构成了潜在的威胁。海缆故障一经出现，将会对通信传输、经济等造成较大影响[2]。利用光纤传感技术对海缆中的光纤振动信号进行监测，可以实现对海缆故障的早期预警和故障类型的识别。这种监测方法可以确保海缆的正常工作，同时减少海缆运维的成本并提高工作效率，因此对海缆健康状态监测具有重要意义。
常规的振动信号识别方法需要对原始信号进行预处理，提取信号的故障特征，如小波变换法(wavelet transform, WT)、集合经验模态分解(ensemble empirical mode decomposition, EEMD)[3]、变分模态分解(variational mode decomposition , VMD) [4]等；然后利用分类算法检测故障类型，其中比较有代表性的分类器有BP神经网络(back propagation, BP)、支持向量机(support vector machine, SVM)[5-6]等。而卷积神经网络融合特征提取及分类识别于一体，节省了时间。近几年基于卷积神经网络（convolution neural network, CNN）的智能故障诊断算法得到了快速发展，CNN的突出优势在于可以直接从输入数据中提取和选择特征，从而减少了工作量[7-8]。2019年，Huang等[9]直接将各类原始振动信号送到一维卷积神经网络（one-dimensional convolution neural network , 1DCNN）中识别，实现了智能故障诊断，提高诊断的准确性和运行效率。2022年，Ma等[10]采用多尺度特征融合的CNN对四类光纤振动信号进行识别，取得了良好的识别效果。2021年，喻后聃等[11]利用一维卷积神经网络提取光纤周界信号的频域特征，对频率成分复杂的信号识别效果显著。2022年，李世晓等[12]基于1DCNN实现了机电振动信号故障诊断，具有较好的识别率、鲁棒性、泛化能力及抗噪性能。
卷积神经网络在小样本情况下容易出现结果的不稳定性，但卷积神经网络训练能很好地适用于大样本条件[10]；SVM对小样本的学习能力强、分类应用较好[5]，但对于大规模数据集计算复杂度高。因此，本文提出了一种BS-1DCNN算法，BS-1DCNN算法利用了1DCNN和SVM互补特性，结合了1DCNN及SVM的优点并改进了各自的局限性。1DCNN自适应地从冲刷、摩擦及锚砸3类海缆振动信号中提取振动信号识别的特征信息，为达到最佳分类效果，更加高效地识别各类海缆故障；通过鸟群算法（bird swarm algorithm, BSA）优化SVM中的相关参数，有效解决局部最优问题，提高分类精度；最后采用鸟群优化的支持向量机分类器对提取的故障特征进行精细识别。将本文算法性能同1DCNN[13]、VMD-GA-SVM[14]、VMD-PSO-SVM[15]、VMD-BSA-SVM[16]进行对比，本文算法在准确率和实时性方面表现良好。
1. 算法原理
1.1 1DCNN算法
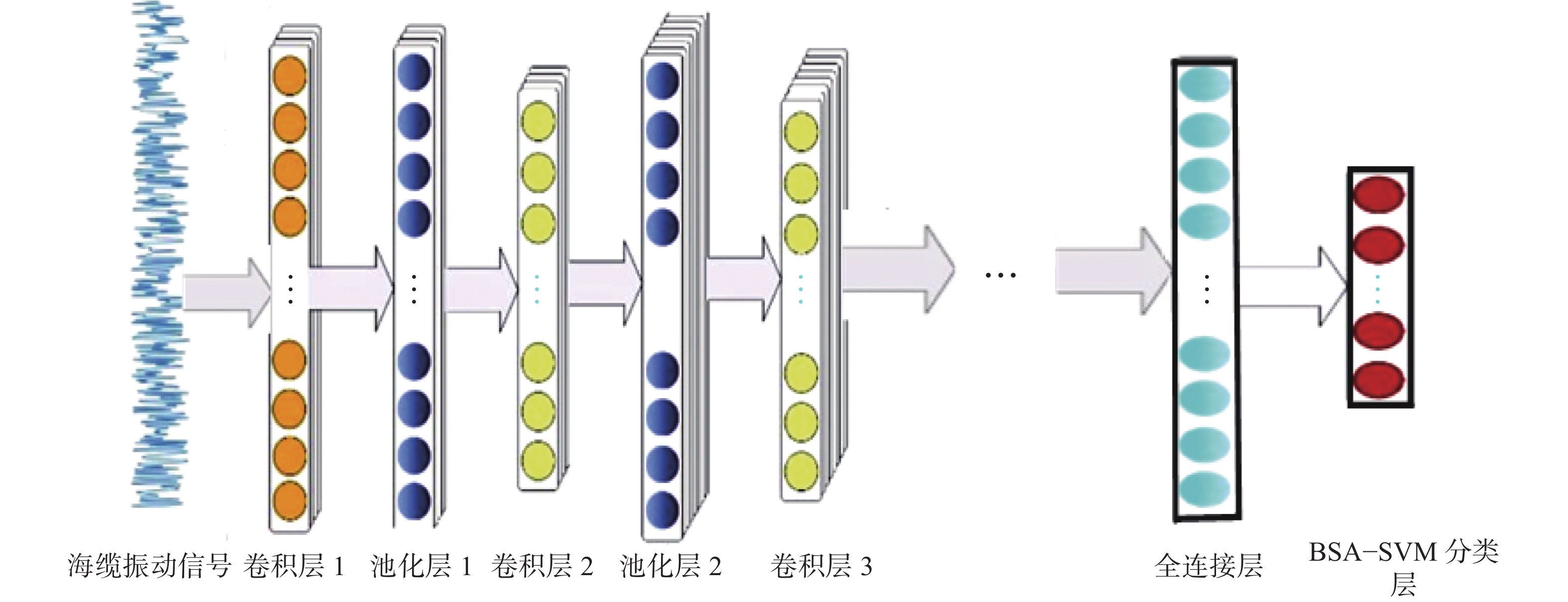
1DCNN的输入是一维数据，其通常由输入层、卷积层、池化层、全连接层和输出层组成[17]。传统1DCNN分类一般在输出层采用Softmax分类器[18]，本文采用鸟群优化的SVM代替传统的Softmax分类器，结构如图1所示。
图 1 1DCNN结构Fig. 1 1DCNN structure
下载:
全尺寸图片
卷积层将一维卷积核同一维的输入信号进行卷积，局部特征可以通过卷积层中激活函数进行提取。本文选择激活函数为ReLu，以避免过拟合[19]。卷积过程为
$$ x_l^j = \sum\limits_{i = 1}^n {{{\rm{conv}}} (\omega _{ik}^{j - 1}} ,s_i^{j - 1}) + b_l^j $$ 式中：第
$ j - 1 $ 层的第i个神经元的输出量用$ s_i^{j - 1} $ 表示；在第j层中，第l个神经元的输出量用$ x_l^j $ 表示，偏移值大小用$ b_l^j $ 表示；同时，第j−1层的第i个神经元和第j层的第k个神经元之间的卷积核用$ \omega _{ik}^{j - 1} $ 表示。其中，i的取值范围是1~n，n代表神经元的数目。通过卷积层提取的海缆振动信号特征引入池化层，保留有用特征，减少不必要特征，使提取的特征更能反映不同类型的海缆故障。平均池化和最大池化是2种常见的池化操作。在本文中，采用最大池化操作，公式为
$$ {\textit{z}}_k^{j(\alpha )} = \mathop {\max }\limits_{(\alpha - 1)r + 1 \leqslant \beta \leqslant \alpha r} \{ y_k^{j(\beta )}\} $$ 式中：第
$ j $ 层中的第$ k $ 个神经元池化以后的第$ \alpha $ 个值用$ {\textit{z}}_k^{j(\alpha )} $ 表示，第$ j $ 层第$ k $ 个神经元内的第$ \beta $ 个激活值用$ y_k^{j(\beta )} $ 表示，池化区域宽度用r表示。全连接层不再对特征进行提取，而是先组合提取到的特征，然后映射至样本标记空间，最后在输出层实现分类结果的输出。
1.2 SVM的BSA优化过程
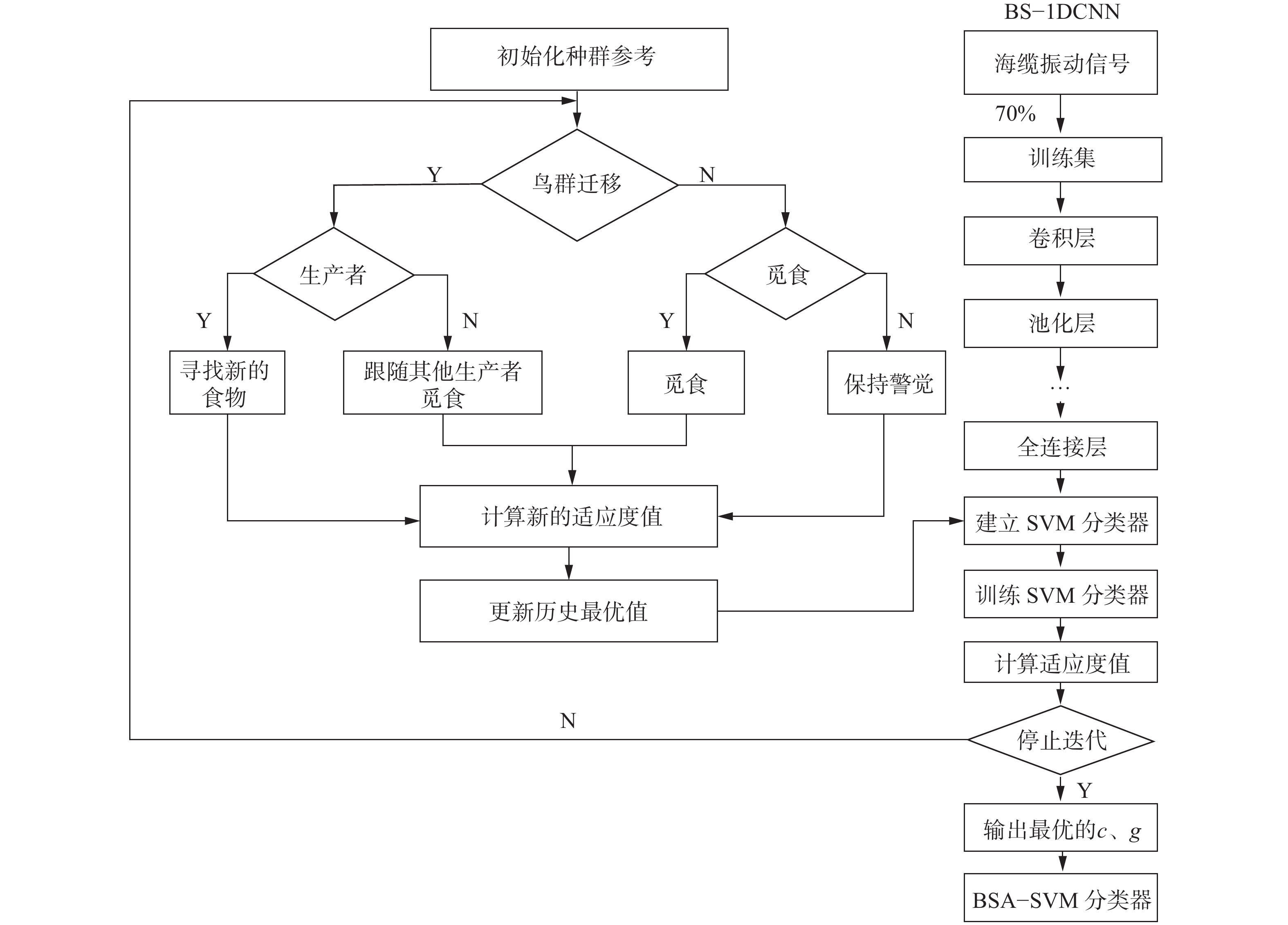
BSA-SVM模型的基本思想是利用鸟群算法来优化SVM模型中的惩罚参数c和径向基核函数的参数g的取值。在BSA-SVM模型中，将c和g作为鸟群的个体位置参数，通过适应度函数来评估每个个体鸟类的位置。适应度函数的值越高，表示个体的位置越优秀。为了更新鸟类的位置信息，BSA-SVM模型采用了觅食行为、警戒行为及飞行行为3种主要行为进行不断迭代和更新，最终BSA-SVM模型能够找到最优的惩罚参数c和径向基核函数的参数g的取值，从而建立一个最优的分类模型。本文中假设鸟群的种群规模初始化为N=30，飞行频率FQ=4，迭代次数M=150。SVM性能受惩罚参数
$ c $ 的影响，$ c $ 越大越容易陷入过拟合[20]，采用鸟群优化算法对参数寻优，找到最佳的($ c $ ，$ g $ )组合，提高准确率的同时避免过拟合。本文惩罚参数起始点$ c $ =0.1，搜索范围是[0.1，1000 ]；核参数$ g $ 起始点为0.01，搜索范围是[0.01，150]，迭代步长均为2，交叉验证次数v=10，认知系数T和社会加速系数S均为1.5。通过优化以输出最优的惩罚参数$ c $ 和核参数$ g $ ，最终分类结果采用$ c $ 和$ g $ 的最佳组合进行分类，具体步骤如下：1）数据标准化：将原始数据进行标准化处理，以避免收敛速度慢等问题。
$${y_i} = \frac{{{x_i} - \mathop {\min }\limits_{1 \leqslant j \leqslant n} \{ {x_j}\} }}{{\mathop {\max }\limits_{1 \leqslant j \leqslant n} \{ {x_j}\} - \mathop {\min }\limits_{1 \leqslant j \leqslant n} \{ {x_j}\} }},\quad i = 1,2, \cdots , n $$ 式中：yi表示归一化值，x表示原始数据，n为序列长度。
2）初始化BSA参数：随机生成个体初始位置的范围，即SVM的参数c和g的取值范围。同时设置种群规模N、迭代次数M、飞行频率
$ {F_Q} $ 、常数T、S等参数。3）训练和测试初始种群：使用SVM模型根据初始种群的参数c和g进行训练，并使用生成的模型对测试集进行分类。将分类精度作为适应度值，用于评估每个个体的位置。
$$ \alpha = \frac{{{n_i}}}{n} $$ 式中：α为分类精度，
$ {n_i} $ 为与实际样本类别一致的样本数，$ n $ 为样本总数。4）更新鸟类种群：根据觅食、警戒和飞行行为的策略，更新鸟类种群的位置。同时对参数c和g进行优化，得到新的参数c和g。
5）训练和测试新的参数：将新的参数c和g代入SVM模型进行训练和测试，得到新的适应度值，并更新历史最佳适应度。
6）判断终止条件：判断是否满足终止条件。如果满足条件，则输出最佳适应度值，并将对应的参数c和g作为最佳组合进行分类；如果不满足条件，则返回步骤4）并继续迭代。
1.3 BS-1DCNN混合模型
训练1DCNN模型，原始信号直接输入到1DCNN中提取与海缆故障诊断相关的特征，然后提取的特征由全连接层输出并送入输出层，最终在1DCNN的输出层使用鸟群优化的SVM分类器替换常规的Softmax分类器，进一步提升分类精度。混合模型训练流程如图2所示。
图 2 混合模型训练流程Fig. 2 Flow chart of the hybrid model training下载:
全尺寸图片
2. 算法性能分析与讨论
2.1 仿真信号获取
根据华北电力大学尚秋峰团队的研究，通过有限元仿真得到了海缆在不同故障情况下的信号[21-23]。以下是每个故障情况的具体描述：
锚砸故障信号：根据文献[21]的设定，船锚的质量为151 kg、下落速率为6.95 m/s、锚砸持续时间为0.05 s。海缆的长度为500 cm，重力加速度为9.8 m/s2。通过使用ANSYS软件进行仿真，提取了光单元的振动数据，进而得到了对应的锚砸故障信号。
冲刷故障信号：根据文献[22]的设定，在波浪高度为100 cm、速度为2 m/s、周期为1 s的匀速海浪条件下，构建了裸露的悬跨海缆的有限元模型。模型中重力加速度设为9.8 m/s2。通过有限元仿真，得到了海缆冲刷故障信号。
摩擦故障信号：根据文献[23]的设定，通过有限元分析法中的瞬态动力学分析方法，构建了岩石与海缆发生摩擦时的二维模型。摩擦时间设定为0.5 s，起始速度为0.25 m/s。通过有限元仿真，得到了海缆摩擦故障信号。
通过以上仿真得到了海缆在锚砸、冲刷和摩擦故障情况下的相应信号。
2.2 实验系统
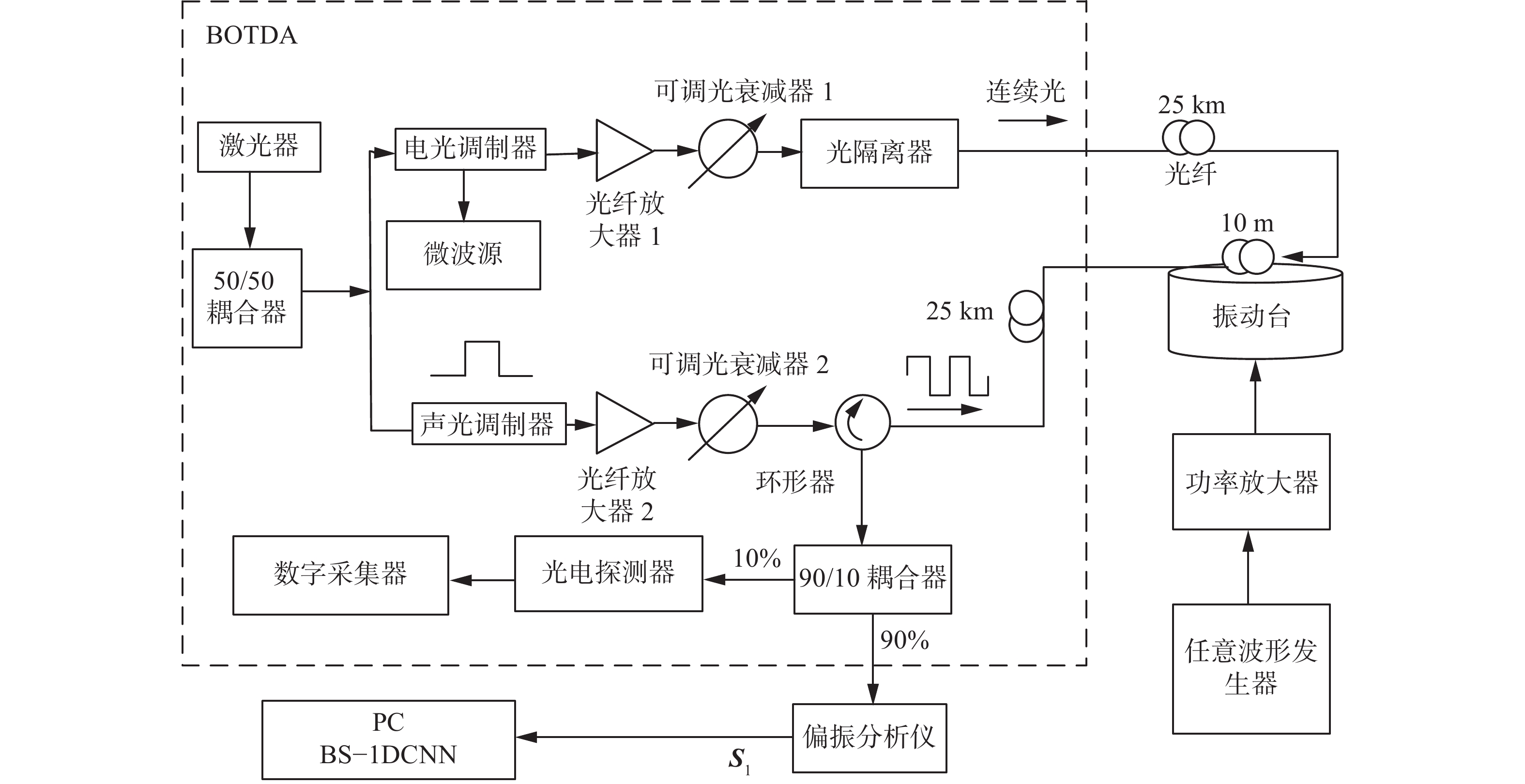
当光纤受到振动时，振动会引起光纤中的光信号偏振态发生变化。偏振分析仪可以测量光信号的偏振态，通过对这些信息的分析可以得到振动信号的变化规律。布里渊光时域分析技术(Brillouin optical time domain analysis，BOTDA)和偏振分析仪的结合可以同时监测海缆的温度、应变和偏振状态，实现对海缆状态的综合监测功能。根据布里渊散射原理，携带受激布里渊散射信息的探测光经环行器和保偏耦合器分光后进入2条路径：一条路径连接到光电探测器以检测温度、应变；另一条路径连接到偏振检测模块用于振动信号监测。实验系统原理如图3所示。
图 3 实验系统Fig. 3 Experimental system下载:
全尺寸图片
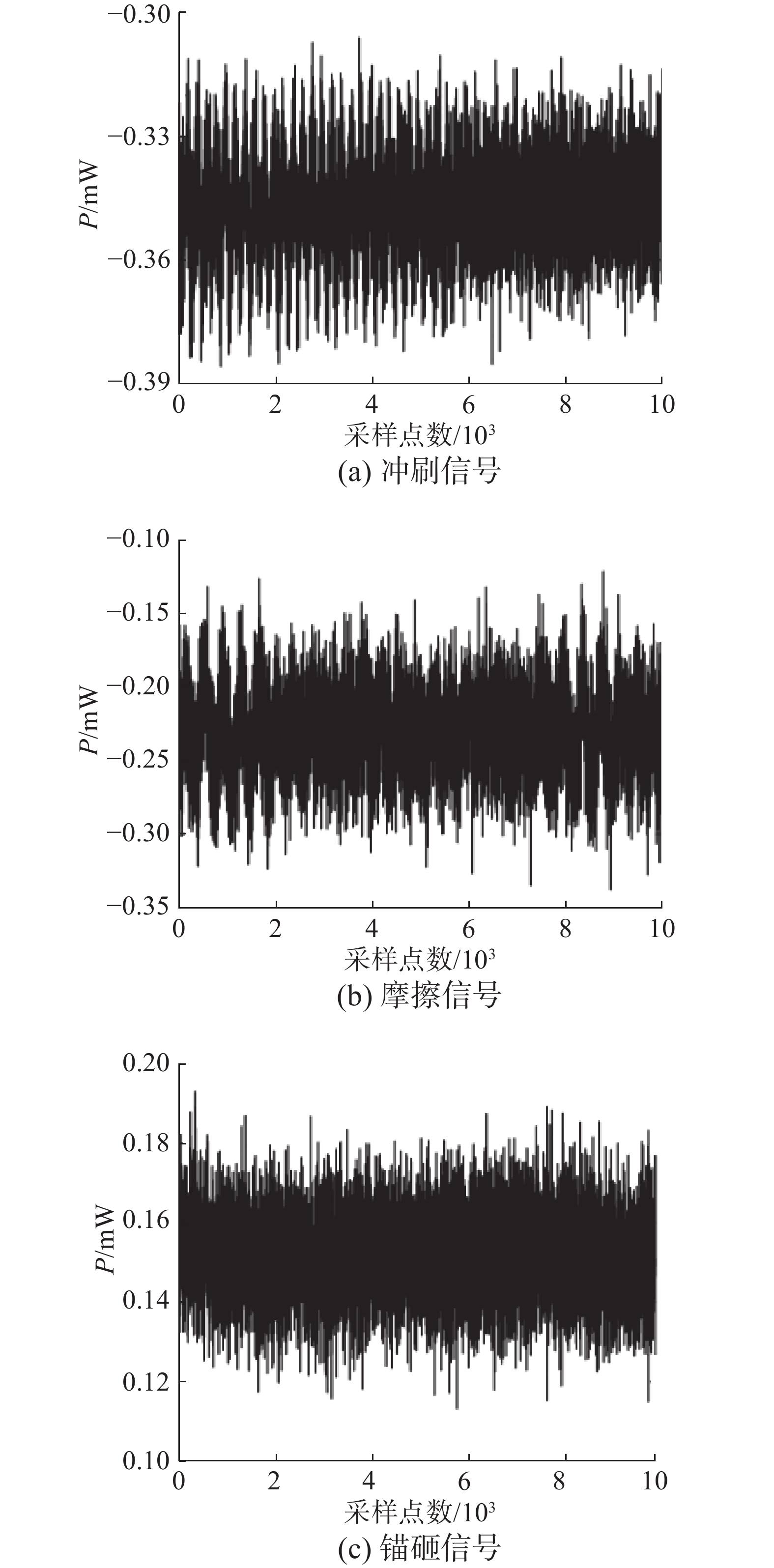
在室温条件下，选择一段长度大约为10 m的光纤跳线及两盘25 km长的光纤，将光纤跳线固定在振动台上，按照图3连接光路，光纤之间用法兰连接。首先打开偏振分析仪，然后打开BOTDA设备。根据第2.1节中得到的3个海缆故障信号，可以将这些信号分别输入到与振动台连接的任意波形发生器中，这样可以模拟实际海缆受到的振动情况，并产生相应的振动信号。其中任意波形发生器的振幅设为1.5 V，重复频率定为2 Hz。在发生SBS时，信号含有大量噪声，不利于对信号的分类识别。分别记录3种工况下在受激布里渊散射之前偏振分析仪输出的斯托克斯矢量S1的光功率。S1信号反映了振动段光纤产生摩擦、冲刷和锚砸3种故障形态对应的偏振态变化。通过实验得到多组海缆在锚砸、冲刷、摩擦工况的数据，以S1作为模型训练的数据集，如图4所示。
图 4 海缆振动信号Fig. 4 Submarine cable vibration signals下载:
全尺寸图片
2.3 实验平台及参数设置
本文硬件环境为64位的Win10操作系统，基于14核酷睿i7处理器，主频为2.6 GHz、内存为16 GB、固态硬盘容量为512 GB。
首先将海缆振动信号划分为训练集和测试集。通过实验共获得冲刷、摩擦及锚砸每类各
1000 组数据，将3000 组海缆振动信号数据的70%作为训练集，30%作为测试集。处理后的数据集有3个不同的类别，共包含2100 组训练集及900组测试集，冲刷信号标签为1，摩擦信号标签为2，锚砸信号标签为3。其中BS-1DCNN算法的参数如表1所示。本算法的全连接层共有64个神经元，分类层采用BSA-SVM分类器以提升分类精度。表 1 BS-1DCNN算法的参数Table 1 Parameters of the BS-1DCNN algorithm层名称 卷积核/池化长度 步长 输出特征 输入层 — — 1× 10000 卷积层1 32个5×1 5 32×2000 最大池化层1 池化长度2 5 32×400 卷积层2 64个3×1 2 64×200 最大池化层2 池化长度2 2 64×100 卷积层3 128个3 × 1 2 128×50 最大池化层3 池化长度2 2 128×25 卷积层4 128个3 × 1 1 128×24 卷积层5 256个3 × 1 4 256×6 最大池化层4 池化长度2 2 256×3 1DCNN模块经过卷积、激活、池化后自适应地提取3类海缆振动信号的相关特征信息，提取的特征信息再送入BSA-SVM分类器进行故障分类。为避免过拟合问题，该模型的损失函数为交叉熵损失函数，附加L2正则化对权重参数进行惩罚 [19]，表示为
$$ L_{{\rm{oss}}} = - \sum\limits_{i = 1}^3 {{y_i}} \log ({p_i}) + \eta {\left\| \theta \right\|^2} $$ 式中:
$ {y_i} $ 为海缆故障信号的实际标签值，$ {p_i} $ 为神经网络的输出，i为海缆故障的类别，$ \eta $ 为正则项系数，$ \left\| \theta \right\| $ 为为防止过拟合添加的正则化项。SVM分类算法典型的核函数有径向基核（radial basis function，RBF）、多项式核（polynomial）及sigmoid核。RBF核是一种应用广泛的核函数，可以适用于各种情况，不论数据规模大小或者数据的维度，RBF核函数都能够有效地进行模式识别和分类[24]。本文分别选用RBF核、多项式核及sigmoid核进行测试，各核函数的初始参数均采用LIBSVM工具箱中设定的默认值。表2为采用不同核函数时BS-1DCNN算法对3类海缆故障的分类结果。结果表明采用RBF核函数算法准确率最高、测试时间最短。因此，本文后面进行不同算法性能比较分析时，选用RBF核作为SVM的核函数。表 2 不同核函数下BS-1DCNN识别结果对比Table 2 Comparison of BS-1DCNN identification results under different kernel functions核函数类型 冲刷准确率/% 摩擦准确率/% 锚砸准确率/% 平均准确率/% 测试时间/s RBF 99.33 99.67 99.33 99.44 153.32 polynomial 99.00 99.33 99.33 99.22 167.58 sigmoid 99.33 99.00 99.00 99.11 159.64 3. 实验结果分析
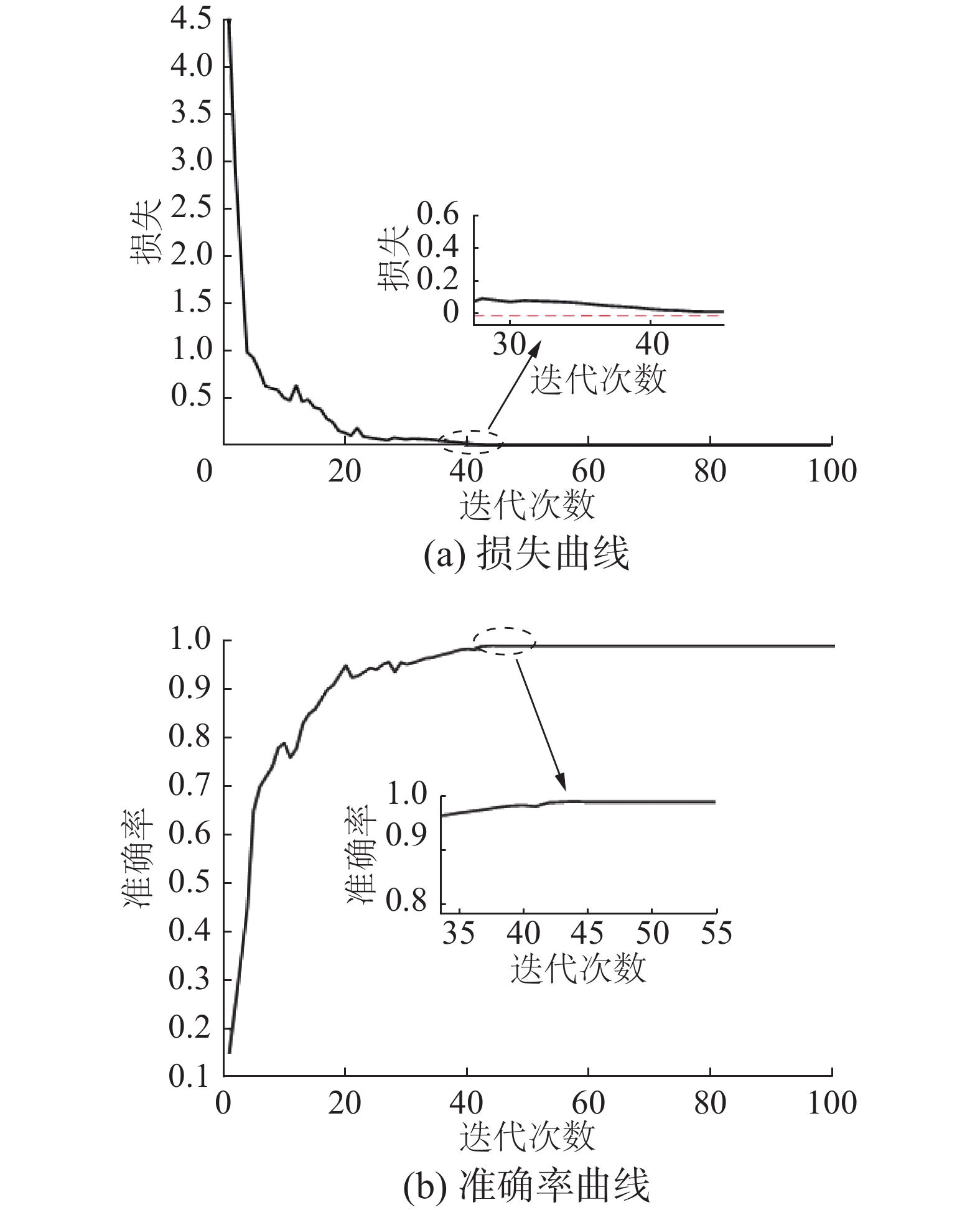
选取70%的样本数据作为混合模型的输入进行训练，剩余30%的样本数据用于测试训练模型的故障识别性能，共计得到
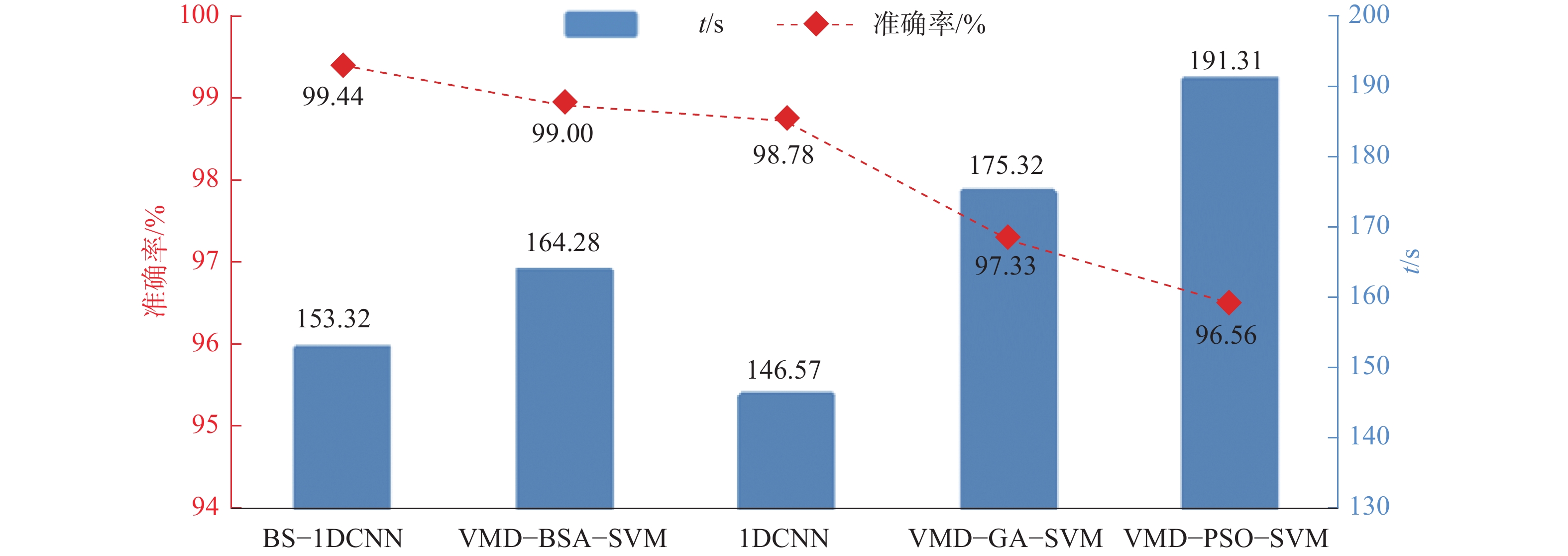
2100 组训练样本和900组测试样本。测试集的准确率曲线和损失曲线如图5所示。
图 5 准确率和损失曲线Fig. 5 Accuracy and loss curve下载:
全尺寸图片
经过100次迭代，在迭代43次左右损失降到最低，准确率基本达到了99.44%。实验将1DCNN、VMD-GA-SVM、VMD-PSO- SVM及VMD-BSA-SVM算法与本文所提出的算法对比。其中，对于VMD-GA-SVM、VMD-PSO-SVM及VMD-BSA-SVM算法，需要事先进行信号分析及特征提取。首先，使用VMD对3类故障信号进行分解，分别得到每个信号的6个模态分量。对于每个模态分量，计算其峭度、能量和能量熵这3个特征值，最终得到18个特征值（6个模态分量，每个模态分量有峭度、能量和能量熵3个特征值），这18个特征值构成每个故障信号的特征向量。为了进行分类训练，给冲刷信号的特征向量标签为1，摩擦信号的特征向量标签为2，锚砸信号的特征向量标签为3，将特征向量和对应的标签用于训练分类模型，以实现对不同故障信号的分类。1DCNN、VMD-GA-SVM、VMD-PSO-SVM 及VMD-BSA- SVM算法的相关参数设置与提出的算法相同（例如VMD分解层数、SVM初始惩罚参数等）。5种算法的准确率及测试时间如图6所示，BS-1DCNN算法在4类海缆振动信号识别算法中具有最高的识别精度，同时测试时间短。
图 6 各类算法比较Fig. 6 Comparison of various algorithms下载:
全尺寸图片
各算法时间复杂度评价如下：首先，对VMD-GA-SVM、VMD-PSO-SVM、VMD-BSA-SVM算法复杂度比较，只需要比较GA (genetic algorithm)、PSO（variational mode decomposition）及BSA算法复杂度即可。3类优化算法时间复杂度均可表示为
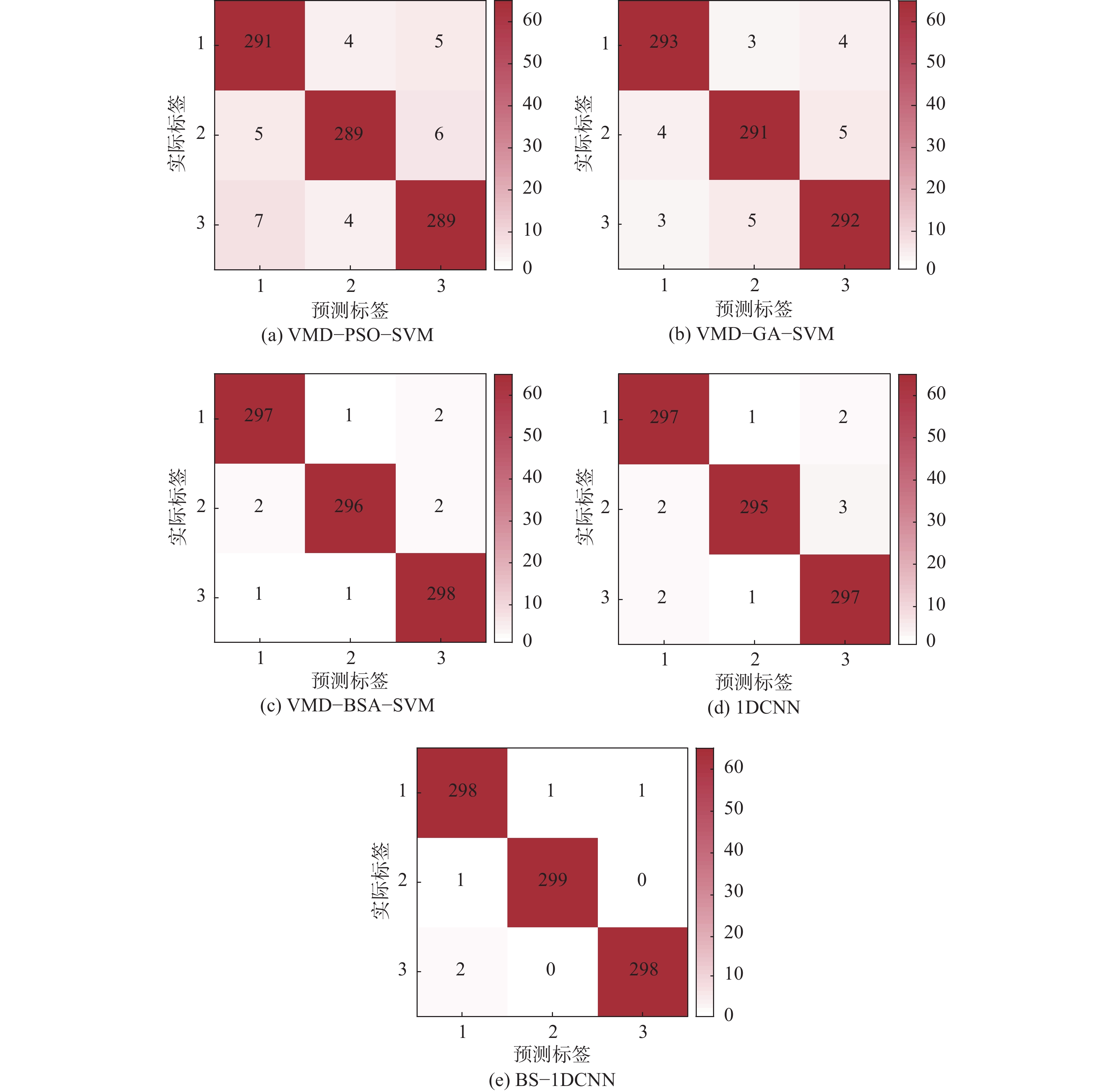
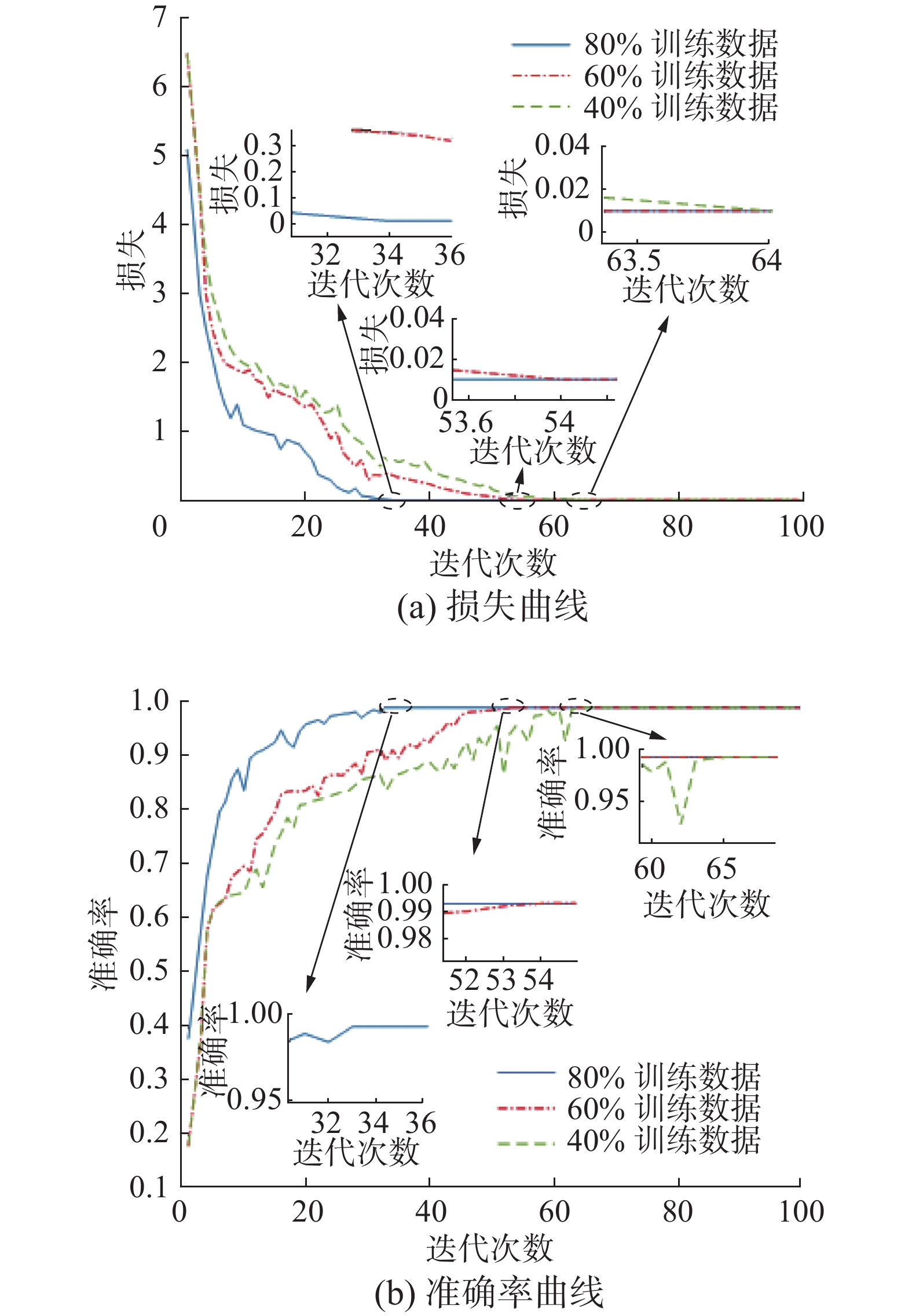
$ O（NM） $ [25-26]，其中，N为种群规模/粒子群数目，本文中3种算法设置相同的N值；M为准确率最佳时所需迭代次数。BSA算法比PSO和DE算法具有更好的优化精度、效率、稳定性和收敛性性能[25]，DE比GA具有更快的收敛速度和更好的准确度[27]。所以，在相同的软硬件配置条件下，VMD-BSA-SVM算法测试时间比VMD-GA-SVM及VMD-PSO-SVM算法时间短。其次，比较BS-1DCNN和VMD-BSA-SVM，主要比较1DCNN及VMD时间复杂度，1DCNN是基于卷积运算[12]，时间复杂度为$O\left({\displaystyle \sum _{l=1}^{5}{K}_{l}}{W}_{l}{}_{}{C}_{l-1}{C}_{l}\right)$ ，其中，$ {K_l} $ 为第$ l $ 个卷积层的卷积核序列维度；$ {W_l} $ 为第$ l $ 个卷积层的输出序列维度；$ {C_l} $ 是神经网络第$ l $ 个卷积层的输出通道数，也即该层的卷积核个数。如表1所示，各层卷积核序列维度均为3，各卷积层输出序列维度依次为2000 、200、50、24及6，各卷积层卷积核个数依次为32、64、128、128及256。VMD是求解变分模型[28-29]，VMD的时间复杂度为$ O(KnN{\log _2}N + N{\log _2}N) $ ，其中，N是序列长度，K是分解层数，n（n>1）是迭代次数，本文中$ N = 10\;000 $ ，$ K = 6 $ ，最大迭代次数为150。基于本文参数及实验环境，BS-1DCNN较VMD-BSA-SVM算法测试时间短。综上所述，和VMD-GA-SVM、VMD-PSO-SVM、VMD-BSA-SVM相比，BS-1DCNN具有最短的测试时间。根据图7中的混淆矩阵可以对算法的分类效果进行评估。混淆矩阵的横坐标代表海缆故障预测的状态类别标签，纵坐标代表海缆故障实际类别标签。混淆矩阵的左对角线上的值表示模型对每种类型的海缆故障状态正确预测的样本数。这些值越大，说明算法对海缆故障分类的准确性越高。通过改变训练样本比例，可以观察算法对不同数量的训练数据的适应能力。将训练样本的比例分别设置为80%、60%和40%，对比在3类训练样本比例下结果的准确率曲线和损失曲线，如图8所示。结果表明，对于损失曲线以及准确率曲线，不同比例下的训练样本分别在迭代34、54和64次左右达到最高识别率及最低损失，80%的训练数据收敛最快，60%的训练数据次之，40%的训练数据收敛最慢，不同比例训练样本下最终都能达到较高的识别率。
图 7 各类模型混淆矩阵Fig. 7 Confusion matrix of various models下载:
全尺寸图片
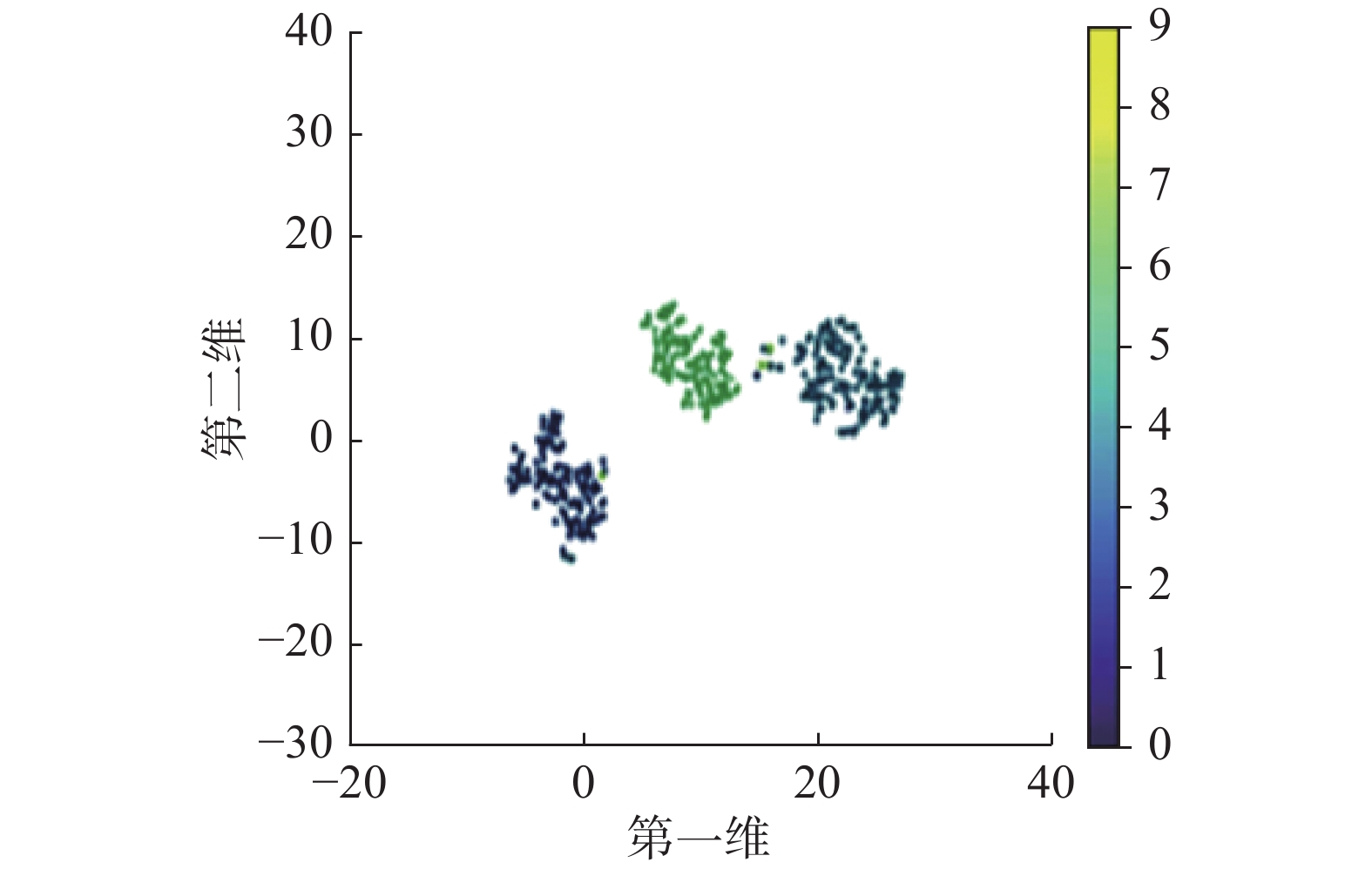
1DCNN的优点是可以自动提取样本数据的特征进行训练。为了验证该模型的特征提取能力，采用t分布随机邻域嵌入（t-SNE）方法将高维数据降维为二维数据并进行可视化[30]。因为混合模型的输出层是采用BSA-SVM分类，所以将上一层的全连接层输出作为模型提取的样本特征，将64维的特征降为二维特征并通过t-SNE方法显示。图9为混合模型提取的特征的可视化，很明显，海缆各类工况特征都很好地聚合在一起，并且不同的特征被有效地分开了。上述结果表明，混合模型具有出色的特征提取能力，能够有效提取故障诊断所需的特征。
图 8 不同训练集下准确率及损失曲线Fig. 8 Accuracy and loss curves under different training sets下载:
全尺寸图片
图 9 t-SNE图Fig. 9 t-SNE diagram下载:
全尺寸图片
4. 结束语
本文提出BS-1DCNN算法用于海缆故障识别。该算法降低了卷积神经网络在小样本情况下出现结果不稳定的概率，同时有效融合了SVM对小样本的学习能力强、分类应用较好的特点，BSA的作用是优化SVM分类器的相关参数，使混合模型工况识别更加准确有效。该方法将原始振动信号直接输入到1DCNN中进行特征提取，在整个识别过程中训练前不需要对原始数据进行信号处理和特征提取操作，该算法能够成功识别海缆振动信号，与其他4类智能诊断方法进行比较，识别率最高并且测试时间短。后续将进一步研究不同信噪比情况下各类海缆故障识别率并进行现场实验。本文工作为利用光纤传感技术进行光纤海缆状态监测提供了有效的分类识别方法。
-
图 1 1DCNN结构
Fig. 1 1DCNN structure
下载:
全尺寸图片
图 2 混合模型训练流程
Fig. 2 Flow chart of the hybrid model training
下载:
全尺寸图片
图 3 实验系统
Fig. 3 Experimental system
下载:
全尺寸图片
图 4 海缆振动信号
Fig. 4 Submarine cable vibration signals
下载:
全尺寸图片
图 5 准确率和损失曲线
Fig. 5 Accuracy and loss curve
下载:
全尺寸图片
图 6 各类算法比较
Fig. 6 Comparison of various algorithms
下载:
全尺寸图片
图 7 各类模型混淆矩阵
Fig. 7 Confusion matrix of various models
下载:
全尺寸图片
图 8 不同训练集下准确率及损失曲线
Fig. 8 Accuracy and loss curves under different training sets
下载:
全尺寸图片
图 9 t-SNE图
Fig. 9 t-SNE diagram
下载:
全尺寸图片
表 1 BS-1DCNN算法的参数
Table 1 Parameters of the BS-1DCNN algorithm
层名称 卷积核/池化长度 步长 输出特征 输入层 — — 1× 10000 卷积层1 32个5×1 5 32×2000 最大池化层1 池化长度2 5 32×400 卷积层2 64个3×1 2 64×200 最大池化层2 池化长度2 2 64×100 卷积层3 128个3 × 1 2 128×50 最大池化层3 池化长度2 2 128×25 卷积层4 128个3 × 1 1 128×24 卷积层5 256个3 × 1 4 256×6 最大池化层4 池化长度2 2 256×3 表 2 不同核函数下BS-1DCNN识别结果对比
Table 2 Comparison of BS-1DCNN identification results under different kernel functions
核函数类型 冲刷准确率/% 摩擦准确率/% 锚砸准确率/% 平均准确率/% 测试时间/s RBF 99.33 99.67 99.33 99.44 153.32 polynomial 99.00 99.33 99.33 99.22 167.58 sigmoid 99.33 99.00 99.00 99.11 159.64 -
[1] 张旭苹, 陈晓红, 梁蕾, 等. 长距离海缆在线监测改进C-OTDR系统[J]. 光学学报, 2021, 41(13): 1306001. doi: 10.3788/AOS202141.1306001 ZHANG Xuping, CHEN Xiaohong, LIANG Lei, et al. Enhanced C-OTDR-based online monitoring scheme for long-distance submarine cables[J]. Acta optica sinica, 2021, 41(13): 1306001. doi: 10.3788/AOS202141.1306001 [2] 张振鹏, 蒙绍新, 胡列翔, 等. 锚害对500 kV海底电缆结构层的影响[J]. 高电压技术, 2020, 46(2): 561–568. ZHANG Zhenpeng, MENG Shaoxin, HU Liexiang, et al. Effect of anchor damage on the structural layer of 500 kV submarine cable[J]. High voltage technology, 2020, 46(2): 561–568. [3] 鄢仁武, 林穿, 宋微浪, 等. 基于EEMD和卷积神经网络的高压断路器故障诊断[J]. 高压电器, 2022, 58(4): 213–220. YAN Renwu, LIN Chuan, SONG Weilang, et al. High voltage circuit fault based on EEMD and Convolutional neural network[J]. High pressure electrical appliances, 2022, 58(4): 213–220. [4] 于淼, 张耀鲁, 何禹潼, 等. 变分模态分解–排列熵方法用于分布式光纤振动传感系统去噪[J]. 光学学报, 2022, 42(7): 0706005. doi: 10.3788/AOS202242.0706005 YU Miao, ZHANG Yaolu, HE Yutong, et al. Variational mode decomposition and permutation entropy method for denoising of distributed optical fiber vibration sensing system[J]. Acta optica sinica, 2022, 42(7): 0706005. doi: 10.3788/AOS202242.0706005 [5] 郑莉, 刘闯, 任姣姣, 等. 基于LDA-CPSO-SVM优化的多层胶接结构脱粘缺陷识别方法[J]. 光子学报, 2021, 50(12): 114–121. ZHENG Li, LIU Chuang, REN Jiaojiao, et al. Based on LDA-CPSO-SVM optimization method[J]. Photonic journal, 2021, 50(12): 114–121. [6] FAN Xin, CHENG Jianyuan, WANG Yunhong, et al. Automatic events recognition in low SNR microseismic signals of coal mine based on wavelet scattering transform and SVM[J]. Energies, 2022, 15(7): 1–13. [7] 朱煜峰, 许永鹏, 陈孝信, 等. 基于卷积神经网络的直流XLPE电缆局部放电模式识别技术[J]. 电工技术学报, 2020, 35(3): 659–66. ZHU Yufeng, XU Yongpeng, CHEN Xiaoxin, et al. Local discharge mode recognition technology of DC XLPE cable based on convolutional neural network[J]. Transactions on China electrotechnical society, 2020, 35(3): 659–66. [8] YAN Sen, SHANG Ying, WANG Chen, et al. Mixed intrusion events recognition based on group convolutional neural networks in DAS system[J]. IEEE sensors journal, 2022, 22(1): 678–684. doi: 10.1109/JSEN.2021.3129473 [9] HUANG Shuzhan, TANG Jian, DAI Juying, et al. Signal status recognition based on 1DCNN and its feature extraction mechanism analysis[J]. Sensors, 2019, 19(9): 1–19. doi: 10.1109/JSEN.2019.2897439 [10] MA Xinrong, MO Jiaqing, ZHANG Jiangwei, et al. Optical fiber vibration signal recognition based on the fusion of multi-scale features[J]. Sensors, 2022, 22(16): 1–16. doi: 10.1109/JSEN.2022.3195413 [11] 喻后聃, 米秋实, 赵栋, 等. 基于一维卷积神经网络的光纤周界入侵模式识别[J]. 光子学报, 2021, 50(9): 95–105. YU Houdan, MI Qiushi, Zhao Dong, et al. Fiber perimeter invasion pattern recognition based on a 1-dimensional convolutional neural network[J]. Photonic journal, 2021, 50(9): 95–105. [12] 李世晓, 杜锦华, 龙云. 基于一维卷积神经网络的机电作动器故障诊断[J]. 电工技术学报, 2022, 37(S1): 62–73. LI Shixiao, DU Jinhua, LONG Yun. Fault diagnosis of electromechanical actuator Based on 1-dimensional convolutional neural network[J]. Transactions on China electrotechnical society, 2022, 37(S1): 62–73. [13] LU Feiyu, TONG Qingbin, FENG Ziwei. Explainable 1DCNN with demodulated frequency features method for fault diagnosis of rolling bearing under time-varying speed conditions[J]. Measurement science and technology, 2022, 33(9): 1–19. [14] 陈建, 姚剑飞, 赵洪杰, 等. 基于GA优化的VMD-SVM识别角度头故障特征[J]. 北京化工大学学报(自然科学版), 2022, 49(3): 47–54. CHEN Jian, YAO Jianfei, ZHAO Hongjie, et al. VMD-SVM identification based on GA optimization[J]. Journal of Beijing University of Chemical Technology (natural science edition), 2022, 49(3): 47–54. [15] YE Maoyou, YAN Xiaoan, JIA Minping. Rolling bearing fault diagnosis based on VMD-MPE and PSO-SVM[J]. Entropy, 2021, 23(6): 1–13. [16] 尚秋峰, 郭家兴. 基于VMD-BSA-SVM的海缆振动信号识别方法[J]. 激光与光电子学进展, 2022, 59(17): 65–74. SHANG Qiufeng, GUO Jiaxing. Marine cable vibration signal identification method based on VMD-BSA-SVM[J]. Progress in laser and optoelectronics, 2022, 59(17): 65–74. [17] 刘立, 朱健成, 韩光洁, 等. 基于1D-CNN联合特征提取的轴承健康监测与故障诊断[J]. 软件学报, 2021, 32(8): 2379–2390. LIU Li, ZHU Jiancheng, HAN Guangjie, etc. Bearing health monitoring and fault diagnosis of sss based on 1D-CNN combined feature extraction[J]. Journal of software, 2021, 32(8): 2379–2390. [18] CAO Jie, HE Zhidong, WANG Jinhua, et al. An antinoise fault diagnosis method based on multiscale 1DCNN[J]. Shock and vibration, 2020, 20(1): 1–17. [19] 崔石玉, 朱志宇. 基于参数迁移和一维卷积神经网络的海水泵故障诊断[J]. 振动与冲击, 2021, 40(24): 180–189. CUI Shiyu, ZHU Zhiyu. Fault diagnosis of seawater pump based on parameter migration and one-dimensional convolutional neural network[J]. Journal of vibration and shock, 2021, 40(24): 180–189. [20] 贾鹤鸣, 李瑶, 孙康健. 基于遗传乌燕鸥算法的同步优化特征选择[J]. 自动化学报, 2022, 48(6): 1601–1615. JIA Heming, LI Yao, SUN Kangjian. Synchronous optimization feature selection based on genetic tern algorithm[J]. Acta automatica sinica, 2022, 48(6): 1601–1615. [21] 尚秋峰, 巩彪, 郑国强. 锚砸作用下光纤复合海底电缆的振动特性分析[J]. 光通信研究, 2021(5): 45–49, 56. SHANG Qiufeng, GONG Biao, ZHENG Guoqiang. Analysis of vibration characteristics of optical fiber composite submarine cable under anchor impact[J]. Optical communication research, 2021(5): 45–49, 56. [22] 冯雨珊, 尚秋峰, 吕安强. 波浪力作用下光纤复合海底电缆动力学有限元分析[J]. 光通信研究, 2017(4): 30–34. FENG Yushang, SHANG Qiufeng, LYU Anqiang. Dynamic finite element analysis of optical fiber composite submarine cable under wave force[J]. Optical communication research, 2017(4): 30–34. [23] 柳小花. 光纤复合海底电缆扭转与磨损特性的有限元分析[D]. 保定: 华北电力大学. 2017. LIU Xiaohua. Finite element analysis of torsion and wear characteristics of optical fiber composite submarine cable [D]. Baoding: North China Electric Power University. 2017. [24] 梁礼明, 陈明理, 刘博文, 等. 基于图论的支持向量机核函数选择[J]. 计算机工程与设计, 2019, 40(5): 1316–1321. LIANG Liming, CHEN Mingli, LIU Bowen, et al. Support vector machine kernel function selection based on graph theory[J]. Computer engineering and design, 2019, 40(5): 1316–1321. [25] MENG Xianbing, LU Lihua, LIU Yu, et al. A new bio-inspired optimisation algorithm: bird swarm algorithm[J]. Journal of experimental & theoretical artificial intelligence, 2016, 28(4): 1–12. [26] 杨帅, 郭茂祖, 赵玲玲, 等. 融合遗传算法与XGBoost的玉米百粒重相关基因挖掘[J]. 智能系统学报, 2022, 17(1): 170–180. YANG Shuai, GUO Maozu, ZHAO Lingling, et al. Fusion genetic algorithm with XGBoost for maize hundred-grain recorrelated gene mining[J]. Journal of intelligent systems, 2022, 17(1): 170–180. [27] 冯雪健, 邓浩川, 韦笑, 等. 基于GA和DE的非均匀等离子体介质参数重构算法研究[J]. 中国传媒大学学报(自然科学版), 2019, 26(3): 33–39. FENG Xuejian, DENG Haochuan, WEI Xiao, et al. Reconstruction algorithm of heterogeneous plasma media parameters based on GA and DE[J]. Journal of the Communication University of China (natural science edition), 2019, 26(3): 33–39. [28] KONSTANTIN Dragomiretskiy, DOMINIQUE Zosso. Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531–544. doi: 10.1109/TSP.2013.2288675 [29] 郭家兴, 钱君霞, 柳瑞, 等. 基于麻雀搜索算法优化支持向量机的海缆振动信号识别方法[J]. 控制与信息技术, 2023(5): 47–54. GUO Jiaxing, QIAN Junxia, LIU Rui, et al. Based on sparrow search algorithm[J]. Control and information technology, 2023(5): 47–54. [30] 王望望, 邓林峰, 赵荣珍, 等. 集成KPCA与t-SNE的滚动轴承故障特征提取方法[J]. 振动工程学报, 2021, 34(2): 431−440. WANG Wangwang, DENG Linfeng, ZHAO Rongzhen, et al. Fault feature extraction method of rolling bearing integrating KPCA and t-SNE[J] Journal of vibration engineering, 2021, 34 (2): 431−440.
