Neural network-based nonsingular terminal sliding mode control of the Stewart platform
-
摘要: 针对Stewart平台的六自由度（six degrees of freedom, 6-DOF）轨迹跟踪问题，提出一种基于神经网络的非奇异终端滑模控制方法并应用于Stewart平台的位置姿态控制中。通过分析Stewart平台的位置反解和速度反解，建立运动学方程，利用牛顿−欧拉方程建立动力学方程，并结合加速度反解得到了平台的状态空间表达式；基于非奇异滑模面函数，设计非奇异终端滑模控制律。考虑到径向基函数（radial Basis function, RBF）神经网络的逼近特性，采用RBF神经网络对模型未知部分进行自适应逼近，并利用Lyapunov第二法设计了自适应律；通过仿真证明控制器设计的有效性。仿真结果表明，相比于比例积分微分（proportional integral derivative, PID）控制器，提出的RBF神经网络非奇异终端滑模控制器具有更好的轨迹跟踪精度和动态特性。Abstract: This paper proposes a solution to the six degrees of freedom trajectory tracking problem of the Stewart platform using a nonsingular terminal sliding mode control method based on a neural network. This method is applied to the position and pose control of the Stewart platform. First, a kinematic equation is established by analyzing the position inverse solution and velocity inverse solution of the Stewart platform. Simultaneously, the dynamic equation is established based on the Newton-Euler equation. By integrating the acceleration inverse solution, we obtain the state–space representation of the platform. Subsequently, a nonsingular terminal sliding mode control law is designed using the nonsingular sliding surface function. Considering the approximation characteristics of the radial basis function (RBF) neural network, we employ this network to adaptively approximate the unknown term of the equation. An adaptive law is then designed based on the second method of Lyapunov. Finally, the effectiveness of the controller design is proved through simulations. The simulation results show that the proposed controller that uses an RBF neural network and nonsingular terminal sliding mode outperforms the proportional integral derivative controller in terms of trajectory tracking accuracy and dynamic characteristics.
-
舰船在航行过程中，由于受到海浪、海风等环境因素的影响，船体会发生横滚、纵摇和艏摇等变化，这些运动对无人机的降落过程、舰船上的一些精密设备的稳定工作等都会造成干扰[1]。为了使得一些作业能够在允许的误差范围内进行，可以在舰船和起降平台（或精密设备的作业平台）之间安装随动稳定装置，依靠该稳定平台的补偿功能，来克服船体横滚、纵摇的偏摆干扰，从而保证无人机在舰船上的安全起降[2]。
不失一般性地，本研究将面向一种Stewart稳定平台展开研究。Stewart平台作为一种六自由度并联机器人，具有结构稳定、刚度大和负载能力强等优势[3-5]，自1965年提出以后，被应用于各个领域的设备运动模拟中[6-7]。针对舰载装备而言，其基座通常与船体固定连接，姿态易受到海洋环境的干扰，为保证装备能够在稳定的工作空间下运行，使用Stewart平台实现舰载装备的姿态控制已经成为了较为普遍选择。Stewart平台是一个多机构，强耦合的非线性系统，当机构快速运动时，其离心力和科氏力对系统的影响将不能忽视[8]，传统的比例积分微分（proportional integral derivative, PID）控制器难以对其进行高精度的控制。因此，研究Stewart平台的轨迹跟踪控制就显得尤为重要。
目前，滑模控制、自适应控制等控制方法均被用于Stewart平台的轨迹跟踪控制。文献[9]提出一种基于模糊滑模的六自由度平台运动控制器，利用模糊原理对变结构控制中的增益进行逼近，提高了轨迹跟踪的精度。文献[10]将反演算法与滑模控制相结合，并改进了经典指数趋近律，削弱了Stewart平台运动过程中的抖振。文献[11]提出一种自适应滑模控制器，在名义动力学模型的基础上，利用自适应函数对建模误差进行补偿，解决了Stewart平台建模不确定性的问题，降低了轨迹跟踪误差。 近些年，一些学者提出了终端滑模控制概念，用非线性函数代替传统的线性滑模函数，使系统状态能在有限时间内收敛到零，动态性能优于普通的滑模控制，并且可以有效消除系统抖振[12-14]。文献[15]为解决普通终端滑模控制的奇异问题，提出了非奇异终端滑模控制策略，并在机器人控制领域得到了应用。文献[16]提出了一种利用遗传算法优化参数的非奇异终端滑模控制方法，可使六自由度并联机器人具有较好的跟踪性能，但是没有解决并联机器人中模型不确定的问题，控制器缺乏自适应能力。本研究在现阶段研究的基础之上，提出一种基于动力学模型的径向基函数（radial Basis function, RBF）神经网络非奇异终端滑模控制方法，首先对Stewart平台的运动学和动力学进行了分析，在利用滑模变结构控制原理实现Stewart平台轨迹跟踪的基础上，将非奇异滑模面函数引入到控制律设计中，并采用RBF神经网络补偿动力学模型中的未知非线性项，最后利用Lyapunov第二法证明了系统的稳定性。仿真结果表明本研究方法可以在较短时间内实现轨迹跟踪，并且有较好的跟踪精度。
1. Stewart平台运动学模型
1.1 坐标系定义
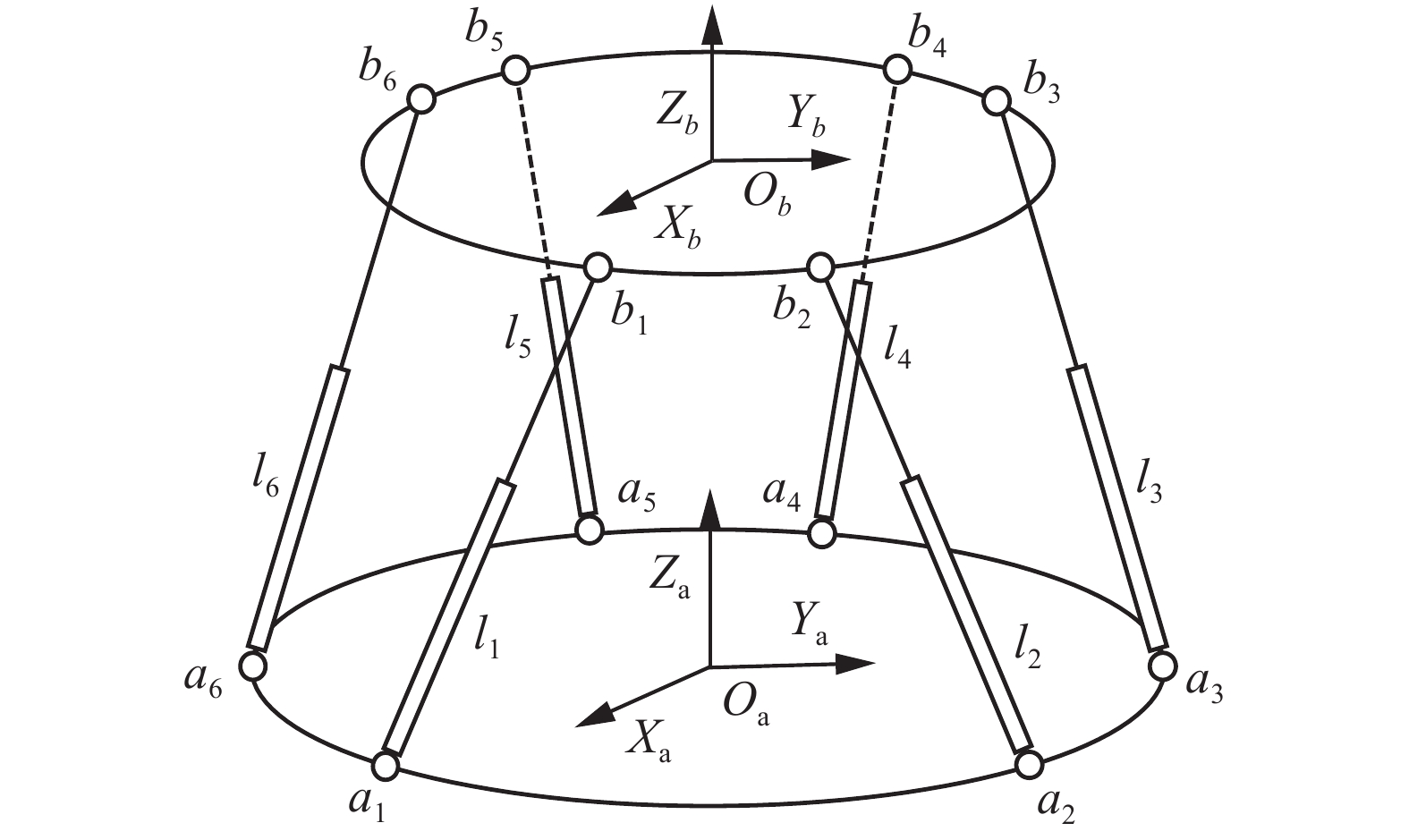
Stewart六自由度平台的结构简图如图1所示，机构整体由上平台、下平台以及连接上下平台的6个支腿组成，支腿与上平台采用球铰连接，与下平台采用虎克铰连接，各支腿采用电动缸来驱动上平台运动[17-18]。分别在上平台质心
${O_b}$ 和下平台质心${O_a}$ 处建立体坐标系${O_b} - {X_b}{Y_b}{Z_b}$ 和惯性坐标系${O_a} - {X_a}{Y_a}{Z_a}$ 。${{\boldsymbol{b}}_i}(i = 1,2,\cdots,6)$ 为上铰点位置在体坐标系中的表示，${{\boldsymbol{a}}_i}(i = 1,2,\cdots,6)$ 为下铰点位置在惯性坐标系中的表示。
图 1 Stewart平台结构Fig. 1 Stewart platform structural diagram
下载:
全尺寸图片
1.2 位置反解
用Z-Y-X欧拉角描述体坐标系相对于惯性坐标系的姿态，上平台绕
${Z_a}$ 轴的旋转角为$\gamma $ ，绕${Y_a}$ 轴的旋转角为$\beta $ ，绕${X_a}$ 轴的旋转角为$\alpha $ ，则上平台相对于惯性坐标系的旋转矩阵可表示为$$ \begin{gathered} {\boldsymbol{R}} = \\ \left[ {\begin{array}{*{20}{c}} {c\beta c\gamma }&{ - c\alpha s\gamma + s\alpha s\beta c\gamma }&{s\alpha s\gamma + c\alpha s\beta c\gamma } \\ {c\beta s\gamma }&{c\alpha c\gamma + s\alpha s\beta s\gamma }&{ - s\alpha c\gamma + c\alpha s\beta s\gamma } \\ { - s\beta }&{s\alpha c\beta }&{c\alpha c\beta } \end{array}} \right] \end{gathered} $$ (1) 式中：
$c\beta = \cos \beta$ ，$s\beta = \sin \beta$ 。根据图1中的各矢量关系可以得出支腿的长度矢量
$$ {{\boldsymbol{l}}_i} = {\boldsymbol{c}} + {\boldsymbol{R}}{{\boldsymbol{b}}_i} - {{\boldsymbol{a}}_i} $$ (2) 式中，c为上平台质心
${O_b}$ 在惯性坐标系中的位置矢量。1.3 速度反解
上平台质心相对于惯性坐标系的角速度为
$$ {\boldsymbol{\omega}} ={\boldsymbol{ R}}\left[ {\begin{array}{*{20}{c}} 1&0&{ - \sin \beta } \\ 0&{\cos \alpha }&{\sin \alpha \cos \beta } \\ 0&{ - \sin \alpha }&{\cos \alpha \cos \beta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \alpha } \\ {\dot \beta } \\ {\dot \gamma } \end{array}} \right] $$ (3) 定义上平台质心在惯性坐标系中的广义速度矢量为
$$ \dot {\boldsymbol{x}} = {[\dot {\boldsymbol{c}},{\boldsymbol{\omega}} ]^{\rm{T}}}_{6 \times 1} $$ (4) 定义广义加速度矢量为
$$ \ddot {\boldsymbol{x}} = {[\ddot {\boldsymbol{c}},\dot {\boldsymbol{\omega}} ]^{\rm{T}}}_{6 \times 1} $$ (5) 上铰点在惯性坐标系中的位置矢量为
$$ {{\boldsymbol{B}}_i} = {\boldsymbol{c}} + {\boldsymbol{R}}{{\boldsymbol{b}}_i} $$ (6) 上铰点在惯性坐标系中的速度矢量为
$$ {{\boldsymbol{v}}_{{\boldsymbol{B}}_i}} = {\dot {\boldsymbol{B}}_i} = \dot {\boldsymbol{c}} + {\boldsymbol{\omega}} \times ({\boldsymbol{R}}{{\boldsymbol{b}}_i}) $$ (7) 上铰点速度与广义速度的关系可表示为
$$ {{\boldsymbol{v}}_{{\boldsymbol{B}}_i}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{I}}_{3 \times 3}}}&{{\boldsymbol{R}}{{\left( {{{\tilde {\boldsymbol{B}}}_i}} \right)}^{\rm{T}}}{{\boldsymbol{R}}^{\rm{T}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot {\boldsymbol{c}}} \\ {\boldsymbol{\omega }} \end{array}} \right] = {{\boldsymbol{J}}_{Bi}}{\dot {\boldsymbol{x}}_i} $$ (8) 式中，
$ {\tilde {\boldsymbol{B}}_i} $ 为矢量$ {{\boldsymbol{B}}_i} $ 的斜对称矩阵。上铰点速度向支腿方向投影可得到支腿的伸长速度：
$$ {\dot l_i} = {\boldsymbol{n}}_i^{\rm{T}}{{\boldsymbol{v}}_{B_i}} = {\boldsymbol{n}}_i^{\rm{T}}[\dot {\boldsymbol{c}} + {\boldsymbol{\omega }}\times ({\boldsymbol{R}}{{\boldsymbol{b}}_i})] $$ (9) 式中
${{\boldsymbol{n}}_i}$ 为支腿的单位矢量。将式(9)写成矩阵形式为
$$ \begin{gathered} \dot {\boldsymbol{L}} = {{\boldsymbol{n}}^{\rm{T}}}{{\boldsymbol{V}}_B} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{n}}^{\rm{T}}}}&{{{({\boldsymbol{RB}} \times {\boldsymbol{n}})}^{\rm{T}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot {\boldsymbol{c}}} \\ {\boldsymbol{ \omega }} \end{array}} \right] = {\boldsymbol{J}}\dot {\boldsymbol{x}} \\ \end{gathered} $$ (10) 式中
$ {\boldsymbol{J }}$ 为6个支腿伸长速度与上平台广义速度间的雅可比矩阵。1.4 加速度反解
对式(10)中的雅可比矩阵
${\boldsymbol{ J}} $ 求导为$$ \dot {\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\rm{d}}{{\boldsymbol{n}}^{\rm{T}}}}}{{{\rm{d}}t}}}&{\dfrac{{{\rm{d}}{{({\boldsymbol{RB}} \times {\boldsymbol{n}})}^{\rm{T}}}}}{{{\rm{d}}t}}} \end{array}} \right] $$ (11) 根据式(10)和式(11)可得6个支腿的加速度为
$$ \ddot {\boldsymbol{L}} = \frac{{{\rm{d}}\left( {{\boldsymbol{J\dot x}}} \right)}}{{{\rm{d}}t}} = {\boldsymbol{\dot J\dot x}} + {\boldsymbol{J\ddot x}} $$ (12) 2. Stewart平台动力学模型
2.1 动力学方程
对于上平台，利用牛顿−欧拉方程可得其动力学方程为
$$ \begin{gathered} {\left[ {\begin{array}{*{20}{c}} {\boldsymbol{n}} \\ {{\boldsymbol{RB}} \times {\boldsymbol{n}}} \end{array}} \right]_{6 \times 6}}{{\boldsymbol{f}}_a} = \left[ {\begin{array}{*{20}{c}} {{m_p}{\boldsymbol{I}}}&0 \\ 0&{{{\boldsymbol{I}}_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\ddot {\boldsymbol{c}}} \\ {\dot {\boldsymbol{\omega}} } \end{array}} \right] + \\ \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{{\boldsymbol{\varOmega}} {{\boldsymbol{I}}_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot {\boldsymbol{c}}} \\ {\boldsymbol{\omega}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{m_p}g} \\ 0 \end{array}} \right] \\ \end{gathered} $$ (13) 式中：
$ {{\boldsymbol{f}}_a} $ 为支腿电动缸的输出力；$ {m_p} $ 为上平台的质量；$ {{\boldsymbol{I}}_p} $ 为上平台的转动惯量；${\boldsymbol{ \varOmega}}$ 为角速度矢量的斜对称矩阵。将式(13)写成一般形式为
$$ {{\boldsymbol{J}}^{\rm{T}}}{{\boldsymbol{f}}_a} = {{\boldsymbol{M}}_p}\ddot {\boldsymbol{x}} + {{\boldsymbol{C}}_p}\dot {\boldsymbol{x}} + {{\boldsymbol{G}}_p} $$ (14) 当上平台运动时，还应考虑各个支腿对系统动力学模型的影响。这时系统不再是一个刚体，而是一个多刚体系统。各支腿的影响包括：支腿的重力、电动缸缸筒的惯性力、活塞杆的惯性力。为计算支腿对上平台的影响，需要计算雅可比矩阵，将支腿上的力投影到上平台质心处。将其与上平台的动力学方程相结合，可得到Stewart平台完整的多刚体动力学方程。
活塞杆质心处速度与上铰点速度间的雅可比矩阵为
$$ {{\boldsymbol{J}}_{di}} = {\boldsymbol{I}} - \frac{{{l_a}}}{{\left| {{{\boldsymbol{l}}_i}} \right|}}{{\boldsymbol{P}}_i} $$ (15) 式中：
$ {l_a} $ 为活塞杆质心到上铰点的距离；${{\boldsymbol{P}}_i} = {\boldsymbol{I}} - {{\boldsymbol{n}}_i}{\boldsymbol{n}}_i^{\rm{T}}$ 。设活塞杆的质量为
$ {m_c} $ ，则活塞杆的重力投影到上平台质心处为$$ {{\boldsymbol{f}}_{ci}} = - {\boldsymbol{J}}_{{\boldsymbol{B}}_i}^{\rm{T}}{\boldsymbol{J}}_{di}^{\rm{T}}{m_c}g $$ (16) 考虑支腿的惯性力，将其投影到上平台质心处，最后的表达形式为
$$ {{\boldsymbol{f}}_g} = {{\boldsymbol{M}}_g}\ddot {\boldsymbol{x}} + {{\boldsymbol{C}}_g}\dot {\boldsymbol{x}} $$ (17) 式中：
$ {{\boldsymbol{M}}_g} $ 为支腿的质量矩阵，$ {{\boldsymbol{C}}_g} $ 为支腿的离心力和科氏力矩阵。将式(16)~(17)代入式(14)即可得到Stewart平台的多刚体动力学方程
$$ {{\boldsymbol{J}}^{\rm{T}}}{{\boldsymbol{f}}_a} = {{\boldsymbol{M}}_\textit{z}}\ddot {\boldsymbol{x}} + {{\boldsymbol{C}}_\textit{z}}\dot {\boldsymbol{x}} + {{\boldsymbol{G}}_\textit{z}} $$ (18) 式中：
$$ \begin{gathered} {{\boldsymbol{M}}_\textit{z}} = {{\boldsymbol{M}}_p} + {{\boldsymbol{M}}_g} \\ {{\boldsymbol{C}}_\textit{z}} = {{\boldsymbol{C}}_p} + {{\boldsymbol{C}}_g} \\ {{\boldsymbol{G}}_\textit{z}} = {{\boldsymbol{G}}_p} + \sum\limits_{i = 1}^6 {{{\boldsymbol{f}}_{ci}}} \\ \end{gathered} $$ (19) 将式(10)~(12)代入式(18)可得
$$ {{\boldsymbol{J}}^{\rm{T}}}{{\boldsymbol{f}}_a} = {{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}\ddot {\boldsymbol{L}} + ({{\boldsymbol{C}}_\textit{z}} - {{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}\dot {\boldsymbol{J}}){{\boldsymbol{J}}^{ - 1}}\dot {\boldsymbol{L}} + {{\boldsymbol{G}}_\textit{z}} $$ (20) 2.2 状态空间方程
设计
${{\boldsymbol{x}}_1} = {\boldsymbol{L}}$ ，${{\boldsymbol{x}}_2} = \dot {\boldsymbol{L}}$ ，根据式(20)可得Stewart平台的状态空间方程：$$ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\boldsymbol{x}}}_1} = {{\boldsymbol{x}}_2} = \dot {\boldsymbol{L}}} \\ \begin{aligned} {{\dot {\boldsymbol{x}}}_2} = &\ddot {\boldsymbol{L}}= - {\left( {{{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}} \right)^{ - 1}}\left( {{{\boldsymbol{C}}_\textit{z}} - {{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}\dot J} \right){{\boldsymbol{J}}^{ - 1}}{x_2} + \\ & {\left( {{{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}} \right)^{ - 1}}{{\boldsymbol{J}}^{\rm{T}}}u - {\left( {{{\boldsymbol{M}}_\textit{z}}{{\boldsymbol{J}}^{ - 1}}} \right)^{ - 1}}{{\boldsymbol{G}}_\textit{z}} \\ \end{aligned} \end{array}} \right. $$ (21) 式中，
${\boldsymbol{u}} = {{\boldsymbol{f}}_a}$ 为控制输入。3. 控制器设计
3.1 非奇异终端滑模控制器的设计
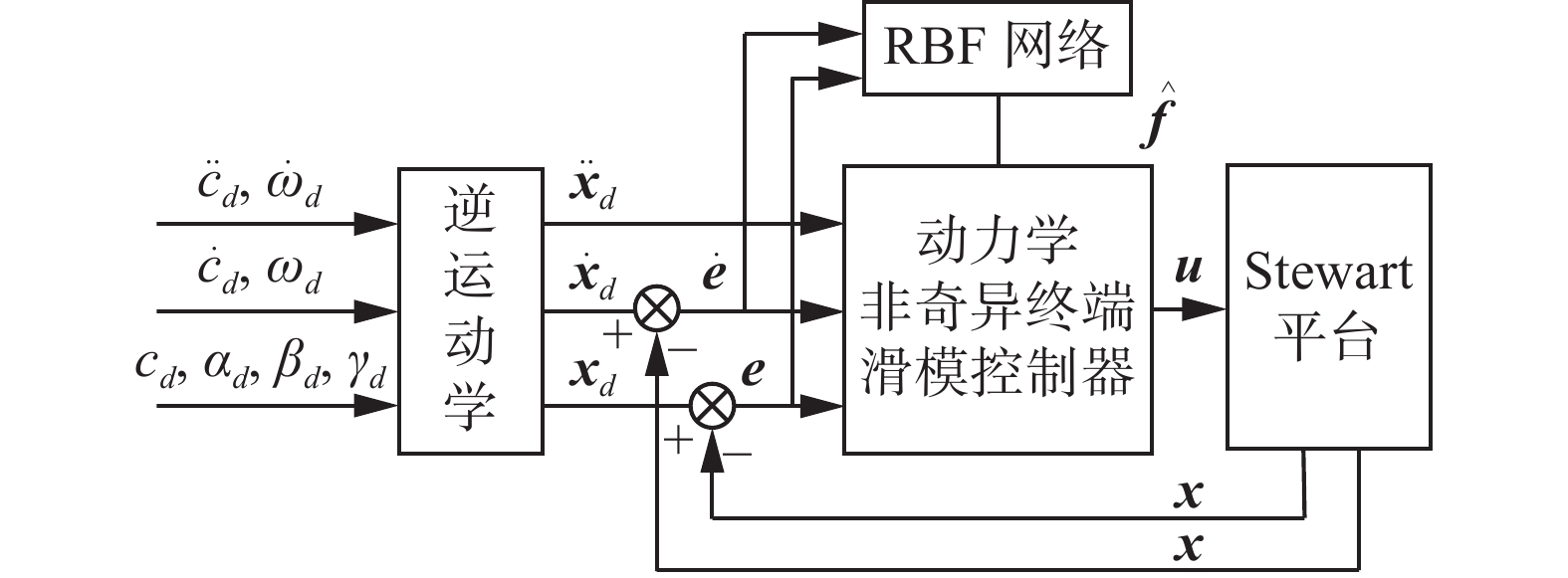
本研究提出一种基于RBF神经网络的非奇异终端滑模控制算法，控制系统结构图如图2所示。
图 2 控制系统结构Fig. 2 Structure of control system下载:
全尺寸图片
由式(21)可以看出，状态
$ {{\boldsymbol{x}}_2} $ 的系数矩阵中存在大量矩阵运算，其中科氏力和离心力矩阵$ {{\boldsymbol{C}}_\textit{z}} $ 通常难以进行精确计算，造成了系统建模的不确定性。考虑将状态方程式(21)写为$$ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\boldsymbol{x}}}_1} = {{\boldsymbol{x}}_2}} \\ {{{\dot {\boldsymbol{x}}}_2} = {\boldsymbol{f}}({\boldsymbol{x}}) + {\boldsymbol{g}}({\boldsymbol{x}}){\boldsymbol{u}} - {\boldsymbol{G}}} \end{array}} \right. $$ (22) 式中：
${\boldsymbol{ f(x) }}$ 为未知非线性函数；$ {\boldsymbol{G}} $ 为重力项。定义系统误差为
${\boldsymbol{e}} = {{\boldsymbol{x}}_d} - {{\boldsymbol{x}}_1}$ ，其中，${{\boldsymbol{x}}_d}$ 为支腿期望长度，${\boldsymbol{e}} = \left[{{e_1}}\;\;{{e_2}}\;\; \cdots\;\;{{e_6}} \right]$ 。考虑支腿
$ i $ ，设计非奇异终端滑模面函数：$$ {s_i} = {e_i} + \frac{1}{\beta }\dot e_i^{p/q}, \;{i = 1,2, \cdots ,6} $$ (23) 其中，
$\beta > 0$ ，$p$ 和$q$ 为正奇数，且$p > q$ 。定义Lyapunov函数为
$$ {V_i} = \frac{1}{2}s_i^2 $$ (24) 为保证
$ {\dot V_i} < 0 $ ，设计非奇异终端滑模控制律为$$ \begin{gathered} {\boldsymbol{u}} = {{\boldsymbol{g}}^{ - 1}}({\boldsymbol{x}})[{{\ddot {\boldsymbol{x}}}_d} - {\boldsymbol{f(x)}} + {\boldsymbol{G}} + \beta \frac{q}{p}\dot {\boldsymbol{e}}^{2 - \tfrac{p}{q}} + \eta {{\rm{sgn}}} ({\boldsymbol{s}}) + k{\boldsymbol{s}}] \\ \end{gathered} $$ (25) 式中：
${\boldsymbol{s}} = \left[ {{s_1}}\;\;\;{{s_2}}\;\;\; \cdots \;\;\;{{s_6}} \right]$ ，$ 1 < p/q < 2 $ ，$ \eta > 0 $ 。对式(23)求导：
$$ \begin{gathered} {{\dot s}_i} = {{\dot e}_i} + \frac{1}{\beta }\frac{p}{q}\dot e_i^{\tfrac{p}{q} - 1}[{{\ddot x}_{di}} - {\boldsymbol{f{(x)}}_i} - {({\boldsymbol{g(x)u}})_i} + {{\boldsymbol{G}}_i}] \\ \end{gathered} $$ (26) 将控制律(25)代入式(26)得：
$$ {\dot s_i} = - \frac{1}{\beta }\frac{p}{q}\dot e_i^{\tfrac{p}{q} - 1}\left( {\eta {\rm{{sgn}}} ({s_i}) + k{s_i}} \right) $$ (27) 对式(24)求导：
$$ {\dot V_i} = {s_i}{\dot s_i} = - \frac{1}{\beta }\frac{p}{q}\dot e_i^{\tfrac{p}{q} - 1}\left( {\eta \left| {{s_i}} \right| + ks_i^2} \right) $$ (28) 定理1 （LaSalle不变性原理）为保证系统的平衡点
$ x = 0 $ 是渐近稳定的，则需存在Lyapunov函数$ V(x) $ 满足：1)
$ V(x) $ 正定；2)
$ \dot V(x) $ 负半定；3)
$ \dot V(x) = 0 $ 当且仅当$ x = 0 $ 。当
$ {\dot e_i} \ne 0 $ 时，显然：$$ \dot e_i^{\tfrac{p}{q} - 1} > 0 $$ (29) 则
$ {\dot V_i} \leqslant 0 $ ，当$ {\dot V_i} \equiv 0 $ 时，$ {s_i} \equiv 0 $ ，根据LaSalle不变性原理，$ t \to \infty $ 时，$ {s_i} \to 0 $ ，$ {e_i} \to 0 $ ，$ {\dot e_i} \to 0 $ ，控制器满足Lyapunov稳定条件。将控制律式(25)代入式(22)有
$$ {\dot {{x}}_{2i}} = {\ddot {{x}}_{di}} + \beta \frac{q}{p}\dot e_i^{2 - \tfrac{p}{q}} + \eta {{\rm{sgn}}} ({s_i}) + k{s_i} $$ (30) 当
${\dot e_i} = 0$ 时$$ {\ddot e_i} = - \eta {{\rm{sgn}}} ({s_i}) - k{s_i} $$ (31) 式中：
${\ddot e_i} = {\ddot {{x}}_{di}} - {\dot {{x}}_{2i}}$ ，当$ {s_i} > 0 $ 时，$ {\ddot e_i} \leqslant - \eta $ ，即$ {\dot e_i} $ 快速减小；当$ {s_i} < 0 $ 时，$ {\ddot e_i} \geqslant \eta $ ，此时$ {\dot e_i} $ 快速上升。可见当$ {\dot e_i} = 0 $ 时，在有限时间内可以实现$ {s_i} = 0 $ 。3.2 径向基神经网络的设计
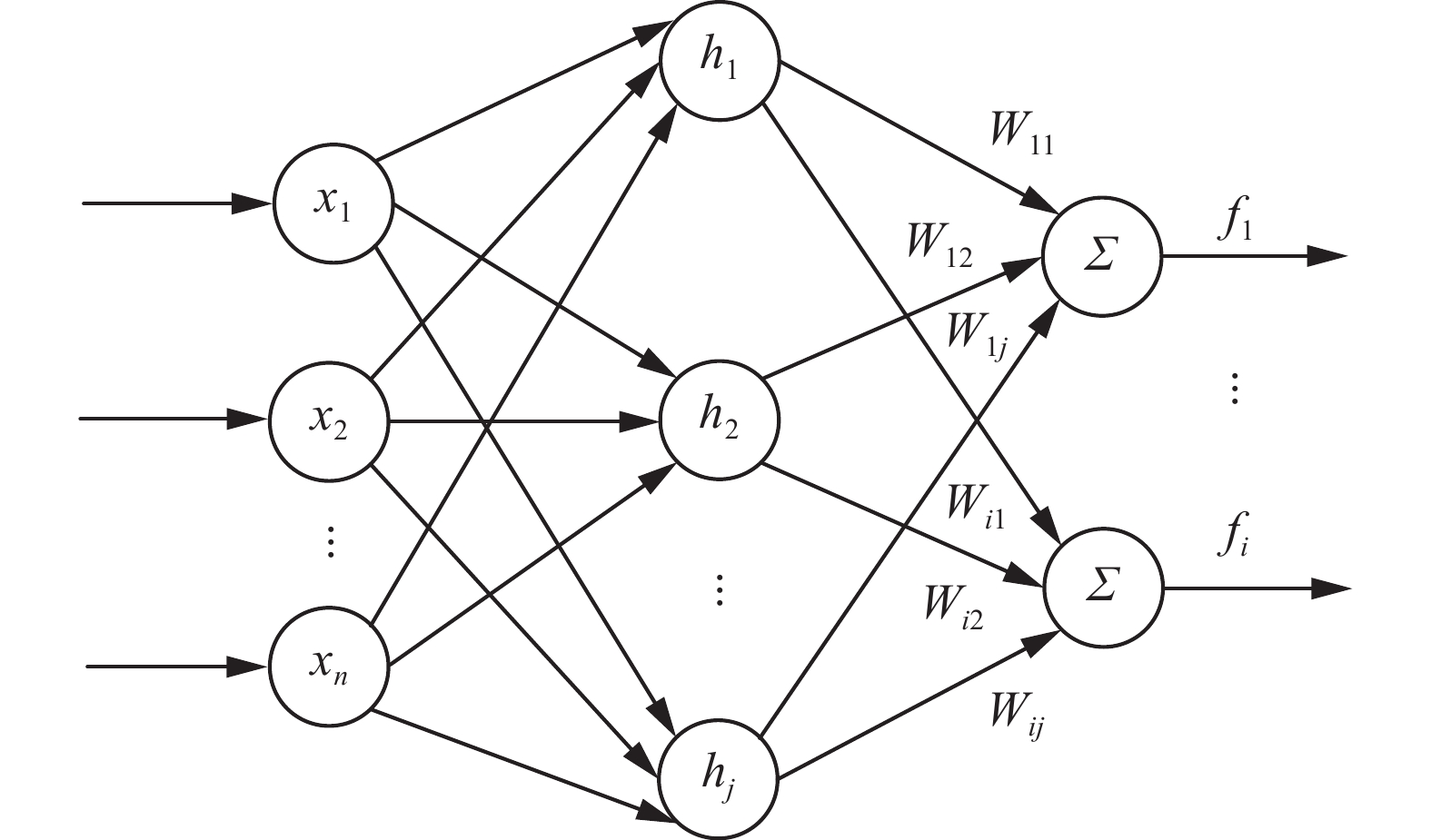
RBF神经网络能够在任意精度下，逼近任何非线性函数，具有良好的泛化能力和鲁棒性，广泛应用于自适应控制和非线性控制领域[19-20]。RBF神经网络分为输入层、隐含层和输出层，其结构如图3所示。
图 3 RBF神经网络拓扑结构Fig. 3 Topology of RBF neural network下载:
全尺寸图片
RBF网络的算法为
$$ {h_j} = \exp \left({\frac{{\left\| {{\boldsymbol{x}} - {{\boldsymbol{c}}_j}} \right\|}}{{2b_j^2}}^2}\right) $$ (32) $$ {\boldsymbol{f}} = {{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{h(x)}} + {\boldsymbol{\varepsilon}} $$ (33) 式中：
$ {\boldsymbol{x}} $ 为网络输入；$ h $ 为网络的高斯基函数；$ {\boldsymbol{W}} $ 为网络的理想权值；$ {\boldsymbol{\varepsilon}} $ 为网络逼近误差；$ {\boldsymbol{f}} $ 为网络理想输出。取网络输入为
${\boldsymbol{x}} = {\left[ {\boldsymbol{e}}\;\;\;{\dot {\boldsymbol{e}}} \right]^{\rm{T}}}$ ，则网络的输出为$$ \hat {\boldsymbol{f}} = {\hat {\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{h(x)}} $$ (34) 利用网络输出
$ \hat {\boldsymbol{f}} $ 逼近未知非线性函数$ {\boldsymbol{f(x)}} $ ，将式(32)代入式(26)得到控制律为$$ \begin{gathered} {\boldsymbol{u}} = {{\boldsymbol{g}}^{ - 1}}({\boldsymbol{x}})[{{\ddot {\boldsymbol{L}}}_d} - \hat {\boldsymbol{f}} + {\boldsymbol{G}} + \beta \frac{q}{p}{{\dot {\boldsymbol{e}}}^{2 - \tfrac{p}{q}}} + \eta {{\rm{sgn}}} ({\boldsymbol{s}}) + k{\boldsymbol{s}}] \end{gathered} $$ (35) 将控制律代入式(24)得：
$$ \dot {\boldsymbol{s}} = \frac{1}{\beta }\frac{p}{q}{\dot {\boldsymbol{e}}^{\tfrac{p}{q} - 1}}\left( { - \tilde {\boldsymbol{f}} - \eta {{\rm{sgn}}} ({\boldsymbol{s}}) - k{\boldsymbol{s}}} \right) $$ (36) 式中：
$$ \begin{gathered} \tilde {\boldsymbol{f}} = {\boldsymbol{f(x)}} - \hat {\boldsymbol{f}}= {{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{h(x)}} + {\boldsymbol{\varepsilon}} - {{\hat {\boldsymbol{W}}}^{\rm{T}}}{\boldsymbol{h(x)}}= {{\tilde {\boldsymbol{W}}}^{\rm{T}}}{\boldsymbol{h(x)}} + {\boldsymbol{\varepsilon}} \end{gathered} $$ (37) 设计Lyapunov函数为
$$ {V_{1i}} = \frac{\beta }{2}\frac{q}{p}{s_i}^2 + \frac{1}{2}\gamma \tilde {\boldsymbol{W}}_i^{\rm{T}}{\tilde {\boldsymbol{W}}_i} $$ (38) 式中：
${\tilde {\boldsymbol{W}}_i} = {\left[ {{{\tilde W}_{i1}}}\;\;\;\;{{{\tilde W}_{i2}}}\;\;\;\; \cdots \;\;\;\;{{{\tilde W}_{ij}}} \right]^{\rm{T}}}$ ；$ \gamma > 0 $ 。对式(38)求导：
$$ \begin{gathered} {{{\dot{V}}}_{1i}}={{s}_{i}}{{{\dot{s}}}_{i}}+\gamma \tilde{{\boldsymbol{W}}}_{i}^{{\rm{T}}}{{{\dot{\tilde{{\boldsymbol{W}}}}}}_{i}} = -\tilde{{\boldsymbol{W}}}_{i}^{{\rm{T}}}\left( \dot{e}_{i}^{\tfrac{p}{q}-1}{{s}_{i}}{\boldsymbol{h(x)}}+\gamma {{{\dot{\hat{{\boldsymbol{W}}}}}}_{i}} \right)- \\ {{{\dot{e}_i}}^{\tfrac{p}{q}-1}}{{s}_{i}}\left( {{\varepsilon }_{i}}+\eta {\rm{sgn}} ({{s}_{i}})+k{{s}_{i}} \right) \end{gathered}$$ (39) 取自适应律为
$$ {{\dot{\hat{{\boldsymbol{W}}}}}_{i}}=-\frac{1}{\gamma }\dot{e}_{i}^{\tfrac{p}{q}-1}{{s}_{i}}{\boldsymbol{h(x)}} $$ (40) 则：
$$ \begin{gathered} {{\dot V}_{1i}} = - \dot e_i^{\tfrac{p}{q} - 1}{s_i}\left( {{\varepsilon _i} + \eta {{\rm{sgn}}} ({s_i}) + k{s_i}} \right) = \\ - \dot e_i^{\tfrac{p}{q} - 1}\left( {{s_i}{\varepsilon _i} + \eta \left| {{s_i}} \right| + ks_i^2} \right) \\ \end{gathered} $$ (41) 显然，
$ {\dot V_{1i}} \leqslant 0 $ ，根据LaSalle不变性原理，闭环系统渐近稳定。自适应控制律中的鲁棒项$\eta {{\rm{sgn}}} ({s_i}) + k{s_i}$ 可以克服神经网络的逼近误差。4. 仿真结果与分析
为验证本研究中控制器设计的有效性，使用MATLAB/Simulink进行仿真测试。Stewart平台的主要参数如表1所示。
表 1 Stewart平台主要参数Table 1 The main parameters of Stewart platform名称 数值 上平台质量/kg 1.65 上平台主惯性矩/(kg·m2) [0.0064;0.0064;0.0124] 上平台外接圆半径/mm 150 下平台外接圆半径/mm 200 活塞杆长度/mm 200 缸筒长度/mm 100 平台初始高度/mm 212 设计非奇异终端滑模控制器参数为：
$ \beta = 10 $ ，$ p = 13 $ ，$ q = 11 $ ，$ \eta = 0.01 $ ，$ k = 70\;000 $ 。设计RBF神经网络参数为：神经元个数$ m = 9 $ ，中心向量$ {{\boldsymbol{c}}_j} = [ - 3:0.75:3] $ ，其中步长为0.75，$ {b_j} = 0.01 $ ，网络权值$\hat{\boldsymbol{ W}}$ 为$ 6 \times 9 $ 的矩阵。为验证所提控制算法的有效性，将提出的RBF神经网络非奇异终端滑模控制器与传统的PID控制器相比较，其中PID控制器的参数设计为：
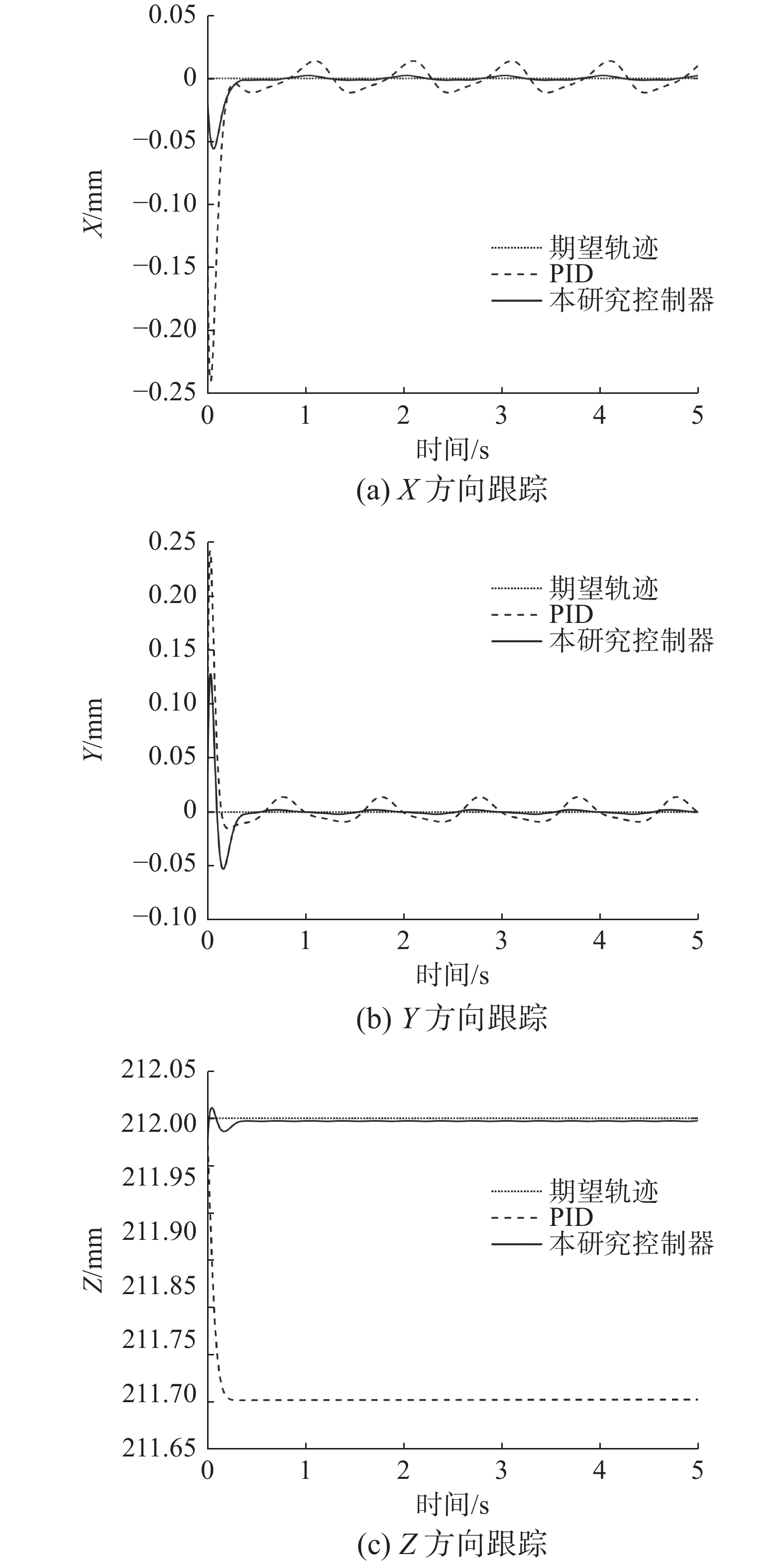
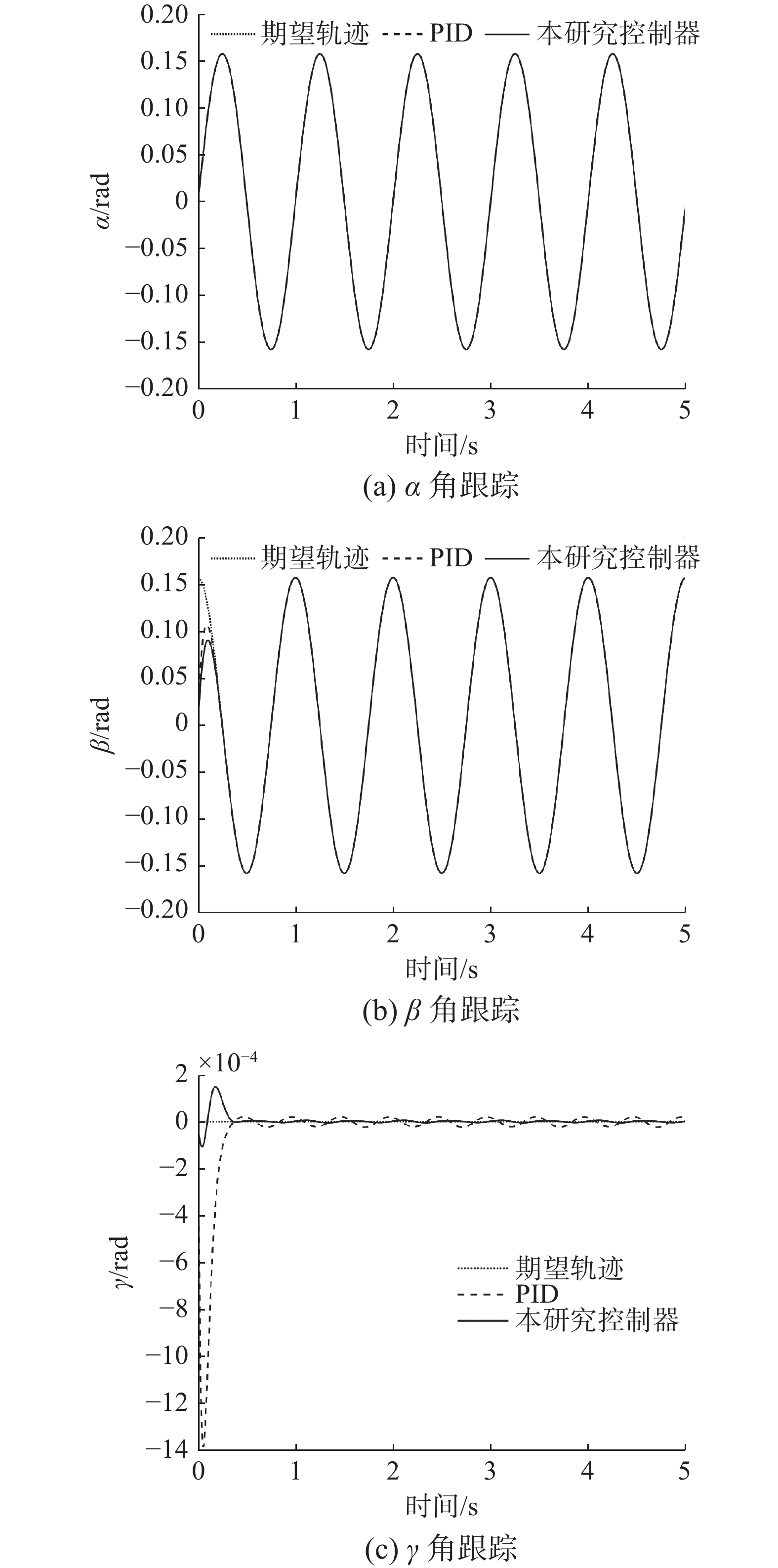
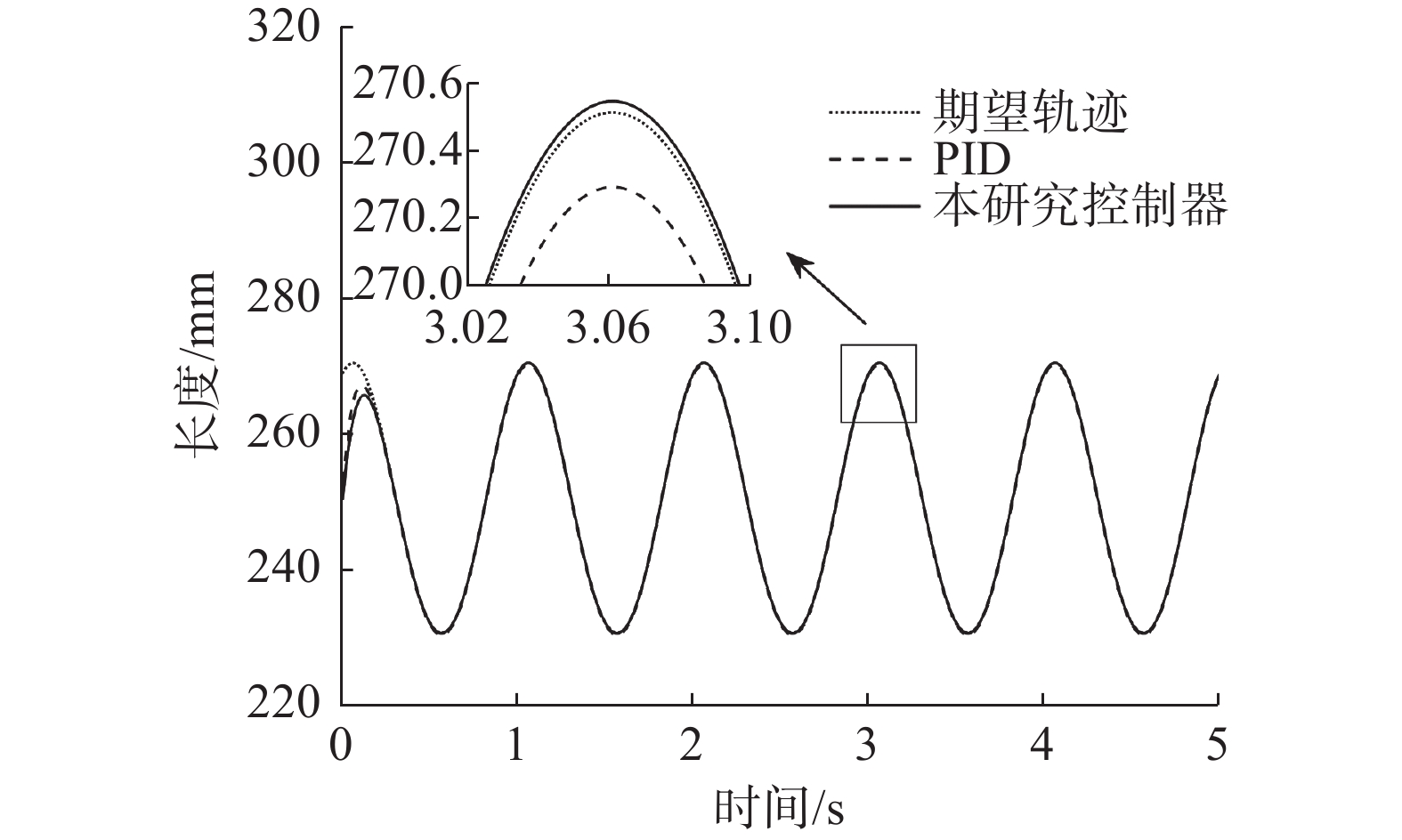
$ {K_p} = 200 $ ，$ {K_i} = 0.1 $ ，$ {K_d} = 10 $ 。设计初始姿态为$ \alpha = \beta = \gamma = 0 $ ，对系统的控制输入进行限幅，即$\left| u \right| \leqslant 30\;{\rm{N}}$ 。期望的上平台运动轨迹为，$\alpha = 0.05\text{π} \; \cdot \sin (2\text{π} t)$ ，$ \beta = 0.05\text{π} \sin (2\text{π} t + 0.5\text{π} ) $ ，其余4个自由度的期望轨迹为0，仿真结果如图4-7所示。
图 4 位置跟踪Fig. 4 Position tracking下载:
全尺寸图片
图 5 角度跟踪Fig. 5 Angle tracking下载:
全尺寸图片
图 6 支腿轨迹跟踪Fig. 6 Trajectory tracking of leg下载:
全尺寸图片
图 7 支腿轨迹跟踪误差Fig. 7 Trajectory tracking error of leg下载:
全尺寸图片
图4和图5分别为上平台位置和姿态的轨迹跟踪曲线，通过图4(a)和(b)可以看出，在给出期望轨迹后，本研究所提控制器能够使上平台质心快速到达期望位置，与PID控制器相比，其在
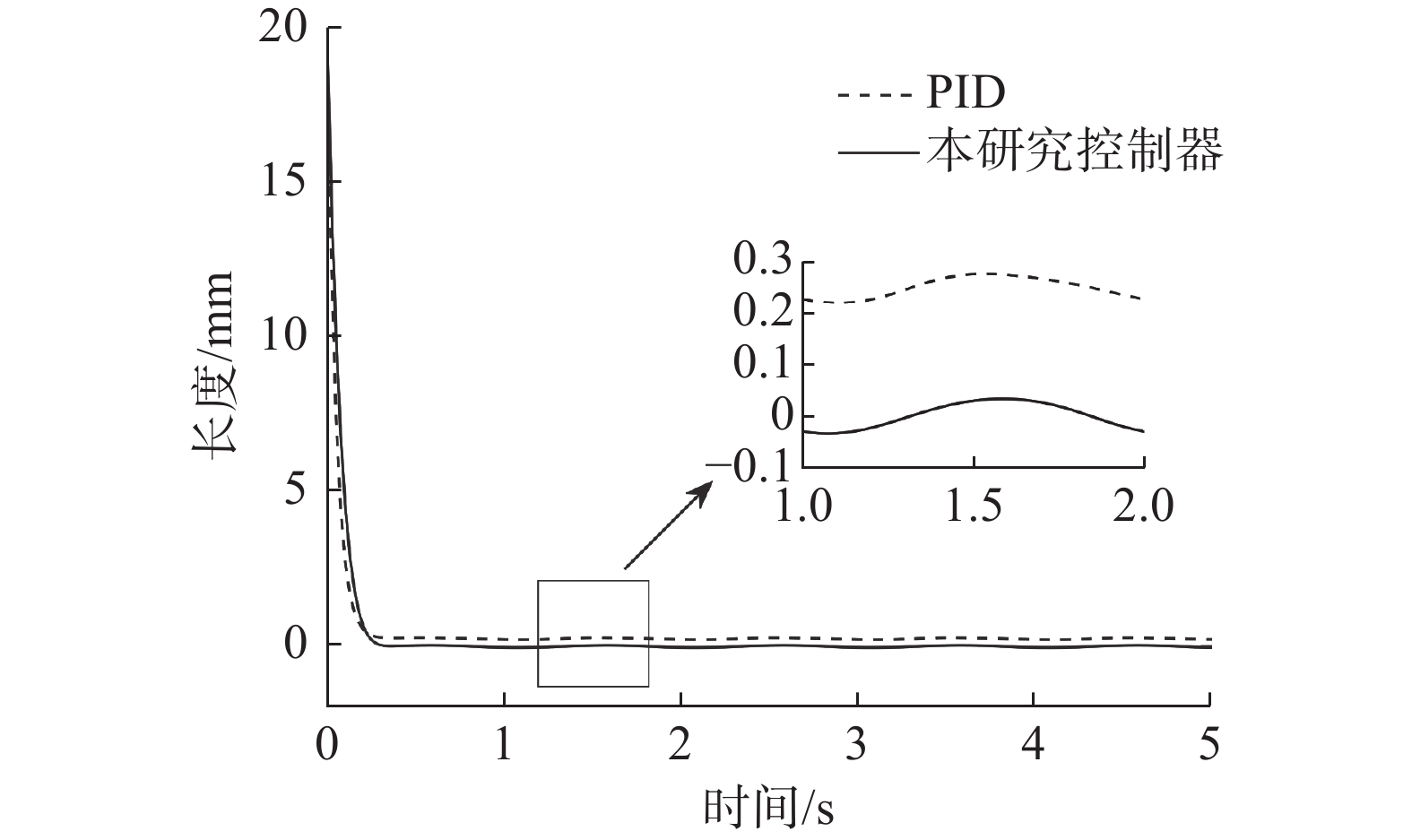
$ {X_a} $ 和$ {Y_a} $ 轴方向上的波动幅度更小。从图4(c)可以看出，在$ {Z_a} $ 轴方向上，PID控制器的控制误差在$ 0.3\;{\text{mm}} $ 左右，本研究所提控制器的控制误差在$ 3 \times {10^{ - 3}}\;{\text{mm}} $ 左右，仅为前者的$ 1\% $ 。通过图5可以看出，本研究所提控制方法能对$ \alpha $ 和$ \beta $ 的轨迹实现快速和精准的跟踪，从图5(c)可以看出，采用本研究所提方法，上平台$ \gamma $ 角的跟踪误差更小。本研究对系统动力学进行了分析，考虑了离心力和科氏力对系统运动的影响，并在控制器设计时进行了补偿，而将非线性系统线性化后设计的PID控制器，无法补偿系统线性化后产生的误差，如图6和图7所示，采用PID控制器，支腿的轨迹跟踪误差均值为
$ 0.22\;{\text{mm}} $ ，而采用本研究所提控制器，轨迹跟踪误差均值仅为$ 0.02\;{\text{mm}} $ ，控制精度得到了显著改善。5. 结束语
本研究针对Stewart六自由度平台的轨迹跟踪问题，提出了RBF神经网络非奇异终端滑模算法。首先分析了由上平台坐标系到6个支腿坐标系的位置反解、速度反解及加速度反解，然后根据牛顿−欧拉方程得到了Stewart平台的多刚体动力学方程，进而得到了系统的状态方程表达式。利用支腿的位置和速度误差设计了非奇异终端滑模控制器，并基于Lyapunov第二法，设计RBF神经网络对状态方程中的未知非线性函数进行逼近，使控制器设计不需要依赖精确的数学模型，具有自适应能力。仿真结果表明：本研究所提控制方法轨迹跟踪精度高，响应速度快，能够达到高性能的位姿动态控制。
-
图 1 Stewart平台结构
Fig. 1 Stewart platform structural diagram
下载:
全尺寸图片
图 2 控制系统结构
Fig. 2 Structure of control system
下载:
全尺寸图片
图 3 RBF神经网络拓扑结构
Fig. 3 Topology of RBF neural network
下载:
全尺寸图片
图 4 位置跟踪
Fig. 4 Position tracking
下载:
全尺寸图片
图 5 角度跟踪
Fig. 5 Angle tracking
下载:
全尺寸图片
图 6 支腿轨迹跟踪
Fig. 6 Trajectory tracking of leg
下载:
全尺寸图片
图 7 支腿轨迹跟踪误差
Fig. 7 Trajectory tracking error of leg
下载:
全尺寸图片
表 1 Stewart平台主要参数
Table 1 The main parameters of Stewart platform
名称 数值 上平台质量/kg 1.65 上平台主惯性矩/(kg·m2) [0.0064;0.0064;0.0124] 上平台外接圆半径/mm 150 下平台外接圆半径/mm 200 活塞杆长度/mm 200 缸筒长度/mm 100 平台初始高度/mm 212 -
[1] 郭立东. 舰载激光武器稳定平台控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. GUO Lidong. The controller of stabilized platform for shipborne laser weapons[D]. Harbin: Harbin Engineering University, 2011. [2] 郑欢. 船用六自由度稳定平台的控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2018. ZHENG Huan. Research on control of shipborne six-degree-of-freedom stabilized platform[D]. Harbin: Harbin Institute of Technology, 2018. [3] INNOCENTI C, PARENTI-CASTELLI V. A novel numerical approach to the closure of the 6-6 Stewart platform mechanism[C]//Fifth International Conference on Advanced Robotics' Robots in Unstructured Environments. Pisa: IEEE, 2002: 851−855. [4] LEBRET G, LIU K, LEWIS F L. Dynamic analysis and control of a Stewart platform manipulator[J]. Journal of robotic systems, 1993, 10(5): 629–655. doi: 10.1002/rob.4620100506 [5] YANG Chifu, HUANG Qitao, HAN Junwei. Decoupling control for spatial six-degree-of-freedom electro-hydraulic parallel robot[J]. Robotics and computer-integrated manufacturing, 2012, 28(1): 14–23. doi: 10.1016/j.rcim.2011.06.002 [6] 赵静一, 张荣兵, 孙龙, 等. Stewart平台位置反解研究[J]. 液压与气动, 2017(12): 40–47. ZHAO Jingyi, ZHANG Rongbing, SUN Long, et al. Position inverse solution of Stewart platform[J]. Chinese hydraulics & pneumatics, 2017(12): 40–47. [7] KOEKEBAKKER S H. Model based control of a flight simulator motion system[D]. Delft: Delft university of technology, 2001. [8] 董彦良, 吴盛林. 一种实用的6-6Stewart平台的实时位置正解法[J]. 哈尔滨工业大学学报, 2002, 34(1): 116–119. DONG Yanliang, WU Shenglin. A hybrid method to solve forward kinematics of general 6-6 Stewart platform[J]. Journal of Harbin Institute of Technology, 2002, 34(1): 116–119. [9] 姚程. 六自由度运动平台的模糊控制策略研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2015. YAO Cheng. Research on fuzzy control strategy of 6 DOF motion platform[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2015. [10] 刘希. 六自由度并联平台位姿跟踪控制研究[D]. 秦皇岛: 燕山大学, 2019. LIU Xi. Research on pose tracking control of six degree of freedom parallel platform[D]. Qinhuangdao: Yanshan University, 2019. [11] 陈泽栋. 六自由度位姿平台机构分析与运动控制策略研究[D]. 北京: 中国运载火箭技术研究院, 2020. CHEN Zedong. Analysis and motion control of 6-DOF position and pose mechanism[D]. Beijing: The first Academy of China Aerospace Science and Technology Corporation, 2020. [12] LIU Jinkun, SUN Fuchun. A novel dynamic terminal sliding mode control of uncertain nonlinear systems[J]. Journal of control theory and applications, 2007, 5(2): 189–193. doi: 10.1007/s11768-005-5275-5 [13] DING Shihong, ZHANG Chi, LI Xuebing. Terminal sliding mode control of second-order systems with bounded input[C]//2013 25th Chinese Control and Decision Conference. Guiyang: IEEE, 2013: 265−269. [14] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407–418. LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control theory & applications, 2007, 24(3): 407–418. [15] FENG Yong, YU Xinghuo, MAN Zhihong. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159–2167. doi: 10.1016/S0005-1098(02)00147-4 [16] 余荣荣, 姚乐. 基于遗传算法优化的机器人非奇异终端滑模控制[J]. 青岛科技大学学报(自然科学版), 2014, 35(4): 422–426. YU Rongrong, YAO Le. Nonsingular terminal sliding mode control of robot based on the genetic algorithm optimization[J]. Journal of Qingdao University of Science and Technology (natural science edition), 2014, 35(4): 422–426. [17] 黄其涛, 韩俊伟, 何景峰. 六自由度并联运动平台动力学建模及分析[J]. 机械科学与技术, 2006, 25(4): 382–385. HUANG Qitao, HAN Junwei, HE Jingfeng. Dynamics modeling of a six-degree-of-freedom parallel platform and its analysis[J]. Mechanical science and technology, 2006, 25(4): 382–385. [18] 杨宇, 郑淑涛, 韩俊伟. 基于动力学的Stewart平台振动控制策略研究[J]. 农业机械学报, 2010, 41(6): 20–24. YANG Yu, ZHENG Shutao, HAN Junwei. Stewart platform vibration control strategy based on dynamics[J]. Transactions of the Chinese society for agricultural machinery, 2010, 41(6): 20–24. [19] PARK J, SANDBERG I W. Approximation and radial-basis-function networks[J]. Neural computation, 1993, 5(2): 305–316. doi: 10.1162/neco.1993.5.2.305 [20] WANG D, HUANG Jie. Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form[J]. IEEE transactions on neural networks, 2005, 16(1): 195–202. doi: 10.1109/TNN.2004.839354
