Autonomous vehicle trajectory planning based on urban overtaking conditions
-
摘要: 在城市道路行驶中，超车驾驶既是常见的驾驶行为，也是常见的交通事故工况之一。基于改进人工势场法（artificial potential field method）与模型预测控制(model predicition control)提出了一种避障规划控制方法。首先，构建目标点引力势场函数、道路及车道线势场函数以及障碍物车辆势场函数；其次，基于势场函数建立统一化模型函数；最后，对系统进行模拟实验评估。结果表明，提出的避障规划控制方法能够生成安全、平滑的路径，其前轮转角变化范围在[−0.67°, 1.02°]，质心侧偏角变化范围在[−0.22°, 0.32°]，具有稳定的控制能力。Abstract: Overtaking is a common driving behavior on urban road. It is also one of the common behaviors in traffic accidents. Based on the improved artificial potential field method (APF) and model prediction control (MPC), a barrier avoidance planning control method was proposed in this study. The method firstly built the gravitational potential field function of the target point, the potential field function of the road & lane line and the potential field function of the obstacle vehicle, then established the unified model function on the basis of the potential field function, and finally evaluated the simulation experiment of the system. The results show that the proposed obstacle avoidance planning control method can generate a safe and smooth path, with the change range of the turning angle of the front wheel within [−0.67°, 1.02°], the change scope of the side slip angle within [−0.22°, 0.32°], having stable control ability.
-
汽车在城市道路行驶过程中超车是一种常见的驾驶行为[1]。由于超车至少涉及到自车和前车，因此存在潜在的碰撞风险。数据统计显示，我国2020年有24万多例交通事故，其中汽车交通事故占比64%。因此提高在超车过程中的行驶安全性成为减少交通事故风险的重要一环。自动驾驶汽车由于自身的优势，包括更好的安全性，更高的交通利用率以及能够减少能源消耗，逐步成为改善交通的良好方案[2-5]。自动驾驶实现超车行为则是需要综合考虑自车路径规划与速度规划以及障碍物车辆的行驶轨迹与速度，因此被称为道路复杂工况之一。
自动驾驶路径规划目的是生成一条无碰撞路径，即车辆行驶安全是主要任务。常见的路径规划方法包括基于图搜索的方法，基于采样的方法，基于插值曲线的方法和基于数值优化的方法等[6-7]。基于图搜索的方法主要包括Dijkstra、A*和D*以及它们的变体[8-10]。采样的方法主要是快速搜索随机树方法[11]。基于插值曲线的方法主要包括多项式曲线、B样条曲线、三次样条曲线插值以及贝塞尔曲线[12-13]等。人工势场方法[14-16]（artificial potential field，APF）通过将车辆所在的运行空间虚拟成一个力存在的场空间，车辆在场中受到引力和斥力共同影响，其具有结构简单、适应性强、实时性好的特点，同时会出现局部最小点的问题。模型预测控制（model prediction control，MPC）方法是一种常见的轨迹规划与跟踪控制方法[17]。综合各种规划方法的特点，本文将采用人工势场法与模型预测控制方法结合的方式进行轨迹规划。
对于自动驾驶的超车问题，张志勇等[18]将超车行为分为变道、匀速、变道3个阶段，并分别进行路径规划。Bhargav等[19]通过策略学习方法融入超车规划与控制中，从而构建一种实现超车行为控制器。张家旭等[20]设计一种动态环境增量的搜索算法，进而规划处汽车弯道超车路径并基于线性鲁棒性控制法保证最优性能控制策略。王树凤等[21]通过构建一种新型人工势场从而实现超车行为。Wu等[22]提出基于冬天太模糊的时间差学习，来判断是否超车，从而降低交通碰撞的可能性。Jeno等[23]构建有限状态机，结合安全，舒适行程效率等特征，从而生成最佳轨迹。
针对超车避障问题，现有研究通常涉及高速公路的工况或静态或前车车速恒定的情况。然而，在实际道路避障过程中，障碍物车辆通常是动态且行驶速度并不是恒定。考虑到时间成本以及行驶稳定性，我们希望在自车安全的前提下，按照预定要求避开障碍物。
本文基于安全距离的方法判断是否符合安全超车行为，根据人工势场法设计引力势场函数、道路势场函数、障碍物势场函数从而构建出车辆行驶可行域，并结合模型预测控制方法进行构建可行轨迹，最终通过模拟实验验证该方法。
1. 问题描述
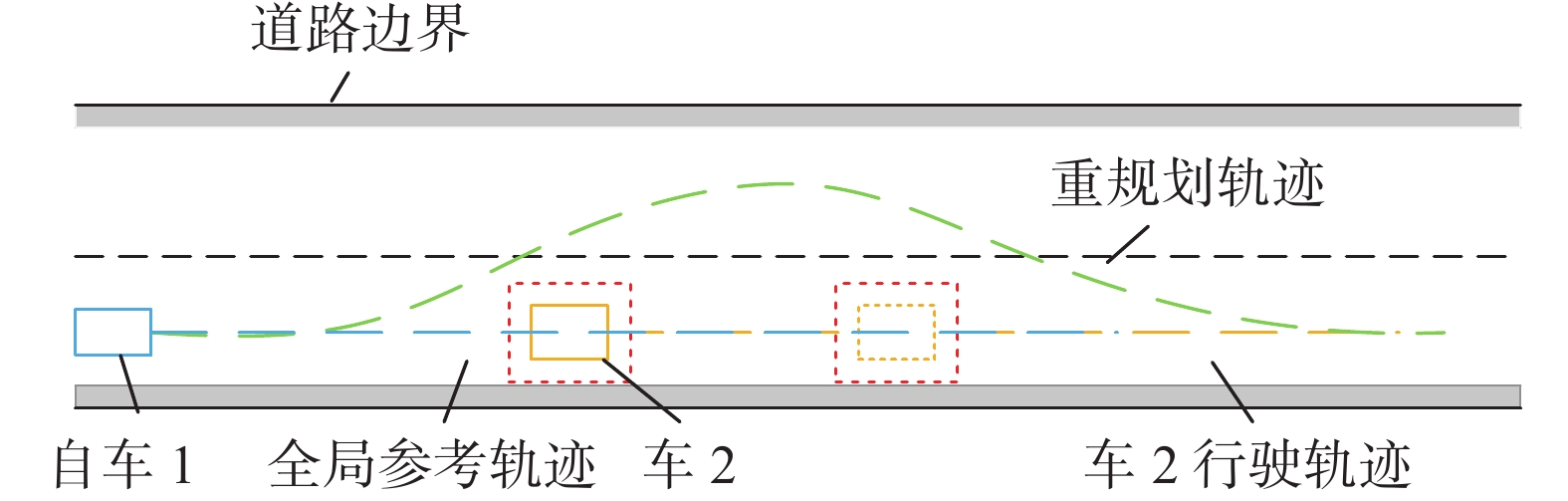
超车场景如图1所示，在城市双向四车道道路工况下（本图只显示一侧），蓝色虚线是自车（蓝色矩形）的全局参考轨迹。由于前方有车辆（橙色矩形），且前车的驾驶行为动态变化。为了保证在安全的情况下处理该场景，自车需要在此阶段判断驾驶行为，进行减速或超车。若进行超车行为，车辆选择合适的超车时机，并选择合适的轨迹。如何选择合适的驾驶行为并生成合适的轨迹（绿色虚线）是解决这个问题的关键。
图 1 超车场景Fig. 1 Overtaking scenario
下载:
全尺寸图片
针对上述所研究的问题，本文提出一种避撞规划策略。在介绍该策略前，首先对于研究问题基于几点假设：
1）在局部路径中，障碍物均可被感知层获取；
2）环境良好，不存在极端天气，道路条件良好，道路摩擦恒定；
3）根据城市道路有关规定，车辆行驶速度不超过60 km/h；
4）初始时刻自车与障碍物车辆保持在安全行驶范围，不存在极端工况。
2. 避撞规划策略
自车在城市工况道路行驶遇到前方有车辆时，会采取减速、跟车行驶、变道或超车等驾驶行为。在与前方车辆行驶路径在未来某时刻可能会发生碰撞危险时，此时车辆的策略很重要，一般有2种选择，减速或者加速超车，在行驶安全的前提下，后者会带来更优的时间成本以及更少的能源消耗。本文基于以下假设：即两车发生碰撞的充分必要条件是两车在同一时刻轨迹空间有交叉或覆盖。
2.1 驾驶行为规划
为了更好地规划车辆超车轨迹，使之与驾驶员超车行为一致，需要分析超车换道行为特点，将其融合到车辆超车换道的路径规划中。发生超车行为需要满足以下条件：当前自车速度大于前方车辆速度，且相邻车道有安全行驶空间；全过程两车保持安全距离，包括横向与纵向安全距离。
基于上述超车行为判据条件，在横向与纵向上基于一种改进的安全距离模型，计算出两车的最短安全距离。
1）若前车以最大减速度制动停车，自车同样制动停车，此时极限工况下纵向安全距离：
$$ \begin{array}{c} {d}_{xs}=\dfrac{1}{2}\left(\dfrac{{v}_{x}^{2}}{{a}_{x\mathrm{m}\mathrm{a}\mathrm{x}}^{2}}-\dfrac{{v}_{Ox}^{2}}{{a}_{Ox\mathrm{m}\mathrm{a}\mathrm{x}}^{2}}\right)+\dfrac{\left(L+{L}_{O}\right)}{2}+{v}_{x}{t}_{0}+{d}_{x}\end{array} $$ (1) 式中：
$ {v}_{x} $ 为自车纵向速度；$ {v}_{{O}x} $ 为障碍物车辆纵向速度；$ {a}_{x\mathrm{m}\mathrm{a}\mathrm{x}} $ 为自车制动最大纵向加速度；$ {a}_{{O}x\mathrm{m}\mathrm{a}\mathrm{x}} $ 为障碍物制动最大纵向加速度；$ L $ 为自车长度；$ {L}_{{O}} $ 为障碍物车辆长度；$ {t}_{0} $ 为自车反应时间,与车辆各组件信息传递相关；$ {d}_{x} $ 为预留最小纵向安全距离。2）自车以最大横向加速度转向行驶，此时极限工况下横向安全距离：
$$ \begin{array}{c}{d}_{ys}=\left(\dfrac{L\mathrm{sin}\;\varphi }{2}+\dfrac{W\mathrm{cos}\;\varphi }{2}\right)+\dfrac{{W}_{\mathrm{o}\mathrm{b}\mathrm{s}}}{2}+{d}_{y}\end{array} $$ (2) 式中：
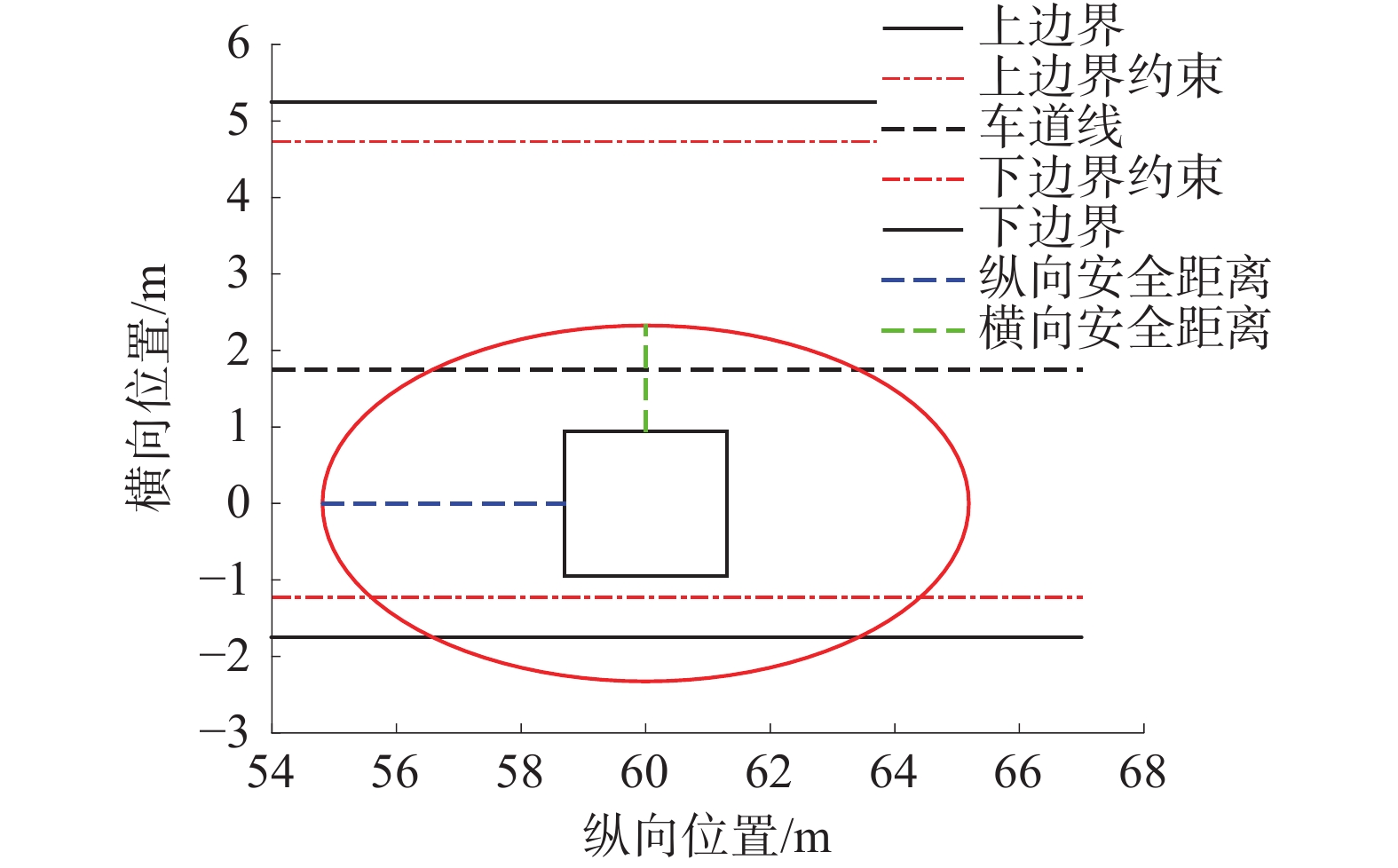
$ L $ 为自车长度；$ W $ 为自车宽度；$ {W}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ 为障碍物车辆宽度；$ {d}_{y} $ 为预留最小横向安全距离。图2中，黑色矩形是障碍物车辆示意图，红色椭圆则为车辆安全距离，此时障碍物车辆安全距离可看作以纵向安全距离为长轴，以横向安全距离为短轴的椭圆。
图 2 障碍物安全距离示意Fig. 2 Obstacle safety distance schematic下载:
全尺寸图片
2.2 车辆模型的建立
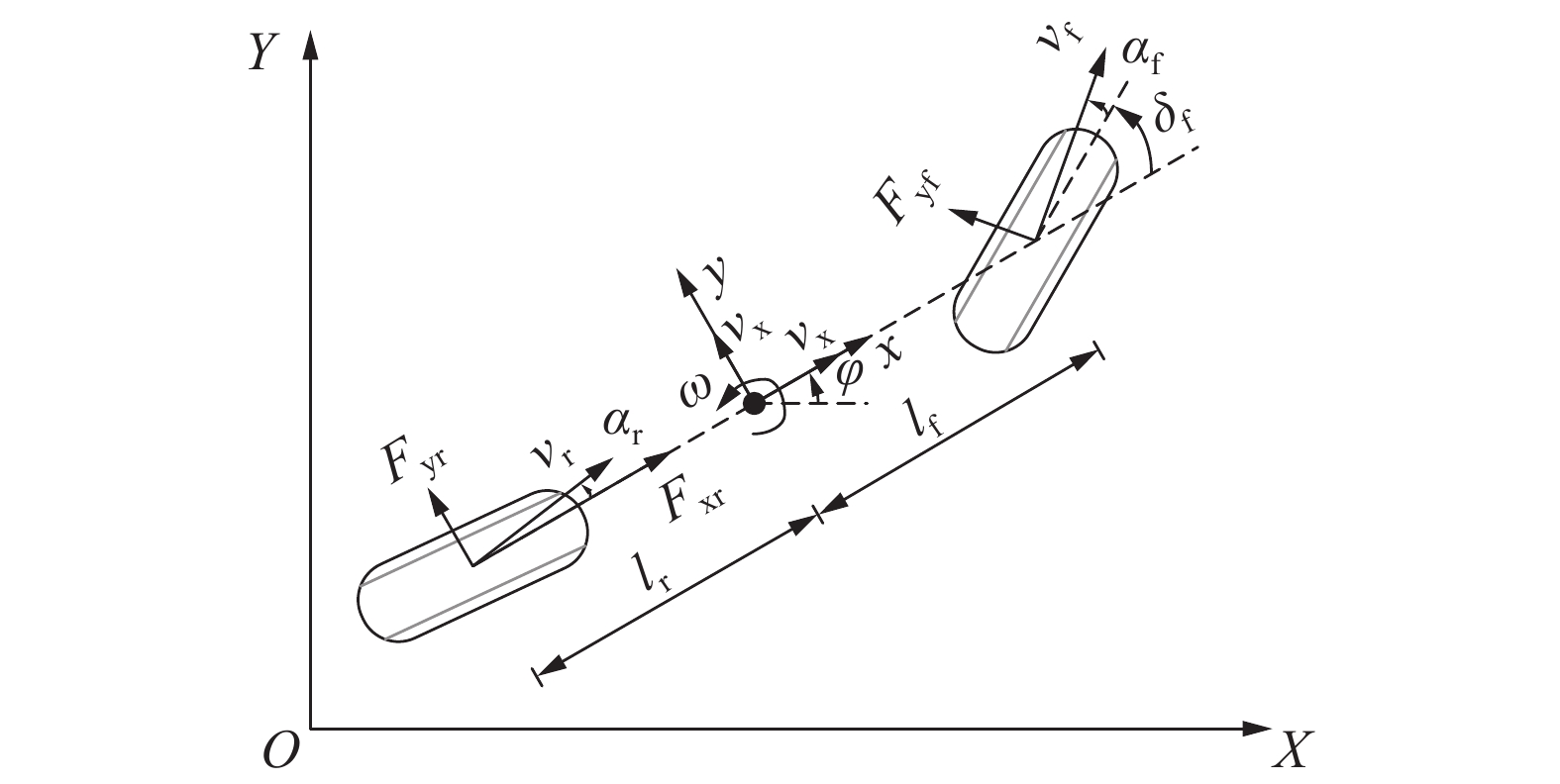
使用复杂的模型能够更好地对车辆输出进行预测，但同时增大了规划控制器的计算量，实时性难以保证，而使用简单的模型有可能导致跟踪失败。Liu等[24]研究证明2自由度模型与14自由度模型在加入约束后具备相近的效果并且计算时间优势明显。本文选择2自由度车辆动力学模型作为车辆动力学模型，如图3所示。
图 3 车辆动力学模型Fig. 3 Vehicle dynamics model下载:
全尺寸图片
在这种情况下，车辆轮胎在小横向加速度下的线性区域运行，可以基于简单的线性轮胎模型计算车辆侧向力，该模型采用等效的轮胎转弯刚度。
$$ \begin{array}{c} m{\dot{v}}_{y}=-m{v}_{x}+ 2\left[{\overline{C}}_{\alpha f}\left({\delta }_{f}-\dfrac{{v}_{y}+{l}_{f}\dot{\varphi }}{{v}_{x}}\right)+{\overline{C}}_{\alpha r}\dfrac{{l}_{r}\dot{\varphi }-{v}_{y}}{{v}_{x}}\right]\end{array} $$ (3) $$ \begin{array}{c} m{\dot{v}}_{x}=m{v}_{y}\dot{\varphi }+2\left[{C}_{lf}{s}_{f}+{\overline{C}}_{\alpha f}\left({\delta }_{f}-\dfrac{{v}_{y}+{l}_{f}\dot{\varphi }}{{v}_{x}}\right){\delta }_{f}+{C}_{lr}{s}_{r}\right]\end{array} $$ (4) $$ \begin{array}{c}{I}_{{\textit{z}}}\ddot{\varphi }=2\left[{l}_{f}{\overline{C}}_{f}\left({\delta }_{f}-\dfrac{{v}_{y}+{l}_{f}\dot{\varphi }}{{v}_{x}}\right)-{l}_{r}{\overline{C}}_{\alpha r}\dfrac{{l}_{r}\dot{\varphi }-{v}_{y}}{{v}_{x}}\right]\end{array} $$ (5) $$ \begin{array}{c}\dot{\varphi }=r\end{array} $$ (6) $$ \begin{array}{c}\dot{Y}={v}_{x}\mathrm{sin}\;\varphi +{v}_{y}\mathrm{cos}\;\varphi \end{array} $$ (7) $$ \begin{array}{c}\dot{X}={v}_{x}\mathrm{cos}\;\varphi -{v}_{y}\mathrm{sin}\;\varphi\end{array} $$ (8) 式中：
$ m $ 是车辆质量，$ {I}_{{\textit{z}}} $ 是车辆绕z轴转动惯量，$ {\overline{C}}_{\alpha f} $ 和$ {\overline{C}}_{\alpha r} $ 分别是车辆模型前后轮的线性侧偏刚度，$ {C}_{lf} $ 和$ {C}_{lr} $ 是车辆前后轮胎的纵向侧偏刚度，$ {\delta }_{f} $ 是前轮偏角，$ {l}_{f} $ 和$ {l}_{r} $ 质心到前后轴的距离。2.3 设计规划控制器
2.3.1 设计人工势场
传统的人工势场法是一种虚拟力方法，根据电荷间相互作用规律演变而来，其基本思想是，在被控对象运动环境人为建立势场，其中障碍物为斥力场，目标点为引力场，分别对被控对象产生斥力和引力，引力和斥力构成的合力控制被控对象的运动方向，其中：
$$ \begin{array}{c}{F}_{\mathrm{a}\mathrm{t}\mathrm{t}}=K\times {\rho }_{g}\times {a}_{g}\end{array} $$ (9) $$ \begin{array}{l}{{F}}_{\text{re}}\text=\left\{\begin{array}{l}\delta \times\left(\dfrac{\text{1}}{\rho _{\text{e}}}-\dfrac{\text{1}}{\rho _{\text{0}}}\right)\times\left(\dfrac{\text{1}}{\rho _{\text{e}}^{\text{2}}}\right),\qquad \rho _{\text{e}}\geqslant \rho _{\text{0}}\\ \text{0}\text{,}\qquad \rho _{\text{e}}\geqslant \rho _{\text{0}}\end{array}\right.\end{array} $$ (10) 式中：
$ {F}_{\mathrm{a}\mathrm{t}\mathrm{t}} $ 为目标点对被控对象的引力，$ {F}_{\mathrm{r}\mathrm{e}} $ 为障碍物对被控对象的斥力。在本文改进的人工势场法中，将势场分为目标引力点势场、道路斥力势场，障碍物斥力势场。在车辆行驶的道路上，基于纵向的安全与横向安全距离不同，其势场范围做相应变化。
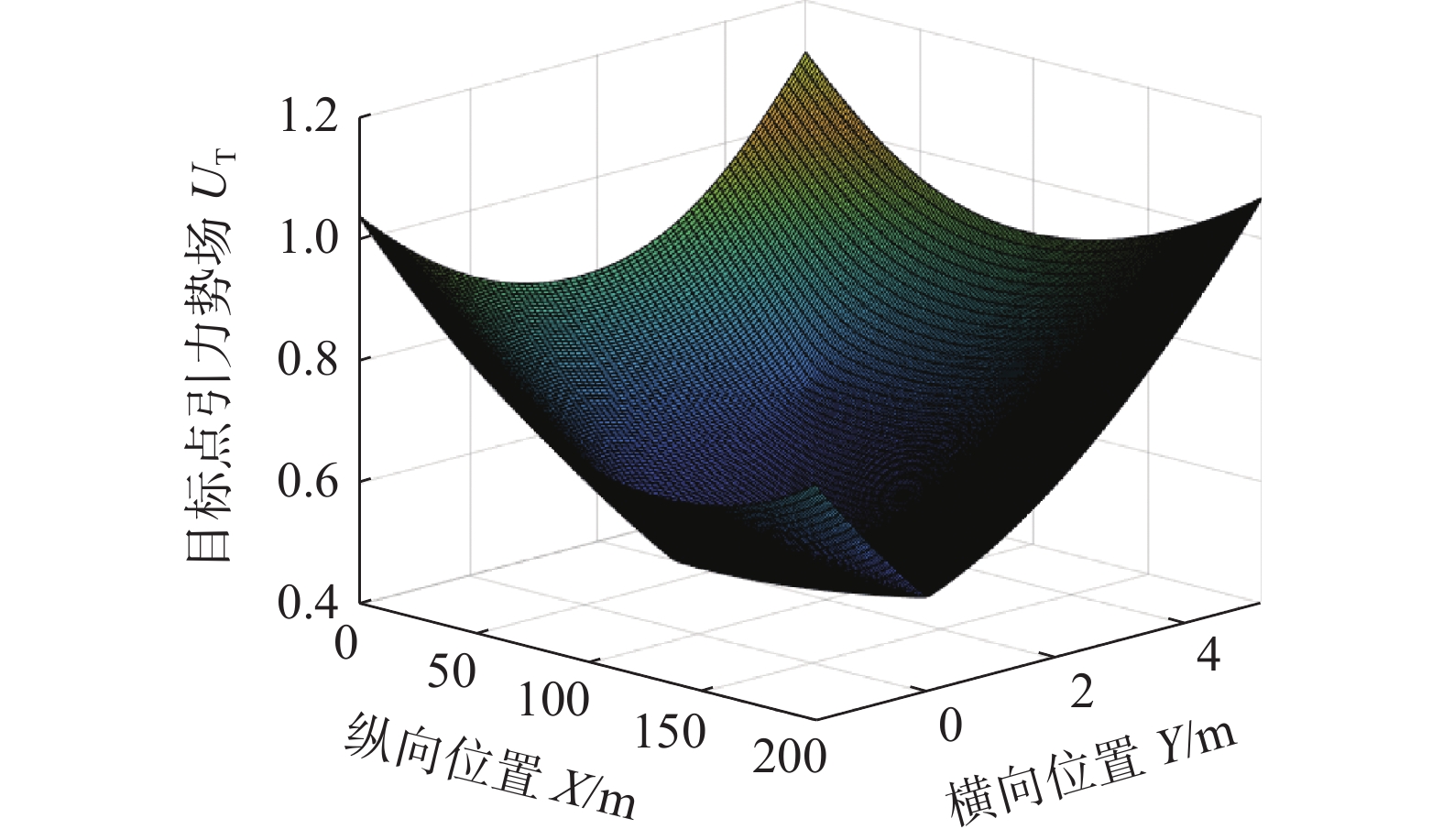
1）目标点引力势场
$ {U}_{\mathrm{T}} $ 构建出虚拟目标点
$ \left({X}_{vt},{Y}_{vt}\right) $ 与实际目标点$ \left({X}_{rt},{Y}_{rt}\right) $ 最终根据虚拟目标点与实际目标点综合影响引力势场，如图4所示。
图 4 目标点引力势场示意Fig. 4 Schematic of the gravitational potential field at the target point下载:
全尺寸图片
$$ \begin{array}{c}{d}_{t}={\left({\left(X-{X}_{rt}\right)}^{2}+{\left(Y-{Y}_{rt}\right)}^{2}\right)}^{\frac{1}{2}}\end{array} $$ (11) $$ {U}_{vt}=\left\{{w}_{td}{d}_{td}+{w}_{tx}{\left({X}_{vt}-X\right)}^{2}+ {{w}_{ty}\left({Y}_{vt}-Y\right)}^{2}\right\}^{\frac{1}{2}} $$ (12) $$ {U}_{rt}=\left\{{w}_{td}{d}_{t}+{w}_{td}{\left({X}_{vt}-X\right)}^{2}+ {\left({Y}_{vt}-Y\right)}^{2}\right\}^{\frac{1}{2}}$$ (13) $$ \begin{array}{c}{U}_{\mathrm{T}}={w}_{vt}{U}_{vt}+{w}_{rt}{U}_{rt}\end{array} $$ (14) 式中：
$ {d}_{t} $ 为自车与实际目标点距离，$ {U}_{vt} $ 为虚拟目标点引力势场，$ {U}_{rt} $ 表示实际目标点引力势场，$ {X}_{vt}、{Y}_{vt} $ 表示虚拟目标点在全局坐标系下的纵、横向位置，$ {w}_{td}、{w}_{tx}、{w}_{ty}、{w}_{vt}、{w}_{rt} $ 表示构建目标点引力势场中权重系数。2）道路及车道线斥力势场
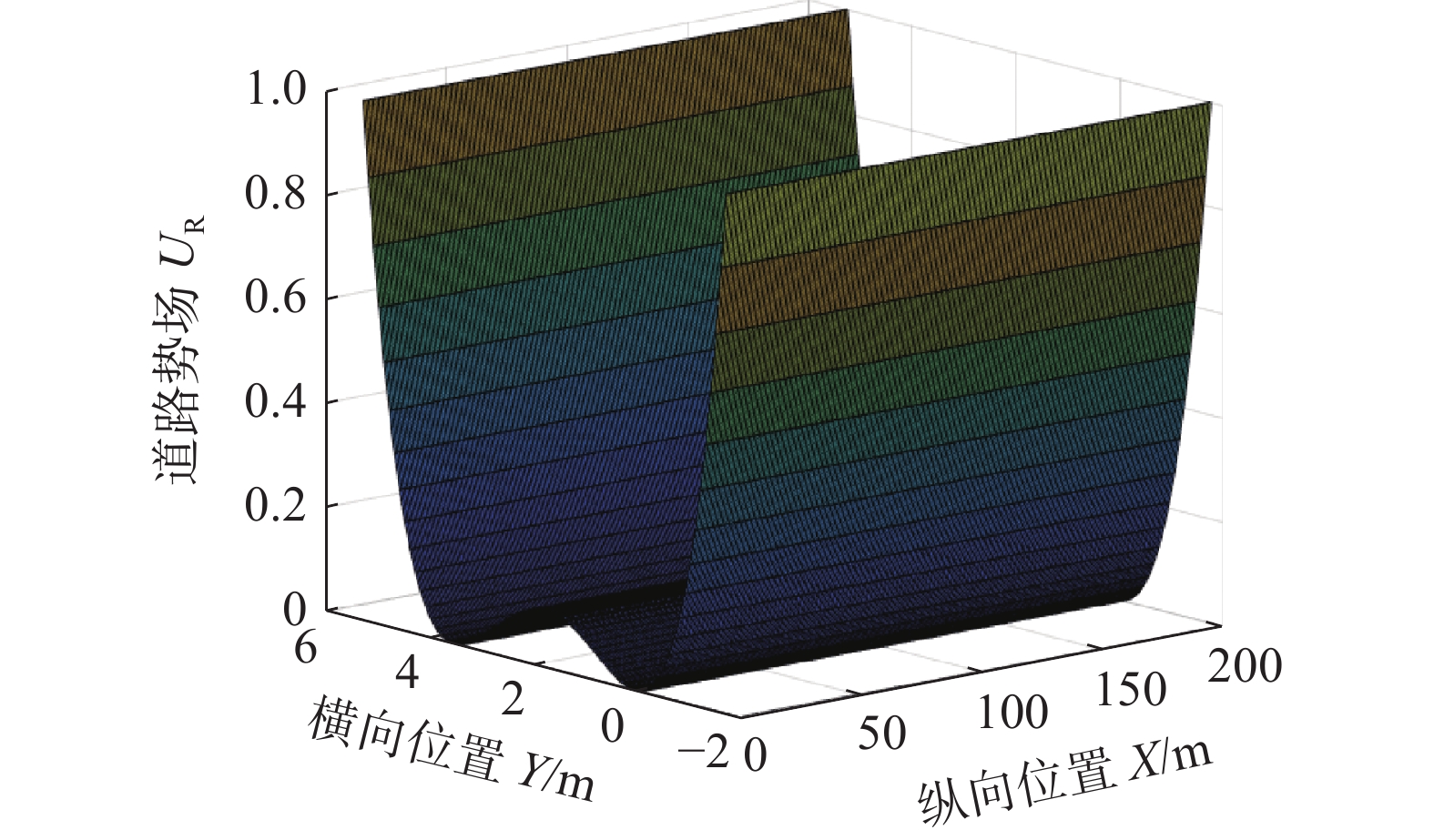
$ {U}_{\mathrm{R}} $ 构建道路以及车道的斥力势场，如图5所示。
图 5 道路及车道线斥力势场示意Fig. 5 Schematic of roadway and lane line repulsive potential field下载:
全尺寸图片
$$ \begin{array}{c}{{U}}_{\text{R}\text{0}}\text={\left(Y-{l}_{l}\right)}^{2}{\left(Y-{l}_{r}\right)}^{2}\end{array} $$ (15) 并将势场归一化：
$$ \begin{array}{c}{U}_{\mathrm{R}}=\dfrac{{U}_{\mathrm{R}0}-{U}_{\mathrm{R}\mathrm{m}\mathrm{i}\mathrm{n}}}{{U}_{\mathrm{R}\mathrm{m}\mathrm{a}\mathrm{x}}-{U}_{\mathrm{R}\mathrm{m}\mathrm{i}\mathrm{n}}}\end{array} $$ (16) 式中：
$ {l}_{l},{l}_{r} $ 分别为左、右车道中心线，$ {U}_{\mathrm{R}\mathrm{m}\mathrm{a}\mathrm{x}}、{U}_{\mathrm{R}\mathrm{m}\mathrm{i}\mathrm{n}} $ 分别为道路势场最大值与最小值。3）障碍物势场
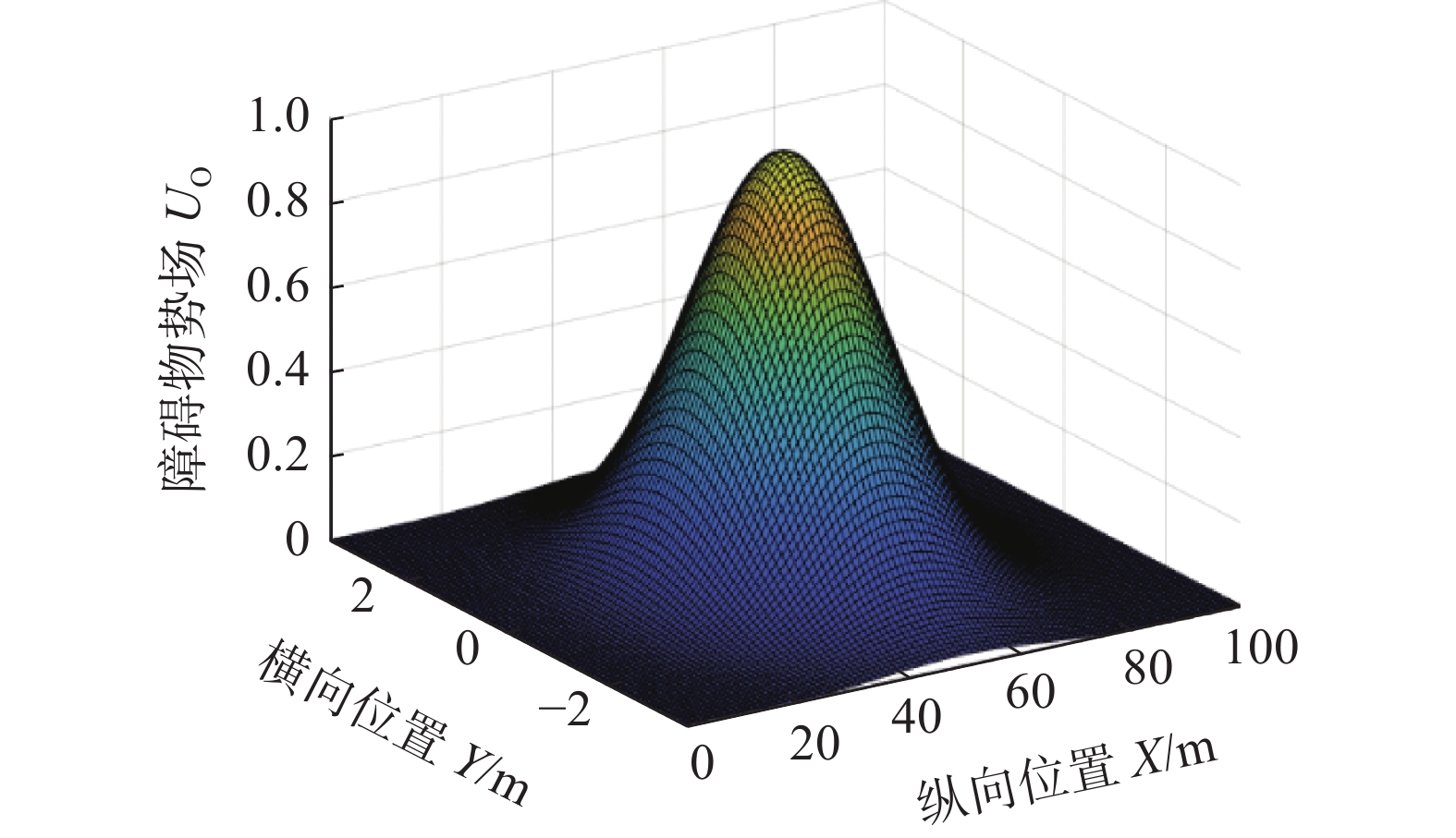
$ {{U}}_{\text{O}} $ ：根据横纵向安全距离构建障碍物的势场，如图6所示。
图 6 障碍物斥力势场示意Fig. 6 Schematic diagram of the obstacle repulsive potential field下载:
全尺寸图片
$$ \begin{array}{c}{w}_{{\rm{O}}X}=-\dfrac{\mathrm{l}\mathrm{n}\left({\varepsilon }_{X}\right)}{{\left(2{X}_{s}\right)}^{2}}\end{array} $$ (17) $$ \begin{array}{c}{w}_{{\rm{O}}Y}=-\dfrac{\mathrm{l}\mathrm{n}\left({\varepsilon }_{Y}\right)}{{\left(2 {Y}_{s}\right)}^{2}}\end{array} $$ (18) $$ \begin{array}{c}{U}_{{\rm{O}}}={w}_{{\rm{O}}}{\mathrm{e}}^{-\left({w}_{{\rm{O}}X}\cdot {\left(X-{X}_{{\rm{O}}}\right)}^{2}+{w}_{{\rm{O}}Y}\cdot {\left(Y-{Y}_{{\rm{O}}}\right)}^{2}\right)}\end{array} $$ (19) 式中：
${w}_{{\rm{O}}X}$ 和${w}_{{\rm{O}}Y}$ 分别为障碍物势场的纵向、横向影响因子；$ {w}_{{\rm{O}}} $ 是障碍物势场期望系数。总势场
$ {U}_{\mathrm{a}\mathrm{l}\mathrm{l}} $ 可以表达为$$ \begin{array}{c}{{U}}_{\text{all}}={{U}}_{\text{T}}+{{U}}_{\text{R}}+{{U}}_{\text{O}}\end{array} $$ (20) 2.3.2 构建模型与目标函数
此时设置状态向量
$\dot{\boldsymbol{\zeta }}={\left[\dot{y}\;\;\dot{x}\varphi\;\; \dot{\varphi }\;\;Y\;\;X\right]}^{\mathrm{T}}$ 和控制向量$ \boldsymbol{u}={\delta }_{f} $ 。$$ \begin{array}{c}\dot{\boldsymbol{\zeta }}={\boldsymbol{f}}\left({\boldsymbol{\zeta}} ,{\boldsymbol{u}}\right)\end{array} $$ (21) 将车辆动力学模型在参考点处用泰勒公式线性化：
$$ \begin{array}{c} {\boldsymbol{\zeta}} \left({k}{+1}\right)={{{\boldsymbol{A}}}}_{{k}} {\boldsymbol{\zeta}} \left({k}\right)+{{{\boldsymbol{B}}}}_{{k}}{{\boldsymbol{u}}}\left({k}\right)\end{array} $$ (22) $$ \begin{array}{c}{\boldsymbol{\eta}} {(}{k}{)}={{{\boldsymbol{C}}}}_{{k}} {\boldsymbol{\zeta}} {(}{k}{)}\end{array} $$ (23) 式中：
${{{\boldsymbol{A}}}}_{{{\boldsymbol{k}}}}{=}{{\boldsymbol{I}}}{+}{{{\boldsymbol{A}}}}_{{t}}，{\boldsymbol{B}}_{k}={\boldsymbol{T}}_{s}{\boldsymbol{B}}_{t}，{{{\boldsymbol{A}}}}_{{t}}{=}{\dfrac{{\partial {\boldsymbol{f}}}}{{\partial {\boldsymbol{\zeta}} }}\Bigg|}_{{ \zeta }_{{t}}{,}{{u}}_{{t}}}，{{{\boldsymbol{B}}}}_{{t}}{=}{ \dfrac{{\partial {\boldsymbol{f}}}}{{\partial {\boldsymbol{u}}}}\Bigg|}_{{ \zeta }_{{t}}{,}{{u}}_{{t}}}， {\boldsymbol{\eta}} {{(}{k}{)}}$ 是输出向量，${{{\boldsymbol{C}}}}_{{k}}$ 是输出选择矩阵。为引进控制量
$\mathrm{\Delta }{\boldsymbol{u}}$ 的增量，简化计算，将状态空间重构为$$ \begin{array}{c}\tilde{ {\boldsymbol{\zeta}} }\left({k}{+1}\right)=\left[\begin{array}{c} {\boldsymbol{\zeta}} {(}{k}{)}\\ {{\boldsymbol{u}}}{(}{k}{-1}{)}\end{array}\right]\end{array} $$ (24) $$ \begin{array}{c}\tilde{{\boldsymbol{\eta}} }\left({k}\right)={\tilde{{{\boldsymbol{C}}}}}_{{k}}\tilde{ {\boldsymbol{\zeta}} }{(}{k}{)}\end{array} $$ (25) 预测状态：
$$ \begin{array}{c}\tilde{\boldsymbol{\zeta }}\left(k+1\right)={\tilde{\boldsymbol{A}}}_{k}\tilde{\boldsymbol{\zeta }}\left(k\right)+{\tilde{\boldsymbol{B}}}_{k}\Delta {\boldsymbol{u}}\left(k\right)\end{array} $$ (26) $$ \begin{array}{c}{\boldsymbol{\eta}} \left(k\right)={\boldsymbol{C}}_{k}{\boldsymbol{\zeta}} \left(k\right)\end{array} $$ (27) 式中：
${\tilde{\boldsymbol{A}}}_{k}=\left[\begin{array}{cc}{\boldsymbol{A}}_{k}& {\boldsymbol{B}}_{k}\\ {{\boldsymbol{0}}}_{m\times n}& {\boldsymbol{I}}_{m}\end{array}\right]，{\tilde{\boldsymbol{B}}}_{k}=\left[\begin{array}{c}{\boldsymbol{B}}_{k}\\ {\boldsymbol{I}}_{m}\end{array}\right]，{\tilde{\boldsymbol{C}}}_{k}=\left[{\boldsymbol{C}}_{k},0\right]， \Delta \boldsymbol{u}\left(k\right)=\boldsymbol{u}\left(k\right)-\boldsymbol{u}\left(k-1\right)，m$ 是控制量维度$ ，n $ 是状态量维度。预测模型可以表达为
$$ \begin{array}{c}{\boldsymbol{\gamma}} \left(k+1\right)={\boldsymbol{\psi}} {\boldsymbol{\zeta}} \left(k\right)+{\boldsymbol{\varTheta}} {{\Delta}} {\boldsymbol{U}}\left(k\right)\end{array} $$ (28) $$ \boldsymbol{\gamma }\left(k+1\right)=\left[\begin{array}{c}{\boldsymbol{\eta}} \left(k+1\right)\\ {\boldsymbol{\eta}} \left(k+2\right)\\ \vdots \\ {\boldsymbol{\eta}} \left(k+{N}_{c}\right)\\ \vdots \\ {\boldsymbol{\eta}} \left(k+{N}_{p}\right)\end{array}\right] $$ $$ \boldsymbol{\psi }=\left[\begin{array}{c}{\tilde{\boldsymbol{C}}}_{k}{\tilde{\boldsymbol{A}}}_{k}\\ {\tilde{\boldsymbol{C}}}_{k}{\tilde{\boldsymbol{A}}_{k}^2}\\ \vdots \\ {\tilde{\boldsymbol{C}}}_{k}{\tilde{\boldsymbol{A}}}_{k}^{{\boldsymbol{N}}_{c}}\\ \vdots \\ {\tilde{\boldsymbol{C}}}_{k}{\tilde{\boldsymbol{C}}}_{k}^{{\boldsymbol{N}}_{p}}\end{array}\right] $$ $$ \Delta \boldsymbol{U}\left(k\right)=\left[\begin{array}{c}\Delta {\boldsymbol{u}}\left(k\right)\\ \Delta {\boldsymbol{u}}(k+1)\\ \vdots \\ \Delta {\boldsymbol{u}}(k+{N}_{c}-1)\end{array}\right] $$ $$ \boldsymbol{\varTheta }=\begin{bmatrix}\tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{B}}_k & \mathbf{0} & \cdots & \mathbf{0}\\ \vdots & \vdots & \vdots & \vdots\\\tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{A}}_k^{\boldsymbol{N}_c}\tilde{\boldsymbol{B}}_k & \tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{A}}_k^{\boldsymbol{N}_c-1}\tilde{\boldsymbol{B}}_k & \cdots & \tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{B}}_k\\ \vdots & \vdots & \ddots & \vdots\\ \tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{A}}_k^{\boldsymbol{N}_p}\tilde{\boldsymbol{B}}_k & \tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{A}}_k^{\boldsymbol{N}_p-1}\tilde{\boldsymbol{B}}_k & \cdots & \tilde{\boldsymbol{C}}_k\tilde{\boldsymbol{A}}_k^{\boldsymbol{N}_p-\boldsymbol{N}_c}\tilde{\boldsymbol{B}}_k\end{bmatrix} $$ 借鉴现有方法[25]设计目标函数：
$$ \begin{array}{c}\boldsymbol{J}\left({\boldsymbol{\zeta}} \left(t\right),{\boldsymbol{u}}\left(t-1\right),\mathrm{\Delta }{\boldsymbol{u}}\left(t\right)\right)={\boldsymbol{J}}_{\varphi }+{\boldsymbol{J}}_{u}+{\boldsymbol{J}}_{{\rm{T}}}+{\boldsymbol{J}}_{{\rm{R}}}+{\boldsymbol{J}}_{{\rm{O}}}\end{array} $$ (29) 其中：
$$ {\boldsymbol{J}}_{\varphi }=\sum _{i=1}^{{\boldsymbol{N}}_{p}}{\left(\varphi \left(t+i|t\right)-{\varphi }_{\mathrm{r}\mathrm{e}\mathrm{f}}(t+i|t)\right)}^{{\rm{T}}}{\lambda }_{\varphi }\left(\varphi \left(t+i|t\right)-{\varphi }_{\mathrm{r}\mathrm{e}\mathrm{f}}(t+i|t)\right) $$ (30) $$ {\boldsymbol{J}}_{u}=\sum _{i=1}^{{\boldsymbol{N}}_{c}-1}\left({\Delta {\boldsymbol{u}}(t+i|t)}^{{\rm{T}}}{\lambda }_{u}\Delta {\boldsymbol{u}}(t+i|t)\right) $$ (31) $$ {\boldsymbol{J}}_{{\rm{T}}}=\sum _{i=1}^{{N}_{p}}{\lambda }_{T}\times {U}_{{\rm{T}}}(t+i|t) $$ (32) $$ {\boldsymbol{J}}_{{\rm{R}}}=\sum _{i=1}^{{N}_{p}}{\lambda }_{R}\times {U}_{{\rm{R}}}(t+i|t) $$ (33) $$ {\boldsymbol{J}}_{{\rm{O}}}=\sum _{i=1}^{{N}_{p}}{\lambda }_{O}\times {U}_{{\rm{O}}}(t+i|t) $$ (34) 式（28）目标函数中，第1、2项保证车辆的稳定性要求，第3、4、5项构建势场影响作用，保证车辆安全性要求。
将式（30）~式（34）带入式（29），把目标函数整理为标准二次形式：
$$ \begin{array}{c} {{\boldsymbol{J}}}\left( {\boldsymbol{\zeta}} \left({t}\right){,}{{\boldsymbol{u}}}\left({t}{-1}\right){,} \Delta {{\boldsymbol{U}}}{(}{t}{)}\right)= \\ \dfrac{{1}}{{2}}{\left[\begin{array}{c} \Delta {{\boldsymbol{U}}}{(}{t}{)}\\ { \varepsilon }\end{array}\right]}^{{{\rm{T}}}}{{\boldsymbol{H}}}\left[\begin{array}{c} \Delta {{\boldsymbol{U}}}{(}{t}{)}\\ { \varepsilon }\end{array}\right]+{{\boldsymbol{f}}}\left[\begin{array}{c} \varDelta {{\boldsymbol{U}}}{(}{t}{)}\\ { \varepsilon }\end{array}\right]+{G}\end{array} $$ (35) 式中：
$ \boldsymbol{H}=\left[\begin{array}{cc}2\times \left({\boldsymbol{\varTheta }}^{\mathrm{T}}{\boldsymbol{Q}}_{1}\boldsymbol{\varTheta }+\boldsymbol{R}\right)& {\boldsymbol{0}}\\ {\boldsymbol{0}}& \rho \end{array}\right]，\boldsymbol{f}=\left[\begin{array}{c}{\boldsymbol{\varepsilon }}^{\mathrm{T}}{\boldsymbol{Q}}_{2}\boldsymbol{\varTheta }\\ {\boldsymbol{0}}\end{array}\right] $ 。2.3.3 优化设计
$$ \begin{gathered} \min_{\Delta {\boldsymbol{U}}_{t,\varepsilon}}{\boldsymbol{J}}_2({\boldsymbol{\zeta}}(t),{{\boldsymbol{u}}}(t-1),\Delta {\boldsymbol{U}}(t),\varepsilon) \\ {\rm{s}}.{\rm{t}}. \; \Delta\boldsymbol{U_\mathrm{min}}\leqslant \Delta \boldsymbol{U_t}\leqslant \Delta\boldsymbol{U_\mathrm{max}} \\ \Delta\boldsymbol{U}_\mathrm{min}\leqslant \boldsymbol{A}\Delta\boldsymbol{U}_t+\boldsymbol{U}_t\leqslant \Delta\boldsymbol{U}_\mathrm{max} \\ y_{\mathrm{hc.min}}\leqslant y_{\mathrm{hc}}\leqslant y_{\mathrm{hc.max}} \\ y_{\mathrm{sc.min}}-\varepsilon\leqslant y_{\mathrm{hc}}\leqslant y_{\mathrm{sc.max}}+\varepsilon \\ \beta_{\mathrm{min}}\leqslant \beta\leqslant \beta_{\mathrm{max}} \\ \varepsilon>0 \end{gathered}$$ (36) 式中：
${y}_{{\rm{hc}}}$ 为硬约束，即不能放宽约束范围的输出量；${y}_{{\rm{sc}}}$ 为软约束，即可以通过松弛因子进行动态调整约束范围的输出量；$ \,\beta $ 为质心侧偏角。使用QuadProg问题解决器，解决方案在时间t对于当前状态和前一时刻的输入。最终规划控制器参数如表1所示。
表 1 规划控制器参数和数值Table 1 Planning controller parameters and values参数 数值 预测时域$ {N}_{p} $ 25 控制时域$ {N}_{c} $ 5 采样时间$ T $ 0.1 $$ \begin{array}{c}{\boldsymbol{u}}\left(t,\zeta \left(t\right)\right)={\boldsymbol{u}}\left(t-1\right)+{\varDelta }_{t,t}^{\mathrm{*}}\left(\boldsymbol{\zeta }\left(t\right)\right)\end{array} $$ (37) 3. 仿真实验
本节通过构建联合模拟实验，验证上述的避障规划控制方法的有效性。模拟实验使用的自车车辆基于CarSim软件中的前驱C级Hatchback模型，前方车辆采用B级Hatchback模型。设置一条直行城市道路。自车的主要参数如表2所示。
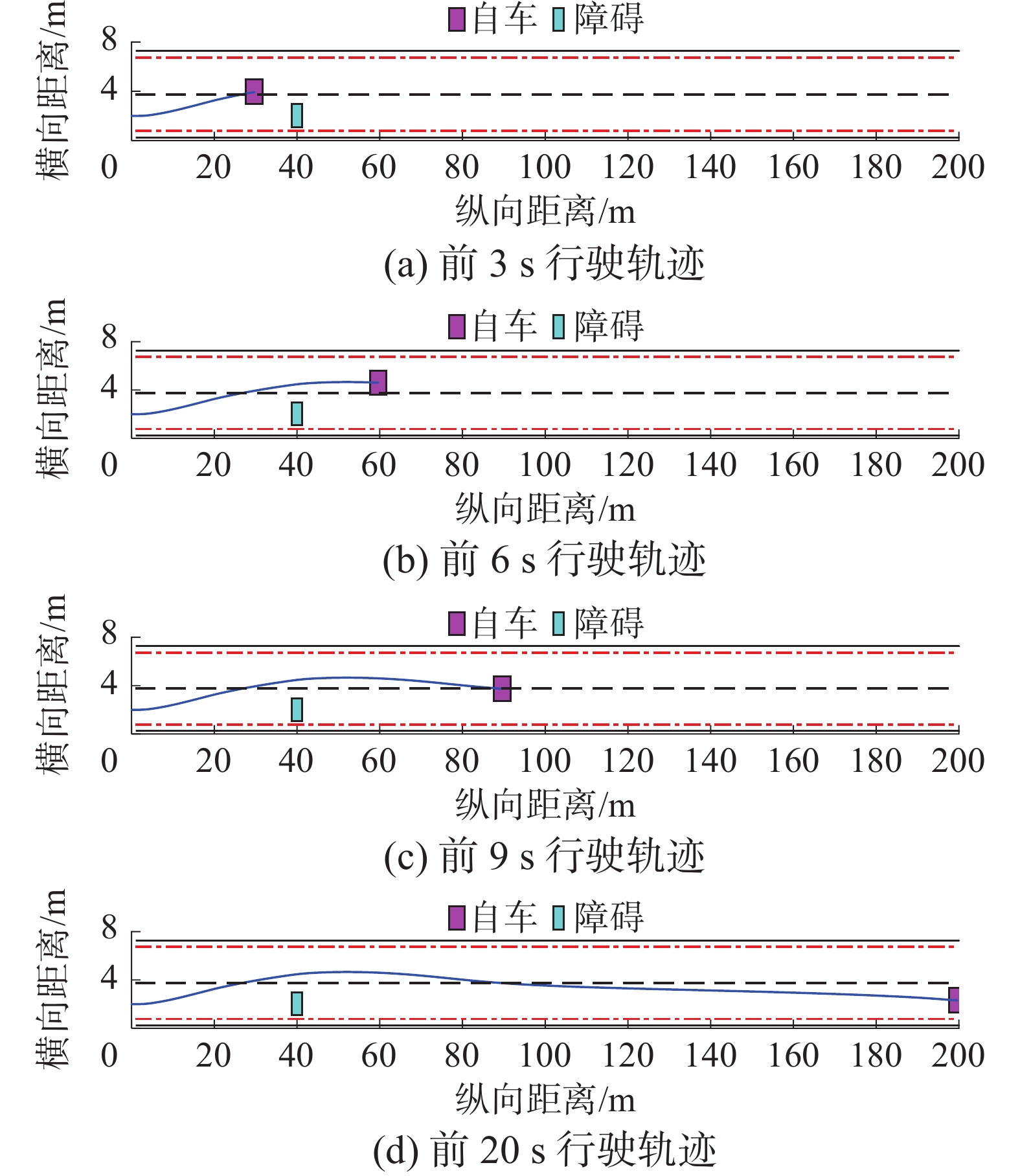
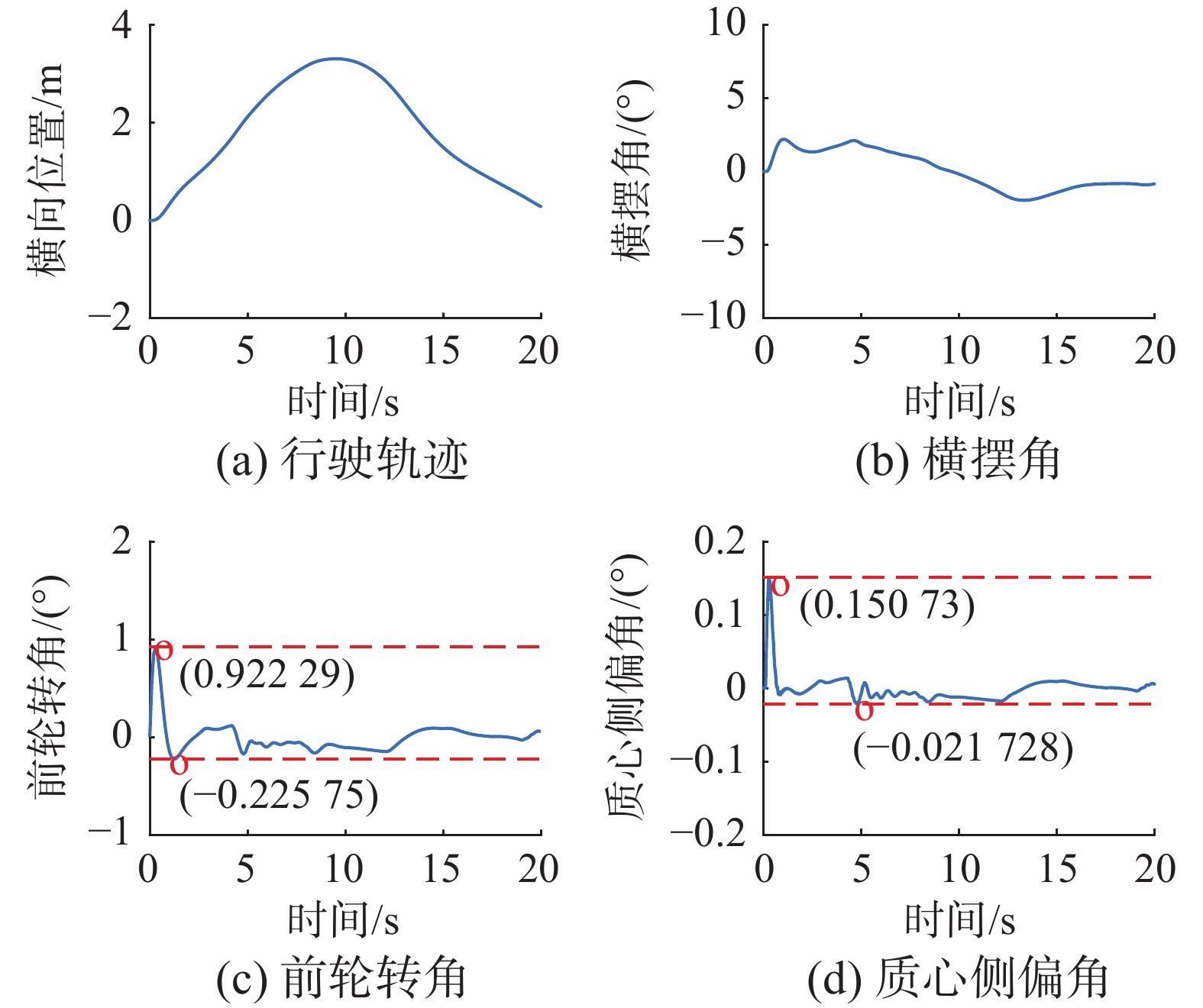
表 2 车辆主要参数Table 2 Main vehicle parameters参数 符号 数值 整车质量/kg m 1723 质心至前轴距离/m $ {l}_{f} $ 1.232 质心至后轴距离/m $ {l}_{r} $ 1.468 前轮侧偏刚度/(N/rad) $ {C}_{f} $ 66 900 后轮侧偏刚度/(N/rad) $ {C}_{r} $ 62 700 重力加速度/(m/s2) g 9.8 滑移率 S 0.2 为验证本文提出的避障控制方法的有效性与普适性，建立3种典型城市路况下超车场景进行实验。场景1中，障碍物静止在自车前方40 m处，自车10 m/s匀速向前行驶。此场景中自车行驶轨迹如图7所示。场景2中，障碍物车辆在自车前方 40 m处并以10 m/s向前匀速行驶，自车以15 m/s匀速行驶，此时自车行驶速度大于障碍物车辆行驶速度，且有超车行驶空间，可以满足超车需求，如图8所示。场景3中，前车在自车前方40 m处并以15 m/s初速度，以加速度−2 m/s2减速行驶，自车以15 m/s行驶，此时满足超车需求，如图9所示。
图 7 障碍物静止自车不同时段超车轨迹Fig. 7 Obstacle stationary self-vehicle overtaking trajectories at different time intervals下载:
全尺寸图片
图 8 前车匀速行驶自车不同时段超车轨迹Fig. 8 Overtaking trajectories at different time intervals of self-vehicle while front vehicle traveling at a constant speed下载:
全尺寸图片
图 9 前车变速行驶自车不同时段超车轨迹Fig. 9 Overtaking trajectories at different time intervals of self-vehicle while front vehicle traveling at variable speeds下载:
全尺寸图片
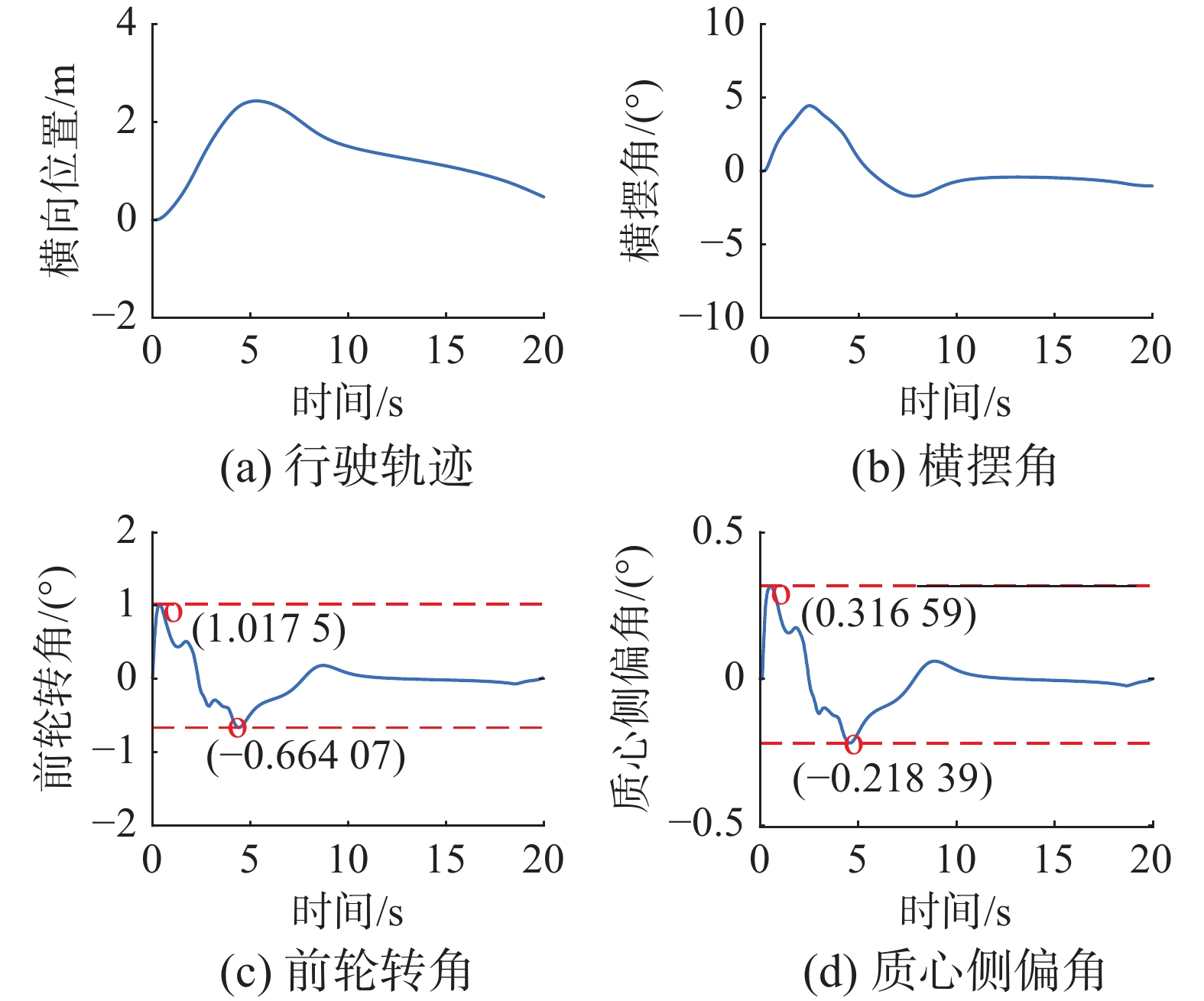
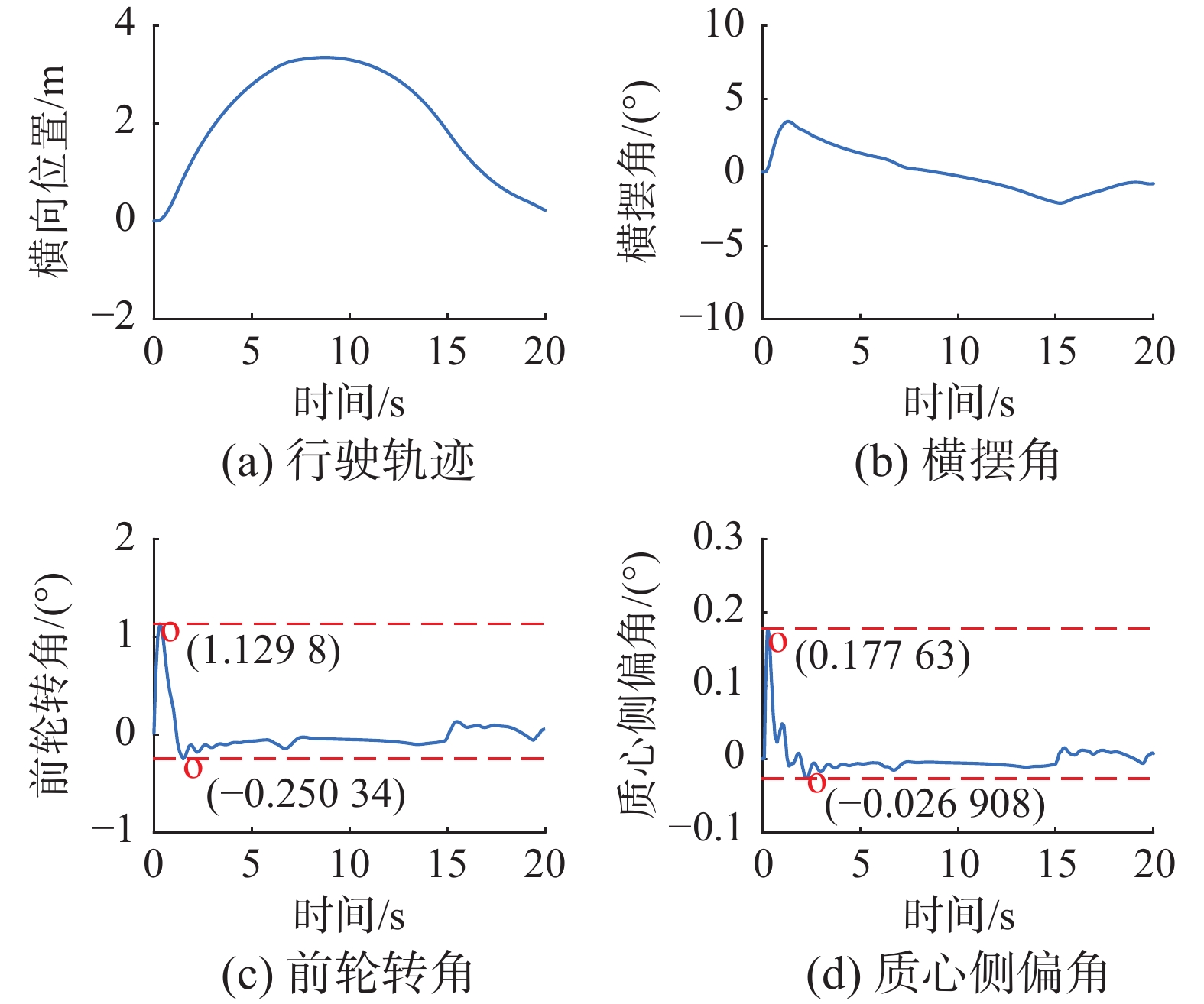
由图7~9可知，本文中提出的规划控制方法可以安全地引导车辆超越同车道较慢的车辆，并在超越后引导车辆安全地行驶回到原来的车道。由图10~12可知，车辆在进行超车过程中，行驶轨迹与横摆角较为平滑，且前轮转角变化范围在[0.67°,1.02°]，质心侧偏角变化范围在[0.22°,0.32°]，且两者长时间保持较低的角度变化，证明本文提出的方法具有很好的稳定性能。通过3种场景对比可以看出，前车的行驶状态的变化导致自车行驶轨迹的变化，当前车变化较小时，自车轨迹平滑性更好，当前车变化较大时，自车的稳定性更优。
图 10 前车静止自车轨迹跟踪结果Fig. 10 Tracking results of self-vehicle trajectory while front vehicle stationary下载:
全尺寸图片
图 11 前车匀速行驶自车轨迹跟踪结果Fig. 11 Tracking result of self-vehicle trajectory while front vehicle traveling at uniform velocity下载:
全尺寸图片
图 12 前车变速行驶自车轨迹跟踪结果Fig. 12 Tracking results of self-vehicle trajectory while front vehicle traveling at variable speed下载:
全尺寸图片
4. 结束语
1）针对城市道路环境中安全超车问题，基于改进人工势场法提出一种避障规划控制方法。构建目标点引力势场、道路边界及车道线斥力势场以及障碍物斥力势场，三者之和构成车辆行驶路径的可行域。
2）基于线性2自由度汽车动力学模型，将改进的人工势场法结合模型预测控制方法构建路径规划与轨迹跟踪统一化的函数模型，引导自车在可行域内安全行驶。
3）论文提出的避障规划控制方法，经城市超车工况模拟验证，能够生成安全、平滑的路径，具有稳定的控制能力。
-
图 1 超车场景
Fig. 1 Overtaking scenario
下载:
全尺寸图片
图 2 障碍物安全距离示意
Fig. 2 Obstacle safety distance schematic
下载:
全尺寸图片
图 3 车辆动力学模型
Fig. 3 Vehicle dynamics model
下载:
全尺寸图片
图 4 目标点引力势场示意
Fig. 4 Schematic of the gravitational potential field at the target point
下载:
全尺寸图片
图 5 道路及车道线斥力势场示意
Fig. 5 Schematic of roadway and lane line repulsive potential field
下载:
全尺寸图片
图 6 障碍物斥力势场示意
Fig. 6 Schematic diagram of the obstacle repulsive potential field
下载:
全尺寸图片
图 7 障碍物静止自车不同时段超车轨迹
Fig. 7 Obstacle stationary self-vehicle overtaking trajectories at different time intervals
下载:
全尺寸图片
图 8 前车匀速行驶自车不同时段超车轨迹
Fig. 8 Overtaking trajectories at different time intervals of self-vehicle while front vehicle traveling at a constant speed
下载:
全尺寸图片
图 9 前车变速行驶自车不同时段超车轨迹
Fig. 9 Overtaking trajectories at different time intervals of self-vehicle while front vehicle traveling at variable speeds
下载:
全尺寸图片
图 10 前车静止自车轨迹跟踪结果
Fig. 10 Tracking results of self-vehicle trajectory while front vehicle stationary
下载:
全尺寸图片
图 11 前车匀速行驶自车轨迹跟踪结果
Fig. 11 Tracking result of self-vehicle trajectory while front vehicle traveling at uniform velocity
下载:
全尺寸图片
图 12 前车变速行驶自车轨迹跟踪结果
Fig. 12 Tracking results of self-vehicle trajectory while front vehicle traveling at variable speed
下载:
全尺寸图片
表 1 规划控制器参数和数值
Table 1 Planning controller parameters and values
参数 数值 预测时域$ {N}_{p} $ 25 控制时域$ {N}_{c} $ 5 采样时间$ T $ 0.1 表 2 车辆主要参数
Table 2 Main vehicle parameters
参数 符号 数值 整车质量/kg m 1723 质心至前轴距离/m $ {l}_{f} $ 1.232 质心至后轴距离/m $ {l}_{r} $ 1.468 前轮侧偏刚度/(N/rad) $ {C}_{f} $ 66 900 后轮侧偏刚度/(N/rad) $ {C}_{r} $ 62 700 重力加速度/(m/s2) g 9.8 滑移率 S 0.2 -
[1] 《中国公路学报》编辑部. 中国交通工程学术研究综述·2016[J]. 中国公路学报, 2016, 29(6): 1–161. doi: 10.3969/j.issn.1001-7372.2016.06.001 Editorial board of the Chinese journal of highways. Review on China’s traffic engineering research progress: 2016[J]. China journal of highway and transport, 2016, 29(6): 1–161. doi: 10.3969/j.issn.1001-7372.2016.06.001 [2] DANIEL W, MARTIN H. Automated driving: safer and more efficient future driving[M]. New Yor: Springer, 2016. [3] ZHAO Can, LI Li, PEI Xin, et al. A comparative study of state-of-the-art driving strategies for autonomous vehicles[J]. Accident analysis & prevention, 2021, 150: 105937. [4] 张新钰, 邹镇洪, 李志伟, 等. 面向自动驾驶目标检测的深度多模态融合技术[J]. 智能系统学报, 2020, 15(4): 758–771. ZHANG Xinyu, ZOU Zhenhong, LI Zhiwei, et al. Deep multi-modal fusion in object detection for autonomous driving[J]. CAAI transactions on intelligent systems, 2020, 15(4): 758–771. [5] 李克强, 戴一凡, 李升波, 等. 智能网联汽车(ICV)技术的发展现状及趋势[J]. 汽车安全与节能学报, 2017, 8(1): 1–14. doi: 10.3969/j.issn.1674-8484.2017.01.001 LI Keqiang, DAI Yifan, LI Shengbo, et al. State-of-the-art and technical trends of intelligent and connected vehicles[J]. Journal of automotive safety and energy, 2017, 8(1): 1–14. doi: 10.3969/j.issn.1674-8484.2017.01.001 [6] GONZÁLEZ D, PÉREZ J, MILANÉS V, et al. A review of motion planning techniques for automated vehicles[J]. IEEE transactions on intelligent transportation systems, 2016, 17(4): 1135–1145. doi: 10.1109/TITS.2015.2498841 [7] KATRAKAZAS C, QUDDUS M, CHEN Wenhua, et al. Real-time motion planning methods for autonomous on-road driving: State-of-the-art and future research directions[J]. Transportation research part C:emerging technologies, 2015, 60: 416–42. doi: 10.1016/j.trc.2015.09.011 [8] ZHOU Yulan, HUANG Nannan. Airport AGV path optimization model based on ant colony algorithm to optimize Dijkstra algorithm in urban systems[J]. Sustainable computing:informatics and systems, 2022, 35: 100716. doi: 10.1016/j.suscom.2022.100716 [9] WANG Xingdong, ZHANG Haowei, LIU Shuo, et al. Path planning of scenic spots based on improved A* algorithm[J]. Scientific reports, 2022, 12(1): 1320. doi: 10.1038/s41598-022-05386-6 [10] LIU Lisang, LIN Jiafeng, YAO Jinxin, et al. Path planning for smart car based on dijkstra algorithm and dynamic window approach[J]. Wireless communications and mobile computing, 2021, 2021: 8881684. [11] 李娟, 张韵, 陈涛. 改进RRT算法在未知三维环境下AUV目标搜索中的应用[J]. 智能系统学报, 2022, 17(2): 368–375. LI Juan, ZHANG Yun, CHEN Tao. Application of the improved RRT algorithm to AUV target search in an unknown 3D environment[J]. CAAI transactions on intelligent systems, 2022, 17(2): 368–375. [12] BAE I, KIM J H, MOON J, et al. Lane change maneuver based on bezier curve providing comfort experience for autonomous vehicle users[C]//2019 IEEE Intelligent Transportation Systems Conference. Auckland: IEEE, 2019: 2272–2277. [13] 王星, 赵海良, 王志刚. 基于邻域系统的智能车辆最优轨迹规划方法[J]. 智能系统学报, 2019, 14(5): 1040–1047. doi: 10.11992/tis.201805004 WANG Xing, ZHAO Hailiang, WANG Zhigang. Optimal trajectory planning method of intelligent vehicles based on neighborhood system[J]. CAAI transactions on intelligent systems, 2019, 14(5): 1040–1047. doi: 10.11992/tis.201805004 [14] ROSTAMI S M H, SANGAIAH A K, WANG Jin, et al. Obstacle avoidance of mobile robots using modified artificial potential field algorithm[J]. EURASIP journal on wireless communications and networking, 2019, 2019(1): 70. doi: 10.1186/s13638-019-1396-2 [15] WANG Pengwei, GAO Song, LI Liang, et al. Obstacle avoidance path planning design for autonomous driving vehicles based on an improved artificial potential field algorithm[J]. Energies, 2019, 12(12): 2342. doi: 10.3390/en12122342 [16] SANG Hongqiang, YOU Yusong, SUN Xiujun, et al. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations[J]. Ocean engineering, 2021, 223: 108709. doi: 10.1016/j.oceaneng.2021.108709 [17] FALCONE. Nonlinear model predictive control for autonomous vehicles [D]. Benevento : University of Sannio, 2007. [18] 张志勇, 龙凯, 杜荣华, 等. 自动驾驶汽车高速超车轨迹跟踪协调控制[J]. 汽车工程, 2021, 43(7): 995–1004. ZHANG Zhiyong, LONG Kai, DU Ronghua, et al. Trajectory tracking coordinated control for autonomous vehicle in high-speed overtaking[J]. Automotive engineering, 2021, 43(7): 995–1004. [19] BHARGAV J, BETZ J, ZEHNG H, et al. Deriving spatial policies for overtaking maneuvers with autonomous vehicles[C]//2022 14th International Conference on COMmunication Systems & NETworkS. Bangalore: IEEE, 2022: 859–864. [20] 张家旭, 王晨, 赵健. 基于改进人工势场法的汽车弯道超车路径规划与跟踪控制[J]. 汽车工程, 2021, 43(4): 546–552. ZHANG Jiaxu, WANG Chen, ZHAO Jian. Path planning and tracking control for vehicle overtaking on curve based on modified artificial potential field method[J]. Automotive engineering, 2021, 43(4): 546–552. [21] 王树凤, 张钧鑫, 刘宗锋. 基于改进人工势场法的智能车辆超车路径规划研究[J]. 汽车技术, 2018(3): 5–9. WANG Shufeng, ZHANG Junxin, LIU Zongfeng. A research on overtaking lane planning for intelligent vehicles based on improved artificial potential field method[J]. Automobile technology, 2018(3): 5–9. [22] WU Qiong, CHENG Shuo, LI Liang, et al. A fuzzy-inference-based reinforcement learning method of overtaking decision making for automated vehicles[J]. Proceedings of the institution of mechanical engineers, part D:journal of automobile engineering, 2022, 236(1): 75–83. doi: 10.1177/09544070211018099 [23] JEON S, LEE K, KUM D. Overtaking decision and trajectory planning in highway via hierarchical architecture of conditional state machine and chance constrained model predictive control[J]. Robotics and autonomous systems, 2022, 151: 104014. doi: 10.1016/j.robot.2021.104014 [24] LIU J C, JAYAKUMAR P, OVERHOLT J L, et al. The role of model fidelity in model predictive control based hazard avoidance in unmanned ground vehicles using LIDAR sensors[C]//Proceedings of ASME 2013 Dynamic Systems and Control Conference, Palo Alto: ASMI, 2014. [25] 石贞洪. 基于模糊MPC和APF的智能汽车转向避撞控制研究[D]. 镇江: 江苏大学, 2020. SHI Zhenhong. Study on steering avoidance control of intelligent vehicle based on fuzzy MPC and APF[D]. Zhenjiang: Jiangsu University, 2020.
