基于多路特征渐进融合和注意力机制的轻量级图像超分辨率重建

刘玉铠,  周登文

downloadPDF
刘玉铠, 周登文. 基于多路特征渐进融合和注意力机制的轻量级图像超分辨率重建 [J]. 智能系统学报, 2024, 19(4): 863-873. doi: 10.11992/tis.202209045
引用本文: 刘玉铠, 周登文. 基于多路特征渐进融合和注意力机制的轻量级图像超分辨率重建 [J]. 智能系统学报, 2024, 19(4): 863-873. doi: 10.11992/tis.202209045
shu
LIU Yukai, ZHOU Dengwen. Lightweight super-resolution reconstruction via progressive multi-path feature fusion and attention mechanism [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 863-873. doi: 10.11992/tis.202209045
Citation: LIU Yukai, ZHOU Dengwen. Lightweight super-resolution reconstruction via progressive multi-path feature fusion and attention mechanism [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 863-873. doi: 10.11992/tis.202209045
shu

基于多路特征渐进融合和注意力机制的轻量级图像超分辨率重建

doi: 10.11992/tis.202209045

  • 华北电力大学 控制与计算机工程学院, 北京 102206

详细信息
    作者简介:

    刘玉铠，硕士，主要研究方向为计算机视觉和深度学习。E-mail：liuyk@ncepu.edu.cn;

    周登文，教授，主要研究方向为图像去噪、图像去马赛克、图像插值和图像超分辨率。发表学术论文50余篇。E-mail：zdw@ncepu.edu.cn.

    通讯作者:

    周登文. E-mail：zdw@ncepu.edu.cn.

  • 中图分类号: TP391

Lightweight super-resolution reconstruction via progressive multi-path feature fusion and attention mechanism

  • School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China

    摘要
  • 摘要: 为进一步探索在计算和存储资源受限设备上应用超分辨率方法的可能性，本研究聚焦于深度卷积神经网络技术在单图像超分辨率中的应用，特别是如何在不显著增加网络规模的情况下，提升网络的性能。 本文提出一种新的基于多路特征渐进融合和注意力机制的轻量级单图像超分辨率方法(multi-path feature fusion and attention mechanism，MPFFA)。MPFFA包括一个多路特征渐进融合块 (multi-path feature progressive fusion，FPF)，可以通过前面的特征，多路渐进地引导和校准后面特征的学习；还包括一个多路特征注意力机制(multi-path feature attention mechanism，FAM)，通过加权拼接多路特征通道，可以提高特征信息的利用率和特征表达能力。实验结果表明：MPFFA显著优于当前其他代表性的方法，在模型复杂度和性能间达到了更好的平衡。本文提出的模型能够更好地应用于计算和资源受限的设备上。

     

    Abstract: In order to further explore the possibility of applying super-resolution methods on computing and storage resource-constrained devices, this study focuses on the application of deep convolutional neural network technology in single-image super-resolution, especially how to improve the performance of the network without significantly increasing the network size. In this paper, a novel lightweight single image super resolution (SISR) method via progressive multi-path feature fusion and attention mechanism (MPFFA) is proposed. MPFFA includes a multi-path FPF module, which can progressively guide and calibrate the learning of the following features through multiple paths. MPFFA also includes a multi-path feature attention mechanism (FAM), which can improve the utilization rate of feature information and the ability of feature expression by splicing multi-path features with weights. The experimental result shows that MPFFA significantly outperforms other representative methods, thus achieves a better balance between model complexity and performance. The proposed model can be better applied to computing and resource-constrained devices.

     

    • HTML全文

  • 单图像超分辨率(single image super-resolution, SISR)[1]旨在从给定的低分辨率(low-resolution, LR)图像恢复对应的高分辨率(high-resolution, HR)图像，已经被广泛用于遥感成像、视频监控和医学成像等计算机视觉领域。然而，SISR是一个经典的病态问题，因为一个LR图像可以对应多个HR图像。

    图像超分辨率(super-resolution, SR)技术的研究有很长的历史[1]，当前，基于深度卷积神经网络[2](convolutional neural network, CNN)的技术主导了SISR技术的研究。直接端到端地学习LR和HR图像之间的映射函数，并革新了SISR的性能。但是，基于CNNs的SISR方法严重依赖于网络的规模，即网络中参数量、深度(层数)和宽度(通道数)等。 要改进SISR的性能，往往需要规模更大的网络，例如：Lim等[3]提出的用于单幅图像超分辨率的增强型深度残差网络(enhanced deep residual networks for single image super-resolution, EDSR)方法，有65个卷积层，参数量达到了43×106；Zhang等[4]提出的非常深的残差通道注意力网络(very deep residual channel attention networks, RCAN)卷积层数超过了800层，参数量约为16×106；EDSR和RCAN等方法虽然有很好的性能，但是需要较高的计算和存储能力，难以在资源受限的设备上应用。 因此，设计轻量级网络(计算和存储需求较低)，对于当前的SISR方法研究是有必要的。但是如何在深度卷积神经网络CNN模型复杂度和SISR的性能之间建立更好的平衡，是一个具有挑战的问题。

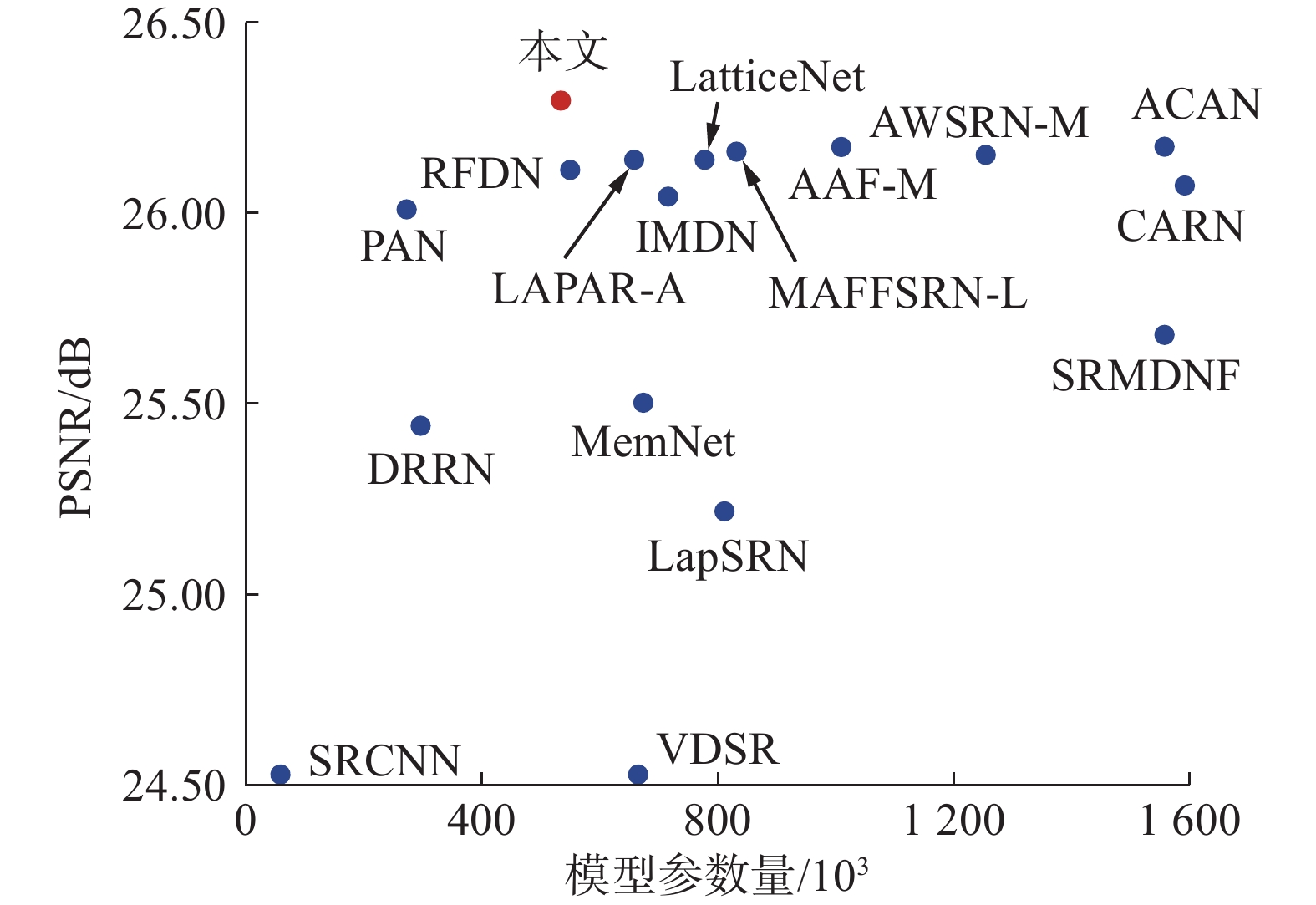
    多路径学习是一种流行的SISR网络架构[5]。 例如：Zhao等[6]提出了一种非常轻量级的SISR网络，称为像素注意力网络 (pixel attention network, PAN)，该网络仅有272×103，却取得了较好的性能。PAN的SC-PA (self-calibrated block with pixel attention)块包含2个分支：一个分支包含像素注意力 (pixel attention，PA)，该分支主要用于提取更高层的特征信息；另一个分支使用标准的卷积层，保持原始的特征信息。2个分支的输出最后进行通道拼接(concatenation)。Wang 等[7]的研究表明：前面层的特征 (即辅助特征)有助于当前层特征的学习；Zhao等[8]的研究表明：采用加权的通道拼接，更符合人脑神经元的行为，可以提高特征的表达能力。本文主要受Zhao等[6]、 Wang等[7]和Zhao 等[8]的工作启发，提出了一个基于多路特征渐进融合和注意力机制的轻量级SISR网络 (multi-path feature fusion and attention mechanism network, MPFFA)。其特点在于：类似于Zhao 等[6]提出的PAN，核心构件采用了多分支结构（3个分支），受Wang等[7]辅助特征学习的启发，渐进地进行特征提取和融合，使用前一个分支的特征引导和校准当前分支的特征学习，并根据Zhao等[8]加权拼接的研究结果，提出了一个多路路注意力机制，最优加权各个分支的特征通道，再进行拼接。MPFFA网络主干的核心构件是多路特征提取块(multi-path feature extraction, MPFE)。MPFE 包括多路特征渐进融合块(multi-path feature progressive fusion, FPF)和多路特征注意力机制(multi-path feature attention mechanism, FAM)2个子块。FPF通过前面的特征，多路渐进地引导后面特征的提取，逐像素预测特征的重要性；FAM则通过通道注意力，加权各路特征通道后，再进行拼接。通过比较其他先进的SISR方法的4倍SR模型在Urban100数据集上的参数量和平均计算峰值信噪比( peak signal to noise ratio, PSNR)结果可以看出，本文提出的模型无论是主观视觉效果，还是客观度量，本文提出的MPFFA方法，显著优于当前其他类似的轻量级方法，把模型复杂度和性能之间的平衡，提升到一个新的水平。

    1.   单图像超分辨网络的相关工作

    1.1   轻量级SISR方法

    Dong等[2]第1个提出了基于CNN的SISR方法(super-resolution using convolutional neural network, SRCNN)。之后，出现了大量基于CNN的SISR方法[9]。 但是，基于CNN的SISR模型严重依赖于网络规模。通常，网络规模越大，表达能力越强，性能也越好，然而，更大的网络往往会急剧增加参数量和计算量，这也限制了它们在计算和存储资源受限的设备上的使用。 为了解决这一问题，出现了大量基于CNN的轻量级SISR方法。递归是一种流行的轻量级SISR网络结构[10-12]。递归的结构，虽然可以减少参数量，但是不能减少计算量。为了进一步解决这一问题，1×1卷积[5-6,13-14]、分组卷积[15]、深度可分离卷积[15]和自校准卷积[6]等也在轻量级SISR网络架构中广泛使用。如图1所示，本文采用了多路径学习和多路注意力机制，设计了一种轻量的构建块，减少了参数量和计算量，提高了 SISR 性能和计算效率。

    图  1  各个先进SISR方法的参数量和平均PSNR结果
    Fig.  1  Average PSNRs and numbers of parameters for each state of the art SISR method
    下载: 全尺寸图片

    1.2   多路径学习

    多路径学习是CNN架构的一个重要形式，残差连接[16]和稠密连接[17]可能是SISR网络架构中最常见的多路径学习。残差连接和稠密连接能够增强特征信息的传播，但是也会造成大量的特征信息冗余。如何改进多路径学习，提高特征信息的利用率和表达能力，持续受到研究人员的重视[13]。

    Wang等[7]提出的注意力辅助特征块A2F (attentive auxiliary features)，包含2个主要分支：一个分支与前面模块的输出特征进行通道拼接和压缩，再使用通道注意力机制，学习各个通道的重要性；另一个分支执行卷积运算。Zhao等[6]提出的PAN，基本组成块是自校准块SC-PA。SC-PA块包含2个分支：一个分支使用PA，用于提取更高层的特征信息；另一个分支使用标准的卷积层，保持原始的特征信息。受到PAN和A2F的启发，本文采用了3条支路，并且可以通过前面的特征，多路渐进地引导后面特征的提取。

    1.3   注意力机制

    注意力机制[15]通常是指人类的视觉系统，能够自动地聚焦于显著的区域。卷积神经网络架构中的注意力机制与其类似，是指能够聚焦于输入的特定部分，提高特征的利用率和表达能力[4,18]。 Zhang等[19] 提出的一个多上下文注意力块 (multi-context attentive block, MCAB)，还可以同时关注通道维度和空间维度之间的依赖关系。本文提出的多路特征注意力机制，通过加权拼接多路通道特征，进一步增强特征表达能力。

    2.   本文方法

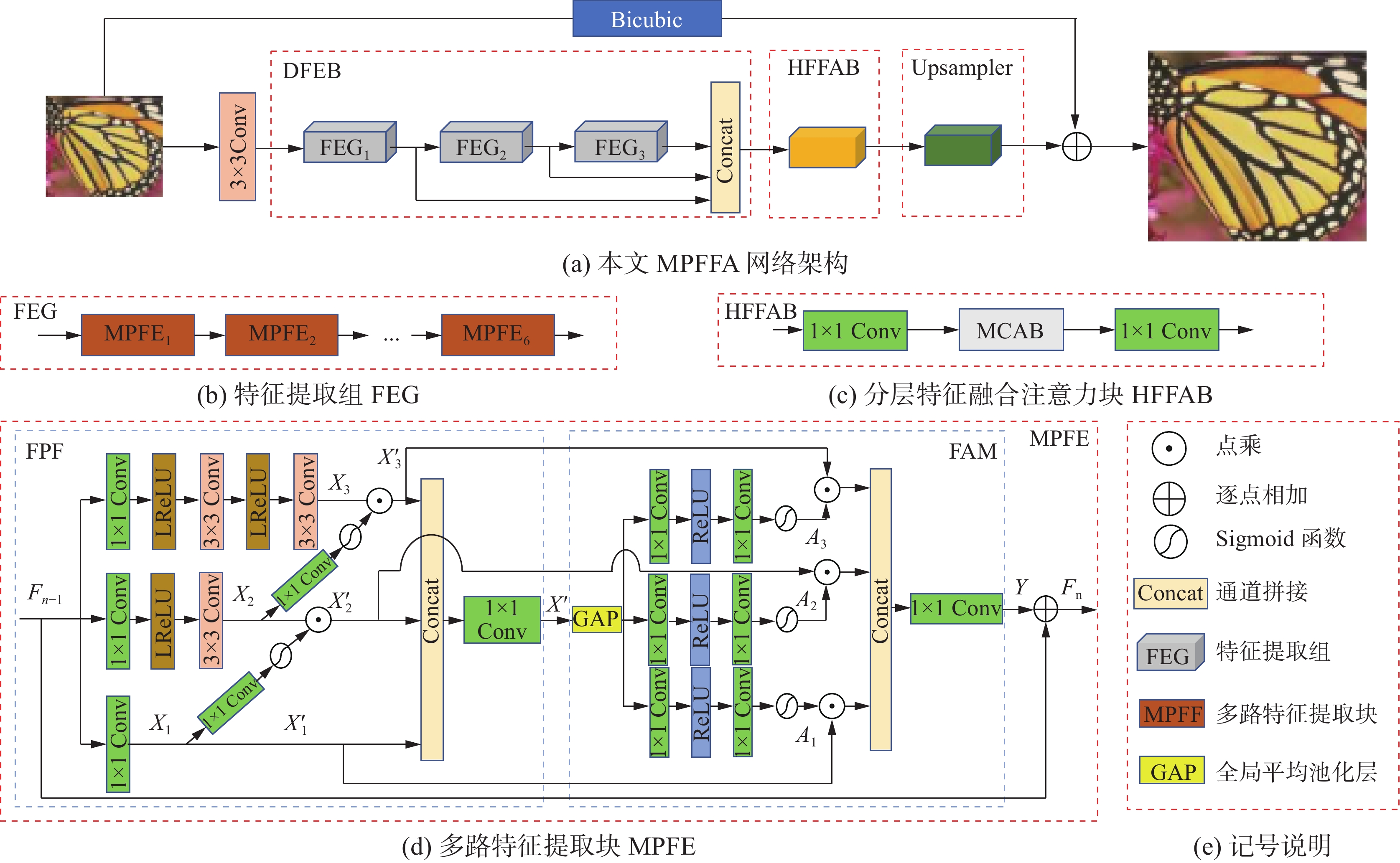
    本文提出的基于多路特征渐进融合和注意力机制的轻量级SISR网络(MPFFA)架构，参见图2(a)。

    图  2  本文模型架构
    Fig.  2  Model architecture of this paper
    下载: 全尺寸图片

    MPFFA 主要包括一个3×3的卷积层、一个深层特征提取块(deep feature extraction block, DFEB)、一个分层特征融合注意力块(hierarchical feature fusion attention block, HFFAB)和一个上采样块(Upsampler)4个部分。3×3的卷积层用于提取浅层特征，Upsampler使用了PAN[6]的上采样块。HFFAB主要使用了用于单张图像超分辨率的两阶段注意力网络（two-stage attentive network for single image super-resolution，TSAN）[19]中的多上下文注意力块MCAB。为了减小计算量，对输入到MCAB的特征通道，用1×1的卷积进行了4倍的压缩和融合；对MCAB的输出特征通道，再用1×1的卷积进行了4倍的扩张。本文工作主要是DFEB，包括3个特征提取组(feature extraction group, FEG)。每个FEG包含6个多路特征提取块(MPFE)，参见图2(b)。FEG提取的分层特征进行拼接，并经HFFAB注意力块进行融合，以更高效地聚焦和利用信息丰富的上下文特征。组成FEG的MPFE是本文模型的核心构件。每个MPFE包括一个多路特征渐进融合块(FPF)和一个多路特征注意力机制(FAM)，参见图2(d)。FPF和FAM的详细介绍，参见下文2.1和2.2节。MPFFA架构也包含一个全局残差连接，LR图像通过双三次插值放大到目标SR图像的大小。下面详细介绍MPFFA的各个部分。

    假定输入的LR图像为${I_{{\text{LR}}}}$,${I_{{\text{LR}}}}$首先通过一个$3 \times 3$的卷积层提取浅层特征。

    $$ {F_0} = {{\rm{Conv}}_{3 \times 3}}\left( {{I_{{\text{LR}}}}} \right) $$

    式中：$ {{\rm{Conv}}_{3 \times 3}}\left( \cdot \right) $为$3 \times 3$的卷积，$ {F_0} $为其输出的特征信息。$ {F_0} $再输入到DFEB，进行深层特征提取。DFEB包含3个FEG，每个FEG又包含6个MPFE。所以，$ {F_0} $共经过18个MPFE，每个MPFE的输出可以表示为

    $$ {F_n} = {H_n}\left( {{F_{n - 1}}} \right),n = 1,2,\cdots ,18 $$ (1)

    式中：$ {H_n}\left( \cdot \right) $为第$n$个MPFE函数，$ {F_n} $为其输出特征信息。每个FEG的输出分别为$ {F_6} $、$ {F_{12}} $和$ {F_{18}} $，进行通道拼接：

    $$ {F_{M0}} = \left[ {{F_6},{F_{12}},{F_{18}}} \right] $$

    式中：[·]为特征通道拼接，$ {F_{M0}} $为拼接后的特征，也是DFEB块的输出特征，再输入到HFFAB：

    $$ {F_M} = {H_{{\text{HFFAB}}}}\left( {{F_{M0}}} \right) $$ (2)

    式中：$ {H_{{\text{HFFAB}}}}\left( \cdot \right) $为HFFAB函数；$ {F_M} $为其输出的特征信息，$ {F_M} $再输入上采样块。

    $$ {I_{{\text{SR}}}} = {H_{{\text{Up}}}}\left( {{F_M}} \right) + {H_{{\text{Bic}}}}\left( {{I_{{\text{LR}}}}} \right) $$

    式中：$ {H_{{\text{Up}}}}\left( \cdot \right) $为上采样块Upsampler函数；$ {H_{{\text{Bic}}}}\left( \cdot \right) $为传统的双三次插值函数，叠加到残差$ {H_{\text{Up}}}\left( \cdot \right) $的输出，得到最终输出的目标SR图像$ {I_{{\text{SR}}}} $。当前SISR方法的上采样块，大多数采用亚像素的卷积[3]或转置的卷积[9]，本文使用了PAN[6]的上采样块。

    2.1   多路特征渐进融合块(FPF)

    FPF主要是受Zhao等[6]和Wang等[7]工作的启发，进行多路(本文使用3路)渐进特征提取和融合，并用前面的特征引导和校准后面的特征学习。 第1条支路仅包含1个$1 \times 1$的卷积层；第2条 支路包含了1个$1 \times 1$的卷积层和1个$3 \times 3$的卷积层，2个卷积层之间包含1个LReLU[15]非线性激活函数，第1条支路的特征通过$1 \times 1$的卷积和Sigmoid函数，引导和校准该支路特征；第3条支路包含1个$1 \times 1$的卷积层和2个$3 \times 3$的卷积层，2个卷积层之间包含1个LReLU非线性激活函数，第2条支路的特征再通过$1 \times 1$的卷积和Sigmoid函数，引导和校准该支路特征。考虑到$ {F_{n - 1}} $和$ {F_n} $分别是第$ n $个MPFE的输入和输出，参见式(1)。3条支路校准前的特征输出分别为(忽略了LReLU非线性激活函数)

    $$ {X_1} = {{\rm{Conv}}_{1 \times 1}}\left( {{F_{n - 1}}} \right) $$
    $$ {X_2} = {{\rm{Conv}}_{3 \times 3}}\left( {{{\rm{Conv}}_{1 \times 1}}\left( {{F_{n - 1}}} \right)} \right) $$
    $$ {X_3} = {{\rm{Conv}}_{3 \times 3}}\left( {{{\rm{Conv}}_{3 \times 3}}\left( {{{\rm{Conv}}_{1 \times 1}}\left( {{F_{n - 1}}} \right)} \right)} \right) $$

    式中：$ {{\rm{Conv}}_{1 \times 1}}\left( \cdot \right) $为$1 \times 1$的卷积，$ {{\rm{Conv}}_{3 \times 3}}\left( \cdot \right) $为$3 \times 3$的卷积，3条支路校准后的特征输出分别为

    $$\begin{gathered} X'_1 = {X_1}\\ X_2' = {X_2} \odot \left( {\sigma \left( {{{\rm{Conv}}_{1 \times 1}}\left( {{X_1}} \right)} \right)} \right) \\ X_3' = {X_3} \odot \left( {\sigma \left( {{{\rm{Conv}}_{1 \times 1}}\left( {{X_2}} \right)} \right)} \right) \end{gathered} $$

    式中：$ \sigma \left( \cdot \right) $为Sigmoid函数，$ \odot $为对应元素相乘。然后，3条支路校准后的输出特征通道进行拼接，并用$1 \times 1$的卷积进行通道压缩和融合。

    $$ {X'} = {{\rm{Conv}}_{1 \times 1}}\left( {\left[ {X_1',X_2',X_3'} \right]} \right) $$

    式中：$ {{\rm{Conv}}_{1 \times 1}}\left( \cdot \right) $为$1 \times 1$的卷积，$ \left[ \cdot \right] $为特征通道拼接。

    2.2   多路特征注意力机制(FAM)

    FAM主要是受Zhao等[8]工作的启发，加权的特征通道拼接，可以提高特征的表达能力。本文算法采用注意力机制，可以最优加权特征通道，并进行拼接。第$ n $个FPF块的输出特征$ {X'} $，通过全局平均池化(global average pooling，GAP)生成初始权重向量。然后，各个支路通过2个$1 \times 1$的卷积(2个$1 \times 1$的卷积之间包含1个ReLU[15]非线性激活函数)进行通道的压缩和扩张，再通过1个Sigmoid函数生成各个支路特征通道的权重向量。

    假定FPF块的特征拼接输出${X'} = \left[ {x_1}, {x_2},\cdots , {x_c}, \cdots {x_C} \right] \in {\bf{R}}^{H \times W \times C}$，GAP运算可表示为

    $$ {{\textit{z}}_c} = {H_\text{GAP}}\left( {{x_c}} \right) = \frac{1}{{H \times W}}\sum\limits_{i = 1}^H {\sum\limits_{j = 1}^W {{x_c}\left( {i,j} \right)} } $$

    式中：$ {H_\text{GAP}}( \cdot ) $为GAP函数，$\boldsymbol{Z} = \left[ {{{\textit{z}}_1},{{\textit{z}}_2}, \cdots ,{{\textit{z}}_c}, \cdots {{\textit{z}}_C}} \right] \in {\bf{R}}^C$，3个支路特征各个通道的权重可表示为(忽略了ReLU 非线性激活函数)

    $$ {A_k} = \sigma \left( {{{\rm{Conv}}_{1 \times 1}}\left( {{{\rm{Conv}}_{1 \times 1}}\left( Z \right)} \right)} \right),k = 1,2,3 $$

    式中$ {{\rm{Conv}}_{1 \times 1}}\left( \cdot \right) $为$1 \times 1$的卷积。第$ n $个FAM的残差输出$ Y $，可表示为

    $$ Y = {{\rm{Conv}}_{1 \times 1}}\left( {\left[ {{A_1} \odot X_1',{A_2} \odot X_2',{A_3} \odot X_3'} \right]} \right) $$

    式中：$ {{\rm{Conv}}_{1 \times 1}}\left( \cdot \right) $为$1 \times 1$的卷积，$ X_k'(k = 1,2,3) $为第$ n $个 FPF块的3条支路输出的特征，$ \left[ \cdot \right] $为特征通道拼接，$ \odot $为权重向量元素与对应特征通道相乘。由于使用了残差连接，第$ n $个FAM 的输出特征$ {F_n} $需要再加上第$ n $个FPF块的输入$ {F_{n - 1}} $，即

    $$ {F_n} = Y + {F_{n - 1}} $$

    2.3   分层特征融合注意力模块(HFFAB)

    MCAB[19]可聚焦信息丰富的上下文特征。HFFAB只是在多上下文注意力块(MCAB)前后各增加一个$1 \times 1$的卷积层。前一个$1 \times 1$的卷积层压缩特征通道，以减少计算量；后一个$1 \times 1$的卷积层再扩张特征通道。HFFAB块的运算，参见式(2)，可进一步表示为

    $$ {F_M} = {{\rm{Conv}}_{1 \times 1}}\left( {{H_{{\rm{MCAB}}}}\left( {{{\rm{Conv}}_{1 \times 1}}\left( {{F_{M0}}} \right)} \right)} \right) $$

    3.   训练MPFFA实验

    3.1   实验设置

    训练阶段，本文采用流行的DIV2K[20]数据集作为训练和验证数据集。前800张图像(001~800)用于训练，10 张图像(821~830)用于验证，标记为DIV2K_val10。为了制作这些训练对，首先从高质量的HR图像开始，然后应用双三次插值法进行下采样，以生成对应的LR图像。除了下采样，为了提高模型的泛化能力，还需要对训练数据集进行数据增强。这包括随机地对图像进行90°、180°、270°的随机旋转以及水平翻转以对图像进行数据增强。首先训练好的×2模型，然后通过预训练的×2模型，训练×3和×4的模型。测试中，使用了 Set5、Set14、B100、Urban100 和Manga109 共5个标准的测试数据集[6]。 为了公正地比较，与之前的方法一样，在YCbCr空间[17]的亮度(Y) 通道上，PSNR和结构相似性(structural similarity index, SSIM)[3]度量。同时本文也计算了学习的感知图像块相似性(learned perceptual im-age patch similarity, LPIPS)[21]度量。

    模型训练中，每批次随机选取32个长和宽均为48的图像块，使用Adam[22]优化器，${\beta _1} = 0.9$、${\beta _2} = 0.999$和$\varepsilon = {10^{ - 8}}$。本文模型训练了1200个迭代周期，初始学习率设置为$2 \times {10^{ - 4}}$，每200个迭代周期衰减一半。使用的损失函数是L1，通过PyTorch[22]框架，一个NVIDIA 2080Ti GPU 实现模型，并进行模型的训练和测试。

    3.2   消融实验

    为了验证FPF、FAM以及HFFAB的有效性，进行了4组对比实验。第1个实验，不包含FAM和HFFAB，FPF块仅包含3个主支路，不包含前面的特征对后面的特征的校准，即不包含2个支路之间的$1 \times 1$的卷积和Sigmoid函数，这个模型称为MPFFA_0；第2个实验，在MPFFA_0 基础上增加包含前面的特征对后面的特征的校准，即完整包含FPF，仍不包含FAM和HFFAB，这个模型称为MPFFA_1；第3个实验，是在MPFFA_1的基础上，增加HFFAB，这个模型称为MPFFA_2；第4个实验，是在MPFFA_2的基础上，再增加FAM，即完整的MPFFA网络模型。4个模型在DIV-2K_val10验证集上，3倍SR的PSNR，参见表1。同时也给出了各个模型的参数量和计算量(即GFLOPs [15]) 和LPIPS度量 [21]结果，以供参考，其中LPIPS值越小越好。可以看到：模型MPFFA_0的PSNR仅29.49 dB；模型MPFFA_1的PSNR增加了0.11 dB，表明多路特征渐进融合，前面特征辅助后面特征的学习，是很有效的；相较于模型MPFFA_1，模型MPFFA_2仅增加了15×103的参数量和1.4 GFLOPs的计算量，使PSNR值增加了0.03 dB。最终的模型MPFFA相较于模型MPFFA_2，PSNR又增加了0.06 dB，表明对各个支路特征通道进行加权拼接的FAM块，是有效的。

    表  1  网络架构不同变种在验证集DIV2K_val10上3倍SR的PSNR、参数量、计算量和LPIPS
    Table  1  Average PSNRs, number of parameters, computational cost and LPIPSs for ×3 SR on validation dataset DIV2K_val10 for different variants of network architecture
    模型FPF校准部分FPF3个主分支HFFABFAMPSNR/dB参数量/103计算量/GFLOPsLPIPS
    MPFFA_0×√××29.4944359.40.1861
    MPFFA_1√√××29.6046561.60.1836
    MPFFA_2√√√×29.6348063.00.1826
    MPFFA√√√√29.6952366.20.1813

    3.3   特征提取组(FEG)实验

    本文模型包含3个FEG，每组内包含相同个数MPFE。MPFE的个数选择，要综合考虑参数量、计算量以及每个FEG输出的不同深度特征拼接后对性能的影响。本文在DIV2K_val10验证集上，进行了3组实验。每组实验中，每个FEG中MPFE个数分别设置为5、6和7。表2给出了模型在DIV2K_val10 上3倍SR 实验，每个 FEG 中不同MPFE 个数对模型平均 PSNR 性能和参数量的影响。

    表  2  不同MPFE个数对模型平均PSNR性能和参数量的影响
    Table  2  Average PSNRs and numbers of parameters for different number of MPFEs
    MPFE/个PSNR /dB参数量/103
    529.55445
    629.69523
    729.74601

    通过结果分析，可以明显观察到随着MPFE个数的增加，模型在3倍超分辨率任务上的性能得到了提升。这表明MPFE能够有效地丰富模型对图像的理解，从而更好地重建高分辨率图像。然而，需要注意的是，随着MPFE个数的增加，模型的参数量也相应增长。这可能会导致模型变得更加复杂，需要更多的计算资源和存储空间。因此，在实际应用中，需要权衡性能提升和参数量增加之间的关系，找到一个合理的平衡点，以确保模型既有较好的性能，又能保持较低的计算成本。 相较于5个MPFE，6个MPFE的PSNR增加了0.14 dB；相较于7个MPFE，6个MPFE的PSNR仅减少了0.05 dB；7个MPFE的PSNR增幅显著减缓，而参数量的增加是一样的，都是78×103。 为了保持网络模型足够轻量，MPFE个数取6 (本文中的设置)，可能是一个合理的折中。

    3.4   多路特征注意力机制(FAM)实验

    3.4.1   多支路的效果

    为了进一步洞察FAM中多支路的效果，本文把FAM块改成了1条支路，在DIV2K_val10验证集上进行实验。3倍SR的PSNR结果为29.56 dB，这比FAM包含3条支路的MPFFA模型的PSNR低0.13 dB。一个有趣的结果是：FAM仅包含一条支路的模型，比MPFFA中去掉FAM块的模型(MPFFA_2)的PSNR还要低0.07 dB。

    3.4.2   参数共享的效果

    参数共享，可以减少参数量。如果FAM中各支路参数共享，在验证集DIV2K_val10上，3倍SR的PSNR结果为29.65 dB，比MPFFA中各支路参数不共享的情形，PSNR低0.04 dB。

    3.5   与先进方法比较

    为了检验本文提出的MPFFA方法的有效性，将其与其他前沿技术进行了客观指标的对比以及从主观视角出发的视觉效果评估的比较。其他代表性的方法包括SRCNN[2]、FSRCNN[9]、VDSR[16]、DRCN[10]、MemNet[11]、IMDN[13]、RFDN[14]、PAN[6]、A2F-M[7]、AWSRN-M、 LapSRN[23]、 DRRN[24]、 SR-MDNF[25]、 CARN[26]、LatticeNet[27]、MAFFSRN-L[28]、ACAN[29]和LAPAR-A[30]。在5个标准测试数据集上，2、3和4倍SR的PSNR/SSIM、参数量和计算量(即GFLOPs [15])结果如表3所示，视觉效果如图3所示。除LatticeNet和PAN以外，其他方法的PSNR/SSIM结果均来自作者的原论文。LatticeNet的结果，源自运行文中提供的训练模型[27]。由于PAN使用了DIV2K和Flickr2K[6]2个训练数据集，为了公平比较，使用了文中提供的代码，在DIV2K 训练集上，重新进行了训练，所以，测试结果与原论文上的结果略有不同。

    表  3  各种先进SISR方法的平均PSNR/SSIM、参数量和计算量结果
    Table  3  Average PSNRs/SSIMs, number of parameters and computational cost of various state-of-the-art SISR methods
    放大倍数模型参数量/
    103    		计算量/
    GFLOPs    		 PSNR/SSIM
    Set5Set14B100Urban100Manga109
    ×2SRCNN5752.736.66/0.952432.42/0.906331.36/0.887929.50/0.894635.74/0.9661
    FSRCNN12637.00/0.955832.63/0.908831.53/0.892029.88/0.902036.67/0.9694
    VDSR665612.637.53/0.958733.03/0.912431.90/0.896030.76/0.914037.22/0.9729
    DRCN17741797437.63/0.958833.04/0.911831.85/0.894230.75/0.913337.63/0.9723
    LapSRN81329.937.52/0.959033.08/0.913031.80/0.895030.41/0.910037.27/0.9740
    DRRN2976796.937.74/0.959133.23/0.913632.05/0.897331.23/0.918837.92/0.9760
    MemNet6772662.437.78/0.959733.28/0.914232.08/0.897831.31/0.919537.72/0.9740
    SRMDNF1513347.737.79/0.960033.32/0.915032.05/0.898031.33/0.920038.07/0.9761
    ×2CARN1592222.837.76/0.959033.52/0.916632.09/0.897831.92/0.925638.36/0.9765
    IMDN694158.838.00/0.960533.63/0.917732.19/0.899632.17/0.928338.88/0.9774
    LAPAR-A54817138.01/0.960533.62/0.918332.19/0.899932.10/0.928338.67/0.9772
    RFDN534123.038.05/0.960633.68/0.918432.16/0.899432.12/0.927838.88/0.9773
    A2F-M999224.238.04/0.960733.67/0.918432.18/0.899632.27/0.929438.87/0.9774
    ACAN800210838.10/0.960833.60/0.917732.21/0.900132.29/0.929738.81/0.9773
    LatticeNet756169.538.06/0.960733.70/0.918732.20/0.899932.25/0.928838.94/0.9774
    AWSRN-M1063244.138.04/0.960533.66/0.918132.21/0.900032.23/0.929438.66/0.9772
    PAN26170.537.99/0.960333.53/0.917432.14/0.899231.93/0.926338.37/0.9766
    MAFFSRN-L790154.438.07/0.960733.59/0.917732.23/0.900532.38/0.9308—/—
    MPFFA (本文方法)523129.438.09/0.960733.70/0.919032.21/0.900032.34/0.929638.98/0.9767
    ×3SRCNN5752.732.75/0.909029.28/0.820928.41/0.786326.24/0.798930.59/0.9107
    FSRCNN124.633.16/0.910429.43/0.824228.53/0.791026.43/0.808030.98/0.9212
    VDSR665612.633.66/0.921329.77/0.831428.82/0.797627.14/0.827932.01/0.9310
    DRCN17741797433.82/0.922629.76/0.831128.80/0.796327.15/0.827632.31/0.9328
    DRRN29767969.034.03/0.924429.96/0.834928.95/0.800427.53/0.837832.74/0.9390
    MemNet6772662.434.09/0.924830.00/0.835028.96/0.800127.56/0.837632.51/0.9369
    SRMDNF1530156.334.12/0.925030.04/0.837028.97/0.803027.57/0.840033.00/0.9403
    CARN1592118.834.29/0.925530.29/0.840729.06/0.803427.38/0.840433.50/0.9440
    IMDN70371.534.36/0.927030.32/0.841729.09/0.804628.17/0.851933.61/0.9445
    LAPAR-A59411434.36/0.926730.34/0.842129.11/0.805428.15/0.852333.51/0.9441
    RFDN54155.434.41/0.927330.34/0.842029.09/0.805028.21/0.852533.67/0.9449
    A2F-M100310034.50/0.927830.39/0.842729.11/0.805428.28/0.854633.66/0.9453
    ACAN11151051.734.46/0.927730.39/0.843529.11/0.805528.28/0.855033.61/0.9447
    LatticeNet76576.334.40/0.927230.32/0.841629.10/0.804928.19/0.851333.63/0.9442
    AWSRN-M1143116.634.42/0.927530.32/0.841929.13/0.805928.26/0.854533.64/0.9450
    PAN26139.034.30/0.926630.30/0.841629.06/0.804228.02/0.849333.34/0.9435
    MAFFSRN-L80768.534.45/0.927730.40/0.843229.13/0.806128.26/0.8552—/—
    MPFFA (本文方法)52366.234.51/0.928330.37/0.842429.13/0.805828.35/0.855033.85/0.9461
    ×4SRCNN5752.730.48/0.862827.49/0.750326.90/0.710124.52/0.722127.66/0.8505
    FSRCNN124.630.71/0.865727.59/0.753526.98/0.715024.62/0.728027.90/0.8517
    VDSR665612.631.35/0.883828.01/0.767427.29/0.725125.18/0.752428.83/0.8809
    DRCN17741797431.53/0.885428.02/0.767027.23/0.723325.14/0.751028.98/0.8816
    LapSRN813149.431.54/0.885028.19/0.772027.32/0.728025.21/0.756029.09/0.8845
    DRRN177417974.331.53/0.885428.02/0.767027.23/0.723325.14/0.751028.98/0.8816
    MemNet6772662.431.74/0.889328.26/0.772327.40/0.728125.50/0.763029.42/0.8942
    SRMDNF155589.331.96/0.893028.35/0.777027.49/0.734025.68/0.773030.09/0.9024
    CARN159290.932.13/0.893728.60/0.780627.58/0.734926.07/0.783730.47/0.9084
    IMDN71540.932.21/0.894828.58/0.781127.56/0.735326.04/0.783830.45/0.9075
    LAPAR-A6599432.15/0.894428.61/0.781827.61/0.736626.14/0.787130.42/0.9074
    RFDN55031.632.24/0.895228.61/0.781927.57/0.736026.11/0.785830.58/0.9089
    A2F-M101056.732.28/0.895528.62/0.782827.58/0.736426.17/0.789230.57/0.9100
    ×4ACAN1556616.532.24/0.895528.62/0.782427.59/0.736626.17/0.789130.53/0.9086
    LatticeNet77743.632.18/0.894328.61/0.781227.57/0.735526.14/0.784430.54/0.9075
    AWSRN-M12547232.21/0.895428.65/0.783227.60/0.736826.15/0.788430.56/0.9093
    PAN27228.232.06/0.893928.56/0.781327.55/0.735226.01/0.783030.33/0.9069
    MAFFSRN-L83038.632.20/0.895328.62/0.782227.59/0.737026.16/0.7887—/—
    MPFFA (本文方法)53443.032.36/0.896828.69/0.783527.61/0.737226.29/0.790230.71/0.9115
    注：加黑代表每列最优值，下同。
    图  3  4倍SR结果的视觉效果比较
    Fig.  3  Visual comparison for ×4 SR
    下载: 全尺寸图片

    在Set5、Urban100和Manga109标准测试数据集上，与其他5个代表方法（CARN[26]、IMDN[13]、LatticeNet[27]、LAPAR-A[30]和PAN[6]）4倍SR的LPIPS结果如表4所示，其值越小越好。

    表  4  不同SISR方法4倍SR的LPIPS值
    Table  4  LPIPSs of ×4 SR for different SISR methods
    模型参数量/
    103    		计算量/
    GFLOPs    		Set5Urban100Manga109
    CARN159290.90.17610.2363—
    IMDN71540.90.17430.23500.1330
    LatticeNet77743.60.17690.24230.1113
    LAPAR-A65994.00.17590.23170.1101
    PAN27228.20.17410.23480.1107
    MPFFA53443.00.17270.22650.1071

    1）定量客观比较。从表3可以看出，本文方法的PSNR/SSIM结果显著优于其他比较的方法。例如，LAPAR-A和RFDN方法比本文的MPFFA模型略大，但是，PSNR的结果一致优于这2个方法。×2、×3、×4的PSNR在各个数据集上，超出LAPAR-A最大值分别为0.31、0.34和0.29 dB；超出RFDN最大值分别为0.22、0.18和0.18 dB。A2F-M方法的参数量大约是MPFFA参数量的2倍，但是，在Manga109数据集上×2、×3、×4的PSNR结果比MPFFA的结果分别低0.11、0.19和0.14 dB。ACAN方法的×4参数量大约是MPFFA参数量的3倍，在Manga109数据集上的PSNR结果，比MPFFA的结果低0.18 dB，而且计算量比MPFFA大约高出了26倍。从表4可以看出，本文方法的LPIPS结果也均优于其他比较的方法。

    2）主观效果比较。图3给出了本文方法与其他先进方法在×4时重建的SR图像结果。本文方法的结果比其他方法的结果更好，是显著可视的。以Urban100数据集中图像img067为例，Bicubic、FSRCNN、CARN、LatticeNet和A2F-M等方法恢复的楼房条纹，均有不同程度的模糊和失真，甚至A2F-M方法恢复的条纹也发生了部分扭曲，本文方法恢复出的条纹很接近于原HR图像。Urban100数据集中图像img089，除LAPAR-A方法和本文网络模型之外，其他方法恢复的条纹基本上过度模糊失真和条纹方向错误。虽然LAPAR-A方法正确地恢复了条纹的方向，但是仍然有明显的模糊，本文方法的结果更加清晰，更接近于原HR图像。Urban100数据集中图像img092，除LAPAR-A、PAN方法和本文网络模型之外，其他方法恢复的条纹，基本上存在过度模糊失真和条纹方向错误的现象。虽然LAPAR-A、PAN正确地恢复了条纹方向，但是仍然有明显的模糊，本文方法的结果更加清晰，与原HR图像更加接近。而对于Set14数据集中的图像barbara，只有本文方法对纹理的重建方向正确，而且视觉效果更加清晰且不失真。

    图4给出了本文方法与其他先进方法在×3时重建的SR图像结果。本文方法的结果比其他方法的结果更好，是显著可视的。以Urban100数据集中图像img011为例，Bicubic、FSRCNN、CARN、LatticeNet和A2F-M等方法恢复的纹理均有不同程度的模糊和失真，本文方法的重建效果很接近于原HR图像。Urban100数据集中图像img024也类似，相较于其他几种方法，本文方法的重建效果比它们更接近于HR图像。

    图  4  3倍SR结果的视觉效果比较
    Fig.  4  Visual comparison for ×3 SR
    下载: 全尺寸图片

    4.   结束语

    本文提出了一个基于多路特征渐进融合和注意力机制的轻量级图像超分辨率网络。本文主要工作是提出了一个FPF和一个FAM，FPF和FAM块配对使用。FPF可以利用前面的特征，多路渐进地引导和辅助后面特征的学习；FAM则可以把多路特征通道，加权拼接，提高特征信息的利用率和表达能力。实验结果表明，本文方法是有效的，无论是客观度量还是主观度量都明显优于其他先进的方法，把轻量级SISR的复杂度和性能平衡提高到了一个新的水平。未来仍考虑进一步优化本文网络结构和损失函数，继续改进其性能。

  • 图  1   各个先进SISR方法的参数量和平均PSNR结果

    Fig.  1   Average PSNRs and numbers of parameters for each state of the art SISR method

    下载: 全尺寸图片

    图  2   本文模型架构

    Fig.  2   Model architecture of this paper

    下载: 全尺寸图片

    图  3   4倍SR结果的视觉效果比较

    Fig.  3   Visual comparison for ×4 SR

    下载: 全尺寸图片

    图  4   3倍SR结果的视觉效果比较

    Fig.  4   Visual comparison for ×3 SR

    下载: 全尺寸图片

    表  1   网络架构不同变种在验证集DIV2K_val10上3倍SR的PSNR、参数量、计算量和LPIPS

    Table  1   Average PSNRs, number of parameters, computational cost and LPIPSs for ×3 SR on validation dataset DIV2K_val10 for different variants of network architecture

    模型FPF校准部分FPF3个主分支HFFABFAMPSNR/dB参数量/103计算量/GFLOPsLPIPS
    MPFFA_0×√××29.4944359.40.1861
    MPFFA_1√√××29.6046561.60.1836
    MPFFA_2√√√×29.6348063.00.1826
    MPFFA√√√√29.6952366.20.1813

    表  2   不同MPFE个数对模型平均PSNR性能和参数量的影响

    Table  2   Average PSNRs and numbers of parameters for different number of MPFEs

    MPFE/个PSNR /dB参数量/103
    529.55445
    629.69523
    729.74601

    表  3   各种先进SISR方法的平均PSNR/SSIM、参数量和计算量结果

    Table  3   Average PSNRs/SSIMs, number of parameters and computational cost of various state-of-the-art SISR methods

    放大倍数模型参数量/
    103    		计算量/
    GFLOPs    		 PSNR/SSIM
    Set5Set14B100Urban100Manga109
    ×2SRCNN5752.736.66/0.952432.42/0.906331.36/0.887929.50/0.894635.74/0.9661
    FSRCNN12637.00/0.955832.63/0.908831.53/0.892029.88/0.902036.67/0.9694
    VDSR665612.637.53/0.958733.03/0.912431.90/0.896030.76/0.914037.22/0.9729
    DRCN17741797437.63/0.958833.04/0.911831.85/0.894230.75/0.913337.63/0.9723
    LapSRN81329.937.52/0.959033.08/0.913031.80/0.895030.41/0.910037.27/0.9740
    DRRN2976796.937.74/0.959133.23/0.913632.05/0.897331.23/0.918837.92/0.9760
    MemNet6772662.437.78/0.959733.28/0.914232.08/0.897831.31/0.919537.72/0.9740
    SRMDNF1513347.737.79/0.960033.32/0.915032.05/0.898031.33/0.920038.07/0.9761
    ×2CARN1592222.837.76/0.959033.52/0.916632.09/0.897831.92/0.925638.36/0.9765
    IMDN694158.838.00/0.960533.63/0.917732.19/0.899632.17/0.928338.88/0.9774
    LAPAR-A54817138.01/0.960533.62/0.918332.19/0.899932.10/0.928338.67/0.9772
    RFDN534123.038.05/0.960633.68/0.918432.16/0.899432.12/0.927838.88/0.9773
    A2F-M999224.238.04/0.960733.67/0.918432.18/0.899632.27/0.929438.87/0.9774
    ACAN800210838.10/0.960833.60/0.917732.21/0.900132.29/0.929738.81/0.9773
    LatticeNet756169.538.06/0.960733.70/0.918732.20/0.899932.25/0.928838.94/0.9774
    AWSRN-M1063244.138.04/0.960533.66/0.918132.21/0.900032.23/0.929438.66/0.9772
    PAN26170.537.99/0.960333.53/0.917432.14/0.899231.93/0.926338.37/0.9766
    MAFFSRN-L790154.438.07/0.960733.59/0.917732.23/0.900532.38/0.9308—/—
    MPFFA (本文方法)523129.438.09/0.960733.70/0.919032.21/0.900032.34/0.929638.98/0.9767
    ×3SRCNN5752.732.75/0.909029.28/0.820928.41/0.786326.24/0.798930.59/0.9107
    FSRCNN124.633.16/0.910429.43/0.824228.53/0.791026.43/0.808030.98/0.9212
    VDSR665612.633.66/0.921329.77/0.831428.82/0.797627.14/0.827932.01/0.9310
    DRCN17741797433.82/0.922629.76/0.831128.80/0.796327.15/0.827632.31/0.9328
    DRRN29767969.034.03/0.924429.96/0.834928.95/0.800427.53/0.837832.74/0.9390
    MemNet6772662.434.09/0.924830.00/0.835028.96/0.800127.56/0.837632.51/0.9369
    SRMDNF1530156.334.12/0.925030.04/0.837028.97/0.803027.57/0.840033.00/0.9403
    CARN1592118.834.29/0.925530.29/0.840729.06/0.803427.38/0.840433.50/0.9440
    IMDN70371.534.36/0.927030.32/0.841729.09/0.804628.17/0.851933.61/0.9445
    LAPAR-A59411434.36/0.926730.34/0.842129.11/0.805428.15/0.852333.51/0.9441
    RFDN54155.434.41/0.927330.34/0.842029.09/0.805028.21/0.852533.67/0.9449
    A2F-M100310034.50/0.927830.39/0.842729.11/0.805428.28/0.854633.66/0.9453
    ACAN11151051.734.46/0.927730.39/0.843529.11/0.805528.28/0.855033.61/0.9447
    LatticeNet76576.334.40/0.927230.32/0.841629.10/0.804928.19/0.851333.63/0.9442
    AWSRN-M1143116.634.42/0.927530.32/0.841929.13/0.805928.26/0.854533.64/0.9450
    PAN26139.034.30/0.926630.30/0.841629.06/0.804228.02/0.849333.34/0.9435
    MAFFSRN-L80768.534.45/0.927730.40/0.843229.13/0.806128.26/0.8552—/—
    MPFFA (本文方法)52366.234.51/0.928330.37/0.842429.13/0.805828.35/0.855033.85/0.9461
    ×4SRCNN5752.730.48/0.862827.49/0.750326.90/0.710124.52/0.722127.66/0.8505
    FSRCNN124.630.71/0.865727.59/0.753526.98/0.715024.62/0.728027.90/0.8517
    VDSR665612.631.35/0.883828.01/0.767427.29/0.725125.18/0.752428.83/0.8809
    DRCN17741797431.53/0.885428.02/0.767027.23/0.723325.14/0.751028.98/0.8816
    LapSRN813149.431.54/0.885028.19/0.772027.32/0.728025.21/0.756029.09/0.8845
    DRRN177417974.331.53/0.885428.02/0.767027.23/0.723325.14/0.751028.98/0.8816
    MemNet6772662.431.74/0.889328.26/0.772327.40/0.728125.50/0.763029.42/0.8942
    SRMDNF155589.331.96/0.893028.35/0.777027.49/0.734025.68/0.773030.09/0.9024
    CARN159290.932.13/0.893728.60/0.780627.58/0.734926.07/0.783730.47/0.9084
    IMDN71540.932.21/0.894828.58/0.781127.56/0.735326.04/0.783830.45/0.9075
    LAPAR-A6599432.15/0.894428.61/0.781827.61/0.736626.14/0.787130.42/0.9074
    RFDN55031.632.24/0.895228.61/0.781927.57/0.736026.11/0.785830.58/0.9089
    A2F-M101056.732.28/0.895528.62/0.782827.58/0.736426.17/0.789230.57/0.9100
    ×4ACAN1556616.532.24/0.895528.62/0.782427.59/0.736626.17/0.789130.53/0.9086
    LatticeNet77743.632.18/0.894328.61/0.781227.57/0.735526.14/0.784430.54/0.9075
    AWSRN-M12547232.21/0.895428.65/0.783227.60/0.736826.15/0.788430.56/0.9093
    PAN27228.232.06/0.893928.56/0.781327.55/0.735226.01/0.783030.33/0.9069
    MAFFSRN-L83038.632.20/0.895328.62/0.782227.59/0.737026.16/0.7887—/—
    MPFFA (本文方法)53443.032.36/0.896828.69/0.783527.61/0.737226.29/0.790230.71/0.9115
    注：加黑代表每列最优值，下同。

    表  4   不同SISR方法4倍SR的LPIPS值

    Table  4   LPIPSs of ×4 SR for different SISR methods

    模型参数量/
    103    		计算量/
    GFLOPs    		Set5Urban100Manga109
    CARN159290.90.17610.2363—
    IMDN71540.90.17430.23500.1330
    LatticeNet77743.60.17690.24230.1113
    LAPAR-A65994.00.17590.23170.1101
    PAN27228.20.17410.23480.1107
    MPFFA53443.00.17270.22650.1071
    • 参考文献(30)
  • [1] PARK S C, PARK M K, KANG M G. Super-resolution image reconstruction: a technical overview[J]. IEEE signal processing magazine, 2003, 20(3): 21–36. doi: 10.1109/MSP.2003.1203207
    [2] DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE transactions on pattern analysis and machine intelligence, 2015, 38(2): 295–307.
    [3] LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Hawaii: IEEE, 2017: 136−144.
    [4] ZHANG Yulun, LI Kunpeng, LI Kai, et al. Image super-resolution using very deep residual channel attention networks[C]//Proceedings of the European Conference on Computer Vision. Munich: ACM, 2018: 286−301.
    [5] HUI Zheng, WANG Xiumei, GAO Xinbo. Fast and accurate single image super-resolution via information distillation network[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 723−731.
    [6] ZHAO Hengyuan, KONG Xiangtao, HE Jingwen, et al. Efficient image super-resolution using pixel attention[C]// European Conference on Computer Vision. Glasgow: ACM, 2020: 56−72.
    [7] WANG Xuehui, WANG Qing, ZHAO Yuzhi, et al. Lightweight single-image super-resolution network with attentive auxiliary feature learning[C]//Proceedings of the Asian Conference on Computer Vision. Kyoto: AFCV, 2021: 268−285.
    [8] ZHAO Xiaole, LIAO Ying, HE Tian, et al. Fc2n: fully channel-concatenated network for single image super-resolution [EB/OL]. (2021−05−05)[2023−06−12].https://arxiv.org/pdf/1907.03221.pdf.
    [9] DONG Chao, LOY C C, TANG Xiaoou. Accelerating the super-resolution convolutional neural network[C]// European Conference on Computer Vision. Amsterdam: ACM, 2016: 391−407.
    [10] KIM J, LEE J K, LEE K M. Deeply-recursive convolutional network for image super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1637−1645.
    [11] TAI Ying, YANG Jian, LIU Xiaoming, et al. MemNet: a persistent memory network for image restoration[C]// Proceedings of the IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 4539−4547.
    [12] 周登文, 赵丽娟. 基于递归残差网络的图像超分辨率重建[J]. 自动化学报, 2019, 45(6): 1157–1165.

    ZHOU Dengwen, ZHAO Lijuan. Image super-resolution based on recursive residual networks[J]. Acta automatica sinica, 2019, 45(6): 1157–1165.
    [13] HUI Zheng, GAO Xinbo, YANG Yuchu, et al. Lightweight image super-resolution with information multi-distillation network[C]//Proceedings of the 27th ACM International Conference on Multimedia. Nice: ACM, 2019: 2024−2032.
    [14] LIU Jie, TANG Jie, WU Gangshan. Residual feature distillation network for lightweight image super-resolution [C]//European Conference on Computer Vision. Glasgow: ACM, 2020: 41−55.
    [15] 周登文, 王婉君. 基于区域互补注意力和多维注意力的轻量级图像超分辨率网络[J]. 模式识别与人工智能, 2022, 35(7): 625–636.

    ZHOU Dengwen, WANG Wanjun. Lightweight image supe-resolution network based on regional complementary attention and multi-dimensional attention[J]. Pattern recognition and artificial intelligence, 2022, 35(7): 625–636.
    [16] KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1646−1654.
    [17] ZHANG Yulun, TIAN Yapeng, KONG Yu, et al. Residual dense network for image super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 2472−2481.
    [18] WOO S, PARK J, LEE J Y, et al. Cbam: convolutional block attention module[C]//Proceedings of the European Conference on Computer Vision. Glasgow: ACM, 2018: 3−19.
    [19] ZHANG Jiqing, LONG Chengjiang, WANG Yuxin, et al. A two-stage attentive network for single image super-resolution[J]. IEEE transactions on circuits and systems for video technology, 2021, 32: 1020–1033.
    [20] TIMOFTE R, AGSTSSON E, VAN GOOL L, et al. Ntire 2017 challenge on single image super-resolution: methods and results[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Hawaii: IEEE, 2017: 114−125.
    [21] ZHANG R, ISOLA P, EFROS A A, et al. The unreasonable effectiveness of deep features as a perceptual metric[C]//Proceedings of the IEEE Conference on Computer VIsion and Pattern Recognition. Salt Lake City: IEEE, 2018: 586−595.
    [22] HUANG Zhiyong, LI Wenbin, LI Jinxin, et al. Dual-path attention network for single image super-resolution[J]. Expert systems with applications, 2021, 169: 114450. doi: 10.1016/j.eswa.2020.114450
    [23] LAI Weisheng, HUANG Jiabin, AHUJA N, et al. Deep laplacian pyramid networks for fast and accurate super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Hawaii: IEEE, 2017: 624−632.
    [24] TAI Ying, YANG Jian, LIU Xiaoming. Image super-resolution via deep recursive residual network[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Hawaii: IEEE, 2017: 3147−3155.
    [25] ZHANG Kai, ZUO Wangmeng, ZHANG Lei. Learning a single convolutional super-resolution network for multiple degradations[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 3262−3271.
    [26] AHN N, KANG B, SOHN K A. Fast, accurate, and lightweight super-resolution with cascading residual network[C]//Proceedings of the European Conference on Computer Vision. Munich: ACM, 2018: 252−268.
    [27] LUO Xiaotong, XIE Yuan, ZHANG Yulun, et al. Latticenet: towards lightweight image super-resolution with lattice block[C]//Computer Vision–ECCV 2020: 16th European Conference. Glasgow: ACM, 2020: 272−289.
    [28] MUQEET A, HWANG J, YANG S, et al. Multi-attention based ultra lightweight image super-resolution[C]// European Conference on Computer Vision. Glasgow: ACM, 2020: 103−118.
    [29] ZHOU Dengwen, CHEN Yiming, LI Wenbin, et al. Image super-resolution based on adaptive cascading attention network[J]. Expert systems with applications, 2021, 186: 115815. doi: 10.1016/j.eswa.2021.115815
    [30] LI Wenbo, ZHOU Kun, QI Lu, et al. Lapar: linearly-assembled pixel-adaptive regression network for single image super-resolution and beyond[C]//Proceedings of the Advances in Neural Information Processing Systems. Chicago: NIPS, 2021: 20343–20355.
WeChat 点击查看大图
图(4)  /  表(4)
出版历程
  • 收稿日期:  2022-09-23
  • 网络出版日期:  2024-04-02

目录

    /

    返回文章
    返回