Salp swarm feature selection algorithm with a hybrid strategy
-
摘要: 近年来,随着计算机和数据库技术的快速发展,大规模数据集迅速增长,利用特征选择技术来筛选信息量大的特征已经变得非常重要。本文提出了一种具有混合策略的樽海鞘群特征选择算法(salp swarm feature selection algorithm with hybrid strategy,HS-SSA)。首先,本文生成一张基于互信息的排序表,并由排序表提出了新的初始化策略。其次,提出一个新颖的并且有条件调用的动态搜索算法。最后在位置更新上结合瞬态搜索算法(transient search algorithm, TSO),改进勘探和开发步骤的效率,增加解空间的灵活性和多样性,从而使算法能够快速定位到全局最优位置。为了验证算法的性能,实验选取14个UCI的数据集,并且与樽海鞘群算法(SSA)以及近几年樽海鞘群的改进算法等多种优化算法进行比较,结果表明HS-SSA在特征选择上具有更强的竞争力。Abstract: In recent years, with the rapid development of computer and database technologies, the number of large-scale datasets has rapidly increased. Thus, the use of feature selection technology is important to screen features with massive amounts of information. In this study, a salp swarm feature selection algorithm with a hybrid strategy (HS-SSA) is proposed. Initially, a sorted table based on mutual information is generated, and a new initialization strategy is proposed on the basis of this sorted table. Furthermore, a novel dynamic search algorithm with conditional call is proposed. With respect to location updates, the efficiency of exploration and development steps is improved, and the flexibility and diversity of the solution space are increased by combining the transient search algorithm (TSO). Consequently, the algorithm can rapidly locate the global optimal location. To verify algorithm performance, 14 UCI datasets were selected for the test. In addition, the proposed algorithm was compared with the salp swarm algorithm (SSA), the improved SSA, and many other improved algorithms in recent years. The results show that HS-SSA is more competitive in feature selection.
-
在过去的几十年中,计算机和数据库技术的快速发展导致了大规模数据集的增长迅速,因此,在使用数据集之前,有必要对数据进行预处理,去除冗余特征。所以特征选择变得越来越重要。它通过消除不相关、冗余或噪声数据来降低数据的维数,是简化数据分析、获取数据关键特征的有效技术[1]。最终从给定的数据集中选择最有用的特征集,这有利于提高机器学习算法的泛化能力,减少训练时间,使模型更具可解释性。基于特征的选择机制,特征选择通常可以分为两类:过滤式(filter)、包裹式(wrapper)。过滤式是根据原始数据上的每个特征的属性直接计算评价指标[2],特征选择过程与后续学习算法无关。包裹式方法首先由John等提出[3]。它需要一个预先设定的学习算法,将特征子集在其算法上的表现作为评估来确定最终的特征子集[4]。基于过滤式方法的特征选择算法的优点是通常比包裹式方法的计算复杂度低得多,但是所选的特征子集在分类准确率方面通常低于包裹式方法。包裹式方法依赖于分类器的优化或所选分类器本身,所以它的特征通用性不强,并且计算复杂度更高。目前基于二者的混合方法已经被提出[5],它结合了上述两种方法的优点。
据报道,特征选择是一个NP难问题,它试图从一个有N个特征的数据集的
$ 2^{n}-1 $ 个可能的特征子集中找到最佳子集。这对特征选择问题的搜索策略提出了很大的挑战[6]。近年来,许多优化算法根据其性能被应用于包裹模式下的特征选择问题,并取得了良好的效果。例如粒子群优化(particle swarm optimization, PSO)[7]、樽海鞘群算法(salp swarm algorithm, SSA)[8]、哈里斯鹰优化 (Harris Hawks optimization, HHO)[9]、灰狼优化器 (grey wolf optimizer, GWO)[10]和遗传算法(genetic algorithms, GA)[11]等。对于每一种优化算法,都存在分类精度低,泛化能力差、勘探与开发不平衡,容易陷入局部最优等缺点。为了克服这些问题,许多优化算法的改进版本被提出。例如Kilic等[12]提出了一种新的基于多种群的粒子群算法(multi population PSO, MPPSO)进行特征选择。在该方法中,多种群从随机生成的初始解和基于Relieff排序生成的初始解同时开始,使用两个种群搜索解空间,使搜索空间多样化。Tu等[13]提出了一种多策略集成GWO,该方法克服了全局优化算法在求解函数优化问题时搜索策略单一的局限性。Mafarja等[14]将8个时变传递函数集成到蜻蜓算法中,实现了勘探与开发之间的稳定平衡。还有Tubishat等[15]提出了一种动态SSA(dynamic SSA, DSSA),在SSA的基础上提出了一个新的位置更新方程,增强了SSA解决方案的多样性,并且开发出了一种新的局部搜索算法来帮助算法跳出局部最优。同时也有不少研究者在先前算法的基础上结合一些启发式算法来解决特征选择问题。例如Zawbaa等[16]开发了一种基于GWO和蚁狮优化器的混合特征选择方法来解决精度、高维数和计算复杂度的问题。Zivkovic等[17]提出了一种具有替换机制的SSA和正弦余弦算法(SSA with replacement mechanism and sine cosine algorithm, SSARM-SCA)。Mafarja等[18]提出了结合鲸鱼优化算法和模拟退火的混合算法。还有Dhal等[19]提出了一种基于PSO和GWO的混合特征选择方法的二进制版本,融合PSO的挖掘能力与GWO探测能力。针对樽海鞘群算法存在在容易陷入局部最优,种群多样性较差等缺点,本文提出了一种具有混合策略的樽海鞘群特征选择算法(salp swarm feature selection algorithm with hybrid strategy,HS-SSA)。在原有的SSA算法的基础上进行了3个改进:
1)利用互信息生成了特征排序表,并提出了新的初始化策略,提高了初始种群的质量和多样性;
2)提出了一个新颖的根据最佳解的改进情况和迭代次数有条件执行的动态搜索算法,来帮助种群在初期淘汰替换较差的种群,后期避免局部最优;
3)结合瞬态搜索算法,随机地选择位置更新方程,这改进了勘探和开发步骤的效率,增加了解空间灵活性和多样性。
1. 背景知识
1.1 樽海鞘群算法
樽海鞘群算法(SSA)在2017年由Mirjalili等[8]提出。它是利用樽海鞘链的概念来模拟樽海鞘在水中的群集行为,这种行为可以用于它们寻找食物的运动中。樽海鞘的链式群行为中,通常个体首尾相接,形成一条“链”,依次跟随进行移动。在樽海鞘链中,第一个个体被划分为领导者,其他的为追随者,领导者不断向着食物移动,并带领其他追随者移动。在搜索空间中每个樽海鞘个体都在n维的搜索空间中搜索,其中n为数据中特征的数量,此外我们用F表示食物的位置,也就是樽海鞘链中个体的最好位置。SSA的领导者位置更新公式为
$$ {X}_{j}^{1}=\left\{\begin{array}{l}{F}_{j}+{r}_{1}\left(\left({u}_{j}-{l}_{j}\right){r}_{2}+{l}_{j}\right),\text{ }{r}_{3}\geqslant 0.5\\ {F}_{j}-{r}_{1}\left(\left({u}_{j}-{l}_{j}\right){r}_{2}+{l}_{j}\right),\text{ }{r}_{3} < 0.5 \end{array}\right. $$ (1) 式中:
$ X_{j}^{1} $ 的上标1表示樽海鞘链中的第一个樽海鞘,也就是领导者;下标j代表第j维,所以它表示领导者在第j维的位置;$ F_{j} $ 代表食物在第j维的位置;$ {u_j} $ 和$ {l_j} $ 分别表示上下边界在第j维的位置,j∈[1,n];$ r_{2} $ 和$ r_{3} $ 是[0,1]之间的随机数,分别表示了领导者在更新时的移动位置大小和移动方向;$ n $ 是收敛因子,起到了平衡全局搜索和局部开发的作用,$ n_{1} $ 的更新公式为$$ {r_1} = 2\exp \left[ { - {{(4l/L)}^2})} \right] $$ (2) 式中:l为当前迭代次数,L表示总共要迭代的次数。SSA追随者的位置更新公式为
$$ X_{j}^{i}=\frac{1}{2}\left(X_{j}^{i}+X_{j}^{i-1}\right), i \geq 2 $$ (3) 式中:
$ X_{j}^{1} $ 表示第i个樽海鞘在第j维的位置,第i个樽海鞘即追随者的位置更新受它前一个樽海鞘$ X^{H} $ 的位置影响,以此类推,都由领导者间接引领。1.2 瞬态搜索算法
瞬态搜索优化算法(transient search optimization, TSO)是于2020年Qais等[20]提出的,是一种新的基于物理的启发式优化算法。该算法的灵感来自于包含电感和电容等存储元件的开关电路的瞬态行为。TSO算法被建模为在搜索区域的下界和上界之间初始化搜索代理;寻找最佳解决方案(探索);达到稳定状态或最佳解决方案(开发)。
TSO搜索代理进行初始化的公式为
$$ Y = l + r \times (u - l){\text{ }} $$ (4) 式中:l是搜索空间的下界,u是搜索空间的上界,r是(0,1)上均匀分布的随机向量。
TSO的探测行为是受到的二阶电路在零点附近振荡的启发。利用随机数
$ n_{1} $ 来平衡勘探($ n_{1} $ ≥0.5)和开发($ n_{1} $ <0.5)之间的关系。TSO算法的开发和探索的数学模型为$$ \begin{array}{c}{Y}_{l+1}=\\ \left\{ \begin{array}{l}{Y}_{l}^{*}\text+({Y}_{l}-{C}_{1}\times Y)\text{exp}(-T)\text{,}\text{ } {r}_{1} < 0.5 \\ {Y}_{l}^{*} + \text{exp}(-T)\left[\mathrm{cos}(2\text{π}T)\text{+sin}(2\text{π}T)\right]\left|({Y}_{l}-{C}_{1}{Y}_{l}^{*})\right|\text{,} {r}_{1} \geqslant \text{0}\text{.5} \end{array}\right. \end{array}$$ (5) $$ T=2 \times {\textit{z}} \times r_{2}-{\textit{z}} $$ (6) $$ C_{1}=k \times {\textit{z}} \times r_{3}+1 $$ (7) $$ {\textit{z}}=2-2\left(\frac{l}{L_{\max }}\right) $$ (8) 式中:
$ Y_{l+1} $ 是当前的搜索代理$ Y_{I} $ 的此次迭代更新的位置,$ Y_{I}^{*} $ 是全局最佳位置,l为当前迭代次数,$ L_{\max } $ 为最大迭代次数,z为从2变为0衰减系数变量。$ n_{1} $ 、$ r_{2} $ 、$ r_{3} $ 为[0,1]内的随机数,T和$ {C_1} $ 为热阻系数,k是一个常数(k = 0,1,…)。2. 提出的方法
2.1 基于互信息的初始化策略
互信息的概念是由Shannon等[21]首先提出,它的引入是用来衡量两个变量间相互依赖的程度,描述了变量之间的公共信息。给定两个变量X和Y,其边缘概率为
$ P(x) $ 和$P(y)$ ,联合概率为$ P(x, y) $ ,条件概率为$ P(x \mid y) $ 。$ H(X) $ 表示随机变量的熵,它度量一个变量的不确定性,$ H(X \mid \boldsymbol{Y}) $ 是条件熵,它们两者之间差值可以表示为互信息$ I(X;Y) $ ,具体表达式为$$ H(X) = - \sum\limits_{x \in X} {P(x){{\log }_2}P(x)} {\text{ }} $$ (9) $$ H(X|Y) = - \sum\limits_{y \in Y} {\sum\limits_{x \in X} {[P(x,y){{\log }_2}P(x|y)]} } {\text{ }} $$ (10) $$ I(X ; Y)=H(X)-H(X \mid Y) $$ (11) 可以取X为某种特征,Y为类标签,用来计算互信息,结果越大,表明该特征与类标签的相关性越大,则认为该特征分类效果更好。并且互信息的有效性已经被证明[6,22-23]。
在本文利用数据集中每个特征与类标签之间的互信息值进行排序,生成一张排序表,排序中数值越大越靠前的特征被认为是和类标签关系越密切,即更加重要。排序表被分成了4个部分,每部分被选中的概率依次减小。通过这种方式既保证每个特征都有机会被选中,继续参加后续迭代,又使得表现良好的特征传给下一代的机会更大。在此策略中60%的初始数据集生成利用此互信息表,另外40%采用随机初始化策略。此划分能使大部分初始种群生成受到互信息表影响,更多的去选择与类标签关系紧密的特征,另外一小部分则保持随机生成,这同时能兼顾初始种群的多样性。
2.2 动态搜索算法
SSA位置更新公式(式(1))仅用于领导者,而追随者的移动依赖于自身和前一个个体,如果该算法幸运地找到了搜索空间中最优解所在区域,那么搜索过程最终会收敛,得到满意的解。相反,搜索将停留在次最优区域,在运行结束时,F将远离全局最优解,为此本文对原始SSA提出的第2种改进为有条件的使用动态搜索算法(dynamic search algorithm, DSA),在每一次迭代结束后,会判断是否调用此算法,这是为了避免多次计算消耗。此算法被调用是根据种群最优解F来判断的,为此在SSA末尾增加了一个计数器count,当F的适应度一次迭代后没有变化时,count就会加1,当count到达3时就会调用DSA,DSA的伪代码如算法1所示。
算法1 动态搜索算法的伪代码
输入 当前种群位置L,当前迭代次数t和最大迭代次数M,后半段动态搜索算法迭代次数K
输出 新的种群位置
1) If t < M/2 /*算法前半段*/
2) Loc = DSA_1(L,t)
3) Else /*算法后半段*/
4) Loc = DSA_2(L,t,K)
5) End If
6) Return Loc
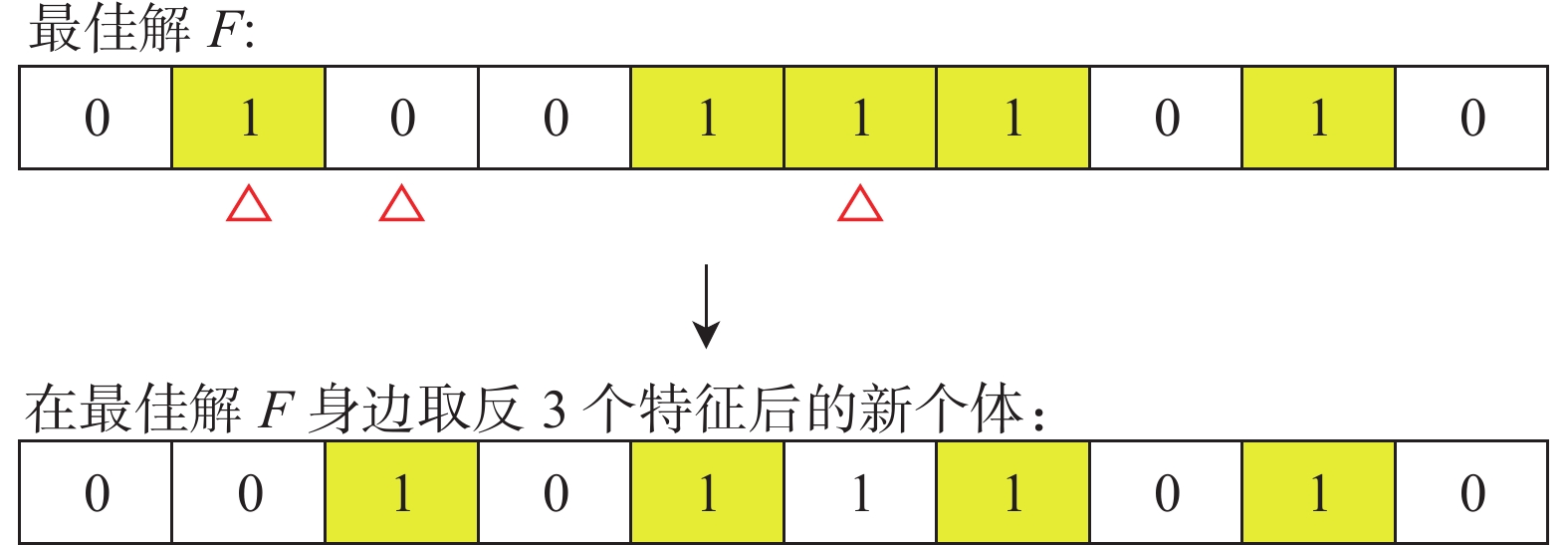
此算法前半段受到进化种群动态机制[24]的启发,此机制是一种通过将最坏的解决方案重新安置在最好的解决方案周围。本文的DSA在迭代次数小于一半时,将适应度后50%的个体淘汰,并将25%的新个体通过在最佳解F周围生成,对F随机取反1~5个特征(小到大的数据集都适用),如图1所示。
另外25%的个体则通过初始化机制生成。此划分以目前种群的最优解作为找到最优可能性较大的位置,在它身边进行发掘,同时考虑了其他位置寻找到最优的可能性。DSA前半段的伪代码如算法2所示。
算法2 DSA_1(L, t)
输入 当前种群位置L,当前迭代次数t
输出 新的种群位置
1) 利用式(12)计算种群适应度,并淘汰较差的50%樽海鞘个体
2) 利用2.1节的策略生成25%×N个新个体到种群
3) For i = 1 to N×25% do
4) 把F的值赋给F_copy,n随机初始化为1~5
5) 从F_copy中随机挑选n个特征
6) For 对于被挑选的特征 in F_copy
7) If 特征的值为1 /*1代表被选择,0为没有*/
8) 特征值改为0
9) Else
10) 特征值改为1
11) End If
12) End For
13) 把F_copy加入到种群中
14) End For
15) 寻找这些新个体的最优适应度值的个体m
16) If f(m) < f(F) /*适应度越小越好*/
17) F = m
18) End If
19) Return Loc
当迭代次数大于一半时,为保持种群的稳定性,此时算法不再大规模地替换种群,而是采取结合互信息排序表,在最佳解F身边寻找,DSA的每一次迭代中都会生成2个新个体,第1个利用互信息排序表,从最佳个体中删除已选择的排序表后端的1~5个特征,增添未选择的排序表前端的1~5个特征。第2个个体从最佳个体上随机挑选1~5个特征取反。之后这两个个体中最好的个体m与种群最佳个体比较,如果m适应度值优于当前的最佳解,则更新F,把F的值更新为m,否则用m去替换当前种群适应度最差的个体。DSA的后半段能够帮助算法避免局部最优。伪代码中的K是后半段DSA的迭代次数,本文K设置为5。DSA后半段的伪代码如算法3所示。
算法3 DSA_2(L, t, K)
输入 当前种群位置L,当前迭代次数t,后半段动态搜索算法的迭代次数K
输出 新的种群位置
1) For i = 1 to k
2) n1、n2和n3分别在1~5中初始化,把F赋给F_copy1、F_copy2,利用排序表从后往前从F_copy1中挑选n1个已选特征,利用排序表从前往后挑选n2个未选特征。从F_copy2随机挑选n3个特征
3) For 对于被挑选的特征 in (F_copy1、F_copy2)
4) If 特征的值为1 /* 1代表被选择,0为没有*/
5) 特征值改为0
6) Else
7) 特征值改为1
8) End If
9) End For
10) 把F_copy1、F_copy2中适应度最佳个体赋给m
11) If f(m) < f(F)
12) 把m赋给F
13) Else
14) 把m赋给种群中最差的个体
15) End If
16) End For
17) Return Loc
2.3 HS-SSA描述
本文对SSA有3个改进:1) 利用互信息生成了特征排序表,并用在新的初始化策略上;2) 提出了动态搜索算法,并且根据计数器count和迭代次数有条件的执行;3) 在位置更新策略上,原SSA追随者更新公式相对简单,算法存在收敛速度较慢、容易陷入局部最优等缺点。为此,本文将追随者的位置更新公式随机的在原式(3)和TSO搜索公式(式(5))中进行选择,这改进了勘探和开发步骤的效率,增加了解空间灵活性和多样性,从而算法能快速定位全局最优。算法4给出了HS-SSA的伪代码。
算法4 HS-SSA的伪代码
输入 最大迭代次数M,种群数量N
输出 最佳适应度值的樽海鞘个体的位置F
1) 用2.1节初始化策略初始化种群
$ X_{i} $ (i = 1, 2, …, N)2) 计算所有个体适应度,并把最佳个体位置赋给F
3) While t < M
4) 更新
$ n $ 、Z,T和$ {C_1} $ 通过式(2)、(8)、(6)和(7)5) For (每一个个体
$ X_{i} $ )6) If i == 1
7) 通过式(1)更新领导者位置
8) Else
9) 生成[0,1]的随机值r
10) If r > 0.5
11) 通过SSA原位置更新公式(式(3))更新追随者
12) Else
13) 通过TSO搜索公式(式(5))更新追随者
14) End If
15) End If
16) End For
17) 更新超出上下边界的樽海鞘个体
18) 更新所有个体适应度,把最佳个体位置赋给F
19) 判断F是否变化从而更新计算器count
20) If(count==3)
21) 在当前种群基础上调用算法1
22) count = 0
23) End If
24) t = t+1
25) End While
26) Return F
2.4 适应度计算函数
适应度计算函数为
$$ f({X_i}) = \alpha \times e({X_i}) + \beta \times \frac{s}{n}$$ (12) 式中:
$ \alpha \in(0,1) $ ,$ \beta=1-\alpha $ ,$ \alpha $ 和$ \beta $ 分别为错误率和选择特征比的权重系数,s表示选择特征的数量,n为数据集的特征维度,$ e({X_i}) $ 表示当前个体放入分类器中得到的错误率。在本文中$ \alpha $ 设置为0.99,则$ \beta $ 为0.01。3. 实验和结果分析
实验中代码运行环境为Python3.9。硬件环境为Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz,RAM为16.0 GB。
3.1 实验描述
为验证本文算法的性能,使用了14个UCI数据集[25]进行实验,表1显示了数据集的基本信息。
表 1 数据集信息Table 1 Information of dataset数据集 特征数 样本数 类别数 BreastEW 30 568 2 CongressEW 16 434 2 Exactly 13 1000 2 HeartEW 13 270 2 Horse 27 368 2 ionosphere 34 351 2 KrVsKpEW 36 3196 2 Lymphography 18 148 4 PenglungEW 325 73 7 Sonar 60 208 2 SpectEW 22 267 2 Tic-tac-toe 9 958 2 vehicle 18 846 4 Zoo 16 101 7 实验采用了80%∶20%的数据集划分,即80%的数据作为训练集,20%数据作为测试集并且使用K近邻(K-nearest neighbor)作为分类器,K=5。同时和SSA算法、SSA变体DSSA[15]和SSARM-SCA[17],还有PSO、HHO和GWO进行了实验对比,表2给出了所有算法的参数设置。为确保结果更精确,减少误差,所有算法在每个数据集上运行20次,取出分类准确率和维度缩减率的平均值,并且做了Wilcoxon秩和检验以确定算法的显著性。
表 2 对比算法的参数设置Table 2 Parameter setting of comparison algorithm算法名称 参数设置 HS-SSA N=30、M=200, SSA中的$ r_{2} $、$ r_{3} $和TSO中的$ r_{2} $和$ r_{3} $为[0,1]中的随机数,TSO中的K取值为3 SSA[8] N=30、M=200, $ r_{2} $、$ r_{3} $为[0,1]中的随机数 DSSA[15] N=30、M=200, $ r_{2} $和$ r_{3} $为[0,1]中的随机数,max_LSA_number_of_iterations=10 SSARM-SCA[17] N=30、M=200,$ r_{2} $和$ r_{3} $为[0,1]中的随机数,替换机制次数设为M/10,最差替换解数设为 N/5 PSO[7] N=30、M=200,设置$ c_{1}=c_{2}=2 $,w=1 HHO[9] N=30,M=200 GWO[10] N=30,M=200 3.2 实验结果与分析
为了使实验结果更具说服力,对每个数据集都运行20次再取平均,HS-SSA和对比算法运行20次以后得到的平均分类准确率和维度缩减率分别统计在表3和表4。每个数据集中表现最好的标粗体。
表 3 HS-SSA与对比算法在运行20次的平均准确率Table 3 Average accuracy of the HS-SSA and competing algorithms in 20 runs数据集 HS-SSA SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 0.971 05 0.959 21 0.959 65 0.961 84 0.952 63 0.952 63 0.957 46 CongressEW 0.985 63 0.971 26 0.975 86 0.978 74 0.977 59 0.966 09 0.975 86 Exactly 1.000 00 0.948 00 0.944 50 0.999 75 0.974 50 0.880 25 0.986 00 HeartEW 0.893 52 0.870 37 0.871 30 0.887 04 0.875 93 0.862 96 0.885 19 Horse 0.871 62 0.802 70 0.798 65 0.847 97 0.820 27 0.786 49 0.847 30 ionosphere 0.973 94 0.928 17 0.922 54 0.960 56 0.946 48 0.940 85 0.960 56 KrVsKpEW 0.985 86 0.971 56 0.975 08 0.984 22 0.981 17 0.971 88 0.980 78 Lymphography 0.948 33 0.918 33 0.923 33 0.931 67 0.930 00 0.896 67 0.923 33 PenglungEW 0.996 67 0.906 67 0.910 00 0.933 33 0.940 00 0.950 00 0.990 00 Sonar 0.982 14 0.923 81 0.922 62 0.966 67 0.961 91 0.938 10 0.972 62 SpectEW 0.921 30 0.906 48 0.900 93 0.919 44 0.912 04 0.880 56 0.912 96 Tic-tac-toe 0.849 48 0.828 39 0.844 01 0.832 81 0.832 29 0.821 09 0.831 51 vehicle 0.775 59 0.747 35 0.746 47 0.759 12 0.757 35 0.729 71 0.770 59 Zoo 0.995 24 0.976 19 0.976 19 0.983 33 0.980 95 0.976 19 0.985 71 表 4 HS-SSA与对比算法在运行20次的平均维度缩减率Table 4 Average dimension reduction rate of HS-SSA and comparison algorithm in 20 runs% 数据集 HS-SSA SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 89.17 73.17 65.00 87.50 84.17 83.00 90.83 CongressEW 72.19 64.06 63.13 70.94 70.94 77.19 74.06 Exactly 53.85 44.23 44.62 53.08 50.38 44.62 53.85 HeartEW 68.08 60.38 56.92 63.85 64.62 66.54 66.54 Horse 85.93 62.96 54.63 69.63 66.30 81.48 82.59 ionosphere 88.53 65.00 63.82 76.32 75.44 82.06 85.15 KrVsKpEW 51.11 43.47 20.14 46.25 46.11 33.19 62.50 Lymphography 69.44 60.28 57.22 66.11 65.28 59.44 69.17 PenglungEW 95.71 58.43 61.09 82.62 70.14 92.66 96.97 Sonar 82.67 57.58 56.17 74.58 69.67 73.50 84.75 SpectEW 72.05 57.73 45.00 60.68 65.23 67.27 71.59 Tic-tac-toe 8.33 14.44 13.33 23.33 13.33 21.67 31.67 vehicle 61.67 48.33 40.56 53.06 50.83 51.94 56.94 Zoo 68.44 60.31 61.88 68.13 64.06 61.88 69.69 从表3中可以看出在准确率上,HS-SSA在所有数据集的平均分类精度优于所有对比算法。与SSA和SSA变体SSARM-SCA相比时更加卓越,在数据集Exactly、Horse、ionosphere、PenglungEW、Sonar上,HS-SSA的准确率都提高了至少4.5%,特别是在PenglungEW分别高达9%和8.67%。对于DSSA、HS-SSA也有稳步提高,特别是在数据集PenglungEW上提高了6%。这说明算法HS-SSA在原始SSA上取得了巨大的突破的同时,还在近几年基于SSA改进的算法中具有较大的竞争力。与其他对比算法相比,HS-SSA也有较好的表现。与HHO对比,除了数据集KrVsKpEW以外HS-SSA都有比较大的提升,特别在数据集Exactly上HS-SSA比HHO的准确率提高了接近12%,而从表4可以看出在数据集KrVsKpEW上HS-SSA比HHO的维度缩减率多了17.92%。在数据集vehicle上HS-SSA的准确率比PSO和GWO提升相对不多,但是在维度缩减方面表现较好,分别多出10.84%和4.73%。对于HS-SSA在维度缩减方面的表现,显然不如它在准确率上的优异,但是也在一半的数据集中表现最好,而且在剩下的一半数据集中维度缩减率也接近最好的。特别是在高维数据集PenglungEW、HS-SSA的维度缩减率高达95.71%。这证明了在不同维度的数据集下算法的降维都具有有效性。在与SSA、DSSA、SSARM-SCA和PSO对比,除了数据集Tic-tac-toe以外,HS-SSA在维度缩减的方面都表现得更佳,可见它的降维能力。
HS-SSA的优势在于利用排序表拥有一个质量更好的初始化种群,并且利用DSA在前期淘汰较差的解决方案,在后期避免局部最优,并且利用瞬态搜索更新公式改进了解的多样性。通过表3和表4可以看出在大部分数据集上HS-SSA展现出来的优越性,同时这些结果也强调了它的稳定性,通过选择信息量大的特征来平衡开发和勘探。为评估实验结果的显著性,采用了Wilcoxon秩和检验,它是通过推断总体的分布是否相同,进而判断两组样本之间的差异是否显著。该测试可以评估HS-SSA相对于对比算法的显著性,在这个测试中,使用的显著性水平是5%。
表5给出了以20次运行准确率为基础的HS-SSA与对比算法的秩和检验的P值,当P小于5%时,说明HS-SSA相对于竞争算法有明显改进,标粗体,当大于5%时则没有。可以看出在大多数数据集上HS-SSA在分类准确率上比其他对比算法有显著提高。特别是与SSA和HHO对比,所有数据集都有显著提高。
表 5 以20次运行准确率为基础的HS-SSA与对比算法的单边 Wilcoxon秩和检验的P值Table 5 Test P-value of unilateral Wilcoxon rank sum test between HS-SSA and comparison algorithm based on the accuracy of 20 runs数据集 SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 2.42×10−2 1.58×10−2 4.05×10−2 6.43×10−4 1.90×10−3 6.41×10−3 CongressEW 4.18×10−3 2.27×10−2 4.17×10−2 1.99×10−2 4.39×10−4 3.82×10−2 Exactly 1.46×10−3 7.62×10−5 3.93×10−1 5.23×10−2 2.19×10−4 3.93×10−1 HeartEW 1.86×10−2 1.04×10−2 3.52×10−1 3.39×10−2 7.18×10−3 2.24×10−1 Horse 6.65×10−8 3.01×10−7 3.50×10−2 5.24×10−7 4.59×10−8 6.66×10−3 ionosphere 1.87×10−6 1.59×10−7 1.37×10−2 5.85×10−4 2.63×10−5 1.24×10−2 KrVsKpEW 4.30×10−6 3.46×10−7 3.52×10−1 1.52×10−2 9.01×10−7 1.69×10−2 Lymphography 4.89×10−3 4.70×10−3 4.42×10−2 4.17×10−2 5.80×10−5 2.34×10−2 PenglungEW 1.55×10−5 1.17×10−4 5.80×10−5 2.56×10−3 1.28×10−3 3.88×10−1 Sonar 1.44×10−6 2.75×10−6 9.48×10−2 3.70×10−3 3.12×10−5 4.95×10−2 SpectEW 4.17×10−2 4.42×10−2 4.46×10−1 1.07×10−1 2.81×10−4 2.54×10−1 Tic-tac-toe 3.28×10−3 1.93×10−1 2.90×10−3 9.30×10−3 5.07×10−4 2.16×10−3 vehicle 6.84×10−5 6.47×10−5 2.57×10−2 1.11×10−2 5.24×10−7 2.05×10−1 Zoo 2.74×10−2 1.52×10−2 8.81×10−2 5.23×10−2 1.52×10−2 2.01×10−1 4. 结束语
本文针对樽海鞘群算法在特征选择上存在容易陷入局部最优和种群多样性较差等缺点,提出了一种具有混合策略的樽海鞘群特征选择算法(HS-SSA)。对于SSA有3点改进:提出了一种基于互信息的排序表并基于此提出了新的初始化策略;提出了一个有条件调用的动态搜索算法;提出了一种让SSA和瞬态搜索(TSO)相结合的更新策略。通过在14个UCI数据集上和6种不同的对比算法进行实验,得出在准确率上优于全部的其他算法,在维度缩减上一半的数据集都是最好的。并且从显著性检验来看,大部分数据集上该算法的性能对于其他算法有显著性的增强。下一步的研究工作重点主要集中在两个方面:进一步增强算法的降维能力;尝试SSA与其他启发式算法相结合。
-
表 1 数据集信息
Table 1 Information of dataset
数据集 特征数 样本数 类别数 BreastEW 30 568 2 CongressEW 16 434 2 Exactly 13 1000 2 HeartEW 13 270 2 Horse 27 368 2 ionosphere 34 351 2 KrVsKpEW 36 3196 2 Lymphography 18 148 4 PenglungEW 325 73 7 Sonar 60 208 2 SpectEW 22 267 2 Tic-tac-toe 9 958 2 vehicle 18 846 4 Zoo 16 101 7 表 2 对比算法的参数设置
Table 2 Parameter setting of comparison algorithm
算法名称 参数设置 HS-SSA N=30、M=200, SSA中的$ r_{2} $、$ r_{3} $和TSO中的$ r_{2} $和$ r_{3} $为[0,1]中的随机数,TSO中的K取值为3 SSA[8] N=30、M=200, $ r_{2} $、$ r_{3} $为[0,1]中的随机数 DSSA[15] N=30、M=200, $ r_{2} $和$ r_{3} $为[0,1]中的随机数,max_LSA_number_of_iterations=10 SSARM-SCA[17] N=30、M=200,$ r_{2} $和$ r_{3} $为[0,1]中的随机数,替换机制次数设为M/10,最差替换解数设为 N/5 PSO[7] N=30、M=200,设置$ c_{1}=c_{2}=2 $,w=1 HHO[9] N=30,M=200 GWO[10] N=30,M=200 表 3 HS-SSA与对比算法在运行20次的平均准确率
Table 3 Average accuracy of the HS-SSA and competing algorithms in 20 runs
数据集 HS-SSA SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 0.971 05 0.959 21 0.959 65 0.961 84 0.952 63 0.952 63 0.957 46 CongressEW 0.985 63 0.971 26 0.975 86 0.978 74 0.977 59 0.966 09 0.975 86 Exactly 1.000 00 0.948 00 0.944 50 0.999 75 0.974 50 0.880 25 0.986 00 HeartEW 0.893 52 0.870 37 0.871 30 0.887 04 0.875 93 0.862 96 0.885 19 Horse 0.871 62 0.802 70 0.798 65 0.847 97 0.820 27 0.786 49 0.847 30 ionosphere 0.973 94 0.928 17 0.922 54 0.960 56 0.946 48 0.940 85 0.960 56 KrVsKpEW 0.985 86 0.971 56 0.975 08 0.984 22 0.981 17 0.971 88 0.980 78 Lymphography 0.948 33 0.918 33 0.923 33 0.931 67 0.930 00 0.896 67 0.923 33 PenglungEW 0.996 67 0.906 67 0.910 00 0.933 33 0.940 00 0.950 00 0.990 00 Sonar 0.982 14 0.923 81 0.922 62 0.966 67 0.961 91 0.938 10 0.972 62 SpectEW 0.921 30 0.906 48 0.900 93 0.919 44 0.912 04 0.880 56 0.912 96 Tic-tac-toe 0.849 48 0.828 39 0.844 01 0.832 81 0.832 29 0.821 09 0.831 51 vehicle 0.775 59 0.747 35 0.746 47 0.759 12 0.757 35 0.729 71 0.770 59 Zoo 0.995 24 0.976 19 0.976 19 0.983 33 0.980 95 0.976 19 0.985 71 表 4 HS-SSA与对比算法在运行20次的平均维度缩减率
Table 4 Average dimension reduction rate of HS-SSA and comparison algorithm in 20 runs
% 数据集 HS-SSA SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 89.17 73.17 65.00 87.50 84.17 83.00 90.83 CongressEW 72.19 64.06 63.13 70.94 70.94 77.19 74.06 Exactly 53.85 44.23 44.62 53.08 50.38 44.62 53.85 HeartEW 68.08 60.38 56.92 63.85 64.62 66.54 66.54 Horse 85.93 62.96 54.63 69.63 66.30 81.48 82.59 ionosphere 88.53 65.00 63.82 76.32 75.44 82.06 85.15 KrVsKpEW 51.11 43.47 20.14 46.25 46.11 33.19 62.50 Lymphography 69.44 60.28 57.22 66.11 65.28 59.44 69.17 PenglungEW 95.71 58.43 61.09 82.62 70.14 92.66 96.97 Sonar 82.67 57.58 56.17 74.58 69.67 73.50 84.75 SpectEW 72.05 57.73 45.00 60.68 65.23 67.27 71.59 Tic-tac-toe 8.33 14.44 13.33 23.33 13.33 21.67 31.67 vehicle 61.67 48.33 40.56 53.06 50.83 51.94 56.94 Zoo 68.44 60.31 61.88 68.13 64.06 61.88 69.69 表 5 以20次运行准确率为基础的HS-SSA与对比算法的单边 Wilcoxon秩和检验的P值
Table 5 Test P-value of unilateral Wilcoxon rank sum test between HS-SSA and comparison algorithm based on the accuracy of 20 runs
数据集 SSA SSARM-SCA DSSA PSO HHO GWO BreastEW 2.42×10−2 1.58×10−2 4.05×10−2 6.43×10−4 1.90×10−3 6.41×10−3 CongressEW 4.18×10−3 2.27×10−2 4.17×10−2 1.99×10−2 4.39×10−4 3.82×10−2 Exactly 1.46×10−3 7.62×10−5 3.93×10−1 5.23×10−2 2.19×10−4 3.93×10−1 HeartEW 1.86×10−2 1.04×10−2 3.52×10−1 3.39×10−2 7.18×10−3 2.24×10−1 Horse 6.65×10−8 3.01×10−7 3.50×10−2 5.24×10−7 4.59×10−8 6.66×10−3 ionosphere 1.87×10−6 1.59×10−7 1.37×10−2 5.85×10−4 2.63×10−5 1.24×10−2 KrVsKpEW 4.30×10−6 3.46×10−7 3.52×10−1 1.52×10−2 9.01×10−7 1.69×10−2 Lymphography 4.89×10−3 4.70×10−3 4.42×10−2 4.17×10−2 5.80×10−5 2.34×10−2 PenglungEW 1.55×10−5 1.17×10−4 5.80×10−5 2.56×10−3 1.28×10−3 3.88×10−1 Sonar 1.44×10−6 2.75×10−6 9.48×10−2 3.70×10−3 3.12×10−5 4.95×10−2 SpectEW 4.17×10−2 4.42×10−2 4.46×10−1 1.07×10−1 2.81×10−4 2.54×10−1 Tic-tac-toe 3.28×10−3 1.93×10−1 2.90×10−3 9.30×10−3 5.07×10−4 2.16×10−3 vehicle 6.84×10−5 6.47×10−5 2.57×10−2 1.11×10−2 5.24×10−7 2.05×10−1 Zoo 2.74×10−2 1.52×10−2 8.81×10−2 5.23×10−2 1.52×10−2 2.01×10−1 -
[1] WANG Changzhong, HU Qinghua, WANG Xizhao, et al. Feature selection based on neighborhood discrimination index[J]. IEEE transactions on neural networks and learning systems, 2018, 29(7): 2986–2999. [2] LI Xiaoping, WANG Yadi, RUIZ R. A survey on sparse learning models for feature selection[J]. IEEE transactions on cybernetics, 2022, 52(3): 1642–1660. doi: 10.1109/TCYB.2020.2982445 [3] JOHN G H, KOHAVI R, PFLEGER K. Irrelevant features and the subset selection problem[M]//Machine learning proceedings 1994. Amsterdam: Elsevier, 1994: 121−129. [4] 董红斌, 滕旭阳, 杨雪. 一种基于关联信息熵度量的特征选择方法[J]. 计算机研究与发展, 2016, 53(8): 1684–1695. DONG Hongbin, TENG Xuyang, YANG Xue. Feature selection based on the measurement of correlation information entropy[J]. Journal of computer research and development, 2016, 53(8): 1684–1695. [5] SONG Xianfang, ZHANG Yong, GONG Dunwei, et al. Feature selection using bare-bones particle swarm optimization with mutual information[J]. Pattern recognition, 2021, 112: 107804. doi: 10.1016/j.patcog.2020.107804 [6] LI Anda, XUE Bing, ZHANG Mengjie. Improved binary particle swarm optimization for feature selection with new initialization and search space reduction strategies[J]. Applied soft computing, 2021, 106: 107302. doi: 10.1016/j.asoc.2021.107302 [7] 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87–94. YANG Wei, LI Qiqiang. Survey on particle swarm optimization algorithm[J]. Engineering science, 2004, 6(5): 87–94. [8] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm[J]. Advances in engineering software, 2017, 114(C): 163–191. [9] 刘骏鹏. 哈里斯鹰算法的改进及应用研究[D]. 杭州: 浙江大学, 2021. LIU Junpeng. Research on improvement and application of Harris eagle algorithm[D]. Hangzhou: Zhejiang University, 2021. [10] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007 [11] HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66–72. doi: 10.1038/scientificamerican0792-66 [12] KILIC F, KAYA Y, YILDIRIM S. A novel multi population based particle swarm optimization for feature selection[J]. Knowledge-based systems, 2021, 219: 106894. doi: 10.1016/j.knosys.2021.106894 [13] TU Qiang, CHEN Xuechen, LIU Xingcheng. Multi-strategy ensemble grey wolf optimizer and its application to feature selection[J]. Applied soft computing, 2019, 76(C): 16–30. [14] MAFARJA M, ALJARAH I, HEIDARI A A, et al. Binary dragonfly optimization for feature selection using time-varying transfer functions[J]. Knowledge-based systems, 2018, 161: 185–204. doi: 10.1016/j.knosys.2018.08.003 [15] TUBISHAT M, JA’AFAR S, ALSWAITTI M, et al. Dynamic salp swarm algorithm for feature selection[J]. Expert systems with applications, 2021, 164: 113873. doi: 10.1016/j.eswa.2020.113873 [16] ZAWBAA H M, EMARY E, GROSAN C, et al. Large-dimensionality small-instance set feature selection: a hybrid bio-inspired heuristic approach[J]. Swarm and evolutionary computation, 2018, 42: 29–42. doi: 10.1016/j.swevo.2018.02.021 [17] ZIVKOVIC M, STOEAN C, CHHABRA A, et al. Novel improved salp swarm algorithm: an application for feature selection[J]. Sensors, 2022, 22(5): 1711. doi: 10.3390/s22051711 [18] MAFARJA M M, MIRJALILI S. Hybrid whale optimization algorithm with simulated annealing for feature selection[J]. Neurocomputing, 2017, 260(C): 302–312. [19] DHAL P, AZAD C. A multi-objective feature selection method using Newton’s law based PSO with GWO[J]. Applied soft computing, 2021, 107: 107394. doi: 10.1016/j.asoc.2021.107394 [20] QAIS M H, HASANIEN H M, ALGHUWAINEM S. Transient search optimization: a new meta-heuristic optimization algorithm[J]. Applied intelligence, 2020, 50(11): 3926–3941. doi: 10.1007/s10489-020-01727-y [21] SHANNON C E. A mathematical theory of communication[J]. The bell system technical journal, 1948, 27(3): 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x [22] 滕旭阳, 董红斌, 孙静. 面向特征选择问题的协同演化方法[J]. 智能系统学报, 2017, 12(1): 24–31. doi: 10.11992/tis.201611029 TENG Xuyang, DONG Hongbin, SUN Jing. Co-evolutionary algorithm for feature selection[J]. CAAI transactions on intelligent systems, 2017, 12(1): 24–31. doi: 10.11992/tis.201611029 [23] LU Huijuan, CHEN Junying, YAN Ke, et al. A hybrid feature selection algorithm for gene expression data classification[J]. Neurocomputing, 2017, 256(C): 56–62. [24] MAFARJA M, ALJARAH I, HEIDARI A A, et al. Evolutionary population dynamics and grasshopper optimization approaches for feature selection problems[J]. Knowledge-based systems, 2018, 145(C): 25–45. [25] DAVIE A, PATRICK M, CHRISTOPHER M, et al. UCI machine learning repository[EB/OL]. [2022–09–19].https://archive.ics.uci.edu/.









































 下载:
下载:












