系统存在的意义是完成预定功能，系统在规定条件下完成预定功能的能力称为可靠性，与之互补的是失效性。那么系统完成预定功能的状态作者定义为系统功能状态^[1-2]，是可靠状态和失效状态的叠加态。这意味着系统功能状态不可能完全是可靠状态或是失效状态。如果设定系统功能状态空间只有可靠和失效状态，则系统功能状态可用可靠状态或失效状态之一表示。又考虑到我们通常更关注系统失效，即系统发生故障的过程，以便干预系统故障使系统安全。因此将系统失效状态作为研究重点，将系统功能状态的变化过程称为系统故障演化过程^[3-4]。系统故障演化过程中的任意时刻，系统功能状态都是确定的。系统故障演化过程是诠释系统在各因素作用下系统功能状态变化的过程。系统在自然状态下功能性逐渐降低，而人的作用是减缓或阻止该过程。这与熵的定义较为一致，即系统在自然状态下存在熵增现象。系统故障演化过程能表示系统在自然情况下的系统功能状态变化。在该变化中系统越混乱，系统的功能状态就趋向于失效状态。因此系统故障演化过程就代表了系统功能状态混乱性的变化过程。该过程是否可以使用熵概念描述，是论文研究的关键问题。

关于熵描述各类系统的混乱性和不确定性的研究较多。目前主要研究包括DSM与信息熵的装备体系结构贡献率^[5]；EWT的压力样本熵分析^[6]；连续−离散系统自适应最大相关熵滤波算法^[7]；皮尔逊系数和信息熵的数据融合^[8]；混合系统线性状态空间模型辨识^[9]；预测不确定性与对抗鲁棒性关系^[10]；逆信息熵因果推理^[11]；熵修正混合人工蜂群−蝙蝠算法^[12]；多粒度形式不确定性度量与最优粒度^[13]；信息熵信息物理系统融合控制^[14]；不确定性空间信息重建^[15]；知识粒度框架的不确定性度量^[16]；改进EMD算法计算熵性能^[17]。国外也对这类问题进行了研究，包括图像熵均衡^[18]；联合图熵知识提取^[19-20]；EEMD信息熵^[21]；信息熵协同理论^[22]；信息熵和灰色关联分析^[23]等。但这些研究一般关注于系统某种条件下的混乱情况或是信息来源的混乱及不确定性。但实际上这种混乱程度通过熵值只能得到一个相对量，缺乏比较性，不能分析熵的具体变化程度。更为有效的方法是度量某演化过程对系统功能状态混乱性的变化程度，即通过系统故障演化过程来衡量系统功能状态混乱性的变化程度。这是一种从演化过程角度研究系统功能状态变化的方法，但类似研究目前仍然鲜见。

根据作者对系统故障演化过程的研究^[3-4]，认为通过系统故障演化过程研究系统功能状态混乱程度是可行的。由此，论文提出了系统故障演化过程熵（下文简称“演化熵”）的概念，衡量演化过程造成系统功能状态下降的程度。演化熵变化越大，系统向着失效状态的变化越大。研究了演化过程中最基本的事件逻辑关系，即“与或”逻辑关系，对演化熵的影响，从而估计系统故障演化过程对演化熵造成的影响。

1.   事件故障概率分布熵的基本概念

在说明演化熵之前，需要论述其基础概念，即事件故障概率分布熵。描述系统故障演化过程中的系统功能状态混乱性，需要确定事件故障概率分布熵和系统故障演化过程熵，前者简称为分布熵，后者简称为演化熵，分布熵是演化熵的基础。

系统功能状态代表了系统在某一演化时刻实现其功能的可能性。或者理解为无数系统功能状态按照演化过程组合在一起形成了系统故障演化过程。而系统功能状态是所有参与系统功能实现的事件的功能性的共同作用。作者为表示这些事件的功能性提出了事件故障概率分布。

事件故障概率分布^[24-25]是空间故障树理论基础的重要概念，空间故障树理论基础^[24]是空间故障树理论体系的第一阶段，因此事件故障概率分布贯穿了整个空间故障树理论体系。事件故障概率分布描述执行该事件元件的故障概率变化情况，该变化受到多因素影响，以这些因素作为坐标轴形成因素空间。则不同因素情况下的事件故障概率就在该因素空间中形成了变化曲面，即事件故障概率分布。事件故障概率分布中，各因素影响下概率变化程度可通过信息熵的形式描述，即形成了上文提到的分布熵。通过分布熵结合系统故障演化过程特征即可得到演化熵。

论述分布熵的构造过程，设因素集合为$F= \left\{ {{f_1},{f_2}, \cdots ,{f_N}} \right\}$，$ n = 1,2, \cdots ,N $，N为因素总数；各因素值域等距划分点数量集合$ D{\text{ = }}\left\{ {{d_1},{d_2}, \cdots ,{d_N}} \right\} $，$ {f_n} $值域的划分点数量为$ {d_n} \in D $；事件故障概率的分类集合$ Q = \left\{ {{q_1},{q_2}, \cdots ,{q_M}} \right\} $，$m=1,2, \cdots, M$，${q_1} = \left[ {0,1/M} \right), {q_2} = \left[ {1/M,2/M} \right), \cdots ,{q_M} = \left[ {(M - 1)/M,M/M} \right]$，${q_1} \cup {q_2} \cdots \cup {q_M} = [0,1]$，$M$是分类总数；$P({x_1},{x_2}, \cdots ,{x_N})$为事件故障概率分布，${x_1}、{x_2}、\cdots、{x_N}$分别为因素${f_1}、{f_2}、\cdots、{f_N}$的具体值。对$P({x_1},{x_2}, \cdots ,{x_N})$中的所有故障概率点按照M类进行归类计数：

式中：$ {N_m} $表示$ P({x_1},{x_2}, \cdots ,{x_N}) $中属于第m类的故障概率点数量，数量集合为$ N = \{ {N_1},{N_2}, \cdots ,{N_M}\} $。

式（1）实现了对事件故障概率分布中所有故障概率点的统计。首先划定了M个分类，主要目的是将故障概率的值域进行划分，从而将落在不同区域的故障点统计出来。在不同故障概率区间中的点的数量是随后计算分布熵的基础。本质上不同概率区间中的点的数量代表了故障概率点在整个故障概率分布中的混乱程度，即为式（1）的基本逻辑意义。

进一步的，设$ {N_m} $与总故障概率点数量${d_1} \times {d_2} \times \cdots \times {d_N}$的比值为$ {b_m} = {N_m}/({d_1} \times {d_2} \times \cdots \times {d_N}) $，比值集合为$ B = \left\{ {{b_1},{b_2}, \cdots ,{b_M}} \right\} $。那么分布熵$\varGamma ({b_1}, {b_2}, \cdots , {b_M})$可表示为

可通过拉格朗日优化函数得到分布熵的最大值是$ {\log _2}M $，最小值为0。

2.   系统故障演化过程熵

系统故障演化过程可理解为按照演化顺序的无数系统功能状态的有序集合，过程中每个时刻都呈现为一个确定的系统功能状态。因此系统功能状态在系统故障演化过程中是连续的，每个时刻的系统功能状态都对应着一个演化熵。

系统故障演化过程是演化开始的原因事件，即边缘事件，以及演化过程中由边缘事件产生的过程事件和演化结果的最终事件组成的。在演化过程中这些事件由于因素作用产生的故障概率变化用事件故障概率分布表示，每个事件都有自己的故障概率分布。边缘事件是演化过程的起始事件，不受任何其他事件影响；过程事件由边缘事件产生，是演化过程的主体事件；最终事件是由过程事件和边缘事件导致的，是演化过程的最终状态事件。由于系统故障演化过程中任何事件都具有事件故障概率分布，所以过程事件的故障概率分布由边缘事件或边缘事件与前继过程事件的故障概率分布共同产生；最终事件故障概率分布由过程事件或过程事件和边缘事件的故障概率分布共同产生。

由上节可知，系统故障演化过程中的所有事件故障概率分布都可计算对应的分布熵。那么边缘事件的分布熵是边缘事件故障概率分布确定的；过程事件的分布熵由过程事件故障概率分布确定；最终事件分布熵由最终事件故障概率分布确定。需注意的事，这些分布熵不是通过前继事件分布熵使用解析方法确定的，而是使用前继事件故障概率分布得到的该时刻事件故障概率分布，再根据式(1)和式(2)确定的。因此系统故障演化过程中事件之间的相互作用和传递是通过事件故障概率分布完成的。分布熵只是对某时刻系统功能状态进行的度量，是通过该状态下事件故障概率分布计算得到的。因此分布熵不具有传递性，只是演化过程中某一时刻的功能状态混乱性的度量。

演化熵能衡量系统故障演化过程中某一时刻的系统功能状态的混乱程度，演化熵是通过该时刻的事件故障概率分布计算得到的，而该事件故障概率分布是通过前期参与演化的所有事件的故障概率分布计算得到的。所以演化熵是演化过程某时刻的分布熵。由于式(1)借助了概率的离散统计方法，因此前继事件的分布熵与当前时刻的演化熵，以及不同时刻的演化熵之间目前没有明确的函数关系。即不能直接通过分布熵或前期的演化熵直接得到后继演化熵。但在系统故障演化过程中，可通过不同时刻的演化熵来衡量系统功能状态的变化程度和趋势。因为各种边缘事件的加入，系统故障演化过程的演化熵必然发生变化。

对演化熵进行总结：1）演化熵表征了系统故障演化过程的某时刻的系统功能状态；2）演化熵不能通过前继演化熵或分布熵直接计算得到，只能通过该时刻事件故障概率分布得到；3）演化熵与分布熵一样，具有确定的值域范围。

3.   与或逻辑的演化熵变化规律

第2节提到演化熵不能通过前继演化熵或分布熵直接计算得到，目前没有明确的解析关系，但演化熵的规律性是研究演化熵的重要前提。系统故障演化过程由经历事件、影响因素、演化条件和事件逻辑关系组成，其中经历事件和影响因素统一由事件故障概率分布表示；演化条件由传递概率表示；逻辑关系是事件间相互作用的逻辑关系。在研究演化熵时，主要考虑事件和事件间逻辑关系，虽然传递概率影响演化熵的数值，但这里假设为1，暂不考虑。

那么演化熵主要受到前期事件故障概率分布和事件逻辑关系影响。第1、2节已说明了分布熵的构造和分布熵与演化熵的关系，这里不再赘述。系统故障演化过程由众多事件组成，虽然这些事件是基础，但演化过程自身的结构才是决定演化本身的关键因素。演化过程结构是这些事件的联系方式，即事件相互作用的方式，这些方式主要通过逻辑关系体现。最一般的逻辑关系是与或非逻辑关系，当然逻辑关系有很多种类和形式。何华灿教授^[26-27]提出了20种柔性逻辑关系，也可作为描述事件间逻辑关系的形式。当逻辑关系复杂时可通过逻辑关系叠加形式进行表示。这里使用二元算子的与或逻辑关系，以3种典型情况为例，进行“与或”演化过程的演化熵性质分析。

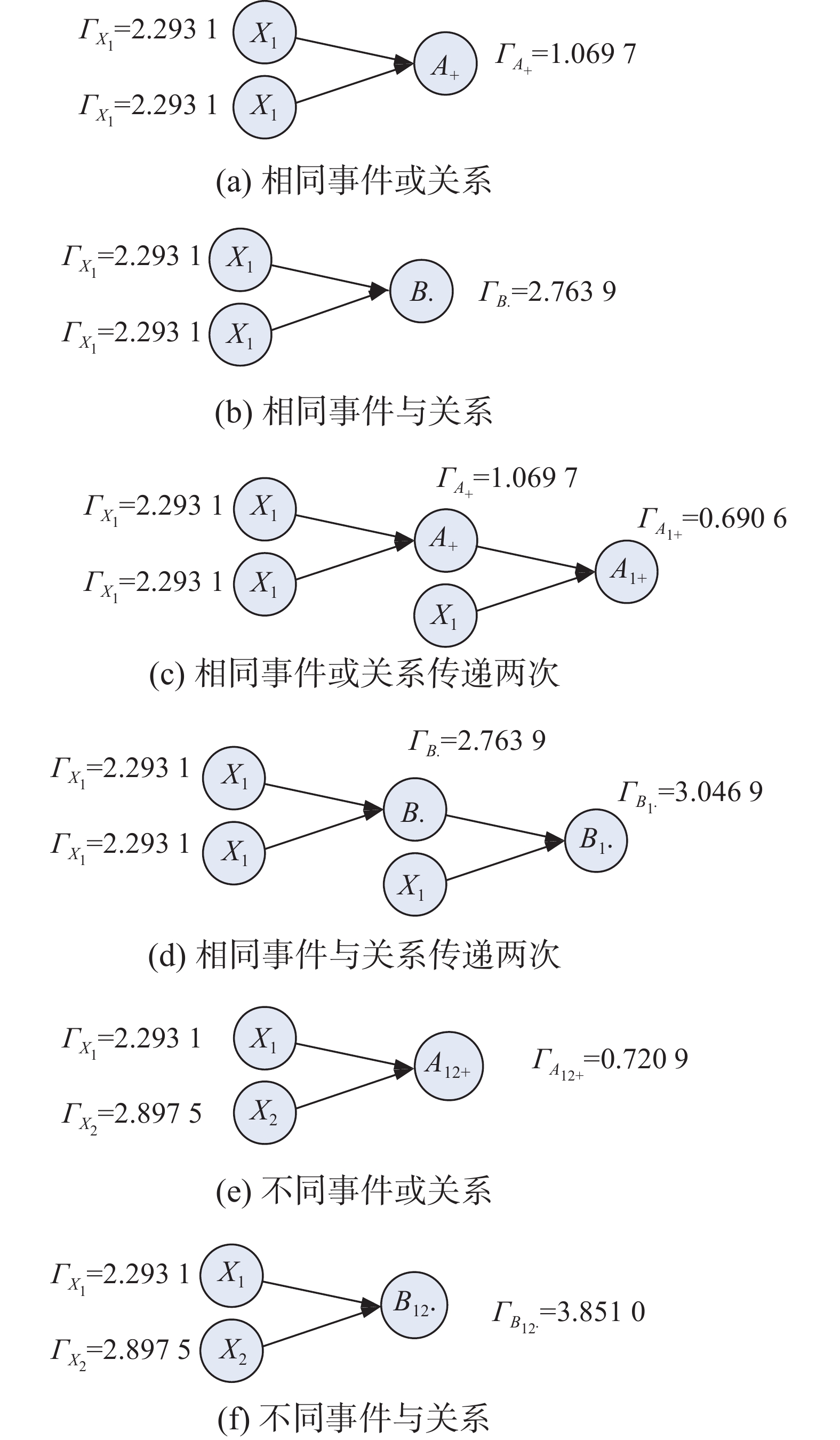
设实例系统受影响的因素集合为$F=\left\{ {f_1} = t, {f_2} = c \right\}$；因素值域划分点数量集合$D{\text{ = }}\left\{ {d_1} = 101, {d_2} = 51 \right\}$，使用时间t为100 d，间隔为1 d，使用温度c为0~50℃，间隔为1℃；故障概率分类为$ {q_1} = \left[ {0,1\% } \right),{q_2} = \left[ {1\% ,2\% } \right), \cdots ,{q_{100}} = \left[ {99\% ,100\% } \right] $；事件故障概率分布$P({x_1},{x_2})$，${x_1}、{x_2}$分别为因素$ {f_1}、 {f_2} $的具体值。图1给出该系统中的5个事件X₁~X₅受因素t和c影响的事件故障概率分布曲面^[25]。

图  1  X₁~X₅的事件故障概率分布曲面

Fig.  1  Event fault probability distribution surface of X₁~X₅

下载: 全尺寸图片

图2给出了与或演化过程的演化熵性质，包括3类演化熵：第1类为相同事件构成的与或关系的演化熵，如图2(a)和2(b)；第2类为相同事件与或关系传递两次的演化熵，如图2(c)和2(d)；第3类为不同事件构成的与或关系的演化熵，如图2(e)和2(f)。

图  2  与或演化过程的演化熵性质

Fig.  2  Evolution entropy property of AND OR evolution process

下载: 全尺寸图片

图2中$\varGamma $为事件的分布熵，如${\varGamma _{{X_1}}}$是图1(a)的事件故障概率分布确定的分布熵。具体过程是，使用图1(a)的概率分布，通过式(1)统计在M=100时各类概率数量，之后再使用式(2)计算得到该事件的分布熵。图2中事件${A}_{+}、{B}_{\cdot }、{A}_{1+}、 {B}_{1\cdot }、 {A}_{12+}、{B}_{12\cdot }$的分布熵都可成为演化熵。例如图2(c)的系统故障演化过程的演化熵就是${A_{1 + }}$的分布熵。它代表了3个边缘事件${X_1}$参与演化过程，传递了两次后展现的该时刻的演化熵${\varGamma _{{A_{1 + }}}}$。${\varGamma _{{A_{1 + }}}}$是通过${A_{1 + }}$的故障概率分布计算得到的，受${X_1}$的故障概率分布、事件间逻辑关系和传递次数等作用。如下对图2中各情况代表的含义进行说明。

相同事件构成的与或关系的演化熵，对比图2(a)与图2(b)，$ {\varGamma _{{X_1}}} = 2.293\;1 $、$ {\varGamma _{{A_ + }}} = 1.069\;7 $、$ {\varGamma _{{B_{{\cdot}}}}} = 2.763\;9 $。说明在相同两边缘事件一次传递条件下，或逻辑使演化熵明显降低，与逻辑明显使演化熵增加。或逻辑使演化熵降低为原有的46%；与逻辑使演化熵增加为原有的120%。或逻辑对演化熵的降低作用大于与逻辑对演化熵的增加作用。因此随着演化过程的延伸，或逻辑将使演化熵逐渐降低，与逻辑使演化熵逐渐增加。

相同事件与或关系传递两次的演化熵，对比图2(c)与图2(d)。当演化过程有两次传递时，对于或逻辑，$ {\varGamma _{{X_1}}} = 2.293\;1 $、$ {\varGamma _{{A_ + }}} = 1.069\;7 $、$ {\varGamma _{{A_{1 + }}}} = 0.690\;6 $，演化熵依次降低为原有演化熵的46.6%和64.5%，可预见随着传递次数的增加，或逻辑关系对演化熵的降低作用逐渐减小。对于与逻辑，$ {\varGamma _{{X_1}}} = 2.293\;1 $、${\varGamma _{{B_{{\cdot}}}}} = 2.763\;9$、$ {\varGamma _{{B_{1 \cdot }}}} = 3.046\;9 $，演化熵依次升高为原有演化熵的120.5%和110.2%，可预见随着传递次数的增加，与逻辑关系对演化熵的提高作用逐渐减小。其原因在于宏观上演化熵的有界性，即[$ {\log _2}M $,0]，因此与或逻辑关对演化熵的改变均在该范围内。

不同事件构成的与或关系的演化熵，对比图2(e)与图2(f)。两个不同边缘事件的分布熵分别为$ {\varGamma _{{X_1}}} = 2.293\;1 $和$ {\varGamma _{{X_2}}} = 2.897\;5 $，或逻辑关系作用下的分布熵，即演化熵为$ {\varGamma _{{A_{12 + }}}} = 0.720\;9 $。这说明或逻辑关系得到的演化熵小于任意参与演化事件的分布熵。与逻辑关系作用下的分布熵，即演化熵为$ {\varGamma _{{B_{{\text{12}} \cdot }}}} = 3.851\;0 $。这说明与逻辑关系得到的演化熵大于任意参与演化事件的分布熵。$ {\varGamma _{{A_{12 + }}}} $/$ {\varGamma _{{A_ + }}} $=67%，$ {\varGamma _{{B_{{\text{12}} \cdot }}}} $/$ {\varGamma _{{B_{{\cdot}}}}} $=139%，这比两边缘事件相同情况下改变演化熵的程度增加了30%~40%。因此，或逻辑关系演化熵小于任意参与演化事件的分布熵；与逻辑关系演化熵大于任意参与演化事件的分布熵。

由于演化熵目前不能使用前继事件的分布熵或演化熵通过解析方法直接得到。因此上述采取了具有特征的举例分析方式，关注的特点在于相同事件构成的与或关系的演化熵、相同事件与或关系传递两次的演化熵、不同事件构成的与或关系的演化熵3种情况。考察两事件与或逻辑关系得到的演化熵与原有分布熵的关系，可得到普遍适用的演化熵变化规律。

4.   两个演化过程的演化熵比较

在研究简单的系统演化过程的演化熵之后，继续研究两个较为复杂的演化过程。接续上节实例，该过程由5个边缘事件组成，它们的事件故障概率分布如图1所示。根据式(1)和式(2)计算得到这5个事件的分布熵，研究的两个演化过程如图3所示。

图  3  多次传递的演化过程

Fig.  3  Evolution process with multiple transfer

下载: 全尺寸图片

图3给出了多次传递的演化过程，它们的边缘事件相同，为事件X₁~X₅。图3(a)经历了两次传递达到最终事件${B_{AB \cdot }}$，${A_{12 + }}$和${B_{45 \cdot }}$是该演化过程的过程事件，它们的分布熵分别为$ {\varGamma _{{B_{AB \cdot }}}} = 4.846\;1 $、$ {\varGamma _{{A_{12 + }}}} = 0.720\;9 $、$ {\varGamma _{{B_{45 \cdot }}}} = 3.980\;7 $。图3(b)经历了3次传递达到最终事件${A_{B5 + }}$，${A_{234 + }}$和${B_{1A \cdot }}$是该演化过程的过程事件，分布熵分别为$ {\varGamma _{{A_{B5 + }}}} = 0.814\;8 $、${\varGamma _{{A_{234 + }}}} = 0.644\;4$、$ {\varGamma _{{B_{1A \cdot }}}} = 2.315\;5 $。

在图3(a)中，系统的演化熵即为${\varGamma _{{B_{AB \cdot }}}} = 4.846\;1$，演化过程由边缘事件X₁~X₅及过程事件${A_{12 + }}$和${B_{45 \cdot }}$共同组成。这时事件${B_{AB \cdot }}$的分布熵就是该时刻系统演化的演化熵。同理在图3(b)中，系统的演化熵即为$ {\varGamma _{{A_{B5 + }}}} = 0.814\;8 $，演化过程由边缘事件X₁~X₅及过程事件${A_{234 + }}$和${B_{1A \cdot }}$共同组成。这时事件${A_{B5 + }}$的分布熵就是该时刻系统演化的演化熵。对于${B_{1A \cdot }}$，系统的演化熵即为$ {\varGamma _{{B_{1A \cdot }}}} = 2.315\;5 $，演化过程由边缘事件X₁~X₄及过程事件${A_{234 + }}$组成。对于${A_{234 + }}$，系统的演化熵即为$ {\varGamma _{{A_{234 + }}}} = 0.644\;4 $，演化过程由边缘事件X₂~X₄组成。将系统故障演化过程中${A_{234 + }}$、${B_{1A \cdot }}$和${A_{B5 + }}$作为演化的3个节点时刻，这3个节点时刻的演化熵就是这些事件的分布熵。由此也可得由${A_{234 + }}$演化到${A_{B5 + }}$的过程中，系统的演化熵增加了$ {\varGamma _{{A_{B5 + }}}} $−$ {\varGamma _{{A_{234 + }}}} $=0.170 4。而且虽然$ {\varGamma _{{A_{B5 + }}}} $和$ {\varGamma _{{A_{234 + }}}} $是熵的相对值，但得到的0.170 4是该过程中演化熵变化的绝对值。这对演化过程中系统功能状态混乱性的变化度量有重要意义。

将熵概念引入系统故障演化过程的研究尚处于起始阶段，存在许多重要问题需要探讨。系统故障演化过程由4部分组成，包括经历事件、影响因素、逻辑关系和演化条件。影响因素对经历事件的影响通过事件故障概率分布描述，引入熵形成了事件故障概率分布熵，在另文中已进行了说明。分布熵是研究演化熵的基础之一。对于逻辑关系，文中研究了最基本的与或逻辑关系对演化熵的影响。但更为复杂的柔性逻辑关系对演化熵的影响有待研究。演化条件在系统故障演化过程中的定义是原因事件引起结果事件的概率，文中没有具体研究，仅设为1，消除其对演化熵的影响，以待后续研究。

因此系统故障演化过程熵至少要从两方面考虑，一是影响因素与经历事件合成的分布熵，二是逻辑关系和演化条件构成的演化熵。前者表示演化的单元，后者表示演化的结构。还有一个值得关注的问题，作为表示系统功能状态混乱程度的演化熵一定随着演化递增吗？文中给出的研究结果显示不一定。如果演化过程中以与逻辑关系主导则演化熵是增加的，以或逻辑关系主导时演化熵减小。这与熵增原理可能不矛盾。与逻辑关系表示事件直接参与演化，共同影响后继事件，与逻辑关系的两个参与事件存在相互通讯，两事件必须合作完成缺一不可，这增加了混乱性使演化熵增加。而或逻辑关系完全不同，因为其中每个参与事件都可引起后继事件发生，因此这些参与事件相互是不通讯的，不知道其他事件的存在，也可理解为两事件完全独立的造成了结果，这的确使演化熵减小了。关于这些问题作者将在后继研究中探讨。

5.   结束语

论文在事件故障概率分布熵的基础上提出了系统故障演化过程熵，用于衡量系统故障演化过程中系统功能状态的混乱性，并研究了演化熵的变化特征。主要结论如下：

1）讨论了使用熵概念描述系统故障演化过程中系统功能状态混乱程度的可行性。研究认为描述系统故障演化过程至少考虑两方面，一是事件和影响因素，二是逻辑关系和演化条件。前者通过事件故障概率分布熵描述，后者通过系统故障演化过程熵描述。某时刻系统故障演化过程的系统功能状态由事件分布熵描述，对演化过程而言该时刻的演化熵就是该分布熵。得到的演化熵性质包括：演化熵表征了系统故障演化过程的某时刻的系统功能状态；演化熵只能通过某时刻的事件故障概率分布得到；演化熵具有确定的值域范围。

2）系统故障演化过程熵受演化过程中事件逻辑关系的直接影响。以最基本的与或逻辑关系为例研究了事件逻辑关系对演化熵的影响。结果表明：或逻辑使演化熵降低，与逻辑使演化熵增加；随传递次数的增加，与逻辑对演化熵的提高作用及或逻辑对演化熵的降低作用均减小；或逻辑的演化熵小于任意参与事件的分布熵；与逻辑的演化熵大于任意参与事件的分布熵。

3）通过两个系统故障演化过程实例给出了演化熵的确定过程。通过演化熵可以确定系统故障演化过程从一个时刻发展到另一时刻的熵的绝对变化量，也表征了该期间系统功能状态混乱程度的绝对变化量。这对演化过程中系统功能状态的变化度量有重要意义。