Finite-time dynamic prescribed performance control for surface unmanned vehicles with unknow disturbances
-
摘要: 本文提出了一种具有动态预设性能的有限时间控制方案，用于解决具有不确定动态和未知时变海洋环境扰动的无人水面艇(unmanned surface vehicles, USVs)的轨迹跟踪问题。传统预设性能采用静态预设性能函数，当外部扰动较大时，跟踪误差有超出预设性能边界的风险。本文设计一种新型的动态预设性能函数，使得USVs跟踪误差始终保持在预设的边界内；基于齐次积分滑模面、有限时间扩张状态观测器和超螺旋积分滑模控制，提出了一种有限时间控制算法。该算法可以实现跟踪误差快速收敛和有界扰动连续补偿，提高了系统鲁棒性并削弱了滑模抖振现象。理论分析证明了USVs闭环系统的全局有限时间稳定性，仿真及比较结果验证了所设计控制方案的有效性和优越性。Abstract: In this paper, a finite-time control scheme with dynamic prescribed performance is proposed to solve the trajectory tracking problem of unmanned surface vehicles (USVs) with uncertain dynamics and unknown time-varying ocean environment disturbances. The conventional prescribed performance adopts a static prescribed performance function, and there is a risk that the tracking error will exceed the prescribed performance boundaries set when external disturbance is large. A new dynamic prescribed performance function is proposed to keep the USVs tracking error within a prescribed range. The proposed finite-time control scheme is based on a combination of homogeneous integral sliding mode surface, finite-time extended state observer and super-twisting integral sliding mode control. The algorithm can achieve fast convergence of tracking errors and continuous compensation of bounded disturbances, improving robustness and reducing sliding mode chatter. The theoretical analysis demonstrates the global finite-time stability of the USVs closed-loop system, and the simulation and comparison results verify effectiveness and superiority of the designed control scheme.
-
由于侦察监视、海上救援、海洋测绘、海洋资源开发等多种任务需求的增加和对任务精度要求的提高，具有高度自主性的无人艇在军事和民用领域发挥着越来越重要的作用[1-2]。在这种背景下，无人水面艇( unmanned surface vehicles, USVs)的运动控制在海洋工程领域起到了至关重要的作用[3]，轨迹跟踪作为USVs运动控制重要的组成部分之一，它不同于路径跟踪任务，轨迹跟踪通过无人艇动力系统跟踪随时间变化的轨迹，对时间有着严格的要求，各种海洋任务的成功与否往往由轨迹跟踪控制系统所决定。然而，众所周知，USVs在航行中会受到风、浪和水流等复杂未知海洋扰动环境影响，并且模型具有强耦合性和非线性特征。这为USVs轨迹跟踪的控制器设计带来巨大挑战。另一方面，使用场景和任务目标也意味着对控制器的性能有更高的要求。
目前，已经有各种控制算法应用于轨迹跟踪控制器的设计，比如反步控制[4-5]、滑模控制[6-7]、鲁棒自适应控制[8-9]和模型预测控制[10-11]。然而，在实践中，为了确保USVs航行的安全，位置误差应保持在预设的有界范围内。因此，将规定的瞬态和稳态控制性能考虑到控制器设计中越来越重要[12]。预设性能函数旨在将预设性能转换为等效的误差范围。文献[13]将预设性能控制(prescribed performance control, PPC)技术集成到反步控制器中，但预设性能函数的设计相当复杂，其中设计了对数型误差变换函数以使控制系统满足预设性能。文献[14]构建了一个非对数分段误差变换函数，为一类严格反馈非线性系统设计具有预设性能的控制律。但是，上述文献使用的对数误差变换函数会导致控制律奇异。障碍Lyapunov函数(barrier Lyapunov function, BLF)具有在其参数接近约束边界时达到无穷大的属性。因此，将BLF与反步技术相结合可以实现预设性能[15]。但是BLF的分段连续性、Lyapunov的连续性和可导性需要得到保证，从而不可避免地增加了控制算法的复杂度，因此设计合适的对数误差变换函数是个值得关注的问题。上述具有预设性能的控制方案只能实现渐进稳定性，近年来，有限时间控制和预设性能控制也受到广泛关注[16]。文献[17]通过结合PPC技术和自适应模糊反步控制方法，引入一个特殊的有限时间预设性能函数,使得动力定位船轨迹跟踪控制问题得到解决。文献[18]针对具有不确定动态和未知干扰的欠驱动水下机器人(autonomous underwater vehicle, AUV)三维轨迹跟踪问题，提出了一种具有预设性能的鲁棒自适应神经网络控制方案。使用的预设性能函数可以设置到达稳态误差边界的时间。此外，大部分文献只能实现实际有限时间收敛[17,19-20]，即系统状态在有限时间内收敛到一个紧集内。目前，上述应用于USVs的PPC技术仍存在问题：1) 跟踪误差存在较大的超调；2) 由于传统PPC技术采用的是静态预设性能函数，当外部扰动较大时，跟踪误差很可能超出预设性能边界，导致传统PPC技术失效[21]。文献[21]针对具有不匹配时变扰动的降压型变换器的电压跟踪控制问题，提出一种动态预设性能函数，保证了跟踪误差始终在预设性能边界内。
基于上述讨论和启发，本文针对具有不确定性动态和未知时变海洋环境扰动的USVs轨迹跟踪问题，设计了一种新的动态预设性能函数，使得USVs跟踪误差始终保持在预设边界内，同时设计新型有限时间扩张观测器来精准估计系统总扰动，并且设计一种超螺旋积分滑模控制律，在消除滑模抖振的同时，提高了系统的鲁棒性。最后提出有限时间控制算法，使得跟踪误差全局收敛到零。
本文的贡献总结如下：
1)基于齐次积分滑模面、有限时间扩张观测器和超螺旋积分滑模控制，解决了具有预设性能的USVs的轨迹跟踪问题，通过与文献[22-23]进行仿真比较，验证了本文所设计的控制算法具有更好的鲁棒性。
2)传统预设性能采用静态预设性能函数，当外部扰动较大时，跟踪误差有超出预设性能边界的风险。本文设计一种新型的动态预设性能函数，使得USVs跟踪误差始终保持在规定的范围内。
1. 问题描述和预备知识
1.1 无人水面艇模型
针对USVs，其数学模型通常需考虑横荡、纵荡和艏摇3个方向的低频运动[3]。为此，建立USVs三自由度非线性数学模型为
$$ \left\{ {\begin{array}{*{20}{l}} {{\dot {\boldsymbol{\eta}} = {\boldsymbol{J}}({\boldsymbol{\eta}} ){\boldsymbol{v}}}} \\ {{{\boldsymbol{M}}\dot {\boldsymbol{v}} = - {\boldsymbol{C}}({\boldsymbol{v}}){\boldsymbol{v}} - {\boldsymbol{D(v)v }}+ {\boldsymbol{\tau}} + {\boldsymbol{d}}}} \end{array}} \right. $$ (1) 式中：向量
${{\boldsymbol{\eta}} }{\text{ = }}{[x\quad y\quad\psi ]^{\rm{T}}} \in {\bf{R}^{\text{3}}}$ 为USVs在大地坐标系下的位置信息$(x,y)$ 和艏摇角$\psi $ ；向量${{\boldsymbol{\nu}} }{\text{ = }}{[u\quad v\quad r]^{\rm{T}}} \in {\bf{R}^{\text{3}}}$ 为USVs在船体坐标系下的速度信息，其中$u、v、r$ 分别表示纵荡速度、横荡速度和艏向角速度；${{\boldsymbol{M}}} \in {{\bf{R}}^{{\text{3}} \times {\text{3}}}}$ 为包含附加矩阵的正定对称惯性矩阵，本文考虑${{\boldsymbol{M}}}$ 已知；${{\boldsymbol{C}}}({\boldsymbol{\nu }})$ 和${{\boldsymbol{D}}}({\boldsymbol{\nu }})$ 分别为由水动力参数组成的科里奥利向心力矩阵和阻尼系数矩阵；${{\boldsymbol{J}}}({{\boldsymbol{\eta}} })$ 为转换矩阵，且具有性质${{{\boldsymbol{J}}}^{\rm{T}}}({{\boldsymbol{\eta}} }) = {{{\boldsymbol{J}}}^{ - 1}}({{\boldsymbol{\eta}} })$ ；${{\boldsymbol{d}}} = {[{d_1}\quad{d_2}\quad{d_3}]^{\rm{T}}} \in {{\bf{R}}^{\text{3}}}$ 表示扰动矢量；${{\boldsymbol{\tau}} } = [{{\boldsymbol{\tau }}_u}\quad{{\boldsymbol{\tau}} _v}\quad {{\boldsymbol{\tau }}_r}]^{\rm{T}} \in {{\bf{R}}^{\text{3}}}$ 为USVs执行器提供的动力矢量。假设1 不确定参数
${{\boldsymbol{C}}}({\boldsymbol{\nu }})$ 和${{\boldsymbol{D}}}({\boldsymbol{\nu }})$ 有界，未知海洋扰动${d_i},i = 1,2,3$ 有界，且存在未知正数$ \varpi $ 使得$ \left| {\dot d} \right| \leqslant \varpi $ 。注1 USVs的水动力系数
${{\boldsymbol{C}}}({\boldsymbol{\nu }})$ 和${{\boldsymbol{D}}}({\boldsymbol{\nu }})$ 是速度的函数，且USVs的航行速度有界，水动力系数有界。由于海洋环境是不断变化的，并且具有有限的能量，因此作用在船舶上的扰动可以看作是具有有限变化率的未知时变但有界的信号，很多文献都做出了同样的假设[23-29]，因此假设是合理的。1.2 动态预设性能函数设计
为了方便后续预设性能函数、误差变换函数和终端滑模面的设计，定义USVs轨迹跟踪控制系统的跟踪误差为
$$ {{\boldsymbol{e}}} = {{\boldsymbol{\eta}} } - {{{\boldsymbol{\eta}} }_{d}} = {[{e_1}\quad{e_2}\quad{e_3}]^{\rm{T}}} $$ (2) USVs轨迹跟踪控制的预设性能体现在跟踪误差满足下列不等式：
$$ - {\rho _{j_{ \min }}}{\zeta _j}(t) < {e_j}(t) < {\rho _{j_{\max} }}{\zeta _j}(t),j = 1,2,3,\forall t > 0 $$ (3) 式中：
${\rho _{j_{\min} }}$ 和${\rho _{j_{\max} }}$ 为设计参数；$ \zeta (t) $ 为预设性能函数，传统预设性能函数表示为[18]$$ {\zeta _j}(t) = ({\zeta _{j0}} - {\zeta _{j\infty }}){{\rm{e}}^{ - {\mu _j}t}} + {\zeta _{j\infty }},j = 1,2,3 $$ (4) 式中：
$ {\mu _j} > 0 $ 为性能函数的收敛速率；$ {\zeta _j}(t) $ 为单调递减的光滑函数，并且有性质$\mathop{\lim\limits_{t \to 0}}{\zeta _j}(t) = {\zeta _{j0}} > 0$ ，$\mathop{\lim\limits_{t \to \infty }}{\zeta _j}(t) = {\zeta _{j\infty }} > 0$ ；$ {\zeta _{j0}} $ 为${{\boldsymbol{e}}}$ 动态过程中最大超调的上界；$ {\zeta _{j\infty }} $ 为跟踪误差的最大稳态误差边界，为了便于控制器设计，将约束条件式(3)转换为无约束情况，引入以下光滑且严格递增的误差变换函数：$$ {{\boldsymbol{\chi}} } = {F^{ - 1}}\left(\frac{{{e_j}}}{{{{\zeta }_j}(t)}}\right) = \frac{1}{2}\ln \frac{{{\theta _j}(t) + {\rho _j}_{{\rm{min}}}}}{{{\rho _j}_{{\rm{min}}} - {\theta _j}(t)}} $$ (5) 式中
$ {\theta _j}(t) = \dfrac{{{e_j}}}{{{{\zeta }_j}(t)}} $ ，可计算$ {{\boldsymbol{\chi }}} $ 的导数为$$ \left\{ \begin{gathered} {{\dot \chi }_j} = {\varepsilon _j}\left( {{{\dot e}_j} - \frac{{{e_j}{{\dot \zeta }_j}}}{{{\zeta _j}}}} \right) \\ {{\ddot \chi }_j} = {{\dot \varepsilon }_j}\left( {{{\dot e}_j} - \frac{{{e_j}{{\dot \zeta }_j}}}{{{\zeta _j}}}} \right) + {\delta _j}\left({{\ddot e}_j} - \frac{{{\dot {\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }} + \frac{{{{\boldsymbol{e}}\ddot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }} - \frac{{{{\boldsymbol{e}}}{{{\dot {\boldsymbol{\zeta}} }}^2}}}{{{{{\boldsymbol{\zeta}} }^2}}}\right) \\ \end{gathered} \right. $$ (6) 其中
${\varepsilon _j} = \dfrac{1}{{{\zeta _j}(t)}}\left( {\dfrac{1}{{{\theta _j} + {\rho _{j_{\min} }}}} - \dfrac{1}{{{\theta _j} - {\rho _{j_{\max }}}}}} \right)$ 。然而在实际系统中，不确定动态和环境干扰是不可避免的。因此，如果采用传统的静态预设性能函数，当系统受到较大干扰时，系统的跟踪误差可能超过预定的误差边界从而导致预设性能失效。为了避免这一问题，本文提出一种动态预设性能函数为
$$ {\zeta _j}(t) = ({\zeta _{ij0}} - {\zeta _{j\infty }}){{\rm{e}}^{ - {\mu _j}(t - {t_i})}} + {\zeta _{j\infty }},j = 1,2,3 $$ (7) 式中：
$t \in [{t_i},{t_{i + 1}})；i = 0,1,\cdots, n$ ，$ i $ 为跟踪误差超出预设边界的第$ i $ 事件；$ {t_i} $ 为事件发生时的时间。并且如果$ {t_0} = 0 $ ，当$ {e_j}({t_0}) > 0 $ 时${\rho _{j_{\max} }}{\zeta _{0j0}} > {e_j}({t_0})$ ，当$ {e_j}({t_0}) < 0 $ 时，$- {\rho _{j_{\min} }}{\zeta _{0j0}} < {e_j}({t_0})$ 。式(7)为一个动态预设性能函数，即当跟踪误差即将超出预设边界时，$ {\zeta _{ij0}} $ 将被重置从而扩大预设边界。引理1[3] 有限时间定理。考虑如下非线性系统系统：
$$ \dot x = f(x),f(0) = 0,x \in U \subset {{{{\rm{R}}}}^n} $$ (8) 式中：
$f(x):U \to {{{{{\rm{R}}}}}^n}$ 是以$ x = 0 $ 为中心的开邻域$ U $ 上$ n $ 维连续的，若存在连续可微的正定函数$V(x):\varOmega\to {{{{{\rm{R}}}}}^ + }$ ，正实数$ c $ 、$ \alpha \in (0,1) $ 和开邻域$\varOmega \in U$ ，使得：$$ \dot V(x) + c{(V(x))^\alpha } \leqslant 0,x \in \varOmega \backslash \{ 0\} $$ (9) 则系统式(8)在平衡点
$ x{\text{ }} = 0 $ 是有限时间稳定的。当$\varOmega = U = {{{{{\rm{R}}}}}^n}$ 成立，在平衡点$ x{\text{ }} = 0 $ 是全局有限时间稳定的，并且有限调节时间。引理2[20] 对于
$ {n_1},{n_2},\cdots,{n_m} \geqslant 0 $ , 如果$ l \in (0,1] $ ，则有${\left( {\displaystyle\sum\limits_{i = 1}^m {{n_i}} } \right)^l} \leqslant \displaystyle\sum\limits_{i = 1}^m {n_i^l}$ 。引理3[22] 考虑如下非线性系统：
$$ \begin{split}& {{\dot \zeta }_1} = {\zeta _2} - {\beta _1}{{{\rm{sig}}} ^{(n + 1)/2}}\left( {{\zeta _1}} \right) \\& {{\dot \zeta }_2} = {\zeta _3} - {\beta _2}{{{\rm{sig}}} ^{(n + 1)/2}}\left( {{\zeta _1}} \right) \\&\;\;\; {{\dot \zeta }_3} = - h - {\beta _3}{{{\rm{sig}}} ^n}\left( {{\zeta _1}} \right) \end{split}$$ (10) 式中：
$ {{{\rm{sig}}} ^\alpha }(x): = |x{|^\alpha }{{\rm{sign}}} (x) $ ；$ h $ 是连续可微并且有界的函数；$0 < n < 1$ ；${\beta _1} $ 、${\beta _2} $ 和$ {\beta _3} $ 是适当的可选参数，则系统全局有限时间稳定的。2. 方案设计与分析
2.1 有限时间扩张状态观测器设计
有限时间扩张状态观测器被设计用于估计和USVs动力学有关的集总未知扰动，以实现精准跟踪。为了方便后续有限时间扩张状态观测器和有限时间控制器的设计，令：
$$ {{{\boldsymbol{x}}}_1} = {{\boldsymbol{\eta}} },{{{\boldsymbol{x}}}_2} = {{\boldsymbol{J\nu}} },{{\boldsymbol{J}}} = {{\boldsymbol{J}}}({{\boldsymbol{\psi}} }) $$ (11) 则系统(1)可以改写为
$$ \left\{ {\begin{array}{*{20}{l}} {{{{\dot {\boldsymbol{x}}}}_1} = {{{\boldsymbol{x}}}_2}} \\ {{{{\dot {\boldsymbol{x}}}}_2} = {{\boldsymbol{f}}}({{{\boldsymbol{x}}}_1},{{{\boldsymbol{x}}}_2}) + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{\tau}} }} \end{array}} \right. $$ (12) 式中：
${{\boldsymbol{f}}}({{{\boldsymbol{x}}}_1},{{{\boldsymbol{x}}}_2}) = ({\boldsymbol{S}}(r) - {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}({{\boldsymbol{C}}}({{{\boldsymbol{J}}}^{\rm{T}}}{{{\boldsymbol{x}}}_2}) + {{\boldsymbol{D}}}({{{\boldsymbol{J}}}^{\rm{T}}}{{{\boldsymbol{x}}}_2}){{{\boldsymbol{J}}}^{\rm{T}}}){{{\boldsymbol{x}}}_2} + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{d}}}$ ${{\boldsymbol{f}}}({{{\boldsymbol{x}}}_1},{{{\boldsymbol{x}}}_2})$ 中包含不确定项$ {{\boldsymbol{C}}} $ 和$ {{\boldsymbol{D}}} $ 、速度项和未知扰动$ {{\boldsymbol{d}}} $ ，根据假设1，可得不确定项的一阶导数有界。因此根据假设1，存在正数$ \xi $ 使得$\left\| {{\dot {\boldsymbol{f}}}} \right\| \leqslant \xi$ 是合理的。然后定义$ {{{\boldsymbol{x}}}_3}{ = {\boldsymbol{f}}} $ 为扩张状态，系统改写为$$ \left\{ {\begin{array}{*{20}{l}} {{{{\dot {\boldsymbol{x}}}}_1} = {{{\boldsymbol{x}}}_2}} \\ \begin{gathered} {{{\dot {\boldsymbol{x}}}}_2} = {{{\boldsymbol{x}}}_3} + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{\tau}} } \\ {{{\dot {\boldsymbol{x}}}}_3} = {\dot {\boldsymbol{f}}} \\ \end{gathered} \end{array}} \right. $$ (13) 文献[22]中设计的有限时间扩张状态观测器可以有效地估计系统的总扰动。但当观测器初始值与系统状态初始值存在较大误差时,会出现微分峰值现象。为了消除观测器微分峰值，引入双曲正切函数
$ \tanh ( \cdot ) $ 抑制观测器初始时刻附近的微分峰值。定理1 对于增广系统式(13)，有限时间扩张状态观测器(extended state observer, ESO)可以设计为
$$ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\hat {\boldsymbol{z}}}}}_1} = {{{\hat {\boldsymbol{z}}}}_2} - {\beta _1}{{{\rm{sig}}} ^{3/4}}\left( {{{{\hat {\boldsymbol{z}}}}_1} - {{{\boldsymbol{x}}}_1}} \right) \\ {{{\dot {\hat {\boldsymbol{z}}}}}_2} = {{{\hat {\boldsymbol{z}}}}_3} - {\beta _2}{{{\rm{sig}}} ^{3/4}}\left( {{{{\hat {\boldsymbol{z}}}}_1} - {{{\boldsymbol{x}}}_1}} \right) + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{\tau}} } \\ {{{\dot {\hat {\boldsymbol{z}}}}}_3} = - {\beta _3}\tanh \left( {{{{\hat {\boldsymbol{z}}}}_1} - {{{\boldsymbol{x}}}_1}} \right) \end{array}} \right. $$ (14) 式中：
$ {\beta _i}{ = }{a_i}\tanh \left( {{b_i}t} \right),i = 1,2,3 $ 是观测器的设计参数，$ {a_i} > 0 $ ，$ {b_i} > 0 $ ，$ i = 1,2,3 $ ；观测器误差${{\tilde {\boldsymbol{z}}}_i} = [{\tilde z_{i1}}\quad{\tilde z_{i2}},\quad{\tilde z_{i3}}]^{\rm{T}}$ 被定义为$ {{\tilde {\boldsymbol{z}}}_i} = {{\hat {\boldsymbol{z}}}_i} - {{{\boldsymbol{x}}}_i},i = 1,2,3 $ ；集总干扰$ {{\boldsymbol{f}}} $ 可以由$ {{\hat {\boldsymbol{z}}}_3} $ 精确估计，并且观测器误差$ {{\tilde {\boldsymbol{z}}}_i} $ 是有限时间稳定的。证明 根据系统式(13)、(14)，可以得到观测器误差动态方程为
$$ \left\{ {\begin{array}{*{20}{l}} {{{\dot {\tilde {\boldsymbol{z}}}}}_1} = {{{\tilde {\boldsymbol{z}}}}_2} - {\beta _1}{{{\rm{sig}}} ^{3/4}}\left( {{{{\tilde {\boldsymbol{z}}}}_1}} \right) \\ {{{\dot {\tilde {\boldsymbol{z}}}}}_2} = {{{\tilde {\boldsymbol{z}}}}_3} - {\beta _2}{{{\rm{sig}}} ^{3/4}}\left( {{{{\tilde {\boldsymbol{z}}}}_1}} \right) + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{\tau}} } \\ {{{\dot {\tilde {\boldsymbol{z}}}}}_3} = - {\beta _3}\tanh \left( {{{{\tilde {\boldsymbol{z}}}}_1}} \right) - {\boldsymbol{f}} \end{array}} \right. $$ (15) 根据引理3，观测器误差
$ {{\tilde {\boldsymbol{z}}}_i} $ 是全局有限时间稳定的，且集总干扰$ {{\boldsymbol{f}}} $ 可以由$ {{\hat {\boldsymbol{z}}}_3} $ 精确估计，证明成立。2.2 有限时间控制算法设计和稳定性分析
本节基于齐次积分滑模面和有限时间扩张状态观测器，结合超螺旋积分算法设计USVs预设性能控制算法。首先，对于非奇异滑模面的设计，已有学者提出了多种设计方法为
1) 非奇异终端滑模(non-singular terminal sliding mode, NTSM) ：
$$ s = e + k{\rm{si}}{{\rm{g}}^\gamma }(\dot e) $$ (16) 式中：
$ k > 0$ ，$1 < \gamma < 2 $ 。2) 非奇异快速异终端滑模(non-singular fast terminal sliding mode, NFTSM)：
$$ s = e + {k_1}{{\rm{sig}}^{{\gamma _1}}}(e) + {k_2}{{\rm{sig}}^{{\gamma _2}}}(\dot e) $$ (17) 式中：
$ {k_1},{k_2} > 0 $ ，${\gamma _1} > {\gamma _2},{\gamma _2} \in (1,2) $ 。尽管上述非奇异滑模面都可以保证跟踪误差在有限的时间收敛到零，但实际应用中存在2个问题: 1)在实际系统中，由于时间延迟和系统惯性，理想的滑模是不存在的。滑模面上的微小扰动将触发不连续控制信号。2)当状态接近切换面时，切换项始终起着恒定的控制作用，即使在切换面
$ s = 0 $ 附近时，也不满足一个好的控制器的性能要求。考虑到以上2个事实，采用积分技术设计具有优异性能的滑模面。受文献[20]启发， 设计如下齐次积分滑模面：
$$ {{\boldsymbol{S}}} = {\dot {\boldsymbol{\chi}} } + \int_0^t {({\lambda _1}} {{\rm{sig}}^{{\alpha _1}}}({{\boldsymbol{\chi}} }) + {\lambda _2}{{\rm{sig}}^{{\alpha _2}}}({\dot {\boldsymbol{\chi}} })){\rm{d}}u $$ (18) 式中：
$ {\lambda _1} > 0 $ ，${\lambda _2} > 0$ ，$0 \leqslant {\alpha _1} \leqslant 1,{\alpha _2} = 2{\alpha _1}/({\alpha _1} + 1) $ ；定义${{\boldsymbol{\chi }}} = {[{\chi _1}\quad{\chi _2}\quad{\chi _3}]^{\rm{T}}}$ ，${{\boldsymbol{\varepsilon }}} = {[{\varepsilon _1}\quad{\varepsilon _2}\quad{\varepsilon _3}]^{\rm{T}}}$ ，${{\boldsymbol{\zeta}} } = {[{\zeta _1}\quad{\zeta _2}\quad{\zeta _3}]^{\rm{T}}}$ 。然后根据式(6)、(12)和(18), 可得$ {{\boldsymbol{S}}} $ 对时间的导数为$$ \begin{split} &\qquad {\dot {\boldsymbol{S}}} = {\ddot {\boldsymbol{\chi}} + }{\lambda _1}{{\rm{sig}}^{{\alpha _1}}}({{\boldsymbol{\chi}} }) + {\lambda _2}{{\rm{sig}}^{{\alpha _2}}}({\dot {\boldsymbol{\chi}} }) = \\& {\dot {\boldsymbol{\varepsilon}} }({\dot {\boldsymbol{e}}} - \frac{{{{\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }}) + {{\boldsymbol{\varepsilon}} }\left({{\boldsymbol{f}}} + {{\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{\tau}} } - \frac{{{\dot {\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }} + \frac{{{{\boldsymbol{e}}\ddot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }} - \frac{{{{\boldsymbol{e}}}{{{\dot {\boldsymbol{\zeta}} }}^2}}}{{{{{\boldsymbol{\zeta}} }^2}}}\right) + \\&\qquad {\lambda _1}{{\rm{sig}}^{{\alpha _1}}}({{\boldsymbol{\chi}} }) + {\lambda _2}{{\rm{sig}}^{{\alpha _2}}}\left({{\boldsymbol{\varepsilon}} }\left({\dot {\boldsymbol{e}}} - \frac{{{{\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }}\right)\right) \end{split} $$ (19) 令
$ {{\boldsymbol{\tau}} } = {{{\boldsymbol{\tau}} }_1} + {{{\boldsymbol{\tau}} }_2} $ ，其中，$ {{{\boldsymbol{\tau}} }_1} $ 和$ {{{\boldsymbol{\tau}} }_2} $ 将在后面进行设计。定义$ {\bar {\boldsymbol{\tau }} = {\boldsymbol{\varepsilon}} {\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}{{{\boldsymbol{\tau }}}_2} $ ，然后建立如下辅助系统：$$\left\{ \begin{array}{c} \sigma = {\boldsymbol{S}} - {\boldsymbol{Z}}\\ \dot {\boldsymbol{Z}} = \bar {\boldsymbol{\tau }} \end{array} \right. $$ 设计
${{{\boldsymbol{\tau }}}_1}$ 为$$\begin{split} & {{{\boldsymbol{\tau}} }_1}= {\left({{\boldsymbol{\varepsilon}} {\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}}\right)^{ - 1}}\left[ - {\dot {\boldsymbol{\varepsilon}} }\left({\dot {\boldsymbol{e}}} - \frac{{{{\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }}\right) - {{\boldsymbol{\varepsilon}} }\left( - \frac{{{\dot {\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta }}}} + \frac{{{e\ddot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }} - \frac{{{e}{{{\dot {\boldsymbol{\zeta}} }}^2}}}{{{{{\boldsymbol{\zeta}} }^2}}}\right) - \right. \\&\qquad {\lambda _1}{{\rm{sig}}^{{\alpha _1}}}\left({{\boldsymbol{\chi}} }\right) - {\lambda _2}{{\rm{sig}}^{{\alpha _2}}}\left({{\boldsymbol{\varepsilon}} }\left({\dot {\boldsymbol{e}}} - \frac{{{{\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta}} }}\right)\right) - {{\boldsymbol{\varepsilon}} }{{{\hat {\boldsymbol{z}}}}_3} - {{{\boldsymbol{k}}}_1}{{\boldsymbol{\sigma}} } - \\&\qquad\qquad\left. {{{\boldsymbol{k}}}_2}{{\rm{sig}}^{1/2}}\left({{\boldsymbol{\sigma}} }\right) - {{{\boldsymbol{k}}}_3}\int_0^t {{\rm{sign}}\left({{\boldsymbol{\sigma}} }\right){\rm{d}}u} \right] \\[-12pt] \end{split} $$ (20) 式中：
$ {{{\boldsymbol{k}}}_1} > 0,{{{\boldsymbol{k}}}_2} > 0,{{{\boldsymbol{k}}}_3} > 0 $ ，结合式(19)、(20)，进一步得：$$ { [\dot{\boldsymbol \sigma}] } = - {{\boldsymbol k}_1}{\boldsymbol \sigma } - {{\boldsymbol k}_2}{{\rm{sig}}^{1/2}}({\boldsymbol \sigma }) - {{\boldsymbol k}_3}\int_0^t {{\rm{sign}}({\boldsymbol \sigma })} {\rm{d}}u - {{\boldsymbol{\varepsilon}} }{{\tilde {\boldsymbol{z}}}_3} $$ (21) 定义
${\bar {\boldsymbol{v}}} = {\left[ {{{{\boldsymbol{\upsilon}}}_2}\quad{{{\boldsymbol{v}}}_3}} \right]^i} = {\left[ {{{\rm{sig}}^{1/2}}({{{\boldsymbol{h}}}_1})\quad{{{\boldsymbol{h}}}_2}} \right]^i}$ ，$ {{{\boldsymbol{h}}}_1} = {\sigma } $ 和${{{\boldsymbol{h}}}_2} = - {{{\boldsymbol{k}}}_1}{{\boldsymbol{\sigma }}} - {{{\boldsymbol{k}}}_3}\int_0^t {{\rm{sign}}({{\boldsymbol{\sigma}} })} {\rm{d}}u - {{\boldsymbol{\varepsilon}} }{{\tilde {\boldsymbol{z}}}_3}$ ，则有：$$ \left\{ {\begin{array}{*{20}{l}} {{{{\dot {\boldsymbol{h}}}}_1} = - {{ {\boldsymbol{k}}}_2}{{\rm{sig}}^{1/2}}({{{\boldsymbol{h}}}_1}) + {{{\boldsymbol{h}}}_2}} \\ {{{{\dot {\boldsymbol{h}}}}_2} = - {{ {\boldsymbol{k}}}_1} - {{ {\boldsymbol{k}}}_3}{\rm{sign}}({{{\boldsymbol{h}}}_1}) - {\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - {\varepsilon }{{{\dot{ \tilde {\boldsymbol{z}}}}}_3}} \end{array}} \right. $$ (22) 对
$ {{{\boldsymbol{k}}}_1} $ 做变换${{{\boldsymbol{k}}}_1} = {{{\boldsymbol{k}}}_1}{\rm{sign}}({{{\boldsymbol{h}}}_1}){\rm{sign}}({{{\boldsymbol{h}}}_1}) = {{{\boldsymbol{k}}}_1}{\rm{sign}}({{{\boldsymbol{h}}}_1})\dfrac{{{{{\boldsymbol{\upsilon}} }_2}}}{{\left| {{{{\boldsymbol{\upsilon}} }_2}} \right|}}$ ，然后${\bar {\boldsymbol{v}}}$ 对时间求导得：$$ \begin{aligned} & \dot{\overline{\boldsymbol{v}}}=\left[\begin{array}{cc} \boldsymbol{\gamma}_1 & \mathbf{0} \\ \mathbf{0} & \boldsymbol{\gamma}_1 \end{array}\right]\left[\begin{array}{cc} -\dfrac{1}{2} \boldsymbol{k}_2 & \dfrac{1}{2} \boldsymbol{I} \\ -\boldsymbol{k}_1 \operatorname{sign}\left(\boldsymbol{h}_1\right)-\boldsymbol{k}_3 & \mathbf{0} \end{array}\right]- \\\;\; & {\left[\begin{array}{l} \mathbf{0} \\ \boldsymbol{I} \end{array}\right]\left(\dot{\dot{{\boldsymbol{\varepsilon}}}} \tilde{{\boldsymbol{z}}}_3-{\boldsymbol{\varepsilon}} \dot{\tilde{{\boldsymbol{z}}}}_3\right)=\overline{\boldsymbol{S}} \boldsymbol{A}_0 \overline{\boldsymbol{v}}-\boldsymbol{B}_0\left(\dot{\dot{\varepsilon}} \tilde{\boldsymbol{z}}_3-\varepsilon \dot{\tilde{{{\boldsymbol{z}}}_3}}\right)} \end{aligned} $$ (23) 式中：
$$\begin{aligned}& {{\bar {\boldsymbol{S}}} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\gamma}} }_1}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{{{{\boldsymbol{\gamma}} }_1}} \end{array}} \right],{{{\boldsymbol{A}}}_0} = \left[ {\begin{array}{*{20}{c}} { - \dfrac{1}{2}{{{\boldsymbol{k}}}_2}}&{\dfrac{1}{2}{{\boldsymbol{I}}}} \\ { - {{{\boldsymbol{k}}}_1}{\rm{sign}}({{{\boldsymbol{h}}}_1}) - {{{\boldsymbol{k}}}_3}}&{\boldsymbol{0}} \end{array}} \right]} \\&\;\;\; {{{{\boldsymbol{B}}}_0} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {{\boldsymbol{I}}} \end{array}} \right],{{{\boldsymbol{\gamma}} }_1} = {\text{diag}}({{\left| {{{\boldsymbol{\sigma}} _1}} \right|}^{ - 1/2}},{{\left| {{{\boldsymbol{\sigma}} _2}} \right|}^{ - 1/2}},{{\left| {{{\boldsymbol{\sigma}} _3}} \right|}^{ - 1/2}})} 。 \end{aligned}$$ (24) 构造如下李雅普诺夫函数:
$${V_2}({\bar {\boldsymbol{v}}}) = {{\bar {\boldsymbol{v}}}^{\rm{T}}}{{{\boldsymbol{P}}}_0}{\bar {\boldsymbol{v}}}$$ 式中：
${{{\boldsymbol{P}}}_0} = \left[ {\begin{array}{*{20}{c}} {({{{\boldsymbol{l}}}_1} + {{\boldsymbol{l}}}_{_2}^2)}&{ - {{{\boldsymbol{l}}}_2}} \\ { - {{{\boldsymbol{l}}}_2}}&{2{{\boldsymbol{I}}}} \end{array}} \right]$ ，将$ {V_2} $ 对时间求导得：$$ \begin{aligned} {{\dot V}_2} =& {[{\bar{\boldsymbol S}}{{A}_0}{\bar{\boldsymbol v}} - {{\boldsymbol B}_0}({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})]^{\rm{T}}}{{\boldsymbol P}_0}{\bar{\boldsymbol v}} + {{{\bar{\boldsymbol v}}}^{\rm{T}}}{{\boldsymbol P}_0}[{\bar{\boldsymbol S}}{{A}_0}{\bar{\boldsymbol v}} - \\& {{\boldsymbol B}_0}({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})] = {{{\bar{\boldsymbol v}}}^{\rm{T}}}({A}_0^{\rm{T}}{\bar{\boldsymbol S}}{{\boldsymbol P}_0} + {{\boldsymbol P}_0}{\bar{\boldsymbol S}}{{A}_0}){\bar{\boldsymbol v}} - \\& 2{({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})^{\rm{T}}}{\boldsymbol B}_{_0}^{\rm{T}}{{\boldsymbol P}_0}{\bar{\boldsymbol v}} \leqslant - \frac{1}{2}{\lambda _{\min }}({\bar{\boldsymbol S}}){{{\bar{\boldsymbol v}}}^{\rm{T}}}{{{\boldsymbol{Q}}}_1}{\bar{\boldsymbol v}} - \\&\qquad\qquad 2{({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})^{\rm{T}}}{\boldsymbol B}_{_0}^{\rm{T}}{{\boldsymbol P}_0}{\bar{\boldsymbol v}} \end{aligned}$$ (25) $$ \begin{aligned}& \;\;\quad {{{\boldsymbol{Q}}}_1} = {{\boldsymbol{A}}}_0^{\rm{T}}{{{\boldsymbol{P}}}_0}{\text{ + }}{{{\boldsymbol{P}}}_0}{{{\boldsymbol{A}}}_0} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{Q}}}_{11}}}&* \\ {{{{\boldsymbol{Q}}}_{21}}}&{2{{{\boldsymbol{}}{\boldsymbol{l}}}_2}} \end{array}} \right] \\& {{{{\boldsymbol{Q}}}_{11}} = 2{{{\boldsymbol{l}}}_1}{{{\boldsymbol{k}}}_2} + 2{{{\boldsymbol{l}}}_2}({{{\boldsymbol{l}}}_2}{{{\boldsymbol{k}}}_2} - 2{{{\boldsymbol{k}}}_3}) - 4{{{\boldsymbol{l}}}_2}{{{\boldsymbol{k}}}_1}{\rm{sign}}({{{\boldsymbol{h}}}_1})} \\&\quad {{{{\boldsymbol{Q}}}_{21}} = (2{{{\boldsymbol{k}}}_3} - {{l}_2}{{{\boldsymbol{k}}}_2} - {{{\boldsymbol{l}}}_1} - {{\boldsymbol{l}}}_2^2) + 2{{{\boldsymbol{k}}}_1}{\rm{sign}}({{{\boldsymbol{h}}}_1})} \\ \end{aligned} $$ (26) 由
$$ \left\{ \begin{gathered} \left\| {{{{\boldsymbol{v}}}_2}} \right\| = {(\left| {{\sigma _1}} \right| + \left| {{\sigma _2}} \right| + \left| {{\sigma _3}} \right|)^{1/2}} \geqslant \\ \min ({\left| {{\sigma _2}} \right|^{ - 1/2}} {\left| {{\sigma _2}} \right|^{ - 1/2}},{\left| {{\sigma _3}} \right|^{ - 1/2}}) = - \lambda _{_{\min }}^{ - 1}({\bar {\boldsymbol{S}}}) \\ \left\| {{{{\boldsymbol{v}}}_2}} \right\|{\lambda _{\min }}({\bar {\boldsymbol{S}}}) \geqslant 1 \\ \end{gathered} \right. $$ (27) 由假设1和式(3)可知，
$({{{\dot {\boldsymbol{\varepsilon}} }{{\tilde {\boldsymbol{z}}}_3} - {{\boldsymbol{\varepsilon }}}{{\dot {\tilde {\boldsymbol{z}}}}_3}}})$ 是有界的，令${{{{\boldsymbol{\varDelta}} } = ({\dot {\boldsymbol{\varepsilon }}}{{\tilde {\boldsymbol{z}}}_3} - {{\boldsymbol{\varepsilon}} }{{\dot {\tilde {\boldsymbol{z}}}}_3})}}$ ，根据引理2与式(27)，可以得到：$$\begin{aligned}& - 2{({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})^{\rm{T}}}{\boldsymbol B}_{_0}^{\rm{T}}{{\boldsymbol P}_0}{\bar{\boldsymbol v}} \leqslant \left\| { - 2{{({\dot {\boldsymbol{\varepsilon}} }{{{\tilde {\boldsymbol{z}}}}_3} - { {\boldsymbol{\varepsilon}} }{{{\dot {\tilde {\boldsymbol{z}}}}}_3})}^{\rm{T}}}{\boldsymbol B}_{_0}^{\rm{T}}{{\boldsymbol P}_0}{\bar{\boldsymbol v}}} \right\| \leqslant \\& \left\| {{\boldsymbol{\varDelta}} } \right\|\left\| { - {{{\boldsymbol{l}}}_2}{{\boldsymbol v}_2} + 2{{\boldsymbol v}_3}} \right\| \leqslant \left\| {{\boldsymbol{\Delta}} } \right\|{\lambda _{\min }}({\bar{\boldsymbol S}})\left\| {{{\boldsymbol v}_2}} \right\|\left\| { - {{{\boldsymbol{l}}}_2}{{\boldsymbol v}_2} + 2{{\boldsymbol v}_3}} \right\| \leqslant \\&\;\; \left\| {{\boldsymbol{\varDelta}} } \right\|{\lambda _{\min }}({\bar{\boldsymbol S}})( - {{{\boldsymbol{l}}}_2}{{\boldsymbol v}_2} + {\boldsymbol v}_2^{\rm{T}}{{\boldsymbol v}_2} + {\boldsymbol v}_3^{\rm{T}}{{\boldsymbol v}_3}) \leqslant {\lambda _{\min }}({\bar{\boldsymbol S}}){{{\bar{\boldsymbol v}}}^{\rm{T}}}{{Q}_2}{\bar{\boldsymbol v}} \end{aligned}$$ (28) 式中
${{{\boldsymbol{Q}}}_2} = \dfrac{1}{2}\left[ {\begin{array}{*{20}{c}} {2\left\| {{\boldsymbol{\varDelta}} } \right\|({{{\boldsymbol{l}}}_2}{\text{ + }}{{\boldsymbol{I}}})}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{ - 2\left\| {{\boldsymbol{\varDelta}} } \right\|{{\boldsymbol{I}}}} \end{array}} \right]$ ，令${{{\boldsymbol{Q}}}^ * } = {{{\boldsymbol{Q}}}_1} - 2{{{\boldsymbol{Q}}}}$ 然后可得：$$ {{\dot V}_2} \leqslant - \frac{1}{2}{\lambda _{\min }}({\bar {\boldsymbol{S}}}){{{\bar {\boldsymbol{v}}}}^{\rm{T}}}{{{\boldsymbol{Q}}}_1}{\bar {\boldsymbol{v}}} - {\lambda _{\min }}({\bar {\boldsymbol{S}}}){{{\bar {\boldsymbol{v}}}}^{\rm{T}}}{{{\boldsymbol{Q}}}_2}{\bar {\boldsymbol{v}}} \leqslant - \frac{{{\lambda _{\min }}({\bar {\boldsymbol{S}}}){{{\bar {\boldsymbol{v}}}}^{\rm{T}}}{{{\boldsymbol{Q}}}^ * }{\bar {\boldsymbol{v}}}}}{2} $$ (29) 设计参数：
$$ \begin{aligned}& {{{\boldsymbol{k}}}_2}{\text{ = }}\frac{{{{({{{\boldsymbol{l}}}_1} + {{\boldsymbol{l}}}_2^2 + 2{{{\boldsymbol{k}}}_1})}^2}}}{{4{{{\boldsymbol{l}}}_1}({{{\boldsymbol{l}}}_2} - \left\| {{\boldsymbol{\varDelta }}} \right\|{{\boldsymbol{I}}})}},{{{\boldsymbol{k}}}_3} = {{{\boldsymbol{l}}}_2}{{{\boldsymbol{k}}}_2}/2 \\&\;\; {{{\boldsymbol{l}}}_2} > \left\| {{\boldsymbol{\varDelta}} } \right\|{I},\left\| {{\boldsymbol{\varDelta}} } \right\|({{{\boldsymbol{l}}}_2} + {{\boldsymbol{I}}}) > 2{{{\boldsymbol{l}}}_2}{{{\boldsymbol{k}}}_1} \end{aligned}$$ (30) 使得
$ {{{\boldsymbol{Q}}}^ * } $ 矩阵正定。为了证明有限时间收敛，考虑如下不等式：
$$ \left\{ \begin{gathered} \lambda _{_{\min }}^{ - 1}({\bar {\boldsymbol{S}}}) \leqslant \left\| {{\bar {\boldsymbol{v}}}} \right\| \leqslant \lambda _{_{\max }}^{ - 1}({\bar {\boldsymbol{S}}}) \\ {\lambda _{\min }}({{{\boldsymbol{P}}}_0}) \leqslant V \leqslant {\lambda _{\max }}({{{\boldsymbol{P}}}_0}){\left\| {{\bar {\boldsymbol{v}}}} \right\|^2} \\ - {\lambda _{\min }}({{{\boldsymbol{Q}}}^ * }) \leqslant - {{{\bar {\boldsymbol{v}}}}^{\rm{T}}}{{{\boldsymbol{Q}}}^ * }{\bar {\boldsymbol{v}}} \leqslant - {\lambda _{\max }}({{{\boldsymbol{Q}}}^ * }){\left\| {{\bar {\boldsymbol{v}}}} \right\|^2} \\ \end{gathered} \right. $$ (31) 结合式(27)~(31)，可得：
$$\begin{split} {{\dot V}_2} \leqslant & - \frac{1}{2}{\lambda _{\min }}({\bar {\boldsymbol{S}}}){{{\bar {\boldsymbol{v}}}}^{\rm{T}}}{{{\boldsymbol{Q}}}^ * }{\bar {\boldsymbol{v}}} \leqslant - \frac{1}{2}{\lambda _{\min }}({\bar {\boldsymbol{S}}}){\lambda _{\max }}({{{\boldsymbol{Q}}}^ * }){\left\| {{\bar {\boldsymbol{v}}}} \right\|^2} \leqslant \\&\qquad - \frac{{\lambda _{_{\min }}^{1/2}({{{\boldsymbol{P}}}_0})}}{{2V_1^{1/2}}}{\lambda _{\max }}({{{\boldsymbol{Q}}}^ * })\frac{{{V_2}}}{{{\lambda _{\max }}({{{\boldsymbol{P}}}_0})}} \end{split}$$ (32) 进一步可得：
$$ {\dot V_2} \leqslant - \xi V_2^{1/2} $$ (33) 式中
$\xi = \dfrac{{\lambda _{{\min }}^{1/2}({{{\boldsymbol{P}}}_0}){\lambda _{\max }}({{{\boldsymbol{Q}}}^ * })}}{{2{\lambda _{\max }}({{{\boldsymbol{P}}}_0})}}$ 。根据式(33)和引理1可得，
$ {\bar {\boldsymbol{v}}{\boldsymbol{S}}{\boldsymbol{Z}}} $ 将在有限时间$ {t_r} $ 内收敛到零，进一步当$ t \geqslant {t_r} $ 时，对于辅助系统式(20)，当$ t \geqslant {t_r} $ 时，可得$ {{\boldsymbol{S}}{\boldsymbol{Z}}} = {{\boldsymbol{Z}}} $ ，因此辅助系统可以改写为$$ \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{S}}} = {{\boldsymbol{Z}}}} \\ {{\dot {\boldsymbol{Z}}} = {\bar {\boldsymbol{\tau}} }} \end{array}} \right. $$ (34) 且有
${{\boldsymbol{S}}} = {{\boldsymbol{Z}}}$ 。注2 由于积分滑模的作用，使得
${{\boldsymbol{\varepsilon}} }{{\tilde {\boldsymbol{z}}}_3}$ 被补偿，因此${\dot {\boldsymbol{S}}}$ 没有干扰项。为了提高
${{\boldsymbol{S}}}$ 的趋近速度并削弱抖振，设计基于$ \arctan ( \cdot ) $ 函数的趋近律，表示为$$ {\dot {\boldsymbol{S}}} = - \frac{1}{{\varUpsilon ({{\boldsymbol{S}}})}}\left[ {{\lambda _3}{{\rm{sig}}^{\frac{{{2_{{r_1}}} - {r_{2}}}}{{r_1}}}}({{\boldsymbol{S}}}) + {\lambda _4}{{\rm{sig}}^{\frac{{{r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right] $$ (35) 式中：
$\varUpsilon ({{\boldsymbol{S}}}) = \left(\dfrac{{\text{π}} }{2} - \arctan (\hbar ){\left\| {{\boldsymbol{S}}} \right\|^\mu }\right)\alpha$ ，$ 0 < \mu < 1 $ ，$\alpha > \dfrac{2}{{{\text{π}}} }$ ；$ {r_1} $ 和$ {r_2} $ 为正奇数且${r_1} > {r_2}; {\lambda _3} > 0 ,{\lambda _4} > 0$ ；由式(35)可知,$\varUpsilon ({{\boldsymbol{S}}})$ 大于零，因此系统稳定性不会受此影响。且当系统初始状态离平衡点较远时，函数$\arctan (\hbar){\left\| {{\boldsymbol{S}}} \right\|^\mu }$ 的值将趋近于$\dfrac{{\text{π}} }{2}$ ，选取合适的$ \mu $ 可使$0 < \varUpsilon ({{\boldsymbol{S}}}) < 1$ 。满足$\left| {\dfrac{{{\lambda _3}}}{{\varUpsilon ({{\boldsymbol{S}}})}}{{\rm{sig}}^{\frac{{2{r_1} - {r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right| > \left| {{\lambda _4}{{\rm{sig}}^{\frac{{2{r_1} - {r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right|$ 。此时，趋近律会相应地提高${{\boldsymbol{S}}}$ 的收敛速度。相反，当$ {{\boldsymbol{S}}} $ 接近于平衡点时，函数$\arctan (\hbar) {\left\| {{\boldsymbol{S}}} \right\|^\mu }$ 趋近于0，$\varUpsilon ({{\boldsymbol{S}}})$ 满足$\varUpsilon ({{\boldsymbol{S}}}) = \dfrac{{{\text{π}} \alpha }}{2} > 1$ ，则有$\left| {\dfrac{{{\lambda _4}}}{{\varUpsilon ({{\boldsymbol{S}}})}}{{\rm{sig}}^{\frac{{{r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right| > \left| {{\lambda _4}{{\rm{sig}}^{\frac{{{r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right|$ ，因有助于削弱抖振。综上可得：$$ {{\tau }_2} = - \frac{{{{({{\boldsymbol{\varepsilon}} {\boldsymbol{J}}}{{{\boldsymbol{M}}}^{ - 1}})}^{ - 1}}}}{{\varUpsilon ({{\boldsymbol{S}}})}}\left[ {{\lambda _3}{{\rm{sig}}^{\frac{{2{r_1} - {r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}}) + {\lambda _4}{{\rm{sig}}^{\frac{{{r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right] $$ (36) 构造李雅普诺夫函数为
$$ {V_3} = \frac{1}{2}{{{\boldsymbol{S}}}^{\rm{T}}{\rm{}}}{{\boldsymbol{S}}} $$ (37) $ {V_3} $ 对时间求导得：$$\begin{gathered} {{\dot V}_3} = - \frac{{{\lambda _3}}}{{\varUpsilon ({\boldsymbol S})}}{\left| {\boldsymbol S} \right|^{\frac{{3{r_1} - {r_2}}}{{r1}}}} - \frac{{{\lambda _4}}}{{\varUpsilon ({\boldsymbol S})}}{\left| {\boldsymbol S} \right|^{\frac{{{r_2} + {r_1}}}{{{r_1}}}}} \leqslant \\ - \frac{{2{\lambda _3}}}{{{\text{π}} \alpha }}{2^{\frac{{3 - {r_2}/{r_1}}}{2}}}{\left( {\frac{1}{2}{{\boldsymbol S}^2}} \right)^{\frac{{3 - {r_2}/{r_1}}}{2}}} - \frac{{2{\lambda _4}}}{{{\text{π}}\alpha }}{2^{\frac{{1 + {r_2}/{r_1}}}{2}}} \\ {\left( {\frac{1}{2}{{\boldsymbol S}^2}} \right)^{\frac{{1 + {r_2}/{r_1}}}{2}}} \leqslant - {\delta _1}V_2^{2 - \frac{{{\mu _4}}}{{{\mu _5}}}} - {\delta _2}V_2^{\frac{{{\mu _4}}}{{{\mu _5}}}} \end{gathered}$$ (38) 式中:
$ {\mu _1} $ 和$ {\mu _2} $ 为正奇数，${\delta _1} = \dfrac{{2{\lambda _3}}}{{{\text{π}}\alpha }}{2^{\frac{{3 - {r_2}/{r_1}}}{2}}}$ ，${\delta _2} = \dfrac{{2{\lambda _4}}}{{{\text{π}} \alpha }}{2^{\frac{{1 + {r_2}/{r_1}}}{2}}}\cdot$ $\dfrac{{{\mu _4}}}{{{\mu _5}}} < \dfrac{{1 + {r_2}/{r_1}}}{2} $ 。根据文献[25]和引理3，
$ {{\boldsymbol{S}}} $ 可以在固定时间内收敛到零, 同时也可保证有限时间内收敛到零点。进一步，根据文献[20]和定理1，在$ {{\boldsymbol{S}}} = 0 $ 的滑动阶段，$ {{\boldsymbol{\chi }}} $ 可以在有限时间内收敛到零，因此，$ {{\boldsymbol{e}}} $ 满足预设性能指标。最后得到有限时间控制律为$$\begin{gathered} \quad\quad {{\boldsymbol{\tau}} } = {({{\boldsymbol{\varepsilon J}}}{{{\boldsymbol{M}}}^{ - 1}})^{ - 1}}\left[ { - {{{\boldsymbol{k}}}_1}{{\boldsymbol{\sigma}} } - {{{\boldsymbol{k}}}_2}{\rm{si}}{{\rm{g}}^{1/2}}({\sigma }) - } \right. \\ \quad {{{\boldsymbol{k}}}_3}\int_0^t {{\rm{sign}}({{\boldsymbol{\sigma}} }){\rm{d}}u} - {{\boldsymbol{\varepsilon}} \hat {\boldsymbol{z}}} - {\dot {\boldsymbol{\varepsilon}} }\left({\dot {\boldsymbol{e}}} - \frac{{{{\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{\zeta }}\right) - {{\boldsymbol{\varepsilon}} }\left( - \frac{{{\dot {\boldsymbol{e}}\dot {\boldsymbol{\zeta}} }}}{{{\boldsymbol{\zeta }}}} + \right. \\\left. \frac{{{{\boldsymbol{e}}\ddot {\boldsymbol{\zeta }}}}}{{{\boldsymbol{\zeta}} }} - \frac{{{{\boldsymbol{e}}}{{{\dot {\boldsymbol{\zeta}} }}^2}}}{{{{{\boldsymbol{\zeta}} }^2}}}\right) - {\lambda _1}{\rm{si}}{{\rm{g}}^{{\alpha _1}}}({{\boldsymbol{\chi}} }) - \left. {{\lambda _2}{\rm{si}}{{\rm{g}}^{{\alpha _2}}}\left({{\boldsymbol{\varepsilon}} }\left({\dot {\boldsymbol{e}}} - \frac{{{e\dot \zeta }}}{{\zeta }}\right)\right)} \right] - \\ \frac{{{{\left({{\boldsymbol{\varepsilon J}}}{{{\boldsymbol{M}}}^{ - 1}}\right)}^{ - 1}}}}{{{\boldsymbol{\varUpsilon}} ({{\boldsymbol{S}}})}}\left[ {{\lambda _3}{\rm{si}}{{\rm{g}}^{\frac{{2{r_1} - {r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right.{\text{ + }}\left. {{\lambda _4}{\rm{si}}{{\rm{g}}^{\frac{{{r_2}}}{{{r_1}}}}}({{\boldsymbol{S}}})} \right] \end{gathered} $$ (39) 定理2 考虑由USVs式(1)、齐次积分滑模面式(30)、有限时间扩张状态观测器式(24)和有限时间控制律式(39)构成的控制算法，在假设1条件下，适当选取齐次积分滑模面参数、有限时间扩张状态观测器和控制律的设计参数。则USVs跟踪误差可以满足式(3)的预设性能，并且在有限时间内快速收敛到零。
3. 数值仿真验证
为了验证所提出控制算法的有效性和优越性, 本文采用经典的Cybership II进行仿真验证。模型水动力参数选取如表1所示[15]。
表 1 CybershipII水动力参数Table 1 Hydrodynamic parameters of the Cybership II参数 数值 参数 数值 参数 数值 $ m $ 23.8000 $ {Y_v} $ −0.8612 $ {X_{\dot u}} $ −2.0000 $ {I_z} $ 1.7600 $ {Y_{\left| v \right|\nu }} $ −36.2823 $ {Y_{\dot v}} $ −10.0000 $ {x_g} $ 0.0460 $ {Y_r} $ 0.1079 $ {Y_{\dot r}} $ 0 $ {X_u} $ −0.7230 $ {N_v} $ 0.1052 $ {N_{\dot v}} $ 0 $ {X_{\left| u \right|u}} $ −1.3270 $ {N_{\left| v \right|v}} $ 5.0437 $ \alpha $ −1.0000 $ {X_{uuu}} $ 1.2550 — — — — 为了验证所设计的控制算法的优越性，采用文献[22]提出的基于扩张状态观测器的非奇异终端滑模控制算法和文献[23]提出的单参数学习控制算法进行仿真比较研究。
文献[22]的控制律为
$$ \begin{gathered} {\tau _{c - I}} = - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{M}}\left( {\frac{{{\gamma _1}p(\alpha + 1)}}{{{\gamma _2}q}}{\rm{diag}}\left( {{{\rm{sig}}^{2 - q/p}}({{\boldsymbol{e}}_2})} \right){{\left\| {{{\boldsymbol{e}}_1}} \right\|}^\alpha }} \right) \\ - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{M}}\left( {\frac{p}{{{\gamma _2}q}}{{\rm{sig}}^{2 - q/p}}({{\boldsymbol{e}}_2}) + {\gamma _3}{\rm{sign}}({\boldsymbol{S}}) + {\gamma _4}{\boldsymbol{S}} - {{\ddot {\boldsymbol{\eta }}}_d} + {{\boldsymbol{z}}_3}} \right) \\ \end{gathered} $$ 式中：
$ S $ 为非奇异终端滑模面；$ {z_3} $ 为观测器的扰动估计值；$ {\gamma _i},i = 1,2,3,4 $ ；$ p $ 和$ q $ 是需要设计的控制器参数。文献[23]的控制律为
$$ \begin{split} {\tau _{c - {\rm{II}}}} = - {k_2}{s_2} - {k_{20}}{{\rm{sig}}^{\frac{1}{2}}}({s_2}) - c{{\hat \varTheta }_2}{\phi ^2}({Z_2}){s_2} \\ {{\dot {\hat \varTheta} }_2} = c{\phi ^2}({Z_2}){\left\| {{s_2}} \right\|^2} - \sigma {{\hat \varTheta }_2},{{\hat \varTheta }_2}(0) \geqslant 0 \\ \end{split} $$ 式中
$ {k_2} $ 、$ {k_{20}} $ 、$ c $ 和$ \sigma $ 为需要设计的控制器参数。公平起见，控制器参数选择与文献[22-23]一致，此处不再给出。参考文献[22]扰动选取，下面在2种扰动情况下对所设计控制方案进行仿真验证。
情况1 海洋环境扰动选取为
$${\boldsymbol{ d}}_1 = \left[ {\begin{array}{*{20}{l}} ({2\cos (0.1{\text{π}} t) + 0.2\sin (1.2{\text{π}} t))({\rm{N}})} \\ ({\sin (0.1{\text{π}} t) + 2\sin (0.5{\text{π}} t))({\rm{N}})} \\ ({\cos (0.2{\text{π}} t) + \sin (0.1{\text{π}} t) + 0.3)({\rm{N}}/{\rm{m}})} \end{array}} \right] $$ 情况2 USVs模型不确定动态部分增加到情况1的30%，同时增大扰动的幅值：
$$ {\boldsymbol{d}}_2 = \left[ {\begin{array}{*{20}{l}} ({15\cos (0.1{\text{π}} t) + 1.2\sin (1.2{\text{π}} t))({\rm{N}})} \\ ({15\sin (0.5{\text{π}} t) + 3\sin (0.1{\text{π}} t))({\rm{N}})} \\ ({10\cos (0.2{\text{π}} t) + 2\sin (0.1{\text{π}} t) + 1.6)({\rm{N}}/{\rm{m}})} \end{array}} \right] $$ 取USVs的初始状态为
${{{\boldsymbol{\eta}} }_0} = {[3\quad - 1\quad0]^{\rm{T}}}$ ；期望轨迹设为${{{\boldsymbol{\eta}} }_d} = {[6\sin (0.1{\text{π}} t)\quad2\sin (0.05{\text{π}} t)\quad0.1t]^{\rm{T}}}$ ；预设性能参数为$ {\zeta }_{0j0}=3$ ，${\zeta }_{ij0}=0.1 $ ，${\zeta }_{j\infty }=0.05 $ ，${\mu }_{j}=0.5 $ ，$j=1, 2, 3$ ，$i = 1,2,\cdots, n$ ，${\rho _{j_{\min }}} = 2/3$ 和${\rho _{j_{\max }}} = 1$ ；观测器参数为$ {a_1} = 20 $ ，$ {a_2} = 50 $ ，$ {a_3} = 40 $ ，$ {b_1} = 1.2 $ ，$ {b_2} = 2 $ ，$ {b_3} = 0.8 $ 。齐次积分滑模面和有限时间控制律的参数选取如表2所示。表 2 齐次积分滑模面和有限时间控制律参数Table 2 Parameters of homogeneous integral sliding mode surface and finite-time control参数 数值 参数 数值 $ {\lambda _1} $ 3 $ {\lambda _2} $ 3 $ {\lambda _3} $ 0.80 $ {\lambda _4} $ 2 $ {\alpha _1} $ 0.60 $ {\alpha _2} $ 0.75 $ {r_1} $ 9 $ {r_2} $ 7 $ \hbar $ 1000 $ \alpha $ 6.50 $ {k_1} $ ${\rm{diag}}(1,1,1)$ $ {k_2} $ ${\rm{diag}}(1.50,1.50,1.50)$ $ {k_3} $ ${\rm{diag}}(0.50,0.50,0.50)$ $ \mu $ 0.80 注3 在使用滑模算法设计控制器的过程中，要求控制器参数大于零，为了抑制海洋环境扰动，选择合适的增益值进行调试，最后达到满意的控制效果。
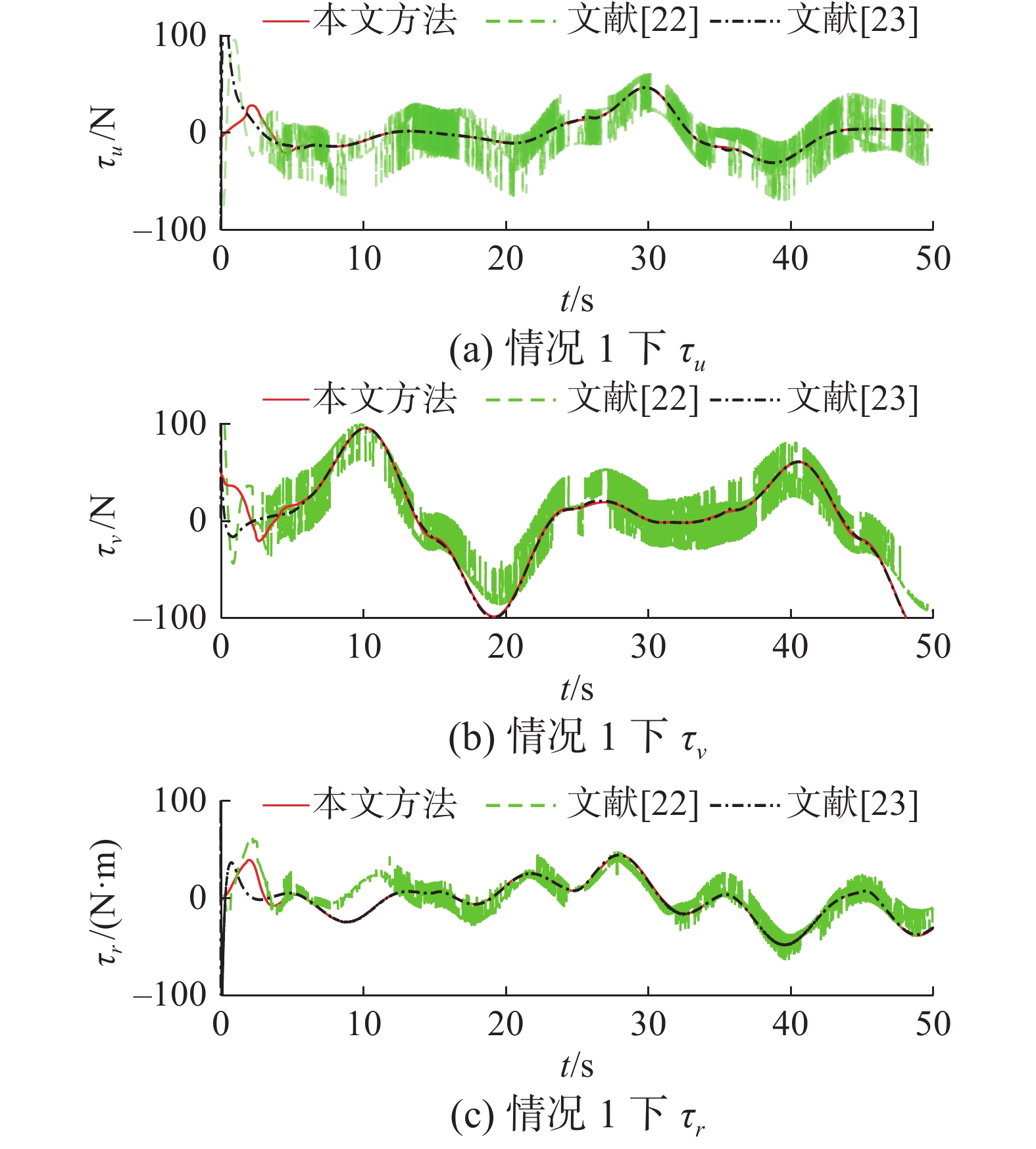
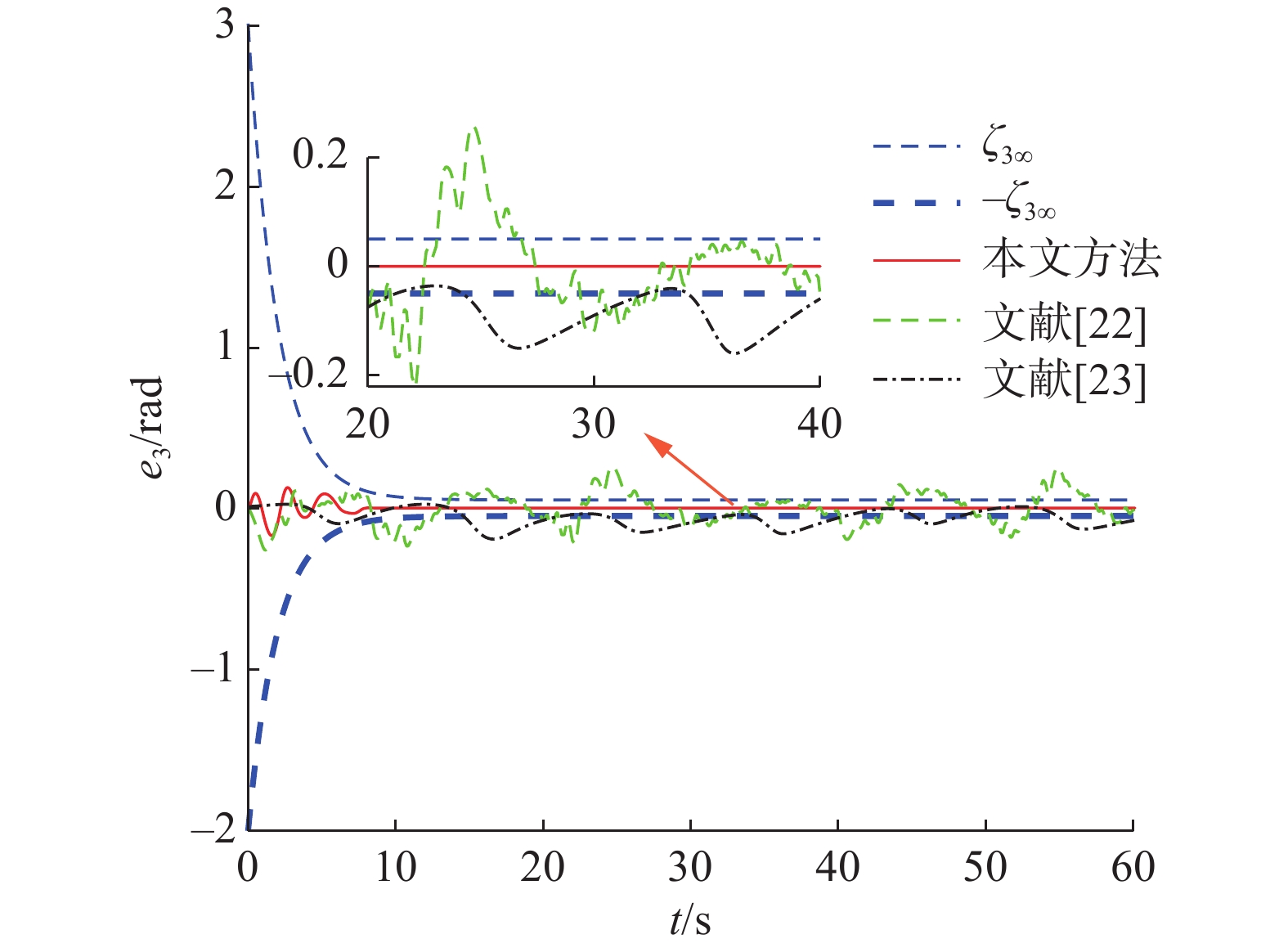
在第3节中对2种情况进行仿真比较，仿真中USVs的期望轨迹和初始状态与3.1节中的相同。仿真结果如图1~8所示。轨迹跟踪误差定量分析如表3所示，其中，定量分析的性能指标选取为
${Q_{{i}}}{\text{ = }}\displaystyle\int_0^{60} {\left| {{e_i}} \right|} {\rm{d}}t $ 。图1为USVs实际轨迹与期望轨迹跟踪示意图。
图 1 USVs期望轨迹和实际轨迹Fig. 1 Desired and actual trajectory of USVs
下载:
全尺寸图片
图 2 情况1下USVs的控制输入Fig. 2 Control input for USVs in case 1下载:
全尺寸图片
图 3 情况1下USVs纵向跟踪误差Fig. 3 Surge direction tracking error of USVs in case 1下载:
全尺寸图片
图 4 情况1下USVs横向跟踪误差Fig. 4 Sway direction tracking error of USVs in case 1下载:
全尺寸图片
图 5 情况1下USVs艏向跟踪误差Fig. 5 Yaw direction tracking error of USVs in case 1下载:
全尺寸图片
图 6 情况2下USVs纵向跟踪误差Fig. 6 Surge direction tracking error of USVs in case 2下载:
全尺寸图片
图 7 情况2下USVs横向跟踪误差Fig. 7 Sway direction tracking error of USVs in case 2下载:
全尺寸图片
图2为在情况1下本文和文献[22-23]提出的控制器的实际输入。图1和图3~5表明，在较小的环境扰动下，本文提出的有限时间控制算法和文献[22-23]的控制算法均能跟踪期望轨迹。为了进一步验证本文控制算法的鲁棒性，不确定动态和环境扰动由情况1增加到情况2。由图6~8和表3中的跟踪误差定量分析结果可见，本文的轨迹跟踪误差量级远小于对比文献的跟踪误差量级，这表明本文的控制算法对USVs存在的不确定动态和未知环境海洋扰动具有更好的鲁棒性。另一方面，由于文献[22-23]提出的控制律没有采用PPC技术，不能保证USVs轨迹跟踪误差始终在稳态误差带内。本文所提出的算法具有更好的瞬态控制性能，可以实现本文的预设性能，避免了使用传统静态预设性能函数导致预设性能失效的问题。此外，从图2可以看出，基于齐次滑模面和超螺旋积分滑模算法，本文的实际控制输入可以有效地削弱抖振现象。然而，基于非奇异终端滑模面设计的实际控制律存在明显抖振现象[22]，这会对推进装置带来很大的挑战，甚至导致控制律失效。因此本文提出的控制方案更便于实际应用。
图 8 情况2下USVs艏向跟踪误差Fig. 8 Yaw direction tracking error of USVs in case 2下载:
全尺寸图片
4. 结束语
本文提出一种动态预设性能函数，可根据系统的性能要求和限制条件，在未知扰动下预先设置USVs轨迹跟踪误差在有限时间内进入并不再超出预设的稳态误差带，提高了系统的响应速度，避免了传统静态预设性能函数失效的问题。为了证明本文所提出有限时间控制算法的优越性，在2种环境扰动情况下，将本文算法与其他具有代表性的控制算法进行了仿真比较。在仿真结果中，本文所提出的控制算法实现了跟踪误差在有限时间内快速收敛到零，具备更好的鲁棒性，同时减弱了控制抖振现象。最终实现了USVs的动态预设性能控制。未来我们计划考虑推进装置的推力分配策略和优化问题。
-
图 1 USVs期望轨迹和实际轨迹
Fig. 1 Desired and actual trajectory of USVs
下载:
全尺寸图片
图 2 情况1下USVs的控制输入
Fig. 2 Control input for USVs in case 1
下载:
全尺寸图片
图 3 情况1下USVs纵向跟踪误差
Fig. 3 Surge direction tracking error of USVs in case 1
下载:
全尺寸图片
图 4 情况1下USVs横向跟踪误差
Fig. 4 Sway direction tracking error of USVs in case 1
下载:
全尺寸图片
图 5 情况1下USVs艏向跟踪误差
Fig. 5 Yaw direction tracking error of USVs in case 1
下载:
全尺寸图片
图 6 情况2下USVs纵向跟踪误差
Fig. 6 Surge direction tracking error of USVs in case 2
下载:
全尺寸图片
图 7 情况2下USVs横向跟踪误差
Fig. 7 Sway direction tracking error of USVs in case 2
下载:
全尺寸图片
图 8 情况2下USVs艏向跟踪误差
Fig. 8 Yaw direction tracking error of USVs in case 2
下载:
全尺寸图片
表 1 CybershipII水动力参数
Table 1 Hydrodynamic parameters of the Cybership II
参数 数值 参数 数值 参数 数值 $ m $ 23.8000 $ {Y_v} $ −0.8612 $ {X_{\dot u}} $ −2.0000 $ {I_z} $ 1.7600 $ {Y_{\left| v \right|\nu }} $ −36.2823 $ {Y_{\dot v}} $ −10.0000 $ {x_g} $ 0.0460 $ {Y_r} $ 0.1079 $ {Y_{\dot r}} $ 0 $ {X_u} $ −0.7230 $ {N_v} $ 0.1052 $ {N_{\dot v}} $ 0 $ {X_{\left| u \right|u}} $ −1.3270 $ {N_{\left| v \right|v}} $ 5.0437 $ \alpha $ −1.0000 $ {X_{uuu}} $ 1.2550 — — — — 表 2 齐次积分滑模面和有限时间控制律参数
Table 2 Parameters of homogeneous integral sliding mode surface and finite-time control
参数 数值 参数 数值 $ {\lambda _1} $ 3 $ {\lambda _2} $ 3 $ {\lambda _3} $ 0.80 $ {\lambda _4} $ 2 $ {\alpha _1} $ 0.60 $ {\alpha _2} $ 0.75 $ {r_1} $ 9 $ {r_2} $ 7 $ \hbar $ 1000 $ \alpha $ 6.50 $ {k_1} $ ${\rm{diag}}(1,1,1)$ $ {k_2} $ ${\rm{diag}}(1.50,1.50,1.50)$ $ {k_3} $ ${\rm{diag}}(0.50,0.50,0.50)$ $ \mu $ 0.80 -
[1] ZHENG Zewei, RUAN Linping, ZHU Ming. Output-constrained tracking control of an underactuated autonomous underwater vehicle with uncertainties[J]. Ocean engineering, 2019, 175: 241–250. doi: 10.1016/j.oceaneng.2019.02.023 [2] ZHENG Zewei, HUANG Yanting, XIE Lihua, et al. Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output[J]. IEEE transactions on control systems technology, 2018, 26(5): 1851–1859. doi: 10.1109/TCST.2017.2728518 [3] FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles. Trondheim[M]. Norway: Marine Cybernetics AS, 2002. [4] LIAO Yulei, WAN Lei, ZHUANG Jiayuan. Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel[J]. Procedia engineering, 2011, 15: 256–263. doi: 10.1016/j.proeng.2011.08.051 [5] WEN Guoxing, GE S S, CHEN C L P, et al. Adaptive tracking control of surface vessel using optimized backstepping technique[J]. IEEE transactions on cybernetics, 2019, 49(9): 3420–3431. doi: 10.1109/TCYB.2018.2844177 [6] LIANG Kun, LIN Xiaogong, CHEN Yu, et al. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation[J]. Ocean engineering, 2020, 206: 107245. doi: 10.1016/j.oceaneng.2020.107245 [7] SUN Yizhuo, GAO Yabin, ZHAO Yue, et al. Neural network-based tracking control of uncertain robotic systems: predefined-time nonsingular terminal sliding-mode approach[J]. IEEE transactions on industrial electronics, 2022, 69(10): 10510–10520. doi: 10.1109/TIE.2022.3161810 [8] 杨迪, 郭晨, 朱玉华, 等. 欠驱动船舶神经网络自适应路径跟踪控制[J]. 智能系统学报, 2018, 13(2): 254–260. YANG Di, GUO Chen, ZHU Yuhua, et al. Neural network adaptive path tracking control for underactuated ships[J]. CAAI transactions on intelligent systems, 2018, 13(2): 254–260. [9] 秦贝贝, 陈增强, 孙明玮, 等. 基于自适应神经模糊推理系统的船舶航向自抗扰控制[J]. 智能系统学报, 2020, 15(2): 255–263. QIN Beibei, CHEN Zengqiang, SUN Mingwei, et al. Active disturbance rejection control of ship course based on adaptive-network-based fuzzy inference system[J]. CAAI transactions on intelligent systems, 2020, 15(2): 255–263. [10] ZHENG Huarong, WU Jun, WU Weimin. Robust dynamic positioning of autonomous surface vessels with tube-based model predictive control[J]. Ocean engineering, 2020, 199: 106820. doi: 10.1016/j.oceaneng.2019.106820 [11] VEKSLER A, JOHANSEN T A, BORRELLI F, et al. Dynamic positioning with model predictive control[J]. IEEE transactions on control systems technology, 2016, 24(4): 1340–1353. doi: 10.1109/TCST.2015.2497280 [12] ZHU Guibing, MA Yong, LI Zhixiong, et al. Adaptive neural output feedback control for MSVs with predefined performance[J]. IEEE transactions on vehicular technology, 2021, 70(4): 2994–3006. doi: 10.1109/TVT.2021.3063687 [13] BECHLIOULIS C P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE transactions on automatic control, 2008, 53(9): 2090–2099. doi: 10.1109/TAC.2008.929402 [14] HAN S I, LEE J M. Recurrent fuzzy neural network backstepping control for the prescribed output tracking performance of nonlinear dynamic systems[J]. ISA transactions, 2014, 53(1): 33–43. doi: 10.1016/j.isatra.2013.08.012 [15] DAI Shilu, HE Shude, WANG Min, et al. Adaptive neural control of underactuated surface vessels with prescribed performance guarantees[J]. IEEE transactions on neural networks and learning systems, 2019, 30(12): 3686–3698. doi: 10.1109/TNNLS.2018.2876685 [16] NA Jing, WANG Shubo, LIU Yanjun, et al. Finite-time convergence adaptive neural network control for nonlinear servo systems[J]. IEEE transactions on cybernetics, 2020, 50(6): 2568–2579. doi: 10.1109/TCYB.2019.2893317 [17] WANG Yuanhui, WANG Haibin, LI Mingyang. Adaptive fuzzy controller design for dynamic positioning ship integrating prescribed performance[J]. Ocean engineering, 2021, 219: 107956. doi: 10.1016/j.oceaneng.2020.107956 [18] LI Jian, DU Jialu, CHEN C L P. Command-filtered robust adaptive NN control with the prescribed performance for the 3-D trajectory tracking of underactuated AUVs[J]. IEEE transactions on neural networks and learning systems, 2022, 33(11): 6545–6557. doi: 10.1109/TNNLS.2021.3082407 [19] JIANG Xiyun, WANG Yuanhui. Prescribed performance control of marine surface vessel trajectory tracking in finite-time with full-state constraints and input saturation[J]. Journal of marine science and engineering, 2021, 9(8): 866. doi: 10.3390/jmse9080866 [20] YAO Qijia. Adaptive finite-time sliding mode control design for finite-time fault-tolerant trajectory tracking of marine vehicles with input saturation[J]. Journal of the franklin institute, 2020, 357(18): 13593–13619. doi: 10.1016/j.jfranklin.2020.10.015 [21] WANG Junxiao, RONG Jiayi, Yu Li. Dynamic prescribed performance sliding mode control for DC-DC buck converter system with mismatched time-varying disturbances[J]. ISA transactions, 2022, 129: 546–557. doi: 10.1016/j.isatra.2022.02.019 [22] WANG Ning, ZHU Zhongben, QIN Hongde, et al. Finite-time extended state observer-based exact tracking control of an unmanned surface vehicle[J]. International journal of robust and nonlinear control, 2021, 31(5): 1704–1719. doi: 10.1002/rnc.5369 [23] ZHU Guibing, DU Jialu. Global robust adaptive trajectory tracking control for surface ships under input saturation[J]. IEEE journal of oceanic engineering, 2020, 45(2): 442–450. doi: 10.1109/JOE.2018.2877895 [24] DU Jialu, HU xin, KRSTI M. Robust dynamic positioning of ships with disturbances under input saturation[J]. Automatica, 2016, 73: 207–214. doi: 10.1016/j.automatica.2016.06.020 [25] WANG Taiqi, LIU Yongtao, ZHANG Xinfeng. Extended state observer-based fixed-time trajectory tracking control of autonomous surface vessels with uncertainties and output constraints[J]. ISA transactions, 2022, 128: 174–183. doi: 10.1016/j.isatra.2021.09.005 [26] LIN Zhi, DU WANG Hongdu, KARKOUB M, et al. Prescribed performance based sliding mode path-following control of UVMS with flexible joints using extended state observer based sliding mode disturbance observer[J]. Ocean engineering, 2021, 240: 109915. doi: 10.1016/j.oceaneng.2021.109915 [27] 刘文吉, 杜佳璐, 李健, 李诤. 基于超螺旋滑模的船载稳定平台镇定控制[J]. 系统工程与电子技术, 2022, 44(5): 1662–1669. LIU Wwenji, DU Jialu, LI Jian, et al. Stabilization control for ship-borne stabilization platform based on super-twisting sliding mode[J]. Systems engineering and electronics, 2022, 44(5): 1662–1669. [28] 杜佳璐, 李健. 欠驱动水下机器人三维轨迹跟踪有限时间预设性能控制[J]. 控制理论与应用, 2022, 39(2): 383–392. DU Jialu, LI Jian. Finite-time prescribed performance control for the three-dimension trajectory tracking of underactuated AUV[J]. Control theory & applications, 2022, 39(2): 383–392. [29] ZHENG Zewei, FEROSKHAN M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances[J]. IEEE/ASME transactions on mechatronics, 2017, 22(6): 2564–2575. doi: 10.1109/TMECH.2017.2756110
