Name disambiguation method based on hyperbolic space feature fusion
-
摘要: 针对传统用户影响力分析等研究遇到姓名重名的挑战，姓名歧义的影响日益严重的问题，本文基于双曲空间结合欧氏空间进行特征融合，提出融合多空间特征的网络对齐方法（geometry interaction network alignment, GINA），有效建模网络结构对用户姓名消歧的主要作用。本文同时使用欧氏空间和双曲空间进行网络表示学习，以获取具有不同空间特点的网络结构信息，使用跨空间网络映射及跨空间特征融合在尽量减少空间映射损失的情况下实现不同空间的信息交互得到最终的网络表示，进行网络对齐，进而实现姓名消歧。本文在中文论文合作网络、英文论文合作网络和中文专利合作网络上，两两对齐构建论文−专利实证数据网络对齐数据集和中文−英文实证数据网络对齐数据集，开展GINA模型在网络对齐数据集上对重名人员身份识别和中外论文身份识别2个实证场景试验验证，双曲空间融合欧氏空间相比单一空间精确率增加了24.9%，验证了GINA方法的有效性。Abstract: In view of the challenge of name duplication and the increasingly serious influence of name ambiguity in traditional user influence analysis and other research, the impact of name ambiguity is becoming increasingly serious. This paper proposes a network alignment model – geometry interaction network alignment (GINA) based on the fusion of hyperbolic space and Euclidean space features, fusing multiple spatial features. It effectively establishes a model to show the main function of a network structure for name disambiguation. The fundamental idea of this paper is to simultaneously utilize both Euclidean space and hyperbolic space for network representation learning, aiming to capture network structural information with distinct spatial characteristics. It employs cross-space network mapping and cross-space feature fusion to realize information exchange among different spaces and final network representation under the situations of reducing loss of spatial mapping as far as possible, implements network alignment and further name disambiguation. By performing network alignment based on the obtained representations, the paper accomplishes name disambiguation. On real datasets, the Chinese paper co-authorship network, English paper co-authorship network, and the Chinese patent co-authorship network are aligned in pair to construct the "Paper-Patent" empirical data network alignment dataset and the "Chinese-English" empirical data network alignment dataset to carry out the test demonstration of GINA model in two empirical scenarios for the identity recognition of the individuals with the same name and Chinese & foreign papers. The results show that the precision in the hyperbolic space combined with the Euclidean space is at least 24.9% higher than that in a single space, confirming effectiveness of the GINA method.
-
随着互联网数据的爆炸式增长，数据库的容量与信息大量增加。由于自然语言的多义性、复杂性和模糊性，出现了许多同名不同义的信息，这使得在数据库中迅速地查找准确信息成为了一项挑战。比如在论文期刊搜索相关专业的研究人员最新研究工作时，会出现属于不同学者，却有着相同学者姓名的文献，从而导致将不同学者所著文献误认为同一个人所写，降低了搜索文献的效率，影响了用户的使用体验。为了降低姓名歧义带来的影响，国内外学者对姓名消歧进行了一系列研究。
姓名消歧是指消除跨文档情况下的人名歧义性，把相同的人名按照现实世界的不同实体进行分类，从而把信息有效地组织和聚类后提供给用户[1]。
目前常见的姓名消歧方法有以下几种：部分研究人员基于数据特征进行姓名消歧[2-6]，他们使用区分度较大的特征（如人物传记、E-mail、职业等），对特征进行提取，排除无关特征，最后选择合适的算法（如聚类算法）得到消歧结果；而部分研究人员基于额外信息进行姓名消歧[7-9]，此类研究大多通过利用网络上的公开资源（如维基百科、Freebase等）构建新的规则和类别，丰富人物特征，结合社会属性进行分类达到消歧的目的；随着网络表示学习的兴起[10-15]，部分研究人员提出使用网络表示方法来进行重名消歧[16]，此研究使用文献数据集构建网络，利用学习得到网络表示的相似性进行作者重名消歧。目前这些方法通常在欧氏空间中嵌入节点，因为欧氏空间具有直观友好的特点，使得模型十分简单并且运行效率可观[17-18]。
在现实世界中，更多的网络会同时包括多种网络结构特征，如Lee等[19]表明大多数机器学习应用中的数据表示分布可能位于平滑流形而非欧氏空间上；Gulcehre等[20]提出的 HAT则使用庞加莱球流形（Poincaré manifold）设计了双曲图注意力操作。实验证明，在低维情况下，双曲模型相对于传统欧氏空间模型可以更好地学习网络表示，得到更优的节点分类和链接预测效果。这表明使用单一网络表示会造成网络表示质量的下降，从而影响网络对齐性能。因此，本文以不同空间的网络表示学习为切入点，提出了融合多空间特征的网络对齐模型（geometry interaction network alignment, GINA），基于多源网络信息，对高度重合的2个网络中的重名人员进行身份识别，并在此基础上细分为中文语境下的重名人员身份识别和英文语境下的中外论文身份识别2个实证场景，利用不同研究成果数据构建科研人员多源合作网络，对重名科研人员身份进行识别。
1. GINA模型
1.1 模型结构
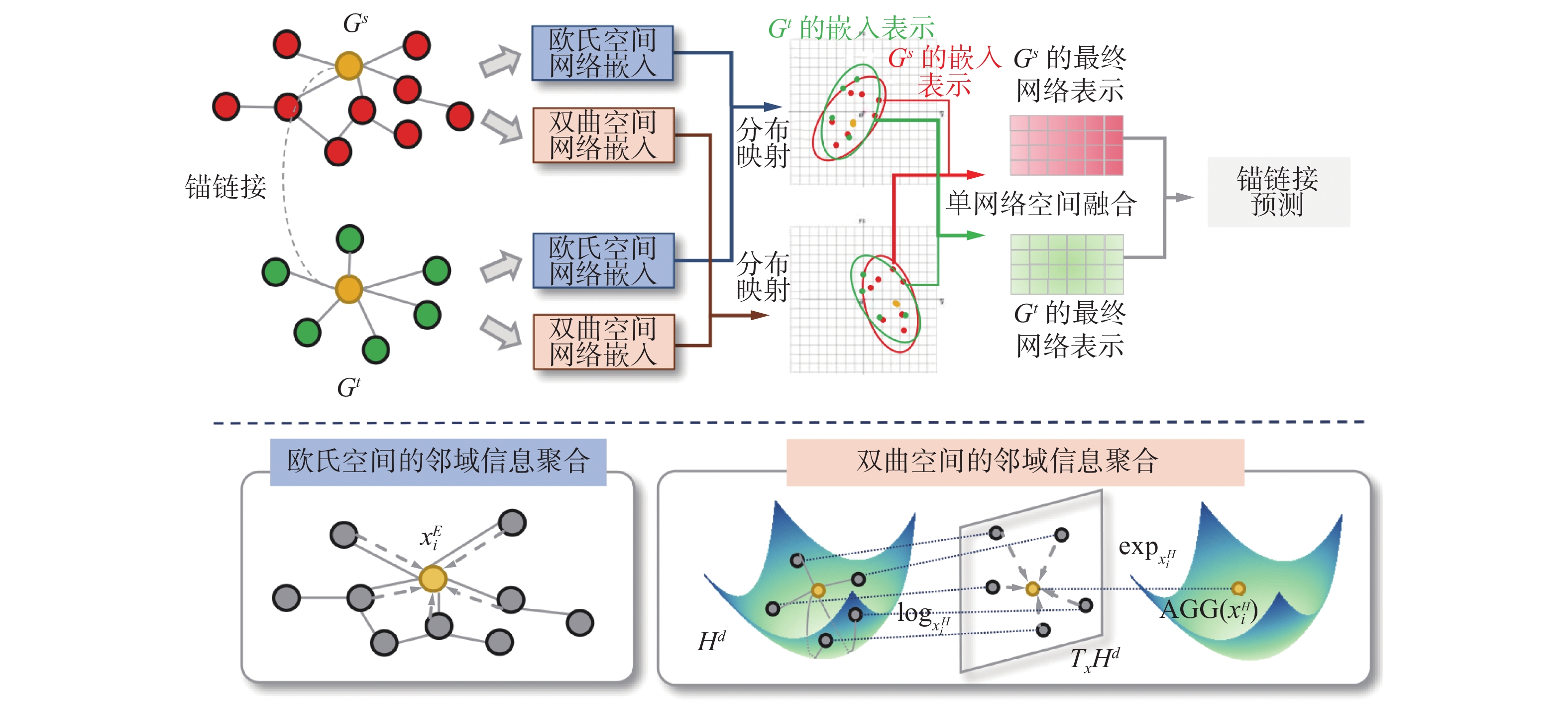
为了解决现有网络对齐方法大多使用欧氏空间网络表示学习来进行网络对齐，不能很好地捕捉现实世界网络中常见的层次结构信息，而仅使用双曲空间又无法较好地区分统一层级的边缘节点这一系列问题，本文通过不同空间的信息交互，提出了融合多空间特征的网络对齐模型GINA。GINA的整体框架如图1所示。
图 1 GINA模型整体框架Fig. 1 Overall framework of GINA model
下载:
全尺寸图片
CINA模型主要由4个部分组成：1) 首先是多空间表示学习，给定2个输入网络Gs和Gt，为了同时学习网络空间中的规则结构和层级结构特征，本模型对原始网络在不同几何空间上进行卷积来获取网络中节点的邻居信息，得到每个节点的欧氏空间嵌入表示和双曲空间嵌入表示。2) 由于Gs和Gt 2个网络的嵌入表示是在不同潜在空间分别学习的，空间分布会有差异，因此本模型实现了跨空间映射，将2个网络的欧氏空间和双曲空间的嵌入分别映射至相同几何空间的潜在空间中。3) 基于映射之后的网络嵌入，本模型对每个网络的欧氏空间网络嵌入和双曲空间网络嵌入进行融合，以促进2个几何空间之间的信息交互，达到捕捉不同结构特征的目的。4) 最后，为了完成网络对齐任务，本文使用一个多层感知机来预测任意一对来自Gs和Gt的节点对之间是否存在锚链接。
1.2 多空间表示学习
不同的几何空间对不同数据的适配程度千差万别。如欧氏空间较为平直，十分适合表示均匀规律的数据结构；而双曲空间随着曲率的变化，空间密度也会发生变化，越靠近边缘空间密度越高，适合表示树状结构或具有一定层次关系的数据。而现实世界中的网络数据往往同时包含多种结构特征，因此本文同时学习网络的欧氏空间嵌入表示和双曲空间嵌入表示来获取不同特征。通常基于网络表示学习的网络对齐方法为了使学到的网络嵌入包含节点之间的关系和网络的结构信息，都会以重建网络为目标来学习网络的嵌入表示。而双曲空间中的网络表示与传统的欧氏空间方法不尽相同，因此接下来本文将分别详细介绍欧氏空间和双曲空间的网络嵌入方法。
欧氏空间网络嵌入 每个网络可以用邻接矩阵A和节点特征矩阵X（如果节点没有特征，可以是单位矩阵）表示，X中的每一行xi表示节点的特征。对邻接矩阵A进行归一化：
$$ \tilde{\boldsymbol{A}}= {{\boldsymbol{D}}^{ - \frac{1}{2}}}({\boldsymbol{A}} + {\boldsymbol{I}}){{\boldsymbol{D}}^{ - \frac{1}{2}}} $$ (1) 式中：I为单位矩阵，D
$ \in {{\bf{R}}^{n \times n}}$ 为对角度矩阵。为了得到欧氏空间中的网络结构表示，本文需要对输入特征矩阵进行图卷积，它遵循以下前馈传递：
$$ {{\boldsymbol{Z}}^l} = \sigma (\tilde {\boldsymbol{A}} {{\boldsymbol{Z}}^{l - 1}}{\boldsymbol{W}}_E^l) $$ (2) 式中：
${\boldsymbol{W}}_E^l$ 为指定层的欧氏空间参数矩阵；$\sigma ( \cdot )$ 为一个非线性函数，如：ReLU(·) = max(0, ·)；${{\boldsymbol{Z}}^l} \in {{\bf{R}}^{n \times d}}$ 为第l层的节点嵌入矩阵，输入层Z0 = X；d为每一个节点嵌入的维度。该前馈传递通过归一化后的邻接矩阵来使每个节点获取其邻居节点的信息，从而学习网络结构。双曲空间网络嵌入 本模型想要得到网络在双曲空间中的嵌入表示，但因为欧氏空间中使用的基本操作（如矩阵的加法、乘法和非线性变换）在双曲空间中不能保持相同的性质，所以无法在双曲空间中直接进行图卷积。如双曲空间的Möbius加法不能保持交换律和结合律的性质[21]。因此，一般的做法是将操作移至“切线空间”[22-23]。
由于初始节点特征属于欧氏空间，本文首先将其映射到双曲空间。使用
${\boldsymbol{o}} = \left\{ {1,0, \cdots ,0} \right\} \in {\boldsymbol{H}^d}$ 表示${\boldsymbol{H}^d}$ 中的原点，满足${\left\langle {{\boldsymbol{o}},(0,{{\boldsymbol{x}}_i})} \right\rangle _\mathcal{L}} = 0$ ，本文将其用作执行切线空间操作的参考点。因此，(0, xi)可以被视为${\boldsymbol{{\mathcal{T}}}_0}{\boldsymbol{H}^d}$ 中的一个点，将其映射至双曲空间${\boldsymbol{H}^d}$ ：$$ {{\boldsymbol{H}}^0} = {\exp _{\boldsymbol{o}}}({\boldsymbol{X}}) $$ (3) 式中
$\exp _{\boldsymbol{o}} $ 是一个指数映射函数。因此，对于给定的网络，一个(l + 1)层GCN在双曲空间中生成节点嵌入矩阵的前馈传递为
$$ {{\boldsymbol{H}}^l} = {\sigma ^ \otimes }\left( {{\rm{AGG}}\left( {{\boldsymbol{W}}_H^l \otimes {{\boldsymbol{H}}^{l - 1}}} \right)} \right) $$ (4) 式中：
${\boldsymbol{W}}_H^l$ 为第l层的双曲空间参数矩阵，$ \otimes $ 为双曲线性变换，AGG(·)为双曲空间的邻域聚合操作，${\sigma ^ \otimes }\left( \cdot \right)$ 为双曲非线性激活函数。接下来本文将详细介绍这几个操作的定义与实现。1）双曲线性变换：欧氏空间的变换是通过矩阵向量乘法来实现的，因此本文利用对数和指数映射来实现双曲流形的线性变换。即先用对数映射将双曲空间中的点映射到切空间，然后在切空间上做线性变换，再用指数映射将切空间中的向量投影回双曲流形：
$$ {{\boldsymbol{W}}_H} \otimes {\boldsymbol{H}} = {\exp _o}({\boldsymbol{W}}{\log _{\boldsymbol{o}}}({\boldsymbol{H}})) $$ (5) 2）双曲邻域聚合：在线性变换后，模型需要通过聚合来获取邻居的结构和特征信息。如节点vi通过权值
${({w_j})_{j \in \mathcal{N}(i)}}$ 聚合来自其邻居的信息${({v_j})_{j \in \mathcal{N}(i)}}$ 。类似于双曲线性变换，对于给定的网络嵌入$({\boldsymbol{x}}_i^H,{\boldsymbol{x}}_j^H)$ ，本文通过将它们映射到原点的切线空间，使用连接和欧几里德多层感知器（multilayer perceptron，MLP）计算它们之间的权重，具体计算方式为$$ {w_{ij}} = {\rm{Softma}}{x_{j \in \mathcal{N}(i)}}\left( {{\rm{MLP}}\left( {{{\log }_{\boldsymbol{o}}}({{\boldsymbol{h}}_i})\left\| {{{\log }_{\boldsymbol{o}}}({{\boldsymbol{h}}_j})} \right.} \right)} \right) $$ (6) $$ {\rm{AGG}}({{\boldsymbol{h}}_i}) = {\exp _{{{\boldsymbol{h}}_i}}}\left( {\sum\limits_{j \in \mathcal{N}(i)} {{w_{ij}}{{\log }_{{{\boldsymbol{h}}_i}}}({{\boldsymbol{h}}_i})} } \right) $$ (7) 3）双曲非线性激活函数：本文使用非线性激活来学习非线性变换，这在GCN中很重要，可以防止多层网络崩溃为单层网络：
$$ {\sigma ^ \otimes }({\boldsymbol{H}}) = {\exp _{\boldsymbol{o}}}(\sigma ({\log _{\boldsymbol{o}}}({\boldsymbol{H}}))) $$ (8) 式中
$\sigma \left( \cdot \right)$ 为一个非线性激活函数，如ReLU(·)。损失函数 对于通过式(2)和式(4)得到的输出嵌入，本模型通过最大化正边的概率和最小化负边的概率来学习网络结构。在对输入网络进行负采样后，损失函数可以定义为
$$ \begin{gathered} {\mathcal{O}_{{\rm{embedding}}}} = - \sum\limits_{({v_i},{v_j}) \in E} {\left[ {\log \;\eta ({\boldsymbol{z}}_i^{\rm{T}}{{\boldsymbol{z}}_j}) + \log \;p({{\boldsymbol{h}}_i},{{\boldsymbol{h}}_j})} \right]}- \\ \;\;\;\;\;\;\; \sum\limits_{{v_k} \in P(v)} {\log \;\eta ( - {\boldsymbol{z}}_i^{\rm{T}}{{\boldsymbol{z}}_k})} - \sum\limits_{{v_k} \in P(v)} {\log \;\eta ( - {\boldsymbol{z}}_j^{\rm{T}}{{\boldsymbol{z}}_k})} - \\ \sum\limits_{{v_k} \in P(v)} {\log \;( - p({{\boldsymbol{h}}_i},{{\boldsymbol{h}}_k})} ) - \sum\limits_{{v_k} \in P(v)} {\log \;( - p({{\boldsymbol{h}}_j},{{\boldsymbol{h}}_k})} ) \\ \end{gathered} $$ (9) 式中：η(·)为计算边(vi , vj)存在概率的欧氏空间sigmoid函数；p(hi, hj) =
$1/({{\rm{e}}^{{d_\mathcal{L}}{{({{\boldsymbol{h}}_i},{{\boldsymbol{h}}_j})}^2} - \tau }} + 1)$ 为计算双曲空间中存在边的概率的函数；τ为超参数；P(v)为噪声分布，一般P(v) ∼$d_v^{3/4}$ ，其中${d_v}$ 为节点v的度。通过不同几何空间的图卷积网络表示学习，可以分别得到网络Gs和Gt在欧氏空间中的节点表示
${{\boldsymbol{Z}}^s}$ 、${{\boldsymbol{Z}}^t}$ 和在双曲空间中的节点表示${{\boldsymbol{H}}^s}$ 、${{\boldsymbol{H}}^t}$ 。1.3 跨空间映射
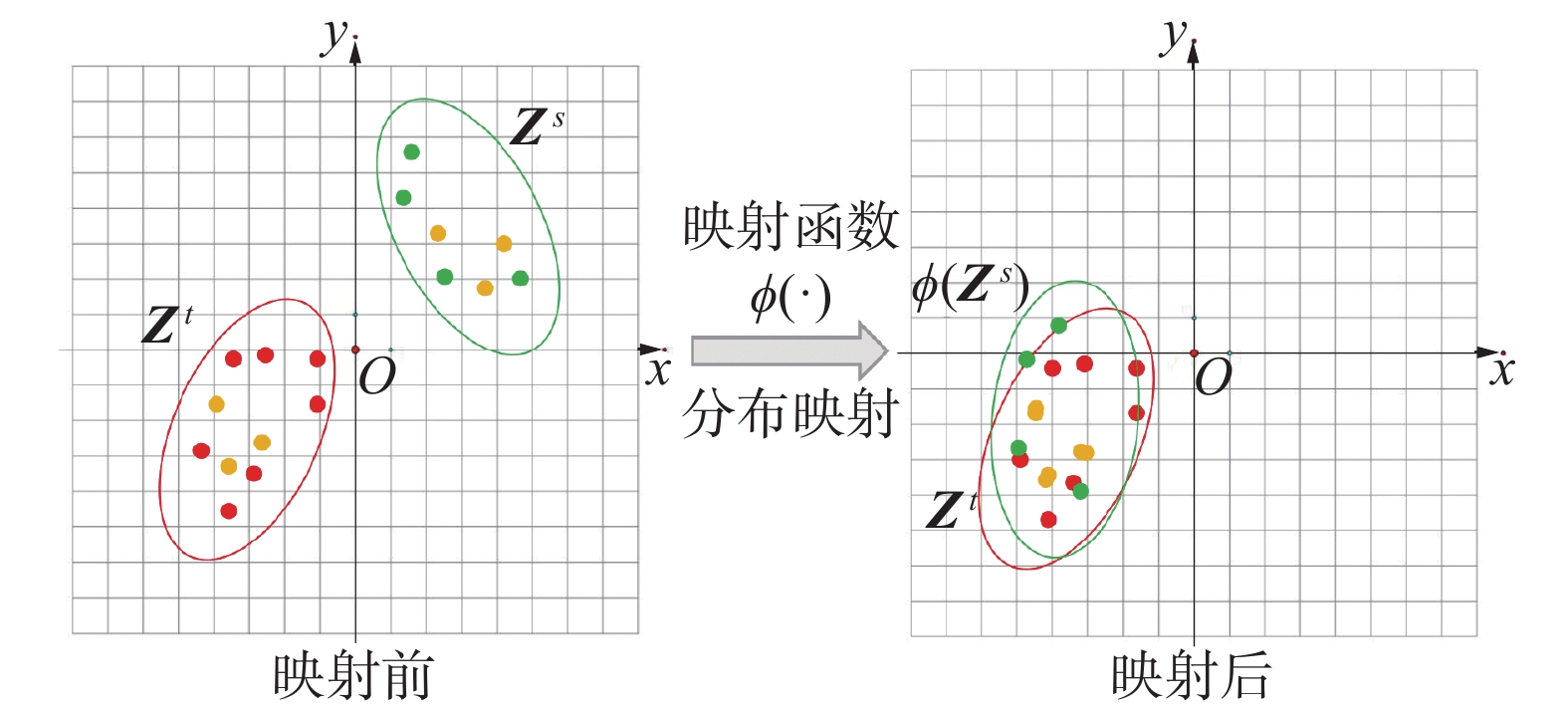
由于节点的嵌入表示
${{\boldsymbol{Z}}^s}$ 和${{\boldsymbol{Z}}^t}$ 、${{\boldsymbol{H}}^s}$ 和${{\boldsymbol{H}}^t}$ 在嵌入过程中被映射到不同的潜在空间，在语义和空间上下文方面可能会有很大的差异，网络对齐模型的常见做法是利用已知锚链接集合M，通过约束锚链接之间的距离学习一个映射函数ϕ(·)，使用ϕ(·)将其中一个网络的嵌入表示映射至另一个网络的空间分布中，如图2所示。由于本模型分别学习了欧氏空间和双曲空间的网络嵌入表示，为了降低模型映射损失，本文对欧氏空间嵌入${{\boldsymbol{Z}}^s}$ 和${{\boldsymbol{Z}}^t}$ 使用欧氏空间映射，对双曲空间嵌入${{\boldsymbol{H}}^s}$ 和${{\boldsymbol{H}}^t}$ 使用双曲空间映射，将其分别映射至相同的潜在空间。
图 2 跨空间映射Fig. 2 Cross-space mapping下载:
全尺寸图片
对于
${{\boldsymbol{Z}}^s}$ 和${{\boldsymbol{Z}}^t}$ ，本方法固定其中一个网络嵌入${{\boldsymbol{Z}}^t}$ 并且通过学习一个映射函数ϕE(·)将另一个网络嵌入${{\boldsymbol{Z}}^s}$ 映射至和${{\boldsymbol{Z}}^t}$ 相同的空间，映射函数通过使用已知的锚链接$(v_i^s,v_j^t) \in M$ 进行约束得到：$$ {\mathcal{O}_{{\rm{ME}}}} = \sum\limits_{(v_i^s,v_j^t) \in M} {{{\left\| {{\boldsymbol{z}}_j^t - {\phi _E}({\boldsymbol{z}}_i^s;{\varGamma _E})} \right\|}_F}} $$ (10) 式中：
${\left\| \cdot \right\|_F}$ 为2个网络嵌入表示之间的欧氏空间距离矩阵，ΓE为ϕE(·)的参数。同理，本文固定
${{\boldsymbol{H}}^t}$ 并将${{\boldsymbol{H}}^s}$ 映射至${{\boldsymbol{H}}^t}$ 相同的空间。不同的是，对于双曲空间网络嵌入需要使用双曲空间映射函数ϕH(·)。双曲空间映射函数类似于式(4)，并且同样通过锚链接约束，利用双曲空间的距离函数${d_\mathcal{L}}$ 得到，具体公式为$$ {\mathcal{O}_{{\rm{MH}}}} = \sum\limits_{(v_i^s,v_j^t) \in M} {{d_\mathcal{L}}({\boldsymbol{h}}_j^t - {\phi _H}(h_i^s;{\varGamma _H}))} $$ (11) 整合2个空间的损失函数可以得到跨空间映射的整体损失函数：
$$ {\mathcal{O}_M} = {\mathcal{O}_{{\rm{ME}}}} + {\mathcal{O}_{{\rm{MH}}}} $$ (12) 该步骤通过最小化锚链接之间的距离，使学习出的4个网络表示尽可能地在各自空间拥有相同的分布和语义。
1.4 跨空间融合
在得到分布映射后的多空间嵌入表示
${{\boldsymbol{Z}}^s}$ 、${{\boldsymbol{Z}}^t}$ 和${{\boldsymbol{H}}^s}$ 、${{\boldsymbol{H}}^t}$ 后，为了同时获取到欧氏空间和双曲空间嵌入网络结构表示的特点，本模型对不同几何空间的嵌入表示进行融合。由于双曲空间的嵌入表示并不能直接与欧氏空间的嵌入表示进行交互，需要将不同空间的嵌入表示进行几何空间映射，而欧氏空间映射至双曲空间会产生较大的信息损失，因此本文采用将双曲空间嵌入表示利用对数映 射映射至切线空间的方式进行空间融合。具体来说，本文分别融合了从欧氏空间和双曲空间中学习到的Gs和Gt的信息：$$ {\boldsymbol{S}} = \lambda {\log _{\boldsymbol{o}}}({{\boldsymbol{H}}^s}) + (1 - \lambda ){{\boldsymbol{Z}}^s} $$ (13) $$ {\boldsymbol{T}} = \lambda {\log _o}({{\boldsymbol{H}}^t}) + (1 - \lambda ){{\boldsymbol{Z}}^t} $$ (14) 本文在其中添加了一个超参数，即融合空间系数λ来控制不同几何空间的构成重要程度。在特征融合之后，节点嵌入不仅通过交互学习整合不同空间的几何特征，而且会保持原始空间的属性和结构信息。因此，本模型就可以得到包含规则结构特征和层级结构特征的2个网络的最终网络嵌入表示S和T。
1.5 锚链接预测
网络对齐的最终目的为预测一对节点
$(v_i^s,v_j^t), v_i^s \in {G^s},v_j^t \in {G^t}$ 是否为一个锚链接，因此本文利用已知锚链接M构造一个判别器。但由于目前已知锚节点的数量一般只是整个网络的一小部分，先前的研究也表明[24-25]现有数据仍存在一些不足，网络对齐方法不应当局限于有限的标记对齐用户。因此为了更好地训练模型，增加模型的鲁棒性，本文首先提出了一种在锚链接较少的情况下的数据补偿方法，根据以下规则构造了一些伪锚链接来提高训练效果：$$ {\rm{sim}}\left( {v_i^s,v_j^t} \right) = \frac{{N_a(v_i^s) \cap N_a(v_j^t)}}{{N(v_i^s) \cup N(v_j^t)}} $$ (15) 式中：
$N_a(v_i^s)$ 和$N_a(v_j^t)$ 分别为$v_i^s$ 和$v_j^t$ 邻居中的已知锚节点，$N(v_i^s)$ 和$N(v_j^t)$ 分别为$v_i^s$ 和$v_j^t$ 的邻居。因此，直观来说sim(·, ·)可以用来衡量$v_i^s$ 和$v_j^t$ 可能是相应锚节点的概率，通过筛选节点间的sim即可对训练节点进行补充。该规则遵循一个直观的假设，即如果不同网络中的2个节点共享更多的公共节点作为它们的邻居，那么它们很有可能成为潜在的锚节点。在数据补偿后，本文利用一个多层感知机来构造判别器：
$$ p\left( {(v_i^s,v_j^t \in Y)\left| {{{{s}}_i},{{{t}}_j}} \right.} \right) = {\rm{ReLU}}({\boldsymbol{W}}\left[ {{s_i}\left\| {{t_j}} \right.} \right] +{{ b}}) $$ (16) 式中：[· || ·]为嵌入的串联，W和b为可训练参数，
$Y = \left\{ {\left( {v_i^s,v_j^t} \right)\left| {v_i^s \in {V^s},} \right.v_j^t \in {V^t},\left( {v_i^s,v_j^t} \right) \notin {M}} \right\}$ 为潜在锚链接集。在判别器中输入节点对的嵌入信息，就可以得到二分类概率，即该节点对是否为锚链接。本文使用已知的锚链接集M和交叉熵作为损失函数来训练此判别器，训练完成后输入待预测节点对的网络嵌入就可以得到网络对齐的最终预测结果。2. 实验与结果
2.1 数据集描述
2.1.1 项目论文数据集与学位论文数据集
论文数据由自然科学基金项目成果论文数据和高校学位论文数据组成。自然科学基金项目成果论文数据爬取于国家自然科学基金基础研究知识库，由2000—2020年间包含2 052所高校及各类研究机构的763 311篇中外论文数据构成，其中包括中文论文335 140篇，英文论文428 171篇。
中文学位论文数据爬取自万方数据网，时间跨度为1980—2020年，涉及全国2 740所高校共计2 258 597条记录。
2.1.2 专利数据集
专利数据由高校中文专利数据和企业中文专利数据组成，数据均爬取自万方数据网。本文主要使用高校中文专利数据，数据时间跨度为1985—2020年，涵盖了全国2 740所高校共计4 206 687条记录。
2.2 数据预处理
本文对上述3个数据集进行数据清洗，对无效数据进行处理，如爬取字段为空、数据间夹杂额外符号以及部分不完整数据等情况，并对分隔符与存储方式等格式进行统一。
而后本文对论文数据依照语言环境进行划分，由于实证场景需要，本文将自然科学基金项目论文数据中的中文论文与英文论文进行筛选分离，同时将学位论文数据与自然科学基金项目中文论文数据合并。由此本文将上述数据重新分为3组：学位论文数据与自然科学基金项目中文论文数据、自然科学基金项目英文论文数据、高校中文专利数据，并将3组数据各自整理为相同的格式以便于构建网络使用。
2.3 网络构建
基于2.2节处理的数据集，本文针对实证场景构建了中文论文合作网络、英文论文合作网络和中文专利合作网络等3个网络。接下来本节将详细介绍这3个网络的构建流程。
2.3.1 中文论文网络与英文论文网络构建
本文基于第1组学位论文数据与自然科学基金项目中文论文数据构建中文论文合作网络Gzh。本文构建网络均为无向图，构建规则遵循：
1）在项目论文中，本文以论文作者为节点，论文合作关系为边，其中节点属性为成果数量、所属机构、学科大类、专业等，边属性为合作关系以及合作次数。
2）在学位论文中，本文以论文作者及其导师为节点，指导关系为边，与项目论文共同构建网络，网络属性与项目论文一致。
3）由于重名现象十分广泛，本文构建的所有网络均以姓名、机构以及学科共同确定一个人员实体。
通过上述规则，本文构建出中文论文合作网络Gzh，包含3 144 640个作者节点及4 660 835条合作边。
本文基于第2组自然科学基金项目英文论文数据构建英文论文合作网络Gen，基本规则与中文项目论文类似，区别在于本文统一将英文姓名处理为全小写名+姓的形式，便于人员实体定位。
通过类似规则，本文构建出英文论文合作网络Gen，包含1 300 145个作者节点及6 506 572条合作边。
2.3.2 专利网络构建
本文基于第3组高校中文专利数据构建中文专利合作网络GP-zh，构建规则与中文论文合作网络类似，以发明人为节点，发明合作关系为边，其中节点属性为发明数量、所属机构（专利权人）、专利分类等，边属性为合作关系及合作次数。
通过上述规则，本文构建出中文专利合作网络GP-zh，包含2 453 313个作者节点及13 248 894条合作边。
2.3.3 基于网络对齐构建实验数据集
本文在中文论文合作网络、英文论文合作网络和中文专利合作网络的基础上，根据实证需求，构建了2个网络对齐数据集。表1总结了数据集的信息。
表 1 网络对齐数据集的描述Table 1 Description of network alignment datasets名称 节点 边 锚链接 重名锚链接 中文论文
合作网络（北京）45 976 134 069 — — 英文论文
合作网络（北京）94 874 864 988 — — 中文专利
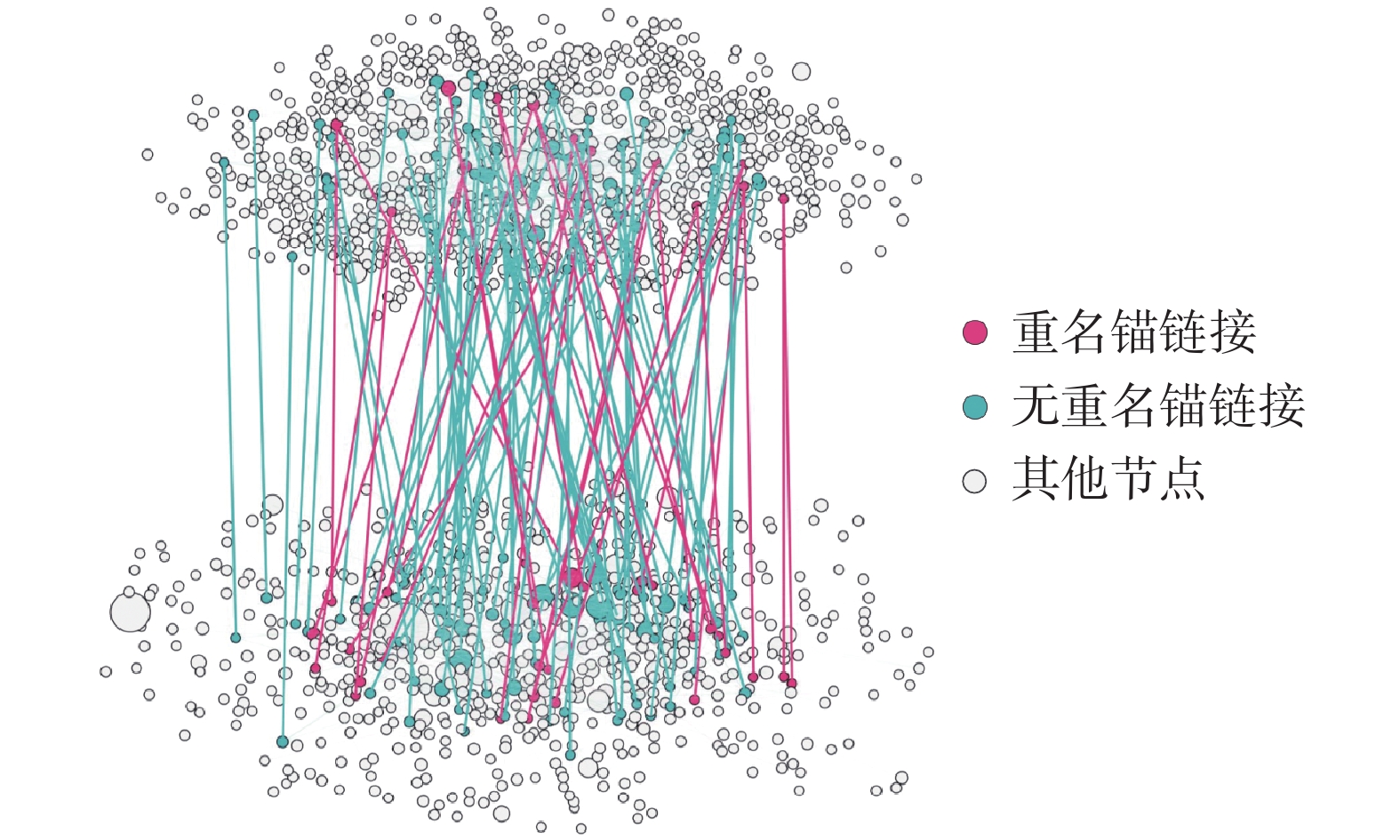
合作网络（北京）76 120 404 211 — — 论文−专利网络 — — 18 965 7 914 中文−英文网络 — — 17 222 10 204 构建论文−专利网络 论文−专利网络使用北京市区域的合作网络。经过区域划分和筛选并利用人员实体构建锚链接后，本文得到了由北京中文论文合作网络和北京中文专利合作网络构成的网络对齐数据集。该网络对齐数据集中2个网络分别包含45 976个节点、134 069条边和76 120个节点、404 211条边，同时该数据集包含18 965个锚链接，其中7 914个锚链接连接的节点为重名人员，部分网络可视化如图3所示，其中上半部分为中文论文合作网络，下半部分为中文专利合作网络。
图 3 论文−专利实证网络对齐Fig. 3 Paper-patent network alignment下载:
全尺寸图片
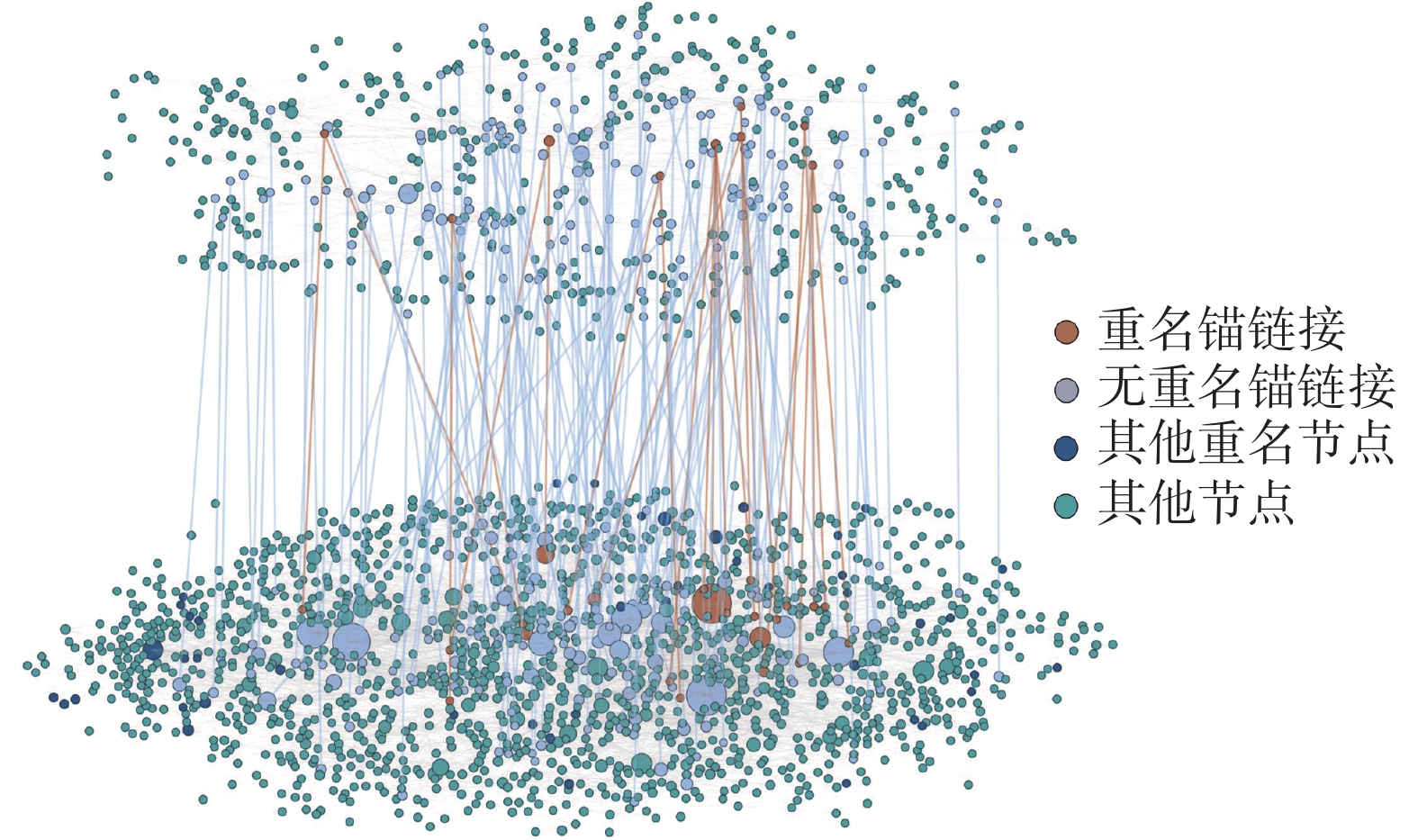
构建中文−英文网络 中文−英文网络使用北京市的中文论文合作网络和英文论文合作网络构建网络对齐数据集。通过划分整理，得到的数据集中2个网络分别包含45 976个节点、134 069条边和94 874个节点、864 988条边。在进行构建锚链接时，本文先将中文姓名转换为与英文论文中姓名格式相同的拼音。在转换过程中本文发现，有2 193个节点出现了拼音重名的现象，常见于“张伟”和“张薇”等姓名，因此本文在节点属性中标注出该节点原有中文名以用于区分。
在转换后，该数据集包含17 222个锚链接，其中10 204个锚链接连接的节点为重名人员，部分网络可视化如图4所示，其中上半部分为中文论文合作网络，下半部分为英文论文合作网络。
图 4 中文−英文实证网络对齐Fig. 4 Chinese-English network alignment下载:
全尺寸图片
2.4 实证方案
针对真实世界人员身份识别这一场景，本文提出了2种实证方案：1)基于中文论文合作网络和中文专利合作网络的网络对齐来探究中文语境下不同网络中的身份识别问题；2)基于中文论文合作网络和英文论文合作网络的网络对齐来探究英文语境下同属性网络中的中英文身份识别问题。接下来本文将分别介绍这2种实证方案。
2.4.1 重名人员身份识别
针对重名人员身份识别这一实证场景，本文利用中文论文合作网络和中文专利合作网络构建了一组网络对齐数据集，并在该数据集上使用本文提出的方法进行实验，探究网络对齐在中文重名人员身份识别中的效果。
本场景实验主要流程如下：首先将输入数据整理为邻接矩阵的形式，将数据输入模型训练，利用训练结果进行网络对齐。为了避免属性对重名人员网络对齐的影响，本实验在训练时将不使用属性信息。本文将锚链接通过是否重名进行划分，无重名人员作为训练集，重名人员作为测试集使用。为了验证重名人员身份识别效果，在锚链接预测时本文对同一姓名的多个节点进行采样，即采样锚节点为正样本、除锚节点外其他同名节点为负样本。
2.4.2 中外论文身份识别
针对中外论文身份识别这一实证场景，本文利用中文论文合作网络和英文论文合作网络构建了一组网络对齐数据集，并在该数据集上使用本文提出的方法进行实验，探究网络对齐对中英文重名人员身份识别的效果。
本节实验流程与2.4.1几乎完全相同，对锚链接依照是否重名进行划分采样，同时使用不同 λ 进行对比实验。唯一的区别是在锚链接预测时，本节使用的是拼音相同的节点采样。
2.5 实验结果分析
2.5.1 重名人员身份识别实验结果分析
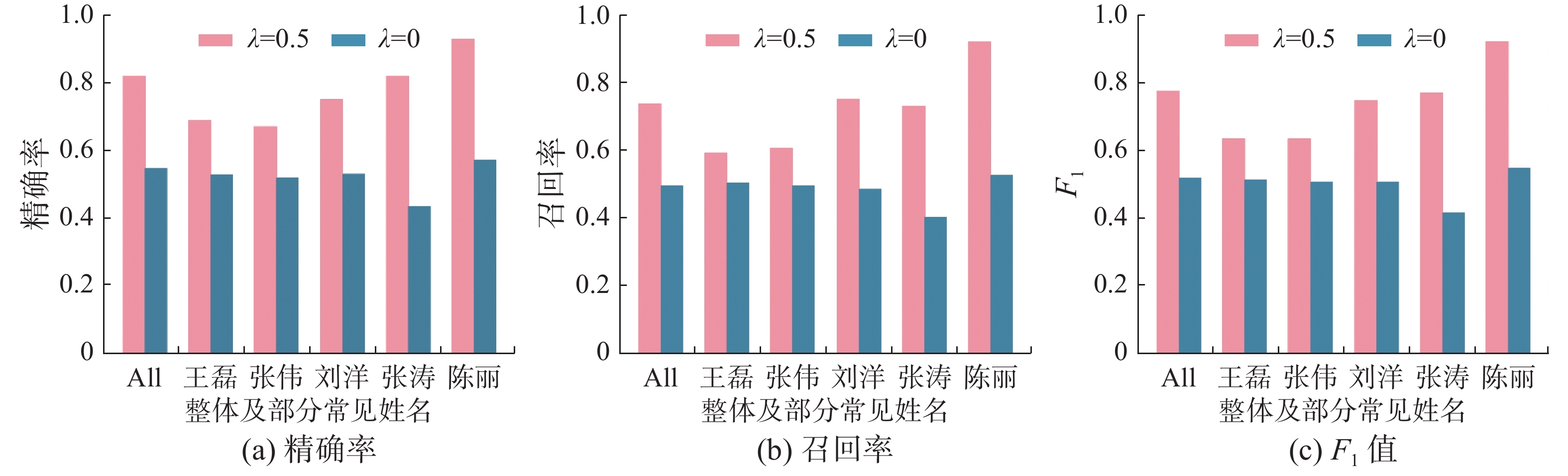
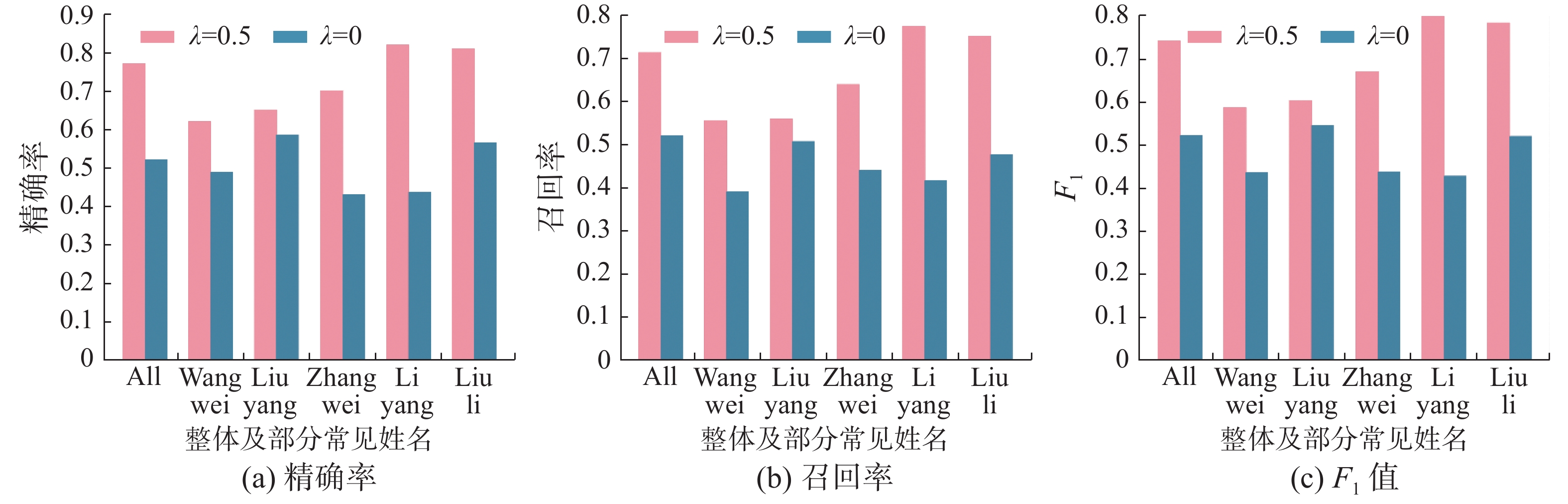
经过实验，本文得到了2种参数下GINA在整体数据和部分常见重名姓名上的实验指标，如图5所示。可以看到，本文模型在仅使用欧氏空间网络表示（λ = 0）进行网络对齐时效果较差，而融合多空间特征（λ = 0.5）的情况下不仅在整体数据上准确率提高了27.2%，在常见姓名上也有不错的表现。并且融合多空间特征网络对齐可以精准地对在层次结构中处于不同层次的人员实体进行区分，如本实验将同名的来自北京航空航天大学的王同学，来自北京交通大学的王老师和来自清华大学的王教授，在另一个网络中的数十个同名人员中精确地匹配到了对应实体。
图 5 论文−专利实证网络对齐结果Fig. 5 Result of paper-patent network alignment下载:
全尺寸图片
同时本文对重名较多的姓名“张某”进行了可视化分析，给出了热度图对比实验结果，如图6所示。图6中横坐标为中文论文合作网络中该姓名的不同人员实体，纵坐标为中文专利合作网络中该姓名的不同人员实体，热度图中的小方块颜色代表该横纵坐标对应2个人员实体的预测值，颜色越深代表该2个人员为同一实体的概率更高。由于热度图横纵坐标的人员排列顺序是一致的，因此在热度图上对角线的方块颜色越深则证明网络对齐的效果越好。其中图6(a)为融合多空间特征网络对齐（λ = 0.5），图6(b)仅使用欧氏空间网络对齐（λ = 0），可以明显看到λ = 0时对角线颜色虽然略深，但与其他节点区分度较小，混淆节点偏多；而λ = 0.5时对角线十分清晰，颜色区分度较高，且混淆节点较少，证明了融合多空间特征网络对齐对处于不同层级的人员实体具有较好的区分能力。
图 6 论文−专利实证网络对齐热力图Fig. 6 Heatmap of paper-patent empirical network alignment下载:
全尺寸图片
在进行细化探究时本文还发现，数据中有部分定义为不同实体的用户，在网络对齐结果中拥有较高的锚链接预测概率。研究发现该现象可能为如下2种原因造成：
1)该实体同时挂名于不同机构，如北京邮电大学的刘某，与同名的来自某电力公司技术研究院的刘某在实验中的锚链接预测概率为83.2%，经调查发现其二人为同一人员实体，在学术研究过程中由于身兼数职或学术合作而挂名至其他机构。
2)该实体由于毕业晋升等原因转换身份，如首都医科大学的张某和首都医科大学附属北京世纪坛医院的张某在实验中的锚链接预测概率为72.5%，调查发现其二人也为同一人员实体。此种现象在医学领域尤其显著，因为在其他领域工作的毕业生大部分不会再以研究人员的身份出现。
根据上述规律，本文对其余预测为锚链接的负样本进行了简单筛查，共找到121名具有上述2种情况的研究人员。因此本文认为，网络对齐在身份识别领域有着十分重要的作用，可以很大程度上消除数据歧义；同时网络对齐还可以帮助识别随时间变化的身份，从而追踪科研人员的职业发展路径。
2.5.2 中外论文身份识别实验结果分析
经过实验，实验结果如图7所示，图7中展示了2种 λ 参数下GINA在整体数据和部分常见重名姓名上的对齐准确率等指标。由图7可知，融合多空间特征（λ = 0.5）的GINA模型在整体数据上比单一空间准确率提高了24.9%。可以看到，虽然为了对齐英文数据集需要将汉字转换为拼音，增加了重名人员数量，提高了对齐难度，如同样来自北京科技大学的王某和汪某均出现在2个网络中，但本文方法依然可以在融合多空间特征时准确地对其进行识别。
图 7 中文−英文实证网络对齐结果Fig. 7 Result of Chinese-English network alignment下载:
全尺寸图片
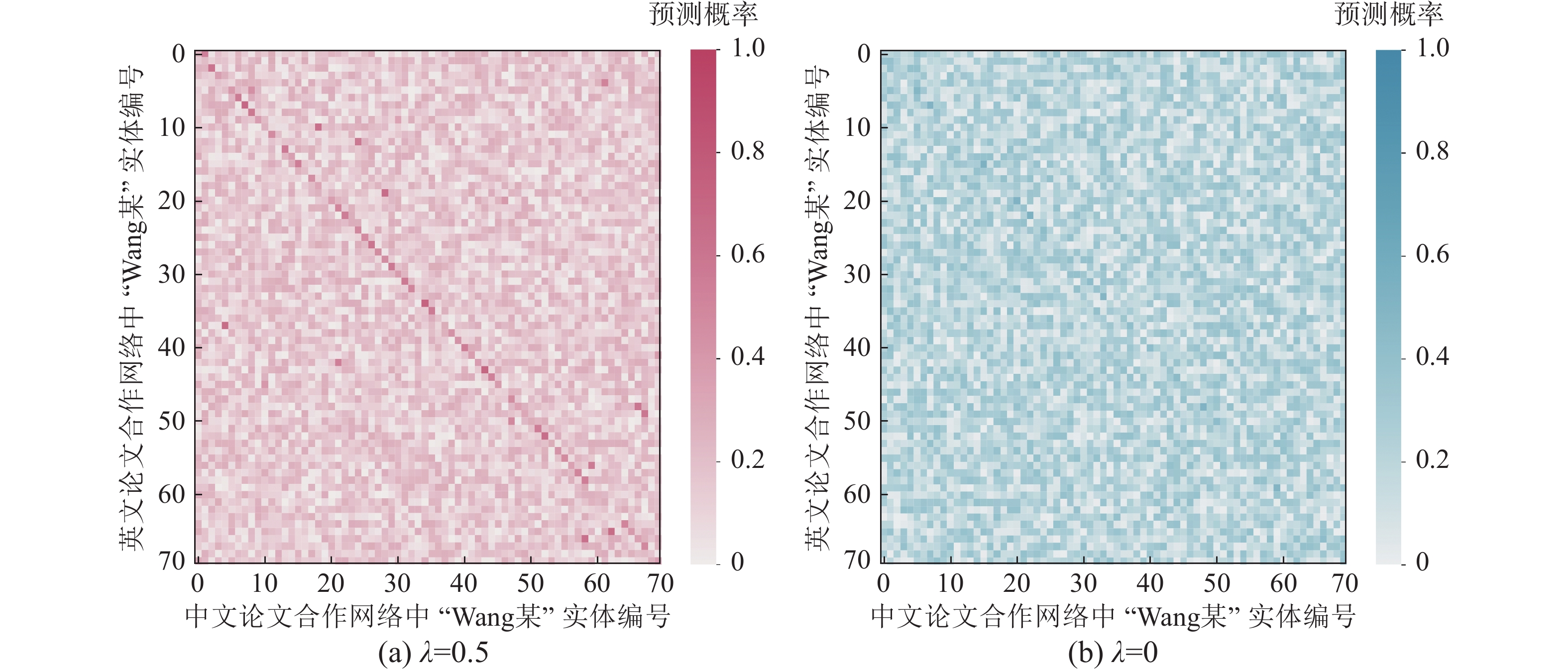
同时本文对中文−英文实证网络中重名较多的“Wang某”使用热力图进行了可视化分析，其中图8(a)为融合多空间特征网络对齐（λ = 0.5），图8(b)仅使用欧氏空间网络对齐（λ = 0）。可以看到结果与上一节类似，λ = 0时节点间区分度较低，对应节点预测准确率较差；λ = 0.5时对应节点预测值与非对应节点区分明显，对应节点预测准确率提升明显。
图 8 中文−英文实证网络对齐热力图Fig. 8 Heatmap of Chinese-English network alignment下载:
全尺寸图片
3. 结束语
本文基于网络表示学习的相关研究，提出了融合双曲空间和欧氏空间特征的网络对齐模型GINA。提出重名人员身份识别和中外论文身份识别2个实证场景，并在构建的中文论文合作网络、中文专利合作网络和英文论文合作网络的基础上，两两对齐分别构建了中文语境和英文语境的网络对齐数据集，使用GINA模型在2个场景上进行实验验证。通过对数据的分析和对实验结果的探究，证明了网络对齐可以帮助姓名消歧和身份识别，也证明了实证场景的有效性以及本文模型的适用性。
-
图 1 GINA模型整体框架
Fig. 1 Overall framework of GINA model
下载:
全尺寸图片
图 2 跨空间映射
Fig. 2 Cross-space mapping
下载:
全尺寸图片
图 3 论文−专利实证网络对齐
Fig. 3 Paper-patent network alignment
下载:
全尺寸图片
图 4 中文−英文实证网络对齐
Fig. 4 Chinese-English network alignment
下载:
全尺寸图片
图 5 论文−专利实证网络对齐结果
Fig. 5 Result of paper-patent network alignment
下载:
全尺寸图片
图 6 论文−专利实证网络对齐热力图
Fig. 6 Heatmap of paper-patent empirical network alignment
下载:
全尺寸图片
图 7 中文−英文实证网络对齐结果
Fig. 7 Result of Chinese-English network alignment
下载:
全尺寸图片
图 8 中文−英文实证网络对齐热力图
Fig. 8 Heatmap of Chinese-English network alignment
下载:
全尺寸图片
表 1 网络对齐数据集的描述
Table 1 Description of network alignment datasets
名称 节点 边 锚链接 重名锚链接 中文论文
合作网络（北京）45 976 134 069 — — 英文论文
合作网络（北京）94 874 864 988 — — 中文专利
合作网络（北京）76 120 404 211 — — 论文−专利网络 — — 18 965 7 914 中文−英文网络 — — 17 222 10 204 -
[1] 付媛, 朱礼军, 韩红旗. 姓名消歧方法研究进展[J]. 情报工程, 2016, 2(1): 53–58. doi: 10.3772/j.issn.2095-915X.2016.01.007 FU Yuan, ZHU Lijun, HAN Hongqi. A survey of name disambiguation[J]. Technology intelligence engineering, 2016, 2(1): 53–58. doi: 10.3772/j.issn.2095-915X.2016.01.007 [2] MANN G S, YAROWSKY D. Unsupervised personal name disambiguation[C]//Proceedings of the Seventh Conference on Natural Language Learning at HLT-NAACL 2003 - Volume 4. New York: ACM, 2003: 33−40. [3] BAGGA A, BALDWIN B. Entity-based cross-document coreferencing using the vector space model[C]//Proceedings of the 36th Annual Meeting of the Association for Computational Linguistics and 17th International Conference on Computational Linguistics - Volume 1. New York: ACM, 1998: 79−85. [4] 朱亮亮. 利用改进的K-means算法实现文献著者人名消歧[J]. 软件导刊, 2013, 12(5): 63–66. ZHU Liangliang. Research on name disambiguation based an improved K-means algorithm[J]. Software guide, 2013, 12(5): 63–66. [5] 肖桐, 朱靖波. 基于多阶段的中文人名消歧聚类技术的研究[C]//第六届全国信息检索学术会议论文集. 牡丹江, 2010: 323−331. XIAO Tong, ZHU Jingbo. A multi-stage clustering approach to Chinese person name disambiguation[C]//The 6th China Conference on Information Retrieval, Mudanjiang: Chinese Information Processing Society of China, 2010: 316−324. [6] 马莹莹, 吴幼龙, 唐华. 基于特征编码和图嵌入的姓名消歧方法[J]. 中国科学院大学学报, 2022, 39(3): 360–368. MA Yingying, WU Youlong, TANG Hua. Name disambiguation based on encoding attributes and graph topology[J]. Journal of University of Chinese Academy of Sciences, 2022, 39(3): 360–368. [7] BUNESCU R, PASCA M. Using encyclopedic knowledge for named entity disambiguation [C]//Conference of the European Chapter of the Association for Computational Linguistics. Trento: DBLP , 2006: 9−16. [8] HAN Xianpei, ZHAO Jun. Named entity disambiguation by leveraging wikipedia semantic knowledge[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management. New York: ACM, 2009: 215−224. [9] HAN Xianpei, ZHAO Jun. Web personal name disambiguation based on reference entity tables mined from the web[C]//Proceedings of the Eleventh International Workshop on Web Information and Data Management. New York: ACM, 2009: 75−82. [10] MAN Tong, SHEN Huawei, LIU Shenghua, et al. Predict anchor links across social networks via an embedding approach[C]//Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence. New York: ACM, 2016: 1823−1829. [11] LIU Li, CHEUNG W K, LI X, et al. Aligning users across social networks using network embedding[C]//Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York: AAAI Press, 2016: 1774–1780. [12] ZHOU Fan, LIU Lei, ZHANG Kunpeng, et al. DeepLink: a deep learning approach for user identity linkage[C]//IEEE INFOCOM 2018 - IEEE Conference on Computer Communications. Piscataway: IEEE, 2018: 1313−1321. [13] LIANG Zhehan, RONG Yu, LI Chenxin, et al. Unsupervised large-scale social network alignment via cross network embedding[C]//Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM, 2021: 1008−1017. [14] DERR T, KARIMI H, LIU Xiaorui, et al. Deep adversarial network alignment[C]//Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: ACM, 2021: 352−361. [15] ZHANG Si, TONG Hanghang, JIN Long, et al. Balancing consistency and disparity in network alignment[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM, 2021: 2212−2222. [16] 余传明, 钟韵辞, 林奥琛, 等. 基于网络表示学习的作者重名消歧研究[J]. 数据分析与知识发现, 2020, 4(S1): 48–59. YU Chuanming, ZHONG Yunci, LIN Aochen, et al. Author name disambiguation with network embedding[J]. Data analysis and knowledge discovery, 2020, 4(S1): 48–59. [17] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2016−09−09)[2022−09−15]. https://arxiv.org/abs/1609.02907.pdf. [18] HAMILTON W L, YING R, LESKOVEC J. Inductive representation learning on large graphs[EB/OL]. (2017−06−07)[2022−09−15]. https://arxiv.org/abs/1706.02216.pdf. [19] LEE J M. Smooth manifolds[M]. Introduction to Smooth Manifolds. New York: Springer New York, 2013: 1−31. [20] GULCEHRE C, DENIL M, MALINOWSKI M, et al. Hyperbolic attention networks[EB/OL]. (2018−05−24)[2022−09−15]. https://arxiv.org/abs/1805.09786.pdf. [21] PENG Wei, VARANKA T, MOSTAFA A, et al. Hyperbolic deep neural networks: a survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 44(12): 10023–10044. [22] CHAMI I, YING R, RÉ C, et al. Hyperbolic graph convolutional neural networks[J]. Advances in neural information processing systems, 2019, 32: 4869–4880. [23] LIU Qi, NICKEL M, KIELA D. Hyperbolic graph neural networks[C]//Proceedings of the 33rd International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc. , 2019: 8230−8241. [24] CHEN Hongxu, YIN Hongzhi, SUN Xiangguo, et al. Multi-level graph convolutional networks for cross-platform anchor link prediction[C]//Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020: 1503−1511. [25] ZHENG Conghui, PAN Li, WU Peng. CAMU: cycle-consistent adversarial mapping model for user alignment across social networks[J]. IEEE transactions on cybernetics, 2022, 52(10): 10709–10720. doi: 10.1109/TCYB.2021.3064294
