Density peaks clustering based on shared nearest neighbor for manifold datasets
-
摘要: 流形数据由一些弧线状或环状的类簇组成，其特点是同一类簇的样本间距离差距较大。密度峰值聚类算法不能有效识别流形类簇的类簇中心且分配剩余样本时易引发样本的连续误分配问题。为此，本文提出面向流形数据的共享近邻密度峰值聚类(density peaks clustering based on shared nearestneighbor for manifold datasets, DPC-SNN)算法。提出了一种基于共享近邻的样本相似度定义方式，使得同一流形类簇样本间的相似度尽可能高；基于上述相似度定义局部密度，不忽略距类簇中心较远样本的密度贡献，能更好地区分出流形类簇的类簇中心与其他样本；根据样本的相似度分配剩余样本，避免了样本的连续误分配。DPC-SNN算法与DPC、FKNN-DPC、FNDPC、DPCSA及IDPC-FA算法的对比实验结果表明，DPC-SNN算法能够有效发现流形数据的类簇中心并准确完成聚类，对真实以及人脸数据集也有不错的聚类效果。Abstract: Manifold data consists of some arc-shaped or ring-shaped clusters, which are characterized by a large distance between samples of the same cluster. Density peaks clustering (DPC) algorithm cannot effectively identify the cluster centers of the manifold clusters and is prone to the problem of continuous misallocation of samples when allocating the remaining samples. To solve these problems, density peaks clustering based on shared nearest neighbor (DPC-SNN) algorithm for manifold data is proposed in this paper. A sample similarity definition based on shared nearest neighbor is proposed to make the similarity between samples of the same manifold cluster as high as possible; Then, the local density is defined based on the above similarity without ignoring the density contribution of samples farther from the cluster centers, which can better distinguish the cluster centers from other samples of manifold cluster; And then, the remaining samples are allocated according to the similarity of samples to avoid continuous misallocation of samples. The comparative experimental results between DPC-SNN and other algorithms of DPC, FKNN-DPC, FNDPC, DPCSA and IDPC-FA show that DPC-SNN can effectively find the cluster centers of manifold data and accurately complete clustering, and has a good clustering effect on real and faces datasets.
-
聚类算法是在不存在先验知识的前提下，依据类簇内样本相似度尽可能大而类簇间的样本相似度尽可能小的原则，将样本划分成多个类簇。迄今为止，聚类算法已被广泛应用于社区检测[1]、生物信息[2]、网络安全[3]、图像处理[4]、模式识别[5]等多种不同领域。
聚类算法问世至今，已有多种聚类算法被陆续提出。这些聚类算法大致分为[6-11]：基于划分的聚类算法、基于密度的聚类算法、基于代表点的聚类算法、基于层次的聚类算法、基于网格的聚类算法、基于图论的聚类算法、基于模型的聚类算法等。其中，基于划分和基于密度的聚类算法由于原理简单、聚类效果好而广受欢迎。K-means算法[12]是经典的基于划分的聚类算法，通过迭代寻找类簇中心，完成最优子类簇划分。K-means算法擅长处理接近正态分布的数据集且对大规模数据集具有良好的适应性，但其初始类簇中心需随机选择、参数K值要人工确定且聚类结果受离群点影响较大。基于密度的噪声应用空间聚类(density based spatial clustering of applications with noise, DBSCAN)算法[13]是一种基于密度的聚类算法，通过空间分布密度有效识别出各种形状的类簇。DBSCAN算法可有效滤除噪音并准确聚类高密度区域的类簇，然而其对参数敏感，不适应密度分布不均等复杂形态数据且不适合大规模数据集聚类。
Rodriguezalex等[14]提出了通过快速搜索和寻找密度峰值聚类(clustering by fast search and find of density peaks, DPC)的方法，简称密度峰值聚类算法。DPC算法通过样本的局部密度和相对距离绘制决策图选择类簇中心，然后通过特定分配策略将剩余样本依次分配给类簇中心所在类簇，从而完成聚类。DPC算法可通过决策图确定类簇个数、找出并排除离群点，可识别任意维度和形状类簇。然而，DPC算法存在如下缺点：1）算法的局部密度定义仅考虑了样本的密度因素而忽略空间分布因素，难以找到复杂数据集的类簇中心；2）在分配剩余样本时，易引发“多米诺骨牌”效应，即一旦某一个样本分配错误，此错误会波及该样本之后的其余样本。
针对DPC算法局部密度存在的问题，Xie等[15]提出了一种基于模糊加权K近邻的密度峰值检测和点赋值的鲁棒聚类 (robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors, FKNN-DPC)算法。FKNN-DPC算法采用基于K近邻的局部密度定义取代基于截断距离的密度定义，缓解了算法参数选取对聚类结果的影响。Du等[16]提出一种基于模糊邻域的鲁棒密度峰值聚类算法(robust density peaks clustering algorithm using fuzzy neighborhood, FNDPC)。FNDPC提出基于模糊邻域的局部密度定义方式，旨在识别任意形状、密度、空间分布和规模数据集的类簇中心，在保持DPC算法高效性的前提下提升了算法鲁棒性。Zhao等[17]提出基于萤火虫算法的改进密度峰值聚类(improved density peaks clustering based on firefly algorithm, IDPC-FA)算法。IDPC-FA算法通过加权因子平衡DPC算法中截断核和高斯核的影响，重新定义了局部密度并通过萤火虫算法科学地选取参数，有效消除了DPC算法面对不同规模数据集时需要更替局部密度定义以及算法参数需要人工指定这2个缺点，极大地提升了算法的鲁棒性。
针对DPC算法分配策略存在的不足，Xu等[18]提出类簇合并策略的密度峰值聚类(feasible density peaks clustering algorithm with a merging strategy, FDPC) 算法。FDPC在分配剩余样本时，通过DPC算法聚类出一定数量的微簇，之后根据各微簇之间的反馈值递归合并微簇，得出最终的聚类结果。Yu等[19]提出基于加权局部密度序列和最近邻分配的密度峰值聚类(density peaks clustering based on weighted local density sequence and nearest neighbor assignment, DPCSA)算法。DPCSA算法采用2阶段动态分配策略，利用最近邻动态表提高效率。Xu等[20]提出基于累积近邻度及微簇合并的密度峰值聚类(density peaks clustering based on cumulative nearest neighbor degree and micro cluster merging, DPC-CNND-MCM)算法。该算法将改进后的图形度连接引入DPC算法，缓解DPC算法引发的“多米诺骨牌”效应。赵嘉等[21]提出基于相互邻近度的密度峰值聚类(density peaks clustering based on mutual neighbor degree, DPC-MND)算法。为应对密度分布不均数据集，该算法引入K近邻思想定义样本的相互邻近度并据此邻近度重新制定样本的分配策略，解决了数据密集程度不统一时聚类效果不理想的问题。上述改进算法都在不同程度上提高了DPC的聚类精度，但对复杂数据效果仍然不佳。
流形数据由一些弧线状或环状的类簇组成，生活中处处有它的影子，如图像分割、Web分析等[22]。流形数据中同簇样本间的距离跨度较大，在确定类簇中心时，由于DPC算法通过核函数将样本间基于欧氏距离的相似度转化成局部密度，而流形数据同一类簇样本间的欧氏距离可能相差极大，因此仅基于欧氏距离的相似度无法使得同一类簇样本间的相似度尽可能高，所以DPC算法的局部密度定义方式不适应流形数据。类簇中心的选择与局部密度高度相关，故DPC算法难以找到流形数据正确的类簇中心。在分配剩余样本时，由于流形数据的类簇中心与簇中部分样本之间距离相距甚远，而根据DPC算法的分配策略，它在确定类簇中心后会将剩余样本依次就近分配给密度较大的样本且是链式分配，此举会造成大量样本的分配错误。
为弥补DPC算法处理流形数据的不足，本文提出一种面向流形数据的共享近邻密度峰值聚类(density peaks clustering based on shared nearest neighbor for manifold datasets, DPC-SNN)算法。首先，提出了基于共享近邻的样本相似度定义规则，使同一类簇中的样本相似度尽可能高；其次，基于上述相似度重新定义局部密度，加强与类簇中心有共享近邻的样本对其密度贡献且不忽略距类簇中心较远样本的贡献，更好地识别出类簇中心；最后，通过样本相似度构造样本相似度矩阵并通过该矩阵完成剩余样本的分配。实验结果表明，DPC-SNN算法在流形数据集以及真实数据集上均表现良好。
1. 密度峰值聚类算法
密度峰值聚类算法基于如下假设：类簇中心被局部密度较低的邻居样本环绕且类簇中心之间相对距离较远。DPC算法的聚类过程可概括为：首先，计算样本的局部密度
${\rho _i} $ 和相对距离$ {\delta _i}$ ；其次，根据局部密度和相对距离绘制决策图并依据决策图选择类簇中心；最后，将剩余样本依次分配给距离其最近且密度较高的样本所在类簇，完成聚类。DPC算法中局部密度定义为
$$ \rho_i=\sum_{i \neq j} \chi\left(d_{i j}-d_c\right), \quad \chi(x)= \begin{cases}1 & x<0 \\ 0 & x \geqslant 0\end{cases} $$ (1) $$\rho_i=\sum_{i \neq j} \exp \left(-\frac{d_{i j}^2}{d_c^2}\right) $$ (2) 式中：
${d_{ij}}$ 为样本$ {x_i} $ 与样本$x_j$ 之间的欧氏距离；$d_c$ 为样本的截断距离，此参数需提前指定。式(1)为基于截断核的局部密度定义，${\rho_i}$ 的值为与样本${x_i}$ 的距离小于截断距离${d_c}$ 的样本个数之和。在此定义下，只有与样本${x_i}$ 距离较近的样本会对其产生密度贡献，而远离样本$ {x_i} $ 的样本对其密度贡献为0。此公式适用于大规模数据。式(2)为基于高斯核的局部密度定义，在此定义下，其余样本对样本$ {x_i} $ 的密度贡献随距离递减，但远离样本$ {x_i} $ 的样本对其仍有密度贡献。此公式适用于小规模数据。DPC算法的相对距离定义为
$$ {\delta _i} = \mathop {\min }\limits_{j:{\rho _j} > {\rho _i}} \left( {{d_{ij}}} \right) $$ (3) $$ {\delta _i} = \mathop {\max }\limits_j \left( {{d_{ij}}} \right) $$ (4) 计算完成后，以
$ {\rho _i} $ 作为横坐标，${\delta _{{i}}}$ 作为纵坐标，建立决策图，选取$ {\rho _i} $ 和${\delta _{{i}}}$ 均较大的样本作为类簇中心。在聚类中心选出后，根据样本的局部密度
$ {\rho _i} $ 和相对距离${\delta _{{i}}}$ ，将剩余样本依次分配给与其距离最近且局部密度更高的样本所在类簇。2. DPC-SNN算法
样本与其大部分邻居往往归属同一类簇，故可通过其邻居的局部信息更好地定义样本局部密度。特别地，样本与其邻居间的共享区包含较多的局部信息，能更准确地反映样本的分布情况。同时，不合适的相似度矩阵往往会引发分配连带错误。样本间共享区对样本相似度和局部密度定义都有着极为重要的作用，故可通过样本与其邻近样本定义样本间的相似度和样本的局部密度。
2.1 共享近邻的样本相似度
本文利用样本近邻信息定义样本间的相似度，使用相似度描述样本间的密度差异，从而确定样本的局部密度。样本的近邻可分为共享区和非共享区。共享区为两样本K近邻的交集，其余部分即非共享区，两区域在不同程度上反映样本间的相似程度，但共享区中样本更能反映样本相似性，故DPC-SNN算法通过共享区样本数计算样本相似度。
定义1 K近邻。升序排列数据集
$ D $ 中样本$ {x_i} $ 与剩余样本距离，前K个样本即样本$ {x_i} $ 的K近邻集合，第K个样本与样本$ {x_i} $ 的距离记作$ {d_{ik}} $ ，定义为$${\rm{ KNN}}({x_i}) = \{ {x_j} \in {\boldsymbol{D}}|{d_{ij}} \leqslant {d_{ik}}\} $$ (5) 定义2 共享近邻。样本
$ {x_i} $ 与${x_{{j}}}$ 的共享近邻集合定义为$$ {\rm{SNN}}({x_i},{x_j}) = {\rm{KNN}}({x_i}) \cap {\rm{KNN}}({x_j}) $$ (6) 定义3 样本相似度
$ {w_{ij}} $ 。对于样本$ {x_i} $ 和${x_{{j}}}$ ，其相似度$ {w_{ij}} $ 定义为$$ {w_{ij}} = {{\rm{e}}^{ - d_{ij}^2}} \times {{\rm{e}}^{\frac{{|{\rm{SNN}}({x_i},{x_j})|}}{k}}} $$ (7) 式中：
$|{\rm{SNN}}({x_i},{x_j})|$ 为样本$ {x_i} $ 和${x_{{j}}}$ 的共享近邻个数，共享近邻个数越多，数据点越相似，故式(7)增强了样本与其共享近邻样本的相似度。指数函数${{\rm{e}}^x}$ 可避免取值过大影响后续计算。2.2 共享近邻的局部密度
定义4 共享近邻的局部密度。对样本
$ {x_i} $ ，其局部密度定义为$$ {\rho _i} = \sum\limits_{j \ne i}^{} {\left( \begin{gathered} \alpha ({d_{ik}} - {d_{ij}}){w_{ij}} + \alpha ({d_{{i_{{\rm{ave}}}}}} - {d_{ij}}){{\rm{e}}^{\frac{{ - {d_{ij}}^2}}{{{{(j - k)}^2}}}}} \end{gathered} \right)} $$ (8) 式中卡方函数定义为
$$ \alpha (x) = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \geqslant 0 \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x < 0 \\ \end{gathered} \right. $$ (9) 式中
${d_{{i_{{\rm{ave}}}}}}$ 的计算公式为$$ {d_{{i_{{\rm{ave}}}}}} = \frac{{\displaystyle\sum\limits_{{x_j} \notin {\rm{KNN}}\left( {{x_i}} \right)}^{} {{d_{ij}}} }}{{N - K}} $$ (10) 式中：
$ {d_{ik}} $ 为样本$ {x_i} $ 到其第$ k $ 个近邻点之间的欧氏距离，${d_{{i_{{\rm{ave}}}}}}$ 为样本$ {x_i} $ 与其K近邻点之外的其余样本间距离之和的平均值，$ N $ 为样本规模，$ K $ 为样本$ {x_i} $ 的K近邻个数。式(8)中，以加号为界可将公式视为2部分。第1部分计算样本
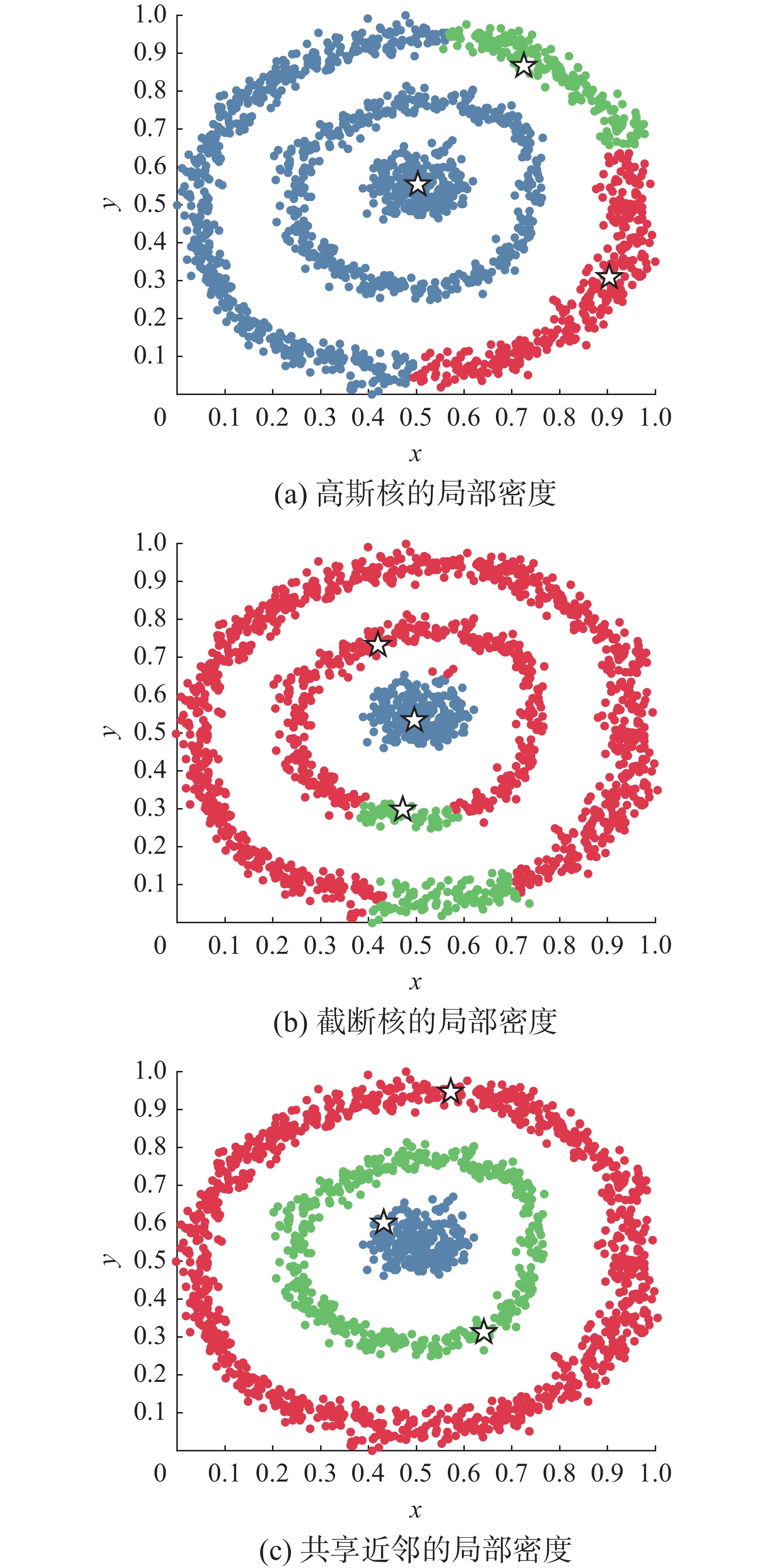
$ {x_i} $ 的K近邻范围内样本对$ {x_i} $ 的密度贡献，由于拥有共享近邻的样本更可能属于同一类簇，所以加强与类簇中心有共享近邻的样本对其密度贡献，增大类簇中心与其他样本的密度差异，能更好地找到类簇中心。第2部分计算其余样本对$ {x_i} $ 的密度贡献，由于流形数据中一些样本距类簇中心较远，故不应忽略这些样本对其密度贡献，样本对类簇中心的密度贡献随距离增大而减小，当样本距类簇中心过远时令其密度贡献为0，可以有效消除离群点的影响。在Circle数据集上作对比实验，验证高斯核、截断核和共享近邻3种方式定义的局部密度对类簇中心选取的影响，结果如图1所示。
图 1 不同局部密度在Circle数据集上获得的类簇中心Fig. 1 Cluster centers obtained from the Circle dataset through different local densities
下载:
全尺寸图片
Circle数据集由2个环形合围着一个团状类簇，共3个类簇。由于截断核的局部密度仅与截断范围内的样本个数相关，而高斯核的局部密度几乎不考虑距离样本较远的其他样本的密度贡献，故这2种局部密度只能较好地识别类似球形簇的类簇中心。可是流形数据中存在一些距离类簇中心较远的样本，故前述2种局部密度定义方式都不适合流形数据。正如图1(a)和(b)所示，类簇中心用空心五角星表示，这2种方式仅识别出2个正确的类簇中心。反观图1(c)，共享近邻的局部密度能准确识别出3个类簇的类簇中心，为之后正确分配剩余样本打好了基础。
2.3 共享近邻的分配策略
DPC 算法的分配策略只考虑样本密度与距离之间的关系，在识别类簇中心后，会将剩余样本依次就近分配给密度较大的样本并且是链式分配，而流形数据的同一类簇中的样本之间往往相距较远，故DPC算法会造成大量样本的分配错误。为此，借助2.1节提出的共享近邻的样本相似度公式计算样本间的相似度，构建样本相似度矩阵，据此进行样本分配。DPC-SNN算法的样本分配过程如下：首先，通过决策图自动选择类簇中心并标为已处理样本；其次，将与已处理样本相似度最高的剩余样本分配给对应已处理样本所在类簇，循环至剩余样本与已处理样本的相似度皆为0或不存在剩余样本；最后，若存在剩余样本，则采用 DPC 算法分配策略分配。
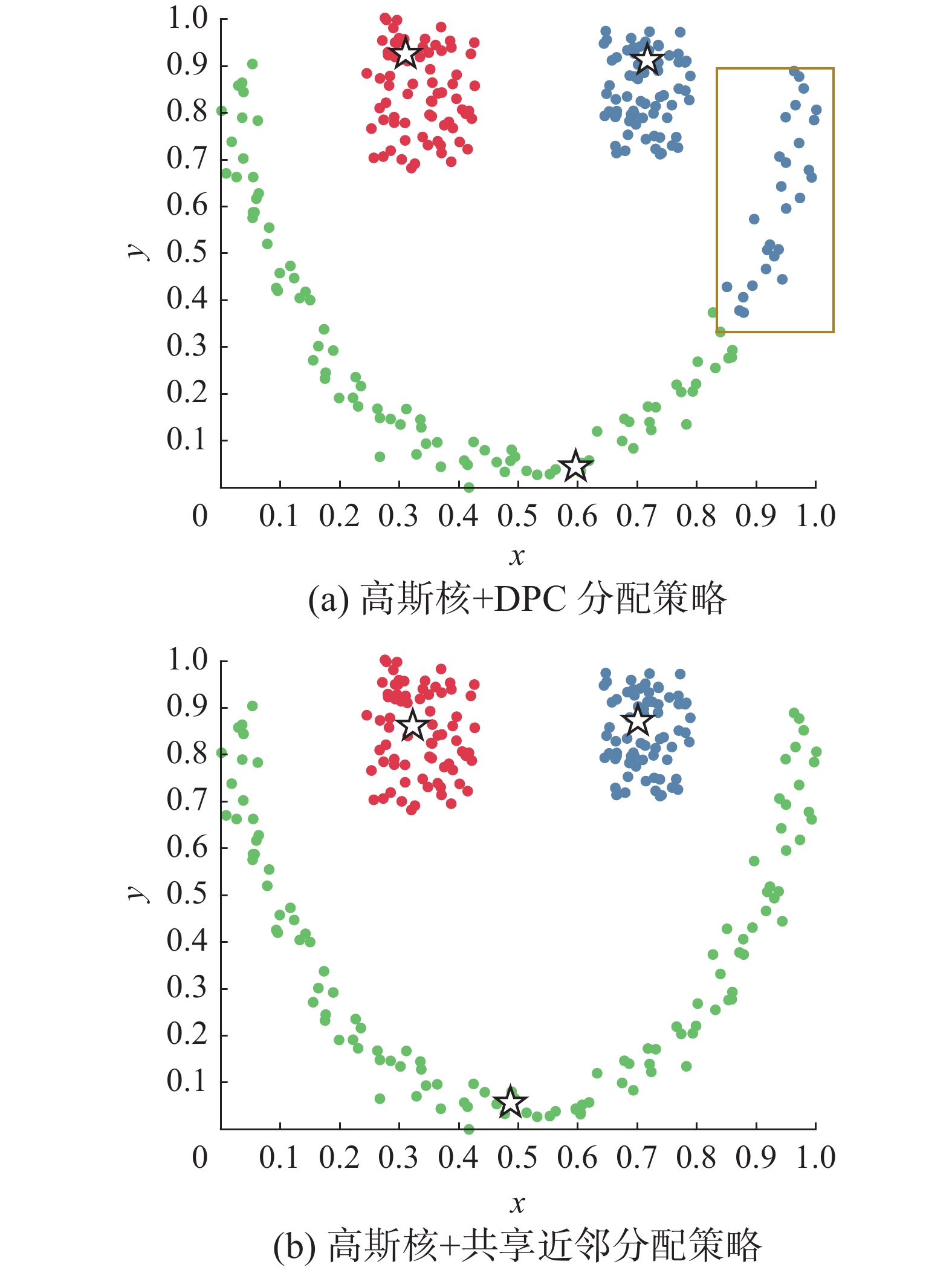
为验证共享近邻的分配策略的有效性，采用高斯核的局部密度分别结合DPC和DPC-SNN算法的分配策略在LineBlobs数据集上进行对比实验，结果见图2。LineBlobs数据集的形状为一个大的半弧形包裹着2个较小的矩形，半弧形和2个矩形各自为一个类簇，共3个类簇。图2(a)为高斯核与DPC算法分配策略结合的聚类结果，可以看到DPC算法通过高斯核计算的局部密度找到了正确的密度中心点，但由于DPC分配策略的局限性，错将半弧形右上方稀疏区域的样本分配给了图中密集的上方右侧矩形所在类簇，导致未能准确归类样本。上述错误发生的原因是：按照DPC算法的分配策略，在找到类簇中心后，会将后续样本就近分配给密度更大的样本所在类簇。具体来说，DPC算法对图2(a)上方右侧框线中样本进行分配时，由于上方右侧矩形类簇的样本距橙框中样本更近，故DPC算法将框线中样本错误地分配给了上方右侧矩形类簇，而不是下方弧形类簇。而如图2(b)所示，本文所提出的共享近邻分配策略在分配样本时克服了上述问题，完美聚类LineBlobs数据集。
图 2 高斯核与2种分配策略组合在LineBlobs数据集上的聚类结果Fig. 2 Clustering results of gaussian kernel and two allocation strategies on LineBlobs dataset下载:
全尺寸图片
2.4 DPC-SNN算法步骤
DPC-SNN算法的流程如下：
输入 数据集
$ D $ ，样本的K近邻参数$ k $ 。输出 最终聚类结果，样本类簇标签。
1) 数据预处理，数据归一化，构造距离矩阵；
2) 利用式(7)计算样本间基于共享近邻的样本相似度并构造相似度矩阵；
3) 利用式(5)~(8)计算样本
$ {x_i} $ 的局部密度$ {\rho _i} $ ，利用式(3)~(4)计算样本$ {x_i} $ 的相对距离$ {\delta _i} $ ；4) 构造决策图，选取类簇中心并标为已处理样本；
5) 将已处理样本相似度最高的剩余样本分配给对应已处理样本所在类簇；
6) 若其余样本与已处理样本相似度均为0，转至步骤7)；否则，转至步骤5)；
7) 若存在剩余样本，则通过DPC算法分配剩余样本；否则结束。
3. 实验结果与分析
3.1 实验设置
本文将DPC-SNN算法与DPC、FKNN-DPC、FNDPC、DPCSA和IDPC-FA算法在8个流形数据集和10个真实数据集上进行实验，验证DPC-SNN算法的性能。数据集信息如表1、表2所示。为更直观观察实验结果，流形数据集均采用二维数据，数据量从266~1897个样本不等。真实数据集相比于流形数据集类簇数更多并且维数也更高，更能检验算法性能。
表 1 流形数据集的基本信息Table 1 Basic information of manifold datasets数据集 样本数 维数 类簇数 Lineblobs 266 2 3 Pathbased 300 2 3 Spiral 312 2 3 Jain 373 2 2 Sticks 512 2 4 Db 630 2 4 Cmc 1 002 2 3 Circle 1 897 2 3 表 2 真实数据集的基本信息Table 2 Basic information of real datasets数据集 样本数 维数 类簇数 Iris 150 4 3 Wine 178 13 3 Seeds 210 7 3 Ecoli 336 8 8 Ionosphere 351 34 2 Libras 360 90 15 WDBC 569 30 2 Segmentation 2310 20 7 算法的参数调校细节如下：DPC算法的截断距离选取的比率以0.1%为步长在0.1%~5%调校；DPC-SNN和FKNN-DPC算法的近邻参数K以1为步长在1~50调校；FNDPC算法的参数以0.01为步长在0.01~1调校，其余算法无需调参。本文实验采用的硬件环境为Intel(R) Core(TM) i5-9400F CPU@2.90 GHz、16G RAM、Windows 10的64位操作系统。为评价聚类结果，本文采用调整互信息( adjusted mutual iformation, AMI)、调整兰德系数( adjusted rand index, ARI)[23]以及Fowlkes-Mallows指数( Fowlkes-Mallows index, FMI )[24]3个评价指标，指标值一般在0~1，值越大则表示聚类结果越好。
3.2 流形数据集的实验结果及分析
为验证DPC-SNN算法在流形数据集上的表现，用6种算法在8个流行数据集上进行实验，结果如表3所示，表中最优的实验结果用加粗字体表示，“Arg-”代表各算法获得最佳聚类结果时的参数取值。表3中，DPC-SNN算法在Lineblobs、Spiral、Jain、Sticks、Db、Cmc和Circle数据集上均得到了指标的最佳值1，在Pathbased上的表现也接近最佳。在聚类Db这一典型流形数据集时，对比算法中效果最好的IDPC-FA的3个评价指标分别为0.6526、0.5033和0.6999，而DPC-SNN的评价指标均为1，相比分别增长了53.23%、98.69%和42.88%；同理，DPC-SNN相较于DPC算法分别增长了92.86%、257.91%和70.85%。综上，DPC-SNN算法处理形状复杂的流形类簇的能力优于其他对比算法。
表 3 6种算法在流形数据集上的比较Table 3 Comparison of six algorithms on manifold datasets数据集 算法 AMI ARI FMI Arg- 数据集 算法 AMI ARI FMI Arg- Lineblobs DPC-SNN 1 1 1 3 Sticks DPC-SNN 1 1 1 2 IDPC-FA 1 1 1 — IDPC-FA 1 1 1 — DPCSA 1 1 1 — DPCSA 0.7634 0.6360 0.7443 — FNDPC 0.6386 0.5769 0.7218 0.21 FNDPC 0.7634 0.6390 0.7467 0.16 FKNN-DPC 1 1 1 12 FKNN-DPC 1 1 1 6 DPC 0.7799 0.7210 0.8166 3.7 DPC 0.8094 0.7534 0.8235 2.1 Pathbased DPC-SNN 0.9651 0.9795 0.9863 17 Db DPC-SNN 1 1 1 8 IDPC-FA 0.8442 0.8593 0.9067 — IDPC-FA 0.6526 0.5033 0.6999 — DPCSA 0.7073 0.6133 0.7511 — DPCSA 0.4136 0.1096 0.4689 — FNDPC 0.5751 0.5067 0.7065 0.01 FNDPC 0.5098 0.2714 0.5803 0.09 FKNN-DPC 0.9305 0.9499 0.9665 9 FKNN-DPC 0.5107 0.2718 0.5793 19 DPC 0.5212 0.4717 0.6664 3.8 DPC 0.5185 0.2794 0.5853 4.0 Spiral DPC-SNN 1 1 1 3 Cmc DPC-SNN 1 1 1 5 IDPC-FA 1 1 1 — IDPC-FA 0.8093 0.8421 0.9027 — DPCSA 1 1 1 — DPCSA 0.6656 0.5761 0.7454 — FNDPC 1 1 1 0.07 FNDPC 0.8093 0.8421 0.9027 0.28 FKNN-DPC 1 1 1 6 FKNN-DPC 1 1 1 49 DPC 1 1 1 1.8 DPC 0.3857 0.2661 0.5377 5 Jain DPC-SNN 1 1 1 2 Circle DPC-SNN 1 1 1 15 IDPC-FA 1 1 1 — IDPC-FA 0.4629 0.4385 0.7652 — DPCSA 0.2167 0.0442 0.5924 — DPCSA 0.2950 0.0833 0.5242 — FNDPC 0.5961 0.7257 0.9051 0.47 FNDPC 0.4236 0.2732 0.5863 0.29 FKNN-DPC 0.7092 0.8224 0.9359 43 FKNN-DPC 0.7063 0.6139 0.7790 32 DPC 0.6183 0.7146 0.8819 0.8 DPC 0.2747 0.0554 0.5005 3.3 下文采用Friedman 检验分析6种算法在流形数据集上的性能差异，结果如表4、表5所示。表4为6种算法在流形数据集上聚类结果的秩均值，秩均值不同说明算法之间性能有差异。表5为DPC-SNN与其他算法在流形数据集上指标差异显著性检验。其中，P值表示DPC-SNN与其他算法具备显著性差异的概率，统计学上认为P小于0.05的事件为小概率事件，即在0.05水平上具备显著性差异。小于0.05的P值在表中用加粗字体表示。
表 4 6种算法在流形数据集上指标的秩均值Table 4 Rank mean of indices of six algorithms on manifold datasets算法 AMI ARI FMI DPC-SNN 5.25 5.25 5.25 IDPC-FA 4.38 4.38 4.38 DPCSA 2.31 2.25 2.25 FNDPC 2.31 2.50 2.62 FKNN-DPC 4.44 4.44 4.31 DPC 2.31 2.19 2.19 表 5 DPC-SNN与其他算法在流形数据集上指标差异显著性检验Table 5 Test for significance of indices difference between DPC-SNN and other algorithms on manifold datasets算法 AMI ARI FMI IDPC-FA 0.350 0.350 0.350 DPCSA 0.002 0.001 0.001 FNDPC 0.002 0.003 0.005 FKNN-DPC 0.385 0.385 0.316 DPC 0.002 0.001 0.001 如表4所示，DPC-SNN算法的秩均值高于其他算法，说明DPC-SNN算法在AMI、ARI和FMI 3个指标上优于其他算法。如表5所示，DPC-SNN与DPCSA、FNDPC、DPC算法的3个指标在0.05水平上具备显著性差异，而与IDPC-FA、FKNN-DPC在0.05水平上不具备显著性差异。综上，DPC-SNN算法在流形数据集上聚类性能优于其他算法。
受篇幅限制，列出6种算法在2种典型流形数据集上的聚类结果图，如图3所示，图中“五角星”表示类簇中心，不同类簇的样本使用不同颜色表示。
图 3 6种算法在Db数据集上的聚类结果Fig. 3 Clustering results of six algorithms on Db dataset下载:
全尺寸图片
如图3所示，包含630个样本的Db数据集的样本分布图由4个弧形类簇组成。其中聚类难度最高的当属图中央的形似“S”的类簇，该类簇不仅在4个类簇中包含样本最多，且样本分布较为分散。观察图3可知，除DPC-SNN算法外，其他各算法均未找到正确的类簇中心。其中，FNDPC、FKNN-DPC和DPC算法由于寻找类簇中心时出错，都将图中下半部分本属于2个类簇的样本错误地归为同一类簇，导致聚类结果不佳。IDPC-FA将右上方区域样本归为一类，而DPCSA算法则将中间区域样本视为一类，降低了聚类质量。DPC-SNN算法在找到正确的类簇中心基础上，运用合适的分配策略准确地对Db数据集完成聚类。
如图4，Jain数据集分布图为上下2个弧形交错，上疏下密。除DPC算法外，其他算法均找到了正确的类簇中心，不过具体位置略有偏差。而DPC找到的类簇中心位置均位于图中下半部分，即位于数据集中的密集区域，聚类结果不佳，这也是DPC算法最大的短板之一。反观其他算法，虽然DPCSA、FKNN-DPC和FNDPC算法找到了正确的类簇中心，但未将2类簇准确区分。聚类结果理想的只有DPC-SNN和IDPC-FA算法，它们类簇中心的寻找和样本分配均准确无误。
图 4 6种算法在Jain数据集上的聚类结果Fig. 4 Clustering results of six algorithms on Jain dataset下载:
全尺寸图片
3.3 真实数据集的实验结果及分析
为进一步验证DPC-SNN算法的有效性，将6种算法在来源于UCI机器学习数据库[25]的8个真实数据集Iris、Wine、Seeds、Ecoli、Ionosphere、WDBC、Libras和Segmentation上进行实验，并计算其结果的秩均值，对比实验结果见表6。
表 6 6种算法在真实数据集上的比较Table 6 Comparison of six algorithms on real datasets数据集 算法 AMI ARI FMI Arg- 数据集 算法 AMI ARI FMI Arg- Iris DPC-SNN 0.8831 0.9038 0.9355 12 Inonsphere DPC-SNN 0.3961 0.5086 0.7954 19 IDPC-FA 0.8623 0.8857 0.9233 — IDPC-FA 0.1355 0.2183 0.6432 — DPCSA 0.8831 0.9038 0.9355 — DPCSA 0.1335 0.2135 0.6390 — FNDPC 0.8831 0.9038 0.9355 0.11 FNDPC 0.1630 0.2483 0.6531 0.06 FKNN-DPC 0.8831 0.9038 0.9355 22 FKNN-DPC 0.3485 0.4790 0.7716 8 DPC 0.8606 0.8857 0.9233 0.2 DPC 0.1376 0.2231 0.6476 0.4 Wine DPC-SNN 0.8598 0.8837 0.9277 45 Libras DPC-SNN 0.5770 0.3639 0.4138 20 IDPC-FA 0.7675 0.7713 0.8478 — IDPC-FA 0.5733 0.3816 0.4247 — DPCSA 0.7480 0.7414 0.8283 — DPCSA 0.5388 0.3095 0.3791 — FNDPC 0.7898 0.8025 0.8686 0.26 FNDPC 0.5494 0.329 0.3869 0.17 FKNN-DPC 0.8481 0.8839 0.9229 8 FKNN-DPC 0.5554 0.3459 0.4044 10 DPC 0.7065 0.6724 0.7835 2 DPC 0.5358 0.3193 0.3717 0.3 Seeds DPC-SNN 0.7500 0.8002 0.8662 34 Segmentation DPC-SNN 0.6035 0.5205 0.5976 44 IDPC-FA 0.7299 0.7670 0.8444 — IDPC-FA 0.7179 0.6493 0.6982 — DPCSA 0.6609 0.6873 0.7918 — DPCSA 0.5130 0.3667 0.4887 — FNDPC 0.7136 0.7545 0.8361 0.07 FNDPC 0.7176 0.6338 0.6859 0.19 FKNN-DPC 0.7757 0.8024 0.8682 9 FKNN-DPC 0.6013 0.4780 0.5695 8 DPC 0.7299 0.7670 0.8444 0.7 DPC 0.6927 0.6004 0.6730 1.5 Ecoli DPC-SNN 0.6781 0.7672 0.8363 60 Wdbc DPC-SNN 0.7540 0.7502 0.9308 41 IDPC-FA 0.6638 0.7561 0.8284 — IDPC-FA 0.6237 0.7423 0.8829 — DPCSA 0.4406 0.4593 0.6467 — DPCSA 0.3361 0.3771 0.7595 — FNDPC 0.4833 0.5618 0.7178 0.35 FNDPC 0.6076 0.3645 0.8758 0.05 FKNN-DPC 0.5878 0.5894 0.7027 2 FKNN-DPC 0.6423 0.7613 0.8894 2 DPC 0.4978 0.4465 0.5775 0.4 DPC 0.4366 0.4964 0.7941 0.5 由表6可知，在小麦种子数据集Seeds上，FKNN-DPC算法的聚类效果最佳，DPC-SNN算法的聚类效果略低于前者，而其他算法的效果皆不如前两者。对于手势数据集Libras，DPC-SNN算法的AMI值是最佳的，而其ARI和FMI值较之IDPC-FA略低，但仍高于其他算法。在数据集Segmentation上，IDPC-FA算法取得了最佳的聚类效果，DPC算法紧随其后，而DPC-SNN算法则表现不佳。除上述3个数据集外，在鸢尾花卉数据集Iris、红酒数据集Wine、大肠杆菌数据集Ecoli、电离层数据集Ionosphere和乳腺癌数据集Wdbc上，DPC-SNN算法均取得了最佳的聚类效果。
表7和表8分别为采用Friedman检验和P值对比分析6种算法在真实数据集上的聚类结果。
表 7 6种算法在真实数据集上指标的秩均值Table 7 Rank mean of indices of six algorithms on real datasets算法 AMI ARI FMI DPC-SNN 5.31 4.94 5.19 IDPC-FA 3.81 3.88 3.88 DPCSA 1.69 1.81 1.81 FNDPC 3.44 3.31 3.69 FKNN-DPC 4.44 4.69 4.31 DPC 2.31 2.38 2.13 表 8 DPC-SNN与其他算法在真实数据集上指标差异显著性检验Table 8 Test for significance of indices difference between DPC-SNN and other algorithms on real datasets算法 AMI ARI FMI IDPC-FA 0.109 0.256 0.161 DPCSA 0.000 0.001 0.000 FNDPC 0.045 0.082 0.109 FKNN-DPC 0.350 0.798 0.350 DPC 0.001 0.006 0.001 如表7所示，DPC-SNN算法在3个指标上的秩均值皆最高。对比算法中结果最好的FKNN-DPC与DPC-SNN的秩均值相差接近1，其他算法则相差更多。如表8所示，DPC-SNN与DPCSA、DPC算法的3个指标和FNDPC算法的AMI指标在0.05水平上具备显著性差异，而与其他算法在0.05水平上不具备显著性差异。综上，DPC-SNN算法不仅能在人工合成的流形数据集上取得极佳的聚类结果，在真实数据集上也有良好的聚类效果。
3.4 人脸图像数据集的实验结果及分析
Olivetti Faces数据集[26]产生于英国剑桥奥利维蒂研究实验室，是典型的流形数据集，已在机器学习领域得到广泛应用。此数据集记录了不同时间、光线、表情、面部细节条件下拍摄的40个受试者共计400幅人脸图像，每幅图像大小为92×112，8位灰度。表9给出了该数据集在6种算法上分别进行聚类实验的结果。
表 9 算法在Olivetti Faces数据集上的比较Table 9 Comparison of algorithms on Olivetti Faces dataset算法 AMI ARI FMI Arg- DPC-SNN 0.8433 0.7330 0.7413 6 IDPC-FA 0.8093 0.6924 0.7029 — DPCSA 0.8254 0.7025 0.7127 — FNDPC 0.7965 0.6652 0.6778 0.44 FKNN-DPC 0.7989 0.6784 0.6885 5 DPC 0.7891 0.6549 0.6701 3.0 为验证DPC-SNN的改进效果，DPC-SNN与DPC在人脸数据集上的聚类结果如图5所示，第1~20号人脸图像依上下顺序排列在左侧，21~40号人脸图像依次右侧排列，不同类簇的人脸图像使用不同的颜色表示，若属于同一个人的图像识别率低于50%则视为未被识别并标记为灰色，类簇中心用白色小圆点表示。
图 5 DPC和DPC-SNN算法在Olivetti Faces数据集上的聚类结果Fig. 5 Clustering results of DPC and DPC-SNN algorithms on Olivetti Faces dataset下载:
全尺寸图片
如图5所示，图5(a)中第9、14、16、19、23、36、38号图像中均有1~5幅数目不等的图像未被DPC算法识别，而如图5(b)所示，上述号码的图像被DPC-SNN算法全部识别并分配到正确类簇；图5(a)中第1、5、39、40号图像中亦有3~10幅图像未被DPC算法识别，DPC-SNN算法虽未完全识别这些图像，但在前者的基础上降低了识别失误率，尤其是第40号图像，直接将未被识别的图像幅数从10降低到4。综上，DPC-SNN算法更能应对人脸数据集的复杂结构，达到良好的聚类效果。
4. 结束语
针对DPC算法聚类流形数据时难以找到准确的类簇中心以及样本分配易引发“多米诺骨牌”效应的问题，本文提出了一种面向流形数据的共享近邻密度峰值聚类算法。首先，提出了基于共享近邻的样本相似度定义方式，确保同一流形类簇中样本间相似度尽可能高；其次，基于上述相似度定义局部密度，不忽略距类簇中心较远样本的密度贡献，结合流形数据的特点能准确地找出流形类簇的类簇中心；最后，根据样本相似度分配剩余样本，采用广度优先搜索策略，有效避免样本的连续误分配。实验结果表明，DPC-SNN算法在流形数据集上聚类效果优秀，在真实以及人脸数据集上综合表现也优于其他对比算法。但是本文算法参数的指定仍需人工干预，如何通过算法自动确定参数将成为下一步研究的重点。同时，群体智能[27-28]的引入有望进一步提升聚类算法的性能，特别是借助群智能进化[29]的途径将使得聚类算法的自适应性更加趋于完善。
-
图 1 不同局部密度在Circle数据集上获得的类簇中心
Fig. 1 Cluster centers obtained from the Circle dataset through different local densities
下载:
全尺寸图片
图 2 高斯核与2种分配策略组合在LineBlobs数据集上的聚类结果
Fig. 2 Clustering results of gaussian kernel and two allocation strategies on LineBlobs dataset
下载:
全尺寸图片
图 3 6种算法在Db数据集上的聚类结果
Fig. 3 Clustering results of six algorithms on Db dataset
下载:
全尺寸图片
图 4 6种算法在Jain数据集上的聚类结果
Fig. 4 Clustering results of six algorithms on Jain dataset
下载:
全尺寸图片
图 5 DPC和DPC-SNN算法在Olivetti Faces数据集上的聚类结果
Fig. 5 Clustering results of DPC and DPC-SNN algorithms on Olivetti Faces dataset
下载:
全尺寸图片
表 1 流形数据集的基本信息
Table 1 Basic information of manifold datasets
数据集 样本数 维数 类簇数 Lineblobs 266 2 3 Pathbased 300 2 3 Spiral 312 2 3 Jain 373 2 2 Sticks 512 2 4 Db 630 2 4 Cmc 1 002 2 3 Circle 1 897 2 3 表 2 真实数据集的基本信息
Table 2 Basic information of real datasets
数据集 样本数 维数 类簇数 Iris 150 4 3 Wine 178 13 3 Seeds 210 7 3 Ecoli 336 8 8 Ionosphere 351 34 2 Libras 360 90 15 WDBC 569 30 2 Segmentation 2310 20 7 表 3 6种算法在流形数据集上的比较
Table 3 Comparison of six algorithms on manifold datasets
数据集 算法 AMI ARI FMI Arg- 数据集 算法 AMI ARI FMI Arg- Lineblobs DPC-SNN 1 1 1 3 Sticks DPC-SNN 1 1 1 2 IDPC-FA 1 1 1 — IDPC-FA 1 1 1 — DPCSA 1 1 1 — DPCSA 0.7634 0.6360 0.7443 — FNDPC 0.6386 0.5769 0.7218 0.21 FNDPC 0.7634 0.6390 0.7467 0.16 FKNN-DPC 1 1 1 12 FKNN-DPC 1 1 1 6 DPC 0.7799 0.7210 0.8166 3.7 DPC 0.8094 0.7534 0.8235 2.1 Pathbased DPC-SNN 0.9651 0.9795 0.9863 17 Db DPC-SNN 1 1 1 8 IDPC-FA 0.8442 0.8593 0.9067 — IDPC-FA 0.6526 0.5033 0.6999 — DPCSA 0.7073 0.6133 0.7511 — DPCSA 0.4136 0.1096 0.4689 — FNDPC 0.5751 0.5067 0.7065 0.01 FNDPC 0.5098 0.2714 0.5803 0.09 FKNN-DPC 0.9305 0.9499 0.9665 9 FKNN-DPC 0.5107 0.2718 0.5793 19 DPC 0.5212 0.4717 0.6664 3.8 DPC 0.5185 0.2794 0.5853 4.0 Spiral DPC-SNN 1 1 1 3 Cmc DPC-SNN 1 1 1 5 IDPC-FA 1 1 1 — IDPC-FA 0.8093 0.8421 0.9027 — DPCSA 1 1 1 — DPCSA 0.6656 0.5761 0.7454 — FNDPC 1 1 1 0.07 FNDPC 0.8093 0.8421 0.9027 0.28 FKNN-DPC 1 1 1 6 FKNN-DPC 1 1 1 49 DPC 1 1 1 1.8 DPC 0.3857 0.2661 0.5377 5 Jain DPC-SNN 1 1 1 2 Circle DPC-SNN 1 1 1 15 IDPC-FA 1 1 1 — IDPC-FA 0.4629 0.4385 0.7652 — DPCSA 0.2167 0.0442 0.5924 — DPCSA 0.2950 0.0833 0.5242 — FNDPC 0.5961 0.7257 0.9051 0.47 FNDPC 0.4236 0.2732 0.5863 0.29 FKNN-DPC 0.7092 0.8224 0.9359 43 FKNN-DPC 0.7063 0.6139 0.7790 32 DPC 0.6183 0.7146 0.8819 0.8 DPC 0.2747 0.0554 0.5005 3.3 表 4 6种算法在流形数据集上指标的秩均值
Table 4 Rank mean of indices of six algorithms on manifold datasets
算法 AMI ARI FMI DPC-SNN 5.25 5.25 5.25 IDPC-FA 4.38 4.38 4.38 DPCSA 2.31 2.25 2.25 FNDPC 2.31 2.50 2.62 FKNN-DPC 4.44 4.44 4.31 DPC 2.31 2.19 2.19 表 5 DPC-SNN与其他算法在流形数据集上指标差异显著性检验
Table 5 Test for significance of indices difference between DPC-SNN and other algorithms on manifold datasets
算法 AMI ARI FMI IDPC-FA 0.350 0.350 0.350 DPCSA 0.002 0.001 0.001 FNDPC 0.002 0.003 0.005 FKNN-DPC 0.385 0.385 0.316 DPC 0.002 0.001 0.001 表 6 6种算法在真实数据集上的比较
Table 6 Comparison of six algorithms on real datasets
数据集 算法 AMI ARI FMI Arg- 数据集 算法 AMI ARI FMI Arg- Iris DPC-SNN 0.8831 0.9038 0.9355 12 Inonsphere DPC-SNN 0.3961 0.5086 0.7954 19 IDPC-FA 0.8623 0.8857 0.9233 — IDPC-FA 0.1355 0.2183 0.6432 — DPCSA 0.8831 0.9038 0.9355 — DPCSA 0.1335 0.2135 0.6390 — FNDPC 0.8831 0.9038 0.9355 0.11 FNDPC 0.1630 0.2483 0.6531 0.06 FKNN-DPC 0.8831 0.9038 0.9355 22 FKNN-DPC 0.3485 0.4790 0.7716 8 DPC 0.8606 0.8857 0.9233 0.2 DPC 0.1376 0.2231 0.6476 0.4 Wine DPC-SNN 0.8598 0.8837 0.9277 45 Libras DPC-SNN 0.5770 0.3639 0.4138 20 IDPC-FA 0.7675 0.7713 0.8478 — IDPC-FA 0.5733 0.3816 0.4247 — DPCSA 0.7480 0.7414 0.8283 — DPCSA 0.5388 0.3095 0.3791 — FNDPC 0.7898 0.8025 0.8686 0.26 FNDPC 0.5494 0.329 0.3869 0.17 FKNN-DPC 0.8481 0.8839 0.9229 8 FKNN-DPC 0.5554 0.3459 0.4044 10 DPC 0.7065 0.6724 0.7835 2 DPC 0.5358 0.3193 0.3717 0.3 Seeds DPC-SNN 0.7500 0.8002 0.8662 34 Segmentation DPC-SNN 0.6035 0.5205 0.5976 44 IDPC-FA 0.7299 0.7670 0.8444 — IDPC-FA 0.7179 0.6493 0.6982 — DPCSA 0.6609 0.6873 0.7918 — DPCSA 0.5130 0.3667 0.4887 — FNDPC 0.7136 0.7545 0.8361 0.07 FNDPC 0.7176 0.6338 0.6859 0.19 FKNN-DPC 0.7757 0.8024 0.8682 9 FKNN-DPC 0.6013 0.4780 0.5695 8 DPC 0.7299 0.7670 0.8444 0.7 DPC 0.6927 0.6004 0.6730 1.5 Ecoli DPC-SNN 0.6781 0.7672 0.8363 60 Wdbc DPC-SNN 0.7540 0.7502 0.9308 41 IDPC-FA 0.6638 0.7561 0.8284 — IDPC-FA 0.6237 0.7423 0.8829 — DPCSA 0.4406 0.4593 0.6467 — DPCSA 0.3361 0.3771 0.7595 — FNDPC 0.4833 0.5618 0.7178 0.35 FNDPC 0.6076 0.3645 0.8758 0.05 FKNN-DPC 0.5878 0.5894 0.7027 2 FKNN-DPC 0.6423 0.7613 0.8894 2 DPC 0.4978 0.4465 0.5775 0.4 DPC 0.4366 0.4964 0.7941 0.5 表 7 6种算法在真实数据集上指标的秩均值
Table 7 Rank mean of indices of six algorithms on real datasets
算法 AMI ARI FMI DPC-SNN 5.31 4.94 5.19 IDPC-FA 3.81 3.88 3.88 DPCSA 1.69 1.81 1.81 FNDPC 3.44 3.31 3.69 FKNN-DPC 4.44 4.69 4.31 DPC 2.31 2.38 2.13 表 8 DPC-SNN与其他算法在真实数据集上指标差异显著性检验
Table 8 Test for significance of indices difference between DPC-SNN and other algorithms on real datasets
算法 AMI ARI FMI IDPC-FA 0.109 0.256 0.161 DPCSA 0.000 0.001 0.000 FNDPC 0.045 0.082 0.109 FKNN-DPC 0.350 0.798 0.350 DPC 0.001 0.006 0.001 表 9 算法在Olivetti Faces数据集上的比较
Table 9 Comparison of algorithms on Olivetti Faces dataset
算法 AMI ARI FMI Arg- DPC-SNN 0.8433 0.7330 0.7413 6 IDPC-FA 0.8093 0.6924 0.7029 — DPCSA 0.8254 0.7025 0.7127 — FNDPC 0.7965 0.6652 0.6778 0.44 FKNN-DPC 0.7989 0.6784 0.6885 5 DPC 0.7891 0.6549 0.6701 3.0 -
[1] SHI Tianhao, DING Shifei, XU Xiao, et al. A community detection algorithm based on Quasi-Laplacian centrality peaks clustering[J]. Applied intelligence, 2021, 51(11): 7917–7932. doi: 10.1007/s10489-021-02278-6 [2] DINOIA A, MARTINO A, MONTANARI P, et al. Supervised machine learning techniques and genetic optimization for occupational diseases risk prediction[J]. Soft computing, 2020, 24(6): 4393–4406. doi: 10.1007/s00500-019-04200-2 [3] BUCZAK A L, GUVEN E. A survey of data mining and machine learning methods for cyber security intrusion detection[J]. IEEE communications surveys & tutorials, 2015, 18(2): 1153–1176. [4] YAN Xiaoqiang. Synergetic information bottleneck for joint multi-view and ensemble clustering[J]. Information fusion, 2020, 56: 15–27. doi: 10.1016/j.inffus.2019.10.006 [5] GAO Miao. Ship-handling behavior pattern recognition using AIS sub-trajectory clustering analysis based on the T-SNE and spectral clustering algorithms[J]. Ocean engineering, 2020, 205: 106919. doi: 10.1016/j.oceaneng.2020.106919 [6] 陈叶旺, 申莲莲, 钟才明, 等. 密度峰值聚类算法综述[J]. 计算机研究与发展, 2020, 57(2): 378–394. doi: 10.7544/issn1000-1239.2020.20190104 CHEN Yewang , SHEN Lianlian, ZHONG Caiming, et al. A review of density peak clustering algorithms[J]. Journal of computer research and development, 2020, 57(2): 378–394. doi: 10.7544/issn1000-1239.2020.20190104 [7] SUN Lin, QIN Xiaoying, DING Weiping, et al. Density peaks clustering based on k-nearest neighbors and self-recommendation[J]. International journal of machine learning and cybernetics, 2021, 12(7): 1913–1938. doi: 10.1007/s13042-021-01284-x [8] XIA Shuyin, PENG Daowan, MENG Deyu, et al. Ball k-means: fast adaptive clustering with No bounds[J]. IEEE transactions on pattern analysis and machine intelligence, 2022, 44(1): 87–99. [9] BU Fanyu, ZHANG Qingchen, YANG L T, et al. An edge-cloud-aided high-order possibilistic c-means algorithm for big data clustering[J]. IEEE transactions on fuzzy systems, 2020, 28(12): 3100–3109. doi: 10.1109/TFUZZ.2020.2992634 [10] DING Jiajun, HE Xiongxiong, YUAN Junqing, et al. Automatic clustering based on density peak detection using generalized extreme value distribution[J]. Soft computing-A fusion of foundations, methodologies and applications, 2018, 22(9): 2777–2796. [11] ABE K, MINOURA K, MAEDA Y, et al. Model-based clustering for flow and mass cytometry data with clinical information[J]. BMC bioinformatics, 2020, 21(suppl 13): 393. [12] CHEUNG Y M, ZHANG Yiqun. Fast and accurate hierarchical clustering based on growing multilayer topology training[J]. IEEE transactions on neural networks and learning systems, 2019, 30(3): 876–890. doi: 10.1109/TNNLS.2018.2853407 [13] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the Second International Conference on Knowledge Discovery and Data Mining. New York: ACM, 1996: 226–231. [14] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. doi: 10.1126/science.1242072 [15] XIE Juanying. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J]. Information sciences, 2016, 354: 19–40. doi: 10.1016/j.ins.2016.03.011 [16] DU Mingjing, DING Shifei, XUE Yu. A robust density peaks clustering algorithm using fuzzy neighborhood[J]. International journal of machine learning and cybernetics, 2018, 9(7): 1131–1140. doi: 10.1007/s13042-017-0636-1 [17] ZHAO Jia, TANG Jingjing, SHI Aiye, et al. Improved density peaks clustering based on firefly algorithm[J]. International journal of bio-inspired computation, 2020, 15(1): 24–42. doi: 10.1504/IJBIC.2020.105899 [18] XU Xiao, DING Shifei, XU Hui, et al. A feasible density peaks clustering algorithm with a merging strategy[J]. Soft computing, 2019, 23(13): 5171–5183. doi: 10.1007/s00500-018-3183-0 [19] YU Donghua, LIU Guojun, GUO Maozu, et al. Density peaks clustering based on weighted local density sequence and nearest neighbor assignment[J]. IEEE access, 2019, 7: 34301–34317. doi: 10.1109/ACCESS.2019.2904254 [20] XU Lizhong, ZHAO Jia, YAO Zhanfeng, et al. Density peak clustering based on cumulative nearest neighbors degree and micro cluster merging[J]. Journal of signal processing systems, 2019, 91(10): 1219–1236. doi: 10.1007/s11265-019-01459-4 [21] 赵嘉, 姚占峰, 吕莉, 等. 基于相互邻近度的密度峰值聚类算法[J]. 控制与决策, 2021, 36(3): 543–552. doi: 10.13195/j.kzyjc.2019.0795 ZHAO Jia, YAO Zhanfeng, LYU Li, at el. Density peaks clustering based on mutual neighbor degree[J]. Control and decision, 2021, 36(3): 543–552. doi: 10.13195/j.kzyjc.2019.0795 [22] DU Mingjing, DING Shifei, XU Xiao, et al. Density peaks clustering using geodesic distances[J]. International journal of machine learning and cybernetics, 2018, 9(8): 1335–1349. doi: 10.1007/s13042-017-0648-x [23] VINH N X, EPPS J, BAILEY J. Information theoretic measures for clusterings comparison: variants, properties, normalization and correction for chance[J]. Journal of machine learning research, 2010, 11: 2837–2854. [24] FOWLKES E B, MALLOWS C L. A method for comparing two hierarchical clusterings[J]. Journal of the American statistical association, 1983, 78(383): 553–569. doi: 10.1080/01621459.1983.10478008 [25] LICHMAN M. UCI machine learning repository[EB/OL]. (2018-09-24)[2022-09-15].http://archive.ics.uci.edu/ml. [26] SAMARIA F S, HARTER A C. Parameterisation of a stochastic model for human face identification[C]//Proceedings of 1994 IEEE Workshop on Applications of Computer Vision. Piscataway: IEEE, 2002: 138−142. [27] 肖人彬. 面向复杂系统的群集智能[M]. 北京: 科学出版社, 2013. [28] 肖人彬, 冯振辉, 王甲海. 群体智能的概念辨析与研究进展及应用分析[J]. 南昌工程学院学报, 2022, 41(1): 1–21. XIAO Renbin, FENG Zhenhui, WANG Jiahai. Collective intelligence: conception, research progresses and application analyses[J]. Journal of Nanchang Institute of Technology, 2022, 41(1): 1–21. [29] 肖人彬, 陈峙臻. 从群智能优化到群智能进化[J]. 南昌工程学院学报, 2023, 42(1): 1–10. XIAO Renbin, CHEN Zhizhen. From swarm intelligence optimization to swarm intelligence evolution[J]. Journal of Nanchang Institute of Technology, 2023, 42(1): 1–10.
