IsomapVSG-LIME: a novel local interpretable model-agnostic explanations
-
摘要: 为了解决局部可解释模型无关的解释(local interpretable model-agnostic explanations, LIME)随机扰动采样方法导致产生的解释缺乏局部忠实性和稳定性的问题,本文提出了一种新的模型无关解释方法IsomapVSG-LIME。该方法使用基于流形学习的等距映射虚拟样本生成 (isometric mapping virtual sample generation, IsomapVSG) 方法代替LIME的随机扰动采样方法来生成样本,并使用凝聚层次聚类方法从虚拟样本中选择具有代表性的样本用以训练解释模型;本文还提出了一种新的解释稳定性评价指标—特征序列稳定性指数 (features sequence stability index, FSSI),解决了以往评价指标忽略特征的序关系和解释翻转的问题。实验结果表明,本文提出的方法在稳定性和局部忠实性上均优于现有的最新模型。
-
关键词:
- 局部可解释模型无关的解释 /
- 机器学习 /
- 等距映射虚拟样本生成 /
- 凝聚层次聚类 /
- 稳定性 /
- 局部忠实性 /
- 随机扰动采样 /
- 特征序列稳定性指数
Abstract: In order to solve the problem of lacking local fidelity and stability caused by local interpretable model-agnostic explanations (LIME) random perturbation sampling method, a new local interpretable model-agnostic explanation, IsomapVSG-LIME is proposed in this paper. In this method, isometric mapping virtual sample generation (IsomapVSG), a virtual sample generation method based on manifold learning, is used in substitution of random perturbation sampling method of LIME to generate samples, and aggregation hierarchical clustering method is used to select representative samples from virtual samples for training explanation model. In addition, this paper also proposes a new explanation stability evaluation index, the features sequence stability index (FSSI), which solves the problem that previous evaluation indexes ignore the sequential relationship of features and the flipping of explanations. Experimental results show that the proposed method outperforms the latest models in terms of stability and local fidelity. -
机器学习是实现人工智能系统的重要方法。然而,由于可解释性的缺乏,一些具有出色性能的机器学习模型在某些特定领域的部署应用受到了严重阻碍,如医疗诊断、司法量刑、金融等关键决策领域。为了克服这一弱点,许多学者对如何提高机器学习模型可解释性进行了深入的研究,并提出了大量的解释方法以帮助用户理解模型内部的工作机制[1]。根据不同的标准[2-4],这些方法可以大致分为以下几类:1) 事前可解释和事后可解释;2) 全局可解释和局部可解释;3) 特定于模型的解释和模型无关的解释。
其中,模型无关解释方法尤其流行。其目标是设计一个能够解释任意机器学习模型决策过程的独立算法。局部可解释模型无关的解释(local interpretable model-agnostic explanations, LIME)[5]是一种著名的模型无关算法,它首先通过随机扰动在实例周围生成模拟数据点,然后用模拟数据拟合一个加权稀疏线性模型来为单个预测提供解释。无论是何种分类器,LIME的解释总是在局部忠实于待解释实例。
由于LIME的灵活性和易用性,其在医疗诊断[6-9]、推荐系统[10-11]、工业[12-13]等领域得到了广泛应用。但LIME 方法本身在解释稳定性和局部忠实性等方面还存在不足之处。局部忠实性指的是解释模型在待解释实例邻域内的行为和黑盒模型的接近程度。稳定性指的是在相同条件下,重复实验在理想情况下应该对相同的实例产生相同的解释。研究发现[14-16],两者都与LIME的随机扰动采样方法有直接关系。首先,该方法产生的样本比较分散,有些样本可能不符合原始数据分布,其严重影响了解释模型的局部忠实性。其次,由于该方法的随机性,重复实验产生的样本也有所不同,其最终导致LIME解释缺乏稳定性。确定性LIME (deterministic LIME, DLIME)[17]首先利用凝聚层次聚类 (agglomerate hierarchical clustering, AHC) 将数据聚类,然后用k近邻 (k-nearest neighbor, KNN) 算法选择待解释实例的相关类簇来代替LIME的随机扰动采样方法,提高了LIME解释的稳定性。贝叶斯LIME (Bayesian LIME, BayLIME)[18]利用贝叶斯修正方法将先验知识融入到LIME中,提高了LIME解释的稳定性和内核设置的鲁棒性。基于自编码器的LIME (autoencoder based LIME, ALIME)[19]用降噪自编码器将数据从原始特征空间映射到隐空间,再进行加权操作,最后根据样本权重选择待解释数据的邻域,提高了LIME解释的局部忠实性。稳定的LIME (stabilized-LIME, S-LIME)[20]利用一个基于中心极限定理的假设检验框架来确定需要扰动的数据点数,以保证结果的稳定性。
此外,如何选择一个合适的指标来评价LIME解释的稳定性也是一个重要的问题。Zafar等[17]用特征稳定性指数 (features stability index, FSI) 指标来评价LIME解释的稳定性。Zhao等[18]用Jaccard系数来评价解释的稳定性。Visani等[21]提出了一种统计稳定性指标变量稳定性指数 (variables stability index, VSI) 来评价解释的稳定性。以上指标均存在2个缺陷: 1) 忽略了特征的序关系; 2) 忽略了特征翻转问题。
等距映射虚拟样本生成 (isometric mapping virtual sample generation, IsomapVSG)[22]是一种基于特征表示的虚拟样本生成(virtual sample generation, VSG)方法,其采用了一种等距映射(isometric mapping, Isomap)[23]的流形学习方法对数据进行降维处理,然后通过插值法和极限学习机(extreme learning machine, ELM)[24]生成虚拟样本。该方法能够在局部生成可靠的、稠密的虚拟样本。受此启发,本文将IsomapVSG引入到LIME框架中代替随机扰动采样方法来生成样本,并用AHC选择具有代表性的样本用以训练解释模型。考虑到特征的序关系和特征翻转问题,本文还提出了一种名为特征序列稳定性指数 (features sequence stability index, FSSI) 的解释稳定性评价指标来更加准确地度量LIME解释的稳定性。
1. LIME模型和IsomapVSG模型
1.1 LIME模型
局部代理模型本身是可解释的模型,用于解释黑盒机器学习模型的单个预测,LIME是Ribeiro等[5]提出的局部代理模型的具体实现。代理模型经过训练可以近似底层黑盒模型的预测。LIME并非训练全局代理模型,而是专注于训练局部代理模型以解释单个预测。
LIME的框架结构如图1所示。上半部分为一个训练好的黑盒分类器,其内部工作机制未知且不限于某种模型。下半部分为LIME产生解释的整个工作流程,解释模型不限于某种模型。对于一个给定的黑盒模型f和一个待解释实例x,LIME通过以下步骤解释x的分类结果f (x):
1) 样本生成:随机扰动x产生一批指定数量的模拟数据Z;
2) 样本加权:根据Z与目标实例x的相似性对样本进行加权,得到样本权重π(Z);
3) 获取标签:将步骤1)产生的样本输入到黑盒模型中获取样本标签信息f (Z);
4) 特征选择:运用某种特征选择方法选择top k特征;
5) 训练解释模型:用加权的样本π(Z)和标签信息f (Z)训练一个可解释的模型g;
6) 解释:通过分析解释模型的系数来解释f (x)。
LIME产生的解释可以表示为
$$ \xi (x) = \mathop {\arg \min }\limits_{g \in G} L(f,g,{\pi _x}) + \varOmega (g) $$ 式中:
$ L $ 为损失函数和;$ \varOmega $ 为解释模型的复杂度,例如解释模型为决策树时,模型复杂度为决策树的深度。损失函数$ L $ 定义为$$ L(f,g,{\pi _x}) = {\sum\limits_{z,z' \in Z} {{\pi _x}(z)(f(z) - g(z'))} ^2} $$ 式中:
$ f $ 为黑盒模型;$ g $ 为解释模型;$ z $ 为采样得到的新数据点;$ z' $ 为$ z $ 的可解释表示;$ \pi $ 为加权函数,其定义为$$ {\pi _x}(z) = \exp ( - D{(x,z)^2}/{\sigma ^2}) $$ 式中:
$ D $ 为欧氏距离,$ \sigma $ 为核宽参数。1.2 IsomapVSG模型
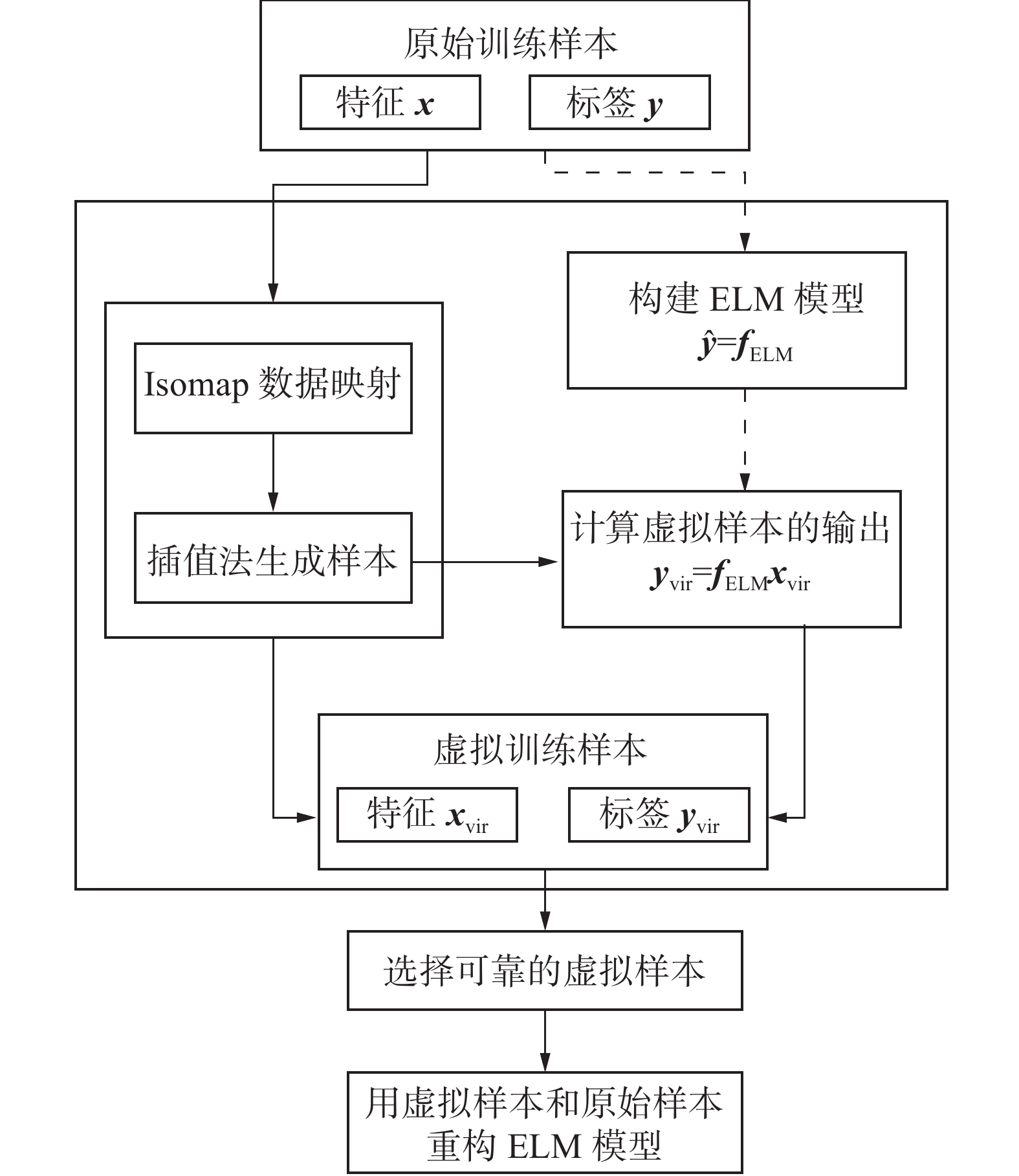
IsomapVSG[22]的目标是通过生成可行的虚拟样本来解决小样本问题,提高软传感模型的精度。整个过程可分为以下步骤:1) 利用小样本构建ELM模型;2) 通过流形学习方法和插值方法生成虚拟样本;3) 选择合适的虚拟样本并将其加入训练样本集对ELM模型进行修改。IsomapVSG的流程如图2所示。
IsomapVSG的数据生成过程分为以下步骤:
1) 利用Isomap方法将所有基样本从原始特征空间映射到二维特征空间,得到二维空间中所有点的坐标
$ {x}_{i}{{'}}=\left\{\right[{x}_{i1}{{'}},{x}_{i2}{{'}}],i=\mathrm{1,2},\cdots,n\} $ 和k个近邻。2) 用插值法生成虚拟样本。根据每个投影点之间的距离和平均距离确定插补点的数量和位置,二维空间中第i个投影点与第j个投影点之间的距离为
$$ {{\rm{dist}}}\left(x_{i}^{\prime}, x_{j}^{\prime}\right)=\sqrt{\left(x_{i 1}^{\prime}-x_{j 1}^{\prime}\right)^{2}+\left(x_{i 2}^{\prime}-x_{j 2}^{\prime}\right)^{2}} $$ 平均距离为
$$A_D = \frac{1}{{k\cdot n}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\rm{dist}}(x_i',x_j')} } $$ 如果2个投影点之间的距离
${\rm{ dist}}({x}_{i}{{'}},{x}_{j}{{'}}) $ 大于所有投影点之间的平均距离,虚拟样本点在这2个投影点之间的直线的t分割处生成产生,t定义为$$ t = \frac{{{\rm{dist}}(x_i',x_j')}}{{{{A_D}}}} $$ 最终,所有的二维虚拟样本点
${{\boldsymbol{x}}}'_{{\rm{vir}}}{}\in {{{{\mathbf{R}}}}}^{V\times 2}$ 被获取,其中V是虚拟样本点的数量。3) 获取虚拟样本在原始特征空间的表示。建立从二维投影点到原始样本点的ELM模型,以所有样本在二维空间的坐标
${{{x}}}_{i}'$ 为输入变量,以所有样本的原始输入$ {{\boldsymbol{x}}}_{i} $ 为输出变量。根据建立的网络模型和${{\boldsymbol{x}}}_{{\rm{vir}}}'$ ,虚拟样本输出${{\boldsymbol{x}}}_{{\rm{vir}}}\in {{\bf{R}}}^{V\times m}$ 可以被计算。4) 选择可靠的虚拟样本。考虑到生成的虚拟样本的可行性,合适的虚拟样本受制于不等式:
$$ {\boldsymbol{L}}{_i} \leqslant {{\boldsymbol{x}}_i} \leqslant {\boldsymbol{U}}{_i},\;\;\;i = 1,2,\cdots,m $$ 式中:
$ {{\boldsymbol{x}}}_{i} $ 为决策变量的第i维向量,${\boldsymbol{L}}{}_{i}\left({\boldsymbol{U}}{}_{i}\right)$ 为i个决策变量的下(上)界。2. IsomapVSG-LIME模型
LIME的目标是在待解释实例的邻域内训练一个简单的可解释的模型,通过分析解释模型的系数来解释单个预测结果。为了训练解释模型,首先需要在待解释实例的邻域内生成一批模拟数据。LIME使用随机扰动采样的方法来生成模拟数据,该方法本身存在一些缺陷。首先,通过随机扰动生成的样本比较分散,并且可能存在一些样本不符合原始数据分布,这严重影响了解释模型的局部忠实性。低的局部忠实性意味着解释方法是不可靠的。其次,由于该方法具有随机性,对于同一待解释实例,在相同条件下重复多次实验所生成样本也会有所不同,这会导致LIME产生不稳定的解释。不稳定的解释意味着解释结果是不可信的。
LIME在邻域数据生成过程中应该考虑3个重要的因素。首先,生成的数据点要尽可能符合原始数据分布。其次,为了获取准确的解释,有必要在待解释实例周围生成稠密的数据。最后,为了获得稳定的解释,样本生成过程的随机性要尽可能小。IsomapVSG采用了一种称为Isomap的流形学习方法对数据进行降维处理,然后通过插值法和极限学习机生成虚拟样本。其可以在局部生成稠密的、符合原始数据分布的虚拟样本。因此,本文将IsomapVSG引入LIME框架中代替随机扰动采样方法进行样本生成,然后用凝聚层次聚类方法从生成的样本中选择具有代表性的样本,最后用选择的样本训练一个可解释的模型来提供解释。
本文提出方法的框架如图3所示。
对于一个给定的黑盒模型f和一个待解释实例x, IsomapVSG-LIME通过以下步骤产生解释:
1) 近邻选择:IsomapVSG生成模型需要一定数量的基样本作为输入,同时,模型生成的样本应该尽可能稠密。因此,通过计算欧氏距离从训练集中选出离待解释实例距离最近的m个样本。
2) 样本生成:设定需要生成的样本数量,然后将步骤1)中选择的近邻数据作为IsomapVSG模型的输入,生成指定数量的样本。
3) 样本选择:这一步的目标是从虚拟样本中选择具有代表性的数据点。给定一个最小样本数量阈值,该方法能够自适应地为待解释实例选择合适的数据点,从而确定其邻域的密度[25]。整个样本选择过程如算法1所示。
算法1 样本选择
① procedure DataSelection(x, f, Z,
$ \tau $ )②
$ {n}_{c}\leftarrow 2 $ ③
${\mathcal{Z}'}\leftarrow \left\{\right\}$ ④ for all
$ l\in \mathcal{L} $ do⑤
$ {\mathcal{G}}_{l}\leftarrow \{z\in Z\mid f(z)=l\} $ ⑥
$ {\mathcal{G}}_{l}\leftarrow x\cup {\mathcal{G}}_{l} $ ⑦ while True do
⑧
${c}_{x},{c}_{\neg x}\leftarrow \text{}{{\rm{AgglomerativeClustering}}}\text{}\left({\mathcal{G} }_{l},{n}_{c}\right)$ ⑨ if
$\left|{c}_{x}\right|\geqslant \tau$ then⑩
$ {\mathcal{G}}_{l}\leftarrow {c}_{x} $ ⑪ else
⑫ break
⑬
${\mathcal{Z} '}\leftarrow {\mathcal{Z} }{ { {'} } }\cup {\mathcal{G} }_{l}$ ⑭ return
$ {\mathcal{Z}}{{{'}}} $ 其中x为待解释实例,f为黑盒模型,
$ \tau $ 为最小样本数量阈值,$ \mathcal{L} $ 为标签集合。该算法可分为3个步骤:①根据样本的标签信息将样本划分为多个集合,每一个集合中的样本的标签相同;
②将每一个集合的样本并上待解释实例,然后用凝聚层次聚类方法将该集合聚为2类:a)包含待解释实例的类簇;b)不包含待解释实例的类簇;
③对待解释实例所属的类簇进行数量判断,如果该类簇样本数量不小于设定的阈值
$ \tau $ ,则保留该部分样本,否则丢弃该部分样本。对每一个样本集合重复上述步骤①~③最终返回挑选出的样本以用作训练解释模型。
4) 获取标签:将步骤3)选出的样本输入黑盒模型中获取标签信息。
5) 样本加权:根据样本和待解释实例的相似程度对样本进行加权,本文使用了RBF (radial basis function)核函数作为加权函数。该函数提供了[0,1]的平滑权重,权重的值通过核宽参数进行调整。
$$ {\rm{RBF}}(z) = \exp \left( {\frac{{\parallel x - z{\parallel ^2}}}{{{\sigma ^2}}}} \right) $$ 6) 样本选择:运用前向特征选择方法从数据中选出最重要的 k个特征;
7) 训练解释模型:利用上述步骤中得到的样本、样本标签信息和样本权重训练一个线性模型作为解释模型,通过分析模型的参数返回解释结果。
本文提出方法的伪代码如算法2所示。
算法2 IsomapVSG-LIME模型
输入 训练集
$ {X}_{\text{train}} $ , 分类器f, 解释实例x, 解释长度K, 样本数量N, 加权函数π。输出 解释模型g。
① 初始化 Y={}, W={}, Z={}, F={}
② Neighbours
$ = $ SelectNeighbors (x,$ {X}_{\text{train}} $ )③ Z = IsomapVSG(Neighbours, N)
④ Z = DataSelection((x, f, Z, t))
⑤ for z in Z:
⑥W = W ∪ π(z)
⑦ Y = Y ∪ f(z) ⑧ F = FeatureSelection(Z, K)
⑨ g = LinearRegression(Z, Y, W, F)
3. 实验结果与分析
3.1 评价指标
LIME返回的解释结果为一个列表:
$$ E = [({e_1},{w_1}),({e_2},{w_2}),\cdots,({e_k},{w_k})] $$ 列表的每个元素为一个元组,元组中的第1个元素表示特征,第2个元素表示特征的权值,且权值大小满足:
$$ |{w_1}| \geqslant |{w_2}| \geqslant ,\cdots, \geqslant |{w_{k - 1}}| \geqslant |{w_k}| $$ FSI[17]、Jaccard系数[18] 和VSI[21]在评估解释稳定性时仅仅考虑特征集合
$ \{{e}_{1},{e}_{2},\cdots,{e}_{k}\} $ ,没有考虑特征的序关系和特征的权值$ \{{w}_{1},{w}_{2},\cdots,{w}_{k}\} $ ,特征的权值对于解释来说是非常重要的信息。特征权重的绝对值越大表示特征越重要,特征在解释列表中的位置越靠前,反之亦然。如果权重的符号为正,表示特征与解释呈正相关关系,反之亦然。因此,以上指标不能准确地评估LIME解释的稳定性。例如,假设LIME 2次重复实验返回的解释结果为$ A=[\left('{\rm{TB}}',0.5\right),\left('{\rm{DB}}',0.4\right),\left('{\rm{TP}}',0.3\right)] $ 和$B= [('{\rm{TP}}', 0.5),\left('{\rm{DB}}',-0.4\right),\left('{\rm{TB}}',0.3\right)]$ ,根据定义计算,VSI(A,B)=FSI(A,B)=J(A,B)=1,但是这并不意味LIME的解释是稳定的。因为特征之间存在序关系,并且第2个特征$ '{\rm{DB}}' $ 的权重由正值变为了负值,即发生了解释翻转。为了更好地量化LIME解释的稳定性,本文提出了一种新的稳定性评价指标FSSI(features sequence stability index)。对于2次重复实验产生的解释结果
$E_{A}=\left[\left({e}_{{a}_{1}},{w}_{{a}_{1}}\right),\left({e}_{{a}_{2}},{w}_{{a}_{2}}\right),\cdots,\left({e}_{{a}_{k}},{w}_{{a}_{k}}\right)\right]$ 和$E_{B}=\left[\left({e}_{{b}_{1}},{w}_{{b}_{1}}\right),\left({e}_{{b}_{2}},{w}_{{b}_{2}}\right),\cdots,\left({e}_{{b}_{k}},{w}_{{b}_{k}}\right)\right]$ ,${\rm{FSSI}}(E_{A}, E_{B})$ 定义为$$ {\rm{FSSI}}(E{_A},E{_B}) = \frac{{\displaystyle\sum\limits_{i = 1}^k {{1_{{e_{{a_i}}} = {e_{{b_i}}}\& \& {w_{{a_i}}} \times {w_{{b_i}}} \geqslant 0}}} }}{k} \in [0,1] $$ 只有在特征序列和特征权值的符号相同时,才认为这2次实验的解释结果是稳定的。FSSI值越大表示解释的稳定性越高。因此,根据定义FSSI(A, B)=0,即LIME产生的解释是不稳定的。算法3给出了FSSI的伪代码。
为了评价模型的局部忠实性,本文选用了R2作为评价指标,R2定义为
$$ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y_i}})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - \overline y )}^2}} }} \in [0,1] $$ 算法3 特征序列稳定性指数 (FSSI)
输入
$E_{A}=\left[\right({e}_{ {a}_{1} },{w}_{ {a}_{1} }),({e}_{ {a}_{2} },{w}_{ {a}_{2} }),\cdots,({e}_{ {a}_{k} },{w}_{ {a}_{k} }\left)\right]$ $E_{B}=\left[\right({e}_{ {b}_{1} },{w}_{ {b}_{1} }),({e}_{ {b}_{2} },{w}_{ {b}_{2} }),\cdots,({e}_{ {b}_{k} },{w}_{ {b}_{k} }\left)\right]$ 输出 FSSI
① foreach i in 1, 2, …, k
② Initialize count=0
③ if
$ {e}_{{a}_{i}} $ =$ {e}_{{b}_{i}} $ and$w_{a_i} \cdot w_{b_i} \geqslant 0$ ④ count++
⑤ return count/k
3.2 数据集和对比算法
本文共使用了6个公开的常用加州大学欧文分校 (university of California Irvine, UCI) 数据集( http://archive.ics.uci.edu/)作为实验数据集:Parkinsons、Breast cancer (BC)、Indian liver patient (ILP)、Wine quality (Wine)、Electrical grid (EG)和Bank marketing (Bank)。数据集的详细统计信息如表1所示。为了评估本文提出方法的性能,本文选择了以下5个最新的方法作为对比算法:LIME[5]、DLIME[17]、BayLIME[18]、ALIME[19]和S-LIME[20]。
表 1 数据集的统计信息Table 1 Statistics of the datasets数据集 样本数 特征数 类别数 任务 Parkinsons 197 22 2 分类 BC 569 30 2 分类 ILP 579 10 2 分类 Wine 4980 11 10 分类 EG 10000 13 2 分类 Bank 45211 20 2 分类 3.3 实验设置
所有的数据集被划分为80%训练集,20%测试集。算法1中参数
$ \tau $ 的值设置为100。算法2中,样本数量N设置为1000,ILP、Wine和EG数据集的解释长度K设置为5,其他数据集设置为10。参照DLIME、BayLIME、LIME、S-LIME均使用了随机森林作为黑盒模型,在后续实验中均使用含500棵树的随机森林[26]模型作为黑盒模型。3.4 局部忠实性评估
为了评估本文提出方法的局部忠实性,以R2为评价指标,将其和其他5种最新方法在6个数据集上进行了详细的对比实验,实验结果如表2所示。从表2中可以看出,针对不同的数据集,LIME、BayLIME、DLIME、ALIME和S-LIME的局部忠实性水平波动很大,而IsomapVSG-LIME比较稳定,R2值均保持在0.7左右,这在一定程度上说明了本文提出方法的泛化性能是比较好的。就R2的平均值而言,IsomapVSG-LIME比其他5种方法的平均值高出46.93%,比局部忠实性最低的DLIME高出67.4%,比局部忠实性最高的BayLIME高出20.27%。在单个数据集上和其他方法相比,IsomapVSG-LIME比局部忠实性最低的DLIME(在EG数据集上)高出77.67%,比局部忠实性最高的BayLIME(在BC数据集上)高出19.18%。综上,本文提出方法有效地提高了LIME解释的局部忠实性。
表 2 局部忠实性实验结果Table 2 Local fidelity experiment results数据集 IsomapVSG-LIME LIME[5] DLIME[17] BayLIME[18] ALIME[19] S-LIME[20] Parkinsons 0.7761 0.3372 0.0613 0.5006 0.3473 0.3250 BC 0.7987 0.2773 0.1361 0.6079 0.2444 0.2602 ILP 0.7933 0.2162 0.0582 0.5929 0.2363 0.2097 Wine 0.6936 0.1426 0.0068 0.3954 0.1775 0.1686 EG 0.7774 0.2520 0.0007 0.5957 0.2524 0.2442 Bank 0.6277 0.2989 0.0943 0.5585 0.3025 0.2888 平均 0.7445 0.2541 0.0705 0.5418 0.2600 0.2494 3.5 稳定性评估
为了评估本文提出方法的稳定性,以FSSI为评价指标,在相同条件下对测试集中的每一条数据重复进行了10次实验,对比实验结果如表3所示。从表3中可以明显地看出,本文所提方法和DLIME一样,是一种稳定的方法,在每一个数据集上的FSSI值都达到了1.0。就FSSI的平均值而言,IsomapVSG-LIME比其他4种方法(DLIME除外)的平均值高出了53.81%,比稳定性最差的LIME高出了62.52%,比稳定性最好的S-LIME高出了49.2%。在单个数据集上和其他方法(DLIME除外)相比,IsomapVSG-LIME比稳定性最低的LIME(在EG数据集上)高出69.18%,比稳定性最高的S-LIME(在ILP数据集上)高出21.49%。综上,本文提出方法有效地提高了LIME解释的稳定性。
3.6 消融实验
为了验证样本选择模块的有效性,本节设置了一个消融实验,将去掉样本选择模块的IsomapVSG-LIME模型(命名为Version1.0)和包含样本选择模块的IsomapVSG-LIME模型(命名为Version2.0)进行局部忠实性对比,实验结果如表4所示。从表4中可以看出,就R2的平均值而言,Version2.0比Version1.0提高了17.15%。在单个数据集上,ILP数据集的提升效果最明显,提高了26.38%。EG的提升效果最差,提高了8.33%。综上,样本选择模块是必要的,其可以有效地提高解释的局部忠实性。
表 4 消融实验结果Table 4 Ablation experiment results数据集 Version1.0 Version2.0 Parkinsons 0.6253 0.7761 BC 0.5747 0.7987 ILP 0.5295 0.7933 Wine 0.5119 0.6936 EG 0.6941 0.7774 Bank 0.5163 0.6416 平均值 0.5753 0.7468 4. 结束语
为了提高LIME解释的局部忠实性和稳定性,本文提出了一种新的局部模型无关解释方法IsomapVSG-LIME。该方法使用基于流形学习的虚拟样本生成方法IsomapVSG代替LIME的随机扰动采样方法来进行样本生成,然后用凝聚层次聚类方法从生成的虚拟样本中选择具有代表性的样本,最后用其训练一个加权稀疏线性模型来解释单个预测实例。此外,本文还提出了一种新的解释稳定性评价指标FSSI,克服了以往评价指标忽略特征序关系和解释翻转的缺陷。在现有的公开数据上进行对比实验,结果表明本文提出的方法在局部忠实性和稳定性上均优于其他方法。
-
表 1 数据集的统计信息
Table 1 Statistics of the datasets
数据集 样本数 特征数 类别数 任务 Parkinsons 197 22 2 分类 BC 569 30 2 分类 ILP 579 10 2 分类 Wine 4980 11 10 分类 EG 10000 13 2 分类 Bank 45211 20 2 分类 表 2 局部忠实性实验结果
Table 2 Local fidelity experiment results
数据集 IsomapVSG-LIME LIME[5] DLIME[17] BayLIME[18] ALIME[19] S-LIME[20] Parkinsons 0.7761 0.3372 0.0613 0.5006 0.3473 0.3250 BC 0.7987 0.2773 0.1361 0.6079 0.2444 0.2602 ILP 0.7933 0.2162 0.0582 0.5929 0.2363 0.2097 Wine 0.6936 0.1426 0.0068 0.3954 0.1775 0.1686 EG 0.7774 0.2520 0.0007 0.5957 0.2524 0.2442 Bank 0.6277 0.2989 0.0943 0.5585 0.3025 0.2888 平均 0.7445 0.2541 0.0705 0.5418 0.2600 0.2494 表 3 稳定性实验结果
Table 3 Stability experiment results
表 4 消融实验结果
Table 4 Ablation experiment results
数据集 Version1.0 Version2.0 Parkinsons 0.6253 0.7761 BC 0.5747 0.7987 ILP 0.5295 0.7933 Wine 0.5119 0.6936 EG 0.6941 0.7774 Bank 0.5163 0.6416 平均值 0.5753 0.7468 -
[1] 纪守领, 李进锋, 杜天宇, 等. 机器学习模型可解释性方法、应用与安全研究综述[J]. 计算机研究与发展, 2019, 56(10): 2071–2096. doi: 10.7544/issn1000-1239.2019.20190540 JI Shouling, LI Jinfeng, DU Tianyu, et al. A review of interpretability methods, applications and security of machine learning models[J]. Journal of computer research and development, 2019, 56(10): 2071–2096. doi: 10.7544/issn1000-1239.2019.20190540 [2] 陈珂锐, 孟小峰. 机器学习的可解释性[J]. 计算机研究与发展, 2020, 57(9): 1971–1986. doi: 10.7544/issn1000-1239.2020.20190456 CHEN Kerui, MENG Xiaofeng. Interpretability of Machine Learning[J]. Journal of computer research and development, 2020, 57(9): 1971–1986. doi: 10.7544/issn1000-1239.2020.20190456 [3] MOLNAR C. Interpretable machine learning[M]. Raleigh: Lulu Press, 2019. [4] 程国建,刘连宏. 机器学习的可解释性综述[J]. 智能计算机与应用, 2020, 10(5): 6–9. doi: 10.1016/j.inffus.2019.12.012 CHENG Guojian , LIU Lianhong. An overview of the inte rpre tability of machine learning[J]. Intelligent computer and applications, 2020, 10(5): 6–9. doi: 10.1016/j.inffus.2019.12.012 [5] RIBEIRO M T, SINGH S, GUESTRIN C. “why should I trust You?”: explaining the predictions of any classifier[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1135–1144. [6] MODHUKUR V, SHARMA S, MONDAL M, et al. Machine learning approaches to classify primary and metastatic cancers using tissue of origin-based DNA methylation profiles[J]. Cancers, 2021, 13(15): 3768. doi: 10.3390/cancers13153768 [7] PAN Pan, LI Yichao, XIAO Yongjiu, et al. Prognostic assessment of COVID-19 in the intensive care unit by machine learning methods: model development and validation[J]. Journal of medical internet research, 2020, 22(11): e23128. doi: 10.2196/23128 [8] SCHULTEBRAUCKS K, CHOI K W, GALATZER-LEVY I R, et al. Discriminating heterogeneous trajectories of resilience and depression after major life stressors using polygenic scores[J]. JAMA psychiatry, 2021, 78(7): 744–752. doi: 10.1001/jamapsychiatry.2021.0228 [9] FAN Yanghua, LI Dongfang, LIU Yifan, et al. Toward better prediction of recurrence for Cushing’s disease: a factorization-machine based neural approach[J]. International journal of machine learning and cybernetics, 2021, 12(3): 625–633. doi: 10.1007/s13042-020-01192-6 [10] NÓBREGA C, MARINHO L. Towards explaining recommendations through local surrogate models[C]//Proceedings of the 34th ACM/SIGAPP Symposium on Applied Computing. New York: ACM, 2019: 1671−1678. [11] ZHU Fan, JIANG Min, QIU Yiming, et al. RSLIME: an efficient feature importance analysis approach for industrial recommendation systems[C]//2019 International Joint Conference on Neural Networks. Piscataway: IEEE, 2019: 1−6. [12] DARIAN M, ONCHIS. Stable and explainable deep learning damage prediction for prismatic cantilever steel beam[J]. Computers in industry, 2021, 125: 103359. doi: 10.1016/j.compind.2020.103359 [13] PANDEY P, RAI A, MITRA M. Explainable 1-D convolutional neural network for damage detection using Lamb wave[J]. Mechanical systems and signal processing, 2022, 164: 108220. doi: 10.1016/j.ymssp.2021.108220 [14] GARREAU D, LUXBURG U. Explaining the explainer: A first theoretical analysis of LIME[C]//International Conference on Artificial Intelligence and Statistics. Palermo: PMLR, 2020: 1287−1296. [15] SLACK D, HILGARD S, JIA E, et al. Fooling LIME and SHAP: adversarial attacks on post hoc explanation methods[C]//Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society. New York: ACM, 2020: 180−186. [16] RAHNAMA A H A, BOSTRÖM H. A study of data and label shift in the LIME framework[EB/OL].(2019-10-31)[2022-09-06].https://arxiv.org/abs/1910.14421. [17] ZAFAR M R, KHAN N. Deterministic local interpretable model-agnostic explanations for stable explainability[J]. Machine learning and knowledge extraction, 2021, 3(3): 525–541. doi: 10.3390/make3030027 [18] ZHAO Xingyu, HUANG Wei, HUANG Xiaowei, et al. Baylime: Bayesian local interpretable model-agnostic explanations[C]//Uncertainty in Artificial Intelligence.Toronto: PMLR, 2021: 887−896. [19] SHANKARANARAYANA S M, RUNJE D. ALIME: autoencoder based approach for local interpretability[M]. Cham: Springer International Publishing, 2019: 454−463. [20] ZHOU Zhengze, HOOKER G, WANG Fei. S-LIME: stabilized-LIME for model explanation[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. New York: ACM, 2021: 2429−2438. [21] VISANI G, BAGLI E, CHESANI F, et al. Statistical stability indices for LIME: obtaining reliable explanations for machine learning models[J]. Journal of the operational research society, 2022, 73(1): 91–101. doi: 10.1080/01605682.2020.1865846 [22] ZHANG Xiaohan, XU Yuan, HE Yanlin, et al. Novel manifold learning based virtual sample generation for optimizing soft sensor with small data[J]. ISA transactions, 2021, 109: 229–241. doi: 10.1016/j.isatra.2020.10.006 [23] TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319–2323. doi: 10.1126/science.290.5500.2319 [24] HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]//2004 IEEE International Joint Conference on Neural Networks. Piscataway: IEEE, 2005: 985−990. [25] RASOULI P, YU I C. EXPLAN: explaining black-box classifiers using adaptive neighborhood generation[C]//2020 International Joint Conference on Neural Networks . Piscataway: IEEE, 2020: 1−9. [26] BREIMAN L. Random forests[J]. Machine learning, 2001, 45(1): 5–32. doi: 10.1023/A:1010933404324


 下载:
下载: