Dual-population co-evolutionary algorithm for solving electric vehicle route problems
-
摘要: 绿色物流领域新兴的电动汽车车辆路径问题，由于需要对车辆路径和充电决策同时优化，搜索空间急剧增大，且需要同时满足容量和电量双重约束，现有方法难以快速找到质量较优的可行解。为此，提出一种基于双种群的协同进化算法，通过忽略电量约束构造简单带容量约束的车辆路径问题，辅助原始复杂问题的快速求解。为实现其间信息交互，设计一种基于改进距离邻接矩阵的解序列特征表示方法，旨在同时获取客户访问顺序和车辆指派信息；利用降噪自编码器构建2个问题解之间转换关系，以实现问题域间知识迁移。将该算法与目前常用的3种启发式算法和2种进化算法在不同规模测试集上进行对比，试验结果表明所提算法具有更快收敛速度且所获解集具有更好收敛性。Abstract: The emerging field of green logistics presents a challenge in the form of electric vehicle routing. This issue requires simultaneous optimization of routing and charging decisions, significantly expanding the search space. Moreover, solutions must comply with capacity and power constraints, making it difficult to quickly find feasible solutions using existing methods. To address these challenges, we propose a dual population-based co-evolutionary algorithm. This approach involves constructing a simpler problem to expedite the solution process for the original, more complicated problem. To facilitate information exchange between these two heterogeneous problems, we designed a solution representation method. This method, which is based on an improved distance adjacency matrix, allows to obtain information on customer visits and vehicle assignments. Subsequently, we employed a commonly used denoising autoencoder to establish the transformation relationship between solutions from these two problems. This step enables knowledge transfer between the two problem domains. Our proposed algorithm was tested against three heuristic methods and two evolutionary algorithms on test sets of different sizes. The experimental results show that the proposed algorithm not only converges faster but also yields solutions with superior convergence.
-
近年来，电动汽车车辆路径问题（electric vehicle route problem, EVRP）作为绿色物流领域新兴的一种复杂组合优化问题，受到众多研究人员的广泛关注[1-4]。不同于传统基于燃油汽车的带容量约束车辆路径问题（capacitated vehicle route problem, CVRP），EVRP除了需要考虑车辆容量约束外，还需要额外考虑电量约束，导致在优化客户访问顺序的同时还需要优化充电调度方案，属于NP-hard问题。目前求解该问题的方法主要分为两大类[4]：精确算法和启发式算法。精确算法是将EVRP转化为混合整数线性规划问题进行求解，如分支定界法[5]和分支切割法[6]。尽管精确算法在中小规模的问题上能够得到比较好的解决方案，但此类算法求解时间随问题规模呈指数级增长，无法有效求解客户数超过50的大规模实例。启发式算法采用基于邻域的局部搜索方式，在有限时间内可以得到有效解，比如模拟退火[7]、禁忌搜索[8]、变邻域搜索（variable neighborhood search, VNS）[9]和自适应大邻域搜索（adaptive large neighborhood search, ALNS）[10]等，但这些算法对初始解和局部搜索算子十分敏感，如果初始解位置或所选搜索算子不当，算法易陷入局部最优。
进化算法作为一种基于种群的启发式算法[11]，以种群并行搜索的方式求解问题的最优解，具有良好的全局搜索特性，被广泛用于求解各类VRP[12-16]。目前已有少量研究工作将进化算法应用于求解EVRP，如Barco等[17]采用差分进化算法同时优化EVRP的路径和充电调度方案，但由于差分进化算法局部开发能力有限，导致无法找到高质量的可行解。Hiermann等[18]提出采用遗传算法，通过实施分层路径评估来解决路径优化和充电调度问题，但这种分层思想忽略了路径优化和充电调度之间的耦合性，易陷入局部最优。Guo等[19]采用基于混合编码的遗传算法对其进行整体求解，但由于其编码方案是同时对客户访问顺序和充电站访问顺序进行统一编码，搜索空间较大，算法很难快速收敛至可行区域。为此，Jia等[20]将EVRP建模成双层优化问题，其中上层为不考虑电量约束和充电站位置的CVRP问题；下层为上层优化后固定路径下的充电调度问题，但由于上层蚁群算法十分耗时且下层只是采用简单的基于插入移除充电站方式满足电量约束，收敛速度较慢。
为了快速收敛至最优可行解，本研究提出一种双种群协同进化算法（dual-population based coevolutionary algorithm, COEA），其核心思想是通过构造与原问题相关的简单问题来辅助原始复杂问题的快速求解，借助简单问题种群快速收敛优势，促进原始问题种群高质量解的快速生成。在本研究中，简单问题构造为EVRP忽略电量约束而保留容量约束的CVRP。由于约束条件不一样，CVRP和EVRP其实是2种不同类型问题。为实现这2个异构问题间的信息交互，引入降噪自编码器（denoising autoencoder, DAE）构建2个问题解之间的转换关系。基于训练后的DAE进行CVRP与EVRP种群中精英解的相互迁移，促进2个种群的协同进化。
1. 问题描述及数学模型
EVRP需要在同时满足车载容量和电量约束的情况下，最小化总行驶距离和使用的车辆数，其目标函数表达式如下
$$ {\rm{minimize}}{\text{ }}{f_1} = \sum\limits_{i \in {V_0},j \in {V_{n + 1}}} {{d_{ij}}{x_{ij}}} $$ (1) $$ {\rm{minimize}}{\text{ }}{f_2} = \sum\limits_{j \in {V_{n + 1}}} {{x_{0j}}} $$ (2) 式中：
$ V = C \cup R $ 表示包括客户点集C和充电站点集R的并集；$ {V_0} $ 表示包括以仓库点为起点的所有点集；$ {V_{n + 1}} $ 表示包括以仓库点为终点的所有点集；$ {d_{ij}} $ 表示在点$ {v_i} $ 和点$ {v_j} $ 之间的距离；$ {x_{ij}} $ 表示是否有车辆从点$ {v_i} $ 行驶到点$ {v_j} $ ，$ {x_{ij}} = 1 $ 表示有，否则$ {x_{ij}} = 0 $ 。EVRP需要满足以下约束条件
$$ {\text{ }}\sum\limits_{j \in {V_{n + 1}},i \ne j} {{x_{ij}} = 1,\quad \forall i \in C} $$ (3) $$ {\text{ }}\sum\limits_{i \in {V_0},i \ne j} {{x_{ij}} \leqslant {y_j},\quad \forall j \in R} $$ (4) $$ {\text{ }}\sum\limits_{i \in {V_{n + 1}},i \ne j} {{x_{ji}} - {\text{ }}\sum\limits_{i \in {V_0},i \ne j} {{x_{ij}}} = 0,\quad \forall j \in V} $$ (5) $$ {\text{ }}\sum\limits_{i \in R} {{y_i} = {O^{{\rm{UB}}}}} $$ (6) $$ {\text{ }}\sum\limits_{j \in {V_{n + 1}}} {{x_{oj}} \leqslant {N^{{\rm{UB}}}}} $$ (7) $$ 0 \leqslant {f_0} \leqslant Q $$ (8) $$ 0 \leqslant {f_0} \leqslant {f_i} - {q_i}{x_{ij}} + Q(1 - {x_{ij}}),\quad \forall j \in {V_{n + 1}},i \ne j $$ (9) $$ {b_i} < B,\quad \forall i \in V $$ (10) $$ {y_i} < {b_i},\quad \forall i \in R $$ (11) $$ 0 < {b_i} \leqslant {b_i} - h{d_{ij}}{x_{ij}} - B(1 - {x_{ij}}),\quad \forall i \in {V_{n + 1}},i \ne j $$ (12) $$ {b_0} \leqslant B $$ (13) $$ {x_{ij}} \in \{ 0;1\} ,{\forall _i} \in {V_0},\quad \forall j \in {V_{n + 1}} $$ (14) $$ {y_i} \in \{ 0;1\} ,\quad \forall i \in R $$ (15) 式中：约束（3）表示每个客户只能由一辆车访问；约束（4）表示电动汽车只能在充电站进行充电，
$ {y}_{i} $ 表示充电站i的使用情况，$ {y_i} = 1 $ 表示被使用，否则$ {y_i} = 0 $ ；式（5）保证结点流量平衡，即每辆车进入某点的次数和离开某点的次数相等；约束（6）表示使用的充电站数最多不能超过$ {O^{{\rm{UB}}}} $ （建设充电站数的上限）；约束（7）表示使用的车辆数最多不能超过$ {N^{{\rm{UB}}}} $ （车辆数的上限）；约束（8）表示车辆从仓库点出发后负载容量不超过车载最大容量，其中$ {f}_{0} $ 表示在车辆起点处的容量，Q表示电动汽车最大负载容量；约束（9）表示车辆装载容量与经过的客户点需求量之间的关系，若$ {x_{ij}} = 1 $ ，则车辆离开j点的最多可剩余货物量至多为车辆离开i点的最多可剩余货物量减去j点的需求，否则该约束松弛；约束（10）表示车辆的电量不能超过车载电池的最大电量，其中，$ {b_j} $ 为车辆到达第j点后的电量水平，B为车载电池的最大电量；约束（11）表示只有当车辆需要充电时才去充电站进行充电，此时电量一定不小于0；约束（12）表示电量与行驶里程之间的关系，如果电动汽车在经过i点之后到达了j点，那么电动汽车刚到达j点的剩余电量$ {b}_{j} $ 为电动汽车离开i点剩余电量$ {b_i} $ 减去i和j之间路程消耗的电量，其中h为电动汽车单位里程电量消耗速度；约束（13）表示电动汽车从仓库点出发后车辆满电，其中$ {b}_{0} $ 为车辆从仓库点出发的电量；约束（14）、（15）定义决策变量是0-1二进制变量。2. 双种群协同进化算法求解EVRP
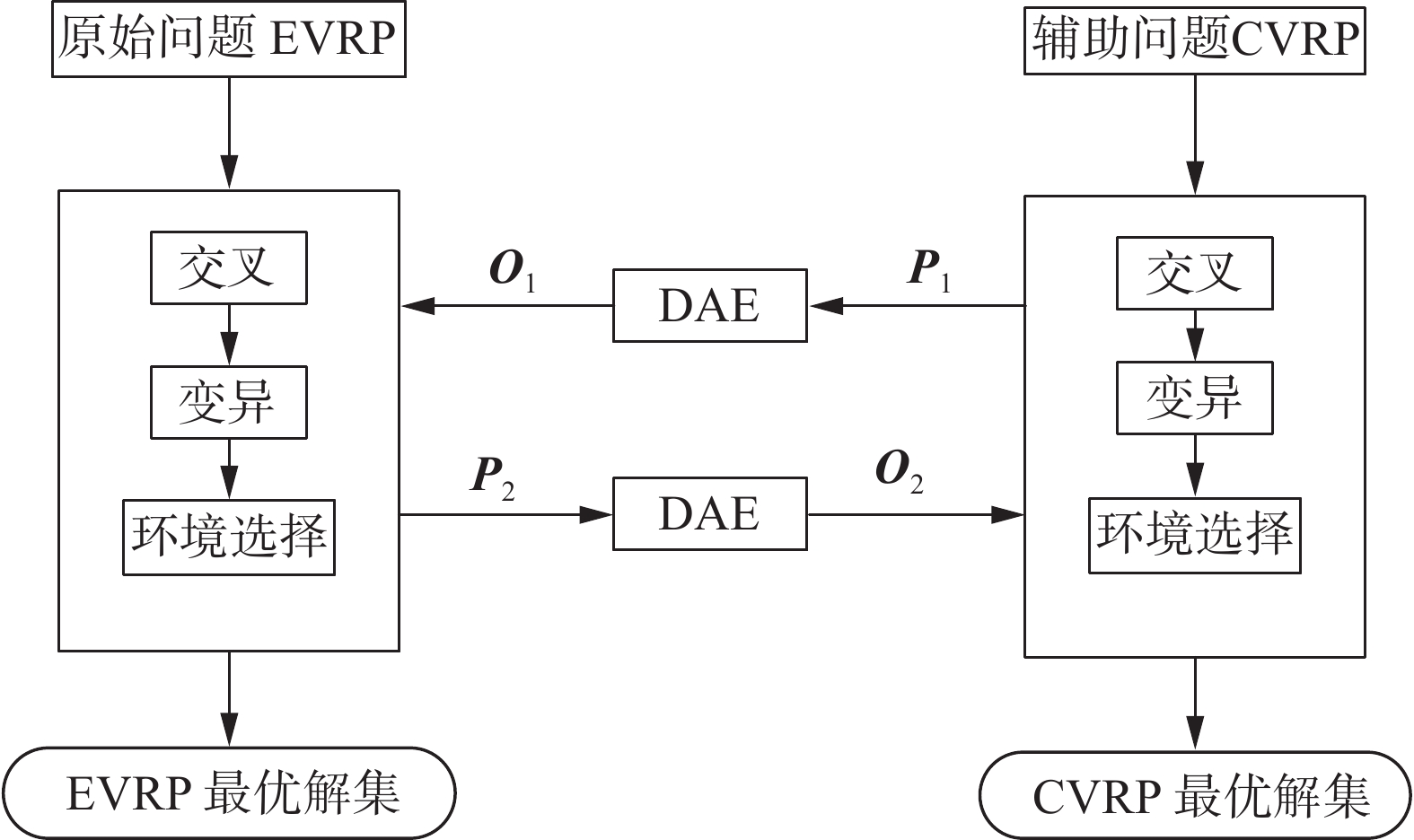
为了提高进化算法求解EVRP的性能和效率，本研究基于双种群协同进化框架，使用一个种群求解EVRP（复杂问题），另一个种群求解CVRP（简单问题），CVRP是EVRP忽略电量约束且将充电站点当成无需求的客户点转化而来的。2个种群单独进化，每隔一定代数先采用改进的距离邻接矩阵对解序列进行表示，使其能蕴含更多问题信息；然后使用降噪自编码器通过应用改进的距离邻接矩阵进行知识转换，构建2个问题间的联系，表征相同客户点和设施点分布在不同场景约束下的转换关系，选择优秀解进行迁移。由于CVRP种群更易搜索到可行解，其种群收敛程度更高，通过将CVRP种群精英解迁移到EVRP种群中，可以加速EVRP求解；反过来，可以将EVRP的精英解迁移到CVRP种群中，引导CVRP种群朝着适合EVRP求解的方向进化。而实现协同进化关键在于2个异构问题间的信息如何交互。
2.1 基于改进距离邻接矩阵的解序列特征表示
为实现2个异构问题间信息迁移，首先构建2个问题解序列统一的特征表示形式，使其蕴含更多问题特征信息。采用整数编码方式对简单CVRP和复杂EVRP进行编码，其中简单CVRP的解由客户点的访问序列和仓库来表示，而EVRP在此基础上多了访问充电站的序列，且不同车辆间用分隔符0隔开。为了保证2个问题解序列编码长度一致，CVRP是将充电站点看作无需求量的客户点，无需服务但需访问。辅助种群CVRP能将EVRP中充电站位置因素考虑到路径规划中，从而为EVRP种群进化提供充电站距离信息，避免绕远充电。
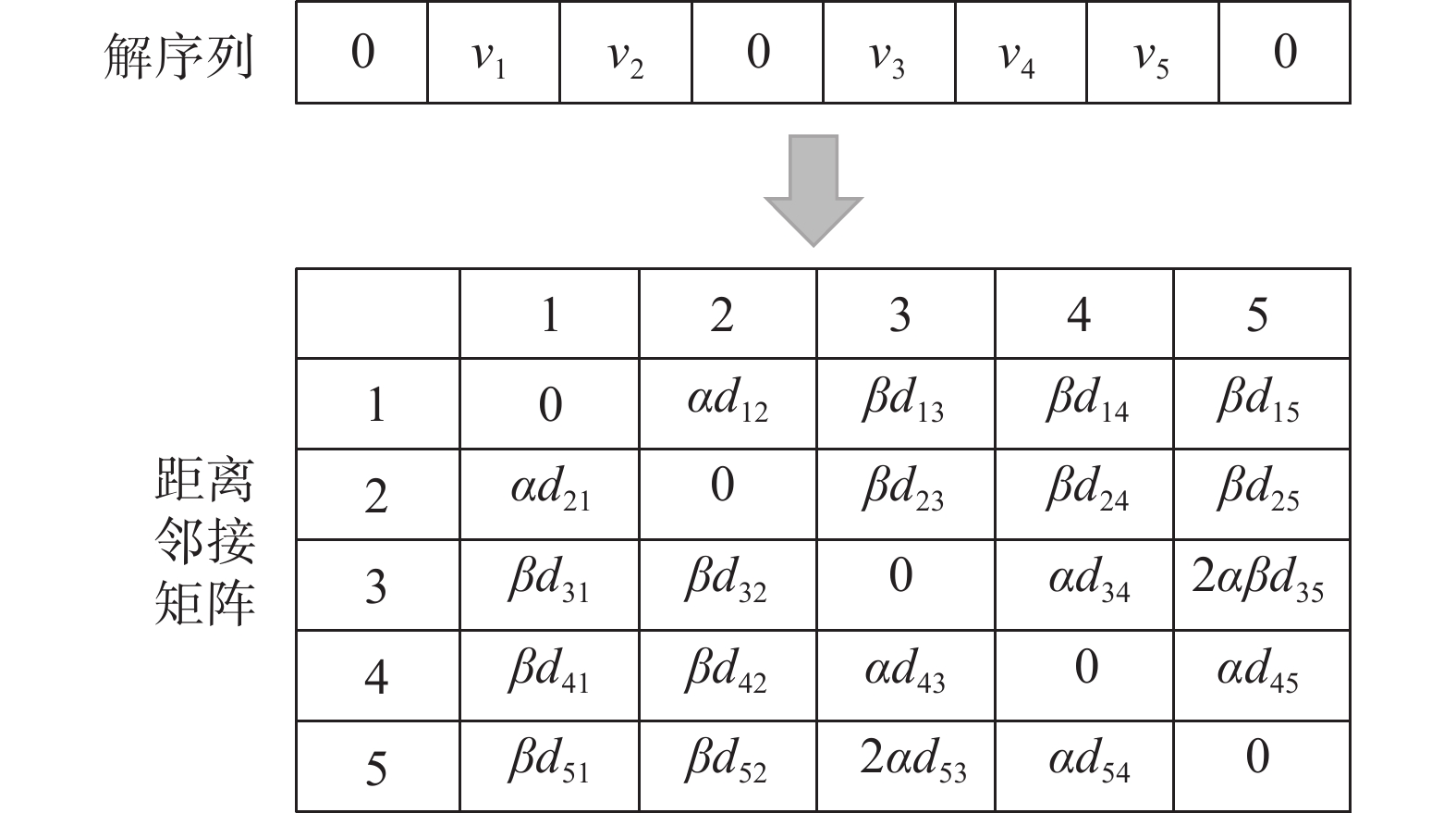
由于上述编码的解序列只是一串序列数字，无法蕴含更多的问题信息，比如客户间距离、客户分配情况等，不便于学习模型进行高效知识迁移。为此，采用改进的距离邻接矩阵对解序列进行特征表示。由图1可知，对于客户数为5的解序列可表示为
$5 \times 5$ 的距离邻接矩阵，不同于传统的距离邻接矩阵，其每一个元素不仅包括原始的真实距离，还包括一个自定义的相对距离，用以体现解序列中不同路径下客户点的分配情况。为了使被同一车辆访问客户距离更近，而不同车辆访问的客户更远，相对距离$ \alpha $ 设置为一个较小的数值，而相对距离$ \beta $ 设置为一较大的数值，用以更快速地进行客户聚类，其中被同一车辆访问的客户，其间距离先后访问顺序线性增加。改进的距离邻接矩阵能同时包含客户间真实距离信息和车辆指派信息，便于之后学习模型更精准拟合解序列间映射关系，在迁移解知识时更加地真实准确。
图 1 基于距离邻接矩阵的解表示Fig. 1 Solution representation based on distance adjacent matrix
下载:
全尺寸图片
值得注意的是，基于距离邻接矩阵，采用K-means方法可以得到相对应的解序列，即将距离邻接矩阵每一列看成是客户的特征向量，对其进行聚类可以得到被同一辆车服务的客户；然后为每个类内客户点确定路径，根据真实距离选择离仓库点最近的客户作为路径内第一个客户，而剩余客户点按照距离邻接矩阵中距离大小进行依次选择。
2.2 基于降噪自编码器的CVRP和EVRP问题间知识迁移
为了能够建立简单CVRP和复杂EVRP解之间的对应关系，采用迁移学习领域常用的降噪自编码器DAE[21]。本研究将CVRP和EVRP分别作为输入输出，通过DAE建立简单CVRP和复杂EVRP解之间的转换关系。具体而言，在进化的每一代，将2个种群的精英解对应距离邻接矩阵表示作为DAE的输入和输出进行训练，间隔数代进行信息交互，即使用训练后的DAE对2个问题的当前最优解进行转换。由图2可知，从右到左，CVRP中当前最好解集
$ {{\boldsymbol{P}}_1} $ 的距离邻接矩阵作为输入，输出为转换后的距离邻接矩阵$ {{\boldsymbol{O}}_1} $ 并作为EVRP问题的子代；从左到右则输入为EVRP问题中当前最好解$ \mathrm{集}{{\boldsymbol{P}}}_{2} $ 的距离邻接矩阵，输出为转换后的距离邻接矩阵$ {{\boldsymbol{O}}_2} $ 并作为CVRP的子代。
图 2 基于DAE的CVRP与EVRP问题间知识迁移示意Fig. 2 Illustration of knowledge transfer process of heterogeneous problem based on DAE下载:
全尺寸图片
基于DAE得到的距离邻接矩阵，按照2.1节中聚类方法将其转化为解序列。值得注意的是，从EVRP到CVRP的解的转换可以通过上述方法实现；但对于从CVRP到EVRP解的转换，还需要进行根据电量约束进行修复：删除解中充电站节点，采用迭代贪婪算法[22]在路径中插入充电站，以得到满足EVRP电量约束的解序列。
2.3 算法总体流程
COEA算法总体流程如下：首先，随机初始化2个大小为N的种群和分别用以求解EVRP和CVRP，每个种群均采用基于分解的多目标进化算法（MOEA/D）[23]进行优化，评价函数分别为
$ {F_o} $ 和$ {F_h} $ 。在优化过程中，每一代选取2个种群中对应权重向量上关联的当前最优解分别作为DAE的输入输出进行训练，然后间隔$ \alpha ·{G_{\max }} $ 代进行预测，即从简单CVRP的种群中选择对应权重向量上的当前解，经过DAE转换后添加到复杂EVRP种群中，作为EVRP的子代；同时从EVRP种群$ {{\boldsymbol{P}}_o} $ 中选择对应权重向量上的当前最优解迁移到CVRP种群中，作为CVRP的子代。然后，分别对生成的子代进行评价，其中$ {{\boldsymbol{O}}_1} $ 中的迁移解是由EVRP问题$ {F_o} $ 进行评估，而$ {{\boldsymbol{O}}_2} $ 中的解是由简单CVRP问题$ {F_h} $ 进行评价。最后，将从$ {F_h} $ 迁移来的解与种群$ {F_o} $ 共同进化，从$ {F_o} $ 迁移来的解与种群$ {F_h} $ 共同进化。由于$ {F_h} $ 比$ {F_o} $ 更加简单，在相同的迭代数下，CVRP种群收敛性更好，能辅助快速收敛，且$ {{\boldsymbol{P}}_h} $ 通常比$ {{\boldsymbol{P}}_o} $ 具有更好的多样性，能避免陷入局部可行区域。3. 试验仿真结果与分析
为测试本研究所提算法性能，选取目前性能优异的5种算法（BACO[20]、KBEA[24]、HVNS[9]、ALNS[10]和TS-MCWS[22]）作为对比算法。
3.1 试验设置
测试问题：选取目前通用的EVRP标准测试集[25]，包含200中等规模客户数和400大规模客户数的测试问题共计18个。
对比算法：所有对比算法参数均按照原始文献设置。COEA中所采用的MOEA/D算法邻域大小
$ T = 10 $ ，邻域内替换解的最大个数设为2，相对距离$ \alpha = 10,\;\beta = 2\;000 $ ，迭代次数比例$ \mu = 0.05 $ 。为了对比公平，所有算法种群大小和最大评价次数均保持一致，其中种群大小$ N=100 $ ，最大迭代次数为1000，每个算例均独立运行20次。评价指标：采用超体积（hypervolume，HV）来评价多目标优化算法COEA和KBEA所获得的解集质量[26]。采用成本函数[22]对COEA和单目标启发式算法BACO、ALNS、HVNS以及TS-MCWS进行比较，其表达式为
$$ C = {f_1} + \theta B{f_2} $$ (16) 式中：
$ \theta $ 为加权系数，参照文献[22]设置为0.35；B为电池最大电量，用以统一2个目标的量纲；f1为总行驶距离；f2为电动车辆数。3.2 算法有效性验证
COEA中有2个核心策略：解序列的距离邻接矩阵表示和基于降噪自编码器的解迁移。为验证两者有效性，将直接采用解序列而不采用距离邻接矩阵的版本称为Variant I，将解直接交换而不采用降噪自编码器进行解迁移的版本称为Variant II，并与采用原始MOEA/D求解EVRP进行对比。试验结果如表1所示，基于4种算法所获最小成本解的目标值优劣验证所提策略有效性。由表2可以看出：在大部分测试实例中，COEA可以在同等车辆数的情况下，获得更短的行驶距离。相比于Variant II，COEA进行解转换迁移可以在13个数据集上有更短的行驶距离，且避免使用过多的车辆数；相比于Variant I，COEA采用距离邻接矩阵表示解序列后，在行驶距离目标上有明显提升；相比于MOEA/D，COEA的双种群协同进化策略在行驶距离和车辆数目标上均有明显提升。
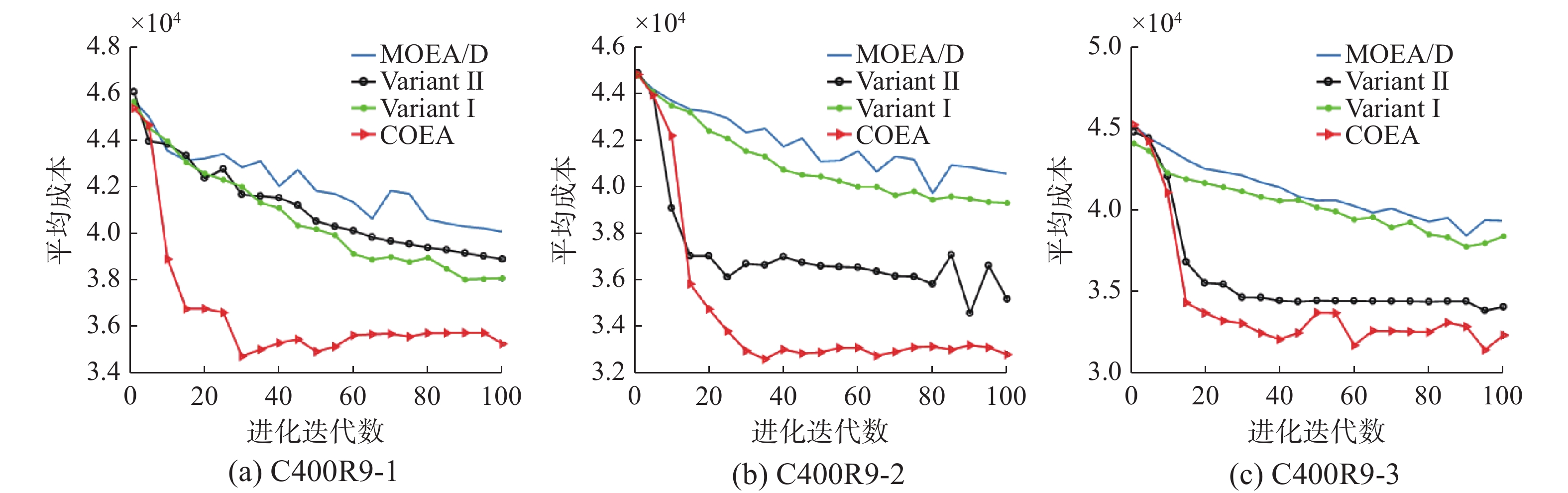
表 1 COEA算法中2种策略有效性验证Table 1 The effectiveness of two strategies of COEA algorithm问题 COEA Variant I Variant II MOEA/D $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 C200R9-1 3494.7 16 3838.3 16 3334.9 19 4142.2 16 C200R9-2 3350.8 16 3690.6 16 3361.0 16 3553.6 16 C200R9-3 3353.9 16 3847.7 16 3367.8 16 4328.4 16 C200R9-4 3306.3 16 4068.1 16 3124.4 18 4380.5 16 C200R5-1 2477.4 16 2707.1 16 2486.7 16 3032.6 17 C200R5-2 2357.2 16 2858.0 15 2390.2 16 2809.8 16 C200R5-3 2509.1 16 2989.7 16 2592.3 16 3219.3 16 C200R5-4 2454.4 16 2971.8 16 2412.1 16 3033.1 16 C400R9-1 6206.6 31 7193.8 31 6484.6 31 8561.5 32 C400R9-2 6161.8 32 6965.5 32 6107.7 32 8349.9 33 C400R9-3 5991.5 31 7014.9 32 6616.4 32 8334.7 31 C400R9-4 6296.7 32 6699.5 32 6439.6 32 8738.5 32 C400R9-5 6046.1 32 7124.3 31 6567.9 32 8296.3 32 C400R5-1 5166.6 32 5824.1 32 4809.0 32 6025.3 31 C400R5-2 4757.5 31 5630.7 31 5021.9 31 5997.3 31 C400R5-3 4992.6 32 5840.6 32 5046.8 32 5792.5 32 C400R5-4 5071.6 32 5793.2 32 5085.0 32 6295.1 32 C400R5-5 4914.4 32 6023.8 32 5512.1 32 5884.2 32 注：黑体代表最优结果，下同。 表 2 6种算法在EVRP标准测试集上所获最优解目标值结果Table 2 Objective values of the optimal solution obtained by the six algorithms on large-scale problems问题 COEA BACO KBEA ALNS HVNS TS-MCWS $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 C200R9-1 3494.7 16 4345.2 16 3348.8 17 3654.6 17 4128.7 16 7405.3 16 C200R9-2 3350.8 16 3823.5 16 3046.4 16 3538.5 16 4161.7 16 6743.1 16 C200R9-3 3353.9 16 4016.7 16 3231.4 16 3852.0 17 4504.2 17 6775.2 16 C200R9-4 3306.3 16 4139.3 16 3319.4 16 3615.9 16 4264.3 16 7043.0 16 C200R5-1 2477.4 16 2876.1 16 2507.8 16 2717.9 17 2851.8 17 4942.2 16 C200R5-2 2357.2 16 2928.3 16 2596.8 16 2518.2 16 2728.9 16 5198.8 16 C200R5-3 2509.1 16 3279.9 16 2789.2 16 2978.8 17 3073.1 17 4784.7 16 C200R5-4 2454.4 16 2830.3 16 2458.5 16 2530.2 17 2813.6 17 4673.1 16 C400R9-1 6206.6 31 7267.8 32 7380.9 31 7417.1 31 9785.2 31 13537.6 33 C400R9-2 6161.8 32 7660.1 32 5873.3 32 7166.9 33 9235.4 33 12259.8 32 C400R9-3 5991.5 31 7820.2 31 6241.9 32 7531.2 32 9443.6 32 13486.8 32 C400R9-4 6296.7 32 7756.3 32 5562.9 32 7102.8 33 9217.9 33 12590.9 32 C400R9-5 6046.1 32 7507.2 32 6786.0 32 6738.8 44 9547.8 32 12399.2 32 C400R5-1 5166.6 32 5892.9 31 4683.3 32 5109.8 36 6369.9 32 9547.2 32 C400R5-2 4757.5 31 6054.7 31 5721.7 32 5181.3 32 6252.1 32 9153.8 32 C400R5-3 4992.6 32 5032.3 32 4690.4 32 6585.8 32 6186.7 32 9331.3 32 C400R5-4 5071.6 32 6189.7 33 5956.1 32 5903.7 33 7163.1 33 9458.1 32 C400R5-5 4914.4 32 5826.2 32 4992.3 32 5051.8 32 6289.8 32 9185.2 32 为了对比收敛速度，绘制出4种算法所获平均成本随迭代次数的曲线图。由图3可知，平均成本是将非支配解集所有解通过式（18）计算出成本除以种群大小得到，其值越小越好。COEA由于采用了距离邻接矩阵和基于降噪自编码器的解迁移策略，具有更快的收敛速度。相比于使用单一策略的2个变体和单种群优化的MOEA/D，COEA所获平均成本大幅度降低。由此说明：基于双种群协同的简单问题辅助复杂问题求解策略是有效的。
图 3 4种算法所获平均成本随迭代次数变化曲线Fig. 3 Average costs of four algorithms over the generation number下载:
全尺寸图片
3.3 COEA与其他算法的对比结果
COEA与BACO、KBEA、ALNS、HVNS和TS-MCWS在EVRP标准测试集上最优解目标值结果如表2所示，其中最优结果以粗体突出显示。由表2中可以看出，COEA在大部分测试实例上所使用车辆数更少，且在行驶距离上更优，在18个算例中的11个上取得了最短行驶路径。具体而言，在
$ {f_1} $ 目标上，COEA明显优于BACO、HVNS、TS-MCWS；相比于KBEA，在11个算例上取得了更好结果；相比于ALNS，在17个算例上取得更好结果。KBEA通过种群历史进化信息挖掘出有用的路径特征，用以指导遗传算子的交叉变异，在400客户的大规模问题上具有较强的搜索能力，并在7个测试实例上获得了最好结果。而COEA通过使用简单CVRP辅助EVRP求解，在相同进化条件下，简单问题的搜索种群能更快收敛，能有效引导复杂问题进化种群快速生成满足容量约束的可行解。所以COEA相比其他算法能在更短的时间内找到可行性更好的解，同时在大规模测试实例最优解目标值上也具有一定竞争优势。COEA及其变种Variant I、Variant II和多目标进化算法KBEA在大规模测试实例上所获HV统计结果如表3所示，分别为20次独立运行结果的平均值和标准差（括号内）。同时，为了比较COEA与另外3种算法所获平均HV值之间差异显著性，采用Wilcoxon秩和检验进行两两比较，显著性水平取5%，表中“+”“−”“≈”分别表示其他算法显著优于、显著劣于和无差别于COEA。COEA在大部分算例上获得了最优解集质量；相比于Variant II，COEA引入基于降噪自编码器的解迁移后，10个算例中取得7个更好结果；与Variant I相比，进行解序列的距离邻接矩阵表示后可以在大规模问题上具有更好的结果；相比于KBEA，在大部分算例上能够获得更好的HV值。总体而言，COEA在大规模EVRP测试实例上能获得多样性和收敛性均佳的解集。
表 3 4种多目标进化算法在大规模测试问题上所获HV结果Table 3 Average and standard deviation of the HV values obtained by the four algorithms on large-scale test problems问题 COEA Variant II Variant I KBEA C400R9-1 1.8070×103(1.95×102) 1.4706×103(1.34×103)− 6.6377×101(4.82×102)− 5.5429×102(1.33×101)− C400R9-2 1.6621×102(1.05×102) 4.0088×102(4.85×102)+ 2.6001×101(1.95×101)− 1.4021×101(2.36×100)− C400R9-3 2.0673×103(8.74×102) 1.5822×103(6.86×102)− 1.0478×102(5.51×101)− 1.2611×101(3.86×10−1)− C400R9-4 3.7079×101(6.57×101) 1.1768×102(4.53×101)+ 3.0047×100(1.60×100)− 1.4371×101(7.73×10−1)− C400R9-5 2.4629×102(7.78×101) 8.0531×101(9.18×101)− 1.9878×101(9.59×100)− 1.9440×101(2.64×10−1)− 续表 3 问题 COEA Variant II Variant I KBEA C400R5-1 6.6082×102(7.45×102) 4.7191×102(1.16×103)− 2.0681×101(1.64×101)− 1.3252×102(1.33×101)− C400R5-2 6.9615×102(1.76×102) 1.9595×101(7.34×100)− 0(0)− 4.7834×100(8.49×10−1)− C400R5-3 4.7101×101(1.22×101) 3.9690×101(2.59×101)− 0(0)− 5.0960×100(3.86×10−1)− C400R5-4 3.6516×101(3.49×101) 9.5989×101(4.17×101)+ 1.0682×100(7.12×10−1)− 0(0)− C400R5-5 8.8559×100(1.74×101) 2.8787×100(3.38×101)− 0(0)− 1.1077×101(2.64×10−1)+ +/−/≈ — 3/7/0 0/10/0 1/9/0 4. 结束语
本研究提出了一种基于双种群的协同进化算法用于求解绿色物流中的电动汽车车辆路径问题，其核心思想是通过构造简单车辆路径问题辅助复杂EVRP快速求解。由于不带电量约束的简单CVRP更容易获得可行解，且收敛速度更快，通过将其精英解迁移到EVRP种群中，用以加速EVRP求解。特别地，为实现两问题种群进化信息的高效交互，首先设计了一种新的距离邻接矩阵表示解序列，使其蕴含更丰富问题特征，便于后续模型学习；其次采用迁移学习模型降噪自编码器实现解的转换，实现异构问题间知识的迁移；最后，迁移解与原种群共同进化，利用CVRP高质量的客户访问顺序促进EVRP的路径规划，提高算法的收敛性能。将所提算法与5种启发式算法在标准EVRP测试集上进行对比，试验结果表明所提算法能更快搜索最优可行解集。
-
图 1 基于距离邻接矩阵的解表示
Fig. 1 Solution representation based on distance adjacent matrix
下载:
全尺寸图片
图 2 基于DAE的CVRP与EVRP问题间知识迁移示意
Fig. 2 Illustration of knowledge transfer process of heterogeneous problem based on DAE
下载:
全尺寸图片
图 3 4种算法所获平均成本随迭代次数变化曲线
Fig. 3 Average costs of four algorithms over the generation number
下载:
全尺寸图片
表 1 COEA算法中2种策略有效性验证
Table 1 The effectiveness of two strategies of COEA algorithm
问题 COEA Variant I Variant II MOEA/D $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 C200R9-1 3494.7 16 3838.3 16 3334.9 19 4142.2 16 C200R9-2 3350.8 16 3690.6 16 3361.0 16 3553.6 16 C200R9-3 3353.9 16 3847.7 16 3367.8 16 4328.4 16 C200R9-4 3306.3 16 4068.1 16 3124.4 18 4380.5 16 C200R5-1 2477.4 16 2707.1 16 2486.7 16 3032.6 17 C200R5-2 2357.2 16 2858.0 15 2390.2 16 2809.8 16 C200R5-3 2509.1 16 2989.7 16 2592.3 16 3219.3 16 C200R5-4 2454.4 16 2971.8 16 2412.1 16 3033.1 16 C400R9-1 6206.6 31 7193.8 31 6484.6 31 8561.5 32 C400R9-2 6161.8 32 6965.5 32 6107.7 32 8349.9 33 C400R9-3 5991.5 31 7014.9 32 6616.4 32 8334.7 31 C400R9-4 6296.7 32 6699.5 32 6439.6 32 8738.5 32 C400R9-5 6046.1 32 7124.3 31 6567.9 32 8296.3 32 C400R5-1 5166.6 32 5824.1 32 4809.0 32 6025.3 31 C400R5-2 4757.5 31 5630.7 31 5021.9 31 5997.3 31 C400R5-3 4992.6 32 5840.6 32 5046.8 32 5792.5 32 C400R5-4 5071.6 32 5793.2 32 5085.0 32 6295.1 32 C400R5-5 4914.4 32 6023.8 32 5512.1 32 5884.2 32 注：黑体代表最优结果，下同。 表 2 6种算法在EVRP标准测试集上所获最优解目标值结果
Table 2 Objective values of the optimal solution obtained by the six algorithms on large-scale problems
问题 COEA BACO KBEA ALNS HVNS TS-MCWS $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 $ {f}_{1} $/m $ {f}_{2} $/辆 C200R9-1 3494.7 16 4345.2 16 3348.8 17 3654.6 17 4128.7 16 7405.3 16 C200R9-2 3350.8 16 3823.5 16 3046.4 16 3538.5 16 4161.7 16 6743.1 16 C200R9-3 3353.9 16 4016.7 16 3231.4 16 3852.0 17 4504.2 17 6775.2 16 C200R9-4 3306.3 16 4139.3 16 3319.4 16 3615.9 16 4264.3 16 7043.0 16 C200R5-1 2477.4 16 2876.1 16 2507.8 16 2717.9 17 2851.8 17 4942.2 16 C200R5-2 2357.2 16 2928.3 16 2596.8 16 2518.2 16 2728.9 16 5198.8 16 C200R5-3 2509.1 16 3279.9 16 2789.2 16 2978.8 17 3073.1 17 4784.7 16 C200R5-4 2454.4 16 2830.3 16 2458.5 16 2530.2 17 2813.6 17 4673.1 16 C400R9-1 6206.6 31 7267.8 32 7380.9 31 7417.1 31 9785.2 31 13537.6 33 C400R9-2 6161.8 32 7660.1 32 5873.3 32 7166.9 33 9235.4 33 12259.8 32 C400R9-3 5991.5 31 7820.2 31 6241.9 32 7531.2 32 9443.6 32 13486.8 32 C400R9-4 6296.7 32 7756.3 32 5562.9 32 7102.8 33 9217.9 33 12590.9 32 C400R9-5 6046.1 32 7507.2 32 6786.0 32 6738.8 44 9547.8 32 12399.2 32 C400R5-1 5166.6 32 5892.9 31 4683.3 32 5109.8 36 6369.9 32 9547.2 32 C400R5-2 4757.5 31 6054.7 31 5721.7 32 5181.3 32 6252.1 32 9153.8 32 C400R5-3 4992.6 32 5032.3 32 4690.4 32 6585.8 32 6186.7 32 9331.3 32 C400R5-4 5071.6 32 6189.7 33 5956.1 32 5903.7 33 7163.1 33 9458.1 32 C400R5-5 4914.4 32 5826.2 32 4992.3 32 5051.8 32 6289.8 32 9185.2 32 表 3 4种多目标进化算法在大规模测试问题上所获HV结果
Table 3 Average and standard deviation of the HV values obtained by the four algorithms on large-scale test problems
问题 COEA Variant II Variant I KBEA C400R9-1 1.8070×103(1.95×102) 1.4706×103(1.34×103)− 6.6377×101(4.82×102)− 5.5429×102(1.33×101)− C400R9-2 1.6621×102(1.05×102) 4.0088×102(4.85×102)+ 2.6001×101(1.95×101)− 1.4021×101(2.36×100)− C400R9-3 2.0673×103(8.74×102) 1.5822×103(6.86×102)− 1.0478×102(5.51×101)− 1.2611×101(3.86×10−1)− C400R9-4 3.7079×101(6.57×101) 1.1768×102(4.53×101)+ 3.0047×100(1.60×100)− 1.4371×101(7.73×10−1)− C400R9-5 2.4629×102(7.78×101) 8.0531×101(9.18×101)− 1.9878×101(9.59×100)− 1.9440×101(2.64×10−1)− 续表 3 问题 COEA Variant II Variant I KBEA C400R5-1 6.6082×102(7.45×102) 4.7191×102(1.16×103)− 2.0681×101(1.64×101)− 1.3252×102(1.33×101)− C400R5-2 6.9615×102(1.76×102) 1.9595×101(7.34×100)− 0(0)− 4.7834×100(8.49×10−1)− C400R5-3 4.7101×101(1.22×101) 3.9690×101(2.59×101)− 0(0)− 5.0960×100(3.86×10−1)− C400R5-4 3.6516×101(3.49×101) 9.5989×101(4.17×101)+ 1.0682×100(7.12×10−1)− 0(0)− C400R5-5 8.8559×100(1.74×101) 2.8787×100(3.38×101)− 0(0)− 1.1077×101(2.64×10−1)+ +/−/≈ — 3/7/0 0/10/0 1/9/0 -
[1] 郭戈, 张振琳. 电动车辆路径优化研究与进展[J]. 控制与决策, 2018, 33(10): 1729–1739. doi: 10.13195/j.kzyjc.2017.1448 GUO Ge, ZHANG Zhenlin. Status and development of electric vehicle routing optimization[J]. Control and decision, 2018, 33(10): 1729–1739. doi: 10.13195/j.kzyjc.2017.1448 [2] SCHIFFER M, WALTHER G. The electric location routing problem with time windows and partial recharging[J]. European journal of operational research, 2017, 260(3): 995–1013. doi: 10.1016/j.ejor.2017.01.011 [3] 刘蓉蓉. 基于进化算法的电动汽车物流调度问题研究[D]. 合肥: 安徽大学, 2021. LIU Rongrong. Research on electric vehicle logistics scheduling problem based on evolutionary algorithms[D]. Hefei: Anhui University, 2021. [4] 吴廷映, 孙灏. 考虑载重影响耗电率的电动车车辆路径问题[J]. 控制与决策, 2023, 38(2): 483–491. doi: 10.13195/j.kzyjc.2021.1050 WU Tingying, SUN Hao. Electric vehicle routing problem with time window and linear weight related discharging[J]. Control and decision, 2023, 38(2): 483–491. doi: 10.13195/j.kzyjc.2021.1050 [5] DESAULNIERS G, ERRICO F, IRNICH S, et al. Exact algorithms for electric vehicle-routing problems with time windows[J]. Operations research, 2016, 64(6): 1388–1405. doi: 10.1287/opre.2016.1535 [6] DUMAN E N, TAŞ D, ÇATAY B. Branch-and-price-and-cut methods for the electric vehicle routing problem with time windows[J]. International journal of production research, 2022, 60(17): 5332–5353. doi: 10.1080/00207543.2021.1955995 [7] OMIDVAR A, TAVAKKOLI-MOGHADDAM R. Sustainable vehicle routing: strategies for congestion management and refueling scheduling[C]//2012 IEEE International Energy Conference and Exhibition. Florence: IEEE, 2012: 1089−1094. [8] PREIS H, FRANK S, NACHTIGALL K. Energy-optimized routing of electric vehicles in urban delivery systems[C]//Operations Research Proceedings 2012. Cham: Springer, 2014: 583−588. [9] SCHNEIDER M, STENGER A, GOEKE D. The electric vehicle-routing problem with time windows and recharging stations[J]. Transportation science, 2014, 48(4): 500–520. doi: 10.1287/trsc.2013.0490 [10] KESKIN M, ÇATAY B. Partial recharge strategies for the electric vehicle routing problem with time windows[J]. Transportation research part C:emerging technologies, 2016, 65: 111–127. doi: 10.1016/j.trc.2016.01.013 [11] RISTO M, STEPHANIE F. A biological perspective on evolutionary computation[J]. Nature machine intelligence, 2021, 3(1): 9–15. doi: 10.1038/s42256-020-00278-8 [12] 彭扬, 陈子侠, 吴承键. 定位−运输路线安排问题的改进离散粒子群优化算法[J]. 智能系统学报, 2010, 5(1): 74–79. doi: 10.3969/j.issn.1673-4785.2010.01.013 PENG Yang, CHEN Zixia, WU Chengjian. Improved discrete particle swarm optimization algorithm for location-routing problems[J]. CAAI transactions on intelligent systems, 2010, 5(1): 74–79. doi: 10.3969/j.issn.1673-4785.2010.01.013 [13] KIM G, ONG Y S, HENG C K, et al. City vehicle routing problem (city VRP): a review[J]. IEEE transactions on intelligent transportation systems, 2015, 16(4): 1654–1666. doi: 10.1109/TITS.2015.2395536 [14] 葛斌, 韩江洪, 魏臻, 等. 最小最大车辆路径问题的动态自适应蚁群优化算法[J]. 模式识别与人工智能, 2015, 28(10): 930–938. doi: 10.16451/j.cnki.issn1003-6059.201510008 GE Bin, HAN Jianghong, WEI Zhen, et al. Dynamic adaptive ant colony optimization algorithm for Min-max vehicle routing problem[J]. Pattern recognition and artificial intelligence, 2015, 28(10): 930–938. doi: 10.16451/j.cnki.issn1003-6059.201510008 [15] 王舜, 赵燕伟, 冷龙龙, 等. 基于蚁群选择超启发算法的低碳选址−路径问题[J]. 计算机集成制造系统, 2020, 26(6): 1702–1716. doi: 10.13196/j.cims.2020.06.026 WANG Shun, ZHAO Yanwei, LENG Longlong, et al. Low carbon location-routing problem based on evolutionary hyper-heuristic algorithm of ant colony selection mechanism[J]. Computer integrated manufacturing systems, 2020, 26(6): 1702–1716. doi: 10.13196/j.cims.2020.06.026 [16] WANG Ling, LU Jiawen. A memetic algorithm with competition for the capacitated green vehicle routing problem[J]. IEEE/CAA journal of automatica sinica, 2019, 6(2): 516–526. doi: 10.1109/JAS.2019.1911405 [17] BARCO J, GUERRA A, MUÑOZ L, et al. Optimal routing and scheduling of charge for electric vehicles: a case study[J]. Mathematical problems in engineering, 2017, 2017: 1–16. [18] HIERMANN G, HARTL R F, PUCHINGER J, et al. Routing a mix of conventional, plug-in hybrid, and electric vehicles[J]. European journal of operational research, 2019, 272(1): 235–248. doi: 10.1016/j.ejor.2018.06.025 [19] GUO Zhenfeng, LI Yang, JIANG Xiaodan, et al. The electric vehicle routing problem with time windows using genetic algorithm[C]//2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference. Chongqing: IEEE, 2017: 635−639. [20] JIA Yahui, MEI Yi, ZHANG Mengjie. A bilevel ant colony optimization algorithm for capacitated electric vehicle routing problem[J]. IEEE transactions on cybernetics, 2022, 52(10): 10855–10868. doi: 10.1109/TCYB.2021.3069942 [21] FENG Liang, ONG Y S, JIANG Siwei, et al. Autoencoding evolutionary search with learning across heterogeneous problems[J]. IEEE transactions on evolutionary computation, 2017, 21(5): 760–772. doi: 10.1109/TEVC.2017.2682274 [22] YANG Jun, SUN Hao. Battery swap station location-routing problem with capacitated electric vehicles[J]. Computers & operations research, 2015, 55: 217–232. [23] ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712–731. doi: 10.1109/TEVC.2007.892759 [24] CHIANG T C, HSU W H. A knowledge-based evolutionary algorithm for the multiobjective vehicle routing problem with time windows[J]. Computers & operations research, 2014, 45: 25–37. [25] FELIPE Á, ORTUÑO M T, RIGHINI G, et al. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges[J]. Transportation research part E:logistics and transportation review, 2014, 71: 111–128. doi: 10.1016/j.tre.2014.09.003 [26] BEUME N, NAUJOKS B, EMMERICH M. SMS-EMOA: Multiobjective selection based on dominated hypervolume[J]. European journal of operational research, 2007, 181(3): 1653–1669. doi: 10.1016/j.ejor.2006.08.008
