Broad collaborative filtering recommendation algorithm combined with matrix completion
-
摘要: 协同过滤是推荐系统中最经典的方法之一，能够满足人们对个性化推荐任务的需求，但许多协同过滤算法在面对评分数据稀疏性问题时推荐效果不佳。为解决此问题，提出一种结合矩阵补全的宽度协同过滤推荐算法。先使用矩阵补全技术对用户项目评分矩阵进行补全，再利用补全后的矩阵对已评分的用户和项目分别寻找其近邻项，进而构造用户与项目的评分协同向量，最后使用宽度学习系统来构建用户项目与评分之间的复杂的非线性关系。在MovieLens和filmtrust数据集上对所提出算法的有效性进行检验。试验结果表明，与当前最先进的方法相比，该方法能够有效地缓解数据稀疏性问题，具有较低的计算复杂度，在一定程度上提升了推荐系统的性能。Abstract: Collaborative filtering is a classic method used in recommendation systems, designed to cater to the need for personalized recommendations. However, many collaborative filtering algorithms struggle when confronted with sparse rating data. To address this issue, we propose a broad collaborative filtering recommendation algorithm that integrates matrix completion. Initially, a matrix completion technique is employed to recover the user–item rating matrix. Subsequently, this completed rating matrix is utilized to identify respective neighbors for a given user–item pair, which in turn helps create the user–item rating collaboration vector. Finally, a broad learning system is employed to establish the complex nonlinear relationship between user-items and ratings. The effectiveness of the proposed algorithm has been validated through tests on MovieLens and Filmtrust data sets. The experimental results show that, compared with state-of-the-art collaborative filtering methods, the proposed method can effectively alleviate the data sparsity problem. It also possesses lower computational complexity and enhances recommendation performance to a certain extent.
-
现今，人们生活在数据爆炸不断加剧的时代[1]。所接收到的巨大的数据量已远超出人们的信息处理的能力范围，且很难从海量数据中挖掘出所需要的信息。因此，从大量数据中过滤出可用数据的技术是非常必要的。推荐系统是挖掘数据以及解决信息过载的有效途径[2]，在音乐、短视频和电影推荐等方面应用广泛[3-4]。
协同过滤（collaborative filtering, CF）是众多个性化推荐方法中最经典且最受欢迎的方法之一[4]，传统的CF推荐算法可分为2类：基于模型和基于邻域。第1类CF方法以矩阵分解（matrix factorization, MF）为主，即将用户项目评分矩阵分解为用户潜在低秩矩阵和项目潜在低秩矩阵的乘积[5]。第2类通过计算用户或项目之间的相似度来帮助其找到若干个合适的近邻。但用户对项目评分数据的长尾分布导致评分矩阵的稀疏性问题，进而严重影响CF算法的推荐性能。
随着深度学习[6]在多个领域中的成熟和发展，人们开发出许多基于深度神经网络(deep neural network, DNN)的CF推荐算法来提高推荐性能[7-9]。He等[10]将MF模型中的内积运算替换为深度神经网络结构，提出了神经协同过滤（neural collaborative filtering, NeuCF）。Xue等[11]将深度神经网络用于学习用户和项目在公共低维空间的表示，提出了深度矩阵分解（deep matrix factorization, DMF）。但由于数据存在稀疏性问题[12]，导致复杂的DNN模型的推荐性能不佳。
宽度协同过滤（broad collaborative filtering, BCF）[13]是一种基于神经网络的CF算法，其采用相似性度量来生成低维的用户与项目联合特征，并基于宽度学习系统（broad learning system, BLS）[14]来建立映射函数，以学习低维用户项目联合特征向量与评分之间的复杂非线性关系。与深度学习和传统的神经网络相比，BCF具有闭形式解，无需使用梯度下降法更新权值，从而具有非常低的计算复杂度。但BCF仍然存在评分数据稀疏性问题[15]。
为了解决前述问题并充分利用用户和项目的近邻信息，本研究提出一种结合矩阵补全的宽度协同过滤(broad collaborative filtering combined with matrix completion, MC+BCF)推荐算法。该算法先利用矩阵补全技术将原始的用户项目评分矩阵补全，再对已评分元素在补全后的矩阵中寻找用户及项目的近邻项，进而构造用户项目评分协同向量。最后将所构建的协同向量作为输入特征、原始用户评分的独热编码作为标签输入到宽度学习系统中，获取用户项目特征与评分之间的复杂非线性关系。
1. 相关工作
为了克服原始评分矩阵的稀疏性问题，使用矩阵补全算法恢复原始评分矩阵；介绍了宽度学习系统，以用于推荐算法。
1.1 矩阵补全
矩阵补全（matrix completion，MC）[16-17]是指矩阵存在缺失元素情况下，根据数据矩阵的低复杂度将其恢复。MC广泛地应用在计算机视觉[18]、推荐系统[19]等领域。通常假设待恢复的矩阵是低秩的，通过低秩矩阵重构来实现缺失元素的恢复。此时，矩阵
$ {\boldsymbol{R}} = {({r_{ij}})_{m \times n}} $ 的补全问题等价于秩最小化模型：$$ \mathop {{\text{min}}}\limits_{\boldsymbol{D}} {\text{rank}}({\boldsymbol{D}}),\quad {\text{s}}{\text{.t}}{\text{.}}\quad {d_{ij}} = {r_{ij}},\quad \forall (i,j) \in \varOmega $$ (1) 式中：
$ \text{rank}(·) $ 表示矩阵的秩；$ {\boldsymbol{R}} $ 为原始的用户项目评分矩阵；$ {\boldsymbol{D}} $ 为补全后的评分矩阵；$ \varOmega $ 为用户已评分项目的用户项目对的下标集；m和n分别为用户数和项目数。上述优化模型是一个非凸的NP难问题，故难以求解。因此，用矩阵核范数将模型(1)凸松弛
$$ \mathop {{\text{min}}}\limits_{\boldsymbol{D}} {\left\| {\boldsymbol{D}} \right\|_*},\quad {\text{s}}{\text{.t}}{\text{.}}\quad {d_{ij}} = {r_{ij}},\quad \forall (i,j) \in \varOmega $$ (2) 其中
$ {\Vert ·\Vert }_{*} $ 为矩阵核范数。使用非精确的增广拉格朗日乘子（inexact augmented lagrange multiplier, IALM）算法[20]求解问题(2)。为此，将该问题重新表示为
$$ \mathop {{\text{min}}}\limits_{{\boldsymbol{D}},{\boldsymbol{E}}} {\left\| {\boldsymbol{D}} \right\|_*},\quad {\text{s}}{\text{.t}}\quad {\boldsymbol{D}} + {\boldsymbol{E}} = {\boldsymbol{R}},\quad {\pi _\varOmega }({\boldsymbol{E}}) = 0 $$ (3) 这里
${\pi }_{\varOmega }：{\bf{R}}^{m\times n}\to {\bf{R}}^{m\times n}$ 是一个正交投影算子，用来保持在$ \varOmega $ 中的条目不变，并将$ \varOmega $ 之外的其他元素设置为0。构造问题(3)的部分增广拉格朗日函数$$ \begin{gathered} L({\boldsymbol{D}},{\boldsymbol{E}},{\boldsymbol{Y}},\mu ) = {\left\| {\boldsymbol{D}} \right\|_*} + \left\langle {{\boldsymbol{Y}},{\boldsymbol{R}} - {\boldsymbol{D}} - {\boldsymbol{E}}} \right\rangle + \\ \frac{\mu }{2}\left\| {{\boldsymbol{R}} - {\boldsymbol{D}} - {\boldsymbol{E}}} \right\|_{\rm{F}}^2 \\ \end{gathered} $$ (4) 式中：
$ {\boldsymbol{Y}} $ 为拉格朗日乘子矩阵；$ \mu > 0 $ 是惩罚项系数；$ {\Vert ·\Vert }_{{\rm{F}}} $ 为矩阵的Frobenius 范数；$ \langle ·,·\rangle $ 表示两矩阵的内积。使用IALM求解问题(3)的算法流程如下。输入 评分矩阵
${\boldsymbol{R}} \in {{\bf{R}}^{m \times n}}$ ，$ {r_{ij}} = 0\left( {\forall (i,j) \notin \varOmega } \right) $ 。1）初始化：
${{\boldsymbol{Y}}_0} = 0,{{\boldsymbol{E}}_0} = 0,{\mu _0} > 0,\rho > 1,k = 0$ ；2）while 未收敛 do：
3）
$ ({\boldsymbol{U}},{\boldsymbol{S}},{\boldsymbol{V}}) = {\text{SVD(}}{\boldsymbol{R}} - {{\boldsymbol{E}}_k}{\text{ + }}\mu _k^{ - 1}{{\boldsymbol{Y}}_k}{\text{)}} $ ；4）
${{\boldsymbol{D}}_{k + 1}} = {\boldsymbol{U}}{\mathcal{S}_{\mu _k^{ - 1}}}[{\boldsymbol{S}}]{{\boldsymbol{V}}^{\text{T}}}$ ；5）
${{\boldsymbol{E}}_{k + 1}} = {\pi _{\bar \varOmega }}({\boldsymbol{R}} - {{\boldsymbol{D}}_{k + 1}} + \mu _k^{ - 1}{{\boldsymbol{Y}}_k})$ ；6）
$ {{\boldsymbol{Y}}_{k + 1}} = {{\boldsymbol{Y}}_k} + {\mu _k}({\boldsymbol{R}} - {{\boldsymbol{D}}_{k + 1}} - {{\boldsymbol{E}}_{k + 1}}) $ ；7）
$ {\mu _{k + 1}} = \min (\rho {\mu _k},\bar \mu ) $ ；8）
$ k: = k + 1 $ ；9）end while
输出
$({{\boldsymbol{D}}_k},{{\boldsymbol{E}}_k})$ 。在上述迭代过程中，算子SVD表示对矩阵进行奇异值分解，
${\mathcal{S}_\lambda }[ \cdot ]$ 是矩阵的绝对值阈值算子[21]，$\bar \varOmega $ 表示$\varOmega $ 的补集，$ \bar \mu $ 为事先给定的正数。1.2 宽度学习系统
宽度学习系统（BLS）[14]是基于随机向量函数连接神经网络[22]的一类轻量级模型。在BLS建模过程中，还可以对新的输入样本采用增量学习算法[23]来更新整个网络结构，且无需重复整个训练过程，从而快速完成模型的重建。BLS主要包括：映射特征层、增强特征层和输出层，其结构如图1所示。
图 1 宽度学习系统网络结构Fig. 1 Network structure of broad learning system
下载:
全尺寸图片
将输入数据集组成矩阵
${\boldsymbol{X}}$ ，其中每行表示一个样本。在映射特征层，先随机生成权重矩阵$ {{\boldsymbol{W}}_{\textit{z}j}} $ 和偏置矩阵$ {{\boldsymbol{\beta }}_{\textit{z}j}} $ ，再建立N个映射$$ {{\boldsymbol{Z}}_j} = {\phi _j}({\boldsymbol{X}}{{\boldsymbol{W}}_{\textit{z}j}} + {{\boldsymbol{\beta }}_{\textit{z}j}}),\quad j = 1,2, \cdots ,N $$ (5) 式中：
$ {\phi _j} $ 为第j个映射的激活函数。对于所得到的N个映射特征节点$ \{ {{\boldsymbol{Z}}_j}\} _{j = 1}^N $ ，在特征维上作连接$$ {{\boldsymbol{Z}}^N} = [{{\boldsymbol{Z}}_1}|{{\boldsymbol{Z}}_2}| \cdots |{{\boldsymbol{Z}}_N}] $$ (6) 类似地，在增强特征层采用M个函数将
${{\boldsymbol{Z}}^N}$ 映射为增强特征节点$$ {{\boldsymbol{H}}_j} = {\xi _j}({{\boldsymbol{Z}}^N}{{\boldsymbol{W}}_{hj}} + {{\boldsymbol{\beta }}_{hj}}),j = 1,2, \cdots ,M $$ (7) 式中：
$ {{\boldsymbol{W}}_{hj}} $ 和$ {{\boldsymbol{\beta }}_{hj}} $ 分别是第j个映射随机生成的权重矩阵和偏置矩阵；$ {\xi _j} $ 为激活函数。同理，将M个增强特征节点$ \{ {{\boldsymbol{H}}_j}\} _{j = 1}^M $ 横向连接起来$$ {{\boldsymbol{H}}^M} = [{{\boldsymbol{H}}_1}|{{\boldsymbol{H}}_2}| \cdots |{{\boldsymbol{H}}_M}] $$ (8) 最后，在输出层对映射特征节点
$ {{\boldsymbol{Z}}^N} $ 和增强特征节点$ {{\boldsymbol{H}}^M} $ 作线性映射$$ {\boldsymbol{Y}} = [{{\boldsymbol{Z}}^N}|{{\boldsymbol{H}}^M}]{\boldsymbol{W}} $$ (9) 式中：
$ {\boldsymbol{W}} $ 表示待求的连接权重矩阵；$ {\boldsymbol{Y}} $ 为所有训练集的输出组成的矩阵。在模型训练过程中，根据最小二乘法求解$ [{{\boldsymbol{Z}}^N}|{{\boldsymbol{H}}^M}] $ 的伪逆得最优权重$ {\boldsymbol{W}} $ 。2. 基于矩阵补全的宽度协同过滤
先给出协同过滤中输入特征与输出特征的构造方式，再建立宽度协同过滤模型。
2.1 特征构造
2.1.1 基于矩阵补全的用户项目评分协同向量
经过矩阵补全技术，所恢复的评分矩阵
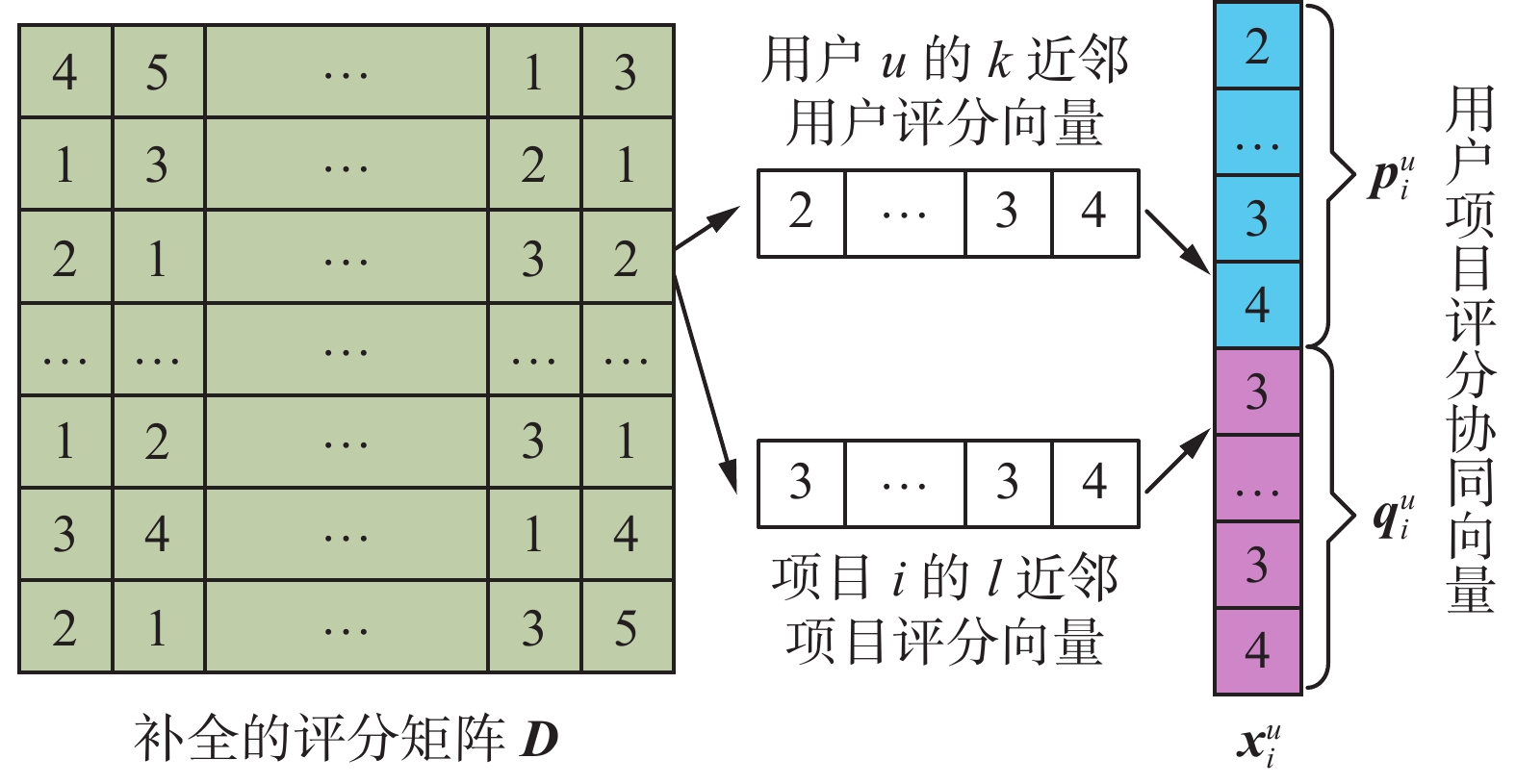
${\boldsymbol{D}}$ 不再是稀疏的。针对已评分的用户项目对(u,i)，通过近邻规则分别寻找用户u的k近邻用户和项目i的l近邻项目，即得到用户低维特征和项目低维特征。将这些近邻项对应的特征进行连接，就得到用户项目的评分协同向量，这种构造方式有效地克服了数据稀疏性问题。图2给出了用户项目评分协同向量的构造示意图。
图 2 用户项目评分协同向量的构造Fig. 2 Construction of user-item rating collaborative vector下载:
全尺寸图片
对于固定的用户u，根据
$ {{\boldsymbol{D}}}_{u·} $ 和$ {{\boldsymbol{D}}}_{j·} $ 的夹角余弦得到用户u与用户j的相似度，其中$ {{\boldsymbol{D}}}_{u·} $ 表示矩阵${\boldsymbol{D}}$ 的第u行。选择用户u的k个最近邻用户，其索引构成的向量记为${{\boldsymbol{n}}^u} = ({{n}}_1^u,\;{{n}}_2^u,\; \cdots ,\;{{n}}_k^u)$ 。考虑用户u对项目i评分时，用户u的k近邻用户的评分向量为$$ {\boldsymbol{p}}_i^u = \left( {{d_{{{n}}_1^u,i}},{d_{{{n}}_2^u,i}},\cdots,{d_{{{n}}_k^u,i}}} \right) $$ (10) 类似地，根据
$ {{\boldsymbol{D}}}_{·i} $ 和$ {{\boldsymbol{D}}}_{·j} $ 可得项目i与项目j的相似度，从而计算出项目i的l个最近邻项目，其索引构成的向量记为${{\boldsymbol{n}}^i} = ({{n}}_1^i,\;{{n}}_2^i,\; \cdots,\;{{n}}_l^i)$ ，其中$ {{\boldsymbol{D}}}_{·i} $ 表示矩阵${\boldsymbol{D}}$ 的第i列。项目i的l近邻项目的评分向量为$$ {\boldsymbol{q}}_i^u = \left( {{d_{u,{{n}}_1^i}},{d_{u,{{n}}_2^i}},\cdots,{d_{u,{{n}}_l^i}}} \right) $$ (11) 最后，将
$ {\boldsymbol{p}}_i^u $ 和$ {\boldsymbol{q}}_i^u $ 连接起来，得到用户项目评分协同向量$$ {\boldsymbol{x}}_i^u = [{\boldsymbol{p}}_i^u|{\boldsymbol{q}}_i^u] \in {{\bf{R}}^{1 \times (k + l)}} $$ (12) 将
$ {\boldsymbol{x}}_i^u $ 作为评分值$ {r_{ui}} $ 的输入特征。2.1.2 用户项目评分的独热向量
考虑评分取值为1到dy的整数。对原始评分矩阵中
${r_{ui}} \ne 0$ 的元素，采用独热（one-hot）编码将其转换为${\boldsymbol{y}}_i^u \in {{\bf{R}}^{1 \times {d_y}}}$ ，其第j个分量定义如下$$ {y}_{i}^{u}[j]=\left\{\begin{array}{l}1,\quad j={r}_{u,i}\\ 0,\quad 其他\end{array}\right. $$ (13) 独热编码的优势是将一维的输出变换成多维输出，从而有益于网络模型的构建。
将用户项目评分协同向量
$ {\boldsymbol{x}}_i^u $ 和用户项目评分的独热向量$ {\boldsymbol{y}}_i^u $ 分别作为训练数据集的输入特征和输出标签，即得到MC+BCF方法的样本集$$ {{T}} = \{ ({\boldsymbol{x}}_i^u,{\boldsymbol{y}}_i^u)|(u,i) \in \varOmega \} $$ (14) 2.2 宽度协同过滤
将样本集
$ {{T}} $ 划分成训练集$ {{{T}}_1} $ 和测试集$ {{{T}}_2} $ 。对于训练集$ {{{T}}_1} $ ，BLS模型的输入矩阵和输出矩阵分别为$$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}_{{i_1}}^{{u_1}}} \\ {{\boldsymbol{x}}_{{i_2}}^{{u_2}}} \\ \vdots \\ {{\boldsymbol{x}}_{{i_{\left| {{{\boldsymbol{T}}_1}} \right|}}}^{{u_{\left| {{{\boldsymbol{T}}_1}} \right|}}}} \end{array}} \right] \in {{\bf{R}}^{\left| {{{{T}}_1}} \right| \times (k + l)}},\quad {\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{y}}_{{i_1}}^{{u_1}}} \\ {{\boldsymbol{y}}_{{i_2}}^{{u_2}}} \\ \vdots \\ {{\boldsymbol{y}}_{{i_{\left| {{{\boldsymbol{T}}_1}} \right|}}}^{{u_{\left| {{{\boldsymbol{T}}_1}} \right|}}}} \end{array}} \right] \in {{\bf{R}}^{\left| {{{{T}}_1}} \right| \times {d_y}}} $$ (15) 式中，
$ \left| {{{{T}}_1}} \right| $ 是训练样本的数量，即对应用户项目对$({u_1},{i_1}),({u_2},{i_2}), \cdots ,({u_{\left| {{{{T}}_1}} \right|}},{i_{\left| {{{{T}}_1}} \right|}})$ 。将
$ {\boldsymbol{X}} $ 和$ {\boldsymbol{Y}} $ 输入到BLS网络中，建立宽度协同过滤模型$$ \left\{ \begin{gathered} {{\boldsymbol{Z}}_j} = {\phi _j}({\boldsymbol{X}}{{\boldsymbol{W}}_{\textit{z}j}} + {{\boldsymbol{\beta }}_{\textit{z}j}}),\quad j = 1,2, \cdots ,N \\ {{\boldsymbol{Z}}^N} = [{{\boldsymbol{Z}}_1}|{{\boldsymbol{Z}}_2} \cdots |{{\boldsymbol{Z}}_N}] \\ {{\boldsymbol{H}}_j} = {\xi _j}({{\boldsymbol{Z}}^N}{{\boldsymbol{W}}_{hj}} + {{\boldsymbol{\beta }}_{hj}}),\quad j = 1,2, \cdots ,M \\ {{\boldsymbol{H}}^M} = [{{\boldsymbol{H}}_1}|{{\boldsymbol{H}}_2} \cdots |{{\boldsymbol{H}}_M}] \\ {\boldsymbol{W}} = {[{{\boldsymbol{Z}}^N}|{{\boldsymbol{H}}^M}]^{\dagger} }{\boldsymbol{Y}} \\ \end{gathered} \right. $$ (16) 式中：
$N$ 、$M$ 分别表示映射特征组和增强特征组的数量；$ {\phi _j} $ 、$ {\xi _j} $ 为非线性激活函数，在实验中选用ReLU；$ {{\boldsymbol{W}}_{\textit{z}j}} \in {{\bf{R}}^{(k + l) \times {d_\textit{z}}}} $ 、$ {{\boldsymbol{W}}_{hj}} \in {{\bf{R}}^{N{d_\textit{z}} \times {d_h}}} $ 为随机权重矩阵，$ {{\boldsymbol{\beta }}_{\textit{z}j}} \in {{\bf{R}}^{\left| {{{{T}}_1}} \right| \times {d_\textit{z}}}} $ 、$ {{\boldsymbol{\beta }}_{hj}} \in {{\bf{R}}^{\left| {{{{T}}_1}} \right| \times {d_h}}} $ 为偏置矩阵；$ {\boldsymbol{W}} \in {{\bf{R}}^{(N{d_\textit{z}} + M{d_h}) \times {d_y}}} $ 为可训练权重矩阵；$ {d}_{\textit{z}}、{d}_{h} $ 分别表示映射特征组和增强特征的维数。假设
$ \max ({d_y},k + l) < N{d_\textit{z}} + M{d_h} $ 。模型（16）的主要计算量集中在求伪逆$ {[{{\boldsymbol{Z}}^N}|{{\boldsymbol{H}}^M}]^{\dagger}} $ ，其复杂度为$ O\left( {{{(N{d_\textit{z}} + M{d_h})}^2} \times (N{d_\textit{z}} + M{d_h} + \left| {{T_1}} \right|)} \right) $ 。所提出的MC+BCF模型的算法求解步骤如下。1）利用矩阵补全（MC）技术，得到补全后的评分矩阵
${\boldsymbol{D}}$ 。2）对于已知的每个评分元素，充分利用邻域信息，基于近邻规则构造相应的用户项目评分协同向量；对输出元素执行独热编码。
3）将用户项目评分协同向量输入到宽度协同过滤网络中，捕获用户项目联合特征与输出编码之间的复杂函数关系。
2.3 评分预测
对于训练集，MC+BCF算法可以确定宽度学习网络的所有权重矩阵和偏置矩阵。在对用户u在项目i的评分进行预测时，先构造用户项目对
$(u,i)$ 的评分协同向量${\boldsymbol{X}}_i^u \in {{\bf{R}}^{1 \times (l + k)}}$ ；再将其输入到BLS模型中，最终得到${\boldsymbol{\hat y}}_i^u = [{{\boldsymbol{\hat Z}}^N}|{{\boldsymbol{\hat H}}^M}]{\boldsymbol{W}} \in {{\bf{R}}^{1 \times {d_y}}}$ ，其中$ {{\boldsymbol{\hat Z}}^N} $ 和$ {{\boldsymbol{\hat H}}^M} $ 均为${\boldsymbol{X}}_i^u$ 对应的行特征向量。记向量${\hat {\boldsymbol{y}}}_i^u$ 的最大值所对应的下标索引为b。考虑评分取值向量${\boldsymbol{L}} = (1,\;2,\; \cdots ,\;{d_y})$ 时，评分预测值为$ {\hat r_{ui}} = {\boldsymbol{L}}[b{\text{]}} $ ，其中$ {\boldsymbol{L}}[b{\text{]}} $ 表示向量$ {\boldsymbol{L}} $ 的第$b$ 个分量。3. 数值试验
先将所提出的MC+BCF在3个基准数据集上与其他5种基线模型的推荐性能进行比较，这些模型分别为矩阵分解（MF）[5]、概率矩阵分解（probabilistic matrix factorization, PMF）[24]、神经协同过滤（NeuCF）[10]、深度矩阵分解（DMF）[11]以及宽度协同过滤（BCF）[13]。然后探讨了MC+BCF模型超参数对推荐性能的影响。
3.1 数据集简介与模型参数设置
数值试验使用公开可获取的3个基准数据集：MovieLens的ml-latest (ml-la)数据集、ml-100k数据集（https://grouplens.org/datasets/movielens）以及filmtrust数据集（https://www.librec.net/datasets.html）。表1列出了这些数据集的相关统计信息，其中前2个数据集的评分为1~5的整数，第3个数据集的评分集合为
$ \{ 0.5i|i = 1,2,…,10\} $ 。矩阵补全算法使用MATLAB2017b进行编程，其余试验代码均使用Python。所有试验均在Intel Core i7-4710MQ CPU 2.50 GHz、GeForce GTX 950 M、RAM 8 GB服务器上进行。表 1 3个基准数据集的相关统计信息Table 1 Statistical information of three benchmark datasets数据集 用户/个 项目/个 评分/条 稀疏度 评分范围/分 ml-la 610 9724 100836 0.0170 1~5 ml-100k 943 1682 100000 0.0630 1~5 filmtrust 1508 2071 35497 0.0114 0.5~5 在MF和PMF 2个模型中，用户和项目潜在因子数均设置为30，且PMF的用户和项目的正则化参数分别设置为0.01和0.001。对于NeuCF模型，广义矩阵分解部分网络各层的特征维数分别为64、32、16、8，用户和项目的嵌入特征维数均设为16。在DMF模型中，用户和项目的隐向量维数均设置为64，网络层数设置为2。对于NeuCF和DMF这2种深度学习模型，批量大小均设置为256，学习率设为0.0001，选择Adam优化器。对于BCF和MC+BCF，将近邻用户和近邻项目的数量设置为5，映射特征组和增强特征组的数量均为25，映射特征维度和增强特征维度分别设为10和15。
3.2 评估指标
使用均方根误差（RMSE）和均值绝对误差（MAE）来评价各模型的性能，MAE或RMSE越小，表明模型推荐性能越好。对于测试集
$ {T_2} $ ，RMSE（式中记为ERMS）和MAE（式中记为EMA）的计算公式如下$$ {E_{{\text{RMS}}}} = \sqrt {\frac{{{\sum _{(i,j) \in {\varOmega _2}}}{{({r_{ij}} - {{\hat r}_{ij}})}^2}}}{{\left| {{T_2}} \right|}}} $$ (17) $$ {E_{{\text{MA}}}} = \frac{{{\sum _{(i,j)\; \in \;{\varOmega _2}}}\left| {{r_{ij}} - {{\hat r}_{ij}}} \right|}}{{\left| {{T_2}} \right|}} $$ (18) 式中：
${\varOmega _2}$ 表示测试集中已评分的下标集合；$ {\hat r_{ij}} $ 表示评分$ {r_{ij}} $ 的预测值。3.3 推荐性能比较
3.3.1 误差比较
在ml-la、ml-100k和filmtrust数据集上比较下列3类模型的推荐性能：浅层矩阵分解（MF、PMF）、深度学习（NeuCF、DMF）和宽度学习（BCF、MC+BCF）。对于每个数据集，按照7∶3的比例随机划分为训练集和测试集，且各基线模型其余超参数按默认值设置。
表2列出了MC+BCF与其他5种基线模型在ml-la、ml-100k和filmtrust数据集上的MAE和RMSE误差。由表2可以看出，与MF、PMF、NeuCF、DMF和BCF相比，MC+BCF的RMSE都有显著地降低；MC+BCF在数据集ml-100k上的MAE稍逊于BCF，但明显优于MF、PMF、NeuCF和DMF。与MF、PMF、NeuCF和DMF相比，BCF和MC+BCF具有较好的推荐效果，且MC+BCF总体上优于BCF。这主要是因为MC+BCF在特征构造阶段，先使用矩阵补全来恢复缺失数据，再使用近邻规则构造训练样本的联合特征，从而有效减小了缺失评分对推荐性能的影响。
表 2 MC+BCF与基线模型的误差比较Table 2 Error comparison of MC+BCF and baseline models数据集 评价误差 MF PMF NeuCF DMF BCF MC+BCF ml-la MAE 0.7663 0.8015 0.7328 0.7704 0.5122 0.4763 RMSE 1.0281 1.0692 0.9559 1.0130 0.8089 0.7615 ml-100k MAE 0.8293 0.7547 0.8140 0.7789 0.6920 0.6546 RMSE 1.0540 0.9623 1.0401 0.9919 1.0354 0.9371 filmtrust MAE 0.7850 0.8375 0.7325 0.7888 0.5135 0.5156 RMSE 1.0568 1.1402 0.9586 0.9954 0.8081 0.7363 对于表2，再比较MC+BCF和BCF的预测误差。对于ml-1a和ml-100k数据集， MC+BCF的MAE比BCF分别下降了7.01%、5.40%，RMSE下降了5.86%、9.49%。而在filmtrust数据集上，MC+BCF的推荐误差RMSE也降低了8.89%，但其MAE比BCF增加了0.0021。在3个基准数据集上，MC+BCF的推荐性能总体上优于BCF，这是由于原始数据评分进行矩阵补全后增加了数据中用户和项目的信息量。综上，前述试验结果验证了MC+BCF能够有效地缓解数据稀疏性问题。
3.3.2 运行时间比较
表3列出了各算法的运行时间，其中MC+BCF包括MC和BCF两部分时间之和。由表3可以看出，与BCF相比，MC的运行时间较短，即MC+BCF在计算复杂度上稍逊于BCF。在ml-la和filmtrust数据集上，MC+BCF的运行时间明显优于MF；在filmtrust数据集上，MC+BCF的运行时间与MF相当。在ml-1a和filmtrust数据集上，PMF的运行时间超过MC+BCF的1.6倍，但在ml-100k数据集上PMF的时间更快一些。与DMF和NeuCF等深度学习的推荐算法相比，在filmtrust数据集上MC+BCF的运行时间与NeuCF相当，MC+BCF的运行时间总体上有显著的优势。
表 3 运行时间比较Table 3 Comparison of running times 模型 MF PMF DMF NeuCF BCF MC+BCF ml-la 91.4234 123.9498 2295.0268 97.5944 45.0166 60.5441 ml-100k 67.4944 43.3328 412.8960 75.3897 32.5498 50.6041 filmtrust 32.0436 54.2636 359.2771 32.5269 22.5786 33.1259 总之，与基于矩阵分解和基于深层神经网络的模型相比，MC+BCF往往具有较低的计算复杂度，这是由于BCF算法使用基于岭回归的伪逆来求解可训练权值，从而避开了梯度下降法或迭代更新。因此，MC+BCF的运行效率比MF、PMF、DMF和NeuCF等模型存在显著优势。
3.4 超参数分析
MC+BCF模型的超参数主要包括用户近邻数量k、项目近邻数量l、映射特征组数N、映射特征组维数
$ {d_\textit{z}} $ 、增强特征组数M和增强特征组维数$ {d_h} $ 。在ml-la、ml-100k和filmtrust数据集上探讨这6个超参数的取值对推荐性能的影响。3.4.1 用户和项目近邻数量
用户近邻数量k和项目近邻数量l是构造用户项目评分协同向量的关键。设置
$ k \in \{ 3,4,5,6\} $ 和$ l \in \{ 3,4,5,6\} $ ，考虑MC+BCF在k和l的16种组合下的测试误差。图3和4分别给出了3个数据集的MAE和RMSE热力图。由这2个图可以看出，对于3个基准数据集，RMSE和MAE值一般会随着k或l的增加而小幅增大，这可能是由于相对较大的用户和项目近邻数量会引入更多的噪声。在ml-100k上，当$ k \in \{ 3,4\} $ 且$ l = 3 $ 时，RMSE和MAE值较大，这可能是由该数据集的稀疏度相对较低所导致的，即邻域信息引入不足可能会影响预测的精度。因此，在后面的试验中将k和l都设置为5。
图 3 不同用户和项目近邻数量下的MAE热力图Fig. 3 MAE heatmap for different number of users and item neighbors下载:
全尺寸图片
图 4 不同用户和项目近邻数量下的RMSE热力图Fig. 4 RMSE heatmap for different number of users and item neighbors下载:
全尺寸图片
3.4.2 映射特征组数量和映射特征组维数
特征映射模块是捕获用户项目协同向量和评分之间的非线性关系的第1步。设置映射特征组数量
$ N \in \{ 15,20,25,30,35\} $ 和映射特征组维数$ {d_{\textit{z}}} \in \{ 5,10,15,20,25\} $ 。图5给出了不同映射特征组数量N下3个数据集对应的MAE和RMSE。由图5可以看出，RMSE和MAE有相同的变化趋势；映射特征组数量$ N \geqslant 20 $ 时，推荐误差趋于稳定，且波动幅度均小于0.01。对于3个数据集，不同映射特征组维数dz下的MAE和RMSE如图6所示。由图6可以发现，随着dz的增加，RMSE和MAE的变化相对平稳，且改变幅度非常小。图5和图6说明MC+BCF对超参数N和dz相对不敏感。在试验中将N和dz分别设置为25和10。
图 5 不同映射特征组数量下的MAE和RMSEFig. 5 MAE and RMSE for different number of mapped feature groups下载:
全尺寸图片
图 6 不同映射特征组维数下的MAE和RMSEFig. 6 MAE and RMSE of different dimension in mapped feature groups下载:
全尺寸图片
3.4.3 增强特征组数量和增强特征组维数
特征增强模块是捕获用户项目协同向量和评分之间的非线性关系的第2步。设置增强特征组数量
$ M \in \{ 15,20,25,30,35\} $ 和增强特征组维数$ {d_h} \in \{ 5,10,15,20,25\} $ 。图7给出了不同增强特征组数量 M下3个数据集对应的MAE和RMSE。由图7可以发现，随着M的增加，RMSE和MAE的变化相对平稳，且波动幅度均小于0.01。对于3个数据集，不同增强特征组维数dh下的MAE和RMSE如图8所示。由图8可以看出，RMSE和MAE有相同的变化趋势，增强特征维数$ {d_h} \geqslant 10 $ 时，推荐误差趋于稳定，且波动幅度均小于0.01。图7和图8说明MC+BCF对超参数M和dh相对不敏感。在试验中将M和dh分别设置为25和10。
图 7 不同增强特征组数量下的MAE和RMSEFig. 7 MAE and RMSE for different number of enhanced feature groups下载:
全尺寸图片
图 8 不同增强特征组维数下的MAE和RMSEFig. 8 MAE and RMSE of different dimension in enhanced feature groups下载:
全尺寸图片
4. 结束语
本研究提出了一种结合矩阵补全和宽度协同过滤的推荐算法。先对原始评分矩阵中的未知数据进行补全，以丰富评分数据的用户和项目的信息量。再使用近邻法则构造用户项目评分协同向量。所提出的算法充分利用了用户和项目补全后的邻域信息，进而有效缓解了数据稀疏性问题。在算法效率方面，MC+BCF也比基于深度学习和矩阵分解的推荐算法的运算效率高。在3个基准数据集上对MC+BCF的推荐性能和算法运算效率进行了验证，试验结果表明，MC+BCF显著地提升推荐性能，且算法效率也更优。
所提算法只对评分数据进行了挖掘，而评分数据的相关辅助信息（如：用户属性、历史访问时间等）对于推荐性能也至关重要。因此，在之后的研究中可以引入相关辅助信息，来提升推荐精度。
-
图 1 宽度学习系统网络结构
Fig. 1 Network structure of broad learning system
下载:
全尺寸图片
图 2 用户项目评分协同向量的构造
Fig. 2 Construction of user-item rating collaborative vector
下载:
全尺寸图片
图 3 不同用户和项目近邻数量下的MAE热力图
Fig. 3 MAE heatmap for different number of users and item neighbors
下载:
全尺寸图片
图 4 不同用户和项目近邻数量下的RMSE热力图
Fig. 4 RMSE heatmap for different number of users and item neighbors
下载:
全尺寸图片
图 5 不同映射特征组数量下的MAE和RMSE
Fig. 5 MAE and RMSE for different number of mapped feature groups
下载:
全尺寸图片
图 6 不同映射特征组维数下的MAE和RMSE
Fig. 6 MAE and RMSE of different dimension in mapped feature groups
下载:
全尺寸图片
图 7 不同增强特征组数量下的MAE和RMSE
Fig. 7 MAE and RMSE for different number of enhanced feature groups
下载:
全尺寸图片
图 8 不同增强特征组维数下的MAE和RMSE
Fig. 8 MAE and RMSE of different dimension in enhanced feature groups
下载:
全尺寸图片
表 1 3个基准数据集的相关统计信息
Table 1 Statistical information of three benchmark datasets
数据集 用户/个 项目/个 评分/条 稀疏度 评分范围/分 ml-la 610 9724 100836 0.0170 1~5 ml-100k 943 1682 100000 0.0630 1~5 filmtrust 1508 2071 35497 0.0114 0.5~5 表 2 MC+BCF与基线模型的误差比较
Table 2 Error comparison of MC+BCF and baseline models
数据集 评价误差 MF PMF NeuCF DMF BCF MC+BCF ml-la MAE 0.7663 0.8015 0.7328 0.7704 0.5122 0.4763 RMSE 1.0281 1.0692 0.9559 1.0130 0.8089 0.7615 ml-100k MAE 0.8293 0.7547 0.8140 0.7789 0.6920 0.6546 RMSE 1.0540 0.9623 1.0401 0.9919 1.0354 0.9371 filmtrust MAE 0.7850 0.8375 0.7325 0.7888 0.5135 0.5156 RMSE 1.0568 1.1402 0.9586 0.9954 0.8081 0.7363 表 3 运行时间比较
Table 3 Comparison of running time
s 模型 MF PMF DMF NeuCF BCF MC+BCF ml-la 91.4234 123.9498 2295.0268 97.5944 45.0166 60.5441 ml-100k 67.4944 43.3328 412.8960 75.3897 32.5498 50.6041 filmtrust 32.0436 54.2636 359.2771 32.5269 22.5786 33.1259 -
[1] SINGH N, SINGH D P, PANT B. Big data knowledge discovery as a service: recent trends and challenges[J]. Wireless personal communications, 2022, 123(2): 1789–1807. doi: 10.1007/s11277-021-09213-5 [2] GUPTA S, DAVE M. An overview of recommendation system: methods and techniques[M]//Advances in Computing and Intelligent Systems. Singapore: Springer Singapore, 2020: 231−237. [3] ASSUNCAO W G, PICCOLO L S G, ZAINA L A M. Considering emotions and contextual factors in music recommendation: a systematic literature review[J]. Multimedia tools and applications, 2022, 81(6): 8367–8407. doi: 10.1007/s11042-022-12110-z [4] LI Xiangpo. Research on the application of collaborative filtering algorithm in mobile E-commerce recommendation system[C]//2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers. Dalian: IEEE, 2021: 924−926. [5] KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems[J]. Computer, 2009, 42(8): 30–37. doi: 10.1109/MC.2009.263 [6] 胡越, 罗东阳, 花奎, 等. 关于深度学习的综述与讨论[J]. 智能系统学报, 2019, 14(1): 1–19. HU Yue, LUO Dongyang, HUA Kui, et al. Overview on deep learning[J]. CAAI transactions on intelligent systems, 2019, 14(1): 1–19. [7] WANG Changdong, XI Wudong, HUANG Ling, et al. A BP neural network based recommender framework with attention mechanism[J]. IEEE transactions on knowledge and data engineering, 2022, 34(7): 3029–3043. [8] XI Wudong, HUANG Ling, WANG Changdong, et al. BPAM: recommendation based on BP neural network with attention mechanism[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. Macao: International Joint Conferences on Artificial Intelligence Organization, 2019: 3905–3911. [9] DENG Zhihong, HUANG Ling, WANG Changdong, et al. DeepCF: a unified framework of representation learning and matching function learning in recommender system[EB/OL]. (2019−01−15)[2022−01−01]. http://arxiv.org/abs/1901.04704V1. [10] HE Xiangnan, LIAO Lizi, ZHANG Hanwang, et al. Neural collaborative filtering[C]//Proceedings of the 26th International Conference on World Wide Web. New York: ACM, 2017: 173−182. [11] XUE Hongjian, DAI Xinyu, ZHANG Jianbing, et al. Deep matrix factorization models for recommender systems[C]//Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. Melbourne: International Joint Conferences on Artificial Intelligence Organization, 2017: 3203−3209. [12] YIN Hongzhi, WANG Qinyong, ZHENG Kai, et al. Overcoming data sparsity in group recommendation[J]. IEEE transactions on knowledge and data engineering, 2022, 34(7): 3447–3460. [13] HUANG Ling, GUAN Canrong, HUANG Zhengwei, et al. Broad recommender system: an efficient nonlinear collaborative filtering approach[EB/OL]. (2022−04−20)[2022−08−29]. https://ar-xiv.org/pdf/2204.11602.pdf. [14] PHILIP CHEN C L, LIU Zhulin. Broad learning system: an effective and efficient incremental learning system without the need for deep architecture[J]. IEEE transactions on neural networks and learning systems, 2018, 29(1): 10–24. doi: 10.1109/TNNLS.2017.2716952 [15] FLETCHER K K. A method for dealing with data sparsity and cold-start limitations in service recommendation using personalized preferences[C]//2017 IEEE International Conference on Cognitive Computing. Honolulu: IEEE, 2017: 72−79. [16] CANDES E J, RECHT B. Exact low-rank matrix completion via convex optimization[C]//2008 46th Annual Allerton Conference on Communication, Control, and Computing. Monticello: IEEE, 2009: 806−812. [17] 陈蕾, 陈松灿. 矩阵补全模型及其算法研究综述[J]. 软件学报, 2017, 28(6): 1547–1564. doi: 10.13328/j.cnki.jos.005260 CHEN Lei, CHEN Songcan. Survey on matrix completion models and algorithms[J]. Journal of software, 2017, 28(6): 1547–1564. doi: 10.13328/j.cnki.jos.005260 [18] WANG Weigang, SONG Wei, WANG Guangyuan, et al. Image recovery and recognition: a combining method of matrix norm regularisation[J]. IET image processing, 2019, 13(8): 1246–1253. doi: 10.1049/iet-ipr.2018.5511 [19] CHEN Zhaoliang, WANG Shiping. A review on matrix completion for recommender systems[J]. Knowledge and information systems, 2022, 64(1): 1–34. doi: 10.1007/s10115-021-01629-6 [20] LIN Zhouchen, CHEN Minming, MA Yi. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[EB/OL]. (2010−09−26)[2022−08−29]. https://arxiv.org/abs/1009.5055.pdf. [21] BIOUCAS-DIAS J M, FIGUEIREDO M A T. A new twist: two-step iterative shrinkage/thresholding algorithms for image restoration[J]. IEEE transactions on image processing, 2007, 16(12): 2992–3004. doi: 10.1109/TIP.2007.909319 [22] PAO Y H, PARK G H, SOBAJIC D J. Learning and generalization characteristics of the random vector functional-link net[J]. Neurocomputing, 1994, 6(2): 163–180. doi: 10.1016/0925-2312(94)90053-1 [23] YANG Qing, GU Yudi, WU Dongsheng. Survey of incremental learning[C]//2019 Chinese Control and Decision Conference. Nanchang: IEEE, 2019: 399−404. [24] SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization[C]//Proceedings of the 20th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2008: 1257−1264.
