Integrated energy multivariate load forecasting combining federated learning with LSTM in privacy-protected and low-data environments
-
摘要: 对于用能数据不足的综合能源系统，借助相似系统的丰富数据可以为其建立高精度的多元负荷预测模型，然而，受数据安全等因素的限制，很多系统并不愿意共享自身数据。联邦学习为处理隐私保护下的少数据综合能源多元负荷预测问题提供了一个重要的思路，但是现有方法依然存在相似参与方识别精度不高等不足。鉴于此，本文提出一种融合联邦学习和长短期记忆网络（long short-term memory, LSTM）的少数据综合能源多元负荷预测方法(multitask learning based on shared dot product confidentiality under federated learning, MT-SDP-FL)。首先，给出一种基于共享向量点积保密协议的相似参与方识别方法，用来从诸多可用的综合能源系统中选出最为相似的参与方；接着，使用参数共享联邦学习算法对选中的各参与方联合训练，结合LSTM和fine-tune技术建立每个参与方的多元负荷预测模型。将所提方法应用于多个实际能源系统，实验结果表明，该方法可以在数据稀疏的情况下取得高精度的多源负荷预测结果。Abstract: For an integrated energy system with insufficient energy consumption data, a high-precision multivariate load forecasting model can be established using data from similar systems. However, due to the limitations of data security and other factors, many systems are unwilling to share data. Federated learning provides an important idea to deal with the problem of multivariate energy load forecast based on a small amount of data under privacy protection. However, the existing methods still exhibit deficiencies, such as low accuracy in identifying similar parties. In this view, a few-data multitask learning based on shared dot product confidentiality under federated learning (MT-SDP-FL) is proposed, combining federated learning and long short-term memory (LSTM). A similar party identification method using a shared vector dot product confidentiality protocol is proposed to select the most similar parties from many available integrated energy systems. Then, the parameter sharing federated learning algorithm is used to jointly train the selected participants, combining the LSTM and fine-tuning technology to establish the multivariate load prediction model for each participant. The proposed method is applied to several energy systems, and the experimental outcomes show that the proposed method can achieve high-precision multi-source load forecasting results in the circumstance of sparse data.
-
自第一次工业革命以来，人类社会在快速发展的同时消耗了大量的化石能源，能源危机问题近年来日益突出。在此背景下，以综合能源系统(integrated energy systems，IES) 为代表的新兴能源使用场景逐渐兴起。目前，已有70余个国家开展了区域综合能源系统研究[1]。针对综合能源负荷预测问题，学者们已经提出了诸多方法，包括以自回归移动平均、灰色模型、卡尔曼滤波器等为代表的传统方法[2-4]，以及以神经网络、决策树、随机森林和支持向量机等为代表的智能方法[5-8]。
由于具有良好的预测能力，近年来智能方法逐渐成为负荷预测的热点方向。Safta等[9]针对蒙特卡罗采样预测可再生能源信息所需采样次数多的问题，采用多项式混沌展开代替蒙特卡罗采样，提升了负荷预测的精度和效率；针对短期光伏功率预测问题，Cheng等[10]建立了一种结合谱图卷积、多图形边和分层输出的混合模型。上述成果进一步提高了负荷预测的精度，但其考虑的客观因素仍然相对较少，而且它们也未考虑能源间的耦合关系。He等[11]采用变模态分解将能源消费时序数据分成若干模态之后，利用贝叶斯优化的长短期记忆网络预测能源消费，给出了一种改进的长短期记忆网络预测模型，提高了模型的预测精度；Potocnik等[12]提出了基于机器学习的区域供热系统短期热需求预测方法，并证实了供热温度与太阳辐射强度、短期热需求的强相关性。这些成果进一步表明，综合考虑负荷间的耦合性以及经济、温度等客观因素能有效提高模型的预测精度。
作为循环神经网络的一类典型改进，长短期记忆网络(long short-term mymory, LSTM)不仅继承了RNN可记忆最近事件的能力，而且有效克服了RNN无法记忆久远信息的缺陷[13-14]。Muzaffar等[15]通过实验表明LSTM的负荷预测效果更优；李鹏等[16]将LSTM用于计及实时电价的短期负荷预测问题，取得较好的预测结果；Somu等[17]利用LSTM构建了一种改进的建筑负荷预测模型。上述研究为综合能源系统负荷预测问题提供了多种高效的处理方法，但是它们都需要依据充足的负荷数据。对于用能数据不足的综合能源系统，它们很难获得理想的负荷预测结果。
然而，随着参与方对自身数据隐私性的重视，孤岛式数据 (即数据孤岛问题)越来越普遍。针对此问题，谷歌提出了联邦学习[18]，其目的是在保证各参与者方数据安全的基础上，共同使用这些数据为它们构建有效的机器学习模型[19]。目前联邦学习已在医疗保健[20]、通信[21]、语言建模[22]、交通[23]等领域得到了广泛应用。在隐私保护需求的推动下，许多学者开始将联邦学习与LSTM相结合用于负荷预测问题。
应用于负荷预测问题，Savi等[24]开发了一个联邦LSTM模型，用于预测单个房屋的电力需求。Chen等[25]设计了一种新的联邦多任务层次注意模型，将注意机制和LSTM网络相结合，对潜在的时间和非线性关系进行建模。在兼顾用户隐私的前提下，这些成果进一步提高了联邦学习模型处理负荷预测问题的性能，但仍缺少对于恶意节点的识别与处理机制。
因此分析恶意节点对联邦训练结果的影响，王鑫等[26]利用区块链技术建立了电能量数据的声望模型，并给出了参与节点的奖励机制。上述方法为负荷预测问题提供了一个重要的思路，但是它们要求参与联邦学习的参与方具有相似的数据分布特征。在处理少数据综合能源系统负荷预测问题时，如何从诸多可用的能源系统中选出与当前系统最为相似的一个或几个参与后续的联邦学习，仍是一个有待解决的问题。在下文中，拥有少量数据的能源系统简称为少数据节点，拥有大量数据的可选能源系统称为多数据节点。
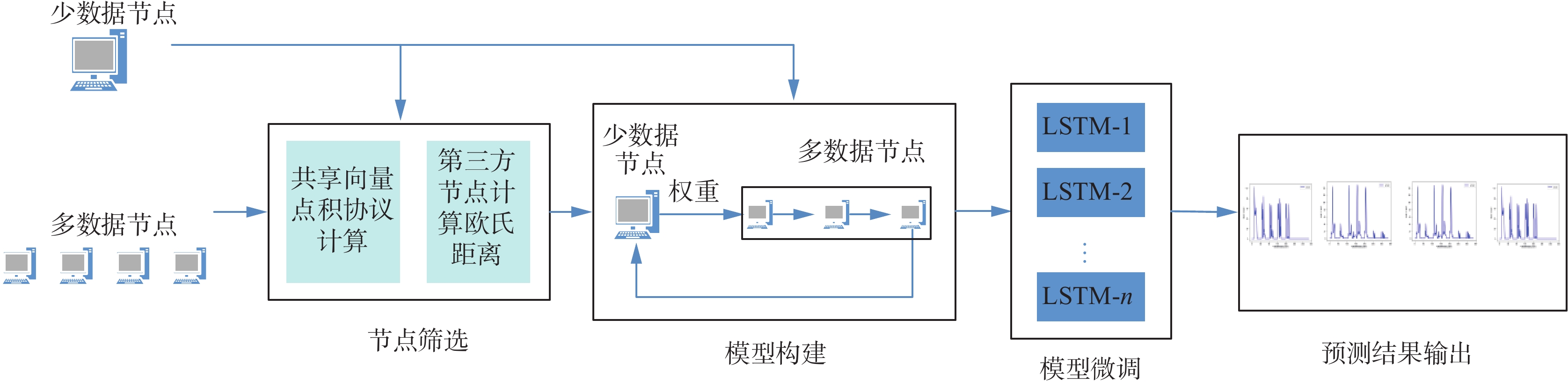
针对少数据综合能源系统的多元负荷预测问题，将点积保密计算协议和LSTM融入联邦学习框架，提出一种改进的多元负荷预测方法，MT-SDP-FL。首先，给出一种基于共享向量点积保密协议的相似参与方识别方法，从诸多可用的多数据节点中选出用能相似的节点；接着，在参数共享联邦学习算法框架下，结合LSTM和fine-tune技术建立每个参与方的多元负荷预测模型。
1. 相关工作
1.1 LSTM
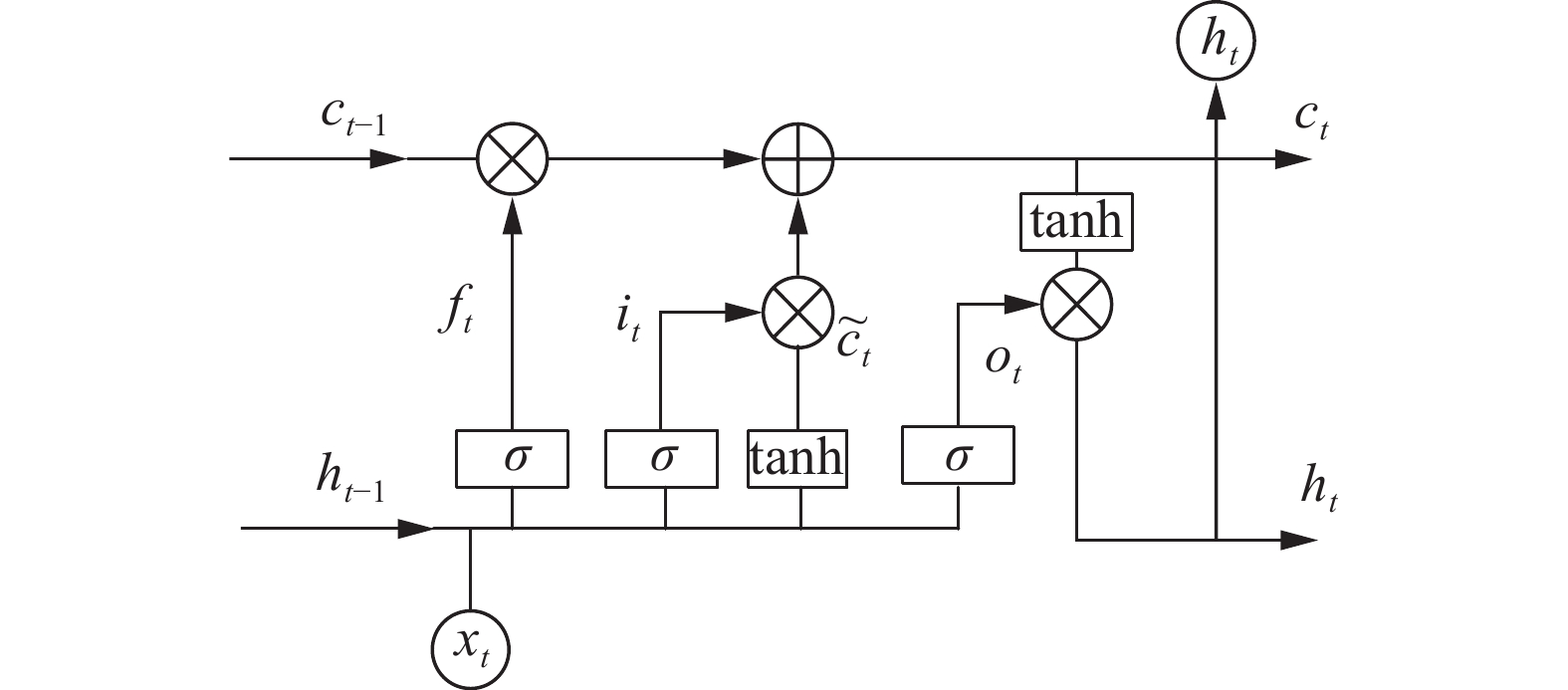
LSTM网络作为一种递归神经网络体系结构由Hochreiter等[27]提出。图1给出了LSTM的单元结构图，每个单元以输入门、遗忘门和输出门作为结构存储信息。其中，
${h_{t - 1}}$ 表示LSTM上一时刻的输出，${x_t}$ 表示当前输入，${h_t}$ 表示当前单元的输出，$ {c_t} $ 和${c_{t - 1}}$ 分别表示存储单元当前时刻以及上一时刻的状态。
图 1 LSTM的基本单元结构Fig. 1 Basic unit structure of LSTM
下载:
全尺寸图片
遗忘门
${f_t}$ 用于对上一单元的信息进行选择性的保留，公式为$$ {f_t} = \sigma ({{\boldsymbol{w}}_f} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_f}) $$ (1) 式中：
${{\boldsymbol{w}}_f}$ 为权重矩阵，${b_f}$ 为偏差，$\sigma $ 为sigmoid函数。输入门
${i_t}$ 用于控制当前输入数据到存储单元状态值的更新，更新公式为$$ {i_t} = \sigma ({{\boldsymbol{w}}_i} \cdot [{h_{t - 1}},{x_t}] + {b_i}) $$ (2) $$ {\tilde c_t} = \tanh ({{\boldsymbol{w}}_c} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_c}) $$ (3) $$ {c_t} = {f_t} \cdot {c_{t - 1}} + {i_t} \cdot {\tilde c_t} $$ (4) 式中：
${{\boldsymbol{w}}_i}$ 为权重矩阵，${b_i}$ 为偏置。同时，新状态信息${\tilde c_t}$ 可由式（3）进行更新，其中，${{\boldsymbol{w}}_c}$ 是权重矩阵，${b_c}$ 是偏置。结合式（2）和（3），可由式（4）得到当前状态$ {c}_{t} $ 。输出门ot用来控制存储单元状态值的输出值，具体计算方式为
$$ {o_t} = \sigma ({{\boldsymbol{w}}_o} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_o}) $$ (5) $$ {h_t} = {o_t} \cdot \tanh ({c_t}) $$ (6) 式中：
${{\boldsymbol{w}}_o}$ 是权重矩阵，${b_o}$ 是偏置。LSTM通过借助上述3个门实现对长时间信息的读取、重置和更新，进而利用历史信息实现对未来进行预测。
1.2 点积保密计算协议
对于A、B两个分别拥有
$n$ 维向量${\boldsymbol{X}} = [{x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_n}]$ 和${\boldsymbol{Y}} = [{y_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_n}]$ 的数据拥有方，双方希望在保护各自数据隐私的情况下计算得到两向量的点积${\boldsymbol{X}} \cdot {\boldsymbol{Y}} = {x_1}{y_1} + {x_2}{y_2} + \cdots + {x_n}{y_n}$ 。其输出结果为${\boldsymbol{X}} \cdot {\boldsymbol{Y}}$ 的协议为向量点积协议。如果协议结束后，其中一方得到$s$ 且$s \ne 0$ ，另一方得到$ s{\boldsymbol{X}} \cdot {\boldsymbol{Y}} $ 或${\boldsymbol{X}} \cdot {\boldsymbol{Y}} + s$ , 则称这样的协议为共享向量点积协议。本文介绍了一个高效的共享向量点积保密计算协议[28]。该协议仅需要基本的算术运算，不使用任何公钥加密方案，具有很高的计算效率。1)将向量
${\boldsymbol{X}} = [{x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_n}]$ 按以下方式进行分解：随机选取有理数${a_i}$ 和有理数向量$ {{\boldsymbol{X}}_i} = [{x_{i1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_{i2}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_{in}}] (i \in (1,2, \cdots ,t),2 \leqslant t \leqslant n + 1) $ ，使得${\boldsymbol{X}} = {a_1}{{\boldsymbol{X}}_1} + {a_2}{{\boldsymbol{X}}_2} + \cdots + {a_n}{{\boldsymbol{X}}_n}$ ，且${a_1} + {a_2} + \cdots + {a_n} \ne 0$ ；A方将$ {{\boldsymbol{X}}}_{1},{{\boldsymbol{X}}}_{2},\cdots ,{{\boldsymbol{X}}}_{i} $ 发送给B方。2)B方随机选取有理数
${b_j}$ 和有理数向量${{\boldsymbol{Y}}_j} = [{y_{j1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {y_{j2}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_{jn}}](j = 1,2)$ ，使得${\boldsymbol{Y}} = {b_1}{{\boldsymbol{Y}}_1} + {b_2}{{\boldsymbol{Y}}_2}$ 。计算完毕后，B方选取非零随机有理数${k_1}、{k_2}、{r_1}、{r_2}$ ，并计算：$$ {{\textit{z}}_{11}} = {k_1}{{\boldsymbol{X}}_1}{{\boldsymbol{Y}}_1} + {r_1}, \cdots ,{{\textit{z}}_{1t}} = {k_1}{{\boldsymbol{X}}_t}{{\boldsymbol{Y}}_1} + {r_1} $$ $$ {{\textit{z}}_{21}} = {k_2}{{\boldsymbol{X}}_1}{{\boldsymbol{Y}}_2} + {r_2}, \cdots ,{{\textit{z}}_{2t}} = {k_2}{{\boldsymbol{X}}_t}{{\boldsymbol{Y}}_2} + {r_2} $$ 随后B方将计算完成后的
$ ({{\textit{z}}_{11}},{{\textit{z}}_{12}}, \cdots ,{{\textit{z}}_{1t}}) $ 和$({{\textit{z}}_{21}},{{\textit{z}}_{22}}, \cdots ,{{\textit{z}}_{2t}})$ 发送给A方。3)A方计算：
$$ {{\textit{z}}_1} = s\left( {{a_1}{{\textit{z}}_{11}} + {a_2}{{\textit{z}}_{12}} + \cdots + {a_t}{{\textit{z}}_{1t}}} \right) $$ $$ \text{ }{{\textit{z}}}_{2}=s\left({a}_{1}{{\textit{z}}}_{21}+{a}_{2}{{\textit{z}}}_{22}+\cdots +{a}_{t}{{\textit{z}}}_{2t}\right) $$ 并将计算后A方的
${{\textit{z}}_1}$ 与${{\textit{z}}_2}$ 分别发送给B方，其中$ s={({a}_{1}+{a}_{2}+\dots +{a}_{n})}^{-1}。 $ 4)B方计算：
$$ {\textit{z}} = {b_1}\frac{{\left( {{{\textit{z}}_1} - r_1} \right)}}{{{k_1}}} + {b_2}\frac{{\left( {{{\textit{z}}_2} - r_2} \right)}}{{{k_2}}} $$ 5)A方输出
$s$ ，B方输出${\textit{z}} = s{\boldsymbol{X}} \cdot {\boldsymbol{Y}}$ 。2. 所提多元负荷预测方法
2.1 算法基本框架
如前所述，对于时序负荷数据，LSTM展现出了优异的预测效果。将LSTM与联邦学习相结合，可以确保多数据节点与少数据节点之间信息迁移的安全性。这其中，相似源域的选择是防止模型负迁移的一个重要方法。
针对少数据综合能源系统的多元负荷预测问题，将点积保密计算协议和LSTM融入到联邦学习框架中，提出一种改进的多元负荷预测方法，即MT-SDP-FL。所提算法的基本框架如图2所示。首先，利用基于共享向量点积保密协议的相似参与方识别方法，从诸多可用的综合能源系统中选出最为相似的参与节点。随后，基于当前少数据综合能源系统与所选多个相似综合能源系统的历史用能数据，执行一种融合参数共享联邦学习和LSTM的综合能源多元负荷预测方法，分别得到这些能源系统的多元负荷预测模型。
图 2 所提算法基本框架Fig. 2 Basic framework of the proposed algorithm下载:
全尺寸图片
2.2 基于共享向量点积保密协议的相似参与方识别
欧氏距离可以用来计算两个向量之间的距离，从而判断它们之间的相似程度，距离越小表明两者间相似度越高。在本文所提的方法中，出于隐私安全的角度考虑，如何在不暴露数据隐私的前提下，选出与少数据节点距离最小的多数据节点，即与少数据节点用能最相似的节点，参与联邦学习训练，是本文解决的主要问题之一。本文所使用的协议通过简单算术运算即可得到两个向量的乘积，无需使用公钥加密，其计算过程更为高效。以
$n$ 维空间为例，两个向量$[{x_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {x_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {x_n}]$ 和$ [{y}_{1}\;\;{y}_{2}\;\;\cdots \;\;{y}_{n}] $ 之间欧氏距离$\,\rho $ 为$$ \rho = \sqrt {{{\left( {{x_1} - {y_1}} \right)}^2} + {{\left( {{x_2} - {y_2}} \right)}^2} + \cdots + {{\left( {{x_n} - {y_n}} \right)}^2}} $$ (7) 将式(7)拆分后可得：
$$ \rho = \sqrt {\mathop \sum \limits_{i=1}^n {x_i}^2 + \mathop \sum \limits_{i=1}^n {y_i}^2 - 2\mathop \sum \limits_{i=1}^n {x_i}{y_i}} $$ (8) 由式(8)可以看出，两个向量彼此之间只知道对方的组成元素的平方和并不会影响自身的隐私。如何在保密的情况下计算
$\displaystyle\sum \limits_{i=1}^n {x_i}{y_i}$ ，是安全计算欧氏距离的关键。基于此，本小节给出一种基于共享向量点积保密协议的相似参与方识别方法，从可用的综合能源系统中选出最为相似的参与节点。不妨设小数据参与方为A方，N个可选的多数据参与方为
${B_i},\;i = 1,2, \cdots ,N,$ 算法1给出了所提相似参与方识别方法的具体步骤。每个${B_i}$ 方在计算得到$s \cdot \left(\displaystyle\sum \limits_{i=1}^n {x_i}{y_i}\right)$ 的基础上，通过第三方可信节点C计算得到它与A方的距离值${\,\rho _v}$ ：$$ {\rho _v} = \sqrt {s \cdot \left(\mathop \sum \limits_{i=1}^n {x_i}^2 + \mathop \sum \limits_{i=1}^n {y_i}^2\right) - 2s \cdot \left(\mathop \sum \limits_{i=1}^n {x_i}{y_i}\right)} $$ (9) 由式(8)和(9)可知，计算后的欧氏距离
${\,\rho _v}$ 与常规欧氏距离$\,\rho $ 的关系为$$ {\rho _v} = \sqrt s \rho $$ (10) 在第三方上比较每个多数据参与方与少数据参与方的距离，从中选出用能最为相近的
$m$ 个B节点。分析上述步骤可知，第三方节点C接受到节点A的随机有理数和
$1/s$ 、平方和$ \displaystyle\sum {x}^{2} $ 、节点$ {B}_{i}的s{\boldsymbol{X}}\cdot {{\boldsymbol{Y}}}_{i} $ 及其平方和$ \displaystyle \sum {y}_{i}{}^{2} $ 。根据接收到的数据，C无法判断出节点A和${B_{\text{i}}}$ 的数据。节点${B_i}$ 会接收到$s{\boldsymbol{X}}$ ，由于不知道$s$ 值，它也无法识别出节点A的数据X。故此，节点A与${B_{\text{i}}}$ 数据是安全的。本文所提基于共享向量点积保密协议的相似参与方识别方法具体步骤如下：
少数据节点A的负荷数据，其他多数据节点的负荷数据作为输入，输出相似数据节点的索引；
1）通过共享点积协议，A方输出随机有理数和 ，每个 方输出其值；
2）A方将随机有理数和、自身数据的平方和发送给可信第三方节点C；
3）每个Bi方将输出
$s{\boldsymbol{X}}\cdot {{\boldsymbol{Y}}}_{i} $ 、自身数据的平方和$\displaystyle \sum {y}_{i}{}^{2} $ 发送给第三方节点C；4）第三方节点C根据公式计算各节点Bi与节点A之间的欧氏距离；
5）跟据欧氏距离大小，选择与少数据节点A最相似的m个节点，并记录节点索引值；
6）输出筛选出的相似节点。
2.3 基于参数共享联邦学习的多元负荷预测模型
由2.2节方法选出相似的多数据节点即拥有大量数据的多个能源系统后，需要利用这些节点的数据辅助当前的少数据综合能源系统，建立其多元负荷预测模型。由于少数据节点只拥有少量的数据，因此少数据节点根据自身数据训练得到的模型缺乏一定的准确性，在只有少量节点参与联邦学习的情况下，通过传统联邦学习的模型融合思想，当本地数据存在数据不平衡问题时，由于本地模型和全局模型之间的权重差异[29]，少数据节点产生的模型会对全局模型产生一定消极影响。因此，给出一种融合参数共享联邦学习（FedPS）[30]和LSTM的综合能源多元负荷预测方法。
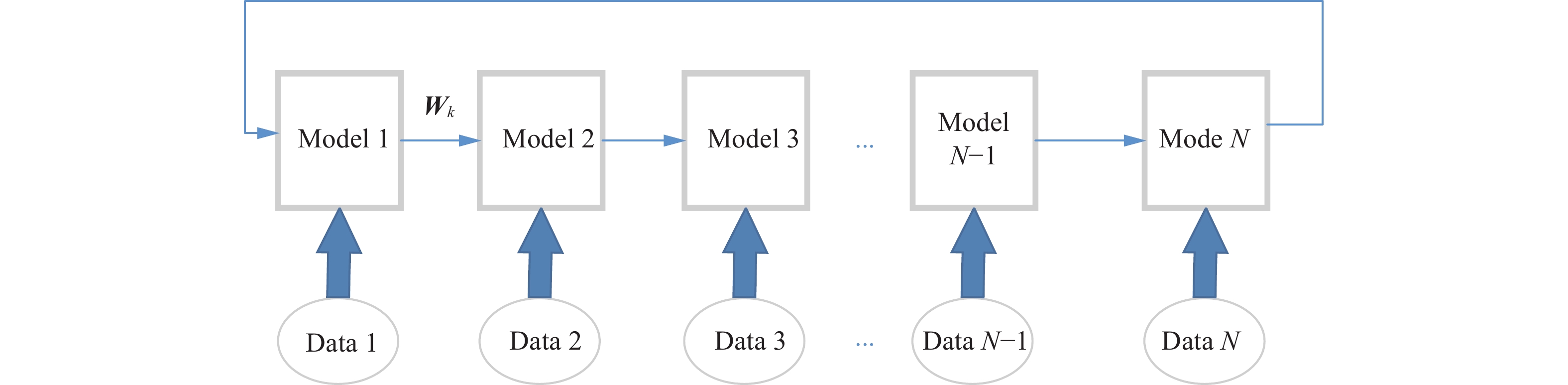
首先，将LSTM作为预测模型，使用FedPS框架对所有参与节点进行融合训练，如图3所示。假设共有
$N$ 个数据拥有方参与联邦训练，在第1次本地训练后，初始化模型以数据Data 1为训练集进行训练更新，得到一组LSTM模型参数为${M_1}$ ，将其传送给第2个数据拥有方；随后执行第2次本地训练更新，经过数据集Data 2的训练，${M_1}$ 更新为${M_2}$ ，并被传递给第3个数据拥有方；以此类推，在第$N$ 次本地训练后，模型参数${M_1}$ 经过$N$ 次训练更新后变为${M_N}$ 。通过上述模型参数更新方式，不仅可以避免少数据参与方对多数据参与方模型的影响，而且能够充分利用各参与节点数据进行联合训练。基于上述方法，包括少数据节点在内的所有参与方都可获得一个初始的LSTM预测模型。
图 3 FedPS的基本流程Fig. 3 Basic process of FedPS下载:
全尺寸图片
随后，每个参与方利用自身拥有的用能数据，采用Fine-tune技术微调初始LSTM模型，进而得到其最终的多元负荷预测模型。LSTM模型的输入分别是数据节点的电和气负荷数据，这意味着电负荷与气负荷数据会在训练的过程中相互影响。相关研究表明，针对多元数据的预测问题，共享隐藏层可以提高模型的预测精度等[27-28]。为此，本文采用基于隐藏层共享的LSTM模型构建预测模型。以第m个数据节点为例，将模型的前n−1层的参数冻结，仅使用当前数据节点的自身数据重新fine-tune初始模型最后一层的参数。
3. 实验部分
本文的实验部分选择在Carbon Culture平台上（https://platform.carbonculture.net1）提供的6所学校作为实验对象。假设出于安全考虑各方之间不能够共享负荷数据；同时，学校1只具备极少量的电和气数据，是一个少数据节点。其余学校都具有较多的负荷数据。本实验的目的是，借助其余学校所持有的数据建立学校1的多元负荷预测模型。
实验中，每个学校以0.5 h为间隔统计用能数据，从而将一天分为48个时刻点。利用拥有的负荷数据来预测后一周的负荷，即预测后面336个时刻的负荷。假设目标学校1仅有4月1—14日两周的电、气负荷数据，其余学校则有4月14日前12周的电、气负荷数据。采用均方根误差（RMSE）和平均绝对误差（MAE）评估预测结果的质量，它们的计算公式为
$$ {R_{{\text{MSE}}}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^n {{\left( {{x_i} - x} \right)}^2}} $$ (11) $$ {M_{{\text{AE}}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left| {{x_i} - x_i'} \right| $$ (12) 式中：
${R_{{\text{MSE}}}}$ 为RMSE值，${M_{{\text{AE}}}}$ 为MAE值，n为预测时刻点的数目，$x_i'$ 为第i时刻的预测值，${x_i}$ 为第i时刻的真实值。本章节实验均取20次结果的${R_{{\text{MSE}}}}$ 、${M_{{\text{AE}}}}$ 平均值作为最终结果进行对比。实验平台的硬件配置如下：AMD Ryzen 5 2400 GB with Radeon Vega Graphics 3.60 GHz处理器，软件采用Windows 10操作系统和PyCharm编译器，其中Python版本为3.8。
3.1 所提相似参与方识别策略的有效性分析
相似节点的选择对少数据节点预测模型的建立至关重要。为此，第3.2节提出了一种基于共享向量点积保密计算协议的节点选择策略。本节实验分析所提相似参与方识别策略的有效性。
以学校1的4月1—14日两周数据参考。表1展示了各校与校1在两周时间内的原始欧氏距离、随机数和
$1/s$ 为3 221.314时点积协议计算出的欧氏距离。可以看出，采用点积协议计算出的欧氏距离与传统方法计算出的欧氏距离有相似的序值关系。这说明，采用本文提出的方法不仅能够较为准确的计算出两个节点所持有数据的相似性，而且可以保证参与方数据的安全性。由表中数据可知，校3、校4与校1的欧氏距离较小，故此本文选择学校3和4作为参与训练的多数据节点。表 1 学校1与各校之间的两种欧氏距离Table 1 Two Euclidean distances between school 1 and each school学校 原始欧氏距离 点击协议计算出的
欧氏距离学校2 758.737 13.368 学校3 487.945 11.070 学校4 518.446 11.762 学校5 1592.331 28.055 学校6 1148.024 20.227 进一步，对比组合{1,3,4}和其他9种组合所建预测模型的预测精度，表2给出了10个预测模型针对少数据学校1的多元负荷预测结果。
表 2 针对少数据学校1的10种组合得到的多元负荷预测结果Table 2 Multivariate load forecasting results for ten combinations of School 1 with a small amount of data学校组合 校1电预测 校1气预测 MAE RMSE MAE RMAE {1，3，4} 0.108 0.202 0.851 1.662 {1，2，3} 0.125 0.243 0.834 1.783 {1，2，4} 0.138 0.222 1.117 2.045 {1，2，5} 0.135 0.230 0.881 1.711 {1，2，6} 0.168 0.266 0.966 1.927 {1，3，5} 0.133 0.246 0.887 1.814 {1，3，6} 0.129 0.215 1.081 2.048 {1，4，5} 0.127 0.260 0.997 1.911 {1，4，6} 0.125 0.242 0.895 1.885 {1，5，6} 0.133 0.233 0.912 1.804 可以看出，采用校3和校4作为参与方时本文算法得到的预测结果大都优于其他节点组合，所提相似参与方识别策略是有效的。
3.2 算法对比
为验证本文所提MT-SDP-FL算法的有效性，本节选择如下3种典型多元负荷预测算法作为对比算法：
联邦平均算法（federated averaging algorithm，FedAvg）[18]。作为一种常用的分布式框架，FedAvg将本地节点训练得到的LSTM参数上传给中心节点，中心节点融合接受到的参数信息并建立一个全局预测模型。
多任务学习算法（Multi-task learning）[31]。该算法是一种集中式多元负荷预测方法，它采用“硬共享机制+长短时记忆共享层”方式，在每个参与方上单独构建一个多元负荷预测模型，各参与不交换任何信息。
基于多源迁移学习和LSTM的集成多元负荷预测方法（multi-task learning of integrated energy by LSTM, MT-E-LSTM）[32]。MT-E-LSTM是一种针对少数据节点提出的迁移学习算法，它使用多个相似节点的负荷数据来改善少数据节点的预测精度。但是，MT-E-LSTM要求各参与方之间能够共享用户负荷数据等敏感信息。
为体现公平性，4种算法都使用相同的LSTM基础算法。本文算法采用提出的相似参与方识别策略选择两个节点参与到最后的联邦训练，但是FedAvg算法中所有节点都参与联邦训练。
为了更直观地比较，本文所提算法与对比算法使用了相同的LSTM模型与参数，如表3所示。为保证公平性，所提MT-SDP-FL算法的本地训练迭代次数、FedAvg的本地训练迭代次数、Multi-task learning算法的单次预测次数皆设为75。
表 3 模型结构与参数Table 3 Model structure and parameters参数名 数值 LSTM层 3 LSTM层输出的空间维数 96 Dropout系数 0.3 batch_size 21 隐藏层 3 优化器 adam 本次实验分为两部分，第1部分比较MT-SDP-FL与MT-E-LSTM的预测结果，其目的是验证在不共享敏感数据的情况下MT-SDP-FL也能得到与MT-E-LSTM相近似的结果。这里，MT-E-LSTM是可以共享敏感数据的。第2部分实验与满足隐私保护需求的剩余两个算法进行对比，说明本文所提MT-SDP-FL算法的高效性。
1）与MT-E-LSTM进行比较
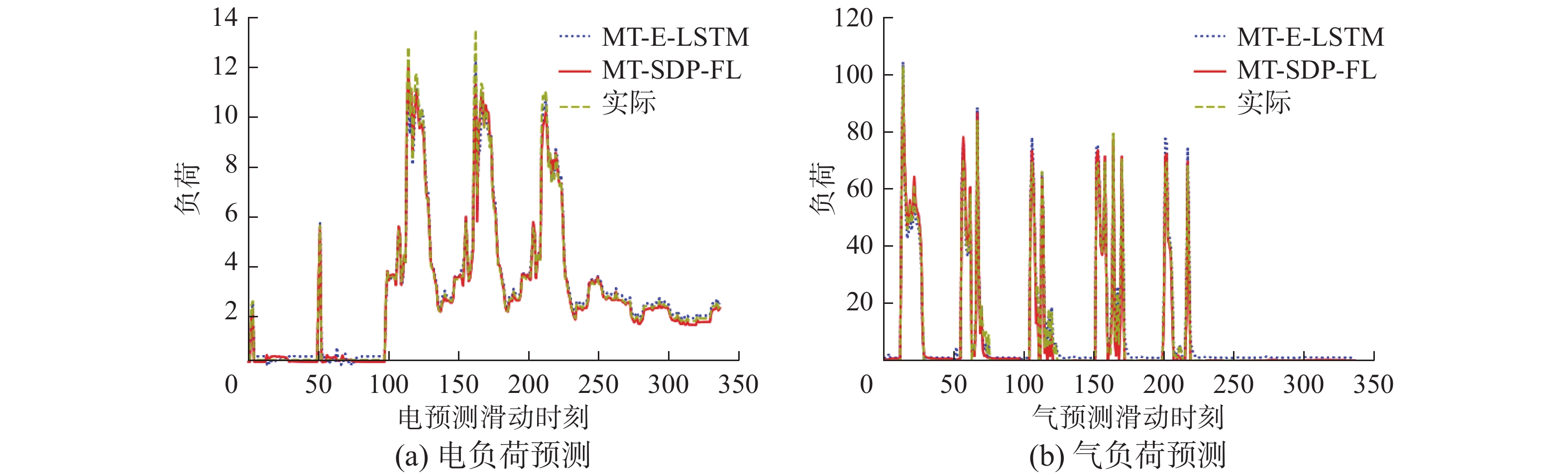
分别采用MT-SDP-FL与MT-E-LSTM预测含少量数据的目标学校1的电、气负荷，表4给出了MT-SDP-FL与MT-E-LSTM得到的RMSE和MAE结果。此次实验同样使用t-test对比本文所提算法MT-SDP-FL 与对比算法MT-E-LSTM结果之间的显著差异性，其中‘+’表示MT-SDP-FL算法显著优于MT-E-LSTM，‘−’表示表示MT-SDP-FL明显劣于MT-E-LSTM，‘≈’表示MT-SDP-FL与MT-E-LSTM之间没有明显差异。可以看出，在MAE和RMSE两个指标上，本文所提算法MT-SDP-FL的结果皆明显优于MT-E-LSTM算法。图4给出了MT-SDP-FL与MT-E-LSTM得到的电、气负荷预测曲线。图中红色实线表示MT-SDP-FL得到的预测结果，蓝色点线表示MT-E-LSTM得到的预测结果，黄色虚线代表真实值。横轴表示时间刻度，即预测的
$n\left( {n \in \left[ {1,336} \right]} \right)$ 个时刻，纵轴表述负荷值。表 4 针对少数据学校1 MT-SDP-FL与MT-E-LSTM得到的多元负荷预测结果Table 4 Multivariate load prediction results obtained by MT-SDP-FL and MT-E-LSTM algorithms for School 1 with a small amount of data学校 电预测 气预测 MT-SDP-FL MT-E-LSTM MT-SDP-FL MT-E-LSTM MAE RMSE MAE RMSE MAE RMSE MAE RMSE 学校1 0.108 0.202 0.168(+) 0.245(+) 0.851 1.6624 1.487(+) 2.084(+) 
图 4 MT-SDP-FL与MT-E-LSTM得到的电、气负荷预测曲线Fig. 4 Electrical load prediction curve obtained by MT-SDP-FL and MT-E-LSTM下载:
全尺寸图片
由表4可以看出，本文算法得到的电和气负荷预测结果都优于MT-E-LSTM。进一步，从图4可以看出，MT-SDP-FL和MT-E-LSTM都得到了较好的电和气预测结果。可见，相对需要共享敏感数据的MT-E-LSTM算法，在不共享敏感数据的情况下MT-SDP-FL也能得到与之相近似的结果。同时，本文所提MT-SDP-FL算法避免了负荷数据的泄露风险，在保障数据的安全性的同时在一定程度上提高了节点的预测精度。
2）与FedAvg和Multi-task learning进行比较
针对上述对象，分别采用MT-SDP-FL、FedAvg和Multi-task learning预测学校1、3、4的电、气负荷，表5给出了3种算法得到的RMSE和MAE结果，同样的，本次实验使用t-test对比本文所提算法MT-SDP-FL 与对比算法结果之间的显著差异性，其中‘+’表示MT-SDP-FL算法显著优于该对比算法，‘−’表示表示MT-SDP-FL明显劣于该对比算法，‘≈’表示MT-SDP-FL与该对比算法之间没有明显差异。可以看出，无论是电负荷还是气负荷，本文所提算法MT-SDP-FL的结果皆明显优于另外两种对比算法，传统Multi-task learning的指标最差，其次是FedAvg算法。
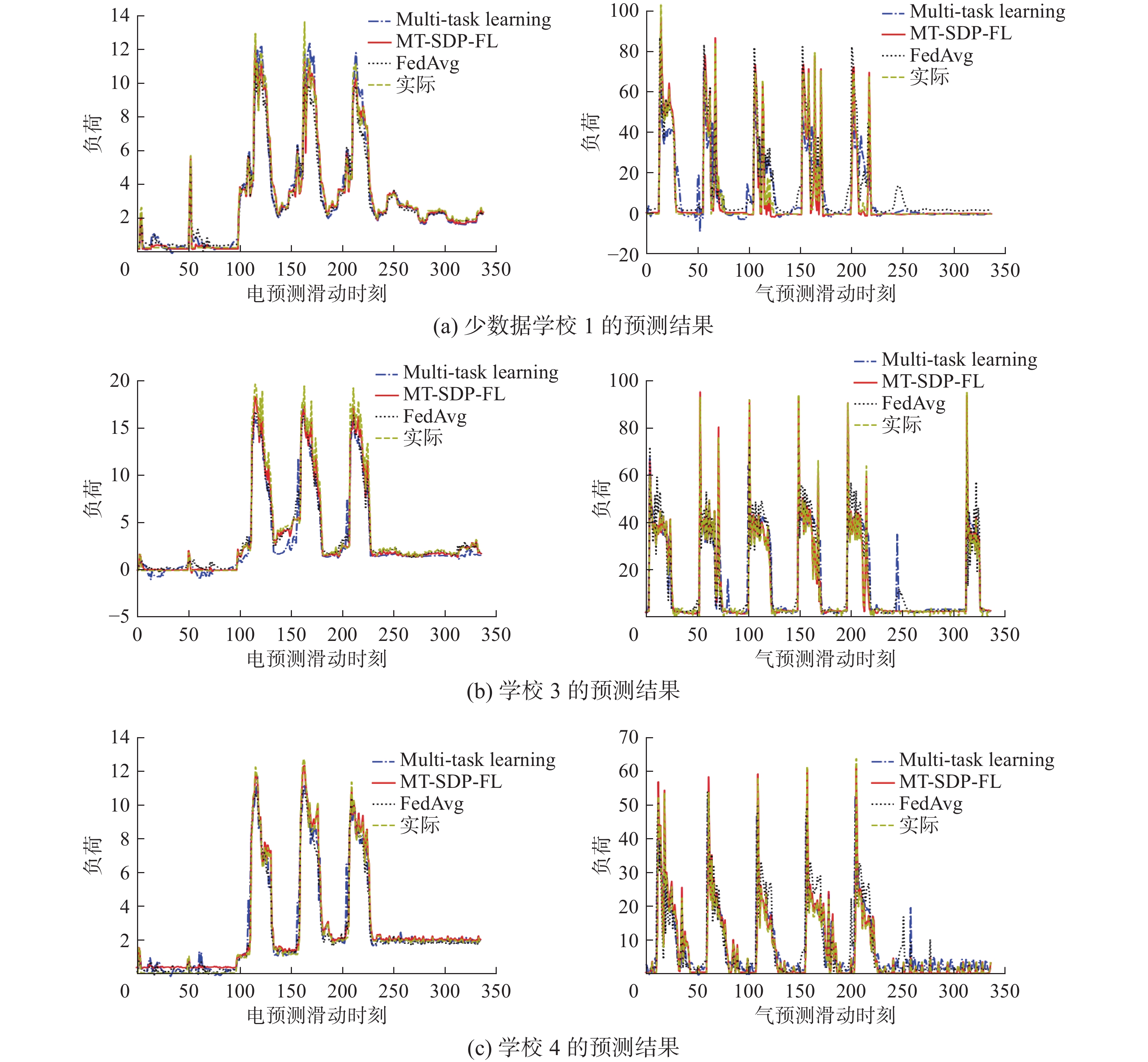
表 5 MT-SDP-FL与对比算法的预测结果Table 5 Prediction results of the comparison algorithm and MT-SDP-FL学校 误差指标 MT-SDP-FL FedAvg Multi-task learning 学校1 电 RMSE 0.202 0.704（+） 0.789（+） MAE 0.108 0.457（+） 0.634（+） 气 RMSE 1.662 8.254（+） 14.180（+） MAE 0.851 5.024（+） 6.583（+） 学校3 电 RMSE 0.543 0.994（+） 1.434（+） MAE 0.303 0.609（+） 0.945（+） 气 RMSE 1.519 6.866（+） 9.453（+） MAE 0.929 3.870（+） 5.041（+） 学校4 电 RMSE 0.188 0.539（+） 0.679（+） MAE 0.126 0.321（+） 0.402（+） 气 RMSE 0.784 5.990（+） 6.925（+） MAE 0.427 3.505（+） 3.482（+） 图5给出了3种算法得到的电、气负荷预测曲线。图中红色实线表示MT-SDP-FL得到的预测结果，蓝色虚点线表示Multi-task learning得到的预测结果，黑色点线代表FedAvg得到的预测结果,黄色虚线则为真实值。横轴表示时间刻度，即预测的
$n\left( {n \in \left[ {1,336} \right]} \right)$ 个时刻，纵轴表述负荷值。由表5可以看出，相对FedAvg和Multi-task learning，本文所提MT-SDP-FL算法在电、气负荷预测精度方面均有所提高。进一步，由图5可知：1）针对少数据学校1，在较为平缓的第1~100时刻，FedAvg和Multi-task learning得到的电负荷预测结果的波动相对较大；同时，由于气负荷波动较大，Multi-task learning算法在极值处出现了明显偏差，而FedAvg算法在220~250时刻也有较大波动。2）针对学校3，在电负荷变化较大的时刻，如第140~160时刻，Multi-task learning算法不能很好地进行预测，而本文所提算法与FedAvg算法的都得到了较好的预测结果。同时，由于气负荷波动频率较高，幅度较大，在极值点附近FedAvg和Multi-task learning都不能很好地对其进行预测，而本文算法得到了相对较好的预测结果。3）针对学校4，在大部分时间段本文所提MT-SDP-FL算法得到的电负荷预测值都好于FedAvg和Multi-task learning。对于气负荷而言，本文算法也展现出了较好的预测能力。综上可见，对于绝大多数时刻，使用MT-SDP-FL得到的负荷预测结果更接近真实值。
图 5 MT-SDP-FL、FedAvg和multi-task learning得到的负荷预测曲线Fig. 5 Load forecasting curve obtained by MT-SDP-FL, FedAvg and multi-Task learning下载:
全尺寸图片
4. 结束语
为在隐私保护的条件下提升少数据参与方的多元负荷预测精度，本文提出了一种融合联邦学习和LSTM的少数据综合能源多元负荷预测方法，MT-SDP-FL。给出的基于共享向量点积保密协议的相似参与方识别方法，能够在确保数据安全的情况下从诸多可用的综合能源系统或节点中选出最为相似的参与方；建立的基于LSTM和fine-tune的多元负荷联邦预测模型，能够在不共享敏感数据的基础上显著提升少数据节点的多元负荷预测精度。实验表明，在数据安全的情况下，所提MT-SDP-FL算法不仅可以使少量数据节点取得优异的预测结果，而且也能提升多数据节点的预测精度。进一步挖掘不同能源间的耦合关系，改善相似节点的选择策略是需要进一步研究的问题。
-
图 1 LSTM的基本单元结构
Fig. 1 Basic unit structure of LSTM
下载:
全尺寸图片
图 2 所提算法基本框架
Fig. 2 Basic framework of the proposed algorithm
下载:
全尺寸图片
图 3 FedPS的基本流程
Fig. 3 Basic process of FedPS
下载:
全尺寸图片
图 4 MT-SDP-FL与MT-E-LSTM得到的电、气负荷预测曲线
Fig. 4 Electrical load prediction curve obtained by MT-SDP-FL and MT-E-LSTM
下载:
全尺寸图片
图 5 MT-SDP-FL、FedAvg和multi-task learning得到的负荷预测曲线
Fig. 5 Load forecasting curve obtained by MT-SDP-FL, FedAvg and multi-Task learning
下载:
全尺寸图片
表 1 学校1与各校之间的两种欧氏距离
Table 1 Two Euclidean distances between school 1 and each school
学校 原始欧氏距离 点击协议计算出的
欧氏距离学校2 758.737 13.368 学校3 487.945 11.070 学校4 518.446 11.762 学校5 1592.331 28.055 学校6 1148.024 20.227 表 2 针对少数据学校1的10种组合得到的多元负荷预测结果
Table 2 Multivariate load forecasting results for ten combinations of School 1 with a small amount of data
学校组合 校1电预测 校1气预测 MAE RMSE MAE RMAE {1，3，4} 0.108 0.202 0.851 1.662 {1，2，3} 0.125 0.243 0.834 1.783 {1，2，4} 0.138 0.222 1.117 2.045 {1，2，5} 0.135 0.230 0.881 1.711 {1，2，6} 0.168 0.266 0.966 1.927 {1，3，5} 0.133 0.246 0.887 1.814 {1，3，6} 0.129 0.215 1.081 2.048 {1，4，5} 0.127 0.260 0.997 1.911 {1，4，6} 0.125 0.242 0.895 1.885 {1，5，6} 0.133 0.233 0.912 1.804 表 3 模型结构与参数
Table 3 Model structure and parameters
参数名 数值 LSTM层 3 LSTM层输出的空间维数 96 Dropout系数 0.3 batch_size 21 隐藏层 3 优化器 adam 表 4 针对少数据学校1 MT-SDP-FL与MT-E-LSTM得到的多元负荷预测结果
Table 4 Multivariate load prediction results obtained by MT-SDP-FL and MT-E-LSTM algorithms for School 1 with a small amount of data
学校 电预测 气预测 MT-SDP-FL MT-E-LSTM MT-SDP-FL MT-E-LSTM MAE RMSE MAE RMSE MAE RMSE MAE RMSE 学校1 0.108 0.202 0.168(+) 0.245(+) 0.851 1.6624 1.487(+) 2.084(+) 表 5 MT-SDP-FL与对比算法的预测结果
Table 5 Prediction results of the comparison algorithm and MT-SDP-FL
学校 误差指标 MT-SDP-FL FedAvg Multi-task learning 学校1 电 RMSE 0.202 0.704（+） 0.789（+） MAE 0.108 0.457（+） 0.634（+） 气 RMSE 1.662 8.254（+） 14.180（+） MAE 0.851 5.024（+） 6.583（+） 学校3 电 RMSE 0.543 0.994（+） 1.434（+） MAE 0.303 0.609（+） 0.945（+） 气 RMSE 1.519 6.866（+） 9.453（+） MAE 0.929 3.870（+） 5.041（+） 学校4 电 RMSE 0.188 0.539（+） 0.679（+） MAE 0.126 0.321（+） 0.402（+） 气 RMSE 0.784 5.990（+） 6.925（+） MAE 0.427 3.505（+） 3.482（+） -
[1] 贾宏杰, 王丹, 徐宪东, 等. 区域综合能源系统若干问题研究[J]. 电力系统自动化, 2015, 39(7): 198–207. JIA Hongjie, WANG Dan, XU Xiandong, et al. Research on some key problems related to integrated energy systems[J]. Automation of electric power systems, 2015, 39(7): 198–207. [2] INFIELD D G, HILL D C. Optimal smoothing for trend removal in short term electricity demand forecasting[J]. IEEE transactions on power systems, 1998, 13(3): 1115–1120. doi: 10.1109/59.709108 [3] LI Yiyan, HAN Dong, YAN Zheng. Long-term system load forecasting based on data-driven linear clustering method[J]. Journal of modern power systems and clean energy, 2018, 6(2): 306–316. doi: 10.1007/s40565-017-0288-x [4] JIN Min, ZHOU Xiang, ZHANG Z M, et al. Short-term power load forecasting using grey correlation contest modeling[J]. Expert systems with applications, 2012, 39(1): 773–779. doi: 10.1016/j.eswa.2011.07.072 [5] 高亚静, 孙永健, 杨文海, 等. 基于新型人体舒适度的气象敏感负荷短期预测研究[J]. 中国电机工程学报, 2017, 37(7): 1946–1955. GAO Yajing, SUN Yongjian, YANG Wenhai, et al. Weather-sensitive load’s short-term forecasting research based on new human body amenity indicator[J]. Proceedings of the CSEE, 2017, 37(7): 1946–1955. [6] PANDEY A S, SINGH D, SINHA S K. Intelligent hybrid wavelet models for short-term load forecasting[J]. IEEE transactions on power systems, 2010, 25(3): 1266–1273. doi: 10.1109/TPWRS.2010.2042471 [7] 曾鸣, 吕春泉, 田廓, 等. 基于细菌群落趋药性优化的最小二乘支持向量机短期负荷预测方法[J]. 中国电机工程学报, 2011, 31(34): 93–99,11. ZENG Ming, LYU Chunquan, TIAN Kuo, et al. Least squares-support vector machine load forecasting approach optimized by bacterial colony chemotaxis method[J]. Proceedings of the CSEE, 2011, 31(34): 93–99,11. [8] 张素香, 赵丙镇, 王风雨, 等. 海量数据下的电力负荷短期预测[J]. 中国电机工程学报, 2015, 35(1): 37–42. ZHANG Suxiang, ZHAO Bingzhen, WANG Fengyu, et al. Short-term power load forecasting based on big data[J]. Proceedings of the CSEE, 2015, 35(1): 37–42. [9] SAFTA C, CHEN R L Y, NAJM H N, et al. Efficient uncertainty quantification in stochastic economic dispatch[J]. IEEE transactions on power systems, 2017, 32(4): 2535–2546. doi: 10.1109/TPWRS.2016.2615334 [10] CHENG Lilin, ZANG Haixiang, DING Tao, et al. Multi-meteorological-factor-based graph modeling for photovoltaic power forecasting[J]. IEEE transactions on sustainable energy, 2021, 12(3): 1593–1603. doi: 10.1109/TSTE.2021.3057521 [11] HE Feifei, ZHOU Jianzhong, FENG Zhongkai, et al. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm[J]. Applied energy, 2019, 237: 103–116. doi: 10.1016/j.apenergy.2019.01.055 [12] POTOČNIK P, ŠKERL P, GOVEKAR E. Machine-learning-based multi-step heat demand forecasting in a district heating system[J]. Energy and buildings, 2021, 233: 110673. doi: 10.1016/j.enbuild.2020.110673 [13] SIMON Haykin. 神经网络原理[M]. 叶世伟, 史忠植, 译. 北京: 机械工业出版社, 2004. [14] CAO Jian, LI Zhi, LI Jian. Financial time series forecasting model based on CEEMDAN and LSTM[J]. Physica A:statistical mechanics and its applications, 2019, 519: 127–139. doi: 10.1016/j.physa.2018.11.061 [15] MUZAFFAR S, AFSHARI A. Short-term load forecasts using LSTM networks[J]. Energy procedia, 2019, 158: 2922–2927. doi: 10.1016/j.egypro.2019.01.952 [16] 李鹏, 何帅, 韩鹏飞, 等. 基于长短期记忆的实时电价条件下智能电网短期负荷预测[J]. 电网技术, 2018, 42(12): 4045–4052. LI Peng, HE Shuai, HAN Pengfei, et al. Short-term load forecasting of smart grid based on long-short-term memory recurrent neural networks in condition of real-time electricity price[J]. Power system technology, 2018, 42(12): 4045–4052. [17] SOMU N, RAMAN M R G, RAMAMRITHAM K. A deep learning framework for building energy consumption forecast[J]. Renewable and sustainable energy reviews, 2021, 137: 110591. doi: 10.1016/j.rser.2020.110591 [18] MCMAHAN H B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[EB/OL]. (2016–02–17)[2022–08–30]. https://arxiv.org/abs/1602.05629. [19] 杨强. 联邦学习: 人工智能的最后一公里[J]. 智能系统学报, 2020, 15(1): 183–186. YANG Qiang. Federated learning: the last on kilometer of artificial intelligence[J]. CAAI transactions on intelligent systems, 2020, 15(1): 183–186. [20] BRISIMI T S, CHEN Ruidi, MELA T, et al. Federated learning of predictive models from federated Electronic Health Records[J]. International journal of medical informatics, 2018, 112: 59–67. doi: 10.1016/j.ijmedinf.2018.01.007 [21] SUBRAMANYA T, RIGGIO R. Centralized and federated learning for predictive VNF autoscaling in multi-domain 5G networks and beyond[J]. IEEE transactions on network and service management, 2021, 18(1): 63–78. doi: 10.1109/TNSM.2021.3050955 [22] WU Xing, LIANG Zhaowang, WANG Jianjia. FedMed: a federated learning framework for language modeling[J]. Sensors, 2020, 20(14): 4048. doi: 10.3390/s20144048 [23] HUA Gaofeng, ZHU Li, WU Jinsong, et al. Blockchain-based federated learning for intelligent control in heavy haul railway[J]. IEEE access, 2020, 8: 176830–176839. doi: 10.1109/ACCESS.2020.3021253 [24] SAVI M, OLIVADESE F. Short-term energy consumption forecasting at the edge: a federated learning approach[J]. IEEE access, 2021, 9: 95949–95969. doi: 10.1109/ACCESS.2021.3094089 [25] CHEN Yujing, NING Yue, CHAI Zheng, et al. Federated multi-task learning with hierarchical attention for sensor data analytics[C]//2020 International Joint Conference on Neural Networks. Glasgow: IEEE, 2020: 1–8. [26] 王鑫, 周泽宝, 余芸, 等. 一种面向电能量数据的联邦学习可靠性激励机制[J]. 计算机科学, 2022, 49(3): 31–38. WANG Xin, ZHOU Zebao, YU Yun, et al. Reliable incentive mechanism for federated learning of electric metering data[J]. Computer science, 2022, 49(3): 31–38. [27] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735 [28] 刘旭红. 高效安全向量计算及其推广[J]. 软件学报, 2021, 32(11): 3628–3645. LIU Xuhong. Efficient secure vector computation and its extension[J]. Journal of software, 2021, 32(11): 3628–3645. [29] 燕忠毅, 曾艳, 赵乃良, 等. 一种基于二阶导数解决联邦学习中数据不平衡问题的方法: CN113691594A[P]. 2021–11–23. YAN Zhongyi, ZENG Yan, ZHAO Nailiang, et al. Method for solving data imbalance problem in federated learning based on second derivative: CN113691594A[P]. 2021–11–23. [30] 刘叶. 数据不平衡的联邦学习方法研究[D]. 北京: 北京邮电大学, 2021. LIU Ye. Research on federatedlearning methods for unbalanced data[D]. Beijing: Beijing University of Posts and Telecommunications, 2021. [31] 孙庆凯, 王小君, 张义志, 等. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63–70. SUN Qingkai, WANG Xiaojun, ZHANG Yizhi, et al. Multiple load prediction of integrated energy system based on long short-term memory and multi-task learning[J]. Automation of electric power systems, 2021, 45(5): 63–70. [32] PENG Chao, TAO Yifan, CHEN Zhipeng, et al. Multi-source transfer learning guided ensemble LSTM for building multi-load forecasting[J]. Expert systems with applications, 2022, 202: 117194. doi: 10.1016/j.eswa.2022.117194
