A spectral clustering based on GCNs and attention mechanism
-
摘要: 经典的谱聚类算法需要计算图拉普拉斯矩阵的特征分解，代价昂贵，学者们将深度学习模型引入谱聚类算法。然而，现有的方法存在一定的局限性。针对现有聚类模型忽略了节点间的关联度信息，导致聚类结果不准确；当图神经网络中的节点数目发生变化时，需要更新整张图，耗费大量存储空间的问题，本文将注意力机制与改进的图卷积神经网络架构相结合，提出了一种基于注意力和图卷积神经网络的谱聚类方法。该方法主要利用注意力机制引导节点聚类，然后建立相应的目标，通过训练神经网络计算出目标最优时对应的聚类分配，并在图重构过程中利用注意力信息和拓扑信息双重引导，从而提升重构的精确度。实验结果显示，本文提出的方法在图分类、图聚类及图重构中具有良好性能。Abstract: The classical spectral clustering algorithm often involves computationally expensive feature decomposition of the Laplacian matrix, prompting researchers to introduce a deep learning model into the spectral clustering algorithm. Nonetheless, the existing methods possess certain limitations. The existing clustering model neglects the information on the correlation degree between nodes, which leads to inaccurate clustering results. Additionally, when the number of nodes in the graph neural network changes, the whole graph requires updating, leading to extensive storage space consumption. By combining the attention mechanism with the improved architecture of graph convolutional neural networks, this paper proposes a spectral clustering method based on the attention and graph convolutional neural network to address these issues. The proposed method mainly utilizes the attention mechanism to guide node clustering, following which it establishes the corresponding target. The corresponding cluster allocation, when the target is optimal, is calculated by training the neural network. Attention information and topological information are used to guide the graph reconstruction process, thereby improving the accuracy of reconstruction. Experimental results reveal that the proposed method exhibits excellent performance in graph classification, graph clustering, and graph reconstruction tasks.
-
聚类是一种通过度量数据点之间的相似性对未标记数据点进行分类的方法。常用的度量数据点之间相似性的方法有欧几里德距离、余弦距离及曼哈顿距离等。经典的聚类算法如K-均值聚类[1]、谱聚类[2]、分层聚类[3]等，近年来已广泛应用于各个领域。然而，经典的聚类方法作用于高维数据时性能较差且计算复杂度较高[4-5]。受到深度学习中一些模型的启发，学者们将深度学习与经典的聚类算法相结合提出了深度聚类的概念。
卷积神经网络（convolutional neural network, CNNs）作为深度学习中一类重要的架构，由于其只能作用于传统的欧几里德数据，且在一般的图结构中定义局部卷积滤波器和池运算符非常困难[6-10]，因此，针对卷积神经网络CNNs的局限性，研究者们提出了图卷积神经网络（GCNs)。图卷积神经网络(graph neural network, GCNs) 继承了卷积神经网络（CNNs）中的池化操作及卷积操作，可以结合局部特征信息，去除冗余信息[4,11-13]，并且将卷积运算扩展到更一般的图结构，可以处理更一般的拓扑结构[5,14-17]。鉴于图卷积神经网络比卷积神经网络更强大的优势，基于图卷积神经网络的各类聚类算法成为研究热点。
经典的谱聚类算法的原理是将样本数据映射到与其拓扑结构相对应的图拉普拉斯矩阵的特征空间，通过对图拉普拉斯矩阵进行特征分解得到相应的聚类结果[18-21]。然而，当图的结构足够复杂时，与图结构对应的图拉普拉斯矩阵的维数会剧增，进行特征分解的代价过高，不适用于具有复杂结构的图数据集和大数据集的聚类分析，因此，研究者们提出了基于深度学习的谱聚类算法并已证明在行为识别[22-23]、社区检测[24]、图像处理[25-27]等任务中体现了良好的性能。有研究者在2020年提出了基于自编码器的生物数据低秩谱集成聚类算法[28-29]，将深度自动编码器同谱聚类算法结合应用于生物领域[30-31]。2019年另有研究者提出了基于深度神经网络的多视图数据光谱聚类[32-33]，利用多个孪生网络（siamese networks）同谱聚类算法结合并应用于多视图数据[34-37]。还有研究者提出了基于图神经网络图池的谱聚类算法，将图拉普拉斯矩阵特征分解导致的高计算量问题转化为目标函数的优化问题[38]，通过优化一个图分割问题得到相应的聚类结果，在一定程度上取得了良好的效果[39-40]。然而上述研究成果仍存在局限性，如忽略了节点之间的关联度信息，使得一些重要性较低的节点被划分到同一簇中，导致聚类结果依然不够准确；使用的网络太浅，不适用于复杂的数据集；经典的图卷积神经网络(GCNs)架构中涉及的节点数量发生变化时，需要更新整张图，导致较高昂的计算成本和存储成本[38,41]。
近年来，注意力机制广泛应用于各类聚类算法中。2021年提出了基于注意力机制的深度子空间应用于多视图数据的分类，将自注意力机制引入深度子空间聚类网络，通过计算节点之间的注意力系数对不同的节点分配不同大小的权重从而给予不同的关注[28,33,42]。2021年提出了具有双重引导自监督的深度注意引导图聚类，动态融合不同层的多尺度特征从而学习更高效的潜在表示[9,40,43]尺度自注意深度聚类方法，利用自注意力机制融合各模块生成语义信息的互补特征表示应用于具有特征缺失的数据[44]。
在前人研究工作的基础上，本文对基于图神经网络图池的谱聚类算法进行改进，提出了一种将注意力机制与改进的图卷积神经网络相结合的谱聚类算法(graph attention spectral clustering，GATSC)。该算法首先利用注意力机制计算节点之间的注意力系数来提高聚类结果的准确性；对传统的图卷积神经网络(GCNs)进行改进，即在神经网络的每一层中围绕每个节点选择一定数量的邻居。然后将聚合的邻居信息与节点在上一层的表示连接起来，形成节点在该层的表示，从而降低经典的图神经网络的存储成本。通过实验表明，与其他谱聚类算法相比，本文提出的模型在图像分类、图像聚类及图重构中具有显著优势。
本文主要贡献如下：1）本文提出了将注意力机制与改进的GCNs相结合的深度谱聚类算法。与现有的方法不同，本文提出的模型在进行聚类操作时需要计算节点之间的注意力系数，通过节点间的注意力系数来引导节点聚类从而提高聚类性能。2）本文模型在进行图重构时，利用注意力机制和拓扑结构信息双重引导重构操作。具体地，将节点之间的注意力信息和图的拓扑结构信息分别作为权重添加在损失函数上，从而不仅在拓扑结构上进行局部保留，而且考虑节点之间的关联度，从而使各部分的重构边缘更加清晰。
1. 相关理论知识
1.1 深度聚类
有研究者在2018年发表了一篇关于深度聚类的综述，包括深度聚类（deep clustering）被提出的原因、原理及经典的一些深度聚类模型[45]。现实中的大多数数据集往往不具有标签或者存在部分的标签缺失，因此，对这类数据进行分类的难度系数较大。而深度聚类算法利用深度学习中的模型将数据进行降维嵌入至低维的特征空间，然后选择适当的相似性度量函数并且制定合理的聚类损失函数，最终通过训练模型最小化聚类损失从而对无标签的数据进行分类。聚类思想见图1，图中每一种颜色代表一种数据类型。
图 1 理想状态下的聚类效果Fig. 1 Clustering diagram under ideal condition
下载:
全尺寸图片
1.2 图卷积神经网络
由于卷积神经网络（CNNs）只能作用于欧几里德域的数据，不适用于更一般的图数据，在对图数据进行处理时效果不佳，因此，有研究者于2019年在ICLR中发表了关于图卷积神经网络（GCNs）的文章[46]。GCNs继承了卷积神经网络的优势，将卷积操作扩展到更一般的图结构中，能够更好地进行图表示学习。具体地讲，GCNs将原始数据输入图卷积神经网络后，图神经网络利用卷积核聚合一阶邻域内所有节点的特征信息作为中心节点的潜在特征、利用池化层的池化操作去掉冗余的特征信息，最终学习到节点的高效表示。
1.3 注意力机制
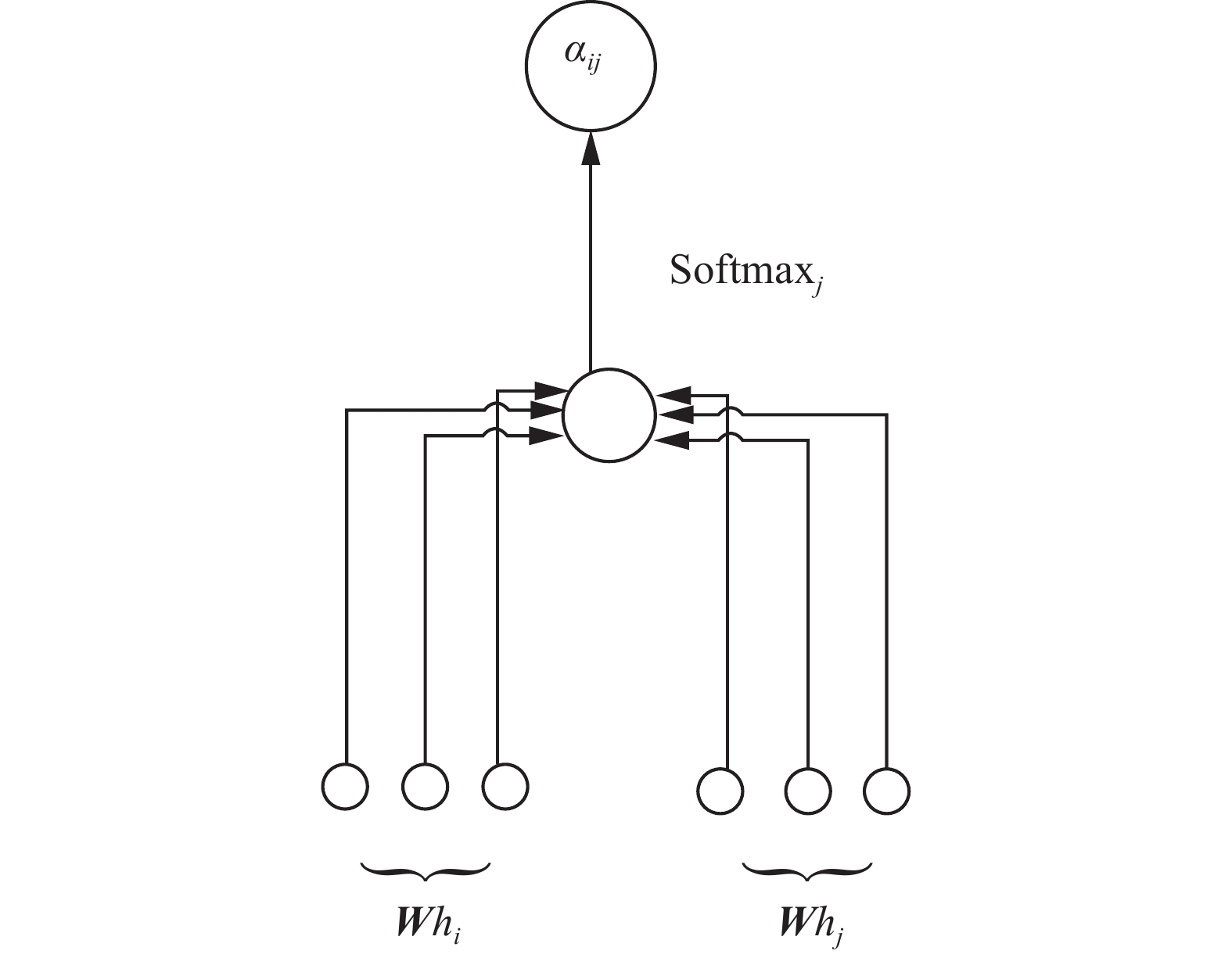
随着神经网络的发展，注意力机制已成为神经网络中的一个重要概念，并在不同领域得到了应用和研究。近年来，注意力机制在语音处理、图像处理等方面得到了越来越广泛的应用。在许多基于序列的任务中，注意力机制已经具有极高的准确性。有研究者在2018年提出了注意力机制并结合图神经网络验证了其效果（注意力机制模型见图2）[47]。
图 2 注意力机制模型Fig. 2 Attention mechanism model下载:
全尺寸图片
注意力机制的核心是计算不同节点之间注意力系数，首先利用卷积操作得到
$ m $ 个节点的特征表示，分别记为${h_1},{h_2},\cdots,{h_m}$ ，然后利用下式计算节点$ i $ 和节点$ j $ 之间的注意力系数：$$ {\alpha _{ij}} = {\rm{Soft}}{\max _j}({e_{ij}}) = \dfrac{{\exp ({e_{ij}})}}{{\displaystyle\sum _{k \in {N_i}}} \exp ({e_{ik}})} $$ (1) 式中：
$a(\cdot):{R}^{F'}\times {R}^{F'}\to R$ 为一个映射函数，$ {\boldsymbol{W}} $ 是权重矩阵，$ {e_{ij}}{\text{ = }}a({\boldsymbol{W}}{\bar h_i},{\boldsymbol{W}}{\bar h_j}) $ 表示节点$ i $ 及节点$ j $ 之间的关联度，$ {\bar h_i} $ 及$ {\bar h_j} $ 分别表示节点$ i $ 及节点$ j $ 进行正则化操作后的特征表示，$ {\alpha _{ij}} $ 利用Softmax函数将节点$ i $ 及节点$ j $ 之间的关联度$ {e_{ij}} $ 作归一化处理。注意力机制将计算得到的节点之间的注意力信息视为权重，并通过权重最大的部分来帮助用户做出决策。然而当输入中不同数据点的尺寸不一致时，往往需要多种类型的卷积块对不同尺寸的输入进行处理，当卷积块类型过多时需要训练大量参数将导致高昂的计算成本。注意力机制不仅充分考虑节点内部的潜在关系，还能处理具有可变大小的输入从而极大地降低了计算成本。当注意力机制被应用于计算一个序列的表示时,它通常被称为自注意力（self-attention）或内部的关注, 当注意力机制与递归神经网络(RNN)或其他卷积神经网络相结合时，这种机制已被证明对机器阅读等任务很有用[48]。
2. 本文提出的模型GATSC
现有的深度谱聚类算法存在一定的局限性如：忽略了节点之间的关联度信息，使得一些重要性较低的节点被划分到同一簇中，导致聚类结果依然不够准确；使用的网络太浅，不适用于复杂的数据集；经典的图卷积神经网络(GCNs)架构中涉及的节点数量发生变化时，需要更新整张图将导致较高昂的计算成本和存储成本。因此，本文提出了基于注意力机制和改进的图卷积神经网络结合的谱聚类算法，记为GATSC。该算法与原有的基于图神经网络图池的谱聚类算法（graph neural networks spectral clustering，GNNSC）相比较，降低了迭代过程中的存储成本，提高聚类准确性。算法流程见图3。
图 3 本文提出的模型框架Fig. 3 Model of the proposed algorithm下载:
全尺寸图片
本文基于文献[39]提出的基于图神经网络图池的谱聚类算法，在原有的模型基础上增加了注意力机制，改进了聚类损失函数和重构损失函数。给定一张图记为
$ {\boldsymbol{G}} $ ，将$ {\boldsymbol{G}} $ 定义为$ {\boldsymbol{G}} = \{ V,E\} $ ，其中$ {\boldsymbol{V}} $ 表示图$ {\boldsymbol{G}} $ 中所有节点构成的集合，且$ \left| V \right| = N $ ，$ V $ 中的每一个节点都是一个$ {{F}} $ 维的向量。$ E $ 代表图$ {\boldsymbol{G}} $ 中所有边的集合。$ {\boldsymbol{A}} $ 是图$ {\boldsymbol{G}} $ 的邻接矩阵，$ {\boldsymbol{A}} \in {{\bf{R}}^{N \times N}} $ 。$ {\boldsymbol{X}} $ 是图$ {\boldsymbol{G}} $ 中节点的特征矩阵，$ {\boldsymbol{H}} \in {{\bf{R}}^{N \times F}} $ ，$ {\boldsymbol{H}} $ 中每一行都是图$ {\boldsymbol{G}} $ 的一个节点。本文提出的模型算法步骤如下：
1)数据预处理。将图像数据进行分割，得到各个节点的特征信息。
2)学习节点的潜在表示。本文利用改进的图卷积神经网络，对于每个节点
$ v \in {\boldsymbol{V}} $ ，聚合节点$ v $ 固定数量的一阶邻居$ \left\{ {u|u \in N(v)} \right\} $ ，利用一个聚合函数$ {\rm{AG}}{{\rm{G}}_l} $ 来进行聚合操作，将聚合后的结果同节点$ v $ 在第$ l - 1 $ 层的潜在表示连接后得到节点$ v $ 在第$ l $ 层的潜在表示：$$ h_u^l = {\rm{AG}}{{\rm{G}}_l}(h_u^{l - 1}) $$ (2) $$ h_v^l = {\rm{combine}}(h_u^{l - 1},h_v^l) $$ (3) 其中
$ u \in N(v) $ 。需要说明的是，
${\rm{AG}}{{\rm{G}}_l}$ 不是聚合拓扑结构意义下的一阶邻居，而是聚合对中心节点贡献大的邻居节点，即对中心节点重要性高的节点作为邻居，其中重要性的大小通过注意力系数衡量。3)计算节点之间的注意力信息。首先定义节点
$ i $ 的特征和节点$ j $ 的特征的关联度如下：$$ {\omega _{ij}} = f({\boldsymbol{W}}{h_i},{\boldsymbol{W}}{h_j}) $$ (4) 其中，
$ f $ 是共享Attention机制，$ f:{{\bf{R}}^F} \times {{\bf{R}}^F} \to {\bf{R}} $ ，$ {\boldsymbol{W}} $ 是一个可训练的权重矩阵。为了更好地比较不同节点特征之间的相关性，并考虑到每一层的共享Attention机制
$ f $ 是被一个权重向量参数${\boldsymbol{W}}$ 所量化的，$\,{\boldsymbol{\beta}} \in {{\bf{R}}^{2F}}$ ，本文对关联度作归一化处理如下。（a）当节点
$ j $ 属于节点$ i $ 的一阶邻域时：$$ {\mu _{ij}} = \dfrac{{\exp ({\rm{LeaklyRELU}}({{\boldsymbol{\beta}} ^{\rm{T}}}[{\boldsymbol{W}}{h_i}||{\boldsymbol{W}}{h_j}]))}}{{\displaystyle\sum\limits_{k \in {\boldsymbol{V}}\backslash {{\boldsymbol{V}}_l}} {\exp ({\rm{LeaklyRELU}}({{\boldsymbol{\beta}} ^{\rm{T}}}[{\boldsymbol{W}}{h_i}||{\boldsymbol{W}}{h_k}]))} }} $$ (5) （b）当节点
$ j $ 不属于节点$ i $ 的一阶邻域时：$$ {\mu _{ij}'} = \dfrac{{\exp ({\rm{LeaklyRELU}}({{\boldsymbol{\beta}} ^{\rm{T}}}[{\boldsymbol{W}}{h_i}||{\boldsymbol{W}}{h_j}]))}}{{\displaystyle\sum\limits_{k \in {\boldsymbol{V}}\backslash {{\boldsymbol{V}}_l}} {\exp ({\rm{LeaklyRELU}}({{\boldsymbol{\beta}} ^{\rm{T}}}[{\boldsymbol{W}}{h_i}||{\boldsymbol{W}}{h_k}]))} }} $$ (6) 式中：
$ {\boldsymbol{V}} $ 是所有节点特征组成的集合，${{\boldsymbol{V}}_l}$ 是节点$ l $ 的一阶邻域的特征组成的集合，$ {h_i} $ 、$ {h_j} $ 及$ {h_k} $ 分别为节点$ i $ 、节点$ j $ 及节点$ k $ 的特征表示，$ {\boldsymbol{W}} $ 是权重矩阵，$ {\boldsymbol{\beta}} $ 是权重系数，LeaklyRELU是激活函数。4)利用本文提出的模型进行聚类。给出了式（7）的损失函数，通过训练神经网络得到每一次迭代后的最优聚类分配结果。
$$ {L_{{\rm{MCP}}}} = {\rm{minimum}} \left( - \dfrac{{{\rm{tr}}({{\boldsymbol{U}}^{{{\rm{T}}}}}\tilde {\boldsymbol{A}}{\boldsymbol{U}})}}{{{\rm{tr}}({{\boldsymbol{U}}^{\rm{T}}}\tilde {\boldsymbol{D}}{\boldsymbol{U}})}} + \left\|\frac{{{{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{U}}}}{\left\|{{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{U}}\right\|_F} - \frac{{{I_K}}}{{\sqrt K }}\right\|_F\right) $$ (7) 式中：
$ {\text{||}} \cdot {\text{|}}{{\text{|}}_F} $ 是Frobenius范数；$ {\boldsymbol{U}} $ 是进行软聚类分配时的分配矩阵，即$ {u_{ij}} \in [0,1] $ ，${\boldsymbol{U}}{{\boldsymbol{1}}_{{K}}}{\text{ = }}{{\boldsymbol{1}}_N}$ ，$ K $ 为强连通分支的个数；$ \tilde {\boldsymbol{D}} $ 为正则化后的节点度矩阵；$ \tilde {\boldsymbol{A}} $ 为正则化后的邻接矩阵，其元素$$ \begin{array}{l}{{\displaystyle \overline{a}}}_{ij}=\left\{\begin{aligned} &{{\displaystyle \mu }}_{ij},\;节点\text{ }j\text{ }在节点\text{ }i\text{ }的一阶邻域内\\ &{{\displaystyle \mu }}_{ij}',\;节点\text{ }j\text{ }不在节点\text{ }i\text{ }的一阶邻域内\end{aligned}\right. \\ \end{array} $$ 其中
$i\ne {j} $ 。图4给出了模型GATSC的池化层模型。
图 4 GATSC的池化层模型Fig. 4 Pooling layer model of GATSC下载:
全尺寸图片
5) 根据聚类结果进行图重构。利用注意力机制和拓扑信息双重引导重构操作，既保留了局部信息，又能准确地勾勒出各部分的边缘。首先利用每次迭代的聚类分配矩阵对节点特征矩阵和邻接矩阵进行迭代操作。每次迭代的邻接矩阵和节点特征矩阵计算如下：
$$ {{\boldsymbol{H}}^{{\rm{ite}}}} = {{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{H}};\;\;{{\boldsymbol{A}}^{{\rm{ite}}}} = {{\boldsymbol{U}}^{\rm{T}}}\bar {\boldsymbol{A}}{\boldsymbol{U}} $$ (8) 式中：
$ {\boldsymbol{U}} $ 为软聚类分配的分配矩阵，$ {\boldsymbol{H}} $ 为图的节点特征矩阵，$ \bar {\boldsymbol{A}} $ 为归一化操作后图的节点邻接矩阵。使用GCNs的自动编码器进行重构操作如下：$$ {{\boldsymbol{H}}^R} = {{\boldsymbol{U}}^{\rm{T}}}{{\boldsymbol{H}}^{{\rm{ite}}}};\;\;{{\boldsymbol{A}}^R} = {{\boldsymbol{U}}^{\rm{T}}}{{\boldsymbol{A}}^{{\rm{ite}}}}{\boldsymbol{U}} $$ (9) 用两种方法定义解码器的重构损失，如下所示：
$$ {L_R} = ||{{\boldsymbol{A}}^R} - {\boldsymbol{A}}||_2^2 $$ (10) 或者
$$ {L_R} = \left\| {{{\boldsymbol{H}}^R} - {\boldsymbol{H}}} \right\|_2^2 $$ (11) 最后将节点之间的注意力系数和拓扑结构信息分别作为权重引入式（10）或（11），计算公式如下：
$$ {L_R} = \lambda \left(\sum\limits_{i,j} {{{\hat \mu }_{ij}}} ||{{\boldsymbol{H}}_i} - {\hat {\boldsymbol{H}}_j}|{|^2}\right) + (1 - \lambda )\left(\sum\limits_{i,t} {{{\hat d}_{ij}}} {\left\| {{\boldsymbol{H}} - {{\tilde {\boldsymbol{H}}}_t}} \right\|^2}\right) $$ (12) 式中：
$ {\hat \mu _{ij}} $ 为正则化操作后的注意力系数；$ {\hat d_{ij}} $ 为正则化操作后的欧氏距离；$ \lambda $ 为一个权衡参数，$\lambda \in (0,1)$ 。${\hat {\boldsymbol{H}}_j}$ 表示数据点${{\boldsymbol{H}}_i}$ 一阶邻域内距离最近的节点的重构结果，${\tilde {\boldsymbol{H}}_t}$ 表示数据点${{\boldsymbol{H}}_i}$ 一阶邻域内关联度最高的节点的重构结果。本段对提出的模型的计算复杂度进行分析。本文采用改进的GCNs中的池化层计算聚类分配矩阵
$ {\boldsymbol{U}} $ ，其中$ {\boldsymbol{U}} \in {{\bf{R}}^{K \times K}} $ 。计算复杂度来源于聚类损失与正则化损失，由式(7)可知聚类损失主要由聚类分配矩阵松弛后的决策邻接矩阵构成，正则化损失主要由聚类分配矩阵构成，因此，主要计算复杂度为$ O(NK(K + N)) $ 。由于图中并非所有节点都高度相关，可以设置一定的阈值，在每一次迭代后，将低于阈值的节点之间的关联度可视为0，即在模型的每次训练过程中会丢弃掉一些相关度不高的节点之间的边，从而对松弛后的节点邻接矩阵进行降维，最终计算复杂度应小于$ O(NK(K + N)) $ 。3. 实验与分析
在本节中，将本文提出的模型与无注意力引导的深度谱聚类模型GNNSC进行比较。本实验每个部分的具体实现建立在Spectral、Tensorflow、Pytorch等架构上。
3.1 无监督聚类实验及分析
3.1.1 引文网络Cora、Citeseer及Pubmed上的聚类比较
首先考虑了在3个引文网络Cora、Citeseer及Pubmed上的聚类任务。这3个引文网络中的节点是各类文献的特征向量构成的集合，这些特征向量包含文献的年份、作者、科目等信息。节点之间的边被定义为文献之间引用或者被引用的关系，且这种关系利用二进制来表示，0代表没有引用关系，1代表具有引用关系。考虑到两种文献之间或许没有直接的引用关系，但是可能存在间接的引用关系。本文利用注意力引导聚类可以关注到多跳节点之间的相关性。每个节点都被标记为文档类型，对各个文档类型进行聚类。利用NMI及CS两种评价指标来评估聚类效果，其中
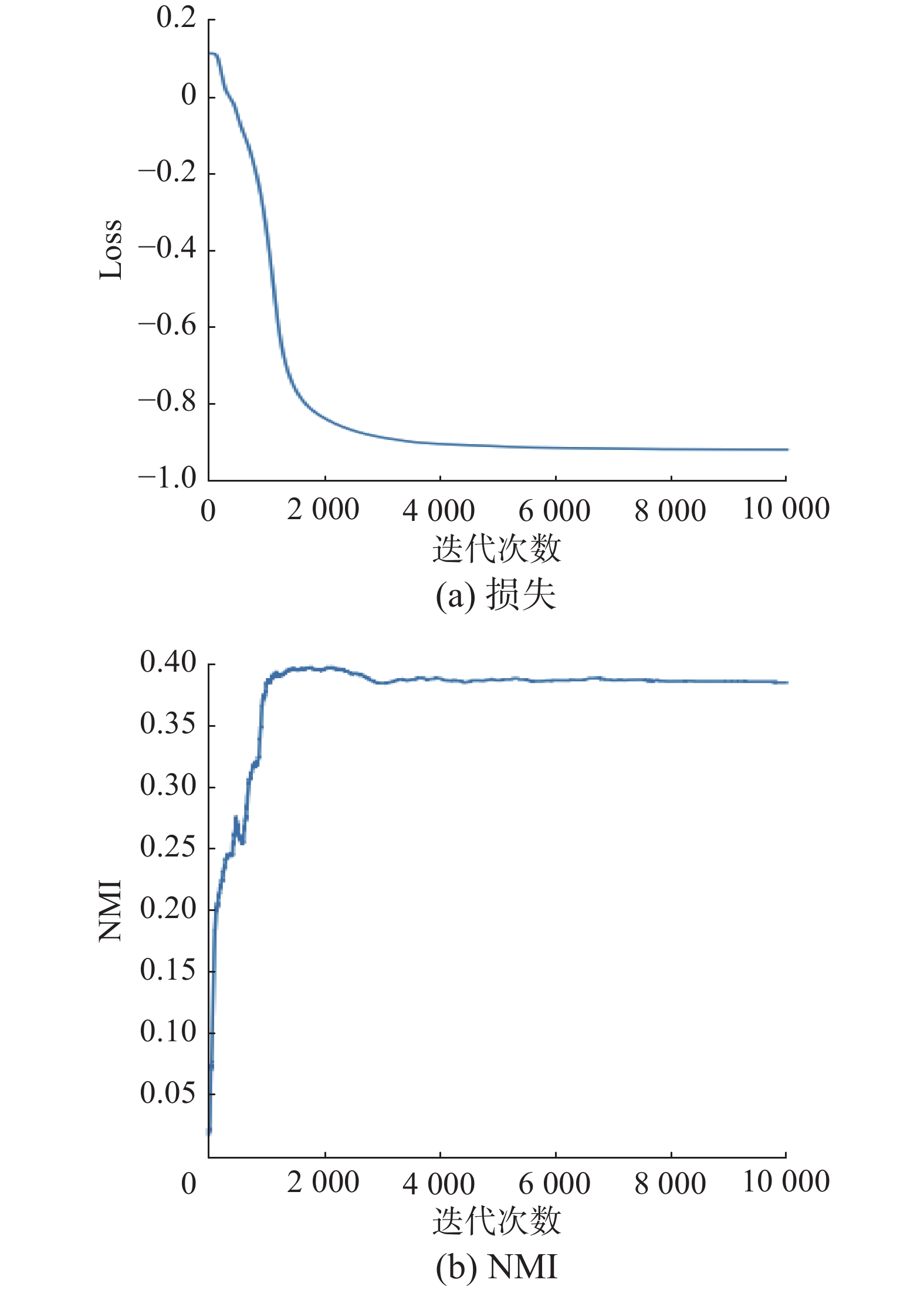
$I_{\rm{NM}}(\hat {\textit{z}},{\textit{z}}) = \dfrac{{H(\hat {\textit{z}}) - H(\hat {\textit{z}}|{\textit{z}})}}{{\sqrt {H(\hat {\textit{z}}) - H({\textit{z}})} }}$ 表示正则化的互信息，${{S}}_{\rm{C}}(\hat {\textit{z}},{\textit{z}}) = 1 - \dfrac{{H(\hat {\textit{z}}|{\textit{z}})}}{{H(\hat {\textit{z}})}}$ 表示完整性得分。将本文GATSC与GNNSC、谱聚类（SC）、基于可微分池化操作的深度谱聚类（DiffPool）进行对比（见表1）。由表1可以看出，本文提出的模型在Cora、Citeseer及Pubmed 3个引文网络上的NMI得分优于SC及DiffPool两个模型，表明本文选取的池化层类型更优。而本文提出的模型的NMI得分优于GNNSC模型表明了注意力机制的强大性。GNNSC模型没有充分考虑节点之间的注意力信息，仅利用节点的拓扑信息寻找强连通分支，进而将节点进行分类。图5及图6分别给出了本文提出的模型与GNNSC的NMI值随着迭代次数的变化、三类损失函数随着迭代次数的变化的曲线图，显示出本文提出的模型获得了更加稳定的集群性能，且迭代收敛的速度更快。
表 1 对不同的引文网络节点聚类得到的NMI值和CS值Table 1 NMI value and CS value obtained by clustering different citation network nodes数据集 K SC Diffpool NMI CS NMI CS Cora 7 0.025 0.126 0.315 0.309 Citeseer 6 0.014 0.033 0.139 0.153 Pubmed 3 0.182 0.261 0.079 0.085 数据集 K GNNSC GATSC NMI CS NMI CS Cora 7 0.404 0.392 0.451 0.437 Citeseer 6 0.287 0.283 0.316 0.312 Pubmed 3 0.200 0.197 0.214 0.212 
图 5 本文提出的模型在Cora数据集上的无监督损失及 NMI值Fig. 5 Unsupervised loss of proposed model and NMI value on Cora dataset下载:
全尺寸图片
图 6 GNNSC在Cora数据集上的无监督损失及NMI值Fig. 6 Unsupervised loss of GNNSC and NMI value on Cora dataset下载:
全尺寸图片
3.1.2 图像分割聚类比较
将本文提出的模型应用于图像分割任务。首先对原图像进行过分割操作，节点特征由过分割后的图像的各个区域的平均值和不同颜色组成，设置聚类数量为4，实验结果如图7所示。实验结果显示，GNNSC总体效果良好，但是图像中各个边缘不够清晰，存在一定的聚类误差。本文提出的模型中由于节点之间的相似性不再纯粹利用拓扑距离来衡量，因此图像中每个部分的边缘会被划分地更清楚，同时也减少了一定的聚类错误。
图 7 图像分割任务效果Fig. 7 Results of image segmentation下载:
全尺寸图片
3.2 图重构实验及分析
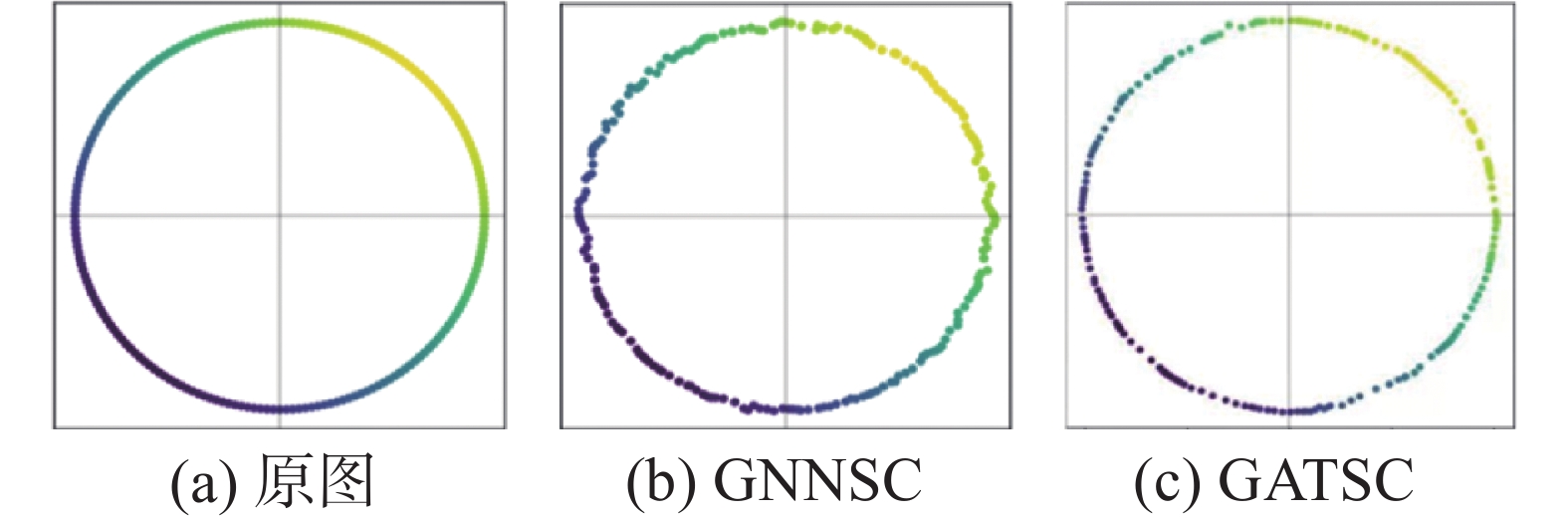
本文利用注意力机制计算节点之间的注意力系数，设计了基于注意力信息和拓扑信息双重引导的自动编码器，并通过最小化重构损失来重建原始输入的节点特征矩阵及原始输入的邻接矩阵，保留25%的原始节点。本文GATSC及GNNSC图重构结果比较如图8。
图 8 环形图重构效果Fig. 8 Results of ring graph reconstruction下载:
全尺寸图片
由图8可以看出，本文提出的模型对于环形图的重构效果更优。虽然GNNSC对于环形的重构较好，但是在环形的边缘重构效果较差。
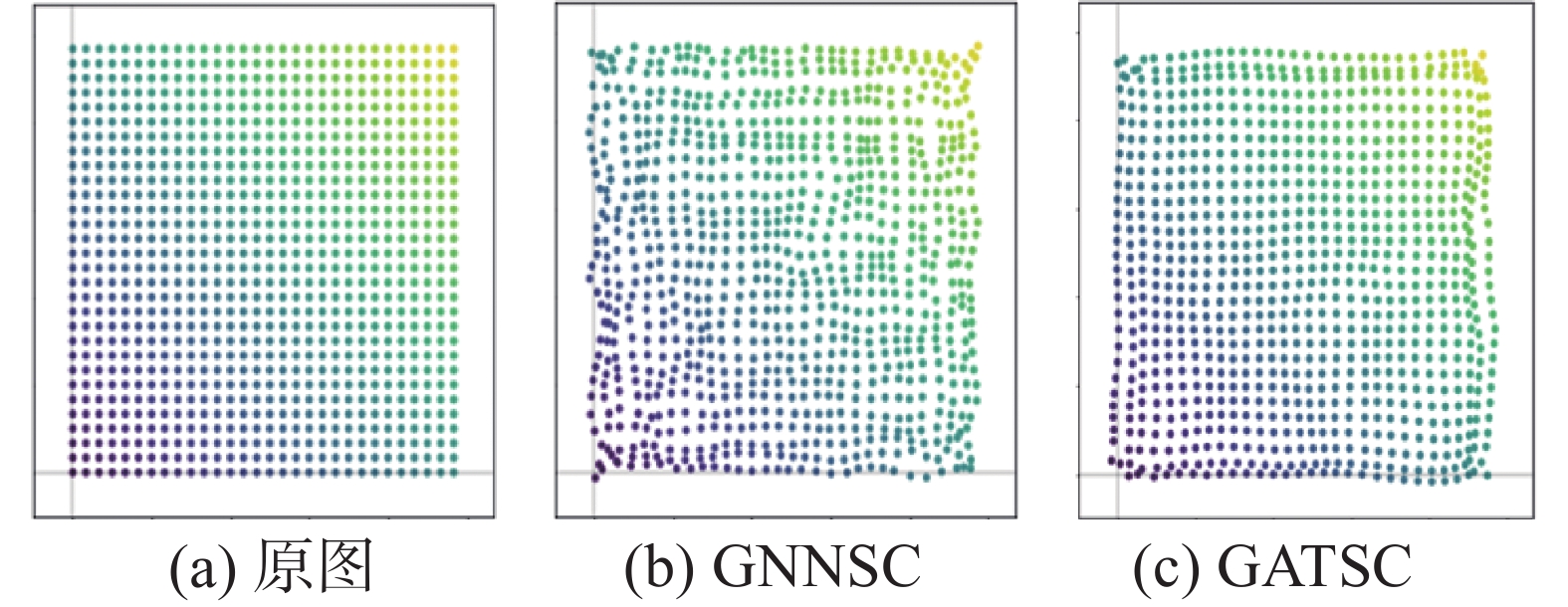
本文提出的模型及GNNSC应用于直方图的重构（见图9）。结果表明，本文提出的模型对于直方图的重构效果更优。GNNSC在重构直方图时，内部节点重构较好，但是对于边缘的节点重构效果不佳。
图 9 方形图的重构效果Fig. 9 Results of grid graph reconstruction下载:
全尺寸图片
3.3 有监督的图像分类实验及分析
在本节实验中，将本文提出的模型及其他模型应用于有监督的图分类任务进行比较分析。本文考虑了WL、Dense、No-pool、Graclus、NDP、DiffPool、Top-K、SAGPool及GNNSC 9种模型，采用了Mutagenicity、Proteins、DD、COLLAB及Reddit-Binary 5种图分类数据集，测试了10种模型的分类精度。对于数据集中没有特征的图数据，借鉴GNNSC模型中的实验，将每个节点的度信息和聚类系数作为节点的特征，使用十折进行训练分割或测试分割来评估模型性能，在每个图像分割任务的每次折叠中使用训练集的10%用于验证模型的优劣性。使用10%的训练集作为早期停止的验证。为了公平比较实验结果，本节中采用一致的网络架构。将GATSC与Graclus、NDP、Top-K、DiffPool及SAGPool进行分类效果比较时，只改变了池化层的选择（结果见表2）。将WL、Dense、No-pool与GATSC模型进行对比，是为了比较有无池化操作是否对分类效果有影响（结果见表2）。
表 2 无监督的图分类精度Table 2 Unsupervised accuracy of graph classification数据集 NDP Graclus Top-K DiffPool SAGPool Mutagenicity 77.8 74.4 71.9 77.6 72.4 Proteins 73.3 68.6 69.6 72.7 70.5 DD 72.0 70.5 69.4 79.3 71.5 COLLAB 79.1 77.1 79.3 81.8 79.2 Reddit-Binary 84.3 79.2 74.7 86.8 73.9 数据集 WL Dense No-Pool GNNSC GATSC Mutagenicity 81.7 68.4 78.0 79.9 84.9 Proteins 71.2 68.7 72.6 76.5 79.1 DD 78.6 70.6 76.8 80.8 81.8 COLLAB 74.8 79.3 82.1 83.4 84.1 Reddit-Binary 68.2 48.5 80.3 91.4 87.7 表2给出了10种模型对于有监督的图分类任务的效果。可以看出，与其他方法相比，本文提出的模型在5种图分类数据集上总能取得良好的结果。同时我们也注意到几个细节，有池化操作的模型不总是优于无池化操作的模型，因为池化操作选择不当可能会适得其反；除此之外，GNNSC在Reddit-Binary数据集上也具有极好的分类精度。综上，本文提出的模型在有监督和无监督任务中均具有良好的性能。
4. 结束语
针对图卷积神经网络的谱聚类算法具有局限性，本文提出了基于注意力机制引导的谱聚类模型GATSC。与无注意力引导的谱聚类模型相比较，本文的模型克服了基于模型的池方法和无模型的拉普拉斯矩阵分解方法的缺点，利用注意力机制提高了聚类的准确性、利用改进的图卷积神经网络降低了存储成本。与传统的解码器重构相比较，本文的重构模块降低了重构错误，提高了重构准确性，缓解了原始重构效果中边缘不清晰的缺陷。实验结果表明，本文提出的模型在Cora、Citeseer、Pubmed 3个引文网络聚类、在环形图和方形图上重构、在Mutagenicity、Proteins、DD、COLLAB及Reddit-Binary 5种图分类数据集上图分类，均显示出良好的性能。然而在进行有监督分类实验时，本文提出的模型在Reddit-Binary数据集上表现一般，且不适用于具有多样性数据集的聚类，因此，下一步的工作是对多样性数据集进行深度聚类研究。
-
图 1 理想状态下的聚类效果
Fig. 1 Clustering diagram under ideal condition
下载:
全尺寸图片
图 2 注意力机制模型
Fig. 2 Attention mechanism model
下载:
全尺寸图片
图 3 本文提出的模型框架
Fig. 3 Model of the proposed algorithm
下载:
全尺寸图片
图 4 GATSC的池化层模型
Fig. 4 Pooling layer model of GATSC
下载:
全尺寸图片
图 5 本文提出的模型在Cora数据集上的无监督损失及 NMI值
Fig. 5 Unsupervised loss of proposed model and NMI value on Cora dataset
下载:
全尺寸图片
图 6 GNNSC在Cora数据集上的无监督损失及NMI值
Fig. 6 Unsupervised loss of GNNSC and NMI value on Cora dataset
下载:
全尺寸图片
图 7 图像分割任务效果
Fig. 7 Results of image segmentation
下载:
全尺寸图片
图 8 环形图重构效果
Fig. 8 Results of ring graph reconstruction
下载:
全尺寸图片
图 9 方形图的重构效果
Fig. 9 Results of grid graph reconstruction
下载:
全尺寸图片
表 1 对不同的引文网络节点聚类得到的NMI值和CS值
Table 1 NMI value and CS value obtained by clustering different citation network nodes
数据集 K SC Diffpool NMI CS NMI CS Cora 7 0.025 0.126 0.315 0.309 Citeseer 6 0.014 0.033 0.139 0.153 Pubmed 3 0.182 0.261 0.079 0.085 数据集 K GNNSC GATSC NMI CS NMI CS Cora 7 0.404 0.392 0.451 0.437 Citeseer 6 0.287 0.283 0.316 0.312 Pubmed 3 0.200 0.197 0.214 0.212 表 2 无监督的图分类精度
Table 2 Unsupervised accuracy of graph classification
数据集 NDP Graclus Top-K DiffPool SAGPool Mutagenicity 77.8 74.4 71.9 77.6 72.4 Proteins 73.3 68.6 69.6 72.7 70.5 DD 72.0 70.5 69.4 79.3 71.5 COLLAB 79.1 77.1 79.3 81.8 79.2 Reddit-Binary 84.3 79.2 74.7 86.8 73.9 数据集 WL Dense No-Pool GNNSC GATSC Mutagenicity 81.7 68.4 78.0 79.9 84.9 Proteins 71.2 68.7 72.6 76.5 79.1 DD 78.6 70.6 76.8 80.8 81.8 COLLAB 74.8 79.3 82.1 83.4 84.1 Reddit-Binary 68.2 48.5 80.3 91.4 87.7 -
[1] SHI Na, LIU Xumin, GUAN Yong. Research on k-means clustering algorithm: an improved k-means clustering algorithm[C]//2010 Third International Symposium on Intelligent Information Technology and Security Informatics. Jian: IEEE, 2010: 63−67. [2] FU Chuanyi, CHEN Huandong, XING Jieqing. Spectral clustering and its research progress[C]//2011 Seventh International Conference on Computational Intelligence and Security: IEEE, 2012: 1367−1369. [3] AGARWAL P, ALAM M A, BISWAS R. A hierarchical clustering algorithm for categorical attributes[C]//2010 Second International Conference on Computer Engineering and Applications. Bali: IEEE, 2010: 365−368. [4] STUDER L, WALLAU J, INGOLD R, et al. Effects of graph pooling layers on classification with graph neural networks[C]//2020 7th Swiss Conference on Data Science. Luzern: IEEE, 2020: 57−58. [5] GAMA F, ISUFI E, LEUS G, et al. Graphs, convolutions, and neural networks: from graph filters to graph neural networks[C]//IEEE Signal Processing Magazine. [S.l.]: IEEE, 2020: 128−138. [6] KHAN A, SOHAIL A, ZAHOORA U, et al. A survey of the recent architectures of deep convolutional neural networks[J]. Artificial intelligence review, 2020, 53(8): 5455–5516. doi: 10.1007/s10462-020-09825-6 [7] BOULEMNADJEL A, HACHOUF F. An improved algorithm for subspace clustering applied to image segmentation[C]//2012 16th International Conference on Information Visualisation. Montpellier: IEEE, 2012: 297−301. [8] XIA Zhile, LI Junmin, LI Jiangrong. Passivity-based resilient adaptive control for fuzzy stochastic delay systems with Markovian switching[J]. Journal of the franklin institute, 2014, 351(7): 3818–3836. doi: 10.1016/j.jfranklin.2013.03.016 [9] YUAN Gonglin, XUE Bing, ZHANG Mengjie. A graph-based approach to automatic convolutional neural network construction for image classification[C]//2020 35th International Conference on Image and Vision Computing New Zealand. Wellington: IEEE, 2020: 1−6. [10] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE transactions on neural networks and learning systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386 [11] LI Yang, ZHANG Jiangzhou, NIE Mingyu, et al. Hessian-regularized spectral clustering for behavior recognition[C]//2020 International Conference on Intelligent Computing and Human-Computer Interaction. Sanya: IEEE, 2021: 156−159. [12] GAO Jianliang, GAO Jun, YING Xiaoting, et al. Higher-order interaction goes neural: a substructure assembling graph attention network for graph classification[J]. IEEE transactions on knowledge and data engineering, 2023, 35(2): 1594–1608. [13] LI Qiuyan, SHANG Yanlei, QIAO Xiuquan, et al. Heterogeneous dynamic graph attention network[C]//2020 IEEE International Conference on Knowledge Graph (ICKG). Nanjing: IEEE, 2020: 404−411. [14] PENG Xi, FENG Jiashi, ZHOU J T, et al. Deep subspace clustering[J]. IEEE transactions on neural networks and learning systems, 2020, 31(12): 5509–5521. doi: 10.1109/TNNLS.2020.2968848 [15] XU Xiaoliang, GAO Tong, WANG Yuxiang, et al. Event temporal relation extraction with attention mechanism and graph neural network[J]. Tsinghua science and technology, 2021, 27(1): 79–90. [16] KIM M, KIM T, KIM D. Spatio-temporal slowfast self-attention network for action recognition[C]//2020 IEEE International Conference on Image Processing. Abu Dhabi: IEEE, 2020: 2206−2210. [17] ZHANG Xuming, SUN Genyun, JIA Xiuping, et al. Spectral–spatial self-attention networks for hyperspectral image classification[J]. IEEE transactions on geoscience and remote sensing, 2022, 60: 1–15. [18] GU Ruijun, WANG Jiacai. An improved spectral clustering algorithm based on neighbour adaptive scale[C]//2009 International Conference on Business Intelligence and Financial Engineering. Beijing: IEEE, 2009: 233−236. [19] NGO M, MAI An, BUI T. On an improvement of Graph Convolutional Network in semi-supervised learning[C]//2020 7th NAFOSTED Conference on Information and Computer Science (NICS). Ho Chi Minh City: IEEE, 2021: 114−117. [20] RUIZ L, GAMA F, RIBEIRO A. Graph neural networks: architectures, stability, and transferability[J]. Proceedings of the IEEE, 2021, 109(5): 660–682. doi: 10.1109/JPROC.2021.3055400 [21] PENG Hongrui. Graph convolutional networks: an analysis of method and applications in different fields and systems[C]//2020 International Conference on Communications, Information System and Computer Engineering (CISCE). Kuala Lumpur: IEEE, 2020: 153−157. [22] CAO Jing, XU Yi, SONG Xuening. First-order meta-learning in node classification with graph convolutional network[C]//2021 4th International Conference on Artificial Intelligence and Big Data. Chengdu: IEEE, 2021: 443−447. [23] XIAO Yi, CHEN Siying, WANG Hao, et al. HSGACN: hyperspectral image classification algorithm based on graph convolutional network[C]//2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. Brussels: IEEE, 2021: 3677−3680. [24] CAI Chengtao, GUO Dongning. CNN-self-attention-DNN architecture for mandarin recognition[C]//2020 Chinese Control and Decision Conference. Hefei: IEEE, 2020: 1190−1194. [25] UEDA T, OKADA M, MORI N, et al. A method to estimate request sentences using LSTM with self-attention mechanism[C]//2019 8th International Congress on Advanced Applied Informatics. Toyama: IEEE, 2020: 7−10. [26] HU Bin, GUO Kehua, WANG Xiaokang, et al. RRL-GAT: graph attention network-driven multilabel image robust representation learning[J]. IEEE Internet of Things journal, 2022, 9(12): 9167–9178. doi: 10.1109/JIOT.2021.3089180 [27] TIAN Long, DU Qian, KOPRIVA I, et al. Spatial-spectral based multi-view low-rank sparse sbuspace clustering for hyperspectral imagery[C]//IEEE International Geoscience and Remote Sensing Symposium. Valencia: IEEE, 2018: 8488−8491. [28] LI He, ZHANG Shiyu, SU Liangcai, et al. GraphSANet: a graph neural network and self attention based approach for spatial temporal prediction in sensor network[C]//2020 IEEE International Conference on Big Data. Atlanta: IEEE, 2021: 5756−5758. [29] ZHANG Jintao, XU Quan. Attention-aware heterogeneous graph neural network[J]. Big data mining and analytics, 2021, 4(4): 233–241. doi: 10.26599/BDMA.2021.9020008 [30] BERIKOV V. Autoencoder-based low-rank spectral ensemble clustering of biological data[C]//2020 Cognitive Sciences, Genomics and Bioinformatics. Novosibirsk: IEEE, 2020: 43−46. [31] SHANTHAMALLU U S, THIAGARAJAN J J, SPANIAS A. A regularized attention mechanism for graph attention networks[C]//2020 IEEE International Conference on Acoustics, Speech and Signal Processing. Barcelona: IEEE, 2020: 3372−3376. [32] CAO Meng, MA Xiying, ZHU Kai, et al. Heterogeneous information network embedding with convolutional graph attention networks[C]//2020 International Joint Conference on Neural Networks. Glasgow: IEEE, 2020: 1−8. [33] 张铭泉, 周辉, 曹锦纲. 基于注意力机制的双BERT有向情感文本分类研究[J]. 智能系统学报, 2022, 17(6): 1220–1227. ZHANG Mingquan, ZHOU Hui, CAO Jingang. Dual BERT directed sentiment text classification based on attention mechanism[J]. CAAI transactions on intelligent systems, 2022, 17(6): 1220–1227. [34] HUANG Shuning, OTA K, DONG Mianxiong, et al. MultiSpectralNet: spectral clustering using deep neural network for multi-view data[J]. IEEE transactions on computational social systems, 2019, 6(4): 749–760. doi: 10.1109/TCSS.2019.2926450 [35] GÜZEL K, KURŞUN O. Improving spectral clustering using path-based connectivity[C]//2015 23nd Signal Processing and Communications Applications Conference. Malatya: IEEE, 2015: 2110−2113. [36] 于润羽, 李雅文, 李昂. 融合领域特征的科技学术会议语义相似性计算方法[J]. 智能系统学报, 2022, 17(4): 737–743. YU Runyu, LI Yawen, LI Ang. Semantic similarity computing for scientific and technological conferences[J]. CAAI transactions on intelligent systems, 2022, 17(4): 737–743. [37] 马甜甜, 杨长春, 严鑫杰, 等. 融合知识图谱和轻量级图卷积网络推荐系统的研究[J]. 智能系统学报, 2022, 17(4): 721–727. MA Tiantian, YANG Changchun, YAN Xinjie, et al. Research on the fusion of knowledge graph and lightweight graph convolutional network recommendation system[J]. CAAI transactions on intelligent systems, 2022, 17(4): 721–727. [38] LI Hongmin, YE Xiucai, IMAKURA A, et al. Ensemble learning for spectral clustering[C]//2020 IEEE International Conference on Data Mining. Sorrento: IEEE, 2021: 1094−1099. [39] BIANCHI F M, GRATTAROLA D, ALIPPI C. Mincut pooling in graph neural networks[EB/OL]. (2020−12−29)[2022−01−01]. https://arxiv.org/abs/1907.00481v2. [40] 杨梦茵, 陈俊芬, 翟俊海. 非对称卷积编码器的聚类算法[J]. 智能系统学报, 2022, 17(5): 900–907. YANG Mengyin, CHEN Junfen, ZHAI Junhai. A clustering method based on the asymmetric convolutional autoencoder[J]. CAAI transactions on intelligent systems, 2022, 17(5): 900–907. [41] SANDFELDER D, VIJAYAN P, HAMILTON W L. Ego-GNNs: exploiting ego structures in graph neural networks[C]//2021 IEEE International Conference on Acoustics, Speech and Signal Processing. Toronto: IEEE, 2021: 8523−8527. [42] LU Runkun, LIU Jianwei, ZUO Xin. Attentive multi-view deep subspace clustering net[J]. Neurocomputing, 2021, 435: 186–196. doi: 10.1016/j.neucom.2021.01.011 [43] PENG Zhihao, LIU Hui, JIA Yuheng, et al. Deep attention-guided graph clustering with dual self-supervision[J]. IEEE transactions on circuits and systems for video technology, 2022: 1. [44] DONG Huihui, MA Wenping, JIAO Licheng, et al. A multiscale self-attention deep clustering for change detection in SAR images[J]. IEEE transactions on geoscience and remote sensing, 2022, 60: 1–16. [45] MIN Erxue, GUO Xifeng, LIU Qiang, et al. A survey of clustering with deep learning: from the perspective of network architecture[J]. IEEE access, 2018, 6: 39501–39514. doi: 10.1109/ACCESS.2018.2855437 [46] XU K, HU WEIHUA, LESKOVEC J, et al. How powerful are graph neural networks? [EB/OL]. (2019−02−22)[2022−01−01]. https://arxiv.org/abs/1810.00826. [47] PETAR V, GUILLEM C, ARANTXA C, et al. Graph attention networks[EB/OL]. (2018−02−04)[2022−01−01].https://arxiv.org/abs/1710.10903. [48] LI Meng, HSU W, XIE Xiaodong, et al. SACNN: self-attention convolutional neural network for low-dose CT denoising with self-supervised perceptual loss network[J]. IEEE transactions on medical imaging, 2020, 39(7): 2289–2301. doi: 10.1109/TMI.2020.2968472
