Adaptive group consensus decision-making method with dynamic update of attribute weights
-
摘要: 为了提高不确定语言环境下异构多属性群决策的质量、效率及可解释性,提出一种属性权重动态更新的自适应群体共识决策方法。首先,定义不确定语言变量与中间值之间的转换函数,发展多级共识测度,建立计算属性初始权重的双目标优化模型;进而,构建包含群体共识自动达成规则和属性权重动态更新机制的自适应共识模型,实现待调整值的精准定位和自动修改,在优化属性权重的同时进一步提升群体共识水平;然后,对于达成共识的群体决策矩阵,先利用转换函数将中间值转换为不确定语言变量,再使用属性权重和集结算子得到各方案的综合评价结果;最后,通过供应商选择实例和实验比较分析验证所提方法的有效性和可行性。本文研究结果为灵活、高效地求解复杂环境下的多属性群决策问题提供了有效途径。Abstract: To improve the quality, efficiency, and interpretability of heterogeneous multi-attribute group decision making in an uncertain linguistic environment, an adaptive group consensus decision-making method with dynamic update of attribute weights is proposed. It first defines the conversion functions between uncertain linguistic variables and median values, and develops the multi-level consensus measures, then calculates the initial weights of attributes by establishing a bi-objective optimization model, and further establishes the group consensus automatic reaching rules and attribute weight dynamic update mechanism to achieve accurate positioning and automatic modification of the values to be adjusted, further improving the level of group consensus while optimizing attribute weights. Furthermore, for the group decision matrix that has reached consensus, the median values in the matrix are first converted into corresponding uncertain linguistic variables by using the conversion function, and then the optimized attribute weight and the uncertain linguistic weighted average operator (ULWA) are used to calculate the overall evaluation results, and the alternatives are ranked and selected by using the dominance index. Finally, the effectiveness and feasibility of the proposed method are verified through the case of supplier selection and experimental comparative analysis. The proposed method has the characteristics of wide application scope, high consensus efficiency, flexibility, practicality, and strong interpretation, which provides an effective approach for solving multi-attribute group decision-making problems in complex environments.
-
多属性群决策是人工智能与决策科学的一个重要研究分支[1-4],作为多属性决策[5-7]与群决策[8]的交叉研究领域,其本质是多个专家从决策问题的多个属性对有限个方案进行判断或评价,进而通过信息集结对方案进行排序或择优[9-10]。目前,多属性群决策的相关理论、方法和模型已在大型项目开发[1]、区域创新资源配置效率评价[2]、融资贷款选择[3]和医疗诊断[11]等真实场景得到了广泛应用。在群决策过程中,若对个体意见不加干预直接集结,可能无法得到有效的决策结果。因此,有必要对群体共识程度进行客观、合理地度量和分析[9-12]。群体共识达成作为群决策领域的热点研究课题[13-15]已被用于应急医疗设施选址[13]、导弹武器选型[14]、城市发展潜力预测[14]等实际问题中。
现有的共识达成方法主要分为交互式和自动式两大类。交互式共识达成方法需要共识度较低的专家根据反馈建议调整个体偏好,直至达到满意的共识水平。文献[16]提出一种专家权重自适应调整的交互式共识达成方法;文献[17]建立了基于妥协度的共识反馈策略。与交互式方法相比,自动式共识达成方法无需专家参与,更加省时高效。文献[14]提出一种基于相似度最大化的共识方法;文献[15]建立了基于最小调整的三支共识反馈机制;文献[18]构建了一种集群体成本最小化和全局共识增量最大化于一体的自动共识模型;文献[19]提出一种两阶段自动共识达成方法。然而,现有的自动式方法普遍存在调整范围过大、针对性不强等局限。此外,目前关于群体共识达成的研究主要集中在同构决策矩阵上,对于属性集或方案集存在差异的异构决策矩阵的研究相对较少。随着异构多属性群决策问题在各个领域的不断涌现[20],决策过程的复杂性和不确定性进一步加剧[11,21],为群体共识达成带来新的挑战。现有的异构多属性群决策共识达成方法大多属于交互式范畴[22-24],不够灵活高效。
通过上述分析可知,面向异构多属性群决策的共识达成方法研究有着很大的发展空间。考虑到现实生活中,人们往往倾向于使用模糊的语言信息[1,8,25-26],尤其是形如[差,一般]、[较好,好]的不确定语言对方案进行评价[27-30],因此,本文围绕不确定语言环境下的异构多属性群决策问题,提出一种属性权重动态更新的自适应群体共识决策方法。该方法由转换函数、多级共识测度、群体共识自动达成规则、属性权重动态更新机制等部分组成。
本文的主要贡献包括以下3个方面:
1) 通过定义多级共识测度,实现对群体共识程度由细到粗多个层次的客观度量,为群体共识水平的高效分析奠定基础;
2) 建立集共识检测、自动调整、权重更新和结果反馈于一体的自适应共识模型,在最大限度保留专家原始意见的同时,提高群体共识达成效率;
3) 结合不确定语言变量的特点设计了相应的转换函数,将方案的综合评价结果以不确定语言的形式展示出来,增强决策结果的直观性和可解释性。
1. 不确定语言变量相关概念
1.1 语言术语集
定义1[27] 设
$ S = \left\{ {{s_\alpha }|\alpha = 0,1, \cdots ,g} \right\} $ 为语言术语集,$g$ 为偶数,${s_\alpha }$ 称为语言术语,α称为语言术语指标,${s_0}$ 和${s_g}$ 分别为语言术语集S的下界和上界。为了避免信息丢失,文献[28]将离散的语言术语集S扩展为连续的语言术语集
$\bar S = \{ {s_\alpha }|\alpha \in [0,g]\}$ 。设$ {s_\alpha } \in \bar S $ ,令$ I({s_\alpha }) = \alpha $ ,相应的逆运算为$ {I^{{{ - }}1}}(\alpha ) = {s_\alpha } $ 。1.2 不确定语言变量
定义2[29] 设
$\tilde s = [{s_L},{s_R}]$ ,其中,${s_L},{s_R} \in \bar S$ 且${s_L} \leqslant {s_R}$ ,则称$\tilde s$ 为不确定语言变量,${s_L}$ 和${s_R}$ 分别为$\tilde s$ 的下界和上界。当${s_L} = {s_R}$ 时,$\tilde s$ 退化为语言术语。设
$ {\tilde s_1} = [{s_{{L_1}}},{s_{{R_1}}}] $ ,$ {\tilde s_2} = [{s_{{L_2}}},{s_{{R_2}}}] $ 是2个不确定语言变量,$\gamma \in [0,1]$ ,则有如下运算法则[29]:$$ {\tilde s_1} \oplus {\tilde s_2} = [{s_{{L_1}}},{s_{{R_1}}}] \oplus [{s_{{L_2}}},{s_{{R_2}}}] = [{s_{{L_1} + {L_2}}},{s_{{R_1} + {R_2}}}] $$ $$ \gamma {\tilde s_1} = \gamma [{s_{{L_1}}},{s_{{R_1}}}] = [\gamma {s_{{L_1}}},\gamma {s_{{R_1}}}] = [{s_{\gamma {L_1}}},{s_{\gamma {R_1}}}] $$ 定义3[30] 设
$\tilde s = [{s_L},{s_R}]$ 为不确定语言变量,其中,${s_L},{s_R} \in \bar S$ 且${s_L} \leqslant {s_R}$ ,则$\tilde s$ 的宽度值定义为$$ w(\tilde s) = {{(I({s_R}) - I({s_L}))} \mathord{\left/ {\vphantom {{(I({s_R}) - I({s_L}))} 2}} \right. } 2} $$ 定义4 [31] 设
$ {\tilde s_j} = [{s_{{L_j}}},{s_{{R_j}}}] $ $ (j = 1,2, \cdots ,n) $ 是一组不确定语言变量,则不确定语言加权平均算子(uncertain linguistic weighted average operator,ULWA)定义为$$ \mathop {{\text{ULWA}}}\nolimits_\omega ({\tilde s_1},{\tilde s_2}, \cdots ,{\tilde s_n}) = \displaystyle\sum\limits_{j = 1}^n {{\omega _j}{{\tilde s}_j}} = \left[\begin{split} s_{\displaystyle\sum\limits_{j = 1}^n {\omega _j} {L_j}},s_{\displaystyle\sum\limits_{j = 1}^n {\omega _j} {R_j}} \end{split}\right] $$ 式中
$ \boldsymbol{\omega} = ({\omega _1},{\omega _2}, \cdots ,{\omega _n}) $ 是$ {\tilde s_j}(j = 1,2, \cdots ,n) $ 的权重向量,且$ {\omega _j} \in [0,1] $ ,$ \displaystyle\sum\limits_{j = 1}^n {{\omega _j}} = 1 $ 。定义5[16] 设
$\tilde s = [{s_L},{s_R}]$ 为不确定语言变量,其中,${s_L},{s_R} \in \bar S$ ,$ \bar S = \{ {s_\alpha }|\alpha \in [0,g]\} $ ,则$\tilde s$ 的优势度定义为$$ {{D}}(\tilde s) = \frac{{\sqrt {{{[I({s_L})]}^2} + {{[I({s_R})]}^2}} }}{{\sqrt {{{[I({s_L}) - g]}^2} + {{[I({s_R}) - g]}^2}} + \sqrt {{{[I({s_L})]}^2} + {{[I({s_R})]}^2}} }} $$ (1) 2. 自适应群体共识决策方法
2.1 问题描述
对于不确定语言环境下的异构多属性群决策问题,令
$X = \{ {x_1},{x_2}, \cdots ,{x_m}\} $ 为方案集,$A = \{ {a_1}, {a_2}, \cdots ,{a_n}\}$ 为属性集,$ \boldsymbol{\tau} = ({\tau _1},{\tau _2}, \cdots ,{\tau _n}) $ 为属性权重向量,$E = \{ {e_1},{e_2}, \cdots ,{e_k}\} $ 为专家集合。设专家使用的语言术语集为$ S{\text{ = }}\{ {s_\alpha }|\alpha = 0,1, \cdots ,g\} $ ,$ {X^h} \subseteq X $ 为专家${e_h}$ 从全部方案集X中选择的部分方案组成的方案子集,$ {A^h} \subseteq A $ 为专家${e_h}$ 从全部属性集A中选择的部分属性组成的属性子集,则专家${e_h}$ 的决策矩阵可表示为$$ {R^h} = {\left[ {\tilde s_{ij}^h} \right]_{|{X^h}| \cdot |{A^h}|}} $$ 式中:
$\tilde s_{ij}^h$ 为不确定语言变量,$ \left| {{X^h}} \right| $ 为$ {X^h} $ 中方案的个数,$ \left| {{A^h}} \right| $ 为$ {A^h} $ 中属性的个数。设
${E_{ij}} = \{ {e_h}|\tilde s_{ij}^h \ne \varnothing ,{e_h} \in E\}$ 表示对方案${x_i}$ 在属性$ {a_j} $ 下进行评价的专家子群体。为保证决策结果的客观性和综合性,异构多属性群决策应满足如下前提条件:1) 所有专家对应的方案子集
${X^h}(h = 1, 2, \cdots , k)$ 的并集应为方案全集$ X $ ,即$ {X^1} \cup {X^2} \cup \cdots \cup {X^k} = X $ 。2) 所有专家对应的属性子集
${A^h}(h = 1,2, \cdots , k)$ 的并集应为属性全集$ A $ ,即$ {A^1} \cup {A^2} \cup \cdots \cup {A^k} = A $ 。3) 每个方案的每个属性至少有3个专家进行评价,即
${E_{ij}}$ 中专家的个数$\left| {{E_{ij}}} \right| \geqslant 3$ $(i = 1,2, \cdots , m,j = 1,2, \cdots ,n)$ 。2.2 转换函数
在决策分析环节,为了方便对不确定语言变量的计算、比较和调整,需将其转换为中间值进行处理;在结果展示环节,为了增强决策结果的直观性和可解释性,又需要将集结后的中间值转换为对应的不确定语言变量。下面给出这2个转换函数。
定义6[30] 设
$\tilde s = [{s_L},{s_R}]$ 为不确定语言变量,其中,${s_L},{s_R} \in \bar S$ ,则将$\tilde s$ 转换为中间值的转换函数定义为$$ m(\tilde s) = {{(I({s_L}) + I({s_R}))} \mathord{\left/ {\vphantom {{(I({s_L}) + I({s_R}))} 2}} \right. } 2} $$ (2) 定义7 给定中间值
$ m(\tilde s) $ ,将其转换成对应的不确定语言变量的转换函数$T(m(\tilde s),\varDelta ,\varLambda )$ 定义如下:$$ \tilde{s}=T(m(\tilde{s}),\varDelta ,\varLambda )=\left\{\begin{array}{l}\text{ }\left[\text{ }{I}^{-1}(\lfloor m(\tilde{s})\rfloor - \lfloor \varLambda \rfloor )\text{ , }{I}^{-1}(\lfloor m(\tilde{s})\rfloor \text{ + }\lfloor \varLambda \rfloor )\text{ }\right]\text{ , }m(\tilde{s})-\lfloor m(\tilde{s})\rfloor \leqslant \varDelta \\ \text{ }\left[\text{ }{I}^{-1}(\lceil m(\tilde{s})\rceil - \lfloor \varLambda \rfloor )\text{ },\text{ }{I}^{-1}(\lceil m(\tilde{s})\rceil \text{ + }\lfloor \varLambda \rfloor )\text{ }\right]\text{ , }\lceil m(\tilde{s})\rceil -m(\tilde{s})\leqslant \varDelta \\ \text{ }\left[\text{ }{I}^{-1}(\lfloor m(\tilde{s})\rfloor - \lfloor \varLambda \rfloor )\text{ },\text{ }{I}^{-1}(\lceil m(\tilde{s})\rceil \text{+ }\lfloor \varLambda \rfloor )\text{ }\right]\text{ },\text{ }其他\end{array}\right. $$ (3) 式中:
$ \left\lfloor {m(\tilde s)} \right\rfloor $ 和$ \left\lceil {m(\tilde s)} \right\rceil $ 分别为中间值$ m(\tilde s) $ 的下整数和上整数;$\varLambda $ 为转换后的不确定语言变量对应的最大宽度值($ \varLambda \in [0,g/2] $ 且$ \varLambda \leqslant \left\lfloor {m(\tilde s)} \right\rfloor $ ),可以由专家直接给出,也可根据${E_{ij}}$ 中各专家初始评价信息的平均宽度值来确定,即$\varLambda = {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {w(\tilde s_{ij}^h)} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {w(\tilde s_{ij}^h)} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}}$ ,$\left\lfloor \varLambda \right\rfloor $ 为$\varLambda $ 的下整数;$\varDelta $ 为偏移量($\varDelta \in (0,0.5)$ ),可以由专家协商给出。2.3 多级共识测度
本节在定义
${E_{ij}}$ 中两两专家关于同一方案${x_i}$ 在同一属性${a_j}$ 下的贴近度的基础上,通过建立多级共识测度实现群体在不同层面共识程度的客观度量。定义8 设专家
${e_h},{e_q} \in {E_{ij}}$ ,则${e_h}$ 与${e_q}$ 关于方案${x_i}$ 在属性${a_j}$ 下评价值之间的贴近度定义为$$ {{U} _{ij}}({e_h},{e_q}) = \frac{{g - |m(\tilde s_{ij}^h) - m(\tilde s_{ij}^q)|}}{g} $$ (4) 式中:
$ m(\tilde s_{ij}^h) $ 和$ m(\tilde s_{ij}^q) $ 分别为专家${e_h}$ 和${e_q}$ 关于方案${x_i}$ 在属性${a_j}$ 下的评价值对应的中间值,$g$ 为语言术语集中术语指标的上界。定义9 专家
${e_h}$ 与其所在的子群体${E_{ij}}$ 之间关于方案${x_i}$ 在属性${a_j}$ 下的共识度(即专家级共识度)定义为$$ {{G} _{ij}}({e_h},{E_{ij}}) = \frac{1}{{\left| {{E_{ij}}} \right|}}\displaystyle\sum\limits_{{e_q} \in {E_{ij}}} {{{U} _{ij}}({e_h},{e_q})} $$ (5) 定义10 子群体
${E_{ij}}$ 关于方案${x_i}$ 在属性${a_j}$ 下的共识度(即属性级共识度)定义为$$ {{G} _{ij}}({E_{ij}}) = \frac{1}{{\left| {{E_{ij}}} \right|}}\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {{{G} _{ij}}({e_h},{E_{ij}})} $$ (6) 定义11 子群体
${E_{ij}}$ 关于方案${x_i}$ 在全部属性下的共识度(即方案级共识度)定义为$$ {G} ({x_i}{\text{) = }}\displaystyle\sum\limits_{j = 1}^n {{\tau _j}{{G} _{ij}}({E_{ij}})} $$ (7) 式中
$ {\tau _j} $ 为属性${a_j}$ 的权重。定义12 全体专家
$E = \{ {e_1},{e_2}, \cdots ,{e_k}\} $ 关于全部方案在全部属性下的共识度(即总体共识度)定义为$$ {{G = }}\frac{1}{m}\displaystyle\sum\limits_{i = 1}^m {{{G}}({x_i})} $$ 2.4 属性初始权重
本节分别从群体共识度和方案差异度2个方面计算属性权重,并通过双目标优化模型实现2类权重的有效融合,从而得到属性的初始权重。
首先,利用式(2)将原始的专家不确定语言决策矩阵
$ {\boldsymbol{R}^h} $ 转换为以中间值形式表示的初始决策矩阵$ {\boldsymbol{M}^{h(0)}} $ ,即$$ {\boldsymbol{M}^{h(0)}} = {\left[ {m(\tilde s_{ij}^{h(0)})} \right]_{|{X^h}| \cdot |{A^h}|}} $$ 然后,基于属性级共识度计算各方案下的属性权重。各属性在方案
${x_i}$ $ (i = 1,2, \cdots ,m) $ 下基于共识度的初始权重$ \tau _{ij}^{c(0)} $ 计算公式为$$ \tau_{i j}^{c(0)}=\frac{{G}_{i j}^{(0)}\left(E_{i j}\right)}{\displaystyle\sum\limits_{j=1}^n {G}_{i j}^{(0)}\left(E_{i j}\right)}$$ (8) 式中
$ {{G}}_{ij}^{(0)}({E_{ij}}) $ 为子群体${E_{ij}}$ 关于方案${x_i}$ 在属性${a_j}$ 下的初始属性级共识度。再利用离差最大化方法[32]计算属性权重。各属性基于离差最大化的初始权重
$\tau _j^{d(0)}$ 计算公式为$$ \tau _j^{d(0)} = \frac{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(0)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(0)})} \right|} } }}{{\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(0)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(0)})} \right|} } } }} $$ (9) 式中
$ m(\tilde s_{ij}^{(0)}) = {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(0)})} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(0)})} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}} $ 为子群体${E_{ij}}$ 关于方案${x_i}$ 在属性${a_j}$ 下的初始平均中间值。式(9)中的
$ \displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(0)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(0)})} \right|} } $ 表示所有方案在属性${a_j}$ 下的差异度之和,则所有方案在全部属性下的总体差异度为$$ {{{D}}^{(0)}} = \displaystyle\sum\limits_{j = 1}^n {\tau _j^{(0)}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(0)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(0)})} \right|} } } $$ 归一化之后的总体差异度为
$$ {{{N}}^{(0)}} = \frac{1}{{{m^2}g}}{{{D}}^{(0)}} $$ 最后,结合上述2类权重信息,建立以离差最大化和共识最大化为目标的属性权重优化模型(M-1):
$$ \begin{gathered} \max [\beta {{{N}}^{(0)}} + (1 - \beta ){{{G}}^{(0)}}] = \\ \frac{\beta }{{{m^2}g}}\displaystyle\sum\limits_{j = 1}^n {\tau _j^{(0)}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(0)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(0)})} \right|} } } + \\ \frac{{1 - \beta }}{m}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\tau _j^{(0)}{{G}}_{ij}^{(0)}({E_{ij}})} } \\ \left\{ \begin{gathered} \min\left\{ {\tau _{1j}^{c(0)},\tau _{2j}^{c(0)}, \cdots ,\tau _{mj}^{c(0)},\tau _j^{d(0)}} \right\} \leqslant \tau _j^{(0)} \leqslant \\ \max \left\{ {\tau _{1j}^{c(0)},\tau _{2j}^{c(0)}, \cdots ,\tau _{mj}^{c(0)},\tau _j^{d(0)}} \right\},\;\;\; j = 1,2, \cdots ,n \\ \displaystyle\sum\limits_{j = 1}^n {\tau _j^{(0)}} = 1 \\ \end{gathered} \right. \\ \end{gathered} $$ 式中:
$ {{{G}}^{(0)}} $ 为初始的总体共识度;$ {{G}}_{ij}^{(0)}({E_{ij}}) $ 为子群体${E_{ij}}$ 关于方案${x_i}$ 在属性${a_j}$ 下的初始共识度;$\beta $ 为比例因子,一般可取0.5。属性权重优化模型(M-1)兼顾了可靠性和重要性2个方面,对决策信息的利用更加充分,有助于得到更加合理、有效的决策结果。
$\beta $ 的设置可以增强优化模型的灵活性和实用性,当决策者对可靠性和重要性的侧重不同时,可根据实际情况调整$\beta $ 。求解模型(M-1)可得到属性的初始权重$\tau _j^{(0)}$ 。2.5 自适应共识模型
为了提高群体共识达成效率,同时最大限度保留专家的原始意见,本节建立了包括群体共识自动达成规则和属性权重动态更新机制的自适应共识模型。
在共识达成过程中,一般需要预先给定共识度阈值
$ {{{G}}^*} $ 及最大迭代次数$ {\lambda _{\max }} $ 。令$ \lambda $ 表示当前迭代轮次,初始值为0。2.5.1 群体共识自动达成规则
规则1 共识判断规则:在第
$ \lambda $ 轮,若对于$\forall {x_i} \in X$ 均有方案级共识度${{{G}}^{(\lambda )}}({x_i}) \geqslant {{{G}}^*}$ ,且$ \lambda \leqslant {\lambda _{\max }} $ ,则共识达成,停止迭代;若$\exists {x_i} \in X$ 对应的${{{G}}^{(\lambda )}}({x_i}) < {{{G}}^*}$ ,而$ \lambda > {\lambda _{\max }} $ ,则共识虽未达成,但已超过最大迭代次数,也停止迭代;否则,继续进行共识达成过程。规则2 共识检测规则。规则2由方案级、属性级和专家级3个由粗到细的共识检测规则构成。
规则2.1 方案级共识检测规则:首先确定待调整评价值对应的方案。对于
$\forall {x_i} \in X$ ,若${{{G}}^{(\lambda )}}({x_i}) < {{{G}}^*}$ ,则该方案下的评价值需要调整。将符合上述条件的方案构成的集合记作$ {X^{(\lambda )}} $ 。规则2.2 属性级共识检测规则:进一步确定待调整的评价值对应方案
${x_i}({x_i} \in {X^{(\lambda )}})$ 下的哪个属性。对于$ \forall {a_j} \in A $ ,若${{G}}_{ij}^{(\lambda )}({E_{ij}})$ $= {\min _{{a_f} \in A}}{{G}}_{if}^{(\lambda )}({E_{if}})$ ,则方案${x_i}({x_i} \in {X^{(\lambda )}})$ 属性$ {a_j} $ 下的评价值需要调整。将符合上述条件的属性构成的集合记作$ A_i^{(\lambda )} $ 。规则2.3 专家级共识检测规则:最后确定待调整评价值对应方案
${x_i}({x_i} \in {X^{(\lambda )}})$ 属性$ {a_j}({a_j} \in A_i^{(\lambda )}) $ 下的哪个专家。对于$\forall {e_h} \in {E_{ij}}$ ,若${{G}}_{ij}^{(\lambda )}({e_h},{E_{ij}}) =$ ${\min _{{e_q} \in {E_{ij}}}}{{G}}_{ij}^{(\lambda )}({e_q},{E_{ij}})$ ,则专家${e_h}$ 关于方案${x_i}({x_i} \in {X^{(\lambda )}})$ 在属性$ {a_j}({a_j} \in A_i^{(\lambda )}) $ 下的评价值需要调整。将符合上述条件的专家构成的集合记作$E_{ij}^{(\lambda )}$ 。规则3 自动调整规则:对于每个需要调整评价值的专家
${e_h}$ $({e_h} \in E_{ij}^{(\lambda )})$ ,利用其所在子群体${E_{ij}}$ $({e_h} \in {E_{ij}})$ 的平均中间值代替原来的中间值,即$$ m({\tilde{s}}_{ij}^{h(\lambda +1)})=\left\{\begin{array}{l}\dfrac{1}{\left|{E}_{ij}\right|}{\displaystyle \displaystyle\sum _{{e}_{q}\in {E}_{ij}}m({\tilde{s}}_{ij}^{q(\lambda )})},{x}_{i}\in {X}^{(\lambda )},{a}_{j}\in {A}_{i}^{(\lambda )},{e}_{h}\in {E}_{ij}^{(\lambda )}\\ m({\tilde{s}}_{ij}^{h(\lambda )}),\begin{array}{cc}其他& \end{array}\end{array}\right. $$ 利用上述规则可实现对待调整评价值的精准定位和自动修改,得到更新后的中间值决策矩阵
$ {\boldsymbol{M}^{h(\lambda + 1)}} $ 。2.5.2 属性权重动态更新机制
在共识达成过程中,若评价值被调整了,则属性权重也需要进行相应的更新。具体的更新机制如下:
首先,对于集合
$ {X^{(\lambda )}} $ 中的各方案,需要重新计算相应的属性级共识度${{G}}_{ij}^{(\lambda + 1)}({E_{ij}})$ $({x_i} \in {X^{(\lambda )}})$ ,进而更新集合$ {X^{(\lambda )}} $ 中各方案下基于共识度的属性权重;对于集合$ X - {X^{(\lambda )}} $ 中各方案下的属性权重则无需更新,即$$ \tau _{ij}^{c(\lambda + 1)} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{G}}_{ij}^{(\lambda + 1)}({E_{ij}})}}{{\displaystyle\sum\limits_{j = 1}^n {{{G}}_{ij}^{(\lambda + 1)}({E_{ij}})} }},{x_i} \in {X^{(\lambda )}}} \\ {\tau _{ij}^{c(\lambda )},{x_i} \in X - {X^{(\lambda )}}} \end{array}} \right. $$ (10) 然后,重新计算各属性基于离差最大化的权重
$\tau _j^{d(\lambda + 1)}$ ,计算公式为$$ \tau _j^{d(\lambda + 1)} = \frac{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(\lambda + 1)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(\lambda + 1)})} \right|} } }}{{\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(\lambda + 1)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(\lambda + 1)})} \right|} } } }} $$ (11) 式中
$ m(\tilde s_{ij}^{(\lambda + 1)}) = {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(\lambda + 1)})} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(\lambda + 1)})} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}} $ 为子群体${E_{ij}}$ 关于方案${x_i}$ 在属性${a_j}$ 下的平均中间值。最后,使用双目标优化模型(M-2)计算更新后的属性权重:
$$\begin{gathered} \max [\beta {{{N}}^{(\lambda + 1)}} + (1 - \beta ){{{G}}^{(\lambda + 1)}}] = \\ \frac{\beta }{{{m^2}g}}\displaystyle\sum\limits_{j = 1}^n {\tau _j^{(\lambda + 1)}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{t = 1}^m {\left| {m(\tilde s_{ij}^{(\lambda + 1)}){\text{ }} - {\text{ }}m(\tilde s_{tj}^{(\lambda + 1)})} \right|} } } + \\ \frac{{1 - \beta }}{m}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {\tau _j^{(\lambda + 1)}{{G}}_{ij}^{(\lambda + 1)}({E_{ij}})} } \\ \left\{ \begin{gathered} \min\left\{ {\tau _{1j}^{c(\lambda + 1)},\tau _{2j}^{c(\lambda + 1)}, \cdots ,\tau _{mj}^{c(\lambda + 1)},\tau _j^{d(\lambda + 1)}} \right\} \leqslant \tau _j^{(\lambda + 1)} \leqslant \\ \max \left\{ {\tau _{1j}^{c(\lambda + 1)},\tau _{2j}^{c(\lambda + 1)}, \cdots ,\tau _{mj}^{c(\lambda + 1)},\tau _j^{d(\lambda + 1)}} \right\},\;\;\; j = 1,2, \cdots ,n \\ {{{G}}^{(\lambda + 1)}}({x_i}) > {{{G}}^{(\lambda )}}({x_i}),{x_i} \in {X^{(\lambda )}} \\ \displaystyle\sum\limits_{j = 1}^n {\tau _j^{(\lambda + 1)}} = 1 \\ \end{gathered} \right.\\ \end{gathered}$$ 式中
$\beta $ 为比例因子,可视具体情况来定。求解模型(M-2)可得到优化后的属性权重。
2.6 属性权重动态更新的自适应群体共识决策过程
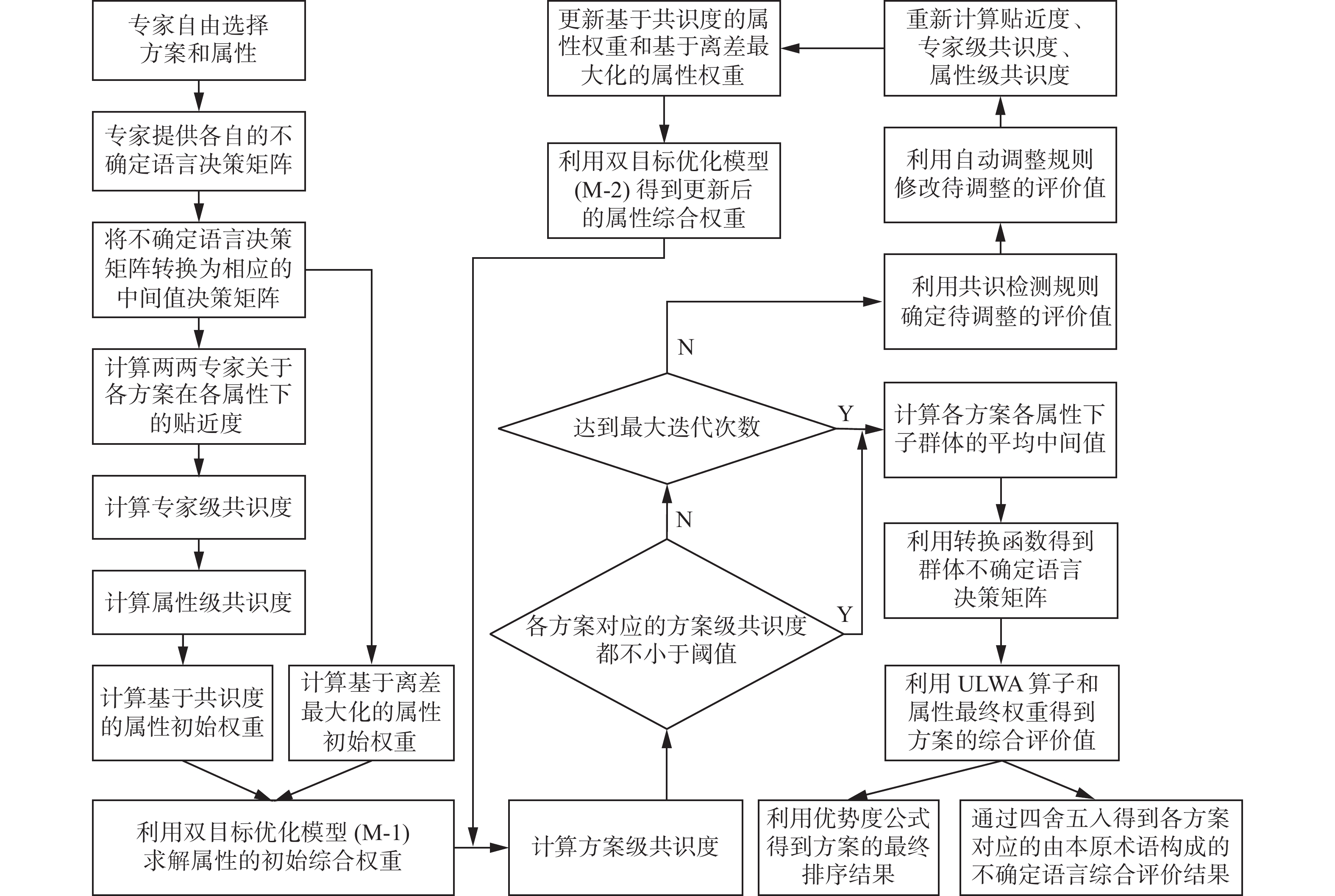
不确定语言环境下属性权重动态更新的自适应群体共识决策过程如下:
1)设语言术语集为
$ S{\text{ = }}\{ {s_\alpha }|\alpha = 0,1, \cdots ,g\} $ ,各专家可选择不同的方案和属性进行评价,并形成各自的不确定语言决策矩阵$ {\boldsymbol{R}^h} $ $ (h = 1,2, \cdots ,k) $ 。2)利用式(2)将
$ {\boldsymbol{R}^h} $ 转换为初始的中间值决策矩阵$ {\boldsymbol{M}^{h(0)}} $ 。3)利用式(4)~(6)计算初始专家级共识度
$ {{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ 和初始属性级共识度$ {{G}}_{ij}^{(0)}({E_{ij}}) $ 。4)利用式(8)、(9)及模型(M-1)计算属性的初始权重
$\tau _j^{(0)}$ 。5)设置共识度阈值
$ {{{G}}^*} $ 及最大迭代次数$ {\lambda _{\max }} $ ,并令$ \lambda $ 表示当前迭代轮次,初始值为0。6) 利用属性权重
$\tau _j^{(\lambda )}$ 及式(7)计算第$ \lambda $ 轮的方案级共识度${{{G}}^{(\lambda )}}({x_i})$ 。7)利用规则1对方案级共识度
${{{G}}^{(\lambda )}}({x_i})$ 及当前迭代轮次$ \lambda $ 进行判断,若停止迭代,则转至步骤12);否则,转至步骤8)。8)利用规则2依次确定第
$ \lambda $ 轮需要调整的评价值所对应的方案集$ {X^{(\lambda )}} $ 、属性集$ A_i^{(\lambda )} $ $({x_i} \in {X^{(\lambda )}})$ 和专家集$E_{ij}^{(\lambda )}$ $({x_i} \in {X^{(\lambda )}},{a_j} \in A_i^{(\lambda )})$ ,进而利用规则3修改待调整的评价值,得到更新后的中间值决策矩阵$ {\boldsymbol{M}^{h(\lambda + 1)}} $ 。9)利用式(4)~(6)对集合
$ {X^{(\lambda )}} $ 中各方案对应的属性级共识度进行更新,得到更新后的属性级共识度${{G}}_{ij}^{(\lambda + 1)}({E_{ij}})$ 。10)利用式(10)、(11)及模型(M-2)对属性权重进行更新,得到优化后的权重
$\tau _j^{(\lambda + 1)}$ 。11)令
$ \lambda = \lambda + 1 $ ,转至步骤6),进入下一轮共识迭代过程。12)利用公式
$ m(\tilde s_{ij}^{(\lambda )}) = {{\displaystyle\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(\lambda )})} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(\lambda )})} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}} $ 得到各方案各属性下子群体${E_{ij}}$ 的平均中间值$ m(\tilde s_{ij}^{(\lambda )}) $ ,进而利用式(3)将$ m(\tilde s_{ij}^{(\lambda )}) $ 转换为相应的不确定语言变量,从而得到群体的不确定语言决策矩阵$ \tilde {\boldsymbol{R}} $ 。13)利用ULWA算子和最终的属性权重对群体决策矩阵
$ \tilde {\boldsymbol{R}} $ 进行集结,得到各方案的不确定语言综合评价值,进而利用式(1)计算各方案的优势度,得到方案的综合排序结果。14)对于综合评价值不是整数的情形,通过四舍五入得到最终的不确定语言综合评价结果。
不确定语言环境下属性权重动态更新的自适应群体共识决策方法流程如图1所示。
3. 实例分析
某电子商务企业经过初步的市场调研,选取了6家物流运输供应商
$X = \{ {x_1},{x_2}, \cdots ,{x_6}\} $ 作为候选供应商。现由5位专家$E = \{ {e_1},{e_2}, \cdots ,{e_5}\} $ 从以下5个评价指标$ A = \{ {a_1},{a_2}, \cdots ,{a_5}\} $ 对各候选供应商进行评价。其中,$ {a_1} $ 为物流服务质量、$ {a_2} $ 为物流服务成本、$ {a_3} $ 为供应商能力、$ {a_4} $ 为信息化程度、$ {a_5} $ 为发展前景。专家采用的语言术语集为S={$ {s_0} $ =极差,${s_1}$ =很差,${s_2}$ =差,${s_3}$ =较差,${s_4}$ =一般,${s_5}$ =较好,${s_6}$ =好,${s_{\text{7}}}$ =很好,${s_{\text{8}}}$ =极好}。各专家给出的不确定语言决策矩阵如表1~5所示。表 1 专家${e_1}$ 给出的决策矩阵${\boldsymbol{R}^1}$ Table 1 Decision matrix$ {\boldsymbol{R}^1} $ given by expert${e_1}$ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ $[{s_1},{s_2}]$ $[{s_6},{s_7}]$ $[{s_5},{s_6}]$ $[{s_3},{s_4}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_4},{s_5}]$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_3},{s_3}]$ $[{s_6},{s_7}]$ ${x_6}$ $[{s_0},{s_2}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_6}]$ $[{s_6},{s_7}]$ 表 2 专家${e_2}$ 给出的决策矩阵$ {\boldsymbol{R}^2} $ Table 2 Decision matrix$ {\boldsymbol{R}^2} $ given by expert${e_2}$ 方案 a2 a3 a4 a5 ${x_2}$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ ${x_3}$ $[{s_5},{s_6}]$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ $[{s_3},{s_5}]$ ${x_4}$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ ${x_6}$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ 表 3 专家${e_3}$ 给出的决策矩阵$ {\boldsymbol{R}^3} $ Table 3 Decision matrix$ {\boldsymbol{R}^3} $ given by expert${e_3}$ 方案 ${a_1}$ ${a_2}$ ${a_4}$ ${a_5}$ ${x_1}$ $[{s_6},{s_8}]$ $[{s_7},{s_8}]$ $[{s_3},{s_4}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_6},{s_7}]$ $[{s_5},{s_6}]$ $[{s_7},{s_8}]$ $[{s_6},{s_8}]$ ${x_3}$ $[{s_1},{s_2}]$ $[{s_2},{s_3}]$ $[{s_3},{s_5}]$ $[{s_4},{s_6}]$ ${x_4}$ $[{s_3},{s_5}]$ $[{s_5},{s_7}]$ $[{s_4},{s_5}]$ $[{s_1},{s_2}]$ ${x_5}$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ 表 4 专家${e_4}$ 给出的决策矩阵$ {\boldsymbol{R}^4} $ Table 4 Decision matrix$ {\boldsymbol{R}^4} $ given by expert${e_4}$ 方案 ${a_1}$ ${a_3}$ ${a_4}$ ${x_1}$ $[{s_6},{s_7}]$ $[{s_6},{s_8}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_6},{s_8}]$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ ${x_3}$ $[{s_4},{s_7}]$ $[{s_4},{s_5}]$ $[{s_3},{s_4}]$ ${x_4}$ $[{s_1},{s_2}]$ $[{s_5},{s_5}]$ $[{s_4},{s_5}]$ ${x_6}$ $[{s_1},{s_2}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ 表 5 专家$ {e_5} $ 给出的决策矩阵$ {\boldsymbol{R}^5} $ Table 5 Decision matrix$ {\boldsymbol{R}^5} $ given by expert$ {e_5} $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_5}$ ${x_1}$ $[{s_6},{s_7}]$ $[{s_6},{s_7}]$ $[{s_6},{s_7}]$ $[{s_2},{s_3}]$ ${x_3}$ $[{s_2},{s_3}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ ${x_4}$ $[{s_1},{s_2}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_2},{s_5}]$ $[{s_3},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_7}]$ ${x_6}$ $[{s_1},{s_2}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ 首先,利用式(2)将各专家给出的不确定语言决策矩阵转换为初始的中间值决策矩阵。限于篇幅,表6仅给出了各专家关于方案
${x_1}$ 的不确定语言评价值$\tilde s_{ij}^{h(0)}$ 及其对应的中间值$m(\tilde s_{ij}^{h(0)})$ 和宽度值$w(\tilde s_{ij}^{h(0)})$ 。然后,利用式(4)、(5)计算初始的专家级共识度$ {{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ 见表7(限于篇幅,表7仅给出了前3个方案的计算结果),再利用式(6)计算初始的属性级共识度$ {{G}}_{ij}^{(0)}({E_{ij}}) $ ,见表8。表 6 方案${x_1}$ 上的初始评价值$ \tilde s_{ij}^{h(0)} $ 对应的中间值$m(\tilde s_{ij}^{h(0)})$ 和宽度值$w(\tilde s_{ij}^{h(0)})$ Table 6 Median value$m(\tilde s_{ij}^{h(0)})$ and width value$ w(\tilde s_{ij}^h) $ corresponding to the initial evaluation value$ \tilde s_{ij}^{h(0)} $ of alternative${x_1}$ 专家 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 ${e_1}$ $[{s_1},{s_2}]$ 1.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 $[{s_5},{s_6}]$ 5.5 0.5 $[{s_3},{s_4}]$ 3.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 ${e_2}$ — — — — — — — — — — — — — — — ${e_3}$ $[{s_6},{s_8}]$ 7 1 $[{s_7},{s_8}]$ 7.5 0.5 — — — $[{s_3},{s_4}]$ 3.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 ${e_4}$ $[{s_6},{s_7}]$ 6.5 0.5 — — — $[{s_6},{s_8}]$ 7 1 $[{s_6},{s_7}]$ 6.5 0.5 — — — ${e_5}$ $[{s_6},{s_7}]$ 6.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 — — — $[{s_2},{s_3}]$ 2.5 0.5 表 7 初始的专家级共识度$ {\text{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ Table 7 Initial expert-level consensus$ {\text{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ 方案 专家 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ ${e_1}$ 0.516 0.958 0.896 0.875 0.833 ${e_2}$ — — — — — ${e_3}$ 0.797 0.917 — 0.875 0.833 ${e_4}$ 0.828 — 0.917 0.75 — ${e_5}$ 0.828 0.958 0.938 — 0.667 ${e_1}$ 0.813 0.833 0.958 0.891 0.896 ${e_2}$ — 0.792 0.958 0.891 0.896 ${x_2}$ ${e_3}$ 0.896 0.875 — 0.766 0.792 ${e_4}$ 0.875 — 0.917 0.859 — ${e_5}$ — — — — — ${e_1}$ — — — — — ${e_2}$ — 0.875 0.917 0.938 0.938 ${x_3}$ ${e_3}$ 0.792 0.75 — 0.958 0.938 ${e_4}$ 0.708 — 0.958 0.938 — ${e_5}$ 0.833 0.875 0.958 — 0.958 注:加黑为共识度的最小值,下同。 表 8 初始的属性级共识度$ {{G}}_{ij}^{(0)}({E_{ij}}) $ Table 8 Initial attribute-level consensus$ {{G}}_{ij}^{(0)}({E_{ij}}) $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ 0.742 0.944 0.917 0.833 0.778 ${x_2}$ 0.861 0.833 0.944 0.852 0.861 ${x_3}$ 0.778 0.833 0.944 0.945 0.945 ${x_4}$ 0.861 0.972 0.972 0.972 0.833 ${x_5}$ 0.833 0.976 0.945 0.917 0.945 ${x_6}$ 0.972 0.944 0.945 0.945 0.944 进而,利用式(8)、(9)及模型(M-1)计算属性的初始权重
$\tau _j^{(0)}$ ,见表9。模型(M-1)中的比例因子$\beta {\text{ = }}0.5$ 。表 9 各轮对应的属性权重$ \tau _j^{(\lambda )} $ Table 9 Comprehensive weight$ \tau _j^{(\lambda )} $ of attribute in each round轮次 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 0 0.237 0.187 0.199 0.196 0.181 1 0.253 0.182 0.199 0.189 0.177 2 0.255 0.182 0.199 0.183 0.181 以下是共识分析与达成的迭代环节。设共识度阈值
$ {{{G}}^*}{\text{ = }}0.9 $ ,最大迭代次数$ {\lambda _{\max }}{\text{ = }}6 $ 。各轮对应的属性权重见表9,各轮对应的方案级共识度见表10。由表10可知,经过2轮调整后,各方案下的子群体都达到了预定的共识水平。表11给出了各轮的待调整值及其对应的方案集、属性集和专家集。
表 10 各轮的方案级共识度$G^{(\lambda )}(x_1)$ Table 10 Alternative-level consensus$G^{(\lambda )}(x_1)$ in each round轮次 $G^{(\lambda )}(x_1) $ $G^{(\lambda )}(x_2) $ $G^{(\lambda )}(x_3) $ $G^{(\lambda )}(x_4) $ $G^{(\lambda )}(x_5) $ $G^{(\lambda )}(x_6) $ 0 0.839 0.871 0.884 0.921 0.919 0.951 1 0.883 0.888 0.915 0.919 0.917 0.951 2 0.919 0.904 0.915 0.919 0.917 0.952 注:加黑为各轮低于共识度阈值0.9的方案级共识度。 表 11 各轮对应的待调整信息Table 11 Information to be adjusted in each round轮次 方案集 属性集 专家集 待调整值 0 $ \{ {x_1},{x_2},{x_3}\} $ $\{ A_1^{(0)} = \{ {a_1}\} ,$ $\{ E_{11}^{(0)} = \{ {e_1}\} ,$ $ \{ s_{11}^{1(0)},s_{22}^{2(0)},s_{31}^{4(0)}\} $ $A_2^{(0)} = \{ {a_2}\} , $ $E_{22}^{(0)} = \{ {e_2}\} , $ $A_3^{(0)} = \{ {a_1}\} \} $ $E_{31}^{(0)} = \{ {e_4}\} \} $ 1 $ \{ {x_1},{x_2}\} $ $\{ A_1^{(1)} = \{ {a_5}\} , $ $\{ E_{15}^{(1)} = \{ {e_5}\} , $ $ \{ s_{15}^{5(1)},s_{24}^{3(1)}\} $ $A_2^{(1)} = \{ {a_4}\} \} $ $E_{24}^{(1)} = \{ {e_3}\} \} $ 共识达成后,利用公式
$ m(\tilde s_{ij}^{(3)}) = {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(3)})} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {m(\tilde s_{ij}^{h(3)})} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}} $ 得到子群体${E_{ij}}$ 最终的平均中间值,进而,利用式(3)将中间值$ m(\tilde s_{ij}^{(3)}) $ 转换为不确定语言变量,从而得到群体的不确定语言决策矩阵$\tilde {\boldsymbol{R}}$ ,见表12。其中,宽度值$\varLambda = {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {w(\tilde s_{ij}^h)} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{{e_h} \in {E_{ij}}} {w(\tilde s_{ij}^h)} } {|{E_{ij}}|}}} \right. } {|{E_{ij}}|}}$ ,偏移量$\varDelta$ 统一赋值为0.25。表 12 群体的不确定语言决策矩阵$ \tilde {\boldsymbol{R}} $ Table 12 Group uncertain linguistic decision matrix$ \tilde {\boldsymbol{R}} $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言${x_1}$ 6.344 0.625 $[{s_6},{s_7}]$ 6.833 0.5 $[{s_7},{s_7}]$ 6.333 0.667 $[{s_6},{s_7}]$ 4.5 0.5 $[{s_4},{s_5}]$ 6.056 0.5 $[{s_6},{s_6}]$ ${x_2}$ 6 0.667 $[{s_6},{s_6}]$ 5.722 0.5 $[{s_5},{s_6}]$ 4.167 0.5 $[{s_4},{s_4}]$ 5.156 0.625 $[{s_5},{s_5}]$ 5.333 0.667 $[{s_5},{s_6}]$ ${x_3}$ 2.389 0.833 $[{s_2},{s_3}]$ 4.5 0.5 $[{s_4},{s_5}]$ 4.167 0.5 $[{s_4},{s_4}]$ 4 0.667 $[{s_4},{s_4}]$ 4.5 0.833 $[{s_4},{s_5}]$ ${x_4}$ 2.333 0.667 $[{s_2},{s_3}]$ 5.667 0.667 $[{s_5},{s_6}]$ 5.333 0.333 $[{s_5},{s_6}]$ 4.667 0.667 $[{s_4},{s_5}]$ 3.5 0.5 $[{s_3},{s_4}]$ ${x_5}$ 5.5 0.833 $[{s_5},{s_6}]$ 4.375 0.625 $[{s_4},{s_5}]$ 5.333 0.667 $[{s_5},{s_5}]$ 4 0.333 $[{s_4},{s_4}]$ 5.875 0.625 $[{s_6},{s_6}]$ ${x_6}$ 1.333 0.667 $[{s_1},{s_2}]$ 4.833 0.5 $[{s_5},{s_5}]$ 4.875 0.625 $[{s_5},{s_5}]$ 5 0.667 $[{s_5},{s_5}]$ 5.833 0.5 $[{s_6},{s_6}]$ 表13给出了各方案对应的综合评价结果及最终的方案排序,其中,方案
$ {x_1} $ 对应“好”,$ {x_2} $ 和$ {x_5} $ 对应 “较好”,$ {x_3} $ 、$ {x_4} $ 和$ {x_6} $ 的综合评价在“一般”附近。表 13 最终决策结果Table 13 Final decision results方案 综合评价值 取整后的不确定
语言变量综合评价
结果优势度 排序 ${x_1}$ $[{s_{5.816}},{s_{6.453}}]$ $[{s_6},{s_6}]$ [好,好] 0.764 1 ${x_2}$ $[{s_{5.056}},{s_{5.419}}]$ $[{s_5},{s_5}]$ [较好,较好] 0.654 2 ${x_3}$ $[{s_{3.49}},{s_{4.108}}]$ $[{s_3},{s_4}]$ [较差,一般] 0.475 6 ${x_4}$ $[{s_{3.69}},{s_{4.69}}]$ $[{s_4},{s_5}]$ [一般,较好] 0.523 5 ${x_5}$ $[{s_{4.816}},{s_{5.253}}]$ $[{s_5},{s_5}]$ [较好,较好] 0.629 3 ${x_6}$ $[{s_{4.161}},{s_{4.416}}]$ $[{s_4},{s_4}]$ [一般,一般] 0.536 4 4. 相关方法比较分析
为了说明本文方法的优势,将其与文献[16]进行比较分析。表14给出了本文方法与文献[16]方法得到的决策结果。
表 14 2种方法得到的决策结果对比Table 14 Comparison of decision results obtained by two methods方案 综合评价值 优势度 方案级共识度 文献[16] 本文方法 文献[16] 本文方法 文献[16] 本文方法 ${x_1}$ $[{s_{2.62}},{s_{4.32}}]$ $[{s_{2.77}},{s_{4.2}}]$ 0.573 0.577 无 0.924 ${x_2}$ $[{s_{2.2}},{s_{5.01}}]$ $[{s_{2.61}},{s_{4.39}}]$ 0.584 0.576 无 0.916 ${x_3}$ $[{s_{2.31}},{s_{4.37}}]$ $[{s_{2.6}},{s_{3.99}}]$ 0.551 0.547 无 0.906 ${x_4}$ $ [{s_{1.83}},{s_{3.71}}] $ $[{s_{2.27}},{s_{4.06}}]$ 0.465 0.525 无 0.902 表15给出了2种方法对应的共识迭代次数、评价值调整个数及方案排序结果。
表 15 2种方法对应的迭代次数、调整个数及排序结果Table 15 Iteration rounds, number of adjustments and ranking results corresponding to the two methods方法 迭代次数 评价值调整个数 方案排序结果 文献[16] 5 40 $ {x_2} > {x_1} > {x_3} > {x_4} $ 本文方法 4 14 $ {x_1} > {x_2} > {x_3} > {x_4} $ 由表15可知,2种方法对方案
$ {x_1} $ 和$ {x_2} $ 的排序有所不同。这主要是因为2种方法所采用的属性赋权方式和共识测度公式均不同。与文献[16]相比,本文所提方法调整轮次更少,调整范围更小,且能够保证每个方案下的子群体都能达到满意的共识水平,因此,得到的决策结果更加合理、可靠。此外,文献[16]方法仅限于同构多属性群决策问题,而本文所提方法的适用情形更加广泛。下面从属性权重、信息类型、适用情形、共识达成方法和综合评价值类型5个方面将本文方法与相关文献进行定性比较分析,见表16所示。
表 16 相关方法比较分析Table 16 Comparative analysis with related methods5. 结束语
针对属性集和方案集都存在差异的不确定语言多属性群决策问题,本文提出一种属性权重动态更新的自适应群体共识决策方法,并通过物流运输供应商选择实例及相关比较分析,验证了所提方法的有效性和实用性。本文所提方法能够更加快速、精准地锁定待调整值,并实现自动修改,具有适用范围广、共识效率高、灵活实用、解释性强等特点,为求解复杂环境下的多属性群决策问题提供了新的思路。下一步将结合信任关系和社会网络,对混合不同类型、不同粒度模糊语言的动态异构多属性群决策问题展开系统、深入的研究。
-
表 1 专家
${e_1}$ 给出的决策矩阵${\boldsymbol{R}^1}$ Table 1 Decision matrix
$ {\boldsymbol{R}^1} $ given by expert${e_1}$ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ $[{s_1},{s_2}]$ $[{s_6},{s_7}]$ $[{s_5},{s_6}]$ $[{s_3},{s_4}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_4},{s_5}]$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_3},{s_3}]$ $[{s_6},{s_7}]$ ${x_6}$ $[{s_0},{s_2}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_6}]$ $[{s_6},{s_7}]$ 表 2 专家
${e_2}$ 给出的决策矩阵$ {\boldsymbol{R}^2} $ Table 2 Decision matrix
$ {\boldsymbol{R}^2} $ given by expert${e_2}$ 方案 a2 a3 a4 a5 ${x_2}$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ ${x_3}$ $[{s_5},{s_6}]$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ $[{s_3},{s_5}]$ ${x_4}$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ ${x_6}$ $[{s_4},{s_5}]$ $[{s_4},{s_6}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ 表 3 专家
${e_3}$ 给出的决策矩阵$ {\boldsymbol{R}^3} $ Table 3 Decision matrix
$ {\boldsymbol{R}^3} $ given by expert${e_3}$ 方案 ${a_1}$ ${a_2}$ ${a_4}$ ${a_5}$ ${x_1}$ $[{s_6},{s_8}]$ $[{s_7},{s_8}]$ $[{s_3},{s_4}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_6},{s_7}]$ $[{s_5},{s_6}]$ $[{s_7},{s_8}]$ $[{s_6},{s_8}]$ ${x_3}$ $[{s_1},{s_2}]$ $[{s_2},{s_3}]$ $[{s_3},{s_5}]$ $[{s_4},{s_6}]$ ${x_4}$ $[{s_3},{s_5}]$ $[{s_5},{s_7}]$ $[{s_4},{s_5}]$ $[{s_1},{s_2}]$ ${x_5}$ $[{s_6},{s_7}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ 表 4 专家
${e_4}$ 给出的决策矩阵$ {\boldsymbol{R}^4} $ Table 4 Decision matrix
$ {\boldsymbol{R}^4} $ given by expert${e_4}$ 方案 ${a_1}$ ${a_3}$ ${a_4}$ ${x_1}$ $[{s_6},{s_7}]$ $[{s_6},{s_8}]$ $[{s_6},{s_7}]$ ${x_2}$ $[{s_6},{s_8}]$ $[{s_3},{s_4}]$ $[{s_4},{s_5}]$ ${x_3}$ $[{s_4},{s_7}]$ $[{s_4},{s_5}]$ $[{s_3},{s_4}]$ ${x_4}$ $[{s_1},{s_2}]$ $[{s_5},{s_5}]$ $[{s_4},{s_5}]$ ${x_6}$ $[{s_1},{s_2}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ 表 5 专家
$ {e_5} $ 给出的决策矩阵$ {\boldsymbol{R}^5} $ Table 5 Decision matrix
$ {\boldsymbol{R}^5} $ given by expert$ {e_5} $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_5}$ ${x_1}$ $[{s_6},{s_7}]$ $[{s_6},{s_7}]$ $[{s_6},{s_7}]$ $[{s_2},{s_3}]$ ${x_3}$ $[{s_2},{s_3}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ ${x_4}$ $[{s_1},{s_2}]$ $[{s_5},{s_6}]$ $[{s_5},{s_6}]$ $[{s_4},{s_5}]$ ${x_5}$ $[{s_2},{s_5}]$ $[{s_3},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_7}]$ ${x_6}$ $[{s_1},{s_2}]$ $[{s_4},{s_5}]$ $[{s_4},{s_5}]$ $[{s_5},{s_6}]$ 表 6 方案
${x_1}$ 上的初始评价值$ \tilde s_{ij}^{h(0)} $ 对应的中间值$m(\tilde s_{ij}^{h(0)})$ 和宽度值$w(\tilde s_{ij}^{h(0)})$ Table 6 Median value
$m(\tilde s_{ij}^{h(0)})$ and width value$ w(\tilde s_{ij}^h) $ corresponding to the initial evaluation value$ \tilde s_{ij}^{h(0)} $ of alternative${x_1}$ 专家 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 评价值 中间值 宽度值 ${e_1}$ $[{s_1},{s_2}]$ 1.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 $[{s_5},{s_6}]$ 5.5 0.5 $[{s_3},{s_4}]$ 3.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 ${e_2}$ — — — — — — — — — — — — — — — ${e_3}$ $[{s_6},{s_8}]$ 7 1 $[{s_7},{s_8}]$ 7.5 0.5 — — — $[{s_3},{s_4}]$ 3.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 ${e_4}$ $[{s_6},{s_7}]$ 6.5 0.5 — — — $[{s_6},{s_8}]$ 7 1 $[{s_6},{s_7}]$ 6.5 0.5 — — — ${e_5}$ $[{s_6},{s_7}]$ 6.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 $[{s_6},{s_7}]$ 6.5 0.5 — — — $[{s_2},{s_3}]$ 2.5 0.5 表 7 初始的专家级共识度
$ {\text{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ Table 7 Initial expert-level consensus
$ {\text{G}}_{ij}^{(0)}({e_h},{E_{ij}}) $ 方案 专家 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ ${e_1}$ 0.516 0.958 0.896 0.875 0.833 ${e_2}$ — — — — — ${e_3}$ 0.797 0.917 — 0.875 0.833 ${e_4}$ 0.828 — 0.917 0.75 — ${e_5}$ 0.828 0.958 0.938 — 0.667 ${e_1}$ 0.813 0.833 0.958 0.891 0.896 ${e_2}$ — 0.792 0.958 0.891 0.896 ${x_2}$ ${e_3}$ 0.896 0.875 — 0.766 0.792 ${e_4}$ 0.875 — 0.917 0.859 — ${e_5}$ — — — — — ${e_1}$ — — — — — ${e_2}$ — 0.875 0.917 0.938 0.938 ${x_3}$ ${e_3}$ 0.792 0.75 — 0.958 0.938 ${e_4}$ 0.708 — 0.958 0.938 — ${e_5}$ 0.833 0.875 0.958 — 0.958 注:加黑为共识度的最小值,下同。 表 8 初始的属性级共识度
$ {{G}}_{ij}^{(0)}({E_{ij}}) $ Table 8 Initial attribute-level consensus
$ {{G}}_{ij}^{(0)}({E_{ij}}) $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${x_1}$ 0.742 0.944 0.917 0.833 0.778 ${x_2}$ 0.861 0.833 0.944 0.852 0.861 ${x_3}$ 0.778 0.833 0.944 0.945 0.945 ${x_4}$ 0.861 0.972 0.972 0.972 0.833 ${x_5}$ 0.833 0.976 0.945 0.917 0.945 ${x_6}$ 0.972 0.944 0.945 0.945 0.944 表 9 各轮对应的属性权重
$ \tau _j^{(\lambda )} $ Table 9 Comprehensive weight
$ \tau _j^{(\lambda )} $ of attribute in each round轮次 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 0 0.237 0.187 0.199 0.196 0.181 1 0.253 0.182 0.199 0.189 0.177 2 0.255 0.182 0.199 0.183 0.181 表 10 各轮的方案级共识度
$G^{(\lambda )}(x_1)$ Table 10 Alternative-level consensus
$G^{(\lambda )}(x_1)$ in each round轮次 $G^{(\lambda )}(x_1) $ $G^{(\lambda )}(x_2) $ $G^{(\lambda )}(x_3) $ $G^{(\lambda )}(x_4) $ $G^{(\lambda )}(x_5) $ $G^{(\lambda )}(x_6) $ 0 0.839 0.871 0.884 0.921 0.919 0.951 1 0.883 0.888 0.915 0.919 0.917 0.951 2 0.919 0.904 0.915 0.919 0.917 0.952 注:加黑为各轮低于共识度阈值0.9的方案级共识度。 表 11 各轮对应的待调整信息
Table 11 Information to be adjusted in each round
轮次 方案集 属性集 专家集 待调整值 0 $ \{ {x_1},{x_2},{x_3}\} $ $\{ A_1^{(0)} = \{ {a_1}\} ,$ $\{ E_{11}^{(0)} = \{ {e_1}\} ,$ $ \{ s_{11}^{1(0)},s_{22}^{2(0)},s_{31}^{4(0)}\} $ $A_2^{(0)} = \{ {a_2}\} , $ $E_{22}^{(0)} = \{ {e_2}\} , $ $A_3^{(0)} = \{ {a_1}\} \} $ $E_{31}^{(0)} = \{ {e_4}\} \} $ 1 $ \{ {x_1},{x_2}\} $ $\{ A_1^{(1)} = \{ {a_5}\} , $ $\{ E_{15}^{(1)} = \{ {e_5}\} , $ $ \{ s_{15}^{5(1)},s_{24}^{3(1)}\} $ $A_2^{(1)} = \{ {a_4}\} \} $ $E_{24}^{(1)} = \{ {e_3}\} \} $ 表 12 群体的不确定语言决策矩阵
$ \tilde {\boldsymbol{R}} $ Table 12 Group uncertain linguistic decision matrix
$ \tilde {\boldsymbol{R}} $ 方案 ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ 中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言中间值 $\varLambda $ 不确定
语言${x_1}$ 6.344 0.625 $[{s_6},{s_7}]$ 6.833 0.5 $[{s_7},{s_7}]$ 6.333 0.667 $[{s_6},{s_7}]$ 4.5 0.5 $[{s_4},{s_5}]$ 6.056 0.5 $[{s_6},{s_6}]$ ${x_2}$ 6 0.667 $[{s_6},{s_6}]$ 5.722 0.5 $[{s_5},{s_6}]$ 4.167 0.5 $[{s_4},{s_4}]$ 5.156 0.625 $[{s_5},{s_5}]$ 5.333 0.667 $[{s_5},{s_6}]$ ${x_3}$ 2.389 0.833 $[{s_2},{s_3}]$ 4.5 0.5 $[{s_4},{s_5}]$ 4.167 0.5 $[{s_4},{s_4}]$ 4 0.667 $[{s_4},{s_4}]$ 4.5 0.833 $[{s_4},{s_5}]$ ${x_4}$ 2.333 0.667 $[{s_2},{s_3}]$ 5.667 0.667 $[{s_5},{s_6}]$ 5.333 0.333 $[{s_5},{s_6}]$ 4.667 0.667 $[{s_4},{s_5}]$ 3.5 0.5 $[{s_3},{s_4}]$ ${x_5}$ 5.5 0.833 $[{s_5},{s_6}]$ 4.375 0.625 $[{s_4},{s_5}]$ 5.333 0.667 $[{s_5},{s_5}]$ 4 0.333 $[{s_4},{s_4}]$ 5.875 0.625 $[{s_6},{s_6}]$ ${x_6}$ 1.333 0.667 $[{s_1},{s_2}]$ 4.833 0.5 $[{s_5},{s_5}]$ 4.875 0.625 $[{s_5},{s_5}]$ 5 0.667 $[{s_5},{s_5}]$ 5.833 0.5 $[{s_6},{s_6}]$ 表 13 最终决策结果
Table 13 Final decision results
方案 综合评价值 取整后的不确定
语言变量综合评价
结果优势度 排序 ${x_1}$ $[{s_{5.816}},{s_{6.453}}]$ $[{s_6},{s_6}]$ [好,好] 0.764 1 ${x_2}$ $[{s_{5.056}},{s_{5.419}}]$ $[{s_5},{s_5}]$ [较好,较好] 0.654 2 ${x_3}$ $[{s_{3.49}},{s_{4.108}}]$ $[{s_3},{s_4}]$ [较差,一般] 0.475 6 ${x_4}$ $[{s_{3.69}},{s_{4.69}}]$ $[{s_4},{s_5}]$ [一般,较好] 0.523 5 ${x_5}$ $[{s_{4.816}},{s_{5.253}}]$ $[{s_5},{s_5}]$ [较好,较好] 0.629 3 ${x_6}$ $[{s_{4.161}},{s_{4.416}}]$ $[{s_4},{s_4}]$ [一般,一般] 0.536 4 表 14 2种方法得到的决策结果对比
Table 14 Comparison of decision results obtained by two methods
方案 综合评价值 优势度 方案级共识度 文献[16] 本文方法 文献[16] 本文方法 文献[16] 本文方法 ${x_1}$ $[{s_{2.62}},{s_{4.32}}]$ $[{s_{2.77}},{s_{4.2}}]$ 0.573 0.577 无 0.924 ${x_2}$ $[{s_{2.2}},{s_{5.01}}]$ $[{s_{2.61}},{s_{4.39}}]$ 0.584 0.576 无 0.916 ${x_3}$ $[{s_{2.31}},{s_{4.37}}]$ $[{s_{2.6}},{s_{3.99}}]$ 0.551 0.547 无 0.906 ${x_4}$ $ [{s_{1.83}},{s_{3.71}}] $ $[{s_{2.27}},{s_{4.06}}]$ 0.465 0.525 无 0.902 表 15 2种方法对应的迭代次数、调整个数及排序结果
Table 15 Iteration rounds, number of adjustments and ranking results corresponding to the two methods
方法 迭代次数 评价值调整个数 方案排序结果 文献[16] 5 40 $ {x_2} > {x_1} > {x_3} > {x_4} $ 本文方法 4 14 $ {x_1} > {x_2} > {x_3} > {x_4} $ 表 16 相关方法比较分析
Table 16 Comparative analysis with related methods
-
[1] PANG Kuo, MARTINEZ Luis, LI Nan, et al. A concept lattice-based expert opinion aggregation method for multi-attribute group decision-making with linguistic information[J]. Expert systems with applications, 2024, 237: 121485. doi: 10.1016/j.eswa.2023.121485 [2] YAO Ruipu, GUO Huijuan. Multiattribute group decision making based on novel score function considering both the angle and fuzzy information under interval-valued intuitionistic fuzzy environment[J]. Information sciences, 2023, 644: 119233. doi: 10.1016/j.ins.2023.119233 [3] 张发明, 张淋茜, 韩江涛. 基于证据理论的多阶段混合型偏好信息群决策方法[J]. 系统工程理论与实践, 2023, 43(12): 3619–3635. doi: 10.12011/SETP2022-2903 ZHANG Faming, ZHANG Linqian, HAN Jiangtao. A method for multi-stage group decision making based on evidence theory under hybrid preference information[J]. Systems engineering-theory & practice, 2023, 43(12): 3619–3635. doi: 10.12011/SETP2022-2903 [4] PANG Jifang, GUAN Xiaoqiang, LIANG Jiye, et al. Multi-attribute group decision-making method based on multi- granulation weights and three-way decisions[J]. International journal of approximate reasoning, 2020, 117: 122–147. doi: 10.1016/j.ijar.2019.11.008 [5] ZHANG Nian, ZHOU Yifan, LIU Jin, et al. VIKOR method for pythagorean hesitant fuzzy multi-attribute decision-making based on regret theory[J]. Engineering applications of artificial intelligence, 2023, 126: 106857. doi: 10.1016/j.engappai.2023.106857 [6] 申情, 蒋云良, 张雄涛. 属性权重未知情况下犹豫模糊多属性决策方法[J]. 智能系统学报, 2022, 17(4): 728–736. SHEN Qing, JIANG Yunliang, ZHANG Xiongtao. A hesitant fuzzy multi-attribute decision making method with unknown attribute weights[J]. CAAI transactions on intelligent systems, 2022, 17(4): 728–736. [7] 崔铁军, 李莎莎. 系统故障影响因素的主客观综合权重确定方法研究[J]. 应用科技. 2022, 49(2):127-132, 139. CUI Tiejun, LI Shasha. Research on the method of determining subjective and objective comprehensive weight for influence factors of system faults[J]. Applied science and technology, 2022, 49(2):127-132, 139. [8] 梁薇, 王应明. 基于可信度的基本不确定区间犹豫模糊广义TODIM 应急群决策方法[J]. 控制与决策, 2023, 38(7): 1988–1996. LIANG Wei, WANG Yingming. Generalized TODIM emergency group decision making method for basic uncertain information interval-valued hesitant fuzzy set based on reliability degree[J]. Control and decision, 2023, 38(7): 1988–1996. [9] ZHAO Chengwei, XU Xuanhua, LIU Ruihuan, et al. A novel multi-attribute group decision-making method for heterogeneous preferences and attribute interaction contexts[J]. Expert systems with applications, 2023, 221: 119752. doi: 10.1016/j.eswa.2023.119752 [10] ZHANG Chao, LI Deyu, LIANG Jiye. Interval-valued hesitant fuzzy multi-granularity three-way decisions in consensus processes with applications to multi-attribute group decision making[J]. Information sciences, 2020, 511: 192–211. doi: 10.1016/j.ins.2019.09.037 [11] YE Jin, SUN Bingzhen, CHU Xiaoli, et al. Valued outranking relation-based heterogeneous multi-decision multi- granulation probabilistic rough set and its use in medical decision- making[J]. Expert systems with applications, 2023, 228: 120296. doi: 10.1016/j.eswa.2023.120296 [12] LI Yanhong, KOU Gang, LI Guangxu, et al. Consensus reaching process in large-scale group decision making based on bounded confidence and social network[J]. European journal of operational research, 2022, 303: 790–802. doi: 10.1016/j.ejor.2022.03.040 [13] 张世涛, 刘小弟, 朱建军, 等. 考虑个体累积共识贡献的犹豫模糊语言自适应共识模型[J]. 控制与决策, 2021, 36(1): 187–195. ZHANG Shitao, LIU Xiaodi, ZHU Jianjun, et al. Adaptive consensus model with hesitant fuzzy linguistic information considering individual cumulative consensus contribution[J]. Control and decision, 2021, 36(1): 187–195. [14] LI Weiwei, YI Pingtao, LI Lingyu. Superiority-comparison- based transformation, consensus, and ranking methods for heterogeneous multi-attribute group decision-making[J]. Expert systems with applications, 2023, 213: 119018. doi: 10.1016/j.eswa.2022.119018 [15] ZHU Jinxing, MA Xueling, KOU Gang, et al. A three-way consensus model with regret theory under the framework of probabilistic linguistic term sets[J]. Information fusion, 2023, 95: 250–274. doi: 10.1016/j.inffus.2023.02.029 [16] PANG Jifang, LIANG Jiye, SONG Peng. An adaptive consensus method for multi-attribute group decision making under uncertain linguistic environment[J]. Applied soft computing, 2017, 58: 339–353. doi: 10.1016/j.asoc.2017.04.039 [17] LIU Xia, XU Yejun, GONG Zaiwu, et al. Democratic consensus reaching process for multi-person multi-criteria large scale decision making considering participants’ individual attributes and concerns[J]. Information fusion, 2022, 77: 220–232. doi: 10.1016/j.inffus.2021.07.023 [18] ZHONG Xiangyu, XU Xuanhua, PAN Bin. A non-threshold consensus model based on the minimum cost and maximum consensus-increasing for multi-attribute large group decision- making[J]. Information fusion, 2022, 77: 90–106. doi: 10.1016/j.inffus.2021.07.006 [19] WAN Shuping, ZOU Wenchang, DONG Jiuying, et al. A consensual method for multi-criteria group decision-making with linguistic intuitionistic information[J]. Information sciences, 2022, 582: 797–832. doi: 10.1016/j.ins.2021.10.030 [20] 庞继芳, 宋鹏, 梁吉业. 面向决策分析的多粒度计算模型与方法综述[J]. 模式识别与人工智能, 2021, 34(12): 1120–1130. PANG Jifang, SONG Peng, LIANG Jiye. Review on multi-granulation computing models and methods[J]. Pattern recognition and artificial intelligence, 2021, 34(12): 1120–1130. [21] SUN Bingzhen, ZHOU Xuemei, LIN Nannan. Diversified binary relation-based fuzzy multigranulation rough set over two universes and application to multiple attribute group decision making[J]. Information fusion, 2020, 55: 91–104. doi: 10.1016/j.inffus.2019.07.013 [22] GAO Yang, LI Dongsheng. A consensus model for heterogeneous multi-attribute group decision making with several attribute sets[J]. Expert systems with applications, 2019, 125: 69–80. doi: 10.1016/j.eswa.2019.01.072 [23] MORENTE-MOLINERA J A, WU X, MORFEQ A, et al. A novel multi-criteria group decision-making method for heterogeneous and dynamic contexts using multi-granular fuzzy linguistic modelling and consensus measures[J]. Information fusion, 2020, 53: 240–250. doi: 10.1016/j.inffus.2019.06.028 [24] DONG Yucheng, ZHANG Hengjie, HERRERA-VIEDMA E. Consensus reaching model in the complex and dynamic MAGDM problem[J]. Knowledge-based systems, 2016, 106: 206–219. doi: 10.1016/j.knosys.2016.05.046 [25] 徐莹莹, 邹丽, 黄志鑫, 等. 基于TOPSIS 的语言真值直觉模糊多属性决策[J]. 智能系统学报, 2017, 12(4): 504–510. XU Yingying, ZOU Li, HUANG Zhixin, et al. Linguistic truth-valued intuitionistic fuzzy multi-attribute decision making based on TOPSIS[J]. CAAI transactions on intelligent systems, 2017, 12(4): 504–510. [26] 薛彦卓, 周莹, 鲁阳, 等. 基于模糊AHP-DEMATEL的北极冰区船舶冰困风险评价[J]. 哈尔滨工程大学学报, 2022, 43(7): 944–949, 992. XUE Yanzhuo, ZHOU Ying, LU Yang, et al. Risk assessment of ships stuck in ice in Arctic ice area based on fuzzy AHP-DEMATEL[J]. Journal of Harbin Engineering University, 2022, 43(7): 944–949, 992. [27] HERRERA F, HERRERA-VIEDMA E, VERDEGAY J L. A sequential selection process in group decision making with a linguistic assessment approach[J]. Information sciences, 1995, 85(4): 223–239. doi: 10.1016/0020-0255(95)00025-K [28] XU Zeshui. A method based on linguistic aggregation operators for group decision making with linguistic preference relations[J]. Information sciences, 2004, 166(1-4): 19–30. doi: 10.1016/j.ins.2003.10.006 [29] XU Zeshui. Induced uncertain linguistic OWA operators applied to group decision making[J]. Information fusion, 2006, 7(2): 231–238. doi: 10.1016/j.inffus.2004.06.005 [30] TSAUR R C. Decision risk analysis for an interval TOPSIS method[J]. Applied mathematics and computation, 2011, 218(8): 4295–4304. doi: 10.1016/j.amc.2011.10.001 [31] XU Zeshui. Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment[J]. Information sciences, 2004, 168(1-4): 171–184. doi: 10.1016/j.ins.2004.02.003 [32] WANG Yingming. Using the method of maximizing deviation to make decision for multi-indices[J]. Journal of systems engineering and electronics, 1997, 8(3): 21–26.









































































































































































































































 下载:
下载:















































































