Research on the construction of the event state connection number in the system fault evolution process
-
摘要: 由于故障数据提取、表示、分析和处理过程存在不确定性，给系统故障演化过程研究带来困难，为此，提出一种基于集对分析联系数的系统故障演化过程事件状态联系数构建方法。基于联系数对多语义状态划分及同异反状态的表示分析能力，以系统安全为目标进行研究。分析已有精确系统故障演化过程分析方法的不足；将事件发生概率分布划分为安全、不确定、不安全三状态等效同异反状态，进而确定状态分项系数得到事件状态联系数；通过同异反真值表确定结果事件状态联系数。结果表明，得到的事件状态联系数符合联系数构造条件和逻辑真值关系，进而获得系统故障演化过程的事件演化表示方法，也可使用集对分析的已有方法进行相关研究。研究搭建集对分析理论与系统安全分析的桥梁，将蕴含不确定数据的定量分析发展为不确定性分析，化简分析过程并体现同异反特征。Abstract: Due to the uncertainty of fault data extraction, representation, analysis, and processing, examining the system fault evolution process is difficult. Herein, we design a construction method of event state connection number in the system fault evolution process based on the set pair analysis connection number. The multisemantic state division, representation, and analysis ability of the identical discrepancy contrary states based on the connection number are explored in terms of system safety. First, the drawbacks of current accurate system fault evolution process analysis methods are analyzed, dividing the probability distribution of event occurrence into three states: safety, uncertainty, and unsafety, which are equivalent to the identical discrepancy contrary states, and then the partial coefficient of the state is determined to obtain the event state connection number. Finally, the state connection number of the result event is determined through the identical discrepancy contrary truth table. It is revealed that the resulting event state connection number conforms to the construction condition of the connection number and logical truth relationship, and then, the event evolution representation method of the system fault evolution process can be acquired. The current methods of set pair analysis can also be employed for related research. The research builds a bridge between set pair analysis theory and system safety analysis. The quantitative analysis with uncertain data is developed into uncertainty analysis, simplifying the analysis process, and embodying the identical discrepancy contrary characteristics.
-
系统故障过程是极其复杂的动态过程，因此研究系统故障过程需要面对的问题很多。根据作者的前期研究成果[1-2]，系统故障过程至少包含四要素，即过程经历的事件、影响过程的因素、过程中的逻辑关系和过程蕴含的演化条件，定义为系统故障演化过程。研究系统故障演化过程的基础是必须获得充分且具有特点的故障数据，而故障数据随着影响因素的变化而变化。影响因素分为内因和外因，内因主要是系统内部元件的性质和这些元件组成系统的结构，其在系统设计期间基本已确定且在运行期间不变；外因是系统运行过程中的环境因素，由于组成系统的基本元件受到外因影响出现故障变化，由这些元件组成的系统故障变化就更为复杂。一般情况下通过监测收集不同因素作用后的故障数据，进而得到因素变化与系统故障概率变化的关系。因此研究系统故障演化过程的关键是故障数据和影响因素。但实际过程中获得故障数据是困难的，一是故障数据特征难以预测；二是故障数据可能是人为或系统随机造成的，难以体现正确性；三是故障数据可能存在冗余和错误，难以使用数据学习方法。因此在实际工况下特别是现场的系统故障难以实现故障数据的精确收集和分析，为后继系统故障演化过程研究带来困难。
关于系统故障过程的研究，以及故障数据的提取、表示和分析在多个领域已有一些研究。较新的国内研究主要在失败故障过程分析[3]、系统故障识别[4-5]、概率共因失效分析[6]和故障诊断方法研究[7-8]等方面展开。国外也使用了广义相关熵滤波[9]、状态评估[10]、特征排序和差分进化[11]、时序数据分析[12]、异常数据分析[13]等方式对上述议题进行了研究。笔者也在相关领域进行了一定研究[2,14]。这些方法从不同角度和不同层次对系统故障过程进行了深入研究，为后继研究提供了大量有参考价值的成果。但正如前述在研究系统故障演化过程中暴露的问题，对最基础的故障数据，其不确定性和因素变化特征是较难确定的。
基于上述问题，借助空间故障网络理论得到的事件发生概率分布描述系统及元件的故障发生概率变化特征，将概率分布按照不同语义划分，并求出不同语义对应概率分布投影下的因素变化区域占比。利用集对分析[15]联系数描述不同语义区域占比并等效为同异反分项系数。从而构建系统故障演化过程中的事件状态联系数，再通过同异反逻辑真值表得到结果事件状态联系数。为克服研究中故障数据等存在的不确定性及变化关系分析提供了有效方法。
1. 系统故障演化过程与空间故障网络
笔者在从事系统安全、故障和可靠性的研究过程中提出了空间故障树理论。经过多年发展空间故障树理论体系形成了几个主要部分，包括空间故障树理论基础[16]、智能化空间故障树[17]、空间故障网络[2]、系统运动空间与系统映射论[18]等。空间故障树理论基础主要从影响因素变化对系统可靠性的影响出发，研究多因素影响下系统可靠性的分布情况。但在研究过程中发现确定影响系统可靠性的因素非常困难，难以确定因素之间的相关性和关联性，对故障数据的分析和提取也存在困难。因此提出了智能化空间故障树用于上述问题的解决，实现了因素与系统故障之间的因果逻辑关系推理和故障大数据表示。但随着研究系统的复杂性增加，原有空间故障树的树形结构难以实现对复杂系统故障过程的研究。因而提出了空间故障网络理论，用于研究系统故障过程中的经历事件、影响因素、逻辑关系和演化条件，从而描述和研究系统故障演化过程。
系统故障演化过程无处不在，无论是自然系统和还是人造系统。自然系统称之为灾害演化过程，人造系统称之为故障演化过程，但两者在结构上是相似的，可以共同抽象为系统故障演化过程。笔者提出的空间故障网络理论利用拓扑结构将系统故障演化过程抽象为经历事件、影响因素、逻辑关系和演化条件，使用网络拓扑形式进行研究。
定性和定量地研究系统故障演化过程使用空间故障网络理论需要解决2个关键问题。一是因素与故障之间的影响关系及其定量方法。主要问题是因素确定、因素与故障定量关系、多因素耦合作用下的故障表示等。目前上述问题已得到初步解决，但对故障数据变化与因素变化的对应关系，因素变化与系统故障等级的界定，及获得相对简单的事件发生概率分布等仍存在困难。二是系统故障演化过程中各事件形成的演化逻辑结构表示，即事件与事件的逻辑关系表示和演化结构表示。
虽然使用空间故障网络理论表示和研究系统故障演化过程的方法已初步形成，并使用了精确的特征函数和事件发生概率分布，但这种精确在数据的获取和分析上比较困难，所得解析式是理想的且蕴含了不确定性。精确的解析式表面上抹杀了数据和结构的不确定性，但实际上增加了分析结果的不确定性，也不利于低复杂性需求的研究环境。因此本研究提出基于集对分析联系数的系统故障演化过程中事件发生状态的表示和分析方法。
2. 事件状态联系数构建
事件发生概率是故障数据统计的基础问题，特别是考虑不同因素及耦合的情况下获取故障数据是比较困难的。另一方面对于实际工程，特别是现场人员的认知而言故障概率不必非常精确，只需要区分安全、不安全和不确定等状态就可指导实际系统操作。因此可将原有事件发生概率分布使用安全、不确定和不安全3种状态进行分区，表示形成3种不同的事件发生概率状态。考虑现有理论和方法，使用集对分析的三元联系数表示较为方便，形成事件发生概率状态联系数，简称事件状态联系数。
设
$F=\left\{{f}_{1},{f}_{2},\cdots ,{f}_{N}\right\},{f}_{o}\in F,o=1,2,\cdots ,N$ ，$ F $ 表示因素的集合，$ {f_o} $ 表示第$ o $ 个因素，$ N $ 表示因素的数量。在$ N $ 个因素影响下的事件发生概率特征函数[16]可分别表示为$p\left( {{f_1}} \right),p\left( {{f_2}} \right), \cdots ,p\left( {{f_N}} \right)$ ，$ p\left( {{f_o}} \right) $ 表示因素$ {f_o} $ 的特征函数。那么根据事件发生概率分布的合成方法[16]，可得如式(1)的$ N $ 因素影响下事件发生概率分布$ P\left( F \right) $ $$ \begin{gathered} P\left( F \right) = \\ 1 - \left[ {\left( {1 - p\left( {{f_1}} \right)} \right)\left( {1 - p\left( {{f_2}} \right)} \right) \cdots \left( {1 - p\left( {{f_N}} \right)} \right)} \right] = \\ 1 - \prod\limits_{o = 1}^N {\left( {1 - p\left( {{f_o}} \right)} \right)} \end{gathered} $$ (1) 进一步设故障概率的不同语义划分，以系统安全为目标，系统状态可划分为安全、不确定和不安全3种语义状态，可根据下式进行语义划分及因素变化区域的划分。
$$ \left\{ \begin{array}{l}\lambda =\left\{{\lambda }_{1},{\lambda }_{2},\cdots ,{\lambda }_{K}\right\},k=1,2,\cdots ,K,{\lambda }_{k}\in \lambda ,{\lambda }_{1}=0,{\lambda }_{K}=1\\ {s}_{a}=\left\{{s}_{u}|P\left(F\right)\leqslant {\lambda }_{2}\right\},安全状态域\\ {s}_{b}=\left\{{s}_{u}|P\left(F\right) >{\lambda }_{2},P\left(F\right) < {\lambda }_{3}\right\},不确定状态域 \\ {s}_{c}={s}_{u}-{s}_{a}-{s}_{b},不安全状态域\end{array}\right. $$ (2) 式中：λ代表了语义划分，
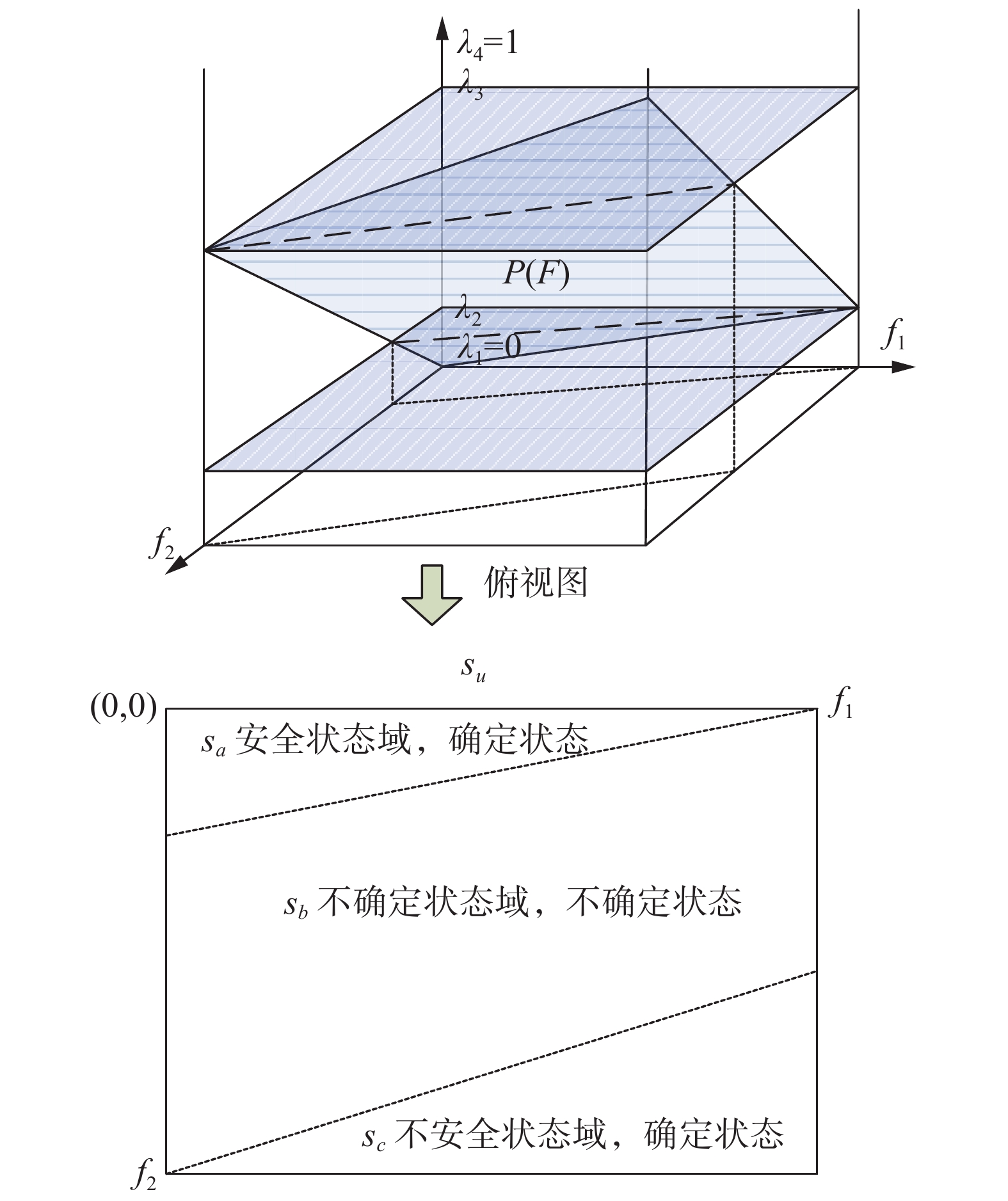
$ {\lambda _1} = 0 $ 表示完全安全的语义，事件发生概率为0；$ {\lambda _K} = 1 $ 表示完全不安全的语义，事件发生概率为100%。由于划分有3种状态，需要将故障概率变化区间[0,1]划分为3部分，因此可设$ K = {\text{4}} $ 。那么安全的故障概率为$ [{\lambda _1} = 0,{\lambda _2}] $ ；不确定安全的故障概率为$ ({\lambda _2},{\lambda _3}) $ ；不安全的故障概率为$ [{\lambda _3},{\lambda _4} = 1] $ 。与上述三状态对应的因素变化范围面积分别为$ {s_a} $ 、$ {s_b} $ 和$ {s_c} $ ，总面积为$ {s_u} $ 。使用图1说明确定的过程和方法。
图 1 三状态的因素变化范围确定Fig. 1 Determination of variation range of factors in three states
下载:
全尺寸图片
图1箭头之上的图是由两因素
$ {f_1} $ 和$ {f_2} $ 以及对应的事件发生概率$ \lambda $ 为三坐标轴形成的事件发生概率空间分布。当然也可讨论多因素影响下的事件发生概率空间分布，但考虑到四维及以上难以绘制的问题，这里使用两因素进行讨论。图1中有浅色阴影区域的部分为事件发生概率空间分布曲面$P\left( F \right) = P({f_1},{f_2}) = 1 - (1 - p({f_1}))(1 - p({f_2}))$ 。其特点是$ P\left( F \right) $ 在概率区间[0,1]中都存在，当因素$ {f_1} $ 和$ {f_2} $ 为最小值时事件发生概率最小值为0；当因素$ {f_1} $ 和$ {f_2} $ 为最大值时事件发生概率最大值为1。当然实际上的事件发生概率分布曲面变化很复杂，这里只应用于举例分析。根据系统安全的语义设定，安全的故障概率为$ [0,{\lambda _2}] $ ；不确定安全的故障概率为$ ({\lambda _2},{\lambda _3}) $ ；不安全的故障概率为$ [{\lambda _3},1] $ 。这时可在概率分布空间中增加2个平面，与$ {f_1} $ 和$ {f_2} $ 变化平面平行，其概率值分别为$ {\lambda _2} $ 和$ {\lambda _3} $ ，见图1中深色阴影区域。这样$ {\lambda _2} $ 和$ {\lambda _3} $ 平面就将分布曲面$ P\left( F \right) $ 划分为3部分，这3部分由下至上分别代表了不同因素条件下的系统故障概率为安全、不确定和不安全的语义。进一步，$ {\lambda _2} $ 和$ {\lambda _3} $ 平面与$ P\left( F \right) $ 分布的交线投影于$ {f_1} $ $ {f_2} $ 平面，2条交线的投影将$ {f_1} $ $ {f_2} $ 平面划分为3部分，如图1中箭头之下的图所示。这3部分分别表示了安全状态、不确定状态和不安全状态，其面积分别是$ {s_a} $ 、$ {s_b} $ 和$ {s_c} $ ，总面积为$ {s_u} $ 。如上过程将原有事件发生概率分布转化成了事件发生状态分布。上述方法的优点如下：
1) 是故障数据的表示无需再使用精确方法。事件发生概率分布使用了事件发生概率特征函数，是精确的事件发生概率表示方法。实际中获得这些数据是困难的，可根据经验和少量数据大体上判断各因素影响下的系统故障状态，得到事件发生状态分布。
2) 事件发生状态分布是一种可扩展的事件发生状态表示方法。见式(2)中的安全、不确定和不安全的状态划分，其不确定状态可进一步划分为如一般安全、临界安全和一般不安全等状态，从而根据实际需要扩展。扩展可通过语义对应的故障概率值
$ \lambda $ 增加水平切面获得对应分布曲面$ P\left( F \right) $ 到因素变化区域投影的面积来代表该语义对应的因素变化区域。也可应用于事件发生概率的确定和不确定性分析，如上面的安全与不安全状态对应了确定状态，而不确定的安全状态对应了不确定状态。可分析系统安全性的确定和不确定状态对应的因素关系，分析确定状态和不确定状态在因素变化中的占比，比例越大说明系统的确定性越大，是有利的情况；反之占比小说明不确定性较大是不利的情况。可确定因素变化过程中确定性与不确定性的变化趋势，这里不做详述。3) 有成熟的理论方法进行表示和研究。可使用集对分析理论中的联系数表示上述事件发生状态分布，形成事件状态联系数。对安全语义的划分不同，可使用三元到多元联系数表示。三元联系数一般表示为
$\mu = a + b{\rm{i}} + c{\rm{j}}$ （1为同/安全状态；i为异/不确定安全状态；j为反/不安全状态，同表2），其中$a$ 、$b$ 、$c$ 分别代表同异反分项系数。即分别代表了集合中与目标相同的对象数量、不确定是否相同的对象数量以及与目标相反的对象数量，使用对象总数进行归一化即为同异反状态的比例。这时$a$ 和$c$ 的和代表确定性比例，$b$ 代表不确定性比例。将系统安全设为目标，则可构建具有安全、不确定和不安全的三元联系数，对应同异反状态。也可将异状态划分为更多状态构建多元联系数，但本质上都是确定和不确定性对象占比变化的博弈过程。因此使用集对分析联系数可很好地表示事件发生状态分布。表 2 状态联系数或逻辑真值表Table 2 Or logical truth table of state connection number状态 1 i j 1 1 1 1 i 1 i i j 1 i j 综上对于一个基本事件
$x$ ，在因素集合$F$ 作用下的事件发生状态分布可表示为事件状态联系数$ u_F^x $ $$ u_F^x = a_F^x + b_F^x{\rm{i}} + c_F^x{\rm{j}} = \left( {s_a^x + s_b^x{\rm{i}} + s_c^x{\rm{j}}} \right)/s_u^x $$ (3) 式中：
$ a_F^x、b_F^x、c_F^x $ 分别表示基本事件x，在因素集合F影响下的安全、不确定和不安全状态的分项系数；三状态对应的因素变化范围面积分别为$ s_a^x、s_b^x、s_c^x $ ；总面积为$ s_u^x $ 。3. 事件间逻辑关系真值表
上述得到了事件状态联系数，解决了因素和事件在系统故障演化过程中的作用表示。进一步需要研究系统故障演化过程中事件之间的逻辑关系表达。从系统故障演化过程的结构看，演化过程是事件与事件的因果关系，是原因事件通过某种形式导致结果事件的过程。最典型的，2个原因事件同时发生导致结果事件发生为与关系，2个原因事件之一发生导致结果事件发生称之为或关系。当然逻辑关系有很多种，甚至出现了可描述连续变化逻辑关系的柔性逻辑的泛逻辑学[19]，但二元与或关系始终是逻辑关系的基础。因此这里以“与或”关系为例构建适合于事件状态联系数的事件间逻辑关系。
事件状态联系数的逻辑关系与一般布尔了逻辑关系既有区别也有联系。联系是仍遵循与或关系的基本逻辑；区别是原逻辑为是非逻辑，而联系数是同异反逻辑。在最基本的两事件作用中，同异反三状态逻辑关系需要制定真值表。根据基本逻辑假设，在与状态下结果事件都偏向于远离目标，因此得到如表1所示的事件状态联系数同异反逻辑真值表；在或状态下结果事件趋近于目标，得到表2的同异反逻辑真值表。
表 1 状态联系数的与逻辑真值表Table 1 And logical truth table of state connection number状态 1 i j 1 1 i j i i i j j j j j 注：1为同/安全状态；i为异/不确定安全状态；j为反/不安全状态，同表2。 在分析2个原因事件以与或逻辑关系导致结果事件时，可使用表1和表2的逻辑真值来运算同异反状态的与或关系，这为系统故障演化过程的事件间逻辑关系描述提供了方法。
4. 结果事件状态联系数构建
上述分别得到了事件状态联系数和状态联系数的逻辑关系，这里以2个原因事件分别以与或关系导致结果事件为例说明结果事件的状态联系数构建过程。对于多原因事件导致结果事件的状态联系数可使用两两复合的方式得到。
设
$$ u_F^1 = a_F^1 + b_F^1{\rm{i}} + c_F^1{\rm{j}} = \left( {s_a^1 + s_b^1{\rm{i}} + s_c^1{\rm{j}}} \right)/s_u^1 $$ $$ u_F^2 = a_F^2 + b_F^2{\rm{i}} + c_F^2{\rm{j}} = \left( {s_a^2 + s_b^2{\rm{i}} + s_c^2{\rm{j}}} \right)/s_u^2 $$ 分别表示原因事件
${x_1}$ 和${x_2}$ 的事件状态联系数，1，2的编号用式中变量的上角标表示，x省略；F表示影响因素的集合；两事件的与关系用“$ \otimes $ ”表示，或关系用“$ \oplus $ ”表示，置于上角标。那么两原因事件以与或关系导致结果事件的状态联系数如下所示$$ \left\{ \begin{gathered} u_F^{1 \otimes 2} = u_F^1 \otimes u_F^2 = {a^1}{a^2} + \left( {{b^1}{a^2} + {b^1}{b^2} + {a^1}{b^2}} \right){\rm{i}} +\\ \left( {{a^1}{c^2} + {b^1}{c^2} + {c^1}{a^2} + {c^1}{b^2} + {c^1}{c^2}} \right){\rm{j}} \\ u_F^{1 \oplus 2} = u_F^1 \oplus u_F^2 = ({a^1}{a^2} + {a^1}{b^2} + {a^1}{c^2} + {b^1}{a^2} + {c^1}{a^2}) +\\ \left( {{b^1}{b^2} + {b^1}{c^2} + {c^1}{b^2}} \right){\rm{i}} + {c^1}{c^2}{\rm{j}} \end{gathered} \right. $$ (4) 式中：
$ u_F^{1 \otimes 2} $ 表示两原因事件以与关系导致结果事件的状态联系数；$ u_F^{1 \oplus 2} $ 表示两原因事件以或关系导致结果事件的状态联系数；由于都在因素集合F的作用下，因此F省略；$ \otimes $ 和$ \oplus $ 分别代表状态联系数的与或运算。由于
$ {a^1} = s_a^1/s_u^1,{b^1} = s_b^1/s_u^1,{c^1} = s_c^1/s_u^1 $ 且${a^2} = s_a^2/s_u^2, {b^2} = s_b^2/s_u^2,{c^2} = s_c^2/s_u^2$ ，代入式(4)得到另一种表达方式$$ \left\{ {\begin{array}{*{20}{c}} {u_F^{1 \otimes 2} = \dfrac{{\left[ s_a^1s_a^2 + \left( {s_b^1s_a^2 + s_b^1s_b^2 + s_a^1s_b^2} \right){\rm{i}} + \left( {s_a^1s_c^2 + s_b^1s_c^2 + s_c^1s_a^2 + s_c^1s_b^2 + s_c^1s_c^2} \right){\rm{j}} \right]}}{{(s_u^1s_u^2)}}} \\ {u_F^{1 \oplus 2} = \dfrac{{\left[ (s_a^1s_a^2 + s_a^1s_b^2 + s_a^1s_c^2 + s_b^1s_a^2 + s_c^1s_a^2) + \left( {s_b^1s_b^2 + s_b^1s_c^2 + s_c^1s_b^2} \right){\rm{i}} + s_c^1s_c^2{\rm{j}} \right]}}{{(s_u^1s_u^2)}}} \end{array}} \right. $$ (5) 式(5)使用了同异反状态占有的因素变化区域面积来表示结果事件的状态联系数，可得结果事件状态联系数的同异反分项系数：
$$ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} a_F^{1 \otimes 2} = s_a^1s_a^2/(s_u^1s_u^2), \\ b_F^{1 \otimes 2} = (s_b^1s_a^2 + s_b^1s_b^2 + s_a^1s_b^2)/s_u^1s_u^2, \\ c_F^{1 \otimes 2} = (s_a^1s_c^2 + s_b^1s_c^2 + s_c^1s_a^2 + s_c^1s_b^2 + s_c^1s_c^2)/s_u^1s_u^2 \\ \end{gathered} \\ \begin{gathered} a_F^{1 \oplus 2} = (s_a^1s_a^2 + s_a^1s_b^2 + s_a^1s_c^2 + s_b^1s_a^2 + s_c^1s_a^2)/s_u^1s_u^2, \\ b_F^{1 \oplus 2} = (s_b^1s_b^2 + s_b^1s_c^2 + s_c^1s_b^2)/s_u^1s_u^2, \\ c_F^{1 \oplus 2} = s_c^1s_c^2/(s_u^1s_u^2) \\ \end{gathered} \end{array}} \right. $$ (6) 因为
$ s_a^1 + s_b^1 + s_c^1 = s_u^1 $ 且$ s_a^2 + s_b^2 + s_c^2 = s_u^2 $ ，可得$ a_F^{1 \otimes 2} + b_F^{1 \otimes 2} + c_F^{1 \otimes 2} = 1 $ 且$ a_F^{1 \oplus 2} + b_F^{1 \oplus 2} + c_F^{1 \oplus 2} = 1 $ ，这满足构建联系数的基本假设。构建的结果事件状态联系数为$ u_F^{1 \otimes 2} = a_F^{1 \otimes 2} + b_F^{1 \otimes 2}i + c_F^{1 \otimes 2}j $ （与关系）及$u_F^{1 \oplus 2} = a_F^{1 \oplus 2} + b_F^{1 \oplus 2}i + c_F^{1 \oplus 2}j$ （或关系）。上述建立了系统故障演化过程中原因事件导致结果事件的事件状态联系数，这是使用联系数思想表示系统故障演化过程的关键。使用空间故障网络表示系统故障演化过程，抽象为由点线构成的拓扑结构。使用上述构造的事件状态联系数表示系统故障演化过程，首先构造原因事件状态联系数，通过同异反逻辑得到结果事件状态联系数，结果事件又作为下一个结果事件的原因事件，如此循环下去即可得到系统故障演化过程的最终结果事件的事件状态联系数，最终确定系统的安全性。
5. 实例分析
根据方法特点和以往研究实例，将实际系统中2个元件在不同因素影响下的故障发生概率分布作为研究对象，将其发生概率分布转化为事件发生状态分布，从而说明上述方法分析过程。
文献[16]给出了实例系统中一些元件随温度和湿度变化的故障概率变化过程，这里使用2个元件的故障情况作为原因事件来描述系统故障演化过程中与或逻辑关系导致结果事件的发生情况。原因事件的发生概率分布仍使用原有的故障概率随温度
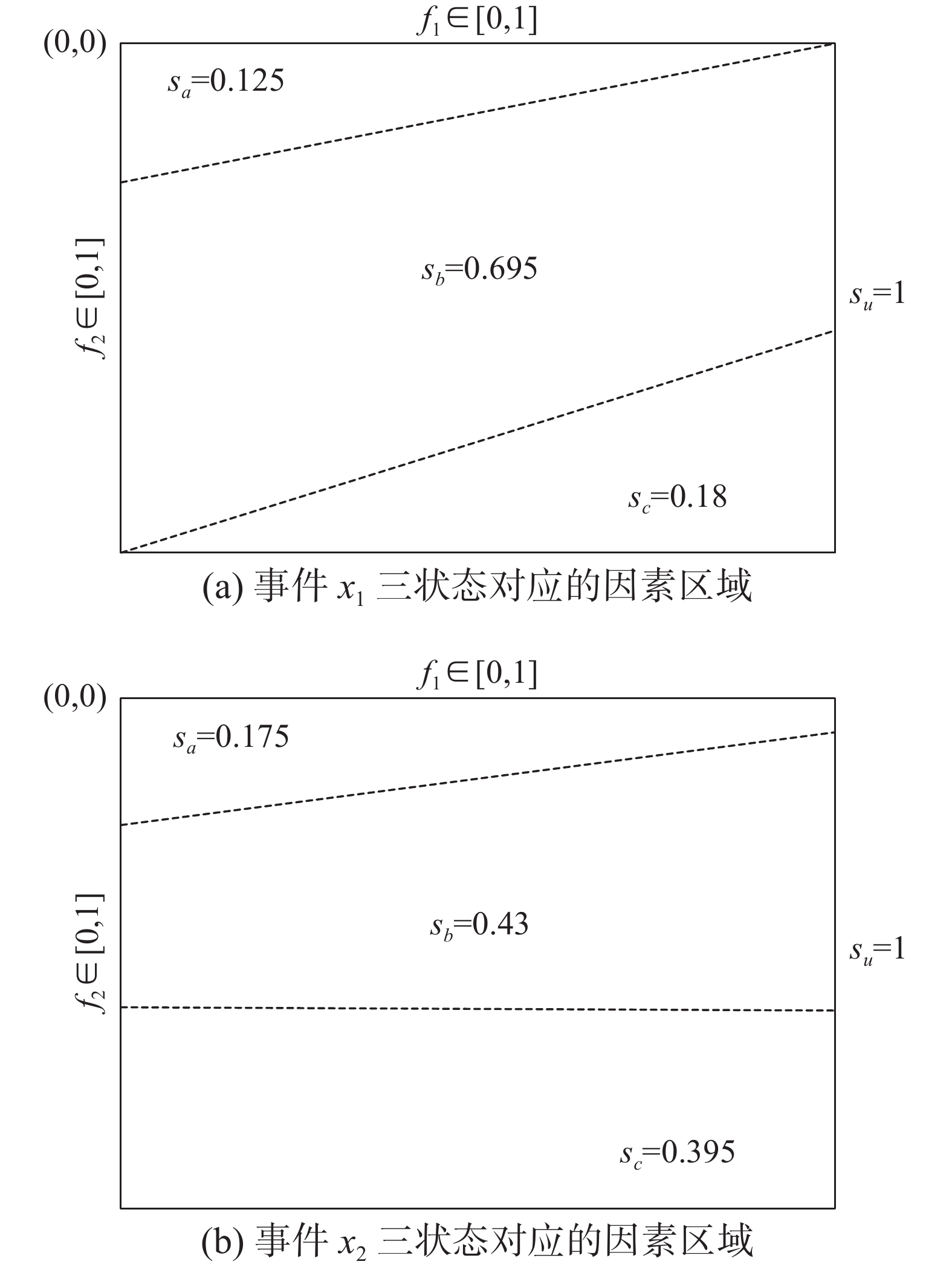
$ {f_1} $ 和湿度$ {f_2} $ 变化得到的特征函数$ p({f_1}) $ 和$ p({f_2}) $ ，由其得到事件发生概率分布$ P\left( F \right) $ 。设系统安全为目标刻画了安全、不确定和不安全3种状态，对应于$\lambda = \{ {\lambda _1}{\text{ = }}0,{\lambda _2}{\text{ = }}0.2,{\lambda _3}{\text{ = }}0.7,{\lambda _4}{\text{ = }}1 \}$ 。那么安全状态的故障概率$ \in \left[ {0,0.{\text{2}}} \right] $ 、不确定状态的故障概率$ \in \left( {0.{\text{2}},0.{\text{7}}} \right) $ 、不安全状态的故障概率$ \in \left[ {0.{\text{7}},{\text{1}}} \right] $ 。由于联系数的同异反状态分项系数是比例，两原因事件的影响因素和变化范围相同且故障概率的变化范围相同，因此可将因素变化区域归一化，$ {f_1} $ ，$ {f_2} $ $ \in \left[ {0,{\text{1}}} \right] $ ，$ P\left( F \right) $ $ \in \left[ {0,{\text{1}}} \right] $ 。化简后两原因事件状态区域如图2所示，并根据式(2)计算同异反状态对应的因素变化范围面积分别为$ {s_a} $ 、$ {s_b} $ 和$ {s_c} $ ，归一化的总面积$ {s_u} $ =1。
图 2 两原因事件状态联系数的同异反因素范围比例Fig. 2 Factor scope proportion of identical discrepancy contrary of state connection number of two cause events下载:
全尺寸图片
根据图2和式(3)得到两原因事件状态联系数分别为
$$ \begin{gathered} u_F^1 = 0.125 + 0.695i + 0.18j \\ u_F^2 = 0.175 + 0.43i + 0.395j \end{gathered}$$ 根据表1和表2及式(4)−(6)的推导过程，可得到结果事件状态联系数的同异反分项系数。如使用原因事件状态联系数的同异反分项系数则根据式（4）求解，如下所示
$$ \left\{ \begin{gathered} {a^1} = 0.125,{b^1} = 0.695,{c^1} = 0.18 \\ u_F^{1 \otimes 2} = a_F^{1 \otimes 2} + b_F^{1 \otimes 2}i + c_F^{1 \otimes 2}j =\\ 0.0219 + 0.4743i + 0.5038j \\ {a^2} = 0.175,{b^2} = 0.43,{c^2} = 0.395 \\ u_F^{1 \oplus 2} = a_F^{1 \oplus 2} + b_F^{1 \oplus 2}i + c_F^{1 \oplus 2}j =\\ 0.2782 + 0.6508j + 0.0710j \end{gathered} \right. $$ (7) 验证式(7)的正确性，其中
$a_F^{1 \otimes 2} + b_F^{1 \otimes 2} + c_F^{1 \otimes 2} = 1$ 且$ a_F^{1 \oplus 2} + b_F^{1 \oplus 2} + c_F^{1 \oplus 2} = 1 $ ，满足联系数分项系数要求；同时与关系使得结果事件同异反状态向着远离目标的方向发展，或关系使结果事件同异反状态向着目标方向发展，满足逻辑真值的设定。因此得到的结果事件状态联系数符合原设定要求。也可根据式（5）和式(6)使用原因事件状态联系数的同异反面积直接计算结果事件状态联系数的同异反分项系数，其结果与式(7)相同，只是形式不同，这里不再论述。图2中同异反状态对应的因素区域是经过化简的简单表示，实际研究中的事件发生概率分布较为复杂，难以使用图2中线性划分表示。应使用统计同异反状态对应点来确定面积，这里不是重点，故不做详述。
本研究分析了如下几个问题：1）利用联系数表示事件发生概率分布的同异反状态，及确定和不确定状态，避免了实际中难以构造事件发生概率分布的情况；2）研究了系统故障演化过程中事件间逻辑关系情况，针对同异反三状态给出了逻辑真值表；3）实现了系统故障演化过程中原因事件以与或逻辑关系导致结果事件的事件状态联系数构造，实现了系统故障演化基本单元的联系数表示。研究成果的应用不限于实例中结果事件状态联系数计算。由于集对分析理论的丰富内涵，可借助联系数的各种分析方法来研究系统故障演化过程。如集对势可分析事件发生状态的优势情况；偏联系数可分析异状态的变化情况；或研究因素对同异反状态变化的影响等。这些研究将在后继论文中呈现。
6. 结束语
1）研究认为系统故障演化过程的定性定量分析存在不足。现有方法研究系统故障演化过程是精确且确定的；抹杀了故障数据和结构的不确定性，因此需要表征不确定性的定性分析方法。建立了事件状态联系数，优点在于故障数据表示无需使用精确方式；可从确定不确定、同异反扩展到更多语义分级并使用多元联系数表示。
2）借助同异反逻辑真值表通过原因事件状态联系数确定了结果事件状态联系数，即确定语义状态和联系数分项系数。语义状态可划分为安全、不确定和不安全使用三元联系数或多元联系数表示。分项系数的本质是不同语义包含对象数量与总数量的比值，得到了原因事件状态联系数分项系数表示结果事件状态联系数分项系数的方法。通过实例演示了方法流程，其符合联系数同异反分项系数性质及同异反逻辑关系特征；最后说明了方法的不足和研究前景。
-
图 1 三状态的因素变化范围确定
Fig. 1 Determination of variation range of factors in three states
下载:
全尺寸图片
图 2 两原因事件状态联系数的同异反因素范围比例
Fig. 2 Factor scope proportion of identical discrepancy contrary of state connection number of two cause events
下载:
全尺寸图片
表 2 状态联系数或逻辑真值表
Table 2 Or logical truth table of state connection number
状态 1 i j 1 1 1 1 i 1 i i j 1 i j 表 1 状态联系数的与逻辑真值表
Table 1 And logical truth table of state connection number
状态 1 i j 1 1 i j i i i j j j j j 注：1为同/安全状态；i为异/不确定安全状态；j为反/不安全状态，同表2。 -
[1] 崔铁军, 李莎莎. 系统故障演化过程最终事件状态及发生概率研究[J]. 中国安全科学学报, 2021, 31(8): 1–7. doi: 10.16265/j.cnki.issn1003-3033.2021.08.001 CUI Tiejun, LI Shasha. Study on target event state and occurrence probability of system fault evolution process[J]. China safety science journal, 2021, 31(8): 1–7. doi: 10.16265/j.cnki.issn1003-3033.2021.08.001 [2] 崔铁军, 李莎莎. 针对不同故障数据特征的SFN最终事件发生概率计算方法研究[J]. 系统科学与数学, 2020, 40(11): 2151–2160. doi: 10.12341/jssms14025 CUI Tiejun, LI Shasha. Research on computing method of target event occurrence probability based on different fault data characteristics in SFN[J]. Journal of systems science and mathematical sciences, 2020, 40(11): 2151–2160. doi: 10.12341/jssms14025 [3] 韩平平, 童青洋, 杨为, 等. UHVDC系统换相失败故障过程分析及运行参数影响研究[J]. 电力系统保护与控制, 2021, 49(18): 25–34. doi: 10.19783/j.cnki.pspc.201498 HAN Pingping, TONG Qingyang, YANG Wei, et al. Analysis of the commutation failure process and a study on the influence of operation parameters on a UHVDC system[J]. Power system protection and control, 2021, 49(18): 25–34. doi: 10.19783/j.cnki.pspc.201498 [4] 马万鹏, 马吉胜, 曹立军, 等. 某火箭炮调炮过程中液压系统故障仿真研究[J]. 机床与液压, 2018, 46(17): 180–184. doi: 10.3969/j.issn.1001-3881.2018.17.040 MA Wanpeng, MA Jisheng, CAO Lijun, et al. Research on fault simulation of hydraulic system in a rocket Gun adjustment process[J]. Machine tool & hydraulics, 2018, 46(17): 180–184. doi: 10.3969/j.issn.1001-3881.2018.17.040 [5] 齐郑, 郑宇航, 杭天琦, 等. 基于暂态过程的非有效接地系统故障相辨识方法[J]. 电力系统自动化, 2018, 42(16): 155–160. doi: 10.7500/AEPS20171202001 QI Zheng, ZHENG Yuhang, HANG Tianqi, et al. Transient process based fault phase identification method for non-effectively grounded system[J]. Automation of electric power systems, 2018, 42(16): 155–160. doi: 10.7500/AEPS20171202001 [6] 蒋子涵, 方志耕, 杨晓钰, 等. 基于GERT网络的非等概率共因失效系统故障间隔期预测[J]. 系统工程, 2018, 36(7): 141–147. JIANG Zihan, FANG Zhigeng, YANG Xiaoyu, et al. MTBF prediction of non-equiprobable common cause failure systems based on GERT network[J]. Systems engineering, 2018, 36(7): 141–147. [7] 袁杰, 王福利, 王姝, 等. 基于D-S融合的混合专家知识系统故障诊断方法[J]. 自动化学报, 2017, 43(9): 1580–1587. doi: 10.16383/j.aas.2017.c160676 YUAN Jie, WANG Fuli, WANG Shu, et al. A fault diagnosis approach by D-S fusion theory and hybrid expert knowledge system[J]. Acta automatica sinica, 2017, 43(9): 1580–1587. doi: 10.16383/j.aas.2017.c160676 [8] 杨懿, 陈文丽, 王永鹏, 等. 基于Hilbert-Huang变换的液体火箭发动机涡轮泵故障分析[J]. 清华大学学报(自然科学版), 2022, 62(3): 540−548. YANG Yi, CHEN Wenli, WANG Yongpeng, et al. Fault analyses of liquid rocket engine turbopumps based on Hilbert-Huang transforms[J]. Journal of Tsinghua University (science and technology edition), 2022, 62(3): 540−548. [9] LI Lifan, YAO Lina. Incipient fault prediction based on generalised correntropy filtering for non-Gaussian stochastic systems[J]. International journal of systems science, 2021, 52(14): 3035–3043. doi: 10.1080/00207721.2021.1918281 [10] LIU Xianzeng. Vibration modelling and fault evolution symptom analysis of a planetary gear train for Sun gear wear status assessment[J]. Mechanical systems and signal processing, 2022, 166: 108403. doi: 10.1016/j.ymssp.2021.108403 [11] LEE Chunyao, HUNG C H. Feature ranking and differential evolution for feature selection in brushless DC motor fault diagnosis[J]. Symmetry, 2021, 13(7): 1291. doi: 10.3390/sym13071291 [12] LUNDGREN A, JUNG D. Data-driven fault diagnosis analysis and open-set classification of time-series data[J]. Control engineering practice, 2022, 121: 105006. doi: 10.1016/j.conengprac.2021.105006 [13] CHEN Xiaogang. Fault detection method and simulation based on abnormal data analysis in wireless sensor networks[J]. Journal of sensors, 2021, 2021: 1–11. [14] 崔铁军, 李莎莎. 少故障数据条件下SFEP最终事件发生概率分布确定方法[J]. 智能系统学报, 2020, 15(1): 136−143. CUI Tiejun, LI Shasha. Determination method of target event occurrence probability in SFEP under the condition of less fault data[J]. CAAI transactions on intelligent systems, 2020, 15(1): 136−143. [15] 赵克勤. 基于集对分析的对立分类、度量及应用[J]. 科学技术与辩证法, 1994, 11(2): 26–30. ZHAO Keqin. Classification, measurement and application of opposites based on set pair analysis[J]. Science technology and dialectics, 1994, 11(2): 26–30. [16] 崔铁军, 马云东. 多维空间故障树构建及应用研究[J]. 中国安全科学学报, 2013, 23(4): 32–37,62. doi: 10.16265/j.cnki.issn1003-3033.2013.04.018 CUI Tiejun, MA Yundong. Research on multi-dimensional space fault tree construction and application[J]. China safety science journal, 2013, 23(4): 32–37,62. doi: 10.16265/j.cnki.issn1003-3033.2013.04.018 [17] 崔铁军, 李莎莎, 韩光, 等. 基于信息增益的SFT中故障影响因素降维方法研究[J]. 安全与环境学报, 2018, 18(5): 1686–1691. doi: 10.13637/j.issn.1009-6094.2018.05.007 CUI Tiejun, LI Shasha, HAN Guang, et al. On the dimensional reduction method for the fault-affecting factors based on the information gain[J]. Journal of safety and environment, 2018, 18(5): 1686–1691. doi: 10.13637/j.issn.1009-6094.2018.05.007 [18] 崔铁军, 李莎莎. 系统运动空间与系统映射论的初步探讨[J]. 智能系统学报, 2020, 15(3): 445–451. CUI Tiejun, LI Shasha. Preliminary study of system movement space and system mapping theory[J]. CAAI transactions on intelligent systems, 2020, 15(3): 445–451. [19] 何华灿. 泛逻辑学理论: 机制主义人工智能理论的逻辑基础[J]. 智能系统学报, 2018, 13(1): 19–36. HE Huacan. Universal logic theory: logical foundation of mechanism-based artificial intelligence theory[J]. CAAI transactions on intelligent systems, 2018, 13(1): 19–36.
