近些年，迅猛发展的信息技术已经被广泛应用在企业和个人生活中，特别是互联网、云计算等技术的发展，促进了大数据产业的稳定增长。由于传感器和数据收集技术的发展，导致数据呈现多源化，如何挖掘多源数据中有价值的信息变得尤为重要。

根据信息的特征，可以把信息分为同构和异构两种数据类型。对于同构多源系统，将多源信息系统集成到单个信息表中是最常见的融合策略。Yu等^[1]针对模糊不完全信息系统提出了基于信息熵的多信息源融合为单信息源的方法；Xu等^[2]通过将每个对象的原始信息转化为三角模糊信息粒，将多个信息源融合为单个源；Sang等^[3]基于决策过程不确定性提出了包括3种多源决策方法，其中包括基于信息熵和均值法融合为单源信息系统的两种方法；Zhang等^[4]提出了多源同构数据的数据级融合模型，并采用无监督的属性选择方法来消除单源信息系统的冗余属性；Zhang等^[5]针对多源不完备区间值数据，提出了基于信息熵的信息融合方法以及4种以信息源和属性变化为特征的增量融合机制。

多粒度粗糙集理论为信息融合提供了一条新的途径。众所周知，人们解决问题时总是从不同的角度进行考虑，借鉴此思想，Qian等^[6]提出了多粒度粗糙集。此后引起大量学者对该模型进行了扩展研究。例如，Yang等^[7]从代价敏感的角度研究了多粒度粗糙集； Liu等^[8]提出了多粒度覆盖粗糙集模型；Qian等^[9]将多粒度思想与贝叶斯决策理论相结合，提出了多粒度决策理论粗糙集模型；Sun等^[10]从单论域扩充到双论域，提出双论域多粒度粗糙集；Liang等^[11]提出了广义优势关系多粒度直觉模糊粗糙集模型及规则获取方法；Yu等^[12]在多粒度近似空间中提出了一种双量化决策理论；Qian等^[13]提出了一个基于多粒度的序贯三支决策模型；Li等^[14]从粒计算的角度对多粒度数据分析方法进行综述；Zhang等^[15]提出了自适应多粒度决策理论粗糙集模型。

在信息融合领域，多粒度粗糙集模型利用一系列源产生的多粒度结构来实现多源信息融合。在这方面，已有许多成果呈现。例如，林国平等^[16]分析了多粒度粗糙集理论和证据理论之间的联系，并提出了基于多粒度视角下的D-S证据理论融合策略；Che等^[17]从多粒度的角度研究了多源信息系统的信息融合及相关数字特征；Sang等^[18]提出了多源信息系统中的广义多粒度双量化决策理论粗糙集模型；Che等^[19]基于多源粗糙近似和证据理论之间的关系，提出了多源粗糙近似下的属性集约简； Wang等^[20]提出了基于多粒度的多源数据知识获取方法；Yang等^[21]通过构造支持聚合算子和可能聚合算子，从多粒度的视角提出了多源决策信息融合方法；Luo等^[22]提出了多源覆盖信息系统下的加权广义多粒度粗糙集模型及其应用；Chu等^[23]针对混合信息系统，提出了多粒度优势粗糙概念及属性约简并应用于实际的中西医临床诊疗决策过程。

根据前文的描述，现有的多源信息融合方法主要分为两种类型。这两种方法都存在一定的局限性，第1种将多源信息表转化为到单信息表的方法，在融合的过程中会导致大量信息丢失；而第2种利用同一阈值的多粒度粗糙集模型进行信息融合的方法没有考虑多源信息的复杂性和多样性。在多源信息系统中，每个子信息系统的采集标准通常不相同，其含有的噪音数据也各不相同。因此，采用相同阈值进行融合多源信息并不合理。

本文的研究动机是获取不同信息源导出的知识粒度对应的阈值对。为此，本文将单参数决策理论粗糙集融入多粒度中，提出了一种广义自适应多粒度粗糙集模型。该模型利用单信息源导出的不可分辨关系构造知识粒度，并通过设置一个补偿系数 $\zeta $ 来自适应获得不同知识粒度的概率阈值对。之后设计了悲观−悲观自适应多粒度粗糙集、乐观−乐观自适应多粒度粗糙集、悲观−乐观自适应多粒度粗糙集和乐观−悲观自适应多粒粗糙集4种经典多粒度粗糙集模型，并讨论了该设计模型的相关性质。最后，在6个数据集上进行实验对比，验证了本模型能够较好实现多源信息融合。

1.   基础知识

本节介绍相关概念^[16,24-26]。

1.1   信息系统和Pawlak粗糙集

定义1^[24] 　信息系统 $ \left( I \right) $ 可用四元组 $(U,A,\{ {V_a}| a \in A\} , \{ {M_a}|a \in A\} )$ 表示，其中 $ U $ 是包含对象 ${x_1},{x_2},\cdots, {x_n}$ 的非空集合，也称为论域； $ A $ 为描述对象的非空有限属性集； $ {V_a} $ 表示属性 $ a $ 的取值，属性集 $ A $ 的取值集合可用 $ V = { \cup _{a \in A}}{V_a} $ 表示； $ M $ 是映射函数， $ {M_a}(x) = {V_a} $ 表示对象 $ x $ 在属性 $ a $ 的取值为 $ {V_a} $ 。信息系统可以简写为 $ (U,A,V,M) $ 。决策信息系统 $ (H) $ 是特殊的信息系统，其属性集 $ A $ 由条件属性集 $C$ 和决策属性集 $D$ 组成，因此也可以表达为 $ (U,C \cup D,V,M) $ 。

定义2^[24] 　设 $ I = (U,A,V,M) $ ，对于 $\forall E \subseteq A,$ $ {R_E} $ 被称为 $ U $ 上的等价关系，定义为

进而得到目标概念 $X(X \subseteq U)$ 关于 $ {R_E} $ 的下近似和上近似分别为

通过 $ {R_E} $ 可将论域 $ U $ 划分为多个块， $ {[x]_E} $ 则指含有对象 $ x $ 的划分块，也称为 $ x $ 的等价类。

1.2   决策理论粗糙集

在概率粗糙集的基础上，Yao等^[25]通过引入贝叶斯风险决策理论提出了决策理论粗糙集 $ ({\text{DTRS}}) $ 。

定义3　设 $ H = (U,C \cup D,V,M) $ ，对于任何一个属性子集 $E \subseteq C,$ 参数满足 $ 0 \leqslant \beta \leqslant \alpha \leqslant 1 $ ，关于目标概念 $X \subseteq U$ 的下近似与上近似分别定义为

式中： $ {[x]_E} $ 为 $E$ 下的等价类， $ P\left( {X|{{[x]}_E}} \right) $ 代表目标概念 $X$ 在 $ {[x]_E} $ 的条件概率，表示为 $P\left( {X|{{[x]}_E}} \right) = \dfrac{{\left|{{[x]}_E} \cap X\right|}}{{\left| {{[x]}_E}\right|}}$ 。

进而可以得到 $X \subseteq U$ 关于 $E$ 的正域、边界域和负域，定义为

在 $ {\text{DTRS}} $ 中，阈值参数是根据最小风险决策准则来获得的。在二分类问题中，假设对象集用 $U = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}$ 来表示；状态集为 $\Lambda = \{ X,\sim X\}$ ， 分别表示对象 $x$ 属于目标概念 $ X $ 和不属于目标概念 $X$ ；行为集表达为 $ a = \{ {a_P},{\text{ }}{a_B},{\text{ }}{a_N}\} $ ，其中 $ {a}_{P}$ 、 ${a}_{B} $ 和 ${a}_{N} $ 分别代表将对象 $x$ 划分到正域 $ \left( {{P_{{\text{OS}}}}} \right) $ 、边界域 $ \left( {{B_{{\text{ND}}}}} \right) $ 和负域 $ \left( {{N_{{\text{EG}}}}} \right) $ 的3种决策行为。 ${\lambda _{\Delta P}}(\Delta = P,B,N)$ 表示 $x$ 属于 $X$ 时采取行为 $\Delta $ 的损失，同理，当 $ x $ 不属于 $ X $ 时，采取行为 $ \Delta $ 的损失为 ${\lambda _{\Delta N}}$ 。则采取3种行为 $ {a}_{P}$ 、 ${a}_{B} $ 和 ${a}_{N} $ 的预期损失可分别表示为

根据贝叶斯风险决策理论，若损失函数满足 ${\lambda }_{PP}\leqslant{\lambda }_{BP} < {\lambda }_{NP}$ ， ${\lambda }_{NN}\leqslant{\lambda }_{BN} < {\lambda }_{PN}$ ，则可获得以下决策规则：

1)若 $P\left(X|{\left[x\right]}_{E}\right)\geqslant \alpha$ ，设定 $x \in {P_{{\text{OS}}}}(X)$ ，表示接受决策；

2)若 $\beta < P\left( {X|{{\left[ x \right]}_E}} \right) < \alpha$ ，设定 $ x \in {B_{{\text{ND}}}} $ ，表示延迟决策；

3)若 $P\left(X|{\left[x\right]}_{E}\right)\leqslant\beta$ ，设定 $x \in {N_{{\text{EG}}}}{\text{(}}X)$ ，表示拒绝决策。

其中阈值对 $(\alpha ,\beta )$ 为

1.3   广义多粒度粗糙集

定义4^[26] 　设信息系统 $ I = (U,A,V,M) $ ， ${E_i} \subseteq A, i = 1,2,\cdots,l(l \leqslant {2^{|A|}})$ 。对于 $X \subseteq U$ ， $\mathcal{S}_X^{{E_i}}(x)$ 称为 $ X $ 的支持特征函数，用于描述等价类 ${[x]_{{E_i}}}$ 和 $ X $ 的包含关系，定义为

定义5^[26] 　设信息系统 $ I = (U,A,V,M) $ ，参数满足 $0.5 \leqslant \beta < 1$ ， ${E_i} \subseteq A,i = 1,2,\cdots,l(l \leqslant {2^{|A|}})$ ， $\mathcal{S}_X^{{E_i}}(x)$ 称为 $ X $ 的支持特征函数。对于 $ X \subseteq U $ ， $ X $ 关于 $\displaystyle\sum\limits_{i = 1}^l {{E_i}}$ 的下近似和上近似分别定义为

1.4   多源信息系统

定义6^[16] 　多源信息系统 $ ({M_S}) $ 由多个信息系统 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ 组成。对于任何 $ i \in s $ ， $ {I_i} $ 表示 $ {M_S} $ 中第 $ i $ 个信息系统。其中论域 $ U $ 是有限非空对象集合； $ {A_i} $ 表示 $ {I_i} $ 下的属性集合； $ {M_i} $ 是 $ {I_i} $ 下的映射函数，用来表示对象和属性之间的关系， $ {V_i} $ 是属性集的值域。则多源信息系统可定义为

特殊地，当 $ {A_i} = {C_i} \cup D $ 时，多源信息系统也称为多源决策信息系统 $ ({M_H}) $ 。其由多个决策信息系统 $ {H_i} = \left( {U,{C_i} \cup D,{V_i},{M_i}} \right) $ 组成，对于任何 $ i \in s $ ， $ {H_i} $ 表示 $ {M_H} $ 中第 $ i $ 个决策信息系统。 $ D $ 表示决策属性， $U/D = \left\{ {{D_1},{\text{ }}{D_2},{\text{ }}\cdots,{\text{ }}{D_m}} \right\}$ 为对 $ U $ 的一个划分，则多源决策信息系统可定义为

2.   广义自适应多粒度粗糙集模型

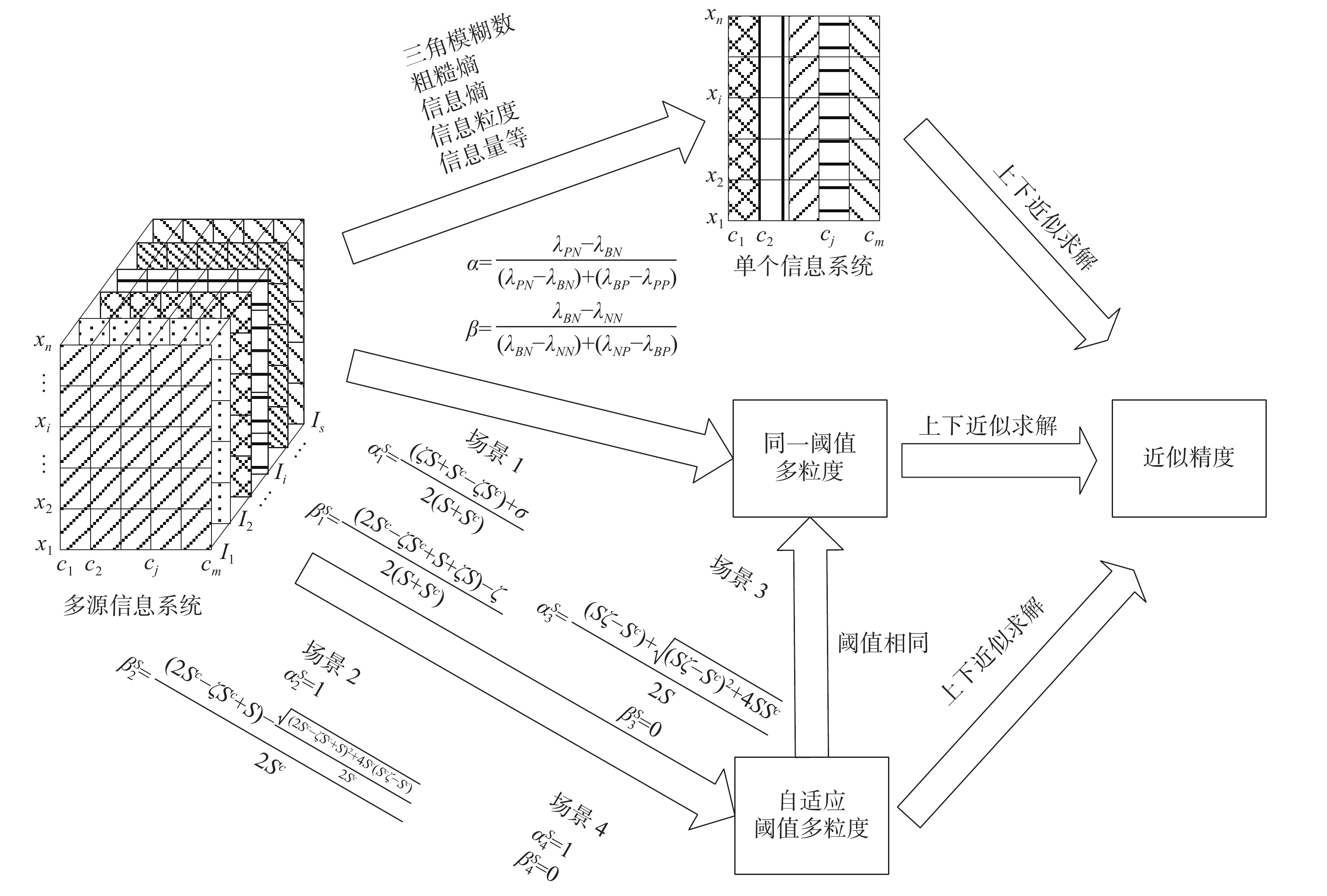
从不同视角和层次采集的多源数据的标准不同，数据的准确性和完备性也不同，因此对多源数据生成的知识粒度采用相同的阈值来获取决策规则并不妥当。为解决这个问题，本文提出了一个用于多源信息系统的广义自适应多粒度粗糙集模型，该模型与传统的两个融合方法对比如图1所示。首先，本文介绍如何在计算3个区域时自适应获得阈值对的方法。

图  1  信息融合方法对比

Fig.  1  Comparison of information fusion methods

下载: 全尺寸图片

2.1   自适应阈值对获取

经典决策理论模型需要预设多个损失参数才能获得阈值对 $ (\alpha, \beta) $ ，在实际中过于复杂，且很难确定参数值。为此，Suo等^[27]提出单参数决策理论粗糙集，只需要预设单个参数，即可获得数据驱动的损失函数矩阵，并计算得到阈值对 $ (\alpha, \beta) $ 。假设 $ H = (U,C \cup D,V,M) $ ，条件属性子集 $E \subseteq C$ ，记 $\Gamma = \{ X,{X^c}\} $ 表示对象状态集，表1为数据驱动的损失函数。其中， $ \zeta $ $ \left( {0 < \zeta \leqslant 1} \right) $ 称为补偿系数，表示对中立的容忍程度。当 $ \left| X \right| \ne 0 $ 和 $ X \cup {X^c}{\text{ = }}U $ 时， $S\left( {X|{{[x]}_E}} \right) = \dfrac{{\left| {X \cap {{[x]}_E}} \right|}}{{\left| X \right|}}$ ， ${S^c}\left( {X|{{[x]}_E}} \right) = \dfrac{{\left| {{X^c} \cap {{[x]}_E}} \right|}}{{\left| X \right|}} $ ，分别代表 $ {[x]_E} $ 中 $ X $ 的重要性和 $ {X^c} $ 的重要性，记 $S = S\left( {X|{{[x]}_E}} \right)$ ， ${S^c} = {S^c}\left( {X|{{[x]}_E}} \right)$ 。

根据表1和式(1)，则新的阈值参数 $\alpha $ 和 $\beta $ 可从以下4种场景计算得到:

1)当 $ P - \zeta > 0 $ 且 $ P + \zeta < 1 $ ，有 $ {\lambda _{BP}} \ne 0 $ 且 $ {\lambda _{BN}} \ne 0 $ ，则阈值参数定义为

式中：

2)当 $ P \leqslant \zeta $ 且 $ P + \zeta < 1 $ ，有 $ {\lambda _{BP}} = 0 $ 且 $ {\lambda _{BN}} \ne 0 $ ，则阈值参数定义为

3)当 $P - \zeta > 0$ 且 $P + \zeta \geqslant 1$ ，有 ${\lambda _{BP}} \ne 0$ 且 ${\lambda _{BN}} = 0$ ，则阈值参数定义为

4)当 $ P \leqslant \zeta $ 且 $ P + \zeta \geqslant 1 $ ，有 $ {\lambda _{BN}} = 0 $ 且 $ {\lambda _{BP}} = 0 $ ，则阈值参数定义为

通过对4种场景下阈值参数 $\alpha $ 和 $\beta $ 求解的描述，我们知道以上两个参数由 $ S $ 、 $ {S^c} $ 和 $\zeta $ 共同决定，因此可表示为 $ {\alpha ^S} = \phi (\zeta ,S,{S^c}) $ ， $ {\beta ^S} = \nu (\zeta ,S,{S^c}) $ ，其中 ${\alpha ^s} = \left\{ {\alpha _1^s,\alpha _2^s,\alpha _3^s,\alpha _4^s} \right\}$ ， ${\beta ^s} = \left\{ {\beta _1^s,\beta _2^s,\beta _3^s,\beta _4^s} \right\}$ 。又因为 $ S $ 、 $ S^{c} $ 只取决于数据本身，则参数又可记为 $ {\alpha ^S} = \phi (\zeta ) $ ， ${\beta ^S} = \nu (\zeta ) $ 。进而单参数决策理论粗糙集模型相应的正域、边界域和负域可表示为

式中： $ 0 < \zeta \leqslant 1 $ ，参数 ${\alpha ^S}$ 和 ${\beta ^S}$ 由上述4种场景可计算得到。由文献[27]的理论4和理论5知道， $0 \leqslant {\beta ^S} < {\alpha ^S} \leqslant 1$ 恒成立。此外，当 $ 0 < {\zeta _2} \leqslant {\zeta _1} \leqslant 1 $ 时，有 $0 \leqslant {\beta ^S}({\zeta _1}) \leqslant {\beta ^S}({\zeta _2}) < {\alpha ^S}({\zeta _2}) \leqslant {\alpha ^S}({\zeta _1})$ 。

2.2   广义自适应多粒度粗糙集模型

多源信息系统本质上是由多个单源信息系统组成，每个源诱导的不可分辨关系都会产生知识粒度。通过采用上节对知识粒度求解阈值的方法，并结合多粒度的思想，我们提出广义自适应多粒度粗糙集模型来实现多源信息系统的知识获取。

定义7　称 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统， ${I_i} = \left( {U,{A_i},{V_i},{M_i}} \right)$ ，参数满足 $ 0 < \zeta \leqslant 1$ ， $ 0 < \varphi \leqslant 1 $ ， $ 0 < \gamma \leqslant 1 $ 。在广义自适应多粒度粗糙集模型MS-AMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的下近似和上近似分别定义为

式中： $ F_X^{{I_i},\zeta } $ 和 $R_X^{{I_i},\zeta }$ 分别为 $ X $ 的支持特征函数和相关特征函数，定义为

其中： $ \zeta $ 称为补偿系数； $\varphi ，\gamma$ 是近似参数。 $[x]_{I_i}$ 表示对象 $ x $ 在信息源 $ {I_i} $ 下所有属性形成的类。 $P(X|{[x]_{{I_i}}})$ 表示条件概率。 ${\alpha _i}^\zeta = \left\{ {\alpha _{i1}^s,\alpha _{i2}^s,\alpha _{i3}^s,\alpha _{i4}^s} \right\}$ ， ${\beta _i}^\zeta = \{ \beta _{i1}^s, \beta _{i2}^s, \beta _{i3}^s, \beta _{i4}^s\}$ 代表知识粒度上的阈值，可由式（2）~（5）得到。

容易看出，广义自适应多粒度粗糙集模型每个知识粒度的对应的阈值都是不尽相同，而且是由数据驱动而自适应得到的。此外，其还可以通过改变两个近似参数 $ \varphi $ 、 $ \gamma $ 调整模型的近似范围，在实际融合过程中更具有灵活性。

定义8　称 $ {M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\} $ 是多源信息系统， $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ，参数满足 $ 0 < \zeta \leqslant 1 $ ， $ 0 < \varphi \leqslant 1 $ ， $ 0 < \gamma \leqslant 1 $ 。在广义自适应多粒度粗糙集模型MS-AMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的正域、边界域和负域分别为

广义自适应多粒度粗糙集模型的有效性通常可以由多源决策信息系统中的融合近似精度来衡量。

定义9　称 ${M_H} = \left\{ {{H_1},{H_2},\cdots,{H_s}} \right\}$ 是多源决策信息系统， $ {H_i} = \left( {U,{C_i} \cup D,{V_i},{M_i}} \right) $ ，参数满足 $ 0 < \zeta \leqslant 1$ ， $0 < \varphi \leqslant 1$ ， $ 0 < \gamma \leqslant 1 $ ，决策等价类 $ U/D $ $= \{ {D_1},{D_2},\cdots,{D_m}\}$ ，对于 $\forall {D_j} \in U/D(j = 1,2,\cdots,m)$ ，融合近似精度定义为

接下来我们设计了算法1来求解自适应多粒度粗糙集模型融合近似精度。

算法1　MS-AMG融合近似精度求解算法

输入　补偿系数 $ \zeta $ ，参数 $ \varphi、\gamma $ 和多源决策信息系统 ${M_H} = \left\{ {{H_1},{H_2},\cdots,{H_s}} \right\}$ ；

输出　融合的近似精度 $ \alpha _{{\text{AMG}}}^\zeta (U/D) $ 。

1）for 每一个 $ {D_j} \subseteq U/D $ do

2）{for 每一个 $ {x_i} \in U $ do

3）{初始化 $ F\left( i \right) = 0,{\text{ }}R\left( i \right) = 0 $ ；

4）{for 每一个 $ {H_k} \in {M_H} $ do

5） 计算对象 $ {x_i} $ 关于决策类 $ {D_j} $ 的条件概率 $ P({D_j}|{[x]_{{H_k}}}) $ 及阈值对 $ {\alpha _k}^\zeta ,{\beta _k}^\zeta $ ；

6） 若 $ P({D_j}|{[x]_{{H_k}}}) \geqslant {\alpha _k}^\zeta $ ，则

7） 若 $P({D_j}|{[x]_{{H_k}}}) > {\beta _k}^\zeta $ ，则

8） 若 $\dfrac{{F(i)}}{s} \geqslant \varphi$ ，则将对象 $ x_{i} $ 划入决策类 $ D_{j} $ 的下近似 $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta ({D_j})$ ；

9） 若 $\dfrac{{R(i)}}{s} \geqslant \gamma$ ，则将对象 $ x_{i} $ 划入决策类 $ D_{j} $ 的上近似 $\overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta ({D_j})$ ;}

10）返回融合近似精度

算法1的时间复杂度为 $ O(|U| \times m \times s) $ ，其中 $ |U| $ 为对象个数， $ m $ 是决策数量， $ s $ 表示信息源的数量。

2.3   经典自适应多粒度粗糙集模型

通过调整参数 $ \varphi $ 、 $ \gamma $ 的取值，广义自适应多粒度粗糙集可以转换为4种经典的多粒度粗糙集模型。根据上下近似采取的策略，可分为悲观−悲观自适应多粒度粗糙集模型MS-PPAMG、乐观−乐观自适应多粒度粗糙集模型MS-OOAMG、悲观−乐观自适应多粒度粗糙集模型MS-POAMG和乐观−悲观自适应多粒度粗糙集模型MS-OPAMG。

假设 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统，其中 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ， $ 0 < \zeta \leqslant 1$ ，则上述4种多粒度粗糙集模型的定义如下。

定义10　在悲观−悲观自适应多粒度粗糙集模型MS-PPAMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的下近似和上近似分别定义为

MS-PPAMG模型的正域、边界域和负域的表达与MS-AMG模型相同。

定义11　在乐观−乐观自适应多粒度粗糙集模型MS-OOAMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的下近似和上近似分别定义为

MS-OOAMG模型的正域、边界域和负域的表达与MS-AMG模型相同。

定义12　在悲观−乐观自适应多粒度粗糙集模型MS-POAMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的下近似和上近似分别定义为

MS-POAMG模型的正域、边界域和负域的表达与MS-AMG模型相同。

定义13　在乐观−悲观自适应多粒度粗糙集模型MS-OPAMG中，对任意的 $X \subseteq U$ ， $X$ 关于 $ {M_S} $ 的下近似和上近似分别定义为

MS-OPAMG模型的正域、边界域和负域的表达与MS-AMG模型相同。然而，MS-OPAMG在某些情况下是不符合粗糙集理论的。例如，假如存在 $ {I_i},{I_j} \in {\text{ }}{M_S} $ ，如果对象 $ x $ 有 $P(X|{[x]_{{I_i}}}) \geqslant {\alpha _i}^\zeta $ ，且 $P(X|{[x]_{{I_j}}}) \leqslant {\beta _j}^\zeta $ ，则 ${F}_{X}^{{I}_{i},\zeta }(x)=1,{R}_{X}^{{I}_{j},\zeta }(x)=0$ 。根据定义13知， $x\in \underline{{M}_{S}-{O}_{\text{PAMG}}}{ }^{\zeta }(X)$ ，并且 $ x\notin \overline{{M}_{S}-{O}_{\text{PAMG}}}{ }^{\zeta }(X) $ 。故 $ \overline{{M}_{S}-{O}_{\text{PAMG}}}{ }^{\zeta }(X)\supseteq $ $\underline{{M}_{S}-{O}_{\text{PAMG}}}{ }^{\zeta }(X)$ 不成立。

根据定义10~13可知，给定不同的近似参数，所提出的广义自适应多粒度粗糙集模型能够退化为经典策略的自适应多粒度粗糙集模型。这也体现所提模型具有灵活性，能适应不同的场景。

2.4   广义自适应多粒度粗糙集模型的相关性质

这部分将介绍广义自适应多粒度粗糙集模型常见性质以及不同自适应多粒度粗糙集模型之间的关系。

定理1　称 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统，其中 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ， $ 0 < \zeta \leqslant 1$ ，如果 $ 0 < \varphi \leqslant 1 $ ， $ 0 < \gamma \leqslant 1 $ ，对于任何 $ X \subseteq U $ ，则广义自适应多粒度粗糙集满足以下常见结论：

1) $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta ( \text{Ø}) = \overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta (X) = \text{Ø}$ ；

2) $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (X) \subseteq X $ ；

3) $\overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta (X) \subseteq X $ ；

4) $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (U) = \overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta (U) = U $ 。

证明　根据定义7，显然结论1)~3)成立。对于结论4， $ \forall x \in U $ ，有 $P(U|{[x]_{{I_i}}}) = 1$ 。则对于 $ \forall {I_i} \in {M_S} $ ，有 $ F_X^{{I_i},{\zeta _1}}\left( x \right) = 1 \geqslant {\alpha _i}^\zeta $ ，进而可以得出

即 $ x \subseteq \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (U) $ ，可证的 $ \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (U) = U $ 。类似地，我们也能证明 $ \overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta (U) = U $ ，则定理1可证。

定理2　称 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统，其中 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ， $ 0 < \zeta \leqslant 1$ ，如果 $ 0 < {\varphi _1} \leqslant {\varphi _2} \leqslant 1 $ ， $ 0 < {\gamma _1} \leqslant {\gamma _2} \leqslant 1 $ ，对于任何 $ X \subseteq U $ ，则以下结论成立：

1) $\underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _1}}^\zeta (X) \supseteq \underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _2}}^\zeta (X) $ ；

2) $\overline {{M_S} - {A_{{\text{MG}}}}} _{{\gamma _1}}^\zeta (X) \supseteq \overline {{M_S} - {A_{{\text{MG}}}}} _{{\gamma _2}}^\zeta (X) $ 。

证明　1)对于 $ \forall x \in \underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _2}}^\zeta (X) $ ，由定义7可知

若存在 $ 0 < {\varphi _1} \leqslant {\varphi _2} \leqslant 1 $ ，则有

即 $ x \subseteq \underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _1}}^\zeta (X) $ ，从而可证 $\underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _1}}^\zeta (X) \supseteq \underline {{M_S} - {A_{{\text{MG}}}}} _{{\varphi _2}}^\zeta (X)$ 。

2）结论2)证明相似。

定理3　称 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统，其中 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ，对于任何 $X \subseteq U$ ，如果 $0 < {\zeta }_{2}\leqslant {\zeta }_{1}\leqslant 1,0 < \varphi \leqslant 1,0 < \gamma \leqslant 1$ ，则以下结论成立：

1) $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^{{\zeta _1}}(X) \subseteq \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^{{\zeta _2}}(X) $ ；

2) $\overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^{{\zeta _1}}(X) \supseteq \overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^{{\zeta _2}}(X) $ ；

3) $\alpha _{{\text{AMG}}}^{{\zeta _1}}(X) \leqslant \alpha _{{\text{AMG}}}^{{\zeta _2}}(X) $ 。

证明　1)对于 $ \forall x \in \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^{{\zeta _1}}(X) $ ，由定义7可知

若存在 $ {\zeta _2} \leqslant {\zeta _1} $ ，则有 $ \alpha _i^{{\zeta _1}} \geqslant \alpha _i^{{\zeta _2}} $ 。因此对于 $ \forall {I_i} \in {M_S} $ ，有 $ F_X^{{I_i},{\zeta _1}}\left( x \right) \leqslant $ $ F_X^{{I_i},{\zeta _2}}\left( x \right) $ ，进而可以得出

即 $ x \subseteq \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^{{\zeta _2}}(X) $ ，则结论1可证明。

2）结论2、3证明相似。

定理4　称 ${M_S} = \left\{ {{I_1},{I_2},\cdots,{I_s}} \right\}$ 是多源信息系统，其中 $ {I_i} = \left( {U,{A_i},{V_i},{M_i}} \right) $ ， $ 0 < \zeta \le 1 $ ， $ 0 < \varphi \leqslant 1, $ $ 0 < \gamma \leqslant 1 $ ，对于任何 $ X \subseteq U $ ，以下结论成立。

1) ${\underline {{M_S} - {P_{{\text{PAMG}}}}} ^\zeta }(X) = {\underline {{M_S} - {P_{{\text{OAMG}}}}} ^\zeta }(X) \subseteq $ 　　　 $\underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (X) \subseteq {\underline {{M_S} - {O_{{\text{OAMG}}}}} ^\zeta }(X) $ ；

2) ${\overline {{M_S} - {P_{{\text{PAMG}}}}} ^\zeta }(X) \subseteq \overline {{M_S} - {A_{{\text{MG}}}}} _\gamma ^\zeta (X) \subseteq $ 　　　 $ {\overline {{M_S} - {O_{{\text{OAMG}}}}} ^\zeta }(X) = {\overline {{M_S} - {P_{{\text{OAMG}}}}} ^\zeta }(X) $ 。

证明　1)对于 $ x \in \underline {{M_S} - {P_{{\text{PAMG}}}}} (X) $ ，由定义10知

则 $ x \in \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (X) $ ，即

${\underline {{M_S} - {P_{{\text{PAMG}}}}} ^\zeta }(X) \subseteq \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (X)$ ；

同理，当 $ x \in \underline {{M_S} - {A_{{\text{MG}}}}} _\varphi ^\zeta (X) $ 时，有

即 $ x \in {\underline {{M_S} - {O_{{\text{OAMG}}}}} ^\zeta }(X) $ ，则结论1可证明。

2）结论2证明类似。

2.5   案例分析

本节将用一个癌症诊断案例来解释广义自适应多粒度粗糙集的应用。假设表2是某医院癌症诊断的多源决策信息表 $ {M_H} $ 。 $ {M_H} = {\text{\{ }}{H_1},{H_2},{H_3}{\text{\} }} $ ，其中 $ {H_i}(i = 1,2,3) $ 分别表示检测团块厚度、细胞大小的均匀性和细胞形状的均匀性得到的单源决策信息系统， $U = \left\{ {{x_1},{x_2},\cdots,{x_{10}}} \right\}$ 是一个包含了10个病人的集合， $ d $ 是决策属性，表示病人是否诊断为癌症。

首先，分别通过3个单源决策信息系统的条件属性集 ${C_i}$ 和决策属性 $ d $ 对 $U$ 进行划分，结果如下：

然后计算 $ {[x]_{{H_i}}} $ 相对于决策属性 $ {D_0}、{D_1} $ 的条件概率 $ {P_0} $ 和 $ {P_1} $ ，如表3所示。

令 $ \zeta {\text{ = }}0.3 $ ，然后根据式（2）到（5）计算 ${[x]_{{{\rm{DIS}}_i}}}$ 相对于决策 $ {D_0}、{D_1} $ 的阈值对，分别如表4和表5所示。

表  4  决策 $ {D_0} $ 上的阈值对

Table  4  A pair of thresholds of $ {D_0} $

$ U $	${H_1}$	${H_2}$	${H_3}$
	$ ({a_1},{b_1}) $	$ ({a_2},{b_2}) $	$ ({a_3},{b_3}) $
$ x_{1} $	(0.71，0.29 )	(0.71，0.29 )	(0.60，0.19 )
$ x_{2} $	(0.71，0.29 )	(0.71，0.29 )	(0.60，0.19 )
$ x_{3} $	(0.71，0.29 )	(1.00，0.47 )	(0.81，0.40 )
$ x_{4} $	(1.00，0.44 )	(0.60，0.19 )	(1.00，0.44 )
$ x_{5} $	(1.00，0.44 )	(1.00，0.47 )	(0.81，0.40 )
$ x_{6} $	(0.71，0.29 )	(0.60，0.19 )	(0.60，0.19 )
$ x_{7} $	(0.71，0.29 )	(1.00，0.47 )	(0.81，0.40 )
$ x_{8} $	(1.00，0.44 )	(1.00，0.47 )	(1.00，0.44 )
$ x_{9} $	(0.71，0.29 )	(1.00，0.47 )	(1.00，0.44 )
$ x_{10} $	(1.00，0.44 )	(0.60，0.19 )	(1.00，0.44 )

表  5  决策 $ {D_1} $ 上的阈值对

Table  5  A pair of thresholds of $ {D_1} $

$ U $	${H_1}$	${H_2}$	${H_3}$
	$ ({a_1},{b_1}) $	$ ({a_2},{b_2}) $	$ ({a_3},{b_3}) $
$ x_{1} $	(0.71，0.29 )	(0.71，0.29 )	(0.81，0.40 )
$ x_{2} $	(0.71，0.29 )	(0.71，0.29 )	(0.81，0.40 )
$ x_{3} $	(0.71，0.29 )	(0.53，0.00 )	(0.60，0.19 )
$ x_{4} $	(0.56，0.00 )	(0.81，0.40 )	(0.56，0.00 )
$ x_{5} $	(0.56，0.00 )	(0.53，0.00 )	(0.60，0.19 )
$ x_{6} $	(0.71，0.29 )	(0.81，0.40 )	(0.81，0.40 )
$ x_{7} $	(0.71，0.29 )	(0.53，0.00 )	(0.60，0.19 )
$ x_{8} $	(0.56，0.00 )	(0.53，0.00 )	(0.56，0.00 )
$ x_{9} $	(0.71，0.29 )	(0.53，0.00 )	(0.56，0.00 )
$ x_{10} $	(0.56，0.00 )	(0.81，0.40 )	(0.56，0.00 )

1）在 $ {M_H} $ 中，令 $\varphi = 0.6,\gamma = 0.2$ ，则MS-AMG模型在每个决策类的下近似和上近似为

对应融合近似精度为

2）在 $ {M_H} $ 中，则MS-PPAMG模型在每个决策类的下近似和上近似分别为

对应融合近似精度为

3）在 $ {M_H} $ 中，则MS-OOAMG模型在每个决策类的下近似和上近似分别为

对应融合近似精度为

4）在 $ {M_H} $ 中，则MS-POAMG模型在每个决策类的下近似和上近似分别为

对应融合近似精度为

5）在 $ {M_H} $ 中，则根据MS-OPAMG模型在每个决策类的下近似和上近似分别为

对应融合近似精度为

通过分析以上结果，所提出的广义自适应多粒度粗糙集MS-AMG可以自适应求得知识粒度 $ {[x]_{{H_i}}} $ 的阈值，相对于取相同阈值的多粒度决策理论粗糙集模型来说更具有合理性。并且与采取4种经典策略的多粒度粗糙集模型相比，模型MS-AMG在决策 $ {D_i}(i = 1,2) $ 的上下近似显然有

此外，对于MS-OPAMG模型，其关于决策 $ {D_i} $ 的下近似并不包含在上近似内，导致其融合近似精度也大于1，这种情况在粗糙集理论中并不合理，而MS-AMG模型可以通过控制参数 $\varphi 、\gamma$ 范围来避免这种情况发生。

3.   实验

为了进一步验证广义自适应多粒度粗糙集模型的有效性，本节选择6个UCI数据集进行实验分析，数据集详细信息如表6所示。在本文中，算法是使用软件IntelliJ IDEA来实现的，实验环境为PC机，其配置为Intel(R) Core(TM) i5-6300HQ @ 2.30 GHz，20 GB内存，Windows 10操作系统。

多源数据集在生活中并不常见，为了建立多源数据集，我们将原始数据添加噪声的方式生成包含15个信息源的多源数据集，添加噪声来扩充为多源数据集的方法可参考文献[21]。

3.1   本文模型与不同集成单源的模型对比分析

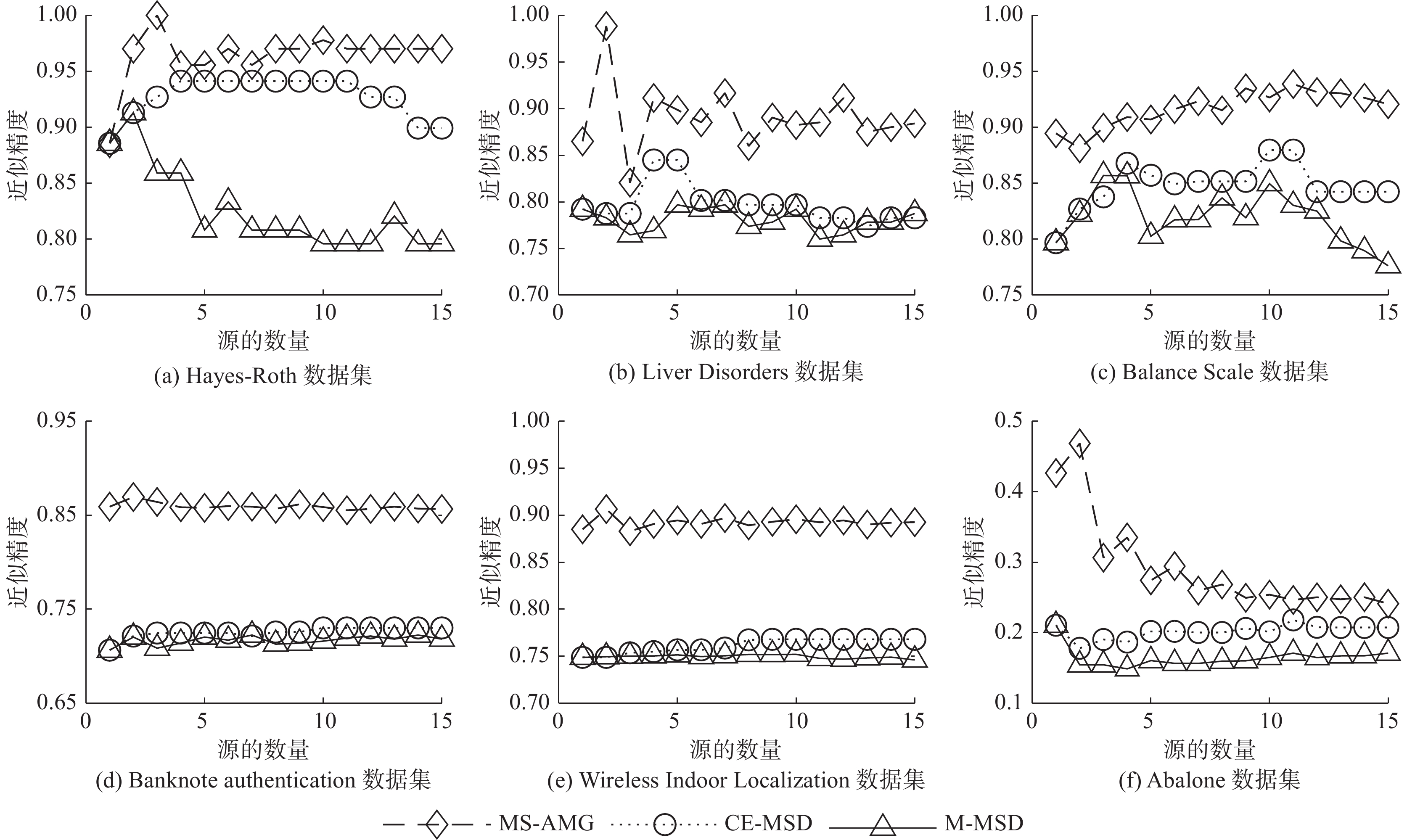
本节主要对比MS-AMG模型与两种集成为单源信息系统的模型之间的融合近似精度，图2显示了3种模型在不同数据集下近似精度的实验结果。

图  2  模型MS-AMG、CE-MSD和M-MSD的近似精度对比

Fig.  2  Comparison of approximation accuracy between MS-AMG、CE-MSD and CE-MSD models

下载: 全尺寸图片

其中，CE-MSD(conditional entropy multi- source decision method) ^[3]是基于条件熵将多源信息系统集成为单源信息系统的模型，M-MSD (mean multi-source decision method) ^[3]是基于均值法合成单源信息系统的模型。MS-AMG的补偿系数设置 $ \zeta {\text{ = }}0.1 $ 。通过实验结果发现，MS-AMG可以在不同的数据集上设置合适的近似参数，使得其融合效果都好于模型CE-MSD和M-MSD。参数具体设置如表7所示。例如，对于“Hayes-Roth”数据集近似参数设置为 $\varphi = 0.3$ 和 $\gamma = 0.7$ ，其融合效果会高于其他两种模型，这也反应了该数据集生成的多个信息系统差异性很大。

由此可知，MS-AMG模型可以针对不同的多源信息系统采取不同的近似参数，从而达到良好的融合效果。

3.2   本文模型与不同多粒度融合模型的对比分析

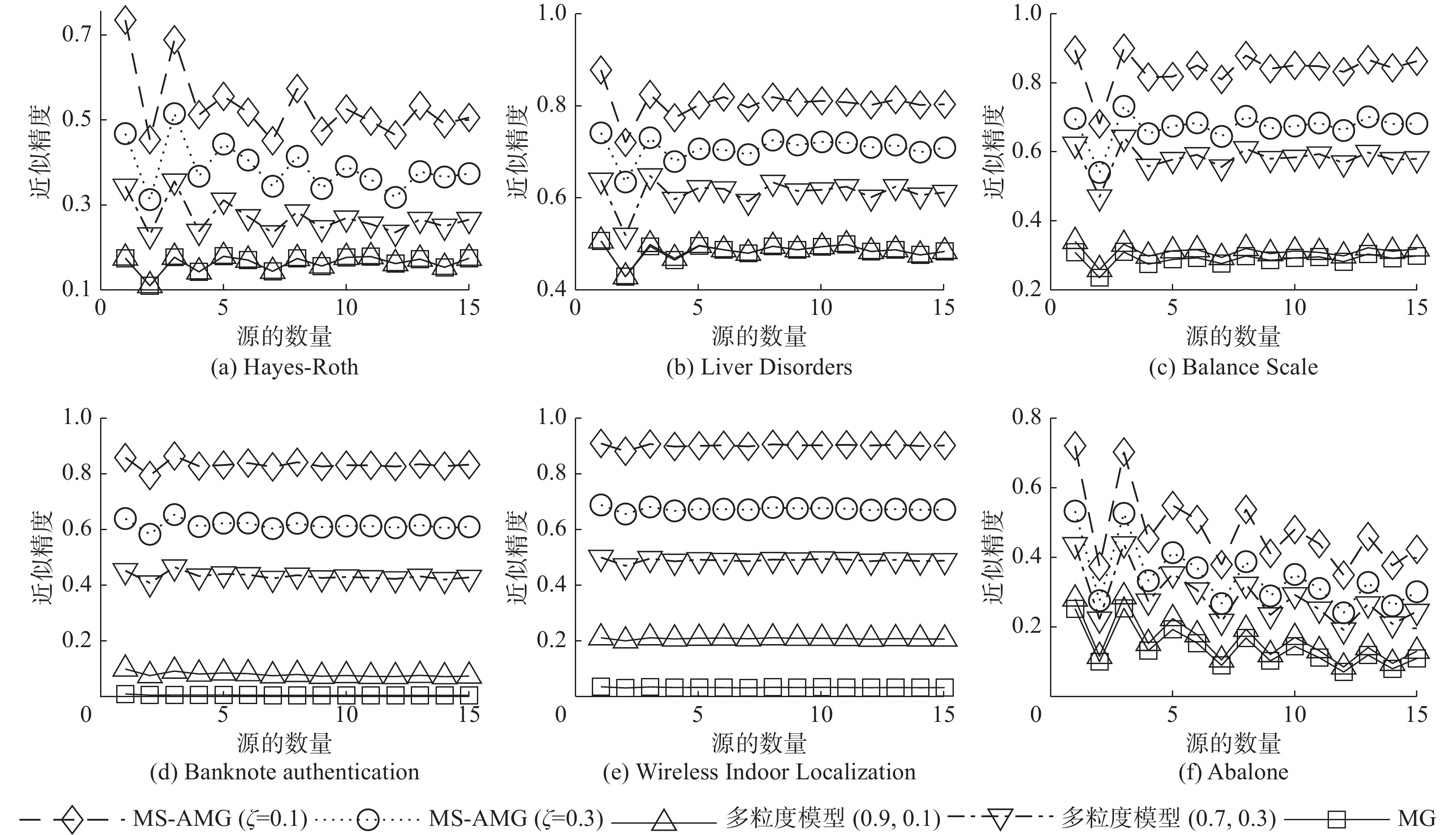
为了进一步验证MS-AMG模型在融合近似精度中的有效性，本节将对不同的多粒度融合模型进行近似精度对比。其中，包括两组补偿系数 $ \zeta $ 分别取为0.1、0.3的MS-AMG模型，两组固定阈值对设置为（0.9, 0.1）和（0.7, 0.3）多粒度模型以及文献[21]提出的多粒度融合模型（MG）。所有多粒度模型的上下近似参数都设置为0.4和0.6。各个模型的近似精度如图3所示。

图  3  不同多粒度模型的融合近似精度比较

Fig.  3  Comparison of fusion approximation accuracy of different multi-granulation models

下载: 全尺寸图片

其中，模型MG的近似精度最低，而采用固定阈值的多粒度模型以及自适应阈值的模型MS-AMG，由于对决策规则具有容忍性，其融合效果相对较好。但从参数数量和实际应用上看，采用自适应阈值的方式的MS-AMG更加具有优越性。此外，实验结果显示MS-AMG模型的近似精度随着 $ \zeta $ 的减少而增大，符合定理3。

3.3   4种广义自适应多粒度粗糙集模型对比分析

在本小节中，我们通过近似精度来比较广义自适应多粒度粗糙集MS-AMG、悲观–悲观自适应多粒度粗糙集MS-PPAMG、乐观–乐观自适应多粒度粗糙集MS-OOAMG和悲观–乐观自适应多粒度粗糙集MS-POAMG。4种模型的补偿系数 $ \zeta {\text{ = }}0.1 $ ，MS-AMG的近似参数为 $\varphi = 0.5$ ， $\gamma = 0.5$ 。上述4种模型的知识粒度对应的阈值都是自适应获得的，并且所有模型可以看为是MS-AMG近似参数取不同值而得到的。从图4展示的结果可以看出，不同近似参数的MS-AMG融合效果也不相同，因而可以根据实际情况选择合适的策略和模型，灵活解决复杂的信息融合问题。

图  4  4种自适应多粒度模型的融合近似精度比较

Fig.  4  Comparison of fusion approximation accuracy of four adaptive multi-granulation models

下载: 全尺寸图片

4.   结束语

本文通过分析认为，现有多粒度粗糙集模型通常采用同一阈值融合多源信息，并没有考虑信息源之间的差异性。本文为解决这个问题，将单参数决策粗糙集理论运用到广义多粒度粗糙集中，提出了广义自适应多粒度粗糙集模型MS-AMG，并且定义了在4种经典多粒度环境下MS-AMG模型的表现形式。所提模型都能够基于数据驱动得到每个知识粒度的阈值，解决了同一阈值多粒度粗糙集实现信息融合的局限性。然后给出了一个例子来说明MS-AMG模型的应用，初步显示了所提出的模型的优越性。最后通过实验进一步表明，我们所提出模型的融合方法更加具有灵活性，能处理好多源信息的融合，为信息融合提供了新的思路。在未来的研究中，将开展基于自适应多粒度序贯三支决策模型的研究。