Construction and application of factor connection distribution formula based on connection number and system function status
-
摘要: 为确定不同因素对系统功能状态的影响趋势，提出并建立了因素联系分布式。论述了联系数与系统功能状态的关系，因素联系分布思想；计算了因素联系分布系数并构建了因素联系分布式。研究表明：以联系数结构为基础可构建因素联系分布式；联系数与系统功能状态具有相同的特点；影响因素与功能状态等级之间存在分布式的联系；可使用一个因素联系分布式表示系统功能状态的所有等级及其比例关系；给出了三元因素联系分布式的构建方法，多元因素联系分布式同理得到。最后研究认为因素联系分布式继承了联系数的特点，并具备了因素分析、动态调整、分布表示等能力，适合于系统安全和可靠性的相关研究。Abstract: The factor connection distributed formula is proposed and established to determine the influence trend of different factors on the system function state. This formula is introduced to discuss the relationship between the connection number and system function state and idea of factor connection distribution, to calculate the factor connection distribution coefficient, and to construct the factor connection distribution formula. The research shows that the factor connection distribution formula can be constructed based on the connection number structure. Furthermore, the connection number has the same characteristics as the system function status. A distribution relationship exists between the influencing factors and function status level. Thus a single-factor connection distribution formula can be used to contact all levels and their proportional relationships of system function status. The construction method for the ternary factor connection distribution formula is given, and the multifactor connection distribution formula is obtained using the same principle. Finally, the factor connection distribution formula inherits the characteristics of the connection number and can perform factor analysis, dynamic adjustment, and distributed representation, which is suitable for related research on system safety and reliability.
-
系统运行期间必然会受到各种因素影响。如果以系统完成功能为目标，那么一些因素的数值增加有利于系统完成功能；一些因素则不利于完成功能，也必然有一些因素对系统完成功能的作用不清楚。这是客观存在的，也影响着系统实现自身功能的能力。对于一种环境，其中蕴含着很多因素，如何判断该环境是否有利于系统实现自身功能成为关键问题。将某一时刻系统实现自身功能的能力状态称为系统功能状态[1-2]，所有时刻的系统功能状态按时间顺序的集合称为系统故障演化过程(system fault evolution process, SFEP)[3-5]。这些定义是作者为了完成对系统故障过程的分析和研究提出的。显然SFEP必然受到因素影响，不同的因素及其数值变化使得SFEP出现多样性、不确定性和随机性。其本质原因就是因素变化与系统功能状态变化，即系统故障特征的变化关系不清造成的。当然这也与测量SFEP的系统有关，其涉及被测SFEP、测量仪器、测量环境和观察者[6-8]，其中最为关键且最易变化的是测量环境，即影响因素。因而无论是系统本身的功能变化或是测量导致的不确定，其主要原因都是因素变化。相较于单因素影响，多因素影响更为复杂。需要确定各因素作用，解决因素的冗余、相关和隐秘性等问题。使用现有方法分析尚存在问题，但因素对系统功能状态、SFEP和系统故障等的影响是普遍、显著和直接的。为使系统实现功能正常运行，确定不同因素在运行环境中对系统功能状态的影响是必须解决的关键科学问题。
就因素对系统功能、故障、安全和风险等的影响研究较多[9-20]。这些研究从不同角度及领域对因素影响系统功能的问题进行了分析。其中有各领域内独特的因素作用分析方法，也有在系统层面给出的通用分析理论，例如因素空间、属性论等。这些成果为研究上述问题提供了有益借鉴，但仍存在难以解决的问题。因素对系统功能状态的影响，应基于因素数值变化与系统功能状态变化之间的关系确定；需要同一函数式对所有因素影响系统功能状态的情况进行表示，而不是复杂的叠加形式；函数式应能动态地进行影响等级合并和扩展；多因素影响能通过简单的统计方法得到。从而构建统一、可变、多因素共同作用的因素变化与系统功能状态变化的关系表达式。该表达式采用上述文献方法显然难以构建。
为解决上述问题，作者基于提出的系统功能状态概念[21-22]，将因素导致系统功能变化的不同等级使用集对分析的联系数形式表示。确定因素联系分布式的因素联系分布系数，最终得到分布式。
1. 联系数与系统功能状态
集对分析理论是处理系统确定性与不确定性的数学理论，是由我国学者赵克勤在1989年提出的[23-25]，其核心工具是联系数。联系数是一种结构函数，其中每一项代表了一类数据对系统的影响程度；所有项代表了系统状态的所有等级；而且所有项在联系数中都是有序的。各项都由分项系数和等级（状态）标记组成。最简单的二元联系数
$\mu = a + bi$ 。一是确定和不确定的对立关系，$a$ 和$b$ 分别代表确定和不确定的占比；二是可靠和失效的对立关系，$a$ 和$b$ 分别代表可靠和失效的占比。三元联系数也是经典联系数，$\mu = a + bi + cj$ 。三元联系数的各项可分别解释为可靠、不确定和失效。$a$ 、$b$ 和$c$ 分别代表可靠、不确定和失效的状态占比。它可退化为二元联系数，将可靠和失效合计为确定状态$a$ ，而$b$ 表示的不确定状态不变。综上可见联系数的特点是二元辩证对立的，是两种基态（可靠和失效）的综合表现；两种状态的比例可以改变；项数代表的不同系统功能状态等级可根据需要拓展或合并。因此联系数是一种动态自适应的结构函数。这与系统功能状态的表示极为契合，系统功能具有可靠和失效两个基态；在不同因素影响下可相互转化；实际的系统功能状态属于在可靠和失效状态之间存在的多种状态等级。
联系数的特点和系统功能状态的特点是对应性，可使用一个联系数统一表示系统功能状态的所有等级，以及这些等级出现的概率、比例或可能性。
2. 因素联系分布的思想
上文论证了联系数可综合的表示系统功能状态。根据定义，系统功能状态是表示某一时刻系统实现功能的能力状态。这意味着对于该时刻的系统功能状态是不变的。但实际上系统工作于环境之中，随着时间发展，影响系统的因素也必然发生变化。将所有系统功能状态组合起来就是一个系统功能的动态变化过程。将多因素影响下系统实现自身功能的能力变化过程定义为SFEP。
SFEP中所有时刻都对应着确定的系统功能状态，而所有系统功状态按照演化时刻能组成SFEP。问题在于如何在SFEP中，研究所有因素对系统功能状态的作用；并根据这些作用将因素按照影响等级进行归类，最终表示在同一个联系数中。由于在多因素影响下，不同因素数值组合必然导致对系统功能状态的影响不同。因此因素联系分布式应该是一个具有因素变量的函数式。将所有因素作为坐标轴构成因素空间[26-27]。空间中不同位置的因素对功能状态的影响不同，因此该函数式表示了在因素空间中的一种随因素变化的数值分布。
对于因素联系分布式的数值表示问题，最直接的方法是确定因素变化与系统功能状态变化的关系，即确定它们单位变化率的关系。可使用求导方法确定它们变化的数值关系。对求导后得到的导数式，将所有因素值代入得到导数值并进行划分，形成多个不同的数值区间。导数为正且值越大者表明因素与系统功能状态的正相关性越强；导数为零表示不相关；导数为负且数值越大代表负相关性越强。将这些划分对应于各系统功能状态等级，即因素联系分布式中的各项。各项的分项系数可根据在该等级的因素数量与总因素数量的比值确定。从而构造同时表示多因素影响的因素联系分布式。
3. 因素联系分布式构建
以确定的系统功能为目标，以可靠、不确定和失效划分系统功能状态等级，考虑所有影响系统功能的因素，确定所有因素同时作用时使系统处于可靠、不确定和失效的因素数量分布情况，利用联系数形式表达分布情况的式子称为三元因素联系分布式。以因素值域为坐标变化区域，以所有影响系统功能的因素作为坐标轴形成了因素空间，影响的作用在空间中可能是点、线、面或更高维度形态。
设影响系统功能状态的因素集合为
$F = \left\{ {f_1},{f_2}, \cdots , {f_N}\right\}$ ，$ n = 1,2, \cdots ,N $ ，$ {f_n} \in F $ ，$ N $ 为因素数量。这些因素对应的因素数值集合为$ X = \left\{ {{x_1},{x_2}, \cdots ,{x_N}} \right\} $ ，$ {x_n} \in X $ ，$ {x_n} $ 为$ {f_n} $ 的一个确定值。所有因素的值域集合为$ A = \left\{ {{a_1},{a_2}, \cdots ,{a_n}} \right\} $ ，$ {x_n} \in {a_n} $ ，$ {a_n} $ 为$ {f_n} $ 的值域。这时三元因素联系分布式$ {\mu _{\text{3}}} $ 为$$\begin{gathered} {\mu _{\text{3}}}\left( {{x_1}, {x_2},\cdots ,{x_N}} \right) = a\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) +\\ b\left( {{x_1}, {x_2},\cdots ,{x_N}} \right)i + c\left( {{x_1},{x_2}, \cdots ,{x_N}} \right)j\end{gathered} $$ (1) 进一步，对式（1）中变量进行解释和计算。上文提到因素联系分布式代表了所有因素
$ {f_1}, {f_2}, \cdots ,{f_N} $ 对系统功能状态的影响。式中$ a $ 代表了使系统功能状态为可靠的因素占比，是以${x_1},{x_2}, \cdots , {x_N}$ 为变量的可靠因素联系分布系数；$ b $ 代表了系统功能状态不确定的因素占比，是不确定因素联系分布系数；$ c $ 代表了系统功能状态为失效的占比，是失效因素联系分布系数。那么确定各因素在其余因素不变情况下对系统功能状态的作用等级是关键问题。对系统功能状态就单一因素值在其余因素值不变时求偏导，得到的偏导式将所有因素数值带入，如果导数值小于0则为可靠状态、等于0不确定、大于0为失效状态。上述对可靠、不确定和失效的划分是由于使用到空间故障树理论基础中的系统故障概率分布
$ p\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) $ 造成的。$ p\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) $ 规定所有影响系统故障的因素作为因素坐标轴，系统故障概率为因素空间中曲面的数值。因此故障概率100%为最大值，即完全失效；故障概率为0是最小值，即完全可靠。因此使用$ p\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) $ 计算因素联系分布式的各分布系数。对于分布系数，导数大于0意味着系统向着失效方向发展，导数小于0代表向着可靠方向发展。式（1）中得到的三元因素联系分布式不是单一值，它代表了在因素空间的不同位置有不同值，空间中的一点是
$ {x_1},{x_2}, \cdots ,{x_N} $ 值的组合，所以因素空间是所有因素值域的组合，设为$\varGamma = {a_1} \times {a_2}\times \cdots \times {a_n}$ 。在多因素影响下，在空间
$ \varGamma $ 中，$ p\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) $ 对因素$ {f_n} $ 的变化率，即为$ p\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) $ 对单一因素$ {f_n} $ 求偏导，偏导式为$ {V_n} $ ：$$ {V_n} = \frac{{\partial P\left( {{x_1},{x_2}, \cdots ,{x_N}} \right)}}{{\partial {x_n}}} $$ (2) 将
$ {x_1},{x_2}, \cdots ,{x_N} $ 值代入式（2）中，如果${{V}_{n}|}_{={x}_{1},{x}_{2},\cdots ,{x}_{N}} > 0$ ，则该时刻$ {f_n} $ 在$\varGamma$ 中使系统故障概率增加；如果$\left. {{V_n}} \right|_ {= {x_1},{x_2}, \cdots ,{x_N} }= 0$ ，则该时刻$ {f_n} $ 在$\varGamma$ 中使系统故障概率不变或不确定；如果$ {\left. {{V_n}} \right|_{ = {x_1},{x_2}, \cdots ,{x_N}}} < 0 $ ，则该时刻$ {f_n} $ 在$\varGamma$ 中使系统故障概率减小。因此设
$ {a'} $ 、$ {b'} $ 和$ {c'} $ 分别是使系统故障概率减小、不确定和增加的因素数量，初始值均为0。那么对于因素$ {f_n} $ ，在因素值为$ {x_1},{x_2}, \cdots ,{x_N} $ 时刻，如果$ {V_n} < 0 $ ，则$ {a'} = {a'} + 1 $ ；如果$ {V_n} = 0 $ ，则$ {b'} = {b'} + 1 $ ；如果$ {V_n} > 0 $ ，则$ {c'} = {c'} + 1 $ 。对于所有因素
$ {f_1},{f_2}, \cdots ,{f_N} $ ，循环$ n = 1,2, \cdots ,N $ ，统计在$ \varGamma $ 中所有位置，即所有因素数值组合情况下，落在$ {a'},{b'},{c'} $ 中的因素数量。在任意$ {x_1},{x_2}, \cdots ,{x_N} $ 数值组合时$ {V_n} $ 的数值只能属于$ {a'},{b'},{c'} $ 之一。统计后即可得三元因素联系分布式$ {\mu _{\text{3}}} $ 的数值表达式为$$ {\mu _{\text{3}}}\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \frac{{{a'}}}{{{a'} + {b'} + {c'}}} + \frac{{{b'}}}{{{a'} + {b'} + {c'}}}i + \frac{{{c'}}}{{{a'} + {b'} + {c'}}}j $$ (3) 设系统可靠为功能目标，那么式(3)中，可靠因素联系分布系数
$a\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{a'}}}{{{a'} + {b'} + {c'}}}$ ；不确定因素联系分布系数$b\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{b'}}}{{{a'} + {b'} + {c'}}}$ ；失效因素联系分布系数$c\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{c'}}}{{{a'} + {b'} + {c'}}}$ ，1、$ i $ 和$ j $ 代表了上述3种系数的标记。从而最终实现了式(1)的定量计算式。4. 多元因素联系分布
第3节确定了三元因素联系分布式，对于二元和多元因素联系分布式的确定如下。
参考二元联系数
${\mu _{\text{2}}} = \left( {a + c} \right) + bi$ ，利用式（1）可得二元因素联系分布式，${\mu _{\text{2}}}\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \left( a\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) + c\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) \right) + b\left( {{x_1},{x_2}, \cdots ,{x_N}} \right)i$ 。对于
$ M $ 元因素联系分布式为$$ \begin{gathered}{\mu _{{M}}} = a\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) + {b_1}\left( {{x_1},{x_2}, \cdots ,{x_N}} \right){i_1} + \\{b_2}\left( {{x_1},{x_2}, \cdots ,{x_N}} \right){i_2} + {b_{M - 3}}\left( {{x_1},{x_2}, \cdots ,{x_N}} \right){i_{M - 3}} +\\c\left( {{x_1},{x_2}, \cdots ,{x_N}} \right)j\end{gathered} $$ (4) 元数不同即表示将因素对系统功能状态影响的等级划分不同。
$ M $ 元将系统功能状态等级划分为$ M $ 级，即在所有因素$ {x_1},{x_2}, \cdots ,{x_N} $ 时刻，将$ {V_n} $ 的值域划分为$ M - 1 $ 个区间。如下对这$ M - 1 $ 个区间的范围进行具体划分，其中$ {\text{Max}}\left\{ {{V_n}} \right\} $ 和$ {\text{Min}}\left\{ {{V_n}} \right\} $ 分别代表着系统功能状态在因素$ {f_n} $ 作用下在$ \varGamma $ 中（所有因素数值组合中$ {V_n} $ ）的最大值和最小值。如果
${V_n} \in \left[ {{\text{Max}}\left\{ {{V_n}} \right\},{\text{Max}}\left\{ {{V_n}} \right\} - \dfrac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}}} \right]$ ，$ {a'} = {a'} + 1 $ ；$$\begin{gathered} {V_n} \in \left[ {{\text{Max}}\left\{ {{V_n}} \right\} - \frac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}},{\text{Max}}\left\{ {{V_n}} \right\} - \frac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}} \times 2} \right] \text{，} {b'_1} = {b'_1} + 1 \text{；}\\ \cdots \\ {V_n} \in \left[ {{\text{Max}}\left\{ {{V_n}} \right\} - \frac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}} \times \left( {M - 3} \right),{\text{Max}}\left\{ {{V_n}} \right\} - \frac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}} \times \left( {M - 2} \right)} \right] \text{，} b_{M - 3}' = b_{M - 3}' + 1 \text{；}\\ {V_n} \in \left[ {{\text{Max}}\left\{ {{V_n}} \right\} - \frac{{{\text{Max}}\left\{ {{V_n}} \right\} - {\text{Min}}\left\{ {{V_n}} \right\}}}{{M - 1}} \times \left( {M - 2} \right),{\text{Min}}\left\{ {{V_n}} \right\}} \right] \text{，} {c'} = {c'} + 1 。\end{gathered} $$ 与三元因素联系分布式的确定方法相同，循环
$ n = 1,2, \cdots ,N $ ，统计$ {a'},{b'_1}, \cdots ,b_{M - 3}',{c'} $ ，则得到式（4）的数值表达形式：$$\begin{gathered}{\mu _M} = \frac{{{a'}}}{{{a'} + \displaystyle\sum\limits_{j = 1}^{M - 3} {b_j' + {c'}} }} + \frac{{{b'}_1}}{{{a'} + \displaystyle\sum\limits_{j = 1}^{M - 3} {b_j' + {c'}} }}{i_1} + \cdots \\ \frac{{{b'}_{M - 3}}}{{{a'} + \displaystyle\sum\limits_{j = 1}^{M - 3} {b_j' + {c'}} }}{i_{M - 3}} + \frac{{{c'}}}{{{a'} + \displaystyle\sum\limits_{j = 1}^{M - 3} {b_j' + {c'}} }}j \end{gathered}$$ (5) 上述过程实现了二元到多元因素联系分布式的推导及计算过程。主要目的在于研究在多因素影响下，所有因素在值域的变化过程中，所有因素对系统功能状态的影响。如果因素空间的某一区域中使系统可靠的因素较多，说明该区域适合系统功能实现；反之使系统失效的因素较多时，该区域则不适合系统功能实现；且一般情况下适合和不适合系统实现功能的区域之间都存在着不确定的区域。因此使用三元因素联系分布的概念和分布式研究因素与系统功能状态的关系是较为理想的。如果试图更为详细的区分因素作用则需要建立多元因素联系分布式。
5. 实例分析
考虑到图像展示，使用三维图像只能考虑两种因素的影响，保留一维用于展示故障概率等曲面信息。因此设有2个因素影响该系统的功能状态，因素集合为
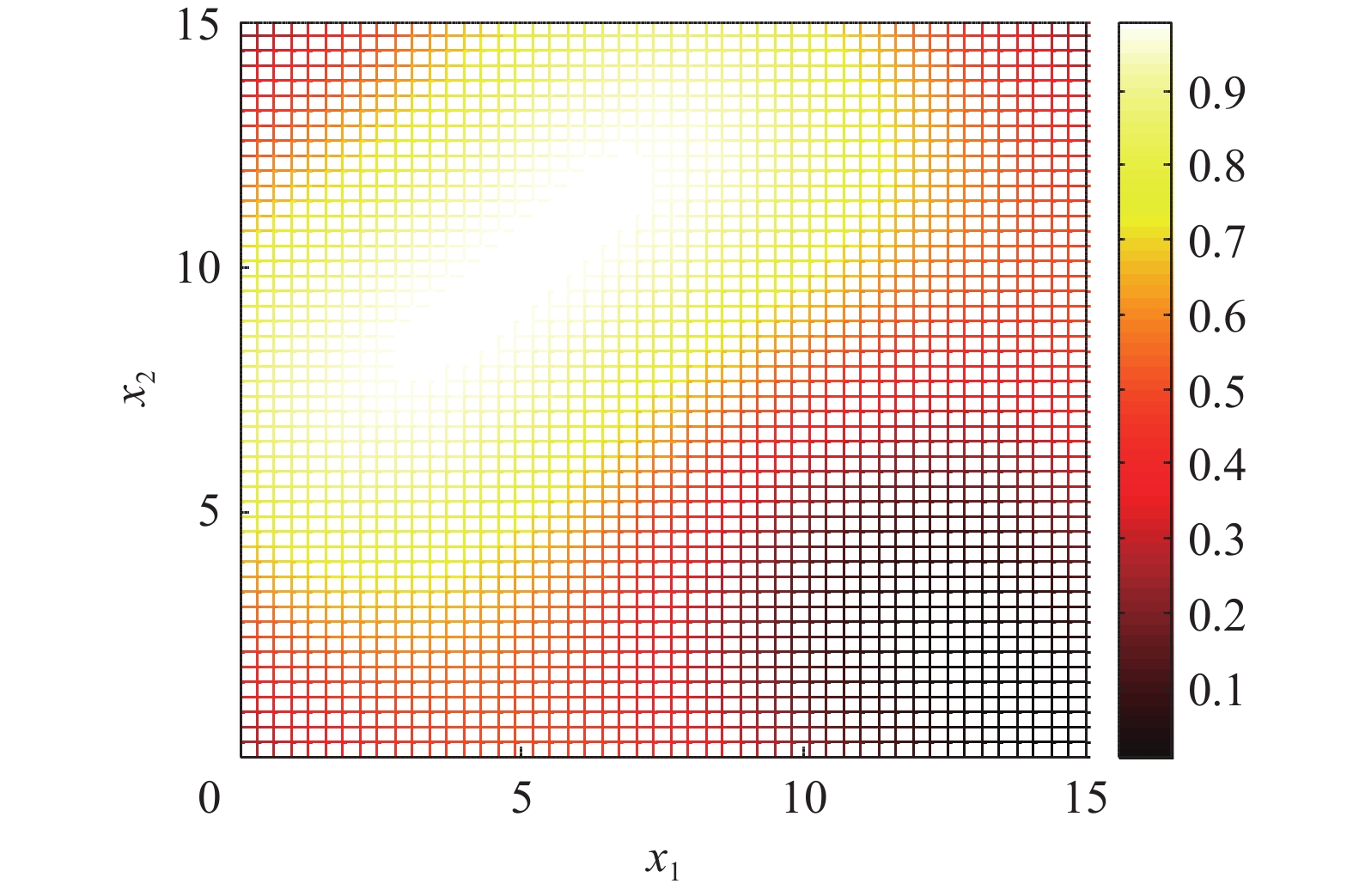
$ F = \left\{ {{f_1},{f_2}} \right\} $ ，因素值集合$ X = \left\{ {{x_1},{x_2}} \right\} $ ，因素值域为$ {x_1} \in {a_1} = \left[ {0,15} \right] $ ，$ {x_2} \in {a_2} = \left[ {0,15} \right] $ ，则因素空间为$ \varGamma = {a_1} \times {a_2} $ 。系统故障概率分布$ P\left( {{x_1},{x_2}} \right) $ 为$$ P\left( {{x_1},{x_2}} \right) = 0.25 \times \left[ {\cos \left( {{x_1}} \right) \times \sin \left( {{x_2}} \right) + \sin \left( {{x_1}} \right) - \cos \left( {{x_2}} \right) + 2} \right] $$ (6) 根据式（2）对式（6）分别就因素
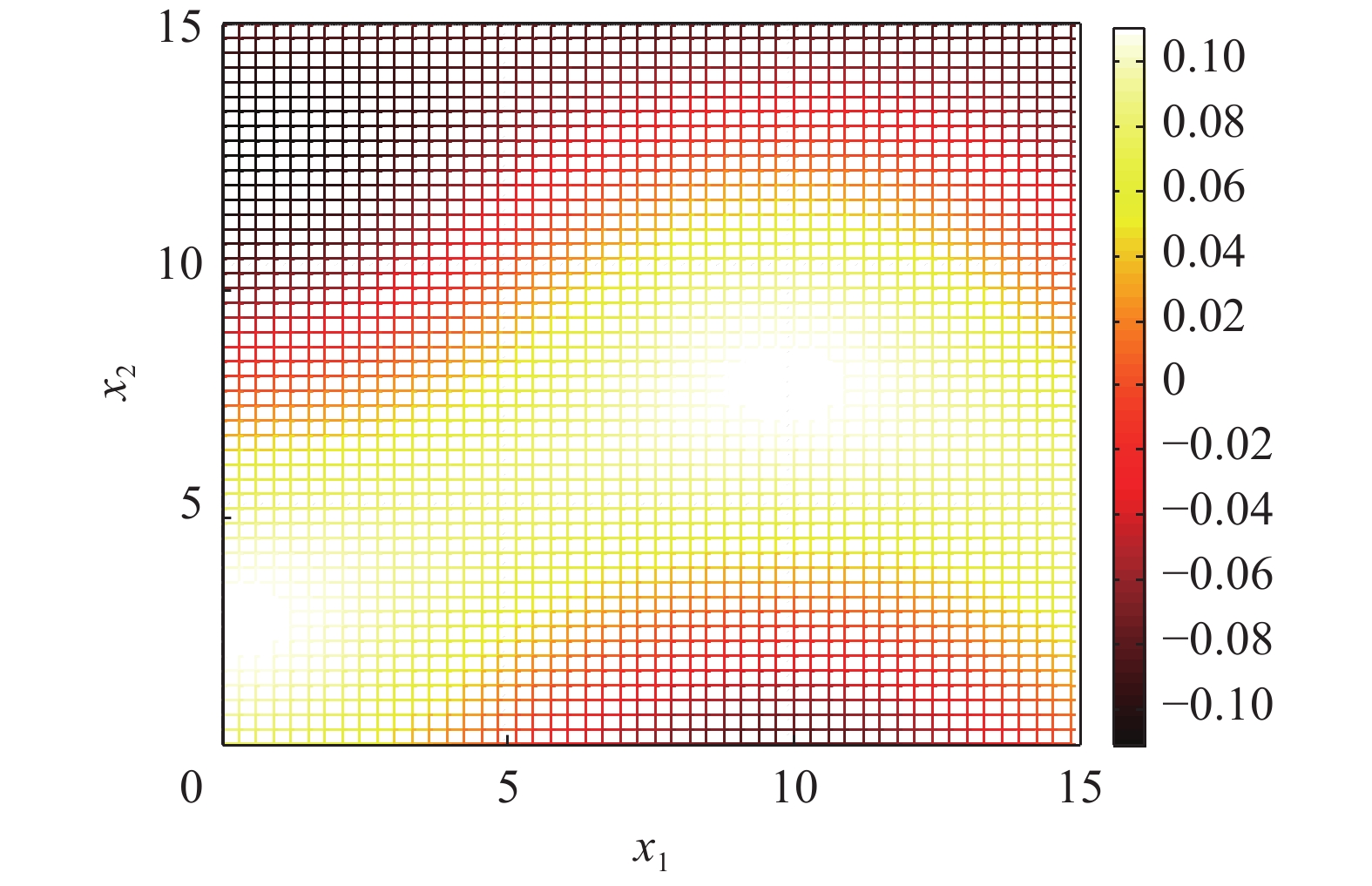
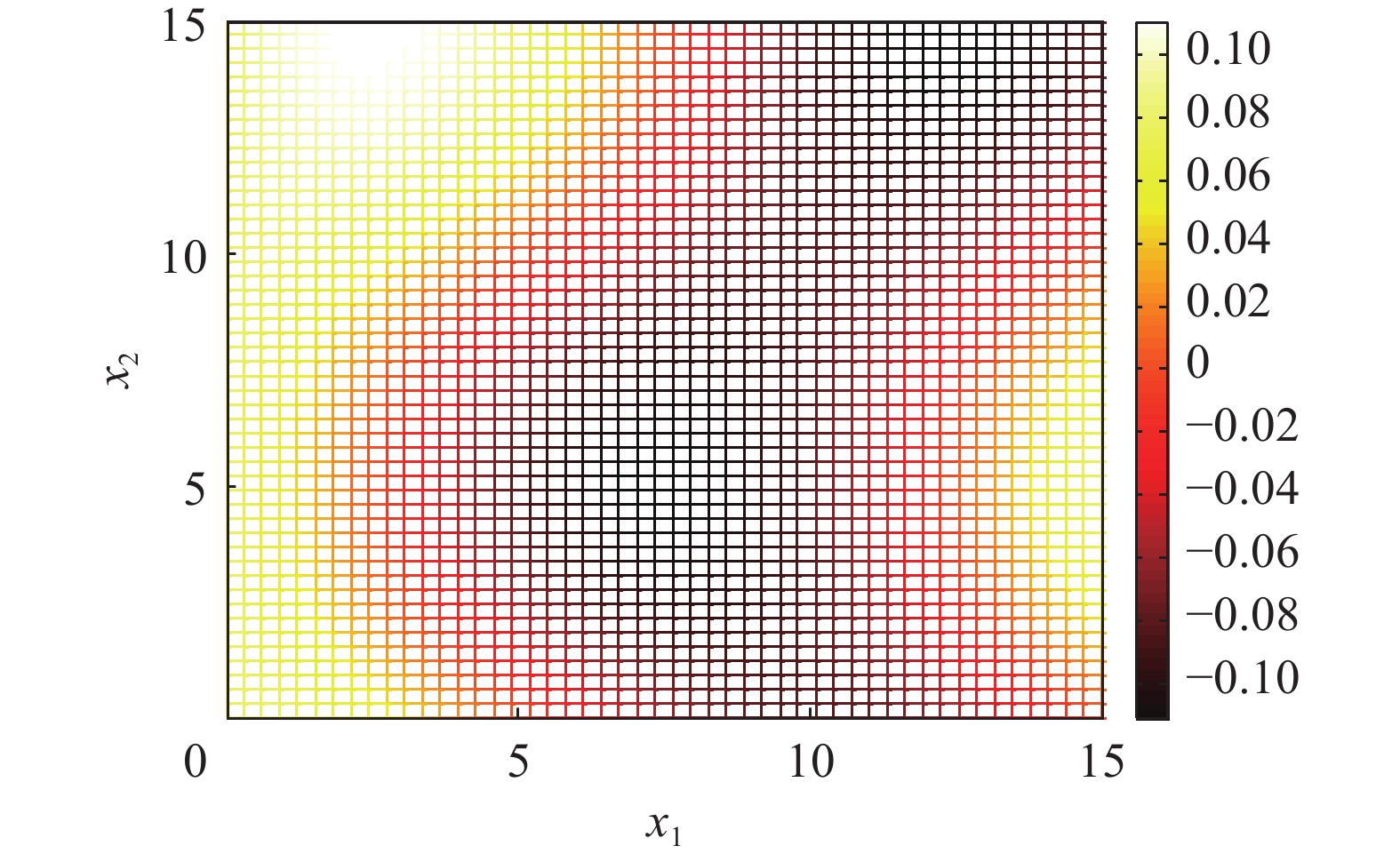
$ {f_1} $ 和$ {f_2} $ 求偏导，得到偏导式$ {V_1} $ 和$ {V_2} $ ，如式（7）、（8）所示。$$ {V_1} = \frac{{\partial P\left( {{x_1},{x_2}} \right)}}{{\partial {x_1}}} = - 0.25 \sin \left( {{x_1}} \right) \times \sin \left( {{x_2}} \right) + 0.25 \cos \left( {{x_1}} \right) $$ (7) $$ {V_2} = \frac{{\partial P\left( {{x_1},{x_2}} \right)}}{{\partial {x_2}}} = 0.25 \cos \left( {{x_1}} \right) \times \cos \left( {{x_2}} \right) + 0.25 \sin \left( {{x_2}} \right) $$ (8) 根据式（6）、（7）和（8），以及
$ {x_1} \in {a_1} = \left[ {0,15} \right] $ ，$ {x_2} \in {a_2} = \left[ {0,15} \right] $ ，得到的系统故障概率分布和偏导式在因素空间中的分布，分别如图1、2、3所示。
图 1 系统故障概率分布Fig. 1 System fault probability distribution
下载:
全尺寸图片
图 2 因素$ f_1$ 偏导式的分布Fig. 2 Distribution of partial derivative of factor$ f_1$ 下载:
全尺寸图片
图 3 因素$ f_2$ 偏导式的分布Fig. 3 Distribution of partial derivative of$ {f_2} $ 下载:
全尺寸图片
将图2和3进行系统功能状态等级划分，以三元因素联系分布式为例。设3个等级为可靠。不确定和失效。图中
$ {V_1} $ 和$ {V_2} $ 大于0的区域是使系统失效的区域，小于0的区域是使系统可靠的区域。因此需要统计上述分布中所有$ {x_1} \in {a_1} = \left[ {0,15} \right] $ ，$ {x_2} \in {a_2} = \left[ {0,15} \right] $ 组合值所对应的$ {V_1} $ 和$ {V_2} $ 数值。当然这些数值不但取决于因素值域，也取决于对因素值域的划分。这里两因素的值域都被划分为49份，50个节点。因此在分布曲面上共有2500个点。统计得到
$ {a'},{b'},{c'} $ 数值，并进行归一化，得到可靠因素联系分布系数$a\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{a'}}}{{{a'} + {b'} + {c'}}}$ ；不确定因素联系分布系数$b\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{b'}}}{{{a'} + {b'} + {c'}}}i$ ；失效因素联系分布系数$c\left( {{x_1},{x_2}, \cdots ,{x_N}} \right) = \dfrac{{{c'}}}{{{a'} + {b'} + {c'}}}j$ 。它们在因素空间中的分布平面图分别如图4的（a）、（b）和（c）。
图 4 各等级因素联系分布Fig. 4 Connection distribution of factors at various levels下载:
全尺寸图片
由于只有两个因素，所以
$ {a'} + {b'} + {c'} = 2 $ ，$ {a'},{b'},{c'} $ 的可能数值为2、1和0。因此图4中，归一化后得到的$ a、b、c $ 值只可能是1、0.5或0。图4（a）和（c）中，黑色为区域为1，橙色区域为0.5，白色区域为0。图4（b）中均为0值，这与分布曲面的变化速度和因素值域划分有关。参照式（3），确定
$ {x_1} = 10 $ 且$ {x_2} = 10 $ 的三元因素联系分布式。根据图4（a），可靠因素联系分布中，当$ {x_1} = 10 $ 且$ {x_2} = 10 $ 时，可靠因素联系分布系数$ a\left( {10,10} \right) = 0.5 $ ；根据图4（b），不确定因素联系分布中，不确定因素联系分布系数$ b\left( {10,10} \right) = 0 $ ；根据图4（c），失效因素联系分布中，失效因素联系分布系数$ c\left( {10,10} \right) = 0.5 $ 。因此最终得到的$ {x_1} = 10 $ 且$ {x_2} = 10 $ 的三元因素分布联系式：$$ {\mu _{\text{3}}}\left( {10,10} \right) = 0.5 + 0i + 0.5j $$ 这也说明了在
$ {x_1} = 10 $ 且$ {x_2} = 10 $ 时，两因素对系统功能状态的影响是均势的。类似可通过上述方法得到所有因素数值组合情况下的三元因素联系分布式。从而确定整个讨论环境条件下的系统功能状态是否有利于系统实现自身功能。当然上述实例是简单的，当因素数量增加，因素值域扩展，划分功能等级数增加时得到的因素联系分布式将变得复杂。但使用的计算方法与上述过程相同。虽然上述方法基于集对分析联系数发展而来，但也有几个明显特点。集对分析联系数是集合对象数量之间的关系，而因素联系分布式代表了不同因素对系统功能状态的影响；前者是单一的计算式，后者是同时表示所有因素值组合情况下的分布式；前者是静态的数量关系，后者是动态的因素与系统功能状态的变化关系；前者是不同等级对象比值关系，后者是不同等级因素对象比例关系。后者在继承了前者统一表示、分类可扩展和收缩等优点后，也具备了上述特点。这使得因素联系分布概念和分布式特别适用于研究因素与系统安全和可靠性之间的关系，也可应用于基于因素分析的系统安全等级研究之中。
6. 结束语
1）论述了联系数与系统功能状态的关系，提出和构建因素联系分布的思想和目的。因素对系统功能状态的作用不同，所有因素的不同值组合必然对应着不同的功能状态等级。因素与等级之间存在联系且以分布形式体现，为此提出因素联系分布的概念和分布式。
2）构建了因素联系分布式。以系统故障概率分布对某因素的导数值代表该因素对系统功能状态的影响。导数值小于0有利于系统可靠，大于0导致系统失效，等于0则代表不确定。统计所有因素值组合情况下的导数值属于三类的数量，归一化得到三元因素联系分布式。多元因素联系分布式可由三元因素联系分布式通过拓展分布得到。通过实例分析说明了方法的分析过程。认为因素联系分布式继承了联系数的特点，并具备了因素分析、动态调整、分布表示等能力，适合于系统安全和可靠性的相关研究。
-
图 1 系统故障概率分布
Fig. 1 System fault probability distribution
下载:
全尺寸图片
图 2 因素
$ f_1$ 偏导式的分布Fig. 2 Distribution of partial derivative of factor
$ f_1$ 下载:
全尺寸图片
图 3 因素
$ f_2$ 偏导式的分布Fig. 3 Distribution of partial derivative of
$ {f_2} $ 下载:
全尺寸图片
图 4 各等级因素联系分布
Fig. 4 Connection distribution of factors at various levels
下载:
全尺寸图片
-
[1] 崔铁军, 李莎莎. 基于集对分析的SFT特征函数重构及性质研究[J]. 智能系统学报, 2022, 17(1): 131–136. CUI Tiejun, LI Shasha. Reconstruction of SFT characteristic function and its properties based on set pair analysis[J]. CAAI transactions on intelligent systems, 2022, 17(1): 131–136. [2] 崔铁军, 李莎莎. 系统可靠−失效模型的哲学意义与智能实现[J]. 智能系统学报, 2020, 15(6): 1104–1112. CUI Tiejun, LI Shasha. Philosophical significance and implementation of an intelligent system based on the system reliability-failure model[J]. CAAI transactions on intelligent systems, 2020, 15(6): 1104–1112. [3] 崔铁军, 李莎莎. 系统故障演化过程最终事件状态及发生概率研究[J]. 中国安全科学学报, 2021, 31(8): 1–7. CUI Tiejun, LI Shasha. Study on target event state and occurrence probability of system fault evolution process[J]. China safety science journal, 2021, 31(8): 1–7. [4] 崔铁军. 空间故障网络理论与系统故障演化过程研究[J]. 安全与环境学报, 2020, 20(4): 1255–1262. CUI Tiejun. Profound trace and exploration into the space fault network theory and the system fault evolution process[J]. Journal of safety and environment, 2020, 20(4): 1255–1262. [5] 李莎莎, 崔铁军. 空间故障网络中单向环转化与事件发生概率计算[J]. 安全与环境学报, 2020, 20(2): 457–463. LI Shasha, CUI Tiejun. Unidirectional ring transformation and the event probability calculation in the space fault network[J]. Journal of safety and environment, 2020, 20(2): 457–463. [6] 乔灵爱, 成素梅. 论量子测量解释中的实在观[J]. 自然辩证法研究, 2005, 21(5): 17–20. QIAO Lingai, CHENG Sumei. On the concept of reality in quantum measurement interpretation[J]. Studies in dialectics of nature, 2005, 21(5): 17–20. [7] 万子谦, 万小龙. 量子力学多世界解释中的概率问题[J]. 自然辩证法研究, 2019, 35(5): 85–90. WAN Ziqian, WAN Xiaolong. Probability issues in the many worlds interpretation of quantum mechanics[J]. Studies in dialectics of nature, 2019, 35(5): 85–90. [8] 万子谦, 万小龙. 量子力学多世界解释视角下的睡美人悖论[J]. 科学技术哲学研究, 2018, 35(6): 26–30. WAN Ziqian, WAN Xiaolong. A many-worlds analysis of the sleeping beauty paradox[J]. Studies in philosophy of science and technology, 2018, 35(6): 26–30. [9] 徐一旻, 田梦莹, 李治, 等. FTA-BN在机场跑道入侵事故影响因素分析中的应用[J]. 安全与环境学报, 2023, 23(5): 1361–1367. XU Yimin, TIAN Mengying, LI Zhi, et al. Analysis of influencing factors of airport runway incursion accident based on FTA-BN[J]. Journal of safety and environment, 2023, 23(5): 1361–1367. [10] 崔铁军, 李莎莎. 基于BQEA的多因素影响下系统故障概率变化范围研究[J]. 安全与环境学报, 2022, 22(2): 642–648. CUI Tiejun, LI Shasha. Study on the change range of systemfault probability under the influence of multiple factors based on BQEA[J]. Journal of safety and environment, 2022, 22(2): 642–648. [11] 邓祥力, 张乾波. 基于ARMA和Copula理论的多因素GIS设备家族性缺陷故障预警[J]. 高压电器, 2022, 58(2): 9–16. doi: 10.13296/j.1001-1609.hva.2022.02.002 DENG Xiangli, ZHANG Qianbo. Fault warning of family defects in multi-factor GIS equipment based on ARMA and copula theory[J]. High voltage apparatus, 2022, 58(2): 9–16. doi: 10.13296/j.1001-1609.hva.2022.02.002 [12] 李浩原, 周国梁, 王刚, 等. 柔直电网阀侧单相接地故障过电压产生及影响因素研究[J]. 电力工程技术, 2021, 40(4): 34–41. LI Haoyuan, ZHOU Guoliang, WANG Gang, et al. Analysis of single-phase-to-ground fault overvoltage at the valve-side of HB-MMCs in bipolar HVDC systems[J]. Electric power engineering technology, 2021, 40(4): 34–41. [13] 胡钋, 李莉莉, 张宝丹, 等. 智能电网中交互级联故障传播的影响因素分析[J]. 智慧电力, 2021, 49(5): 69–76. HU Po, LI Lili, ZHANG Baodan, et al. Influence analysis of interactive cascading failures in smart grid[J]. Smart power, 2021, 49(5): 69–76. [14] 袁长峰, 张玉龙, 呼义超, 等. 基于模糊动态故障树的油气储运火灾事故应急过程致因因素评价[J]. 大连海事大学学报, 2021, 47(1): 92–100. YUAN Changfeng, ZHANG Yulong, HU Yichao, et al. Evaluation on causal factors in emergency processes of fire accidents for oil-gas storage and transportation based on fuzzy dynamic fault tree[J]. Journal of Dalian Maritime University, 2021, 47(1): 92–100. [15] 李钰洋, 王增平, 赵乔. 基于贝叶斯全解析模型与多因素降维的有源配电网分布式故障区段定位方法[J]. 电网技术, 2021, 45(10): 3917–3927. LI Yuyang, WANG Zengping, ZHAO Qiao. Distributed fault section location for ADN based on Bayesian complete analytic model and multi-factor dimension reduction[J]. Power system technology, 2021, 45(10): 3917–3927. [16] 张明奇, 刘麒麟, 张英敏. MMC型换流器双极故障电流影响因素分析及其优化[J]. 电力建设, 2020, 41(5): 124–132. ZHANG Mingqi, LIU Qilin, ZHANG Yingmin. Analysis and optimization of factors influencing current during MMC bipolar fault[J]. Electric power construction, 2020, 41(5): 124–132. [17] 罗静, 李豪. 基于系统因素分析法和优劣解距离法的全寿命周期故障排序[J]. 科学技术与工程, 2020, 20(7): 2694–2699. doi: 10.3969/j.issn.1671-1815.2020.07.024 LUO Jing, LI Hao. Life cycle fault sequencing study based on DEMATEL weight-TOPSIS method[J]. Science technology and engineering, 2020, 20(7): 2694–2699. doi: 10.3969/j.issn.1671-1815.2020.07.024 [18] 金闪, 许志红. 故障电弧模拟测试系统及不确定因素的研究[J]. 电力自动化设备, 2019, 39(1): 205–210. JIN Shan, XU Zhihong. Research on fault arc simulation test system and its uncertain factors[J]. Electric power automation equipment, 2019, 39(1): 205–210. [19] 范瀚文, 常征, 王聪. 海上运输通道关键节点安全韧性影响因素及评价[J]. 上海海事大学学报, 2022, 43(2): 40–46. FAN Hanwen, CHANG Zheng, WANG Cong. Influencing factors and evaluation of safety resilience of key nodes in maritime transportation channels[J]. Journal of Shanghai Maritime University, 2022, 43(2): 40–46. [20] 田水承, 孙雯, 杨鹏飞, 等. 煤矿班组不安全状态影响因素及评价[J]. 西安科技大学学报, 2022, 42(3): 405–412. TIAN Shuicheng, SUN Wen, YANG Pengfei, et al. Connotation and influencing factors of coal mine team unsafe state[J]. Journal of Xi’an University of Science and Technology, 2022, 42(3): 405–412. [21] 崔铁军, 马云东. 基于多维空间事故树的维持系统可靠性方法研究[J]. 系统科学与数学, 2014, 34(6): 682–692. CUI Tiejun, MA Yundong. Research on the maintenance method of system reliability based on multi-dimensional space fault tree[J]. Journal of systems science and mathematical sciences, 2014, 34(6): 682–692. [22] 崔铁军, 马云东. 多维空间故障树构建及应用研究[J]. 中国安全科学学报, 2013, 23(4): 32–37,62. CUI Tiejun, MA Yundong. Research on multi-dimensional space fault tree construction and application[J]. China safety science journal, 2013, 23(4): 32–37,62. [23] 赵克勤. 基于集对分析同一度的方案综合评价决策[J]. 决策探索, 1994(2): 14–15,46. ZHAO Keqin. Scheme comprehensive evaluation decision based on set pair analysis identity[J]. Police research and exploration, 1994(2): 14–15,46. [24] 赵克勤. 集对分析与熵的研究[J]. 浙江大学学报(社会科学版), 1992, 22(2): 68–75. ZHAO Keqin. Research on set pair analysis and entropy[J]. Journal of Zhejiang University (sicoal sciences edition), 1992, 22(2): 68–75. [25] 赵克勤. 集对分析与同异反决策[J]. 决策探索, 1992(2): 14–15. ZHAO Keqin. Set pair analysis and same-but-different decision-making[J]. Policy research & exploration, 1992(2): 14–15. [26] 汪培庄. 因素空间与因素库[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(10): 1297–1304. WANG Peizhuang. Factor spaces and factor data-bases[J]. Journal of Liaoning Technical University (natural science edition), 2013, 32(10): 1297–1304. [27] 汪培庄. 因素空间与概念描述[J]. 软件学报, 1992, 3(1): 30–40. WANG Peizhuang. Factor space and description of concepts[J]. Journal of software, 1992, 3(1): 30–40.
