多移动机器人固定时间编队控制

李洁; 师五喜; 李宝全

doi:10.11992/tis.202208021

多移动机器人固定时间编队控制

doi: 10.11992/tis.202208021

天津工业大学控制科学与工程学院, 天津 300387

基金项目: 国家自然科学基金项目（61973234）；天津市自然科学基金项目（20JCYBJC00180）.

详细信息

作者简介:
李洁，硕士研究生，主要研究方向为机器人控制;

师五喜，教授，博士生导师，博士，主要研究方向为机器人控制、飞行器控制、智能控制理论及应用。发表学术论文 100 余篇;

李宝全，教授，博士生导师，博士，主要研究方向为机器人控制、飞行器控制、计算机视觉.

通讯作者:
师五喜. E-mail： shiwuxi@tiangong.edu.cn.

中图分类号: TP242
出版历程
- 收稿日期: 2022-08-15
- 网络出版日期: 2023-07-19

Fixed-time formation control of multimobile robots

School of Control Science and Engineering, Tiangong University, Tianjin 300387, China

摘要

摘要: 为了减少初始位置对编队系统收敛时间的影响，本文提出了一种多移动机器人系统的固定时间编队控制方法。该方法依据领航−跟随法，将n个机器人的编队控制问题转化为n−1对跟随者与其指定领航者之间的跟踪控制问题。在领航−跟随结构模型下，设计了基于反步法的固定时间控制器使跟随机器人与领航机器人保持固定的距离与角度。基于李雅普诺夫稳定性理论，对编队控制系统的稳定性进行了分析。仿真和实验结果验证了本文方法的有效性。
- 编队控制 /
- 固定时间控制 /
- 领航−跟随 /
- 反步法 /
- 稳定性分析 /
- 移动机器人 /
- 运动学模型 /
- 图论
Abstract: In order to reduce the influence of initial position on the convergence time of formation systems, a fixed-time formation control method is presented in this paper for multimobile robot systems. Based on the leader-following structure, the formation control problem of n robots is decomposed into the tracking control problem between (n – 1) pairs of followers and their designated leader. In this structure, a fixed-time controller based on backstepping is designed to maintain the desired distance and angle between the followers and leader. Furthermore, the stability of the formation control system is analyzed using the Lyapunov stability theory, and the effectiveness of this method is verified through simulation and experimental results.
- formation control /
- fixed-time control /
- leader-following /
- backstepping /
- stability analysis /
- mobile robot /
- kinematics modeling /
- graph theory

HTML全文

当面对高并行性和高实时性的任务时,多机器人能更好地克服单个机器人的功能缺陷和执行效率低的不足,多机器人系统编队问题因其广泛的潜在应用价值引起了学者们的广泛关注。编队控制是一个典型的多机器人协调问题^[1]，基于行为的方法^[2]控制精度较低，基于人工势场的方法^[3]容易陷入局部最小陷阱中，基于虚拟结构的方法^[4]通过图论理论把多机器人系统视为刚体，因此任一机器人出现故障都会导致编队失败。由于领航−跟随方法^[5-6]容易实现，目前得到了比较广泛的研究。文献[7]在领航−跟随编队问题中用图论方法来表示机器人之间的通信。文献[8]设计了一种能够以任何平滑的领航者轨迹实现编队跟踪控制方法。文献[9]提出了一种利用模型预测控制(model predictive control)和自适应终端滑模控制(adaptive terminal sliding mode control)技术的轮式移动机器人编队复合控制策略。文献[10]在两个不同的自适应耦合增益基础上设计了一种仅依赖于相对状态信息和智能体自身的一般动力学的自适应算法。在文献[11]中，基于领航−跟随者的神经网络自适应观测器将受约束的误差动力学转化为新的二阶欧拉−拉格朗日无约束的误差动力学。但这些领航−跟随编队控制方法都是基于机器人动力学模型设计的。而与动力学控制方法相比，基于运动学模型的控制方法可以降低对机器人的硬件要求，所以此方法也是目前的一个研究热点。文献[12]提出了基于运动学模型具有路径参数同步和干扰抑制的编队系统分布式控制。文献[13]提出了一种基于具有饱和角速度和区间内有界线速度的单循环模型的独轮车运动学模型的新型滑模控制。文献[14]在领航−跟随策略中，基于每个跟随者未知领航者的完整状态的假设，提出了一种利用机器人间协调误差的分布式编队控制策略。

然而，以上编队控制方法仅仅保证了跟踪误差的渐近收敛。为了获得更快的收敛速度，文献[15]提出了有限时间收敛方法。应用此方法，文献[16] 利用添加功率积分器法和反步技术研制出一组能够保证闭环系统有限时间稳定的齐次控制器。文献[17]为了保持领航−跟随轮式移动机器人系统，提出了基于降低刚度的矩阵估计器和控制器保证在有限时间内收敛，并且可以在代理的局部坐标系内实现。然而，有限时间控制中存在收敛时间依赖于初始条件的问题，而文献[18]提出的固定时间控制方法是解决此问题的有效方法。文献[19]将现有的固定时间控制方法推广到具有死区输入和输出约束的非严格反馈系统中。文献[20]解决了一种不确定链式非完整系统的固定时间控制问题。文献[21]在反步递归设计技术的基础上，设计了一种结构简单的自适应模糊固定时间控制器。但是，这些固定时间控制方法并未应用到多移动机器人编队控制中。

本文提出了基于运动学模型的固定时间编队控制方法。该方法应用领航−跟随法将全局编队任务转化为局部跟踪问题。利用反步法技巧设计了固定时间控制器来实现轨迹跟踪。文中证明了该方法可使机器人系统所有信号有界，且使跟踪误差在固定时间收敛。实验结果验证了本文方法的有效性。

1. 问题描述

1.1 图论相关知识

多机器人系统由n个机器人和一个动态虚拟领航者组成。 $n + 1$ 个机器人之间的通信可以用一个无向图 ${\boldsymbol{G}} = \left( {N,E,A} \right)$ 来描述，其中 $N = \left\{ {0,1,\cdots,n} \right\}$ 为机器人集， $E \subseteq N \times N$ 为边缘集， ${\boldsymbol{A}} = \left[ {{a_{ij}}} \right] \subseteq R \times R$ 为邻接矩阵。当 $(i,j) \in E$ 时， ${a_{ij}} > 0$ ，否则 $ {a}_{ij}=0 $ 。动态虚拟机器人 ${R_0}$ 确定整个多机器人系统的运动轨迹，不跟踪任何机器人，其余 $ n $ 个机器人 ${R_i}$ $\left( {i = 1,2,\cdots,n} \right)$ 以固定的距离 ${\lambda _i}$ 、角度 ${\varphi _i}$ 跟踪其给定的领航者 ${R_j}$ $\left( {j = 0,1,\cdots,n - 1} \right)$ ，形成 $ n $ 对领航−跟随子结构。

假设1^[7] 　至少有一个机器人跟踪动态虚拟机器人 ${R_0}$ 。

1.2 领航−跟随编队运动学模型

在世界坐标系 $ XOY $ 中，引入的虚拟领航机器人 ${R_{{{{\rm{d}}j}}}}$ 、领航机器人 $ {R_j} $ 和跟随机器人 $ {R_i} $ 的位姿分别为 ${\left[ {{x_{{\rm{d}}j}}\quad{y_{{\rm{d}}j}}\quad{\theta _{{\rm{d}}j}}} \right]^{\rm{T}}}$ 、 ${\left[ {{x_j}\quad{y_j}\quad{\theta _j}} \right]^{\rm{T}}}$ 、 ${\left[ {{x_i}\quad{y_i}\quad{\theta _i}} \right]^{\rm{T}}}$ ，线速度分别用 ${v_{{\rm{d}}j}}$ 、 $ {v_j} $ 、 ${v_i}$ 来表示，角速度分别用 ${\omega _{{\rm{d}}j}}$ 、 ${\omega _j}$ 、 $ {\omega _i} $ 来表示。其位置关系如图1所示。

图 1 领航−跟随者结构模型

Fig. 1 Leader-follower structure model

下载: 全尺寸图片

假设2　领航机器人与虚拟领航机器人姿态一致。

则机器人 ${R_{{\rm{d}}j}}$ 、 $ {R_j} $ 之间的位置关系可表示为

$$ \begin{gathered} {x_{{\rm{d}}j}} = {x_j} + {\lambda _i}\cos ({\varphi _i} + {\theta _j}) \\ {y_{{\rm{d}}j}} = {y_j} + {\lambda _i}\sin ({\varphi _i} + {\theta _j}) \\ {\theta _{{\rm{d}}j}} = {\theta _j} \end{gathered} $$

(1)

式中： ${\varphi _i}$ 为领航机器人和虚拟领航机器人的距离， ${\lambda _i}$ 所在线段与领航机器人速度方向之间的角度。

领航机器人的运动学模型为

$$ \begin{gathered} {{\dot x}_j} = {v_j}\cos {\theta _j} \\ {{\dot y}_j} = {v_j}\sin {\theta _j} \\ {{\dot \theta }_j} = {\omega _j} \end{gathered} $$

(2)

结合式(1)、(2)可得

$$ \begin{gathered} {{\dot x}_{{\rm{d}}j}} = {v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j}) \\ {{\dot y}_{{\rm{d}}j}} = {v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos ({\varphi _i} + {\theta _j}) \\ {{\dot \theta }_{{\rm{d}}j}} = {\kern 1pt} {\kern 1pt} {\omega _j} \end{gathered} $$

(3)

跟随机器人运动学模型为

$$ \begin{gathered} {{\dot x}_i} = {v_i}\cos {\theta _i} \\ {{\dot y}_i} = {v_i}\sin {\theta _i} \\ {{\dot \theta }_i} = {\omega _i} \end{gathered} $$

(4)

假设3^[22] 　机器人 ${R_i}$ 满足以下速度约束： $ 0 < {v_i} \leqslant {v_{\max }},\left| {{\omega _i}} \right| \leqslant {\omega _{\max }} $ ，其中 ${v_{\max }}$ 、 ${\omega _{\max }}$ 为常数。

假设4^[23] 　领航机器人的 $ {v}_{j}、{\omega }_{j} $ 及其一阶导数是有界的，即 ${v_j}、{\omega _j}、{\dot v_j}、{\dot \omega _j}$ 有界。

1.3 相关引理

引理1^[18,24] 　对于系统

$$ \dot x\left( t \right) = f\left( {x\left( t \right)} \right),x\left( 0 \right) = 0,f\left( 0 \right) = 0 \text{，} $$

存在正实数 ${\mu _1},{\mu _2} > 0$ ， ${\xi _1} \in \left( {1, + \infty } \right)$ ， $ {\xi _2} \in \left( {0,1} \right) $ 和连续可微正定函数 $V\left( x \right)$ ，有

$$ \dot V\left( x \right) \leqslant - {\mu _1}{V^{{\xi _1}}}\left( x \right) - {\mu _2}{V^{{\xi _{\text{2}}}}}\left( x \right) $$

则该系统是全局固定时间稳定的且收敛时间 ${T_s}$ 满足 ${T_s} \leqslant \dfrac{1}{{{\mu _1}({\xi _1} - 1)}} + \dfrac{1}{{{\mu _2}(1 - {\xi _2})}}$ 。

引理2^[25] 　若 ${\gamma _1} > 1$ ，则以下不等式成立：

$$ {N^{\frac{{1 - {\gamma _1}}}{2}}}{\left(\sum\limits_{i = 1}^N {{{\left| {{y_i}} \right|}^2}} \right)^{\frac{{1 + {\gamma _1}}}{2}}} \leqslant \sum\limits_{i = 1}^N {{{\left| {{y_i}} \right|}^{{\gamma _1} + 1}}} $$

若 $ {\gamma _2} < 1 $ ，则以下不等式成立：

$$ {\left( {\sum\limits_{i = 1}^N {{{\left| {{y_i}} \right|}^2}} } \right)^{\frac{{1 + {\gamma _2}}}{2}}} \leqslant \sum\limits_{i = 1}^N {{{\left| {{y_i}} \right|}^{{\gamma _2} + 1}}} $$

2. 固定时间控制器设计

2.1 领航−跟随子结构的跟踪控制

$n$ 个机器人系统编队控制的目标是使机器人之间保持一定编队同时跟踪给定轨迹。由1.1节可知，给定轨迹由动态虚拟机器人 ${R_0}$ 确定， $ n $ 个机器人 ${R_i}$ $\left( {i = 1,2,\cdots,n} \right)$ 以固定的距离 ${\lambda _i}$ 、角度 ${\varphi _i}$ 跟踪其给定的领航者 ${R_j}$ $\left( {j = 0,1,\cdots,n - 1} \right)$ ，从而形成 $ n $ 对领航−跟随子结构，这样将编队问题转换成局部轨迹跟踪问题。而本节的控制目标是使机器人 ${R_i}$ 以固定的距离 ${\lambda _i}$ 、角度 ${\varphi _i}$ 跟踪领航者 ${R_j}$ 。为此引入虚拟领航机器人 ${R_{{\rm{d}}j}}$ ，将机器人 ${R_i}$ 、 ${R_j}$ 的跟踪问题转化为跟随机器人 ${R_i}$ 与虚拟领航机器人 ${R_{{\rm{d}}j}}$ 轨迹跟踪问题。 ${R_i}$ 、 ${R_{{\rm{d}}j}}$ 的误差定义为

$$ \begin{gathered} {x_e}{\text{ = }}{x_{{\rm{d}}j}} - {x_i} \\ {y_e}{\text{ = }}{y_{{\rm{d}}j}}{\kern 1pt} - {y_i} \\ {\theta _e}{\text{ = }}{\theta _{{\rm{d}}j}} - {\theta _i} \\ \end{gathered} $$

(5)

利用反步法技巧引入虚拟输入 ${\alpha _i}$ ，根据式(4)有

$$ \begin{gathered} {{\dot x}_i} = {v_i}\cos {\alpha _i} \\ {{\dot y}_i} = {v_i}\sin {\alpha _i} \\ \end{gathered} $$

(6)

结合式(3)、(5)、(6)可得

$$ \begin{gathered} {{\dot x}_e} = {v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j}) - {v_i}\cos {\alpha _i} \\ {{\dot y}_e} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos ({\varphi _i} + {\theta _j}) - {v_i}\sin {\alpha _i} \\ {{\dot \theta }_e} = {\kern 1pt} {\kern 1pt} {\omega _j} - {\omega _i}{\kern 1pt} {\kern 1pt} {\kern 1pt} \end{gathered} $$

(7)

取李雅普诺夫函数为

$$ {V_1} = \frac{1}{2}x_e^2 + \frac{1}{2}y_e^2 $$

(8)

对式(8)求导并代入式(7)得

$$\begin{gathered} {{\dot V}_1} = {x_e}{{\dot x}_e} + {y_e}{{\dot y}_e} = \\ {x_e}\left( {{v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin \left( {{\varphi _i} + {\theta _j}} \right) - {v_i}\cos {\alpha _i}} \right) +\\ {y_e}\left( {{v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos \left( {{\varphi _i} + {\theta _j}} \right) - {v_i}\sin {\alpha _i}} \right) \\ \end{gathered} $$

(9)

设计虚拟输入 ${\alpha _i}$ ，使得满足

$$ \begin{gathered} {v_i}\cos {\alpha _i} = {v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j}) +\\ {k_{1i}}x_e^{\beta _1} + {k_{2i}}x_e^{\beta _2} \\ \end{gathered} $$

(10)

$$ \begin{gathered} {v_i}\sin {\alpha _i} = {\kern 1pt} {\kern 1pt} {v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos ({\varphi _i} + {\theta _j}) +\\ {k_{3i}}y_e^{{\beta _1}} + {k_{4i}}y_e^{{\beta _2}} \\ \end{gathered} $$

(11)

其中 ${k_{1i}},{k_{2i}},{k_{3i}},{k_{4i}} > 0$ ， ${\beta _1} > 1$ ， $0 < {\beta _2} < 1$ 。

由式(10)、(11)可得线速度和虚拟输入：

$$ {v_i} = \sqrt {m_x^2 + m_y^2} $$

(12)

$$ {\alpha _i} = \arctan \frac{{{m_y}}}{{{m_x}}} $$

(13)

其中

$$ {m_x} = {v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j}) + {k_{1{{i}}}}x_e^{{\beta _1}} + {k_{2{{i}}}}x_e^{{\beta _2}} $$

(14)

$$ {m_y} = {v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos ({\varphi _i} + {\theta _j}) + {k_{3{{i}}}}y_e^{{\beta _1}} + {k_{4{{i}}}}y_e^{{\beta _2}} $$

(15)

将式(10)、(11)代入式(9)可得

$$ \begin{gathered} {{\dot V}_{\text{1}}} = - {k_{1{{i}}}}x_e^{{\beta _1} + 1} - {k_{2{{i}}}}x_e^{{\beta _2} + 1} - {k_{3{{i}}}}y_e^{{\beta _1} + 1} - {k_{4{{i}}}}y_e^{{\beta _2} + 1} \leqslant \\ -{p_1}\left( {x_e^{{\beta _1} + 1} + y_e^{{\beta _1} + 1}} \right) - {p_2}\left( {x_e^{{\beta _2} + 1} + y_e^{{\beta _2} + 1}} \right) \\ \end{gathered} $$

(16)

其中 ${p_1} = \min \left\{ {{k_{1{{i}}}},{k_{3{{i}}}}} \right\},{p_2} = \min \left\{ {{k_{2{{i}}}},{k_{4{{i}}}}} \right\}$ 。由引理2，式(16)还可以写成

$$ \begin{gathered} {{\dot V}_1} \leqslant - {2^{\frac{{1 - {\beta _1}}}{2}}}{p_1}{\left( {x_e^2 + y_e^2} \right)^{\frac{{1 + {\beta _1}}}{2}}} - {p_2}{\left( {x_e^2 + y_e^2} \right)^{\frac{{1 + {\beta _2}}}{2}}} = \\ - 2{p_1}{V_1}^{\frac{{1 + {\beta _1}}}{2}} - {2^{\frac{{1 + {\beta _2}}}{2}}}{p_2}{V_1}^{\frac{{1 + {\beta _2}}}{2}} \leqslant 0 \end{gathered} $$

(17)

由式(17)得， ${x_e}、{y_e}$ 有界，由引理1知跟踪误差 ${x_e}、{y_e}$ 固定时间收敛。当 ${x_e}、{y_e}$ 收敛到零时，由式(3)、(14)和(15)得， ${\alpha _i}=\arctan$ $\dfrac{{{v_j}\sin {\theta _j} + {\omega _j}{\lambda _i}\cos ({\varphi _i} + {\theta _j})}}{{{v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j})}}= \dfrac{{{{\dot y}_{{\rm{d}}j}}}}{{{{\dot x}_{{\rm{d}}j}}}}$ 。由于机器人 ${R_{{\rm{d}}j}}$ 运动学模型可以写为

$$ \begin{gathered} {{\dot x}_{{\rm{d}}j}} = {v_{{\rm{d}}j}}\cos {\theta _{{\rm{d}}j}} \\ {{\dot y}_{{\rm{d}}j}} = {\kern 1pt} {v_{{\rm{d}}j}}\sin {\theta _{{\rm{d}}j}} \\ {{\dot \theta }_{{\rm{d}}j}} = {\kern 1pt} {\kern 1pt} {\omega _{{\rm{d}}j}} \end{gathered} $$

(18)

所以 ${\alpha _i} = \arctan \dfrac{{{v_{{\rm{d}}j}}\sin {\theta _{{\rm{d}}j}}}}{{{v_{{\rm{d}}j}}\cos {\theta _{{\rm{d}}j}}}} = {\theta _{{\rm{d}}j}}$ 。故要实现 ${\theta _i}$ 固定时间内跟踪 ${\theta _{{\rm{d}}j}}$ 就必须要保证 ${\theta _i}$ 在固定时间内跟踪 ${\alpha _i}$ 。为此定义 $e = {\alpha _i} - {\theta _i}$ ，设计角速度控制律为

$$ {\omega _i} = {\dot \alpha _i} + {k_{5{{i}}}}e_{}^{{\beta _1}} + {k_{6{{i}}}}e_{}^{{\beta _2}} $$

(19)

其中 ${k_{5{{i}}}},{k_{6{{i}}}} > 0$ 。

定理1　对于领航−跟随子系统，控制输入式(12)、(19)可使闭环系统的所有信号有界，且跟踪误差在固定时间内收敛，其收敛时间 $ {T_i} $ 满足

$$ {T_i} \leqslant \frac{2}{{{a_1}({\beta _1} - 1)}} + \frac{2}{{{a_2}(1 - {\beta _2})}} $$

其中 ${a_1}、{a_2}$ 为常数。

证明　取李雅普诺夫函数为

$$ {V_2} = {V_1} + \frac{1}{2}e_{}^2 $$

(20)

对式(20)求导并代入式(16)得

$$ \begin{gathered} {{\dot V}_2} ={{\dot V}_1} + e\dot e =- {k_{1{{i}}}}x_e^{{\beta _1} + 1} - {k_{2{{i}}}}x_e^{{\beta _2} + 1} - {k_{3{{i}}}}y_e^{{\beta _1} + 1} -\\ {k_{4{{i}}}}y_e^{{\beta _2} + 1} + e\left( {{{\dot \alpha }_i} - {\omega _i}} \right) \\ \end{gathered} $$

(21)

将式(19)代入式(21)，可得

$$ \begin{gathered} {{\dot V}_2} = - {k_{1{{i}}}}x_e^{{\beta _1} + 1} - {k_{2{{i}}}}x_e^{{\beta _2} + 1} - {k_{3{{i}}}}y_e^{{\beta _1} + 1} - {k_{4{{i}}}}y_e^{{\beta _2} + 1} - {k_{{{5i}}}}{e^{{\beta _1} + 1}} -\\ {k_{6{{i}}}}{e^{{\beta _2} + 1}} \leqslant - {p_3}(x_e^{{\beta _1} + 1} + y_e^{{\beta _1} + 1} + {e^{{\beta _1} + 1}}) -{p_4}(x_e^{{\beta _2} + 1} + y_e^{{\beta _2} + 1} + {e^{{\beta _2} + 1}}) \end{gathered} $$

(22)

其中 ${p_3} = \min \{ {k_{1{{i}}}},{k_{3{{i}}}},{k_{5{{i}}}}\}$ ， ${p_4} = \min \{ {k_{2{{i}}}},{k_{4{{i}}}},{k_{6{{i}}}}\}$ 。由引理2、式(22)得

$$ \begin{gathered} {{\dot V}_2} \leqslant - {3^{\frac{{1 - {\beta _1}}}{2}}}{p_3}{(x_e^2 + y_e^2 + {e^2})^{\frac{{{\beta _1} + 1}}{2}}} - {p_4}{(x_e^2 + y_e^2 + {e^2})^{\frac{{{\beta _2} + 1}}{2}}} = \\ - {3^{\frac{{1 - {\beta _1}}}{2}}}{2^{\frac{{{\beta _1} + 1}}{2}}}{p_3}V_2^{\frac{{{\beta _1} + 1}}{2}} - {2^{\frac{{{\beta _2} + 1}}{2}}}{p_4}V_2^{\frac{{{\beta _2} + 1}}{2}} \end{gathered} $$

(23)

令 $ {a_1} = {3^{\frac{{1 - {\beta _1}}}{2}}}{2^{\frac{{{\beta _1} + 1}}{2}}}{p_3} > 0,{a_2} = {2^{\frac{{{\beta _2} + 1}}{2}}}{p_4} > 0 $ ，式(23)可化简为

$$ {\dot V_2} \leqslant - {a_1}V_2^{\frac{{{\beta _1} + 1}}{2}} - {a_2}V_2^{\frac{{{\beta _2} + 1}}{2}} \leqslant {\text{0}} $$

(24)

由此可得 ${x_e}、{y_e}、e$ 是有界的。

将式(14)和式(15)求导得

$$\begin{gathered} {{\dot m}_x} ={{\dot v}_j}\cos {\theta _j} - {v_j}{\omega _j}\sin {\theta _j} - \omega _j^2{\lambda _i}\cos \left( {{\varphi _i} + {\theta _j}} \right) -\\{{\dot \omega }_j}{\lambda _i}\sin \left( {{\varphi _i} + {\theta _j}} \right) + {k_{1{{i}}}}{\beta _1}x_e^{{\beta _1} - 1}{{\dot x}_e} + {k_{2{{i}}}}{\beta _2}x_e^{{\beta _2} - 1}{{\dot x}_e} \\ \end{gathered}$$

(25)

$$ \begin{gathered} {{\dot m}_y} = {{\dot v}_j}\sin {\theta _j} + {v_j}{\omega _j}\cos {\theta _j} - \omega _j^2{\lambda _i}\sin \left( {{\varphi _i} + {\theta _j}} \right) +\\ {{\dot \omega }_j}{\lambda _i}\cos \left( {{\varphi _i} + {\theta _j}} \right) + {k_{3{{i}}}}{\beta _1}y_e^{{\beta _1} - 1}{{\dot y}_e} + {k_{4{{i}}}}{\beta _2}y_e^{{\beta _2} - 1}{{\dot y}_e} \end{gathered} $$

(26)

由假设3、假设4和式(25)、(26)，可以得到 $ {m}_{x}、{m}_{y} $ 、 $ {\dot{m}}_{x}、{\dot{m}}_{y} $ 有界。式(13)对时间求导，代入式(12)得

$$ \mathop {{\alpha _i}}\limits^. = \frac{{{{\dot m}_y}{m_x} - {{\dot m}_x}{m_y}}}{{m_x^2 + m_y^2}} = \frac{{{{\dot m}_y}{m_x} - {{\dot m}_x}{m_y}}}{{v_i^2}} $$

(27)

由假设3和式(27)，可得 $ {\dot \alpha _i} $ 有界，因此， ${v_i},{\omega _i}$ 有界，因此闭环系统所有信号均有界。由引理1，跟踪误差 $ {x}_{e},{y}_{e},e $ 在固定时间 $ {T}_{i} $ 内收敛。

2.2 编队控制

以下把领航−跟随子结构模型推广到 $n$ 个机器人的编队控制。在实现领航−跟随子结构轨迹跟踪后，基于图论知识确定机器人之间的领航−跟随关系就可以实现机器人编队。无向图中的节点为动态虚拟机器人 ${R_0}$ 和 $n$ 个机器人，无向图的边表示两个机器人间的跟踪关系。 $(i,j) \in E$ 表示机器人 ${R_i}$ 以固定的距离 ${\lambda _i}$ 、角度 ${\varphi _i}$ 跟踪跟随机器人 ${R_j}$ ，此时，取 ${a_{ij}} = 1$ 。邻接矩阵 ${\boldsymbol{A}}$ 为

$$ \begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {{R_0}}&{{R_1}}& \cdots &{{R_n}} \end{array}} \\ {\begin{array}{*{20}{c}} {{R_0}} \\ {{R_1}} \\ \vdots \\ {{R_n}} \end{array}}&{\left[ {\begin{array}{*{20}{c}} {{a_{00}}}&{{a_{01}}}& \cdots &{{a_{0n}}} \\ {{a_{10}}}&{{a_{11}}}& \cdots &{{a_{1n}}} \\ \vdots & \vdots &\ddots & \vdots \\ {{a_{n0}}}&{{a_{n1}}}& \cdots &{{a_{nn}}} \end{array}} \right]} \end{array} $$

邻接矩阵表示了机器人之间的相互联系，其中每一行表示一个跟随者，每一列表示它的候选领航者。如果第 $i$ 行在第 $j$ 列中有一个非零项，则机器人 ${R_i}$ 跟随机器人 ${R_j}$ 。由于动态虚拟机器人 $ {R}_{0} $ 没有跟随任何机器人，因此第1行中全为零。 $n$ 对领航者和跟随者中，两个关键参数 ${\lambda _i}$ 和 ${\varphi _i}$ 决定了机器人子系统的几何形状，进而确定编队队形。当队形变化时，只需改变 ${\boldsymbol{A}}$ ， ${\lambda _i}$ ， ${\varphi _i}$ 的对应值。本文基于领航−跟随法将多机器人编队控制转化为多个领航−跟随子结构轨迹跟踪问题，根据定理1，每个领航−跟随子结构都存收敛时间的上界 $ {T}_{i} $ ，多机器人系统编队控制的收敛时间上界 $ T $ 为 $ T=\mathrm{max}\left\{{T}_{i}\right\}，i\in N $ ，且与控制律的参数有关。

3. 仿真与实验验证

3.1 仿真验证

为了验证所设计控制器的有效性，在本节中，给出了数值仿真来验证从上一节得出的理论结果。考虑10个机器人( $ {R}_{1} $ , $ {R}_{\text{2}} $ , $ {R}_{\text{3}} $ , $ {R}_{\text{4}} $ , $ {R}_{\text{5}} $ , $ {R}_{\text{6}} $ , $ {R}_{\text{7}} $ , $ {R}_{\text{8}} $ , $ {R}_{\text{9}} $ , $ {R}_{\text{10}} $ )和一个虚拟领航者 ${R_0}$ ，编队队形如图2所示。

图 2 机器人无向拓扑连接图

Fig. 2 Undirected topology connection diagram of robots

下载: 全尺寸图片

为了直观地表示队形，为每一个跟随机器人 ${R_i}$ 引入的虚拟机器人 ${R_{{\rm{d}}j}}$ 未在图2中体现。由图2可得

$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \end{array}} \right] $$

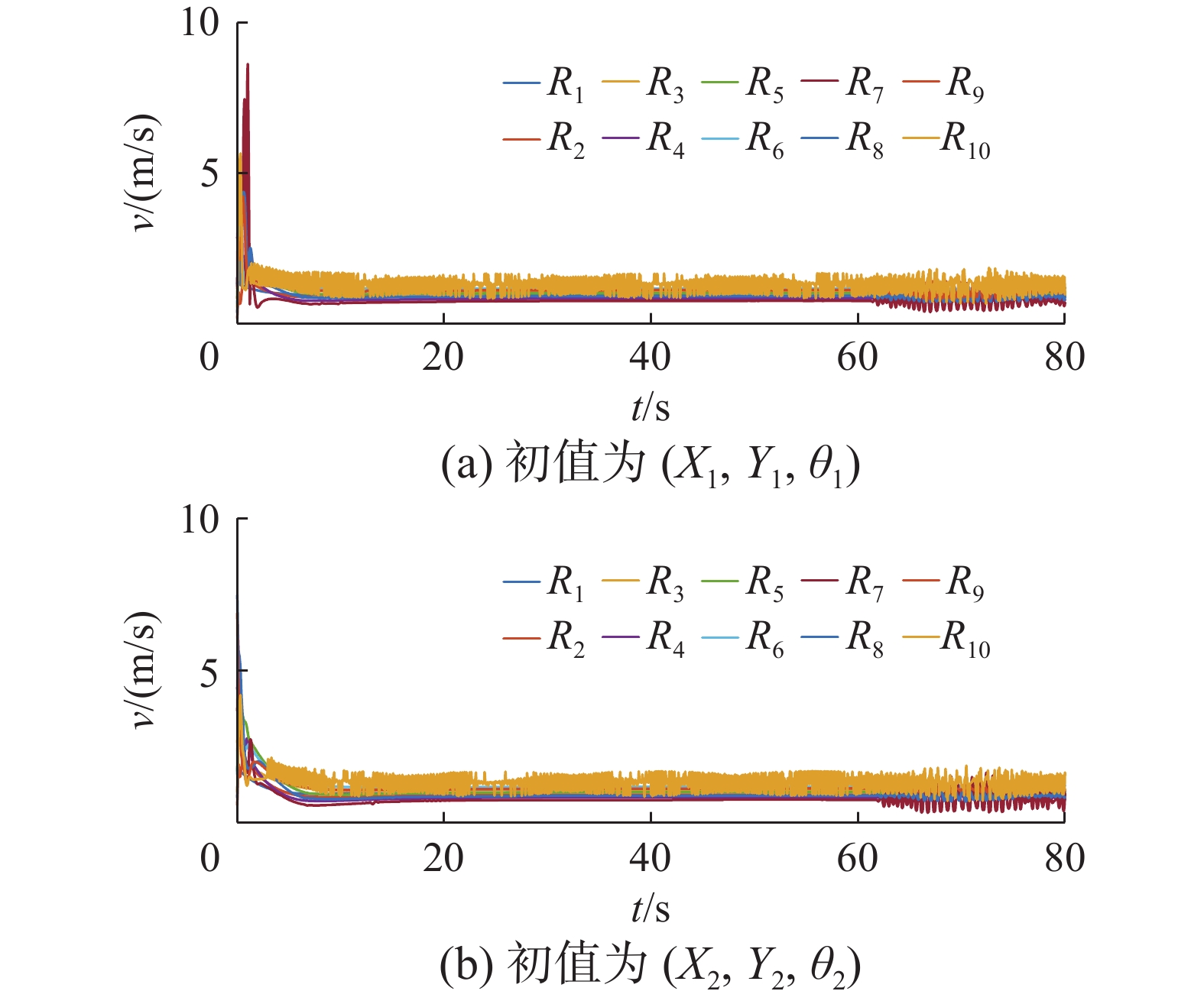
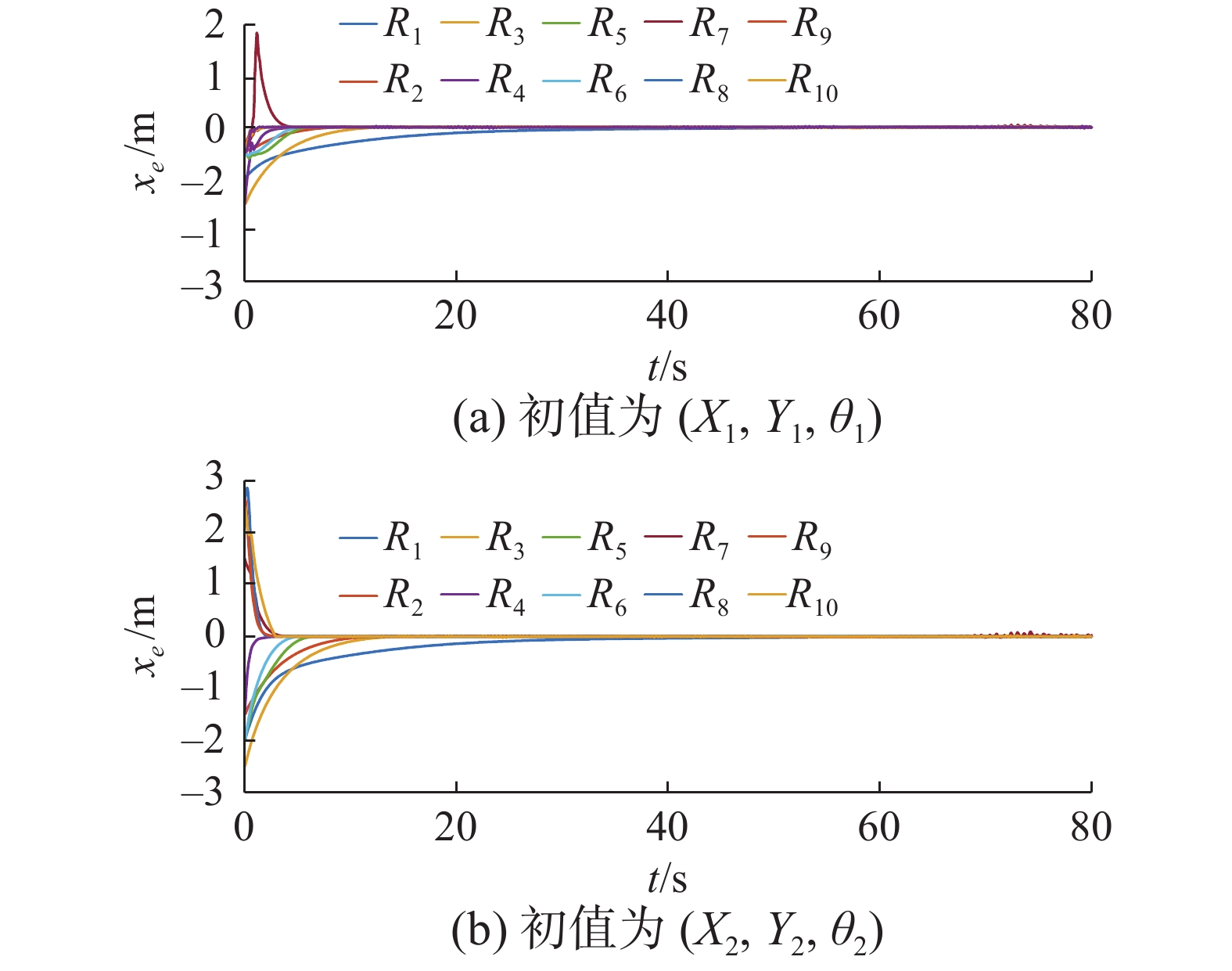
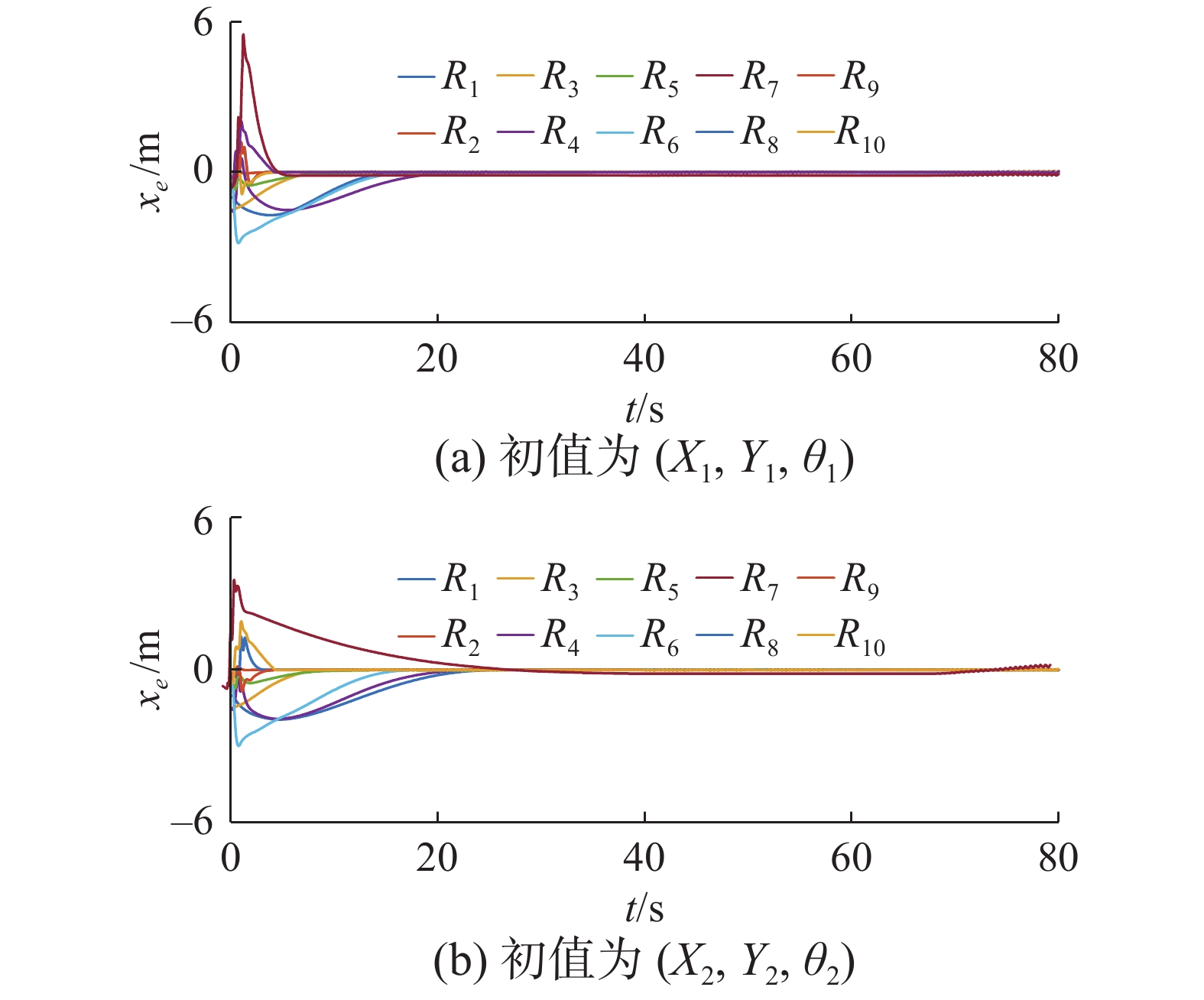
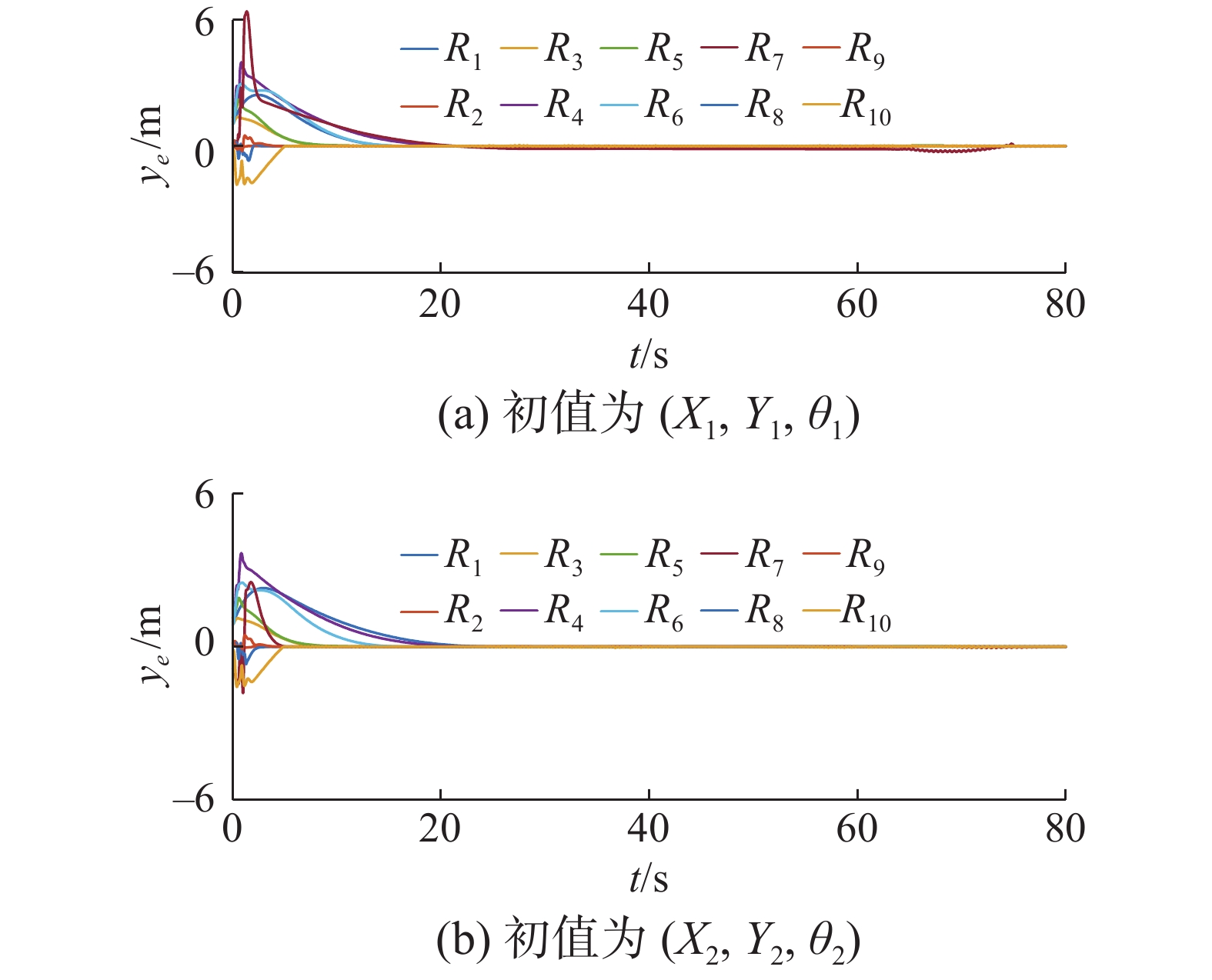
期望轨迹定义为动态虚拟领航者 $ {R_0} $ ， ${v_0} = {\text{1}}\;{\rm{m }}/{{\rm{s}}}$ ， ${\omega _0} = {\text{0}}{\text{.1}}\;{\rm{rad}} /{\rm{s}}$ 。为了验证本文方法的跟踪性能不依赖于初始位置，给出了不同的初始位置下的仿真结果，记两个初始位置为 $ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $ 、 $ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $ 。初始位置和编队期望距离及角度 $\left( {{\lambda _i},{\varphi _i}} \right)$ 如表1所示。控制律的参数如表2所示。由2.2节的讨论和表2可得仿真系统的收敛时间上界为机器人 $ {R_{\text{2}}} $ 跟随 $ {R_{\text{1}}} $ 的收敛时间上界45 s。仿真结果如图3~图8所示。根据仿真图3、4可以得出，控制器可满足编队的要求，跟踪效果显著。图5、6为机器人速度。如图7、8所示，在初始位置变化时，控制器都可以在30 s左右实现编队，该仿真结果符合上文讨论的系统收敛时间上界。

表 1 机器人初始位姿和编队参数表

Table 1 Initial pose and formation parameters of the robot

机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
R₀	$ \left( {0, - 10,0} \right) $	$ \left( {0, - 10,0} \right) $	—
R₁	$\left( { {{ - 1} }, - {\text{9} },0} \right)$	$\left( { {- 2 }, - {\text{8} },0} \right)$	$\left( {0,0} \right)$
R₂	$ \left( { - {\text{2}}, - {\text{8}},0} \right) $	$ \left( { - {\text{4}}, - 6,0} \right) $	$\left( {1,0.6\text{π} } \right)$
R₃	$ \left( { - {\text{3}}, - 9,0} \right) $	$ \left( { - {\text{5}}, - {\text{7}},0} \right) $	$\left( {1, - 0.6\text{π} } \right)$
R₄	$ \left( { - {\text{4}}, - 6,0} \right) $	$ \left( { - {\text{6}}, - {\text{4}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₅	$ \left( { - {\text{4}}, - 7,0} \right) $	$ \left( { - {\text{7}}, - {\text{4}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₆	$ \left( { - {\text{4}}, - {\text{9}},0} \right) $	$ \left(-\text{7},-\text{7},0\right) $	$ \left(1,-0.6\text{π} \right) $
R₇	$ \left(-\text{5},-\text{5},0\right) $	$ \left( { - {\text{5}}, - {\text{5}},0} \right) $	$\left( {1,0.6\text{π} } \right)$

续表 1
机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
R₈	$ \left(-\text{5},-\text{6},0\right) $	$ \left(-\text{5},-\text{6},0\right) $	$\left( {1,0.6\text{π} } \right)$
R₉	$ \left( { - {\text{5}}, - {\text{8}},0} \right) $	$ \left( { - {\text{5}}, - {\text{8}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₁₀	$ \left( { - {\text{5}}, - 10,0} \right) $	$ \left( { - {\text{5}}, - 10,0} \right) $	$\left( {1, - 0.6\text{π} } \right)$

表 2 固定时间控制参数表

Table 2 Parameters of fixed-time control

机器人	${k_{1{{i}}} }$	${k_{2{{i}}}}$	${k_{3{{i}}}}$	${k_{4{{i}}}}$	${k_{5{{i}}}}$	${k_{6{{i}}}}$	${\beta _1}$	${\beta _2}$
R₁	0.2	0.5	0.2	0.5	0.2	0.2	1.2	0.5
R₂	0.2	0.1	0.2	0.1	1.0	1.0	1.2	0.5
R₃	0.2	0.1	0.2	0.1	2.0	0.1	1.2	0.5
R₄	1.0	0.5	1.0	0.5	2.0	2.0	1.2	0.7
R₅	0.2	1.0	0.2	1.0	1.0	1.0	1.2	0.7
R₆	0.2	1.0	0.2	1.0	2.0	2.0	1.2	0.7
R₇	0.5	0.7	0.5	0.7	2.0	2.0	1.2	0.7
R₈	0.7	1.5	0.7	1.5	2.0	2.0	1.2	0.7
R₉	0.7	1.5	0.7	1.5	3.0	3.0	1.2	0.9
R₁₀	0.5	0.5	0.5	0.5	2.0	2.0	1.2	0.1

图 3 初始位置为 $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $ 固定时间控制机器人轨迹

Fig. 3 Trajectories of fixed-time control with $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $

下载: 全尺寸图片

图 4 初始位置为 $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $ 固定时间控制机器人轨迹

Fig. 4 Trajectories of fixed-time control with $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $

下载: 全尺寸图片

图 5 固定时间控制机器人线速度

Fig. 5 Robots’ linear velocity of fixed-time control

下载: 全尺寸图片

图 6 固定时间控制机器人角速度

Fig. 6 Robots’ angle velocity of fixed-time control

下载: 全尺寸图片

图 7 固定时间控制的误差 ${x_e}$

Fig. 7 Error ${x_e}$ of fixed-time control

下载: 全尺寸图片

图 8 固定时间控制的误差 ${y_e}$

Fig. 8 Error ${y_e}$ of fixed-time control

下载: 全尺寸图片

为了比较控制律的有效性，给出有限时间控制律：

$$ \begin{gathered} {v_i} = \sqrt {m_{xx}^2 + m_{yy}^2} \\[-1pt] {\alpha _i} = \arctan \frac{{{m_{yy}}}}{{{m_{xx}}}} \\[-1pt] {\omega _i} = {{\dot \alpha }_i} + {c_{3{{i}}}}{e^{{\beta _2}}} \end{gathered} $$

(28)

其中： ${m_{xx}} = {v_j}\cos {\theta _j} - {\omega _j}{\lambda _i}\sin ({\varphi _i} + {\theta _j}) + {c_{1{{i}}}}x_e^{{\beta _2}}$ ， ${m_{yy}} = $ ${\omega _j}{\lambda _i} \cos ({\varphi _i} + {\theta _j}) + {v_j}\sin {\theta _j} + {c_{2{{i}}}}y_e^{{\beta _2}}$ 。参数如表3所示。

表 3 有限时间控制参数表

Table 3 Parameters of finite-time control

机器人	${c_{1{{i}}} }$	${c_{2{{i}}} }$	${c_{3{{i}}} }$	${\beta _2}$
R₁	0.8	0.8	0.5	0.6
R₂	0.2	0.2	1.0	0.5
R₃	0.3	0.3	0.5	0.5
R₄	0.6	0.6	1.5	0.6
R₅	0.5	0.5	1.0	0.9
R₆	0.5	0.5	0.5	0.7
R₇	0.1	0.1	3.0	0.6
R₈	1.5	1.5	2.0	0.7
R₉	1.5	1.5	3.0	0.9
R₁₀	0.5	0.5	2.0	0.1

控制律与固定时间控制律采用相同的期望轨迹和初始位置。该实验可以实现不同初始值下机器人的编队轨迹，为了比较系统收敛时间的变化，只给出图9和图10所示的编队误差，当机器人初始位置发生变化时，收敛时间从20 s变化到25 s左右。而本文控制器的系统收敛时间相对固定。

图 9 有限时间控制的误差 $ {x}_{e} $

Fig. 9 Error $ {x}_{e} $ of finite-time control

下载: 全尺寸图片

图 10 有限时间控制的误差 $ {y}_{e} $

Fig. 10 Error ${y_e}$ of finite-time control

下载: 全尺寸图片

3.2 实验验证

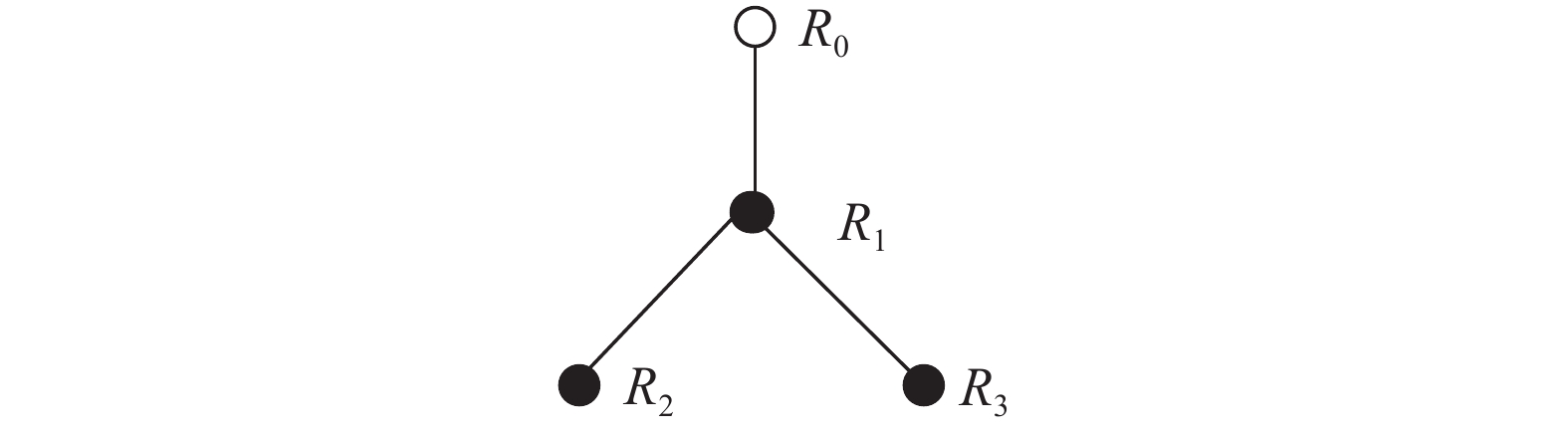
实验平台为Turtlebot3 Waffle Pi，如图11所示。为了验证本文所设计控制方法的有效性，在本节中，考虑3个Turtlebot3( $ {R}_{1} $ , $ {R}_{\text{2}} $ , $ {R}_{\text{3}} $ )和一个虚拟领航者 ${R_0}$ ，编队队形如图12所示。为了直观地表示队形，为每一个跟随机器人 ${R_i}$ 引入的虚拟机器人 ${R_{{\rm{d}}j}}$ 未在图12中体现。由图12可得邻接矩阵为

图 11 Turtlebot3 Waffle Pi机器人

Fig. 11 Turtlebot3 Waffle Pi robots

下载: 全尺寸图片

图 12 机器人无向拓扑连接图

Fig. 12 Undirected topology connection diagram of robots

下载: 全尺寸图片

$${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{1}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{1}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{1}}&{\text{0}}&{\text{0}} \end{array}} \right] $$

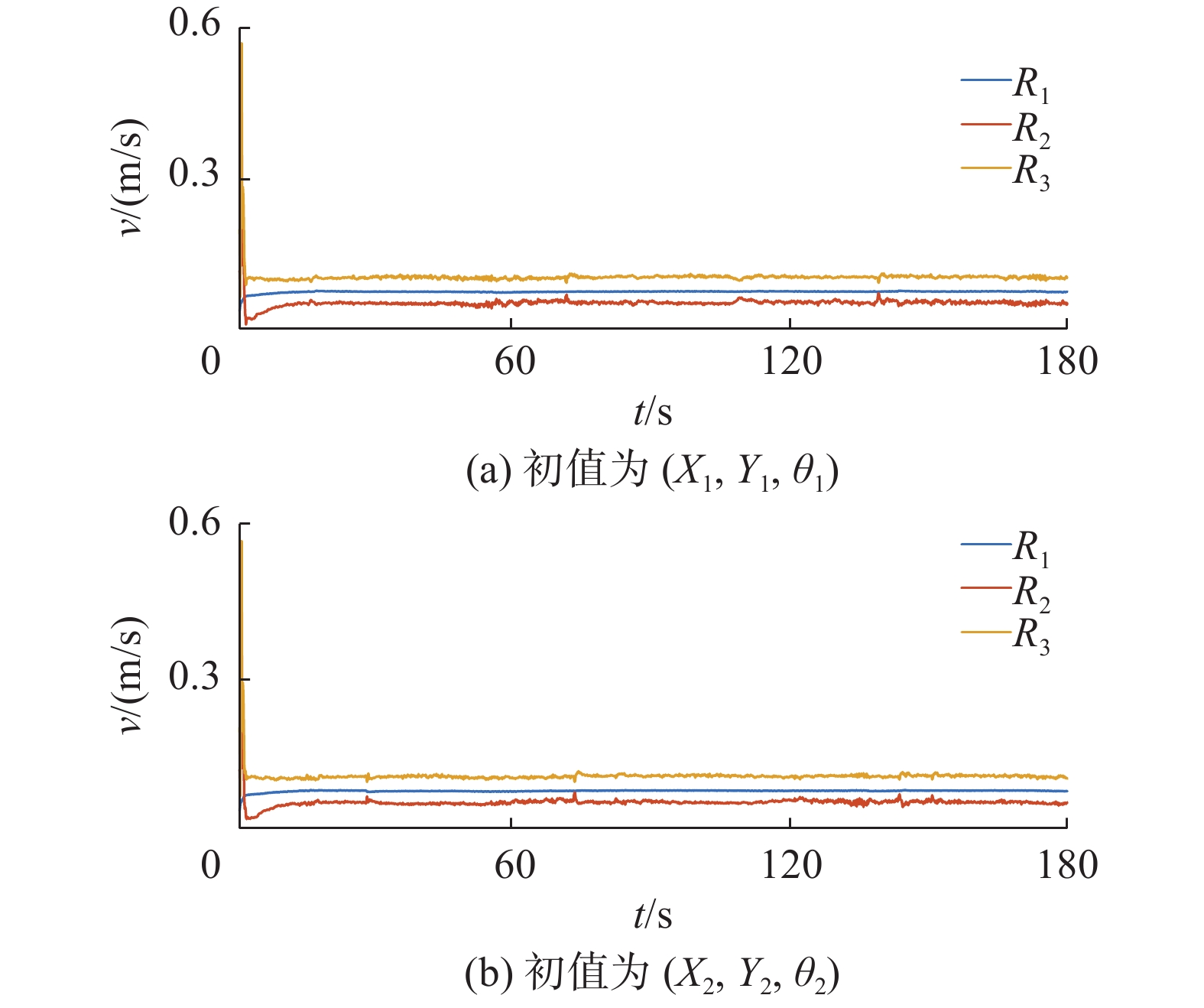
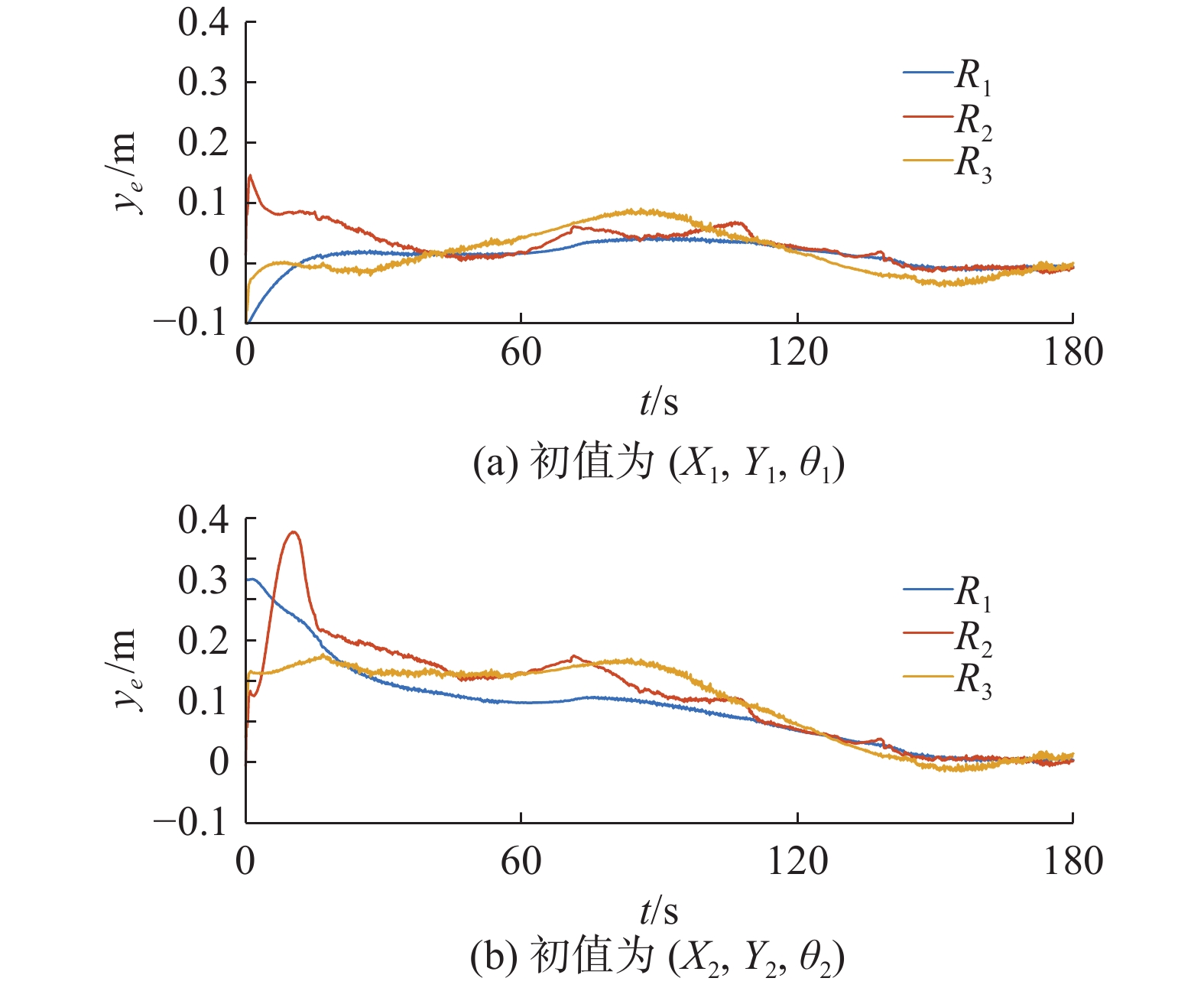
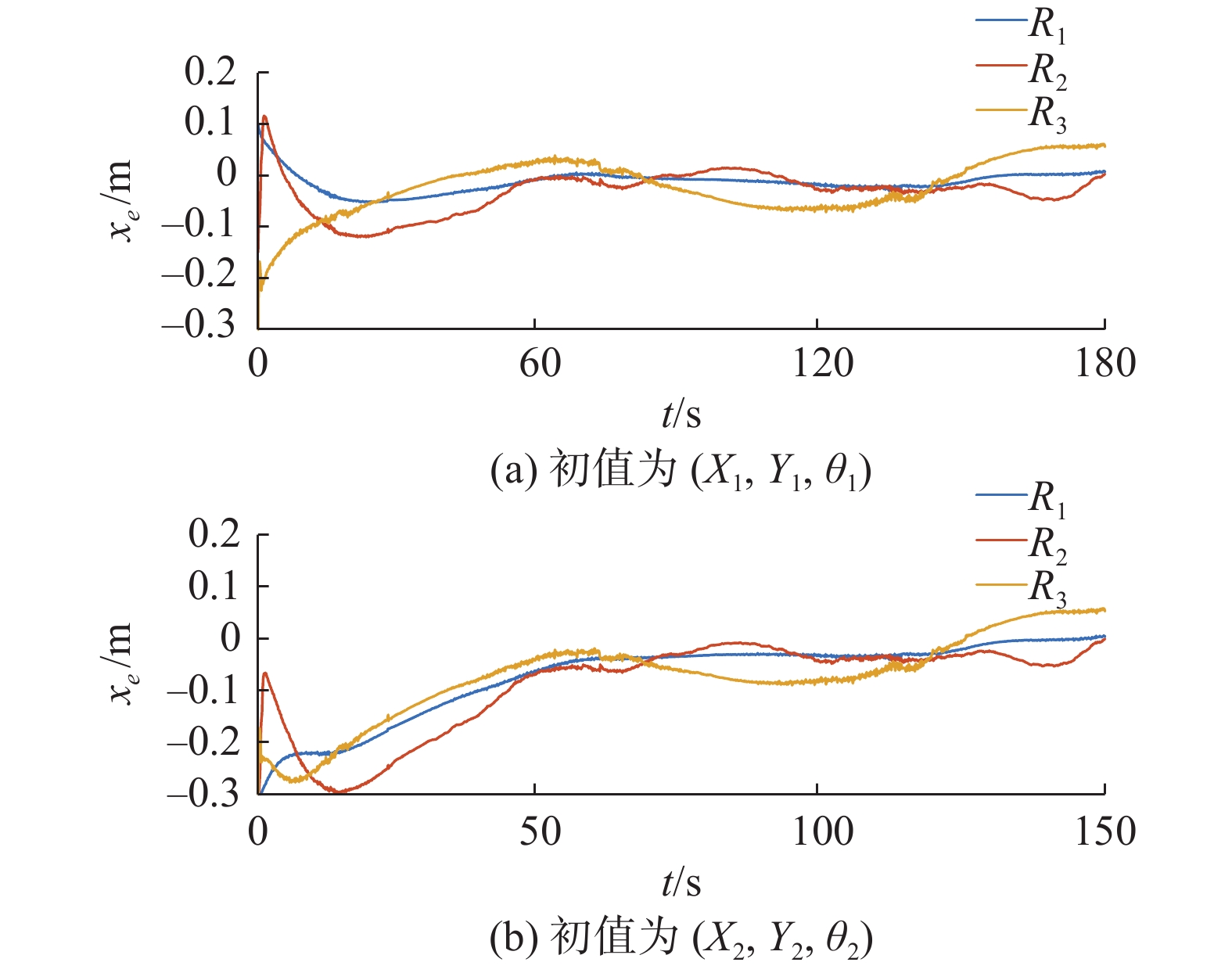
期望轨迹由动态虚拟领航者 $ {R_0} $ 确定，选取 ${v_0} = 0.{\text{07}}5 \;{{\rm{m}}/{\rm{s}}}$ ， ${\omega }_{0}=0.05\;{\rm{rad}}/{{\rm{s}}}$ 。初始位置和编队期望距离及角度 $\left({\lambda }_{i},{\varphi }_{i}\right)$ 如表4所示，图13为实验环境。控制器的参数选取如表5所示。由2.2节和表5可以获得的系统收敛时间上界为机器人 ${R_1}$ 跟踪 ${R_0}$ 的收敛时间上界240 s。实验结果如图14~图19所示，其中图14、15为不同初始值下机器人的编队轨迹，图16、17为机器人速度，图18、19为编队误差。本文的控制算法是基于理想状态的运动学模型设计的,未考虑机器人自身的机械结构、载重等因素,且由图13可得本实验环境中不可避免出侧滑等情况，本文虽然在运动学模型中未考虑以上不确定性，但通过实验结果可以看出，对侧滑等不确定性有较强的鲁棒性，在初始位置变化时，本文所提出的方法仍然可以在120 s内实现编队，该仿真结果符合上文讨论的系统收敛时间上界。

表 4 机器人初始位姿和编队参数表

Table 4 Initial pose and formation parameters of the robot

机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
${R_0}$	$ \left( { - 0.1,0.1,0} \right) $	$ \left( { - 0.2,0.2,0} \right) $	—
${R_1}$	$ \left( {0,0,0} \right) $	$ \left( {0,0,0} \right) $	$\left( {0,0} \right)$
${R_2}$	$ \left( { - 0.4,0.6,0} \right) $	$ \left( { - 0.5,0.5,0} \right) $	$\left( {0.6,0.6\text{π} } \right)$
${R_3}$	$ \left( { - 0.5, - 0.6,0} \right) $	$ \left( { - 0.4, - 0.7,0} \right) $	$\left( {0.8, - 0.6\text{π} } \right)$

图 13 实验环境

Fig. 13 Experimental environment

下载: 全尺寸图片

表 5 固定时间控制参数表

Table 5 Parameters of fixed-time control

机器人	${k_{1{{i}}}}$	${k_{2{{i}}}}$	${k_{3{{i}}}}$	${k_{4{{i}}}}$	${k_{5{{i}}}}$	${k_{6{{i}}}}$	${\beta _1}$	$ {\beta }_{2} $
R₁	0.05	0.01	0.05	0.01	0.10	0.10	1.20	0.70
R₂	0.05	0.05	0.05	0.05	0.05	0.05	1.20	0.70
R₃	0.10	0.10	0.10	0.10	0.10	0.10	1.20	0.70

图 14 初始位置为 $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $ 固定时间控制机器人轨迹

Fig. 14 Trajectories of fixed time control with $ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $

下载: 全尺寸图片

图 15 初始位置为 $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $ 固定时间控制机器人轨迹

Fig. 15 Trajectories of fixed-time control with $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $

下载: 全尺寸图片

图 16 固定时间控制机器人线速度

Fig. 16 Robots’ linear velocity of fixed-time control

下载: 全尺寸图片

图 17 固定时间控制机器人角速度

Fig. 17 Robots’ angle velocity of fixed-time control

下载: 全尺寸图片

图 18 固定时间控制的误差 ${x_e}$

Fig. 18 Error ${x_e}$ of fixed-time control

下载: 全尺寸图片

图 19 固定时间控制的误差 ${y_e}$

Fig. 19 Error $ {y}_{e} $ of fixed-time control

下载: 全尺寸图片

下面再对本文方法和有限时间控制方法进行实验对比，参数选取如表6所示。期望轨迹和初始位置的选取和以上固定时间控制相同。该实验可以实现不同初始值下机器人的编队轨迹，为了比较系统收敛时间的变化,只给出图20、图21所示的编队误差,当机器人初始位置发生变化时，收敛时间从80 s变化到120 s，系统的收敛速度显然受到初始位置的影响，而从实验结果可知本文方法系统的收敛速度不受初始值影响。

表 6 有限时间控制参数表

Table 6 Parameters of finite-time control

机器人	${c_{1{{i}}} }$	${c_{2{{i}}} }$	${c_{3{{i} } } }$	${\beta _2}$
R₁	0.01	0.05	0.10	0.70
R₂	0.01	0.05	0.10	0.70
R₃	0.10	0.05	0.10	0.70

图 20 有限时间控制的误差 $ {x}_{e} $

Fig. 20 Error $ {x}_{e} $ of finite-time control

下载: 全尺寸图片

图 21 有限时间控制的误差 ${y_e}$

Fig. 21 Error $ {y}_{e} $ of finite-time control

下载: 全尺寸图片

4. 结束语

本文提出一种固定时间编队控制方法。该方法参照领航−跟随策略，利用反步法技巧基于运动学模型的设计固定时间控制器来实现轨迹跟踪，进而实现编队控制。仿真结果表明，本文控制方法对初始位置不同的多机器人系统收敛时间基本一致，控制器很好地消除初始值对系统性能的影响。

图 1 领航−跟随者结构模型

Fig. 1 Leader-follower structure model

下载: 全尺寸图片

图 2 机器人无向拓扑连接图

Fig. 2 Undirected topology connection diagram of robots

下载: 全尺寸图片

图 3 初始位置为 $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $ 固定时间控制机器人轨迹

Fig. 3 Trajectories of fixed-time control with $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $

下载: 全尺寸图片

图 4 初始位置为 $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $ 固定时间控制机器人轨迹

Fig. 4 Trajectories of fixed-time control with $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $

下载: 全尺寸图片

图 5 固定时间控制机器人线速度

Fig. 5 Robots’ linear velocity of fixed-time control

下载: 全尺寸图片

图 6 固定时间控制机器人角速度

Fig. 6 Robots’ angle velocity of fixed-time control

下载: 全尺寸图片

图 7 固定时间控制的误差 ${x_e}$

Fig. 7 Error ${x_e}$ of fixed-time control

下载: 全尺寸图片

图 8 固定时间控制的误差 ${y_e}$

Fig. 8 Error ${y_e}$ of fixed-time control

下载: 全尺寸图片

图 9 有限时间控制的误差 $ {x}_{e} $

Fig. 9 Error $ {x}_{e} $ of finite-time control

下载: 全尺寸图片

图 10 有限时间控制的误差 $ {y}_{e} $

Fig. 10 Error ${y_e}$ of finite-time control

下载: 全尺寸图片

图 11 Turtlebot3 Waffle Pi机器人

Fig. 11 Turtlebot3 Waffle Pi robots

下载: 全尺寸图片

图 12 机器人无向拓扑连接图

Fig. 12 Undirected topology connection diagram of robots

下载: 全尺寸图片

图 13 实验环境

Fig. 13 Experimental environment

下载: 全尺寸图片

图 14 初始位置为 $ \left( {{X_1},{\text{ }}{Y_1},{\text{ }}{\theta _1}} \right) $ 固定时间控制机器人轨迹

Fig. 14 Trajectories of fixed time control with $ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $

下载: 全尺寸图片

图 15 初始位置为 $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $ 固定时间控制机器人轨迹

Fig. 15 Trajectories of fixed-time control with $ \left( {{X_2},{\text{ }}{Y_2},{\text{ }}{\theta _2}} \right) $

下载: 全尺寸图片

图 16 固定时间控制机器人线速度

Fig. 16 Robots’ linear velocity of fixed-time control

下载: 全尺寸图片

图 17 固定时间控制机器人角速度

Fig. 17 Robots’ angle velocity of fixed-time control

下载: 全尺寸图片

图 18 固定时间控制的误差 ${x_e}$

Fig. 18 Error ${x_e}$ of fixed-time control

下载: 全尺寸图片

图 19 固定时间控制的误差 ${y_e}$

Fig. 19 Error $ {y}_{e} $ of fixed-time control

下载: 全尺寸图片

图 20 有限时间控制的误差 $ {x}_{e} $

Fig. 20 Error $ {x}_{e} $ of finite-time control

下载: 全尺寸图片

图 21 有限时间控制的误差 ${y_e}$

Fig. 21 Error $ {y}_{e} $ of finite-time control

下载: 全尺寸图片

表 1 机器人初始位姿和编队参数表

Table 1 Initial pose and formation parameters of the robot

机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
R₀	$ \left( {0, - 10,0} \right) $	$ \left( {0, - 10,0} \right) $	—
R₁	$\left( { {{ - 1} }, - {\text{9} },0} \right)$	$\left( { {- 2 }, - {\text{8} },0} \right)$	$\left( {0,0} \right)$
R₂	$ \left( { - {\text{2}}, - {\text{8}},0} \right) $	$ \left( { - {\text{4}}, - 6,0} \right) $	$\left( {1,0.6\text{π} } \right)$
R₃	$ \left( { - {\text{3}}, - 9,0} \right) $	$ \left( { - {\text{5}}, - {\text{7}},0} \right) $	$\left( {1, - 0.6\text{π} } \right)$
R₄	$ \left( { - {\text{4}}, - 6,0} \right) $	$ \left( { - {\text{6}}, - {\text{4}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₅	$ \left( { - {\text{4}}, - 7,0} \right) $	$ \left( { - {\text{7}}, - {\text{4}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₆	$ \left( { - {\text{4}}, - {\text{9}},0} \right) $	$ \left(-\text{7},-\text{7},0\right) $	$ \left(1,-0.6\text{π} \right) $
R₇	$ \left(-\text{5},-\text{5},0\right) $	$ \left( { - {\text{5}}, - {\text{5}},0} \right) $	$\left( {1,0.6\text{π} } \right)$

续表 1
机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
R₈	$ \left(-\text{5},-\text{6},0\right) $	$ \left(-\text{5},-\text{6},0\right) $	$\left( {1,0.6\text{π} } \right)$
R₉	$ \left( { - {\text{5}}, - {\text{8}},0} \right) $	$ \left( { - {\text{5}}, - {\text{8}},0} \right) $	$ \left(1,0.6\text{π} \right) $
R₁₀	$ \left( { - {\text{5}}, - 10,0} \right) $	$ \left( { - {\text{5}}, - 10,0} \right) $	$\left( {1, - 0.6\text{π} } \right)$

表 2 固定时间控制参数表

Table 2 Parameters of fixed-time control

机器人	${k_{1{{i}}} }$	${k_{2{{i}}}}$	${k_{3{{i}}}}$	${k_{4{{i}}}}$	${k_{5{{i}}}}$	${k_{6{{i}}}}$	${\beta _1}$	${\beta _2}$
R₁	0.2	0.5	0.2	0.5	0.2	0.2	1.2	0.5
R₂	0.2	0.1	0.2	0.1	1.0	1.0	1.2	0.5
R₃	0.2	0.1	0.2	0.1	2.0	0.1	1.2	0.5
R₄	1.0	0.5	1.0	0.5	2.0	2.0	1.2	0.7
R₅	0.2	1.0	0.2	1.0	1.0	1.0	1.2	0.7
R₆	0.2	1.0	0.2	1.0	2.0	2.0	1.2	0.7
R₇	0.5	0.7	0.5	0.7	2.0	2.0	1.2	0.7
R₈	0.7	1.5	0.7	1.5	2.0	2.0	1.2	0.7
R₉	0.7	1.5	0.7	1.5	3.0	3.0	1.2	0.9
R₁₀	0.5	0.5	0.5	0.5	2.0	2.0	1.2	0.1

表 3 有限时间控制参数表

Table 3 Parameters of finite-time control

机器人	${c_{1{{i}}} }$	${c_{2{{i}}} }$	${c_{3{{i}}} }$	${\beta _2}$
R₁	0.8	0.8	0.5	0.6
R₂	0.2	0.2	1.0	0.5
R₃	0.3	0.3	0.5	0.5
R₄	0.6	0.6	1.5	0.6
R₅	0.5	0.5	1.0	0.9
R₆	0.5	0.5	0.5	0.7
R₇	0.1	0.1	3.0	0.6
R₈	1.5	1.5	2.0	0.7
R₉	1.5	1.5	3.0	0.9
R₁₀	0.5	0.5	2.0	0.1

表 4 机器人初始位姿和编队参数表

Table 4 Initial pose and formation parameters of the robot

机器人	$ \left({X}_{1},\text{ }{Y}_{1},\text{ }{\theta }_{1}\right) $	$ \left({X}_{2},\text{ }{Y}_{2},\text{ }{\theta }_{2}\right) $	$\left( {{\lambda _i},{\varphi _i}} \right)$
${R_0}$	$ \left( { - 0.1,0.1,0} \right) $	$ \left( { - 0.2,0.2,0} \right) $	—
${R_1}$	$ \left( {0,0,0} \right) $	$ \left( {0,0,0} \right) $	$\left( {0,0} \right)$
${R_2}$	$ \left( { - 0.4,0.6,0} \right) $	$ \left( { - 0.5,0.5,0} \right) $	$\left( {0.6,0.6\text{π} } \right)$
${R_3}$	$ \left( { - 0.5, - 0.6,0} \right) $	$ \left( { - 0.4, - 0.7,0} \right) $	$\left( {0.8, - 0.6\text{π} } \right)$

表 5 固定时间控制参数表

Table 5 Parameters of fixed-time control

机器人	${k_{1{{i}}}}$	${k_{2{{i}}}}$	${k_{3{{i}}}}$	${k_{4{{i}}}}$	${k_{5{{i}}}}$	${k_{6{{i}}}}$	${\beta _1}$	$ {\beta }_{2} $
R₁	0.05	0.01	0.05	0.01	0.10	0.10	1.20	0.70
R₂	0.05	0.05	0.05	0.05	0.05	0.05	1.20	0.70
R₃	0.10	0.10	0.10	0.10	0.10	0.10	1.20	0.70

表 6 有限时间控制参数表

Table 6 Parameters of finite-time control

机器人	${c_{1{{i}}} }$	${c_{2{{i}}} }$	${c_{3{{i} } } }$	${\beta _2}$
R₁	0.01	0.05	0.10	0.70
R₂	0.01	0.05	0.10	0.70
R₃	0.10	0.05	0.10	0.70

参考文献(25)

[1]	李苗, 刘忠信, 陈增强. 一种多非完整移动机器人分布式编队控制方法[J]. 智能系统学报, 2017, 12(1): 88–94. doi: 10.11992/tis.201512021 LI Miao, LIU Zhongxin, CHEN Zengqiang. A distributed formation control method for multiple nonholonomic mobile robots[J]. CAAI transactions on intelligent systems, 2017, 12(1): 88–94. doi: 10.11992/tis.201512021
[2]	HACENE N, MENDIL B. Fuzzy behavior-based control of three wheeled omnidirectional mobile robot[J]. International journal of automation and computing, 2019, 16(2): 163–185. doi: 10.1007/s11633-018-1135-x
[3]	谌海云, 陈华胄, 刘强. 基于改进人工势场法的多无人机三维编队路径规划[J]. 系统仿真学报, 2020, 32(3): 414–420. CHEN Haiyun, CHEN Huazhou, LIU Qiang. Multi-UAV 3D formation path planning based on improved artificial potential field[J]. Journal of system simulation, 2020, 32(3): 414–420.
[4]	CHEN Xuanlin, HUANG Fanghao, ZHANG Yougong, et al. A novel virtual-structure formation control design for mobile robots with obstacle avoidance[J]. Applied sciences, 2020, 10(17): 5807. doi: 10.3390/app10175807
[5]	罗京, 刘成林, 刘飞. 多移动机器人的领航−跟随编队避障控制[J]. 智能系统学报, 2017, 12(2): 202–212. LUO Jing, LIU Chenglin, LIU Fei. Piloting-following formation and obstacle avoidance control of multiple mobile robots[J]. CAAI transactions on intelligent systems, 2017, 12(2): 202–212.
[6]	CAI He, HUANG Jie. Leader-following attitude consensus of multiple rigid body systems by attitude feedback control[J]. Automatica, 2016, 69: 87–92. doi: 10.1016/j.automatica.2016.02.010
[7]	HAN Tao, GUAN Zhihong, CHI Ming, et al. Multi-formation control of nonlinear leader-following multi-agent systems[J]. ISA transactions, 2017, 69: 140–147. doi: 10.1016/j.isatra.2017.05.003
[8]	YAN Lixia, MA Baoli. Adaptive practical leader-following formation control of multiple nonholonomic wheeled mobile robots[J]. International journal of robust and nonlinear control, 2020, 30(17): 7216–7237. doi: 10.1002/rnc.5165
[9]	LIN Sida, JIA Ruiming, YUE Ming, et al. On composite leader–follower formation control for wheeled mobile robots with adaptive disturbance rejection[J]. Applied artificial intelligence, 2019, 33(14): 1306–1326. doi: 10.1080/08839514.2019.1685182
[10]	DAI Shilu, HE Shude, CHEN Xin, et al. Adaptive leader–follower formation control of nonholonomic mobile robots with prescribed transient and steady-state performance[J]. IEEE transactions on industrial informatics, 2020, 16(6): 3662–3671. doi: 10.1109/TII.2019.2939263
[11]	SHOJAEI K, ABDOLMALEKI M. Saturated observer-based adaptive neural network leader-following control of N tractors with n-trailers with a guaranteed performance[J]. International journal of adaptive control and signal processing, 2021, 35(1): 15–37. doi: 10.1002/acs.3188
[12]	LIU Andong, ZHANG Wenan, YU Li, et al. Formation control of multiple mobile robots incorporating an extended state observer and distributed model predictive approach[J]. IEEE transactions on systems, man, and cybernetics:systems, 2020, 50(11): 4587–4597. doi: 10.1109/TSMC.2018.2855444
[13]	WANG Xiangke, YU Yangguang, LI Zhongkui. Distributed sliding mode control for leader-follower formation flight of fixed-wing unmanned aerial vehicles subject to velocity constraints[J]. International journal of robust and nonlinear control, 2021, 31(6): 2110–2125. doi: 10.1002/rnc.5030
[14]	MIAO Zhiqiang, LIU Yunhui, WANG Yaonan, et al. Distributed estimation and control for leader-following formations of nonholonomic mobile robots[J]. IEEE transactions on automation science and engineering, 2018, 15(4): 1946–1954. doi: 10.1109/TASE.2018.2810253
[15]	BHAT S P, BERNSTEIN D S. Continuous finite-time stabilization of the translational and rotational double integrators[J]. IEEE transactions on automatic control, 1998, 43(5): 678–682. doi: 10.1109/9.668834
[16]	LI Yongming, YANG Tingting, LIU Lu, et al. Finite-time optimal control for interconnected nonlinear systems[J]. International journal of robust and nonlinear control, 2020, 30(8): 3451–3470. doi: 10.1002/rnc.4944
[17]	HERNÁNDEZ-LEÓN P, DÁVILA J, SALAZAR S, et al. Distance-based formation maneuvering of non-holonomic wheeled mobile robot multi-agent system[J]. IFAC-PapersOnLine, 2020, 53(2): 5665–5670. doi: 10.1016/j.ifacol.2020.12.1588
[18]	POLYAKOV A. Nonlinear feedback design for fixed-time stabilization of linear control systems[J]. IEEE transactions on automatic control, 2012, 57(8): 2106–2110. doi: 10.1109/TAC.2011.2179869
[19]	NI Junkang, WU Zhonghua, LIU Ling, et al. Fixed-time adaptive neural network control for nonstrict-feedback nonlinear systems with deadzone and output constraint[J]. ISA transactions, 2020, 97: 458–473. doi: 10.1016/j.isatra.2019.07.013
[20]	GAO Fangzheng, HUANG Jiacai, SHI Xinxin, et al. Nonlinear mapping-based fixed-time stabilization of uncertain nonholonomic systems with time-varying state constraints[J]. Journal of the franklin institute, 2020, 357(11): 6653–6670. doi: 10.1016/j.jfranklin.2020.04.028
[21]	ZHOU Qi, DU Peihao, LI Hongyi, et al. Adaptive fixed-time control of error-constrained pure-feedback interconnected nonlinear systems[J]. IEEE transactions on systems, man, and cybernetics:systems, 2021, 51(10): 6369–6380. doi: 10.1109/TSMC.2019.2961371
[22]	CONSOLINI L, MORBIDI F, PRATTICHIZZO D, et al. Leader-follower formation control of nonholonomic mobile robots with input constraints[J]. Automatica, 2008, 44(5): 1343–1349. doi: 10.1016/j.automatica.2007.09.019
[23]	LU Peifen, WANG He, ZHANG Fan, et al. Formation control of nonholonomic mobile robots using distributed estimators[J]. IEEE transactions on circuits and systems II:express briefs, 2020, 67(12): 3162–3166. doi: 10.1109/TCSII.2020.2973773
[24]	苏博, 王洪斌, 王跃灵, 等. 基于固定时间滑模干扰观测器的AUVs事件触发编队控制[J]. 控制与决策, 2022, 37(5): 1116–1126. SU Bo, WANG Hongbin, WANG Yueling, et al. Event-triggered formation control for AUVs with fixed-time sliding mode disturbance observer[J]. Control and decision, 2022, 37(5): 1116–1126.
[25]	ZUO Zongyu, TIE Lin. A new class of finite-time nonlinear consensus protocols for multi-agent systems[J]. International journal of control, 2014, 87(2): 363–370. doi: 10.1080/00207179.2013.834484

点击查看大图

图(21) / 表(7)

摘要

多移动机器人固定时间编队控制

doi: 10.11992/tis.202208021

通讯作者: 师五喜. E-mail： shiwuxi@tiangong.edu.cn.

出版历程

Fixed-time formation control of multimobile robots

1. 问题描述

1.1 图论相关知识

1.2 领航−跟随编队运动学模型

1.3 相关引理

2. 固定时间控制器设计

2.1 领航−跟随子结构的跟踪控制

2.2 编队控制

3. 仿真与实验验证

3.1 仿真验证

3.2 实验验证

4. 结束语

出版历程

目录

通讯作者:
师五喜. E-mail： shiwuxi@tiangong.edu.cn.