基于脑电（electroencephalogram，EEG）信号的运动想象任务^[1-2]通过解码大脑运动想象过程中的放电信号，实现对外部设备的直接控制，是脑机接口领域^[3-5]的一个重要研究方向。然而，受肌电、情绪等诸多因素影响，被试者之间数据分布不一致^[6-8]。传统微调算法(vanilla fine-tuning)^[9]通过预训练、微调的二阶段策略实现跨领域知识迁移，在计算机视觉、自然语言处理等领域得到了广泛的应用，显著提高了下游任务的预测精度。由于神经网络不具备记忆功能，拟合下游任务数据分布的过程中常伴随着对上游任务的遗忘^[10]。在样本稀疏的场景下，灾难性遗忘问题常常导致模型过拟合下游任务。运动想象EEG分类任务数据采集和标注成本昂贵^[11]，单一被试仅有少量标注样本。传统微调算法直接应用于EEG运动想象任务，往往由于灾难性遗忘问题^[12-14]导致模型在目标任务上过拟合^[14]。

传统微调算法^[9]预训练所得到的模型参数保留了源域数据潜在信息。因此，主流的方法通过抑制微调阶段参数更新^[15-19]缓解传统微调算法在微调过程中的灾难性遗忘问题。Top-K^[15]仅仅微调最后K层网络参数，减少了可调参数数量，固定参数保留了源域数据潜在信息。权重衰减(weight decay)^[16]算法添加模型参数与预训练参数之差的L2损失函数作为正则化项，抑制微调阶段参数更新。RecAdam^[17]基于权重衰减算法^[16]，针对L2损失构建了随循环次数不断衰减的权重项，提高了模型对下游任务的拟合能力。Child-Tuning^[19]借鉴了随机失活^[20]的思想，在微调过程中仅更新深度神经网络部分参数。抑制参数更新的方式，虽然能够缓解传统微调算法在目标域样本稀疏情况下的灾难性遗忘问题，却牺牲了模型对下游任务的拟合能力。

邻域风险最小化策略^[21]基于标注数据邻域值训练模型参数，可以在不牺牲模型拟合能力的基础上，提高模型的泛化性能。Mixup^[22]凸组合域内数据，构造标注数据邻域分布，缓解了经验风险最小化策略所引发的过拟合问题。为了缓解传统微调算法在目标域样本稀疏场景下的灾难性遗忘问题，同时提高模型对下游任务的拟合能力，本文提出基于域间Mixup微调策略的跨被试运动想象脑电信号分类算法Mix-Tuning，在微调阶段引入源域数据潜在信息。

Mix-Tuning沿用了传统微调算法预训练、微调的二阶段策略。预训练阶段，Mix-Tuning使用源域数据初始化模型参数，挖掘源域数据潜在信息；微调阶段，Mix-Tuning通过域间Mixup得到合成样本训练模型参数。合成样本引入了源域数据潜在信息，缓解了微调过程中的灾难性遗忘问题，提高了模型的泛化性能。Mix-Tuning被进一步应用于运动想象脑电信号分类任务，实现了跨被试正向知识迁移。

本文的贡献点主要有:

1）提出了域间Mixup微调策略，缓解了传统微调算法在目标域样本稀疏场景下的灾难性遗忘问题。

2）域间Mixup微调策略通过数据合成对模型施加正则化约束，为缓解微调阶段灾难性遗忘问题贡献了一种新的思路。

3）将Mix-Tuning方法应用于运动想象脑电信号分类任务，在BMI数据集达到了85.50%的平均分类准确率。

1.   运动想象EEG训练方式

运动想象脑机接口^[3-4]近年来在运动康复、游戏等领域取得了诸多实质性的进展，受到了学术界和工业界越来越多的关注。然而，脑电信号采集和标注过程繁琐、代价昂贵^[11]，单一被试往往只有少量样本。此外，脑电信号作为生物信号的一种，不同被试数据分布不一致。运动想象脑电信号数据稀疏、跨被试数据分布不一致的特点，促使脑电信号的深度学习研究主要采用被试–依赖^[23–26]、被试–独立^[26-28]和被试–自适应^[29]3种训练方式。

被试–依赖^[23-26]使用目标被试标注数据训练模型参数，其经验风险公式为

式中：$ {R_{{\text{spe}}}} $为被试–依赖训练方式经验风险；$ \mathcal{F}\left( {;\theta } \right) $为预测模型，$ \theta $为模型的参数；$ \ell $为风险函数；$ {{\boldsymbol{D}}_l} $为目标被试标注数据；$ ({x_i},{y_i}) $为$ {{\boldsymbol{D}}_l} $中第i个样本的数据和标签；E为数学期望。

由于单一目标被试数据非常稀少，为了降低过拟合风险，采用被试–依赖训练方式的模型往往容量较小。文献[26]模仿滤波器组共空间模式（filter bank common spatial pattern，FBCSP）^[2]的特征提取过程，设计了模型Shallow ConvNet。Shallow ConvNet使用时域卷积和空域卷积提取特征，并使用1层全连接层完成分类任务，其在多个数据集上取得了超越传统EEG信号处理方法的精度。文献[23]引入深度可分离卷积（depthwise separable convolution）^[30]，提出了紧凑型的卷积神经网络EEGNet。EEGNet在保证模型表达能力的基础上，进一步减少了模型参数。然而，受限于单个被试数据规模，被试–依赖训练方式容易导致模型过拟合^[23-26]。

被试–独立^[26-28]忽略不同被试者数据分布的差异，组合多个被试者数据得到训练数据，其经验风险表示为

式中：$ {R_{{\text{ind}}}} $为被试–独立训练方式经验风险，$ {{\boldsymbol{D}}_s} $为非目标被试标注数据，$ ({x_i},{y_i}) $为$ ({{\boldsymbol{D}}_s} \cup {{\boldsymbol{D}}_l}) $中第i个样本的输入和标签。

为了匹配训练数据规模，采用被试–独立训练方式的模型通常有着更大的容量。文献[26]提出一个层次化特征提取模型，称作Deep ConvNet。Deep ConvNet使用4个卷积–池化块实现特征提取和降维，并使用1层全连接层完成分类任务。文献[27]提出了模型TIDNet，引入卷积网络中的残差模块（residual block）^[31]和密集模块（dense block）^[32]，进一步加深了模型的深度。然而，被试–独立训练方式假设不同被试EEG数据服从独立同分布假设，不符合EEG真实数据分布^[27-28]。

被试–自适应^[29]通过预训练、微调的二阶段策略，挖掘源域数据潜在信息，实现跨被试知识迁移，有望解决被试–依赖和被试–独立训练方式所面临的困境。被试–自适应训练方式预训练和微调阶段的经验风险公式为

式中：$ {R_{{\text{pre}}}} $为预训练阶段经验风险，$ {R_{{\text{tuning}}}} $为微调阶段经验风险。

文献[29]通过调低学习率和早停策略成功将传统微调算法应用于EEG领域，实现了跨被试正向知识迁移。然而，EEG标注数据获取成本昂贵，早停策略需要划分验证集^[33]。这将进一步减少标注样本的数量，增加模型的过拟合风险。为了缓解传统微调算法在目标域样本稀疏时出现的过拟合问题，本文提出了基于域间Mixup微调策略的跨被试运动想象脑电信号分类算法Mix-Tuning。微调阶段，Mix-Tuning通过域间Mixup，生成域间插值数据微调模型参数。域间Mixup引入了源域数据潜在信息，缓解了微调阶段的过拟合问题。

2.   域间Mixup微调算法

在EEG运动想象跨被试知识迁移的场景中，数据分别来自源域$ {{\boldsymbol{D}}_s} = \{ (x_i^s,y_i^s)\} _i^{{n_s}} $和目标域${{\boldsymbol{D}}_t} = \{ (x_i^t,y_i^t)\} _i^{{n_t}}$，$ {n_s} $和$ {n_t} $分别表示源域和目标域样本数量。目标域数据又可分为标注数据$ {{\boldsymbol{D}}_l} = \{ (x_i^l,y_i^l)\} _i^{{n_l}} $和未标注数据$ {{\boldsymbol{D}}_u} = \{ (x_i^u)\} _i^{{n_u}} $，$ {n_l} $和$ {n_u} $分别表示目标域标注样本和未标注样本数量。源域数据和目标域数据共享输入空间$\mathcal{X} \in {\bf{R}}^{C \times T}$和标签空间$\mathcal{Y} \in {\bf{R}}^{\textit{z}}$。源域数据和目标域数据分别服从数据分布$ P $和$ {\boldsymbol{Q}} $，并且$ P \ne {\boldsymbol{Q}} $。源域含有大量标注数据，而目标域仅有少量样本，$ {n_s} \gg {n_t} = {n_l} + {n_u} $。

2.1   模型介绍

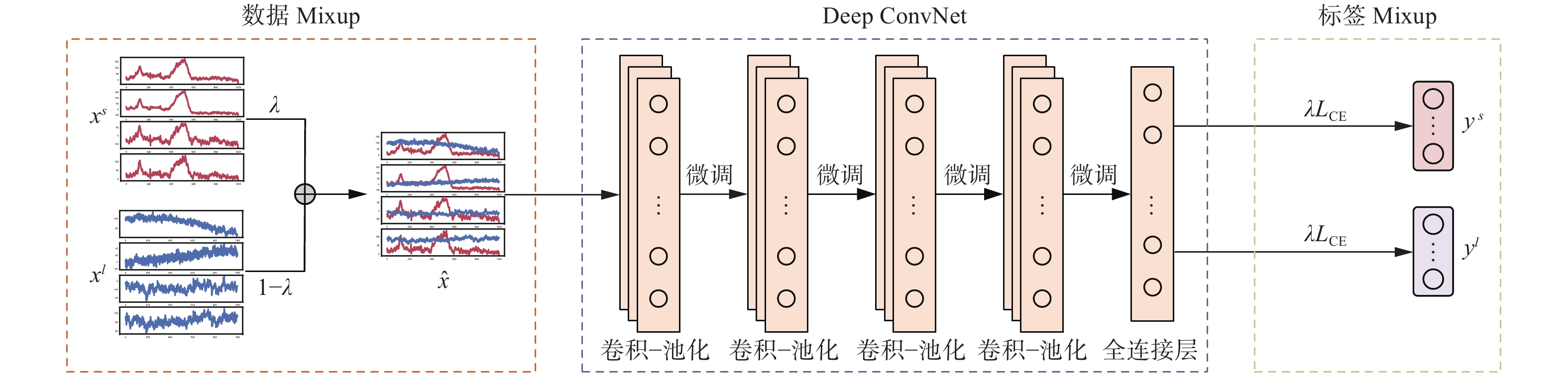
本文选择Deep ConvNet^[26]作为主干网络。Deep ConvNet由4个卷积–池化块和1层全连接层构成。第1个卷积–池化块使用时域卷积和空域卷积分别提取EEG原始数据时序特征和空间特征，并通过最大值池化对特征进行降采样。后3个卷积–池化块由时域卷积层和最大值池化层构成，进一步提取任务相关特征。EEG数据经过4个卷积–池化块完成特征提取后，送入最后1层全连接层。全连接层神经元数量与类别数量相等，其输出经过Softmax函数，转化为对每个类别的预测概率。Deep ConvNet网络结构如图1所示，其中，$ \lambda $为域间插值系数，$ \lambda \sim {\rm{Beta}}(\alpha ,\alpha ) $，$ \alpha $为贝塔分布参数，$ {{L}_{{\rm{CE}}}} $表示交叉熵损失函数。

图  1  Mix-Tuning微调过程

Fig.  1  Mix-Tuning fine-tuning process

下载: 全尺寸图片

2.2   训练过程

EEG信号跨被试数据分布不一致。Mix-Tuning通过预训练、微调的二阶段策略，实现跨被试知识迁移。预训练阶段，Mix-Tuning使用源域数据初始化模型参数，挖掘源域数据潜在信息；微调阶段，源域数据和目标域数据通过域间Mixup生成域间插值数据微调模型参数。其中，数据Mixup通过按维度加权相加得到，标签Mixup通过分类损失函数的加权和替代。Mix-Tuning微调阶段训练过程如图1所示。Mix-Tuning预训练–微调训练方式的训练步骤如下所示。

1）预训练。源域数据与目标域数据共享输入空间$\mathcal{X} \in {\bf{R}}^{C \times T}$和标签空间$\mathcal{Y} \in {\bf{R}}^{\textit{z}}$，且数据之间有着接近的数据分布$ P(x_i^s,y_i^s) \approx P(x_i^l,y_i^l) = P(x_i^u,y_i^u) $。卷积神经网络浅层部分提取通用的特征，网络浅层部分参数可迁移至相关任务。为了充分利用源域数据潜在信息，提高模型的泛化性能，Mix-Tuning使用源域数据预训练模型参数。预训练阶段损失函数表示为

式中：$ \mathbb{I} $为指示函数，当$ y_i^s = c $时，$ \mathbb{I} $取值为1，否则取值为0；z为类别数量；$ {n_s} $为源域样本数量，$ (x_i^s,y_i^s) $为源域的第i个样本。

2）微调。EEG标注数据获取成本昂贵，单一被试无法提供充足的样本微调模型参数。经验风险最小化倾向于记忆目标域标注数据，所训练的模型泛化性能较差。Mix-Tuning通过Mixup凸组合域间数据，构造了源域数据和目标域标注数据的邻域分布$ {P_v}(\hat x,\hat y) $。

式中：$ \delta $为狄拉克函数，$ {\mathbb{H}_\lambda }[ \cdot ] $为取全体$ \lambda $取值的集合。

Mix-Tuning采样邻域分布构建了一个新的数据集${{\boldsymbol{D}}_v}: = \{ ({\hat x_k}, {\hat y_k})\} _k^m$，m表示样本数量，$ ({\hat x_k},{\hat y_k}) $表示第k个合成样本，$ {\hat y_k} = y_k^s + y_k^l $。微调阶段，每次迭代独立采样数据集$ {{\boldsymbol{D}}_v} $得到训练数据。确定交叉熵需要标签为独热码方可计算，Mix-Tuning微调阶段分别计算预测标签$ \mathcal{F}({\hat x_k};\theta ) $与源域标签$ y_k^s $和目标域标签$ y_k^l $的交叉熵函数，二者加权和构成微调阶段的损失函数为

式中：Mix-Tuning通过域间Mixup微调策略，实现跨被试正向知识迁移，伪代码如算法1所示。

算法1　Mix-Tuning

输入　源域数据$ {{\boldsymbol{D}}_s} = \{ (x_i^s,y_i^s)\} _i^{{n_s}} $，目标域标注数据$ {{\boldsymbol{D}}_l} = \{ (x_i^l,y_i^l)\} _i^{{n_l}} $，Deep ConvNet参数$ \theta $，超参数$ \alpha $，预训练迭代次数$ {T_1} $，微调迭代次数$ {T_2} $；

输出　Deep ConvNet最优参数$ \hat \theta $;

1) 随机初始化$ \theta $

2) WHILE $ t < {T_1} $ DO

3)$ t \leftarrow t + 1 $

4) $ (x_i^s,y_i^s) \leftarrow {\text{RANDOM}}({{\boldsymbol{D}}_s}) $

5) ${\theta _{t + 1}} \leftarrow {\theta _t} - {\nabla _\theta }\mathcal{L}(\mathcal{F}(x_i^s,\theta ),y_i^s)$

6) ENDWHILE

7) WHILE $ t < {T_2} $ DO

8) $ t \leftarrow t + 1 $

9) $ (x_i^s,y_i^s) \leftarrow {\text{RANDOM}}({{\boldsymbol{D}}_s}) $

10) $ (x_i^l,y_i^l) \leftarrow {\text{RANDOM}}({{\boldsymbol{D}}_l}) $

11) $ \lambda \sim {\text{Beta}}(\alpha ,\alpha ) $

12) $ \hat x \leftarrow \lambda x_i^l + (1 - \lambda )x_j^s $

13) $\begin{gathered} {\theta _{t + 1}} \leftarrow {\theta _t} - \lambda {\nabla _\theta }\mathcal{L}(\mathcal{F}(\hat x,\theta ),y_i^l) - \\ \;\;\;\;\;\;\;\;\;(1 - \lambda ){\nabla _\theta }\mathcal{L}(\mathcal{F}(\hat x,\theta ),y_i^s) \\ \end{gathered}$

14) ENDWHILE

2.3   邻域风险最小化

目标域真实数据分布$ P(x,y) $通常是未知的。传统微调算法在微调阶段基于目标域标注数据，通过经验风险最小化^[12]搜索最优假设。微调阶段经验风险$ {R_{{\text{tuning}}}}(\theta ) $如式(1)所示。经验风险最小化策略^[12]在样本稀疏场景下倾向于简单记住训练数据，导致模型泛化性能不足^[21,33]。域间Mixup数据增强策略通过凸组合域间数据得到合成样本微调模型参数，将经验风险最小化转变为邻域风险最小化，从而降低了模型微调过程中的过拟合风险。邻域风险$ {R_v}(\theta ) $为

邻域风险$ {R_v}(\theta ) $可以进一步划分为目标域标注数据邻域风险$ {R_l}(\theta ) $和源域数据邻域风险$ {R_s}(\theta ) $：

$ {R_s}(\theta ) $、$ {R_l}(\theta ) $分别促使模型拟合源域和目标域邻域数据分布。$ {R_s}(\theta ) $可以看作Mix-Tuning微调阶段的正则化项，促使模型偏好于有效拟合源域数据分布的参数。Mix-Tuning通过域间Mixup生成域间插值数据微调模型参数，在微调阶段引入源域数据邻域风险最小化策略，缓解了传统微调算法在微调阶段的灾难性遗忘问题，提高了模型的泛化性能。

3.   实验结果与分析

3.1   数据集和数据预处理

本文采用韩国高丽大学大脑与认知工程系发布的BMI数据集^[11]的运动想象部分作为实验数据。BMI数据集通过62个电极，以1000 Hz频率采样被试脑电信号。数据集采集自54个被试（S1~S54），执行左、右手2类运动想象任务。每个被试数据分为2个会话，每个会话包含200个类别平衡样本。目标被试第1个会话数据作为目标域训练集$ {{\boldsymbol{D}}_l} = \{ (x_i^l,y_i^l)\} _i^{{n_l}} $，目标被试第2个会话数据作为目标域测试集$ {{\boldsymbol{D}}_u} = \{ (x_i^u)\} _i^{{n_u}} $，非目标被试的其余53个被试所有数据组合构成源域数据$ {{\boldsymbol{D}}_s} = \{ (x_i^s,y_i^s)\} _i^{{n_s}} $。

本文所选择的对比模型包括深度学习模型^{[23, 26-27]}和传统脑电数据处理模型^[1-2]。对于深度学习模型，保留数据集所有电极采样的脑电信号，截取被试执行运动想象任务的4 s采集的脑电信号作为输入数据，并将其频率降采样为250 Hz。因此，深度学习模型输入数据$\mathcal{X} \in {\bf{R}}^{C \times T}, C = 62,\;T = 1\;000$。传统的脑电模型对噪声比较敏感^[34]，本文沿用数据集发布方^[11]所选择与运动想象任务相关的20个电极作为输入信号，并将数据采样频率降采样至250 Hz。为了进一步提高数据的信噪比，本文选择8~30 Hz的带通滤波器对数据滤波。因此，传统的机器学习方法输入数据$\mathcal{X} \in {\bf{R}}^{C \times T},\;C = 20,\;T = 1\;000$。

3.2   实验设置

本文算法Mix-Tuning基于Pytorch机器学习库实现。所有实验均在同一设备运行，处理器为Intel(R) Xeon(R) Silver 4214，图形处理器为Nvidia Tesla V100，操作系统为CentOS Linux release 7.9.2009。本文中深度神经网络均采用小批次梯度下降算法训练，除样本数量实验外，批次大小（batch size）统一设置为50。优化器选择Adam^[35]，相应的参数分别设置为0.9和0.99。本文中所有采用被试–独立训练方式的模型，学习率和迭代次数统一设置为0.01和200。本文中采用被试–自适应训练方式的算法学习率和迭代次数保持一致。预训练阶段，学习率和迭代次数分别被设置为0.01和200； 微调阶段，学习率和迭代次数分别被设置为0.003和300。本文采用准确率和F₁值作为评价指标，F₁值是精确率和召回率的调和平均。

3.3   对比实验

为了验证Mix-Tuning的有效性，本文选择采用被试–依赖、被试–独立和被试–自适应3种训练方式的多个算法与本文算法进行比较。

1）被试–依赖：共空间模式（comon spatial pattern，CSP）^[1]通过最大化2类信号的方差值，得到多通道脑电信号在空间中的最优投影。FBCSP^[2]首先划分脑电数据为多个不同的频带，然后针对每个频带的数据使用共空间模式提取特征。共空间模式和滤波器组共空间模式完成EEG数据的特征提取，线性判别分析对所提取特征执行分类任务。

2）被试–独立：EEGNet^[23]、Shallow ConvNet^[26]、Deep ConvNet^[26]和TIDNet^[27]采用被试–独立训练方式，作为 Mix-Tuning的对比算法。EEGNet、Shallow ConvNet、Deep ConvNet和TIDNet除失活概率^[20]外，均采用默认参数设置。EEGNet、Shallow ConvNet和Deep ConvNet所有失活层^[20]的失活概率均设置为0.5。TIDNet包括5层失活层，其失活概率分别设置为{0, 0, 0.4, 0.4, 0}。

3）被试–自适应：运动想象EEG领域采用被试–自适应训练方式的算法还比较稀少。为了验证Mix-Tuning方法的有效性，本文选用了部分已经在计算机视觉和自然语言处理领域取得成功的预训练–微调算法，迁移至运动想象EEG领域，作为Mix-Tuning的对比算法。

权重衰减算法^[16]：添加模型当前参数与预训练参数之差的L2范数作为正则化项，抑制微调阶段参数更新，从而缓解模型在微调过程中出现的灾难性遗忘问题，提高模型泛化性能。对比实验中，文中通过网格搜索超参数的最优值。

RecAdam^[17]：在权重衰减算法的基础上，借鉴模拟退火公式，构建随迭代次数逐渐衰减的L2正则化项，提高了模型对下游任务的拟合能力。对比实验中，文中通过网格搜索RecAdam超参数的最优值。

Child-Tuning^[19]：借鉴了随机失活^[20]方法，在微调过程中仅更新部分参数，从而达到抑制参数更新的目的。Child-Tuning设定一个概率值，每一次迭代依据概率值生成伯努利矩阵$ {{\boldsymbol{M}}_t} $，$ {{\boldsymbol{M}}_t} $维度与参数维度相匹配。对比实验中，文中在{0.1，0.3，0.5，0.7，0.9}中网格搜索概率值的最优值。

本次实验中所有的被试–自适应方法均采用Deep ConvNet^[26]作为模型的主干网络。为了能够公平地比较不同算法的实验结果，除算法特定参数外，学习率、迭代次数等参数的设置均保持一致。被试–依赖、被试–独立、被试–自适应3种训练方式的模型所对应在BMI数据集^[11]上54个被试的平均准确率和F₁值如表1，括号中的内容表示标准差。

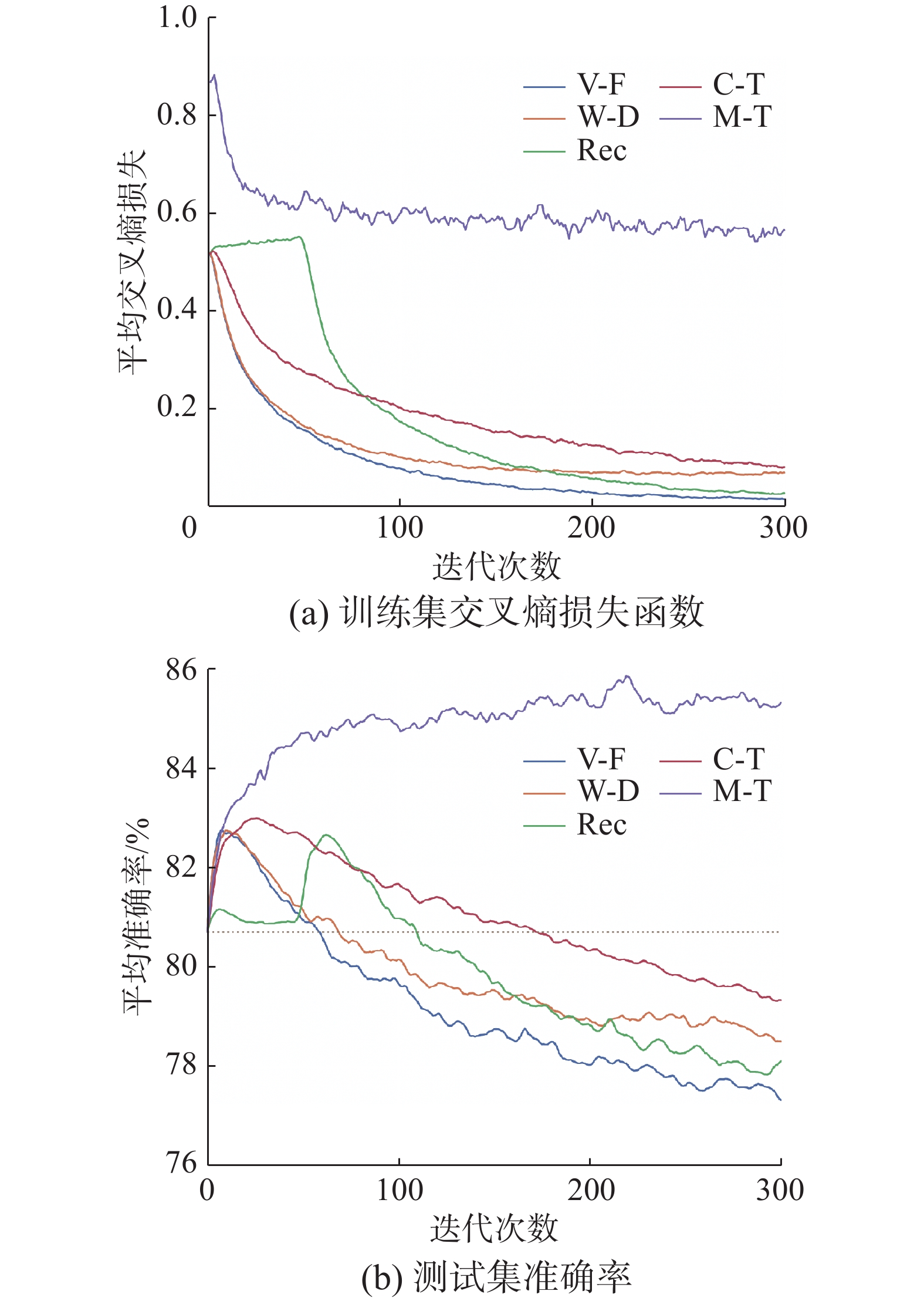
被试–依赖实验中，由于目标域数据训练集和测试集来自不同的会话，数据分布之间存在一定的差异，传统的脑电数据处理方法CSP和FBCSP表现较差。由于标注数据样本极其稀疏，Deep ConvNet采用被试–依赖训练方式出现了严重的过拟合问题，仅取得了58.72%的平均准确率。被试–独立实验中，Deep ConvNet取得了最高的准确率84.01%。EEGNet和Shallow ConvNet网络规模较小，拟合能力较弱，二者预测准确率低于Deep ConvNet。TIDNet由于参数量过大，出现了过拟合问题，导致准确率偏低。被试–自适应实验采用Deep ConvNet网络结构，预训练模型在54个被试测试数据上的平均准确率为80.71%。本次实验中，采用了BMI数据集作为数据集。其中，源域数据整合了53个非目标被试2个会话的数据，样本数量达到21200个。目标域仅选取单一被试第1个会话的200个标注样本。受到数据规模的影响，预训练模型展示了较强的泛化性能，同时，模型在微调阶段将面临较高的过拟合风险。传统微调算法未采用任何正则化策略，在目标域微调过程中出现了严重的过拟合问题，平均准确率降为77.23%。相较于预训练模型，传统微调算法微调之后平均准确率下降了3.48%。权重衰减算法、RecAdam和Child-Tuning通过抑制微调过程中的参数更新，缓解了模型微调过程中的灾难性遗忘问题。相较于传统微调算法，其准确率均有小幅度提高。然而，权重衰减算法、RecAdam和Child-Tuning在微调后平均准确率仍低于预训练模型准确率。Mix-Tuning通过域间Mixup生成域间插值数据微调模型参数，其平均准确率达到了85.50%。相较于预训练模型，Mix-Tuning平均准确率提高了4.79%，实现了目标域样本稀疏场景下跨被试正向知识迁移。

不同的被试–自适应算法在微调过程中的训练集交叉熵损失函数（权重被置为1）和测试集准确率随迭代次数变化情况如图2所示，算法{传统微调算法，权重衰减算法，RecAdam，Child-Tuning，Mix-Tuning}分别简记为{V-F，W-D，Rec，C-T，M-T}。图2中，曲线均采用指数移动平均平滑化处理，平滑因子设置为0.8。交叉熵损失函数均值随迭代次数变化情况如图2（a）所示，传统微调算法方法未采用正则化方法，其损失函数曲线随迭代次数快速下降，直至逼近于0。权重衰减算法、RecAdam和Child-Tuning添加了正则化项，限制了微调阶段的参数更新，其损失函数曲线下降至一定程度后便不再继续下降。Mix-Tuning采样源域和目标域邻域分布，在微调阶段引入源域数据邻域风险最小化，其损失函数曲线下降幅度最小，缓解了传统微调算法在样本稀疏场景下的过拟合问题。目标域测试数据平均准确率随迭代次数变化曲线如图2（b）所示。预训练模型在BMI数据集上的平均准确率为80.71%，在图2中以虚线表示，作为被试–自适应方法的基准模型。随着迭代次数的增加，传统微调算法、权重衰减算法、RecAdam和Child-Tuning的准确率均经历了短暂的上升，随后由于过拟合开始下降。权重衰减算法、RecAdam和Child-Tuning通过抑制参数更新的策略，缓解了微调阶段的过拟合问题，准确率下降幅度低于传统微调算法。然而，由于目标被试仅有200个标注样本，在标注样本如此稀疏的场景下微调模型参数有很高的过拟合风险。权重衰减算法、RecAdam和Child-Tuning的准确率仍低于预训练模型，微调过程反而导致模型预测精度下降。Mix-Tuning的准确率随着迭代次数的增加逐渐升高，直至趋于稳定。Mix-Tuning很好地缓解了模型在目标域样本稀疏场景下的过拟合问题，提高了模型的泛化性能。

图  2  被试–自适应算法损失函数和准确率变化曲线

Fig.  2  Subject-adaptive algorithm loss function and accuracy curves

下载: 全尺寸图片

3.4   样本数量实验

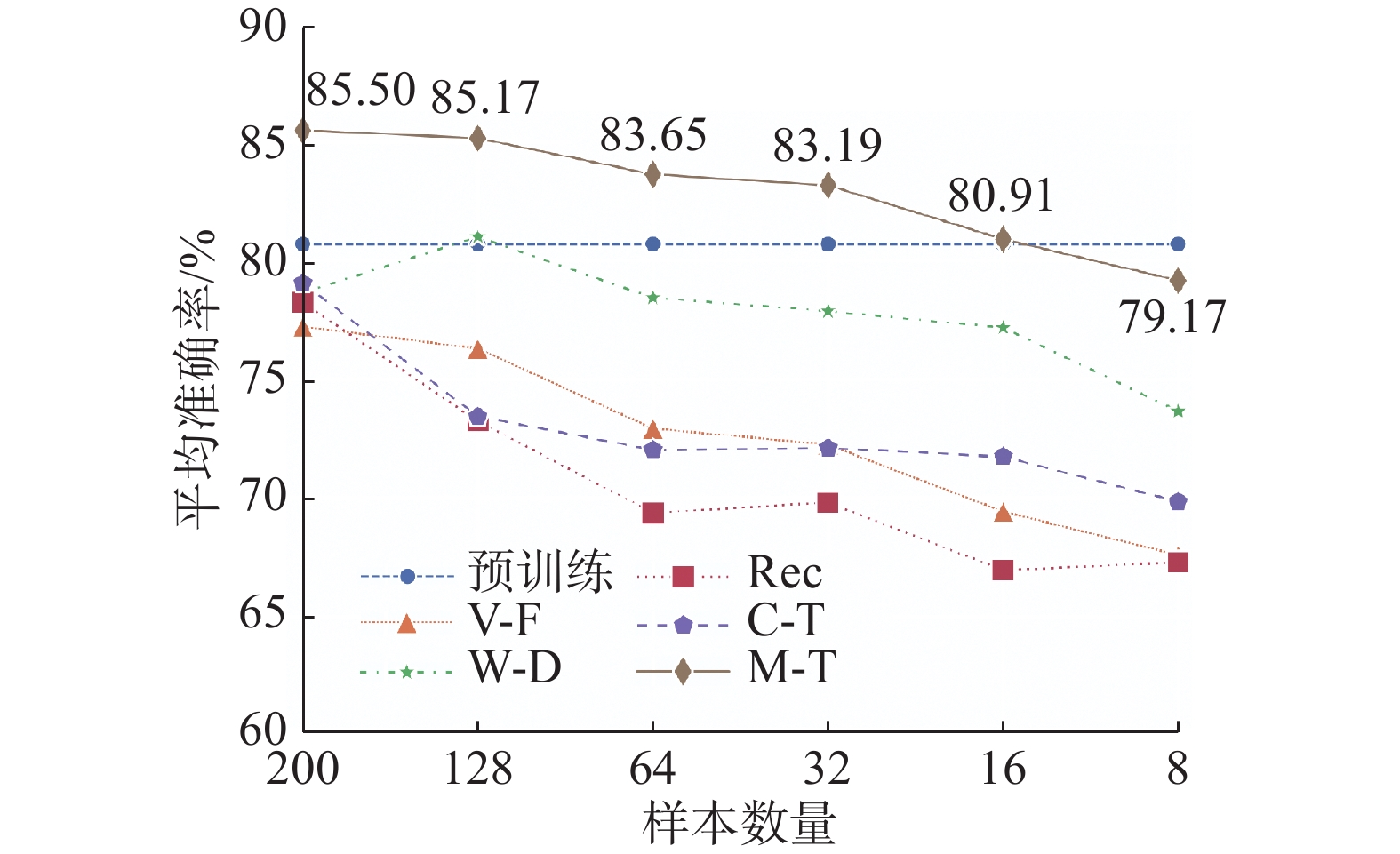
EEG标注数据的成本昂贵，某些现实场景中单一被试无法提供200个标注数据。为了观察本文算法Mix-Tuning在目标被试标注样本极端稀疏时的表现，本文组织了样本数量实验，从目标域标注数据$ {{\boldsymbol{D}}_l} $随机选取{200，128，64，32，16，8}个类别平衡样本进行实验。为了保证模型在目标域微调过程中参数更新次数一致，此次实验中批次大小被设置为样本数的四分之一。即当样本分别为{200，128，64，32，16，8}时，批次大小分别设置为{50，32，16，8，4，2}。不同的被试–自适应算法在不同样本数量下的平均准确率绘制折线如图3 所示。不同样本数量下被试–自适应算法的平均准确率如表2所示。

图  3  不同样本数量下被试–自适应算法准确率对比

Fig.  3  Comparison of the accuracy of subject-adaptive algorithm under different sample sizes

下载: 全尺寸图片

如图3所示，随着样本数量的减少，传统微调算法在目标域测试集上的准确率极速衰减。权重衰减算法、RecAdam和Child-Tuning抑制微调过程中参数更新，缓解了微调过程中的过拟合问题。随着样本数量的减少，权重衰减算法和Child-Tuning下降幅度明显低于传统微调算法。然而，当样本数取值为{200，128，64，32，16，8}时，权重衰减算法、RecAdam和Child-Tuning微调后的准确率普遍低于预训练模型准确率，微调过程反而导致预测准确率下降。随着样本数量的减少，模型过拟合风险逐渐增加，Mix-Tuning平均准确率也随之下降。当样本数量仅为16时，Mix-Tuning仍取得了80.91%的平均准确率，略高于预训练模型80.71%的准确率，实现了跨被试正向知识迁移。样本数量实验表明，本文算法Mix-Tuning能够应对目标域标注样本极其稀疏的场景，实现跨被试正向知识迁移。

3.5   自适应网络层实验

为了观察本文算法Mix-Tuning应用于具有不同拟合能力的模型时的表现，本文设计了网络自适应层的实验。网络自适应实验通过固定Deep ConvNet部分参数，调节Deep ConvNet对下游任务的拟合能力。Deep ConvNet由4个卷积–池化块和1层全连接层组成，其网络参数$ \theta $由卷积–池化块参数$ \{ {\theta _1},\;{\theta _2},\;{\theta _3},\;{\theta _4}\} $和全连接层参数$ \{ {\theta _c}\} $构成，$ \theta = \{ {\theta _1},\;{\theta _2},\;{\theta _3},\;{\theta _4},\;{\theta _c}\} $。微调阶段，本文固定Deep ConvNet预训练模型的前h个卷积–池化块参数，得到具有不同拟合能力的模型Frozen-h，$ h \in \{ 0,\;1, 2,\;3,\;4\} $。h的取值决定了微调阶段模型可调参数数量，影响模型对下游任务的拟合能力。本文统计了当输入空间$ \mathcal{X} \in {\bf{R}^{62 \times 100}} $和标签空间$ \mathcal{Y} \in {\bf{R}^2} $时，Frozen-h可调参数数量如表3所示。

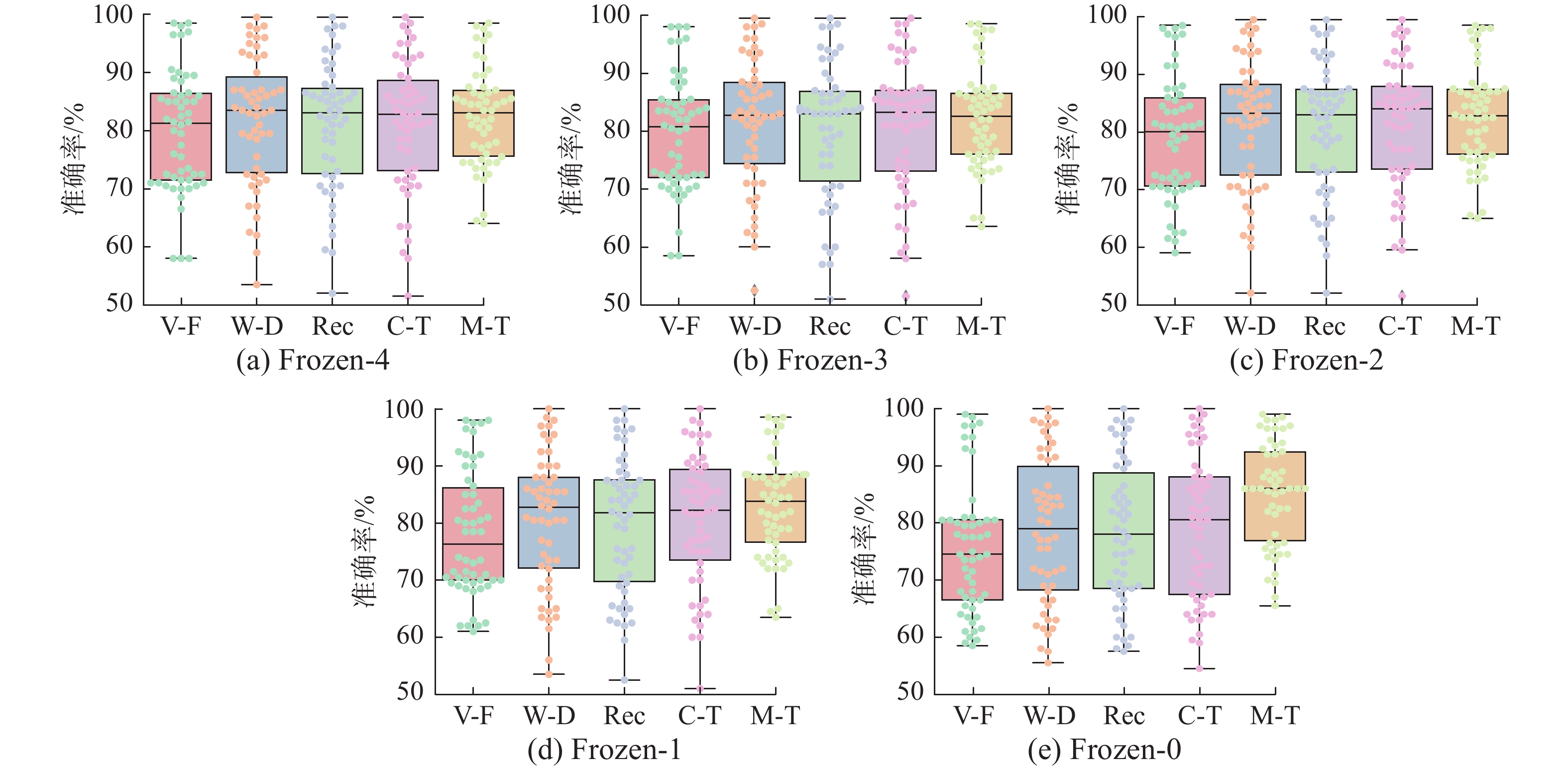
当$ h = 4 $时，Deep ConvNet前4个卷积–池化块参数被固定，只剩下最后1层全连接层参数可调，可调参数量为2802。随着h取值变小，模型可调参数数量逐渐增加，模型对下游任务拟合能力逐渐增加; 与此同时，微调阶段过拟合风险也随之增加。本文设计了网络自适应层实验，观察不同被试–自适应算法在Frozen-h下的表现，$ h \in \{ 0,\;1,\;2,\;3,\;4\} $。不同被试–自适应算法在模型 Frozen-h 的准确率绘制箱线如图4 所示，54个被试平均准确率和标准差如表4所示。

图  4  被试–自适应算法在 Frozen-h 下的表现，$ h \in \{ 0,\;1,\;2,\;3,\;4\} $

Fig.  4  Performance of different subject-adaptive algorithms with different Frozen-h, $ h \in \{ 0,\;1,\;2,\;3,\;4\} $

下载: 全尺寸图片

如图4所示，本文算法Mix-tuning在Frozen-h中正确率分布更为集中，有着更高的准确率下界。如表4所示，随着h取值变小，Frozen-h对下游任务拟合能力增强，过拟合风险逐渐增加。传统微调算法、权重衰减算法、RecAdam、Child-Tuning由于缺少有效的正则化策略，随着模型可调参数增加，正确率却随之下降。从Frozen-4~Frozen-0，传统微调算法、权重衰减算法和Child-Tuning平均正确率分别下降了2.56%、3.22%和2.15%。与此同时，Mix-Tuning平均正确率却随着模型拟合能力的增强而逐渐增加。Mix-Tuning在Frozen-4的正确率仅为82.32%，在Frozen-0时却取得了最高正确率85.50%。网络自适应层实验表明，本文算法Mix-Tuning在模型参数量较大、过拟合风险较高的场景下，所训练模型仍保持了良好的泛化性能。

3.6   参数敏感性实验

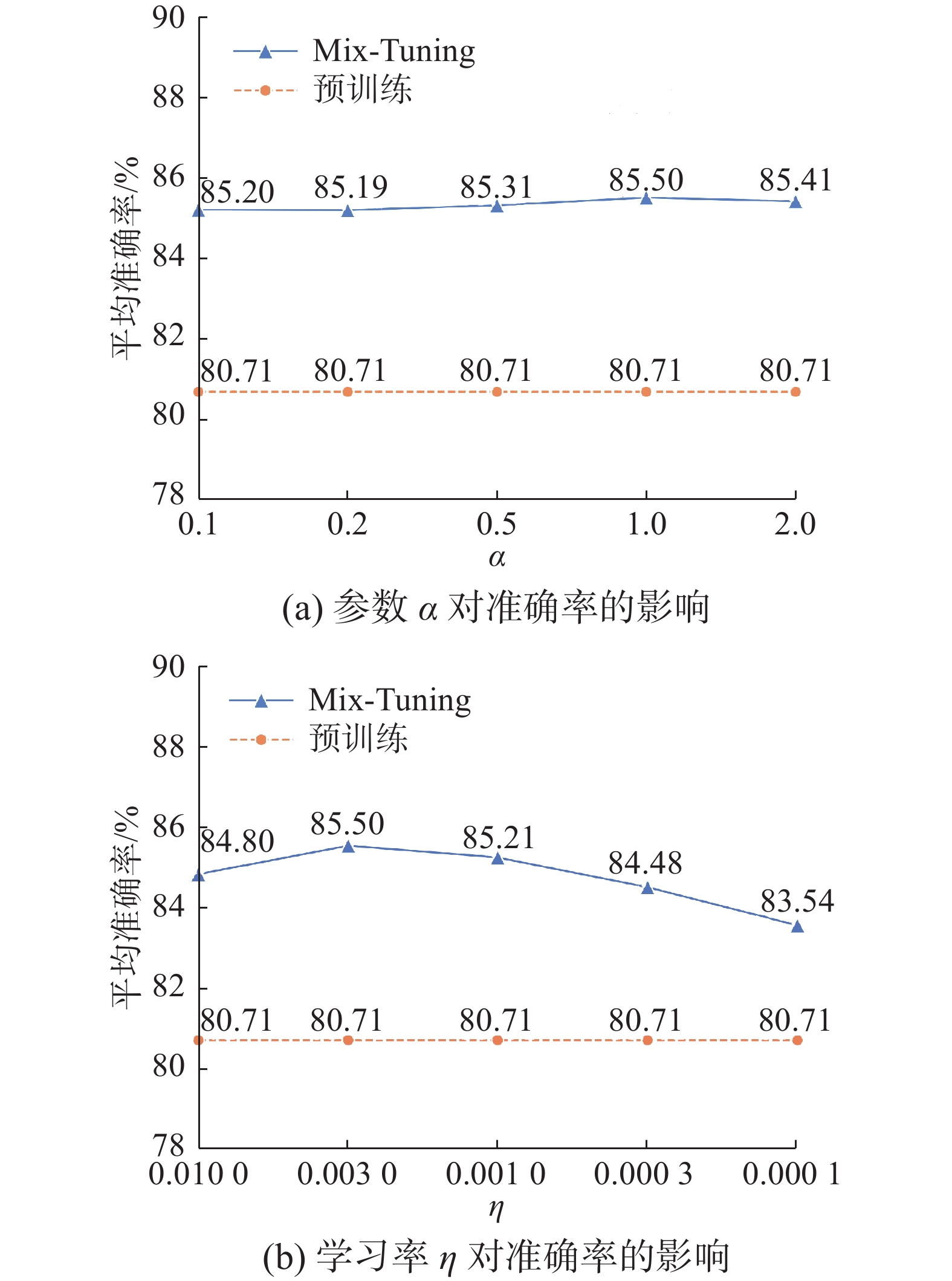
Mix-Tuning包括贝塔分布中$ \alpha $的取值和模型微调阶段学习率$ \eta $共2个超参数。参数敏感性实验通过手动设置$ \alpha $和$ \eta $不同取值，寻找Mix-Tuning在BMI数据集上的最优参数，同时观察Mix-Tuning方法对参数的敏感程度。参数$ \alpha $决定贝塔分布密度函数，进而影响$ \lambda $分布情况。固定学习率为0.003，当$ \alpha $的取值分别为{0.1，0.2，0.5，1.0，2.0}时，Mix-Tuning的平均准确率如图5（a）所示。为了提高模型泛化性能，Mix-Tuning预训练阶段学习率被设置为0.01。微调阶段，为了充分拟合目标域数据分布，学习率$ \eta $需要设置为一个小于0.01的值。当贝塔分布的参数$ \alpha $被固定为1，微调阶段学习率$ \eta $分别设置为{0.01，0.003，0.001，0.0003，0.0001}时，Mix-Tuning的平均准确率如图5（b）所示。

图  5  Mix-Tuning参数敏感性实验

Fig.  5  Mix-Tuning parameter sensitivity experiment

下载: 全尺寸图片

图5（a）表明，平均准确率随$ \alpha $取值变动幅度很小，Mix-Tuning方法对贝塔分布的参数$ \alpha $不敏感。图5（b）显示，当学习率$ \eta $设置为0.003时，模型得到最高的准确率85.50%；当学习率高于0.003时，Mix-Tuning不能够充分拟合目标域数据；学习率$ \eta $低于0.003时，模型参数更新步长过小，模型参数不能得到充分训练。本文其他实验，学习率$ \eta $和$ \alpha $分别固定为0.003和1。

4.   结束语

本文提出了一种基于域间Mixup微调策略的跨被试运动想象脑电信号分类算法Mix-Tuning。Mix-Tuning基于预训练、微调的二阶段策略训练模型参数。域间Mixup引入源域数据潜在信息，缓解了传统微调算法在样本稀疏场景下的灾难性遗忘问题，提高了模型的泛化性能，实现了EEG运动想象跨被试正向知识迁移。在BMI数据集运动想象部分实验结果验证了本文所提算法的有效性。

Mix-Tuning在预训练和微调阶段均需要源域数据的参与，与其他微调算法一样，其预测精度受源域数据规模影响。此外，域间Mixup通过凸组合得到域间插值数据，要求源域和目标域共享输入空间和标签空间。然而，采样自不同设备的EEG数据通常数据维度不一致。因此，Mix-Tuning方法无法直接实现跨设备、跨任务知识迁移。这将是本文未来的一个研究方向。