多标记分类^[1-2]由于示例与标记的多重性而被广泛研究，学习任务通常描述为判定示例与候选标记的相关性。受标记语义的约束，传统多标记分类假设相关标记（不相关标记）对示例描述的相关性程度相同，这显然不能满足人类复杂的认知需求^[3]。例如，在图像检索^[4]时，人们更多希望排名靠前的图片与检索关键词具有更强的关联性。这使得同样具有“天空”“森林”“水”和“云”等多个标记的两个自然场景的图片由于检索策略的不同而具有不同的排序；在文本情感分析^[5]中，文章中蕴含的情绪通常是几种基础情感(如快乐、悲伤、惊讶、愤怒、厌恶和恐惧)的混合呈现，若不加以区分情绪的组成，则无法满足图书推荐等精准营销应用。上述实例表明，仅以逻辑相关与否作为多标记分类的监督信息使得分类器在优化学习过程中损失了许多深层次语义信息。为了有效弥补分类器的学习能力缺陷，标记分布学习^[6]被提出。通过引入描述度这个度量，标记分布学习将标记描述示例的能力从“是否”拓展成了“多少”。

然而，获得大规模精准描述示例的数值标记是实施标记分布学习的前提，而人工形式标注下，数值标记的标注成本将显著高于逻辑标记的标注成本，极大地制约标记分布学习在多标记学习场景的推广。针对上述问题，一些学者从标记增强角度出发，试图学习多标记上隐含的数值型标记分布。代表性模型有一阶段标记增强图模型^[7](label enhanced multi-label learning, LEMLL)、模糊辨识关系的标记增强算法^[8]、图拉普拉斯标记增强^[9](graph Laplacian label enhancement, GLLE)。除了上述显式的标记增强方法外，也有前人提出的模糊方法FCM^[10]和KM^[11]模型恢复标记重要程度，以及基于图的标记传播的方法LP^[12] 和ML^[13]模型。尽管上述研究对深入理解多标记数据有重要意义，然而并没有深入地分析数据标记相关性在示例集上的分布，使得分类准确性不够精细。

粒计算^[14-18]是近年来涌现出的一类模拟人类认知复杂概念的方法论，其主要观点是概念可以逐层粒化，在粒化分析过程中处理概念的不确定性。在粒计算框架下，表示学习可体现为一个由细到粗，由具象到抽象的过程。从粒计算视角看表示学习，是标记分布学习的新视角。已有一些基于粒的思想进行多标记数据的研究。本文作者^[19-21]是国内较早系统地从粒的角度研究多标记学习的学者之一，在全局标记相关性假设下构造的模型已经在多标记的监督学习、增量学习和主动学习等方面证明了粒计算的有效性。

在多标记数据的研究中，标记相关性局部成立是一种更为广泛的情形，是标记相关性在示例集上从“必然”向“或然”的拓展^[22]。标记局部相关性在标记分布学习中已有一些研究，如贾修一等^[23-24]将标记局部相关性引入标记分布学习的预测模型中，在优化目标函数的正则化项中加入标记局部相关性信息。在一定的聚类假设下，示例自动地形成了信息粒，刻画出潜在的主题。聚类/邻域粗糙集是利用特征空间信息形成粒的有效手段^[25]。这些类簇形成一系列粒，在粒的层面上进行局部处理。在每一个粒上，通过利用示例的特征空间的拓扑性质和逻辑标记的信息恢复隐含的数值型标记分布。在粒化得到的局部标记分布基础上，结合具体聚类策略，可构造一个新的标记分布表示。

本文的主要创新点：1）在优化多标记数据的标记分布时，引入粒计算的思想，通过粒化与融合策略，能更全面地刻画示例标记分布，减少由于具有相似局部相关性过少导致标记分布均匀化现象。2）根据局部标记相关性假设，利用聚类策略构造了示例的粒结构，增强了示例表示的鲁棒性。提出了一个基于粒的标记增强标记分布学习模型(granule-graph Laplacian label enhancement, G-GLLE)。

为了验证模型的有效性，我们与现有的标记增强算法在多个数据集下展开了性能对比。同时分析了在局部标记相关性假设下，各模型所重构的数值标记关于示例的描述拟合程度以及粒化本身对多标记学习的贡献。实验结果均表明，本文所构造的模型在3个评测上均能取得较好的学习效果。

1.   相关工作

1.1   符号表示

首先，本文先给出主要符号解释和定义^[8]。示例记为 $ x $ ,第 $ i $ 个示例记为 $ {{\boldsymbol{x}}_i} $ ，标记变量记为 $ y $ ，第 $ j $ 个标记值记为 $ {y_j} $ ， $ {{\boldsymbol{x}}_i} $ 的逻辑标记向量记为 ${{\boldsymbol{l}}_i} = {\left[ {l_{{{{x}}_i}}^{{y_1}}\;l_{{{{x}}_i}}^{{y_2}}\;\cdots\;l_{{{{x}}_i}}^{{y_c}}} \right]^{\rm T}}$ ，其中 $ c $ 是可能的标记个数， ${\boldsymbol{l}}_{{{{x}}_i}}^{{y_1}} \in \left\{ {0,1} \right\}$ 。 $ y $ 对 $ x $ 的描述度记为 $ d_x^y $ ， $ {{\boldsymbol{x}}_i} $ 的标记分布记为 ${{\boldsymbol{d}}_{{i}}} = {\left[ {d_{{{{x}}_i}}^{{y_1}}\;d_{{{{x}}_i}}^{{y_2}}\;\cdots\;d_{{{\boldsymbol{x}}_i}}^{{y_c}}} \right]^{\rm T}}$ ，其中 $ d_{{{\boldsymbol{x}}_i}}^{{y_c}} \in \left[ {0,1} \right] $ 。令 $ \mathcal{X} $ $= {{\bf{R}}^q}$ 表示 $ q $ 维特征空间，则标记增强形式化表示如下：

给定训练集 ${\boldsymbol{S}} = \{ \left( {{{{x}}_i},{{{l}}_i}} \right)\left| {1 \leqslant i} \right. \leqslant n\}$ ，其中 $ {{\boldsymbol{x}}_i} \in \mathcal{X} $ ， $ {{\boldsymbol{l}}_i} \in {\left\{ {0,1} \right\}^c} $ ， 标记增强从逻辑标记向量 $ {{\boldsymbol{l}}_i} $ 中恢复 $ {{\boldsymbol{x}}_i} $ 的标记分布 $ {{\boldsymbol{d}}_i} $ ，此时， $ {\boldsymbol{S}} $ 转化为标记分布学习的训练集。

1.2   经典标记增强算法

1.2.1   模糊标记增强

FCM^[10]模型是基于模糊聚类(FCM)的标记增强算法，采用模糊C-均值聚类，该方法试图通过迭代最小化一个目标函数来聚类特征向量。

KM^[11]模型是基于核函数的方法，根据逻辑标记将特征空间划分为两个集合，分别将两个集合样本点映射到高维特征空间，根据高维特征空间的拓扑性质计算每个示例到每个标记的隶属度，最后作softmax标准化得到标记分布。

基于模糊的标记增强方法对参数的鲁棒性强，不易受参数变化的影响，但对于不同类型数据的敏感性低，难以根据数据类型特点，形成独特的模型，缺少模糊隶属度与标签对应的数学理论依据。

1.2.2   基于图的标记增强

LP^[12]模型是基于标记传播的算法。它构建所有示例的图模型，通过迭代标记传播技术得到标记重要性信息，最后经softmax标准化得到标记分布。

ML^[13]模型是基于流形学习的算法。它根据示例的特征空间的拓扑性质构造图模型，在示例可以通过邻域中其他示例的线性组合构造的平滑假设下，构造有约束的二次规划，通过优化参数得到标记分布，最后作softmax的标准化。

GLLE^[9]模型是基于图拉普拉斯模型的标记增强算法，它依据平滑假设在根据示例的特征空间构造的图模型性质计算图拉普拉斯标记特征函数，利用特征空间映射的高维空间拓扑性质构造损失函数，通过优化目标函数的参数，得到标记分布，最后进行softmax标准化。

2.   基于粒的标记增强模型

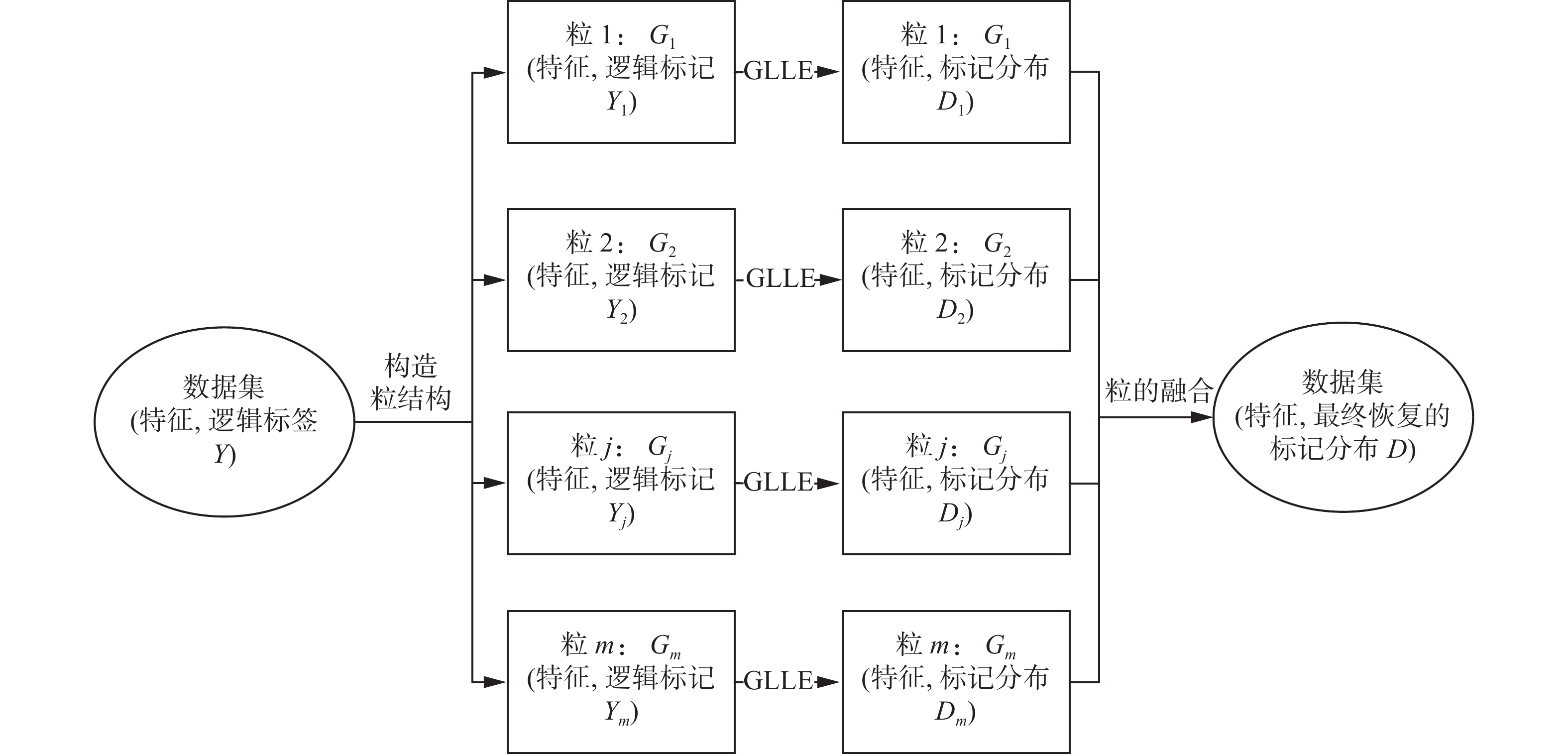
本节将详述如何根据聚类方法构造粒给出基于粒的标记增强模型。本文试图改进GLLE^[9]的标记增强模型，提升预测效果。图1给出了基于粒的标记增强模型的整体框架。

图  1  基于粒的标记增强标记模型G-GLLE的整体框架

Fig.  1  Framework of granule-based label enhancement for label distribution learning (G-GLLE)

下载: 全尺寸图片

不同的多标记数据的多个标记之间具有不同的局部相关性。若对所有数据采用同一标准整体处理标记相关性，不能精确描述不同示例的多标记之间的相关性，导致实验结果不佳。对于大规模数据集，若找到具有相似局部相关性的示例，对它们进行局部统一处理，挖掘该类簇中示例的隐含的数值型标记分布，再在粒的基础上进行标记分布的融合，将会大大提升工作效率，并提高分类精度。

因为标记相关性局部成立，所以， $ \left( {{\boldsymbol{w}},{\boldsymbol{b}}} \right) $ 序偶关系是多组的，我们用聚类方法找到哪些示例具有局部相关性，划分到同一粒中。局部相关性下，标记之间的相关关系并非对所有示例都成立，而一个 $ \left( {{\boldsymbol{w}},{\boldsymbol{b}}} \right) $ 能表示的标记相关性是单一的，不能体现标记之间局部相关性。解决的策略为，寻找一组关于示例子集的表示，每组表示用一个图去刻画。策略上可使用类似于聚类的方法获得这样的表示，根据表示之间的示例分布，增加其他的正则项，以体现同一个示例在不同类簇间标记相关的一致性。在类簇的基础上，作带逻辑标记数据的数值型标记挖掘，得到的标记分布再作融合，体现粒的思想。

所以，本文提出的G-GLLE模型在训练阶段有两个问题需要解决。

1） 如何构造粒？

2） 如何在粒的基础上挖掘隐含的数值型标记信息？

幸运的是，我们可以参考一些前人处理多标记数据的方法。Zhu等^[25]认为“属性特征相似的示例，拥有相似的标记描述”。依据流形假设，本文进一步假设示例的某个标记只能属于一个局部标记相关假设，并对数据集的属性空间进行聚类处理，将属性特征相似的示例划分到相同类簇中，构成不相交的示例粒。由上述操作过程可知，同一粒中示例具有相似的特征，即有相似的标记描述，那么同一粒中示例的标记的相关性应该是一致的，所以先从局部开始处理，对同一粒 ${G_i} = [{{\bf{Idx}}_{\boldsymbol{i}}},{{\boldsymbol{C}}_{\boldsymbol{i}}}]$ 中的示例进行建模，结合该粒中示例的属性空间的拓扑性质和逻辑标记空间的特性，在G-GLLE模型下求解，该粒 ${G_i} = [{{\bf{Idx}}_{\boldsymbol{i}}},{{\boldsymbol{C}}_{\boldsymbol{i}}}]$ 的参数 $\left( {{{\boldsymbol{w}}_i},{{\boldsymbol{b}}_i}} \right),i = 1,2,\cdots,m$ 。当得到每个粒中示例的数值型标记分布时，在粒的基础上，对所有粒进行融合，得到整个数据集的粒的标记分布。

上述过程分为以下3个阶段。G-GLLE模型1）希望建立一个映射 $\varphi :X \to \left\{ {{G_1},{G_2},\cdots,{G_m}} \right\}$ ，从原始的 $ q $ 维输入示例空间到 $ m $ 个新的 $ q $ 维空间 ${G_j}, j = 1, 2,\cdots,m$ ；2）然后在每个粒 $ {G_j} $ 上，训练基于粒的 $ c $ 维逻辑标记 $ y $ 到 $ c $ 维数值型标记分布 $ {D_j} $ 的转化映射 $ {f_k}:{G_j} \to {D_j} $ ；3）在整个示例空间，将每个粒 $ {G_j} $ 上的示例标记分布 $ {D_j} $ 进行融合， $r:\{ {D_1},{D_2},\cdots,{D_m}\} \to D$ 。

下面具体阐述这3个阶段。

阶段1　基于簇的粒结构。

为了找到具有相似局部相关性的标记的示例，需要对示例划分成不同的粒。根据流形假设，以示例的属性空间的拓扑性质为依据，度量示例构成粒。本文不研究如何构造粒结构，只从一个新颖的角度探讨如何在粒结构上以标记分布方式的标注。为了便于理解，选择符合文本假设的经典的构成粒的方式——聚类算法。粒结构形成过程中希望捕捉可识别的特征，刻画具有相似局部标记相关性的示例。为了实现这个过程，本文运用k-means聚类技术，来挖掘数据隐藏的结构。形式化地，将 $ X $ 划分到 $ m $ 个互不相交的簇 $ {G_i} $ ，示例类别和簇中心分别用 ${{\bf{Idx}}_i}$ 和 $ {{\boldsymbol{C}}_i} $ 表示， $ i = 1, 2,\cdots,m $ 。

给定训练集 $ S $ ,特征矩阵 ${\boldsymbol{X}} = [{{\boldsymbol{x}}_1}\;{{\boldsymbol{x}}_2}\;\cdots\;{{\boldsymbol{x}}_n}]$ ，逻辑标记矩阵 ${\boldsymbol{L}} = [{{\boldsymbol{l}}_1}\;{{\boldsymbol{l}}_2}\;\cdots\;{{\boldsymbol{l}}_n}]$ ，本文目的是从逻辑标记矩阵 $ {\boldsymbol{L}} $ 恢复标记分布矩阵 ${\boldsymbol{D}} = [{{\boldsymbol{d}}_1}\;{{\boldsymbol{d}}_2}\;\cdots\;{{\boldsymbol{d}}_n}]$ 。根据标记相关性局部假设，我们希望将具有相似标记相关性的示例放在一起，划分成粒，分别局部处理，在每个粒上单独处理将属于此粒中的示例，从逻辑标记矩阵 $ {\boldsymbol{L}} $ 中恢复出标记分布矩阵 $ {{\boldsymbol{D}}_i} $ 。

具体地，对于训练集 $ S $ ,运用k-means聚类算法，根据特征矩阵 ${\boldsymbol{X}} = [{{\boldsymbol{x}}_1}\;{{\boldsymbol{x}}_2}\;\cdots\;{{\boldsymbol{x}}_n}]$ 的拓扑信息，将 $ {\boldsymbol{S}} $ 划分为 $ m $ 个互不相交的簇，根据粒计算^[13]的思想，这些簇构成了 $ m $ 个q维粒空间 $\left\{ {{G_1},{G_2},\cdots,{G_m}} \right\}$ ：

每个粒 ${G_i},i = 1,2,\cdots,m$ 中的示例的特征空间拓扑性质相似。根据流形假设，粒 $ {G_i} $ 中的示例具有相似的局部标记相关性。因此，下一步我们分别在每个粒 $ {G_i} $ 上局部地从示例的逻辑标记中恢复隐藏的数值型标记分布，这样可更充分地利用标记间的相关性。

阶段2　基于粒的图拉普拉斯标记增强模型（G-GLLE）。

给定粒 ${G_h},h = 1,2,\cdots,m$ ，假设 $ {G_h} $ 中的示例为 $[{{\boldsymbol{x}}_1}\;{{\boldsymbol{x}}_2}\;\cdots\;{{\boldsymbol{x}}_h}]$ 。我们首先要恢复粒 $ {G_h} $ 中示例的逻辑标记矩阵 $ {{\boldsymbol{L}}_h} $ 中隐藏的标记分布矩阵 ${{\boldsymbol{D}}_h} = [{d_{h1}}\; {d_{h2}}\;\cdots\;{d_{hc}}]$ 。G-GLLE模型假设参数模型为

式中： ${{\boldsymbol{W}}^h} = [{{\boldsymbol{w}}^{h1}}\;{{\boldsymbol{w}}^{h2}}\;\cdots\;{{\boldsymbol{w}}^{hc}}]$ 是一个权重矩阵； ${{\boldsymbol{b}}^h} \in {{\bf{R}}^C}$ 是偏置向量。 $ {\varphi ^h}\left( x \right) $ 是把 $ x $ 转化到高维特征空间的非线性转化。为了方便描述，令 ${{\boldsymbol{\hat W}}^h} = [{{\boldsymbol{W}}^h}\; {{\boldsymbol{b}}^h}],$ $ {\phi _i}^h = [{\varphi ^h}\left( {{x_i}} \right);1] $ 。我们方法的目的是求解最优的参数 $ {{\boldsymbol{W}}^{h*}} $ ，使得粒 $ {G_h} $ 中的示例 $ {{\boldsymbol{x}}_i} $ 产生合理的标记分布 $ {\boldsymbol{d}}_i^h $ 。因此学习目标转化为找到最优模型 $ {{\boldsymbol{W}}^{h*}} $ ，可最小化下列目标函数：

式中： $ \lambda $ 是权重参数， ${{\boldsymbol{\varPhi }}^h} = [\varPhi _1^h\;\varPhi _2^h\;\cdots\;\varPhi _n^h]$ ， $ {{\boldsymbol{G}}_L} = {{\hat {\boldsymbol{A}}}} - {\boldsymbol{A}} $ 是图拉普拉斯矩阵， $ {{\hat {\boldsymbol{A}}}} $ 是对角矩阵，

其中： $ N\left( i \right) $ 是 $ {{\boldsymbol{x}}_i} $ 的k近邻的集合，宽度系数 $ \sigma {\text{ = 1}} $ ， ${a_{ii}} = \displaystyle \sum\limits_{j = 1}^n {{a_{ij}}}$ 。

阶段2的优化求解过程主要参考徐宁等^[9]提出的标记增强模型(GLLE)，求解最优的参数 $ {{\boldsymbol{W}}^{h*}} $ ，使得粒 $ {G_h} $ 中的示例 $ {{\boldsymbol{x}}_i} $ 产生合理的标记分布 $ {\boldsymbol{d}}_i^h $ 。

阶段3　基于粒的标记分布融合。

上述两阶段已经求出粒 $ {G_h} $ 对应的最优参数 $ {{\boldsymbol{W}}^{h*}} $ 以及标记分布 ${D^h},h = 1,2,\cdots,m$ 。由于本文采用k-means聚类，得到的粒是关于原数据集的一个划分，任意两个粒之间不相交，不存在共有的示例，使得每个示例对应的标记分布唯一，所以在基于粒的标记分布融合过程中，为了求出整体训练集 $ S $ 中所有示例的标记分布，只需要在粒的层面将每个粒 $ {G_h} $ 对应的标记分布 $ {D^h},h = 1,2,\cdots,m $ 拼接在一起即可。因此，恢复出最终的标记分布为 $D = \left\{ {D^1}, \right. \left.{D^2},\cdots,{D^h}, \cdots ,{D^m} \right\}$ 。

3.   实验及结果

3.1   数据集

实验在6个真实数据集(http://cse.seu.edu.cn/PersonalPage/xgeng/LDL/index.htm)上进行，涉及人脸表情图像，自然场景图象等领域。数据集具体描述如表1所示。

3.2   评价指标

为了估计恢复后的标记分布的效果，本文采用5个指标度量恢复标记分布和真实标记分布的平均距离和相似性。5个评价指标分别为切比雪夫距离(Chebyshev, 简记为Cheb)、克拉克距离(Clark)、KL散度(KL Divergence, 简记为KL)、余弦距离(Cosine)以及交叉相似性(Intersection, 简记为Intersec)。假设真实的标记分布是 ${\boldsymbol{d}} = ({d_1},{d_2},\cdots, {d_c})$ ，预测的标记分布是 ${{\hat {\boldsymbol{d}}}}= ({\hat d_1},{\hat d_2},\cdots,{\hat d_c})$ ，5个指标的定义如表2所示。↑表示指标值越大，预测效果越好；↓表示指标值越小，预测效果越好。

3.3   实验结果

3.3.1   标记分布恢复能力对比

为了评价G-GLLE在标记增强方面的能力，我们设计了如下实验比较不同标记增强算法在标记分布恢复方面的能力。首先生成6个标记分布数据集对应的逻辑标记。在多标记分类指标上评测，对于训练集中的示例，采用如下方式完成从数值标记到逻辑标记的二值化：若标记分布值相对大，且和超过0.5的标记，则标为1；其余标记标为0。

基于所获得的逻辑标记，实验选取了6个对比的标记增强学习代表性算法（GLLE^[9]、LEMLL^[7]、FCM^[10]、KM^[11]、LP^[12]、ML^[13]）和本文提出的算法G-GLLE。比较上述算法在标记增强后获得的数值标记与真实的数值标记之间的相似性。

对G-GLLE和GLLE模型，参数 $ \lambda $ 设置为0.01并且邻域数k设为数据集标记个数加1（记为 $ c + 1 $ ）。GLLE的核函数是高斯核函数。LP的参数设为0.5。ML的邻域数k设为 $ c + 1 $ 。FCM的参数 $ \beta $ 设为2。KM的核函数设为线性核函数。LEMLL中 k 设为 10，ε 设为0.1， $\alpha $ 、 $ \beta $ 和 $\gamma $ 从集合{ 1/ 64, 1/ 16, 1 /4, 1, 4, 16, 64}中选择。

十折交叉验证下，所有算法恢复的标记分布在5个度量下的平均性能如表3~8所示，其中无法得到指标结果的值标注为NaN。

通过表3~8可以看出，G-GLLE算法有良好的恢复标记分布的能力，恢复标记分布标记的效果至少与现有的恢复标记分布算法的效果相当。本文对每个数据集的每个度量指标排在第1、第2、第3的算法结果分别以同时加粗和下划线、仅加粗、仅下划线的形式高亮显示，发现G-GLLE算法的恢复标记分布的效果排名前3名的概率在28/36，而且与第1名和第2名的在各指标上的效果相差不大。G-GLLE在图像数据集3DFE、Natural、SPO、SPOEM 4个数据集上排名基本上都排在前3名。

3.3.2   标记分布学习能力对比

为了进一步测试对逻辑标记数据集在标记增强预处理后作标记分布学习的有效性，我们从基于所选数据集的逻辑分布出发，经7个标记增强算法（G-GLLE、GLLE^[9]、LEMLL^[7]、ML^[13]、LP^[12]、KM^[11]、FCM^[10]）得到数值标记分别作为训练集，在标记分布学习基准算法SA-BFGS^[26]上训练标记分布学习模型，并用所训练的LDL模型测试数据集标记分布学习效果。

预测实验的对比结果如图2所示。由5个对比图可以直观地看出，在所比较的6个数据集分别对应的6种数值标记恢复监督信息下，G-GLLE算法恢复的标记分布对于提升LDL算法的运算效果整体上效果更好。特别是在2个图像数据集3DFE和Natural上优势更明显。

图  2  各算法在5个指标上的标记分布学习能力对比

Fig.  2  Comparisons on capability of label distribution learning on five indexes

下载: 全尺寸图片

进一步对比G-GLLE和GLLE时发现，对于3DFE、Natural Scene和Movie数据集，从粒的角度挖掘数据特征的算法G-GLLE效果好。这可能是由于3DFE、Natural Scene和Movie数据集的标记局部相关性的不一致性明显，所以由标记局部相关性为依据划分知识粒的效果好，能较大可能性地划分出标记局部一致性的相关性的示例构成的粒。在各个一致性粒的基础上，粒间示例的标记局部相关差异性强，粒内示例的标记局部相关一致性强，此时对于同一粒上的示例求解关于示例的标记分布表示知识比较一致，可求得相似的参数，且符合平滑假设。

而在SJAFFE数据集上，2个算法在5个指标上的效果相差不大，并且从示例挖掘标记特性的GLLE算法效果略好些。这可能是由于标记局部相关性的不一致性差异不大，各标记的重要性相似，使得通过诸如k-means聚类方式，较难得到有效的标记分布表示知识粒，当强制将示例划分为几类时，标记局部语义信息可能不完整，导致数据集的标记分布学习效果不佳。

4.   结束语

现有的标记增强学习仅降低了大规模标记分布标注的必要性，而没有进一步研究示例层次的局部相关性。本文提出的算法G-GLLE从粒的角度处理数据，利用了标记分布的局部性信息，提供了恢复多标记信息的新视角。已有实验结果证明本文方法能有效地挖掘标记局部相关性。未来可以在粒的构造上作进一步的研究，设计不同的粒化策略以进一步优化标记分布的局部性形态，提升标记分布学习的有效性。