Robust unsupervised feature selection via multistep Markov probability and latent representation
-
摘要: 无监督特征选择是机器学习和数据挖掘中的一种重要的降维技术。然而当前的无监督特征选择方法侧重于从数据的邻接矩阵中学习数据的流形结构，忽视非邻接数据对之间的关联。其次这些方法都假设数据实例具有独立同一性，但现实中的数据样本其来源是不同的，这样的假设就不成立。此外，在原始数据空间中特征重要性的衡量会受到数据和特征中的噪声影响。基于以上问题，本文提出了潜在多步马尔可夫概率的鲁棒无监督特征选择方法（unsupervised feature selection via multi-step Markov probability and latent representation, MMLRL），其思想是通过最大多步马尔可夫转移概率学习数据流形结构，然后通过对称非负矩阵分解模型学习数据的潜在表示，最后在数据的潜在表示空间中选择特征。同时在6个不同类型的数据集上验证了所提出算法的有效性。Abstract: Unsupervised feature selection is a significant dimensionality reduction technique in machine learning and data mining. However, current unsupervised feature selection methods primarily focus on learning the manifold structure of the data from the adjacency matrix, ignoring the association between non-adjacent data pairs. Second, these methods often assume that the data instances are independent and identically distributed, but in reality, the data samples originate from heterogeneous sources, and this assumption is often untenable. Additionally, the measure of feature importance in the original data space is affected by noise in the data and features. To address the aforementioned problems, this study proposes a robust unsupervised feature selection method based on multistep Markov probability and latent representation (MMLRL). The key idea is to learn the manifold structure between the data points through the maximum multistep Markov transition probability. Subsequently, a symmetric non-negative matrix factorization model was used to learn the latent representation of the data. Finally, the feature selection is performed in the latent representation space. At the same time, the proposed algorithm is evaluated on six different types of datasets to validate its effectiveness.
-
随着信息技术的发展，机器学习在实际应用中受到越来越多的关注[1-5]。与此同时机器学习处理的数据维度也越来越高，高维数据中的冗余特征和噪声也越来越多，因此有必要剔除数据中的冗余和不相关特征[6]。数据降维是一种寻找数据重要特征并降低维度的数据挖掘技术，通常数据降维方法有特征选择[7]和特征提取[8]两种。特征选择根据学习规则从高维数据中选取重要特征子集[9]，因此不会改变数据的原始特征；特征提取是通过学习高维数据在低维空间中的转换表达来降低数据维度[10]。根据有无数据标签，特征选择方法可分为有监督[11]、半监督[12]和无监督[13]3种。本文中主要研究无监督特征选择方法。
无监督特征选择方法可分为过滤式[14]、包裹式[15]和嵌入式[16]3种。过滤式特征选择方法是根据评估指标给特征赋权重，按权重大小选择重要特征，整个过程独立于学习算法，常见的评估指标有拉普拉斯分数(Laplacian score for feature selection, LS)[14]和特征相似度。包裹式特征选择方法是根据学习器的性能从原始特征子集中选择最优特征子集。嵌入式特征选择方法[17-18]是学习特征权重，然后根据排序后的特征权重选择最优特征子集。与前两者方法相比，嵌入式方法考虑了不同的数据属性，如流形结构和数据的先验分布等，因而性能更好。
近年来，无监督特征选择方法得到迅速发展。例如，Cai等[16]利用图拉普拉斯算子的特征向量来捕获数据的多簇类结构，提出用于多类数据的特征选择方法(unsupervised feature selection for multi-cluster data, MCFS)。但该方法会独立进行流形结构表示和特征选择，这样特征选择的性能在很大程度上取决于图的构造效率。因此Hou等[13]提出一种基于联合嵌入学习和稀疏回归(joint embedding learning and sparse regression: a framework for unsupervised feature selection, JELSR)的无监督特征选择框架，通过学习稀疏变换矩阵来进行特征选择。Zhu等[19]提出特征自表示模型(unsupervised feature selection by regularized self-representation, RSR)，通过对特征矩阵本身进行表示，找出具有代表性的特征分量。为了使特征选择过程不过度依赖最初学到的流形结构，Nie等[20]提出了自适应的特征选择方法(unsupervised feature selection with structured graph optimization, SOGFS)，该方法将特征选择和局部结构学习相结合。Li等[21]则提出自适应广义不相关的无监督特征选择方法(generalized uncorrelated regression with adaptive graph for unsupervised feature selection, URAFS)，在广义不相关模型中添加基于最大熵原理的图正则化项，从而将数据局部几何结构嵌入流形学习中。目前大部分算法都是在欧氏距离的基础上学习数据的流形结构，而Min等[22]通过多步马尔可夫概率关系来描述数据结构从而进行无监督特征选择(unsupervised feature selection via multi-step Markov probability relationship, MMFS)。
虽然以上无监督特征选择方法在各种应用中取得一定的效果，但是这些方法还存在一些不足。首先，这些方法都假设数据是独立同分布的，然而现实中的数据来源不同，即使同源数据也会受到外部条件（如光照、角度）影响，因而真实的数据实例不仅与高维特征相关，还与数据之间的内在联系有关。其次，大多数方法都是度量原始数据空间中的特征重要性，这些方法的性能通常受到噪声特征和样本的影响。而且，这些方法在数据流形学习中都只利用相邻数据点之间的信息，忽略不相邻数据对之间可能存在的关联。基于以上问题，本文提出了一种新颖且简洁的潜在多步马尔可夫概率的鲁棒无监督特征选择方法。
该方法借助多步马尔可夫转移概率构造数据间的亲和矩阵，充分挖掘数据之间的流形结构。然后利用对称非负矩阵分解(symmetric nonnegative matrix factorization, SymNMF)学习原始数据的潜在表示，最后将潜在表示学习嵌入到稀疏回归模型(sparse regression model)中进行特征选择。多步马尔可夫转移概率矩阵可以描述数据与相邻数据点和非相邻数据点之间的关系，在基于这种关系构造的潜在表示空间中进行特征选择，不仅能选择重要特征还能去除冗余特征和噪声，增强算法的鲁棒性。
1. 相关工作
1.1 符号的定义
在本文中，矩阵用粗斜体大写字母表示，向量用粗斜体小写字母表示。
${\boldsymbol{X}} = [{{\boldsymbol{x}}_1}\quad{{\boldsymbol{x}}_2}\quad \cdots \quad {{\boldsymbol{x}}_n}] \in {{\bf{R}}^{d \times n}}$ 是数据矩阵，$ d $ 是样本维度，即特征数，$ n $ 是样本个数。对于任意矩阵${\boldsymbol{X}} \in {{\bf{R}}^{d \times n}}$ ，$ {x_{ij}} $ 是$ {\boldsymbol{X}} $ 的第$ i $ 行第$ j $ 列元素，矩阵${{\boldsymbol{X}}^{{\rm{T}}}}$ 为$ {\boldsymbol{X}} $ 的转置矩阵，${\rm{tr}}({\boldsymbol{X}})$ 为$ {\boldsymbol{X}} $ 的迹。$ {\boldsymbol{X}} $ 的F-范数定义为${\left\| {\boldsymbol{X}} \right\|_F} = \sqrt {\displaystyle\sum_{i = 1}^n {\displaystyle\sum_{j = 1}^d {x_{ij}^2} } }$ ，$ {\boldsymbol{X}} $ 的$ {L_{2,1}} $ 范数定义为${\left\| {\boldsymbol{X}} \right\|_{2,1}} = \displaystyle\sum_{i = 1}^n {\sqrt {\displaystyle\sum_{j = 1}^d {x_{ij}^2} } }$ 。1.2 多步马尔可夫转移概率
高维空间中数据点可视为一个节点或状态，数据
$ {{\boldsymbol{x}}_i} $ 到数据$ {{\boldsymbol{x}}_j} $ 的一步转移概率定义为$$ {{\boldsymbol{P}}_{ij}} = \dfrac{{{{\boldsymbol{M}}_{ij}}}}{{\displaystyle\sum_{r = 1}^n {{{\boldsymbol{M}}_{ir}}} }} $$ (1) 其中
$$ {{\boldsymbol{M}}_{ij}} = \left\{\;\; {\begin{aligned} & 1\Biggr/\left({{{\dfrac{{{{\boldsymbol{D}}_{ij}}}}{{\displaystyle\sum_{r = 1}^n {{{\boldsymbol{D}}_{ir}}} }} + \varepsilon }}}\right)\;,\quad {{\text{ }}{{\boldsymbol{x}}_j} \in {N_k}({{\boldsymbol{x}}_i})} \\ & 0\;,\quad {其他} \end{aligned}} \right. $$ (2) 式中
$ {\boldsymbol{D}} $ 是欧氏距离矩阵。式（1）和（2）有两点值得注意：1）任意数据点的自转移概率为0，即$ {{\boldsymbol{P}}_{ii}} = 0 $ ；2）随着数据维度的增加欧氏距离并不能很好反映所有数据点之间的关系，但流形的局部微小结构同构于欧氏空间，因此非常接近的数据点之间的一步转移概率是可以借助欧氏距离来计算的。从式(1)和式(2)可知两个数据的关系越近，数据的一步转移概率越大。由定理1得数据的$ u $ 步转移概率为$$ {{\boldsymbol{P}}^{(u)}} = {{\boldsymbol{P}}^{(u - 1)}}{{\boldsymbol{P}}^{(1)}} $$ (3) 定理1 设
$ \left\{ {{{\boldsymbol{X}}_u},u \in T} \right\} $ 为马尔可夫链，则对任意整数$ u \geqslant 0,i,j \in I $ ，$ u $ 步转移概率$ p_{ij}^{(u)} $ 具有性质$ {{\boldsymbol{P}}^{(u)}} = {{\boldsymbol{P}}^{(u - 1)}}{{\boldsymbol{P}}^{(1)}} $ 。定义1 若随机过程
$ \left\{ {{{\boldsymbol{X}}_u},u \in T} \right\} $ 对于任意的非负整数$ u \in T $ 和任意的${i_0},{i_1},\cdots,{i_{u + 1}} \in I$ ，其条件概率满足$$ \begin{gathered} P\left\{ {{X_{u + 1}} = {i_{u + 1}}\left| {{X_0} = {i_0},{X_1} = {i_1},\cdots{\text{ , }}{X_u} = {i_u}} \right.} \right\}=\\ P\left\{ {{X_{u + 1}} = {i_{u + 1}}\left| {{X_u} = {i_u}} \right.} \right\} \end{gathered} $$ (4) 则称
$ \left\{ {{{\boldsymbol{X}}_u},{\text{ }}u \in T} \right\} $ 为马尔可夫链。定义1中马尔可夫过程
$ \left\{ {{{\boldsymbol{X}}_u},u \in T} \right\} $ 的参数集$ T $ 是离散的时间集合，即$T = \left\{ {0,1,2,\cdots} \right\}$ ，$ {{\boldsymbol{X}}_u} $ 取值的状态空间是离散的状态集$I = \left\{ {{i_0},{i_1},{i_2},\cdots} \right\}$ 。定理1证明：利用全概率公式及定义1中的马尔可夫性，有：
$$ \begin{gathered} p_{ij}^{(u)} = P\left\{ {{X_{m + u}} = j\left| {{X_m} = i} \right.} \right\} = \dfrac{{P\left\{ {{X_m} = i,{X_{m + u}} = j} \right\}}}{{P\left\{ {{X_m} = i} \right\}}} = \\ \displaystyle\sum\limits_{{\textit{z}} \in I} {\dfrac{{P\left\{ {{X_m} = i,{X_{m + l}} = {\textit{z}},{X_{m + u}} = j} \right\}}}{{P\left\{ {{X_m} = i,{X_{m + l}} = {\textit{z}}} \right\}}} \cdot } \dfrac{{P\left\{ {{X_m} = i,{X_{m + l}} = {\textit{z}}} \right\}}}{{P\left\{ {{X_m} = i} \right\}}} = \\ \displaystyle\sum\limits_{{\textit{z}} \in I} {P\left\{ {{X_{m + u}} = j\left| {{X_{m + l}} = {\textit{z}}} \right.} \right\}} P\left\{ {{X_{m + l}} = {\textit{z}}\left| {{X_m} = i} \right.} \right\} = \\ \displaystyle\sum\limits_{{\textit{z}} \in I} {p_{{\textit{z}}j}^{(u - l)}(m + l){p^{(l)}}(m)} = \displaystyle\sum\limits_{{\textit{z}} \in I} {p_{i{\textit{z}}}^{(l)}p_{{\textit{z}}j}^{(u - l)}} \end{gathered} $$ (5) 令
$ l = 1 $ ，根据定义2及矩阵乘法的运算法则得$ {{\boldsymbol{P}}^{(u)}} = {{\boldsymbol{P}}^{(u - 1)}}{{\boldsymbol{P}}^{(1)}} $ ，定理1得证。定义2 若对任意的
$ i,j \in I $ ，马尔可夫链$\{ {{\boldsymbol{X}}_u}, u \in T \}$ 的转移概率$ p_{ij}^{(u)} $ 与$ u $ 无关，则称马尔可夫链$\{ {{\boldsymbol{X}}_u}, u \in T \}$ 是齐次的，并记$ p_{ij}^{(u)} $ 为$ {p_{ij}} $ 。设
$ {{\boldsymbol{P}}^{(1)}} $ 为一步转移概率所组成的矩阵，且状态空间$T = \left\{ {1,2,\cdots} \right\}$ ，那么系统状态的一步转移概率为$$ {{\boldsymbol{P}}^{(1)}} = \left( {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}& \cdots &{{p_{1n}}} & \cdots \\ {{p_{21}}} & {{p_{22}}}&\cdots&{{p_{2n}}}&\cdots\\ \cdots &\cdots & \cdots & \cdots &\cdots \end{array}} \right) $$ (6) 数据
$ {{\boldsymbol{x}}_i} $ 和数据$ {{\boldsymbol{x}}_j} $ 的$ t $ 步最小多步马尔可夫转移概率为$$ {{\boldsymbol{V}}_1}_{ij} = \min {\boldsymbol{P}}_{ij}^{(t)}\quad {\rm{s}}.{\rm{t}}. i \ne j,t \leqslant u,{{\boldsymbol{V}}_1}_{ii} = 0,\sum\limits_{j = 1}^n {{{\boldsymbol{V}}_1}_{ij} = 1} $$ (7) $ {{\boldsymbol{V}}_1} $ 描述了数据点与其他$ u $ 步可达的数据点之间的最小转移关系，即松散关系。而数据间的最大多步马尔可夫转移概率关系，即紧密关系为$$ {{\boldsymbol{V}}_2}_{ij} = \max {\boldsymbol{P}}_{ij}^{(t)}\quad {\rm{s}}.{\rm{t}}.{\text{ }}i \ne j,t \leqslant u,{{\boldsymbol{V}}_2}_{ii} = 0,\sum\limits_{j = 1}^n {{{\boldsymbol{V}}_2}_{ij} = 1} $$ (8) 详细过程可见算法1，算法中学习数据流形结构的核心是多步马尔可夫转移概率，一定步数可达的最大马尔可夫转移概率描述了该数据对间的紧凑结构，而在一定步数可达的最小马尔可夫转移概率则描述该数据对间的松散结构。因此马尔可夫步[23]描述两个数据样本间的松紧关系，可进一步应用到聚类或分类任务中。
MMFS[22]方法在获得多步马尔可夫转移概率矩阵V1或V2后，直接将其应用于特征选择模板
$ {{\boldsymbol{F}}_1} = {{\boldsymbol{V}}_1}{{\boldsymbol{X}}^{{\rm{T}}}} $ 或$ {{\boldsymbol{F}}_2} = {{\boldsymbol{V}}_2}{{\boldsymbol{X}}^{{\rm{T}}}} $ 中选择特征。该方法虽然能自然地表征数据的流形结构，但是算法的特征选择能力很容易受噪声或异常值的影响，随着数据维度和特征维度的不断增加，从原始数据空间选择的特征质量会下降。如果从潜在表示空间中选择特征，就能很好地减弱噪声对算法模型的影响，提高算法的鲁棒性。算法1 求数据
$ {\boldsymbol{X}} $ 的$ u $ 步最大马尔可夫转移概率关系矩阵$ {{\boldsymbol{V}}_{\text{2}}} $ 输入 数据矩阵
${\boldsymbol{X}} \in {{\bf{R}}^{d \times n}}$ ，马尔可夫步数$ u $ 初始化 马尔可夫步数
$ t = 0 $ ，计算数据间的欧氏距离
${\boldsymbol{D}} \in {{\bf{R}}^{n \times n}}$ ；计算一步马尔可夫转移概率
$ {{\boldsymbol{P}}^{(1)}} $ ：$$ {{\boldsymbol{P}}_{ij}}^{(1)} = \dfrac{{{{\boldsymbol{M}}_{ij}}}}{{\displaystyle\sum\limits_{r = 1}^n {{{\boldsymbol{M}}_{ir}}} }} \text{，} {{\boldsymbol{M}}_{ij}} = 1\Biggr/\left(\dfrac{{\boldsymbol{D}}_{ij}}{\displaystyle\sum\limits_{r = 1}^n {{{\boldsymbol{D}}_{ir}}} } + \varepsilon \right) $$ 其中
$ {{\boldsymbol{P}}_{ii}} = 0 $ 且$ {{\boldsymbol{P}}_{ij}} = 0,{\text{ if }}{{\boldsymbol{x}}_j} \notin {N_k}({{\boldsymbol{x}}_i}) $ While
$ t < u $ do1)
$ {{\boldsymbol{P}}^{(t)}} = {{\boldsymbol{P}}^{(t - 1)}}{{\boldsymbol{P}}^{(1)}} $ ；2)
$ {{\boldsymbol{V}}_2}_{ij} = \max {\boldsymbol{P}}_{ij}^{(t)} $ ${\rm{s}}.{\rm{t}}.{\text{ }}i \ne j,{{\boldsymbol{V}}_2}_{ii} = 0,\displaystyle\sum\limits_{j = 1}^n {{{\boldsymbol{V}}_2}_{ij} = 1}$ 3)
$ t = t + 1 $ End while
输出 关系矩阵
$ {{\boldsymbol{V}}_{\text{2}}} $ 1.3 潜在表示学习
潜在表示学习[24](latent representation learning, LRL)有利于数据挖掘和机器学习任务，特别是对于网络数据的处理。非负矩阵分解(nonnegative matrix factorization, NMF)[25-26]主要是围绕具有线性结构的数据进行聚类，但其并不适用于所有类型的数据聚类，例如，一组图像会形成多个一维非线性流形。
而SymNMF模型不仅继承了NMF的可解释性[27]，还挖掘了数据的潜在聚类结构。假设同类数据的相似度更大，异类数据的相似度更小，
$ \left\| {{\boldsymbol{A}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}} \right\|_{F}^2 $ 越小，非负矩阵$ {\boldsymbol{H}} $ 捕捉的聚类结构越完整。SymNMF过程就是对数据进行潜在表示学习的过程，其目标是将相似性矩阵$ {\boldsymbol{A}} \in {{\bf{R}}^{n \times n}} $ 进行对称非负分解，分解为低维潜在空间中非负矩阵$ {\boldsymbol{H}} $ 与其转置矩阵$ {{\boldsymbol{H}}^{{\rm{T}}}} $ 的乘积：$$ \mathop {{\text{min}}}\limits_{\boldsymbol{A}} \left\| {{\boldsymbol{A}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{\rm{T}}}} \right\|_F^2 \quad {\rm{s}}.{\rm{t}}.{\text{ }}{\boldsymbol{H}} \geqslant 0 $$ (9) 式中：
$ {\boldsymbol{H}} \in {{\bf{R}}^{n \times c}} $ 是$ n $ 个数据的潜在表示矩阵；c是潜在因子数，且$ c < \min \{ d,n\} $ ；$$ {{\boldsymbol{A}}_{ij}} = \exp \left( - \left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|_2^2/2{\sigma ^2}\right) $$ (10) 其中
$ \sigma > 0 $ 为宽度参数。由于SymNMF模型在线性和非线性流形上都能获得更好的聚类结构，因此可以借用该思想从数据样本的亲和矩阵中学习潜在表示并进行无监督特征选择。
2. 模型和算法
2.1 模型建立
在潜在表示中，潜在因子对样本的一些隐藏属性进行编码，而这些隐藏属性与数据样本的某些特征（或属性）是相关的。因此，对潜在表示矩阵进行稀疏多元线性回归模型得：
$$ \mathop {\min }\limits_{\boldsymbol{W}} {\kern 1pt} \left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {\boldsymbol{H}}} \right\|_F^2 + a{\left\| {\boldsymbol{W}} \right\|_{2,1}} $$ (11) 式中：
$ {\boldsymbol{W}} \in {{\bf{R}}^{d \times c}} $ 是回归系数矩阵；矩阵$ {\boldsymbol{H}} \in {{\bf{R}}^{n \times c}} $ 可作为伪标签矩阵，可为特征选择提供判别信息。参数$ \alpha $ 控制模型稀疏度。将潜在表示学习的式(9)与稀疏回归模型式(11)相结合，得到基于稀疏正则化的潜在表示学习的特征选择模型：
$$\begin{gathered} \mathop {\min }\limits_{{\boldsymbol{W}},{\boldsymbol{H}}} \left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {\boldsymbol{H}}} \right\|_F^2 + \beta \left\| {{\boldsymbol{A}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}} \right\| + \alpha {\left\| {\boldsymbol{W}} \right\|_{2,1}}\\ {\rm{s.t.}}{\text{ }}{\boldsymbol{H}} \geqslant {\text{0}}\end{gathered} $$ (12) 式中：
$ {\boldsymbol{A}} $ 是如式(10)定义的数据相似性对称矩阵。但是，这种相似性矩阵$ {\boldsymbol{A}} $ 只保留了邻接数据点之间的相似关系，而没有考虑非邻接数据对之间可能存在的关系，即相似矩阵不能真实反映数据实例之间的关系。前文提到最大多步马尔可夫转移概率在保留任意数据对的局部流形结构的同时，还能描述该数据与较远点数据间的紧密关系。因此最大马尔可夫转移概率矩阵比相似性矩阵更适合潜在表示学习。基于以上分析，本文将最大多步马尔可夫转移概率与潜在表示的稀疏回归模型相结合，给出一个简洁新颖的无监督特征选择模型(unsupervised feature selection via multi-step Markov probability and latent representation, MMLRL)：
$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{W}},{\boldsymbol{H}}} \;\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {\boldsymbol{H}}} \right\|_F^2 + \alpha {\left\| {\boldsymbol{W}} \right\|_{2,1}} + \beta \left\| {{\boldsymbol{V}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}} \right\| \\ {\rm{s.t.}}{\text{ }}{\boldsymbol{H}} \geqslant {\text{0}} \end{gathered} $$ (13) 式中
${\boldsymbol{V}} \in {{\bf{R}}^{n \times n}}$ 是最大多步马尔可夫转移概率关系矩阵，可由算法$ \mathrm{Ⅰ} $ 学习得到。2.2 优化算法
式(13)用交替方向法（alternating direction minimizing, ADM）求解[28]，使用交替迭代优化策略逐个迭代更新模型中的变量。
2.2.1 固定
$ {\boldsymbol{W}} $ 更新$ {\boldsymbol{H}} $ 当
$ {\boldsymbol{W}} $ 固定时，目标函数(式(11))改写为$$\begin{gathered} \mathop {\min }\limits_{\boldsymbol{H}} \;\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} - {\boldsymbol{H}}} \right\|_F^2 + \beta \left\| {{\boldsymbol{V}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}} \right\|_F^2{\text{ }}\\ {\rm{s.t.}}{\text{ }}{\boldsymbol{H}} \geqslant {\text{0}} \end{gathered}$$ (14) 于是，使用拉格朗日乘子法求解问题(式(14))。设约束
$ {\boldsymbol{H}} \geqslant {\text{0}} $ 的拉格朗日乘子为$ {\boldsymbol{\varTheta }} \in {{\bf{R}}^{c \times n}} $ ，则式(14)中目标函数的拉格朗日函数为$$ \begin{gathered} L({\boldsymbol{H}},{\boldsymbol{\varTheta }}) = \;\;\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} - {\boldsymbol{H}}} \right\|_F^2 + \beta \left\| {{\boldsymbol{V}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}} \right\|_F^2 + {\rm{tr}}({\boldsymbol{\varTheta }}{{\boldsymbol{H}}^{{\rm{T}}}}) =\\ {\rm{tr}}\left[ {{{\left({{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} - {\boldsymbol{H}}\right)}^{{\rm{T}}}}\left({{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} - {\boldsymbol{H}}\right)} \right] + \\ {\rm{tr}}\left({\boldsymbol{\varTheta }}{{\boldsymbol{H}}^{{\rm{T}}}}\right) + \beta \cdot {\rm{tr}}\left[ {{{\left({\boldsymbol{V}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}\right)}^{{\rm{T}}}}\left({\boldsymbol{V}} - {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}\right)} \right] = \\ {\rm{tr}}\left({{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} - 2{{\boldsymbol{W}}^{(t)}}^{^{{\rm{T}}}}{\boldsymbol{XH}} + {{\boldsymbol{W}}^{(t)}}^{^{{\rm{T}}}}{\boldsymbol{X}}{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}}\right) + \\ {\text{ }}{\rm{tr}}\left({\boldsymbol{\varTheta }}{{\boldsymbol{H}}^{{\rm{T}}}}\right) + \beta \cdot {\rm{tr}}\left({\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}} - 2{{\boldsymbol{V}}^{{\rm{T}}}}{\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}} + {{\boldsymbol{V}}^{{\rm{T}}}}{\boldsymbol{V}}\right){\text{ }} \end{gathered} $$ (15) 对
$ L({\boldsymbol{H}},{\boldsymbol{\varTheta }}) $ 关于$ {\boldsymbol{H}} $ 求导数并令其等于0得:$$ \begin{gathered} \frac{{\partial {\text{ }}L({\boldsymbol{H}},{\boldsymbol{\varTheta }})}}{{\partial {\text{ }}{\boldsymbol{H}}}} = \frac{{\partial {\rm{tr}}\left({{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} - 2{{\boldsymbol{W}}^{(t)}}^{^{{\rm{T}}}}{\boldsymbol{XH}}\right)}}{{\partial {\text{ }}{\boldsymbol{H}}}} + \frac{{\partial {\text{ }}{\rm{tr}}\left({\boldsymbol{\varTheta }}{{\boldsymbol{H}}^{{\rm{T}}}}\right)}}{{\partial {\text{ }}{\boldsymbol{H}}}} + \\ \beta \frac{{\partial {\text{ }}{\rm{tr}}\left({\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}} - 2{{\boldsymbol{V}}^{{\rm{T}}}}{\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}\right)}}{{\partial {\text{ }}{\boldsymbol{H}}}} \Rightarrow \\ - 2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} + 2{\boldsymbol{H}} - 4\beta {\boldsymbol{VH}} + 4\beta {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} + {\boldsymbol{\varTheta }} = 0 \end{gathered} $$ (16) 由Kuhn-Tucker条件
$ {{\boldsymbol{\varTheta }}_{ij}}{{\boldsymbol{H}}_{ij}} = 0 $ 及定理2得$ {\boldsymbol{H}} $ 的更新规则为[29]$$ {\boldsymbol{H}}_{ij}^{(t + 1)} \leftarrow {\boldsymbol{H}}_{ij}^{(t)}\frac{{{{(2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}} + 4\beta {\boldsymbol{V}}{{\boldsymbol{H}}^{(t)}})}_{ij}}}}{{{{(2{{\boldsymbol{H}}^{(t)}} + 4\beta {{\boldsymbol{H}}^{(t)}}{{\boldsymbol{H}}^{(t)}}^{\rm{T}}{{\boldsymbol{H}}^{(t)}})}_{ij}}}} $$ (17) 其中
$ \leftarrow $ 是赋值符号。定理2 如果
$ {\boldsymbol{H}} $ 是式(14)中目标函数的一个局部最小值，那么：$$ (4\beta {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} + 2{\boldsymbol{H}}) \otimes {\boldsymbol{H}} - (4\beta {\boldsymbol{VH}} + 2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}}) \otimes {\boldsymbol{H}} = {\text{0}} $$ (18) 其中
$ \otimes $ 为Hadamard积。证明
${\boldsymbol{\varTheta }} \in {{\bf{R}}^{c \times n}}$ 为约束$ {\boldsymbol{H}} \geqslant {\text{0}} $ 的拉格朗日乘子，拉格朗日函数为$ L({\boldsymbol{H}},{\boldsymbol{\varTheta }}) $ ，Kuhn-Tucker条件有：$$ {{\partial L({\boldsymbol{H}},{\boldsymbol{\varTheta }})} \mathord{\left/ {\vphantom {{\partial L({\boldsymbol{H}},{\boldsymbol{\varTheta }})} {\partial {\boldsymbol{H}}}}} \right. } {\partial{\boldsymbol{H}}}} = {\text{0}} $$ (19) $$ {\boldsymbol{\varTheta }} \otimes {\boldsymbol{H}} = {\text{0}} $$ (20) 对式(19)等号两边关于
$ {\boldsymbol{H}} $ 求导得：$$ \left(4\beta {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} + 2{\boldsymbol{H}}\right) - \left(4\beta {\boldsymbol{VH}} + 2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}}\right) + {\boldsymbol{\varTheta }} = 0{\text{ }} $$ (21) 等式(21)两边同时与
$ {\boldsymbol{H}} $ 进行Hadamard积运算得：$$ \begin{gathered} \left(4\beta {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} + 2{\boldsymbol{H}}\right) \otimes {\boldsymbol{H}} + {\boldsymbol{\varTheta }} \otimes {\boldsymbol{H}} - \\ \left(4\beta {\boldsymbol{VH}} + 2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}}\right) \otimes {\boldsymbol{H}} = 0 \otimes {\boldsymbol{H}} \\ \end{gathered} $$ (22) 由式(20)的
$ {\boldsymbol{\varTheta }} \otimes {\boldsymbol{H}} = {\text{0}} $ 得：$$ \left(4\beta {\boldsymbol{H}}{{\boldsymbol{H}}^{{\rm{T}}}}{\boldsymbol{H}} + 2{\boldsymbol{H}}\right) \otimes {\boldsymbol{H}} - \left(4\beta {\boldsymbol{VH}} + 2{{\boldsymbol{X}}^{{\rm{T}}}}{{\boldsymbol{W}}^{(t)}}\right) \otimes {\boldsymbol{H}} = {\text{0}} $$ (23) 2.2.2 固定
$ {\boldsymbol{H}} $ 更新$ {\boldsymbol{W}} $ 当H固定时，可得以下关于
$ {\boldsymbol{W}} $ 的优化问题：$$ \mathop {{\text{min}}}\limits_{\boldsymbol{W}} \;\;\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}} \right\|_F^2 + \alpha {\left\| {\boldsymbol{W}} \right\|_{2,1}} $$ (24) 对于问题式（24）使用迭代加权（iterative reweighted least-squares, IRLS）最小二乘法[19,30]求解。先引入对角矩阵
${{\boldsymbol{\varLambda }}^{(t)}} \in {{\bf{R}}^{d \times d}}$ ，${\boldsymbol{\varLambda }}_{ii}^{(t)} = 1\bigg/ \left(2{\left\| {{\boldsymbol{W}}{{(i,:)}^{(t)}}} \right\|_2}\right)$ ，如果$ {\left\| {{\boldsymbol{W}}{{(i,:)}^{(t)}}} \right\|_2} $ 为 0，则${\boldsymbol{\varLambda }}_{ii}^{(t)} = 1\bigg/ \left(2{\left\| {{\boldsymbol{W}}{{(i,:)}^{(t)}}} \right\|_2} + \varepsilon \right)$ 。因此式(24)转化为以下问题：$$ \mathop {\min }\limits_{\boldsymbol{W}} \;\;\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}} \right\|_F^2 + \alpha \cdot {\rm{tr}}\left({{\boldsymbol{W}}^{{\rm{T}}}}{{\boldsymbol{\varLambda }}^{(t)}}{\boldsymbol{W}}\right) $$ (25) 式(25)中的目标函数的第一项为
$$ \begin{gathered} {\text{ }}\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}} \right\|_F^2 = {\rm{tr}}\left[ {{{\left({{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}\right)}^{{\rm{T}}}}\left({{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}\right)} \right] = \\ {\rm{tr}}\left({{\boldsymbol{W}}^{{\rm{T}}}}{\boldsymbol{X}}{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - 2{{\boldsymbol{W}}^{{\rm{T}}}}{\boldsymbol{X}}{{\boldsymbol{H}}^{(t + 1)}} + {{\boldsymbol{H}}^{(t + 1)}}{{\boldsymbol{H}}^{(t + 1)}}^{{{\rm{T}}}}\right){\text{ }} \end{gathered} $$ (26) 然后对式(25)中的目标函数所有项关于
$ {\boldsymbol{W}} $ 求导并令其为0解得：$$ \begin{gathered} \frac{{\partial {\text{ }}\left\| {{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - {{\boldsymbol{H}}^{(t + 1)}}} \right\|_F^2}}{{\partial {\text{ }}{\boldsymbol{W}}}} + \alpha \frac{{\partial {\rm{tr}}({{\boldsymbol{W}}^{{\rm{T}}}}{{\boldsymbol{\varLambda }}^{(t)}}{\boldsymbol{W}})}}{{\partial {\text{ }}{\boldsymbol{W}}}} = \\ \frac{{\partial {\text{ }}{\rm{tr}}({{\boldsymbol{W}}^{{\rm{T}}}}{\boldsymbol{X}}{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}})}}{{\partial {\text{ }}{\boldsymbol{W}}}} - 2\frac{{\partial {\text{ }}{\rm{tr}}({{\boldsymbol{W}}^{{\rm{T}}}}{\boldsymbol{X}}{{\boldsymbol{H}}^{(t + 1)}})}}{{\partial {\text{ }}{\boldsymbol{W}}}} + \\ \alpha \frac{{\partial {\rm{tr}}({{\boldsymbol{W}}^{{\rm{T}}}}{{\boldsymbol{\varLambda }}^{(t)}}{\boldsymbol{W}})}}{{\partial {\text{ }}{\boldsymbol{W}}}} = 0 \Rightarrow \\ 2{\boldsymbol{X}}{{\boldsymbol{X}}^{{\rm{T}}}}{\boldsymbol{W}} - 2{\boldsymbol{X}}{{\boldsymbol{H}}^{(t + 1)}} + 2\alpha {{\boldsymbol{\varLambda }}^{(t)}}{\boldsymbol{W}} = 0 \Rightarrow\\ {\boldsymbol{W}} = {\left(\alpha {{\boldsymbol{\varLambda }}^{(t)}} + {\boldsymbol{X}}{{\boldsymbol{X}}^{{\rm{T}}}}\right)^{ - 1}}{\boldsymbol{X}}{{\boldsymbol{H}}^{(t + 1)}} \end{gathered} $$ (27) 以上求解
$ {\boldsymbol{H}} $ 和$ {\boldsymbol{W}} $ 过程交替地重复进行，直到满足终止条件，详细过程见算法2。在求得矩阵$ \overline {\boldsymbol{W}} $ 之后，可根据其行向量的2-范数来衡量数据中对应特征的重要性，如果$ \overline {\boldsymbol{W}} $ 中某行的2-范数趋于0，则对应的特征为冗余或不相关特征。因此将$ \overline {\boldsymbol{W}} $ 所有行向量的2-范数进行排序，值越大代表数据相应特征越重要。最后，对特征选择后所得到的样本进行聚类或分类。算法2 MMLRL用于求解问题式(13)
输入 数据矩阵
$ {\boldsymbol{X}} \in {{\bf{R}}^{d \times n}} $ ，马尔可夫步数$ u $ ，正则化参数$ \alpha $ ，$ \beta $ 初始化
$ {{\boldsymbol{W}}^{(0)}} \in {{\boldsymbol{I}}_{n \times n}} $ ，随机矩阵$ {{\boldsymbol{H}}^{(0)}} \in {{\bf{R}}^{n \times c}} $ ，迭代次数$ t = 0 $ 根据算法1计算
$ {\boldsymbol{X}} $ 的$ u $ 步最大马尔可夫转移概率关系矩阵$ {\boldsymbol{V}} $ ；While 不收敛 do
1) 计算对角矩阵
$ {{\boldsymbol{\varLambda }}^{(t)}} $ 2) 根据乘法法则式(17)更新
$ {{\boldsymbol{H}}^{(t + 1)}} $ ；3) 根据式(27)更新
$ {{\boldsymbol{W}}^{(t + 1)}} $ 4)
$ t = t + 1 $ End while
输出 变换矩阵
$\overline {\boldsymbol{W}} = {{\boldsymbol{W}}^{(t + 1)}} \in {{\bf{R}}^{d \times c}}$ 3. 实验分析
本节将MMLRL算法在7个公开数据集上进行特征选择实验，并与8个特征选择算法对比，全面评估和验证MMLRL算法的性能和有效性。
3.1 数据集
实验中的数据集包括两个人脸数据集ORL-32[31]和warpAR10P[19]，物体数据集COIL-20[32],手写字体数据集USPS[33],语音数据集Isolet[34]以及两个生物数据集Lung[35]和CLL_SUB_111[36]。数据集的具体信息如表1所示。
表 1 数据集具体信息Table 1 Specific information of data sets数据集 样本数 特征数 类别数 样本类型 ORL 400 1024 40 人脸 warpAR10P 130 2400 10 人脸 COIL_20 1440 1024 20 物体 USPS 9298 256 10 手写字体 Isolet 1560 617 26 语音 Lung 203 3312 26 生物 CLL_SUB 111 11340 3 生物 3.2 对比算法及实验设置
实验中的对比算法包括：拉普拉斯算子(LS)[14]、多聚类特征选择(MCFS)[16]、嵌入式稀疏正则化(JELSR)[13]；自表示特征选择(RSR)[19]、结构图优化(SOGFS)[20]、广义不相关的自适应图特征选择(URAFS)[21]、潜在表示与流形正则化(unsupervised feature selection via latent representation learning and manifold regularization, LRLMR)[37]、基于多步马尔可夫概率的无监督特征选择(MMFS)[22]。
为保证实验公正性，近邻数
$ k $ 设置为5，通过网格搜索策略确定每个算法的最优参数组，参数范围为{10−3, 10−2, 10−1, 1, 10, 102, 103}。除了USPS数据集的特征选择范围为{50, 80, 110, 140, 170, 200}，其余数据集上特征选择的范围为{50, 100, 150, 200, 250, 300}。聚类实验的评价指标通常有聚类精度(clustering accuracy, ACC)和标准化互信息(normalized mutual information, NMI)，ACC的定义如下：
$$ {C_{{{{\rm{AC}}}}}} = \dfrac{{\displaystyle\sum_{i = 1}^n {\delta ({p_i},{\rm{map}}({q_i}))} }}{n} $$ (28) 式中：
$ {q_i} $ 为数据$ {{\boldsymbol{x}}_i} $ 的聚类标签，$ {p_i} $ 为$ {{\boldsymbol{x}}_i} $ 的真实标签。当$ x = y $ 时，$ \delta (x,y) = 1 $ ，否则$ \delta (x,y) = 0 $ 。$ {\text{map}}({q_i}) $ 为最佳映射函数，该函数通过最大权匹配(Kuhn-Munkres)算法将聚类标签与真实标签进行匹配。NMI表示聚类结果与真实标签的同一性，其定义为$$ I_{{{\rm{NM}}}}(P{\text{,}}Q{\text{)}} = \frac{{I_{\text{M}}(P,Q)}}{{\sqrt {H(P)H(Q)} }} $$ (29) 式中：
$ H(P) $ 和$ H(Q) $ 分别为变量$ P $ 和变量$ Q $ 的熵，聚类中$ P $ 和$ Q $ 分别为聚类结果和真实标签，$I_{\rm{M}}(P,Q)$ 为$ P $ 和$ Q $ 的互信息。$$ {I_{{{\rm{M}}}}}(P,Q) = \sum\limits_{{p_i} \in P,{q_j} \in Q} {P({p_i},{q_j})\lg \frac{{P({p_i},{q_j})}}{{P({p_i})P({q_j})}}} $$ (30) 式中：
$ P({p_i}) $ 为样本属于$ {p_i} $ 类的概率，$ P({q_j}) $ 为样本属于$ {q_j} $ 类的概率。$ P({p_i},{q_j}) $ 为样本同属于$ {p_i} $ 类和$ {q_j} $ 类的联合概率。分类实验的评价指标为分类精度(classification accuracy, ACA)，定义如下：
$$ A_{{{\rm{CA}}}} = \frac{1}{n}\sum\limits_{i = 1}^T {\delta ({y_i},{{\hat y}_i})} $$ (31) 式中：
$ {y_i} $ 是数据$ {{\boldsymbol{x}}_i} $ 的真实标签，$ {\hat y_i} $ 是数据$ {{\boldsymbol{x}}_i} $ 的预测标签。$ T $ 是测试样本数，$ {y_i} = {\hat y_i} $ 时，$ \delta ({y_i},{\hat y_i}) = 1 $ ，否则$ \delta ({y_i},{\hat y_i}) = 0 $ 。3.3 聚类性能与分析
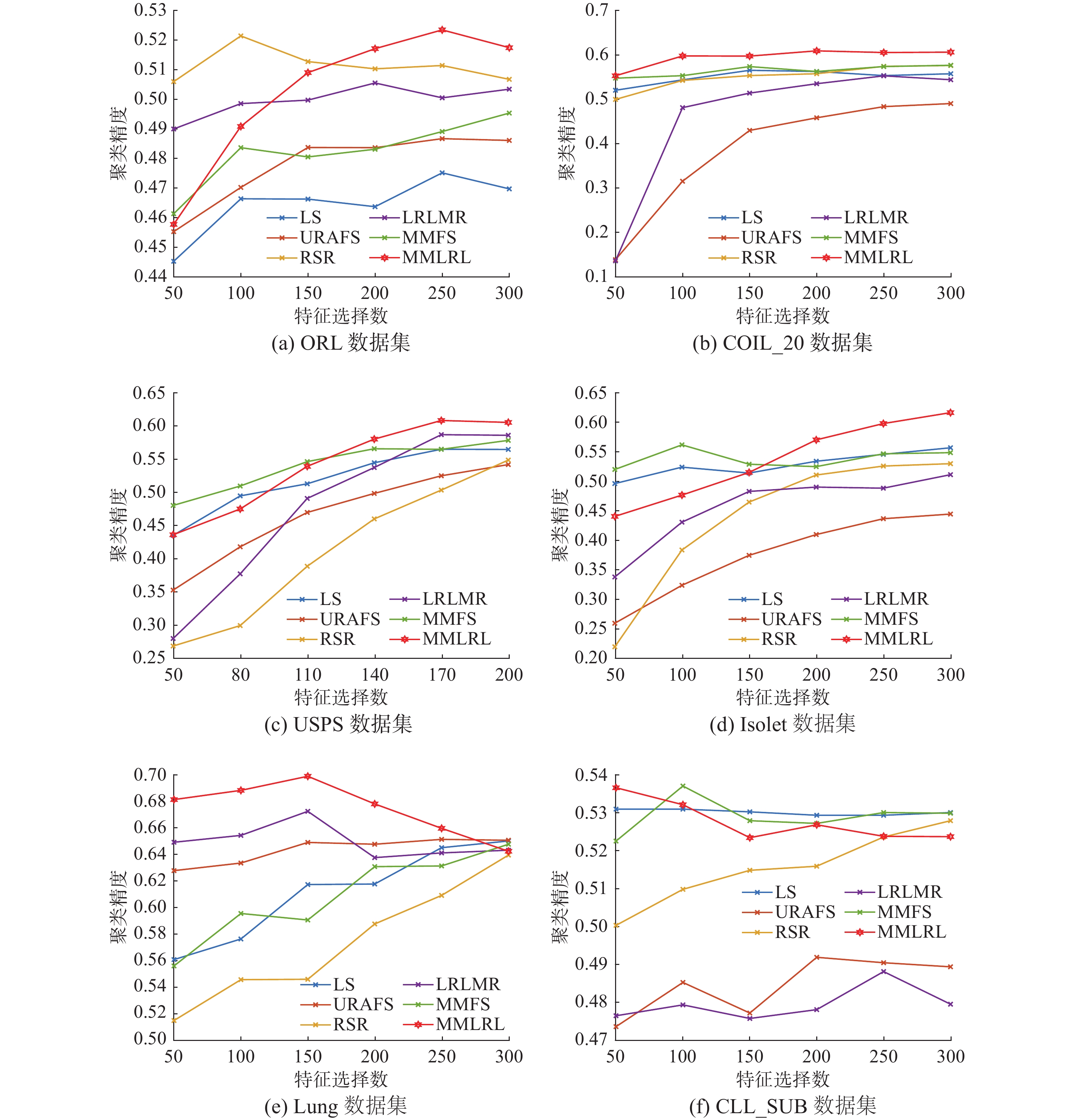
算法获取带有重要特征的数据后，用K均值方法对这些数据进行聚类，通过聚类效果反映算法的性能。通常用聚类精度和标准化互信息来衡量聚类效果，ACC值或NMI值越大，算法聚类性能越好。实验重复运行20次K均值聚类，从而消除初始点对聚类效果的影响。
表2和表3分别列出了所有算法在不同数据集上进行特征选择的ACC和NMI的平均值和标准差，以及取得最好效果时所选的特征数，最优结果用粗体突出标示，次优结果用下划线标出。
表 2 不同方法在6个数据集上的聚类精度(ACC±std)及所选特征数Table 2 Clustering accuracies (ACC ± std) and the numbers of selected features of different algorithms on six datasets% 数据集 ORL COIL_20 USPS Isolet Lung CLL_SUB LS 47.51±0.83 (250) 56.51±1.46 (150) 56.43±1.41 (250) 55.82±1.11 (300) 65.01±2.41 (300) 53.12±0.07 (50) MCFS 52.19±1.12 (100) 58.81±1.22 (100) 58.91±1.57 (50) 59.31±0.74 (50) 69.86±2.12 (100) 53.15±0 (100) JELSR 53.08±0.64 (100) 57.67±1.66 (250) 59.71±1.21 (150) 57.36±1.36 (300) 66.68±1.63 (200) 53.15±0 (300) RSR 52.14±0.95 (100) 57.59±1.54 (300) 54.79±0.82 (300) 53.12±1.29 (300) 63.95±1.87 (300) 52.81±0.31 (300) SOGFS 50.80±0.89 (150) 59.18±0.74 (100) 55.60±0.89 (300) 59.09±1.37 (100) 67.60±2.16 (50) 53.15±0 (50) URAFS 48.67±0.95 (250) 48.99±1.22 (300) 54.12±0.64 (300) 44.56±0.65 (300) 65.14±2.65 (250) 49.19±1.58 (200) LRLMR 50.55±1.07 (200) 55.25±0.73 (250) 58.63±0.93 (250) 51.25±0.92 (300) 67.26±2.38 (150) 48.81±0.73 (250) MMFS 49.53±0.87 (300) 57.65±1.36 (300) 57.77±0.28 (300) 56.31±0.72 (100) 64.77±2.48 (300) 53.63±0.74 (100) MMLRL 52.34±0.96 (250) 60.91±1.10 (200) 60.77±0.64 (250) 61.78±0.60 (300) 69.92±2.15 (150) 53.68±0.44 (50) 表 3 不同方法在6个数据集上的归一化互信息(NMI±std)及所选特征数Table 3 NMI values (NMI ± std) and the number of selected features of different algorithms on six datasets% 数据集 ORL COIL_20 USPS Isolet Lung CLL_SUB LS 71.42±0.49 (250) 71.90±0.63 (200) 55.57±0.42 (250) 73.10±0.31 (300) 63.01±0.82 (250) 19.05±0.62 (50) MCFS 74.57±0.51 (100) 73.72±0.44 (250) 56.27±0.32 (100) 75.94±0.36 (200) 67.37±2.09 (50) 18.74±0 (100) JELSR 74.73±0.31 (100) 71.91±0.65 (250) 56.97±0.38 (200) 74.55±0.40 (300) 65.07±1.02 (200) 19.34±0.75 (200) RSR 74.00±0.40 (100) 72.81±0.57 (300) 51.09±0.31 (300) 68.72±0.49 (300) 61.81±1.54 (300) 18.46±1.42 (300) SOGFS 74.16±0.47 (150) 72.44±0.46 (200) 54.07±0.40 (300) 73.49±0.47 (100) 64.54±1.70 (50) 18.96±0.59 (100) URAFS 71.89±0.49 (300) 66.68±0.85 (300) 52.07±1.01 (300) 63.82±0.28 (300) 63.24±1.72 (200) 15.41±4.84 (200) LRLMR 73.38±0.68 (200) 71.87±0.36 (250) 55.48±0.17 (300) 69.67±0.49 (300) 64.77±1.87 (150) 9.71±1.41 (250) MMFS 72.82±0.61 (300) 74.35±0.39 (300) 55.28±0.14 (300) 72.02±0.34 (100) 62.53±1.93 (300) 20.39±0.59 (300) MMLRL 74.32±0.44 (250) 75.43±0.62 (300) 57.01±6.09 (300) 77.66±0.32 (300) 68.31±1.61 (150) 23.09±1.20 (50) 由表2和表3可知，MMLRL除了在ORL数据集上取得次优的ACC和较优的NMI外，在其他数据集上均取得最好的ACC和NMI。这是因为MMLRL算法通过多步马尔可夫转移概率不仅得到数据点与其相邻点间的关系，还得到了该数据点与其较远点之间的关系，充分利用和保持了流形上的数据结构；同时在纯净的潜在表示空间中选择特征，减少了噪声或异常值的影响。
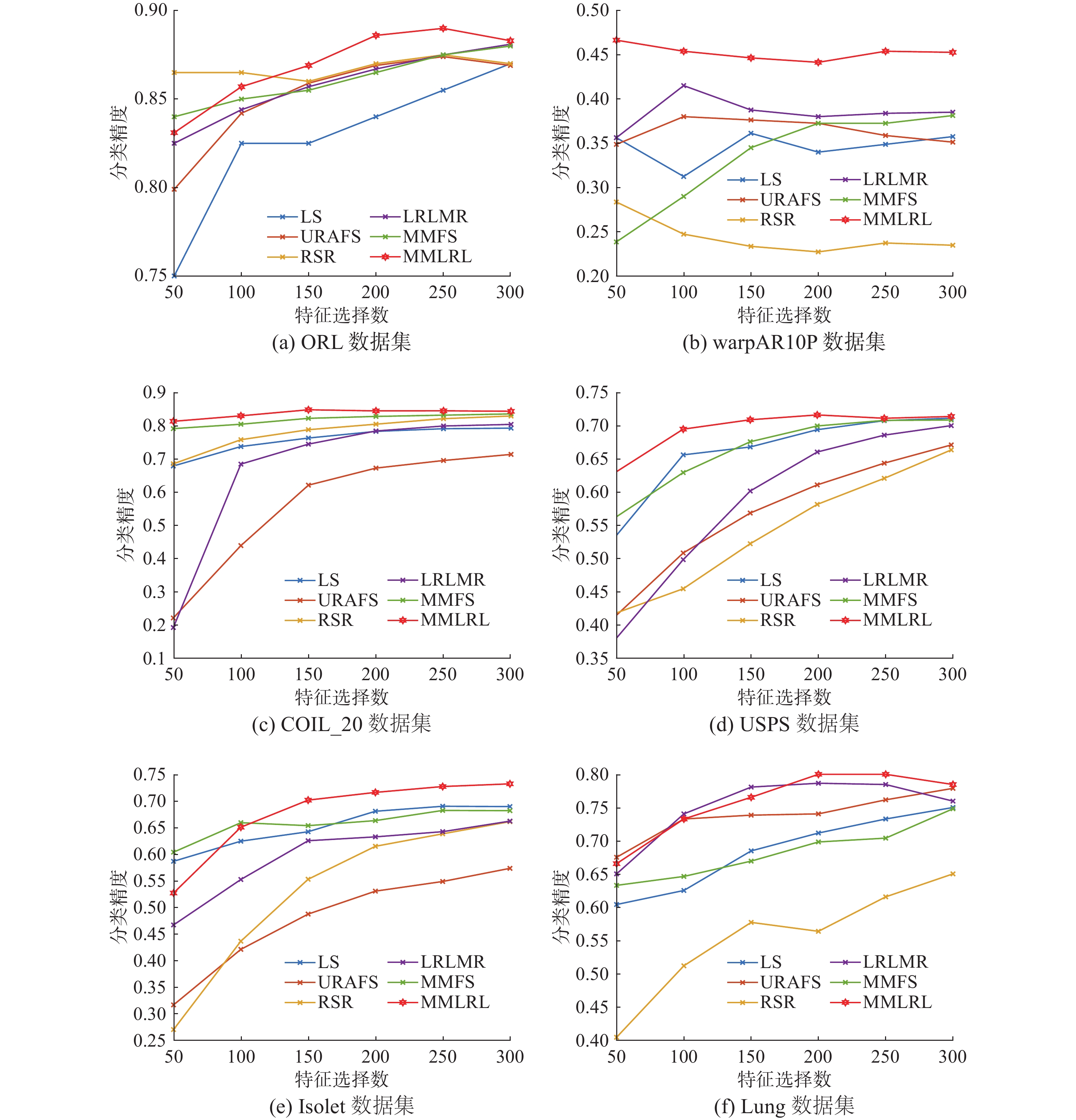
其次，考虑特征选择数对聚类精度的影响，图1给出6种算法在不同数据集上选择不同特征数时ACC值的变化曲线。由图1可见，随着特征选择数的增加，MMLRL算法的聚类精度稳定地优于其他对比算法，从而可以通过选择合适的特征个数来获得比其他算法更好的聚类精度。尤其在COIL_20数据集上，不管选择多少数目的特征，其ACC都优于其他对比算法，这说明可以选择最小的特征数来得到最好的聚类效果，从而减少计算时间。
图 1 不同方法选择不同特征数时的聚类精度(ACC)Fig. 1 ACC of all the algorithms for different numbers of selected features on the six datasets
下载:
全尺寸图片
3.4 运行时间
本节比较了8种算法在ORL、COIL_20、USPS、Isolet和Lung5个数据集上进行聚类实验的运行时间，实验结果如表4所示。从表4可以看出，本文提出的算法MMLRL同MCFS、SOGFS和MMFS算法相比，运行时间更短，与其他对比算法相比运行时间相当。MMLRL算法在学习非邻接数据点间的流形关系时会消耗些许时间，但增加的时间很少，而且这步有利于数据潜在表示学习。因此以很少的时间换取更好的特征选择效果是可取的。
表 4 不同方法运行时间Table 4 Running time of different methods数据集 ORL COIL_20 USPS Isolet Lung MCFS 4.0403±0.2224 9.8950±0.1231 4.2758±0.5543 8.5937±0.0597 1.2706±0.0591 JELSR 0.0751±0.0017 1.3437±0.0071 1.4832±0.0489 1.0359±0.0373 0.8310±0.0068 RSR 0.0815±0.0012 0.2041±0.0017 0.1524±0.0039 0.1500±0.0157 1.1157±0.0080 SOGFS 1.2373±0.0226 1.9632±0.0345 1.4661±0.0259 1.1818±0.0114 46.9287±0.1577 URAFS 0.4691±0.0034 0.9525±0.0085 1.0501±0.0470 0.7301±0.0065 9.1499±1.3109 LRLMR 0.0874±0.0037 0.3795±0.0047 0.3574±0.0052 0.3099±0.0156 1.0482±0.0155 MMFS 0.1404±0.0107 1.8099±0.0235 4.2048±0.1717 2.1244±0.0239 1.2276±0.0193 MMLRL 0.1184±0.0107 1.51426±0.0132 3.5231±0.0823 1.8243±0.0536 0.8613±0.0122 3.5 分类性能与分析
本节通过KNN分类法对6个数据集上的多类数据进行分类。除了USPS数据集，其他数据集都随机选择每类的7个样本作为训练集，为了防止过拟合现象，在USPS数据集中会随机选择每类的70个样本做为测试集，剩余的样本作为测试集。由于CLL_SUB数据集的类别数较少，因此将该数据集替换为10类的warpAR10P数据集。同时为了消除数据集划分过程中可能存在的误差，会随机划分数据集5次，然后取5次结果的平均值作为最终结果。通常平均分类精度(ACA)用于衡量分类效果，ACA值越大说明算法分类越精确。表5给出了不同方法在6个数据集上的分类精度(ACA)以及对应的特征数，最好的结果用粗体表示。图2则为不同算法在6个数据集上选择不同特征数时的分类精度曲线。从表5和图2可以看出，MMLRL方法在COIL_20、USPS和Isolet数据集上取得显著的分类效果，这说明该方法在预处理多类数据时更具优势。
表 5 不同方法在6个数据集上的分类精度(ACA±std)及所选特征数Table 5 Classification accuracies (ACA ± std) and the numbers of selected features of different algorithms on six datasets% 数据集 ORL warpAR10P COIL_20 USPS Isolet Lung LS 87.00±0.00 (300) 44.60±4.88 (150) 79.19±1.20 (300) 71.11±2.47 (300) 69.85±1.13 (300) 75.00±4.15 (300) JELSR 88.00±0.00 (200) 36.00±5.57 (100) 79.53±1.16 (300) 71.14±2.18 (150) 71.75±0.78 (300) 77.88±5.31 (250) RSR 87.50±0.00 (250) 48.00±2.24 (50) 82.84±1.97 (300) 66.35±2.50 (300) 66.59±0.21 (300) 65.00±6.95 (300) SOGFS 88.50±0.00 (100) 24.20±3.11 (50) 80.16±1.35 (300) 69.85±2.16 (300) 71.90±1.24 (100) 76.92±3.01 (150) URAFS 87.40±1.24 (250) 32.60±4.77 (100) 71.32±1.74 (300) 67.09±2.04 (300) 58.66±2.01 (300) 77.88±5.23 (300) LRLMR 88.10±0.82 (300) 39.20±4.76 (200) 80.32±1.10 (300) 69.99±2.60 (300) 65.79±1.14 (300) 78.65±2.64 (200) MMFS 88.00±0.00 (300) 34.40±4.10 (300) 83.47±1.28 (300) 70.83±2.38 (300) 70.60±1.28 (300) 74.81±5.98 (300) MMLRL 89.00±0.79 (250) 43.00±6.63 (200) 84.71±1.07 (150) 71.60±2.21 (200) 72.70±1.88 (300) 80.00±2.90 (200) 
图 2 6个数据库上选择不同特征数时的分类精度Fig. 2 ACA of all the algorithms for different numbers of features on the six datasets下载:
全尺寸图片
3.6 噪声对聚类精度的影响
为验证MMLRL算法在噪声下的鲁棒性，本节研究算法在噪声数据集中聚类精度的变化情况，主要有两种噪声：在图像中随机加不同像素大小的遮挡块和不同比例的点噪声（如椒盐噪声），以COIL_20数据集和Isolet数据集为例。表6给出了9种算法在有遮挡块的COIL_20数据集上的聚类精度变化情况，表7则是8种方法在包含不同比例椒盐噪声的Isolet数据集上的聚类结果。
表 6 不同算法在有遮挡块的COIL_20数据集上的聚类精度(ACC)Table 6 Clustering accuracies of different methods to block occlusion with different sizes on COIL_20dataset% 算法 遮挡快大小 0×0 3×3 4×4 5×5 6×6 7×7 LS 57.74 53.42 54.52 51.51 52.25 50.60 MCFS 59.58 58.92 57.65 54.46 56.69 52.20 JELSR 58.32 59.19 56.19 53.19 51.74 46.83 RSR 58.05 56.81 50.61 44.74 34.81 28.05 SOGFS 59.74 56.81 56.99 52.28 50.50 48.77 URAFS 50.43 47.76 48.01 47.20 48.50 47.37 LRLMR 55.62 55.94 55.23 56.03 51.83 50.17 MMFS 58.29 59.49 61.90 58.43 51.96 49.72 MMLRL 64.09 59.86 61.65 60.28 57.10 50.47 由表6可知，给COIL_20数据集图像随机添加遮挡块时，算法的聚类精度受到较大的影响，尤其是对RSR算法的影响，到后期ACC值降低到很小，而MMLRL算法得到的ACC值减少幅度很小，且能持续取得高于对比算法的聚类精度。表7则表明，随着Isolet数据集中噪声比例不断加，MMLRL算法取得的ACC值波动很小，而且聚类效果优于其他对比算法。这说明 MMLRL算法学习有噪声数据样本的特征时具有一定的鲁棒性，在噪声特征或数据中依然能选择出重要特征。
表 7 不同方法在有点噪声的Isolet数据集上的聚类精度(ACC)Table 7 Clustering accuracies of different methods to different densities of salt and pepper noise on Isolet dataset% 算法 点噪声比例 0 10 20 30 40 50 60 LS 55.58 55.86 54.12 54.66 54.39 55.26 54.48 JELSR 57.79 57.58 57.08 57.65 57.72 58.01 58.35 RSR 52.67 53.22 54.03 52.65 52.44 53.00 52.53 SOGFS 58.19 57.06 50.40 52.58 49.43 50.17 49.94 URAFS 45.26 43.69 45.01 44.75 45.94 45.89 47.46 LRLMR 50.75 53.90 54.60 53.87 55.66 58.57 56.45 MMFS 56.45 52.67 52.50 51.96 52.25 55.12 53.56 MMLRL 60.47 60.22 59.94 59.96 58.11 58.05 56.76 3.7 特征选择图
图3给出了6种算法关于ORL数据集侧脸图像的特征选择图。
图 3 不同算法对ORL数据集的特征选择图Fig. 3 Feature selected images of partial ORL data set by different algorithms下载:
全尺寸图片
图3(a)是原始侧脸图像，(b)~(g)是不同算法在原始图像上选择不同特征数时的图像，特征选择的范围为{200, 250, 300, 350, 400, 450, 500}。观察图3(b)~(d)得知， LS和SOGFS算法的特征选择效果最差，随着特征选择数的增加，只选择面部特征，而重要五官特征都未被选择。在图3(c)~(e)中，MCFS和LRLMR算法虽然选择特征均匀，但不是重要的五官特征。相比于其他算法，MMLRL算法最后能选出重要的五官特征（眼、口、鼻），这也是MMLRL算法在不同数据集上取得较好聚类效果的原因。
3.8 参数对聚类精度的影响
本节讨论模型式(11)中正则化参数
$ \alpha $ 与$ \beta $ 对聚类精度的影响，图4给出了MMLRL算法在不同数据集上取不同参数值时聚类精度图。
图 4 不同参数组合下MMLRL在6个数据集上聚类精度Fig. 4 Clustering accuracy of MMLRL algorithm with respect to$ \alpha $ and$ \beta $ on six data sets下载:
全尺寸图片
观察图4得知，在除ORL和Isolet数据集外的其他数据集上，一个参数固定而另一参数变化时，ACC都相对稳定，这说明在大部分情况下MMLRL算法受参数的影响较小。在ORL数据集上，当
$ \alpha \geqslant {\text{1}}，\beta \leqslant 0.1 $ 时参数对算法的学习效果影响较小；在Isolet数据集上，参数对聚类效果的影响较大。从以上分析可知，在实际情况下应选择合适的参数组来提高平均聚类精度。4. 结束语
本文提出了一种更为简洁的潜在多步马尔可夫概率的无监督特征选择模型。该模型利用多步马尔可夫概率学习数据更为广义的流形结构，在学习相邻数据点流形信息的同时充分挖掘非相邻数据点之间的结构信息；通过对称非负矩阵分解模型来学习数据的潜在表示，并在潜在表示空间中选择数据特征。模型在参数少和结构更为简单的情况下能取得更好的聚类效果。实验表明，MMLRL算法能快速而有效地选择数据的重要特征，降低噪声或异常值的影响，证明了所提算法的有效性。
以上模型是在数据空间中学习潜在表示的，为进一步提高特征选择和聚类的性能，也可以在特征空间中学习潜在表示，从而同时学习数据和特征的内在互联信息。因此可以对模型结构进行扩展以提高聚类效果。
-
图 1 不同方法选择不同特征数时的聚类精度(ACC)
Fig. 1 ACC of all the algorithms for different numbers of selected features on the six datasets
下载:
全尺寸图片
图 2 6个数据库上选择不同特征数时的分类精度
Fig. 2 ACA of all the algorithms for different numbers of features on the six datasets
下载:
全尺寸图片
图 3 不同算法对ORL数据集的特征选择图
Fig. 3 Feature selected images of partial ORL data set by different algorithms
下载:
全尺寸图片
图 4 不同参数组合下MMLRL在6个数据集上聚类精度
Fig. 4 Clustering accuracy of MMLRL algorithm with respect to
$ \alpha $ and$ \beta $ on six data sets下载:
全尺寸图片
表 1 数据集具体信息
Table 1 Specific information of data sets
数据集 样本数 特征数 类别数 样本类型 ORL 400 1024 40 人脸 warpAR10P 130 2400 10 人脸 COIL_20 1440 1024 20 物体 USPS 9298 256 10 手写字体 Isolet 1560 617 26 语音 Lung 203 3312 26 生物 CLL_SUB 111 11340 3 生物 表 2 不同方法在6个数据集上的聚类精度(ACC±std)及所选特征数
Table 2 Clustering accuracies (ACC ± std) and the numbers of selected features of different algorithms on six datasets
% 数据集 ORL COIL_20 USPS Isolet Lung CLL_SUB LS 47.51±0.83 (250) 56.51±1.46 (150) 56.43±1.41 (250) 55.82±1.11 (300) 65.01±2.41 (300) 53.12±0.07 (50) MCFS 52.19±1.12 (100) 58.81±1.22 (100) 58.91±1.57 (50) 59.31±0.74 (50) 69.86±2.12 (100) 53.15±0 (100) JELSR 53.08±0.64 (100) 57.67±1.66 (250) 59.71±1.21 (150) 57.36±1.36 (300) 66.68±1.63 (200) 53.15±0 (300) RSR 52.14±0.95 (100) 57.59±1.54 (300) 54.79±0.82 (300) 53.12±1.29 (300) 63.95±1.87 (300) 52.81±0.31 (300) SOGFS 50.80±0.89 (150) 59.18±0.74 (100) 55.60±0.89 (300) 59.09±1.37 (100) 67.60±2.16 (50) 53.15±0 (50) URAFS 48.67±0.95 (250) 48.99±1.22 (300) 54.12±0.64 (300) 44.56±0.65 (300) 65.14±2.65 (250) 49.19±1.58 (200) LRLMR 50.55±1.07 (200) 55.25±0.73 (250) 58.63±0.93 (250) 51.25±0.92 (300) 67.26±2.38 (150) 48.81±0.73 (250) MMFS 49.53±0.87 (300) 57.65±1.36 (300) 57.77±0.28 (300) 56.31±0.72 (100) 64.77±2.48 (300) 53.63±0.74 (100) MMLRL 52.34±0.96 (250) 60.91±1.10 (200) 60.77±0.64 (250) 61.78±0.60 (300) 69.92±2.15 (150) 53.68±0.44 (50) 表 3 不同方法在6个数据集上的归一化互信息(NMI±std)及所选特征数
Table 3 NMI values (NMI ± std) and the number of selected features of different algorithms on six datasets
% 数据集 ORL COIL_20 USPS Isolet Lung CLL_SUB LS 71.42±0.49 (250) 71.90±0.63 (200) 55.57±0.42 (250) 73.10±0.31 (300) 63.01±0.82 (250) 19.05±0.62 (50) MCFS 74.57±0.51 (100) 73.72±0.44 (250) 56.27±0.32 (100) 75.94±0.36 (200) 67.37±2.09 (50) 18.74±0 (100) JELSR 74.73±0.31 (100) 71.91±0.65 (250) 56.97±0.38 (200) 74.55±0.40 (300) 65.07±1.02 (200) 19.34±0.75 (200) RSR 74.00±0.40 (100) 72.81±0.57 (300) 51.09±0.31 (300) 68.72±0.49 (300) 61.81±1.54 (300) 18.46±1.42 (300) SOGFS 74.16±0.47 (150) 72.44±0.46 (200) 54.07±0.40 (300) 73.49±0.47 (100) 64.54±1.70 (50) 18.96±0.59 (100) URAFS 71.89±0.49 (300) 66.68±0.85 (300) 52.07±1.01 (300) 63.82±0.28 (300) 63.24±1.72 (200) 15.41±4.84 (200) LRLMR 73.38±0.68 (200) 71.87±0.36 (250) 55.48±0.17 (300) 69.67±0.49 (300) 64.77±1.87 (150) 9.71±1.41 (250) MMFS 72.82±0.61 (300) 74.35±0.39 (300) 55.28±0.14 (300) 72.02±0.34 (100) 62.53±1.93 (300) 20.39±0.59 (300) MMLRL 74.32±0.44 (250) 75.43±0.62 (300) 57.01±6.09 (300) 77.66±0.32 (300) 68.31±1.61 (150) 23.09±1.20 (50) 表 4 不同方法运行时间
Table 4 Running time of different methods
数据集 ORL COIL_20 USPS Isolet Lung MCFS 4.0403±0.2224 9.8950±0.1231 4.2758±0.5543 8.5937±0.0597 1.2706±0.0591 JELSR 0.0751±0.0017 1.3437±0.0071 1.4832±0.0489 1.0359±0.0373 0.8310±0.0068 RSR 0.0815±0.0012 0.2041±0.0017 0.1524±0.0039 0.1500±0.0157 1.1157±0.0080 SOGFS 1.2373±0.0226 1.9632±0.0345 1.4661±0.0259 1.1818±0.0114 46.9287±0.1577 URAFS 0.4691±0.0034 0.9525±0.0085 1.0501±0.0470 0.7301±0.0065 9.1499±1.3109 LRLMR 0.0874±0.0037 0.3795±0.0047 0.3574±0.0052 0.3099±0.0156 1.0482±0.0155 MMFS 0.1404±0.0107 1.8099±0.0235 4.2048±0.1717 2.1244±0.0239 1.2276±0.0193 MMLRL 0.1184±0.0107 1.51426±0.0132 3.5231±0.0823 1.8243±0.0536 0.8613±0.0122 表 5 不同方法在6个数据集上的分类精度(ACA±std)及所选特征数
Table 5 Classification accuracies (ACA ± std) and the numbers of selected features of different algorithms on six datasets
% 数据集 ORL warpAR10P COIL_20 USPS Isolet Lung LS 87.00±0.00 (300) 44.60±4.88 (150) 79.19±1.20 (300) 71.11±2.47 (300) 69.85±1.13 (300) 75.00±4.15 (300) JELSR 88.00±0.00 (200) 36.00±5.57 (100) 79.53±1.16 (300) 71.14±2.18 (150) 71.75±0.78 (300) 77.88±5.31 (250) RSR 87.50±0.00 (250) 48.00±2.24 (50) 82.84±1.97 (300) 66.35±2.50 (300) 66.59±0.21 (300) 65.00±6.95 (300) SOGFS 88.50±0.00 (100) 24.20±3.11 (50) 80.16±1.35 (300) 69.85±2.16 (300) 71.90±1.24 (100) 76.92±3.01 (150) URAFS 87.40±1.24 (250) 32.60±4.77 (100) 71.32±1.74 (300) 67.09±2.04 (300) 58.66±2.01 (300) 77.88±5.23 (300) LRLMR 88.10±0.82 (300) 39.20±4.76 (200) 80.32±1.10 (300) 69.99±2.60 (300) 65.79±1.14 (300) 78.65±2.64 (200) MMFS 88.00±0.00 (300) 34.40±4.10 (300) 83.47±1.28 (300) 70.83±2.38 (300) 70.60±1.28 (300) 74.81±5.98 (300) MMLRL 89.00±0.79 (250) 43.00±6.63 (200) 84.71±1.07 (150) 71.60±2.21 (200) 72.70±1.88 (300) 80.00±2.90 (200) 表 6 不同算法在有遮挡块的COIL_20数据集上的聚类精度(ACC)
Table 6 Clustering accuracies of different methods to block occlusion with different sizes on COIL_20dataset
% 算法 遮挡快大小 0×0 3×3 4×4 5×5 6×6 7×7 LS 57.74 53.42 54.52 51.51 52.25 50.60 MCFS 59.58 58.92 57.65 54.46 56.69 52.20 JELSR 58.32 59.19 56.19 53.19 51.74 46.83 RSR 58.05 56.81 50.61 44.74 34.81 28.05 SOGFS 59.74 56.81 56.99 52.28 50.50 48.77 URAFS 50.43 47.76 48.01 47.20 48.50 47.37 LRLMR 55.62 55.94 55.23 56.03 51.83 50.17 MMFS 58.29 59.49 61.90 58.43 51.96 49.72 MMLRL 64.09 59.86 61.65 60.28 57.10 50.47 表 7 不同方法在有点噪声的Isolet数据集上的聚类精度(ACC)
Table 7 Clustering accuracies of different methods to different densities of salt and pepper noise on Isolet dataset
% 算法 点噪声比例 0 10 20 30 40 50 60 LS 55.58 55.86 54.12 54.66 54.39 55.26 54.48 JELSR 57.79 57.58 57.08 57.65 57.72 58.01 58.35 RSR 52.67 53.22 54.03 52.65 52.44 53.00 52.53 SOGFS 58.19 57.06 50.40 52.58 49.43 50.17 49.94 URAFS 45.26 43.69 45.01 44.75 45.94 45.89 47.46 LRLMR 50.75 53.90 54.60 53.87 55.66 58.57 56.45 MMFS 56.45 52.67 52.50 51.96 52.25 55.12 53.56 MMLRL 60.47 60.22 59.94 59.96 58.11 58.05 56.76 -
[1] BRUNETTI A, BUONGIORNO D, TROTTA G F, et al. Computer vision and deep learning techniques for pedestrian detection and tracking: a survey[J]. Neurocomputing, 2018, 300: 17–33. doi: 10.1016/j.neucom.2018.01.092 [2] JORDAN M I, MITCHELL T M. Machine learning: trends, perspectives, and prospects[J]. Science, 2015, 349(6245): 255–260. doi: 10.1126/science.aaa8415 [3] LI H, HE X, TAO D, et al. Joint medical image fusion, denoising and enhancement via discriminative low-rank sparse dictionaries learning[J]. Pattern recognition, 2018, 79: 130–146. doi: 10.1016/j.patcog.2018.02.005 [4] QURESHI R, UZAIR M, KHURSHID K, et al. Hyperspectral document image processing: applications, challenges and future prospects[J]. Pattern recognition, 2019, 90: 12–22. doi: 10.1016/j.patcog.2019.01.026 [5] VADIM K. Overview of different approaches to solving problems of data mining[J]. Procedia computers, 2018, 123: 234–239. doi: 10.1016/j.procs.2018.01.036 [6] PENG H C, LONG F H, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(8): 1226–1238. doi: 10.1109/TPAMI.2005.159 [7] 朱星宇, 陈秀宏. 联合不相关回归和非负谱分析的无监督特征选择[J]. 智能系统学报, 2022, 17(2): 303–313. ZHU X Y, CHEN X H. Joint uncorrelated regression and non-negative spectral analysis for unsupervised feature selection[J]. CAAI Transactions on Intelligent Systems, 2022, 17(2): 303–313. [8] 白圣子, 降爱莲. 基于特征正则稀疏关联的无监督特征选择方法[J]. 计算机工程与设计, 2022, 43(04): 969–976. BAI S Z, JIANG A L. Unsupervised feature selection method based on feature regularized sparse association[J]. Computer engineering and eesign, 2022, 43(04): 969–976. [9] PENG C, GAO X, WANG N, et al. Face recognition from multiple stylistic sketches: scenarios, datasets, and evaluation[J]. Pattern recognition, 2018, 84: 262–272. doi: 10.1016/j.patcog.2018.07.014 [10] FU Y, YAN S, HUANG T S. Correlation metric for generalized feature extraction[J]. IEEE transactions on pattern analysis and machine intelligence, 2008, 30(12): 2229–2235. doi: 10.1109/TPAMI.2008.154 [11] JAIN A, ZONGKER D. Feature selection: Evaluation, application, and small sample performance[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(2): 153–158. doi: 10.1109/34.574797 [12] ZHAO J D, LU K, HE X F. Locality sensitive semi-supervised feature selection[J]. Neurocomputing, 2008, 71(10-12): 1842–1849. doi: 10.1016/j.neucom.2007.06.014 [13] HOU C P, NIE F P, LI X L, et al. Joint embedding learning and sparse regression: a framework for unsupervised feature selection[J]. IEEE transactions on cybernetics, 2014, 44(6): 793–804. doi: 10.1109/TCYB.2013.2272642 [14] HE X F, CAI D, NIYOGI P. Laplacian Score for feature selection[C]//Advances in Neural Information Processing Systems. Vancouver: NIPS, 2005: 507−514. [15] TABAKHI S, MORADI P, AKHLAGHIAN F. An unsupervised feature selection algorithm based on ant colony optimization[J]. Engineering applications of artificial intelligence, 2014, 32: 112–123. doi: 10.1016/j.engappai.2014.03.007 [16] CAI D, ZHANG C Y, HE X F. Unsupervised feature selection for multi-cluster data[C]// Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, DC: ACM, 2010, 333−342. [17] NIE F P, WANG X Q, HUANG H. Clustering and projected clustering with adaptive neighbors[C]// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Arlington: ACM, 2014: 977−986. [18] MOHSENZADEH Y, SHEIKHZADEH H, Reza A M, et al. The relevance sample-feature machine: A sparse bayesian learning approach to joint feature-sample selection[J]. IEEE transactions on cybernetics, 2014, 43(6): 2241–2254. [19] ZHU P F, ZUO W M, ZHANG L, et al. Unsupervised feature selection by regularized self-representation[J]. Pattern recognition, 2015, 48(2): 438–446. doi: 10.1016/j.patcog.2014.08.006 [20] NIE F P, ZHU W, LI X L. Unsupervised feature selection with structured graph optimization[C]// Proceedings of Thirtieth AAAI Conference on Artificial Intelligence. Phoenix: AAAI Press, 2016: 1302−1308. [21] LI X L, ZHANG H, ZHANG R, et al. Generalized uncorrelated regression with adaptive graph for unsupervised feature selection[J]. IEEE transactions on neural network and learning systems, 2019, 30(5): 1587–1595. doi: 10.1109/TNNLS.2018.2868847 [22] MIN Y, YE M, TIAN L, et al. Unsupervised feature selection via multi-step Markov probability relationship[J]. Neurocomputing, 2021, 453: 241–253. doi: 10.1016/j.neucom.2021.04.073 [23] SZUMMER M, JAAKKOLA T. Partially labeled classification with markov random walks[C]//Proceedings of the 14th International Conference on Neural Information Processing System: Natural and Synthetic. Cambridge: MIT Press, 2001, 945−952. [24] CAI J F, CANDES E J, SHEN Z W. A singular value thresholding algorithm for matrix completion[J]. SIAM journal on optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970 [25] HE Z S, XIE S L, ZDUNEK R, et al. Symmetric nonnegative matrix factorization: algorithms and applications to probabilistic clustering[J]. IEEE transactions on neural networks, 2011, 22(12): 2117–2131. doi: 10.1109/TNN.2011.2172457 [26] 徐慧敏, 陈秀宏. 图正则化稀疏判别非负矩阵分解[J]. 智能系统学报, 2019, 14(6): 1217–1224. XU H M, CHEN X H. Graph-regularized, sparse discriminant, non-negative matrix factorization[J]. CAAI Transactions on Intelligent Systems, 2019, 14(6): 1217–1224. [27] KUANG D, DING C, PARK H. Symmetric nonnegative matrix factorization for graph clustering[C]// Proceedings of the SIAM International Conference on Data Mining. Anaheim: SDM, 2012, 1(2): 106−117. [28] BOYD S, PARIKH N, ERIC C, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and trends in machine learning, 2010, 3(1): 1–122. doi: 10.1561/2200000016 [29] LONG B, ZHANG Z, YU P S. Co-clustering by block value decomposition[C]// Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Chicago: ACM, 2005: 635−640. [30] LANGE K, HUNTER D R, YANG L. Optimization transfer using surrogate objective functions[J]. Journal of computational and graphical statistics, 2000, 9(1): 1–20. [31] SAMARIA F S, HARTER A C. Parameterisation of a stochastic model for human face identification[C]// Proceedings of 1994 IEEE Workshop on Applications of Computer Vision. Sarasota: IEEE, 1994, 138−142. [32] RATE C, RETRIEVAL C. Columbia object image library(COIL-20)[EB/OL]. (2011−12−12)[2020−01−01]. http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php. [33] HULL J. A database for handwritten text recognition research[J]. IEEE transactions on pattern analysis and machine intelligence, 1994, 16(5): 550–554. doi: 10.1109/34.291440 [34] FANTY M A, COLE R A. Spoken Letter Recognition[C]// Advances in Neural Information Processing Systems. Stroudsburg: Association for Computational Linguistics, 1990, 220−226. [35] BHATTACHARJEE A, RICHARDS W G, STAUNTON J, et al. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses[J]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(24): 13790–13795. doi: 10.1073/pnas.191502998 [36] HASLINGER C, SCHWEIFER N, STILGENBAUER S, et al. Microarray gene expression profiling of B-cell chronic lymphocytic leukemia subgroups defined by genomic aberrations and VH mutation status[J]. Journal of clinical oncology, 2004, 22(19): 3937–49. doi: 10.1200/JCO.2004.12.133 [37] TANG C, BIAN M, LIU X W, et al. Unsupervised feature selection via latent representation learning and manifold regularization[J]. Neural network, 2019, 117: 163–17. doi: 10.1016/j.neunet.2019.04.015
