基于邻域互信息与K-means特征聚类的特征选择

孙林,  梁娜,  徐久成

downloadPDF
孙林, 梁娜, 徐久成. 基于邻域互信息与K-means特征聚类的特征选择 [J]. 智能系统学报, 2024, 19(4): 983-996. doi: 10.11992/tis.202208012
引用本文: 孙林, 梁娜, 徐久成. 基于邻域互信息与K-means特征聚类的特征选择 [J]. 智能系统学报, 2024, 19(4): 983-996. doi: 10.11992/tis.202208012
shu
SUN Lin, LIANG Na, XU Jiucheng. Feature selection using neighborhood mutual information and feature clustering with K-means [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 983-996. doi: 10.11992/tis.202208012
Citation: SUN Lin, LIANG Na, XU Jiucheng. Feature selection using neighborhood mutual information and feature clustering with K-means [J]. CAAI Transactions on Intelligent Systems, 2024, 19(4): 983-996. doi: 10.11992/tis.202208012
shu

基于邻域互信息与K-means特征聚类的特征选择

doi: 10.11992/tis.202208012
  • 1.

    天津科技大学 人工智能学院, 天津 300457;

  • 2.

    河南师范大学 计算机与信息工程学院, 河南 新乡 453007

基金项目: 国家自然科学基金项目（62076089, 61772176, 61976082）；河南省科技攻关计划项目(212102210136).
详细信息
    作者简介:

    孙林，教授，博士生导师，博士，计算机学会会员，主要研究方向为粒计算、大数据挖掘和机器学习。发表学术论文60余篇。E-mail：sunlin@tust.edu.cn;

    梁娜，硕士研究生，主要研究方向为数据挖掘。E-mail：ms_liangna@126.com;

    徐久成，教授，博士生导师，博士，计算机学会高级会员，主要研究方向为粒计算、大数据挖掘和智能信息处理。E-mail：xjc@htu.edu.cn.

    通讯作者:

    孙林. E-mail：sunlin@tust.edu.cn.

  • 中图分类号: TP181

Feature selection using neighborhood mutual information and feature clustering with K-means

  • 1.

    College of Artificial Intelligence, Tianjin University of Science and Technology, Tianjin 300457, China;

  • 2.

    College of Computer and Information Engineering, Henan Normal University, Xinxiang 453007, China

    摘要
  • 摘要: 针对多数邻域系统通过人工调试很难搜索到最佳邻域半径，以及传统的K-means聚类需要随机选取簇中心和指定簇的数目等问题，提出了一种基于邻域互信息与K-means特征聚类的特征选择方法。首先，将样本在各特征下与其他样本距离的平均值作为自适应邻域半径，确定样本的邻域集，并由此构建自适应邻域熵、邻域互信息、归一化邻域互信息等度量，反映特征之间的相关性；然后，基于归一化邻域互信息构建自适应K近邻集合，利用Pearson相关系数表示特征的权重定义加权K近邻密度，实现自动选取K-means算法的簇中心，进而完成K-means特征聚类；最后，给出加权平均冗余度，选出每个特征簇中加权平均冗余度最大的特征构成最优特征子集。实验结果表明所提算法不仅可以有效提升特征选择的分类结果而且可以获得更好的聚类效果。

     

    Abstract: Aiming at the problems that it is difficult to search the optimal neighborhood radius through manual debugging in most neighborhood systems, and that traditional K-means clustering requires random selection of cluster centers and the number of specified clusters, this paper proposed a feature selection method using neighborhood mutual information and feature clustering with K-means. Firstly, the average distance of the sample from other samples under each feature is taken as the adaptive neighborhood radius, and the neighborhood set of the sample is determined. Then to reflect the correlation between features, some metrics are presented, such as adaptive neighborhood entropy, neighborhood mutual information, normalized neighborhood mutual information, etc. Secondly, an adaptive K neighbor set is constructed based on the normalized neighborhood mutual information, and the weighted K neighbor density is defined by using the feature weight with the Pearson correlation coefficient so that the K-means algorithm can automatically select the cluster center. The K-means feature clustering is completed well. Finally, the weighted average redundancy degree is given, and the feature with the largest weighted average redundancy in each feature cluster is selected to form the optimal subset of features. Experimental results show that the developed algorithm can not only effectively improve the classification results of feature selection, but also obtain better clustering effects.

     

    • HTML全文

  • 随着大数据时代的快速发展，特征选择寻找最小特征子集提高模型分类精度和运行时效[1-3]。作为一种有效的特征选择模型，邻域粗糙集理论是处理连续型数据的高效工具之一[4]。Hu等[5]提出了基于邻域互信息的特征选择算法。但是其性能受邻域半径的影响较大。孙林等[6]提出了基于自适应邻域互信息与谱聚类的特征选择算法，引入标准差自适应地确定邻域半径。但是在一定范围内仍然需要调试邻域半径改进分类性能。Rahmanian等[7]通过正则化回归模型提出了一种子空间聚类的无监督特征选择算法。但是，该算法在特征聚类时需要固定K近邻，且不适应于高维数据集。孙林等[8]提出了基于K近邻和优化分配策略的密度峰值聚类算法。但是K近邻数需要通过网格搜索策略在一定范围内调试，因而未凸显每个样本的局部几何结构。张新元等[9]提出了共享K近邻和多分配策略的密度峰值聚类算法。但是其邻域半径仍需要预先指定或者在一定范围内通过不断的人工调试才能获取较优值。为了解决上述问题，受文献[6, 10]自适应邻域的启发，在邻域决策系统中，本文将样本在特征子集下到其他样本距离的平均值作为邻域半径，自适应地确定样本在不同特征下的自适应邻域半径，设计归一化邻域互信息，有效度量特征之间的相关性。

    截至目前，从聚类角度进行特征选择已经逐渐引起学者们的关注[11-13]。Chen等[14]提出了基于冗余互补维度分析的聚类特征子集选择算法。但是，该算法在处理连续型数据时需要对数据进行离散化处理。Sun等[15]提出了基于最近邻优化分配策略的自适应密度峰值聚类算法。但是仍需要指定簇的数目，导致聚类性能受人的主观影响较大。辛永杰等[16]提出来一种基于跨结构特征选择和图循环自适应学习的多视图聚类。但是该算法忽略了特征间的权重。Song等[1]提出了基于相关性引导聚类和粒子群优化的高维数据特征选择算法。但是该算法在对特征进行聚类时需要预先指定阈值。总的来说，尽管上述算法在性能上有一定的提升，但是一些问题并未得到有效解决，如需预先指定簇的数目、随机选取簇中心以及处理连续型数据需要预先进行离散化等。

    为解决邻域粗糙集需要调试邻域参数的问题，计算样本与其他样本间距离，定义自适应邻域半径，实现自动选择最优邻域半径；针对互信息通常选择多值特征的问题，定义归一化邻域互信息计算特征间的对称不确定性，度量特征间的相关性；为弥补 K-means需要指定簇数目和随机选取簇中心的缺陷，将K近邻集与自适应邻域集结合，构建自适应K近邻集和加权K近邻密度，自动选取K-means的簇中心，实现K-means特征聚类，由此设计基于邻域互信息与K-means特征聚类的特征选择算法。

    1.   邻域粗糙集与K-means聚类

    1.1   邻域粗糙集

    假设邻域决策系统I = <U, C, D, H >，其中，U为m个样本构成的集合，C为含连续型属性的条件属性集，D为决策属性集，A = C$ \cup $D，V为属性的值域，H为U$ \times $A$ \to $V的映射函数。对于任意样本xi，xj$ \in $U，B$ \subseteq $C，xi在B下的邻域集[5]表示为

    $$ {{N}_B}({x_i}) = \{ {x_j} \in U|{d_B}({x_i},{x_j}) \leqslant \delta \} $$

    式中：预设邻域半径δ$ > $0，d表示任意2个样本xi和xj在属性at$ \in $B下的欧氏距离，其表达式为

    $$ {d_B}({x_i},{x_j}) = \sqrt {\displaystyle\sum\limits_{t = 1}^{|B|} {{{(H({x_i},{a_t}) - H({x_j},{a_t}))}^2}} } $$

    在I = <U, C, D, H >中，样本子集X$ \subseteq $U，B$ \subseteq $C，X关于B的邻域下近似、上近似集[17]为

    $$ \underline {N_B^\delta } (X) = \{ {x_i} \in U|{\delta _B}({x_i}) \subseteq X\} $$
    $$ \overline {N_B^\delta } (X) = \{ {x_i} \in U|{\delta _B}({x_i}) \cap X \ne \varnothing \} $$

    1.2   K-means聚类

    假设簇中心为F1, F2, ···, Fc，随机选择c个样本点作为初始簇中心，计算其他每个样本到各个簇中心的距离[18]表示为

    $$ {d_B}({x_i},{F_{{b}}}) = \sqrt {{{({x_i} - {F_b})}^2}} $$

    式中：Fb为第b个簇中心，b = 1, 2, ···, c；xi为第i个样本，根据距离远近将它们划分到距离其最近的簇中。根据每个簇中所有样本点的均值，更新调整簇中心的计算公式[19]表示为

    $$ F_b^{{\rm{new}}} = \frac{{\displaystyle\sum\limits_{{x_i} \in {F_b}} {{x_i}} }}{{|{F_b}|}} $$

    式中：|Fb|为划分到簇Fb中的样本数目，$F_b^{{\rm{new}}}$为新的簇中心。如果$F_b^{{\rm{new}}}$和Fb不相同，需要不断更新调整簇中心，重新划分样本点到距离其最近的簇中，迭代结束的条件[19]表示为

    $$ F_b^{{\rm{new}}} = F_b^{{\rm{old}}} $$

    2.   提出的特征选择算法

    2.1   邻域互信息

    为了解决传统的邻域互信息中邻域半径在一定范围内不断调试的问题，将样本在特征子集下到其他样本距离的平均值作为邻域半径，基于此可以自适应确定样本在不同特征下的自适应邻域半径，并确定样本的自适应邻域集。

    定义1　在I = <U, C, D, H>中，特征子集B$ \subseteq $C，则其他所有样本到xi之间的距离表示为

    $$ {P_B}({x_i}) = \{ {d_B}{x_{(i,1)}},{d_B}{x_{(i,2)}}, \cdots ,{d_B}{x_{(i,j)}}, \cdots ,{d_B}{x_{(i,m)}}\} $$

    式中：dBx(i, j)表示在特征子集B上样本xi和xj之间的欧氏距离，j = 1, 2, ···, m。

    定义2　在I = <U, C, D, H>中，特征子集B$ \subseteq $C，对于任意样本xi$ \in $U，样本xi在B上的自适应邻域半径δB(xi)和邻域集NB(xi)表示为

    $$ {\delta _B}({x_i}) = \frac{{\displaystyle\sum\limits_{j = 1}^m {{d_B}({x_i},{x_j})} }}{{(m - 1)}} $$ (1)
    $$ {N}_{B}({x}_{i})=\left\{{x}_{p}\right| {d}_{B}({x}_{i},{x}_{p})\leqslant {\delta}_{B}({x}_{i})\} $$ (2)

    Hu等[5]构建邻域互信息度量特征与决策之间的相关性。受此启发，基于自适应邻域集研究邻域熵及其互信息等度量方法。

    定义3　在I = <U, C, D, H>中，A和B是C的2个特征子集，对于任意样本xi$ \in $U，B上的自适应邻域熵、A和B的邻域联合熵、B相对于A的邻域条件熵、B和A的自适应邻域互信息分别表示为

    $$ {E_\delta }(B) = - \frac{1}{{|U|}}\displaystyle\sum\limits_{i = 1}^{|U|} {{{\rm{log}}_2}\left(\frac{{|{N_B}({x_i})|}}{{|U|}}\right)} $$ (3)
    $$ {E_\delta }(A,B) = - \frac{1}{{|U|}}\displaystyle\sum\limits_{i = 1}^{|U|} {{{\rm{log}}_2}\left(\frac{{|{N_{A \cup B}}({x_i})|}}{{|U|}}\right)} $$
    $$ {E_\delta }(B|A) = - \frac{1}{{|U|}}\displaystyle\sum\limits_{i = 1}^{|U|} {{{\rm{log}}_2}\left(\frac{{|{N_{A \cup B}}({x_i})|}}{{|{N_A}({x_i})|}}\right)} $$
    $$ {E}_{\delta }(B;A)=-\frac{1}{\left|U\right|}{\displaystyle \displaystyle\sum _{i=1}^{\left|U\right|}{\mathrm{log}}_{2}}\left(\frac{|{N}_{A}({x}_{i})|\text{|}{N}_{B}({x}_{i}\text{)|}}{\left|U\right||{N}_{A\cup B}({x}_{i})|}\right) $$ (4)

    性质1　互信息与熵满足的关系为

    $$ {E_\delta }(B;A) = {E_\delta }(B) + {E_\delta }(A) - {E_\delta }(B,A) $$
    $$ {E_\delta }(B;A) = {E_\delta }(B) - {E_\delta }(B|A) = {E_\delta }(A) - {E_\delta }(A|B) $$

    文献[20]强调：对称不确定性克服互信息对具有更多值要素的偏向。为了弥补这种偏差，基于自适应邻域互信息定义归一化邻域互信息。

    定义4　在I = <U, C, D, H >中，A和B是C的2个特征子集，则特征A和B的归一化邻域互信息表示为

    $$ M(A,B) = \frac{{2 \times {E_\delta }(B;A)}}{{{E_\delta }(A) + {E_\delta }(B)}} $$ (5)

    式中：Eδ(A)和Eδ(B)分别是A和B的自适应邻域熵，Eδ(B; A)是A和B的自适应邻域互信息。M(A, B)的值越大，表示A和B越相似。

    定义5　对于任意特征fs$ \in $C，则特征fs与其他所有特征的归一化邻域互信息的有序序列表示为

    $$ {\boldsymbol{L}}(f_{s}) = (M(f_{s}, f_{(s, 1)}),M(f_{s}, f_{(s, 2)}),\cdots ,M(f_{s}, f_{(s, n-1)})) $$

    式中：M(fs, f(s, 1)) ≥ M(fs, f(s, 2)) ≥ ··· ≥ M(fs, f(s, n−1))，f(s, r)是特征fs降序序列的第r个特征，s = 1, 2, ···, n，r = 1, 2, ···, n−1。为了表述方便，用Ms(f(s, r))表示M(fs, f(s, r))。

    2.2   K-means特征聚类

    文献[21]基于归一化互信息度量特征之间的对称不确定性，通过K近邻关系和K近邻密度实现对特征的聚类。但是，其需要预先指定k的数目，并且也忽略了特征之间的影响。因此，为了解决这些缺点，本文提出自适应K近邻集和加权K近邻密度，实现K-means特征聚类。

    定义6　在I = <U, C, D, H >中，任意特征fs$ \in $C，特征fs的K近邻集和自适应邻域集分别为

    $$ \gamma (f_{s}) = {f_{(s, k)}| k \in M_{s}(f_{(s, k)}), 1\leqslant k \leqslant \sqrt n } $$
    $$ \varepsilon (f_{s}) = {f_{(s, r)}|M_{s}(f_{(s, r)}) > Q_\text{avg}(f_{s})} $$

    式中：1 ≤ r ≤ n−1，Qavg(fs)为特征fs与其他特征的对称不确定性平均值。

    文献[9]表明K近邻在稀疏密度区域表现不佳，自适应邻域关系在高密度区域表现不佳。由此将K近邻集与自适应邻域集结合，提出自适应K近邻集。

    定义7　在I = <U, C, D, H >中，任意特征fs$ \in $C，则特征fs的自适应K近邻集合表示为

    $$ \zeta(f_{s})={f_{(s,l)}|f_{(s,l)} \in (\gamma (f_{s}) \cap \varepsilon(f_{s}))} $$ (6)

    式中1 ≤ l ≤ n−1。

    由定义6至定义7可知，如果满足Ms(f(s, l)) > M(fs)且f(s, l)$ \in $γ(fs)，则特征f(s, l)属于特征fs的近邻；否则，特征f(s, l)不属于特征fs的近邻。

    借鉴文献[22]加权K近邻思想，基于Pearson相关系数定义近邻特征之间的权重，并由此设计加权K近邻密度与加权平均冗余度。

    定义8　在I = <U, C, D, H >中，任意特征fs$ \in $C，特征f(s, l)是特征fs的第l个近邻，则特征f(s, l)相对于特征fs的权重表示为

    $$ \omega ({f_s},{f_{(s,l)}}){\text{ = }}\left|\frac{{R({f_s}{f_{(s,l)}}) - R({f_s}) \times R({f_{(s,l)}})}}{{\sqrt {R({f_s}^2) - {R^2}({f_S})} \times \sqrt {R({f_{(s,l)}}^2) - {R^2}({f_{(s,l)}})} }}\right| $$

    式中：w(fs, f(s, l))度量2个变量fs和f(s, l)之间的相关程度，R()为数学期望值。

    文献[21]中定义的K近邻密度、平均冗余度假设特征之间的影响是相同的。为了克服该局限性，受文献[8]中加权K近邻思想的启发，考虑特征之间的影响存在不一定相同的情形，将基于Pearson相关系数表示的特征权重与特征的密度、平均冗余度分别进行结合，定义加权K近邻密度。

    定义9　在I = <U, C, D, H >中，任意特征fs$ \in $C，则特征fs的加权K近邻密度表示为

    $$ Z({f_s}) = \frac{{\displaystyle\sum\limits_{l = 1}^{|\zeta ({f_s})|} {\omega ({f_s},{f_{(s,l)}}) \times M({f_s},{f_{(s,l)}})} }}{{|\zeta ({f_s})|}} $$ (7)

    由定义9可知，加权K近邻密度Z(fs)反映了特征fs与其K个近邻的冗余程度，因此，近邻密度越大，越有可能成为簇中心。

    定义10　在I = <U, C, D, H >中，任意特征fs$ \in $C(s = 1, 2, ···, n)，则所有特征自适应加权K近邻密度的有序序列表示为

    $$ L(Z) = (f_{1}, f_{2}, \cdots, f_{n}) $$ (Z)

    式中Z(f1) >Z (f2) > ··· > Z(fn)。

    依据定义10，L(Z)中的第一个特征f1添加到特征簇中心集合Fc中，对于任意特征fs$ \in $C – Fc和ft$ \in $Fc，如果特征fs$ \in $ζ(ft)且ft$ \in $ζ(fs)，那么fs将被放到特征簇中心集合Fc中，依次重复上述步骤直到结束，特征簇中心集Fc实现了初始化。因此，根据特征的自适应K近邻集合、加权K近邻密度来确定簇中心，使得提出的K-means特征聚类既不需要随机选取也不需要预先确定簇中心的数目。由此，对于任意特征簇Fe (e = 1, 2, ···, g)，若任意特征fs、ft、fp和fq属于特征簇Fe，且M(fs, ft) ≥ M (fp, fq)，那么M(fs, ft) = maxM(Fe)，否则M(fs, ft) = minM(Fe)。假设Fc是初始特征簇中心集合，对于任意特征fs$ \in $C–Fc和ft$ \in $Fc，并且ft属于特征簇Ft，如果fs和ft具有最大对称不确定性且M(fs, ft) > maxM(Ft)，则将fs放到特征簇Ft中，否则fs将被放到Fc中成为一个新的簇中心。由此可知，对于任意特征fs$ \in $Fs和ft$ \in $Ft，如果fs和ft是簇中心，则M(fs, ft) < minM(Ft)且M(fs, ft) < minM(Fs)，这表示簇中心之间的对称不确定性小于特征簇的最小对称不确定性。通过上述过程，将相似度较大的特征分配到一个簇中，将相似度较小的特征分配到其他的不同簇中，进而实现K-means特征聚类。

    2.3   特征选择算法描述

    文献[21]指出：特征聚类之后，冗余特征被分到同一个特征簇中，具有最大平均冗余度的特征包含了同一簇中其他特征的大多数信息量。由此将同一簇中每个特征相对于其他特征的权重引入到平均冗余度中，定义加权平均冗余度，选出每个特征簇中加权平均冗余度最大特征构成所选特征子集。

    定义11　在I = <U, C, D, H >中，任意特征fs和ft属于特征簇Fe(e = 1, 2, ···, g)，则特征fs的加权平均冗余度表示为

    $$ T({f_s},{F_e}) = \frac{{\displaystyle\sum\limits_{t = 1}^{|{F_e}|} {\omega ({f_s},{f_t}) \times M({f_s},{f_t})} }}{{|{F_e}|}} $$

    式中：|Fe|是特征簇Fe中包含的特征数，w(fs, ft)为ft相对于fs的权重。

    由定义11可知，在一个特征簇中，具有最大加权平均冗余度T(fs, Fe)的特征fs比同一个特征簇中的其他特征更重要。由此，选择特征簇Fe中的特征fs作为代表特征，而Fe中的其余特征作为冗余特征而被剔除。从每个特征簇选出具有最大T(fs, Fe)的特征，构成最终所选特征集。

    为了提高其计算效率，对于高维数据集使用文献[17]Fisher得分算法对高维数据集进行初步降维处理，利用文献[23]中的数据离散度代替类内散度与类间散度，避免不同量纲对统计结果的影响。

    定义12　在I = <U, C, D, H >中，任意特征fs$ \in $C，U/D = {D1, D2, ···, Dd}，假设样本xi$ \in $Da，则决策类Da中的样本在特征fs上的Fisher得分和离散度分别表示为

    $$ W({f_s}) = \frac{{\displaystyle\sum\limits_{a = 1}^d {|{D_a}|} \times \frac{{{{(R(f_s^a) - R({f_s}))}^2}}}{{R({f_s})}}}}{{\displaystyle\sum\limits_{a = 1}^d {|{D_a}|} \times {{(Y_s^a)}^2}}} $$ (8)
    $$ Y_s^a = \frac{{\sqrt {\displaystyle\sum\limits_{{x_i} \in {D^a}} {{{(H({x_i},{f_s}) - R(f_s^a))}^2}} } }}{{|{D^a}||R(f_s^a)|}} $$

    式中：|Da|为决策类Da中样本的数目，1≤a≤c，$ R(f_s^a) $为决策类Da中样本在特征fs下的平均值，H(xi, fs)为样本xi在特征fs上的值，R(fs)为全部样本在特征fs下的平均值，$ Y_s^a $为决策类Da中样本在特征fs下的离散度。

    接下来，基于邻域互信息与K-means特征聚类设计特征选择算法(feature selection algorithm using neighborhood mutual information and feature clustering with K-means, FSNFK)，其伪代码描述如算法1所示。

    算法1　FSNFK算法

    输入　I = <U, C, D, H >

    输出　最优特征子集S

    1) 初始化特征簇中心Fc = $\varnothing $，特征子集Jsub = S = $\varnothing $

    2) 依据式(1)和式(2)计算每个样本xi的自适应邻域集

    3) For任意特征fs、ft$ \in $C且s$ \ne $t do

    4) 根据式(3)计算fs和ft的自适应邻域熵

    5) 根据式(4)计算fs和ft的自适应邻域互信息

    6) 根据式(5)计算fs和ft的归一化邻域互信息M(fs, ft)

    7) End for

    8) For任意特征fs do

    9) 降序排序fs与其他特征的归一化邻域互信息得到L(fs)

    10) 根据式(6)计算fs的自适应K近邻集合

    11) 根据式(7)计算fs的加权K近邻密度Z(fs)

    12) 降序排序所有特征的加权K近邻密度得到L(Z)

    13) End for

    14) 降序排序所有特征的加权K近邻密度对应的特征集为Jsub = {f1, f2, ···, fn}，并且Z(fs) > Z(ft), 其中，s＜t≤n，特征簇中心Fc = Fc$ \cup ${f1}

    15) For任意特征fs$ \in $ Jsub do

    16) For任意特征ft$ \in $ Jsub do

    17) If ft$ \in $ζ(fs)且fs$ \in $ζ(ft)

    18) 特征簇中心Fc = Fc$ \cup ${fs}

    19) maxM(Fc) = max(maxM(Fc), M(fs , ft))

    20) End if

    21) End for

    22) End for

    23) For d = 1：length(Fc) do

    24) 特征子集Fd = fd，其中，特征fd是Fc中的第d个特征

    25) End for

    26) For任意特征fs$ \in $ Jsub且fs$ \in $ Fc do

    27) $ d = {\rm{argma}}{x_{{f_d} \in {F_c}}}(M({f_s},{f_d})) $

    28) If M(fs, fd)$ > $maxM(Fc) then

    29) 特征子集Fd = Fd$ \cup ${fs}

    30) Else 特征簇中心Fc = Fc$ \cup ${fs}，跳转到步骤23)

    31) End if

    32) End for

    33) For 任意特征簇Fd do

    34) 特征$ {f_s} = {\rm{argma}}{x_{{f_s} \in {F_d}}}(T({f_s},{F_d})) $

    35) 特征子集S = fs$ \cup $S

    36) End for

    37) 返回最优特征子集S

    2.4   计算复杂度分析与比较

    假若一个数据集含有m个样本和n个特征，步骤1)~2)的计算复杂度为O(mn2)，步骤3)~7)的复杂度为O(n2/2)。步骤8)~13)的复杂度为O(n|ζ(fs)|)，这里|ζ(fs)| << n。步骤14)~32)中最多有n个特征不属于聚类中心，则将特征分配到所在簇中的计算复杂度最差为O(n + m + n2)，因而其计算复杂度是O(n2)。如果特征簇的数量是w，步骤33)~36)计算加权平均冗余度的复杂度是O(w2)；如果所有特征都被划分为一个特征簇，步骤32)~步骤36)计算加权平均冗余度的复杂度是O(n2)。因此，FSNFK算法的计算复杂度为O(mn2)。由分析可知，FSNFK算法的计算复杂度明显低于MSU-FS[7]、FMSU-FS[7]、FSFC[21]、MICIMR[24]、IG-RFE[25]、GSMI[26]和UFSMI[27]，与DRGS[28]和MRI[29]相同，略高于K-means[30]、K-medoids[31]、DBSCAN[32]、OPTICS[33]、IWFS[34]和CRFS[35]。

    3.   实验和结果分析

    3.1   实验准备

    实验配置为Windows 7操作系统、Intel(R) i7 CPU 3.20 GHz处理器，8 GB内存。依据文献[7, 24, 26]，本文选用19个实验数据集(https://archive. ics.uci.edu/ml和http://portals.broadinstitute.org/cgi- bin/cancer/datasets. cgi)，如表1所示。对于特征数大于500的高维数据集，采用式(9)进行初步降维提升算法的计算效率，由此设置Ovarian-PBSII 数据集为10维，Isolet、CLL-SUB-111、lung、lung-cancer-203、ALLAML、COLON、warpPIE10P和warpAR10P这8个数据集为50维，TOX171数据集为200维。

    表  1  19个数据集的描述
    Table  1  Description of nineteen datasets
    编号数据集样本数属性数类别数
    1Wpbc198312
    2Isolet156061726
    3CLL-SUB-1111440102420
    4lung20333125
    5movement-libras3609015
    6SPAMBASE4601572
    7lung-cancer-203203126005
    8ALLAML7271292
    9COLON6220002
    10TOX17117157484
    11Ovarian-PBSII253151552
    12Wine178133
    13Sonar208602
    14Breast Cancer569312
    15Breast Tissue10696
    16Parkinsons197222
    17warpPIE10P21024202
    18warpAR10P130240010
    19Lung cancer32562

    3.2   特征选择结果分析

    为了验证FSNFK在不同数据集上选择特征进行分类的有效性，第一部分选择FSNFK与文献[24]中的6种方法进行对比，包括MICIMR[24]、IG-RFE[25]、DRGS[28]、MRI[29]、IWFS[34]和CRFS[35]。为了与文献[24]实验保持一致，采用10折交叉验证，从表1中选择6个数据集，选用K最近邻(K-nearest neighbor, KNN)、决策树(C4.5)和随机森林(random forest, RF)作为分类器，使用文献[24]中的F1_Macro作为特征选择分类结果的评价指标，其中F1_Macro越大则分类效果越好。表2给出了3种分类器下8种算法在6个数据集上的F1_Macro，其中Fullset表示直接对原始数据集处理的算法。

    表  2  3种分类器下8种算法在6个数据集上的F1_Macro
    Table  2  F1_Macro of eight algorithms on six datasets under three classifiers %
    分类器数据集FullSetMICIMRIG-RFEIWFSCRFSDRGSMRIFSNFK
    KNNWpbc10.5114.239.1511.2010.3114.8010.3161.02
    ISOLET26.7666.0846.8237.0544.5855.9456.9672.72
    CLL-SUB-11168.3076.6666.0260.7064.1175.6764.4377.75
    lung62.4875.4266.6352.4268.4376.2376.3482.89
    movement-libras68.0382.5770.5267.6574.0774.6574.0784.13
    SPAMBASE81.3789.7786.7881.3287.1983.0288.2188.56
    平均52.9167.4657.6551.7258.1263.3961.7277.85
    C4.5Wpbc13.4314.6612.4111.8110.0413.9312.1160.60
    ISOLET26.1466.4042.2638.2238.9750.9750.7266.42
    CLL-SUB-11162.7168.9562.4563.3064.6267.6057.1061.50
    lung58.2881.5774.9454.8366.3568.1970.6582.60
    movement-libras56.7566.5363.3357.3159.5262.3362.4268.03
    SPAMBASE87.3390.2889.3686.1188.9989.4589.6891.18
    平均50.7764.7357.4651.9354.7558.7557.1169.55
    RFWpbc16.6317.6216.8217.5116.1417.1014.5064.25
    ISOLET29.0171.2847.6847.9846.5857.0760.2582.80
    CLL-SUB-11168.3076.6666.0260.7064.1175.6764.4372.85
    lung60.6480.1370.8151.3564.4773.1174.9687.02
    movement-libras65.5576.0167.8362.9469.3771.4966.3884.27
    SPAMBASE89.8692.5691.8589.6891.8490.8992.0293.70
    平均55.0069.0460.1755.0358.7564.2262.0980.82
    注：加黑代表最优结果，下同。

    根据表2可知，在KNN分类器下，在Wpbc、ISOLET、CLL-SUB-111、lung和movement-libras这5个数据集上，FSNFK的F1_Macro优于其他对比算法，尤其是在Wpbc、ISOLET和lung这3个数据集上优势非常明显，其F1_Macro值分别比其他算法优46.22%~51.87%、6.64%~45.96%与6.25%~30.47%；在SPAMBASE数据集上，FSNFK取得了次优的F1_Macro，比最优的MICIMR低1.21%，但是比其他算法高0.35%~7.24%。究其原因可能是因为FSNFK在SPAMBASE数据集上丢失了个别重要特征而造成的。在C4.5分类器下，在5个数据集Wpbc、ISOLET、lung、movement-libras和SPAMBASE上，FSNFK的F1_Macro优于其他对比算法，特别是在Wpbc、lung和movement-libras这3个数据集上优势非常明显；在CLL-SUB-111数据集上，FSNFK的F1_Macro尽管比最优的MICIMR低7.45%，但是比MRI高4.4%。在RF分类器下，在Wpbc、ISOLET、lung、movement-libras和SPAMBASE这5个数据集上，FSNFK的F1_Macro优于其他对比算法，特别是在Wpbc、ISOLET和lung数据集上优势非常明显；在CLL-SUB-111数据集上，FSNFK尽管比表现最好的MICIMR低3.81%，但是比FullSet、IG-RFE、IWFS、CRFS和MRI这5种对比算法高4.55%~12.15%。在C4.5和RF这2种分类器下CLL-SUB-111数据集，MICIMR均比FSNFK优秀，究其原因是FSNFK在CLL-SUB-111数据集上未充分考虑类与特征的相关性与冗余性而导致的。综合分析可知，FSNFK的性能表现良好。

    实验的第2部分选择FSNFK与文献[26]中的5种方法进行对比，包括：基于目标函数驱动的2种特征选择算法（K-means[30]和K-medoids[31]）、基于密度的2种特征选择算法（DBSCAN[32]和OPTICS[33]）和文献[26]的多元归一化互信息的无监督基因选择算法(unsupervised gene selection algorithm based on multivariate normalized mutual information of genes, GSMI )[26]。为了与文献[26]实验保持一致，从表1中选择5个数据集，选用文献[26]的分类精度指标，使用支持向量机(support vector machine, SVM)、 KNN和RF分类器评估所有对比算法，采用5折交叉验证。表3给出了3种分类器下6种算法在5个数据集上的分类精度。

    表  3  3种分类器下6种算法在5个数据集上的分类精度
    Table  3  Classification accuracy of six algorithms on five datasets under three classifiers %
    分类器数据集K-meansK-medoidsDBSCANOPTICSGSMIFSNFK
    SVMlung-cancer-20390.12±03.9287.67±03.4390.62±04.8578.33±02.3978.33±00.8693.07±02.88
    ALLAML65.24±01.1780.38±11.5181.90±11.6276.38±09.6483.1±10.8490.18±06.45
    COLON78.97±06.7167.56±12.1578.97±08.5474.49±08.3977.38±15.1485.26±08.13
    TOX17119.88±05.7046.20±07.7155.58±10.7856.81±09.9446.73±10.5397.06±02.63
    Ovarian97.63±01.4898.81±00.9699.60±00.8077.04±10.2997.64±02.2897.22±03.12
    平均70.37±03.8076.12±07.1581.33±07.3272.61±08.0776.64±07.9392.56±04.64
    KNNlung-cancer-20392.57±04.2189.64±05.7290.59±08.0988.17±01.0589.17±04.5591.12±03.25
    ALLAML68.09±05.0977.61±07.3181.81±09.7380.38±11.5177.90±10.9683.14±05.53
    COLON80.25±16.5179.23±07.6777.43±08.0672.56±08.4279.10±06.0183.33±10.54
    TOX17153.78±05.2045.00±03.6850.27±10.4547.36±04.5944.45±06.2594.12±04.92
    Ovarian95.24±01.6294.88±02.9297.23±02.0479.84±04.9094.88±04.2196.04±02.81
    平均77.99±06.5377.27±05.4679.47±07.6773.66±06.0977.10±06.4089.55±05.41
    RFlung-cancer-20386.21±01.1982.78±02.9982.28±03.5578.83±00.9682.28±01.6990.60±04.71
    ALLAML69.33±09.4186.00±12.0195.81±03.4287.33±09.4593.14±04.2291.43±07.00
    COLON82.05±12.3973.97±06.7785.38±06.3274.36±07.3977.56±09.1786.67±08.50
    TOX17149.78±11.6954.45±06.5053.88±13.3445.04±05.5353.83±05.9992.94±04.40
    Ovarian97.61±01.9494.87±03.6497.62±02.3278.65±05.4396.05±04.1197.22±03.47
    平均77.00±07.3278.41±06.3882.99±05.7972.84±05.7580.57±05.0491.77±05.62

    由表3可以看出，在SVM分类器下，在lung- cancer-203、ALLAML、COLON和TOX171这4个数据集上，FSNFK的分类精度优于其他算法，特别是在ALLAML、COLON和TOX171数据集上优势明显；在Ovarian数据集上，FSNFK的分类精度比最优的DBSCAN低2.38%，但是比OPTICS高20.18%。同时，FSNFK的平均分类精度优势明显。在KNN分类器下，在ALLAML、COLON和TOX171这3个数据集上，FSNFK优于其他5种对比算法，特别是在TOX171数据集上优势明显；在lung-cancer-203和Ovarian数据集上，FSNFK取得了次优的分类精度，分别比最优的K-means与DBSCAN低1.45%和0.41%，但是比其他算法分别高0.53%~2.95%和0.8%~16.2%。究其原因是FSNFK选取的特征仍存在部分冗余特征。同时，FSNFK的平均分类精度优势凸出。在RF分类器下，在lung-cancer-203、COLON和TOX171这3个数据集上，FSNFK的分类精度优于其他对比算法，特别是在lung-cancer-203和TOX171这2个数据集上，优势显著；在ALLAML和Ovarian这2个数据集上，FSNFK的分类精度分别比最优的DBSCAN低4.38和0.40，但是比其他3种算法分别高4.1%~22.1%和1.17%~18.57%。同时，FSNFK的平均分类精度表现最佳。另外，在这3种分类器下的Ovarian数据集以及在RF分类器下ALLAML数据集，FSNFK均略次于最优的DBSCAN，究其原因是这2个数据集存在个别异常值样本，而DBSCAN对异常值不敏感造成的。综合来看，FSNFK能够表现出良好的分类性能。

    3.3   聚类分析结果

    为了充分展示在不同数据集上实施FSNFK后对所选特征进行K-means聚类的效果，本节实验第1部分选择FSNFK与文献[26]中的5种方法进行对比，包括：K-means[30]、K-medoids[31]、DBSCAN[32]、OPTICS[33]和GSMI[26]。为了确保与文献[26]实验结果的一致性，从表1中选择5个数据集，在3.2节第2部分特征选择的基础上，首先对上述6种算法选择的特征子集实施K-means聚类分析，指定簇数为数据集中类的数目，然后选用文献[26]中标准互信息(normalized mutual information, NMI)、调整兰德系数(adjusted rand index, ARI)和F–分数(F-Score)这3种聚类指标评价所有对比算法的聚类效果，采用10折交叉实现实验验证。表4给出了3种聚类指标下6种算法在5个数据集上的聚类结果。

    表  4  3种聚类分析指标下6种算法在5个数据集上的聚类结果
    Table  4  Clustering results of six algorithms on five datasets under three clustering analysis metrics
    聚类指标数据集K-meansK-medoidsDBSCANOPTICSGSMIFSNFK
    NMIlung-cancer-2030.4860.3920.4170.3000.2250.492
    ALLAML0.0220.1360.1790.0330.2060.220
    COLON−0.001−0.007−0.0080.0070.0070.115
    TOX1710.0260.1930.1630.2580.2440.325
    Ovarian0.0630.0020.0040.004−0.0030.119
    平均0.1190.1430.1510.1200.1360.254
    ARIlung-cancer-2030.3360.2130.2360.1620.0760.371
    ALLAML0.0370.210−0.0190.0870.1610.233
    COLON0.018−0.0160.0050.011−0.006−0.021
    TOX1710.0190.1290.1350.1580.2900.232
    Ovarian0.0620.0060.021−0.001−0.0040.071
    平均0.0940.1080.0760.0830.1030.177
    F-Scorelung-cancer-2030.1380.3150.0300.2220.2120.702
    ALLAML0.6110.2640.4310.6670.7080.745
    COLON0.4030.5160.4190.4190.4520.608
    TOX1710.2920.3330.2110.3280.1350.525
    Ovarian0.3720.4510.5890.5300.5060.642
    平均0.3630.3760.3360.4330.4030.644

    由表4分析可知，在NMI指标下，FSNFK优于其他5种对比算法，特别是在COLON、TOX171和Ovarian数据集上，FSNFK优势明显，其NMI值比其他对比算法分别高0.108~0.123、0.067~0.299与0.056~0.122。同时，FSNFK的平均NMI优势明显。在ARI指标下，FSNFK在lung-cancer-203、ALLAML和Ovarian数据集上表现最优，特别是在lung-cancer-203和ALLAML数据集上，FSNFK的优势极为明显；在COLON与TOX171数据集上未能表现最优，究其原因为噪声点导致了实例类别划分与聚类划分的重叠程度较小而引起。同时，FSNFK的平均ARI明显最优。在F-Score指标下，FSNFK在这5个数据集上表现最优，特别是在lung-cancer-203、COLON和TOX171数据集上，其F-Score值比其他对比算法分别高0.387~0.672、0.092~0.205与0.192~0.390。同时，FSNFK的平均F-Score最优。总的来说，FSNFK在这5个数据集上的聚类效果优于其他5种算法，这表明该算法在特征选择之后有效提升了数据集的聚类分析性能。

    本节实验的第2部分选择FSNFK与文献[7]中4种方法进行对比，包括：UFSMI[27]、FSFC[21]、FMSU-FS[7]和MSU-FS[7]。为了与文献[7]实验保持一致，首先从表1中选择了9个数据集，对上述5种算法选择的特征子集实施K-means聚类分析，指定簇数为数据集中类的数目，然后使用NMI、ARI和F-Score这3种聚类分析指标评价所有对比算法，采用5折交叉验证方法实现。表5给出了3种聚类指标下5种算法在9个数据集上的聚类结果。

    表  5  3种聚类分析指标下5种算法在9个数据集上的聚类结果
    Table  5  Clustering results of five algorithms on nine datasets under three clustering analysis metrics
    聚类指标数据集UFSMIFSFCMSU-FSFMSU-FSFSNFK
    NMIWine0.13950.19530.08250.15700.3288
    Sonar0.00360.00850.01160.20580.3331
    Breast Cancer0.50230.28500.04560.37420.2400
    Breast Tissue0.40750.32530.23010.32950.5505
    Parkinsons0.19600.06930.0911−0.00580.2925
    warpPIE10P0.12400.25790.24620.09310.4535
    warpAR10P0.12720.14420.18940.28360.5103
    TOX1710.19250.24680.23480.05890.3570
    Lung-cancer−0.0188−0.03040.08570.37080.1470
    平均0.18600.16690.13520.23410.3570
    ARIWine0.10990.19690.05220.09110.3060
    Sonar−0.00300.01260.01580.04830.3181
    Breast Cancer0.55610.28190.08360.39630.3000
    Breast Tissue0.24800.21040.09390.22890.2987
    Parkinsons0.14620.16670.05400.06550.3854
    warpPIE10P0.05980.10170.11040.02950.2162
    warpAR10P0.06510.07400.10710.15530.2485
    TOX1710.14660.11090.18310.05460.2661
    Lung-cancer−0.0098−0.02940.07470.30960.1727
    平均0.16520.12510.08610.15320.2791
    F-ScoreWine0.18580.22340.32280.38030.6607
    Sonar0.45680.44810.48080.52080.6772
    Breast Cancer0.10520.64770.54710.68880.7550
    Breast Tissue0.06710.06290.08170.01470.5618
    Parkinsons0.63870.18880.26110.22660.8276
    warpPIE10P0.11410.07740.14660.11300.4624
    warpAR10P0.10760.11410.12630.09930.4855
    TOX1710.17340.18730.12960.29210.5602
    Lung-cancer0.14060.29740.24550.40180.7343
    平均0.22100.24970.26020.30420.6361

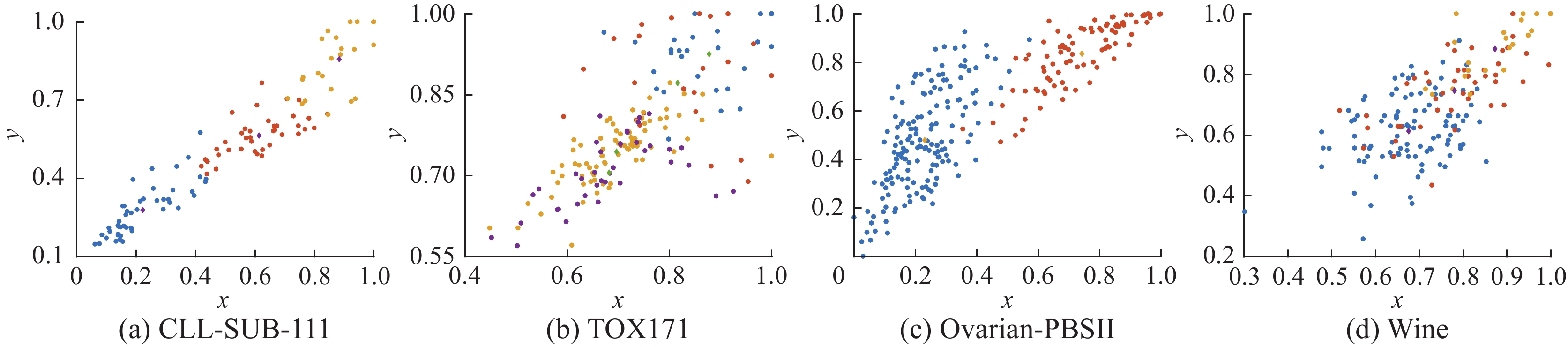
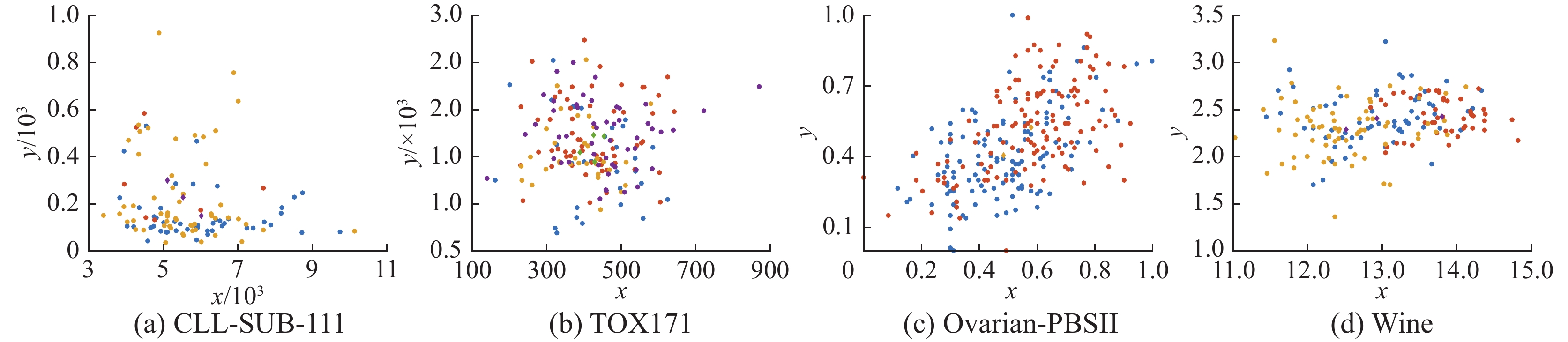
    根据表5可知，在NMI指标下，Wine、Sonar、Breast Tissue、Parkinsons、warpPIE10P、warp-AR10P和TOX171数据集上，FSNFK优于其他4种对比算法，特别是在Breast Tissue、warp-PIE10P和warpAR10P数据集上，其NMI值分别比其他对比算法高0.143~0.3204、0.1956~0.3604与0.2267~ 0.3831；在Breast Cancer数据集上，FSNFK的NMI值尽管比最优的UFSMI低0.2623，但是比MSU-FS高0.1944；在Lung-cancer数据集上，FSNFK的NMI值比最优的FMSU-FS低0.2238，但是比其他算法高0.0613~0.1774。同时，FSNFK的平均NMI优势明显。在ARI指标下，FSNFK在Wine、So-nar、Breast Tissue、Parkinsons、warpPIE10P、warpAR10P和TOX171数据集上的表现最佳，特别是在Wine、Sonar和Parkinsons这3个数据集上，FSNFK的优势明显；在Breast Cancer数据集上，FSNFK的ARI值尽管比最优的UFSMI低0.2561，但是比FSFC和MSU-FS分别高0.0181和0.2164；在Lung-cancer数据集上，FSNFK的ARI值为次优，比最优的FMSU-FS低0.1369，但比其他对比算法高0.098~0.2021。同时，FSNFK的平均ARI优势凸出。在F-Score指标下，FSNFK在9个数据集上的表现均最优，尤其是在Breast Tissue、warpPIE10P、warpAR10P和Lung-cancer数据集上，优势特别明显。另外，在Breast Cancer数据集上，UFSMI的NMI和ARI均比FSNFK优秀，究其原因是UFSMI采用互信息标准测量特征之间的统计相关性并去除不相关的特征。在Lung-cancer数据集上，FMSU-FS的NMI和ARI均比FSNFK优秀，究其原因是FSNFK在进行特征选择时丢失了个别关键特征造成的。总的来说，FSNFK在9个数据集上的3种聚类分析指标表现均优于其他对比算法，这说明通过FSNFK算法的特征选择之后能够有效提升聚类分析的性能。

    最后，由于篇幅限制，为了直观展示在代表性数据集上实施FSNFK算法前后的聚类效果，从表1中选择CLL-SUB-111、TOX171、Ovarian-PBSII和Wine共4个代表性数据集，图1和图2分别给出了在4个数据集上未使用FSNFK和使用FSNFK的K-means聚类结果，其中，指定簇的数目为数据集中的类别数。通过比较图1和图2的聚类效果，当实施FSNFK后，在这4个数据集上的K-means聚类效果更优，不同簇之间的区分更明显。

    图  1  4个数据集上的K-means聚类结果
    Fig.  1  K-means clustering results of four datasets
    下载: 全尺寸图片
    图  2  4个数据集上实施FSNFK算法之后的K-means聚类结果
    Fig.  2  K-means clustering results of four datasets after performing FSNFK algorithm
    下载: 全尺寸图片

    3.4   运行时间对比

    为了说明FSNFK算法的运行效率，从表1中选择6个代表性数据集，与文献[26]中的3种算法(K-means[30]、DBSCAN[32]和OPTICS[33])和FSFC[21]算法对比运行时间，如表6所示。根据表6分析可知，FSNFK的运行时间最低，明显优于其他4种对比算法，说明FSNFK具有很好的时效性。

    表  6  5种算法在8个数据集上的运行时间
    Table  6  Running time of five algorithms on eight datasets s
    数据集FSFCOPTICSDBSCANK-meansFSNFK
    warpPIE10P12.81514.02010.40010.7069.089
    lung-cancer-203151.281179.581142.383153.62655.964
    ALLAML47.80766.21048.00546.5527.568
    Ovarian-PBSII245.426328.027339.360248.6253.990
    Isolet94.777336.25663.123111.53330.957
    CLL-SUB-111102.180101.186103.766101.77616.038

    3.5   统计分析

    采用文献[17]中Friedman检验与Nemenyi测试展示对比算法的统计性能。根据文献[36]中统计方法，CD图展示算法之间的差异性。表7给出了表2中8种算法在 KNN、C4.5和RF分类器下F1_Macro的统计结果。表8给出了表3中6种算法在SVM、KNN和RF分类器下分类精度的统计结果。表9给出了表4中6种算法在NMI、ARI和F-Score指标下聚类的统计结果。表10给出了表5中5种算法在NMI、ARI和F-Score指标下聚类的统计结果。

    表  7  8种算法在 KNN、C4.5和RF分类器下F1_Macro的统计结果
    Table  7  Statistical results of eight algorithms in terms of F1_Macro under the KNN, C4.5 and RF classifiers
    分类器FullSetMICIMRIG-RFEIWFSCRFSDRGSMRIFSNFK$ \chi _F^2 $FF
    KNN6.332.335.837.175.333.504.331.1729.7812.18
    C4.56.501.834.506.835.833.674.832.0025.397.64
    RF6.501.835.006.676.003.834.831.3328.8911.02
    表  8  6种算法在SVM、KNN和RF分类器下分类精度的统计结果
    Table  8  Statistical results of six algorithms in terms of classification accuracy under the SVM, KNN and RF classifiers
    分类器K-meansK-medoidsDBSCANOPTICSGSMIFSNFK$ \chi _F^2 $FF
    SVM4.204.202.404.603.801.809.112.30
    KNN2.84.22.854.81.414.035.11
    RF3.64.22.25.43.81.812.544.03
    表  9  6种算法在NMI、ARI和F-Score指标下聚类的统计结果
    Table  9  Clustering statistical results of six algorithms in terms of the NMI, ARI and F-Score metrics
    指标K-meansK-medoidsDBSCANOPTICSGSMIFSNFK$ \chi _F^2 $FF
    NMI4.004.404.003.604.001.0011.173.23
    ARI3.204.003.803.804.002.203.510.65
    F-Score5.003.404.403.403.801.0013.464.66
    表  10  5种算法在NMI、ARI和F-Score指标下聚类的统计结果
    Table  10  Clustering statistical results of five algorithms in terms of the NMI, ARI and F-Score metrics
    指标UFSMIFSFCMSU-FSFMSU-FSFSNFK$ \chi _F^2 $FF
    NMI3.443.333.663.111.4411.473.74
    ARI3.333.563.673.111.3313.164.61
    F-Score3.893.893.113.11120.1810.20

    当显著性水平为0.1时，临界值为1.90，表2对应的Nemenyi测试结果如图3所示。由图3(a)可知，FSNFK优于其他7种算法，尽管FSNFK与DRGS、IWFS之间不存在显著性差异。在图3(b)中，尽管FSNFK排名略次于MICIMR，但是明显优于CRFS、FullSet和IWFS，另外FSNFK与CRFS之间不存在显著性差异。在图3(c)中，FSNFK明显优于其他7种算法，尽管FSNFK与IG-RFE之间不存在显著性差异。当显著性水平为0.1时，临界值为2.16，表3对应的Nemenyi测试结果如图4所示。由图4可以看出，FSNFK在SVM、KNN和RF分类器下表现最优。在图4(b)和图4(c)中，FSNFK与K-medoids之间不存在显著性差异。当显著性水平为0.1时，临界值为2.16，表4对应的Nemenyi测试结果如图5所示。由图5看出，FSNFK在NMI、ARI和F-Score指标下表现最优。在图5(a)中，FSNFK与K-means之间不存在显著性差异；在图5(c)中，FSNFK与GSMI不存在显著性差异。当显著性水平为0.1时，临界值为1.87，表5对应的Nemenyi测试结果如图6所示。由图6可以看出，FSNFK在NMI、ARI和F-Score指标上表现最佳。在图6(a)中，FSNFK与K-means不存在显著性差异。在图6(c)中，FSNFK与GSMI不存在显著性差异。总的来说，FSNFK表现均优于其他对比算法。

    图  3  8种算法在 KNN、C4.5和RF分类器下F1_Macro的Nemenyi测试结果
    Fig.  3  Nemenyi test results of eight algorithms in terms of F1_Macro under the KNN, C4.5 and RF classifiers
    下载: 全尺寸图片
    图  4  6种算法在SVM、KNN和RF分类器下分类精度的Nemenyi测试结果
    Fig.  4  Nemenyi test results of six algorithms in terms of classificaiton accuracy under the SVM, KNN and RF classifiers
    下载: 全尺寸图片
    图  5  6种算法在NMI、ARI和F-Score指标下的Nemenyi测试结果
    Fig.  5  Nemenyi test results of six algorithms in terms of the NMI, ARI and F-Score metrics
    下载: 全尺寸图片
    图  6  5种算法在NMI、ARI和F-Score指标下的Nemenyi测试结果
    Fig.  6  Nemenyi test results of five algorithms in terms of the NMI, ARI and F-Score metrics
    下载: 全尺寸图片

    4.   结束语

    本文提出了基于邻域互信息与K-means特征聚类的特征选择方法。首先，定义了每个样本的自适应邻域半径，由此找到每个样本的邻域集，并在此基础上构建了归一化邻域互信息度量特征之间的相关性。然后，定义了自适应K近邻集合，基于Pearson相关系数提出了加权K近邻密度，进而实现K-means特征聚类。最后，给出了加权平均冗余度，选出每个特征簇中加权平均冗余度最大的特征构成特征子集。但是，所提算法未充分考虑特征之间的相关性、冗余性与互补性等问题，导致未能在所有数据集上取得最优的分类效果，因而，在未来的研究工作中将注重解决上述问题。

  • 图  1   4个数据集上的K-means聚类结果

    Fig.  1   K-means clustering results of four datasets

    下载: 全尺寸图片

    图  2   4个数据集上实施FSNFK算法之后的K-means聚类结果

    Fig.  2   K-means clustering results of four datasets after performing FSNFK algorithm

    下载: 全尺寸图片

    图  3   8种算法在 KNN、C4.5和RF分类器下F1_Macro的Nemenyi测试结果

    Fig.  3   Nemenyi test results of eight algorithms in terms of F1_Macro under the KNN, C4.5 and RF classifiers

    下载: 全尺寸图片

    图  4   6种算法在SVM、KNN和RF分类器下分类精度的Nemenyi测试结果

    Fig.  4   Nemenyi test results of six algorithms in terms of classificaiton accuracy under the SVM, KNN and RF classifiers

    下载: 全尺寸图片

    图  5   6种算法在NMI、ARI和F-Score指标下的Nemenyi测试结果

    Fig.  5   Nemenyi test results of six algorithms in terms of the NMI, ARI and F-Score metrics

    下载: 全尺寸图片

    图  6   5种算法在NMI、ARI和F-Score指标下的Nemenyi测试结果

    Fig.  6   Nemenyi test results of five algorithms in terms of the NMI, ARI and F-Score metrics

    下载: 全尺寸图片

    表  1   19个数据集的描述

    Table  1   Description of nineteen datasets

    编号数据集样本数属性数类别数
    1Wpbc198312
    2Isolet156061726
    3CLL-SUB-1111440102420
    4lung20333125
    5movement-libras3609015
    6SPAMBASE4601572
    7lung-cancer-203203126005
    8ALLAML7271292
    9COLON6220002
    10TOX17117157484
    11Ovarian-PBSII253151552
    12Wine178133
    13Sonar208602
    14Breast Cancer569312
    15Breast Tissue10696
    16Parkinsons197222
    17warpPIE10P21024202
    18warpAR10P130240010
    19Lung cancer32562

    表  2   3种分类器下8种算法在6个数据集上的F1_Macro

    Table  2   F1_Macro of eight algorithms on six datasets under three classifiers %

    分类器数据集FullSetMICIMRIG-RFEIWFSCRFSDRGSMRIFSNFK
    KNNWpbc10.5114.239.1511.2010.3114.8010.3161.02
    ISOLET26.7666.0846.8237.0544.5855.9456.9672.72
    CLL-SUB-11168.3076.6666.0260.7064.1175.6764.4377.75
    lung62.4875.4266.6352.4268.4376.2376.3482.89
    movement-libras68.0382.5770.5267.6574.0774.6574.0784.13
    SPAMBASE81.3789.7786.7881.3287.1983.0288.2188.56
    平均52.9167.4657.6551.7258.1263.3961.7277.85
    C4.5Wpbc13.4314.6612.4111.8110.0413.9312.1160.60
    ISOLET26.1466.4042.2638.2238.9750.9750.7266.42
    CLL-SUB-11162.7168.9562.4563.3064.6267.6057.1061.50
    lung58.2881.5774.9454.8366.3568.1970.6582.60
    movement-libras56.7566.5363.3357.3159.5262.3362.4268.03
    SPAMBASE87.3390.2889.3686.1188.9989.4589.6891.18
    平均50.7764.7357.4651.9354.7558.7557.1169.55
    RFWpbc16.6317.6216.8217.5116.1417.1014.5064.25
    ISOLET29.0171.2847.6847.9846.5857.0760.2582.80
    CLL-SUB-11168.3076.6666.0260.7064.1175.6764.4372.85
    lung60.6480.1370.8151.3564.4773.1174.9687.02
    movement-libras65.5576.0167.8362.9469.3771.4966.3884.27
    SPAMBASE89.8692.5691.8589.6891.8490.8992.0293.70
    平均55.0069.0460.1755.0358.7564.2262.0980.82
    注：加黑代表最优结果，下同。

    表  3   3种分类器下6种算法在5个数据集上的分类精度

    Table  3   Classification accuracy of six algorithms on five datasets under three classifiers %

    分类器数据集K-meansK-medoidsDBSCANOPTICSGSMIFSNFK
    SVMlung-cancer-20390.12±03.9287.67±03.4390.62±04.8578.33±02.3978.33±00.8693.07±02.88
    ALLAML65.24±01.1780.38±11.5181.90±11.6276.38±09.6483.1±10.8490.18±06.45
    COLON78.97±06.7167.56±12.1578.97±08.5474.49±08.3977.38±15.1485.26±08.13
    TOX17119.88±05.7046.20±07.7155.58±10.7856.81±09.9446.73±10.5397.06±02.63
    Ovarian97.63±01.4898.81±00.9699.60±00.8077.04±10.2997.64±02.2897.22±03.12
    平均70.37±03.8076.12±07.1581.33±07.3272.61±08.0776.64±07.9392.56±04.64
    KNNlung-cancer-20392.57±04.2189.64±05.7290.59±08.0988.17±01.0589.17±04.5591.12±03.25
    ALLAML68.09±05.0977.61±07.3181.81±09.7380.38±11.5177.90±10.9683.14±05.53
    COLON80.25±16.5179.23±07.6777.43±08.0672.56±08.4279.10±06.0183.33±10.54
    TOX17153.78±05.2045.00±03.6850.27±10.4547.36±04.5944.45±06.2594.12±04.92
    Ovarian95.24±01.6294.88±02.9297.23±02.0479.84±04.9094.88±04.2196.04±02.81
    平均77.99±06.5377.27±05.4679.47±07.6773.66±06.0977.10±06.4089.55±05.41
    RFlung-cancer-20386.21±01.1982.78±02.9982.28±03.5578.83±00.9682.28±01.6990.60±04.71
    ALLAML69.33±09.4186.00±12.0195.81±03.4287.33±09.4593.14±04.2291.43±07.00
    COLON82.05±12.3973.97±06.7785.38±06.3274.36±07.3977.56±09.1786.67±08.50
    TOX17149.78±11.6954.45±06.5053.88±13.3445.04±05.5353.83±05.9992.94±04.40
    Ovarian97.61±01.9494.87±03.6497.62±02.3278.65±05.4396.05±04.1197.22±03.47
    平均77.00±07.3278.41±06.3882.99±05.7972.84±05.7580.57±05.0491.77±05.62

    表  4   3种聚类分析指标下6种算法在5个数据集上的聚类结果

    Table  4   Clustering results of six algorithms on five datasets under three clustering analysis metrics

    聚类指标数据集K-meansK-medoidsDBSCANOPTICSGSMIFSNFK
    NMIlung-cancer-2030.4860.3920.4170.3000.2250.492
    ALLAML0.0220.1360.1790.0330.2060.220
    COLON−0.001−0.007−0.0080.0070.0070.115
    TOX1710.0260.1930.1630.2580.2440.325
    Ovarian0.0630.0020.0040.004−0.0030.119
    平均0.1190.1430.1510.1200.1360.254
    ARIlung-cancer-2030.3360.2130.2360.1620.0760.371
    ALLAML0.0370.210−0.0190.0870.1610.233
    COLON0.018−0.0160.0050.011−0.006−0.021
    TOX1710.0190.1290.1350.1580.2900.232
    Ovarian0.0620.0060.021−0.001−0.0040.071
    平均0.0940.1080.0760.0830.1030.177
    F-Scorelung-cancer-2030.1380.3150.0300.2220.2120.702
    ALLAML0.6110.2640.4310.6670.7080.745
    COLON0.4030.5160.4190.4190.4520.608
    TOX1710.2920.3330.2110.3280.1350.525
    Ovarian0.3720.4510.5890.5300.5060.642
    平均0.3630.3760.3360.4330.4030.644

    表  5   3种聚类分析指标下5种算法在9个数据集上的聚类结果

    Table  5   Clustering results of five algorithms on nine datasets under three clustering analysis metrics

    聚类指标数据集UFSMIFSFCMSU-FSFMSU-FSFSNFK
    NMIWine0.13950.19530.08250.15700.3288
    Sonar0.00360.00850.01160.20580.3331
    Breast Cancer0.50230.28500.04560.37420.2400
    Breast Tissue0.40750.32530.23010.32950.5505
    Parkinsons0.19600.06930.0911−0.00580.2925
    warpPIE10P0.12400.25790.24620.09310.4535
    warpAR10P0.12720.14420.18940.28360.5103
    TOX1710.19250.24680.23480.05890.3570
    Lung-cancer−0.0188−0.03040.08570.37080.1470
    平均0.18600.16690.13520.23410.3570
    ARIWine0.10990.19690.05220.09110.3060
    Sonar−0.00300.01260.01580.04830.3181
    Breast Cancer0.55610.28190.08360.39630.3000
    Breast Tissue0.24800.21040.09390.22890.2987
    Parkinsons0.14620.16670.05400.06550.3854
    warpPIE10P0.05980.10170.11040.02950.2162
    warpAR10P0.06510.07400.10710.15530.2485
    TOX1710.14660.11090.18310.05460.2661
    Lung-cancer−0.0098−0.02940.07470.30960.1727
    平均0.16520.12510.08610.15320.2791
    F-ScoreWine0.18580.22340.32280.38030.6607
    Sonar0.45680.44810.48080.52080.6772
    Breast Cancer0.10520.64770.54710.68880.7550
    Breast Tissue0.06710.06290.08170.01470.5618
    Parkinsons0.63870.18880.26110.22660.8276
    warpPIE10P0.11410.07740.14660.11300.4624
    warpAR10P0.10760.11410.12630.09930.4855
    TOX1710.17340.18730.12960.29210.5602
    Lung-cancer0.14060.29740.24550.40180.7343
    平均0.22100.24970.26020.30420.6361

    表  6   5种算法在8个数据集上的运行时间

    Table  6   Running time of five algorithms on eight datasets s

    数据集FSFCOPTICSDBSCANK-meansFSNFK
    warpPIE10P12.81514.02010.40010.7069.089
    lung-cancer-203151.281179.581142.383153.62655.964
    ALLAML47.80766.21048.00546.5527.568
    Ovarian-PBSII245.426328.027339.360248.6253.990
    Isolet94.777336.25663.123111.53330.957
    CLL-SUB-111102.180101.186103.766101.77616.038

    表  7   8种算法在 KNN、C4.5和RF分类器下F1_Macro的统计结果

    Table  7   Statistical results of eight algorithms in terms of F1_Macro under the KNN, C4.5 and RF classifiers

    分类器FullSetMICIMRIG-RFEIWFSCRFSDRGSMRIFSNFK$ \chi _F^2 $FF
    KNN6.332.335.837.175.333.504.331.1729.7812.18
    C4.56.501.834.506.835.833.674.832.0025.397.64
    RF6.501.835.006.676.003.834.831.3328.8911.02

    表  8   6种算法在SVM、KNN和RF分类器下分类精度的统计结果

    Table  8   Statistical results of six algorithms in terms of classification accuracy under the SVM, KNN and RF classifiers

    分类器K-meansK-medoidsDBSCANOPTICSGSMIFSNFK$ \chi _F^2 $FF
    SVM4.204.202.404.603.801.809.112.30
    KNN2.84.22.854.81.414.035.11
    RF3.64.22.25.43.81.812.544.03

    表  9   6种算法在NMI、ARI和F-Score指标下聚类的统计结果

    Table  9   Clustering statistical results of six algorithms in terms of the NMI, ARI and F-Score metrics

    指标K-meansK-medoidsDBSCANOPTICSGSMIFSNFK$ \chi _F^2 $FF
    NMI4.004.404.003.604.001.0011.173.23
    ARI3.204.003.803.804.002.203.510.65
    F-Score5.003.404.403.403.801.0013.464.66

    表  10   5种算法在NMI、ARI和F-Score指标下聚类的统计结果

    Table  10   Clustering statistical results of five algorithms in terms of the NMI, ARI and F-Score metrics

    指标UFSMIFSFCMSU-FSFMSU-FSFSNFK$ \chi _F^2 $FF
    NMI3.443.333.663.111.4411.473.74
    ARI3.333.563.673.111.3313.164.61
    F-Score3.893.893.113.11120.1810.20
    • 参考文献(36)
  • [1] SONG Xianfang, ZHANG Yong, GONG Dunwei, et al. A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high- dimensional data[J]. IEEE transactions on cybernetics, 2022, 52(9): 9573–9586. doi: 10.1109/TCYB.2021.3061152
    [2] 梁云辉, 甘舰文, 陈艳, 等. 基于对偶流形重排序的无监督特征选择算法[J]. 计算机科学, 2023, 50(7): 72–81. doi: 10.11896/jsjkx.221000143

    LIANG Yunhui, GANJianwen, CHEN Yan, et al. Unsupervised feature selection algorithm based on dual manifold re-ranking[J]. Computer science, 2023, 50(7): 72–81. doi: 10.11896/jsjkx.221000143
    [3] 侯天宝, 王爱银. 基于Stacking特征增强多粒度联级Logistic的个人信用评估[J]. 河南师范大学学报(自然科学版), 2023, 51(3): 111–122.

    HOU Tianbao, WANG Aiyin. Personal credit evaluation based on stacking feature enhancing multi-grained cascade logistic[J]. Journal of Henan Normal University (natural science edition), 2023, 51(3): 111–122.
    [4] 杨洁, 匡俊成, 王国胤, 等. 代价敏感的多粒度邻域粗糙模糊集的近似表示[J]. 计算机科学, 2023, 50(5): 137–145. doi: 10.11896/jsjkx.220500268

    YANG Jie, KUANG Juncheng, WANG Guoyin, et al. Cost-sentitive multigranulation approximation of neighborhood rough fuzzy sets[J]. Computer science, 2023, 50(5): 137–145. doi: 10.11896/jsjkx.220500268
    [5] HU Qinghua, ZHANG Lei, ZHANG David, et al. Measuring relevance between discrete and continuous features based on neighborhood mutual information[J]. Expert systems with applications, 2011, 38: 10737–10750. doi: 10.1016/j.eswa.2011.01.023
    [6] 孙林, 梁娜, 徐久成. 基于自适应邻域互信息与谱聚类的特征选择[J]. 山东大学学报(理学版), 2022, 57(12): 13–24.

    SUN Lin, LIANG Na, XU Jiucheng. Feature selection using adaptive neighborhood mutual information and spectral clustering[J]. Journal of Shandong University (nature science edition), 2022, 57(12): 13–24.
    [7] RAHMANIAN M, MANSOORI E. Unsupervised fuzzy multivariate symmetric uncertainty feature selection based on constructing virtual cluster representative[J]. Fuzzy sets and systems, 2022, 438: 148–163. doi: 10.1016/j.fss.2021.07.015
    [8] 孙林, 秦小营, 徐久成, 等. 基于K近邻和优化分配策略的密度峰值聚类算法[J]. 软件学报, 2022, 33(4): 1390–1411.

    SUN Lin, QIN Xiaoying, XU Jiucheng, et al. Density peak clustering algorithm based on k-nearest neighbors and optimized allocation[J]. Journal of software, 2022, 33(4): 1390–1411.
    [9] 张新元, 贠卫国. 共享K近邻和多分配策略的密度峰值聚类算法[J]. 小型微型计算机系统, 2023, 44(1): 75–82.

    ZHANG Xinyuan, YUN Weiguo. Sharing K-nearest neighbors and multiple assignment policies density peaks[J]. Journal of chinese computer systems, 2023, 44(1): 75–82.
    [10] 孙林, 李梦梦, 徐久成. 二进制哈里斯鹰优化及其特征选择算法[J]. 计算机科学, 2023, 50(5): 277–291. doi: 10.11896/jsjkx.220300269

    SUN Lin, LI Mengmeng, XU Jiucheng. Binary Harris hawk optimization and its feature selection algorithm[J]. Computer science, 2023, 50(5): 277–291. doi: 10.11896/jsjkx.220300269
    [11] 曹栋涛, 舒文豪, 钱进. 基于粗糙集与密度峰值聚类的特征选择算法[J]. 计算机科学, 2023, 50(10): 37–47. doi: 10.11896/jsjkx.230600038

    CAO Dongtao, SHU Wenhao, QIAN Jin. Feature selection algorithm based on rough setand density peak clustering[J]. Computer science, 2023, 50(10): 37–47. doi: 10.11896/jsjkx.230600038
    [12] 徐天杰, 王平心, 杨习贝. 基于人工蜂群的三支k-means聚类算法[J]. 计算机科学, 2023, 50(6): 116–121. doi: 10.11896/jsjkx.220800150

    XU Tianjie, WANG Pingxin, YANG Xibei. Three-way k-means clustering based on artificial bee colony[J]. Computer science, 2023, 50(6): 116–121. doi: 10.11896/jsjkx.220800150
    [13] 李冰晓, 万睿之, 朱永杰, 等. 基于种群分区的多策略综合粒子群优化算法[J]. 河南师范大学学报(自然科学版), 2022, 50(3): 85–94.

    LI Bingxiao, WAN Ruizhi, ZHU Yongjie, et al. Multi-strategy comprehensive particle swarm optimization algorithm based on population partition[J]. Journal of Henan Normal University (natural science edition), 2022, 50(3): 85–94.
    [14] CHEN Zhijun, CHEN Qiushi, ZHANG Yishi, et al. Clustering-based feature subset selection with analysis on the redundancy-complementarity dimension[J]. Computer communications, 2021, 168: 65–74. doi: 10.1016/j.comcom.2021.01.005
    [15] SUN Lin, QIN Xiaoying, DING Weiping, et al. Nearest neighbors-based adaptive density peaks clustering with optimized allocation strategy[J]. Neurocomputing, 2022, 473: 159–181. doi: 10.1016/j.neucom.2021.12.019
    [16] 辛永杰, 蔡江辉, 贺艳婷, 等. 基于跨结构特征选择和图循环自适应学习的多视图聚类[J/OL]. 计算机科学, 2024. [2024−05−14]. https://link.cnki.net/urlid/50.1075.tp.20240513.1427.017.

    XIN Yongjie, CAI Jianghui, HE Yanting et al. Multi-view clustering based on cross-structural feature selection and graph cycle adaptive learning[J/OL]. Computer science, 2024. [2024−05−14]. https://link.cnki.net/urlid/50.1075.tp.20240513.1427.017.
    [17] 孙林, 马天娇. 基于中心偏移的Fisher score与直觉邻域模糊熵的多标记特征选择[J/OL]. 计算机科学, (2023-11-14)[2023-12-06]. https://link.cnki.net/urlid/50.1075.TP.20231113.1009.012.

    SUN Lin, MA Tianjiao. Multilabel feature selection using fisher score with center shift and neighborhood intuitionistic fuzzy entropy[J/OL]. Computer science, (2023-11-14)[2023-12-06].https://link.cnki. net/urlid/50.1075.TP.20231113.1009.012.
    [18] 赵燕伟, 朱芬, 桂方志, 等. 基于可拓距的改进K-means聚类算法[J]. 智能系统学报, 2020, 15(2): 344–351.

    ZHAO Yanwei, ZHU Fen, GUI Fangzhi, et al. Improved K-means algorithm based on extension distance[J]. CAAI transactions on intelligent systems, 2020, 15(2): 344–351.
    [19] 王雷, 杜亮, 周芃. 基于稀疏连接的层次化多核K-Means算法[J]. 计算机科学, 2023, 50(2): 138–145.

    WAND Lei, DU Liang, ZHOU Peng. Hierarchical multiple kernel K-means algorithm based on sparse connectivity[J]. Computer science, 2023, 50(2): 138–145.
    [20] GUSTAVO S C, MIGUEL G T, SANTIAGO G G, et al. A multivariate approach to the symmetrical uncertainty measure: Application to feature selection problem[J]. Information sciences, 2019, 494: 1–20. doi: 10.1016/j.ins.2019.04.046
    [21] ZHU Xiaoyan, WANG Yu, LI Yingbin, et al. A new unsupervised feature selection algorithm using similarity-based feature clustering[J]. Computational intelligence, 2019, 35(1): 2–22. doi: 10.1111/coin.12192
    [22] ALHELALI B, CHEN Qi, XUE Bing, et al. A new imputation method based on genetic programming and weighted KNN for symbolic regression with incomplete data[J]. Soft computing, 2021, 25(8): 5993–6012. doi: 10.1007/s00500-021-05590-y
    [23] SUN Lin, ZHANG Jiuxiao, DING Weiping, et al. Mixed measure-based feature selection using the Fisher score and neighborhood rough sets[J]. Applied intelligence, 2022, 52: 17264–17288. doi: 10.1007/s10489-021-03142-3
    [24] ZHANG Li, CHEN Xiaobo. Feature selection methods based on symmetric uncertainty coefficients and independent classification information[J]. IEEE access, 2021, 9: 13845–13856. doi: 10.1109/ACCESS.2021.3049815
    [25] LIN Xiaohui, LI Chao, REN Wenjie, et al. A new feature selection method based on symmetrical uncertainty and interaction gain[J]. Computational biology and chemistry, 2019, 83: 107149. doi: 10.1016/j.compbiolchem.2019.107149
    [26] RAHMANIAN M, MANSOORI E G. An unsupervised gene selection method based on multivariate normalized mutual information of genes[J]. Chemometrics and intelligent laboratory systems, 2022, 222: 104512. doi: 10.1016/j.chemolab.2022.104512
    [27] FAIVISHEVSKY L, GOLDBERGER J. Unsupervised feature selection based on non-parametric mutual information[C]// 2012 IEEE international workshop on machine learning for signal processing. Santander: IEEE, 2012: 1−6.
    [28] SUN Xin, LIU Yanheng, WEI Da, et al. Selection of interdependent genes via dynamic relevance analysis for cancer diagnosis[J]. Journal of biomedical informatics, 2013, 46(2): 252–258. doi: 10.1016/j.jbi.2012.10.004
    [29] WANG Jun, WEI Jinmao, YANG Zhenglu, et al. Feature selection by maximizing independent classification information[J]. IEEE transactions on knowledge and data engineering, 2017, 29(4): 828–841. doi: 10.1109/TKDE.2017.2650906
    [30] MACQUEEN J. B. Some methods for classification and analysis of multivariate observations[C]//Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. Los Angeles: University of California Press, 1967: 281−297.
    [31] KAUFMAN L, ROUSSEEUW P J. Finding groups in data: an introduction to cluster analysis[M]. Hoboken: Wiley Online Library, 1991.
    [32] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2th International Conference on Knowledge Discovery and Data Mining. Muenchen: AAAI Press, 1996: 226–231.
    [33] ANKERST M, BREUNIG M M, KRIEGEL H P, et al. OPTICS: ordering points to identify the clustering structure [C]//Proceedings of ACM SIGMOD International Conference on Management of Data. New York: ACM, 1999: 49–60.
    [34] ZENG Zilin, ZHANG Hongjun, ZHANG Rui, et al. A novel feature selection method considering feature interaction[J]. Pattern recognition, 2015, 48(8): 2656–2666. doi: 10.1016/j.patcog.2015.02.025
    [35] 刘杰, 张平, 高万夫. 基于条件相关的特征选择方法[J]. 吉林大学学报(工学版), 2018, 48(3): 874–881.

    LIU Jie, ZHANG Ping, GAO Wanfu. Feature selection method based on conditional relevance[J]. Journal of Jilin University (engineering and technology edition), 2018, 48(3): 874–881.
    [36] 孙林, 徐枫, 李硕, 等. 基于ReliefF和最大相关最小冗余的多标记特征选择[J]. 河南师范大学学报(自然科学版), 2023, 51(6): 21–29.

    SUN Lin, XU Feng, LI Shuo, et al. Multilabel feature selection algorithm using ReliefF and mRMR[J]. Journal of Henan Normal University (natural science edition), 2023, 51(6): 21–29.
WeChat 点击查看大图
图(6)  /  表(10)
出版历程
  • 收稿日期:  2022-08-12
  • 网络出版日期:  2024-04-10

目录

    /

    返回文章
    返回