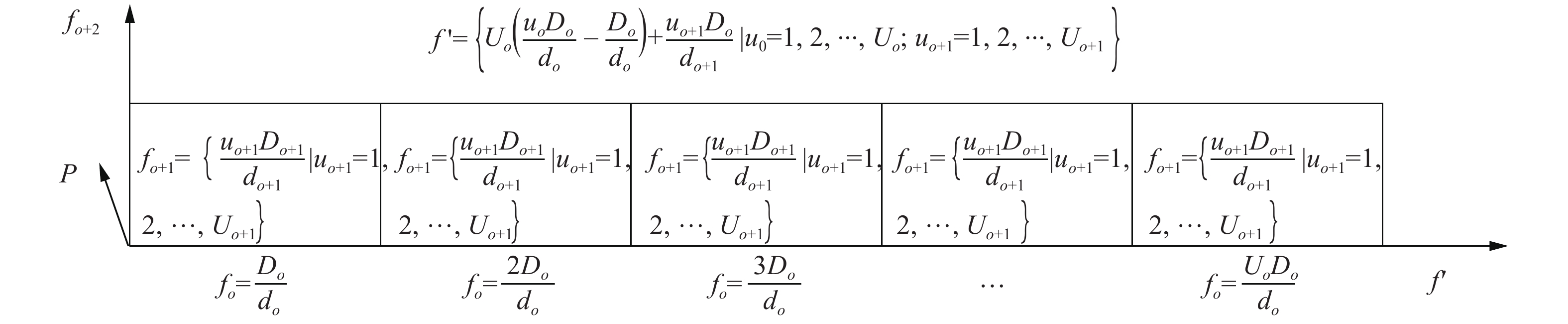Research on the connection number representation of event states under the influence of multi-factor fluctuations
-
摘要: 为研究在因素波动影响下事件状态变化和不同状态出现的可能性,本文将语义划分与集对分析联系数的多级状态对应,建立因素波动影响下的事件状态联系数表示方法。制定了单因素波动情况下事件状态联系数的构建方法,以单位因素区间对因素平面进行离散,分别计算各离散区域的联系数,综合所有联系数形成事件状态联系数。根据数值逻辑的或关系和联系数运算法则耦合单因素事件状态联系数得到2因素事件状态联系数。多因素通过切片法降维至2因素才可使用上述方法。本文证明了离散求解与整体求解的等价性,使用各语义划分面积比例计算联系数较离散法更为方便。实例中使用整体求解法计算了2因素事件状态联系数。最后说明了本文方法面临的问题、原因和解决方法。Abstract: In order to study the possibility of event state change and different states under the influence of factor fluctuation, this paper establishes the representation method of event state connection number under the influence of factor fluctuations by corresponding semantic partition with multi-level state of set pair analysis connection number. The construction method of event state connection number under single factor fluctuation is established. The factor plane is discretized by unit factor interval, the connection numbers of each discrete region is calculated respectively. All the connection numbers are integrated to form the event state connection numbers. According to the OR relationship of numerical logic and the algorithm of connection number, the connection number of single-factor event state is coupled to obtain the connection number of two-factor event state. The method described above can only be used only when the multiple factors is reduced to two factors by slicing. This paper proves the equivalence between discrete solution and global solution, and it is more convenient to calculate the connection number by using the area proportion of each semantic division than by the discrete method. In the example, the global solution method is used to calculate the connection number of two-factor event states. Finally, the problems, reasons and solutions of this method are illustrated.
-
系统存在的目的是完成预定功能且必须在规定的条件下。该条件实际是对系统功能有影响的内外部因素的集合。以系统是否能完成预定功能为目标,可将系统状态进行划分,如安全状态、不安全状态、不确定状态等,称为事件状态,其中事件表示系统的行为,状态表示系统行为与目的一致性。影响事件状态的内因主要是组成系统的元件及其结构,在系统设计期间内因基本确定,在运行过程中很少变化。影响事件状态的外因指影响系统运行期间系统功能的各类因素,主要是外部环境因素。由于外因影响了组成系统基本元件的基本性能,在外因波动过程中元件实现自身功能的能力也发生变化。由这些元件组成的系统在外因波动过程中的事件状态变化更为复杂。另一方面,如果因素波动过程中事件状态虽然变化但未脱离原有事件状态类别和程度,则原有的各类措施和方法仍有效无需调整;但当事件状态变化超过了原有事件状态的类别和程度,发生跃迁至其他状态类别和程度,则原有措施和方法失效需按照新的事件状态类别进行调整。状态跃迁是通过某种语义程度出现的概率是否占优体现的,即不同状态出现的可能性。因此必须了解系统在不同因素波动过程中的系统功能的变化情况,即事件状态变化情况。为在多因素波动中事件状态变化的提前感知和优劣性判断提供依据和方法。
多因素对系统安全及功能状态的影响已成为系统工程和智能分析领域的研究重点。目前最新的主要研究包括崔铁军等[1]基于量子粒子群优化(quantum particle swarm optimization,QPSO)研究了多因素影响下系统故障概率变化;卢颖等[2]研究了多因素影响的踩踏生成特征与集群风险关联;崔铁军等[3]使用联系数和属性多边形识别了系统故障模式;朱晶等[4]对堤防安全稳定影响的多因素进行了综合分析;靳文舟等[5]进行了多因素耦合作用下的车辆群事故分析;王燕语等[6]基于多因素、多层次评判研究了多灾种下城市安全韧性评价指标;岳仁田等[7]基于多因素耦合分析了航空运输系统脆弱性;李路等[8]研究了多因素耦合作用下的边坡滑动机理;王晨宇等[9]研究了面向多网关的无线传感器网络多因素认证;陈蔚等[10]基于层次分析法研究了车联网多因素信誉评价模型;陈艳等[11]基于动态激励视角进行了建筑工人不安全行为演化博弈分析;罗科等[12]在多因素耦合下研究了采空区上覆岩层安全厚度;王景春等[13]研究了多因素影响下的地铁车站深基坑韧性;裴兴旺等[14]基于熵权物元可拓方法评价了桥梁检测作业危险性;李文龙等[15]基于多因素耦合评价了山区道路系统脆弱性等。这些研究针对各领域的系统在不同因素影响下的功能状态变化及其特征进行了分析。明显的,不同系统对于不同因素的敏感性不同,因而被影响的系统功能状态的变化也不同。这些工作都在各自领域发挥了积极作用,但在系统层面缺乏抽象能力,难以形成具有通用性的理论方法。也难以分析上述多因素波动过程中的事件状态变化及不同状态出现的可能性。
为研究多因素波动影响下事件状态的表示,从而分析不同事件状态在不同语义划分中出现的概率,本文使用集对分析中的联系数来描述和表达事件状态变化和不同状态出现的可能性。利用三元联系数的同异反状态表达事件状态的不同语义划分。对单因素、两因素和多因素波动影响下的事件状态进行三元联系数表达,同时证明了离散求解与整体求解法的等效性,而整体求解法更为简便。最终为多因素波动过程中事件状态变化和不同状态出现的可能性提供分析方法。
1. 多因素波动对事件状态的影响
多因素波动对事件状态的影响是一种抽象表述,涉及多因素波动和事件状态2部分内容。
因素波动指因素值的变化过程。在因素变化范围内的所有对象都将受到因素变化的影响,只是影响程度和变化速率不同。如文献[16-18]所示,系统中多个元件在不同因素影响下的故障概率不同,在其余因素不变时,可将某一因素波动过程与元件故障概率变化过程形成对应函数称为特征函数,来描述因素波动与故障概率变化的关系。进一步如果有多个因素共同作用于该元件,且各因素波动时对元件的故障概率影响都不同,这时元件故障概率变化就更为复杂了。耦合特征函数建立元件故障概率分布,表示多因素波动与元件故障概率变化的关系。因此因素波动是元件故障概率变化的直接原因,元件故障是事件状态变化的直接原因。
事件状态是具有预期目标的事件状态。事件是抽象描述,对象及其动作或状态变化都可称为事件。事件必然对应着一个目标,例如系统故障、元件失效都可称为事件,而状态则是故障或失效程度的描述。例如以安全为目标,系统出现了故障称为事件,故障的程度称为事件状态。
事件状态由于因素波动而变化,如果以系统安全为目标可将系统状态划分为安全、不确定和不安全,它们组成了事件状态的全集。针对这3种状态系统将采取不同措施使系统保持安全或向着安全状态发展。确定的安全状态为最佳状态,确定的不安全状态也可采取确定的措施转变为安全状态;而不确定状态则相对难以处理。因为不确定状态难以采取具体措施,因此是最不利状态。而且随着因素波动,事件状态也会在3种状态内变化或发生跃迁,因此如何界定这些状态以及在多因素波动范围内确定各状态出现比例是判断事件状态是否有利的关键。
实际中因素波动是恒定的,因素不变是相对的。因素波动必将导致2种情况:1)事件状态变化未超出现有状态程度,即状态不变;2)超过了现有状态程度,发生了状态跃迁。例如元件故障概率随因素波动而变化,设故障概率在[0,30)%时事件状态为安全,[30,70)%时事件状态为不确定,[70,100]%时事件状态为不安全。如果因素波动使元件故障发生概率(事件状态)一直属于安全状态,则该事件状态未改变;如果因素波动使元件故障概率超过30%,则事件状态跃迁到不确定状态。这时难以判断事件的具体状态,也难以实施具体措施进行调整。
可见多因素波动对事件状态的影响应从事件状态是否变化及状态出现的可能性角度进行研究。其次需确定在多因素波动范围内事件状态属于不同语义划分的程度,即事件状态在不同语义程度出现的概率。以此判断该事件状态在因素波动过程中是否确定,是否有利或不利于预定目标的实现。而不同状态出现的可能性,即状态跃迁也是通过某语义程度出现的概率是否占优体现的。
根据作者已有研究[19-21]可使用集对分析的联系数来表示上述问题中的事件状态变化及出现可能性,构造事件状态联系数。集对分析理论是我国著名学者赵克勤教授[22-23]在1989年提出的。联系数具有从二元到多元的多种联系数形式。二元联系数是确定和不确定状态占比的博弈;三元联系数是与目标同异反状态占比的博弈;而多元联系数是对异状态的进一步划分,产生不同程度的异状态。
本文研究主要解决单因素波动下的事件状态联系数表示、两因素波动下的联系数表示、离散求解与整体求解的等价性证明以及多因素波动下的事件状态联系数表示。
2. 单因素波动下的事件状态联系数表示
将单因素波动下的事件状态联系数简称为单因素事件状态联系数。为说明单因素、两因素和多因素事件状态联系数,建立如下系统对该问题进行描述。设因素集合
$F = \{ {f_1},{f_2},\cdots,{f_N}\} , {f_o} \in F, o = 1,2,\cdots,N$ ,且这些因素同时存在;事件状态语义划分集合$S = \{ {s_1},{s_2},\cdots,{s_K}\} ,{s_k} \in S,k = 1,2,\cdots,K$ ;事件状态划分值集合$\lambda = \{ {\lambda _0} = 0,{\lambda _1},{\lambda _2},\cdots, {\lambda _K},{\lambda _{K + 1}} = 1\} , {\lambda _k} \in \lambda$ ;因素取值间隔集合$d = \{ {d_1},{d_2},\cdots,{d_N}\} ,{d_o} \in d$ ;因素值域集合$D = \{ {D_1},{D_2},\cdots,{D_N}\} ,{D_o} \in D$ ;因素${f_o}$ 间隔划分后的离散值${f_o} = \left\{ { \dfrac{{{u_o}{D_o}}}{{{d_o}}}\bigg|{u_o} = 1,2,\cdots,{U_o}} \right\} ,\dfrac{{{D_o}}}{{{d_o}}} = {U_o}$ ,${U_o}$ 为因素${f_o}$ 的值域划分数量。考虑到研究的复杂性和呈现研究过程的需要,使用两因素说明事件状态联系数的形成过程。设
${f_o}$ 和${f_{o + 1}}$ 两因素影响着事件X的状态$P$ ,根据空间故障树和空间故障网络理论[24-25],参照特征函数的构造方法可得到这2个因素对事件X的发生概率影响,形成2个特征函数分别为${p_X}({f_o})$ 和${p_X}({f_{o + 1}})$ ,使用它们可构建事件X的发生概率分布${P_X} = 1 - (1 - {p_X}({f_o}))(1 - {p_X}({f_{o + 1}}))$ 。发生概率分布${P_X}$ 是以${f_o}$ 和${f_{o + 1}}$ 两因素和事件发生概率构建的三维空间曲面,如文献[16-18]中给出的各元件和系统的故障发生概率分布。可见这些从实际数据得来的分布在空间内的变化是非常复杂的,并不利于直观地解析说明,因此将概率分布抽象为平面,如图1所示,以方便过程论述。图1中左图为简化的故障概率分布,即事件状态分布,简化为由平面
${M_1}$ 和${M_2}$ 组成的空间分布曲面。考虑联系数特征使用最简单的三元联系数描述事件状态变化特征,即$\mu = a + b{\rm{i}} + c{\rm{j}}$ 。设$ S=\{{s}_{1}=安全,{s}_{2}=不确定,{s}_{3}=不安全\},K\text{=}3 $ ,即以安全为目标将事件状态的语义划分为安全、不确定和不安全,对应三元联系数中同异反状态。也可划分多级语义对应多元联系数,但过程相对复杂且与三元联系数构造同理。三元联系数将事件发生概率$P$ 划分为3种状态,${s_1}$ 状态对应的值域为$\lambda ({s_1}) = [{\lambda _0},{\lambda _1})$ ,$\lambda ({s_2}) = [{\lambda _1},{\lambda _2})$ ,$\lambda ({s_3}) = [{\lambda _2},{\lambda _3}]$ ,形成2个平面$P = {\lambda _1}$ 和$P = {\lambda _2}$ 。平面${M_1}$ 与$P = {\lambda _2}$ 平面交线为${l_1}$ ;${M_1}$ 与$P = {\lambda _1}$ 交线为${l_2}$ ;${M_2}$ 与$P = {\lambda _1}$ 交线为${l_3}$ ;${M_2}$ 与$P = {\lambda _2}$ 交线为${l_4}$ ,将这些交线投影到${f_o}$ ${f_{o + 1}}$ 平面上,如图1中右图所示。在图1右图中对因素
${f_o}$ 坐标轴进行划分,设单位距离$\Delta {f_o}({u_o})$ 为$\left[ {\dfrac{{{u_o}{D_o}}}{{{d_o}}},\dfrac{{({u_o} + 1){D_o}}}{{{d_o}}}} \right]$ ,${u_o} = 1,2,\cdots, {U_o}$ 。图1右图阴影区域的面积可分为5部分(这取决于语义划分和空间曲面形态),其面积由下至上分别为${Z_o}({u_o},{l_1},0) = \int\limits_{\Delta {f_o}({u_o})} {({l_1} - 0){\rm{d}}{f_o}}$ ;${Z_o}({u_o},{l_2},{l_1}) = \int\limits_{\Delta {f_o}({u_o})} {({l_2} - }$ ${l_1}){\rm{d}}{f_o}$ ;${Z_o}({u_o},{l_3},{l_2}) = \int\limits_{\Delta {f_o}({u_o})} {({l_3} - {l_2}){\rm{d}}{f_o}}$ ;${Z_o}({u_o},{l_4},{l_3}) = \int\limits_{\Delta {f_o}({u_o})}({l_4} -$ ${l_3}){\rm{d}}{f_o} $ ;${Z_o}({u_o},{D_{o + 1}},{l_4}) = \int\limits_{\Delta {f_o}({u_o})} {({D_{o + 1}} - {l_4}){\rm{d}}{f_o}}$ ,总面积为${Z_o}({u_o}) = \Delta {f_o}({u_o}) \times {D_{o + 1}} = {Z_o}({u_o},{l_1},0)+{Z_o}({u_o},{l_2},{l_1})+ {Z_o}({u_o},{l_3},{l_2}) + {Z_o}({u_o},{l_4},{l_3}) + {Z_o}({u_o},{D_{o + 1}},{l_4})$ 。又因为${Z_o} ({u_o},{l_1}, 0)$ 对应的发生概率根据语义划分属于$\lambda ({s_3}) = [{\lambda _3}, {\lambda _2}]$ ;${Z_o}({u_o}, {l_2},{l_1}) \in \lambda ({s_2}) = ({\lambda _2},{\lambda _1})$ ;${Z_o}({u_o},{l_3},{l_2}) \in \lambda ({s_1}) = [{\lambda _1},{\lambda _0}]$ ;${Z_o}({u_o}, {l_4},{l_3}) \in \lambda ({s_2}) = ({\lambda _2},{\lambda _1})$ ;${Z_o}({u_o},{D_{o + 1}},{l_4}) \in \lambda ({s_3}) = [{\lambda _3},{\lambda _2}]$ ,可合并为${Z_o}({u_o},{l_1},0)$ +${Z_o}({u_o},{D_{o + 1}},{l_4})$ $ \in \lambda ({s_3})$ 表示不安全的面积,${Z_o}({u_o},{l_2},{l_1})$ +${Z_o}({u_o},{l_4},{l_3}) \in \lambda ({s_2})$ 表示不确定的面积,${Z_o}({u_o},{l_3},{l_2}) \in \lambda ({s_1})$ 表示安全状态的面积。形成三元联系数${\mu _o}({u_o}) = {a_o}({u_o}) + {b_o}({u_o}){\rm{i}} +{c_o}({u_o}){\rm{j}}$ ,${a_o}({u_o}) = {Z_o} ({u_o},{l_3},{l_2}) / {Z_o} ({u_o})$ ,${b_o} ({u_o}) = ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o}, {l_4}, {l_3})) / {Z_o}({u_o})$ ,${c_o}({u_o}) = ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4}))/{Z_o}({u_o})$ 。得到针对因素${f_o}$ 在$\Delta {f_o}({u_o})$ 上的事件状态联系数为$$ {\mu _o}({u_o}) = \dfrac{{{Z_o}({u_o},{l_3},{l_2}) + ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3})){\rm{i}} + ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4})){\rm{j}}}}{{{Z_o}({u_o})}} $$ (1) ${f_o}$ 在${D_o}$ 全域的事件状态联系数可表示为$$ \begin{array}{c} {\mu _o} = \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {{\mu _o}({u_o})} = \\ \dfrac{{\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {\dfrac{{{Z_o}({u_o},{l_3},{l_2}) + ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3})){\rm{i}} + ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4})){\rm{j}}}}{{{Z_o}({u_o})}}} }}{{{U_o}}} = \\ \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {\dfrac{{{Z_o}({u_o},{l_3},{l_2}) + ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3})){\rm{i}} + ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4})){\rm{j}}}}{{{Z_o}({u_o}){U_o}}}} = \\ \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {\frac{{{Z_o}({u_o},{l_3},{l_2}) + ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3})){\rm{i}} + ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4})){\rm{j}}}}{{{D_{o + 1}}\Delta {f_o}({u_o}){U_o}}}} = \\ \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {\dfrac{{{Z_o}({u_o},{l_3},{l_2}) + ({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3})){\rm{i}} + ({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4})){\rm{j}}}}{{{D_{o + 1}}{D_o}}}} = \\ \dfrac{1}{{{D_{o + 1}}{D_o}}}\left( {\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {{Z_o}({u_o},{l_3},{l_2}) +\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3}))} {\rm{i}} + \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4}))}{\rm{ j}}} } \right) \\ \end{array} $$ (2) 式中:
${a_o} = \dfrac{1}{{{D_{o + 1}}{D_o}}}\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {{Z_o}({u_o},{l_3},{l_2})}$ ;${b_o} = \dfrac{1}{{{D_{o + 1}}{D_o}}} \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} ({Z_o}({u_o}, {l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3}))$ ;${c_o} = \dfrac{1}{{{D_{o + 1}}{D_o}}}\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} ({Z_o}({u_o},{l_1}, 0) +{Z_o}({u_o}, {D_{o + 1}},{l_4}))$ 。式(2)代表了该事件在因素${f_o}$ 作用下的状态波动情况,其中同分项系数$ {a_o} $ 代表了事件状态为安全的概率,异分项系数$ {b_o} $ 代表了不确定的事件状态概率,反分项系数$ {c_o} $ 代表了事件状态为不安全的概率。同理对于因素
${f_{o + 1}}$ 在${D_{o + 1}}$ 全域的事件状态,可将式(2)下角标“$ o $ ”替换为“$ {o + 1} $ ”为$$ {\mu _{o + 1}} = {a_{o + 1}} + {b_{o + 1}}{\rm{i}} + {c_{o + 1}}{\rm{j}} $$ (3) 式中:
${a_{o+1}} = \dfrac{1}{{{D_{o + 1}}{D_o}}}\displaystyle \sum\limits_{{u_{o+1}} = 1}^{{U_{o+1}}} {{Z_{o+1}}({u_{o+1}},{l_3},{l_2})}$ ;${b_{o+1}} = \dfrac{1}{{{D_{o + 1}}{D_o}}} \cdot \displaystyle \sum\limits_{{u_{o+1}} = 1}^{{U_{o+1}}} \;{({Z_{o+1}}({u_{o+1}},\;{l_2},\;{l_1})\; +\; {Z_{o+1}}\;({u_{o+1}},\;{l_4},\;{l_3}))}$ ;${c_{o+1}} \;=\; \dfrac{1}{{{D_{o + 1}}{D_o}}}\cdot$ $\displaystyle \sum\limits_{{u_{o+1}} = 1}^{{U_{o+1}}} \;{({Z_{o+1}}({u_{o+1}},{l_1},0) + {Z_{o+1}}({u_{o+1}},{D_o},{l_4}))}$ 3. 两因素波动下的事件状态联系数表示
当
${f_o}$ 和${f_{o + 1}}$ 共同作用时,根据已有研究[16-18]两者是“或”逻辑关系,参照文献[16-18]给出的多因素耦合影响关系有:$$ {\mu _F} = 1 - [(1 - {\mu _1})(1 - {\mu _2}) \cdots (1 - {\mu _N})] = 1 - \prod\limits_{o = 1}^N {(1 - {\mu _o})} $$ 对于
$F = \{ {f_o},{f_{o + 1}}\} $ ,有:${\mu _F} = 1 - [(1 - {\mu _o}){\rm{ }}(1 - {\mu _{o + 1}})] = {\mu _o} + {\mu _{o + 1}} - {\mu _o}{\mu _{o + 1}}, $ 根据联系数的运算法则:$$ \left\{ {\begin{array}{*{20}{l}} {{\mu _o} + {\mu _{o + 1}} = \dfrac{{({a_o} + {a_{o + 1}}) + ({b_o} + {b_{o + 1}}){\rm{i}} + ({c_o} + {c_{o + 1}}){\rm{j}}}}{{{a_o} + {a_{o + 1}} + {b_o} + {b_{o + 1}} + {c_o} + {c_{o + 1}}}}} \\ {{\mu _o} - {\mu _{o + 1}} = \dfrac{{({a_1} - {a_{o + 1}}) + ({b_1} + {b_{o + 1}}){\rm{i}} + ({c_1} - {c_{o + 1}}){\rm{j}}}}{{{a_o} - {a_{o + 1}} + {b_o} + {b_{o + 1}} + {c_o} - {c_{o + 1}}}}} \\ {\mu _o}{\mu _{o + 1}}={a_o}{a_{o + 1}} + ({a_o}{b_{o + 1}} + {a_{o + 1}}{b_o} + {b_o}{b_{o + 1}} + {b_o}{c_{o + 1}} + {b_{o + 1}}{c_o}){\rm{i}} + ({a_o}{c_{o + 1}} + {a_{o + 1}}{c_o} + {c_o}{c_{o + 1}}){\rm{j}} \end{array}} \right. $$ (4) 可设
${\mu _o} = {a_o} + {b_o}{\rm{i}} + {c_o}{\rm{j}}$ 和${\mu _{o + 1}} = {a_{o + 1}} + {b_{o + 1}}{\rm{i}} + {c_{o + 1}}{\rm{j}}$ ,则${f_o}$ 和${f_{o + 1}}$ 共同作用产生的事件状态联系数$ {\mu _F} $ 为$$ {\mu _F} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\dfrac{{{a_o} + {a_{o + 1}}}}{{{\sigma ^ + }}} - {a_o}{a_{o + 1}}}}{{{\sigma ^ - }}} + \dfrac{{\dfrac{{{b_o} + {b_{o + 1}}}}{{{\sigma ^ + }}} + {a_o}{b_{o + 1}} + {a_{o + 1}}{b_o} + {b_o}{b_{o + 1}} + {b_o}{c_{o + 1}} + {b_{o + 1}}{c_o}}}{{{\sigma ^ - }}}{\rm{i}} + \dfrac{{\dfrac{{{c_o} + {c_{o + 1}}}}{{{\sigma ^ + }}} - ({a_o}{c_{o + 1}} + {a_{o + 1}}{c_o} + {c_o}{c_{o + 1}})}}{{{\sigma ^ - }}}{\rm{j}}} \\ {{\sigma ^ + } = {a_o} + {a_{o + 1}} + {b_o} + {b_{o + 1}} + {c_o} + {c_{o + 1}}} \\ {{\sigma ^ - } = \dfrac{{{a_o} + {a_{o + 1}}}}{{{\sigma ^ + }}} - {a_o}{a_{o + 1}} + \dfrac{{{b_o} + {b_{o + 1}}}}{{{\sigma ^ + }}} + {a_o}{b_{o + 1}} + {a_{o + 1}}{b_o} + {b_o}{b_{o + 1}} + {b_o}{c_{o + 1}} + {b_{o + 1}}{c_o} + \dfrac{{{c_o} + {c_{o + 1}}}}{{{\sigma ^ + }}} - ({a_o}{c_{o + 1}} + {a_{o + 1}}{c_o} + {c_o}{c_{o + 1}})} \end{array}} \right. $$ (5) 由于同异反分项系数的具体形式较为繁琐,不代入式(5),可参考式(2)和式(3)。
4. 离散求解与整体求解的等价性证明
显然第2和第3节给出的分析过程是比较繁琐的,关键问题集中在需要对因素值域进行划分
${f_o} = \left\{ { \dfrac{{{u_o}{D_o}}}{{{d_o}}}|{u_o} = 1,2,\cdots,{U_o}} \right\} ,\dfrac{{{D_o}}}{{{d_o}}} = {U_o}$ ,划分后针对$\Delta {f_o}({u_o}) \cdot {D_{o + 1}}$ 计算三元联系数${\mu _o}({u_o})$ ,再对因素值域${D_o}$ 上的所有三元联系数${\mu _o}({u_o})$ 进行综合得到$ {\mu _o} $ 。这是将值域${D_o}$ 对$\Delta {f_o}({u_o})$ 进行离散,是$ {\mu _o} $ 的离散化求解方法。在${f_o}$ ${f_{o + 1}}$ 平面上进行的离散化语义划分所得面积在最终$ {\mu _o} $ 计算过程中进行了合并。因此考虑是否可以直接使用各语义划分面积整体作为比例得到$ {\mu _o} $ 的同异反分项系数,这将比离散求解法更为简单。按该思路接续式(2)进行推导:$$ \begin{gathered} {\mu _o} = \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {{\mu _o}({u_o})} = \dfrac{1}{{{D_{o + 1}}{D_o}}}\left( {\displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {{Z_o}({u_o},{l_3},{l_2}) + \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {({Z_o}({u_o},{l_2},{l_1}) + {Z_o}({u_o},{l_4},{l_3}))} {\rm{i}} + \displaystyle \sum\limits_{{u_o} = 1}^{{U_o}} {({Z_o}({u_o},{l_1},0) + {Z_o}({u_o},{D_{o + 1}},{l_4}))} {\rm{j}}} } \right) =\\ \dfrac{{\int_0^{{D_o}} {{l_3} - {l_2}{\rm{d}}{f_0}} }}{{{D_{o + 1}}{D_o}}} + \dfrac{{\int_0^{{D_o}} {({l_3} - {l_2}) + ({l_4} - {l_3}){\rm{d}}{f_0}} }}{{{D_{o + 1}}{D_o}}}{\rm{i}} + \dfrac{{\int_0^{{D_o}} {({l_1} - 0) + ({D_{o + 1}} - {l_4}){\rm{d}}{f_0}} }}{{{D_{o + 1}}{D_o}}}{\rm{j }} \end{gathered} $$ (6) 结合图1右图所示,式(6)可进一步改写为
$$ \begin{array}{c} {\mu _o} = \dfrac{{{s_1}}}{{{D_{o + 1}}{D_o}}} + \dfrac{{{s_2}}}{{{D_{o + 1}}{D_o}}}{\rm{i }}+ \dfrac{{{s_3}}}{{{D_{o + 1}}{D_o}}}{\rm{j}},{s_1} + {s_2} + {s_3} =\\ {D_{o + 1}}{D_o},{a_o} = \dfrac{{{s_1}}}{{{D_{o + 1}}{D_o}}},{b_o} = \dfrac{{{s_2}}}{{{D_{o + 1}}{D_o}}},{c_o} = \dfrac{{{s_3}}}{{{D_{o + 1}}{D_o}}} \end{array} $$ (7) 图1右图中
${f_o} = 0$ 、${l_1}$ ~${l_4}$ 和${f_o} = {D_o}$ 的相邻2线之间区域分别隶属于${s_1},{s_2},{s_3}$ ,因此在${D_o} {D_{o + 1}}$ 区域内不同语义划分形成的面积也都确定的属于${s_1},{s_2},{s_3}$ 。因此式(2)等价于式(7),即离散求解与整体求解等价,而后者较前者计算更为方便。进一步的,发现在分布空间中计算
$ {\mu _{o + 1}} $ 使用了与$ {\mu _o} $ 相同的语义及其划分。因此事件状态分布、截平面、交线投影等均相同,导致各语义划分的面积也相同,从而得到的单因素事件状态联系数也相同。具体的,对于因素${f_o}$ 及${f_{o + 1}}$ 构成的事件发生概率分布曲面是相同的,均为${P_X} = 1 - (1 - {p_X}({f_o})) (1 - {p_X}({f_{o + 1}}))$ 。所以当语义相同且划分相同时2个截平面$P = {\lambda _1}$ 和$P = {\lambda _2}$ 相同,进一步导致${l_1}$ 、${l_2}$ 、${l_3}$ 和${l_4}$ 相同,所以最终得到$ {\mu _{o + 1}} = {\mu _o} $ 的结论。5. 多因素波动下的事件状态联系数表示
当有多个因素作用于事件状态时,可将2个因素的波动耦合为一个因素的波动。如此耦合可将任意多因素的波动影响转化为一个因素的波动影响。例如考虑三因素
${f_o}$ 、${f_{o + 1}}$ 、${f_{o + 2}}$ 及其事件发生概率分布$P = P({f_o},{f_{o + 1}},{f_{o + 2}})$ ,它们构成了四维空间曲面,显然使用上述分析方法是难以计算事件状态联系数的。考虑将${f_o}$ 、${f_{o + 1}}$ 2个因素合并为一个因素,即将2个变量的变化过程一一对应的转化为一个变量的变化过程达到降维目的。本文给出一种适合于上述过程的降维方法,利用空间切片方式按顺序排布改变四维空间曲面为三维空间曲面。具体地将${f_o}$ 、${f_{o + 1}}$ 因素降维至因素$f'$ ,对${f_o}$ 进行切分,以${f_o}$ 的单位长度$\Delta {f_o}({u_o})$ 及${f_o}$ ${f_{o + 1}}$ 平面组成新的以${f_{o + 2}}$ 、$f'$ 和P为坐标轴构成的三维空间,得到事件状态分布,过程如图2所示。新因素
$f'$ 划分后的离散值$f' = \Bigg\{ {U_o}\Bigg( \dfrac{{{u_o}{D_o}}}{{{d_o}}} -\dfrac{{{D_o}}}{{{d_o}}} \Bigg) + \dfrac{{{u_{o+1}}{D_o}}}{{{d_{o+1}}}}\bigg|{u_o} = 1,2,\cdots,{U_o};{u_{o + 1}} = 1,2,\cdots,{U_{o + 1}} \Bigg\}$ 。进而$f'$ ,${f_{o + 2}}$ 与$P = P(f',{f_{o + 2}}) = P({f_o},{f_{o + 1}},{f_{o + 2}})$ 组成了新的三维空间,这时$f'$ ,${f_{o + 2}}$ 为坐标轴,$P$ 为事件状态分布曲面。与原四维空间曲面的特征相同,可使用离散求解或整体求解方法计算多因素事件状态联系数。6. 实例分析
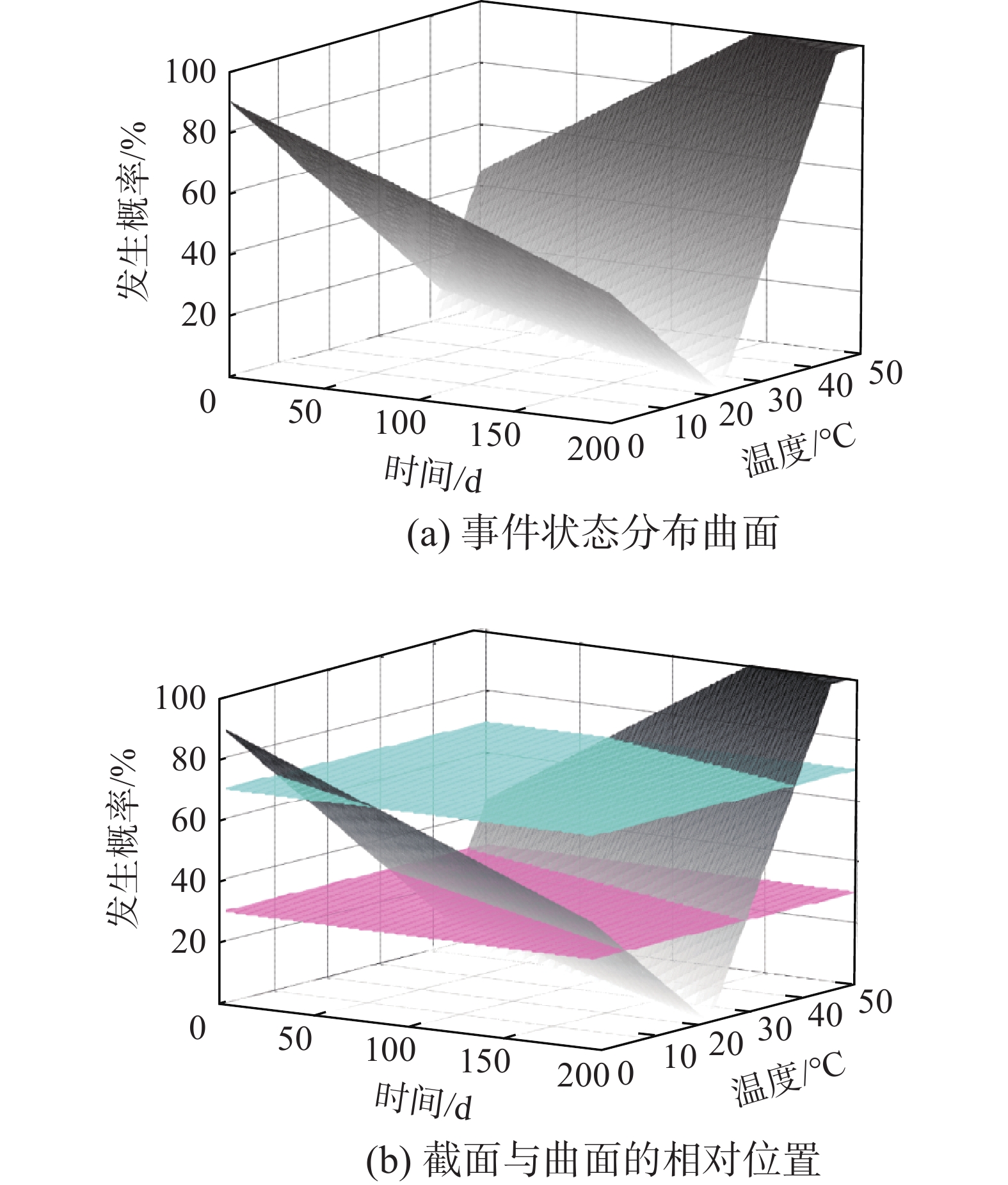
根据图1设置参数进行实例分析。根据文献[16-18]给出的元件故障发生概率空间分布,设影响故障发生的因素为时间
${f_1} \in$ [0,200 d]和温度${f_2} \in $ [0,50 ℃],图3给出了不同时间和温度情况下的该元件故障发生概率分布,即事件状态分布情况。如图3(a)所示,前侧平面方程为
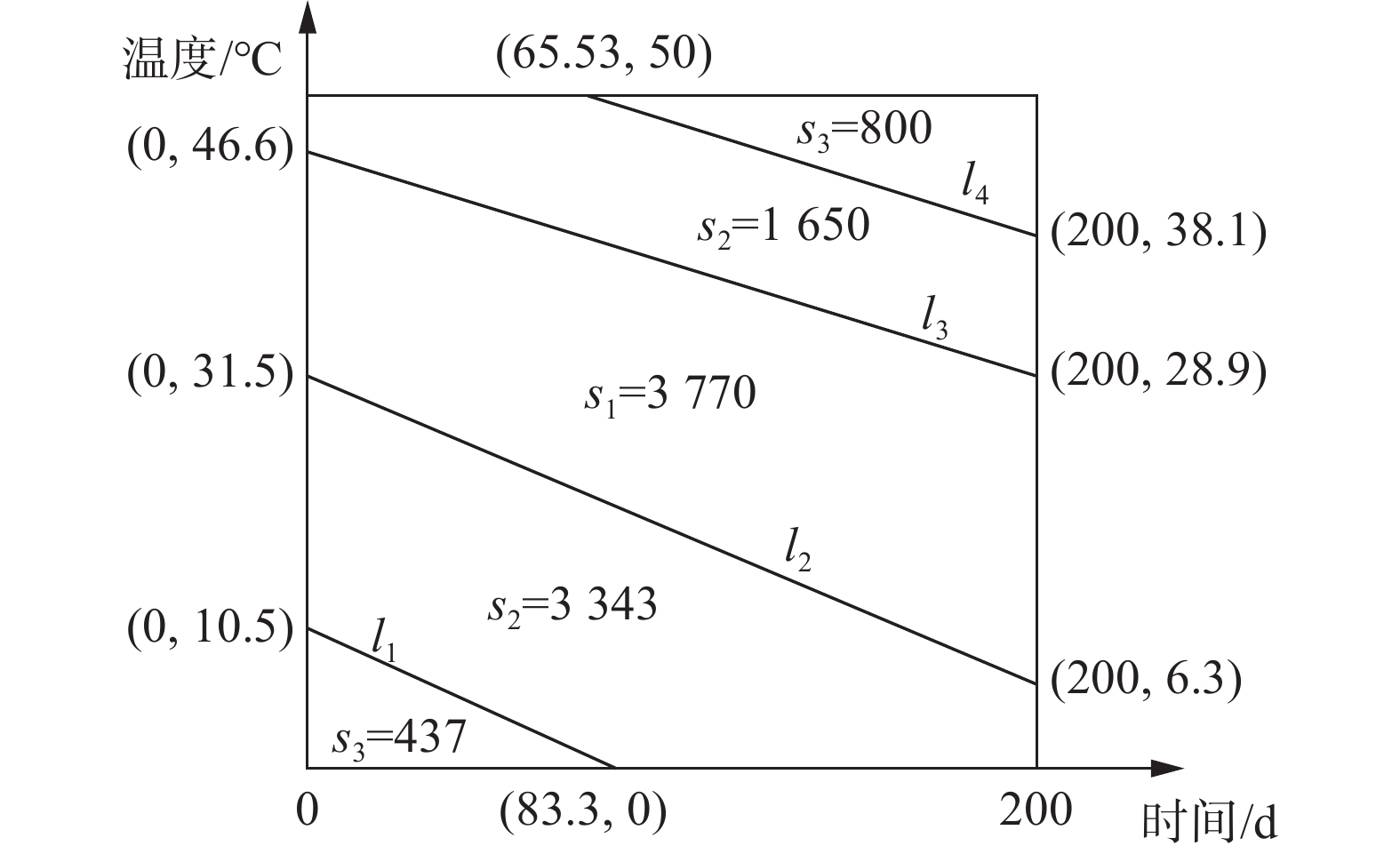
${M_1}: - 7\;560 + 20.2x + 160y + 8\;400z = 0$ ,后侧平面方程为${M_2}: - 7\;940 + 17.7x + 200y - 4\;600z = 0$ 。以系统安全为目标,设同异反状态集合为$S=\{{s}_{1} = 安全(同) ,r {s}_{2} = 不确定 (异), {s}_{3}=不安全(反)\}, K=3$ ,则状态划分值集合为$\lambda = \{ {\lambda _0} = 0, {\lambda _1} = 0.3,{\lambda _2} = 0.7,{\lambda _4} = 1\} $ 。2个截平面$P = {\lambda _1} = 0.3$ 和$P = {\lambda _2} = 0.7$ ,与${M_1}$ 和${M_2}$ 相交形成4条交线,并向${f_1} {f_2}$ 平面投影得到4条直线,分别为${l_1}$ 、${l_2}$ 、${l_3}$ 和${l_4}$ 。方程为${l_4} = {\lambda _2} \cap {M_2} = - 0.088\;5x + 55.8$ 、${l_3} = {\lambda _1} \cap {M_2} = - 0.088\;5x + 46.6$ 、${l_2} = {\lambda _1} \cap {M_1} = - 0.126x + 31.5$ 和${l_1} = {\lambda _2} \cap {M_1} = - 0.126x + 10.5$ ,相对位置如图4所示。考虑离散求解与整体求解的等价性,使用第4节方法计算单因素和两因素事件状态联系数。图4中,
${s_1} = 3\;770$ 、${s_2} = 3\;343 + 1\;650 = 4\;993$ ,${s_3} = 437 + 800 = 1\;237$ ,${s_1} + {s_2} + {s_3} = {D_1}{D_2} = 200 \times 50 = 10\;000$ 。又因为$ {\mu _1} = {\mu _2} $ ,根据式(7)可得2个因素波动分别对该事件状态影响的三元联系数为$$ \left\{ {\begin{array}{*{20}{c}} {{\mu _1}{\text{ = }}0.377 + 0.499{\rm{i}} + 0.124{\rm{j}}} \\ {{\mu _2}{\text{ = }}0.377 + 0.499{\rm{i}} + 0.124{\rm{j}}} \end{array}} \right. $$ (8) 考虑
${f_1}、{f_2}$ 同时作用,${\mu _F} = 1 - [(1 - {\mu _1})(1 - {\mu _2})] = {\mu _1} + {\mu _2} - {\mu _1}{\mu _2}$ ,根据式(4)并将式(8)代入得:$$ \begin{array}{c} {\mu _F} = {\mu _1} + {\mu _2} - {\mu _1}{\mu _2} = \\ 0.377 + 0.499{\rm{i}}+ 0.124{\rm{j}} + 0.377 + 0.499{\rm{i}}+ 0.124{\rm{j}} - \\ (0.377 + 0.499{\rm{i}}+ 0.124{\rm{j}})(0.377 + 0.499{\rm{i}}+ 0.124{\rm{j}}) = \\ 0.377 + 0.499{\rm{i}}+ 0.124{\rm{j}} - (0.1421 + 0.749{\rm{i}}+ 0.108\;9{\rm{j}})= \\ 0.156\;8 + 0.833\;1{\rm{i}}+ 0.01{\rm{j}} \\ \end{array} $$ (9) 式(9)得到了两因素事件状态的三元联系数,表示了该元件在规定的时间和温度变化过程中处于安全、不确定和不安全状态的可能性。为在因素波动情况下分析不同语义对应的事件状态可能性提供基础方法。基于上述计算结果可分析
$ {\mu _1} $ 、$ {\mu _2} $ 和$ {\mu _F} $ 的事件状态特征。如$ {\mu _1} $ 和$ {\mu _2} $ 都是异状态占优,即不确定性安全状态占优,其次是同的安全状态,最后是反的不安全状态。$ {\mu _F} $ 也是不确定性安全状态占优,不安全状态可能性很低。由于事件状态联系数也是联系数的一种,它符合所有的联系数分析方法。可借助这些方法分析事件状态特征,例如判断事件是否发生状态跃迁可通过集对势函数,从而确定事件状态的发展趋势等。总结上述工作和面临的问题。因素波动对事件状态的影响可从2方面描述,一是状态值,即元件发生故障概率变化的绝对值;二是语义状态跃迁,即不同事件状态出现的可能性变化,当事件状态在因素变化时占优的语义发生变化就产生了跃迁。当状态值波动但未发生跃迁时表明这部分因素变化虽然使状态值波动但并未导致语义状态变化,是可以接受的,原有各种方式和措施仍然适用。而当因素变化过程中状态值从一种语义跃迁到另一种语义已达到质变发生跃迁,原有各类措施和方法不再适用必须调整。另外事件状态联系数可表示在因素波动中事件状态属于安全状态、不确定状态和不安全状态的比例,即各种状态出现的可能性。当然安全状态分项系数越高系统状态越好;安全状态分项系数和不安全状态分项系数越大说明系统状态越具有确定性。在某些因素作用下系统如果确定不安全也可采取确定的措施转变为安全状态。最不可控的是不确定状态,不能确定是否安全或不安全,也难以采取措施进行调整。
研究可能存在的问题,1)状态语义划分,本文划分状态语义为3类对应三元联系数,也可进行多类语义划分对应多元联系数,这与三元联系数的构造方式相同。2)事件状态分布(故障发生概率分布)的形态,文中给出的分布以2个平面组合的形式呈现,但实际分布比较复杂,如文献[16-18]给出的元件和系统故障概率分布。这里是为直观展示得到线性交线,实际交线变化多样但与线性交线计算思路相同。3)高维状态分布曲面降维,超过三维难以展示,但文中方法可通过解析方式完成计算。
7. 结论
1)实现了单因素和两因素波动下的事件状态联系数表示。将事件发生概率分布与语义划分值平面相交,投影交线到因素平面,对目标因素等距划分,计算相邻交线之间的面积,将相同语义面积相加即可代表语义安全、不确定和不安全所占比例。这等同于联系数的同异反分项系数,进而构建单因素事件状态联系数。两因素事件状态联系数是由两个单因素事件状态联系数耦合形成的,耦合方式是数值逻辑“或”关系,同时根据联系数运算法则可得到两因素事件状态联系数。
2)证明了离散求解与整体求解的等价性。对离散求解的单因素事件状态联系数继续推导,发现因素离散化语义划分面积在最终的联系数计算过程中进行了合并。因此直接使用各语义划分的因素面积与总面积的比例即是事件状态联系数的同异反分项系数,较离散求解更为简便。
3)实现了多因素波动下的事件状态联系数表示。由于通过面积比例确定分项系数,当因素超过2时难以适用,因此提出对应的因素降维方法。利用空间切片方式排布改变四维空间曲面为三维空间曲面,将两因素降维形成一个新因素,以剩余因素、新因素和故障概率为坐标轴构成三维空间,可得降维后事件状态分布。
4)通过实例使用整体求解法进行了两因素事件状态联系数构建。论述了面临的问题和解决方法。状态语义划分不限于三元联系数,可使用多元联系数对应多语义划分;实际事件状态分布形态复杂,可能是非线性交线,但由于使用面积作为计算基础与线性交线的分析方法相同;高维事件状态分布曲面可通过降维后的解析方式计算。
-
[1] 崔铁军, 李莎莎. 基于QPSO的多因素影响下系统故障概率变化程度研究[J]. 安全与环境学报, 2021, 21(5): 1905–1910. CUI Tiejun, LI Shasha. On the changing degree of the system fault probability under the impact of the multiple factors based on the QPSO[J]. Journal of safety and environment, 2021, 21(5): 1905–1910. [2] 卢颖, 仇乐, 吕希凡, 等. 基于ISODATA的踩踏生成特征与集群风险关联性研究[J]. 安全与环境学报, 2022, 22(3): 1459–1466. LU Ying, QIU Le, LYU Xifan, et al. Analysis of correlation between stampede generation characteristics and clustering risk using ISODATA algorithm[J]. Journal of safety and environment, 2022, 22(3): 1459–1466. [3] 崔铁军, 李莎莎. 联系数和属性多边形的系统故障模式识别[J]. 智能系统学报, 2022, 17(3): 568–575. CUI Tiejun, LI Shasha. System fault pattern recognition based on connection number and attribute polygon[J]. CAAI transactions on intelligent systems, 2022, 17(3): 568–575. [4] 朱晶, 仲静文, 徐海峰, 等. 基于水平定向钻施工对堤防安全稳定影响的多因素综合分析[J]. 水利水电技术, 2021, 52(6): 67–75. ZHU Jing, ZHONG Jingwen, XU Haifeng, et al. Analysis of the comprehensive influence of multiple factors based on the horizontal directional drilling construction on the safety and stability of levee[J]. Water resources and hydropower engineering, 2021, 52(6): 67–75. [5] 靳文舟, 姚尹杰. 多因素耦合作用下的车辆群事故伤害程度估计[J]. 郑州大学学报(工学版), 2021, 42(3): 1–7. JIN Wenzhou, YAO Yinjie. Estimation of accident injury severity of vehicle groups considering multi-factor coupling[J]. Journal of Zhengzhou University (engineering science edition), 2021, 42(3): 1–7. [6] 王燕语, 范圣权, 范乐. 基于多因素、多层次评判的多灾种下城市安全韧性评价指标研究[J]. 建筑科学, 2021, 37(1): 82–88. Wang Yanyu, Fan Shengquan, Fan Le. Research on assessment index of urban safety resilience under multi-hazards based on multi-factors and multi-level evaluation[J]. Building science, 2021, 37(1): 82–88. [7] 岳仁田, 李君尉. 基于多因素耦合的航空运输系统脆弱性分析[J]. 中国安全生产科学技术, 2020, 16(12): 150–156. YUE Rentian, LI Junwei. Vulnerability analysis of air transportation system based on multi-factor coupling[J]. Journal of safety science and technology, 2020, 16(12): 150–156. [8] 李路, 贺超, 徐鹏, 等. 多因素耦合作用下的边坡滑动机理研究[J]. 矿业研究与开发, 2020, 40(4): 79–84. doi: 10.13827/j.cnki.kyyk.2020.04.015 Li Lu, He Chao, Xu Peng, et al. Study on the slope sliding mechanism under multi-factor coupling[J]. Mining research and development, 2020, 40(4): 79–84. doi: 10.13827/j.cnki.kyyk.2020.04.015 [9] 王晨宇, 汪定, 王菲菲, 等. 面向多网关的无线传感器网络多因素认证协议[J]. 计算机学报, 2020, 43(4): 683–700. WANG Chenyu, WANG Ding, WANG Feifei, et al. Multi-factor user authentication scheme for multi-gateway wireless sensor networks[J]. Chinese journal of computers, 2020, 43(4): 683–700. [10] 陈蔚, 刘雪娇, 夏莹杰. 基于层次分析法的车联网多因素信誉评价模型[J]. 浙江大学学报(工学版), 2020, 54(4): 722–731. doi: 10.3785/j.issn.1008-973X.2020.04.011 CHEN Wei, LIU Xuejiao, XIA Yingjie. Multi-factor reputation evaluation model based on analytic hierarchy process in vehicle Ad-hoc networks[J]. Journal of Zhejiang University (engineering science edition), 2020, 54(4): 722–731. doi: 10.3785/j.issn.1008-973X.2020.04.011 [11] 陈艳, 吕云翔, 柴访, 等. 动态激励视角下建筑工人不安全行为演化博弈分析[J]. 安全与环境工程, 2020, 27(1): 197–203. Chen Yan, LYU Yunxiang, Chai Fang, et al. Evolutionary game analysis of unsafe behavior of construction workers from the perspective of dynamic incentives[J]. Safety and environmental engineering, 2020, 27(1): 197–203. [12] 罗科, 李胤达, 王振. 多因素耦合下的采空区上覆岩层安全厚度分析[J]. 煤矿安全, 2019, 50(12): 223–226. LUO Ke, LI Yinda, WANG Zhen. Research on safety thickness of overlying strata in goaf under multi-factor coupling[J]. Safety in coal mines, 2019, 50(12): 223–226. [13] 王景春, 赵福全, 王炳华, 等. 多因素影响下的地铁车站深基坑韧性评估[J]. 中国安全科学学报, 2019, 29(10): 154–159. WANG Jingchun, ZHAO Fuquan, WANG Binghua, et al. Resilience evaluation for deep foundation pit of metro station under influence of multiple factors[J]. China safety science journal, 2019, 29(10): 154–159. [14] 裴兴旺, 李慧民, 李文龙, 等. 基于熵权物元可拓的桥梁检测作业危险性评价[J]. 中国安全科学学报, 2019, 29(8): 42–48. PEI Xingwang, LI Huimin, LI Wenlong, et al. Risk assessment of bridge detection operation based on entropy weight and matter-element extension theory[J]. China safety science journal, 2019, 29(8): 42–48. [15] 李文龙, 李慧民, 裴兴旺, 等. 基于多因素耦合的山区道路系统脆弱性评估[J]. 中国安全科学学报, 2019, 29(5): 165–170. LI Wenlong, LI Huimin, PEI Xingwang, et al. Vulnerability assessment of mountainous road system based on multiple-factor coupling[J]. China safety science journal, 2019, 29(5): 165–170. [16] 崔铁军, 马云东. 基于多维空间事故树的维持系统可靠性方法研究[J]. 系统科学与数学, 2014, 34(6): 682–692. CUI Tiejun, MA Yundong. Research on the maintenance method of system reliability based on multi-dimensional space fault tree[J]. Journal of systems science and mathematical sciences, 2014, 34(6): 682–692. [17] 崔铁军, 马云东. 空间故障树的径集域与割集域的定义与认识[J]. 中国安全科学学报, 2014, 24(4): 27–32. CUI Tiejun, MA Yundong. Defining and understanding both size set domain and cut set domain for multi-dimensional space fault tree[J]. China safety science journal, 2014, 24(4): 27–32. [18] 崔铁军, 马云东. 多维空间故障树构建及应用研究[J]. 中国安全科学学报, 2013, 23(4): 32–37,62. CUI Tiejun, MA Yundong. Research on multi-dimensional space fault tree construction and application[J]. China safety science journal, 2013, 23(4): 32–37,62. [19] 崔铁军, 李莎莎. 基于集对分析的SFT特征函数重构及性质研究[J]. 智能系统学报, 2022, 17(1): 131–136. CUI Tiejun, LI Shasha. Reconstruction of SFT characteristic function and its properties based on Set Pair Analysis[J]. CAAI transactions on intelligent systems, 2022, 17(1): 131–136. [20] 崔铁军, 李莎莎. 多因素集对分析的系统故障模式识别方法研究[J]. 智能系统学报, 2022, 17(2): 387–392. CUI Tiejun, LI Shasha. Research on system fault pattern recognition based on set pair analysis with multi factor[J]. CAAI transactions on intelligent systems, 2022, 17(2): 387–392. [21] 崔铁军, 李莎莎. 基于特征函数和联系数的系统故障模式识别[J]. 中国安全科学学报, 2021, 31(6): 1–6. doi: 10.16265/j.cnki.issn1003-3033.2021.06.001 CUI Tiejun, LI Shasha. Research on system fault pattern recognition based on characteristic function and connection number[J]. China safety science journal, 2021, 31(6): 1–6. doi: 10.16265/j.cnki.issn1003-3033.2021.06.001 [22] 赵克勤, 黄德才, 陆耀忠. 基于a+bi+cj型联系数的网络计划方法初探[J]. 系统工程与电子技术, 2000, 22(2): 29–31. doi: 10.3321/j.issn:1001-506X.2000.02.009 ZHAO Keqin, HUANG Decai, LU Yaozhong. A new network planning method based on the connection number a+bi+cj[J]. Systems engineering and electronics, 2000, 22(2): 29–31. doi: 10.3321/j.issn:1001-506X.2000.02.009 [23] 赵克勤. 集对分析对不确定性的描述和处理[J]. 信息与控制, 1995, 24(3): 162–166. ZHAO Keqin. Disposal and description of uncertainties based on the set pair analysis[J]. Information and control, 1995, 24(3): 162–166. [24] 崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J]. 安全与环境学报, 2019, 19(2): 399–405. CUI Tiejun, LI Shasha. Revision of the space fault tree and the space fault network system[J]. Journal of safety and environment, 2019, 19(2): 399–405. [25] 崔铁军, 李莎莎, 朱宝艳. 含有单向环的多向环网络结构及其故障概率计算[J]. 中国安全科学学报, 2018, 28(7): 19–24. CUI Tiejun, LI Shasha, ZHU Baoyan. Multidirectional ring network structure with one-way ring and its fault probability calculation[J]. China safety science journal, 2018, 28(7): 19–24.




















 下载:
下载: