对于航天器而言，良好的轨迹跟踪控制能力是其开展目标跟踪、交会对接、空间站建设和太空垃圾清理等任务的前提^[1-4]。近年来，随着空间技术的不断发展，航天器的集成度越来越高，组成机构日益复杂，所涉及的领域也在不断增多。人们对在轨服务的需求急剧上升，进一步对航天器的快速性和通信网络的稳定性提出了更高的要求。因此，航天器轨道动力学建模、控制及仿真方面的研究逐渐受到了广大科研工作者的青睐^[5]。

随着通信技术的不断发展，越来越多控制信号的远程传输主要基于信息网络实现^[6-7]。作为一种典型的信息物理系统(cyber-physical system, CPS)，航天器控制系统也不例外。对于通信能力受限下的航天器控制问题，通常有两种不同的控制方案。其一是提高信号的编/解码效率，如选择合适的量化器^{[8- 9]}；其二便是降低非必要信号的传输频率，较为典型的便是引入事件触发机制^[10-11]。事件触发机制的底层逻辑是控制信号的传输与否不由时间决定，而是由事先设计好的触发条件决定^[12]。和基于采样时间的触发方式相比，事件触发往往可以节约更多的计算资源、通信资源，减少能源消耗^[13]。在航天器编队协同控制方面，Xu等^[14]提出了一种分布式事件触发方案，以减少编队成员间的通信压力。为了实现欧拉–拉格朗日系统的协同控制，Shi等^[15]提出了一种基于周期性采样的事件触发算法。该控制方案不仅可以保证系统无Zeno现象，还可以避免编队成员过多造成的通信阻塞。

值得注意的是，大部分现有的航天器跟踪控制算法只能实现控制系统的渐进稳定，这意味着系统的收敛时间过长，无法实现航天器的快速机动^[16-17]。为此，Zhang等^[18]提出了一种新的非奇异快速终端滑模，为航天器协同控制系统有向和无向通信连接下的有限时间控制问题提供了思路。Huang等^[19]针对航天器姿态协同控制问题提出了基于旋转矩阵的自适应有限时间控制策略。实际上，无论是渐进稳定还是有限时间稳定，系统收敛到误差带的时间总是正相关于系统初值。系统实际的收敛时间只能通过后验的方式获得，不可提前预知和设定^[20]。因此，探究如何实现航天器控制系统的预设时间收敛有着重要的理论意义和工程价值。

受到上述研究工作的启发，本文主要研究基于事件触发的预设时间航天器轨迹跟踪控制算法。文中所提算法的创新之处在于：

1) 不同于文献[21-22]，本文在反步法框架的基础上实现了航天器轨迹跟踪控制系统的预设时间稳定，并通过改进的低通滤波器避免“微分爆炸”问题；

2) 考虑到控制系统通信带宽有限，本文提出了一种基于动态参数的事件触发控制策略。不同于文献[14-15, 23]中的静态事件触发策略，该策略在保证系统控制精度的同时，拥有更大的事件触发间隔，因此在降低通信频率方面更具优势。

1.   准备工作与相关模型

1.1   准备工作

在控制器设计之前，首先给出如下预设时间引理和假设。

引理^[24]　如果存在李雅普诺夫函数$V{\text{:}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\bf{R}}^n} \to {{\bf{R}}_ + } \cup \left\{ 0 \right\}$满足：

则控制系统是预设时间稳定的，即系统的状态误差可以在预设的时间内收敛。式中K和$\varDelta$是正常数；$ a\left( t \right) $是预设时间动态增益，满足：

式中：$ 0 < \sigma \ll {T_s} $，$ \bar a = 1 + {{{T_s}} \mathord{\left/ {\vphantom {{{T_s}} \sigma }} \right. } \sigma } $；$ {T_s} $是预设时间参数。为了简便起见，在之后的控制器设计过程中将使用a代替$ a\left( t \right) $。

假设^[25]　对于时变的期望轨迹$\,{{\boldsymbol{\rho }}_d} $，其一阶导数存在且满足$ \left\| {{{{\boldsymbol{\dot \rho }}}_d}} \right\| \leqslant {\rho _M} $，$ \,{\rho _M} $是正常数。

1.2   航天器轨道动力学模型

假设航天器运行在椭圆轨道上，令$\,{\boldsymbol{\rho }} $和$ {\boldsymbol{v}} $分别表示航天器相对于参考轨迹的位置和速度矢量，则航天器在赤道惯性坐标系和轨道坐标系下的运动方程可以表示为^[26-27]

其中：$ M $和$ {\boldsymbol{\tau }} $分别表示航天器的质量和控制力矩；C、D和n的完整形式为

式中：$ \mu $为地球引力常数；R为地心到航天器的距离；$ \theta $是参考航天器的真近地角，其一阶和二阶导数分别满足：

其中：$ {n_c} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu {a_c^3}}} \right. } {a_c^3}}} $是参考航天器的平均角速度，$ {a_c} $和$ {e_c} $分别为参考航天器的半长轴和偏心率。

2.   基于事件触发的预设时间跟踪控制器设计

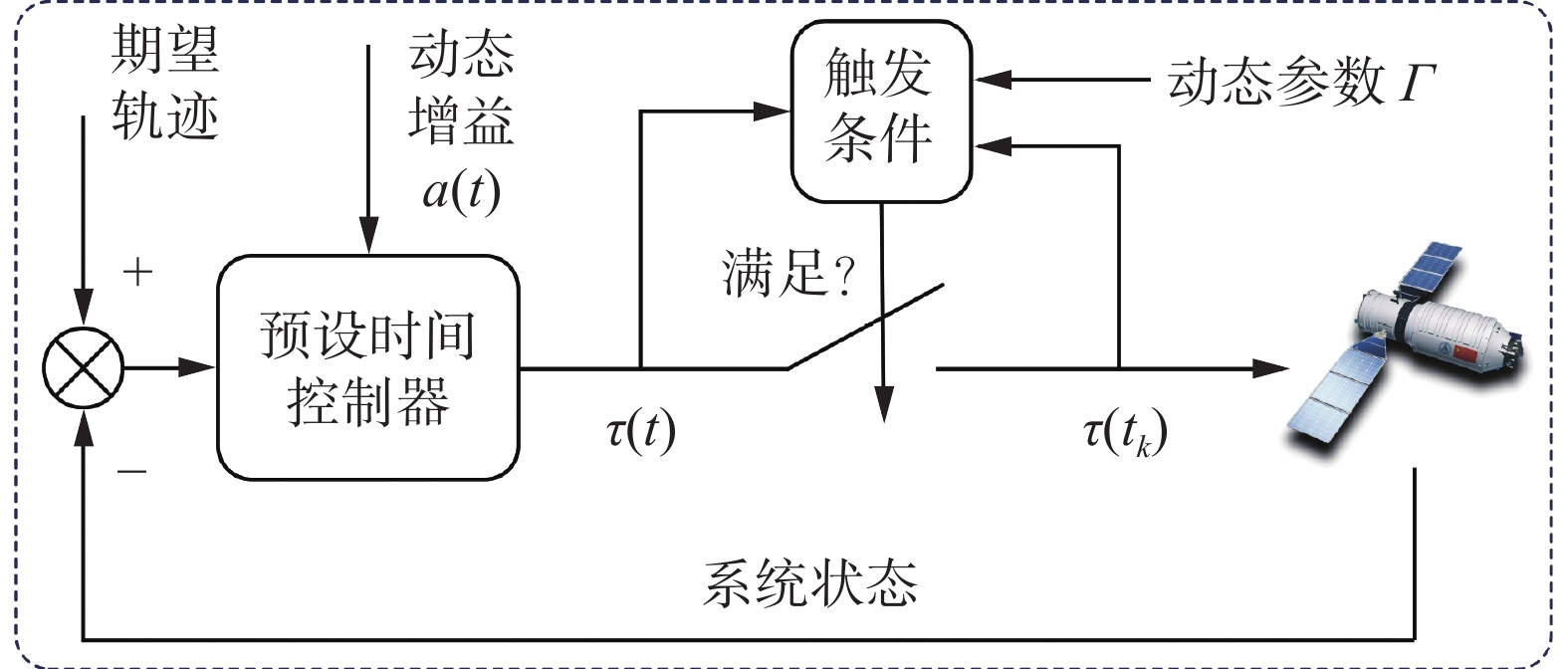
首先，本节以引理1作为理论依据设计了一种预设时间轨迹跟踪控制器。接着，针对控制系统部分信道上的通信受限问题，提出了一种基于动态参数的事件触发算法。航天器控制系统的整体设计流程如图1所示。

图  1  控制系统结构框

Fig.  1  Conceptual structure of the control system

下载: 全尺寸图片

2.1   预设时间控制器设计

首先，定义系统状态误差变量：

其中：$ \,{{\boldsymbol{\rho }}_d} $表示期望轨迹；$ {{\boldsymbol{v}}_d} $是经过滤波后的虚拟指令。一阶低通滤波器的表达式为

其中：$ \varepsilon $是滤波系数满足$ 0 < \varepsilon < {a^2} $；$ {{\boldsymbol{v}}_c} $是待设计的虚拟指令。定义滤波误差$ {\boldsymbol{y}} = {{\boldsymbol{v}}_d} - {{\boldsymbol{v}}_c} $，根据式(7)可知，滤波误差的导数满足：

注释 1　为了避免对虚拟指令的直接微分，本节通过引入一阶低通滤波器间接得到虚拟指令的导数。这不仅在一定程度上避免“微分爆炸”的问题，还可以平滑指令信号。其次，为了提高系统的瞬态性能，我们在滤波器中加入动态增益a，以确保当时间$ t \to {T_s} $时，滤波误差$ {\boldsymbol{y}} $实现收敛。

至此，本文的控制目标可以被描述为

其中$ {{\boldsymbol{\varTheta }}_i}{\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} i = \rho {\text{,}}v{\kern 1pt} $表示原点所在的邻域。

2.2   基于反步的控制器设计

本小节主要基于反步的设计框架，具体的预设时间控制器设计过程分为以下两个步骤：

1) 为了实现轨迹跟踪误差$ \,{{\boldsymbol{\rho }}_e} $的预设时间稳定，设计如下虚拟指令：

其中$ {k_\rho } $为正常数。由假设1可知，$ {{\boldsymbol{\dot \rho }}_d} $存在且有界。

2) 考虑到实际的航天器系统中，由于测量误差、燃料消耗等因素影响，航天器质量往往会在一定范围内波动，为此式(3)中航天器轨道动力学模型可进一步写为

式中：$ {M_0} + \Delta M = M $，$ {{\boldsymbol{C}}_0} + \Delta {\boldsymbol{C}} = {\boldsymbol{C}} $，$ {{\boldsymbol{D}}_0} + \Delta {\boldsymbol{D}} = {\boldsymbol{D}} $和$ {{\boldsymbol{n}}_0} + \Delta {\boldsymbol{n}} = {\boldsymbol{n}} $。其中$ {M_0} $、$ {{\boldsymbol{C}}_0} $、$ {{\boldsymbol{D}}_0} $和$ {{\boldsymbol{n}}_0} $为系统标称部分（已知），$ \Delta M $、$ \Delta {\boldsymbol{C}} $、$ \Delta {\boldsymbol{D}} $和$ \Delta {\boldsymbol{n}} $为不确定部分。从式(4)中可知，C、D和n是关于质量M的函数。因此这里同样考虑它们对应的不确定部分$ \Delta {\boldsymbol{C}} $、$ \Delta {\boldsymbol{D}} $和$ \Delta {\boldsymbol{n}} $。式(11)可进一步简写为

其中$ {\boldsymbol{Y}}\left( {{\boldsymbol{\rho }},{\kern 1pt} {\kern 1pt} {\boldsymbol{v}},{\kern 1pt} {\kern 1pt} {\boldsymbol{\dot v}}} \right) = \Delta M{\kern 1pt} {\boldsymbol{\dot v}} + \Delta {\boldsymbol{Cv}} + \Delta {\boldsymbol{D\rho }} + \Delta {\boldsymbol{n}} $。根据系统的动力学特性，不确定项Y满足如下不等式：

其中$ c = {\text{max}}\left( {{c_1},{\kern 1pt} {\kern 1pt} {c_2},{\kern 1pt} {\kern 1pt} {c_3},{\kern 1pt} {\kern 1pt} {c_4}} \right) $是不确定项的系数，$ \varPhi = 1 + \left\| {\boldsymbol{\rho }} \right\| + \left\| {\boldsymbol{v}} \right\| + \left\| {{\boldsymbol{\dot v}}} \right\| $为复合系统状态。针对系数项，这里设计自适应更新律保证$ c \to \hat c $：

其中${k}_{c}，{k}_{\hat{c}} > 0$为自适应增益。$ \tilde c = c - \hat c $为逼近误差。基于此，设计自适应控制器，具体形式如下：

其中$ {k_v} $为正常数。

注释 2　在实际的工程应用中，航天器动力学参数M、C、D和n的变化往往会影响系统的稳定性和控制精度。本小节中通过使用自适应算法，对未知项$ {\boldsymbol{Y}}{\text{(}}{\boldsymbol{\rho }},{\kern 1pt} {\kern 1pt} {\boldsymbol{v}},{\kern 1pt} {\kern 1pt} {\boldsymbol{\dot v}}{\text{)}} $进行一定程度的补偿，从而减少参数摄动对于系统控制性能的影响，提高轨迹跟踪系统的鲁棒性。

注释 3　从式(15)中不难看出，低通滤波器的使用避免了对虚拟指令$ {{\boldsymbol{v}}_c} $的直接微分。控制指令式(15)中的$ {{\boldsymbol{\dot v}}_d} $可以从滤波器式(7)中直接得到，即$ {{\boldsymbol{\dot v}}_d} = {{a\left( {{{\boldsymbol{v}}_c} - {{\boldsymbol{v}}_d}} \right)} \mathord{\left/ {\vphantom {{a\left( {{{\boldsymbol{v}}_c} - {{\boldsymbol{v}}_d}} \right)} \varepsilon }} \right. } \varepsilon } $，因此系统的计算复杂度得到进一步减小，避免了“微分爆炸”问题。此外，符号函数$ {\text{sign}}\left( \cdot \right) $的使用可能会引起抖振现象，所以在仿真中往往使用饱和函数或双曲正切函数进行替换。

2.3   事件触发机制

首先，定义如下误差方程：

其中$ {\boldsymbol{\tau }}\left( {{t_k}} \right) $表示第k次事件触发时的控制力矩。由于零阶保持器的作用，控制力矩在$ \left[ {{t_k},{t_{k + 1}}} \right) $时间区间内保持不变。在本节中采用如下事件触发机制：

式中：$ \alpha $和$ \beta $是正常数，为事件触发的动态参数，满足：

其中设计参数$ \theta ,{\kern 1pt} {\kern 1pt} \mu > 0 $。从式(18)中可以知道$ \varGamma \in \left[ {1,{\kern 1pt} {\kern 1pt} 1 + \theta } \right) $。

注释 4　不同于静态事件触发的设计：

本节中的事件触发策略包含动态参数$ \varGamma $，且$ \varGamma $具有以下两个重要性质：

1) 当$ \left\| {{{\boldsymbol{\rho }}_e}} \right\| + \left\| {{{\boldsymbol{v}}_e}} \right\| $增大时，$ \varGamma $值增大，$ \varGamma \to 1 + \theta $；

2) 当$ \left\| {{{\boldsymbol{\rho }}_e}} \right\| + \left\| {{{\boldsymbol{v}}_e}} \right\| $减小时，$ \varGamma $值减小，$ \varGamma \to 1 $。

在系统到达稳定状态之前($ {T_s} $时刻)，误差函数的模值$ \left\| {\boldsymbol{e}} \right\| $和系统控制力矩$ {\boldsymbol{\tau }} $往往较大。这意味着式(17)中的触发条件更容易达到，系统将在较大的控制力矩作用下多次重置${\text{[}}{\boldsymbol{\tau }}{\text{(}}{t_1}{\text{)}},{\kern 1pt} {\kern 1pt} {\boldsymbol{\tau }}{\text{(}}{t_2}{\text{)}}, \cdots , {\boldsymbol{\tau }}{\text{(}}{t_k}{\text{)}}, \cdots {\text{]}}$的值。显而易见的缺点有：1) 过于密集的通信次数将增加通信阻塞的风险；2) 多次在控制力矩较大的情况下进行系统切换会大幅增加执行器故障的风险。为此，本文在事件触发条件中引入动态参数$ \varGamma $，目的是在系统未达到稳定状态之前，有目的地提高事件触发阈值，从而降低执行器故障的风险，同时一定程度上避免由信道阻塞造成通信时延和丢包等问题。

2.4   稳定性分析

为了说明文中所提控制算法的有效性，现给出如下定理及证明过程：

定理　对于航天器控制系统式(3)，在满足假设1的前提下，如果预设时间控制器的设计如式(10)和(15)所示，采用式(17)中所述的事件触发机制，若系统控制参数满足$ {k_\rho } > {{{\text{(}}2 + \alpha \varGamma {\text{)}}} \mathord{\left/ {\vphantom {{{\text{(}}2 + \alpha \varGamma {\text{)}}} 4}} \right. } 4} $，${k_v} > \dfrac{{{\text{(}}a + 1{\text{)}}\alpha \varGamma + {1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}}{{{a^2}}}$，则航天器可以在预设时间$ {T_s} $内跟踪上期望轨迹，也即$\mathop {{\rm{lim}}}\limits_{t \to {T_s}} {\text{[}}{{\boldsymbol{\rho }}_e}{\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\boldsymbol{v}}_e}{\text{]}} \in {\text{[}}{{\boldsymbol{\varTheta }}_\rho }{\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\boldsymbol{\varTheta }}_v}{\text{]}}$，且系统不存在Zeno现象。

证明　首先构建李雅普诺夫方程：

结合式(6)和(8)，可算得$ {V_1} $的导数为

代入虚拟指令式(10)，可得：

考虑实际控制指令式(15)，结合式(13)和式(16)，有如下关系成立：

根据$ \tilde c $的定义可知$ \dot {\tilde c} = \dot c - \dot{ \hat c} = - \dot {\hat c }$，结合自适应律式(14)有：

由式(17)中的触发条件可知，式(24)中$ {\boldsymbol{v}}_e^{\text{T}}{\boldsymbol{e}} $满足不等式：

参考文献[28]，可知对于虚拟指令有$\left\| { - {{{\boldsymbol{\dot v}}}_c}} \right\| \leqslant \varLambda$。结合杨氏不等式，有如下关系式成立：

将式(25)和式(26)代入式(23)，可得：

其中

$ {\lambda _{{\text{max}}}}\left( {\boldsymbol{M}} \right) $表示矩阵M的最大特征值。系统控制参数满足$ {k_\rho } > {{{\text{(}}2 + \alpha \varGamma {\text{)}}} \mathord{\left/ {\vphantom {{{\text{(}}2 + \alpha \varGamma {\text{)}}} 4}} \right. } 4} $，${k_v} > \dfrac{{{\text{(}}a + 1{\text{)}}\alpha \varGamma + {1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}}{{{a^2}}}$。

由引理1可知，系统跟踪误差可以在预设时间$ {T_s} $内收敛。至此，完成定理1的证明。

2.5   Zeno现象分析

Zeno现象是指系统的控制行为在有限时间内被无限次触发^[13]。想要证明系统不存在Zeno现象，只需要证明相邻两次事件触发的间隔大于正常数$ \kappa $，也即$ {t_{k + 1}} - {t_k} > \kappa $。

对于任意$ t \in \left[ {{t_k},{\kern 1pt} {\kern 1pt} {t_{k + 1}}} \right) $，由式(16)中e的定义可知：

因此，对于$ \left\| e \right\| $的导数，有：

对不等式两边积分可得：

其中正常数$ \varsigma \geqslant \left\| {{\boldsymbol{\dot \tau }}\left( t \right)} \right\| $。进一步可得事件触发间隔：

即本文中提出的事件触发算法可以有效避免Zeno现象。

注释 5　对一般的静态时间触发算法，由上述方法可求得其事件触发间隔为

观察式(32)和(33)，动态参数$ \varGamma \in {\text{[}}1,{\kern 1pt} {\kern 1pt} 1 + \theta {\text{)}} $显然在一定程度上增加了触发间隔，使得$ T \geqslant {T'} $。因此本文中的事件触发策略能够更加有效地降低系统通信频率，避免通信阻塞。

3.   仿真与分析

为了验证文中预设时间和事件触发算法在航天器轨迹跟踪控制中的有效性，本节对所提控制算法进行仿真验证。

3.1   基础仿真

仿真所用的航天器模型参数同文献[15]：

质量变化范围设置为$ \Delta M \in {\text{[}} - {\text{3}},{\kern 1pt} {\kern 1pt} {\text{3]kg}} $。不失一般性，系统的初始状态和期望轨迹分别设置为

在稳定性分析部分可知，系统控制增益需满足$ {k_\rho } > {{{\text{(}}2 + \alpha \varGamma {\text{)}}} \mathord{\left/ {\vphantom {{{\text{(}}2 + \alpha \varGamma {\text{)}}} 4}} \right. } 4} $，${k_v} > \dfrac{{{\text{(}}a + 1{\text{)}}\alpha \varGamma + {1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}}{{{a^2}}}$。通过简单的调试与计算，相关控制参数设置为

事件触发参数：

由式(32)可知，事件触发间隔$ T $与上述参数的值息息相关。相对激进的参数选取会得到较大的触发间隔，大幅降低通信频率，此时系统的跟踪控制性能也会随之下降。因此事件触发参数的选取应遵守以下两个原则：

1) 系统通信频率是否得到大幅降低，如降低90%以上；

2) 系统的性能指标是否满足任务要求，如超调是否过大、理论跟踪精度能否达到毫米级等。

基于以上两个原则，在保证控制性能的前提下逐渐由小及大地调整$ \alpha {\kern 1pt} $、$ {\kern 1pt} \beta $、$ \theta $和$ \mu $的值。

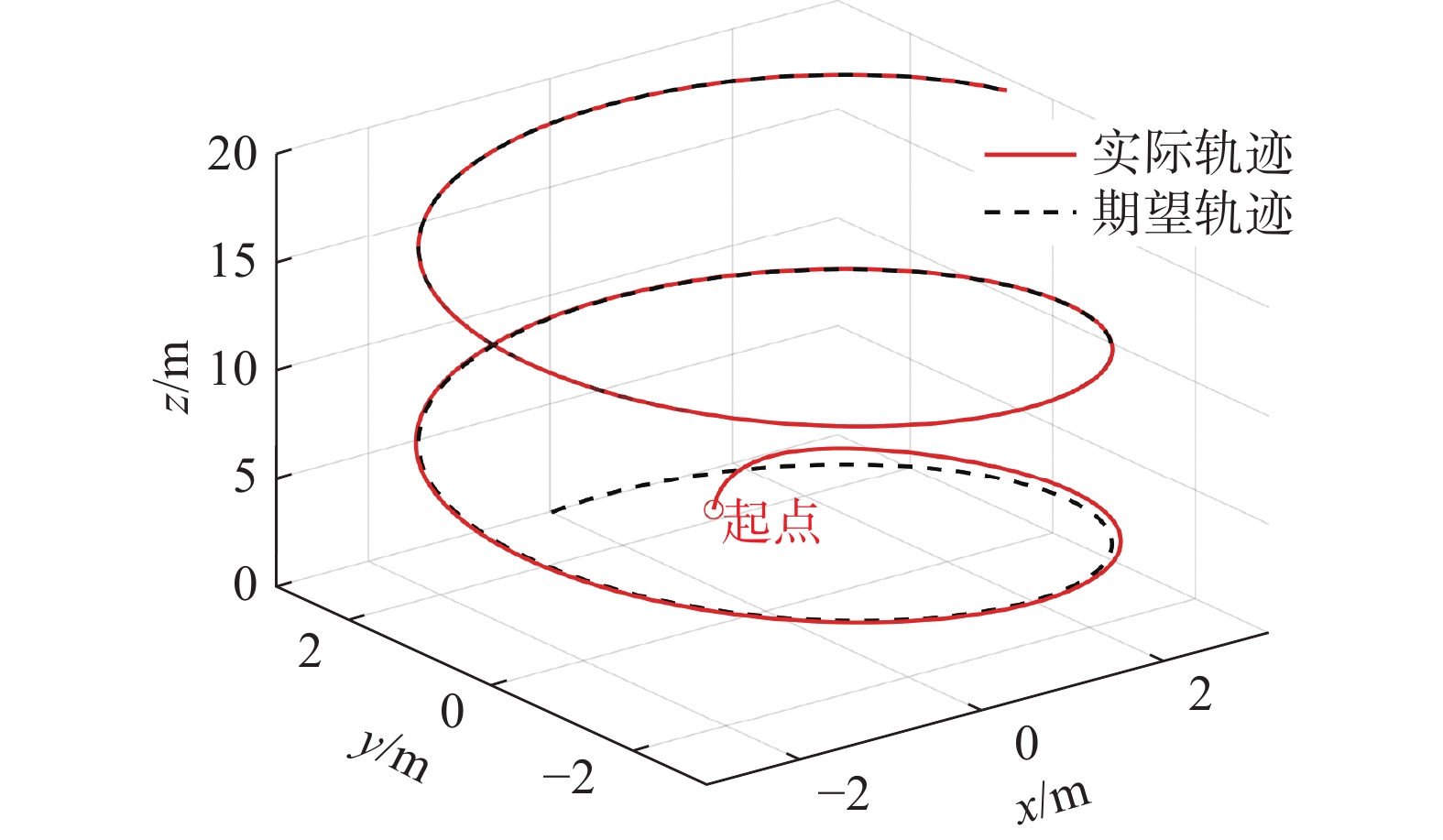
系统仿真时间为20 s，仿真步长为${t_{{\text{s}}{\text{t}} {\text{e}} {\text{p}}}} = 2 \times {10^{ - 3}}{\kern 1pt} {\kern 1pt} {\text{s}}$，预设时间参数设为$ {T_s} = 15{\kern 1pt} {\kern 1pt} {\text{s}} $。据此，我们得到图2~6中所示的仿真结果。

图  2  航天器轨迹跟踪效果

Fig.  2  Trajectory tracking result of spacecraft

下载: 全尺寸图片

图  3  轨迹跟踪误差变化曲线

Fig.  3  Curves of trajectory tracking error

下载: 全尺寸图片

图  4  速度跟踪误差变化曲线

Fig.  4  Curves of velocity tracking error

下载: 全尺寸图片

图  5  控制力矩变化曲线

Fig.  5  Curves of control torque

下载: 全尺寸图片

图  6  触发误差及其阈值

Fig.  6  Trigger error and its threshold

下载: 全尺寸图片

图2给出了航天器的曲线跟踪效果，虚线表示期望轨迹，可以看出，所采用的反步控制方案可以取得较好的轨迹跟踪效果。

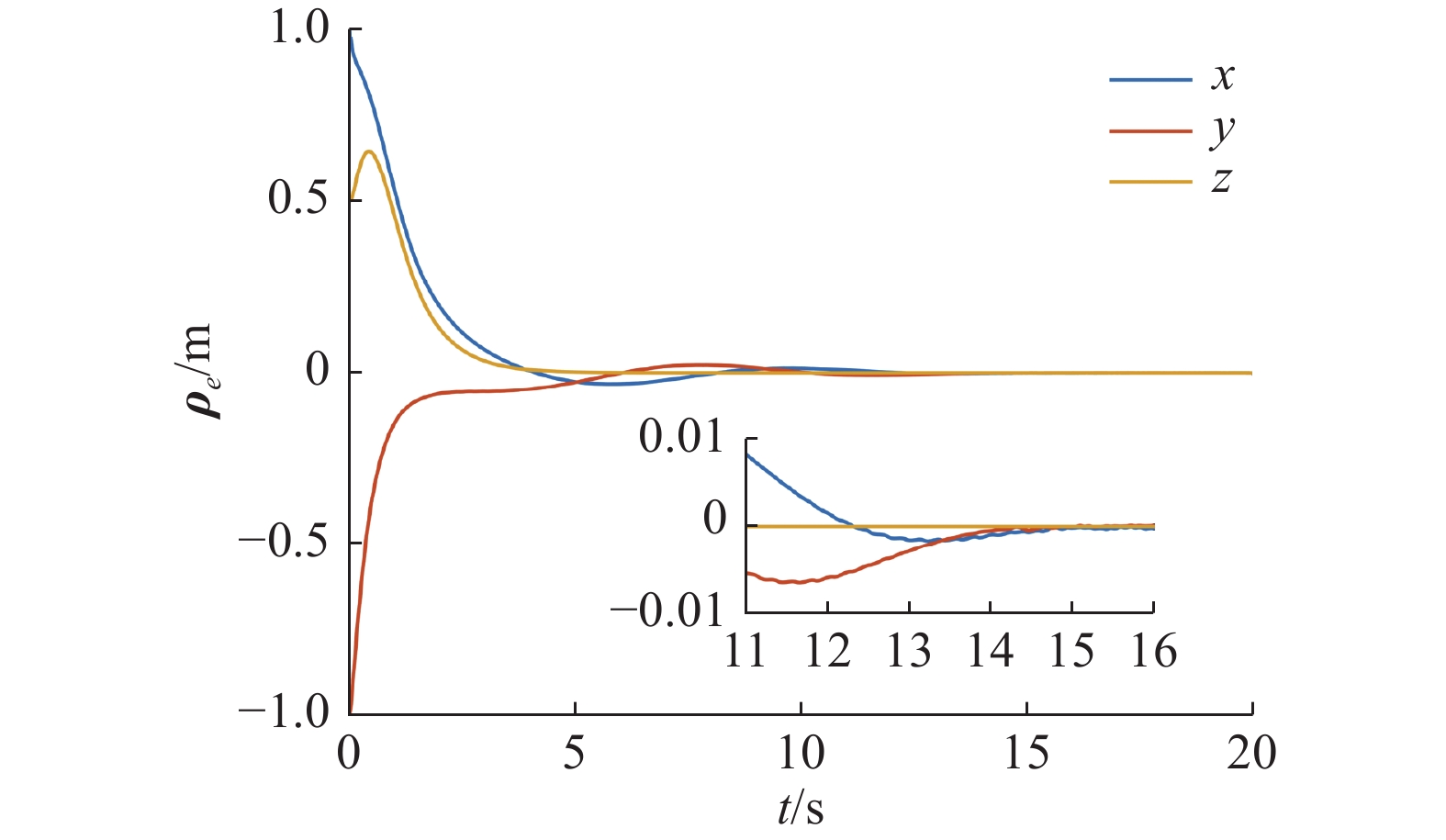
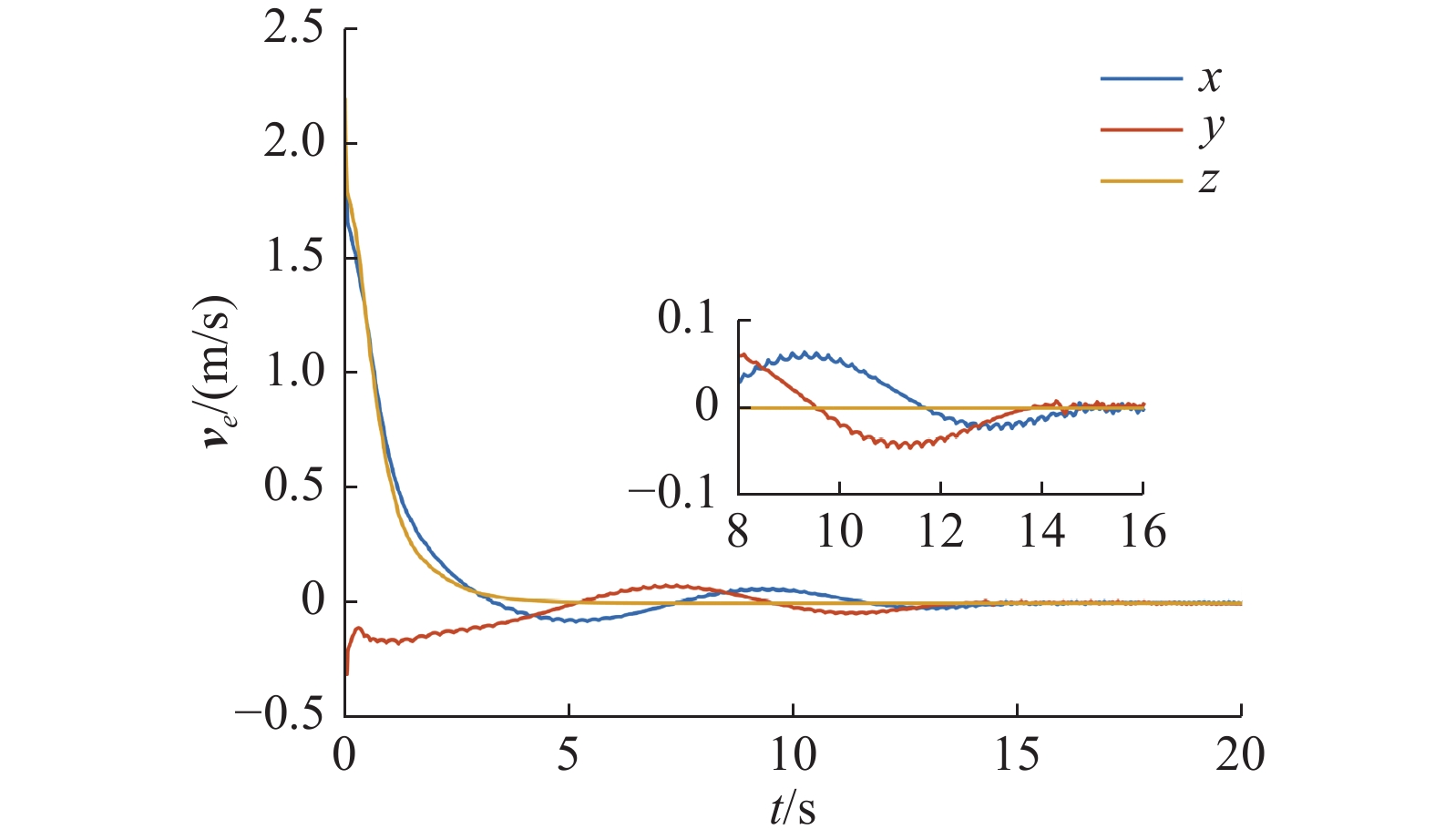
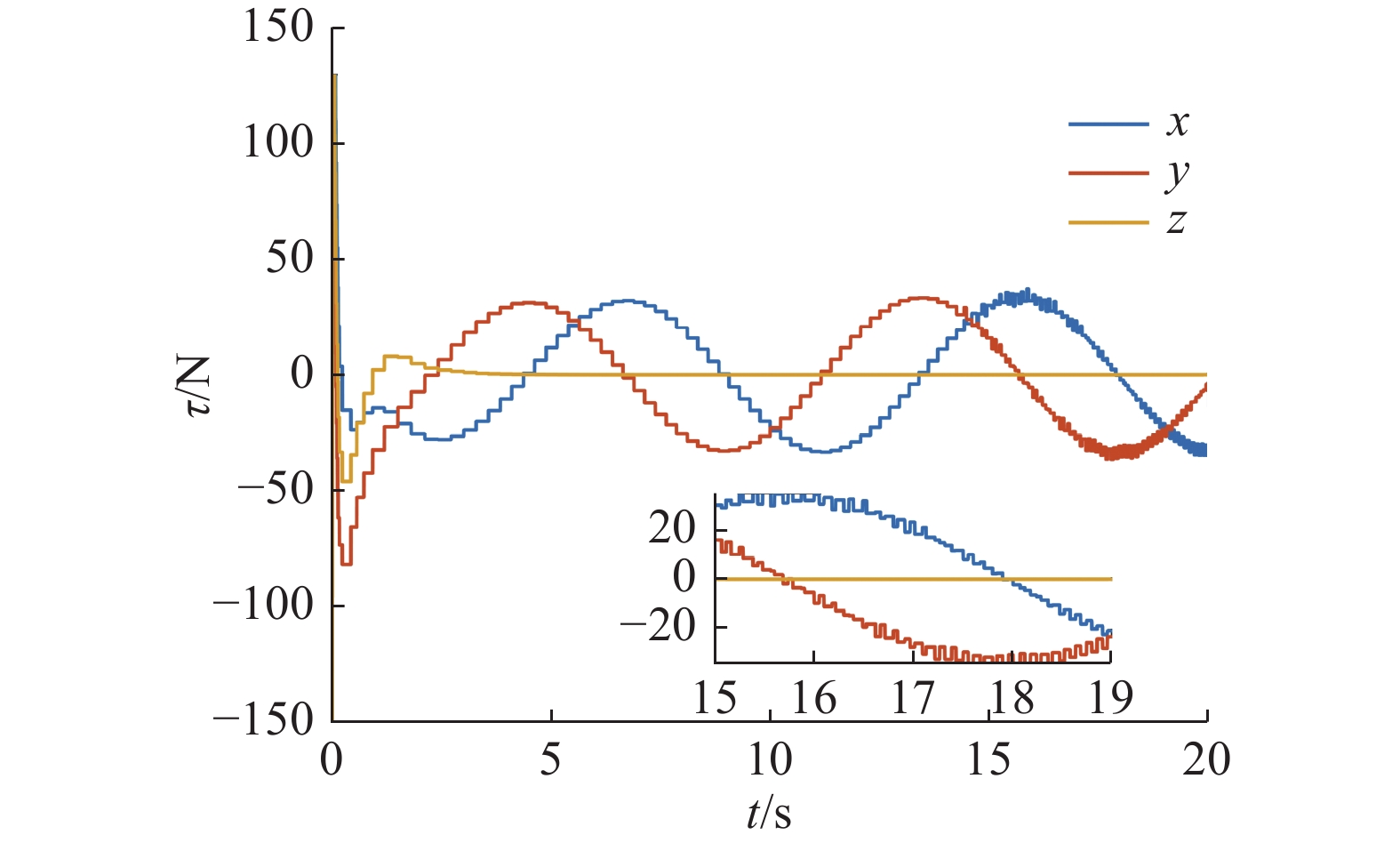
轨迹跟踪误差和速度跟踪误差曲线如图3和图4所示。从图中不难看出，在预设时间控制器的作用下，轨迹跟踪误差$ {{\boldsymbol{\rho }}_e} $和速度跟踪误差$ {{\boldsymbol{v}}_e} $均在15 s内收敛，且稳态误差分别控制在$2 \times {10^{{{ - }}4}}\;{\text{m}}$和$7 \times {10^{{{ - 3}}}}\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. } {\text{s}}}$之内，能够满足一般的轨迹跟踪控制任务需求。

图5中给出了系统在事件触发机制下系统的控制力矩。由于只有满足事件触发条件式(17)时，系统控制指令才会得到更新。因此图5中的控制指令具有明显的离散化特征，这进一步说明控制中心与航天器之间的通信频率得到降低。

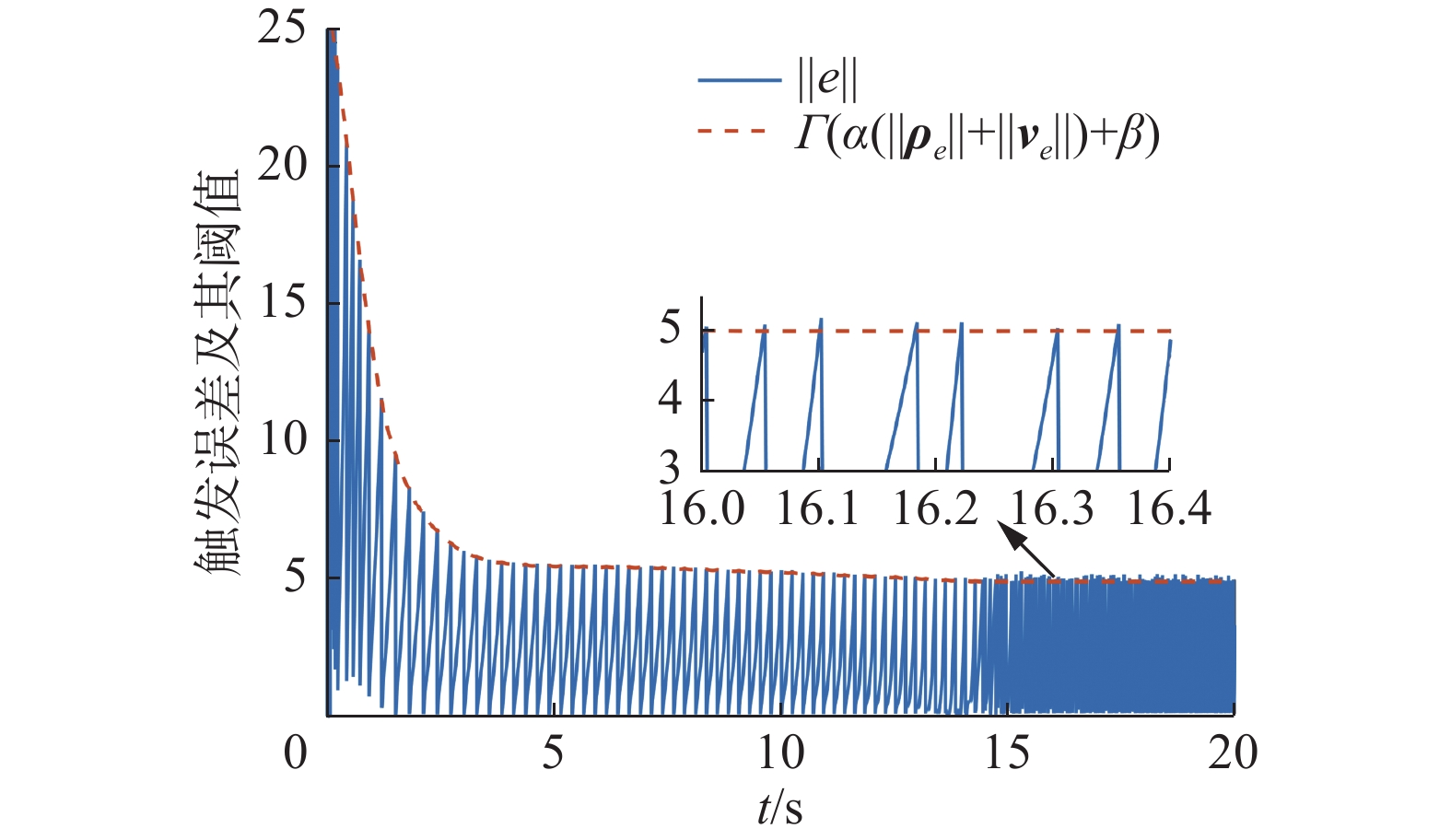
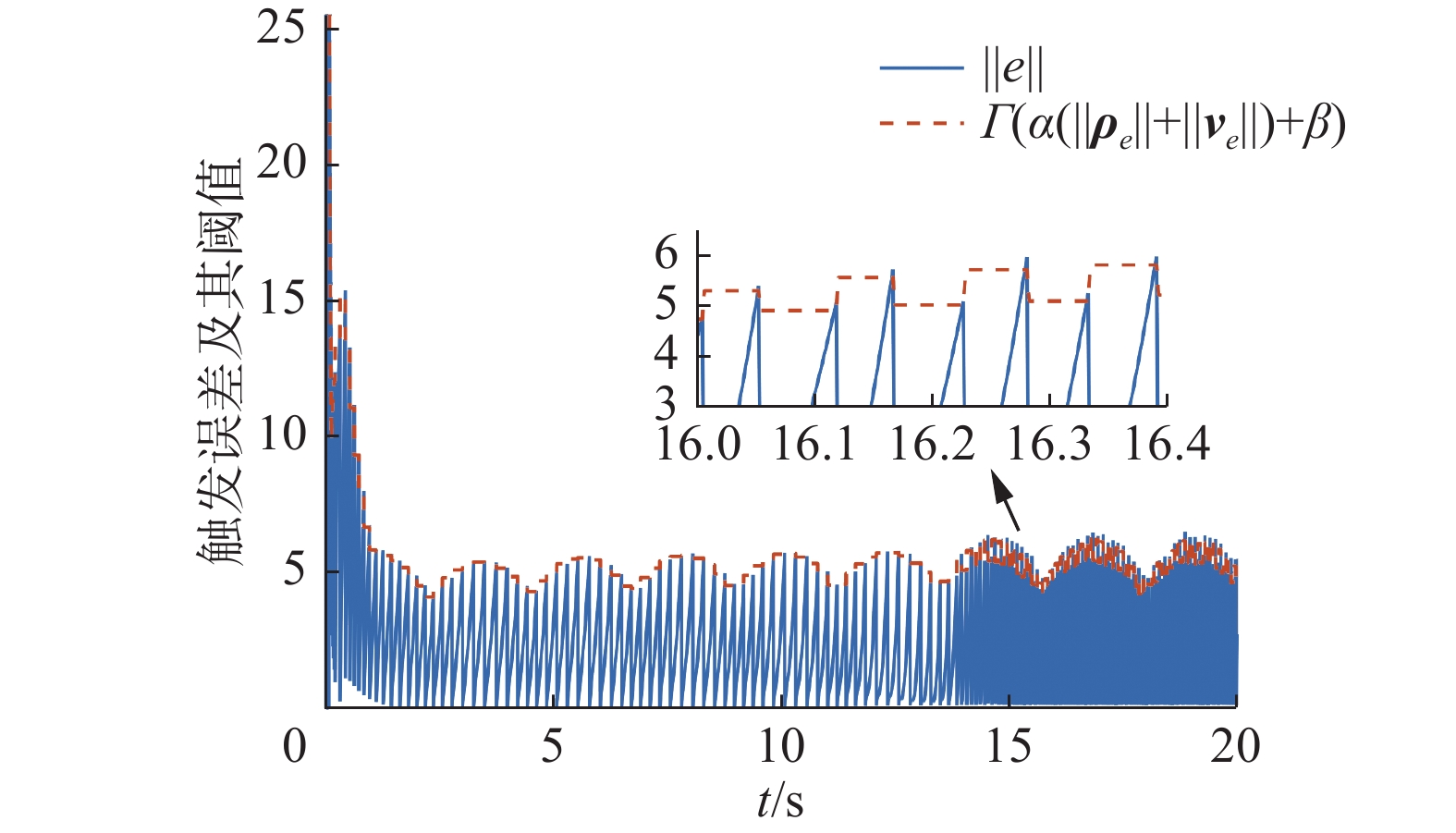
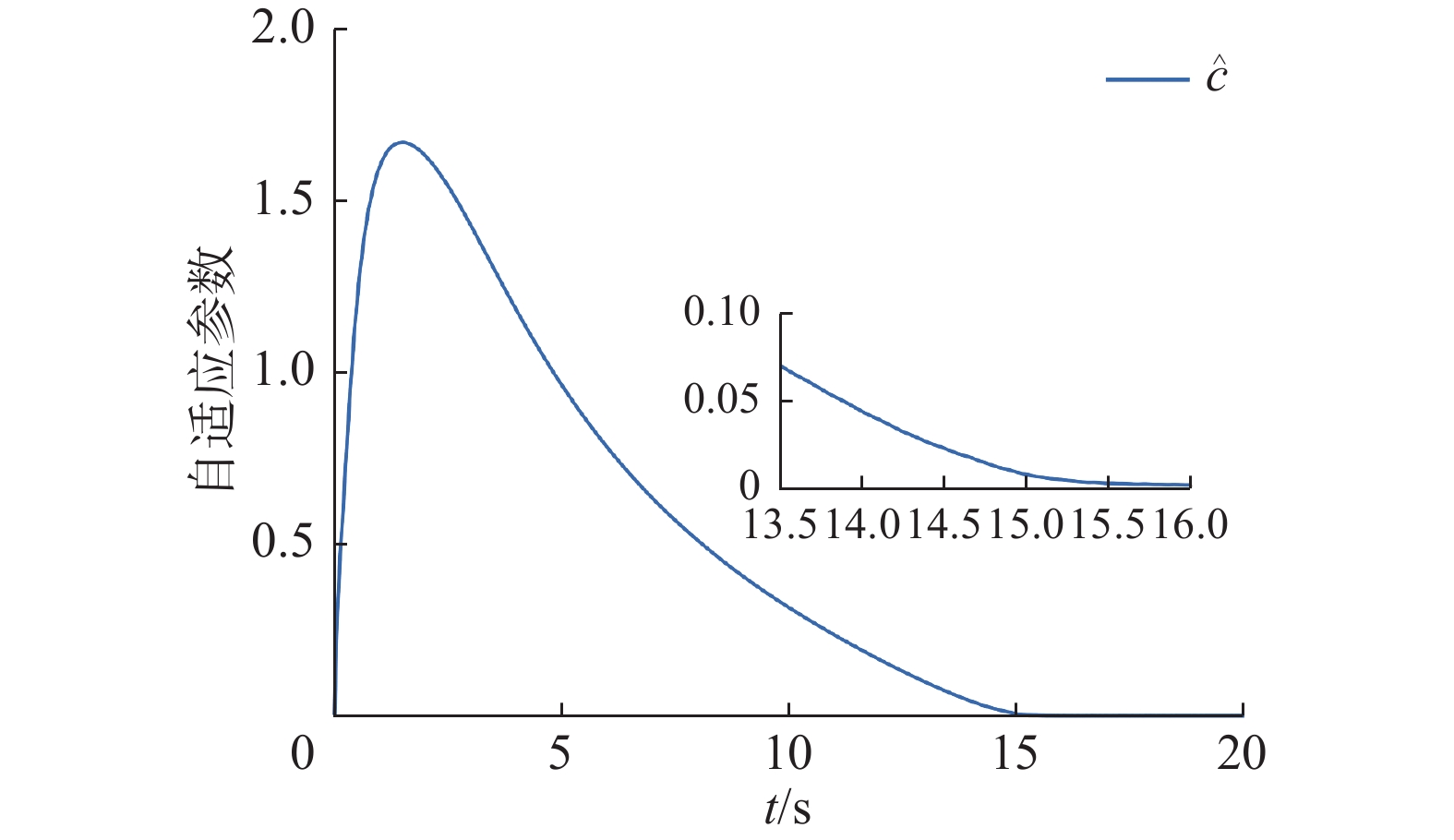
触发误差及其阈值的变化曲线如图6所示。可以看到，每当触发误差增大并逼近触发边界后，系统将完成一次触发，$ {\boldsymbol{\tau }}{\text{(}}{t_{k - 1}}{\text{)}} $被重置为$ {\boldsymbol{\tau }}{\text{(}}{t_k}{\text{)}} $。$ \left\| {\boldsymbol{e}} \right\| $在$ {t_k} $时刻被重置为0，在触发间隔$ {\text{[}}{t_k},{\kern 1pt} {\kern 1pt} {t_{k + 1}}{\text{)}} $误差$ \left\| {\boldsymbol{e}} \right\| $持续积累，直到满足下一次触发条件。在20 s的仿真时间内，系统通信总数为163次，其中前5 s内触发30次，平均触发间隔为0.12 s，远大于系统采样周期$ {t_{{\text{s}} {\text{t}} {\text{e}} {\text{p}}}} $。相较于无事件触发的控制策略(触发次数10 000次)，本文所提的事件触发方法可以在20 s的仿真时长内减少98.37%的通信量。通过理论分析可知，由于事件触发参数$ \varGamma {\text{,}}{\kern 1pt} {\kern 1pt} \alpha {\text{,}}{\kern 1pt} {\kern 1pt} \beta > 0 $，所以触发阈值$ \varGamma {\text{(}}\alpha {\text{(}}\left\| {{{\boldsymbol{\rho }}_e}} \right\| + \left\| {{{\boldsymbol{v}}_e}} \right\|{\text{)}} + \beta {\text{)}} > 0 $始终成立。当系统稳定时，$ \left\| {{{\boldsymbol{\rho }}_e}} \right\| + \left\| {{{\boldsymbol{v}}_e}} \right\| $的值减小，但稳态误差始终存在。此时触发阈值$ \varGamma {\text{(}}\alpha {\text{(}}\left\| {{{\boldsymbol{\rho }}_e}} \right\| + \left\| {{{\boldsymbol{v}}_e}} \right\|{\text{)}} + \beta {\text{)}} $会逐渐收敛到某一常值附近，而不会趋于零。因此一定程度上避免了Zeno现象。

自适应参数的变化曲线如图7所示，可以看到随着系统的稳定自适应参数的值逐渐收敛，最终保持有界。

图  7  自适应参数变化曲线

Fig.  7  Curve of adaptive parameter

下载: 全尺寸图片

3.2   控制参数有效性验证

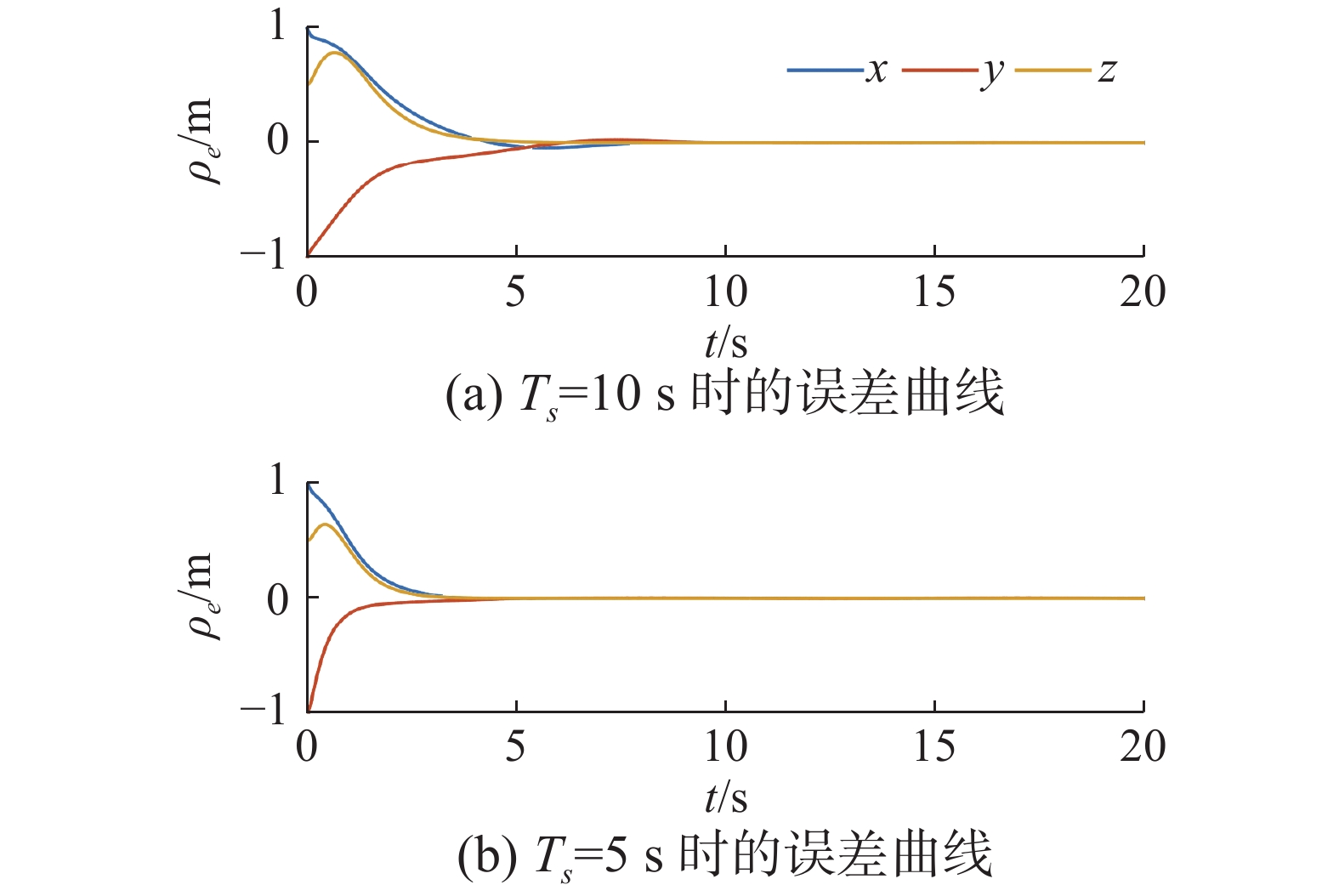
为了进一步说明所提预设时间和事件触发控制算法的优越性，在接下来的对比仿真中分别将：1) 预设时间参数设置为$ {T_s} = 10{\text{ s}} $和$ {T_s} = 5{\text{ s}} $；2) 事件触发的动态参数设置为$ \varGamma {{ = 1}} $； 3) 与其他相关算法进行仿真对比。得到以下3组仿真结果。

1) 改变预设时间参数$ {T_s} $。

从图8中不难看出，系统的跟踪误差总是在预设的时间$ {T_s} $内收敛到原点所在的邻域内。因此，本文中的预设时间算法能够满足多种任务场景下对于系统快速性的要求。

图  8  不同预设时间参数下轨迹跟踪误差变化曲线

Fig.  8  Curves of trajectory tracking error with different prescribed-time parameters

下载: 全尺寸图片

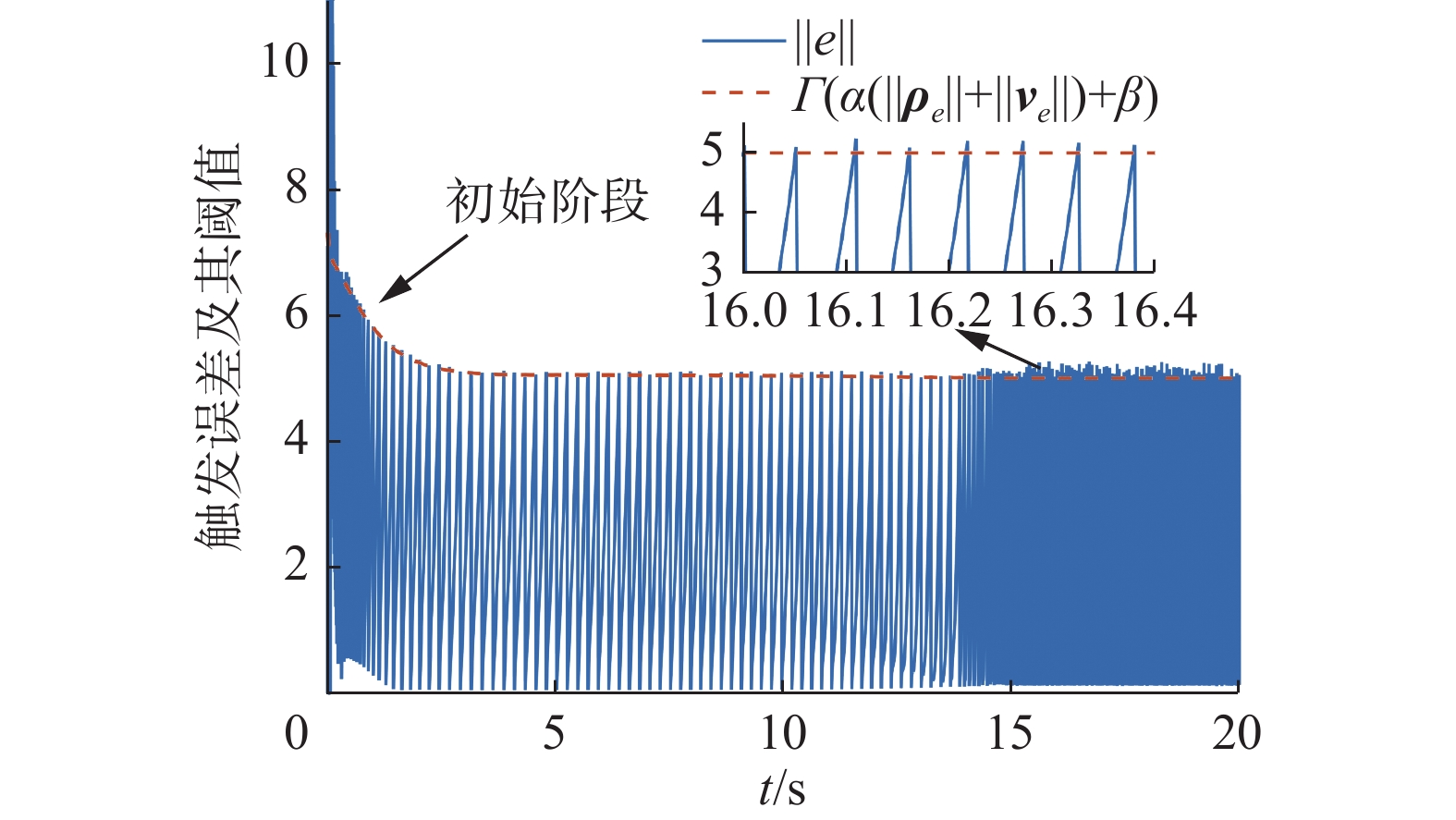
2) 改变动态参数$ \varGamma $。

当动态参数$ \varGamma = 1 $时，文中的事件触发控制算法即变成式(19)中所示的静态事件触发算法。由于系统状态在初始阶段变化相对剧烈，且静态事件触发算法无法自动调节触发阈值，因此初始阶段系统触发频率更高，如图9所示。在20 s的仿真时间内，系统通信次数为207次。相较于本文中的事件触发策略，通信总次数增加了约26.99%；在初始阶段(前5 s内)，通信频率提高了103.33%，同前文中的理论分析结果一致。因此，基于动态参数的事件触发控制策略在减少通信频率方面有着较为明显的优势，特别是在系统的初始阶段。

图  9  静态事件触发误差及其阈值

Fig.  9  Trigger error and its threshold of static event trigger

下载: 全尺寸图片

3) 对比仿真。

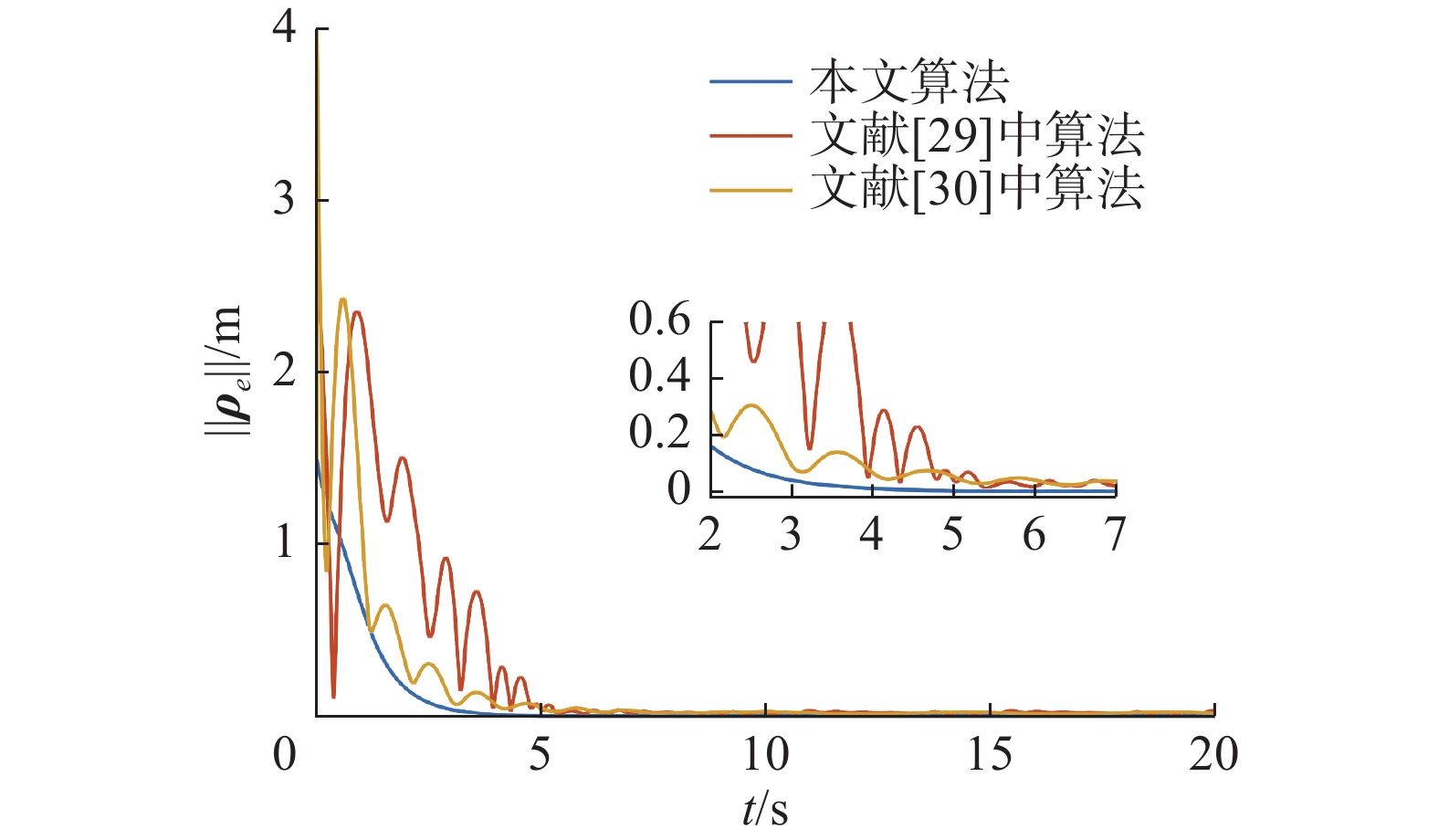
本小节分别通过与有限时间控制算法和静态参数事件触发算法进行对比，进一步突出文中所提算法的优越性。文献[29]和文献[30]中的分别提出了两种基于终端滑模的航天器有限时间控制算法。在对比仿真过程中，容易发现该算法中存在控制参数过多，不同参数间相互关联，不利于参数整定的问题。而本文中控制参数较少，且相关参数的物理意义明确，为参数整定提供了便利。在这里以跟踪误差范数$ \left\| {{{\boldsymbol{\rho }}_e}} \right\| $的时间响应为例，将预设时间参数设置为$ {T_s} = 5{\text{ s}} $，得到图10所示对比仿真结果。

图  10  与有限时间算法的对比仿真

Fig.  10  Comparative results with finite-time control algorithm

下载: 全尺寸图片

从图10可以看出，本文所提基于反步的预设时间控制算法拥有更好的瞬态和稳态性能，特别是在系统超调和稳态精度方面具有明显优势。文献[31]中的基于静态参数的事件触发的仿真结果如图11所示。同$ \varGamma = 1 $时的仿真结果相似，系统事件触发频率较高，特别是在初始阶段。与基于动态参数的事件触发算法相比，初始阶段通信频率提高了46.67%。这进一步说明本文所提算法在降低通信频率方面的明显优势。

图  11  与静态参数事件触发算法的对比仿真

Fig.  11  Comparative results with static parameter-based event-trigger algorithm

下载: 全尺寸图片

4.   结束语

本文主要研究了基于事件触发的航天器预设时间轨迹跟踪控制问题。相比于现有的航天器轨迹跟踪控制策略，本研究：1) 实现了航天器轨迹跟踪控制系统的预设时间稳定，2) 将预设时间增益与一阶低通滤波器结合以避免“微分爆炸”问题，3) 设计了基于动态参数的事件触发机制。理论分析和仿真结果都表明，所提的控制策略能够在通信频率大大降低的情况下实现轨迹跟踪系统的预设时间稳定，同时保持较高的控制精度。下一步计划将文中所提算法扩展到航天器编队协同控制领域中去，以提高编队系统执行任务的灵活性、容错性和可靠性。