Self-organizing rule generation method for a general type-2 fuzzy system
-
摘要: 针对广义二型模糊系统在复杂情况中因缺乏专家经验而难以构建合适模糊规则的问题，提出了一种基于输入数据的激活强度来生成广义二型模糊集以及模糊规则的方法。通过数据驱动自组织构建广义二型模糊系统模糊规则，并且使用迭代最小二乘法和梯度下降法优化系统前后件参数。最后，分别在无扰动和施加噪声情况下进行了非线性系统的跟踪仿真，实验结果证明了自组织规则生成的广义二型模糊系统的有效性，并能够以较高精度跟踪参考轨迹。Abstract: To solve the problem of difficult construction of appropriate fuzzy rules in the generalized type-2 fuzzy system due to a lack of expertise in complex situations, a method for generating generalized type-2 fuzzy sets and fuzzy rules based on the activation intensity of input data was proposed. The fuzzy rules of generalized type-2 fuzzy systems were constructed by a data-driven self-organization strategy, and the parameters of the front and rear parts of the system were optimized by the iterative least squares and gradient descent methods. Finally, the tracking simulation of the nonlinear system was conducted in the conditions of no disturbance and noise disturbance . The experimental results revealed that the generalized type-2 fuzzy system generated by the self-organizing rules is effective, and the reference trajectory can be tracked with high accuracy.
-
二型模糊系统最早主要由Mendel等[1]得以推广，其主要思想是对模糊集进行再次模糊化，从而使得模糊系统更加有效处理实际应用中的高度不确定性。二型模糊集的三维结构特性极大地提高了设计的自由度，在高度不确定场合，二型模糊集往往可以获得比一型模糊集更好地效果。其中，二型模糊集也可以分为两类，区间二型模糊集与广义二型模糊集。故而从模糊系统的类型上来说，可以分为一型模糊系统(type-1 fuzzy logic system, T1FLS)、区间二型模糊系统(interval type-2 fuzzy logic system, IT2FLS)和广义二型模糊系统(general type-2 fuzzy logic system, GT2FLS)3种。其模糊系统的结构主要由模糊器、模糊规则库、降型器(IT2FLS、GT2FLS)以及解模糊器组成。
基于模糊逻辑的智能控制系统广泛地应用在移动机器人[2-3]、工业生产过程[4]、模式识别和智能家居等领域。但是传统的模糊控制器依赖先验知识来设计模糊规则。当在复杂情况中缺乏专家经验时，便无法设计模糊系统。由于区间二型模糊系统兼顾了复杂度和性能的要求，目前已经被广泛研究。随着需要处理的问题不断复杂化，广义二型模糊控制作为一种先进的智能控制算法，在过去的几年中逐渐引起人们的注意。广义二型模糊系统有潜力比一型模糊系统与区间二型模糊系统具有更强大的处理不确定性的能力，但广义二型模糊系统的设计尚缺乏系统性设计方法，还有待进一步的研究。
传统二型模糊系统的建立主要分为两种：一种是基于模型衍生的模糊系统，另一种是基于数据驱动的模糊系统。其中，基于数据驱动的模糊系统因其不依赖于人工建立的模型，更加贴合数据集本身内在的一些数据规律，故而现在越来越受到广大学者的欢迎。文献[5]提出了一种动态演化神经模糊推理系统，根据新输入数据和现有聚类中心之间的欧氏距离添加新的模糊规则；文献[6]通过激活强度来对模糊规则的添加做出决策；文献[7]提出了一种数据驱动的区间二型模糊系统，该系统通过数据自组织构建模糊系统，使得模糊系统在保持较高的准确率的同时提高了其可解释性。
本文将通过数据驱动的方式自组织构建广义二型模糊系统，提出了一种基于输入数据的激活强度来生成广义二型模糊集以及模糊规则的方法，避免依赖于专家知识的同时使广义二型模糊系统的性能得到保证。
1. 广义二型模糊系统
1.1 广义二型模糊集
现有的二型模糊系统主要分为两种：第1种是广义二型模糊系统，其主要特点是二型模糊系统的次隶属度函数为其他非常值函数；第2种是区间二型模糊系统，其与广义二型模糊系统的不同之处是次隶属度函数为常值函数，区间二型模糊系统可以看作是广义二型模糊系统的一个特例。在二型模糊系统的降型过程中，广义二型模糊系统的降型结果为一个一型的隶属度函数。
一般来说，广义二型模糊集可定义如下：
$$ \tilde A = \{ (x,u),{\mu _{\tilde A}}(x,u)|\forall x \in X|\forall u \in [0,1]\} $$ (1) 式中：
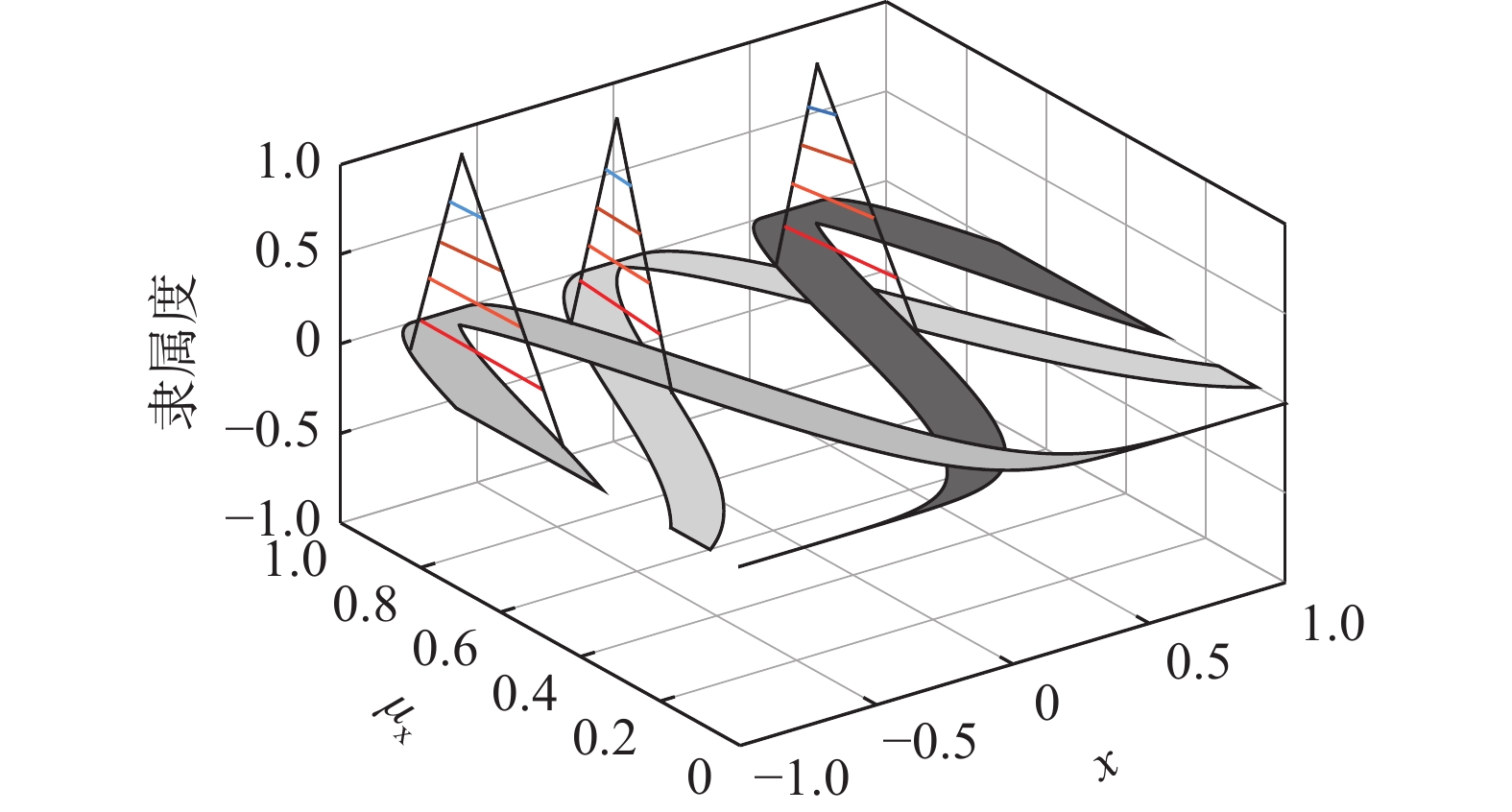
$ {\mu _{\tilde A}}(x,u) $ 为次隶属度；$ X $ 是主变量$ x $ 的定义域，次变量$ u $ 的定义域在0~1；次隶属度的支撑域称为不确定性轨迹，记为${F_{{\text{OU}}}}(\tilde A)$ ，即$$ {F_{{\text{OU}}}}(\tilde A) = \{ (x,u) \in X \times [0,1]|{\mu _{\tilde A}}(x,u) > 0\} $$ (2) 如图1所示，
$ \tilde A $ 的一个不确定轨迹被上隶属函数和下隶属函数所包含，上、下隶属函数分别记为${U_{{\text{MF}}}}(\tilde A)$ 和${L_{{\text{MF}}}}(\tilde A)$ ，即：
图 1 不确定轨迹Fig. 1 The footprint of uncertain
下载:
全尺寸图片
$$ {U_{{\text{MF}}}}(\tilde A) = \overline {{F_{{\text{OU}}}}(\tilde A)} $$ (3) $$ {L_{{\text{MF}}}}(\tilde A) = \underline {{F_{{\text{OU}}}}(\tilde A)} $$ (4) 虽然广义二型模糊集的概念很早就被提出，但是由于其拥有三维隶属度结构导致相关的广义二型模糊系统的运算很复杂，因此很难运用到需要实时计算的实际工程中。由于区间二型模糊集的次隶属度函数
$ {\mu _{\tilde A}}(x,u) $ 恒为1，与广义二型模糊集相比拥有着更简单的结构[8-10]，通过牺牲一部分的性能来提高系统的运算速度，在实际工程中取得了大量的应用[11-17]。为减少整个系统的计算负担，本文考虑在广义二型模糊系统中使用
$ \alpha $ 平面表示法。通过使用$ \alpha $ 平面，整个广义二型模糊系统可以被划分为若干个类区间二型模糊系统，而每个区间二型模糊系统可以分别进行运算。显然，计算量被大大降低了。有相关文献证明，只需要5~10个$ \alpha $ 平面就足够表示一个广义二型模糊系统[18]。图2为具有5个$ \alpha $ 平面的广义二型模糊系统的隶属函数图。
图 2 具有5个$ \alpha $ 平面的广义二型模糊系统隶属函数Fig. 2 Membership functions of GT2FLS with 5$ \alpha $ -planes下载:
全尺寸图片
基于
$ \alpha $ 平面法表示的广义二型模糊集$ \tilde A $ 可表述为$$ \tilde A = \mathop \cup \limits_{\alpha \in [1,0]} \frac{\alpha }{{{{\tilde A}_\alpha }}} $$ (5) 从式 (5) 中可以看到，通过使用
$ \alpha $ 平面表示法，广义二型模糊系统可以被认为是由若干个区间二型模糊系统组成的。进而不难猜想出，除解模糊过程外，基于$ \alpha $ 平面法表示的广义二型模糊系统的计算方法与区间二型模糊系统是类似的。1.2 广义二型模糊系统
一般来说，广义二型模糊系统由模糊器、模糊规则表、模糊推理机、降型器和解模糊器组成。模糊规则是由if-then规则所组成的，可以表示为
$$ {R^i}:{\text{If}}\,\,{x_{ij}}{\kern 1pt} {\kern 1pt} {\text{is}}\;\tilde F_1^i{\kern 1pt} {\text{and}}\, \cdots \,{\text{and}}\;{x_{ij}}{\kern 1pt} {\text{is}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde F_j^i\;{\text{then}}\;{y_i}\;{\text{is}}\;{\tilde G^i} $$ (6) 式中：
$ {x_{ij}} $ 是第$ i $ 条规则的$ j $ 个输入，$ {y_i} $ 是第$ i $ 条规则的输出。$ \tilde F_j^i $ 和$ {\tilde G^i} $ 是广义二型模糊系统的前件和后件。模糊推理机主要用于建立输入与输出之间的映射，本文采用的是乘积推理机。由于本文采用了
$ \alpha $ 平面法，每个$ \alpha $ 平面对应的隶属度要被首先计算出来。本文采用三角形次隶属函数，可按照下式来计算每一个$ \alpha $ 平面对应的隶属度。$$ \mu _j^i{(X)_{{a_k}}} = [\underline \mu _j^i{(X)_{{a_k}}},\bar \mu _j^i{(X)_{{a_k}}}] $$ (7) $$ \underline \mu _j^i{(X)_{{a_k}}} = \underline \mu _j^i(X) + \omega \cdot (\bar \mu _j^i(X) - \underline \mu _j^i(X)) \cdot {a_k} $$ (8) $$ \bar \mu _j^i{(X)_{{a_k}}} = \bar \mu _j^i(X) - (1 - \omega ) \cdot (\bar \mu _j^i(X) - \underline \mu _j^i(X)) \cdot {a_k} $$ (9) 其中
$\underline \mu _j^i(X)$ 和$\bar \mu _j^i(X)$ 分别是当$\alpha = 0$ 时的上、下隶属度。$ \omega $ 可以决定三角形次隶属函数的顶点位置，当$\omega 为0或1$ 时，次隶属函数就成为了直角三角形，当$\omega 为 0.5$ 时，次隶属函数就成为了等腰三角形。在本文中$ \omega $ 取固定值0.5。$\underline \mu _j^i{(X)_{{\alpha _k}}}$ 和$\bar \mu _j^i{(X)_{{\alpha _k}}}$ 是对应每一$ \alpha $ 平面的隶属度。当所有的隶属度计算出来之后，每个$ \alpha $ 平面的激活区间可由下式进行计算：$$ F_\alpha ^j(X) = [\underline f _\alpha ^j(X),\bar f_\alpha ^j(X)] $$ (10) $$ \underline f _\alpha ^j(X) = \underline \mu _\alpha ^1(X) \cdot \underline \mu _\alpha ^2(X) \cdots \underline \mu _\alpha ^j(X) $$ (11) $$ \bar f_\alpha ^j(X) = \bar \mu _\alpha ^1(X) \cdot \bar \mu _\alpha ^2(X) \cdots \bar \mu _\alpha ^j(X) $$ (12) 本文使用KM(Karnik–Mendel)算法进行降型[19]。KM算法是最主流的降型算法之一，与其他降型算法相比，KM降型算法结果更具准确性。对于每一个
$ \alpha $ 平面，其终止点可由下式计算：$$ {y_{l\alpha }} = \frac{{\displaystyle\sum\limits_{j = 1}^L {\bar f_\alpha ^j\underline \theta _\alpha ^j} + \displaystyle\sum\limits_{j = L + 1}^M {\underline f _\alpha ^j\underline \theta _\alpha ^j} }}{{\displaystyle\sum\limits_{j = 1}^L {\bar f_\alpha ^j} + \displaystyle\sum\limits_{j = L + 1}^M {\underline f _\alpha ^j} }} $$ (13) $$ {y_{r\alpha }} = \frac{{\displaystyle\sum\limits_{j = 1}^R {\underline f _\alpha ^j\bar \theta _\alpha ^j} + \displaystyle\sum\limits_{j = R + 1}^M {\bar f_\alpha ^j\bar \theta _\alpha ^j} }}{{\displaystyle\sum\limits_{j = 1}^R {\underline f _\alpha ^j} + \displaystyle\sum\limits_{j = R + 1}^M {\bar f_\alpha ^j} }} $$ (14) 式中：
$ \underline \theta _\alpha ^j $ 是第$ j $ 个后件的左终止点，$ \bar \theta _\alpha ^j $ 是其右终止点。在计算出每一个$ \alpha $ 平面的左右终止点之后，解模糊器可以建立模糊集到确定输出值之间的映射。文献[20]中也同样总结了多种解模糊的方法，本文采用的为终止点平均值解模糊化，可按照下式进行计算：$$ y = \frac{{\displaystyle\sum\limits_{p = 1}^k {{\alpha _p}({y_{l\alpha }} + {y_{r\alpha }})} }}{{2\displaystyle\sum\limits_{p = 1}^k {{\alpha _p}} }} $$ (15) 2. 广义二型模糊系统规则生成方法
相较于一型或区间二型模糊系统，广义二型模糊系统在复杂度较高的环境中，能更好地处理较强不确定性的非线性系统。然而，由于广义二型模糊系统本身三维结构的特性，并且模糊系统规则数会随着输入的增加而呈指数性的增长，进而产生规则爆炸，计算复杂度会变得非常大。
为了解决这一问题，可以将基于激活强度生成模糊规则的方法应用到广义二型模糊系统，大大减少模糊集数量和规则数量。假设最开始规则库中没有规则和事先收集的训练数据，控制开始时输入输出数据会被用来构建广义二型模糊集和模糊规则。在每一个采样时刻，由式(7)~(9)计算输入数据在模糊集中每一个
$ \alpha $ 平面对应的上、下隶属度，本文中广义二型模糊集的次隶属度参数$ \omega $ 取固定值0.5。对于每一个
$ {\alpha _{ {k}}} $ 平面的上下隶属度，都分配一个权重$p = \dfrac{{1 - {\alpha _{ {k}}}}}{{\displaystyle\sum \limits_{k = 1}^n (1 - {\alpha _{ {k}}})}}$ ，则合成的广义二型模糊集的上下隶属度可以表示为$$ \mu _j^i(X) = \frac{{\displaystyle\sum\limits_{k = 1}^n {(1 - {\alpha _k}) \cdot } \mu _j^i{{(X)}_{{\alpha _k}}}}}{{\displaystyle\sum\limits_{k = 1}^n {(1 - {\alpha _k})} }} $$ (16) 进而求出最大规则激活强度：
$$ {f_{\max }} = \mathop {\max }\limits_{1 \leqslant i \leqslant R(t)} {f_i}(x) $$ (17) 如果最大规则激活强度
$ {f_{\max }} $ 小于阈值$ {f_{{\text{th}}}} $ 意味着没有合适的规则可以覆盖输入数据，因而需要增加一个新的规则。阈值$ {f_{{\text{th}}}} $ 的大小决定了生成模糊规则的数量，较小的阈值会生成较少数量的规则。对于每个新生成的规则，计算
$$ {I_j} = \arg \,\mathop {\max }\limits_{1 \leqslant i \leqslant {k_j}(t)} \mu _{A_j^i}^c,\quad \quad j = 1,2, \cdots ,n $$ (18) 其中
$ {k_j}(t) $ 是输入变量$ k $ 的模糊集数。如果$\mu _{A_j}^{I_j} > \rho $ ,其中$ \rho \in [0,1] $ 是预先设定的阈值，则使用现有的模糊集$\tilde A_j^{I_j} $ 作为输入变量$ j $ 中新规则的前件。否则，在输入变量$ k $ 中生成一个新的模糊集并设置$ {k_j}(t + 1) = {k_j}(t) + 1 $ 。参数$ \rho $ 决定了每个输入变量中模糊集的数量，较小的$ \rho $ 值会产生较少的模糊集。如果设定$ \rho = 1 $ ，则每个输入变量中的模糊集数等于规则数；而如果设定$ \rho = 0 $ ，则每个输入变量只生成一个模糊集。一旦生成了新的模糊集，输入变量
$ j $ 中新模糊集的方差取决于输入数据$ {x_j} $ 与该模糊集均值之间的距离。广义二型模糊集的不确定均值和方差前件参数初始化如下：$$ {m}_{j}^{i}\in [{x}_{j}-0.1\text{，}{x}_{j}+0.1] $$ (19) $$ {\sigma _{{k_j}(t + 1)j}} = \beta |{x_j} - \frac{1}{2}(m_{j1}^{{I_j}} + m_{j2}^{{I_j}})| $$ (20) 其中参数
$ \beta $ 决定两个模糊集之间的重叠程度。本文将$ \beta $ 设为0.5使得新模糊集的宽度为新模糊集平均均值与模糊集$ {I_j} $ 之间距离的一半，在两个模糊集之前产生适当的重叠。3. 广义二型模糊系统的前后件参数优化
广义二型模糊系统隶属函数具有完整的三维结构，在提升系统处理不确定性的能力的同时，也会给广义二型模糊系统的设计带来更大的压力。系统参数的好坏会影响到整个系统的性能，传统的参数设置方法，如平均分配法和试错法都难以达到所期望的要求。有些文献通过智能算法对区间二型模糊集参数进行优化，例如文献[21]采用分别采用遗传算法、粒子群算法和蚁群算法用来设计最佳的区间二型模糊系统，并对不同的优化方法进行了比较。
本文所提出的广义二型模糊系统的参数优化阶段与自组织规则优化是同时发生的。对于每个输入数据，除了决定广义二型模糊集次隶属度形状的参数
$ \omega $ 以外，所有广义二型模糊集的不确定均值$ m_{j1}^i $ ，$ m_{j2}^i $ 和方差$ \sigma _j^i $ 参数都会进行调整。由于是单个输出情况，将系统误差设定为最小化误差函数$$ E = \frac{1}{2}{[y(t) - {y_d}(t)]^2} $$ (21) 其中，
$ y(t) $ 和$ {y_d}(t) $ 分别表示实际输出和期望输出。式(13)和(14)中计算$ {y_{l\alpha }} $ 和$ {y_{{\text{r}}\alpha }} $ 的KM算法的前提是$ \underline \theta _\alpha ^j $ 和$ \bar \theta _\alpha ^j $ 按升序重新排列。在参数优化过程中，$ \underline \theta _\alpha ^j $ 和$ \bar \theta _\alpha ^j $ 的值会发生变化，计算式(13)和(14)时它们的顺序和相应的规则顺序也会相应变化。广义二型模糊系统的后件$ {\tilde G^i} $ 可以进一步表示为$$ {\tilde{G}}^{i}={\tilde{a}}_{0}^{i}+{\displaystyle \displaystyle\sum _{j=1}^{n}{\tilde{a}}_{j}^{i}{x}_{j}}\text{，}i=1,2,\cdots ,M $$ (22) $$ \tilde a_j^i = [c{}_j^i - s{}_j^i,c{}_j^i + s{}_j^i],\quad j = 0,1, \cdots ,n $$ (23) 令
${{\boldsymbol{w}}_{{\text{TSK}}}} \in {{\text{R}}^{2M(n + 1) \times 1}}$ 表示所有后件参数，即$$ {{\boldsymbol{w}}_{{\text{TSK}}}} = {[c_0^1c_1^1 \cdots c_n^1\quad s_0^1s_1^1 \cdots s_n^1 \cdots c_0^Mc_1^M \cdots c_n^M\quad s_0^Ms_1^M \cdots s_n^M]^{\text{T}}} $$ (24) 其中参数根据规则顺序放置，以便在规则生成期间随着规则数量的增加时位置保持不变。等式 (15) 转换为
$$ y = \frac{{\displaystyle\sum\limits_{p = 1}^k {{\alpha _p}({\boldsymbol{\varphi }}_{{\text{TSK}}}^{\text{T}}{{\boldsymbol{w}}_{{\text{TSK}}}})} }}{{\displaystyle\sum\limits_{p = 1}^k {{\alpha _p}} }} $$ (25) 文献[22]中同样运用了迭代最小二乘法来更新后件参数，通过执行以下规则排序的迭代最小二乘算法来更新后件参数向量：
$$ \begin{gathered} {{\boldsymbol{w}}_{{\text{TSK}}}}(t + 1) = {{\boldsymbol{w}}_{{\text{TSK}}}}(t) + {\boldsymbol{S}}(t + 1){{\boldsymbol{\varphi }}_{{\text{TSK}}}}(t + 1)({y_d}(t + 1) -\\ {\boldsymbol{\varphi }}_{{\text{TSK}}}^{\text{T}}(t + 1){{\boldsymbol{w}}_{{\text{TSK}}}}(t)) {\boldsymbol{S}}(t + 1) =\\ \frac{1}{\lambda }\left[{\boldsymbol{S}}(t) - \frac{{{\boldsymbol{S}}(t){{\boldsymbol{\varphi }}_{{\text{TSK}}}}({\text{t}} + 1){\boldsymbol{\varphi }}_{{\text{TSK}}}^{\text{T}}({\text{t}} + 1){\boldsymbol{S}}(t)}}{{\lambda + {\boldsymbol{\varphi }}_{{\text{TSK}}}^T(t + 1){\boldsymbol{S}}(t){{\boldsymbol{\varphi }}_{{\text{TSK}}}}(t + 1)}}\right] \end{gathered}$$ (26) 其中
$0 < \lambda \leqslant 1$ 是一个遗忘因子（本文中$\lambda = 0.999{\kern 1pt} {\kern 1pt} {\kern 1pt} 5$ ）。对于广义二型模糊系统的前件参数不确定均值、方差部分，通过梯度下降法来法进行调整，广义二型模糊集的不确定均值和方差前件参数调整为
$$ m_{j1}^i(t + 1) = m_{j1}^i(t) - \eta \frac{{\partial E}}{{\partial m_{j1}^i}} $$ (27) $$ m_{j2}^i(t + 1) = m_{j2}^i(t) - \eta \frac{{\partial E}}{{\partial m_{j2}^i}} $$ (28) $$ \sigma _j^i(t + 1) = \sigma _j^i(t) - \eta \frac{{\partial E}}{{\partial \sigma _j^i}} $$ (29) 4. 仿真结果与分析
本节仿真主要使用上述基于自组织规则生成的广义二型模糊系统来辨识非线性系统，示例包括无扰动和施加噪声两种情况，并将此系统与同样方法生成的区间二型模糊系统进行了比较。
该非线性系统的函数为
$$ {y_d}(t + 1) = \frac{{{y_d}(t)}}{{1 + y_d^2(t)}} + {u^3}(t) $$ (30) $$ u(t)=\mathrm{sin}(2\text{π}/100)\text{，}t=1,2,\cdots ,200 $$ (31) 其中：
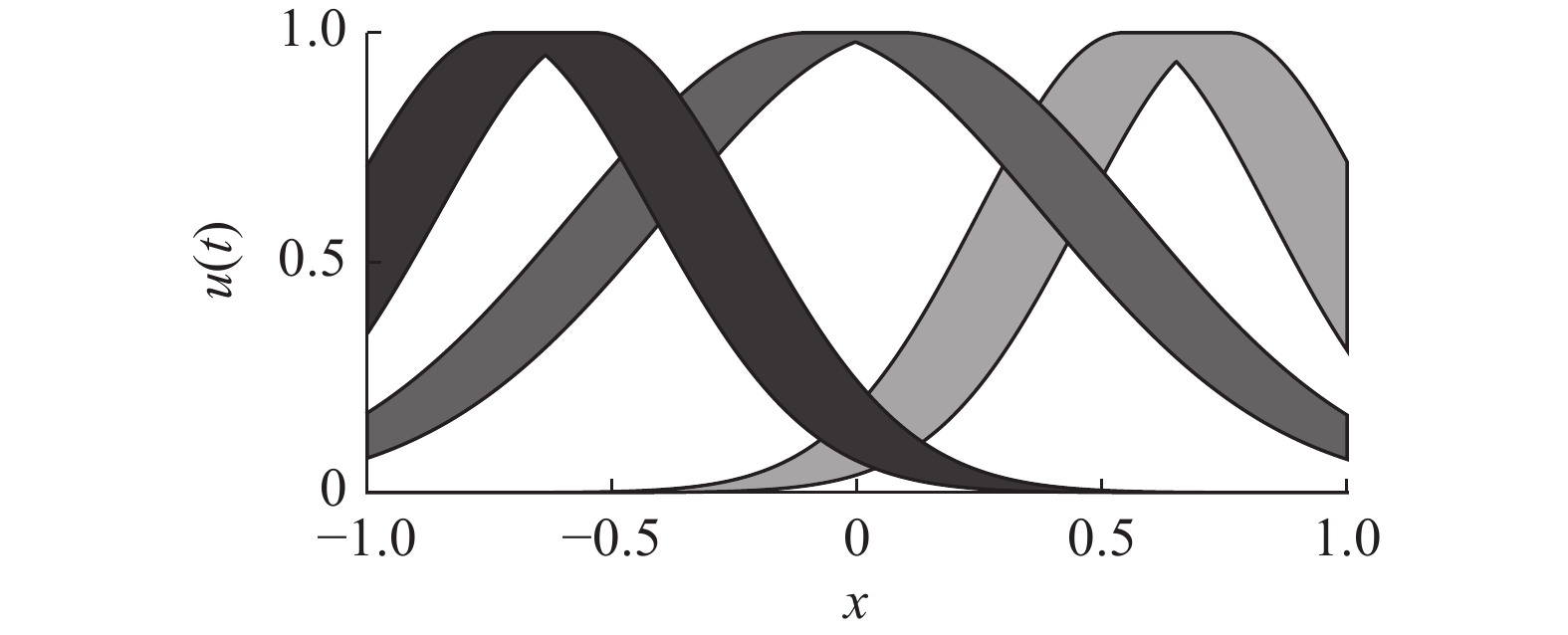
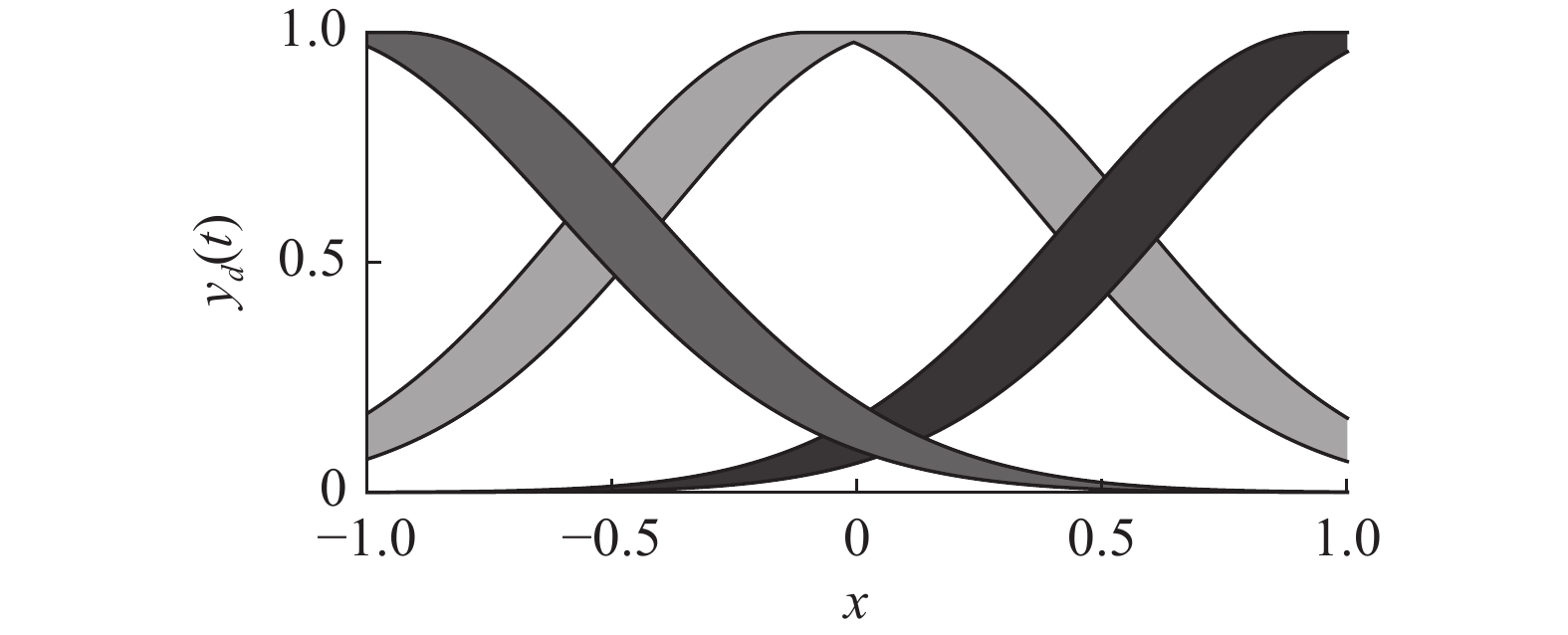
$ {y_d}(t) $ 和$ u(t) $ 作为系统的输入，期望输出为$ {y_d}(t + 1) $ 。运行过程中产生的广义二型模糊集对应的FOU如图3和图4所示。
图 3$u(t) $ 对应的FOUFig. 3 The FOU for$u(t) $ 下载:
全尺寸图片
图 4$y_d(t) $ 对应的FOUFig. 4 The FOU for$y_d(t) $ 下载:
全尺寸图片
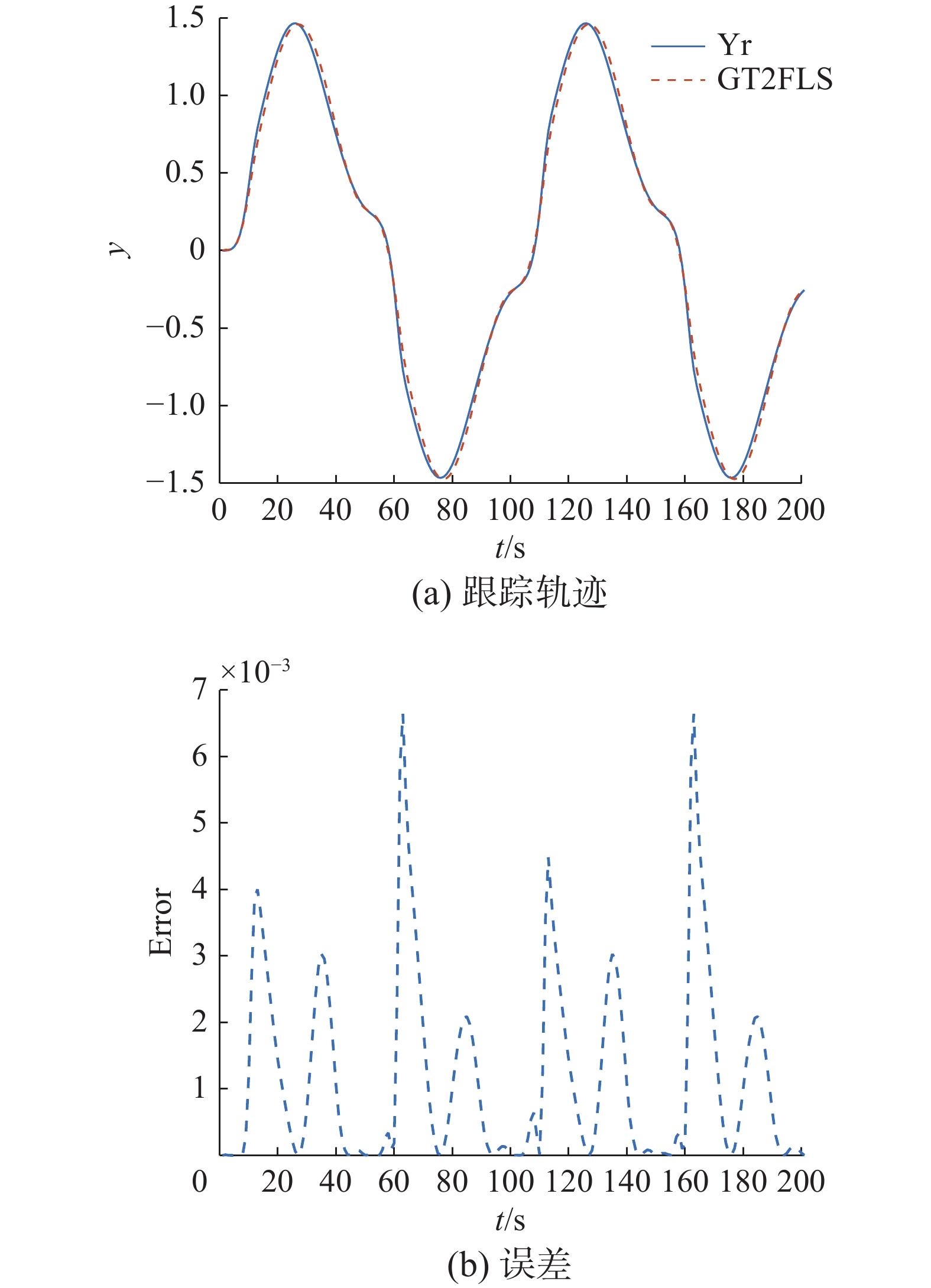
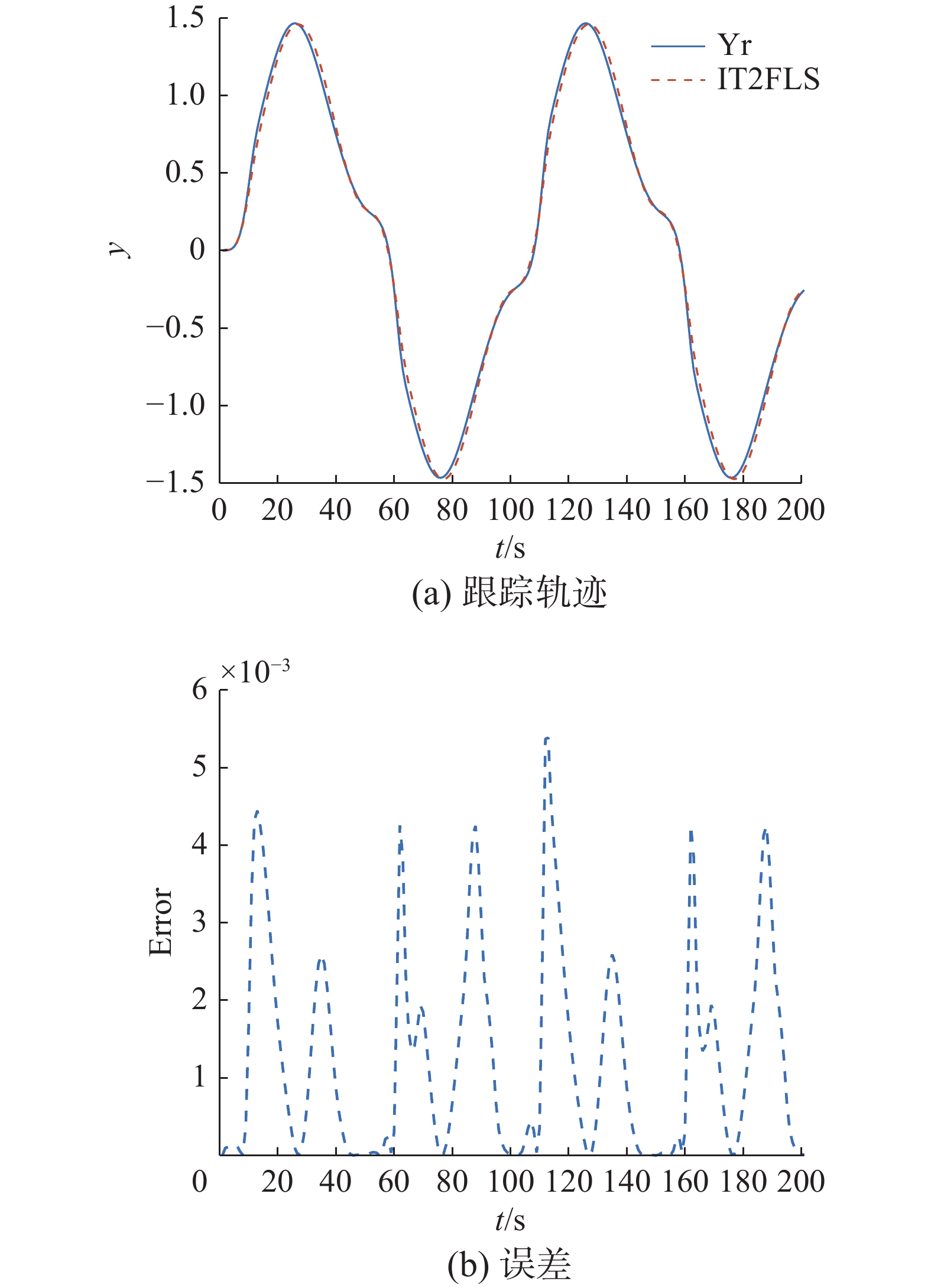
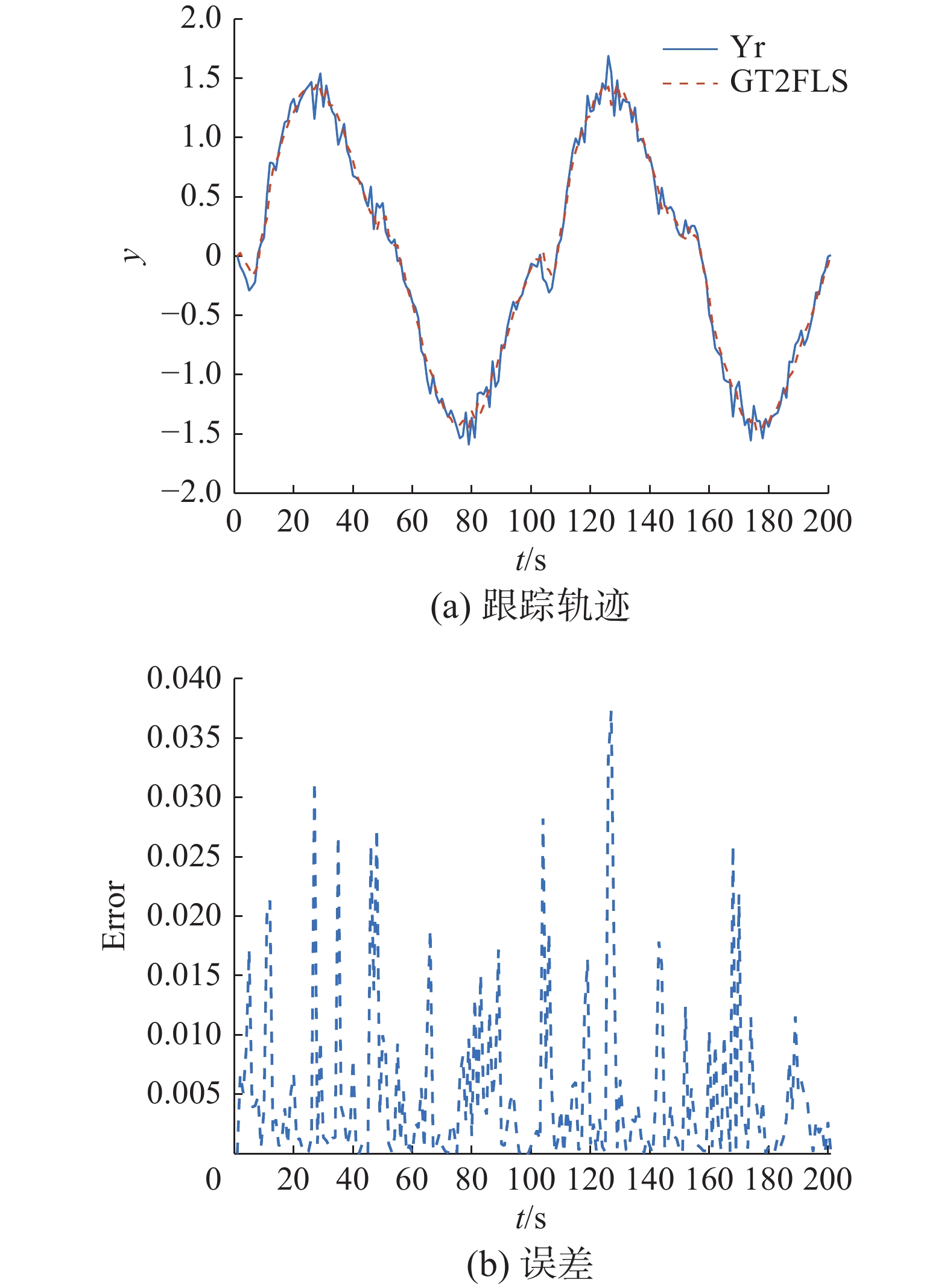
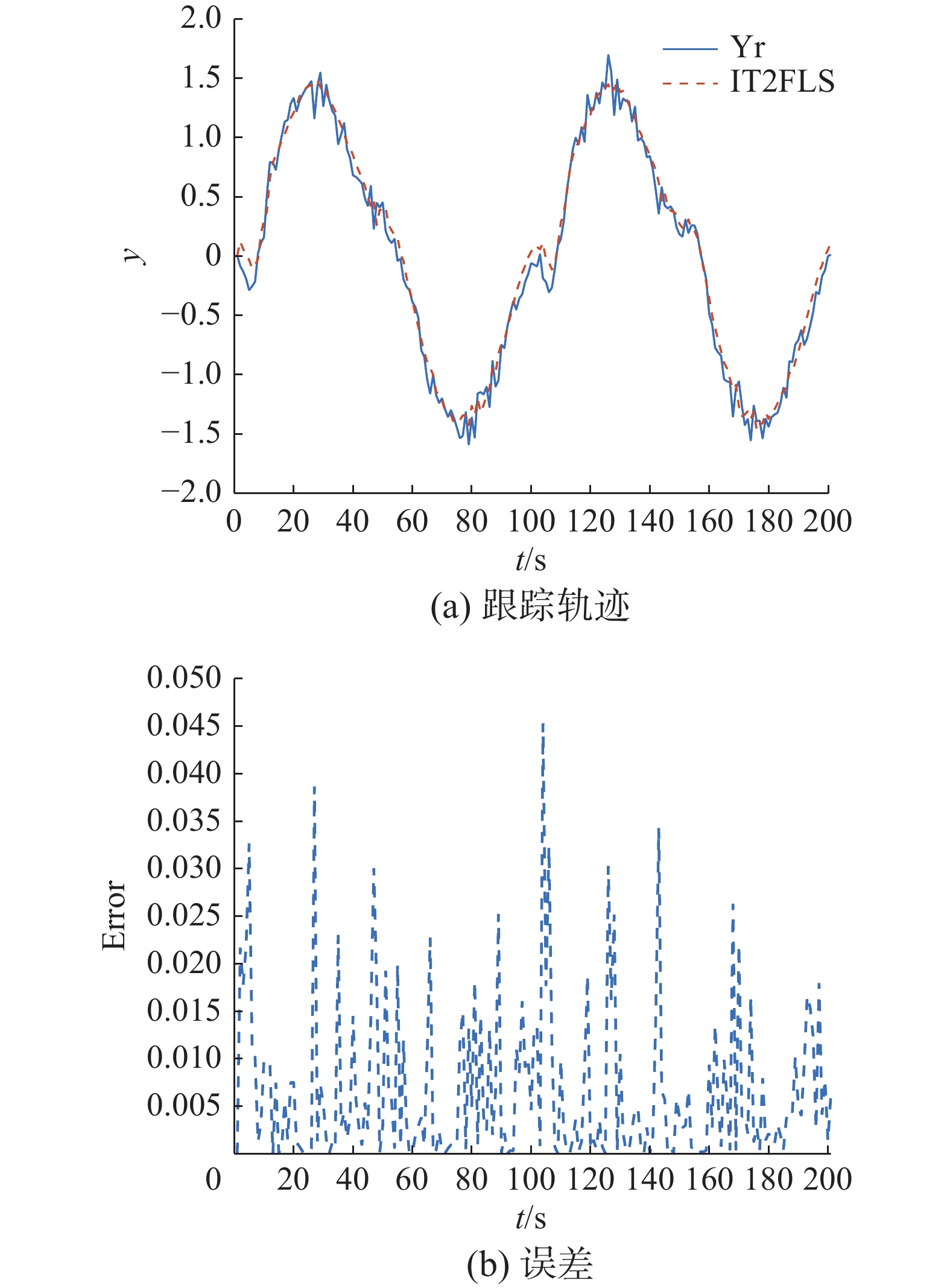
首先考虑在没有任何外部干扰的情况下，对比基于自组织规则生成的GT2FLS以及IT2FLS的控制效果。跟踪效果和误差如图5和图6所示，可以看出在无扰动的条件下通过数据驱动生成的IT2FLS和GT2FLS均对给定的非线性系统轨迹有着良好的跟踪效果，说明了这种自组织规则生成方法的有效性。在施加噪声情况下，基于自组织规则生成GT2FLS以及IT2FLS与非线性系统的期望输出跟踪效果和误差如图7和图8所示。显然GT2FLS相较于IT2FLS具有更好的处理不确定性的能力，非线性系统轨迹与GT2FLS跟踪轨迹的吻合程度更高，对不确定情况的改善更明显。
图 5 无扰动情况GT2FLS跟踪及误差Fig. 5 Tracking and error of GT2FLS without disturbance下载:
全尺寸图片
图 6 无扰动情况IT2FLS跟踪及误差Fig. 6 Tracking and error of IT2FLS without disturbance下载:
全尺寸图片
图 7 施加噪声情况GT2FLS跟踪及误差Fig. 7 Tracking and error of GT2FLS with disturbances下载:
全尺寸图片
图 8 施加噪声情况IT2FLS跟踪及误差Fig. 8 Tracking and error of IT2FLS with disturbances下载:
全尺寸图片
为了对提出的自组织规则生成广义二型模糊系统性能进行评价并验证这种方法的优越性，本文通过评价函数对跟踪误差进行计算来量化控制效果，分别选择标准差(STD)DST、均方根误差(RMSE)EMSE、平均绝对误差(MAE)EMA这3个性能指标进行评估。
$$ {D_{{\rm{ST}}}} = \sqrt {\frac{1}{{n - 1}}\displaystyle\sum\limits_{i = 1}^n {|{{\hat y}_i} - \bar y{|^2}} } $$ (32) $$ {E_{{\rm{MSE}}}} = \sqrt {\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} } $$ (33) $$ {E_{{\rm{MA}}}} = \frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {|{{\hat y}_i} - {y_i}|} $$ (34) 评价指标越小证明系统具有更好的性能。表1和表2给出了自组织IT2FLS、自组织GT2FLS以及非自组织GT2FLS分别在无扰动和施加噪声情况下跟踪效果对比，加粗表示效果最好。
表 1 无扰动情况下平均性能指标Table 1 Average performance index without disturbance方法 STD RMSE MAE IT2FLS 0.0292 0.0354 0.0408 GT2FLS
(非自组织)0.0327 0.0496 0.0622 GT2FLS 0.0305 0.0347 0.0386 表 2 施加噪声情况下平均性能指标Table 2 Average performance index with disturbances方法 STD RMSE MAE IT2FLS 0.0671 0.0817 0.0942 GT2FLS
(非自组织)0.0623 0.0734 0.0832 GT2FLS 0.0596 0.0700 0.0793 从表1~2中可以看出，在无扰动情况下，除STD外自组织GT2FLS的预测性能指标都要优于自组织IT2FLS和非自组织GT2FLS；而在施加噪声情况下，自组织GT2FLS的所有预测性能指标都要明显优于其他模糊系统。仿真实验结果证实了基于自组织规则生成的GT2FLS更能提升系统处理不确定性的能力，提高了系统运行的效率。
5. 结束语
本文针对广义二型模糊系统结构复杂难以建立构建适当模糊规则的问题，设计了一个GT2FLS、提出了一种基于输入数据的激活强度来生成广义二型模糊集以及模糊规则的方法，并使用迭代最小二乘法和梯度下降法优化系统前后件参数。在无扰动和施加噪声两种情况下，与区间二型模糊系统进行比较，仿真结果证明了这种基于自组织规则生成的广义二型模糊系统的有效性。
-
图 1 不确定轨迹
Fig. 1 The footprint of uncertain
下载:
全尺寸图片
图 2 具有5个
$ \alpha $ 平面的广义二型模糊系统隶属函数Fig. 2 Membership functions of GT2FLS with 5
$ \alpha $ -planes下载:
全尺寸图片
图 3
$u(t) $ 对应的FOUFig. 3 The FOU for
$u(t) $ 下载:
全尺寸图片
图 4
$y_d(t) $ 对应的FOUFig. 4 The FOU for
$y_d(t) $ 下载:
全尺寸图片
图 5 无扰动情况GT2FLS跟踪及误差
Fig. 5 Tracking and error of GT2FLS without disturbance
下载:
全尺寸图片
图 6 无扰动情况IT2FLS跟踪及误差
Fig. 6 Tracking and error of IT2FLS without disturbance
下载:
全尺寸图片
图 7 施加噪声情况GT2FLS跟踪及误差
Fig. 7 Tracking and error of GT2FLS with disturbances
下载:
全尺寸图片
图 8 施加噪声情况IT2FLS跟踪及误差
Fig. 8 Tracking and error of IT2FLS with disturbances
下载:
全尺寸图片
表 1 无扰动情况下平均性能指标
Table 1 Average performance index without disturbance
方法 STD RMSE MAE IT2FLS 0.0292 0.0354 0.0408 GT2FLS
(非自组织)0.0327 0.0496 0.0622 GT2FLS 0.0305 0.0347 0.0386 表 2 施加噪声情况下平均性能指标
Table 2 Average performance index with disturbances
方法 STD RMSE MAE IT2FLS 0.0671 0.0817 0.0942 GT2FLS
(非自组织)0.0623 0.0734 0.0832 GT2FLS 0.0596 0.0700 0.0793 -
[1] MENDEL J M. Type-2 fuzzy sets and systems: an overview[J]. IEEE computational intelligence magazine, 2007, 2(1): 20–29. doi: 10.1109/MCI.2007.380672 [2] 钱殿伟. 基于模糊滑模的多机器人系统编队控制[J]. 智能系统学报, 2016, 11(5): 641–647. QIAN Dianwei. Formation control of multi-robot systems in a fuzzy sliding mode[J]. CAAI transactions on intelligent systems, 2016, 11(5): 641–647. [3] MA Zhiqiang, HUANG Panfeng, KUANG Zhian. Fuzzy approximate learning-based sliding mode control for deploying tethered space robot[J]. IEEE transactions on fuzzy systems, 2021, 29(9): 2739–2749. doi: 10.1109/TFUZZ.2020.3006583 [4] 秦贝贝, 陈增强, 孙明玮, 等. 基于自适应神经模糊推理系统的船舶航向自抗扰控制[J]. 智能系统学报, 2020, 15(2): 255–263. QIN Beibei, CHEN Zengqiang, SUN Mingwei, et al. Active disturbance rejection control of ship course based on adaptive-network-based fuzzy inference system[J]. CAAI transactions on intelligent systems, 2020, 15(2): 255–263. [5] KASABOV N K, SONG Qun. DENFIS: dynamic evolving neural-fuzzy inference system and its application for time-series prediction[J]. IEEE transactions on fuzzy systems, 2002, 10(2): 144–154. doi: 10.1109/91.995117 [6] SILVA A M, CAMINHAS W, LEMOS A, et al. A fast learning algorithm for evolving neo-fuzzy neuron[J]. Applied soft computing, 2014, 14: 194–209. doi: 10.1016/j.asoc.2013.03.022 [7] SU W C, JUANG C F, HSU C M. Multiobjective evolutionary interpretable type-2 fuzzy systems with structure and parameter learning for hexapod robot control[J]. IEEE transactions on systems, man, and cybernetics:systems, 2022, 52(5): 3066–3078. doi: 10.1109/TSMC.2021.3063778 [8] LIANG Qilian, MENDEL J M. Interval type-2 fuzzy logic systems: theory and design[J]. IEEE transactions on fuzzy systems, 2000, 8(5): 535–550. doi: 10.1109/91.873577 [9] MENDEL J M, JOHN R I, LIU Feilong. Interval type-2 fuzzy logic systems made simple[J]. IEEE transactions on fuzzy systems, 2006, 14(6): 808–821. doi: 10.1109/TFUZZ.2006.879986 [10] MENDEL J M, LIU Xinwang. Simplified interval type-2 fuzzy logic systems[J]. IEEE transactions on fuzzy systems, 2013, 21(6): 1056–1069. doi: 10.1109/TFUZZ.2013.2241771 [11] ZHAO Tao, LIU Jiahao, DIAN Songyi. Finite-time control for interval type-2 fuzzy time-delay systems with norm-bounded uncertainties and limited communication capacity[J]. Information sciences:an international journal, 2019, 483(C): 153–173. [12] ZHAO Tao, DIAN Songyi. State feedback control for interval type-2 fuzzy systems with time-varying delay and unreliable communication links[J]. IEEE transactions on fuzzy systems, 2018, 26(2): 951–966. doi: 10.1109/TFUZZ.2017.2699947 [13] LIN Yangyin, LIAO S H, CHANG J Y, et al. Simplified interval type-2 fuzzy neural networks[J]. IEEE transactions on neural networks and learning systems, 2014, 25(5): 959–969. doi: 10.1109/TNNLS.2013.2284603 [14] HWANG C, RHEE F C H. Uncertain fuzzy clustering: interval type-2 fuzzy approach to C-means[J]. IEEE transactions on fuzzy systems, 2007, 15(1): 107–120. doi: 10.1109/TFUZZ.2006.889763 [15] PUJIANTARA M, ABDILLAH M. Intelligent over current relays based on interval type 2 fuzzy logic approach[C]//2012 International Conference on Green and Ubiquitous Technology. Bandung: IEEE, 2012: 58−61. [16] BIGLARBEGIAN M, MELEK W W, MENDEL J M. Design of novel interval type-2 fuzzy controllers for modular and reconfigurable robots: theory and experiments[J]. IEEE transactions on industrial electronics, 2011, 58(4): 1371–1384. doi: 10.1109/TIE.2010.2049718 [17] CHEN C S. Supervisory adaptive tracking control of robot manipulators using interval type-2 TSK fuzzy logic system[J]. IET control theory & applications, 2011, 5(15): 1796–1807. [18] LIU Feilong. An efficient centroid type-reduction strategy for general type-2 fuzzy logic system[J]. Information sciences:an international journal, 2008, 178(9): 2224–2236. doi: 10.1016/j.ins.2007.11.014 [19] MENDEL J M, Uncertain rule-based fuzzy logic system: introduction and new directions[M]. New York: Springer, 2001. [20] KARNIK N N, MENDEL J M. Type-2 fuzzy logic systems: type-reduction[C]//SMC'98 Conference Proceedings. 1998 IEEE International Conference on Systems, Man, and Cybernetics. San Diego: IEEE, 2002: 2046−2051. [21] CASTILLO O, MELIN P. Optimization of type-2 fuzzy systems based on bio-inspired methods: a concise review[J]. Information sciences:an international journal, 2012, 205: 1–19. doi: 10.1016/j.ins.2012.04.003 [22] JUANG C F, TSAO Y W. A self-evolving interval type-2 fuzzy neural network with online structure and parameter learning[J]. IEEE transactions on fuzzy systems, 2008, 16(6): 1411–1424. doi: 10.1109/TFUZZ.2008.925907
