Electroencephalogram emotion recognition method using multitask feature integration
-
摘要: 特征选择与融合是提升脑电信号情绪解码精度的重要手段之一。然而，当前脑电情绪解码中的特征选择方法常忽略了脑电信号内在数据结构的隐含信息。该文提出一种基于近邻传播聚类的多任务特征融合方法，通过
${L_{2,1}}$ 范数约束实现稀疏特征选择，同时利用图拉普拉斯正则化保持不同子类间的潜在关系。该算法在不揭示真实样本标签的情况下，在子任务空间有效融合脑网络空间拓扑结构信息和微分熵信息，为高精度脑电信号情绪解码提供具有更高情绪表征能力的特征。DEAP和SEED数据集以及本实验室数据集的分析结果表明，该文提出的方法能显著提高脑电情绪解码的精度。Abstract: Feature selection and integration is one of the crucial approaches to improving the emotion decoding accuracy of electroencephalogram (EEG) signals. However, current methods often neglect the implicit information of the intrinsic data structure in EEG signals. Herein, a multitask feature integration method is proposed based on affinity propagation clustering. This method uses the L2,1-norm constraint to select sparse features and uses graph Laplacian regularization to maintain potential relationships among different subclasses. In case of not disclosing real sample labels, the method has effectively integrated the spatial topology information of brain networks and differential entropy information in the subtask space, providing features with higher emotional characterization ability for the emotional decoding of high-accuracy EEG signals. The analytic results on DEAP and SEED datasets and the dataset of the laboratory show that the proposed method can markedly improve the decoding accuracy of EEG emotional decoding. -
情感脑机接口是一种对人的情绪进行识别和调控的脑机接口[1]，在人机交互领域中有着重要应用。在脑电 (electroencephalogram, EEG)，心电、肌电和皮肤温度等生理信号中，基于EEG的情绪识别具有时间分辨率高、成本低廉、设备便携性好、操作简单的优势，近年来得到广泛关注[2]。
基于EEG的情绪识别主要从EEG的时域、频域、时频域3个维度提取特征。同时，脑区的不对称性也反映情绪信息[3]。常见的时域特征包括EEG的信号统计量（如均值、方差等）、Hjorth参数特征、分形维数等。频域特征常通过傅里叶变换将原有的EEG信号分解到若干个子频带，再分别提取功率、功率谱密度、高阶谱、微分熵等特征。由于傅里叶变换从全局上进行信号分析，存在时域和频域的局部化矛盾，研究者们进一步使用短时傅里叶变换，Hilbert-Huang方法和小波包变换等方法提取EEG的时频域特征。在上述特征中，微分熵(differential entropy, DE)具有区分低频和高频能量之间的EEG模式的平衡能力，能根据EEG信号的不规则程度有效地解码各种情绪，被广泛应用于情绪识别[4-6]。
认知科学和神经生理学的研究已表明，大脑的情绪活动体现出功能整合的特性。脑网络通过研究脑功能连通性的全局和局部拓扑结构，能够表示不同情绪状态下，不同大脑区域传输信息的能力之间的差异[7]。脑电信号构建脑网络的方法是以脑电电极为节点，并通过线性或非线性相关、相干函数、相位同步和互信息等方法度量节点间的连接强度。Zhang等[8]利用通道之间的互信息构建基于最小生成树的脑网络，提取7种特征融合后反馈给随机森林分类器进行情感识别。Kang等[9]利用锁相值(phase-locking value, PLV)计算脑电通道之间的相关性，通过双阈值构造脑网络，融合平均最短路径、全局效率和聚类系数等网络属性特征进行情绪解码。脑网络蕴含的空间拓扑结构信息提高了情绪解码精度，然而，在脑网络构建过程中，阈值的选择没有具体的标准，且脑网络属性难以完全表征不同情绪状态下的脑网络空间拓扑结构差异。为了更好地提取脑网络的信息，Xu等[10]提出一种基于共空间模式(common spatial pattern, CSP)提取脑网络信息的方法鉴别癫痫发作方式，结果表明，基于CSP的脑网络特征的解码性能远远高于脑网络属性值。
不同的特征之间具有互补性，融合特征在脑电解码上有着较好的自适应性和较高的识别精度[11]。Gao等[12]连接融合了功率谱和小波能量熵两类EEG特征，并采用主成分分析进行降维和特征选择，结果表明融合特征相比于单一特征具有更好的情绪表征能力。Gao等[13]提出了一种基于多层卷积神经网络并融合DE和脑网络的情感分类方法，验证了DE和脑网络之间存在互补特性，两者的融合能有效地提升脑电情绪解码精度。目前的特征降维和选择方法(如主成分分析、最大相关最小冗余[14]、归一化互信息[15]等)常通过计算特征与情感标签之间的相关性进行特征排序和选择，忽略了EEG信号本身的数据结构。Zhang等[16]的研究表明，EEG数据中的固有子类为特征学习提供了更多的先验信息，对脑电解码有着重要的意义。
为有效地探索捕获真实EEG样本分布的重要数据结构，本文利用近邻传播(affinity propagation, AP)聚类[17]构造多任务特征融合方法，充分挖掘EEG数据子类任务的隐含信息。该方法能有效地降低特征维数，且具有更优的情感解码性能。本文贡献包括：1) 利用DE和脑网络的互补特性，融合两类特征提升脑电情绪解码精度。2) 提出基于AP聚类的多任务特征融合算法，通过
$ {L_{2,1}} $ 范数约束实现了稀疏特征选择，并利用图拉普拉斯正则化保持子类间的潜在关系，为基于EEG的高精度情绪解码提供有效特征选择与融合方法。1. 脑电情绪识别方法
1.1 算法框架
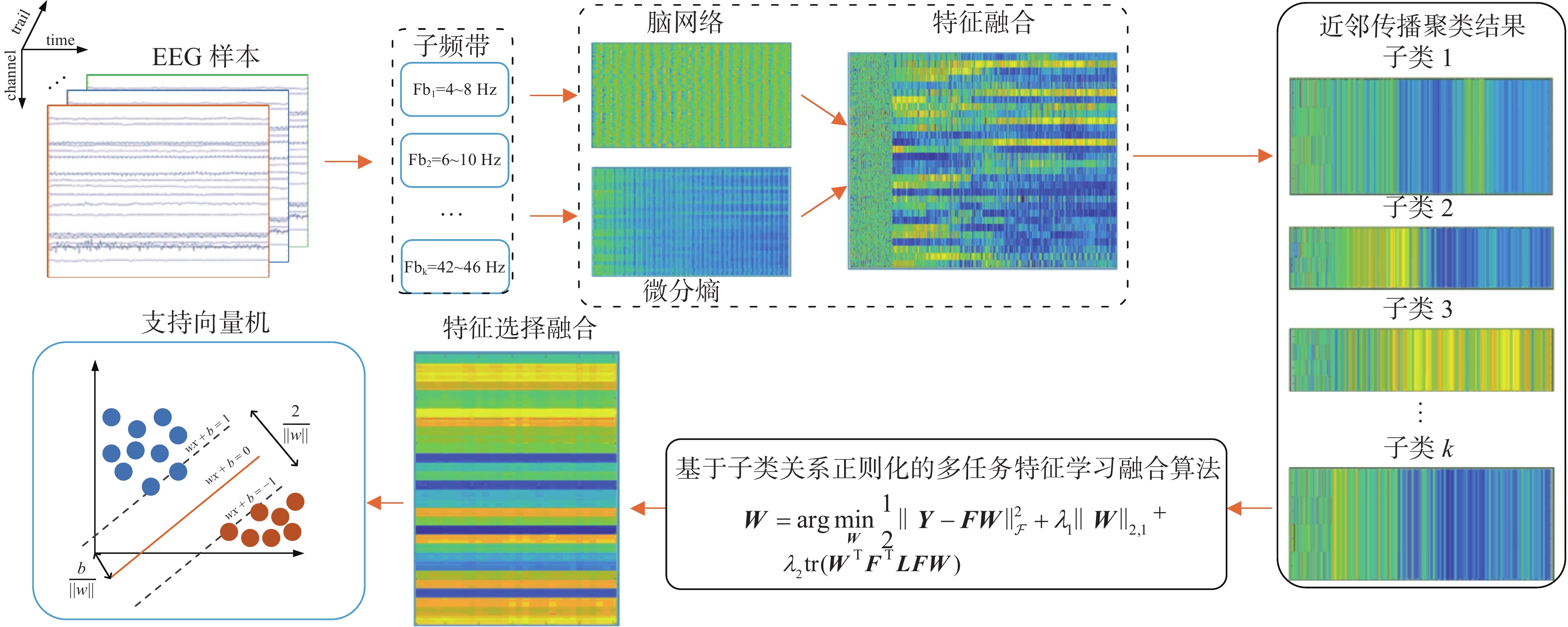
本文首先提取脑电情绪不同频段的脑网络和DE组成EEG特征向量，然后利用近邻传播聚类获取EEG数据隐含的分类信息，构造基于子类关系正则化的多任务特征融合算法(subclass relationship regularized multi-task learning and fusion, srMTLF)来提升脑电情绪识别的准确率，算法流程如图1所示。
图 1 srMTLF算法流程Fig. 1 Flow of srMTLF algorithm
下载:
全尺寸图片
1.2 特征提取
1.2.1 PLV
由于PLV具有聚焦于脑电波动的同步性，降低数据本身振幅影响的优点，因此是常用度量脑功能网络的方法[18]。具体来讲，对于EEG信号
$x(t)$ 和$y(t)$ ，其希尔伯特变换(HT)为$$ \left\{ \begin{gathered} {T_{H^x}}(t) = \frac{{\text{1}}}{{\text{π}}}P\int_{ - \infty }^\infty {\frac{{x({t'})}}{{t - {t'}}}{\text{d}}{t'}} \\ {T_{H^{\text{y}}}}(t) = \frac{{\text{1}}}{{\text{π}}}P\int_{ - \infty }^\infty {\frac{{y({t'})}}{{t - {t'}}}{\text{d}}{t'}} \\ \end{gathered} \right. $$ (1) 其中
$P$ 是柯西主值。对应解析信号为$$ \left\{ \begin{gathered} Z_x(t) = x(t) + {\rm{i}}H_x(t) \\ Z_y(t) = y(t) + {\rm{i}}H_y(t) \\ \end{gathered} \right. $$ (2) 根据解析信号，得到两个信号的瞬时相位
$\varphi_x(t)$ 和$\varphi_y(t)$ 为$$ \left\{ \begin{gathered} \varphi_x = \arctan \frac{{{T_{H^x}}(t)}}{{x(t)}} \\ \varphi_y = \arctan \frac{{{T_{H^{\text{y}}}}(t)}}{{y(t)}} \\ \end{gathered} \right. $$ (3) 根据
$\varphi_x(t)$ 和$\varphi_y(t)$ ，PLV定义为$$ {{\boldsymbol{W}}^{{\text{PLV}}}} = \left| {\frac{1}{{{N_0}}}\sum\limits_{j = 0}^{{N_0} - 1} {{{\text{e}}^{{\rm{i}}({\varphi _x}(j\Delta t) - {\varphi _y})}}} } \right| $$ (4) 式中：
$ {{\boldsymbol{W}}^{{\text{PLV}}}} $ 表示信号间的连接权重，$\Delta t$ 是采样周期，${N_0}$ 表示采样点。根据式(4)依次计算EEG电极间的连接权重，构建PLV脑功能连接矩阵。本文利用CSP[19]分析提取脑网络的空间拓扑结构信息。假设
${{\boldsymbol{X}}_{i{\text{,l}}}} \in {\bf{R}}^{N \times N}$ 表述被试第$i$ 个trial的第$l$ 类PLV连接矩阵，不同类的协方差矩阵计算方式为$$ {{\boldsymbol{\varSigma }}_l} = \sum\limits_{i = 1}^{{N_l}} {{{\boldsymbol{X}}_{i{\text{,l}}}}} {\boldsymbol{X}}_{i{\text{,l}}}^{\text{T}},\quad l = 1,2 $$ (5) 式中
${N_l}$ 代表被试第$l$ 类的trial总数。CSP主要用于二分类，本文通过一对一策略解决多分类问题。CSP空域滤波器通过下式求解：$$ \begin{gathered} {\boldsymbol{w}} = \arg \mathop {\max }\limits_{\boldsymbol{w}} \frac{{{{\boldsymbol{w}}^{\text{T}}}{{\boldsymbol{\varSigma }}_1}{\boldsymbol{w}}}}{{{{\boldsymbol{w}}^{\text{T}}}{{\boldsymbol{\varSigma }}_2}{\boldsymbol{w}}}} \\ {\text{ s}}{\text{.t}}{\text{. }}{\left\| {\boldsymbol{w}} \right\|_2} = 1 \end{gathered} $$ (6) 式中
${\boldsymbol{w}} \in {\bf{R}}^{N \times 1}$ 为CSP空间滤波器，该文选择广义特征值分解中最大M个和最小M个特征值对应的特征向量构建空间滤波器。M对最大和最小广义特征值对应的特征向量构成CSP滤波，而${\boldsymbol{W}} = \left[ {{{\boldsymbol{w}}_1}{\kern 1pt} {{\boldsymbol{w}}_2} \cdots {\kern 1pt} {{\boldsymbol{w}}_{2M}}} \right]$ ，${{\boldsymbol{w}}_m} \in {\bf{R}}^{N \times 1}$ 表示第$ m $ 个滤波器。给定脑功能连接矩阵${\boldsymbol{X}} \in {\bf{R}}^{N \times N}$ ，${\boldsymbol{z}} = {\left[ {{{\textit{z}}_1}{\kern 1pt} {{\textit{z}}_2}{\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {{\textit{z}}_{2M}}} \right]^{\text{T}}} \in {\bf{R}}^{2M \times 1}{\kern 1pt}$ 为求解的特征向量$$ {{\textit{z}}_m} = \log \left({{\rm{var}}} \left({\boldsymbol{w}}_m^{\text{T}}{\boldsymbol{X}}\right)\right),m = 1,2, \cdots ,2M $$ (7) 其中
$\log ( \cdot )$ 和${{\rm{var}}} ( \cdot )$ 分别为对数算子和方差算子。1.2.2 DE
DE是香农信息熵在连续变量上的扩展。用于测量随机变量的复杂性。对于一段特定长度的近似服从高斯分布
$ \mathcal{N}(\mu ,\sigma _i^2) $ 的EEG，其DE特征为[20]$$ \begin{gathered} {\text{DE}} = - \int_a^b {\frac{1}{{\sqrt {2{\text{π}}{\sigma _i}^2} }}} {{\text{e}}^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma _i}^2}}}}\log \left(\frac{1}{{\sqrt {2{\text{π}}{\sigma _i}^2} }}{{\text{e}}^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma _i}^2}}}}\right){\text{d}}x = \\ \frac{1}{2}\log (2{\text{πe}}{\sigma _i}^2) \end{gathered} $$ (8) 1.3 特征选择与融合
1.3.1 AP聚类
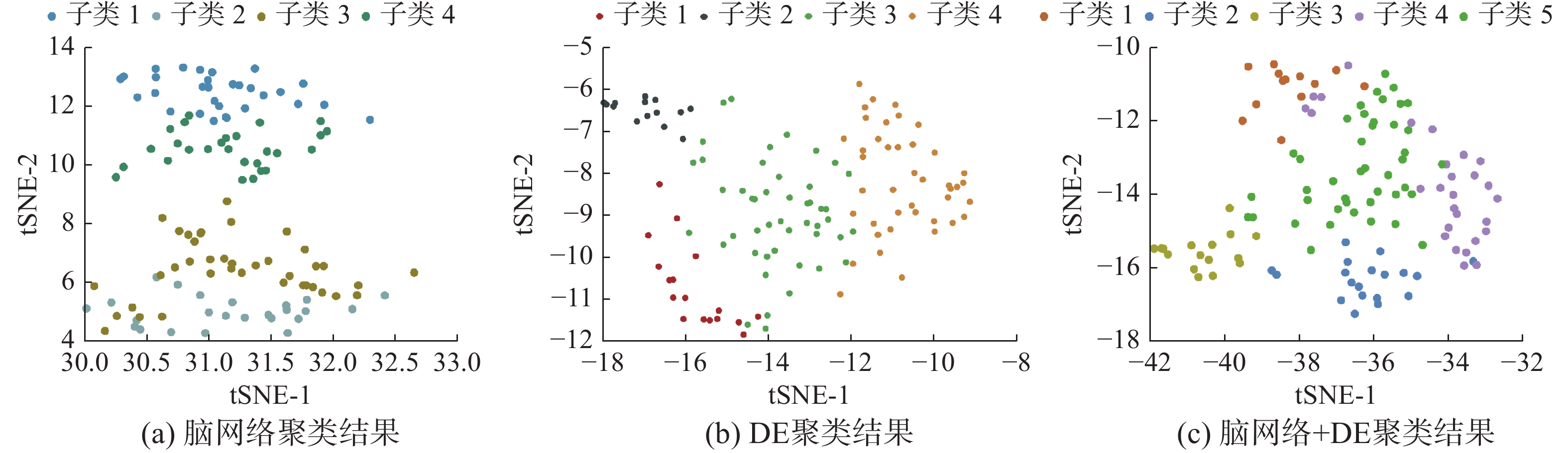
虽然融合多频带特征方法在一定程度上能提高解码精度，但在特征选择方法上EEG数据结构本身隐含的信息未被充分地挖掘。在不揭示真实样本标签分布的情况下，目前大多数方法所建立的特征优化模型只能得到次优结果。此外，融合特征在实验间存在高度的可变性，具体来说，部分实验的融合特征相较于同类别的特征与不同类别的更加相似，简单地以二进制的方式进行特征选择不能提供最佳的解码精度。为挖掘EEG数据的内在结构信息，更准确地解码神经模式，本文应用AP聚类来探索每个特征集的潜在子类。如图2所示，不同的簇揭示了隐藏在1原始类中的内在样本分布。通过将每个簇视为一个子类，然后根据one-hot编码策略对每个子类进行编码，从而构建标签矩阵
$ {\boldsymbol{Y}} $ 。假设发现K个子类，标签矩阵编码为${\boldsymbol{Y}} = {[{y_1}{\kern 1pt} {y_2}{\kern 1pt} \cdots {\kern 1pt} {y_N}]^{\text{T}}} \in {\bf{R}}^{N \times K}$ ，其中$N$ 表示样本个数，${y_i}$ 中的第$k$ 个元素定义为
图 2 DEAP数据集被试s01-tSNE聚类结果Fig. 2 tSNE clustering results of subject s01 in DEAP dataset下载:
全尺寸图片
$$ {y}_{ik}=\left\{\begin{array}{l}1, \qquad\text{ }{x}_{i}\in 集群\text{ }k\\ 0,\qquad \text{ 其他} \end{array} \right. $$ (9) 1.3.2 基于
${L_{2,1}}$ 范数约束的稀疏特征选择为实现AP聚类后子类空间上的特征选择，本文根据式(9)重构子类的标签矩阵
$ {\boldsymbol{Y}} $ ，并利用$ {L}_{2,1} $ 范数约束实现稀疏特征选择：$$ {\boldsymbol{W}}=\mathrm{arg}\underset{{\boldsymbol{W}}}{\mathrm{min}}\frac{1}{2}\Vert {\boldsymbol{Y}}-{\boldsymbol{F}}{\boldsymbol{W}}{\Vert }_{\mathcal{F}}^{2}+\lambda \Vert {\boldsymbol{W}}{\Vert }_{2,1} $$ (10) 式中：
${\left\| \cdot \right\|_\mathcal{F}}$ 表示Frobenius范数，${\boldsymbol{W}} \in {\bf{R}}^{D \times K}$ 为权重矩阵，${\boldsymbol{F}} \in {\bf{R}}^{N \times D}$ 为式(7)和式(8)提取的特征拼接矩阵。$$ \Vert {\boldsymbol{W}}{\Vert }_{2,1}={\displaystyle \sum _{i}\sqrt{{\displaystyle \sum _{j}{{\boldsymbol{W}}}_{ij}^{2}}}} $$ (11) 式（11）使得
${\boldsymbol{W}}$ 的某些行为零，实现基于子类的特征选择。$\lambda $ 控制${\boldsymbol{W}}$ 的稀疏性。1.3.3 基于子类关系正则化多任务学习
在利用近邻传播聚类获取EEG数据隐含的分类信息后，我们认为表示子类流形结构的内在子类关系也有助于提高情绪解码。如果样本
$i$ 、$j$ 属于AP聚类后的同一个子类，那么其对应的特征$ {{\boldsymbol{f}}_{i,:}} $ 和${{\boldsymbol{f}}_{j,:}}$ (分别对应特征矩阵的第$i$ 和第$j$ 行)投影到编码的标签空间后也应该彼此接近。为保持潜在的子类关系，本文在式(10)基础上引入图拉普拉斯正则化：$$ \begin{gathered} {\boldsymbol{\varOmega}} = \sum\limits_{i,j}^N {{s_{i,j}}} \left\| {{{\boldsymbol{W}}^{\text{T}}}{{\boldsymbol{f}}_{i,:}} - {{\boldsymbol{W}}^{\text{T}}}{{\boldsymbol{f}}_{j,:}}} \right\|_2^2 = {\text{ tr}}({{\boldsymbol{W}}^{\text{T}}}{{\boldsymbol{F}}^{\text{T}}}{\boldsymbol{LFW}}) \end{gathered} $$ (12) 式中：
$\text{tr}(\cdot)$ 表示矩阵的迹，${\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{S}}$ ，${\boldsymbol{S}} = [{s_{ij}}] \in {\bf{R}}^{N \times N}$ 为子类间关系的相似矩阵，${\boldsymbol{D}} \in {\bf{R}}^{N \times N}$ 是对角矩阵，且${d_{ii}} = \displaystyle\sum_j {{s_{ij}}}$ ，${s_{ij}}$ 定义为$$ {s}_{ij}=\left\{\begin{array}{l}1, \qquad \text{ }{{\boldsymbol{f}}}_{i}\text{ }和\text{ }{{\boldsymbol{f}}}_{j}是同一集群\\ 0, \qquad 其他\end{array} \right.$$ (13) 将
${\boldsymbol{\varOmega}}$ 作为惩罚项引入多任务学习模型[21]，得到基于子类关系正则化的多任务特征学习算法算法模型：$$ \begin{array}{c}{\boldsymbol{W}}=\mathrm{arg}\underset{{\boldsymbol{W}}}{\mathrm{min}}\dfrac{1}{2}\Vert {\boldsymbol{Y}}-{\boldsymbol{FW}}{\Vert }_{\mathcal{F}}^{2}+{\lambda }_{1}\Vert {\boldsymbol{W}}{\Vert }_{2,1}+ {\lambda }_{2}\text{tr}({{\boldsymbol{W}}}^{\text{T}}{{\boldsymbol{F}}}^{\text{T}}{\boldsymbol{LFW}})\end{array} $$ (14) srMTLF算法利用加速近端梯度实现权重矩阵
${\boldsymbol{W}}$ 的估计。具体来讲，将代价函数(14)分成光滑部分：$$ f({\boldsymbol{W}})=\frac{1}{2}\Vert {\boldsymbol{Y}}-{\boldsymbol{FW}}{\Vert }_{\mathcal{F}}^{2}+{\lambda }_{2}\text{tr}({{\boldsymbol{W}}}^{\text{T}}{{\boldsymbol{F}}}^{\text{T}}{\boldsymbol{LFW}}) $$ (15) 和非光滑部分：
$$ \mathcal{L}({\boldsymbol{W)}}={\lambda }_{1}\Vert {\boldsymbol{W}}{\Vert }_{2,1} $$ (16) 并利用下式近似
$ f({\boldsymbol{W}}) + \mathcal{L}({\boldsymbol{W}}) $ ：$$ \begin{array}{c}\mathcal{G}({\boldsymbol{W}})=f({\boldsymbol{W}}(t))+\langle {\boldsymbol{W}}-{\boldsymbol{W}}(t),\nabla f({\boldsymbol{W}}(t))\rangle +\\ \dfrac{\mu }{2}\Vert {\boldsymbol{W}}-{\boldsymbol{W}}(t){\Vert }_{\mathcal{F}}^{2}+\mathcal{L}({\boldsymbol{W}})\end{array} $$ (17) 式中：
${\boldsymbol{W}}(t)$ 表示${\boldsymbol{W}}$ 的第$t$ 次迭代值，$\nabla f({\boldsymbol{W}}(t))$ 表示$ f({\boldsymbol{W}}) $ 在点${\boldsymbol{W}}(t)$ 的梯度，$\langle \cdot , \cdot \rangle $ 表示内积算子，$\mu $ 表示步长。基于近似代价函数，权重矩阵${\boldsymbol{W}}$ 可以通过近似算子迭代：$$ {\boldsymbol{W}}(t+1)=\mathrm{arg}\underset{{\boldsymbol{W}}}{\mathrm{min}}\frac{1}{2}\Vert {\boldsymbol{W}}-{\boldsymbol{V}}(t){\Vert }_{\mathcal{F}}^{2}+\frac{1}{\mu }\mathcal{L}({\boldsymbol{W}}) $$ 其中
${\boldsymbol{V}}(t) = {\boldsymbol{W}}(t) - (1/\mu )\nabla f({\boldsymbol{W}}(t))$ 。因为${\boldsymbol{W}}$ 的每一行相互独立，可以分别迭代更新：$$ \begin{array}{c} {{\boldsymbol{w}}}^{{d}}(t+1)=\mathrm{arg}\underset{{{\boldsymbol{w}}}^{{d}}}{\mathrm{min}}\dfrac{1}{2}\Vert {{\boldsymbol{w}}}^{{d}}-{{\boldsymbol{v}}}^{{d}}(t){\Vert }_{2}^{2}+\dfrac{1}{\mu }\Vert {{\boldsymbol{w}}}^{{d}}{\Vert }_{2}=\\ \left\{\begin{array}{l}\left(1-\dfrac{{\lambda }_{1}}{\mu \Vert {{\boldsymbol{v}}}^{{ {d}}}(t){\Vert }_{2}^{2}}\right){{\boldsymbol{v}}}^{{ {d}}}(t),\qquad \Vert {{\boldsymbol{v}}}^{{ {d}}}(t){\Vert }_{2}^{2} > \dfrac{{\lambda }_{1}}{\mu }\\ 0,\qquad 其他\end{array} \right. \end{array} $$ (18) 其中
${{\boldsymbol{v}}^{{d}}}(t)$ 表示${\boldsymbol{V}}(t)$ 的第$d$ 行。为加速近似算子迭代，进一步将${\boldsymbol{W}}(t)$ 替换为$$ {\boldsymbol{\tilde W}}(t)={\boldsymbol{W}}(t){\text{ + }}\frac{{\alpha ({{t}}- 1) - 1}}{{\alpha ({{t)}}}}({\boldsymbol{W}}(t)-{\boldsymbol{W}}(t{-1})) $$ (19) 其中
$\alpha ({{{{t}}) = }}\dfrac{{1 + \sqrt {1 + 4\alpha {{({{{{t}} - 1)}}}^2}} }}{2}$ （初始值$\alpha (0) = 1$ ）交替迭代求解式(18)、(19),直到代价函数(14)收敛后得到最终的权重矩阵${\boldsymbol{W}}$ 。1.3.4 特征融合
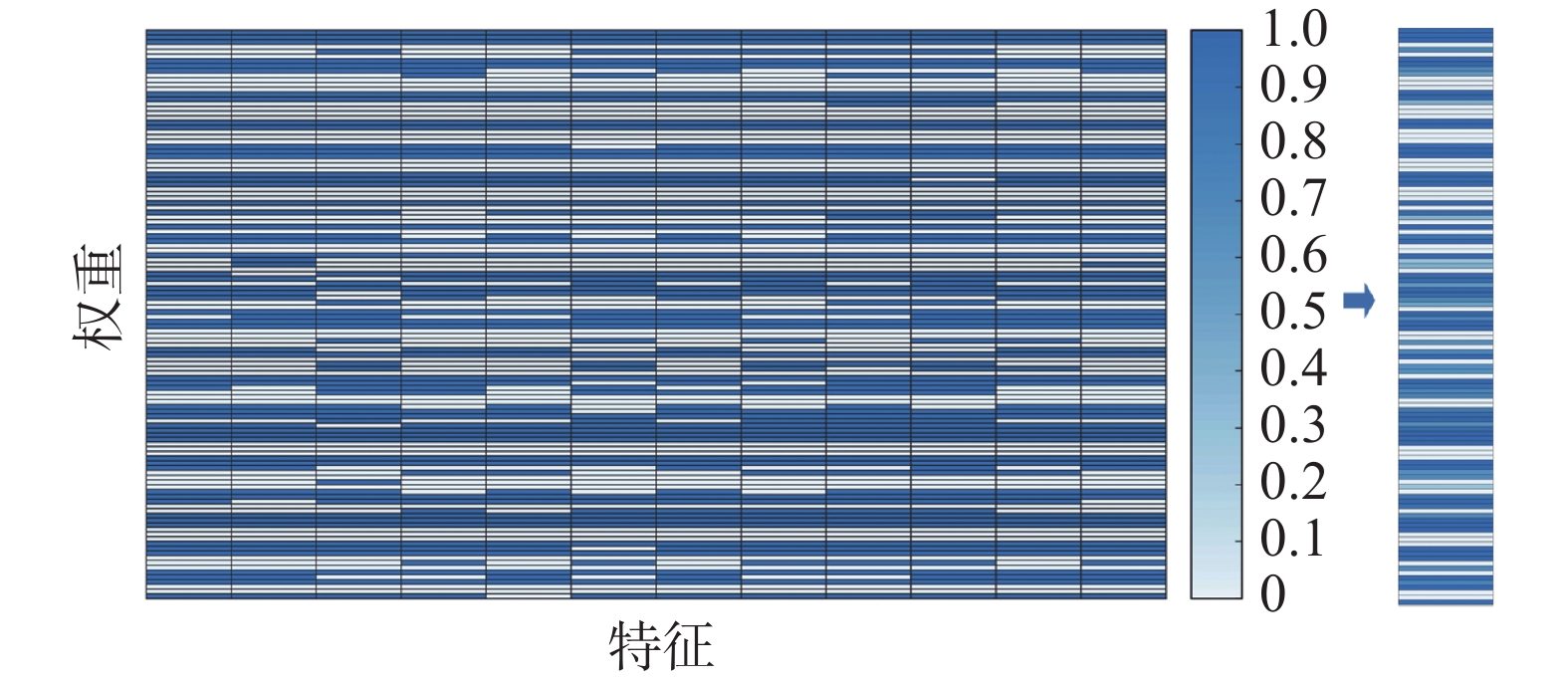
通过srMTLF算法，实现了不同特征在AP聚类后子任务的联合特征学习。得到权重矩阵
${\boldsymbol{W}}$ 后，本文发现简单地根据特征在各个子类的权重信息的汇总进行选择，没有充分利用每个子类任务的信息。如图3所示，不同特征在不同子类任务下的权重不同，但最后的特征选择忽略单个子类任务选择出来的特征信息。因此，本文把特征数降维成聚类后的子类数，并在每一个子类任务上实现特征的加权选择和融合[22-24]，构造srMTLF算法不仅能够有效降低特征维数，而且保留了所有子类任务的先验信息，从而为情绪解码提供表征能力较强的特征。
图 3 权重矩阵可视化Fig. 3 Visualization of the weight matrix下载:
全尺寸图片
2. 实验评价及结果
2.1 实验数据
2.1.1 DEAP数据集
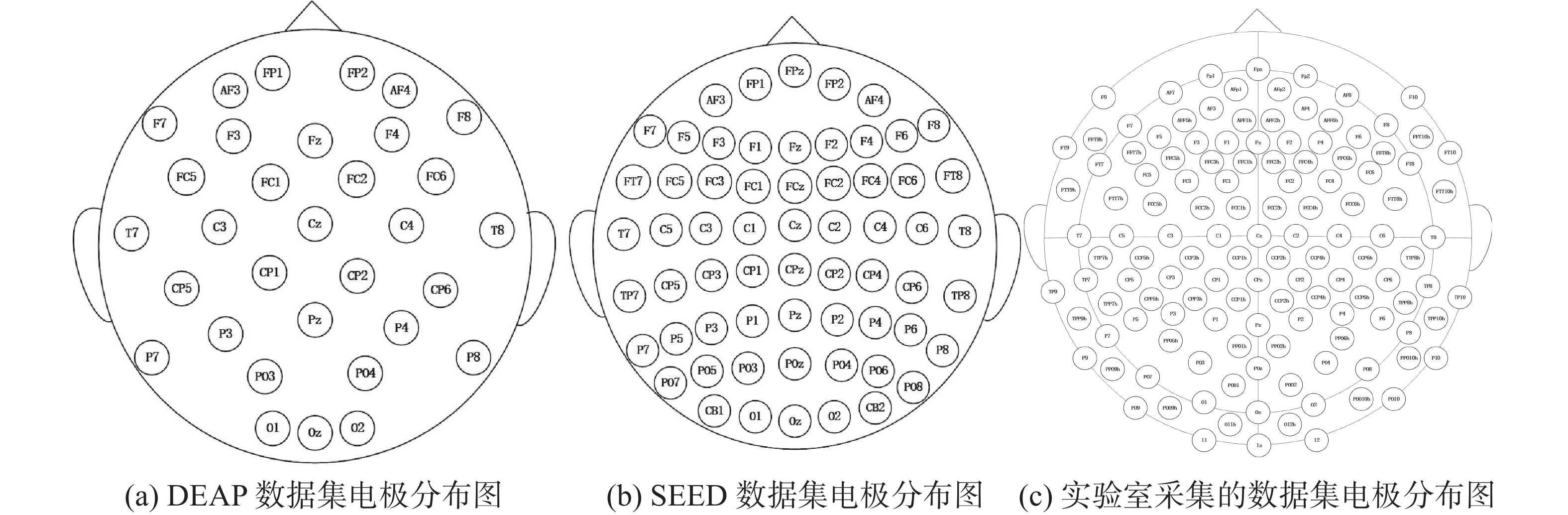
DEAP是Koelstra等[25]建立的公开情感数据库，包括32名（16名男性和16名女性）参与者观看40 min音乐视频的生理信号和受试者对视频的Valence、Arousal、Dominance、Liking的心理量表，其中EEG信号由32个活动电极按照国际10-20系统记录，如图4(a)所示。实验采用官方预处理后的EEG数据。
图 4 数据集的电极分布Fig. 4 Electrode distribution map of the data sets下载:
全尺寸图片
2.1.2 SEED数据集
SEED(SJTU Emotion EEG Dataset)由上海交通大学吕宝粮课题组[20]发布，包括15名受试者（7男8女，23.27±2.37岁）进行的62通道(如图4(b)所示)EEG记录。该数据集主要测量3种类型的情绪（积极、中性、消极），每一类情绪都与5个视频镜头相关。实验采用官方预处理后的EEG数据。
2.1.3 CEED数据集
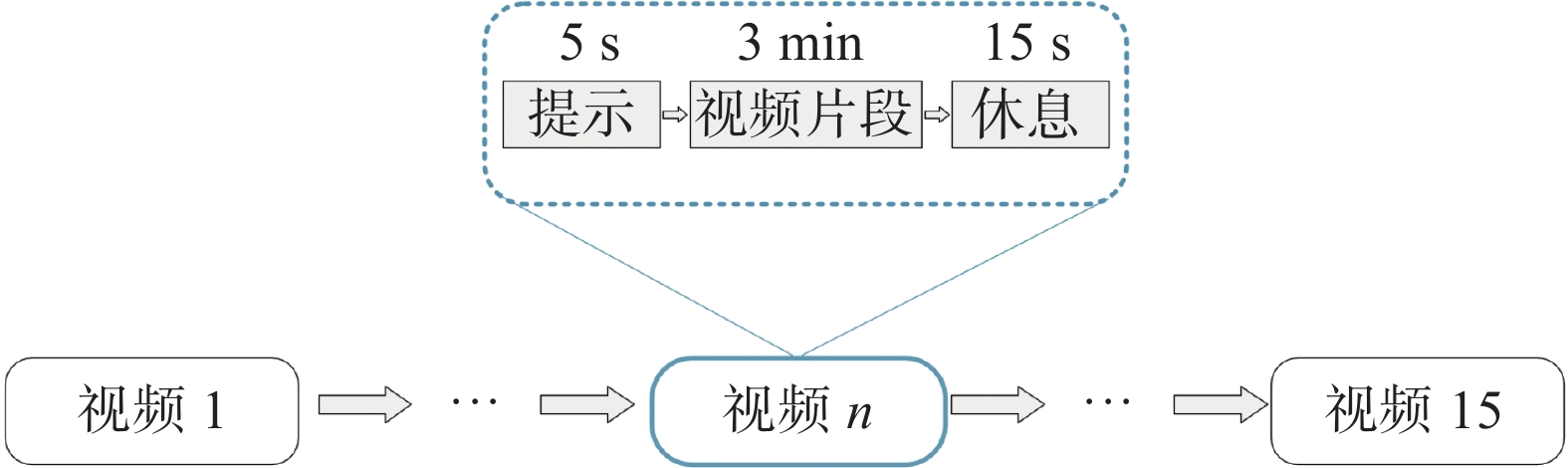
CEED(CQUPT Emotion EEG Dataset)是本实验室采集的基于视频刺激诱发的情感脑电数据集。利用实验室的Brain Products脑电采集放大系统对14名受试者（9男5女，24±1.38岁）进行的128通道(图4(c))EEG记录。被试的一次实验由3种情绪（积极、中性、消极）各5种剪辑片段组合而成。具体的采集流程和视频剪辑片段选择如图5和表1所示，实验采用预处理（降采样256 Hz，0.1~50 Hz带通滤波），去除眼电后的EEG数据。
图 5 实验采集流程Fig. 5 Experimental acquisition process下载:
全尺寸图片
表 1 情绪刺激视频选择Table 1 Selection of emotionally stimulating videos序号 标签 电影剪辑源 片段个数 1 积极 大学宿舍生活图鉴 1 2 中性 河西走廊 3 3 消极 亲爱的 1 4 积极 岳云鹏小品精选 2 续表 1 序号 标签 电影剪辑源 片段个数 5 中性 航拍中国 2 6 消极 盲山 1 7 积极 缝纫机乐队 1 8 积极 雪天搞笑行为图鉴 1 9 消极 唐山大地震 2 10 消极 成年人崩溃瞬间 1 2.2 实验评价以及结果
为验证提出的基于srMTLF的情绪识别的有效性，本文将以下方法作为对比算法：
1) Feature Fusion: 提取每个子频带的脑网络和微分熵，对两种向量进行拼接融合后作为新的特征向量进行分类。
2) Lasso: 利用L1正则化(式（14）)对连接融合后的特征向量进行选择，用选择特征进行分类。
$$ {\boldsymbol{w}}=\mathrm{arg}\underset{{\boldsymbol{w}}}{\mathrm{min}}\frac{1}{2}\Vert {\boldsymbol{y}}-{\boldsymbol{Fw}}{\Vert }_{2}^{2}+{\lambda }_{1}\Vert {\boldsymbol{w}}{\Vert }_{1} $$ (20) 3) Group Lasso(GL): AP聚类重构原始标签后，利用
${L_{2,1}}$ 对权重矩阵进行约束，构造基于子类的多任务学习算法(式（10）)优化原始特征向量。4) 基于Group Lasso的特征融合学习算法(GLF): 在GL基础上，在聚类后的子类空间进行特征的选择和融合优化多频带特征向量。
5) 基于子类关系正则化的多任务特征学习算法(srMTL)：在GL的基础上，利用图拉普拉斯正则化保持子类间潜在的关系，构造多任务学习算法(式（13）)去优化多频带特征向量。
6) srMTLF: 在srMTL的基础上，基于聚类后每个子类的进行特征的选择和融合，构造多任务特征融合算法优化多频带特征向量。
为避免出现“数据泄露”导致的测试集准确率虚高的情况，本文采用“同源样本捆绑”[26]的方式来对单个被试的数据进行训练集和测试集的划分。由于每次刺激视频的开头有可能出现上一段视频中的情绪波动，类似于文献[27]的研究方法，本文采用截取DEAP数据集中间40 s的数据，并使用大小为10 s滑动窗口(不重叠)分割数据。每个样本数据大小为32×1280（通道数×采样点）。样本标签根据[7]丢弃掉评分在4.8~5.2的模糊样本，之后以5为阈值在效价和唤醒维度上进行分类[28]。为保持数据的一致性，SEED和实验室的数据集采取类似的处理方法。本文采用小波包变换[29]的方式对实验数据进行20个重叠子频带(4~8 Hz, 6~10 Hz, …, 42~45 Hz)的划分，接着提取各个子频带对应的脑网络和DE特征组成融合特征向量，用于后续的特征优化和分类。
本文采用五折交叉验证对情绪解码精度进行评价。在交叉验证的每一次运行中，通过内环交叉验证确定最优超参数。分类模型支持向量机[30]的软边界参数C设为默认值(C = 1)。
表2~5中，∗和∗∗分别代表srMTLF和其他方法成对进行t检验时不同，p<0.05和p<0.01的情况。对于公开EEG数据集和本实验室采集的情绪EEG数据集，在单一特征和融合特征下，srMTLF学习到的特征均具有更强的情绪表征能力和稳定的分类性能。脑网络的空间拓扑结构信息和差分熵进行特征融合后，蕴含更丰富的情绪解码信息，两者分别刻画EEG数据的空间和非线性特征，在结构与内容上互相补充，所以相较于单一特征具有更高的解码精度。和其他特征选择算法的对比，本文使用的srMTLF算法进一步提高脑电情绪的解码精度，显示出其在EEG情绪解码上的优势。
表 2 DEAP数据集效价维度分类准确率Table 2 Classification accuracy for the valence dimension of the DEAP dataset% 方法 脑网络 DE 脑网络+DE Feature Fusion 62.94±11.96** 61.19±10.80** 62.08±11.17** Lasso 68.23±10.33** 69.56±9.99** 69.00±10.67** GL 70.17±10.34** 73.29±8.83** 68.34±9.09** GLF 71.12±10.02** 70.88±8.23** 68.11±10.74** srMTL 72.23±9.07** 74.85±9.52** 73.30±9.10** srMTLF 74.49±8.60 81.58±5.19 86.29±5.84 表 3 DEAP数据集唤醒维度分类准确率Table 3 Classification accuracy for the arousal dimension of the DEAP dataset% 方法 脑网络 DE 脑网络+ DE Feature Fusion 61.19±8.38** 60.61±10.30** 62.53±10.55** Lasso 66.86±7.46** 69.66±9.08** 69.34±8.34** GL 70.00±7.47** 71.45±7.09** 69.66±8.17** GLF 70.57±7.08** 73.46±7.87** 70.26±8.86** srMTL 71.58±7.08** 74.58±7.19** 73.98±7.30** srMTLF 75.29±6.49 81.34±7.14 87.74±4.51 表 4 SEED数据集分类准确率Table 4 SEED dataset Classification accuracy% 方法 脑网络 DE 脑网络+ DE Feature Fusion 62.19±12.18** 66.67±9.75** 68.30±12.11** Lasso 67.93±10.89** 74.00±9.44 ∗ 73.78±11.35** GL 68.19±10.21** 77.63±7.40 74.89±12.03** GLF 70.44±11.47 ∗ 82.81±7.39 79.30±8.76** srMTL 71.74±11.79 ∗ 79.52±7.81 76.89±9.89** srMTLF 72.15±11.01 78.07±9.11 92.67±3.79 表 5 实验室采集的数据集分类准确率Table 5 Classification accuracy for laboratory-collected data sets% 方法 脑网络 DE 脑网络+ DE Feature Fusion 43.37±8.05** 42.05±18.41** 41.29±18.16** Lasso 44.42±8.65** 41.67±17.93** 48.48±15.56** GL 44.89±8.78** 48.30±19.41** 62.31±19.85** GLF 50.19±11.78** 60.42±17.25 ∗ 63.26±20.14** srMTL 51.70±14.08** 60.42±17.67 ∗ 62.50±18.39** srMTLF 66.67±10.59 68.75±12.40 88.89±11.87 为进一步验证本文方法的优势，将本文方法与近几年代表的分类方法进行了对比（如表6所示）。与其他方法相比较，srMTLF方法脑电解码精度最高，进一步说明DE和脑网络的融合提高了情绪解码的精度，利用子类之间的关系进行多任务特征融合算法的优越性。
表 6 不同特征提取算法的脑电情绪解码准确率对比Table 6 Comparison of EEG emotion decoding accuracy with different feature extraction algorithms作者 数据集 方法/特征 准确率/% Liu等, 2022[24] DEAP DE 85.6(Valence)/84.3(Arousal) Ding等, 2021[26] DEAP TSception 62.27(Valence)/63.75(Arousal) Yin等, 2017[31] DEAP EEG、EOG/EMG、GSR 83.0(Valence)/84.2(Arousal) Li等, 2021[32] SEED PSD、DE、DASM、RASM、DCAU 89.65 Song等, 2020[6] SEED DE、PSD、DASM、RASM、DCAU 90.94 Gao等,2021[13] SEED DE、Spearman 91.45 本文算法 SEED srMTLF 92.67 本文算法 DEAP srMTLF 86.29(Valence)/87.74(Arousal) 3. 算法评估
3.1 混淆矩阵
本文针对公开数据集SEED对上述实验涉及到的模型的混淆矩阵进行了可视化分析，如图6所示，在进行加权融合后的模型，在各种类型的情绪识别准确率上都有着提升。srMTLF模型在区分消极情绪和中性情绪方面则相对较差，这也与Zhou等[33]的研究结果一致。加权融合后的srMTLF在各类情绪识别的解码精度都有所提升，特别在中性和消极情绪识别的精度有着更明显的提升。
图 6 不同特征选择与融合模型的混淆矩阵Fig. 6 Confusion matrix for different feature selection and fusion models下载:
全尺寸图片
3.2 参数敏感性
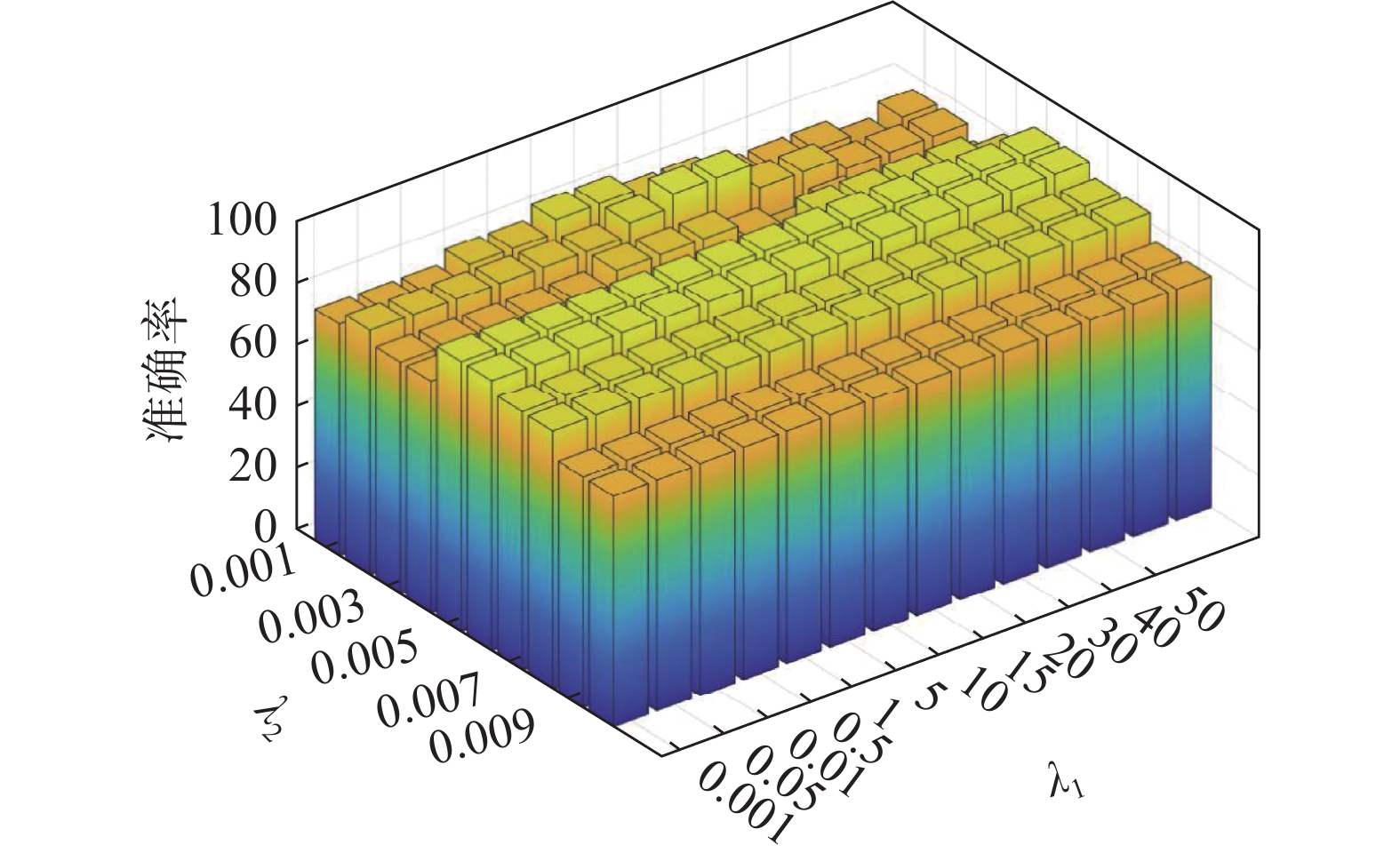
srMTLF（式（12））中有两个超参数
${\lambda _1}$ 和${\lambda _2}$ 需要手动选择。图7是在不同超参数值下的测试准确率，其中${\lambda _1}$ 在对数坐标轴上取值，${\lambda _2}$ 在线性坐标轴上取值。如图7所示，srMTLF算法对于超参数具有较高的稳定性和鲁棒性。
图 7 srMTLF在不同超参数下的解码精度Fig. 7 Decoding accuracy of srMTLF under different hyperparameters下载:
全尺寸图片
3.3 收敛性与计算时间
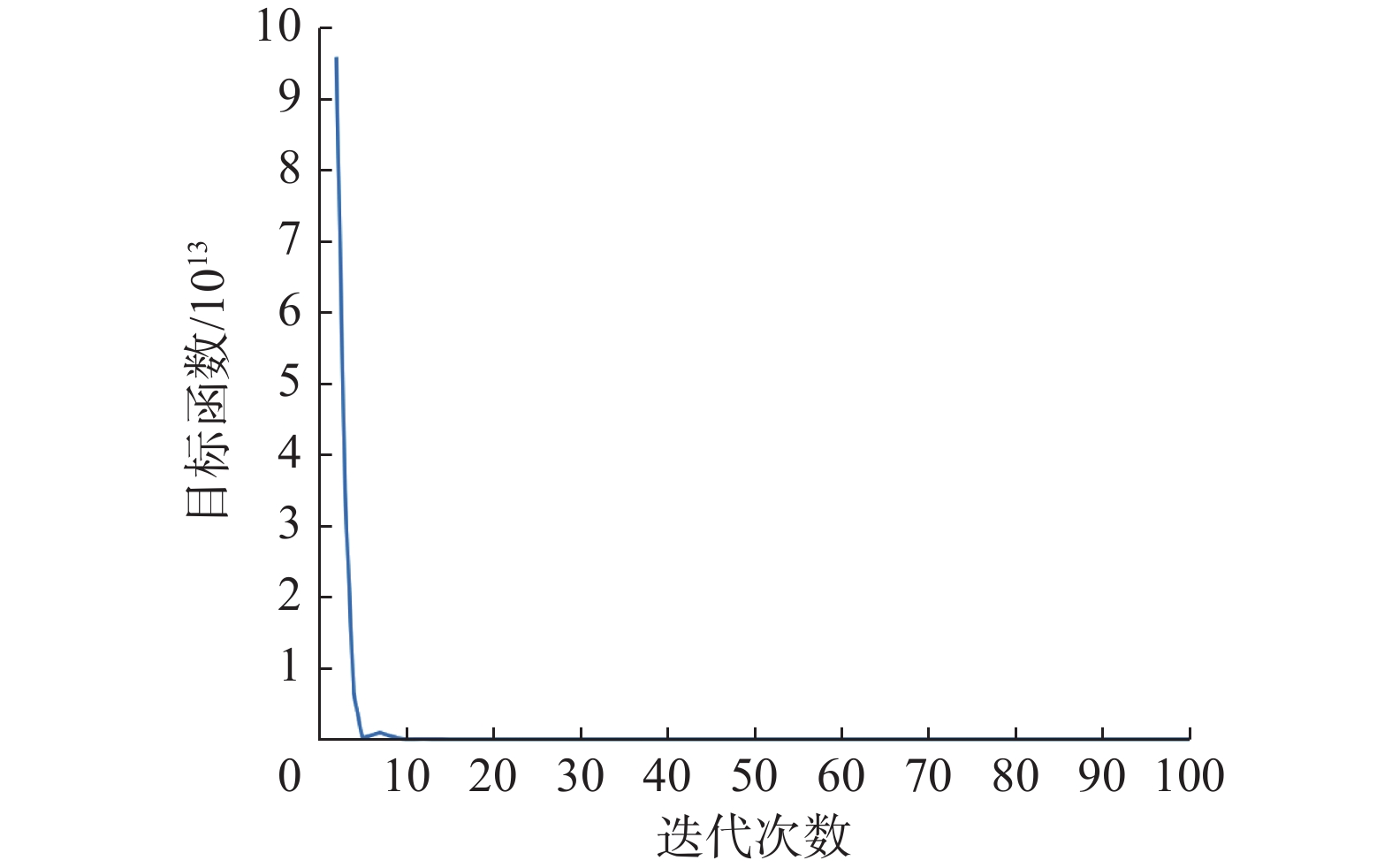
srMTLF算法利用加速近端梯度实现权重矩阵
${\boldsymbol{W}}$ 的估计。图8表明，srMTLF在20次迭代左右即收敛。图9是不同算法的训练时间。所有方法均在台式机(i5-10400 CPU@2.90 GHz, 64 GB RAM)上进行五折交叉验证，虽然本文的方法相对于其他方法来说时间成本有所增加，但srMTLF算法显著提升情绪解码精度且在分类准确率上具有更高的稳定性，满足脑机接口系统的实际需要。此外，利用训练数据离线估计${\boldsymbol{W}}$ 后，可以实现高效的在线情绪解码。
图 8 srMTLF算法收敛曲线Fig. 8 Convergence curve of srMTLF algorithm下载:
全尺寸图片
图 9 不同算法训练时间Fig. 9 Training time for different algorithms下载:
全尺寸图片
4. 结束语
本文提出了基于子类关系的多任务特征融合算法，融合EEG的脑网络和DE特征，显著提高了脑电情绪解码的精度。深度学习方法利用其深层非线性结构，能够数据自驱动地挖掘EEG信号的特征信息。与人工构造特征相比，利用大量数据学习到的特征更能反映数据的内在本质，提高情绪识别的智能和普适性，因此我们下一步的工作是利用深度神经网络去提取上述特征组合的非线性特征信息。此外由于容积传导效应，EEG信号空间分辨率较低，一定程度上限制了基于头皮EEG信号的情绪解码精度。我们将进一步利用EEG源成像技术，获取具有更高时空分辨率的皮层神经活动信号，在皮层源信号空间进行EEG信号分析和情绪解码，以进一步提高基于EEG的情绪解码性能。
-
图 1 srMTLF算法流程
Fig. 1 Flow of srMTLF algorithm
下载:
全尺寸图片
图 2 DEAP数据集被试s01-tSNE聚类结果
Fig. 2 tSNE clustering results of subject s01 in DEAP dataset
下载:
全尺寸图片
图 3 权重矩阵可视化
Fig. 3 Visualization of the weight matrix
下载:
全尺寸图片
图 4 数据集的电极分布
Fig. 4 Electrode distribution map of the data sets
下载:
全尺寸图片
图 5 实验采集流程
Fig. 5 Experimental acquisition process
下载:
全尺寸图片
图 6 不同特征选择与融合模型的混淆矩阵
Fig. 6 Confusion matrix for different feature selection and fusion models
下载:
全尺寸图片
图 7 srMTLF在不同超参数下的解码精度
Fig. 7 Decoding accuracy of srMTLF under different hyperparameters
下载:
全尺寸图片
图 8 srMTLF算法收敛曲线
Fig. 8 Convergence curve of srMTLF algorithm
下载:
全尺寸图片
图 9 不同算法训练时间
Fig. 9 Training time for different algorithms
下载:
全尺寸图片
表 1 情绪刺激视频选择
Table 1 Selection of emotionally stimulating videos
序号 标签 电影剪辑源 片段个数 1 积极 大学宿舍生活图鉴 1 2 中性 河西走廊 3 3 消极 亲爱的 1 4 积极 岳云鹏小品精选 2 续表 1 序号 标签 电影剪辑源 片段个数 5 中性 航拍中国 2 6 消极 盲山 1 7 积极 缝纫机乐队 1 8 积极 雪天搞笑行为图鉴 1 9 消极 唐山大地震 2 10 消极 成年人崩溃瞬间 1 表 2 DEAP数据集效价维度分类准确率
Table 2 Classification accuracy for the valence dimension of the DEAP dataset
% 方法 脑网络 DE 脑网络+DE Feature Fusion 62.94±11.96** 61.19±10.80** 62.08±11.17** Lasso 68.23±10.33** 69.56±9.99** 69.00±10.67** GL 70.17±10.34** 73.29±8.83** 68.34±9.09** GLF 71.12±10.02** 70.88±8.23** 68.11±10.74** srMTL 72.23±9.07** 74.85±9.52** 73.30±9.10** srMTLF 74.49±8.60 81.58±5.19 86.29±5.84 表 3 DEAP数据集唤醒维度分类准确率
Table 3 Classification accuracy for the arousal dimension of the DEAP dataset
% 方法 脑网络 DE 脑网络+ DE Feature Fusion 61.19±8.38** 60.61±10.30** 62.53±10.55** Lasso 66.86±7.46** 69.66±9.08** 69.34±8.34** GL 70.00±7.47** 71.45±7.09** 69.66±8.17** GLF 70.57±7.08** 73.46±7.87** 70.26±8.86** srMTL 71.58±7.08** 74.58±7.19** 73.98±7.30** srMTLF 75.29±6.49 81.34±7.14 87.74±4.51 表 4 SEED数据集分类准确率
Table 4 SEED dataset Classification accuracy
% 方法 脑网络 DE 脑网络+ DE Feature Fusion 62.19±12.18** 66.67±9.75** 68.30±12.11** Lasso 67.93±10.89** 74.00±9.44 ∗ 73.78±11.35** GL 68.19±10.21** 77.63±7.40 74.89±12.03** GLF 70.44±11.47 ∗ 82.81±7.39 79.30±8.76** srMTL 71.74±11.79 ∗ 79.52±7.81 76.89±9.89** srMTLF 72.15±11.01 78.07±9.11 92.67±3.79 表 5 实验室采集的数据集分类准确率
Table 5 Classification accuracy for laboratory-collected data sets
% 方法 脑网络 DE 脑网络+ DE Feature Fusion 43.37±8.05** 42.05±18.41** 41.29±18.16** Lasso 44.42±8.65** 41.67±17.93** 48.48±15.56** GL 44.89±8.78** 48.30±19.41** 62.31±19.85** GLF 50.19±11.78** 60.42±17.25 ∗ 63.26±20.14** srMTL 51.70±14.08** 60.42±17.67 ∗ 62.50±18.39** srMTLF 66.67±10.59 68.75±12.40 88.89±11.87 表 6 不同特征提取算法的脑电情绪解码准确率对比
Table 6 Comparison of EEG emotion decoding accuracy with different feature extraction algorithms
作者 数据集 方法/特征 准确率/% Liu等, 2022[24] DEAP DE 85.6(Valence)/84.3(Arousal) Ding等, 2021[26] DEAP TSception 62.27(Valence)/63.75(Arousal) Yin等, 2017[31] DEAP EEG、EOG/EMG、GSR 83.0(Valence)/84.2(Arousal) Li等, 2021[32] SEED PSD、DE、DASM、RASM、DCAU 89.65 Song等, 2020[6] SEED DE、PSD、DASM、RASM、DCAU 90.94 Gao等,2021[13] SEED DE、Spearman 91.45 本文算法 SEED srMTLF 92.67 本文算法 DEAP srMTLF 86.29(Valence)/87.74(Arousal) -
[1] 吕宝粮, 张亚倩, 郑伟龙. 情感脑机接口研究综述[J]. 智能科学与技术学报, 2021, 3(1): 36–48. doi: 10.11959/j.issn.2096-6652.202104 LYU Baoliang, ZHANG Yaqian, ZHENG Weilong. A survey of affective brain-computer interface[J]. Chinese journal of intelligent science and technology, 2021, 3(1): 36–48. doi: 10.11959/j.issn.2096-6652.202104 [2] ALARCÃO S M, FONSECA M J. Emotions recognition using EEG signals: a survey[J]. IEEE transactions on affective computing, 2019, 10(3): 374–393. doi: 10.1109/TAFFC.2017.2714671 [3] 张冠华, 余旻婧, 陈果, 等. 面向情绪识别的脑电特征研究综述[J]. 中国科学: 信息科学, 2019, 49(9): 1097–1118. doi: 10.1360/N112018-00337 ZHANG Guanhua, YU Minjing, CHEN Guo, et al. A review of EEG features for emotion recognition[J]. Scientia sinica informationis, 2019, 49(9): 1097–1118. doi: 10.1360/N112018-00337 [4] PATEL P, R R, ANNAVARAPU R N. EEG-based human emotion recognition using entropy as a feature extraction measure[J]. Brain informatics, 2021, 8(1): 20. doi: 10.1186/s40708-021-00141-5 [5] ZHENG Weilong, LIU Wei, LU Yifei, et al. EmotionMeter: a multimodal framework for recognizing human emotions[J]. IEEE transactions on cybernetics, 2019, 49(3): 1110–1122. doi: 10.1109/TCYB.2018.2797176 [6] SONG Tengfei, ZHENG Wenming, SONG Peng, et al. EEG emotion recognition using dynamical graph convolutional neural networks[J]. IEEE transactions on affective computing, 2020, 11(3): 532–541. doi: 10.1109/TAFFC.2018.2817622 [7] 孙岩, 薄思雨, 吕娇娇. 认知重评和表达抑制情绪调节策略的脑网络分析: 来自 EEG 和 ERP 的证据[J]. 心理学报, 2020, 52(1): 12. SUN Yan, BO Siyu, LYU Jiaojiao. Brain network analysis of cognitive reappraisal and expressive suppression emotion regulation strategies: evidence from EEG and ERP[J]. Acta psychologica sinica, 2020, 52(1): 12. [8] ZHANG Shilin, HU Bin, BIAN Ji, et al. A novel emotion recognition method incorporating MST-based brain network and FVMD-GAMPE[C]//2021 IEEE International Conference on Bioinformatics and Biomedicine. Houston: IEEE, 2021: 1153–1158. [9] KANG Qiaoju, GAO Qiang, SONG Yu, et al. Emotion recognition from EEG signals of hearing-impaired people using stacking ensemble learning framework based on a novel brain network[J]. IEEE sensors journal, 2021, 21(20): 23245–23255. doi: 10.1109/JSEN.2021.3108471 [10] XU Peng, XIONG Xiuchun, XUE Qing, et al. Differentiating between psychogenic nonepileptic seizures and epilepsy based on common spatial pattern of weighted EEG resting networks[J]. IEEE transactions on bio-medical engineering, 2014, 61(6): 1747–1755. doi: 10.1109/TBME.2014.2305159 [11] ZHANG Junan, GU Liping, CHEN Yongqiang, et al. Multi-feature fusion emotion recognition based on resting eeg[J]. Journal of mechanics in medicine and biology, 2022, 22(3): 2240002. doi: 10.1142/S0219519422400024 [12] GAO Qiang, WANG Chuhan, WANG Zhe, et al. EEG based emotion recognition using fusion feature extraction method[J]. Multimedia tools and applications, 2020, 79(37): 27057–27074. [13] GAO Zhongke, LI Rumei, MA Chao, et al. Core-brain-network-based multilayer convolutional neural network for emotion recognition[J]. IEEE transactions on instrumentation and measurement, 2021, 70: 2510209. [14] ZHENG Weilong, ZHU Jiayi, LU Baoliang. Identifying stable patterns over time for emotion recognition from EEG[J]. IEEE transactions on affective computing, 2019, 10(3): 417–429. doi: 10.1109/TAFFC.2017.2712143 [15] WANG Zhongmin, HU Shuyuan, SONG Hui. Channel selection method for EEG emotion recognition using normalized mutual information[J]. IEEE access, 2019, 7: 143303–143311. doi: 10.1109/ACCESS.2019.2944273 [16] ZHANG Yu, ZHOU Tao, WU Wei, et al. Improving EEG decoding via clustering-based multitask feature learning[J]. IEEE transactions on neural networks and learning systems, 2022, 33(8): 3587–3597. doi: 10.1109/TNNLS.2021.3053576 [17] FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972–976. doi: 10.1126/science.1136800 [18] LI Fali, WANG Jiuju, LIAO Yuanyuan, et al. Differentiation of schizophrenia by combining the spatial EEG brain network patterns of rest and task P300[J]. IEEE transactions on neural systems and rehabilitation engineering, 2019, 27(4): 594–602. doi: 10.1109/TNSRE.2019.2900725 [19] RAMOSER H, MULLER-GERKING J, PFURTSCHELLER G. Optimal spatial filtering of single trial EEG during imagined hand movement[J]. IEEE transactions on rehabilitation engineering, 2000, 8(4): 441–446. doi: 10.1109/86.895946 [20] ZHENG Weilong, LYU Baoliang. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE transactions on autonomous mental development, 2015, 7(3): 162–175. doi: 10.1109/TAMD.2015.2431497 [21] LIU Jun, JI Shuiwang, YE Jieping. Multi-task feature learning via efficient l2, 1-norm minimization[EB/OL]. (2012–05–09)[2022–06–14]. http://arxiv.org/abs/1205.2631. [22] LI Yazhou, DAI Wei, ZHANG Weifang. Bearing fault feature selection method based on weighted multidimensional feature fusion[J]. IEEE access, 2020, 8: 19008–19025. doi: 10.1109/ACCESS.2020.2967537 [23] WU Xun, ZHENG Weilong, LI Ziyi, et al. Investigating EEG-based functional connectivity patterns for multimodal emotion recognition[J]. Journal of neural engineering, 2022, 19(1): 016012. doi: 10.1088/1741-2552/ac49a7 [24] LIU Wei, QIU Jielin, ZHENG Weilong, et al. Comparing recognition performance and robustness of multimodal deep learning models for multimodal emotion recognition[J]. IEEE transactions on cognitive and developmental systems, 2022, 14(2): 715–729. doi: 10.1109/TCDS.2021.3071170 [25] KOELSTRA S, MUHL C, SOLEYMANI M, et al. DEAP: a database for emotion analysis; using physiological signals[J]. IEEE transactions on affective computing, 2012, 3(1): 18–31. doi: 10.1109/T-AFFC.2011.15 [26] DING Yi, ROBINSON N, ZHANG Su, et al. TSception: capturing temporal dynamics and spatial asymmetry from EEG for emotion recognition[EB/OL]. (2021–04–07) [2022–06–14]. http://arxiv.org/abs/2104.02935. [27] NAWAZ R, CHEAH K H, NISAR H, et al. Comparison of different feature extraction methods for EEG-based emotion recognition[J]. Biocybernetics and biomedical engineering, 2020, 40(3): 910–926. doi: 10.1016/j.bbe.2020.04.005 [28] LI Xiang, SONG Dawei, ZHANG Peng, et al. Exploring EEG features in cross-subject emotion recognition[J]. Frontiers in neuroscience, 2018, 12: 162. doi: 10.3389/fnins.2018.00162 [29] RAHMAN M A, KHANAM F, AHMAD M, et al. Multiclass EEG signal classification utilizing Rényi min-entropy-based feature selection from wavelet packet transformation[J]. Brain informatics, 2020, 7(1): 7. doi: 10.1186/s40708-020-00108-y [30] KHATUN S, MORSHED B I, BIDELMAN G M. A single-channel EEG-based approach to detect mild cognitive impairment via speech-evoked brain responses[J]. IEEE transactions on neural systems and rehabilitation engineering, 2019, 27(5): 1063–1070. doi: 10.1109/TNSRE.2019.2911970 [31] YIN Zhong, ZHAO Mengyuan, WANG Yongxiong, et al. Recognition of emotions using multimodal physiological signals and an ensemble deep learning model[J]. Computer methods and programs in biomedicine, 2017, 140: 93–110. doi: 10.1016/j.cmpb.2016.12.005 [32] LI Yang, ZHENG Wenming, ZONG Yuan, et al. A Bi-hemisphere domain adversarial neural network model for EEG emotion recognition[J]. IEEE transactions on affective computing, 2021, 12(2): 494–504. doi: 10.1109/TAFFC.2018.2885474 [33] ZHOU Rushuang, ZHANG Zhiguo, FU Hong, et al. PR-PL: a novel transfer learning framework with prototypical representation based pairwise learning for EEG-based emotion recognition[EB/OL]. (2022–02–14) [2022–06–14]. http://arxiv.org/abs/2202.06509.
