Improved slime mould algorithm with multistrategy integration and its application
-
摘要: 针对黏菌算法存在自适应能力有限，抗停滞能力弱等不足，提出多策略融合的改进黏菌算法。采用Bernoulli混沌初始化，丰富种群多样性，提升算法优化精度和收敛速度；提出动态非线性递减策略，动态调节黏菌个体探索幅度，协调并优化算法全局搜索与局部开发能力；结合麻雀算法的预警机制与折射反向学习策略，优化黏菌个体分离觅食过程，防止前期优质个体流失以及后期种群多样性匮乏，提升算法整体抗停滞能力。通过对基准测试函数及部分CEC2017测试函数进行寻优对比实验，测试结果表明改进算法具有更好的寻优精度、稳定性。利用改进算法优化XGBoost参数并将其用于变压器故障诊断，进一步验证了改进策略的有效性及算法的工程实用性。Abstract: In order to address the disadvantages of the slime mold algorithm, such as limited adaptive ability and weak antistagnation capability, we propose an improved slime mold algorithm with multistrategy integration. Bernoulli chaos is used to generate the initial population, which enriches the population diversity, improves the optimization accuracy, and enhances the convergence speed of the algorithm. A dynamic nonlinear decreasing strategy is proposed to adjust the exploration range of slime mold individuals dynamically; this strategy coordinates and optimizes the global exploration and local exploitation capabilities of the algorithm. By combining the early warning mechanism of the sparrow search algorithm and refracted opposition-based learning, the foraging process of slime mold individuals is optimized, preventing the loss of high-quality individuals in the early stage and ensuring population diversity in the later stage, thereby improving the overall antistagnation capability of the algorithm. Comparative optimization experiments are conducted on benchmark functions and some CEC2017 test functions, demonstrating that the improved algorithm exhibits superior optimization accuracy and stability. Furthermore, the improved algorithm is used to optimize XGBoost parameters and is applied to transformer fault diagnosis, which further verifies the effectiveness of the improved strategy and the practicality of the algorithm in engineering applications.
-
随着优化算法的不断深入发展，基于随机算子实现的元启发式算法，因其简单灵活、不需梯度的优势，近些年来受到了众多相关学者的关注。常见元启发式算法包括粒子群算法[1] (particle swarm optimization, PSO)，麻雀搜索算法[2] (sparrow search algorithm, SSA)，海洋捕食者算法[3] (marine predators algorithm, MPA)，算术优化算法[4] (arithmetic optimization algorithm, AOA)、樽海鞘群算法[5] 、蚁群算法[6]等，在绝缘子绝缘状态评估[7]、故障诊断[8]、光伏模型参数规划[9]等实际工程领域得到了广泛应用和研究。
黏菌算法[10] (slime mould algorithm, SMA)是由Li等于2020年基于自然界黏菌的振荡捕食行为提出的元启发式算法，黏菌主要依靠生物振荡器产生的传播波来改变静脉内的细胞质流动，使其倾向于处于较好的食物富集位置，从而达到寻优效果。相较于其他群体智能优化算法具有参数少，寻优能力强的特点。但黏菌算法也同其他算法均存在依赖初始解、后期种群多样性骤降、容易陷入局部最优值等问题。因此，相关学者针对上述问题对黏菌算法进行了相关改进研究。Yu等[11]利用小幅度量子旋转门和水循环机制分别增强算法搜索与开发能力；Alfadhli等[12]通过自适应波动调整种群大小，平衡算法搜索与开发并缩减算法运行时间；Naik等[13]利用自适应方法控制反向学习的使用，增强算法寻优精度；肖亚宁等[14]将Tent混沌映射引入初始化阶段提升初始种群丰富度，利用精英反向学习策略扩大搜索范围；贾鹤鸣等[15]引入AOA算法中的乘法搜索策略改进位置更新方式；刘成汉等[16]添加交叉算子增强个体变异能力，结合自适应反馈因子和人工蜂群算法，增强算法搜索能力。上述文献从不同角度对黏菌算法进行改进，针对丰富初始种群多样性、改进位置更新方式、修改黏菌个体依据概率的变异方式或添加变异扰动环节等单一部分的优化尽管能提升算法优化能力，但依然存在顾此失彼，在复杂多峰寻优中易陷入局部最优，增加算法复杂度的情况，造成改进算法在寻优中出现收敛效果不理想，全局搜索能力和局部开发能力不协调，后期抗停滞能力弱等问题。
因此，针对黏菌算法的特性和不足，提出一种Bernoulli混沌初始化策略、动态非线性递减策略和融合麻雀预警机制与折射反向学习策略的改进黏菌算法(improved slime mould algorithm with multi-strategy, ISMA)。通过基准测试函数、部分CEC2017测试函数以及1个工程实际问题验证ISMA性能。通过实验对比分析，证明ISMA能更好兼顾全局搜索和局部开发的能力，具有良好的寻优能力与工程实用性。本文主要贡献如下：
1)设计多策略融合的改进黏菌算法。将Bernoulli混沌映射引入黏菌算法的种群初始化进程中，使初始解分布更均匀，丰富种群多样性；设计两种非线性递减策略，通过b、c参数控制黏菌觅食振荡幅度，解决算法全局搜索与局部寻优的平衡问题；结合黏菌算法特点，在分离觅食环节融合麻雀预警机制与折射反向学习，前期保证优质个体不被重新初始化行为降为非优质个体，后期避免算法早熟、陷入局部最优。
2)为了避免人工选择分类模型超参数的随机性、盲目性，利用ISMA优化XGBoost参数，基于油中溶解气体分析技术以及变压器故障特点，提出并建立ISMA-XGBoost模型进行变压器故障诊断。
1. 黏菌搜索算法分析
搜索空间中有
$N$ 个黏菌个体，黏菌个体$i$ 在$d$ 维空间中位置表示为${{\boldsymbol{X}}_{{i}}} = \left[x_i^1\quad x_i^2\quad \cdots \quad x_i^d\right]\quad \forall i \in [1,N]$ ，适应度表示为${f_i} = f({{\boldsymbol{X}}_{{i}}}),\forall i \in [1,N]$ 。则黏菌种群在迭代$t$ 次的位置和适应度表示为$$ {\boldsymbol{X}}(t) = \left[ {\begin{array}{*{20}{c}} {x_1^1(t)}&{x_1^2(t)}& \cdots &{x_1^d(t)} \\ {x_2^1(t)}&{x_2^2(t)}& \cdots &{x_2^d(t)} \\ \vdots & \vdots & \ddots & \vdots \\ {x_N^1(t)}&{x_N^2(t)}& \cdots &{x_N^d(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{X}}_{\text{1}}}(t)} \\ {{{\boldsymbol{X}}_{\text{2}}}(t)} \\ \vdots \\ {{{\boldsymbol{X}}_{\text{N}}}(t)} \end{array}} \right] $$ (1) $$ f({\boldsymbol{X}}(t)) = [f({{\boldsymbol{X}}_{\text{1}}}(t)),f({{\boldsymbol{X}}_{\text{2}}}(t)), \cdots ,f({{\boldsymbol{X}}_{\text{N}}}(t))] $$ (2) 模拟黏菌捕食行为的位置更新公式:
$$ {{\boldsymbol{X}}_{{i}}}(t + 1) = \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{X}}_{{b}}}(t) + {{{{\boldsymbol{v}}}}_{{b}}}(W{{\boldsymbol{X}}_{{A}}}(t) - {{\boldsymbol{X}}_{{B}}}(t))},\quad {{r_1} \geqslant {\textit{z}},\; {r_2} < {p_i}} \\ {{{{{\boldsymbol{v}}}}_{{c}}}{{\boldsymbol{X}}_{{i}}}(t)}, \quad {{r_1} \geqslant {\textit{z}},\; {r_2} \geqslant {p_i}} \\ {{\rm{rand}}({\boldsymbol{U}} - {\boldsymbol{L}}) + {\boldsymbol{L}}}, \quad {{r_1} < {\textit{z}}} \end{array}} \right. $$ (3) 式中：
${{\boldsymbol{X}}_b}$ 表示当前发现的食物浓度最高的个体位置；${{\boldsymbol{X}}_{{A}}}$ 和${{\boldsymbol{X}}_{{B}}}$ 表示种群中任意两个个体的位置；${\boldsymbol{W}}$ 表示黏菌的质量。${\boldsymbol{v}}_{{b}}$ 和${{\boldsymbol{v}}}_{{c}}$ 为振荡参数，可使黏菌个体形成任意角度的搜索向量，即在任意方向搜索解空间。${\boldsymbol{U}}$ 与${\boldsymbol{L}}$ 分别为上界、下界。$ {r_1} $ 与${r_2}$ 为均匀分布定义域；为[0,1]的随机数；$z$ 为黏菌分离个体搜索其他食物源的概率，即产生变异的概率，根据实验研究[10]设置其为0.03。${p_i}$ 为条件参数，用于控制黏菌位置更新方式。在下一次迭代中使用最佳个体或当前位置，其更新公式:$$ {p_i} = \tanh (\left| {{f_i} - {f_b}} \right|{\text{)}},\;i \in \{ 1,2, \cdots ,n\} $$ (4) 式中：tanh表示双曲正切函数；
${f_b}$ 表示所有迭代中获得的最佳适应度。重量${\boldsymbol{W}}$ 更新公式如下:$$ {\boldsymbol{W}}({S_{ {\rm{Index}}}}(i)) = \left\{ {\begin{split} {1 + r \cdot \log \left(\dfrac{{{f_b} - f({{\boldsymbol{X}}_{{i}}})}}{{{f_b} - {f_w}}} + 1\right),{\text{ }}i = C} \\ {1 - r \cdot \log \left(\dfrac{{{f_b} - f({{\boldsymbol{X}}_{{i}}})}}{{{f_b} - {f_w}}} + 1\right),{\text{ }}i = O} \end{split}} \right. $$ (5) 式中：
$r$ 为$[0,1]$ 的随机数用于模拟静脉收缩模式的不确定性；$\log $ 用于缓和数值的变化率使收缩频率数值变化较小；$ {f_w} $ 表示最劣适应度值，$i = C$ 表示适应度$S(i)$ 排序为前50%的黏菌个体，$i = O$ 表示其余个体。黏菌种群根据食物的质量来调整自身搜索模式。当食物浓度较高时，该区域附近的重量${\boldsymbol{W}}$ 越大；当食物浓度较低时，区域的权重会降低，从而转向其他区域的探索。${S_{ {\rm{Index}}}}(i)$ 为适应度值序列，在求极小值问题时为递增序列，公式描述为$$ {S_{ {\rm{Index}}}}(i) = {\rm{sort}}(S) $$ (6) ${{{{\boldsymbol{v}}}}_{{b}}}$ 和${{{{\boldsymbol{v}}}}_{{c}}}$ 分别是范围为$[ - b,b]$ 和$[ - c,c]$ 的振荡向量，随着迭代次数增加最终趋于0，其中第$t$ 次迭代的参数$ b、c $ 分别描述为$$ b = \arctan \left( - \left(\dfrac{t}{T}\right) + 1\right) $$ (7) $$ c = 1 - \dfrac{t}{T} $$ (8) 其中
$T$ 为最大迭代次数。${{{\nu }}_{{b}}}$ 和${{{\nu }}_{{c}}}$ 的协同作用模拟黏菌的选择性行为。$ {{{\nu }}_{\text{b}}} $ 的振荡模拟黏菌选择接近食物或者继续探寻的状态，进一步增强算法摆脱局部最优解能力。标准黏菌算法也存在一定局限性，由于黏菌种群多样性较低，故而易陷入局部极值；更新策略中振荡幅度控制探索能力，在后期迭代中收敛较慢，并且难以在开发和探索之间保持平衡；在迭代过程中仅利用固定概率使随机黏菌个体分离觅食，造成优质个体流失。
2. 多策略融合的改进黏菌算法
鉴于如上分析，对SMA算法进行如下改进：1)采用Bernoulli混沌映射进行种群初始化，丰富黏菌种群多样性；2)提出动态非线性递减策略协调算法探索与开发能力；3)融合麻雀预警机制与折射反向学习，提升个体变异能力，防止前期优质个体流失后期种群多样性匮乏。
2.1 Bernoulli混沌初始化策略
黏菌种群初始状态对最终优化结果存在较大影响，标准黏菌算法在初始化过程中使用随机生成种群初始位置，存在种群分布不均、多样性低以及易陷入局部极值等问题。故引入Bernoulli混沌映射[17]初始化种群，使黏菌种群具备遍历均匀性。公式如下:
$$ y_{i + 1}^j = \left\{ {\begin{split} &{y_i^j/(1 - \lambda ),} \quad {0 < y_i^j \leqslant 1 - \lambda } \\ &{\left( {y_i^j - 1 + \lambda } \right)/\lambda ,}\quad {1 - \lambda < y_i^j < 1} \end{split}} \right. $$ (9) $$ x_i^j = {\boldsymbol{L}^j} + ({\boldsymbol{U}^j} - {\boldsymbol{L}^j}) \times y_i^j $$ (10) 式中，
$i = 1,2, \cdots ,N$ 表示个体编号，$j = 1,2, \cdots ,d$ 表示空间维数，$ \lambda $ 为混沌映射参数设置为0.4，${\boldsymbol{U}^j}$ 和${\boldsymbol{L}^j}$ 分别表示第$j$ 维的上下界。初始化具体过程为：随机在$[0,1]$ 生成一个$d$ 维向量作为初始个体${{\boldsymbol{X}}_{\text{1}}}$ (即${\boldsymbol{X}}_{\text{1}}^{{{{\rm{chaos}}}}}$ )，代入式(9)中生成下一个体$d$ 维位置信息${{\boldsymbol{y}}_2} = [y_2^1 \quad y_2^2 \quad \cdots \quad y_2^d]$ ，循环最终得到$N - 1$ 个新黏菌个体，代入式(10)逆映射到个体的搜索空间中，得到黏菌种群${{\boldsymbol{X}}^{{\rm{chaos}}}} = [{\boldsymbol{X}}_1^{{\rm{chaos}}}\quad{\boldsymbol{X}}_2^{{\rm{chaos}}}\quad \cdots \quad {\boldsymbol{X}}_N^{{\rm{chaos}}}{{]}}$ 。2.2 动态非线性递减策略
在SMA迭代优化过程中，当
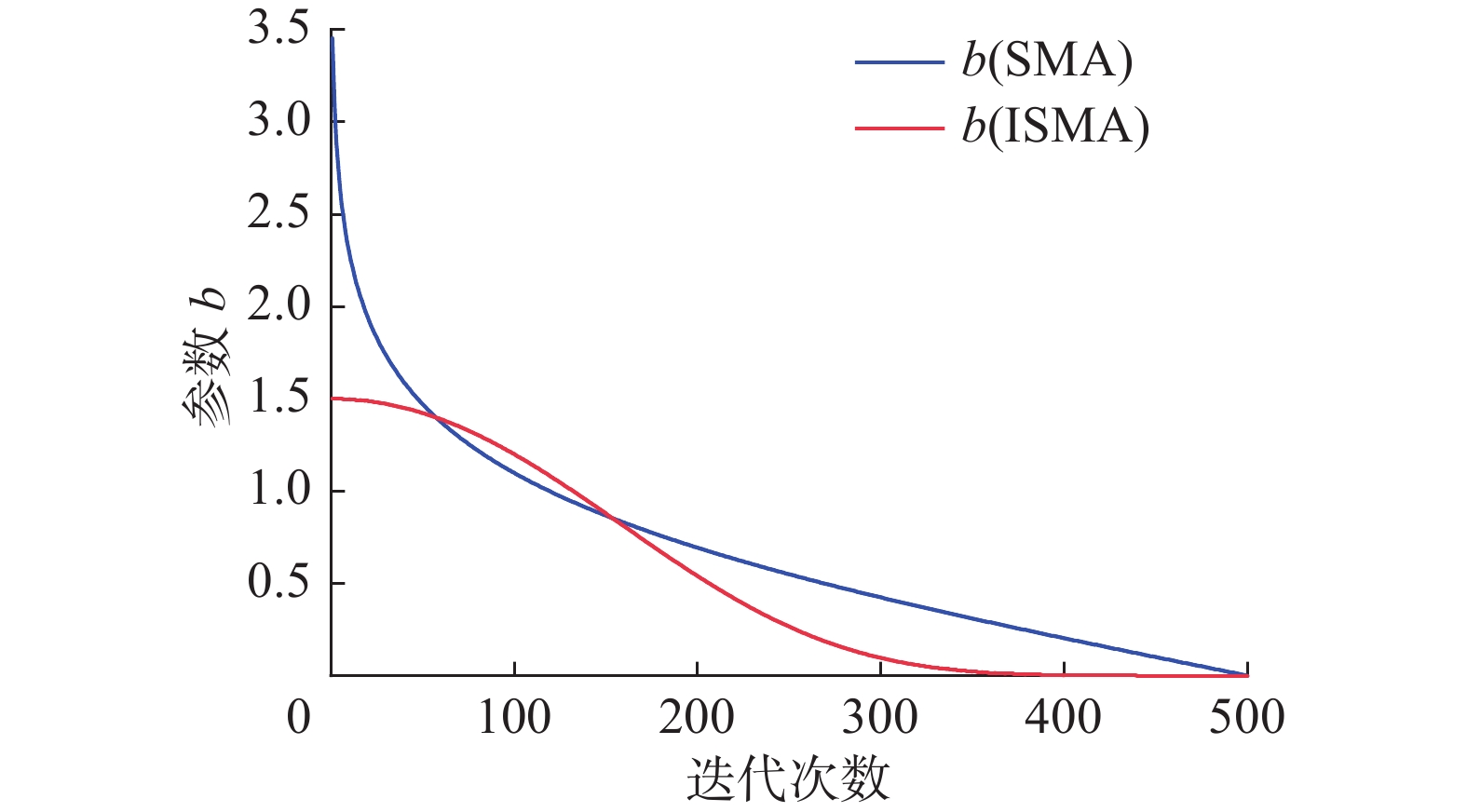
$ {r_1} \geqslant {\textit{z}} $ 及$ {r_2} <{p_i} $ 时，黏菌搜索轨迹由最佳个体${{\boldsymbol{X}}_b}$ 、两个随机个体${{\boldsymbol{X}}_{{A}}}$ 、${{\boldsymbol{X}}_{{B}}}$ 所引导，以向量${{{\boldsymbol{v}}}_{{b}}}$ 决定黏菌移动方向，参数$b$ 的变化对搜索与开发的平衡有重要影响。标准黏菌算法中，参数$b$ 在迭代前期迅速减小，迭代后期数值较小。前期较小的$b$ 值不利于算法的摆脱局部极值进行全局搜索[18]。故提出非线性递减策略，参数$b$ 重新定义如下:$$ b = {k_1}{\left(1 - \dfrac{t}{T}\right)^{\left({k_2}\tfrac{t}{T}\right)}} $$ (11) 式中：
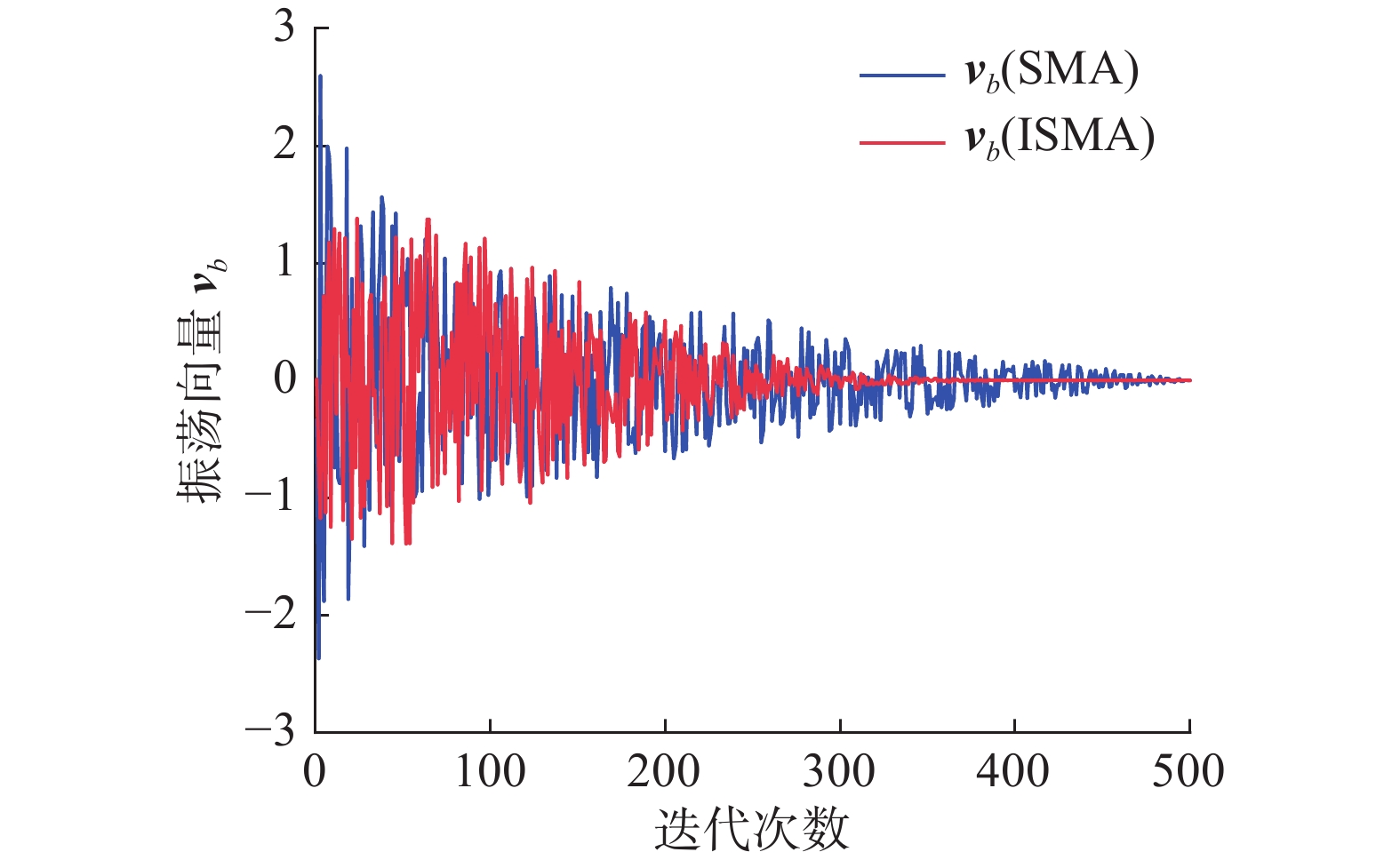
$ {k}_{1}、{k}_{2} $ 为幅值系数及调节系数，控制参数$b$ 的幅值及下降速度。$b$ 值幅值与下降速度分别随${k_1}$ 、${k_2}$ 的增大而增加。根据实验分析，最终取值分别为1.5和5。将新参数$b$ 与原始更改策略进行比较如图1所示。在前期缓慢减少，增加了全局搜索范围。在后期迭代中较小$b$ 值限制振荡向量${{{{\boldsymbol{v}} }}_{{b}}}$ 大小，有助于算法达到更高精度，更加快速的开发，振荡向量${{{{\boldsymbol{v}} }}_{{b}}}$ 如图2所示。
图 1 参数b曲线Fig. 1 Curves of b
下载:
全尺寸图片
图 2 振荡向量vb趋势Fig. 2 Trend of vibration vector vb下载:
全尺寸图片
当
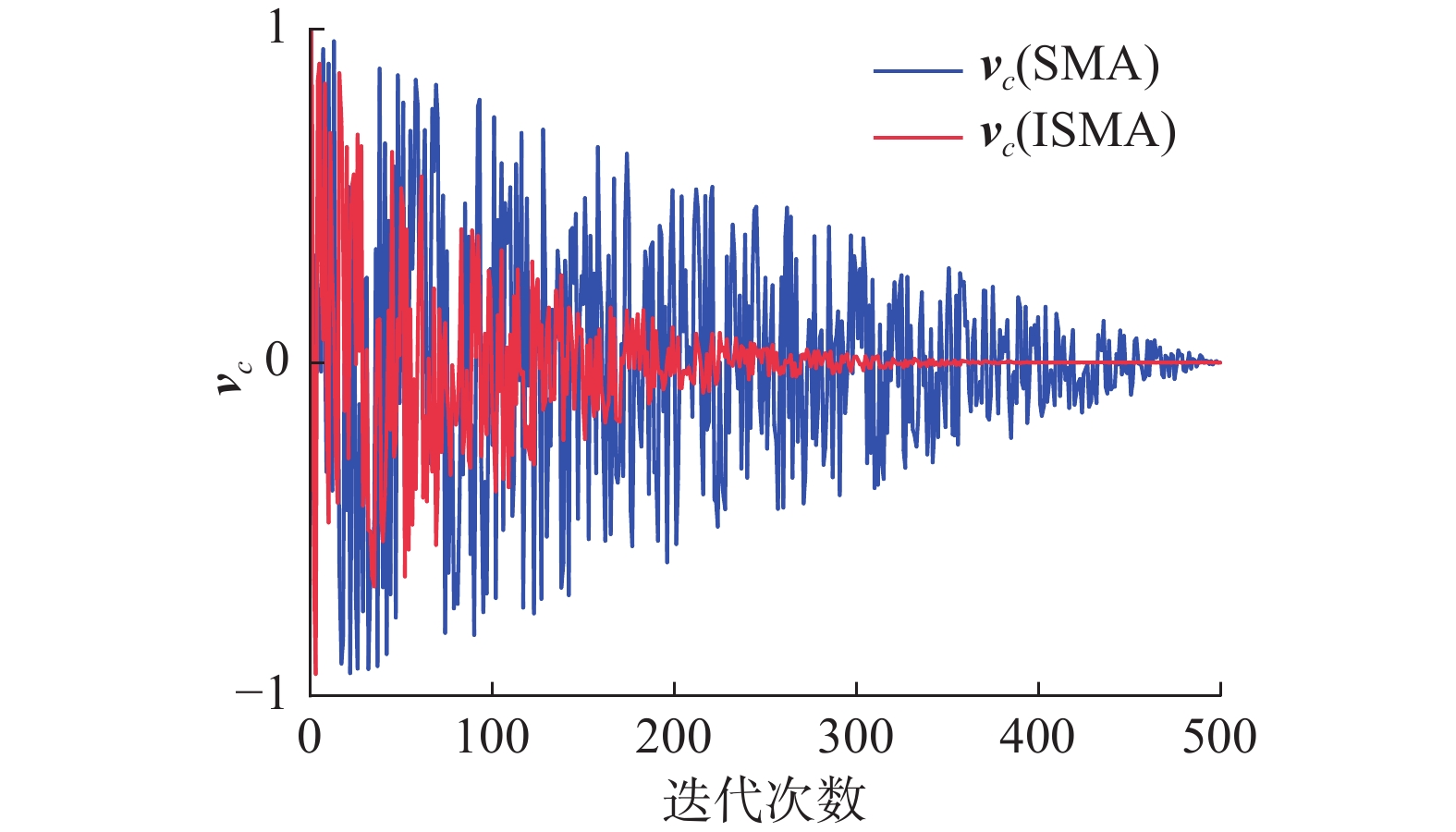
$ {r_1} \geqslant {\textit{z}} $ 及$ {r_2} \geqslant {p_i} $ 时，黏菌搜索轨迹由自身位置${\boldsymbol{X}}(t)$ 和速度${{{{\boldsymbol{v}} }}_{{c}}}$ 决定，此情况下算法主要进行开发阶段，参数$ c $ 主要用于约束振荡向量${{{{\boldsymbol{v}} }}_{\text{c}}}$ 的大小。标准SMA中参数$ c $ 从1线性减小到0，开发阶段中过大的$ c $ 值不利于算法进行局部开发，需要使$ c $ 值迅速下降，防止振荡幅值过大，错过最优解。参数$ c $ 定义如下：$$ c = {\left({c_{\max }} - \frac{{t({c_{\max }} - {c_{\min }})}}{T}\right)^k} $$ (12) 根据标准黏菌算法将
$ {c}_{\mathrm{max}}、{c}_{\mathrm{min}} $ 分别取值为1、0，$k$ 为调节参数，分别取2、4和6时参数$ c $ 变化曲线如图3所示。$k$ 值过小将造成前期振荡幅度过大，$k$ 值过大将造成后期振动幅度过小，最终都将降低收敛速度。为平衡算法整个过程中的开发能力，通过实验分析最终取$k = 4$ ，振动向量${{{{\boldsymbol{v}} }}_{{c}}}$ 如图4所示。
图 3 参数c曲线Fig. 3 Curves of c下载:
全尺寸图片
图 4 振荡向量${\boldsymbol{v}}_c$ 趋势Fig. 4 Trend of vibration vector${\boldsymbol{v}}_c$ 下载:
全尺寸图片
通过引入动态非线性递减策略调节参数
$ b $ 、$c $ ，最终使振荡向量${\boldsymbol{v}}_{{b}}$ 、${\boldsymbol{v}}_{{c}}$ 实现动态变化，从而协调并优化算法搜索与开发能力，在一定程度上加快算法收敛。2.3 融合麻雀预警机制与折射反向学习
标准黏菌算法中当
$ {r_1} < {\textit{z}} $ 时，黏菌种群由解空间随机生成黏菌个体，模拟黏菌分离部分个体搜索其他可能存在的其他食物源的行为。以上黏菌搜索特性虽能起到避免算法早熟的作用，却在前期可能造成已处于较优位置的黏菌个体重新初始化，使优质个体信息得不到充分利用。麻雀搜索算法中，麻雀侦查预警行为能引导麻雀个体向最优个体前进加快算法收敛速度。麻雀位置更新如下：
$$ {\boldsymbol{X}}_{{i}}(t+1)=\left\{\begin{split} &{\boldsymbol{X}}_{{b}}(t)+\beta \cdot ({\boldsymbol{X}}_{{i}}(t)-{\boldsymbol{X}}_{{b}}(t))\text{，}{f}_{i}\ne {f}_{b}\\ &{\boldsymbol{X}}_{{i}}(t)+K\frac{{\boldsymbol{X}}_{{i}}(t)-{\boldsymbol{X}}_{{w}}(t)}{\left|{f}_{i}-{f}_{w}\right|+\varepsilon }\text{，}{f}_{i}={f}_{b}\end{split}\right.$$ (13) 式中：
$\,\beta $ 为高斯分布的随机数；$K$ 为$[ - 1,1]$ 的均匀随机数；$\varepsilon $ 是防止分母为0的较小值。将麻雀预警机制引入黏菌算法，在迭代前期预警行为充分利用优质黏菌个体位置信息，提高算法收敛速度。黏菌个体若处于最优位置，则躲避到自身附近的位置，距离为自身位置距离最差位置和适应度差的比值；若个体不处于最优位置，则迁移到最优位置附近。麻雀预警机制在寻优迭代后期可能造成黏菌个体趋于同质化，故融合折射反向学习(refracted opposition-based learning， ROBL)[19]策略解决黏菌个体因趋同而陷入局部最优的问题。
$$ {\boldsymbol{X}}_{{i}}^{{{{\rm{robl}}}}} = \frac{{{\boldsymbol{L}} + {\boldsymbol{U}}}}{2} + \frac{{{\boldsymbol{L}} + {\boldsymbol{U}}}}{{2m}} - \frac{{{\boldsymbol{X}}_{{i}}^{{{{\rm{chaos}}}}}}}{m} $$ (14) 相较于传统反向学习，ROBL可以通过调整折射率参数
$m$ 获得不同的反向黏菌个体，扩大种群搜索范围。迭代后期利用折射反向学习，生成反向黏菌个体搜寻更优位置，增强算法摆脱局部最优的抗停滞能力。最终改进后黏菌种群更新公式如下：$$ {\boldsymbol{X}}_{{i}}(t+1)=\left\{\begin{split} &{\boldsymbol{X}}_{{b}}(t)+\beta \cdot ({\boldsymbol{X}}_{{i}}(t)-{\boldsymbol{X}}_{{b}}(t))\text{，}\frac{t}{T} < \alpha ,\; {f}_{i}\ne {f}_{b}\\ &{\boldsymbol{X}}_{{i}}(t)+K\frac{{\boldsymbol{X}}_{{i}}(t)-{\boldsymbol{X}}_{{w}}(t)}{\left|{f}_{i}-{f}_{w}\right|+\varepsilon }\text{，}\frac{t}{T} < \alpha ,\;{f}_{i}={f}_{b}\\ &\frac{\boldsymbol{L}+\boldsymbol{U}}{2}+\frac{\boldsymbol{L}+\boldsymbol{U}}{2k}-\frac{{\boldsymbol{X}}_{{i}}(t)}{k}\text{，}\frac{t}{T} > \alpha \end{split} \right.$$ (15) 式中：
$\alpha $ 为变异策略间分隔比例，取黄金分割比约为0.618033。2.4 ISMA伪代码
综合上述改进方法，ISMA伪代码如下:
开始
设置种群规模
$N$ ，最大迭代次数$T$ ，变异参数${\textit{z}}$ ；通过式(9)、(10) Bernoulli混沌映射初始化黏菌种群
${{\boldsymbol{X}}^{{{{\rm{chaos}}}}}}$ ；while (
$t \leqslant T$ )计算适应度
$ {f_i} $ 并排序，得最优及最差适应度$ {f_b} $ 、$ {f_w} $ ；通过式(5)计算黏菌质量
${\boldsymbol{W}}$ ；分别通过式(11)、(12)计算
$b$ 、$c$ ；for (i=1:N)
产生随机数
${r_1}$ 、$ {r_2} $ ；通过式(4)计算条件参数
${p_i}$ 、振荡向量${{{{\boldsymbol{v}}}}_{{b}}}$ 、${{{{\boldsymbol{v}} }}_{{c}}}$ ；if
$ {r_1} \geqslant {\textit{z}} $ 通过式(3)更新黏菌个体位置；
else
通过式(15)更新黏菌个体位置；
end if
end for
t = t + 1
end while
结束
算法结束，返回最优位置及适应度。
2.5 时间复杂度分析
时间复杂度[20]是反映算性能的重要指标。设
$N$ 表示黏菌个体数量，$D$ 表示解空间维数，$T$ 表示最大迭代次数。在标准SMA算法中，初始化复杂度为$O(N D)$ ，适应度评估和排序的复杂度为$O((N + N N) T)$ ，黏菌质量更新复杂度为$O(N D T)$ ，黏菌个体位置更新复杂度$O(N D T)$ 。可知标准SMA算法的总时间复杂度为$O(N \times (D + (1 + N + 2D) T))$ 。ISMA时间复杂度分析如下:1)初始化参数所需时间为
${\alpha _0}$ ，利用式(9)每一维进行混沌映射迭代的时间为${\alpha _1}$ ，式(10)逆映射到搜索空间的时间为${\alpha _2}$ 。初始化时间复杂度为$O({\alpha _0} + N D({\alpha _1} + {\alpha _2})) = O(N D)$ 。适应度评估和排序的复杂度与标准黏菌算法保持一致为$O((N + N N) T)$ 。2)通过动态非线性递减策略按式(11)、(12)计算时间分别为
${\alpha _3}$ 、${\alpha _4}$ ，黏菌个体位置更新复杂度$O(N D T + ({\alpha _1} + {\alpha _2}) T) = O(N D \times T)$ 。3)引入麻雀预警机制与折射反向学习，迭代前期按式(13)进行位置更新，时间复杂度为
$O(N D T)$ ；迭代后期按式(14)生成每个反向个体所需时间为${\alpha _5}$ ，时间复杂度为$O(N D T + N T \times {\alpha _5}) = O(N D T)$ 。综上可知，针对SMA算法缺陷的改进，并未增加时间复杂度。ISMA算法的时间复杂度为
$ O(N (D + (1 + N + 2D) T)) $ ，与标准SMA算法时间复杂度一致。3. ISMA算法性能测试与分析
3.1 测试函数的选取
为了评估改进黏菌算法的优化效果和稳定性，利用基准测试函数以及部分CEC2017测试函数进行优化对比测试。基准测试函数中单峰测试函数具有唯一的全局最优解，这有助于理解优化算法的开发能力。多峰测试函数具有多个局部极小值，该特性有助于理解优化算法摆脱局部极值的能力。基准测试函数及其具体信息如表1。
表 1 基准测试函数Table 1 Benchmark function类型 编号 函数名称 维数D 搜索范围 最优值 单峰 F1 Step Function 30 [−100,100] 0 多峰 F2 Generalized
Schwefel's
Problem 2.2630 [−500,500] −418.9829D F3 Generalized
Penalized
Function 130 [−50,50] 0 F4 Generalized
Penalized
Function 230 [−50,50] 0 3.2 改进策略的有效性分析
为检验不同策略对改进黏菌算法的作用，采用测试函数对标准SMA、仅采用混沌初始化的SMA(slime mould algorithm based on Bernoulli chaos initialization, BCSMA)、仅采用动态非线性递减策略的SMA(slime mould algorithm based on Dynamic nonlinear decline strategy, DNSMA)、仅采用融合麻雀预警机制与折射反向学习策略的SMA(slime mould algorithm based on Sparrow early warning mechanism and refracted opposition-based learning, SRSMA)与ISMA算法进行寻优对比实验。为准确验证所提算法与对比算法之间的优劣，设定种群规模均为50，迭代次数为500。结果如表2所示。
表 2 不同改进策略寻优结果Table 2 Optimization results of different improvement strategies函数 算法 D=10 D=30 D=100 最优值 平均值 标准差 最优值 平均值 标准差 最优值 平均值 标准差 F1 SMA 9.04×10−6 3.44×10−5 2.04×10−5 3.26×10−1 6.11×10−1 2.35×10−1 2.12×101 2.17×101 3.99×100 ISMA 3.35×10−15 1.50×10−13 3.16×10−13 2.68×10−4 1.06×10−3 7.58×10−4 4.26×10−3 2.66×100 2.06×100 BCSMA 2.16×10−11 2.27×10−10 2.40×10−10 7.67×10−4 5.39×10−3 4.03×10−3 2.83×100 3.31×100 5.97×10−1 DNSMA 9.31×10−6 3.26×10−5 2.61×10−5 3.83×10−1 5.92×10−1 1.77×10−1 1.82×101 2.07×101 1.35×100 SRSMA 5.00×10−1 9.15×10−1 2.63×10−1 3.74×100 4.30×100 4.90×10−1 1.46×100 1.72×100 5.70×10−1 续表 2 函数 算法 D=10 D=30 D=100 最优值 平均值 标准差 最优值 平均值 标准差 最优值 平均值 标准差 F2 SMA −3.83×103 −3.50×103 2.55×102 −1.03×104 −9.64×103 4.80×102 −2.82×104 −2.62×104 1.08×103 ISMA −4.10×103 −3.81×103 2.40×102 −1.16×104 −1.02×104 6.86×102 −4.09×104 −3.78×104 5.16×103 BCSMA −3.85×103 −3.65×103 1.87×102 −1.05×104 −9.56×103 5.17×102 −2.66×104 −2.51×104 9.43×102 DNSMA −3.95×103 −3.85×103 1.39×102 −1.02×104 −9.35×103 4.18×102 −2.88×104 −2.66×104 1.10×103 SRSMA −3.60×103 −3.35×103 1.74×102 −9.84×103 −9.08×103 5.41×102 −3.94×104 −3.10×104 9.39×102 F3 SMA 6.29×10−8 3.43×10−7 2.23×10−7 3.22×10−3 7.56×10−3 3.08×10−3 3.26×10−1 4.00×10−1 4.07×10−2 ISMA 4.33×10−18 6.61×10−16 1.34×10−15 5.07×10−4 1.05×10−3 5.18×10−4 2.59×10−2 1.41×10−1 8.78×10−2 BCSMA 1.04×10−7 4.50×10−7 4.38×10−7 5.72×10−3 1.28×10−2 5.32×10−3 3.38×10−1 4.21×10−1 7.48×10−2 DNSMA 1.77×10−13 2.52×10−12 3.25×10−12 2.97×10−4 1.34×10−3 1.28×10−3 1.90×10−1 2.57×10−1 5.93×10−2 SRSMA 1.58×10−8 1.18×10−2 1.37×10−2 1.76×10−1 3.06×10−1 1.13×10−1 3.36×10−1 3.76×10−1 3.53×10−2 F4 SMA 4.47×10−5 1.77×10−4 1.30×10−4 2.59×10−3 5.79×10−3 3.60×10−3 6.25×100 7.42×100 5.97×10−1 ISMA 1.93×10−8 1.75×10−7 2.32×10−7 1.24×10−6 2.20×10−3 2.33×10−3 3.32×10−1 3.34×100 2.63×100 BCSMA 5.10×10−5 1.28×10−4 6.27×10−5 3.03×10−3 6.53×10−3 2.48×10−3 5.36×100 7.47×100 9.85×10−1 DNSMA 4.62×10−8 2.47×10−6 3.11×10−6 5.10×10−6 1.12×10−3 3.47×10−3 1.11×100 3.82×100 1.91×100 SRSMA 1.67×10−4 1.59×10−1 1.43×10−1 1.69×100 2.32×100 2.77×10−1 9.48×10−1 7.30×100 2.30×100 表2中给出5种算法独立运行30次在10维、30维及100维下对部分函数的测试结果。随着函数维度增加，寻优难度上升，求解精度随之下降，但ISMA算法在整体上呈现更好的寻优性能。对于单峰测试函数F1，ISMA算法寻优精度均最高，在维度为10及30时，BCSMA表现较好。维度为100时，SRSMA拥有更高的寻优精度及稳定性。表明引入Bernoulli混沌初始化、融合麻雀预警机制与折射反向学习能在不同维度的寻优中有效提升算法收敛性能。对于多峰测试函数F2、F3及F4，对比SMA、BCSMA和SRSMA，DNSMA算法表现突出，表现动态非线性递减策略能有效协调算法全局搜索和局部开发，增加算法寻优能力。
相较于标准SMA算法，3种单一策略改进SMA算法在最优值、平均值及标准差上均有不同程度提升，但单一策略对SMA的提升有限，对不同维度及测试函数的寻优效果不能保持。融合3种策略的ISMA算法在10、30和100维寻优中，大部分寻优精及稳定性优于单策略优化算法，验证了多策略融合对标准SMA算法的全方位提升。其中动态非线性递减策略协调算法的全局搜索和局部开发能力起主导作用，Bernoulli混沌初始化及融合麻雀预警机制与折射反向学习进一步提升算法寻优性能。
3.3 ISMA与其他改进SMA的对比
为进一步验证多策略融合改进黏菌算法对复杂函数的寻优性能。与文献[13-15]中所提出的改进黏菌算法AOSMA(adaptive opposition slime mould algorithm)、CESMA(chaotic elite slime mould algorithm)、HSMAAOA(hybrid algorithm of slime mould algorithm and arithmetic optimization algorithm based on random opposition-based learning)对选取的CEC2017测试函数分别进行寻优对比实验。其中包含多峰(CEC05、CEC06)，混合(CEC11、CEC16)、复合(CEC23、CEC24、CEC25)类型函数。选取测试函数信息如表3所示。
表 3 CEC2017测试函数Table 3 CEC2017 test function函数名称 类型 维数 搜索范围 最优值 CEC05 MF 30 [−100,100] 500 CEC06 MF 30 [−100,100] 600 CEC11 HF 30 [−100,100] 1100 CEC16 HF 30 [−100,100] 1600 CEC23 CF 30 [−100,100] 2300 CEC24 CF 30 [−100,100] 2400 CEC25 CF 30 [−100,100] 2500 CEC2017测试函数中具有许多局部最优解，包括混合复合移位、旋转和扩展的多模态测试函数，它们模拟了搜索领域中的高度复杂性。这些组合测试函数有助于理解开发和探索之间的权衡能力，通过摆脱局部最优最终获得全局最优解。设置维度为30，黏菌个体数量为50，迭代次数为500，各算法对每个测试函数分别进行30次寻优，结果如表4所示。由表4可知，ISMA算法在多峰、混合及复合函数的寻优中都能达到较好的效果。与其他3种改进黏菌算法相比，ISMA从种群初始化、个体迭代和变异更新3个方面着手，提出更符合黏菌算法的改进。在种群初始化方面，标准SMA、AOSMA以及HSMAAOA算法均采用随机生成， ISMA则采用Bernoulli混沌序列进行种群初始化，相较于其他方式，该方式使种群分布均匀，增强了种群多样性。个体迭代阶段， AOSMA、CESMA分别在个体位置移动后添加自适应反向学习、精英反向学习，却在自适应判断及精英策略筛选过程中容易陷入局部极值，并在时间复杂度上有所增加，HSMAAOA引入AOA算法乘法搜索策略替换原有开发阶段增强算法搜索能力，却削弱算法的开发能力，存在迭代速度慢的问题，ISMA通过动态非线性递减策略调节振荡参数，在不增加时间复杂度的前提下，协调算法局部开发与全局搜索能力，使收敛速度提升。变异更新方面，其余算法均保留标准黏菌算法的分离黏菌个体并随机生成个体位置的方式，极可能造成优质个体分离，ISMA引入麻雀预警机制及折射反向学习，前期防止优质个体分离，后期通过折射反向学习增强黏菌种群局部极值逃逸能力。
表 4 不同改进SMA算法寻优对比Table 4 Optimization results of different improved SMA函数 SMA算法 ISMA算法 AOSMA算法 CESMA算法 HSMAAOA算法 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 CEC05 6.07×102 3.01×101 5.80×102 2.50×101 6.07×102 4.10×101 5.89×102 2.63×101 5.96×102 3.66×101 CEC06 6.33×102 1.52×101 6.26×102 6.74×100 6.33×102 1.32×101 6.26×102 7.11×100 6.29×102 8.70×100 CEC11 1.26×103 7.16×101 1.21×103 3.33×101 5.92×103 9.67×102 1.28×103 3.80×101 1.28×103 6.59×101 CEC16 2.48×103 2.84×102 2.41×103 2.74×102 2.46×103 4.20×102 2.41×103 2.53×102 2.50×103 3.81×102 CEC23 2.78×103 1.87×101 2.75×103 1.73×101 3.49×103 7.59×101 2.75×103 2.53×101 2.75×103 2.47×101 CEC24 2.95×103 3.10×101 2.94×103 3.14×101 3.69×103 7.42×101 2.95×103 3.11×101 2.94×103 3.58×101 CEC25 2.93×103 1.98×100 2.89×103 1.38×101 2.92×103 4.47×102 2.90×103 1.40×101 2.89×103 9.67×10−1 4. 变压器故障诊断实验
极致梯度提升[21] (extreme gradient boosting, XGBoost)以分类回归树CART为基分类器，利用集成学习中加法模型形成集成分类器，拥有极高的分类速度与精度[22-24]。其中分类器抗干扰能力[20]主要受到学习率η、树的最大深度max_depth、基分类器随机采样比例subsample、权重L1正则化惩罚系数α、权重L2正则化惩罚系数λ影响。选取PSO、MPA、SMA、ISMA算法分别对上述参数进行优化，利用变压器绝缘油中溶解气体数据，进行变压器故障诊断实验，反映ISMA算法的工程实用性。
4.1 实验数据集的建立
变压器故障发生时，绝缘油中溶解气体
$ {\text{(H}}_{\text{2}}、 {\text{CH}}_{\text{4}}、{\text{C}}_{\text{2}}{\text{H}}_{\text{2}}、{\text{C}}_{\text{2}}{\text{H}}_{\text{4}}、{\text{C}}_{\text{2}}{\text{H}}_{\text{6}}\text{)} $ 含量将发生变化，气体含量较为分散，将其直接作为模型输入无法充分利用特征信息，故采用无编码比值法[25]形成9维特征:$ {\text{C}}{{\text{H}}_{\text{4}}}{\text{/ }}{{\text{H}}_{\text{2}}} $ 、$ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}{\text{/}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}} $ 、$ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{/}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}} $ 、$ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}{\text{/}}\left( {{\text{TH}}} \right) $ 、$ {{\text{H}}_{\text{2}}}{\text{/}}\left( {{{\text{H}}_{\text{2}}}{\text{ + TH}}} \right) $ 、$ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{/}}\left( {{\text{TH}}} \right) $ 、$ {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}}{\text{/}}\left( {{\text{TH}}} \right) $ 、$ {\text{C}}{{\text{H}}_{\text{4}}}{\text{/}}\left( {{\text{TH}}} \right) $ 、$ \left( {{\text{C}}{{\text{H}}_{\text{4}}}{\text{ + }}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}} \right){\text{/}}\left( {{\text{TH}}} \right) $ ，其中TH 为总烃，值为$( {\text{C}}{{\text{H}}_{\text{4}}}{\text{ + }} {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}{\text{ + }}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{ + }}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}} )$ 。变压器故障类型分为正常运行、低能放电、高能放电、局部放电、中低温过热及高温过热6种，分别编号为0~5。从辽宁省某供电公司监测数据中随机选取600组按照4∶1的比例划分训练集及测试集，如表5所示。表 5 样本数据分布Table 5 Distribution of sample data故障类型 训练样本 测试样本 样本总数 正常运行 80 20 100 低能放电 72 18 90 高能放电 76 19 95 局部放电 84 21 105 中低温过热 80 20 100 高温过热 88 22 110 4.2 仿真结果与分析
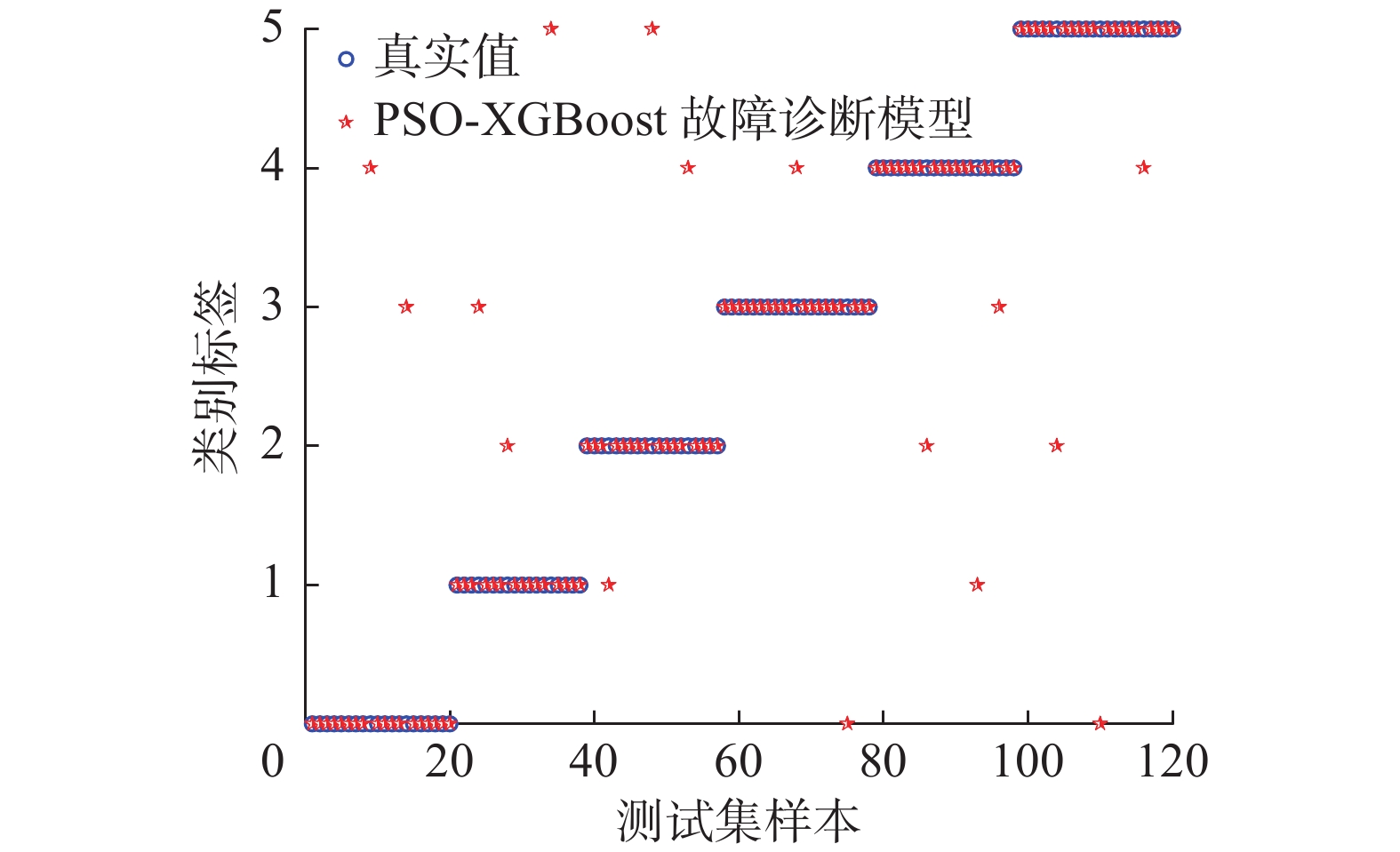
本文实验仿真均在Intel Core i7、2.7 GHz、内存16 GB、在Anaconda环境下，利用Python3编程。各算法优化XGBoost参数进行变压器故障诊断实验。实验结果如图5~9所示。
图 5 XGBoost故障诊断结果(准确率84.71%)Fig. 5 Fault diagnosis result of XGBoost (accuracy is 84.17%)下载:
全尺寸图片
图 6 PSO-XGBoost故障诊断结果(准确率86.67%)Fig. 6 Fault diagnosis result of PSO-XGBoost (accuracy is 86.67%)下载:
全尺寸图片
图 7 MPA-XGBoost故障诊断结果(准确率87.50%)Fig. 7 Fault diagnosis result of MPA-XGBoost (accuracy is 87.50%)下载:
全尺寸图片
图 8 SMA-XGBoost故障诊断结果(准确率90.00%)Fig. 8 Fault diagnosis result of SMA-XGBoost (accuracy is 90.00%)下载:
全尺寸图片
图 9 ISMA-XGBoost故障诊断结果(准确率94.17%)Fig. 9 Fault diagnosis result of ISMA-XGBoost (accuracy is 94.17%)下载:
全尺寸图片
由图可知，ISMA-XGBoost变压器故障诊断中对正常运行较为灵敏，低能放电诊断效果不佳，但综合诊断精度最高为94.17%、XGBoost、PSO-XGBoost、MPA-XGBoost及SMA-XGBoost的变压器故障诊断准确率分别为84.17%、86.67%、87.50%、90.00%。ISMA优化后故障诊断精度提升10%，表明多策略融合改进的黏菌算法对XGBoost参数进行寻优，建立故障诊断模型能有效提升诊断精度。
5. 结束语
本文根据对标准黏菌算法不足的分析，提出多策略融合的改进黏菌算法，引入Bernoulli混沌初始化丰富黏菌种群多样性，提出动态非线性递减策略协调并优化算法探索与开发能力，融合麻雀预警机制与折射反向学习前期保留优质个体、后期增强算法抗停滞能力，有效提升算法寻优精度。对基准测试函数及CEC2017测试函数进行寻优仿真实验，实验结果表明ISMA各改进策略具有一定协作互补性，针对标准SMA各阶段的缺陷均有较好的改进作用，较其他改进黏菌算法能达到更好的寻优效果。ISMA优化的XGBoost进行变压器故障诊断准确率为94.17%，较XGBoost准确率提升10%，进一步验证了ISMA算法优越的寻优能力及工程实用性。未来的研究考虑采用不同改进策略以期达到更为有效的优化效果，并将ISMA结合其他工程实际问题作进一步研究。
-
图 1 参数b曲线
Fig. 1 Curves of b
下载:
全尺寸图片
图 2 振荡向量vb趋势
Fig. 2 Trend of vibration vector vb
下载:
全尺寸图片
图 3 参数c曲线
Fig. 3 Curves of c
下载:
全尺寸图片
图 4 振荡向量
${\boldsymbol{v}}_c$ 趋势Fig. 4 Trend of vibration vector
${\boldsymbol{v}}_c$ 下载:
全尺寸图片
图 5 XGBoost故障诊断结果(准确率84.71%)
Fig. 5 Fault diagnosis result of XGBoost (accuracy is 84.17%)
下载:
全尺寸图片
图 6 PSO-XGBoost故障诊断结果(准确率86.67%)
Fig. 6 Fault diagnosis result of PSO-XGBoost (accuracy is 86.67%)
下载:
全尺寸图片
图 7 MPA-XGBoost故障诊断结果(准确率87.50%)
Fig. 7 Fault diagnosis result of MPA-XGBoost (accuracy is 87.50%)
下载:
全尺寸图片
图 8 SMA-XGBoost故障诊断结果(准确率90.00%)
Fig. 8 Fault diagnosis result of SMA-XGBoost (accuracy is 90.00%)
下载:
全尺寸图片
图 9 ISMA-XGBoost故障诊断结果(准确率94.17%)
Fig. 9 Fault diagnosis result of ISMA-XGBoost (accuracy is 94.17%)
下载:
全尺寸图片
表 1 基准测试函数
Table 1 Benchmark function
类型 编号 函数名称 维数D 搜索范围 最优值 单峰 F1 Step Function 30 [−100,100] 0 多峰 F2 Generalized
Schwefel's
Problem 2.2630 [−500,500] −418.9829D F3 Generalized
Penalized
Function 130 [−50,50] 0 F4 Generalized
Penalized
Function 230 [−50,50] 0 表 2 不同改进策略寻优结果
Table 2 Optimization results of different improvement strategies
函数 算法 D=10 D=30 D=100 最优值 平均值 标准差 最优值 平均值 标准差 最优值 平均值 标准差 F1 SMA 9.04×10−6 3.44×10−5 2.04×10−5 3.26×10−1 6.11×10−1 2.35×10−1 2.12×101 2.17×101 3.99×100 ISMA 3.35×10−15 1.50×10−13 3.16×10−13 2.68×10−4 1.06×10−3 7.58×10−4 4.26×10−3 2.66×100 2.06×100 BCSMA 2.16×10−11 2.27×10−10 2.40×10−10 7.67×10−4 5.39×10−3 4.03×10−3 2.83×100 3.31×100 5.97×10−1 DNSMA 9.31×10−6 3.26×10−5 2.61×10−5 3.83×10−1 5.92×10−1 1.77×10−1 1.82×101 2.07×101 1.35×100 SRSMA 5.00×10−1 9.15×10−1 2.63×10−1 3.74×100 4.30×100 4.90×10−1 1.46×100 1.72×100 5.70×10−1 续表 2 函数 算法 D=10 D=30 D=100 最优值 平均值 标准差 最优值 平均值 标准差 最优值 平均值 标准差 F2 SMA −3.83×103 −3.50×103 2.55×102 −1.03×104 −9.64×103 4.80×102 −2.82×104 −2.62×104 1.08×103 ISMA −4.10×103 −3.81×103 2.40×102 −1.16×104 −1.02×104 6.86×102 −4.09×104 −3.78×104 5.16×103 BCSMA −3.85×103 −3.65×103 1.87×102 −1.05×104 −9.56×103 5.17×102 −2.66×104 −2.51×104 9.43×102 DNSMA −3.95×103 −3.85×103 1.39×102 −1.02×104 −9.35×103 4.18×102 −2.88×104 −2.66×104 1.10×103 SRSMA −3.60×103 −3.35×103 1.74×102 −9.84×103 −9.08×103 5.41×102 −3.94×104 −3.10×104 9.39×102 F3 SMA 6.29×10−8 3.43×10−7 2.23×10−7 3.22×10−3 7.56×10−3 3.08×10−3 3.26×10−1 4.00×10−1 4.07×10−2 ISMA 4.33×10−18 6.61×10−16 1.34×10−15 5.07×10−4 1.05×10−3 5.18×10−4 2.59×10−2 1.41×10−1 8.78×10−2 BCSMA 1.04×10−7 4.50×10−7 4.38×10−7 5.72×10−3 1.28×10−2 5.32×10−3 3.38×10−1 4.21×10−1 7.48×10−2 DNSMA 1.77×10−13 2.52×10−12 3.25×10−12 2.97×10−4 1.34×10−3 1.28×10−3 1.90×10−1 2.57×10−1 5.93×10−2 SRSMA 1.58×10−8 1.18×10−2 1.37×10−2 1.76×10−1 3.06×10−1 1.13×10−1 3.36×10−1 3.76×10−1 3.53×10−2 F4 SMA 4.47×10−5 1.77×10−4 1.30×10−4 2.59×10−3 5.79×10−3 3.60×10−3 6.25×100 7.42×100 5.97×10−1 ISMA 1.93×10−8 1.75×10−7 2.32×10−7 1.24×10−6 2.20×10−3 2.33×10−3 3.32×10−1 3.34×100 2.63×100 BCSMA 5.10×10−5 1.28×10−4 6.27×10−5 3.03×10−3 6.53×10−3 2.48×10−3 5.36×100 7.47×100 9.85×10−1 DNSMA 4.62×10−8 2.47×10−6 3.11×10−6 5.10×10−6 1.12×10−3 3.47×10−3 1.11×100 3.82×100 1.91×100 SRSMA 1.67×10−4 1.59×10−1 1.43×10−1 1.69×100 2.32×100 2.77×10−1 9.48×10−1 7.30×100 2.30×100 表 3 CEC2017测试函数
Table 3 CEC2017 test function
函数名称 类型 维数 搜索范围 最优值 CEC05 MF 30 [−100,100] 500 CEC06 MF 30 [−100,100] 600 CEC11 HF 30 [−100,100] 1100 CEC16 HF 30 [−100,100] 1600 CEC23 CF 30 [−100,100] 2300 CEC24 CF 30 [−100,100] 2400 CEC25 CF 30 [−100,100] 2500 表 4 不同改进SMA算法寻优对比
Table 4 Optimization results of different improved SMA
函数 SMA算法 ISMA算法 AOSMA算法 CESMA算法 HSMAAOA算法 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 平均值 标准差 CEC05 6.07×102 3.01×101 5.80×102 2.50×101 6.07×102 4.10×101 5.89×102 2.63×101 5.96×102 3.66×101 CEC06 6.33×102 1.52×101 6.26×102 6.74×100 6.33×102 1.32×101 6.26×102 7.11×100 6.29×102 8.70×100 CEC11 1.26×103 7.16×101 1.21×103 3.33×101 5.92×103 9.67×102 1.28×103 3.80×101 1.28×103 6.59×101 CEC16 2.48×103 2.84×102 2.41×103 2.74×102 2.46×103 4.20×102 2.41×103 2.53×102 2.50×103 3.81×102 CEC23 2.78×103 1.87×101 2.75×103 1.73×101 3.49×103 7.59×101 2.75×103 2.53×101 2.75×103 2.47×101 CEC24 2.95×103 3.10×101 2.94×103 3.14×101 3.69×103 7.42×101 2.95×103 3.11×101 2.94×103 3.58×101 CEC25 2.93×103 1.98×100 2.89×103 1.38×101 2.92×103 4.47×102 2.90×103 1.40×101 2.89×103 9.67×10−1 表 5 样本数据分布
Table 5 Distribution of sample data
故障类型 训练样本 测试样本 样本总数 正常运行 80 20 100 低能放电 72 18 90 高能放电 76 19 95 局部放电 84 21 105 中低温过热 80 20 100 高温过热 88 22 110 -
[1] HOU Jue, LIU Zhou, WANG Shaorong, et al. Intelligent coordinated damping control in active distribution network based on PSO[J]. Energy reports, 2022, 8: 1302–1312. doi: 10.1016/j.egyr.2021.11.161 [2] XUE Jiankai, SHEN Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems science & control engineering, 2020, 8(1): 22–34. [3] FARAMARZI A, HEIDARINEJAD M, MIRJALILI S, et al. Marine predators algorithm: a nature-inspired metaheuristic[J]. Expert systems with applications, 2020, 152: 113377. doi: 10.1016/j.eswa.2020.113377 [4] ABUALIGAH L, DIABAT A, MIRJALILI S, et al. The arithmetic optimization algorithm[J]. Computer methods in applied mechanics and engineering, 2021, 376: 113609. doi: 10.1016/j.cma.2020.113609 [5] 赵文超, 郭鹏, 王海波, 等. 改进樽海鞘群算法求解柔性作业车间调度问题[J]. 智能系统学报, 2022, 17(2): 376–386. ZHAO Wenchao, GUO Peng, WANG Haibo, et al. Improved slap swarm algorithm for scheduling of flexible job shop[J]. CAAI transactions on intelligent systems, 2022, 17(2): 376–386. [6] 蒲兴成, 宋欣琳. 分组教学蚁群算法改进及其在机器人路径规划中应用[J]. 智能系统学报, 2022, 17(4): 764–771. PU Xingcheng, SONG Xinlin. Improvement of ant colony algorithm in group teaching and its application in robot path planning[J]. CAAI transactions on intelligent systems, 2022, 17(4): 764–771. [7] 刘云鹏, 李泳霖, 裴少通, 等. 基于紫外光辐射照度特征的污秽瓷绝缘子绝缘状态评估方法[J]. 高电压技术, 2023, 49(4): 1622–1631. LIU Yunpeng, LI Yonglin, PEI Shaotong, et al. Evaluation of the insulation state of contaminated porcelain insulators based on characteristics of ultraviolet irradiance[J]. High voltage engineering, 2023, 49(4): 1622–1631. [8] WANG Rui, SUN Wanting. Fault diagnosis of electrical automatic control system of hydraulic support based on particle swarm optimization algorithm[J]. Journal of ambient intelligence and humanized computing, 2022, 228: 1–7. [9] LIU Yun, HEIDARI A A, YE Xiaojia, et al. Boosting slime mould algorithm for parameter identification of photovoltaic models[J]. Energy, 2021, 234: 121164. doi: 10.1016/j.energy.2021.121164 [10] LI Shimin, CHEN Huiling, WANG Mingjing, et al. Slime mould algorithm: a new method for stochastic optimization[J]. Future generation computer systems, 2020, 111: 300–323. doi: 10.1016/j.future.2020.03.055 [11] YU C, HEIDARI A A, XUE X, et al. Boosting quantum rotation gate embedded slime Mould algorithm[J]. Expert systems with applications, 2021, 181: 115082. doi: 10.1016/j.eswa.2021.115082 [12] ALFADHLI J, JARAGH A, ALFAILAKAWI M G, et al. FP-SMA: an adaptive, fluctuant population strategy for slime mould algorithm[J]. Neural computing and applications, 2022, 34(13): 11163–11175. doi: 10.1007/s00521-022-07034-6 [13] NAIK M K, PANDA R, ABRAHAM A. Adaptive opposition slime mould algorithm[J]. Soft computing, 2021, 25(22): 14297–14313. doi: 10.1007/s00500-021-06140-2 [14] 肖亚宁, 孙雪, 李三平, 等. 基于混沌精英黏菌算法的无刷直流电机转速控制[J]. 科学技术与工程, 2021, 21(28): 12130–12138. doi: 10.3969/j.issn.1671-1815.2021.28.028 XIAO Yaning, SUN Xue, LI Sanping, et al. Speed control of brushless direct current motor based on chaotic elite slime mould algorithm[J]. Science technology and engineering, 2021, 21(28): 12130–12138. doi: 10.3969/j.issn.1671-1815.2021.28.028 [15] 贾鹤鸣, 刘宇翔, 刘庆鑫, 等. 融合随机反向学习的黏菌与算术混合优化算法[J]. 计算机科学与探索, 2022, 16(5): 1182–1192. doi: 10.3778/j.issn.1673-9418.2105016 JIA heming, LIU yuxiang, LIU Qingxin, et al. Hybrid algorithm of slime mould algorithm and arithmetic optimization algorithm based on random opposition-based learning[J]. Journal of frontiers of computer science and technology, 2022, 16(5): 1182–1192. doi: 10.3778/j.issn.1673-9418.2105016 [16] 刘成汉, 何庆. 改进交叉算子的自适应人工蜂群黏菌算法[J]. 小型微型计算机系统, 2023, 44(2): 263–268. doi: 10.20009/j.cnki.21-1106/TP.2021-0451 LIU Chenghan, HE Qing. Adaptive artificial bee colony slime mold algorithm with improved crossover operator[J]. Journal of Chinese computer systems, 2023, 44(2): 263–268. doi: 10.20009/j.cnki.21-1106/TP.2021-0451 [17] YU Yang, GAO Shangce, CHENG Shi, et al. CBSO: a memetic brain storm optimization with chaotic local search[J]. Memetic computing, 2018, 10(4): 353–367. doi: 10.1007/s12293-017-0247-0 [18] TANG Andi, TANG Shangqin, HAN Tong, et al. A modified slime mould algorithm for global optimization[J]. Computational intelligence and neuroscience, 2021, 2021: 1–22. [19] 范千, 陈振健, 夏樟华. 一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法[J]. 哈尔滨工业大学学报, 2020, 52(10): 183–191. FAN Qian, CHEN Zhenjian, XIA Zhanghua. A modified salp swarm algorithm based on refracted opposition-based learning mechanism and adaptive control factor[J]. Journal of Harbin Institute of technology, 2020, 52(10): 183–191. [20] 何庆, 罗仕杭. 混合改进策略的黑猩猩优化算法及其机械应用[J]. 控制与决策, 2023, 38(2): 354–364. doi: 10.13195/j.kzyjc.2021.1108 HE Qing, LUO Shihang. Chimp optimization algorithm based on hybrid improvement strategy and its mechanical application[J]. Control and decision, 2023, 38(2): 354–364. doi: 10.13195/j.kzyjc.2021.1108 [21] CHEN Tianqi, GUESTRIN C. XGBoost: a scalable tree boosting system[EB/OL]. (2016−06−10)[2022−01−01].https://arxiv.org/abs/1603.02754. [22] 张又文, 冯斌, 陈页, 等. 基于遗传算法优化XGBoost的油浸式变压器故障诊断方法[J]. 电力自动化设备, 2021, 41(2): 200–206. doi: 10.16081/j.epae.202012021 ZHANG Youwen, FENG Bin, CHEN Ye, et al. Fault diagnosis method for oil-immersed transformer based on XGBoost optimized by genetic algorithm[J]. Electric power automation equipment, 2021, 41(2): 200–206. doi: 10.16081/j.epae.202012021 [23] 朱圳, 刘立芳, 齐小刚. 基于数据挖掘的通信网络故障分类研究[J]. 智能系统学报, 2022, 17(6): 1228–1234. ZHU Zhen, LIU Lifang, QI Xiaogang. Research on communication network fault classification based on data mining[J]. CAAI transactions on intelligent systems, 2022, 17(6): 1228–1234. [24] 杨帅, 郭茂祖, 赵玲玲, 等. 融合遗传算法与XGBoost的玉米百粒重相关基因挖掘[J]. 智能系统学报, 2022, 17(1): 170–180. YANG Shuai, GUO Maozu, ZHAO Lingling, et al. The method of 100-kernel weight related genes mining in maize mixed with genetic algorithm and XGboost[J]. CAAI transactions on intelligent systems, 2022, 17(1): 170–180. [25] 王雨虹, 王志中, 付华, 等. 多策略改进麻雀算法与BiLSTM的变压器故障诊断研究[J]. 仪器仪表学报, 2022, 43(3): 87−97. WANG Yuhong, WANG Zhizhong, FU Hua, et al, Research on transformer fault diagnosis based on the improved multi-strategy sparrow algorithm and BiLSTM[J]. Chinese Journal of scientific instrument, 2022, 43(3): 87−97.
