A self-supervised data-driven particle swarm optimization approach for large-scale feature selection
-
摘要: 大规模特征选择问题的求解通常面临两大挑战:一是真实标签不足,难以引导算法进行特征选择;二是搜索空间规模大,难以搜索到满意的高质量解。为此,提出了新型的面向大规模特征选择的自监督数据驱动粒子群优化算法。第一,提出了自监督数据驱动特征选择的新型算法框架,可不依赖于真实标签进行特征选择。第二,提出了基于离散区域编码的搜索策略,帮助算法在大规模搜索空间中找到更优解。第三,基于上述的框架和方法,提出了自监督数据驱动粒子群优化算法,实现对问题的求解。在大规模特征数据集上的实验结果显示,提出的算法与主流有监督算法表现相当,并比前沿无监督算法具有更高的特征选择效率。Abstract: Large-scale feature selection problems usually face two challenges: 1) Real labels are insufficient for guiding the algorithm to select features, and 2) a large-scale search space encumbers the search for a satisfactory high-quality solution. To this end, in this paper, a novel self-supervised data-driven particle swarm optimization algorithm is proposed for large-scale feature selection, including three contributions. First, a novel algorithmic framework named self-supervised data-driven feature selection is proposed, which can perform the feature selection without real labels. Second, a discrete region encoding-based search strategy is proposed, which helps the algorithm to find better solutions in a large-scale search space. Third, based on the above framework and method, a self-supervised data-driven particle swarm optimization algorithm is proposed to solve the large-scale feature selection problem. Experimental results on datasets with large-scale features show that the proposed algorithm performs comparably to the mainstream supervised algorithms and has higher feature selection efficiency than state-of-the-art unsupervised algorithms.
-
在现实世界中,人工智能问题的求解和模型的应用往往涉及大量的数据特征[1-4]。然而,并非所有的特征都有考虑的必要。在实际问题中,许多特征的相关性很低,甚至与问题不相关。因此,使用这些特征容易误导算法模型,降低模型的泛化能力、鲁棒性等性能[5-8]。特征选择的目的正是解决这个问题。特征选择旨在从原来的大规模特征集中选出合适的一部分相关特征。通过去除不相关和多余的特征,特征选择可以降低数据特征的维度,简化学习模型,加快学习过程,提高模型性能[9-12]。
然而,由于数据特征的众多,特征选择的搜索空间规模巨大。因此,特征选择是一个难以求解的优化问题。例如,对于有D个特征的数据集,可能的特征选择方案总数为2D个[1]。而且,随着大数据技术的发展进步和现实问题复杂性的增加,数据的特征数量D越来越大,特征选择问题的搜索空间规模呈指数级急剧上升。当问题规模D大于1000时,这样的特征问题被称为大规模特征选择问题。在解决大规模特征选择问题时,由于问题潜在的解有2D个,通过穷举式搜索找到给定的数据集的最佳特征子集十分不切实际。因此,许多学者提出了各种搜索技术求解大规模特征选择问题,如贪婪搜索、启发式搜索和随机搜索[13-18]。近年来,进化计算(evolutionary computation, EC)方法因其全局搜索能力和搜索效率而广为人知,被广泛应用在特征选择问题之中[19-23]。其中,作为进化计算中群体智能的代表算法,粒子群优化算法(particle swarm optimization, PSO)在大规模特征选择问题中表现出了巨大的优势和发展潜力,受到了越来越多专家学者的关注[24-27]。因此,本文主要考虑利用PSO求解大规模特征选择问题。
目前,已有很多专家学者提出新型的PSO算法及其变种来求解大规模特征选择问题[28-29]。这些研究主要可以分为两类。第一类是设计适合求解特征选择问题的PSO算法。由于初始提出的PSO是用于求解连续优化问题的算法,而特征选择问题是典型的离散优化问题,因此需要将PSO转变为适用于求解离散优化问题的算法。这些研究包括粒子的编码方式(解码方式),离散的粒子速度和位置更新策略[1]。其中,二进制PSO (binary PSO, BPSO)受到了广泛的关注和研究[25]。第二类研究关注如何让算法更高效地求解特征选择问题。例如,Gu等[26]将擅于求解大规模优化问题的竞争粒子群优化算法(competitive swarm optimizer, CSO)用于求解特征选择优化问题,而Tran等[27]提出可变长度的PSO以避开局部最优和增强搜索效率。Xue等[28]提出基于自适应参数和策略的PSO,用于对大规模特征选择问题进行自适应求解。Luo等[29]提出混合粗糙超立方体方法与BPSO的算法来对大规模特征选择问题进行高效求解。
尽管已有不少相关的研究,使用PSO进行大规模特征选择时仍然存在以下两个问题。第一,现有的PSO算法都是在有监督的条件下执行,需要依赖数据的真实标签。然而,在大多数实际场景中,由于真实标签的获取十分困难而且成本高昂,数据只有很少的真实标签,甚至没有标签。因此,现有的算法无法很好地求解这类缺乏真实标签的大规模特征选择问题。第二,在处理大规模特征时,由于搜索空间巨大,粒子很容易陷入局部最优,导致搜索性能不佳,即PSO面临着“维度诅咒”的挑战,因此非常需要高效的搜索机制[1]。
为此本文提出了自监督数据驱动粒子群优化算法(self-supervised data-driven PSO, SDPSO)来高效地求解大规模特征选择问题。本文的贡献和创新之处主要有以下三点。
1)本文提出了自监督数据驱动特征选择(self-supervised data-driven feature selection, SDFS)的新型算法框架,可通过自监督任务生成数据标签,从而使用生成的标签来驱动算法进行特征选择,避免了对真实标签的依赖。另外,为了实现数据标签生成,本文提出了基于多模态聚类的任务生成方法(multi-modal clustering-based task generation, MCTG)来生成自监督任务,从而对数据赋予合适的标签。
2)近期研究工作发现,基于区域编码的PSO能够高效求解大规模连续优化问题[30]。受此启发,本文提出了基于离散区域编码的搜索策略(discrete region encoding-based search, DRES)来辅助PSO在大规模离散搜索空间中搜索到更优解,提升PSO求解大规模特征选择问题的性能。
3)基于上述提出的框架和方法,本文提出了完整的SDPSO算法,从而实现对大规模特征选择问题的高效求解。
为了验证算法性能,本文采用了领域内通用的6个大规模数据集(人脸数据集Yale[31]和ORL[32],物品识别数据集COIL20[33],以及3个基因数据集Leukemia[34]、DLBCL[34]和Braintumor[34])进行实验分析,并与主流和前沿算法进行对比。
1. 背景知识与相关工作
1.1 大规模特征选择问题
有D维特征的特征选择问题可表示为
$$ \begin{gathered} \underset{O}{\rm{max}}f(O)\\ {\rm{s.t.}}\quad {O}_{d}\in \{0,1\},\quad 1\leqslant d\leqslant D\end{gathered} $$ (1) 式中:Od为1表示第d维特征被选择,Od为0表示第d维特征不被选择;f是衡量特征组合的性能的函数,例如,f可以是基于特征组合进行分类时的准确率。由式(1)可见,特征选择问题是一个0/1组合优化问题,其候选解集合的规模为2D。因此,随着问题规模增大,即特征数量D增加(例如D>1000),问题的候选解数量呈指数型上升,给优化算法带来巨大挑战,这样的特征选择问题通常被称为大规模特征选择问题。
1.2 二进制粒子群优化算法
Kennedy等[24]提出的PSO算法是求解复杂优化问题的高效群体智能算法。然而,最初提出的PSO算法只适用于求解连续搜索空间的优化问题,不能直接用于求解特征选择等离散二进制搜索空间的优化问题。因此,研究者们提出了离散的PSO算法来对这类离散优化问题进行求解。其中,比较著名的是BPSO算法[25]。与原始的PSO一样,BPSO中每个粒子个体都带有1个位置向量X和1个速度向量V。其中X和V的维度与问题维度一致。然而,与原始的PSO不同的地方是,BPSO中每一个X对应一个问题的候选解,因此,针对特征选择问题,X中的每一维取值只能是0或1,即位置向量X的每一维都是离散的值。然而,V中的每一维仍然是连续值,以便粒子个体在优化过程中进行位置更新。在优化过程中,BPSO使用Sigmoid函数将V的每一维取值映射到[0, 1], 从而决定粒子位置X对应维度取值为1的概率。
速度V的更新公式可以表示为
$$ \begin{gathered} {{\boldsymbol{V}}_{i,d}} = w \cdot {{\boldsymbol{V}}_{i,d}} + {c_1} \cdot r_{1_{i,d}} \cdot ({\boldsymbol{X}}_{i,d}^{{\rm{pbest}}} - {{\boldsymbol{X}}_{i,d}})+\\ {c_2} \cdot r_{2_{i,d}} \cdot ({\boldsymbol{X}}_d^{{\rm{gbest}}} - {{\boldsymbol{X}}_{i,d}}) \\ \end{gathered} $$ (2) 式中:i是个体的索引;d代表维度;w是惯性权重参数;c1和c2是加速因子;
$r_{1_{i,d}}$ 和$r_{2_{i,d}}$ 是不同的属于[0, 1]区间的随机数;${\boldsymbol{X}}^{{\rm{pbest}}}_{i,d}$ 是个体i的历史最优位置;${\boldsymbol{X}}^{{\rm{gbest}}}_d$ 是所有个体的最优位置。在更新速度V后,位置X根据V的值和Sigmoid函数(以ϕ表示)取值为
$$ {{\boldsymbol{X}}}_{i,d}=\left\{\begin{split} &1,\quad {r}_{i,d} < \phi ({{\boldsymbol{V}}}_{i,d})\\ &0,\quad 其他\end{split} \right.$$ (3) 式中:i是个体的索引;d是维度索引;ri,d是[0, 1]区间的随机数;而ϕ的表达式为
$$ \varphi (z) = \frac{1}{{1 + {{\rm{e}}^{ - z}}}} $$ (4) 在位置X更新后,算法评估新个体的适应值,然后更新对应的
${\boldsymbol{X}}^{{\rm{pbest}}}$ 和${\boldsymbol{X}}^{{\rm{gbest}}}$ 。式(2)~(4)不断重复,直到算法满足停止条件。1.3 基于二进制粒子群优化算法的特征选择
由于特征选择问题是一个0/1组合优化问题,使用基于二进制的粒子群优化算法(例如BPSO算法)进行求解非常合适、直观。为了实现有效的特征选择,通常需要两个不重叠的数据集:用于进行特征选择的数据集(后文简称为特征选择数据集)和用于测试所选特征的效果的数据集(后文简称为测试集)。因此,BPSO等算法只使用特征选择数据集进行特征选择,然后在测试集上测试选出特征的性能。基于BPSO求解特征选择问题的经典算法步骤如算法1所示。
算法 1 求解特征选择的经典BPSO算法
输入 种群规模N,特征数目(问题维度)D,样本数据S,对应S的真实标签数据L,最大的适应值评估次数Zmax;
输出 搜索到的最优特征选择方案
${\boldsymbol{X}}^{{\rm{gbest}}}$ 。1) 初始化N个粒子的速度V和位置X;
2) 设真实标签数据L为计算适应值时的标签数据T;
3) 计算每个粒子的适应值;//算法2
4) Z=N; //N个个体消耗了N次适应值评估次数
5) 记录个体的历史最优
${\boldsymbol{X}}^{{\rm{pbest}}}$ 和种群全局最优${\boldsymbol{X}}^{{\rm{gbest}}}$ ;6) WHILE(Z<Zmax)DO
7) 更新粒子速度V和位置X;
8) 计算每个粒子的适应值;//算法2
9) Z=Z +N;
10) 更新个体的历史最优
${\boldsymbol{X}}^{{\rm{pbest}}}$ 和种群全局最优${\boldsymbol{X}}^{{\rm{gbest}}}$ ;11) END WHILE
12) 输出
${\boldsymbol{X}}^{{\rm{gbest}}}$ 。在特征选择的优化过程中,需要计算每个粒子个体的适应值。此处的适应值可设置为特征组合的性能指标。本文以分类准确率作为粒子个体的适应值。为了计算适应值,特征选择数据集S及S中各个数据对应的分类标签T将被划分成训练集和验证集,分别记为Strain和Svalid以及标签集合Ttrain和Tvalid。在现有的研究中,分类标签数据T都是直接使用数据S对应的真实分类标签数据L(即将L当作T)。然而,如果将真实标签L当作T,需要确保特征选择数据集S中的样本都有对应的真实标签,否则,没有对应真实标签的样本将不可使用。因此,L中真实标签的数量决定了特征选择数据集中可用样本的数量,这会导致在真实标签数据不足的情况下,特征选择数据集的可用样本过少,算法无法很好地进行特征选择。这也是本文提出可不依赖真实标签L的自监督特征选择框架的研究动机。即在真实标签L不足、甚至没有的情况下,本文的自监督特征选择框架仍然可以通过采用基于多模态聚类的任务生成方法生成标签T,以辅助特征选择。
在划分特征数据集后,对于需要计算适应值的个体X,将其转换为对应的特征组合(X第d维取值为1则表示第d维特征被选中并使用,否则不使用),并基于划分后的训练集Strain和对应的标签集Ttrain建立和训练分类器G。分类器可以选择使用任意的分类模型,例如经典的K最邻近分类方法。
为了避免上述划分的偶然性导致适应值计算偏差,通常使用H–折交叉验证法对S和T进行H次的划分并计算分类准确率在H次划分情况下的平均结果,其中H为一个正整数参数,常设为H=5或H=10。H–折交叉验证法计算适应值的过程如下:1)数据集S和对应的标签集T会被均分成H份,每一份也称为一折。其中,根据粒子个体的X, S中的数据只保留被X选中的特征列。2)对于第h次划分,第h份数据集及对应的第h份标签分别被用作验证集Svalid和Tvalid,而剩余的(H–1)份数据(包括第1到第(h–1)份和第(h+1)份到第H份的数据及对应标签)被合并用作训练集Strain和Ttrain。从而训练得到模型Gh。基于Svalid和Tvalid以及模型Gh,计算本次(第h次)划分的分类准确率Ah,计算过程为
$$ {A_h} = \frac{1}{{|{S_{{\text{valid}}}}|}}\sum\limits_{j = 1}^{|{S_{{\text{valid}}}}|} {I({G_h}({S_{{\text{valid}},j}}),{T_{{\text{valid}},j}})} $$ (5) 式中:|Svalid|为验证集Svalid的总样本数(也即第h份数据的样本数),Svalid,j为Svalid中第j个样本数据,Tvalid,j为对应Svalid中第j个样本数据的分类标签,Gh (Svalid,j)为分类模型Gh对样本Svalid,j的预测分类标签,函数I的定义为
$$ I(a,b)=\left\{\begin{split} & 1,\quad a==b\\ & 0,\quad 其他\end{split}\right. $$ (6) 将2)的过程执行H次,得到H个准确率的结果。
3)计算H次准确率结果的均值作为粒子X的适应值f(X):
$$ f({\boldsymbol{X}}) = \frac{1}{H}\sum\limits_{h = 1}^H {{A_h}} $$ (7) 式中Ah表示第h次的分类准确率。适应值计算过程如算法2所示。
算法 2 适应值评估
输入 数据集S,标签数据T,交叉验证折数H,候选解X。
输出 候选解X的适应值。
1) 根据X将S中未被选中的特征列去掉;
2) 将数据集S和对应的标签数据T均分成H份;
3) FOR h=1 to H
4) 将第h份样本数据作为Svalid;
5) 将除第h份外的所有样本数据作为Strain;
6) 将第h份数据对应的标签作为Tvalid;
7) 将除第h份外所有数据对应的标签作为Ttrain;
8) 基于Strain和Ttrain建立并训练分类器G;
9) 式(5)计算Ah;
10) END FOR
11) 公式(7)计算并输出X的适应值。
1.4 针对大规模特征选择的PSO算法
在求解大规模特征选择问题时,传统的PSO经常面临着“维度诅咒”的挑战,性能不佳。因此,很多专家学者提出了针对大规模特征选择的PSO算法及其变种[26-27]。Xue等[28]提出基于自适应参数和策略的PSO(Self-adaptive Parameter and Strategy based PSO,SPS-PSO),用于对大规模特征选择问题进行自适应求解。Luo等[29]提出混合粗糙超立方体方法与BPSO的算法(Hybridization of the Rough Hypercuboid Approach and BPSO,RH-BPSO)来对大规模特征选择问题进行高效求解。
虽然国内外的专家学者们已经提出许多针对大规模特征选择的PSO算法及其变种,但是这些算法都需要在有监督的条件下执行,即算法搜索过程中需要用到具有真实标签的数据。然而,在实际应用中,监督信息(真实标签)的获取十分困难且成本很高,很多情况下只有一部分的数据带有真实标签,甚至没有数据带有真实标签。因此,有监督算法在这些应用中很难取得良好的表现。与现有的有监督算法不同,本文提出了自监督数据驱动的算法框架,通过自监督学习来进行特征选择,不用依赖于真实标签等监督信息。另外,本文还提出了新型的离散区域搜索策略,以辅助PSO对大规模特征选择问题进行求解。
2. 自监督数据驱动粒子群优化算法
2.1 自监督数据驱动特征选择算法框架
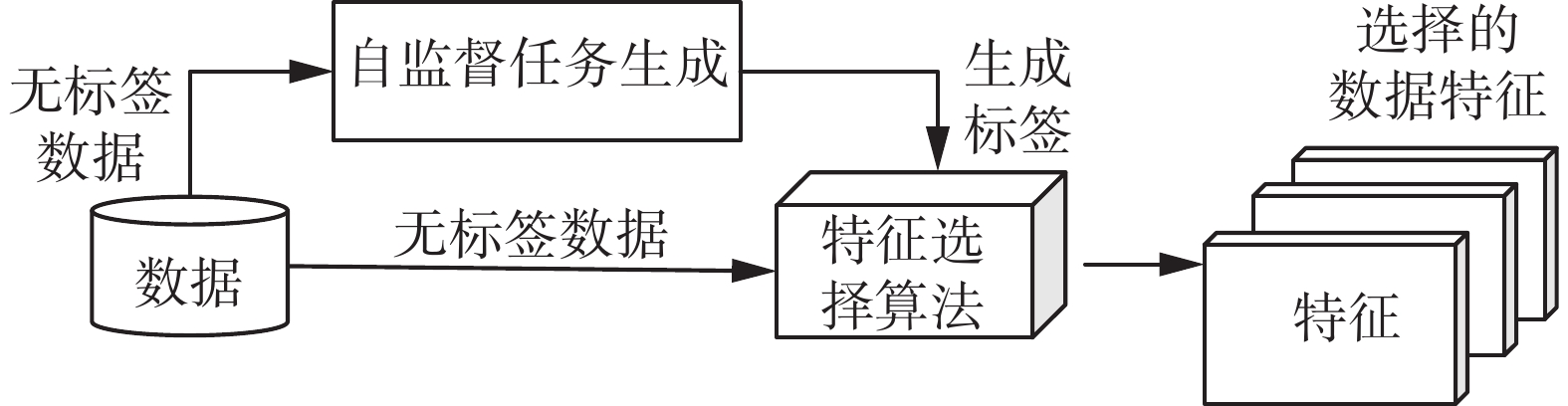
为了实现不依赖标签等真实监督信息来进行高效的特征选择,本文提出新型算法框架SDFS。如图1所示,该算法框架可利用自监督任务生成数据标签,并使用生成的标签来驱动算法对特征进行选择。因此,该框架不用依赖真实的数据标签亦可完成特征选择过程。
然而,如何基于无监督的数据获取或构建合适的自监督信息是一个关键的难题。在现有的研究中,有许多学者研究和提出了不同的方法生成自监督分类任务,从而对数据赋予标签,例如基于数据重建方式生成分类任务(如图像着色和分辨率辨别)[35],基于任务知识生成分类任务(如几何变换识别和噪声数据辨别)[36-37]和自动任务生成(如使用聚类算法和矩阵分解)[38-41]。这些方法都可以用于生成自监督任务,从而对数据赋予标签。由于基于聚类的方法相比其他方法具有较好的通用性且较为常用[42],本文也采用聚类的方式生成自监督分类任务,并赋予数据对应的标签。为此,本文提出了基于多模态聚类的任务生成方法(MCTG),对数据进行自动化的自监督分类任务生成,并基于生成任务对数据赋予标签。不同于现有采用单一聚类赋予数据标签的方法,MCTG的创新之处在于它旨在利用多种聚类方法,对数据进行多种模态的分类,并通过对不同分类结果的关联综合结果作为生成的标签信息替代原来有监督搜索中所需的真实标签信息。
具体地,MCTG使用Q个不同的聚类方法,其中每个聚类方法都将数据分成两类,类别记为0或1。记对第i个样本数据的第q个分类结果为ti,q (ti,q∈{0,1}),则对于该样本的自监督任务分类标签Ti为
$$ {T_i} = \sum\limits_{q = 1}^Q {({2^{Q - 1}} \cdot {t_{i,q}})} $$ (8) 可见,生成的任务最终共有2Q个类别(Ti的取值有2Q种),即类别0,1,…, 2Q–1。因此,每个数据都将属于2Q个类别中的一个类别,这些类别标签可用于后续的特征选择过程。不失一般性,本文在算法实现中采用了3种(Q=3)较为常见的聚类方法来进行任务生成,分别是基于欧式距离、基于曼哈顿距离(绝对值距离)和基于余弦值的K-means聚类方法。具体的MCTG伪代码如算法3所示。基于MCTG,可以用生成的标签评估特征组合的优劣(即候选解的适应值),该计算过程如前文的算法2所示,其中T为生成的分类标签而非真实分类标签。
算法 3 MCTG
1) FOR q=1 to Q
2) 使用第q个聚类方法将样本数据集S聚成两类
3) FOR i=1 to |S| //|S|为数据集S的总样本数
4) IF Si 被分到第一类 THEN
5) ti,q = 0
6) ELSE
7) ti,q = 1
8) END IF
9) END FOR
10) END FOR
11)根据式(8)计算每个样本数据的T结果作为标签。
2.2 离散区域编码的搜索策略
近期的研究工作发现,基于区域编码的PSO在求解大规模连续优化问题中有很好的效果[30]。受此启发,本文提出DRES来提升PSO求解大规模特征选择优化问题的性能。
首先,在区域编码的PSO中,每个粒子不仅仅表示一个点,还表示以该点为中心,r为半径的覆盖区域。然而,针对离散问题,粒子覆盖的区域需要重新定义。因此,首先定义粒子的离散区域编码。给定区域半径r,每个粒子Xi所对应的一个离散区域集合,记为κ(Xi, r),可表示为
$$ \kappa ({{\boldsymbol{X}}_i},r) = \{ U\left| {\gamma (U,{{\boldsymbol{X}}_i}) \leqslant r} \right.\} $$ (9) 其中γ计算两个向量的汉明距离。使用κ(Xi, r)中的随机个体替换当前个体位置,从而增加搜索的多样性。综上,DRES的伪代码如算法4所示。
算法 4 DRES
1) FOR现有种群中的每个个体Xi;
2) 任意生成一个属于κ(Xi, r)的个体,记为Ui;
3) 用Ui替换Xi;
4) END FOR。
2.3 完整算法
基于上述方法和策略,并结合BPSO中的速度(式(2))和位置更新(式(3)),本文提出了完整SDPSO算法。SDPSO的算法伪代码如算法5所示。算法5主要分为2个部分。第1部分是算法5的第1行,对于无标签数据通过MCTG(即算法3)生成数据的标签,以进行后续的特征选择。第2部分是基于自监督数据驱动的特征选择优化,即算法5的第2~15行。该过程包括粒子的初始化(算法5的第2~6行)和演化搜索(算法5的第7~15行)。其中,第10行会执行DRES(算法4)以增强算法搜索的多样性和效率。第7~15行将不断迭代执行直到满足算法停止条件(此处为适应值评估次数Z达到预设的最大次数Zmax)。最后,算法输出找到的最优解
${\boldsymbol{X}}^{{\rm{gbest}}}$ 。算法 5 SDPSO
输入 种群规模N,特征数目(问题维度)D,样本数据S,最大的适应值评估次数Zmax。
输出 搜索到的最优特征选择方案
${\boldsymbol{X}}^{{\rm{gbest}}}$ 。1) 对S中的数据生成标签T;//算法3
2) 随机初始化N个粒子的速度V和位置X;
3) 计算N个粒子的适应值;//算法2, 基于生成的标签T
4) Z=N; //已消耗N次适应值评估次数
5) 记录每个个体的历史最优
${\boldsymbol{X}}^{{\rm{pbest}}}$ ;6) 记录全局最优
${\boldsymbol{X}}^{{\rm{gbest}}}$ ;7) WHILE(Z < Zmax)DO
8) 根据式(2)更新粒子速度V;
9) 根据式(3)更新粒子位置X;
10)执行DRES得到新的粒子位置X;//算法4
11)计算新粒子的适应值;//算法2, 基于生成的标签T
12) Z=Z +N;
13)更新每个个体的历史最优
${\boldsymbol{X}}^{{\rm{pbest}}}$ ;14)更新全局最优
${\boldsymbol{X}}^{{\rm{gbest}}}$ ;15) END WHILE
16)输出
${\boldsymbol{X}}^{{\rm{gbest}}}$ 。本节对SDPSO(即算法5)的时间复杂度进行分析。由上文可知,算法5主要有2个部分,第1部分为算法5的第1行,第2部分算法5的第2~15行。
在算法5的第1部分,SDPSO通过算法3对数据进行标签生成。算法3的第1~10行需执行Q次循环。每次循环中,算法3的第2行执行一次Kmeans算法。Kmeans算法的时间复杂度为O(G×t×|S|×D),其中G为聚类的迭代次数,t为聚类的类别数,|S|为S中样本数,D为样本特征数。由于算法3中Kmeans聚类类别均为2类(即t=2),执行的Kmeans算法的时间复杂度可简化为O(G×|S|×D)。算法3的第3~9行执行|S|次循环,每次循环执行一次判断和一次赋值,因此|S|次循环的时间复杂度为O(|S|)。因此,算法3第2~9行的时间复杂度合并为O(G×|S|×D)。由于算法3第1~10行需执行Q次循环,因此其时间复杂度为O(Q×G×|S|×D)。算法3的11行计算式(8),由于式(8)包含Q次乘法和加法,因此该行的时间复杂度为O(Q)。综上,算法3的总时间复杂度合并为O(Q×G×|S|×D)。由于Q为常数参数且本文中Q=3,因此算法3的时间复杂度可简化为O(G×|S|×D)。
算法5的第2部分包括其第2~15行。第2行初始化N个粒子个体的速度和位置,时间复杂度度为O(N×D)。第3行计算N个个体的适应值。由算法2可见,适应值计算的时间复杂度与所采用的分类器相关。因此,为了不失一般性,此处假设每次适应值评估的时间复杂度为O(E),则第3行的时间复杂度为O(N×E)。第4行为赋值操作,时间复杂度为O(1),而第5和第6行是寻找并记录最优个体,因此时间复杂度为O(N×D)。因此,第3~6行的时间复杂度为O(N×(E+D))。在第7~15行的WHILE循环中,第8、9行更新粒子的速度和位置,时间复杂度为O(N×D);第10行执行算法4,对每个个体进行DRES,时间复杂度也为O(N×D);第11~14行与第3~6行相同,因此时间复杂度也为O(N×(E+D))。综上,第8~14行的时间复杂度可合并为O(N×(E+D))。由于WHILE循环将循环执行第8~14行ν=(Zmax/N–1)次,其中Zmax为最大的适应值评估次数,WHILE循环的时间复杂度为 O(ν×N×(E+D))。则算法5第2部分(第2~14行)的总时间复杂度为O(N×(E+D)+ν×N×(E+D))=O(Zmax×(E+D))。
综合算法5的第1部分和第2部分,算法5的总时间复杂度为O(G×|S|×D+ Zmax×(E+D))。
3. 实验分析
3.1 实验设置
为了对算法性能进行测试,本文采用了领域内常见的6个具有大规模特征的数据集进行实验。这6个数据集分别是人脸数据集Yale [31]和ORL [32],物品识别数据集COIL20[33]以及3个基因数据集Leukemia [34]、DLBCL [34]、Braintumor [34]。这些数据集已被研究者收集整理,其中前3个数据集在文献[43]中公开,而后3个数据集在文献[34]中公开。表1提供了这些数据集的相关信息。此外,图2也给出了3个图片数据集的部分样例图片,以供参考。
为了对比SDPSO的性能,本文使用目前主流的代表性有监督算法BPSO[25]和CSO[26]作为对比算法。对于参数设置,为了公平起见,SDPSO与BPSO采用相同的参数,即种群规模为20,速度的最大值和最小值分别为6和−6,加速因子c1和c2均为2.01,惯性权重w为1。上述这些参数也是BPSO论文的推荐值[25]。对于SDPSO中DRES的设置,因为在大规模问题中,κ(Xi, r)包含的候选解会随着r增大急剧增多,所以DRES中的r设置为较小的值,即r=1。CSO的参数设置也按其论文的推荐进行设置[26]。此外,本文也将全选所有特征的方法(简记为FULL方法)和随机分类的方法(简记为RAND)作为基准结果与提出的算法进行对比。
所有进行特征选择的算法在优化过程中的最大评估次数被设定为Zmax=5000。在每个数据集上,每个算法独立运行30次,采用平均结果(在测试集上的分类准确率)作为最终结果。为了保持公平性,每个数据集也进行30次的随机划分,每次将90%的样本作为特征选择数据集和10%的样本作为测试集。因此,每个算法在第i次运行时使用第i次划分的数据集。即使用第i次划分的特征选择数据集进行特征选择,然后将选择的特征在第i次划分的测试集上进行测试。另外,在特征选择阶段,SDPSO、BPSO和CSO的每个粒子使用常用的H=5的H–折交叉验证法来获得基于选择特征的平均分类准确率作为适应值。为了体现本文提出方法的实用性,在实验中特征选择数据集中只有20%的数据带有真实分类标签。由于SDPSO不需要依赖真实标签,因此SDPSO可以在整个特征数据集上进行特征选择,而BPSO与CSO只能使用特征选择数据集中带真实标签的数据(即20%的数据)进行特征选择。此外,为了更准确地评估选出的特征的效果,实验在测试集上使用留一验证法计算分类的准确率。其中,留一验证法是H设置为数据样本数的H–折交叉验证法,即有多少个数据,就需计算多少次分类准确率再求平均。因此,相比于H更小的交叉验证法版本(如H=5),留一验证法计算误差更小,但因为需要计算更多次的准确率(即A值)以取平均,所以计算量更大。另外,由于FULL和RAND算法不需要进行特征选择,因此在计算其第i次结果的时候,只需直接使用第i次划分的测试集通过留一验证法来计算分类准确率。在实验中,本文选择K最邻近分类方法作为分类器来计算实验中所选特征的分类准确率,其中参数K被设置为5。此外,当得到的分类准确率相近时,只需更少特征数量的特征选择组合比需要更多特征数量的特征选择组合更优。
此外,本文采用Wilcoxon符号秩检验(显著性水平α=0.05)来检验SDPSO与其他对比算法之间的显著差异。在实验统计结果中,符号 “+”表示SDPSO明显优于对比算法,符号“−”表示SDPSO明显劣于对比算法,符号“=”表示SDPSO与对比算法在当前显著水平上没有明显差异。所有的算法实验均在配置Intel Core i7-7700F CPU @ 3.60 GHz和总内存为8 GB的集群服务器上运行。
3.2 与主流经典方法的实验对比
表2给出了SDPSO与主流经典算法的对比结果。对比结果显示SDPSO能取得与使用了真实标签的有监督算法相当的结果。根据Wilcoxon符号秩检验,SDPSO在Yale数据集上取得了比CSO显著好的结果,并在剩下的数据集上取得与BPSO和CSO相当的结果。除此之外,SDPSO在2个数据集上取得最优的均值(已在表2中加粗),在数量上与BPSO和CSO相当。而在选择出来的特征数量方面,SDPSO和对比的BPSO和CSO在6个数据集上都没有明显差别。可见,SDPSO具有与基于真实标签的算法相当,甚至更好的性能。而且,SDPSO的运行并不需要真实的标签。因此,相比于基于真实标签的算法,SDPSO具有更加通用、成本更低(获取真实标签的成本)的优势。这些都表明了SDPSO的优越性。
表 2 SDPSO与经典算法的实验结果Table 2 The experimental results of SDPSO and classical algorithms数据集 SDPSO
(特征选择不
需真实标签)BPSO
(特征选择基
于真实标签)CSO
(特征选择基
于真实标签)FULL
(不进行特征选择)RAND
(随机进行分类)准确率 特征数 准确率 特征数 准确率 特征数 准确率 特征数 准确率 Yale 0.150±0.142 511.6 0.150±0.133(=) 510.1 0.138±0.141(+) 510.6 0.144±0.134(=) 1024 0.070±0.004(+) ORL 0.151±0.081 509.0 0.149±0.090(=) 511.0 0.143±0.086(=) 508.3 0.154±0.085(=) 1024 0.025±0.001(+) COIL20 0.721±0.035 512.1 0.722±0.042(=) 508.9 0.723±0.042(=) 511.2 0.722±0.041(=) 1024 0.050±0.001(+) Leukemia 0.462±0.285 2661.2 0.463±0.320(=) 2664.3 0.468±0.265(=) 2669.0 0.452±0.293(+) 5327 0.333±0.002(+) DLBCL 0.671±0.229 2735.8 0.663±0.222(=) 2720.2 0.670±0.226(=) 2736.2 0.671±0.229(=) 5469 0.500±0.002(+) Braintumor 0.652±0.184 2960.2 0.671±0.157(=) 2965.7 0.662±0.186(=) 2965.0 0.648±0.187(=) 5920 0.200±0.001(+) +/=/− NA 0/6/0 1/5/0 1/5/0 6/0/0 此外,跟全选所有特征的FULL方法相比,SDPSO在Leukemia数据集上取得显著好的结果,并在剩下5个数据集上与FULL表现相当。同时,SDPSO在这6个数据集上选择的特征数量约占FULL的50%。即,SDPSO只用50%的特征就能取得与FULL相当,甚至更好的分类结果。可见,SDPSO具有较强的特征选择能力。另外,与RAND相比,SDPSO在全部的数据集上都得到显著更优的结果,即SDPSO取得了比随机分类显著更高的准确率,甚至在COIL20数据集上的准确率比随机分类的准确率超过13倍,表明了特征选择进行分类的有效性。
综上所述,对比实验结果表明了SDPSO不依赖真实标签进行特征选择的性能。
3.3 SDFS框架的作用分析
为了对SDFS框架的作用进行分析,本文将SDPSO与不使用SDFS框架的SDPSO变种(简记为SDPSO-w/o-SDFS)进行对比。具体地,SDPSO-w/o-SDFS使用真实的标签数据代替SDFS得到的生成标签数据。除此之外,SDPSO-w/o-SDFS在设置上与SDPSO一致。表3给出了对比实验的结果。由表3可知,SDPSO在Leukemia数据集上得到的结果显著优于SDPSO-w/o-SDFS。此外,在另外5个数据集上SDPSO与SDPSO-w/o-SDFS取得的结果没有显著性差异。同时,SDPSO与SDPSO-w/o-SDFS在每个数据集上所选择的特征数量也基本相当。这说明SDFS能够免除算法对真实标签的依赖,同时对算法的效果有一定程度的提升,表明了SDFS的有效性。
表 3 SDPSO与SDPSO-w/o-SDFS的实验结果Table 3 Experimental results of SDPSO and SDPSO-w/o-SDFS数据集 SDPSO
(不需真实标签)SDPSO-w/o-SDFS
(基于真实标签)准确率 特征数 准确率 特征数 Yale 0.150±0.142 511.6 0.143±0.143(=) 512.4 ORL 0.151±0.081 509.0 0.143±0.091(=) 510.1 COIL20 0.721±0.035 512.1 0.720±0.040(=) 508.8 Leukemia 0.462±0.285 2661.2 0.443±0.278(+) 2664.4 DLBCL 0.671±0.229 2735.8 0.663±0.245(=) 2741.5 Braintumor 0.652±0.184 2960.2 0.652±0.184(=) 2959.4 +/=/- NA 1/5/0 3.4 基于离散区域编码的搜索策略的作用分析
为了对DRES进行性能分析,本文将SDPSO与不使用DRES的SDPSO变种(简记为SDPSO-w/o-DRES)进行对比。表4给出了SDPSO与SDPSO-w/o-DRES的对比结果。从表4可知,SDPSO在Yale数据集和Leukemia数据集上得到的结果显著优于SDPSO-w/o-DRES。在另外的4个数据集上,SDPSO取得的结果也与SDPSO-w/o-DRES相当。即,在总体上SDPSO有比SDPSO-w/o-DRES更好的性能。这说明了DRES有助于算法在大规模搜索空间中找到更好的候选解。
表 4 SDPSO与SDPSO-w/o-DRES的实验结果Table 4 Experimental results of SDPSO and SDPSO-w/o-DRES数据集 SDPSO SDPSO-w/o-DRES 准确率 特征数 准确率 特征数 Yale 0.150±0.142 511.6 0.132±0.142(+) 511.8 ORL 0.151±0.081 509.0 0.150±0.084(=) 505.9 COIL20 0.721±0.035 512.1 0.721±0.032(=) 509.9 Leukemia 0.462±0.285 2661.2 0.445±0.295(+) 2662.6 DLBCL 0.671±0.229 2735.8 0.678±0.230(=) 2735.2 Braintumor 0.652±0.184 2960.2 0.647±0.195(=) 2963.0 +/=/- NA 2/4/0 3.5 真实标签比例对特征选择的影响
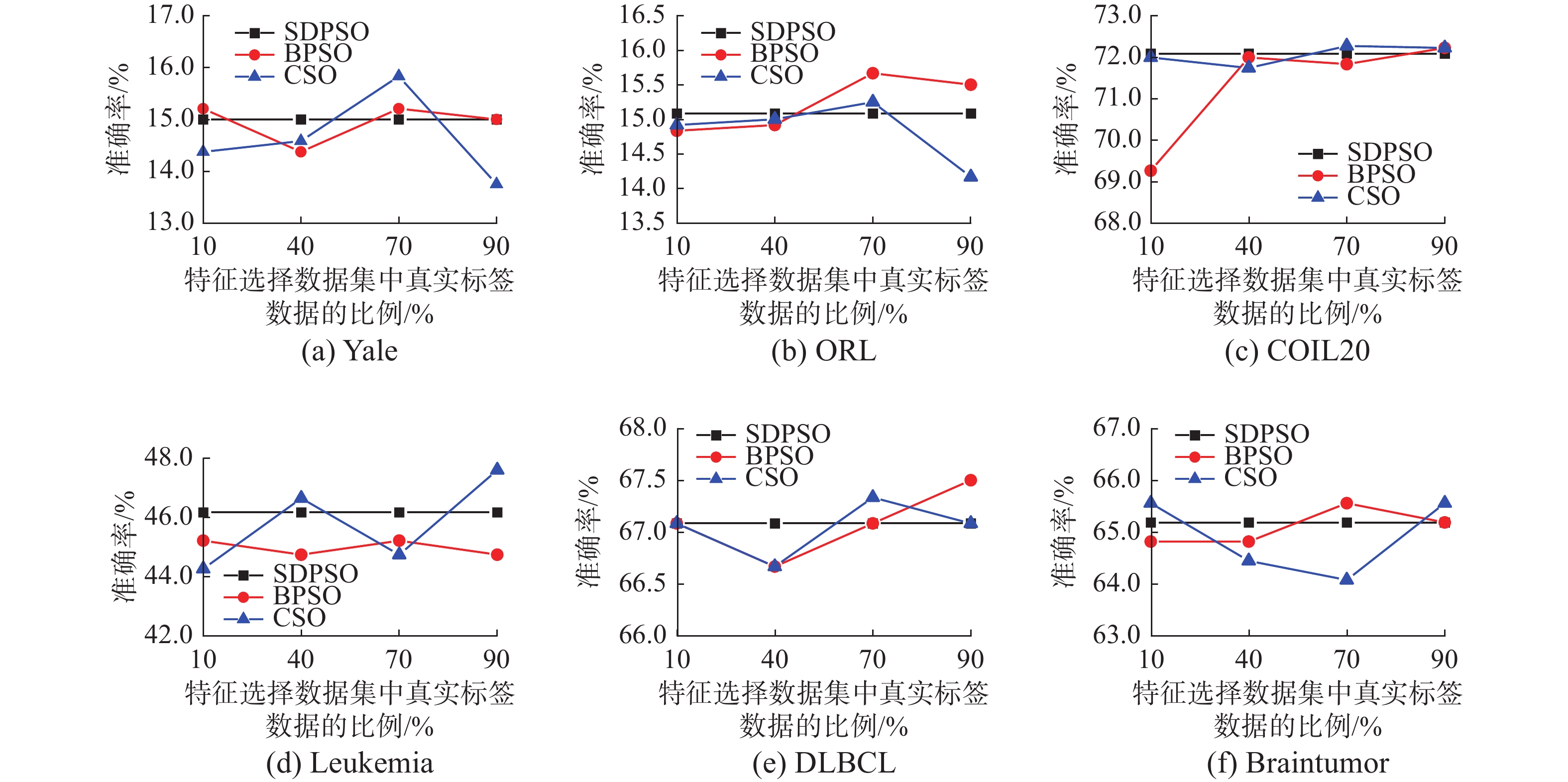
为了探究真实标签比例对特征选择的影响,通过实验测试对比SDPSO与其他算法在不同情况下的优化结果。测试了SDPSO、BPSO和CSO在特征选择数据集中真实标签数据比例变化时的特征选择效果。由于SDPSO在特征选择过程中不需要依赖真实标签数据,因此真实标签数据比例的变化不会影响SDPSO的结果。
3个算法在不同真实标签数据比例情况下的结果如图3所示。由图3可见,在真实标签数据比例较小时(如不大于40%),SDPSO在大部分问题上都能取得比BPSO和CSO更高的准确率,说明在真实标签数据样本较少时,SDPSO相比BPSO与CSO具有总体更优越的性能。而且,在真实标签数据比例变化的情况下,SDPSO的结果波动比BPSO与CSO更小,说明了SDPSO具有更好的稳定性和通用性。综上所述,真实标签对SDPSO的影响要比对BPSO和CSO的影响小得多。而且,基于SDPSO的特征选择在真实标签不足的情况下仍能有很好的表现,说明了SDPSO的通用性。
3.6 与前沿方法的实验对比
为了进一步测试SDPSO的性能优势,本节将SDPSO与6个前沿的特征选择方法进行实验对比。这6个前沿方法分别为:引言中提到的SPS-PSO[28]和RH-BPSO[29],结合凸非负矩阵分解和自适应图约束的特征选择方法(convex non-negative matrix factorization with an adaptive graph constraint feature selection, CNAFS)[38]、多组自适应图表示方法(multi-group adaptive graph representation, MGAGR)[39]、基于嵌入图学习和约束的无监督特征选择方法(unsupervised feature selection via embedded graph learning and constraint method, EGCFS)[40]和结合可分性的无监督特征选择方法(unsupervised feature selection with separability, UFS2)[41]。其中,CNAFS和UFS2主要基于生成标签进行无监督特征选择,MGAGR和EGCFS主要利用图学习与几何约束进行无监督特征选择。由于CNAFS、MGAGR、EGCFS和UFS2方法均需预先确定需要选择的特征数,而现有文献通常采用穷举法确定最佳选择特征数[38-41],本文也采用穷举法确定这4种方法的最佳选择特征数。在穷举法过程中,需要对不同特征数设置下的选取特征进行评估和比较,以确定最佳特征数。因此,在实验中,采用基于真实标签的算法2作为穷举法过程中的特征评估方式。另外,由于SPS-PSO和RH-BPSO需要标签信息进行特征搜索,为了公平比较算法的搜索效率,SPS-PSO和RH-BPSO也使用与SDPSO相同的生成标签,并使用算法2作为搜索过程中粒子的适应值评估方式。所有对比算法的参数均采用其对应论文的推荐设置。每个算法独立运行30次并使用平均结果进行比较。
各个算法在6个数据集上的平均准确率如表5所示。在6个不同数据集的特征选择问题上,SDPSO能在Yale、ORL、COIL20、Leukemia和Braintumor 这5个不同数据集上取得比其他对比算法都更好的结果,表明了SDPSO具有比其他算法更好的综合性能。而且,Yale、ORL和COIL20是样本类别数分别为15、40和20的多类别数据集,要对样本实现准确分类十分困难。然而,SDPSO在这3个数据集上都能得到比其他算法更好的分类准确率,说明SDPSO选择的特征能够应对复杂的分类任务。综上所述,实验对比结果表明了SDPSO进行特征选择的优越性。
表 5 SDPSO算法与前沿算法的平均准确率结果Table 5 Average accuracy results of SDPSO and state-of-the-art algorithms数据集 SDPSO SPS-PSO RH-BPSO CNAFS MGAGR EGCFS UFS2 Yale 0.150 0.145 0.142 0.124 0.117 0.121 0.113 ORL 0.151 0.148 0.144 0.115 0.129 0.123 0.136 COIL20 0.721 0.658 0.658 0.633 0.643 0.660 0.568 Leukemia 0.462 0.437 0.410 0.430 0.423 0.437 0.417 DLBCL 0.671 0.693 0.687 0.683 0.687 0.683 0.723 Braintumor 0.652 0.648 0.640 0.652 0.623 0.643 0.623 最优结果数 5 0 0 0 0 0 1 本节也对算法的运行时间进行比较。其中,CNAFS、MGAGR、EGCFS和UFS2方法的运行时间包括使用穷举法选取最优特征数所需的时间。各个算法的平均运行时间如表6所示。由表6可见,在特征数较小的数据集上,如Yale、ORL和COIL20,CNAFS的运行时间最短,而在特征数较多的数据集上,如Leukemia,DLBCL和Braintumor,SDPSO算法所需的运行时间最短。尽管在Yale、ORL和COIL20上,SDPSO的运行时间多于CNAFS,但SDPSO得到的分类准确率明显优于CNAFS(如表5所示)。此外,与SPS-PSO和RH-BPSO相比,SDPSO使用简单且高效的DRES进行高效的搜索,因此在大规模问题上只需更少的平均运行时间。与CNAFS、MGAGR、EGCFS和UFS2相比,SDPSO能够在搜索最优特征组合的同时确定最优特征数,而CNAFS、MGAGR、EGCFS和UFS2在确定特征的优劣和选择顺序之后,还需再寻找最优的选择特征数。因此,随着问题特征数不断增加,SDPSO的运行时间效率优势更加明显。综上所述,算法运行时间的比较结果表明了SDPSO的高效性。
表 6 SDPSO算法与前沿算法的平均运行时间Table 6 Average running time of SDPSO and state-of-the-art algorithmss 数据集(总特征数) SDPSO SPS-PSO RH-BPSO CNAFS MGAGR EGCFS UFS2 Yale(1024) 108.376 107.471 107.123 22.756 110.726 43.912 372.168 ORL(1024) 22.385 22.950 22.446 4.817 20.156 24.775 179.095 COIL20(1024) 950.269 926.013 926.361 202.682 1490.019 212.838 1530.091 Leukemia(5327) 59.313 61.276 59.451 66.717 275.612 2357.183 5982.512 DLBCL(5469) 64.378 66.325 64.779 75.146 343.659 4311.511 6527.624 Braintumor(5920) 83.871 85.479 84.113 105.956 538.061 5460.928 7882.529 4. 结束语
本文提出了面向大规模特征选择问题的SDPSO算法。首先,SDPSO算法基于本文提出SDFS框架和MCTG方法,可以在不依赖真实标签的情况下进行特征选择。其次,SDPSO使用了本文提出的DRES,能够高效地在大规模搜索空间中找到更好的候选解。实验结果表明,本文提出的SDPSO能在不使用真实标签的情况下依然与使用真实标签的对比算法表现相当,并比前沿无监督算法具有更高的特征选择效率。
在未来工作中,我们希望进一步增强 SDPSO算法及SDFS框架在复杂特征选择问题上的求解性能,包括带有多目标、多任务、小样本和数据不平衡等特点的特征选择问题。而且,如何基于无监督的数据获取或构建合适的自监督信息也是未来值得研究的科学问题。此外,我们也会将相关算法应用到智慧城市的复杂智能应用问题。
-
表 1 6个数据集的具体信息
Table 1 Information of the six datasets
表 2 SDPSO与经典算法的实验结果
Table 2 The experimental results of SDPSO and classical algorithms
数据集 SDPSO
(特征选择不
需真实标签)BPSO
(特征选择基
于真实标签)CSO
(特征选择基
于真实标签)FULL
(不进行特征选择)RAND
(随机进行分类)准确率 特征数 准确率 特征数 准确率 特征数 准确率 特征数 准确率 Yale 0.150±0.142 511.6 0.150±0.133(=) 510.1 0.138±0.141(+) 510.6 0.144±0.134(=) 1024 0.070±0.004(+) ORL 0.151±0.081 509.0 0.149±0.090(=) 511.0 0.143±0.086(=) 508.3 0.154±0.085(=) 1024 0.025±0.001(+) COIL20 0.721±0.035 512.1 0.722±0.042(=) 508.9 0.723±0.042(=) 511.2 0.722±0.041(=) 1024 0.050±0.001(+) Leukemia 0.462±0.285 2661.2 0.463±0.320(=) 2664.3 0.468±0.265(=) 2669.0 0.452±0.293(+) 5327 0.333±0.002(+) DLBCL 0.671±0.229 2735.8 0.663±0.222(=) 2720.2 0.670±0.226(=) 2736.2 0.671±0.229(=) 5469 0.500±0.002(+) Braintumor 0.652±0.184 2960.2 0.671±0.157(=) 2965.7 0.662±0.186(=) 2965.0 0.648±0.187(=) 5920 0.200±0.001(+) +/=/− NA 0/6/0 1/5/0 1/5/0 6/0/0 表 3 SDPSO与SDPSO-w/o-SDFS的实验结果
Table 3 Experimental results of SDPSO and SDPSO-w/o-SDFS
数据集 SDPSO
(不需真实标签)SDPSO-w/o-SDFS
(基于真实标签)准确率 特征数 准确率 特征数 Yale 0.150±0.142 511.6 0.143±0.143(=) 512.4 ORL 0.151±0.081 509.0 0.143±0.091(=) 510.1 COIL20 0.721±0.035 512.1 0.720±0.040(=) 508.8 Leukemia 0.462±0.285 2661.2 0.443±0.278(+) 2664.4 DLBCL 0.671±0.229 2735.8 0.663±0.245(=) 2741.5 Braintumor 0.652±0.184 2960.2 0.652±0.184(=) 2959.4 +/=/- NA 1/5/0 表 4 SDPSO与SDPSO-w/o-DRES的实验结果
Table 4 Experimental results of SDPSO and SDPSO-w/o-DRES
数据集 SDPSO SDPSO-w/o-DRES 准确率 特征数 准确率 特征数 Yale 0.150±0.142 511.6 0.132±0.142(+) 511.8 ORL 0.151±0.081 509.0 0.150±0.084(=) 505.9 COIL20 0.721±0.035 512.1 0.721±0.032(=) 509.9 Leukemia 0.462±0.285 2661.2 0.445±0.295(+) 2662.6 DLBCL 0.671±0.229 2735.8 0.678±0.230(=) 2735.2 Braintumor 0.652±0.184 2960.2 0.647±0.195(=) 2963.0 +/=/- NA 2/4/0 表 5 SDPSO算法与前沿算法的平均准确率结果
Table 5 Average accuracy results of SDPSO and state-of-the-art algorithms
数据集 SDPSO SPS-PSO RH-BPSO CNAFS MGAGR EGCFS UFS2 Yale 0.150 0.145 0.142 0.124 0.117 0.121 0.113 ORL 0.151 0.148 0.144 0.115 0.129 0.123 0.136 COIL20 0.721 0.658 0.658 0.633 0.643 0.660 0.568 Leukemia 0.462 0.437 0.410 0.430 0.423 0.437 0.417 DLBCL 0.671 0.693 0.687 0.683 0.687 0.683 0.723 Braintumor 0.652 0.648 0.640 0.652 0.623 0.643 0.623 最优结果数 5 0 0 0 0 0 1 表 6 SDPSO算法与前沿算法的平均运行时间
Table 6 Average running time of SDPSO and state-of-the-art algorithms
s 数据集(总特征数) SDPSO SPS-PSO RH-BPSO CNAFS MGAGR EGCFS UFS2 Yale(1024) 108.376 107.471 107.123 22.756 110.726 43.912 372.168 ORL(1024) 22.385 22.950 22.446 4.817 20.156 24.775 179.095 COIL20(1024) 950.269 926.013 926.361 202.682 1490.019 212.838 1530.091 Leukemia(5327) 59.313 61.276 59.451 66.717 275.612 2357.183 5982.512 DLBCL(5469) 64.378 66.325 64.779 75.146 343.659 4311.511 6527.624 Braintumor(5920) 83.871 85.479 84.113 105.956 538.061 5460.928 7882.529 -
[1] XUE Bing, ZHANG Mengjie, BROWNE W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE transactions on evolutionary computation, 2016, 20(4): 606–626. doi: 10.1109/TEVC.2015.2504420 [2] ZHAN Zhihui, SHI Lin, TAN K C, et al. A survey on evolutionary computation for complex continuous optimization[J]. Artificial intelligence review, 2022, 55(1): 59–110. doi: 10.1007/s10462-021-10042-y [3] WANG Peng, XUE Bing, LIANG Jing, et al. Differential evolution based feature selection: a niching-based multi-objective approach[J]. IEEE transactions on evolutionary computation, PP(99): 1. [4] ZHAN Zhihui, LI Jianyu, ZHANG Jun. Evolutionary deep learning: a survey[J]. Neurocomputing, 2022, 483: 42–58. doi: 10.1016/j.neucom.2022.01.099 [5] CHENG Fan, CUI Junjie, WANG Qijun, et al. A variable granularity search based multi-objective feature selection algorithm for high-dimensional data classification[EB/OL].(2022–03–18)[2022–06–01].https://ieeexplore.ieee.org/abstract/document/9737335. [6] LI Jianyu, ZHAN Zhihui, XU Jin, et al. Surrogate-assisted hybrid-model estimation of distribution algorithm for mixed-variable hyperparameters optimization in convolutional neural networks[EB/OL]. (2021–09–20)[2022–06–01].https://ieeexplore.ieee.org/document/9540902. [7] SONG Xianfang, ZHANG Yong, GONG Dunwei, et al. Surrogate sample-assisted particle swarm optimization for feature selection on high-dimensional data[EB/OL]. (2022–05–18)[2022–06–01].https://ieeexplore.ieee.org/abstract/document/9775183 [8] 李永豪, 胡亮, 高万夫. 基于稀疏系数矩阵重构的多标记特征选择[J]. 计算机学报, 2022, 45(9): 1827–1841. doi: 10.11897/SP.J.1016.2022.001827 LI Yonghao, HU Liang, GAO Wanfu. Multi-label feature selection based on sparse coefficient matrix reconstruction[J]. Chinese journal of computers, 2022, 45(9): 1827–1841. doi: 10.11897/SP.J.1016.2022.001827 [9] LI Junyu, CHEN Jiazhou, QI Fei, et al. Two-dimensional unsupervised feature selection via sparse feature filter[EB/OL]. (2022–04–11)[2022–06–01].https://ieeexplore.ieee.org/abstract/document/9754711. [10] WANG Peng, XUE Bing, LIANG Jing, et al. Multiobjective differential evolution for feature selection in classification[EB/OL]. (2021–12–07) [2022–06–01].https://pubmed.ncbi.nlm.nih.gov/34874881. [11] 陈彤, 陈秀宏. 特征自表达和图正则化的鲁棒无监督特征选择[J]. 智能系统学报, 2022, 17(2): 286–294. doi: 10.11992/tis.202012043 CHEN Tong, CHEN Xiuhong. Feature self-representation and graph regularization for robust unsupervised feature selection[J]. CAAI transactions on intelligent systems, 2022, 17(2): 286–294. doi: 10.11992/tis.202012043 [12] LI Xiaoping, WANG Yadi, RUIZ R. A survey on sparse learning models for feature selection[J]. IEEE transactions on cybernetics, 2022, 52(3): 1642–1660. doi: 10.1109/TCYB.2020.2982445 [13] 李顺勇, 王改变. 一种新的最大相关最小冗余特征选择算法[J]. 智能系统学报, 2021, 16(4): 649–661. doi: 10.11992/tis.202009016 LI Shunyong, WANG Gaibian. New MRMR feature selection algorithm[J]. CAAI transactions on intelligent systems, 2021, 16(4): 649–661. doi: 10.11992/tis.202009016 [14] LIU Shulei, WANG Handing, PENG Wei, et al. A surrogate-assisted evolutionary feature selection algorithm with parallel random grouping for high-dimensional classification[J]. IEEE transactions on evolutionary computation, 2022, 26(5): 1087–1101. doi: 10.1109/TEVC.2022.3149601 [15] 曾毓菁, 姜勇. 一种融入注意力和预测的特征选择SLAM算法[J]. 智能系统学报, 2021, 16(6): 1039–1044. doi: 10.11992/tis.202010036 ZENG Yujing, JIANG Yong. Feature selection simultaneous localization and mapping algorithm incorporating attention and anticipation[J]. CAAI transactions on intelligent systems, 2021, 16(6): 1039–1044. doi: 10.11992/tis.202010036 [16] ZHANG N, GUPTA A, CHEN Zefeng, et al. Evolutionary machine learning with minions: a case study in feature selection[J]. IEEE transactions on evolutionary computation, 2022, 26(1): 130–144. doi: 10.1109/TEVC.2021.3099289 [17] YANG Jiaquan, CHEN Chunhua, LI Jianyu, et al. Compressed-encoding particle swarm optimization with fuzzy learning for large-scale feature selection[J]. Symmetry, 2022, 14(6): 1142. doi: 10.3390/sym14061142 [18] CHEN Ke, XUE Bing, ZHANG Mengjie, et al. Correlation-guided updating strategy for feature selection in classification with surrogate-assisted particle swarm optimisation[EB/OL]. (2021–12–13)[2022–06–01].https://ieeexplore.ieee.org/abstract/document/9647020. [19] WANG Zijia, JIAN Junrong, ZHAN Zhihui, et al. Gene targeting differential evolution: a simple and efficient method for large scale optimization[EB/OL]. (2022–06–23)[2022–06–23].https://ieeexplore.ieee.org/abstract/document/9804806. [20] ZHANG Yong, WANG Yanhu, GONG Dunwei, et al. Clustering-guided particle swarm feature selection algorithm for high-dimensional imbalanced data with missing values[J]. IEEE transactions on evolutionary computation, 2022, 26(4): 616–630. doi: 10.1109/TEVC.2021.3106975 [21] WANG Yequn, LI Jianyu, CHEN Chunhua, et al. Scale adaptive fitness evaluation-based particle swarm optimisation for hyperparameter and architecture optimisation in neural networks and deep learning[EB/OL]. (2022–06–02)[2022–06–02].https://ietresearch.onlinelibrary.wiley.com/doi/full/10.1049/cit2.12106. [22] HE Chunlin, ZHANG Yong, GONG Dunwei, et al. A multi-task bee colony band selection algorithm with variable-size clustering for hyperspectral images[EB/OL]. (2022–03–14) [2022–06–02].https://ieeexplore.ieee.org/abstract/document/9733922. [23] 陈宗淦, 詹志辉. 面向多峰优化问题的双层协同差分进化算法[J]. 计算机学报, 2021, 44(9): 1806–1823. doi: 10.11897/SP.J.1016.2021.01806 CHEN Zonggan, ZHAN Zhihui. Two-layer collaborative differential evolution algorithm for multimodal optimization problems[J]. Chinese journal of computers, 2021, 44(9): 1806–1823. doi: 10.11897/SP.J.1016.2021.01806 [24] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN’95-International Conference on Neural Networks. Perth: IEEE, 1995: 1942–1948. [25] KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm algorithm[C]//1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation. Orlando: IEEE, 1997: 4104–4108. [26] GU Shenkai, CHENG Ran, JIN Yaochu. Feature selection for high-dimensional classification using a competitive swarm optimizer[J]. Soft computing, 2018, 22(3): 811–822. doi: 10.1007/s00500-016-2385-6 [27] TRAN Binh, XUE Bing, ZHANG Mengjie. Variable-length particle swarm optimization for feature selection on high-dimensional classification[J]. IEEE transactions on evolutionary computation, 2019, 23(3): 473–487. doi: 10.1109/TEVC.2018.2869405 [28] XUE Yu, TANG Tao, PANG Wei, et al. Self-adaptive parameter and strategy based particle swarm optimization for large-scale feature selection problems with multiple classifiers[J]. Applied soft computing, 2020, 88: 106031. doi: 10.1016/j.asoc.2019.106031 [29] LUO Chuan, WANG Sizhao, LI Tianrui, et al. Large-scale meta-heuristic feature selection based on BPSO assisted rough hypercuboid approach[EB/OL]. (2022–05–12) [2022–06–02].https://ieeexplore.ieee.org/abstract/document/9773310. [30] JIAN Junrong, CHEN Zonggan, ZHAN Zhihui, et al. Region encoding helps evolutionary computation evolve faster: a new solution encoding scheme in particle swarm for large-scale optimization[J]. IEEE transactions on evolutionary computation, 2021, 25(4): 779–793. doi: 10.1109/TEVC.2021.3065659 [31] HE Xiaofei, YAN Shuicheng, HU Yuxiao, et al. Face recognition using Laplacianfaces[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(3): 328–340. doi: 10.1109/TPAMI.2005.55 [32] CAI Deng, HE Xiaofei, HAN Jiawei, et al. Orthogonal laplacianfaces for face recognition[J]. IEEE transactions on image processing, 2006, 15(11): 3608–3614. doi: 10.1109/TIP.2006.881945 [33] CAI Deng, HE Xiaofei, HAN Jiawei, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(8): 1548–1560. doi: 10.1109/TPAMI.2010.231 [34] CHEN Ke, XUE Bing, ZHANG Mengjie, et al. An evolutionary multitasking-based feature selection method for high-dimensional classification[J]. IEEE transactions on cybernetics, 2022, 52(7): 7172–7186. doi: 10.1109/TCYB.2020.3042243 [35] JING Longlong, TIAN Yingli. Self-supervised visual feature learning with deep neural networks: a survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 43(11): 4037–4058. doi: 10.1109/TPAMI.2020.2992393 [36] SARKAR P, ETEMAD A. Self-supervised ECG representation learning for emotion recognition[J]. IEEE transactions on affective computing, 2022, 13(3): 1541–1554. doi: 10.1109/TAFFC.2020.3014842 [37] HSU W N, BOLTE B, TSAI Y H H, et al. HuBERT: self-supervised speech representation learning by masked prediction of hidden units[J]. IEEE/ACM transactions on audio, speech, and language processing, 2021, 29: 3451–3460. doi: 10.1109/TASLP.2021.3122291 [38] YUAN Aihong, YOU Mengbo, HE Dongjian, et al. Convex non-negative matrix factorization with adaptive graph for unsupervised feature selection[J]. IEEE transactions on cybernetics, 2022, 52(6): 5522–5534. doi: 10.1109/TCYB.2020.3034462 [39] YOU Mengbo, YUAN Aihong, ZOU Min, et al. Robust unsupervised feature selection via multi-group adaptive graph representation[EB/OL]. (2021–11–08)[2022–06–1].https://ieeexplore.ieee.org/abstract/document/9606609. [40] ZHANG Rui, ZHANG Yunxing, LI Xuelong. Unsupervised feature selection via adaptive graph learning and constraint[J]. IEEE transactions on neural networks and learning systems, 2022, 33(3): 1355–1362. doi: 10.1109/TNNLS.2020.3042330 [41] CHANG Heng, GUO Jun, ZHU Wenwu. Rethinking embedded unsupervised feature selection: a simple joint approach[EB/OL]. (2022–05–30)[2022–06–01].https://ieeexplore.ieee.org/abstract/document/9784919. [42] SOLORIO-FERNÁNDEZ S, CARRASCO-OCHOA J A, MARTÍNEZ-TRINIDAD J F. A review of unsupervised feature selection methods[J]. Artificial intelligence review, 2020, 53(2): 907–948. doi: 10.1007/s10462-019-09682-y [43] LI Jundong, CHENG Kewei, WANG Suhang, et al. Feature selection: a data perspective[J]. ACM computing surveys, 2018, 50(6): 94.




















 下载:
下载: