A causal probabilistic inference classification algorithm based on factor space theory
-
摘要: 机器学习方法与因果推理结合能极大地提升方法性能。为探究因果概率正逆向推理的分类效果,基于因素空间理论下的因素概率论,利用条件概率,研究正向因素概率推理原理及模型并提出正向因果概率推理分类法(forward causal probabilistic inference classification algorithm, FCPIC)和简化条件的可取度分类法;研究逆向因素概率推理原理及模型并结合贝叶斯网络提出逆向因果概率推理分类法(reverse causal probabilistic inference classification algorithm, RCPIC)。将3个分类算法与KNN(K-Nearest neighbor)和SVM(support vector machine)算法进行实例对比验证,研究结果表明:FCPIC算法、可取度分类算法和RCPIC算法简单有效、具有可行性和实用性,且可取度分类法和RCPIC算法性能优于SVM和KNN算法,FCPIC算法对实际数据预测中必要类有查全需求的情况更优。研究结论丰富了因素空间的理论研究和应用价值。Abstract: The integration of machine learning techniques with causal reasoning can significantly enhance method performance. To investigate the classification effect of positive and reverse causal probability inferences, we rely our study on factor probability theory under factor space theory. Using conditional probability, we examined the principles and model of positive-factor probabilistic reasoning. This led to the proposal of the forward causal probabilistic inference classification algorithm (FCPIC) and a desirability classification method of simplified conditions. We also explored the principles and model of inverse factor probabilistic inference, which resulted in the proposal of the reverse causal probabilistic inference classification algorithm (RCPIC) along with a Bayesian network. The three classification algorithms were compared with the K-nearest neighbor (KNN) and support vector machine (SVM) algorithms. The results demonstrate that the FCPIC algorithm, the desirability classification algorithm, and the RCPIC algorithm are simple, effective, feasible, and practical. The performance of the desirability classification method and RCPIC algorithm surpasses those of both SVM and KNN. Additionally, the FCPIC algorithm is better when dealing with cases where the necessary classes in actual data prediction have full demand. These research findings contribute to the theoretical research and application value of factor space.
-
1982年,汪培庄等[1]提出了因素空间,用来剖析事物的因果联系,创建了因素空间理论[2],是国际智能数学最早同时问世的三个学派之一。相关学者扩展了因素空间理论,并作了应用研究[3-14],其中因素之间的因果关系分析[5-6]为人工智能、数据挖掘提供了重要工具,例如,刘海涛等[8]为因果分析提出了推理模型;曾繁慧等[9]用因果推理算法与云模型相结合得到连续变量的决策树算法,这些研究都体现了一个重要的思想:背景关系决定因果推理。
因果推理在机器人技术研究中发挥了重要作用[12],因果推理分为从因到果和从果到因两个方面,其中,从因到果是一种正向思维,从果到因则是一种逆向思维。如果把“推理”二字泛化,从因到果可以叫做正向推理,从果到因也可以叫做逆向推理。正向推理是从事物的表面出发,逆向推理是智能问题求解的普遍形式。智能问题是如何行动以达到目标,目标就是所希望达到的结果,例如,要使身体强健,首先就要反问:怎样才能使身体强健?身体强健是要达到的结果。在因素空间中,正向因果分析的条件因素是因,结果因素是果,而逆向因果分析是从果倒过来求因,也就是说,此时的结果因素是“因”,条件因素是“果”。
正向思维更专注表面的东西,追求的是短期的解决方案,而逆向思维可能更接近问题的本质,以找到恰当的方案,从长期来看会更有效果,所以正向和逆向推理思维都具有研究意义。 Reichenbach等[15]试图在概率术语中定义因果关系。Hájek等[16]在概率因果关系一章中使用因果贝叶斯网表示因果关系,加强了概率到因果关系的推断。Sprenger[17]给出了因果强度作为差异制造的概率理论的公理化基础,Faghihi等[18]认为概率模糊逻辑是在机器中实现因果关系的更好选择,并将因果关系整合到机器中的理论框架,这是创建可解释人工智能的关键一步。本文基于因素空间理论下的因素概率论,利用条件概率,首先研究了正向因素概率推理模型,结合贝叶斯网络[19],得到正向因果概率推理分类法(forward causal probabilistic inference classification algorithm,FCPIC);并根据正向因果推理,提出相的可取度,得到可取度分类法;其次根据逆向思维,提出逆向因素概率推理原理,建立逆向因素概率推理模型,结合贝叶斯网络,提出逆向因果概率推理分类法;最后进行实例验证。
1. 预备知识
1.1 可测因素概率场
因素是描述万事万物的一把钥匙,可以理解为广义的基因。基因是生物的质根,就像每个基因串出一列生物形态一样,每个因素串出事物的一列相或属性。例如颜色这个因素就可以串出红、黄、蓝等性状(相)。从数学观点来看,因素是一种特殊的映射,把对象映射到其相上。因素空间[1-2]相关基础理论如下:
定义1 设非空集合D为论域,I为论域上一类性状的集合,从论域D到I的一个满射f:
$$ f:D \to I $$ 称为D上一个因素,论域D就是一群实体或对象的集合,叫做f的定义域。
定义2 (性状空间)记
$$ I = I(f) = \left\{ {{a_1},{a_2}, \cdots , {a_k}} \right\} $$ 叫做f的性状空间(或相域),其中各相彼此不同,或记作
$X(f)$ 。将f1, f2, ···, fn的性状空间$I(f)$ 记为$I({f_j}) = \left\{ {a_1^j, a_2^j, \cdots , a_k^j} \right\}(j = 1, 2, \cdots , n)$ 。相域
$I(f) = \left\{ {{a_1},{a_2} \cdots , {a_k}} \right\}$ ,记$$ [a_{t}]={d∈D|f(d)=a_{t}}, t=1, 2, \cdots , k $$ 叫做相的反馈外延。
定义3 给定因素空间
$ (D, F) $ ,如果f1, f2, ···, f n∈F两两的析取为零因素,${f_i} \vee {f_j} = 0(1 \leqslant i \ne j \leqslant n)$ ,则$$ I({f_1} \wedge{f_2} \wedge \cdots \wedge {f_n}) = I({f_1}) \times I({f_2}) \times \cdots \times I({f_n}) $$ 称
$ (D, F) $ 是一个简单因素空间。定义4 (背景关系)给定因素空间
$(D, F)$ ,记I=I(f1)×I(f2)×···×I(fn),$R=c=(c_{1}, c_{2}, \cdots, c_{n})\in I|\exists $ $ d\in D;f_{1}(d)=c_{1}, f_{2}(d)=c_{2}, \cdots, f_{n}(d)=c_{n}$ 称R为f1, f2, ···, fn的背景关系或背景集。其中,因素f1, f2, ···, fn互不相关。
定义5 考虑因素
$ F = \left\{ {{f_1}, {f_2}, \cdots , {f_n}} \right\} $ ,性状空间:$$ I(F) = I({f_1}) \times I({f_2}) \times \cdots \times I({f_n}) $$ 若对任意c={c1, c2, ···, cn}∈I(F)都有[c]=F−1(c)={d∈D|F(d)=c},则称F是可测因素。即f1, f2, ···, fn∈F可测,将I(F)记为IF。
因素空间可测是解决不确定背景关系的基础。因素可测时,可以将每个因素都理解为随机变量,将每个因素中的各相理解为随机事件。例如,射击靶子的结果ξ具有相域I(ξ)={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}。其中,因素为随机变量ξ,该因素的11个相为随机事件,即环数。
定义6 称
$\psi = (D, {I_F})$ 为因素空间上所定义的可测空间,简称可测因素空间,对于定义于其上的概率测度p,称$(D, {I_F}, p)$ 为因素空间上所定义的概率场,简称可测因素概率场[20-21]。1.2 因果分析表
一个以对象为行(即论域),以条件因素和结果因素(最后一列)为列,表中第i行第j列元素是第i对象在第j因素下的状态,称这个表为因果分析表,表头记作
$$ (D, {f_1},{f_2}, \cdots , {f_n};g) $$ 因果分析表的每一行是一个对象在因素空间中的坐标;一张因素分析表就是由有限个对象在因果空间中所形成的一个背景样本,其样式见表1。
表 1 因果分析表Table 1 Causal analysis tableD F$ \rightarrow $g f1 f2 ··· fn g d1 f1(d1) f2(d1) ··· fn(d1) g(d1) d2 f1(d2) f2(d2) ··· fn(d2) g(d2) $ \vdots $ $ \vdots $ $ \vdots $ ··· $ \vdots $ $ \vdots $ dm f1(dm) f2(dm) ··· fn(dm) g(dm) 1.3 贝叶斯网络
贝叶斯网络是一种概率图模型,是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓扑结构是一个有向无环图。
贝叶斯网络的有向无环图中:节点(圈)表示随机变量;箭头表示条件依赖,连接有因果关系、非条件独立的变量或命题。若两个节点间以单箭头连接在一起,其中一个节点是“因”,另一个节点是“果”,则两节点产生一个条件概率值。
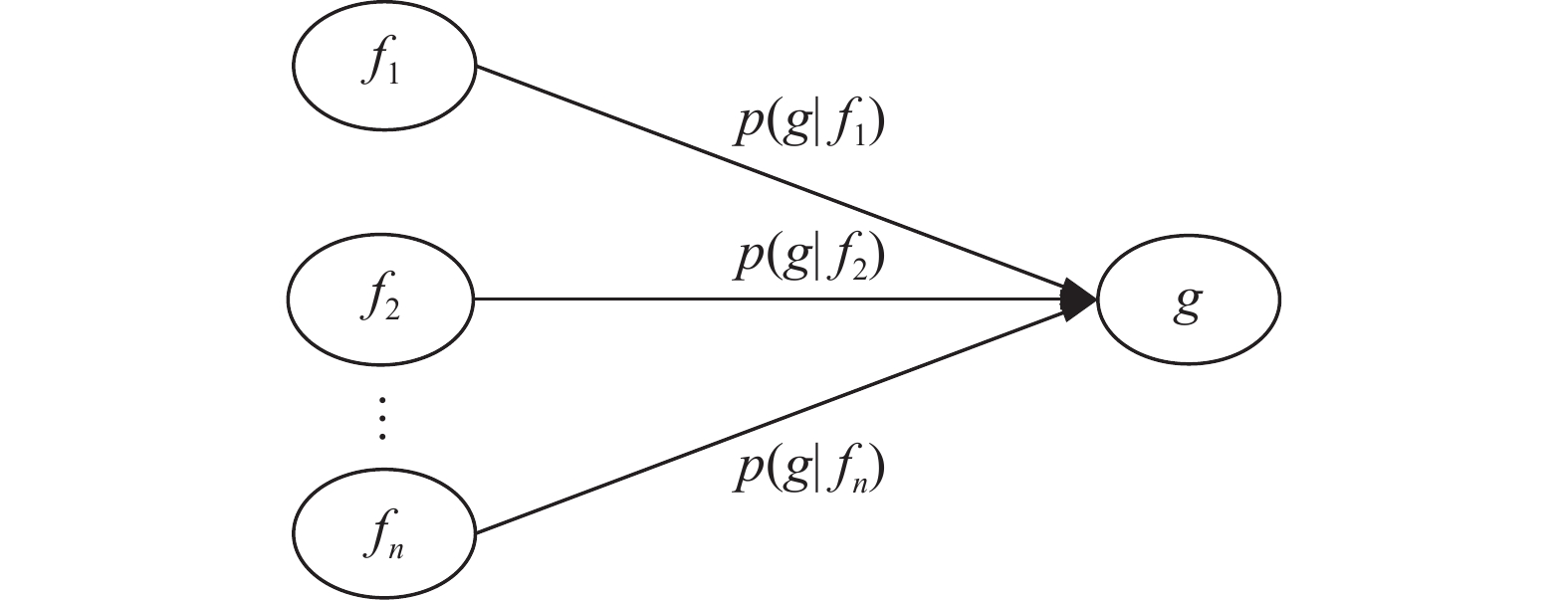
例如,假设节点A直接影响到节点B,即A→B,则用从A指向B的箭头建立结点A到结点B的有向弧(A, B),权值(连接强度)用条件概率p(B|A)来表示,如图1所示。
根据图1可得p(AB)=p(B|A)p(A)。
简言之,将研究系统中所涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
2. 正向因果概率推理分类法
表 2 因果分析简表Table 2 Causal analysis tableD F$ \rightarrow $g f1 f2 … fn g d c1 c2 … cn gi 由表2可得:
条件因素F={f1, f2, ···, fn},
$I({f_j}) = \left\{ a_1^j, a_2^j, \cdots , a_k^j \right\}(j = 1, 2, \cdots , n)$ 。结果因素g={g1, g2, ···, gs},当s=2时,称为二分类问题,当s>2时,则称为多分类问题。
对象d(即样本)为一个n维向量,记d=[c1 c2 ··· cn],其中c1, c2, ···, cn分别表示对象d在f1, f2, ···, fn下对应的相。如
$I({f_1}) = \left\{ {a_1^1,a_2^1, \cdots , a_k^1} \right\}$ ,则${c_1} = a_t^1(t = 1, 2, \cdots , k)$ 。2.1 正向因素概率推理
2.1.1 条件概率
设A, B为两个事件,且p(B)>0,则在事件B发生的条件下,事件A发生的条件概率为
$$ p(A|B){\text{ = }}\dfrac{{p(AB)}}{{p(B)}} $$ 当A和B事件相互独立时,p(AB)=p(A)p(B)。条件概率包含了正向与逆向思维。当事件A为结果,事件B为条件时,则为正向分析,即正向推理;当事件A为条件,事件B为结果时,则为逆向分析,即逆向推理。
2.1.2 正向因素概率推理原理
推理有确定性推理和不确定性推理之分。例如,“若太阳升起,则天会亮”,这是一个推理句,它是确定性推理句,其真值(即正确率)是百分之百100%=1;“若同时掷两颗骰子,则两颗骰子点数之和大于2”,这是不确定性推理句,它多半是对的,但也有不对的时候。不确定性推理被概率论提升到科学的高度,因为这句话的正确率可以非常精确地表达成35/36!
在因素概率论中,条件概率就是不确定性推理句的真值:
$$ p(B|A)=t(A→B)(t表示真值) $$ 定义7 在因素空间(D, F)中,由已知的条件因素
$ {f_1}, {f_2}, \cdots , {f_n} $ 寻找结果类别g的过程,即某对象由已知各因素fj(j=1, 2, ···, n)所对应的相寻求结果类别的过程称为由因寻果。2.1.3 正向因素概率推理模型
正向推理是有目标的求索。
给定事件列a(a为因素对应的相)和结果类g1, g2, …, gs,已知条件概率
$p({g_i}|a)$ 。若a已经发生,要问g类事件中,哪个事件最有可能发生?这就是正向因素概率推理。
定理1 给定事件列a和结果类g1, g2, …, gs,已知结果g类事件中每个事件在a下的条件概率为
$p({g_i}|a)$ ,若$$ i^* = {\rm{argmax}}\left\{ {p\left( {{g_i}|a} \right)|i = {\text{1}}, 2, \cdots , s} \right\} $$ 则事件
$ {f_1} $ 最有可能发生。按照条件概率的定义,证明是显然的。
2.2 正向因果概率推理分类法——FCPIC
根据正向因素概率推理原理,利用正向因素概率推理模型,下面研究正向因果概率推理分类法(FCPIC)。
假设1 因素空间(D, F)中因素f1, f2, ···, fn之间相互条件独立。
假设2 因素f1, f2, ···, fn对应的各相转换的数据均是离散型数据。
正向因素概率推理分类是由因寻果,即由已知条件寻找结果,也即某对象由已知各因素fj (j=1, 2, ···, n)所对应的相寻求结果类别。
1)正向因果概率推理分类法。
在因素空间中,条件因素f1, f2, ···, fn与结果因素g对应的正向贝叶斯网络可由图2表示。
当分析对象d时,d=[c1 c2 ··· cn],即I(f1)=c1, I(f2)=c2, ···, I(fn)=cn有
$$ \begin{gathered} p(g|I({f_1})) = p(g|I({f_1}) = {c_1}){\text{ }} \\ p(g|I({f_2})) = p(g|I({f_2}) = {c_2}) \\ {\text{ }}\qquad\qquad\quad \vdots \\ p(g|I({f_n})) = p(g|I({f_n}) = {c_n}) \\ \end{gathered} $$ 为了简便,简记为
$$ p(g|{c_1}), p(g|{c_2}), \cdots , p(g|{c_n}) $$ (1) 由图2的正向贝叶斯网络可得
$$ \begin{gathered} p(g_{i}, c_{1}, c_{2}, \cdots, c_{n})=p(c_{1}) \times p(c_{2}) \times \cdots \times\\ p(c_{n}) \times p(g_{i}|c_{1}) \times p(g_{i}|c_{2}) \times \cdots \times p(g_{i}|c_{n}) \end{gathered} $$ (2) 由正向推理模型和式(2)可得
$$ p({g_i}{\text{|}}{c_1}, {c_2}, \cdots , {c_n}) = \dfrac{{p({g_i}, {c_1}, {c_2}, \cdots , {c_n})}}{{p({c_1}, {c_2}, \cdots , {c_n})}} = $$ $$ \begin{gathered} (p({c_1}) \times p({c_2}) \times \cdots \times p({c_n}) \times p({g_i}|{c_1}) \times p({g_i}|{c_2}) \times \\ \cdots \times p({g_i}|{c_n}))/ p({c_1}) \times p({c_2}) \times \cdots \times p({c_n}){\text{ }} \end{gathered} $$ 即
$$ p({g_i}{\text{|}}d) = \prod\limits_{j = 1}^n {p({g_i}|{c_j})},\;\;i = 1, 2, \cdots , s $$ (3) 称式(3)是正向因果概率推理分类公式,表示对象d为结果gi时发生的可能性。
式(3)中,cj表示对象d在第j个因素上的相取值;
$ p({g_i}|{c_j}) = \dfrac{{|{D_{{g_i}, {c_j}}}|}}{{|{D_{{c_j}}}{\text{|}}}} $ ,其中$ |{D_{{g_i}, {c_j}}}| $ 表示在因素$ {f}_{j}相 值为{c}_{j} $ 的训练集中类别为gi的样本数量,$ {\text{|}}{D_{{c_j}}}{\text{|}} $ 表示D中$ {f}_{j}相值为{c}_{j} $ 的样本数量。设N(d,
${g_i^*}$ )为对象d的最终判定类别,则正向因果概率推理分类公式为$$ N(d, {g_i^*}) = {\rm{argmax}}\prod\limits_{j = 1}^n {p({g_i}|{c_j})},\;\; i = 1, 2, \cdots , s $$ (4) 正向因果概率推理分类法是通过计算对象在不同结果类别下发生的可能性来达到预测结果分类的目的。
2)正向因果概率推理分类公式的修正。
如果
$ {\text{|}}{D_{{g_i}, {c_j}}}{\text{|}} = 0 $ ,即cj为结果类gi的数量为0,根据式(3),不论其他因素的相如何,对于这一结果类的对象发生概率值都为0。为避免这种情况,提出了解决办法,对其进行“平滑”处理,使用“拉普拉斯修正”法:$$ p({g_i}|{c_j}) = \dfrac{{{\text{|}}{D_{{g_i}, {c_j}}}{\text{|}} + 1}}{{{\text{|}}{D_{{c_j}}}{\text{| + |}}{N_g}{\text{|}}}} $$ (5) 式中|Ng|表示研究系统的结果类别个数。
利用修正的正向因果概率推理分类法解决例1问题。
例1 电风扇质量检测结果的因果分析见表3。其中,f1为扇叶数量,f2为每分钟转速,f3为散热性能,g为检测结果。
表 3 电风扇质量因果分析表Table 3 Electric fan quality causal analysis tableD F→g f1 f2 f3 g d c1 c2 c3 gi d1 1 3 1 2 d2 1 2 3 2 d3 2 1 3 2 d4 2 1 1 1 d5 2 2 1 1 d6 2 3 2 2 d7 2 1 2 1 d8 1 1 1 1 d9 2 3 1 2 d10 1 2 2 2 I(f1)={五扇叶, 七扇叶}=
$ \left\{ {a_1^1, a_2^1} \right\} $ ={1, 2};I(f2)={高速, 中速, 低速}=
$ \left\{ {a_1^2, a_2^2, a_3^2} \right\} $ = {1, 2, 3};I(f3)={好, 中, 差}=
$ \left\{ {a_1^3, a_2^3, a_3^3} \right\} $ ={1, 2, 3};I(g)={好, 差}=
$\left\{ {{g_1}, {g_2}} \right\}$ ={1, 2}。利用修正的正向因果概率推理分类公式,在
$j = 1, \; i = 1, 2$ 时,即因素为f1,对g1=1,g2=2的计算结果分别为①
${c_1} = 1, p({g_1}|{c_1}) = \dfrac{{|{D_{{g_1}, {c_1}}}| + 1}}{{|{D_{{c_1}}}| + |{N_g}|}} = \dfrac{{1 + 1}}{{4 + 2}}{\text{ = }}\dfrac{2}{6} $ ;$p({g_2}|{c_1}) = \dfrac{{|{D_{{g_2}, {c_1}}}| + 1}}{{|{D_{{c_1}}}| + |{N_g}|}} = \dfrac{{3{\text{ + }}1}}{{4 + 2}}{\text{ = }}\dfrac{4}{6}$ 。②
$ {c_1} = 2, p({g_1}|{c_1}) = \dfrac{{3{\text{ + }}1}}{{6{\text{ + }}2}}{\text{ = }}\dfrac{4}{8} $ ;$ p({g_2}|{c_1}) = \dfrac{{3{\text{ + }}1}}{{6{\text{ + }}2}}{\text{ = }}\dfrac{4}{8} $ 。以此类推,计算过程省略,针对d1:
$$ N({d_1}) = \left[ {\dfrac{2}{6} \times \dfrac{1}{5} \times \dfrac{4}{7}, } \right.\left. {\dfrac{4}{6} \times \dfrac{4}{5} \times \dfrac{3}{7}} \right]{\text{ = }}\left[ {\dfrac{4}{{105}}, \dfrac{8}{{35}}} \right] $$ 即d1发生时,结果为g2的可能性更大,所以将d1判定为g2类。
3. 可取度分类法
当
$ {\text{|}}{D_{{g_i}, {c_j}}}{\text{|}} = 0 $ 时,利用式(3)求得对象的这一结果类概率必为0,进而影响分类预测结果的准确性,为了避免这种情况,除了平滑处理外,运用正向推理思想,考虑各因素的各相对各结果类的影响程度作为分类标准,给出相的可取度,提出适用范围更广的可取度分类法。3.1 相对结果因素的可取度
定义8 (相可取度)给定一个条件因素fj及该因素所取的一个状态a,记[a]={d|I(fj(d))=a},对结果因素的状态gi,使得[gi]={d|I(g(d))=gi}
$ {\text{|}}{D_{{g_i}}}{\text{|}} $ [a](i=1, 2, ···, s),则称[a]为gi的一个单可取相。结果类为gi的相a所占行数h与gi所占的行数|$ {\text{|}}{D_{{g_i}}}{\text{|}} $ |之比称为a对结果gi的可取度,记为q(a, gi)=h/$ {\text{|}}{D_{{g_i}}}{\text{|}} $ 。相可取度是由条件因素对结果因素的正向推理,因此可称为由因寻果。
3.2 可取度分类方法
根据相可取度定义,引申为对象可取度。
定义9 对于一个对象d,d=(c1, c2, ···, cn),结果因素的状态为gi。将c1, c2, ···, cn对结果类gi的可取度之和称为对象d对结果类gi的可取度。
定理2 给定事件列a1, a2, ···, ak和结果类g1, g2, ···, gs,已知a1, a2, ···, ak对结果g类事件的可取度q(aq, gi),若
$$ {a_{q*}} = {\rm{argmax}}\dfrac{{{\text{|}}{a_q} \cap {g_i}{\text{|}}}}{{{\text{|}}{D_{{g_i}}}{\text{|}}}},\;\;i = 1, 2, \cdots , s, q = 1, 2, \cdots , k $$ (6) 则事件
$ {a_{q*}} $ 最有可能发生。根据定理2,得到可取度分类公式为
$$ q(d, {g_i^*}) = {\rm{argmax}}\sum\limits_{j = 1}^n {\dfrac{{{\text{|}}{c_j} \cap {g_i}{\text{|}}}}{{{\text{|}}{D_{{g_i}}}{\text{|}}}}} ,\;\;i = 1, 2, \cdots , s, j = 1, 2, \cdots , n $$ (7) 式中:
$ {\text{|}}{c_j} \cap {g_i}{\text{|}} $ 表示相cj为结果类gi所占的行数,${g_i^*}$ 为对象d的最终判定类别。可取度分类法是通过计算对象在不同结果类别下的可取度大小,从而判别d的类别。
注:可取度分类法不需要条件因素相互条件独立,因此该算法适用范围更广。
例2 利用可取度分类法解决例1问题。
首先计算所有条件因素的相可取度,以因素f1扇叶数量为例,将论域D分为2类:
$a_1^1$ =五扇叶:{d1, d2, d8, d10},$a_2^1$ =七扇叶:{d3, d4, d5, d6, d7, d9}。1)
$a_1^1$ 类中对象对应的结果有好有坏,可继续划分:五扇叶
$a_1^1$ |→g1:{d8},五扇叶
$a_1^1$ |→g2:{d1, d2, d10}。相
$a_1^1$ 五扇叶对结果g1的可取度为q($a_1^1$ , g1)=h/$ |{D_{{g_1}}}| $ =1/4(h=1);相
$a_1^1$ 五扇叶对结果g2的可取度为q($a_1^1$ , g2)=h/$ |{D_{{g_2}}}| $ =3/6(h=3)。2)
$ |{D_{{g_1}}}| $ 类中对象对应的结果有好有坏,可继续划分:七扇叶
$a_2^1$ |→g1:{d4, d5, d7},七扇叶
$a_2^1$ |→g2:{d3, d6, d9}。相
$a_2^1$ 七扇叶对结果g1的可取度为q($a_2^1$ , g1)=h/$ |{D_{{g_1}}}| $ =3/4(h=3);相
$a_2^1$ 七扇叶对结果g2的可取度为q($a_2^1$ , g2)=h/$ |{D_{{g_2}}}| $ =3/6(h=3)。以此类推,计算过程省略,针对d1:
$$ q({d_1}) = \left[ {\dfrac{1}{4} + \dfrac{0}{4} + \dfrac{3}{4}, \dfrac{3}{6} + \dfrac{3}{6} + \dfrac{2}{6}} \right] = \left[ {1, \dfrac{4}{3}} \right] $$ 即对象d1对结果类g1的可取度为1,对结果类g2的可取度为4/3,因此对象d1判别为g2类。
4. 逆向因果概率推理分类法
正向推理是无目标的求索,目标锁定时,可进行逆向推理,因此本节探讨逆向因素概率推理原理、逆向因素概率推理模型以及逆向因果概率推理分类法。
4.1 逆向因素概率推理
2.1节是由已知的条件a寻求结果g,下面要由已知的结果g返回寻找条件a。
4.1.1 逆向因素概率推理原理
给定事件列a1, a2, ···, ak以及结果列g,其中a1, a2, ···, ak是某因素的全相列。已知条件概率p(g|aq)(q=1, 2, ···, k),现在要反过来问:在g发生的条件下哪个事件最有可能发生?
若
$ q* = {\rm{argmax}}\left\{ {p\left( {g|{a_q}} \right)|q = {\text{1}}, 2, \cdots , k} \right\} $ ,则得出结论aq*最有可能发生。该结论不一定成立,因为从p(g|aq*)最大推出p(aq*|g)最大是没有根据的。例如,一个班里10名女生,其中4名数学得优,p(g|a1)=2/5,有20名走读生,有5名得优,p(g|a2)=1/4,p(g|a1)高于p(g|a2);但全班共8名得优,p(a1|g)=4/8,p(a2|g)=5/8。p(a1|g)低于p(a2|g),这就是一个反例。定义10 在因素空间
$(D, F)$ 中,由已知的结果类别g寻找条件因素f1, f2, ···, fn的过程,即由已知结果类别寻求某对象各因素fj(j=1, 2, ···, n)所对应的相的过程称为由果寻因。4.1.2 逆向因素概率推理模型
一般来讲,最有可能发生的事件是谁?给定事件列a1, a2, ···, ak、结果列g,已知g类事件的概率
$ q* = {\rm{argmax}}\left\{ {p\left( {{a_q}|g} \right)p(g)|q = {\text{1}}, 2, \cdots , k} \right\} $ 以及条件概率$ q* = {\rm{argmax}}\left\{ {p\left( {{a_q}|g} \right)p(g)|q = {\text{1}}, 2, \cdots , k} \right\} $ ,现在g已经发生,最有可能发生的事件是谁?根据条件概率公式,可知
$$ p({a_q}|g) = \dfrac{{p(g, {a_q})}}{{p(g)}} $$ (8) 定理3 给定事件列a1, a2, ···, ak、结果列g,已知g类事件的概率
$q* = {\rm{argmax}}\left\{ p\left( {{a_q}|g} \right)p(g)|q = {\text{1}}, \right. \left.2, \cdots , k \right\}$ 以及条件概率$ p({a_q}|g) $ ,g发生时,若$$ q* = {\rm{argmax}}\left\{ {p\left( {{a_q}|g} \right)p(g)|q = {\text{1}}, 2, \cdots , k} \right\} $$ (9) 则最有可能发生的事件是
${a_{q*}}$ 。按照条件概率的定义,证明是显然的。
4.2 逆向因果概率推理分类法——RCPIC
根据逆向因素概率推理原理,利用逆向因素概率推理模型,下面研究逆向因果概率推理分类法RCPIC。
假设1 因素空间(D, F)中因素f1, f2, ···, fn之间相互条件独立。
假设2 因素f1, f2, ···, fn对应的各相转换的数据均是离散型数据。
逆向因素概率推理分类法是由果寻因,即由已知结果寻找条件,也即由结果类别寻求对象各因素fj(j=1, 2, ···, n)所对应的相。
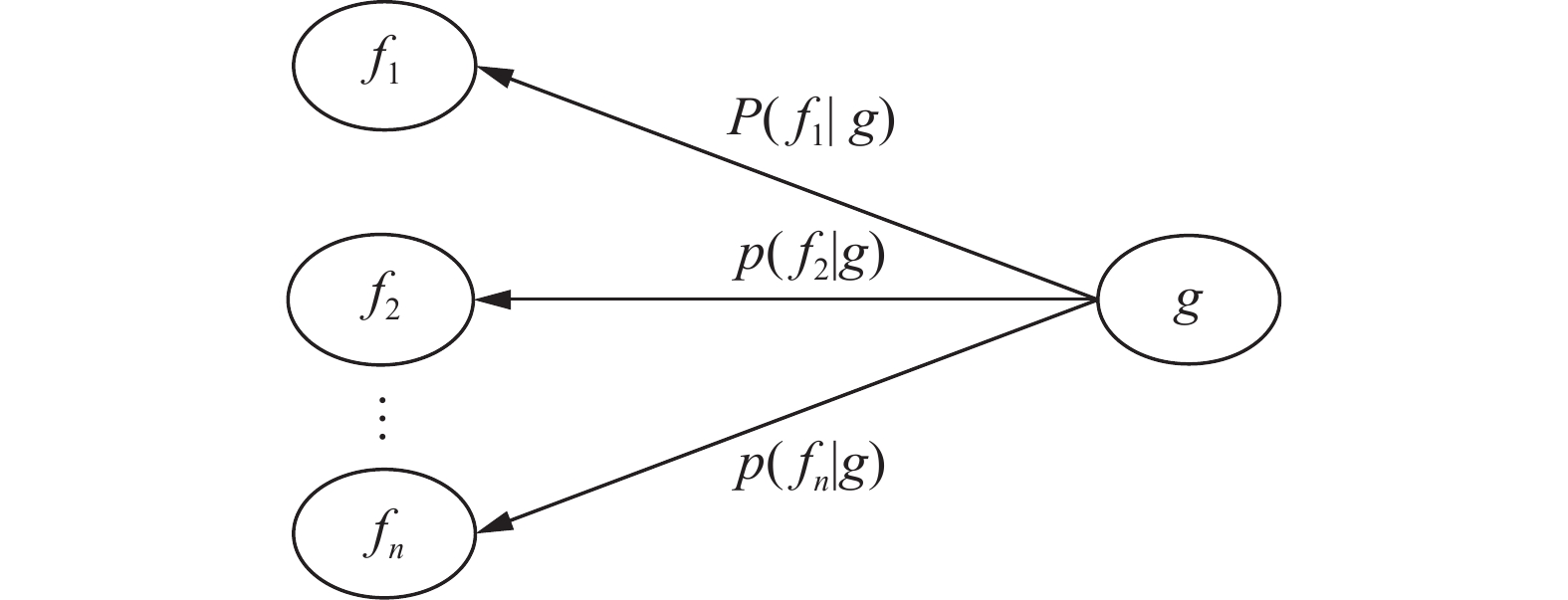
在因素空间中,条件因素f1, f2, ···, fn与结果因素g对应的逆向贝叶斯网络可由图3表示。
根据表2,分析对象d时,因d=[c1 c2 ··· cn], 即I(f1(d))=c1, I(f2(d))=c2, ···, I(fn(d))=cn有
$$ \begin{gathered} p(I({f_1})|g) = p(I({f_1}) = {c_1}|g){\text{ }} \\ p(I({f_2})|g) = p(I({f_2}) = {c_2}|g) \\ {\text{ }}\qquad\qquad\quad \vdots \\ p(I({f_n})|g) = p(I({f_n}) = {c_n}|g) \\ \end{gathered} $$ 为了简便,简记为
$$ p({c_1}|g), p({c_2}|g), \cdots , p({c_n}|g) $$ (10) 由图3的逆向贝叶斯网络可得
$$ \begin{aligned} & p(g_{i}, c_{1}, c_{2}, \cdots, c_{n})=p(g_{i})\times p(c_{1}|g_{i})\times p(c_{2}|g_{i}) \times \cdots \times p(c_{n}|g_{i})\\ & \end{aligned} $$ (11) 由逆向推理模型和式(11)可得
$$ \begin{gathered} p({c_1}, {c_2}, \cdots , {c_n}|{g_i})p({g_i}) = \dfrac{{p({g_i}, {c_1}, {c_2}, \cdots , {c_n})}}{{p({g_i})}}p({g_i}) =\\ p(g_{i})\times p(c_{1}|g_{i}) \times p(c_{2}|g_{i}) \times \cdots \times p(c_{n}|g_{i}) \end{gathered}$$ 即
$$ p(d|{g_i})p({g_i}) = p({g_i})\prod\limits_{j = 1}^n {p({c_j}|{g_i})} ,\;\; i = 1, 2, \cdots , s $$ (12) 称式(12)是逆向因果概率推理分类公式,为结果g发生时对象d发生的可能性。
式(12)中,cj表示对象d在第j个因素上的相取值。
$ p({g_i}) = \dfrac{{|{D_{{g_i}}}|}}{{|D|}} $ ,其中$ |D| $ 为研究的论域中总对象数量,$ |{D_{{g_i}}}| $ 为研究的论域中结果类别为gi的对象数量。$ p({c_j}|{g_i}) = \dfrac{{|{D_{{c_j}, {g_i}}}|}}{{|{D_{{g_i}}}|}} $ ,其中$ |{D_{{c_j}, {g_i}}}| $ 表示在研究的论域中,结果类别为gi时,因素${f_j} = {c_j}$ 的对象数量。设
$T(d, g_i^*)$ 为对象d的最终判定类别,则逆向因果概率推理分类法的表达式为$$ T({\boldsymbol{d}}, g_i^*) = {\rm{argmaxp}}({g_i})\prod\limits_{j = 1}^n {p({c_j}|{g_i})} ,\;\; i = 1, 2, \cdots , s $$ (13) 逆向因果概率推理分类法是通过计算在不同结果类别下对象发生的可能性来达到预测结果分类的目的。
同理,在类别为gi时,如果出现cj的样本个数是0, 即
$ |{D_{{c_j}, {g_i}}}| = 0 $ 的情况,根据式(12)不论其他因素相如何,那么对于类别gi的选择概率值都会是0。为避免这种情况,可进行“平滑”处理,使用“拉普拉斯修正”法,计算公式为$$ p({c_j}|{g_i}) = \dfrac{{|{D_{{c_j}, {g_i}}}| + 1}}{{|{D_{{g_i}}}| + |{N_j}|}} $$ (14) 式中:|Nj|表示因素fj的类别个数,如f1的相取值包括1和2,那么此时的|N1|=2。
例3 利用逆向因果概率推理分类法解决例1问题。
$$ p({g_1}) = \dfrac{{|{D_{{g_1}}}|}}{{|D|}} = \dfrac{4}{{10}} \text{,} p({g_2}) = \dfrac{{|{D_{{g_2}}}|}}{{|D|}} = \dfrac{6}{{10}} $$ $ i = 1, j = 1, 2, 3 $ 时,即$ g{}_1{\text{ = }}1 $ 时对各条件因素的计算结果分别为①
$ {c_1} = 1, p({c_1}|{g_1}) = \dfrac{{|{D_{{c_1}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_1}|}} = \dfrac{{1 + 1}}{{4 + 2}} = \dfrac{2}{6} $ ${c_1} = 2, p({c_1}|{g_1}) = \dfrac{{|{D_{{c_1}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_1}|}} = \dfrac{{3 + 1}}{{4 + 2}} = \dfrac{4}{6} $ ②
$ {c_2} = 1, p({c_2}|{g_1}) = \dfrac{{|{D_{{c_2}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_2}|}} = \dfrac{{3 + 1}}{{4 + 3}} = \dfrac{4}{7} $ $ {c_2} = 2, p({c_2}|{g_1}) = \dfrac{{|{D_{{c_2}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_2}|}} = \dfrac{{1 + 1}}{{4 + 3}} = \dfrac{2}{7} $ $ {c_2} = 3, p({c_2}|{g_1}) = \dfrac{{|{D_{{c_2}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_2}|}} = \dfrac{{0 + 1}}{{4 + 3}} = \dfrac{1}{7} $ ③
$ {c_3} = 1, p({c_3}|{g_1}) = \dfrac{{|{D_{{c_3}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_3}|}} = \dfrac{4}{7} $ $ {c_3} = 2, p({c_3}|{g_1}) = \dfrac{{|{D_{{c_3}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_3}|}} = \dfrac{2}{7} $ $ {c_3} = 3, p({c_3}|{g_1}) = \dfrac{{|{D_{{c_3}, {g_1}}}| + 1}}{{|{D_{{g_1}}}| + |{N_3}|}} = \dfrac{1}{7} $ 以此类推,计算过程省略,针对d1:
$$ T({d_1}) = \left[ {\dfrac{4}{{10}} \times \dfrac{2}{6} \times \dfrac{1}{7} \times \dfrac{4}{7}, \dfrac{6}{{10}} \times \dfrac{4}{8} \times \dfrac{4}{9} \times \dfrac{3}{9}} \right] = \left[ {\dfrac{8}{{735}}, \dfrac{2}{{45}}} \right] $$ 即与结果g1相比,结果为g2时,d1发生的可能更大,所以将d1判定为g2类。
注:本文提出FCPIC、RCPIC、可取度分类算法的时间复杂度均为O(mns)。
KNN的算法复杂度为O(mn), SVM的算法复杂度为O(m2)~O(m3)。
其中m是训练集中对象个数,n是条件因素的个数,s是结果因素的相的个数。有O(mn)< O(mns)< O(m2)。
5. 实例应用
为了验证FCPIC、RCPIC、可取度分类算法在实际数据中的预测性能,使用UCI数据库中的3个分类数据集并进行学习,与KNN和SVM分类算法分别进行结果和时间复杂度对比。
各数据集信息如下:
Heart数据集是诊断是否患有心脏病,患病为正类,不患病为负类。
Breast cancer数据集是通过肿瘤的团块厚度、细胞大小的均匀性、细胞形状的均匀性等来判断是恶性还是良性,恶性为正类,良性为负类。
Australian数据集是澳大利亚信贷批准,批准为正类,不批准为负类。
各数据集的具体结构见表4。
表 4 数据集信息Table 4 Dataset information数据集 样本数 因素个数 结果类别 正类 负类 Heart 297 13 2 150 120 Breast cancer 683 9 2 239 444 Australian 690 14 2 383 307 分别对5种分类算法采用十折交叉验证,得到准确率Acc(accuracy)、精确率Pre(precision)、召回率Rec(recall)、F1和AUC,其中精确率表示识别为正类的对象中正确的比例,召回率表示正类对象被识别出的比例,实验结果见表5。
表 5 实验结果对比Table 5 Comparison of experimental results数据集 指标 FCPIC RCPIC 可取度
分类法KNN SVM Heart Acc 0.8148 0.863 0.8704 0.8074 0.8481 Pre 0.7632 0.8228 0.8365 0.8365 0.8717 Rec 0.9667 0.8833 0.8833 0.8133 0.8533 F1 0.8528 0.8511 0.8581 0.8243 0.8620 AUC 0.9144 0.9411 0.9467 0.9115 0.9272 Breast cancer Acc 0.9809 0.9839 0.9252 0.9649 0.9589 Pre 0.9757 0.9977 0.9081 0.9752 0.9052 Rec 0.9707 0.9775 0.9865 0.9243 0.9875 F1 0.9727 0.9874 0.9454 0.9472 0.9438 AUC 0.9882 0.9969 0.9872 0.9805 0.9879 Aust-
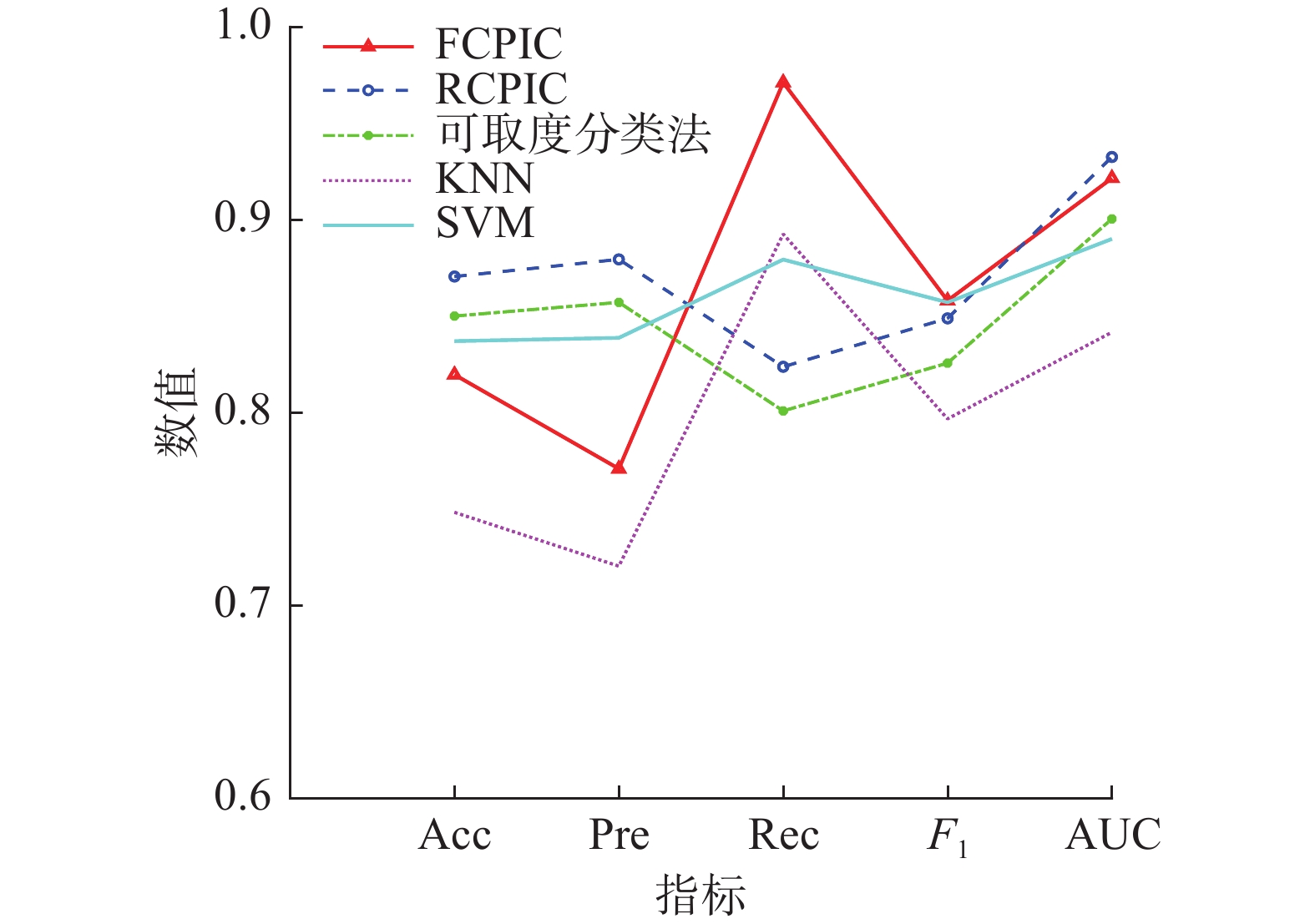
ralianAcc 0.8197 0.8706 0.8501 0.7483 0.8371 Pre 0.7709 0.8795 0.8572 0.7204 0.8388 Rec 0.9712 0.8238 0.8009 0.8926 0.8794 F1 0.8581 0.8489 0.8257 0.7968 0.8572 AUC 0.9216 0.9326 0.9005 0.8417 0.8901 为直观地展示算法实验结果,对比分析5种算法在不同数据集上的指标。
实验1
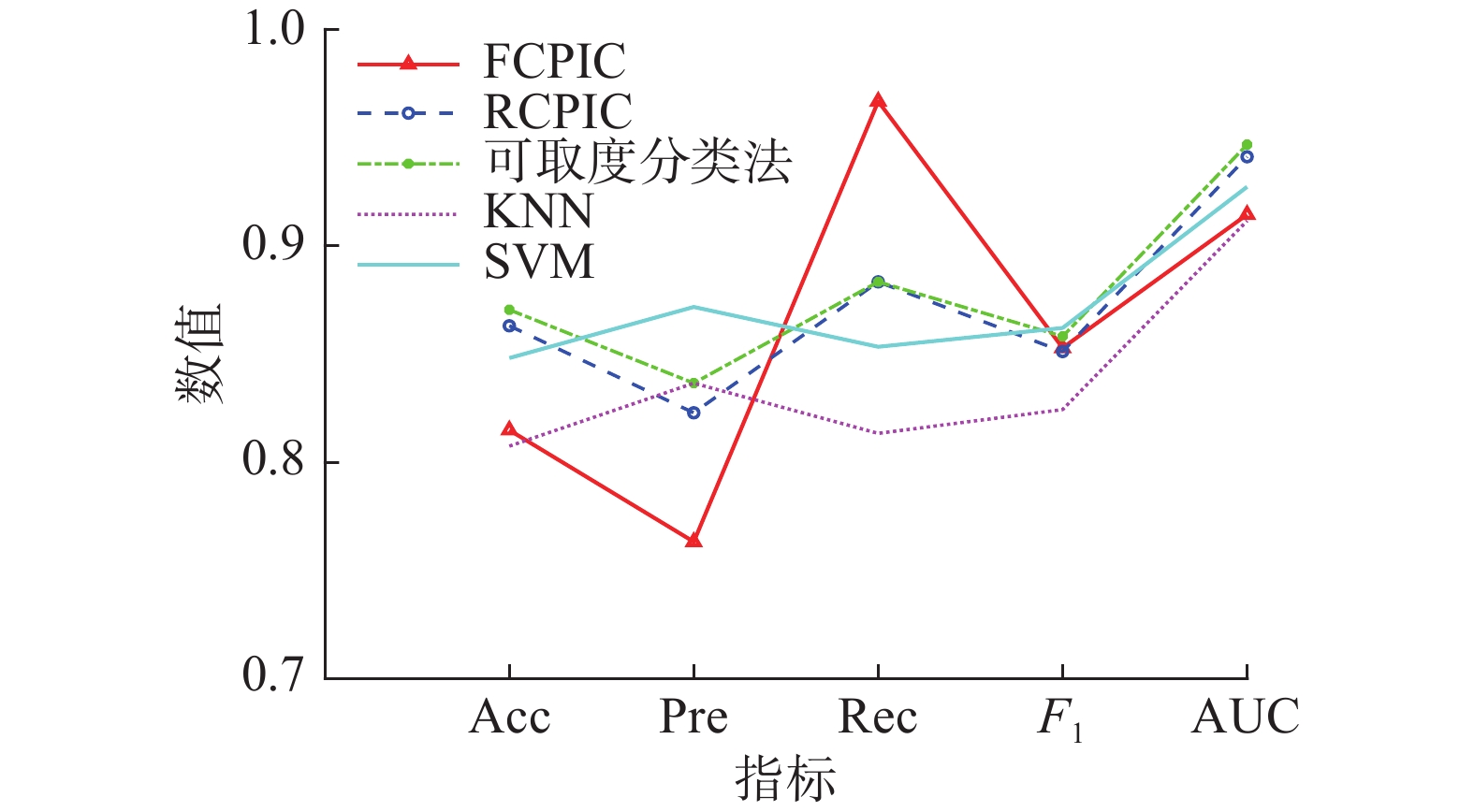
对于Heart数据集,各分类算法的准确率、精确率、召回率、F1和AUC的指标对比关系见图4。
由图4和表5可知,对于Heart数据集,RCPIC算法和可取度分类法的准确率、召回率以及AUC都优于KNN和SVM算法;FCPIC的性能优于KNN且召回率最高。
实验2
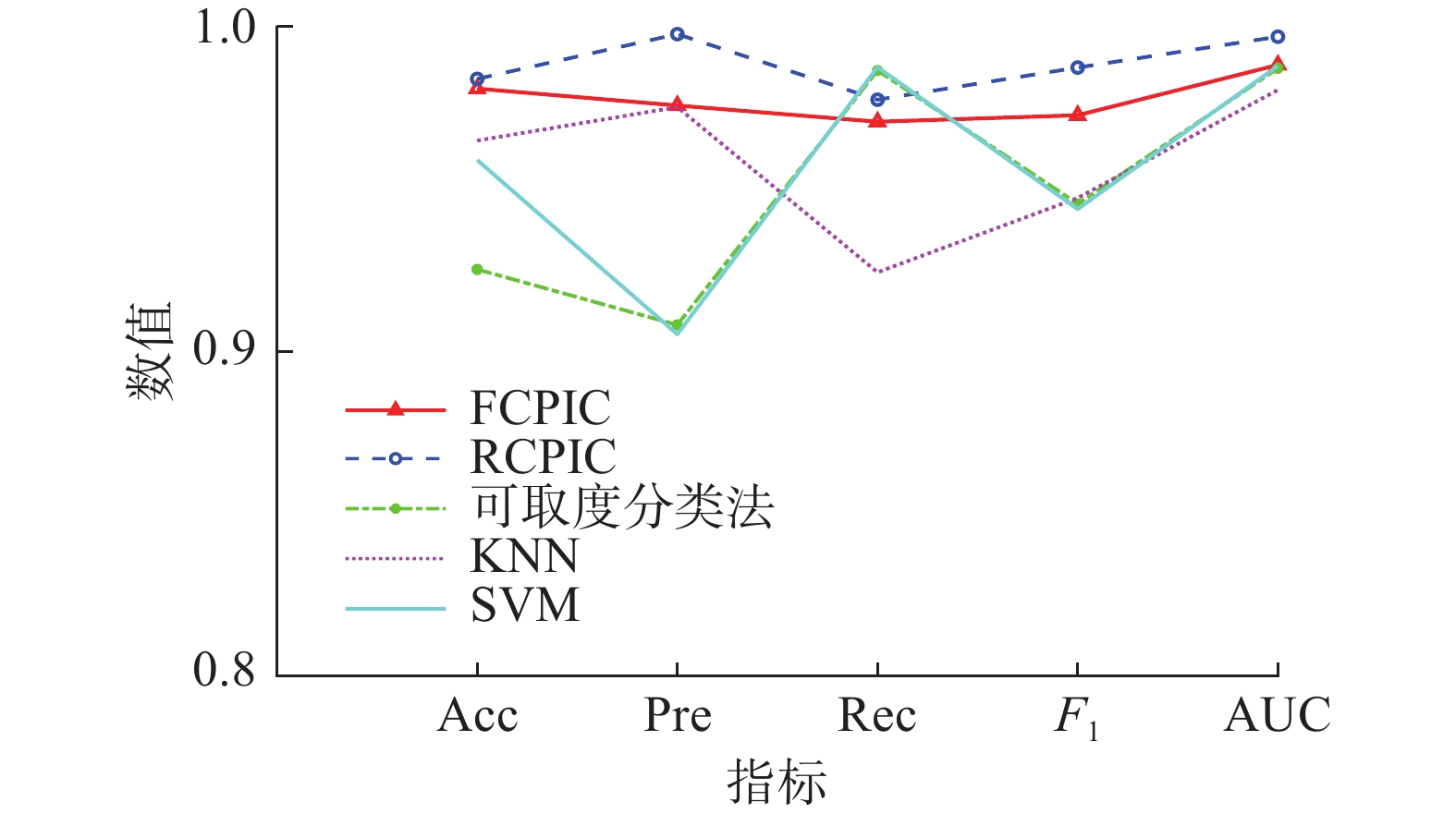
对于Breast cancer数据集,各分类算法的准确率、精确率、召回率、F1和AUC的指标对比关系见图5。
由图5和表5可知,对于Breast cancer数据集,FCPIC和RCPIC算法的准确率、精确率、F1以及AUC都优于KNN和SNM算法;可取度分法具有较高的召回率,其性能优于KNN算法。
实验3
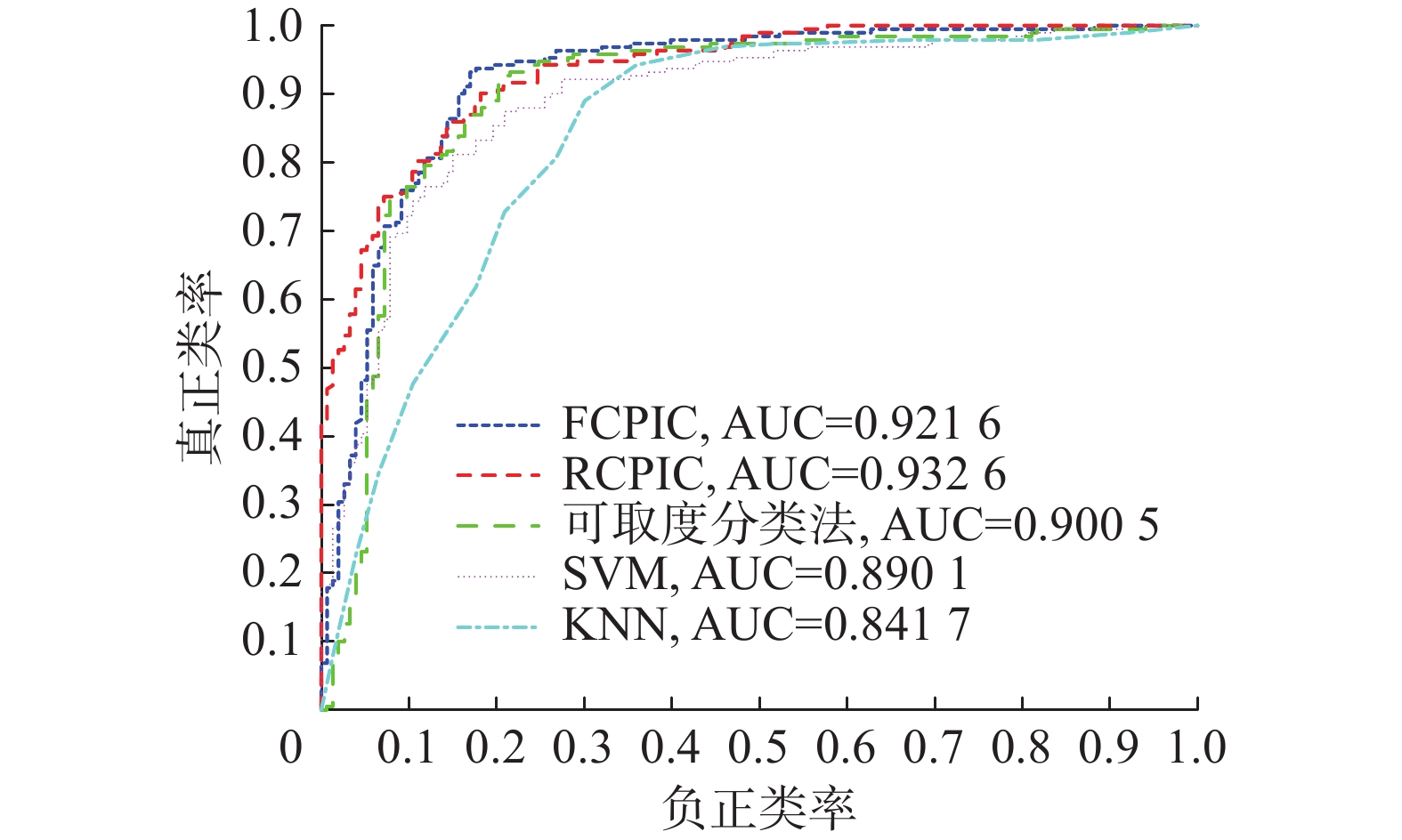
对于Australian数据集,各分类算法的准确率、精确率、召回率、F1和AUC的指标对比关系见图6,ROC曲线见图7。
由图6和表5可知,对于Australian数据集,FCPIC、RCPIC和可取度分类法的的性能都优于KNN和SNM算法,且FCPIC的召回率最高,即更多地找到可以批准的信贷用户。
由图7和表5可知,RCPIC算法的ROC曲线最凸,完全“包住”SVM和KNN,即随着算法划分对象为正类的个数增多时,划错的个数少于SVM和KNN算法;可取度分类法的ROC曲线没有完全“包住”SVM,但AUC值大于SVM和KNN算法,即性能优于SVM和KNN算法;FCPIC算法的预测准确率低于SVM算法,但其左上方的ROC曲线更凸,性能更优。
综上分析,相较于KNN和SVM算法,FCPIC具有较高的召回率,在查找患者等重要的数据时,漏查率较低。RCPIC算法的准确率和性能都优于KNN和SVM算法,4个评价指标相对其他算法更平稳。可取度分类算法对不同数据集精确率或召回率较高,且性能也好。
算法复杂度对比
FCPIC、RCPIC和可取度分类算法的时间复杂度低于SVM算法。
FCPIC、RCPIC和可取度分类算法的时间复杂度稍高于KNN算法,即O(mns)>O(mn),但算法分类预测性能优于KNN算法。
6. 结束语
本文基于因素空间理论下的因素概率论及条件概率,提出因果概率推理分类法,该算法能够清晰地阐述研究系统的构成,即由条件因素、结果因素及各因素的相构成。提出3种时间复杂度为O(mns)的分类算法,与SVM和KNN算法进行比较,并用实例验证得到结论:
1)FCPIC算法原理是由原因寻找结果的正向概率推理,与KNN和SVM算法相比具有较高的召回率,针对实际数据预测中必要类有查全需求的情况,优先选择该算法。
2)可取度分类法原理是计算原因对结果的影响程度的正向推理,可取度分类法的性能优于KNN算法,且与SVM算法相当。该算法无因素相互独立条件,适用范围更广。
3)RCPIC算法原理是由结果寻找原因的逆向概率推理,其性能优于KNN和SVM算法,准确率、精确率、召回率和F1 4个指标相对其他算法更平稳。
综上,本文在理论和实际层面分析了算法的有效性,在未来将进一步研究正逆向概率推理结合的情况。
-
表 1 因果分析表
Table 1 Causal analysis table
D F$ \rightarrow $g f1 f2 ··· fn g d1 f1(d1) f2(d1) ··· fn(d1) g(d1) d2 f1(d2) f2(d2) ··· fn(d2) g(d2) $ \vdots $ $ \vdots $ $ \vdots $ ··· $ \vdots $ $ \vdots $ dm f1(dm) f2(dm) ··· fn(dm) g(dm) 表 2 因果分析简表
Table 2 Causal analysis table
D F$ \rightarrow $g f1 f2 … fn g d c1 c2 … cn gi 表 3 电风扇质量因果分析表
Table 3 Electric fan quality causal analysis table
D F→g f1 f2 f3 g d c1 c2 c3 gi d1 1 3 1 2 d2 1 2 3 2 d3 2 1 3 2 d4 2 1 1 1 d5 2 2 1 1 d6 2 3 2 2 d7 2 1 2 1 d8 1 1 1 1 d9 2 3 1 2 d10 1 2 2 2 表 4 数据集信息
Table 4 Dataset information
数据集 样本数 因素个数 结果类别 正类 负类 Heart 297 13 2 150 120 Breast cancer 683 9 2 239 444 Australian 690 14 2 383 307 表 5 实验结果对比
Table 5 Comparison of experimental results
数据集 指标 FCPIC RCPIC 可取度
分类法KNN SVM Heart Acc 0.8148 0.863 0.8704 0.8074 0.8481 Pre 0.7632 0.8228 0.8365 0.8365 0.8717 Rec 0.9667 0.8833 0.8833 0.8133 0.8533 F1 0.8528 0.8511 0.8581 0.8243 0.8620 AUC 0.9144 0.9411 0.9467 0.9115 0.9272 Breast cancer Acc 0.9809 0.9839 0.9252 0.9649 0.9589 Pre 0.9757 0.9977 0.9081 0.9752 0.9052 Rec 0.9707 0.9775 0.9865 0.9243 0.9875 F1 0.9727 0.9874 0.9454 0.9472 0.9438 AUC 0.9882 0.9969 0.9872 0.9805 0.9879 Aust-
ralianAcc 0.8197 0.8706 0.8501 0.7483 0.8371 Pre 0.7709 0.8795 0.8572 0.7204 0.8388 Rec 0.9712 0.8238 0.8009 0.8926 0.8794 F1 0.8581 0.8489 0.8257 0.7968 0.8572 AUC 0.9216 0.9326 0.9005 0.8417 0.8901 -
[1] 汪培庄, SUGENO M. 因素场与模糊集的背景结构[J]. 模糊数学, 1982(2): 45–54. WANG Peizhuang, SUGENO M. The factors field and background structure for fuzzy subsets[J]. Fuzzy mathematics, 1982(2): 45–54. [2] 汪培庄, 李洪兴. 知识表示的数学理论[M]. 天津: 天津科学技术出版社, 1994. [3] 李洪兴. 因素空间与模糊决策[J]. 北京师范大学学报(自然科学版), 1994, 30(1): 41–46. LI Hongxing. Factor spaces and fuzzy decision making[J]. Journal of Beijing Normal University (natural science edition), 1994, 30(1): 41–46. [4] 袁学海, 汪培庄. 因素空间和范畴[J]. 模糊系统与数学, 1995, 9(2): 25–33. YUAN Xuehai, WANG Peizhuang. Factor spaces and categories[J]. Fuzzy systems and mathematics, 1995, 9(2): 25–33. [5] WANG Peizhuang, LIU Zengliang, SHI Yong, et al. Factor space, the theoretical base of data science[J]. Annals of data science, 2014, 1(2): 233–251. doi: 10.1007/s40745-014-0017-5 [6] 汪培庄, 郭嗣琮, 包研科, 等. 因素空间中的因素分析法[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(7): 865–870. WANG Peizhuang, GUO Sicong, BAO Yanke, et al. Causality analysis in factor spaces[J]. Journal of Liaoning Technical University (natural science edition), 2014, 33(7): 865–870. [7] 于福生, 罗承忠. 粒子因素空间与智能诊断专家系统[C]// 第七届全国电工数学学术年会论文集. 北京: 科学技术出版社, 1999: 24−27. YU Fusheng, LUO Chengzhong. Granule factors space and intelligent diagnostic expert systems[C]//Proceedings of the 7th National Conference on Electric Mathematics. Beijing: China Science & Technology Press, 1999: 24−27. [8] 刘海涛, 郭嗣琮. 因素分析法的推理模型[J]. 辽宁工程技术大学学报(自然科学版), 2015, 34(1): 124–128. LIU Haitao, GUO Sicong. Reasoning model of causality analysis[J]. Journal of Liaoning Technical University (natural science edition), 2015, 34(1): 124–128. [9] 曾繁慧, 李艺. 因素空间理论的决策树C4.5算法改进[J]. 辽宁工程技术大学学报(自然科学版), 2017, 36(1): 109–112. ZENG Fanhui, LI Yi. An improved decision tree algorithm based on factor space theory[J]. Journal of Liaoning Technical University (natural science edition), 2017, 36(1): 109–112. [10] 汪华东, 郭嗣琮. 基于因素空间反馈外延外包络的DFE决策[J]. 计算机工程与应用, 2015, 51(15): 148–152,156. WANG Huadong, GUO Sicong. DFE decision-making based on outer-enveloping of feedback extension in factor spaces[J]. Computer engineering and applications, 2015, 51(15): 148–152,156. [11] 孙慧, 曾繁慧, 蒲凌杰. 因素空间理论下多目标因果分析的降维算法[J]. 辽宁工程技术大学学报(自然科学版), 2021, 40(5): 466–472. SUN Hui, ZENG Fanhui, PU Lingjie. Research on dimension reduction algorithm of multiple targets causal analysis based on factor space theory[J]. Journal of Liaoning Technical University (natural science edition), 2021, 40(5): 466–472. [12] HELLSTRÖM T. The relevance of causation in robotics: a review, categorization, and analysis[J]. Paladyn, journal of behavioral robotics, 2021, 12(1): 238–255. doi: 10.1515/pjbr-2021-0017 [13] 蒲凌杰, 曾繁慧, 汪培庄. 因素空间理论下基点分类算法研究[J]. 智能系统学报, 2020, 15(3): 528–536. PU Lingjie, ZENG Fanhui, WANG Peizhuang. Base point classification algorithm based on factor space theory[J]. CAAI transactions on intelligent systems, 2020, 15(3): 528–536. [14] 刘海涛, 郝传波, 傅贵. 因素空间下的煤与瓦斯突出预测方法[J]. 黑龙江科技大学学报, 2017, 27(4): 354–358. LIU Haitao, HAO Chuanbo, FU Gui. Study on factor space- based prediction method of coal and gas outburst[J]. Journal of Heilongjiang University of Science & Technology, 2017, 27(4): 354–358. [15] REICHENBACH H, REICHENBACH M. The direction of time[M]. Berkeley: University of California Press, 1956. [16] HÁJEK A, HITCHCOCK C. The Oxford handbook of probability and philosophy[M]. New York: Oxford University Press, 2016. [17] SPRENGER J. Foundations of a probabilistic theory of causal strength[J]. The philosophical review, 2018, 127(3): 371–398. doi: 10.1215/00318108-6718797 [18] FAGHIHI U, BOUCHARD S M, BISKRI I. Science of data: a new ladder for causation[M]//Sayed-Mouchaweh M. Explainable AI Within the Digital Transformation and Cyber Physical Systems. Cham: Springer, 2021: 33−45. [19] 黄影平. 贝叶斯网络发展及其应用综述[J]. 北京理工大学学报, 2013, 33(12): 1211–1219. HUANG Yingping. Survey on Bayesian network development and application[J]. Transactions of Beijing Institute of Technology, 2013, 33(12): 1211–1219. [20] 曲国华, 曾繁慧, 刘增良, 等. 因素空间中的背景分布与模糊背景关系[J]. 模糊系统与数学, 2017, 31(6): 66–73. QU Guohua, ZENG Fanhui, LIU Zengliang, et al. Background distribution and fuzzy background relation in factor spaces[J]. Fuzzy systems and mathematics, 2017, 31(6): 66–73. [21] 张艳妮, 曾繁慧, 郭嗣琮. 因素空间理论的因素Markov过程[J]. 辽宁工程技术大学学报(自然科学版), 2019, 38(4): 385–389. ZHANG Yanni, ZENG Fanhui, GUO Sicong. Factor Markov process of factor space theory[J]. Journal of Liaoning Technical University (natural science edition), 2019, 38(4): 385–389.




















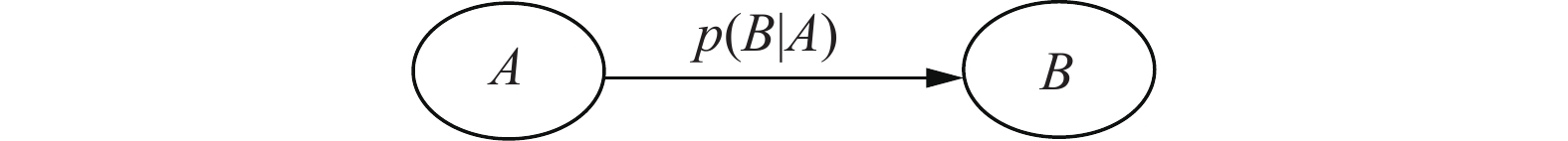
 下载:
下载: