Path planning of a meal delivery robot based on an improved ant colony algorithm
-
摘要: 蚁群算法拥有良好的全局性、自组织性、鲁棒性，但传统蚁群算法存在许多不足之处。为此，针对算法在路径规划问题中的缺陷，在传统蚁群算法的状态转移公式中，引入目标点距离因素和引导素，加快算法收敛性和改善局部最优缺陷。在带时间窗的车辆路径问题（vehicle routing problem with time windows，VRPTW）上，融合蚁群算法和遗传算法，并将顾客时间窗宽度以及机器人等待时间加入蚁群算法状态转移公式中，以及将蚁群算法的解作为遗传算法的初始种群，提高遗传算法的初始解质量，然后进行编码，设置违反时间窗约束和载重量的惩罚函数和适应度函数，在传统遗传算法的交叉、变异操作后加入了破坏−修复基因的操作来优化每一代新解的质量，在Solomon Benchmark算例上进行仿真，对比算法改进前后的最优解，验证算法可行性。最后在餐厅送餐问题中把带有障碍物的仿真环境路径规划问题和VRPTW问题结合，使用改进后的算法解决餐厅环境下送餐机器人对顾客服务配送问题。Abstract: The ant colony algorithm has advantages, such as good global ability, self-organization, and robustness, but the conventional ant colony algorithm has several drawbacks. Herein, with the goal of addressing these drawbacks, in the path planning problem, according to the conventional ant colony algorithm, the distance factor of the target point and the guide element are added to the state transition formula to optimize the convergence of the ant colony algorithm in the path planning and enhance the defect of local optimal point. On the vehicle routing problem with time window (VRPTW), the ant colony algorithm and genetic algorithm are combined, and the customer time window width and robot waiting time are added to the state transition formula of the ant colony algorithm. The solution of the ant colony algorithm is taken as the initial population of the genetic algorithm to enhance the quality of the initial solution of the genetic algorithm, and subsequently, coding is conducted. The penalty function and fitness function violating the time window constraint and load are set. After the mutation and crossover operation of the conventional genetic algorithm, the damage and repair gene operation is added to optimize the quality of each generation of new solutions. Simulations are performed on the Solomon benchmark example, and the optimal solutions before and after enhancement of the algorithm are compared to confirm the feasibility of the algorithm. To apply this to a real-world problem, the path planning problem in a simulative environment with obstacles and the VRPTW problem are joined using the enhanced algorithm to solve the customer service delivery problem of the restaurant delivery robot.
-
餐饮服务越来越强调无接触式的用餐服务，而智能送餐机器人能够完美解决餐馆的无接触送餐服务的问题。这类机器人的优点在于开发高效、使用方便，对硬件要求不高[1]。但是现在市面上的送餐机器人也还存在不足之处，一些普通餐厅中的送餐机器人仅仅能实现简单循迹。而且现在大多数的送餐机器人只能单对单的服务，这种机器人需要前台在上位机上进行操作才能送达，并不能对多位顾客的需求和等待时长进行实时分析。因此，设计一种能够对餐厅多位顾客的需求和点餐顺序进行分析并规划出合理的配送顺序和最优路径的算法具有一定意义。机器人规划路径的优劣需要综合考虑多种因素，如路径长度、运行时间和算法的迭代次数等[2-4]。早期使用的路径规划方法有人工势场法[5]、A*算法[6]和Dijkstra算法[7]等，这些方法在实际应用中表现出了很大的不足。遗传算法[8-9]、蚁群算法[10]、粒子群算法[11-12]、萤火虫算法[13]、果蝇优化算法[14]和灰狼算法[15]等属于智能优化算法，与传统路径最优算法相比也有很多传统算法没有的优势。蚁群算法作为经典智能优化算法，因其正反馈性和并行性等优势，被广泛应用于移动机器人路径规划问题中[16-18]。Cao[19]在改进的蚁群算法中，每个周期的一些短路径上增加了信息素数量，并动态调整了其蒸发率，从而提高转移概率，结果证明算法的全局寻优能力增强，搜索速度明显提高。Tsai等[20]提出了一种新的多目标灰狼优化算法解决移动机器人路径规划问题。张毅等[21]将A*算法和改进的人工鱼群方法相结合，先采用A*算法规划出次优路径，然后在基本鱼群方法中提出了非线性惯性权重因子的自适应行为，引入衰减函数，优化算法的全局搜索能力和局部搜索能力，得到更优的路径，且收敛速度也更快。Brand等[22]将萤火虫算法应用在动态空间中移动机器人路径规划，仿真证明这个算法能够成功规划出可行路径，并且在长度和计算成本方面都比较低。
虽然上述改进策略能够在一定程度上改善蚁群算法的不足，但蚁群算法的收敛速度慢和易陷入局部最优仍是该算法的缺陷。针对以上缺陷，本研究提出了一种蚂蚁引导素，引导素能够让蚂蚁对自己走过的路径进行分析，对规划效果更好的路径留下引导素，能让后续蚂蚁倾向于更优的路径，避开相对较差的路径来改进局部最优的缺陷。
而餐厅多位顾客的配送顺序实际就是解决带时间窗的车辆路径（vehicle routing problem with time windows，VRPTW）问题。VRPTW问题可描述为：若干车辆从某个确定的节点出发，为该节点周围的其他节点提供一次服务(如配送货物)，已知各个节点处在不同的地理位置，并且具有不同的货物需求和不同的服务时间段(即时间窗)要求，车辆服务完毕返回始发节点。在该问题上，本研究将蚁群算法和遗传算法进行融合，用蚁群算法的初始解代替遗传算法的初始种群，并提出一种破坏基因和修复基因的操作，利用相关性公式找出所有基因与被破坏掉的基因的相关性，对基因进行删减，然后利用最远插入式思想将删掉的基因进行插回，提高了算法鲁棒性。通过破坏基因和修复基因的操作能够有效提高组合优化问题的求解质量。
将上述的路径规划和配送顺序问题结合就是本研究拟解决的送餐机器人的路径规划问题。通过对比试验证明了改进后算法能够规划出最优配送方案以及最优的实际路线。
1. 蚁群算法
蚁群算法（ant colony，ACO）最初是由意大利的研究学者Dorigo等[23-24]在1992年期间第一次提出来的。蚂蚁在寻找食物的过程中，会在每条走过的路径下留下自己的信息素从而来引导其他的蚂蚁。随着各个蚂蚁经过不同的路径到达食物点时，每条路径上留下的信息素浓度各不相同，后面的蚂蚁更多地会选择信息素浓度更高的一条路径去移动。其中每条路径信息素的浓度与经过该路径的蚂蚁数量和路径长短有关。当路径较远时，同一只蚂蚁留下的信息素浓度越低，经过蚂蚁不断探索路径，最终蚂蚁会更加倾向信息素浓度最高路径。蚂蚁们最终通过这种方式来找到一条通往食物的最短路径。在t时刻蚂蚁从位置i到未知位置j的转移概率为
$$ p_{ij}^k = \left\{ \begin{split} &\frac{{\tau _{ij}^\alpha (t)\eta _{ij}^\beta (t)}}{{\displaystyle\sum\limits_{s \in A{_k}} {\tau _{is}^\alpha (t)\eta _{is}^\beta (t)} }},\quad j \in A{_k} \\ & 0, \quad 其他 \end{split} \right. $$ (1) 式中：
$ \tau_{i j}^{\alpha} $ 为信息素；α为信息素的启发因子；$\eta_{ij}^{\beta}$ 为节点i到节点j的期望函数；β为期望启发因子；Ak为蚂蚁可以选择的下一个点的所有集合。其中期望函数表达式为$$ {\eta _{ij}} = \frac{1}{{{d_{ij}}}} $$ (2) 式中dij为i，j两地之间的距离。
信息素的更新公式为
$$ {\tau _{ij}}(t + n) = (1 - \rho ){\tau _{ij}}(t) + \Delta {\tau _{ij}} $$ (3) $$ \Delta {\tau _{ij}}(t + n) = \sum\limits_{k = 1}^K {\Delta \tau _{ij}^k} $$ (4) 式中：ρ为信息素挥发系数；
$ \Delta \tau_{i j}^{k} $ 为信息素增量，信息素增量具体表达式为$$ \Delta {\tau }_{ij}^{k}=\left\{\begin{array}{l}\dfrac{Q}{{L}_{k}}\text{，}蚂蚁k从节点i\text{ }至\text{ }j\\ 0\text{，}其他\end{array}\right. $$ (5) 式中：Q为一个常数；Lk为每一只蚂蚁从起点走到目的地的总路程。通过该方式进行信息素增量的计算加强了蚁群算法的全局性。
2. 改进应用于路径规划的蚁群算法
2.1 考虑目标点距离因素的概率转移函数
在传统的蚁群算法转移概率式(1)中的启发信息
$\eta_{is}^{\beta}$ 是当前蚂蚁所在点到下一步的各个可选点之间的距离的倒数。这样的转移概率没有考虑到蚂蚁的下一个可选点离目标点的距离，算法缺乏全局性。因此将可选点集合中各个点与目标点的欧几里得距离的倒数代替该期望函数。改进后的概率公式为$$ p_{ij}^k = \left\{ \begin{split} &\frac{{\tau _{ij}^\alpha (t){{[{d^{ - 1}}(j,e)]}^\beta }}}{{\displaystyle\sum\limits_{s \in A{_k}} {\tau _{is}^\alpha (t){{[{d^{ - 1}}(s,e)]}^\beta }} }},\quad j \in A{_k} \\ &0\;, \quad 其他 \end{split} \right. $$ (6) 式中：d(j, e)为可选点j与目标点e之间的欧几里得距离。
2.2 加入引导素改进局部最优
蚁群算法中使用的轮盘赌法使得该算法在复杂环境下，有低概率选择相对较差的位置。由于蚁群算法的信息素正反馈机制会使得蚂蚁在该位置留下信息素，导致后代蚂蚁选择该位置的几率增加，反而降低了最优解质量。针对该缺陷，提出一种引导素。当第一只蚂蚁到达终点之后开始分析从起点到达目的地的路径上有无相对较差的点位，对这些点位，找到适当的新路线并留下一种引导素，以此来引导后续的蚂蚁在寻找最优路径时避开那些相对较差的点位，从而提高最优解的质量，改善蚁群算法陷入局部最优的问题。加入引导素后蚁群算法的状态转移概率公式为
$$ p_{ij}^k = \left\{ \begin{split} & \frac{{\tau _{ij}^\alpha (t){{[{d^{ - 1}}(j,e)]}^\beta }\upsilon _{ij}^\gamma }}{{\displaystyle\sum\limits_{s \in A{_k}} {\tau _{is}^\alpha (t){{[{d^{ - 1}}(s,e)]}^\beta }\upsilon _{is}^\gamma } }},\quad j \in A{_k} \\ &0\;, \quad 其他 \end{split} \right. $$ (7) 式中：
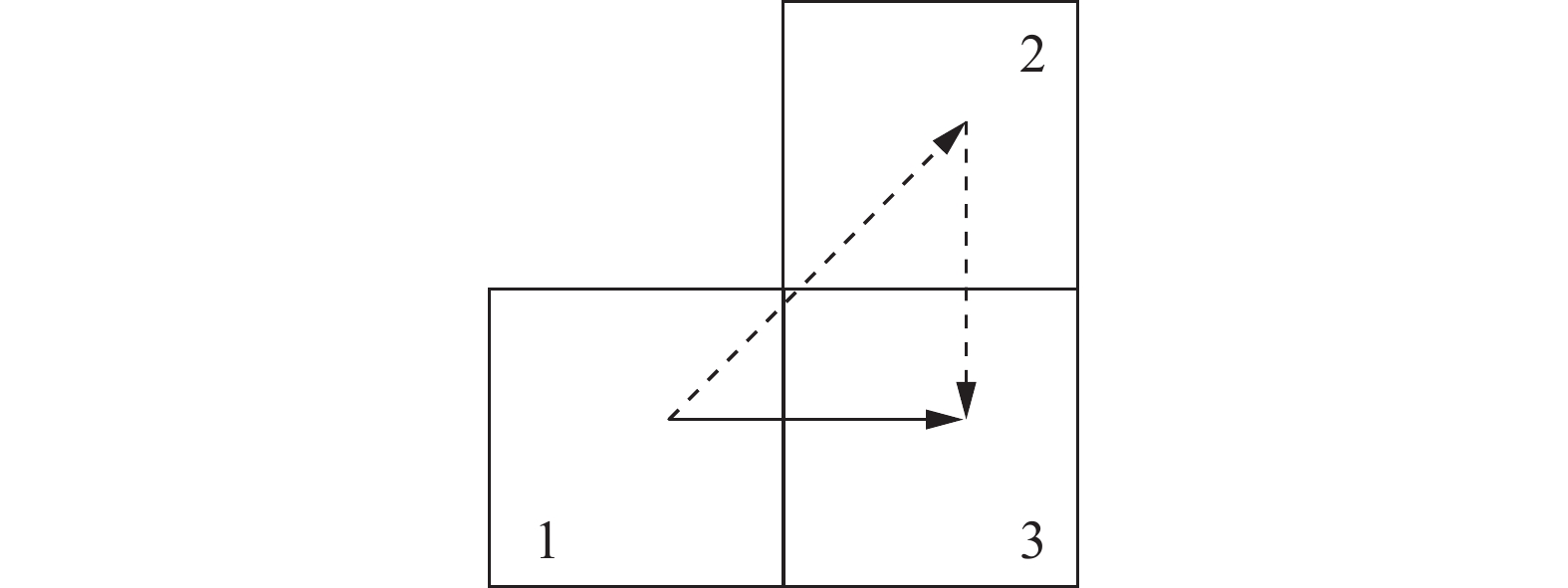
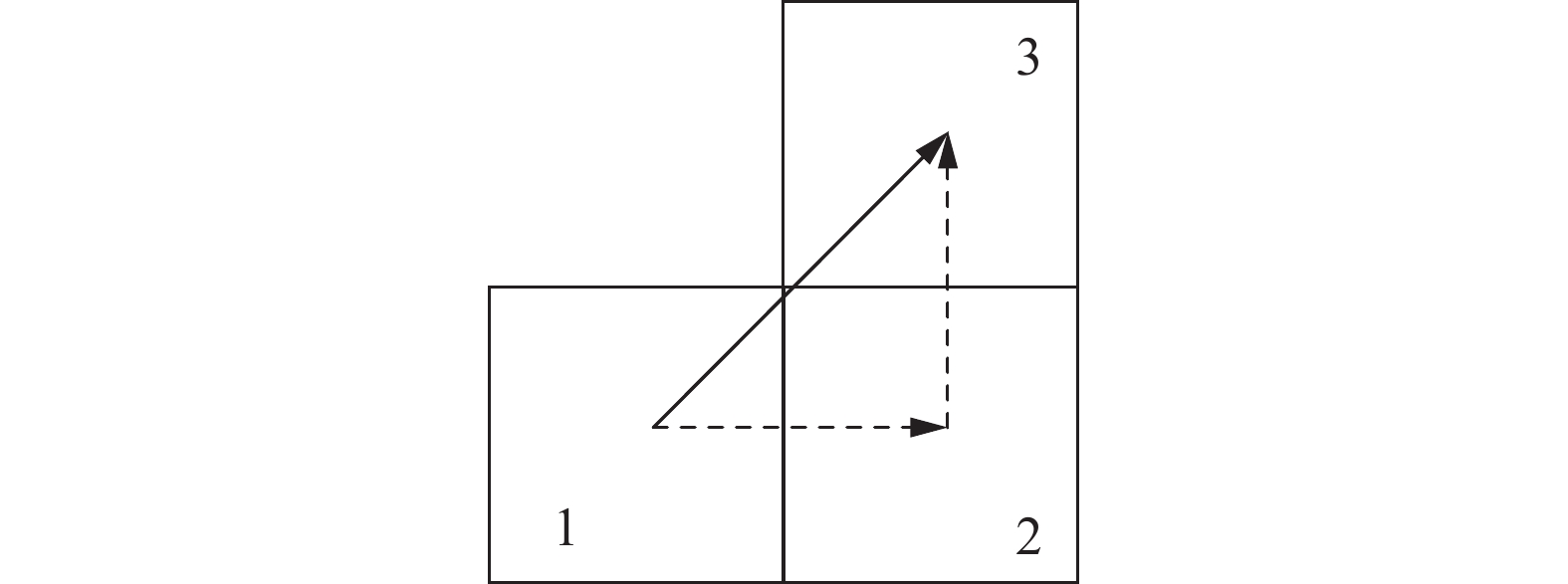
$ v_{i j} $ 代表i点到j点的引导素浓度；γ为引导素启发因子。引导素对于相对较差点位的更改情况可分为3类。第1种情况如图1所示，虚线为蚂蚁实际路线。若蚂蚁从栅格1直接前往栅格3的距离小于实际路线距离，则增加栅格1到栅格3的引导素浓度。
图 1 第1种情况Fig. 1 Case 1
下载:
全尺寸图片
公式可以表示为
$$ {d_{1 - 3}} < {d_{1 - 2}} + {d_{2 - 3}},\quad {\upsilon _{13}} = {\upsilon _{13}} + \Delta \upsilon $$ (8) 式中：d为两点之间的距离；
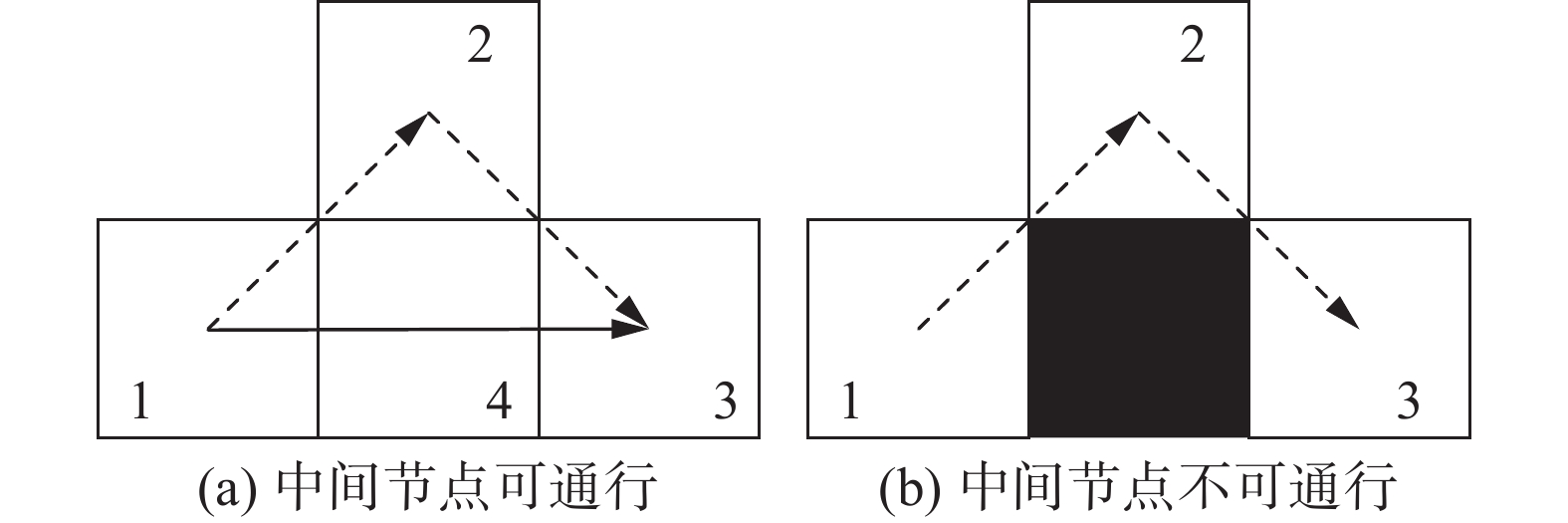
$ \Delta \upsilon $ 为增加的引导素。第2种情况如图2所示，原理与第1种情况一样且公式也可以用式(8)表示。
图 2 第2种情况Fig. 2 Case 2下载:
全尺寸图片
第3种情况如图3所示，在前面2种的基础上需要多出一个对格子1和格子3之间的中间格子进行有否具有障碍物的判定，如果中间格子为可通行格，则增加格子1到格子4的引导素浓度；反之则保持原始的引导素浓度。公式如下所示
图 3 第3种情况Fig. 3 Case3下载:
全尺寸图片
$$ {d_{1 - 3}} < {d_{1 - 2}} + {d_{2 - 3}}\;\;\&\& G({\rm{mid}})\text{!}= 1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\upsilon _{14}} = {\upsilon _{14}} + \Delta \upsilon \\ $$ (9) 式中：d为两点之间的距离；G表示格子的障碍物状态；0表示可通行状态；1表示存在障碍物；&&表示与运算；mid表示节点1与节点3直线上的中间节点。
2.3 蚁群算法参数整定
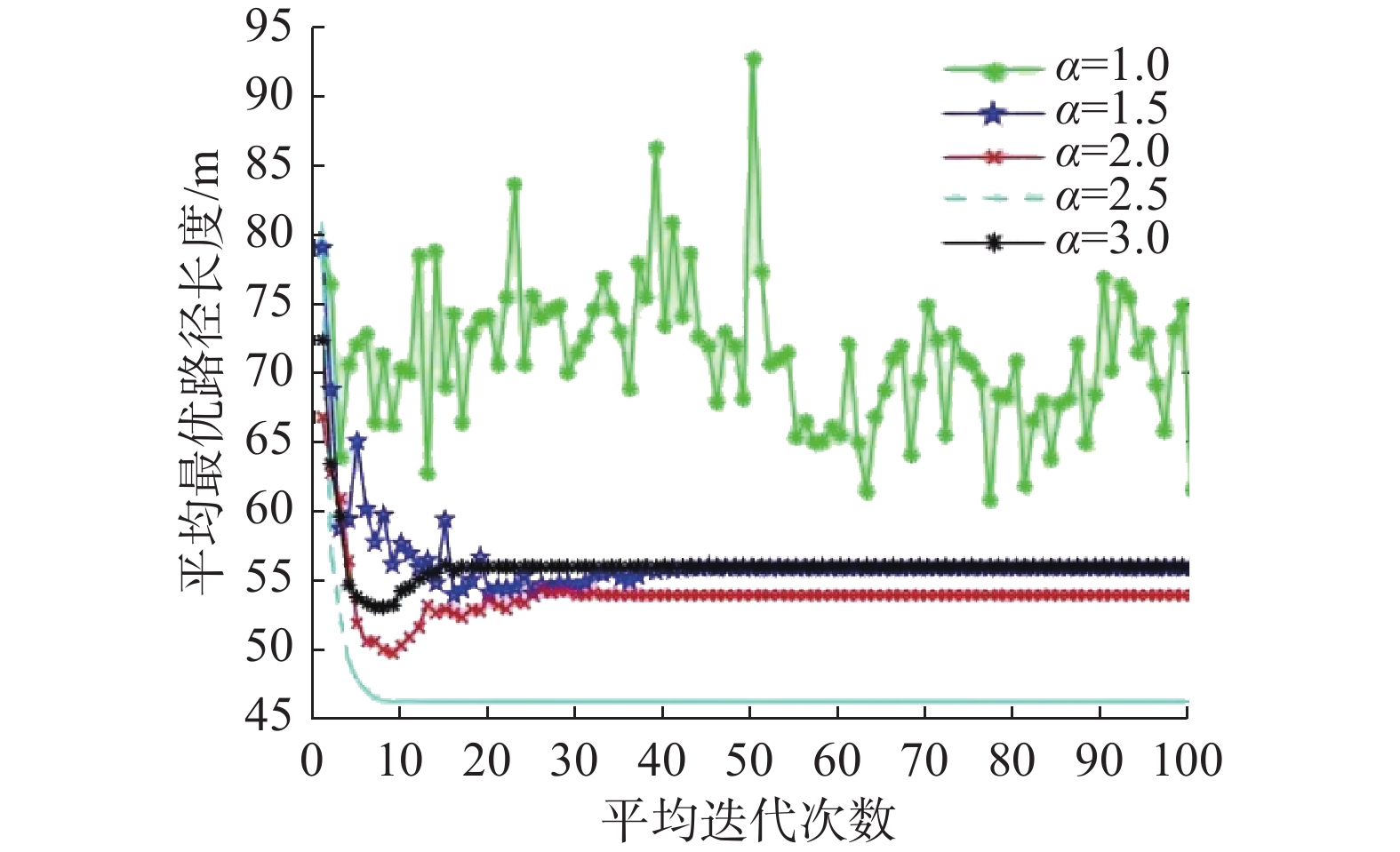
为了整定蚁群算法的试验参数，首先采用文献[25]的试验参数，挥发系数ρ=0.3、信息素启发因子α=2、启发信息影响因子β=6。随后用控制变量法，控制如：挥发因子ρ、信息素启发因子α、启发信息影响因子β等参数值固定不变，依次改变α的取值为{1.0，1.5，2.0，2.5，3.0}，分批进行20次试验，其余参数为固定值将20次的5批数据取其平均值，不同α值的平均最优路径长度随平均迭代次数的变化图如图4所示。
图 4 不同$ \alpha $ 参数实验结果Fig. 4 Different$ \alpha $ parameter experiment results下载:
全尺寸图片
由图4中可以看出，当α=2.5时，算法得到的平均最优路径同时也是最快收敛的，于是取α=2.5。
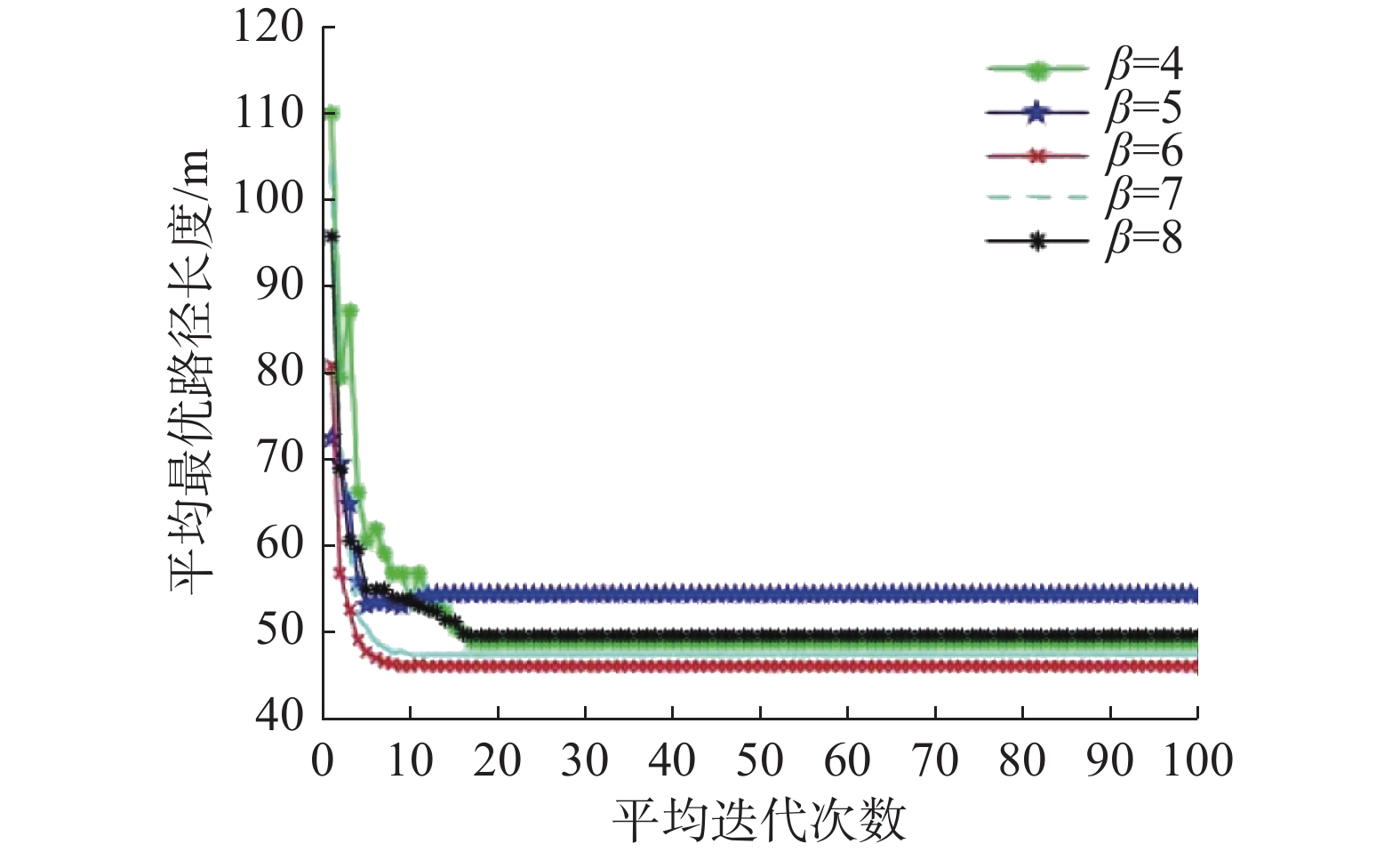
随后取α=2.5，其他参数值固定不变，依次改变β的取值为{4，5，6，7，8}，分批进行20次试验，不同β的平均最优路径长度随平均迭代次数的变化图如图5所示。
图 5 不同β参数实验结果Fig. 5 Different β parameter experiment results下载:
全尺寸图片
由图5中可以看出，当β=6时，算法得到的最优路径长度最小同时也是收敛最快的，于是取β=6。
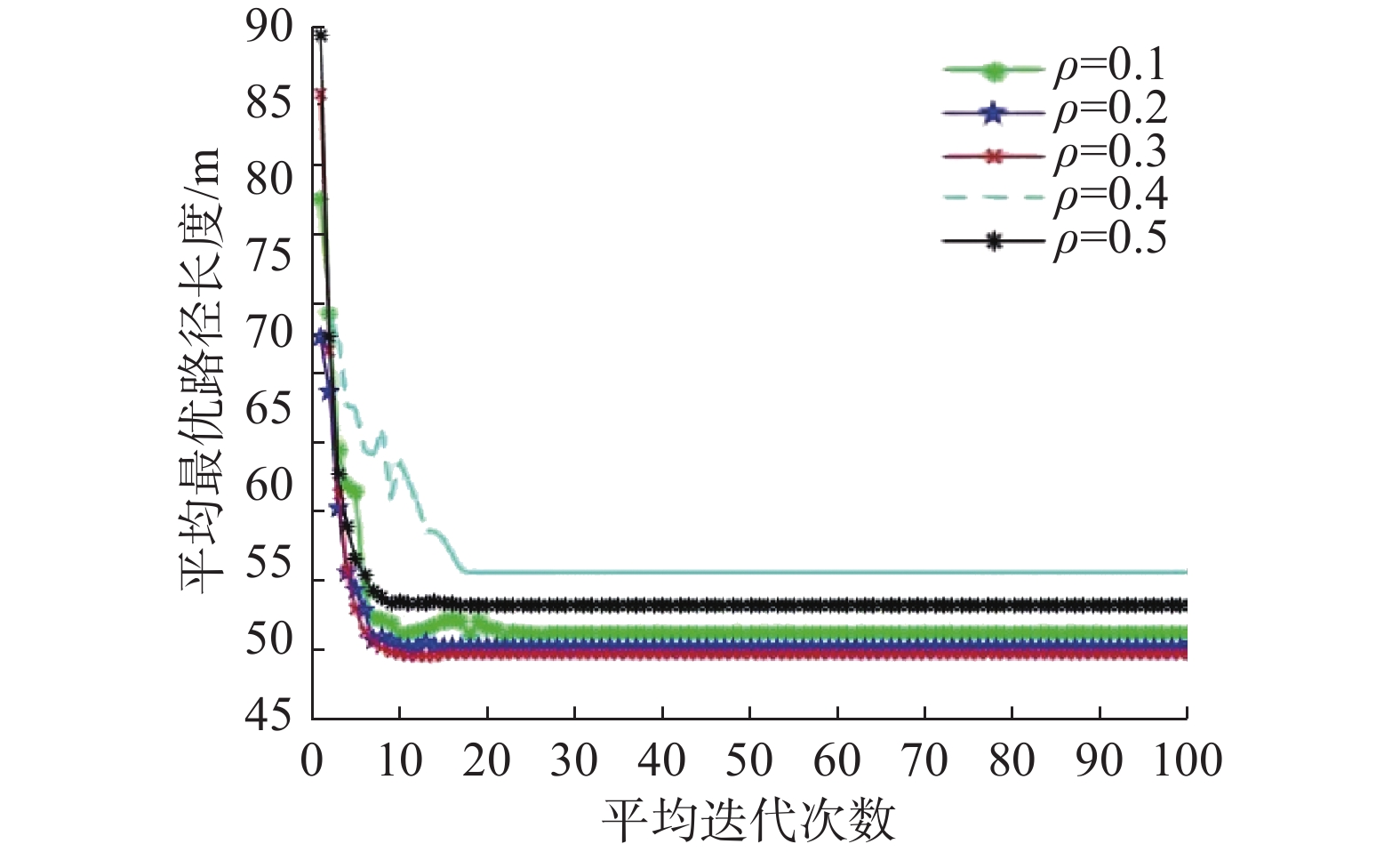
随后取α=2.5，β=6，其他参数值固定不变，依次改变ρ的取值为{0.1，0.2，0.3，0.4，0.5}，进行分批多次试验，不同α的平均最优路径长度随平均迭代次数的变化图如图6所示。
图 6 不同ρ参数实验结果Fig. 6 Different ρ parameter experiment results下载:
全尺寸图片
由图6中可以看出，当ρ=0.3时，算法得到的平均最优路径同时也是最快收敛的，于是取ρ=0.3。
2.4 蚁群算法改进前后仿真对比
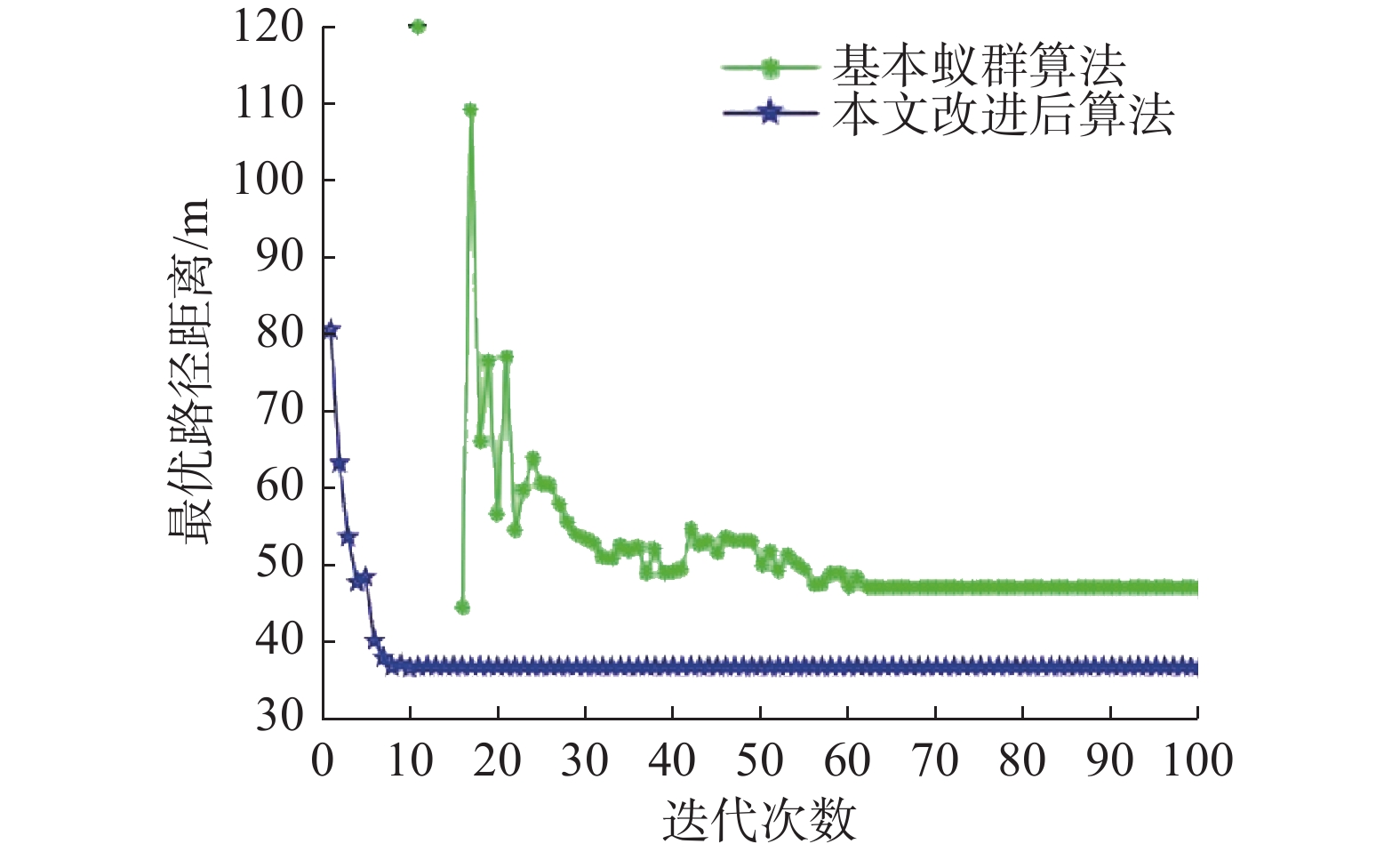
在构建20×20的栅格环境进行仿真对比验证，以下所有对比试验都把起点设置为(0.5，19.5)，终点设置为(19.5，0.5)，试验中的信息素影响因子α=1.5、启发信息影响因子β=6、引导素影响因子γ=6，挥发系数ρ=0.3、信息素浓度Q=100。在该栅格环境下分别使用基本蚁群算法和改进后的蚁群算法进行路径规划，最优规划路径仿真结果如图7所示。各算法仿真结果的路径长度随迭代次数的变化过程对比如图8所示。
图 7 基本蚁群算法与改进后的蚁群算法对比Fig. 7 Comparison between basic ant colony algorithm and improved ant colony algorithm下载:
全尺寸图片
图 8 2种不同算法对比Fig. 8 Comparison of two different algorithms下载:
全尺寸图片
通过基本蚁群算法和改进后蚁群算法的最优路径规划图以及各个算法的最优路径长度随迭代次数变化对比曲线可以看出，基本蚁群算法经过50多次迭代之后规划的最优路径规划效果十分不理想，这是因为基本蚁群算法在算法初期信息素浓度的缺乏，导致不能对蚂蚁进行有效的路径搜索引导，使得蚂蚁在前期的搜索陷入盲目状态，经过算法初期的盲目搜索导致许多不合理的路径上留下了一定量的信息素，使得算法中期蚂蚁在信息素的正反馈机制下极易陷入此局部最优而无法跳出。相较于基本蚁群算法，本研究改进后的算法在栅格环境中路径规划效果较好。因为该算法的状态转移公式考虑了目标点距离和引导素，让蚂蚁避免了许多相对较差的点位，改进了局部最优的缺陷。经计算，基本蚁群算法最优路径长度为48.623 m，本研究改进后算法最优路径长度为36.552 m。本研究改进后算法最优路径长度比基本蚁群算法减少了24.83%。
3. 餐厅服务机器人配送问题
在餐厅中的服务机器人配送问题可以看作是一个经典的VRPTW问题。VRPTW问题可描述为：若干车辆从某个确定的节点出发，为该节点周围的其他节点提供一次服务(如配送货物)，已知各个节点处在不同的地理位置，并且具有不同的货物需求和不同的服务时间段(即时间窗)要求，车辆服务完毕返回始发节点。设K为送餐中心拥有的机器人集合；设N为需要送餐服务的n个顾客点的集合，N = {1,2,···,n}；Vk为机器人k访问顾客的集合；V={0}∪N。设0为餐饮中心； i、j表示顾客编号；
$x_{ij}^k$ 表示机器人k服务完顾客i以后是否服务顾客j；$y_i^k$ 表示顾客i是否被机器人k服务；Q表示服务机器人的装载能力约束；${q_i}$ 表示顾客i的需求量,且${q_0}$ = 0。${C_{ij}}$ 为机器人从i点走向j点的运输成本，运输成本在不同的情况下，实际意义也不一样，需要以实际情况来确定运输成本。餐厅服务机器人配送问题可以描述为
$$ \min \sum\limits_{k \in K} {\sum\limits_{i \in {V_k}} {\sum\limits_{j \in {V_k}\backslash \{ i\} } {{C_{ij}}x_{ij}^k} } } $$ (10) $$ \sum\limits_{j \in {V_k}\backslash \{ i\} } {x_{ij}^k = y_i^k,\forall i \in V,} \forall k \in K $$ (11) $$ \sum\limits_{i \in {V_k}\backslash \{ j\} } {x_{ij}^k = y_j^k,\forall j \in V,} \forall k \in K $$ (12) $$ \sum\limits_{i \in {V_k}} {{q_i}y_i^k \leqslant Q,} \forall k \in K $$ (13) $$ \sum\limits_{j \in N} {x_{0j}^k = \sum\limits_{i \in N} {x_{i0}^k = 1,} } \forall k \in K $$ (14) $$ \sum\limits_{k \in K} {y_i^k = 1,} \forall i \in N $$ (15) $$ \sum\limits_{i,j \in {V_k}} {x_{ij}^k \leqslant \left| {{V_k}} \right| - 1,} \forall k \in K $$ (16) $$ x_{ij}^k \in \{ 0,1\} ,\forall i,j \in V,\forall k \in K $$ (17) $$ y_i^k \in \{ 0,1\} ,\forall i \in N,\forall k \in K $$ (18) 目标函数(10)表示费用最小的目标函数；约束(11)表示机器人在服务完顾客i后直接服务一个顾客j；式(12)表示机器人在服务顾客j之前只服务一个顾客i；式(13)表示每个机器人k运送的顾客需求总量不超过机器人的最大容量；式(14)表示每个机器人从中心出发最终必须回到中心；式(15)指每个顾客i只能由一位机器人服务；式(16)是避免配送过程中产生子回路；
$x_{ij}^k$ 、$y_i^k$ 为决策变量。当机器人k服务完顾客i后直接服务顾客j时，$x_{ij}^k$ = 1;否则$x_{ij}^k$ =0。当顾客i由机器人k服务时，$y_i^k$ =1；否则$y_i^k$ =0。在餐厅服务机器人配送过程中涉及到时间窗问题。通常时间窗可分为软时间窗约束和硬时间窗约束，在餐厅送餐问题中没有涉及到惩罚费用，故在该问题中采用硬时间窗约束，即服务机器人一定要在顾客的容忍时间范围到达并开始服务。容忍时间范围可以用[ETi，LTi]来表达，其中ETi是左时间窗，代表顾客能够容忍的最早服务的时间点；LTi是右时间窗，代表顾客能容忍的最晚服务的时间点。
4. 混合蚁群−遗传算法解决餐厅服务机器人配送问题
4.1 改进蚁群算法的概率转移函数
利用第2章的改进蚁群算法求解机器人中心点位（即配送餐饮中心）和所有餐位点互相之间的最短距离和最优路径并进行保存，本研究采用文献[26]在硬时间窗约束改进，由于顾客只接受在时间窗约束内的服务，所以当送餐机器人到达顾客j的时间
$ a_{j} $ 早于左时间窗ETj，意味着机器人需要等待时间${w_{tj}} = {E_{Tj}} - {a_j}$ 。除此之外还要考虑每位顾客j的时间窗宽度${w_d} = {L_{Tj}} - {E_{Tj}}$ 。由此可以改进蚁群算法，蚂蚁选择下一个顾客j的状态转移概率公式为$$ p_{ij}^k = \frac{{{\tau '}_{ij}^{\alpha '}\eta _{ij}^{\beta '}{[1/{w_d}_j]^\varepsilon }{[1/{w_t}_j]^\delta }}}{{\displaystyle\sum\limits_{s \in N_{ik}} {({\tau'}{ _{is}} ^{\alpha '}\eta _{is}^{\beta '}{[1/{w_d}_s]^\varepsilon }{[1/{w_t}_s]^\delta })} }} $$ (19) 式中：
$\tau_{ij}^{\prime}$ 是机器人在顾客i选择下一个顾客j的信息素浓度；$ \alpha^{\prime} $ 是信息素启发因子；$ \eta_{i j} $ 是顾客i到顾客j的最短距离的倒数；$ \beta^{\prime} $ 是最短距离启发因子；$ {w_{dj}} $ 是顾客j的时间窗宽度；$ {\varepsilon} $ 是时间窗宽度启发因子；${w_{tj}}$ 是机器人将要在顾客j等待的时间；$ \delta $ 是机器人等待时间启发因子；Nik为可选顾客点集合。4.2 混合蚁群遗传算法
4.2.1 提高初始种群质量
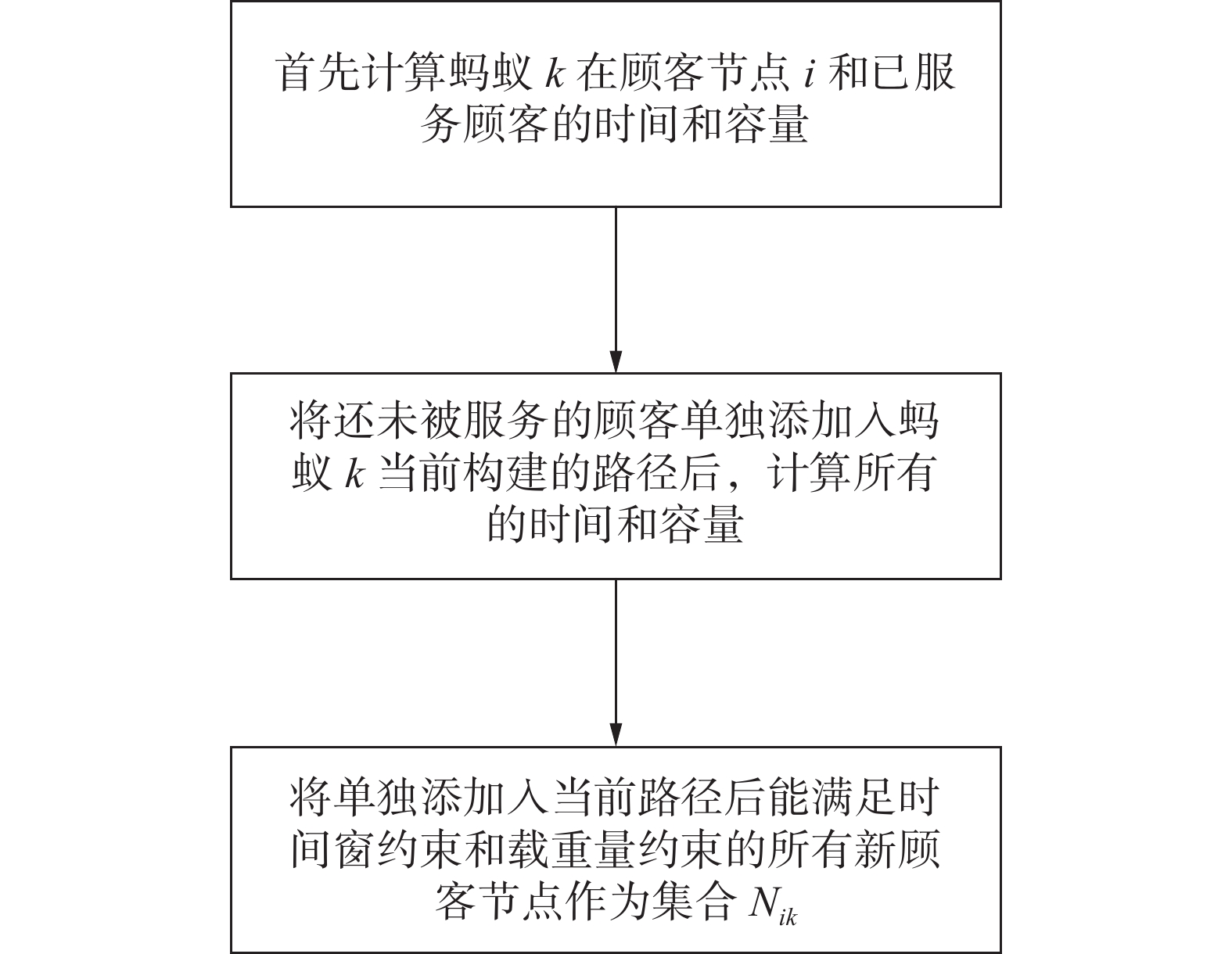
为了提高混合蚁群遗传算法的初始种群质量，本研究提出了让蚂蚁自主构建当前的可行顾客点集合。蚂蚁k在顾客i时的可选顾客点集合Nik的确定方式如图9所示。
图 9 Nik的确定方法Fig. 9 Method for determining Nik下载:
全尺寸图片
通过可行路径的构建方法，让蚂蚁在选择下一位顾客时，只会在考虑满足所有约束条件的顾客中进行选择。利用能够自主构建可选顾客节点的改进蚁群算法的解作为遗传算法的初始种群，提高初始种群的质量。
4.2.2 编码操作
混合蚁群遗传算法需要对蚁群算法得到的解首先进行编码操作才能进行后续操作。本研究编码方式为当顾客数目为N且最大车辆使用数目为K时，染色体长度为N+K−1，染色体表达形式为（1，2，…，N，N+1，N+2，…，N+K−1）。例如一共5位顾客，3辆车的第1条路径为0−1−2−0，第2条路径为0−3−4−0，第3条路径为0−5−0。最终路径用染色体编码为1263475，其中6和7代表配送中心。
4.2.3 制定适应度函数
为了解决在混合蚁群遗传算法中经过变异、交叉操作之后不满足约束条件的情况，制定惩罚函数，惩罚函数为
$$ f(s) = c(s) + \chi q(s) + \phi w(s) $$ (20) 式中：
$ c(s) $ 表示机器人总行走距离；$ q(s) $ 表示各条路径违反的容量约束之和；$ w(s) $ 表示所有顾客违反的时间窗约束之和；$ \chi $ 表示违反载重量约束的惩罚系数；$ \phi $ 表示违反时间窗约束的惩罚系数。$$ q(s) = \sum\limits_{i = 1}^m {\max \{ ({L_i} - {c_{ap}}),0\} } $$ (21) $$ w(s) = \sum\limits_{i = 1}^m {\max \{ ({a_i} - {l_i}),0\} } $$ (22) 式中：
$ {L_i} $ 表示该机器人的载重量；cap表示该机器人的最大载重量；$ {a_i} $ 表示机器人达到顾客的时间；$ {l_i} $ 表示顾客i的右时间窗。通过惩罚函数可知，该问题需要得到最小的惩罚函数，所以应度应该为惩罚函数的倒数，适应度函数应该为
$1/f(s)$ 。4.2.4 选择操作
对初始种群进行编码以及计算初始种群的适应度函数之后，需要进行选择操作。通过对初始种群中每个个体都计算它的适应度函数值，并对初始种群的适应度函数值进行归一操作，通过轮盘赌法选择出种群中的90%的个体进行后续操作。
4.2.5 加入破坏基因操作
针对传统遗传算法经过变异和交叉操作之后的求解质量低的问题，本研究提出破坏基因的操作，对经过变异和交叉操作之后得到的新路径上的顾客进行移除。首先对机器人所有路径中随机选择一位顾客进行移除，假如构建的100位顾客的配送首先移除顾客9，然后通过相关性计算公式，计算出顾客9与其他99为顾客的相关性值R。相关性计算公式如下所示
$$ R(i,j) = 1/(c'_{ij} + {v_{ij}}) $$ (23) $$ c'_{ij} = \frac{{{c_{ij}}}}{{\max {c_{ik}}}},k \in N $$ (24) 式中：
${v_{ij}}$ 表示顾客j与顾客i是否由同一个机器人服务，如果是同一个机器人服务为0，否则为1；$ {c_{ij}} $ 代表顾客i与j的距离；$ \max {c_{ik}} $ 代表离顾客i最远的顾客k的距离；N属于顾客集合。由相关性公式可知，顾客i与j的相关性的值越大则代表顾客i与顾客j的相关性越大。假如一共排除10个顾客，首先随机排除一位，通过计算已移除的第一位顾客与其他所有顾客的相关性值，并进行归一处理通过轮盘赌法排除另外9个顾客点位。将该10位顾客从遗传算法种群中移除。
4.2.6 加入修复基因操作
修复基因的思想为最远插入启发式思想，即求到移除的顾客依次添加回各个机器人服务的顾客中间的最小距离增量，找到移除顾客中的最小距离增量中最大的顾客重新插回顾客服务顺序中。例如已经移除了10位顾客，将移除的9号顾客点依次添加回每一个机器人服务的顾客点位中间去，一共有NV+90种情况，NV为机器人的数量。依次计算NV+90种情况中机器人到达每位顾客的时间和该机器人的载重量，判断插入顾客后的机器人到达每位顾客的时间是否满足每位的时间窗约束和载重量约束，如果同时满足记录下插入顾客前后的距离增量，如果不满足其中之一的约束，就派出新的机器人进行服务该新增顾客。由此可以得到NV+90个距离增量，从中找出最小距离增量的插入点和机器人序号。由此可以得到之前移除的10位顾客的最小距离增量。找到10位顾客中最小距离增量最大的移除顾客，将其重新添加回对应的最小距离增量的插入点和机器人序号。重新插回一位已移除的顾客后，把剩下的9位已移除的顾客代入新解中，继续重新计算的最小距离增量，再进行比较，重新插回种群中。直至10位顾客都重新插回到新解中得到新的100位顾客的新解。
4.3 混合蚁群−遗传算法解决配送顾客的算法步骤
1）初始化顾客点信息、机器人信息以及蚁群算法和遗传算法实验参数。
2）首先设置m只蚂蚁利用改进状态转移公式(20)来得到每只蚂蚁遍历完100位顾客点的机器人配送方案，由此得到m个100位顾客的机器人配送方案。
3）对m个100位顾客的机器人配送方案进行编码，以此作为遗传算法的初始种群。
4）对初始种群计算种群的各个目标函数值，并进行归一操作，运用轮盘赌法从m个基因片段中选择出NP个进行交叉操作和变异操作得到新种群。
5）对新种群进行解码，并随机移除一位顾客，并计算该移除顾客和其余99位顾客的相关性值，进行归一处理，用轮盘赌法得到一共移除的D个顾客。
6）计算D个顾客重新插回到新解中的最小距离增量。并从D个最小距离增量中找到最大的增量值并插回到相应插入顾客点以及服务机器人序号，直到D个顾客被重新插回到新解中。
7）重新将新解编码重插入子代形成新种群并删除种群中重复个体，并补齐删除的个体。
8）是否达到遗传算法最大迭代值，如果没有达到就返回4），达到最大迭代值则停止算法并输出最优配送方案。
4.4 混合蚁群−遗传算法解决配送顾客的算法试验验证
针对传统的蚁群算法和遗传算法在求解大规模VRPTW问题质量低下的问题，本研究提出混合蚁群遗传算法，将蚁群算法初代解用作遗传算法的初始种群。随后在传统的遗传算法的变异交叉操作外新加入本研究提出的破坏−修复基因操作，并引入基因相关性的因素丰富了求解的多样性，提高了求解质量。为了验证本研究改进算法的优越性，本次实验选用Solomon Benchmark中的C101.100的数据集进行仿真验证。对试验中应用最优路径的改进蚁群算法中的应用机器人对顾客服务分配顺序的蚁群算法中时间窗宽度启发因子
$ {\varepsilon} $ =2、机器人等待时间启发因子$ \delta $ =3，每台机器人的容量cap=200。违反容量约束的惩罚函数系数为1，违反时间窗约束的惩罚函数系数为6，迭代次数为100，交叉概率Pc=0.9，变异概率Pm=0.05。在参数一致的情况下，将基本蚁群算法、文献[26]算法、以及本研究改进算法在C101.100算例中进行对比分析，各算法的最小总距离迭代图如图10所示，机器人配送方案如表1所示。表 1 机器人配送方案Table 1 Robot distribution scheme编号 路径顾客点 1 0 32 33 31 35 37 38 39 36 34 0 2 0 43 42 41 40 44 46 45 48 51 50 52 49 47 0 3 0 98 96 95 94 92 93 97 100 99 0 4 0 90 87 86 83 82 84 85 88 89 91 0 5 0 57 55 54 53 56 58 60 59 0 6 0 67 65 63 62 74 72 61 64 68 66 69 0 7 0 20 24 25 27 29 30 28 26 23 22 21 0 8 0 81 78 76 71 70 73 77 79 80 0 9 0 5 3 7 8 10 11 9 6 4 2 1 75 0 10 0 13 17 18 19 15 16 14 12 0 
图 10 最小总距离迭代图Fig. 10 Iteration diagram of minimum total distance下载:
全尺寸图片
混合蚁群算法、基本蚁群算法以及文献[26]算法的车辆行驶最小总距离分别为828.9396、1200.5268、860.2051 m。在距离方面混合蚁群算法有了显著降低。在C101.100中，随着顾客数量变多，文献[26]算法最优解的质量出现下滑并且算法的收敛性也十分差，算法一直到迭代次数到了80代以后才收敛。由图10可以看出，本研究改进算法无论是在最小总距离的长度还是在迭代次数方面都要比基本蚁群算法和文献[26]算法有所改善。
其次，Solomon Benchmark的网站给出了各个算例历来使用启发式算法求解得到的最优路径,将其与本次改进后得到的最优解对比，在C101.100算例中历来最短行驶距离为828.94 m，本研究算法的数据为828.94 m，虽然在试验数据上的一些精确值上存在略微差异，但可以看出本研究改进的算法结果能够与历年最优路径值一致，证明了算法的可行性。
本研究改进算法在C101.100算例中得到的最优方案配送路线图如图11所示。其中得到的最优解为机器人使用数目为10，车辆行驶总距离为828.9369 m。配送路线如图11所示。
图 11 最优方案配送路线Fig. 11 distribution route of the optimal scheme下载:
全尺寸图片
5. 餐厅环境下仿真试验
餐厅配送的问题实际就是基于将有障碍物的实际环境中每位顾客点之间和送餐中心的最短距离求出并记录实际路线，将有障碍物的实际最短距离融入VRPTW问题中解出最优配送方案并通过实际路线进行配送。所以在实际问题中不仅要得到合理的顾客配送顺序，还要得到用最少的机器人去服务以减少成本。本研究的成本函数公式为
$$ {C_t}{\text{ = 1 000}}\cdot {N_V}{\text{ + 1}}\cdot{T_D} $$ (25) 式中：NV代表本次送餐一共派出的机器人数目；TD代表所有机器人行走的距离。
首先要进行对餐厅环境的建模，这里通过栅格法，并且修改c101.25的一些顾客点位置信息后作为餐厅顾客点。在仿真餐厅环境下的算法步骤为：
1）初始化顾客点信息、机器人信息以及混合蚁群算法试验参数，对餐厅环境进行建模。
2）通过前文应用于路径规划的改进蚁群算法找到顾客点之间和顾客点与送餐中心之间的最短距离，并记录下来其之间互相的实际路线。
3）通过前文的混合蚁群算法，将其中最短距离替换为前文的顾客点之间和顾客点与送餐中心之间的最短距离，解出餐厅中顾客的最优配送方案。
4）结合配送方案以及前文解出的实际路线，完成整个餐厅的机器人送餐配送调度。
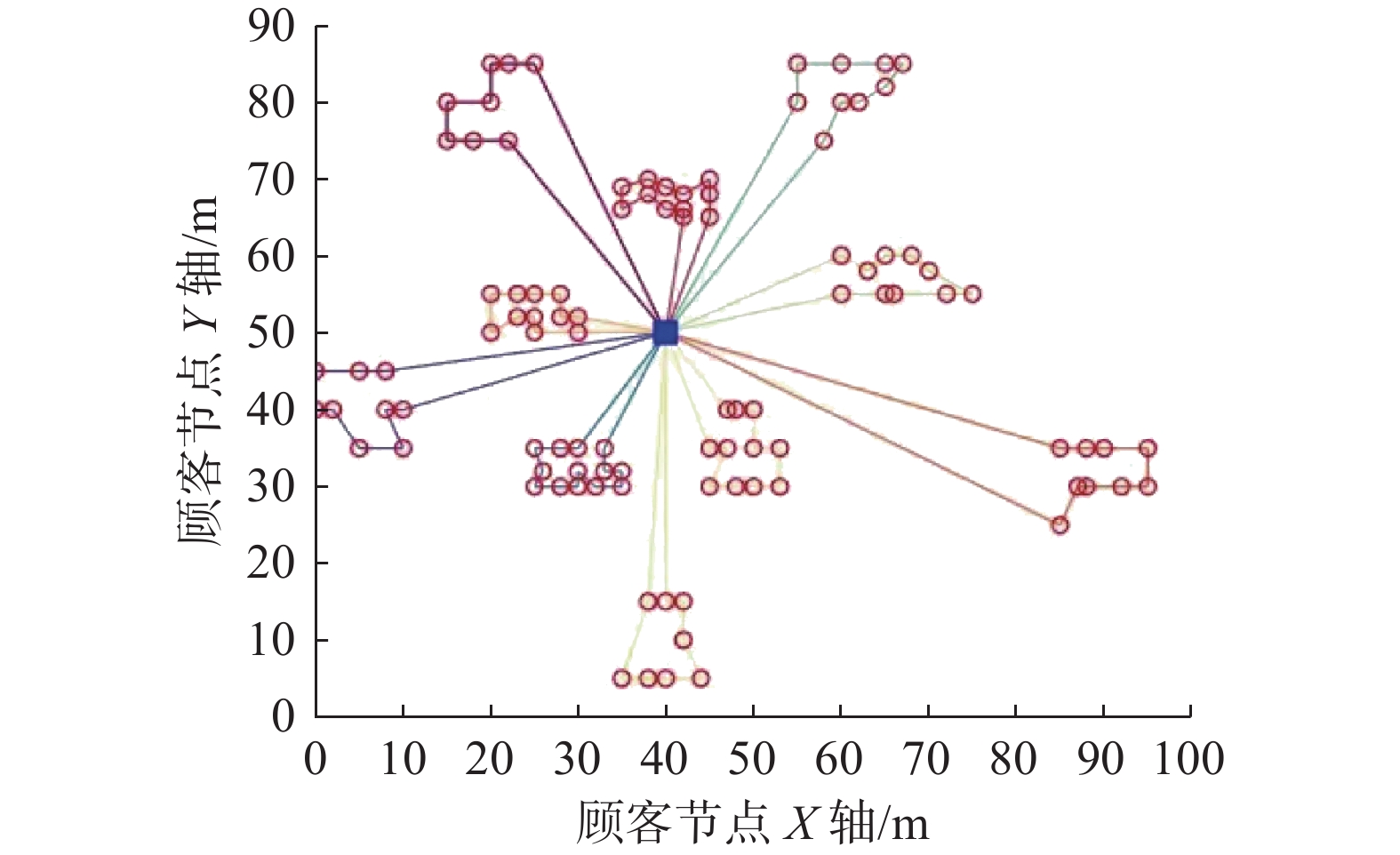
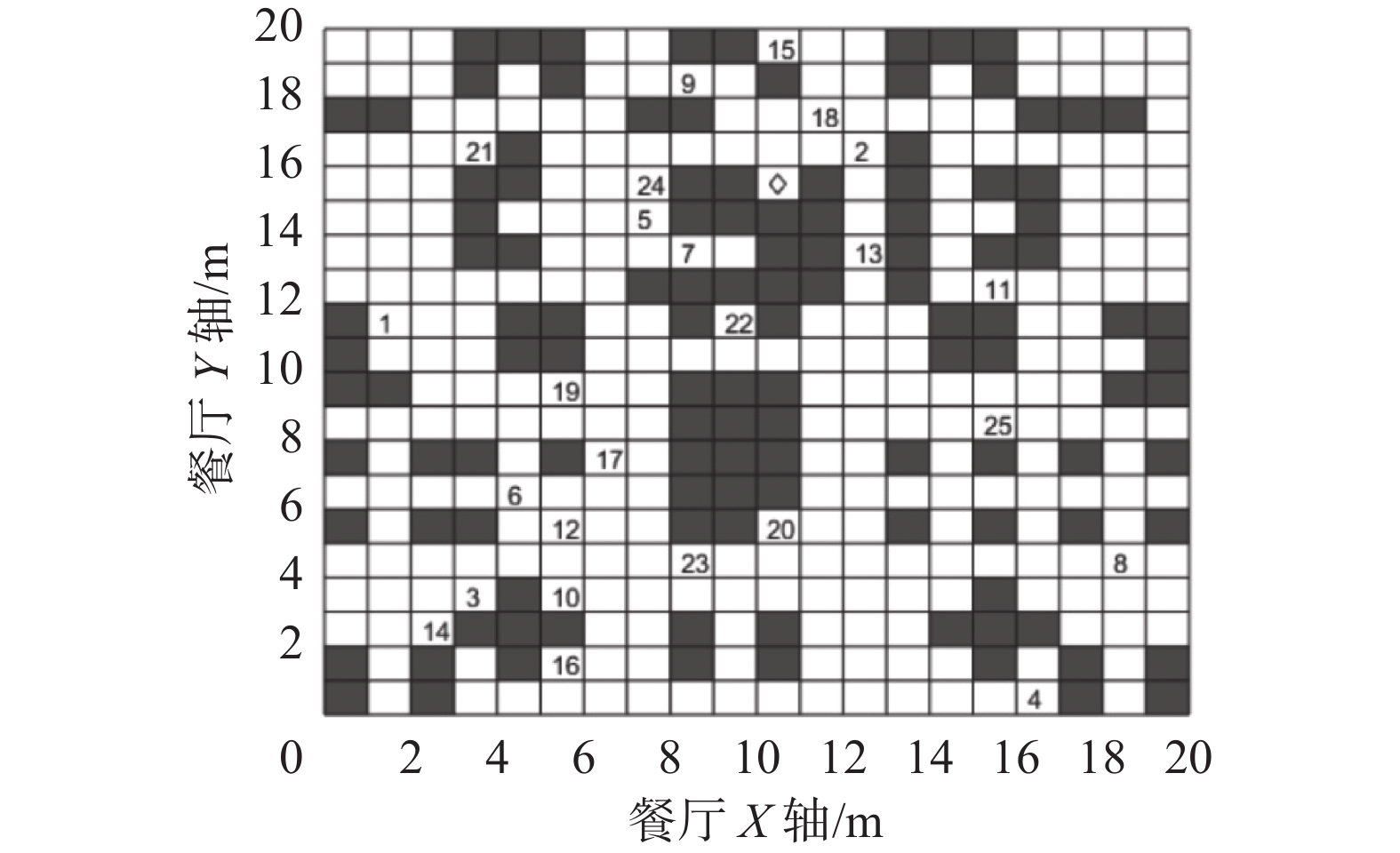
一共25位顾客点的点位以及机器人送餐中心和餐厅的仿真环境如图12所示。
图 12 餐厅仿真环境Fig. 12 Restaurant simulation environment下载:
全尺寸图片
本研究选取C101.25的数据集，并根据实际生活情况修改其顾客坐标、顾客需求以及机器人的容量。设◇为餐饮中心，需求量单位为0.1 kg，时间窗单位取30 s，送餐机器人最大载重量为20 kg。具体数据如表2所示。
表 2 餐厅信息表Table 2 Restaurant information sheet序号 X坐
标/mY坐
标/m需求量/
kg左时间窗/
s有时间窗/
s服务时间/
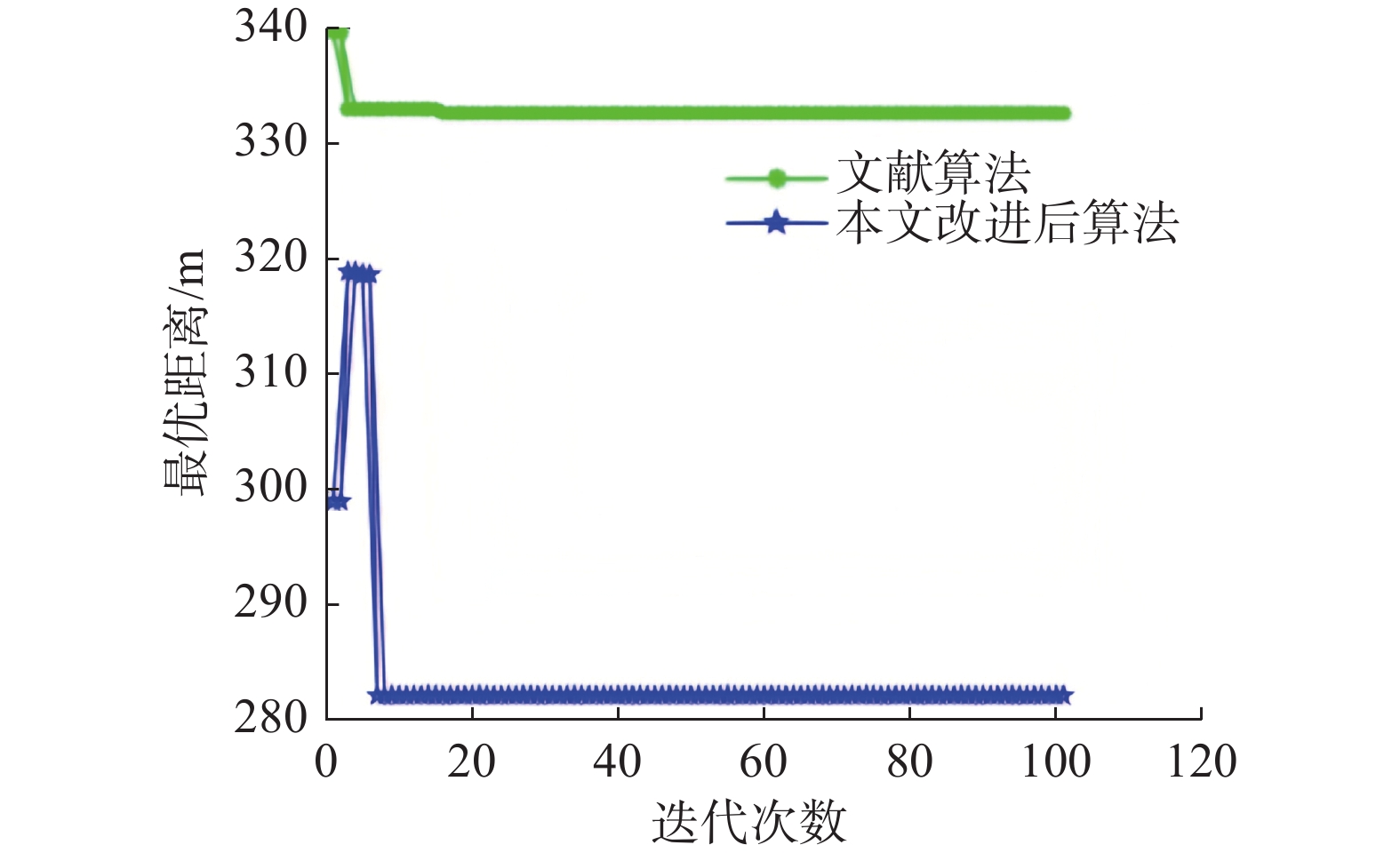
s0 10.5 15.5 0 0 1236 0 1 1.5 11.5 1 912 967 90 2 12.5 16.5 3 825 870 90 3 3.5 3.5 1 65 146 90 4 16.5 0.5 1 727 782 90 5 7.5 14.5 1 15 67 90 6 4.5 6.5 2 621 702 90 7 8.5 13.5 2 170 225 90 8 18.5 4.5 2 255 324 90 9 8.5 18.5 1 534 605 90 10 5.5 3.5 1 357 410 90 11 15.5 12.5 1 448 505 90 12 5.5 5.5 2 652 721 90 13 12.5 13.5 3 30 92 90 14 2.5 2.5 1 567 620 90 15 10.5 19.5 4 384 429 90 16 5.5 1.5 4 475 528 90 17 6.5 7.5 2 99 148 90 18 11.5 17.5 2 179 254 90 19 5.5 9.5 1 278 345 90 20 10.5 5.5 1 10 73 90 21 3.5 16.5 2 914 965 90 22 9.5 11.5 2 812 883 90 23 8.5 4.5 1 732 777 90 24 7.5 15.5 1 65 144 90 25 15.5 8.5 4 169 224 90 前面已经分别进行了带有障碍物的栅格环境下的路径规划算法验证对比和在VRPTW问题上各算法的配送方案算法的验证对比。在本节餐厅仿真环境下，进行25位顾客在餐厅用餐的送餐仿真算法对比。在同一仿真环境和顾客信息一致情况下，将基本蚁群算法和文献[26]算法结合后得到的送餐机器人最小距离迭代图与本研究算法实验得到的最小距离迭代图对比，如图13所示。两种算法的最小距离和最小成本对比如表3所示。
图 13 2种算法最优距离对比Fig. 13 Comparison diagram of optimal distance of two algorithms下载:
全尺寸图片
表 3 2种算法的最小距离和最小成本对比表Table 3 Comparison table of minimum distance and minimum cost of two algorithms文献算法最小距离/m 本研究算法最小距离/m 文献算法最小成本 本研究算法最小成本 332.7696 282.2498 4332.7696 3282.2498 由图13中2种算法的对比可以看出，由于本研究算法构建了满足约束条件的可选顾客集，因此只用了较少的迭代次数就寻到了最优解，并且由于本研究算法添加了适应度函数，在算法寻到了最优解时，收敛速度会加快，因此出现了最优解迅速收敛的现象。在25位顾客的餐厅送餐问题下，本研究算法相比文献算法得到的机器人最小总距离结果更好，并且从2种算法的最小成本上来看，本研究算法只需要3个机器人便可以完成25位顾客的配送。而结合了基本蚁群算法的文献[26]算法需要4个机器人进行配送。这主要是因为基本蚁群算法在计算25位顾客之间的最优路径效果不如本研究在第2章改进的算法得到最优路径。并且文献算法在25位顾客之间的分配问题中，算法迭代次数在接近20代收敛，而本研究算法在10代以前收敛，在本研究算法的收敛性上也体现本研究算法的优越性。
通过本研究改进后算法得到25位最优配送方案如表4所示。
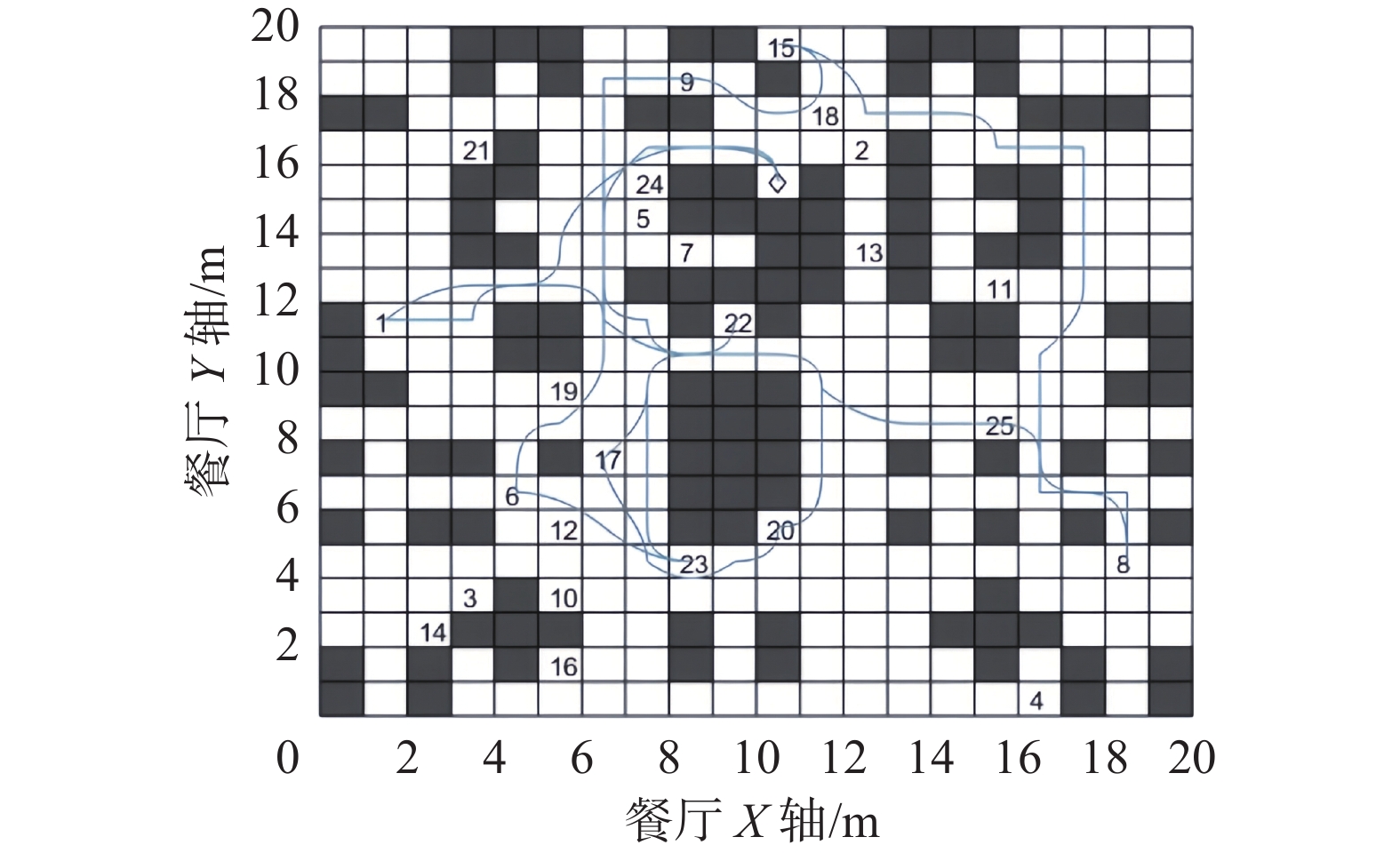
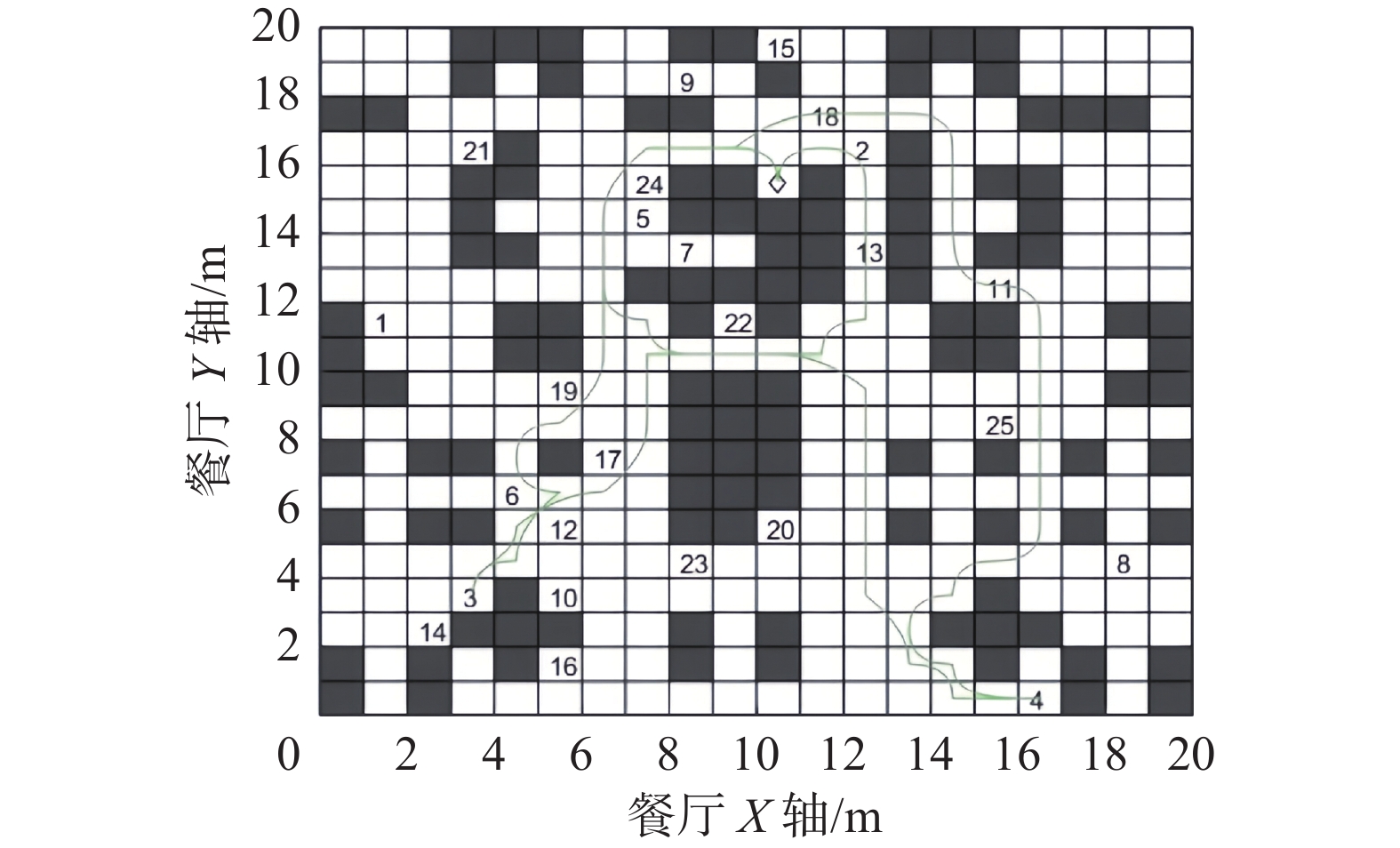
表 4 餐厅最优配送方案表Table 4 Optimal distribution scheme of restaurant机器人编号 配送的顾客点 1 0 20 17 25 8 15 9 6 23 22 1 0 2 0 5 24 7 19 10 16 14 12 2 21 0 3 0 13 3 18 11 4 0 机器人送餐配送仿真图如图14-16所示。图中◇为机器人的出发点，即餐饮配送中心。1−25的数字分别代表该餐厅中，不同的顾客所在的位置信息。
图 14 一号机器人的配送方案Fig. 14 Distribution scheme of robot 1下载:
全尺寸图片
图 15 二号机器人的配送方案Fig. 15 Distribution scheme of robot 2下载:
全尺寸图片
图 16 三号机器人的配送方案Fig. 16 Distribution scheme of robot 3下载:
全尺寸图片
6. 结束语
本研究首先介绍了蚁群算法的原理和公式，将目标点对地图上每个点的距离因素以及引导素加入到蚁群算法的状态转移公式中，对比仿真验证了算法能够在栅格环境下得到良好的路径规划。接着提出了混合蚁群−遗传算法，通过加入顾客点的时间窗宽度和机器人等待时间因素到状态转移公式中，将蚁群算法得出的解作为遗传算法的初始种群，并加入了破坏和修复基因操作，得到了跟Solomon Benchmark的网站给出的历代最优解一致的结果，验证了改进算法的可行性。最后结合餐厅仿真环境通过仿真结果表明，改进后的算法能够在餐厅复杂环境下，规划出多位顾客合理配送方案以及最优路径规划路线。
-
图 1 第1种情况
Fig. 1 Case 1
下载:
全尺寸图片
图 2 第2种情况
Fig. 2 Case 2
下载:
全尺寸图片
图 3 第3种情况
Fig. 3 Case3
下载:
全尺寸图片
图 4 不同
$ \alpha $ 参数实验结果Fig. 4 Different
$ \alpha $ parameter experiment results下载:
全尺寸图片
图 5 不同β参数实验结果
Fig. 5 Different β parameter experiment results
下载:
全尺寸图片
图 6 不同ρ参数实验结果
Fig. 6 Different ρ parameter experiment results
下载:
全尺寸图片
图 7 基本蚁群算法与改进后的蚁群算法对比
Fig. 7 Comparison between basic ant colony algorithm and improved ant colony algorithm
下载:
全尺寸图片
图 8 2种不同算法对比
Fig. 8 Comparison of two different algorithms
下载:
全尺寸图片
图 9 Nik的确定方法
Fig. 9 Method for determining Nik
下载:
全尺寸图片
图 10 最小总距离迭代图
Fig. 10 Iteration diagram of minimum total distance
下载:
全尺寸图片
图 11 最优方案配送路线
Fig. 11 distribution route of the optimal scheme
下载:
全尺寸图片
图 12 餐厅仿真环境
Fig. 12 Restaurant simulation environment
下载:
全尺寸图片
图 13 2种算法最优距离对比
Fig. 13 Comparison diagram of optimal distance of two algorithms
下载:
全尺寸图片
图 14 一号机器人的配送方案
Fig. 14 Distribution scheme of robot 1
下载:
全尺寸图片
图 15 二号机器人的配送方案
Fig. 15 Distribution scheme of robot 2
下载:
全尺寸图片
图 16 三号机器人的配送方案
Fig. 16 Distribution scheme of robot 3
下载:
全尺寸图片
表 1 机器人配送方案
Table 1 Robot distribution scheme
编号 路径顾客点 1 0 32 33 31 35 37 38 39 36 34 0 2 0 43 42 41 40 44 46 45 48 51 50 52 49 47 0 3 0 98 96 95 94 92 93 97 100 99 0 4 0 90 87 86 83 82 84 85 88 89 91 0 5 0 57 55 54 53 56 58 60 59 0 6 0 67 65 63 62 74 72 61 64 68 66 69 0 7 0 20 24 25 27 29 30 28 26 23 22 21 0 8 0 81 78 76 71 70 73 77 79 80 0 9 0 5 3 7 8 10 11 9 6 4 2 1 75 0 10 0 13 17 18 19 15 16 14 12 0 表 2 餐厅信息表
Table 2 Restaurant information sheet
序号 X坐
标/mY坐
标/m需求量/
kg左时间窗/
s有时间窗/
s服务时间/
s0 10.5 15.5 0 0 1236 0 1 1.5 11.5 1 912 967 90 2 12.5 16.5 3 825 870 90 3 3.5 3.5 1 65 146 90 4 16.5 0.5 1 727 782 90 5 7.5 14.5 1 15 67 90 6 4.5 6.5 2 621 702 90 7 8.5 13.5 2 170 225 90 8 18.5 4.5 2 255 324 90 9 8.5 18.5 1 534 605 90 10 5.5 3.5 1 357 410 90 11 15.5 12.5 1 448 505 90 12 5.5 5.5 2 652 721 90 13 12.5 13.5 3 30 92 90 14 2.5 2.5 1 567 620 90 15 10.5 19.5 4 384 429 90 16 5.5 1.5 4 475 528 90 17 6.5 7.5 2 99 148 90 18 11.5 17.5 2 179 254 90 19 5.5 9.5 1 278 345 90 20 10.5 5.5 1 10 73 90 21 3.5 16.5 2 914 965 90 22 9.5 11.5 2 812 883 90 23 8.5 4.5 1 732 777 90 24 7.5 15.5 1 65 144 90 25 15.5 8.5 4 169 224 90 表 3 2种算法的最小距离和最小成本对比表
Table 3 Comparison table of minimum distance and minimum cost of two algorithms
文献算法最小距离/m 本研究算法最小距离/m 文献算法最小成本 本研究算法最小成本 332.7696 282.2498 4332.7696 3282.2498 表 4 餐厅最优配送方案表
Table 4 Optimal distribution scheme of restaurant
机器人编号 配送的顾客点 1 0 20 17 25 8 15 9 6 23 22 1 0 2 0 5 24 7 19 10 16 14 12 2 21 0 3 0 13 3 18 11 4 0 -
[1] 陶永, 王田苗, 刘辉, 等. 智能机器人研究现状及发展趋势的思考与建议[J]. 高技术通讯, 2019, 29(2): 149–163. doi: 10.3772/j.issn.1002-0470.2019.02.006 TAO Yong, WANG Tianmiao, LIU Hui, et al. Insights and suggestions on the current situation and development trend of intelligent robots[J]. Chinese high technology letters, 2019, 29(2): 149–163. doi: 10.3772/j.issn.1002-0470.2019.02.006 [2] KUANG Hua, XU Zhipeng, LI Xingli, et al. An extended car-following model accounting for the average headway effect in intelligent transportation system[J]. Physica A:statistical mechanics and its applications, 2017, 471: 778–787. doi: 10.1016/j.physa.2016.12.022 [3] POOLE A, KOTSIALOS A. Swarm intelligence algorithms for macroscopic traffic flow model validation with automatic assignment of fundamental diagrams[J]. Applied soft computing, 2016, 38: 134–150. doi: 10.1016/j.asoc.2015.09.011 [4] CHMIEL W, DAŃDA J, DZIECH A, et al. INSIGMA: an intelligent transportation system for urban mobility enhancement[J]. Multimedia tools and applications, 2016, 75(17): 10529–10560. doi: 10.1007/s11042-016-3367-5 [5] 程志, 张志安, 李金芝, 等. 改进人工势场法的移动机器人路径规划[J]. 计算机工程与应用, 2019, 55(23): 29–34. doi: 10.3778/j.issn.1002-8331.1904-0472 CHENG Zhi, ZHANG Zhian, LI Jinzhi, et al. Mobile robots path planning based on improved artificial potential field[J]. Computer engineering and applications, 2019, 55(23): 29–34. doi: 10.3778/j.issn.1002-8331.1904-0472 [6] WANG Xiuhong, LIU Xuehao, WANG Yongcheng, et al. Research on path planning of mobile robot based on improved A* algorithm[C]//IE&EM 2019. Singapore: Springer, 2020: 153−161. [7] WANG Huijuan, YU Yuan, YUAN Quanbo. Application of Dijkstra algorithm in robot path-planning[C]//2011 Second International Conference on Mechanic Automation and Control Engineering. Hohhot. IEEE, 2011: 1067−1069. [8] ELHOSENY M, THARWAT A, HASSANIEN A E. Bezier curve based path planning in a dynamic field using modified genetic algorithm[J]. Journal of computational science, 2018, 25: 339–350. doi: 10.1016/j.jocs.2017.08.004 [9] SONG Baoye, WANG Zidong, SHENG Ligang. A new genetic algorithm approach to smooth path planning for mobile robots[J]. Assembly automation, 2016, 36: 138–145. doi: 10.1108/AA-11-2015-094 [10] FERNANDES C M, MORA A M, MERELO J J, et al. KANTS: a stigmergic ant algorithm for cluster analysis and swarm art[J]. IEEE transactions on cybernetics, 2014, 44(6): 843–856. doi: 10.1109/TCYB.2013.2273495 [11] 陈嘉林, 魏国亮, 田昕. 改进粒子群算法的移动机器人平滑路径规划[J]. 小型微型计算机系统, 2019, 40(12): 2550–2555. doi: 10.3969/j.issn.1000-1220.2019.12.014 CHEN Jialin, WEI Guoliang, TIAN Xin. Smooth path planning for mobile robots based on improved particle swarm optimization algorithm[J]. Journal of Chinese computer systems, 2019, 40(12): 2550–2555. doi: 10.3969/j.issn.1000-1220.2019.12.014 [12] ALAM M S, RAFIQUE M U, KHAN M U. Mobile robot path planning in static environments using particle swarm optimization[EB/OL]. (2020−08−23)[2021−01−01].https://arxiv.org/abs/2008.10000.pdf. [13] PATLE B K, PANDEY A, JAGADEESH A, et al. Path planning in uncertain environment by using firefly algorithm[J]. Defence technology, 2018, 14(6): 691–701. doi: 10.1016/j.dt.2018.06.004 [14] JIANG Tao, WANG Jianzhong. Study on path planning method for mobile robot based on fruit fly optimization algorithm[J]. Applied mechanics and materials, 2014, 536/537: 970–973. doi: 10.4028/www.scientific.net/AMM.536-537.970 [15] PANDA M, DAS B, PATI B B. Grey wolf optimization for global path planning of autonomous underwater vehicle[C]//Proceedings of the Third International Conference on Advanced Informatics for Computing Research. New York: ACM, 2019: 1−6. [16] 楼传炜, 葛泉波, 刘华平, 等. 无人机群目标搜索的主动感知方法[J]. 智能系统学报, 2021, 16(3): 575–583. doi: 10.11992/tis.202009012 LOU Chuanwei, GE Quanbo, LIU Huaping, et al. Active perception method for UAV group target search[J]. CAAI transactions on intelligent systems, 2021, 16(3): 575–583. doi: 10.11992/tis.202009012 [17] 徐玉琼, 娄柯, 李志锟. 基于变步长蚁群算法的移动机器人路径规划[J]. 智能系统学报, 2021, 16(2): 330–337. doi: 10.11992/tis.202004011 XU Yuqiong, LOU Ke, LI Zhikun. Mobile robot path planning based on variable-step ant colony algorithm[J]. CAAI transactions on intelligent systems, 2021, 16(2): 330–337. doi: 10.11992/tis.202004011 [18] 夏小云, 周育人. 蚁群优化算法的理论研究进展[J]. 智能系统学报, 2016, 11(1): 27–36. doi: 10.11992/tis.201510002 XIA Xiaoyun, ZHOU Yuren. Advances in theoretical research of ant colony optimization[J]. CAAI transactions on intelligent systems, 2016, 11(1): 27–36. doi: 10.11992/tis.201510002 [19] CAO Jingang. Robot global path planning based on an improved ant colony algorithm[J]. Journal of computer and communications, 2016, 4(2): 11–19. doi: 10.4236/jcc.2016.42002 [20] TSAI P W, NGUYEN T T, DAO T K. Robot path planning optimization based on multiobjective grey wolf optimizer[C]// International Conference on Genetic and Evolutionary Computing. Cham: Springer, 2017: 166−173. [21] 张毅, 杨光辉, 花远红. 基于改进人工鱼群算法的机器人路径规划[J]. 控制工程, 2020, 27(7): 1157–1163. doi: 10.14107/j.cnki.kzgc.170847 ZHANG Yi, YANG Guanghui, HUA Yuanhong. Robot path planning based on improved artificial fish swarm algorithm[J]. Control engineering of China, 2020, 27(7): 1157–1163. doi: 10.14107/j.cnki.kzgc.170847 [22] BRAND M, YU Xiaohua. Autonomous robot path optimization using firefly algorithm[C]//2013 International Conference on Machine Learning and Cybernetics. Tianjin: IEEE, 2014: 1028−1032. [23] DORIGO M, MANIEZZO V, COLORNI A. The ant system: an autocatalytic optimizing process Technical Report91-O16[R]. Milan: Dipartimento di Elettronica, Politecnicl di Milano, 1991. [24] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agents[C]//IEEE Transactions on Systems, Man, and Cybernetics, Part B. Cybernetics: IEEE, 2002: 29−41. [25] 董炫良, 赵桂清. 人工势场引导蚁群算法的机器人导航路径规划[J]. 机械设计与制造, 2021(6): 169–173. doi: 10.3969/j.issn.1001-3997.2021.06.039 DONG Xuanliang, ZHAO Guiqing. Robot navigation path planning based on ant colony algorithm guided by artificial potential field[J]. Machinery design & manufacture, 2021(6): 169–173. doi: 10.3969/j.issn.1001-3997.2021.06.039 [26] 李琳, 刘士新, 唐加福. 改进的蚁群算法求解带时间窗的车辆路径问题[J]. 控制与决策, 2010, 25(9): 1379–1383. doi: 10.13195/j.cd.2010.09.102.lil.012 LI Lin, LIU Shixin, TANG Jiafu. Improved ant colony algorithm for solving vehicle routing problem with time windows[J]. Control and decision, 2010, 25(9): 1379–1383. doi: 10.13195/j.cd.2010.09.102.lil.012
