Transition process identification based on the long and short sliding windowed slow feature analysis and time series association rule mining
-
摘要: 工况过渡过程与异常状态（故障）的数据特性极为相似。如果不对过渡过程加以辨识，极易导致过程监测系统频繁误报警，进而可能引发不适当的人工操作而严重破坏生产的稳定性。本文提出一种基于长短滑窗慢特征分析（slow feature analysis, SFA）与时序关联规则挖掘的过渡过程识别方法。首先，依据稳态工况和过渡工况在时间跨度上的差异性，提出一种长短滑窗与SFA相结合的多工况过程建模方法，将工况状态细分为多个稳态阶段与过渡阶段，并分别建立相应的离线SFA模型；然后，提出一种多时序多时间区间的同步频繁树构建方法，挖掘每种状态转变在多个时间序列与多个时间区间内的关联规则，以实现工况过渡过程的准确辨识。针对田纳西伊斯曼（Tennessee Eastman, TE）过程生成一组包含多模态相互转变的过程数据对所提方法进行实验验证，结果表明所提方法能够在频繁发生过程转变的过程数据中有效识别过渡过程，降低故障误报率，提高过程监测水平。Abstract: The transition process of working condition has similar data characteristics with process anomalies or faults. Thus, it is prone to cause frequent false alarms in the process monitoring if the transition process cannot be identified, which may lead to inappropriate manual operations and consequently destroy production stability. This paper proposes a transition process identification method based on the long and short sliding windowed slow feature analysis (SFA) and time series association rules mining approach. First, a multi-mode process modeling method based on the SFA associated with long and short sliding window processing is proposed according to the time-span difference between steady and transition conditions. The working condition state is divided into multiple sub-stages of steady or transition states, and then corresponding offline SFA models are established, respectively. Then, a synchronous frequent tree construction method with multi-time series and multi-time intervals is proposed, which can mine the association rules of each transition state in multi-time series and multi-time intervals, so as to accurately identify transition processes. Based on the Tennessee Eastman (TE) process, a set of process data, including all modal transitions, is established to verify the proposed method. The results show that the proposed method can effectively identify the transition process with frequent transitions, reducing the false alarm rate and improving the level of process monitoring.
-
因生产原材料来源的多样性和成分的复杂多变性、人们对于产品质量需求的个性化改变以及机器设备使用中的老化损耗等多重因素影响，现代工业往往处于多模态工况下运行，给工业过程的稳定生产和安全管理带来巨大挑战[1-2]。过程监测作为一种实现安全生产、保证产品质量以及降低生产中资源能源消耗的有效手段，成为工业生产中不可或缺的一环[3]。
研究者往往通过建立多个局部模型来对多模态工业过程进行异常检测与故障诊断[4]。然而，实际的多模态工况状态并不能仅归结为一些独立工况的简单组合。因为生产工况的转换不可能一蹴而就，任何两个稳态工况之间都会包含一个短暂的中间过渡过程。过渡过程作为稳定工况间的过渡状态广泛存在于复杂多工况工业过程中。过渡过程具有较高的时变特征，与过程故障所表现出来的数据特点极为相似，极易被误判为故障[5-6]。
先对过渡过程进行辨识再进行异常检测是降低故障误报警的有效方法。比如Zhao等[7]通过建立不同的在线质量预测模型，实现对过渡过程的监测识别；Zhang等[8]研究了随机扰动下的过渡过程识别问题。然而，上述方法没有注意到过程数据特别是过渡过程数据中存在的快速时变特点，以至于对数据的利用不够充分，过程状态识别准确性有待进一步提升。在复杂多工况工业过程监测中，稳态过程类似于物理中的“位置”概念，而动态变化的过渡过程则更类似于“速度”的概念[8]，两者携带信息不同，应使用不同的检测变量对动态变化与静态变化进行监测。
慢特征分析(slow feature analysis, SFA)将数据投影到显示其变化快慢的低维空间来分析过程的动态信息。由于SFA充分考虑了过程数据中的时变特性，在过程监测中受到广泛关注。如Dong等[9]提出了基于SFA与K最近邻(k-nearest neighbor, KNN)的故障监测框架；Zhao等[10]提出了一种基于SFA和高斯混合模型(Gaussian mixture model, GMM)[11]的条件驱动的数据重组策略，可以实现多模态工况的识别，但是该方法更多的是关注过程的条件切片，并没有充分注意到数据中包含的时变以及时序特性。
过程数据的时序关联特性在一定程度上能够反映出过程随时间变化的情况，因而通过挖掘时间序列中存在的关联关系，能判断过程的变化趋势[12]。时序关联规则是一种增加了时间约束的关联规则，不仅要找到相同属性与时间之间的关联关系，还要找到时域下不同属性之间的关联关系[13]。常见的关联规则挖掘算法有基于Apriori的算法[14]、基于FP-tree的算法[15]和基于频繁树的算法。
Apriori算法需要多次扫描单个模式实现对频繁项的识别，势必会造成大量的候选频繁项集，导致运行效率低下[16]。为了克服Apriori算法的不足，一些学者提出了FP-Growth算法[17]。FP-Growth基于压缩的FP-tree结构，递归挖掘频繁项集，可以有效减少候选项集的数量[18]。然而，FP-Growth的算法不能直接对时序数据挖掘关联规则，因而有学者提出基于频繁树的关联规则挖掘算法，通过生成频繁树直接从时序数据中挖掘关联规则。比如，Wang等[16]提出了一种基于频繁项集树的时态关联规则挖掘算法；李海林等[19]则通过定义趋势项−位置表示法创建同步频繁树(synchronize frequent tree, SFT)，避免在构建树结构的过程中占用大量的数据内存，但是该方法没有关注到不同时序不同时间区间下的关联规则挖掘且没有描述支持度与置信度的计算方法。
考虑到复杂多工况过程往往具有丰富的过程数据，这些过程数据反映的是多种复杂的时变工况特性[20-22]，如果直接对整个数据集进行SFA操作，可能会受到全局变量中波动值较大的对象的影响，进而导致时变工况监测性能下降。因而，本文将SFA与滑窗方法相结合，通过结合长短滑窗和自适应滑窗处理方式，对过程运行模态进行动态智能划分；同时将SFT与不同时间序列和不同时间区间下的置信度与支持度计算相结合，提出一种基于长短滑窗SFA与时序关联规则挖掘的工业过渡过程识别方法，对模态转换建立不同的识别规则，以适应对在线数据的模态转换识别。
1. 相关工作
本节简要回顾SFA、基于SFT的时序规则挖掘以及自适应滑窗算法的基本原理和主要步骤。
1.1 SFA
从数学上来说，SFA是要找到一个映射函数
${g_i}( \cdot )$ ，将一包含$m$ 个变量的输入数据${X}(t) = [{x_1}(t), {x_{_2}}(t), \cdots ,{x_m}(t)]$ 转化为表示时间变化快慢的慢特征数据$ {S}(t) = [{s_1}(t),{s_2}(t), \cdots ,{s_m}(t)] $ ，使其中的特征${s_i}(t)$ 具有尽可能慢的变化。因而，对于一包含
$n$ 条数据的过程数据矩阵，其目标函数可以表示为$$ \min \Delta ({s_i}(t)) = {\left\langle {{{\dot s}_i}^2} \right\rangle _t}{\text{ = }}\frac{1}{n}\sum\limits_{t = 1}^n {{{\dot s}_i}(t)} = \int_1^n {\frac{{{{\dot s}_i}(t)}}{{n - 1}}} {\rm{d}}t $$ (1) 式中
${\dot s_i}(t)$ 表示${s_i}(t)$ 的一阶导数，即$$ {\dot s_i}(t) = {s_i}(t) - {s_i}(t - 1) $$ 用来表示数据的变化程度，
${\dot s_i}(t)$ 的值越小表明数据变化越缓慢；同时，式(1)需满足以下3个约束：$$ \left\{ \begin{gathered} {\left\langle {{s_i}} \right\rangle _t} = 0 \\ {\left\langle {{s_i}^2} \right\rangle _t} = 1 \\ \forall i \ne j,{\left\langle {{s_i}{s_j}} \right\rangle _t} = 0 \\ \end{gathered} \right. $$ (2) 约束条件1强制数据保持零均值，用来简化问题并且保障一般性；约束条件2用于避免产生
${s_j}(t)$ 恒等于常数的情况发生；约束条件3则用来保证慢特征携带着不同的信息。考虑线性映射，每个慢特征
${s_i}(t)$ 都是所有输入变量的线性组合：$$ {s_i}(t) = {{\boldsymbol{W}}_i}{\boldsymbol{X}}{(t)^{\text{T}}} $$ 式中
${{{\boldsymbol{W}}}_i} \in {{\bf{R}}^{1 \times m}}$ 为特征映射向量。此时从${{\boldsymbol{X}}}(t)$ 到${{\boldsymbol{S}}}(t)$ 的映射可以表示为$$ {{\boldsymbol{S}}}(t) = {[{{\boldsymbol{WX}}}{(t)^{\rm{T}}}]^{\text{T}}} $$ 式中
${{\boldsymbol{W}}} = {[{{{\boldsymbol{W}}}_1}^{\text{T}}\;{{{\boldsymbol{W}}}_2}^{\text{T}}\; \cdots \;{{{\boldsymbol{W}}}_m}^{\text{T}}]^{\text{T}}}$ 为系数矩阵。对于式（1）所述的优化问题，可以使用拉格朗日乘子法，将目标函数视为广义特征值分解(GED)问题，即
$$ {{{\boldsymbol{R}}}_{\dot x\dot x}}{{\boldsymbol{W}}} = {{{\boldsymbol{R}}}_{xx}}{{\boldsymbol{W\varOmega}} } $$ 式中：
${{{\boldsymbol{R}}}_{\dot x\dot x}} = {\left\langle {{{{\dot {\boldsymbol{X}}}}^{\text{T}}}{\dot {\boldsymbol{X}}}} \right\rangle _t}$ ，${{{\boldsymbol{R}}}_{xx}} = {\left\langle {{{{\boldsymbol{X}}}^{\text{T}}}{{\boldsymbol{X}}}} \right\rangle _t}$ 为两个协方差矩阵的时间平均，${{\boldsymbol{W}}}$ 是矩阵对$\{ {{{\bf{R}}}_{\dot x\dot x}},{{{\bf{R}}}_{xx}}\}$ 的$m$ 维广义特征向组成的矩阵，${{\boldsymbol{\varOmega }}} = {\text{diag}}\{ {\omega _1},{\omega_2}, \cdots ,{\omega_m}\}$ 是一个广义特征值对角矩阵。与PCA类似，在进行SFA计算时，先对协方差矩阵的时间平均
${\left\langle {{{{\boldsymbol{X}}}^{\text{T}}}{{\boldsymbol{X}}}} \right\rangle _t}$ 进行奇异值分解：$$ {\left\langle {{{{\boldsymbol{X}}}^{\text{T}}}{{\boldsymbol{X}}}} \right\rangle _t} = {{\boldsymbol{V\varLambda}} }{{{\boldsymbol{V}}}^{\text{T}}} $$ (3) 这样原始输入数据就可以球化处理为
$$ {{\boldsymbol{Z}}} = {[{{{\boldsymbol{\varLambda}} }^{ - 1/2}}{{{\boldsymbol{V}}}^T}{{{\boldsymbol{X}}}^{\text{T}}}]^{\text{T}}} = {[{{\boldsymbol{Q}}}{{{\boldsymbol{X}}}^{\text{T}}}]^{\text{T}}} $$ (4) 式中
${{\boldsymbol{Q}}} = {{{\boldsymbol{\varLambda }}}^{ - 1/2}}{{{\boldsymbol{V}}}^{\text{T}}}$ 表示球化矩阵。由式(3)和(4)可知${\left\langle {{{{\boldsymbol{Z}}}^{\text{T}}}{{\boldsymbol{Z}}}} \right\rangle _t} = {{\boldsymbol{Q}}}{\left\langle {{{{\boldsymbol{X}}}^{\text{T}}}{{\boldsymbol{X}}}} \right\rangle _t}{{{\boldsymbol{Q}}}^{\text{T}}} = {{\boldsymbol{I}}}$ ，其中I为单位矩阵，并且${\left\langle {{\boldsymbol{Z}}} \right\rangle _t} = 0$ ，满足式(2)中的约束条件。令
${{\boldsymbol{P}}} = {{\boldsymbol{W}}}{{{\boldsymbol{Q}}}^{ - 1}}$ ，则矩阵可以表示为$$ {{\boldsymbol{S}}} = {[{{\boldsymbol{W}}}{{{\boldsymbol{X}}}^{\text{T}}}]^{\text{T}}} = {[{{\boldsymbol{W}}}{{{\boldsymbol{Q}}}^{ - 1}}{{{\boldsymbol{Z}}}^{\text{T}}}]^{\text{T}}} = {[{{\boldsymbol{P}}}{{{\boldsymbol{Z}}}^{\text{T}}}]^{\text{T}}} $$ 根据约束条件1和约束条件2可知
${\left\langle {{{{\boldsymbol{S}}}^{\rm{T}}}{{\boldsymbol{S}}}} \right\rangle _t} = {{\boldsymbol{I}}}$ ，则，$$ {\left\langle {{{{\boldsymbol{S}}}^{\text{T}}}{{\boldsymbol{S}}}} \right\rangle _t} = {{\boldsymbol{P}}}{\left\langle {{{{\boldsymbol{Z}}}^{\text{T}}}{{\boldsymbol{Z}}}} \right\rangle _t}{{{\boldsymbol{P}}}^{\text{T}}} = {{\boldsymbol{P}}}{{{\boldsymbol{P}}}^{\text{T}}} = {{\boldsymbol{I}}} $$ 说明矩阵
${{\boldsymbol{P}}}$ 是一个正交矩阵，此时，则SFA算法的目标函数变为$$ \min \Delta ({s_i}(t)) = {\left\langle {{{\dot s}_i}^2} \right\rangle _t} = {{{\boldsymbol{P}}}_i}^{\text{T}}{\left\langle {{{{{\dot {\bf{Z}}}}}^{\text{T}}}{{\dot {\bf{Z}}}}} \right\rangle _t}{{{\boldsymbol{P}}}_i}$$ 只需要计算
${\left\langle {{{{\dot {\boldsymbol{Z}}}}^T}{{\dot {\bf{Z}}}}} \right\rangle _t}$ 并进行奇异值分解即可：$$ {\left\langle {{{{\dot {\boldsymbol{Z}}}}^{\text{T}}}{\dot {\boldsymbol{Z}}}} \right\rangle _t} = {{{\boldsymbol{P}}}^{\text{T}}}{{\boldsymbol{\varOmega P}}} $$ 此时，
${\left\langle {{{{\dot {\boldsymbol{S}}}}^{\text{T}}}{\dot {\boldsymbol{S}}}} \right\rangle _t} = {{\boldsymbol{\varOmega }}}$ ，并且最后系数矩阵${{\boldsymbol{W}}}$ 可以表示为$$ {{\boldsymbol{W}}} = {{\boldsymbol{PQ}}} = {{\boldsymbol{P}}}{{{\boldsymbol{\varLambda}} }^{ - 1/2}}{{{\boldsymbol{V}}}^{\text{T}}} $$ (13) 此时广义特征向量
${{\boldsymbol{W}}} = [{{{\boldsymbol{W}}}_1}\;{{{\boldsymbol{W}}}_2}\;\cdots\;{{{\boldsymbol{W}}}_m}]$ ，其中的每个元素都对应了一个线性映射的系数向量。广义特征值对角矩阵${{\boldsymbol{\varOmega}} }={\text{diag}}\{ {\omega _1},{\omega _2},\cdots,{\omega _m}\}$ 中的元素则按照升序的方式排列，保证变化最慢的特性具有最低的索引。进而将数据转化为按照时变快慢排列的数据空间。1.2 同步频繁树时序关联方式挖掘
为从时序数据中挖掘出数据变化的关联方式，本文使用基于SFT的时序关联挖掘算法找到每种数据变化的关联规则。
1） 数据序列时序表示
对于数据的时序变化特征，可以采用趋势项–位置的表示方法，其表示规则为：趋势项+位置列表。对于趋势项的表示，采用斜率的大小作为趋势项的值，而时序表示则只保留一个趋势项的名称，相同的趋势项使用位置索引代替。
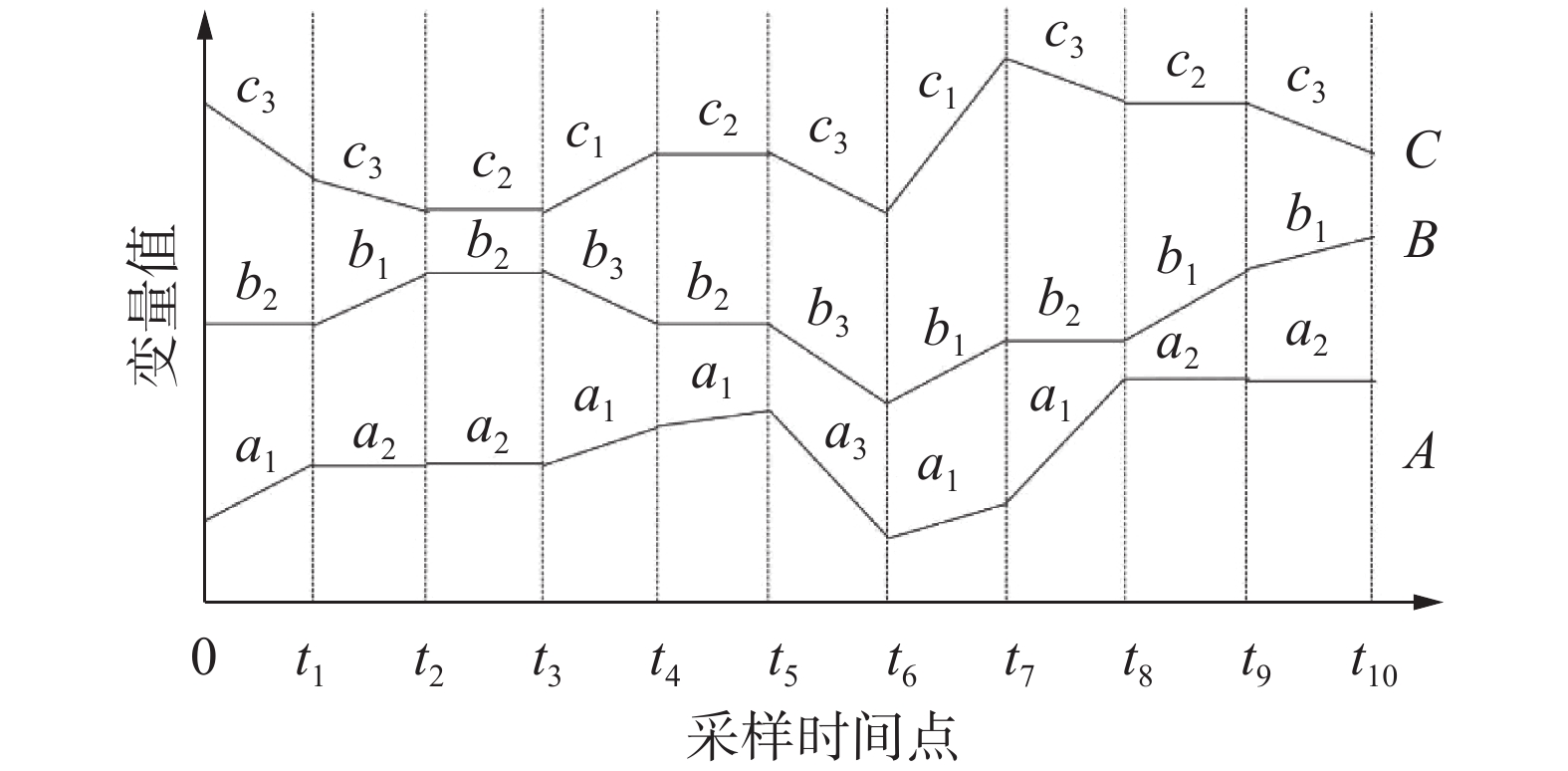
图1给出了3组时序数据
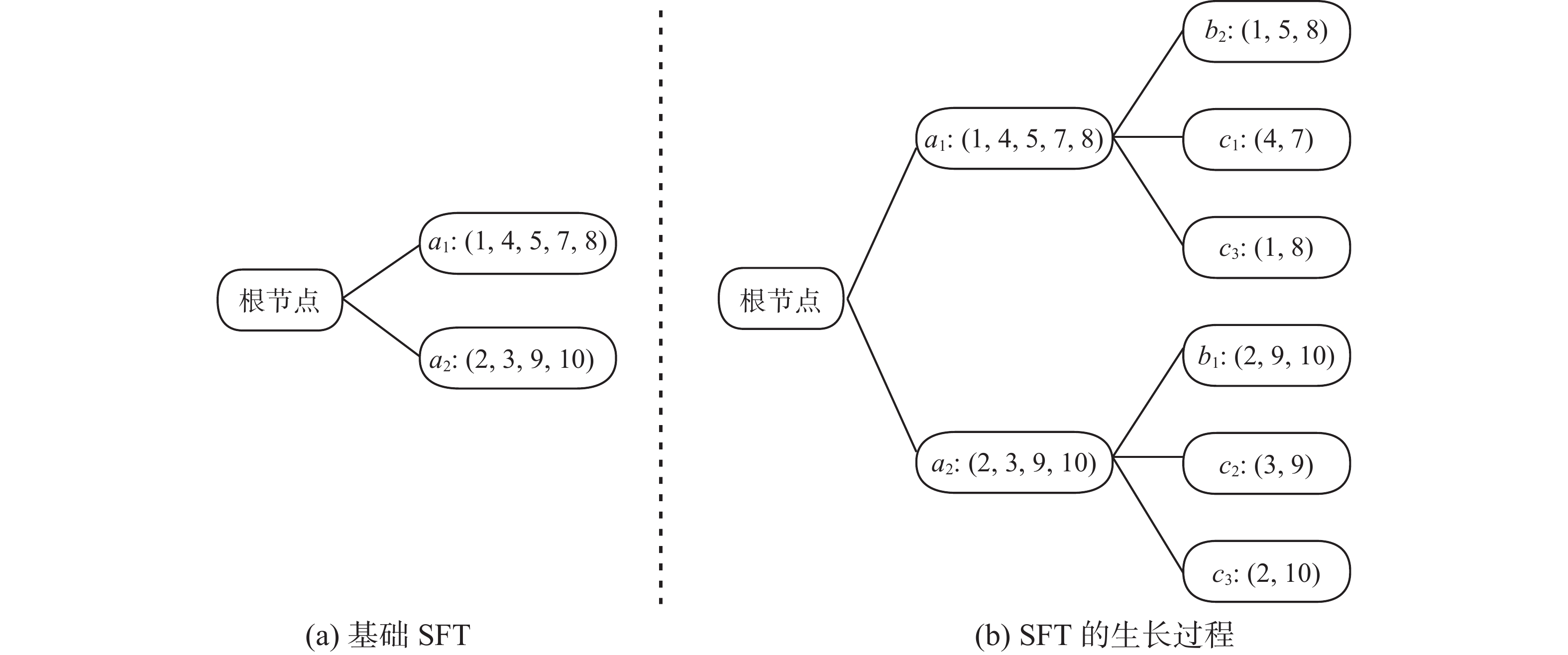
${\text{A}}$ 、${\text{B}}$ 、${\text{C}}$ 的趋势项变化情况，其中${{{a}}_1}$ 、${b_1}$ 、${c_1}$ 代表数据的上升趋势，$ {{{a}}_2} $ 、$ {b_2} $ 、$ {c_2} $ 代表数据的平稳趋势，${{{a}}_3}$ 、${b_3}$ 、${c_3}$ 代表数据的下降趋势。使用趋势项−位置表示法对3条时序数据表示为
图 1 实例数据趋势项Fig. 1 Illustrative data-trend items
下载:
全尺寸图片
$$ {T_A} = \{ {a_1}:(1,4,5,7,8),{a_2}:(2,3,9,10),{a_3}:(6)\} \text{；} $$ $$ {T_B} = \{ {b_1}:(2,7,9,10),{b_2}:(1,3,5,8),{b_3}:(4,6)\} \text{；} $$ $$ {T_C} = \{ {c_1}:(4,7),{c_2}:(3,5,9),{c_3}:(1,2,6,8,10)\} 。 $$ 使用趋势项−位置表示法只需要简单的几个数组就能够存储大量的变化数据。与传统时序规则挖掘方法使用的数据表达相比，趋势项−位置表示法有效节约了内存占用。
2） SFT构建
SFT是在生成树结构的同时挖掘出频繁项集的一种算法。SFT的构建依赖数据的频繁项，所谓频繁项指的是在一条时序数据中频繁出现的趋势项。对于如图1所示的时序数据
${T_A}$ ，若最小频繁项的频繁数设为2，则只有趋势项${a_1}$ 、${a_2}$ 是符合要求的频繁项而${a_3}$ 为非频繁项。SFT的构建步骤如下：①将时间序列转化为趋势项−位置表示，并设置最小频繁数
$l$ 和计数器$k = 0$ ；② 针对首条时间序列的趋势项，去除位置数量小于
$l$ 的非频繁项，将剩余趋势项作为叶子节点构建基础树，并将计数器$k + 1$ ；③ 取下一条时间序列的趋势项，依次与现有叶子节点的位置信息进行匹配计算，若位置信息相同的数量
$i > l$ ，则转④；否则转⑤;④ 将该趋势项作为新的叶子节点插入树中，将计数器
$k + 1$ ，同时生成频繁$k$ 项集，并更新叶子节点的位置信息；⑤ 判断当前时间序列是否为最后一条时间序列，若不是最后一条时间序列，则转③；否则完成同步频繁树的建立，并生成所有频繁项集。
针对图1给出的3组时序数据按照上述步骤构建SFT树如下：
设最小频繁数
$l = 2$ ，针对第一条时间序列${T_A}$ ，去除非频繁项${a_3}$ 构建基础树如图2（a）所示。接下来将所有叶子节点${a_1}$ 、${a_2}$ 与后续时间序列${T_B}$ 和${T_C}$ 进行位置信息匹配计算。首先将${b_1}$ 的位置信息与${a_1}$ 进行匹配可得二者只有一个相同的位置信息，小于最小频繁数$l$ ，因此${b_1}$ 不能作为${a_1}$ 的叶子节点。接下来判断${b_2}$ 与${a_1}$ 的位置信息可得二者有相同的位置$(2,9,10)$ 共3个，大于最小频繁数$l$ ，作为叶子节点生成频繁2项集的第一个元素：${a_1} \to {b_2}$ 。同样地，分别将${b_3}$ 、${c_1}$ 、${c_2}$ 、${c_3}$ 与${a_1}$ 的位置信息进行对比计算，生成以${a_1}$ 为根节点的分叉树。再将${T_B}$ 和${T_C}$ 的趋势项分别与叶子节点${a_2}$ 的位置信息进行对比计算，生成另一边的分叉树。最终生成的2层SFT如图2（b）所示。最终统计频繁2项集：${a_1} \to {b_2}$ ，${a_1} \to {c_1}$ ，${a_1} \to {c_3}$ ，${a_2} \to {b_1}$ ，${a_2} \to {c_2}$ ，${a_2} \to {c_3}$ 。
图 2 SFT构造过程Fig. 2 SFT’s construction process下载:
全尺寸图片
对于趋势项为
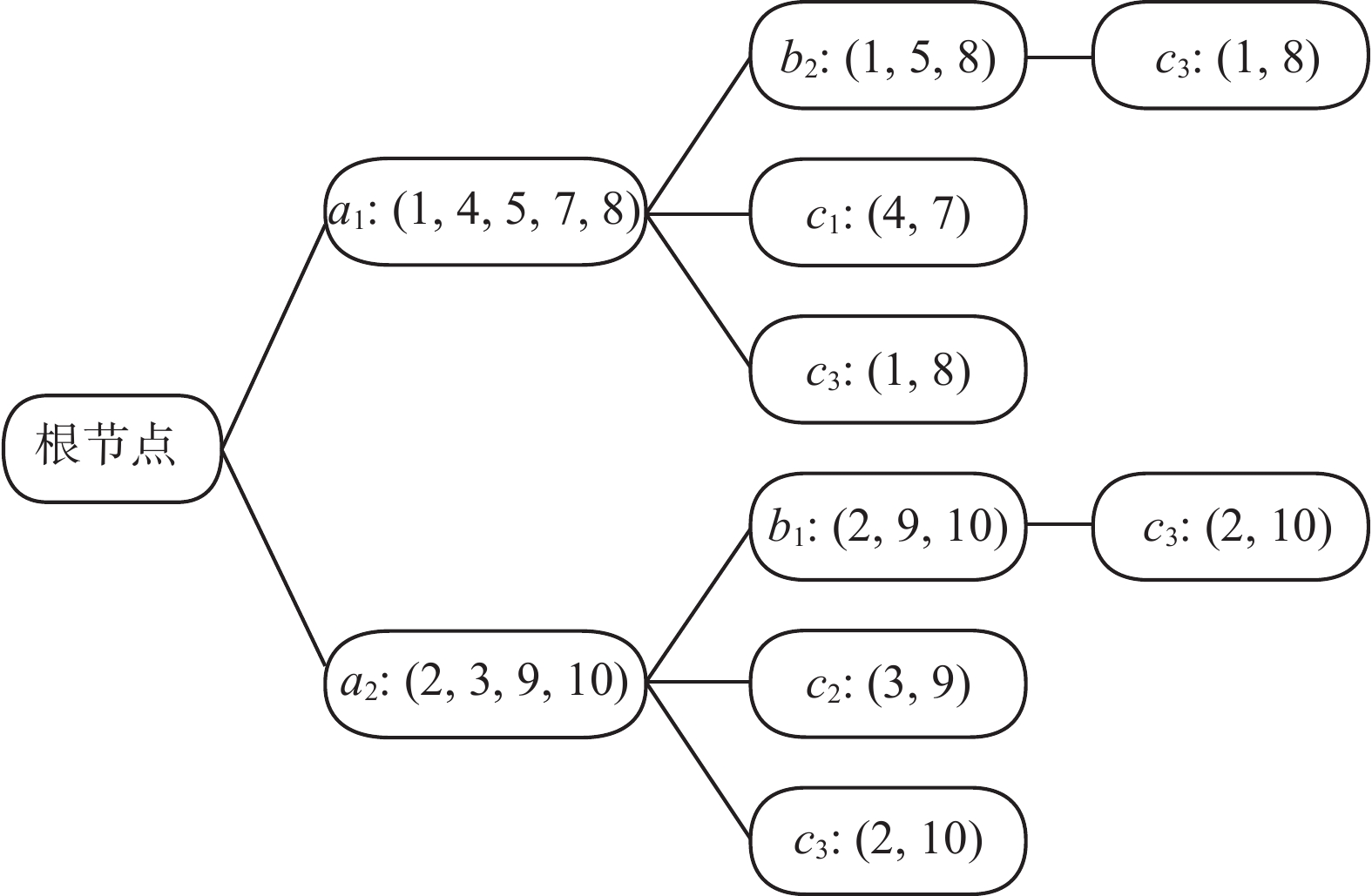
${b_i}$ （其中$i = 1,2,3$ ）的叶子节点，由于${T_B}$ 不是最后一个时间序列，所以在此节点的基础上还要对时序${T_C}$ 进行位置信息匹配计算，完善SFT并生成频繁三项集：${a_1}{b_2} \to {c_3}$ 和${a_2}{b_1} \to {c_3}$ 。由于${T_C}$ 为最后一个时间序列，所以最终的SFT如图3所示。
图 3 完整的SFTFig. 3 Complete SFT下载:
全尺寸图片
1.3 自适应滑窗算法
传统的滑窗处理方法通过设置初始窗口大小和增幅窗口大小实现窗口滑动，但是该处理方法非常依赖窗口大小的合理设置，若窗口过大会忽略数据的内部变化，若窗口过小则会导致计算量激增，并且受局部数据变化的影响增大。
1）自适应滑窗处理算法原理
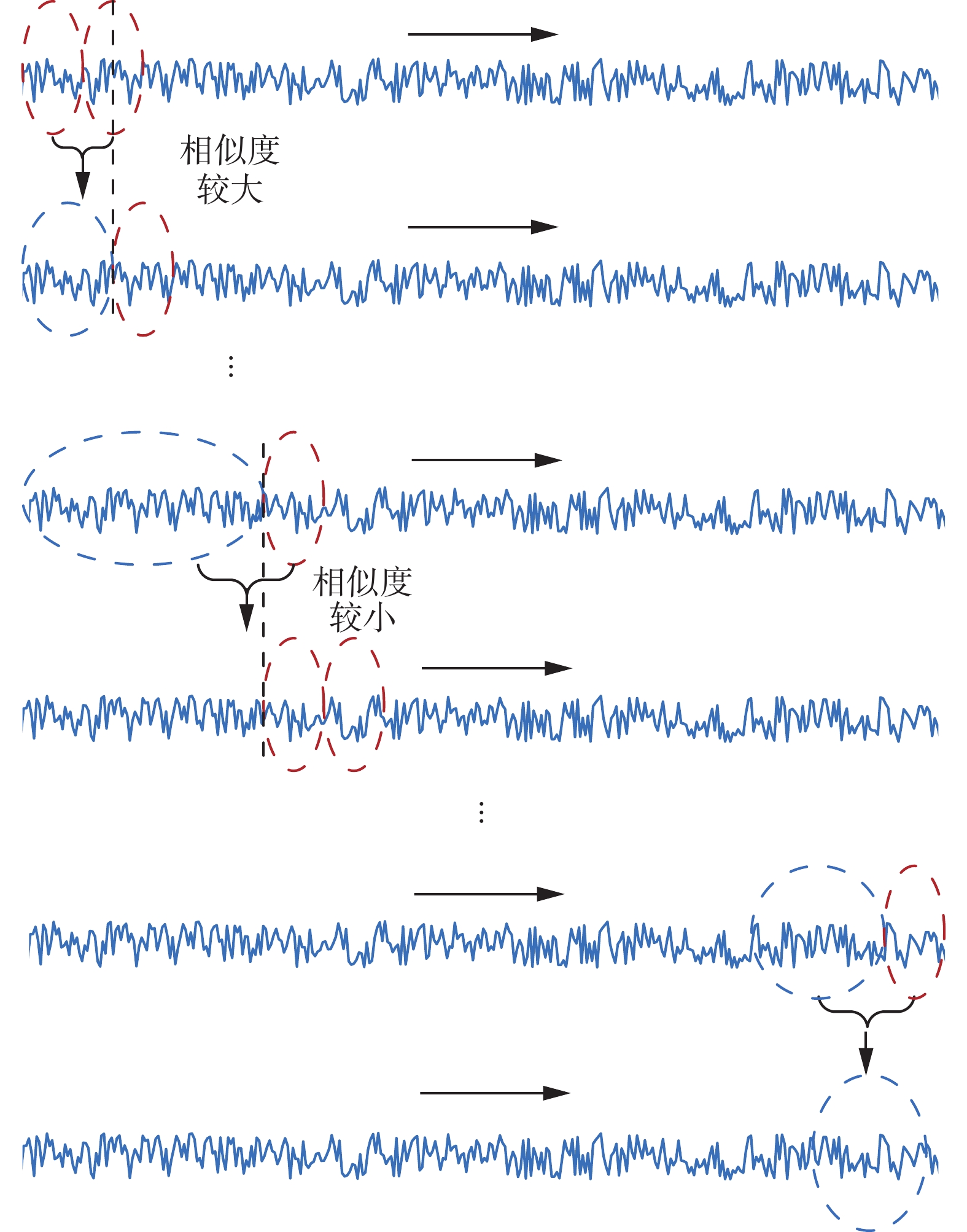
自适应滑窗处理方法根据相邻数据块之间的相似性判断窗口向前滑动距离，可以尽可能地将相似数据划分到同一个数据块中，有效降低了初始化窗口大小带来的影响。与传统滑窗法相比，自适应滑窗算法基于数据自身特点实现窗口滑动，可以提高数据块中数据的相似性。自适应滑窗算法的示意图如图4所示。
图 4 自适应滑窗算法示意Fig. 4 Illustrative diagram of adaptive sliding window algorithm下载:
全尺寸图片
图4中，每行为一次窗口相似度对比计算，其中左侧为原始滑窗或者自适应滑动之后的窗口，右侧为增幅窗口。第1行的2个窗口通过计算相似度获取遗忘数据长度，然后将2个窗口合并，同时遗忘左侧滑动窗口最前面的部分数据，实现窗口向前滑动。如果后续还有数据，继续添加增幅窗口并计算2个窗口数据的相似度，完成窗口自适应滑动。在自适应滑窗算法中，窗口长度随着两个窗口的相似度发生变化。若两个窗口相似度较大，则遗忘数据较多，窗口长度相对较小；相反则遗忘数据较少，窗口长度相对较大。
2）窗口相似度计算
设自适应滑窗算法的初始窗口长度为
$L$ ，滑窗的增幅为$Z$ ，${l_i}$ 表示第$i$ 个窗口的长度。${{{\boldsymbol{X}}}_i} =[ {{{\boldsymbol{X}}}_{{s_{i-1}} + 1}}, {{{\boldsymbol{X}}}_{{s_{i-1}} + 2}},\cdots,{{{\boldsymbol{X}}}_{{s_{i-1}} + {l_i}}} ] \in {{\bf{R}}^{m \times {l_i}}}$ 表示第$i$ 个滑窗，其中${s_i} = \displaystyle\sum_{k = 1}^{i - 1} {{l_k}}$ ，对应的增幅矩阵为${{\boldsymbol{Y}}} = \left[ {{{{\boldsymbol{X}}}_{{s_i} + 1}},{{{\boldsymbol{X}}}_{{s_i} + 2}},\cdots,{{{\boldsymbol{X}}}_{{s_i} + Z}}} \right] \in {{\bf{R}}^{m \times Z}}$ ，其中${s_i} = {s_{i - 1}}{\text{ + }}{l_i}$ 。初始窗口的统计特征值由均值${\overline {{\boldsymbol{X}}} _k}$ 和标准差矩阵${{\Sigma }_k}$ 表示，两者的定义为$$ \left\{ \begin{aligned} &{\overline {{\boldsymbol{X}}} _k} = \frac{{{{{\boldsymbol{X}}}_1}^{\rm{T}}{{{\boldsymbol{I}}}_L}}}{L} \\ &{{{\boldsymbol{\Sigma}} }_k} = {\text{diag}}\left( {\sigma _k^1,\sigma _k^2, \cdots, \sigma _k^m} \right) \\ &\sigma _k^i = \sqrt {{{\left( {{X_{1j}} - {{\overline {{\boldsymbol{X}}} }_{kj}}} \right)}^2}/L} ,\;\;i = 1,2, \cdots ,L,\;\;j = 1,2, \cdots ,m \\ \end{aligned} \right. $$ 其中
${{{\boldsymbol{I}}}_L}$ 为单位列向量。对于所有的滑窗数据均采用初始窗口的统计特征进行标准化处理，然后计算Gram矩阵
${{{\boldsymbol{G}}}_i}$ ：$$ {{{\boldsymbol{G}}}_i} = {\tilde {\boldsymbol{X}}}_i^{\rm{T}}{{\tilde {\boldsymbol{X}}}_i} $$ 其中
${{\tilde {\boldsymbol{X}}}_i}$ 是第$i$ 个滑窗矩阵${{{\boldsymbol{X}}}_i}$ 经过标准化处理后的数据矩阵。为了反映新数据窗口相对于旧数据窗口数据特征的变化，采用相似度分析的方法建立一个量化的窗口遗忘指标来判断两个窗口之间的相似度信息。定义窗口
${{{\boldsymbol{X}}}_i}$ 和${{\boldsymbol{Y}}}$ 的混合Gram矩阵为$$ {{{\boldsymbol{G}}}_{\varOmega }} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{G}}}_i}} \\ {{{{\boldsymbol{G}}}_H}} \end{array}} \right] $$ 其中
${{{\boldsymbol{G}}}_H}$ 是窗口${{\boldsymbol{Y}}}$ 的Gram矩阵。对${{{\boldsymbol{G}}}_{\varOmega }}$ 进行特征值分解，分别采用${{{\boldsymbol{\varLambda}} }_\varOmega }$ 和${{{\boldsymbol{P}}}_\varOmega }$ 表示特征值对角矩阵和特征向量。定义转换矩阵${{{\boldsymbol{P}}}_0}$ 为$$ {{{\boldsymbol{P}}}_0} = {{{\boldsymbol{P}}}_\varOmega }{{\boldsymbol{\varLambda}} }_\varOmega ^{ - \tfrac{1}{2}} $$ (6) 使用转换矩阵
${{{\boldsymbol{P}}}_{\text{0}}}$ 对${{{\boldsymbol{G}}}_i}$ 和${{{\boldsymbol{G}}}_H}$ 进行变换可得：$$ \left\{ {\begin{split} &{{{\boldsymbol{G}}}_i' = {{\boldsymbol{P}}}_0^{\rm{T}}{{{\boldsymbol{G}}}_i}{{{\boldsymbol{P}}}_0}} \\ &{{{\boldsymbol{G}}}_H' = {{\boldsymbol{P}}}_0^{\rm{T}}{{{\boldsymbol{G}}}_H}{{{\boldsymbol{P}}}_0}} \end{split}} \right. $$ (7) 由式(6)和(7)可得到转换后的矩阵满足：
$$ {{\boldsymbol{P}}}_0^{\rm{T}}{{{\boldsymbol{G}}}_{\varOmega }}{{{\boldsymbol{P}}}_0} = {{\boldsymbol{G}}}_i' + {{{\boldsymbol{G}}}_H} = {{\boldsymbol{I}}} $$ (8) 然后对转换后的两个Gram矩阵
${{\boldsymbol{G}}}_i'$ 和${{\boldsymbol{G}}}_H'$ 分解特征值得到$\varUpsilon _k^i$ 和$\varUpsilon _k^H$ ，其中$k = 1,2, \cdots ,m$ ，$m$ 是特征值的个数。由式(8)可知
$\varUpsilon _k^i + \varUpsilon _i^H = 1$ 。由于特征值$\varUpsilon _k^i$ 和$\varUpsilon _k^H$ 是关于0.5对称的，因此$\varUpsilon _k^i$ 越接近0.5，说明$ {{\boldsymbol{G}}_H} $ 与${{\boldsymbol{G}}_i}$ 的相似度越高。文献[23]中给出了一个可以判别两组数据相似度的指标：$$ U=1 - \dfrac{{4\displaystyle\sum\limits_{k = 1}^m {(\varUpsilon _k^i - 0.5)} }}{m} $$ 本文使用
$U$ 作为滑窗相似度判别标准，$U$ 越大说明两个滑动窗口的数据越相似。当$ U $ 逼近1时，两组数据趋于一致，可以认定为同一工况下产生的数据。因此预设一个临界值$ c $ ，当$U$ 超过$ c $ 时，认为滑窗${{{\boldsymbol{X}}}_i}$ 与滑窗${{\boldsymbol{Y}}}$ 之间相似度较大，两者有$U$ 概率属于同一个工况，将矩阵${{\boldsymbol{Y}}}$ 的前$\ell = |U \times {l_i}|$ 个对象划分到矩阵${{{\boldsymbol{X}}}_i}$ 所属的子阶段中，窗口长度增加，新的窗口数据为$$ {{{\boldsymbol{X}}}_i} = \left[ {{{{\boldsymbol{X}}}_{{\Sigma _1} + 1}},{{{\boldsymbol{X}}}_{{\Sigma _1} + 2}}, \cdots ,{{{\boldsymbol{X}}}_{{\Sigma _2}}},{{{\boldsymbol{X}}}_{{\Sigma _2} + 1}}, \cdots ,{{{\boldsymbol{X}}}_{{\Sigma _2} + \ell }}} \right] $$ 其中
${\Sigma _1} = \displaystyle\sum\limits_{k = 1}^{i - 1} {{l_k}}$ 是当前滑窗前面其他滑窗的长度之和，${\Sigma _2} = \displaystyle\sum\limits_{k = 1}^i {{l_k}}$ 是增幅窗口之前滑窗数据的长度之和。当
$U$ 小于临界值$ c $ 时，认为两个滑动窗之间相似度较小，应该分别属于两个不同的阶段。按照这种判断方法，依次将过程数据划分成不同的阶段。2. 基于长短滑窗SFA与SFT的时序关联规则挖掘
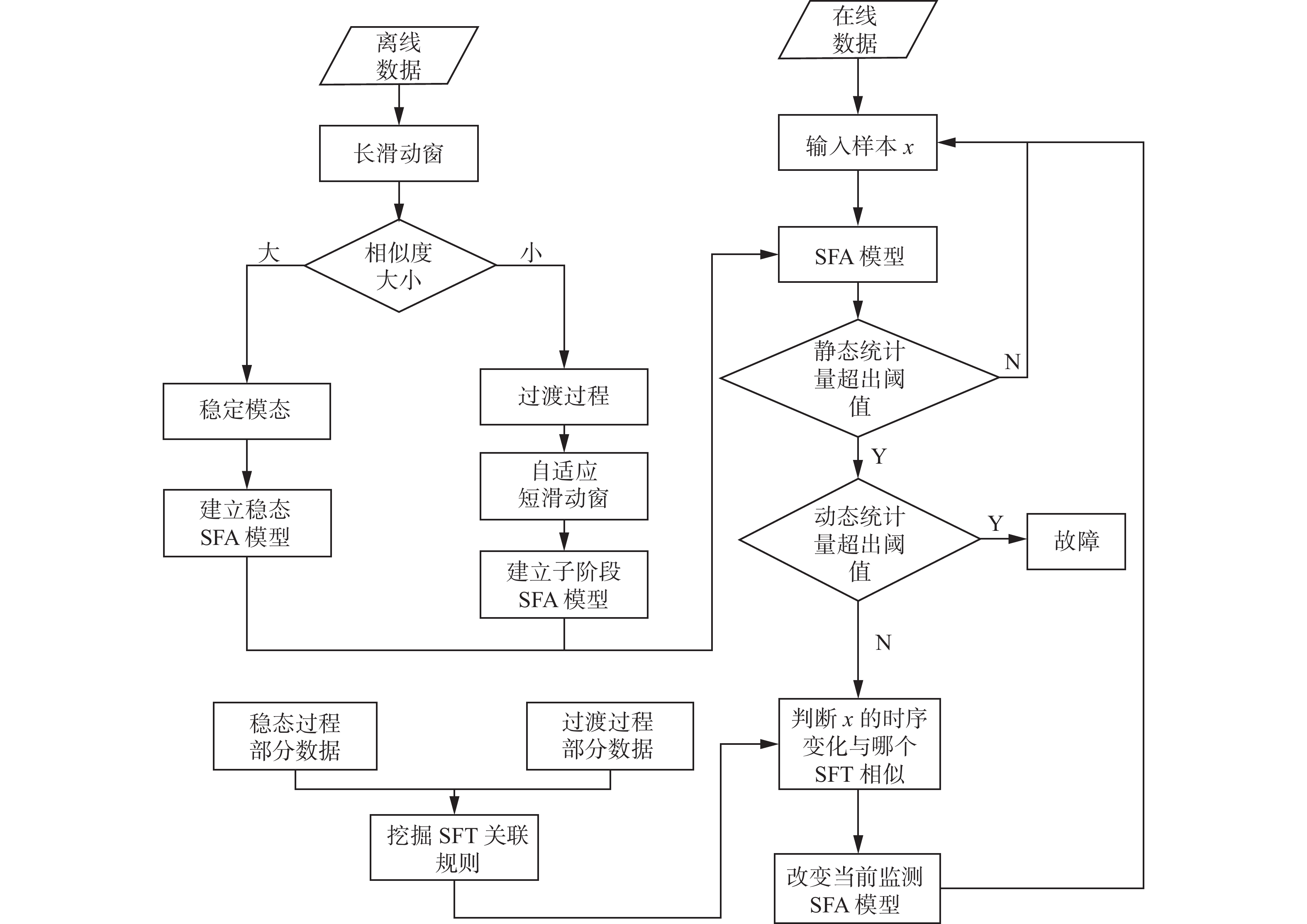
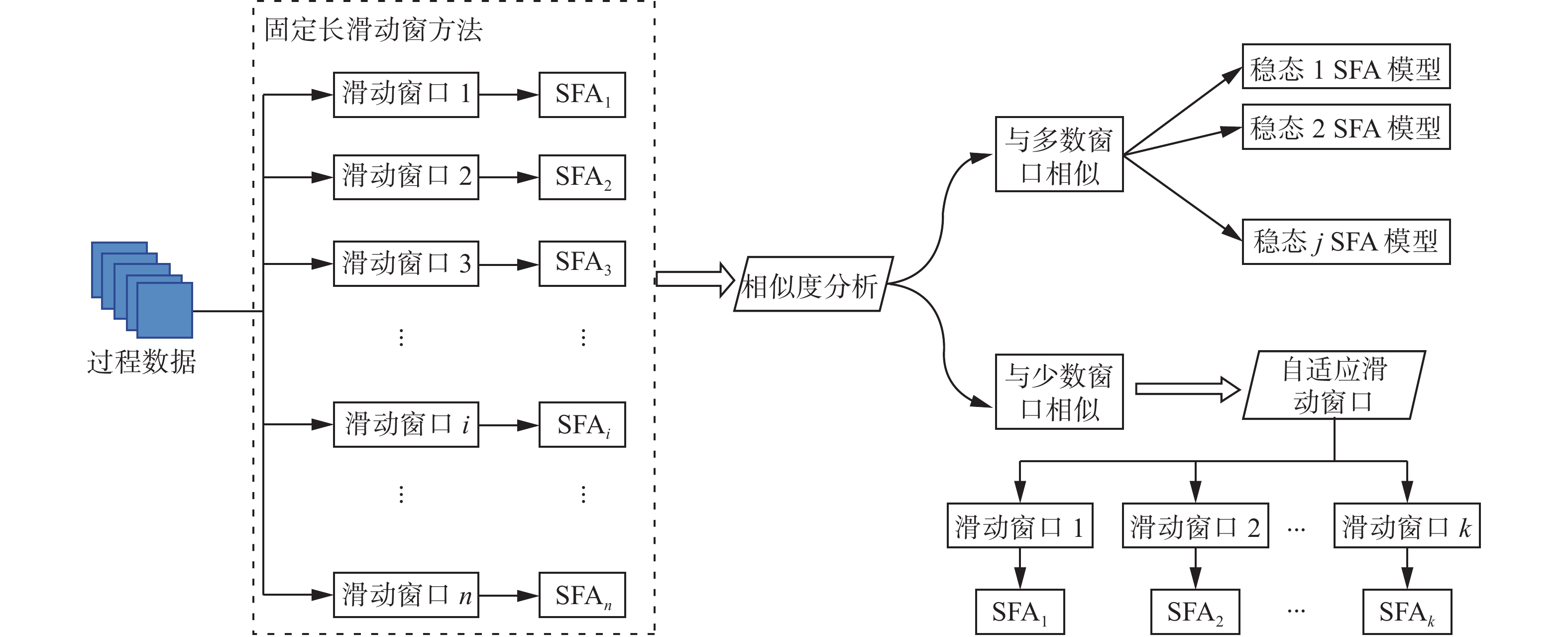
本文提出一种基于长短滑窗慢特征分析与同步频繁树（long-short sliding windowed SFA with SFT，LSSW-SFA-SFT）时序规则挖掘的复杂工业过渡过程识别方法。LSSW-SFA-SFT首先将长短滑窗与SFA相结合将数据划分成多个稳态阶段与过渡过程子阶段并建立对应的SFA模型；然后挖掘多时序多时间区间的SFT时序关联规则，为每种状态转变建立不同的关联规则；而对于在线数据则利用SFA模型进行过程监测，并使用SFT方法对过程转换进行在线识别，以提高过程监测准确率。过程监测流程如图5所示。
图 5 基于LSSW-SFA-SFT的过程监测Fig. 5 LSSW-SFA-SFT-based process monitoring下载:
全尺寸图片
2.1 基于LSSW-SFA的离线建模
本节详细描述长短滑窗−慢特征分析(LSSW-SFA)方法的原理、在过程监测中进行离线建模的步骤以及相应统计量的计算。
2.1.1 基本思想
LSSW-SFA的处理流程如图6所示。由于稳态工况数据在生产中占比大，在进行稳态识别时，为了提高监测效率可以使用长度较大的滑动窗口进行数据块的对比。由于自适应滑窗处理法需要经过相似度对比与窗口滑动，会产生重复计算，因此本文采用固定长度的长滑窗结合SFA算法进行稳态过程识别。
图 6 LSSW-SFA处理流程Fig. 6 Processing flow of LSSW-SFA下载:
全尺寸图片
过渡过程数据变化快，存在时间跨度小是其主要特点。此时固定长度的长滑窗将会受到数据变化的影响，造成模型不匹配，误报率上升的情况。自适应滑窗可以根据数据的相关性，自适应的调整窗口的大小，降低初始窗口长度与固定滑动步长对数据块划分结果产生的影响。因此，本文使用自适应短滑窗对过渡数据进行子阶段划分，然后分别针对每个子阶段建立SFA模型，分段计算统计量，实现过渡过程的动态监测。
2.1.2 离线建模
LSSW-SFA离线建模的主要步骤如下：
1）采集正常工作条件下的训练样本数据集，设置初始化滑动数据窗口大小为
$L$ ，滑动步长为$Z$ ；2）计算滑动窗口数据集的均值和方差，并对窗口数据进行标准化处理；
3） 对滑窗建立SFA模型，完成特征映射与降维；
4）对所有SFA模型进行相似度分析，生成相似度谱图和聚类图谱判断相似数据块；
5） 将滑窗数据转化为实际数据分类情况，在相似度图谱中，相似度大的大段连续窗口为稳态数据，转6）；相似度小的少部分窗口为非稳态数据，转7）；
6）对稳态数据整体重新建立SFA模型，共形成
$j$ 个稳态SFA监测模型；7）设置初始短滑窗大小
$L$ ，滑动步长$Z$ 和相似度阈值$U$ ；8） 对当前窗口与滑动窗口计算相似度
$u$ ，若$u > U$ ，说明两个窗口相似度较大，转9）；否则转10）；9） 计算窗口合并长度
$\ell = u \times Z$ ，将增量窗口的前$\ell $ 个数据合并到当前滑动窗中，更新当前窗口与滑动窗口数据，转8）；10）将当前窗口划分为一个子阶段，对其建立SFA模型；
11） 判断后面是否还有未建模数据，若有，则用初始滑窗长度
$L$ 与滑动步长$Z$ 划分数据块，转8）；否则，结束过渡过程子阶段建模，转12）；12） 取每个过渡过程第一个子阶段与前一个稳态的最后
$k$ 个数据建立SFT，挖掘该状态转变的关联规则；13） 取每个过渡过程的最后一个子阶段与后一个稳态的最初
$k$ 个数据建立SFT，挖掘状态转变的关联规则。12）和13）中提到的SFT建立过程如图7所示。
图 7 离线建模中SFT构建示意Fig. 7 Schematic diagram of SFT construction in offline modeling下载:
全尺寸图片
2.1.3 过程监测统计量计算
SFA将整个数据空间转化为表示数据变化快慢的潜变量空间
${{\boldsymbol{S}}}(t)$ 。本节利用累计贡献率方法对SFA映射后的潜变量空间${{\boldsymbol{S}}}(t)$ 进行降维处理并建立过程监测模型。首先，在式(5)的基础上，采用累计贡献率的方法取前$r$ 个特征值作为慢特征分量，实现数据降维的同时将数据空间划分为慢特征子空间${{{\boldsymbol{S}}}_d}$ 和残差空间${{{\boldsymbol{S}}}_e}$ 。对于测试集数据${{{\boldsymbol{X}}}_{{\text{test}}}}$ ，使用训练集${{{\boldsymbol{X}}}_{{\text{train}}}}$ 计算得到的广义特征向量矩阵${{\boldsymbol{W}}}$ 对${{{\boldsymbol{X}}}_{{\text{test}}}}$ 进行映射，映射结果为${{{\boldsymbol{S}}}_{{\text{test}}}} = {[{{\boldsymbol{WX}}}_{{\text{test}}}^{\text{T}}]^{\text{T}}} = [{{{\boldsymbol{S}}}_{{d_{{\text{test}}}}}},{{\boldsymbol{S}}}{}_{{e_{{\text{test}}}}}]$ ，得到慢特征空间${{{\boldsymbol{S}}}_{{d_{{\text{test}}}}}}$ 与残差空间${{\boldsymbol{S}}}{}_{{e_{{\text{test}}}}}$ 。为了监测过程运行状态，对于一个
$n \times m$ 的数据矩阵，分别针对两个数据空间计算静态统计量$T_d^2$ 和$T_e^2$ ，对于第$i$ 个样本的静态统计量的计算方法如下：$$ T_d^2(i) = {{{\boldsymbol{S}}}_d}(i){{{\boldsymbol{S}}}_d}{(i)^{\text{T}}} $$ $$ T_e^2(i) = {{{\boldsymbol{S}}}_e}(i){{{\boldsymbol{S}}}_e}{(i)^{\text{T}}} $$ 式中：
${{{\boldsymbol{S}}}_d} = {{{\boldsymbol{S}}}_{{d_{{\text{train}}}}}}$ 或${{{\boldsymbol{S}}}_{{d_{{\text{test}}}}}}$ ；${{{\boldsymbol{S}}}_e} = {{\boldsymbol{S}}}{}_{{e_{{\text{train}}}}}$ 或${{\boldsymbol{S}}}{}_{{e_{{\text{test}}}}}$ ；${{{\boldsymbol{S}}}_d} = {[{{{\boldsymbol{W}}}_r}{{{\boldsymbol{X}}}^{\text{T}}}]^{\text{T}}}$ 为经过SFA计算得到的慢特征空间的分量；${{{\boldsymbol{S}}}_e} = {[{{{\boldsymbol{W}}}_{m - r}}{{{\boldsymbol{X}}}^{\text{T}}}]^{\text{T}}}$ 为残差空间的分量，其中${{\boldsymbol{X}}}$ 为原始数据。两个静态统计量符合${\chi ^2}$ 分布，由给定的贡献率水平确定阈值：$$ \left\{ {\begin{aligned} &{T_d^2 \sim \chi _r^2} \\ &{T_e^2 \sim \chi _{m - r}^2} \end{aligned}} \right. $$ 同时，为了监测数据的动态特性，针对两个数据空间的一阶导数，计算动态统计量
$S_d^2$ 和$S_e^2$ ：$$ S_d^2(i) = {{\dot {\boldsymbol{S}}}_d}(i){{\boldsymbol{\varOmega}} }_d^{ - 1}{{\dot {\boldsymbol{S}}}_d}{(i)^{\text{T}}} $$ $$ S_e^2(i) = {{\dot {\boldsymbol{S}}}_e}(i){{\boldsymbol{\varOmega}} }_e^{ - 1}{{\dot {\boldsymbol{S}}}_e}{(i)^{\text{T}}} $$ 式中
${{{\boldsymbol{\varOmega}} }_d} = {\left\langle {{{{\dot {\boldsymbol{S}}}}_d}^{\rm{T}}{{{\dot {\boldsymbol{S}}}}_d}} \right\rangle _t}$ ，${{{\boldsymbol{\varOmega}} }_e} = {\left\langle {{{{\dot {\boldsymbol{S}}}}_e}^{\rm{T}}{{{\dot {\boldsymbol{S}}}}_e}} \right\rangle _t}$ 代表两个数据空间的时变特征，可以用来检测数据的动态异常。两个动态统计量的阈值可以通过核密度估计(kernel density estimation, KDE)方法估算出来。当静态统计量
$T_d^2$ 和$T_e^2$ 超出阈值时，说明系统发生了波动，与正常运行状态有偏差，此时需要借助动态统计量$S_d^2$ 和$S_e^2$ 才能对系统状态进行判定。如果此时$S_d^2$ 和$S_e^2$ 都没有超出阈值，说明系统只是发生了数据波动，并未产生动态异常。此时只需要对过程转变情况进行判断，不需要产生故障报警。相反，如果$S_d^2$ 或者$S_e^2$ 超出阈值，说明系统发生了动态异常，即有故障发生。2.2 基于时序关联规则挖掘的故障在线监测
本节主要描述多时序多时间区间的同步频繁树(SFT with multi time sequence and multi time interval, SFT-MTSI)时序关联规则挖掘方法对过程工况状态转变进行辨识以及进行在线过程监测的步骤。
2.2.1 SFT-MTSI算法原理
基于第1.2节提到的SFT算法，为了对每种时序规则进行选择区分，使用支持度(support)和置信度(confidence)来对每种规则进行标记。
受到文献[13]的启发，对时序规则的挖掘，不仅关注相同时间下的不同序列的相关变化趋势类型的频繁程度，还关注在相邻的两个时间区间内，一个序列的某种变化趋势引起另一个序列的某种变化趋势的频繁程度。此外，在关注两个不同序列之间的关联关系的同时，还关注两个不同序列导致其他序列变化的关联关系。为此，对于一个
$n$ 个时间样本$m$ 个属性的数据矩阵，使用如下4种关联规则标识数据的时序关联规则：1） 两个属性序列同时发生变化。
定义对应的规则支持度和置信度计算方式为
$$ {S_{{\text{supp}}}}({a_{1i}} \to {a_{2j}}) = \frac{{N({a_{1i}} \wedge {a_{2j}})}}{{|T|}} $$ $$ {C_{{\text{conf}}}}({a_{1i}} \to {a_{2j}}) = \frac{{N({a_{1i}} \wedge {a_{2j}})}}{{N({a_{1i}})}}$$ 2）两个属性序列同时发生变化导致另一个不同的属性序列发生变化。
定义对应的规则支持度和置信度计算方式为
$$ {S_{{\text{supp}}}}({a_{1i}} \wedge {a_{2j}} \to {a_{3k}}) = \frac{{N({a_{1i}} \wedge {a_{2j}} \wedge {a_{3k}})}}{{|T|}} $$ $$ {C_{{\text{conf}}}}({a_{1i}} \wedge {a_{2j}} \to {a_{3k}}) = \frac{{N({a_{1i}} \wedge {a_{2j}} \wedge {a_{3k}})}}{{N({a_{1i}} \wedge {a_{2j}})}} $$ 3）一个属性序列发生变化导致另一个属性序列紧接着发生变化。
定义对应的规则支持度和置信度计算方式为
$$ {S_{{\text{supp}}}}({a_{1i}} \to ({a_{2j}})') = \frac{{N({a_{1i}} \wedge ({a_{2j}})')}}{{|T|}} $$ $$ {C_{{\text{conf}}}}({a_{1i}} \to ({a_{2j}})') = \frac{{N({a_{1i}} \wedge ({a_{2j}})')}}{{N({a_{1i}})}} $$ 4）两个属性序列同时发生变化导致另一个不同的属性序列紧接着发生变化。
定义对应的规则支持度和置信度计算方式为
$$ {S_{{\text{supp}}}}({a_{1i}} \wedge {a_{2j}} \to ({a_{3k}})') = \frac{{N({a_{1i}} \wedge {a_{2j}} \wedge ({a_{3k}})')}}{{|T|}} $$ $$ {C_{{\text{conf}}}}({a_{1i}} \wedge {a_{2j}} \to ({a_{3k}})') = \frac{{N({a_{1i}} \wedge {a_{2j}} \wedge ({a_{3k}})')}}{{N({a_{1i}} \wedge {a_{2j}})}} $$ 式中：
${a_{1i}}$ 表示属性${a_1}$ 取值为$i$ 的元素；$({a_{2j}})'$ 表示属性${a_2}$ 在下一个时间取值为$j$ 的元素；$i = 1,0, - 1$ 且$j = 1, 0, - 1$ ；$ N({a_{1i}} \wedge {a_{2j}}) $ 表示${a_1}$ 取值为$i$ 的同时${a_2}$ 取值为$j$ 的个数；$ |T| $ 表示整个时间区间内${a_1}$ 的个数；$ N({a_{1i}}) $ 表示${a_1}$ 取值为$i$ 的个数；$ N({a_{1i}} \wedge {a_{2j}} \wedge ({a_{3k}})') $ 表示${a_1}$ 取值为$i$ 同时${a_2}$ 取值为$j$ 时${a_3}$ 在下一个时间取值为$k$ 的个数。2.2.2 在线过程识别与故障检测步骤
在离线建模的基础上，结合过渡过程识别结果，对复杂工况在线数据进行过程识别。算法步骤如下：
1）取第1个样本依次代入每个SFA模型，计算该模型下的统计量的值，并初始化计数器
$ k = 0 $ ；2） 判断统计量是否超出对应模型的统计量阈值。若超出阈值说明该模态不是初始运行模态，否则说明该模态有可能是初始运行模态，记录该模型并将计数器
$k + 1$ ；3） 判断当前对比模型是否为最后一个SFA模型，如果是最后一个，则转4），否则转1）；
4）判断初始运行模态，若
$k = 1$ 则确定在线数据初始模态为该SFA模型所示模态；若$k > 1$ 说明存在多个SFA模型都不超出阈值，依次对记录的SFA模型带入后续数据，直到$k = 1$ ；5）将下一个数据带入该SFA模型，计算统计量并与阈值进行比较；
6）若静态统计量
$T_d^2$ 和$T_e^2$ 都超出阈值，转7），否则转5）；7）判断动态统计量
$S_d^2$ 和$S_e^2$ 是否存在超出阈值情况出现，若都没有超出控制线，则发生过程转变，转8）；否则说明当前数据为故障样本，产生故障报警；8）将当前数据与其前后的
$p$ 个数据构建SFT，挖掘该转变的关联规则；9）将该转变的关联规则与离线建模的过程转变规则进行对比，找到最为相似的SFT模型，取该SFT模型的转变后运行模态为过程转变的最终模态；
10）以该模态SFA为新的过程监测模型，转5）。
在离线建模中，为了保证统计量阈值关注到整个过程数据的特点，对每个完整的稳态数据建立一个SFA模型。而对于过渡过程数据而言，由于数据的变化较大，如果依然对整体数据建立一个SFA模型，则会导致阈值偏高，使得过程监测不够准确。因此，对于过渡过程而言依据自适应滑动窗口的数据块划分情况，分别建立子阶段SFA模型，实现对过渡过程数据的动态监测。
在进行在线监测时，如果当前模态是稳态，则直接对后续数据进行统计量计算与监测。由于相同的过渡过程通常具有相同的数据变化和时间跨度，因此如果当前模态是过渡过程，则依次使用过渡过程的每个子阶段对在线数据进行监测。
2.3 算法复杂度分析
本文所提方法的时间复杂度主要取决于SFA离线建模与SFT的树生成过程。对于一个
$n \times m$ 的样本矩阵来说，其中$n$ 为样本数量，$m$ 为属性数量，所提算法的时间复杂度计算如下。对于SFA算法，在离线建模阶段使用两步奇异值分解(singular value decomposition, SVD)方法求解优化问题。其中每一步的SVD时间复杂度均为
$O({m^3})$ 。因此所提算法在SFA阶段的时间复杂度为$2O({m^3})$ 。虽然该时间复杂度是属性数量的三阶函数，但是当进行在线监测时则无需再进行SVD分解，可以直接使用离线模型实现在线监测。对于SFT算法，其时间复杂度主要为树的生成过程。在生成完整的SFT过程中，除了基础树的建立只考虑一个时间序列以外，其余树的生成都需要对剩余所有时间序列进行分析。因此对于频繁
$k$ 项树而言，从基础树到完整树的建立所需的时间为等差数列的前$k - 1$ 项和：${S_k} = n + $ $\dfrac{{k[(m - 1)n + (m - k - 1)n]}}{2}$ ，最终的SFT算法时间复杂度为$O((km - {k^2} + 1)n)$ ，与样本个数与变量数目乘积相关。此外，由于在生成SFT的时候使用趋势项−位置表示法，将时序数据用数值型(int)数据进行保存，因此减少了内存的占用，降低了方法的空间复杂度。
3. 实验验证
本文使用田纳西伊斯曼(Tennessee Eastman, TE)过程[24]生成多模态工业过程仿真数据，对所提算法进行实验验证。
3.1 实验设计
由于TE过程能对实际复杂工业过程中存在的许多典型特征进行较好的模拟，因此常被用来评估过程监测结果，以及故障诊断方法的优劣性。TE过程通过反应器、冷凝器、循环压缩机、分离器和汽提塔5个操作单元，将4种气态反应物转化成2种气态生成物G和H以及副产物F和惰性气体B。TE过程的流程在文献[25]中有详细介绍。在整个TE过程中，共有53个变量，包括12个操作变量和41个测量变量。在整个TE过程中共存在21种故障，所以在公共数据集中共存在22组不同的数据，其中包含一组正常数据和21组带有不同故障的数据集。TE过程的故障类型如表1所示。
表 1 TE过程故障类型Table 1 Fault types in TE process故障 故障描述 故障类型 1 A/C进料比变化，B不变（流4） 阶跃 2 B含量变化，A/C进料比不变（流4） 阶跃 3 D的进料温度变化（流2） 阶跃 4 反应器冷却水的入口温度变化 阶跃 5 冷凝器冷却水的入口温度变化 阶跃 6 A进料损失（流1） 阶跃 7 C压力损失（流4） 阶跃 8 A、B、C进料变化（流4） 随机变化 9 D的进料温度变化（流2） 随机变化 10 C的进料温度变化（流2） 随机变化 11 反应器冷却水的入口温度变化 随机变化 12 冷凝器冷却水的入口温度变化 随机变化 13 反应动力学常数变化 慢偏移 14 反应器冷却水阀门 黏滞 15 冷凝器冷却水阀门 黏滞 16~21 未知 未知 为了充分验证所提方法的有效性，本文使用TE过程的Simulink仿真程序生成包含频繁过程转变的多模态过程数据。表2列出了TE过程中存在的6种不同的运行模态。不同运行模态之间最大的区别在于两种产物G和H的生产比率。由于产品生产的主要过程在反应器中，因此通过调节反应器的等级、压力和温度3个参数达到改变运行模态的目的。以上3个参数在6种运行模态下的设定值如表3所示。
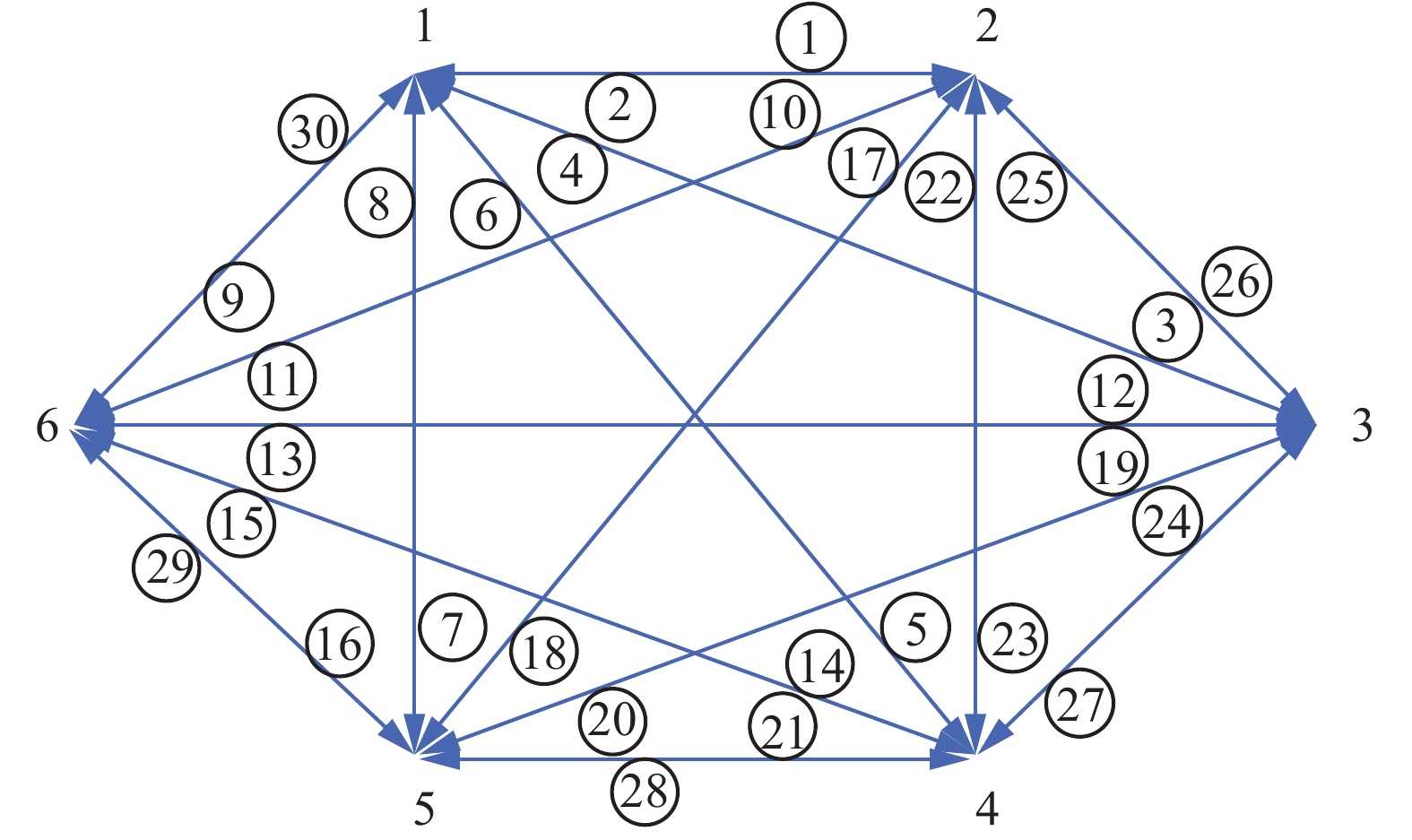
表 2 TE过程生产模式Table 2 Operating modes in TE process模式 G/H率 产品生产率/(kg·h−1) 1 50/50 7038G和7038H 2 10/90 1048G和12669H 3 90/10 10000G和1111H 4 50/50 最大生产率 5 10/90 最大生产率 6 90/10 最大生产率 表 3 不同运行模态参数设置Table 3 Parameter settings of different operating modes工况编号 1 2 3 4 5 6 反应器等级 75 65 75 85 70 80 反应器压力 2705 2805 2905 2855 2805 2755 反应器温度 120.4 125.4 130 135 120 125 为了对每种运行模态以及其中的过渡转变进行分析，本文在仿真系统中进行设计使生产过程在6种运行模态之间都发生转变，转变情况如图8所示。共生成31种稳态工况和30种过渡过程，包含了所有可能的模态转变。由于每种稳态都有其独特的数据特点，因此从稳态1转到稳态2所经过的数据过渡转变，与从稳态2转到稳态1所经过的数据过渡转变，存在差别，用SFT可以挖掘出相应的关联规则。
图 8 仿真系统模态转变Fig. 8 Modal transitions in simulation system下载:
全尺寸图片
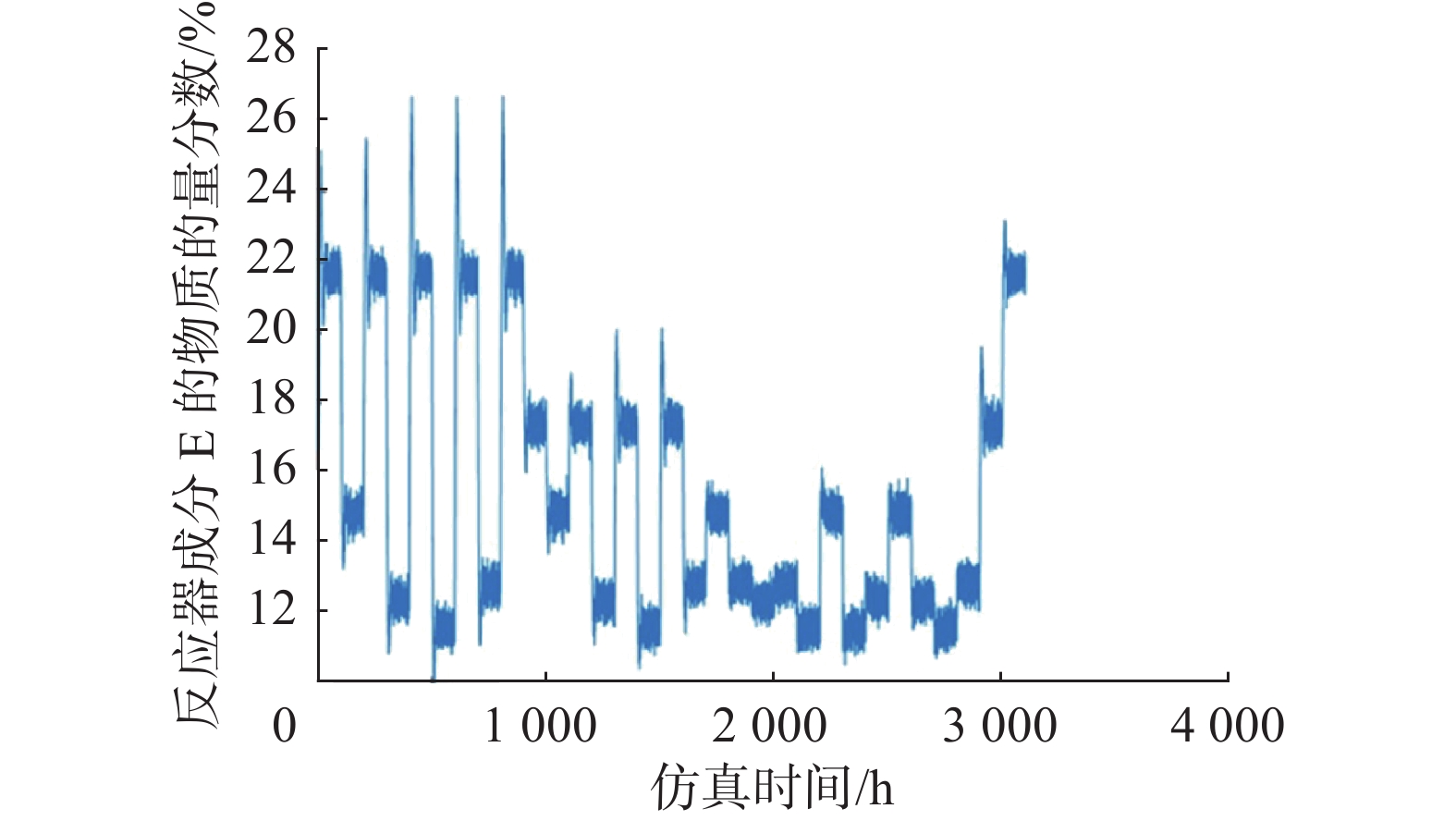
设计训练集每100 h转换一种稳态，整个仿真时常为3100 h。设置采样率为0.1，即每6 min采样一次。因此共产生31 000个训练样本数据。由仿真数据得到的反应器中成分E的变化曲线如图9所示。
图 9 反应器成分E变化曲线Fig. 9 Variation curve of component E in the reactor下载:
全尺寸图片
3.2 验证性实验
为了验证所提方法的有效性，使用上一节生成的数据作为训练集
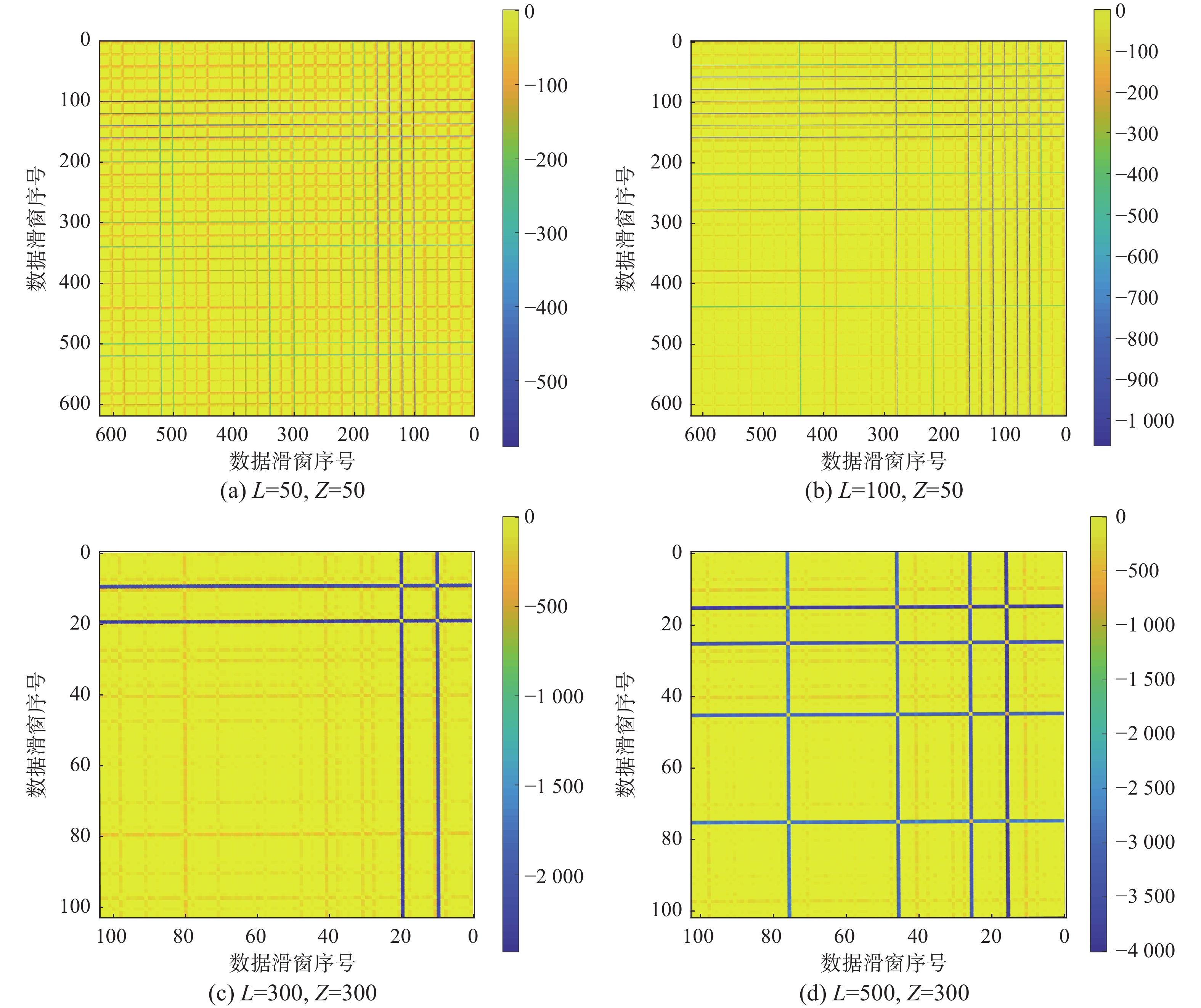
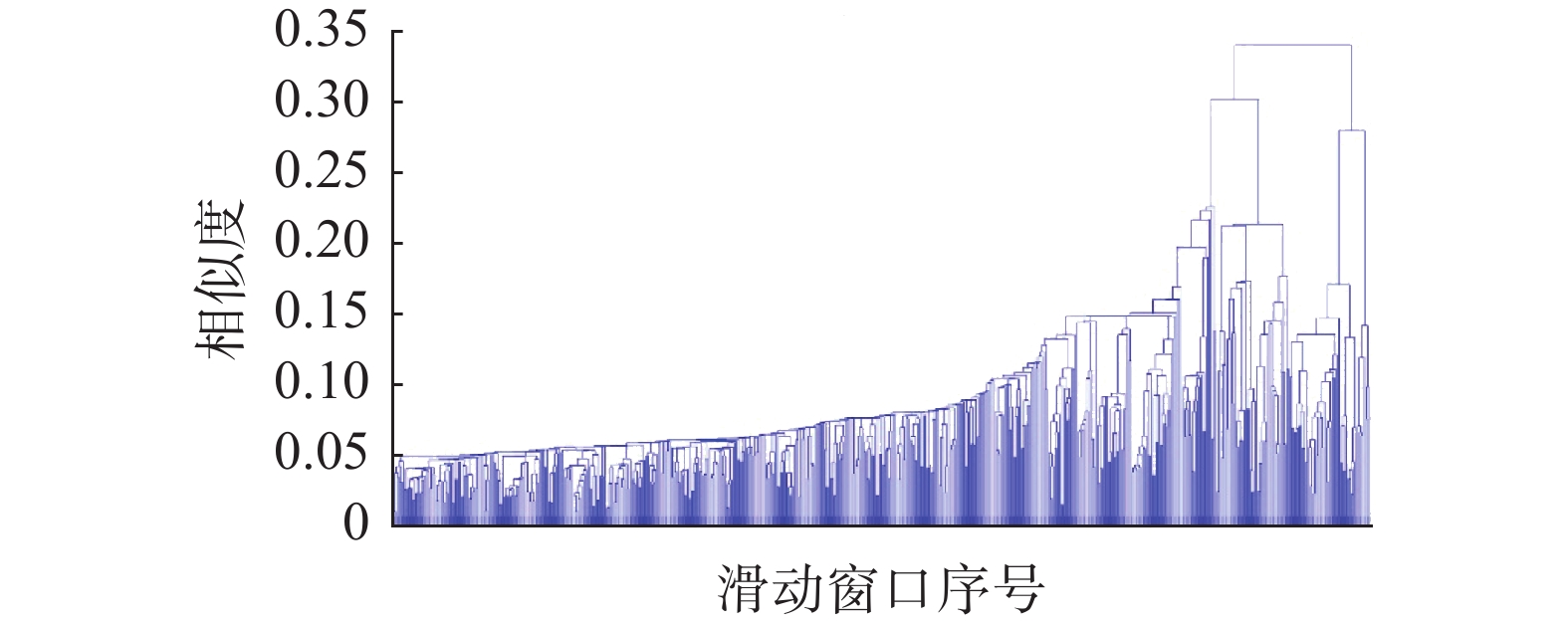
${{\boldsymbol{X}}_{{\rm{train}}}}$ ，同时生成一组从稳态1转变到稳态3，再从稳态3转变到稳态4的数据作为测试集${{\boldsymbol{X}}_{{\rm{test}}}}$ ，验证LSSW-SFA-SFT方法在多模态频繁转变的复杂生产过程中实现模态划分与过程识别的有效性。由于自适应短滑动窗口根据窗口数据之间的相似性可以动态改变窗口大小所以不需要过于依赖初始值，但是长滑动窗算法非常依赖窗口长度和滑动步长的设置。因此本节首先对长滑动窗的窗口长度取值进行分析，通过几种不同窗口长度的长滑动窗划分结果相似度图谱的对比，选择最优的窗口长度。图10给出了4种窗口长度的数据块相似度图谱。
图 10 相似度图谱Fig. 10 Similarity map下载:
全尺寸图片
从图10(a)可以看出，由于窗口长度设置太小，窗口之间的相似度分布不明显，不易对稳态数据进行划分。在图10(b)中，由于窗口长度
$L$ 增大，数据窗口之间相似性有了较大区分，数据可以被明显的划分成多个不同的数据块。而当窗口长度$L$ 和滑动步长$Z$ 继续增加时（如图10(c)和(d)所示），由于窗口长度过大，数据之间的相似性反而不能被有效识别，导致数据划分偏离正常分布情况，不利于模态识别与过程监测。因此，最终设置长滑窗长度
$L$ 为100，滑动步长$Z$ 为50，在整个长滑窗稳态识别过程中共获得了619个长滑窗。分别对每个滑动窗口建立SFA模型并计算相似度。然后使用层次聚类的方法对所有长滑窗进行层次聚类，生成如图11所示的聚类树。依据相似度图谱，可以将相似度大的长滑窗划分得到31组数据块，结合图11所示聚类树可以得到31组稳态数据。对于这31组数据，分别对每种稳态建立一个对应的SFA模型，生成用于在线监测的31个稳态的SFA模型。而剩余部分相似度很小的滑窗数据则被认为是非稳态数据，需要使用自适应短滑动窗进行过渡过程子阶段识别。
图 11 聚类树Fig. 11 Clustering tree下载:
全尺寸图片
接下来先初始化自适应短滑动窗的初始窗口大小
$L$ 为50，滑动步长$Z$ 为50，对剩余非稳态数据进行自适应窗口划分，将每一个滑动窗口作为一个过渡过程子阶段。然后针对每个过渡过程子阶段建立一个SFA模型。由于实验中相同的过程转变产生的过渡过程是相同的，因此对每个过渡过程只使用第1个子阶段SFA模型对过程状态转变结果进行判断。由于在31个稳态过程中存在30种过渡过程，因此共生成61个用于在线过程监测的SFA模型。然后利用过渡过程前后数据对每种过程转变建立一个SFT并使用第2.2.1节中提到的4种关联规则对过渡转变进行标识，得到61种转变规则，用于对在线数据过程转变方向进行判断。再选用一个训练集
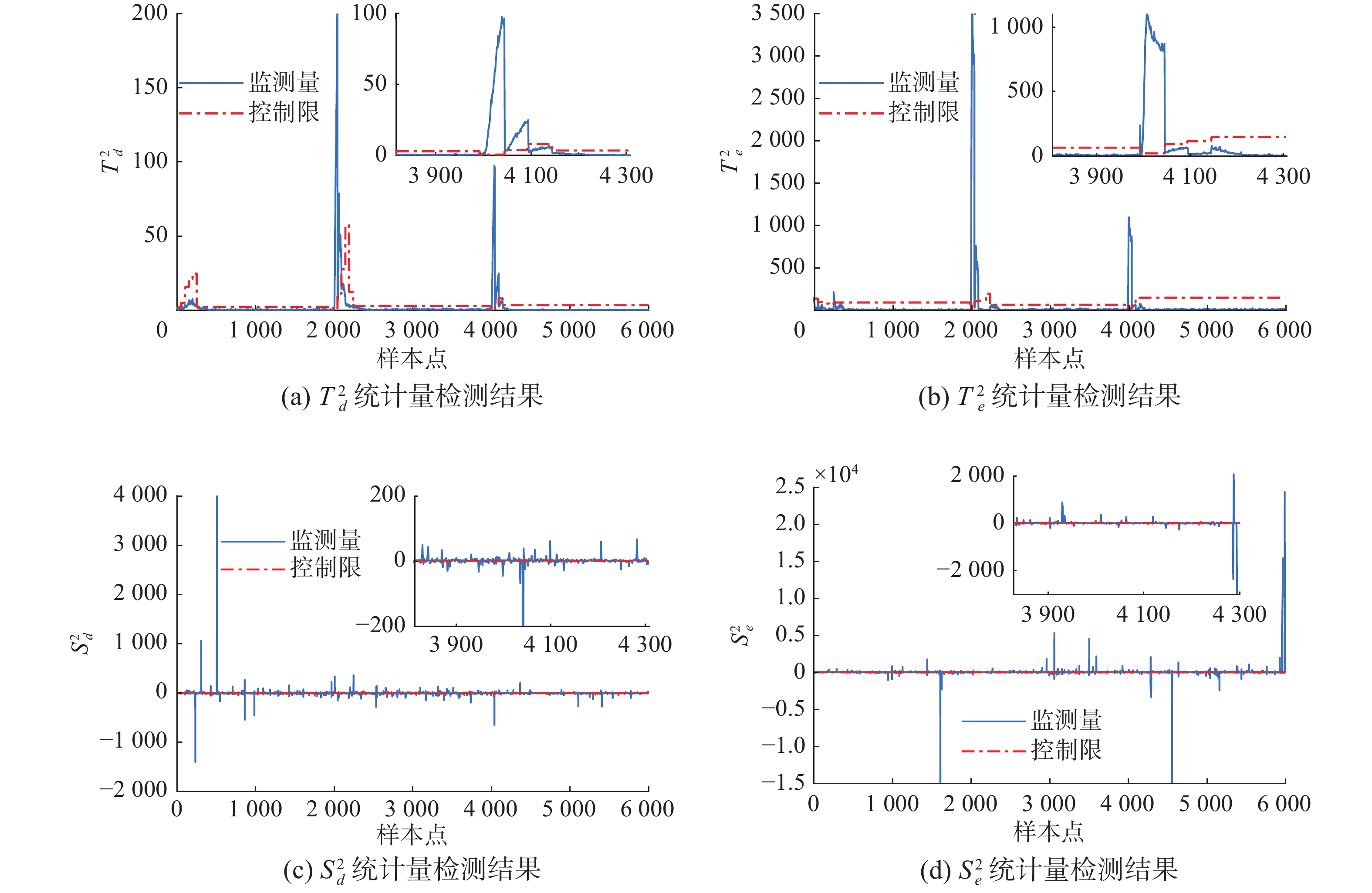
${X_{{\rm{train}}}}$ （从稳态1转稳态3，再从稳态3转稳态4的过程转变，其中每200 h进行一次模态转换，采样率依然为0.1，共生成6000个样本点），使用LSSW-SFA-SFT方法进行实验，在线监测的结果如图12所示。图12(a)和(b)为静态统计量，(c)和(d)为动态统计量。
图 12 LSSW-SFA-SFT过程监测结果Fig. 12 LSSW-SFA-SFT-based process monitoring results下载:
全尺寸图片
从图12可以看出，过程起始阶段会产生数据波动，因此测试集的起始运行模态是一个数据波动较大的过渡过程，所提方法的静态统计量能够较好地识别出该波动，不会产生故障误报警。对于中间两个过渡过程，所提的LSSW-SFA-SFT方法能够检测出过程转变，并使用对应的过渡过程子阶段SFA模型进行动态过程监测。从图12的(a)和(b)中可以看出，虽然静态统计量
$T_d^2$ 和$T_e^2$ 在该阶段产生了较大波动，出现了部分数据统计量超出阈值的情况，但在图12(c)和(d)中，只有少数几个样本点存在统计量超出阈值的情况。在基于SFA的过程监测中，只有当静态统计量都超出控制限，同时有动态统计量超出控制限时，才会判定为发生了故障。如果只有静态统计量超出控制限，则认为过程发生了波动，而不会产生故障报警。因此，LSSW-SFA-SFT方法对于每个过渡阶段都能够有效识别不会产生故障报警。综上所述，所提LSSW-SFA-SFT方法能够有效识别不同稳态工况转变产生的过渡过程，并且对初始阶段的波动也能够有效识别，减少误报警情况的发生，有效提高过程监测率。
3.3 对比性实验
为了验证所提LSSW-SFA-SFT方法在故障检测领域的有效性，以及与其他故障检测方法的对比效果。本节根据表2所列前20种故障类型，在Simulink仿真系统中生成20组带有不同故障的测试集样本。测试集数据的过程转变为：从稳态1转到稳态3，再从稳态3转到稳态4。每200 h进行一次模态转换，设置采样率为0.1，并在第550 h处引入故障。因此本节实验所用测试集分别为20组带不同种类故障的数据，每组数据包含6000个样本，每个样本包含53个属性。
由于所提出的LSSW-SFA-SFT方法需要综合静态统计量
$T_d^2$ 、$T_e^2$ 与动态统计量$S_d^2$ 、$S_e^2$ 4个统计量才能判断是否为故障，使得每种故障的检测图较多。所以本节通过列表的方式将所提方法与MS-DSFA[25]和SFA-MDKNN[9]两种故障检测方法的检测结果进行对比。使用故障检测率(FDR)、误报率(FAR)和ROC曲线下面积(AUC)作为客观评价指标。FDR表示将故障数据准确检测出来的概率，FAR则表示正常数据被误认为故障而产生误报警的概率，因此在检测效果对比中FDR越高，同时FAR越低说明效果越好。但是FDR和FAR较难达到一致的表达效果，因此同时使用AUC进一步评估检测性能。AUC的值越大说明正观测值大于负观测值越多，检测越准确，检测性能越好。
3种检测方法的FDR对比结果如表4所示。故障3和故障9都是由于流2中进料D的温度发生变化。故障10是由于流2中的进料C的温度发生了变化。由于原料D和C均为气态反应物，对温度不敏感，对数据影响小所以不易检测。故障5为冷凝器冷却水的入口温度发生阶跃变化产生的故障，故障15为冷凝器阀门黏滞故障。由于这两种故障都发生在冷凝器，对过程变化影响较小，所以不容易被检测到。因此这3种检测方法对所列几种故障的FDR都比较低。除此之外，LSSW-SFA-SFT方法对其他故障都具有较高的FDR，能够有效识别故障的发生。虽然MS-DSFA和SFA-MDKNN方法采用了SFA建模进行故障检测，有效关注到数据的时变特性，提高了故障检测率，但是由于整体数据波动较大，SFA-MDKNN方法只建立一个SFA模型会受到整体数据的影响；MS-DSFA方法虽然建立多个模型，但是数据块划分过大，使得统计量阈值偏高，所以造成部分故障未能及时识别。LSSW-SFA-SFT先对模态进行划分识别，然后进行故障检测，使用不同阶段的SFA模型对故障进行检测，能够有效降低波动数据产生的影响，提高故障检测率。
表 4 3种方法的FDR对比Table 4 Comparative FDR results of three methods故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.970 0.978 0.998 IDV2 0.978 0.971 0.998 IDV3 0.021 0.039 0.047 IDV4 1.000 0.996 1.000 IDV5 0.183 0.182 0.257 IDV6 0.997 1.000 1.000 IDV7 1.000 1.000 1.000 IDV8 0.975 0.979 0.990 IDV9 0.48 0.451 0.460 IDV10 0.65 0.783 0.88. IDV11 0.792 0.593 1.000 IDV12 0.891 0.952 0.981 IDV13 0.957 0.951 1.000 IDV14 1.000 0.769 0.960 IDV15 0.081 0.083 0.120 IDV16 0.83 0.847 0.835 IDV17 0.859 0.925 0.972 IDV18 0.925 0.911 0.940 IDV19 0.762 0.762 0.720 IDV20 0.873 0.881 0.980 表4给出了3种检测方法的FAR结果对比情况。从表5中可以看到LSSW-SFA-SFT方法的误报率最低，只有0.0123。虽然MS-DSFA和SFA-MDKNN方法考虑到了数据时变特性，综合了多个统计量进行分析，有效降低误报情况的发生，但是由于都忽略了过渡过程的辨识，在发生过程转变的过渡过程处会产生故障误报警，因此提高了FAR，故障检测效果没有LSSW-SFA-SFT方法理想。表6给出了3种检测方法的AUC对比结果。从表中可以看到所提出的LSSW-SFA-SFT在大多数种类的故障上具有较好的表现。由于AUC同时兼顾了FDR和FAR的检测情况，因此部分故障MS-DSFA或者SFA-MDKNN方法有更好的表现。但是对于表6中所列的大多数故障，LSSW-SFA-SFT方法无疑具有更好的检测结果。综上所述，对于大多数故障而言，LSSW-SFA-SFT方法都能够及时检测到故障发生，并且由于准确识别了过渡过程，使得对于过渡过程产生的数据波动能被有效辨识，从而降低了故障误报警情况的产生，同时避免了误报警带来的不利影响。
表 5 3种方法的FAR对比Table 5 Comparative FAR results of three methods故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.047 0.015 0.0123 IDV2 0.047 0.015 0.0123 IDV3 0.047 0.018 0.0123 IDV4 0.043 0.022 0.0123 IDV5 0.047 0.022 0.0123 IDV6 0.052 0.008 0.0123 IDV7 0.043 0.015 0.0123 IDV8 0.047 0.015 0.0123 IDV9 0.047 0.018 0.0123 IDV10 0.047 0.022 0.0123 IDV11 0.046 0.018 0.0123 IDV12 0.047 0.033 0.0123 IDV13 0.047 0.008 0.0123 IDV14 0.046 0.018 0.0123 IDV15 0.047 0.015 0.0123 IDV16 0.047 0.080 0.0123 IDV17 0.047 0.033 0.0123 IDV18 0.047 0.018 0.0123 IDV19 0.047 0.008 0.0123 IDV20 0.047 0.015 0.0123 表 6 3种方法的AUC对比Table 6 Comparative AUC results of three methods故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.977 0.983 0.990 IDV2 0.980 0.980 0.990 IDV3 0.842 0.841 0.847 IDV4 0.985 0.99 0.998 IDV5 0.910 0.917 0.968 IDV6 0.985 0.993 0.998 IDV7 0.989 0.993 0.998 IDV8 0.978 0.984 0.988 IDV9 0.931 0.930 0.951 IDV10 0.958 0.965 0.950 IDV11 0.988 0.987 0.998 IDV12 0.963 0.967 0.984 IDV13 0.969 0.987 0.998 IDV14 0.987 0.967 0.993 IDV15 0.875 0.853 0.939 IDV16 0.971 0.952 0.947 IDV17 0.975 0.957 0.994 IDV18 0.965 0.956 0.992 IDV19 0.976 0.989 0.969 IDV20 0.962 0.958 0.984 4. 结束语
针对传统过程监测方法忽视数据变化快慢，进而导致数据利用不充分，无法处理包含复杂过程频繁转变的过程数据的问题，提出一种基于长短滑窗慢特征分析与时序规则挖掘的复杂工业过渡过程识别方法（LSSW-SFA-SFT）。主要研究工作和创新点总结如下：
1）提出一种LSSW-SFA方法，能对复杂的多工况状态进行智能划分。基于稳态运行时间长和过渡过程运行时间短的特点，使用长短滑窗相结合的方法进行运行模态定位，再结合SFA提取数据中的时变特征，可以准确描述每种运行模态的动态时变特性。
2）提出一种基于SFT-MTSI的时序关联规则提取算法。采用SFT构建关联规则树，并结合多种模式下的置信度和支持度，为每种状态转变建立不同的关联规则，实现工况状态转变的在线辨识。
3）以TE过程为基础建立了复杂的频繁过程转变模型，对TE过程中可能出现的各种过程转变进行实验分析。通过对在线数据的过程识别，验证了本文方法的可行性。同时对带故障的在线数据进行实验，证实了本文方法在故障监测方面的有效性。
所提出的LSSW-SFA-SFT适用于带有频繁过渡过程转变的复杂多模态工业过程监测。对于过程监测，不仅需要判断出故障的产生，还要能够判断出故障的类型，以便有针对性的进行调整操作，避免持续故障带来的损失。因此在接下来的研究中，将考虑如何将本文所提方法应用与故障类型辨识中，进一步研究数据的时变特征在故障诊断中的作用。
-
图 1 实例数据趋势项
Fig. 1 Illustrative data-trend items
下载:
全尺寸图片
图 2 SFT构造过程
Fig. 2 SFT’s construction process
下载:
全尺寸图片
图 3 完整的SFT
Fig. 3 Complete SFT
下载:
全尺寸图片
图 4 自适应滑窗算法示意
Fig. 4 Illustrative diagram of adaptive sliding window algorithm
下载:
全尺寸图片
图 5 基于LSSW-SFA-SFT的过程监测
Fig. 5 LSSW-SFA-SFT-based process monitoring
下载:
全尺寸图片
图 6 LSSW-SFA处理流程
Fig. 6 Processing flow of LSSW-SFA
下载:
全尺寸图片
图 7 离线建模中SFT构建示意
Fig. 7 Schematic diagram of SFT construction in offline modeling
下载:
全尺寸图片
图 8 仿真系统模态转变
Fig. 8 Modal transitions in simulation system
下载:
全尺寸图片
图 9 反应器成分E变化曲线
Fig. 9 Variation curve of component E in the reactor
下载:
全尺寸图片
图 10 相似度图谱
Fig. 10 Similarity map
下载:
全尺寸图片
图 11 聚类树
Fig. 11 Clustering tree
下载:
全尺寸图片
图 12 LSSW-SFA-SFT过程监测结果
Fig. 12 LSSW-SFA-SFT-based process monitoring results
下载:
全尺寸图片
表 1 TE过程故障类型
Table 1 Fault types in TE process
故障 故障描述 故障类型 1 A/C进料比变化，B不变（流4） 阶跃 2 B含量变化，A/C进料比不变（流4） 阶跃 3 D的进料温度变化（流2） 阶跃 4 反应器冷却水的入口温度变化 阶跃 5 冷凝器冷却水的入口温度变化 阶跃 6 A进料损失（流1） 阶跃 7 C压力损失（流4） 阶跃 8 A、B、C进料变化（流4） 随机变化 9 D的进料温度变化（流2） 随机变化 10 C的进料温度变化（流2） 随机变化 11 反应器冷却水的入口温度变化 随机变化 12 冷凝器冷却水的入口温度变化 随机变化 13 反应动力学常数变化 慢偏移 14 反应器冷却水阀门 黏滞 15 冷凝器冷却水阀门 黏滞 16~21 未知 未知 表 2 TE过程生产模式
Table 2 Operating modes in TE process
模式 G/H率 产品生产率/(kg·h−1) 1 50/50 7038G和7038H 2 10/90 1048G和12669H 3 90/10 10000G和1111H 4 50/50 最大生产率 5 10/90 最大生产率 6 90/10 最大生产率 表 3 不同运行模态参数设置
Table 3 Parameter settings of different operating modes
工况编号 1 2 3 4 5 6 反应器等级 75 65 75 85 70 80 反应器压力 2705 2805 2905 2855 2805 2755 反应器温度 120.4 125.4 130 135 120 125 表 4 3种方法的FDR对比
Table 4 Comparative FDR results of three methods
故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.970 0.978 0.998 IDV2 0.978 0.971 0.998 IDV3 0.021 0.039 0.047 IDV4 1.000 0.996 1.000 IDV5 0.183 0.182 0.257 IDV6 0.997 1.000 1.000 IDV7 1.000 1.000 1.000 IDV8 0.975 0.979 0.990 IDV9 0.48 0.451 0.460 IDV10 0.65 0.783 0.88. IDV11 0.792 0.593 1.000 IDV12 0.891 0.952 0.981 IDV13 0.957 0.951 1.000 IDV14 1.000 0.769 0.960 IDV15 0.081 0.083 0.120 IDV16 0.83 0.847 0.835 IDV17 0.859 0.925 0.972 IDV18 0.925 0.911 0.940 IDV19 0.762 0.762 0.720 IDV20 0.873 0.881 0.980 表 5 3种方法的FAR对比
Table 5 Comparative FAR results of three methods
故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.047 0.015 0.0123 IDV2 0.047 0.015 0.0123 IDV3 0.047 0.018 0.0123 IDV4 0.043 0.022 0.0123 IDV5 0.047 0.022 0.0123 IDV6 0.052 0.008 0.0123 IDV7 0.043 0.015 0.0123 IDV8 0.047 0.015 0.0123 IDV9 0.047 0.018 0.0123 IDV10 0.047 0.022 0.0123 IDV11 0.046 0.018 0.0123 IDV12 0.047 0.033 0.0123 IDV13 0.047 0.008 0.0123 IDV14 0.046 0.018 0.0123 IDV15 0.047 0.015 0.0123 IDV16 0.047 0.080 0.0123 IDV17 0.047 0.033 0.0123 IDV18 0.047 0.018 0.0123 IDV19 0.047 0.008 0.0123 IDV20 0.047 0.015 0.0123 表 6 3种方法的AUC对比
Table 6 Comparative AUC results of three methods
故障序号 MS-DSFA SFA-MDKNN LSSW-SFA-SFT IDV1 0.977 0.983 0.990 IDV2 0.980 0.980 0.990 IDV3 0.842 0.841 0.847 IDV4 0.985 0.99 0.998 IDV5 0.910 0.917 0.968 IDV6 0.985 0.993 0.998 IDV7 0.989 0.993 0.998 IDV8 0.978 0.984 0.988 IDV9 0.931 0.930 0.951 IDV10 0.958 0.965 0.950 IDV11 0.988 0.987 0.998 IDV12 0.963 0.967 0.984 IDV13 0.969 0.987 0.998 IDV14 0.987 0.967 0.993 IDV15 0.875 0.853 0.939 IDV16 0.971 0.952 0.947 IDV17 0.975 0.957 0.994 IDV18 0.965 0.956 0.992 IDV19 0.976 0.989 0.969 IDV20 0.962 0.958 0.984 -
[1] LIU Jinping, XU Longcheng, XIE Yongfang, et al. Toward robust fault identification of complex industrial processes using stacked sparse-denoising autoencoder with softmax classifier[J]. IEEE transactions on cybernetics, 2023, 53(1): 428–442. doi: 10.1109/TCYB.2021.3109618 [2] LIU Jinping, WANG Jie, LIU Xianfeng, et al. MWRSPCA: online fault monitoring based on moving window recursive sparse principal component analysis[J]. Journal of intelligent manufacturing, 2022, 33(5): 1255–1271. doi: 10.1007/s10845-020-01721-8 [3] SUN Dongdong, GONG Xiaofeng, CHEN Yonglu. Integrating canonical variate analysis and kernel independent component analysis for Tennessee Eastman process monitoring[J]. Journal of chemical engineering of Japan, 2020, 53(3): 126–133. doi: 10.1252/jcej.19we085 [4] SU Hao, YANG Xin, XIANG Ling, et al. A novel method based on deep transfer unsupervised learning network for bearing fault diagnosis under variable working condition of unequal quantity[J]. Knowledge-based systems, 2022, 242: 108381. doi: 10.1016/j.knosys.2022.108381 [5] 何雨辰, 葛志强, 宋执环. 基于动态信息的过渡过程辨识方法[J]. 上海交通大学学报, 2017, 51(6): 686–692. doi: 10.16183/j.cnki.jsjtu.2017.06.007 HE Yuchen, GE Zhiqiang, SONG Zhihuan. A new method for transition identification by using dynamic information[J]. Journal of Shanghai Jiao Tong university, 2017, 51(6): 686–692. doi: 10.16183/j.cnki.jsjtu.2017.06.007 [6] 赵健程, 赵春晖. 面向全量测点耦合结构分析与估计的工业过程监测方法[J/OL]. 自动化学报. (2022−10−08)[2023−03−07]. http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c220090. ZHAO Jiancheng, ZHAO Chunhui. An industrial process monitoring method based on total measurement point coupling structure analysis and estimation[J/OL]. Acta automatica sinica. (2022−10−08)[2023−03−07]. http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c220090. [7] ZHAO Chunhui, GAO Furong. Between-phase-based statistical analysis and modeling for transition monitoring in multiphase batch processes[J]. AIChE journal, 2012, 58(9): 2682–2696. doi: 10.1002/aic.12783 [8] ZHANG Hanwen, SHANG Jun, YANG Chunjie, et al. Conditional random field for monitoring multimode processes with stochastic perturbations[J]. Journal of the franklin institute, 2020, 357(12): 8229–8251. doi: 10.1016/j.jfranklin.2020.05.039 [9] DONG Jie, WANG Yaqi, PENG Kaixiang. A novel fault detection method based on the extraction of slow features for dynamic nonstationary processes[J]. IEEE transactions on instrumentation and measurement, 2022, 71: 1–11. [10] ZHAO Chunhui, CHEN Junhao, JING Hua. Condition-driven data analytics and monitoring for wide-range nonstationary and transient continuous processes[J]. IEEE transactions on automation science and engineering, 2021, 18(4): 1563–1574. doi: 10.1109/TASE.2020.3010536 [11] CAI Meiling, SHI Yaqin, LIU Jinping, et al. DRKPCA-VBGMM: fault monitoring via dynamically-recursive kernel principal component analysis with variational Bayesian Gaussian mixture model[J]. Journal of intelligent manufacturing, 2022: 1−29. [12] 王雪平, 林甲祥, 巫建伟, 等. 基于可决系数的自适应关联规则挖掘算法[J]. 智能系统学报, 2020, 15(2): 352–359. WANG Xueping, LIN Jiaxiang, WU Jianwei, et al. Adaptive-association-rule mining algorithm based on determination coefficient[J]. CAAI transactions on intelligent systems, 2020, 15(2): 352–359. [13] WANG Ling, MENG Jianyao, XU Peipei, et al. Mining temporal association rules with frequent itemsets tree[J]. Applied soft computing, 2018, 62: 817–829. doi: 10.1016/j.asoc.2017.09.013 [14] PANJAITAN S, SULINDAWATY, AMIN M, et al. Implementation of apriori algorithm for analysis of consumer purchase patterns[J]. Journal of physics:conference series, 2019, 1255(1): 012057. doi: 10.1088/1742-6596/1255/1/012057 [15] THURACHON W, KREESURADEJ W. Incremental association rule mining with a fast incremental updating frequent pattern growth algorithm[J]. IEEE access, 2021, 9: 55726–55741. doi: 10.1109/ACCESS.2021.3071777 [16] WANG Huanbin, GAO Yangjun. Research on parallelization of Apriori algorithm in association rule mining[J]. Procedia computer science, 2021, 183: 641–647. doi: 10.1016/j.procs.2021.02.109 [17] LI Yuanyuan, YIN Shaohong. Mining algorithm for weighted FP-growth frequent item sets based on ordered FP-tree[J]. International journal of engineering and management research, 2019, 9(5): 154–158. doi: 10.31033/ijemr.9.5.22 [18] WU J M T, LIN J C W, TAMRAKAR A. High-utility itemset mining with effective pruning strategies[J]. ACM transactions on knowledge discovery from data, 2019, 13(6): 1–22. [19] 李海林, 龙芳菊. 基于同步频繁树的时间序列关联规则分析[J]. 智能系统学报, 2021, 16(3): 502–510. doi: 10.11992/tis.202008012 LI Hailin, LONG Fangju. Association rules analysis of time series based on synchronization frequent tree[J]. CAAI transactions on intelligent systems, 2021, 16(3): 502–510. doi: 10.11992/tis.202008012 [20] 闫浩, 王福利, 孙钰沣, 等. 基于贝叶斯网络参数迁移学习的电熔镁炉异常工况识别[J]. 自动化学报, 2021, 47(1): 197–208. doi: 10.16383/j.aas.c200104 YAN Hao, WANG Fuli, SUN Yufeng, et al. Abnormal condition identification based on Bayesian network parameter transfer learning for the electro-fused magnesia[J]. Acta automatica sinica, 2021, 47(1): 197–208. doi: 10.16383/j.aas.c200104 [21] 姜庆超, 颜学峰. 基于局部−整体相关特征的多单元化工过程分层监测[J]. 自动化学报, 2020, 46(9): 1770–1782. doi: 10.16383/j.aas.c190671 JIANG Qingchao, YAN Xuefeng. Hierarchical monitoring for multi-unit chemical processes based on local-global correlation features[J]. Acta automatica sinica, 2020, 46(9): 1770–1782. doi: 10.16383/j.aas.c190671 [22] KE Yun, YAO Chong, SONG Enzhe, et al. An early fault diagnosis method of common-rail injector based on improved CYCBD and hierarchical fluctuation dispersion entropy[J]. Digital signal processing, 2021, 114: 103049. doi: 10.1016/j.dsp.2021.103049 [23] KANO M, HASEBE S, HASHIMOTO I, et al. Statistical process monitoring based on dissimilarity of process data[J]. AIChE journal, 2002, 48(6): 1231–1240. doi: 10.1002/aic.690480610 [24] HE Yuchen, ZHOU Le, GE Zhiqiang, et al. Distributed model projection based transition processes recognition and quality-related fault detection[J]. Chemometrics and intelligent laboratory systems, 2016, 159: 69–79. doi: 10.1016/j.chemolab.2016.10.001 [25] MA Xin, SI Yabin, YUAN Zeyi, et al. Multistep dynamic slow feature analysis for industrial process monitoring[J]. IEEE transactions on instrumentation and measurement, 2020, 69(12): 9535–9548. doi: 10.1109/TIM.2020.3004681
